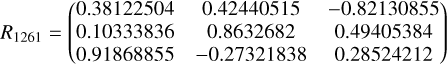| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202451930 | |
| Published online | 03 January 2025 | |
S5: New insights from deep spectroscopic observations of the tidal tails of the globular clusters NGC 1261 and NGC 1904
1
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV
Groningen,
The Netherlands
2
Bernoulli Institute for Mathematics, Computer Science and Artificial Intelligence, University of Groningen,
9700 AK
Groningen,
The Netherlands
3
Department of Astronomy and Astrophysics, University of Toronto,
50 St. George Street,
Toronto,
ON
M5S 3H4,
Canada
4
Department of Physics, University of Surrey,
Guildford
GU2 7XH,
UK
5
Universidad Technica Frederico de Santa Maria,
Avenida Vicuña Mackenna 3939,
San Joaquín, Santiago,
Chile
6
University of Birmingham, School of Computer Science,
B15 1TT,
Birmingham,
UK
7
Institute for Astronomy, University of Edinburgh,
Royal Observatory, Blackford Hill,
Edinburgh
EH9 3HJ,
UK
8
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
9
Kavli Institute for Cosmology, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
10
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
11
Research School of Astronomy and Astrophysics, Australian National University,
Canberra,
ACT 2611,
Australia
12
Centre of Excellence for All-Sky Astrophysics in Three Dimensions (ASTRO 3D),
Australia
13
Department of Astronomy & Astrophysics, University of Chicago,
5640 S Ellis Avenue,
Chicago,
IL
60637,
USA
14
Kavli Institute for Cosmological Physics, University of Chicago,
Chicago,
IL
60637,
USA
15
Lowell Observatory,
1400 W Mars Hill Rd,
Flagstaff,
AZ
86001,
USA
16
Sydney Institute for Astronomy, School of Physics, A28, The University of Sydney,
NSW 2006,
Australia
17
McWilliams Center for Cosmology, Carnegie Mellon University,
5000 Forbes Ave,
Pittsburgh,
PA
15213,
USA
18
School of Mathematical and Physical Sciences, Macquarie University,
Sydney,
NSW 2109,
Australia
19
Macquarie University Research Centre for Astrophysics and Space Technologies,
Sydney,
NSW 2109,
Australia
20
Universidade de São Paulo, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Departamento de Astronomia,
SP 05508-090,
São Paulo,
Brazil
21
School of Physics, University of New South Wales,
Sydney,
NSW 2052,
Australia
★ Corresponding author; p.awad@rug.nl
Received:
19
August
2024
Accepted:
8
November
2024
As globular clusters (GCs) orbit the Milky Way, their stars are tidally stripped and form tidal tails that follow the orbit of the cluster around the Galaxy. The morphology of these tails is complex and shows correlations with the phase of orbit and the orbital angular velocity, especially for GCs on eccentric orbits. Here we focus on two GCs, NGC 1261 and NGC 1904, that were potentially accreted alongside Gaia-Enceladus and that have shown signatures of having, in addition to tidal tails, structures formed by distributions of extra-tidal stars that are misaligned with the general direction of the clusters’ respective orbits. To provide an explanation for the formation of these structures, we made use of spectroscopic measurements from the Southern Stellar Stream Spectroscopic Survey (S5) as well as proper motion measurements from Gaia’s third data release (DR3), and applied a Bayesian mixture modelling approach to isolate high-probability member stars. We recovered extra-tidal features surrounding each cluster matching findings from previous work. We then conducted N-body simulations and compared the expected spatial distribution and variation in the dynamical parameters along the orbit with those of our potential member sample. Furthermore, we used Dark Energy Camera (DECam) photometry to inspect the distribution of the member stars in the colour-magnitude diagram (CMD). We find that potential members agree reasonably with the N-body simulations, and that the majority follow a simple stellar population distribution in the CMD, which is characteristic of GCs. We link the extra-tidal features with their orbital properties and find that the presence of the tails agrees well with the theory of stellar stream formation through tidal disruption. In the case of NGC 1904, we clearly detect the tidal debris escaping the inner and outer Lagrange points, which are expected to be prominent when at or close to the apocentre of its orbit. Our analysis allows for further exploration of other GCs in the Milky Way that exhibit similar extra-tidal features.
Key words: stars: kinematics and dynamics / Galaxy: halo / globular clusters: individual: NGC 1261 / globular clusters: individual: NGC 1904
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Globular clusters (GCs) are densely packed, spheroidal distributions of stars bound together by their gravity. Milky Way GCs can mostly be found within its halo or the bulge in orbit around the Galaxy. During a GC s orbit, the Galactic tidal interaction leads to a gradual loss of member stars. According to Reina-Campos et al. (2020) who used 25 present-day Milky Way-mass zoom simulations from the E-MOSAICS project to estimate the fraction of GC stars within the halo, ~0.3% of the stars in the halo can be attributed to disrupted GCs. Meanwhile, 2.3% can be attributed to other star clusters, and the majority of the halo is formed by the accretion of dwarf galaxies. Observationally, around 2% of halo field stars show the chemical abundance anomalies of second-generation GC stars (Martell & Grebel 2010; Martell et al. 2011, 2016; Schiavon et al. 2017; Koch et al. 2019; Horta et al. 2021). Converting this into a fraction of the halo that originally formed in GCs is strongly influenced by the model one uses for the star formation history in a GC and the extent of early first-generation mass loss, but estimates have ranged from 11% (Horta et al. 2021) to 50% (Martell & Grebel 2010).
The gradual loss of mass that GCs undergo can be the result of several mechanisms. In the outskirts of a GC, stars can be stripped away by the Galaxy’s potential, therefore gaining energy above the critical energy level needed for their escape from the GC’s potential. This leads to the formation of a diffuse stellar envelope surrounding the cluster beyond its tidal radius (Fukushige & Heggie 2000; Baumgardt 2001; Claydon et al. 2017; Daniel et al. 2017). Other mechanisms that lead to the ejection of stars from within GCs are possible (Leigh & Sills 2011; Grondin et al. 2023). These processes include natal kicks (Merritt et al. 2004); ejections via supernova events (Shen et al. 2018; Kounkel et al. 2022); or three-body encounters that can result in the ejection of one of the stars, thus leaving behind a binary (Stone & Leigh 2019; Manwadkar et al. 2020; Montanari & García-Bellido 2022; Grondin et al. 2023). The main depopulation mechanism of GCs is the escape of stars through the Lagrange points, formed by the combined potentials of a given GC and the Galaxy (e.g. Küpper et al. 2008; Weatherford et al. 2023; Xu et al. 2024). This mechanism results in the formation of long streams of stars sometimes referred to as tidal tails (e.g. Ibata et al. 2021, and references therein).
Uncovering these streams is of great importance as they provide a means of probing the acceleration field of the Galaxy (e.g. Johnston et al. 1999; Ibata et al. 2001; Fellhauer et al. 2009), which can then constrain the dark matter distribution within the halo. Given the hierarchical merging scenario, the detection of stellar streams also reveals past merger events. Additionally, dark matter subhalos can be studied using stellar streams by examining gaps in the streams that could have resulted from impacts with these halos (e.g. Ibata et al. 2002; Johnston et al. 2002; Carlberg 2012; Bovy 2016; Erkal et al. 2016; Banik et al. 2018; Bonaca et al. 2019; Montanari & García-Bellido 2022) allowing for tests of ACDM itself.
Tidal tails of GCs have complex morphologies, and the orientation of the tails is correlated with the phase of orbit around the Galaxy, especially for GCs with eccentric orbits (Capuzzo Dolcetta et al. 2005; Montuori et al. 2007). We refer to Fig. 5 in Montuori et al. (2007) for a schematic of all forces acting on a tidally disrupted GC that lead to the formation of tidal tails. Palomar 5 is a well-studied example of a GC with prominent tidal tails (Odenkirchen et al. 2001, 2003; Ibata et al. 2016; Bonaca et al. 2020). The outer parts of the tails of Palomar 5 align with the direction of the orbit. The leading tail has a slightly lower energy and thus orbits closer to the Milky Way, while the trailing tail has a higher energy and thus orbits further from the Milky Way; the two tails form the characteristic S-shape centred on the cluster. Since the location of the Sun is above the orbital plane of Palomar 5, the difference in the tails’ distances from the Galactic centre is projected onto the sky and is thus easily detectable. The orientation of the tails of GCs is also correlated with the location of the GC along its orbit and its eccentricity. The outer tails, or parts of the tidal tails that are further away from the cluster, always align with the path of the orbit. On the other hand, the inner tails (i.e. the parts of the tidal tails close to the GC) roughly align with the orbital path only when the cluster is near the pericentre (Capuzzo Dolcetta et al. 2005; Montuori et al. 2007). When the cluster approaches apocentre, the inner tails point in the direction of the Galactic centre and anti-centre. This distinction between the orientation of the inner and outer tails when the cluster is at apocentre then gives the impression that the GC has multiple tidal tails surrounding it. The same morphology dependence has been demonstrated for dwarf galaxies accreted onto the Milky Way in Klimentowski et al. (2009). Finally, a GC that has spent a long time in the Galactic halo will undergo several orbital periods, potentially leading to the production of many streams within the halo. This mechanism also leads to more than one pair of streams that can be observed when probing an area on the sky surrounding such a GC. Some GCs that have been found with such structures surrounding them include NGC 288 (Leon et al. 2000; Sollima 2020) and NGC 2298 (Balbinot et al. 2011).
In this work, we explore two other GCs, NGC 1261 and NGC 1904, which have also shown multiple stream-like structures surrounding them. Both GCs are relatively metal-rich with mean metallicities of −1.33 ± 0.02 and −1.66 ± 0.01, respectively (Wan et al. 2023), and are thought to have been accreted alongside the Gaia-Enceladus event (Limberg et al. 2022). NGC 1261 has a present-day mass of 1.67 × 105 M⊙ with a heliocentric distance of 16.4 kpc and a galactocentric distance of 18.28 kpc (Baumgardt & Hilker 2018). Based on the simulations of Wan et al. (2023), the orbital period of NGC 1261 is ~170 Myr, with a pericentre distance of ~2 kpc, and an apocentre distance of ~20 kpc. With such an orbital period, NGC 1261 is likely to have completed more than 10 full orbits around the galaxy within 2 Gyr and lost a large portion (~50%) of its mass due to stellar evolution and the frequent interaction with the Galaxy’s tidal field (e.g. Balbinot & Gieles 2017). NGC 1904 (M 79), has a present-day mass of 1.69 × 105 M⊙ with heliocentric and galactocentric distances of 13.08 kpc and 19.1 kpc, respectively (Baumgardt & Hilker 2018). It has a small pericentre with a galactocentric radius of ~0.33 kpc where the tidal effect from the Galaxy is strong. At the present, this GC lies very close to the apocentre of its orbit.
Leon et al. (2000) pointed out the existence of a tidal tail for NGC 1261 oriented in the direction of the Galactic centre, and works including Kuzma et al. (2017) and Wan et al. (2023) pointed out the existence of a stellar envelope surrounding this cluster. Similarly, an extended halo of stars was found around NGC 1904, first in Grillmair et al. (1995) and also in Leon et al. (2000), Zhang et al. (2022), Wan et al. (2023), and Xu et al. (2024). In Shipp et al. (2018), data from the first three years of the Dark Energy Survey (DES: Abbott et al. 2018) were used to identify stellar streams in the Milky Way halo. Their results also include evidence for extra-tidal features around four Milky Way GCs, namely NGC 288, NGC 1261, NGC 1851, and NGC 1904. Shipp et al. (2018) found stellar overdensities associated with NGC 1261 and NGC 1904 that do not align with the general direction of their orbits, and that in fact form a cross-shaped pattern centred on the clusters. Though they pointed out these overdensities, they left further exploration to future work. More recently, Sollima (2020) has found three extra-tidal structures surrounding NGC 1904 that point in multiple directions, and Ibata et al. (2024) suggested that two streams could be associated with NGC 1261. In this paper we focus on these two GCs, and perform the subsequent analysis hinted at by Shipp et al. (2018) to provide further clarity pertaining to the origin of the clusters’ extra-tidal features.
Given the detection of these features in the aforementioned works, and the current location of NGC 1904 along its orbit, it seems possible that multiple stream-like features can be associated with these GCs, though more work is required to make that connection. Consequently, the Southern Stellar Stream Spec-troscopic Survey (S5 ; Li et al. 2019), has performed follow-up observations of these two clusters and in the fields surrounding them to expand on the findings of Shipp et al. (2018). The survey has targeted regions on the sky along the expected orbit of the clusters and in the regions where the extra-tidal features from Shipp et al. (2018) were found. The survey provides radial velocities as well as metallicity measurements to help constrain extra-tidal member stars associated with these clusters in the targeted fields.
The goal of this paper is to explore the cross-shaped features reported by Shipp et al. (2018) around the GCs NGC 1261 and NGC 1904, making use of the deep spectroscopic observations of S 5. We employed a Bayesian mixture modelling technique that incorporates proper motion measurements as well as radial velocity and metallicity values to isolate the GC and stream stars from the surrounding field stars within an area spanning ~10 rJ, where rJ is the Jacobi radius of each cluster. After extracting the studied structures, we compared their spatial distribution and properties to what is expected when running N-body simulations of the two GCs. We primarily attempted to link the substructure found surrounding the clusters to their orbits around the Galaxy.
This paper is organized as follows. In Sect. 2, we explain the data collected by S5, specifically the target selection during the follow-up observations and the processing that the measurements undergo. In Sect. 3, we describe the methodology applied to the selected sample of stars for each GC to distinguish high-probability member stars. We also explain how the N-body simulations are constructed for comparison with our results. Sect. 4 describes our results pertaining to the detected streams or substructure detected around the studied GCs. We then discuss these results in Sect. 5. In particular, we discuss the reliability of our methodology as well as the formation mechanisms of any uncovered substructure. Sect. 6 then summarizes our results and presents the future prospects of this work.
2 Data
Observations of these two GCs were taken as part of S5, which was initiated in 2018 using the Two-degree Field (2dF) fiber positioner (Lewis et al. 2002) coupled with the dual-arm AAOmega spectrograph (Sharp et al. 2006) on the 3.9m Anglo-Australian Telescope (AAT). This ongoing survey pursues a complete census of known streams in the Southern hemisphere. GCs and dwarf galaxies experiencing tidal disruption are also targeted, for example the Crater II and Antlia II dwarf galaxies (Ji et al. 2021). We refer to Li et al. (2019) and Li et al. (2022) for a detailed description of the instrument setup, observations, data reduction, and validation for S5. The first public data release (DR1) was made available in 2021 (Li & S5 Collaboration 2021), containing data collected from 2018 to 2020. The specific catalog used in this analysis is based on an internal data release, iDR3.7 of S5, which is slated to become the second public data release (DR2) in 2025, with a more detailed description to be provided therein (Li et al., in prep.).
We provide a brief summary of the reduction pipeline here. As described in S5 DR1 (Li et al. 2019; Li & S5 Collaboration 2021), the rvspecfit pipeline (Koposov 2019) is used to determine radial velocity (RV) and other stellar parameters, such as metallicity ([Fe/H]), effective temperature, and surface gravity for each star. The pipeline uses the PHOENIX-2.0 highresolution stellar spectra library (Husser et al. 2013), truncates the template spectra to the AAOmega wavelength range, and convolves them to match the AAOmega spectral resolution (R ~ 1300 for the blue arm at 3700–5700 Å and R ~ 10000 for the red arm at 8400–8800 Å), followed by multi-dimensional interpolation between templates. The fitting process involves a Nelder-Mead optimization to find the maximum likelihood point in the space of stellar atmospheric parameters and RVs, with subsequent Markov Chain Monte Carlo sampling to derive the full posterior distribution for each parameter. Moreover, the data reduction pipeline for DR2 has undergone significant improvements compared to DR1, most notably through the simultaneous modelling of multiple spectra, fitting both the blue-arm and red-arm spectra, as well as repeated observations of the same object from different nights, with proper consideration of the heliocentric correction for each observation.
The observations for these two GCs were mostly taken in 2020–2021, with some added in 2023. The GC targets are selected using parallax and proper motions from either Gaia DR2 (for observations taken before Dec. 2020) or Gaia DR3. For parallax, we select stars with ϖ − 3σϖ < 0.2 to remove nearby disk contaminants. For proper motions, we select targets with |µ – µ0| < 1.6 mas yr−1, where µ0 is the proper motion of each GC from Vasiliev (2019, for observations taken before March 2021) and Vasiliev & Baumgardt (2021, for observations taken after March 2021). The targets were further selected to have similar colour and magnitude as known GC members using the photometry from DES DR2 (Abbott et al. 2021). Specifically, dereddened ɡ and r magnitudes are used for target selection, using the dust maps from Schlegel et al. (1998). A total of 7 AAT fields were observed for NGC 1261, and 9 fields for NGC 1904 (Fig. 1). Observations of the central regions (Wan et al. 2023) were added to the S5 observations and processed using the same data reduction pipeline.
The radial velocities are converted from heliocentric to the galactic standard of rest (gsr) using the latest galactocen-tric frame parameters from astropy v5.1. We also use the coordinate system (ϕ1, ϕ2) defined using the rotation matrices provided in Appendix A for the two GCs, where ϕ1 is directed along the expected orbit of the clusters and ϕ2 is orthogonal to that direction. We select stars with radial velocity −250 < v𝑔sr/km s−1 < 250 and metallicity [Fe/H]< 0 to remove stars with radial velocities and metallicities very far away from any known measurements for the GCs. Additionally, we enforce quality cuts to keep stars that have good measurements by the survey (i.e. stars with the flag good_star = 1), and stars with small measurement errors on the radial velocity and metallicity (i.e. vel_calib_std < 20 km s−1 and feh_calib_std < 1). In total, we retain 938 and 1706 stars in the 7 and 9 AAT fields surrounding NGC 1261 and NGC 1904, respectively. We subsequently apply the procedure described in Sect. 3 to analyse these samples.
 |
Fig. 1 3D sky plots for NGC 1261 (top) and NGC 1904 (bottom). The position of each GC is shown as a red star and the particles from the N-body simulations are shown in blue throughout the paper. The insets show the distribution of particles close to the clusters and the outlines of the fields targeted by S5 (black circles). We also plot in purple the integrated orbit of each GC given the gravitational potential described in Sect. 3.1, and the direction of motion of the cluster is indicated by the red arrow. |
3 Methods
3.1 N-body simulations
In order to compare the observations with theoretical predictions, we perform N-body simulations of both GCs. This approach is similar to Massari et al. (2025), who studied NGC 6254 and NGC 6397 with Euclid. These simulations are performed with the N-body part of GADGET-3, which is an improved version of GADGET-2 (Springel 2005). We model the Milky Way gravitational potential using the three component MWPotential2014 model from Bovy (2015). This consists of an NFW halo (Navarro et al. 1996) with a mass of 8 × 1011 M⊙, a scale radius of 16 kpc, and a concentration of 15.3, a Miyamoto-Nagai disk (Miyamoto & Nagai 1975) with a mass of 6.8 × 1010 M⊙, a scale radius of 3 kpc, and a scale height of 0.28 kpc, and a broken power-law bulge with a mass of 5 × 109 M⊙, a power-law exponent of −1.8, and a cutoff radius of 1.9 kpc.
In addition to the Milky Way, we also include the Large Magellanic Cloud (LMC), which has been shown to have a significant effect on the orbits and physical properties of streams in the Milky Way (e.g. Erkal et al. 2019; Erkal & Belokurov 2020; Patel et al. 2020; Vasiliev et al. 2021; Pace et al. 2022; Correa Magnus & Vasiliev 2022; Koposov et al. 2023). We take a similar approach to Erkal et al. (2019) and model the LMC as a particle sourcing a Hernquist potential (Hernquist 1990) with a mass of 1.5 × 1011 M⊙ and a scale radius of 17.13 kpc motivated by the LMC mass measured in Erkal et al. (2019). We include the effect of dynamical friction on the LMC using the results of Jethwa et al. (2016). We also account for the reflex motion of the Milky Way in response to the LMC. This is done using the approach of Vasiliev et al. (2021) where the simulation is performed in the non-inertial Milky Way frame and the acceleration of the LMC on the Milky Way is subtracted off the LMC and the GC particles. As a sanity check, we integrated the GC orbits using the approach of Erkal et al. (2019) where the Milky Way is included as a particle that moves in response to the LMC and we verified that the orbits relative to the Milky Way are identical.
In order to perform our simulations, we first rewind NGC 1261 and NGC 1904 in the combined potential of the Milky Way and the LMC for 2 Gyr. The present-day phase space coordinates of each GC (i.e. on-sky angles, proper motions, radial velocity, and distance) are taken from Vasiliev & Baumgardt (2021). For the LMC’s present-day phase-space coordinates we use the proper motions, distance, and radial velocity from Kallivayalil et al. (2013); Pietrzyński et al. (2019), and van der Marel et al. (2002), respectively. After rewinding, we track the orbit of each GC and determine when they reach apocentre. For both GCs, we choose to simulate them forward from four apoc-entres ago. For NGC 1904 and NGC 1261 this corresponds to 0.97 Gyr and 1.19 Gyr ago, respectively. We choose to inject the GCs at apocentre to give them time to adjust to the tidal field before pericentre.
We then inject the GCs at their respective locations and simulate them forward to the present day in the combined potential of the Milky Way and the LMC. Each GC is modelled as a King profile with 105 particles where the profile can be characterized by the profile normalization factor W, the tidal radius rt, and the mass m. We extract from de Boer et al. (2019) the values of W and rt and from Baumgardt & Hilker (2018) the values for the masses of each cluster. For NGC 1261, we use W = 6.8, rt = 37.81 pc, and a mass of 1.67 × 105 M⊙. For NGC 1904, we use W = 7.93, a tidal radius of rt = 38.32 pc, and a mass of 1.69 × 105 M⊙. For the softening, we simulate both GCs in isolation for 2 Gyr with a range of softening parameters, (2.5, 5, 10, 20) × 10−2 pc, and find that a softening of 5 × 10−2 pc maintains the initial King profile with the smallest change. Both GCs are simulated forward to the present day, and both experience significant tides during their pericentric passages with the Milky Way1. Both clusters end up close to their present-day location, with offsets of only 0.18° and 0.57° for NGC 1904 and NGC 1261, respectively. We therefore correct for this offset by shifting the position of the stars in right ascension α and declination δ so that the GCs match their observed present-day positions. This slight shift has a minimal effect on the proper motions and radial velocities of the simulated particles. We note that in these simulations, NGC 1904 and NGC 1261 lose 11% and 2% of their mass due to tidal stripping. Since this mass loss is comparable to the uncertainty on their present mass (Baumgardt & Hilker 2018), we do not iterate the procedure to match their present-day mass.
In Fig. 1, we provide 3D sky plots for NGC 1261 (top) and NGC 1904 (bottom). The red star indicates the current position of the GCs, and the blue dots indicate the results of the N-body simulations. We also overplot the outline of the measured fields done by S5 for both of these clusters in the zoom plot shown in the top and bottom panels. Furthermore, we show the expected orbit of each GC integrated using the same gravitational potential described above. The direction of the orbit is indicated by the arrow. The simulations will be used to compare the properties of the stars classified as probable cluster members and for further discussion in Sect. 5.
3.2 Mixture model description
We aim to detect members of each GC separately, within the regions observed by S5 which extend beyond the tidal radius of each cluster as explained in Sect. 2. We therefore employ a mixture modelling approach whereby we disentangle stars that have similar properties to the clusters from the surrounding field stars (hereafter referred to as the background). Such probabilistic approaches have been used previously such as in the work of Sollima (2020) for searching for tidal tails around a sample of 18 GCs, or Kuzma et al. (2021) for finding tidal extensions to Omega Centauri. Similarly, the works of Pace & Li (2019) and McConnachie & Venn (2020) apply a probabilistic modelling approach on data from Gaia DR2 to study ultra-faint dwarf galaxies. Earlier work includes Walker et al. (2009), Koposov et al. (2011), and Walker & Peñarrubia (2011) who use a probabilistic approach for studying the Milky Way’s dwarf spheroidal galaxies. Similarly to Kuzma et al. (2021), in this work we model the different properties of the GCs with Gaussian mixture modelling, while fitting for the parameters that optimize a log-likelihood function within a Bayesian framework.
We assume that for each star we have the following information: star positional coordinates ϕ1 and ϕ2, proper motions along right ascension and declination (µα and µδ, respectively), radial velocity v and the [Fe/H] abundance. We note that µα always contains the cos δ term. We also assume knowledge of the measurement errors 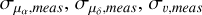 and
and ![${\sigma _{[{\rm{Fe}}/{\rm{H}}]{\rm{,meas}}}}$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq2.png) for the above quantities, as well as the correlation coefficient p linking the measurement noise of the two proper motions. We build a density model for u = (µα, µδ, v, [Fe/H]), given the positional information ϕ1 and measurement noise characteristics collected in
for the above quantities, as well as the correlation coefficient p linking the measurement noise of the two proper motions. We build a density model for u = (µα, µδ, v, [Fe/H]), given the positional information ϕ1 and measurement noise characteristics collected in ![$\zeta = \left( {{\sigma _{{\mu _\alpha },{\rm{}}meas{\rm{}}}},{\sigma _{{\mu _\delta },{\rm{}}meas{\rm{}}}},{\sigma _{v,{\rm{}}meas{\rm{}}}},{\sigma _{[{\rm{Fe}}/{\rm{H}}],{\rm{}}meas{\rm{}}}},\rho } \right)$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq3.png) . The use of ϕ2 is defined later in the modelling.
. The use of ϕ2 is defined later in the modelling.
Our two-component mixture model p(u | ϕ1, ζ) mixes a stream component ps(u | ϕ1, ζ) with a background component pb𝑔 (u|ζ) as
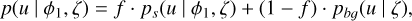 (1)
(1)
where 0 ≤ f ≤ 1 is the mixture coefficient of the stream component. The stream component models properties of stars belonging to GCs, while the background component models other contaminant stars within the field. In both GC and background component models the distribution over u is factorized into three independent factors – two univariate ones over radial velocity and metallicity, pv and p[Fe/H], respectively, and a bivari-ate one, ppm, for proper motions. All component factors will be formulated as Gaussians fully specified by their means and (co)variance structures.
The kinematics along the stream vary as a function of the position on the sky, and this variation can be small or large depending on how far or close a GC is from its turning points on the orbit. To include this variation in our modelling, the mean vs of the velocity factor of the stream mixture component pv, s will therefore be modelled as a quadratic function vs (x) = v1 + v2x + v3 x2 of the position within the stream, x = ϕ1/10º, parametrized by the coefficients (v1, v2, v3). A similar dependence on the stream-position can be argued for the mean µs(x) = (µα, S(x), µδ, s(x))T of the proper motion factor ppm, s of the stream component,
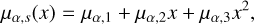 (2)
(2)
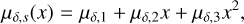 (3)
(3)
parametrized by the coefficients (µα, 1, µα, 2, µα, 3, µδ, 1, µδ, 2, µδ, 3).
No such dependence on the stream-position needs to be captured by the background component, hence, the means vb𝑔 and µbg = (µα, b𝑔, µδ, b𝑔) of the velocity and proper motion factors, respectively, of the background mixture component can be considered constant parameters of our mixture model.
Finally, the evolution of a GC within the Galaxy does not change its initial metallicity. Hence, the mean metallicity for both the stream, and background components, ![$\overline {{{\left[ {{\rm{Fe}}/{\rm{H}}} \right]}_s}} $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq7.png) and
and ![$\overline {{{\left[ {{\rm{Fe}}/{\rm{H}}} \right]}_{bg}}} $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq8.png) , respectively, are considered constant parameters.
, respectively, are considered constant parameters.
Having specified the mean structure of our mixture model, we now focus on the (co)variance one. For the univariate (v and [Fe/H]) and bivariate factors (µα and µδ), the variance is a superposition of the intrinsic and measurement dispersions. Hence,
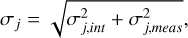 (4)
(4)
where j is an element of u. Again, the intrinsic dispersions are free parameters of the model. For proper motions, we also impose a full bivariate Gaussian model with covariance structure
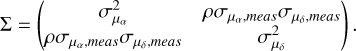 (5)
(5)
The above treatments are done for both the stream and background component which will be indicated by the subscripts s and b𝑔 where needed. We are now ready to fully specify the model of Eq. (1):
![${p_s}\left( {u\mid {\phi _1},\zeta } \right) = {p_{v,s}}\left( {v\mid {\phi _1},\zeta } \right) \cdot {p_{[{\rm{Fe}}/{\rm{H}}],s}}([{\rm{Fe}}/{\rm{H}}]\mid \zeta ) \cdot {p_{pm,s}}\left( {\mu \mid {\phi _1},\zeta } \right).$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq11.png) (6)
(6)
Each of the factors is provided here:
![${p_{v,s}}\left( {\upsilon \mid {\phi _1},\zeta } \right) = {1 \over {{\sigma _{v,s}}\sqrt {2\pi } }}\exp \left[ { - {1 \over 2}{{\left( {{{\upsilon - {\upsilon _s}(x)} \over {{\sigma _{v,s}}}}} \right)}^2}} \right],$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq12.png) (7)
(7)
![$\matrix{ {{p_{[{\rm{Fe}}/{\rm{H}}],s}}([{\rm{Fe}}/{\rm{H}}]\mid \zeta )} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over {{\sigma _{[{\rm{Fe}}/{\rm{H}}],s}}\sqrt {2\pi } }}\exp \left[ { - {1 \over 2}{{\left( {{{[{\rm{Fe}}/{\rm{H}}] - \overline {[{\rm{Fe}}/{\rm{H}}]} } \over {{\sigma _{[{\rm{Fe}}/{\rm{H}}],s}}}}} \right)}^2}} \right],} \hfill \cr } $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq13.png) (8)
(8)
![$\matrix{ {{p_{pm,s}}\left( {\mu \mid {\phi _1},\zeta } \right)} \hfill \cr {\quad = {1 \over {\sqrt {{{(2\pi )}^2}\left| {{\Sigma _s}} \right|} }}\exp \left[ { - {1 \over 2}{{\left( {\mu - {\mu _s}(x)} \right)}^T}\Sigma _s^{ - 1}\left( {\mu - {\mu _s}(x)} \right)} \right].} \hfill \cr } $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq14.png) (9)
(9)
For the background component we have a similar scheme except our parameters do not vary with ϕ1 but are constant values:
![${p_{bg}}(u\mid \zeta ) = {p_{v,bg}}(v\mid \zeta ) \cdot {p_{[{\rm{Fe}}/{\rm{H}}],bg}}([{\rm{Fe}}/{\rm{H}}]\mid \zeta ) \cdot {p_{pm,bg}}(\mu \mid \zeta ).$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq15.png) (10)
(10)
Similarly the factors are detailed here:
![${p_{v,bg}}(v\mid \zeta ) = {1 \over {{\sigma {v,bg}}\sqrt {2\pi } }}\exp \left[ { - {1 \over 2}{{\left( {{{v - {v_{bg}}} \over {{\sigma {v,bg}}}}} \right)}^2}} \right],$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq16.png) (11)
(11)
![$\matrix{ {{p_{[{\rm{Fe}}/{\rm{H}}],bg}}([{\rm{Fe}}/{\rm{H}}]\mid \zeta )} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad = {1 \over {{\sigma _{[{\rm{Fe}}/{\rm{H}}],bg}}\sqrt {2\pi } }}\exp \left[ { - {1 \over 2}{{\left( {{{[{\rm{Fe}}/{\rm{H}}] - \overline {{\rm{Fe}}/{\rm{H}}} {]_{bg}}} \over {{\sigma _{[{\rm{Fe}}/{\rm{H}}],bg}}}}} \right)}^2}} \right],} \hfill \cr } $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq17.png) (12)
(12)
![$\matrix{ {{p_{pm,bg}}(\mu \mid \zeta )} \hfill \cr {\quad = {1 \over {\sqrt {{{(2\pi )}^2}\left| {{\Sigma _{bg}}} \right|} }}\exp \left[ { - {1 \over 2}{{\left( {\mu - {\mu _{bg}}} \right)}^T}\Sigma _{bg}^{ - 1}\left( {\mu - {\mu _{bg}}} \right)} \right]} \hfill \cr } $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq18.png) (13)
(13)
There is a final nuance to our probabilistic modelling. We, in fact, have two models, one operating within the present-day Jacobi radius rJ of the GC, the other outside of it, both identical up to a mixing coefficient or fraction f. The separation is necessary as maintaining a single fraction of member stars for the whole setup would artificially increase the membership likelihood of stars within the stream component far away from the GC centre. It is thus more realistic to assume two different fractions of member stars for the areas within and outside the Jacobi radius of each cluster. The two models can therefore be given by the following:
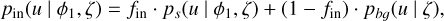 (14)
(14)
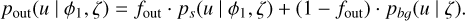 (15)
(15)
The coefficients 0 < fin, fout < 1 are free model parameters. Given a star with distance 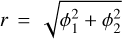 to the cluster’s centre and measurements u = (µα, µδ, v, [Fe/H]), together with positional information ϕ1 and measurement noise characteristics
to the cluster’s centre and measurements u = (µα, µδ, v, [Fe/H]), together with positional information ϕ1 and measurement noise characteristics ![$\zeta = \left( {{\sigma _{{\mu _\alpha },{\rm{}}meas{\rm{}}}},{\sigma _{{\mu _\delta },{\rm{}}meas{\rm{}}}},{\sigma _{v,{\rm{}}meas{\rm{}}}},{\sigma _{[{\rm{Fe}}/{\rm{H}}],{\rm{}}meas{\rm{}}}},\rho } \right)$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq22.png) , the overall model likelihood reads
, the overall model likelihood reads
![$p\left( {u\mid r,{\phi _1},\zeta } \right) = {\left[ {{p_{{\rm{in}}}}\left( {u\mid {\phi _1},\zeta } \right)} \right]^{I\left( {r < {r_J}} \right)}} \cdot {\left[ {{p_{{\rm{out}}}}\left( {u\mid {\phi _1},\zeta } \right)} \right]^{1 - I\left( {r < {r_J}} \right)}},$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq23.png) (16)
(16)
where I(r < rJ) is an indicator function equal to 1 when r < rJ and 0 otherwise. We note that this is the only step that requires the knowledge of ϕ2 in the mixture model.
In total, we have 24 parameters that we attempt to fit. These consist first of the coefficients for the quadratic functions parametrizing the change of radial velocity and proper motions of the stream component: {v1, v2, v3}, {µα, 1, µα, 2, µα, 3}, and {µδ, 1, µδ, 2, µδ, 3}, and the respective means for the background component: {vb𝑔, µα, b𝑔, µδ, b𝑔}. With regard to the metal-licity, the mean stream and background metallicities ![$\overline {{{\left[ {{\rm{Fe}}/{\rm{H}}} \right]}_s}} $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq24.png) and
and ![$\overline {{{\left[ {{\rm{Fe}}/{\rm{H}}} \right]}_{bg}}} $](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq25.png) , respectively, are fit. We also fit the intrinsic dispersions of the radial velocities, proper motions and metallicities for both the stream and background components:
, respectively, are fit. We also fit the intrinsic dispersions of the radial velocities, proper motions and metallicities for both the stream and background components: ![$\left\{ {{\sigma _{v,s}},{\sigma _{{\mu _\alpha },s}},{\sigma _{{\mu _\delta },s}},{\sigma _{[{\rm{Fe}}/{\rm{H}}],s}}} \right\}\quad {\rm{and}}\quad \left\{ {{\sigma _{v,bg}},{\sigma _{{\mu _\alpha },bg}},{\sigma _{{\mu _\delta },bg}},{\sigma _{[{\rm{Fe}}/{\rm{H}}],bg}}} \right\}$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq26.png) , respectively. We have dropped the subscript int for better readability, but stress that we fit the intrinsic and not total dispersion. Finally, we also fit for the fraction of GC members parameter in and outside of the respective Jacobi radius of each GC, namely fin and fout.
, respectively. We have dropped the subscript int for better readability, but stress that we fit the intrinsic and not total dispersion. Finally, we also fit for the fraction of GC members parameter in and outside of the respective Jacobi radius of each GC, namely fin and fout.
For the computation of the present-day Jacobi radius, we use the result of King (1962):
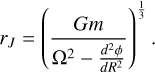 (17)
(17)
Here m is the mass of the GC, Ω is its angular velocity with respect to the Milky Way, and 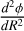 is the second derivative of the Milky Way’s gravitational potential with respect to the distance from the Milky Way. We compute this Jacobi radius while rewinding each cluster’s orbit in the presence of the Milky Way and the LMC. To account for uncertainties in the Milky Way and LMC potential, we use the same approach as Pace et al. (2022, see their Sect. 3.1), who sampled over the Milky Way potential uncertainties using the results of McMillan (2017). We also sample over the uncertainties in the present-day phase-space of both clusters (i.e. their proper motions, distances, and radial velocities). For NGC 1261, we obtain for the present-day Jacobi radius
is the second derivative of the Milky Way’s gravitational potential with respect to the distance from the Milky Way. We compute this Jacobi radius while rewinding each cluster’s orbit in the presence of the Milky Way and the LMC. To account for uncertainties in the Milky Way and LMC potential, we use the same approach as Pace et al. (2022, see their Sect. 3.1), who sampled over the Milky Way potential uncertainties using the results of McMillan (2017). We also sample over the uncertainties in the present-day phase-space of both clusters (i.e. their proper motions, distances, and radial velocities). For NGC 1261, we obtain for the present-day Jacobi radius 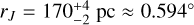 given a distance of 16.4 kpc. For NGC 1904, we obtain
given a distance of 16.4 kpc. For NGC 1904, we obtain 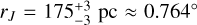 given a distance of 13.07 kpc. These values are comparable to those detailed in Balbinot & Gieles (2017). We note that with this calculation, we can also extrapolate estimates of the pericentre of each cluster’s orbit found to be 0.6 ± 0.1 kpc for NGC 1261 and 0.12 ± 0.06 kpc for NGC 1904. These values along with the other orbital parameters pertaining to these clusters will be discussed in Sect. 5.
given a distance of 13.07 kpc. These values are comparable to those detailed in Balbinot & Gieles (2017). We note that with this calculation, we can also extrapolate estimates of the pericentre of each cluster’s orbit found to be 0.6 ± 0.1 kpc for NGC 1261 and 0.12 ± 0.06 kpc for NGC 1904. These values along with the other orbital parameters pertaining to these clusters will be discussed in Sect. 5.
In fitting the mixture model parameters, we assume log-flat priors for the sampling of the dispersions and flat priors for all other parameters. In Table 1, we provide the prior ranges assumed for each of the parameters in obtaining the results for NGC 1261 and NGC 1904. The sampling and optimization of the log-likelihood function is performed using the emcee package with 100 walkers and 3000 steps each for the burn-in process and the actual run. Once the best-fit parameters are found, they are substituted within Eqs. (1–19) and the GC membership probability for each star is calculated as the posterior probability of the star to belong to the stream component,
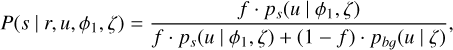 (18)
(18)
where f is either fin or fout depending on stars’ positions with respect to rJ:
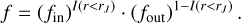 (19)
(19)
By applying a threshold cut on this membership probability, we are able to separate stars that have a high likelihood of belonging to the GC from the background distribution of stars. In Table 1, we provide the best-fit values for the quantities we fit for, both for NGC 1261 and NGC 1904, as well as their respective errors. This includes our estimates for the velocities as well as the mean metallicities for each GC which are in excellent agreement with the literature. Further discussion around our estimates of the mean metallicity as well as the metallicity and velocity dispersions will be provided in Sect. 5.4.
4 Results
In Fig. 2, we show the distribution of stars for each of our samples for NGC 1261 (left) and NGC 1904 (right). We colour each star by the membership probability achieved after a full run of the methodology described in Sect. 3. Stars with the highest probability of belonging to the respective GC are those in yellow. All stars with a membership probability of less than 20% are shown in solid grey.
The first thing we observe is that the stars immediately surrounding the centres of the clusters are retrieved with very high probability (>90%). Aside from the stars in the immediate vicinity of the GCs, we also detect high membership probability stars within each of the fields observed by S5 several degrees away from the clusters. For NGC 1261, we observe that the most probable member stars populate the target fields aligned with the direction of the GC’s orbit around the Galaxy (i.e. direction of increasing ϕ1) as well as the fields that are orthogonal to the orientation of the orbit (direction of increasing ϕ2). This hints at the intersecting double stream feature that has been reported for this GC in works such as Shipp et al. (2018) and Ibata et al. (2024). However, we caution that this could also be a result of limited sky coverage by S5 such that the debris from NGC 1261 could have a much wider coverage and happens to be present in all the S5 fields.
For NGC 1904, we also see probable member stars in all target fields observed by S5. We observe the alignment of several high-probability stars extending both to the left and right of the GC, specifically stars with ϕ1 < −1° and ϕ1 > 1°, indicating the presence of a stream of stars aligned with the direction of orbit of the GC. In addition to this feature, we also observe two groups of high-probability stars above and below the cluster in ϕ2 with −1° < ϕ1 < 1°. This is a sign of an inner stream to the GC referenced in Grillmair et al. (1995), Carballo-Bello et al. (2017), and Shipp et al. (2018). We elaborate on these features for both GCs further later in this section and provide a discussion of their nature and origin in Sect. 5.
In Fig. 3, we display the distributions of v𝑔sr, µα, µδ and [Fe/H] as a function of ϕ1 for all stars in our sample for NGC 1261 (left) and NGC 1904 (right). Each star is coloured by the probability of belonging to the respective cluster as computed via Eq. (18) in Sect. 3. In the bottom panels of the same figure, we also show the distributions of the membership probabilities for each GC. In order to isolate the stars that have a high probability of belonging to the respective GC, we enforce a threshold on the membership probability. By inspecting the probability distributions shown in the bottom panels of Fig. 3, we choose a threshold as high as possible as long as it does not eliminate clear members in the colour-magnitude diagram (CMD, discussed further in Figs. 4 and 5). This also corresponds approximately to the points at which we start seeing an increase in the number of stars with a larger probability in the bottom panels of Fig. 3. We therefore choose a threshold of 60% as is indicated by the dashed line. Bins with probabilities <20% again are shown in grey. With this preliminary cut, we assess in what follows the true membership of the remaining stars by tracing their position in the CMD as well as comparing their spatial distributions and properties to what is expected from N-body simulations of the two GCs. We further discuss robustness of this technique and possible contamination in our samples in Sect. 5.
Another step is performed to ascertain the membership of the selected sample of stars to the two studied GCs, through inspecting their distribution within the CMD. To construct the CMDs of the two clusters, we make use of the bands available from DECam photometry, particularly the dereddened ɡ and r bands which provide a much narrower CMD for the GC stars than what is possible using Gaia photometry given the larger depth that DECam photometry is able to probe. In Figs. 4 and 5 we analyse the distributions in the CMD for NGC 1261 and NGC 1904, respectively. The left panel of these two figures shows all stars in our original sample coloured by cluster membership probability. Similarly here, we plot all stars with probabilities of less than 20% in solid grey. We expect that for GCs, all member stars should follow a thin isochrone-like distribution in the CMD. It is therefore significantly noteworthy to see that the majority of the stars highlighted as high-probability members have such a distribution in the CMD, especially since no information about the colour or magnitude of the stars has been involved in the modelling. The middle and right panels show the remaining stars after enforcing the thresholds on the probability. In the middle panel, we show the potential members that lie within rJ while the right panel shows all potential members outside of this region. We also plot PARSEC isochrones with mean metal-licities taken from Table 1, and ages 11.2 Gyr for NGC 1261 and 11.7 Gyr for NGC 1904 (Baumgardt & Hilker 2018). These isochrones are also shifted using the respective distances of each GC (i.e. 16.4 kpc and 13.08 kpc for NGC 1261 and NGC 1904, respectively).
The middle panel shows that the majority of stars within the central region around the GC follow closely the isochrone. This is a good indication that the potential members we have in this region are true members. We also expect stream stars of a GC to follow the same isochrone. The right panel shows that many of the stars found in the stream indeed show this overlap with the isochrone though we see a slight scatter compared to the middle panel. The stars marked in red in Fig. 4 will be further introduced and discussed through Fig. 6. Using the dashed line in the middle and right panels, we define regions where the stars outside rJ have similar colour and magnitude properties as the respective clusters. These lines are defined such that the stars that are clearly far away from the isochrone are not included. Stars that lie outside the dashed lines are therefore contaminants and are indicated using a square marker. These stars are also plotted in the same way in Fig. 6 to track their spatial positions and properties.
We present the same analysis for NGC 1904 in Fig. 5. Similarly, we observe a strikingly narrow isochrone-like distribution of the potential members in the CMD. Similar to NGC 1261, the potential members are divided between those that lie within and outside of rJ and we observe near-perfect overlap between these stars and the GC isochrone. As for the stars outlined in magenta, they will be further introduced and discussed through Fig. 7. The stars outside of the chosen limits are shown by a square marker and are plotted in Fig. 7 as well.
The remaining stars after enforcing our selection threshold are shown in Figs. 6 and 7 for NGC 1261 and NGC 1904, respectively. In both figures, we display the observed stars in yellow and what is expected from the N-body simulations in blue. The top middle panel of both figures shows the spatial distribution of the remaining stars. The dashed circles outline the target fields observed by S5 and the solid circle shows the area outlined by the Jacobi radius. In the top right panel, we show the density plot for the remaining sample stars (shown again in yellow in this figure) by applying kernel density estimation (KDE) using an Epaneshnikov kernel with 1.5° for the bandwidth. We note that we take out the stars within rJ of the GC in order to enhance the density contrast.
The bottom right panel in both figures shows a 2D histogram plot of what we would expect to see from our N-body simulations with the red vertical lines indicating the same area on the sky as the above panels. Lighter colours represent regions of higher density, while darker colours similarly represent regions of lower density. In the left panels, the dashed black lines show the best-fit polynomial tracks defined in Sect. 3 that trace the mean variation of v𝑔sr, µα and µδ as a function of φ1. We emphasize that the polynomial tracks are solely a fit to the data without any assumption or knowledge of the GC orbits or Milky Way potential. In the bottom left panel, the horizontal dashed line similarly defines the best-fit mean metallicity ![${\overline {[{\rm{Fe}}/{\rm{H}}]} _s}$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq40.png) as our estimate for the mean metallicity of each GC.
as our estimate for the mean metallicity of each GC.
For NGC 1261 (Fig. 6), we find 88 potential members within rJ and 28 outside rJ. We observe that the best-fit track and the recovered member stars are quite similar to the results of the N- body simulation within ~2° of the cluster. The properties of the potential member stars also lie within the ranges defined by the simulation to within two standard deviations. The metallicity for each star is also consistent within two standard deviations from the best-fit mean metallicity of the cluster. For the region with ϕ1 < −2.5°, however, the best-fit tracks begin to diverge from the expected distribution. Since the potential members in this region are questionable, we mark these stars with a red border in both the left and top right panels, and track them further in the rest of the analysis. With regard to the position of these stars in the CMD, we observe that two of the stars marked in red do not differ in their distribution within the CMD from the remaining potential members, showing that they have properties similar to those of the stars within rJ from the cluster. The mismatch seen in Fig. 6 between the expected properties of these stars in the simulations and their observed properties may imply that the Milky Way potential assumed for the N-body simulations is not accurate enough to reproduce the properties of the stream far away from the cluster. For example, we have ignored the effect of the Milky Way bar (e.g. Hattori et al. 2016; Price-Whelan et al. 2016; Erkal et al. 2017; Pearson et al. 2017). Within ±2° from this GC (roughly 4rJ), however, we can confidently say that we detect highly probable member stars that are also expected from the simulations. We also discuss the divergence of the tracks in Sect. 5. In total, we observe a broad distribution of stars that overlaps with the regions where the cross-shaped structures were observed in Shipp et al. (2018). Although this similarity could be a consequence of the fields chosen by S5, we do confirm the existence of potential member stars in all fields.
For NGC 1904 (Fig. 7), we find 143 potential members within rJ and 51 outside rJ . We see that the best-fit tracks agree with the N-body simulation, and the likely cluster and stream members also have similar properties to what is expected from the simulation, considering the measurement uncertainties. We note the groups of stars on the top and bottom of the GC that seem to form an inner set of tidal tails that along with the horizontal distribution of stars along the cluster’s orbit, give the appearance of "multiple-tidal tails" associated with this cluster. Such substructure is expected when a GC is very close to apocentre, which is the case for NGC 1904. To trace the properties of the potential member stars of the inner stream, we mark these stars with magenta outlines. These stars are also indicated in Fig. 5 where we observe that they all align perfectly with the isochrone indicating that they are likely to be true members. The left panel of Fig. 7 shows that the properties of these stars directly overlap with the properties of stars close to the GC. To further evidence the existence of the top and bottom overdensities of stars, they are shown in the top right panel as overdensities on the top and bottom of the cluster and a stream component along ϕ1 . This distribution matches the results of Shipp et al. (2018) with respect to this cluster. This extension in the ϕ2 direction is also visible in the N -body simulations, as shown in the bottom right panel of Fig. 7. There too, the simulations predict the existence of an outer stream with ϕ1 < −2° or ϕ1 > 2°, and an inner stream in the region in between. We provide in Appendix B some of the potential members identified in this work for NGC 1261 and NGC 1904, respectively, with the full lists made available online. In the following section, we further discuss our methodology and the possible origin scenarios explaining the observed structures.
Prior range and best-fit values for the mixture model parameters for NGC 1261 and for NGC 1904.
 |
Fig. 2 Spatial distribution of the targeted stars, each colour-coded according to their membership probability of belonging to NGC 1261 (left) and NGC 1904 (right). All stars with probabilities of less than 20% are shown in grey. The solid circles outline the region within the Jacobi radius of each cluster and show that we detect many probable members outside of these regions. |
 |
Fig. 3 Modelled properties of stars within the sample (left for NGC 1261 and right for NGC 1904) as a function of ϕ1. As in Fig. 2, each point is colour-coded according to its membership probability of belonging to the respective cluster. The bottom two panels show the histograms of all probabilities in the sample. The vertical lines at 0.6 (60%) represent the threshold on the probability. |
 |
Fig. 4 Dereddened colour-magnitude diagram for likely NGC 1261 cluster and stream members using the g and r bands from the available DECam photometric measurements. Left panel: all stars in our sample for this cluster are colour-coded according to the calculated membership probability; grey indicates stars with probabilities of less than 20%. We observe a very narrow distribution that emerges within the whole sample. Middle panel: high-probability member stars are extracted using the threshold of 60% and considering only stars within a radius r = rJ around the cluster. An isochrone is also added for comparison. The dashed lines separate stars with CMD properties similar to those of the cluster from likely contaminants (square markers). Right panel: similarly, we plot high-probability stars that lie outside of r = rJ. The stars outlined in red are the same stars selected in Fig. 6 as having different vgsr from the N-body simulation prediction. |
 |
Fig. 5 Same as Fig. 4, but for NGC 1904. The results for this GC show very little contamination as most potential members align well in the CMD. The stars outlined in magenta are the same as those selected in Fig. 7 for their extension in ϕ2. These stars align well with the rest of the selection, indicating that they are likely to be true members of NGC 1904. |
 |
Fig. 6 Main results for NGC 1261. Left: distribution of the modelled properties of the stars belonging to NGC 1261 and its stream as a function of ϕ1 after enforcing a 60% lower limit on the membership probability. The error bars represent the measurement uncertainties. The black dashed line represents the best-fit track used to model the mean value for the respective property at a given ϕ1. The results from the N-body simulation in each of the four dimensions are in blue. Stars with v𝑔sr values inconsistent with the N-body simulation are outlined in red. Top middle: spatial distribution of the same stars plotted in the left panel. The dashed circles show the outlines of the fields targeted by S5. The solid circle shows the extent of rJ. Stars plotted using the square markers are those that show different CMD properties from the cluster, as shown in Fig. 4. Top right: 2D density plot of the distribution of potential member stars around NGC 1261. Stars within rJ were removed when creating this plot to enhance the density contrast. Bottom right: 2D histogram showing the density of simulation particles on the sky. The vertical red lines indicate the same window on the sky as shown in the top panels. |
 |
Fig. 7 Same as Fig. 6, but for NGC 1904. In the top middle panel we show the stars that form overdensities above and below the cluster in ϕ2 (in magenta). They are also highlighted in the left panel, showing that they have similar properties to the other likely cluster and stream stars. These overdensities are clearly visible in the density plot provided in the top right panel. The 2D histogram of the N-body simulation shown in bottom right panel also shows a clear distinction between the inner tails, which correspond to our detected overdensities, and the outer tails. |
5 Discussion
5.1 Contamination and robustness of findings
In the Gaussian mixture modelling approach (Sect. 3), we fit for a stream and a background component in the data. The properties of stars belonging to the stream component are assumed to vary along a polynomial as a function of its coordinate ϕ1 , while stars belonging to the background have non-varying Gaussian distributions modelling their properties. A concern therefore could be that since we assume that a stream component exists, the algorithm will likely find a set of stars that have streamlike properties when the structures found are not necessarily real. In this case, the stream-like property would be the variation of the parameters modelling the extra-tidal GC stars along a thin polynomial distribution dependent on ϕ1. To address this concern we therefore repeat the mixture model runs we have performed while not fitting for one of the parameters available. In other words, we remove any information we have on one of our modelled parameters that shows a dependence on ϕ1 , and repeat the runs with this information missing. Specifically, we fit for the distribution in v𝑔sr, μα and [Fe/H] and take out any information about µδ. Hence, the 2-dimensional Gaussian modelling of the proper motion space of the GCs is now a 1-dimensional Gaussian modelling of the distribution in μα alone. In this way the correlation between μα and µδ is also not considered, and therefore a large portion of the information that could constrain a stream component is removed. If the new high-probability member stars in these runs show a narrow distribution of µδ even though no assumption is made on this parameter, this shows that the retrieved stars indeed follow a stream-like distribution that is not artificially invented. Additionally, if we retrieve the same high-probability members from the previous runs, this shows that our results are highly robust against missing information and large changes in the methodology.
The same range of priors assumed for the full-fit runs are used (see Table 1). The results from the new runs are displayed in Fig. 8 for NGC 1261 (left) and NGC 1904 (right). The best- fit tracks from the full-fit runs are shown by the dashed black line while the solid red line represents the best-fit tracks from the new runs excluding µδ. For both NGC 1261 and NGC 1904, we see great overlap between the two runs. We also extract the potential members from the new runs by enforcing a limit on the membership probability. Since by removing any information of µδ, we are using less information than when applying the full- fit runs, this increases the variation and the uncertainty of the outcomes. As a result, it is expected that the membership probability for originally high-probability member stars will decrease. Therefore, to extract potential members, we enforce a 50% lower limit instead of the 60% we used before. The stars that remain from this cut are shown in blue open circles in Fig. 8 and the common stars between these runs and the full-fit ones are shown using yellow open circles. As expected, since the runs excluding µδ use less information, we find more stars that are more likely contaminants than when using the full-fit runs. These are the stars that were not common between the new and full-fit runs (blue points). However, the majority of potential members found using the full-fit runs have been retrieved by the new runs as well. This includes stars present in the extra-tidal structures found surrounding the two GCs. Most importantly, the stars that we retrieve with the less informative runs still follow the track found for µδ even though no assumptions were made for this parameter. We repeat this same analysis now removing any information on μα instead of µδ and arrive at similar conclusions: we retrieve the potential members found using the full-fit runs though with expected larger contamination, and the retrieved stars follow a narrow distribution in μα though no assumption was made on this parameter.
Regarding contamination, Figs. 4 and 5 have shown that some stars we retrieve do not align with the GCs’ isochrones. These stars have been plotted in Figs. 6 and 7 to inspect their spatial distributions. We can also assess the contamination by taking parameter samples from the chains of the mixture model defined in Sect. 3. We therefore sample 100 values of each mixture model parameter, and using each of these samples, the membership probability of the stars in our original selection is then calculated thus obtaining 100 probabilities for each star. The thresholds on the probability defined in Sect. 4 are then applied and the fraction of samples in which each star passes the thresholding is counted. The results of this procedure are shown in Fig. 9 for NGC 1261 (top) and NGC 1904 (bottom). The potential members for each GC are coloured by the fraction of samples in which they had a membership probability greater than the threshold. Stars identified as contaminants given their position in the CMD are indicated with a square marker. We see that in the case of NGC 1261, one star with ϕ1 < −2.5 previously highlighted in red appears as potential members ≈80% of the time, other stars closer to the cluster have a smaller fraction. The majority of the stars for this GC, however, have robust membership probabilities. In the case of NGC 1904 (lower panel) we see that stars farthest away from the cluster in ϕ1 have probabilities that are not as robust as the other stars. These stars could therefore be contaminants. The majority of the stars forming the overdensities we detect on the top and bottom of this cluster, however, have survived the thresholding 100% of the time showing robust high probabilities against changes in the best-fit model parameters.
We therefore find that our method is detecting true structures surrounding the GCs which extend several degrees away from their centres. Additionally, although contamination is present, we find that it is minimal. This is also supported by previous work which have made note of the presence of these structures, primarily Shipp et al. (2018), but have not studied them using proper motion or radial velocity and metallicity information.
 |
Fig. 8 Comparison between the full-fit runs described in Sect. 3, and the new runs where µδ is not taken into account. The best-fit tracks from the full-fit runs, first shown in Figs. 6 and 7, are re-plotted here using the dashed line. The best-fit tracks from the new runs are shown using the solid red line. A new lower limit is enforced on the membership probability from the new runs and the remaining stars are cross-matched with the potential members from the full-fit results of Sect. 4. The common members between the two runs are shown in yellow and those that are not common are shown in dark blue. In this plot we see that the distribution of stars in µδ follows the same track as the original runs, even though it was not taken into account. |
 |
Fig. 9 An assessment of the contamination within the samples of possible members. This is calculated by sampling 100 values from the posterior distributions of our mixture model parameters and checking how many times each star survives our cut using the model parameters from each of the 100 samples. The potential members (in yellow) survived 100% of the time, while those closer to blue survived the corresponding fraction of times. Contaminants identified through their position in the CMD are indicated using the square markers. |
5.2 Understanding the tidal disruption of NGC 1261 and NGC 1904
In order to better understand why NGC 1261 and NGC 1904 are tidally disrupting, we can compare their Jacobi radii to their present-day half-mass radius and the observed extent of the GC, which is parametrized by the tidal radius (de Boer et al. 2019). This is useful since the cluster is expected to strip heavily when the Jacobi radius is comparable to the half-mass radius. In addition, stars beyond the Jacobi radius are unbound so if the tidal radius is larger than the Jacobi radius, then there are stars to strip.
As calculated in Sect. 3, NGC 1261’s present-day Jacobi radius is 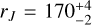 pc. This is much larger than its half-mass radius of 4.86 pc (Baumgardt & Hilker 2018) and its observed extent (i.e. tidal radius) of 51.51 pc (de Boer et al. 2019) suggesting that NGC 1261 is currently in a relatively weak tidal field. However, at its pericentre of 0.6 ± 0.1 kpc, NGC 1261’s Jacobi radius was
pc. This is much larger than its half-mass radius of 4.86 pc (Baumgardt & Hilker 2018) and its observed extent (i.e. tidal radius) of 51.51 pc (de Boer et al. 2019) suggesting that NGC 1261 is currently in a relatively weak tidal field. However, at its pericentre of 0.6 ± 0.1 kpc, NGC 1261’s Jacobi radius was 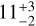 pc: only ~2.2 half-mass radii, and significantly smaller than its present-day tidal radius. This suggests that stars in the outskirts of NGC 1261 would have stripped at its previous pericentre.
pc: only ~2.2 half-mass radii, and significantly smaller than its present-day tidal radius. This suggests that stars in the outskirts of NGC 1261 would have stripped at its previous pericentre.
For NGC 1904, the present-day Jacobi radius is 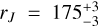 pc. This is significantly larger than the half-mass radius of 4.33 pc (Baumgardt & Hilker 2018) and the tidal radius of 108.73 pc (de Boer et al. 2019) suggesting that NGC 1904 is currently in a weak tidal field. However, at its pericentre of 0.12 ± 0.06 kpc, its Jacobi radius was
pc. This is significantly larger than the half-mass radius of 4.33 pc (Baumgardt & Hilker 2018) and the tidal radius of 108.73 pc (de Boer et al. 2019) suggesting that NGC 1904 is currently in a weak tidal field. However, at its pericentre of 0.12 ± 0.06 kpc, its Jacobi radius was 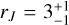 pc. This is only ~0.7 half-mass radii, suggesting that it experienced strong stripping at pericentre. Indeed, the dipole-like morphology of the tidal debris seen in the top and bottom right panels of Fig. 7 was likely stripped at the previous pericentre. Thus, although both GCs are currently in a weak tidal field, they both experienced much stronger tides at pericentre.
pc. This is only ~0.7 half-mass radii, suggesting that it experienced strong stripping at pericentre. Indeed, the dipole-like morphology of the tidal debris seen in the top and bottom right panels of Fig. 7 was likely stripped at the previous pericentre. Thus, although both GCs are currently in a weak tidal field, they both experienced much stronger tides at pericentre.
5.3 Further insights into the extra-tidal features of the GCs
In Sect. 1, we introduced the physical mechanism behind which tidal tails around GCs form and the characteristic S-shaped morphology that they take. When a GC is not at pericentre, the inner-most parts of the tails point towards the Galactic centre, with the outer parts of the tails (at larger distances from the cluster centre) moving towards the orbital path (Montuori et al. 2007; Klimentowski et al. 2009). In Fig. 10, we study this behaviour in more detail by looking at the radial velocity of each star with respect to the radial velocity of the cluster 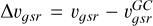 , where
, where  is the mean radial velocity of each GC taken from (Baumgardt & Hilker 2018) and transformed to the galactic standard of rest. Figure 10 shows the distribution of stars within ±2° around NGC 1261 (top row) and NGC 1904 (bottom row) for our potential members (left) and simulations (right). Each star is coloured by its value of Δv𝑔sr. For NGC 1261, the simulations predict a gradient in Δv𝑔sr along ϕ1, which is also visible using the observed sample from the corresponding left panel. For NGC 1904, we observe a clear change in the direction of Δv𝑔sr for the inner tidal tails evidenced by the switching of the sign of Δv𝑔sr between ϕ2 < 0 and ϕ2 > 0. This behaviour is compatible between the observational sample (left) and the simulations (right). This therefore shows that the top and bottom overdensities of stars (in both the observations and simulations) are moving in opposite directions, pointing towards the apparent rotational motion undergone by these stars as they escape the cluster’s potential (Montuori et al. 2007).
is the mean radial velocity of each GC taken from (Baumgardt & Hilker 2018) and transformed to the galactic standard of rest. Figure 10 shows the distribution of stars within ±2° around NGC 1261 (top row) and NGC 1904 (bottom row) for our potential members (left) and simulations (right). Each star is coloured by its value of Δv𝑔sr. For NGC 1261, the simulations predict a gradient in Δv𝑔sr along ϕ1, which is also visible using the observed sample from the corresponding left panel. For NGC 1904, we observe a clear change in the direction of Δv𝑔sr for the inner tidal tails evidenced by the switching of the sign of Δv𝑔sr between ϕ2 < 0 and ϕ2 > 0. This behaviour is compatible between the observational sample (left) and the simulations (right). This therefore shows that the top and bottom overdensities of stars (in both the observations and simulations) are moving in opposite directions, pointing towards the apparent rotational motion undergone by these stars as they escape the cluster’s potential (Montuori et al. 2007).
Further inspection of the top and bottom overdensities of stars can be performed by looking at their corresponding distances. In the left-most panel of Fig. 11, we colour the particles in the N-body simulation with their heliocentric distances in the same area on the sky as shown in Fig. 10. We observe an expected distance gradient along ϕ2 with ≈ 2 kpc difference between stars in the top and bottom overdensities. To check whether this gradient is also detected within our sample, we select the stars in the top (cyan) and bottom (magenta) overdensities, as well as the stars within rJ (grey) as shown in the middle left panel of the same figure. We then plot the CMD of these stars in the middle right panel zooming in on the main sequence and subgiant branches. We observe a difference in magnitude detected as a vertical offset in this panel between the three selected groups of stars. To further confirm this distance gradient, we attribute a distance measure to each star in our sample equal to the distance of its nearest neighbor in the simulation particles. By correcting the magnitudes of the potential members given their distances, we then obtain a measure of their absolute magnitudes M𝑔. The right panel of the figure shows the result of this procedure where we observe that the three selected groups of stars now overlap after this correction, supporting the presence of the distance gradient predicted by the simulations and further consolidating the true membership of these stars to the GC.
Additionally, as mentioned, there exists a strong correlation between the orientation of inner tidal tails and the position of the GC along the orbit. For near-circular orbits, the angular velocity is constant and therefore results in an almost constant orientation of the tails with respect to the direction of the cluster orbit and the Galactic centre. For eccentric orbits, however, the behaviour becomes more complicated. When approaching the apocentre, the stars between the cluster and the Galactic centre reach their apocentres before the GC does, and decelerate because they are on tighter orbits than the rest of the tail. On the other hand, stars between the cluster and the Galactic anti-centre will not have yet reached their apocentres and so will be moving faster. The resulting effect seen is that near apocentres, the inner tails are oriented along the direction to the Milky Way centre. When approaching pericentre, stars between the GC and the Galactic centre speed up with respect to the GC, again being on tighter orbits, while those on the opposite side of the GC slow down. This leads the tails to become elongated along the direction of the GC orbit (Montuori et al. 2007; Klimentowski et al. 2009; Küpper et al. 2012).
This dynamic can be probed by inspecting the orientation of tails with respect to the current phases of the GCs along the orbit. In Fig. 12, we plot in red and using galactocentric coordinates the current position of each GC along its integrated orbit plotted in purple. The upper row refers to NGC 1261 and the bottom row to NGC 1904. Each column is a projection on one of the planes defined in this coordinate system. The orbit has been integrated using the gravitational potential defined in Sect. 3.1. Arrows in the middle panels show the direction in which the clusters are moving. The orange line connects the cluster to the centre of the Galaxy, and the respective N-body simulation scatter is also plotted in blue. From Fig. 12, we can see that NGC 1261 has recently passed apocentre and is heading towards pericentre, while NGC 1904 is close to reaching apocentre. The difference in the tidal tails can then clearly be seen as explained by the theory: the inner tails for NGC 1261 point towards the orbit while in the case of NGC 1904, we see the dipole morphology of the inner tails pointing in the direction of the Milky Way centre. This shows that the overdensities we detect on the top and bottom of NGC 1904 are a result of this cluster approaching apocentre and the reason we do not see these overdensities in the case of NGC 1261 is because this GC is in a different phase in its orbit where it has passed its apocentre and is now heading towards pericentre2. Finally, we also note that the Sun’s location relative to the orbital plane of NGC 1904 is crucial in order to see the radially extended debris on the sky. Since the Sun sits ~4 kpc above the orbital plane of NGC 1904, we can see this radial extension projected onto the sky instead of only being able to see it with precise distances.
We also compare our potential members detected for NGC 1261 with the results presented in Ibata et al. (2024). In the latter work, two streams were speculated to be related to NGC 1261 given that they share the same position on the sky. The streams were labelled NGC 1261a and NGC 1261b. In Fig. 13 we plot the stellar streams detected in Ibata et al. (2024) that surround NGC 1261, where we colour each star in the figure according to its corresponding stream index. We observe that at least two streams crisscross this area. We also overplot in yellow the potential members detected in the current work, with the stars common with Ibata et al. (2024) outlined in black. The fields surveyed by S5 are indicated by the dashed circles. In total, we find 34 common stars, 20 of which are within rJ and 14 are outside. From this figure we see the extent of the extra- tidal features around NGC 1261 which goes beyond the fields probed by S5. This also supports the presence of a wide distribution of member stars surrounding this GC. We note that for NGC 1261, our simulations do not reproduce the double stream morphology inspected in this work and seen in Shipp et al. (2018) and Ibata et al. (2024). This therefore points towards more complex dynamics that serve to form this second stream that should be incorporated in the simulations to retrieve the structures observed in these several works. One possible explanation of this complex morphology is the Milky Way bar. Previous works have found that the rotating bar can have a significant effect on stellar streams (e.g. Hattori et al. 2016; Price-Whelan et al. 2016; Erkal et al. 2017; Pearson et al. 2017), and can create complex morphology in the tidal debris close to the cluster (e.g. Dillamore et al. 2024). Given that the orbit of NGC 1261 is highly eccentric with a small pericentre, this makes the interaction of this GC with the Milky Way bar very possible and also frequent given its small orbital period. Additionally, NGC 1261 is known to have undergone more than 10 orbital laps around the Galaxy in the past 2 Gyr (Wan et al. 2023) similarly due to its short orbital period. At each pericentre passage, the GC sheds some of its stars producing a new stream that follows its orbit as a result. These streams can overlap on the long run and produce “multiple tidal tail” features around GCs, and could be the case explaining the extra-tidal features seen for NGC 1261.
 |
Fig. 10 A closer look at the radial velocities in comparison between observed members and simulation predictions. The upper and lower rows refer to NGC 1261 and NGC 1904, respectively. Left panels: potential member stars within ±2° around the clusters coloured by the radial velocity shifted with respect to the radial velocity of the cluster (Δv𝑔sr). Right panels: same property as left panels, but displayed using particles from the N-body simulation. |
 |
Fig. 11 Confirmation of the distant gradient along ϕ2 for NGC 1904. Left: distance gradient along ϕ2 seen in the simulations of NGC 1904. Middle left: Top and bottom overdensities of stars (in cyan and magenta, respectively). Potential GC members that fall within rJ are shown as empty black circles, while those outside rJ are shown in yellow. Middle right: distance gradient can be seen in the main sequence and subgiant branches given the observed differences in magnitude. Right: correcting for the distance differences leads to the overlapping of selected stars within the CMD supporting the present of the distance gradient. |
5.4 GC properties
Given that we fit the mean and intrinsic dispersions for the properties of the GCs while fitting for the stream and background components, we can compare our measured values to previous literature estimates. For NGC 1261, we measure a radial velocity dispersion of σv = 2.82 ± 0.32 km s−1 which is in agreement with Wan et al. (2023) within 2 standard deviations. For NGC 1904, we measure σv = 3.06 ± 0.30 km s−1 which is smaller than that measured by Wan et al. (2023) of 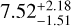 km s−1, though in the latter work it is mentioned that the last two stars in their radial bins contribute the most to the dispersion, and when excluded from their sample, the dispersion drops to
km s−1, though in the latter work it is mentioned that the last two stars in their radial bins contribute the most to the dispersion, and when excluded from their sample, the dispersion drops to 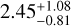 km s−1 which then becomes in good agreement with our estimate. We note that Wan et al. (2023) consider an area of 1° around their sample of GCs which is ≈rJ in the case of NGC 1904.
km s−1 which then becomes in good agreement with our estimate. We note that Wan et al. (2023) consider an area of 1° around their sample of GCs which is ≈rJ in the case of NGC 1904.
In terms of the mean metallicity, we measure ![$\overline {[{\rm{Fe}}/{\rm{H}}]} = - 1.29 \pm 0.02$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq49.png) for NGC 1261 and
for NGC 1261 and ![$\overline {[{\rm{Fe}}/{\rm{H}}]} = - 1.61 \pm 0.02$](/articles/aa/full_html/2025/01/aa51930-24/aa51930-24-eq50.png) for NGC 1904. These estimates are in excellent agreement with works such as Harris (1996, 2010 edition), Ferraro et al. (1999), Muñoz et al. (2021), and Wan et al. (2023). As for the metallic- ity dispersion, we measure σ[Fe/H] = 0.19 ± 0.02 for NGC 1261 and σ[Fe/H] = 0.21 ± 0.02 for NGC 1904. These values are larger than what is presented in works such as Muñoz et al. (2021), Limberg et al. (2022), and Wan et al. (2023) which can be an indication of high contamination in our sample or an underestimation of the measurement errors. We argue here that the issue is an underestimation of measurement uncertainties.
for NGC 1904. These estimates are in excellent agreement with works such as Harris (1996, 2010 edition), Ferraro et al. (1999), Muñoz et al. (2021), and Wan et al. (2023). As for the metallic- ity dispersion, we measure σ[Fe/H] = 0.19 ± 0.02 for NGC 1261 and σ[Fe/H] = 0.21 ± 0.02 for NGC 1904. These values are larger than what is presented in works such as Muñoz et al. (2021), Limberg et al. (2022), and Wan et al. (2023) which can be an indication of high contamination in our sample or an underestimation of the measurement errors. We argue here that the issue is an underestimation of measurement uncertainties.
To gain better understanding of the source of the issue, we split the detected potential members (i.e. stars that have passed the probability threshold) between stars within rJ and those outside and repeat the calculation of the intrinsic metallicity dispersion on both these groups. We also exclude the stars that have been deemed as contaminants given their positions in the CMD (i.e. stars indicated throughout this work with a square marker). The calculation is performed by fitting a Gaussian function to the distribution of metallicities of either group following an MCMC framework using the emcee package with 100 walkers and 1000 steps. Specifically, we fit for the mean metallicity and intrinsic metallicity dispersion. The same analysis is performed for the velocity dispersion. In other words, we calculate the velocity dispersion of the stars within and outside rJ , by fitting a Gaussian function to the distribution of v𝑔sr − v(x), where we remind v(x) is the best-fit polynomial for the variation of v𝑔sr against ϕ1.
The results are presented in Table 2 for both GCs where the total number of stars in each region is also indicated. For NGC 1261, we observe that the metallicity dispersions for stars inside and outside rJ are compatible. This indicates low contamination in the stream component and instead points towards an underestimation of the measurement uncertainties. Additionally, the dispersions are now smaller and in agreement with previous work now that a threshold on the probability has been applied. Similarly, we retrieve comparable velocity dispersions for stars inside and outside rJ which remain consistent with values present in the literature with an slight increase from 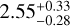 km s−1 to
km s−1 to 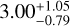 km s−1 which is expected as we move rad−ally away from the cluster centre. For NGC 1904, σ[Fe/H] inside rJ stayed the same as when fitting for the entire set-up
km s−1 which is expected as we move rad−ally away from the cluster centre. For NGC 1904, σ[Fe/H] inside rJ stayed the same as when fitting for the entire set-up 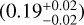 . Given the low level of contamination in this region, especially that evidenced by the CMD distribution in Fig. 5, we expect that the measurement errors for the stars inside rJ are underestimated leading to the inflated dispersion. We thus suspect that the rvspecfit metallicities have a systematic accuracy floor of ~0.2 dex, but might be the best that can be done with a low-resolution spectrograph like AAOmega. For stars outside rJ, however, we see that the metallicity dispersion drops to
. Given the low level of contamination in this region, especially that evidenced by the CMD distribution in Fig. 5, we expect that the measurement errors for the stars inside rJ are underestimated leading to the inflated dispersion. We thus suspect that the rvspecfit metallicities have a systematic accuracy floor of ~0.2 dex, but might be the best that can be done with a low-resolution spectrograph like AAOmega. For stars outside rJ, however, we see that the metallicity dispersion drops to 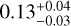 which is now consistent with estimates provided in Wan et al. (2023) and therefore consistent with an unresolved dispersion. For the velocity dispersion we measure
which is now consistent with estimates provided in Wan et al. (2023) and therefore consistent with an unresolved dispersion. For the velocity dispersion we measure 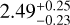 km s−1 which is still in agreement with the estimate of Limberg et al. (2022) and Wan et al. (2023) when the latter exclude the outermost two stars in their analysis of this cluster. For stars outside rJ, we measure a radial velocity dispersion of
km s−1 which is still in agreement with the estimate of Limberg et al. (2022) and Wan et al. (2023) when the latter exclude the outermost two stars in their analysis of this cluster. For stars outside rJ, we measure a radial velocity dispersion of 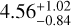 km s−1, an expected increase which then is in agreement with the estimate of Wan et al. (2023) within the given error margins.
km s−1, an expected increase which then is in agreement with the estimate of Wan et al. (2023) within the given error margins.
 |
Fig. 12 Orbits of NGC 1261 (upper row) and NGC 1904 (lower row). Each column presents a different plane projection in galactocentric coordinates. The red star indicates the present position of each GC and the simulation particles are overplotted in this coordinate system. The purple line represents the integrated orbit of each cluster where the direction of orbit is indicated by the red arrow in the middle panels. The orange line connects the cluster to the centre of the Galaxy. We see that NGC 1261 is close to apocentre, but has passed it and is moving closer to pericentre, while NGC 1904 is approaching and is very close to its orbit’s apocentre. |
 |
Fig. 13 Comparison with the results of Ibata et al. (2024) around NGC 1261. Streams found by Ibata et al. (2024) surrounding NGC 1261 and thought to be associated with the GC are plotted here colour-coded according to the corresponding stream ID. We overplot the potential members for NGC 1261 found in this paper in yellow, and outline the common ones between the two works in black. We also show the areas inspected by S5 (dashed circles). |
Recalculated metallicity and velocity dispersions for stars inside and outside rJ of NGC 1261 and of NGC 1904.
6 Conclusions
In this work, we have explored the extra-tidal features of the globular clusters (GCs) NGC 1261 and NGC 1904. Given the interesting morphology of the features surrounding the two GCs, the Southern Stellar Stream Spectroscopic Survey (S5) performed follow-up observations of fields surrounding the clusters where radial velocity and metallicity measurements were gathered for the target stars. In this work we have used these observations to gather new information about the structures surrounding the two GCs and linked their presence to their dynamical properties. The analysis performed and results obtained can be summarized as follows:
With the use of information on the proper motion, radial velocity, and metallicity of the targeted stars, we applied a Bayesian mixture modelling approach to provide a membership probability thereby separating high-probability stars from others that are more likely field stars;
We identified potential member stars associated with these two GCs within an area spanning ten times their Jacobi radius. By inspecting the spatial distribution of the potential members, we confirmed the results of Shipp et al. (2018). In the case of NGC 1904, we observed stars distributed along the direction of the cluster’s orbit, as well as distributions of stars not aligned with this direction and forming a cross-shaped pattern with the previous distribution. As for NGC 1261, we observed a broad distribution of member stars surrounding the cluster;
We performed N-body simulations of the two GCs and compared what is expected from the simulations with regard to the evolution of the properties of the escaped cluster stars along the orbit and the properties of the detected potential members from our sample. It is clear that there is good agreement between the observational sample and the simulation predictions for NGC 1904, but a clear comment cannot be made with respect to NGC 1261;
Using DECam photometry, we inspected the colourmagnitude diagrams of the potential member stars and confirmed that the majority of them lie along an isochrone-like distribution, which is expected for GCs. This final check is a powerful independent confirmation that we are correctly identifying members and the structures in which they are now found;
We discussed the origin of the observed structures and linked their presence to the phase of orbit of each GC. Given that NGC 1904 is approaching apocentre, we expect a clear distinction between the inner and outer tidal tails, where the inner parts of its tidal tails are expected to point towards the Milky Way centre. On the other hand, NGC 1261 has recently passed its apocentre passage and is now on its way to pericentre. Therefore, the inner parts of its tidal tails are expected to have closer alignment with its orbit instead. We discussed that the remaining stream for this cluster can be associated instead with the fact that NGC 1261 has undergone several orbits around the galaxy and its possible interaction with the Milky Way bar.
Similar to NGC 1261 and NGC 1904, other Milky Way GCs exhibit signs of multiple tails, such as NGC 288 and NGC 2298. Therefore, it is possible to perform the analysis presented here for these systems as well. Additionally, given that the studied GCs are found close to their apocentre passages, the epicyclic motion within their tidal tails would be theoretically prominent and so one can attempt to look for periodicity in the distribution and dynamics of the stars in the tails. Moreover, follow-up high- resolution spectroscopic measurements of the potential members found in this work could help confirm membership and improve the precision of our estimates. We leave such explorations for future work.
Data availability
The full versions of Tables B.1 and B.2 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/693/A69
Simulation videos are available at https://www.aanda.org and at https://www.youtube.com/watch?v=R-zooau62hk, https://www.youtube.com/watch?v=Gr8legg0QeQ, https://www.youtube.com/watch?v=ITUK1mfpM70, and https://www.youtube.com/watch?v=8bHzEqXmwZU
Acknowledgements
This work is supported by the DSSC Doctoral Training Program of the University of Groningen. T.S.L. acknowledges financial support from Natural Sciences and Engineering Research Council of Canada (NSERC) through grant RGPIN-2022-04794. DBZ, GFL and SLM acknowledge support from the Australian Research Council through Discovery Program grant DP220102254. SK acknowledges support from the Science & Technology Facilities Council (STFC) grant ST/Y001001/1. This paper includes data obtained with the Anglo-Australian Telescope in Australia. We acknowledge the traditional owners of the land on which the AAT stands, the Gamilaraay people, and pay our respects to elders past and present. This work was supported by the Australian Research Council Centre ofExcellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. This project used public archival data from the Dark Energy Survey (DES). Funding for the DES Projects has been provided by the U.S. Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desen- volvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft, and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the OzDES Membership Consortium, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. Based in part on observations at Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
Appendix A Rotation matrices
Appendix B Potential members
Potential members of NGC 1261 (extract).
Potential members of NGC 1904 (extract).
References
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [Google Scholar]
- Abbott, T. M. C., Adamów, M., Aguena, M., et al. 2021, ApJS, 255, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Balbinot, E., & Gieles, M. 2017, MNRAS, 474, 2479 [Google Scholar]
- Balbinot, E., Santiago, B. X., da Costa, L. N., Makler, M., & Maia, M. A. G. 2011, MNRAS, 416, 393 [NASA ADS] [Google Scholar]
- Banik, N., Bertone, G., Bovy, J., & Bozorgnia, N. 2018, J. Cosmol. Astropart. Phys., 2018, 061 [CrossRef] [Google Scholar]
- Baumgardt, H. 2001, MNRAS, 325, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
- Bonaca, A., Hogg, D. W., Price-Whelan, A. M., & Conroy, C. 2019, ApJ, 880, 38 [Google Scholar]
- Bonaca, A., Pearson, S., Price-Whelan, A. M., et al. 2020, ApJ, 889, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J. 2016, Phys. Rev. Lett., 116, 121301 [NASA ADS] [CrossRef] [Google Scholar]
- Capuzzo Dolcetta, R., Di Matteo, P., & Miocchi, P. 2005, AJ, 129, 1906 [CrossRef] [Google Scholar]
- Carballo-Bello, J. A., Martínez-Delgado, D., Navarrete, C., et al. 2017, MNRAS, 474, 683 [Google Scholar]
- Carlberg, R. G. 2012, ApJ, 748, 20 [Google Scholar]
- Claydon, I., Gieles, M., & Zocchi, A. 2017, MNRAS, 466, 3937 [CrossRef] [Google Scholar]
- Correa Magnus, L., & Vasiliev, E. 2022, MNRAS, 511, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, K. J., Heggie, D. C., & Varri, A. L. 2017, MNRAS, 468, 1453 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T. J. L., Gieles, M., Balbinot, E., et al. 2019, MNRAS, 485, 4906 [Google Scholar]
- Dillamore, A. M., Belokurov, V., & Evans, N. W. 2024, MNRAS, 532, 4389 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., & Belokurov, V. A. 2020, MNRAS, 495, 2554 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., Belokurov, V., Bovy, J., & Sanders, J. L. 2016, MNRAS, 463, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., Koposov, S. E., & Belokurov, V. 2017, MNRAS, 470, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., Belokurov, V., Laporte, C. F. P., et al. 2019, MNRAS, 487, 2685 [Google Scholar]
- Fellhauer, M., Wilkinson, M. I., & Kroupa, P. 2009, MNRAS, 397, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Messineo, M., Fusi Pecci, F., et al. 1999, AJ, 118, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushige, T., & Heggie, D. C. 2000, MNRAS, 318, 753 [CrossRef] [Google Scholar]
- Grillmair, C. J., Freeman, K. C., Irwin, M., & Quinn, P. J. 1995, AJ, 109, 2553 [Google Scholar]
- Grondin, S. M., Webb, J. J., Leigh, N. W. C., Speagle, J. S., & Khalifeh, R. J. 2023, MNRAS, 518, 4249 [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Hattori, K., Erkal, D., & Sanders, J. L. 2016, MNRAS, 460, 497 [CrossRef] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2021, MNRAS, 500, 13 85 [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibata, R., Lewis, G. F., Irwin, M., Totten, E., & Quinn, T. 2001, ApJ, 551, 294 [Google Scholar]
- Ibata, R. A., Lewis, G. F., Irwin, M. J., & Quinn, T. 2002, MNRAS, 332, 915 [Google Scholar]
- Ibata, R. A., Lewis, G. F., & Martin, N. F. 2016, ApJ, 819, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Malhan, K., Martin, N., et al. 2021, ApJ, 914, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Malhan, K., Tenachi, W., et al. 2024, ApJ, 967, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Jethwa, P., Erkal, D., & Belokurov, V. 2016, MNRAS, 461, 2212 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, A. P., Koposov, S. E., Li, T. S., et al. 2021, ApJ, 921, 32 [CrossRef] [Google Scholar]
- Johnston, K. V., Zhao, H., Spergel, D. N., & Hernquist, L. 1999, ApJ, 512, L109 [Google Scholar]
- Johnston, K. V., Spergel, D. N., & Haydn, C. 2002, ApJ, 570, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., Besla, G., Anderson, J., & Alcock, C. 2013, ApJ, 764, 161 [Google Scholar]
- King, I. 1962, AJ, 67, 471 [Google Scholar]
- Klimentowski, J., Lokas, E. L., Kazantzidis, S., et al. 2009, MNRAS, 400, 2162 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Grebel, E. K., & Martell, S. L. 2019, A&A, 625, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koposov, S. E. 2019, RVSpecFit: Radial velocity and stellar atmospheric parameter fitting, Astrophysics Source Code Library [record ascl:1907.013] [Google Scholar]
- Koposov, S. E., Gilmore, G., Walker, M. G., et al. 2011, ApJ, 736, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Erkal, D., Li, T. S., et al. 2023, MNRS, 521, 4936 [NASA ADS] [CrossRef] [Google Scholar]
- Kounkel, M., Mcbride, A., Stassun, K. G., & Leigh, N. 2022, MNRAS, 517, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Küpper, A. H. W., MacLeod, A., & Heggie, D. C. 2008, MNRAS, 387, 1248 [Google Scholar]
- Küpper, A. H. W., Lane, R. R., & Heggie, D. C. 2012, MNRAS, 420, 2700 [Google Scholar]
- Kuzma, P. B., Da Costa, G. S., & Mackey, A. D. 2017, MNRAS, 473, 2881 [Google Scholar]
- Kuzma, P. B., Ferguson, A. M. N., & Peñarrubia, J. 2021, MNRAS, 507, 1127 [CrossRef] [Google Scholar]
- Leigh, N., & Sills, A. 2011, MNRAS, 410, 2370 [NASA ADS] [CrossRef] [Google Scholar]
- Leon, S., Meylan, G., & Combes, F. 2000, A&A, 359, 907 [NASA ADS] [Google Scholar]
- Lewis, I. J., Cannon, R. D., Taylor, K., et al. 2002, MNRAS, 333, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T., & S5 Collaboration 2021, Southern Stellar Stream Spectroscopic Survey: The First Public Data Release [Google Scholar]
- Li, T. S., Koposov, S. E., Zucker, D. B., et al. 2019, MNRAS, 490, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. S., Ji, A. P., Pace, A. B., et al. 2022, ApJ, 928, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Limberg, G., Souza, S. O., Pérez-Villegas, A., et al. 2022, ApJ, 935, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Manwadkar, V., Trani, A. A., & Leigh, N. W. C. 2020, MNRAS, 497, 3694 [CrossRef] [Google Scholar]
- Martell, S. L., & Grebel, E. K. 2010, A&A, 519, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., Smolinski, J. P., Beers, T. C., & Grebel, E. K. 2011, A&A, 534, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., Shetrone, M. D., Lucatello, S., et al. 2016, ApJ, 825, 146 [Google Scholar]
- Massari, D., Dalessandro, E., Erkal, D., et al. 2025, A&A, in press, https://doi.org/10.1051/0004-6361/202449696 [Google Scholar]
- McConnachie, A. W., & Venn, K. A. 2020, AJ, 160, 124 [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Milosavljevic, M., Favata, M., Hughes, S. A., & Holz, D. E. 2004, ApJ, 607, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Montanari, F., & García-Bellido, J. 2022, Phys. Dark Universe, 35, 100978 [NASA ADS] [CrossRef] [Google Scholar]
- Montuori, M., Capuzzo-Dolcetta, R., Di Matteo, P., Lepinette, A., & Miocchi, P. 2007, ApJ, 659, 1212 [Google Scholar]
- Muñoz, C., Geisler, D., Villanova, S., et al. 2021, MNRAS, 506, 4676 [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., et al. 2003, AJ, 126, 2385 [Google Scholar]
- Pace, A. B., & Li, T. S. 2019, ApJ, 875, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, A. B., Erkal, D., & Li, T. S. 2022, ApJ, 940, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, E., Kallivayalil, N., Garavito-Camargo, N., et al. 2020, ApJ, 893, 121 [Google Scholar]
- Pearson, S., Price-Whelan, A. M., & Johnston, K. V. 2017, Nat. Astron., 1, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzynski, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Sesar, B., Johnston, K. V., & Rix, H.-W. 2016, ApJ, 824, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Reina-Campos, M., Hughes, M. E., Kruijssen, J. M. D., et al. 2020, MNRAS, 493, 3422 [Google Scholar]
- Schiavon, R. P., Zamora, O., Carrera, R., et al. 2017, MNRAS, 465, 501 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Sharp, R., Saunders, W., Smith, G., et al. 2006, Proc. SPIE, 6269, 62690G [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Boubert, D., Gänsicke, B. T., et al. 2018, ApJ, 865, 15 [Google Scholar]
- Shipp, N., Drlica-Wagner, A., Balbinot, E., et al. 2018, ApJ, 862, 114 [Google Scholar]
- Sollima, A. 2020, MNRAS, 495, 2222 [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Stone, N. C., & Leigh, N. W. C. 2019, Nature, 576, 406 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E. 2019, MNRAS, 489, 623 [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E., Belokurov, V., & Erkal, D. 2021, MNRAS, 501, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., & Peñarrubia, J. 2011, ApJ, 742, 20 [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Sen, B., & Woodroofe, M. 2009, AJ, 137, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, Z., Arnold, A. D., Oliver, W. H., et al. 2023, MNRAS, 519, 192 [Google Scholar]
- Weatherford, N. C., Kiroglu, F., Fragione, G., et al. 2023, ApJ, 946, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C., Tang, B., Li, C., et al. 2024, A&A, 684, A205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, S., Mackey, D., & Da Costa, G. S. 2022, MNRAS, 513, 3136 [NASA ADS] [CrossRef] [Google Scholar]
Videos for the NGC 1904 and NGC 1261 simulations are available at https://www.youtube.com/watch?v=R-zooau62hk and https://www.youtube.com/watch?v=Gr8legg0QeQ, respectively.
See https://www.youtube.com/watch?v=lTUK1mfpM70 and https://www.youtube.com/watch?v=8bHzEqXmwZU for movies showing the 3d view of NGC 1904 and NGC 1261, respectively.
All Tables
Prior range and best-fit values for the mixture model parameters for NGC 1261 and for NGC 1904.
Recalculated metallicity and velocity dispersions for stars inside and outside rJ of NGC 1261 and of NGC 1904.
All Figures
 |
Fig. 1 3D sky plots for NGC 1261 (top) and NGC 1904 (bottom). The position of each GC is shown as a red star and the particles from the N-body simulations are shown in blue throughout the paper. The insets show the distribution of particles close to the clusters and the outlines of the fields targeted by S5 (black circles). We also plot in purple the integrated orbit of each GC given the gravitational potential described in Sect. 3.1, and the direction of motion of the cluster is indicated by the red arrow. |
| In the text | |
 |
Fig. 2 Spatial distribution of the targeted stars, each colour-coded according to their membership probability of belonging to NGC 1261 (left) and NGC 1904 (right). All stars with probabilities of less than 20% are shown in grey. The solid circles outline the region within the Jacobi radius of each cluster and show that we detect many probable members outside of these regions. |
| In the text | |
 |
Fig. 3 Modelled properties of stars within the sample (left for NGC 1261 and right for NGC 1904) as a function of ϕ1. As in Fig. 2, each point is colour-coded according to its membership probability of belonging to the respective cluster. The bottom two panels show the histograms of all probabilities in the sample. The vertical lines at 0.6 (60%) represent the threshold on the probability. |
| In the text | |
 |
Fig. 4 Dereddened colour-magnitude diagram for likely NGC 1261 cluster and stream members using the g and r bands from the available DECam photometric measurements. Left panel: all stars in our sample for this cluster are colour-coded according to the calculated membership probability; grey indicates stars with probabilities of less than 20%. We observe a very narrow distribution that emerges within the whole sample. Middle panel: high-probability member stars are extracted using the threshold of 60% and considering only stars within a radius r = rJ around the cluster. An isochrone is also added for comparison. The dashed lines separate stars with CMD properties similar to those of the cluster from likely contaminants (square markers). Right panel: similarly, we plot high-probability stars that lie outside of r = rJ. The stars outlined in red are the same stars selected in Fig. 6 as having different vgsr from the N-body simulation prediction. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for NGC 1904. The results for this GC show very little contamination as most potential members align well in the CMD. The stars outlined in magenta are the same as those selected in Fig. 7 for their extension in ϕ2. These stars align well with the rest of the selection, indicating that they are likely to be true members of NGC 1904. |
| In the text | |
 |
Fig. 6 Main results for NGC 1261. Left: distribution of the modelled properties of the stars belonging to NGC 1261 and its stream as a function of ϕ1 after enforcing a 60% lower limit on the membership probability. The error bars represent the measurement uncertainties. The black dashed line represents the best-fit track used to model the mean value for the respective property at a given ϕ1. The results from the N-body simulation in each of the four dimensions are in blue. Stars with v𝑔sr values inconsistent with the N-body simulation are outlined in red. Top middle: spatial distribution of the same stars plotted in the left panel. The dashed circles show the outlines of the fields targeted by S5. The solid circle shows the extent of rJ. Stars plotted using the square markers are those that show different CMD properties from the cluster, as shown in Fig. 4. Top right: 2D density plot of the distribution of potential member stars around NGC 1261. Stars within rJ were removed when creating this plot to enhance the density contrast. Bottom right: 2D histogram showing the density of simulation particles on the sky. The vertical red lines indicate the same window on the sky as shown in the top panels. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for NGC 1904. In the top middle panel we show the stars that form overdensities above and below the cluster in ϕ2 (in magenta). They are also highlighted in the left panel, showing that they have similar properties to the other likely cluster and stream stars. These overdensities are clearly visible in the density plot provided in the top right panel. The 2D histogram of the N-body simulation shown in bottom right panel also shows a clear distinction between the inner tails, which correspond to our detected overdensities, and the outer tails. |
| In the text | |
 |
Fig. 8 Comparison between the full-fit runs described in Sect. 3, and the new runs where µδ is not taken into account. The best-fit tracks from the full-fit runs, first shown in Figs. 6 and 7, are re-plotted here using the dashed line. The best-fit tracks from the new runs are shown using the solid red line. A new lower limit is enforced on the membership probability from the new runs and the remaining stars are cross-matched with the potential members from the full-fit results of Sect. 4. The common members between the two runs are shown in yellow and those that are not common are shown in dark blue. In this plot we see that the distribution of stars in µδ follows the same track as the original runs, even though it was not taken into account. |
| In the text | |
 |
Fig. 9 An assessment of the contamination within the samples of possible members. This is calculated by sampling 100 values from the posterior distributions of our mixture model parameters and checking how many times each star survives our cut using the model parameters from each of the 100 samples. The potential members (in yellow) survived 100% of the time, while those closer to blue survived the corresponding fraction of times. Contaminants identified through their position in the CMD are indicated using the square markers. |
| In the text | |
 |
Fig. 10 A closer look at the radial velocities in comparison between observed members and simulation predictions. The upper and lower rows refer to NGC 1261 and NGC 1904, respectively. Left panels: potential member stars within ±2° around the clusters coloured by the radial velocity shifted with respect to the radial velocity of the cluster (Δv𝑔sr). Right panels: same property as left panels, but displayed using particles from the N-body simulation. |
| In the text | |
 |
Fig. 11 Confirmation of the distant gradient along ϕ2 for NGC 1904. Left: distance gradient along ϕ2 seen in the simulations of NGC 1904. Middle left: Top and bottom overdensities of stars (in cyan and magenta, respectively). Potential GC members that fall within rJ are shown as empty black circles, while those outside rJ are shown in yellow. Middle right: distance gradient can be seen in the main sequence and subgiant branches given the observed differences in magnitude. Right: correcting for the distance differences leads to the overlapping of selected stars within the CMD supporting the present of the distance gradient. |
| In the text | |
 |
Fig. 12 Orbits of NGC 1261 (upper row) and NGC 1904 (lower row). Each column presents a different plane projection in galactocentric coordinates. The red star indicates the present position of each GC and the simulation particles are overplotted in this coordinate system. The purple line represents the integrated orbit of each cluster where the direction of orbit is indicated by the red arrow in the middle panels. The orange line connects the cluster to the centre of the Galaxy. We see that NGC 1261 is close to apocentre, but has passed it and is moving closer to pericentre, while NGC 1904 is approaching and is very close to its orbit’s apocentre. |
| In the text | |
 |
Fig. 13 Comparison with the results of Ibata et al. (2024) around NGC 1261. Streams found by Ibata et al. (2024) surrounding NGC 1261 and thought to be associated with the GC are plotted here colour-coded according to the corresponding stream ID. We overplot the potential members for NGC 1261 found in this paper in yellow, and outline the common ones between the two works in black. We also show the areas inspected by S5 (dashed circles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.