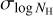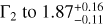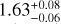| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A399 | |
| Number of page(s) | 31 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202451045 | |
| Published online | 29 October 2024 | |
The SRG/eROSITA diffuse soft X-ray background
I. The local hot bubble in the western Galactic hemisphere
1
Max-Planck-Institut für extraterrestrische Physik,
Gießenbachstraße 1,
85748
Garching,
Germany
2
INAF-Osservatorio Astronomico di Brera,
Via E. Bianchi 46,
23807
Merate (LC),
Italy
3
Department of Astronomy, University of Science and Technology of China,
Hefei
230026,
China
4
School of Astronomy and Space Science, University of Science and Technology of China,
Hefei
230026,
China
5
Dr. Karl Remeis Observatory, Erlangen Centre for Astroparticle Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg,
Sternwartstraße 7,
96049
Bamberg,
Germany
★ Corresponding author; myeung@mpe.mpg.de
Received:
9
June
2024
Accepted:
15
August
2024
Context. The SRG/eROSITA All-Sky Surveys (eRASSs) combine the advantages of complete sky coverage and the energy resolution provided by the charge couple device and offer the most holistic and detailed view of the diffuse soft X-ray background (SXRB) to date. The first eRASS (eRASSl) was completed at solar minimum, when solar wind charge exchange emission was minimal, providing the clearest view of the SXRB.
Aims. We aim to extract spatial and spectral information from each constituent of the SXRB in the western Galactic hemisphere, focusing on the local hot bubble (LHB).
Methods. We extracted and analysed eRASSl spectra from almost all directions in the western Galactic hemisphere by dividing the sky into equal signal-to-noise bins. We fitted all bins with fixed spectral templates of known background constituents.
Results. We find the temperature of the LHB exhibits a north-south dichotomy at high latitudes (|b| > 30°), with the south being hotter, with a mean temperature at kT = 121.8 ± 0.6 eV and the north at kT = 100.8 ± 0.5 eV. At low latitudes, the LHB temperature increases towards the Galactic plane, especially towards the inner Galaxy. The LHB emission measure (EMLHB) enhances approximately towards the Galactic poles. The EMLHB map shows clear anti-correlation with the local dust column density. In particular, we found tunnels of dust cavities filled with hot plasma, potentially forming a wider network of hot interstellar medium. We also constructed a three-dimensional LHB model from EMLHB, assuming constant density. The average thermal pressure of the LHB is Pthermal/k = 10100−1500+1200 cm−3 K, a lower value than typical supernova remnants and wind-blown bubbles. This could be an indication of the LHB being open towards high Galactic latitudes.
Key words: ISM: bubbles / ISM: structure / local insterstellar matter / solar neighborhood / X-rays: diffuse background / X-rays: ISM
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
The diffuse soft X-ray background (SXRB) is known to be a superposition of emission components spanning from the length scale of AU to cosmic distances (e.g. McCammon & Sanders 1990; Kuntz & Snowden 2000). All-sky analyses of the SXRB have largely relied on ROSAT/PSPC broadband count rates and ratios (e.g. Snowden et al. 1997, 1998; Kuntz & Snowden 2000), especially for studies on the local hot bubble (LHB; e.g. Snowden et al. 2000; Liu et al. 2017), as background photons with energies ≲0.3 keV (R1: 0.11–0.284 keV; R2: 0.140.284 keV) are readily absorbed by the wall of the local bubble and all R12 counts are effectively of local origin. The brightest soft X-ray line feature in the SXRB is the O VII triplet at 0.57 keV. This is an important diagnostic, as it encapsulates emissions from the LHB; the background Galactic emission, including the Milky Way circum-galactic medium (MW CGM); and depending on sight lines, intervening Galactic structures.
Hence, extracting information for a particular component using broadband count rates and ratios alone becomes challenging and heavily dependent on the knowledge and the accurate subtraction of the rest. Notably, the discovery of the time-variable solar wind charge exchange (SWCX) component has aggravated the issue even further (Lisse et al. 1996; Cravens 1997; Dennerl et al. 1997).
X-ray observatories with charge couple device (CCD) cameras, such as XMM-Newton/EPIC, Chandra/ACIS, and Suzaku/XIS, have demonstrated the importance of spectral resolution to decompose the SXRB into their respective components (e.g. Lumb et al. 2002; Markevitch et al. 2003; Henley & Shelton 2008; Yoshino et al. 2009), but they are restricted to limited ‘pencil-beam’ sight lines due to their relatively small fields of view (FoVs) and observing strategies. Only since the last decade have a substantial number of pointings been accumulated to enable a more holistic view of the SXRB (Henley & Shelton 2010, 2012, 2013; Nakashima et al. 2018; Gupta et al. 2023; Pan et al. 2024). A notable exception is Halosat, where a large portion of the sky is covered in 333 pointings by virtue of its large FoV (~10°) whilst achieving CCD-type energy resolution using non-imaging silicon drift detectors (Kaaret et al. 2019, 2020; Ringuette et al. 2021; Bluem et al. 2022).
Currently, high spectral resolution observations of the SXRB remain extremely difficult to obtain without telescopes of a large grasp1. However, successive sounding rocket launches of the X-ray Quantum Calorimeter (XQC) (McCammon et al. 2002; Crowder et al. 2012; Wulf et al. 2019) have shown promise of being able to separate the SWCX contribution from the LHB emission beyond CCD energy resolution using C VI Ly-α, γ and the fine structure lines within the O VII triplet, despite their short exposure times.
The local interstellar medium (LISM) is known to be a volume devoid of neutral gas – also known as the local cavity (LC) or the local bubble (LB) (e.g. see a review by Frisch et al. 2011). This cavity is instead filled by a ~0.1 keV (~106 K) plasma (e.g. Snowden et al. 1990, 1997; McCammon et al. 2002; Liu et al. 2017; Yeung et al. 2023). The electron density of this plasma is uncertain without the assumption of its line-of-sight density profile. However, shadowing studies of molecular clouds on the wall of the LC at different distances have consistently shown that a uniform electron density of ~4 × 10–3 cm–3 is a reasonable assumption, as probed by various sight lines (Snowden et al. 2014; Yeung et al. 2023). There is a growing number of studies that support a formation scenario where dozens of supernova explosions create and sustain the LHB (e.g. Fuchs et al. 2006; Zucker et al. 2022; Schulreich et al. 2023), employing a combination of star cluster traceback, numerical simulations, and matching supernova-produced radioisotopes found in Earth’s crust.
Solar wind charge exchange has long been the biggest source of uncertainty revolving around the X-ray measurements of the LHB, as its spectrum resembles that of the LHB despite being non-thermal in nature (see reviews by Dennerl 2010; Kuntz 2019, and references therein). SWCX can be broadly separated into two categories: magnetospheric and heliospheric. The former refers to the emission from solar wind ions interacting with neutrals in Earth’s exosphere and the latter with the inflowing neutral interstellar medium (ISM) into the solar system. Observations conducted by most X-ray missions are prone to both kinds of SWCX emissions. An exception is eROSITA (Predehl et al. 2021), which is on board the Spectrum-Roentgen-Gamma (SRG) (Sunyaev et al. 2021) observatory. SRG orbits around the Sun-Earth Lagrangian point L2. SRG/eROSITA always pointed perpendicular to the Sun-Earth line during all-sky surveys (eRASSs). Hence, it never looked through the Earth’s exosphere, avoiding the magnetospheric SWCX. No evidence of SWCX emission from the magnetotail has been found thus far (Yeung et al. 2023; Dennerl et al., in prep.). Heliospheric SWCX indeed caused variations in the SXRB in eRASSs, and it correlates with the solar cycle and ecliptic latitudes (Ponti et al. 2023; Yeung et al. 2023). Studies using other soft X-ray instruments have found the same correlation between solar cycles and heliospheric SWCX (Qu et al. 2022; Ueda et al. 2022; Pan et al. 2024). The first eRASS (eRASS1) was completed during solar minimum and, on average, exhibits a low amount of heliospheric SWCX (Ponti et al. 2023; Yeung et al. 2023). A parallel work (Dennerl et al., in prep.) will rigorously present and discuss the SWCX contributions in eRASSs. In this work, we leverage this advantage and model the SXRB in eRASS1 without the SWCX contribution, which became non-negligible in later eRASSs.
The hot phase of the CGM in a spiral galaxy is believed to trace gas from both feedback processes and the shock-heated intergalactic medium out to its virial radius (e.g. see Putman et al. 2012, for a review). The hot halo gas is also predicted to be at approximately the virial temperature (for the MW, ~0.2 keV) and holds a large fraction of its baryons. Numerous X-ray observations have confirmed the existence of this phase via both emission (e.g. Yoshino et al. 2009; Henley & Shelton 2010, 2012, 2013; Miller & Bregman 2015; Nakashima et al. 2018; Kaaret et al. 2020; Ponti et al. 2023) and absorption studies (e.g. Bregman & Lloyd-Davies 2007; Yao & Wang 2007; Yao et al. 2008; Sakai et al. 2012; Miller & Bregman 2013; Fang & Jiang 2014; Fang et al. 2015). Recently, there have been growing reports of the presence of an additional thermal component in the CGM, at ~0.7 keV (e.g. Das et al. 2019; Bluem et al. 2022; Ponti et al. 2023), which could alternatively be attributed to coronal emission from M-dwarfs (Wulf et al. 2019). One of the prime goals of our spectral analysis is the characterisation of the two CGM components. The results and discussion concerning the MW CGM will be presented in Paper II (Ponti et al. in prep.) of the series.
Our understanding of the cosmic X-ray background (CXB) at the low-energy end (0.5-2 keV) has taken a giant leap forward with Chandra and XMM-Newton surveys, resolving ~80% of the CXB sources (De Luca & Molendi 2004; Luo et al. 2017; Cappelluti et al. 2017). The resolved sources are mostly identified as active galactic nuclei (AGNs). Still, contributions from galaxies, galaxy groups, and clusters are expected to rise below 1 keV, steepening the slope at the softest end (Gilli et al. 2007). eROSITA is an instrument specialised in the soft X-ray band. As a result, we expect to be able to measure such a steepening and subsequently apply the result to refine our measurements on the Galactic components.
In this work, we report on the spectral analysis of the eRASS1 data in the western Galactic hemisphere, being as spatially continuous as possible by extracting a large number (~2000 bins) of high S/N spectra. This work is the first of a series focusing on the various components of the SXRB seen by eROSITA. In particular, this paper lays out the data extraction and the general methodology adopted in the spectral modelling in Sect. 2 and 3, which is the backbone for the series. Then, in Sect. 4, we report on the results, which are mainly focused on, but not limited to, the LHB and the hot LISM, with intervening discussions and interpretations. The results on the CGM, the Galactic corona, and the eROSITA bubbles will mainly be presented in other works in the series (Ponti et al., in prep.; Yeung et al., in prep.). Hence, they are only mentioned in this work when they directly affect results on the LHB.
2 Data selection and spectral extraction
We study the diffuse soft X-ray background from the eRASS1 data of processing version c020 of the western Galactic hemisphere (180° < l < 360°). We cleaned the data following a few criteria. First, we discarded the data from TM5 and TM7 due to optical light-leak (Predehl et al. 2021), and removed goodtime-intervals (GTIs) with count rates >1.435 counts s–1 deg–2 in the 4–9 keV band to minimise contaminations by flares. The particle background dominates this band, and the threshold corresponds to 1.5 times the level of particle background in this band (Yeung et al. 2023). The eROSITA-DE consortium has also released a list of temperature-sensitive or bright pixels that occasionally produce artefacts but are not officially flagged as bad pixels. They are mostly from TM4, which suffered from a major micrometeoroid hit (Freyberg et al. 2022). We rejected these sensitive pixels in addition. Last but not least, we masked regions with overdense source detection (Merloni et al. 2024) and positions of known galaxy clusters with R500 ≳ 3′ as described in Bulbul et al. (2024, and references therein). The overdense source detection regions could be regions within or near extended sources, such as supernova remnants or artefacts caused by bright point sources, which triggered a high density of spurious source detections.
Subsequently, we defined our spatial binning of spectral extraction using the software contbin (Sanders 2006), with the primary aim of dividing the western Galactic hemisphere into bins of approximately constant S/N in the diffuse soft X-ray emission, instead of imposing a regular grid system such as the skytile system adopted by the standard products of eROSITA. For our analysis, contbin also has the advantage of defining bins with edges more closely following distinct features (for example, from superbubbles, supernova remnants etc.) and being computationally efficient compared to traditional Voronoi binning codes. The binning was done on the eRASS1 0.2–0.6 keV diffuse emission count map (all detected sources masked2) after subtracting the expected counts from the non-X-ray background measured from the filter-wheel-closed data (Yeung et al. 2023), as this band contains the bulk of the emissions from the LHB that eROSITA observes. This can be written explicitly as
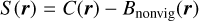 (1)
(1)
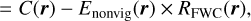 (2)
(2)
where r, S , C and Bnonvig denote the sky position, signal, total counts from diffuse emission, non-X-ray or non-vignetted background counts respectively. Bnonvig can be further written as a product of non-vignetted exposure time (Enonvig) and the count rate of the filter-wheel-closed background (RFWC). We estimate the corresponding noise map N(r) for the S/N calculation using equation (4) of Sanders (2006) as adopted from Gehrels (1986), that is,
![$N(r) = \sqrt {g[C(r)] + g\left[ {{B_{nonvig}}(r)} \right]} ,$](/articles/aa/full_html/2024/10/aa51045-24/aa51045-24-eq4.png) (3)
(3)
is an estimation of the upper limit of the squared uncertainty on c counts in Poissonian statistics. Before binning, the maps were projected into the zenithal equal area (ZEA) projection. Contour-binning yielded 2010 bins larger than 1 deg2, which we consider valid bins for spectral analysis. 1 deg2 is approximately the eROSITA field-of-view. This selection primarily removed areas near the south ecliptic pole and the Large Magellanic Cloud where the exposure time is maximal due to the overlapping of the scanning loci in eRASSs but are not representative of the general SXRB.
Fig. 1 shows the contour-binned eRASS1 0.2–0.6 keV band surface brightness map of the valid bins. Large soft X-ray emitting structures such as the eROSITA bubbles (a pair of bubbles at l ≳ 290° in the north and l ≳ 320° in the south), Antlia supernova remnant (l, b)~(275°, 15°), Monogem Ring (l, b)~(200°, 8°) and Orion-Eridanus Superbubble (l, b)~(205°, –30°), and the Galactic disc stand out in stark relief. The sky area distribution of the valid contour bins is shown in Fig. 2. The median bin size is ~7 deg2. All bins with an area less than 1 deg2 were removed. The distribution can be well approximated by a log-normal function, as shown by the red line.
Possible fluctuations contributed by bright X-ray sources should be removed from the analysis of diffuse emission. However, as is discussed in more detail in Sect. 3.2, removing sources alters the shape and normalisation of the cosmic X-ray background (CXB). Masking sources above a flux limit threshold substantially higher than the eRASS1 flux limit (Flim,0.5–2keV ~ 10–14erg s–1 cm–2; Merloni et al. 2024) could avoid the problem of having an exposure-dependent CXB component in the spectra. In order words, if one were to mask all detected sources, the CXB resolve fraction would depend on the exposure depth, causing spatially correlated CXB normalisation and photon index variations. As such, we chose to mask only sources with fluxes F0.5–2keV > 10–12 erg s–1 cm–2 and detection likelihood of DET_LIKE_0 > 10 in the eRASS1 source catalogue (Merloni et al. 2024), using circular masks of radius four times their aperture photometry extraction radii (4 × APE_RADIUS_1 ≃2′)3 during spectral extraction. This choice minimises the spectral fluctuations introduced by bright sources while maintaining a largely uniform CXB component in all spectra. This masking was applied during spectral extraction and differs from the one used to create the diffuse emission map for contour-binning.
We extracted the spectrum and its auxiliary response file for events of all valid patterns (pat=15) of each contour bin by providing a point source cheesemask and a contour bin mask that demarcates the bin profile to the eSASS task srctool. They serve as the basis of all analyses in this work.
Last but not least, we also utilised publicly available ROSAT R1 and R2 diffuse background maps in our spectral fitting (Snowden et al. 1997). Despite ROSAT/PSPC’s poor spectral resolution, it provides a larger grasp than eROSITA at energies ≲0.3 keV (see Fig. 10 of Predehl et al. 2021). We found the addition of ROSAT data helps break the degeneracies between the LHB and the CGM components that arose in some low absorption regions (see Sect. 4.3).
The R1 and R2 band count rate and sigma maps were used to provide two more data points in each spectrum, with some manipulations. In detail, we began by binning the maps using the same set of contour bins, then we converted the map unit of count Ms–1 arcmin–2 to a flux unit of erg s–1 cm–2 by assuming a 0.1 keV apec spectral model and multiplication with the bin area. The use of a apec model (Smith et al. 2001) is motivated by the approximation that the contribution from the LHB dominates R1 and R2 counts. As the last step, we used the ftflx2xsp task in FTOOLS to create Xspec/PyXspec-ready spectra and diagonal response matrices to enable simultaneously fitting with the eROSITA spectra. The bin edges of the R1 and R2 maps were taken from (Snowden et al. 1994) where the band response drops to 10% of the peak values, namely, 0.11-0.284 keV for R1 and 0.14-0.284 keV for R2.
 |
Fig. 1 Contour-binned eRASS1 0.2–0.6 keV band surface brightness map in zenithal equal-area projection. Locations of big galaxy clusters, overdense regions in source detection, and bins with sky area less than 1 deg2 were masked. Counts from the non-X-ray background and all eRASS1-catalogued sources (Merloni et al. 2024) were also removed from this image (but not in the spectra; see Sect. 2 for more details). |
 |
Fig. 2 Sky area distribution of the contour bins. It can be approximated by a log-normal distribution, as shown with the red line. |
 |
Fig. 3 Example spectra outside (left) and inside (right) of the eROSITA bubbles, overlaid with the best-fit spectral models labelled in the legends. We modelled the eROSITA bubbles with an additional thermal component in brown. Both spectra have been divided by the effective area, aiming to bring the ROSAT R1 and R2 count rates into a reasonable range. This has the disadvantage of creating the fictitious jump of the instrumental background component above the gold absorption edge at ~2 keV. The horizontal error bars at the top left corners of the figures reflect the width of the ROSAT R1 and R2 bands. |
3 Spectral analysis
Attempting to decompose the diffuse emission from half the sky both spatially and spectrally is an ambitious task. As the first study to do so, we decided to employ a more conventional approach in the analysis, whereby treating the contour bins as independent during spectral fitting. Additionally, we adopted a fixed number of spectral components to fit the spectra from all contour bins. These components include four conventional X- ray background components (e.g. Gupta et al. 2021; Bluem et al. 2022; Ponti et al. 2023; Yeung et al. 2023): (1) the local hot bubble (LHB), (2) the Milky Way’s halo or (warm-hot) CGM, (3) the Galactic corona or the hot component of the CGM (COR) and (4) the cosmic X-ray background (CXB), and the non-X-ray background modelled by (5) the eROSITA filter-wheel-closed (FWC) background models (Yeung et al. 2023). The SWCX emission during eRASS1 was weak, as it was the time of solar minimum, as shown by Dennerl et al. (in prep.) in a detailed eRASS1– eRASS4 half-sky analysis, Ponti et al. (2023) in the eFEDS field, and Yeung et al. (2023) in three giant molecular cloud sight lines. Therefore, we did not include an SWCX component in our spectral fits. In addition, we included an extra thermal component for contour bins overlapping with the eROSITA bubbles (eROBub) (Sect. 3.4).
3.1 Description of model components
Fig. 3 shows two example spectra to illustrate our spectral templates, one outside the eROSITA bubbles and one inside.
The discussion in the remainder of this Section deals with the detailed description of these model components.
3.1.1 Local hot bubble
The LHB is a foreground component and was thus modelled as an unabsorbed optically thin plasma in collisional ionisation equilibrium (CIE) using the apec model (Smith et al. 2001) using AtomDB version 3.0.9 (Foster et al. 2012). Its temperature is allowed to vary freely only below 0.15 keV, for contour bins that have log10 (NH/cm–2) < 20.5, estimated from a combination of HI4PI and Planck dust radiance map (see Sect. 3.1.2). The introduction of this bound was to prevent the LHB component from ‘switching’ with the CGM component in low column density (NH) regions. We refer the reader to Sect. 4.3 for a detailed discussion. While this effect was mitigated by introducing the ROSAT R1 and R2 bands into the spectral fitting, this degeneracy remained in some low NH regions and necessitated the use of a hardbound. Its emission measure (EM) was left to vary in all locations. The abundance of the LHB is assumed to be solar.
In Appendix A, we loosen our CIE prescription of LHB to see if there is evidence of non-equilibrium ionisation (NEI) in our data. In short, we did not find a clear indication of NEI despite it being the general expectation from simulations of the ISM (e.g. de Avillez & Breitschwerdt 2012; Breitschwerdt & de Avillez 2021). We attribute this to the insufficient spectral resolution to resolve the emission lines and their ratios, which are crucial diagnostics of NEI.
3.1.2 Absorption of background components
For the X-ray background components (CGM, COR, CXB and eRObub), we adopted the simplifying assumption that they are absorbed by the same NH layer within each bin. In addition, their absorption was modelled by the disnht model (Locatelli et al. 2022), which behaves identically to tbabs (Wilms et al. 2000) but with a lognormal distribution with mean log NH and width 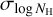 . We believe this treatment is more realistic than a single NH as some of our bins cover a large sky area and a range of NH within the field. While log NH is left to vary during the spectral fits, we fixed the value of
. We believe this treatment is more realistic than a single NH as some of our bins cover a large sky area and a range of NH within the field. While log NH is left to vary during the spectral fits, we fixed the value of 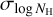 in each contour bin according to the following estimation.
in each contour bin according to the following estimation.
We estimated NH independently from our X-ray spectral measurement assuming 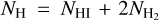 . We adopted the NHI information from 21 cm line measurement by HI4PI Collaboration (2016), while NH2 was estimated using the conversion given in Willingale et al. (2013):
. We adopted the NHI information from 21 cm line measurement by HI4PI Collaboration (2016), while NH2 was estimated using the conversion given in Willingale et al. (2013):
![${N_{{{\rm{H}}_2}}} = 7.2 \times {10^{20}}{\left[ {1 - \exp \left( { - {{{N_{HI}}E(B - V)} \over {3 \times {{10}^{20}}c{m^{ - 2}}}}} \right)} \right]^{1.1}},$](/articles/aa/full_html/2024/10/aa51045-24/aa51045-24-eq9.png) (5)
(5)
where E(B – V) was taken from the conversion from the Planck dust radiance (R) map using E(B – V)/R = 5.4 × 105 given in Planck Collaboration XI (2014). We refer to this NH estimation simply by HI4PI NH hereafter for brevity. We then estimated 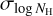 as the standard deviation of HI4PI NH within the area of each contour bin. In other words, our estimated value of
as the standard deviation of HI4PI NH within the area of each contour bin. In other words, our estimated value of 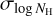 accounts only for the spatial variation in the column density and can be treated as a lower limit to the ‘genuine’ variation, which should include the line-of-sight component.
accounts only for the spatial variation in the column density and can be treated as a lower limit to the ‘genuine’ variation, which should include the line-of-sight component.
We have indeed attempted to let 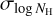 freely vary in the fits. However, this choice brought about two unforeseen issues:
freely vary in the fits. However, this choice brought about two unforeseen issues:
1) We found the fitted log NH to be higher than total HI4PI NH by ≳0.3 dex, usually at high 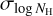 areas (≳0.6 dex) near (l,b)~(300°, –20°), and consequently, boosted the CXB above a level allowed by cosmic variance.
areas (≳0.6 dex) near (l,b)~(300°, –20°), and consequently, boosted the CXB above a level allowed by cosmic variance.
2) A significant number of contour bins resulted in a vanishing LHB component, which we considered unphysical, especially since their occurrences appear random.
On the other hand, these issues were not present when 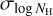 was fixed using the aforementioned method. Therefore, we kept
was fixed using the aforementioned method. Therefore, we kept 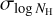 fixed throughout our spectral analysis.
fixed throughout our spectral analysis.
Fig. 4 shows the values of 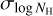 in all contour bins. A clear decreasing trend can be seen as a function of Galactic longitude. This is primarily caused by the larger contour bins away from the Galactic centre, capturing larger spatial spread in NH. The scatter plot in Fig. 5 demonstrates this correlation. Of course, the areas of the contour bins are dictated by the S/N in the soft band, affected by both exposure time and soft band intensity in the sky, which happens to be lower between 250° ≲ l ≲ 180°.
in all contour bins. A clear decreasing trend can be seen as a function of Galactic longitude. This is primarily caused by the larger contour bins away from the Galactic centre, capturing larger spatial spread in NH. The scatter plot in Fig. 5 demonstrates this correlation. Of course, the areas of the contour bins are dictated by the S/N in the soft band, affected by both exposure time and soft band intensity in the sky, which happens to be lower between 250° ≲ l ≲ 180°.
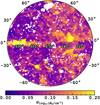 |
Fig. 4 Values of |
3.1.3 Milky Way’s circum-galactic medium
The CGM component was modelled using an apec model with the abundance fixed at 0.1 Z⊙. The low abundance was found to be required by the eFEDS data (Ponti et al. 2023) and is shown to be stable against the choice of the emission models of optically thin plasma in CIE (for example, Raymond-Smith, Mekal) in Paper II (Ponti et al., in prep.). The main impact of assuming a different abundance is reflected primarily in the emission measure. The behaviour is fairly linear; for instance, the conventional choice of Z = 0.3 Z⊙ would lower the emission measure by about three times compared to Z = 0.1 Z⊙.
Several recent publications have found a Galactic corona or a hotter CGM component necessary to reproduce the spectra of the SXRB (e.g. Gupta et al. 2021; Bluem et al. 2022; Ponti et al. 2023). We refer the reader to Paper II for an in-depth discussion. In this paper, it suffices to note that this component was necessary for reproducing the spectra. We modelled the Galactic corona component using an apec model with solar abundance. Our choice of S/N = 80 at the 0.2–0.6 keV band did not usually provide sufficient constraints on the Galactic corona component in the spectral fitting. Hence, throughout this paper, we kept its temperature fixed at kTCOR = 0.7 keV.
 |
Fig. 5 Scatter plot of |
3.1.4 Instrumental background
For the instrumental background, the spectrum for each TM was modelled by its own FWC model to account for any TM-specific features. The normalisation of the FWC model in the sky spectrum is related to that of the FWC spectrum by the ratio of their BACKSCAL header keywords and was fixed accordingly in the spectral fit. However, we noticed the Al -Kα fluorescence line at 1.49 keV in the CXB regions (see Fig. 6 and Sect. 3.2) is always weaker than that in the FWC data for all TMs, by -20%-60% depending on the TM. The precise cause of this phenomenon is unknown. Still, it is suspected to be linked to the extra Aluminium put above the CCD when the filter wheel was rotated to the CLOSED position compared to the FILTER position. However, this explanation cannot explain the relatively large spread in the deficit between the TMs. To compensate for the Al-Kα line deficit in the sky spectra, we singled out this line and refitted its normalisation of all TMs as the first step of all our spectral fits. It was then frozen in the subsequent optimisation of the rest of the free parameters.
3.1.5 Summary of model parameters
We elaborate on the description of the CXB in Sect. 3.2. In summary, two parametrisations (single (Γ = 1.7) and broken power-law (Γ = 1.9, Γ2 = 1.6, Eb = 1.2 keV)) of the CXB component could reproduce the data equally well at high Galactic latitudes. Therefore, both were used in the spectral fits, and the differences between the two were considered to be systematic uncertainties.
There are a total of 7 or 9 free parameters in the spectral fits: kTLHB, EMLHB, kTCGM, EMCGM, EMCOR, normCXB and log NH for contour bins outside the eROSITA bubbles; and an addition of kTeRObub and EMeRObub for bins inside the eROSITA bubbles.
 |
Fig. 6 Similar to Fig. 1 but showing only regions selected to determine the spectral shape of the CXB. |
3.2 Treatment of the cosmic X-ray background
In our spectral analysis, detected sources with F0.5–2keV > 10–12erg s–1 cm–2 as well as known clusters from X-ray cluster catalogues with R500 ≳ 3′ were masked (Liu et al. 2022; Merloni et al. 2024; Bulbul et al. 2024, and references therein). The choice of the flux threshold is more than an order of magnitude higher than the eRASS1 flux limit. With this limit, we can assume eROSITA is complete in detecting sources above this threshold in all look directions, and the corresponding resolved fraction across the western Galactic hemisphere is uniform. Masking of sources is expected to change the photon index of the cosmic X-ray background (CXB) from the canonical value of Γ ~ 1.4–1.5 (Vecchi et al. 1999; Kushino et al. 2002; Hickox & Markevitch 2006; Cappelluti et al. 2017); however, the high flux threshold guarantees this change is not spatially dependent.
Fig. 6 shows the regions we chose to determine the CXB model. These regions correspond to the spatial bins with centres located above |b| > 30°, and are free of large-scale foreground structures upon binning the western Galactic hemisphere using contbin (Sanders 2006) with a target S/N of 400. In addition to the CXB model we focus on, we fitted the spectrum of each region independently with freely varying LHB, CGM, Galactic corona and absorption column densities similar to the description in Sect. 3.1, with the omission of SWCX since the contribution of SWCX in eRASS1 is low (Dennerl et al., in prep.).
From the spectral analysis of the regions shown in Fig. 6, we found that simple power-law and broken power-law models perform equally well in reproducing the data, but a double broken power-law was unnecessary. Therefore, both simple and broken power-laws were adopted as our CXB models. We delay the details of this CXB analysis to Sect. 4.8.1.
3.3 Fitting procedures
Spectral fitting was done in PyXspec version 2.1.0 (Arnaud 1996; Gordon & Arnaud 2021). Lodders (2003) was used as the reference for abundance, and absorption cross-sections from Verner et al. (1996) were assumed.
We repeated the following fitting procedure for all the 2010 contour bins. After determining the normalisation of the Al-Kα line (Sect. 3.1), we made a simultaneous fit of 5 eROSITA spectra (5 TMs) and 2 ROSAT band fluxes (R1 and R2) for each contour bin. The eROSITA spectra were fitted in the energy range 0.2–5 keV using Poissonian statistics (cstat) (Cash 1979), and as the R1 and R2 data points were fluxes, χ2-statistics was used. We minimised the total statistics using the Levenberg-Marquardt algorithm. Then, we ran a MCMC with 64 walkers, each with 1.6k steps, giving a total of 102.4k steps, using the Goodman- Weare method (Goodman & Weare 2010). The walkers were initially distributed in a Gaussian distribution around the best fit from the minimisation. We found discarding the initial 80k steps, albeit aggressive, was a conservative and uniform way to ensure all parameters had moved past the burn-in phase and reached convergence in the vast majority of bins. In this paper, we report the median, 16th and 84th percentiles of the posterior distribution as the most probable value, the lower and the upper errors, respectively. If the posterior distribution is Gaussian, these reduce to the mean and ±1σ errors.
 |
Fig. 7 Finding chart for features discussed mainly in Sect. 3.4 and 4.2. The background image shows the emission measure of the LHB, which is a proxy of the extent of the LHB and is relevant for discussions (Sect. 4.2) on interstellar tunnels and anti-correlation with dust. The demarcation of the eROSITA bubbles is shown by the turquoise line, based on the 0.6–1.0 keV intensity map. |
3.4 Treatment of the eROSITA bubbles
The enigmatic eROSITA bubbles (Predehl et al. 2020) emit thermally in the soft X-rays at ~0.3 keV, and we modelled it using the apec model at solar abundance4. Combining with the LHB and CGM, the multi-component spectral analysis in eRASS exposure depth and spectral resolution inescapably entails model degeneracies because of their similar spectral shapes (0.1, 0.2 and 0.3 keV plasma in CIE). As such, we implemented a two-step approach in fitting spectra within the eROSITA bubbles region, where some spectral parameters outside the eROSITA bubbles were passed in the form of Gaussian priors into spectral fits within the eROSITA bubbles.
We began by defining the demarcation of the eROSITA bubbles using the 0.6–1.0 keV intensity map, where the eROSITA bubbles are the most prominent. The turquoise line in Fig. 7 shows the demarcation. We fitted the spectra of the contour bins outside the eROSITA bubbles before those inside, following the procedure described in Sect. 3.3. Subsequently, we fitted the contour bins within the eROSITA bubbles by passing Galactic latitude-dependent priors based on the fit results. More precisely, for a given contour bin within the eROSITA bubbles centred at (l,b), we created a Gaussian prior for each relevant parameter based on fitting results of all the bins outside the eROSITA bubbles centred within the range of b ± 5°. This implementation reflects our recurring observation with the eROSITA data that most spectral parameters are either constant (for example, the CXB) or exhibit primarily Galactic latitudinal dependence (for example, kTLHB , see Fig. 8). These priors were only applied on kTLHB, kTCGM, EMCGM, EMCOR, normCXB. We did not impose Galactic latitude-dependent priors on EMLHB, kTeRObub, EMeRObub because in this paper, we primarily focus on inferring the 3-dimensional (3D) structure of the LHB. The eROSITA bubbles will be the focus of a forthcoming paper in the series (Yeung et al., in prep.).
 |
Fig. 8 Spatial distribution of kTLHB in the high latitude regions (|b| > 30°). |
3.5 Limitations of the current method
At the end of this section, we would like to emphasise the data obtained by eROSITA is rich, especially for diffuse emission. A weakness of our method is that the inference of spectral parameters was independent of locations. However, some parameters, such as the LHB temperature, are likely correlated for bins in proximity based on the intuitive consideration that the local ISM would preferentially be in similar conditions the closer they are in space. There exist some potential methods that could take this into account. For instance, one idea is to use Bayesian hierarchical modelling and treat the proximity of bins as a hyperprior. Another potentially interesting method is to utilise an algorithm called the generalised morphological components analysis (GMCA) or its variants (sGMCA, pGMCA) to decompose the spectral components with the help of each component’s intrinsically unique spatial distribution, which has recently been demonstrated to disentangle spectral components remarkably well in extended X-ray sources (Bobin et al. 2015; Picquenot et al. 2019, 2021, 2023; Carloni Gertosio et al. 2023).
4 Results and discussion
The sheer number of spectra we analysed prevents us from discussing them individually. Therefore, we provide a webpage hosted on the eROSITA Data Release 1 server that provides all the relevant information, including visualisations and the fitting results organised in downloadable tables, for readers who are interested in the spectra, their associated model parameters, uncertainties or fit quality of any our contour bins (Sect. 5).
4.1 Evidence of a variable LHB temperature
Fig. 8 shows the spatial distribution of kTLHB in the high latitude regions, where the Galactic plane (|b| < 30°) and regions overlapping with the Large Magellanic Cloud, known supernova remnants or superbubbles (Antlia, Orion-Eridanus, Monogem Ring, Vela; masked also in other parameter maps) and the recently discovered structure surrounding the LMC, dubbed the ‘Goat Horn Complex’ (Locatelli et al. 2024), were ignored. In addition, regions with 1σ LHB temperature or emission measure fitting uncertainty 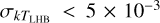 keV or
keV or 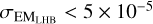 cm−6 pc were removed. These criteria are possible indications of sub-optimal spectral fits; the former is to avoid regions with kTLHB pegged at edges of the uniform prior, and the latter is useful for removing regions with EMLHB pegged close to zero. A total of 788 valid bins remained following the screening (36 bins were screened out).
cm−6 pc were removed. These criteria are possible indications of sub-optimal spectral fits; the former is to avoid regions with kTLHB pegged at edges of the uniform prior, and the latter is useful for removing regions with EMLHB pegged close to zero. A total of 788 valid bins remained following the screening (36 bins were screened out).
The histogram of kTLHB of all the valid bins is shown in the black line in Fig. 9. We report a median (and the 0.16 and 0.84 quantiles) kTLHB of 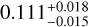 keV. The observation of the mean 1σ fitting uncertainty (0.010 keV), as shown in the black error bar, being significantly smaller than the σ of the distribution (0.018 keV) indicates a variable kTLHB. An inspection of Fig. 8 shows the primary origin of this variation is a large-scale temperature gradient, with the northern Galactic hemisphere being cooler than the south by ~0.02 keV. This is further demonstrated by dividing the histogram in Fig. 9 into the north (orange) and south (green). The north-south temperature dichotomy is evident. By overlaying the typical spectral fitting uncertainties within each hemisphere on the figure, one can notice the width of the temperature distributions within both hemispheres could be attributed mainly to their respective spectral fitting uncertainties, especially in the north. Hence, the dominating factor of the spread in the LHB temperature is a large-scale temperature gradient, but not bin-to-bin fluctuations. To complement the systematic change in kTLHB observed from the projected map and histogram, Appendix D highlights the spectral signature that determines the LHB temperature using high-S/N spectra from each hemisphere.
keV. The observation of the mean 1σ fitting uncertainty (0.010 keV), as shown in the black error bar, being significantly smaller than the σ of the distribution (0.018 keV) indicates a variable kTLHB. An inspection of Fig. 8 shows the primary origin of this variation is a large-scale temperature gradient, with the northern Galactic hemisphere being cooler than the south by ~0.02 keV. This is further demonstrated by dividing the histogram in Fig. 9 into the north (orange) and south (green). The north-south temperature dichotomy is evident. By overlaying the typical spectral fitting uncertainties within each hemisphere on the figure, one can notice the width of the temperature distributions within both hemispheres could be attributed mainly to their respective spectral fitting uncertainties, especially in the north. Hence, the dominating factor of the spread in the LHB temperature is a large-scale temperature gradient, but not bin-to-bin fluctuations. To complement the systematic change in kTLHB observed from the projected map and histogram, Appendix D highlights the spectral signature that determines the LHB temperature using high-S/N spectra from each hemisphere.
We tested if the northern and southern temperature distributions could be drawn from the same underlying distribution using the two-sample Kolmogorov-Smirnov test. The test returned a statistic of 0.693 and a p-value in the order of 10−102 ≪ 0.01. Thus, we can safely reject the null hypothesis that the temperature dichotomy occurs by chance.
To quantify the intrinsic temperature distributions in each hemisphere, we used a maximum likelihood approach to identify the mean and width of the Gaussian distributions, which best reproduce the observed temperature measurements, including their statistical errors. We constrained the mean temperature in the northern and southern Galactic hemispheres to be kTN = 100.8 ± 0.5 eV and kTS = 121.8 ± 0.6 eV, respectively. We also extracted the widths (1σ) of the intrinsic temperature distributions, which are 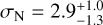 eV in the north and
eV in the north and  eV in the south. This result reiterates the temperature dichotomy is highly significant, as is evident from the precision with which we can determine the mean temperature of each hemisphere. It is also clear that the southern hemisphere exhibits a larger intrinsic temperature scatter than the northern counterpart. We would like to emphasise that the statistical uncertainty of the means and the widths of the intrinsic temperature distributions should not be confused with the fitting uncertainty of each bin. The temperature dichotomy is highly significant because of the large number of bins that sampled each hemispheric distribution well despite the individual bin having a median fitting uncertainty (⋍0.01 keV; see Fig. 9) larger than the intrinsic widths of the distributions.
eV in the south. This result reiterates the temperature dichotomy is highly significant, as is evident from the precision with which we can determine the mean temperature of each hemisphere. It is also clear that the southern hemisphere exhibits a larger intrinsic temperature scatter than the northern counterpart. We would like to emphasise that the statistical uncertainty of the means and the widths of the intrinsic temperature distributions should not be confused with the fitting uncertainty of each bin. The temperature dichotomy is highly significant because of the large number of bins that sampled each hemispheric distribution well despite the individual bin having a median fitting uncertainty (⋍0.01 keV; see Fig. 9) larger than the intrinsic widths of the distributions.
Having established a temperature dichotomy at high Galactic latitudes, it is natural to ask if a smooth transition across the Galactic plane connects them. We separated the discussion of high latitude regions since we believe our measurement there is relatively secure. Still, it is unclear how close to the Galactic plane one can venture before one is heavily biased by complexities such as multiple line-of-sight emitting and absorbing components. We relax the |b| > 30° limit and plot all the valid bins, including those on the Galactic plane in Fig. 10, using the same screening applied to Fig. 8. Fig. 10 shows a remarkable temperature enhancement towards the Galactic plane, especially at l ≳ 270°. Inspection of the spectra and their posterior distributions suggests the spectra have significant constraining power on kTLHB down to at least 10° of the Galactic plane, albeit a subjective choice. The column densities in these regions (≳ 1021 cm−2; see Fig. 11 for NH information) are adequate and peak strongly at the first wall of LB absorption (~100–200 pc) (Lallement et al. 2022; Edenhofer et al. 2024), enabling us to differentiate between the unabsorbed LHB and the absorbed components, primarily the CGM. Therefore, we argue the temperature enhancement towards the inner Galaxy is a real feature of the LHB.
First, we must address why earlier studies did not observe the north-south LHB temperature gradient using ROSAT data (see Sect. 4.1.2 for a deeper literature discussion). The R2/R1 band ratio is the main tracer of LHB temperature using ROSAT data, commonly assumed to be only contributed by the LHB emission. Fig. 12 shows the R2/R1 band ratio as a function of plasma temperature at solar abundance, using three common plasma models, Raymond-Smith (Raymond & Smith 1977), Mekal (Mewe et al. 1985, 1986; Liedahl et al. 1995) and apec (Smith et al. 2001). The Raymond-Smith model was commonly used by studies before and around the millennium (e.g. Snowden et al. 1990, 1997, 1998) to infer the temperature of the LHB. The calibration curve of the Raymond-Smith model in Fig. 12 shows the R2/R1 ratio is insensitive to temperatures above 0.13 keV. This could be one of the reasons why the LHB temperature was not found to be ~0.2 keV in earlier LHB temperature measurements using ROSAT.
Another possibly more important reason is the flawed assumption that only the LHB emission contributes to the R1 and R2 bands. To demonstrate this, we forward-modelled the same models used to extract Fig. 10, using the R1 and R2 band responses. The resulting R2/R1 band ratio map is shown in the left panel of Fig. 13. The eROSITA bubbles appear distinctly on the map, indicating that absorbed background structures can shine through and alter the R2/R1 ratio. The north-south LHB temperature dichotomy also disappears. It is fair to suggest the forward-modelled R2/R1 map does not capture the primary morphological features of the kTLHB map, and conversely, kTLHB directly inferred from R2/R1 without contributions from the background components could be biased. Furthermore, regions within the eROSITA bubbles in the forward-modelled map commonly show R2/R1 > 1.4, a limit according to the calibration curves in Fig. 12 that should not be crossed for an unabsorbed plasma. This is another evidence of the absorbed components contributing to the R1 and R2 bands, boosting the R2/R1 ratio. The right panel of Fig. 13 displays the binned R2/R1 ratio of the original ROSAT maps presented in Snowden et al. (1997), which can be directly compared to our forward-modelled map. Their resemblance reiterates that our kTLHB measurement is not at odds with the ROSAT data, and including background components in the modelling is essential to extract information on the LHB.
Merely showing our measurement is consistent with ROSAT does not necessarily mean it is robust, especially towards the inner Galaxy at low latitudes. We want to show that the LHB emission we measured at low latitudes must be local and not heavily contaminated by background ISM. Fig. 14 shows the corresponding EMLHB map. The details of it are discussed in Sect. 4.2, but for the current purpose, it suffices to note the EM at low latitudes within the Loop I contour in Fig. 7 is one of the lowest in this hemisphere. Our LHB component is unlikely to capture extra emission from the background ISM and returns a lower EM. Fig. 15 demonstrates the column density reaches 1020 cm−2 at a very close distance (~100 pc) and inspection of the local dust radial profiles suggests most of the total NH is located within the first 250 pc, corroborating that very few background ISM photons can contaminate our LHB measurement. Indeed, because of the lower EMLHB, the uncertainties of the kTLHB is larger (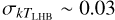 keV), which is a well-known anticorrelation that can also be readily observed from their posterior distributions. These regions, excluding the ones that are exactly lying on the Galactic plane, do not show poorer fit statistics than the rest of the sky (see Sect. 4.9 and Fig. 16). Even if they do, they are mostly due to larger residuals above ≳0.6 keV, and not at energies where the LHB dominates. Therefore, we conservatively consider our inferred LHB temperature credible at |b| > 10°and characterise it using spherical harmonics in the next Section.
keV), which is a well-known anticorrelation that can also be readily observed from their posterior distributions. These regions, excluding the ones that are exactly lying on the Galactic plane, do not show poorer fit statistics than the rest of the sky (see Sect. 4.9 and Fig. 16). Even if they do, they are mostly due to larger residuals above ≳0.6 keV, and not at energies where the LHB dominates. Therefore, we conservatively consider our inferred LHB temperature credible at |b| > 10°and characterise it using spherical harmonics in the next Section.
 |
Fig. 9 Distribution of kTLHB in the high latitude regions (|b| > 30°). The unfilled histogram outlined in black displays the distribution of all the high latitude bins displayed in Fig. 8. The black dashed line shows the Gaussian best fit for the distribution. The black data point with error bars shows the typical (median) 1σ spectral fitting uncertainty, centred at the mean of the fitted Gaussian. It is plotted at a height of exp (−1/2)Ngauss,peak = 0.606 Ngauss,peak for proper comparison between the spectral fitting uncertainty and the width of the distribution. The former (0.010 keV) is approximately half of the latter (0.018 keV), demonstrating a genuine variation in the LHB temperature. The sample is divided into the northern (orange) and the southern (green) Galactic hemispheres to demonstrate the primary source of variation is a large-scale gradient instead of small-scale fluctuations. The northern hemisphere is cooler (0.100 keV) than the south (0.122 keV), and comparing their distributions with the respective typical spectral fitting uncertainties shows that each hemisphere exhibits approximately constant LHB temperature. |
 |
Fig. 10 Map of kTLHB including low latitude regions. We note that the colour bar is scaled differently from Fig. 8. The thermal pressure is also shown under the assumption of constant ne = 4 × 10−3 cm−3. |
4.1.1 Spherical harmonic analysis
In Figs. 8 and 10, an apparent gradient or dichotomy in approximately the north-south direction and an enhancement towards the Galactic plane can be observed, respectively. One way to quantify a gradient in the sky is by fitting a combination of spherical harmonics to the data given the uncertainties, and the simplest case of a gradient is a dipole. We decided to separate the analysis of the high latitude regions (|b| > 30°) from the ‘full sample’ down to |b| > 10°, because we want to tackle two different issues: 1) quantify the significance of the (high latitude) north-south gradient as modelled by a dipole, and 2) produce an empirical multipole model that captures the main kTLHB profile.
The significance of the high latitude north-south gradient can be evaluated by independently fitting a monopole and dipole model to the data. Then, the F-test could determine if the improvement of using a dipole is statistically significant over the null hypothesis of a uniform kTLHB model (monopole).
The expansion of any well-behaved functions (in our case, the LHB temperature) on a sphere can be expanded into spherical harmonics Ylm up to degree lmax by
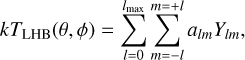 (6)
(6)
where alm is the complex coefficient associated with each Ylm. The question is finding the set of alm that minimises the χ2 between the observed data and spherical harmonic model kTLHB(θ, ϕ), which can be written explicitly as
![${\chi ^2} = \sum\limits_i {{{\left[ {{{d\left( {{\theta _i},{\phi _i}} \right) - \sum\nolimits_{l = 0}^{{l_{{\rm{max }}}}} {\sum\nolimits_{m = - l}^{m = + l} {{a_{lm}}} } {Y_{lm}}\left( {{\theta _i},{\phi _i}} \right)} \over {\sigma \left( {{\theta _i},{\phi _i}} \right)}}} \right]}^2}} ,$](/articles/aa/full_html/2024/10/aa51045-24/aa51045-24-eq28.png) (7)
(7)
where d(θi, ϕi) and σ(θi, ϕi) represent the ith data point and uncertainty associated with it. In our convention, ϕi = li and θi = 90 – bi, where li and bi are the Galactic longitude and latitude. For real-valued functions, the conjugate property of spherical harmonics means that  , where the * denotes the complex conjugate. It follows that al0 has no imaginary part, and the number of independent parameters required to describe each spherical harmonics of degree l is 2l + 1 (each complex alm requires two).
, where the * denotes the complex conjugate. It follows that al0 has no imaginary part, and the number of independent parameters required to describe each spherical harmonics of degree l is 2l + 1 (each complex alm requires two).
The most probable alm coefficients and their associated uncertainties are found by running MCMC using the emcee package (Foreman-Mackey et al. 2013), with the walkers initialised (with a small spread) at the minimum χ2 position found by the Levenberg-Marquardt algorithm implemented in lmfit (Newville et al. 2016).
We begin with evaluating the significance of the north-south gradient, using the same regions (|b| > 30°) shown in Fig. 8.
We began by modelling kTLHB as a constant (monopole) in the unmasked regions. We found a median kTLHB of 0.1154 ± 0.0003 keV with χ2/d.o.f = 6.36 (915 d.o.f), a unacceptable fit. Subsequently, we fitted the data with a dipole (lmax ≤ 1). The most probable model and the corresponding residual normalised by the bins’ fitting uncertainty are shown in Fig. 17. The χ2/d.o.f decreased to 4.01 (912d.o.f) compared to the monopole. Using the F-test and a significance level of 0.001, we deduced an F- statistic of 179.7 > Fcrit = 5.5 with a p-value in the order of 10−16. This suggests the dipole model is strongly preferred over the constant model, and the presence of a north-south gradient is statistically significant. However, one could still recognise systematic residuals in the northern hemisphere by inspecting the residual image, reflecting the north–south gradient is not simply a dipole.
Naturally, raising lmax can improve the fidelity of our spherical harmonics model to reproduce the data more closely. We included data as close as 10° from the Galactic plane for this empirical model. With multiple trials of different lmax values, we arrived at a lmax = 6 model that captures the main large-scale features in the data reasonably well, presented in Fig. 18. It has a χ2/d.o.f of 3.11 (1560 d.o.f.). We emphasise that we do not associate any physical interpretations with the multipoles. It merely serves as an empirical model for the LHB temperature profile. However, we speculate on the origin of the gradient in Sect. 4.1.4. The model parameters can be found in Appendix B. Appendix C presents the latitudinal profiles of kTLHB, where both the uncertainties and scatters of kTLHB are shown to compare with the spherical harmonics models.
 |
Fig. 11 Comparison of fitted NH and independent estimate of NH from H I and dust measurements. Left: fitted NH. Right: estimate of NH combining neutral hydrogen information from HI4PI (HI4PI Collaboration 2016) and E(B – V) information derived from Planck radiance map (Planck Collaboration XI 2014). |
 |
Fig. 12 Calibration curves of R2/R1 band ratio of the Raymond-Smith (Raymond & Smith 1977), Mekal (Mewe et al. 1985, 1986; Liedahl et al. 1995), and apec (Smith et al. 2001) models as a function of the temperature of an unabsorbed plasma at solar abundance. |
 |
Fig. 13 Comparison of our forward-modelled R2/R1 band ratio map with the observation. Left: R2/R1 band ratio map calculated by folding our best-fit (median) spectral models with the ROSAT R1 and R2 band responses. Right: R2/R1 data binned to the same contour-binning scheme (Snowden et al. 1997). |
 |
Fig. 14 Spatial distribution of EMLHB. Regions with EMLHB uncertainty < 5 × 10−5 cm−6 pc were also masked. The solid black line indicates the position of the ecliptic, and the two dashed lines represent a range of ±25° around it in ecliptic latitude where the solar wind density is expected to be high. The extent of the LHB under the assumption of ne = 4 × 10−3 cm−3 is also shown. |
4.1.2 Comparison with past observations
The most relevant references on the large-scale temperature variations of the LHB are Snowden et al. (1990), Snowden et al. (2000) and Liu et al. (2017). Snowden et al. (1990) inferred a temperature gradient of the LHB for the first time using the Wisconsin B/C band intensity ratio. They reported a mean temperature of 0.097 keV (106.05 K), and a dipole gradient pointing towards (l,b) = (348°.7,−11°.2) going from 0.064 keV (105.87 K; near Galactic anti-centre) to 0.127 keV (106.17 K; near Galactic centre). With the advent of ROSAT All-Sky Survey data (RASS), Snowden et al. (2000) compiled a catalogue of X- ray shadows at high Galactic latitudes (|b| > 20°). With these X-ray shadows and taking the simplifying assumption similar to us, that all components except the LHB are absorbed by the total Galactic NH , they arrived at an LHB temperature dipole in a similar direction, but with the dipole spanning the range of 0.094(106.04 K)−0.116 (106.13 K), only ~1/3 of that of Snowden et al. (1990). We note that our dipole model has the dipole amplitude in between the two studies (Adi = 0.0133 ± 0.0004 keV5; Table B.1). Liu et al. (2017) make use of both the RASS R2/R1 band ratio as well as the estimation of the SWCX contribution from the DXL sounding rocket (Galeazzi et al. 2012) mission to conclude that kTLHB is fairly uniform over the sky at 0.097 ± 0.019 keV (Bluem et al. (2022) recently lower this estimate to 0.084 ± 0.019 keV using AtomDB version 3.0.9). Inspection of the kTLHB map (left panel of their Fig. 6) from Liu et al. (2017) shows enhanced temperature in the Galactic south pole, but the enhancement appeared more localised than we observed using eROSITA, possibly caused by the unsubtracted eROSITA bubbles component.
Snowden et al. (1990, 2000) and our work show markedly different dipole direction of the LHB temperature. While a quantitative comparison of Snowden et al. (1990, 2000)’s dipole models with our dipole model is problematic because we found the LHB temperature profile not fully following a dipole, a qualitative comparison suggests our observed dipole axis is almost ~60° away from Snowden et al. (1990, 2000)’s. In contrast, despite being similar to Snowden et al. (1990, 2000) in using band ratio as a proxy of LHB temperature, Liu et al. (2017) reports a temperature map that resembles ours more closely. For Snowden et al. (1990), Wisconsin B (0.13–0.188 keV) and C (0.16–0.284 keV) bands match the peak emitting energies of a ~0.1 keV plasma and are largely (but not completely) unaffected by the hotter emission from the CGM when taking the band ratio as a proxy of LHB temperature. However, it was completed by 10 sounding rocket flights in ~8 years, sampling various parts of a solar cycle. We note that the analysis was done before the realisation that the SWCX process could contaminate the SXRB. Thus, how much of the B/C band ratio genuinely traced the LHB emission is unclear. ROSAT R1 (0.11–0.284keV) and R2 (0.14–0.284 keV) bands have similar energy coverage to the B and C bands and are similarly sensitive to the LHB temperature. Subtraction of the SWCX (comparing Fig. 11a of Snowden et al. 1997 and Fig. 3 of Liu et al. 2017) and background absorbed emission (see Sect. 4.1) can significantly change the profile of the R2/R1 band ratio. The dipole gradient Snowden et al. (2000) found could be plagued by SWCX as RASS was conducted near solar maximum.
Despite only covering the western Galactic hemisphere, it is a positive sign that our LHB temperature profile shows compatible morphology to the Liu et al. (2017)’s map, but with adequate significance to suggest a gradient. However, the spherical harmonic models we presented are a partial view without information from the eastern Galactic hemisphere. The low-order spherical harmonics would almost certainly change significantly should this information become available, as they are most sensitive to features spanning large angular scales by definition. Nevertheless, we suspect the change is unlikely to reconcile our model with Snowden et al. (1990, 2000)’s dipole as there is only a very weak sign of longitudinal temperature dependence from the eROSITA data.
 |
Fig. 15 Distance at which the integration of NH reaches 1020 cm−2 in the Lallement et al. (2022) (left) and Edenhofer et al. (2024) (right) dust cubes, as proxies of the extent of the local bubble. The empty regions in the map indicate that the integration does not reach NH ≥ 1020 cm−2 before 400 pc. |
 |
Fig. 16 Map of reduced-χ2 (χ2/d.o.f) after rebinning each spectrum, imposing that each spectral bin receives at least ten counts. |
 |
Fig. 17 Dipole model and residual. Left: dipole model of kTLHB. Right: residual normalised by the 1 σ fitting uncertainty of each valid bin. The black cross in both panels shows the direction of the dipole towards (l, b) = (291°, −26°). |
 |
Fig. 18 Similar to Fig. 17 but for the spherical harmonics model of lmax = 6. The data were fitted down to 10° from the Galactic plane. We note that the colour bar of the left panel was scaled up to 0.2 keV, identical to Fig. 10 for comparison. |
4.1.3 Temperature anti-correlation with absorption column density
The left panel of Fig. 11 shows the distribution of log10(NH/cm−2) inferred from our spectral fitting.
Neglecting the Galactic plane where both our and HI4PI NH measurements are not particularly accurate due to modelling simplification and self-absorption, the two NH maps possess almost identical morphology, with the X-ray absorption inferring a lower NH at high Galactic latitudes. By comparing the kTLHB maps in Figs. 8 and 10 with the NH maps, one can immediately notice the anti-correlation between the kTLHB and NH, especially in the southern Galactic hemisphere. The hottest regions of the LHB above b < −30° are where the NH are the lowest. Interestingly, as is described in more detail in Sect. 4.2, the hottest regions correspond to the largest EMLHB .
Given the morphological similarity of the southern hot patch and the low NH region and the observation that the X-ray absorption column density there is consistently lower than the HI4PI measurement, we suspected the cause of the hot patch was the result of our inaccuracies in fitting the NH, biasing kTLHB in the process. Therefore, we reran the spectral modelling of all contour bins and imposed the condition that the NH must be fixed at the HI4PI values.
We show the resulting map on kTLHB in Fig. 19. The kTLHB gradient remains, with similar amplitude and direction. The anti-correlation with NH remains clear. Not surprisingly, the quality of the spectral fits became increasingly worse towards the Galactic plane, as the assumption of using total NH alone the line-of-sight becomes questionable. The result of this test indicates the LHB temperature gradient is unlikely to be caused by our NH determination, and in addition, leaving NH free during spectral fitting was appropriate and necessary.
 |
Fig. 19 Map of kTLHB upon fixing the NH to the HI4PI NH. The colour scaling conforms to Fig. 8 to highlight the high latitude temperature dichotomy. |
4.1.4 Speculations on the source of temperature gradient
The mechanism that set up this temperature gradient is unclear. Still, it is not completely unexpected. Schulreich et al. (2023) demonstrate in a sophisticated numerical study that sequential supernova explosions could have created the LHB, with some possibly exploding in the last ~1–2 Myr. In their simulation, the LHB temperature is not uniform in the present day; instead, it shows a large-scale gradient that could span approximately an order of magnitude. Therefore, the scenario of recent off-centre supernova explosions can, in principle, explain our measured temperature contrast. However, their simulated temperature gradient direction differs from our measurement. They back-traced the trajectories of the stellar populations, which most likely hosted massive stars that expanded the LB using Gaia EDR3 data. Further, they predicted the massive stars’ explosion times and positions by considering the initial mass function and stellar isochrones. They used these informed explosion sites and times as input parameters of their simulation; thus, the simulation’s gradient direction is not arbitrary. Judging from their Fig. 4, the simulated temperature gradient is primarily along the Galactic centre-anticentre line, in contrast to our measurement in the north-south direction. Whilst the uncertainty of the stellar trace-back does not allow for the explosion sites in the south, shock reflections from the thick LB shell and gas sloshing following any explosions could easily change the direction of the temperature gradient (Pacicco, M. & Schulreich, M., priv. comm.). Pressure gradients in the LHB are washed out following the sound crossing timescale (a few 0.1–1 Myr). Transient shocks within the LHB exist in the simulation of Schulreich et al. (2023). These shocks create hotter and denser plasma layers and can be preferentially picked up in their X-ray emissions as emission measure scales as n2. The temperature dichotomy we observe could be caused by these shocks in the south. It is likely a matter of fine-tuning the simulations and choosing a correct time stamp to reproduce the current LHB observables so that these shocks appear in the right place and time. Last but not least, the density of the plasma also displays a similar gradient as the temperature in their simulation, which we do not see or have not seen with the current instrumental sensitivity in shadowing experiments (e.g. Yeung et al. 2023) that probed only very few sight lines. Future observations in this direction will be essential to confirm or reject this scenario.
The second possible scenario hinges on more assumptions, including the density of the LHB and magnetic pressure within it do not vary significantly in different directions. Consider a simple static scenario where the LHB is not expanding and is in pressure equilibrium with the surrounding ISM. The temperature gradient, in this case, reflects a pressure gradient set up by the surrounding ISM, where its profile can be traced by the thermal pressure of the LHB, given by
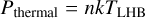 (8)
(8)
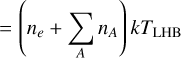 (9)
(9)
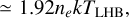 (10)
(10)
where nA is number density of the Ath element and n = 1.92ne is a common estimation of the total particle density6 (e.g. Galeazzi et al. 2007; Snowden et al. 2014). The colour bar in the kTLHB map in Fig. 10 shows also the resulting thermal pressure, assuming ne = 4 × 10−3 cm−3 (Yeung et al. 2023). An enhancement of pressure near the Galactic disc can be observed, and the pressure decreases rapidly away from it. It makes intuitive sense that the Galactic disc exerts a larger pressure on the LHB. Indeed, the vertical pressure profile in the Solar neighbourhood is approximately an exponentially decaying function from the midplane, with a scale height of ~500 pc (Cox 2005). The smaller high latitude temperature or pressure gradient could also be explained if the initial surrounding medium was not uniform before the formation of the LHB. This scenario does not necessarily conflict with the off-centre supernova explosions scenario in the simulation of Schulreich et al. (2023) and could both be at work.
4.2 Emission measure and extent of the local hot bubble
Fig. 14 shows the spatial distribution of the emission measure of the LHB, EMLHB. In addition to masking known large super-bubbles and supernova remnants, we also excluded regions with 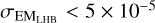 cm−6 pc. Regions that make up the latter are usually biased, possibly spectral fits with vanishing LHB components or MCMC chains that did not converge well. Before delving into the correlation or anti-correlation of EMlhb with other parameters, it is best to discuss EMlhb in the context of the extent of the LHB.
cm−6 pc. Regions that make up the latter are usually biased, possibly spectral fits with vanishing LHB components or MCMC chains that did not converge well. Before delving into the correlation or anti-correlation of EMlhb with other parameters, it is best to discuss EMlhb in the context of the extent of the LHB.
EMlhb is directly related to the extent of the LHB in a given look direction if one knows the line-of-sight density profile, which is given by the following equation:
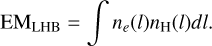 (11)
(11)
By adopting the assumption of a fully ionised solar abundance plasma (see Leahy et al. 2023, for caveats of this assumption), ne/nH ≃ 1.2 and further assuming a constant density profile, we obtained a simple relation between EMlhb and the extent of the LHB L:
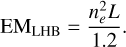 (12)
(12)
One could calibrate ne under the constant density assumption using sight lines through various molecular clouds on the surface of the LHB. Recent work suggests ne ≃ (4 ± 0.5) × 10−3 cm−3, moderately independent of the look direction (Yeung et al. 2023), which is the number we adopted in converting EMlhb to the extent of the LHB. This is smaller than ne = (4.68 ± 0.47) × 10−3 cm−3 inferred by Snowden et al. (2014), but within the uncertainties. The assumed electron density gives rise to the largest systematic uncertainty in our 3D LHB model. The difference between the two numbers alone entails a 37% difference in estimating the LHB distance.
Figs. 14 and 20 show the structure of the LHB assuming ne = 4 × 10−3 cm−3, in the ZEA projection and a 3D-rendered surface respectively. For the latter, the LHB surface is smoothed and interpolated into the masked regions using radial basis function interpolation (scipy.interpolate.rbf(*, smooth=0.3)) implemented in the Python package scipy (Virtanen et al. 2020).
Despite its irregular shape, the LHB is systematically more extended away from the disk, presumably because the denser medium permeated along the Galactic plane prohibits its expansion. The conventional picture of1 MK plasma displacing colder ISM phases in the solar neighbourhood first put forward by Sanders et al. (1977) appears to explain our result excellently, especially in the southern Galactic hemisphere. An almost perfect anti-correlation with Galactic NH can be observed in the southern Galactic hemisphere, slightly less so in the northern hemisphere.
For a more comprehensive view of the multiphase ISM in the solar neighbourhood, we also compared our spatial model of the hot phase of the ISM to the local dust maps, inferred primarily from Gaia extinction data by Lallement et al. (2022) and Edenhofer et al. (2024) independently. A sophisticated method was used by Pelgrims et al. (2020) to trace the inner surface of the local bubble (LB) from 3D dust maps, involving identifying inflexion points in the differential extinction radial profiles and an iterative refining process. In our analysis, we took a simpler approach by identifying the LB extent at which the integration of dust maps reaches a column density of NH = 1020 cm−2, where the optical depth is approximately unity at 0.2 keV. Both the extinction cubes of Lallement et al. (2022) and Edenhofer et al. (2024) were converted from AV to NH cubes using the conversion NH = 2.21 × 1021 AV (Güver & Özel 2009). The extent of the LB inferred from these two cubes is shown in Fig. 15.
We could see excellent agreement in a few areas (see the finding chart in Fig. 7):
- 1)
in the general direction of the Loop I superbubble or the eROSITA bubbles, both the LHB plasma and dust cubes show distances in the order of 100 pc. The LHB emission appears to be absorption-bounded.
- 2)
The LHB is much more extended in the low NH regions in the southern Galactic hemisphere.
- 3)
Around 240° ≲ l ≲ 270° on the Galactic plane (~ β Canis Majoris interstellar tunnel; Gry et al. 1985; Welsh 1991), one could match the larger extent of the LHB well with the dust maps, both in position and morphology, especially when compared with Edenhofer et al. (2024).
- 4)
In the northern Galactic polar cap (l ≳ 60°), the LHB is more extended when there is low NH.
- 5)
Towards the constellation Centaurus at (l, b) ≃ (315°, 25°), one can see a hint of an extended tunnel, possibly connecting to the Loop I superbubble. This feature can also be seen when integrating the Edenhofer et al. (2024)’s cube in the right panel of Fig. 15.
- 6)
On the other hand, we could see in the region of (180° ≲ l ≲ 240°, 15° ≲ b ≲ 45°), little absorbing material is present within 400 pc, yet the LHB does not extend as freely as in regions towards the LoopI/eROSITA bubbles and the Galactic poles. This could be a hint that the hot plasma is not completely volume-filling, or its density is lower in this general direction, or the dust wall of the LB in this direction is very low in density. Indeed, a peak of low-density dust at ~150 pc could be present there as found by the recent work by O’Neill et al. (2024). We elaborate on the interstellar tunnels in Sect. 4.6.
The anti-correlation of EMLHB and dust can also be appreciated by looking at slices of 3D dust cubes. Fig. 21 shows the shape of the LHB shell overlaid on the y = 0 slice in the Edenhofer et al. (2024) dust cube. The extent of the LHB matches the onset of extinction extremely well, filling gaps of low dust density.
Liu et al. (2017) produced the latest X-ray LHB model before our work. Consulting their EM map and great-circle cuts (their Figs. 6 and 7), one can see despite the difference in methodology (spectral-fitting versus band-ratio) and instrument, the inferred EM and shape of the LHB are remarkably similar. Nevertheless, we have identified some areas that are interestingly different:
(i) at l ~ 240° we found a more distinct transition in LHB extent between the Galactic plane (b ~ 0, region of the β Canis-Majoris tunnel) and a large-scale protrusion in the southern Galactic hemisphere (b ≲ −30°) than Liu et al. (2017).
(ii)The aforementioned channel around (l,b)=(315°, 25°) did not appear in the Liu et al. (2017)’s EM map. It was because that region was categorised as contaminated by the background Loop I superbubble and was excluded from the analysis. In fact, the appearance of the tunnel was seen in the ROSAT R1+R2 band map even after the SWCX subtraction (Liu et al. 2017, their Fig. 2).
 |
Fig. 20 Three-dimensional structure of the LHB in the western Galactic hemisphere assuming a constant density of 4 × 10−3 cm−3. The inner (opaque, coloured) and the outer (grey, translucent) surfaces show the ±1 σ uncertainty bounds of the distance under the constant ne assumption. We note that the two surfaces only reflect the uncertainty in the spectral fitting but not in ne. We note that kTLHB is also colour-coded on the inner surface. A sphere of 100 pc radius is shown around the Sun (yellow) as a ruler. An interactive version of this figure, including the comparison with dust maps (not shown) can be accessed from online or the accompanying website (Sect. 5). |
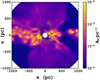 |
Fig. 21 A slice of the Edenhofer et al. (2024) cube at the x-z plane overplotted with the silhouette of the LHB. |
4.3 Degeneracy between the local hot bubble and the Milky Way’s circum-galactic medium components
This Section discusses the degeneracy between the LHB and CGM components and our mitigation methods. We begin by laying out the observations that demonstrate this degeneracy. In summary, this led us to incorporate ROSAT R1 and R2 bands into our analysis, as well as imposing a uniform prior to limit kTLHB < 0.15 keV for regions of low NH.
Inspecting the spectral fitting results with only eROSITA data revealed a degeneracy between the LHB and the CGM components in some contour bins. An example of this degeneracy can be seen in Fig. 22, where we show the parameter correlations in the spectral fits of Bin476 and Bin1875, located at (l, b)=(257°.9, 59°.6) and (296°.7, 47°.6) respectively. Both regions have log (NH/cm−2) ≃ 20.5 as traced by the HI4PI survey (HI4PI Collaboration 2016) using Eq. (5). One can see the posterior distributions of KTCGM are bimodal in both bins. The lower KTCGM peak is contributed by either partially in Bin476, or completely in Binl875, by samples that have kTLHB > KTCGM. Similarly, the posterior distributions of kTLHB show either an extended tail in Bin476 or a second peak in Binl875, at temperatures at least doubled of the main peak. We believe these solutions are unlikely to represent the real picture, but are caused by the similarity of the LHB’s and CGM’s apec models observed at eROSITA’s energy resolution. The main differentiating factor of LHB and CGM is the absorption that causes CGM component to drop off at the low energy end. Therefore, one would expect the two to exhibit some levels of degeneracy at regions of low NH. To help break the degeneracy, one would ideally go to energies lower than 0.2keV, but eROSITA’s effective area there is small. However, ROSAT maintains significant effective area until ~0.1 keV, and is therefore more sensitive to detect the drop off caused by absorption in the CGM component. The details of how the ROSAT data were used were described in Sect. 2. We note that ideally, one should subtract the heliospheric SWCX contributions from the ROSAT R1 and R2 band maps as in Uprety et al. (2016), who reported an all-sky average SWCX contribution of 30 ± 8% in R1 and 8 ± 10% in R2. However, given that the average relative uncertainties in Rl and R2 are 37% and 31% in our contour bins and that they only contributed to two spectral bins in the fitting, we believe the bias introduced by neglecting SWCX in ROSAT data is vastly subdominant to the resulting fit parameters of our full spectral analysis. Perhaps a more pertinent question would be whether a pair of data points from ROSAT possesses sufficient capability to resolve the degeneracy between the LHB and CGM components.
The answer is largely affirmative in many contour bins plagued by the degeneracy. For a specific example and a direct comparison, the top panel of Fig. 23 shows the corner plot of Bin476 after including the ROSAT data. The high temperature tail in the posterior of kTLHB vanished and samples with kTLHB > kTCGM disappeared. Motivated by the positive results, we incorporated the ROSAT R1 and R2 bands into the spectral analysis.
Nonetheless, cases remained where this was inadequate, especially at low NH regions. For instance, in Bin1875 (lower panel of Fig. 23), the degeneracy remained. The posterior distributions remained highly bimodal, albeit a longer MCMC chain was needed to sample the second peak (kTLHB > kTCGM). Unfortunately, we could not break this degeneracy using the currently available data. Therefore, we decided to forbid kTLHB to go above 0.15 keV by imposing a uniform prior between 0.07–0.15 keV on kTLHB. Not surprisingly, the resulting posterior distributions no longer show a second peak, as shown in Fig. 24. This prior was used in the fitting of all the contour bins where log (NH /cm−2) < 20.5. To our knowledge, the LHB temperature has seldomly been measured to be higher than 0.15 keV (e.g. Snowden et al. 1990, 2000; McCammon et al. 2002; Liu et al. 2017), and conversely, the CGM seldomly below 0.15keV (e.g. McCammon et al. 2002; Yoshino et al. 2009; Gupta et al. 2021; Bluem et al. 2022; Ponti et al. 2023), justifying our choice of prior in the low NH regions.
 |
Fig. 22 Corner plots showing LHB and CGM parameters are degenerate in regions of low NH. Top: Bin476 at (l, b)=(257°.9, 59°.6). Bottom: Binl875 at (l, b)=(296°.7, 47°.6). |
 |
Fig. 24 Corner plot of Bin1875 after using ROSAT data and imposing a uniform prior on kTLHB below 0.15 keV. |
4.4 Solar wind charge exchange
The halo orbit of SRG/eROSITA around the Sun-Earth Lagrangian point L2 (Freyberg et al. 2020) avoids much of the magnetospheric SWCX that originates from the interaction of the solar wind ions with neutrals in the Earth’s exosphere (Kuntz 2019). An image of the Earth’s exosphere in Ly-α taken from 2348 R⊕ away shows that it is contained within 94 R⊕ (Kameda et al. 2017), while SRG never ventured within 175 R⊕ from the Earth (Freyberg et al. 2020), effectively immune to the magnetospheric SWCX emission since it is always pointing perpendicular to the Sun-Earth-L2 line. Even avoiding the bulk of the exosphere, in principle, SWCX can also occur on the surface of the magnetotail, but we expect its effect to be small since such a thin interaction and emission layer would incur brightness variation in short timescales (minutes to hours), and we do not observe obvious stripes along the ecliptic longitude lines in the soft band in eRASS1 (eROSITA completes scanning a great circle primarily along this direction every four hours).
We further ignored the effect of heliospheric SWCX in our spectral analysis, which can indeed contaminate eROSITA data in general. We verify that this is at least a satisfactory assumption by looking at the EMLHB map a posteriori. It is well-known that the solar wind density is higher at low heliographic latitudes than the poles, especially around solar minima (e.g. Porowski et al. 2022). Therefore, unlike pointed observations, eRASS provides a way of estimating the heliospheric SWCX contribution from detecting extra emission preferentially along the ecliptic plane. In Fig. 14, we overlaid the ecliptic in black on the EMLHB map, and the dashed black lines mark the range of ±25° within the ecliptic, where the denser, slow solar wind dominates during solar minima (e.g. McComas et al. 1998, 2003). The fact that there is no obvious enhancement within this ecliptic latitude range suggests the heliospheric SWCX contamination in our results is minor. Indeed, as we gradually approached solar maximum, eRASS3 and 4 data clearly show enhancement in this band, but the presentation and the detailed analysis of this effect will be presented in another work (Dennerl et al., in prep.).
4.5 Energetics and pressure balance within the local hot bubble
We estimated the thermal energy of the LHB as follows:
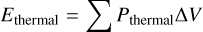 (13)
(13)
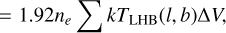 (14)
(14)
where ΔV is the volume occupied by the LHB plasma within a contour bin. The EMLHB information is implicitly passed into ΔV in the form of the extent of the LHB. We have incomplete coverage of the sky. Hence, we scaled up our estimation of Ethermal to a total of 4π solid angle. Finally, we estimated 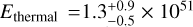 erg, where we have assumed ne = 4 × 10−3 cm−3. This is in the order of the energy released by a supernova explosion. However, one must consider that the LHB’s size (radius) is >100 pc, which is too large for a single explosion. Therefore, the LHB is more likely to have been episodically reheated and expanded by successive supernova explosions and simultaneously radiated its energy away to produce the current energy content.
erg, where we have assumed ne = 4 × 10−3 cm−3. This is in the order of the energy released by a supernova explosion. However, one must consider that the LHB’s size (radius) is >100 pc, which is too large for a single explosion. Therefore, the LHB is more likely to have been episodically reheated and expanded by successive supernova explosions and simultaneously radiated its energy away to produce the current energy content.
We presented the thermal pressure map in Fig. 10, using Pthermal/k = nT. We found the mean pressure of the LHB is 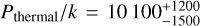 cm−3 K. These numbers are consistent with pressure measured in the sight line of (l,b)=(144°,0°) by Snowden et al. (2014), hence supporting their finding of the LHB being in pressure equilibrium with the local interstellar clouds (LICs), after accounting for magnetic pressure as measured by Voyager I outside of the heliosphere Burlaga & Ness (2014). But we also point out that Snowden et al. (2014)’s sight line lies on the Galactic plane, which we found to have systematically higher thermal pressure. This pressure is also fully consistent with measurements based on X-ray shadowing using eRASS:4 data (Yeung et al. 2023).
cm−3 K. These numbers are consistent with pressure measured in the sight line of (l,b)=(144°,0°) by Snowden et al. (2014), hence supporting their finding of the LHB being in pressure equilibrium with the local interstellar clouds (LICs), after accounting for magnetic pressure as measured by Voyager I outside of the heliosphere Burlaga & Ness (2014). But we also point out that Snowden et al. (2014)’s sight line lies on the Galactic plane, which we found to have systematically higher thermal pressure. This pressure is also fully consistent with measurements based on X-ray shadowing using eRASS:4 data (Yeung et al. 2023).
Compared with the latest numerical simulation of the LHB by Schulreich et al. (2023), our measured pressure is consistent with their simulated present-day pressure of 10100 cm−3 K. However, this results from combining their n and T, which are lower and higher by roughly an order of magnitude compared to our results, respectively. Despite the apparent coincidence, their simulation shows how successive supernova explosions in the Sco-Cen complex can lead to the large-scale temperature gradient within the LHB, as we found in this work (Sect. 4.1).
The estimated Galactic midplane total ISM pressure is P/k ~ (2.8 ± 0.7) × 104 cm−3 K, about two to three times the thermal pressure we estimated from the LHB on the plane (Boulares & Cox 1990; Cox 2005). As already put forth at the time, one can approximate the cosmic rays, magnetic and dynamical (possibly thermal) pressure as equipartition. This yields a thermal pressure from the ISM about Pthermal/k ~ 104cm−3K, consistent with our measurement. Finally, we would like to highlight the LHB pressure of Pthermal/k ~ 104 cm−3 K is lower than the typical values seen in superbubbles, supernova remnants or wind-blown bubbles (e.g. Oey & García-Segura 2004; Sasaki et al. 2011; Kavanagh et al. 2012; Sasaki et al. 2022). This may indicate the LHB being open towards higher Galactic latitudes.
 |
Fig. 25 Zoom-in of the Centaurus tunnel in the smoothed EMlhb map (left) and dust distance map by integrating the dAv map up to 1020 cm−2 (right) (Edenhoſer et al. 2024). The contour line outlining the region where the NH does not reach 1020cm−2 in 400 pc is overlaid on the EMLHB map. |
4.6 Interstellar tunnel network
Cox & Smith (1974) famously postulated supernovae can generate and maintain an interstellar tunnel network in the Galaxy, filled with ~0.1 keV gas. Mapping the hot phase structure of the LB/LHB in emission has more limitations than mapping the cold phase of the local ISM with stellar extinction or line absorption because one has to assume a model of the emitting components and the absorption they are subject to. This makes inference of the LHB shape on the Galactic plane difficult as one expects many line-of-sight emitting and absorbing components. Also, extensions and possible connecting tunnels of the LHB that are not aligned with the radial direction are difficult to infer. Nevertheless, as mentioned in Sect. 4.2, we found evidence of hot gas filling nearby channels that lack neutral material.
The most convincing evidence of such a channel is the β CMa tunnel (l ~ 250°, b ~ 0°), where even the projected morphology of the tunnel in EMLhb (see Fig. 14) is similar to the dust map (especially, the right panel of Fig. 15). Historically, ROSAT did not provide enough evidence of the tunnel being filled by hot gas (Welsh & Shelton 2009, and references therein)7. However, Dupin & Gry (1998) and Gry & Jenkins (2001) found the intervening absorbing clouds to the stars β CMa and ϵ CMa to show absorptions from high ionisation species such as С iv and Si in, but comparison with the cloud turbulent temperature (~7000 K) demonstrated that they are likely partially ionised due to photoionisation of the hot stars and/or the interaction with the hot LHB gas in the surrounding. Our observation confirms the presence of the surrounding hot gas in the tunnel. Indeed, both the UV and our soft X-ray observations corroborate the scenario where the warm gas in LICs forms a conductive layer between themselves and the surrounding hot gas (see e.g. Cowie & McKee 1977; Slavin 1989). Welsh (1991) suggested this tunnel is connected to the Gum nebula (Gum 1952), which lies in the same direction at 400 pc (Brandt et al. 1971). The Gum nebula is likely part of a large superbubble GSH 238+00+09 (Heiles 1998), which the LHB could also connect to.
In addition, we report on a possible channel filled by hot plasma towards the direction (l ~ 315°, b ~ 25°), in the constellation Centaurus. A zoom-in view of the EMLhb and dust map tracing the neutral matter in the region is shown in Fig. 25. There is an enhancement in EMlhb in this direction, which anti-correlates with the amount of dust extinction. This implies the presence of extra path length of the LHB plasma, possibly filling the tunnel. It might be another channel connecting to the Loop I superbubble (Egger & Aschenbach 1995), in addition to the Lupus tunnels first discovered from Na I absorption lines (Welsh et al. 1994; Lallement et al. 2003). The latter are, unfortunately, located on the Galactic plane and, thus, are difficult to identify in our spectral analysis. The Centaurus tunnel region is located on the edge of the eROSITA bubbles, further complicating the spectral fitting. A dedicated spectral analysis, with a tailored spectral extraction region, of this region will likely help disentangle the emission from the Loop I superbubble (its nature or existence has become unclear after the discovery of the eROSITA bubbles) from the eROSITA bubbles, in terms of spectral properties and distance. This analysis is currently ongoing.
The Antlia supernova remnant (l, b)~(275°, 15°) (e.g. Fesen et al. 2021), Monogem Ring (l, b)~(200°,8°) (e.g. Knies et al. 2024) and Orion-Eridanus superbubble (l, b)~(205°, −30°) (e.g. Pon et al. 2016) are other nearby bubbles that our data suggest the LHB could be touching or connected to. Monogem Ring is arguably even more interesting because there is a lack of dust (Lallement et al. 2022; Edenhofer et al. 2024) in the line-of-sight up to its distance of ≃300 pc (Knies et al. 2024, we refer to the closest components in the whole Gemini-Monoceros X-ray enhancement), consistent with the eROSITA spectral analysis of it (Knies et al. 2024). The LHB might be currently merging or about to interact with it.
On the other hand, there is the presence of channels of low NH that do not seem to be filled with soft X-ray-emitting plasma. The more obvious one is located at (l, b)~(260°, 29°), which can be seen in the right panel of Fig. 15. The EMlhb map in Fig. 14 does not show an anti-correlated enhancement.
In summary, our data demonstrates that the displacement model in which the LHB plasma fills the LC works well overall. Only a few regions seemingly do not abide by the displacement model.
 |
Fig. 26 Comparison of the local (hot) bubble extent from X-ray and dust. Left: extent of the local hot bubble under the constant ne = 4 × 10−3 cm−3 assumption. Right: local bubble shell tracing the closest extinction peak inferred by O’Neill et al. (2024). An interactive comparison in 3D can be accessed from the accompanying website (Sect. 5). |
4.7 Beyond constant density of the local hot bubble
We have discussed the close anti-correlation between the local dust map and the emission measure of the LHB in Sect. 4.2. The dust maps (Fig. 15) we compared our LHB shape to were inferred from integrating the NH up to 1020 cm−2 (an optical depth for a 0.2 keV photon) from our position. An alternative way of locating the shell of the LB is by finding the first peak of the extinction as adopted by Pelgrims et al. (2020) and O’Neill et al. (2024). This might be more physically motivated as the expansion on the LB is expected to create a shell of denser material at its boundary that is not necessarily dense enough to be opaque to soft X-ray.
A comparison of the inferred LB shell from O’Neill et al. (2024) using Edenhofer et al. (2024) data to our constant density LHB model is shown in Fig. 26. For this comparison, we adopted their A′0.5 peak density distance as the extent of the LB. Their shapes are significantly different, most notably at b > 60°, where the apparent enhancement in EMlhb (hence extent) lacks a counterpart in the LB. Below b ≲ 30°, the LHB and the LB are both more extended but with a fairly different morphology. The clear tunnel in the LB at (l, b) ≃ (250°, −20°) is not shared by the LHB. There is a reasonable agreement for regions between −30° ≲ b ≲ 60°, ignoring the various tunnels discussed in Sect. 4.6. The simplest reason for the discrepancy between the two maps is the constant density assumption is inaccurate, given 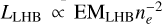 , which means the extent of the LHB is more sensitive to ne than EMlhb.
, which means the extent of the LHB is more sensitive to ne than EMlhb.
One can work conversely, assuming the LB shell is the true extent of the LHB and estimate the electron density of the LHB plasma using Eq. (12), as well as its thermal pressure by Eq. (10) subsequently. We show the resulting electron density and thermal pressure maps in Fig. 27. Clearly, much of the modulation in EMlhb is transferred to the variation in density, especially in regions where the LHB extent derived from the constant density assumption differs much from the extent of the LB. This causes the average LHB density at b > 60° to be higher than the rest of the areas by ~40%. The extensions towards β CMa (at least the part on the Galactic plane) and Centaurus tunnels mentioned in Sect. 4.6 do not have direct counterparts in the LB map, and thus they are taken as high-density regions of the LHB. The thermal pressure map slightly differs from the constant density case shown in Fig. 10, where the former displays a weaker north-south gradient because of the higher electron density in the northern polar cap balancing the lower LHB temperature, and it produces a more uniform pressure profile on the largest scale. Indeed, being in pressure equilibrium with its surroundings would be the expectation for an old bubble such as the LHB. From the two maps, the half-sky median electron density and thermal pressure are 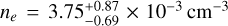 and
and 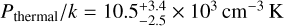 .
.
Assuming the LHB extends up to the first extinction peak is a sound assumption, but it is not without challenges. The hardest part to reconcile is the presence of tunnels that seem independent of the LB shell. We suggest it is unlikely a coincidence that EMlhb shows a better anti-correlation to the local dust column density (Fig. 15) than the extent of the LB shell, especially when the LB shell peak density is the lowest in these regions (see Fig. 4 in O’Neill et al. 2024). Not accepting it as a coincidence entails hot plasma located beyond the first wall of absorption. They could have the same origin as the LHB or had other heating mechanisms. One possibility is shown by the LB simulation by Schulreich et al. (2023) (third and fourth columns of their Fig. 4), in which pockets of hot plasma could be formed beyond the main LB cavity because of the LHB anisotropic expansion into the inhomogeneous surrounding materials that were already stirred up during the wind-driven phase.
 |
Fig. 27 Electron density (left) and thermal pressure (right) of the local hot bubble assuming it extends up to the local bubble shell (O’Neill et al. 2024). |
4.8 Cosmic X-ray background
4.8.1 Determination of the cosmic X-ray background photon indices
Ponti et al. (2023) adopts a double-broken power-law model to describe the CXB in the eFEDS field, following the CXB synthesis model by Gilli et al. (2007), which produces a steepening CXB slope ≲ 1 keV from galaxy groups and clusters. The double-broken power-law8 (bkn2pow in Xspec/PyXspec) can be written as
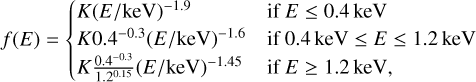 (15)
(15)
where K is the normalisation of the power-law at 1 keV in the unit of photons s−1 cm−2 keV−1 and the first and second break energies are located at 0.4 and 1.2 keV.
From the spectral fitting of the regions shown in Fig. 6, we found that the first break energy at 0.4 keV is redundant as the photon indexes below 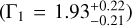 and above
and above 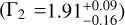 this energy are consistent within 1 σ when we left all three photon indexes free to vary in the spectral fitting. Therefore, we subsequently replace the double-broken power-law model with a single-broken power-law model, which can be treated as a special case of Eq. (15). It has the form
this energy are consistent within 1 σ when we left all three photon indexes free to vary in the spectral fitting. Therefore, we subsequently replace the double-broken power-law model with a single-broken power-law model, which can be treated as a special case of Eq. (15). It has the form
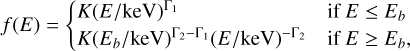 (16)
(16)
where Eb is the break energy and Г1 and Г2 are the photon indexes below and above Eb. Another iteration of the spectral fitting with the single-broken power-law model indicates 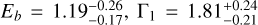 and
and 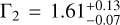 . This result suggests a change of slope in the CXB at 1.2 keV, below which the slope is possibly steeper from the contributions from active galactic nuclei, galaxy groups and galaxy clusters (Hasinger et al. 1993; Smith et al. 2007; Yoshino et al. 2009). Nonetheless, the transition of the CXB slope is only significant on ~1 σ level9 and is not strictly required by the data. Additionally, the uncertainties of the parameters are dominated by the spread from multiple regions instead of the statistical uncertainties within each region. A simple power-law fit yields
. This result suggests a change of slope in the CXB at 1.2 keV, below which the slope is possibly steeper from the contributions from active galactic nuclei, galaxy groups and galaxy clusters (Hasinger et al. 1993; Smith et al. 2007; Yoshino et al. 2009). Nonetheless, the transition of the CXB slope is only significant on ~1 σ level9 and is not strictly required by the data. Additionally, the uncertainties of the parameters are dominated by the spread from multiple regions instead of the statistical uncertainties within each region. A simple power-law fit yields 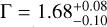 , in good agreement with Г2 in the single-broken power-law model. This is steeper than the canonical photon index of 1.4–1.5. Calibration issues could partly cause this, as eROSITA indeed tends to measure cooler cluster temperature than Chandra and XMM-Newton for massive clusters (Liu et al. 2023; Migkas et al. 2024)10. Both treatments of the CXB reproduce the data almost equiva-lently, with the simple power-law and single-broken power-law resulting in an average C-statistic/d.o.f in the Markov chain Monte Carlo (MCMC) runs of all regions of
, in good agreement with Г2 in the single-broken power-law model. This is steeper than the canonical photon index of 1.4–1.5. Calibration issues could partly cause this, as eROSITA indeed tends to measure cooler cluster temperature than Chandra and XMM-Newton for massive clusters (Liu et al. 2023; Migkas et al. 2024)10. Both treatments of the CXB reproduce the data almost equiva-lently, with the simple power-law and single-broken power-law resulting in an average C-statistic/d.o.f in the Markov chain Monte Carlo (MCMC) runs of all regions of 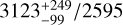 and
and 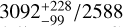 , respectively. Therefore, we adopted both in our full western Galactic hemisphere analysis and discuss the systematic uncertainties associated with either choice in Sect. 4.8.3. Based on this analysis of the CXB, we froze Г1, Г2 and Eb to be 1.9, 1.6 and 1.2 keV of the single-broken power-law model, Г to 1.7 for the simple power-law model as the CXB model in the full spectral analysis.
, respectively. Therefore, we adopted both in our full western Galactic hemisphere analysis and discuss the systematic uncertainties associated with either choice in Sect. 4.8.3. Based on this analysis of the CXB, we froze Г1, Г2 and Eb to be 1.9, 1.6 and 1.2 keV of the single-broken power-law model, Г to 1.7 for the simple power-law model as the CXB model in the full spectral analysis.
4.8.2 Normalisation
Fig. 28 shows the normalisation of the CXB, taken from the simple power-law model of Г = 1.7. Ignoring the Galactic plane, the normalisation of the CXB is extremely uniform. At |b| > 30°, it has a median of 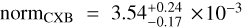 photons cm−2 s−1 keV−1 deg−2 at 1 keV. This means the fluctuation of the CXB is ≲ 10%, on the angular scales of ~1°.5–4° that we probe set by the contour binning scheme. The enhancement on the Galactic plane is likely due to the Galactic ridge emission.
photons cm−2 s−1 keV−1 deg−2 at 1 keV. This means the fluctuation of the CXB is ≲ 10%, on the angular scales of ~1°.5–4° that we probe set by the contour binning scheme. The enhancement on the Galactic plane is likely due to the Galactic ridge emission.
Our main finding on the CXB is that eROSITA observes a steeper photon index than the conventional value of 1.45 (Cappelluti et al. 2017) (Sect. 4.8.1). It might be due to calibration issues (Migkas et al. 2024) or caused by the steepening of the CXB slope at soft energies. A newer processing version of eROSITA data will potentially mitigate or resolve the calibration issue. Given the steeper slope of Г ~ 1.6-1.7, the normalisation we found is also slightly higher compared to Chandra ((3.32 + 0.05) × 10¯3 photons cm−2 s¯1 keV¯1 deg¯2, Cappelluti et al. 2017). In addition, the uniformity of the CXB demonstrates the robustness of our spectral fitting to differentiate multiple sky components.
 |
Fig. 28 Normalisation of the cosmic X-ray background assuming a simple power-law of Г = 1.7. |
4.8.3 Systematic uncertainties associated with the choice of cosmic X-ray background model
As described in Sect. 4.8.1, the power-law and the broken power-law model could reproduce the diffuse X-ray spectra equally well. So far, we have been discussing the results using a CXB described by a simple power-law model. To test the systematic effect caused by the CXB model, we fitted all spectra again in the same way but using a broken-power-law CXB component. We then plotted the 2D maps and inspected the histograms of the other components. We observed that the distributions of most of the components were unaffected except for the LHB.
Fig. 29 shows the difference in distributions of kTLнв and EMlhb by using the two CXB models for regions above |b| > 10°. The broken power-law model appears to raise the temperature of the LHB systematically by 0.02 keV in terms of the median. On the other hand, the impact of such temperature change on the EM is small (~0.3 × 10−3 cm−6 pc) compared to the width of the EMLhb distribution (~1.5 × 10−3cm−6pc). Inspection of the spectra suggests this is the result of the intricate balancing at the softest end of the spectra (~0.2 keV). By increasing the temperature slightly, the LHB could lower its flux density at this energy to accommodate the steepening slope of the CXB.
Fig. 30 demonstrates this is indeed a systematic effect by showing the ubiquitous under-subtraction in the residual map made from subtracting the LHB temperature map determined by the simple power-law model from that of the broken power-law model. The broken power-law model consistently predicts a higher LHB temperature than the simple power-law model, and the difference is more enhanced towards the Galactic plane. We computed the median differences below and above |b| = 30°. For |b| > 30°, the median difference between the two CXB models is 0.009 keV, about the same as the 1 σ statistical fitting uncertainty in this region. Between 10° < |b| < 30°, the median difference rises to 0.029 keV, about 1.5 times the statistical uncertainty in this region. We consider these to be the systematic uncertainties of the absolute values of the temperature of the LHB. However, we emphasise that the temperature gradient reported in Sect. 4.1 is still present, as this systematic effect only steers the absolute value of kTLHB in a single direction and is only very weakly dependent on location.
4.9 Robustness of the spectral fits
The use of cstat in evaluating the goodness of fit is possible but not straightforward, as the expected value and the variance of cstat depend on the number of counts in each spectral bin (Kaastra 2017). Instead of the rule-of-thumb χ2/d.o.f. ~ 1 indicating a good fit, one needs to compare the fitted cstat with the expected value and variance of cstat in each spectrum, which is a variable number dependent on counts. Therefore, while the spectral fitting was done using cstat (the eROSITA part), we report the χ2/d.o.f after rebinning each spectrum to have at least 10 counts in each spectral bin using the same model. The rebinning was done following the scheme presented by Kaastra & Bleeker (2016). We present the map of the resulting χ2/d.o.f. values in Fig. 16.
We would like to remind the reader that the relatively small and narrow range of χ2/d.o.f. results partly from fitting the spectra up to 5 keV, where the instrumental background dominates with a small CXB contribution. The wide energy range between ~2–5 keV can almost always be well-modelled by the dominating, but fixed, FWC model, thus inclined to result in low χ2/d.o.f. However, this energy range has strong constraining power on the subdominant CXB component, which is the only contributing component and was thus included in our spectral fitting.
To better understand the robustness of the spectral fits, we show four spectra with increasing values of χ2/d.o.f. in Fig. 31 and 32, from ~1.0–1.7. Fig. 31 shows spectra in the range of 1.0 ≲ χ2/d.o.f. ≲ 1.1, where no major discrepancies between data and model could be seen. Fig. 16 demonstrates these values are typical of spectra away from the Galactic plane and the central part of the Galaxy. On the Galactic plane, poorer spectral fits are expected because of the definite presence of multiple line-of-sight structures, both in emission and absorption, which are not part of our model template. Towards the inner part of the Galaxy (310° ≲ l ≲ 360°), this scenario exacerbates, and poorer fits begin to be prevalent to even high Galactic latitudes around −20° ≲ b ≲ 30°. There are many ways to obtain poor fits, but one of the most common ways is the poor reproduction between ~0.7–1 keV, where the Fexvii, Neix and Nex lines dominate. The reproduction is usually imperfect when these lines are bright, especially at the base of the eROSITA bubbles. However, it is currently difficult to distinguish between calibration imperfections and real variations in the astrophysical source. The upcoming pipeline processing version c030 will address the former slightly in terms of including a more accurate energy resolution in the redistribution matrix.
The robustness of each region’s fit and MCMC chain could be inspected by its associated corner plot and steps plot in the choropleth maps on our website (Sect. 5).
 |
Fig. 29 Distributions of kTLHB (left) and EMLHB(right) using either a simple power-law (pow) or a broken power-law (bknpow) parametrisation of the CXB. |
 |
Fig. 30 Difference in the LHB temperature in assuming a simple power-law CXB model and a broken power-law model, namely, kTLHB,bknpow – kTLHB,pow· |
5 Conclusion
In this work, we binned the western Galactic hemisphere into ~2000 regions. We extracted their spectra at solar minimum (eRASS1), where the heliospheric SWCX emission was negligible (Dennerl et al., in prep.). These spectra were fitted with a model template consisting of the LHB, the Milky Way’s CGM, the Galactic corona, the CXB, and, depending on the location, the eROSITA bubbles. This resulted in maps of the parameters, primarily the temperature and emission measure maps for the thermal plasma. We focused on the results regarding the LHB. We summarise our main findings below:
We found the median temperature of the LHB to be
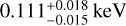 . Much of the spread comes from the approximately north-south gradient above Galactic latitudes of 30°, with the south being hotter (121.8 ± 0.6 eV) than the north (100.8 ± 0.5 eV). Venturing closer to the Galactic plane, there seems to be an increase in LHB temperature, especially at l ≳ 270°. The origin of the temperature gradient is unclear, but it could be set up by more recent supernova explosions within the LHB. The enhancement in temperature towards the Galactic plane could be due to the enhanced thermal pressure needed in the Galactic plane for the LHB to maintain pressure equilibrium with the surroundings;
. Much of the spread comes from the approximately north-south gradient above Galactic latitudes of 30°, with the south being hotter (121.8 ± 0.6 eV) than the north (100.8 ± 0.5 eV). Venturing closer to the Galactic plane, there seems to be an increase in LHB temperature, especially at l ≳ 270°. The origin of the temperature gradient is unclear, but it could be set up by more recent supernova explosions within the LHB. The enhancement in temperature towards the Galactic plane could be due to the enhanced thermal pressure needed in the Galactic plane for the LHB to maintain pressure equilibrium with the surroundings;The emission measure of the LHB is higher towards high latitudes in both hemispheres. It entails that the LHB is more extended towards high latitudes, assuming a constant electron density. The emission measure is also spatially anti-correlated with the local dust column density, consistent with the displacement model put forth by Sanders et al. (1977). We produced a 3D model of the LHB in the western Galactic hemisphere;
We found two tunnels with a low local column density that appear to be filled by hot plasma. One is the well-known β CMa tunnel, and the other is towards (l, b)~(315°, 25°), in the constellation Centaurus. This hints at the possibility ofa widespread tunnel network connecting regions filled by the hot phase of the ISM;
-
Both a simple and broken power law could fit the cosmic X-ray background well, but with a steeper slope (Г ≃ 1.61.7 above 1.2keV) than the conventional value (Г = 1.45). Whether this represents a genuine steepening of the CXB slope below ~1 keV or is caused by calibration inaccuracies is uncertain. It will likely become clear with a forthcoming new calibration version.
From this study, it is clear that eROSITA and its all-sky surveys provide a valuable dataset for studying the SXRB. Future papers will follow to discuss other aspects of the SXRB.
 |
Fig. 31 Example spectra having χ2/d.o.f = 0.99 and 1.10. |
 |
Fig. 32 Example spectra having χ2/d.o.f of 1.50 and 1.70, respectively. They are commonly found near the Galactic plane, towards the inner part of the Galaxy and the base of the eROSITA bubbles. The models usually cannot predict the spectrum between ~0.7–1 keV well. |
Interactive figure
Interactive 3D version of Fig. 20 Access here
Data availability
The results of the spectral fits can be accessed and visualised as choropleth maps via the website https://erosita.mpe.mpg.de/dr1/AllSkySurveyData_dr1/DiffuseBkg/ hosted on the eROSITA DR1 server. An interactive version of the 3D model of the LHB (Fig. 20) and structures in the solar neighbourhood can also be accessed there, as well as the spherical harmonics models of LHB temperature presented in Sect. 4.1.1 and Appendix B. Xspec model files are also available through the website for readers interested in particular regions in the western Galactic hemisphere. The 3D interactive map in Fig. 20 is also available at https://www.aanda.org.
Acknowledgements
MY thanks Mattia Pacicco and Michael Schulreich for their in-depth explanations of their LB simulations during the EAS meeting 2024 in Padova, which has greatly improved the interpretation of the results. MY extends his gratitude to Susanne Friedrich and Harald Baumgartner for their guidance and help in setting up the accompanying website on the eROSITA DR1 server. MY appreciates the helpful discussion on cluster masks and measurement of cluster temperature provided by Ang Liu. MY and MF acknowledge support from the Deutsche Forschungsgemeinschaft through the grant FR 1691/2-1. GP acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 865637). MS acknowledges support from the Deutsche Forschungsgemeinschaft through the grants SA 2131/13-1, SA 2131/14-1, and SA 2131/15-1. This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft- und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors, and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. The eROSITA data shown here were processed using the eSASS/NRTA software system developed by the German eROSITA consortium. MY thanks the developers of the following software and packages that made this work possible: numpy (Harris et al. 2020), matplotlib (Hunter 2007), astropy (Astropy Collaboration 2013, 2018, 2022), PyXspec (Arnaud 1996), HEAsoft (Nasa High Energy Astrophysics Science Archive Research Center (Heasarc) 2014), FTOOLS (Blackburn 1995), contbin (Sanders 2006), lmfit (Newville et al. 2016), emcee (Foreman-Mackey et al. 2013), corner.py (Foreman-Mackey 2016), plotly (Plotly Technologies Inc. 2015), folium (Filipe et al. 2021), K3D–jupyter (Trzesiok et al. 2022), OpenCV (Bradski 2000) and scipy (Virtanen et al. 2020).
Appendix A Test for non-equilibrium ionisation
Non-equilibrium ionisation (NEI) can happen in the LHB if there were recent rapid heating or cooling events. Electrons respond quickly to temperature change via collisions, but ionisation and recombination of the ions lag behind (e.g. see a review by Breitschwerdt & de Avillez 2021). As a result, the line intensities under the assumption of collisional ionisation equilibrium (CIE) do not reflect the real temperature of the gas. If a recent supernova exploded within the LHB, parts or all of LHB could be under-ionised due to rapid shock-heating. On the other hand, if the LHB spawned from a dense cloud, it could undergo rapid adiabatic cooling when it bursts out of the cloud, resulting in an over-ionised plasma (Breitschwerdt & Schmutzler 1994). Henley et al. (2007) investigated both scenarios using a combination of XMM-Newton/EPIC-MOS and ROSAT/PSPC data and concluded the data could not distinguish between CIE and under-ionised plasma but disfavoured the over-ionised scenario.
We used a simple test to evaluate whether our data (eRASS1+ROSAT R12) are sensitive to the signature of NEI. We chose the same regions that were used to determine the spectral shape of the CXB (Fig. 6) for this analysis. They have high S/N (400) in the soft band. This minimises the statistical uncertainty and boosts any potential signatures of NEI. We refitted the spectra by replacing the CIE LHB model (apec) with a NEI LHB model (nei).
We summarise the fitting results in Table A.1. Six of the seven regions have the fitted density-weighted ionisation timescale τ > 1012 cm−3 s. At τ > 1012 cm−3 s, Smith & Hughes (2010) showed that 90% of carbon and oxygen ions (which dominate the observed LHB emission) would reach CIE for plasma at ~0.1 keV. The one exception is the region centred at (l, b)=(241°, 45°), which returns 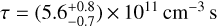 , suggesting a small under-ionisation. Fig. A.1 compares the CIE and NEI models in this region. From the residual spectra, one can see the improvement below ~0.5 keV. Nevertheless, because the NEI models of most regions reduce to the CIE case even at a high S/N of 400, we conclude our data can be sufficiently explained by CIE and keep this assumption throughout our analysis in the main text.
, suggesting a small under-ionisation. Fig. A.1 compares the CIE and NEI models in this region. From the residual spectra, one can see the improvement below ~0.5 keV. Nevertheless, because the NEI models of most regions reduce to the CIE case even at a high S/N of 400, we conclude our data can be sufficiently explained by CIE and keep this assumption throughout our analysis in the main text.
Fitted LHB parameters of the seven high-SN spectra under the NEI and CIE assumptions. All but one region show an ionisation timescale of τ > 1012 cm−3 s, essentially reducing to the CIE case.
 |
Fig. A.1 Comparison of spectral fits assuming the LHB in CIE (left) and NEI (right) of the region showing a potential NEI signature. The residual highlights the improvement below 0.5 keV. |
Appendix B Posterior distributions of the dipole and lmax = 6 models of local hot bubble temperature
The best-fit parameters of the dipole model in Fig. 17 are presented in Table B.1. The z-axis points towards the Galactic north pole in our convention, and the x-axis points towards the Galactic centre. Two equivalent representations are presented: the complex alm coefficients and the dipole vector. In the complex representation, each multipole gives 2l + 1 free parameters; Each al|m| contributes to two, one for the real part and one for the imaginary part, except from al0 coefficients, which do not have a complex part for real-valued functions.
For the dipole, it can be shown that a10 and a11 are related to the dipole vector by the following equations:
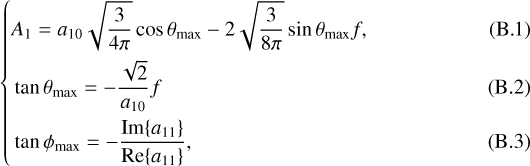
where f = Re{a11} cos ϕmax − Im{a11} sin ϕmax, A is the amplitude of the dipole and (θmax, ϕmax; colatitude and azimuth in spherical coordinates) is the direction where this amplitude is obtained.
The posterior distributions of the dipole are shown in Fig. B.1 both in complex and dipole vector representations.
We list the best-fit parameters of the lmax = 6 spherical harmonics model (Fig. 18) in Table B.2.
Best-fit parameters of the dipole (lmax = 1) model of kTLHB. The resulting temperature model is in units of keV.
 |
Fig. B.1 Posterior distributions of the dipole (lmax = 1) model in complex (top) and multipole vector (bottom) representations. The contours show the 1, 2, and 3 σ uncertainties. |
Best-fit parameters of the lmax = 6 model of kTLHB. The resulting temperature model is in units of keV.
Appendix C Latitudinal profiles of local hot bubble temperature
Fig. C.1 shows the kTLHB data in another light by dividing the western Galactic hemisphere in 15°-wide longitudinal stripes and shows kTLHB as a function of latitude. This presentation has the advantage of enabling visual inspection of the uncertainty associated with individual contour bins and their comparison with the large-scale gradient. Lines of the monopole (orange), dipole (red) and lmax = 6 (blue) models are overlaid in addition. With the help of the best-fit monopole model line, it is apparent that kTLHB is higher in the southern hemisphere than in the north. The dipole model can capture the primary latitudinal gradient, especially in the south, but fails to follow the data closely above b > 30°. While the model complexity can increase to accommodate the temperature variation on a smaller scale, we note the presence of a temperature gradient in LHB is clear. The scatter is large in the region (270° ≲ l ≲ 300°, −40° ≲ b ≲ −10°), which partially covers the Large Magellanic Cloud but cannot be fully attributed to it. The relatively large scatter below 10° < b < 30° and l > 300° is caused by the lower EMLHB in this direction, resulting in higher uncertainties in the determination of kTLHB.
 |
Fig. C.1 Latitudinal profiles of kTLHB with their 1 σ error bars in all longitudinal stripes of 15° width in the western Galactic hemisphere. The vertical orange, red and blue lines show the corresponding monopole, dipole and lmax = 6 models, respectively. The black region indicates the Galactic plane region, which we masked for the temperature gradient analysis. Regions plotted on the white background indicate where the dipole model was fitted (|b| > 30°). The lmax model was fitted with the inclusion of data from the shaded region (|b| > 10°). |
Appendix D Local hot bubble temperature dichotomy seen from high S/N spectra
Sect. 4.1 demonstrated the north-south dichotomy of the LHB temperature, mainly by the systematic temperature offset between the hemispheres. However, this offset is difficult to appreciate purely by looking at individual spectra of S/N ≃ 80 because the temperature difference of 0.02 keV is only approximately twice the typical fitting uncertainty, as shown in Fig. 9.
To highlight the spectral difference, we took two examples of high-S/N spectra (S/N = 400), one from each hemisphere. Fig. D.1 shows the spectrum in the south. The difference in the left and right panels lies only with the model: the left panel has the kTLHB kept at the northern value, while all model parameters were allowed to vary in the right panel. Fig. D.2 shows the reverse: showing the northern spectrum and keeping the southern temperature of the LHB in the left panel. The comparisons demonstrate the incompatibility of the spectrum from either hemisphere with the LHB temperature measured from the opposite hemisphere. This lends further support for a real LHB temperature dichotomy in the hemispheres.
 |
Fig. D.1 North-south temperature dichotomy shown by a high S/N spectra in the south. Left: Spectrum in the southern hemisphere fitted while keeping kTLHB fixed at the northern value (kTLHB = 0.10 ke V). Right: Same as on the left but all the parameters were allowed to vary while fitting. |
 |
Fig. D.2 Similar to Fig. D.1, but showing a high S/N spectra in the north. Left: Spectrum in the northern hemisphere fitted while keeping kTLHB fixed at the southern value (kTLHB = 0.12 ke V). Right: Same as on the left but all the parameters were allowed to vary while fitting. |
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, Astronomical Society of the Pacific Conference Series, 101, 17 [NASA ADS] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Blackburn, J. K. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, Astronomical Society of the Pacific Conference Series, 77, 367 [NASA ADS] [Google Scholar]
- Bluem, J., Kaaret, P., Kuntz, K. D., et al. 2022, ApJ, 936, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bobin, J., Rapin, J., Larue, A., & Starck, J.-L. 2015, Trans. Sig. Proc., 63, 1199-1213 [CrossRef] [Google Scholar]
- Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Bradski, G. 2000, Dr. Dobb’s Journal of Software Tools [Google Scholar]
- Brandt, J. C., Stecher, T. P., Crawford, D. L., & Maran, S. P. 1971, ApJ, 163, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. N., & Lloyd-Davies, E. J. 2007, ApJ, 669, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D., & Schmutzler, T. 1994, Nature, 371, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D., & de Avillez, M. A. 2021, Ap&SS, 366, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Liu, A., Kluge, M., et al. 2024, A&A, 685, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burlaga, L. F., & Ness, N. F. 2014, ApJ, 784, 146 [CrossRef] [Google Scholar]
- Cappelluti, N., Li, Y., Ricarte, A., et al. 2017, ApJ, 837, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Carloni Gertosio, R., Bobin, J., & Acero, F. 2023, Signal Process., 202, 108776 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [Google Scholar]
- Cox, D. P., & Smith, B. W. 1974, ApJ, 189, L105 [CrossRef] [Google Scholar]
- Cravens, T. E. 1997, Geophys. Res. Lett., 24, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Crowder, S. G., Barger, K. A., Brandl, D. E., et al. 2012, ApJ, 758, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Das, S., Mathur, S., Nicastro, F., & Krongold, Y. 2019, ApJ, 882, L23 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2012, A&A, 539, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dennerl, K. 2010, Space Sci. Rev., 157, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Dennerl, K., Englhauser, J., & Trümper, J. 1997, Science, 277, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Dupin, O., & Gry, C. 1998, A&A, 335, 661 [NASA ADS] [Google Scholar]
- Edenhofer, G., Zucker, C., Frank, P., et al. 2024, A&A, 685, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Egger, R. J., & Aschenbach, B. 1995, A&A, 294, L25 [NASA ADS] [Google Scholar]
- Fang, T., & Jiang, X. 2014, ApJ, 785, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, T., Buote, D., Bullock, J., & Ma, R. 2015, ApJS, 217, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Drechsler, M., Weil, K. E., et al. 2021, ApJ, 920, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Filipe, Journois, M., Frank, et al. 2021, https://doi.org/10.5281/zenodo.4447642 [Google Scholar]
- Foreman-Mackey, D. 2016, corner.py: Scatterplot matrices in Python [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [Google Scholar]
- Freyberg, M., Perinati, E., Pacaud, F., et al. 2020, SPIE Conf. Ser., 11444, 114441O [Google Scholar]
- Freyberg, M. J., Müller, T., Perinati, E., et al. 2022, SPIE Conf. Ser., 12181, 1218155 [NASA ADS] [Google Scholar]
- Frisch, P. C., Redfield, S., & Slavin, J. D. 2011, ARA&A, 49, 237 [CrossRef] [Google Scholar]
- Fuchs, B., Breitschwerdt, D., de Avillez, M. A., Dettbarn, C., & Flynn, C. 2006, MNRAS, 373, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Galeazzi, M., Gupta, A., Covey, K., & Ursino, E. 2007, ApJ, 658, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Galeazzi, M., Collier, M. R., Cravens, T., et al. 2012, Astron. Nachr., 333, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Computat. Sci., 5, 65 [Google Scholar]
- Gordon, C., & Arnaud, K. 2021, PyXspec: Python interface to XSPEC spectral-fitting program, Astrophysics Source Code Library [record ascl:2101.014] [Google Scholar]
- Gry, C., & Jenkins, E. B. 2001, A&A, 367, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gry, C., York, D. G., & Vidal-Madjar, A. 1985, ApJ, 296, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, L., Mao, J., Costantini, E., & Kaastra, J. 2016, A&A, 594, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gum, C. S. 1952, The Observatory, 72, 151 [NASA ADS] [Google Scholar]
- Gupta, A., Kingsbury, J., Mathur, S., et al. 2021, ApJ, 909, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Kingsbury, J., Das, S., & Krongold, Y. 2023, Nat. Astron., 7, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Burg, R., Giacconi, R., et al. 1993, A&A, 275, 1 [NASA ADS] [Google Scholar]
- Heiles, C. 1998, ApJ, 498, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Henley, D. B., & Shelton, R. L. 2008, ApJ, 676, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Henley, D. B., & Shelton, R. L. 2010, ApJS, 187, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Henley, D. B., & Shelton, R. L. 2012, ApJS, 202, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Henley, D. B., & Shelton, R. L. 2013, ApJ, 773, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Henley, D. B., Shelton, R. L., & Kuntz, K. D. 2007, ApJ, 661, 304 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Zajczyk, A., LaRocca, D. M., et al. 2019, ApJ, 884, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Koutroumpa, D., Kuntz, K. D., et al. 2020, Nat. Astron., 4, 1072 [CrossRef] [Google Scholar]
- Kaastra, J. S. 2017, A&A, 605, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kameda, S., Ikezawa, S., Sato, M., et al. 2017, Geophys. Res. Lett., 44, 11,706 [Google Scholar]
- Kataoka, J., Tahara, M., Totani, T., et al. 2013, ApJ, 779, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Kavanagh, P. J., Sasaki, M., & Points, S. D. 2012, A&A, 547, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knies, J. R., Sasaki, M., Becker, W., et al. 2024, A&A, 688, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuntz, K. D. 2019, A&A Rev., 27, 1 [CrossRef] [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2000, ApJ, 543, 195 [Google Scholar]
- Kushino, A., Ishisaki, Y., Morita, U., et al. 2002, PASJ, 54, 327 [CrossRef] [Google Scholar]
- Lallement, R., Welsh, B. Y., Vergely, J. L., Crifo, F., & Sfeir, D. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
- Lallement, R., Snowden, S., Kuntz, K. D., et al. 2016, A&A, 595, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J. L., Babusiaux, C., & Cox, N. L. J. 2022, A&A, 661, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, D., Foster, A., & Seitenzahl, I. 2023, arXiv e-prints [arXiv:2311.11181] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [CrossRef] [Google Scholar]
- Lisse, C. M., Dennerl, K., Englhauser, J., et al. 1996, Science, 274, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Chiao, M., Collier, M. R., et al. 2017, ApJ, 834, 33 [Google Scholar]
- Liu, A., Bulbul, E., Ghirardini, V., et al. 2022, A&A, 661, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, A., Bulbul, E., Ramos-Ceja, M. E., et al. 2023, A&A, 670, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Locatelli, N., Ponti, G., & Bianchi, S. 2022, A&A, 659, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Locatelli, N., Ponti, G., Merloni, A., et al. 2024, A&A, 688, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
- Lumb, D. H., Warwick, R. S., Page, M., & De Luca, A. 2002, A&A, 389, 93 [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
- Markevitch, M., Bautz, M. W., Biller, B., et al. 2003, ApJ, 583, 70 [Google Scholar]
- McCammon, D., & Sanders, W. T. 1990, ARA&A, 28, 657 [NASA ADS] [CrossRef] [Google Scholar]
- McCammon, D., Almy, R., Apodaca, E., et al. 2002, ApJ, 576, 188 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Bame, S. J., Barraclough, B. L., et al. 1998, Geophys. Res. Lett., 25, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Elliott, H. A., Schwadron, N. A., et al. 2003, Geo-phys. Res. Lett., 30, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Lamer, G., Liu, T., et al. 2024, A&A, 682, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511 [NASA ADS] [Google Scholar]
- Migkas, K., Kox, D., Schellenberger, G., et al. 2024, A&A, 688, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, M. J., & Bregman, J. N. 2013, ApJ, 770, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. J., & Bregman, J. N. 2015, ApJ, 800, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, E. D., Tsunemi Hiroshi, Bautz, M. W., et al. 2008, PASJ, 60, S95 [CrossRef] [Google Scholar]
- Mou, G., Sun, D., Fang, T., et al. 2023, Nat. Commun., 14, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Nakashima, S., Inoue, Y., Yamasaki, N., et al. 2018, ApJ, 862, 34 [CrossRef] [Google Scholar]
- Nasa High Energy Astrophysics Science Archive Research Center (Heasarc). 2014, HEAsoft: Unified Release of FTOOLS and XANADU [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., et al. 2016, Lmfit: Non-Linear Least-Square Minimization and Curve-Fitting for Python, Astrophysics Source Code Library [record ascl:1606.014] [Google Scholar]
- Oey, M. S., & García-Segura, G. 2004, ApJ, 613, 302 [NASA ADS] [CrossRef] [Google Scholar]
- O’Neill, T. J., Zucker, C., Goodman, A. A., & Edenhofer, G. 2024, ApJ, 973, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Z., Qu, Z., Bregman, J. N., & Liu, J. 2024, ApJS, 271, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Pelgrims, V., Ferrière, K., Boulanger, F., Lallement, R., & Montier, L. 2020, A&A, 636, A17 [EDP Sciences] [Google Scholar]
- Picquenot, A., Acero, F., Bobin, J., et al. 2019, A&A, 627, A139 [EDP Sciences] [Google Scholar]
- Picquenot, A., Acero, F., Holland-Ashford, T., Lopez, L. A., & Bobin, J. 2021, A&A, 646, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Picquenot, A., Williams, B. J., Acero, F., & Guest, B. T. 2023, A&A, 672, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plotly Technologies Inc. 2015, Collaborative data science [Google Scholar]
- Pon, A., Ochsendorf, B. B., Alves, J., et al. 2016, ApJ, 827, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Zheng, X., Locatelli, N., et al. 2023, A&A, 674, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porowski, C., Bzowski, M., & Tokumaru, M. 2022, ApJS, 259, 2 [Google Scholar]
- Predehl, P., Sunyaev, R. A., Becker, W., et al. 2020, Nature, 588, 227 [CrossRef] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Putman, M. E., Peek, J. E. G., & Joung, M. R. 2012, ARA&A, 50, 491 [Google Scholar]
- Qu, Z., Koutroumpa, D., Bregman, J. N., Kuntz, K. D., & Kaaret, P. 2022, ApJ, 930, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Ringuette, R., Koutroumpa, D., Kuntz, K. D., et al. 2021, ApJ, 918, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, K., Mitsuda, K., Yamasaki, N. Y., et al. 2012, in Suzaku 2011: Exploring the X-ray Universe: Suzaku and Beyond, eds. R. Petre, K. Mitsuda, & L. Angelini, American Institute of Physics Conference Series, 1427, 342 [NASA ADS] [Google Scholar]
- Sanders, J. S. 2006, MNRAS, 371, 829 [Google Scholar]
- Sanders, W. T., Kraushaar, W. L., Nousek, J. A., & Fried, P. M. 1977, ApJ, 217, L87 [Google Scholar]
- Sasaki, M., Breitschwerdt, D., Baumgartner, V., & Haberl, F. 2011, A&A, 528, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sasaki, M., Knies, J., Haberl, F., et al. 2022, A&A, 661, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulreich, M. M., Feige, J., & Breitschwerdt, D. 2023, A&A, 680, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, J. D. 1989, ApJ, 346, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., & Hughes, J. P. 2010, ApJ, 718, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [Google Scholar]
- Smith, R. K., Bautz, M. W., Edgar, R. J., et al. 2007, PASJ, 59, 141 [Google Scholar]
- Snowden, S. L., Schmitt, J. H. M. M., & Edwards, B. C. 1990, ApJ, 364, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., McCammon, D., Burrows, D. N., & Mendenhall, J. A. 1994, ApJ, 424, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Egger, R., Freyberg, M. J., et al. 1997, ApJ, 485, 125 [Google Scholar]
- Snowden, S. L., Egger, R., Finkbeiner, D. P., Freyberg, M. J., & Plucinsky, P. P. 1998, ApJ, 493, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Freyberg, M. J., Kuntz, K. D., & Sanders, W. T. 2000, ApJS, 128, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Chiao, M., Collier, M. R., et al. 2014, ApJ, 791, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trzesiok, A., Tgandor, Kostur, M., et al. 2022, K3D-tools/K3D-jupyter: 2.12.0 [Google Scholar]
- Ueda, M., Sugiyama, H., Kobayashi, S. B., et al. 2022, PASJ, 74, 1396 [CrossRef] [Google Scholar]
- Uprety, Y., Chiao, M., Collier, M. R., et al. 2016, ApJ, 829, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Vecchi, A., Molendi, S., Guainazzi, M., Fiore, F., & Parmar, A. N. 1999, A&A, 349, L73 [NASA ADS] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261 [CrossRef] [Google Scholar]
- Welsh, B. Y. 1991, ApJ, 373, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., & Shelton, R. L. 2009, Ap&SS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., Craig, N., Vedder, P. W., & Vallerga, J. V. 1994, ApJ, 437, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Wulf, D., Eckart, M. E., Galeazzi, M., et al. 2019, ApJ, 884, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, Y., & Wang, Q. D. 2007, ApJ, 666, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, Y., Nowak, M. A., Wang, Q. D., Schulz, N. S., & Canizares, C. R. 2008, ApJ, 672, L21 [Google Scholar]
- Yeung, M. C. H., Freyberg, M. J., Ponti, G., et al. 2023, A&A, 676, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoshino, T., Mitsuda, K., Yamasaki, N. Y., et al. 2009, PASJ, 61, 805 [NASA ADS] [Google Scholar]
- Zucker, C., Goodman, A. A., Alves, J., et al. 2022, Nature, 601, 334 [NASA ADS] [CrossRef] [Google Scholar]
More precisely, the masking of ‘all’ detected sources is done by merging the CheeseMask images from the standard eSASS pipeline from all the skytiles and project them into a HEALPix map of Nside = 4096 (pixel size ≃51″) using nearest-neighbour interpolation. Contribution from the masked pixels is then removed from the final diffuse emission count map after downsampling the HEALPix map from N side = 4096 to N side = 256.
We assumed solar abundance for simplicity, following Lallement et al. (2016). Indeed, there are reports of sub-solar abundances both from observations (e.g. Miller et al. 2008; Kataoka et al. 2013; Gu et al. 2016) and as expectations from simulations (e.g. Mou et al. 2023). We defer the abundance measurement in eROSITA to an ongoing work (Yeung et al., in prep.).
The factor of 1.92 assumes the abundance in Anders & Grevesse (1989). Opting for the abundance of Lodders (2003) (the abundance reference we use for spectral fitting) results in a factor closer to 1.9. The difference is dominated by the difference in Helium abundance: (nHe/nH)AnGr = 0.0977 versus (nHe/nH)Lodd = 0.0792.
Closer inspection of the R12 band count rate map suggests there is indeed a weak enhancement, independent of the subtraction of SWCX (Snowden et al. 1997; Uprety et al. 2016).
Three models of CXB were used in Ponti et al. (2023). We refer to their ‘CXB’ model here.
All Tables
Fitted LHB parameters of the seven high-SN spectra under the NEI and CIE assumptions. All but one region show an ionisation timescale of τ > 1012 cm−3 s, essentially reducing to the CIE case.
Best-fit parameters of the dipole (lmax = 1) model of kTLHB. The resulting temperature model is in units of keV.
Best-fit parameters of the lmax = 6 model of kTLHB. The resulting temperature model is in units of keV.
All Figures
 |
Fig. 1 Contour-binned eRASS1 0.2–0.6 keV band surface brightness map in zenithal equal-area projection. Locations of big galaxy clusters, overdense regions in source detection, and bins with sky area less than 1 deg2 were masked. Counts from the non-X-ray background and all eRASS1-catalogued sources (Merloni et al. 2024) were also removed from this image (but not in the spectra; see Sect. 2 for more details). |
| In the text | |
 |
Fig. 2 Sky area distribution of the contour bins. It can be approximated by a log-normal distribution, as shown with the red line. |
| In the text | |
 |
Fig. 3 Example spectra outside (left) and inside (right) of the eROSITA bubbles, overlaid with the best-fit spectral models labelled in the legends. We modelled the eROSITA bubbles with an additional thermal component in brown. Both spectra have been divided by the effective area, aiming to bring the ROSAT R1 and R2 count rates into a reasonable range. This has the disadvantage of creating the fictitious jump of the instrumental background component above the gold absorption edge at ~2 keV. The horizontal error bars at the top left corners of the figures reflect the width of the ROSAT R1 and R2 bands. |
| In the text | |
 |
Fig. 4 Values of |
| In the text | |
 |
Fig. 5 Scatter plot of |
| In the text | |
 |
Fig. 6 Similar to Fig. 1 but showing only regions selected to determine the spectral shape of the CXB. |
| In the text | |
 |
Fig. 7 Finding chart for features discussed mainly in Sect. 3.4 and 4.2. The background image shows the emission measure of the LHB, which is a proxy of the extent of the LHB and is relevant for discussions (Sect. 4.2) on interstellar tunnels and anti-correlation with dust. The demarcation of the eROSITA bubbles is shown by the turquoise line, based on the 0.6–1.0 keV intensity map. |
| In the text | |
 |
Fig. 8 Spatial distribution of kTLHB in the high latitude regions (|b| > 30°). |
| In the text | |
 |
Fig. 9 Distribution of kTLHB in the high latitude regions (|b| > 30°). The unfilled histogram outlined in black displays the distribution of all the high latitude bins displayed in Fig. 8. The black dashed line shows the Gaussian best fit for the distribution. The black data point with error bars shows the typical (median) 1σ spectral fitting uncertainty, centred at the mean of the fitted Gaussian. It is plotted at a height of exp (−1/2)Ngauss,peak = 0.606 Ngauss,peak for proper comparison between the spectral fitting uncertainty and the width of the distribution. The former (0.010 keV) is approximately half of the latter (0.018 keV), demonstrating a genuine variation in the LHB temperature. The sample is divided into the northern (orange) and the southern (green) Galactic hemispheres to demonstrate the primary source of variation is a large-scale gradient instead of small-scale fluctuations. The northern hemisphere is cooler (0.100 keV) than the south (0.122 keV), and comparing their distributions with the respective typical spectral fitting uncertainties shows that each hemisphere exhibits approximately constant LHB temperature. |
| In the text | |
 |
Fig. 10 Map of kTLHB including low latitude regions. We note that the colour bar is scaled differently from Fig. 8. The thermal pressure is also shown under the assumption of constant ne = 4 × 10−3 cm−3. |
| In the text | |
 |
Fig. 11 Comparison of fitted NH and independent estimate of NH from H I and dust measurements. Left: fitted NH. Right: estimate of NH combining neutral hydrogen information from HI4PI (HI4PI Collaboration 2016) and E(B – V) information derived from Planck radiance map (Planck Collaboration XI 2014). |
| In the text | |
 |
Fig. 12 Calibration curves of R2/R1 band ratio of the Raymond-Smith (Raymond & Smith 1977), Mekal (Mewe et al. 1985, 1986; Liedahl et al. 1995), and apec (Smith et al. 2001) models as a function of the temperature of an unabsorbed plasma at solar abundance. |
| In the text | |
 |
Fig. 13 Comparison of our forward-modelled R2/R1 band ratio map with the observation. Left: R2/R1 band ratio map calculated by folding our best-fit (median) spectral models with the ROSAT R1 and R2 band responses. Right: R2/R1 data binned to the same contour-binning scheme (Snowden et al. 1997). |
| In the text | |
 |
Fig. 14 Spatial distribution of EMLHB. Regions with EMLHB uncertainty < 5 × 10−5 cm−6 pc were also masked. The solid black line indicates the position of the ecliptic, and the two dashed lines represent a range of ±25° around it in ecliptic latitude where the solar wind density is expected to be high. The extent of the LHB under the assumption of ne = 4 × 10−3 cm−3 is also shown. |
| In the text | |
 |
Fig. 15 Distance at which the integration of NH reaches 1020 cm−2 in the Lallement et al. (2022) (left) and Edenhofer et al. (2024) (right) dust cubes, as proxies of the extent of the local bubble. The empty regions in the map indicate that the integration does not reach NH ≥ 1020 cm−2 before 400 pc. |
| In the text | |
 |
Fig. 16 Map of reduced-χ2 (χ2/d.o.f) after rebinning each spectrum, imposing that each spectral bin receives at least ten counts. |
| In the text | |
 |
Fig. 17 Dipole model and residual. Left: dipole model of kTLHB. Right: residual normalised by the 1 σ fitting uncertainty of each valid bin. The black cross in both panels shows the direction of the dipole towards (l, b) = (291°, −26°). |
| In the text | |
 |
Fig. 18 Similar to Fig. 17 but for the spherical harmonics model of lmax = 6. The data were fitted down to 10° from the Galactic plane. We note that the colour bar of the left panel was scaled up to 0.2 keV, identical to Fig. 10 for comparison. |
| In the text | |
 |
Fig. 19 Map of kTLHB upon fixing the NH to the HI4PI NH. The colour scaling conforms to Fig. 8 to highlight the high latitude temperature dichotomy. |
| In the text | |
 |
Fig. 20 Three-dimensional structure of the LHB in the western Galactic hemisphere assuming a constant density of 4 × 10−3 cm−3. The inner (opaque, coloured) and the outer (grey, translucent) surfaces show the ±1 σ uncertainty bounds of the distance under the constant ne assumption. We note that the two surfaces only reflect the uncertainty in the spectral fitting but not in ne. We note that kTLHB is also colour-coded on the inner surface. A sphere of 100 pc radius is shown around the Sun (yellow) as a ruler. An interactive version of this figure, including the comparison with dust maps (not shown) can be accessed from online or the accompanying website (Sect. 5). |
| In the text | |
 |
Fig. 21 A slice of the Edenhofer et al. (2024) cube at the x-z plane overplotted with the silhouette of the LHB. |
| In the text | |
 |
Fig. 22 Corner plots showing LHB and CGM parameters are degenerate in regions of low NH. Top: Bin476 at (l, b)=(257°.9, 59°.6). Bottom: Binl875 at (l, b)=(296°.7, 47°.6). |
| In the text | |
 |
Fig. 23 The same plots and panel configuration as Fig. 22 but with ROSAT R1 and R2 data. |
| In the text | |
 |
Fig. 24 Corner plot of Bin1875 after using ROSAT data and imposing a uniform prior on kTLHB below 0.15 keV. |
| In the text | |
 |
Fig. 25 Zoom-in of the Centaurus tunnel in the smoothed EMlhb map (left) and dust distance map by integrating the dAv map up to 1020 cm−2 (right) (Edenhoſer et al. 2024). The contour line outlining the region where the NH does not reach 1020cm−2 in 400 pc is overlaid on the EMLHB map. |
| In the text | |
 |
Fig. 26 Comparison of the local (hot) bubble extent from X-ray and dust. Left: extent of the local hot bubble under the constant ne = 4 × 10−3 cm−3 assumption. Right: local bubble shell tracing the closest extinction peak inferred by O’Neill et al. (2024). An interactive comparison in 3D can be accessed from the accompanying website (Sect. 5). |
| In the text | |
 |
Fig. 27 Electron density (left) and thermal pressure (right) of the local hot bubble assuming it extends up to the local bubble shell (O’Neill et al. 2024). |
| In the text | |
 |
Fig. 28 Normalisation of the cosmic X-ray background assuming a simple power-law of Г = 1.7. |
| In the text | |
 |
Fig. 29 Distributions of kTLHB (left) and EMLHB(right) using either a simple power-law (pow) or a broken power-law (bknpow) parametrisation of the CXB. |
| In the text | |
 |
Fig. 30 Difference in the LHB temperature in assuming a simple power-law CXB model and a broken power-law model, namely, kTLHB,bknpow – kTLHB,pow· |
| In the text | |
 |
Fig. 31 Example spectra having χ2/d.o.f = 0.99 and 1.10. |
| In the text | |
 |
Fig. 32 Example spectra having χ2/d.o.f of 1.50 and 1.70, respectively. They are commonly found near the Galactic plane, towards the inner part of the Galaxy and the base of the eROSITA bubbles. The models usually cannot predict the spectrum between ~0.7–1 keV well. |
| In the text | |
 |
Fig. A.1 Comparison of spectral fits assuming the LHB in CIE (left) and NEI (right) of the region showing a potential NEI signature. The residual highlights the improvement below 0.5 keV. |
| In the text | |
 |
Fig. B.1 Posterior distributions of the dipole (lmax = 1) model in complex (top) and multipole vector (bottom) representations. The contours show the 1, 2, and 3 σ uncertainties. |
| In the text | |
 |
Fig. C.1 Latitudinal profiles of kTLHB with their 1 σ error bars in all longitudinal stripes of 15° width in the western Galactic hemisphere. The vertical orange, red and blue lines show the corresponding monopole, dipole and lmax = 6 models, respectively. The black region indicates the Galactic plane region, which we masked for the temperature gradient analysis. Regions plotted on the white background indicate where the dipole model was fitted (|b| > 30°). The lmax model was fitted with the inclusion of data from the shaded region (|b| > 10°). |
| In the text | |
 |
Fig. D.1 North-south temperature dichotomy shown by a high S/N spectra in the south. Left: Spectrum in the southern hemisphere fitted while keeping kTLHB fixed at the northern value (kTLHB = 0.10 ke V). Right: Same as on the left but all the parameters were allowed to vary while fitting. |
| In the text | |
 |
Fig. D.2 Similar to Fig. D.1, but showing a high S/N spectra in the north. Left: Spectrum in the northern hemisphere fitted while keeping kTLHB fixed at the southern value (kTLHB = 0.12 ke V). Right: Same as on the left but all the parameters were allowed to vary while fitting. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.