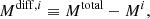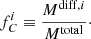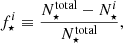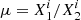| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A255 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202449164 | |
| Published online | 15 October 2024 | |
Carbon envelopes around merging galaxies at z ∼ 4.5
1
Dipartimento di Fisica, Sapienza, Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
2
INFN, Sezione di Roma I, Piazzale Aldo Moro 2, 00185 Roma, Italy
3
INAF/Osservatorio Astronomico di Roma, Via di Frascati 33, 00078 Monte Porzio Catone, Italy
4
Institute of Science and Technology Austria (ISTA), Am Campus 1, 3400 Klosterneuburg, Austria
5
Dipartimento di Fisica e Astronomia, Università di Firenze, Via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
6
INAF/Osservatorio Astrofisico di Arcetri, Largo E. Femi 5, 50125 Firenze, Italy
7
Sapienza School for Advanced Studies, Viale Regina Elena 291, 00161 Roma, Italy
8
National Centre for Nuclear Research, ul. Pasteura 7, 02-093 Warsaw, Poland
9
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
10
European Southern Observatory, Karl-Schwarzschild-Str. 2, D-85748 Garching, Germany
Received:
5
January
2024
Accepted:
6
August
2024
Context. Galaxies evolve through a dynamic exchange of material with their immediate surrounding environment, the so-called circumgalactic medium (CGM). Understanding the physics of gas flows and the nature of the CGM is fundamental to studying galaxy evolution, especially at 4 ≤ z ≤ 6 (i.e., after the Epoch of Reionization) when galaxies rapidly assembled their masses and reached their chemical maturity. Galactic outflows are predicted to enrich the CGM with metals, although it has also been suggested that gas stripping in systems undergoing a major merger may play a role.
Aims. In this work, we explore the metal enrichment of the medium around merging galaxies at z ∼ 4.5, observed by the ALMA Large Program to INvestigate [CII] at Early times (ALPINE). To do so, we study the nature of the [CII] 158 μm emission in the CGM around these systems, using simulations to help disentangle the mechanisms contributing to the CGM metal pollution.
Methods. By adopting an updated classification of major merger systems in the ALPINE survey, we selected and analyzed merging galaxies whose components can be spatially and/or spectrally resolved in a robust way. This makes it possible to distinguish between the [CII] emission coming from the single components of the system and that coming from the system as a whole. We also made use of the dustyGadget cosmological simulation to select synthetic analogs of observed galaxies and guide the interpretation of the observational results.
Results. We find a large diffuse [CII] envelope (≳20 kpc) embedding all the merging systems, with at least 25% of the total [CII] emission coming from the medium between the galaxies. Using predictions from dustyGadget, we suggest that this emission has a multi-fold nature, with dynamical interactions between galaxies playing a major role in stripping the gas and enriching the medium with heavy elements.
Key words: galaxies: evolution / galaxies: formation / galaxies: high-redshift / galaxies: interactions / early Universe
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The circumgalactic medium (CGM) is a buffer medium between interstellar and intergalactic media (ISM, IGM). It regulates gas flows, stellar feedback, and, consequently, star formation activity and galaxy growth. Generally, one refers to the CGM as the gas outside the galaxy, but indicatively within one virial radius, Rvir, of its dark matter (DM) halo. However, it is important to keep in mind that some of the processes involving the CGM (e.g., galactic outflows) can reach larger radii (Tumlinson et al. 2017; Faucher-Giguère & Oh 2023). The CGM is a fundamental component in galaxy evolution and studying it in terms of both emission and absorption provides hints on how galaxies assemble their masses through cosmic time. To understand the cycle of baryons between the ISM and the CGM, we need observations of the stellar component and of the multiple gas phases both within and around galaxies (see Péroux & Howk 2020 for a review on the baryon and metal cycles in galaxies). In this context, the Atacama Large Millimeter/submillimeter Array (ALMA) has recently opened a window to explore the cold neutral and molecular gas in early galaxies with unprecedented levels of detail (Capak et al. 2015; Le Fèvre et al. 2020; Bouwens et al. 2022). On the other hand, we need simulations able to resolve the characteristic scales of CGM/ISM, which usually adopt zoom-in refinement schemes1 (see Pallottini et al. 2017, 2022; Lupi & Bovino 2020; Lupi et al. 2020), or cosmological boxes with a moderate (∼100 pc) spatial resolution (see, e.g., Katz et al. 2017 where the authors include on-the-fly radiative transfer and detailed non-equilibrium chemistry, to self-consistently model the ISM of high redshift galaxies). Finally, we refer to Faucher-Giguère & Oh (2023) for a recent general review of the key physical processes that operate in the CGM from a theoretical point of view.
In the last decades, theories of galaxy evolution and cosmological numerical simulations have predicted that high-z galaxies assemble their masses via both cold gas accretion from the IGM (Dekel et al. 2009; Topping et al. 2022) and major mergers, namely, dynamical interactions between galaxies of nearly equal stellar masses (Hopkins et al. 2010; Schaye et al. 2015; Duncan et al. 2019; Romano et al. 2021). In particular, dynamical interactions between galaxies can drive a significant amount of gas towards the center of the interacting system boosting the efficiency of star formation (up to a factor of two for major mergers) and also trigger starburst and active galactic nuclei (AGN) activity (Oser et al. 2012; López-Sanjuan et al. 2012; Kaviraj et al. 2014; Behroozi et al. 2015; Reeves & Hudson 2024). Moreover, ongoing and post-mergers episodes can disturb and change the morphology of the galaxies involved, leading to tails of stripped material (i.e., tidal tails), irregular shapes, and disturbed velocity fields (Conselice et al. 2003, 2008; Casteels et al. 2014). Tidal tails are challenging to observe at high redshift because of the diffuse and faint nature of the stripped gas. However, thanks to ALMA we can study the efficiency of gas stripping and circumgalactic gas mixing in the early Universe by mapping the morphology and the kinematics of the CGM around merging galaxies using bright far-infrared (FIR) lines. One such line is the singly ionized carbon, hereafter denoted as [CII] at 158 μm, which is generally the brightest FIR emission line for star-forming galaxies (Carilli & Walter 2013). [CII] 158 μm is an important tracer of the ISM in the local and high-z galaxies and, thanks to the low ionization potential (11.26 eV) of the neutral carbon, it is abundant in both the cold and warm ISM, as well as in the molecular ISM. Via its fine structure emission line at 158 μm (2P3/20→2P1/20), it acts as a coolant in the cold ISM, thus it is considered as one of the main tracer of cold gas in galaxies, star-forming regions, and molecular clouds. As a consequence, many studies have been focused on the investigation of the [CII] emission and, in particular, the [CII] and star formation rate (SFR) relation in the local Universe and at high-redshift, using both observations (De Looze et al. 2014; Herrera-Camus et al. 2015, 2018; Carniani et al. 2018; Schaerer et al. 2020; Romano et al. 2022) and simulations (Katz et al. 2017; Popping et al. 2019; Ferrara et al. 2019; Lupi & Bovino 2020; Vallini et al. 2020; Schimek et al. 2024).
Observations of [CII] in early main sequence galaxies led to the discovery of extended [CII] envelopes (up to 10 kpc) around these systems. These envelopes were at first found by stacking the [CII] emission in 18 ALMA-detected star-forming galaxies at 5 < z < 7 (Fujimoto et al. 2019) and in a large sample of normal star-forming galaxies at 4 < z < 6 (Ginolfi et al. 2020a). This was later confirmed, on an individual basis, by Fujimoto et al. (2020) and Lambert et al. (2023). These extended emissions have been found also at higher redshifts, up to z ∼ 7 (see e.g., Herrera-Camus et al. 2021; Fudamoto et al. 2022; Akins et al. 2022). However, we refer to Posses et al. (2023) for an example of a normal star-forming galaxy at z ∼ 7 where no extended [CII] has been detected.
In this paper, we present a study on the properties of [CII] emission around major merging systems at z ∼ 4.5, with the aim of characterizing the metal enrichment of their inner CGM and investigating its dependence on the dynamical interaction between the galaxies. Our target systems are drawn from the ALMA Large Program to INvestigate [CII] at Early times (ALPINE), an ALMA large program that observed [CII] and thermal dust continuum emission for a large sample of main sequence galaxies in the redshift range 4.4 < z < 5.9. The interested reader can find more information on the detection strategy, the data processing, and the ancillary data of the ALPINE sample in Le Fèvre et al. (2020), Béthermin et al. (2020), Faisst et al. (2020), respectively. The analysis of the [CII] emission has revealed a diverse distribution of morphological and kinematical properties in the ALPINE sample (Faisst et al. 2020; Jones et al. 2021), with the detection of signatures of metal-enriched gas outflows powered by star formation activity in the high-velocity tails of the stacked [CII] emission spectrum (Ginolfi et al. 2020a). Also, a detailed morpho-spectral decomposition analysis in one of the ALPINE systems undergoing major merging has revealed the presence of a widespread [CII] emission component, extending to scales of a few tens of kpc. This emission has been interpreted as a possible signature of processed ISM stripped by the strong gravitational interaction, suggesting that mergers could be an efficient mechanism of metal enrichment and gas mixing in the CGM around high-z galaxies (Ginolfi et al. 2020b; Jones et al. 2020).
Motivated by these findings, we apply a similar morpho-spectral decomposition analysis on additional systems classified as mergers in the ALPINE sample. To this aim, we made use of the merger classification of ALPINE galaxies carried out by Romano et al. (2021). The observational part of this work is complemented with predictions from cosmological simulations run with the hydrodynamical code dustyGadget (Graziani et al. 2020), which guide our interpretation of the results. We would like to clarify that throughout the paper when presenting results based on simulations, we used the mass of carbon in the cold ISM medium (T ≲ 104 K) as a proxy to estimate the expected [CII] emission. Thus, we did not employ any radiative transfer code to predict the [CII] luminosity and we did not assume any empirical relation to link the physical properties of galaxies with the expected [CII] luminosity.
The paper is organized as follows. In Sect. 2, we describe the selected observational sample and the analysis we carried out. Sect. 3 presents the [CII] diffuse emission that we found in the observed candidates and its interpretation. In Sect. 4, we introduce the hydrodynamical code dustyGadget, explain the adopted procedure to identify synthetic major mergers, their time evolution, and their gas distribution. Finally, we exploit the predictions from dustyGadget to interpret the observed [CII] diffuse emission in Sect. 5. We present our conclusions in Sect. 6.
Throughout the paper, we assume a flat ΛCDM cosmology with cosmological parameters from Planck Collaboration XIII (2016) consistent with that assumed by dustyGadget simulation (see Sect. 4) and adopt a Salpeter (1955) initial mass function (IMF). All the stellar masses and star formation rates in this paper have been converted to a Salpeter (1955) IMF following the conversion factors from Madau & Dickinson (2014). At z ∼ 4.6, which is the mean redshift of our sample, 1 arcsec corresponds to 6.69 proper kpc.
2. Observational sample and data processing
In this section, we first briefly introduce the ALPINE survey and the properties of the target galaxy sample, then we discuss the classification established by Romano et al. (2021) on merging systems and how we used it to select major mergers needed for the aim of this work. Finally, we describe the ALMA data reduction procedure and the analysis we performed on our sample of major merging galaxies.
2.1. Targets selection
The ALPINE survey is designed to detect the [CII] line at 158 μm rest-frame and the surrounding FIR continuum emission for a sample of 118 normal galaxies at 4.4 < z < 5.9. Its targets are selected from the Cosmic Evolution Survey (COSMOS; Scoville et al. 2007a,b) and Extended Chandra Deep Field South (E-CDFS; Giavalisco et al. 2004; Cardamone et al. 2010) fields. In the following, we use “vc” and “DC” to respectively refer to vuds_cosmos and DEIMOS_COSMOS sources. Since these fields have been targeted by several observational campaigns, a wealth of ancillary multi-wavelength photometric data (from rest-frame UV to FIR) is available, which made it possible to recover physical properties such as stellar masses (M⋆) and SFR through spectral energy distribution (SED)-fitting; these estimates have been performed adopting a Chabrier IMF (Chabrier 2003, see Faisst et al. 2020 for a detailed description). With stellar masses in the range 9 ≤ Log(M⋆/M⊙)≤11 and star formation rates of 1 ≤ Log(SFR/M⊙ yr−1)≤3, ALPINE galaxies lie on the so-called main sequence of star-forming galaxies (Rodighiero et al. 2011; Tasca et al. 2015); thus, they are representative of the underlying galaxy population at z ∼ 5 (Speagle et al. 2014).
To study the metal enrichment of the CGM around high-z merging galaxies, we exploit the work of Romano et al. (2021). These authors combined the morpho-kinematic information provided by the [CII] emission with archival multi-wavelength photometry to identify merging systems in the ALPINE sample, along with the fraction of major mergers within this subset (see also Le Fèvre et al. 2020; Jones et al. 2021). According to their classification criteria, Romano et al. (2021) found that the ALPINE sample is composed of 31% of mergers (23 out of 752) leading to a major merger fraction of fMM ∼ 0.44 (0.34) at z ∼ 4.5 (5.5). This result is in good agreement with morphological studies by Conselice & Arnold (2009) at the same redshift and, when combined with other works down to the Local Universe, suggests a rapid increase in the cosmic merger fraction from z = 0 to z ∼ 2, a peak at z ∼ 2 − 3, and a possible slow decline for z ≥ 3.
For the aim of this study, starting from the classification by Romano et al. (2021), we selected major merging systems that are spatially and/or spectrally separated in a robust way. In particular, we looked for merging systems with:
-
a velocity separation Δv ≤ 500 km/s, so that the two systems can be considered as gravitationally bound (see Patton et al. 2000; Lin et al. 2008; Ventou et al. 2017);
-
a projected distance of rp > 4 kpc, where rp = θ × dA(zm), θ is the angular separation in arcsec in the sky between the two galaxies, and dA(zm) is the angular diameter distance (in kpc arcsec−1) calculated at the mean redshift zm of the two sources (see Romano et al. 2021 for more details). With this condition, the projected distance between the merging systems is larger than the typical [CII] size of individual galaxies, which (on average) is estimated to be ∼2.1 kpc for ALPINE galaxies at these redshifts (Fujimoto et al. 2020; Romano et al. 2021). Indeed, closer components could just be clumps of star formation within the same galaxy, affecting the morphology and kinematics of [CII] emission;
-
a relative stellar mass ratio of 1 < μK < 4. Here, μK is defined as the ratio between the UltraVista Ks-band fluxes of the merging components3, which is used as a proxy for the mass ratio of galaxies (hereafter, μK ≡ μ⋆) since the Ks-band flux is a good tracer of the stellar mass of galaxies up to z ∼ 4 (Laigle et al. 2016).
By applying these criteria to the 23 merging systems selected by Romano et al. (2021), we ended up with a sample of six targets. We note that the Ks-band ratio is available for 9 out of 23 merging systems; for the other 14 systems, only the [CII] flux ratio, μ[CII], is available, from which Romano et al. (2021) was not able to draw any specific conclusions about the nature of the merger (see their Sect. 4 for more details). Table 1 lists the six observational targets selected for our study and summarizes their merging properties (Δv, rp, μ[CII], μK; Romano et al. 2021), as well as their M⋆ and SFR, as estimated by Faisst et al. (2020).
Physical parameters of the major merging galaxies selected for this work.
2.2. Observational analysis
In this section, we describe the processing and analysis performed on the major merging systems whose properties are reported in Table 1.
Firstly, we reduce the ALMA data for these targets using the Common Astronomy Software Applications (CASA; McMullin et al. 2007) pipeline. Each data cube is continuum-subtracted using the CASA task uvcontsub over the line-free visibilities in all spectral windows to obtain line-only cubes. The [CII] datacubes are generated from the continuum-subtracted visibilities using the task tclean until we reach a signal-to-noise ratio of S/N < 2 for the residuals. We choose a natural weighting of the visibilities to maximize the sensitivity, a common pixel size of 0.15″, and a common spectral bin of 25 km s−1 (beam size of ∼1″).
Secondly, we visually inspect ALMA datacubes, looking for [CII] emissions coming from the components of each merging system. Every time we find such an emission, we adopt a 1″ aperture centered on the emitting galaxy to extract a preliminary [CII] spectrum, which is then fitted using a single 1D Gaussian model.
Finally, we consider the 2σ confidence interval of the Gaussian fit to get the min-max frequency range, which we collapse to generate the moment-0 (i.e., velocity integrated) maps of each merging component (dubbed as #A, #B, etc.) using the CASA immoments task. The moment-0 map of the entire system is then obtained by collapsing the absolute minimum and maximum of the previously obtained frequency (i.e., min[minfreqA, minfreqB] and max[maxfreqA, maxfreqB]).
Fig. 1 shows the total velocity-integrated [CII] maps for our sample; white contours indicate the 2σ region4 and black crosses are the centers of each emitting component (see procedure in the following) and all the S/N are consistent with those of the ALPINE survey (Béthermin et al. 2020). Having the moment-0 maps, we then fit a single 2D Gaussian model to each merging component, masking it, and retrieving morphological information such as the coordinates of the [CII] emission peak, the full-width half maximum (FWHM) of the major and minor axis of the Gaussian, and its position angle (PA). For one system, DC_873321, we had to perform a two 2D Gaussian components fit, because of the small spatial separation and similar [CII] luminosity (μ[CII] ∼ 1; see Table 1) of the merging galaxies, which prevented us from fitting single 2D Gaussian models. Once we estimate the coordinates of the [CII] emission peaks of each source, we use it to center different size apertures. In particular, we employed a 1″ aperture, a 2 × 2 pixel square aperture5 (hereafter “peak”), and FWHMx × FWHMy aperture (hereafter, “FWHM-based”), with x and y as the major and minor axis of the 2D Gaussian model, respectively. From these apertures, we extracted the [CII] fluxes in mJy km/s. In this analysis, we assume that all the [CII] emission coming from the apertures is associated with the merging galaxies, while that coming from the 2σ contour is the total emission (galaxies + diffuse [CII] emission).
 |
Fig. 1. Total velocity integrated [CII] map of the six selected systems. At the top of each panel, the ID of the source is given. White contours indicate the positive significant level at 2σ of [CII] emission. Black crosses mark the center of each galaxy (see the text for more information). The ALMA beam size is given in the bottom-left corners. |
Fig. 2 shows (in the upper panels) the total velocity-integrated [CII] maps for two systems highlighting the FWHM-based apertures for each merging component (dashed black lines), the center of each galaxy (black crosses), and the 2σ regions (white contours). In the lower panels, we give the [CII] flux density. In particular, different line styles correspond to each merging component, while different colors (orange, green, and pink) to line spectra extracted considering 1″, FWHM-based and peak apertures, respectively. Looking at the spectra, we note that the brightest emission is the one coming from the peak aperture (pink), namely, the center of each galaxy, while 1″ and FWHM-based apertures in some cases have comparable emissions (see e.g., component #A of both DC_818760 and vc_5101209780).
 |
Fig. 2. Same as Fig. 1, but for two specific systems: (a) DC_818760 (top-left) and (b) vc_5101209780 (top-right). The white contour indicates the positive significant level at 2σ of [CII] flux, where σ[CII] = 84 mJy km/s in (a) and σ[CII] = 95 mJy km/s in (b). The dashed black ellipses indicate the FWHMx × FWHMy regions obtained by 2D Gaussian models and correspond to the apertures used to extract the [CII] spectra of (a) and (b). Finally, the black crosses mark the center of each ellipse (i.e., center of each galaxy). The ALMA beam size is given in the bottom-left corners. The lower panel shows the [CII] spectra for each component of the merging system (different line styles) extracted using 1″ (orange), FWHM-based (green), and peak apertures (pink). |
The merging system DC_818760 is the only triple merger in our sample. The bottom-left panel of Fig. 2 shows that the emission coming from component #C is about four and five times dimmer than the one coming from components #A and #B, respectively. The major merger is indeed underway between galaxies #A and #B, which are closely associated both spatially and in velocity, while #C is identified as an upcoming minor merger (see Jones et al. 2020 for a detailed discussion about this system).
Finally, Fig. 3 shows the [CII] emission arising from the total system (black) together with the sum of the emissions arising from each component of the merging system when we adopt the FWHM-based aperture (green). The difference between these two emissions (green hatched area) can be interpreted as due to the diffuse [CII] envelope around the galaxies. Previously, in Ginolfi et al. (2020b), the authors analyzed the merging system vc_5101209780 in detail, finding that about 50% of the total [CII] emission arises from a gaseous envelope distributed between the individual components of the system. From the analysis of the observational sample used in this work, we find that a consistent fraction of the total [CII] emission arises from the diffuse gas between the galaxies, as qualitatively shown in Fig. 3.
 |
Fig. 3. [CII] flux density in mJy as a function of frequency (GHz) for the galaxies in our sample. Black lines are the total [CII] emission arising from the full system (galaxy + diffuse [CII] halo) and green solid lines are the sum of the emissions coming from each component of the merging system when we consider the FWHMx × FWHMy aperture. Green hatched areas show the emission coming from the diffuse [CII] halo and the [CII] fraction is in green boxes (see Sect. 3 for the definition of this quantity and discussion). |
DC_873321 is the system with the least [CII] emission associated with the diffuse component, according to Fig. 3 (top right panel) and it is also the only system where we had to perform a two-component 2D Gaussian fit, instead of two single-component 2D Gaussian models (see previous discussion). Because of the difficulty in separating the emission from the galaxies and that of the surrounding medium, it is likely that part of the [CII] emission from the diffuse halo is associated with the individual components of the system. We note that systems for which it is more difficult to separate the components may be in a more advanced phase of the merger (i.e., a closer interaction). In Appendix A, we test the presence (if any) of a velocity shift among the diffuse and galactic components of the [CII] emission.
3. [CII] emission from the CGM
In this section, we investigate the amount of [CII] emission arising from the diffuse halo in a more quantitative way with the aim to identify possible trends between the diffuse emission and the physical properties of the merging galaxies, such as their [CII] luminosity (L[CII]), M⋆, and SFR. We also explore possible trends between the fraction of [CII] emission associated with the diffuse component or inner CGM of the galaxies and the relative properties of the merging systems, such as rp, μ⋆, and μ[CII]. Indeed, these trends can give us hints about the nature of the diffuse [CII] envelope that we observe, helping us to understand whether it originates from metal-enriched gas outflows, or from tidally stripped material during the gravitational interaction between the merging galaxies, and/or it pertains to small satellites lying around the merging galaxies (see the discussion in Ginolfi et al. 2020b).
To estimate the total [CII] fluxes – in Jy km/s – we extract the emission from the 2σ region and fit it using a single Gaussian model. We then convert the measured fluxes in [CII] luminosity using the following relation (Solomon et al. 1992; Carilli & Walter 2013):
where L[CII] is in L⊙, DL(z) is the luminosity distance (in Mpc) at the redshift of the merging system and νobs(z) is the observed frequency of the [CII] line (in GHz). We dub the total luminosity of the merging system ![$ {L}^{2\sigma}_{\mathrm{[CII]}} $](/articles/aa/full_html/2024/10/aa49164-24/aa49164-24-eq14.gif) and we estimate the error associated with this luminosity as
and we estimate the error associated with this luminosity as 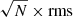 of the moment-0 map, where N is the number of ALMA beams enclosed in that region. To quantify the emission associated with the individual merging galaxies, we extract the spectra of each component using three different apertures centered on each galaxy (see Sect. 2.2 for a description of the adopted method). For a fixed aperture, we sum together the spectrum of each component and integrate it into the 2σ confidence interval found before. Using Eq. (2), we obtain the luminosity from the galaxies for each of the three apertures (1″, FWHM-based, peak). We use the formalism
of the moment-0 map, where N is the number of ALMA beams enclosed in that region. To quantify the emission associated with the individual merging galaxies, we extract the spectra of each component using three different apertures centered on each galaxy (see Sect. 2.2 for a description of the adopted method). For a fixed aperture, we sum together the spectrum of each component and integrate it into the 2σ confidence interval found before. Using Eq. (2), we obtain the luminosity from the galaxies for each of the three apertures (1″, FWHM-based, peak). We use the formalism ![$ {L}^{i}_{\mathrm{[CII]}} $](/articles/aa/full_html/2024/10/aa49164-24/aa49164-24-eq16.gif) , with i = {1″, FWHM-based, peak}. The error associated with the flux coming from these apertures is consistent with the rms of the moment-0 map since the apertures are comparable to the ALMA beam.
, with i = {1″, FWHM-based, peak}. The error associated with the flux coming from these apertures is consistent with the rms of the moment-0 map since the apertures are comparable to the ALMA beam.
Having estimated the total [CII] luminosity of the merging system and the luminosity coming from the galaxies, we can then compute the [CII] emission coming from the diffuse medium as:
where we have dropped the subscript [CII]. We also define the fraction of [CII] emission coming from the inner CGM of the merging system (hereafter, f[CII]) as:
Fig. 4 shows the relation between Ldiff and some integrated properties of the system, such as the total [CII] luminosity associated with galaxies, the star formation rate, and the stellar mass of the entire merging system listed in Table 1 (see Faisst et al. 2020 for the discussion on photometry and SED fitting procedure). For each of these relations, we compute the Spearman coefficient, ρ, to see how reliable the suggested trend is: if ρ ∼ 1 a strong correlation between the quantities is present, while for ρ ∼ −1 there is a strong anti-correlation. Although we report the results obtained for each of the three apertures, we primarily base our conclusions on the more appropriate FWHM-based method. However, this method needs to be revised to account for possible contamination of the ALMA beam, as discussed below. In particular, we applied a correction to address the potential flux loss (associated with individual galaxies) that might be located in the tails of the ALMA beam during the 2D Gaussian fit on the velocity-integrated maps to define the FWHM-based aperture (see Figs. 2 and 3). This effect could enhance the [CII] emission linked to the diffuse envelope. To address this issue, we simulated artificial velocity-integrated maps of point-like sources by injecting the ALMA beams and the measured noise of the ALPINE observations, thereby matching the depth of the observed maps and replicating the same peak S/N and separations as in the observations. We then performed the same analysis on these simulated maps as we do for the FWHM-based case in the observations. Our findings indicate that the tails of the PSF indeed enhance the [CII] emission from the diffuse medium. Consequently, our FWHM-based results need to be corrected by a factor of 0.58 (i.e., on average, about 58% of the extended emission can be attributed to the tails of the PSF). The revised values are shown as filled green pentagons in Figs. 4 and 5. We note that this results in a conservative correction as it is based on the moment-0 maps of the entire emitting regions (Fig. 1) which are not optimized for the extended emission.
 |
Fig. 4. Trends among the [CII] luminosity coming from the diffuse halo around merging systems, Ldiff, and their integrated physical properties. Different colors refer to different apertures adopted to extract the emission from the merging galaxies, Ldiff, i, with i = 1″ (orange border), FWHM-based (green border), and peak (pink border). In each panel, the filled green pentagons are the estimates obtained after applying the correction for the tails of the ALMA PSF (see text for discussion). The green solid line and shaded areas are respectively the linear fit and the associated error for these estimates. We also report the Spearman coefficient (ρ) of the analyzed relation. Left: Ldiff is shown as a function of the [CII] luminosity coming from the galaxies, Lgal. The black dot-dashed line is the 1:1 relation. Middle and right: Ldiff as a function of the total SFR and total M⋆ of the merging systems (see Table 1). DC_873321 is highlighted in gray; see the main text for the discussion on this candidate. |
 |
Fig. 5. Trends between the fraction of [CII] emission coming from the inner CGM (f[CII]; see Eq. 4) and the properties of the merging systems, such as the projected distance (rp) between the galaxies (left), the stellar mass ratio (μ⋆, middle), and the [CII] emission ratio (μ[CII], right). We show the results obtained when adopting different apertures (1″ orange border, and FWHM-based green border) needed to define the [CII] emission associated with each component of the merger. Filled green pentagons are the estimates obtained after applying the correction for the tails of the ALMA PSF (see Sect. 3 for a discussion). In each panel, the green solid line and shaded areas are respectively the linear fit and the associated error for the more conservative estimates, and we specify the Spearman coefficient (ρ) of the corresponding relation. The horizontal dot-dashed black line indicates the 0.5 value and the system DC_873321 is highlighted in gray (see text). |
Fig. 4 shows that there is a strong positive correlation (ρ = 0.8) between the [CII] luminosity of the diffuse medium and that of the merging components. This suggests that the objects with higher L[CII] result in a more carbon-polluted medium (i.e., higher values of diffuse L[CII]). This is not unexpected, as more massive (luminous) galaxies are more star-forming and gas-rich, resulting in stronger outflows (Ginolfi et al. 2020b). Moreover, as most of the points in the 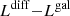 plane, place themselves above the 1:1 relation (black dot-dashed line), we can conclude that most of the [CII] emission is associated with the diffuse medium.
plane, place themselves above the 1:1 relation (black dot-dashed line), we can conclude that most of the [CII] emission is associated with the diffuse medium.
We also find a tentative (ρ = 0.3) relation between the diffuse [CII] luminosity and the SFR of the system, as well as a stronger positive correlation (ρ = 0.5) between Ldiff and the stellar mass of the system (see the middle and right panels of Fig. 4). These results provide some tentative indications of the origin of the metal-enriched gas powering the diffuse [CII] luminosity. In fact, stronger gas outflows are expected in more star-forming systems (Ginolfi et al. 2020b), while more massive galaxies trace the possible presence of small unresolved satellite galaxies and/or a stronger dynamical interaction between the merging components and are associated with more star forming (SF) galaxies resulting in a greater outflows activity. The tentative trends found so far suggest that the inner CGM is polluted with heavy elements by means of outflows, dynamical interactions, and small star-forming satellites. In particular, stripping mechanisms seem to have an important role in this scenario as we observed more extended [CII] envelopes in interacting systems, compared to non-interacting galaxies with similar SFR (and, thus, with comparable outflow activity; see, e.g., [CII] size estimates in Fujimoto et al. 2020). This is also supported by the relation between f[CII] and μ⋆ (see Fig. 5 and the relevant discussion), which suggests that systems with the strongest gravitational interaction (i.e., with μ⋆ closer to unity) have a higher fraction of [CII] emission coming from the diffuse envelope.
In Fig. 5, we further explore the dependence of the fraction of [CII] emission coming from the inner CGM of the merging systems, f[CII], and the properties of the merging pairs, such as rp between the galaxies, μ⋆, and μ[CII]. In each panel, the green solid line and shaded areas are respectively the linear fit and the associated error when considering the ALMA PSF tails contribution to the diffuse emission. In Fig. 5, we do not include the peak aperture as we obtain f[CII] ∼ 0.95 in all the systems given that in this case (i.e., unresolved merging galaxies), most of the [CII] emission is associated with the inner CGM. From this figure, we note that the fraction of [CII] emission coming from the inner CGM of the merging systems is in the range f[CII] ≃ 0.14 − 0.30 (∼25%, on average) when accounting for the possible effect of the PSF broadening (as discussed in Sect. 3). The black horizontal line corresponds to f[CII] = 0.50.
The left panel of Fig. 5 indicates that there is a strong positive correlation (ρ = 0.9) between f[CII] and rp. This demonstrates that merging systems with larger projected separations appear to have a larger f[CII] compared to systems with smaller rp, where a clear separation between the emission coming from the diffuse component and that coming from the galaxies is more challenging. However, it could also be that galaxies that are interacting for a longer period of time result in a more carbon-rich envelope (see Appendix C). To investigate this possibility, we would need to have information on the time evolution of the system, which is beyond the scope of the present work.
We also find an anti-correlation (ρ = −0.8) between the fraction of [CII] emission coming from the inner CGM and the mass ratio of the galaxies: the larger μ⋆ the smaller f[CII]. This may suggest that the dynamical interaction between mergers where galaxies have similar masses (μ⋆ ∼ 1) results in stronger tidal stripping and, as a consequence, in a more polluted CGM. Finally, we analyzed the relation between f[CII] and ![$ \mu_{[\rm CII]} $](/articles/aa/full_html/2024/10/aa49164-24/aa49164-24-eq20.gif) (right panel), finding a mild correlation, ρ = 0.5, which suggests that the fraction of [CII] emission from the diffuse envelope does not depend on the ratio between the L[CII] associated with the galaxies.
(right panel), finding a mild correlation, ρ = 0.5, which suggests that the fraction of [CII] emission from the diffuse envelope does not depend on the ratio between the L[CII] associated with the galaxies.
The DC_873321 system is highlighted in gray in Figs. 4 and 5. It is the only one for which we had to perform a two 2D Gaussian components fit instead of two single 2D Gaussian models (see Sect. 2.2). This was because of the difficulty in separating the emission from the galaxies and that of the diffuse envelope.
In summary, our observational analysis shows that a consistent part (∼25%, at least) of the [CII] emission of major merging galaxies identified in the ALPINE survey originates from a diffuse gas envelope around the merging galaxies or inner CGM. Also, we find tentative trends between the emission arising from the diffuse envelope and the physical properties of the merging systems, which provide some indication of the possible mechanisms that are responsible for the presence of a diffuse metal-enriched cold gas component surrounding these galaxies, such as small satellite companions, gravitational interaction resulting in tidal stripping, and outflow activity.
In the next section, we compare the above findings and observational sample with synthetic merging systems at similar redshift selected from a cosmological hydrodynamical simulation. This allows us to gain a more in-depth understanding of the physical processes shaping the origin and metal enrichment of their inner CGM.
4. Comparison with simulations
The results obtained from ALMA observations suggest that a fraction of the [CII] emission originates from the gas between merging galaxies and that different mechanisms (i.e., outflows, star-forming satellites, and tidal interactions) may be responsible for such emission. Thus, we employed cosmological simulations to gain more insights into the nature of [CII] emission. In the following, we first provide a brief presentation of the simulations used in our analysis. These have been thoroughly presented in Di Cesare et al. (2023) and have been run using the hydrodynamical code dustyGadget (Graziani et al. 2020). We then illustrate our analysis of the simulation results aimed at interpreting the nature of the observed [CII] envelopes. To this aim, we identify simulated galaxies with properties similar to the observed systems and we use the carbon mass in their cold ISM medium (T ≲ 104 K) as a proxy for their [CII] emission. Our goal is to investigate whether the simulated galaxies follow the relations presented in Sect. 3. We remark here that our qualitative analysis6 is meant to provide indications on the physical processes that may be responsible for the extended emission in merging systems, supporting the interpretation of ALMA observations.
4.1. dustyGadget
In this section, we provide a synthetic summary of the key features of the cosmological hydrodynamical code dustyGadget. We refer the to Graziani et al. (2020) for a detailed description of the code, and to Di Cesare et al. (2023), Venditti et al. (2024, 2023) for its latest results.
In brief, dustyGadget is an extension of the particle-based smoothed particle hydrodynamics (SPH) code Gadget-2/3 (Springel 2005; Springel et al. 2021) and provides a self-consistent implementation of dust production and evolution, on top of the improvements to the chemical evolution module from Tornatore et al. (2007a,b) and to molecular chemistry and cooling from Maio et al. (2007). In particular, the gas chemical evolution scheme is inherited from Tornatore et al. (2007a) (see also Maio et al. 2010): it follows the metal release from stars of different masses, metallicity, and lifetimes. Yields depending on mass and metallicity are implemented for both PopII and PopI stars and stars with masses ≥40 M⊙ are assumed to collapse into black holes and do not contribute to metal enrichment. PopIII stars with masses inside the range 140 M⊙ ≤ M⋆ ≤ 260 M⊙ are expected to explode as pair-instability SNe (PISN), while those with masses outside the PISN range are assumed to collapse into black holes. We caution that the formation of AGN is not modeled in our simulations; thus we do not account for mechanical or radiative feedback from accreting nuclear black holes. Moreover, as already stated, [CII] emission is not followed in the simulation; hence, we used the carbon mass in the cold gas phase as a proxy for the emission (see the discussion in Sect. 4.4). Following Maio et al. (2007), the chemical network in dustyGadget also includes the evolution of both H and H+, He, D, and primordial molecules by relying on the standard Gadget implementation of the cosmic UV background as a photo-heating mechanism, first introduced by Haardt & Madau (1996). Star formation occurs in the cold gas phase, once the gas density exceeds a value of nth = 132 h−2 cm−3 (physical). The IMF of the stellar populations, each represented by stellar particles, is assigned according to their metallicity, Z⋆, given a gas critical metallicity, Zcrit = 10−4 Z⊙, where Z⊙ = 0.02 (Grevesse & Anders 1989). When Z⋆ < Zcrit, we adopted a Salpeter IMF (Salpeter 1955) in the mass range [100 − 500] M⊙; otherwise, the stars were assumed to form according to a Salpeter IMF in the mass range of [0.1 − 100] M⊙.
The production of dust grains by stars in SNe explosion and asymptotic giant branch (AGB) stellar winds is described by means of a set of mass- and metallicity-dependent yields (Bianchi & Schneider 2007; Marassi et al. 2014, 2015; Bocchio et al. 2016; Ginolfi et al. 2018; Graziani et al. 2020; Pizzati et al. 2020; Romano et al. 2023), which closely follow the chemical network adopted for metal yields (Tornatore et al. 2007a). Once the grains produced by stars are released in the ISM, they can undergo diverse physical processes that can alter their mass, relative abundances, chemical properties, charge, and temperature. Generally, it is assumed that the dust-to-light interactions (e.g., photo-heating, grain charging) alter the thermodynamic and electrical properties of the grains (see e.g., Glatzle et al. 2019, 2022); however, these processes have a negligible impact on the total dust mass unless the grain temperatures reach the sublimation threshold (Td, s ≳ 103 K). Other physical processes (i.e., sputtering and grain growth) can alter the total dust mass (Mdust) and the grain size distribution (Draine 2011; Aoyama et al. 2020). In the version of dustyGadget adopted in this work, we only consider physical processes which alter the dust mass (i.e., grain growth, destruction by interstellar shocks, and sublimation)7 in the hot and cold phases of the ISM (Springel & Hernquist 2003). The spreading of dust grains and atomic metals in the ISM, CGM, and IGM is done through galactic winds, which are modeled with a fixed initial velocity following the implementation of Tornatore et al. (2010). Also, we refer to Maio et al. (2011) for the interplay between chemical and mechanical feedback in simulations. In dustyGadget, the initial velocity is fixed to 500 km/s, following typical outflow velocities observed in main sequence galaxies at z ≳ 4 (Gallerani et al. 2018; Sugahara et al. 2019; Ginolfi et al. 2020a). Finally, the identification of DM halos and their substructures is performed in post-processing with the AMIGA halo finder (AHF, Knollmann & Knebe 2009).
In this work, we make use of one of the eight statistically independent cosmological simulations (U6–U13) analyzed in Di Cesare et al. (2023), where we investigated the redshift evolution of the SFR, stellar mass density, stellar mass function, and galaxy scaling relations, at z ≥ 4, comparing our results with observational data.
The physical setup of the runs and simulated cosmic volumes are the same as in Di Cesare et al. (2023). In particular, we considered a cubic volume with 50 h−1 cMpc (∼74 cMpc) side length, with 2 × 6723 particles, corresponding to a mass resolution of 5.2 × 107 M⊙ for DM particles, and of 8.2 × 106 M⊙ for gas particles. Using the current version of dustyGadget, we were able to resolve down to the scale of a giant molecular cloud (a few tens up to hundreds of pc); however, for the purposes of this work, we are only interested in scales on the order of tens of kpc.
Finally, the simulations adopt a flat ΛCDM cosmology with ΩΛ = 0.6911, Ωm = 0.3089, Ωb = 0.0486, and h = 0.6774 (Planck Collaboration XIII 2016). The simulations start at z = 100, assuming neutral pristine gas, and evolve all particle components down to z = 4. In the following, whenever we refer to units we mean physical ones (unless otherwise stated).
4.2. Identifying galaxy mergers
Di Cesare et al. (2023) already compared the integrated properties (SFR, M⋆, Mdust) of synthetic galaxies from dustyGadget with those observed in the ALPINE survey. They found a remarkable agreement between the two (see, e.g., their Figs. 3 and 8).
In this work, we started from the galaxy catalogs generated by the simulation and select synthetic merging galaxies whose physical, integrated properties resemble the observed ones, as described in Sect. 2.1. We analyzed the simulation snapshots (hereafter referred as snap) from snap = 041 (z = 4.495) to snap = 035 (z = 5.098), which encompass the redshift range of the observed systems (z = 4.5 − 5.1; see Table 1), and a physical time interval of ΔtH = (1.338 − 1.145) Gyr = 193 Myr, for our assumed cosmology. Hence, we ended up having six galaxy catalogs, with Δz = 0.1, containing simulated systems with masses in the range M⋆ ∼ 108 − 1011 M⊙ (∼14 000 objects at snap = 041, and ∼9400 at snap = 035). Among these, we considered only the galaxies with stellar mass of M⋆ ≥ 1010 M⊙, to match the properties of the observed systems (see Table 1), ending up with ∼40 galaxies at snap = 041 and ∼15 galaxies at snap = 035. Within these smaller samples of objects, which match the observed systems in terms of redshift and stellar mass, our aim was to identify possible galaxy mergers.
Mergers were identified considering galaxies at z ≃ 4.5 and reconstructing their merger trees (i.e., their past assembly histories in gas, dark matter, and stellar particles) up to z ≃ 5.1. Fig. 6 shows a schematic view of a merger tree reconstruction: we started at z = 4.495 (snap = 041) with a galaxy dubbed “a” and went backward in time up to z = 5.1 (snap = 035); at each intermediate redshift step, we identify the ancestors of “a” (i.e., halos “b” and “c” contributing particles to “a” at z = 4.6). Once we have reconstructed the merger tree of each galaxy, we can then follow its evolution forward in time and characterize the origin of its mass assembly and establish whether this is the result of a major merger, smooth accretion, or minor mergers.
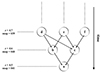 |
Fig. 6. Illustration of an example of merger tree reconstruction. Starting from galaxy “a” at z = 4.5 (snap = 041), its progenitors at the previous snapshot are “b” and “c”. Merger trees have been reconstructed all simulated galaxies at z = 4.5 with masses of M⋆ ≥ 1010 M⊙, up to z = 5.1 (snap = 035). This allows us to reconstruct the mass assembly history of the simulated galaxies, identifying those systems that undergo major mergers, defined as galaxy interactions where the relative stellar mass ratio of the merging pair is 1 < μ⋆ < 4 (see text). |
In particular, we followed the same criterion adopted for the observed systems and we assumed that two ancestors undergo a major merger when their relative stellar mass ratio (defined as the ratio between the most massive and the least massive) is 1 < μ⋆ < 4.
After applying this condition and checking that we were not double counting merging episodes8, we ended up with eight unique candidates (7 at z ≃ 4.5 and one at z ≃ 5.0), which undergo major mergers during their history. In Table 2, we provide a summary of their physical properties, where each row corresponds to one of these synthetic major mergers; in particular: their IDs, redshift, mean projected (rm)9 distance in kpc, relative carbon mass ratio of the merging pair (μC), relative stellar mass ratio of the merging pair, μ⋆, total M⋆ in M⊙, and the SFR in M⊙ yr−1.
Properties of the eight simulated systems classified as major mergers and the two galaxies that are not involved in any major mergers.
Compared to the observed sample (see Table 1), the simulated systems appear to span a similar range of properties and can be considered as good synthetic analogs of the systems we analyze in Sect. 2. This sample of synthetic galaxies can help us interpret the observed trends that we presented in Sect. 3. As an illustrative example, in the next section, we discuss the time evolution of the simulated system H4 at z = 4.495, which provides the best synthetic analog of vc_5100822662.
4.3. Time evolution of a representative merger
The simulated system H4 at z = 4.495 and the observed system vc_5100822662 (hereafter, vc_662) at z = 4.5210 have stellar mass and SFR which are consistent within the errors: log(M⋆/M⊙) = 10.6 (H4) and log(M⋆/M⊙) = 10.4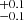 (vc_662); log(SFR/M⊙ yr−1) = 2.0 and log(SFR/M⊙ yr−1) = 2.0
(vc_662); log(SFR/M⊙ yr−1) = 2.0 and log(SFR/M⊙ yr−1) = 2.0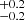 , respectively. Moreover, H4 and vc_662 have similar stellar mass ratios μH4 = 1.5 and μvc_662 = 1.7, and projected distance of 16 kpc and 11 kpc, respectively. It is important to keep in mind that the simulation not only offers information on the projected distances, but also on the physical (3D) distance between the merging galaxies, which we compute as r = 21 kpc for this synthetic system.
, respectively. Moreover, H4 and vc_662 have similar stellar mass ratios μH4 = 1.5 and μvc_662 = 1.7, and projected distance of 16 kpc and 11 kpc, respectively. It is important to keep in mind that the simulation not only offers information on the projected distances, but also on the physical (3D) distance between the merging galaxies, which we compute as r = 21 kpc for this synthetic system.
Fig. 7 shows the merger tree reconstruction for H4 (see Table 2 for its integrated physical properties) from z = 4.5 to z = 5.1, together with maps (80 × 80) kpc and (60 × 60) kpc, respectively showing the (x, y) projection of the dark matter particles and stellar particles. These maps are centered respectively in the center of mass of the dark matter halo and of the baryonic component. Here, we dubbed the merging galaxies H4 and H98 at z = 4.5 as “a” and “b”, respectively, so that it is easier to follow their past history along the merger tree reconstruction. In the illustration provided, we connected with solid black lines each component of the merging pair to its main galaxy progenitor at the preceding redshift10: as an example, the galaxy dubbed as “a” at z = 4.6 (H3) is considered to be the main progenitor of galaxy “a” at z = 4.5 (H4). At each redshift, we also indicate the μ⋆ of the galaxies undergoing the major merger. For the sake of clarity, the projections of the dark matter and baryonic components in the middle and right panels of Fig. 7 are shown only at four redshifts, while particles belonging to each merging component are color-coded to match those in the corresponding merger tree. In the following section, we discuss how the spatial distribution of the gaseous component is generated.
 |
Fig. 7. History of two merging galaxies, H4 and H98 (dubbed as “a” and “b”) shown in the left panel, reconstructed along their past merger tree, starting from z = 4.5 up to z = 5.1. At each redshift, we show both the main progenitor (black solid line) and secondary progenitor (black dashed lines), we also report the stellar mass ratio μ⋆ of the primary (green) and secondary (magenta) merging galaxies. In the middle and right panels, we show the projection on the (x, y) plane of the merging galaxies as seen in dark matter and baryonic matter components, respectively. For the sake of clarity, we only show the maps at four redshift steps (z = 5.1, 4.9, 4.7, and 4.5, from top to bottom) and galaxies are color-coded the same way as in the merger tree. |
Looking at the dark matter and baryonic matter visualizations (in the middle and right panels of Fig. 7), it is interesting to note how dark matter halos merge and coalesce in a shorter time compared to galaxies themselves (i.e., to the baryonic components). Indeed, by z = 4.5, the dark matter halos of the two systems can be considered as a single virialized object, while the baryonic components are still largely spatially segregated, and undergoing the merger. Moreover, as soon as the gravitational interaction between galaxies becomes stronger (i.e., they move closer), galaxies appear to be clumpier and richer in satellites and undergo disruption events, leading to filamentary structures by z = 4.5. In addition, we also have to consider that the merger between the dark matter halos of the galaxies may lead to the formation of overdense regions, thereby resulting in dense clouds where star formation can be triggered.
All this qualitative information coming from the simulation provides us with fundamental indications on the evolution of merging pairs, inaccessible using only observations, and helps us interpret the results from the observational part of this work. In fact, simulated galaxies have higher spatial resolution compared to ALPINE observations and we are able to resolve small satellite galaxies and filamentary structures. This allows us to infer the origin of the enriched diffuse gas surrounding the galaxies, which powers the observed [CII] emission coming from the inner CGM of merging galaxies. We can also infer whether this is due to unresolved satellites galaxies, filamentary structures, outflows, or perhaps a combination of the three. In the following, we explore these options in a more quantitative way.
4.4. Dependence of galaxy properties and their CGM on the mass ratio of merging pairs
In this section, we focus on two synthetic candidates (H2 and H10) at z = 4.5, selected on the basis of their merging pairs being characterized by the highest (μ⋆ = 4.1) and lowest (μ⋆ = 1.3) stellar mass ratios, respectively, in our sample. Our aim is to investigate whether systems with extreme μ⋆ may be characterized by different morphological properties of the stellar and gas components, on scales comparable to the diffuse [CII] emission component quantified in Sect. 3.
Fig. 8 shows the stellar particle distributions (first row) and carbon surface density maps (ΣC, second and third rows) for H2 and H10 projected on the plane perpendicular to the line of sight along the x-axis. Specifically, the orange and violet tones show the carbon in regions with gas temperature T < 5 × 104 K, used as a proxy for L[CII] (see the discussion below).
 |
Fig. 8. Properties of two synthetic merging systems with high (μ⋆ = 4.1, H2, left panels) and low (μ⋆ = 1.3, H10, right panels) stellar mass ratios at z = 4.5. First row: Maps of the stellar surface density projected along a line-of-sight parallel to the x-axis. Stellar particles are color-coded according to their age, with age ≤ 10 Myr in dark blue, age ≤ 100 Myr in light blue, and 100 Myr < age ≤ 1 Gyr in red color scale. Second row: Same as above, but for the carbon surface density distribution of H10 (μC = 3.6) and H2 (μC = 1.5), respectively. The green color map shows the total carbon surface density distribution and overplotted on that, in orange tones, is the carbon distribution in the cold gas phase (i.e., with T < 5 × 104 K). Third row: Carbon in the cold gas phase surface density distribution once we convolve the original simulated map with the ALMA PSF. Black ellipses indicate the FWHM-based apertures used to extract the carbon content associated with each merging galaxy. In the bottom left corner is a beam of ∼1″ as a reference. Black (first row) and white (second and third rows) dashed contours indicate the positive significant level at 2σ. |
In general, to characterize the gas and metals spatial distributions, we projected the gas and metal particles onto Cartesian grids with 256 or 512 cells on each side. Each particle contribution was weighted with the SPH kernel adopted in dustyGadget. These maps are centered either in the halo mass center (H2, H4, H5, H6, H10, and H0) or in the center of mass of the merging system (H25, H28), depending on how diverse these two values are; whereas the side of the Cartesian grid was chosen to capture the whole merging system. Specifically, we chose a box side of 60 kpc (256 cells/side) for all the synthetic candidates but for H25 and H28 for which we adopted a side length of 100 kpc (512 cells/side). Both grids have a spatial resolution (pixel dimension) of ∼0.2 kpc, thus a factor of ∼20−30 more resolved than the ALPINE-ALMA beam.
As for the panels showing stellar particles (scatter plots), in red we color-coded their ages, in dark blue stellar populations with ages of ≤10 Myr, and in light blue those with ages of ≤100 Myr. This is done in order to characterize younger populations and star-forming regions (blue) in contrast to more mature stellar populations in red. Observations interpreted with photo-ionization models suggest that the bulk of [CII] emission is coming from neutral atomic gas clouds in photo-dissociation regions (PDRs) surrounding young stars (Hollenbach & Tielens 1999); thus, we anticipated that a consistent part of the carbon mass predicted by dustyGadget simulations would be associated with young stellar populations (ages ≤ 10 Myr; see the discussion in Sect. 5).
In the second row of Fig. 8, blue and green tones show the total carbon surface density, while orange and violet show the carbon surface density found in regions with gas temperature of T < 5 × 104 K11. This cut was done as the [CII] emission is expected to be associated with cold-warm gas phases and, at higher temperatures, we expect the C atoms to be in higher ionization states.
The third row of Fig. 8 shows the surface density distribution of the carbon associated with gas at a temperature below the adopted cut (hereafter, “cold” gas phase) once it is convolved with the ALMA PSF (i.e., we applied a Gaussian smoothing with FWHM ∼1″). This step is needed since we want to compare the results from simulations with those from observations (see Sect. 4.5). The black crosses mark the center of the two interacting galaxies and the gray circle in the bottom-left corner shows a reference beam of ∼1″.
The comparison among two merging systems in Fig. 8 highlights the different environments these systems belong to. In fact, H2 is characterized by a dominant component and several smaller satellites (μ⋆ ∼ 4), while H10 is characterized by an almost equal mass merging pair (μ⋆ ∼ 1). This translates into different stellar and metal-enriched gas spatial distributions in the two cases. Also, it is interesting to note how diverse scenarios appear when comparing carbon maps with and without the convolution with ALMA PSF, with the latter lacking the detailed spatial distribution inferred from the simulation.
4.5. Statistical properties
Here, we analyze the relations between the carbon mass (in the cold phase) present in the diffuse envelope around merging galaxies and the integrated properties of such systems to identify possible trends. The aim is to derive scaling relations that can be compared to the observational ones (see Figs. 4 and 5) using the carbon in the cold gas phase as a proxy for [CII] luminosity. In fact, once similar relations are recovered, predictions from dustyGadget can help us interpret the observations and help us gain insights into the nature of the extended emission.
Henceforth, whenever we talk about the carbon mass, we are referring to the MC in the cold phase, T < 5 × 104 K, shown as orange and violet tones in Fig. 8. As previously stated, this cut in temperature is necessary in order to highlight the regions from which we expect [CII] emission to be more likely. Briefly, we generated the gas and carbon 3D distributions, applied the cut in temperature to these cubes, and then projected this result on planes perpendicular to the lines of sight parallel to the z, y, and x-axis. We repeated this procedure to all our selected synthetic galaxies (see Table 2) and once we had an image for each candidate and its three plane projections, we convolved the image with the ALMA PSF and fit a 2D Gaussian model to it. This allowed us to retrieve morphological information such as the coordinate of the main MC clumps that are associated with the major merging galaxies. Then, we used the mean value of all the FWHM-based apertures adopted for the observational part as the standard aperture to be used in simulations (black dashed circles in Fig. 8, last row) and associated all the carbon inside the aperture with belonging to the galaxy.
Knowing the coordinates of the center and the dimensions of all the apertures, for each 2D projection (lines of sight, i = z, y, x), we can distinguish between the carbon mass associated with the galaxies (sum of the carbon mass inside the apertures) and the total one (sum over the entire plane projection). At this point, we can define the MC associated with the diffuse halo as:
where we dropped the subscript C. The fraction of MC in the envelope around merging systems (hereafter, fC) is:
Fig. 9 shows the relation between Mdiff and some integrated properties of the systems, such as the total carbon mass, SFR, and stellar mass. For each relation, we calculated the Spearman coefficient to understand how reliable the suggested trend is. Moreover, different colors correspond to projected quantities along lines of sight parallel to the z (blue), y (pink), and x (red) axis, and projections associated with the same system are connected by gray vertical lines quantifying the variation of Mdiff.
 |
Fig. 9. Trends between the carbon mass in the cold gas phase (T < 5 × 104 K) coming from the diffuse halo around merging systems, Mdiffuse, and their integrated physical properties. Different colors refer to projected quantities along different lines of sight parallel to the z (blue), y (pink), and x (red) axis. In each panel, white dots are Mavg (i.e., the average among the three projections), the black dashed line is the linear fit once we consider Mavg, and ρ is the Spearman coefficient corresponding to the analyzed relation. Left: Mdiffuse is shown as a function of the total carbon mass in the cold gas phase (Mtotal). Middle and right panels: Mdiffuse as a function of the total SFR and total M⋆ of the merging systems. Highlighted in gray: H2 and H6, which have peculiar structures, and for this reason, they have not been included in the fit. Green triangles are single non-interacting galaxies (see the end of this section for discussion). |
The black dashed line is the result of the linear fit once we consider the carbon mass value in the diffuse halo averaged on the three projections (hereafter, Mavg shown as white dots in the figures) and the corresponding x-axis quantity. Finally, H2, which displays a peculiar morphological structure rich in clumps and satellites (see the left panels of Fig. 8), and H6, whose galaxies are closely interacting (see Appendix B) are highlighted in gray. For these reasons, they have been considered as not belonging to the fiducial simulated sample and are not included in the fit.
The figure shows a positive ρ = 0.4 and strong positive ρ = 0.8 and 0.9 correlations in the first, second, and third panels, respectively. These results suggest that their inner CGM is characterized by a significant carbon mass, which appears to be well correlated with the SFR and stellar mass of the systems, indicating the important role that current and past star formation activity has in enriching the inner CGM with outflows from the merging pairs and smaller satellite systems. This conclusion strengthens the tentative trends between diffuse [CII] emission and star formation rate and stellar mass of merging systems (ρ = 0.3 and 0.5, respectively) we found in Sect. 3.
In Fig. 10, we explore the dependence between the fraction of carbon mass in the diffuse halo (fC) and rm, μ⋆ and μC. In the middle and right panels, different colors correspond to different projections, with those associated with the same system connected by gray vertical lines. In each panel, we specify the Spearman coefficient of the corresponding relation and the black dashed line is the linear fit once we consider the fraction of carbon in the diffuse envelope averaged on the three projections (favg) and the corresponding x-axis quantity. Then, favg is shown with a violet squares and stars in the left panel and with white dots in the middle and right panels. The synthetic galaxy H2 has not been included in these plots, as it is considered an outlier, with fC ∼ 0.8, and thus out of scale. H6, instead, has been highlighted in gray and not considered in the fits and computation of the Spearman coefficients.
 |
Fig. 10. Trends between the fraction of carbon mass in the cold gas phase (T < 5 × 104 K) in the diffuse halo (fC) and the distance (r) between the galaxies (left), the stellar mass ratio (μ⋆, middle), and the carbon mass ratio (μC, right). In particular, on the left, we show favg (i.e., the average among the three projections) as a function of both the distance averaged on the three projections (rm, violet squares) and the physical distance between the galaxies (R, violet stars). In the middle and right panels, different colors refer to fC estimated by projecting the carbon surface density along the lines of sight parallel to the z (blue), y (pink), and x (red) axis. In each panel, white dots are favg, the black line is the linear fit considering favg versus rm, μ⋆, μC, respectively. We also specify the Spearman coefficient (ρ) of each relation. H2 is not included in these plots as this system is characterized by an out-of-scale value of fC = 0.8 and H6 is highlighted in gray. The horizontal gray dot-dashed line shows the value of fC = 0.5. |
On average, we find that, when considering the entire simulated sample, ∼59% of carbon mass resides in the envelope around merging systems. By excluding H2, which has been considered an outlier (being particularly rich in star-forming satellites; see the left panels of Fig. 8), this value becomes ∼57%. Both cases are indicative of the presence of carbon in the cold gas phase in the inner CGM of the merging systems, according to dustyGadget.
In the left panel of Fig. 10, we show favg as a function of the mean projected distance (violet square) and physical distance (violet stars) between merging galaxies, with the physical distance being larger than the projected one in all the systems. The Spearman coefficient for the favg − rm relation is ρ = −0.5 suggesting a correlation with negative trend between these two quantities. This result, which points to a negative trend among favg − rm, appears to be in disagreement with what has been found in observations (see Fig. 5). However, in the simulations, we are considering systems with mean distances rm up to ∼50 kpc; whereas, in the ALPINE sample, the projected distance goes up to ∼16 kpc. This is further discussed in Appendix C, where we show that a positive correlation among favg − rm, similar to that found in observations, is recovered when we consider galaxies with rm ≲ 16 kpc. This highlights the role of interactions in polluting the diffuse medium.
The middle panel suggests an anti-correlation between the fraction of carbon mass in the diffuse halo and the stellar mass ratio of the merging galaxies, indicating that systems with μ⋆ closer to unity have stronger interactions, which result in more metal-enriched inner CGM. This may be a clue that dynamical interaction at high-z can be an efficient mechanism for extracting material out of galaxies and mixing it in the CGM. Finally, the right panel shows fC as a function of μC, suggesting that there is not a correlation between the amount of MC found in the diffuse halo and the ratio between carbon masses of each merging component.
5. Discussion
In this section, we interpret the observations using our simulated galaxies and discuss the results obtained from the analyzed merging systems at z ∼ 4 − 6. First and foremost, it is important to bear in mind that the comparison between the results from observations and those from simulations is not straightforward. In fact, in simulations, we consider the carbon mass in the cold gas phase which is more likely to emit in [CII], but not the actual [CII] luminosity. In fact, to recover luminosity information from simulations we would need to couple our result with radiative transfer codes, such as Cloudy (for line transfer, Ferland et al. 2017) and SKIRT (for dust continuum, Baes & Camps 2015). These features will be implemented as a follow-up work. Thus, preliminarily, we assume that the carbon mass in the cold gas phase (T < 5 × 104 K) can be considered as a good proxy for [CII] luminosity, to guide the interpretation of the observational results (illustrated in Sect. 3).
On the one hand, [CII] envelopes have been observed at first in non-interacting galaxies (e.g., Fujimoto et al. 2019, 2020; Ginolfi et al. 2020a; Herrera-Camus et al. 2021), where they extend up to ∼10−15 kpc outside the galaxies. A possible explanation has been provided by Pizzati et al. (2020, 2023), who adopted a semi-analytical model to interpret the presence of [CII] halos in high-z galaxies concluding that they can be produced by ongoing (or past) starburst-driven outflows, which transport carbon and other heavy elements in the CGM. Recently, Romano et al. (2023, 2024) analyzed Herschel (Pilbratt et al. 2010) data of local dwarf galaxies finding that the observed [CII] emission (the size of which agrees with that measured for star-forming galaxies at z > 4) can be attributed to the presence of galactic outflows. On the other hand, Ginolfi et al. (2020b) found an even more extended (> 20 kpc) emission in one interacting system from the ALPINE sample, arguing that most of the detected circumgalactic emission is a consequence of the effect of gas stripping induced by strong gravitational interaction.
In this work, by analyzing major merging systems in the ALPINE survey, we confirm the presence of extended [CII] envelopes around interacting galaxies, finding that around 25% of the total [CII] emission comes from the medium between the galaxies. All the analyzed systems have an extended emission (mean value of ∼27 kpc), suggesting that the gravitational interaction between galaxies (which results in tidal tails) is responsible for their extended carbon-enriched envelope. This scenario has been investigated using the hydrodynamical simulation dustyGadget and comparing merging and not merging systems (see the discussion in the following). Specifically, the anti-correlation between fC and μ⋆ (shown in Fig. 10) indicates that systems that interact more strongly result in a more enriched halo (i.e., higher fC), supporting the conclusion from Ginolfi et al. (2020b). Starburst-driven outflows, which spread metals outside the galaxies, are still at work in interacting systems. In fact (as shown in the middle panel of Fig. 9), there is a correlation between the carbon in the diffuse medium and the SFR of galaxies that may be associated with outflows. To quantify the importance of that mechanism compared to others, we need to look at galactic winds of interacting galaxies, which is beyond the scope of this paper.
Predictions from dustyGadget not only helped us corroborate and interpret the observational results, but we also used them to disentangle the different mechanisms that contribute to the metal enrichment of the inner CGM of interacting galaxies. To do so, we considered SFR, M⋆, and μ⋆ as proxies for outflows, SF clumps, and tidal interactions, respectively, and studied their contribution to the carbon-enriched envelope.
As mentioned above, H2 is considered an outlier in the synthetic sample, because of its high fC, which is due to its peculiar morphology rich in satellites/star-forming clumps. To further investigate this hypothesis (i.e., that star-forming clumps play a role in the observed [CII] diffuse emission), we studied the relation among fC and the fraction of young, age ≤ 10 Myr, stellar populations (f⋆) that reside in the inner CGM of the systems. This quantity is defined as:
with N⋆total being the total number of young stellar populations and N⋆i the sum of stellar particles associated with merging galaxies for each projection (i = z, y, x).
In Fig. 11, we show the mean values for f⋆ and fC for interacting, in orange, and non-interacting, in green, systems; error bars on both axes give us an idea of the variations of f⋆ and fC among different projections. This figure shows a linear relation and positive trend between the fraction of carbon and that of young stellar populations in the diffuse halo, suggesting that clumps of star-forming regions, unresolved by ALMA, can play a role in enriching the gas envelope with carbon. Moreover, as shown in Fig. 7, the merger between dark matter halos happens on smaller timescales compared to those needed for the merger in the baryonic component and may lead to the formation of overdense regions at the periphery of merging systems triggering star formation and enriching their surrounding medium with carbon and other heavy elements.
 |
Fig. 11. Relation between the fraction of carbon mass (fC) and the fraction of young (age ≤ 10 Myr) stellar populations (f⋆) present in the diffuse halo of interacting (orange stars) and non-interacting (green triangles) systems. We show the mean value of fC and f⋆ of all the simulated galaxies, along with the error bars representative of the variations in different projections and the linear fit. |
In addition to the previous analysis, by comparing results from major merging systems (dubbed “interacting”) with those from systems which are not in major mergers (dubbed as “non-interacting” or “single”12), we can obtain an estimate of the importance of gravitational interactions that result in tidal stripping, for the enrichment of the inner CGM. To do so, we selected two non-interacting galaxies with stellar masses and SFRs similar to the interacting synthetic candidates (see Table 2). These two galaxies are also representative of other synthetic single galaxies at the same redshift that we find in our simulation.
In the single-galaxy case, we recovered an extended carbon-rich envelope going up to ∼10 kpc, in agreement with the estimations from Fujimoto et al. (2019, 2020), Ginolfi et al. (2020a), Herrera-Camus et al. (2021). As shown in Fig. 12, this confirms that the diffuse halo in non-interacting galaxies is less extended than the one estimated for interacting systems (> 20 kpc).
 |
Fig. 12. Example of the surface density distribution of carbon in the cold gas phase once we convolve the original simulated map with the ALMA PSF, for interacting (left) and non-interacting (right) systems. The line of sight is chosen parallel to the x-axis, in the bottom left corner is a beam of ∼1″ as a reference. |
In Fig. 9, we compare Mdiff in interacting (colored pentagons) and non-interacting (green triangles) galaxies. In general, we note that single galaxies have lower Mdiff values than interacting systems; also, they result in similar diffuse carbon masses no matter the adopted line of sight, indicating a more compact and regular morphology, namely, one that is not disturbed by dynamical interactions. The first panel of Fig. 9 suggests that both interacting and non-interacting systems follow a similar trend when comparing Mdiff and the total carbon mass. On the one hand, the relation between the diffuse carbon mass and the SFR (second panel) shows that for non-interacting systems, the ongoing SFR is not a good proxy for the amount of carbon mass in the inner CGM. We also note that H6, which is an interacting system in an advanced phase of the merger, ends up placed close to non-interacting systems on the Mdiff–SFR relation. On the other hand, looking at the third panel, which shows Mdiff as a function of M⋆, we see that interacting systems have ∼1.4× more carbon mass in the diffuse halo than single galaxies. This result suggests that stripping mechanisms seem to be responsible for bringing metals into the CGM of the analyzed systems. This conclusion is further corroborated by the fact that the fraction of SF clumps and carbon mass present in the diffuse halo of non-interacting galaxies is comparable to that of interacting galaxies, as shown in Fig. 11.
In summary, it seems that for the interacting systems analyzed in this work, stripping mechanisms are responsible not only for bringing carbon into larger scales but also for enhancing [CII] emission possibly via shocks (see also Ginolfi et al. 2020b).
The interacting systems we analyze in this work could be considered as high-z analogs of circumgalactic stripped carbon and shock-induced [CII] emission in local studies (Appleton et al. 2013; Velusamy & Langer 2014). These are qualitative conclusions, based on a comparison between the properties of the inner CGM found around single and major merging galaxies in our simulation. These results need to be reinforced by performing a more quantitative analysis of the specific effects of all feedback processes at play, both mechanical and radiative, in a future work.
6. Summary and conclusions
In this paper, we analyze a sample of merging galaxies observed by the ALMA-ALPINE survey at a redshift of 4.5 < z < 5.1, to investigate the [CII] emission coming from the gas between the galaxies. We complement the observational analysis with cosmological simulations, specifically the hydrodynamical code dustyGadget, looking for synthetic merging systems that helped us interpret the nature of such emission. Our main results can be summarized as follows:
-
We analyze major merging systems in the ALPINE survey and confirmed the presence of an extended (> 20 kpc) [CII] halo in interacting galaxies. This extended halo is larger than the one observed in isolated galaxies as a consequence of the dynamic interaction between galaxies.
-
We found that at least 25% of the total [CII] emission associated with these systems comes from the medium surrounding the merging system, thus being located between the galaxies.
-
We establish the presence of correlations, either strong or tentative, between the amount (fraction) of [CII] emission from the diffuse halo and integrated (relative) properties of galaxies.
-
We find that an extended carbon-rich envelope is also present in interacting systems selected from the dustyGadget simulation. In particular, extended emissions of around 10 kpc and larger than 20 kpc have been found in non-interacting and interacting systems, respectively. Also, we found strong correlations between diffuse carbon in the cold gas phase (used as a proxy for [CII] emission) and the physical properties of galaxies; in particular, with their total carbon mass, SFR, and stellar mass. This suggests that there are different mechanisms at work behind [CII] emission.
-
Using dustyGadget, we investigate the nature of the metal-enriched envelope, which (apart from outflow mechanisms) can be attributed to dynamical interaction between merging galaxies that extract carbon-rich gas out of galaxies and the presence of star-forming satellites that enrich the inner CGM with newborn stellar populations. We argue that most of the [CII] emission observed in the ALPINE systems originates from gas stripping mechanisms in turbulent collisional environments (see discussion in Sect. 5), analogously to broad [CII] emission observations of tidal tails of shock-excited carbon in local groups (Appleton et al. 2013).
Taken altogether, our findings suggest that dynamical interactions and star-forming clumps at high-z can be an efficient mechanism for extracting gas out of galaxies and enriching the CGM with chemically evolved material. Deeper and higher resolution ALMA data along with state-of-the-art simulations with refined sub-grids models are necessary to study the key role of mergers in the baryon cycle of distant galaxies in greater detail, as well as to understand the specific role of outflows, tidal interactions, and star-forming satellites in the observed [CII] diffuse emission. Concerning the observations, the first results from the ALMA-CRISTAL survey (PI: Herrera-Camus) have already provided substantial details on the extended [CII] emission from high-z galaxies (see e.g., Solimano et al. 2024; Posses et al. 2024), laying the groundwork for even more in-depth observations and analyses. Moreover, ALMA observations together with future sub-mm information from single-antenna telescopes (e.g., AtLAST; Mroczkowski et al. 2024; van Kampen et al. 2024; Lee et al. 2024) would significantly improve our knowledge of the CGM and of the [CII] emission in the high-z Universe.
Such as Adaptive Mesh Refinement (Hummels et al. 2019; Peeples et al. 2019) and moving mesh codes (van de Voort et al. 2019).
Among the 118 main sequence galaxies of the ALPINE sample, 75 are detected in [CII] at S/N > 3.5 (Béthermin et al. 2020).
Radiative transfer codes are indeed needed to estimate the proper [CII] luminosity from synthetic galaxies; see the discussion in Sect. 5.
We do not consider the evolution of grain sizes, and the grains are assumed to be spherical, with a static, average size of 0.1 μm (Graziani et al. 2020).
Acknowledgments
The authors would like to thank the anonymous referee for the useful suggestions which improved this article. This paper is based on data obtained with the ALMA Observatory, under Large Program 2017.1.00428.L. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. CDC would like to thank the GESO group at the European Southern Observatory (ESO) for the useful discussions while preparing this manuscript. The simulated data underlying this article will be shared on reasonable request to the corresponding author. CDC acknowledged support from Sapienza University of Rome program “Bando per la mobilità individuale all’estero” (DR n. 1607 del 14 June 2021) during the visiting period (June-November 2022) at ESO Garching, Germany. LG and RS acknowledge support from the PRIN 2022 MUR project 2022CB3PJ3 – First Light And Galaxy aSsembly (FLAGS) funded by the European Union – Next Generation EU, and from the Amaldi Research Center funded by the MIUR program “Dipartimento di Eccellenza” (CUP:B81I18001170001). MR acknowledges support from the Narodowe Centrum Nauki (UMO-2020/38/E/ST9/00077) and support from the Foundation for Polish Science (FNP) under the program START 063.2023. We have benefited from the publicly available software CASA and CARTA and programming language Python, including the numpy (https://numpy.org), matplotlib (https://matplotlib.org), scipy (https://scipy.org) and astropy (http://www.astropy.org) packages.
References
- Akins, H. B., Fujimoto, S., Finlator, K., et al. 2022, ApJ, 934, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Aoyama, S., Hirashita, H., & Nagamine, K. 2020, MNRAS, 491, 3844 [NASA ADS] [Google Scholar]
- Appleton, P. N., Guillard, P., Boulanger, F., et al. 2013, ApJ, 777, 66 [CrossRef] [Google Scholar]
- Baes, M., & Camps, P. 2015, Astron. Comput., 12, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Zhu, G., Ferguson, H. C., et al. 2015, MNRAS, 450, 1546 [CrossRef] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchio, M., Marassi, S., Schneider, R., et al. 2016, A&A, 587, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Smit, R., Schouws, S., et al. 2022, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Cardamone, C. N., van Dokkum, P. G., Urry, C. M., et al. 2010, ApJS, 189, 270 [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Maiolino, R., Smit, R., & Amorín, R. 2018, ApJ, 854, L7 [Google Scholar]
- Casteels, K. R. V., Conselice, C. J., Bamford, S. P., et al. 2014, MNRAS, 445, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Conselice, C. J., & Arnold, J. 2009, MNRAS, 397, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [CrossRef] [Google Scholar]
- Conselice, C. J., Rajgor, S., & Myers, R. 2008, MNRAS, 386, 909 [CrossRef] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Duncan, K., Conselice, C. J., Mundy, C., et al. 2019, ApJ, 876, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L., Schaerer, D., Lemaux, B. C., et al. 2020, ApJS, 247, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Oh, S. P. 2023, ARA&A, 61, 131 [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Ferrara, A., Vallini, L., Pallottini, A., et al. 2019, MNRAS, 489, 1 [Google Scholar]
- Fudamoto, Y., Smit, R., Bowler, R. A. A., et al. 2022, ApJ, 934, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Ouchi, M., Ferrara, A., et al. 2019, ApJ, 887, 107 [Google Scholar]
- Fujimoto, S., Silverman, J. D., Bethermin, M., et al. 2020, ApJ, 900, 1 [Google Scholar]
- Gallerani, S., Pallottini, A., Feruglio, C., et al. 2018, MNRAS, 473, 1909 [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Ginolfi, M., Graziani, L., Schneider, R., et al. 2018, MNRAS, 473, 4538 [NASA ADS] [CrossRef] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020a, A&A, 633, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020b, A&A, 643, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glatzle, M., Ciardi, B., & Graziani, L. 2019, MNRAS, 482, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzle, M., Graziani, L., & Ciardi, B. 2022, MNRAS, 510, 1068 [Google Scholar]
- Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Anders, E. 1989, AIP Conf. Ser., 183, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [Google Scholar]
- Herrera-Camus, R., Sturm, E., Graciá-Carpio, J., et al. 2018, ApJ, 861, 95 [Google Scholar]
- Herrera-Camus, R., Förster Schreiber, N., Genzel, R., et al. 2021, A&A, 649, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [Google Scholar]
- Hummels, C. B., Smith, B. D., Hopkins, P. F., et al. 2019, ApJ, 882, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, G. C., Béthermin, M., Fudamoto, Y., et al. 2020, MNRAS, 491, L18 [Google Scholar]
- Jones, G. C., Vergani, D., Romano, M., et al. 2021, MNRAS, 507, 3540 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Kimm, T., Sijacki, D., & Haehnelt, M. G. 2017, MNRAS, 468, 4831 [Google Scholar]
- Kaviraj, S., Huertas-Company, M., Cohen, S., et al. 2014, MNRAS, 443, 1861 [CrossRef] [Google Scholar]
- Knollmann, S. R., & Knebe, A. 2009, ApJS, 182, 608 [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Lambert, T. S., Posses, A., Aravena, M., et al. 2023, MNRAS, 518, 3183 [Google Scholar]
- Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [Google Scholar]
- Lee, M. M., Schimek, A., Cicone, C., et al. 2024, ArXiv e-prints [arXiv:2403.00924] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [Google Scholar]
- Lupi, A., & Bovino, S. 2020, MNRAS, 492, 2818 [Google Scholar]
- Lupi, A., Pallottini, A., Ferrara, A., et al. 2020, MNRAS, 496, 5160 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Maio, U., Dolag, K., Ciardi, B., & Tornatore, L. 2007, MNRAS, 379, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Maio, U., Ciardi, B., Dolag, K., Tornatore, L., & Khochfar, S. 2010, MNRAS, 407, 1003 [CrossRef] [Google Scholar]
- Maio, U., Khochfar, S., Johnson, J. L., & Ciardi, B. 2011, MNRAS, 414, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Marassi, S., Chiaki, G., Schneider, R., et al. 2014, ApJ, 794, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Marassi, S., Schneider, R., Limongi, M., et al. 2015, MNRAS, 454, 4250 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mroczkowski, T., Gallardo, P. A., Timpe, M., et al. 2024, A&A, submitted [arXiv:2402.18645] [Google Scholar]
- Oser, L., Naab, T., Ostriker, J. P., & Johansson, P. H. 2012, ApJ, 744, 63 [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2017, MNRAS, 465, 2540 [CrossRef] [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Peeples, M., Behroozi, P., Bordoloi, R., et al. 2019, BAAS, 51, 368 [NASA ADS] [Google Scholar]
- Péroux, C., & Howk, J. C. 2020, ARA&A, 58, 363 [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 495, 160 [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2023, MNRAS, 519, 4608 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Narayanan, D., Somerville, R. S., Faisst, A. L., & Krumholz, M. R. 2019, MNRAS, 482, 4906 [Google Scholar]
- Posses, A. C., Aravena, M., González-López, J., et al. 2023, A&A, 669, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posses, A., Aravena, M., González-López, J., et al. 2024, A&A, submitted [arXiv:2403.03379] [Google Scholar]
- Reeves, A. M. M., & Hudson, M. J. 2024, MNRAS, 527, 2037 [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [Google Scholar]
- Romano, M., Cassata, P., Morselli, L., et al. 2021, A&A, 653, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, M., Morselli, L., Cassata, P., et al. 2022, A&A, 660, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, M., Nanni, A., Donevski, D., et al. 2023, A&A, 677, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, M., Donevski, D., Junais, et al. 2024, A&A, 683, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schaerer, D., Ginolfi, M., Béthermin, M., et al. 2020, A&A, 643, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schimek, A., Decataldo, D., Shen, S., et al. 2024, A&A, 682, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007a, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007b, ApJS, 172, 1 [Google Scholar]
- Solimano, M., González-López, J., Aravena, M., et al. 2024, A&A, 689, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., Downes, D., & Radford, S. J. E. 1992, ApJ, 398, L29 [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Springel, V., Pakmor, R., Zier, O., & Reinecke, M. 2021, MNRAS, 506, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Sugahara, Y., Ouchi, M., Harikane, Y., et al. 2019, ApJ, 886, 29 [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Hathi, N. P., et al. 2015, A&A, 581, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Topping, M. W., Stark, D. P., Endsley, R., et al. 2022, MNRAS, 516, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007a, MNRAS, 382, 1050 [Google Scholar]
- Tornatore, L., Ferrara, A., & Schneider, R. 2007b, MNRAS, 382, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Borgani, S., Viel, M., & Springel, V. 2010, MNRAS, 402, 1911 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., Carniani, S., & Gallerani, S. 2020, MNRAS, 495, L22 [Google Scholar]
- van de Voort, F., Springel, V., Mandelker, N., van den Bosch, F. C., & Pakmor, R. 2019, MNRAS, 482, L85 [NASA ADS] [CrossRef] [Google Scholar]
- van Kampen, E., Bakx, T., De Breuck, C., et al. 2024, Open Research Europe, submitted [arXiv:2403.02806] [Google Scholar]
- Velusamy, T., & Langer, W. D. 2014, A&A, 572, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venditti, A., Graziani, L., Schneider, R., et al. 2023, MNRAS, 522, 3809 [NASA ADS] [CrossRef] [Google Scholar]
- Venditti, A., Bromm, V., Finkelstein, S. L., Graziani, L., & Schneider, R. 2024, MNRAS, 527, 5102 [Google Scholar]
- Ventou, E., Contini, T., Bouché, N., et al. 2017, A&A, 608, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: [CII] velocity shifts
In this section we test the presence, in any, of a velocity shift among the diffuse [CII] component and that associated with the merging galaxies. Fig. A.1 shows the [CII] flux density as a function of velocity for our sample: the diffuse component (after accounting for the possible effect of the PSF broadening; see the discussion in Sect. 3) is shown in dark green while that associated with galaxies in light green. We fit these emissions with a 1D-Gaussian function and look for any shift among its central values. The velocity shift (Δv[CII]) is reported in the top right corner of each panel. In general, we find Δv[CII] ≲ 19 km/s which suggests a small difference in the kinematics of the [CII] emission associated with the diffuse medium and that coming from the galaxies. This result is in line with what has been found previously for ALMA-ALPINE galaxies (see, e.g., Ginolfi et al. 2020a for merging systems and Fujimoto et al. 2020 for individual galaxies), and suggests that these two regions have a similar bulk motion.
 |
Fig. A.1. [CII] flux density (mJy) as a function of velocity (km/s) for our observational sample. The [CII] emission from the diffuse gas (i.e., envelope) is depicted in dark green, while in light green is the emission associated with the galaxies - assuming the FWHM-based aperture case. The emission associated with the envelope has been corrected for the 0.58 factor which takes into account that part of the emission can attributed to the tails of the PSF (see Sect. 3 for a discussion). Gaussian fits for the emission associated with the diffuse gas component and galactic one are in orange and pink respectively. The dashed vertical lines show the central values of the Gaussian fits. The velocity shift (Δv[CII]) between these two components is displayed on the top right side of each panel. |
Appendix B: Merging system H6
The synthetic merging system H6 has been considered as a peculiar system and excluded from the statistical analysis previously performed, as the two interacting galaxies are very close to each other (mean distance value: rm = 5.3 kpc; see Table 2) resulting in a smaller fraction of carbon associated with the diffuse envelope. Indeed, it is difficult to distinguish the two merging galaxies, as shown by the x-projection in the smoothed case (see the bottom right panel in Fig. B1). For this reason, we do not consider it as belonging to the "fiducial sample" of galaxies. In this system the interaction between galaxies is in such an advanced phase that the carbon mass belonging to or associated with the galaxies and that of the diffuse envelope are mixed together, leading to a tricky analysis and interpretation. Moreover, the system appears differently depending on the chosen projection, resulting in large error bars (see Figs. 9 and 10). This peculiar system, which can be considered as the synthetic counterpart of DC_873321 (see Sect. 3) needs to be treated and interpreted with care.
 |
Fig. B.1. Carbon surface density distribution in the synthetic merging system H6, each column is a projection. Top row: Green color map showing the total surface density distribution of carbon. Overplotted in orange tones is the carbon distribution in the cold gas phase (T < 5 × 104 K). Bottom row: Surface density distribution of carbon once we convolve the original map with the ALPINE-ALMA PSF. Black crosses indicate each merging galaxy and in the bottom left corner is a beam of ∼1” as a reference. The x-projection in the bottom-right panel shows that it is difficult to discriminate between the two interacting galaxies. |
Appendix C: Carbon fraction versus average distance between galaxies
In the left panel of Fig. 10 we show the correlation between the fraction of carbon in the cold gas phase that resides in the diffuse envelope and the mean distance between the merging galaxies (rm, averaged between three projections). The relation between these two quantities leads to a correlation with ρ = −0.5 and a negative trend which seems to disagree with what has been found from the analysis of the observational sample (ρ = 0.9). However, by further investigating this trend we find that the positive or negative correlation depends on the considered range of values for rm. In fact, as shown in Fig. C1, if we only consider rm up to ∼16 kpc (maximum value for the projected distance in the ALPINE sample), we recover the positive trend (ρ = 0.8) found in observations. This result highlights that the distance between the galaxies, thus the amount of time galaxies have been interacting, plays a fundamental role in the pollution of their inner CGM, suggesting that systems in their early phase of interaction (at larger distances) have less carbon-rich envelopes.
 |
Fig. C.1. Fraction of carbon mass in the cold gas phase as a function of the mean distance (rm, violet square) and physical distance (R, violet stars) between the galaxies. The horizontal and vertical gray dot-dashed lines show the fC = 0.5 value and r = 21.5 kpc, the maximum value for the x-axis in Fig. 5, respectively. |
All Tables
Properties of the eight simulated systems classified as major mergers and the two galaxies that are not involved in any major mergers.
All Figures
 |
Fig. 1. Total velocity integrated [CII] map of the six selected systems. At the top of each panel, the ID of the source is given. White contours indicate the positive significant level at 2σ of [CII] emission. Black crosses mark the center of each galaxy (see the text for more information). The ALMA beam size is given in the bottom-left corners. |
| In the text | |
 |
Fig. 2. Same as Fig. 1, but for two specific systems: (a) DC_818760 (top-left) and (b) vc_5101209780 (top-right). The white contour indicates the positive significant level at 2σ of [CII] flux, where σ[CII] = 84 mJy km/s in (a) and σ[CII] = 95 mJy km/s in (b). The dashed black ellipses indicate the FWHMx × FWHMy regions obtained by 2D Gaussian models and correspond to the apertures used to extract the [CII] spectra of (a) and (b). Finally, the black crosses mark the center of each ellipse (i.e., center of each galaxy). The ALMA beam size is given in the bottom-left corners. The lower panel shows the [CII] spectra for each component of the merging system (different line styles) extracted using 1″ (orange), FWHM-based (green), and peak apertures (pink). |
| In the text | |
 |
Fig. 3. [CII] flux density in mJy as a function of frequency (GHz) for the galaxies in our sample. Black lines are the total [CII] emission arising from the full system (galaxy + diffuse [CII] halo) and green solid lines are the sum of the emissions coming from each component of the merging system when we consider the FWHMx × FWHMy aperture. Green hatched areas show the emission coming from the diffuse [CII] halo and the [CII] fraction is in green boxes (see Sect. 3 for the definition of this quantity and discussion). |
| In the text | |
 |
Fig. 4. Trends among the [CII] luminosity coming from the diffuse halo around merging systems, Ldiff, and their integrated physical properties. Different colors refer to different apertures adopted to extract the emission from the merging galaxies, Ldiff, i, with i = 1″ (orange border), FWHM-based (green border), and peak (pink border). In each panel, the filled green pentagons are the estimates obtained after applying the correction for the tails of the ALMA PSF (see text for discussion). The green solid line and shaded areas are respectively the linear fit and the associated error for these estimates. We also report the Spearman coefficient (ρ) of the analyzed relation. Left: Ldiff is shown as a function of the [CII] luminosity coming from the galaxies, Lgal. The black dot-dashed line is the 1:1 relation. Middle and right: Ldiff as a function of the total SFR and total M⋆ of the merging systems (see Table 1). DC_873321 is highlighted in gray; see the main text for the discussion on this candidate. |
| In the text | |
 |
Fig. 5. Trends between the fraction of [CII] emission coming from the inner CGM (f[CII]; see Eq. 4) and the properties of the merging systems, such as the projected distance (rp) between the galaxies (left), the stellar mass ratio (μ⋆, middle), and the [CII] emission ratio (μ[CII], right). We show the results obtained when adopting different apertures (1″ orange border, and FWHM-based green border) needed to define the [CII] emission associated with each component of the merger. Filled green pentagons are the estimates obtained after applying the correction for the tails of the ALMA PSF (see Sect. 3 for a discussion). In each panel, the green solid line and shaded areas are respectively the linear fit and the associated error for the more conservative estimates, and we specify the Spearman coefficient (ρ) of the corresponding relation. The horizontal dot-dashed black line indicates the 0.5 value and the system DC_873321 is highlighted in gray (see text). |
| In the text | |
 |
Fig. 6. Illustration of an example of merger tree reconstruction. Starting from galaxy “a” at z = 4.5 (snap = 041), its progenitors at the previous snapshot are “b” and “c”. Merger trees have been reconstructed all simulated galaxies at z = 4.5 with masses of M⋆ ≥ 1010 M⊙, up to z = 5.1 (snap = 035). This allows us to reconstruct the mass assembly history of the simulated galaxies, identifying those systems that undergo major mergers, defined as galaxy interactions where the relative stellar mass ratio of the merging pair is 1 < μ⋆ < 4 (see text). |
| In the text | |
 |
Fig. 7. History of two merging galaxies, H4 and H98 (dubbed as “a” and “b”) shown in the left panel, reconstructed along their past merger tree, starting from z = 4.5 up to z = 5.1. At each redshift, we show both the main progenitor (black solid line) and secondary progenitor (black dashed lines), we also report the stellar mass ratio μ⋆ of the primary (green) and secondary (magenta) merging galaxies. In the middle and right panels, we show the projection on the (x, y) plane of the merging galaxies as seen in dark matter and baryonic matter components, respectively. For the sake of clarity, we only show the maps at four redshift steps (z = 5.1, 4.9, 4.7, and 4.5, from top to bottom) and galaxies are color-coded the same way as in the merger tree. |
| In the text | |
 |
Fig. 8. Properties of two synthetic merging systems with high (μ⋆ = 4.1, H2, left panels) and low (μ⋆ = 1.3, H10, right panels) stellar mass ratios at z = 4.5. First row: Maps of the stellar surface density projected along a line-of-sight parallel to the x-axis. Stellar particles are color-coded according to their age, with age ≤ 10 Myr in dark blue, age ≤ 100 Myr in light blue, and 100 Myr < age ≤ 1 Gyr in red color scale. Second row: Same as above, but for the carbon surface density distribution of H10 (μC = 3.6) and H2 (μC = 1.5), respectively. The green color map shows the total carbon surface density distribution and overplotted on that, in orange tones, is the carbon distribution in the cold gas phase (i.e., with T < 5 × 104 K). Third row: Carbon in the cold gas phase surface density distribution once we convolve the original simulated map with the ALMA PSF. Black ellipses indicate the FWHM-based apertures used to extract the carbon content associated with each merging galaxy. In the bottom left corner is a beam of ∼1″ as a reference. Black (first row) and white (second and third rows) dashed contours indicate the positive significant level at 2σ. |
| In the text | |
 |
Fig. 9. Trends between the carbon mass in the cold gas phase (T < 5 × 104 K) coming from the diffuse halo around merging systems, Mdiffuse, and their integrated physical properties. Different colors refer to projected quantities along different lines of sight parallel to the z (blue), y (pink), and x (red) axis. In each panel, white dots are Mavg (i.e., the average among the three projections), the black dashed line is the linear fit once we consider Mavg, and ρ is the Spearman coefficient corresponding to the analyzed relation. Left: Mdiffuse is shown as a function of the total carbon mass in the cold gas phase (Mtotal). Middle and right panels: Mdiffuse as a function of the total SFR and total M⋆ of the merging systems. Highlighted in gray: H2 and H6, which have peculiar structures, and for this reason, they have not been included in the fit. Green triangles are single non-interacting galaxies (see the end of this section for discussion). |
| In the text | |
 |
Fig. 10. Trends between the fraction of carbon mass in the cold gas phase (T < 5 × 104 K) in the diffuse halo (fC) and the distance (r) between the galaxies (left), the stellar mass ratio (μ⋆, middle), and the carbon mass ratio (μC, right). In particular, on the left, we show favg (i.e., the average among the three projections) as a function of both the distance averaged on the three projections (rm, violet squares) and the physical distance between the galaxies (R, violet stars). In the middle and right panels, different colors refer to fC estimated by projecting the carbon surface density along the lines of sight parallel to the z (blue), y (pink), and x (red) axis. In each panel, white dots are favg, the black line is the linear fit considering favg versus rm, μ⋆, μC, respectively. We also specify the Spearman coefficient (ρ) of each relation. H2 is not included in these plots as this system is characterized by an out-of-scale value of fC = 0.8 and H6 is highlighted in gray. The horizontal gray dot-dashed line shows the value of fC = 0.5. |
| In the text | |
 |
Fig. 11. Relation between the fraction of carbon mass (fC) and the fraction of young (age ≤ 10 Myr) stellar populations (f⋆) present in the diffuse halo of interacting (orange stars) and non-interacting (green triangles) systems. We show the mean value of fC and f⋆ of all the simulated galaxies, along with the error bars representative of the variations in different projections and the linear fit. |
| In the text | |
 |
Fig. 12. Example of the surface density distribution of carbon in the cold gas phase once we convolve the original simulated map with the ALMA PSF, for interacting (left) and non-interacting (right) systems. The line of sight is chosen parallel to the x-axis, in the bottom left corner is a beam of ∼1″ as a reference. |
| In the text | |
 |
Fig. A.1. [CII] flux density (mJy) as a function of velocity (km/s) for our observational sample. The [CII] emission from the diffuse gas (i.e., envelope) is depicted in dark green, while in light green is the emission associated with the galaxies - assuming the FWHM-based aperture case. The emission associated with the envelope has been corrected for the 0.58 factor which takes into account that part of the emission can attributed to the tails of the PSF (see Sect. 3 for a discussion). Gaussian fits for the emission associated with the diffuse gas component and galactic one are in orange and pink respectively. The dashed vertical lines show the central values of the Gaussian fits. The velocity shift (Δv[CII]) between these two components is displayed on the top right side of each panel. |
| In the text | |
 |
Fig. B.1. Carbon surface density distribution in the synthetic merging system H6, each column is a projection. Top row: Green color map showing the total surface density distribution of carbon. Overplotted in orange tones is the carbon distribution in the cold gas phase (T < 5 × 104 K). Bottom row: Surface density distribution of carbon once we convolve the original map with the ALPINE-ALMA PSF. Black crosses indicate each merging galaxy and in the bottom left corner is a beam of ∼1” as a reference. The x-projection in the bottom-right panel shows that it is difficult to discriminate between the two interacting galaxies. |
| In the text | |
 |
Fig. C.1. Fraction of carbon mass in the cold gas phase as a function of the mean distance (rm, violet square) and physical distance (R, violet stars) between the galaxies. The horizontal and vertical gray dot-dashed lines show the fC = 0.5 value and r = 21.5 kpc, the maximum value for the x-axis in Fig. 5, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} {L_{\rm [CII]}} = 1.04 \times 10^{-3} \, {F_{\rm [CII]}} \, D_{\rm L}^2(z) \, \nu _{\rm obs}(z), \end{aligned} $$](/articles/aa/full_html/2024/10/aa49164-24/aa49164-24-eq13.gif)
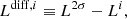
![$$ \begin{aligned} f_{\rm [CII]}^i \equiv \frac{L^{\mathrm{diff},i}}{L^{2\sigma }}\cdot \end{aligned} $$](/articles/aa/full_html/2024/10/aa49164-24/aa49164-24-eq18.gif)