| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 28 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202346945 | |
| Published online | 06 February 2024 | |
High resolution modelling of [CII], [CI], [OIII], and CO line emission from the interstellar medium and circumgalactic medium of a star-forming galaxy at z ∼ 6.5
1
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
e-mail: alice.schimek@astro.uio.no
2
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching bei München, Germany
3
UK Astronomy Technology Centre, Royal Observatory Edinburgh, Blackford Hill, Edinburgh, UK
4
Department of Astronomy & Astrophysics, University of California, 1156 High Street, Santa Cruz, CA 95064, USA
5
Astronomy Unit, Department of Physics, University of Trieste, Via Tiepolo 11, 34131 Trieste, Italy
6
INAF – Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34131 Trieste, Italy
7
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
8
Center for Theoretical Astrophysics and Cosmology, Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
Received:
19
May
2023
Accepted:
20
November
2023
The circumgalactic medium (CGM) is a crucial component of galaxy evolution, but thus far its physical properties are highly unconstrained. As of yet, no cosmological simulation has reached convergence when it comes to constraining the cold and dense gas fraction of the CGM. Such components are also challenging to observe directly, as they require sub-millimetre (sub-mm) instruments with a high sensitivity to extended and mostly diffuse emission. We present a state-of-the-art theoretical effort at modelling the [CII] 158 μm, [CI](1−0) 609 μm, [CI](2−1) 370 μm, CO(3−2) 867 μm, and [OIII] 88 μm line emissions that arise from the interstellar medium (ISM) and CGM of galaxies, with the goal of studying the contribution from different cold (T < 104 K) components of galaxy halos. We used the high-resolution cosmological zoom-in simulation PONOS (mgas = 883.4 M⊙), which represents a typical star-forming galaxy system at z = 6.5, composed of a main disc with stellar mass M* = 2 × 109 M⊙ that is undergoing a major merger. We adopted different modelling approaches based on the photoionisation code CLOUDY. Our fiducial model uses radiative transfer post-processing with RAMSES-RT and KROME (KRAMSES-RT) to create more realistic far-ultraviolet (FUV) radiation fields, which we then compared to other sub-grid modelling approaches adopted in the literature. We find significant differences in the luminosity and in the contribution of different gas phases and galaxy components between the different modelling approaches. [CII] is the least model-dependant gas tracer, while [CI](1−0) and CO(3−2) are very model-sensitive. In all models, we find a significant contribution to the emission of [CII] (up to ∼10%) and [OIII] (up to ∼21%) from the CGM. Our fiducial global radiative transfer (RT) model produces a lower density, T ∼ 104 K tail of [CII] emission that is not seen in the other more simplistic models and that resides entirely in the CGM, ionised by the FUV background and producing the extended halos observed in [CII] at high-z. Notably, [CII] and [OIII] trace different regions of the CGM: [CII] arises from an accreting filament and from the tidal tails connecting the main disc and its merging satellites, while [OIII] traces a puffy halo surrounding the main disc, probably linked to supernova feedback. We discuss our results in the context of sub-mm observations. Using simulated spectra and mock maps, we show that, despite the rather compact angular extent of PONOS’s CGM, deep ALMA observations would not detect this component, even in [CII] which is the brightest available tracer. Instead, a next generation single-dish observatory such as the Atacama Large Aperture Submillimeter Telescope (AtLAST) could detect PONOS’ CGM in [CII] at a high signal-to-noise ratio, and possibly even in [OIII].
Key words: methods: numerical / galaxies: halos / galaxies: high-redshift / galaxies: ISM / submillimeter: galaxies / submillimeter: ISM
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
We loosely define the circumgalactic medium (CGM) of a galaxy as the gaseous halo surrounding the disc and extending up to the virial radius (Rvir). It is often assumed that the CGM consists of mostly hot and warm gas (Tumlinson et al. 2017). However, the discoveries of massive (up to a few ∼109 M⊙) and fast (v > 1000 km s−1) outflows of cold and dense molecular gas extending by kpc in local starbursts and active galaxies (Feruglio et al. 2010; Fischer et al. 2010; Sturm et al. 2011; Veilleux et al. 2020; Herrera-Camus et al. 2021), and of halos of cold atomic and molecular gas extending from tens to hundreds of kiloparsecs (kpc) at high redshift (Cicone et al. 2015, 2021; Emonts et al. 2016, 2023; Ginolfi et al. 2017; Fujimoto et al. 2020; Li et al. 2021; Meyer et al. 2022; De Breuck et al. 2022; Scholtz et al. 2023; Jones et al. 2023), strongly suggest that there could be a significant cold (T < 104 K) gas component in the CGM. In the current model of galaxy formation and evolution, the CGM consists of (i) gas that has been expelled from galaxies by outflows, (ii) inflows from the intergalactic medium (IGM), and (iii) gas stripped from the interstellar medium (ISM) of satellites and merging companions (Dekel et al. 2009; Tumlinson et al. 2017; Cicone et al. 2019). Feedback processes inside galaxies, their merger histories, accretion, inflow and outflow events all leave their imprint in the CGM, which makes it a key component to study the baryonic cycle of galaxies and thus decipher galaxy evolution. In a parallel struggle to observational efforts, cosmological simulations have not been able to reproduce cold (T < 104 K) gas beyond the inner ISM region of galaxies, because of limited resolution, and so have had little to no predicting power on the presence of a cold and dense CGM or IGM components. However, the situation is improving, thanks to increased resolution and improved modelling techniques (Scannapieco & Brüggen 2015; Schneider & Robertson 2017; Mandelker et al. 2018; McCourt et al. 2018; Hummels et al. 2019; Suresh et al. 2019; van de Voort et al. 2019; Sparre et al. 2019; Nelson et al. 2021; Rey et al. 2023).
Because of the diffuse and low surface brightness nature of the ionised medium that – up to now – has been believed to account for most of the CGM mass, the CGM has been studied preferentially by analysing absorption lines in the spectra of background sources (e.g. Prochaska et al. 2014; Werk et al. 2014; Lehner et al. 2015; Bowen et al. 2016; Cooper et al. 2019; Dutta et al. 2020). However, any denser neutral and ionised CGM components could be observed in emission through atomic fine structure lines and molecular rotational transitions at far-infrared (FIR) and sub-mm wavelengths. In particular, many FIR lines such as [CII] λ158 μm that are not observable from ground at z ∼ 0 due to the Earth’s atmospheric absorption, get red-shifted into the sub-millimetre (sub-mm) atmospheric windows at higher-z, hence becoming observable with ground-based telescopes such as the Atacama Large Millimeter/Submillimeter Array (ALMA), the Atacama Pathfinder Experiment (APEX), the Northern Extended Millimeter Array (NOEMA) and, in the future, the Atacama Large Aperture Submillimetre Telescope (AtLAST)1 (Carilli & Walter 2013; Klaassen et al. 2020; Cicone et al. 2019).
Our study is part of a larger effort dedicated to deriving theoretical predictions for future AtLAST observations. AtLAST is a concept for a 50-m-class, single dish, (sub-)mm telescope to be built in the 2030 s in the Atacama desert, powered by renewable energy (Klaassen et al. 2020). Interferometers such as ALMA are ideal to study at sub-arcsec resolution targets that have a projected size of at most a few arcseconds (arcsec) on the sky, but the small field of view (FoV) and poor sensitivity to low surface brightness emission make even a powerful telescope such as ALMA inadequate to capture diffuse emission on scales of ≳10 arcsec at sub-mm wavelengths or to perform a swift and extensive mapping (Carniani et al. 2020; Cicone et al. 2019)2. AtLAST will fill this technological gap and enable us to map portions of the sky that are tens of degrees in size at an angular resolution better than < 5 arcsec at sub-mm wavelengths, by also capturing the diffuse large-scale structures (Klaassen et al. 2020; Ramasawmy et al. 2022). One of the scientific drivers of AtLAST is the study of the CGM of galaxies, which is the focus of this paper.
Because AtLAST will be able to directly image extended reservoirs – including the cold and dense gas – from ISM to IGM scales, providing robust constraints on future AtLAST line observations requires an investigation that embraces both the galaxies and their surrounding halos, as well as their cosmological context, with the highest possible resolution. It is clear that for this particular science goal, we can neither give up the resolution, because we need a realistic treatment of cold gas, nor the cosmological context, since explaining the origin of cold gas in the CGM requires tracking mergers, outflows, accreting filaments, and the interaction of these processes across cosmic times.
In this work we trace cold and warm gas components by modelling the following emission lines: [CII] λ158 μm, [CI](1−0) λ609 μm, [CI](2−1) λ370 μm, CO(3−2) λ867 μm, and [OIII] λ88 μm.
Modelling FIR/sub-mm lines presents many challenges, as they arise from a multi-phase medium (HII, HI, H2), and depend on a wide range of physical processes acting from sub-parsec (pc) to megaparsecs (Mpc) scales. In recent years there have been several efforts focusing on the exploration and analysis of cold gas tracers in galaxies, although they focused on reproducing the emission of the ISM, not the extended CGM. These studies were done by using semi-analytical models (e.g. Lagache et al. 2018; Popping et al. 2019; Pizzati et al. 2020, 2023), applying complex sub-grid modelling on lower resolution (mgas ∼ 105 − 109 M⊙) simulations to model the dense gas and to reflect a Milky Way (MW)-like population of giant molecular clouds (GMC; e.g. Olsen et al. 2015, 2017; Vallini et al. 2018; Leung et al. 2020), using radiative transfer post-processing (e.g Vallini et al. 2015; Arata et al. 2020), applying state of the art on-the-fly radiative transfer on high resolution (spatial resolution ∼10 pc) simulations (e.g. Pallottini et al. 2019, 2022; Katz et al. 2019, 2022; Lupi et al. 2020), and trying to refine the sub-grid cold gas cloud modelling (e.g. Vallini et al. 2018; Pallottini et al. 2019, 2022). Even for high resolution, state-of-the-art simulations, sub-grid modelling is necessary when trying to model the cold gas that resides in temperature and density regimes not probed by the simulation. Such sub-grid models can suffer from confirmation biases. It is worth stressing that the choice of sub-grid models can affect strongly the results, as shown by for example Popping et al. (2019), who compared the emission of GMCs by assuming different internal density profiles. In the current generation of high resolution simulations, it became evident that previous sub-grid recipes could not be applied in the same way and that new modelling approaches are needed (e.g. more refined sub-grid recipes and on-the-fly radiative transfer), which come with their own complications and challenges (Vallini et al. 2017; Bisbas et al. 2023).
We use the PONOS simulation (Fiacconi et al. 2017) at z = 6.5, which represents the high-z progenitor of a local massive galaxy. PONOS has a resolution high enough (< 4 pc) to begin to resolve GMCs, which is crucial for modelling cold gas, although the simulation is still far from reaching typical GMC densities, or from resolving the complex sub-pc filaments within GMCs (e.g. Arzoumanian et al. 2011). In this work, we apply different models for unresolved GMC structures via sub-grid density profiles, and compare their results with more recent approaches of radiative transfer calculations, by studying the effects on the derived synthetic emission lines within the same simulation. The results are then used to produce theoretical predictions that can inform future sub-mm observations. In contrast to previous modelling efforts, we especially focus on the emission originating from the CGM component of the galaxy.
This paper is structured as follows. We introduce the PONOS simulation in Sect. 2, and then detail the modelling approaches of the emission lines in Sect. 3. In Sect. 4 we discuss the differences on the resulting emission entailed by different models, and set a range of emission line luminosities that can be expected from a similar source. In Sect. 5 we compare our results with currently available observational and theoretical constraints from the literature. In Sect. 6 we discuss our results in the framework of other simulation studies. Finally, in Sect. 7 we discuss future prospects in this field, specifically in the context of the AtLAST project. Our conclusions are summarised in Sect. 8.
2. Simulation
2.1. The PONOS simulation
In this study we analyse the PONOS simulation by Fiacconi et al. (2017), which is a high-resolution cosmological zoom-in simulation run with the GASOLINE smoothed particle hydrodynamics (SPH) code (Wadsley et al. 2004) down to z = 6.5. The simulation has a gas mass resolution of mgas = 883.4 M⊙, a stellar particle mass of m* = 0.4 ⋅ mgas = 353.4 M⊙, and uses WMAP 7/9 cosmology (Ωm, 0 = 0.272, ΩΛ, 0 = 0.728, Ωb, 0 = 0.0455, σ8 = 0.807, ns = 0.961, and H0 = 70.2 km s−1 Mpc−1; Komatsu et al. 2011; Hinshaw et al. 2013). This leads to a minimum smoothing length of around 3.6 pc in the disc of the galaxy. The simulation includes a non-equilibrium chemical network for HI, HII, HeI, HeII and HeIII, and a uniform redshift-dependent ultraviolet (UV) radiation background (UVB) due to stellar and quasar reionisation, according to Haardt & Madau (2012). Cooling due to metals under the UVB is calculated and tabulated using the photoionisation code CLOUDY (last described in Ferland et al. 2017) assuming photoionisation equilibrium (Shen et al. 2010). A turbulent diffusion model is included for thermal energy and metals (Shen et al. 2010), which reduces artificial surface tension near strong density gradients and allows instabilities to develop (Agertz et al. 2007; Wadsley et al. 2017). Star formation occurs when the gas density exceeds a threshold nSF = 10 cm−3 and the gas flow is converging and Jeans unstable. Star formation is modelled with a stochastic approach, where the SFR follows the local Schmidt–Kennicutt relation 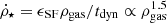 , with a star formation efficiency parameter ϵSF = 0.05. Each stellar particle represents a stellar population with a Kroupa (2001) initial mass function. Feedback due to Type Ia and Type II Supernovae is modelled following Stinson et al. (2006). The simulation tracks metal production from stellar winds, SN Ia and SN II with yields detailed in Raiteri et al. (1996). We track the α-elements and iron-peak elements separately, an approach that has been adopted with previous simulations (Guedes et al. 2011; Shen et al. 2014; Kim et al. 2014, AGORA comparison project). However, abundances between different α-elements are assumed to follow the solar abundance ratio (Asplund et al. 2009).
, with a star formation efficiency parameter ϵSF = 0.05. Each stellar particle represents a stellar population with a Kroupa (2001) initial mass function. Feedback due to Type Ia and Type II Supernovae is modelled following Stinson et al. (2006). The simulation tracks metal production from stellar winds, SN Ia and SN II with yields detailed in Raiteri et al. (1996). We track the α-elements and iron-peak elements separately, an approach that has been adopted with previous simulations (Guedes et al. 2011; Shen et al. 2014; Kim et al. 2014, AGORA comparison project). However, abundances between different α-elements are assumed to follow the solar abundance ratio (Asplund et al. 2009).
PONOS is the progenitor of a massive galaxy with a mass of Mvir(z = 0) = 1.2 × 1013 M⊙ at z = 0 (Mvir(z = 6.5) = 1.22 × 1011 M⊙ at z = 6.5). For the analysis presented in this paper, we chose the snapshot at z = 6.5, where the galaxy is undergoing a merger (stellar mass merger ratio 1:2.7). In this snapshot, the central simulated galaxy has a stellar mass of M* = 2 × 109 M⊙, a virial radius of Rvir = 21.18 kpc, and a star formation rate SFR = 20 M* yr−1. These properties make PONOS a typical star-forming galaxy at z = 6.5.
The simulation data were analysed using Pynbody (Pontzen et al. 2013). In Fig. 1 we show maps of the dark matter surface density (ΣDM), gas surface density (Σgas), and stellar surface density (Σ*) in the PONOS simulation snapshot studied in this work. The maps capture the chaotic state of the galaxy, due to the ongoing major merger.
 |
Fig. 1. Maps of the PONOS simulation at redshift z = 6.5, showing the dark matter surface density (top panel), the gas surface density (middle panel), and the stellar surface density (bottom panel). The white circle marks Rvir. The highest density structures trace the central disc and the three major satellites, two of which are close to the disc and merging with each other (merger B). Another merger can be seen in the south (A). Extended structures embedding both gas and stars lie between the main disc and the mergers. |
2.2. Component separation
In order to analyse the ISM in the galaxy and its satellites separately from the diffuse CGM, we categorise the gas in the simulation into different components: main galaxy disc, mergers, CGM. We ascribe all the particles contained within twice the half-light radius to the main galaxy disc. The mergers are masked out using a sphere with a 2 kpc radius for the southern merging companion (merger A), centred on the nucleus of the satellite, and a sphere with a 3 kpc radius for the two merging satellites closer to the disc (merger B), which are also in the process of merging with each other, and thus can not be de-blended. These spherical regions are chosen to include 98% of the stars of merger A, and 91% of the stars of merger B. The diffuse CGM is defined as all the remaining gas particles contained within the Rvir, excluding the already classified particles belonging to the main disc and to the ISM of the merging companions. Therefore, in our analysis, the definition of CGM does not include the discs of the main halo and its satellites, although observationally small merging companions would probably be unresolved and so ascribed to the CGM. Figure 2 illustrates the results of this classification in the PONOS snapshot, where the top panel shows the gas density as a contour, overlaid with the masked areas defining the ISM components due to the main disc and to the discs of the merging satellites, while the bottom panel shows the gas density map of the CGM components.
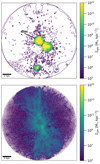 |
Fig. 2. Gas density maps, showing the identification and de-blending of ISM and CGM gas components in the PONOS simulation snapshot. The top panel shows the ISM components, which include the main galaxy disc (including all gas particles within twice the half light radius) and the discs of the merging satellites. The gas density of the “non-ISM” particles is shown by the purple contours. The bottom panel shows the CGM component, made up by all gas within the Rvir after masking out the galaxy discs. |
Throughout this paper we divide gas particles into two phases, based on their temperature and density. Particles with temperatures T ≲ 104 K and densities nH ≳ 10 cm−3 are classified to be dense, and trace gas that would fall into the star formation criteria in the simulation. The diffuse phase traces gas particles that would not form stars. We use the terms of dense gas phase and star-forming gas interchangeably, and use the term diffuse gas for all gas that is not classified as dense and cold, even though it might be dense and hot. This definition is used for all models, although these two gas phases are only treated separately in the multi-phase model approach in Sect. 3.2. Additionally, we define the diffuse gas to be ionised, when the gas particle has an electron fraction ≥0.5. The dense, star-forming gas makes up around 20% of the total baryon mass of the simulation.
3. Modelling
In this study, we are comparing three different approaches for modelling the unresolved gas phases in the PONOS simulation, with varying levels of complexity, which in total deliver six different predictions for the explored emission lines. For all models, the CLOUDY photoionisation code was used to derive synthetic line emission based on gas properties. The following sections will describe each model in detail. Figure 3 illustrates the steps of the different approaches.
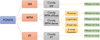 |
Fig. 3. Flowchart illustrating our three different modelling approaches: simple model (SM), multi-phase model (MPM), and global radiative transfer (RT) approach, which are described in detail in Sects. 3.1–3.3. The RT is our fiducial model. The corresponding CLOUDY parameters are reported in Table 1. |
3.1. Simple model
In the simple model (SM), we take the gas properties (density, temperature, metallicity) directly from the simulation, and use those as an input for CLOUDY. This will mainly serve as a simple test for the comparison with more advanced models. Instead of carrying out a CLOUDY run for every single gas particle in the simulation, multi-dimensional grids were created, spanning over parameter ranges taken from the simulation (see Table 1), and then interpolated over the values of SPH particles. Such grid approach is commonly used in studies to create synthetic emission of galaxies (Olsen et al. 2015, 2018; Pallottini et al. 2019, 2022; Katz et al. 2019, 2022; Lupi et al. 2020).
CLOUDY grid values for all different models.
We use a slab geometry, so that each particle is considered as a gas slab using the given density, temperature and metallicity from the grid. CLOUDY divides the computational domain (i.e. one cloud) into thin layers (concentric shells for spherical geometry, thin layers for slab geometry), called “zones”. For the SM, we use the thickness of the cloud as a stop criterion, setting it equal to the maximal smoothing length, and we iterate until convergence. The depletion of heavier elements onto dust is self-consistently included in the CLOUDY model, and is set to scale linearly with the metallicity of the particles, which is used as an input parameter in our grid. The size distribution and abundances of the dust are appropriate for a MW-like galaxy, and reproduce observed extinction properties, with the assumption of a MW-like gas to dust ratio and solar abundance ratios (Ferland et al. 2017). At the redshift of the PONOS snapshot, the cosmic microwave background (CMB) temperature is around 20 K, which is quite high in relation to the temperature of the gas emitting the FIR and sub-mm lines targeted in this study. Therefore CMB radiation is included in the models, and assumed to be isotropic.
The radiation field G0, bg, which is defined to be the ionising FUV radiation field between 6 and 13.6 eV in units of Habing (1.6 × 10−3 erg cm−2 s−1; Habing 1968), is assumed to be uniform and it is scaled to the average star formation rate density of the galaxy ΣSFR following:
where G0, MW = 9.6 × 10−4 erg cm−2 s−1 ( = 0.6 Habing) and ΣSFR, MW = 0.0024 M* yr−1 kpc−3 are the average FUV flux and the average SFR density in the MW (Seon et al. 2011). Including FUV radiation in the modelling of emission lines originating from photo-dissociation regions (PDRs) is necessary, as photons in this energy range are responsible for the photo-dissociation and ionisation of molecules and atoms. Additionally, FUV radiation is important for regulating the temperature in PDRs (Hollenbach & Tielens 1999; Wolfire et al. 2022). The FUV field, determined with the CLOUDY ISM table, has the spectral shape of the solar neighbourhood, and is considered to be the interstellar radiation field (ISRF) of the galaxy. We note that this is different from the SIGAME approach by Olsen et al. (2017), where the FUV radiation field for the dense phase also includes fluxes from individual star particles within the smoothing length of each gas particle, without absorption. While this approach is likely accurate for lower resolution simulations where individual gas particles have a similar or larger mass than a GMC, it cannot be directly applied to PONOS, in which each gas particle is a part of a larger GMC complex structure, and absorption along the line of sight would be important. Indeed, simply counting radiation from within the smoothing length results in a significant overestimation of the local radiation field. Within the framework of post-processing, the most accurate way to compute the FUV field (both intensity and spectra shape) is the global radiative transfer modelling, and we explore this in our fiducial model (Sect. 3.3). Thus, for simplicity, our simple and multi-phase model only includes the ISRF. We stress that these two models only serve as a first (and rather crude) exploration of the challenges of modelling FIR/sub-mm line emission without a global RT calculation for simulations that start to resolve the GMC structure. They are not intended to replicate Olsen et al. (2017, 2018). Cosmic rays are included, with a rate ζCR scaled to G0, bg:
where ζCR, MW = 3 × 10−17 s−1 is the average CR rate in the MW (Webber & Soutoul 1998). The parameters used for the CLOUDY runs for the SM are summarised in Table 1.
3.2. Multi-phase model
The multi-phase model (MPM), which is loosely based on the approach by Olsen et al. (2017), differs from the SM in the sense that the particles are already divided into a dense and a diffuse phase before the CLOUDY grid is applied, using the same dense gas criterion that was introduced in Sect. 2.2. The two gas phases are treated differently, and separate CLOUDY grids are applied. For the diffuse phase, we use the same approach as in the SM, interpolating over CLOUDY runs across the same parameter grid created previously for the SM.
For the dense phase, we adopt a different approach. Every gas particle that has been classified as being dense and cold is interpreted as an individual GMC. This approach is commonly adopted in lower resolution simulations, as typical local GMC masses range from 104 − 106 M⊙, whereas the mass resolution of PONOS is mgas = 883.4 M⊙. As mentioned in the previous section, precisely due to this resolution challenge, there exist substantial differences in the calculation of FUV field between our MPM model and SIGAME. Nevertheless, we still find it instructive to assess the performance of such MPM model applied to PONOS, and compare the results obtained with different sub-grid GMC density models. We consider four possible sub-grid density profiles3 for the GMCs, hence each giving rise to a different MPM “sub-model”: (1) a Plummer sphere profile, (2) a logotropic profile, (3) a power-law profile and (4) a two-component Gaussian. Profiles 1, 2 and 3 have already been tested by Popping et al. (2019) in their semi-analytical models (SAMs). Since these authors found that even small changes in the sub-grid prescription can lead to significant differences in the FIR line emission, we want to test here how the use of different density profiles affect the emission in the context of a galaxy simulation. Each of the profiles is described in more detail below. We also include turbulence within the CLOUDY model, adopting the internal velocity dispersion σv derived by Olsen et al. (2015):
where P is the pressure of the SPH particle and RGMC is the cloud radius, derived from the SPH particle mass and the pressure, following the pressure-normalised scaling relation for virialised GMCs (e.g. Field et al. 2011):
Figure 4 shows a comparison of the different radial density profiles. We implement these profiles in CLOUDY using 30 radial bins, and using the “dlaw” CLOUDY parameter, which allows to input custom density profiles (Ferland et al. 2017, see CLOUDY documentation). In contrast to the diffuse phase, for the GMCs we assumed a spherical geometry, and derived the emission in each shell as a function of the radius, which was summed up to give the total emission of the cloud.
 |
Fig. 4. Qualitative representation of the different sub-grid cloud density profiles applied in the MPM. |
3.2.1. Plummer profile
The Plummer profile (Plummer 1911), first introduced to fit observations of globular clusters, was suggested by Whitworth & Ward-Thompson (2001) to also fit GMCs (Zucker et al. 2021), pre-stellar core and class 0 proto-star density profiles (Popping et al. 2019). The density n as a function of radius R is given by:
where Rp = 0.1 RGMC, MGMC is the cloud mass (i.e. the SPH particle mass from the simulation).
3.2.2. Logotropic profile
A logotrope is a limiting form of a polytrope, where the polytropic index γ = 0 (Chavanis & Sire 2007). A logotropic profile was used by Olsen et al. (2015, 2017) in their modelling, using the SIGAME approach. The larger particle mass allowed the authors to divide their gas particles or fluid elements into GMCs according to the GMC mass function. The higher resolution of PONOS does not allow us to apply this method, and instead we ascribe one individual cloud to each gas particle. The radial density profile is given by:
where:
is the external density. We note that in this recipe, the density is infinite at the centre of the cloud (see also Fig. 4).
3.2.3. Power law profile
The third density profile that we explore is a power law profile:
using an with exponent of α = 2. According to the findings by Walker et al. (1990), this type of profile fits the density profiles of molecular cloud cores, which was also tested by Popping et al. (2019). Similar to the logotropic profile, the power law profile has an infinite central density, which needs to be handled properly when using these profiles in CLOUDY, by choosing some ‘cut off’ density value. We found that the results are very sensitive to the choice of such a parameter, and a slight difference can change the resulting integrated line luminosity even by three orders of magnitude. We calculated the value of the cut-off density by choosing a radius close to the centre of the cloud, where the density values are within realistic central densities of 105 − 106 cm−3 (e.g. see findings by Bergin et al. 1997 and recent observations by Zhang et al. 2018), and allowing densities up to 109 cm−3. This was done by estimating if the most inner radial bin still had realistic density values. If the density was too high, a radius half way between the last and second to last radial bin value was chosen, to calculate the density, which was used as the cut-off density.
3.2.4. Two-component Gaussian profile
Finally, we also explored a two-component Gaussian (2CG) profile, motivated by Zucker et al. (2021), who found that this provides a good fit to local GMCs measured with the Gaia satellite (Gaia Collaboration 2018; Leike et al. 2020). This profile is described by:
The four free parameters (a1, a2, σ1, σ2) were made dependent on cloud properties. In particular, σ1 and σ2 depend on the cloud radius (σ1 = 0.05 R and σ2 = 0.2 R), while a1 and a2 were set to depend on the central density of the Plummer profile (a1 being equal to the central density in the Plummer profile, and 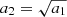 ). Both the Plummer profile and the 2CG profile have finite central densities and, based on Zucker et al. (2021), we set them to reach the same central densities, as shown in Fig. 4. Physically, the transition between the inner and outer Gaussians in the 2CG profile represent a shift in temperature, density, or chemical composition of the gas in the cloud (Zucker et al. 2021). The shift in density could represent the transition between the molecular and atomic gas phases, and the one in temperature could be a transition between an unstable warm neutral medium and a cold neutral medium.
). Both the Plummer profile and the 2CG profile have finite central densities and, based on Zucker et al. (2021), we set them to reach the same central densities, as shown in Fig. 4. Physically, the transition between the inner and outer Gaussians in the 2CG profile represent a shift in temperature, density, or chemical composition of the gas in the cloud (Zucker et al. 2021). The shift in density could represent the transition between the molecular and atomic gas phases, and the one in temperature could be a transition between an unstable warm neutral medium and a cold neutral medium.
3.3. Global radiative transfer model
The global radiative transfer (RT) approach provides our fiducial modelling of the FIR and sub-mm line emissions from PONOS. Although the post-processing with CLOUDY is also a RT technique, we now apply a global RT calculation over the whole simulation, taking into account the propagation of photons from all emitting sources, so that we can have a more accurate estimate of the UV flux in each point of the simulation box. The PONOS simulation was post-processed with KRAMSES-RT (Pallottini et al. 2019; Decataldo et al. 2019, 2020), a customised version of RAMSES-RT (Teyssier 2002; Rosdahl et al. 2013) where a non-equilibrium chemical network generated via the package KROME (Grassi et al. 2014) has been implemented. In this way, the radiation field in each grid cell is computed with an accurate scheme of radiative transport accounting for gas self-shielding. This is different from using a uniform background radiation scaled with ΣSFR, which was done in the simpler SM and MPM approaches. The resulting radiation flux is then directly used as input in the CLOUDY grid, after being sampled using ten flux bins. In the RT approach, a sub-grid modelling of the dense gas phase (GMCs) is not necessary, since the RT naturally creates a multi-phase medium, and so the temperature, metallicity and density values needed to compute the resulting line emissions are taken directly from the post-processed simulation data. However, due to the finite resolution, our maximal reachable density is n ∼ 103 cm−3, hence, despite having mitigated this issue compared to lower-resolution cosmological simulation, the resulting molecular gas fractions should be regarded as lower limits.
3.3.1. RT post-processing
To post-process the PONOS simulation with KRAMSES-RT, we first convert the SPH simulation into an adaptive-mesh-refinement (AMR) grid. To do this, we select particles with coordinates within a box of size 50 kpc, which is slightly larger than twice the Rvir and thus encompasses the whole region defined as the CGM. The simulation box is initially tiled with 323 cells (coarse resolution). We assign values of density, thermal pressure, metallicity and different elements abundances (HI, HII, He, HeI, HeII, electrons) from the SPH particles to the cells using a cloud-in-cell (CIC) scheme. The resolution is increased whenever the gas mass in a cell is larger than 32 times the gas mass resolution in the original SPH simulation, by using up to ten additional levels of refinements and repeating recursively the CIC interpolation to assign values to the refined cells. This is designed to always resolve the smoothing length of each particle in the SPH simulation. The final AMR grid has a resolution ranging from 195.3 pc in the outer low density regions, to a maximum of 1.52 pc in the dense disc gas.
Since the original PONOS simulation does not include H−, H2 and 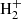 , which are instead accounted for in KROME, we assume initial zero abundance for those species, and then run the chemical network over the whole box for a time t = 20 Myr in isothermal conditions and with a uniform UVB as the only radiation source (from the Haardt & Madau 2012, tables at z = 6.49) attenuated according to the cell’s optical depth. The chemical evolution is accomplished in small time-steps of dt = 0.1 Myr, and the flux in each cell is attenuated at every time-step according to the opacity of the cell. We verified in single-cell tests with KROME that 20 Myr are enough to reach the equilibrium abundances for all chemical species, for a range of initial temperature and gas densities that represent the values found in PONOS.
, which are instead accounted for in KROME, we assume initial zero abundance for those species, and then run the chemical network over the whole box for a time t = 20 Myr in isothermal conditions and with a uniform UVB as the only radiation source (from the Haardt & Madau 2012, tables at z = 6.49) attenuated according to the cell’s optical depth. The chemical evolution is accomplished in small time-steps of dt = 0.1 Myr, and the flux in each cell is attenuated at every time-step according to the opacity of the cell. We verified in single-cell tests with KROME that 20 Myr are enough to reach the equilibrium abundances for all chemical species, for a range of initial temperature and gas densities that represent the values found in PONOS.
After these preparation steps, we let the simulation evolve with radiative transfer and chemical evolution, but no dynamical evolution (RT post-process step). Stellar spectra are computed with STARBURST 99 (SB99; Leitherer et al. 1999), according to the age and the metallicity of the stellar particle, and then rescaled to its mass. To reduce the computational cost of loading photons for each stellar particle, particles located in the same cell are merged together, reducing the number of particles by 65%, without changing the results as the total amount of photons propagated into the surrounding cells are unchanged. Stellar radiation propagates into the grid according to RAMSES-RT’s moment-based scheme, with full speed of light (we do not use a reduced speed of light).
Additionally to stellar radiation, a uniform UVB (Haardt & Madau 2012, tables at z = 6.49) is included and attenuated in each cell according to the column density of each chemical species. Since the density of cells at the centre of the box (i.e. in the galaxy disc) is high enough to completely absorb the UVB, this approach is meant to approximate a more realistic model where the UVB radiation is propagating inwards from the outside of the galaxy and absorbed on its way to the center. We notice that including an UVB is important especially for low density CGM gas, yielding lower H2 abundances in the outskirts of the galaxy. We allow the temperature to evolve together with the abundances during the post-process, but we do not allow gas hotter than T = 106 K to cool down, since we assume that such gas was heated because of shocks due to stellar mechanical feedback (which was included in the original SPH simulation, while there is no dynamical evolution in the RT post-process) and we do not want to loose its imprint on gas temperature and chemical composition. We evolve in this way until the variation of chemical abundances is less than 0.1% in two consecutive timesteps, which was around t ∼ 1 Myr, more than five times the light-crossing time of the entire box.
The results of the post-processing are shown in Fig. 5, reporting the surface density map of the H2 gas fraction, and in Fig. 6, showing the gas mass weighted distribution of G0, divided into the different galaxy components. Most of the H2 resides inside the main disc and in the close merging companion (component B in Fig. 1), with some filaments and clouds in the CGM also displaying a non-negligible H2 fraction. Due to the radiation of young stars, the highest G0 values are found in the disc and in the merger components, while the radiation field in the CGM is weaker.
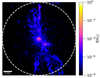 |
Fig. 5. H2 gas fraction in PONOS obtained from the RT post-processing with KRAMSES-RT. Most of the H2 resides in the main disc and in the merging component B, although clouds of molecular gas are also formed in the CGM, especially in the northern accreting filament. |
 |
Fig. 6. Distribution of the log(G0) values of the PONOS simulation after RT post-processing. In black the distribution for the whole halo is shown, while in purple the disc, in orange the merger component, and in pink the CGM is represented. The high log(G0) values are part of the disc and mergers, where the gas experiences UV radiation from young stars. The black dashed line represents the background radiation used in the SM and MPM. |
3.3.2. CLOUDY post-processing
It has to be noted that there are some inconsistencies when combining the post-processing with KRAMSES-RT and CLOUDY. More specifically, RAMSES-RT in combination with KROME solves non-equilibrium photo-chemistry, while CLOUDY (which we use for further analysis) assumes a photoionisation equilibrium. The parameters of the CLOUDY grid used in the RT model are reported in Table 1. With respect to previous models, the FUV flux G0 is not assumed proportional to the ΣSFR, but it can be inferred from the RT simulation. Since adding another parameter for each radiation band is computationally expensive, we compute the FUV flux into the range [6, 13.6] eV and add the corresponding G0 as parameter to the CLOUDY grid models. In this way, the total amount of CLOUDY models is 42560. Nevertheless, we retain the information about the shape of the spectra, by computing the median spectra among all fluid elements residing within a G0 bin and importing it in CLOUDY via the “table SED” command (which allows to import a custom spectrum). To account for the AMR structure of the grid, we integrate the emission originating from CLOUDY to a depth corresponding to the cell size, multiplying it by the surface area of the cell:
where J is the total integrated emission, I(l) is the emission of a thin slab at distance l, li is the size of a cell at the refinement level i, and 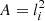 is the surface of a grid cell. Temperatures, gas densities, and metallicities are taken from the KRAMSES-RT post-processed simulation. Emission line luminosities are derived from the simulation by interpolating over the CLOUDY grid, accounting for the cell size.
is the surface of a grid cell. Temperatures, gas densities, and metallicities are taken from the KRAMSES-RT post-processed simulation. Emission line luminosities are derived from the simulation by interpolating over the CLOUDY grid, accounting for the cell size.
4. Results
4.1. Comparison of the six different model results
Figure 7 shows the total luminosities in each line ([CII], [CI]609 μm, [CI]370 μm, CO(3−2) and [OIII]) obtained with the six different models. The different symbols represent the different halo components, with circles corresponding to the total line luminosity from the whole computational box. The corresponding luminosity values for all models are listed in Table B.1.
 |
Fig. 7. Comparison of line luminosities (in solar luminosities) obtained with our six modelling strategies (see summary in Fig. 3), computed for different halo components. Each model is represented by a different colour: SM (grey), MPM+Plummer (purple), MPM+Logotropic (yellow), MPM+Power law (magenta), MPM+2-component Gaussian (orange), and RT (black). Different halo components are indicated using symbols: circle markers for the whole PONOS halo, crosses for the main disc, pentagons for the mergers, and diamonds for the CGM (see Sect. 2.2 or the definition of the components). For the SM, dense gas tracers such as CO are unrealistically low and outside the ranges shown in this plot. |
The left-most panel of Fig. 7 shows the [CII] luminosity values obtained with the different models. The [CII] emission line is one of the brightest gas tracers in the FIR, accounting for 0.1−1% of the total FIR emission of a star-forming galaxy (Stacey et al. 1991). Single ionised carbon has a lower ionisation potential (11.6 eV) than hydrogen (13.6 eV), and is sensitive to the UV radiation emitted by young, massive stars. [CII] is one of the main coolants in the ISM (Tielens & Hollenbach 1985; Wolfire et al. 2022), the main cooling transition for the cold atomic medium (Veilleux et al. 2020), and traces both the neutral and ionised gas. C+ is collisionally excited by molecules, atoms or electrons, depending on its environment, as it can reside co-spatially with molecular, neutral atomic and ionised hydrogen, due to its low ionisation potential (Olsen et al. 2015, 2017; Leung et al. 2020; Lupi et al. 2020). In the figure, it can be seen that the [CII] luminosity values obtained with the different models are not too dissimilar from each other, differing at most by one and a half orders of magnitude. The RT model (plotted in black) produces the lowest [CII] emission, with over 60% originating from the disc, and 56% originating from the gas classified as dense. The second lowest [CII] emission results from the MPM that employs a logotropic density profile for the dense gas in GMCs (plotted in yellow in Fig. 7). In this model, most of [CII] originates from the disc, and over two thirds of the emission arises from gas classified as dense. We thus obtain the opposite trend with respect to Popping et al. (2019), who found the logotropic density profile to produce the highest luminosities, followed by the power law profile and finally the Plummer profile. Instead, in our study, the 2CG and Plummer profile result in the highest [CII] luminosity values. We ascribe such effect to (i) the increased PDR covering fraction, which is seen in all MPM models, and is due to the assumption that every SPH particle represents a GMC; and (ii) to the shape of the density profile itself. Indeed, both the Plummer and the 2CG profile have large wings spanning densities of nH ∼ 100 − 104 cm−3, which are typical densities for [CII] emission for the temperatures where the sub-grid density profiles are applied (Goldsmith et al. 2012).
The atomic carbon ([CI]) lines, shown in the second and third columns of Fig. 7, display large differences between the tested models, especially in the lowest frequency transition ([CI](1−0) 609 μm). Atomic carbon is thought to reside mostly in molecular gas, as it needs some degree of shielding due to the low ionisation potential of C+ of hν = 11.6 eV. [CI] lines are optically thin and usually do not trace a large reservoir of carbon, as most is either ionised to C+, or bounded into a CO molecule (Popping et al. 2019; Valentino et al. 2020; Dunne et al. 2022). Papadopoulos et al. (2022) found that the [CI](2−1) and (1−0) lines are sub-thermally excited, and their ratio thus does not reflect the molecular gas temperatures of galaxies. Although classically believed to arise from a narrow layer in PDRs, it has been shown that [CI] emission is well mixed and co-spatial with CO, thus confirming that [CI] represents a valid alternative H2 tracer (Papadopoulos et al. 2022; Thi et al. 2009; Hartigan et al. 2022; Montoya Arroyave et al. 2023). In our modelling, the SM produces the lowest [CI] emission in all components. In all four MPM models, [CI]609 μm is brighter than [CI]370 μm, which is an opposite trend to the one produced by the SM and RT models. This is due to the fact that [CI](1−0) probes higher densities than [CI](2−1), which are reached in the MPM but not in the SM and RT. The MPM models do not show significant differences from one another in [CI] line emission. [CI]370 μm appears to be less model sensitive than [CI]609 μm.
The fourth column of Fig. 7 shows the synthetic emission of CO(3−2), which also displays a strong model dependency. Carbon monoxide (CO) rotational lines are the best proxies for tracing the cold H2 gas in external galaxies, as they are bright, and can be studied over a wide range of redshifts. When available in combination with [CII] data, CO(3−2) line observations can help us determine what fraction of the [CII] emission originates from molecular gas. We choose the CO(3−2) line as it is the lowest-J CO transition that is observable with sub-mm telescopes at z > 6. CO(3−2) traces the surface of warmer and denser molecular gas, compared to lower J transitions (Wilson et al. 2008; Carilli & Walter 2013; Leroy et al. 2022). Despite its higher excitation requirements compared to lower-J CO lines, in starburst galaxies this line can trace the bulk of the H2 gas reservoir (Bothwell et al. 2013; Montoya Arroyave et al. 2023), and it has the advantage of a higher contrast against the CMB (da Cunha et al. 2013; Zhang et al. 2016).
The large variance of [CI] and CO values delivered by the different models is expected, since these low energy transitions are produced in the densest gas (concomitant with H2), which is very sensitive to post-processing recipes in all cosmological simulations as they cannot resolve the scales relevant for H2 formation (< 0.1 pc). As a result, the MPM models, which include ad-hoc sub-resolution treatments of dense gas, estimate higher [CI] and CO values than the other models. The SM values of CO(3−2) are so low that they are outside the lower range included in the plot (LCO(3 − 2) = 4.3 × 10−4 L⊙ for the SM). The MPM approach produces reasonable values of CO luminosity, as in the MPM models every dense cloud (particle) is assigned a sub-grid density profile that reaches densities high enough for sizable molecular gas emission. Instead, the RT model relies on the post-processed density values of shielded clouds, which do not reach the typical densities expected in GMCs (n ∼ 104 − 105 cm−3) because of the finite resolution limit of PONOS, which results in low CO emission. Thus, the resulting CO values in the fiducial model should be interpreted as lower limits.
The right-most panel of Fig. 7 shows the results of our modelling of the [OIII]88 μm line, the only tracer of warm ISM included in our analysis (T ∼ 104 − 5 × 105 K). [OIII] is a common tracer of HII regions, as O++ has a high ionisation potential of 35 eV and so it needs hot, massive stars to be ionised. Thus, this line can be used to map recent star formation, and it is an extinction-free probe for the conditions of the gas (Ferkinhoff et al. 2010). [OIII]88 μm is one of the brightest FIR fine structure lines and it can be observed with ease from ground from z ≥ 8, hence it is, together with [CII], a major player in follow-ups of very high-z candidates (De Looze et al. 2014; Inoue et al. 2016; Carniani et al. 2018, 2020; Hashimoto et al. 2018, 2019; Harikane et al. 2020; Fujimoto et al. 2022; Witstok et al. 2022; Algera et al. 2024; Popping 2023; Ren et al. 2023). In contrast to the often used optical [OIII] emission lines (e.g. 5007 Å), the FIR [OIII] lines have a different dependence on the physical conditions of the gas, being less sensitive to the gas electron temperature and most sensitive to the electron density, as their critical density for collisional de-excitation to dominate is quite low (Dinerstein et al. 1985). Since [OIII] probes warm gas in HII regions, this tracer is not affected by the implementation of sub-grid density profiles in our study, and as a consequence all four MPM models deliver the same [OIII] luminosity values (as shown by the overlapping MPM symbols in Fig. 7). The [OIII] values produced by the RT model are lower than in the SM and MPM models because [OIII] emission is weakened by the heating and cooling processes in place during in the post-processing of the RT run, which is investigated further below.
Figure 8 shows the density–temperature (n − T) phase diagrams resulting from the different models, colour-coded according by line luminosities. Each column represents a different emission line, and the rows show the different models. The phase diagram allows us to to understand which portion of the gas (in terms of densities and temperatures) is responsible for the emission of each line. For the MPM models, it is important to note that the densities shown in Fig. 8 are those taken directly from the simulations, so they do not correspond to the values passed to CLOUDY in order to model unresolved GMCs, which have sub-grid density profiles. Because of this, the diagrams look quite similar for all models except for the RT one, due to the temperature evolution of the gas during the post-processing where heating and cooling processes are at work. In particular, the hot and dense gas phase (top-right corner of each sub-plot) has disappeared after the RT post-processing due to cooling, while some gas at lower densities is heated up by stellar radiation. The hot and dense phase is a result of the stellar feedback in the simulation, where SNe shocks heat up the gas in the ISM. Such gas has a very short cooling time, and thus would not be long lasting. In the PONOS simulation a blast wave SNe feedback is employed, where the cooling is delayed (Stinson et al. 2006), leading to this gas phase being present in the snapshot. During the RT post-processing this hot dense gas is allowed to cool. Additionally, the cold and diffuse gas phase is heated up by stellar radiation.
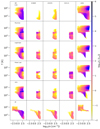 |
Fig. 8. Density–temperature (n − T) phase diagram of all six models used in this analysis. The rows show the different models, while the columns represent the different synthetic emission lines. The colours represent the emission in a particular line. For the MPM the densities do not directly correspond to those taken directly from the simulations, as they are given sub-grid density profiles, as described in Sect. 3.2. The bottom row corresponds to the fiducial RT model, and it shows how the RT post-processing produces densities and temperatures that differ from the original simulation. |
The first column of Fig. 8 confirms the multi-phase origin of the [CII] emission, which traces gas spanning at least three orders of magnitude in T and n, with a major contribution from denser gas. It can also be seen that while the emission varies between the models, the differences are, as was already seen in Fig. 7, not as strong as for other lines, and [CII] retains its multi-phase nature in all modelling approaches. Interestingly, the RT run produces a lower density, T ∼ 104 K tail of [CII] emission that is not seen in the other models, and which resides entirely in the CGM component. The latter corresponds to cold streams accreting onto the main disc, and to tidal tails connecting the main disc and the mergers (which can also be seen in the H2 structure in Fig. 5). This gas is mostly ionised by the UVB, and not stellar radiation.
The [CI] lines (second and third column in Fig. 8) are weaker than [CII] and less-multi-phase, but still probe a wide range of densities and temperature especially in the RT model, where however most of the [CI] emission arises from high density gas. In the MPM models, [CI] comes only from the particles classified as dense (nH > 10 cm−3) which undergo our sub-grid density profile modelling, hence the sharp transition seen in the phase diagrams.
A similar effect can be seen for the CO(3−2) emission, which is actually only sizeable in the MPM models, as already discussed in relation to Fig. 7. Compared to [CI], CO emission is spread more uniformly across the particles classified as dense (log10(nH) > 1). In our fiducial RT model, CO emission is weak, and originates mostly from the densest and coldest gas in the simulation, where we also find a low radiation field.
As already pointed out, [OIII] emission is almost model-independent in our study, as most of it originates from gas phases that are not affected by the additional sub-grid models. In the SM and MPM models, [OIII] is dominated by hot and dense gas, in addition to a more diffuse and colder gas phase, with a star-forming gas contribution of less than 0.01%, except for the SM where it is around 17%. The RT model on the other hand differs from the previous models, as after the post-processing the hot and dense gas disappears, due to the cooling of gas previously heated up by supernova feedback. Such hot and dense phase erased by the RT model had an artificially delayed cooling according to the sub-grid blast wave feedback model of PONOS, as described above. At the same time, the RT run removes also the [OIII] contribution from colder gas at lower densities thanks to heating by stellar radiation. We consider the [OIII] values delivered by the RT model to be more realistic than the enhanced [OIII] values produced by the other models. O++ needs a certain excitation energy to be ionised, and thus re-emitted as [OIII], hence a lower emission from low temperature gas is expected. Since gas temperature and density in the RT model are also linked to the G0 value, higher radiation leads to higher temperatures, explaining the lower [OIII] emission rate generated by the RT approach. The FIR [OIII] emission line is sensitive to the critical density of the gas (i.e. the density where collisional de-excitation becomes the dominant de-excitation method; Dinerstein et al. 1985), so together with the needed high excitation energy for [OIII] we expect lower emission for gas at high densities, and at low temperatures. Most of the [OIII] emission originates from gas at T ∼ 1.5 × 104 K and nH ∼ 10 cm−3, which is in the range of typical values for HII regions (see Table 2).
Line luminosities (in units of L⊙) obtained from the fiducial RT model, divided by halo component.
4.2. Results from the fiducial RT model
In this section we analyse in more detail the results of our fiducial RT model. Figure 9 shows the different line luminosities plotted as a function of gas density, radial distance (where R is computed from the centre of the PONOS simulation), Habing radiation field, and gas temperature. The contributions from the main disc and from the minor mergers (B at r ∼ 6 kpc and A at r ∼ 16 kpc) are clearly seen as peaks in [CII], [OIII], [CI] and CO in the radial profiles (top-right panel of Fig. 9).
 |
Fig. 9. [CII], [CI], CO, and [OIII] line luminosities of the RT model as a function of gas number density (nH, top-left panel), distance from the centre of the simulation box (top-right panel), radiation field (bottom-left panel), and gas temperature (bottom-right panel). |
Focusing on [CII], we observe stronger emission from denser gas, though the dependence on density is not as steep as for other lines, which again hints at the multi-phase nature of [CII]. The [CII] emission peaks at log(G0) = 1.5. Only over half of [CII] (around 56%) originates from the dense, star-forming phase, while such dense and cold gas makes up 20% of the total baryon mass. The [CII] emission peaks at a temperature of T ∼ 104 K.
[OIII] also seems insensitive to gas density at lower densities, but drops noticeably towards high densities, where [CII], [CI] and CO peak. Compared to the other lines, [OIII] emits strongly from high temperature gas that experiences a high radiation field. 99% of [OIII] emission originates from the diffuse gas phase (nH < 10 cm−3).
The two [CI] transitions behave similarly in the RT model, with their luminosities deviating in median by 2.5 and by a factor of 9 at most, especially from the high-n, lower-T gas, where the [CI]370 μm shows slightly stronger emission especially towards low temperatures, high radiation field strength and high densities. Over 90% of the [CI] emission in both transitions originates from dense gas (nH > 10 cm−3). Compared to [CII], the [CI] transitions clearly rise in emission towards higher densities.
Even though the CO emission is weak, it can be clearly seen that it peaks towards high densities and low temperatures (over 99% of the emission originates from gas classified as cold and dense). Compared to the other lines, there is little emission of CO in the CGM and between the galaxies (around 0.01%), and the emission clearly peaks in the main disc and the mergers. The resolution within the CGM and the tidal tails is lower than in the main disc, suggesting that CO emission inside the CGM could be underestimated.
Figure 10 shows the different line luminosity profiles as a function of gas number density, temperature, and incident radiation field, plotted separately for each morphological component. The main disc, the mergers, and the CGM are plotted using dashed lines, while the total emission from the PONOS halo is reported as a solid black line. In all these sub-mm/FIR tracers, the CGM component is by far the dominant emitter at low densities and low radiation fields. The density value below which the CGM becomes the dominant emitting component is equivalent for CO and [CI] (n ∼ 3 cm−3), higher for [CI] than for [CII] (n ∼ 1 cm−3), and higher for [CII] than [OIII] (n ∼ 0.2 cm−3). The CGM contribution to the total [CII] emission is around 10%, and it dominates at low densities and low radiation fields. For the [CI] lines, the contribution from lower density gas located in the CGM is ∼1.3% for the [CI]609 μm transition and ∼0.8% for the [CI]370 μm one. [CI] peaks at similar radiation field strengths as [CII]. As expected from the resolution limitations discussed earlier (which, unfortunately, not even the RT approach can mitigate for the higher density molecular gas with n > 103 cm−3), the CO(3−2) emission is weak and peaks at the highest densities, lowest temperatures, and lower radiation field values. As a consequence, CO(3−2) exhibits a very small contribution from the CGM, equal to 0.01%. Most of the CO(3−2) emission originates from the main disc, making up 70% of the total CO line luminosity. [OIII] is less sensitive to the density, compared to other lines, but it shows a clear uptrend towards higher temperatures and higher radiation fields, which is due to the already discussed higher excitation energy needed for doubly ionised oxygen. The highest temperature, lowest density and lowest radiation field emission is dominated by the CGM, making up 21% of the total [OIII] emission. For all analysed lines we find stronger emission for higher metallicity gas. At higher metallicities there are more metals in the gas that can emit in the analysed emission lines (Vallini et al. 2015).
 |
Fig. 10. Line luminosities plotted as a function of gas number density (left column), gas temperature (middle column) and incident radiation field (right column). The lines are also divided into the contribution from different halo components, where the black solid line shows the total emission from the whole simulation box, the dashed purple line shows the main disc emission, the two mergers are plotted using a magenta dashed line, and the CGM is plotted using a dashed orange line. |
The emission line maps obtained using the RT approach are shown in Fig. 11. The corresponding maps obtained from one of the alternative models, the MPM 2CG model, are reported in Fig. A.1 for comparison. Because of the compactness of the CO emission, for this tracer we also plotted a version of the map zoomed-in on the central galaxy disc of PONOS galaxy (bottom left panel of Fig. 11). The white dashed circle in each plot of Fig. 11 shows the virial radius (Rvir). Figure 12 shows the [CII] and [OIII] maps obtained by selecting only the CGM components of PONOS.
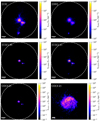 |
Fig. 11. Line emission maps obtained with the fiducial RT model. The circles in each plot mark Rvir. The top-left panel shows [CII], which is clearly extended and clumpy in appearance, with most of its emission originating from the main disc and merger components, and bridges of gas in between. The top-right panel shows the [OIII] map, which is fainter than in the other models tested in this study (see e.g. Fig. A.1 showing the same maps obtained for the MPM 2-component Gaussian model). [OIII] is extended, although less than [CII], and traces warm-ionised gas rather than the cold neutral gas traced by [CII]. The central maps show the [CI]609 μm and [CI]370 μm transitions, which are also extended, although fainter than [CII] (note the different surface luminosity scaling). The bottom panels show the CO(3−2) maps. The lowest plot on the right shows the CO(3−2) emission zoomed in on the main disc. As discussed in the main text, CO is faint in the RT model, and concentrated in the main disc and merger components. There are faint clouds of CO(3−2) emission in the CGM, overlapping with regions with relatively high [CI] emission. |
 |
Fig. 12. Line emission maps obtained with the fiducial RT model, only showing the CGM emission of Ponos for [CII] and [OIII]. |
For [CII] (top-left panels of Figs. 11 and 12), the maps clearly show extended emission in the CGM, both in a diffuse halo around the central disc and in the gas bridges and tidal tails connecting the merging galaxies. The accreting filament (which hosts H2 gas, see Fig. 5) is responsible for the northern asymmetric extension of [CII], which is more visible in the CGM-only map. These results are nicely consistent with recent observations of [CII] emission extending up to 10−15 kpc around high-z galaxies, reported by several authors (Fujimoto et al. 2019, 2020, 2022; Ginolfi et al. 2020a,b; Fudamoto et al. 2022). Additionally there is a bright CGM contribution south of the main disc, which is gas being accreted from merger B onto the central disc.
The [OIII] maps (top-right panels of Figs. 11 and 12) show extended emission, although less extended than [CII]. Notably, the CGM emission in [OIII] arises from different places than the CGM emission seen in [CII]. According to our computation and component separation, the CGM contribution to [OIII] is 21%, while this number is lower (10%) for [CII]. However, Fig. 12 shows that the northern accreting filament, and the bridges and tails connecting the merging galaxies are much brighter in [CII] than in [OIII], and [CII] extends as far as Rvir. Instead, [OIII] appears more puffy and concentrated in a halo surrounding the galaxy discs, possibly also due to SN feedback processes. [OIII] needs the presence of young, massive stars to be excited, so this is expected. Previous studies, both observational (Carniani et al. 2020; Fujimoto et al. 2020, 2021; Ginolfi et al. 2020a,b; Fudamoto et al. 2022) and theoretical (Arata et al. 2020; Pallottini et al. 2019; Katz et al. 2019; Pizzati et al. 2020, 2023), have indeed found [CII] to be more extended than rest-frame UV discs, sub-mm continuum emission from dust, and than [OIII] emission. We find the same result in our simulation, both for the main disc and for mergers A and B. Fujimoto et al. (2019) investigated the origin of the extended [CII] emission, dismissing the idea of satellite galaxies as a cause, and focusing of circumgalactic PDR and HII regions, as well as cold streams and outflows. In our study we find that the extended emission originates from cold gas falling into the galaxy from the filament and from tidal tails between the main disc and the satellites, similar to Ginolfi et al. (2020b), who estimated that 50% of the [CII] emission of a high-z merger originated from the regions between the nuclei. Ginolfi et al. (2020a) detected broad [CII] wings ascribed to outflows in normal high-z galaxies from the ALPINE sample, especially for SFR > 25 M⊙ yr−1, and more extreme [CII] outflows have been observed in the luminous quasar population at these redshifts (Maiolino et al. 2012; Cicone et al. 2015; Bischetti et al. 2019; Izumi et al. 2021; Meyer et al. 2022). While PONOS has star formation driven outflows, is not affected by extreme AGN driven outflows, which could lead to a higher fraction of extended emission. Moreover, how to address the formation and survival of molecular gas within the multi-phase outflow environments is still an open question for cosmological simulations, as this task requires extremely high resolutions that can only be achieved in idealised simulations (Decataldo et al. 2019; Nelson et al. 2021).
Both the [CI] and CO maps in Fig. 11 show mainly compact emission, tracing the dense and cold gas within the disc and merger components, with only minor contribution from the gas that we ascribe to the CGM. Therefore, the CGM of PONOS does not appear to be detectable in molecular gas tracers. However, there are two caveats to consider: (i) the lower numerical resolution on CGM scales which, as already mentioned, can lead to underestimating its H2 content; and (ii) components that we ascribe to the ISM of the mergers (e.g. tidal tails, bridges, and the minor merging satellites themselves) and so we do not count as “CGM”, may appear blended or unresolved in the observational data, and so they can contribute to what observations detect as a “diffuse” CGM emission. A more in depth discussion of observations is addressed in Sects. 5 and 7.
4.2.1. Kinematics of the CGM traced by FIR/sub-mm lines
While the PONOS simulation does not have extreme, AGN driven outflows, there are outflows caused by stellar feedback processes, pushing gas from the ISM into the CGM. To study the CGM emission in the different lines in detail, we divided the gas into “inflows” and “outflows”. This was done by selecting gas at velocities of v > 200 km s−1 (which is higher than the rotational velocity of the main disc, and is also in the range of velocities found by Pizzati et al. 2023 for outflowing [CII] bright gas in their semi-analytical modelling) which we defined as being high velocity gas, and then dividing this high velocity gas into gas that is flowing away from the main disc (outflowing), and gas that is flowing towards the main disc (inflowing). As shown in Fig. 13 we plot the emission of the CGM (solid black), the high velocity CGM (dashed black), the inflows (dashed blue) and the outflow (dashed red) together with the disc/ISM emission (dashed green) as functions of the gas density, the gas temperature and the gas metallicity for the individual emission lines.
 |
Fig. 13. Line luminosities of the CGM plotted as a function of gas number density (left column), gas temperature (middle column) and gas metallicity (right column). The lines are also divided into the contribution from different CGM components as well as the main disc, where the black solid line shows the total CGM emission, the dashed black line shows the emission of high velocity CGM gas (v > 200 km s−1), outflowing high velocity gas in the dashed red line, inflowing high velocity gas in the blue dashed line and as a reference the disc/ISM component in dashed green. |
In all lines (except CO, where we do not see significant emission from the outflowing component) the outflowing gas has low densities, high temperatures and high metallicity, which is consistent with gas expelled by stellar feedback. The outflowing gas is only dominant in emission in the CGM for the highest metallicities. The outflows within the PONOS are dominated by hot gas, but cold clouds within the outflows could be unresolved, which would lead to a stronger [CII] emission from the outflowing gas. It has to be noted, that outflowing gas very close to the disc, would not fall into the definition of the CGM in our study, as it would reside within twice the effective radius of the main disc. The inflowing gas has a wider range of densities, temperatures and metallicites, as it represents both pristine gas flowing in from the IGM, as well as gas accreted to the main disc from merger components in the form of gas bridges and tidal tails. The inflowing gas is the dominating component emitting in the CGM, which can also be seen in Figs. 11 and 12, where the a accreting stream in the north and the gas bridges between the merging galaxies are bright in [CII]. At high redshift the cold gas is dominated by accreting gas (e.g. Decataldo et al. 2023), so it is not surprising that the inflows dominate in luminosity. For [OIII] the inflowing component is dominating as well, but this inflowing gas is mostly found within the bright tidal bridge between the main disc and merger B (see Fig. 12), where there is ongoing star formation and SN events that are traced by [OIII]. The rest of the emission originates from the outflowing gas.
Without additional information about the gas velocity and the chemistry, the interpretation of the CGM component is not straightforward. In our analysis we find that no gas tracer can be said to definitely trace inflows and outflows. A more statistical analysis of the CGM emission of similar systems could help to disentangle the different line tracers better.
4.2.2. The [OIII]/[CII] ratio map
Emission line ratios are a common tool to explore galaxy properties (Rubin et al. 1994; Nagao et al. 2011, 2013; Pereira-Santaella et al. 2017; Díaz-Santos et al. 2017; Rigopoulou et al. 2018; Killi et al. 2023). The L[OIII]/L[CII] ratio is especially interesting, as it involves two prominent FIR emission lines that arise from gas with different properties, and thus can be used to constrain the physical conditions of the high-z ISM and, potentially, CGM (Carniani et al. 2018; Hashimoto et al. 2019; Harikane et al. 2020; Arata et al. 2020; Vallini et al. 2021; Fujimoto et al. 2022; Katz et al. 2019, 2022). At z ≥ 6 the measured L[OIII]/L[CII] ratios are typically high (between 1 and 20), due to a deficit in [CII] emission compared to local galaxies (Inoue et al. 2016; Hashimoto et al. 2019; Carniani et al. 2020; Harikane et al. 2020; Vallini et al. 2021; Witstok et al. 2022; Kumari et al. 2024). This deficit is generally ascribed to extreme physical conditions of the ISM in early galaxies, such as very low PDR covering fractions due to compact morphologies and high densities, strong radiation fields and high turbulence, as well as different abundance ratios and low metallicities (Vallini et al. 2015, 2021; Olsen et al. 2017; Pallottini et al. 2017, 2019; Lagache et al. 2018; Lupi et al. 2020; Arata et al. 2020; Katz et al. 2022). Due to their different wavelengths, angular resolution and sensitivity effects can bias the ratios measured by observations. In particular, the more extended nature of [CII] compared to [OIII], makes it more prone to its flux being underestimated by interferometric observations performed with high angular resolution (the surface brightness dimming discussed by Carniani et al. 2020).
To calculate the L[OIII]/L[CII] ratio for PONOS, we first mask out gas with weak emission (Σline < 1 L⊙ kpc−2) in either of the lines. Such cut has a negligible effect on the total ratio, but it affects spatially resolved ratio maps. We note that this effect applies to observational data as well, as they all have a sensitivity threshold. Because of the relative compactness of [OIII] and of the above cut, our line ratio map, reported in Fig. 14 (computed from the fiducial RT run), shows only the main disc and merger B, which are the regions from which most of the [OIII] emission originates (see Fig. 11). The total L[OIII]/L[CII] ratio measured in PONOS is around 0.17, which is lower than reported by observations at similar redshifts, and more in line to the ≤1 values typically measured in local starburst galaxies (Brauher et al. 2008; De Looze et al. 2014; Cormier et al. 2015). Katz et al. (2022) found that using different abundance ratios in the CLOUDY modelling, which would be more representative of the early Universe, can lead to lower [CII] and higher [OIII] emission, thus delivering higher L[OIII]/L[CII] ratios more similar to the values observed at high redshift.
 |
Fig. 14. [OIII]/[CII] surface brightness ratio map obtained from the RT run. The right panels show the [CII], [OIII], and [OIII]/[CII] plots in a zoomed-in portion of the main disc, to highlight the spatial offset between [OIII] and [CII]. The units of Σline are [L⊙ kpc−2]. |
In addition, as also pointed out by Pallottini et al. (2019), the line ratios can vary within the galaxy itself, depending on the radiation field experienced by the gas and other gas properties. The [OIII]/[CII] ratio map in Fig. 14 shows a clear offset between these two tracers in the dense star-forming regions in the PONOS main disc. In the densest portions of the disc, [CII] appears more widespread, while [OIII] is bright in compact regions that corresponds to cavities of the [CII] map, possibly created by SN feedback (see comparison between the two zoomed-in panels on the right showing the [CII] and [OIII] maps). There is a clear morphological difference between the two tracers, with [OIII] appearing “puffier” and more concentrated around the main galaxy and the ISM material of the mergers, and [CII] being more extended and also tracing filamentary structures between the mergers (as also found by e.g. Ginolfi et al. 2020b). In summary, higher L[OIII]/L[CII] are found in regions with higher G0 values within the main disc and merger B, coinciding with areas of high star formation. Our results support the use of spatially resolved observational studies of the L[OIII]/L[CII] ratio to study the physical properties of the ISM in high-z galaxies. Line ratios, including different tracers, will be further explored in a follow-up publication.
5. Discussing our results in the context of observational works
When comparing theoretical predictions with observational results, it is important to keep in mind that the observational setup plays a major role in the outcome of the observation. As discussed and demonstrated in Sect. 7.2 through ALMA mock observations of PONOS, the choice of a single dish telescope vs an interferometer, the array configuration (which determines the angular resolution and the maximum recoverable scale of the source), the integration time, and the observed frequency, all have a major impact on the recovery of the physical properties of the target. For the comparison between our results and observational constraints available in the literature, it is also important to note that, while our PONOS modelling delivers several data points (for the disc, merging companions, CGM, and total halo of the simulation), high-redshift observations usually only provide one data point per target, with only one associated estimate of SFR (or M*, etc). There could be several minor mergers and CGM components contributing to those single data points, which went undetected by the observation.
5.1. [CII] vs SFR
The empirical correlation between [CII] luminosity and SFR of galaxies has been extensively investigated in the literature (De Looze et al. 2014; Herrera-Camus et al. 2015; Capak et al. 2015; Schaerer et al. 2020; Carniani et al. 2020), and widely used to validate theoretical predictions against observational constraints. This relation is explored in Fig. 15 for our six different models, where the left panel focuses on the comparison with available high-redshift observational constraints, and the right panel on the comparison with simulation data and other theoretical models. The large coloured markers in both plots represent the data from our study, using the intrinsic SFR of PONOS and the derived line luminosities. As it was done in Fig. 7, different components are represented with different symbols (the circles represent the total luminosity). The observational data and the simulation data of other studies are plotted in grey, while relations derived by other studies are plotted with grey and purple lines, the shaded areas representing their corresponding scatter. All observational and simulation data points are obtained for high-z objects, with the exact references and redshifts reported in the caption of Fig. 15. The relations on the left panel are taken from De Looze et al. (2014) for starburst galaxies, which Schaerer et al. (2020) found to hold up for high-redshift galaxies, and from Carniani et al. (2020) for high-redshift galaxies. The relations on the right panel are by Olsen et al. (2017), Arata et al. (2020), and Leung et al. (2020), based on their simulations, and by Vallini et al. (2015) based on their theoretical modelling.
 |
Fig. 15. [CII] line luminosity as a function of the SFR. In the left panel, our models are compared with observational constraints available from the literature at a similar redshift, while the right panel shows the comparison with other theoretical works. The circles represent the whole halo, crosses represent the main disc, and the pentagon the merging companions A and B. The CGM is shown using diamond symbols. The observational data are taken from: Kanekar et al. (2013) at z = 6.5, Ouchi et al. (2013) at z = 6.5, González-López et al. (2014) at z = 6.5 − 11, Ota et al. (2014) at z = 6.9, Schaerer et al. (2015)z = 6.8 − 7.5, Capak et al. (2015) for z = 5.1 − 5.7, Willott et al. (2015) for z = 6, Maiolino et al. (2015) for z = 6.8 − 7.1, Knudsen et al. (2016, 2017) for z = 6 − 7.6, Pentericci et al. (2016) for z = 6.6 − 7.1, Bradač et al. (2017) for z = 6.7, Decarli et al. (2017) for z = 6 − 6.6, Khusanova et al. (2022) for z = 6, Vanderhoof et al. (2022) for z = 4.5, Fujimoto et al. (2021) for z = 6, Witstok et al. (2022) for z = 6 − 7, Hashimoto et al. (2019) for z ∼ 7, Harikane et al. (2020) for z ∼ 6, the ALPINE data for z = 4 − 8, Schaerer et al. (2020), Algera et al. (2024) for z = 7.3, Fujimoto et al. (2022) for z = 8.4, Ren et al. (2023) for z = 7.2, and Carniani et al. (2018) for z = 5 − 7. The relation shown in grey is by De Looze et al. (2014) for SB galaxies, and the relation shown in purple by Carniani et al. (2020) for high-redshift galaxies. In addition, on the right panel, we compare our results to simulation data by Pallottini et al. (2019, 2022); Katz et al. (2022) and Lupi et al. (2020). The relation by Vallini et al. (2015) based on physical motivated models for a metallicity of Z = 0.5 Z⊙ can be seen in grey dashed, the relation by Arata et al. (2020) in dot-dashed, the relation found by Leung et al. (2020) in purple, and the Olsen et al. (2018) data in grey dot-dashed. |
By focusing on the comparison with observational data (left panel of Fig. 15), we note that our SM, MPM power law, and MPM logotropic models lie above the Schaerer et al. (2020) relation obtained for ALPINE data, but are still consistent with the upper envelope of the distributions of observational data points. In contrast, the MPM Plummer and MPM 2CG models strongly overestimate the total [CII] emission compared to available observational constraints. Our fiducial RT model is the most consistent with observations, and it even broadly follows the Schaerer et al. (2020) [CII]–SFR best-fit relation, except for the CGM component, which lies above the relation. This could indicate that star formation (SFR ∼ 1 M⊙ yr−1 in the CGM) is not the only source of ionisation of the extended gas component, but that the UVB plays a vital role, as also suggested by other studies (Fujimoto et al. 2019; Pizzati et al. 2020).
In the right panel of Fig. 15, we compare our results to other theoretical works. The RT model, represented by the same black symbols as in the left panel of Fig. 15, is consistent with the relation by Vallini et al. (2015), except for its CGM component which lies above this relation. Our other models lie all above the results from other theoretical works, as explained in Sect. 6.
5.2. [OIII] vs SFR
Figure 16 shows the [OIII] 88 μm luminosity as a function of SFR, compared with observational data on the left panel, and with theoretical predictions on the right panel. The left panel of Fig. 16 reports the comparison with the empirical relations derived by De Looze et al. (2014) and Harikane et al. (2020), while the right panel shows the theoretical relations from Olsen et al. (2017) and Arata et al. (2020). Because of the scarcity of observational constraints, there are only few data points reported in the left panel, all from observations at z ≳ 6 (including an upper limit at z ∼ 13 by Popping 2023), hence they are not necessarily representative of the normal z ∼ 6 galaxy population that we probe with the PONOS simulation, since they could be biased towards the brightest [OIII] emitters. Our fiducial RT model lies slightly below the De Looze et al. (2014) relation, and has a lower SFR than most of the observations of high-redshift galaxies. The few observations of galaxies with similar SFR show higher [OIII] emission. Additional observations of a broader population of high-redshift galaxies are needed to further constrain the [OIII]–SFR relation.
 |
Fig. 16. [OIII]88 μm line luminosity as a function of SFR. Our modelling results based on the PONOS simulation are compared with observations in the left panel, and with other theoretical works in the right panel. Symbols and colour-coding are the same as in Fig. 15. As was also seen in Fig. 7, the [OIII] luminosities of the MPMs does not change much for different sub-grid density profiles for the dense gas, and thus we show the MPM emission in one data point. The MPMs are represented in indigo. The observational data in the left panel are taken from: Popping (2023; upper limit of a z = 13 galaxy), Witstok et al. (2022; z = 6 − 7), Hashimoto et al. (2019; z ∼ 7), Hashimoto et al. (2018; z = 9), Inoue et al. (2016; z ∼ 7), Algera et al. (2024; z = 7.3), Fujimoto et al. (2022; z = 8.4), Ren et al. (2023; z = 7.2), and Harikane et al. (2020; z ∼ 6). The relation reported in the left panel are the one derived by De Looze et al. (2014) and by Harikane et al. (2020). On the right panel, we compare our results to the simulation results by Pallottini et al. (2019, 2022), Katz et al. (2022), and Lupi et al. (2020), the relation by Arata et al. (2020) in dot-dashed, and the relation reported is the one fitted by Olsen et al. (2017) for their z = 6 simulated galaxies. |
As shown in the right panel of Fig. 16, most other theoretical predictions lie below the observational data in the SFR–[OIII] relation, and indeed our RT model is in good agreement with them (Olsen et al. 2017; Katz et al. 2022; Pallottini et al. 2019, 2022). Instead, our SM and MPM models produce higher [OIII] luminosity values compared to other theoretical studies, which we ascribe to the hot and dense gas component created by the sub-grid blast wave feedback model of PONOS that, as already discussed in Sect. 4.1, is cooled down by the RT post-processing.
5.3. CO(3−2) vs IR luminosity
To compare our CO(3−2) predictions with observational data, we computed the brightness-temperature dependent line luminosity ( , often used by observational works), using the following equation by Solomon et al. (1997):
, often used by observational works), using the following equation by Solomon et al. (1997):
where νobs is the observed frequency in units of GHz (νrest = νobs ⋅ (1 + z)), ∫ΔνSνdv is the velocity integrated flux in units of Jy km s−1 (see Eq. (13)), and DL is the luminosity distance in units of Mpc (calculated with the Cosmology Calculator by Wright 2006 for a flat Universe). This results in 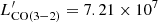 K km s−1 pc2, which is significantly lower than observations. Indeed, at z > 1, the measured values are in the range
K km s−1 pc2, which is significantly lower than observations. Indeed, at z > 1, the measured values are in the range 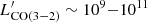 K km s−1 pc2 (Yang et al. 2017; Strandet et al. 2017; Lenkić et al. 2020; Decarli et al. 2020; Boogaard et al. 2023). Knudsen et al. (2017) reports a (3σ) upper limit of ∼109 K km s−1 pc2 for a dusty lensed z = 7.5 galaxy with stellar mass of ∼109 M⊙ and SFR ∼ 12 M⊙ yr−1. Such discrepancy with observational data is expected, as we known that our fiducial model underestimates CO emission.
K km s−1 pc2 (Yang et al. 2017; Strandet et al. 2017; Lenkić et al. 2020; Decarli et al. 2020; Boogaard et al. 2023). Knudsen et al. (2017) reports a (3σ) upper limit of ∼109 K km s−1 pc2 for a dusty lensed z = 7.5 galaxy with stellar mass of ∼109 M⊙ and SFR ∼ 12 M⊙ yr−1. Such discrepancy with observational data is expected, as we known that our fiducial model underestimates CO emission.
For a further comparison, we plot in Fig. 17 the 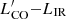 relation. For this, we have assumed the LIR to relate to the SFR following a Chabrier initial mass function, as often done in observational works (Chabrier 2003; Gowardhan et al. 2019):
relation. For this, we have assumed the LIR to relate to the SFR following a Chabrier initial mass function, as often done in observational works (Chabrier 2003; Gowardhan et al. 2019):
 |
Fig. 17. CO(3−2) line luminosity as a function of total infrared luminosity of PONOS, obtained with the different models, compared with observational data. Symbols and colour-coding are as in Fig. 15. The SM was not included because of its very low CO luminosity. Due to the scarcity of observations CO(3−2) data at z ≳ 6, most data shown in this figure (except for Strandet et al. 2017 at z = 6.9) represent galaxies at z = 1 − 4: Gowardhan et al. (2019) at z ∼ 3.2, Tacconi et al. (2013) at z = 1 − 3, Daddi et al. (2015) at z = 1.5, Yang et al. (2017) at z = 2 − 4, Circosta et al. (2021) at z = 2 − 2.5 and Zanella et al. (2023) at z ∼ 1. |
Due to the scarcity of z > 6 observations, we compare our results with literature data between z = 1 − 4. As expected, the RT model lies below the observed values, as we do not reach the necessary densities in the RT model to fully represent molecular gas. All the MPM models lie within the scatter of the observations, with the MPM power law profile resembling the findings of Tacconi et al. (2013) most closely, once again showing that for the modelling of molecular gas, sub-grid models are necessary. Vallini et al. (2018) simulated the high-z CO emission for various transitions by modelling the emission from individual GMCs, and then applying this to a cosmological zoom-in simulation. Our RT model has lower emission in CO(3−2) in comparison.
6. Discussing our results in the context of theoretical studies
In this section we discuss how different modelling approaches and sub-grid recipes can affect the resulting emission line luminosities. In literature there are currently two main approaches. The first one includes global radiative transfer and non-equilibrium chemistry of primordial gas (e.g. Pallottini et al. 2019, 2022; Katz et al. 2019, 2022) or (non)-equilibrium chemistry tracing the main coolants (Arata et al. 2020; Lupi et al. 2020), which are most comparable to our fiducial RT model. The second approach includes more advanced sub-grid modelling of the dense gas, but usually with more approximative estimations of the FUV radiation field (e.g. Olsen et al. 2015, 2017, 2018; Leung et al. 2020) which are most comparable to our MPM model, next to some semi-analytical approaches (e.g. Popping et al. 2019; Pizzati et al. 2023). We focus on the [CII] and [OIII] emission lines, because, being the most prominent coolants of the ISM, and being observable at high-z using sub-mm ground-based telescopes, these lines have been modelled in a variety of theoretical studies. Important to note is that none of the following studies focus on the CGM emission in the same extent as we do, where we find 10% of [CII] and 21% of [OIII].
6.1. Global radiative transfer studies
Our fidicual RT model is most similar to the studies by Pallottini et al. (2019, 2022) using the SERRA cosmological zoom-in simulations. Their simulations have resolution of ∼25 pc, somewhat lower but similar to PONOS. The simulations are performed with RAMSES-RT with on-the-fly radiative transfer and also used KROME for primordial non-equilibrium chemistry. For the modelling of FIR emission lines, the authors use CLOUDY grids for the density, metallicility and radiation field with a slab geometry similar to our grid. In addition, they employ a sub-grid log-normal density distribution profiles, to account for the clumpy structure of the ISM. Comparing to their model, PONOS does not have on-the-fly RT, which may result in inconsistencies in gas dynamics. Nevertheless, our post-processing with KRAMSES-RT do capture the ionisation sates and the FUV radiation accurately at a specific snapshot. Moreover, we include the radiation from the UVB for the first time to investigate the extended emission from the CGM.
Regarding [CII] emission, we have shown that over half of the emission originates from the dense phase, and the emission peaks at intensity log(G0) ∼ 1.5. This is in partial agreement with Pallottini et al. (2019), where the authors found that predominant [CII] emission originates from their denser gas phase with n ≃ 160 cm−3, irradiated by an average radiation field of ∼20 G0, with a subdominant contribution for the low density gas. However, unlike Pallottini et al. (2019) and the previous work by Pallottini et al. (2017), our results indicate a significant fraction (44%) of [CII] emission from the more diffuse gas (in neutral and ionised phase), and this diffuse phase [CII] dominates the CGM emission (see Fig. 10). From our definition of components, the CGM component accounts for about 10% of the total [CII] emission, whereas Pallottini et al. (2019) only find a very faint [CII] halo of Σ[CII] = 5 × 104 L⊙ kpc−2. In Pallottini et al. (2022), where the authors found majority of [CII] emission originated from the central disc, they also do not find [CII] halos which are as extended as high redshift observations. This is most likely due the inclusion of the UVB in our modelling, which is demonstrated to be important in producing extended [CII] emission. Another possible reason is the sub-grid modelling of log-normal density distribution in Pallottini et al. (2019, 2022). This can potentially result in more [CII] emission from the dense phase, because the high density gas beyond the resolution limit of the hydrodynamic simulation is sampled in such sub-grid models. Last but not least, we note that PONOS is one single system undergoing major merger, and mergers may enhance extended emission due to the large-scale flows they induce.
Pallottini et al. (2019) found that in their models the [OIII] emission line peaks in dense but ionised regions, which is again in agreement with our findings, where most of the [OIII] originates in denser gas, but at higher temperatures compared to the other modelled emission lines, and in regions with higher G0 values. The [OIII] emission modelled by Pallottini et al. (2019) is mostly concentrated around the main galaxy, which is also where we find a significant fraction in our model, but we also find extended emission tracing the gas bridge between merger B and the main disc, as well as some outflowing gas. Similarly, Pallottini et al. (2022) find a concentrated emission of [OIII], tracing the HII regions of the galaxies in their sample, which is similar to what we find in PONOS.
Katz et al. (2019) investigated [CII] and [OIII] line emissions using the Aspen cosmological radiation hydrodynamics zoom-in simulation of a massive Lyman-break galaxy at z = 12 − 9. The simulation was performed with the RAMSES-RT code with on-the-fly RT and non-equilibrium chemistry, and it reaches a resolution of 13.6 pc. FIR line emissions were calculated using CLOUDY (with grids for density, temperature, metallicity and radiation field, calculated with constant temperature) and machine learning. The authors found that the [CII] emission origins predominantly from the cold molecular disc, while [OIII] is concentrated around SF regions. Extended emissions are found to be connected to merger activities. While we also find that a significant amount of emission originates from tidal tails between the merging components, the extended emission in PONOS also traces inflowing and outflowing gas. Katz et al. (2019) found outflowing gas in their z = 10 galaxies traced by [OIII] but not by [CII], and there is a clear spatial offset between the two lines which was confirmed by a later study with the same simulation, in Katz et al. (2022). The spatial offset is also observed in our study (see Fig. 14) and [OIII] in PONOS is puffy in appearance. However, we do not find a significant difference in velocities between gas that is bright in [OIII] and gas that is bright in [CII]. In fact, inflowing gas dominates both [OIII] and [CII] systems in our simulation, except for the lowest density n ≲ 0.01 cm−3 and high metallicity (Z ≳ Z⊙) gas (Fig. 13). As noted in a previous section, this inflowing gas is mainly found in the tidal bridge where ongoing star formation and SN events are located. Comparing the phase diagram for the RT model in Fig. 8 to the results of Katz et al. (2019) at redshift z = 10, we find that the peaks of [CII] and [OIII] emissions in our simulation in the density–temperature space coincide those in Katz et al. (2019), although we also find emission from lower density gas. Their total [CII] and [OIII] luminosities are comparable to our derived values at z = 6.
Lupi et al. (2020) compared various emission line luminosities ([CII] 158 μm, [OI] 63 μm, [OI] 146 μm, [OIII] 88 μm) computed based on established CLOUDY models with the ones computed from on-the-fly non-equilibrium chemical network, using a GIZMO cosmological zoom-in simulation of a galaxy at z = 6 (with a stellar mass of M* = 1.6 × 1010 M⊙). The simulation has resolution mgas = 2 × 104 M⊙, and includes on-the-fly RT coupled with non-equilibrium chemistry using KROME, following 16 chemical species. In their models, the [CII] line luminosities derived with their “KROME approach” differ from their CLOUDY based models by about a factor of 3. The authors conclude that, because the effect of very different approaches on the [CII] luminosity is not very strong, [CII] is a good tool for constraining physics included in cosmological simulations. This is in agreement with our findings, which also suggest [CII] emission is rather insensitive to models. Nevertheless, the highest line luminosity found by Lupi et al. (2020) in their KROME approach (L[CII] = 5.12 × 107 L⊙) is lower than our results (L[CII] = 1.95 × 109 L⊙) by over an order of magnitude. This is also shown in Figs. 15 and 16, where the [CII] and [OIII] luminosities from Lupi et al. (2020) for all their modelling approaches are lower compared to our models, even though their simulated galaxy is more massive and has a higher SFR (∼50 M⊙ yr−1) than PONOS. This is likely to be caused by the difference in resolution, as the contrast in luminosities is stronger in [CII], which is multi-phase and sensitive to resolution, than in [OIII], which originates from diffuse, warm gas which converges at lower resolutions.
Arata et al. (2020) applied global radiative transfer in post-processing using the ART2 code onto a suite of Gadget-3 cosmological zoom-in simulations of galaxies at z = 6 − 15 where they traced 9 chemical species. They derived the emission of [OIII] and [CII] based on equilibrium heating and cooling calculations of O++ and C+, consistent with the equations used in CLOUDY. The authors found the results from their modelling approach consistent with CLOUDY modelling. They found [CII] to be more extended than [OIII], and exhibit less variation with time, whereas [OIII] emission varies more significantly with time, and is brighter in eras of high star formation. Their [CII] luminosity is consistent with the results of our study (see Fig. 15), once again showing that [CII] is less model sensitive, while their [OIII] emission is higher, which could be due to the direct tracing of chemical species, and thus the more accurate treatment of abundance ratios within the gas.
6.2. Sub-grid modelling of dense gas
By using a model based on cosmological simulations run with Gadget-2 (resolution of 60 pc), RT post-processing (using the UV RT code LICORICE) and sub-grid ISM modelling to account for a two-phase ISM, Vallini et al. (2015) found that the PDR regions in their models of high-redshift galaxies dominate the [CII] emission, while diffuse cold neutral gas only accounts for 10%, and the authors attributed this behaviour to the high CMB temperature at these epochs, which suppress the flux contrast. The neutral diffuse gas in our RT model accounts for around 18% of the [CII] emission. The two-phase ISM model in Vallini et al. (2015) does not include a hot-ionised gas phase, and hence there is no contribution from ionised gas to [CII] luminosity. In our fiducial RT model such ionised gas makes up 25% of the emission, comparable to the contribution from the neutral diffuse phase.
Olsen et al. (2017, 2018) used the Mufasa cosmological simulations (Davé et al. 2016, 2017; mgas = 1.9 × 105 h−1 M⊙) together with the SIGAME approach (applying sub-grid GMCs to their simulation using the GMC mass function) to study [CII] emission from high-redshift galaxies. They find the average contribution of GMCs to the [CII] emission to be around 50% for galaxies at z = 6, with 44% originating from the diffuse ionised gas, and only 6% from the diffuse neutral gas. In our fiducial model, more than half of the [CII] emission originates from the gas defined as a GMC, and 25% from the diffuse ionised gas, with the remaining emission originating from the diffuse neutral gas. However, it is important to note that Olsen et al. (2017, 2018) base their GMCs on the H2 fraction, calculated according to Krumholz et al. (2009), and not directly from the gas density and temperature, as was done in our model. They also did not directly account for the propagation of radiation via RT, but use an algorithm to find the closest stars, to estimate the radiation field experienced by the gas. As stated in Sect. 3.1, this method was unphysical to be applied in a simulation such as PONOS. In comparison with our MPM model, they have much lower luminosities, in [CII]. The main reason for this is the resolution, as our assumptions, where we treat every particle as an individual GMC, and not as part of a GMC structure, lead to an increased PDR covering fraction. In addition, the non-inclusion of a local-radiation field could lead to an increased [CII] emission. Without global RT the approximation used to estimate the local radiation field by Olsen et al. (2017, 2018) would overestimate the radiation experienced by the gas in PONOS, and thus would be unphysical, as mentioned previously. Our results show that when reaching a certain mass and spatial resolution, global RT and a different sub-grid approach are necessary to reproduce the [CII] emission.
6.3. Semi-analytical modelling
In the sphere of semi-analytical modelling, Popping et al. (2019) discussed at length the strong dependence on the implemented sub-grid cloud density profiles, and suggested that the Plummer profile leads to line luminosities that best reproduce current observational constraints. In our study, however, we do not find the Plummer profile to be the best at matching observations, which we ascribe to the high resolution of the simulation. Indeed, assuming every high density particle to be a GMC, creates an artificially high PDR covering fraction, and thus strong [CII] emission, especially if the radiation field is approximated. Without RT to calculate the radiation field experienced in different parts of the galaxy, the emission will be overestimated for high resolution simulations, and thus lead to high PDR emission.
Pizzati et al. (2023) find in their semi-analytical modelling, which they applied to ALPINE data, that extended [CII] halos are a natural by-product of starburst-driven outflows. The outflows in their model are launched by SNe, expanding into the CGM with velocities of 200−500 km s−1, where they first cool down to a few 100 K, before being heated up again by the UVB. This is in agreement with our results, where we find the UVB to be necessary for the extended [CII] emission. Pizzati et al. (2023) also state that the ALMA sensitivity threshold for ALPINE observations explains the non-detections of the faint, extended emission.
7. Discussion on future theoretical and observational prospects
7.1. Challenges in modelling CGM emission
Since the CGM is shaped by galaxy mergers, interactions, and cosmic accretion, as well as by internal feedback processes, only simulations of galaxies within a cosmological context can produce realistic predictions on the CGM properties, which is something idealised disc simulations cannot tackle. As of yet, no cosmological simulation has reached convergence when it comes to resolving the structure of cold gas in the CGM (Scannapieco & Brüggen 2015; Schneider & Robertson 2017; Mandelker et al. 2018; McCourt et al. 2018; Hummels et al. 2019; Suresh et al. 2019; van de Voort et al. 2019; Sparre et al. 2019; Nelson et al. 2021; Rey et al. 2023). A higher resolution leads to more substructures in the cold gas, hence high resolution simulations investigating the survival of cold streams and cold clumps including RT and chemistry (e.g. Rey et al. 2023), magnetic fields (e.g. Ponnada et al. 2022; Heesen et al. 2023) and cosmic rays (e.g. Butsky et al. 2023) are needed to get a better understanding of CGM properties.
In addition, better-resolved sub-structures will also affect the predicted emission of cold gas tracers, being highly sensitive to gas density, temperature, and ionisation state. As an example of this, we find [CI](1−0) emission line to be weaker than [CI](2−1) line for the RT model, which is the opposite trend than in the MPM model: indeed [CI](1−0) traces denser gas than [CI](2−1), which is not resolved in PONOS, but it is accounted for in analytical sub-grid density profiles. For the same reason, CO emission is weak in the RT model, since the maximum resolved density (nmax ∼ 2 × 103 cm−3) is still not enough to allow for CO formation. According to Seifried et al. (2020), in order to have H2 formation convergence and properly account for the H2 non-equilibrium state, a resolution of at least 0.1 pc is needed, which is currently unattainable in cosmological simulations or even idealised disc simulations. Therefore, while RT post-processing seems to be an accurate way to estimate the radiation field in the simulation, multi-phase analytical sub-grid models allow to explore the contribution of dense and otherwise unresolved gas to the emission. In this respect, a promising approach could be to combine the two approaches, as we plan to investigate in a future study.
Finally, we also point out that two other ingredients could improve the results: (1) accounting for variation of the stellar IMF through cosmic time and (2) including turbulent mixing effects on line emission. Neither the original PONOS simulation nor our post-processing take into account the time-dependency and metallicity-dependency of the stellar IMF. This is relevant since some observations have found a deficit in [CII] emission at high redshift (e.g. Ota et al. 2014; Maiolino et al. 2015; Schaerer et al. 2015; Pentericci et al. 2016; Knudsen et al. 2016; Bradač et al. 2017), which could be explained by a different C/O abundance ratio, caused by a top-heavy IMF in the early universe, enriching the ISM by low-metallicity core-collapse SNe (Katz et al. 2022). While turbulent mixing is included in the SPH simulation, it is not accounted in any of our sub-grid models (CLOUDY post-processing includes some turbulence, but not accurate turbulent mixing on a global scale). One consequence of this is that the [CI] emission only comes from PDR layers, and not from the molecular gas phase, as found in some observations (Hartigan et al. 2022; Papadopoulos 2004) and ascribed to turbulent mixing and cosmic rays (Papadopoulos et al. 2018; Zhang et al. 2018; Bisbas et al. 2018). This could explain why [CI] emission falls off for high values of the density (see Fig. 9). We also do not resolve the very dense gas in PONOS, which also lead to the very low CO emission.
Despite these unavoidable limitations, the PONOS simulation, thanks to its high resolution in combination with RT modelling similar to state-of-the-art studies (Pallottini et al. 2019, 2022; Katz et al. 2019, 2022; Lupi et al. 2020), produces reasonable theoretical predictions of sub-mm and FIR line emission from the ISM and CGM of a high redshift galaxy, showing extended emission in filaments and tidal tales in [CII], consistent with observations. Furthermore, comparing multiple modelling recipes within the same simulation has provided insights on the effect of each model on the resulting emission, factoring out differences that would arise when comparing results from different simulation setups. In the next section we exploit our results to discuss future avenues of observational astronomy.
7.2. Future observational avenues and relevance to AtLAST
Detecting and imaging the cold (T < 104 K) and dense gas residing in extended CGM reservoirs is extremely challenging at high redshift and impossible for local galaxies, because of the aforementioned limitations of current interferometric facilities such as ALMA, which have a limited sensitivity to large angular scale structures. In this context, AtLAST will revolutionise this field, as it will be the first sub-mm telescope capable of detecting and imaging the cold diffuse and extended (by ≳50 kpc) CGM at all redshifts and in multiple gas tracers. In this section we discuss in more detail how a system such as PONOS – that is a typical star-forming galaxy at z ∼ 6 – would be observed by current sub-mm facilities. To simulate sub-mm observations, we need to derive observed fluxes (in units of Jy km s−1) from the line luminosity values predicted by our models. We chose to focus on the fiducial RT model. We use the following relation (see e.g. Solomon & Vanden Bout 2005):
where νrest is the rest-frame frequency in units of GHz, and DL is the luminosity distance in units of Mpc. The luminosity distance was calculated with the Cosmology Calculator by Wright (2006) for a flat Universe.
PONOS is a small system, and, although it shows FIR/sub-mm line emission extending on scales of r ∼ 10 kpc or more due to merging companions, filaments, and other diffuse CGM components (see Fig. 12), these physical scales translate to rather compact angular sizes on the sky. At z = 6.5, assuming the same WMAP cosmological parameters as the simulation (see Sect. 2), which deliver a scale of 5.627 kpc arcsec−1, the virial halo of PONOS (2 ⋅ Rvir = 42 kpc) would have a projected angular diameter of 7.46″. The following considerations focus on the central 25 kpc region of PONOS, corresponding to 4.4 arscec on the sky.
7.2.1. Spectroscopy: simulated emission line spectra
Using the projected velocities from the simulation, we generated emission line spectra for each of the transitions modelled, which are reported in Fig. 18. Here, we show the total spectra (in purple) as well as the spectral decomposition of the different gas components: main disc (in orange), ISM of the merger companions (indigo), and CGM (in yellow). The spectra display clear spectral differences between the different components, in particular for the mergers, which can be easily resolved spectroscopically into two distinct peaks, as they orbit around the main disc of the central galaxy in PONOS. The CGM shows a broader spectrum than the disc, with clear asymmetries. The CO line profiles are narrower than the other lines, especially than [CII] and [OIII] which present broader spectra with high-velocity wings due to the mergers and to the CGM components.
 |
Fig. 18. Simulated spectra of each of the modelled emission lines (fiducial RT model). The total emission is shown in purple, the emission from the central disc in orange, the ISM of the merger components in indigo, and the CGM in yellow. The dotted lines show the multi-component Gaussian line fits performed separately for the spectra of each component. The purple dashed lines show single-Gaussian fits of the total integrated spectra, which we executed with the goal of obtaining an FWHM and peak density value. |
It is evident from Fig. 18 that, considering the tracers explored in this work and our fiducial RT model, the CGM emission from a system like PONOS may be detected only in [CII] and [OIII] emission. To test this hypothesis, we used the ALMA Cycle 10 observing tool and the new AtLAST sensitivity calculator4 to estimate the observing time needed to detect the CGM emission from PONOS in these two lines. Through a Gaussian spectral fit (see yellow dotted curves in Fig. 18), we obtain peak CGM flux densities of 3.8 mJy and 1.34 mJy, with full-width at half maximum (FWHM) values of ∼230 km s−1 and ∼280 km s−1, respectively for [CII] and [OIII]. Because of its roughly uniform brightness that fills this entire area (see Fig. 12), to calculate the sensitivity per beam required to detect such a CGM component, we need to scale down the sensitivity required to detect the total CGM component by the number of ALMA (or AtLAST) resolution elements (beams) contained in the imaged region. Carniani et al. (2020) dubbed this effects as “surface brightness dimming”.
As a result, we obtain that, to detect the CGM in [CII] at a signal-to-noise ratio S/N = 10 measured in Δv = 50 km s−1 channels, AtLAST would employ 9.7 h (5.1″ beam), while ALMA would use 48 h in the most compact configuration (C-1, 1.4″ beam), and > 3550 days in the C-5 configuration (0.24″ beam). Detecting the CGM of PONOS in [OIII]5 would be a much more challenging task even for AtLAST, due to the faintness of this line (compared to [CII]) and to the low atmospheric transmission at its observing frequency. In the case of [OIII], we relax our sensitivity goal to a S/N = 3 in Δv = 100 km s−1 channels, and obtain an integration time of ∼55 h with AtLAST (2.9″ beam), and 211 days with ALMA in compact configuration (0.77″ beam).
This exercise showed that – despite the rather compact angular extent of PONOS’s CGM (a few arcsec), ALMA would struggle to observe it, even in [CII] which is the brightest available tracer. Instead, AtLAST can easily detect the CGM component in [CII] at high S/N in just a few hours. For the much more challenging [OIII] line, tracing the ionised gas in the CGM, AtLAST can deliver a low S/N detection in about two days of integration, while this would be an impossible task for ALMA.
7.2.2. Imaging: mock maps
To image the ISM components of a system such as PONOS at z = 6.5, most observers would use intermediate-resolution ALMA configurations (∼0.2 − 0.3″ resolution). In Fig. 19 we display ALMA mock observations of the emission lines observable from ground at this redshift, that is [CI](2−1), [CII], and [OIII]6 For [CII] and [OIII], we also report ALMA mock observations of only the CGM component of PONOS (see Fig. 12). In all mocks, we simulated the central 50 km s−1, a spectral range where the CGM contribution relative to the ISM is maximised. In this velocity range, the ISM contribution arises from the main disc of the PONOS system. With a total integration time of 10 h per line (not including overheads), ALMA can detect well the ISM of the main disc all three transitions, without however revealing any extended halo component. Only the [CII] map (top-central panel) shows an additional extended feature that is not ascribable to the disc, tracing the brightest CGM spot emitting in this transition. This component is however only marginally detected when removing the ISM contribution from the maps (bottom left panel). The CGM is not detected at all in [OIII], despite contributing to ∼20% of the total flux in this tracer. These results are consistent with what discussed in Sect. 7.2.1. This exercise showed that the detection of extended CGM components does not come for free with deep ALMA observations optimised for imaging the ISM of high-z galaxies, and dedicated efforts are needed. As mentioned earlier, Pizzati et al. (2023) find in their semi-analytical model, that all high-z galaxies should have a [CII] halo, which would fall below the ALMA detection limit for lower masses. This can also be seen in our mock-observation, where the extended emission is too faint to be fully detected.
 |
Fig. 19. Simulated ALMA observations of PONOS, performed using CASA. The field of view of the input image includes the main disc, and mergers A and B. Note that the output CASA mocks are flipped and rotated by 180 deg with respect to the maps shown in Figs. 11 and 12: in these mocks, merger A is to the north and the accreting filament to the south, while the main galaxy disc is still to the left (east) and merger B to the right (west). Upper left: ALMA mock map of the total [CI](2−1) line emission, at an observed frequency of 107.91 GHz (Band 5). The simulation uses the ALMA C-5 array configuration (0.30″ angular resolution, 3.62″ maximum recoverable scale (MRS)). Upper middle: total [CII] line mock map, at an observed frequency of 253.40 GHz (Band 6). The simulation uses the ALMA C-5 array configuration (0.24″ angular resolution, 2.91″ MRS). Upper right: total [OIII] line mock map, at an observed frequency of 460 GHz (Band 8). The simulation uses the ALMA C-3 array configuration (0.31″ angular resolution, 3.51″ MRS). Bottom panels: show the corresponding [CII] and [OIII] mocks obtained for the CGM component only (see Fig. 12). In all CASA simulations, the total integration time was set equal to 10 h (without overheads), and we simulated one velocity channel of 50 km s−1 centred at v = 0 km s−1. |
8. Conclusions
We presented a state-of-the-art theoretical effort at modelling the emission of several FIR/sub-mm cold and warm gas tracers ([CII], [CI](1−0), [CI](2−1), CO(3−2), [OIII]) in the ISM and CGM of galaxies. We have used the high-resolution (1.5 pc) cosmological zoom-in simulation PONOS, which represents a typical star-forming galaxy system at z = 6.5, composed of a main disc with M* = 2 × 109 M⊙ and SFR = 20 M⊙ yr−1, and several merging companions. We have explored different modelling approaches based on the photoionisation code CLOUDY, including recipes commonly adopted in the literature. Our fiducial model includes RT post-processing using KRAMSES-RT, allowing us to include heating by radiation and cooling via different species of H and He. Our main results can be summarised as follows:
-
The [CII] line is the least sensitive to the underlying modelling approach, as it is by nature multi-phase, and can be found co-spatially with ionised, neutral and molecular gas, due to the low excitation energy of carbon. As it does not trace the densest gas phases, the emission can be modelled without additional sub-grid models; even the simplest modelling approach (denoted simple model, SM) yields reasonable results that are consistent with more sophisticated approaches. In our modelling we found [CII] to be sensitive to the PDR covering fraction.
-
Radiative transfer (RT) calculations are needed, as the gas emission is dependant on the underlying radiation field the gas experiences, and to account for the cooling and self-shielding that can occur; this can especially be seen for [OIII], where the RT process allows for heating and cooling, thus lowering the [OIII] emission compared to other models.
-
The [CI](1−0) and CO(3−2) lines are very sensitive to post-processing recipes as PONOS, like any other cosmological simulation, cannot resolve the scales relevant for H2 formation (< 0.1 pc). For the CO(3−2) line, only the multi-phase model (MPM) approach, which includes ad-hoc sub-resolution treatments of dense gas, produces reasonable results. Future efforts should explore combining RT calculations with multi-phase analytical sub-grid models to explore the contribution of dense, otherwise unresolved, gas.
-
More than half of [CII] in our fiducial model (∼55%) originates from gas at T ≤ 104 K and nH ≥ 10 cm−3. Our fiducial RT model produces a lower density, T ∼ 104 K tail of [CII] emission that is not seen in the other more simplistic models and that resides entirely in the CGM. This gas is ionised by the UV background.
-
Both [CII] and [OIII] have a non-negligible contribution from the CGM (10% and 21% respectively in the fiducial RT model), but trace different components of the CGM. In particular, [CII] is brighter in the accreting filaments and in the merging companions and connected tidal features. The CGM contribution to [OIII] resides instead in puffy halo surrounding the main galaxy disc, ionised by newly formed stars and possibly linked to supernova feedback.
-
In our study of the CGM emission, no gas tracer can be exclusively connected to in- or outflowing gas, showing that the interpretation of the origin of the extended emission is not straightforward.
These results are highly relevant to the interpretation of current and future sub-mm observations, with ALMA and with the planned AtLAST. In particular, observations need to take into account that a significant (∼10% and above) portion of the emission from typically employed sub-mm and FIR lines such as [CII] and [OIII] arises in the CGM component and not in galaxies’ discs. This contribution increases if the angular resolution of the observations is insufficient for deblending the discs of merging satellites from the diffuse CGM emission. We have shown, that even for a relatively compact system such as PONOS at z ∼ 6.5 whose entire halo is contained within a < 10″ angular region, imaging extended ISM and CGM components is extremely challenging with ALMA in [CII] and unfeasible in [OIII]. This is due to the diffuse and low surface brightness nature of these components. For this type of experiments, it will be crucial to build AtLAST: a new large-aperture, large-FoV sub-mm single-dish telescope, in a site with excellent atmospheric transmission at sub-mm wavelengths as to enable multi-tracer observations of the ISM and CGM of galaxies.
See also Table 7.1 of the ALMA Cycle 9 Technical Handbook (https://almascience.nrao.edu/documents-and-tools/cycle9/alma-technical-handbook).
We note that, in contrast to Pallottini et al. (2019) and Vallini et al. (2018) we do not include density distribution profiles in our analysis, as this is a different modelling approach from the sub-grid density profiles that we apply in this model.
Acknowledgments
This project has received funding from the European Unions Horizon 2020 research and innovation program under grant agreement No. 951815 (AtLAST). D. Decataldo, S. Shen and B. Baumschlager acknowledge the support from the Research Council of Norway through NFR Young Research Talents Grant 276043. L.D.M. is supported by the ERC-StG “ClustersXCosmo” grant agreement 716762 and acknowledges financial contribution from the agreement ASI-INAF n.2017-14-H.0. We thank the anonymous referee for providing insightful and constructive comments that significantly helped us improve the analysis and the overall presentation of the results. We thank Gergö Popping for his helpful input during the early stages of this study. We also thank Carlos De Breuck for helping us navigate the observational results in literature. We acknowledge usage of the Python programming language (Van Rossum & Drake 1995, 2009), Matplotlib (Hunter 2007), NumPy (van der Walt et al. 2011), Pynbody (Pontzen et al. 2013), of the CASA simulator (CASA Team 2022) and of the AtLAST sensitivity calculator.
References
- Agertz, O., Moore, B., Stadel, J., et al. 2007, MNRAS, 380, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Algera, H. S. B., Inami, H., Sommovigo, L., et al. 2024, MNRAS, 527, 6867 [Google Scholar]
- Arata, S., Yajima, H., Nagamine, K., Abe, M., & Khochfar, S. 2020, MNRAS, 498, 5541 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Goldsmith, P. F., Snell, R. L., & Langer, W. D. 1997, ApJ, 482, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Bisbas, T. G., Tan, J. C., Csengeri, T., et al. 2018, MNRAS, 478, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Bisbas, T. G., van Dishoeck, E. F., Hu, C.-Y., & Schruba, A. 2023, MNRAS, 519, 729 [Google Scholar]
- Bischetti, M., Maiolino, R., Carniani, S., et al. 2019, A&A, 630, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogaard, L. A., Decarli, R., Walter, F., et al. 2023, ApJ, 945, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Bowen, D. V., Chelouche, D., Jenkins, E. B., et al. 2016, ApJ, 826, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Garcia-Appadoo, D., Huang, K.-H., et al. 2017, ApJ, 836, L2 [Google Scholar]
- Brauher, J. R., Dale, D. A., & Helou, G. 2008, ApJS, 178, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Butsky, I. S., Nakum, S., Ponnada, S. B., et al. 2023, MNRAS, 521, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Maiolino, R., Amorin, R., et al. 2018, MNRAS, 478, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Ferrara, A., Maiolino, R., et al. 2020, MNRAS, 499, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- CASA Team (Bean, B., et al.) 2022, PASP, 134, 114501 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H., & Sire, C. 2007, Phys. A: Stat. Mech. Appl., 375, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Gallerani, S., et al. 2015, A&A, 574, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., De Breuck, C., Chen, C.-C., et al. 2019, BAAS, 51, 82 [NASA ADS] [Google Scholar]
- Cicone, C., Mainieri, V., Circosta, C., et al. 2021, A&A, 654, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Circosta, C., Mainieri, V., Lamperti, I., et al. 2021, A&A, 646, A96 [EDP Sciences] [Google Scholar]
- Cooper, T. J., Simcoe, R. A., Cooksey, K. L., et al. 2019, ApJ, 882, 77 [CrossRef] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [CrossRef] [EDP Sciences] [Google Scholar]
- da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
- Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davé, R., Thompson, R., & Hopkins, P. F. 2016, MNRAS, 462, 3265 [Google Scholar]
- Davé, R., Rafieferantsoa, M. H., Thompson, R. J., & Hopkins, P. F. 2017, MNRAS, 467, 115 [NASA ADS] [Google Scholar]
- De Breuck, C., Lundgren, A., Emonts, B., et al. 2022, A&A, 658, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- Decarli, R., Walter, F., Venemans, B. P., et al. 2017, Nature, 545, 457 [Google Scholar]
- Decarli, R., Aravena, M., Boogaard, L., et al. 2020, ApJ, 902, 110 [Google Scholar]
- Decataldo, D., Pallottini, A., Ferrara, A., Vallini, L., & Gallerani, S. 2019, MNRAS, 487, 3377 [Google Scholar]
- Decataldo, D., Lupi, A., Ferrara, A., Pallottini, A., & Fumagalli, M. 2020, MNRAS, 497, 4718 [NASA ADS] [CrossRef] [Google Scholar]
- Decataldo, D., Shen, S., Mayer, L., Baumschlager, B., & Madau, P. 2023, A&A, submitted [arXiv:2306.03146] [Google Scholar]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2017, ApJ, 846, 32 [Google Scholar]
- Dinerstein, H. L., Lester, D. F., & Werner, M. W. 1985, ApJ, 291, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Maddox, S. J., Papadopoulos, P. P., Ivison, R. J., & Gomez, H. L. 2022, MNRAS, 517, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, R., Fumagalli, M., Fossati, M., et al. 2020, MNRAS, 499, 5022 [CrossRef] [Google Scholar]
- Emonts, B. H. C., Lehnert, M. D., Villar-Martín, M., et al. 2016, Science, 354, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Emonts, B. H. C., Lehnert, M. D., Yoon, I., et al. 2023, Science, 379, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Ferkinhoff, C., Hailey-Dunsheath, S., Nikola, T., et al. 2010, ApJ, 714, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiacconi, D., Mayer, L., Madau, P., et al. 2017, MNRAS, 467, 4080 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Blackman, E. G., & Keto, E. R. 2011, MNRAS, 416, 710 [NASA ADS] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fudamoto, Y., Smit, R., Bowler, R. A. A., et al. 2022, ApJ, 934, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Ouchi, M., Ferrara, A., et al. 2019, ApJ, 887, 107 [Google Scholar]
- Fujimoto, S., Silverman, J. D., Bethermin, M., et al. 2020, ApJ, 900, 1 [Google Scholar]
- Fujimoto, S., Oguri, M., Brammer, G., et al. 2021, ApJ, 911, 99 [Google Scholar]
- Fujimoto, S., Ouchi, M., Nakajima, K., et al. 2022, ApJ, submitted [arXiv:2212.06863] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginolfi, M., Maiolino, R., Nagao, T., et al. 2017, MNRAS, 468, 3468 [CrossRef] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020a, A&A, 633, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020b, A&A, 643, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Langer, W. D., Pineda, J. L., & Velusamy, T. 2012, ApJS, 203, 13 [Google Scholar]
- González-López, J., Riechers, D. A., Decarli, R., et al. 2014, ApJ, 784, 99 [Google Scholar]
- Gowardhan, A., Riechers, D., Pavesi, R., et al. 2019, ApJ, 875, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [Google Scholar]
- Guedes, J., Callegari, S., Madau, P., & Mayer, L. 2011, ApJ, 742, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 2012, ApJ, 746, 125 [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Neth., 19, 421 [Google Scholar]
- Harikane, Y., Ouchi, M., Inoue, A. K., et al. 2020, ApJ, 896, 93 [Google Scholar]
- Hartigan, P., Hummel, M., Isella, A., & Downes, T. 2022, AJ, 164, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, T., Laporte, N., Mawatari, K., et al. 2018, Nature, 557, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019, PASJ, 71, 71 [Google Scholar]
- Heesen, V., O’Sullivan, S. P., Brüggen, M., et al. 2023, A&A, 670, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [Google Scholar]
- Herrera-Camus, R., Förster Schreiber, N., Genzel, R., et al. 2021, A&A, 649, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Hummels, C. B., Smith, B. D., Hopkins, P. F., et al. 2019, ApJ, 882, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Tamura, Y., Matsuo, H., et al. 2016, Science, 352, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Izumi, T., Matsuoka, Y., Fujimoto, S., et al. 2021, ApJ, 914, 36 [CrossRef] [Google Scholar]
- Jones, G. C., Maiolino, R., Carniani, S., et al. 2023, MNRAS, 522, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., Wagg, J., Chary, R. R., & Carilli, C. L. 2013, ApJ, 771, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Galligan, T. P., Kimm, T., et al. 2019, MNRAS, 487, 5902 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Rosdahl, J., Kimm, T., et al. 2022, MNRAS, 510, 5603 [NASA ADS] [CrossRef] [Google Scholar]
- Khusanova, Y., Bañados, E., Mazzucchelli, C., et al. 2022, A&A, 664, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Killi, M., Watson, D., Fujimoto, S., et al. 2023, MNRAS, 521, 2526 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-H., Abel, T., Agertz, O., et al. 2014, ApJS, 210, 14 [Google Scholar]
- Klaassen, P. D., Mroczkowski, T. K., Cicone, C., et al. 2020, SPIE Conf. Ser., 11445, 114452F [NASA ADS] [Google Scholar]
- Knudsen, K. K., Richard, J., Kneib, J.-P., et al. 2016, MNRAS, 462, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Knudsen, K. K., Watson, D., Frayer, D., et al. 2017, MNRAS, 466, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 699, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Kumari, N., Smit, R., Leitherer, C., et al. 2024, MNRAS, in press https://doi.org/10.1093/mnras/stae252 [Google Scholar]
- Lagache, G., Cousin, M., & Chatzikos, M. 2018, A&A, 609, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehner, N., Howk, J. C., & Wakker, B. P. 2015, ApJ, 804, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Leike, R. H., Glatzle, M., & Enßlin, T. A. 2020, A&A, 639, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Lenkić, L., Bolatto, A. D., Förster Schreiber, N. M., et al. 2020, AJ, 159, 190 [CrossRef] [Google Scholar]
- Leroy, A. K., Rosolowsky, E., Usero, A., et al. 2022, ApJ, 927, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, T. K. D., Olsen, K. P., Somerville, R. S., et al. 2020, ApJ, 905, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Emonts, B. H. C., Cai, Z., et al. 2021, ApJ, 922, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Lupi, A., Pallottini, A., Ferrara, A., et al. 2020, MNRAS, 496, 5160 [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [Google Scholar]
- Maiolino, R., Carniani, S., Fontana, A., et al. 2015, MNRAS, 452, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelker, N., van Dokkum, P. G., Brodie, J. P., van den Bosch, F. C., & Ceverino, D. 2018, ApJ, 861, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McCourt, M., Oh, S. P., O’Leary, R., & Madigan, A.-M. 2018, MNRAS, 473, 5407 [Google Scholar]
- Meyer, R. A., Walter, F., Cicone, C., et al. 2022, ApJ, 927, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Montoya Arroyave, I., Cicone, C., Makroleivaditi, E., et al. 2023, A&A, 673, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagao, T., Maiolino, R., Marconi, A., & Matsuhara, H. 2011, A&A, 526, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagao, T., Maiolino, R., De Breuck, C., et al. 2013, in New Trends in Radio Astronomy in the ALMA Era: The 30th Anniversary of Nobeyama Radio Observatory, eds. R. Kawabe, N. Kuno, & S. Yamamoto, ASP Conf. Ser., 476, 29 [NASA ADS] [Google Scholar]
- Nelson, D., Byrohl, C., Peroux, C., Rubin, K. H. R., & Burchett, J. N. 2021, MNRAS, 507, 4445 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, K. P., Greve, T. R., Narayanan, D., et al. 2015, ApJ, 814, 76 [CrossRef] [Google Scholar]
- Olsen, K., Greve, T. R., Narayanan, D., et al. 2017, ApJ, 846, 105 [Google Scholar]
- Olsen, K., Pallottini, A., Wofford, A., et al. 2018, Galaxies, 6, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, K., Walter, F., Ohta, K., et al. 2014, ApJ, 792, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ellis, R., Ono, Y., et al. 2013, ApJ, 778, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., Ferrara, A., Bovino, S., et al. 2017, MNRAS, 471, 4128 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., Ferrara, A., Decataldo, D., et al. 2019, MNRAS, 487, 1689 [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
- Papadopoulos, P. 2004, in The Neutral ISM in Starburst Galaxies, eds. S. Aalto, S. Huttemeister, & A. Pedlar, ASP Conf. Ser., 320, 101 [NASA ADS] [Google Scholar]
- Papadopoulos, P. P., Bisbas, T. G., & Zhang, Z.-Y. 2018, MNRAS, 478, 1716 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P., Dunne, L., & Maddox, S. 2022, MNRAS, 510, 725 [Google Scholar]
- Pentericci, L., Carniani, S., Castellano, M., et al. 2016, ApJ, 829, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Rigopoulou, D., Farrah, D., Lebouteiller, V., & Li, J. 2017, MNRAS, 470, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 495, 160 [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2023, MNRAS, 519, 4608 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
- Ponnada, S. B., Panopoulou, G. V., Butsky, I. S., et al. 2022, MNRAS, 516, 4417 [NASA ADS] [CrossRef] [Google Scholar]
- Pontzen, A., Roškar, R., Stinson, G., & Woods, R. 2013, Astrophysics Source Code Library [record ascl:1305.002] [Google Scholar]
- Popping, G. 2023, A&A, 669, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Narayanan, D., Somerville, R. S., Faisst, A. L., & Krumholz, M. R. 2019, MNRAS, 482, 4906 [Google Scholar]
- Prochaska, J. X., Lau, M. W., & Hennawi, J. F. 2014, ApJ, 796, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., & Navarro, J. F. 1996, A&A, 315, 105 [NASA ADS] [Google Scholar]
- Ramasawmy, J., Klaassen, P. D., Cicone, C., et al. 2022, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy XI, eds. J. Zmuidzinas, & J. R. Gao, SPIE Conf. Ser., 12190, 1219007 [Google Scholar]
- Ren, Y. W., Fudamoto, Y., Inoue, A. K., et al. 2023, ApJ, 945, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Rey, M. P., Katz, H. B., Cameron, A. J., Devriendt, J., & Slyz, A. 2023, ArXiv e-prints [arXiv:2302.08521] [Google Scholar]
- Rigopoulou, D., Pereira-Santaella, M., Magdis, G. E., et al. 2018, MNRAS, 473, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., & Teyssier, R. 2013, MNRAS, 436, 2188 [Google Scholar]
- Rubin, R. H., Simpson, J. P., Lord, S. D., et al. 1994, ApJ, 420, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E., & Brüggen, M. 2015, ApJ, 805, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., Boone, F., Zamojski, M., et al. 2015, A&A, 574, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Ginolfi, M., Béthermin, M., et al. 2020, A&A, 643, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, E. E., & Robertson, B. E. 2017, ApJ, 834, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Scholtz, J., Maiolino, R., Jones, G. C., & Carniani, S. 2023, MNRAS, 519, 5246 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Haid, S., Walch, S., Borchert, E. M. A., & Bisbas, T. G. 2020, MNRAS, 492, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Seon, K.-I., Witt, A., Kim, I.-J., et al. 2011, ApJ, 743, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Wadsley, J., & Stinson, G. 2010, MNRAS, 407, 1581 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Madau, P., Conroy, C., Governato, F., & Mayer, L. 2014, ApJ, 792, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Pfrommer, C., & Vogelsberger, M. 2019, MNRAS, 482, 5401 [Google Scholar]
- Stacey, G., Townes, C., Poglitsch, A., et al. 1991, ApJ, 382, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Stinson, G., Seth, A., Katz, N., et al. 2006, MNRAS, 373, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Suresh, J., Nelson, D., Genel, S., Rubin, K. H. R., & Hernquist, L. 2019, MNRAS, 483, 4040 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W. F., van Dishoeck, E. F., Bell, T., Viti, S., & Black, J. 2009, MNRAS, 400, 622 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]
- Vallini, L., Gallerani, S., Ferrara, A., Pallottini, A., & Yue, B. 2015, ApJ, 813, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., & Gallerani, S. 2017, MNRAS, 467, 1300 [NASA ADS] [Google Scholar]
- Vallini, L., Pallottini, A., Ferrara, A., et al. 2018, MNRAS, 473, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., Carniani, S., & Gallerani, S. 2021, MNRAS, 505, 5543 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderhoof, B. N., Faisst, A. L., Shen, L., et al. 2022, MNRAS, 511, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- van de Voort, F., Springel, V., Mandelker, N., van den Bosch, F. C., & Pakmor, R. 2019, MNRAS, 482, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Van Rossum, G., & Drake, F. L., Jr. 1995, Python Reference Manual (Amsterdam: Centrum voor Wiskunde en Informatica) [Google Scholar]
- Van Rossum, G., & Drake, F. L. 2009, Python 3 Reference Manual (Scotts Valley: CreateSpace) [Google Scholar]
- Veilleux, S., Maiolino, R., Bolatto, A. D., & Aalto, S. 2020, A&ARv, 28, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wadsley, J. W., Stadel, J., & Quinn, T. 2004, New Astron., 9, 137 [Google Scholar]
- Wadsley, J. W., Keller, B. W., & Quinn, T. R. 2017, MNRAS, 471, 2357 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, C. K., Adams, F. C., & Lada, C. J. 1990, ApJ, 349, 515 [Google Scholar]
- Webber, W. R., & Soutoul, A. 1998, ApJ, 506, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Werk, J. K., Prochaska, J. X., Tumlinson, J., et al. 2014, ApJ, 792, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Whitworth, A. P., & Ward-Thompson, D. 2001, ApJ, 547, 317 [Google Scholar]
- Willott, C. J., Carilli, C. L., Wagg, J., & Wang, R. 2015, ApJ, 807, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D., Petitpas, G. R., Iono, D., et al. 2008, ApJS, 178, 189 [Google Scholar]
- Witstok, J., Smit, R., Maiolino, R., et al. 2022, MNRAS, 515, 1751 [Google Scholar]
- Wolfire, M. G., Vallini, L., & Chevance, M. 2022, ARA&A, 60, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanella, A., Valentino, F., Gallazzi, A., et al. 2023, MNRAS, 524, 923 [CrossRef] [Google Scholar]
- Zhang, Z.-Y., Papadopoulos, P. P., Ivison, R. J., et al. 2016, R. Soc. Open Sci., 3, 160025 [Google Scholar]
- Zhang, G.-Y., Xu, J.-L., Vasyunin, A. I., et al. 2018, A&A, 620, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucker, C., Goodman, A., Alves, J., et al. 2021, ApJ, 919, 35 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Multiphase model maps
In Fig. A.1 we show the different emission line maps obtained with the 2CG MPM, to compare it with the corresponding maps obtained with our fiducial RT model, that can be seen in Fig. 11. All maps of the MPMs look very similar in morphology, so we selected to only show one example. In the MPM we see a far more extended emission in [OIII] compared to the RT model, due to the contribution of cold and diffuse, as well as hot and dense gas, which heats up and cools down in the RT post-processing respectively, as commented in Section 4.1 and as shown in the phase diagram in Fig. 8.
 |
Fig. A.1. Line emission maps obtained with the MPM 2CG model. The circles in each plot mark Rvir. |
The [CII] and [CI] line emission in the MPM model do not trace the filaments as well as the RT model, and their resulting emission are very clumpy in appearance and less concentrated to the central disc of the galaxy than in the RT model, which is due to the assumption of every dense gas particle being treated as a GMC. The same behaviour can be seen in the CO(3-2) maps, which is shown in the bottom panel of Fig. A.1, where the left plot shows the map in the same scaling as the RT CO map, while the right panel shows a rescaled map to be able to see the differences in emission within the model. The reasons for this differences are explained in more detail in the main text of this paper.
As in our modelling the dense gas is defined according to the star formation criteria of PONOS, the particles where a sub-grid model was applied are the same particles that are able to form stars. Thus, the particles traced by CO in the MPM emission maps are also the places where we found recent star formation, including inside the CGM.
Appendix B: Emission line table
Table B.1 lists the line luminosities in units of L⊙ for all models discussed in this paper, together with the corresponding fractions for gas phase and morphology. We use the same definitions for the dense and diffuse gas in all models for consistency, which is described in detail in Section 2.2.
Line luminosities for all models.
All Tables
Line luminosities (in units of L⊙) obtained from the fiducial RT model, divided by halo component.
All Figures
 |
Fig. 1. Maps of the PONOS simulation at redshift z = 6.5, showing the dark matter surface density (top panel), the gas surface density (middle panel), and the stellar surface density (bottom panel). The white circle marks Rvir. The highest density structures trace the central disc and the three major satellites, two of which are close to the disc and merging with each other (merger B). Another merger can be seen in the south (A). Extended structures embedding both gas and stars lie between the main disc and the mergers. |
| In the text | |
 |
Fig. 2. Gas density maps, showing the identification and de-blending of ISM and CGM gas components in the PONOS simulation snapshot. The top panel shows the ISM components, which include the main galaxy disc (including all gas particles within twice the half light radius) and the discs of the merging satellites. The gas density of the “non-ISM” particles is shown by the purple contours. The bottom panel shows the CGM component, made up by all gas within the Rvir after masking out the galaxy discs. |
| In the text | |
 |
Fig. 3. Flowchart illustrating our three different modelling approaches: simple model (SM), multi-phase model (MPM), and global radiative transfer (RT) approach, which are described in detail in Sects. 3.1–3.3. The RT is our fiducial model. The corresponding CLOUDY parameters are reported in Table 1. |
| In the text | |
 |
Fig. 4. Qualitative representation of the different sub-grid cloud density profiles applied in the MPM. |
| In the text | |
 |
Fig. 5. H2 gas fraction in PONOS obtained from the RT post-processing with KRAMSES-RT. Most of the H2 resides in the main disc and in the merging component B, although clouds of molecular gas are also formed in the CGM, especially in the northern accreting filament. |
| In the text | |
 |
Fig. 6. Distribution of the log(G0) values of the PONOS simulation after RT post-processing. In black the distribution for the whole halo is shown, while in purple the disc, in orange the merger component, and in pink the CGM is represented. The high log(G0) values are part of the disc and mergers, where the gas experiences UV radiation from young stars. The black dashed line represents the background radiation used in the SM and MPM. |
| In the text | |
 |
Fig. 7. Comparison of line luminosities (in solar luminosities) obtained with our six modelling strategies (see summary in Fig. 3), computed for different halo components. Each model is represented by a different colour: SM (grey), MPM+Plummer (purple), MPM+Logotropic (yellow), MPM+Power law (magenta), MPM+2-component Gaussian (orange), and RT (black). Different halo components are indicated using symbols: circle markers for the whole PONOS halo, crosses for the main disc, pentagons for the mergers, and diamonds for the CGM (see Sect. 2.2 or the definition of the components). For the SM, dense gas tracers such as CO are unrealistically low and outside the ranges shown in this plot. |
| In the text | |
 |
Fig. 8. Density–temperature (n − T) phase diagram of all six models used in this analysis. The rows show the different models, while the columns represent the different synthetic emission lines. The colours represent the emission in a particular line. For the MPM the densities do not directly correspond to those taken directly from the simulations, as they are given sub-grid density profiles, as described in Sect. 3.2. The bottom row corresponds to the fiducial RT model, and it shows how the RT post-processing produces densities and temperatures that differ from the original simulation. |
| In the text | |
 |
Fig. 9. [CII], [CI], CO, and [OIII] line luminosities of the RT model as a function of gas number density (nH, top-left panel), distance from the centre of the simulation box (top-right panel), radiation field (bottom-left panel), and gas temperature (bottom-right panel). |
| In the text | |
 |
Fig. 10. Line luminosities plotted as a function of gas number density (left column), gas temperature (middle column) and incident radiation field (right column). The lines are also divided into the contribution from different halo components, where the black solid line shows the total emission from the whole simulation box, the dashed purple line shows the main disc emission, the two mergers are plotted using a magenta dashed line, and the CGM is plotted using a dashed orange line. |
| In the text | |
 |
Fig. 11. Line emission maps obtained with the fiducial RT model. The circles in each plot mark Rvir. The top-left panel shows [CII], which is clearly extended and clumpy in appearance, with most of its emission originating from the main disc and merger components, and bridges of gas in between. The top-right panel shows the [OIII] map, which is fainter than in the other models tested in this study (see e.g. Fig. A.1 showing the same maps obtained for the MPM 2-component Gaussian model). [OIII] is extended, although less than [CII], and traces warm-ionised gas rather than the cold neutral gas traced by [CII]. The central maps show the [CI]609 μm and [CI]370 μm transitions, which are also extended, although fainter than [CII] (note the different surface luminosity scaling). The bottom panels show the CO(3−2) maps. The lowest plot on the right shows the CO(3−2) emission zoomed in on the main disc. As discussed in the main text, CO is faint in the RT model, and concentrated in the main disc and merger components. There are faint clouds of CO(3−2) emission in the CGM, overlapping with regions with relatively high [CI] emission. |
| In the text | |
 |
Fig. 12. Line emission maps obtained with the fiducial RT model, only showing the CGM emission of Ponos for [CII] and [OIII]. |
| In the text | |
 |
Fig. 13. Line luminosities of the CGM plotted as a function of gas number density (left column), gas temperature (middle column) and gas metallicity (right column). The lines are also divided into the contribution from different CGM components as well as the main disc, where the black solid line shows the total CGM emission, the dashed black line shows the emission of high velocity CGM gas (v > 200 km s−1), outflowing high velocity gas in the dashed red line, inflowing high velocity gas in the blue dashed line and as a reference the disc/ISM component in dashed green. |
| In the text | |
 |
Fig. 14. [OIII]/[CII] surface brightness ratio map obtained from the RT run. The right panels show the [CII], [OIII], and [OIII]/[CII] plots in a zoomed-in portion of the main disc, to highlight the spatial offset between [OIII] and [CII]. The units of Σline are [L⊙ kpc−2]. |
| In the text | |
 |
Fig. 15. [CII] line luminosity as a function of the SFR. In the left panel, our models are compared with observational constraints available from the literature at a similar redshift, while the right panel shows the comparison with other theoretical works. The circles represent the whole halo, crosses represent the main disc, and the pentagon the merging companions A and B. The CGM is shown using diamond symbols. The observational data are taken from: Kanekar et al. (2013) at z = 6.5, Ouchi et al. (2013) at z = 6.5, González-López et al. (2014) at z = 6.5 − 11, Ota et al. (2014) at z = 6.9, Schaerer et al. (2015)z = 6.8 − 7.5, Capak et al. (2015) for z = 5.1 − 5.7, Willott et al. (2015) for z = 6, Maiolino et al. (2015) for z = 6.8 − 7.1, Knudsen et al. (2016, 2017) for z = 6 − 7.6, Pentericci et al. (2016) for z = 6.6 − 7.1, Bradač et al. (2017) for z = 6.7, Decarli et al. (2017) for z = 6 − 6.6, Khusanova et al. (2022) for z = 6, Vanderhoof et al. (2022) for z = 4.5, Fujimoto et al. (2021) for z = 6, Witstok et al. (2022) for z = 6 − 7, Hashimoto et al. (2019) for z ∼ 7, Harikane et al. (2020) for z ∼ 6, the ALPINE data for z = 4 − 8, Schaerer et al. (2020), Algera et al. (2024) for z = 7.3, Fujimoto et al. (2022) for z = 8.4, Ren et al. (2023) for z = 7.2, and Carniani et al. (2018) for z = 5 − 7. The relation shown in grey is by De Looze et al. (2014) for SB galaxies, and the relation shown in purple by Carniani et al. (2020) for high-redshift galaxies. In addition, on the right panel, we compare our results to simulation data by Pallottini et al. (2019, 2022); Katz et al. (2022) and Lupi et al. (2020). The relation by Vallini et al. (2015) based on physical motivated models for a metallicity of Z = 0.5 Z⊙ can be seen in grey dashed, the relation by Arata et al. (2020) in dot-dashed, the relation found by Leung et al. (2020) in purple, and the Olsen et al. (2018) data in grey dot-dashed. |
| In the text | |
 |
Fig. 16. [OIII]88 μm line luminosity as a function of SFR. Our modelling results based on the PONOS simulation are compared with observations in the left panel, and with other theoretical works in the right panel. Symbols and colour-coding are the same as in Fig. 15. As was also seen in Fig. 7, the [OIII] luminosities of the MPMs does not change much for different sub-grid density profiles for the dense gas, and thus we show the MPM emission in one data point. The MPMs are represented in indigo. The observational data in the left panel are taken from: Popping (2023; upper limit of a z = 13 galaxy), Witstok et al. (2022; z = 6 − 7), Hashimoto et al. (2019; z ∼ 7), Hashimoto et al. (2018; z = 9), Inoue et al. (2016; z ∼ 7), Algera et al. (2024; z = 7.3), Fujimoto et al. (2022; z = 8.4), Ren et al. (2023; z = 7.2), and Harikane et al. (2020; z ∼ 6). The relation reported in the left panel are the one derived by De Looze et al. (2014) and by Harikane et al. (2020). On the right panel, we compare our results to the simulation results by Pallottini et al. (2019, 2022), Katz et al. (2022), and Lupi et al. (2020), the relation by Arata et al. (2020) in dot-dashed, and the relation reported is the one fitted by Olsen et al. (2017) for their z = 6 simulated galaxies. |
| In the text | |
 |
Fig. 17. CO(3−2) line luminosity as a function of total infrared luminosity of PONOS, obtained with the different models, compared with observational data. Symbols and colour-coding are as in Fig. 15. The SM was not included because of its very low CO luminosity. Due to the scarcity of observations CO(3−2) data at z ≳ 6, most data shown in this figure (except for Strandet et al. 2017 at z = 6.9) represent galaxies at z = 1 − 4: Gowardhan et al. (2019) at z ∼ 3.2, Tacconi et al. (2013) at z = 1 − 3, Daddi et al. (2015) at z = 1.5, Yang et al. (2017) at z = 2 − 4, Circosta et al. (2021) at z = 2 − 2.5 and Zanella et al. (2023) at z ∼ 1. |
| In the text | |
 |
Fig. 18. Simulated spectra of each of the modelled emission lines (fiducial RT model). The total emission is shown in purple, the emission from the central disc in orange, the ISM of the merger components in indigo, and the CGM in yellow. The dotted lines show the multi-component Gaussian line fits performed separately for the spectra of each component. The purple dashed lines show single-Gaussian fits of the total integrated spectra, which we executed with the goal of obtaining an FWHM and peak density value. |
| In the text | |
 |
Fig. 19. Simulated ALMA observations of PONOS, performed using CASA. The field of view of the input image includes the main disc, and mergers A and B. Note that the output CASA mocks are flipped and rotated by 180 deg with respect to the maps shown in Figs. 11 and 12: in these mocks, merger A is to the north and the accreting filament to the south, while the main galaxy disc is still to the left (east) and merger B to the right (west). Upper left: ALMA mock map of the total [CI](2−1) line emission, at an observed frequency of 107.91 GHz (Band 5). The simulation uses the ALMA C-5 array configuration (0.30″ angular resolution, 3.62″ maximum recoverable scale (MRS)). Upper middle: total [CII] line mock map, at an observed frequency of 253.40 GHz (Band 6). The simulation uses the ALMA C-5 array configuration (0.24″ angular resolution, 2.91″ MRS). Upper right: total [OIII] line mock map, at an observed frequency of 460 GHz (Band 8). The simulation uses the ALMA C-3 array configuration (0.31″ angular resolution, 3.51″ MRS). Bottom panels: show the corresponding [CII] and [OIII] mocks obtained for the CGM component only (see Fig. 12). In all CASA simulations, the total integration time was set equal to 10 h (without overheads), and we simulated one velocity channel of 50 km s−1 centred at v = 0 km s−1. |
| In the text | |
 |
Fig. A.1. Line emission maps obtained with the MPM 2CG model. The circles in each plot mark Rvir. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



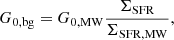
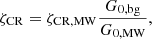
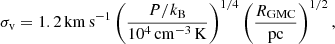
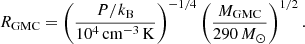
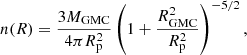
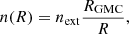
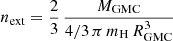
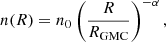
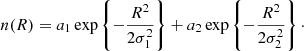
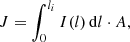
![$$ \begin{aligned} L^{\prime }_{\rm CO} [\mathrm{K\,km\,s^{-1}\,pc^{2}}] = (3.25 \times 10^{7}) \nu _{\rm obs}^{-2} D_{\rm L}^{2} (1+z)^{-3} \int _{\Delta \nu } {S\!}_{\nu }\mathrm{d}v \end{aligned} $$](/articles/aa/full_html/2024/02/aa46945-23/aa46945-23-eq16.gif)
![$$ \begin{aligned} \mathrm{SFR}\,[M_{\odot }\,\mathrm{yr}^{-1}] = 1.09 \times 10^{-10}\,\mathrm{L_{\rm IR}}\,[L_{\odot }]. \end{aligned} $$](/articles/aa/full_html/2024/02/aa46945-23/aa46945-23-eq20.gif)
![$$ \begin{aligned} L_{\rm Line} [L_{\odot }] = (1.04 \times 10^{-3}) \frac{\nu _{\rm rest}}{(1 + z)} D_{\rm L}^{2} \int _{\Delta \nu } {S\!}_{\nu }\mathrm{d}v, \end{aligned} $$](/articles/aa/full_html/2024/02/aa46945-23/aa46945-23-eq21.gif)