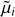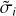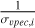| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 25 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202346288 | |
| Published online | 30 October 2023 | |
Statistically bias-minimized peculiar velocity catalogs from Gibbs point processes and Bayesian inference
1
Univ. Lille, CNRS, Centrale Lille, UMR 9189 CRIStAL,
59000
Lille, France
e-mail: jenny.sorce@univ-lille.fr; jenny.sorce@universite-paris-saclay.fr
2
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale,
91405
Orsay, France
3
Leibniz-Institut für Astrophysik,
An der Sternwarte 16,
14482
Potsdam, Germany
4
Université de Lorraine, CNRS, IECL, Inria,
54000
Nancy, France
5
Tartu Observatory, University of Tartu,
Observatooriumi 1,
61602
Tõravere, Estonia
6
Estonian Academy of Sciences,
Kohtu 6,
10130
Tallinn, Estonia
Received:
1
March
2023
Accepted:
16
August
2023
The peculiar velocities of galaxies can serve as excellent cosmological probes provided that the biases inherent to their measurements are contained prior to the start of any study. This paper proposes a new algorithm based on an object point process model whose probability density is built to statistically reduce the effects of Malmquist biases and uncertainties due to lognormal errors in radial peculiar velocity catalogs. More precisely, a simulated annealing algorithm allows for the probability density describing the point process model to be maximized. The resulting configurations are bias-minimized catalogs. We conducted tests on synthetic catalogs mimicking the second and third distance modulus catalogs of the Cosmicflows project from which peculiar velocity catalogs are derived. By reducing the local peculiar velocity variance in catalogs by an order of magnitude, the algorithm permits the recovery of the expected one, while preserving the small-scale velocity correlation. It also allows for the expected clustering to be retrieved. The algorithm was then applied to the observational catalogs. The large-scale structure reconstructed with the Wiener-filter technique applied to the bias-minimized observational catalogs matches that of the local cosmic web well, as supported by redshift surveys of local galaxies. These new bias-minimized versions of peculiar velocity catalogs can be used as a starting point for several studies, from plausible estimations of the most probable value for the Hubble constant, H0, to the production of simulations constrained to reproduce the local Universe.
Key words: methods: statistical / techniques: radial velocities / catalogs / Galaxy: kinematics and dynamics
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The peculiar velocities of galaxies result from the action of the entire underlying gravitational field. Additionally, they are linear and correlated on large scales. As such, they are excellent cosmological probes for studying the dark side of the Universe. However, peculiar velocity catalogs are also grandly affected by different sources of biases. Some are known, some are not. In any case accounting for their effects is not completely mastered. Disentangling the true underlying signal from noises in radial peculiar velocity catalogs has become a major issue within the last decade with the advent of using them to derive cosmological parameters (e.g., Nusser & Davis 2011; Feix et al. 2017; Howlett et al. 2017; Nusser 2017; Wang et al. 2018), to map the local distribution of matter (e.g., Tully et al. 2014; Hoffman et al. 2018), and to constrain initial conditions that evolve into our local neighborhood, the Local Universe (e.g., Gottlöber et al. 2010; Sorce et al. 2014a, 2016b).
Tully et al. (2013) and later Tully et al. (2016) released two large peculiar velocity catalogs. The second improves on the first one with additional major contributions from the 6dF Galaxy Survey (e.g., Wakamatsu et al. 2003; Campbell et al. 2014) and two Spitzer surveys: CosmicFlows with Spitzer (CFS, Sorce et al. 2014b) and the Spitzer Survey of Stellar Structure in Galaxies (S4G, Sheth et al. 2010). However, with the increasing distance coverage, the impact of biases affecting the catalogs has grown stronger. Sorce (2015) proposed a technique to minimize the biases in such peculiar velocity catalogs. It permitted their effects, such as a spurious strong infall onto the reconstructed Local Volume, to be eliminated. Later, it allowed for simulations of local clusters such as our closest neighbor, the Virgo cluster of galaxies (Sorce et al. 2016a, 2019, 2021), as well as other local clusters (e.g., Centaurus, Coma, and Perseus, Sorce 2018; Sorce et al. 2023). Even more recently, Graziani et al. (2019); Boruah et al. (2022) and Valade et al. (2022), borrowing from Lavaux (2016), proposed Bayesian techniques that could reasonably reduce the infall onto the reconstructed Local Volume. As with any Bayesian techniques, they relied on theoretical expectations, in their case: those mostly coming from the ΛCDM cosmological paradigm. However, they also relied (heavily) on prior knowledge of the dataset. They invoke multiple functions making it difficult to disentangle what can really be deduced from the data from what is included as a prior to correct the data. On the other hand, although Sorce (2015) relied only on the expected radial peculiar velocity 1D distribution, they neglected the 3D small-scale correlations related to the 3D spatial distributions of galaxies.
In this paper, we propose to focus on the 3D small-scale correlations using a probabilistic approach. More precisely, considering the finite size of the peculiar velocity catalogs of galaxies in a finite region (the Local Universe), we base our approach on an object point process model that is built in a way that its probability density tends to be maximal when bias effects are minimal. The configurations (or realizations) maximizing the probability density are then bias-minimized radial peculiar velocity catalogs. From a broad point of view, it is a typical inverse problem regularly solved in various fields (including in astrophysics), for instance, for image restoration (e.g. Van Lieshout 1994; Bijaoui 2013).
In our case, functions used within the core of the algorithm should not rely heavily on the cosmological model nor on the dataset configuration. This makes it easier to: 1) change for another cosmological model; 2) change for another dataset; and 3) disentangle the underlying signal in the data from the signal that is induced by priors.
More specifically, galaxy radial peculiar velocities are derived via a cosmological model from galaxy distance moduli and observational redshifts, with the latter being far more precisely determined than the former and uncertainties on the latter usually considered negligible. Galaxy observational redshifts are thus assumed to be fixed. The algorithm should then output the most probable location of the galaxies given the uncertainty on their distance modulus measurements and the associated derived radial peculiar velocities. This kind of configuration should be likely to maximize the proposed probability density. We note that it is possible to advocate for using observational redshifts as proxies for distances. Radial peculiar velocities derived from such distances would all be zero, which would be an unrealistic result. Thus, the resulting configuration should not maximize the proposed probability density.
To include 3D small-scale correlations, for a set of galaxy distance moduli and uncertainties (μ, σ), the algorithm should consider for each galaxy a pre-determined spatial region that characterize a zone of interactions. This zone should depend on the galaxy distance modulus and uncertainty and, by extension, on its radial peculiar velocity. The algorithm should rely on the underlying correlation, in the catalog of galaxy distance moduli, between the directly derived peculiar velocities of galaxies. Radial peculiar velocities of galaxies sharing a same local region in space are indeed linked to the local underlying gravitational field, namely, the local structure. As mentioned above, given our spatial data set (a distribution of galaxies in a finite Local Volume), we assume that the realization that maximizes the probability density of our point process model should permit retrieving the underlying correlation. The probability density, p, with respect to the unit intensity Poisson reference measure, should depend on the data, (μ, σ), and the model parameters, (c), (see Stoica 2010, and references therein for detailed explanations). Given the intractability of the underlying probability density, to derive the configuration that maximizes it, we need instead to construct a function, U(μ|d, c), where d = (μinit, σinit, zobs), and sample from it (cf. Metropolis-Hastings algorithm). This function should reach its maximum for a realization (set of distance moduli μi and associated uncertainties σi) that minimizes the biases. Moreover, since the function is not a priori convex (i.e., not a single maximum), the realization should be obtained with a global optimization technique through a simulated annealing to sample a probability law in the form p(μ|d, c)1/T ∝ exp(−U(μ|d, c)/T) with T slowly going to zero.
Such techniques have been used in the past in astronomy to find, for instance, filaments and groups in redshift surveys (Tempel et al. 2016b, 2018) as well as to build maps of optimal tile distributions for efficiently observing multi-source catalogs (Tempel et al. 2020). However, in these examples, celestial object (galaxy and star) distributions are considered fixed.
Considering these distributions, one of the realizations maximizing the probability gives one of the optimal arrangement of filaments, groups and tiles. In our case, the galaxy distribution is not fixed but constitutes a realization by itself. One of the galaxy distributions that maximizes the probability can be retrieved, in particular, thanks to the local underlying velocity correlations. Contrary to Sorce (2015), bias-minimized radial peculiar velocities of galaxies are not obtained on a one-to-one basis (probability of the velocity to exist given the 1D velocity probability distribution) but collectively (probability of the velocity to exist given the 1D velocity probability distribution and given the 3D velocity local variance probability). In both cases, the resulting bias-minimized peculiar velocity catalog should be considered as a whole; namely, the data points cannot be considered individually as better estimates. The realization, namely, the full catalog, constitutes a statistically improved representation of the true data point distribution. This concept is at the core of the algorithm we propose in this work.
This paper starts with a description of the biases affecting the catalogs and the computation of radial peculiar velocities. The third section builds the probability law as well as the algorithm and the associated inference processes. The algorithm is subsequently applied to mock catalogs mimicking observational ones. The building of the latter is also detailed. The results of the application of the algorithm to the synthetic catalogs are analyzed. For the sake of concision, plots are shown for one of the mock catalogs. To show one use-example of the bias-minimized catalogs, they are plugged into a Wiener-filter algorithm to recover the full 3D velocity and density fields. This technique is chosen as a case study because of its sensitivity to biases. The technique was then applied to the observational catalogs. Again, for concision, results are shown only for one of them: the third catalog of the Cosmicflows project, namely, cosmicflows-3 (Tully et al. 2016). The Wiener-filter is also applied to the initial and post-treatment observational catalogs to validate further the bias-minimization algorithm. We quantified the influence of the H0 parameter value on the results using both the synthetic and observational catalogs, and we present our conclusions.
2 Biases and uncertainties
2.1 Biases and effects
The matter of peculiar velocity measurements1 and their collection into catalogs are complicated by several biases described at length in Sorce (2015) and references therein. Whilst they are generally all gathered under the term “Malmquist bias,” three types of Malmquist bias can, in fact, be distinguished. In addition to these biases, there is a lognormal error distribution, which requires some attention. Here, we present only a short description of these biases below.
- b1.
The Malmquist bias: due to selection effects, it is usually taken care of when calibrating distance indicators. The latter are then used to derive distances and then velocities (Kapteyn 1914; Malmquist 1922; Han 1992; Sandage 1994; Teerikorpi 1997, 1995, 1993, 1990; Hendry & Simmons 1994; Willick 1994). This is the case in the catalogs use here (e.g., Tully & Courtois 2012; Sorce et al. 2013, 2014b).
- b2.
The homogeneous Malmquist bias: due to a higher probability of scattering galaxies further away closer than the opposite (increasing surface of shells centered on us with the distance), this aspect needs to be dealt with (Kapteyn 1914; Malmquist 1922; Lynden-Bell et al. 1988; Han 1992; Sandage 1994; Teerikorpi 1990, 1993, 1995, 1997; Hendry & Simmons 1994; Strauss & Willick 1995). When considering a complete up-to-a-given-distance galaxy sample, on average, post-bias-minimized galaxies should end up with larger distance estimates than originally measured. Although it must not be an explicit requirement of the algorithm (i.e., no function should directly enforce larger distances per se), it must be checked that it ends up being the case when comparing the initial and bias-minimized catalogs that are mainly constituted of complete galaxy surveys2.
- b3.
The inhomogeneous Malmquist bias: due to a higher probability of scattering galaxies from high density regions to low density regions, it is not taken into account either (e.g., Dekel 1994; Hudson 1994). Similarly, post-bias-minimized galaxies should be more numerous in high density regions than initially. We thus check that although it is not a direct requirement, the algorithm tends to cluster galaxies. We note that we group galaxies gathered into one group/cluster to derive a unique distance or velocity estimate, that of the group or cluster. This permits the removal of non-linear virial motions from the catalog (Sorce & Tempel 2017, 2018), which is a source of biases for the Wiener-filter technique. Clustering will thus be smoothed out on very small scales.
- b4.
The logarithmic relation between distance moduli and distances (hence, the velocities too) introduces a non-Gaussian distribution of errors on velocities, called the lognormal error distribution. Typically, an overestimated distance modulus results in a higher error on the velocity estimate than would an underestimated distance modulus (e.g., Tully et al. 2016). Thus, over- and underestimates of distance must not be considered in the same way. There are analytical and ad hoc solutions to take care of this bias (e.g., Landy & Szalay 1992; Hoffman et al. 2021). We note although that unlike the errors on the distances, the errors on the distance moduli can be considered symmetric. We thus ensured that the distance moduli – rather than distances – are the starting point of the algorithm. There will be no need to deal with this bias at the distance modulus level.
2.2 Main source of uncertainties
To obtain the 3D galaxy distribution from observations (= initial realization) and to control any additional source of systematics when deriving peculiar velocities (cf. bias b4 above), we began directly with the catalog of galaxy distance moduli (µ) and observational redshifts (zobs, Davis & Scrimgeour 2014) to which we added supergalactic longitude and latitude coordinates. This allows us to derive galaxy cartesian Supergalactic coordinates. A cosmological model is then required to determine peculiar velocities. While we use ΛCDM in this work, another model can easily substitute it for future works.
In the following, we recall the different relations between distance moduli, observational, and cosmological redshifts, luminosity distances and radial peculiar velocities. From observations of all the galaxies in the catalog, thanks to distance indicators and the Doppler effect, we can access two independent measurements:
Distance modulus measurements, µ;
Observational redshifts, zobs.
Then, we want to obtain the:
Luminosity distances, dlum, which are obtained via distance moduli,
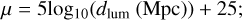 (1)
(1)-
Cosmological redshifts, zcos, which are derived with luminosity distances using the equation:
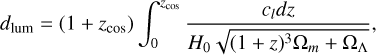 (2)
(2)where H0 is the Hubble constant, c is the speed of light, and Ωm and ΩΛ are the cosmological parameters corresponding to the matter and the dark energy, respectively.
-
Radial peculiar velocity estimates, υpec, which are finally obtained using the observational zobs and cosmological zcos redshifts according to the following formula:
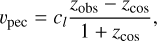 (3)
(3)where υpec always refers to the radial peculiar velocity in this paper.
Among all the parameters used to derive the galaxy peculiar velocities, the largest source of uncertainties unquestionably comes from their distance estimates. This reinforces our original idea to minimize biases in peculiar velocity catalogs through the minimization of biases in distance (modulus) catalogs. We reiterate that starting from distance moduli allows us to avoid the lognormal error distribution (bias b4 above) in the initial setting. Considering their precision with respect to that of distance moduli, Supergalactic latitude and longitude coordinates as well as the observational redshift are considered to be error free in a first approximation. Our goal is thus designed to provide a new distance modulus estimate for each galaxy of the catalog. These new distance moduli will give new distances (cf. Eq. (1)) thus radial peculiar velocities (cf. Eqs. (2) and (3)).
3 Model construction: A new Gibbs field model for minimizing biases
- 3.1.
The main goal of the algorithm is to find the position of galaxies that results, given their distance modulus (by extension peculiar velocity) and uncertainty on the latter, in the highest probability density of a point process.
To reach that goal, the principle is as follows, for each galaxy:
- 3.2.
The distance modulus is slightly perturbed from its initial estimate inducing a new distance estimate, thus a new peculiar velocity (cf. Eqs. (1)–(3)). The distance modulus is modified proportionally to its uncertainty to be more conservative towards distance modulus measurements with higher confidence level than others (e.g., obtained with supernovae against Tully-Fisher relation).
- 3.3.
The resulting new distance modulus and associated peculiar velocity of a galaxy are compared to the initial and previous distance modulus and velocity to ensure their likelihood given the uncertainty.
- 3.4.
The resulting new peculiar velocity of a galaxy has to be compared to the peculiar velocities of surrounding galaxies. To that end, a 3D local region shape is required to identify which velocities should be compared. To avoid rounded structures in density fields reconstructed with catalogs, clear signs of bias residuals as observed with other proposed bias minimizations, the shape should be extended along the line-of-sight with a short coverage tangentially. This prevents fortuitous transversal unrealistic correlations. This volumetric shape is essential to ensure that both the homogeneous (further to closer positions as per bias b2) and inhomogeneous (higher to lower densities as per bias b3) Malmquist effects are probed during the algorithm run. Hence, although there is an explicit requirement of the algorithm to increase neither distances on average nor clustering, it can have an impact on these two aspects. Whether this results in the desired effect constitutes a proof of concept that the algorithm reaches the bias-minimization goal.
- 3.5.
Additionally, to be able to use the newly derived distance modulus (i.e., distance and velocity as per Eqs. (1)–(3)) for various studies, a new uncertainty must be assigned. In the following, the first subsection sets the basis of the point process model, that is, its density probability and the technique to find a realization that corresponds to a maximum of the latter. The next subsections define the different terms required to propose new configurations. They also build the terms of the density probability function.
3.1 Maximized probability density and bias-minimized catalog
The algorithm should give the most probable location of a galaxy within a pre-determined spatial region given the uncertainty on its distance modulus measurement and (by extension) the associated radial peculiar velocity with respect to the entire catalog. Because supergalactic longitude and latitude coordinates are considered to be error free in a first approximation, the spatial region is shaped along the line of sight to retrieve the distances. In future developments, they could be relaxed alongside observational redshift measurements and the Hubble constant, H0, or (more generally) the cosmology. In other words, considering a finite volume (the Local Universe), the algorithm, input with a given set of n (µinit,i,σinit,i) with n fixed (= initial configuration), will result in a new set of n (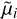 ,
,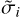 ) (one realization maximizing the probability density). Since our number of galaxies is fixed, we construct the probability density, p, for a Gibbs point process (Chiu et al. 2013) with the objective that this probability density is maximal when the effects of the biases are minimal. The realization corresponding to the bias-minimized catalog is thus obtained by maximizing the probability density of the point process where:
) (one realization maximizing the probability density). Since our number of galaxies is fixed, we construct the probability density, p, for a Gibbs point process (Chiu et al. 2013) with the objective that this probability density is maximal when the effects of the biases are minimal. The realization corresponding to the bias-minimized catalog is thus obtained by maximizing the probability density of the point process where:
![$p\left( {\left. \mu \right|{\bf{d}},c} \right) \propto \,{\rm{exp}}\left[ { - U\left( {\left. \mu \right|{\bf{d}},c} \right)} \right],$](/articles/aa/full_html/2023/11/aa46288-23/aa46288-23-eq6.png) (4)
(4)
with d = (µinit, σinit, zobs), c = {ci}i∈ℕ a set of positive parameters, µ = (µ1, µ2,…,µn) the set of distance moduli, n the number of galaxies (data points), and U the energy function. Again, given the intractability nature of p, building U permits us to sample and thus to propose new sets.
In addition to the standard likelihood included via a data energy term, UD, the energy function must take into account the local peculiar velocity correlation via an interaction energy term, UI. The energy function, U can thus be written:
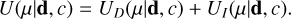 (5)
(5)
More specifically, UD is required to control the galaxy position (distance modulus) and associated uncertainty and, by extension, the velocity. It depends on the distance modulus, its uncertainty and the derived velocity; namely, for a given galaxy, it depends only on its associated properties. Here, UI allows controlling the probability that the object is at this position given its peculiar velocity (i.e., would it be at this distance modulus) in conjunction with its neighboring galaxies. It thus builds also upon the neighboring galaxy properties of a given galaxy. In that respect, the aim of the algorithm is to obtain a result that is a statistically bias-minimized catalog, but with no information on individual galaxies per se.
Notes. When a range is given, tests with the parameter values in this range do not demonstrate any major change in the final datasets. For results presented in this paper, the bold values have been used. The constants are calibrated only once on one mock catalog and are kept unchanged for all the other synthetic catalogs and a fortiori for the observational catalogs. The γ parameter serves the only purpose of speeding up the algorithm.
Subsequently, the minimization of both energy terms for a given realization of the dataset corresponds to a maximum of the probability density, that is, to a bias-minimized catalog: a new set of distance moduli and their uncertainties, (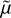 ,
, 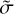 ). In other words, we need to minimize with a given set of parameters:
). In other words, we need to minimize with a given set of parameters:
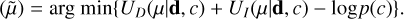 (6)
(6)
This can be solved sampling the Gibbs point process (Chiu et al. 2013) within a simulated annealing algorithm.
Parameters used in the algorithm.
3.2 New distance modulus, 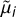
A new distance modulus, 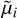 is drawn as follows:
is drawn as follows:
![${\tilde \mu _i} = {\mu _i} + {U_n}\left[ { - 0.5,\, + 0.5} \right] \times \gamma \,{\sigma _i},$](/articles/aa/full_html/2023/11/aa46288-23/aa46288-23-eq13.png) (7)
(7)
where Un[−0.5, +0.5] defines a random number from a uniform distribution between -0.5 and 0.5, γ is set between 1 and 3 (see Table 1). Choosing a uniform distribution, centered on the previous distance modulus, with a variance proportional to the uncertainty, allows for this process to be computationally faster than when using a fixed step (slower convergence). We note that this choice does not affect the results.
3.3 Data energy term, UD
The data energy term controls that new drawn distance moduli and newly derived velocities are probable given the initial and previous distance modulus and velocity values. It can be decomposed into a first term controlling the newly assigned distance moduli, UD1, and a second term controlling the associated newly derived velocities, UD2:
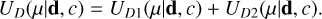 (8)
(8)
3.3.1 Data energy term 1, UD1
The data energy term 1 for each data point, e1, is associated to the likelihood. It must ensure that any new drawn distance modulus, µi, for a galaxy is contained within a restricted range of values imposed by its uncertainty, σinit, i. In particular, a term preserving a relative memory with respect to the initial distance modulus and its related uncertainty value is essential to prevent an infall onto the observer (at the center of the catalog by definition). Since the probability distribution of a galaxy distance modulus follows a Gaussian of variance σinit, i, centered on µinit,i, the term e1 can be written:
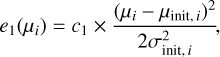 (9)
(9)
where c1 is a constant (see Table 1 for its value), σis are the uncertainties on the µis, and the subscript init refers to the initial values in the catalog. The derivation of new uncertainty estimates, σis, is detailed in Sect. 3.5. While theoretically σis can be equal to zero, in practice, it is never the case; thus, hereafter, we do not specify a special treatment. We again note that since distance moduli constitute the starting point of the algorithm, we avoid bias b4 mentioned above. That is to say, it is possible to use a Gaussian for the probability distribution of a galaxy distance modulus without any approximation.
The total data energy term 1, UD1, is then:
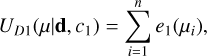 (10)
(10)
where n is the total number of galaxies. We note that in practice at a given time, this term is different from that of the previous time step only for the point perturbed from its previous step position.
3.3.2 Data energy term 2, UD2
A second data energy term is essential to encourage the decrease of high velocities in absolute value when initializing the Metropolis-Hastings random sampling. Indeed, initially the interaction term (cf. next subsection) can be null because galaxies are either isolated or clustered but biased in the same way; namely, with matching velocities and associated uncertainties (cf. biases b2 and b3). It needs also to prevent points at the edge of the sample to simply flee away where they would have no interaction (cf. next subsection).
The data energy term 2 for each data point, e2, can thus be written as:
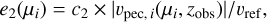 (11)
(11)
with c2 as a constant (see Table 1 for its value) and υref a reference velocity set to 10 000 km s−1. We note that υref allows us to ensure that all the constants have no physical unit. In addition, υref value is chosen so that when all the constants are of the same order of magnitude, all the terms in U are also of the same order of magnitude. All the terms weight similarly in U. The total data energy term 2, UD2, is then:
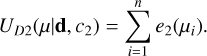 (12)
(12)
Currently, the energy terms are simple. Later H0, etc could vary to include their uncertainties. We might also consider a different cosmology. In the current paper, we consider though that H0, zobs (and so on) are constants. The line-of-sight position (distance modulus and radial peculiar velocity) and its uncertainty are the only measurements allowed to vary. In particular, we assume that distance moduli (and, by extension, the peculiar velocities) are the only measurements with an error. Therefore, a likelihood term needs to be written only for them. Nonetheless, Appendix A presents results using another set of cosmological parameters and Sect. 3.5 quantifies the significance of H0 value (and associated cosmological parameters) change on the results.
As an aside note, we define the decrease of velocity in absolute value parameter.
The decrease of velocity in absolute value for the ith galaxy:
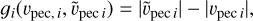 (13)
(13)
with υpec i the initial or another previous peculiar velocity, 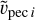 , the new peculiar velocity. Then, gi will appear when comparing the probabilities between ancient and new data points in the Markov chain (see below), more specifically in ∆UD2. We note that the symmetric uncertainty on the distance modulus propagates to an asymmetric uncertainty on the peculiar velocity. In particular, the new peculiar velocity, obtained with the distance modulus, is not strictly the mean of the peculiar velocities obtained with distance modulus plus and minus the uncertainty,
, the new peculiar velocity. Then, gi will appear when comparing the probabilities between ancient and new data points in the Markov chain (see below), more specifically in ∆UD2. We note that the symmetric uncertainty on the distance modulus propagates to an asymmetric uncertainty on the peculiar velocity. In particular, the new peculiar velocity, obtained with the distance modulus, is not strictly the mean of the peculiar velocities obtained with distance modulus plus and minus the uncertainty, 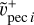 and
and 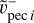 Tests conducted using
Tests conducted using 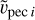 or 〈
or 〈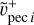 ,
,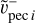 〉 reveal that results are unchanged given the precision reached when sampling. Indeed, this term mostly acts as a regulator not to have very large velocities. The sign of gi is statistically unchanged when using 〈
〉 reveal that results are unchanged given the precision reached when sampling. Indeed, this term mostly acts as a regulator not to have very large velocities. The sign of gi is statistically unchanged when using 〈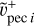 ,
, 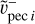 〉 rather than
〉 rather than 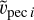 . In the future, increasing precision of the algorithm might require this distinction.
. In the future, increasing precision of the algorithm might require this distinction.
3.4 Interaction energy term, UI, step by step
The sole data energy term does not give much information on where it is best to locate the data points (i.e., their true location). The role of the interaction energy term is to favor configurations with plausible peculiar velocities in a statistical sense. It is essential to enforce the small-scale correlations. It should result in dealing with the effects of biases b2 and b3. It will be checked as a proof-of-concept of the algorithm. The interaction energy term thus compares peculiar velocities of interacting galaxies. It must permit distinguishing between “positive” and “negative” interactions. “Positive” means that one or both peculiar velocities are unlikely given the proximity of the two galaxies, namely, one or both galaxies are likely not to be at the proper distance, while “negative” indicates the opposite3. Consequently, in order to define the interaction energy term, we first need to introduce an interaction shape (Sect. 3.4.1) that permits a determination of interacting galaxies and a function accounting for the small-scale velocity correlation (Sect. 3.4.2) that allows us to attribute a state to the interactions.
3.4.1 Interaction shape, S
The shape, S, allows us to determine whether two galaxies must be considered as interacting. The shape length and size depend on the galaxy distance and associated uncertainty. However, its direction is always aligned with the line-of-sight. It is a 3D region shown in 2D in Fig. 1 top with the following properties: dmin/max are the distances obtained with µi ± nσσinit,i (see Table 1 for nσ value) to prevent introducing the lognormal error effect (bias b4) at this stage. We note that to ensure a minimum size for the shape, the initial uncertainty is used. The final uncertainty within a single run of the algorithm (see the detailed explanation below) indeed tends toward zero, thus decreasing the size of the shape and preventing any interaction. M is the projection of a given point, j, on the line of sight of the perturbed point, i. r is equivalent to the aperture of the shape and is defined by r = αpc × dM (see Table 1 for αpc value) with dM as the distance of a point, M.
Any point, j, within the region of another point, i, is then considered to be interacting and their velocities are compared. The only difficulty is to check that the origin (us) is not in the shape. If this is the case, a point, j, on the opposite side of the origin with respect to the point, i should not be considered as an interacting point. Consequently if the dot product between the direction of the two points is -1, then there is no interaction by definition. Figure 1 (bottom) shows three types of situations: a) i and j are in each others’ shapes; b) k is in the shape of j, but j is not in the shape of k; and c) l and k are not in each others’ shapes.
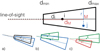 |
Fig. 1 Schematic view of the interaction shape. Top: interaction shape in 2D showing how i’s shape is derived. j belongs to i’s shape. Bottom: examples of interactions: a) i and j are both within one another shapes; b) k is in the shape of j, but j is not in that of k; c) l and k are not in one another shapes. |
3.4.2 Small-scale velocity variance function, σv
The small-scale velocity variance, συ, and its fit are shown in Fig. 2 with filled circles and a solid line respectively. The filled circle values and their standard deviations are obtained by throwing randomly shapes, S, of different hypothetical sizes onto a mock catalog of radial peculiar velocities free of any errors. Each size corresponds to a given uncertainty, σ. The velocity variance συ of objects within each shape is then derived. We note that changing the value of the parameters defining the shape (e.g., αpc) requires us to re-derive the corresponding correlation of velocities at small-scale. In practice, small variations of the parameter values do not drastically modify the relation. We note that modifying the cosmological model implies also re-deriving the small-scale velocity variance using a mock catalog without errors from the corresponding model for consistency.
The small-scale velocity variance function, συ, is a polynomial fitting of the small-scale velocity variance:
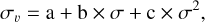 (14)
(14)
where a = 64, b = 70 and c = 22 km s−1 assuming uncertainty magnitudes (Mag) in dex. It determines the average maximum authorized difference between velocities of galaxies belonging to the same shape as a function of the size of the shape. This shape is itself related to uncertainties on distance moduli. We note that the small-scale velocity correlations, obtained by casting shapes onto different synthetic catalogs (either mimicking the second or third Cosmicflows catalog distributions but without error; see the description below) are within their 3σ uncertainty range. Using fitted parameters within their 3σ uncertainty range does not drastically impact the final output new distance modulus catalog. However, it certainly depends on the cosmological model. In the future, they will need to be relaxed together with the latter.
 |
Fig. 2 Correlation between the velocity variance and the uncertainty. More precisely, variance between velocities of objects in the same shape S whose size is defined by the uncertainty. Filled circles are obtained throwing shapes, as defined in Fig. 1, onto mock catalogs without errors. The solid line is the polynomial fitting a+bx+cx2 with a = 64, b = 70, c = 22 km s−1 assuming uncertainty magnitudes (Mag) in dex. |
3.4.3 Interaction functions, h, f, and q
The shape and the velocity correlation allows us to define the interaction functions those values depend on the galaxy positions (shape membership) and velocity values (difference). Additionally, an interaction with a galaxy, j, that has a small distance uncertainty must have a higher weight than that with a galaxy with a large distance uncertainty. The inverse of the uncertainty is thus used as a weight.
The interaction between two points (galaxies), i and j, exists, i ~s j, if:
i ∈ Sj and j ∉ Si, or
j ∈ Si and i ∉ Sj, or
j ∈ Si and i ∈ Sj.
The weighted “positive” interaction function, h, between point, i, and the other points, j, with which it interacts, is then defined as4:
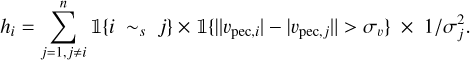 (15)
(15)
The weighted total – “positive or negative” – interaction function, f between point, i, and other points, j, with which it interacts, is then defined as:
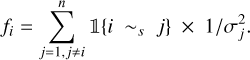 (16)
(16)
The absence of interaction function, namely, if i ≁s j, q between point, i, and the other points, j, is then defined as:
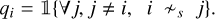 (17)
(17)
Here, is an indicator function equal to 1 if the condition within is met and 0 otherwise. In particular, in the f case, 𝟙{i ~s j} equals 1 if the interaction between i and j exists (cf. conditions above). In h case, 𝟙{‖υpec,i| − |υpec,j‖ > συ} equals 1 if i and j velocities differ by more than συ(σi). We note that the qi = 1 choice when there is no interaction induces a constant penalization of isolated points. While values between 0.5 and 1 do not drastically change the results, we stick to 1 to prevent potential fleeing away points. We avoid values between 0 and 0.5 to prevent ending up with an almost repulsive configuration (especially with the 0 value).
3.4.4 Interaction energy term, UI
Finally, the energy term ensures that, for objects that are close-by transversally and with position uncertainties on the line-of-sight allowing them to be within the range of distances of one another (given dmin and dmax), their peculiar velocities in absolute value are on the same order.
The pairwise interaction process, e3, in the interaction energy term for each point is then defined as follows:
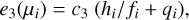 (18)
(18)
where c3 is a constant (see Table 1 for its value) and with the convention hi/fi = 0 when fi = 0, namely, there is no interaction.
The total interaction energy term is:
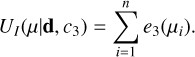 (19)
(19)
We note that this term has to be computed for every point because their interaction term can be affected by the perturbed point. In practice, we considered only the interaction between the perturbed point and each other point because of the required reciprocity of the interaction (see the interaction requirements with the “or” condition).
3.5 New uncertainty on distance moduli, 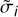
New distance modulus uncertainties must be assigned to the data points. Typically, new uncertainties should depend on the probability of the new data point position thus peculiar velocity with respect to the entire catalog. Since the catalog is statistically bias-minimized but not individual data points, new uncertainty and distance modulus cannot be used individually but within the context of the entire catalog.
We thus first define pυ as the cumulative distribution function of the velocity value probability given the theory. Indeed, Sheth & Diaferio (2001) proved that the distribution of radial peculiar velocities considering groups and clusters (virial motions removed) is a Gaussian. Unless the Milky Way is at a peculiar position in the Universe, the distribution of radial peculiar velocities obtained from our position should be close to a Gaussian too. This was verified by Sorce (2015) with constrained simulations of the Local Universe.
The (cumulative distribution function of the) probability of a peculiar velocity (in absolute value), pυ, is then defined as follows:
 (20)
(20)
with συ′, derived from mock catalogs mimicking the distribution of the observational catalog to be bias-minimized. Its value is given in Table 1. For the sake of simplicity, in the following we will refer to pυ as the probability of a given velocity value. We note that here again because of the precision with which the current algorithm computes this integral, using υpec instead of 〈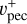 ,
, 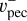 〉 does not impact the final result. In future developments, if this precision were to increase, this lognormal distribution effect on the peculiar velocity value might need to be taken into account. Then,
〉 does not impact the final result. In future developments, if this precision were to increase, this lognormal distribution effect on the peculiar velocity value might need to be taken into account. Then,
The higher the probability, the more the uncertainty should decrease. Thus, the term, (1 – pυ), must appear to derive the new uncertainty from the previous step uncertainty.
However, since the maximum probability, pυ, is at a zero velocity value, the interaction term h/f (see previous subsection) is also required. The text in the previous sub-subsection explains this term in more detail. In brief, the smaller the value of h/f is, the less “positive” (in the sense of “more unrealistic”) interactions, the data point has with its neighbors (with respect to all its interactions). Thus, the more probable the velocity is and the smaller the uncertainty may be.
Still, with the increasing probability pυ of the velocity, the interaction term h/f should have an increasing weight with respect to the probability term (1 – pυ) (from (i)) and vice versa. This prevents the gathering of wrongly high absolute velocity values that have a low probability, pυ, but few “positive” interactions (small h/f) because together they form an isolated ensemble of high velocity values. The weight on the probability (i) and interaction (ii) terms is thus simply the probability pv for the interaction term (ii) and, by extension, (1 – pυ) for the probability term (i). Since the individual probability of the velocity appears in the uncertainty term, it can reasonably reduce the small-scale correlation of the errors on distance moduli (by extension, the peculiar velocities) inherent to the interaction shape. In any case, this small-scale correlation of errors has no impact on large-scale studies because of the small sizes of the shapes.
The new uncertainty, 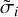 , is thus:
, is thus:
![${\tilde \sigma _i} = {\sigma _i}\,\left[ {\left. {{{\left( {1 - {p_\upsilon }} \right)}^2} + {p_\upsilon }\left( {{{{h_i}} \mathord{\left/ {\vphantom {{{h_i}} {{f_i}}}} \right. \kern-\nulldelimiterspace} {{f_i}}} + {q_i}} \right)} \right)} \right],$](/articles/aa/full_html/2023/11/aa46288-23/aa46288-23-eq42.png) (21)
(21)
where hi, fi and qi are the interaction and absence of interaction functions defined in the previous subsubsection.
 |
Fig. 3 Details of the steps to obtain the new set of (µi, σi), namely ( |
3.6 Simulation method
We used a Metropolis-Hastings sampling embedded into a simulated annealing algorithm (as detailed by Fig. 3) with blue and orange colors, respectively. The first yellow panel gives the initialization with the initial realization and the last yellow panel gives the resulting realization (one maximum of the density probability). More precisely, the steps are as follows:
- Step i.
We compute the data and interaction energy terms.
- Step ii.
We perturb the distance moduli, µis using a draw from a uniform distribution between [−0.5,0.5[ given the σis to get
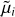 s. For each perturbed distance modulus, we compute the corresponding new distance, dlum, velocity, υpec, energy term, U and uncertainty,
s. For each perturbed distance modulus, we compute the corresponding new distance, dlum, velocity, υpec, energy term, U and uncertainty, 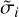 . We define
. We define 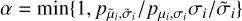 , where p is the Bayesian probability. We draw a number R from a uniform distribution between [0,1[ if α ≥ R, accepting the modification or else keeping the previous configuration. We repeat the process, for every single point (n points), nmh times.
, where p is the Bayesian probability. We draw a number R from a uniform distribution between [0,1[ if α ≥ R, accepting the modification or else keeping the previous configuration. We repeat the process, for every single point (n points), nmh times. - Step iii.
We decrease the probability ratio as follows:
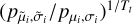 with Tt going slowly to zero at each end of [Step iii] according to the equation defined below. Then we go back to [Step ii]. Again, we repeat this process nsa times.
with Tt going slowly to zero at each end of [Step iii] according to the equation defined below. Then we go back to [Step ii]. Again, we repeat this process nsa times. - Step iv.
We exit with a new catalog of data points with new positions along the line of sight and, thus new peculiar velocities and new uncertainties - more precisely a new inseparable (µ,σ) set.
The temperature, Tt, required by the simulated annealing algorithm after each loop of the Metropolis-Hastings algorithm times the number of galaxies, n, is defined as follows:
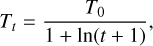 (22)
(22)
with t the time-step. The initial temperature T0 is given in Table 1 together with the number of steps of the two embedded algorithms: nmh and nsa.
To speed up of the process, we implemented slight modifications as follows. We emphasize that they have no impact on the final result.
We parallelized the algorithm using both MPI and openMP to run on several points from different part of the Local Volume at the same time and to speed up the interaction term calculation. That is to say, we perturbed several points simultaneously (points sufficiently far away do not interact) and we derived their interaction energy term cumulatively and respectively. We split points on processors depending on their Supergalactic longitude.
Points with an uncertainty below a certain threshold are not perturbed anymore. The threshold is determined as max{(σi)}/10 × (10 − m) where m is increased by one unit each nmh/10 iterations of the Metropolis-Hastings algorithm. Additionally, the minimum is set to 10−4. This limit is just above the minimum change possible on the distance moduli given the precision of our algorithm. It thus prevents irrelevant iterations on data points those distance moduli would end up unchanged at the given precision in [Step ii].
Also, γ is used to draw a new distance modulus decreases each nmh/10 iterations as γ = 1 + 2/10 × (10 − m), m as defined before. It drastically decreases the number of rejected new points in [Step ii] thus the number of irrelevant iterations.
If 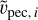 is greater in absolute value than the largest initial peculiar velocity absolute value in the catalog, we immediately reject the new distance modulus.
is greater in absolute value than the largest initial peculiar velocity absolute value in the catalog, we immediately reject the new distance modulus.
If the new distance modulus is smaller than 25 (i.e., di < 1 Mpc), we immediately reject it since it is the size of the Local Group (Milky Way, Andromeda, and their satellites).
4 Application to synthetic catalogs
In this section, we apply the newly developed algorithm and test it on synthetic catalogs. For the sake of concision, given the results are identical for all the synthetic catalogs, we offer details for one of the mock catalogs.
4.1 Building synthetic catalogs
To build mock catalogs matching our observational catalogs, we used a CLONE (Constrained LOcal & Nesting Environment) simulation obtained with the technique described in Sorce (2018). It contains 20483 particles in a ~738 Mpc box and it ran from z = 120 to z = 0 in the Planck cosmology framework (Ωm = 0.307 ; ΩΛ = 0.693 ; H0 = 67.77 km s−1 Mpc−1).
To obtain the different synthetic catalogs (hereafter dubbed “true” and “biased” with the latter used as input for the algorithm), we proceeded as follows:
We cut the catalog in mass and remove substructures to mimic grouping. We are not interested in testing again the grouping technique here (see e.g., Sorce & Tempel 2017, for such tests). Only dark matter halos with masses greater than 1012 M⊙ are preserved.
We set an observer at the center of the box. From the x, y, z coordinates and υx, υy, υz velocity components derive the distance, d, Supergalactic longitude and latitude, sgl, sgb, and radial peculiar velocity, υpec, of each halo with respect to the observer.
We compute cosmological redshifts, zcos with 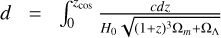 We compute luminosity distances, dlum = (1 + zcos) d, distance moduli, µ = 5 × log10(dlum) + 25, and observational redshifts, zobs = υpec/c (1 + zcos) + zcos.
We compute luminosity distances, dlum = (1 + zcos) d, distance moduli, µ = 5 × log10(dlum) + 25, and observational redshifts, zobs = υpec/c (1 + zcos) + zcos.
We build a mock zone of avoidance by removing any halo, at more than dlum = 10 Mpc from the center of the box, within a cone which apex is the box origin and, whose aperture is 0.2 radian assuming the same orientation within the XYZ simulated volume as the observational one in the Supergalactic XYZ volume.
For each data point in the observational catalog, we find all the halos such that |zobs − Zobs, datapoint| < 0.01, then sort these points by this value and by |sgl − sgldatapoint| and |sgb − sgbdatapoint|. We take the first halo of the sorted list as the mock point for the observational data point. The obtained (sgl,sgb,zobs,µ) set constitutes the true synthetic catalog.
We add an uncertainty to the halo distance modulus as µ = µ + R σdatapoint. We assign σdatapoint as the uncertainty for the halo distance modulus, then R is drawn from a Gaussian distribution of mean zero and variance one. We note that because the observational catalogs consist in a collection of distance moduli obtained with different indicators, coupled with the fact that several distance modulus estimates may be available for a given galaxy and a fortiori for groups and clusters, the σdatapoint ensemble spreads over a large range of values rather than being unique for all the data points. The obtained (sgl,sgb,zobs,µ,σdatapoint) set constitutes the biased synthetic catalog. The goal of the algorithm is to retrieve a statistically bias-minimized synthetic catalog starting from the biased one.
 |
Fig. 4 Galaxies in 5 h−1 Mpc thick slices of the XY supergalactic plane. From left to right: black lines show the projected distances between true (yellow filled circles) and biased (black filled diamonds), after nmh. Metropolis Hastings loops but no cooling for the n data points (in the text iteration 1, blue-filled square) and, at the end of all loops (red-filled circles), data point positions. The filled symbol sizes are proportional to velocities in a logarithmic scale. Because errors are large in the left panel, yellow filled circles are harder to distinguish. The algorithm reduces on average errors on data point positions thus on their peculiar velocities, namely, on average, shorter black lines and, by extension, better matching filled symbol sizes of different colors. |
4.2 Results
Figures 4–7 present the results of the above-described algorithm applied to one of the biased mock catalog mimicking cosmicflows-3. The yellow color stands for true data points, namely, without errors (true catalog), while the black color is used for the catalog with errors (biased catalog) used as input for the algorithm. The blue color is used for data points after nmh Metropolis-Hastings iterations of every single one of the n points (called iteration 1) and the red color after nmh × nsa iterations, namely, the Metropolis Hastings samplings embedded into the simulated annealing algorithm (in other words, iteration nsa, hereafter denoted as “corrected”). In the following, figures and the associated results are described more thoroughly. We note that although the ultimate goal is to obtained bias-minimized peculiar velocity catalogs, since the input consists in distance moduli (that permit deriving ultimately peculiar velocities), analyses are conducted on the former as well as on the latter and on distances.
Figure 4 shows the data points in the mock catalog (from left to right) at their true positions with symbol sizes proportional, on a logarithmic scale, to their true peculiar velocities (yellow filled circles) alongside the initial biased positions and associated velocities (black filled diamonds), after iteration 1 (blue filled squares) and, finally, the recovered or corrected positions and associated velocities (red filled circles). The solid black lines connect the true data point positions to their biased, after iteration 1 and corrected positions. The mean length of these lines and its standard deviation starts from 18 ± 19 h−1 Mpc to decrease to 3.1 ± 5.4 h−1 Mpc and ends at 2.9 ± 3.7 h−1 Mpc. The algorithm after iteration 1 already minimizes on the average errors on data point positions. According to the definitions given in Eqs. (1)–(3) and the propagation of uncertainty, it statistically reduces the errors on luminosity distances, cosmological redshifts, and peculiar velocities. The cooling process allows for small refinements on a point-to-point basis, but still to be considered within the full catalog environment.
Figure 5 confirms that errors on distance moduli are statistically reduced. The left panel shows that true and bias-minimized distance moduli differ (on average) by less than 1% (blue and red dashed and dotted lines) against 3-4% without corrections (black solid line). More precisely, the middle panel shows that true and biased minimized distance moduli (blue and red squares and triangles) differ at most by about 0.5 mag against twice, up to four times, that value for biased distance moduli (black diamonds) especially at large distances. At small distances, the average error becomes more centered on zero, a clear indication that a systematic – galaxies too close on average as per bias b2 – has been decreased. We note that the more data points there are in a given region, the better the algorithm performs. This is in agreement with the data interaction energy term. It proves that this term is essential and that it enforces the small-scale velocity correlation in the interaction shapes. It also confirms that data points cannot be considered individually but together as a whole: the bias-minimized catalog. The right panel shows for information that newly assigned uncertainties and true errors on data points are consistent as they differ at most by a few percent of the true error.
Finally, the two left panels of Fig. 6 highlight that peculiar velocities (dotted and dashed blue and red versus solid black lines), derived from statistically reduced-error distance moduli, also have (on average) reduced errors. In the left panel, the underlying Gaussian radial peculiar velocity distribution (thick solid yellow line) is recovered (dashed red line), as in Sorce (2015). However, unlike in the latter case, it is not the main aim as efforts are focused on converging toward the most probable distance modulus distribution. It just so happens that peculiar velocities derived from such a new distance modulus catalog have this property. Additionally, the expected small-scale velocity variance in different shape sizes (corresponding to different uncertainties and shown by a color gradient) at various distances from the center of the box is almost recovered: warm-color dashed lines (corrected) versus warm-color solid lines (true) with respect to cold color solid lines (biased) versus warm color solid lines (true).
To confirm that the algorithm is not equivalent to a naive decrease of all the peculiar velocities that would also result in a reduced peculiar velocity variance (but fully intentional), we proceeded with the following Gedanken experiment:
peculiar velocities, rather than distance moduli, constitute the starting point;
all the peculiar velocities are reduced by a constant factor chosen to find back the expected variance5;
new distance moduli are derived from these new peculiar velocities.
We find that although the resulting peculiar velocity distribution presents the expected variance (by construction), close-by galaxies and groups have strongly biased distance moduli. Moreover, the correlation of velocities on small-scale velocity reaches extremely low values that are well below the expected values. In addition, bias b4 is fully present and more difficult to deal with. While it is possible to prevent from having it when starting from distance moduli to derive peculiar velocities, it is more difficult to extract non-b4-biased distance moduli from peculiar velocities as only one uncertainty is available (assumption of a symmetric distribution of the uncertainty). The consistency seen among all the panels of Figs. 5 and 6 is another strong argument in favor of the algorithm capability.
Figure 7 shows additional verifications of the algorithm results. In particular, it checks the reduction of the effects of biases b2 and b3 (homogeneous and heterogeneous Malmquist biases). Bias b2 tends to scatter galaxies and groups closer to, rather than further away from, us. Although no data term enforces new distance moduli to be larger than starting ones, corrected distances should statistically be larger than biased ones. The left panel of the figure shows that indeed the median differences between after iteration 1 (filled blue squares) and corrected (filled red circles) distances and biased distances (that have been used as a starting point) are statistically positive but at large distances. Errors on the median show that neither a positive nor a negative difference stands out at large distances. The effects of the catalog edges (e.g., sharp cut-off) do indeed dominate over bias b2. Then, bias b3 reduces galaxy clustering by scattering objects from high- to low-density regions. Although no data term enforces data points to be close to each others6, corrected distance moduli should increase back clustering.
To derive an estimate of clustering, we built grids to split the Supergalactic coordinate space uniformly. We then filled in the grids with the catalog data points and proceed with a count-in-cell. The top-right panel of Fig. 7 shows the resulting histograms of the number of data points per grid cells for the true (thick solid yellow line), biased (solid black line), after iteration 1 (dotted blue line), and the final or corrected (dashed red line) catalogs. The bottom panel shows the ratio of the different histograms to the true one (same color and line style codes). The thickness of the lines refers to the different grid-cell sizes. From the thickest to the thinner lines, the cell size ranges from ~4.6 to 6.9 h−1 Mpc. Because the catalogs are incomplete by construction, cells with zero data points are removed. On a few-megaparsecs scale, the biased catalog presents a strong excess (deficit) of cells with only one (several) data point(s) with respect to the true catalog. Conversely, the after iteration 1 and corrected catalogs exhibit only a very small (if any) clustering difference with the true catalog.
Figure 7 confirms that the algorithm reduces the effects of biases b2 and b3. Nonetheless, theoretically, the Metropolis-Hastings algorithm output is a sample distributed according to the probability distribution of interest. Similarly, the simulated annealing algorithm output is a sample distributed uniformly over the configuration subspace maximizing the probability distribution of interest. Under these circumstances, averaging realizations reduces the stochastic effects (variance) inherent to a single proposed solution.
We stacked several realizations of the corrected catalog obtained with the algorithm (i.e., slightly different realizations with a slightly different minimized energy term – maximized probability density – because of the a priori non-concavity of the function). We treated each one of these realizations independently, thus deriving a simple mean of their distance moduli and assigned uncertainties for each data point. We then derived the corresponding new velocities. Figure 8 shows the same plots as the right panel of Fig. 4 and Figs. 5 and 6 for five (left column) and ten (right column) stacked realizations. Small additional improvements are visible on a point-to-point basis. The mean length of the lines and its standard deviation are further decreased from 2.9 ± 3.7 h−1 Mpc to 2.2 ± 2.7 h−1 Mpc and 2.1 ± 2.3 h−1 Mpc, respectively. It is interesting to note that this is the characteristic average size of galaxy clusters. Overall, the major improvement is on the small-scale velocity variance (last panel of the last row in both columns). We note that stacking ten realizations (rather than five) does not seem to improve the small-scale velocity variance. It might even smooth the velocities a bit too much, at least in the synthetic catalog case (see next section for the observational catalog). Stacking realizations also allows us to get more realistic uncertainties on the new distance moduli rather than globally converging towards zero ones. On the whole, the algorithm thus allows for the recovery of statistically better distance moduli and, hence, the peculiar velocities for galaxies as per the peculiar velocity definition.
 |
Fig. 5 Comparisons of spatial distribution properties in the datasets. Left: histograms of the ratio of the differences between biased (black solid line), after iteration 1 (see text for a definition, blue dotted line), corrected (red dashed line), and true distance moduli to the true distance moduli, namely, the errors in percent on distance moduli. Middle: difference between true and biased (black diamonds), after iteration 1 (blue square) and at the end of the process or corrected (red circles) distance moduli versus true distance moduli. Right: ratio of the difference between assigned uncertainties and true errors to the true errors on distance moduli. Same colors and line styles as the left panel. |
 |
Fig. 6 Comparisons of velocity properties in the datasets. Left: true (thick yellow solid line) and biased (black solid line) peculiar velocity distributions vs. those derived from after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) distance moduli. Middle: histograms of errors in absolute value on peculiar velocities derived from before correction, after iteration 1 and after correction distance moduli. Same color and line style codes. Right: local velocity variance in different shape S elongations (one line per elongation) for a catalog free of errors (solid lines with warm colors), with errors (solid lines with cold colors), after applying the algorithm (dashed lines with warm colors). The variance is defined as the standard deviation between peculiar velocities of galaxies belonging to a same, elongated along the line-of-sight, shape S (see exact definition in the text). Shape elongations at given distances are obtained ranging fictively distance modulus uncertainties from 0.2 (orange, red, black) to 1.8 (green, orange, light blue) mag. |
 |
Fig. 7 Comparisons of dataset properties. Left: median of the difference between distances obtained from after iteration 1 (filled blue squares) and at the end of the process or corrected (filled red circles) distance moduli and those derived from biased distance moduli as a function of the true distances. Errors on the median are obtained with bootstrapping. New distances tend to be larger than initial ones. This is in agreement with the reduction of the homogeneous Malmquist bias that statistically tends to put objects closer than they are. After bias-minimization of distance modulus catalog, new distances are indeed statistically larger than initial ones derived from biased distance moduli. At large distances, effects of the catalog edges, like sharp cut-off, are preponderant. Top-right panel: histograms of the number of data points per grid cells obtained from true (thick yellow solid line), biased (black solid line), after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) distance modulus catalogs. Grids are built to split the Supergalactic coordinate space uniformly. Since catalogs are not complete, cells with no data point have been removed. The histograms represent a measurement of the clustering. The more clustered the data points in a catalog are, the more data points there can be per grid cells. Bottom-right panel: ratios between the biased (black solid line), after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) histograms and the true one. These right panels show that data points in the biased catalog are statistically less clustered than in the true and corrected ones. This is in agreement with the reduction of the heterogeneous Malmquist bias. Indeed, the latter tends to reduce clustering by statistically scattering objects from high density regions to low ones. The line thickness stands for the grid-cell size. From the thicker to the thinner lines, the cell sizes are ~4.6, 5.5 and 6.9 h−1 Mpc. |
 |
Fig. 8 Same as Fig. 4 (right panel) as well as Figs. 5 and 6 for five (left column) and ten (right column) stacked realizations of the corrected catalog obtained with the algorithm. |
4.3 Mock field reconstructions
Before applying the algorithm to the observational catalog, this subsection gives an example of how valuable the corrected catalog is as a whole. To that end, we reconstructed the density and 3D velocity fields from the true, biased, and corrected (both single and stacked) catalogs using the Wiener-filter technique (Zaroubi et al. 1999). This technique is known for its lack of capacity to deal with the different biases. Reconstructed fields are then compared to the initial simulation from which the synthetic catalog is built. Figure 9 shows the three Supergalactic slices of the reconstructed Local Universe obtained with the different catalogs of peculiar velocities. Black contours stand for the overdensity field. The thick blue solid lines delimit the over-density from the underdensity. Arrows stand for the velocities. Yellow dots are data points constituting the synthetic catalogs. The biased catalog results in the worst reconstruction with round structures at the edge and a large infall onto the observer (i.e., the center of the box). Reconstructions based on corrected catalogs present more defined structures like for the reconstruction obtained with the true catalog. In addition, the major infall onto the Local Volume is suppressed.
To quantify the similarity between the reconstructed fields and the simulation, cell-to-cell comparisons between simulated and reconstructed velocity fields were conducted. For each successive cell-to-cell comparison between two velocity fields, cells are selected in a larger and larger sub-volume of the reconstruction and simulation boxes. A linear fit to each one of the cell-to-cell comparison plots (reconstructed vs. simulated velocities) permits the derivation of the slope of the correlation between simulated and reconstructed x, y, z velocity components as well as its variance. Figure 10 left shows the variances (black lines and symbols) and slopes (red lines and symbols) of the linear fits to the relations between reconstructed and simulated velocities. They are obtained by comparing cells in different sub-volumes of the boxes. As expected, the best (worst) reconstruction is obtained with the true (biased) catalog: the variance, namely, the difference between reconstructed and simulated velocity fields, is the smallest (largest) being below 50 km s−1 (about 100-170 km s−1) and the slope is the closest to 1 (i.e., almost a perfect match); varying the most (i.e., no correlation) as shown by the open black and red circles (crosses) respectively. We note that the slopes overall decrease with the increasing compared subvolumes. As for reconstructions obtained with bias-minimized catalogs, those obtained with stacked realizations present linear fits to cell-to-cell comparison plots with smaller variances than that obtained with a single realization: 80 against 100 km s−1 (black squares and diamonds with respect to stars). Slopes (same red symbols) present the same trend as for the true catalog. That is to say, the larger the sub-boxsize considered for the cell-to-cell comparison is, the smaller the slope. This is a Wiener-filter known effect as it goes to the mean field in absence of data. Indeed, the number of data points (N) per Unit of Volume drastically decreases with the distance to the center of the box (top axis of the figure).
To confirm this effect, Fig. 10 (right panel) compares velocities only at selected-for-the-mock-catalog halo positions in the simulation and in the reconstructions. It highlights that indeed reconstructed velocities with the biased catalog are too large at large distances and too small close by with a large disparity (black dotted line). Reconstructed velocities obtained with the true and corrected catalogs are alternatively slightly too small or slightly too large (yellow and dashed red lines). Those obtained from the corrected stacked-realization catalogs are overall too small (dotted-dashed and three-dots-dashed red lines). Interestingly the ratio between reconstructed and simulated velocities has the smallest variance for the reconstructions obtained with stacked realizations making it easier to correct for the smoothing effect of the Wiener-filter.
Indeed, in a previous work, to obtain better 3D reconstructed velocities, Sorce (2015) multiplied all the mock-catalog velocities by the average decrease caused by the Wiener-filter technique. Then, by applying the Wiener-filter technique to this mock catalog, they got an average slope of 1 for the linear fits to the cell-to-cell comparisons between the simulated and reconstructed velocity fields. To obtain a slope value of 1 independently of the sub-boxsize used for the cell-to-cell comparisons, Sorce (2018) considered the 3D volume and applied an additional smoothing (uncertainties) inversely proportional to the number of points per sub-volume. We leave further comparisons as well as these additional steps with potential new improvements for the next paper of the series. The major improvement in the reconstructions obtained with the corrected catalogs is already visible: the difference between the reconstructed and simulated velocity fields or variance is drastically reduced whatever the subvolume considered.
 |
Fig. 9 Supergalactic slices of the simulated (first column) and reconstructed (second to sixth columns) density and velocity fields. Contours show the overdensities and arrows indicate the velocities. The blue contours delimit the underdensities from the overdensities. Yellow points show halos constituting the different catalogs. The peculiar velocities of these halos, obtained from distance moduli, are actually used for the different reconstructions. |
5 Application to the observational catalogs
In this section, the algorithm is applied to the second and third catalogs of the Cosmicflows project. Again, for the sake of concision and the results being identical for the two catalogs, the results are shown only for the third catalog.
5.1 Observational catalog
We apply the algorithm to the third dataset of the Cosmicflows project (Tully et al. 2016). This catalog contains 17 649 galaxy distance moduli. Using several distance estimators, mostly from the Tully-Fisher (Tully & Fisher 1977) and fundamental plane (Colless et al. 2001) relations, this catalog allows us to probe distances as large as 500 Mpc. Still, 50% (90 and 99 %) of the data are within 120 Mpc (225 and 330 Mpc). The other distance indicators are Cepheids (Freedman et al. 2001), tip of the red giant branch (Lee et al. 1993), surface brightness fluctuation (Tonry et al. 2001), supernovae of type Ia (Jha et al. 2007), and other miscellaneous methods. We group the distance moduli into 15 050 galaxy and group distance moduli using the grouping technique of Tempel et al. (2016a), as described in Sorce & Tempel (2017), using Planck cosmology in this paper. In a future paper of this series, we will study the impact of the cosmological parameter value choice in thorough details. Still, since Tully et al. (2016) estimate the third dataset of the Cosmicflows project to be compatible with H0 = 75 ± 2 km s−1 Mpc−1, Appendix A shows the result obtained with WMAP7-like parameters: H0 = 74 km s−1 Mpc−1, Ωm = 0.27, and ΩΛ = 0.73. Additionally, Sect. 6 presents a quantification of the significance of the difference between results obtained with this second choice of cosmo-logical parameter set values versus the first one (Planck-like).
 |
Fig. 10 Comparisons of the velocity fields reconstructed from the different datasets. Left: variances (black color) and slopes (red color) of linear fits to cell-to-cell simulated/reconstructed velocity field comparisons considering larger and larger sub-volumes of the total boxes. The variance, namely, the difference between the reconstructed and simulated velocities, is the greatest when using the biased catalog (black crosses) - especially when considering the largest sub-volumes - and the smallest when using the true catalog (black circles) to reconstruct the fields. It has intermediate values when the corrected catalogs (black stars, squares, and diamonds) are used to reconstruct the fields. The slopes are smaller than 1 in all but one point for the biased-catalog-based reconstruction. It represents a well-known effect of the Wiener-filter technique that goes to the mean field in absence of data, implying reconstructed velocities with null values to be compared to simulated velocities in this case. Right: ratio between reconstructed and simulated velocities at the sole positions of the selected-for-the-mock-catalog halos as a function of the latter’s distance. If the Wiener-filter tends to underestimate velocities when using corrected stacked-realization catalogs (dotted-dashed and three-dots-dashed red lines) for reconstruction, it does so quasi uniformly in the whole volume. It makes further corrections of Wiener-filter reconstructions easier than when using the biased catalog for the reconstructions. In the latter case (black dotted line), velocities are indeed alternatively under and overestimated with large fluctuations. |
5.2 Results
Figure 11 presents the results obtained applying the algorithm to the observational catalog described above. The top row shows one realization of the catalog that maximizes the probability density of the point process model. The bottom row shows five (ten) stacked realizations. In the first panel of each three-panel gathering, the distance modulus histograms reveal that indeed the Malmquist bias is overall corrected: objects those distances were underestimated (black solid line) are now further away (dashed and dotted blue and red lines). The sharp cut in distances due to the Fundamental plane-based 6-degree Field Galaxy Survey peculiar velocity sample (Springob et al. 2014), one of the main components of the cosmicflows-3 catalog, is also recovered. We note that unlike other bias-minimization techniques, we did not use a prior on this sharp cut-off. In the second panel of each one of these three-panel gatherings, the 1D peculiar velocity distribution is also less flattened. The expected 1D Gaussian distribution is recovered. Finally, the last panel of each three-panel gathering shows that the small-scale velocity variance is reduced to reach values in better agreement with expectations. We note that contrary to realizations obtained with the mock catalog, stacking five or ten realizations does not further change the small-scale velocity variance in a significant way.
In addition, Fig. 12 shows the distribution of galaxies in the three 40 h−1 Mpc thick Supergalactic slices. Galaxies are represented as blue (filled red) circles when their associated velocities are negative (positive). While the top row shows galaxies in the raw third catalog of the Cosmicflows project, the second (third) row highlights the galaxy distribution in the corrected (ten stacked realization) catalog. No pattern emerges in the raw catalog distribution, except for the biases, namely: there are solely negative velocities at large distances. Conversely, in the corrected catalogs, the filamentary structure of the cosmic web starts to emerge: well-defined filaments with infalling galaxies on both side appear delimiting voids. We note that while assuming redshift distances would also result in a filamentary like structure of the cosmic web, it would lack any information on peculiar velocities and thus on the true nature of the filamentary structures.
 |
Fig. 11 Comparisons between spatial distribution and velocity properties of the observed catalog before and after bias-minimization. From left to right: distance modulus histograms, peculiar velocity distributions obtained from the raw (black solid line) and corrected (blue and red dotted and dashed lines) observational catalogs as well as the small-scale velocity variance (solid cold color vs. dashed warm color lines respectively). Top to bottom left and right: results for one distribution, for five and ten stacked realizations. |
5.3 Reconstruction
Wiener-filter reconstructions of the density and velocity fields are built from the biased and corrected (both single and stacked realizations) observational catalogs. Supergalactic slices of these reconstructions are shown on Figs. 13 and 14, with the latter a zoom on the inner part of the box with respect to the former. Galaxies and groups from the 2MASS Galaxy Redshift Catalog (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018) are overplotted as red dots for comparison purposes solely. The yellow dots indicate galaxies those peculiar velocities have been used for the reconstructions. The large infall onto the center of the box and the observer and the rounded structures observed in the reconstruction obtained with the biased velocity catalog are suppressed in reconstructions obtained with corrected catalogs. These infalls and rounded structures are the result of biases that the Wiener-filter cannot not take into account by itself. In reconstructions obtained with bias-minimized catalogs, structures are more sharply defined. The velocity field presents several islands of convergence or divergence, in agreement with the clustering of galaxies as given by the redshift survey.
We note that the central outflow is more pronounced than the overall infall in the reconstruction obtained with the biased observational catalog than in that obtained with the biased synthetic catalog. This is because we use in both cases the same Planck Hubble constant value, while the cosmicflows-3 catalog zeropoint is set to a higher local Hubble constant value. The detailed effect of the Hubble constant choice and a possible estimation of the best fit to the data will be thoroughly investigated in a subsequent paper. Sorce & Tempel (2017) already showed the impact of the Hubble constant value and the capabilities of bias minimization techniques in standardizing the results to suppress at several levels and first order this dependence. Appendix A seems to further comfort this capability, while Sect. 6 quantifies the significance of the differences between results obtained assuming different H0 values. In any case, we can notice that both outflow and infall are drastically reduced in reconstructions obtained with bias-minimized catalogs.
6 The choice of H0
This section aims at quantifying the impact of H0 value on the results shown in this paper. It starts with quantifying differences and estimating their significance using synthetic catalogs before propagating the study to the observational catalogs.
6.1 Synthetic catalogs
To conduct this study, we built two synthetic catalogs following the procedure we described hereabove (in Sect. 4.1). One catalog uses H0 = 67.77 km s−1 Mpc−1, the other uses H0 = 74 km s−1 Mpc−1. This constitutes two true catalogs containing (sgl,sgb,zobs,µ) that are denoted T67 and T74, respectively. Our building procedure implies that selected halo-points are not identical in both catalogs. From these two catalogs, we built three biased catalogs. Two of them are obtained adding uncertainties as detailed in Sect. 4.1 to the two true catalogs. The third one is obtained from the T67-catalog but assuming H0 = 74 km s−1 Mpc−1 and propagating uncertainties. This configuration allows us to have the same selected halo-points in both biased catalogs. These biased catalogs are called B67, B74, and B74with67, respectively. Only B67 and B74with67 share the same ground truth in terms of catalogs. However, there is only one ground truth in terms of the reference simulation. We note that we could have instead built B67with74 without affecting the following conclusions. Since H0 = 67.77 km s−1 Mpc−1 is not favored for the observational catalogs, presenting the results for B74with67 is more relevant.
We applied the algorithm to the three biased catalogs to get the (stacked) bias-minimized catalogs called ‘H0_N’, where the ‘H0’ string is 67 or 74 and ‘_N’ is used only for the stacked realizations with N = 5 or 10.
Table 2 compiles the average variance (V) of the distance moduli between the ten different realizations used for the stacked version of the bias-minimized catalogs. Namely, the algorithm is applied ten times with a different initial seed on B67 (or B74 or B74with67). The variance between the distance moduli obtained for a halo-point in ten resulting bias-minimized catalogs, C67 (or C74 or C74with67) is then derived. The average of the variances for all halo-points is then reported in Table 2. Additionally, the variance of the residuals between the distance moduli is computed for pairs of realizations. The average variance of the residuals (VoR) is then reported in Table 2. The same can be done for pairs made of one C67 and one C74with67 as they share exactly the same halo-points. We note that the mean of these residuals is zero in all the cases, except for C67 versus C74with67. Final distance moduli are on average slightly smaller (~0.18 ± 0.05) for C74with67. This change of zeropoint is related to the larger assumed value of H0 but it is still smaller than the initial uncertainties on average (~0.5 against ~0.18 mag).
It is notable that the average variance (V) between the different realizations is almost an order of magnitude smaller than initial uncertainties on average (~0.5 against ~0.06 mag). Although slightly higher, the average variance of the residuals (VoR) is also about the same order of magnitude (~0.09 mag). The most interesting fact is that this average variance of the residuals is not larger when using pairs of realizations obtained with the algorithm assuming the same H0 value with respect to using pairs based on different H0 values. Statistically, the differences between distance moduli have the same variance (~0.09 mag).
To understand better the impact of these slight differences, comparisons can be extended to the Wiener-filter reconstructed velocity fields obtained with the different catalogs. They can be compared between themselves or with the reference simulation velocity field smoothed at the same scale. Indeed, in order to determine whether the difference between counterparts (i.e., fields obtained with the same type, namely, true, biased, bias-minimized, of the catalogs but different H0 values) is significant or not, we need first to estimate by how much the reconstructed field obtained with the true catalog differs from the simulated field.
Figure 15 top shows the variance (filled circle) between the reference simulation velocity field and that reconstructed from the different synthetic catalogs, that is, from the true ones to the bias-minimized ones through the biased ones. The solid red line highlights the average variance between the simulated velocity field and a reconstruction obtained with a true synthetic catalog. The velocity fields are compared in the full box as well as in different sub-boxes (gradient of gray).Velocity fields obtained from both true synthetic catalogs differ from the simulated velocity field at the same level. Fields reconstructed with the biased catalogs differ the most from the simulated one. Variances derived from the bias-minimized catalogs are all of the same order and are intermediate between those derived using the true catalogs and those obtained with the biased ones.
Figure 15 (bottom) goes further by showing the variance (filled circle) between reconstructed velocity fields obtained from T67 and from all the other catalogs. The same color and line style code as in the top panel applies. The additional dashed blue line highlights the variance between reconstructed velocity fields obtained with both true catalogs built out of different H0 values. Notably, velocity fields reconstructed with the bias-minimized catalogs (especially the stacked ones) differ from that obtained with the true catalog (T67) by the same amount that the latter differs from the reference simulated field (solid red line).
Finally, Fig. 16 compares pairs of velocity fields obtained with the same type of catalogs but different H0 values. It looks not only at the total velocity fields but also only at its divergent part denoted by the additional “d” letter at the end of the name for “divergent.” Fields reconstructed with the ten stacked bias-minimized realizations but different H0 values differ no more than those obtained from the true catalogs but different H0 values (dashed blue line). In any case, they differ less than the reconstructed velocity field obtained from the true catalog differs from the reference field (solid red line) or than the reconstructed fields derived from the bias-minimized catalogs differ from that reconstructed from the true catalog. Such differences can thus be considered insignificant at this first order.
 |
Fig. 12 Distribution of galaxies. From top to bottom: in the raw, corrected, ten stacked realization third catalog of the Cosmicflows project in the three supergalactic 40 h−1 Mpc thick slices (from left to right). Blue circles stand for galaxies with negative peculiar velocities. Red filled circles represent galaxies with positive peculiar velocities. The strong biases affecting the raw catalog (top) is clearly visible with negative velocities at large distances. The filamentary structure of the cosmic web is visible in the corrected catalogs. |
 |
Fig. 13 Supergalactic slices of reconstructed density (contours) and velocity (arrows) fields of the Local Universe. The blue color delimits over-from under- densities. Red points are galaxies (small filled circles) and groups (larger filled circles) from the 2MRS Galaxy Redshift Catalog for comparison purposes only (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018). Yellow points show galaxies whose peculiar velocities obtained from distance moduli are actually used for the reconstructions. The bias effects are reduced in reconstructed fields obtained with corrected catalogs. |
Variance between synthetic catalogs.
6.2 Observational catalogs
In this section, the study is repeated on the observational catalog with the exception that the ground truth is unknown. Neither the true field nor the true catalog are available. The letter “o” is added to the names of the different catalogs for “observed.” Table 3 reports the average variance between distance moduli (V) and the average variance of the residuals (VoR). As for the synthetic catalogs, the mean of the residuals is zero but when comparing C67o with C74o. Final distance moduli are (on average) slightly smaller (~0.16 ± 0.09) for C74o. All the values are very similar to those obtained with the synthetic catalogs and in that respect the same conclusions can be drawn.
Wiener-filter reconstructed velocity fields are also compared. Variances are shown on Fig. 17 in the same fashion as Fig. 16. The solid red line highlights the average variance found when comparing the velocity field reconstructed with the true synthetic catalog and the reference simulated field. The dashed blue line shows the average variance between the reconstructed velocity fields obtained with the true synthetic catalogs but different H0 values. Conclusions are similar to those drawn with the synthetic catalogs. Differences between reconstructed velocity fields derived from the stacked bias-minimized realizations obtained with different H0 values are insignificant at this first order.
Finally, Fig. 18 shows the three supergalactic slices of the overdensity and velocity fields reconstructed from the biased, bias-minimized assuming H0 = 67.77 km s−1 Mpc−1 and H0 = 74 km s−1 Mpc−1 observational catalogs. The color gradient from red to violet-white highlights high over- to underdensities. Names of structures are visible. White is used for superclusters, grey for clusters, dark green for walls and black with smaller character sizes for voids. Red points are still galaxies (small filled circles) and groups (larger filled circles) from the 2MRS Galaxy Redshift Catalog for comparison purposes only (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018). Yellow points still show those galaxies whose peculiar velocities obtained from distance moduli were actually used for the reconstructions.
Clearly the reconstruction obtained with the original catalog is biased although high density regions and structures are not completely off in the sense that there are over- and under-densities where expected although too pronounced. The velocity field though is clearly wrong. On the contrary, reconstructions obtained with the ten-stacked bias-minimized catalogs present several zones of velocity convergence and divergence. The agreement with known structures is good with both values of H0. The overall fields are very similar in agreement with the variance obtained when comparing the velocity fields. Over- and under-densities are at similar locations with tiny fluctuations that may hint at a better reconstruction alternatively using one or the other value of H0 with some difficulties in concluding in absence of ground truth. Future constrained simulations obtained with these catalogs will however also provide us with the mass of the clusters that can be compared with the observational mass estimates. Because the major differences between the reconstructions seems to be at the level of the intensities of the over- and under-densities, simulations seem like an excellent alternative to push further this study. We will certainly do so in a subsequent paper.
This section can be concluded comparing reconstructed structures from this paper to those obtained, for instance, by Graziani et al. (2019). Structures are named just as in their Fig. 8 to ease the comparisons and similar structures can indeed be found. Additionally, the residual spherical imprint of biases in the structures centered on the observer seems more dissipated. Several radial structures make their apparition. This similarity between reconstructions is to be pointed out especially because: Their grouping is different from ours and we showed in Sorce & Tempel (2017) that it may lead to drastic changes in the reconstruction. Their reconstruction technique is different (Wiener-filter vs. Hamiltonian Monte-Carlo, HMC), leading to maximum a posteriori fields versus mean of HMC sampling fields.
Variance between observational catalogs.
 |
Fig. 15 Comparisons between reconstructed velocity fields. Top: variance (filled circles) between the velocity field of the reference simulation and those reconstructed from the different catalogs. Bottom: variance (filled circles) between the reconstructed velocity field obtained with the true catalog T67 and those derived from the other catalogs. Detailed explanations of the different catalogs are given in the text. Names are given as follows: the letter indicates the type - T for True, B for biased and C for bias-minimized; the number gives the Hubble constant value −67 for 67.77 km s−1 Mpc−1, 74 for 74 km s−1 Mpc−1 and 74with67 when assuming 74 km s−1 Mpc−1 but for a 67.77 km s−1 Mpc−1 based true catalog; any additional suffix means that several realizations have been stacked (either 5 or 10). The size and color of the filled circles stand for the sub-box size within which fields are compared. The solid red line stands for the average variance between the reference simulated velocity field and that reconstructed from T67. The dashed blue line shows the average variance between the reconstructed fields obtained from both true catalogs with different H0 values (T67 and T74). Fields reconstructed from the bias-minimized catalogs differ from those obtained with the true catalog by the same amount as the latter differs from the reference field. |
 |
Fig. 16 Same as Fig. 15, but comparing reconstructed velocity fields obtained from the same type, namely, true, biased, and bias-minimized, of the catalogs but with different H0 values. The additional “d” suffix stands for divergent to be opposed to full velocity field. Fields reconstructed from the ten stacked bias-minimized realizations but different H0 values differ on average by the same order of magnitude as those obtained from the true catalogs but different H0 values. |
 |
Fig. 17 Same as Fig. 16 but for the observational catalog (hence the additional letter ‘o’). Fields reconstructed from the ten stacked bias-minimized realizations but different H0 values differ on average by the same order of magnitude than those obtained from the true synthetic catalogs, but different H0 values. Stacked bias-minimized catalogs permit obtaining reconstructions that differ at most by the same amount as the reconstructed field from the true synthetic catalog differs from the reference simulated field. |
 |
Fig. 18 Supergalactic slices of reconstructed density (filled contours) and velocity (arrows) fields of the Local Universe. Hot to cold colors go from over- to under- densities. Red points are galaxies (small filled circles) and groups (larger filled circles) from the 2MRS Galaxy Redshift Catalog for comparison purposes only (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018). Yellow points show galaxies whose peculiar velocities obtained from distance moduli are actually used for the reconstructions. Names indicate superclusters (white), clusters (grey), walls (dark green), and voids (smaller size characters in black). The bias effects are reduced in reconstructed fields obtained with corrected catalogs using either H0 = 67.77 km s−1 Mpc−1 or H0 = 74 km s−1 Mpc−1. |
7 Conclusion
As a response to the full underlying gravitational field, galaxy peculiar velocities can be extraordinary cosmological probes provided that biases inherent to their catalog construction are controlled. To minimize the effect of the different biases, this paper proposes a new technique based on a point process model whose density probability is maximized with Metropolis-Hastings samplings embedded into a simulated annealing scheme. The algorithm determines realizations maximizing the density probability. They correspond to sets of galaxy distance moduli and uncertainties with the highest probabilities given their corresponding radial peculiar velocities.
This new algorithm builds on our 2015 work (Sorce 2015) and improves it by determining the most probable position of a galaxy and its associated peculiar velocity given not only the 1D peculiar velocity probability distribution but also the 3D small-scale velocity correlation. This concept is at the core of the algorithm proposed.
Moreover, the model, tailored for this purpose, does not rely on very detailed prior knowledge of the catalog nor prior hypotheses specific to the catalog:
It offers a great flexibility,
It does not require as many priors as usual Bayesian techniques used in the field,
These priors are independent on the datasets unless the data sampling in space varies from one extreme to another,
The algorithm thus makes it possible to easily switch from one dataset to another,
The cosmological model and its parameters can also be modified in the most convenient way7.
The proposed method diminishes the effects of the biases. The obtained results and the conducted statistical tests show the reduction of the effects of the biases in two situations. Applied to synthetic catalogs8, when comparisons with both the true and biased data are possible, the algorithm results in statistically corrected datasets, namely, the distance moduli (thus distances and peculiar velocities) are in agreement at better than an average 1%. This step also permits us to set the parameters of the algorithm.
Subsequently, as applied to observational catalogs of the Cosmicflows project, the algorithm gives datasets that are input into the Wiener-filter technique to reconstruct the Local Universe. The Wiener-filter technique, a classical restoration method, is specifically chosen for its inefficiency in taking into account the biases. Resulting reconstructed density fields are a great match to the 2MASS Galaxy Redshift Catalog (2MRS) and the velocity field does not present any significant outflow or infall, signs of biases, out of or onto the Local Volume. Within this context, the new proposed method improves the quality of the peculiar velocity catalogs as a whole.
The newly derived version of the peculiar velocity datasets will be used for future constrained simulations of the Local Universe. Nevertheless, reducing biases in cosmological data and those appearing while exploiting the data is still an open and challenging problem. It leads to new questions, which we will tackle in future works. For instance, following Sorce (2018), the extra-smoothing of the velocity field by the Wiener-filter technique, due to the fading of the number of data points with the distance from the observer, will be taken care of.
In the meantime, subsequent studies will also focus on using different H0 values to probe on the possibility to extract an estimate of the H0 value directly from the data. A first quantitative study based on the fields reconstructed from the bias-minimized catalogs obtained with different H0 values hints at insignificant changes at first order that could become significant with deeper studies like going to constrained simulations and looking at the resulting cluster mass function.
Later on, the cosmological model itself could be relaxed. In addition, the observational redshift, zobs, assumed to have negligible errors with respect to distance moduli, might also be unfixed in future developments.
Acknowledgements
The authors would like to thank the referee for their careful reading of the manuscript and their sensible comments that helped improved its quality. The authors acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) and GENCI (https://www.genci.fr/) for funding this project by providing computing time on the GCS Supercomputer SuperMUC-NG at Leibniz Supercomputing Centre (www.lrz.de) and Joliot-Curie at TGCC (http://www-hpc.cea.fr). J.S. acknowledges support from the ANR LOCALIZATION project, grant ANR-21-CE31-0019 of the French Agence Nationale de la Recherche. E.T. acknowledges support by ETAg grant PRG1006 and by the EU through the ERDF CoE grant TK133. This work was supported by the Programme National Cosmologie et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES.
Appendix A H0=74 km s−1 Mpc−1
This appendix reports the results obtained for the third catalog of the Cosmicflows project when using WMAP7-like cosmological parameter values rather than Planck values. Indeed, Tully et al. (2016) estimate the third dataset of the Cosmicflows project to be compatible with H0=75±2 km s−1 Mpc−1, this appendix thus uses WMAP7-like parameters: H0=74 km s−1 Mpc−1, Ωm = 0.27, and ΩΛ = 0.73. Figures presented in the paper core for the observational catalog are reproduced in this appendix (Figs. A.1 to A.4). No drastic changes appear when using either set of cosmological parameter values. It confirms that this kind of bias minimization techniques seems prone to smooth any effect due to the Hubble constant value choice. A further work will consist of determining whether this could also permit estimating the Hubble constant value that is a best fit to the data.
References
- Bijaoui, A. 2013, in EAS Pub. Ser., 59, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boruah, S. S., Lavaux, G., & Hudson, M. J. 2022, MNRAS, 517, 4529 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, L. A., Lucey, J. R., Colless, M., et al. 2014, MNRAS, 443, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, S. N., Stoyan, D., Kendall, W. S., & Mecke, J. 2013, Stochastic Geometry and its Applications, Wiley Series in Probability and Statistics (John Wiley & Sons, Ltd) [Google Scholar]
- Colless, M., Saglia, R. P., Burstein, D., et al. 2001, MNRAS, 321, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. M., & Scrimgeour, M. I. 2014, MNRAS, 442, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A. 1994, ARA&A, 32, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Feix, M., Branchini, E., & Nusser, A. 2017, MNRAS, 468, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [Google Scholar]
- Gottlöber, S., Hoffman, Y., & Yepes, G. 2010, ArXiv e-prints, [arXiv:1005.2687] [Google Scholar]
- Graziani, R., Courtois, H. M., Lavaux, G., et al. 2019, MNRAS, 488, 5438 [NASA ADS] [CrossRef] [Google Scholar]
- Han, M. 1992, ApJ, 395, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hendry, M. A., & Simmons, J. F. L. 1994, ApJ, 435, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, Y., Carlesi, E., Pomarède, D., et al. 2018, Nat. Astron., 2, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, Y., Nusser, A., Valade, A., Libeskind, N. I., & Tully, R. B. 2021, MNRAS, 505, 3380 [NASA ADS] [CrossRef] [Google Scholar]
- Howlett, C., Staveley-Smith, L., & Blake, C. 2017, MNRAS, 464, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [Google Scholar]
- Hudson, M. J. 1994, MNRAS, 266, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kapteyn, J. C. 1914, Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington, 82, 3 [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1992, ApJ, 391, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G. 2016, MNRAS, 457, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, ApJ, 417, 553 [Google Scholar]
- Lynden-Bell, D., Faber, S. M., Burstein, D., et al. 1988, ApJ, 326, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Malmquist, K. G. 1922, Meddelanden fran Lunds Astronomiska Observatorium Serie I, 100, 1 [Google Scholar]
- Nusser, A. 2017, MNRAS, 470, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A., & Davis, M. 2011, ApJ, 736, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. 1994, ApJ, 430, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Diaferio, A. 2001, MNRAS, 322, 901 [Google Scholar]
- Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [Google Scholar]
- Sorce, J. G. 2015, MNRAS, 450, 2644 [CrossRef] [Google Scholar]
- Sorce, J. G. 2018, MNRAS, 478, 5199 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., & Tempel, E. 2017, MNRAS, 469, 2859 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., & Tempel, E. 2018, MNRAS, 476, 4362 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Courtois, H. M., Tully, R. B., et al. 2013, ApJ, 765, 94 [Google Scholar]
- Sorce, J. G., Courtois, H. M., Gottlöber, S., Hoffman, Y., & Tully, R. B. 2014a, MNRAS, 437, 3586 [CrossRef] [Google Scholar]
- Sorce, J. G., Tully, R. B., Courtois, H. M., et al. 2014b, MNRAS, 444, 527 [Google Scholar]
- Sorce, J. G., Gottlöber, S., Hoffman, Y., & Yepes, G. 2016a, MNRAS, 460, 2015 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Gottlöber, S., Yepes, G., et al. 2016b, MNRAS, 455, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Blaizot, J., & Dubois, Y. 2019, MNRAS, 486, 3951 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Dubois, Y., Blaizot, J., et al. 2021, MNRAS, 504, 2998 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Mohayaee, R., Aghanim, N., Dolag, K., & Malavasi, N. 2023, MNRAS, submitted, [arXiv:2301.01305] [Google Scholar]
- Springob, C. M., Magoulas, C., Colless, M., et al. 2014, MNRAS, 445, 2677 [Google Scholar]
- Stoica, R. S. 2010, Eur. Phys. J. Spec. Top., 186, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., & Willick, J. A. 1995, Phys. Rep., 261, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Teerikorpi, P. 1990, A&A, 234, 1 [NASA ADS] [Google Scholar]
- Teerikorpi, P. 1993, A&A, 280, 443 [NASA ADS] [Google Scholar]
- Teerikorpi, P. 1995, Astrophys. Lett. Commun., 31, 263 [NASA ADS] [Google Scholar]
- Teerikorpi, P. 1997, ARA&A, 35, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Kipper, R., Tamm, A., et al. 2016a, A&A, 588, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Stoica, R. S., Kipper, R., & Saar, E. 2016b, Astron. Comput., 16, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Kruuse, M., Kipper, R., et al. 2018, A&A, 618, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tuvikene, T., Muru, M. M., et al. 2020, MNRAS, 497, 4626 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [Google Scholar]
- Tully, R. B., & Courtois, H. M. 2012, ApJ, 749, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H., Hoffman, Y., & Pomarède, D. 2014, Nature, 513, 71 [Google Scholar]
- Tully, R. B., Courtois, H. M., & Sorce, J. G. 2016, AJ, 152, 50 [Google Scholar]
- Valade, A., Hoffman, Y., Libeskind, N. I., & Graziani, R. 2022, MNRAS, 513, 5148 [NASA ADS] [CrossRef] [Google Scholar]
- Van Lieshout, M. 1994, Adv. Appl. Prob., 26, 281 [CrossRef] [Google Scholar]
- Wakamatsu, K., Colless, M., Jarrett, T., et al. 2003, ASP Conf. Ser., 289, The 6dF Galaxy Survey, eds. S. Ikeuchi, J. Hearnshaw, & T. Hanawa, 97 [NASA ADS] [Google Scholar]
- Wang, Y. Y., Wang, F. Y., & Zou, Y. C. 2018, Phys. Rev. D, 98, 063503 [NASA ADS] [CrossRef] [Google Scholar]
- Willick, J. A. 1994, ApJS, 92, 1 [CrossRef] [Google Scholar]
- Zaroubi, S., Hoffman, Y., & Dekel, A. 1999, ApJ, 520, 413 [NASA ADS] [CrossRef] [Google Scholar]
Notably, ~50% of the third cosmicflows dataset is constituted of the 6-degree Field Galaxy Survey peculiar velocity sample (Springob et al. 2014), a complete up-to-a-given-distance survey.
As a matter of fact, Appendix A gives the results for the observational catalogs using a set of cosmological parameter values consistent with WMAP7 while Planck values are used in the core of the paper.
All Tables
All Figures
 |
Fig. 1 Schematic view of the interaction shape. Top: interaction shape in 2D showing how i’s shape is derived. j belongs to i’s shape. Bottom: examples of interactions: a) i and j are both within one another shapes; b) k is in the shape of j, but j is not in that of k; c) l and k are not in one another shapes. |
| In the text | |
 |
Fig. 2 Correlation between the velocity variance and the uncertainty. More precisely, variance between velocities of objects in the same shape S whose size is defined by the uncertainty. Filled circles are obtained throwing shapes, as defined in Fig. 1, onto mock catalogs without errors. The solid line is the polynomial fitting a+bx+cx2 with a = 64, b = 70, c = 22 km s−1 assuming uncertainty magnitudes (Mag) in dex. |
| In the text | |
 |
Fig. 3 Details of the steps to obtain the new set of (µi, σi), namely ( |
| In the text | |
 |
Fig. 4 Galaxies in 5 h−1 Mpc thick slices of the XY supergalactic plane. From left to right: black lines show the projected distances between true (yellow filled circles) and biased (black filled diamonds), after nmh. Metropolis Hastings loops but no cooling for the n data points (in the text iteration 1, blue-filled square) and, at the end of all loops (red-filled circles), data point positions. The filled symbol sizes are proportional to velocities in a logarithmic scale. Because errors are large in the left panel, yellow filled circles are harder to distinguish. The algorithm reduces on average errors on data point positions thus on their peculiar velocities, namely, on average, shorter black lines and, by extension, better matching filled symbol sizes of different colors. |
| In the text | |
 |
Fig. 5 Comparisons of spatial distribution properties in the datasets. Left: histograms of the ratio of the differences between biased (black solid line), after iteration 1 (see text for a definition, blue dotted line), corrected (red dashed line), and true distance moduli to the true distance moduli, namely, the errors in percent on distance moduli. Middle: difference between true and biased (black diamonds), after iteration 1 (blue square) and at the end of the process or corrected (red circles) distance moduli versus true distance moduli. Right: ratio of the difference between assigned uncertainties and true errors to the true errors on distance moduli. Same colors and line styles as the left panel. |
| In the text | |
 |
Fig. 6 Comparisons of velocity properties in the datasets. Left: true (thick yellow solid line) and biased (black solid line) peculiar velocity distributions vs. those derived from after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) distance moduli. Middle: histograms of errors in absolute value on peculiar velocities derived from before correction, after iteration 1 and after correction distance moduli. Same color and line style codes. Right: local velocity variance in different shape S elongations (one line per elongation) for a catalog free of errors (solid lines with warm colors), with errors (solid lines with cold colors), after applying the algorithm (dashed lines with warm colors). The variance is defined as the standard deviation between peculiar velocities of galaxies belonging to a same, elongated along the line-of-sight, shape S (see exact definition in the text). Shape elongations at given distances are obtained ranging fictively distance modulus uncertainties from 0.2 (orange, red, black) to 1.8 (green, orange, light blue) mag. |
| In the text | |
 |
Fig. 7 Comparisons of dataset properties. Left: median of the difference between distances obtained from after iteration 1 (filled blue squares) and at the end of the process or corrected (filled red circles) distance moduli and those derived from biased distance moduli as a function of the true distances. Errors on the median are obtained with bootstrapping. New distances tend to be larger than initial ones. This is in agreement with the reduction of the homogeneous Malmquist bias that statistically tends to put objects closer than they are. After bias-minimization of distance modulus catalog, new distances are indeed statistically larger than initial ones derived from biased distance moduli. At large distances, effects of the catalog edges, like sharp cut-off, are preponderant. Top-right panel: histograms of the number of data points per grid cells obtained from true (thick yellow solid line), biased (black solid line), after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) distance modulus catalogs. Grids are built to split the Supergalactic coordinate space uniformly. Since catalogs are not complete, cells with no data point have been removed. The histograms represent a measurement of the clustering. The more clustered the data points in a catalog are, the more data points there can be per grid cells. Bottom-right panel: ratios between the biased (black solid line), after iteration 1 (blue dotted line) and at the end of the process or corrected (red dashed line) histograms and the true one. These right panels show that data points in the biased catalog are statistically less clustered than in the true and corrected ones. This is in agreement with the reduction of the heterogeneous Malmquist bias. Indeed, the latter tends to reduce clustering by statistically scattering objects from high density regions to low ones. The line thickness stands for the grid-cell size. From the thicker to the thinner lines, the cell sizes are ~4.6, 5.5 and 6.9 h−1 Mpc. |
| In the text | |
 |
Fig. 8 Same as Fig. 4 (right panel) as well as Figs. 5 and 6 for five (left column) and ten (right column) stacked realizations of the corrected catalog obtained with the algorithm. |
| In the text | |
 |
Fig. 9 Supergalactic slices of the simulated (first column) and reconstructed (second to sixth columns) density and velocity fields. Contours show the overdensities and arrows indicate the velocities. The blue contours delimit the underdensities from the overdensities. Yellow points show halos constituting the different catalogs. The peculiar velocities of these halos, obtained from distance moduli, are actually used for the different reconstructions. |
| In the text | |
 |
Fig. 10 Comparisons of the velocity fields reconstructed from the different datasets. Left: variances (black color) and slopes (red color) of linear fits to cell-to-cell simulated/reconstructed velocity field comparisons considering larger and larger sub-volumes of the total boxes. The variance, namely, the difference between the reconstructed and simulated velocities, is the greatest when using the biased catalog (black crosses) - especially when considering the largest sub-volumes - and the smallest when using the true catalog (black circles) to reconstruct the fields. It has intermediate values when the corrected catalogs (black stars, squares, and diamonds) are used to reconstruct the fields. The slopes are smaller than 1 in all but one point for the biased-catalog-based reconstruction. It represents a well-known effect of the Wiener-filter technique that goes to the mean field in absence of data, implying reconstructed velocities with null values to be compared to simulated velocities in this case. Right: ratio between reconstructed and simulated velocities at the sole positions of the selected-for-the-mock-catalog halos as a function of the latter’s distance. If the Wiener-filter tends to underestimate velocities when using corrected stacked-realization catalogs (dotted-dashed and three-dots-dashed red lines) for reconstruction, it does so quasi uniformly in the whole volume. It makes further corrections of Wiener-filter reconstructions easier than when using the biased catalog for the reconstructions. In the latter case (black dotted line), velocities are indeed alternatively under and overestimated with large fluctuations. |
| In the text | |
 |
Fig. 11 Comparisons between spatial distribution and velocity properties of the observed catalog before and after bias-minimization. From left to right: distance modulus histograms, peculiar velocity distributions obtained from the raw (black solid line) and corrected (blue and red dotted and dashed lines) observational catalogs as well as the small-scale velocity variance (solid cold color vs. dashed warm color lines respectively). Top to bottom left and right: results for one distribution, for five and ten stacked realizations. |
| In the text | |
 |
Fig. 12 Distribution of galaxies. From top to bottom: in the raw, corrected, ten stacked realization third catalog of the Cosmicflows project in the three supergalactic 40 h−1 Mpc thick slices (from left to right). Blue circles stand for galaxies with negative peculiar velocities. Red filled circles represent galaxies with positive peculiar velocities. The strong biases affecting the raw catalog (top) is clearly visible with negative velocities at large distances. The filamentary structure of the cosmic web is visible in the corrected catalogs. |
| In the text | |
 |
Fig. 13 Supergalactic slices of reconstructed density (contours) and velocity (arrows) fields of the Local Universe. The blue color delimits over-from under- densities. Red points are galaxies (small filled circles) and groups (larger filled circles) from the 2MRS Galaxy Redshift Catalog for comparison purposes only (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018). Yellow points show galaxies whose peculiar velocities obtained from distance moduli are actually used for the reconstructions. The bias effects are reduced in reconstructed fields obtained with corrected catalogs. |
| In the text | |
 |
Fig. 14 Same as Fig. 13 but zoomed on the inner part of the box. |
| In the text | |
 |
Fig. 15 Comparisons between reconstructed velocity fields. Top: variance (filled circles) between the velocity field of the reference simulation and those reconstructed from the different catalogs. Bottom: variance (filled circles) between the reconstructed velocity field obtained with the true catalog T67 and those derived from the other catalogs. Detailed explanations of the different catalogs are given in the text. Names are given as follows: the letter indicates the type - T for True, B for biased and C for bias-minimized; the number gives the Hubble constant value −67 for 67.77 km s−1 Mpc−1, 74 for 74 km s−1 Mpc−1 and 74with67 when assuming 74 km s−1 Mpc−1 but for a 67.77 km s−1 Mpc−1 based true catalog; any additional suffix means that several realizations have been stacked (either 5 or 10). The size and color of the filled circles stand for the sub-box size within which fields are compared. The solid red line stands for the average variance between the reference simulated velocity field and that reconstructed from T67. The dashed blue line shows the average variance between the reconstructed fields obtained from both true catalogs with different H0 values (T67 and T74). Fields reconstructed from the bias-minimized catalogs differ from those obtained with the true catalog by the same amount as the latter differs from the reference field. |
| In the text | |
 |
Fig. 16 Same as Fig. 15, but comparing reconstructed velocity fields obtained from the same type, namely, true, biased, and bias-minimized, of the catalogs but with different H0 values. The additional “d” suffix stands for divergent to be opposed to full velocity field. Fields reconstructed from the ten stacked bias-minimized realizations but different H0 values differ on average by the same order of magnitude as those obtained from the true catalogs but different H0 values. |
| In the text | |
 |
Fig. 17 Same as Fig. 16 but for the observational catalog (hence the additional letter ‘o’). Fields reconstructed from the ten stacked bias-minimized realizations but different H0 values differ on average by the same order of magnitude than those obtained from the true synthetic catalogs, but different H0 values. Stacked bias-minimized catalogs permit obtaining reconstructions that differ at most by the same amount as the reconstructed field from the true synthetic catalog differs from the reference simulated field. |
| In the text | |
 |
Fig. 18 Supergalactic slices of reconstructed density (filled contours) and velocity (arrows) fields of the Local Universe. Hot to cold colors go from over- to under- densities. Red points are galaxies (small filled circles) and groups (larger filled circles) from the 2MRS Galaxy Redshift Catalog for comparison purposes only (2MRS, Huchra et al. 2012; groups from Tempel et al. 2018). Yellow points show galaxies whose peculiar velocities obtained from distance moduli are actually used for the reconstructions. Names indicate superclusters (white), clusters (grey), walls (dark green), and voids (smaller size characters in black). The bias effects are reduced in reconstructed fields obtained with corrected catalogs using either H0 = 67.77 km s−1 Mpc−1 or H0 = 74 km s−1 Mpc−1. |
| In the text | |
 |
Fig. A.1 Same as Fig. 12 but using WMAP7-like cosmological parameter values in the algorithm. |
| In the text | |
 |
Fig. A.2 Same as Fig. 11 but using WMAP7-like cosmological parameter values in the algorithm. |
| In the text | |
 |
Fig. A.3 Same as Fig. 13 but using WMAP7-like cosmological parameter values in the algorithm. |
| In the text | |
 |
Fig. A.4 Same as Fig. 14 but using WMAP7-like cosmological parameter values in the algorithm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.