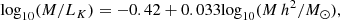EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A169 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A169
Number of page(s) 16
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202346213
Published online 20 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

The neighborhood in the immediate vicinity of the Milky Way (MW) is known as the Local Group. It is a binary system composed of two average-sized galaxies (the MW and Andromeda) that occupies a volume that is roughly ∼7 Mpc in diameter. At a distance of around 16 Mpc, the Virgo cluster comes into view as the main defining feature of our neighborhood on these scales. Beyond Virgo, a number of well-known and well-observed clusters, such as Centaurus, Fornax, Hydra, Norma, Perseus, and Coma, dominate the local volume, among them a significant number of very massive clusters.

Therefore, our local Universe, which is centered on us and extends over 150 h−1 Mpc, is not only a formidable site for detailed observations, but also appears to be a very particular region of the Universe. Starting from the Local Void (Tully & Fisher 1987), bordered by the Local Sheet (Tully et al. 2008), there are also a large number of supercluster structures identified within the local Universe, among them Perseus-Pisces, Centaurus, Coma, and Hercules (see recent work by Böhringer & Chon 2021, and references therein). Several of these most prominent structures in the local Universe form what is called the supergalactic plane, which was already recognized by de Vaucouleurs (1953; see also Lahav et al. 2000; Peebles 2022 for a summary of our current understanding of these structures, as well as Flin 1986; Rubin 1989 for historical reviews). The impact of these structures is also recognized to form a global pancake-like structure out to a scale of ∼100 Mpc (Einasto & Miller 1983; Einasto et al. 1994; Böhringer et al. 2021) as well as large differences in the mean stellar density between the northern and southern hemispheres (Karachentsev & Telikova 2018) out to distances of ∼60 Mpc. It is often argued that such particular structures show an unusual overdensity (Makarov & Karachentsev 2011) or underdensity (Böhringer et al. 2020) when using luminous matter on different scales; different conclusions are reached when evaluating the underlying dark matter density field from them. As this could play a significant role in some of the current tensions in cosmology, for example the larger H0 value locally inferred compared to CMB measurements (see Freedman 2021, for a most recent compilation of the values), it is important to understand how galaxies and galaxy clusters with different masses and properties trace the underlying dark matter density field. In addition, the selection effect of different observations has to be understood in detail to answer such questions.

Trying to understand such features in the local Universe motivated various campaigns producing constrained simulations in the past. However, for a more detailed study it is necessary to cover a large enough volume, covering several hundred megaparsec and initial conditions that are not directly based on the distribution of the traces to allow an independent comparison. In addition, it is necessary to include galaxy formation physics into the simulation to properly select objects by observables, such as stellar masses of galaxies or X-ray luminosity of galaxy clusters. Here we present simulations that for the first time match all three criteria.

The paper is structured as follows. Section 2 gives an extended summary of previous constrained simulations followed by Sect. 3, which describes the details of the simulations used, the galaxy formation physics included, and details on the building of the initial conditions, followed by a qualitative comparison to observations in Sect. 4. In Sect. 5, we then present the predicted, spatial distribution of matter, halos, and galaxies from the simulations, and compare the peculiar features extensively with various observations in Sect. 6. In addition to the conclusions presented in Sect. 7, we also repeated some of the analysis on previous constrained simulations, which are presented in Appendix A to demonstrate the potential inherent in our constrained simulations, which does not depend on assuming a bias between tracer particles and dark matter, but rather predicts this bias quite accurately.

2. Constrained simulations

There are two approaches to study the problems mentioned above with numerical simulations. The first is to run simulations of very large volumes with very high resolution, and to find the objects of interest in these simulations in environments similar to the observed ones. For example, in a statistical approach, the scatter in the H0 value locally inferred can be studied in a box of (6 h−1 Gpc)3 (Wojtak et al. 2014) or Local Group candidates can be drawn from a large sample of isolated halo pairs identified in a set of cosmological simulations (APOSTLE, Fattahi et al. 2016). An alternative approach is to use constrained cosmological simulations. The goal of these simulations is to reproduce as closely as possible the positions, velocities, masses, and internal properties of the objects of interest (i.e., to reduce the cosmic variance in the region of interest as much as possible). Then the simulations can go well beyond the statistical approach and even trace back the evolutionary paths of the studied objects. The constrained simulations are based on observations. There are two different approaches to obtaining the initial conditions of cosmological simulations based on the observed matter distribution at present. The first goes backward in time and is based on the Hoffman-Ribak algorithm (Hoffman & Ribak 1991). We use this algorithm throughout our paper. An alternative approach to studying the local Universe with constrained simulations was developed during the last decade, namely a Bayesian forward modeling (e.g., Kitaura et al. 2012, [ELUCID] Wang et al. 2016, [SIBELIUS] Sawala et al. 2022; McAlpine et al. 2022; for a recent comprehensive discussion of this Bayesian modeling, see Jasche & Lavaux 2019). The quality of the constrained simulations depends on the number and the quality of the constraints (see, e.g., the discussion of the optimal sampling of velocity constraints for Wiener Filter reconstructions by Sorce et al. 2017).

One of the first constrained simulations was based on data derived from redshift surveys that estimate the local total matter density from the distribution of galaxies using their observed redshift. Here, the main uncertainties are the assumed constant relation between galaxy density and total density as well as the imposed uncertainty in the distances by the presence of peculiar line-of-sight velocity. The initial conditions for a 240 h−1 Mpc box were constructed, which contains a sphere of 160 h−1 Mpc diameter sampled with higher resolution (Mathis et al. 2002). Simulations based on these initial conditions cover dark matter-only simulations combined with semianalytic models were used to study the local galaxy population (Mathis et al. 2002), and pure magneto-hydrodynamics simulations were used to study the propagation of cosmic rays in the local Universe (CORUSCANT1; Dolag et al. 2004a) as well as the imprint of the local supercluster onto the CMB (Dolag et al. 2005a). Subsequently, these initial conditions were evolved with more advanced physics including radiative cooling, star-formation, stellar evolution, and chemical enrichment to study density and temperature fluctuations in the local and prominent galaxy clusters (SALACIOUS2; Kawahara et al. 2007), including AGN feedback from supermassive black holes; subsequent simulations based on these initial conditions were used to contrast the observed Sunyaev–Zel’dovich effect (SZ) of the Coma and Virgo clusters, as measured by the Planck satellite (Planck Collaboration X 2013; Planck Collaboration XL 2016).

The other method used to constrain the initial conditions is based on peculiar velocities derived from direct distance measures. This has the advantage that tracing the velocity field is independent of the tracer population and that the velocity traces the potential caused by the large-scale density field of all matter. However, the data sets of galaxies with measured distance indicators are much smaller, and the intrinsically large uncertainties associated with these distance indicators have to be dealt with in a very careful way. Early attempts therefore tried a hybrid approach using velocity data combined with constraints coming from local galaxy clusters, which allowed large enough spans in volume to cover the most important galaxy clusters like Virgo, Perseus, and Coma. This led to the CLUES3 (Yepes et al. 2009) dark matter-only simulation of a 160 h−1 Mpc box centered on the MW position to study the local galaxy population (Klypin et al. 2003) and a nonradiative hydrodynamic simulation of the Virgo cluster within that box to study the properties of the intergalactic medium (Kravtsov et al. 2002). Based on the same constraints, high-resolution simulations of a 64 h−1 Mpc box (Gottlöber et al. 2010) were performed and used, for example to study the reionization of the Local Group (Dixon et al. 2018), while zoomed-in full hydrodynamics simulations within a central region, a few megaparsec in size, of the same box were used for many studies of the Local Group, including simulations following in detail the formation of isolated dwarfs in the neighborhood of the Local Group (see, e.g., Benítez-Llambay et al. 2015).

The growing data of direct distances from the CosmicFlow project (e.g., Courtois et al. 2012; Tully et al. 2013, 2016, 2023) has driven new approaches within the CLUES project since then. In a series of papers, techniques were developed to deal with the increasing number of constraints and to handle the biases inherent to velocity data (Doumler et al. 2013a,b,c; Sorce et al. 2014, 2016a; Sorce 2015). Based on this approach, initial conditions for a 64 h−1 Mpc box were constructed. They were used within the CosmicDawn project to run a fully coupled radiation-hydrodynamics simulation of cosmic reionization and galaxy formation until redshift z = 6 (Ocvirk et al. 2020) and to run a dark matter-only simulation with 40963 particles down to redshift z = 0 within the MultiDark project. In this simulation the Milky Way and Andromeda galaxies can be identified so that their reionization history can be inferred from the radiation-hydrodynamics simulation (Sorce et al. 2022). Moreover, initial conditions based on the same approach were used to simulate a 100 h−1 Mpc box, where a high-resolution region of about 10 h−1 Mpc is placed in the central region around the Local Group, including detailed galaxy formation physics (HESTIA; Libeskind et al. 2020). The first dark matter-only simulations based on a larger 500 h−1 Mpc box already allowed us to reproduce the Virgo cluster and its formation history (LU2016, Sorce et al. 2016b). The consecutive improvements of dark matter simulations of this volume allowed us to reproduce ever more prominent galaxy clusters like Perseus and Coma (Constrained LOcal and Nesting Environment Simulations, CLONES; Sorce 2018), to study the formation history of clusters (Olchanski & Sorce 2018; Sorce et al. 2020), and to study the large-scale cosmic web in which clusters like Coma are embedded by comparing observations (Malavasi et al. 2020) and simulations (Malavasi et al. 2023). Subsequent placing high-resolution regions around such prominent clusters allowed the direct comparison of galaxy properties within the Virgo cluster via hydrodynamics simulations with full galaxy formation physics with their observed counterparts (Sorce et al. 2021). For the first time, the CLONES results undoubtedly show that the constrained formation history of the Virgo cluster significantly differs from averaged clusters of the same mass (Sorce et al. 2021). Moreover, the simulations indicate phase-space positions of recently in-falling galaxy groups. It also matches the specific amplitude and shapes of the appearing velocity waves on the lines of sight toward various well-known galaxy clusters (Sorce et al. 2023).

The Simulating the Local Web (SLOW) procedure4 is a 500 h−1 Mpc box using realization number 8 of CLONES, as described in Sect. 3.3, and assumes a Planck like cosmology (Planck Collaboration XVI 2014), with a Hubble constant H0 = 67.77 km s−1 Mpc−1, a total matter density of ΩMatter = 0.307115, a cosmological constant of ΩΛ = 0.692885, and a baryon fraction corresponding to Ωbaryon = 0.0480217. It follows the evolution of dark and baryonic matter within a (500 h−1 Mpc)3 simulation volume centered on the position of the MW and that stands for our cosmic neighborhood. The initial conditions for these simulations are obtained with sophisticated algorithms (see Sect. 3.3) that take into account the position and motion estimates of thousands of galaxies within our local volume. These local measurements allow us to constrain the initial conditions that, in turn, lead to the observed local large-scale structure, when motions from early times until today are followed according to the gravity laws. In addition, the baryonic matter is treated via hydrodynamics together with various state-of-the-art subgrid models (see Sect. 3.2). There are variants that follow the evolution of the magnetic field and cosmic rays; others follow the formation of the stellar population as well as black holes (BHs) and associated active galactic nucleus (AGN) physics. Here we follow the prescriptions used for the Magneticum simulations (see Hirschmann et al. 2014; Dolag et al. 2016). This first paper in the series mainly introduces the general properties based on the simulation following galaxy formation processes, and therefore a realistic galaxy population is present in the simulations as well as galaxy clusters with proper intracluster medium (ICM) properties. Therefore, galaxies together with the population of galaxy clusters can be directly compared by the same means to the observed counterparts. This also allows us to study the effects of the local environment on observational properties and their cosmological impact.

However, comparing clusters from constrained simulations with their observational counterparts needs a cross-identification, which itself is subject to evaluating differences in observed and simulated positions and masses. Such differences in positions have different origins. Simulations performing density reconstruction based on redshift surveys typically need to apply a relatively large smoothing (e.g., 5−10 Mpc in the case of CORUSCANT) to the reconstructed density field, while the bulk velocity at which the halo is moving over cosmic time is largely unconstrained and leads to additional displacement of the halo in the simulation. In simulations based on peculiar velocities, uncertainties from distance moduli propagate to radial velocities and, when applying a Poisson equation, propagate further into uncertainties on the reconstructed density and the total velocity field. Therefore, uncertainties in the observed distance (which could be as large as several tens of megaparsec for distant clusters) are coupled directly with displacements of the three-dimensional positions within the evolved simulation.

To give a better impression on the differences in some of the constrained simulations, we show the predicted distribution of galaxies from the three simulations SLOW, SIBELIUS, and SALACIOUS compared to the galaxies from the 2MRS catalog in Fig. 1. In addition, the positions of Coma, Perseus, and Virgo within the simulations and observations are shown. In general, the environments of these clusters are similar in the different simulations, for example the large-scale structure leaving Perseus to the lower left, or the horizontal structures leaving Virgo and Coma. However, the details in these structures are different, and there are striking differences between the massive clusters and their immediate environments. In SLOW/CLONES for example, the immediate outskirts of Perseus indicate a quiet fossil, a relaxed system with a mass that is very close to that expected from observations, where Perseus is characterized by a strong cool-core feature associated with overall relaxed systems (see Fabian et al. 1981; Böhringer et al. 1993). In contrast, within the CORUSCANT/SALACIOUS simulation the Perseus structure appears as a twin system with an even more massive companion, while in the SIBELIUS simulation Perseus appears to be three times too massive. The obtained virial masses of these clusters in the different simulations and their positions are listed in Table 1, where we also listed the observational findings. For the masses, we converted all values to the same mass definition using the scaling relations given in Ragagnin et al. (2021) and Planck Collaboration XL (2016).

thumbnail Fig. 1.

Positions in supergalactic x/y coordinates of all galaxies in the simulations, compared to galaxies from the 2MRS catalog. To make the simulations comparable, the galaxies are restricted to stellar masses above 1010 M⊙ within a 50 Mpc thick slice around the center of the simulation volume. A lighter color means galaxies more distant than 130 Mpc. For the observation, only galaxies with log(LK) > 10.25 are plotted to match the mass cut. In addition, the positions of Coma, Virgo, and Perseus are labeled. The virial masses of the halos in the simulations are listed in Table 1. From top to bottom: SLOW, SIBELIUS, CORUSCANT, and 2MRS.

Table 1.

Observational properties of Coma, Perseus, and Virgo showing the radial velocity and two estimates of their virial mass Mvir.

3. Simulations

3.1. Magneticum simulations

The Magneticum5 simulations follow for the first time the evolution of up to 1011 particles in a series of hydrodynamics simulations of cosmological volumes ranging in size from (68 Mpc)3 to almost (4 Gpc)3. To evaluate the significance of features in the Local Universe, we use the largest simulation volume, Box0/mr of the Magneticum simulation, set as reference for the general presence of such features within the Lambda-cold dark matter (ΛCDM) cosmological model. This simulation covers a box of 2.688 h−1 GPc in size, resolved with a total of 2 × 45363 dark matter and gas resolution elements, having a mass resolution of 1.3 × 1010 h−1 M⊙ and 2.6 × 109 h−1 M⊙, respectively, and featuring full galaxy formation physics. It is therefore well equipped to reflect galaxy cluster and group properties. Having ≈150 times the volume of the 500 h−1 Mpc box, Box0/mr of the Magneticum simulations allows us to compare a large number of random patches with the constrained part of SLOW to very high statistical significance. The cosmology adopted for these simulations is slightly different than for SLOW as it follows the WMAP7 from Komatsu et al. (2011), with Hubble constant H0 = 70.4 km s−1 Mpc−1, a total matter density of ΩMatter = 0.272, a cosmological constant of ΩΛ = 0.728 and a baryon fraction corresponding to Ωbaryon = 0.0459, as well as an overall normalization of the power spectrum of σ8 = 0.809 and a slope of the primordial fluctuation spectra of n = 0.963. However, these small differences do not play a significant role in the comparisons presented in this study.

3.2. The subgrid model used

The SLOW and the Magneticum simulations both use an updated formulation of SPH (Beck et al. 2016) with modern high-order Kernels (Dehnen & Aly 2012) and include the treatment of the relevant models to describe the physical processes needed for galaxy formation, such as cooling, star formation, and winds. This is based on the multi-phase model (Springel & Hernquist 2003), but is extended to follow in detail the stellar population and chemical enrichment by SN-Ia, SN-II, AGB (Tornatore et al. 2003, 2007); uses metal-dependent cooling tables from Wiersma et al. (2009) and a galactic wind velocity of 350 km s−1 for the kinetic feedback. Other important aspects to follow are the evolution of supermassive black holes and the associated AGN feedback, where we follow for the treatment of the black hole sink particles Springel et al. (2005), with various improvements for the different feedback modes as described in Fabjan et al. (2010), Hirschmann et al. (2014). Importantly for the treatment of the ICM, they include isotropic thermal conduction of 1/20 of the standard Spitzer value (Dolag et al. 2004b) and a low-viscosity scheme to track turbulence (Dolag et al. 2005b; Beck et al. 2016).

It has been intensively demonstrated that this subgrid model leads to galaxy and ICM properties in galaxy clusters that largely follow the observational trends and properties. The Magneticum simulations have been compared to Sunyaev–Zel’dovich (SZ) data from Planck (Planck Collaboration V 2013) and SPT (McDonald et al. 2014). It has been demonstrated that they reproduce the observable X-ray luminosity relation (Biffi et al. 2013), the chemical composition (Dolag et al. 2017; Biffi et al. 2018a) of the ICM, and the high concentration observed in fossil groups (Ragagnin et al. 2019). On larger scales, the Magneticum simulations were shown to reproduce the observed SZ power spectrum (Dolag et al. 2016) as well as the observed thermal history of the Universe (Young et al. 2021) and the gas properties between galaxy clusters (Biffi et al. 2022). On galaxy scales, the simulations lead to an overall successful reproduction of the basic galaxy properties, such as the stellar mass function at low (Naab & Ostriker 2017) and high (Lustig et al. 2023; Remus et al. 2023) redshifts, the environmental impact of galaxy clusters on galaxy properties (Lotz et al. 2019; Lustig et al. 2023), the azimuthal distribution of matter around clusters compared with findings in SDSS (Gouin et al. 2020) and the appearance of post-starburst galaxies (Lotz et al. 2021), and the associated AGN population at various redshifts (Hirschmann et al. 2014; Steinborn et al. 2016; Biffi et al. 2018b).

3.3. SLOW

The large-scale structure of the Universe is effectively described by the (peculiar) velocity and real space distribution of observable galaxies. A Wiener filter (WF) algorithm6 is needed to reconstruct the true underlying cosmography from the noisy and incomplete galaxy data reaped from surveys. The first attempt to construct constrained realizations of Gaussian random fields subject to linear constraints was made by Hoffman & Ribak (1991). In the intervening two decades the technique and the input constraints have been refined; peculiar velocity surveys, in particular distance modulus surveys such as CosmicFlows-2 (CF2, Tully et al. 2013), are particularly useful since the cosmic velocity field is directly related to the matter density field in the linear regime. Wiener Filter reconstructions of CF2 have already been carried out successfully estimating the density field within ∼100 Mpc (e.g., Laniakea, Tully et al. 2014). Sorce (2018) describes in details the steps of the method to build the constrained initial conditions and introduces those used in this paper. The main steps are summarized here.

First, before deriving the peculiar velocities, grouping (Sorce & Tempel 2018) of the distance modulus catalog is performed to remove nonlinear virial motions that would affect the linear reconstruction obtained with the linear method (e.g., Sorce et al. 2017; Sorce & Tempel 2017). Typically, when several distance moduli are available for several galaxies within the same galaxy cluster, they are replaced by the distance modulus of the cluster. Second, the biases (Sorce 2015) inherent to any observational radial peculiar velocity catalog (e.g., Malmquist biases and lognormal error) are minimized. An iterative algorithm permits the retrieval of the Gaussian radial peculiar velocity distribution expected from the theory from a flat distribution with large tails. Additionally, uncertainties are derived for these new peculiar velocities to filter the smoothing effect with the distance (dilution of the information with the distance) of the subsequent algorithms (Sorce et al. 2016a; Sorce 2018). Third, the cosmic displacement field is reconstructed with the WF technique applied to the peculiar velocity constraints. Fourth, the cosmic displacement is accounted for by relocating constraints to the positions of their progenitors using the Reverse Zel’dovich Approximation and the reconstructed cosmic displacement field (Doumler et al. 2013a,b,c), and replacing noisy radial peculiar velocities by their WF 3D reconstructions (Sorce et al. 2014). Fifth, density fields constrained by the modified observational peculiar velocities are combined with a random realization to restore statistically the missing structures using the technique of constrained realization (CR; Hoffman & Ribak 1991, 1992). Finally, the density fields are rescaled to build constrained initial conditions7, where increasing the resolution implies adding random small-scale features.

Here, and for the actual simulations, we assume the standard ΛCDM cosmological model with the Hubble constant H0 = 67.77 km s−1 Mpc−1, a total matter density of ΩMatter = 0.307115, a cosmological constant of ΩΛ = 0.692885, and a baryon fraction corresponding to Ωbaryon = 0.0480217. We also assume an overall normalization of the power spectrum of σ8 = 0.829 and a slope of the primordial fluctuation spectra of n = 0.961 (Planck Collaboration XVI 2014).

3.4. SLOW set of simulations

To create the initial conditions, SLOW uses the CLONE-500 Mpc/h–5123 grid, realization number 8, to which different small-scale features for different resolutions are added with GINNUNGAGAP. Simulations are then performed with different levels of additional physics:

  • Dark matter-only simulations using 7683, 15763, 30723, and 61443 particles;

  • Magneto-hydrodynamic nonradiative simulations, but also following a cosmic ray component (Böss et al. 2023) using 2 × 30723 gas and dark matter particles;

  • Hydrodynamic full galaxy formation physics simulation using 2 × 7683, 2 × 15763, and 2 × 30723 gas and dark matter particles (the last only down to z = 2).

Halos are identified using SUBFIND (Springel et al. 2001; Dolag et al. 2009) which detects halos based on the standard friends-of-friends algorithm (Davis et al. 1985) and subhalos as self-bound regions around local density peaks within the main halos. The center of a halo or subhalo is defined as the position of the particle with the (local) minimum of the gravitational potential. The virial mass Mvir is defined through the spherical overdensity around a halo, as predicted by the generalized top-hat spherical collapse model (Eke et al. 1996) with an overdensity for the chosen cosmology following Bryan & Norman (1998). For subhalos, individual properties are computed based on the particles that are associated with the individual subhalos. To compute the K-band magnitudes in our simulation, which include galaxy formation physics, we used the K-band stellar mass-to-light ratio, as obtained from SDSS (Bell et al. 2003)

(1)

while in the case of dark matter-only simulations, we used the corresponding Tully–Fisher relation based on the maximum circular velocity computed within the subhalos.

4. Qualitative comparison with observations

Within the SLOW simulations, more than 40 local clusters have been cross-identified with their observational counterpart, showing good agreement in global properties (e.g., total mass) as well as profiles of the ICM properties (e.g., pressure and temperature; see Hernández-Martínez et al., in prep. for details). All the results presented in this paper are based on the hydrodynamic full galaxy formation simulation with 2 × 15763 particles. In Fig. 2 we show the distribution of the dark matter within the SLOW simulation as a full-sky map up to a distance of 350 Mpc, color-coded according to the total matter content in each pixel. This shows how the constrained region of the Local Universe (where we labeled a subset of the cross-identified clusters) is embedded in the larger cosmological structures. In Fig. 3 we show a collection of observations. First, we show the distribution of galaxies in the 2MRS catalog. We note that here the observations are limited to more local galaxies as the 2MRS becomes very sparse at distances beyond 100 Mpc. On the other hand, the X-ray and Compton-Y map contain significant foreground and other noncluster related emission. Here the selection of the 1.5 keV (R6 + R7 = 0.76 − 2.04 keV) band for the X-ray surface brightness map, based on the data of the ROSAT All-Sky Survey (RASS, Snowden et al. 1997), maximizes the visibility of the cluster signal. In the Compton-Y map the exclusion of regions with significant CO emission (according to the mask by Khatri 2016) from the Planck data (produced with the MILCA algorithm; Planck Collaboration XXII 2016) reduces the noncluster related foreground. Therefore, it should be kept in mind that both observational tracers contain objects that are outside the distance range of the simulation counterparts (some prominent ones are marked with yellow labels), and even some much more distant objects, even outside the simulation volume, as well as residuals of local galactic foreground features and are limited on the faint end by the observational noise. This can be compared with the according counterparts as derived from the simulation shown in Fig. 4. Here we show the distribution of the stellar component (upper panel), the X-ray surface brightness (middle panel), and the Compton-Y map (lower panel) as obtained from the SLOW simulation. The maps are created from the simulations using SMAC (Dolag et al. 2005a), where for the X-ray map the emissivity for each SPH particle is computed following Bartelmann & Steinmetz (1996). Here we can use a much larger dynamic ranges in the color scaling to emphasize the large angular imprint on the very local galaxy clusters. Again, here we always used the full simulation volume out to the distance of 350 Mpc to produce the counterpart sky maps from the simulations. In addition, we show two special regions (Perseus and Hercules) in more detail in the insets. Therefore we always center on the cross-identified halo of the prominent cluster (e.g., Perseus and A2147) and used a much narrower range around them (e.g., 10 and 40 Mpc, respectively) to emphasize the local structures. The virial masses (in solar masses) are given as labels for the cross-identified halos, while in addition the radial velocity (in km s−1) is given as a distance indicator. A more detailed comparison of the individual cluster properties across multiple wavebands will be released in a series of papers. In Table 1 we give the virial masses for Coma, Virgo, and Perseus as a reference. As can be seen when comparing the full sky maps from the observations and the simulations, uncertainties in the constraints that went into the construction of the initial condition lead to a noticeable shift in the positions (see also Sorce 2018). The largest contributions to this positional discrepancies are the still relatively large uncertainties in the observed distance modules. This becomes even more evident when comparing the insets. For example, in the Hercules region A2147 has a clear match, and A2107 also has a corresponding halo. There is also a halo resembling the A2063/A2052 complex, but this is only a single halo in the simulation and shows also a significant shift (e.g., several degrees on sky). A similar situation arises for the Perseus region. Perseus itself has a quite well matching counterpart; however, a possible counterpart to AWM7 is already significantly displaced. Nevertheless, this comparison across multiple wavebands clearly reveals that the appearance of clusters can look significantly different across the different wavebands and demonstrates the need of full hydrodynamics simulations for such a comparison, as the apparent significance of structures often largely differs when comparing galaxy and ICM properties. Even so, overall clear similarities in the large-scale structure and the appearance of galaxy clusters are visible across the different wavebands when comparing the SLOW simulations with the observations, confirming the Sorce (2018) and Sorce et al. (2023) assertions.

thumbnail Fig. 2.

Full-sky map of the projected dark matter distribution from SLOW up to a distance of 350 Mpc. To distinguish the constrained part of the Local Universe simulation, some of the cross-identified clusters in the Local Universe are indicated.

thumbnail Fig. 3.

Observations in different wavebands. From top to bottom: distribution of galaxies in the 2MRS catalog, X-ray surface brightness in the ROSAT 1.5 keV band (R6 + R7 = 0.76 − 2.04 keV), and Compton-Y map based on Planck data (produced with the MILCA algorithm Planck Collaboration XXII 2016) with the CO mask by Khatri (2016). The insets show zoomed-in images of the Perseus and Hercules regions. The labels in the insets give the Name together with radial velocity (in km s−1) as redshift distance indicator. The yellow labels indicate clusters that are outside the slice used in the simulations shown in Fig. 4.

thumbnail Fig. 4.

SLOW in different wavebands. From top to bottom: distribution of stellar mass in SLOW, X-ray surface brightness, and Compton-Y. A much larger dynamic range than in the observations shown on Fig. 3 are used here for the color scaling to emphasize the large angular imprint on the very local galaxy clusters. The full simulation volume out to a distance of 350 Mpc is always shown. The insets show zoomed-in images of the Perseus and Hercules regions. Here a much narrower range around Perseus and A2147 is used (respectively 10 and 40 Mpc thick) to emphasize the local structures. The labels in the insets give the virial mass (in M⊙) of the halos, together with radial velocity (in km s−1) as redshift distance indicator.

5. Mean density for Halos in SLOW

There are various density anomalies reported in the Local Universe, ranging from the Council of Giants (McCall 2014), the local void (Tully & Fisher 1987), close structures, a local deficit of galaxy clusters (Böhringer et al. 2020), and an overabundance of very massive galaxy clusters like Norma, Perseus, Coma, Ophiuchus, and A2199 or A119. As SLOW is a constrained simulation, based on peculiar velocity observations, we can investigate how these structures are present in the predicted density field. Given the large volume of (500 h−1 Mpc)3 covered by the simulation, we can investigate the full range of observed anomalies, given the resolution it is now possible to reach for such volumes. Having a full galaxy formation physics run also allows us to distinguish between the dark matter density field, halos, and galaxies, including observational properties like stellar mass for galaxies and properties of the intracluster medium (ICM) within galaxy clusters (e.g., their temperature and X-ray luminosity).

Figure 5 shows the cumulative number density within spheres with growing radius centered on the position of the MW. Here the left panel uses the distribution of halos with different lower limits in their virial mass as indicated by the legend, while the right panel uses the galaxies (e.g., subhalos) with different lower limits in stellar mass. In both cases the spacing of the lines corresponds to a change in the mass threshold of Δlog10(M) = 0.05. The solid black line is obtained directly from the dark matter particles within the simulation.

thumbnail Fig. 5.

Cumulative relative number density of halos (left) and number density of galaxies (right) as a function of distance from the MW position, obtained from the SLOW simulation. The different colors are lines obtained for different lower mass cuts, as indicated in the color bars: virial masses of the halos (left) and stellar masses of the galaxies (right). The black line in each panel is the same when directly using dark matter distribution.

Several features are immediately visible. Starting with a quite empty region within the very close vicinity around the MW position8, there are several relatively massive galaxies at a distance of 5 Mpc, which build the equivalent of the Council of Giants, which are observed at ≈3.75 Mpc (McCall 2014). After that, the local void is clearly visible and fills the space until the Virgo galaxy cluster at ≈16 Mpc and the associated supercluster (the Virgo supercluster) comes into place. Then, between ≈30 and 140 Mpc, a clear underdensity is present in all tracers, except the very massive galaxies and massive galaxy clusters, which is in agreement with our findings based on the halo mass functions as presented in Sorce et al. (2016a). The high start of the blue upper lines reflects the fact that we have a very massive cluster like Virgo very close. We note that a typical mean separation of clusters with a virial mass of 1015 M⊙ is ≈180 Mpc. These lines stay high as we approach other very massive clusters (among them Perseus and Coma) well before the distance reflecting the mean density of such systems. The main obstacle in relating the density of tracers to the underlying dark matter distribution depends on the physics of gravitational clustering and the more complex physics of galaxy formation and is often referred generically as “bias” (see, e.g., Weinberg et al. 2004, and references therein). It is interesting to note that the bias between the tracer population and the dark matter for the galaxy population in the normal mass-range shows the expected regular behavior with only a mild dependence on actual mass. In contrast, the bias using halos shows a strong mass dependence and also large fluctuations in relative amplitude when comparing halos to the dark matter distribution. It is equally interesting to note that the factor of 2 overdensity associated with the Virgo supercluster structure as seen in dark matter only shows up in galaxies, and only if galaxies down to stellar masses of at least 1011 M⊙ are used, and does not show up in the halo number density distribution at all. This means that in this case, the halo of the Virgo clusters seems generally quite isolated, and therefore the halo itself traces the general overdensity, but not the associated structures in the environment. At the very high-mass end the galaxies and halos align, which just reflects that the central very massive galaxies are strictly related to massive galaxy clusters and their halo, marking the point where galaxies of a certain mass can no longer be formed by internal processes, but mainly grow by mostly dry mergers.

6. Comparison to observations

As discussed in the previous section, the different features in the Local Universe can be compared more directly to observations to understand better how unique our Local Universe is. Figure 6 shows the comparison to different observational tracers as discussed in the following subsections in detail.

thumbnail Fig. 6.

Cumulative relative density of halos and galaxies of different masses as a function of distance (computed from redshift) compared to different observations. Top panel: comparison of galaxy clusters to the X-ray sample from Böhringer et al. (2021), using the same mass cut (solid) and the same X-ray luminosity cut (dashed line). Middle panel: comparison of massive galaxy clusters (Mvir > ;1015 blue line, T500c > ;5 keV red line) to the five closest clusters exceeding this mass or temperature from the Tully catalog (Tully 2015) or the BAX database Sadat et al. (2004), respectively. Bottom panel: comparison of our simulated galaxies with the results on the stellar mass density presented in Karachentsev & Telikova (2018). In the upper two panels, the gray shaded regions indicate the 1, 2, and 3σ lines obtained from the Magneticum simulation and the black line indicates the median (to display the cosmic variance left).

6.1. X-ray cluster sample

The upper panel of Fig. 6 compares the results from the SLOW simulation to the findings by Böhringer et al. (2020), who reported a 50% underdensity of X-ray selected galaxy cluster from the CLASSIX catalog (shown as blue data points). The luminosity cut of 1042 erg s−1 in the (0.1−2.4) keV band translates into a virial mass of ≈1013.4 M⊙ when using a canonical X-ray luminosity-mass relation (Böhringer et al. 2014). The blue solid line resembles the result from the SLOW simulation for halos with this mass threshold, nicely reproducing the data points. However, having a full hydrodynamics simulation we can also directly use the predicted X-ray luminosity of the clusters in the simulations. Here, we started from the predicted bolometric luminosity within R500c and applied the correction for the used energy band based on the mass weighted T500c of the cluster. When applying the X-ray luminosity cut to the simulated clusters, we get the dashed line, which is very close to the one where we used the virial mass cut to select the clusters. This shows that the observed signal in the simulation, and therefore also the signal in the real data, is not driven by the X-ray selection of galaxy clusters.

Given this signal, it is interesting to investigate how peculiar it is to have a local environment that features such a 50% underdensity within the given volume. Therefore, we took the very large, general cosmological simulation from the Magneticum simulations set, namely Box0/mr, which covers a volume of (2688 h−1 Mpc)3. Here we randomly selected more than 15 000 points within the volume, and computed the cumulative overdensity profiles out to 360 Mpc radius. The gray shaded regions mark the one-, two-, and three-sigma regions occupied by these profiles from a random cosmological simulation. The black solid line is the median of the distribution to indicate the statistical error left due to the still somewhat limited sample size from the large simulation. We clearly see that the underdensity we live in is not very uncommon in the cosmological sense, representing a ≈1.5σ event, similar to what Sorce et al. (2016a) concluded from comparing the halo mass function.

6.2. Massive galaxy clusters

Although we are living in a large-scale underdense region, there are several very massive galaxy clusters within that region that exceed virial masses of 1015 M⊙, among them Coma, Perseus, and Ophiuchus. Using the five closest galaxy clusters from the Tully galaxy groups catalog (Tully 2015) with masses above 1015 M⊙, the middle part of Fig. 6 shows that this corresponds to a very large overdensity in the Local Universe (blue diamonds). We also selected the five closest galaxy clusters from the BAX9 database with X-ray measured temperatures exceeding 5 keV and showing (red triangles), basically confirming the presence of an overdensity of high-mass systems. Selecting such clusters predicted by the SLOW simulation (blue line for the mass selection, red line for the temperature selection) again follows the observational data points extremely well, confirming this significant overdensity of massive clusters, as was already clearly visible in Fig. 5. We note that there is a large overlap between the selected clusters when switching the selection criteria in observations (4/5) and in simulations (3/5). We note that the closest cluster in the simulation exceeding 1015 M⊙ is at a distance of ≈40 Mpc (as can be seen in Fig. 5). Furthermore, many of these prominent, massive, and/or hot clusters can be cross-identified between the simulations and observations, among them Perseus, Coma, A119, and A85; they even show very similar virial masses and temperatures (see Sorce 2018; Sorce et al. 2023, and for more details Hernández-Martínez et al., in prep.). Only Norma and Ophiuchus are not very well reproduced in the simulations, due to their position in or close to the zone of avoidance, because no data are available. Nevertheless, there is a significant overlap between the two sets of most massive and/or hot clusters in simulations and observations. Therefore, we expect similar properties of the clusters in the two sets, as was already shown for example for the Virgo cluster (Sorce et al. 2021).

Again we investigate the statistical significance of this excess of massive systems. Here the gray shaded regions again indicate the one-, two-, and three-sigma regions, as obtained from the large cosmological simulation Box0/mr from the Magneticum set. The comparison indicates that this excess in massive system is approximately a 1.5σ coincidence. The black line marks the median from the 15 635 samples we used and gives an indication of the remaining statistical uncertainty, which in this case is somewhat larger due to the general low number density of such massive galaxy clusters.

One might speculate that the general underdensity of clusters might be related to the overdensity of massive systems; however, a closer investigation based on Box0/mr indicates the opposite. In fact, when requiring a very conservative limit to have at 90 Mpc a mean density below 0.65 for clusters with viral masses of ≈1013.4 M⊙ and having an overdensity of massive systems of 2.3 at 160 Mpc (corresponding to the observational value of the closest system), we find that only 44 out of the 15635 samples match. This corresponds to a more than 3σ case. In addition, it clearly demonstrates that these two peculiarities of the Local Universe are not related.

It is worth noting that in addition, at distances in the range ≈(240 − 330) Mpc, the simulation predicts a ∼(20 − 30)% overdensity of massive galaxy clusters, as visible in the middle panel of Fig. 6 and in the left panel of Fig. 5. At these distances, which are beyond the radial distance for which peculiar velocities are mainly constrained, some of the very massive galaxy clusters can be cross-matched between simulations and observations, among them A3266 for example, which is also labeled in Figs. 3 and 4.

6.3. Galaxies

Finally we can also compare the density fields traced with galaxies as this might be closer to the actual underlying distribution of dark matter, as shown in the previous section. In the lower panel of Fig. 6 we compare the stellar mass in all simulated galaxies in SLOW (solid blue line) with the observed stellar density, as reported in Karachentsev & Telikova (2018). Here the red band corresponds to the overall mean stellar density reported in Karachentsev & Telikova (2018), normalized to the global stellar density of Ω* = 0.0027 (Fukugita & Peebles 2004) or to the value at the largest distance. The orange and dark orange bands correspond respectively to the observed stellar density for the northern and southern hemispheres (Karachentsev & Telikova 2018), normalized to these two general values. In addition, the blue dashed line marks the relative mean number density of galaxies with M* > ;1010 M⊙, while the gray line is the relative dark matter density. Comparing to the expectations from the SLOW simulation in both cases matched quite well the large overdensity feature of a factor of ≈2 of the local structures associated with the Virgo cluster at distances around ≈16 Mpc. It also shows a very similar shape farther out with two minima and two maxima, although the first underdensity in the simulation appears at a distance of ≈40 Mpc, while in the observations the minimum in the relative density is at ≈55 Mpc. As seen in comparison with the dark matter density, these features are clearly directly related to the underlying dark matter density field. Closer than the distance to Virgo, the simulations show a very prominent large underdensity of the local void (already visible in Fig. 5); however, the stellar density reported in Karachentsev & Telikova (2018) features a larger, local density. Interestingly, SLOW predicts a global stellar density of Ω* = 0.0031, which is close to the value of Ω* = 0.0027, as reported in Fukugita & Peebles (2004). In general, the good match of the gray line for the dark matter density in the bottom panel with the observed and with the simulated stellar density at distances beyond ≈20 Mpc indicates that the observed stellar densities obtained from galaxies quite robustly trace the underlying dark matter field, which is not the case when using galaxy clusters as tracers, as shown in the previous subsections.

6.4. Anisotropies

As mentioned in the Introduction, the local structures also lead to observed nonisotropic distribution of tracers of the large-scale structures. Here we want to compare the results from SLOW with two of these reported features. In Fig. 7 we compare the distribution of galaxy clusters in the simulations to the pancake-like structure out to a scale of ≈100 Mpc, as reported in Böhringer et al. (2021). We follow the characterization of the flattened superstructure in the observations. Starting from a cylinder with 100 Mpc radius, centered at the MW position and oriented along the supergalactic SGY direction, we compute the overdensity within slices of thickness ±w1/2 Mpc and compare this with the mean density of the same objects within a sphere of 100 Mpc radius, centered on the MW. To mimic the observational selection of clusters we selected clusters either by their X-ray luminosity (e.g., 1042 erg s−1 as in the observations) or by the corresponding virial mass (e.g., Mvir = 1013.4 M⊙) as shown by the blue and black solid line, respectively. This qualitatively agrees well with the observational data points (blue symbols with error bars), which are also shown. In addition, the blue dashed and dash-dotted lines show the dependence on the luminosity threshold used, indicating that choosing a slightly higher luminosity would further increase the agreement with the observational data. To strengthen this result, the red dashed and dash-dotted lines show the absence (or even reverse signal) obtained when doing the split along the supergalactic SGZ and SGX coordinate, respectively. We can conclude here, that the pancake-like structure is a solid prediction by SLOW and aligns well qualitatively with the observational finding without fine-tuning selection parameters.

thumbnail Fig. 7.

Comparison of the flattening of the galaxy cluster distribution to the X-ray sample from Böhringer et al. (2021, see text for description) and to the simulation using the same mass (black) and the same X-ray luminosity (blue solid line) cut. The dashed and the dash-dotted red lines apply the same measurement in the other supergalactic coordinates for comparison. The dashed and dash-dotted blue lines are slightly different cuts in X-ray luminosity.

In Fig. 8 we repeat the comparison of the stellar density within the Local Universe with the finding of Karachentsev & Telikova (2018), where a large difference between the northern and southern Galactic hemisphere was reported. Splitting our galaxies from SLOW in the same way (red and blue solid lines), the SLOW simulation shows some features very similar to the observations (red and blue bands). Clearly, there is an overdensity (underdensity) present in the northern (southern) hemisphere at large distances. This qualitatively agrees with observations, although here the quantitative agreement is not as good as for the pancake-like structure traced by galaxy clusters. Here too we add a split along the supergalactic x and z coordinates (dashed and dash-dotted lines) to show the dependence of the signal onto the directional split. As seen before, the lower stellar density within SLOW out to a distance of ≈15 Mpc is present and independent of the direction. Interestingly, the split along the supergalactic x coordinate follows the observations even better and may indicate that the positional uncertainty of some prominent structure in the simulated Local Universe might influence the actual selection and might be worth further studies.

thumbnail Fig. 8.

Comparison of our simulated galaxies with the results of the stellar mass density presented in Karachentsev & Telikova (2018) divided in the northern Galactic hemisphere (blue) and southern Galactic hemisphere (red). As comparison, the thinner red dashed and dash-dotted line show the results when splitting along supergalactic SGX and SGZ coordinates.

7. Conclusions

We presented the first results from a long-standing initiative to perform hydrodynamic cosmological simulations of the Local Universe (a) with high enough resolution and detailed enough galaxy formation physics to reproduce reliable galaxies and intracluster medium properties; (b) that extends to large distances to properly cover the transition of the local structures toward the cosmological average properties; and (c) that are not constructed on total density estimates based on galaxy densities in redshift surveys. The last makes the comparisons with the observed galaxy distribution and galaxy clusters properties independent from observations, which were already used to construct the constraints for the initial condition, and also allows us to better compare their evolution. Initial conditions of our SLOW simulation are based on peculiar velocities (more precisely, a complex interplay and combination of observed redshift and distance modulus from the CosmicFlows-2 catalog), applying various improvements in their creation over the last years (Sorce & Tempel 2018; Sorce 2020) leading to a simulation that captures a volume of (500 h−1 Mpc)3 in which various clusters of the Local Universe can be cross-identified (see Sorce 2018; Hernández-Martínez et al., in prep. for details).

The predicted density field of the simulation shows various distinct features and indicates that the Local Universe transits into the cosmic mean at a distance of ≈200 Mpc (with significant variances depending on the tracers used). Within this region several ranges with relative under- and overdensity are present that can be compared to observational indications. In particular, we find that the following:

  1. Up to the distance of Virgo cluster (i.e., ≈16 Mpc), the SLOW simulation predicts the mean dark matter density in the Local Universe to be at ≈0.5 of the mean value. With the Virgo supercluster this transits into a factor of two overdensity region until ≈30 Mpc, after which the Local Universe seems to be ≈20% underdense out to ≈200 Mpc.

  2. While this is traced by normal galaxies within the simulation with an expected bias on the order of 30%, using halos or galaxy clusters can result in quite different, sometimes even opposite conclusions, depending on the halo mass cut.

  3. Applying the same mass cut (or alternatively X-ray luminosity cut) as in the CLASSIX galaxy cluster sample, the simulation very closely reproduces the observed 50% underdensity of galaxy clusters in the Local Universe.

  4. Using clusters with virial masses above 1015 M⊙, simulations and observations consistently show a significant overdensity of such objects within the same volume out to ≈200 Mpc within the Local Universe. In addition, at distances in the range ≈(240 − 330) Mpc, the simulation predicts a ≈(20 − 30)% overdensity of such massive galaxy clusters.

  5. Using a comparison with hydrodynamics simulations of very large cosmological volumes, we find that these two features individually are not so uncommon, and correspond to ≈18% of cases (e.g., they fall into the ≈1.5σ region). However, they appear to be unrelated to each other and the combination is only found in ≈0.28% of random selections from our (4 Gpc)3 reference simulation Box0/mr of the Magneticum simulation set, and therefore would correspond to a 3σ case.

  6. The SLOW simulation also shows the pancake-like distribution of galaxy clusters within 100 Mpc of the Local Universe (Böhringer et al. 2021). Thus, the radial distribution of the number counts of galaxy clusters follows quite closely the observations when splitting in supergalactic north–south direction.

  7. The SLOW simulation predicts a global stellar density of Ω* = 0.0031, which is close to the value of Ω* = 0.0027 reported in Fukugita & Peebles (2004). At distances larger than ≈15 Mpc the stellar density obtained from the SLOW simulation follows the value reported in Karachentsev & Telikova (2018) remarkably well, and confirms both the large relative overdensity induced by Virgo and the ≈20% underdensity beyond distances of 100 Mpc.

  8. At distances between ≈15 and 100 Mpc, the predicted stellar density in the SLOW simulation also shows a qualitatively similar difference between the northern and southern Galactic hemisphere to that reported in Karachentsev & Telikova (2018).

The presented SLOW simulation of the Local Universe reproduces some of the main features of the local density field, and therefore opens a new window for local field cosmology. It allows us to better verify and interpret observations of the local structures and their tracers. In the future this will allow us to evaluate in detail the imprint of the specific density field of the Local Universe on the local estimations of cosmological parameters such as H0 and to perform detailed studies of the imprint of the formation history on actual properties of galaxy clusters.

6

Linear minimum variance estimator, in abridged form WF (Zaroubi et al. 1995, 1999).

8

Here we defined the position of the MW in this realization, so that the Virgo cluster is exactly at the correct position.

9

http://bax.irap.omp.eu and references therein.

Acknowledgments

We want to thank T. Hoffmann for the help when extracting observational data points from the according publication and McAlpine for providing the mean dark matter density profile of the Sibelius simulation, which we added to complete the figures in the appendix. This work was supported by the grant agreements ANR-21-CE31-0019/490702358 from the French Agence Nationale de la Recherche/DFG for the LOCALIZATION project. N.A. acknowledges support from the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2015-AdG 695561. K.D. and M.V. acknowledge support by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311 and funding for the COMPLEX project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2019-AdG 882679. M.V. also acknowledges support from the Alexander von Humboldt Stiftung and the Carl Friedrich von Siemens Stiftung. The calculations for the hydrodynamics simulations were carried out at the Leibniz Supercomputer Center (LRZ) under the project pr83li (Magneticum) and pn68na (SLOW). We are especially grateful for the support by M. Petkova through the Computational Center for Particle and Astrophysics (C2PAP).

References

  1. Bartelmann, M., & Steinmetz, M. 1996, MNRAS, 283, 431 [NASA ADS] [Google Scholar]
  2. Beck, A. M., Murante, G., Arth, A., et al. 2016, MNRAS, 455, 2110 [Google Scholar]
  3. Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [Google Scholar]
  4. Benítez-Llambay, A., Navarro, J. F., Abadi, M. G., et al. 2015, MNRAS, 450, 4207 [CrossRef] [Google Scholar]
  5. Biffi, V., Dolag, K., & Böhringer, H. 2013, MNRAS, 428, 1395 [Google Scholar]
  6. Biffi, V., Mernier, F., & Medvedev, P. 2018a, Space Sci. Rev., 214, 123 [NASA ADS] [CrossRef] [Google Scholar]
  7. Biffi, V., Dolag, K., & Merloni, A. 2018b, MNRAS, 481, 2213 [Google Scholar]
  8. Biffi, V., Dolag, K., Reiprich, T. H., et al. 2022, A&A, 661, A17 [Google Scholar]
  9. Böhringer, H., & Chon, G. 2021, A&A, 656, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Böhringer, H., Voges, W., Fabian, A. C., Edge, A. C., & Neumann, D. M. 1993, MNRAS, 264, L25 [NASA ADS] [CrossRef] [Google Scholar]
  11. Böhringer, H., Chon, G., & Collins, C. A. 2014, A&A, 570, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Böhringer, H., Chon, G., & Collins, C. A. 2020, A&A, 633, A19 [EDP Sciences] [Google Scholar]
  13. Böhringer, H., Chon, G., & Trümper, J. 2021, A&A, 651, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Böss, L. M., Steinwandel, U. P., Dolag, K., & Lesch, H. 2023, MNRAS, 519, 548 [Google Scholar]
  15. Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
  16. Courtois, H. M., Hoffman, Y., Tully, R. B., & Gottlöber, S. 2012, ApJ, 744, 43 [NASA ADS] [CrossRef] [Google Scholar]
  17. Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [Google Scholar]
  18. Dehnen, W., & Aly, H. 2012, MNRAS, 425, 1068 [NASA ADS] [CrossRef] [Google Scholar]
  19. de Vaucouleurs, G. 1953, AJ, 58, 30 [Google Scholar]
  20. Dixon, K. L., Iliev, I. T., Gottlöber, S., et al. 2018, MNRAS, 477, 867 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2004a, Sov. J. Exp. Theor. Phys. Lett., 79, 583 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dolag, K., Jubelgas, M., Springel, V., Borgani, S., & Rasia, E. 2004b, ApJ, 606, L97 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dolag, K., Hansen, F. K., Roncarelli, M., & Moscardini, L. 2005a, MNRAS, 363, 29 [Google Scholar]
  24. Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005b, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]
  25. Dolag, K., Borgani, S., Murante, G., & Springel, V. 2009, MNRAS, 399, 497 [Google Scholar]
  26. Dolag, K., Komatsu, E., & Sunyaev, R. 2016, MNRAS, 463, 1797 [Google Scholar]
  27. Dolag, K., Mevius, E., & Remus, R.-S. 2017, Galaxies, 5, 35 [NASA ADS] [CrossRef] [Google Scholar]
  28. Doumler, T., Hoffman, Y., Courtois, H., & Gottlöber, S. 2013a, MNRAS, 430, 888 [NASA ADS] [CrossRef] [Google Scholar]
  29. Doumler, T., Courtois, H., Gottlöber, S., & Hoffman, Y. 2013b, MNRAS, 430, 902 [NASA ADS] [CrossRef] [Google Scholar]
  30. Doumler, T., Gottlöber, S., Hoffman, Y., & Courtois, H. 2013c, MNRAS, 430, 912 [NASA ADS] [CrossRef] [Google Scholar]
  31. Einasto, J., & Miller, R. H. 1983, in Early Evolution of the Universe and its Present Structure, eds. G. O. Abell, & G. Chincarini, 104, 405 [NASA ADS] [CrossRef] [Google Scholar]
  32. Einasto, M., Einasto, J., Tago, E., Dalton, G. B., & Andernach, H. 1994, MNRAS, 269, 301 [Google Scholar]
  33. Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [CrossRef] [Google Scholar]
  34. Fabian, A. C., Hu, E. M., Cowie, L. L., & Grindlay, J. 1981, ApJ, 248, 47 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fabjan, D., Borgani, S., Tornatore, L., et al. 2010, MNRAS, 401, 1670 [Google Scholar]
  36. Fattahi, A., Navarro, J. F., Sawala, T., et al. 2016, MNRAS, 457, 844 [NASA ADS] [CrossRef] [Google Scholar]
  37. Flin, P. 1986, Acta Cosmol., 14, 7 [NASA ADS] [Google Scholar]
  38. Freedman, W. L. 2021, ApJ, 919, 16 [NASA ADS] [CrossRef] [Google Scholar]
  39. Fukugita, M., & Peebles, P. J. E. 2004, ApJ, 616, 643 [Google Scholar]
  40. Gottlöber, S., Hoffman, Y., & Yepes, G. 2010, arXiv e-prints [arXiv:1005.2687] [Google Scholar]
  41. Gouin, C., Aghanim, N., Bonjean, V., & Douspis, M. 2020, A&A, 635, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Hirschmann, M., Dolag, K., Saro, A., et al. 2014, MNRAS, 442, 2304 [Google Scholar]
  43. Hoffman, Y., & Ribak, E. 1991, ApJ, 380, L5 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hoffman, Y., & Ribak, E. 1992, ApJ, 384, 448 [NASA ADS] [CrossRef] [Google Scholar]
  45. Jasche, J., & Lavaux, G. 2019, A&A, 625, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Karachentsev, I. D., & Telikova, K. N. 2018, Astron. Nachr., 339, 615 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kawahara, H., Suto, Y., Kitayama, T., et al. 2007, ApJ, 659, 257 [NASA ADS] [CrossRef] [Google Scholar]
  48. Khatri, R. 2016, A&A, 592, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Kitaura, F.-S., Erdoǧdu, P., Nuza, S. E., et al. 2012, MNRAS, 427, L35 [NASA ADS] [Google Scholar]
  50. Klypin, A., Hoffman, Y., Kravtsov, A. V., & Gottlöber, S. 2003, ApJ, 596, 19 [NASA ADS] [CrossRef] [Google Scholar]
  51. Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [Google Scholar]
  52. Kravtsov, A. V., Klypin, A., & Hoffman, Y. 2002, ApJ, 571, 563 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lahav, O., Santiago, B. X., Webster, A. M., et al. 2000, MNRAS, 312, 166 [NASA ADS] [CrossRef] [Google Scholar]
  54. Libeskind, N. I., Carlesi, E., Grand, R. J. J., et al. 2020, MNRAS, 498, 2968 [NASA ADS] [CrossRef] [Google Scholar]
  55. Lotz, M., Remus, R.-S., Dolag, K., Biviano, A., & Burkert, A. 2019, MNRAS, 488, 5370 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lotz, M., Dolag, K., Remus, R.-S., & Burkert, A. 2021, MNRAS, 506, 4516 [NASA ADS] [CrossRef] [Google Scholar]
  57. Lustig, P., Strazzullo, V., Remus, R.-S., et al. 2023, MNRAS, 518, 5953 [Google Scholar]
  58. Makarov, D., & Karachentsev, I. 2011, MNRAS, 412, 2498 [NASA ADS] [CrossRef] [Google Scholar]
  59. Malavasi, N., Aghanim, N., Tanimura, H., Bonjean, V., & Douspis, M. 2020, A&A, 634, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Malavasi, N., Sorce, J. G., Dolag, K., & Aghanim, N. 2023, A&A, 675, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Mathis, H., Lemson, G., Springel, V., et al. 2002, MNRAS, 333, 739 [NASA ADS] [CrossRef] [Google Scholar]
  62. McAlpine, S., Helly, J. C., Schaller, M., et al. 2022, MNRAS, 512, 5823 [CrossRef] [Google Scholar]
  63. McCall, M. L. 2014, MNRAS, 440, 405 [NASA ADS] [CrossRef] [Google Scholar]
  64. McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2014, ApJ, 794, 67 [Google Scholar]
  65. Naab, T., & Ostriker, J. P. 2017, ARA&A, 55, 59 [Google Scholar]
  66. Ocvirk, P., Aubert, D., Sorce, J. G., et al. 2020, MNRAS, 496, 4087 [NASA ADS] [CrossRef] [Google Scholar]
  67. Olchanski, M., & Sorce, J. G. 2018, A&A, 614, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Peebles, P. J. E. 2022, MNRAS, 511, 5093 [NASA ADS] [CrossRef] [Google Scholar]
  69. Planck Collaboration V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Planck Collaboration X. 2013, A&A, 554, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Planck Collaboration XL. 2016, A&A, 596, A101 [EDP Sciences] [Google Scholar]
  74. Ragagnin, A., Dolag, K., Moscardini, L., Biviano, A., & D’Onofrio, M. 2019, MNRAS, 486, 4001 [Google Scholar]
  75. Ragagnin, A., Saro, A., Singh, P., & Dolag, K. 2021, MNRAS, 500, 5056 [Google Scholar]
  76. Remus, R.-S., Dolag, K., & Dannerbauer, H. 2023, ApJ, 950, 191 [NASA ADS] [CrossRef] [Google Scholar]
  77. Rubin, V. C. 1989, in World of Galaxies (Le Monde des Galaxies), eds. J. Corwin, G. Harold, & L. Bottinelli, 431 [CrossRef] [Google Scholar]
  78. Sadat, R., Blanchard, A., Kneib, J. P., et al. 2004, A&A, 424, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Sawala, T., McAlpine, S., Jasche, J., et al. 2022, MNRAS, 509, 1432 [Google Scholar]
  80. Snowden, S. L., Egger, R., Freyberg, M. J., et al. 1997, ApJ, 485, 125 [Google Scholar]
  81. Sorce, J. G. 2015, MNRAS, 450, 2644 [CrossRef] [Google Scholar]
  82. Sorce, J. G. 2018, MNRAS, 478, 5199 [NASA ADS] [CrossRef] [Google Scholar]
  83. Sorce, J. G. 2020, MNRAS, 495, 4463 [CrossRef] [Google Scholar]
  84. Sorce, J. G., & Tempel, E. 2017, MNRAS, 469, 2859 [NASA ADS] [CrossRef] [Google Scholar]
  85. Sorce, J. G., & Tempel, E. 2018, MNRAS, 476, 4362 [NASA ADS] [CrossRef] [Google Scholar]
  86. Sorce, J. G., Courtois, H. M., Gottlöber, S., Hoffman, Y., & Tully, R. B. 2014, MNRAS, 437, 3586 [CrossRef] [Google Scholar]
  87. Sorce, J. G., Gottlöber, S., Yepes, G., et al. 2016a, MNRAS, 455, 2078 [NASA ADS] [CrossRef] [Google Scholar]
  88. Sorce, J. G., Gottlöber, S., Hoffman, Y., & Yepes, G. 2016b, MNRAS, 460, 2015 [NASA ADS] [CrossRef] [Google Scholar]
  89. Sorce, J. G., Hoffman, Y., & Gottlöber, S. 2017, MNRAS, 468, 1812 [NASA ADS] [CrossRef] [Google Scholar]
  90. Sorce, J. G., Gottlöber, S., & Yepes, G. 2020, MNRAS, 496, 5139 [NASA ADS] [CrossRef] [Google Scholar]
  91. Sorce, J. G., Dubois, Y., Blaizot, J., et al. 2021, MNRAS, 504, 2998 [NASA ADS] [CrossRef] [Google Scholar]
  92. Sorce, J. G., Ocvirk, P., Aubert, D., et al. 2022, MNRAS, 515, 2970 [NASA ADS] [CrossRef] [Google Scholar]
  93. Sorce, J. G., Mohayaee, R., Aghanim, N., Dolag, K., & Malavasi, N. 2023, MNRAS, submitted [arXiv:2301.01305] [Google Scholar]
  94. Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
  95. Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
  96. Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [Google Scholar]
  97. Steinborn, L. K., Dolag, K., Comerford, J. M., et al. 2016, MNRAS, 458, 1013 [Google Scholar]
  98. Tornatore, L., Borgani, S., Springel, V., et al. 2003, MNRAS, 342, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  99. Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007, MNRAS, 382, 1050 [Google Scholar]
  100. Tully, R. B. 2015, AJ, 149, 171 [NASA ADS] [CrossRef] [Google Scholar]
  101. Tully, R. B., & Fisher, J. R. 1987, Atlas of Nearby Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
  102. Tully, R. B., Shaya, E. J., Karachentsev, I. D., et al. 2008, ApJ, 676, 184 [Google Scholar]
  103. Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
  104. Tully, R. B., Courtois, H., Hoffman, Y., & Pomarède, D. 2014, Nature, 513, 71 [Google Scholar]
  105. Tully, R. B., Courtois, H. M., & Sorce, J. G. 2016, AJ, 152, 50 [Google Scholar]
  106. Tully, R. B., Kourkchi, E., Courtois, H. M., et al. 2023, ApJ, 944, 94 [NASA ADS] [CrossRef] [Google Scholar]
  107. Wang, H., Mo, H. J., Yang, X., et al. 2016, ApJ, 831, 164 [Google Scholar]
  108. Weinberg, D. H., Davé, R., Katz, N., & Hernquist, L. 2004, ApJ, 601, 1 [Google Scholar]
  109. Wiersma, R. P. C., Schaye, J., Theuns, T., Dalla Vecchia, C., & Tornatore, L. 2009, MNRAS, 399, 574 [NASA ADS] [CrossRef] [Google Scholar]
  110. Wojtak, R., Knebe, A., Watson, W. A., et al. 2014, MNRAS, 438, 1805 [CrossRef] [Google Scholar]
  111. Yepes, G., Martínez-Vaquero, L. A., Gottlöber, S., & Hoffman, Y. 2009, in 5th International Workshop on the Dark Side of the Universe, eds. C. Balazs, & F. Wang, AIP Conf. Ser., 1178, 64 [CrossRef] [Google Scholar]
  112. Young, S., Komatsu, E., & Dolag, K. 2021, Phys. Rev. D, 104, 083538 [NASA ADS] [CrossRef] [Google Scholar]
  113. Zaroubi, S., Hoffman, Y., Fisher, K. B., & Lahav, O. 1995, ApJ, 449, 446 [Google Scholar]
  114. Zaroubi, S., Hoffman, Y., & Dekel, A. 1999, ApJ, 520, 413 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Comparison to other simulations

Here we present some comparisons with other previous or more recent constrained simulations, such as CORUSCANT (Dolag et al. 2004a) and its SALACIOUS variant (Kawahara et al. 2007), which includes galaxy formation physics; the early CLUES (Klypin et al. 2003) simulation (labeled B160_WM3); and the SIBELIUS (McAlpine et al. 2022) simulation.

A.1. Dark matter distribution

Similarly to figure 5, figure A.1 shows the dark matter density in the Local Universe, but compares different simulation: SLOW, CORUSCANT, B160_WM3, and SIBELIUS. For SIBELIUS the dark matter data are not publicly available; however, the dark matter profiles were provided by McAlpine on our request. All simulations show the overdensity related to the Virgo complex, but SIBELIUS shows only a very mild signal. On the other hand, SIBELIUS shows a significant underdensity at scales of 30-60 Mpc, while only SLOW shows the large-scale underdensity toward a distance of 100 Mpc. For B160_WM3 and CORUSCANT this is mainly because these simulations cover a too small volume, while there is a very tiny underdensity visible in SIBELIUS. However, B160_WM3 shows a significant overdensity within a spherical region of 100 Mpc radius. Interestingly, both SLOW and B160_WM3 show a clear local underdensity in dark matter within 10 Mpc, while CORUSCANT shows a larger overdensity in this region.

thumbnail Fig. A.1.

Cumulative relative dark matter density as a function of distance from the MW position. Shown are the values obtained from the simulations: SLOW (black), CORUSCANT (blue), early CLUES (red), and SIBELIUS (orange).

A.2. Galaxy cluster distribution

Similar to figure 6, in figure A.2 we show the density of galaxy clusters in the Local Universe as obtained from the different simulations, divided into massive clusters (blue) and all clusters (red), compared to the observational data points. While SLOW and B160_WM3 reproduce the high number of local very massive systems, CORUSCANT and SIBELIUS fall somewhat short in having the unusual large number of such massive systems. We note however that this is not really significant, given the low number of halos in this case. However, when comparing to the CLASSIX sample, only SLOW is able to match the reported significant underdensity out to a distance of 100 Mpc.

thumbnail Fig. A.2.

Same as figure 6, top and middle panels, but for the different simulations. Shown are the cumulative relative cluster density as a function of distance from the MW position obtained from the simulations: SLOW (solid), CORUSCANT (dashed), SIBELIUS (long dashed), and early CLUES (dash-dotted). The blue lines are for very massive halos and the red lines are for clusters and correspond to the observations from the CLASSIX Böhringer et al. (2020) sample.

A.3. Galaxy density profiles

Finally, we repeat the right panel of figure 5 for SIBELIUS (left panel) and SALACIOUS (right panel) in figure A.3. We show (as before) the mean density of galaxies as a function of distance for different stellar masses, as indicated in the color bar. We note that from this we obtain a Ω* = 0.0014 for SIBELIUS and Ω* = 0.0021 for CORUSCANT, compared to Ω* = 0.0031 for SLOW and the observed value of Ω* = 0.0027 reported in Fukugita & Peebles (2004). Compared to the SLOW simulations, both simulations display significantly less variation in the mean density, and especially SIBELIUS does not show a one-sided deviation from the mean density over very large scales. As already discussed in figure A.2, SIBELIUS does not show the large-scale underdensity out to a distance of 100 Mpc, as reported in the CLASSIX sample of galaxy clusters. Here it is clear that contrary to SLOW, no galaxy or galaxy cluster selection in SIBELIUS features this observed anomaly in the Local Universe. Once more, this demonstrates that the assumption of a constant bias within reconstructions based on galaxy densities limits the predictive power of the resulting constrained simulations. The significant differences of the bias and its environmental dependence visible in simulations based on semi-analytic modeling (like SIBELIUS) and the full hydrodynamics simulations (like SLOW or CORUSCANT) emphasize that this is a nontrivial obstacle for reconstructions of the Local Universe. This can in principle be overcome with reconstructions based on the observed velocity field, as demonstrated through the SLOW simulation, which seems to closely match the observational findings of various different tracers of the large-scale structure. However, as shown, they come with their own obstacles that are difficult to overcome in a satisfactory manner, as demonstrated by the overall effort made to bring forward the constrained simulations to this point.

thumbnail Fig. A.3.

Same as right panel of figure 5, but for SIBELIUS (left panel) and SALACIOUS (right panel). Shown is the mean density of galaxies within the Local Universe for different stellar masses (as indicated in the color bar). The dark matter density is also shown in both cases.

A.4. Weighting halos by mass

We also tested if the mass weighting of halos would result in densities closer to the dark matter density, especially for the peak created by the Virgo cluster region, where one could think that in the case of using groups and clusters, this might give a better result. The result is shown in figure A.4, which is identical to the left part of figure 5, except that we used mass weighting to compute the densities instead of number densities. Especially for the nearby structures, like the local void and the peak dominated by the Virgo cluster region, the mass weighting even overshoots the feature. However, the mass weighting creates a very sharp feature at a distance of ≈40 Mpc, even when using very small halos, which is similar to the sharp feature visible in the stellar density at distance of ≈30 Mpc found by Karachentsev & Telikova (2018) (see lower panel of figure 6), which is obtained by integrating the observed stellar mass function.

thumbnail Fig. A.4.

Same as left panel of figure 5, but using mass weighting to compute the density, instead of number density.

All Tables

Table 1.

Observational properties of Coma, Perseus, and Virgo showing the radial velocity and two estimates of their virial mass Mvir.

In the text

All Figures

thumbnail Fig. 1.

Positions in supergalactic x/y coordinates of all galaxies in the simulations, compared to galaxies from the 2MRS catalog. To make the simulations comparable, the galaxies are restricted to stellar masses above 1010 M⊙ within a 50 Mpc thick slice around the center of the simulation volume. A lighter color means galaxies more distant than 130 Mpc. For the observation, only galaxies with log(LK) > 10.25 are plotted to match the mass cut. In addition, the positions of Coma, Virgo, and Perseus are labeled. The virial masses of the halos in the simulations are listed in Table 1. From top to bottom: SLOW, SIBELIUS, CORUSCANT, and 2MRS.
In the text
thumbnail Fig. 2.

Full-sky map of the projected dark matter distribution from SLOW up to a distance of 350 Mpc. To distinguish the constrained part of the Local Universe simulation, some of the cross-identified clusters in the Local Universe are indicated.
In the text
thumbnail Fig. 3.

Observations in different wavebands. From top to bottom: distribution of galaxies in the 2MRS catalog, X-ray surface brightness in the ROSAT 1.5 keV band (R6 + R7 = 0.76 − 2.04 keV), and Compton-Y map based on Planck data (produced with the MILCA algorithm Planck Collaboration XXII 2016) with the CO mask by Khatri (2016). The insets show zoomed-in images of the Perseus and Hercules regions. The labels in the insets give the Name together with radial velocity (in km s−1) as redshift distance indicator. The yellow labels indicate clusters that are outside the slice used in the simulations shown in Fig. 4.
In the text
thumbnail Fig. 4.

SLOW in different wavebands. From top to bottom: distribution of stellar mass in SLOW, X-ray surface brightness, and Compton-Y. A much larger dynamic range than in the observations shown on Fig. 3 are used here for the color scaling to emphasize the large angular imprint on the very local galaxy clusters. The full simulation volume out to a distance of 350 Mpc is always shown. The insets show zoomed-in images of the Perseus and Hercules regions. Here a much narrower range around Perseus and A2147 is used (respectively 10 and 40 Mpc thick) to emphasize the local structures. The labels in the insets give the virial mass (in M⊙) of the halos, together with radial velocity (in km s−1) as redshift distance indicator.
In the text
thumbnail Fig. 5.

Cumulative relative number density of halos (left) and number density of galaxies (right) as a function of distance from the MW position, obtained from the SLOW simulation. The different colors are lines obtained for different lower mass cuts, as indicated in the color bars: virial masses of the halos (left) and stellar masses of the galaxies (right). The black line in each panel is the same when directly using dark matter distribution.
In the text
thumbnail Fig. 6.

Cumulative relative density of halos and galaxies of different masses as a function of distance (computed from redshift) compared to different observations. Top panel: comparison of galaxy clusters to the X-ray sample from Böhringer et al. (2021), using the same mass cut (solid) and the same X-ray luminosity cut (dashed line). Middle panel: comparison of massive galaxy clusters (Mvir > ;1015 blue line, T500c > ;5 keV red line) to the five closest clusters exceeding this mass or temperature from the Tully catalog (Tully 2015) or the BAX database Sadat et al. (2004), respectively. Bottom panel: comparison of our simulated galaxies with the results on the stellar mass density presented in Karachentsev & Telikova (2018). In the upper two panels, the gray shaded regions indicate the 1, 2, and 3σ lines obtained from the Magneticum simulation and the black line indicates the median (to display the cosmic variance left).
In the text
thumbnail Fig. 7.

Comparison of the flattening of the galaxy cluster distribution to the X-ray sample from Böhringer et al. (2021, see text for description) and to the simulation using the same mass (black) and the same X-ray luminosity (blue solid line) cut. The dashed and the dash-dotted red lines apply the same measurement in the other supergalactic coordinates for comparison. The dashed and dash-dotted blue lines are slightly different cuts in X-ray luminosity.
In the text
thumbnail Fig. 8.

Comparison of our simulated galaxies with the results of the stellar mass density presented in Karachentsev & Telikova (2018) divided in the northern Galactic hemisphere (blue) and southern Galactic hemisphere (red). As comparison, the thinner red dashed and dash-dotted line show the results when splitting along supergalactic SGX and SGZ coordinates.
In the text
thumbnail Fig. A.1.

Cumulative relative dark matter density as a function of distance from the MW position. Shown are the values obtained from the simulations: SLOW (black), CORUSCANT (blue), early CLUES (red), and SIBELIUS (orange).
In the text
thumbnail Fig. A.2.

Same as figure 6, top and middle panels, but for the different simulations. Shown are the cumulative relative cluster density as a function of distance from the MW position obtained from the simulations: SLOW (solid), CORUSCANT (dashed), SIBELIUS (long dashed), and early CLUES (dash-dotted). The blue lines are for very massive halos and the red lines are for clusters and correspond to the observations from the CLASSIX Böhringer et al. (2020) sample.
In the text
thumbnail Fig. A.3.

Same as right panel of figure 5, but for SIBELIUS (left panel) and SALACIOUS (right panel). Shown is the mean density of galaxies within the Local Universe for different stellar masses (as indicated in the color bar). The dark matter density is also shown in both cases.
In the text
thumbnail Fig. A.4.

Same as left panel of figure 5, but using mass weighting to compute the density, instead of number density.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.