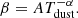| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202346804 | |
| Published online | 04 October 2023 | |
z-GAL: A NOEMA spectroscopic redshift survey of bright Herschel galaxies
II. Dust properties⋆
1
Aix-Marseille Université, CNRS and CNES, Laboratoire d’Astrophysique de Marseille, 38 rue Frédéric Joliot-Curie, 13013 Marseille, France
e-mail: diana.ismail@lam.fr
2
Institut de Radioastronomie Millimétrique (IRAM), 300 rue de la Piscine, 38400 Saint-Martin-d’Hères, France
3
Sorbonne Université, UPMC Université Paris 6 and CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
4
Department of Physics and Astronomy, Rutgers, The State University of New Jersey, 136 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA
5
Cosmic DAWN Centre Radmandsgade 62, 2200 Copenhagen N, Denmark
6
Departement of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 439 92 Onsala, Sweden
7
Division of Particle and Astrophysical Science, Graduate School of Science, Nagoya University, Aichi 464-8602, Japan
8
National Astronomical Observatory of Japan, 2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan
9
Instituto Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
10
Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
11
University of California Irvine, Department of Physics & Astronomy, FRH 2174, Irvine, CA 92697, USA
12
National Centre for Nuclear Research, ul. Pasteura 7, 02-093 Warsaw, Poland
13
INAF – Osservatorio astronomico d’Abruzzo, Via Maggini, SNC 64100 Teramo, Italy
14
Department of Physical Sciences, The Open University, Milton Keynes MK7 6AA, UK
15
Leiden University, Leiden Observatory, PO Box 9513 2300 RA Leiden, The Netherlands
16
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
17
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
18
Department of Physics and Astronomy, University of the Western Cape, Robert Sobukwe Road, Bellville 7535, South Africa
19
UK ALMA Regional Center Node, Jodrell Bank Center for Astrophysics, Department of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
20
Dipartimento di Fisica & Astronomia “G. Galilei”, Università di Padova, vicolo dell’Osservatorio 3, Padova 35122, Italy
21
School of Physics and Astronomy, University of Nottingham, University Park, Notthingham NG7 2RD, UK
22
School of Physics and Astronomy, Cardiff University, Queens Building, The Parade, Cardiff CF24 3AA, UK
23
Instituto Nacional de Astrofísica, Óptica y Electrónica, Astrophysics Department, Apdo 51 y 216, Tonantzintla, Puebla 72000, Mexico
24
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
25
Department of Physics and Astronomy, Macquarie University, North Ryde, New South Wales, Australia
26
School of Cosmic Physics, Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin D02 XF86, Ireland
27
Institut for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
28
I. Physikalisches Institut, Iniversität zu Köln, Zülpicher Strasse 77, 50937 Köln, Germany
29
Centre de Recherche Astrophysique de Lyon – CRAL, CNRS UMR 5574, UCBL1, ENS Lyon, 9 avenue Charles André, 69230 Saint-Genis-Laval, France
30
Department of Physics and Astronomy, University of the Western Cape, Private Bag X17, Bellville, 7535 Cape Town, South Africa
31
Istituto Nazionale di Astrofisica, Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
32
Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura, 763-0355 Santiago de Chile, Chile
33
European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla, 19001 Santiago de Chile, Chile
Received:
3
May
2023
Accepted:
5
July
2023
We present the dust properties of 125 bright Herschel galaxies selected from the z-GAL NOEMA spectroscopic redshift survey. All the galaxies have precise spectroscopic redshifts in the range 1.3 < z < 5.4. The large instantaneous bandwidth of NOEMA provides an exquisite sampling of the underlying dust continuum emission at 2 and 3 mm in the observed frame, with flux densities in at least four sidebands for each source. Together with the available Herschel 250, 350, and 500 μm and SCUBA-2 850 μm flux densities, the spectral energy distribution (SED) of each source can be analyzed from the far-infrared to the millimeter, with a fine sampling of the Rayleigh-Jeans tail. This wealth of data provides a solid basis to derive robust dust properties, in particular the dust emissivity index (β) and the dust temperature (Tdust). In order to demonstrate our ability to constrain the dust properties, we used a flux-generated mock catalog and analyzed the results under the assumption of an optically thin and optically thick modified black body emission. The robustness of the SED sampling for the z-GAL sources is highlighted by the mock analysis that showed high accuracy in estimating the continuum dust properties. These findings provided the basis for our detailed analysis of the z-GAL continuum data. We report a range of dust emissivities with β ∼ 1.5 − 3 estimated up to high precision with relative uncertainties that vary in the range 7%−15%, and an average of 2.2 ± 0.3. We find dust temperatures varying from 20 to 50 K with an average of Tdust ∼ 30 K for the optically thin case and Tdust ∼ 38 K in the optically thick case. For all the sources, we estimate the dust masses and apparent infrared luminosities (based on the optically thin approach). An inverse correlation is found between Tdust and β with β ∝ Tdust−0.69, which is similar to what is seen in the local Universe. Finally, we report an increasing trend in the dust temperature as a function of redshift at a rate of 6.5 ± 0.5 K/z for this 500 μm-selected sample. Based on this study, future prospects are outlined to further explore the evolution of dust temperature across cosmic time.
Key words: galaxies: high-redshift / galaxies: evolution / infrared: galaxies / submillimeter: galaxies
Full Tables A.1 and B.1 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/678/A27
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Following the detection of luminous infrared galaxies at high redshift with the IRAS satellite (e.g., Rowan-Robinson et al. 1991, 1993), the first observations at 850 μm with the Submillimeter Common-User Bolometer Array (SCUBA; Holland et al. 1999), and later at 1.2 mm with the Max-Planck Millimeter Bolometer Array (MAMBO; Kreysa et al. 1999), uncovered a population of very luminous dusty star-forming galaxies (DSFGs; with infrared luminosities in excess of ≥1012 L⊙) at high redshifts (z ≥ 1; see reviews by Blain et al. 2002; Carilli & Walter 2013; Casey et al. 2014; Hodge & da Cunha 2020). Subsequent extragalactic imaging surveys carried out with the Herschel Space Observatory (Pilbratt et al. 2010) increased the number of known DSFGs from hundreds to several hundreds of thousands (e.g., Eales et al. 2010; Oliver et al. 2012; Ward et al. 2022). These dust-enshrouded luminous galaxies absorb ∼99% of the light emitted by young, forming stars (e.g., Clements et al. 1996; Lagache et al. 2005; Buat et al. 2010), and thermally radiate the reprocessed ultraviolet–optical light in the far-infrared (FIR) and submillimeter (submm) regimes. The discovery of this population of DSFGs has changed our understanding of galaxy evolution in the early Universe, and the advent of facilities such as the Atacama Large Millimeter/submillimeter Array (ALMA), the IRAM Northern Extended Millimeter Array (NOEMA), and the Karl G. Jansky Very Large Array (VLA) have enabled follow-up observations of large samples of DSFGs to study their physical properties by probing the molecular and atomic gas (Hodge & da Cunha 2020, and references therein), and tracing the FIR/submm spectral energy distribution (SED) of the dust emission up to z ∼ 7 (e.g., Riechers et al. 2013; Reuter et al. 2020; Bouwens et al. 2021; Sommovigo et al. 2022).
Bright DSFGs are known to have very large dust reservoirs, with typical dust masses Mdust > 108 M⊙ (e.g., Swinbank et al. 2014; Reuter et al. 2020; Dudzevičiūtė et al. 2021; da Cunha et al. 2021). Dust grains, which are abundant in the interstellar medium (ISM) of galaxies in the local and distant Universe (e.g., Smail et al. 1997; Blain et al. 1999), play a vital role in many astrophysical processes, including the onset of the star-formation process. However, the origin of these large dust masses in DSFGs, particularly at high redshift, has been a matter of debate over the years. The mass buildup occurs mainly in the ejecta of supernovae (SNe) and in the envelopes of asymptotic giant branch (AGB) stars, but also via grain growth by accretion in the ISM (e.g., see the review by Galliano et al. 2018). However, these mechanisms cannot fully explain the amount of dust available in these high-z galaxies given the short timescales involved (Michałowski 2015; Nanni et al. 2020). It is therefore crucial to derive dust properties in DSFGs across cosmic time to search for any sign of evolution that could provide constraints on how the dust grains were formed in the early Universe.
Dust masses are commonly estimated by fitting a modified blackbody that best describes the thermal emission of dust in the FIR/submm domain. However, one of the caveats of this fitting method is the dependence of dust mass on the dust temperature estimates. For instance, Casey (2012) pointed out that a 4 K difference in temperature could result in a 150% increase in dust mass. Therefore, it is important to quantify as well as constrain the dust properties in DSFGs from which we can derive the star formation rates (SFRs; Sanders & Mirabel 1996; Kennicutt 1998) and estimate the gas masses (e.g., Eales et al. 2010; Scoville 2013).
To derive precise dust parameters, it is crucial to have a good coverage of the SED. With facilities like ALMA and NOEMA, follow-up observations of previously FIR/submm detected DSFGs have been carried out to measure the continuum emission along the Rayleigh-Jeans (RJ) tail from submm wavelengths down to 3 mm, which enabled a precise fitting of the FIR/submm SEDs (e.g., Reuter et al. 2020; Berta et al. 2021; da Cunha et al. 2021; Bendo et al. 2023). However, uncertainties in measuring dust temperatures still exist, and arise from (i) the opacity (in other words, on the assumptions of optical depth), and (ii) the degeneracy with the dust emissivity index β. The wavelength at which the optical depth (τ) becomes unity is often assumed to be λthick ∼ 100 μm (Draine 2006), although some galaxies have been found to have higher values, with λthick ∼ 200 μm (Conley et al. 2011; Riechers et al. 2013, 2017). For simplicity, some works assume that the dust emission in DSFGs can be approximated with an optically thin modified blackbody (τ ≪ 1), which can also lead to an underestimation of the dust temperature (e.g., up to ΔTdust ∼ 20 K as shown by da Cunha et al. 2021). To overcome these assumptions, high-resolution imaging is essential in order to derive robust values of dust opacities by recovering the galaxy size (e.g., Spilker et al. 2016). On the other hand, a degeneracy has been found for β and Tdust (Dupac et al. 2003; Shetty et al. 2009; Paradis et al. 2010; Planck Collaboration XXIII 2011; Juvela et al. 2011), which is further amplified by a lack of photometric data at longer wavelengths. To avoid the effects of this degeneracy, the emissivity index β is generally fixed based on measurements of the Milky Way (β = 1.5 − 2, e.g., Magnelli et al. 2012). However, recent studies show that dust emissivities of DSFGs diverge from the classical values (e.g., da Cunha et al. 2021; Cooper et al. 2022), which would in turn affect the dust temperature estimate. Bendo et al. (2023) found a difference of up to ∼9 K when fixing β for a sample of 37 Herschel-selected galaxies observed with ALMA at 3 and 2 mm. With a good sampling of photometric data at longer wavelengths, the dust temperature estimate becomes isolated from the effect of fixing (or deriving) an inadequate value for β, thus breaking the degeneracy.
Nonetheless, the growing number of surveys with FIR/submm observations has resulted in an abundance of dust temperature measurements in the literature that span a wide range of redshifts, reaching z ∼ 8 (e.g., Reuter et al. 2020; Bakx et al. 2021; Sommovigo et al. 2022). However, contradictory claims of dust temperature trends across cosmic time have been reported. Some studies argue that dust becomes hotter at higher redshifts as compared to the local Universe, which is attributed to higher specific star formation rates (sSFR; e.g., Magnelli et al. 2014; Magdis et al. 2012; Béthermin et al. 2015; Schreiber et al. 2018; Zavala et al. 2018; Liang et al. 2019; Faisst et al. 2020; Sommovigo et al. 2020, 2022). Conversely, Dudzevičiūtė et al. (2020) argue that there is no evidence of temperature evolution, and the observed correlation is solely due to selection biases that limit observations to the brightest galaxies, especially at higher redshifts.
Recently, Neri et al. (2020) demonstrated the capability of the broadband receivers and the Polyfix correlator at NOEMA to measure up to ten continuum flux densities in the millimeter bands per source by observing 13 bright high-zHerschel-selected galaxies. Reliable spectroscopic redshifts were obtained for 11 of the selected sources, and by combining the available continuum flux densities from the Herschel-Spire, SCUBA-2, and the 2 and 3 mm NOEMA data, well-sampled SEDs for each source were obtained from which the dust properties were derived (infrared luminosities, dust masses, and temperatures; Neri et al. 2020; Berta et al. 2021). Based on the successful NOEMA Pilot Program, the z-GAL Large Program has extended this work by observing 126 high-redshift Herschel-selected galaxies in the 2 and 3 mm NOEMA wavebands (Cox et al. 2023; hereafter Paper I) with the goal to measure precise spectroscopic redshifts. In addition to the molecular and atomic emission lines that were detected in all the sources, the continuum emission flux densities were extracted for each source in at least four, and up to ten, sidebands. The combined Pilot Program and z-GAL Large Program constitutes the final z-GAL sample of 137 sources, for which robust redshifts were derived for 135 sources, spanning the range 0.8 < z < 6.5. The present study of the dust properties of high-z galaxies is based on this sample, the largest with precise redshifts to date.
This paper (Paper II) is part of a series of three papers reporting the results of the z-GAL project. Paper I gives an overview of the Herschel-selected sources of this program and presents the overall properties of the molecular and atomic emission lines, as well as the derived spectroscopic redshifts. In Paper III, Berta et al. (2023) analyze and describe the physical properties of the molecular and atomic gas in the z-GAL sources using both the continuum and emission lines. Here, we study the continuum data of the z-GAL sources. Our main goal is to derive the dust properties, taking advantage of the exquisite coverage in frequency of the SED. In order to demonstrate our ability to constrain the essential dust properties, such as dust temperature and emissivity index, we used a flux-generated mock catalog and analyzed the results under the assumptions of an optically thick and optically thin modified blackbody emission. We then performed a detailed analysis of the z-GAL continuum data informed by the findings of the mock simulation. The main results focus on the optically thin approximation, which will serve as a basis for our analysis (specifically the dust masses and inferred FIR luminosities) in Paper III.
The paper is organized as follows. In Sect. 2, we give a brief overview of the z-GAL sample selected from the Herschel catalog and the NOEMA observations in the 2 and 3 mm wavebands, and provide a detailed explanation of the continuum data reduction as well as an overview of the data that form the basis of this paper. In Sect. 3, we describe the optically thin approximation of the modified blackbody used to determine the continuum dust properties and analyze the model effects on each term. In Sect. 4, we present the optically thin dust properties of the z-GAL sample of sources. In Sect. 5, we present the general modified blackbody (GMBB) model, and our derivation of parameters and z-GAL dust properties. In Sect. 6, we discuss the derived results and their evolution with redshift. Finally, in Sect. 7, we summarize our main conclusions and outline future studies. Throughout the paper, we adopt a spatially flat ΛCDM cosmology with H0 = 67.4 km s−1 Mpc−1 and ΩM = 0.315 (Planck Collaboration I 2020).
2. z-GAL sample
The aim of the z-GAL project is to measure robust spectroscopic redshifts of a sample of 137 Herschel-selected galaxies. The details of the sample selection are provided in Paper I. The 126 sources for the z-GAL Large Program (carried out under projects M18AB and D20AB – PI: P. Cox, T. Bakx & H. Dannerbauer) were selected from the Herschel Bright Sources (HerBS) sample, the HerMES Large Mode Survey (HeLMS), and the Herschel Stripe 82 (HerS) Survey (Nayyeri et al. 2016; Bakx et al. 2018), and also include the 11 sources of the Pilot Program (Neri et al. 2020) from the HerBS sample. The HeLMS and HerS fields cover 372 deg2, and HerBS sources were selected from the NGP and GAMA fields that cover 170.1 and 161.6 deg2, respectively. The selection was based on the 500 μm flux limit with S500 μm > 80 mJy for the HerBS sources and S500 μm > 100 mJy for both HeLMS and HerS sources, as well as photometric redshifts zphot > 2 (see Cox et al. 2023, for the sample selection and references therein). The z-GAL sources were observed using NOEMA by scanning the 2 and 3 mm wavebands, which successfully resulted in deriving spectroscopic redshifts based on at least two emission lines for all but two of the selected sources (Neri et al. 2020; Cox et al. 2023). The frequency setup for the 3 mm observations covers the range from 75.874 to 106.868 GHz and the 2 mm setup covers the range from 127.377 to 158.380 GHz. The fields of view at 2 and 3 mm are ∼33″ and ∼50″, respectively, and the angular resolutions were in between 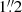 and
and 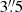 at 2 mm and between
at 2 mm and between 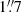 and ∼6″ at 3 mm. Alongside the line emission measurements, all sources were detected in the continuum in at least four sidebands thanks to the broad band receiver of NOEMA. The z-GAL sources span the redshift range 1 < z < 6 (see Fig. 1), peaking at the peak of cosmic evolution at z ∼ 2 − 3, making it an ideal large sample with which to explore eventual changes of dust properties with redshift.
and ∼6″ at 3 mm. Alongside the line emission measurements, all sources were detected in the continuum in at least four sidebands thanks to the broad band receiver of NOEMA. The z-GAL sources span the redshift range 1 < z < 6 (see Fig. 1), peaking at the peak of cosmic evolution at z ∼ 2 − 3, making it an ideal large sample with which to explore eventual changes of dust properties with redshift.
 |
Fig. 1. Redshift distribution of the galaxies used in this study, which includes 125 out of the 137 sources from the z-GAL sample. In our analysis, we exclude multiples at different redshifts in the field of view observed by NOEMA, which are unresolved in the Herschel field of view, as well as problematic sources (see details in Sect. 2.2). |
2.1. Data reduction
The NOEMA data were reduced and calibrated with the GILDAS1 package and uv-tables of each sideband were produced in the standard way. The main calibrators adopted were MWC349 and LkHα101. More details are provided in Paper I. The absolute flux uncertainty is 10% and the positional error is 0.2 arcsec.
For each z-GAL target, stacked maps were produced combining all channels of all available sidebands, including both continuum and spectral lines (hereafter called all-channels maps). Such stacked maps were then used as reference for the detection of sources in the NOEMA fields centered on the Herschel positions. Continuum maps of each sideband were produced by combining all channels of the given sideband, but excluding the spectral ranges including the emission lines. As an example, Fig. 2 shows the ten sidebands observed for one of the sources, HeLMS-1, at 2 and 3 mm, each one with a bandwidth of approximately 8 GHz.
 |
Fig. 2. NOEMA spectral coverage and bandwidth of the 2 and 3 mm bands for the source HeLMS-1 at z = 1.905. The ten alternating colors are the lower and upper sidebands for each setup. The black points show the flux density extracted in each band along with their uncertainties (very small error bars). The 12CO(4-3) and (2-1) emission lines detected in this source are identified in the figure. |
Source extraction and continuum measurements were conducted in the following way. For each target, the all-channels maps were used to identify all sources in the field of view of NOEMA using 3σ threshold contours as guidance to define the aperture. The maps were cleaned using natural weights and support masks including all detected sources. The individual continuum maps were also cleaned with natural weight, adopting support masks re-adapted because of different beam size, orientation, and shape. In cases where sources were not detected in individual sidebands, the support masks follow the size and orientation of the beam.
The measurement of continuum fluxes was then performed on the cleaned continuum maps of each individual sideband for the sources identified in the all-channels map. Aperture fluxes were measured using ad hoc extraction polygons and corrected for primary beam losses. Flux statistical uncertainties were computed by rescaling the map noise to the effective extraction aperture size. Source positions were computed as signal barycenters within the same extraction apertures.
2.2. Continuum flux densities of the z-GAL sample
The continuum flux densities are listed in Table A.1 along with their uncertainties. The uncertainties listed are the ones estimated in the data reduction process, but in our subsequent analysis (Sects. 3 and 5), we add a 10% error in quadrature to each flux density uncertainty to account for calibration uncertainty. Flux densities with S/N > 3 are considered detections, listed as the measured flux followed by the 1σ uncertainty, and non-detections (S/N < 3) are listed with a “< ” sign followed by the measured flux and the 3σ uncertainty. The flux densities of the multiple sources detected in the NOEMA field that are unresolved by Herschel and SCUBA-2 are listed individually and, in the case where sources are at the same z (a total of 15 sources), as the sum of all components (see Notes of Table A.1). A total of 12 sources from 137 were discarded from our further analysis, 9 of which are multiple sources in the field of view at different redshifts (including 3 sources from the Pilot Program, i.e., HerBS-43, 70, 95), another two sources have tentative redshifts (HerS-19 and HerBS-82), and HerS-9 is a foreground galaxy at z = 0.853. This brings the total number of sources retained in order to study their continuum and to extract dust-emission properties to 125. The selected sources span the redshift range 1.3 < z < 5.4 (Fig. 1).
In the top panel of Fig. 3, we summarize the signal-to-noise ratios of each of the wavebands, where the continuum coverage of the z-GAL sample ranges from the FIR to the millimeter, with all sources having Herschel-SPIRE 250, 350, and 500 μm flux densities with 7 < S/N < 10. The 850 μm SCUBA-2 flux density is only available for the HerBS sources (Bakx et al. 2018, 2000) with 1.5 < S/N < 7 (see Cox et al. 2023, for a table of the Herschel and SCUBA-2 flux densities). The NOEMA 2 and 3 mm flux densities for all sources have been measured with 1 < S/N < 9. For two sources in the sample, additional data in the 1 mm band are available, namely for HeLMS-17 (see Paper I) and HerBS-89 (Berta et al. 2021). In the bottom panel of Fig. 3, we summarize the z-GAL millimeter sampling, illustrating the uniqueness of the z-GAL sources that have up to ten measured continuum flux densities in the 2 and 3 mm bands. In our further analysis, we use data below 1 mm in the rest-frame (see Sect. 3.1) so that the effective number of flux density measurements varies between 2 and 8 data points in the millimeter, where most of the sources have two or more detections (S/N > 3).
 |
Fig. 3. Sampling and S/N of the flux densities of the z-GAL galaxies. Top panel: signal-to-noise ratio of the z-GAL data split into Herschel 250, 350, and 500 μm flux densities shown in indigo, which varies between 6 and 10; SCUBA-2 850 μm flux density, in orange, which varies between 1.5 and 7; and NOEMA 2 and 3 mm flux densities, which varies between 1 and 9, shown in black. Bottom panel: distribution of the number of millimeter flux data points available for each z-GAL source shown in gray; all sources have at least 2, and up to 10, measurements. The cyan histogram shows the number of millimeter measurements used in the fitting procedure (below 1 mm in the rest-frame; see Sect. 3) with a median of 5 data points sampling the Rayleigh-Jeans of the z-GAL sources. The indigo-lined histogram shows the number of data points with signal-to-noise ratio > 3. |
3. Modeling the optically thin dust emission
The main goal of this study is to estimate the properties of the dust continuum emission of the z-GAL sample that covers the observed wavelength range from 250 μm to 3 mm. In this section, we present the dust emission model, the modified blackbody (MBB), used to fit the cold dust component between rest-frame wavelengths of 50 and 1000 μm, excluding the warm dust and radio (free-free and synchrotron) emission, respectively. Our main focus is on the optically thin approximation of the MBB, which is presented in Sect. 3.1, which serves as a basis for the z-GAL sample results presented in Sect. 4. We also study the robustness of the sampling and discuss parameter estimation in detail in Sect. 3.2.
3.1. Optically thin modified blackbody
The thermal dust emission is most simplistically described by a single-temperature MBB. This is the solution to the radiative transfer equation where dust grains are in thermal equilibrium with the radiation field with an emergent flux density:
where Bν(Tdust) is Planck’s blackbody radiation, Ω is the solid angle of emission: 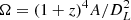 , A, and DL are the physical area of the galaxy and luminosity distance, respectively, μ is the magnification factor for the sources that are gravitationally lensed, ϵν is the emissivity coefficient at rest-frame frequency ν: ϵν = (1 − e−τν), and τν is the frequency-dependent optical depth that is written in terms of the dust mass surface density Σdust and the mass absorption coefficient (e.g., Beelen et al. 2006):
, A, and DL are the physical area of the galaxy and luminosity distance, respectively, μ is the magnification factor for the sources that are gravitationally lensed, ϵν is the emissivity coefficient at rest-frame frequency ν: ϵν = (1 − e−τν), and τν is the frequency-dependent optical depth that is written in terms of the dust mass surface density Σdust and the mass absorption coefficient (e.g., Beelen et al. 2006):
where κν can be approximated by a power law at our wavelength of interest: κν = κ0(ν/ν0)β with κ0 being the mass absorption coefficient at frequency ν0 and β the dust emissivity index. Σdust(=Mdust/A) is the dust mass density, with Mdust being the dust mass. We adopt the values computed by Draine et al. (2014) for the mass absorption coefficient: ν0 = 353 GHz (i.e., λ0 = 850μm), κ0 = 0.047 m2/kg. Berta et al. (2016) and Bianchi (2013) pointed out that a correction is needed when using the tabulated κν values and fitting with β ≠ 2.08 due to a dependence on the normalization (Mdust in this case), and so we correct Mdust by a factor of (850 μm/500 μm)β − 2.08.
When assuming an optically thin medium in the observed frequencies, the optical depth τν ≪ 1, and therefore the emissivity coefficient will simplify to: ϵν = (1 − e−τν)≈τν using Taylor’s expansion. The observed flux can therefore be written:
Hereafter, we refer to this form as MBB, which we correct for the cosmic microwave background (CMB) effects throughout this study, as described by da Cunha et al. (2013).
The FIR luminosity of the cold dust component is estimated by integrating the fitted modified blackbody between rest-frame 50 and 1000 μm:
3.2. SED fitting and parameter estimation
With the frequency coverage of the z-GAL sample, especially along the RJ tail, we cover the millimeter wavebands with a varying number of flux measurements along with the FIR Herschel and, when available, SCUBA-2 flux densities. This confers an advantage in that it allows us to measure the dust parameters with greater accuracy, especially β, which is governed by the RJ tail, without the need to fix them to an average standard (e.g., β is usually fixed to 1.5 or 2, e.g., Magnelli et al. 2012). Here, we create a mock catalog using the MBB of simulated flux densities that mimic those in our sample in order to explore how well we can retrieve the dust parameters β, Tdust, and Mdust, which are recovered from the SED fit of Eq. (3), as well as LFIR, which is the integrated area under the curve using Eq. (4).
To generate a mock catalog of flux densities using the MBB, we choose a range of initial parameters, with β varying between 1 and 3, Tdust between 15 and 70 K, Mdust between 108 − 1011 M⊙, and a redshift range chosen between 1.3 and 6 that is representative of the z-GAL sample (see Fig. 1). Given the dust parameter ranges mentioned, we generate a grid of 124 mock sources, without any prior correlation between the dust parameters and uniformly spread over the parameter space. Using Eq. (3), the mock flux densities are then computed – accounting for the CMB effect – with these parameters and we add a random error bar (equivalent to 1σ) for each waveband, which was chosen to be similar to the real data signal-to-noise ratio (S/N), where the S/N varies between 6 and 10 for the Herschel flux densities, between 1.5 and 7 for the SCUBA-2 flux density, and between 1 and 9 for the NOEMA flux densities. To mimic real observations, we perturb the flux densities on a normal distribution with 1σ, which is equivalent to the error bar of each flux point. The final mock catalog covers the 250, 350, and 500 μmHerschel flux densities, the 850 μm SCUBA-2 flux, and five millimeter data points that vary between 79.76 and 162.32 GHz (or 3.7 and 1.8 mm).
We then fit the SEDs to estimate the output dust parameters of the mock galaxies using the MBB. Throughout this paper, we use the EMCEE package (Foreman-Mackey et al. 2013), which is a Markov chain Monte Carlo sampler, to fit the SEDs using the MBB corrected for CMB effects. We introduce the MCMC sampler with flat priors for each dust parameter: (i) 0 < Tdust < 100 K, (ii) 0 < β < 4, and (iii) 105 < Mdust (M⊙) < 1015. Given the flux densities with their uncertainties, we run the code with 150 walkers and 2000 steps with a 1000 burn-in phase and verify the chains converged (Nsteps > 10× auto-correlation time). In the following subsections, we present a detailed study of how well the dust parameters are recovered (focusing mainly on the dust emissivity index in Sect. 3.2.1 and dust temperatures in Sect. 3.2.2) and the impact of different aspects (redshift, intrinsic dust temperature, and S/N) on the accuracy of their estimates.
3.2.1. Dust emissivity index β
We find good agreement between true and output β values as shown in Fig. 4 (first panel on the left) where the mean of each bin, represented by the black points, lies on the one-to-one relation, and is recovered with a standard deviation of between (output – input) ±0.18. We also find good agreement in recovering β irrespective of the redshift or the recovery of the dust temperatures. Within different redshift bins, as shown in Fig. D.1, we see changes in the accuracy and scatter of the temperature, but we do not see any direct impact on the β estimation.
 |
Fig. 4. Input (true) vs. output dust properties of the mock-generated catalog of sources. The black line is the identity line and the black dots show the median within the bins and the error bars represent the standard deviation in these bins. The boxes in the lower right corner describe the accuracy of the fitting method when using the optically thin MBB for this mock sample. |
To look in more detail at the estimation of β, we show the posterior likelihood distributions of estimated parameters of a mock source chosen at z = 4.29 in Fig. 5. We still find a slight degeneracy between dust temperature and β, even with a large number of data points sampling the RJ tail (see Sect. 6.4, for the discussion on the origin of this degeneracy). However, Fig. 5 clearly shows that the dust emissivity is well constrained and independent of the peak sampling (or in other words, independent of the temperature estimate). Nevertheless, it is dependent on the quality of the data used to minimize the width of the posterior distribution (shown in red for S/N < 3 and black for S/N > 3 in Fig. 5), an effect that was also described by Shetty et al. (2009). Unlike z-GAL sources, many previous studies had a sampling of no more than two data points along the RJ tail, which results in a larger degeneracy between dust temperature and β (illustrated in teal contours in Fig. 5) especially when the peak is less well sampled. This result further underlines the robustness of the z-GAL coverage for constraining the dust emissivity index β.
 |
Fig. 5. Corner plot of the posterior distribution and SED fit of a mock galaxy at redshift z = 4.29. The posterior distribution shows dust parameter estimates: (i) with five flux points in the millimeter domain with S/N > 3 in black, (ii) five flux points in the millimeter domain with S/N < 3 in red, and (iii) two flux points in the millimeter domain with S/N > 3 in teal; over-plotted in gray are the true values. |
3.2.2. Dust temperature Tdust
The dust temperature output is, on average, in good agreement with the true temperature and we recover it to within ±6.8 K, as shown in the second panel of Fig. 4. The significant dispersion in the estimates of Tdust is primarily related to the intrinsic temperature; that is, the higher the temperature, the lower the accuracy as the peak shifts towards shorter wavelengths, as shown in the right panel of Fig. 6. Another important factor is the redshift, where the peak becomes poorly constrained at lower redshifts; given the wavelength coverage of our sample, we lose sensitivity and accuracy in recovering Tdust as illustrated in the left panel of Fig. 6 and in the redshift-binned histogram in Fig. D.1.
 |
Fig. 6. Coverage of the z-GAL sample flux densities as a function of the physical properties of a galaxy. Left: when varying the redshift, we lose peak sensitivity at lower redshifts, which limits the recovery of the true Tdust of the SED. Right: with an intrinsically higher Tdust, we lose peak sensitivity as well and we no longer recover the true temperature of the SED. |
Figure 7 displays the root mean square (RMS) of the ΔTdust(=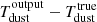 ) distribution as a function of the estimated Tdust and redshift. Coupling both redshift and temperature, Tdust, is best recovered between redshifts 2 and 4, and with more precision toward higher temperatures. However, this precision slightly drops at z > 4 because of the effect of our fitting method, where we remove any contribution from warm dust (λrest < 50 μm); that is, the Herschel 250 μm flux point falls below that limit starting at z ≥ 4, resulting in a lower accuracy in recovering Tdust.
) distribution as a function of the estimated Tdust and redshift. Coupling both redshift and temperature, Tdust, is best recovered between redshifts 2 and 4, and with more precision toward higher temperatures. However, this precision slightly drops at z > 4 because of the effect of our fitting method, where we remove any contribution from warm dust (λrest < 50 μm); that is, the Herschel 250 μm flux point falls below that limit starting at z ≥ 4, resulting in a lower accuracy in recovering Tdust.
 |
Fig. 7. Root mean square of (output – true) Tdust distribution as a function of the estimated dust temperatures and redshift. |
Finally, the dust mass estimates are found to be in good agreement with the mock values and are recovered to within ±0.066 dex. In the MBB, this parameter acts as a normalization in the equation, but is also dependent on the dust temperature estimates. However, with good constraints on the dust temperature, we are able to obtain robust dust mass estimates. Furthermore, the dust luminosity that we recover is in very good agreement with mock values (to within ±0.056 dex on average), as shown in the right panel of Fig. 4, and is determined by the data rather than the fitting method.
We performed a final check to measure the effect of the lack of a flux density measurement at 850 μm. Only the HerBS sources in the z-GAL sample were observed at this wavelength with SCUBA-2 (Bakx et al. 2018), whereas the HeLMS and HerS sources lack an 850 μm measurement (representing a total of 56 sources). To this effect, we fit the SEDs of the mock catalog generated using the same strategy but removing the flux density at 850 μm; however, we do not find any significant change in the output. The standard deviation of the (output − input) parameters is only slightly higher, with ±0.2 for β, ±7.07 K for Tdust, ±0.069 dex for Mdust, and ±0.059 dex for LFIR. Therefore, we do not distinguish between sources with and without this measurement because NOEMA data cover observations along the RJ tail, which allows us to constrain the dust parameters well.
4. z-GAL optically thin dust properties
In this section, we present the continuum dust properties of the z-GAL sources using the MBB approach, which will provide the basis for the analysis presented in the series of z-GAL papers; in particular, their infrared luminosities, which are used to derive the physical properties of these galaxies (Berta et al. 2023). The dust parameters are derived by fitting the SED of each source following the method described in Sect. 3.2.
In Fig. 8, we summarize the distribution of the dust parameters for all the sources of the z-GAL sample selected for this study (gray histogram). The results show a wide range of values around the median values of the dust emissivity index β (2.16 ± 0.27), the dust temperatures (30 ± 4.37 K), the apparent dust masses (0.58 ± 0.16) × 1010 M⊙, and the inferred apparent dust luminosities (1.8 ± 0.52) × 1013 L⊙. With the given z-GAL sampling at the peak and the RJ tail of the SED, we find that on average, we recover robust dust parameters, as shown by the mock results, especially the dust masses and the infrared luminosities across all redshift bins. However, the accuracy of Tdust changes within each bin, as does the accuracy of the dust emissivity index β.
 |
Fig. 8. Distribution of the dust properties of the z-GAL sources derived from the MBB shown in gray. The median value of each parameter is plotted with a dashed line whose value is given in the upper right corner of each plot along with the median absolute deviation. The black contour histogram shows the distribution of each parameter within the redshift subset 2 < z < 4. |
One of the great advantages of the z-GAL sample is the excellent coverage in the millimeter domain, which allows us to constrain the dust emissivity index with high accuracy. Indeed, we recover β to within 10% for most of the sources (the relative uncertainty varies in the range of approximately 7%−15%); however, we still find some sources whose β is less well constrained, with a relative uncertainty of Δβ/β > 15%. In Sect. 3.2.1, we show that the main reasons for a low precision in estimating β come from a low S/N or poor-quality measurements, which also increases the degeneracy with dust temperatures. We show the distribution of estimated dust emissivity indices versus dust temperatures for our sample in Fig. 9, where a total of 14 sources show a poorly constrained β.
 |
Fig. 9. β − Tdust relation and precision in estimating these parameters. The black squares, blue diamonds, and yellow circles show the output for sources in the redshift ranges of 2 < z < 4, z < 2, and z > 4, respectively. |
The dust emissivity indices and dust temperatures clearly show an intrinsic relation between these parameters. In order to fully understand whether or not the uncertainties on β are related to Tdust, we looked at the dust temperature estimate and its accuracy, which we categorize into three subsamples. The first subsample is the most dominant in our sample, and covers the redshift range 2 < z < 4, amounting to 101 of the total sample. This redshift subset gives the most robust constraints on parameter estimates, especially Tdust up to intrinsic temperatures of 40 K. Our results show that only five sources have temperatures above this limit, and that they vary between 42 and 47 K, as shown in Fig. 9. After inspecting their posterior distribution in Fig. F.1 (particularly, HerBS-78, and HerBS-204), we find that the degeneracy is small and we find β to be well constrained for those sources. We also checked whether the use of upper limits (as measured flux densities) biases the high β values (β ≥ 3); however, Fig. F.3 shows that excluding them does not have a significant effect on the estimation of β where the posterior distributions are overlapping.
The second subset is for sources at z < 2, which turned out to be more challenging in constraining Tdust beyond 30 K. In our sample, 18 galaxies (at z < 2) have estimated temperatures that reach ∼30 K and are recovered to within 15% (denoted by blue diamonds in Fig. 9), placing them in the unbiased region. Three sources in this subset show a poor constraint on β, while two of these (HeLMS-35 and HeLMS-44) have only two millimeter data points sampling the RJ tail, resulting in a lower precision, and HerBS-199 has poor millimeter data quality (low S/N).
The third subset is for sources at z > 4. In our sample, there are six sources within this range with estimated temperatures that vary between 33 and 56 K (shown as yellow filled circles in Fig. 9). Similarly to the first subset, sources with Tdust > 40 K show lower precision in estimating dust temperatures. The relative uncertainties on these sources (HeLMS-19, HeLMS-24, and HeLMS-45) are due to a larger degeneracy with Tdust, which is caused by a poorly sampled peak.
5. Exploring the general modified blackbody model
Given its simplicity, the most commonly used model is the optically thin approximation, but it is nevertheless important to explore the general form of the modified blackbody (GMBB). Although the GMBB is also a simplification, where a single temperature is assumed, we need to take into consideration the fact that some sources could be optically thick up to ∼200 μm (e.g., Riechers et al. 2017; Casey et al. 2019; Dudzevičiūtė et al. 2021). It also has been shown that Tdust tends to be underestimated by up to ∼20 K when using the optically thin model (e.g., da Cunha et al. 2021; Cortzen et al. 2020). In this section, we explore the GMBB SED fitting and show the accuracy and the different biases in estimating dust properties.
We start by modeling the GMBB using Eq. (1) and the expression of the optical depth in Eq. (2). The observed flux in its expanded form can now be written as:
and we refer to this equation as GMBB-Sizes hereafter. The GMBB-Sizes contains an extra parameter, namely the source size, which we set as a free parameter along with β, Tdust, and Mdust.
It is also common to represent the optical depth as τν = (ν/νthick)β, where νthick is the frequency at which the optical depth is unity (Spilker et al. 2016; Draine 2006). Substituting this equation of the optical depth into Eq. (1), the observed flux can be written as:
and we refer to this equation as GMBB-Lambda hereafter. λthick (=c/νthick) is usually set to 100 μm, but estimates go as low as 55 μm (Simpson et al. 2017, derived a range between 55 and 90 μm), and could reach as high as 200 μm (Riechers et al. 2017, 2021). Spilker et al. (2016) also find a median of 140 μm with a range between ∼50 and 250 μm. λthick is dependent on intrinsic dust properties (dust mass absorption coefficient κ0 and dust mass surface density Σdust) and by equating the two forms of optical depth (τν = (ν/νthick)β and Eq. (2)), it can be expressed as
This means that for a given dust mass, λthick decreases as a function of source size (R; A = 4πR2) and the medium becomes optically thin at shorter wavelengths. Taking the median apparent dust mass derived for z-GAL sources, namely Mdust = 109.7 M⊙, and a median β = 2, the medium becomes optically thin at 33 μm for an apparent source size of 5 kpc and at 165 μm for a size of 1 kpc.
5.1. SED fitting and parameter estimation with GMBB
We perform similar tests for GMBB as done for the optically thin mock catalog and explore how well we can constrain the dust parameters when using the general opacity model in both its forms (Eqs. (5) and (6)) to re-estimate the GMBB-generated mock catalog. We also show the degeneracies that arise when using a general model (GMBB-Sizes and GMBB-Lambda) as well as the biases when assuming solely an optically thin approximation by fitting MBB to the GMBB-generated mock catalog.
To generate the mock catalog of flux densities, we follow the same procedure as in Sect. 3.2 and choose the same range of initial parameters. In addition to z, β, Tdust, and Mdust, we need to choose a range of the intrinsic size (R) of the emission region. ALMA observations show that the typical FIR/submm dusty galaxies have R = 1–5 kpc (e.g., Hodge et al. 2015, 2016, 2019; Simpson et al. 2015; Rujopakarn et al. 2016; Fujimoto et al. 2017,) which will be the basis of the range chosen here. We then generate a grid of 95 mock sources and estimate the corresponding λthick values of the parameter space, which varies between 0.02 and 731 μm, but we narrow it down to sources within the range of 40 < λthick < 300 μm, keeping only the physical values, giving a total of 27,054 mock sources in this catalog. Finally, we compute the flux densities using Eq. (5), and we follow the procedure in Sect. 3.2 to derive their respective uncertainties and scatter to mimic real observations.
Figure 10 summarizes the output versus true parameters of the SED fits using GMBB-Sizes by setting the size as a free parameter with a prior between 0.1 and 9 kpc in the MCMC sampler. On average, we find good agreement in recovering the dust parameters using GMBB-Sizes where β is recovered to within ±0.23, dust temperatures within ±6.9K, dust masses within ±0.1 dex, and dust luminosity within ±0.067 dex. However, the ratio of output/input LFIR is on average overestimated by ∼10%−15% (the reason for this is explained in the following paragraph). We also looked at the generated catalog split into two categories: where the medium becomes optically thin (i) at lower wavelengths (λthick < 100 μm), and (ii) at higher wavelengths (λthick > 100 μm). GMBB-Sizes results in estimated parameters that agree with the true ones in both scenarios, as shown in the density histogram of Figs. E.1 and E.2 (first row).
 |
Fig. 10. Ratio of output and true parameters to the true dust parameters of the GMBB mock-generated catalog of sources. The median within each bin is shown as a black filled square, an empty square, and an empty circle for the results fitted with GMBB-Sizes, GMBB-Lambda, and the MBB, respectively, with the error bars representing the standard deviation within each bin. With the z-GAL sampling, β is recovered very well with all methods. Fitting with GMBB-Sizes can overestimate the inferred luminosity by ∼10%–15% due to an unrecovered source size (see Sect. 5.1). Fitting with GMBB-Lambda can overestimate the dust temperatures by 10%−20% and consequently the dust masses become underestimated by up to 40%. When fitting with MBB, the dust temperatures can be underestimated by 20%−30% and consequently the dust masses become overestimated by up to 75%. |
We note that having the source size as an extra free parameter gives rise to a new type of covariance between parameters. In Fig. 11, we demonstrate the posterior distribution of the output parameters of a mock source when using GMBB-Sizes, which shows that we recover the dust emissivity index, the dust temperature, and dust masses with high accuracy, but not the true size where the likelihood shows a flat distribution. Moreover, the output sizes show a flat distribution for almost all cases where R (output) ∼4.5 kpc (midpoint of the range set for the prior). This, in turn, affects the FIR luminosity overestimation by ∼10% on average. To explain the flat distribution, we illustrate the variation of the SED fit as a function of source size (R) in Fig. 12, which shows that for a source size at R > 3 kpc (for a given Mdust), the medium becomes optically thin at λthick ∼ 50 μm. But for R < 1 kpc, the variation at the peak is very large, and the medium is optically thick up to longer wavelengths for all Mdust, which creates a degeneracy between the source size and dust temperature, as well as between the source size and dust mass. Nevertheless, the derived λthick remains close to the true value with a systematic shift of ∼30 μm, as shown in the left panel of Fig. 13, although with a large scatter.
 |
Fig. 11. Corner plot of the posterior distribution and SED fit of a mock source at redshift z = 3.06. The posterior distribution shows dust parameter estimation using (i) GMBB-Sizes (green) and (ii) GMBB-Lambda (red), which are over-plotted with the true values in black. In this fit, λthick for GMBB-Sizes is estimated using Eq. (7) given the posterior distribution of the output parameters (β, Mdust and A), and Mdust distribution for GMBB-Lambda is also estimated with Eq. (7) using the posterior distribution of the output parameters (β, A = 4πR2, and λthick). |
 |
Fig. 12. Effect of the source-size variation on SED fitting. Left: Effect of source size variation on the SED of a galaxy. Orange indicates the variation when the size R < 1 kpc, and a gradient of blues indicates the variation when R > 1 kpc. On the right side, we plot λthick (wavelength at which optical depth is unity) versus source size (R), color coded according to dust mass. These two figures show that for source sizes R < 1 kpc, there is a large effect on the peak of the SED, where the medium is optically thick, reaching higher values of λthick. |
 |
Fig. 13. Output versus true λthick estimation. The left figure shows the accuracy of estimating λthick when using GMBB-Sizes to fit the SED, in which it is derived using Eq. (7). The right figure shows the accuracy of estimating λthick when using GMBB-Lambda to fit the SED, in which it is a free parameter in the equation. The black dashed line is the identity line and the black squares show the median within each bin. |
We also fit the SEDs using GMBB-Lambda – which is a more common way to use the GMBB (e.g., Cortzen et al. 2020; da Cunha et al. 2021) – by setting λthick as a free parameter that varies between 50 and 250 μm. Results show (Fig. 10) that dust temperatures are (on average) always overestimated, which is a result of the large degeneracy between λthick and Tdust, where λthick is poorly constrained (as illustrated in the corner plot of Fig. 11). With the given sampling of the peak, the likelihood shows a preference for the longer wavelengths, with a consequent rise in dust temperatures by up to 20%. Especially in the region where the medium becomes optically thin at lower wavelengths (λthick < 100μm), this method does not prove to be a reliable way to constrain dust parameters, and the output λthick is overestimated by a factor of ∼1.5 − 2, as shown in Fig. 13 (right panel). However, it holds true for an optically thick medium for all output parameters and especially Tdust, where the output λthick appears to be slightly better constrained between 125 and 200 μm, as also shown in Fig. 13 (see also density histograms of Appendix E). In addition, we see the effect on the dust mass estimate, which is underestimated by 1.5 times2 on average.
Finally, we fit the GMBB-generated catalog using the MBB, which shows on average an underestimation of the dust temperatures, as expected, with an increasing offset towards higher intrinsic temperatures and consequently an overestimation of dust masses, which can reach 1.5 times the true value. These trends become even more evident when we check the split catalog, where the optically thin approximation holds true when λthick < 100 μm. Otherwise, the dust temperatures are underestimated with an offset of ∼10 K for an intrinsic Tdust = 30 K, which increases to an offset of ∼25 K for intrinsic Tdust = 60 K (see Figs. E.1 and E.2 for density histograms).
5.2. z-GAL dust properties using the GMBB
Following the results of the GMBB mock analysis in Sect. 5.1, the GMBB-Sizes provides more accurate results, especially for Tdust (and consequently Mdust), where we are also able to quantify the optical depth to a certain level of accuracy, unlike with GMBB-Lambda. Based on this result, we estimate the dust properties of the z-GAL sample using GMBB-Sizes alone. In Fig. F.2, we demonstrate the posterior likelihood for one of the sources, HeLMS-48, with a corner plot. The results of GMBB-Sizes versus MBB are displayed in Fig. 14, where the red dots represent z-GAL sources with their respective uncertainties; over-plotted are the output results of the mock sample, which clearly show the similarity in trends between real and synthetic data. Shown in black circles are the problematic sources with two probable solutions (a double-peaked posterior distribution) because of the degeneracy between the source size and dust temperature, as illustrated in Fig. 12. For these sources, we constrain the prior additionally by choosing the highest probability values between the dust temperature and dust masses from the first run, then rerun the MCMC sampler with an additional Gaussian prior on dust temperatures. The Gaussian is centered on the maximum probability from the previous chains with a width of 7K.
 |
Fig. 14. Dust properties of the z-GAL sample of sources derived using GMBB-Sizes versus MBB shown in red squares with the derived error bars. Sources denoted in black are some of the problematic sources that we treated with an extra step (discussed in Sect. 5.2). For comparison, in the background, we show the output results of the mock catalog when computing the dust parameters using MBB versus GMBB-Sizes. The black dotted line is the identity line. |
We find β to lie on the identity relation when using either method with a slight systematic shift when β ∼ 3 and a median β = 2.17 (βMBB = 2.16), which underlines once more the robustness of the z-GAL sampling in constraining the value of β. As expected, the dust temperatures are higher when using the GMBB with ΔTdust = 5 − 15 K where the median 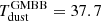 K (7.7 K higher than
K (7.7 K higher than 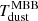 ). With the data in hand, we cannot confirm that the derived temperatures using GMBB are correct until the source size is known. Consequently, the difference in the derived dust temperatures affects the estimated dust masses as shown in the third panel of Fig. 14, where the MBB-derived Mdust are lower than the GMBB-derived ones. Finally, we find that the inferred apparent dust luminosities are in very good agreement between MBB and GMBB-Sizes.
). With the data in hand, we cannot confirm that the derived temperatures using GMBB are correct until the source size is known. Consequently, the difference in the derived dust temperatures affects the estimated dust masses as shown in the third panel of Fig. 14, where the MBB-derived Mdust are lower than the GMBB-derived ones. Finally, we find that the inferred apparent dust luminosities are in very good agreement between MBB and GMBB-Sizes.
Similar to the mock output results, our sources show a flat distribution when setting the size as a free parameter with R(output) varying between 3 and 4.5 kpc for most sources. In Fig. 15, we plot the derived λthick values using the output parameters we fit for our SEDs, and we find that it varies between 25 and 75 μm for most sources, but with very low precision resulting from a flat distribution in the derived source sizes. As we find similar trends between the mock and the z-GAL sources, we cannot distinguish whether our sources are optically thick or thin until we have new high-angular resolution data that will constrain their sizes.
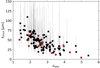 |
Fig. 15. Distribution of derived λthick values using Eq. (7) and the output results of GMBB-Sizes as a function of redshift for the z-GAL sample of galaxies. In red, we show the problematic sources (see Sect. 5.2). |
A decreasing trend with redshift is also observed –although statistically insignificant because of the large uncertainties– which appears to be influenced by the trend in β values. λthick is dependent on three free parameters (see Eq. (7)), namely the dust mass, which does not exhibit a clear evolution with redshift (slope = − 0.05 ± 0.026); the source size, which shows a flat distribution with a rather constant value; and the dust emissivity index (β) with a slight slope of −0.3 ± 0.014. However, this trend cannot be regarded as real because the source size is not actually constant for all sources. Additionally, the mock results show no clear evidence of the evolution of λthick either.
6. Discussion
In the previous sections, we estimate the dust properties using the optically thin MBB of the z-GAL sample of galaxies, which covers a wide range of redshifts from 1.3 to 6. We also explore the general opacity model that has shown that additional information is needed (i.e., the source size) in order to be certain about the dust parameters. In this section, we focus on the results of the MBB and compare them to other samples found in the literature. We first present a comparison of the dust masses and FIR luminosities of the z-GAL sample with sources similarly selected from the literature in Sect. 6.1. In Sect. 6.2, we discuss the dust emissivity indices derived in Sect. 4. In Sect. 6.3, the dust temperature evolution derived for the z-GAL sample is estimated. Finally, in Sect. 6.4, we discuss the β − Tdust relation.
6.1. Dust masses and far-infrared luminosities
We compare the dust parameters of the z-GAL sample with those of 37 gravitationally lensed galaxies selected by Bendo et al. (2023) from the BEARS sample (Urquhart et al. 2022). BEARS sources, similarly to the z-GAL HerBS sources, were selected from the same Herschel catalog (Bakx et al. 2018), with S500 μm > 80 mJy, and have continuum flux density measurements in the FIR/submm wavelength range including 250, 350, and 500 μmHerschel-SPIRE, SCUBA-2 850 μm data, and two millimeter measurements at 101 and 151 GHz (≥5σ detections). The sources have spectroscopic redshifts in the range 1.5 < z < 4.5. Bendo et al. (2023) report dust emissivity indices and dust temperature values derived by fitting a MBB using a similar method to ours; for consistency, we refit the BEARS sources to include the dust masses and dust luminosities in our comparison. In Fig. 16, we show the distribution of the apparent dust masses and inferred FIR luminosities across different redshifts, which demonstrates the Malmquist bias for the selection at 500 μm, which approximately samples the peak. The BEARS sources follow the same trend as the z-GAL sources, as expected given that they were selected in a similar way to the z-GAL sources. At this stage, we cannot say much about the intrinsic trends due to gravitational lensing effects, which will change the intrinsic relation depending on the magnification factors that are still unknown for both the z-GAL and BEARS samples.
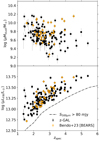 |
Fig. 16. Evolution of z-GAL apparent dust mass (upper panel) and apparent FIR luminosity (lower panel) with redshift for the optically thin MBB, shown in black squares. The BEARS sample (Bendo et al. 2023) is over-plotted in orange diamonds. In the lower panel, the black dashed line shows the lower limit resulting from the 500 μm flux density selection. |
6.2. Dust emissivity index β
In addition to the BEARS sample, we compare the results from z-GAL to the dust emissivities derived by Cooper et al. (2022) for the bright 850 μm-selected sample of 39 sources (SSA) for which AzTEC 1.1 mm and ALMA 2 mm flux densities are available with reported detections at S/N > 3 (and a few non-detections). It is important to mention that our comparison to the SSA sample (throughout the discussion) is restricted to the dust emissivity results, as only photometric redshifts (1.2 < zphot < 4.7) are available.
Our findings show a distribution of β of the z-GAL sample that varies between roughly 1.5 and 3 for the majority of the sources, with an average uncertainty of 0.25 and 0.3 using the MBB and GMBB, respectively. However, we derived unusually high dust emissivities, β ≥ 3, for a total of five sources, which is not common in the literature. While degeneracies exist in the MBB fit in the presence of noise and lack of data, the millimeter coverage of NOEMA has demonstrated that we can reach high precision in estimating β and thus lift this degeneracy; in particular, we find that there are only slight to no differences in the β estimates when fitting with either MBB or GMBB (see Fig. 14). Intrinsic degeneracy could also be affecting β, depending on the grain type or composition and its environment (see our discussion on the β − Tdust relation in Sect. 6.4).
In Fig. 17, we plot the dust emissivity indices as a function of redshift, which agree with the BEARS sample between redshifts 2 and 4. The SSA sample β estimates follow a similar distribution to those of the z-GAL sources, apart from a few sources with very large uncertainties. In general, we note that we do not find an evolution of β; for the sources in the populated redshift range (2 < z < 3), the dust emissivities follow a similar variation to the total sample. With all three samples across a wide redshift range, dusty galaxies tend to show a wider distribution of β values than the range generally assumed in the literature (1.5 < β < 2, e.g., Magnelli et al. 2012; Scoville et al. 2016) based on the Milky Way estimates.
 |
Fig. 17. Dust emissivity index (β) derived using MBB as a function of redshift of the z-GAL sample in black squares, Bendo et al. (2023) BEARS sample in orange diamonds, and Cooper et al. (2022) SSA sample in red circles. |
The dust emissivity index could potentially provide information about the dust grain composition and/or size (e.g., Ysard et al. 2019). However, at this stage, this may be an over-interpretation of the results, because the MBB model is a simplification of the true dust emission, which is spatially heterogeneous and more complex. Nevertheless, the findings reported suggest that we cannot limit β to 2 because of the possible variety of grain properties. Moreover, steeper dust emissivities could be due to growth of icy mantles on dust grains. Aannestad (1975) found that silicate grains coated with icy mantles could have β ∼ 3 and could reach as high as 3.5. Kuan et al. (1996) also reported a high dust emissivity measured for Sgr B2 (β = 3.7 ± 0.7) fitted to the millimeter data.
6.3. Dust temperature Tdust
The distribution of the z-GAL dust temperatures –derived using MBB and as a function of redshift– is shown in Fig. 18, which exhibits an increasing trend with redshift. Fitting a linear model accounting for intrinsic scatter, Tdust = az + b + ϵ, we find a = 6.5 ± 0.5 K/z and 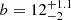 K with a minimal intrinsic scatter of
K with a minimal intrinsic scatter of 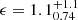 K/z3. A similar trend is found for the temperatures derived with the GMBB, but shifted ∼7 K higher. The shaded region in Fig. 18, representing the 500 μm selection effect on dust temperatures, shows no clear evidence of bias towards the trend.
K/z3. A similar trend is found for the temperatures derived with the GMBB, but shifted ∼7 K higher. The shaded region in Fig. 18, representing the 500 μm selection effect on dust temperatures, shows no clear evidence of bias towards the trend.
 |
Fig. 18. z-GAL MBB dust temperatures as a function of redshift shown in gray squares with their respective uncertainties. Best-fit slope estimated for the MBB is plotted with a solid black line and for GMBB with a dotted black line with the confidence interval shaded in blue. The median binned temperatures are plotted in black circles up to redshift z = 4 with a bin size of Δz = 0.5. The selection effect is shown with a gray shaded region. For comparison, we over-plot the BEARS-derived MBB dust temperatures by Bendo et al. (2023) shown as orange diamonds. Evolutionary trends from the literature are also plotted in purple (Viero et al. 2022), in red (Schreiber et al. 2018, extrapolated to z = 6), and in green (Magnelli et al. 2014, extrapolated to z = 6). |
In general, our result agrees with the increasing Tdust versus z evolutionary trends, which are attributed to higher specific star formation rates (sSFRs) at higher redshift (Liang et al. 2019; Magdis et al. 2012). However, the rate we find for this evolution is steeper than that found by Magnelli et al. (2014, for main sequence galaxies) and Schreiber et al. (2018, for Herschel-like galaxy models), but is comparable to that found by Viero et al. (2022, for the stacked COSMOS galaxies) between redshifts 2 and 4 (see Fig. 18). Moreover, all three trends show temperatures that are ∼7 − 10 K higher than the z-GAL ones at lower redshifts. Although more compatible with the GMBB intercept, all three samples used the optically thin approximation to estimate dust temperatures. Schreiber et al. (2016) demonstrated that more massive star-forming galaxies tend to have lower dust temperatures at lower redshifts as compared to main sequence galaxies, suggesting that they are undergoing a decline in star-formation activity.
On the other hand, there is contradictory evidence in the literature of a lack of evolution of dust temperatures over cosmic time. Drew & Casey (2022) argue that dust temperatures do not evolve, based on samples from IRAS, H-ATLAS, and COSMOS surveys at z = 0 − 2. Similarly, Reuter et al. (2020) do not provide any conclusive evidence about the evolution trend for the SPT sample of 81 gravitationally lensed galaxies selected in the millimeter (S1.4 μm > 20 mJy and S870 μm > 25 mJy) that cover the redshift range between 1.9 and 6.9. It is also argued that selection effects could induce an increasing trend that limits observations to the brightest galaxies, especially at higher redshifts (e.g., Dudzevičiūtė et al. 2020; Riechers et al. 2020). The strong cut on the luminosity induced by the 500 μm selection of the z-GAL sources (as shown in Fig. 16) could explain the observed increasing trend in Tdust following the temperature–luminosity relation (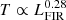 and
and 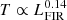 , as shown by Chapman et al. 2005; Casey et al. 2012, respectively). However, this needs to be further checked after obtaining the magnification factors for the z-GAL galaxies.
, as shown by Chapman et al. 2005; Casey et al. 2012, respectively). However, this needs to be further checked after obtaining the magnification factors for the z-GAL galaxies.
Due to the various aspects that influence the dust temperature estimates, such as the fitting method (e.g., MBB, GMBB-Sizes, GMBB-Lambda) and observational limits, which make each sample significantly different, we intend to compare our results to other samples (e.g., Béthermin et al. 2015; Zavala et al. 2018; Reuter et al. 2020; Sommovigo et al. 2020) in a forthcoming paper. This will help us to identify the main cause, or causes, of the differences, which cannot be achieved using a homogeneous flux-generated catalog that does not represent the real galaxy emission.
6.4. β − Tdust relation
In Fig. 19, we show the distribution of dust emissivity β versus dust temperature for the z-GAL sample derived from the optically thin MBB in Sect. 4. We see a clear anti-correlation between the two parameters. It has been argued that there is an intrinsic relation between β and Tdust (e.g., Désert et al. 2008; Paradis et al. 2010; Smith et al. 2012; Juvela et al. 2013; Kirkpatrick et al. 2014; Cortese et al. 2014), which was also found in laboratory experiments using interstellar grain analogs (Agladze et al. 1996; Mennella et al. 1998). We derive an empirical relation between the two parameters described by the following equation:
 |
Fig. 19. β − Tdust distribution for the z-GAL sources (black squares) compared to the BEARS sources (orange diamonds; Bendo et al. 2023). The solid black line is the fitted relation we find for the z-GAL sources with α = 0.69 ± 0.04 (see Sect. 6.4) and the shaded region is the confidence level. We over-plot the trend found by Yang & Phillips (2007) for local LIRGs in black dashed line. The 1σ level distribution of the MCMC chains is represented by the red contours for a few sources, that demonstrate a high level constraint. The lighter pink contour demonstrates one of the few cases where the 1σ level shows large degeneracy. |
We find α = 0.69 ± 0.04 for the z-GAL sources, which is shallower than the one found by Yang & Phillips (2007; α = 1.07) estimated for a sample of 18 local luminous infrared galaxies (LIRGs). We over-plot the results found for the BEARS sample, which also follow a very similar trend to ours. We note that our fitting method did not introduce any bias towards the trend (a systematic study was performed by Juvela et al. 2013, who show that both the fitting method and the noise increase the degeneracy between β and Tdust). Using the mock catalog, we found a uniform distribution in the resulting β − Tdust parameter space, resulting from the fact that our mock catalog is uniformly distributed over a grid with no prior relations between parameters.
Additionally, we checked the 1σ contours of the z-GAL sources (a few of the contours are shown in red in Fig. 19) and we find that for the bulk of them, the degeneracy is very minimal; it only becomes evident for sources with noisy (or poor-quality) continuum data or when the peak is a poorly sampled (e.g., HeLMS-19), but such cases do not dominate our sample. Fitting this relation to the well-constrained sample (a total of 27 sources), where the relative uncertainties are within 10%, yields a result of α = 0.57 ± 0.09, which falls within the confidence range. The underlying nature of the β − Tdust relation, whether it is physical or is a result of parameter degeneracy, remains an open question. Previous studies used a hierarchical Bayesian fitting method (e.g., Kelly et al. 2012; Juvela et al. 2013; Lamperti et al. 2019), which resulted in a significantly reduced degeneracy. However, these studies focused on datasets with limited millimeter data that cover the RJ tail. In the case of z-GAL, the rich sampling along the RJ tail provides better constraints and larger weights on the derived β values, which reduces the necessity for more complex statistical approaches.
The β − Tdust relation has been studied in more detail in our Galaxy (e.g., Juvela et al. 2011; Planck Collaboration XXIII 2011; Planck Collaboration Int. XVII 2014). The value of α could carry physical information about the cloud metallicity (Cortese et al. 2014), and could also explain the physical conditions that dust grains are exposed to in different parts of the galaxy (such as heating in star-forming clouds in the outskirts of a galaxy; Smith et al. 2012). However, it is challenging to retrieve the properties of the environments where the dust grains are located at this stage in the z-GAL sources, and more in-depth studies are needed to confirm the extreme dust emissivities.
7. Summary and conclusions
In this paper, we present the continuum dust properties of 125 galaxies selected from the z-GAL sample that cover the redshift range 1.3 < z < 5.4 and are centered around z ∼ 2 − 3 at the peak epoch of cosmic SFR density. To explore how the derivation of the dust parameters is influenced by the data that are available along the SED from the FIR to the millimeter wavelengths, we performed an in-depth mock-data analysis using both the general opacity and optically thin approximation modified blackbody models. Our principal findings and conclusions are as follows:
-
We demonstrate the unique wavelength sampling of the z-GAL sample of galaxies in the FIR/submm regime through a detailed mock analysis. The Herschel-SPIRE flux densities, together with the SCUBA-2 850 μm data, when available, which sample roughly the peak of the SED, and the NOEMA 2 and 3 mm fluxes, which sample the RJ tail, allowed us to constrain the dust properties β, Tdust, and Mdust with great precision.
-
The dust emissivity index is derived with high confidence based on the sampling of an average of five NOEMA flux densities along the RJ tail. β estimates show no change (within error bars) when using either the optically thin approximation or the general opacity modified blackbody, even though the dust temperatures vary from one model to the other. We report an average value of β = 2.2 ± 0.3 and a range of between roughly 1.5 and 3 with relative uncertainties that vary in the range 7% − 15%. This range is wider than previous Milky Way estimates (β = 1.5 − 2); however, it coincides with more recent DSFG studies (Cooper et al. 2022).
-
We find an average
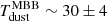 K and
K and 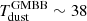 K when fitting with a MBB and a GMBB, respectively. Although the temperature estimate is decoupled from the uncertainties on β, this parameter is still dependent on the optical depth assumptions. Our mock analysis shows that accurate Tdust values can be estimated using GMBB with a measured source size. While many studies are based on the use of λthick, the wavelength at which the optical depth reaches unity, the results remain degenerate with Tdust and could overestimate the dust temperatures by ∼20%. Consequently, the change in Tdust affects the Mdust estimates, leading to an overestimation that varies between 10%−75% depending on the opacity model assumed.
K when fitting with a MBB and a GMBB, respectively. Although the temperature estimate is decoupled from the uncertainties on β, this parameter is still dependent on the optical depth assumptions. Our mock analysis shows that accurate Tdust values can be estimated using GMBB with a measured source size. While many studies are based on the use of λthick, the wavelength at which the optical depth reaches unity, the results remain degenerate with Tdust and could overestimate the dust temperatures by ∼20%. Consequently, the change in Tdust affects the Mdust estimates, leading to an overestimation that varies between 10%−75% depending on the opacity model assumed. -
We find an anti-correlation between β and Tdust following the trend
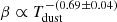 . The flux-generated mock catalog shows that this relation is induced neither by the sample selection nor the fitting method. This confirms that the relation is intrinsic, as shown previously by Juvela et al. (2013). The relationship between β and Tdust has direct implications on the nature of dust grains and the physical environment to which they are exposed.
. The flux-generated mock catalog shows that this relation is induced neither by the sample selection nor the fitting method. This confirms that the relation is intrinsic, as shown previously by Juvela et al. (2013). The relationship between β and Tdust has direct implications on the nature of dust grains and the physical environment to which they are exposed. -
We find an evolution of the dust temperature with redshift given by
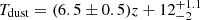 K. However, this trend cannot represent the entire galaxy population, because the z-GAL sample is flux limited. A deeper sample, covering a large redshift range, will be needed to complement the bright zGAL and BEARS Herschel-selected sources in order to verify this evolutionary trend across cosmic time. This study will be presented in a following paper.
K. However, this trend cannot represent the entire galaxy population, because the z-GAL sample is flux limited. A deeper sample, covering a large redshift range, will be needed to complement the bright zGAL and BEARS Herschel-selected sources in order to verify this evolutionary trend across cosmic time. This study will be presented in a following paper. -
Due to potential gravitational lensing, the dust masses and inferred luminosities are only apparent values. However, once the magnification factor is derived, we will be able to add the intrinsic properties for the lensed sources in the z-GAL sample, and compare them with those of other samples for which this information is available in order to further explore the nature of the dust grains and their evolution across cosmic time.
This work has highlighted the robustness of the z-GAL flux sampling from the FIR to the millimeter regime in determining dust properties, particularly the dust emissivity index β, whose value could vary significantly from the Milky Way range, leading to biased dust temperature estimates. The results from our mock analysis indicate that the accurate measurement of dust temperatures requires estimates of the source sizes with high-resolution imaging of the continuum, and that this will result in a well-constrained dust mass. Future work will focus on exploring the evolution of the dust temperature across cosmic time and comparing the z-GAL sample with other similar samples of high-z dusty star-forming galaxies in order to further explore the cause or causes of the differences, which cannot be well understood with a flux-generated mock catalog.
In the case of GMBB-Lambda, Mdust is not a parameter used in the fit, but is estimated afterwards. We use Eq. (7) to calculate the dust masses using the derived parameters (λthick, β, Mdust, and area (A)).
Acknowledgments
This work is based on observations carried out under project numbers M18AB and, subsequently D20AB, with the IRAM NOEMA Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). The authors are grateful to IRAM for making this work possible and for the continuous support that we received over the past four years to make this large program a success. The authors are also grateful to the IRAM director for approving the DDT proposal that enabled to complete the survey. This work benefited from the support of the project Z-GAL ANR-AAPG2019 of the French National Research Agency (ANR). The anonymous referee is thanked for providing useful comments that helped to improve the contents of this paper. The authors would like to thank I. Cortzen and Cynthia Herrera for their contributions in the early stages of this project and recognise the essential work of the z-GAL Cat-Team and Tiger-Team, who performed the reduction, calibration and delivery of the z-GAL data. D.I. extends her heartfelt appreciation to Alfred Gulum for being a pillar of support. A.J.B. and A.J.Y acknowledge support from the National Science Foundation grant AST-1716585. A.N. acknowledges support from the Narodowe Centrum Nauki (UMO-2020/38/E/ST9/00077). D.A.R. acknowledges support from the National Science Foundation under grant numbers AST-1614213 and AST-1910107 and from the Alexander von Humboldt Foundation through a Humboldt Research Fellowship for Experienced Researchers. SS was partly supported by the ESCAPE project. ESCAPE – The European Science Cluster of Astronomy & Particle Physics ESFRI Research Infrastructures has received funding from the European Union’s Horizon 2020 research and innovation program under Grant Agreement no. 824064. C.Y. acknowledges support from ERC Advanced Grant 789410. H.D. acknowledges financial support from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (AEI-MCINN) under grant (La evolución de los cíumulos de galaxias desde el amanecer hasta el mediodía cósmico) with reference (PID2019-105776GB-I00/DOI:10.13039/501100011033) and acknowledge support from the ACIISI, Consejería de Economía, Conocimiento y Empleo del Gobierno de Canarias and the European Regional Development Fund (ERDF) under grant with reference PROID2020010107. T.B. acknowledges support from NAOJ ALMA Scientific Research Grant Nos. 2018-09B and JSPS KAKENHI No. 17H06130, 22H04939, and 22J21948. A.N. acknowledges support from INAF – Osservatorio astronomico d’Abruzzo Via maggini SNC 64100 Teramo. RJI acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311.
References
- Aannestad, P. A. 1975, ApJ, 200, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Agladze, N. I., Sievers, A. J., Jones, S. A., Burlitch, J. M., & Beckwith, S. V. W. 1996, ApJ, 462, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Eales, S. A., Negrello, M., et al. 2018, MNRAS, 473, 1751 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Eales, S. A., Negrello, M., et al. 2020, MNRAS, 494, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Sommovigo, L., Carniani, S., et al. 2021, MNRAS, 508, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Urquhart, S. A., Serjeant, S., et al. 2023, MNRAS, 522, 2995 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A&A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Young, A. J., Cox, P., et al. 2021, A&A, 646, A122 [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Stanley, F., Ismail, D., et al. 2023, A&A, 678, A28 (Paper III) [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [Google Scholar]
- Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., & Kneib, J. P. 1999, MNRAS, 302, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J. P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., van Dokkum, P. G., et al. 2021, AJ, 162, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Giovannoli, E., Burgarella, D., et al. 2010, MNRAS, 409, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]
- Casey, C. M., Berta, S., Béthermin, M., et al. 2012, ApJ, 761, 139 [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
- Casey, C. M., Zavala, J. A., Aravena, M., et al. 2019, ApJ, 887, 55 [Google Scholar]
- Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Clements, D. L., Sutherland, W. J., McMahon, R. G., & Saunders, W. 1996, MNRAS, 279, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Cooray, A., Vieira, J. D., et al. 2011, ApJ, 732, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, O. R., Casey, C. M., Zavala, J. A., et al. 2022, ApJ, 930, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Fritz, J., Bianchi, S., et al. 2014, MNRAS, 440, 942 [Google Scholar]
- Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A&A, 634, L14 [EDP Sciences] [Google Scholar]
- Cox, P., Neri, R., Berta, S., et al. 2023, A&A, 678, A26 (Paper I) [Google Scholar]
- da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
- da Cunha, E., Hodge, J. A., Casey, C. M., et al. 2021, ApJ, 919, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, F. X., Macías-Pérez, J. F., Mayet, F., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
- Drew, P. M., & Casey, C. M. 2022, ApJ, 930, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2020, MNRAS, 494, 3828 [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2021, MNRAS, 500, 942 [Google Scholar]
- Dupac, X., Bernard, J. P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L., Fudamoto, Y., Oesch, P. A., et al. 2020, MNRAS, 498, 4192 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [Google Scholar]
- Hodge, J. A., & da Cunha, E. 2020, R. Soc. Open Sci., 7, 200556a [CrossRef] [Google Scholar]
- Hodge, J., Riechers, D. A., Decarli, R., et al. 2015, Am. Astron. Soc. Meet. Abstr., 225, 251.11 [NASA ADS] [Google Scholar]
- Hodge, J. A., Swinbank, A. M., Simpson, J. M., et al. 2016, ApJ, 833, 103 [Google Scholar]
- Hodge, J. A., Smail, I., Walter, F., et al. 2019, ApJ, 876, 130 [Google Scholar]
- Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pelkonen, V. M., et al. 2011, A&A, 527, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Montillaud, J., Ysard, N., & Lunttila, T. 2013, A&A, 556, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelly, B. C., Shetty, R., Stutz, A. M., et al. 2012, ApJ, 752, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
- Kirkpatrick, A., Calzetti, D., Kennicutt, R., et al. 2014, ApJ, 789, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Kreysa, E., Gemünd, H. P., Gromke, J., et al. 1999, Infrared Phys. Technol., 40, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Kuan, Y.-J., Mehringer, D. M., & Snyder, L. E. 1996, ApJ, 459, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lamperti, I., Saintonge, A., De Looze, I., et al. 2019, MNRAS, 489, 4389 [Google Scholar]
- Liang, L., Feldmann, R., Kereš, D., et al. 2019, MNRAS, 489, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, V., Brucato, J. R., Colangeli, L., et al. 1998, ApJ, 496, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M. J. 2015, A&A, 577, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, A., Burgarella, D., Theulé, P., Côté, B., & Hirashita, H. 2020, A&A, 641, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nayyeri, H., Keele, M., Cooray, A., et al. 2016, ApJ, 823, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Neri, R., Cox, P., Omont, A., et al. 2020, A&A, 635, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2011, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reuter, C., Vieira, J. D., Spilker, J. S., et al. 2020, ApJ, 902, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Riechers, D. A., Leung, T. K. D., Ivison, R. J., et al. 2017, ApJ, 850, 1 [Google Scholar]
- Riechers, D. A., Hodge, J. A., Pavesi, R., et al. 2020, ApJ, 895, 81 [Google Scholar]
- Riechers, D. A., Cooray, A., Pérez-Fournon, I., & Neri, R. 2021, ApJ, 913, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Broadhurst, T., Lawrence, A., et al. 1991, Nature, 351, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Efstathiou, A., Lawrence, A., et al. 1993, MNRAS, 261, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Rujopakarn, W., Dunlop, J. S., Rieke, G. H., et al. 2016, ApJ, 833, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2016, A&A, 589, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N. Z. 2013, in Secular Evolution of Galaxies, eds. J. Falcón-Barroso, & J. H. Knapen (Cambridge University Press), 491 [CrossRef] [Google Scholar]
- Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009, ApJ, 696, 2234 [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015, ApJ, 807, 128 [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2017, ApJ, 839, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Eales, S. A., Gomez, H. L., et al. 2012, ApJ, 756, 40 [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 497, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Carniani, S., et al. 2022, MNRAS, 517, 5930 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Marrone, D. P., Aravena, M., et al. 2016, ApJ, 826, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Simpson, J. M., Smail, I., et al. 2014, MNRAS, 438, 1267 [Google Scholar]
- Urquhart, S. A., Bendo, G. J., Serjeant, S., et al. 2022, MNRAS, 511, 3017 [CrossRef] [Google Scholar]
- Viero, M. P., Sun, G., Chung, D. T., Moncelsi, L., & Condon, S. S. 2022, MNRAS, 516, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, B. A., Eales, S. A., Pons, E., et al. 2022, MNRAS, 510, 2261 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, M., & Phillips, T. 2007, ApJ, 662, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Koehler, M., Jimenez-Serra, I., Jones, A. P., & Verstraete, L. 2019, A&A, 631, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zavala, J. A., Aretxaga, I., Dunlop, J. S., et al. 2018, MNRAS, 475, 5585 [Google Scholar]
Appendix A: z-GAL NOEMA continuum flux densities
Millimeter continuum flux densities of the z-GAL sources (extract only(1)).
Appendix B: Dust continuum properties
Dust continuum properties of the 125 z-GAL sources derived using the optically thin modified blackbody in Section 4. The best-fit values indicate the 50th percentile and their corresponding uncertainties; i.e., the 16th and 84th percentiles of the posterior likelihood distribution. μ is the magnification factor for the gravitationally lensed sources. (Only extract(1))
Appendix C: z-GAL sources spectral energy distribution
 |
Fig. C.1. Spectral energy distributions of the HeLMS sources. The observed flux densities that are used in the computation of the dust properties are shown as black dots and the error bars correspond to their 1σ uncertainties. We also plot the millimeter flux densities at which the wavelength is above 1000 μm in rest-frame as open red circles and the flux densities at which the rest-frame wavelength is below 50 μm as open green circles. The solid gray line is the MBB best fit and the orange lines are the output sampling of 100 random walks from the EMCEE output. The names of the sources and their spectroscopic redshifts are given in the lower right corner of each panel. |
 |
Fig. C.1. continued, for the HerS sources. |
 |
Fig. C.1. continued, for the HerBS sources. |
 |
Fig. C.1. continued, for the Pilot Program sources. |
Appendix D: MBB redshift-binned results
Appendix E: GMBB details
 |
Fig. E.1. Same as Fig. 10 but binned to where the medium becomes optically thin at lower wavelengths (λthick < 100 μm). This shows that GMBB-Sizes (first row) estimates the output parameters with good accuracy, as does the MBB (third row), but that GMBB-Lambda (second row) will always overestimate the dust temperatures within this range of λthick. |
 |
Fig. E.2. Same as Fig. 10 but binned to where the medium becomes optically thick at higher wavelengths(λthick > 100 μm). This shows us that the optically thin method will always underestimate the dust temperatures and consequently Mdust. On the other hand, both versions of the GMBB are able to retrieve (on average) the true dust parameters within this range of λthick. |
Appendix F: z-GAL sources posterior distribution
 |
Fig. F.1. β − Tdust posterior distribution plots for sources whose δβ/β > 15%. The yellow names represent sources at z > 4, the blue names are sources at z < 2, and black names are sources at 2 ≤ z ≤ 4. |
 |
Fig. F.2. Corner plot of HeLMS-48 demonstrating the posterior likelihood distribution of estimated parameters using GMBB-Sizes and the SED fit. In the corner plot, the vertical lines represent the 16th, 50th, and 84th percentiles, respectively. The flux densities are shown as black dots in the SED, and the black line is the best fit. |
 |
Fig. F.3. Posterior distribution of β as estimated when using the measured flux densities (which include those that are upper limits) along the RJ tail in black and when removing them in red, for eight sources whose β≥ 3. This shows that the large β estimate is not biased by the use of measured flux densities of non-detections. |
All Tables
Dust continuum properties of the 125 z-GAL sources derived using the optically thin modified blackbody in Section 4. The best-fit values indicate the 50th percentile and their corresponding uncertainties; i.e., the 16th and 84th percentiles of the posterior likelihood distribution. μ is the magnification factor for the gravitationally lensed sources. (Only extract(1))
All Figures
 |
Fig. 1. Redshift distribution of the galaxies used in this study, which includes 125 out of the 137 sources from the z-GAL sample. In our analysis, we exclude multiples at different redshifts in the field of view observed by NOEMA, which are unresolved in the Herschel field of view, as well as problematic sources (see details in Sect. 2.2). |
| In the text | |
 |
Fig. 2. NOEMA spectral coverage and bandwidth of the 2 and 3 mm bands for the source HeLMS-1 at z = 1.905. The ten alternating colors are the lower and upper sidebands for each setup. The black points show the flux density extracted in each band along with their uncertainties (very small error bars). The 12CO(4-3) and (2-1) emission lines detected in this source are identified in the figure. |
| In the text | |
 |
Fig. 3. Sampling and S/N of the flux densities of the z-GAL galaxies. Top panel: signal-to-noise ratio of the z-GAL data split into Herschel 250, 350, and 500 μm flux densities shown in indigo, which varies between 6 and 10; SCUBA-2 850 μm flux density, in orange, which varies between 1.5 and 7; and NOEMA 2 and 3 mm flux densities, which varies between 1 and 9, shown in black. Bottom panel: distribution of the number of millimeter flux data points available for each z-GAL source shown in gray; all sources have at least 2, and up to 10, measurements. The cyan histogram shows the number of millimeter measurements used in the fitting procedure (below 1 mm in the rest-frame; see Sect. 3) with a median of 5 data points sampling the Rayleigh-Jeans of the z-GAL sources. The indigo-lined histogram shows the number of data points with signal-to-noise ratio > 3. |
| In the text | |
 |
Fig. 4. Input (true) vs. output dust properties of the mock-generated catalog of sources. The black line is the identity line and the black dots show the median within the bins and the error bars represent the standard deviation in these bins. The boxes in the lower right corner describe the accuracy of the fitting method when using the optically thin MBB for this mock sample. |
| In the text | |
 |
Fig. 5. Corner plot of the posterior distribution and SED fit of a mock galaxy at redshift z = 4.29. The posterior distribution shows dust parameter estimates: (i) with five flux points in the millimeter domain with S/N > 3 in black, (ii) five flux points in the millimeter domain with S/N < 3 in red, and (iii) two flux points in the millimeter domain with S/N > 3 in teal; over-plotted in gray are the true values. |
| In the text | |
 |
Fig. 6. Coverage of the z-GAL sample flux densities as a function of the physical properties of a galaxy. Left: when varying the redshift, we lose peak sensitivity at lower redshifts, which limits the recovery of the true Tdust of the SED. Right: with an intrinsically higher Tdust, we lose peak sensitivity as well and we no longer recover the true temperature of the SED. |
| In the text | |
 |
Fig. 7. Root mean square of (output – true) Tdust distribution as a function of the estimated dust temperatures and redshift. |
| In the text | |
 |
Fig. 8. Distribution of the dust properties of the z-GAL sources derived from the MBB shown in gray. The median value of each parameter is plotted with a dashed line whose value is given in the upper right corner of each plot along with the median absolute deviation. The black contour histogram shows the distribution of each parameter within the redshift subset 2 < z < 4. |
| In the text | |
 |
Fig. 9. β − Tdust relation and precision in estimating these parameters. The black squares, blue diamonds, and yellow circles show the output for sources in the redshift ranges of 2 < z < 4, z < 2, and z > 4, respectively. |
| In the text | |
 |
Fig. 10. Ratio of output and true parameters to the true dust parameters of the GMBB mock-generated catalog of sources. The median within each bin is shown as a black filled square, an empty square, and an empty circle for the results fitted with GMBB-Sizes, GMBB-Lambda, and the MBB, respectively, with the error bars representing the standard deviation within each bin. With the z-GAL sampling, β is recovered very well with all methods. Fitting with GMBB-Sizes can overestimate the inferred luminosity by ∼10%–15% due to an unrecovered source size (see Sect. 5.1). Fitting with GMBB-Lambda can overestimate the dust temperatures by 10%−20% and consequently the dust masses become underestimated by up to 40%. When fitting with MBB, the dust temperatures can be underestimated by 20%−30% and consequently the dust masses become overestimated by up to 75%. |
| In the text | |
 |
Fig. 11. Corner plot of the posterior distribution and SED fit of a mock source at redshift z = 3.06. The posterior distribution shows dust parameter estimation using (i) GMBB-Sizes (green) and (ii) GMBB-Lambda (red), which are over-plotted with the true values in black. In this fit, λthick for GMBB-Sizes is estimated using Eq. (7) given the posterior distribution of the output parameters (β, Mdust and A), and Mdust distribution for GMBB-Lambda is also estimated with Eq. (7) using the posterior distribution of the output parameters (β, A = 4πR2, and λthick). |
| In the text | |
 |
Fig. 12. Effect of the source-size variation on SED fitting. Left: Effect of source size variation on the SED of a galaxy. Orange indicates the variation when the size R < 1 kpc, and a gradient of blues indicates the variation when R > 1 kpc. On the right side, we plot λthick (wavelength at which optical depth is unity) versus source size (R), color coded according to dust mass. These two figures show that for source sizes R < 1 kpc, there is a large effect on the peak of the SED, where the medium is optically thick, reaching higher values of λthick. |
| In the text | |
 |
Fig. 13. Output versus true λthick estimation. The left figure shows the accuracy of estimating λthick when using GMBB-Sizes to fit the SED, in which it is derived using Eq. (7). The right figure shows the accuracy of estimating λthick when using GMBB-Lambda to fit the SED, in which it is a free parameter in the equation. The black dashed line is the identity line and the black squares show the median within each bin. |
| In the text | |
 |
Fig. 14. Dust properties of the z-GAL sample of sources derived using GMBB-Sizes versus MBB shown in red squares with the derived error bars. Sources denoted in black are some of the problematic sources that we treated with an extra step (discussed in Sect. 5.2). For comparison, in the background, we show the output results of the mock catalog when computing the dust parameters using MBB versus GMBB-Sizes. The black dotted line is the identity line. |
| In the text | |
 |
Fig. 15. Distribution of derived λthick values using Eq. (7) and the output results of GMBB-Sizes as a function of redshift for the z-GAL sample of galaxies. In red, we show the problematic sources (see Sect. 5.2). |
| In the text | |
 |
Fig. 16. Evolution of z-GAL apparent dust mass (upper panel) and apparent FIR luminosity (lower panel) with redshift for the optically thin MBB, shown in black squares. The BEARS sample (Bendo et al. 2023) is over-plotted in orange diamonds. In the lower panel, the black dashed line shows the lower limit resulting from the 500 μm flux density selection. |
| In the text | |
 |
Fig. 17. Dust emissivity index (β) derived using MBB as a function of redshift of the z-GAL sample in black squares, Bendo et al. (2023) BEARS sample in orange diamonds, and Cooper et al. (2022) SSA sample in red circles. |
| In the text | |
 |
Fig. 18. z-GAL MBB dust temperatures as a function of redshift shown in gray squares with their respective uncertainties. Best-fit slope estimated for the MBB is plotted with a solid black line and for GMBB with a dotted black line with the confidence interval shaded in blue. The median binned temperatures are plotted in black circles up to redshift z = 4 with a bin size of Δz = 0.5. The selection effect is shown with a gray shaded region. For comparison, we over-plot the BEARS-derived MBB dust temperatures by Bendo et al. (2023) shown as orange diamonds. Evolutionary trends from the literature are also plotted in purple (Viero et al. 2022), in red (Schreiber et al. 2018, extrapolated to z = 6), and in green (Magnelli et al. 2014, extrapolated to z = 6). |
| In the text | |
 |
Fig. 19. β − Tdust distribution for the z-GAL sources (black squares) compared to the BEARS sources (orange diamonds; Bendo et al. 2023). The solid black line is the fitted relation we find for the z-GAL sources with α = 0.69 ± 0.04 (see Sect. 6.4) and the shaded region is the confidence level. We over-plot the trend found by Yang & Phillips (2007) for local LIRGs in black dashed line. The 1σ level distribution of the MCMC chains is represented by the red contours for a few sources, that demonstrate a high level constraint. The lighter pink contour demonstrates one of the few cases where the 1σ level shows large degeneracy. |
| In the text | |
 |
Fig. C.1. Spectral energy distributions of the HeLMS sources. The observed flux densities that are used in the computation of the dust properties are shown as black dots and the error bars correspond to their 1σ uncertainties. We also plot the millimeter flux densities at which the wavelength is above 1000 μm in rest-frame as open red circles and the flux densities at which the rest-frame wavelength is below 50 μm as open green circles. The solid gray line is the MBB best fit and the orange lines are the output sampling of 100 random walks from the EMCEE output. The names of the sources and their spectroscopic redshifts are given in the lower right corner of each panel. |
| In the text | |
 |
Fig. C.1. continued, for the HerS sources. |
| In the text | |
 |
Fig. C.1. continued, for the HerBS sources. |
| In the text | |
 |
Fig. C.1. continued, for the Pilot Program sources. |
| In the text | |
 |
Fig. D.1. Same as Fig. 4 but redshift-binned results of the mock catalog. |
| In the text | |
 |
Fig. E.1. Same as Fig. 10 but binned to where the medium becomes optically thin at lower wavelengths (λthick < 100 μm). This shows that GMBB-Sizes (first row) estimates the output parameters with good accuracy, as does the MBB (third row), but that GMBB-Lambda (second row) will always overestimate the dust temperatures within this range of λthick. |
| In the text | |
 |
Fig. E.2. Same as Fig. 10 but binned to where the medium becomes optically thick at higher wavelengths(λthick > 100 μm). This shows us that the optically thin method will always underestimate the dust temperatures and consequently Mdust. On the other hand, both versions of the GMBB are able to retrieve (on average) the true dust parameters within this range of λthick. |
| In the text | |
 |
Fig. F.1. β − Tdust posterior distribution plots for sources whose δβ/β > 15%. The yellow names represent sources at z > 4, the blue names are sources at z < 2, and black names are sources at 2 ≤ z ≤ 4. |
| In the text | |
 |
Fig. F.2. Corner plot of HeLMS-48 demonstrating the posterior likelihood distribution of estimated parameters using GMBB-Sizes and the SED fit. In the corner plot, the vertical lines represent the 16th, 50th, and 84th percentiles, respectively. The flux densities are shown as black dots in the SED, and the black line is the best fit. |
| In the text | |
 |
Fig. F.3. Posterior distribution of β as estimated when using the measured flux densities (which include those that are upper limits) along the RJ tail in black and when removing them in red, for eight sources whose β≥ 3. This shows that the large β estimate is not biased by the use of measured flux densities of non-detections. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



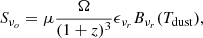
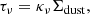
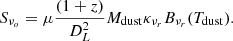
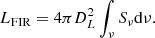
![$$ \begin{aligned} S_{\nu _o} = \mu \frac{A}{D_L^2} (1+z) \left( 1 - \exp \left[ - (\nu _r/\nu _0)^\beta \kappa _0 \frac{M_{\rm dust}}{A}\right]\right) B_{\nu _r}(T_{\rm dust}) ,\end{aligned} $$](/articles/aa/full_html/2023/10/aa46804-23/aa46804-23-eq11.gif)
![$$ \begin{aligned} S_{\nu _o} = \mu \frac{A}{D_L^2} (1+z) \left( 1 - \exp \left[ - (\nu _r/\nu _{\rm thick})^\beta \right]\right) B_{\nu _r}(T_{\rm dust}) ,\end{aligned} $$](/articles/aa/full_html/2023/10/aa46804-23/aa46804-23-eq12.gif)