| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | A154 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244790 | |
| Published online | 20 March 2023 | |
A full transit of v2 Lupi d and the search for an exomoon in its Hill sphere with CHEOPS★,★★
1
Observatoire astronomique de l’Université de Genève,
chemin Pegasi 51,
1290
Versoix,
Switzerland
e-mail: david.ehrenreich@unige.ch
2
Centre Vie dans l’Univers, Faculté des sciences de l’Université de Genève,
Quai Ernest-Ansermet 30,
1205
Geneva,
Switzerland
3
Astrobiology Research Unit, Université de Liège,
Allée du 6 Août 19C,
4000
Liège,
Belgium
4
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août 19C,
4000
Liège,
Belgium
5
Centre for Exoplanet Science, SUPA School of Physics and Astronomy, University of St Andrews,
North Haugh,
St Andrews KY16 9SS,
UK
6
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz,
Austria
7
Physikalisches Institut, University of Bern,
Sidlerstrasse 5,
3012
Bern,
Switzerland
8
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern,
Switzerland
9
Aix-Marseille Univ, CNRS, CNES, LAM,
38 rue Frédéric Joliot-Curie,
13388
Marseille,
France
10
ETH Zurich, Department of Physics,
Wolfgang-Pauli-Strasse 2,
8093
Zurich,
Switzerland
11
Cavendish Laboratory,
JJ Thomson Avenue,
Cambridge
CB3 0HE
UK
12
Université de Paris, Institut de physique du globe de Paris, CNRS,
1 Rue Jussieu,
75005
Paris,
France
13
Department of Astronomy, Stockholm University, AlbaNova University Center,
106 91
Stockholm,
Sweden
14
Instituto de Astrofísica e Ciencias do Espaco, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto,
Portugal
15
Instituto de Astrofísica de Canarias,
38200
La Laguna, Tenerife,
Spain ;
Departamento de Astrofísica, Universidad de La Laguna,
38206
La Laguna, Tenerife,
Spain
16
Institut de Ciencies de l’Espai (ICE, CSIC), Campus UAB,
Can Magrans s/n,
08193
Bellaterra,
Spain
17
Institut d’Estudis Espacials de Catalunya (IEEC),
Carrer del Gran Capità, 2,
08034
Barcelona,
Spain
18
Depto. de Astrofísica, Centro de Astrobiologia (CSIC-INTA), ESAC campus,
28692
Villanueva de la Cañada (Madrid),
Spain
19
Departamento de Fisica e Astronomia, Faculdade de Ciencias, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto,
Portugal
20
INAF, Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
21
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
22
Admatis,
5. Kandó Kálmán Street,
3534
Miskolc,
Hungary
23
Institute of Planetary Research, German Aerospace Center (DLR),
Rutherfordstraße 2,
12489
Berlin,
Germany
24
Science and Operations Department - Science Division (SCI-SC), Directorate of Science, European Space Agency (ESA), European Space Research and Technology Centre (ESTEC),
Keplerlaan 1,
2201 -
Noordwijk,
The Netherlands
25
Centre for Mathematical Sciences, Lund University,
Box 118,
221 00
Lund,
Sweden
26
Leiden Observatory, University of Leiden,
PO Box 9513,
2300
RA Leiden,
The Netherlands
27
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala,
Sweden
28
Dipartimento di Fisica, Universita degli Studi di Torino,
via Pietro Giuria 1,
10125
Torino,
Italy
29
Division Technique INSU, CS20330,
83507
La Seyne-sur-Mercedex,
France
30
Department of Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
31
Department of Physics, University of Warwick, Gibbet Hill Road,
Coventry
CV4 7AL,
UK
32
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
1121
Budapest,
Konkoly Thege Miklós út 15-17,
Hungary
33
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
34
IMCCE, UMR8028 CNRS, Observatoire de Paris, PSL Univ.,
Sorbonne Univ., 77 av. Denfert-Rochereau,
75014
Paris,
France
35
Institut d’astrophysique de Paris, UMR7095 CNRS, Université Pierre et Marie Curie,
98bis blvd. Arago,
75014
Paris,
France
36
Astrophysics Group, Keele University,
Staffordshire,
ST5 5BG,
UK
37
INAF, Osservatorio Astrofísico di Catania,
Via S. Sofia 78,
95123
Catania,
Italy
38
Institute of Optical Sensor Systems, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin,
Germany
39
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova,
Italy
40
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
D-10623
Berlin,
Germany
41
Institut für Geologische Wissenschaften, Freie Universität Berlin,
12249
Berlin,
Germany
42
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory,
9700
Szombathely,
Szent Imre h. u. 112,
Hungary
43
MTA-ELTE Exoplanet Research Group,
9700
Szombathely,
Szent Imre h. u. 112,
Hungary
44
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge,
CB3 0HA,
UK
45
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA 02138,
USA
46
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
77 Massachusetts Avenue,
Cambridge,
MA 02139,
USA
47
Noqsi Aerospace Ltd.,
15 Blanchard Avenue,
Billerica,
MA 01821,
USA
48
NASA Ames Research Center,
Moffett Field,
CA 94035,
USA
49
Department of Astrophysical and Planetary Sciences, University of Colorado,
Boulder,
CO 80309,
USA
Received:
22
August
2022
Accepted:
3
December
2022
The planetary system around the naked-eye star v2 Lupi (HD 136352; TOI-2011) is composed of three exoplanets with masses of 4.7, 11.2, and 8.6 Earth masses (M⊕). The TESS and CHEOPS missions revealed that all three planets are transiting and have radii straddling the radius gap separating volatile-rich and volatile-poor super-earths. Only a partial transit of planet d had been covered so we re-observed an inferior conjunction of the long-period 8.6 M⊕ exoplanet v2 Lup d with the CHEOPS space telescope. We confirmed its transiting nature by covering its whole 9.1 h transit for the first time. We refined the planet transit ephemeris to P = 107.1361−0.0022+0.0019 days and Tc = 2459009.7759−0.0096+0.0101 BJDTDB, improving by ~40 times on the previously reported transit timing uncertainty. This refined ephemeris will enable further follow-up of this outstanding long-period transiting planet to search for atmospheric signatures or explore the planet’s Hill sphere in search for an exomoon. In fact, the CHEOPS observations also cover the transit of a large fraction of the planet’s Hill sphere, which is as large as the Earth’s, opening the tantalising possibility of catching transiting exomoons. We conducted a search for exomoon signals in this single-epoch light curve but found no conclusive photometric signature of additional transiting bodies larger than Mars. Yet, only a sustained follow-up of v2 Lup d transits will warrant a comprehensive search for a moon around this outstanding exoplanet.
Key words: planets and satellites: detection / planets and satellites: individual: HD 136352 / planets and satellites: general
Undetrended and detrended light curves are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/671/A154
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Exoplanets with masses intermediate between that of terrestrial planets and icy giants are mysterious objects. Some, dubbed ‘rocky super-earths’, have bulk densities compatible with the composition of terrestrial planets (Mayor et al. 2011; Dressing et al. 2015) and could thus be scaled-up versions of Earth or Mercury (Valencia et al. 2006; Elkins-Tanton & Seager 2008; Dorn et al. 2019). Other, larger, objects have lower densities that are compatible with the presence of a volatile (ice or steam) or gas (hydrogen and helium) envelope. Depending on authors, these have been called ‘ocean-planets’, ‘volatile-rich super-earths’, ‘mini-neptunes’ or ‘sub-neptunes’ (Kuchner 2003; Léger et al. 2004; Santos et al. 2004; Grasset et al. 2009); the lack of a universally accepted designation illustrates their uncertain nature. These two groups of objects appear to be separated by a radius gap in the exoplanet population (Fulton et al. 2017, 2018), which indicates different histories (Owen & Wu 2017): formerly gas-or volatile-rich planets could have lost their envelopes via photo-evaporation or core-powered mass-loss to become volatile-poor planets (Venturini et al. 2020; Rogers et al. 2021). Alternatively, the latter could have formed intrinsically devoid of ice or gas.
The origin of rocky super-earths as a product of the evolution of sub-neptunes largely depends on the level of high-energy stellar irradiation received by the planets, which is driving the escape of their gaseous envelope (Lammer et al. 2003; Lecavelier Des Etangs 2007). However, the planet irradiation history is challenging to reconstruct and tricky to compare across different systems. In this respect, multi-planet systems are critically important; they give access to exoplanets with irradiation history that can be compared accurately. In addition, when planets in such system transit their stars, it becomes possible to measure their densities and surface gravities, and probe their atmospheres. This provides inestimable insights into their present-day composition and, by comparing them together, their past evolution (Lopez et al. 2012).
The system of three planets around the naked-eye star v2 Lupi (v2 Lup, also known as HD 136352, HR 5699 or TOI-2011; Udry et al. 2019) offers one of the best known opportunities for comparative studies of super-earth evolution. v2 Lupi is a close-by (14.7 pc), old (11.7 ± 2 Gyr) solar-type (G4V) star (see Table 2). Its three planets provide huge dynamics in terms of stellar irradiation, ranging from ~100 times the insolation of the Earth at planet b to ~5 times at planet d, which could have been spared by intense photoevaporation, 0.425 au away from its star (between Mercury and Venus in the Solar System), and still possess a low gas content of primordial origin (Delrez et al. 2021).
Interest in the v2 Lup system exploded when the Transiting Exoplanet Survey Satellite (TESS) detected transits by the two inner planets b and c (Kane et al. 2020). Planet b has an orbital period of 11.6 d and a mass of 4.72 ± 0.42 Earth masses (M⊕), while planet c is 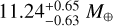 at 27.6 d, which is relatively long for a transiting planet. Kane et al. (2020) measured largely different densities of
at 27.6 d, which is relatively long for a transiting planet. Kane et al. (2020) measured largely different densities of 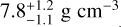 for b and
for b and 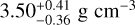 for c, placing these planets on opposite sides of the radius valley.
for c, placing these planets on opposite sides of the radius valley.
Delrez et al. (2021) followed up the transits of v2 Lup b and v2 Lup c with the Characterising Exoplanets Satellite (CHEOPS). Their observations (see their Figs. 1 and S1) serendipitously revealed a third transit-like event, attributed to planet d passing in front of the star altogether with planet c. This was a fortunate finding, because planet d – with a mass of 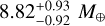 – has a 107 d period that made its transit unlikely to be seen. However, Delrez et al. (2021) showed that the transitlike event is compatible with the radial-velocity-based (hence, relatively loose) ephemeris for planet d, has a depth compatible with a planet of ~2.6 Earth radii (R⊕), and exhibits an in-transit curvature consistent with the known limb-darkening profile of the host star; all these elements are in favour of planet d being transiting in spite of an incomplete observation: CHEOPS stopped collecting data before the egress. As a result, the transit duration and mid-transit time are loosely constrained. This makes any follow-up attempts of this unusually long-period transiting planet risky, whilst the scarce opportunities are costly in observing time (the transit duration is estimated to be longer than 8 h). A robust ephemeris is sorely needed to achieve the follow-up v2 Lup d deserves.
– has a 107 d period that made its transit unlikely to be seen. However, Delrez et al. (2021) showed that the transitlike event is compatible with the radial-velocity-based (hence, relatively loose) ephemeris for planet d, has a depth compatible with a planet of ~2.6 Earth radii (R⊕), and exhibits an in-transit curvature consistent with the known limb-darkening profile of the host star; all these elements are in favour of planet d being transiting in spite of an incomplete observation: CHEOPS stopped collecting data before the egress. As a result, the transit duration and mid-transit time are loosely constrained. This makes any follow-up attempts of this unusually long-period transiting planet risky, whilst the scarce opportunities are costly in observing time (the transit duration is estimated to be longer than 8 h). A robust ephemeris is sorely needed to achieve the follow-up v2 Lup d deserves.
Here, we report on a second-epoch CHEOPS observation specifically designed to confirm the transit of v2 Lup d and to obtain precise transit parameters and a reliable ephemeris. The analysis of the observations (Sect. 2) shows a clear detection and confirmation of a complete transit of v2 Lup d, enabling us to derive a precise ephemeris and refine the planet properties (Sect. 3). Furthermore, this 8.6 M⊕ planet located relatively far from its host star has a Hill sphere similar in size to that of the Earth (Fig. 1), allowing for the presence of satellites that could transit alongside the planet. As our observations cover the full transit of the Hill sphere of v2 Lup d, we investigate the presence of moons in Sect. 4.
2 Observations and data reduction
2.1 New data
2.1.1 CHEOPS
CHEOPS (Benz et al. 2021) initially observed v2 Lup in its early science programme (CH_PR100041), which was part of the guaranteed time observations (GTO), from April to July 2020. v2 Lup d was first detected in transit on 9 June 2020 (Delrez et al. 2021). The first window of opportunity for a confirmation was in late April 2021. We scheduled a new CHEOPS visit from 24 April to 28 April 2021 to cover both the 3σ window on the transit-timing uncertainty and the transit of the planet Hill sphere, as part of the GTO programme CH_PR100031. The visit represents 56 CHEOPS orbits (3.85 days).
A total of 4 720 images were obtained; each image is a 200×200-pixel subarray resulting from the co-addition, performed on board, of 26 exposures of 1.7 s; one such image is obtained every 44.2 s. Images were processed by the CHEOPS data reduction pipeline (DRP v13.1.0; Hoyer et al. 2020). The DRP calibrates the raw images (event flagging, bias and gain corrections, linearisation, dark current, and flat-field corrections), corrects for environmental effects (smearing trails, jitter, background, and stray light), and performs a photometric extraction using several circular apertures (Hoyer et al. 2020), out of which we selected the default aperture size (25 pixels in radius), following Delrez et al. (2021). The output is the photometric time series reproduced in the upper panel of Fig. 2. Contamination of the photometric aperture by background stars is automatically estimated by the DRP and is typically small (0.027–0.031%) for these observations of v2 Lup. The resulting light curve features interruptions due to Earth occultations and passages throughout the South Atlantic Anomaly. The CHEOPS light curve has an RMS of 48 ppm (unbinned cadence of 44.2 s), 28 ppm (binned by 2 min), and 9 ppm (binned by 20 min).
2.1.2 TESS
TESS first observed v2 Lup during sector 12 of its primary mission, between 21 May 2019 and 18 June 2019. The transits of planets b and c were discovered in these observations (Kane et al. 2020), which did not cover an inferior conjunction of planet d. TESS observed the system again during cycle 3 in sector 38 of its extended mission, from 28 April to 26 May 2021. Both 2-min and 20-s cadence observations are available for this new sector, which covers two transits of planet b and one transit of planet c. However, these observations again did not cover a transit of planet d, according to the ephemeris of Delrez et al. (2021). The data were processed by the Science Processing Operations Center (SPOC) pipeline at NASA Ames Research Center (Jenkins et al. 2010, 2016). We retrieved the presearch data conditioning simple aperture photometry (PDC_SAP, Stumpe et al. 2012, 2014; Smith et al. 2012) from the Mikulski Archive for Space Telescopes (MAST1) and removed all data points for which the quality flag was not zero.
Huber et al. (2022) recently reported that TESS 20-s light curves show a ~10–25% improvement in photometric precision compared to the 2-min data for bright stars (T-mag ≲ 8), when binned to the same cadence. This is consistent with pre-flight expectations and related to differences in the cosmic-ray rejection algorithms applied to the 20-s and 2-min data. According to their Fig. 2, this improvement can even be as large as ~30% for very bright stars with T-mag~5, such as v2 Lup (T-mag = 5.05). Checking this for the v2 Lup PDC_SAP photometry, we indeed found a ~29% improvement when comparing the RMS of the 20-s light curve binned into 2-min intervals (103 ppm) with the one of the 2-min light curve (146 ppm). We thus decided to use the binned 20-s light curve in our analysis. This light curve consists of 18 482 data points and is shown in the top panel of Fig. 3.
 |
Fig. 1 Comparison of the sizes of the Hill spheres (dashed circles) for the three v2 Lup planets. Planet d is represented while transiting the star (ivory white disc). The respective orbital positions of the planets are not representative of their positions during the observations; only their transit impact parameters are considered. The Hill sphere radius of v2 Lup d (1.87 R★ or 0.0092 au or 9.1 h) is almost equal to the length of the planet transit chord. Because the Hill sphere of v2 Lup d is larger than the star, some parts of it (hatched areas) do not transit: a highly inclined exomoon in these regions, close to maximum apparent separation, could remain undetectable during this single visit. Such a distant moon would most likely be on a stable retrograde orbit, as these non-transiting regions are mostly beyond the stability limit for prograde (circular) orbits, represented at half the Hill sphere radius (Domingos et al. 2006) by the dotted circle. The diameters of the Hill spheres of Mercury, Venus, and Earth are shown for comparison; the location of the Moon within Earth’s Hill sphere is indicated. |
2.2 Archival data
To derive the strongest constraints on the system parameters, we also included the data previously published in Udry et al. (2019), Kane et al. (2020), and Delrez et al. (2021) in our combined analysis. These data sets are (i) the 246 radial velocities obtained between 27 May 2004 and 4 August 2017 with the HARPS spectrograph on ESO 3.6 m telescope (La Silla, Chile), (ii) the TESS 2-min-cadence photometry obtained during sector 12 of its primary mission (21 May-18 June 2019), covering two transits of planet b and one transit of planet c, and (iii) the six CHEOPS visits obtained between 4 April and 6 July 2020 and covering in total four transits of planet b (one of which is partial), three transits of planet c, and one partial transit of planet d. We refer to the studies cited above for more details about these data and their reduction. A log of the photometric observations can be found in Table 1.
3 Analysis
3.1 Stellar properties
We determined the radius of v2 Lup (Gaia EDR3 5902750168276592256) in a similar manner as in Delrez et al. (2021), using updated Gaia EDR3 photometry and parallax, which allowed us to refine the radius value compared to the literature. In brief, we used a Markov Chain Monte Carlo (MCMC) modified infrared-flux method (IRFM; Blackwell & Shallis 1977; Schanche et al. 2020) to compute the bolometric flux of the target by fitting Gaia, 2MASS, and WISE broadband photometry (Gaia Collaboration 2021; Skrutskie et al. 2006; Wright et al. 2010) with stellar atmospheric models (Castelli & Kurucz 2003) and converting the bolometric flux into stellar effective temperature and angular diameter. Using the offset-corrected Gaia EDR3 parallax (Lindegren et al. 2021), we determine the stellar radius of v2 Lup to be 1.054 ± 0.014 R⊙.
The stellar radius R★ together with the effective temperature Teff and metallicity [Fe/H] (Sousa et al. 2008; Delrez et al. 2021) constitute the basic input set to then derive the isochronal mass M★ and age t★, for which we employed two different stellar evolutionary models. A first pair of mass and age values was computed through the isochrone placement algorithm (Bonfanti et al. 2015, 2016) using its capability of fitting the input parameters to pre-computed grids of the Padova and Trieste stellar evolutionary code (PARSEC2; Marigo et al. 2017) isochrones and tracks. The stellar υ sin i was also added to the basic input set to improve the routine convergence as detailed in Bonfanti et al. (2016). To compute the second pair of mass and age values, we applied another code, namely the code liégeois d’évolution stellaire (CLES; Scuflaire et al. 2008). It uses the constraints given by the input parameters to produce the best-fit evolutionary tracks of the target star following the Levenberg-Marquadt minimisation scheme (see Salmon et al. 2021, for further details). After confirming the mutual consistency of the two respective pairs of outcomes through the χ2-based criterion described in Bonfanti et al. (2021), we finally merged the pairs of output distributions and obtained 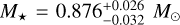 and
and 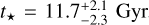 . The uncertainties on M★ and t★ were propagated from the uncertainties on R★, Teff and [Fe/H], as described in Bonfanti et al. (2015, 2016) for the isochrone placement and in Scuflaire et al. (2008) and Salmon et al. (2021) for the CLES code. All stellar parameters we used and derived are listed in Table 2.
. The uncertainties on M★ and t★ were propagated from the uncertainties on R★, Teff and [Fe/H], as described in Bonfanti et al. (2015, 2016) for the isochrone placement and in Scuflaire et al. (2008) and Salmon et al. (2021) for the CLES code. All stellar parameters we used and derived are listed in Table 2.
 |
Fig. 2 New CHEOPS transit light curve of v2 Lup d. Top panel: the light curve reduced with the CHEOPS automated DRP (blue points with error bars), modelled with a combination of instrumental effects (blue curve), stellar noise (green curve), and a transit. The model including all these effects is shown in orange. Middle panel: light curve corrected for the instrumental and stellar noise models (blue points), together with the best-fit transit model (orange curve). See Fig. 4 for a zoom on the transit itself. Bottom panel: residuals resulting from the difference between the detrended light curve and the transit model. For all panels, the error bars of the data points include the fitted additional jitter term added in quadrature. The open black circles show the light curve binned into 20-min intervals. |
3.2 Combined data analysis
We performed a combined analysis of the whole data set using the juliet python package (Espinoza et al. 2019), which is built on several publicly available tools such as batman (Kreidberg 2015) for the modelling of transits, radvel (Fulton et al. 2018) for radial velocities, celerite (Foreman-Mackey et al. 2017) for Gaussian processes (GPs), and dynesty (Speagle 2020) for estimating Bayesian posteriors and evidence via dynamic nested sampling. Our analysis is very similar to the one presented in Delrez et al. (2021) and simply incorporating the new CHEOPS and TESS light curves.
The fitted system parameters were, for each planet: the orbital period P, the mid-transit time T0, the radiai velocity semi-amplitude K and the parameters r1 and r2, which are connected to the planet-to-star radius ratio p and the transit impact parameter b via Eqs. (1)–(4) in Espinoza (2018). This parametrisation was shown to allow an efficient sampling of the physically plausible values in the (b, p) plane. We parametrised the stellar density ρ★ which, together with the orbital period P of each planet, defines a value for the scaled semi-major axis a/R★ of each planet through Kepler’s third law, where R★ is the stellar radius. This parametrisation offers the advantage of defining a single common value of the stellar density for the system, rather than fitting for the scaled semi-major axis of each planet, thus reducing the number of fitted parameters. We placed a normal prior 𝒩(μ = 1 052 kg m−3, σ2 = (56 kg m−3)2) (i.e. ρ★ = 0.746 ± 0.041 ρ⊙) on the stellar density based on the stellar mass 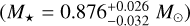 and radius (R★ = 1.054 ± 0.014 R⊙) that we derived previously (Sect. 3.1). Finally, for each band pass (CHEOPS and TESS), two quadratic limb-darkening coefficients were parametrised using the (q1, q2) triangular sampling scheme of Kipping (2013). All these parameters were sampled from wide uniform priors, except for the stellar density (see above). We assumed circular orbits for the three planets, as justified in Delrez et al. (2021).
and radius (R★ = 1.054 ± 0.014 R⊙) that we derived previously (Sect. 3.1). Finally, for each band pass (CHEOPS and TESS), two quadratic limb-darkening coefficients were parametrised using the (q1, q2) triangular sampling scheme of Kipping (2013). All these parameters were sampled from wide uniform priors, except for the stellar density (see above). We assumed circular orbits for the three planets, as justified in Delrez et al. (2021).
We modelled the correlated noise present in the light curves simultaneously with the planetary signals to ensure a full propagation of the uncertainties. To this end, we first performed individual analyses of each light curve in order to select the best correlated noise model for each of them based on Bayesian evidence. The new CHEOPS visit shows some typical flux variations phased with the spacecraft roll angle ϕ (also seen for all previous visits; Delrez et al. 2021), which we modelled using linear functions of sin(nϕ) and cos(nϕ), where n = 1, 2, 3 (blue model in Fig. 2). In addition, the CHEOPS light curve also shows some higher-frequency stellar noise, which we modelled using a GP with a stochastically driven damped simple harmonic oscillator (SHO) kernel (Foreman-Mackey et al. 2017), with a quality factor of  . As described in Delrez et al. (2021), this stellar variability is seen in all the CHEOPS light curves, therefore we fitted a single common SHO GP across the seven CHEOPS visits in our combined analysis (green model in Fig. 2). We modelled the correlated noise in TESS sector 38 light curve with an exponential GP (Foreman-Mackey et al. 2017) and used the noise models detailed in Delrez et al. (2021) for the archival data. Finally, we also fitted an additional jitter term for each of our photometric and radial velocity data sets that was added quadratically to the error bars of the data points to account for any underestimation of the uncertainties or any excess noise not captured by our modelling.
. As described in Delrez et al. (2021), this stellar variability is seen in all the CHEOPS light curves, therefore we fitted a single common SHO GP across the seven CHEOPS visits in our combined analysis (green model in Fig. 2). We modelled the correlated noise in TESS sector 38 light curve with an exponential GP (Foreman-Mackey et al. 2017) and used the noise models detailed in Delrez et al. (2021) for the archival data. Finally, we also fitted an additional jitter term for each of our photometric and radial velocity data sets that was added quadratically to the error bars of the data points to account for any underestimation of the uncertainties or any excess noise not captured by our modelling.
The best-fit models for the new CHEOPS and TESS light curves are shown in Figs. 2 and 3, respectively. A close-up of the CHEOPS transit of v2 Lup d is shown in Fig. 4. The medians and 1σ credible intervals of the system parameter posterior distributions are given in Table 3. The posterior distributions of all parameters are shown as a corner plot in Fig. A.1.
Log of photometric observations.
Stellar parameters of v2 Lup.
 |
Fig. 3 TESS sector 38 light curve of v2 Lup. Top panel: raw light curve obtained by binning the 20-s cadence data into 2-min intervals (blue points with error bars), together with our best-fit model (orange curve), which includes the transits of planets b and c, and the GP model used to account for the correlated noise. Middle panel: light curve obtained after subtracting the GP component of our model, together with our best-fit transit model (orange curve). Bottom panel: residuals resulting from the difference between the detrended light curve and the transit model. For all panels, the error bars of the data points include the fitted additional jitter term added in quadrature. The open black circles show the light curve binned into one-hour intervals. |
 |
Fig. 4 Zoom on the detrended transit of v2 Lup d from the middle panel of Fig. 2. Unbinned exposures are shown as sky blue points with error bars, and white points show a binning by a factor of 15 (or lower depending on how many exposures there are between two light-curve interruptions). The transit model is represented by an orange curve. |
4 Searching for a moon
4.1 Motivations and limitations
v2 Lup d has one of the longest known periods of all transiting planets. With an orbital period of 107.1 days and a low eccentricity, its orbit would be located between those of Mercury and Venus in the Solar System. Because it is much more massive than Mercury or Venus, v2 Lup d might have retained one or several satellites within its larger Hill sphere. Assuming a circular orbit, the Hill sphere radius can be approximated as 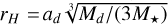 . For v2 Lup d, rH = 0.0092 au (~1.4 × 106 km), almost identical to the Hill sphere radius of Earth (0.0098 au) and substantially larger than that of Mercury (0.0012 au) and Venus (0.0067 au). By comparison, the two inner planets b and c have rH values of 0.0017 au and 0.0040 au, respectively (Fig. 1). Therefore, v2 Lup d could have retained one or several moons. In the Solar System, the highest moon-to-planet size ratio is ~5% for icy giants (Triton to Neptune) and ~27% for terrestrial planets (Moon to Earth). For the 2.51 R⊕ and 8.66 M⊕ v2 Lup d, whose size and mass are intermediate between those of the Earth (1 R⊕, 1 M⊕) and Neptune (3.9 R⊕, 17.2 M⊕), this range would translate into a moon size range of 0.13–0.68 R⊕. The larger end of this range roughly corresponds to a Mars-size body, whose transit might be detectable given the brightness of the star and the excellent photometric precision it allows us to reach. This motivates the search for one or several moons that transit together with the planet.
. For v2 Lup d, rH = 0.0092 au (~1.4 × 106 km), almost identical to the Hill sphere radius of Earth (0.0098 au) and substantially larger than that of Mercury (0.0012 au) and Venus (0.0067 au). By comparison, the two inner planets b and c have rH values of 0.0017 au and 0.0040 au, respectively (Fig. 1). Therefore, v2 Lup d could have retained one or several moons. In the Solar System, the highest moon-to-planet size ratio is ~5% for icy giants (Triton to Neptune) and ~27% for terrestrial planets (Moon to Earth). For the 2.51 R⊕ and 8.66 M⊕ v2 Lup d, whose size and mass are intermediate between those of the Earth (1 R⊕, 1 M⊕) and Neptune (3.9 R⊕, 17.2 M⊕), this range would translate into a moon size range of 0.13–0.68 R⊕. The larger end of this range roughly corresponds to a Mars-size body, whose transit might be detectable given the brightness of the star and the excellent photometric precision it allows us to reach. This motivates the search for one or several moons that transit together with the planet.
Our observations lasted for over 84 h, roughly centred on the mid-transit time of v2 Lup d. This is largely sufficient to cover the entire transit of the planet Hill sphere in front of the stellar disc, which takes 27.3 h3. Because the Hill sphere of v2 Lup d is larger than the star, however, our transit observation cannot probe the fraction of the Hill sphere that does not transit the star; this would correspond to highly inclined moon orbits with respect to the planetary orbital plan (Fig. 1). As can be seen in Fig. 1, most such orbits would have to be retrograde; in fact, prograde moons are only gravitationally stable out to ~0.5 rH (for circular orbits), while only retrograde moons are stable out to 1 rH (Domingos et al. 2006). Most of the large satellites in the Solar System have prograde orbits, with the notable exception of the Neptune moon Triton.
The existence of several apparent small transit-like features in the CHEOPS light curves has motivated several independent analyses of light curves obtained with different pipelines. We summarise two of these efforts below. These efforts converged to conclude that there is no evidence for an exomoon signal in these data. However, a series of transit observations is needed to explore the full extent of the orbital parameter space of a moon.
4.2 Alternative photometric extractions
In addition to the standard DRP reduction of CHEOPS data (Sect. 2.1.1; Hoyer et al. 2020), which uses aperture photometry, we ran an alternative and independent pipeline based on point spread function (PSF) fitting, called the PSF Imagette Photometric Extraction pipeline (PIPE4; see Morris et al. 2021; Szabó et al. 2021; Deline et al. 2022; Brandeker et al. 2022). We ran PIPE on the CHEOPS stacked subarray images (the same input as for the DRP) as well as on the imagettes, which are small stamps centred on the target, extracted on-board directly out of the unstacked subarray images. While the subarray images result from the on-board co-addition of 26 individual 1.7 s exposures (performed to save bandwidth), the imagettes are only stacked in groups of two, allowing us to retrieve a sampling close to the actual observing cadence. We produced two alternative light curves, one based on PSF-fitting of the subarray images, and another based on PSF-fitting of the imagettes. They are shown in Fig. D.1. While these light curves are largely compatible with each other and with the DRP light curve, the PIPE photometry has a slightly better dispersion. More importantly, these different light-curve extractions allowed us to test for the robustness of shallow transit signatures such as those we search for below.
4.3 Upper limits on the size of a moon from one transit of v2 Lup d Hill sphere
Modelling the transit light curve of an exomoon around v2 Lup d while exploring the whole parameter space of its orbital properties would require the use of six (eight) parameters, assuming a circular (an eccentric) orbit: the exomoon radius, orbital period, orbital inclination, longitude of the ascending node, true anomaly at a given epoch (e.g. the mid-transit time of the planet), the moon-to-planet mass ratio, and for an eccentric orbit, the eccentricity and argument of periastron. The sensitivity of our moon search, based on only a single-epoch observation, is limited by the fact that the gravitational pull of the moon on the planet could induce planetary transit-timing variations and transit duration variations (Szabó et al. 2006; Simon et al. 2007; Kipping 2013), and also by the existence of possible planet-moon eclipses (Simon et al. 2009; Kipping 2011; Hippke & Heller 2022; Gordon & Agol 2022). We thus caution that a deep, rigorous search for a moon requires additional epoch and follow-up observations (see Simon et al., for a CHEOPS-specific analysis). Nevertheless, determining the time investment represented by such a future follow-up requires us to quantify the sensitivity reached in a single epoch. We therefore opted to simplify the problem by reducing the number of dimensions of our parameter space in the following way: We parametrised box-shape moon transits with the mid-transit time shift ∆T0 with respect to the planet, the transit duration W, and a transit depth 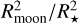 . We scanned a grid of ∆T0 and W values, covering the full Hill sphere radius (−9.1 ≤ ∆T0 ≤ +9.1 h) and considering possible transit durations 0 < W ≤ 12 h. We measured the upper limit at 3 σ on Rmoon by trying to fit additional box-shaped transits to the residuals of the DRP light curve and report the values in Fig. 5.
. We scanned a grid of ∆T0 and W values, covering the full Hill sphere radius (−9.1 ≤ ∆T0 ≤ +9.1 h) and considering possible transit durations 0 < W ≤ 12 h. We measured the upper limit at 3 σ on Rmoon by trying to fit additional box-shaped transits to the residuals of the DRP light curve and report the values in Fig. 5.
The tighter detection limit on a moon radius is obtained for configurations with a long moon-transit duration. In these cases, it is possible to exclude moons with radii larger than ~0.6 R⊕ (roughly Mars-size) from the regions of the Hill sphere that are transiting the star (see Fig. 1). Larger moons at long periods (likely on retrograde orbits, as discussed in Sect. 4.1) could still hide in the parts of the Hill sphere that do not transit the star during our observation (they could transit at another epoch, however). Short moon transits allow for larger objects (up to ~2 R⊕) to fit into light curve gaps or that could be due to outlying points in the light curve. Short transits like this could happen for instance when a transiting moon is eclipsed by the planet, or for a moon that grazes the edge of the stellar disc. The region of the parameter space with small W and large |∆T0| is less likely because when the moon is far from the planet, it implies a rapidly transiting moon on the stellar disc or a moon transiting close to the stellar limb, which are not properly modelled when using box-shaped transits. A similar but independent search (see Appendix B) yielded similar results. We also conducted further explorations of our CHEOPS light curve using more realistic transit models with simpler models for the moon orbit (see Appendices C and D); these efforts did not allow us to find any compelling evidence for a moon larger than Mars. A comprehensive future search will require additional epochs of observation.
Parameters of the v2 Lup planets.
 |
Fig. 5 3σ upper limit on the moon radius as a function of the mid-transit time shift ∆T0 with respect to the planet and the transit duration W. The dotted white lines indicate the transit duration and location of planet v2 Lup d. The horizontal axis spans the whole diameter of the Hill sphere (seen in projection on the stellar disc), where ∆T0 < 0 indicates that the moon lags the planet. The bottom lines of the map show short transits that could represent a moon transiting shortly before being hidden by the planet, or transiting close to the limb of the star. Such short transits allow for larger moons to exist while remaining undetectable in our single-epoch data set. |
5 Conclusion
We observed a complete transit of v2 Lup d with the CHEOPS space telescope. We substantially refined the planet transit ephemeris to 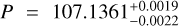 days and
days and 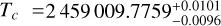 BJDTBD, which improves by ~40× on the previously reported transit-timing uncertainty (projected in June 2022). The total transiting duration is 9.1 h. The CHEOPS observations cover the transit of the Hill sphere of the planet, which is large for a transiting exoplanet, as large as that of Earth, and might host one or several transiting moons. Throughout several independent searches, we concluded that there is no evidence for additional transits of objects with radii ≲0.6 R⊕, demonstrating that CHEOPS is precise enough to hunt for exomoons that have about the size of Mars. Nonetheless, the best candidate signals did not pass our reproducibility tests. We emphasise that even if they had, confirming the presence of an exomoon around v2 Lup d would require additional epochs of observations to validate a circumplanetary orbit in any case. Such a follow up, by CHEOPS or other telescopes, is now enabled by the refined ephemeris we provide in this work. This will enable performing a deeper search of the planetary Hill sphere, or spectroscopically probing the atmosphere of this warm subneptune, which has one of the highest transit spectroscopy metrics (TSM) of its temperature class (Delrez et al. 2021, see their Fig. 2d and discussion), including at wavelengths, such as that of the Lyman-α line of atomic hydrogen, that are obscured by the interstellar medium in more distant systems.
BJDTBD, which improves by ~40× on the previously reported transit-timing uncertainty (projected in June 2022). The total transiting duration is 9.1 h. The CHEOPS observations cover the transit of the Hill sphere of the planet, which is large for a transiting exoplanet, as large as that of Earth, and might host one or several transiting moons. Throughout several independent searches, we concluded that there is no evidence for additional transits of objects with radii ≲0.6 R⊕, demonstrating that CHEOPS is precise enough to hunt for exomoons that have about the size of Mars. Nonetheless, the best candidate signals did not pass our reproducibility tests. We emphasise that even if they had, confirming the presence of an exomoon around v2 Lup d would require additional epochs of observations to validate a circumplanetary orbit in any case. Such a follow up, by CHEOPS or other telescopes, is now enabled by the refined ephemeris we provide in this work. This will enable performing a deeper search of the planetary Hill sphere, or spectroscopically probing the atmosphere of this warm subneptune, which has one of the highest transit spectroscopy metrics (TSM) of its temperature class (Delrez et al. 2021, see their Fig. 2d and discussion), including at wavelengths, such as that of the Lyman-α line of atomic hydrogen, that are obscured by the interstellar medium in more distant systems.
Acknowledgements
We thank the anonymous referee for their time spent reviewing the manuscript. CHEOPS is a European Space Agency (ESA) mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden and the United Kingdom. The Swiss participation in CHEOPS has been supported by the Swiss Space Office in the framework of PRODEX and the Activités Nationales Complémentaires and the Universities of Bern and Geneva as well as the NCCR PlanetS and the Swiss National Science Foundation. The MOC activities have been supported by ESA contract 4000124370. This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. D.G., X.B., S.C., M.F. and J.L. acknowledge their roles as ESA-appointed CHEOPS science team members. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES; grant agreement No 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). DE acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation; L.D. is an F.R.S.-FNRS Postdoctoral Researcher. A.C.C. and T.W. acknowledge support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. S.H. gratefully acknowledges CNES funding through the grant 837319. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). Y.A. and M.J.H. acknowledge the support of the Swiss National Fund under grant 200020_172746. M.L. and B.A. acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. S.G.S. acknowledges support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). We acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grants ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R, PGC2018-098153-B-C33, PGC2018-098153-B-C31, ESP2017-87676-C5-1-R, MDM-2017-0737 Unidad de Excelencia Maria de Maeztu-Centro de Astrobiología (INTA-CSIC), as well as the support of the Generalitat de Catalunya/CERCA programme. The MOC activities have been supported by the ESA contract No. 4000124370. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. A.Br. was supported by the SNSA. This project was supported by the CNES. This work was supported by FCT - Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 - Programa Operacional Competitividade e Internacionalizaç ao by these grants: UID/FIS/04434/2019, UIDB/04434/2020, UIDP/04434/2020, PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113, PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953, PTDC/FIS-AST/28987/2017 & POCI-01-0145-FEDER-028987, O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. B.-O.D. acknowledges support from the Swiss National Science Foundation (PP00P2-190080). M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). D.G. gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseousor rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. This work was granted access to the HPC resources of MesoPSL financed by the Région Île-de-France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. P.M. acknowledges support from STFC research grant number ST/M001040/1. L.Bo., G.Br., V.Na., I.Pa., G.Pi., R.Ra., G.Sc., V.Si., and T.Zi. acknowledge support from CHEOPS ASI-INAF agreement n. 2019-29-HH.0. K.G.I. is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. I.R.I. acknowledges support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant PGC2018-098153-B-C33, as well as the support of the Generalitat de Catalunya/CERCA programme. Gy.M.Sz. acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S-FNRS Research Associate. N.A.W. acknowledges UKSA grant ST/R004838/1. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). Funding for the TESS mission is provided by the NASA’s Science Mission Directorate. We acknowledge the use of public TESS data from pipelines at the TESS Science Office and at the TESS Science Processing Operations Center. Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center for the production of the SPOC data products.
Appendix A Corner plot of the combined data analysis
The posterior distributions of all parameters from the combined data analysis (Sect. 3.2) are shown in Fig. A.1.
 |
Fig. A.1 Corner plot showing the posterior distributions of all parameters of the combined fit. |
Appendix B Alternative search for moon(s) 1
We fitted the CHEOPS light curve with a model including a planet and a moon that took Keplerian motion and moon-planet eclipses into account. The moon was assumed (1) to have a circular orbit beyond the planet’s Roche limit, but inside the planet’s Hill sphere; (2) to be co-aligned with the orbit of the planet; and (3) to have an arbitrary transit depth from 10 to 1 000 pm. The moon orbit is thus parametrised with only two parameters (P, θ): the moon orbital period P and its orbital phase θ at mid-transit. This choice is motivated by the fact that our single 9.1 h planetary transit represents only a small fraction of the hypothetical moon orbit: at the Roche limit, we have P = 0.3 d, while at the Hill sphere radius, P = 115 d), preventing any accurate fit of the six orbital elements of the moon. We considered 100 values for θ from 0 to 360 deg. For P, we considered 100 values from −115 to +115 d (negative values represent a retrograde orbit). For every pair of values (Pi, θi), we calculated the moon transit depth Di that best fit the data following a χ2 minimisation and the value of 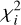 .
.
Among the 10 000 combinations tested, the best fit was obtained for P = +1.766 d, θ = 198.36 deg and D = 23 ppm 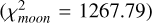 . However, this solution does not appear better than a simple χ2 fit to the data without a moon (the null hypothesis). This null hypothesis results in
. However, this solution does not appear better than a simple χ2 fit to the data without a moon (the null hypothesis). This null hypothesis results in 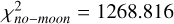 . The difference between the two best fits is barely visible by eye. While the ‘moon model’ has a slightly lower χ2 than the ‘no-moon model’, this improvement is not significant because the ‘moon model’ has a larger number of free parameters than the ‘no-moon model’. Two models with different degrees of freedom can be compared with the Akaike information criterion (AIC; Burnham & Anderson 2002),
. The difference between the two best fits is barely visible by eye. While the ‘moon model’ has a slightly lower χ2 than the ‘no-moon model’, this improvement is not significant because the ‘moon model’ has a larger number of free parameters than the ‘no-moon model’. Two models with different degrees of freedom can be compared with the Akaike information criterion (AIC; Burnham & Anderson 2002),
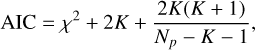 (B.1)
(B.1)
where K is the number of model parameters and NP is the number of data points in the fit. The AIC can be qualitatively interpreted as the χ2, but with a penalty proportional to the number of degrees of freedom. The model with the smallest AIC is the preferred hypothesis. In this case, we obtain AICmoon = 1278.07 and AICno-moon = 1268.81. The ‘no-moon model’ is thus preferred to the ‘moon model’. No moon seems necessary to fit the data. We emphasise, however, that this does imply there is no moon around v2 Lup d, given the limitations expressed in Sect. 4.1.
Appendix C Alternative search for moon(s) 2
We searched the light curve for additional dips that might be caused by a transiting moon. This was done by adding a second (moon) transit model to the planet transit model (both created using batman) to generate a simple planet-moon transit model. The planet model parameters are those from Table 3 (right column).
We assumed that the moon is co-moving with the planet across the stellar disc and thus has the same transit duration. Therefore, several parameters remain the same for the moon and the planet transits (Kipping 2011) (e.g. we fitted for only one stellar density value). The planet and moon also share the same impact parameter that was considered to be the impact parameter of the planet-moon barycenter across the stellar surface (Kipping 2010). Thus, the only moon parameters we fitted for were its mid-transit time 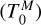 and radius ratio (pM = RM/R★). We allowed for a nonphysical negative-radius moon (inverted transit) to avoid biasing towards a detection and allowed for a good sampling of values around 0. Based on the Hill radius of the planet, the maximum separation of a plausible moon from the planetary transit is ±0.37 d (leading or lagging the planet). We used this range as prior bounds on the expected mid-transit time of the moon, but we also relaxed this constraint to search for any such dips outside the Hill radius that might indicate that a dip found within the Hill radius is spurious.
and radius ratio (pM = RM/R★). We allowed for a nonphysical negative-radius moon (inverted transit) to avoid biasing towards a detection and allowed for a good sampling of values around 0. Based on the Hill radius of the planet, the maximum separation of a plausible moon from the planetary transit is ±0.37 d (leading or lagging the planet). We used this range as prior bounds on the expected mid-transit time of the moon, but we also relaxed this constraint to search for any such dips outside the Hill radius that might indicate that a dip found within the Hill radius is spurious.
We used a linear function of time and Fourier functions as in Sect. 3.2 to model the temporal trend and roll-angle variations in the light curve. We used the SHO kernel that was also employed to model the stellar noise (§3.2) and the dynesty nested-sampling routine to sample the parameter space for the planet-only and planet-moon models. This procedure was performed on the different light curve extractions mentioned above (DRP, PIPE-imagette and PIPE-subarray).
The analysis of the PIPE-subarray data reveals a dip within the Hill radius with a depth corresponding to a body of radius 0.61 ± 0.1 R⊕. This dip is found regardless of whether we constrain the search region to be within the Hill radius. Figure C.1 shows the maximum likelihood planet-moon fit to the PIPE-subarray transit light curve of v2 Lup d. Comparing the Bayesian evidence of the planet-moon model to the planet-only model, we obtain a Bayes factor of 9.6, which is in strong favour of the planet-moon model (the threshold to reject the null hypothesis lies at a Bayes factor of ~5; Kass & Raftery 1995). In the case of the planet-only model fit, the GP is able to absorb any variation or moon-like dip that is not modelled.
The existence of the shallow transit that is clearly visible in the GP-detrended light curve (Fig. C.1, second panel) seems statistically sound based on Bayesian evidence. However, because fools rush in where angels fear to tread, we wished to further assess how reproducible and robust this signature, a product of a sophisticated detrending, really is. Rodenbeck et al. (2018) have previously shown that light-curve detrending processes can result in the injection of spurious moon transits to the data. Thus, to test whether this dip could have been induced by the GP that we used to model the stellar noise, we performed the same fit without the GP. We obtained a similar result, albeit with less precision on the transit depth. When we re-fitted the data after removing the detected shallow transit signal, we found additional dips outside the Hill sphere of v2 Lup d. This indicates that a shallow transit signal found within the Hill radius could well be an artefact due to systematics (stellar noise, instrumental noise, a spurious signal created by the data reduction process or a combination of all of these). A good test for the latter scenario is to perform a similar detrending and fitting procedure to the product of the alternative data reduction pipeline mentioned in Sect. 4.2. We might expect that different kinds of systematic effects would be created or amplified differently with two different extraction methods (aperture photometry vs. PSF fitting).
This proved an efficient test to refute our candidate exomoon, as we simply were unable to retrieve the same signal in these alternative light curves. Instead, we detected several transit-like dips outside the Hill sphere, at different times from the initial candidate signal, in the DRP light-curve, while an inverted transit was detected in both the PIPE imagette and DRP data. The prevalence of these transit-like dips at different times in independent data reductions indicates that they are likely artefacts produced by the stellar noise, instrumental noise, the data reduction procedure or a combination of the three.
 |
Fig. C.1 Planet-moon model fit to the CHEOPS light curve of v2 Lup. Top panel: PIPE-subarray light curve (blue points with error bars) modelled with a combination of instrumental effects (blue curve), stellar noise (green curve) and transits of a planet and moon. The model including all these effects is shown in orange. The shaded grey region shows the physically plausible moon mid-transit times within the planet’s Hill sphere. Middle panel: Light curve corrected for the instrumental and stellar noise models (blue points), together with the best-fit planet-moon transit model (orange curve). The dashed black curve shows the isolated moon component. Bottom panels: Residuals from the planet-model fit and planet-only fit. The open black circles show the light curve binned into 20-minute intervals. As described in Sect. C, the shallow transit feature clearly appearing in the second panel from top is an artefact. |
Appendix D Alternative search for moon(s) 3
A second, independent search for a shallow signal resulting from the transit of a moon similarly failed to provide convincing evidence. For this second attempt, we conducted a statistically robust analysis of the CHEOPS visit by constructing the most complete noise model to remove systematics from the data and thus optimise our search for transit-like features. The noise model contained the instrumental vectors of the visit (background, contamination, smearing, roll angle, change in temperature, and x and y centroid offset positions) that were retrieved using the pycheops Python package (Maxted et al. 2021)5. Previous CHEOPS studies have found that the telescope temperature can alter the shape of the CHEOPS PSF, which in turn produces flux variation at the beginning of a visit (the so-called ‘ramp’); another source of flux variations on the orbital timescale of CHEOPS is the presence of nearby contaminants (Maxted et al. 2021; Morris et al. 2021; Wilson et al. 2022). To assess and remove this potential flux modulation, we used a novel PSF-based detrending method that was recently reported in Wilson et al. (2022) to remove these effects in the CHEOPS light curves of TOI-1064. We refer to that paper for the full mathematical description of the algorithm. In brief, the tool conducts a principal component analysis (PCA) on the auto-correlation function of either the CHEOPS subarrays or imagettes, depending on the light curve of interest, to assess any subtle change in the PSF shape. To find the most significant components that should be included in the overall noise model, the algorithm uses a leave-one-out cross-validation method. Fig. D.1 shows the results of this process on the CHEOPS subarrays or imagettes for the DRP and PIPE light curves. We find that the PSF PCA method (Wilson et al. 2022) removes a subtle flux ramp at the beginning of the dataset.
Satisfied that we constructed a noise model that can account for as much of the systematic flux variation as possible, we fit the data with this model simultaneously with either N = 0, 1, and 2 transit models in order to determine the true inclusion probabilities (TIP; Hara et al. 2021). Therefore, we can statistically verify the presence of one or two transits in the CHEOPS light curves. For the first transit model, we took priors on v2 Lup d from the results of our global analysis (see Table. 3), whereas for the second transit model, we assumed a similar orbital period and impact parameter as v2 Lup d, and left uniform priors on the transit depth and centre time. An example result from the N = 1 fit using the DRP fluxes is shown in Fig. D.2. By comparing the Bayes evidence and posterior distributions of the N = 0 and N = 1 fits, we find TIPs ~ 1 for a transit at BJD 2459 331.1875 in the DRP light curve, and at BJD 2459 331.1877 and BJD 2459 331.1876 in the PIPE subarray and imagette light curves. This corresponds to the transit of v2 Lup d. Confident that our process can statistically detect transits in the detrended light curves, we computed the TIP for the N = 1 versus N = 2 case in order to search for an additional transit that could be caused by an exomoon. For all light curves, we find TIPs ~ 0 for all transit centre times within the data. Based on this analysis, we therefore cannot statistically confirm the presence of a transiting exomoon around v2 Lup d in these data.
 |
Fig. D.1 Results of the PSF PCA process. Top: Subarrays and DRP fluxes. Middle: Subarrays and PIPE fluxes. Bottom: Imagettes and PIPE fluxes. Blue represents the raw DRP or PIPE fluxes; orange shows the combined PSF shape-change noise model from the 127, 127, and 210 principal components, respectively; and green shows detrended fluxes. In the TIP analysis, we included all the individual components that comprise the orange curves and the blue raw fluxes. |
 |
Fig. D.2 Example result of the fitting method described in Sect. D with one transit (N = 1). Top: DRP fluxes for the visit of v2 Lup d. Middle upper: Linear model of the instrumental vectors and the components of the PSF PCA, Middle lower: N = 1 transit model. Bottom: Residuals to linear model plus N = 1 transit model. |
References
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Blackwell, D.E., & Shallis, M.J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfanti, A., Ortolani, S., Piotto, G., & Nascimbeni, V. 2015, A&A, 575, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Ortolani, S., & Nascimbeni, V. 2016, A&A, 585, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfanti, A., Delrez, L., Hooton, M.J., et al. 2021, A&A, 646, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandeker, A., Heng, K., Lendl, M., et al. 2022, A&A, 659, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burnham, K.P., & Anderson, D.R. 2002, Model Selection and Multimodel Inference : A Practical Information-Theoretic Approach (New York: Springer) [Google Scholar]
- Castelli, F., & Kurucz, R.L. 2003, IAU Symp., 210, A20 [NASA ADS] [Google Scholar]
- Deline, A., Hooton, M.J., Lendl, M., et al. 2022, A&A, 659, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Ehrenreich, D., Alibert, Y., et al. 2021, Nat. Astron., 5, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Domingos, R.C., Winter, O.C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Harrison, J.H.D., Bonsor, A., & Hands, T.O. 2019, MNRAS, 484, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C.D., Charbonneau, D., Dumusque, X., et al. 2015, ApJ, 800, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Elkins-Tanton, L.T., & Seager, S. 2008, ApJ, 688, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N. 2018, Res. Notes Am. Astron. Soc., 2, 209 [Google Scholar]
- Espinoza, N., Kossakowski, D., & Brahm, R. 2019, MNRAS, 490, 2262 [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
- Fulton, B.J., Petigura, E.A., Howard, A.W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B.J., Petigura, E.A., Blunt, S., & Sinukoff, E. 2018, PASP, 130, 044504 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordon, T.A., & Agol, E. 2022, AJ, 164, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Grasset, O., Schneider, J., & Sotin, C. 2009, ApJ, 693, 722 [Google Scholar]
- Hara, N.C., Unger, N., Delisle, J.-B., Díaz, R., & Ségransan, D. 2021, A&A, 663, A14 [Google Scholar]
- Hippke, M., & Heller, R. 2022, A&A, 662, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, D., White, T.R., Metcalfe, T.S., et al. 2022, AJ, 163, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J.M., Caldwell, D.A., Chandrasekaran, H., et al. 2010, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J.M., Twicken, J.D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [NASA ADS] [Google Scholar]
- Kane, S.R., Yalçinkaya, S., Osborn, H.P., et al. 2020, AJ, 160, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kass, R.E., & Raftery, A.E. 1995, J. Am. Stat. Assoc., 90, 90 [Google Scholar]
- Kipping, D.M. 2010, MNRAS, 409, 409 [Google Scholar]
- Kipping, D.M. 2011, MNRAS, 416, 416 [NASA ADS] [Google Scholar]
- Kipping, D.M. 2013, MNRAS, 435, 2152 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
- Kuchner, M.J. 2003, ApJ, 596, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [Google Scholar]
- Lecavelier Des Etangs, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Léger, A., Selsis, F., Sotin, C., et al. 2004, Icarus, 169, 499 [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lopez, E.D., Fortney, J.J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
- Maxted, P.F.L., Ehrenreich, D., Wilson, T.G., et al. 2021, MNRAS, 514, 77 [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Morris, B.M., Delrez, L., Brandeker, A., et al. 2021, A&A, 653, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J.E., & Wu, Y. 2017, ApJ, 847, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Rodenbeck, K., Heller, R., Hippke, M., & Gizon, L. 2018, A&A, 617, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, J.G., Gupta, A., Owen, J.E., & Schlichting, H.E. 2021, MNRAS, 508, 5886 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, S.J.A.J., Van Grootel, V., Buldgen, G., Dupret, M.A., & Eggenberger, P. 2021, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N.C., Bouchy, F., Mayor, M., et al. 2004, A&A, 426, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schanche, N., Hébrard, G., Collier Cameron, A., et al. 2020, MNRAS, 499, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [Google Scholar]
- Simon, A., Szatmáry, K., & Szabó, G.M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, A.E., Szabó, G.M., & Szatmáry, K. 2009, Earth Moon Planets, 105, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, A.E., Szabó, G.M., Kiss, L.L., Fortier, A., & Benz, W. 2015, PASP, 127, 1084 [CrossRef] [Google Scholar]
- Skrutskie, M.F., Cutri, R.M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J.C., Stumpe, M.C., Van Cleve, J.E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S.G., Santos, N.C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speagle, J.S. 2020, MNRAS, 493, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M.C., Smith, J.C., Van Cleve, J.E., et al. 2012, PASP, 124, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M.C., Smith, J.C., Catanzarite, J.H., et al. 2014, PASP, 126, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G.M., Szatmáry, K., Divéki, Z., & Simon, A. 2006, A&A, 450, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, G.M., Gandolfi, D., Brandeker, A., et al. 2021, A&A, 654, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Dumusque, X., Lovis, C., et al. 2019, A&A, 622, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valencia, D., O’Connell, R.J., & Sasselov, D. 2006, Icarus, 181, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., Guilera, O.M., Haldemann, J., Ronco, M.P., & Mordasini, C. 2020, A&A, 643, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T.G., Goffo, E., Alibert, Y., et al. 2022, MNRAS, 511, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E.L., Eisenhardt, P.R.M., Mainzer, A.K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison of the sizes of the Hill spheres (dashed circles) for the three v2 Lup planets. Planet d is represented while transiting the star (ivory white disc). The respective orbital positions of the planets are not representative of their positions during the observations; only their transit impact parameters are considered. The Hill sphere radius of v2 Lup d (1.87 R★ or 0.0092 au or 9.1 h) is almost equal to the length of the planet transit chord. Because the Hill sphere of v2 Lup d is larger than the star, some parts of it (hatched areas) do not transit: a highly inclined exomoon in these regions, close to maximum apparent separation, could remain undetectable during this single visit. Such a distant moon would most likely be on a stable retrograde orbit, as these non-transiting regions are mostly beyond the stability limit for prograde (circular) orbits, represented at half the Hill sphere radius (Domingos et al. 2006) by the dotted circle. The diameters of the Hill spheres of Mercury, Venus, and Earth are shown for comparison; the location of the Moon within Earth’s Hill sphere is indicated. |
| In the text | |
 |
Fig. 2 New CHEOPS transit light curve of v2 Lup d. Top panel: the light curve reduced with the CHEOPS automated DRP (blue points with error bars), modelled with a combination of instrumental effects (blue curve), stellar noise (green curve), and a transit. The model including all these effects is shown in orange. Middle panel: light curve corrected for the instrumental and stellar noise models (blue points), together with the best-fit transit model (orange curve). See Fig. 4 for a zoom on the transit itself. Bottom panel: residuals resulting from the difference between the detrended light curve and the transit model. For all panels, the error bars of the data points include the fitted additional jitter term added in quadrature. The open black circles show the light curve binned into 20-min intervals. |
| In the text | |
 |
Fig. 3 TESS sector 38 light curve of v2 Lup. Top panel: raw light curve obtained by binning the 20-s cadence data into 2-min intervals (blue points with error bars), together with our best-fit model (orange curve), which includes the transits of planets b and c, and the GP model used to account for the correlated noise. Middle panel: light curve obtained after subtracting the GP component of our model, together with our best-fit transit model (orange curve). Bottom panel: residuals resulting from the difference between the detrended light curve and the transit model. For all panels, the error bars of the data points include the fitted additional jitter term added in quadrature. The open black circles show the light curve binned into one-hour intervals. |
| In the text | |
 |
Fig. 4 Zoom on the detrended transit of v2 Lup d from the middle panel of Fig. 2. Unbinned exposures are shown as sky blue points with error bars, and white points show a binning by a factor of 15 (or lower depending on how many exposures there are between two light-curve interruptions). The transit model is represented by an orange curve. |
| In the text | |
 |
Fig. 5 3σ upper limit on the moon radius as a function of the mid-transit time shift ∆T0 with respect to the planet and the transit duration W. The dotted white lines indicate the transit duration and location of planet v2 Lup d. The horizontal axis spans the whole diameter of the Hill sphere (seen in projection on the stellar disc), where ∆T0 < 0 indicates that the moon lags the planet. The bottom lines of the map show short transits that could represent a moon transiting shortly before being hidden by the planet, or transiting close to the limb of the star. Such short transits allow for larger moons to exist while remaining undetectable in our single-epoch data set. |
| In the text | |
 |
Fig. A.1 Corner plot showing the posterior distributions of all parameters of the combined fit. |
| In the text | |
 |
Fig. C.1 Planet-moon model fit to the CHEOPS light curve of v2 Lup. Top panel: PIPE-subarray light curve (blue points with error bars) modelled with a combination of instrumental effects (blue curve), stellar noise (green curve) and transits of a planet and moon. The model including all these effects is shown in orange. The shaded grey region shows the physically plausible moon mid-transit times within the planet’s Hill sphere. Middle panel: Light curve corrected for the instrumental and stellar noise models (blue points), together with the best-fit planet-moon transit model (orange curve). The dashed black curve shows the isolated moon component. Bottom panels: Residuals from the planet-model fit and planet-only fit. The open black circles show the light curve binned into 20-minute intervals. As described in Sect. C, the shallow transit feature clearly appearing in the second panel from top is an artefact. |
| In the text | |
 |
Fig. D.1 Results of the PSF PCA process. Top: Subarrays and DRP fluxes. Middle: Subarrays and PIPE fluxes. Bottom: Imagettes and PIPE fluxes. Blue represents the raw DRP or PIPE fluxes; orange shows the combined PSF shape-change noise model from the 127, 127, and 210 principal components, respectively; and green shows detrended fluxes. In the TIP analysis, we included all the individual components that comprise the orange curves and the blue raw fluxes. |
| In the text | |
 |
Fig. D.2 Example result of the fitting method described in Sect. D with one transit (N = 1). Top: DRP fluxes for the visit of v2 Lup d. Middle upper: Linear model of the instrumental vectors and the components of the PSF PCA, Middle lower: N = 1 transit model. Bottom: Residuals to linear model plus N = 1 transit model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


