| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 18 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202245269 | |
| Published online | 20 February 2023 | |
High-resolution X-ray spectra of RS Ophiuchi (2006 and 2021): Revealing the cause of SSS variability★
1
European Space Agency (ESA), European Space Astronomy Centre (ESAC),
Camino Bajo del Castillo s/n,
28692
Villanueva de la Canada, Madrid, Spain
e-mail: jan.uwe.ness@esa.int
2
School of Physics & Astronomy, University of Leicester,
University Rd,
Leicester
LE1 7RH, UK
3
Astrophysics Research Institute, Liverpool John Moores University,
IC2 Liverpool Science Park,
Liverpool
L3 5RF, UK
4
Vice Chancellor’s Office, Botswana International University of Science and Technology,
Private Bag 16,
Palapye, Botswana
5
Advanced Technologies Research Institute, Faculty of Materials Science and Technology in Trnava, Slovak University of Technology in Bratislava,
Bottova 25,
917 24
Trnava, Slovakia
6
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge, MA
02138, USA
7
INAF Astronomical Observatory of Padova,
Via Osservatorio Astronomico 8,
36012
Asiago (VI), Italy
8
Dept. of Astronomy, University of Wisconsin,
475 N. Charter Str.,
Madison,
WI 53706, USA
9
INAF-Osservatorio di Padova,
Vicolo Osservatorio 5,
35122
Padova, Italy
10
School of Earth and Space Exploration, Arizona State University,
781 Terrace Mall,
Tempe, AZ
85287-1404, USA
Received:
23
October
2022
Accepted:
13
December
2022
Context. The ~ 10–20 yr recurrent symbiotic nova RS Oph exploded on 2021 August 9, the seventh confirmed recorded outburst since 1898. During the previous outburst in 2006, the current fleet of X-ray space observatories was already in operation, and thanks to the longevity of Swift, XMM-Newton, and Chandra, a direct comparison between these two outbursts is possible. The Swift monitoring campaign revealed similar behaviour during the early shock phase but very different behaviour during the super-soft source (SSS) phase. Two XMM-Newton observations were made during the 2021 SSS phase on days 37.1 and 55.6 after the 2021 optical peak. We focus in this work on the bright SSS observation on day 55.6 and compare to SSS Chandra and XMM-Newton grating observations made on days 39.7, 54, and 66.9 after the 2006 optical peak.
Aims. By exploring the reasons for the differences between the 2006 and 2021 outbursts, we aim to obtain a better general understanding of the emission and absorption mechanisms. While the emission mechanisms hold the key to the physics of novae and nuclear burning, absorption processes may dominate what we observe, and we aim to explore the cause of the gross initial variability in the observed SSS emission.
Methods. We present a novel approach to down-scaling the observed (brighter) 2006 SSS spectra to match the 2021 day 55.6 spectrum by parameter optimisation of: (1) a constant factor (representing fainter source emission, smaller radius, eclipses, etc.), (2) a multi-ionisation photoelectric absorption model (representing different line-of-sight absorption), and (3) scaling with a ratio of two blackbody models with different effective temperatures (representing different brightness and colours). This model approach does not depend on a source model assuming the intrinsic source to be the same. It is therefore more sensitive to incremental changes than modelling approaches where source and absorption are modelled simultaneously.
Results. The 2021d55.6 spectrum can be reproduced remarkably well by multiplying the (brighter) 2006d39.7 and 2006d54 spectra with the absorption model, while the 2006d66.9 spectrum requires additional colour changes to match the 2021.d55.6 spectrum. The 2006d39.7 spectrum much more closely resembles the 2021d55.6 spectrum in shape and structure than the same-epoch 2006d54 spectrum: The spectra on days 2006d39.7 and 2021d55.6 are richer in absorption lines with a deeper O I absorption edge, and blueshifts are higher (~1200 km s−1) than on day 2006d54 (~700 km s−1). In the SSS light curves on days 2006d39.7, 2006d54, and 2021d55.6, brightness and hardness variations are correlated, indicating variations of the O I column density. Only on day 2006d39.7, a 1000 s lag is observed. The 35 s period was detected on day 2021d55.6 with lower significance compared to 2006d54.
Conclusions. We conclude that the central radiation source is the same, while absorption is the principal reason for observing lower soft-X-ray emission in 2021 than in 2006. This is consistent with a similar 2006 and 2021 [Fe X] line-flux evolution. We explain the reduction in line blueshift, depth in O I edge, and number of absorption lines from day 2006d39.7 to 2006d54 by deceleration and heating of the ejecta within the stellar wind of the companion. In 2021, less such deceleration and heating was observed, which we interpret as due to viewing at different angles through an inhomogeneous density distribution of the stellar wind, allowing free expansion in some directions (probed in 2021) and a higher degree of deceleration in others (probed in 2006). The higher absorption in 2021 can then be explained by the lower-temperature absorbing plasma being more opaque to soft X-rays. Our approach of scaling observations against observations is free of ambiguities from imperfect source models and can be applied to other grating spectra with complex continuum sources.
Key words: novae, cataclysmic variables / X-rays: binaries / stars: winds, outflows
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
During a typical nova outburst, hydrogen is fused to helium on the surface of a white dwarf star. The burning material is obtained from a companion star via accretion, and a variety of companion stars can act as hydrogen donors. Over a period of continuous accretion, hydrogen accumulates on the surface of the white dwarf until ignition conditions are reached leading to thermonuclear runaway reactions. While explosive nuclear burning is highly energetic, white dwarfs are sufficiently sturdy to survive a nova outburst. As opposed to supernovae, novae are thus cataclysmic rather than catastrophic events, and the pre-outburst configuration is essentially preserved. After a nova outburst, accretion continues, eventually leading to another outburst once the ignition conditions are reached again. The recurrence timescale is highly sensitive to the mass of the white dwarf, which determines the ignition conditions and how quickly they can be reached. This means that the interoutburst time for a given white dwarf mass depends to the highest degree on the accretion rate, which is not necessarily constant, and interoutburst times can therefore vary.
While all novae are recurrent, the class of recurrent novae is defined as those for which at least two outbursts have been observed. RS Oph is one of the most famous recurrent novae, having been observed in outburst with roughly 10–20 yr recurrence time since 1898, and the seventh1 confirmed outburst was reported by the AAVSO (American Association of Variable Star Observers) network with Alert Notice 752 on 2021 August 9. The optical peak magnitude of 4.5 was reached around 2021-08-09.5417 UT, which is used as the reference time tref for this work. Munari & Valisa (2022) performed weighted spline fitting to the whole set of AAVSO data resulting in 2021-08-09.58 UT (±0.05 days), that is, 0.04 days (=55 min) later than our value of tref but within the error uncertainty.
Nuclear reactions occur in the form of hydrogen burning via the CNO cycle and the energy produced is initially dissipated as high-energy radiation, powering a radiation-driven wind. During the early fireball phase, super-soft-source (SSS) emission is expected to be observable for a short time and was recently observed in serendipitous eROSITA observations (König et al. 2022). Shortly after the initial detonation, the white dwarf will be surrounded by an optically thick ejecta envelope that is initially opaque to high-energy radiation. At the pseudo-photosphere of this envelope, the energy escapes and becomes observable to us in lower-energy bands, depending on the extent of the optically thick part of the ejecta. As the expansion continues and the mass-ejection rate slows down, the pseudo-photospheric radius decreases with time, and the peak of the spectral energy distribution (SED) moves into the UV and soft X-ray bands. Initially, a nova is brightest in the optical bands, later moving into the UV bands, and is ultimately brightest in the soft X-rays, when an atmospheric spectrum of several 105 K is emitted and observed as an SSS X-ray spectrum. For more details, we refer to Bode & Evans (2008).
The intense SSS radiation affects the surrounding medium in ways that facilitate indirect observational evidence for the presence of SSS emission. Munari & Valisa (2022) present the evolution of coronal iron lines ([Fe X], [Fe XI], [Fe XIV]) and of O VI 1032 Å, 1036 Å, which are Raman-scattered to 6825 Å, 7088 Å by neutral hydrogen in the ground state (see their Fig. 5, and Schmid 1989 for identification of the Raman line). All of these lines rose substantially after day ≳ 20 after maximum optical brightness of the 2021 outburst of RS Oph where for lines in higher ionisation stages, this rise was observed later. For RS Oph in 2021, the coronal lines remained stable through days 30–86, as if the number of ionising photons fed to the expanding medium remained stable until the nuclear burning was switched off. All coronal lines further decline in parallel with the declining continuum, as if governed only by dilution in the ejecta under stable illumination by the central source. Figure 14 of Page et al. (2022) shows a comparison between the evolution of the [Fe X] emission line flux (6375 Å) and the Swift/XRT soft-X-ray count rate, demonstrating the temporal correlation of SSS emission and coronal emission line intensity.
Until the start of the SSS phase, the pseudo-photosphere is X-ray dark, but other processes less directly related to the white dwarf can produce X-rays. The companion in RS Oph is a red giant and so produces a dense stellar wind. The nova ejecta interact with this wind to give rise to a forward shock running into this wind with a reverse shock running into the ejecta. Some of the kinetic energy of the ejecta is thus converted to thermal energy and particle acceleration leading in turn to line and continuum emission across the electromagnetic spectrum, including the X-ray (e.g. Bode & Kahn 1985; O’Brien et al. 1994; Vaytet et al. 2007). The sweeping up of the wind of the companion red giant in symbiotic systems such as RS Oph, plus the emission of some of the initial energy imparted by the ejecta, lead to deceleration and hence lower-than-usual expansion velocities compared to novae occurring in non-symbiotic systems later in their evolution. This was seen in the 2006 outburst of RS Oph by Ness et al. (2007) for example.
Radio interferometric imaging of the 2006 and 2021 outbursts reveals the structure of the ejecta. A more accurate Gaia astrometric position allowed Munari et al. (2022) to obtain a more concise model, which indicates two lobes east and west of the white dwarf, expanding perpendicular to the orbital plane. These lobes evolved similarly in 2006 and 2021. Figure 2 in Munari & Valisa (2022) indicates that the flux ratio between blue- and redshifted peaks reversed between 2006 and 2021, which can be explained by the orbital phases differing by nearly 180 degrees. Possibly, circular symmetry does not hold along the inner wall of the density enhancement in the orbital plane, and this may influence how SSS radiation reached us in 2006 and 2021.
During the sixth recorded outburst in 2006, the evolution of RS Oph in X-rays was intensively followed with Swift (Bode et al. 2006; Osborne et al. 2011), guiding deeper high-resolution spectroscopy observations with Chandra and XMM-Newton (Drake et al. 2009; Ness et al. 2007, 2009; Nelson et al. 2008). Until day ~25 after optical peak, only the shock emission was observed with, after an initial peak, ultimately a slowly declining brightness, while the distribution of electron temperatures gradually shifted, indicating a cooling plasma. Around day 26, the SSS was first observed with a highly variable Swift count rate, which was a great surprise at the time. High-amplitude variations were thought to be caused by occultations by clumps within inhomogeneous outer ejecta, although this has been the subject of great debate, and previous studies have proven inconclusive (Osborne et al. 2011). The SSS high-resolution grating spectra contained deep absorption lines originating from highly ionised elements that were blueshifted by ~800–1000 km s−1, which is slow compared to other novae. The slower expansion velocity could be explained by substantial amounts of kinetic energy having been dissipated within the stellar wind of the companion star.
The seventh outburst of RS Oph met us with essentially the same X-ray observing capabilities in space, giving us the unique opportunity to study two outbursts with the same instrumentation. With our observing strategy, we aimed to identify similarities and differences but also to follow up questions that remained from the 2006 observation campaigns. The Swift observing campaign is described by Page et al. (2022), while the Chandra and XXMM-Newton observations during the shock phase are described by Orio et al. (2022). The expectations motivating the observing strategy are described in Sect. 2.1 where we also describe instrumental issues and how we solved them (with more details in Appendix A). In Sect. 3, we describe the methods with which we analyse our observations, combined with the results obtained from the data studying variability (Sect. 3.1), spectra (Sect. 3.2, and short-term spectral variability within the observation (Sect. 3.3). Our results are discussed in Sect. 4 and summarised with conclusions in Sect. 5.
Journal of exposures taken with XMM-Newton and Chandra (last rows) used in this work.
2 Observations
The details of all observations with exposures used in this work are listed in Table 1. XXMM-Newton consists of five X-ray telescopes operating in parallel behind three focusing mirrors: The European Photon Imaging Cameras (EPIC) consist of three detectors, the pn detector collecting all the light from one mirror (Strüder et al. 2001) and two MOS detectors MOS1 and MOS2 (Turner et al. 2001) sharing the light of the respective other two mirrors with two Reflection Grating Spectrometers (RGS1 and RGS2; den Herder et al. 2001). The two dispersive RGS spectrometers yield high-resolution spectra capable of resolving emission and absorption lines. In addition, there is an Optical Monitor (OM; Talavera 2009), a 30 cm telescope with a CCD detector, six filters, and two grisms. There are two readout modes, an Imaging mode reading out full or parts of the CCD chip of an entire exposure, and a Timing (=Fast) mode, reading out a small area of the chip in event counting mode, recording the coordinates and arrival time of each photon, allowing the construction of a light curve.
To distinguish 2006 from 2021 observations, we adopt the naming terminology of year followed by d and the day after the respective optical peak, for example 2021d37.1 for the observation taken on day 37.1 after the 2021 optical peak. In addition to the new observations taken on days 2021d37.1 and 2021:55.6, exposure details of RGS exposures for the two archival observations taken on days 2006d26.1 and 2006d54 and the Chandra observations taken on days 2006d39.7 and 2006d66.9 are included. The available information for the 2006 outburst gave us a novel opportunity to schedule deeper X-ray grating observations in a pro-active rather than re-active manner in 2021, that is we did not wait until phase changes (such as the start of the SSS phase) were demonstrated with Swift but assumed the Swift light curve would evolve the same way as in 2006. This enabled us to avoid the delay between trigger and actual XMM-Newton or Chandra observations. However, we depended on the reality of our assumption, and the strengths and weaknesses of this approach are described in the following section.
2.1 Expectations motivating the observing strategy
As reported in AAVSO Alert notice 752, the duration of the inter-outburst interval in RS Oph varies greatly, but the shape of the outburst in optical light and recovery to quiescence is remarkably similar from outburst to outburst. Our baseline expectation was therefore to also see similar behaviour between the 2006 and 2021 outbursts in X-rays and was supported by seeing the results of the first two weeks of Swift X-ray monitoring (Page et al. 2022). Figure 1 shows the 2006 and 2021 Swift light curves in black and orange colours, respectively, with the times of Chandra and XMM-Newton observations in 2006 and 2021 marked with the same colours. During the shock phase in 2021, Chandra and XMM-Newton observations were obtained on days 2021d17.5 and 2021d21.1, respectively, yielding high-resolution X-ray spectra that perfectly fit into the cooling trend seen in 2006 (Orio et al. 2022). During the SSS phase, two XMM-Newton observations were obtained on days 2021d37.1 and 2021d55.6; these are described in the present work.
Assuming the same SSS evolution as in 2006, we made a scheduling request for day 37.1 (ObsID 0841930501, 100ks) with the goal to probe spectral changes during the early SSS phase that had displayed high-amplitude variations in 2006 (Osborne et al. 2011). As the peaks of emission were expected to be extremely bright, we selected the most conservative instrumental setup with RGS in Small Window mode, both MOS instruments turned off to use their telemetry allocation for downlinking all RGS data, and the pn in burst mode. Unfortunately, the nova did not behave as expected, yielding a much lower count rate, and rendering the restrictive instrumental setup unnecessary. Nevertheless, important new insights can be gathered from this observation when comparing to the observation on 2006d26.1, which will be described in more detail in an upcoming publication.
Under the same proposal, we had requested a shorter follow-up observation (approved 47 ks) in order to determine the spectral shape after the early variability phase. We scheduled a 56ks observation under ObsID 0841930901 (see Table 1) starting on day 55.6 in order to compare it with the 2006 observation on day 54, thus obtaining two SSS spectra of the same nova during the same epoch of the evolution. Expecting a higher brightness than on day 37, we initially chose the same restrictive instrumental setup of the RGS Small Window Mode and pn burst mode. However, between days 45 and 50, a gradual decline was observed (Page et al. 2022), and we therefore changed the instrumental setup to standard RGS spectroscopy mode for the benefit of adding the MOS cameras. Also, because the pn burst mode is not sensitive below 0.7 keV, we changed the pn to Timing mode. Unfortunately, the brightness started to increase again just hours before the start of the XMM-Newton observation, and the RGS suffered some problems owing to the soft brightness, which we describe in Sect. 2.2.
 |
Fig. 1 Comparison of long-term Swift X-ray light curves obtained during the 2006 (black) and 2021 (orange) outbursts (Page et al. 2022). The similar behaviour during the early shock phase until ~30 days after tref can be seen while the remarkable differences during the SSS- and decline phases after day ~30 are evident. Vertical lines mark the times of deeper Chandra (dotted) and XMM-Newton (solid) observations for the outbursts in 2006 (orange) and 2021 (black) as marked in the upper right legend. In this work, the two XMM-Newton observations taken on days 37.1 and 55.6 are discussed. |
2.2 Data processing
The uncalibrated observation data (Observation Data File=ODF) were downloaded from the ESA XMM-Newton archive and processed with the Science Analysis Software (SAS) version 19.0.0 and the latest version of calibration files. For the data of the OM, the two standard chains omichain and omfchain were run to produce image and fast-mode data, respectively. Owing to the brightness in the soft-X-ray band, all X-ray exposures suffered some type of anomalies, which we dealt with thanks to the help of the XMM-Newton helpdesk as described in this section, with more details in the Appendix.
The RGS Small Window mode data in ObsID 0841930501 suffered some issues with an inconsistency flagged in the SAS terminology as ‘GTI&EXPOSU Inconsistency’, which cannot be handled by the SOC. A workaround was found to obtain calibrated spectra and light curves and will be described in an upcoming paper. Our choice of instrument setup for ObsID 0841930901 was strongly influenced by these issues, coupled with the declining rather than increasing Swift count rate. As described above, the source became brighter again just before the start of the XMM-Newton observation, and although the source was nowhere near as bright on day 2021d55.6 as it was on day 2006d54 (see Fig. 1), we suffered more problems with ObsID 0841930901 than we had in 2006 with ObsID 0410180301.
The RGS2 spectrum is not usable owing to excessive pile up in addition to the loss of an unknown number of events. The XMM-Newton helpdesk provided the following background information: Since August 2007, the RGS2 CCDs are read via a single node because of an electronics malfunction. RGS2 frame times are therefore twice as long as before this change, now with an accumulation time of 9.6 s in normal spectroscopy mode and 2.4 s for Small Window mode when reading the eight CCDs. Therefore, the RGS2 is now more vulnerable to excessive pileup.
Also, the RGS1 is affected by pileup, but due to the still shorter readout time, not in a way that photons were lost in an uncontrollable way as in the RGS2. As photons are only redistributed, we can correct the RGS1 data for pile up as described in Appendix A.1. We therefore only use the pile-up-corrected RGS1 spectrum. Unfortunately, this leaves a larger number of gaps in the grating spectrum, because the RGS1 bad pixels cannot be filled with information from the RGS2. We note that the fluxed RGS spectrum in the pipeline products for ObsID 0841930901, P0841930901RGX000FLUXED1003.FTZ is invalid, yielding an artificial flux reduction in the range 24–28 Å. As reported by Ness et al. (2007), the 2006d54 spectrum was also piled up, but both RGS2 and RGS1 spectra could be corrected with the same approach, which is described in Appendix A.1.
Another issue is telemetry losses that can lead to aliases in the period analysis. In Appendix A.2, we describe our checks, finding aliases at ~24s and ~28s in the pn light curve, while there is no other alias expected, and therefore the feature in the periodogram at 35.47-s period is not related to the telemetry dropouts and can be associated to the source (see Sect. 3.1).
3 Analysis and results
3.1 Variability studies
Figure 2 shows the X-ray and UV light curves extracted from the pn, RGS1, and OM exposures as labelled in the respective panel legends. The hard-X-ray light curve (top panel) whose emission originates in the shocks is flat, demonstrating that all variability originates in the SSS component. Between days 55.6 and 56.3, random variability of a factor of <2 can be seen consistently in the soft pn and RGS light curves. Towards the end of the observation, the RGS1 and pn count rates are ~20% lower, starting with a continuous decline around day 56, slowly rising again around day 56.2, and dropping slightly back again. The scaled hardness ratio curve is overplotted in the second panel (see discussion in Sect. 3.3). The RGS2 light curve on day 55.6 (not shown) is severely compromised by telemetry losses and pile up, yielding count rates of between 8 and 16 counts per second (cps). This is much lower than the count rate in the RGS1 light curve of namely 30–40 cps, and the trends seen in the RGS1 and pn light curves in Fig. 2 are not seen in the RGS2 light curve.
Figure 3 shows the power density spectrum (PDS) describing random variability in the pn light curve of timescales longer than 100 s. The light curve was split into four2 subsamples, a log-log periodogram3 was calculated from each subsample, and the resulting periodogram points were binned with a bin width of 0.2 in dex. All periodogram points within a bin were averaged and the error of the mean was calculated. It can be seen that the low-frequency part of the PDS is dominated by red noise4 up to frequency log(f/Hz) = −3.17, which corresponds to a timescale of 0.017 days (25 min). All variability longer than this timescale belongs to this red noise. No break or other characteristic frequencies are detected.
The UVW2 Image mode magnitudes are shown in the bottom panel of Fig. 2 with 11 red horizontal bars whose lengths correspond to the respective integration times of 4400 s each. These magnitudes vary in a narrow range of 11.27–11.26 mag (red dotted horizontal lines), and within this range, no systematic decline or increase can be identified. We further found no periodic variability in the OM Fast mode light curve (black) as can be seen from the power spectrum shown in Fig. 4. The highest peak is below 70% confidence and is therefore probably a random event. In particular, there is no signal at the 35 s period that was seen in X-ray light curves.
During the 2006 outburst, transient 35 s periodic oscillations were detected with both Swift (Osborne et al. 2006, 2011) and XMM-Newton (Nelson et al. 2008; Ness et al. 2007, 2015). This period was only present in the plasma that emits the SSS spectrum (Ness et al. 2007). This period was again found with Swift during the 2021 outburst (Page et al. 2022), indicating that it is related to system parameters. We searched for this period in the soft pn and RGS1 light curves from day 55.6. As it was transient, we studied the time evolution following the methods described in Ness et al. (2015), splitting each light curve into 54 (soft pn) and 55 (RGS1) adjacent overlapping subintervals of 2000 s duration with 50% overlap. For each of these subintervals, we calculated separate Lomb-Scargle power spectra with the method of Scargle (1982). In Fig. 5, period time maps are shown where a clear transient period can be seen around 35 s in both RGS1 and pn light curves. We repeated the same study with different bin sizes, all yielding consistent results. We also detected 35 s oscillations in the RGS2 light curve, even though it is seriously compromised by pile up and telemetry losses. The trends in the RGS2 light curve are different from those in the pn and RGS1 light curves, which we attribute to the higher levels of pile up and telemetry loss due to the longer read-out time.
The period is variable in strength but this variability is not obviously correlated with the count rate. Towards the end of the observation, the strongest signal is detected, when the count rate was ~20% lower. During this last part of the observation, a small rise in count rate is seen that seems to correlate with a much lower power of the period. It is possible that during the last part of the observation, the variability behaviour changed, yielding an anti-correlation between period power and count rate. We remind the reader that the correlation between hardness and count rate was less clear towards the end of the observation (see Fig. 2).
The total pn light curve shows two strong signals around 24 s and 28 s not seen in the RGS1 data. This is caused by the pn instrument reaching telemetry saturation (see Sect. 2.2 and Fig. A.2).
 |
Fig. 2 XMM-Newton X-ray and UV light curves (units counts per second, cps) extracted from the pn, RGS1, and OM instruments taken on day 2021d55.6 (see x-axis labels). The photon arrival times were converted to days after tref = 2021-08-09.5417. The pn light curve is broken into a hard (top) and a soft (second panel) band split at 1.5 keV (see legends for individual energy bands), probing shock and SSS emission, respectively. The soft band is split into two bands, H and S, with the split at 0.54keV, and the orange curve in the second panel represents the scaled hardness ratio (HR) constructed from countrates recorded in the energy bands H and S as given in the legend. The shaded coloured area in the third panel marks light-curve segments discussed separately in Sect. 3.3. In the bottom panel, the OM UVM2 filter (~2070–2170 Å range) light curves are shown from the Image mode (red horizontal bars for each exposure) and Fast mode (black) data. Count rates are plotted, and corresponding magnitude values are included on the left, which correspond to the lowest and highest Image mode count rates (marked with the dotted horizontal red lines). |
 |
Fig. 3 PDS calculated from the pn data (20 s binning) where the red solid line is a broken power-law fit. The circles are average values within the frequency bin with error bars as error of the mean. The frequency range corresponds to a period range of 100-32 000 s. |
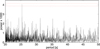 |
Fig. 4 Periodogram calculated from the OM data with 70% and 50% confidence levels as upper and lower horizontal dashed lines, respectively. The PDS standard normalisation of the Lomb–Scargle algorithm was used for the confidence level calculation. |
3.2 Spectral studies
The two spectra taken on days 2021d37.1 and 2021d55.6 probe different phases of the evolution. In Fig. 6 we compare the RGS spectrum from day 2021d37.1 (grey shading) with the same-epoch 2006d39.7 spectrum down-scaled by a factor five (red), and the earlier 2006d26.1 spectrum extracted from the times after a sudden brightness increase (black). The top panel shows a larger wavelength range demonstrating that the same-epoch 2006d39.7 spectrum is very different, while more, qualitative similarities are seen with the 2006d26.1 spectrum. The shock emission was the same, while the soft component with many unidentified narrow emission features was much brighter on day 2021d37.1. The bottom panel zooms into the soft range, demonstrating that qualitatively, many of the unknown features on day 2006d26.1 were also present on day 2021d37.1. Many of the unknown features are also present in the 2006d39.7 spectrum. These spectra demonstrate that a dedicated publication is needed to discuss these complex spectra in sufficient depth. The 2021d37.1 data are therefore not discussed further in this work with reference to an upcoming publication.
In this work, we concentrate on the day 2021d55.6 spectrum, focusing on identifying reasons for the lower brightness of the SSS emission compared to 2006d39.7, 2006d54, and 2006d66.9. We test three hypotheses and any combination of them: simply scaling with a constant factor (e.g. caused by occultations or eclipses or by a lower nuclear burning rate), a change of effective temperature (or colour change), and more absorption.
We present a novel approach, applying relatively simple models to observations rather than source models to scale observations against observations. With this approach, all the known and unknown details that are present in both observed spectra are mapped against each other without needing a full description of the processes leading to all observed details.
The standard approach is to fit spectral models to the data comparing model with data. Physical quantities such as the effective temperatures or mass of the underlying white dwarf can be determined this way, which in turn are useful for constraining evolutionary models needed to obtain a full understanding of the nova phenomenon. However, robust physical conclusions are only possible if the spectral models reproduce the data in full detail, which has so far not been achieved with the SSS grating spectra. The calculation of robust parameter uncertainties is needed for the interpretation of best-fit parameters, and this is only possible if a formally acceptable fit (not just ‘best’ fit) is found, indicated by finding a value of reduced χ2 near unity. The most promising results have been achieved with the SPEX model first attempted by Pinto et al. (2012) and more recently by Ness et al. (2022). While the agreement of model with data is the best ever achieved for an SSS spectrum, formal statistical values of reduced χ2 still range around six, and the models make some simplifying assumptions, only allowing insights into the properties of the absorbing layers without allowing determination of the mass of the white dwarf. We do not follow this approach in this work. It is desirable to conduct a systematic, homogeneous analysis of a sample of SSS spectra with the same analysis strategy, the same version of SPEX, and so on to enable comparison of different systems.
Our novel approach is only possible with the grating spectra because of their low degree of photon energy redistribution compared to the XMM-Newton EPIC cameras or the Swift/XRT. The instrumental response characterises photon redistribution and calibrates physical flux to instrumental counts. The conversion from a fluxed model spectrum to a predicted count spectrum is done via matrix multiplication of the model with a response matrix that is the result of the instrument calibration. This matrix contains the largest conversion values on its diagonal, and the lower the spectral resolution (and thus the larger the amount of photon redistribution), the more off-diagonal positions are populated with non-zero values. Near-diagonal response matrices can be inverted, and high-resolution spectra such as optical spectra or X-ray grating spectra can be converted to physical flux spectra by multiplying an observed count spectrum with the inverse response matrix. For highly populated response matrices of low-resolution instruments, such as the XMM-Newton EPIC cameras or the Swift/XRT, the inversion solutions are far less unique, and models have to be converted to instrumental units by smearing out sharp features to the low instrumental resolution.
Our novel approach is to break the separation of models and data and multiply a multiplicative scaling model (without units) with an observation in physical flux units (converted from the instrumental counts) and compare this with another observed spectrum in physical flux units.
We performed parameter optimisation, yielding a minimum value of 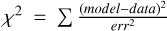 , where model is a 2006 observed spectrum multiplied by the down-scaling model: either a wavelength-independent (i.e. grey) constant factor, the ratio of two blackbodies (BB-ratio, described in Sect. 3.2.2), or an absorption model (described in Sect. 3.2.3). Here, data is the 2021d55.6 spectrum; as it has hot pixel gaps at different wavelengths from the 2006 spectra, we interpolated each 2006 spectrum to the wavelength grid of day 2021d55.6. The measurement errors err were combined as the summed squared errors from day 2021d55.6 and the respective 2006 errors.
, where model is a 2006 observed spectrum multiplied by the down-scaling model: either a wavelength-independent (i.e. grey) constant factor, the ratio of two blackbodies (BB-ratio, described in Sect. 3.2.2), or an absorption model (described in Sect. 3.2.3). Here, data is the 2021d55.6 spectrum; as it has hot pixel gaps at different wavelengths from the 2006 spectra, we interpolated each 2006 spectrum to the wavelength grid of day 2021d55.6. The measurement errors err were combined as the summed squared errors from day 2021d55.6 and the respective 2006 errors.
 |
Fig. 5 XMM-Newton RGS (left) and pn (right, soft 0.2–1.5 keV range) periodogram time maps illustrating the evolution of periods focusing on the 35 s period detected during the 2006 outburst. Each graph consists of four panels: in the main (bottom left) panel, time is running down and the tested periods run from left to right, while the panel above shows representative Lomb–Scargle periodograms on the same shared horizontal axis. The bottom-right panel shows the light curve along the same vertical time axis. The colour bar in the top right allows conversion of colours in the main panel to the units of power used for the periodograms. The vertical time axis is in units of elapsed hours since the start of the RGS1 exposure (left panel), and the pn exposure (right panel) which started 2250 s (0.6 h) later than the RGS1 exposure owing to the higher pn overhead. In the respective top panels, the black curves show the periodograms from the respective entire light curves and the colour-shaded curves are periodograms from the selected 2000 s time intervals marked with horizontal lines of the same colour as the dashed lines in the panels below. The time bin sizes of the light curves are included in the respective top-left panels. The same time maps were produced with different bin sizes, yielding similar results. |
 |
Fig. 6 XMM-Newton RGS spectra in photon flux units per 103 s (=ks). The 2021d37.1 spectrum (grey shading) is compared to the same-epoch 2006d39.7 spectrum (down-scaled by factor 5; red) and the bright-only 2006 spectrum on day 26.1 (black). The top panel shows a larger wavelength range while the bottom panel zooms into the variable soft excess with several unknown narrow emission and absorption features, where only the corresponding wavelength is indicated. |
3.2.1 Scaling by a constant factor
In order to account for wavelength-independent effects, such as eclipses or other grey occultations, we allow the application of a constant factor. This is the simplest scaling process. This factor can also be interpreted as a luminosity change; for example, if there is a temperature change (Sect. 3.2.2) combined with a change of radius, the scaling factor would correspond to a ratio in radius 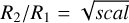 . As the approaches of temperature change (Sect. 3.2.2) and absorption (Sect. 3.2.3) combine brightness changes with spectral changes, we keep grey scaling fixed at unity during initial experiments with those models while testing the additional scaling only to judge the quality of the other approaches.
. As the approaches of temperature change (Sect. 3.2.2) and absorption (Sect. 3.2.3) combine brightness changes with spectral changes, we keep grey scaling fixed at unity during initial experiments with those models while testing the additional scaling only to judge the quality of the other approaches.
3.2.2 Blackbody scaling
Given the Stefan-Boltzmann law of L ∝ T4 × R2, a temperature change at the same emitting radius not only shifts the spectrum to the red or blue but also leads to a substantial change in brightness. Without the need for a constant scaling factor (Sect. 3.2.1), small temperature changes can therefore already lead to large changes in flux. If temperature changes were the cause of the lower fluxes in 2021 compared to 2006, this would be detectable as different spectral shapes. This is illustrated in the top panel of Fig. 7 where the observed RGS1 spectrum of RS Oph on day 2021d55.6 (black) is compared with the same spectrum multiplied by the ratio of two blackbody curves corresponding to Tref,1 = 5 × 105 K and Tref,2 = 4 × 105 K, respectively (labelled in the legend in units kK= 103 K). The resulting spectrum is 20 times brighter at the peak, and it is therefore renormalised by a factor 0.05 to show that it is harder than the original spectrum. Multiplication of such ratio curves to the 2006 spectra can therefore probe whether the 2021d55.6 spectrum might be the result of lower effective temperature by fitting the two temperatures to yield a best fit of scaled 2006 spectra to the observed 2021d55.6 spectrum. To understand the behaviour of such fits, we stepped through a grid of fixed values of Tref,1 and fitted T2,best to obtain the closest match to the 500 kK/400 kK ratio curve and found that with any value of Tref,1 that yields significant flux within the RGS spectral range (Teff ≈ (3−25) × 105 K) a value of T2,best can be found to almost exactly reproduce the 500 kK/400 kK ratio curve. While fitting both reference temperatures (Sect. 3.2.4), we indeed encountered no convergence, and we only managed to constrain one temperature value if the other is assumed fixed. The respective best-fit values of T2,best are shown in the bottom panel of Fig. 7. The results are very close when allowing additional renormalisation (orange curves). The bottom panel shows that with higher values of Tref,1, higher values of T2,best are also needed. There is no linear relationship, and the bottom-right legend provides empirical relationships, and these relationships are in fact independent of the original choices of Tref,1 and Tref,2.
The conclusion that we draw from this study can be summarised as follows:
Down-scaling the 2006 spectra with the ratio of two black-body curves corresponding to different temperatures can explain the lower fluxes in 2021 if a good match can be found after iterating Tref,1 and Tref,2.
The values of Tref,1 and Tref,2 are degenerate, and therefore many pairs of Tref,1 and Tref,2 can produce the same blackbody ratio curve; one of these two values has to be fixed to any value within the range of ~(8−25) × 105 K.
When applying this method to data (Sect. 3.2.4), the resulting values of temperature only inform us as to whether the compared spectra are qualitatively cooler or hotter. The method does not provide any concrete values of respective effective temperatures, and also differences or relative changes in temperature cannot be quantified.
 |
Fig. 7 Illustration of the scaling method with the ratio of two different blackbody curves and that many pairs of Tref,1 and Tref,2 can produce the same blackbody ratio curve. In the top panel, the RGS1 spectrum of RS Oph from 2021d55.6 (black) is multiplied with the ratio of two blackbody models corresponding to Tref,1 = 5 × 105 K (=500 kK) and Tref,2 = 4 × 105 K (=400 kK), respectively and normalised (see legend). The resulting spectrum (orange) is a factor 20 brighter but is also harder. The bottom panel shows the results of fitting only Tref,2 with (black) and without (orange) additional normalisation while Tref,1 is fixed at given grid values (x-axis) to reproduce the 500 kK/400 kK ratio curve. The bottom right legend provides empirical analytic relationships between fixed grid value and T2,best values reproducing the same ratio curve. The same relationships are found for any other pairs of reference temperatures Tref,1 and Tref,2; see Sect. 3.2.2 for details. |
 |
Fig. 8 Illustration of how to down-scale an observed source spectrum, assuming higher absorption. In the top panel, transmission curves are shown assuming an arbitrary value of neutral hydrogen column density NH and cosmic abundances of other elements. Different colours represent a pure (neutral) interstellar absorption model (black) and modifications when successively adding (hot) absorption edges at the respective ionisation energies of O VII, N VII, and N VI (see labels); thus, the red curve represents the absorption model accounting for all edges. In the bottom panel, the effect of absorption is illustrated for the example of a blackbody source with an effective temperature of 500,000K. These absorption models were designed to be applied to emission models but can also be applied to data of sufficiently high spectral resolution; see Sect. 3.2.3 for details. |
3.2.3 Absorption scaling
Photoelectric absorption affects photons with energies higher than the ionisation energies of the intervening material. The ionisation energies increase with the stage of ionisation, and an ionised plasma is more transparent to X-rays than neutral material. To test a higher degree of photoelectric absorption as the cause of the differences, we multiply the brighter 2006 spectra on days 39.7, 54, and 66.9 with a photoelectric absorption model. We use the ionabs absorption model, which is part of the PintOfAle package (Kashyap & Drake 2000) and is illustrated in Fig. 8. Assuming elemental abundances and an ionisation balance for each element, ionabs calculates cross sections from which transmission factors at each wavelength can be computed that are to be multiplied with a source spectrum. This model works similarly to the better-known multiplicative model tbvarabs in xspec, which is designed to be applied to additive source models (in flux units) before folding through an instrumental response and comparison to an observed spectrum in instrumental units.
As the RGS response matrix is sufficiently diagonal, we can afford to apply the absorption model to the fluxed RGS spectra without the need for defining (and understanding) a model of an emission source. As an approximation of the small amount of photon redistribution, we fold the absorption model with a Gaussian filter of 0.05 Å width, which smoothes out the sharp edges and absorption lines to roughly RGS resolution. This is not possible with CCD spectra as the much larger photon redistribution is a statistical process that needs to be modelled.
The ionabs model calculates photoelectric absorption cross sections σλ (in units cm2) for a given photon energy E = h × c/λ for specified chemical composition (we used here Anders & Grevesse 1989) and ion fractions. It uses ground-state photoionisation cross sections computed using the fortran code of Verner et al. (1996) and is supplemented with high-resolution cross sections in the vicinity of 1s–2p resonances for O from García et al. (2005).
From σλ, transmission curves 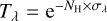 as shown in the top panel of Fig. 8 can be computed for an assumed column density NH in units of cm−2. The vector Τλ consists of factors ≤1 for each wavelength value λ to be multiplied with a source spectrum to simulate what would be observed behind an assumed equivalent hydrogen column of NH. The column densities of other elements are scaled by the assumed abundance relative to hydrogen when computing σλ.
as shown in the top panel of Fig. 8 can be computed for an assumed column density NH in units of cm−2. The vector Τλ consists of factors ≤1 for each wavelength value λ to be multiplied with a source spectrum to simulate what would be observed behind an assumed equivalent hydrogen column of NH. The column densities of other elements are scaled by the assumed abundance relative to hydrogen when computing σλ.
The black curve in the top panel of Fig. 8 represents Τλ, assuming a neutral absorber with ion fraction values of one for all neutral ionisation stages and zero for higher ionisation stages. For illustration purposes (to better see the ionisation edges at shorter wavelengths), the O I edge was decreased by reducing the oxygen abundance. In our analysis, we test such modifications equivalent to a change of the O I column density. A shallower O I edge can be interpreted as a reduced oxygen abundance but may also mean that oxygen is ionised, thus only reducing the column density of neutral oxygen. We tested the behaviour of the transmission curve when the column densities of correspondingly higher ionisation stages increase, finding that the edge shifts to shorter wavelengths. If this is not observed, then a reduced O I edge could be produced by fully ionising oxygen. Oxygen may also be hidden in other ways; for example, if locked in dust grains that change the absorbing behaviour to not affect the O I edge. We further include absorption by highly ionised material, primarily leading to edges at 16.77 Å (O VII), 18.64 Å (N VII), and 22.46 Å (N VI), which are marked by red labels in Fig. 8. While ionabs allows neutral and ionised absorption to be included in one model, we define separate models for each ion, meaning that we obtain the product of up to four ionabs components. One reason for the separation is that the interstellar matter contains no O VII and so on, and the ionised material must be based on a different value of NH. It would be more self-consistent to combine at least the N VI and N VII edges into one component. Fine-tuning the ionisation balance would also require assuming less-ionised nitrogen, which increases complexity. This would be a different study from that presented here, where our goal is to identify the role of absorption as an explanation for the lower fluxes in 2021 compared to 2006. In the bottom panel of Fig. 8, we demonstrate the effects of the absorption models from the top panel of the same figure on a blackbody source spectrum with Teff = 5 × 105 K.
3.2.4 Results
The RGS spectrum for day 2021d55.6 is shown with grey shadings in photon flux units in Fig. 9 in comparison to the bright SSS continuum spectra taken on days 2006d39.7, 2006d54, and 2006d66.9 using orange and red lines for the original spectra and the down-scaled spectra, respectively. We experimented with various ways to down-scale the 2006 spectra to match the day 2021d55.6 spectrum as described in Sect. 3.2, namely any combination of: (1) constant scaling factor (Sect. 3.2.1), (2) multiplication by the ratio of two different blackbody models (probing temperature changes, Sect. 3.2.2), and (3) multiplication with an absorption model (probing higher absorption in 2021 compared to 2006, Sect. 3.2.3). For the ratio of two black-body models, we fixed the first temperature to 5 × 105 K given the degeneracy that for any temperature value, a second temperature value can be found yielding the same ratio curve (see Sect. 3.2.2). As on days 2006d54 and 2006d66.9 the O I absorption edge was considerably reduced compared to 2006d39.7 (Ness et al. 2007), we allow changes in the depth of the O I edge when fitting the neutral absorption model.
We present graphical representations of the results of two selected approaches with the red curves in Fig. 9: In the left column, we show the results of assuming pure photoelectric absorption by neutral and ionised material, and in the right column with additional emission-spectrum temperature changes, both without scaling. The agreement between the scaled 2006 and 2021d55.6 is remarkable, lending significant credibility to our novel approach and demonstrating its ability to provide useful information within a certain scope: For days 2006d39.7 and 2006d54, the agreement of the unscaled absorption model is already excellent without the need for the additional BB ratio. For day 2006d66.9, the pure absorption model (bottom left) clearly leaves room for improvement, which can be achieved by the additional assumption of a temperature change (bottom right).
Table 2 lists best-fit parameters testing various combinations of scaling, temperature-changes (BB ratio), and absorption. The 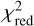 values in the last row of each respective section indicate how well the scaled 2006 spectra in each column reproduce the 2021d55.6 spectrum. A graphical illustration of these values is shown in Fig. 10. The different combinations are ordered in Table 2 and Fig. 10 (see legend) by degree of complexity. Pure scaling factor and scaled and unscaled BB-ratio fits yield rather poor agreement in all cases, while the pure absorption model alone, without any scaling (fourth section in Table 2; see also left panel of Fig. 9), leads to much better agreement with the data on 2021d55.6, except for the scaling from day 2006d66.9. Adding a scaled or unscaled BB ratio (fifth section in Table 2) only leads to improvement for day 2006d66.9, while for day 2006d39.7 there is no improvement. The combined absorption plus BB-ratio model for day 2006d66.9 works better than a pure BB-ratio model. No neutral ΔΝΗ is needed, while the improvement is driven by the ionisation edges, where the N VII edge is found to be shallower (negative value) on day 2021d55.6 than on day 2006d66.9. Additional scaling (last section in Table 2) leads to only small improvements in fit in all three cases. For day 2006d66.9, we can therefore conclude that a temperature change must be responsible for the difference in brightness, while different absorption edges of ionised material are also important. We note that we cannot quantify the temperature difference as the fitted temperature depends on the choice of the first temperature. Also, the ratio of temperatures is not meaningful as it also depends on the choice of the first temperature (see Fig. 7). All we can conclude with this method is that the effective temperature of the underlying source in the 2006d66.9 spectrum was higher than on day 2021d55.6, although we are not able to quantify by how much.
values in the last row of each respective section indicate how well the scaled 2006 spectra in each column reproduce the 2021d55.6 spectrum. A graphical illustration of these values is shown in Fig. 10. The different combinations are ordered in Table 2 and Fig. 10 (see legend) by degree of complexity. Pure scaling factor and scaled and unscaled BB-ratio fits yield rather poor agreement in all cases, while the pure absorption model alone, without any scaling (fourth section in Table 2; see also left panel of Fig. 9), leads to much better agreement with the data on 2021d55.6, except for the scaling from day 2006d66.9. Adding a scaled or unscaled BB ratio (fifth section in Table 2) only leads to improvement for day 2006d66.9, while for day 2006d39.7 there is no improvement. The combined absorption plus BB-ratio model for day 2006d66.9 works better than a pure BB-ratio model. No neutral ΔΝΗ is needed, while the improvement is driven by the ionisation edges, where the N VII edge is found to be shallower (negative value) on day 2021d55.6 than on day 2006d66.9. Additional scaling (last section in Table 2) leads to only small improvements in fit in all three cases. For day 2006d66.9, we can therefore conclude that a temperature change must be responsible for the difference in brightness, while different absorption edges of ionised material are also important. We note that we cannot quantify the temperature difference as the fitted temperature depends on the choice of the first temperature. Also, the ratio of temperatures is not meaningful as it also depends on the choice of the first temperature (see Fig. 7). All we can conclude with this method is that the effective temperature of the underlying source in the 2006d66.9 spectrum was higher than on day 2021d55.6, although we are not able to quantify by how much.
These results lead us to the conclusion that absorption is the dominant factor explaining the lower fluxes in 2021 compared to 2006, while a temperature change is only detectable in the last 2006 observation, which was taken after the peak of the SSS emission was reached (see Fig. 1).
Another interesting result is that the agreement between day 2021d55.6 and 2006d39.9 is actually better than that with the same-epoch observation 2006d54. While in 2006, the neutral oxygen column density decreased substantially by day 54, possibly by continuous photoionisation (Ness et al. 2007), the same process leading to this reduction apparently did not take place during the 2021 outburst (or was slower). Figure 11 shows that also on the sub-Å level, 2021d55.6 agrees better with 2006d39.7 than with the same-epoch 2006d54 spectrum, both yielding deeper absorption lines with more similar blueshifts. Unfortunately, due to the missing information from the RGS2, the day 2021d55.6 spectrum contains a lot of gaps, and few absorption line profiles qualify for direct comparison with all three spectra. In the top panel of Fig. 12, we show a comparison of the (normalised) O VII (λ0 = 21.6 À) line region in velocity space, again showing much more similarity between days 2021d55.6 and 2006d39.7. As discussed by Ness et al. (2007), the early 2006 SSS spectra still contained P-Cyg-type line profiles, while the emission line component disappeared in the later observations. It can be seen in Fig. 12 that an O VII emission line was clearly present on day 2021d55.6, while not on days 2006d54 and 2006d66.9. Also, the observed blueshift was much lower on day 2006d54 than on both 2006d39.7 and 2021d55.6. Another absorption feature suitable for comparison is an unknown absorption feature observed at 26.83 Å. In the bottom panel of Fig. 12, we show the profile assuming a rest wavelength of 26.93 Å (yielding about the same blueshift as for O VII on day 2021d55.6). This line has no emission line component, and it is only present on days 2006.39.7 and 2021d55.6, again showing these two observations are more similar than the same-epoch observation on day 2006d54. We note that the blueshift for the 26.83-Å line is different on days 2006.39.7 and 2021d55.6, while for O VII this blueshift is consistent on both days. The day 2021d55.6 spectrum therefore resembles an absorbed version of the 2006d39.7 spectrum, suggesting that the opacity of the ejecta to soft X-rays may have evolved more slowly during the 2021 outburst.
 |
Fig. 9 XMM-Newton RGS1 spectrum obtained on 2021d55.6 (grey shadings) compared to the 2006 spectra obtained on 2006d39.7 (top), 2006d54 (middle), and 2006d66.9 (bottom). The orange lines represent the unscaled (brighter) 2006 spectra as observed, while the respective red lines are the results of applying an absorption model to the observed 2006 spectra assuming the absorption parameters given in Table 2: ΔNH of an absorption model of only neutral absorbers with modification of the depth of the O I absorption edge at 22.8 Å and the parameters of three absorption edges of highly ionised ions with values of optical depths and column density. A scaling factor was not applied. In the left panel, the result from scaling only with an absorption model is shown, while in the right panel, additional scaling with blackbody ratio has been applied, thus assuming a change in temperature between the spectra. The parameters of these and more models are given in Table 2. |
3.3 Spectral variations
In Fig. 2, variability can be seen to correlate with variations in the hardness ratio. Such variations may be due to variations in the O I column density that would cause variations in the depth of the absorption edge at 540 eV, the minimum energy needed to ionise O I out of the inner (K) shell. To test this hypothesis, we extracted the hardness-ratio light curve from the pn data split at the energy 540 eV defining the hardness ratio as HR = (H − S)/(H + S) with H and S being count rates extracted from the respective energy bands H = 540–800 eV and S = 300–540 eV. The hardness ratio varies between values of −0.580 and −0.397 on day 2021d55.6, and for comparison with the brightness evolution, we have scaled the hardness ratio curve to a curve with the same median value and dynamic range (thus the same minimum and maximum values) and overplot the thus-scaled hardness curve in the second panel of the right graph in Fig. 2 with the brown curve. Here, we see that brightness and hardness variations are directly correlated, indicating that the depth of the O I absorption edge has caused the variations.
Figure 13 shows hardness (separated at the O I ionisation edge at 540 eV) and brightness light curves for all SSS observations in the order of epoch, starting with the two early SSS observations on days 2006d26.1 and 2021d37.1 until the post-peak observation taken on day 2006d66.9. During the early-SSS observations, hardness and brightness are strongly anti-correlated, reflecting that all variability happened in the soft band while the hard band represented only the more constant shock emission. We note that during these early SSS observations, there was no SSS emission shortward of the O I absorption edge (Fig. 6).
Changes of the O I absorption edge proportional to brightness changes were already found during the 2006 outburst on day 39.7 (Ness et al. 2007), where the hardness evolution lagged 1000 s behind the brightness evolution. Ness et al. (2007); Schönrich & Ness (2008) interpreted this lag as owing to density-dependent changes in the ionisation or recombination timescales. In the fourth panel of Fig. 13, it can be seen that on day 2006d54, variations were almost exactly coincident with possibly a small lag of hardness following brightness changes. Such a small lag may actually also be present in the day 2021d55.6 observation (fifth panel). However, towards the end of the day 55.6 observation, the correlation seems to break down, where we remind the reader that the 35 s period seems to be strongest; see Fig. 5. After the peak of SSS emission on day 2006d66.9, we see no variability (bottom panel). If nuclear burning had already turned off, this would indicate that the variability observed in the other SSS light curve depends on active central burning. A similar behaviour was seen in M31N 2008-12a by Darnley et al. (2016) with the SSS light curve becoming smoother with the transition from a burning white dwarf to a cooling white dwarf.
To visualise the spectral evolution in a continuous manner, we use the concept of spectral time maps. The general concept of these spectral time maps is described in Ness (2012), for example. In the spectral time map shown in Fig. 14, it can be seen that the emission around 20 Å increased by more during the brighter phases than the emission above 22.8 Å (blue and red spectra in the top panel). The variations therefore appear to be related to changes in the O I absorption edge: during brighter episodes, the O I column density was lower and thus more transparent to harder emission. The coloured bars in Fig. 2 mark the time intervals from which spectra were extracted, representing selected activity episodes that are shown in the top panel of Fig. 14. During the last episode of lower count rates (yellow spectrum), the count rate is not only lower at λ < 22.8 Å but also above, and the origin of this reduction in flux is therefore different.
Parameters of down-scaling 2006 spectra to the 2021d55.6 spectrum.
 |
Fig. 10 Reduced values of χ2 for the six down-scaling models listed in Table 2. The dotted line in the bottom represents |
 |
Fig. 11 XMM-Newton RGS1 spectrum taken on 2021d55.6 compared to 2006 spectra scaled with the pure absorption model (left column in Fig. 9). The lower panels show details, and although the 2021d55.6 spectrum has a lot of gaps, one can see that the same-epoch 2006 spectrum (blue) contains much weaker absorption lines, while on the sub-Å level, there is a greater resemblance to the 2006d39.7 spectrum. |
 |
Fig. 12 Comparison in velocity space of line profiles of the O VII line at rest wavelength 21.6 Å (top) and an unknown absorption line observed at 26.83 Å (bottom) for the 2021d55.6 observation and the 2006d39.7, 2006d54, and 2006d66.9 observations. Assuming a similar blueshift for the unidentified line, we adopt a rest wavelength of 26.96 Å. Data are shown in histogram style and Gaussian fits to the absorption lines with solid lines. Values of best-fit blueshift are given in the bottom right legend. Observed spectra and models are normalised to the respective median values of the plot range. |
 |
Fig. 13 Comparisons of 2006 and 2021 light curves with the respective hardness-ratio light curves (see respective horizontal axes labels). In the third panel (2006d39.7), the observed hardness ratio light curve is shown with a dotted line while the solid line represents the hardness ratio light curve shifted by −1000 s (see Ness et al. 2007; Schönrich & Ness 2008; Ness 2015). No such lag is seen on days 2006d54 and 2021d55.6, although a small lag might be present. On days 2006d26.1 and 2021d37.1 (top two panels), hardness and brightness are anti-correlated, reflecting the appearance and disappearance of the complex soft emission component, while much less variability is seen during the decline observed on day 2006d66.9 (bottom panel). |
4 Discussion
We present a novel data-to-data scaling approach enabling us to compare different data sets with minimal model assumptions. This approach does not require a full description of all features, because those appearing in both spectra cancel out. The fact that we find both differences in absorption and changes in intrinsic properties demonstrates the ability of this approach to distinguish absorption from intrinsic changes.
This method can be applied to all SSS spectra extracted from different brightness phases of the same system, testing whether fainter SSS emission was due to higher absorption of different temperature or lower intrinsic luminosity. For example, we applied this test to the high-flux and low-flux XXMM-Newton spectra of V2491 Cyg, ObsID 0552270501 (Ness et al. 2011), clearly finding that a small temperature change can fully account for the brightness change, even without re-scaling. A systematic study of all SSS spectra would therefore likely be fruitful.
4.1 Explaining the lower SSS flux in 2021
The 2006 spectra on days 39.7 and 54 can be brought into agreement with the 2021 spectrum on day 55.6 by down-scaling them with a relatively simple absorption model involving cold and hot overlying material (top two panels on the left of Fig. 9). It is worth noting that no additional scaling is required, and therefore the lower total flux on day 2021d55.6 is consistent with the spectral changes expected from more photoelectric absorption. The addition of changes of temperature (top two panels in the right of Fig. 9) only improves the agreement of the re-scaled 2006 spectra with the 2021d55.6 spectrum by a minimal amount. The fact that the best-fit temperatures for blackbody scaling are so close to each other supports absorption as the dominant factor for the reduced brightness in 2021.
The intrinsic source was then equally bright in both outbursts. This is supported by the observation that the line flux light curves of the coronal [Fe X] emission line (6375 Å) shown in Fig. 14 by Page et al. (2022) are similar in the two outbursts. The [Fe X] line is a forbidden line and as such is optically thin; it is therefore more capable of escaping much denser plasma without re-absorption or scattering than resonance lines. We are therefore seeing the sum of [Fe X] emission from all regions, and line-of-sight effects are irrelevant as local inhomogeneities balance out. Radiative decays of forbidden lines occur on long timescales, and the higher the plasma density (and therefore the collision rate), the higher the number of excited states that are depopulated by collisions rather than the radiative de-excitations that produce the line photons. While a higher plasma density increases the population of the ionisation stage such as Fe X, the same higher density reduces the production efficiency of forbidden lines such as the [Fe X] line at 6375 Å. Meanwhile, photoionisation can increase the Fe X number density without decreasing the strength of forbidden lines, and the intensity of coronal lines such as [Fe X] are therefore indicators of the local presence of a strong central ionising radiation source, even if this latter does not materialise as observed soft-X-ray emission. [Fe X] line measurements catch photoionising radiation emitted in all directions, which is the SSS intensity averaged over 4π. Meanwhile, soft-X-ray observations can be compromised by line-of-sight effects, such as angle-dependent emission and/or absorption in different directions. We therefore consider [Fe X] measurements to be an important source of complementary information to soft-X-ray observations. From Fig. 14 in Page et al. (2022) and Fig. 5 in Munari & Valisa (2022), we highlight
The steep increase in [Fe X] intensity between days ~23 and 30 indicates that the SSS phase already started a few days before soft-X-ray emission was detected.
No high-amplitude variations in the [Fe X] line.
The [Fe X] line fluxes are similar in 2006 and 2021.
These differences support the conclusion of intrinsically the same SSS emission, while emission and absorption are not spherically symmetric, which means that what we see in soft X-rays depends on the viewing angle. The Swift/XRT analysis carried out by Page et al. (2022) does not obviously support significant differences in absorption, while the grating spectra analysed with our approach of data scaling provide strong evidence for absorption being the dominant factor explaining the lower observed flux in 2021 compared to 2006. We interpret these differences as due to the lower spectral resolution of the Swift/XRT data and the limitations on the analysis methods that are possible under the circumstances of a high degree of statistical photon redistribution: Page et al. (2022) fitted blackbody and atmosphere models to the XRT spectra taken at similar epochs in 2006 and 2021 and compared the resulting parameters of source and absorption models. While these source models fit the 2021 XRT spectra well (see Fig. 9 in Page et al. 2022) both blackbody and atmosphere models are only approximations and have never reproduced X-ray high-resolution grating spectra. The good agreement between these models and the Swift/XRT spectra is therefore mostly owing to the low resolution of the XRT ‘washing out’ narrow features that would be difficult to reproduce with models. At the low spectral resolution, any deficiencies in the source models will be washed out and can easily be compensated for by the absorption model; this freedom reduces the sensitivity to differences in absorption. By replacing the source model with the 2006 data, this freedom is being removed, which substantially increases the sensitivity of the differences in absorption.
As discussed by Page et al. (2022), the finding that absorption is the reason for the lower soft-X-ray flux in 2021 compared to 2006 is a challenge to the geometry. One could argue that the different orbital phases in 2006 (0.26) and 2021 (0.72) may imply a different portion of phase-aligned absorbing structures such as the accretion stream or overlying envelope of the companion star to be located within the line of sight. However, Page et al. (2022) argue that the 1985 EXOSAT soft-X-ray observations were taken during a similar orbital phase (0.32) to in 2006 while even lower soft-X-ray fluxes were seen; however, it should be noted that the temporal coverage of the 1985 outburst in the X-ray was far sparser, and gross variability may again have played a part in the observed difference in flux. Phase-aligned large-scale structures are therefore less likely to be accountable for the differences in absorption. However, we note that a phase difference of 0.26−0.32 = 0.06 translates to a duration of 27.2 days assuming an orbital period of 453.6 ± 0.4 days (Brandi et al. 2009) which is of order of the same timescale as the evolution of the nova outburst. We also note that the uncertainty of the orbit of 0.4 days accumulates to an uncertainty in phase of 2% after 17 orbits between 1985 and 2006. The overlap in phase is therefore marginal with a range of 0.28–0.34 in 1985 and 0.24–0.28 in 2006. Comparison of the 2006 and 2021 [Fe X] line fluxes suggests that the overall SSS brightness was similar in these two outbursts, and we searched for similar diagnostics for the 1985 outburst. [Fe X] line fluxes are given by Anupama & Prabhu (1989), but even if reversing their de-reddening, they are not consistent with the 2006 and 2021 fluxes. We attribute these inconsistencies to high uncertainties owing to the non-linear behaviour complicating the conversion from photographic density integrated over a line profile into a linear flux value. Unfortunately, we found no publication covering the 1985 event where the spectra were recorded with other than photographic plates. We inspected the Asiago photographic plate archive finding 38 spectra of RS Oph in 1985 (cf Rosino & Iijima 1987). From these original plates, we found that in most observations, the [Fe X] line suffers saturation in its core, making an accurate flux calibration impossible during the most interesting brightest time interval of the evolution. We then scaled the [Fe X] fluxes against He I, finding that the 1985 spectra agree relatively well with the 2006 and 2021 data.
We therefore cannot clarify whether or not the large differences are phase-dependent. The assumption that the surrounding material is randomly inhomogeneous (independent of phase) has the weakness of not being testable, but it could lead to small changes in viewing angle, causing large changes in the SSS intensity and spectral shape. This could also explain the highamplitude variations during the first ~3 weeks of the SSS phase in 2006 that Osborne et al. (2011) concluded to be caused, at least partly, by clumpy ejecta. While we have no grating observations covering the low- and high states of these variations, it appears possible that spectra extracted from low-flux episodes can be reproduced by application of similarly simple absorption models to the spectra from the high-flux episodes. This would need to be tested with a long grating observation covering low-and high-flux episodes. The XMM-Newton proposal under which this was attempted led to the observation on day 2021d37.1; however, the early variability phase was not observed as expected, and confirming this hypothesis will require a high-risk (but also highly rewarding) target-of-opportunity observation of a future nova in outburst.
 |
Fig. 14 Spectral time map based on 281 RGS spectra extracted from adjacent 200 s time intervals from the 2021d55.6 observation. The main panel shows the spectra with wavelength from left to right, time from top to bottom, and colours representing flux following the (non-linear) bar in the top right panel along the vertical flux axis. The dashed horizontal lines and shadings with the same colours in the bottom right panel indicate time intervals from which the spectra shown with the same colour shadings in the top left panel were extracted. The brown dotted line in the light curve panel in the bottom right represents the hardness light curve extracted from the pn where hardness is scaled to fit into the graph while varying between values −0.580 and −0.397. |
4.2 Explaining post-peak differences
The 2006d66.9 spectrum that was obtained after the peak of SSS emission (see Fig. 1) cannot reproduce the 2021d55.6 spectrum with only absorption (bottom left panel in Fig. 9), and the addition of a temperature change is required (bottom right panel in Fig. 9). The resulting temperature parameters indicate that the effective temperature at the pseudo-photosphere was higher on day 2006d66.9 than it was on 2021d55.6. As nuclear burning may have already turned off after the peak of SSS emission was reached, one might naively expect the temperature to start decreasing. However, our observations are not driven by the temperature of the central source but by the radiation transport behaviour of the higher layers, and we may be seeing deeper into the outflow.
4.3 Explaining the different spectral structures
Figure 11 demonstrates that the shape and structure of the SSS spectrum on 2021d55.6 more closely resembles the 2006d39.7 spectrum than the same-epoch 2006d54 spectrum. Specifically, the following items were found to be common to 2006d39.7 and 2021d55.6 while different from 2006d54:
The O I absorption edge was much deeper in 2006d39.7 and 2021d55.6.
The 2006d39.7 and 2021d55.6 spectra contain more and deeper absorption lines (Fig. 11).
The absorption lines of O VII (Fig. 12), for example, were blueshifted by ~1200 km s−1 on days 2006d39.7 and 2021d55.6 but only by ~700 km s−1 on day 2006d54.
The deeper O I absorption edge on day 2021d55.6 compared to day 2006d54 can be interpreted as the absorbing plasma having been hotter in 2006, leading to oxygen being ionised to higher ionisation stages or even being fully ionised (discussed in more detail in Sect. 4.4). Also the presence of more absorption lines on day 2021d55.6 compared to day 2006d54 can be interpreted as a higher temperature on day 2006d54 causing absorption lines from low-ionisation elements to disappear, while the fully ionised (higher) fraction of the material in the line of sight produces no absorption lines. Meanwhile, the observed expansion velocity was lower on day 2006d54 than on day 2021d55.6, indicating that slower-moving material was hotter, while the plasma containing lower-temperature spectral features moved at higher velocities.
Concentrating on the 2006 evolution for a moment, the evolution from day 2006d39.7 to 2006d54 can be understood as follows:
The nova ejecta decelerate while transferring their kinetic energy to the stellar wind of the giant companion star, and this kinetic energy feeds the observed shock emission.
While the outflow was decelerated, it was also heated and (collisionally) ionised, which is a natural consequence of the evolution of shock systems generated by the interaction of the nova ejecta with the pre-existing stellar wind.
The higher degree of ionisation on day 2006d54 compared to the earlier day 2006d39.7 made the absorbing plasma more transparent leading to the higher observed flux on day 2006d54.
In this picture, originally lower-temperature ejecta with a higher opacity were moving at ~1200 km s−1 before entering the regions of the stellar wind where they gradually decelerated to ~700 km s−1 while increasing the degree of ionisation and thus transparency to soft X-rays. Meanwhile, in 2021, this process was less efficient, as on day 2021d55.6 we see more absorption, no reduction in velocity, and no reduction in the number of low-temperature absorption lines. If this is due to the different viewing angles in 2006 and 2021, the interactions between nova ejecta and stellar wind are not homogeneous in all directions, which could be caused by an inhomogeneous density distribution of the wind of the stellar companion for example. In this picture, the line of sight coincided in 2021 with lower-density regions of the stellar wind, and the plasma could expand more freely in that direction without detectable deceleration and heating via collisions.
4.4 Variations in the O I edge depth
In this section, we discuss possible interpretations for the observed variations in the depth of the O I K-shell absorption edge at 540 eV (22.8 Å), which implies variations in the O I column density. These could either be caused by ionisation of O I to higher ionisation stages or a more radical change of the entire oxygen abundance.
In the 2006 observations of RS Oph, Ness et al. (2007); Schönrich & Ness (2008); Ness (2015) found variations in the absorption edge to correlate with source brightness, and concluded that ionising O I is responsible for the variable transparency for hard emission. However, there are a few potential issues with this interpretation. With the brightness variations as the trigger for changes in the ionisation balance, independent intrinsic brightness variations have to be assumed. In this scenario, the brightness variations cannot be a consequence of variable absorption, at least not fully. Meanwhile, correlated hardness and brightness changes are interpreted as a consequence of variable absorption, and cause and effect are in conflict.
If O I is ionised, the number density of higher ionisation stages increases. While Ness et al. (2007) identified absorption lines from O II and higher ionisation stages of oxygen (see their Table 3), we find from the ionabs model that there will be ionisation edges at higher energies that we do not observe. The only way to avoid additional edges would be to ionise all the way to O VII or higher.
For the absorbing material to respond to the brightness changes, some time is needed. While there should be enough time for ionisation between days 2006d39.7 and 2006d54, more rapid variations of the O I column density are observed within all SSS observations (Fig. 13). There must be some response time leading to a lag between brightness and hardness changes, but we only observe such a lag in the observation on day 2006d39.7. This lag could therefore be explained as a response time to intrinsic brightness changes, but the lack of lag in all the other observations is then difficult to explain.
Interestingly, the lag duration of 1000 s corresponds to a light travel spatial scale of ~2 AU; however, the absorber must be in the same line of sight as the continuum source, and if it is the source of ionisation, any brightness changes would be delayed by the same light travel time.
If oxygen is photoionised by an increased level of radiation intensity, then also hydrogen, helium, and other elements with lower ionisation energies than 540 eV should be ionised. However, the depth of the O I edge was observed to vary more strongly than the low-energy slope of the continuum, indicating that the O I edge variations are decoupled from changes of ΝΗ. The likelihood of a photon ionising oxygen or hydrogen decreases exponentially with the difference between photon energy and ionisation energy, and 540 eV photons ionise oxygen much more efficiently than hydrogen. An unabsorbed SSS spectrum approximated by a blackbody with Teff = 5 × 105 K peaks at 200 eV with 540 eV in the Wien tail with ~6% intensity relative to the peak. The same 6% intensity level is encountered in the Rayleigh–Jeans tail at 54.7 eV, not far from the 13.6 eV ionisation energy of hydrogen. It is therefore not conceivable for oxygen to be photoionised while hydrogen is not. A way out may be that circumstellar hydrogen, helium, and so on is already fully ionised, while some neutral oxygen is initially still present in the local circumstellar material.
On the other hand, to produce the Raman-scattered O VI line observed by Munari & Valisa (2022), a great amount of neutral gas is required (at least neutral hydrogen), and the evolution of this line suggests that the global amount of neutral hydrogen remained fairly constant during the SSS phase.
An alternative explanation for changes in the O I column density could be found by reducing the overall oxygen abundance in general by condensation of oxygen into dust grains. This would reduce the number of oxygen atoms that can absorb photons above 540 eV. While some of the issues with the ionisation hypothesis could be avoided, there are also arguments against dust formation.
Dust grains may lead to other observable features in the X-ray spectra. These features can be studied with the SPEX model as has been demonstrated by Pinto et al. (2012). We have not performed such modelling as it is beyond the scope of this work. We can therefore at present not decide whether or not dust formation is consistent with the SSS spectra.
As the O I absorption edge not only decreased but also increased on short timescales, a dissociation mechanism is also needed. It appears unlikely that the number of oxygen atoms locked in dust can vary as quickly as we observe the depth of the O I edge to vary. A possible explanation of the strictly correlated hardness and brightness variations may be that clumps with oxygen already locked in grains moved into and out of the line of sight and all variability that correlates with hardness would then be due to variations in obscuration with a reduced O I column density. This would also be a way out for the ionisation hypothesis.
There is no evidence from either excess infrared emission or breaks in the optical light curve of any large-scale dust formation following the outburst (Evans et al. 1988). While there will be some destruction of dust in the pre-existing stellar wind of the companion star, some of it survives (Evans et al. 2007), but whether or not that is sufficient to explain changes in the O I edge on the observed timescales would require studies beyond the scope of this work.
Cyclic creation and destruction of dust seed nuclei were found by Harvey et al. (2018) for the DQ Hercules-like nova V5668 Sagittarii (2015), but again the timescales on which this can lead to destruction and replenishment of oxygen may be longer than the fast changes in O I that we observed.
Photon-induced condensation and dissociation would actually lead to an anti-correlation of hardness ratio and brightness as a higher radiation intensity would lead to increased dissociation and thus a deeper O I edge.
We cannot fully rule out nor confirm either mechanism. We lean towards the ionisation hypothesis.
5 Summary and conclusions
The results from this study can be summarised as follows:
The significantly lower emission during the SSS phase in 2021 reported by Page et al. (2022) can be explained by absorption from cold (neutral) and hot (ionised) material in the line of sight. This can be demonstrated by application of a relatively simple absorption model to the bright 2006 SSS spectra taken on days 39.7 and 54, which leads to almost perfect agreement with the RGS1 spectrum taken on day 55.6 after the 2021 optical peak. The direct inference is that the intrinsic SSS emission, and thus energy production, was the same in 2006 and 2021. This is consistent with similar [Fe X] fluxes observed in 2006 and 2021.
The post-peak SSS spectrum on day 2006d66.9 can also be rescaled to match the 2021d55.6 spectrum, but in addition to absorption, we also detect a higher effective temperature in 2006.d66.9. We conclude that after the SSS peak, we can see hotter layers after the pseudo-photosphere has receded further inside.
The 2021d55.6 spectrum more closely resembles the 2006d39.7 spectrum than the same-epoch 2006d54 spectrum: the scaling by a simple absorption model works better; the O I absorption edge is deeper than on day 2006d54; the spectrum on day 2006d54 contains fewer absorption lines; similar P-Cyg-like absorption line profiles are observed, while on day 2006d54 no emission line components were present, and the blueshift on days 2006d39.7 and 2021d55.6 was ~1200 km s−1 while on day 2006d54 we find only ~700 km s−1. From our discussion, we conclude from these differences that the deceleration of the nova ejecta was not the same in all directions owing to an inhomogeneous density distribution of the wind of the stellar companion. The total amount of dissipated energy must have been the same in 2006 and 2021 because the intensity of bremsstrahlung emission radiated in all directions was the same (Page et al. 2022; Orio et al. 2022). Meanwhile, the small portion of the nova ejecta propagating in the direction of the line of sight underwent a different degree of deceleration and heating between days ~40 and 60, depending on the density of the stellar wind in the respective directions probed in 2006 and 2021.
The X-ray light curves taken during the bright SSS phase (days 2006d39.7, 2006d54, and day 2021d55.6) are mildly variable, and the hardness ratio is correlated with the brightness changes. The hardness changes are caused by variability in the column density of neutral oxygen.
The hardness changes lag behind the brightness changes by 1000 s only on day 2006d39.7 but by at most marginal lags on days 2006d54 and 2021d55.6.
Attributing variations in the O I absorption edge to ionisation may have some issues. Ionising O I to O II-V would lead to other features that we do not observe. A reduction in the O I edge without seeing other edges at higher energies could be achieved by immediate ionisation to O VII or higher; however, this should take more time than the 1000 s lag observed on day 2006d39.7 and appears inconsistent with the instantaneous hardness and brightness variations seen in all other observations. If oxygen is photoionised, elements with lower ionisation energies such as hydrogen and helium must also be photoionised, and fully ionised material would be fully transparent. An alternative to ionisation may be condensation and/or dissociation of oxygen into dust grains but this is inconsistent with infrared observations. Further studies are required to investigate other potential inconsistencies, such as needing to see dust features in the X-ray spectra (testable with SPEX models) or timescales for condensation and dissociation of dust compared to observed timescales of variations.
In the new 2021 data, we find the 35 s period with a lower duty cycle compared to the brighter day 2006d54 light curve. This suggests that the period is more difficult to detect in obscured data, which is consistent with its origin towards the surface of the white dwarf.
Our novel approach to rescaling a grating spectrum with (a) a single scaling factor, (b) an absorption model, or (c) the ratio of two blackbody models proves to be a powerful tool for understanding brightness changes more generally. This approach can be applied to revisit all variable SSS observations in the archive, and as an example, we already find that the deep dip in the Slight curve of V2491 Cyg (Ness et al. 2011) can be explained by a small temperature change.
Acknowledgements
A.P. Beardmore, K.L. Page acknowledge support from the UK Space Agency. M.J. Darnley receives funding from UKRI grant number ST/S505559/1. A. Dobrotka and J. Magdolen were supported by the Slovak grant VEGA 1/0408/20, and by the European Regional Development Fund, project No. ITMS2014+: 313011W085. S. Starrfield gratefully acknowledges partial support from NSF and NASA grants to ASU.
Appendix A Appendix
Appendix A.1 Correction for pileup in RGS
Pileup is an effect caused by two (or more photons) arriving at the same position within the same readout time, and instead of registering two photons with their respective energies, a single photon with the sum of their energies is recorded. This is an issue for particularly bright sources with photon arrival rates that are faster than the readout time of the recording detector. Photon pileup is usually not an issue for the RGS because the source photons are distributed over a large area on the detector following the dispersion relation, and therefore soft photons are recorded further away from the zeroth order than higher-energy photons. However, SSS belong to the rare class of sources for which even the RGS suffers pile up at those positions of the recording CCD chip array where the dispersed spectrum is brightest.
Fortunately, owing to the extreme softness of the source, the photons are not lost. At each chip position, dispersed photons can be identified from their photon energies in the pi column of the events file to be consistent with the wavelengths computed from their angular distance from the zero-th order. Discrepancies in pi energy and wavelength from the dispersion relation can be used to filter out background events. If a pi energy yields twice the value of the corresponding wavelength, there are two possibilities, either the photon belongs to the second dispersion order, or two photons of the same energy have arrived at the same time, thus pile up.
The default rgsproc pipeline assumes no pile-up and registers all photons with twice the pi energies than the corresponding wavelength values in a separate second-order spectrum assuming the wavelength values to be the correct ones. This spectrum is a mix of piled photons and second dispersion order but for soft sources such as SSS, the number of second-order photons at high energies is small, and the second-order spectrum essentially consists of half the number of all piled photons at half their wavelength values. For these photons, the values in the pi column can be corrected to half their value, and as two photons had originally arrived, all photons for which the pi energy was corrected need to be duplicated, preserving energy, which means additional rows added to the events file.
This is illustrated in Fig. A.1 where the RGS1 and RGS2 first-order spectra are shown with black and orange, respectively. For the RGS2, only the range up to 19 Å is shown as it has not operated correctly at longer wavelengths. The RGS1 second-order spectrum, shown with light blue, can be seen to be much brighter between 8 Å and 14 Å than the RGS2 first-order spectrum5. All emission in excess of the RGS2 first-order spectrum in this range is therefore due to photon pile up, and the correction procedure adds a small amount of emission from the Ne X line at 24 Å.
Specifically, the steps to correct for photon pileup in the RGS are:
Regular rgsproc run
In the events files P0841930901R1S002EVENLI0000.FIT and P0841930901R2S004EVENLI0000.FIT, identify all events satisfying the following conditions for their column values m_lambda (in Å) and pi (in eV):
18 < m_lambda < 28
Ratio of column values pi/(12398.5/m_lambda) = 2 ± 0.2
where 12398.5/m_lambda represents the conversion from wavelength in Å to photon energy in eV.
For each of these events, change the value of pi to half its value.
To conserve the total energy, duplicate all these modified events.
Based on the modified events file, produce all follow-up products with rgsproc entrystage=4:spectra.
These manipulations can be performed with any software allowing fits file editing; we used IDL6.
 |
Fig. A.1 Illustration of RGS pileup correction for ObsID 0841930901 (see Sect. A.1. The Black spectrum shows the uncorrected RGS1 first-order spectrum, and the uncorrected RGS1 second order spectrum (light blue), a fainter clone of first-order spectrum can be seen at half the wavelengths. The second order spectrum captures the pileup photons that need to be moved into the first order, which then leads to the read curve, the corrected RGS1 spectrum. |
Appendix A.2 Aliases from Telemetry Drops in the pn light curve ObsID 0841930901
Another issue are telemetry losses owing to full memory buffer. For very bright sources, not all events can be downlinked before the onboard memory is full. This has occurred in the second observation (day 55.6) for the pn in a quasi-periodic manner as illustrated in the top panel of Fig. A.2. Close inspection shows that during time segments with lower count rate, the short time intervals during which data could be obtained were slightly longer while the gaps between these data chunks remained roughly the same. The evolution of the durations of gaps and times during which data were downlinked (good time intervals) are illustrated in the second panel, clearly showing an anti-correlation of count rate (grey) and duration of continuous good times (black). Therefore, when the count rate is lower, the capability to take continuous data is higher. However, once a gap is reached, its duration varies only very little, that is, by 13 – 15 s. The distribution of durations of good-times (black), gaps (red), and times between start times of good-time-intervals (blue) are shown in the third panel, where the (count rate independent) distribution of gaps is strongly peaked at 14 ± 1 seconds. The bottom panel shows the periodogram that does not contain a peak at the 14s gap duration but two peaks at ~24s and ~28s, that coincide with the peaks in the panel above showing the distribution of differences of start times of good-time intervals. These peaks in the periodogram are therefore not related to the source but are induced by the telemetry gaps, while the 35.47s period is not related to the telemetry dropouts and can therefore be associated to the source (see Sect. 3.1).
 |
Fig. A.2 Illustration of telemetry losses in the soft (0.2–1.5 keV) pn light curve taken on day 2021d55.6. Top: First and last 600s time segments of the light curve showing regular gaps between time intervals taking data. During the last 600s segment, with a lower count rate, the duration of continuous good times are slightly longer, illustrating the dependence of losses with count rate. Second panel: time evolution of durations of continuous good time intervals (black) and gaps without data (red) in comparison to the (re-scaled) count rates (grey). The durations of continuous data-taking were longer while the source was fainter. Third panel: Histogram distributions of durations of goodtimes (black), gaps (red), and times between starting good-time intervals (blue). The durations of gaps vary within very small margins, independent of count rate, between 13 – 15 s while the durations of good times vary between ~10 – 20 s (dependent on count rate, see panel above). The distribution of times between start times of data-taking intervals cluster at 24s and 28s, and these peaks introduce an alias to period studies as seen in the bottom panel where the periodogram contains peaks at these periods. |
References
- Adamakis, S., Eyres, S. P. S., Sarkar, A., & Walsh, R. W. 2011, MNRAS, 414, 2195 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmoch. Acta, 53, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Anupama, G. C., & Prabhu, T. P. 1989, J. Astrophys. Astron., 10, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, M. F., & Evans, A. 2008, Classical Novae, eds. Bode, M. F., & Evans, A. (Cambridge University Press) [CrossRef] [Google Scholar]
- Bode, M. F., & Kahn, F. D. 1985, MNRAS, 217, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, M. F., O’Brien, T. J., Osborne, J. P., et al. 2006, ApJ, 652, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Brandi, E., Quiroga, C., Mikołajewska, J., Ferrer, O. E., & García, L. G. 2009, A&A, 497, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darnley, M. J., Henze, M., Bode, M. F., et al. 2016, ApJ, 833, 149 [NASA ADS] [CrossRef] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drake, J. J., Laming, J. M., Ness, J.-U., et al. 2009, ApJ, 691, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A., Callus, C. M., Albinson, J. S., et al. 1988, MNRAS, 234, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A., Woodward, C. E., Helton, L. A., et al. 2007, ApJ, 671, L157 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Mendoza, C., Bautista, M. A., et al. 2005, ApJS, 158, 68 [CrossRef] [Google Scholar]
- Harvey, E. J., Redman, M. P., Darnley, M. J., et al. 2018, A&A, 611, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashyap, V., & Drake, J. J. 2000, Bull. Astron. Soc. India, 28, 475 [NASA ADS] [EDP Sciences] [Google Scholar]
- König, O., Wilms, J., Arcodia, R., et al. 2022, Nature, 605, 248 [CrossRef] [Google Scholar]
- Miyamoto, S., Kimura, K., Kitamoto, S., Dotani, T., & Ebisawa, K. 1991, ApJ, 383, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., & Valisa, P. 2022, ArXiv e-prints [arXiv:2203.01378] [Google Scholar]
- Munari, U., Giroletti, M., Marcote, B., et al. 2022, A&A, 666, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, T., Orio, M., Cassinelli, J. P., et al. 2008, ApJ, 673, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J. U. 2012, Bull. Astron. Soc. India, 40, 353 [NASA ADS] [Google Scholar]
- Ness, J.-U. 2015, Acta Polytech. CTU Proc., 2, 222 [CrossRef] [Google Scholar]
- Ness, J., Starrfield, S., Beardmore, A., et al. 2007, ApJ, 665, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J. U., Drake, J. J., Starrfield, S., et al. 2009, AJ, 137, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Osborne, J. P., Dobrotka, A., et al. 2011, ApJ, 733, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Beardmore, A. P., Osborne, J. P., et al. 2015, A&A, 578, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ness, J. U., Beardmore, A. P., Bezak, P., et al. 2022, A&A, 658, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Brien, T. J., Lloyd, H. M., & Bode, M. F. 1994, MNRAS, 271, 155 [CrossRef] [Google Scholar]
- Orio, M., Behar, E., Luna, G. J. M., et al. 2022, ApJ, 938, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, J., Page, K., Goad, A. B. M., et al. 2006, The Astronomer’s Telegram, 770, 1 [Google Scholar]
- Osborne, J. P., Page, K. L., Beardmore, A. P., et al. 2011, ApJ, 727, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Beardmore, A. P., Osborne, J. P., et al. 2022, MNRAS, 514, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, C., Ness, J.-U., Verbunt, F., et al. 2012, A&A, 543, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosino, L., & Iijima, T. 1987, in RS Ophiuchi (1985) and the Recurrent Nova Phenomenon, ed. M. F. Bode (VNU Science Press), 27 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schmid, H. M. 1989, A&A, 211, L31 [NASA ADS] [Google Scholar]
- Schönrich, R. A., & Ness, J.-U. 2008, ASP Conf. Ser., 401, 291 [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
- Talavera, A. 2009, APSS, 320, 177 [NASA ADS] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N. M. H., O’Brien, T. J., & Bode, M. F. 2007, ApJ, 665, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
A further possible eruption took place in 1945 (Adamakis et al. 2011) and was greatly obscured by the seasonal gap.
The Lomb-Scargle algorithm in the Python package Astropy (Astropy Collaboration 2013, 2018, 2022) was used. Periodograms were rms normalised (Miyamoto etal. 1991).
We refer also to a technical note by Cor de Vries: https://xmmweb.esac.esa.int/docs/documents/CAL-TN-0075-1-0.pdf
All Tables
Journal of exposures taken with XMM-Newton and Chandra (last rows) used in this work.
All Figures
 |
Fig. 1 Comparison of long-term Swift X-ray light curves obtained during the 2006 (black) and 2021 (orange) outbursts (Page et al. 2022). The similar behaviour during the early shock phase until ~30 days after tref can be seen while the remarkable differences during the SSS- and decline phases after day ~30 are evident. Vertical lines mark the times of deeper Chandra (dotted) and XMM-Newton (solid) observations for the outbursts in 2006 (orange) and 2021 (black) as marked in the upper right legend. In this work, the two XMM-Newton observations taken on days 37.1 and 55.6 are discussed. |
| In the text | |
 |
Fig. 2 XMM-Newton X-ray and UV light curves (units counts per second, cps) extracted from the pn, RGS1, and OM instruments taken on day 2021d55.6 (see x-axis labels). The photon arrival times were converted to days after tref = 2021-08-09.5417. The pn light curve is broken into a hard (top) and a soft (second panel) band split at 1.5 keV (see legends for individual energy bands), probing shock and SSS emission, respectively. The soft band is split into two bands, H and S, with the split at 0.54keV, and the orange curve in the second panel represents the scaled hardness ratio (HR) constructed from countrates recorded in the energy bands H and S as given in the legend. The shaded coloured area in the third panel marks light-curve segments discussed separately in Sect. 3.3. In the bottom panel, the OM UVM2 filter (~2070–2170 Å range) light curves are shown from the Image mode (red horizontal bars for each exposure) and Fast mode (black) data. Count rates are plotted, and corresponding magnitude values are included on the left, which correspond to the lowest and highest Image mode count rates (marked with the dotted horizontal red lines). |
| In the text | |
 |
Fig. 3 PDS calculated from the pn data (20 s binning) where the red solid line is a broken power-law fit. The circles are average values within the frequency bin with error bars as error of the mean. The frequency range corresponds to a period range of 100-32 000 s. |
| In the text | |
 |
Fig. 4 Periodogram calculated from the OM data with 70% and 50% confidence levels as upper and lower horizontal dashed lines, respectively. The PDS standard normalisation of the Lomb–Scargle algorithm was used for the confidence level calculation. |
| In the text | |
 |
Fig. 5 XMM-Newton RGS (left) and pn (right, soft 0.2–1.5 keV range) periodogram time maps illustrating the evolution of periods focusing on the 35 s period detected during the 2006 outburst. Each graph consists of four panels: in the main (bottom left) panel, time is running down and the tested periods run from left to right, while the panel above shows representative Lomb–Scargle periodograms on the same shared horizontal axis. The bottom-right panel shows the light curve along the same vertical time axis. The colour bar in the top right allows conversion of colours in the main panel to the units of power used for the periodograms. The vertical time axis is in units of elapsed hours since the start of the RGS1 exposure (left panel), and the pn exposure (right panel) which started 2250 s (0.6 h) later than the RGS1 exposure owing to the higher pn overhead. In the respective top panels, the black curves show the periodograms from the respective entire light curves and the colour-shaded curves are periodograms from the selected 2000 s time intervals marked with horizontal lines of the same colour as the dashed lines in the panels below. The time bin sizes of the light curves are included in the respective top-left panels. The same time maps were produced with different bin sizes, yielding similar results. |
| In the text | |
 |
Fig. 6 XMM-Newton RGS spectra in photon flux units per 103 s (=ks). The 2021d37.1 spectrum (grey shading) is compared to the same-epoch 2006d39.7 spectrum (down-scaled by factor 5; red) and the bright-only 2006 spectrum on day 26.1 (black). The top panel shows a larger wavelength range while the bottom panel zooms into the variable soft excess with several unknown narrow emission and absorption features, where only the corresponding wavelength is indicated. |
| In the text | |
 |
Fig. 7 Illustration of the scaling method with the ratio of two different blackbody curves and that many pairs of Tref,1 and Tref,2 can produce the same blackbody ratio curve. In the top panel, the RGS1 spectrum of RS Oph from 2021d55.6 (black) is multiplied with the ratio of two blackbody models corresponding to Tref,1 = 5 × 105 K (=500 kK) and Tref,2 = 4 × 105 K (=400 kK), respectively and normalised (see legend). The resulting spectrum (orange) is a factor 20 brighter but is also harder. The bottom panel shows the results of fitting only Tref,2 with (black) and without (orange) additional normalisation while Tref,1 is fixed at given grid values (x-axis) to reproduce the 500 kK/400 kK ratio curve. The bottom right legend provides empirical analytic relationships between fixed grid value and T2,best values reproducing the same ratio curve. The same relationships are found for any other pairs of reference temperatures Tref,1 and Tref,2; see Sect. 3.2.2 for details. |
| In the text | |
 |
Fig. 8 Illustration of how to down-scale an observed source spectrum, assuming higher absorption. In the top panel, transmission curves are shown assuming an arbitrary value of neutral hydrogen column density NH and cosmic abundances of other elements. Different colours represent a pure (neutral) interstellar absorption model (black) and modifications when successively adding (hot) absorption edges at the respective ionisation energies of O VII, N VII, and N VI (see labels); thus, the red curve represents the absorption model accounting for all edges. In the bottom panel, the effect of absorption is illustrated for the example of a blackbody source with an effective temperature of 500,000K. These absorption models were designed to be applied to emission models but can also be applied to data of sufficiently high spectral resolution; see Sect. 3.2.3 for details. |
| In the text | |
 |
Fig. 9 XMM-Newton RGS1 spectrum obtained on 2021d55.6 (grey shadings) compared to the 2006 spectra obtained on 2006d39.7 (top), 2006d54 (middle), and 2006d66.9 (bottom). The orange lines represent the unscaled (brighter) 2006 spectra as observed, while the respective red lines are the results of applying an absorption model to the observed 2006 spectra assuming the absorption parameters given in Table 2: ΔNH of an absorption model of only neutral absorbers with modification of the depth of the O I absorption edge at 22.8 Å and the parameters of three absorption edges of highly ionised ions with values of optical depths and column density. A scaling factor was not applied. In the left panel, the result from scaling only with an absorption model is shown, while in the right panel, additional scaling with blackbody ratio has been applied, thus assuming a change in temperature between the spectra. The parameters of these and more models are given in Table 2. |
| In the text | |
 |
Fig. 10 Reduced values of χ2 for the six down-scaling models listed in Table 2. The dotted line in the bottom represents |
| In the text | |
 |
Fig. 11 XMM-Newton RGS1 spectrum taken on 2021d55.6 compared to 2006 spectra scaled with the pure absorption model (left column in Fig. 9). The lower panels show details, and although the 2021d55.6 spectrum has a lot of gaps, one can see that the same-epoch 2006 spectrum (blue) contains much weaker absorption lines, while on the sub-Å level, there is a greater resemblance to the 2006d39.7 spectrum. |
| In the text | |
 |
Fig. 12 Comparison in velocity space of line profiles of the O VII line at rest wavelength 21.6 Å (top) and an unknown absorption line observed at 26.83 Å (bottom) for the 2021d55.6 observation and the 2006d39.7, 2006d54, and 2006d66.9 observations. Assuming a similar blueshift for the unidentified line, we adopt a rest wavelength of 26.96 Å. Data are shown in histogram style and Gaussian fits to the absorption lines with solid lines. Values of best-fit blueshift are given in the bottom right legend. Observed spectra and models are normalised to the respective median values of the plot range. |
| In the text | |
 |
Fig. 13 Comparisons of 2006 and 2021 light curves with the respective hardness-ratio light curves (see respective horizontal axes labels). In the third panel (2006d39.7), the observed hardness ratio light curve is shown with a dotted line while the solid line represents the hardness ratio light curve shifted by −1000 s (see Ness et al. 2007; Schönrich & Ness 2008; Ness 2015). No such lag is seen on days 2006d54 and 2021d55.6, although a small lag might be present. On days 2006d26.1 and 2021d37.1 (top two panels), hardness and brightness are anti-correlated, reflecting the appearance and disappearance of the complex soft emission component, while much less variability is seen during the decline observed on day 2006d66.9 (bottom panel). |
| In the text | |
 |
Fig. 14 Spectral time map based on 281 RGS spectra extracted from adjacent 200 s time intervals from the 2021d55.6 observation. The main panel shows the spectra with wavelength from left to right, time from top to bottom, and colours representing flux following the (non-linear) bar in the top right panel along the vertical flux axis. The dashed horizontal lines and shadings with the same colours in the bottom right panel indicate time intervals from which the spectra shown with the same colour shadings in the top left panel were extracted. The brown dotted line in the light curve panel in the bottom right represents the hardness light curve extracted from the pn where hardness is scaled to fit into the graph while varying between values −0.580 and −0.397. |
| In the text | |
 |
Fig. A.1 Illustration of RGS pileup correction for ObsID 0841930901 (see Sect. A.1. The Black spectrum shows the uncorrected RGS1 first-order spectrum, and the uncorrected RGS1 second order spectrum (light blue), a fainter clone of first-order spectrum can be seen at half the wavelengths. The second order spectrum captures the pileup photons that need to be moved into the first order, which then leads to the read curve, the corrected RGS1 spectrum. |
| In the text | |
 |
Fig. A.2 Illustration of telemetry losses in the soft (0.2–1.5 keV) pn light curve taken on day 2021d55.6. Top: First and last 600s time segments of the light curve showing regular gaps between time intervals taking data. During the last 600s segment, with a lower count rate, the duration of continuous good times are slightly longer, illustrating the dependence of losses with count rate. Second panel: time evolution of durations of continuous good time intervals (black) and gaps without data (red) in comparison to the (re-scaled) count rates (grey). The durations of continuous data-taking were longer while the source was fainter. Third panel: Histogram distributions of durations of goodtimes (black), gaps (red), and times between starting good-time intervals (blue). The durations of gaps vary within very small margins, independent of count rate, between 13 – 15 s while the durations of good times vary between ~10 – 20 s (dependent on count rate, see panel above). The distribution of times between start times of data-taking intervals cluster at 24s and 28s, and these peaks introduce an alias to period studies as seen in the bottom panel where the periodogram contains peaks at these periods. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.