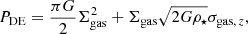| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202243395 | |
| Published online | 30 September 2022 | |
Stellar feedback in M 83 as observed with MUSE
II. Analysis of the H II region population: Ionisation budget and pre-SN feedback
1
The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
e-mail: adamo@astro.su.se
2
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
3
Institute for Computational Cosmology, Department of Physics, University of Durham, South Road, Durham DH1 3LE, UK
4
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
5
Département de physique, de génie physique et d’optique, Université Laval, Québec, Canada
6
Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, ON L8S 4M1, Canada
7
Canadian Institute for Theoretical Astrophysics (CITA), University of Toronto, 60 St George Street, Toronto, ON M5S 3H8, Canada
8
Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
9
Aix-Marseille Université, CNRS, CNES, LAM, Marseille, France
10
The William H. Miller III Department of Physics and Astronomy, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
11
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
12
Eureka Scientific, Inc. 2452 Delmer Street, Suite 100, Oakland, CA 94602-3017, USA
13
Department of Astronomy and Theoretical Physics, Lund Observatory, Box 43, 221 00 Lund, Sweden
14
Department of Astronomy, New Mexico State University, Las Cruces, NM 88001, USA
Received:
22
February
2022
Accepted:
17
June
2022
Context. Energy and momentum injected by young, massive stars into the surrounding gas play an important role in regulating further star formation and in determining the galaxy’s global properties. Before supernovae begin to explode, stellar feedback consists of two main processes: radiation pressure and photoionisation.
Aims. We study pre-supernova feedback and constrain the leakage of Lyman continuum (LyC) radiation in a sample of ∼4700 H II regions in the nearby spiral galaxy M 83. We explore the impact that the galactic environment and intrinsic physical properties (metallicity, extinction, and stellar content) have on the early phases of H II region evolution.
Methods. We combined VLT/MUSE observations of the ionised gas with young star cluster physical properties derived from HST multiwavelength data. We identified H II regions based on their Hα emission, and cross-matched the sample with planetary nebulae and supernova remnants to assess contaminant sources and identify evolved H II regions. We also spectroscopically identified Wolf-Rayet (WR) stars populating the star-forming regions. We estimated the physical properties of the H II regions (luminosity, size, oxygen abundance, and electron density). For each H II region, we computed the pressure of ionised gas (Pion) and the direct radiation pressure (Pdir) acting in the region, and investigated how they vary with galactocentric distance, with the physical properties of the region, and with the pressure of the galactic environment (PDE). For a subset of ∼500 regions, we also investigated the link between the pressure terms and the properties of the cluster population (age, mass, and LyC flux). By comparing the LyC flux derived from Hα emission with the one modelled from their clusters and WRs, we furthermore constrained any escape of LyC radiation (fesc).
Results. We find that Pion dominates over Pdir by at least a factor of 10 on average over the disk. Both pressure terms are strongly enhanced and become almost comparable in the central starburst region. In the disk (R ≥ 0.15 Re), we observe that Pdir stays approximately constant with galactocentric distance. We note that Pdir is positively correlated with an increase in radiation field strength (linked to the negative metallicity gradient in the galaxy), while it decreases in low extinction regions, as is expected if the amount of dust to which the momentum can be imparted decreases. In addition, Pion decreases constantly for increasing galactocentric distances; this trend correlates with the decrease in extinction – indicative of more evolved and thus less compact regions – and with changes in the galactic environment (traced by a decrease in PDE). In general, we observe that H II regions near the centre are underpressured with respect to their surroundings, whereas regions in the rest of the disk are overpressured and hence expanding. We find that regions hosting younger clusters or those that have more mass in young star clusters have a higher internal pressure, indicating that clustered star formation likely plays a dominant role in setting the pressure. Finally, we estimate that only 13% of H II regions hosting young clusters and WR stars have fesc ≥ 0, which suggests that star formation taking place outside young clusters makes a non-negligible contribution to ionising H II regions.
Key words: HII regions / galaxies: star formation / galaxies: individual: NGC 5236 / ISM: structure / galaxies: star clusters: general
© L. Della Bruna et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Stellar feedback consists of a variety of processes (see Krumholz et al. 2014; Dale 2015, for a review), the most important mechanisms being photoionisation, direct radiation pressure, and mechanical feedback via stellar winds and supernovae (SNe) explosions. The combined effect of these mechanisms results in a multi-scale phenomenon, ranging from scales of a few parsec – surrounding the stars – to galactic-wide scales.
Stellar feedback originates from massive stars, forming in the densest cores of giant molecular clouds (GMCs). Therefore, studying stellar feedback and its regulatory role in the star formation cycle of galaxies requires access to a large dynamical range of observations and simulations that capture processes happening over five orders of magnitude in physical scales. One of the key questions currently focusses on the timescales necessary to dissolve GMCs. These timescales are fundamental because they determine the resulting efficiency of the star formation process in the region, as well as how energy and momentum stream away from these regions maintaining a multi-phase interstellar medium (ISM).
Numerical approaches are typically focussed on simulating isolated star-forming regions, but including detailed treatment of star formation and stellar feedback (e.g. Kim et al. 2018, 2021; Olivier et al. 2021; Grudić et al. 2021, 2022, among the latest); or they probe the feedback in isolated galaxy simulations by focusing on different feedback processes, while simplifying other physical processes happening at small physical scales (e.g. Hopkins et al. 2018; Bending et al. 2020; Jeffreson et al. 2021); or re-simulating regions of galaxies (e.g. a fraction of spiral arms) to preserve the regulatory role of galactic scale dynamics, while improving the details of feedback prescriptions (e.g. Gatto et al. 2017; Ali 2021; Ali et al. 2022; Bending et al. 2022). Overall, these diverse approaches reach a similar conclusion regarding the importance that photionisation from massive stars has in the evolution of the star-forming regions by lowering the gas density and, therefore, pre-processing the surrounding gas where SNe explode.
From the observational side, great advancements have recently been made thanks to the advent of sensitive integral field spectrographs (IFSs) with wide field of views, enabling large portions of local galaxies to be covered at reasonable high spatial resolution. It is now possible to directly study the impact of different types of feedback on the star-forming regions, and to trace their rapid evolution. Two instruments that have been playing an important role in this sense are: the multi-unit spectroscopic explorer (MUSE) IFS (Bacon et al. 2010) at ESO’s Very Large Telescope and the SITELLE imaging Fourier transform spectrograph at the Canada-France-Hawaii Telescope (Drissen et al. 2019). Using these instruments, two large ongoing surveys targeting H II regions in nearby galaxies at scales relevant for these types of studies are the PHANGS-MUSE (Emsellem et al. 2022) and SITELLE-SIGNALS (Rousseau-Nepton et al. 2019) surveys, which are mapping ∼20 and 40 nearby galaxies at a median physical scale of 50 pc, respectively. These surveys provide us with a statistical sample of H II regions, enabling us to study their overall properties, such as luminosity, metallicity, and ionisation state, indirectly derive their internal pressure, and determine how they depend on the galactic environment (e.g. galactocentric distance or arm-interarm environment), on changes in local environmental conditions and on the average properties of the stellar populations hosted by the regions (e.g. Rousseau-Nepton et al. 2018; Kreckel et al. 2019, 2020; Barnes et al. 2021). These studies, however, do not allow to resolve sizes and determine electron densities for a large fraction of their H II regions, requiring indirect methods and assumptions to estimate different pressure terms and resulting in degeneracies not easy to disentangle (e.g. Barnes et al. 2021, 2022).
On the other hand, very high-resolution (∼ 10 pc scale) studies of smaller samples of H II regions are allowing us to resolve the star-forming regions in their details. This makes possible investigations of the impact of the different stellar feedback mechanisms on individual regions (e.g. Lopez et al. 2014; McLeod et al. 2019, 2020, 2021), and how they are related to the properties of the regions (e.g. metallicity or extinction) and of their environment. If the stellar population of the regions is accessible, by modelling the expected ionising photon flux Q(H0) and comparing it to the observed ionised gas emission, one can infer whether the regions are leaking hydrogen ionising radiation (Lyman continuum photons, LyC, hν > 13.6 eV; e.g. McLeod et al. 2019, 2020; Della Bruna et al. 2021). By constructing a ‘ionisation budget’ for the full sample, one can assess whether ionising photons escaping from the H II region population can explain the amount of diffuse ionised gas (DIG) emission outside the H II regions, shedding light on the origin of this emission component of the interstellar medium (ISM, see e.g. the review of Haffner et al. 2009).
Another open question is how the LyC escape fraction (fesc) is linked to the properties of the regions, such as their ionisation structure (e.g. the presence of optically thin ‘channels’), or the stellar population they host. Recent high-resolution cosmological simulations of Ma et al. (2020) seem to indicate for example that regions with an age spread in their stellar population are advantaged in leaking ionising photons. Namely, feedback from clustered SNe can result in the creation of a superbubble; a second generation of stars is then able to ionise pre-cleared lower density channels, and leak LyC photons into the surrounding ISM. In a previous publication (Della Bruna et al. 2021) we investigated this in a sample of 8 H II regions in the nearby galaxy NGC 7793, finding a significant leakage of ionising photons but no conclusive evidence of a trend with age spread.
In this work, we study a sample of ∼4700 H II regions across the stellar disk (R ≲ 1.1 Re) of the nearby galaxy M 83, a grand design barred spiral at a distance ≃5 Mpc (Jacobs et al. 2009, see Table 1). In Della Bruna et al. (2022, henceforth Paper I) we have presented a large MUSE mosaic of M 83 (3.8 × 3.8 kpc), with a spatial resolution of 20 pc. In Paper I, we discussed the large scale kinematics of the gas and the stars. Here, we focus on the individual H II regions. With the spatial resolution of our data, we are able to resolve most individual regions. We have access to their stellar population thanks to HST observations of the young star cluster (YSC) population (Silva-Villa et al. 2014; Adamo et al. 2015). We investigate the relative importance of different feedback mechanisms and constrain the escape of ionising radiation from the regions. We then investigate how these quantities are linked to the region properties and the stellar population they host.
Overview of the H II regions sample.
This work is organised as follows: in Sect. 2 we briefly describe the dataset. In Sect. 3 we summarise the selection steps and properties of the H II regions sample. In Sect. 4 we describe the stellar population in the regions, and in Sect. 5 we summarise their physical properties. In Sects. 6 and 7 we investigate the contribution of different pressure terms in the regions and compute their ionisation budget. We discuss the results in Sect. 8, and conclude with a summary in Sect. 9.
2. Data description
We summarise the main physical properties adopted for M 83 in Table 1. The dataset is described in detail in Paper I. Briefly, we constructed a large mosaic of 26 MUSE pointings, combining a total of 65 single exposures1. The data are obtained in Wide-Field Mode (WFM), and extended wavelength mode (4650−9300 Å), and cover a galactocentric radius of ∼3.8 kpc (1.1 × Re), for a total area of 40.5 kpc2. The median point spread function (PSF) measured at 7000 Å is 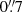 (17 pc); we refer to Paper I for details on PSF variation with wavelength and across the mosaic tiles.
(17 pc); we refer to Paper I for details on PSF variation with wavelength and across the mosaic tiles.
We combine the information on the ionised gas from MUSE with HST data tracing the star cluster population (Silva-Villa et al. 2014; Adamo et al. 2015). M 83 was first observed during the WFC3 Early release science programme (GO11360, PI O’Connell). The coverage was later extended to a galactocentric radius of 4.5 kpc (1.3 × Re, GO12513, PI Blair). The final HST mosaic2 (7 pointings) is described in Blair et al. (2014), and the data have a FWHM of 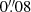 (1.9 pc).
(1.9 pc).
3. H II regions, SNR, PNe sample
3.1. Identification of the H II regions
The identification of the boundaries of the H II regions and other emission regions has been performed using the Python package ASTRODENDRO3 as described in Paper I. In summary, the dendrogram tree was computed down to a surface brightness (SB) of 1.23 × 10−15 erg s−1 cm−2 arcsec−2. This threshold was estimated as the brightness of an H II region of 10 pc radius ionised by a single low-luminosity star, adopting the luminosity of a O9.5 main sequence star (Martins et al. 2005). We set the minimum leaf size of the tree to a square of width 4.3 pixel, corresponding to the typical FWHM of the PSF at Hα (see Paper I). The outcome of ASTRODENDRO is a tree structure, consisting of leaves and branches organised hierarchically according to their flux. In crowded H II region complexes however, this is often not sufficient to disentangle single regions. This is less of an issue in flocculent spiral galaxies (NGC 7793, Della Bruna et al. 2020, or NGC 300, McLeod et al. 2021), where H II complexes are not too large, but can be a cause of concern in grand-design spirals such as M 83, where the spiral arms consist of tightly packed H II regions.
Breaking up H II region complexes into single regions has therefore required additional steps. We first tested the approach of McLeod et al. (2021), where hierarchical structures identified with ASTRODENDRO are divided into sub-structures using the SCIMES algorithm (Colombo et al. 2015). Hereby, relevant sub-structures are identified and grouped by determining their ‘affinity’ with a spectral clustering approach. However, the SCIMES algorithm did not perform optimally for our dataset, due to the wide range in luminosity of the H II regions and the lack of flexibility in the code parameters. Namely, the code starts by identifying sub-structures in the most luminous complexes. Increasing the user_k parameter (expected number of clusters) only results in an over-shredding of the bright complexes, and a lack of substructures in the less luminous ones.
We obtain optimal results using the first version of the code developed by Savard et al. (in prep.) which is based on the algorithm described in Rousseau-Nepton et al. (2018). For details on the working principles of the code, we refer the reader to Rousseau-Nepton et al. (2018) and the upcoming work of Savard et al. (in prep.), while we summarise here principal steps. The algorithm works as follows: in a first step, peaks of emission are identified in a Hα linemap by computing a Laplacian map. Relevant peaks of emission are identified using the peak_finder function, which takes as input: (1) the size of a (square) detection box; (2) the standard deviation of the Gaussian filter used by the Laplacian function to convolve the image, (3) the coordinates of a ‘background’ box, located in an area with little to no emission; (4) a constant fnoise, which determines the relative importance of the local noise variations and uncertainties on the Hα emission (see Eq. (1)). After detecting all relevant peaks of emission in the Laplacian image, the desired peaks are selected based on a detection threshold t. The latter is determined as a function of the background and peak emission level, as well as the local noise variation and the uncertainty on the emission peak in the detection box:
where mdetec, mbkg and σdetec, σbkg are the median and standard deviation of the input map within the detection box and in the background box, respectively, and Adetec is the area of the detection box. In a second step, each spaxel is assigned to the peak minimising 1/r3, where r indicates the distance to the peak. This metric was found to prevent bright emission peaks from embedding spaxels physically linked to dimmer peaks.
As input to the code, we provide the (non continuum subtracted) map of the Hα emission, obtained by integration of the datacube around the Hα line in the (restframe) wavelength range 6559−6569 Å, and a ‘continuum map’ obtained as the median of the data in the range around the line (stacking the regions 6529−6539 Å and 6599−6609 Å). We used a peak detection box size of 2 pixels (limited by the seeing) and a background detection box size of ∼130 × 160 arcsec2 situated in an interarm region with little Hα emission. We set the standard deviation of the Laplacian filter to 1.5. This value has been determined by visually inspecting the location of the resulting peaks. A lower value results in the detection of noise peaks, whereas a larger one retains only the strongest peaks of emission. We tested several value of fnoise. By visual inspection, we found the optimal value to be around 1. Higher fnoise values lead to missed detections of relevant peaks of emission, resulting in irregularly shaped and unrealistic region boundaries. Lower fnoise values, on the other hand, do not impact the distribution of the peaks within the dendrogram contours, but only result in a deeper detection limit below the adopted minimum SB threshold. In Appendix A, we illustrate an example of boundaries, luminosity, and sizes of regions identified using different values of fnoise. The change in fnoise affects the detection of faint H II regions, while it does not affect the recovered size distributions. To define the final domain of the regions, we set a termination criterion by multiplication with the mask obtained from ASTRODENDRO.
We note that throughout this work we do not correct the H II region emission for background emission caused for example by the DIG or other nearby regions. This emission varies significantly with distance from the regions, and is therefore very hard to estimate in crowded areas. DIG contamination by itself should not strongly affect the Hα luminosity, but can explain for example why some regions are beyond the extreme starburst line in the BPT diagrams in Fig. 10 and have a [S II] λλ6716,31 ratio above the sensitivity limit to the electron density (e.g. Belfiore et al. 2022). We also would like to point out that, despite our best efforts, not all regions will have well physically motivated boundaries in crowded areas. Nevertheless, the flux of each region will be dominated by the peak of Hα emission contained within it.
The resulting regions and an enlargement of a H II region complex are shown in Fig. 1. We identify a total of 4687 candidate regions. However, other classes of objects such as supernova remnants (SNRs) and planetary nebulae (PNe) emit in Hα. In the following we therefore cross-match the H II candidates with SNRs and PNe catalogues to remove such contaminants.
 |
Fig. 1. Map of Hα emission (extinction corrected) with the boundaries of the identified H II regions. Bottom panel: enlargement of one of the star-forming complexes. |
3.2. Identification of SNR
We cross-match our H II region catalogue with SNR identified in the MUSE M 83 dataset by Long et al. (2022) and based on the [S II]/Hα line ratio. The catalogue consists of 228 SNR in the region covered by the MUSE data. We find that 149 of our emission regions host a SNR (within a distance of 0.2″). We keep these in our H II region sample but flag them as ‘evolved’ H II regions throughout our analysis.
3.3. Identification of PNe
PNe are emission nebulae arising from an old stellar population that we wish to exclude from our H II region study. In the Milky Way and local galaxies, they are observed to have enhanced [O III]/Hα ratios (see e.g. Ciardullo et al. 2002; Magrini et al. 2005; Kniazev et al. 2008). Here we use two different methods to identify them.
The first method makes use of the spectral information contained in the MUSE datacubes (e.g. Kreckel et al. 2017; McLeod et al. 2021). Using the (reddening corrected) [O III]/Hα emission line map, we extract compact sources using ASTRODENDRO, requiring a minimum ratio value for [O III]/Hα of 0.45 and a minimum number of 8 pixels per leaf. Before extracting the regions of interest, we smooth the map with a 2D Gaussian filter with a kernel standard deviation of 1σ. This is done in order to prevent ASTRODENDRO from detecting noise in the map. We only consider leaves in the tree and obtain an initial sample of 3978 potential candidates.
Once the positions of the regions of interest are known, we extract spectra with a circular aperture of r = 1″, (5 px), using the leaf centres estimated from the ASTRODENDRO PPStatistic module, on the continuum-subtracted datacube. The spectra are dereddened using the E(B − V) estimated from the Balmer decrement (see Paper I) at the centre of the aperture. Confirmed candidates must then fulfil four criteria. First of all, have f([O III] λ5007)aperture ≥ 2 f([O III] λ5007)bkg, where the background flux is estimated in an annulus of (r + 4, r + 6) pixels. Secondly, have a ratio of f([O III] λ5007)/f(Hα) > 0.5. We use this as a lower limit threshold; previously known PNe are generally observed to have much higher ratios (∼2, Ciardullo et al. 2002). Thirdly, have a ratio of f([S II] λ6731)/f(Hα) < 0.5. This is done in order to exclude SNR from the sample, which notoriously have a high ratio of [S II]/Hα (> 0.4, Mathewson & Clarke 1973). We remark that here we use a less strict limit as a first filtering step, but that the candidates are later cross-checked with SNR identified based on a threshold of 0.4. Finally, they must also be unresolved in HST [O III] continuum subtracted imaging (Blair et al. 2014). The HST WFC3 pixel size of 0.04″ corresponds to ∼1.1 pc, so PNe will remain point-like while most compact emission nebulae will be resolved. We note that in the second and third criterium, the [O III]/Hα and [S II]/Hα ratios are background corrected by subtracting from each linemap a first order estimate of the emission background, computed over the entire FoV (via sigma clipping) rather than locally. This is done in order to avoid contamination by surrounding bright regions.
Of the initial 3978 candidates, 131 pass all four selection criteria. We cross-match this catalogue with the sample of SNR by Long et al. (2022) and exclude 11 more candidates coincident with the location of a SNR (within 0.4″). We are left with 120 confirmed PNe. Five of these were previously catalogued by Herrmann & Ciardullo (2009), all located in the outer disk. Two additional candidates from Herrmann & Ciardullo (2009, M 83-100 and M 83-195) are located at the very edge of the MUSE FoV and are not picked up by our selection criteria. The 115 new sources reported here highlight the capability of MUSE (combined with HST) in detecting this type of objects even at the distance of M 83. We inspected the confirmed PN sample for the presence of He IIλ4686; this line traces extremely high energetic photons with hν ≥ 54.4 eV and, when detected, is a robust confirmation of the presence of a PN (Frew & Parker 2010). We find He II emission in 15 of the objects. The position and coordinates of the 120 confirmed PNe can be found in Fig. B.1 and Table B.1.
The second method relies on the superior spatial resolution of the HST data. We use continuum subtracted [O III] and Hα data (Blair et al. 2014) to create a line ratio map. The latter is visually inspected to identify potential PNe candidates that have been missed in the MUSE extraction above. The selected candidates appear as point-like [O III] emission sources without stellar counterparts in the HST dataset. However, WFC3 data alone has some limitations. Faint stellar residuals in the subtracted emission line images and other artefacts such as cosmic ray residuals or hot camera pixels can be mistaken for real objects. MUSE data and HST WFC3 imaging used in conjunction are much more powerful for identifying PNe at the distance of M 83 than either dataset is alone.
We visually inspected the candidates using the display programme SAOimage ds9, simultaneously displaying the MUSE Hα, and [O III]/Hα map alongside the subtracted WFC3 [O III] and the WFC3 V-band images during the search for potential candidates. Point-like sources in the WFC3 [O III] image are compared against the continuum band to remove stellar residuals from further consideration and against the aligned MUSE data to verify the presence of a corresponding emission nebula at the position, thus eliminating cosmic ray residuals. We show an example of the search technique applied to a small 6″ region of M 83 in Fig. B.2. Using this approach, we identify 124 new PNe candidates. We then extract the spectra of the candidates from the continuum subtracted MUSE datacube and estimate line ratios as described in the first method. Of the 124 candidates, 81 are detected in all the emission lines of interest (Hα, Hβ, [O III], [S II]). Of these 81 candidates, only 28 have f([O III] λ5007)/f(Hα) ratios greater than 0.5. We do not require the f([S II] λ6731)/f(Hα) < 0.5 criterion as in these cases we use the prior knowledge of the SNR positions. These 28 candidates have therefore been included into the sample of spectroscopically confirmed PNe. The remaining sources are listed and referred to as candidates in Table B.1 and in Figs. B.1 and 2.
 |
Fig. 2. Location of spectroscopically confirmed PNe (filled red points), PNe candidates (filled orange points) and H II regions (open blue circles) in a diagram of [O III] λλ4959,5007/Hβ versus [S II] λλ6716,6731/[O III] λλ4959,5007. We applied a first order background correction to the PN fluxes as described in Sect. 3.3. We observe that the confirmed PNe occupy a well-defined region in the diagram. |
In Appendix B we plot the positions of the confirmed and candidate PNe on the MUSE [O III]/Hα map. We see that spectroscopically confirmed PNe are preferentially located outside the bright H II regions (purple contours in Fig. B.1), whereas PNe candidates are distributed throughout the disc. This indicates that in bright, crowded regions the superior spatial resolution of HST data can improve the detection of PNe over low-spatial resolution 3D spectroscopy.
In Fig. 2 we show the position of the confirmed PNe (in red), candidate PNe (in orange) and H II regions (in blue) in an [O III]/Hβ versus [S II]/[O III] diagram. We see that the spectroscopically confirmed PNe occupy a well-defined region in the diagram, as recently observed by McLeod et al. (2021) in NGC 300. In contrast, candidate PNe tend to have less extreme line ratios that overlap with the H II region portion of the diagram. However, the candidate PNe are so few in number and so low in flux levels that the contamination of the H II region assessments can be ignored in what follows. We cross match our sample of Hα bright regions with the spectroscopically confirmed PNe, and remove from the H II region sample eight regions that coincide with the position of a confirmed PN along the line of sight.
4. Stellar population in the H II regions
4.1. Young star clusters
Using HST narrow and broad band imaging ranging from the UV to near-infrared (NIR), Silva-Villa et al. (2014) and Adamo et al. (2015) identified YSCs in the radial range 0.45−4.5 kpc (0.1−1.3 Re). This catalogue is complete down to a few thousand of M⊙ in the age range 1−10 Myr (see Adamo et al. 2015). In this paper, we extend the analysis of the cluster population to the inner 0.45 kpc of the galaxy, which was previously excluded due to its high luminosity gradient. We use the same dataset as in Adamo et al. (2015), consisting of the F336W, F438W, F555W, F657N, and F814W WFC3 bands. Cluster candidate identification and extraction has been performed with the same software developed to analyse star cluster populations in the HiPEEC sample (Adamo et al. 2020).
In short, the extraction step is performed with the source extraction software SEXTRACTOR (Bertin & Arnouts 1996) on the reference frame (F555W). The settings are optimised to extract point-like sources in crowded regions (see Adamo et al. 2020). We limit the extraction region to 0.47 kpc (corresponding to a radius of 500 native pixels from the centre). Aperture photometry is performed in all the bands at the positions determined in the reference frame. We use a radius of 5 pixels (0.2″) and a local sky background annulus of 6 pixels (0.25″) radius and of 2 pixel width (0.08″). We assume Vegamag as reference system, correct all the photometry for foreground galactic extinction (Schlafly & Finkbeiner 2011), and apply an aperture correction in all the bands, using as reference tabulated stellar encircled energy distributions. In this initial catalogue, we retain only sources with photometric error better than 0.3 mag in F438W, F555W, F814W.
In total, the positions of 3133 sources are extracted. Because of the close distance of M 83, we use a concentration index (CI) criterion to separate stars (PSF-like appearance) from cluster candidates (the FWHM is larger than the stellar PSF). Following Adamo et al. (2017), we estimate the CI in the reference frame (F555W) as the difference between the magnitude of the source extracted with aperture photometry of radius 1 pixels and at 3 pixels. From the distributions of the CI, we apply a CI ≥1.2 mag criterion to separate stars from cluster candidates. The final automatic catalogue includes only sources that have CI ≥1.2 mag, an absolute magnitude in the F555W band brighter than −6 mag, and that are also detected in the F336W with a photometric error better than 0.3 mag. This selection results in ∼300 sources.
Visual inspection of these sources was performed in the same way as done in the previous star cluster catalogue published by Adamo et al. (2015), where ‘Class 1’ corresponds to compact and symmetric clusters, ‘Class 2’ to concentrated but with some degree of asymmetry systems and ‘Class 3’ to not-cluster (stars, interlopers, artefacts in the image, etc.). In total, 179 sources have been classified as class 1 and 2 in the inner region of M 83. From the combined cluster catalogue covering the entire HST mosaic, we select exclusively class 1 and 2 clusters, that is 7459 systems. Of these, 4317 clusters are located in the MUSE FoV. We cross-match the location of the YSCs with the sample of H II regions determined in Sect. 3 and find that 1251 regions host at least one YSC.
To include stochastic effects that arise when sampling the initial mass function (IMF) of YSCs, we used the Bayesian code SLUG (see da Silva et al. 2012; Krumholz et al. 2015a, v2). The photometric tables, containing the spectral energy distributions (SEDs) of class 1 and 2 clusters are analysed using cluster_slug (Krumholz et al. 2015a). We compute probability distribution functions (PDFs) of clusters physical parameters based on their observed HST photometry in the five filters listed above (see Krumholz et al. 2015b), using a library of clusters simulated with SLUG. We consider age t, mass M and visual extinction AV as free parameters, and assume a flat prior in AV and in log t, and a log(M)∼1/M prior on the mass. We use the library of mock star clusters described in Ashworth et al. (2018), a Milky Way extinction law by Fitzpatrick (1999) and the non-rotating solar metallicity stellar population models from Ekström et al. (2012). As a proxy for the best value of each cluster physical properties, we use the median and quartiles of the relevant PDF, following the method tested by Krumholz et al. (2015b). Naturally, reducing a full PDF to a single best value can lead to biased results, especially in the case of a non-Gaussian PDF. For a detailed study on the use of different proxies, we refer to the work of Krumholz et al. (2015a). Cluster ages, masses and ionising photon luminosity (Q(H0)) are recovered directly from the PDFs of single clusters and will be widely used in the following analyses.
In Fig. 3 we show the age and mass of the YSCs as function of galactocentric radius. We observe that the cluster age does not correlate with radius, whereas the central region hosts more massive clusters. We notice that near the galactic centre, due to crowding, the low mass distribution is less complete than in the rest of the disk. In Fig. 4 we also show the combined PDFs of young clusters (age t ≤ 10 Myr) located inside (in blue) and outside the H II regions (in orange). The combined PDFs are obtained by summing the fractional probability contribution of each cluster in each logarithmic age, mass and Q(H0) bin and re-normalising the overall distribution. We observe that the age PDF is double peaked, due to the degeneracy between age and extinction. Overall, clusters populating the H II regions are on average younger (median age of 4.7 vs. 8.23 Myr) and slightly more massive (median mass of 1.7 vs. 1.4 × 103 M⊙), and they emit an order of magnitude more ionising photons (median log Q(H0) of 48.5 vs. 47.4 s−1).
 |
Fig. 3. Age and mass of the YSCs as function of galactocentric radius. The black dots indicate the median (±quartiles) over radial bins with equal number of objects (≃20). |
 |
Fig. 4. Combined posterior probability distributions of age, mass and ionising photon flux obtained with SLUG for young clusters (t ≤ 10 Myr) populating H II regions (in blue) and located outside the H II regions (‘field’ clusters, in orange). The vertical lines and shaded areas indicate the median and quartiles of each distribution. |
For the remaining analysis4, we only consider YSC of age ≤10 Myr populating the H II regions, as older clusters are generally not associated with H II regions and are more likely line-of-sight objects. We find 885 clusters of age t ≤ 10 Myr in the MUSE FoV, populating 532 H II regions. Most regions host one or two clusters, but we observe up to six clusters per region in a few cases. We also find that ∼10% of the YSCs with t ≤ 10 Myr are located outside an H II region. These clusters have on average a low mass (∼1000 M⊙), indicating that they have a low probability of forming massive stars. The cluster population across the MUSE FoV is shown in the top panel of Fig. 5; we observe that the clusters trace quite closely the location of the H II regions.
 |
Fig. 5. Stellar population in the MUSE FoV. Top panel: extinction-corrected Hα map with the location of YSCs of age ≤10 Myr (green triangles). Bottom panel: enlargement of one of the H II region complexes. Green triangles indicate the position of YSCs observed with HST (Adamo et al. 2015), blue crosses and red stars indicate respectively WR stars and PNe identified in the MUSE dataset and orange squares are SNR from Long et al. (2022). |
4.2. WR stars
Hadfield et al. (2005) identified WR stars in M 83 by observing photometrically selected candidates using multi-object spectroscopy. We confirm and add to this sample using spectroscopic information from the MUSE data. We identify candidate WR stars in a He IIλ4686 linemap, obtained by integrating the gas cube over the (restframe) wavelength range 4686−4695 Å. We select sources using ASTRODENDRO, with a flux threshold of 7.85 × 10−19 erg s−1 cm−2 (10σ above the mean background across the map), and with a minimum leaf area of 5 × 5 spaxels. We also add to this sample candidates from Hadfield et al. (2005) that we missed. For each of the 457 candidates, we extract spectra with a circular aperture of 1″ on the full datacube (without continuum subtraction). We visually inspect the spectra, looking for characteristic features: the blue bump (BB) of He IIλ4686, C III/C IVλ4650/4658 and the red bump (RB) of C IVλ5801,5812. We also determine if other characteristic lines, such as C IIIλ5696, N Vλ4603–20 and N IIIλ4634–41 are present. We confirm 68 candidates, of which 27 already identified by Hadfield et al. (2005). We further classify the spectra into helium-dominated WN type and carbon-dominated WC type, based on their spectral features. Like Hadfield et al. (2005), we find that most of the confirmed WR are late WC stars with C IIIλ5696 present in their spectra. The position and coordinates of the confirmed WR and their spectral classification can be found in Fig. C.1 and Table C.1. We find that 64 of the confirmed WR are located in an H II region. As already reported in Della Bruna et al. (2021) for one WR, we postulate that the remaining 4 WRs, which do not coincide with the position of H II regions along the line of sight, are probably runaway stars.
In the bottom panel of Fig. 5, we show an overview of the stellar population of a single H II region complex. We indicate the position of YSCs (t ≤ 10 Myr, green triangles), Wolf-Rayet stars (WR, blue crosses), SNR (yellow squares) and PNe (red stars).
5. Physical properties of the H II regions
In Table 1, we summarise our H II region sample. After removing for PNe contaminants the final catalogue contains a total number of 4679 regions. Of these regions, 531 host at least 1 YSC of age ≤10 Myr, and 64 host a WR star (of which 10 regions do not contain a YSC). The fact that many regions do not host YSCs might be partly due to a bias in detecting low mass clusters, as well as the fact that many star-forming regions host less compact clustered star formation (e.g. OB associations). In general, the cluster formation efficiency varies between 30 and 8% from the centre to the disk of M 83 (Adamo et al. 2015) and overall it can explain why only about ∼10% of the regions host compact young clusters.
In total, we have access to the stellar population of 541 regions (42 of which are evolved regions hosting a SNR5). This is the subset of regions used in most of the remaining analysis, whose properties are highlighted in light green in Figs. 6–8 and 10.
 |
Fig. 6. Luminosity function (top) and size distribution (bottom) of the final sample of H II regions. In blue we show the total distribution, and in green the distribution for regions hosting either a YSC younger than 10 Myr or a WR star. The vertical lines and shaded areas indicate the median and quartiles of each distribution. The grey dashed lines in the top panel indicate the minimum luminosity of a region of radius 10 and 50 pc based on the SB threshold used for the H II region selection. Bottom panel: the grey dashed line corresponds to the spatial resolution limit of the MUSE data (regions below this line are unresolved in our dataset). |
 |
Fig. 7. Luminosity (top panel) and size (bottom panel) of the final sample of H II regions as function of galactocentric radius. Green stars indicate regions hosting either a YSC younger than 10 Myr or a WR star. The large black dots indicate the median (±quartiles) in radial bins with equal number of objects (≃120). The dashed line in the bottom plot indicates the spatial resolution limit of the MUSE data. |
 |
Fig. 8. Same as Fig. 7 but showing the extinction (top), oxygen abundance (centre) and density (bottom panel) of the H II regions. Central panel: a linear fit to the data (in black) with a 95% confidence interval (shaded grey area). We also indicate the best fit parameters in the upper right corner. Bottom panel: the grey dashed line in the bottom panel indicates the sensitivity limit of the density determination method: points below this lines are consistent – within measurement uncertainty – with ne ≃ 1 cm−3. Error bars span the first to third quartile of a distribution of ne obtained from 1000 Monte Carlo realisations of the [S II] ratio (see Sect. 5). |
In Fig. 6 we show the luminosity function (top panel) and size distribution (bottom panel) of the regions. The radius of each H II region is estimated by approximating the area enclosed by the boundaries determined in Sect. 3.1 to a circular area. We observe that regions with YSCs (in light green) are on average more luminous and larger in size. The recovered luminosity distribution is comparable to the range reported by Kreckel et al. (2019) and Santoro et al. (2022) for the PHANGS-MUSE sample. The ‘turnover’ at Lmin ∼ 2 × 1037 erg s−1 is due to incompleteness (see Kennicutt et al. 1989) and is consistent with the values of Lmin obtained by Santoro et al. (2022) in nine of the PHANGS galaxies. The incompleteness originates on one hand from the non-detection of faint regions, due to both instrumental sensitivity limit and the SB threshold used in the H II regions detection. On the other hand, there are blending effects of low-luminosity regions with neighbouring bright objects, especially in crowded and luminous region complexes, for example near the galactic centre. The distribution of radii peaks at much smaller sizes than in PHANGS-MUSE (Kreckel et al. 2019), as a result of the higher spatial resolution of our dataset (∼20 pc) compared to the average resolution of PHANGS-MUSE (∼50 pc). The distribution of radii observed in this work is comparable with sizes reported in other local galaxies at resolution < 20 pc (e.g. Sivan et al. 1990; McLeod et al. 2021). Finally, we assess that (for r > 20 pc) the frequency distribution of diameters is well fitted by a van den Bergh (1981) exponential law
with N0 ∼ 8 and D0 ∼ 45 pc. This is in agreement with observations in most spiral galaxies (Ye 1992; Gutiérrez et al. 2011; Azimlu et al. 2011; Araújo de Souza et al. 2018).
In Fig. 7, we show how the size and luminosity of the regions vary as function of galactocentric radius. The most luminous regions are located within the inner 0.5 kpc (R ≤ 0.15 Re) of the galaxy, coincident with the starburst region (see Paper I). A noticeable increase in H II region luminosity is also observed in correspondence of the highly star-forming regions located at the end of the bar at ∼2.3 kpc (0.7 Re), the same region where the cluster formation efficiency is observed to increase as reported in Adamo et al. (2015). We observe that the radius of the regions does not change significantly as a function of galactocentric distance.
Figure 8 shows the average extinction, oxygen abundance and electron density of the H II regions as function of galactocentric radius. In order to compute these quantities, we first obtained an integrated spectrum for each region. We then fit single Gaussian profiles to the emission lines (see Paper I for details). In the case of the [S III] λ9069 line, which was not in the wavelength range for which we had removed the stellar continuum (see Paper I), we manually subtracted a median stellar continuum determined in the (restframe) wavelength range 9034−9054 Å and 9079−9099 Å.
We determine the extinction (top panel in Fig. 8) from the Hα/Hβ ratio using PYNEB (Luridiana et al. 2015), assuming an intrinsic ratio of 2.863 (case B recombination with Te = 104 K, ne = 100 cm−3, Osterbrock & Ferland 2006) and a Cardelli et al. (1989) extinction law. We see that the average extinction peaks within the circumnuclear starburst region (E(B − V)∼0.6) and decreases slightly with radius, down to ∼0.4 mag.
The oxygen abundance (central panel in Fig. 8) was determined from the [N II] λ6584/Hα := N2 ratio, using the calibration from Denicoló et al. (2002):
We decided to use the N2 ratio for two reasons. First of all, Bresolin et al. (2016) studied the metallicity of H II regions in M 83 using different line ratios and calibrations, and found that the N2 ratio with the calibration above gives an excellent agreement with the metallicity recovered using direct methods and determined from observations of blue supergiants. Secondly, we wanted to avoid using multiple lines which would result in stronger degeneracies with temperature and density (see e.g. Ercolano et al. 2012; McLeod et al. 2016, 2019; Della Bruna et al. 2021). The recovered range in oxygen abundance agrees well with the results of Bresolin et al. (2016) for the radial range probed by the MUSE data (corresponding roughly to 0.4 R25 in their work). We perform a linear fit to the data and obtain
in very good agreement with the central abundance of 8.87 and slope of −0.09 reported by Bresolin et al. (2016) for the radial range 0−3 R25 (0−8 Re) using the N2 ratio. We note large variations as a function of galactocentric distance. The abundance peaks at 12 + log(O/H) ∼ 9.0 at about 0.14 Reff, declines to an average value of 12 + log(O/H) ∼ 8.7 in the interarm region (0.3−0.6 Reff) and plateaus around 8.8 at larger radii, which are dominated by the presence of the spiral arms. Further analysis of the metallicity distribution as a function of spatial position will be presented in an upcoming work (Adamo et al., in prep.).
Finally, the electron density (bottom panel in Fig. 8) is determined from the ratio of [S II] λλ6716,6731, using PYNEB. We remark that densities below ≲40 cm−3 (grey dashed line in the figure) are in the asymptotic part of the [S II] versus ne curve and are consistent – within the uncertainties – with the lowest density limit probed by the ratio, ne ∼ 1 cm−3 (see e.g. Kewley et al. 2019a). To take into account uncertainties on the method, we considered 1000 Monte Carlo realisations of the [S II] ratio within the measurement errors, adopt as fiducial value the median of the resulting distribution and indicate the first to third quartile as grey error bars. The density of the H II regions decreases by almost two orders of magnitude between the centre of the galaxy and the outer regions. This trend seems to tightly follow the decline in the gas surface density of the molecular gas reported in Lundgren et al. (2004) and Adamo et al. (2015), as well as in the average midplane pressure reported in Fig. 15, suggesting that the ambient environment where H II regions form might be responsible for some of their key physical properties (Smith et al. 2006).
In Fig. 9 we furthermore inspect the ionisation state of the regions as function of radius. We use as tracer the ratio of [S III]/[S II]. A high ratio indicates gas with a high ionisation state, where doubly ionised sulphur is dominant, whereas a low ratio is indicative of singly ionised ions (low ionisation state). In general, we observe that regions at larger radii have a higher ratio of [S III]/[S II] (higher ionisation state). This is expected based on the slight decrease in metallicity with radius, as shown in the colour axis, and is due to the fact that stars at lower metallicity are hotter and therefore emit harder ionising radiation.
 |
Fig. 9. Ratio of [S III] λ9069/[S II] λλ6716,31 (reddening corrected) of each H II region as function of galactocentric radius. This ratio is a tracer of the hardness of the radiation field within the H II regions. |
Finally, in Fig. 10 we place the H II regions on N2- and S2-‘BPT’ emission line diagrams (Baldwin et al. 1981; Veilleux & Osterbrock 1987). As described in Kewley et al. (2019b), the position occupied by an object in these diagrams is a function of many different parameters, such as the density, radiation strength and hardness and metallicity. These diagrams were originally devised to identify the source of ionisation in single aperture spectra of galaxies but are today also used to determine the source of ionisation in different emission line regions within galaxies. Kewley et al. (2001) determined using models of star forming galaxies and shocks what is the upper limit spanned by purely star-forming galaxies in the diagrams (‘extreme starburst line’). In Fig. 10 we confirm that all the regions lie below or very close to this limit. We observe that most regions beyond the extreme starburst line are evolved H II regions hosting one or more SNR (red triangles), and that regions hosting young clusters or WR stars (green dots) are all located below this threshold.
 |
Fig. 10. Location of the final sample of H II regions in BPT emission line diagrams. Green stars indicate the subset of regions hosting either a YSC younger than 10 Myr or a WR star. Red triangles indicate evolved regions hosting a SNR. The black dashed line indicate the ‘extreme starburst line’ from Kewley et al. (2001), denoting the upper limit for gas purely excited by star-formation. |
6. Pressure analysis
In order to investigate which feedback mechanisms are dominant in each region, we study the contribution of the two main pre-SN feedback mechanisms (ionised gas pressure and radiation pressure) to the region’s internal pressure. We then compare how these vary with radial position in the galaxy and with the properties of the YSCs powering the regions.
6.1. Ionised gas pressure
The pressure exerted by the warm ionised gas is simply described by the ideal gas law:
where THII is the temperature of the H II gas. Assuming singly ionised Helium, this simplifies into Pion ≈ 2nekBTe. We computed the electron density using PYNEB and the ratio of [S II] λ6716,6731. Given that in the MUSE dataset we do not detect any temperature sensitive line with sufficient signal-to-noise (S/N), we assume a constant temperature Te = 104 K.
6.2. Direct radiation pressure
Direct radiation pressure is the pressure exerted by the momentum of the photons in the region. The volume-averaged direct radiation pressure can be derived from the observed total (bolometric) reddening-corrected luminosity Lbol as described by Lopez et al. (2014):
where R is the radius of the region. We note that this is an upper limit to the effective radiation pressure in the region, assuming a ‘classic’ Strömgren sphere morphology with an optically thick envelope (ionisation bounded region). To determine Lbol we use the relation between the bolometric luminosity and the Hα luminosity, Lbol = 138 L(Hα), derived by Kennicutt & Evans (2012), under the assumption of a stellar population with a fully sampled6 IMF in the age range 0−10 Myr.
6.3. Trends with galactic radius
In this work we focus on global environmental dependencies described by trends as a function of 1D galactocentric distance. In a follow-up paper we will investigate the impact of spiral arms by performing a 2D analysis which retains the azimuthal information about arm and interarm environments.
In Fig. 11, we show Pion (in blue), Pdir (in orange) and their ratio (in green) as function of galactocentric radius. In general, Pion dominates over Pdir, with a median ratio ≃13 across our sample. This is in agreement with observations of nearby galaxies (Lopez et al. 2011, 2014; McLeod et al. 2019, 2020, 2021; Barnes et al. 2021) at scales of 10−100 s parsec. Environmental dependencies are also observed. Both pressure terms are enhanced in regions located within the central starburst (Dgc ≲ 0.15 Re). In particular, Pdir is up to to 2 order of magnitude higher with respect to H II regions located in the disk, becoming comparable to Pion. An increase in Pdir is also observed in the end-of-bar region at ∼0.7 Reff. Outside the central starburst, we observe that Pion is decreasing as a function of radius (linear fit slope a ≃ −0.6, Pearson’s correlation coefficient r = −0.48), whereas Pdir stays approximately constant (a ≃ 0.0, r = −0.15).
 |
Fig. 11. Ionised gas pressure (in blue), direct radiation pressure (in orange) and their ratio (in green, values indicated on the right axis) as function of galactocentric radius. Red and dark blue triangles indicate evolved H II regions (hosting a SNR). The black dots indicate the median (±first and third quartile) pressure in radial bins containing an equal number of points (∼120). On top of the figure, we indicate the coefficients of a linear fit to the data. |
In Figs. 8 and 9 we see that – despite strong local variations – overall the extinction is decreasing and the radiation field hardness is increasing with galactocentric radius. In order to investigate whether radial trends observed in the pressure terms could be related to the radial variation in these quantities, in Fig. 12 we plot the pressure against the average reddening and radiation field hardness of each H II region.
 |
Fig. 12. Pressure terms as function of average reddening (top panels) and radiation field hardness (bottom panels) in the regions. Red and blue triangles indicate evolved H II regions (hosting a SNR). The black dots indicate the median (±quartiles) pressure in radial bins containing an equal number of points. On the top right, we indicate the value of the Pearson’s correlation coefficient r. |
For Pdir we observe both a positive correlation with reddening (r = 0.19) and with radiation field hardness (r = 0.21). Similar trends have also been reported by McLeod et al. (2021) for the flocculent galaxy NGC 300. The positive correlation between Pdir and reddening is produced by a positive correlation between Lbol and E(B − V). In general, we find that luminous H II regions have higher reddening and harbour a harder radiation field, resulting therefore in higher Pdir exerted within the H II regions.
On the other hand, the trends with Pion require a more complex interpretation. We see a positive correlation with extinction (r = 0.18) and a weak anti-correlation with radiation field hardness (r = −0.08). In this case, the correlation with extinction can be interpreted in the light of the fact that regions with higher values of E(B − V) are typically at a younger evolutionary stage (see also Sect. 6.4) and are hence more compact, resulting in a higher ne and therefore an increase in Pion (at constant temperature). The results of radiation-hydrodynamical models from Ali (2021) discussed in McLeod et al. (2021) agree with this scenario, indicating that an increase in UV photon extinction results in smaller regions. We directly investigate the correlation between H II region radius and Pion, finding a modest negative correlation (r = −0.13). The trend is probably weakened by the presence of both very young and compact regions as well as the smaller H II regions surrounding older stars. The anti-correlation with radiation field hardness can be understood in the light of two factors. First, a harder radiation field is caused by a lower metallicity (Fig. 9), which in turn results in higher electron temperatures (whereas we have assumed a constant Te in the computation of Pion). Taking this effect into consideration will weaken the observed correlation. Second, the regions with the highest metallicity are on average located closer to the centre of the galaxy (see central panel Fig. 8), where ne is also enhanced (bottom panel Fig. 8). Thus, the observed trend between Pion and [S III]/[S II] is likely in large part driven by the dramatic impact that the galactic environment has on the physical properties of rapidly evolving star-forming regions and only to a second degree to variations in the intrinsic properties of the regions. We discuss this further in Sect. 8.
6.4. Trends with YSC properties
As observed in Fig. 6, H II regions containing YSCs are brighter and larger in size with respect to regions that do not host any compact detected cluster. When considering the physical properties and ionisation state of these H II regions (Figs. 8 and 10), those hosting YSCs do not show any significant deviations from the average properties. We investigate here to what extent the pressure terms are linked to the star cluster physical properties. Extrapolating from Adamo et al. (2015), we know that cluster formation efficiency changes between 8 and 30% from the outer disk to the centre of M 83. This means that star clusters represent only a fraction of the stars forming and powering the H II regions. However, it is important to notice, as reported in several numerical simulations (e.g. Kim et al. 2017; Gentry et al. 2017; Fielding et al. 2018; Bending et al. 2020) that because of the compact configuration of the stars within star clusters we expect that stellar feedback couples more efficiently with the surrounding H II region.
Because multiple YSCs can be found within the same H II region, we plot in Fig. 13 the pressure terms against the age of the youngest cluster (top panels), assuming that the cluster with the youngest age has the most significant contribution to the LyC photon production in the region. We find that regions hosting younger clusters have both a higher Pdir (r = −0.47) and Pion (r = −0.34). The two pressure terms peak in regions containing very young clusters (∼1 Myr), although there is some scatter, probably due to the simplifying assumption that the youngest cluster is the one producing the highest photoionisation rates. We also see that after 1 to 2 Myr, Pion remains constant, suggesting that – whereas cluster feedback dominates the pressure terms at very young ages – in regions hosting more evolved clusters the ionising photon flux is maintained by the young stars surrounding the clusters. On the other hand, Pdir continues to decrease with cluster age, as expected if dust is destroyed in more evolved regions, thus reducing the coupling efficiency between dust and photons flux. Moreover, as we remarked in Sect. 6.2, Pdir is an upper limit assuming an ideal ionisation bounded region, which might not be the case for more evolved regions. In the bottom panels of Fig. 13, we plot the pressure terms as a function of the total stellar mass in clusters (of age t ≤ 10 Myr). We observe that a higher total mass in young clusters correlates with a steady increase in the pressure terms (r = 0.36 and 0.24, respectively). This is true especially for Pdir. We discuss these trends further in Sect. 8.
 |
Fig. 13. Pressure terms as function of the age of the youngest cluster in the region (top) and the total mass of clusters younger than 10 Myr (bottom). Red and blue triangles indicate evolved regions hosting a SNR. The black dots and line indicate the median (±quartiles, shaded in grey) in radial bins of 1 Myr (top) and in mass bins with equal number of objects (bottom, ≃40 objects/bin). On the top right, we indicate the value of the Pearson’s correlation coefficient r. |
7. Photoionisation budget
In the previous section, we identified a coupling between the physical properties of the very young star clusters and the pressure exerted on their host H II regions. In this section, we evaluate whether this coupling between star cluster physical properties and pressure terms leads also to a correlation between cluster physical properties and escape of ionising radiations from the H II regions. In Weilbacher et al. (2018), the authors report that the ionising radiation produced by the star cluster population in the Antennae merger system is sufficient to produce the ionising radiation observed in the emitting ISM. We assess here whether this is the case also in the spiral galaxy M 83.
Given that we lack a catalogue of young, massive stars outside clusters, we limit the ionisation budget analysis to regions hosting at least one YSC. For completeness, we also include in the budget the ionising radiation produced by the spectroscopically confirmed WR stars, even if they do not reside in regions containing YSCs. In the latter case, we assign the region an age of 4 Myr. In total, we perform the budget analysis on 541 regions, 531 hosting YSCs and 10 hosting exclusively WR stars, as summarised in Table 1.
In general, the rate of hydrogen ionising photons emitted from a region, Q(H0), is defined as the total number of LyC photons emitted per unit time
We infer an ‘observed’ Q(H0), hereafter Qobs, for each region from the Hα flux, and compare it to the ‘expected’ Q(H0), hereafter Qexp, obtained by modelling the ionising photon rate produced by YSCs and WR stars within the region. We then compare the two quantities to compute an escape fraction
A value of fesc > 0 indicates that the observed emission is lower than the expected emission, indicating that some radiation might have escaped the region. We caution however that other effects can mimic an fesc > 0. One of these is the absorption of LyC radiation by dust: dust can absorb the LyC photons before they can ionise the hydrogen atoms, and re-emit them at longer wavelength. The typical fraction of LyC radiation absorbed by dust has been constrained to be of the order of 30−50% in observations of nearby galaxies (Inoue et al. 2001; Hirashita et al. 2003; Iglesias-Páramo et al. 2004; Salim et al. 2016) as well as in simulations (Tacchella et al. 2022).
In the following, we summarise how we estimate Qobs and Qexp for each H II region.
7.1. Observed ionising photon flux
We compute the observed ionising photon flux from the (dereddened) Hα luminosity. We use the following conversion factor from Draine (2011), which assumes case B recombination with an electron temperature of Te ∼ 104 K and a density of ne = 103 cm−3:
7.2. modelling YSC ionising radiation output
We model the emission of YSCs with the SLUG Bayesian stellar population synthesis code based on their observed HST photometry, as described in Sect. 4.1. We obtain the total ionising flux of a region by constraining a PDF of Q(H0) for each cluster, sampling one value from each one of these PDFs and repeating this procedure during 1000 Monte Carlo realisations, to obtain a distribution of the total flux. We then report the median and quartiles of the total distribution as best value and related uncertainty.
7.3. modelling WR stars
WR stars emit very powerful radiation, and a single WR star can substantially contribute to the ionisation budget of a region (see e.g. Della Bruna et al. 2021). We constrain Qexp for each star using values tabulated by Smith et al. (2002, Tables 3 and 4 in their work). We use the WR spectral types listed in Table C.1 and assume a temperature range T = [40 − 80]×103 K for WN-type stars and T = [100 − 140]×103 K for WC-type stars. We obtain a distribution of Q(H0) from 1000 Monte Carlo realisations of T and we consider its median and quartiles as best value and associated uncertainty.
7.4. Resulting budget
Figure 14 shows the resulting budget for all the regions analysed. Points above the black dashed line indicate regions with an fesc > 0. Overall, we observe escape only for ∼13% of the regions (69 out of 541), pointing to the fact that only a fraction of YSCs does produce enough ionising radiations to match the observed Hα luminosity of H II regions. In the majority of the leaking regions, that is 80%, the youngest cluster has an age tmin < 2 Myr (top panel). In order to quantify the effect of dust absorption, we colour code each region by its average E(B − V). We do not observe an excess in extinction among the regions with fesc > 0, indicating that dust is likely not playing a dominant role, and that these escape fractions are significant.
 |
Fig. 14. Ratio of expected to observed Q(H0) for all the H II regions hosting YSCs or WR stars. The black dashed line indicates a ratio of 1 (fesc = 0). Top panel: Q ratio as function of the age of the youngest cluster (tmin) hosted in each region, colour coded by the region’s average extinction. Bottom panel: Q ratio as function of the total mass in clusters younger than 10 Myr, colour coded by galactocentric distance. |
We also investigate whether regions that have been forming stars for a longer time are advantaged in leaking ionising photons, motivated by the recent results of high resolution simulations from Ma et al. (2020, see Sect. 1). We assume that the age of the oldest star cluster in the H II region is an indicator of how long star formation has been active in the region (duration of star formation, tSF). This assumption is also justified by studies of star-forming region complexes in local spirals (e.g. Bastian et al. 2005, and references therein). In the case of a region hosting only one (or more) WRs, we assume a fiducial age of 4 Myr. In general, we find that only 35% of the regions with fesc > 0 have tSF larger than the age of the youngest hosted clusters. This result is driven by the fact that most of the regions host single clusters (hence, tSF = tmin by definition).
Finally, we do not see strong dependencies between the Q ratio and the total mass in YSCs (bottom plot in Fig. 14, r = 0.08), suggesting that while star cluster mass seems to have a strong impact on the pressure terms at work within H II regions, it does not drive the escape of ionising radiation. Similarly, we do not observe dependencies between the Q ratio and Rgc (colour bar in the bottom plot of Fig. 14). This suggests that none of the physical variations in the H II regions which host star clusters is driving LyC escape from the regions. Taking into account that the observed Q ratio ≥1 would somewhat be affected by dust reprocessed light, especially at the youngest ages, these results point towards the scenario where star clusters are not the main responsible for LyC radiation leakage from H II regions in M 83. We discuss this further in Sect. 8.
8. Discussion
8.1. Pressure terms as function of YSC properties
In the past decades, HST narrow-band imaging observations centred on Hα emission, combined with broadband photometry of YSCs have been widely employed to study the evolution of H II regions in nearby galaxies. Various studies find for example that after being initially embedded in their natal gas, clusters emerge after < 4−5 Myr, and according to the latest optically centred analyses (Whitmore et al. 2011; Hollyhead et al. 2015; Hannon et al. 2019, 2022; Grasha et al. 2019; Messa et al. 2021) this process can be as fast as 2−3 Myr. Whereas high-resolution imaging can inform us about the evolution of the H II regions associated with star cluster properties, spectroscopy provides the key to actually sample H II regions physical properties while they evolve. Combining HST imaging of YSCs with MUSE spectroscopy of the ionised gas, we observed that indeed the properties of star clusters have a strong coupling with the pressure terms tracing stellar feedback exerted in H II regions (Fig. 13), and this despite the fact that in M 83 YSCs only make up a fraction of the stars forming in the galaxy (< 30%). We suggest that these trends are driven by the effect of clustering, that is the fact that feedback from stars tightly packed in clusters (having a size of a few parsecs) has a higher impact on the host H II region, as observed in numerical simulations (e.g. Kim et al. 2017; Gentry et al. 2017; Fielding et al. 2018; Bending et al. 2020).
8.2. Relative strength of the pressure terms
In Fig. 11, we found that Pion is predominant over Pdir, with a median Pion/Pdir ≃ 13, but with significant variations in specific regions of the galaxy (like the central starburst at Re ≤ 0.15). These results are in agreement with what is reported in the literature for lower mass and metallicity galaxies (Large and Small Magellanic Cloud, NGC 300 at 2 Mpc), thus extending the range of galactic environment to massive, highly star-forming and metal-rich grand-design spiral galaxies. Lopez et al. (2011) studied the 30 Dor giant H II region (∼300 pc in size) in the Large Magellanic Cloud, finding that Pion is predominant over Pdir at d > 75 pc from the central star cluster. Lopez et al. (2014) performed a similar study in a sample of ∼30 H II regions in the Small and Large Magellanic clouds, finding that Pdir is one or two order of magnitude smaller than Pion in all regions. More recently, McLeod et al. (2020, 2021) reported a median Pion/Pdir ∼ 60 in a sample of ∼100 H II regions in NGC 300.
In another recent study, Barnes et al. (2021) computed pressure terms for ∼5800 regions in the PHANGS-MUSE sample, which consists of 19 spiral galaxies sampled from the local main-sequence of galaxies (Emsellem et al. 2022) at an average distance of 15 Mpc. According to their selection criteria, M 83 would nicely fit the sample. The authors obtain an upper and a lower limit for each pressure term, by considering the extreme cases of a perfectly smooth H II region (with a pressure Pmin) and a clumpy H II region, where all the clumps are located near the region’s centre (with a pressure Pmax). Whereas in the upper limit case Pdir is observed to be ∼Pion, in the lower limit case Pion is up to a factor four higher.
In order to better compare our results with the study of Barnes et al. (2021), here we very briefly compare the adopted methodologies. For Barnes et al. (2021), the lower limit case the region radius corresponds to the measured effective radius (Re), while the lower limit for ne is computed as a function of Qobs and Re. In the upper limit case, ne is estimated from the [S II] line ratio and the radius of the clumpy region is derived as function of Qobs and ne. In this work, on the other hand, we do not attempt to compute a lower and an upper limit. Our H II region sizes are comparable to the radii estimated for the lower limit case in Barnes et al. (2021), and agree with the size distribution of H II regions observed in NGC 300 by McLeod et al. (2021, ∼10 pc resolution). We point out that, even if the sizes in Fig. 6 are overestimated by a factor three, Pion would still be the dominant term. Secondly, we compute pressure terms only for regions for which we have a density estimated from the [S II] line ratio (this approach removes about 30 regions from the 4684 extracted). Therefore, the luminosity, size and density of the regions are computed independently, and our estimates of Pion and Pdir are independent from each other. Overall, our results are closer to those that Barnes et al. (2021) obtain by using the lower limit case (smooth H II region assumption), reinforcing the conclusion that, for average star formation conditions representative of galaxies in the local universe, pre-SN feedback within H II region is dominated by the thermal pressure exerted by photoionisation.
8.3. Pressure terms as function of galactocentric radius
In Fig. 11, we showed that – outside of the inner region – Pdir is approximately constant with radius, whereas Pion decreases. The pressure terms appear to be correlated both with changes in the intrinsic properties of the H II regions (metallicity and thus radiation field strength, and extinction) and with changes in the galactic environmental conditions. While the trend in Pdir can be explained purely with changes in the region intrinsic properties, the decrease in Pion with radius seems to be fully dominated by changes in the galactic environment. This is in agreement with what observed by Barnes et al. (2021), where the pressure (both in their lower and upper limit) shows a systematic increase towards the galaxy centres, despite the higher metallicities. On the other hand, McLeod et al. (2021) find that in NGC 300 both Pdir and Pion mildly increase with radius, and link these trends to the negative metallicity gradient and positive extinction gradient observed in the galaxy.
We suggest that this could be due either to the overall lower metallicity of NGC 300 with respect the metallicity measured in M 83 and the majority of the PHANGS-MUSE galaxies, or to the fact that the environmental conditions are not significantly changing across the NGC 300 disk.
In order to study the dependency on the environment, adopting an approach similar to Barnes et al. (2021), we compare the pressure of the H II regions with the pressure of their surrounding environment, namely the midplane pressure measured at different distance from the centre of the galaxy. We use the environmental pressure PDE derived by Sun et al. (2022) following the definition in Leroy et al. (2008) and Sun et al. (2020):
where Σgas = Σmol + Σatom is the total gas surface density, ρ⋆ the stellar mass volume density near the galaxy mid-plane, and σgas, z the vertical velocity dispersion of the gas. The values of PDE reported by Sun et al. (2022) were estimated within 500 pc wide radial bins across M 83, using PHANGS-ALMA CO (2 − 1) data (Leroy et al. 2021a,b), THINGS HI data (Walter et al. 2008), and S4G IRAC 3.6 μm data (Sheth et al. 2010). There, Σmol was derived from CO line intensity with a radially varying CO-to-H2 conversion factor (following Sun et al. 2020). A stellar mass surface density Σ⋆ was derived from 3.6 μm SB with a varying stellar mass-to-light ratio (following Leroy et al. 2021b), and then it was converted to ρ⋆ with an estimated stellar disk scale height from the disk radial scale length H⋆ = R⋆/7.3 (van der Kruit & Searle 1981; Sun et al. 2020). A fixed gas velocity dispersion of σgas, z = 10 km s−1 was adopted following Leroy et al. (2008). We remark that some of the assumptions that went into the calculation of PDE might not hold well in the circumnuclear star-forming regions (innermost radial bin), where the stellar disk scale height could get larger, whereas the CO-to-H2 conversion factor might be smaller than the adopted value.
In Fig. 15 we compare PDE with the internal pressure terms Pion and Pdir. We average all pressure terms in six radial bins of width 0.15 Re. The resulting median Pdir and Pion are shown as orange and blue filled circles, respectively, and their sum is shown as black open circles. The median PDE are shown as green stars. We observe that PDE increases dramatically towards the galactic centre, where both the gas and stellar surface densities are higher. Its increase is strongly connected with the increase in the H II region internal pressure terms. As a consequence, near the centre the total internal pressure is lower than the environmental pressure, that is, H II regions are underpressured, whereas in the rest of the disk the regions are overpressured, and are therefore expanding. This is in agreement with what reported by Barnes et al. (2021) from the PHANGS data. The authors conclude that – both in their lower and upper limit estimate – increases in environmental pressure are driving the change in pressure terms. Namely, ne increases by up to an order of magnitude (as indicated in the bottom panel of Fig. 8), whereas the change in metallicity has a smaller impact on Te.
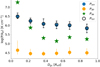 |
Fig. 15. Comparison between the H II region internal pressure terms (Pion and Pdir, in blue and orange, and their sum in black) and the environmental pressure (PDE, green stars). The pressure terms are binned in radial bins of width 0.15 Re. |
In the literature, the physical conditions of the ISM in the central region of spiral galaxies, such as the Milky Way or M 83, have often been compared to the star formation conditions of main-sequence galaxies at the peak of the cosmic star formation history (redshift ∼2, Kruijssen & Longmore 2013; Ginsburg et al. 2019; Callanan et al. 2021). In light of these similarities, our results suggest that pre-SN feedback drives the expansion of H II regions, and therefore plays a significant role in dissolving the parent GMC in galactic environments where the star formation conditions are representative of galaxies in the local universe (e.g. the galactic disk in M 83, see also Chevance et al. 2022). On the other hand, this might not be the case in galactic environments where the gas conditions probe extreme pressure and turbulence (e.g. Leroy et al. 2015a,b; Callanan et al. 2021), as is often seen in high-redshift clumpy disk galaxies (Dessauges-Zavadsky et al. 2019; Tacconi et al. 2020). In the circumnuclear starburst region of M 83, H II regions appear to be underpressured and therefore stable against expansion. A similar behaviour has also been observed in H II regions around massive star clusters in M 82 (Smith et al. 2006), where Pion/kB has measured values of ∼107 K cm−3.
Unlike Barnes et al. (2021), we have not attempted to estimate the pressure exerted by stellar winds, which do contribute to the total pressure exerted by pre-SN feedback in the early evolution stages of H II regions. However, winds are unlikely to be a dominant factor in the expansion of the H II regions (e.g. Dale et al. 2014). Overall, Barnes et al. (2021) find that Pwind is comparable to Pdir under the assumption of smooth H II regions, or comparable to the Pion term under the assumption of clumpy H II regions. If we extrapolate these considerations for the H II regions in the nuclear regions of M 83 – even in the extreme assumption of doubling the Pion term to account for the missing Pwind – we would get an average Ptot that would be (within uncertainties) still comparable to the midplane pressure. This suggests that pre-SN feedback might not be sufficient to drive the expansion and evolution of H II regions in galaxies (or regions of galaxies) with more extreme gas conditions, both in the local universe as well as in high-redshift, gas-rich and highly turbulent disk galaxies.
8.4. Ionisation budget
In the ionisation budget analysis in Sect. 7, we found that ionising radiation escaped from only ∼13% of the H II regions. The large majority of them appears instead to be ‘missing’ ionising photons. Dust can also mimic escape fraction, since it reprocesses LyC photons to emission at longer wavelengths. However, we do not see evidence that the H II regions with Q ratios higher than 1 have higher extinction in general. As a result, we conclude that the energy input by YSCs and WR stars alone is insufficient to explain the Hα emission, both within and outside the H II regions (in the DIG, see Paper I).
However, it is well known that very young star clusters are rarely isolated. As found in the analysis of star-forming regions in the Local Group (Gouliermis 2018, and references therein), these clusters always sit in stellar overdensities; young, massive stars form around gravitationally bound clusters. Thus, to fully determine if there is escape of LyC photons from the H II regions, we would also need to account for the contribution of the resolved stellar population surrounding the clusters. This is in apparent contrast with the results of Weilbacher et al. (2018), who compared the H II region emission and star cluster population in the Antennae galaxy merger. Weilbacher et al. (2018) found that ∼20% of the regions are leaking LyC photons, and that leakage from the H II regions was sufficient to explain the DIG observed in the system. However, most regions leaking LyC photons were found to populate the centre of the merger, indicating that environmental conditions are playing a role.
Finally, our analysis does not show any direct relation between star cluster mass and escape fraction of LyC (bottom panel in Fig. 14), although in the high mass range (mtot > 104 M⊙) between 30 and 50% of the regions hosting YSC leak ionising continuum radiation. The low number statistics do not allow us to draw any conclusion. A way forward to test whether regions forming higher mass clusters favour escape of ionising radiation is to extend this type of analysis to other local spirals with elevated SFR to ensure an increase in the number of massive star clusters sampled.
In the near future, the NIR and MIR wavelength that will be imaged by the James Webb Space Telescope (JWST) will allow us to trace emission reprocessed by dust (e.g. FEAST programme, PI Adamo, ID 1793; the public treasury programme ID 2107, PI Lee; among several others). We will be able to study the early phases of star formation and interaction with the parent GMC; account for the amount of LyC photons absorbed by dust, to improve cluster physical properties constraints in very young star clusters, as well as to account for the physical properties of very embedded H II regions that are found to have high nebular extinction (e.g. Messa et al. 2021). The large variety of galactic environments that will be probed by different programs will also enable us to study environmental dependencies and constraint the time scales and stellar feedback processes that are relevant for H II region evolution and GMC dissolution. These time scales are fundamental because they are the link between stellar feedback originating at parsec scale and galactic scale properties of the gas that will regulate the future generation of star formation.
9. Summary and conclusions
We present the analysis of ∼4700 H II regions observed with MUSE across the disk of M 83. We identify the H II regions based on their Hα emission. We then cross-match the initial catalogue with a sample of 148 PNe identified in the MUSE dataset (listed in Table B.1), to assess potential contaminant sources. We also match the H II regions with the SNR catalogue of Long et al. (2022), finding that 149 regions are evolved regions hosting a SNR.
We compare the emission of the H II regions with the stellar population they host. We spectroscopically identify in the MUSE data a total of 68 WR stars (listed in Table C.1). We furthermore complement our data with a sample of ∼7500 YSCs observed with HST (Silva-Villa et al. 2014; Adamo et al. 2015). In total, we had access to the star cluster and WR star population of ∼540 H II regions.
We study the overall properties of the regions, finding that regions hosting YSCs are on average larger and more luminous (Fig. 6), but that they otherwise have properties comparable to the rest of the sample. The average extinction peaks within the starburst region (at R ∼ 0.14 Re) and then decreases with radius (Fig. 8, top panel). A similar trend also exists in in oxygen abundance, and we obtain a gradient in very good agreement with that determined by Bresolin et al. (2016, Fig. 8, middle panel). Consequently, we find that the hardness of the radiation field increases with radius (Fig. 9). Also the electron density decreases with radius, and is ≃2 dex higher in the central starburst region (R ≤ 0.15 Re) than in the rest of the disk (Fig. 8, bottom panel). Finally, the location of the H II regions in a ‘BPT’ emission line diagram confirms that they are compatible with pure photoionisation (Fig. 10).
We investigate the impact of two feedback mechanisms on the regions: the pressure exerted by the ionised gas (Pion) and directly from the radiation (Pdir). Overall, Pion dominates over Pdir (Fig. 11), in agreement with observations in the literature. Both internal pressure terms are enhanced in the nuclear region of the galaxy. The relative increase in Pdir is the strongest (≃2 dex). Outside the central region, Pdir stays approximately constant with radius: we interpret this as a combination of two factors: (1) a decrease in dust content (lowering the pressure) and (2) an increase in radiation field hardness (enhancing it), as shown in Fig. 12. On the other hand, Pion decreases with radius. In this case, we explain the trend with a decrease in dust content (pointing to more evolved and hence less compact regions), and with the impact of the galactic environment. We investigate this further in Fig. 15, by comparing the internal pressure to the environmental pressure PDE (Sun et al. 2022). We find that regions in the galactic disk are over pressured and therefore expanding. On the other hand, for regions near the central starburst PDE is almost one order of magnitude higher than the internal pressure, pointing to the fact that in extreme gas conditions pre-SN feedback is not sufficient to drive H II region expansion.
We constrain the age, mass and ionising photon flux of the YSCs based on their photometry, using a Bayesian fitting analysis and stochastically populated cluster models. We observe that YSCs populating the H II regions are on average younger (median age of 4.7 vs. 8.2 Myr), more massive (median mass of 1.7 vs. 1.4 × 103 M⊙), and emit an order of magnitude more ionising photons (median log Q(H0) of 48.5 vs. 47.4 s−1) than field clusters. We then investigate how the pressure terms are impacted by the stellar population powering the regions. We find that regions hosting younger clusters have higher internal pressure, peaking at tmin, YSC ≃ 1 Myr (Fig. 13).
Whereas Pion flattens after 2 Myr, the decreasing trend in Pdir continues up to 10 Myr, suggesting that the coupling between the pressure terms and the H II regions grows steadily weaker with age. Regions hosting a higher mass in young clusters (t ≤ 10 Myr) have a higher internal pressure, with a more pronounced trend for Pdir. These trends have never been observed before, and seem to suggest that young, clustered star formation has a stronger impact on the H II regions than distributed star formation, in agreement with the results of numerical simulations. This seems to hold despite the fact that the fraction of stars formed in compact, gravitationally-bound clusters in M 83 is low (< 30%, Adamo et al. 2015).
Finally, we have computed a photoionisation budget for the regions for which we have access to the stellar population (limiting our analysis to the YSCs and WR stars). We compare the modelled flux to the observed Hα emission to compute an escape fraction. Overall, we detect escaping radiation in only ∼13% of the regions. The majority of these regions host clusters younger than 2 Myr. The fesc does not seem to positively correlate either with the duration of star formation in the regions, or with the total mass in young clusters (Fig. 14). We conclude that the energy input of YSCs and WR stars by itself is not sufficient to explain the observed Hα emission, both within the regions and in the DIG. Further analysis, including the assessment of the resolved stellar population surrounding each cluster, is needed to complete the physical picture.
Publicly available at https://archive.stsci.edu/prepds/m83mos/
With the exception of the ionisation budget analysis in Sect. 7, where we sample the PDFs of all the clusters in a region, in order to not exclude YSCs with a biased median estimate. Clusters which effectively have an age t > 10 Myr will not contribute significantly to the total budget.
Acknowledgments
We thank the anonymous referee for suggestions and comments that have improved the manuscript. A. A. acknowledges support of the Swedish Research Council, Vetenskapsrådet (2016-05199), and the Swedish National Space Agency (SNSA, Dnr140). The work of J. S. is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship, and by the National Science Foundation (NSF) under Grants No. 1615105, 1615109, and 1653300. This work is based on observations collected at the European Southern Observatory under ESO programmes 096.B-0057(A), 0101.B-0727(A), 097.B-0899(B), 097.B-0640(A). This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
References
- Adamo, A., Kruijssen, J. M. D., Bastian, N., Silva-Villa, E., & Ryon, J. 2015, MNRAS, 452, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Ryon, J. E., Messa, M., et al. 2017, ApJ, 841, 131 [Google Scholar]
- Adamo, A., Hollyhead, K., Messa, M., et al. 2020, MNRAS, 499, 3267 [Google Scholar]
- Ali, A. A. 2021, MNRAS, 501, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Ali, A. A., Bending, T. J. R., & Dobbs, C. L. 2022, MNRAS, 510, 5592 [NASA ADS] [CrossRef] [Google Scholar]
- Araújo de Souza, A., Martins, L. P., Rodríguez-Ardila, A., & Fraga, L. 2018, AJ, 155, 234 [CrossRef] [Google Scholar]
- Ashworth, G., Fumagalli, M., Adamo, A., & Krumholz, M. R. 2018, MNRAS, 480, 3091 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Azimlu, M., Marciniak, R., & Barmby, P. 2011, AJ, 142, 139 [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Proc. SPIE, 7735, 773508 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Barnes, A. T., Glover, S. C. O., Kreckel, K., et al. 2021, MNRAS, 508, 5362 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, A. T., Chandar, R., Kreckel, K., et al. 2022, A&A, 662, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastian, N., Gieles, M., Efremov, Y. N., & Lamers, H. J. G. L. M. 2005, A&A, 443, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belfiore, F., Santoro, F., Groves, B., et al. 2022, A&A, 659, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bending, T. J. R., Dobbs, C. L., & Bate, M. R. 2020, MNRAS, 495, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Bending, T. J. R., Dobbs, C. L., & Bate, M. R. 2022, MNRAS, 513, 2088 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blair, W. P., Chandar, R., Dopita, M. A., et al. 2014, ApJ, 788, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kudritzki, R.-P., Urbaneja, M. A., et al. 2016, ApJ, 830, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Callanan, D., Longmore, S. N., Kruijssen, J. M. D., et al. 2021, MNRAS, 505, 4310 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Krumholz, M. R., et al. 2022, MNRAS, 509, 272 [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [Google Scholar]
- Colombo, D., Rosolowsky, E., Ginsburg, A., Duarte-Cabral, A., & Hughes, A. 2015, MNRAS, 454, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, R. L., Fumagalli, M., & Krumholz, M. 2012, ApJ, 745, 145 [CrossRef] [Google Scholar]
- Dale, J. E. 2015, New Astron. Rev., 68, 1 [CrossRef] [Google Scholar]
- Dale, J. E., Ngoumou, J., Ercolano, B., & Bonnell, I. A. 2014, MNRAS, 442, 694 [Google Scholar]
- Della Bruna, L., Adamo, A., Bik, A., et al. 2020, A&A, 635, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Bruna, L., Adamo, A., Lee, J. C., et al. 2021, A&A, 650, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Bruna, L., Adamo, A., Amram, P., et al. 2022, A&A, 660, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [CrossRef] [Google Scholar]
- Dessauges-Zavadsky, M., Richard, J., Combes, F., et al. 2019, Nat. Astron., 3, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Drissen, L., Martin, T., Rousseau-Nepton, L., et al. 2019, MNRAS, 485, 3930 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., Dale, J. E., Gritschneder, M., & Westmoquette, M. 2012, MNRAS, 420, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Fielding, D., Quataert, E., & Martizzi, D. 2018, MNRAS, 481, 3325 [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Frew, D. J., & Parker, Q. A. 2010, PASA, 27, 129 [CrossRef] [Google Scholar]
- Gatto, A., Walch, S., Naab, T., et al. 2017, MNRAS, 466, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Gentry, E. S., Krumholz, M. R., Dekel, A., & Madau, P. 2017, MNRAS, 465, 2471 [NASA ADS] [CrossRef] [Google Scholar]
- Ginsburg, A., Mills, E. A. C., Battersby, C. D., Longmore, S. N., & Kruijssen, J. M. D. 2019, BAAS, 51, 220 [NASA ADS] [Google Scholar]
- Gouliermis, D. A. 2018, PASP, 130, 072001 [NASA ADS] [CrossRef] [Google Scholar]
- Grasha, K., Calzetti, D., Adamo, A., et al. 2019, MNRAS, 483, 4707 [NASA ADS] [CrossRef] [Google Scholar]
- Grudić, M. Y., Guszejnov, D., Hopkins, P. F., Offner, S. S. R., & Faucher-Giguère, C.-A. 2021, MNRAS, 506, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Grudić, M. Y., Guszejnov, D., Offner, S. S. R., et al. 2022, MNRAS, 512, 216 [CrossRef] [Google Scholar]
- Gutiérrez, L., Beckman, J. E., & Buenrostro, V. 2011, AJ, 141, 113 [CrossRef] [Google Scholar]
- Hadfield, L. J., Crowther, P. A., Schild, H., & Schmutz, W. 2005, A&A, 439, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haffner, L. M., Dettmar, R. J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [CrossRef] [Google Scholar]
- Hannon, S., Lee, J. C., Whitmore, B. C., et al. 2019, MNRAS, 490, 4648 [NASA ADS] [CrossRef] [Google Scholar]
- Hannon, S., Lee, J. C., Whitmore, B. C., et al. 2022, MNRAS, 512, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Herrmann, K. A., & Ciardullo, R. 2009, ApJ, 703, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., Buat, V., & Inoue, A. K. 2003, A&A, 410, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollyhead, K., Bastian, N., Adamo, A., et al. 2015, MNRAS, 449, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Wetzel, A., Kereš, D., et al. 2018, MNRAS, 480, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Páramo, J., Boselli, A., Gavazzi, G., & Zaccardo, A. 2004, A&A, 421, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, A. K., Hirashita, H., & Kamaya, H. 2001, ApJ, 555, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, B. A., Rizzi, L., Tully, R. B., et al. 2009, AJ, 138, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreson, S. M. R., Krumholz, M. R., Fujimoto, Y., et al. 2021, MNRAS, 505, 3470 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Edgar, B. K., & Hodge, P. W. 1989, ApJ, 337, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., Sutherland, R., et al. 2019a, ApJ, 880, 16 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., & Sutherland, R. S. 2019b, ARA&A, 57, 511 [Google Scholar]
- Kim, C.-G., Ostriker, E. C., & Raileanu, R. 2017, ApJ, 834, 25 [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2018, ApJ, 859, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Ostriker, E. C., & Filippova, N. 2021, ApJ, 911, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Kniazev, A. Y., Pustilnik, S. A., & Zucker, D. B. 2008, MNRAS, 384, 1045 [Google Scholar]
- Kreckel, K., Groves, B., Bigiel, F., et al. 2017, ApJ, 834, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2020, MNRAS, 499, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2013, MNRAS, 435, 2598 [Google Scholar]
- Krumholz, M. R., Bate, M. R., Arce, H. G., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 243 [Google Scholar]
- Krumholz, M. R., Fumagalli, M., da Silva, R. L., Rendahl, T., & Parra, J. 2015a, MNRAS, 452, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Adamo, A., Fumagalli, M., et al. 2015b, ApJ, 812, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Bolatto, A. D., Ostriker, E. C., et al. 2015a, ApJ, 801, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Martini, P., et al. 2015b, ApJ, 814, 83 [Google Scholar]
- Leroy, A. K., Hughes, A., Liu, D., et al. 2021a, ApJS, 255, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021b, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Blair, W. P., Winkler, P. F., et al. 2022, ApJ, 929, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., Prochaska, J. X., & Ramirez-Ruiz, E. 2011, ApJ, 731, 91 [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., et al. 2014, ApJ, 795, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lundgren, A. A., Wiklind, T., Olofsson, H., & Rydbeck, G. 2004, A&A, 413, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, X., Quataert, E., Wetzel, A., et al. 2020, MNRAS, 498, 2001 [Google Scholar]
- Magrini, L., Leisy, P., Corradi, R. L. M., et al. 2005, A&A, 443, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathewson, D. S., & Clarke, J. N. 1973, ApJ, 180, 725 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Weilbacher, P. M., Ginsburg, A., et al. 2016, MNRAS, 455, 4057 [CrossRef] [Google Scholar]
- McLeod, A. F., Dale, J. E., Evans, C. J., et al. 2019, MNRAS, 486, 5263 [Google Scholar]
- McLeod, A. F., Kruijssen, J. M. D., Weisz, D. R., et al. 2020, ApJ, 891, 25 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Ali, A. A., Chevance, M., et al. 2021, MNRAS, 508, 5425 [NASA ADS] [CrossRef] [Google Scholar]
- Messa, M., Calzetti, D., Adamo, A., et al. 2021, ApJ, 909, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Olivier, G. M., Lopez, L. A., Rosen, A. L., et al. 2021, ApJ, 908, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito: University Science Books) [Google Scholar]
- Rousseau-Nepton, L., Robert, C., Martin, R. P., Drissen, L., & Martin, T. 2018, MNRAS, 477, 4152 [NASA ADS] [Google Scholar]
- Rousseau-Nepton, L., Martin, R. P., Robert, C., et al. 2019, MNRAS, 489, 5530 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Santoro, F., Kreckel, K., Belfiore, F., et al. 2022, A&A, 658, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [Google Scholar]
- Silva-Villa, E., Adamo, A., Bastian, N., Fouesneau, M., & Zackrisson, E. 2014, MNRAS, 440, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Sivan, J. P., Petit, H., Comte, G., & Maucherat, A. J. 1990, A&A, 237, 23 [Google Scholar]
- Smith, L. J., Norris, R. P. F., & Crowther, P. A. 2002, MNRAS, 337, 1309 [CrossRef] [Google Scholar]
- Smith, L. J., Westmoquette, M. S., Gallagher, J. S., et al. 2006, MNRAS, 370, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, J., Leroy, A. K., Ostriker, E. C., et al. 2020, ApJ, 892, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, J., Leroy, A. K., Rosolowsky, E., et al. 2022, AJ, 164, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Smith, A., Kannan, R., et al. 2022, MNRAS, 513, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1981, AJ, 86, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1981, A&A, 95, 105 [NASA ADS] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [Google Scholar]
- Weilbacher, P. M., Monreal-Ibero, A., Verhamme, A., et al. 2018, A&A, 611, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitmore, B. C., Chandar, R., Kim, H., et al. 2011, ApJ, 729, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ye, T. 1992, MNRAS, 255, 32 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: H II region selection
In this appendix we expand on the H II region selection procedure described in Sect. 3.1. In particular, we show the impact of the fnoise parameter (see Eq. 1) on the boundaries, luminosity and size of the recovered regions. In Fig. A.1 we show the emission peaks (black ‘+’) and region boundaries (thin black lines) identified with three different values of fnoise. By visual inspection, we find that a value of fnoise = 1 (left panel) delivers an optimal division of the regions, as it detects all relevant peaks of emission within the adopted SB limit (thick black contour in Fig. A.1). We find that values of fnoise < 1 do not change the number and distribution of peaks within the SB contours, but only lead to the detection of additional fainter peaks. A progressive increase of fnoise (central and right panel in Fig. A.1), on the other hand, results in the missed detection of relevant emission peaks and therefore in unrealistic region boundaries.
 |
Fig. A.1. Emission peaks (black ‘+’) and boundaries (thin black lines) of regions identified in a large H II complex with three different values of the fnoise parameter (Eq. 1). The thick black contours indicate the SB threshold adopted for the H II regions (see Sect. 3.1). |
Fig. A.2 illustrates the luminosity function (left panel) and size distribution (right panel) of the three resulting samples of H II regions (across the full disk). In the luminosity function, we observe that the distributions match for L(Hα) > 5 × 1037, but that with increasing fnoise the histogram cuts off at a progressively higher threshold. The size distributions, on the other hand, match well at all radii.
 |
Fig. A.2. Luminosity function (left panel) and size distribution (right panel) for the samples of H II regions obtained with three different values of the fnoise parameter (Eq. 1). The grey dashed lines indicate, respectively, the adopted adopted H II SB threshold and the spatial resolution limit of the MUSE data. |
Appendix B: PNe sample
In this appendix we provide some complementary information related to the PNe detection and confirmation. As discussed in Sect. 3.3, we use two different methods to detect PNe candidates. In the first method, we use the [O III]/Hα map extracted from the MUSE mosaic. In the second method, we complement the purely spectroscopic-based selection by visually inspecting HST images. The second method enables us to detect PNe candidates that would otherwise be missed in our initial selection. We use the position of these targets to extract their spectra and verify whether their line ratios would confirm their nature or not. We find an additional 28 PNe that are spectroscopically confirmed and are therefore included in the confirmed sample. The remaining targets are retained as candidate PNe. Unfortunately the comparatively low spatial resolution of the MUSE data does not allow us to fully confirm the nature of the latter systems.
We show an example of the search technique applied to a small 6″ region of M83 in Fig. B.2. The positions of all spectroscopically confirmed and candidate PNe are shown in Fig. B.1. Their coordinates and detection class are listed in Table B.1.
 |
Fig. B.1. Location of the identified PNe on a map of [O III]/Hα. The coordinates of all objects are given in Table B.1. Blue and red circles indicate spectroscopically confirmed candidates (Class 1 and 2 in Table B.1) with and without He IIλ4686 detection, respectively. The orange squares indicate candidates visually identified in the HST+MUSE dataset (Class 3 in Table B.1). In purple we indicate the outer boundaries of the H II regions. |
 |
Fig. B.2. Example of the visual inspection technique applied to a small 6″ region of M83. The small magenta circle (0.6″ diameter) shows a confirmed PN candidate, which appears as a point-like source of [O III] emission in the HST data. The yellow square shows an object that looks very similar in the MUSE data but is clearly extended in the HST data, thus disqualifying it from further consideration. Likewise, the cyan square shows an object with [O III] emission, which however aligns with a stellar source in V band. This demonstrates the power of using MUSE and WFC3 together to identify candidate PN at the distance of M83. |
Coordinates of the PNe identified in the MUSE+HST dataset. In the third column we report a classification score, indicating whether the PNe is spectroscopically confirmed (class 1, additional He IIλ4686 detection, and 2), or whether it remains a candidate PNe (class 3, visually identified). In the last column we cross reference our sample with PN catalogued by Herrmann & Ciardullo (2009).
Appendix C: WR sample
 |
Fig. C.1. Location of the identified WR on a map of He IIλ4686. The source that appears out of the MUSE FoV was observed in the non-extended wavelength mode. It was extracted as part of the Hadfield et al. (2005) catalogue and, despite the lack of He IIλ4686 emission, featured emission lines characteristic of a WR. |
Coordinates of the confirmed WR candidates and cross-match with the catalogue of Hadfield et al. (2005).
All Tables
Coordinates of the PNe identified in the MUSE+HST dataset. In the third column we report a classification score, indicating whether the PNe is spectroscopically confirmed (class 1, additional He IIλ4686 detection, and 2), or whether it remains a candidate PNe (class 3, visually identified). In the last column we cross reference our sample with PN catalogued by Herrmann & Ciardullo (2009).
Coordinates of the confirmed WR candidates and cross-match with the catalogue of Hadfield et al. (2005).
All Figures
 |
Fig. 1. Map of Hα emission (extinction corrected) with the boundaries of the identified H II regions. Bottom panel: enlargement of one of the star-forming complexes. |
| In the text | |
 |
Fig. 2. Location of spectroscopically confirmed PNe (filled red points), PNe candidates (filled orange points) and H II regions (open blue circles) in a diagram of [O III] λλ4959,5007/Hβ versus [S II] λλ6716,6731/[O III] λλ4959,5007. We applied a first order background correction to the PN fluxes as described in Sect. 3.3. We observe that the confirmed PNe occupy a well-defined region in the diagram. |
| In the text | |
 |
Fig. 3. Age and mass of the YSCs as function of galactocentric radius. The black dots indicate the median (±quartiles) over radial bins with equal number of objects (≃20). |
| In the text | |
 |
Fig. 4. Combined posterior probability distributions of age, mass and ionising photon flux obtained with SLUG for young clusters (t ≤ 10 Myr) populating H II regions (in blue) and located outside the H II regions (‘field’ clusters, in orange). The vertical lines and shaded areas indicate the median and quartiles of each distribution. |
| In the text | |
 |
Fig. 5. Stellar population in the MUSE FoV. Top panel: extinction-corrected Hα map with the location of YSCs of age ≤10 Myr (green triangles). Bottom panel: enlargement of one of the H II region complexes. Green triangles indicate the position of YSCs observed with HST (Adamo et al. 2015), blue crosses and red stars indicate respectively WR stars and PNe identified in the MUSE dataset and orange squares are SNR from Long et al. (2022). |
| In the text | |
 |
Fig. 6. Luminosity function (top) and size distribution (bottom) of the final sample of H II regions. In blue we show the total distribution, and in green the distribution for regions hosting either a YSC younger than 10 Myr or a WR star. The vertical lines and shaded areas indicate the median and quartiles of each distribution. The grey dashed lines in the top panel indicate the minimum luminosity of a region of radius 10 and 50 pc based on the SB threshold used for the H II region selection. Bottom panel: the grey dashed line corresponds to the spatial resolution limit of the MUSE data (regions below this line are unresolved in our dataset). |
| In the text | |
 |
Fig. 7. Luminosity (top panel) and size (bottom panel) of the final sample of H II regions as function of galactocentric radius. Green stars indicate regions hosting either a YSC younger than 10 Myr or a WR star. The large black dots indicate the median (±quartiles) in radial bins with equal number of objects (≃120). The dashed line in the bottom plot indicates the spatial resolution limit of the MUSE data. |
| In the text | |
 |
Fig. 8. Same as Fig. 7 but showing the extinction (top), oxygen abundance (centre) and density (bottom panel) of the H II regions. Central panel: a linear fit to the data (in black) with a 95% confidence interval (shaded grey area). We also indicate the best fit parameters in the upper right corner. Bottom panel: the grey dashed line in the bottom panel indicates the sensitivity limit of the density determination method: points below this lines are consistent – within measurement uncertainty – with ne ≃ 1 cm−3. Error bars span the first to third quartile of a distribution of ne obtained from 1000 Monte Carlo realisations of the [S II] ratio (see Sect. 5). |
| In the text | |
 |
Fig. 9. Ratio of [S III] λ9069/[S II] λλ6716,31 (reddening corrected) of each H II region as function of galactocentric radius. This ratio is a tracer of the hardness of the radiation field within the H II regions. |
| In the text | |
 |
Fig. 10. Location of the final sample of H II regions in BPT emission line diagrams. Green stars indicate the subset of regions hosting either a YSC younger than 10 Myr or a WR star. Red triangles indicate evolved regions hosting a SNR. The black dashed line indicate the ‘extreme starburst line’ from Kewley et al. (2001), denoting the upper limit for gas purely excited by star-formation. |
| In the text | |
 |
Fig. 11. Ionised gas pressure (in blue), direct radiation pressure (in orange) and their ratio (in green, values indicated on the right axis) as function of galactocentric radius. Red and dark blue triangles indicate evolved H II regions (hosting a SNR). The black dots indicate the median (±first and third quartile) pressure in radial bins containing an equal number of points (∼120). On top of the figure, we indicate the coefficients of a linear fit to the data. |
| In the text | |
 |
Fig. 12. Pressure terms as function of average reddening (top panels) and radiation field hardness (bottom panels) in the regions. Red and blue triangles indicate evolved H II regions (hosting a SNR). The black dots indicate the median (±quartiles) pressure in radial bins containing an equal number of points. On the top right, we indicate the value of the Pearson’s correlation coefficient r. |
| In the text | |
 |
Fig. 13. Pressure terms as function of the age of the youngest cluster in the region (top) and the total mass of clusters younger than 10 Myr (bottom). Red and blue triangles indicate evolved regions hosting a SNR. The black dots and line indicate the median (±quartiles, shaded in grey) in radial bins of 1 Myr (top) and in mass bins with equal number of objects (bottom, ≃40 objects/bin). On the top right, we indicate the value of the Pearson’s correlation coefficient r. |
| In the text | |
 |
Fig. 14. Ratio of expected to observed Q(H0) for all the H II regions hosting YSCs or WR stars. The black dashed line indicates a ratio of 1 (fesc = 0). Top panel: Q ratio as function of the age of the youngest cluster (tmin) hosted in each region, colour coded by the region’s average extinction. Bottom panel: Q ratio as function of the total mass in clusters younger than 10 Myr, colour coded by galactocentric distance. |
| In the text | |
 |
Fig. 15. Comparison between the H II region internal pressure terms (Pion and Pdir, in blue and orange, and their sum in black) and the environmental pressure (PDE, green stars). The pressure terms are binned in radial bins of width 0.15 Re. |
| In the text | |
 |
Fig. A.1. Emission peaks (black ‘+’) and boundaries (thin black lines) of regions identified in a large H II complex with three different values of the fnoise parameter (Eq. 1). The thick black contours indicate the SB threshold adopted for the H II regions (see Sect. 3.1). |
| In the text | |
 |
Fig. A.2. Luminosity function (left panel) and size distribution (right panel) for the samples of H II regions obtained with three different values of the fnoise parameter (Eq. 1). The grey dashed lines indicate, respectively, the adopted adopted H II SB threshold and the spatial resolution limit of the MUSE data. |
| In the text | |
 |
Fig. B.1. Location of the identified PNe on a map of [O III]/Hα. The coordinates of all objects are given in Table B.1. Blue and red circles indicate spectroscopically confirmed candidates (Class 1 and 2 in Table B.1) with and without He IIλ4686 detection, respectively. The orange squares indicate candidates visually identified in the HST+MUSE dataset (Class 3 in Table B.1). In purple we indicate the outer boundaries of the H II regions. |
| In the text | |
 |
Fig. B.2. Example of the visual inspection technique applied to a small 6″ region of M83. The small magenta circle (0.6″ diameter) shows a confirmed PN candidate, which appears as a point-like source of [O III] emission in the HST data. The yellow square shows an object that looks very similar in the MUSE data but is clearly extended in the HST data, thus disqualifying it from further consideration. Likewise, the cyan square shows an object with [O III] emission, which however aligns with a stellar source in V band. This demonstrates the power of using MUSE and WFC3 together to identify candidate PN at the distance of M83. |
| In the text | |
 |
Fig. C.1. Location of the identified WR on a map of He IIλ4686. The source that appears out of the MUSE FoV was observed in the non-extended wavelength mode. It was extracted as part of the Hadfield et al. (2005) catalogue and, despite the lack of He IIλ4686 emission, featured emission lines characteristic of a WR. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



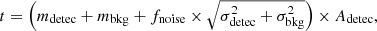
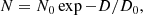
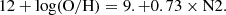
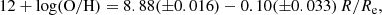
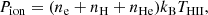
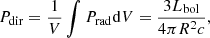
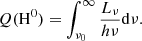
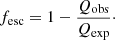
![$$ \begin{aligned} Q(\mathrm{H}^0)_{\rm obs}\;[\mathrm{s}^{-1}] = 7.31 \times 10^{11} L(\mathrm{H}\alpha ) \quad [\mathrm{erg\,s}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2022/10/aa43395-22/aa43395-22-eq11.gif)