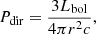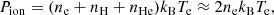| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348029 | |
| Published online | 06 May 2024 | |
Pre-supernova stellar feedback in nearby starburst dwarf galaxies
1
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
e-mail: lrowland@strw.leidenuniv.nl
2
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
3
Institute for Computational Cosmology, Department of Physics, University of Durham, South Road, Durham DH1 3LE, UK
4
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
5
Research School of Astronomy and Astrophysics, Australian National University, Cotter Rd, Weston, ACT 2611, Australia
6
ARC Centre of Excellence for Astronomy in Three Dimensions (ASTRO-3D), Canberra, ACT 2600, Australia
7
AURA for European Space Agency (ESA), ESA Office, Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
8
INAF – Padova Astronomical Observatory, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
9
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
10
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
Received:
19
September
2023
Accepted:
30
January
2024
Context. Stellar feedback in dwarf galaxies remains, to date, poorly explored, yet is crucial to understanding galaxy evolution in the early Universe. In particular, pre-supernova feedback has recently been found to play a significant role in regulating and disrupting star formation in larger spiral galaxies, but it remains uncertain if it also plays this role in dwarfs.
Aims. We study the ionised gas properties and stellar content of individual star-forming regions across three nearby, low-metallicity (12 + log(O/H)∼7.5), dwarf (M* ∼ 40 × 106 M⊙), starburst (log(SFR)∼ − 2.8) galaxies (J0921, KKH046, and Leo P) to investigate how massive stars influence their surroundings and how this influence changes as a function of environment.
Methods. We extracted integrated spectra of 30 HII regions from archival VLT/MUSE integral field spectroscopic observations of these three dwarf starburst galaxies. We fitted the HII regions’ main emission lines with Gaussian profiles to derive their oxygen abundances, electron densities, and luminosities, and we used the Stochastically Ligthing Up Galaxies (SLUG) code to derive the stellar mass, age, and bolometric luminosity of the stellar populations driving the HII regions. We quantified two pre-supernova stellar feedback mechanisms, namely the direct radiation pressure and photoionisation feedback, and explored how feedback strength varies with HII region properties.
Results. Our findings suggest that stellar feedback has less of an impact on evolved regions, with both the pressure of the ionised gas and the direct radiation pressure decreasing as a function of HII region size (i.e. the evolutionary stage). We find that these stellar feedback mechanisms are also dependent on the metallicity of the HII regions. These findings extend results from stellar feedback studies of more massive star-forming galaxies to the low-mass, low-metallicity regime. In addition, we conclude that the use of stochastic stellar population models significantly affects the relationships found between feedback-related pressure terms and HII region properties, and in particular that non-stochastic models can severely underestimate the bolometric luminosity of low-mass stellar populations.
Key words: HII regions / galaxies: dwarf / galaxies: star formation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The effect that stars have on their surroundings is a multi-scale and multi-physics process known as stellar feedback. Massive stars (≳8 M⊙) are, by far, the dominant sources of stellar feedback (e.g. Abbott 1982), emitting vast quantities of ionising photons into the interstellar medium (ISM), imparting momentum via radiation pressure and ultimately ending their lives in supernova (SN) explosions (Krumholz et al. 2014). Radiative and mechanical feedback mechanisms from massive stars have been shown to drive the expansion of HII regions (e.g. Lopez et al. 2011, 2014; McLeod et al. 2019, 2020, 2021; Olivier et al. 2021), enrich the ISM (e.g. Maiolino & Mannucci 2019), regulate and disrupt star formation (e.g. Ostriker et al. 2010; Chevance et al. 2020), and even govern the dark matter distribution within dwarf galaxies (e.g. Mashchenko et al. 2006; Pontzen & Governato 2014). Stellar feedback physics is therefore a central topic in galaxy formation and evolution, and understanding it is a critical step towards creating realistic simulations from the scales of individual star-forming regions and giant molecular clouds (GMCs) up to the scales of entire galaxies (e.g. Kim et al. 2018; Dale et al. 2014; Hopkins et al. 2018).
Recently, focus has shifted from the effects of SNe, which are generally thought to be the dominant stellar feedback mechanism in shaping galaxies on large scales, to so-called pre-SN mechanisms. These mechanisms have been shown to play a significant role in the regulation of star formation prior to the first SN events (Lucas et al. 2020; McLeod et al. 2021; Chevance et al. 2022). Whilst significant progress has been made in recent years in the incorporation of these stellar feedback mechanisms into simulations (e.g. FIRE, Hopkins et al. 2023), we currently lack a detailed understanding of their dependence on the physical properties of the ISM. This is particularly the case for dwarf galaxies, which are largely absent from recent large extragalactic surveys (e.g. SAMI, Bryant et al. 2015; CALIFA, Sánchez et al. 2012; PHANGS, Emsellem et al. 2022; Barnes et al. 2021).
Dwarf galaxies are interesting targets for feedback studies for a number of reasons. Firstly, they are the most abundant type of galaxy in the Universe (e.g. Phillipps et al. 1998), and yet their formation and evolution is still not completely understood (Tolstoy et al. 2009). Secondly, at the low-mass regime of dwarfs, it is well known that the effects of feedback processes are more dramatic due to galaxies’ shallow gravitational potentials (e.g. Hopkins et al. 2014). Finally, based on the mass-metallicity relation (e.g. Lequeux et al. 1979), we can also expect the HII regions within a sample of low-mass galaxies to be metal-poor, providing a comparison sample to the more metal-rich HII regions in recent works (e.g. Barnes et al. 2021; Della Bruna et al. 2022) and allowing us to extend the study of stellar feedback effects across a wider range of environments. This makes nearby dwarf galaxies critical laboratories for providing observational constraints necessary for more realistic simulations.
In the past decade or so, observational studies of stellar feedback have been made increasingly more detailed by the development of integral field unit (IFU) spectroscopy. IFU instruments are ideal to study the gaseous and stellar components of resolved star-forming regions, allowing us to derive the properties and kinematics of the feedback-affected ionised gas, to derive the properties of the feedback-driving stellar populations, and to quantify the feedback mechanisms themselves. This use of IFU spectroscopy has been demonstrated in recent works, including Lopez et al. (2014), McLeod et al. (2021), Barnes et al. (2021), and Della Bruna et al. (2022). This ever-increasing number of spatially resolved studies of star-forming regions within our own Galaxy and in nearby star-forming galaxies has created a vast database of HII regions, which in this paper we extend to low-mass, low-metallicity host galaxies.
Consequently, in this work we aim to investigate a sample of nearby, low-metallicity dwarf starburst galaxies observed with the Multi Unit Spectroscopic Explorer (MUSE, Bacon et al. 2010) IFU instrument mounted on the Very Large Telescope (VLT). We then make comparisons to similar studies in more massive systems, for example, the sample of more massive galaxies from the Physics at High Angular resolutions in Nearby GalaxieS (PHANGS) MUSE survey (Emsellem et al. 2022 and the corresponding stellar feedback studies of Barnes et al. 2021, 2022), in order to contribute to the ongoing investigation of the environmental dependence of stellar feedback.
This paper is organised as follows. We give a brief overview of our selection of dwarf galaxies and of the VLT/MUSE observations in Sect. 2, followed by Sect. 3 where we describe the techniques used to select, classify, and extract the integrated spectra from our sample of 30 HII regions. In Sect. 4, we describe the methods used to derive the ionised gas properties of these regions. In Sect. 5, we discuss the stellar population synthesis modelling, and how we used these libraries of simulations to derive star cluster properties within our regions. We then explain how we derived two pre-SN stellar feedback mechanisms in Sect. 6, and discuss our findings and compare them to those of other works in Sect. 7 in order to quantify these mechanisms as a function of environmental properties. Finally, in Sect. 8 we give a summary of our work and conclusions.
2. Observations and target selection
The dwarf galaxies analysed in this paper were selected from the DWarf galaxies Archival Local survey for Ism iNvestigation (DWALIN, Marasco et al. 2023; Cresci et al., in prep.) galaxy sample. DWALIN consists of 40 nearby (median distance D ∼ 9.3 Mpc), low stellar mass (median M* ∼ 108 M⊙), highly star-forming (median specific star formation rate, sSFR ∼ 10−9.44 yr−1) galaxies with archival VLT/MUSE data. MUSE is an optical IFU, with a wavelength range of 4600−9350 Å and a 1′×1′ field-of-view in its extended wide field mode (WFM), a pixel scale of 0.2″ pixel−1, and a resolving power of ∼1770−3590. As described in Marasco et al. (2023), the data reduction for the DWALIN sample was carried out via the MUSE pipeline (Weilbacher et al. 2020), v2.8.1. Full details of the sample and data reduction will be given by Cresci et al. (in prep.).
From the DWALIN sample, we have selected three dwarf galaxies, namely AGC 193816 (also known as J0921+0721 and henceforth referred to as J0921), KKH046 and Leo P. These three galaxies show clearly visible ionised gas bubbles, which are the signatures of feedback and hence suitable for this study. Observations were taken under programmes 096.B-0212 (PI: James), 0104.D-0199 (PI: Brinchmann), and 094.D-0346 (PI: Evans) for J0921, KKH046 and Leo P, respectively. In Figs. 1 and 2, we show three-colour composite images of these galaxies. The images in Fig. 1, which trace the stellar populations of these galaxies, are produced by dividing the wavelength range of MUSE intro three arbitrary colour ranges (blue = 4650−5800 Å, green = 5800−7000 Å, red = 7000−8200 Å) and integrating the cubes across these three ranges to produce and combine the images in each custom filter. We exclude the red channels at 8200−9350 Å and the blue edge channels at 4600−4650 Å, where there are some residual background effects, from our analysis. In Fig. 2, we combine three different emission line maps (red = [SII]λ6717, green = Hα, blue = [OIII]λ5007) to trace the ionised gas within these galaxies. These emission maps are obtained by integrating the MUSE cube over a 6 Å wide spectral window centred on the corresponding emission line. The Hα emission maps are also shown in Fig. 3. We selected these three galaxies from the DWALIN sample on the basis that they are observed with < 100 pc resolution, and the importance of this is apparent from the emission maps, which at this resolution show clearly distinct bubbles of ionised gas.
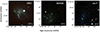 |
Fig. 1. Three-colour composite images of the three dwarf galaxies (left: J0921, centre: KKH046, right: Leo P) collapsed across three arbitrary wavelength ranges and coloured blue (4650−5800 Å), green (5800−7000 Å), and red (7000−8200 Å). |
 |
Fig. 2. Same as Fig. 1, except here red corresponds to [SII]λ6716, green to Hα, and blue to [OIII]λ5007 emission. |
 |
Fig. 3. Hα emission maps of J0921 (left), KKH046 (centre), and Leo P (right), with the dendrogram structures identified in this work as HII regions outlined in red. Each HII region is labelled by a number on its right or via a line. |
The gas-phase metallicities of these galaxies, as measured by their oxygen abundance (12 + log(O/H)), are given in Table 1, along with other key properties. We also give the spatial resolutions, Θ, of the VLT/MUSE observations used in this work as determined from the distance to each galaxy, D, and the reported seeing of the observations. We note that the seeing for the observations of KKH046 were considerably improved by the use of the VLT/MUSE Adaptive Optics (AO) system. As in Marasco et al. (2023), the distances for KKH046 and J0921 are taken from Kourkchi et al. (2020, where distances are determined using the local peculiar velocity model of Masters 2005) and for Leo P we use the value determined by McQuinn (2015) for reasons described therein.
Properties of the target dwarf galaxies in this paper.
3. Data analysis
3.1. HII region selection
As in McLeod et al. (2021), we use Hα emission line maps with the ASTRODENDRO1 Python package to trace the boundaries of HII regions within the target galaxies and extract their spatially integrated spectra. These emission maps are continuum corrected by subtracting a continuum map, obtained by integrating a small section of the continuum level either side of the Hα line with no other significant nebular emission or sky lines. The ASTRODENDRO package then takes these 2D emission maps and returns tree-like hierarchical structures called dendrograms, with areas of bright emission called “leaves”. These structures are strongly dependent on user-defined parameters, namely the minimum flux threshold necessary for a pixel to be added to a structure, Fmin, and the minimum number of pixels contained within an independent structure, Nmin.
As can be seen in Figs. 2 and 3, there are some clear bright clumps of ionised gas in each galaxy, along with fainter diffuse ionised gas (DIG) emission surrounding these clumps. This surrounding DIG can represent a significant fraction of the total Hα emission (Oey et al. 2007; Kumari et al. 2020). For example, in their recent analysis of MUSE data of M83, Della Bruna et al. (2021) find a DIG fraction of ∼27 − 42%. In comparison to HII regions, DIG is found to have a lower surface brightness, lower electron density (∼0.1 cm−3) and slightly lower ionisation states (e.g. Mannucci et al. 2021; Belfiore et al. 2022, and references therein). The origin of the DIG found in the ISM of galaxies is still not fully understood, though suggested explanations include the leakage of photons from HII regions (e.g. Weilbacher et al. 2018), ionisation by shocks (e.g. Dopita & Sutherland 1995), and ionisation by evolved, post AGB stars (e.g. Byler et al. 2019), or a combination of the above (Flores-Fajardo et al. 2011; Belfiore et al. 2022). The DIG can therefore show line ratios that differ significantly from those seen in HII regions, and contamination from DIG can substantially impact the physical properties derived from these line ratios for both HII regions, and for galaxies as a whole (Zhang et al. 2016). To limit this contamination, we therefore only consider regions with significant Hα emission and of reasonable physical size (exact thresholds described below).
For KKH046 and Leo P, we set the minimum number of pixels within a region (Nmin) to be comparable to the size of the seeing disc for the reported seeing of each observation, and we set the minimum flux threshold (Fmin) to twice the standard deviation of the Hα flux within each galaxy. These Fmin values correspond to emission measures of ∼120 pc cm−6, which are greater than the cutoff values used in McLeod et al. (2021) for NGC 300 (∼60 pc cm−6) and in Della Bruna et al. (2021) for NGC 7793 (∼82 pc cm−6). However, a test of lower thresholds for KKH046 produced large, irregularly shaped structures and multiple small leaves found to have negative electron densities, which could indicate potential contamination from DIG. We find that the criteria stated above produce regions of reasonable size around each visibly distinguishable ionised gas bubble within KKH046 and Leo P, that is, greater than the spatial resolution of the observations and comparable to similar studies of extragalactic HII regions. For example, Barnes et al. (2021) find a range in HII region radii of 16.6−388.2 pc in PHANGS-MUSE galaxies, which is comparable to the sizes obtained for HII regions in this study (22−270 pc).
The emission maps of J0921 reveal a more complex structure of multiple scattered HII regions that are less well defined by eye, likely due to it being the most distant galaxy selected. For an initial estimate of the number of regions within this galaxy, we consider the analysis of J0921 carried out by James et al. (2020, hereafter J20), who found 30 HII regions with the same MUSE data. A discussion of this paper with a comparison to some of our results is given in Appendix A. With an input of Fmin of three standard deviations above the median Hα flux, or 6.90 × 10−18 erg s−1 cm−2, and an Nmin of 6 pixels, we find 25 HII regions, comparable to those found by J20. This flux threshold corresponds to an emission measure of 82 cm pc−6, that is, comparable to values used in McLeod et al. (2021) and Della Bruna et al. (2021) for NGC 300 and NGC 7793, respectively. However, as we progressed through our analysis, we found that four of these J0921 regions seemingly had unphysical, negative electron densities. This could be for a number of reasons, including contamination from DIG. For two of these regions, numbered 6 and 20 in Fig. 3, we found that the dendrogram regions were too large compared to their discernible size, and we therefore use smaller, by eye, circular apertures. We discard the other two regions from subsequent calculations, although further investigation into their sources of ionisation would be interesting for future study. This results in 23 HII regions for J0921, though we note that four regions are smaller than the spatial resolution of the observations, increasing the uncertainty in the properties we have derived.
To test our confidence in the sizes of the dendrogram leaves, we calculated the radius that encompasses 90% of the Hα flux (R90) of each visible clump; an example of this process is given Appendix B. The R90 of each clump are found to be comparable to the radius of our final dendrogram structures (measured by the geometric mean of the major and minor axes), which are listed in Col. 2 of Table 2. We note that we do not apply a PSF correction due to the lack of high resolution imaging available for all three galaxies, but the observations are seeing-limited and at the spatial resolution of J0921, these HII regions are more likely to be unresolved.
Properties of the 30 HII regions across the three dwarf galaxies in this sample.
In order to confirm our classification of these dendrogram leaves as HII regions, rather than supernova remnants (SNRs) or planetary nebulae (PNe), we investigate their location in Baldwin, Phillips and Terlevich (BPT) diagrams (Baldwin et al. 1981). These diagnostic plots were initially introduced to separate star-forming galaxies from objects excited by harder ionising sources (e.g. active galactic nuclei, AGNs), but are also useful to investigate the ionisation state and nature of individual regions of ionised gas within galaxies (e.g. Espinosa-Ponce et al. 2020; McLeod et al. 2021; Belfiore et al. 2022). SNRs typically show higher [NII]/Hα ratios, while PNe tend to show enhanced [OIII]/Hβ ratios (e.g. Baldwin et al. 1981). We do not find evidence of these enhanced ratios, and all our regions are found to lie below the theoretical “starburst” lines from Kewley et al. (2001) and Kauffmann et al. (2003, Fig. 4), indicating that the dominant source of ionisation within these regions is photoionisation, as expected for HII regions.
 |
Fig. 4. Classical emission line diagnostic diagrams of the HII regions defined in this paper. Theoretical maximum starburst lines plotted by the solid and dashed black lines are taken from literature (Kewley et al. 2001; Kauffmann et al. 2003, respectively). Low-metallicity photoionisation models from CLOUDY are also plotted, coloured by ionisation parameter (log U). |
However, since the interpretation of these diagrams is dependent on a number of factors (see Kewley et al. 2019a) and due to the low metallicity of these systems, further investigation with photoionisation modelling is necessary to more confidently infer their ionisation states (Plat et al. 2019). We have made some comparisons to low-metallicity CLOUDY (Ferland et al. 2017) photoionisation models from the Mexican Million Models database (Morisset et al. 2015), shown by the small circular markers in Fig. 4 coloured in terms of their ionisation parameter, log U. We choose to plot only models with HII regions aged 6 Myr, since this is closest to the median age found for our clusters (see Sect. 5). We plot models for 12 + log(O/H) ranging from 7.0 to 8.0, although we note that the models in this database have a gap between 7.0 and 7.4, which is the metallicity range that covers Leo P. In general, however, we find that the flux ratios of the regions studied in this work appear to be compatible with low-metallicity photoionisation models, supporting their classification as HII regions.
Overall, our selection strategy produces 23 HII regions within J0921, six within KKH046, and one in Leo P, with sizes ranging from 22 to 270 pc. These HII regions are outlined by red contours and numbered in Fig. 3.
We note that when making comparisons between these three galaxies, and with HII regions in the literature, the change in the spatial resolution of the observations may introduce some bias to the interpretations. For example, the derived radii of HII regions in nearby targets, such as the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC), or within the Milky Way, are more likely to appear smaller than regions in more distant targets due to the ability to resolve finer detail. This study would therefore benefit from higher spatial resolution follow-up observations to reduce the uncertainty on the sizes of these regions and to reveal more details of their morphology, for example, as carried out with Hubble Space Telescope (HST) high-resolution observations in Barnes et al. (2022). We also introduce a bias by selecting only the brightest Hα emission regions, as we could be missing weak HII regions. These biases must be especially considered in Sect. 7, where we make comparisons to studies with smaller and more compact HII regions.
3.2. Emission line fitting
We next use the SpectralCube package (Ginsburg et al. 2019) to extract the spectra of the individual regions within the dendrogram leaf contours shown in Fig. 3. We continuum-correct the spectra by subtracting a linear baseline fit using the PYSPECKIT Python package (Ginsburg & Mirocha 2011). Figure 5 shows a portion of the MUSE spectrum for region 1 in KKH046, as an example. We note that the hashed rectangle in the spectrum indicates a gap in the spectral coverage due to the notch filter from the AO system used for the observations of KKH046. We fit the key nebular lines (e.g. Hα, Hβ, [OIII]λ5007,4959, [NII]λ6548,6584, and [SII]λ6716,6731) with Gaussians using PYSPECKIT, and we show an example fit to the [OIII] doublet and Hβ line in Fig. 5. To correct for attenuation, we assume an attenuation curve for the continuum of starburst galaxies empirically derived in Calzetti et al. (2000), and calculate the colour excess, E(B − V), from the Balmer decrement of each HII region assuming Case B recombination with an intrinsic ratio of 2.86 (Osterbrock & Ferland 2006). Calzetti et al. (1994) showed that HII regions are more heavily attenuated than the stellar continuum, and so we adopt their derived conversion factor of 2.27 between the stellar continuum attenuation curve and the nebular attenuation. The continuum-subtracted, attenuation-corrected fluxes are then used for all following calculations, with the uncertainties returned by PYSPECKIT propagated through. We also determine the visual extinction, AV, for each of our HII regions from the product of the colour excess and the total-to-selective attenuation, for which we adopt the value of 4.1 ± 0.8 derived by Calzetti et al. (2000) for nearby starbursts. We note that the results presented in this paper do not significantly change when a Milky Way extinction curve (Cardelli et al. 1989) or LMC extinction curve (Fitzpatrick 1999) are used.
 |
Fig. 5. Portion of the MUSE spectrum of HII region 1 in KKH046 which covers the key nebular emission lines studied in this paper, with the PYSPECKIT Gaussian fit plotted in red. The hashed region indicates the AO notch filter. In the overlaying panel outlined in blue, we show a closer look at the Hβ and [OIII]λ4959, 5007 doublet lines. |
4. Ionised gas properties
In this section, we focus on the methods used to derive the electron densities, luminosities, and oxygen abundances of the HII regions in our sample. These properties, along with the region size, extinction, and stellar content, are of particular interest for the purpose of studying feedback as a function of environment. We list some of the key ionised gas properties, the feedback-related pressure terms, and the stellar population properties derived in this work in Table 2, along with their estimated uncertainties. For a more in-depth discussion of our estimated uncertainties, see Appendix C.
4.1. Electron densities
We derive the electron density (ne) from the line ratio R[SII] = [SII]λ6716/[SII]λ6731 using the calibration of McCall (1984), given by
This assumes an electron temperature of 104 K, which is typical of nearby HII regions (e.g. Peimbert et al. 2017), including some studies of low-metallicity HII regions (e.g. James et al. 2020). As listed in Table 2, we find an electron density range of ∼5−260 cm−3. Kewley et al. (2019b) find that the use of R[SII] as an electron density diagnostic is most effective within the range ∼40−104 cm−3. For the HII regions with densities below this lower threshold, these values are likely to be more uncertain.
4.2. Luminosities
We derive the Hα luminosities, LHα, from the total integrated Hα flux of each HII region and assuming distances as given in Table 1. In order to derive the direct radiation pressure, Pdir (see Sect. 6.1), for each HII region, we are also interested in deriving a value for the bolometric luminosity, Lbol, of the stellar population within each region. Kennicutt & Evans (2012) defines a method of estimating the bolometric luminosity from the observed, extinction-corrected Hα luminosity, as
We note that Lbol, IMF refers to the assumption that the stellar population fully samples the initial mass function (IMF). This relationship also assumes a continuous star formation history over a range of 0−100 Myr. However, individual star-forming regions are unlikely to fully sample the IMF and stellar age distribution. Lopez et al. (2014) and references therein find that, for low-mass regions, Lbol, IMF is likely to be an underestimate of the true bolometric luminosity, whilst for particularly young regions (T ≲ 5 Myr), Lbol, IMF is likely to be an overestimate. In Fig. 6, we use the stellar population synthesis code, SLUG (see Sect. 5), to illustrate this using 100 synthesised stellar populations of varying stellar mass (103 − 104.5 M⊙), where we calculate the fractional difference between using Eq. (2) to calculate the bolometric luminosity and the true bolometric luminosity of the synthesised stellar population. Positive values correspond to cases where Eq. (2) overestimates the true bolometric luminosity, and negative values to cases where it underestimates the true value. Here, the median fractional error for all masses is above 0 for populations younger than ∼4 Myr, indicating that using Eq. (2) is likely to overestimate Lbol. However, for more evolved regions, Eq. (2) is more likely to be an underestimate, regardless of mass. We also see that there is a greater amount of stochastic variation for the low-mass, younger regions. In Sect. 5 we compare the Lbol values derived from Eq. (2) to those determined from a stochastically sampled stellar population, without assuming a fully sampled IMF, for the 30 HII regions analysed in this paper.
 |
Fig. 6. Fractional error when using Eq. (2) to determine Lbol compared to the true Lbol for synthesised stellar populations with different cluster masses as a function of time. To create these synthesised populations, we used SLUG with the median metallicity, extinction, and electron density found for the HII regions in this sample. The solid lines indicate the median of 100 simulations and the shaded region indicates the spread between the fifth and 95th percentiles for each cluster stellar mass. The dashed black line shows where the IMF-averaged estimate given by Eq. (2) is equivalent to the true bolometric luminosity from SLUG, Lbol, SLUG. Above this line, Eq. (2) overestimates the true Lbol of these synthesised populations. |
4.3. Oxygen abundances
To derive oxygen abundances in HII regions as a measure of metallicity, the direct method is generally preferred (e.g. Peimbert et al. 2017; Kewley et al. 2019a). However, the MUSE wavelength range does not cover the most commonly used auroral line, [OIII]λ4363, and whilst it covers some of the others, these are typically very faint (Curti et al. 2016). We do not achieve a high enough signal-to-noise (3σ level) to measure these auroral lines for many of the HII regions. To make consistent metallicity estimates, we therefore use strong line calibrations to derive oxygen abundances.
The review of Kewley et al. (2019a) discusses various empirical and theoretical strong-line calibrations for deriving oxygen abundances, with often large discrepancies found between them. It is also well known that strong line abundances show a systematic offset to direct method abundances (e.g. Pilyugin & Grebel 2016; Kumari et al. 2017), and selecting a strong line calibration that minimises this offset is an oft-used strategy (e.g. Yin et al. 2007, and references therein). For this study, we tested four different strong line calibrations, namely the S calibration method of Pilyugin & Grebel (2016), the empirical N2 index and O3N2 index calibrations of Pérez-Montero & Contini (2009), and the theoretical calibration of Dopita et al. (2016). These were selected both due to the wavelength coverage of the HII regions studied in this paper and for their being commonly used in recent studies relevant to this work (e.g. Kreckel et al. 2019; McLeod et al. 2021, 2019; James et al. 2020). We compared the results of these different calibrations to available direct method values in order to determine which is the optimal method for our sample. For J0921, there are ten HII regions cross-matched to those in J20 with direct method abundances, and for Leo P we take the value given by McQuinn (2015).
In Fig. 7, we plot the oxygen abundances determined from the different calibrations against the direct method abundances for the ten corresponding regions in J0921 and the single region in Leo P. Here we see that the S calibration produces values of 12 + log(O/H) (abbreviated to (O/H)S cal in Table 2), closest to those available that are determined via the direct method. The direct method and S calibration abundance values also show a similarly large spread for J0921 (∼0.6 dex), indicating that this galaxy may be particularly chemically inhomogeneous, as discussed in J20. The S calibration is an empirical calibration that relies on the following line ratios:
 |
Fig. 7. Oxygen abundances as determined from the strong-line calibration methods described in the Sect. 4.3 against the direct method oxygen abundance for ten regions in J0921 (from J20) and the Leo P HII region (taken from Skillman et al. 2013), with the single Leo P region having the lowest 12 + log(O/H)direct. The dashed black line indicates where the derived abundances are equivalent to the direct, temperature-based values. |
where each of the flux terms are the Gaussian-fitted, continuum-subtracted and reddening-corrected integrated fluxes in each HII region for the corresponding emission line. This calibration is split into two branches; a lower branch (for low-metallicity objects), where log(N2) < − 0.6, given by Eq. (7) in Pilyugin & Grebel (2016); and an upper branch (for high-metallicity objects) where log(N2)≥ − 0.6, given by Eq. (6) in Pilyugin & Grebel (2016). We find that the majority of our HII regions sit on the lower branch; that is to say, these are low metallicity regions.
We note that the use of different calibrations can, in some cases, produce conflicting findings, for example in searching for metallicity gradients and in quantifying values as a function of metallicity. We discuss some of these potential biases in Sect. 7.2, and in Appendices A and D. Given the large discrepancies found between the various calibrations for our sample (up to ∼1 dex), and also for HII regions in the literature, deep spectroscopic observations of auroral lines will likely be necessary for future investigations of the dependence of stellar feedback on metallicity.
5. Stellar population synthesis with SLUG
In the previous sections of this paper, we have mainly focused on the ionised gas within HII regions. However, a more complete understanding of stellar feedback requires some information on the feedback-driving stellar populations within these regions. When studying stellar populations, it is important to consider the limitations of the oft-used assumption that the stellar IMF is always fully sampled, so that population synthesis models can use IMF-averaged quantities. This is a poor assumption for low-mass galaxies, and for resolved, individual star-forming regions (da Silva et al. 2012, and references therein). For this reason, we have opted to use the stellar population synthesis (SPS) code SLUG (Stochastically Lighting Up Galaxies, da Silva et al. 2012; Krumholz et al. 2015a, v2.0) to model stochastically sampled stellar populations within our sample of dwarf galaxies. In this section, we will discuss the use of this code for deriving the properties of the stellar populations within our HII regions.
For the purpose of this study, the main properties we are interested in deriving are the current stellar masses (M*), ages (T), and bolometric luminosities (Lbol, SLUG). In order to use SLUG to estimate these properties, we produce a library of 106 simulations for each HII region in our sample, run in SLUG’s “cluster” mode. For each library, we input the properties already derived for each HII region; namely the electron density, extinction, and metallicity. We note that each inputted metallicity is interpolated by SLUG to the nearest value available in the MESA Isochrones and Stellar Tracks (MIST; Dotter 2016) and stellar atmosphere models, and therefore does not represent our full sample of metallicities. We use a Chabrier (2005) IMF and a Calzetti et al. (2000) starburst attenuation curve with a factor of 2.27 between nebular and stellar attenuation (Calzetti et al. 1994). We sample cluster masses and ages from distributions:
We initially set the maximum stellar mass, Mmax, to 5 × 105 M⊙, similar to the maximum mass found in Barnes et al. (2021) and Della Bruna et al. (2022), for example. Upon inspection of the resulting posterior distributions and considering its lower total stellar mass, we then limit this to 104 M⊙ for Leo P. The choice to limit the cluster age distribution between 1 and 10 Myr is based on the expectation that stellar populations older than 10 Myr are not typically associated with HII regions (e.g. Kennicutt & Evans 2012).
The power laws of these distributions are selected to increase sampling of younger, less massive clusters, where there is a larger amount of stochastic variation in the resulting spectra and photometry. This sampling density is accounted for when deriving cluster properties, and therefore should not affect the physical results derived.
We then follow the methods described in Krumholz et al. (2015b), whereby we use the cluster_slug2 function to perform Bayesian inference of the cluster properties using a set of observed photometric values for each HII region and a physically motivated estimate of the prior probability given by:
Since high resolution imaging is not available for KKH046 and J0921, photometric values are calculated using a set of four custom filters to create mock photometric images using the MUSE data for each galaxy. For J0921 and Leo P, these images are created by collapsing the MUSE cubes over three broad wavelength ranges, 4650−5800 Å, 5800−7000 Å, and 7000−8200 Å, and additionally 10 Å around the redshifted Hα emission line to create a mock narrow-band Hα image. Whilst MUSE does cover redder wavelength ranges, we find that for these data cubes there may be residual emission from poor sky subtraction at wavelengths > 8200 Å. For the KKH046 observations with AO correction, we use the same four mock filters but with an inputted transmission of zero over the AO notch filter indicated in Fig. 5. Photometry values for these custom filters are also then outputted for each of our SLUG libraries, and compared to the observed values.
We take the median of the resulting posterior probability distribution functions (PDFs) as our estimated values for the mass, age and bolometric luminosity. To estimate the uncertainty on these values, we use the difference between the 84th and 16th percentiles (68% confidence interval, CI).
In Fig. 8, we show the posterior PDFs for the mass, age and bolometric luminosity of KKH046 region 1 as an example of the capabilities of cluster_slug. From this plot, and from similar plots of all other regions, we see that in the majority of cases, the posterior PDFs returned by cluster_slug have a well-defined peak within the range of values tested for the cluster mass and bolometric luminosity. In the case where the distribution is bimodal, the median typically sits somewhere between these peaks, as in Krumholz et al. (2015a). However, the ages of these clusters are not as well constrained with these observations, likely due to the limited wavelength range of the mock photometry.
 |
Fig. 8. Corner plot for KKH046 region 1 showing the 1D posterior probability distribution functions (PDFs) for the stellar mass (log M*), age (log T) and bolometric luminosity (log Lbol) of this region in the top, centre, and bottom right panels, respectively. The vertical solid and dashed lines indicate the median values and their 68% confidence interval (CI), respectively. The bottom left panels show the joint posterior PDFs, with the intensity indicating the probability density. The five crosses indicate the five best photometric matches in the library to the observed photometry. All PDFs are normalised to have unit integral. |
We find that the star clusters powering these HII regions have estimated stellar masses (M*) within the range of 500 to 104 M⊙, and estimated ages between 4.5 and 7.3 Myr. In Fig. 8 we also plot the joint posterior PDF for the cluster properties, along with the five best photometric matches in this library to the observed photometry of KKH046 region 1. We find that for all regions, a minimum of two best matches lies within the 3σ contour level of the joint PDFs.
In this paper, we have determined two different values for the bolometric luminosity of each HII region, the first using the approximation given by Eq. (2) (Lbol, IMF) and the second estimated with SLUG (Lbol, SLUG). We plot in Fig. 9 a comparison of these two methods. These data points are coloured by age, and their size corresponds to their mass. We find that for the majority of our regions, Lbol, IMF < Lbol, SLUG. This follows from our finding that these regions are low mass (M* ≲ 6 × 104 M⊙) and not particularly young (T ≳ 4.5 Myr). The uncertainty in using Eq. (2) to estimate the bolometric luminosity, as discussed in Sect. 4.2, is therefore likely to be dominated by the assumption that the IMF is fully sampled, leading to an underestimation of the bolometric luminosity, and consequently the direct radiation pressure.
 |
Fig. 9. Comparison plot for the two methods used to calculate the bolometric luminosity for the 30 HII regions in this sample, where for Lbol, IMF we have assumed a fully sampled IMF, and for Lbol, SLUG we have used the median of the posterior PDF returned by SLUG. The colours indicate the age of the regions, and the size of each point is a representation of their mass. The dashed black line indicates where these values are equivalent; points above this line show where Lbol, IMF is greater than Lbol, SLUG – that is to say, where assuming a fully sampled IMF with Eq. (2) overestimates the bolometric luminosity. The Leo P data point has been labelled for visual clarity. |
An additional useful parameter returned by SLUG is the mass of the most massive star currently present within the stellar population. This parameter is of particular interest for our investigation of Leo P, since pre-existing studies (Evans et al. 2019; Telford et al. 2021, 2023) have identified a single O-type star within this HII region of mass 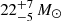 and age
and age 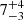 Myr (Telford et al. 2021). To make an estimate from SLUG, we create 20 libraries each of 1000 simulations and find the best photometric match for each library to the star cluster in the Leo P HII region. We then record the mass and age of the most massive star in that best match. We find a median and 68% confidence interval of
Myr (Telford et al. 2021). To make an estimate from SLUG, we create 20 libraries each of 1000 simulations and find the best photometric match for each library to the star cluster in the Leo P HII region. We then record the mass and age of the most massive star in that best match. We find a median and 68% confidence interval of 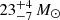 for the mass of the most massive star and an age of
for the mass of the most massive star and an age of 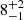 Myr. This shows that our photometric method yields results consistent with spectroscopic studies.
Myr. This shows that our photometric method yields results consistent with spectroscopic studies.
6. Quantifying the mechanisms of stellar feedback
In this work, we focus on two pre-SN stellar feedback mechanisms, namely photoionisation and direct radiation pressure. These mechanisms can be quantified by their corresponding pressure terms, that is, the thermal pressure of the ionised gas and the mechanical direct radiation pressure resulting from the momentum imparted by the stellar light output (as in e.g. Lopez et al. 2014; McLeod et al. 2021). There exist other pre-SN mechanisms of interest, including stellar winds and the dust-processed radiation pressure. We do not attempt to derive stellar wind pressure, since this derivation often depends on models that may not be valid at the low-metallicity regime (e.g. Rickard et al. 2022, and references therein). Follow-up X-ray observations of our sample would allow us to better assess the hot gas pressure attributed to shock-heating by stellar winds (and SNe), and follow-up infrared observations would enable us to quantify the dust-processed radiation pressure (e.g. as in the PHANGS-JWST programme for massive star-forming galaxies, Lee et al. 2023).
Despite a number of feedback-related pressure terms being outside the scope of this work, it is likely that the ionised gas pressure (together with stellar winds) will be more dominant within this sample, as previously found for evolved HII regions (e.g. McLeod et al. 2021; Lopez et al. 2014).
6.1. Direct radiation pressure
We determine the total volume-averaged direct radiation pressure, Pdir, as
where c is speed of light and r is the radius of the HII region.
Two different values for the direct radiation pressure of each HII region are calculated, the first using the approximation for Lbol, IMF given by Eq. (2) and the second using the value of Lbol, SLUG estimated with SLUG, referred to as Pdir, IMF and Pdir, SLUG, respectively. The overall effect of using Lbol, SLUG instead of Lbol, IMF is that it shifts the direct radiation pressure values up for most of the HII regions in this sample.
For visual clarity, we show only the Pdir, SLUG points in all of our subsequent figures. However, we show the corresponding best-fit lines found using Pdir, IMF in some figures by a dashed teal line for comparison.
6.2. Pressure of the ionised gas
We compute the ionised gas pressure from the ideal gas law,
where ne, nH and nHe are the electron, hydrogen, and helium number densities, respectively, and kB is the Boltzmann constant. As with our derivation of the electron density, ne, in Eq. (1), we assume that the temperature of the HII regions is 104 K. We also assume that these regions are neutral and that helium is singly ionised, so that ne + nH + nHe ≈ 2ne.
7. Discussion
We now explore our findings and their implications for the relationships between stellar feedback and environmental properties in HII regions. We compare to studies with similar spatial resolution, including from the LMC (McLeod et al. 2019; HII region radii of 3.4−45.7 pc), the SMC (Lopez et al. 2014; HII region radii ranging from 10−112 pc), and the PHANGS-MUSE survey (Barnes et al. 2021; spatial resolution ranging from 50−100 pc) in order to investigate a wider range of physical properties in star-forming galaxies. The range of ≈7 − 8 in 12 + log(O/H) in our sample allows us to expand these studies into the less studied, low-metallicity regime.
The Pion values for the regions in the LMC from McLeod et al. (2019) are determined using the same methods as described in Sect. 6.2. However, the Pdir values are determined using the ionising photon flux, Q0, *, of the stellar populations identified within the regions. McLeod et al. (2019) state that if Eq. (6) and Lbol, IMF from Eq. (2) is used, the Pdir values would be around an order of one magnitude higher. However, since these regions are young, it is likely that Lbol, IMF would be an overestimate. If the Pdir values for the LMC regions were higher, this would only strengthen the trends observed in the following discussions. For the HII regions in the SMC taken from Lopez et al. (2014), and for the region SMC N76 (McLeod et al., in prep.), the pressure terms are determined using the same methods as described in Sect. 6, but with a fully sampled IMF assumed when determining Lbol, increasing their uncertainty. For the PHANGS-MUSE sample, we take the median pressure terms for each of the 19 galaxies in Barnes et al. (2021). In Barnes et al. (2021), two values are calculated for both Pdir (which is called Prad in Barnes et al. 2021) and for Pion (which is called Ptherm instead). We take the minimum Pdir values (Prad, min) and the maximum values of Pion (Ptherm, max), since the methods used to determine these are consistent with those used for the 30 HII regions in this study, and with the other literature studies described above. We note that taking the minimum values for both pressure terms, or the maximum values for both pressure terms, would strengthen the findings discussed in Sect. 7.2. A lower conversion of 88 between LHα and Lbol is used instead of Eq. (2) to better account for the likely young ages of these regions. However, Barnes et al. (2021) state that around 20% of the 5810 regions in their sample have a mass < 103 M⊙, where stochastic effects have a more significant effect on the bolometric luminosity. By using the median for each galaxy, we limit the effect of these potential biases.
In Fig. 10, we plot the two pressure components quantified in this work against the radii of the 30 HII regions in this study, along with the values taken from the aforementioned literature sources. Linear fits are plotted for each relationship, with a separate fit for each derivation of the direct radiation pressure. We find that the HII region SMC N76 and the region within Leo P show a significantly higher Pdir than the other regions in this sample. These larger values for Pdir are likely driven by the fact that these observations have a higher spatial resolution (≲10 pc), and Pdir ∝ r−2. Therefore, we do not include these regions in the fits for Pdir, although further study could make comparisons to observations at similar resolution.
 |
Fig. 10. Panel a: photoionisation pressure (Pion) and direct radiation pressure (Pdir) of the HII regions in various galaxies (see legend) plotted as a function of region size. The Pion values occupy the top half of the plot, and Pdir values the bottom half. SMC points are taken from Lopez et al. (2014), SMC N76 from McLeod et al. (in prep.), and the LMC points from McLeod et al. (2019). We note that uncertainties in the radii values are not given in the literature, and we therefore assume a generous 20%. We also plotted the median values from the PHANGS-MUSE survey as given in Barnes et al. (2021) by the grey diamond marker. The solid black lines indicate the linear best fits for Pion and Pdir, SLUG, with shaded grey areas for the 95% confidence regions. The dashed teal line and shaded area depict the linear fit when using Pdir, IMF. The black dotted line indicates the r−2 proportionality from Eq. (6) used to calculate Pdir. Panel b: correlation coefficient analysis for the Pdir, SLUG − log10(r) relation (see Sect. 7). The histogram shows the probability density distribution of the Pearson correlation coefficient using the bootstrapping and perturbation method from Curran (2014). The solid black line is the median correlation coefficient, C, found for this relation and the dashed lines show the 16th and 84th percentiles used to determine the uncertainty. |
To explore the statistical significance of the relationships investigated in this paper, we perform correlation coefficient analyses using pymccorrelation (Curran 2014; Privon et al. 2020), whereby we compute the Pearson correlation coefficient, p-value and associated uncertainties for each relationship using a Monte Carlo routine. With pymccorrelation we perform 1000 bootstrap iterations and 1000 perturbations, according to the “composite method” described in Curran (2014). The quoted values and their uncertainties for the Pearson correlation coefficients and p-values are the median and the range between the 16th and 84th percentiles of the resulting PDFs.
7.1. Feedback evolution
As found in other works (e.g. Lopez et al. 2014; McLeod et al. 2019, 2021; Barnes et al. 2021; Olivier et al. 2021), we see that the pressure of the ionised gas is roughly a few orders of magnitude greater than the direct radiation pressure for HII regions ∼10 − 100 pc in size, suggesting that photoionisation drives the expansion of these evolved (T ≳ 4.5 Myr) HII regions. Similarly to Olivier et al. (2021) and Barnes et al. (2021), we find that the pressure terms decrease with HII region size, with a correlation coefficient of 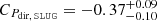 and a p-value of
and a p-value of 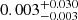 for Pdir, SLUG, and with CPion = −0.3 ± 0.1 and a p-value of
for Pdir, SLUG, and with CPion = −0.3 ± 0.1 and a p-value of 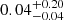 for Pion. This indicates only weak negative correlations, and the p-values mean we can only confidently reject the null hypothesis for the direct radiation pressure. We also find that Pdir falls more sharply than Pion in Fig. 10. If we take the size of each region as a proxy for its evolutionary stage, we therefore find that as HII regions evolve and expand, the feedback-driven pressure drops, and the direct radiation pressure becomes less important relative to the ionised gas pressure.
for Pion. This indicates only weak negative correlations, and the p-values mean we can only confidently reject the null hypothesis for the direct radiation pressure. We also find that Pdir falls more sharply than Pion in Fig. 10. If we take the size of each region as a proxy for its evolutionary stage, we therefore find that as HII regions evolve and expand, the feedback-driven pressure drops, and the direct radiation pressure becomes less important relative to the ionised gas pressure.
We note that there are caveats with taking HII region size as a proxy for its evolutionary stage. For example, this approach assumes that these HII regions are able to freely expand, and that they have similar stellar populations. There exist other sources of bias in these relationships with r; namely that we have used r−2 to calculate our Pdir values, and also that the size of the regions is in part limited by the spatial resolution of the observations, as discussed in Sect. 3.1. The Milky Way objects studied by Olivier et al. (2021), for example, are much smaller and much more compact (r ≲ 0.5 pc) than the HII regions in this study.
Olivier et al. (2021) and Barnes et al. (2020), who both studied compact HII regions within the Milky Way, also find that the degree of scatter around these pressure–size relationships is more significant for large HII regions, particularly for Pdir. Olivier et al. (2021) find Pdir ∝ r−1.36 ± 0.16, which is significantly steeper than our slopes of Pdir, IMF ∝ r−0.49(±0.1) and Pdir, SLUG ∝ r−0.66(±0.1). However, our shallower gradients could be a consequence of this increased degree of scatter and of our sampling. Due to the limits of our spatial resolution, we are unable to sample any compact HII regions where these pressure terms have been found to have more importance, and where these relationships have been found to show less scatter. This is particularly true for J0921, at a distance of 21 Mpc and spatial resolution of ∼83 pc.
An example of the effect of potential biases when using Eq. (2) and Pdir, IMF to investigate the relationship between the direct radiation pressure and the size of the HII regions is shown in Fig. 11 for the HII regions in J0921. Here, we can see that the size of the HII regions is positively correlated to their stellar mass, and therefore for the smaller (and less massive) regions we are likely underestimating Lbol when assuming a fully sampled IMF. In this case, this leads to a strong positive correlation (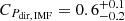 with a p-value of
with a p-value of 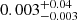 ) when using Pdir, IMF, as opposed to the negative trend described above.
) when using Pdir, IMF, as opposed to the negative trend described above.
 |
Fig. 11. Pdir, IMF values for J0921 against their HII region radii with red star-shaped markers sized according to their stellar mass. The solid black line and shaded area indicate the Pdir, SLUG fit from Fig. 10a. The dashed red line and shaded area indicate the Pdir, IMF fit for the HII regions in J0921 only. |
7.2. Stellar feedback in the low-mass, low-metallicity regime
In Fig. 12a, we have plotted the feedback-related pressure components as a function of metallicity, as measured by their oxygen abundance. For this plot, we have also included data from the LMC (McLeod et al. 2019), the SMC (Lopez et al. 2014, where the oxygen abundance is not measured for each HII region individually but for the SMC as a whole), SMC N76 (McLeod et al., in prep.) and from more massive star-forming galaxies from the PHANGS-MUSE survey (Barnes et al. 2021). We note that each of the PHANGS-MUSE data points represents the median and standard deviation of multiple HII regions within each of the 19 galaxies in their sample, rather than for an individual HII region as for all the other data points. Since the inclusion of these literature values is intended to show the continuation of the global trends in the pressure terms as a function of metallicity, and since there are > 5000 HII regions in the PHANGS-MUSE catalogue, we choose to only plot these median values for visual clarity. We add that none of the individual PHANGS-MUSE HII regions have an oxygen abundance less than 12 + log(O/H)S cal ∼ 8.1.
 |
Fig. 12. Panel a: similar to Fig. 10a, but with the pressure components plotted as a function of their oxygen abundance, 12 + log(O/H), with all markers coloured by their extinction and sized according to the HII region radii, where we take the median radii and extinction for the PHANGS data points (Barnes et al. 2021). Panel b: similar to panel a, but with only the 30 HII regions from the three dwarfs in this sample plotted against their cluster mass and coloured by their oxygen abundance. |
The oxygen abundances of the HII regions in the LMC in McLeod et al. (2019) are determined using the average values given from the N2 and O3N2 indices using equations from Marino et al. (2013), based on a comparison to values obtained via the direct method. Based on Fig. 7, these values could be as much as 0.3 dex higher than if the S calibration method was used, which would not change the main conclusions of this work. For the SMC, Lopez et al. (2014) assume a metallicity of 20% solar, which is consistent with the average value obtained from individual regions within the SMC from the direct method (e.g. Toribio San Cipriano Cipriano et al. 2017). From Fig. 7, the S calibration method can overestimate the direct method oxygen abundance by as much as 0.6 dex. Again, this would not change our main conclusions. For the PHANGS-MUSE sample, we take the average oxygen abundance for each galaxy given in Table 1 in Barnes et al. (2021), which are determined using the same calibration (the S calibration of Pilyugin & Grebel 2016) as used for the 30 HII regions in the metal-poor dwarf galaxies studied here.
We also plot these pressure terms for the 30 HII regions studied in this work against their cluster mass in Fig. 12b. We do not include literature values in this plot since in most cases they are not quantified, or are derived from different methods that may introduce further biases.
7.2.1. Direct radiation pressure
We find a correlation coefficient of 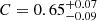 with a p-value of
with a p-value of 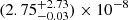 for Pdir, SLUG against the oxygen abundance for the HII regions in this study and from the literature listed above. This positive correlation is likely driven by two trends: (1) the weak positive correlation we find between Lbol and metallicity (
for Pdir, SLUG against the oxygen abundance for the HII regions in this study and from the literature listed above. This positive correlation is likely driven by two trends: (1) the weak positive correlation we find between Lbol and metallicity (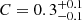 ), and (2) the moderate negative correlation we find between the metalllicity and the HII region radius (
), and (2) the moderate negative correlation we find between the metalllicity and the HII region radius (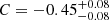 ). More luminous regions are more metal-rich, and HII regions in metal-poor galaxies tend to be larger.
). More luminous regions are more metal-rich, and HII regions in metal-poor galaxies tend to be larger.
The second finding may be expected since HII regions with lower metallicities have higher temperatures (due to less metal-line cooling, e.g. Bresolin et al. 1999; Kennicutt et al. 2000), and also since low-metallicity stellar populations, at fixed stellar mass, produce more ionising photons (e.g. McLeod et al. 2021). These effects increase the thermal pressure, and therefore cause the HII regions to expand faster (Ali 2021). Furthermore, the global properties of the host galaxies are also related to the gas-phase metallicity. Metal-poor galaxies tend to be dwarfs with lower ISM pressure and density, which makes it easier for HII regions to expand.
We would also expect the metallicity of HII regions to impact their dust content, and so further impact their size and therefore the direct radiation pressure. One would expect that as the metallicity of a HII region increases, so too does its dust content (Rémy-Ruyer et al. 2014), meaning that there is greater extinction of UV photons and the intensity of the ionising spectrum is reduced. A recent study based on radiation-hydrodynamical models of star-forming regions (Ali 2021) finds that the presence of dust hinders the expansion of these regions due to this greater extinction of UV photons. That is to say, for a greater dust content, HII regions are smaller, leading to greater values of Pdir. This predicted positive correlation between dust and Pdir is supported by observations of the HII regions within the LMC, SMC and NGC 300 (Lopez et al. 2014; Roman-Duval et al. 2014; McLeod et al. 2021). However, for the 30 HII regions in this study we find no correlation for size (C = −0.0 ± 0.2) nor Pdir (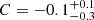 , i.e., consistent with zero) as a function of the dust content, as measured by the visual extinction, AV (assuming that the extinction, measured from the Balmer decrement, is mainly originating from dust within the galaxies rather than foreground material). It is therefore unclear whether a change in the dust content is driving these trends, although we note that the unknown extinction curve for these galaxies is a source of uncertainty when determining the extinction. However, a test with the Cardelli et al. (1989) Galactic extinction curve produces similar findings to those presented here.
, i.e., consistent with zero) as a function of the dust content, as measured by the visual extinction, AV (assuming that the extinction, measured from the Balmer decrement, is mainly originating from dust within the galaxies rather than foreground material). It is therefore unclear whether a change in the dust content is driving these trends, although we note that the unknown extinction curve for these galaxies is a source of uncertainty when determining the extinction. However, a test with the Cardelli et al. (1989) Galactic extinction curve produces similar findings to those presented here.
Due to the high uncertainty in the derived mass values, the trends observed with the cluster mass show a high degree of scatter. However, as with Fig. 11, we see that different conclusions can be drawn from HII region studies if stochastic effects are not taken into account. A moderate correlation is found between Pdir, IMF and the cluster mass with C = 0.4 ± 0.2. However, when Pdir, SLUG is used, C is consistent with zero. This is again likely driven by the consequences of using Eq. (2) to estimate Lbol. Lbol of the lower mass regions is underestimated, and likely overestimated for the higher mass and younger regions, particularly in KKH046 (Fig. 9).
Overall, we tentatively see that HII regions in low-mass, low-metallicity host galaxies tend to have a larger radius and hence a lower value of Pdir. A larger sample and higher resolution observations would be needed to investigate these trends fully.
7.2.2. Pressure of the ionised gas
The trend found for Pion as a function of metallicity in Fig. 12a, is found to be much weaker than for Pdir, though we see a slight negative correlation with 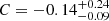 and a p-value of
and a p-value of 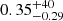 . Whilst we cannot reject the null hypothesis, a negative correlation between photoionisation pressure and metallicity follows from the expectation that metal-poor HII regions should have a higher temperature (e.g. Kennicutt et al. 2000), and then Pion ∝ Te. In terms of investigating Pion as a function of metallicity, and other quantities, we are limited by assuming an electron temperature of 104 K for all HII regions. To further investigate these relationships, we would benefit from deeper spectra that would allow us to determine the electron temperature, and also use the direct method for determining the oxygen abundance.
. Whilst we cannot reject the null hypothesis, a negative correlation between photoionisation pressure and metallicity follows from the expectation that metal-poor HII regions should have a higher temperature (e.g. Kennicutt et al. 2000), and then Pion ∝ Te. In terms of investigating Pion as a function of metallicity, and other quantities, we are limited by assuming an electron temperature of 104 K for all HII regions. To further investigate these relationships, we would benefit from deeper spectra that would allow us to determine the electron temperature, and also use the direct method for determining the oxygen abundance.
For Pion as a function of cluster mass in Fig. 12b, we find a weak negative correlation with C = −0.2 ± 0.1 and a p-value of 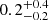 . Based on the p-value and the large uncertainties in the cluster mass, we again cannot reject the null hypothesis. However, in Fig. 12b, we see that the more massive regions tend to have a larger radius. Following from the trend in Fig. 10a, this may then drive a decrease in Pion with increasing mass.
. Based on the p-value and the large uncertainties in the cluster mass, we again cannot reject the null hypothesis. However, in Fig. 12b, we see that the more massive regions tend to have a larger radius. Following from the trend in Fig. 10a, this may then drive a decrease in Pion with increasing mass.
We note that the relationships between Pdir and Pion also persist when only the regions with direct method metallicities are considered (see Appendix D). However, a more statistically significant sample with direct method metallicities is necessary to investigate these trends further.
8. Summary and conclusions
In this paper, we have presented the results of a stellar feedback study of HII regions within three nearby, low-metallicity, dwarf starburst galaxies (J0921, KKH046, and Leo P), which were observed with the IFU spectrograph, MUSE, and collected by the DWALIN collaboration. We have discussed the methods used to select and extract the integrated spectra of these HII regions via the ASTRODENDRO Python package, and the methods used to derive their key ionised gas properties. We have also presented the use of stochastically sampled stellar population synthesis models using the SLUG package to investigate the properties of the ionising stellar populations within these HII regions. Finally, we have quantified two pre-SN stellar feedback mechanisms and quantified them as a function of the selected environmental properties. This has allowed us to investigate the evolution of stellar feedback within low-mass, low-metallicity HII regions, and make comparisons to observations of more massive, metal-rich star-forming galaxies from the recently published results of the PHANGS-MUSE survey (Barnes et al. 2021).
The key findings of this paper are summarised as follows:
-
There are considerable discrepancies between the different methods for determining the oxygen abundance using strong-line ratios. To increase our confidence in the oxygen abundance values we have reported, and therefore in our interpretations of the results, deeper spectra of these galaxies covering temperature-sensitive auroral lines for the direct method would be necessary.
-
We estimate that the HII regions within our sample are low-mass (M* ≲ 6 × 104 M⊙) and evolved (T ≳ 4.5 Myr) regions and we therefore believe that their bolometric luminosities are underestimated in most cases if one assumes a fully sampled IMF.
-
We see that stochastic sampling effects can significantly affect the trends observed between feedback-related pressure terms and properties of the HII regions. This stresses the importance of stochastic sampling in the low-mass regime.
-
Our simulated SLUG libraries for Leo P are consistent with a previously reported late O-type star within Leo P’s HII region, which we find to be of mass
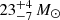 and age
and age 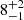 Myr. This illustrates the success of SLUG at identifying massive stars from observations that may not have the necessary spatial resolution for traditional techniques.
Myr. This illustrates the success of SLUG at identifying massive stars from observations that may not have the necessary spatial resolution for traditional techniques. -
For all HII regions in our sample, the pressure of the ionised gas is greater than the direct radiation pressure. This supports the findings of feedback studies of other giant HII regions, such as in Olivier et al. (2021) and Barnes et al. (2021). This suggests that photoionisation is more dominant than the direct radiation pressure within these evolved HII regions.
-
The two feedback mechanisms that we have quantified are shown, overall, to decrease with region size, supporting literature findings that these feedback mechanisms have less of an importance in giant, evolved HII regions when compared to ultra-compact HII regions.
-
We find that the direct radiation pressure within HII regions increases with metallicity. In some cases, this may follow from more rapid expansion in metal-poor, and hence hotter regions.
-
Deeper spectra covering the auroral lines necessary for determining the electron temperature and the oxygen abundance via the direct method are required to fully investigate relationships between Pion and the ionised gas and stellar properties of HII regions.
In conclusion, we find that an investigation of stellar feedback in the extreme environments of low-metallicity, dwarf starburst galaxies, along with comparisons to more massive systems, can provide a wide range of physical properties to probe the environmental dependence of stellar feedback mechanisms. Follow-up investigations, that is, deeper spectroscopic observations, IR, and X-ray data, and investigations into the full sample of star-forming galaxies provided by DWALIN and other upcoming surveys will provide further observational constraints on these mechanisms of stellar feedback and how they affect the evolution of galaxies.
Acknowledgments
The authors thank the anonymous referee for their constructive comments that have improved the clarity and quality of the paper. The authors also thank Eve Cully for work on the analysis of the HII region SMC N76. This paper made use of the following software packages: Astropy (Astropy Collaboration 2013, 2018), Matplotlib (Hunter 2007), NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), spectral-cube (Ginsburg et al. 2019), and ASTRODENDRO (http://www.dendrograms.org/). A.F. is supported by a UKRI Future Leaders Fellowship (grant no. MR/T042362/1). F.B. acknowledges support from the INAF Ricerca Fondamentale 2022 Grant. M.R.K. acknowledges funding from the Australian Research Council through its Laureate Fellowship scheme, award FL220100020. G.V. acknowledges support from ANID programme FONDECYT Postdoctorado 3200802.
References
- Abbott, D. C. 1982, ApJ, 263, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Ali, A. A. 2021, MNRAS, 501, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, eds. I. S. McLean, S. K. Ramsay, & H. Takami, SPIE Conf. Ser., 7735, 773508 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Barnes, A. T., Longmore, S. N., Dale, J. E., et al. 2020, MNRAS, 498, 4906 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, A. T., Glover, S. C. O., Kreckel, K., et al. 2021, MNRAS, 508, 5362 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, A. T., Chandar, R., Kreckel, K., et al. 2022, A&A, 662, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belfiore, F., Santoro, F., Groves, B., et al. 2022, A&A, 659, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., & Garnett, D. R. 1999, ApJ, 510, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Bryant, J. J., Owers, M. S., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2857 [Google Scholar]
- Byler, N., Dalcanton, J. J., Conroy, C., et al. 2019, AJ, 158, 2 [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Vazquez-Semadeni, E., et al. 2020, Space Sci. Rev., 216, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Krumholz, M. R., et al. 2022, MNRAS, 509, 272 [Google Scholar]
- Curran, P. A. 2014, arXiv e-prints [arXiv:1411.3816] [Google Scholar]
- Curti, M., Cresci, G., Mannucci, F., et al. 2016, MNRAS, 465, 1384 [Google Scholar]
- D’Agostino, J. J., Kewley, L. J., Groves, B., et al. 2019, ApJ, 878, 2 [CrossRef] [Google Scholar]
- Dale, J. E., Ngoumou, J., Ercolano, B., & Bonnell, I. A. 2014, MNRAS, 442, 694 [Google Scholar]
- da Silva, R. L., Fumagalli, M., & Krumholz, M. 2012, ApJ, 745, 145 [CrossRef] [Google Scholar]
- Della Bruna, L., Adamo, A., Lee, J. C., et al. 2021, A&A, 650, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Bruna, L., Adamo, A., McLeod, A. F., et al. 2022, A&A, 666, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 1995, ApJ, 455, 468 [Google Scholar]
- Dopita, M., Kewley, L., Sutherland, R., & Nicholls, D. 2016, Astrophys. Space Sci., 361, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa-Ponce, C., Sánchez, S. F., Morisset, C., et al. 2020, MNRAS, 494, 1622 [Google Scholar]
- Evans, C. J., Castro, N., Gonzalez, O. A., et al. 2019, A&A, 622, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Flores-Fajardo, N., Morisset, C., Stasińska, G., & Binette, L. 2011, MNRAS, 415, 2182 [Google Scholar]
- Ginsburg, A., & Mirocha, J. 2011, Astrophysics Source Code Library [record ascl:1109.001] [Google Scholar]
- Ginsburg, A., Koch, E., Robitaille, T., et al. 2019, https://doi.org/10.5281/zenodo.2573901 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., Giovanelli, R., Kent, B. R., et al. 2018, ApJ, 861, 49 [Google Scholar]
- Hopkins, P. F., Kereš, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Wetzel, A., Kereš, D., et al. 2018, MNRAS, 480, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Wetzel, A., Wheeler, C., et al. 2023, MNRAS, 519, 3154 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2012, A&A, 546, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, B. L., Koposov, S., Stark, D. P., et al. 2015, MNRAS, 448, 2687 [NASA ADS] [CrossRef] [Google Scholar]
- James, B. L., Koposov, S. E., Stark, D. P., et al. 2017, MNRAS, 465, 3977 [NASA ADS] [CrossRef] [Google Scholar]
- James, B. L., Kumari, N., Emerick, A., et al. 2020, MNRAS, 495, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Bresolin, F., French, H., & Martin, P. 2000, ApJ, 537, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., & Sutherland, R. S. 2019a, ARA&A, 57, 511 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., Sutherland, R., et al. 2019b, ApJ, 880, 16 [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2018, ApJ, 859, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kourkchi, E., Courtois, H. M., Graziani, R., et al. 2020, AJ, 159, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I.-T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Bate, M. R., Arce, H. G., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 243 [Google Scholar]
- Krumholz, M. R., Fumagalli, M., da Silva, R. L., Rendahl, T., & Parra, J. 2015a, MNRAS, 452, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Adamo, A., Fumagalli, M., et al. 2015b, ApJ, 812, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Kumari, N., James, B. L., & Irwin, M. J. 2017, MNRAS, 470, 4618 [NASA ADS] [CrossRef] [Google Scholar]
- Kumari, N., Irwin, M. J., & James, B. L. 2020, A&A, 634, A24 [EDP Sciences] [Google Scholar]
- Lee, J. C., Sandstrom, K. M., Leroy, A. K., et al. 2023, ApJ, 944, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., Prochaska, J. X., & Ramirez-Ruiz, E. 2011, ApJ, 731, 91 [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., et al. 2014, ApJ, 795, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, W. E., Bonnell, I. A., & Dale, J. E. 2020, MNRAS, 493, 4700 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
- Mannucci, F., Belfiore, F., Curti, M., et al. 2021, MNRAS, 508, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Belfiore, F., Cresci, G., et al. 2023, A&A, 670, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, R. A., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2013, A&A, 559, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashchenko, S., Couchman, H. M. P., & Wadsley, J. 2006, Nature, 442, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, K. L. 2005, Proceedings of the 22nd Texas Symposium on Relativistic Astrophysics at Stanford, 374 [Google Scholar]
- McCall, M. L. 1984, MNRAS, 208, 253 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Dale, J. E., Evans, C. J., et al. 2019, MNRAS, 486, 5263 [Google Scholar]
- McLeod, A. F., Kruijssen, J. M. D., Weisz, D. R., et al. 2020, ApJ, 891, 25 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Ali, A. A., Chevance, M., et al. 2021, MNRAS, 508, 5425 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, Skillman E. D., Dolphin, A., et al. 2015, ApJ, 812, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Monreal-Ibero, A., Weilbacher, P. M., Micheva, G., Kollatschny, W., & Maseda, M. 2023, A&A, 674, A210 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morisset, C., Delgado-Inglada, G., & Flores-Fajardo, N. 2015, Rev. Mex. Astron. Astrofis., 51, 103 [Google Scholar]
- Oey, M. S., Meurer, G. R., Yelda, S., et al. 2007, ApJ, 661, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Olivier, G. M., Lopez, L. A., Rosen, A. L., et al. 2021, ApJ, 908, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D., & Ferland, G. 2006, The Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito: University Science Books) [Google Scholar]
- Ostriker, E. C., McKee, C. F., & Leroy, A. K. 2010, ApJ, 721, 975 [CrossRef] [Google Scholar]
- Peimbert, M., Peimbert, A., & Delgado-Inglada, G. 2017, PASP, 129, 082001 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Montero, E., & Contini, T. 2009, MNRAS, 398, 949 [CrossRef] [Google Scholar]
- Phillipps, S., Driver, S. P., Couch, W. J., & Smith, R. M. 1998, ApJ, 498, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
- Plat, A., Charlot, S., Bruzual, G., et al. 2019, MNRAS, 490, 978 [Google Scholar]
- Pontzen, A., & Governato, F. 2014, Nature, 506, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Privon, G. C., Ricci, C., Aalto, S., et al. 2020, ApJ, 893, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
- Rickard, M. J., Hainich, R., Hamann, W. R., et al. 2022, A&A, 666, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roman-Duval, J., Gordon, K. D., Meixner, M., et al. 2014, ApJ, 797, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., de Paz, A. G., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skillman, E. D., Salzer, J. J., Berg, D. A., et al. 2013, AJ, 146, 3 [CrossRef] [Google Scholar]
- Telford, O. G., Chisholm, J., McQuinn, K. B. W., & Berg, D. A. 2021, ApJ, 922, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Telford, O. G., McQuinn, K. B. W., Chisholm, J., & Berg, D. A. 2023, ApJ, 943, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [Google Scholar]
- Toribio San Cipriano, L., Domínguez-Guzmán, G., Esteban, C., et al. 2017, MNRAS, 467, 3759 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Weilbacher, P. M., Monreal-Ibero, A., Verhamme, A., et al. 2018, A&A, 611, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yin, S. Y., Liang, Y. C., Hammer, F., et al. 2007, A&A, 462, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, K., Yan, R., Bundy, K., et al. 2016, MNRAS, 466, 3217 [Google Scholar]
Appendix A: J0921 – Comparison with previous studies
Here, we focus on some of the ionised gas properties derived for one of our target dwarf galaxies, J0921, since it contains ∼77% of the HII regions in our sample and has also been the focus of a previous study, J20. J20 used the same MUSE data to explore the chemical homogeneity of J0921, referred to as JKB 18 in their study (from the JKB catalogue presented in James et al. 2015 and James et al. 2017).
In J20, an IFAUNAL binning algorithm with an optimum bin size of seven pixels and a minimum flux threshold of 10−19 erg s−1 is used to select HII regions (i.e. a lower flux threshold then in our methods described in Section 3.1). This resulted in 30 HII regions. All 23 HII regions identified in this study have a match within J20 (note region 14 in J20 encompasses both regions 20 and 22 in this study) and the derived values of LHα and ne between J20 and this study are comparable (within the uncertainties). Oxygen abundance values were determined using the O3N2 index in J20, however in this study we instead use the S calibration method.
We carried out similar tests as in J20 to search for evidence of a metallicity gradient within this galaxy. In J20, the centre of the galaxy is taken to be the centre of the brightest HII region. We investigated additional galactic centres, with 5 centres tested in total: (1) an estimated kinematic centre (Figure A.1a), (2) the centre of the brightest region, (3) the geometric centre of all HII regions, (4) the geometric centre of all pixels with Hα emission above a 3σ detection and (5) the HI centroid from Haynes et al. (2018). The position of these centres are labelled in Figure A.1b. For all of these potential galactic centres, a slight negative metallicity gradient is found when the S calibration method is used (Figure A.2a; note that the galactocentric radii, Rgal, values are projected on the plane of the sky due to the unknown inclination of the system). However, when the direct method metallicity values for the subsample of 11 HII regions with a > 3σ detection of the auroral [SII]λ6312 line (given by J20) are used with these galactic centres, no convincing gradient is found (Figure A.2b). Similarly to J20, we therefore conclude that there is insufficient evidence to support the presence of a negative metallicity gradient within this galaxy. The weak correlation found when using the strong line methods is perhaps driven by some other radial change within this galaxy, such as a change in the ionisation parameter.
 |
Fig. A.1. Panel (a) shows the Hα emission map of J0921, with each region coloured according to its radial velocity (not inclination-corrected due to the unknown inclination of the system). Red indicates regions moving away from us, and blue indicates regions moving towards us. Here we can see evidence that J0921 is rotating as a large body, as discussed in J20 and also illustrated in Marasco et al. (2023). Panel (b): Similar to (a), but regions are instead coloured by their oxygen abundance (using the S calibration) to indicate the spatial distribution of metals in J0921. Also plotted are the various galactic centres tested in this work, as listed in the text. |
 |
Fig. A.2. Panel (a): Oxygen abundance against projected galactocentric distance for the 23 HII regions within J0921. Horizontal teal lines indicate the change in the position of each region when different galactic centres were used, and the shaded grey area shows the spread of metallicity gradients for the five galactic centres tested. The points plotted in red are for the fourth centre, which is the geometric centre of all pixels containing Hα emission above three standard deviations. Panel (b): Similar to panel (a) but with the direct method oxygen abundance for the ten regions from J20. |
In Monreal-Ibero et al. (2023), a similar discrepancy is found when studying the spatial distribution of metals within the nearby dwarf galaxy UM 462. When using the direct method oxygen abundance, the galaxy appears chemically homogeneous. However, when using strong-line methods, chemical inhomogeneities were identified. We therefore support Monreal-Ibero et al. (2023) in stating that further work is necessary to determine the optimal method for calculating the oxygen abundance at any point within a galaxy.
Appendix B: Radial intensity profiles
To test the sizes of the HII regions studied here, radial flux profiles for a box (of size judged by eye) surrounding each visibly distinguishable ionised gas clump in the Hα emission maps were plotted. The radius that encompasses 90% of the Hα flux in each box, R90, was then calculated and compared to the radius of the region returned by ASTRODENDRO. An example radial flux profile for region KKH046 1 is shown in Figure B.1. The R90 values for all regions across all three galaxies were found to be comparable to the radius of our final dendrogram structures (measured by the geometric mean of the major and minor axes), which are listed in column 2 of Table 2. However, it must be noted that ASTRODENDRO calculates the radius using the geometric mean of the major and minor axes, whereas the R90 calculation assumes the regions are circular.
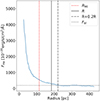 |
Fig. B.1. Radial flux profile for KKH046 region 1. The dashed red line is the radius that encompasses 90% of the Hα emission and the solid black line is the radius returned by ASTRODENDRO. The horizontal line depicts where the flux profile reaches the background level, Fbl (median of the emission). This line was used to determine the uncertainty in the size of these regions, which we determined to be 20%. |
Appendix C: Uncertainty estimation
The uncertainties in this work consist of those returned by PYSPECKIT for the Gaussian-fit parameters of each emission line, the uncertainties in each of the calibrations we use based on emission lines, the 20% uncertainty on the radius, r, of our regions (as estimated by the radius at which the radial intensity profiles reach the background level, see Figure B.1), the uncertainty in the extinction correction, and the 68% confidence intervals of our posterior PDFs for the cluster mass, age and bolometric luminosity. We note that there is an additional uncertainty in the true extinction curves of these galaxies, which could in fact be different from that given by Calzetti et al. (2000), and additional uncertainties in the calibrations using emission line ratios. In particular, studies have found that stochasticity may have an effect on all of these calibrations, for example readers can refer to D’Agostino et al. (2019). We also note that different papers often use different methods and calibrations, and there will therefore exist some discrepancies between values. This must be taken into account when making comparisons between different literature values.
Appendix D: Oxygen abundance calibration tests
In Section 4.3 we derived the oxygen abundances of our HII regions using the S calibration method of Pilyugin & Grebel (2016). In Section 4.3, we discussed some of the discrepancies between different calibrations. Here, we continue this discussion.
We investigated the effect of the calibration method when quantifying the feedback-related pressure terms as a function of metallicity. For the overall trends including literature values, the different calibrations have little effect and are similar to those in Figure 12a. However, when only considering the 30 HII regions in this study, the N2 and O3N2 abundances show a slight negative gradient for Pdir against 12+log(O/H), whereas the S cal, Dopita et al. (2016) and direct method abundances show a slight positive gradient. We show the trends when using the available direct method abundances and when using the N2 index in Figures D1 and D2, respectively. We expect that the N2 and O3N2 indices are not a good measure of the oxygen abundance for these regions due to their dependence on the ionisation parameter, as discussed in Kewley et al. (2019a).
 |
Fig. D.1. Similar toFigure 12a, but with the available direct method oxygen abundances from J20 and McQuinn (2015) (11 HII regions within this study). |
 |
Fig. D.2. Similar to Figure 12a, but with the pressure components instead plotted against the oxygen abundance derived using the N2 index. |
All Tables
Properties of the 30 HII regions across the three dwarf galaxies in this sample.
All Figures
 |
Fig. 1. Three-colour composite images of the three dwarf galaxies (left: J0921, centre: KKH046, right: Leo P) collapsed across three arbitrary wavelength ranges and coloured blue (4650−5800 Å), green (5800−7000 Å), and red (7000−8200 Å). |
| In the text | |
 |
Fig. 2. Same as Fig. 1, except here red corresponds to [SII]λ6716, green to Hα, and blue to [OIII]λ5007 emission. |
| In the text | |
 |
Fig. 3. Hα emission maps of J0921 (left), KKH046 (centre), and Leo P (right), with the dendrogram structures identified in this work as HII regions outlined in red. Each HII region is labelled by a number on its right or via a line. |
| In the text | |
 |
Fig. 4. Classical emission line diagnostic diagrams of the HII regions defined in this paper. Theoretical maximum starburst lines plotted by the solid and dashed black lines are taken from literature (Kewley et al. 2001; Kauffmann et al. 2003, respectively). Low-metallicity photoionisation models from CLOUDY are also plotted, coloured by ionisation parameter (log U). |
| In the text | |
 |
Fig. 5. Portion of the MUSE spectrum of HII region 1 in KKH046 which covers the key nebular emission lines studied in this paper, with the PYSPECKIT Gaussian fit plotted in red. The hashed region indicates the AO notch filter. In the overlaying panel outlined in blue, we show a closer look at the Hβ and [OIII]λ4959, 5007 doublet lines. |
| In the text | |
 |
Fig. 6. Fractional error when using Eq. (2) to determine Lbol compared to the true Lbol for synthesised stellar populations with different cluster masses as a function of time. To create these synthesised populations, we used SLUG with the median metallicity, extinction, and electron density found for the HII regions in this sample. The solid lines indicate the median of 100 simulations and the shaded region indicates the spread between the fifth and 95th percentiles for each cluster stellar mass. The dashed black line shows where the IMF-averaged estimate given by Eq. (2) is equivalent to the true bolometric luminosity from SLUG, Lbol, SLUG. Above this line, Eq. (2) overestimates the true Lbol of these synthesised populations. |
| In the text | |
 |
Fig. 7. Oxygen abundances as determined from the strong-line calibration methods described in the Sect. 4.3 against the direct method oxygen abundance for ten regions in J0921 (from J20) and the Leo P HII region (taken from Skillman et al. 2013), with the single Leo P region having the lowest 12 + log(O/H)direct. The dashed black line indicates where the derived abundances are equivalent to the direct, temperature-based values. |
| In the text | |
 |
Fig. 8. Corner plot for KKH046 region 1 showing the 1D posterior probability distribution functions (PDFs) for the stellar mass (log M*), age (log T) and bolometric luminosity (log Lbol) of this region in the top, centre, and bottom right panels, respectively. The vertical solid and dashed lines indicate the median values and their 68% confidence interval (CI), respectively. The bottom left panels show the joint posterior PDFs, with the intensity indicating the probability density. The five crosses indicate the five best photometric matches in the library to the observed photometry. All PDFs are normalised to have unit integral. |
| In the text | |
 |
Fig. 9. Comparison plot for the two methods used to calculate the bolometric luminosity for the 30 HII regions in this sample, where for Lbol, IMF we have assumed a fully sampled IMF, and for Lbol, SLUG we have used the median of the posterior PDF returned by SLUG. The colours indicate the age of the regions, and the size of each point is a representation of their mass. The dashed black line indicates where these values are equivalent; points above this line show where Lbol, IMF is greater than Lbol, SLUG – that is to say, where assuming a fully sampled IMF with Eq. (2) overestimates the bolometric luminosity. The Leo P data point has been labelled for visual clarity. |
| In the text | |
 |
Fig. 10. Panel a: photoionisation pressure (Pion) and direct radiation pressure (Pdir) of the HII regions in various galaxies (see legend) plotted as a function of region size. The Pion values occupy the top half of the plot, and Pdir values the bottom half. SMC points are taken from Lopez et al. (2014), SMC N76 from McLeod et al. (in prep.), and the LMC points from McLeod et al. (2019). We note that uncertainties in the radii values are not given in the literature, and we therefore assume a generous 20%. We also plotted the median values from the PHANGS-MUSE survey as given in Barnes et al. (2021) by the grey diamond marker. The solid black lines indicate the linear best fits for Pion and Pdir, SLUG, with shaded grey areas for the 95% confidence regions. The dashed teal line and shaded area depict the linear fit when using Pdir, IMF. The black dotted line indicates the r−2 proportionality from Eq. (6) used to calculate Pdir. Panel b: correlation coefficient analysis for the Pdir, SLUG − log10(r) relation (see Sect. 7). The histogram shows the probability density distribution of the Pearson correlation coefficient using the bootstrapping and perturbation method from Curran (2014). The solid black line is the median correlation coefficient, C, found for this relation and the dashed lines show the 16th and 84th percentiles used to determine the uncertainty. |
| In the text | |
 |
Fig. 11. Pdir, IMF values for J0921 against their HII region radii with red star-shaped markers sized according to their stellar mass. The solid black line and shaded area indicate the Pdir, SLUG fit from Fig. 10a. The dashed red line and shaded area indicate the Pdir, IMF fit for the HII regions in J0921 only. |
| In the text | |
 |
Fig. 12. Panel a: similar to Fig. 10a, but with the pressure components plotted as a function of their oxygen abundance, 12 + log(O/H), with all markers coloured by their extinction and sized according to the HII region radii, where we take the median radii and extinction for the PHANGS data points (Barnes et al. 2021). Panel b: similar to panel a, but with only the 30 HII regions from the three dwarfs in this sample plotted against their cluster mass and coloured by their oxygen abundance. |
| In the text | |
 |
Fig. A.1. Panel (a) shows the Hα emission map of J0921, with each region coloured according to its radial velocity (not inclination-corrected due to the unknown inclination of the system). Red indicates regions moving away from us, and blue indicates regions moving towards us. Here we can see evidence that J0921 is rotating as a large body, as discussed in J20 and also illustrated in Marasco et al. (2023). Panel (b): Similar to (a), but regions are instead coloured by their oxygen abundance (using the S calibration) to indicate the spatial distribution of metals in J0921. Also plotted are the various galactic centres tested in this work, as listed in the text. |
| In the text | |
 |
Fig. A.2. Panel (a): Oxygen abundance against projected galactocentric distance for the 23 HII regions within J0921. Horizontal teal lines indicate the change in the position of each region when different galactic centres were used, and the shaded grey area shows the spread of metallicity gradients for the five galactic centres tested. The points plotted in red are for the fourth centre, which is the geometric centre of all pixels containing Hα emission above three standard deviations. Panel (b): Similar to panel (a) but with the direct method oxygen abundance for the ten regions from J20. |
| In the text | |
 |
Fig. B.1. Radial flux profile for KKH046 region 1. The dashed red line is the radius that encompasses 90% of the Hα emission and the solid black line is the radius returned by ASTRODENDRO. The horizontal line depicts where the flux profile reaches the background level, Fbl (median of the emission). This line was used to determine the uncertainty in the size of these regions, which we determined to be 20%. |
| In the text | |
 |
Fig. D.1. Similar toFigure 12a, but with the available direct method oxygen abundances from J20 and McQuinn (2015) (11 HII regions within this study). |
| In the text | |
 |
Fig. D.2. Similar to Figure 12a, but with the pressure components instead plotted against the oxygen abundance derived using the N2 index. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} n_{\rm e} = \frac{R_{\rm [SII]}-1.49}{5.6713-12.8\,R_{\rm [SII]}}\cdot \end{aligned} $$](/articles/aa/full_html/2024/05/aa48029-23/aa48029-23-eq41.gif)
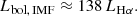
![$$ \begin{aligned}&N_2= \frac{F_{\rm [NII]\lambda 6548+\lambda 6584}}{F_{\rm H\beta }},\\&{S\!}_2= \frac{F_{\rm [SII]\lambda 6716+\lambda 6731}}{F_{\rm H\beta }},\\&R_3= \frac{F_{\rm [OIII]\lambda 4959+\lambda 5007}}{F_{\rm H\beta }}, \end{aligned} $$](/articles/aa/full_html/2024/05/aa48029-23/aa48029-23-eq43.gif)
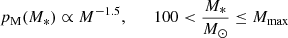
![$$ \begin{aligned}&p_{\rm T}(T) \propto T^{-0.5}, \qquad 10^6 < T\,[\mathrm{yr}] \le 10^7. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48029-23/aa48029-23-eq45.gif)