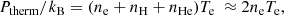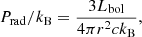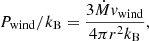| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202243766 | |
| Published online | 17 June 2022 | |
Letter to the Editor
Linking stellar populations to H II regions across nearby galaxies
I. Constraining pre-supernova feedback from young clusters in NGC 1672
1
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: ashleybarnes.astro@gmail.com
2
Ritter Astrophysical Research Center, The University of Toledo, Toledo, OH 43606, USA
3
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
4
Institut für Theoretische Astrophysik, Zentrum für Astronomie der Universität Heidelberg, Albert-Ueberle-Str 2, 69120 Heidelberg, Germany
5
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
6
The Observatories of the Carnegie Institution for Science, 813 Santa Barbara Street, Pasadena, CA 91101, USA
7
Departamento de Astronomía, Universidad de Chile, Camino del Observatorio 1515, Las Condes, Santiago, Chile
8
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
9
Department of Physics and Astronomy, University of Wyoming, Laramie, WY 82071, USA
10
TAPIR, California Institute of Technology, Pasadena, CA 91125, USA
11
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
12
Univ Lyon, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval, France
13
Research School of Astronomy and Astrophysics, Australian National University, Weston Creek, ACT 2611, Australia
14
International Centre for Radio Astronomy Research, University of Western Australia, 7 Fairway, Crawley, 6009 WA, Australia
15
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, 69120 Heidelberg, Germany
16
Department of Physics and Astronomy, University of California, Riverside, CA, USA
17
Department of Physics, University of Alberta, Edmonton, AB T6G 2E1, Canada
18
Gemini Observatory/NSF’s NOIRLab, 950 N. Cherry Avenue, Tucson, AZ 85719, USA
19
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
20
Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
21
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
22
Institute for Computational Cosmology, Department of Physics, University of Durham, South Road, Durham DH1 3LE, UK
23
Department of Physics, Tamkang University, No.151, Yingzhuan Road, Tamsui District, New Taipei City 251301, Taiwan
24
Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Cantoblanco, Spain
25
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
26
Department of Physics and Astronomy, Bloomberg Center for Physics and Astronomy, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
27
Space Telescope Science Institute, Baltimore, MD 21218, USA
Received:
12
April
2022
Accepted:
11
May
2022
Context. Stellar feedback is one of the fundamental factors regulating the evolution of galaxies. However, we still do not have access to strong observational constraints on the relative importance of the different feedback mechanisms (e.g. radiation, ionised gas pressure, stellar winds) in driving H II region evolution and molecular cloud disruption. To quantify and compare the different feedback mechanisms, the size of an H II region is crucial, whereas samples of well-resolved H II regions are scarce.
Aims. We constrain the relative importance of the various feedback mechanisms from young massive star populations by resolving H II regions across the disk of the nearby star-forming galaxy NGC 1672.
Methods. We combined measurements of ionised gas nebular lines obtained by PHANGS-MUSE, with high-resolution (PSF FWHM ∼ 0.1″; ∼10 pc) imaging from Hubble Space Telescope (HST) in both the narrow-band Hα and broad-band (NUV, U, B, V, I) filters. We identified a sample of 40 isolated, compact H II regions in the HST Hα image. We measured the sizes of these H II regions, which were previously unresolved in seeing-limited ground-based observations. In addition, we identified the ionisation source(s) for each H II region from catalogues produced as part of the PHANGS-HST survey. In doing so, we were able to link young stellar populations with the properties of their surrounding H II regions.
Results. The HST observations allowed us to resolve all 40 regions, with radii between 5 and 40 pc. The H II regions investigated here are mildly dominated by thermal or wind pressure, yet their elevation above the radiation pressure is within the expected uncertainty range. We see that radiation pressure provides a substantially higher contribution to the total pressure than previously found in the literature over similar size scales. In general, we find higher pressures within more compact H II regions, which is driven by the inherent size scaling relations of each pressure term, albeit with significant scatter introduced by the variation in the stellar population properties (e.g. luminosity, mass, age, metallicity).
Conclusions. For nearby galaxies, the combination of MUSE/VLT observations with stellar population and resolved Hα observations from HST provides a promising approach that could yield the statistics required to map out how the importance of different stellar feedback mechanisms evolve over the lifetime of a H II region.
Key words: H II regions / galaxies: evolution / galaxies: star clusters: general
© A. T. Barnes et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
High-mass stars (> 8 M⊙) are fundamental in driving the evolution of galaxies, due to the large amounts of energy and momentum (i.e. stellar feedback) that they inject into the interstellar medium (ISM) during their short lifetimes (e.g. Krumholz et al. 2014). Recent simulations (e.g. Dale et al. 2012, 2013; Raskutti et al. 2016; Gatto et al. 2017; Rahner et al. 2017, 2019; Kim et al. 2018, 2021a; Kannan et al. 2020; Jeffreson et al. 2021) and observational evidence (e.g. Grasha et al. 2018, 2019; Kruijssen et al. 2019; Chevance et al. 2020a,b; Kim et al. 2021b; McLeod et al. 2021; Barrera-Ballesteros et al. 2021a,b; Hannon et al. 2019, 2022) suggest that, in particular, feedback in the early, pre-supernovae (pre-SNe) stages of high-mass stars (i.e. within H II regions) plays a critical role in driving the evolution of both its local and larger scale environment. Hence, there has been considerable interest in observationally quantifying the impact of the various early (pre-SN) feedback mechanisms in H II regions (e.g. Pellegrini et al. 2011; Lopez et al. 2014; McLeod et al. 2019, 2021; Kruijssen et al. 2019; Chevance et al. 2022a,b; Olivier et al. 2021; Barnes et al. 2020, 2021).
The dynamics and expansion of H II regions may be driven by several possible sources of internal energy and momentum injection. A useful quantity to observationally constrain and compare these different feedback mechanisms is the pressure. For example, H II regions are filled with warm (Te ∼ 104 K) ionised hydrogen, which imparts an outward gas pressure (e.g. Spitzer 1978). This thermal pressure of this photoionised gas, Ptherm, is set by the ideal gas law:
where ne, nH, and nHe are the electron, H and He number densities, respectively; Te is the electron temperature and kB is the Boltzmann constant. Here, all He is assumed to be singly ionised. Constraints on the electron density, ne, can be obtained from e.g. a Strömgren sphere approximation with accurate measurements of the source radius, r, and ionisation rate, Q (ne ∝ r3/2; Stromgren 1939).
An additional source of feedback is the intense radiation field produced by young, massive stellar populations. Assuming the stellar population’s bolometric luminosity (Lbol) emerges in the UV or optical and that the photons are absorbed once at the H II region inner shell (for alternative see e.g. Krumholz & Matzner 2009; Draine 2011; Reissl et al. 2018), the volume-averaged direct radiation pressure is given as (e.g. Lopez et al. 2014):
where c is the speed of light.
Lastly, in their early evolutionary stages, high-mass stars produce strong stellar winds that can result in mechanical pressure within H II regions. The wind ram pressure is calculated as:
where Ṁ is the mass loss rate and vwind is the wind velocity (Sect. 4).
Based on the assumptions above, Barnes et al. (2021) recently assessed the magnitudes of feedback mechanisms acting within a sample of ∼6000 H II regions identified from the PHANGS-MUSE survey of 19 nearby (< 20 Mpc) star-forming main sequence spiral galaxies (Emsellem et al. 2022). However, in this work, the majority of the H II regions remained unresolved by the ∼50 − 100 pc resolution of the ground-based observations, only allowing for limits to be placed on the size of these H II regions. These broad uncertainties on size measurements and the lack of knowledge regarding the detailed morphology (such as broken shells, suggestive of a large escape fraction of ionising gas and winds), result in a large uncertainty (of about two orders of magnitude) in their pressure calculations. In this work, we directly address this uncertainty by introducing new size measurements from high-resolution HST data that are key for constraining the above pressure terms and apply them to a subsample of isolated, compact H II regions (see Fig. 1).
 |
Fig. 1. H II regions identified towards NGC 1672. The three colour images are composed of 814 nm, 555 nm, and 435 nm wideband filters from the HST (Jenkins et al. 2011; Lee et al. 2022); and in red, we display the HST continuum-subtracted 658 nm (Hα) narrow-band emission (Jenkins et al. 2011). Map of the galaxy disc overlaid with the boxes showing the positions of the H II region sample (upper left). Image cutouts for a subset of the H II regions (right and below). The region ID is shown in the upper left of each panel (Table A.1). Overlaid as a red contour is the boundary of each H II region (Sect. 3.1). At the lower left of each panel, we show a scale bar, and a circle denoting the approximate HST PSF size (0.1″, 9 pc). |
2. Observations of NGC 1672
We make use of HST and VLT/MUSE observations towards a single galaxy: NGC 1672 (see Emsellem et al. 2022; Lee et al. 2022 for survey overviews). NGC 1672 is a nearby (19.4 ± 2.9 Mpc; Anand et al. 2021), strongly-barred, and actively star-forming spiral galaxy. It is a good candidate for this initial study thanks to its high star formation rate (7.6 M⊙ yr−1; Leroy et al. 2021), which yields a large sample of H II regions to study, and moderate inclination (i ∼ 40°; Lang et al. 2020), which limits the effects of extinction and line-of-sight confusion.
2.1. HST
We make use of HST observations from Jenkins et al. (2011) and the PHANGS-HST survey (Lee et al. 2022). The PSF of these observations has a FWHM of ∼0.07−0.1″ (7 −9 pc) depending on the filter and the field of view (FOV) covers the majority of the galaxy disc.
Broad-band observations: We use observations taken with the F435W and F814W (I) filters on the Advanced Camera for Surveys (ACS) taken from project 10354 (Jenkins et al. 2011), and with the F275W (NUV),F336W (U), and F555W (V) filters using the Wide Field Camera 3 (WFC3; UVIS) taken as part of the PHANGS-HST treasury program 15654 (Lee et al. 2022). The PHANGS-HST UVIS and archival ACS data were both reduced as part of the PHANGS survey (see Lee et al. 2022).
Narrow/medium-band observations: We also include archival ACS observations using the F658N (i.e. including Hα) and F550M filters taken as part of project 10354. The narrow-band F658N map is continuum subtracted using an image formed from a combination of the F814W and F550M maps, appropriately scaled using their AB zero-points (see Hannon et al. 2022 for methods).
2.2. PHANGS-MUSE
We make use of VLT/MUSE observations from the PHANGS-MUSE survey (see Emsellem et al. 2022 for a complete discussion of the processing and reduction of the MUSE observations). The PSF of these observations has a FWHM of 0.96″ (90 pc), and the FOV is comparable to the HST observations. The MUSE Integral Field Unit provides a typical spectral resolution (FWHM) of ∼2.5 Å (or ∼100 km s−1) covering lines (e.g. Hα, Hβ, [S II]) within the spectral range 4800 − 9300 Å. In this Letter, we include properties (e.g. extinction corrected intensities) of individual H II regions measured from their integral spectra from MUSE, as presented in the ionised nebula catalogue from Santoro et al. (2022).
3. Properties of H II regions and their ionising sources
3.1. Properties of H II regions
We used the high-resolution continuum subtracted HST Hα map to resolve the structure of the H II regions identified in the PHANGS-MUSE nebula catalogue (Santoro et al. 2022; see Fig. 2). Based on the following criteria, we selected a sample of isolated 40 H II regions out of the 1581 nebulae identified across NGC 1672 in this catalogue (Fig. 1) which:
-
(i)
Meet the BPT and Hα velocity dispersion criteria to be classified as a H II region (e.g. see Barnes et al. 2021);
-
(ii)
Are sufficiently isolated such that they dominate the emission in MUSE line maps, which are clearly uncontaminated by other sources, based on a manual inspection of the maps;
-
(iii)
Contain a single H II region with a compact morphology in the HST Hα map, which has an apparent circular or simple shell-like profile in the image;
-
(vi)
Are spatially resolved (i.e. more extended than the PSF FWHM) in the HST Hα map, so that we can make a direct measurement of the radius1.
 |
Fig. 2. Comparison between the HST and MUSE observations towards one of the H II regions in our sample. HST Hα narrowband emission overlaid with a contour outlining the isophotal boundary as defined from our dendrogram analysis, shown on the left. We show the intensity-weighted second order moment of the structure within this boundary as a dashed ellipse, which we use to define the radius of the H II region (Sect. 3.1). A star marks the position of the identified ionising stellar population (Sect. 3.2). The region ID is shown in the upper left (Table A.1). Hα emission observed with MUSE (Emsellem et al. 2022), overlaid with white contours showing the boundaries of sources identified as part of the nebula catalogue from Santoro et al. (2022), shown on the right. In the lower right of each panel, we show a scale bar and a circle denoting the approximate PSF size. |
Our regions appear in the HST Hα images as discrete, well-defined sources. To measure their sizes, we measured the noise in the Hα images from a 5″ cutout around each H II MUSE region, and assigned the contiguous region of pixels with S/N > 5 to represent the H II region (see the red contours in Figs. 1 and 2). Then we measured their radius (r) by taking the geometric mean of the intensity-weighted spatial second moment using the Hα intensity and assigned pixels (i.e. mean of the semi-major and semi-minor axis of ellipse shown in Fig. 2)2. This radius approximately corresponds to the inner portion of the H II region shell for extended sources, or one standard deviation around the peak of compact sources (see Fig. 2). This definition is physically motivated given that for H II regions with shell-like morphologies, the centre is likely devoid of gas. To estimate the feedback process that is dominating their expansion, we compared the pressures at the inner edge of the shell (see Sect. 4). Comparisons between the measured size and flux radial profile for each H II region suggest that, depending on geometry, the uncertainties in our radius measurements are no greater than 50%.
3.2. Properties of ionising sources
We used broad-band HST imaging to determine the stellar sources responsible for the ionisation of each H II region. These sources are typically close to the centre of each H II region. We assume that even the most compact H II regions in our sample are being ionised by a young stellar population rather than by an individual massive star. This is justified as the Hα luminosity completeness limit in the MUSE nebula catalogue for NGC 1672 is ∼1037 erg s−1, which is higher than what can be produced by a single massive (e.g. O7V) star (see Santoro et al. 2022).
We followed the general procedure described in Turner et al. (2021) to estimate the age and mass of each ionising stellar population; in other words, we used aperture photometry in each band performed through the PHANGS-HST pipeline using a 4-pixel radius (which is large enough to capture most of the light from a cluster, yet small enough to avoid much contamination from nearby sources in crowded regions). The pipeline applies an aperture correction to each filter determined from several isolated stellar populations, as described in Deger et al. (2022). After correcting for the foreground extinction based on a Milky Way extinction law (Fitzpatrick 1999) and the foreground value given in NED, we fit the measured magnitudes with those predicted by the Bruzual & Charlot (2003) population synthesis models, assuming solar metallicity and a Chabrier stellar initial mass function (IMF; Chabrier 2003). Predictions from the solar metallicity model provide a better overall fit than those from other metallicities to the measured broad-band colors of very young clusters (the ionising sources of H II regions) in NGC 1672, consistent with the mean H II region value of 12 + log(O/H) ≈ 8.56 measured from the MUSE spectra. The age estimates are mostly unchanged if we assume the 1/2× solar metallicity model instead. We perform spectral energy distribution fitting using the publicly available CIGALE fitting package (e.g. Boquien et al. 2019) to determine the best combination of age and local reddening (assuming a Galactic extinction law; Fitzpatrick 1999) for each stellar population (Turner et al. 2021). The predicted mass-to-light ratio and extinction-corrected luminosity give an estimate of the stellar population mass.
We find the ionising sources all have estimated ages younger than 5 Myr (i.e. pre-SN feedback), and stellar masses in the range from 103 to 105 M⊙. Based on previous experiments, uncertainties in the age and mass of each young stellar population is approximately Δlog10(t)≈Δlog10(M)≈0.3 dex, that is, a factor of ∼2 (e.g. Chandar et al. 2010). In addition to these uncertainties, the lowest mass stellar populations within our sample (< 104 M⊙) may suffer from stochastic sampling effects of the IMF (e.g. Krumholz et al. 2019). However, there is a limit to how deficient low mass clusters could be in high mass stars while still producing enough ionising radiation to produce a detectable H II region, and all the H II regions within our sample sit above this (bolometric luminosity) threshold; namely, where stochastic effects are less significant (Lbol > 1039 erg s−1; da Silva et al. 2012).
4. Pressure calculations
We determined Ptherm (Eq. (1)) using values of the electron temperature (Te) based on the MUSE nitrogen auroral lines finding a range of 7000–11 000 K or, for the 20 H II regions without a significant Te measurement (i.e. where the auroral N II emission is too faint to be detected), we adopted a value of Te = 8000 K, corresponding approximately to the mean value of all H II regions in NGC 1672 with well-determined temperatures. We estimated the electron density assuming a smooth, spherical geometry as 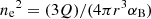 , where Q is the ionisation rate (also determined using MUSE) and αB is the temperature-dependent case B recombination coefficient, which is taken from Ferland et al. (1992). Here,
, where Q is the ionisation rate (also determined using MUSE) and αB is the temperature-dependent case B recombination coefficient, which is taken from Ferland et al. (1992). Here, 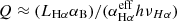 , where the effective recombination coefficient (i.e. the rate coefficient for recombinations resulting in the emission of an Hα photon) is
, where the effective recombination coefficient (i.e. the rate coefficient for recombinations resulting in the emission of an Hα photon) is  cm3 s−1 (Osterbrock & Ferland 2006); νHα is the frequency of the Hα emission line; and h is the Planck constant. For comparison, for the five sources for which we can derive a reliable estimate of ne from the [S II] emission line ratio, we find that ne([S II]) > ne(r) by factors of ∼2–3, which is expected given that the H II regions show clumpy sub-structure (see discussion in Barnes et al. 2021). Given this bias, we use only our spherical geometry estimates of the electron density in our calculations of Ptherm.
cm3 s−1 (Osterbrock & Ferland 2006); νHα is the frequency of the Hα emission line; and h is the Planck constant. For comparison, for the five sources for which we can derive a reliable estimate of ne from the [S II] emission line ratio, we find that ne([S II]) > ne(r) by factors of ∼2–3, which is expected given that the H II regions show clumpy sub-structure (see discussion in Barnes et al. 2021). Given this bias, we use only our spherical geometry estimates of the electron density in our calculations of Ptherm.
To calculate Prad (Eq. (2)), we compute Lbol following Barnes et al. (2021, see their Fig. 7), where we used STARBURST99 models (Leitherer et al. 1999) to determine a relation between the age of the stellar population (t) and Lbol/LHα, where LHα is the extinction corrected Hα luminosity from the MUSE observations.
To calculate Pwind (Eq. (3)), we estimate the wind velocity as, vwind = (2Lmech/Ṁ)0.5, where Lmech is the mechanical luminosity. Both Lmech and Ṁ taken from STARBURST99 models (Leitherer et al. 1999), where they vary as a function of the stellar population mass (M) and age (t) (see e.g. Fig. 8 Barnes et al. 2021). To constrain Lmech and Ṁ and, hence, determine Pwind for each H II region, we make use of the stellar population M and t determined from the HST broadband maps (Sect. 3.2).
It is worth noting that Eqs. (1)–(3) intrinsically impose a radial dependence on all the pressure terms, and, in addition, both Ptherm and Prad also depend on the Hα luminosity. We discuss this in more detail when interpreting the correlated axes in the plots of the following section.
5. Discussion and summary
We investigated how the different pressure terms vary as a function of the determined H II region properties (Fig. 3) and we find that in most cases, either thermal pressure (median 105.74 K cm−3) or wind ram pressure (105.71 K cm−3) is mildly dominant. The radiation pressure is typically lower (105.47 K cm−3), albeit within an uncertainty of around 2 on these measurements. These results are in broad agreement with those in the literature made for H II regions with sizes up to 10 pc (e.g. Lopez et al. 2011; Rahner et al. 2017; McLeod et al. 2019, 2020). Interestingly, however, the direct radiation pressure determined here for NGC 1672 provides a substantially higher contribution to the total pressure than previous sources studied in the literature (e.g. LMC/SMC, NGC 300; Lopez et al. 2014; McLeod et al. 2021). This could be a result of our sample bias toward luminous and compact H II regions within this actively star-forming galaxy (7.6 M⊙ yr−1; Leroy et al. 2021), or differences in H II region properties (e.g. metallicity).
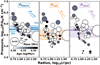 |
Fig. 3. Distribution of the pressures due to the various feedback mechanisms as a function of H II region radius, as well as stellar population mass (circle size) and age (circle colour). We show a key for the size (i.e. mass) and a colour bar denoting the age at the bottom of the left panel. The horizontal lines show the 25, 50 (median), and 75 percentiles for each pressure. The intrinsic relations of each pressure term are shown as a short dashed line in the upper right of each panel. |
Figure 3 also shows a trend towards increasing pressure with decreasing radius. In other words, smaller H II regions are typically more highly pressurised. However, by definition (Sect. 4), the pressure terms are not independent of the radius (see intrinsic relations shown as dashed lines in Fig. 3). The significant observed scatter away from these simple power-law dependencies may then be introduced by the variation in the stellar population properties (e.g. luminosity). We see that trends with the mass (i.e. circle size in Fig. 3) or age (circle colour) of the ionising stellar population responsible for the H II regions are, however, less clear than with size. There is tentative evidence for a correlation between the stellar population age and Pwind, with older stellar populations having lower pressures for the same radius and mass.
We expect that the radius and luminosity of the H II regions are correlated as r ∝ Q1/3 ∝ 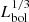 for a constant ne (e.g. Stromgren 1939). This could complicate our interpretation of how the H II regions evolve through the r − P parameter space; namely, for fixed age and ne, a more luminous stellar population will produce a larger H II region. Normalising r by
for a constant ne (e.g. Stromgren 1939). This could complicate our interpretation of how the H II regions evolve through the r − P parameter space; namely, for fixed age and ne, a more luminous stellar population will produce a larger H II region. Normalising r by 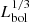 accounts for differences in ionising photon production between regions without assuming a single representative value of ne, which our observations show varies from region to region. We see a tight correlation between r/
accounts for differences in ionising photon production between regions without assuming a single representative value of ne, which our observations show varies from region to region. We see a tight correlation between r/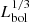 and P for all terms (Fig. 4). Moreover, we find weak trends that for a given r/
and P for all terms (Fig. 4). Moreover, we find weak trends that for a given r/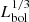 and mass, younger H II regions appear to have systematically higher P (again this is most evident for Pwind).
and mass, younger H II regions appear to have systematically higher P (again this is most evident for Pwind).
 |
Fig. 4. Pressures from the various feedback mechanisms as a function of radius normalised to the bolometric luminosity from the ionising stellar population. We show a key for the size (i.e. mass) and a colour bar denoting the age in the left panel. |
We also investigate how the local environment affects the various feedback mechanisms. Figure 5 shows the pressures as a function of the galactocentric radius (Rgal). We see a weak trend of increased pressure at higher Rgal. These higher pressures correlate with a weak decrease in the metallicity or an increase in extinction. The increase of Ptherm and Prad with Rgal could be due to higher photon fluxes from lower metallicity stellar populations (cf. McLeod et al. 2021). The increase in Pwind at lower metallicity is, however, not expected (e.g. Kudritzki 2002), but more data is needed to further explore this trend.
 |
Fig. 5. Distribution of the pressures due to the various feedback mechanisms as a function of galactocentric radius (normalised to the effective radius of 3.5 kpc; Leroy et al. 2021), as well as extinction (size) and metalicity (colour). We show a key for the size (i.e. extinction) reference of each data point and a colour bar denoting the metalicity at the bottom of the left panel. The overlaid lines and shaded area show the mean and standard deviation of the data within equally spaced bins. |
We compare the pressures determined in this work to those estimated in the literature (Fig. 6). Here, we compare only the thermal (shown in blue) and radiation (shown in orange) pressure terms, which are typically calculated in a similar manner as in this work. We see that the pressures determined here are consistent with those in the literature. In Fig. 6, we also indicate the size-pressure relations from Olivier et al. (2021), for which the Prad ∝ R−0.74 and Ptherm ∝ R−1.36 appear to be in good agreement with both our literature compilation and measured values3. These relations are traversed at sizes similar to our smallest H II region (∼5 pc). Therefore, we are probing an interesting part of parameter space, where the single scattering radiation pressure and thermal pressure of ionised gas make comparable (to within a factor of a few) contributions to the expansion of H II regions.
 |
Fig. 6. Thermal (left panel) and direct radiation (right panel) pressure terms. Coloured points are H II regions studied in this work, grey points are measurements from the literature (Lopez et al. 2014; McLeod et al. 2019, 2020, 2021; Barnes et al. 2020; Olivier et al. 2021), and the contours show the upper and lower limits for all galaxies studied by Barnes et al. (2021). The dashed lines show the power law relations from Olivier et al. (2021). |
In the lower-left panels of Fig. 6 we also show a representative uncertainty range spanned by the limits calculated just using ground-based observations (Barnes et al. 2021), which can be compared to the error range of the estimates from this work. The order of magnitude reduction error is primarily due to the inclusion of the resolved size measurements from the HST Hα maps, which all the pressure terms depend on to a large extent. An additional gain is also achieved by the inclusion of the stellar population information, which is included within all the pressure terms. Specifically, the stellar population age associated with each H II region is used (with the extinction corrected Hα luminosity from MUSE) to determine its bolometric luminosity that is used in the calculation of Ptherm and Prad, and both the stellar population age and mass are to infer the mechanical luminosity and mass loss rate that are used in the calculation of Pwind.
In summary, we demonstrate in this Letter that, altogether, HST and MUSE significantly improved our constraints on the feedback pressures dominating within H II regions across nearby galaxies (cf. Fig. 3). This represents an important step in directly connecting how young stars destroy their host environments, which can, in the future, be expanded to larger samples of H II regions and in a greater number of galactic environments, and provide a statistical benchmark for the inclusion of pre-SNe stellar feedback in theory and simulations; for instance, from resolved planet, disc, and star formation simulations to large-scale galaxy dynamic and evolution simulations, as well as cosmological simulations.
We can robustly measure sizes that are fractions of a pixel broader than the PSF. For example, the Ishape software (Larsen 1999) can reliably measure the radii of compact sources with good S/N that are only ∼0.2 pix broader than the PSF, which is less than 1 pc at the distance of NGC 1672.
We carry out these calculations using the ASTRODENDRO software, though we do not use the full hierarchical information (see Rosolowsky et al. 2008), only the outer contour.
We note that the range of bolometric luminosities of the H II regions studied in this work (105.5 − 7.3 L⊙) are at the upper end of the range from the Olivier et al. (2021) sample (103.5 − 6.4 L⊙).
Acknowledgments
We would like to thank the referee for their constructive feedback that helped improve the quality of this paper. This work was carried out as part of the PHANGS collaboration, based on observations collected at the European Southern Observatory under ESO programmes 1100.B-0651 (PHANGS–MUSE; PI Schinnerer). ATB and FB would like to acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 726384/Empire). MB gratefully acknowledges support by the ANID BASAL project FB210003 and from the FONDECYT regular grants 1211000. RSK & SCOG acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) via SFB 881 ‘The Milky Way System’ (subprojects A1, B1, B2 and B8) and from the Heidelberg Cluster of Excellence STRUCTURES in the framework of Germany’s Excellence Strategy (grant EXC-2181/1 – 390900948). They also acknowledge support from the European Research Council in the ERC synergy grant ‘ECOGAL’ Understanding our Galactic ecosystem: From the disk of the Milky Way to the formation sites of stars and planets’ (project ID 855130). HAP acknowledges support by the Ministry of Science and Technology of Taiwan under grant 110-2112-M-032-020-MY3. EC acknowledges support from ANID project Basal AFB-170002. MC and JMDK gratefully acknowledge funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (grant number KR4801/1-1), as well as from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme via the ERC Starting Grant MUSTANG (grant agreement No. 714907). KK, FS and OE gratefully acknowledge funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (grant No. KR4598/2-1, PI Kreckel). ES and TGW acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694343).
References
- Anand, G. S., Lee, J. C., Van Dyk, S. D., et al. 2021, MNRAS, 501, 3621 [Google Scholar]
- Barnes, A. T., Longmore, S. N., Dale, J. E., et al. 2020, MNRAS, 498, 4906 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, A. T., Glover, S. C. O., Kreckel, K., et al. 2021, MNRAS, 508, 5362 [NASA ADS] [CrossRef] [Google Scholar]
- Barrera-Ballesteros, J. K., Sánchez, S. F., Heckman, T., et al. 2021a, MNRAS, 503, 3643 [NASA ADS] [CrossRef] [Google Scholar]
- Barrera-Ballesteros, J. K., Heckman, T., Sánchez, S. F., et al. 2021b, ApJ, 909, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chandar, R., Whitmore, B. C., Kim, H., et al. 2010, ApJ, 719, 966 [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Vazquez-Semadeni, E., et al. 2020a, Space Sci. Rev., 216, 50 [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Hygate, A. P. S., et al. 2020b, MNRAS, 493, 2872 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Krumholz, M. R., et al. 2022a, MNRAS, 509, 272 [Google Scholar]
- Chevance, M., Krumholz, M. R., McLeod, A. F., et al. 2022b, ArXiv e-prints [arXiv:2203.09570] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2012, MNRAS, 424, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2013, MNRAS, 430, 234 [Google Scholar]
- da Silva, R. L., Fumagalli, M., & Krumholz, M. 2012, ApJ, 745, 145 [CrossRef] [Google Scholar]
- Deger, S., Lee, J. C., Whitmore, B. C., et al. 2022, MNRAS, 510, 32 [Google Scholar]
- Draine, B. T. 2011, ApJ, 732, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Peterson, B. M., Horne, K., Welsh, W. F., & Nahar, S. N. 1992, ApJ, 387, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Gatto, A., Walch, S., Naab, T., et al. 2017, MNRAS, 466, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Grasha, K., Calzetti, D., Bittle, L., et al. 2018, MNRAS, 481, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Grasha, K., Calzetti, D., Adamo, A., et al. 2019, MNRAS, 483, 4707 [NASA ADS] [CrossRef] [Google Scholar]
- Hannon, S., Lee, J. C., Whitmore, B. C., et al. 2019, MNRAS, 490, 4648 [NASA ADS] [CrossRef] [Google Scholar]
- Hannon, S., Lee, J. C., Whitmore, B. C., et al. 2022, MNRAS, 512, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreson, S. M. R., Krumholz, M. R., Fujimoto, Y., et al. 2021, MNRAS, 505, 3470 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, L. P., Brandt, W. N., Colbert, E. J. M., et al. 2011, ApJ, 734, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kannan, R., Marinacci, F., Simpson, C. M., Glover, S. C. O., & Hernquist, L. 2020, MNRAS, 491, 2088 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2018, ApJ, 859, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Ostriker, E. C., & Filippova, N. 2021a, ApJ, 911, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J., Chevance, M., Kruijssen, J. M. D., et al. 2021b, MNRAS, 504, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Schruba, A., Chevance, M., et al. 2019, Nature, 569, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Matzner, C. D. 2009, ApJ, 703, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Bate, M. R., Arce, H. G., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 243 [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, P., Meidt, S. E., Rosolowsky, E., et al. 2020, ApJ, 897, 122 [CrossRef] [Google Scholar]
- Larsen, S. S. 1999, A&AS, 139, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J. C., Whitmore, B. C., Thilker, D. A., et al. 2022, ApJS, 258, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., Prochaska, J. X., & Ramirez-Ruiz, E. 2011, ApJ, 731, 91 [Google Scholar]
- Lopez, L. A., Krumholz, M. R., Bolatto, A. D., et al. 2014, ApJ, 795, 121 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Dale, J. E., Evans, C. J., et al. 2019, MNRAS, 486, 5263 [Google Scholar]
- McLeod, A. F., Kruijssen, J. M. D., Weisz, D. R., et al. 2020, ApJ, 891, 25 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A. F., Ali, A. A., Chevance, M., et al. 2021, MNRAS, 508, 5425 [NASA ADS] [CrossRef] [Google Scholar]
- Olivier, G. M., Lopez, L. A., Rosen, A. L., et al. 2021, ApJ, 908, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei, (Sausalito: University Science Books) [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., & Ferland, G. J. 2011, ApJ, 738, 34 [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2017, MNRAS, 470, 4453 [NASA ADS] [CrossRef] [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2019, MNRAS, 483, 2547 [NASA ADS] [CrossRef] [Google Scholar]
- Raskutti, S., Ostriker, E. C., & Skinner, M. A. 2016, ApJ, 829, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Reissl, S., Klessen, R. S., Mac Low, M.-M., & Pellegrini, E. W. 2018, A&A, 611, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [Google Scholar]
- Santoro, F., Kreckel, K., Belfiore, F., et al. 2022, A&A, 658, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium, (New York: Wiley) [Google Scholar]
- Stromgren, B. 1939, ApJ, 89, 526 [CrossRef] [Google Scholar]
- Turner, J. A., Dale, D. A., Lee, J. C., et al. 2021, MNRAS, 502, 1366 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Sample properties and data
In table A.1, we summarise the properties of the H II region sample studied in this work.
Properties of the H II region sample.
Science-level MUSE mosaicked datacubes and high-level analysis products (e.g. emission line fluxes) are provided via the ESO archive phase 3 interface.4 A full description of the first PHANGS-MUSE data release is presented in Emsellem et al. (2022). Science-level HST broadband images and higher-level data products are available in the MAST archive,5. A full description of the first PHANGS-HST data release is presented in Lee et al. (2022). The HST Hα images are publicly available in the Hubble Legacy Archive.6
All Tables
All Figures
 |
Fig. 1. H II regions identified towards NGC 1672. The three colour images are composed of 814 nm, 555 nm, and 435 nm wideband filters from the HST (Jenkins et al. 2011; Lee et al. 2022); and in red, we display the HST continuum-subtracted 658 nm (Hα) narrow-band emission (Jenkins et al. 2011). Map of the galaxy disc overlaid with the boxes showing the positions of the H II region sample (upper left). Image cutouts for a subset of the H II regions (right and below). The region ID is shown in the upper left of each panel (Table A.1). Overlaid as a red contour is the boundary of each H II region (Sect. 3.1). At the lower left of each panel, we show a scale bar, and a circle denoting the approximate HST PSF size (0.1″, 9 pc). |
| In the text | |
 |
Fig. 2. Comparison between the HST and MUSE observations towards one of the H II regions in our sample. HST Hα narrowband emission overlaid with a contour outlining the isophotal boundary as defined from our dendrogram analysis, shown on the left. We show the intensity-weighted second order moment of the structure within this boundary as a dashed ellipse, which we use to define the radius of the H II region (Sect. 3.1). A star marks the position of the identified ionising stellar population (Sect. 3.2). The region ID is shown in the upper left (Table A.1). Hα emission observed with MUSE (Emsellem et al. 2022), overlaid with white contours showing the boundaries of sources identified as part of the nebula catalogue from Santoro et al. (2022), shown on the right. In the lower right of each panel, we show a scale bar and a circle denoting the approximate PSF size. |
| In the text | |
 |
Fig. 3. Distribution of the pressures due to the various feedback mechanisms as a function of H II region radius, as well as stellar population mass (circle size) and age (circle colour). We show a key for the size (i.e. mass) and a colour bar denoting the age at the bottom of the left panel. The horizontal lines show the 25, 50 (median), and 75 percentiles for each pressure. The intrinsic relations of each pressure term are shown as a short dashed line in the upper right of each panel. |
| In the text | |
 |
Fig. 4. Pressures from the various feedback mechanisms as a function of radius normalised to the bolometric luminosity from the ionising stellar population. We show a key for the size (i.e. mass) and a colour bar denoting the age in the left panel. |
| In the text | |
 |
Fig. 5. Distribution of the pressures due to the various feedback mechanisms as a function of galactocentric radius (normalised to the effective radius of 3.5 kpc; Leroy et al. 2021), as well as extinction (size) and metalicity (colour). We show a key for the size (i.e. extinction) reference of each data point and a colour bar denoting the metalicity at the bottom of the left panel. The overlaid lines and shaded area show the mean and standard deviation of the data within equally spaced bins. |
| In the text | |
 |
Fig. 6. Thermal (left panel) and direct radiation (right panel) pressure terms. Coloured points are H II regions studied in this work, grey points are measurements from the literature (Lopez et al. 2014; McLeod et al. 2019, 2020, 2021; Barnes et al. 2020; Olivier et al. 2021), and the contours show the upper and lower limits for all galaxies studied by Barnes et al. (2021). The dashed lines show the power law relations from Olivier et al. (2021). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.