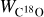EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 663 (July 2022) A&A, 663 (2022) A82 Full HTML
Open Access

This article has an erratum: [https://doi.org/10.1051/0004-6361/202142713e]

Issue
A&A
Volume 663, July 2022
Article Number A82
Number of page(s) 15
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202142713
Published online 18 July 2022

© Y. Gong et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Open Access funding provided by Max Planck Society.

1 Introduction

Turbulence plays an important role in controlling star formation (e.g., Elmegreen & Scalo 2004). Observations suggest that molecular clouds show supersonic line widths, which are always interpreted as a sign of supersonic turbulence (e.g., Zuckerman & Palmer 1974). Further studies have established an empirical size-line width relationship which is widely known as the Larson’s relation (Larson 1981), and the relationship is revised to be σ ∝ R0.5 (σ is the velocity dispersion and R is the cloud radius, e.g., Heyer et al. 2009). This suggests that turbulence energy will decay with decreasing scales. Based on the scale-dependent turbulence energy cascade processes, we would expect to detect (sub)sonic motions at small scales (e.g., McKee & Ostriker 2007). Such sonic motions at a typical scale of ~0.1 pc have been detected in the so-called “coherent cores” where stars are born (e.g., Goodman et al. 1998; Pineda et al. 2010). More recent studies have shown that such sonic motions can appear on a larger scale (e.g., Hacar & Tafalla 2011; Tafalla & Hacar 2015; Hacar et al. 2017; Gong et al. 2018; Li et al. 2020) with an extreme case up to 6.5 pc (Hacar et al. 2016); this is where all large-scale sonic motions have been found in the dense filamentary structures. It remains to be seen whether large-scale (sub)sonic motions may be present in different environments or not. Furthermore, the reason for the formation of large-scale (sub)sonic turbulence remains inconclusive. Large-scale mappings of nearby molecular clouds provide enough information to tackle these questions.

2 Oph N1 as a Nearby Quiescent Cloud

Ophiuchus North 1 (Oph N1) is selected to investigate the turbulence properties in this study. Based on stellar photometric data with Gaia DR2 parallax measurements, the distance to Oph N1 is found to be 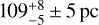109−5+8±5 pc$109_{- 5}^{ + 8} \pm 5\,{\rm{pc}}$ (Zucker et al. 2020), and a distance of 110 pc is adopted in this work. Because of its proximity, this cloud can be well resolved even by single-dish telescopes, allowing for in-depth investigations of the physics of interstellar turbulence. Oph N1, also known as L260, is a part of Ophiuchus North (Nozawa et al. 1991; Tachihara et al. 2000, 2002; Hatchell et al. 2012), where molecular clouds were first mapped in the J = 1−0 transition of 12C16O (hereafter CO) with the 1.2 m Columbia University Sky Survey Telescope (denoted Complex 4 in de Geus et al. 1990), revealing a filamentary structure. The molecular cloud complex shows as a dark patch on the Hα nebula, indicating that this cloud is situated at the edge of the Sh 2−27 Hii region around an O9.5V runaway star ζ Oph (Hubrig et al. 2011), which is located at 113 pc (e.g., van Leeuwen 2007), strongly suggesting that the Hii region ionized by ζ Oph is physically associated with the molecular clouds in Ophiuchus North.

Figure 1 presents an overview of the Ophiuchus North region where the Stockert-25m 11 cm continuum emission mainly arises from the free-free emission of the extended Hii region Sh 2−27, the IRAS 100 μm emission is mainly attributed to cold dust emission and the WISE 12 μm emission is dominated by hot dust emission. Oph N l presents a cometary head-tail morphology projected on the periphery of the extended Hii region Sh 2−27. Oph N l appears to protrude more deeply into the Sh 2−27 Hii region than L134E and OphN2. Such a protruding morphology is commonly observed in irradiated structures (e.g., White et al. 1997; Schneider et al. 2016; Su et al. 2020), thus, the morphology further supports the existence of an interaction between Oph N l and Sh 2–27.

The Ophiuchus North region has also been mapped in CO isotopic lines with the 4 m millimeter telescope of the Nagoya University (Nozawa et al. 1991; Tachihara et al. 2000). Their observations suggest that star formation in Oph N l is inactive in contrast to the ρ Oph cloud core and most of 12C180 (hereafter C180) cores are starless. Hence, gas properties are less affected by internal stellar feedback. Two Planck Galactic cold clumps, G008.52+21.84 and G008.67+22.14, were found in Oph Ν 1 (Planck Collaboration XXIII 2011 ; Planck Collaboration XXVIII 2016). Higher angular resolution observations of sub-millimeter continuum emission resolve G008.67+22.14 into two dense cores, L260-SMM1 and L260-SMM2 (e.g., Visser et al. 2002). L260-SMM1, also denoted SCO 01 in Mottram et al. (2017), was found be a Class I protostar associated with outflows (Bontemps et al. 1996; Visser et al. 2002; Hatchell et al. 2012), but was reclassified to be a Class II protostar without associated outflows (Mottram et al. 2017). Its submilimeter emission is likely dominated by its disk with a mass of <0.05 Μ⊙ (e.g., Visser et al. 2002). L260-SMM2 is a starless core with a mass of ~10 Μ⊙ (e.g., Visser et al. 2002; Hatchell et al. 2012), which is confirmed by Spitzer nondetection of 70 μm emission. Both Planck cold clumps are found to show quite narrow line widths of ~0.4 km s−1 in either C18O (J = 1−0) or NH3 (2, 2) (Wu et al. 2012; Benson & Myers 1989), demonstrating low levels of turbulence. However, the large-scale turbulence properties of Oph N l have been poorly explored. This is why we have carried out dedicated observations to characterize the dynamics of this cloud in detail.

Our observations are described in Sect. 3. In Sect. 4, we report our discoveries. The results are discussed in Sect. 5. Our summary and conclusions are presented in Sect. 6.

thumbnail Fig. 1

Three-color composite image of the Stockert-25m 11 cm (red; Reif et al. 1987), IRAS 100 μm (green; Miville-Deschênes & Lagache 2005), and the WISE 12 μπι (blue; Wright et al. 2010) emission toward Ophiuchus North. The Sh 2-27 Hii region is ionized by ζ Oph that is indicated by the black cross. The observed region Oph Nl is indicated by the white dashed box, while the other regions are indicated by the white solid boxes.

3 Observations and Data Reduction

3.1 PMO-13.7 m Observations

Because of their high abundances and low critical densities, the J= 1−0 transitions of 12CO, 13CO, and C18O are ideal tracers of the large-scale gas distribution of molecular clouds. Since C18O (J= 1−0) has lower opacities than the other two, it is best suited to investigate the turbulence properties in Oph Nl. We carried out simultaneous imaging observations of CO (J = 1−0) and C18O (J = 1 −0) toward Oph Ν 1 with the Purple Mountain Observatory 13.7m (PMO-13.7 m) telescope during 2021 May 31 June 30 (project code: 21A011). We used 3×3 beam sideband separation Superconducting Spectroscopic Array Receiver as the front end and fast Fourier transform spectrometers (FFTSs) as the back ends (Shan et al. 2012). Then, FFTSs with instantaneous bandwidths of 1 GHz and 200 MHz were used to record the CO (J= 1−0) and C180 (J= 1−0) signals, respectively. Each FFTS consists of 16,384 channels, and the resulting channel widths are 61.0 kHz and 12.2 kHz for the two FFTS modes. The corresponding velocity spacings are 0.16 km s−1 and 0.03 km s−1 at the rest frequencies of CO (J= 1−0) and C18O (J= 1−0) for the two FFTS modes, respectively. The on-the-fly method was employed to map Oph N l at a scanning rate of 50″ s−1 and a dump time of 0.3 s (Sun et al. 2018). The mapping was performed alternatively along the right ascension and declination directions in order to reduce striping effects. These observations took about 80 hours in total.

The standard chopper wheel method was used for calibrations and correcting the atmospheric attenuation (Ulich & Haas 1976). The antenna temperature, 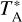TA*$T_{\rm{A}}^*$, was converted to the main beam temperature, Tmb, by applying the relation, 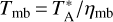Tmb=TA*/ηmb${T_{{\rm{mb}}}} = T_{\rm{A}}^*/{\eta _{{\rm{mb}}}}$, where ηmb is the main beam efficiency. Then, ηmb is taken to be 49% and 54% for CO (J= 1−0) and C180 (J= 1−0) according to the telescope’s status report1. The half-power beam widths (HPBWs) are 46″ and 50″ for CO (J = 1−0) and C180 (J = 1−0), respectively. Pointing accuracy is within 5″. The uncertainties of the absolute flux calibration are assumed to be 10% in this work. During the observations, the typical system temperatures were 315-390 Κ and 141–221 Κ on a 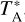TA*$T_{\rm{A}}^*$ scale for CO (J= 1−0) and C180 (J= 1−0), respectively. The median rms noise levels are 0.10 Κ at a channel width of 0.16 km s−1 for CO (J= 1−0) and 0.28 Κ at a channel width of 0.03 km s−1 for C180 (J= 1−0). The C180 (J = 1−0) spectra were binned to a channel width of 0.05 km s−1 in order to improve the signal-to-noise ratios of the resulting effective channels. Throughout this paper, velocities are given with respect to the local standard of rest (LSR) while the rest frequencies of CO (7 = 1−0) and C18O (7 = 1−0) are set to be 115271.202 MHz and 109782.173 MHz (Müller et al. 2005).

The spectra were reduced with the GILDAS software (Pety 2005), and a first-order baseline was subtracted from each spectrum. Raw data were regridded by convolving with a Gaussian kernel of 1/3 of the HPBWs. After regridding, the effective angular resolutions become 52″ and 55″ for CO (J= 1−0) and C18O (J= 1−0), respectively.

thumbnail Fig. 2

Distribution of CO, C18O and H2 gas. (a) CO (J = 1−0) integrated intensity map, Wco, is overlaid with the C18O (J= 1−0) integrated intensity contours. The integrated velocity ranges are [1.3, 6.1] km s−1 for CO (J = 1−0) and [2.5, 4.2] km s−1 for C18O (J= 1−0). The color bar represents the CO (J = 1−0) integrated intensity in units of Κ km s−1, while the contours start at 0.54 Κ km s−1 and increase by 0.54 Κ km s−1. (b) C18O (J = 1−0) integrated intensity map, WCO${W_{{\rm{CO}}}}$ is overlaid with the H2 column density black contours from the near infrared extinction map (Juvela & Montillaud b2016). The color bar represents the C18O (J = 1−0) integrated intensity in units of Κ km s−1. The black contours start at 3 × 1021 cm-2 and increase by 3 × 1021 cm-2, (c) Extinction-based H2 column density map. In each panel, the beam size is shown in the lower right corner, and the two Planck cold clumps are indicated by the two blue open circles.

3.2 Archival Data

The Planck submillimter continuum polarization data2 at 353 GHz were employed to study the polarization properties (Planck Collaboration XI 2014; Planck Collaboration Int. XX 2015; Planck Collaboration Int. XIX 2015). Following previous studies (e.g., Soler 2019), we smoothed the data to an effective angular resolution of 10′ to achieve P/σP >3, where Ρ is the linear polarization magnitude and σP is the 1σ rms level of P. In order to be consistent with the IAU convention, the polarization angle of E-vector is calculated with 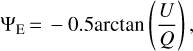ΨE=−0.5arctan(UQ),${{\rm{\Psi }}_{\rm{E}}} = - 0.5\arctan \left( {{U \over Q}} \right),$(1)

and the direction of magnetic field, ΨB, is perpendicular to the E-vector, that is 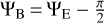ΨB=ΨE−π2.${\Psi _{\rm{B}}} = {\Psi _{\rm{E}}} - {\pi \over 2}.$

We also made use of the near-infrared extinction map to trace the H2 column density. The extinction map is derived using the reddening of the light of background stars (Juvela & Montillaud b2016). The near-infrared extinction map with an angular resolution of 3′ was used in this study. We converted the near-infrared extinction, AJ, to visual extinction, Av, by multiplying by 3.55 (Juvela & Montillaud 2016a), where the extinction curve, Rv =Av/E(B − V), is set to 3.1 (Cardelli et al. 1989) and E(B − V) is the degree of redenning. We adopted the relationship of Güver & Özel (2009) to convert Av to H2 column density: 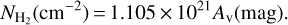NH2(cm−2)=1.105×1021Av(mag).${N_{{{\rm{H}}_2}}}\left( {{\rm{c}}{{\rm{m}}^{ - 2}}} \right) = 1.105 \times {10^{21}}{A_{\rm{v}}}\left( {{\rm{mag}}} \right).$(2)

Oph N1 is a high-latitude molecular cloud, and our molecular line observations suggest only one coherent velocity component (see Sect. 4). This supports the finding that there are no additional foreground or background molecular clouds along the line of sight. Hence, the extinction map can aptly trace the H2 column density distribution in Oph Nl.

4 Results

4.1 Molecular Distribution

Our observed integrated-intensity maps of CO (J = 1 −0) and C18O (J = 1 −0), Wco and 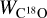WC18O${W_{{{\rm{C}}^{18}}{\rm{O}}}}$, are shown in Figs. 2a, 2b, which provide angular resolutions a factor of ≳3 finer than previous CO surveys (Nozawa et al. 1991; Tachihara et al. 2000, 2002). The CO (J = 1 −0) integrated-intensity map shows an extended distribution in Fig. 2a. The CO (J = 1−0) emission above 1 Κ km s−1 (3σ) has a size of about 1.8 pc × 1.1 pc with a position angle of ~135°, which is similar to the morphology traced by the IRAS 100 μm emission (see Fig. 1). The distribution presents a rift in the northwest, where the C18O (J = 1 −0) emission is prominent. This is indicative of the CO (J = 1 −0) self-absorption which can even result in the line ratio [C18O/CO] of >1 toward G008.52+21.84 (see Appendix B). As shown in Figs. 3a–c, the CO spectra exhibit narrow dips that coincide with the peaks of the corresponding C180 (J = 1 −0) spectra, confirming the presence of CO (J = 1 −0) self-absorption. However, the CO (J = 1 −0) self-absorption features are too narrow to be well resolved due to the insufficient spectral resolutions.

In addition to the difference in the emitting size, the C180 (J = 1 −0) morphology is also quite different from that of CO (J = 1 −0). Unlike the extended CO (J = 1 −0) emission, the C18O (J = 1 −0) emission exhibits a northwest-southeast filamentary structure with two enhancements at the northwest end and the center where the extinction-based H2 column densities exceed 1 × 1022 cm-2. The two enhancements correspond to the two Planck Galactic cold clumps, G008.52+21.84 and G008.67+22.14 (Planck Collaboration XXIII 2011; Planck Collaboration XXVIII 2016). The morphology coincides with the infrared extinction map (see Fig. 2b).

thumbnail Fig. 3

CO (J = 1 −0) and C18O (J = 1 −0) spectra of the selected positions indicated in the central map that is the same as Fig. 2a. CO (J = 1 −0) and C18O (J = 1 −0) are indicated by the black and blue lines, respectively.

4.2 Excitation

Assuming that CO (J = 1 −0) is optically thick (i.e., τ12 ≫ 1, where τ12 is the optical depth) and neglecting the beam dilution effects, we are able to derive the excitation temperature, Tex, from the CO (J = 1 −0) peak main beam temperature, Tp(CO), with the radiative transfer equation (e.g., Mangum & Shirley 2015): 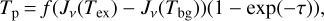Tp=f(Jv(Tex)−Jv(Tbg))(1−exp(−τ)),${T_{\rm{p}}} = f\left( {{J_v}\left( {{T_{{\rm{ex}}}}} \right) - {J_v}\left( {{T_{{\rm{bg}}}}} \right)} \right)\left( {1 - \exp \left( { - \tau } \right)} \right),$(3) Jv(T)=hv/kexp(hv/k)−1,${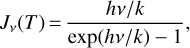J_v}\left( T \right) = {{hv/k} \over {\exp \left( {hv/k} \right) - 1}},$(4)

where the beam dilution factor, f, is assumed to be unity, exp(−τ12) ~0, the background temperature, Tbg, is set to be 2.73 Κ (Fixsen 2009), the Planck constant, h, is 6.626 × 10-27 erg s, the Boltzmann constant, k, is 1.38 × 10−16 erg K−1, and y is the rest frequency. Oph Nl is seen as a dark patch on the Ha nebula of Sh 2–27 (de Geus et al. 1990), supporting the notion that Oph Nl lies in front of Sh 2–27. Therefore, the continuum emission from the Sh 2–27 Hii region may contribute to the background temperature term. Based on the 11 cm continuum map (Reif et al. 1987), the brightness temperatures are about 0.4 K. Assuming a typical spectral index for the optically thin free-free continuum emission (i.e., TΒ ~ v-2.1, where TΒ is the brightness temperature and y is the frequency; Condon 1992), we obtained about 0.1 mK at 115 GHz. Hence, the free-free background contribution from the Sh 2–27 Hii region is negligible in the estimate of the excitation temperature.

Because the noise distribution is not homogeneous across the observed map, we first estimated the 1σ rms noise level of each pixel from emission-free channels, and only took the pixels with CO (J = 1 −0) peak main beam temperatures higher than 5σ into account. The derived excitation temperature map is shown in Fig. 4a. We find that 72% of pixels have excitation temperatures of 7.5–12.0 Κ with a median value of 8.5 Κ (see the distribution within the contour in Fig. 4a), which is well consistent with the kinetic temperature of 8.8 Κ derived from previous ammonia observations (Benson & Myers 1989). We also note that the excitation temperatures can be underestimated if the beam dilution effects and CO self-absorption become important.

Molecular gas with excitation temperatures of > 10 Κ tends to be clumpy. If the high excitation temperatures are caused by the irradiation from ζ Oph, this would support a clumpy geometry for photon dominated regions (PDRs; see Andree-Labsch et al. 2017, for instance). It is also evident that high excitation molecular gas is in the outer regions within the boundary, which is supportive of external heating. The rest 28% pixels with lower excitation temperatures lie at its outskirt outside the 7.5 Κ contour boundary in Fig. 4a. Toward this outskirt, the excitation temperatures drop sharply to ~4 K. This indicates that molecular gas in the outskirt tends to be more diffuse. Furthermore, the optical depths of CO (J = 1 −0) become lower in the outskirt than in the inner regions, possibly violating the optically thick assumption. Therefore, the derived excitation temperatures might be underestimated in the outskirt. Furthermore, the H2 number densities become lower, making CO subthermal in the outskirt. One more possibility is that the beam dilution factor becomes significantly lower than unity for CO (1 −0) at the very edge of this cloud.

thumbnail Fig. 4

Distribution of the physical and chemical properties of C18O in Oph N l. (a) Excitation temperature map derived from the CO peak main beam temperature. The color bar represents the excitation temperature in units of K, while the contour represents an excitation temperature of 7.5 K. (b) Peak C18O (J = 1 −0) opacity map. (c) C18O column density map at an angular resolution of 3′ (d) C18O fractional abundance map. The contours represent the C18O fractional abundances of 5 × 10-8 and 1 × 10-7. The two dashed circles represent the observed CO depletion holes. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two blue open circles.

4.3 Molecular Abundance

Assuming C18O (J = 1 -0) excitation temperature to be the same as CO (J = 1 −0) excitation temperature in Fig. 4a, we derived the peak C18O (J = 1 −0) opacity, τ18, from its peak main beam temperatures above 3σ with the radiative transfer equation (see Eq. (3)) and the derived peak C18O (J = 1 −0) opacity map is shown in Fig. 4b. Most of the opacities are greater than unity toward the two Planck cold clumps, suggesting that the opacity cannot be neglected to estimate the C18O column density in the hubs. In order to improve the signal-to-noise ratios and derive the C18O fractional abundance with respect to H2, we first smooth the CO (J = 1 −0) and C18O (J = 1 −0) data cubes to an angular resolution of 3′, and recalculate the excitation temperature and C18O (J = 1 −0) opacity maps using the same method described above.

Assuming local thermodynamic equilibrium (LTE), the C18O column density, Ν18, can be calculated by using Eqs. (102) and (103) in Mangum & Shirley (2015): N18=3h8π3μ2Ju(kTexhv+1/3)exp(EukTex)[ exp(hvkTex)−1 ]−1×WC18OJv(Tex)−Jv(Tbg)τ181−exp−(−τ18)cm−2,$\matrix{ {{N_{18}} = {{3h} \over {8{\pi ^3}{\mu ^2}{J_{\rm{u}}}}}\left( {{{k{T_{{\rm{ex}}}}} \over {hv}} + 1/3} \right)\exp \left( {{{{E_{\rm{u}}}} \over {k{T_{{\rm{ex}}}}}}} \right){{\left[ {\exp \left( {{{hv} \over {k{T_{{\rm{ex}}}}}}} \right) - 1} \right]}^{ - 1}}} \cr { \times {{{W_{{{\rm{C}}^{18}}{\rm{O}}}}} \over {{J_v}\left( {{T_{{\rm{ex}}}}} \right) - {J_v}\left( {{T_{{\rm{bg}}}}} \right)}}{{{\tau _{18}}} \over {1 - \exp - \left( { - {\tau _{18}}} \right)}}{\rm{c}}{{\rm{m}}^{ - 2}},} \cr }$(5)

where the dipole moment, μ, is 0.1098 D, Ju is the quantum number of the upper level,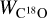WC18O${W_{{{\rm{C}}^{18}}{\rm{O}}}}$ is the C18O integrated intensity. The resulting map is shown in Fig. 4c. The derived C18O column densities are within the range of (0.7−15.4) × 1014 cm-2. The C18O fraction abundance with respect to H2 is directly determined by the ratio of the C18O and H2 column densities, and the H2 column densities are derived from the extinction. The C18O fractional abundance map is shown in Fig. 4d. The derived abundances are within the range of (0.2–1.7) × 10-7.

Most emitting regions are consistent with the typical abundance of (1–2) × 10-7 in nearby dark clouds (Frerking et al. 1982; Blake et al. 1987; Lada et al. 1994). The C18O fractional abundance of <5 × 10-8 is only present in the edge of the cloud (see Fig. 4d), which is likely caused by the far ultraviolet (FUV) photodissociation of C18O (e.g., van Dishoeck & Black 1988; Shimajiri et al. 2014; Wang et al. 2019). On the other hand, the C18O fractional abundances become higher in the two Planck cold clumps, because FUV radiation is well shielded by their high extinctions (i.e., corresponding H2 column densities of ≳7 × 1021 cm-2). Ring-like structures are revealed toward the two Planck cold clumps (see the two dashed circles in Fig. 4d), which can be readily explained by the CO depletion onto dust grains in dense regions (e.g., Bergin & Tafalla 2007). Both the depletion holes have radii of about 0.1 pc, similar to the typical depletion size in prestellar cores (~0.1 pc; Bergin & Tafalla 2007). Because of the abundance variations caused by photodissociation and CO depletion, the mass is estimated using the extinction-based H2 column density instead. Using the same mask in Fig. 4a, we derived the total molecular gas mass to be 132 M⊙

4.4 Velocity Field

4.4.1 Decomposition

Because CO (J = 1 −0) is likely optically thick and suffers from self-absorption, CO (J = 1 −0) spectra cannot adequately trace the velocity field of Oph Nl. In contrast, C18O (J = 1 −0) has much lower opacities, so its spectra can better trace intrinsic velocity centroids and velocity dispersions of molecular clouds. Therefore, we use C18O (J = 1 −0) data to study the kinematics of Oph N l.

A Gaussian decomposition allows us to study the kinematic properties of C18O (J = 1 −0) data across Oph Nl. We manually examined the data cube which appears to display only one single Gaussian component for the whole region. Therefore, we assumed a single Gaussian component to decompose the C18O (J = 1 −0) spectra with peak intensities higher than 3σ. Figures 5a–c present the distribution of the peak intensities, LSR velocities, and velocity dispersions. We also performed Gaussian convolution on the C18O data cube to improve the signal-to-noise ratios at the expense of angular resolution. The C18O data cube is smoothed to a beam size of 180″. We carried out the same decomposition to the smoothed data cube, and the results are shown in Figs. 5d–f. The distributions of the peak intensities, LSR velocities, and velocity dispersions are similar to Figs. 5a–c, except that the velocity dispersions are slightly higher than the values derived from the data cube with a beam size of 55″. This is because the velocity gradients tend to be larger in a larger beam.

thumbnail Fig. 5

Maps of peak intensities (Fig. 5a), LSR velocities (Fig. 5b), and velocity dispersions (Fig. 5c) derived from single-component Gaussian fits to our C18O (J = 1 −0) data cube. Figures 5d–f are similar to Figs. 5a–c, but at a smoothed angular resolution of 180″. In each panel, the beam size is shown in the lower right corner, and the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.

4.4.2 Local Velocity Gradient

In the velocity-centroid maps (see Figs. 5b and e), velocity centroids range from 3.1 km s−1 to 3.95 km s−1. The narrow and continuous distribution suggests that Oph Nl is velocity-coherent. Furthermore, different velocity gradients are evident in different regions. In order to better visualize the local velocity gradients, VV, we use the definition of the local velocity gradients by Goodman et al. (1993): 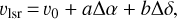υlsr=υ0+aΔα+bΔδ,${\upsilon _{{\rm{lsr}}}} = {\upsilon _0} + a{\rm{\Delta }}\alpha + b{\rm{\Delta }}\delta ,$(6)

where vlsr is the observed LSR velocity centroid, υ0 is the systemic LSR velocity, Δα and Δδ are the offsets in right ascension and declination, and a and b are the components of ∇V along the directions of right ascension and declination. The magnitude of ∇V is 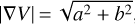|∇V|=a2+b2$\left| {\nabla V} \right| = \sqrt {{a^2} + {b^2}}$, and the position angle is θpa = arctan(a / b) where θpa increases counter-clockwise with respect to the north. Following Gong et al. (2021), we used the Levenberg-Marquardt algorithm to fit this function toward each square block with adjacent 3 × 3 pixels toward Figs. 5b and e. The distribution of the local velocity gradients, ∇υ, is shown in Fig. 6.

Figures 6a and b mainly trace the ∇υ distributions around the two Planck cold clumps, while Figs. 6c and d can better trace ∇υ in more extended regions. In Fig. 6a, high |∇υ| of ≳5 km s−1 pc−1 are found in a shell that has a radius of ~0.1 pc centered at G008.52+21.84, but |∇υ| decreases toward the center. Figure 6b exhibits a converging morphology toward G008.52+21.84, indicating core accretion from ambient clouds. The trend of having a decreasing |∇υ| towards the center of the cores has also been detected in other studies (Chen et al. 2020; Gong et al. 2021). Because the decreasing ∇υ trend is opposite to the prediction by the gravity-driven accretion model (e.g., Heitsch et al. 2009), Chen et al. (2020) proposed that the accretion can be damped by the high-density materials. The other possibility is at least partially due to the geometric effect (Gong et al. 2021). For a spherically collapsing core, the observed LSR velocity should be constant across the core, because the observed LSR velocity is actually density-weighted 3D velocity average over the line of sight. On the other hand, the velocity gradient should be more significant for other geometry such as sheets (see Fig. 1 in Shimajiri et al. 2019 for example). Hence, the decreasing Vu toward the center of G008.52+21.84 could be due to the fact that the structure becomes more symmetric toward dense regions. In Fig. 6b, the Vu converging morphology toward G008.67+22.14 is not as evident as G008.52+21.84, which is likely dominated by the large-scale east-west velocity gradient (see Fig. 6d).

The representation of Vu in the red and blue dashed boxes appears to be dominated by a northeast-southwest velocity gradient which is almost perpendicular to the filament’s long axis and the plane-of-the-sky magnetic field. Such transverse velocity gradients can be caused by filament rotation (e.g., Zhang et al. 2020; Stewart & Federrath 2022). However, ∇υ in the red and blue dashed boxes show opposite directions, ruling out the filament’s rigid rotation. Instead, such a ∇υ morphology can be explained by differential rotation or shear motions that would indeed be expected in turbulence vorticity (e.g., Fiege & Pudritz 2000; Lesieur 2008; Banda-Barragán et al. 2018).

Comparing the results at different angular resolutions, we find that the magnitude of ∇υ in Fig. 6c is lower than Fig. 6a due to its lower spatial resolution, while the opposite directions of ∇υ (indicated by the arrows in Fig. 6a) are largely retained, as seen in Fig. 6d. Another interesting feature is that three regions show higher ∇υ magnitudes than ambient regions and the three regions are nearly parallel to each other (see the black dashed boxes in Fig. 6c). The high ∇υ magnitudes contribute to the velocity dispersion measured within a beam, leading to the higher velocity dispersions of the corresponding pixels in Fig. 5f than in Fig. 5c. Such sharp variations have been detected and interpreted as velocity shear by previous studies (Hily-Blant & Falgarone 2009; Falgarone et al. 2009). Hence, this implies that the observed velocity field is partially regulated by shear motions.

On the other hand, simulations have shown that turbulence can also cause small-scale fluctuations on the measured velocity centroids (Stewart & Federrath 2022), which should affect the patterns in our ∇υ maps (Fig. 6). However, it is difficult to quantify the contributions of the ordered motions and turbulent motions in Fig. 6 based on our current observations. Nevertheless, large-scale velocity gradients should be much less affected by turbulence than small-scale velocity gradients.

thumbnail Fig. 6

Distribution of local velocity gradients derived from C18O velocity centroids. (a) Local velocity gradient magnitude map derived from Fig. 5b. (b) C18O (J = 1 −0) peak intensity map is overlaid with the normalized velocity gradient vectors. The blue and red arrows represent the average directions of the local velocity gradients in sub-regions indicated by the blue and red dashed boxes, respectively. Figures 6c and d is similar to Figs. 6a and b, but derived from Fig. 5e. In Fig. 6c, the three regions showing high velocity gradients are indicated by the three black dashed boxes. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.

4.4.3 Widespread Subsonic Turbulence

In Fig. 5c, we can see that all the derived velocity dispersions are lower than 0.25 kms−1. The fitting errors in the derived velocity dispersion range from 0.004 km s−1 to 0.04 kms−1. Hence, the derived velocity dispersions should be robust. The observed velocity dispersions come from thermal and nonthermal motions. The non-thermal velocity dispersion, σnt, can be estimated by subtracting the thermal velocity dispersion, σt, from the observed total velocity dispersion3,σobs, 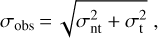σobs=σnt2+σt2,${\sigma _{{\rm{obs}}}} = \sqrt {\sigma _{{\rm{nt}}}^2 + \sigma _{\rm{t}}^2} ,$(7)

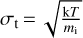where σobs=kTmi,k${\sigma _{{\rm{obs}}}} = \sqrt {{{{\rm{k}}T} \over {{m_i}}}} ,{\rm{k}}$ k is the Boltzmann constant, and mi is the mass weight that is 30 for C18O. Here, we adopt a kinetic temperature of 10 Κ for the fiducial case, which results in σt = 0.05 km s−1 for C18O and a sound speed, cs, of 0.19 kms−1 where mi = 2.37 (Kaufmiann et al. 2008). The observed Mach number, 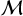M${\cal M}$, is determined by 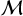M${\cal M}$ = σnt/cs. As shown in Fig. 7, we find that more than 85% and 70% of the fitted pixels that have 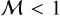M<1${\cal M} &lt; 1$ at the angular resolutions of 55″ and 180″, respectively.

The observed σnt can also be higher than the intrinsic turbulence velocity dispersion, because the variation of LSR velocity centroids within the beam can partially arise from the ordered motions (e.g., rotation, shear motions) rather than pure turbulence (see also Stewart & Federrath 2022). Making use of the derived local velocity gradients, we could roughly estimate the contributions to the observed σnt. The observed |∇υ| vary from 1 kms−1 pc−1 to 10 kms−1 pc−1 in Figs. 6a and c, suggesting a plane-of-sky contribution of 0.1 km s−1 to 0.3 km s−1 to observed line widths within the beam sizes of 55″ and 180″, respectively. If we assume that the observed |∇υ| is not attributed to turbulence, we can subtract the contributions of ordered motions from the velocity dispersions for each pixel. This correction leads to more than 92% and 82% of the fitted pixels showing the subsonic level of turbulence at the angular resolutions of 55″ and 180″, respectively, which further reinforces the widespread subsonic turbulence in Oph Nl.

Such subsonic turbulence has also been reported in L1517 (Hacar & Tafalla 2011), but the prevalence of subsonic motions is up to about 0.5 pc. In contrast, our observations demonstrate large-scale subsonic motions up to a scale of ≳1.5 pc, greater than the previous study. Based on the classic size-line width relations (e.g., Larson 1981; Heyer et al. 2009), sonic motions are expected on scales of ≲0.3 pc. Therefore, the turbulence properties of Oph Nl apparently violate the classic size-line width scaling relationship.

We also investigated the CO (J = 1−0) spectra on the outskirts of Oph Nl (Figs. 3d−e). These spectra are found to have line widths of 0.64−0.81 km s−1. Removing the broadening effects caused by the channel width and thermal motions, we obtained the nonthermal velocity dispersions of 0.26−0.37 kms−1, corresponding to 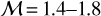M=1.4−1.8${\cal M} = 1.4 - 1.8$, that is, transonic. Because of the potential opacity broadening effects in CO (J= 1−0) and local velocity gradients within the beam, the derived M are upper limits, and the intrinsic motions can be actually more quiescent. Gaussian decomposition to the whole CO (J= 1−0) data cube confirms the quiescent motions in a larger region (see Appendix A). In combination with our C18O measurements, our observations indicate that the entire cloud could be fully decoupled from the supersonic environment.

thumbnail Fig. 7

Histogram and cumulative distribution of the nonthermal velocity dispersion derived from C18O (J = 1−0) at the angular resolutions of 55″ and 180″, respectively. The vertical dashed lines represent the sonic speed and the thermal velocity dispersion of C18O at a kinetic temperature of 10 K. This figure is suggestive of widespread subsonic turbulence.

4.4.4 Steep Velocity Structure Function

Velocity structure functions are useful to study the dynamical state of molecular clouds (e.g., Miesch & Bally 1994; Ossenkopf & Mac Low 2002; Heyer & Brunt 2004; Esquivel & Lazarian 2005; Chira et al. 2019; Henshaw et al. 2020). Following previous studies (e.g., Chira et al. 2019), the second-order velocity structure function, S 2, is a two-point correlation function that quantifies the mean velocity difference: 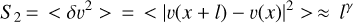S2=〈 δυ2 〉=〈 | υ(x+l)−υ(x) |2 〉≈ly${S_2} = \left\langle {\delta {\upsilon ^2}} \right\rangle = \left\langle {{{\left| {\upsilon \left( {x + l} \right) - \upsilon \left( x \right)} \right|}^2}} \right\rangle \approx {l^y}$(8)

where l is the spatial lag between two positions, χ and χ + l, and γ is the power-law index.

Because Fig. 5e has a higher dynamical range than Fig. 5b and the bulk motions are nearly identical at large scales, we made use of Fig. 5e to derive the second-order velocity structure function for Oph Nl, and the result is shown in Fig. 8. The distribution appears to be linear at the spatial lag of l < 0.5 pc, because the completeness limit is about 0.5 pc in our study. Hence, a linear fit is performed on the data in the logarithmic form in order to derive 7 in the spatial range of 0.03−0.5 pc. The resulting γ is 1.30 ± 0.03, which is steeper than previous reported values of molecular clouds in the Galactic disk (see Table 1 in Chira et al. 2019) and the classical Larson relation (e.g., Larson 1981; Heyer et al. 2009), but is similar to the reported size-line width relations in the Rosette molecular cloud (Heyer et al. 2006), Taurus 13CO cores (γ ~ 1.4; Qian et al. 2012), the central molecular zone (γ= 1.32 ± 0.36; Kauffmann et al. 2017), and nearby young stellar object associations measured with the Gaia proper motions (γ ~ 1.3; Zhou et al. 2022).

The derived γ cannot be explained by the classic energy cascade that predicts γ = 2/3 (Kolmogorov 1941). Kauffmann et al. (2017) proposed the decay of gas motions to transonic velocities in strong shocks to explain the observed steep size-line width relation. This scenario appears to contradict widespread subsonic motions observed in Oph Nl. However, we cannot rule out the possibility that the observed structure is a fossil of shocks, in which kinetic energies have been already dissipated. Based on the comparison of clouds inside and outside the ionization front induced by the Rosette clusters (Heyer et al. 2006), the steep index is thought to arise from the expansion of ionized gas. Because Oph Nl is interacting with the Sh 2-27 Hii region, this scenario is favored to explain our case. On the other hand, the steep index indicates that Oph Nl is dissipating more efficiently than the classic energy cascade. In the frame of incompressible turbulence that is expected in the subsonic regime, the index in the dissipative range is steeper than in the inertial range. Furthermore, filamentary structures are known to be typical structures of turbulence dissipation for low Mach numbers (e.g., de Avillez & Breitschwerdt 2007; Zybin & Sirota 2015; Childress & Gilbert 2020). Hence, we suggest that the steep velocity structure function can be caused by the expansion of the Sh 2−27 Hii region or the dissipative range of incompressible turbulence.

thumbnail Fig. 8

Second-order velocity structure function of Oph Nl derived from Fig. 5b as a function of the spatial lag, l. The gray-shaded region is the spatial-resolution limit which corresponds to 55″. The power-law fitting result is indicated by the black dashed line. The orange, red, and blue dashed lines represent the observed relation in Musca (Hacar et al. 2016) and Rossete (Heyer et al. 2006), the classic Larson relation (γ = 0.76; Larson 1981), and the revised relation, σ ∝ R0.5 (γ = l; Heyer et al. 2009), respectively.

4.5 Magnetic Field Strength

The large-scale magnetic field of Oph Nl has not been reported by previous Planck studies (e.g., Soler 2019). We present the distribution of the plane-of-the-sky magnetic field toward Oph Nl in Fig. 9a. The plane-of-the-sky magnetic field is nearly parallel to the elongation direction of Oph Nl, which is different from the polarization configuration in OphN2 (L204) where the plane-of-the-sky magnetic field is perpendicular to its elongation direction (McCutcheon et al. 1986; Heiles 1988). The large-scale magnetic field morphology is confirmed by the Planck dust polarization measurements (see Fig. C.1). This is consistent with previous Planck results that the relative orientation is commonly observed to change progressively with increasing H2 column densities, from mostly parallel to mostly perpendicular, which was interpreted a signature of Alfvénic or sub-Alfvénic turbulence (e.g., Planck Collaboration Int. XXXV 2016).

As shown in Fig. 9a, the dispersion of the polarization angles is small, indicating that its magnetic field plays an important role in this region. We adopt the Davis-Chandrasekhar-Fermi (DCF) method to estimate the magnetic field strength of the plane-of-sky component, Bpos, in this region using the following formula (Davis 1951; Chandrasekhar & Fermi 1953; Crutcher 2012): 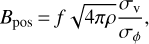Bpos=f4πρσvσϕ,${B_{{\rm{pos}}}} = f\sqrt {4\pi \rho } {{{\sigma _{\rm{v}}}} \over {{\sigma _\phi }}},$(9)

where f is the correction factor, ρ is the cloud density, σv is the one-dimensional turbulence velocity dispersion, and σϕ is the dispersion in polarization angle.

Based on numerical simulations (Ostriker et al. 2001; Heitsch et al. 2001), f is assumed to be 0.5 when σϕ <25°. Because C18O (J = 1−0) emission is widespread in the observed region, we use the critical density of C18O (J = 1−0) to represent the cloud density. Following the method introduced by Shirley (2015), we estimate the optical thin critical density of C18O (J = 1−0) to be 7×l02 cm−3 at a kinetic temperature of 10 K. On the other hand, we can roughly estimate the average cloud density by assuming a nearly prolate 3D shape, that is, the depth is close to its width (~1.1 pc) of the cometary cloud. This leads to an average cloud volume density of 7.4 × 102 cm−2, which is in agreement with the optical thin critical density of C18O (J = 1−0). Hence, a cloud density of 7 × 102 cm−3 is adopted in our estimate. For σv, the median value of the non-thermal velocity dispersions is adopted (i.e., σv = 0.14 ± 0.04 kms−1). We estimate σϕ from the histogram distribution of the polarization angle which is shown in Fig. 9b. We perform a single-component Gaussian fitting on the histogram distribution, and this gives σϕ = 3.0° ± 0.3°. Consequently, we obtain Bpos = 28 + 9 μΟ. The errors are derived with the Monte Carlo error analysis where 10 000 Monte Carlo simulations are carried out. The derived Bpos is slightly higher than other nearby molecular clouds' values which are calculated with the same method (5−20 μG; Planck Collaboration Int. XXXV 2016). This indicates that magnetic support might be important for this cloud.

The DCF method is based on the assumption of the isotropic turbulent motions. However, our target may violate the assumption, which might overestimate Bpos. Based on magnetohy-drodynamic simulations, Skalidis & Tassis (2021) propose an alternative relation to estimate Bpos, 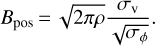Bpos=2πρσvσϕ.${B_{{\rm{pos}}}} = \sqrt {2\pi \rho } {{{\sigma _{\rm{v}}}} \over {\sqrt {{\sigma _\phi }} }}.$(10)

Skalidis & Tassis (2021) compared the method with the simulations, and found a deviation of 17% in Bpos. Using Eq. (10) and including the uncertainty of 17%, we obtain Bpos = 9 ± 3 ± 2 μG. Although this method takes the anisotropic properties of turbulence into account, the estimated value from this method could be biased to lower values (Skalidis & Tassis 2021), because gravity cannot be neglected in our case (see the discussion in Sect. 5.1).

Based on the two methods mentioned above, we can give a lower limit of ~9 μG for Bpos, which provides a lower limit for the total magnetic field strength, Bt that is, Bt >9 μG. In order to obtain the total magnetic field strength, one needs the magnetic field strength of the line-of-sight component, Blos. Heiles (1988) measured the nearby cloud OphN2 (L204) with the HI Zeeman splitting, and found about 4.2 μG for the average Blos. If the same Blos is assumed for Oph Nl, we arrive at Bt ≳10 μG, which is comparable to the reported Bt of about 12 μG in OphN2 (Heiles 1988). A study of polarized radio emission toward Sh 2−27 indicates the line-of-sight magnetic strengths of −15 μG and +30 μG in the near and far cloud (Thomson et al. 2019). Because Oph Nl is located in front of Sh 2−27 as mentioned above, we assume −15 μG for the line-of-sight component toward Oph Nl, which leads to Bt ≳18 μG. On the other hand, Crutcher et al. (2004) derived the statistical average relation, 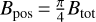Bpos=π4Btot${B_{{\rm{pos}}}} = {\pi \over 4}{B_{{\rm{tot}}}}@$ which gives Bt ≳ 11 μG for our case. Hence, these different assumptions support Bt ≳ 10 μG for Oph Nl. The Bt values give a three-dimensional Alfvén velocity of ≳0.5 kms−1, where the three-dimensional Alfvén velocity is defined as 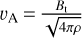υA=Bt4πρ${\upsilon _{\rm{A}}} = {{{B_{\rm{t}}}} \over {\sqrt {4\pi \rho } }}@$ The corresponding Alfvén Mach number 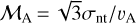MA=3σnt/υA${{\cal M}_{\rm{A}}} = \sqrt 3 {\sigma _{{\rm{nt}}}}/{\upsilon _{\rm{A}}}$ is about 0.5. Since the derived υA is a lower limit, the corresponding 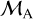MA${{\cal M}_{\rm{A}}}$ is an upper limit. Hence, 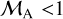MA<1${{\cal M}_{\rm{A}}} &lt; 1$ is robust. Therefore, we conclude that Oph Nl is globally sub-Alfvénic.

thumbnail Fig. 9

(a) Planck Stokes I continuum emission at 353 GHz is overlaid with magnetic field orientations, (b) Histogram distribution of the polarization angle fitted with a single Gaussian component.

5 Discussion

5.1 Magnetically Supported Cloud

We tested the cloud stability by comparing the observed properties with the magnetic critical condition which takes the projection effects into account (e.g., Li et al. 2014): 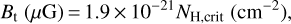Bt(μG)=1.9×10−21NH,crit(cm−2),${B_{\rm{t}}}\left( {\mu {\rm{G}}} \right) = 1.9 \times {10^{ - 21}}{N_{{\rm{H,crit}}}}\left( {{\rm{c}}{{\rm{m}}^{ - 2}}} \right),$(11)

where NH,crit is the critical hydrogen column density. Adopting Bt = 10 μG, we obtain NH,crit = 5.3 × 1021 cm−2. The average H2 column density is found to be 2.5 × 1021 cm−2, which is equivalent to NH = 5 × 1021 cm−2 that is comparable to NH,crit This indicates that magnetic field is at least comparable to gravity in Oph Nl. Because Bt = 10 μG is a lower limit (see Sect. 4.5), the magnetic field should be even more important.

We also compare the magnetic pressure with thermal and turbulent pressures in order to estimate their relative roles in stabilizing the cloud. Magnetic pressure, 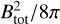Btot2/8π$B_{{\rm{tot}}}^2/8\pi$, is estimated to be 4.0 × 10−12 erg cm−3 when Btot is set to be 10 μG. Adopting the C18O (J = 1−0) critical density of 7 × 102 cm−2 and a kinetic temperature of 10 Κ (see discussions above), we derive thermal pressure to be 7 × 103 cm−3 Κ (i.e., 9.7 × 10−13 erg cm−3). Turbulent pressure is determined by 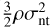32ρσnt2${3 \over 2}\rho \sigma _{{\rm{nt}}}^2$, where ρ is the density and σnt is the nonthermal velocity dispersion. Adopting a H2 number density of 7 × 102 cm−2 and σnt = 0.14 km s−1 (see Sect. 4.4), we arrive at the turbulent pressure of 3.3 × 10−12 erg cm−3. Because the adopted Btot is a lower limit, this comparison suggests that magnetic pressure should be higher than thermal pressure and turbulent pressure. This result is also supported by our observed morphology that the cloud elongation is parallel to the plane-of-the-sky magnetic field, because such a configuration is expected in sub-Alfvénic turbulence where the magnetic energy is above or comparable to the kinetic energy (Soler et al. 2013). Oph Nl is therefore supported against gravity mainly by the magnetic field.

5.2 Energy Dissipation

The widespread narrow line widths suggest large-scale subsonic turbulence in Oph Nl, which tends to be more quiescent than most molecular clouds. A question can be raised here regarding how the cloud reaches the current dynamic state. We find that energy injection and dissipation should be the key to the question.

Because Oph Nl lies at the edge of the Sh 2-27 Hii region, the Hii region may input kinetic energies into the clouds. However, the Sh 2−27 Hii region has a large projected diameter of ~15 pc (see Fig. 1). Following the method used in Brand et al. (2011) and assuming an initial density of 1 × 103 cm−3, we estimate the dynamic age of the Sh 2−27 Hii region to be about 4 Myr, in agreement with the age (~3 Myr) of ζ Oph derived from evolutionary models (Tetzlaff et al. 2011). The numerical simulations of Mackey et al. (2013) suggest that the kinetic energy input from the Sh 2−27 region becomes negligible after the first 1.5 Myr (see their Fig. 9). This confirms that, at 4 Myr, Sh 2−27 is an old Hii region that has already lost most of its kinetic energy. Oph Nl is about 4 pc away from ζ Oph, and the radiation from OB stars varies as the inverse square of distance, so the radiation should not play an important role. On the other hand, Oph Nl is also not active in star formation, so its internal feedback is also not important. Since the cloud is likely stabilized by magnetic fields (see Sect. 5.1), the energy input from gravity should be also negligible. These facts suggest that there are no considerable internal and external kinetic energy input toward Oph Nl recently.

Energy dissipation by turbulent cascade might cause the low level of turbulence. We estimate the timescale of energy dissipation via a turbulence cascade in order to evaluate its role. The timescale is characterized by the crossing time, τc, which is determined by the size of the cloud, L, and velocity dispersion, 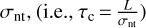σnt,(i,e.,τc=Lσnt)${\sigma _{{\rm{nt}}}},\left( {{\rm{i,e}}{\rm{.,}}{\tau _{\rm{c}}} = {L \over {{\sigma _{{\rm{nt}}}}}}} \right)$ In our case, we adopt the width of 1.1 pc and the median non-thermal velocity dispersion of 0.14 km s−1, which results in about 8 Myr for the crossing time. Because this process can cause lower σnt with time, σnt should be higher in earlier stages, which implies that the timescale of about 8 Myr can be overestimated.

Alternatively, the energy dissipation by the ion-neutral friction can be potentially more important, since the cloud is globally sub-Alfvénic. We can estimate the timescale for energy dissipation by the ion-neutral friction, τdiss,amb, with Eq. (13) in Hennebelle & André (2013): 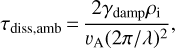τdiss,amb=2γdampρiυA(2π/λ)2,${\tau _{{\rm{diss,amb}}}} = {{2{\gamma _{{\rm{damp}}}}{\rho _{\rm{i}}}} \over {{\upsilon _{\rm{A}}}{{\left( {2\pi /\lambda } \right)}^2}}},$(12)

We adopt the damping rate, γdamp, as 3.5 × 1013 cm3 g−1 s−1 and the ion density, ρi, to be 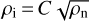ρi=Cρn${\rho _{\rm{i}}} = C\sqrt {{\rho _{\rm{n}}}}$ (Elmegreen 1979; Hennebelle & André 2013), where C = 3 × l0−16 cm−3/2 g1/2 and the neutral density, ρn, is assumed to be the C18O (J = 1−0) critical density of 7 × 102 cm−2. The Alfvénic speed is set to be 0.5 kms−1 (see Sect. 4.5), and the wavelength, λ, is assumed to be equal to the width (~ 1.1 pc) of Oph Nl. This gives a timescale of 2.7 Myr. If we take the Alfvénic speed of >0.5 km s−1 and the wavelength of <1.1 pc, the timescale can become significantly shorter.

If we believe that the structure is formed after the interaction with the Hii region, the age of the Hii region allows us to set an upper limit on the formation of the structure (i.e., ≳3 Myr). The age is much lower than the timescale of energy dissipation resulting from a turbulent cascade, but it is comparable to or higher than the timescale of energy dissipation by ion-neutral friction. As discussed in Sect. 4.4.4, a classic turbulent cascade cannot solely explain the observed velocity structure function, which is indicative of additional dissipation mechanisms. Therefore, we suggest that the energy dissipation via the ion-neutral friction should play an important role in forming the observed large-scale subsonic turbulence.

6 Summary

We simultaneously mapped Ophiuchus North 1 (Oph Nl) in CO (J = 1−0) and C18O (J = 1−0) with the PMO−13.7 m telescope to study its physical properties. Our main findings are summarized as follows:

  1. We find that most of the whole C18O emitting regions have Mach numbers of ≲1, demonstrating the extended subsonic turbulence up to a scale of ≳1.5 pc. Based on the measurements of the local velocity gradients, the velocity field indicates the presence of velocity shear, while the contributions of turbulence on the local velocity gradients should not be neglected.

  2. Oph Nl exhibits a head-tail morphology at the edge of the Sh 2−27 Hii region. The excitation temperatures are within the range of 7.5−12.0 Κ with a median value of 8.4 K. High-excitation molecular gas is found in the outer regions, which might be caused by external heating. The C18O fractional abundances with respect to H2 are within the range of (0.2−1.7) × 10−7. We show the presence of regions of C18O depletion towards the center of the two Planck cold clumps.

  3. The plane-of-the-sky magnetic field is nearly parallel to the long axis of Oph Nl. Based on the polarization measurements at 353 GHz, we estimate the magnetic field strength of the plane-of-sky component to be ≳9 μG, and the total magnetic field strength should be ≳ 10 μG. We find that Oph Nl is globally sub-Alfvénic and supported against gravity mainly by the magnetic field.

  4. We construct the second-order velocity structure function of Oph Nl from the C18O (J= 1−0) velocity centroids. The power-law index is found to be 1.30 ± 0.03 in the spatial range of 0.03−0.5 pc. We suggest that the steep velocity structure function can be caused by the expansion of the Sh 2−27 Hii region or the dissipative range of incompressible turbulence. Comparing the different timescales of dissipation, we suggest that the energy dissipation by ion-neutral friction should play an important role in forming the observed widespread subsonic turbulence.

Our observations have demonstrated the presence of widespread subsonic turbulence in Oph Nl that is sub-Alfvénic. However, it is not known how common are subsonic turbulence in molecular clouds. Further observations of nearby molecular clouds within the Gould Belt (distances of <500 pc) should shed light on this question.

Acknowledgements

We acknowledge the PMO-13.7 m staff for their assistance with our observations. This work was partially supported by the National Key R&D Program of China under grant 2017YFA0402702. W.S.Z. is supported by NSFC grant 12173102. GXL acknowledges supports from NSFC grant W820301904 and 12033005. This research has made use of NASA's Astrophysics Data System. This work also made use of Python libraries including Astropy (https://www.astropy.org/) (Astropy Collaboration 2013), NumPy (https://www.numpy.org/) (van der Walt et al. 2011), SciPy (https://www.scipy.org/) (Jones et al. 2001), Matplotlib (https://matplotlib.org/) (Hunter 2007), APLpy (Robitaille & Bressert 2012), GaussPy+ (https://github.com/mriener/gausspyplus) (Riener et al. 2019), and magne-tar (https://github.com/solerjuan/magnetar) (Soler et al. 2013). This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. We would like to thank the anonymous referee for a careful review of this article and valuable comments.

Appendix A Decomposition of CO (J = 1−0) Spectra

We fit the Gaussian profiles to the CO (J = 1−0) data cube, using the fully automated Gaussian decomposition package, GAUSSPY+ (Riener et al. 2019) that is based on the GAUSSPY algorithm (Lindner et al. 2015). We successfully obtained the fitting results toward 6395 spectra, and the results are presented in Fig. A.1. In Fig. A.1a, We find that 3521 spectra show one single velocity component and the rest 2874 display multiple velocity components. Because we cannot disentangle whether the multiple velocity components are caused by self-absorption (see Sect. 4.1) or multiple gas structures, we only investigated the spectral results showing a single velocity component, and the fitted results are shown in Figs. A.1b−A.1d. In Fig. A.1d, we find 1106 pixels with velocity dispersions of <0.38 km s−1, suggesting that 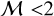M<2${\cal M} &lt; 2$ even without taking opacity broadening and local velocity gradients into account. Therefore, the results further support the low level of turbulence across Oph N1.

thumbnail Fig. A.1

Decomposition of CO (J = 1 – 0) data (a) Distribution of the number of the fitted velocity components, (b) Fitted peak intensities for the pixels showing a single velocity component, (c) Fitted velocity centroids for the pixels showing a single velocity component, (d) Fitted velocity dispersions for the pixels showing a single velocity component. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.)

Appendix B Line-ratio Map

We first derived the peak intensity map of C18O (J = 1−0) that is clipped at 3σ. The corresponding peak intensity map of CO (J = 1−0) is obtained at the peak velocity of C18O (J = 1−0). The line-ratio map is directly estimated by the ratio of the two maps, and Fig. B.1 presents the distribution of the line ratios between C18O and CO. The line ratios of >1 are found toward G008.52+21.84, which is caused by the significant CO self-absorption (see Fig. 3c). There are also high line ratios of >0.5 toward G008.67+22.14, which can also be caused by CO self-absorption (see Fig. 3a). This indicates widespread 12CO (1−0) self-absorption in observed regions (see also Sect. 4.1).

thumbnail Fig. B.1

Decomposition of CO (J=1−0) data, (a) Distribution of the number of the fitted velocity components, (b) Fitted peak intensities for the pixels showing a single velocity component, (c) Fitted velocity centroids for the pixels showing a single velocity component, (d) Fitted velocity dispersions for the pixels showing a single velocity component. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.

Appendix C Large-scale magnetic field morphology toward Ophiuchus North

Figure C.1 presents the large-scale magnetic field morphology of Ophiuchus North that is traced by the Planck dust polarization data. This figure shows that the plane-of-the-sky magnetic field is nearly parallel to the elongation direction of Oph Nl and becomes perpendicular to the elongation directions of L234E and OphN2.

thumbnail Fig. C.1

Plane-of-the-sky magnetic field and τ345 measured by Planck toward Ophiuchus North. The overlaid pattern, produced using the line integral convolution (LIC) method (Cabrai & Leedom 1993), indicates the orientation of magnetic field lines. The marked regions are the same as in Fig. 1.

References

  1. Andree-Labsch, S., Ossenkopf-Okada, V., & Röllig, M. 2017, A&A, 598, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Astropy Collaboration (Robitaille, T.P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Banda-Barragân, W.E., Federrath, C., Crocker, R.M., & Bicknell, G.V. 2018, MNRAS, 473, 3454 [CrossRef] [Google Scholar]
  4. Benson, P.J., & Myers, P.C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bergin, E.A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blake, G.A., Sutton, E.C., Masson, C.R., & Phillips, T.G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bontemps, S., Andre, P., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 [NASA ADS] [Google Scholar]
  8. Brand, J., Massi, F., Zavagno, A., Deharveng, L., & Lefloch, B. 2011, A&A, 527, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cabral, B., & Leedom, L.C. 1993, in Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH '93 (New York, NY, USA: Association for Computing Machinery), 263 [CrossRef] [Google Scholar]
  10. Cardelli, J.A., Clayton, G.C., & Mathis, J.S. 1989, ApJ, 345, 245 [CrossRef] [Google Scholar]
  11. Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [Google Scholar]
  12. Chen, M.C.-Y., Di Francesco, J., Rosolowsky, E., et al. 2020, ApJ, 891, 84 [NASA ADS] [CrossRef] [Google Scholar]
  13. Childress, S., & Gilbert, A.D. 2020, Fluid Dyn. Res., 52, 035502 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chira, R.A., Ibânez-Mejia, J.C., Mac Low, M.M., & Henning, T. 2019, A&A, 630, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Condon, J.J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [Google Scholar]
  16. Crutcher, R.M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
  17. Crutcher, R.M., Nutter, D.J., Ward-Thompson, D., & Kirk, J.M. 2004, ApJ, 600, 279 [NASA ADS] [CrossRef] [Google Scholar]
  18. Davis, L. 1951, Phys. Rev., 81, 890 [Google Scholar]
  19. de Avillez, M.A., & Breitschwerdt, D. 2007, ApJ, 665, L35 [NASA ADS] [CrossRef] [Google Scholar]
  20. de Geus, E.J., Bronfman, L., & Thaddeus, P. 1990, A&A, 231, 137 [NASA ADS] [Google Scholar]
  21. Elmegreen, B.G. 1979, ApJ, 232, 729 [NASA ADS] [CrossRef] [Google Scholar]
  22. Elmegreen, B.G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
  23. Esquivel, A., & Lazarian, A. 2005, ApJ, 631, 320 [NASA ADS] [CrossRef] [Google Scholar]
  24. Falgarone, E., Pety, J., & Hily-Blant, P. 2009, A&A, 507, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Fiege, J.D., & Pudritz, R.E. 2000, MNRAS, 311, 85 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fixsen, D.J. 2009, ApJ, 707, 916 [NASA ADS] [CrossRef] [Google Scholar]
  27. Frerking, M.A., Langer, W.D., & Wilson, R.W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gong, Y., Li, G.X., Mao, R.Q., et al. 2018, A&A, 620, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gong, Y., Belloche, A., Du, F.J., et al. 2021, A&A, 646, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Goodman, A.A., Benson, P.J., Fuller, G.A., & Myers, P.C. 1993, ApJ, 406, 528 [CrossRef] [Google Scholar]
  31. Goodman, A.A., Barranco, J.A., Wilner, D.J., & Heyer, M.H. 1998, ApJ, 504, 223 [CrossRef] [Google Scholar]
  32. Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [Google Scholar]
  33. Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Hacar, A., Tafalla, M., & Alves, J. 2017, A&A, 606, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Hatchell, J., Terebey, S., Huard, T., et al. 2012, ApJ, 754, 104 [NASA ADS] [CrossRef] [Google Scholar]
  37. Heiles, C. 1988, ApJ, 324, 321 [CrossRef] [Google Scholar]
  38. Heitsch, F., Zweibel, E.G., Mac Low, M.-M., Li, P., & Norman, M.L. 2001, ApJ, 561, 800 [NASA ADS] [CrossRef] [Google Scholar]
  39. Heitsch, F., Ballesteros-Paredes, J., & Hartmann, L. 2009, ApJ, 704, 1735 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hennebelle, P., & André, P. 2013, A&A, 560, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Henshaw, J.D., Kruijssen, J.M.D., Longmore, S.N., et al. 2020, Nat. Astron., 4, 1064 [CrossRef] [Google Scholar]
  42. Heyer, M.H., & Brunt, C.M. 2004, ApJ, 615, L45 [NASA ADS] [CrossRef] [Google Scholar]
  43. Heyer, M.H., Williams, J.P., & Brunt, C.M. 2006, ApJ, 643, 956 [NASA ADS] [CrossRef] [Google Scholar]
  44. Heyer, M., Krawczyk, C., Duval, J., & Jackson, J.M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
  45. Hily-Blant, P., & Falgarone, E. 2009, A&A, 500, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Hubrig, S., Oskinova, L.M., & Schöller, M. 2011, Astron. Nachr., 332, 147 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hunter, J.D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  48. Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
  49. Juvela, M., & Montillaud, J. 2016a, A&A, 585, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Juvela, M., & Montillaud, J. 2016b, A&A, 585, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Kauffmann, J., Bertoldi, F., Bourke, T.L., Evans, N.J.I., & Lee, C.W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017, A&A, 603, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Kolmogorov, A. 1941, Akad. Nauk SSSR Dokl., 30, 301 [Google Scholar]
  54. Lada, C.J., Lada, E.A., Clemens, D.P., & Bally, J. 1994, ApJ, 429, 694 [NASA ADS] [CrossRef] [Google Scholar]
  55. Larson, R.B. 1981, MNRAS, 194, 809 [Google Scholar]
  56. Lesieur, M. 2008, Turbulence in Fluids, Fluid Mechanics and Its Applications (Springer Netherlands) [CrossRef] [Google Scholar]
  57. Li, H.B., Goodman, A., Sridharan, T.K., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R.S. Klessen, C.P. Dullemond, & T. Henning, 101 [Google Scholar]
  58. Li, S., Zhang, Q., Liu, H.B., et al. 2020, ApJ, 896, 110 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lindner, R.R., Vera-Ciro, C., Murray, C.E., et al. 2015, AJ, 149, 138 [NASA ADS] [CrossRef] [Google Scholar]
  60. Mackey, J., Langer, N., & Gvaramadze, V.V. 2013, MNRAS, 436, 859 [NASA ADS] [CrossRef] [Google Scholar]
  61. Mangum, J.G., & Shirley, Y.L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
  62. McCutcheon, W.H., Vrba, F.J., Dickman, R.L., & Clemens, D.P. 1986, ApJ, 309, 619 [NASA ADS] [CrossRef] [Google Scholar]
  63. McKee, C.F., & Ostriker, E.C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
  64. Miesch, M.S., & Bally, J. 1994, ApJ, 429, 645 [NASA ADS] [CrossRef] [Google Scholar]
  65. Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [Google Scholar]
  66. Mottram, J.C., van Dishoeck, E.F., Kristensen, L.E., et al. 2017, A&A, 600, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Müller, H.S.P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [CrossRef] [Google Scholar]
  68. Nozawa, S., Mizuno, A., Teshima, Y., Ogawa, H., & Fukui, Y. 1991, ApJS, 77, 647 [NASA ADS] [CrossRef] [Google Scholar]
  69. Ossenkopf, V., & Mac Low, M.M. 2002, A&A, 390, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Ostriker, E.C., Stone, J.M., & Gammie, C.F. 2001, ApJ, 546, 980 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pety, J. 2005, in SF2A-2005: Semaine de l'Astrophysique Francaise, eds. F. Casoli, T. Contini, J.M. Hameury, & L. Pagani, 721 [Google Scholar]
  72. Pineda, J.E., Goodman, A.A., Arce, H.G., et al. 2010, ApJ, 712, L116 [NASA ADS] [CrossRef] [Google Scholar]
  73. Planck Collaboration XXIII. 2011, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Planck Collaboration XXVIII. 2016, A&A, 594, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Planck Collaboration Int. XX. 2015, A&A, 576, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Planck Collaboration Int. XXXV. 2016, A&A, 586, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Qian, L., Li, D., & Goldsmith, P.F. 2012, ApJ, 760, 147 [CrossRef] [Google Scholar]
  80. Reif, K., Reich, W., Steffen, P., Müller, P., & Weiland, H. 1987, Mitteil. Astron. Gesell. Hamburg, 70, 419 [NASA ADS] [Google Scholar]
  81. Riener, M., Kainulainen, J., Henshaw, J.D., et al. 2019, A&A, 628, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Robitaille, T., & Bressert, E. 2012, APLpy: Astronomical Plotting Library in Python Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
  83. Schneider, N., Bontemps, S., Motte, F., et al. 2016, A&A, 591, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Shan, W., Yang, J., Shi, S., et al. 2012, IEEE Trans. Terahertz Sci. Technol., 2, 593 [Google Scholar]
  85. Shimajiri, Y., Kitamura, Y., Saito, M., et al. 2014, A&A, 564, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Shimajiri, Y., André, P., Palmeirim, P., et al. 2019, A&A, 623, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Shirley, Y.L. 2015, PASP, 127, 299 [NASA ADS] [CrossRef] [Google Scholar]
  88. Skalidis, R., & Tassis, K. 2021, A&A, 647, A186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Soler, J.D. 2019, A&A, 629, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Soler, J.D., Hennebelle, P., Martin, P.G., et al. 2013, ApJ, 774, 128 [NASA ADS] [CrossRef] [Google Scholar]
  91. Stewart, M., & Federrath, C. 2022, MNRAS, 509, 5237 [Google Scholar]
  92. Su, Y., Yang, J., Yan, Q.-Z., et al. 2020, ApJ, 893, 91 [Google Scholar]
  93. Sun, J.X., Lu, D.R., Yang, J., et al. 2018, Acta Astron. Sinica, 59, 3 [Google Scholar]
  94. Tachihara, K., Mizuno, A., & Fukui, Y. 2000, ApJ, 528, 817 [NASA ADS] [CrossRef] [Google Scholar]
  95. Tachihara, K., Onishi, T., Mizuno, A., & Fukui, Y. 2002, A&A, 385, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Tafalla, M., & Hacar, A. 2015, A&A, 574, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Tetzlaff, N., Neuhäuser, R., & Hohle, M.M. 2011, MNRAS, 410, 190 [NASA ADS] [CrossRef] [Google Scholar]
  98. Thomson, A.J.M., Landecker, T.L., Dickey, J.M., et al. 2019, MNRAS, 487, 4751 [NASA ADS] [CrossRef] [Google Scholar]
  99. Ulich, B.L., & Haas, R.W. 1976, ApJS, 30, 247 [NASA ADS] [CrossRef] [Google Scholar]
  100. van der Walt, S., Colbert, S.C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [NASA ADS] [CrossRef] [Google Scholar]
  101. van Dishoeck, E.F., & Black, J.H. 1988, ApJ, 334, 771 [NASA ADS] [CrossRef] [Google Scholar]
  102. van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
  103. Visser, A.E., Richer, J.S., & Chandler, C.J. 2002, AJ, 124, 2756 [NASA ADS] [CrossRef] [Google Scholar]
  104. Wang, C., Yang, J., Su, Y., et al. 2019, ApJS, 243, 25 [NASA ADS] [CrossRef] [Google Scholar]
  105. White, G.J., Lefloch, B., Fridlund, C.V.M., et al. 1997, A&A, 323, 931 [NASA ADS] [Google Scholar]
  106. Wright, E.L., Eisenhardt, P.R.M., Mainzer, A.K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
  107. Wu, Y., Liu, T., Meng, F., et al. 2012, ApJ, 756, 76 [CrossRef] [Google Scholar]
  108. Zhang, G.-Y., André, P., Men'shchikov, A., & Wang, K. 2020, A&A, 642, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Zhou, J.-X., Li, G.-X., & Chen, B.-Q. 2022, MNRAS, 513, 638 [NASA ADS] [CrossRef] [Google Scholar]
  110. Zucker, C., Speagle, J.S., Schlafly, E.F., et al. 2020, A&A, 633, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Zuckerman, B., & Palmer, P. 1974, ARA&A, 12, 279 [NASA ADS] [CrossRef] [Google Scholar]
  112. Zybin, K.P., & Sirota, V.A. 2015, Phys. Uspekhi, 58, 556 [NASA ADS] [CrossRef] [Google Scholar]
2

The maps can be obtained from the public Planck Legacy Archive http://pla.esac.esa.int/

3

In this work, σnt, σt and σobs refer to one-dimensional velocity dispersions rather than three-dimensional velocity dispersions.

All Figures

thumbnail Fig. 1

Three-color composite image of the Stockert-25m 11 cm (red; Reif et al. 1987), IRAS 100 μm (green; Miville-Deschênes & Lagache 2005), and the WISE 12 μπι (blue; Wright et al. 2010) emission toward Ophiuchus North. The Sh 2-27 Hii region is ionized by ζ Oph that is indicated by the black cross. The observed region Oph Nl is indicated by the white dashed box, while the other regions are indicated by the white solid boxes.
In the text
thumbnail Fig. 2

Distribution of CO, C18O and H2 gas. (a) CO (J = 1−0) integrated intensity map, Wco, is overlaid with the C18O (J= 1−0) integrated intensity contours. The integrated velocity ranges are [1.3, 6.1] km s−1 for CO (J = 1−0) and [2.5, 4.2] km s−1 for C18O (J= 1−0). The color bar represents the CO (J = 1−0) integrated intensity in units of Κ km s−1, while the contours start at 0.54 Κ km s−1 and increase by 0.54 Κ km s−1. (b) C18O (J = 1−0) integrated intensity map, WCO${W_{{\rm{CO}}}}$ is overlaid with the H2 column density black contours from the near infrared extinction map (Juvela & Montillaud b2016). The color bar represents the C18O (J = 1−0) integrated intensity in units of Κ km s−1. The black contours start at 3 × 1021 cm-2 and increase by 3 × 1021 cm-2, (c) Extinction-based H2 column density map. In each panel, the beam size is shown in the lower right corner, and the two Planck cold clumps are indicated by the two blue open circles.
In the text
thumbnail Fig. 3

CO (J = 1 −0) and C18O (J = 1 −0) spectra of the selected positions indicated in the central map that is the same as Fig. 2a. CO (J = 1 −0) and C18O (J = 1 −0) are indicated by the black and blue lines, respectively.
In the text
thumbnail Fig. 4

Distribution of the physical and chemical properties of C18O in Oph N l. (a) Excitation temperature map derived from the CO peak main beam temperature. The color bar represents the excitation temperature in units of K, while the contour represents an excitation temperature of 7.5 K. (b) Peak C18O (J = 1 −0) opacity map. (c) C18O column density map at an angular resolution of 3′ (d) C18O fractional abundance map. The contours represent the C18O fractional abundances of 5 × 10-8 and 1 × 10-7. The two dashed circles represent the observed CO depletion holes. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two blue open circles.
In the text
thumbnail Fig. 5

Maps of peak intensities (Fig. 5a), LSR velocities (Fig. 5b), and velocity dispersions (Fig. 5c) derived from single-component Gaussian fits to our C18O (J = 1 −0) data cube. Figures 5d–f are similar to Figs. 5a–c, but at a smoothed angular resolution of 180″. In each panel, the beam size is shown in the lower right corner, and the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.
In the text
thumbnail Fig. 6

Distribution of local velocity gradients derived from C18O velocity centroids. (a) Local velocity gradient magnitude map derived from Fig. 5b. (b) C18O (J = 1 −0) peak intensity map is overlaid with the normalized velocity gradient vectors. The blue and red arrows represent the average directions of the local velocity gradients in sub-regions indicated by the blue and red dashed boxes, respectively. Figures 6c and d is similar to Figs. 6a and b, but derived from Fig. 5e. In Fig. 6c, the three regions showing high velocity gradients are indicated by the three black dashed boxes. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.
In the text
thumbnail Fig. 7

Histogram and cumulative distribution of the nonthermal velocity dispersion derived from C18O (J = 1−0) at the angular resolutions of 55″ and 180″, respectively. The vertical dashed lines represent the sonic speed and the thermal velocity dispersion of C18O at a kinetic temperature of 10 K. This figure is suggestive of widespread subsonic turbulence.
In the text
thumbnail Fig. 8

Second-order velocity structure function of Oph Nl derived from Fig. 5b as a function of the spatial lag, l. The gray-shaded region is the spatial-resolution limit which corresponds to 55″. The power-law fitting result is indicated by the black dashed line. The orange, red, and blue dashed lines represent the observed relation in Musca (Hacar et al. 2016) and Rossete (Heyer et al. 2006), the classic Larson relation (γ = 0.76; Larson 1981), and the revised relation, σ ∝ R0.5 (γ = l; Heyer et al. 2009), respectively.
In the text
thumbnail Fig. 9

(a) Planck Stokes I continuum emission at 353 GHz is overlaid with magnetic field orientations, (b) Histogram distribution of the polarization angle fitted with a single Gaussian component.
In the text
thumbnail Fig. A.1

Decomposition of CO (J = 1 – 0) data (a) Distribution of the number of the fitted velocity components, (b) Fitted peak intensities for the pixels showing a single velocity component, (c) Fitted velocity centroids for the pixels showing a single velocity component, (d) Fitted velocity dispersions for the pixels showing a single velocity component. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.)
In the text
thumbnail Fig. B.1

Decomposition of CO (J=1−0) data, (a) Distribution of the number of the fitted velocity components, (b) Fitted peak intensities for the pixels showing a single velocity component, (c) Fitted velocity centroids for the pixels showing a single velocity component, (d) Fitted velocity dispersions for the pixels showing a single velocity component. In each panel, the beam size is shown in the lower right corner, the two Planck cold clumps (G008.67+22.14 and G008.52+21.84) are indicated by the two open blue circles.
In the text
thumbnail Fig. C.1

Plane-of-the-sky magnetic field and τ345 measured by Planck toward Ophiuchus North. The overlaid pattern, produced using the line integral convolution (LIC) method (Cabrai & Leedom 1993), indicates the orientation of magnetic field lines. The marked regions are the same as in Fig. 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.