| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 23 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202140863 | |
| Published online | 11 February 2022 | |
The SAPP pipeline for the determination of stellar abundances and atmospheric parameters of stars in the core program of the PLATO mission
1
Max Planck Institute for Astronomy, 69117 Heidelberg, Germany
e-mail: gent@mpia-hd.mpg.de
2
Niels Bohr International Academy, NBI, University of Copenhagen, Blegdamsvej 17, 2100 Copenhagen, Denmark
3
Institute of Space Sciences (ICE, CSIC), Carrer de Can Magrans s/n, 08193 Cerdanyola del Valles, Spain
4
Institut d’Estudis Espacials de Catalunya (IEEC), Carrer Gran Capita 2, 08034 Barcelona, Spain
5
Space Sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège, Quartier Agora, Allée du 6 Août 19c, Bât. B5C, 4000 Liège, Belgium
6
Observational Astrophysics, Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
7
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Lagrange, CS 34229, Nice, France
8
Research School of Astronomy & Astrophysics, Mount Stromlo Observatory, Australian National University, ACT 2611, Australia
9
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, Boulevard du Triomphe, 1050 Brussels, Belgium
10
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory, Szent Imre H. St. 112, 9700 Szombathely, Hungary
11
MTA-ELTE Exoplanet Research Group, Hungary
12
MTA-ELTE Lendület Milky Way Research Group, Hungary
13
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
14
Observatoire Paris-Site de Meudon, LESIA, 5 Pl Jules Janssen, 92195 Meudon Cedex, France
15
Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro 1, Sta. Ma. Tonantzintla, Puebla CP 72840, Mexico
16
Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
17
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
18
Istituto Nazionale di Astrofisica – INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
19
Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
20
Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
21
CNRS, IRAP, 9 Av. Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
22
LUPM, Univ. Montpellier, CNRS, Montpellier, France
23
Yunnan Observatories, Chinese Academy of Sciences, PO Box 110 Kunming 650216, PR China
24
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120/1520, 8000 Aarhus, Denmark
25
Space Science Institute, 4765 Walnut Street, Boulder, CO 80301, USA
26
LESIA, Observatoire de Paris, Bât. 14 – Soleil-Planètes, 5 Place Jules Janssen, 92195 Meudon, France
Received:
23
March
2021
Accepted:
8
November
2021
We introduce the SAPP (Stellar Abundances and atmospheric Parameters Pipeline), the prototype of the code that will be used to determine parameters of stars observed within the core program of the PLATO space mission. The pipeline is based on the Bayesian inference and provides effective temperature, surface gravity, metallicity, chemical abundances, and luminosity. The code in its more general version has a much wider range of potential applications. It can also provide masses, ages, and radii of stars and can be used with stellar types not targeted by the PLATO core program, such as red giants. We validate the code on a set of 27 benchmark stars that includes 19 FGK-type dwarfs, 6 GK-type subgiants, and 2 red giants. Our results suggest that combining various observables is the optimal approach, as this allows the degeneracies between different parameters to be broken and yields more accurate values of stellar parameters and more realistic uncertainties. For the PLATO core sample, we obtain a typical uncertainty of 27 (syst.) ± 37 (stat.) K for Teff, 0.00 ± 0.01 dex for log g, 0.02 ± 0.02 dex for metallicity [Fe/H], −0.01 ± 0.03 R⊙ for radii, −0.01 ± 0.05 M⊙ for stellar masses, and −0.14 ± 0.63 Gyr for ages. We also show that the best results are obtained by combining the νmax scaling relation with stellar spectra. This resolves the notorious problem of degeneracies, which is particularly important for F-type stars.
Key words: surveys / stars: fundamental parameters / stars: solar-type / stars: abundances / stars: atmospheres
© M. R. Gent et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The past decade has seen revolutionary developments in astronomical surveys and large-scale observational programs which are assembling high-quality data for millions of stars in our Galaxy. Many of the ongoing efforts are motivated by the potential of using stars as tracers of Galaxy structure and evolution (e.g. HIPPARCOS: Perryman et al. 1997, 2MASS: Skrutskie et al. 2006, SDSS/SEGUE: Yanny et al. 2009, GCS: Nordström et al. 2004, Gaia-ESO: Gilmore et al. 2012; Randich et al. 2013, LAMOST: Cui et al. 2012, RAVE: Steinmetz et al. 2006, Gaia: Gaia Collaboration 2016, APOGEE: Majewski et al. 2017, GALAH: De Silva et al. 2015). With the advent of exoplanet science, the role of stars as exoplanet hosts is becoming increasingly important. Space-based missions – CoRoT, Kepler, and TESS – are discovering new exoplanets at an astonishing rate (e.g. Borucki et al. 2010; Buchhave et al. 2014; Ricker et al. 2015), but also yield precise data for the study of stellar interiors with asteroseismology techniques (e.g. Christensen-Dalsgaard 2002; Huber et al. 2013; Serenelli et al. 2017). Future facilities, such as PLATO (Rauer et al. 2014), are opening entirely new perspectives for studies of exoplanets in different environments and for studies of stars at a level of detail that has so far only been possible for our Sun.
In this work, we introduce the SAPP pipeline1, which will be used for the determination of atmospheric parameters of stars observed within the core program of the PLATO space mission (Montalto et al. 2021). The code will provide stellar effective temperature (Teff), metallicity ([Fe/H]), surface gravity (log g), radial velocities, and detailed chemical composition, among other parameters. Our ambitious goal is to reach uncertainties as low as 1% on Teff and [Fe/H], for instance, in order to match the high spectral data quality provided by upcoming ground-based facilities, such as WEAVE and 4MOST. The SAPP is written in Python and the source code is public and available for use2.
Our approach to the analysis of our targets is somewhat different from other available pipelines and codes (e.g. SME: Valenti & Piskunov 1996; Piskunov & Valenti 2017, The Cannon: Ness et al. 2015, The Payne: Ting et al. 2016; Rix et al. 2016; Ting et al. 2019, MATISSE: Recio-Blanco et al. 2006, CNN StarNet: Bialek et al. 2020), although our analysis shares many of the elements with these software units. It is beyond the scope of this paper to provide a detailed comparison of our code with the other programs, as ultimately the design of a computer program follows the needs and objectives of a given research project, and this sets the conceptual and numerical basis of a code. In our case, motivated by the need to provide accurate and precise astrophysical parameters for several 105 (and more) stars to enable their exploitation in studies of exoplanets, we have chosen a Bayesian inference method as the basis of the code (see, e.g. Jofré et al. 2019, for a review of methods and models). The idea of using Bayesian techniques is not new, and has already featured in a number of studies (e.g. Pont & Eyer 2004; Jørgensen & Lindegren 2005; Serenelli et al. 2013; Schönrich & Bergemann 2014; Bailer-Jones et al. 2018; McMillan et al. 2018; del Burgo & Allende Prieto 2018; Steinmetz et al. 2020). In this work, we closely follow the methodology outlined in Schönrich & Bergemann (2014) and combine various sources of observational information, including electromagnetic spectra, parallaxes, photometry, and seismic constraints to determine astrophysical parameters of stars. The benefits of using a Bayesian approach for the analysis of fundamental parameters of stars, such as masses and metallicities, have already been demonstrated (e.g. Pont & Eyer 2004; Jørgensen & Lindegren 2005; Gruberbauer et al. 2012; Bazot et al. 2012). Therefore, in order to take full advantage of the Bayesian formalism, we also include stellar evolution models that give us the ability to determine masses, luminosities, radii, and ages of stars in a single consistent framework that takes into account the correlations between all relevant parameters.
The paper is organised as follows. Section 2 gives an overview of the observed sample of stars that are used to validate the approach developed in this work. In Sect. 3 we outline the basic concepts behind the numerical part of the code and review the input parameters and input models, including stellar structure models, stellar atmospheres, and the grids of stellar spectra. In Sect. 4 we present the results of the analysis of the benchmark stars, as well as clusters and in Sect. 5 we describe the operation of SAPP briefly in the context of the PLATO space mission (Rauer et al. 2014). We close the paper with a discussion of forthcoming improvements to the pipeline in Sect. 6 and draw conclusions in Sect. 7.
2. Observations
2.1. Observational data
The core PLATO sample focuses on main sequence stars and subgiants (Montalto et al. 2021). Therefore, we first focus on these types of stars, but owing to the versatility of the code and input physics, we also present in Sect. 4.6 the performance of the code when combined with spectra of red giants in the Galactic field and in stellar clusters.
Our core validation stellar sample includes Gaia benchmark stars (Heiter et al. 2015), Kepler legacy stars (Silva Aguirre et al. 2017; Nissen et al. 2017), and the very metal-poor star ν ind (Chaplin et al. 2020). These stars are shown in the Teff − log g plane in Fig. 1, and provide a representative coverage of the current PLATO input catalogue (PIC; Montalto et al. 2021). The stars cover a broad range in effective temperature from 5022 K (δ Eri) to 6635 K (HD 49933), and surface gravity from log g = 3.46 (ν Ind) to log g = 4.53 dex (α Cen B). One of the stars in the sample (η Boo) is a relatively fast rotator (for FGK-type stars) with a projected equatorial rotational velocity v sin i = 12.7 km s−1. Some of the stars have a super-solar metallicity, in excess of +0.2 dex (η Boo, α Cen A,B system), whereas the most metal-poor star in the sample is ν Ind with [Fe/H] = −1.43 dex (Chaplin et al. 2020).
 |
Fig. 1. Teff − log g relation of the benchmark targets. The colour scale represents metallicity (the blue end is metal poor and the red end is just above solar metallicity). Each star is plotted with its reference values (Table 1) on top of a solar isochrone. |
The spectra of the benchmark stars are taken from the ESO public archive. Spectra obtained with the high-resolution UVES spectrograph mounted on the VLT are available for the majority of the stars from our sample. For the Kepler stars, reduced combined spectra taken with the HARPS-N facility were kindly provided by P. E. Nissen (priv. comm.). The UVES spectra (4800 to 6800 Å) have a resolving power of λ/δλ ≈ 47 000 (Dekker et al. 2000) and the HARPS data have a resolving power of 115 000 (Mayor et al. 2003). The signal-to-noise ratio (S/N) of the UVES and HARPS spectra is in the range from 200 to over 1000. The spectra are all pre-processed (described in Appendix B.1) by the SAPP using different developed procedures, which include continuum normalisation, radial velocity correction, and contaminant treatment. We then degrade the resolving power of the spectra to R = 20 000 and reduce the wavelength coverage to 5300−5600 Å in the optical spectral window. This is done to ensure that our tests are as predictive as possible: spectra with such characteristics represent a plausible scenario, in which only spectra observed with medium-resolution (R ≈ 20 000) facilities, such as 4MOST, WEAVE, and APOGEE, will be available for the vast majority of PLATO targets.
Reference parameter sample of benchmark stars.
The observed photometry for these stars was extracted from the Gaia EDR3 catalogue Gaia Collaboration (2016, 2018, 2020), which we supplemented with 2MASS magnitudes (JHKs) and Johnson-Cousins photometric data, where available. For most stars in the sample, we used the photo-geometric distances from the Bailer-Jones et al. (2021) catalogue. If they were not available (see Table 1), then Gaia parallaxes π are converted into distances via d [pc] = 1/π. This is a suitable approximation in this work, because the benchmark stars are all nearby targets, with the most distant system being KIC 10162436 at around 138 pc. If Gaia parallaxes were not available, then values from the HIPPARCOS catalogue were supplemented (Perryman et al. 1997; van Leeuwen 2007). The largest percentage difference between distances from Bailer-Jones et al. (2021) and using the inverse parallax values are 0.02% for Gaia EDR3 and 0.39% for HIPPARCOS, respectively. The comparison between EDR3 and HIPPARCOS parallaxes can be seen in Fig. 2, where it can be seen that the maximum propagated percentage difference for Kepler legacy stars is ∼5% and that for Gaia-ESO is less than 0.5%.
 |
Fig. 2. Percentage difference between Gaia EDR3 parallax and HIPPARCOS parallax (van Leeuwen 2007) with respect to Gaia EDR3 in mas. The error represents the uncertainty of EDR3 parallaxes and HIPPARCOS parallaxes propagated through the percentage difference. The open circles represent the Kepler legacy stars, the solid black circles represent Gaia-ESO stars, and the single open square represents our metal-poor star ν Ind. The average uncertainties for the Kepler legacy and Gaia ESO stars are shown in the bottom right corner. |
The observed magnitudes were corrected for interstellar extinction using the Stilism tool (Capitanio et al. 2017). The tool provides line-of-sight reddening interpolated on a given distance with associated uncertainties. For the benchmark stars, the reddening is small (E(B − V)≲0.015 mag) and is implemented via the extinction correction (see Eq. (9)).
2.2. Stellar parameters of the benchmark stars
Stellar parameters for our benchmark stars were obtained from several literature sources, the priority being given to Jofré et al. (2018), because these authors provide a comprehensive homogeneous analysis of all classical stellar parameters, including metallicity and detailed chemical abundances derived with constraints from independent data. This study is based on the analysis presented by Jofré et al. (2014) and Heiter et al. (2015). All parameters for ν Ind were adopted from Chaplin et al. (2020).
Briefly, the determination of parameters for the Gaia benchmark stars is as follows. The Teff values rely on interferometric angular diameters measured with CHARA and VLTI facilities and bolometric fluxes obtained either via integrating the observed spectral energy distributions (SEDs) or indirectly by converting the photometry into Fbol using synthetic calibrations. δ Eri is the only star for which we give a preference to the recent accurate Teff and radius values based on the interferometric angular diameter measured with VLTI/PIONEER (Rains et al. 2020). The surface gravities were determined using masses estimated from evolutionary tracks, angular diameters, and HIPPARCOS parallaxes, which are mostly in excellent agreement with Gaia DR2 and Gaia EDR3 values for the reference sample (see Fig. 2). The surface gravities were verified using asteroseismic scaling relations where possible. Metallicities are model-dependent quantities: here we adopt the non-local thermodynamic equilibrium (NLTE) estimates. Luminosity measurements are taken from Heiter et al. (2015), whereas masses are adopted from different sources. For δ Eri, mass is taken from Bruntt et al. (2010) with age adopted from Thévenin et al. (2005). α Cen A and B have masses and radii from Kervella et al. (2017) with ages from Joyce & Chaboyer (2018). The mass and age of ν Ind are taken from Chaplin et al. (2020), but no luminosity or radius is provided in that study. HD 49933 has mass, age, and radius estimated by Liu et al. (2013). The age and radius sources vary star-by-star: for 18 Sco, age is taken from Monroe et al. (2013) and radius from Bazot et al. (2018); for β Hyi age and radius are adopted from Brandão et al. (2011); for β Vir age is taken from Eggenberger & Carrier (2006) and radius from Boyajian et al. (2012); for η Boo age is adopted from Carrier et al. (2005) and radius from van Belle et al. (2007); and for Procyon age is from Liebert et al. (2013) and radius from Kervella et al. (2004).
For the Kepler legacy sample, stellar parameters were adopted from Nissen et al. (2017), except the 16 Cyg A and B binary, for which the interferometric Teff estimate from White et al. (2013) is given preference. We do not use ν Ind or the Kepler stars in the analysis of Teff (except 16 Cyg A and B), because their Teff were not determined in the same fundamental way as those of Gaia benchmark stars and large scatter exists between different estimates (e.g. Wu & Li 2017 for KIC 6225718). The interferometric angular diameter (AD) measurements for KIC 6225718 and KIC 6106415 exist, but the errors of the Teff estimates are too large (70 to 90 K) to provide a meaningful constraint on the methods. The estimates of mass (M), radius (R), luminosity (L), and age (τ) for the majority of these stars come from Serenelli et al. (2017; KIC 10162436, KIC 10644253, KIC 3427720, KIC 9139151) and Creevey et al. (2017; 16 Cyg A and B, KIC 12258514, KIC 6106415, KIC 6225718, KIC 7940546).
3. Methods
3.1. Bayesian probability approach
The conditional probability of a set of model parameters X = X1, …, Xn given a set of observations O = O1, …, Om is given by Bayes theorem and results from the combined probability P(X,O) = P(X|O)P(O). Hence,
where P(X|O) is the posterior probability, that is the conditional probability of the parameter set X given the set of observables O; P(O|X) is the likelihood, i.e. the probability of the observations occurring given the set of parameters X; P(X) is the prior probability ascribed to a set of predefined parameters; and the denominator P(O) is function only of the observations, and is not relevant for determination of stellar model parameters, as it only acts as a normalisation factor. Therefore, the expression above can be simplified to
where the posterior P(X|O) is a probability distribution function (PDF) on the chosen parameter space. For the remainder of this paper, the observational likelihoods are abbreviated by a prime given the set of parameters, i.e. P′(X). The current implementation of SAPP assumes observables are statistically independent, which allows P(O1, …, Om|X) to be decomposed as,
More specifically, based on the observables used in this work,
where the subscripts refer to a specific observable, j: ‘spec’ for stellar spectra (fluxes against wavelength), ‘mag’ for photometric magnitudes and their products, ‘seism’ for asteroseismic quantities (Δν, νmax), and ‘prior’ for any priors. Here Pprior(X) is the prior probability distribution, which can represent the initial mass function (IMF), selection function, or any other source of information that further constrains the parameter space. All observables are assumed to be normally distributed, i.e.
where Nj is the number of parameter points (index running over k) for the given observable j. Therefore,
It is easy to modify the expression for the likelihood to include statistically dependent observables by introducing the use of their correlation matrix. This is usually not necessary, but in this work we explore the influence of covariance in the analysis (see Sect. 4.5) and therefore we also perform additional calculations with Eq. (6) modified to
where Σ is the covariance matrix. The individual likelihoods are described in the following sections. Similar to Schönrich & Bergemann (2014), we include spectra, photometry, parallax, stellar evolution models, and asteroseismic constraints, when available.
The core parameter space is defined as follows. The quantities Teff, log g, and [Fe/H] represent the key parameter space shared by all the grids of the SAPP (photometric, asteroseismic, spectroscopic). On the other hand, mass M, age τ, radius R, Luminosity L, and abundances are secondary parameters. They can only be inferred from some of the grids and so have dependencies on each of the three parameters in the key parameter space.
3.2. Synthetic photometry
The photometry PDF P(Omag, dist|X) relates magnitudes and parallaxes to the model predictions. We denote the stellar model magnitudes at model point i and magnitude k1 by mi, k1 and the photometric observation in the filter k1 (such as G, GBP or GRP) with Ok1:
in accordance with Eq. (6),
where the extinction value Ak1(r) is a function of reddening (r), μ(d) = 5 log(d)–5 is the distance modulus, and σk1 is the photometric error combined for the k1 band.
The extinction in an individual photometric band is calculated using:
where the values of R were adopted from Casagrande et al. (2011):
For the Gaia EDR3 dataset, the AG value can be given, but is not always available. In the case where it is not available, (GBP − GRP) colour-dependent extinction coefficients presented in Casagrande et al. (2021) are used for G, GBP, and GRP. For the magnitudes, we separate the PDFs entirely, that is (G, GBP, GRP) and (H, J, Ks, B, V).
3.3. Distance and extinction uncertainties with respect to photometry
To include the uncertainty on distance modulus and extinction in computing the photometric PDF, μ(d) and Ak1 must be considered as separate quantities. In Eq. (9), μ(d) and Ak1 enter as parameters in each band with no error. To account for the measured value and error, an additional factor in the likelihood is introduced:
where Pi, α, β is marginalised over parameters μα and Ak1, β which vary over a large range in values centering around the observed quantities μ(d) and Ak1.
3.4. Asteroseismic constraints
Cool stars, typically FGK, show ubiquitous oscillations which are excited by convective motions in their envelopes, the same mechanism responsible for solar oscillations. These so-called solar-like oscillations are characterised by a regular pattern, with modes of consecutive radial order that are almost equally spaced in frequency. The difference in frequency values of such consecutive modes determines the large frequency separation Δν. Moreover, the distribution of power as a function of frequency shows a well-defined peak at the so-called frequency of maximum power, νmax. These two quantities are related through standard asteroseismic scaling relationships (e.g. Chaplin & Miglio 2013; Serenelli et al. 2017) to fundamental stellar parameters as follows:
where Δν⊙ = 135.1 μHz (Huber et al. 2011), ρ is the mean density of the star, and ρ⊙ is the solar mean density, and the last equality assumes the stellar mass M and radius R are expressed in solar units.
For νmax, the relation is:
where the solar values are ν⊙ = 3090 μHz (Huber et al. 2011), log g⊙ = 4.44, and Teff, ⊙ = 5777 K (Heiter et al. 2015) and, again, the last expression assumes solar units for M and R.
The νmax taken from the stellar evolution model is calculated using the aforementioned relationship, given the model values of Teff, M, and R. However, Δν is computed from the radial orders (l = 0) according to the prescription in White et al. (2011). We denote the stellar model asteroseismic quantities at model point i and quantity k2 by νseism, i, k2. It should be stressed that νmax and Δν are, strictly speaking, not direct observables. The analysis of light curves and the oscillation power spectrum is a complex and non-trivial procedure that involves a number of parameters, and it is far beyond the scope of this work to incorporate it into the present scheme3. We therefore refer to these quantities as observables (Belkacem et al. 2011). The asteroseismology likelihood is constructed as:
3.5. Spectroscopy
3.5.1. Spectroscopic models
The main difference between our approach and that outlined in Schönrich & Bergemann (2014) is our code does not use synthetic grids directly, but relies on the Payne algorithm. This is a fast model-reconstruction technique, which is based on artificial neural networks (ANNs; Ting et al. 2016, 2019). The conceptual idea of the method is to use an ANN (or a set of ANNs) to represent how the flux at each point across the stellar spectrum varies with each individual stellar parameter; for example the Teff (but the number of parameters is only limited by the dimensionality of the spectral grids). Once trained, the ANN layers, which act like a function that predicts a flux value at each point, can be used to quickly re-create an almost exact copy of the original spectrum. The typical error of the flux is ≲10−3, which corresponds to the interpolation error of ≲0.1% (Kovalev et al. 2019). Such ‘generic’ spectra can be used to quickly create analogues of stellar spectra computed ab initio. The input training grids of synthetic spectra must be computed on a random mesh and must be uniformly distributed in the full space of parameters.
Here we use the Payne model trained on an 8D grid (Teff, log g, [Fe/H], micro-turbulence vmic, vbrd (which accounts for macro-turbulence and projected rotation velocity v sin i), [Mg/Fe], [Ti/Fe], [Mn/Fe]). The training grids (see Kovalev et al. 2019, for more details) cover the entire parameter space of FGKM-type main sequence stars, subgiants, and red giants, that is 4000 ≤ Teff ≤ 7000 and 1.0 ≤ log g ≤ 5.0, and metallicity −2.6 ≤ [Fe/H] ≤ +0.5. Here, vbrd is used because it is not possible to resolve the separate influence of macro-turbulence and rotation broadening components at the typical resolving power of observed stellar spectra (see also Mashonkina et al. 2017; Kovalev et al. 2019). Both vmic and vbrd are randomly and evenly distributed in the parameter space, corresponding to typical values measured for FGK stars. vmic varies from 0.5 to 2 km−1, whereas vbrd varies from 5 to 25 km−1. The elements are chosen, because for them reliable NLTE atomic models were available to us at the stage of model grid development. The reference solar composition adopted in that grid was taken from Grupp (2004a) and scaled-solar abundances were used for all elements, except Mg, Ti, Fe, and Mn, for which the meteoritic values from Grevesse & Sauval (1998) were used. The main advantage of this approach compared to classical methods is the significant improvement in performance. The standard method, which relies on symmetric grids with an equidistant step size, is computationally very costly and does not allow separate grids to be computed for all possible detailed abundances while still keeping up with the rapid developments in atomic and molecular physics (e.g. Belyaev & Voronov 2020; Den Hartog et al. 2021) and 3D NLTE radiative transfer methods (e.g. Bergemann et al. 2019, 2021; Gallagher et al. 2020). The current grids allow us to determine [Mg/Fe], [Ti/Fe], and [Mn/Fe], but this can be extended to an arbitrary number of chemical elements in future.
The physics of the input model spectra was extensively described in Kovalev et al. (2019). Briefly, these are synthetic spectra models computed using 1D NLTE radiative transfer for Fe, Mg, Ti, and Mn. The MAFAGS-OS (Grupp 2004a,b) 1D hydrostatic model atmospheres with opacity sampling (OS) were used, owing to their more extended parameter coverage (up to mid A-type) and denser grid sampling. However, we note that extensive comparative tests were performed in different studies, showing that the MAFAGS-OS and MARCS models (Gustafsson et al. 2008) provide very similar thermodynamic structures, and results based on these models are almost identical (Bergemann et al. 2012, 2019). Owing to the assumption of hydrostatic equilibrium, the transport of energy by convection has to be parametrised. In the MAFAGS-OS model, the latter is computed using the mixing-length theory (Böhm-Vitense 1958; Cox & Giuli 1968; Canuto & Mazzitelli 1991). Microturbulence, the parameter that –for the lack of full 3D radiation-hydrodynamics (RHD) treatment– approximates the effect of velocities on scales smaller than the photon mean free path, is a free parameter in the grid. However, we note that the calculations of new multi-dimensional NLTE grids with average 3D models are already in progress, and the grids will make the use of ad hoc adjustable parameter vmic obsolete.
3.5.2. Model-data comparison
In the spectroscopic module, the SAPP relies on the gradient descent method, a standard first-order iterative optimisation algorithm that allows the user to locate the global minimum in the parameter space. As shown in Kovalev et al. (2019), the main advantage of the gradient descent method is that it allows to greatly speed-up the spectroscopic analysis compared to other methods. The average run time of this module is about 0.4 s per star, and this procedure yields all spectroscopic quantities, including Teff, metallicity, and detailed chemical abundances.
Once the global minimum in the 8D parameter space is found, we construct the spectroscopic PDF P(Ospec|X) by assuming a normal distribution with the 1σ uncertainty for 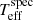 , log gspec, and [Fe/H]spec which are provided by the gradient descent method. Other types of spectroscopic PDFs were extensively studied in Schönrich & Bergemann (2014). The other derived spectroscopic parameters (chemical abundances, vbrd, vmic) are kept at their best-fit values. The discretisation and parameter space of the spectroscopic PDF follow the grid points defined by the tracks. However, we note that the latter has no influence on the shape or amplitude of P(Ospec|X).
, log gspec, and [Fe/H]spec which are provided by the gradient descent method. Other types of spectroscopic PDFs were extensively studied in Schönrich & Bergemann (2014). The other derived spectroscopic parameters (chemical abundances, vbrd, vmic) are kept at their best-fit values. The discretisation and parameter space of the spectroscopic PDF follow the grid points defined by the tracks. However, we note that the latter has no influence on the shape or amplitude of P(Ospec|X).
Hence, P(Ospec|X) for a given parameter space point i is indexed over quantity k3,
for each spectroscopic parameter Ok3,
where Ospec = 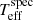 , log gspec, [Fe/H]spec and Xi = Teff, i, log gi, [Fe/H]i, respectively.
, log gspec, [Fe/H]spec and Xi = Teff, i, log gi, [Fe/H]i, respectively.
For the case of covariance, Eq. (7) is used instead of Eq. (5).
3.5.3. Error model
As our model grids have only eight dimensions, we implemented a more restrictive approach with respect to the statistical analysis of individual observations. Kovalev et al. (2019) used the full spectrum fit, but this is suboptimal because different spectral lines correspond to the abundances of different chemical elements across the entire periodic table, and using low-dimensional training grids does not allow the true chemical abundance patterns of the star to be accounted for, which are in most cases not scaled with solar values (Bergemann et al. 2014).
Therefore, in this work, instead of pre-selecting spectral lines by eye, as is common elsewhere in the literature, we resort to a robust statistical procedure. The procedure entails a comparison of the reference synthetic spectra of the benchmark stars (using the reference stellar parameters and abundances obtained as described in Sect. 2.2) with the observed spectra, which allows us to find the wavelength regions that are poorly described by our synthetic models. These regions are not masked, but rather we evaluate the residuals between the model flux and observed flux at each wavelength point. These monochromatic residuals, which we refer to as the error model, serve as systematic uncertainties, so that the total combined error per wavelength point is determined by adding the error model in quadrature with the observed flux error.
3.5.4. Correlation
It shall be pointed out that some spectroscopic parameters are highly correlated with each other, owing to the underlying physics of energy transfer in stellar atmospheres. Figure 3 shows the covariances for all eight parameters in the spectroscopic module. The core parameters – Teff, log g, and [Fe/H] show the most significant correlation, but also the α-enhancement (e.g. [Mg/Fe] or [Ti/Fe]) and micro-turbulence correlate with metallicity in different regimes of parameter space. This is why it is often necessary to use alternative constraints on the core parameter space. The impact of covariance on the final results is discussed in Sect. 4.5.
 |
Fig. 3. Correlation coefficient tables. Each table has a colour scale that represents the correlation coefficient, which ranges from −1 (negatively correlated) through 0 (no correlation) to 1 (positively correlated). This number informs how each spectroscopic parameter is correlated with the others. The top table shows the coefficients for a K-type star (δ Eri) and the bottom table for a F-type star (HD 49933). The vertical and horizontal axes for both depict the eight spectroscopic parameters from the SAPP spectroscopy module. |
3.6. Infrared flux method
The infrared flux method (IRFM) is another efficient method to determine the effective temperature and angular diameter of a star (e.g. Blackwell & Shallis 1977; Casagrande et al. 2006; González Hernández & Bonifacio 2009). The IRFM does not depend to a great extent on the physics of the stellar model atmospheres employed (see e.g. Casagrande et al. 2006, 2010, for a discussion of H− opacity and the use of MARCS vs ATLAS9 models across FGK dwarfs, and Asplund & García Pérez 2001; Chiavassa et al. 2018 for an analysis of the use of 3D vs 1D models). An estimate of log g and [Fe/H] is also required, but has minimal impact on the methodology (see e.g. Casagrande et al. 2006; González Hernández & Bonifacio 2009, for a discussion)
However, the adopted interstellar reddening and absolute flux calibration can easily introduce systematic errors of the order of ∼100 K (Casagrande et al. 2006; Ruchti et al. 2013). In the context of this work, the use of IRFM is limited to stars with reliable 2MASS photometry, which is about half of those in Table 1 due to their brightness and 2MASS saturation. For some of the remaining stars with good photometry in fewer bands, we tested the colour–Teff relations derived from the same implementation of the IRFM (Casagrande et al. 2021). These calibrations are available in up to 12 different colour combinations, with extra quality cuts based on photometry and realistic errors from a Monte Carlo approach4. The sensitivity of these relations to the adopted input parameters varies depending on the colour indices.
In Sect. 4.2 we compare the results of 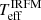 with our spectroscopic Teff values. This allows us to test the precision with which we can determine the Teff by means of the IRFM method. This is important because we expect that this method, along with the surface-brightness–colour relationships (SBCRs), will be the source of constraints on Teff for those PLATO targets that do not have spectra.
with our spectroscopic Teff values. This allows us to test the precision with which we can determine the Teff by means of the IRFM method. This is important because we expect that this method, along with the surface-brightness–colour relationships (SBCRs), will be the source of constraints on Teff for those PLATO targets that do not have spectra.
3.7. Surface-brightness–colour relationships
Surface-brightness–colour relationships allow the limb-darkened angular diameter of the star to be easily and independently estimated. Combining the latter with the distance to the star, the linear radius can be computed. Furthermore, the combination with the bolometric flux yields the effective temperature.
Many SBCRs exist in the literature, but all of them are empirical and are calibrated on interferometric measurements (see Nardetto 2018; Salsi et al. 2020 for a short review) or on Galactic eclipsing binaries (Graczyk et al. 2017, 2019). For example, Pietrzyński et al. (2019) derived the distance to the Large Magellanic Cloud with a precision of 1% using eclipsing binaries as distance indicators. In order to achieve such precision, they used a dedicated SBCR based on observations of 48 red clump stars with the PIONIER/VLTI instrument (Gallenne et al. 2018). Assuming the expected 1% precision and accuracy of angular diameters expected from CHARA/SPICA (see Sect. 6), we estimate that the method will provide a precision of 50 to 100 K in Teff and 1% to 2% in radii.
The main advantage of the method is its simplicity: only two magnitudes (usually V and K) are required and it is not very sensitive to reddening, because the surface brightness and the colours have a similar sensitivity to extinction. For example, a difference of 0.2 mag in the visual extinction translates into a difference of 2% on the radius and 60 K on the temperature. For comparison, a 2% error on Fbol translates into an error of 30 K on temperature. The main limitation of the method in the context of PLATO is likely its sensitivity to the uncertainty on the K magnitude. A 0.03 mag error in the K band magnitude causes an 80 K uncertainty in Teff and a 2% uncertainty on the radius. The results also depend on the spectral type and luminosity class (Salsi et al. 2020). Additionally, the method cannot be used for stars that show a significant activity level, have a companion(s), are flattened due to rotation (Challouf et al. 2014, 2015), and show signatures of wind and/or circumstellar shells.
In this work, we employ the SBCR relationships from Salsi et al. (2021), which were derived for F5-K7 IV/V stars using the methodology described in Salsi et al. (2020). The relationships are based on a careful selection of the interferometric data, suitable sample selection (no activity), and a homogeneous set of 2MASS photometry.
In Sect. 4.2, we compare our SBCR estimates obtained with these relationships with the reference values. The bolometric fluxes, which are needed in the SBCR method to determine Teff from the linear radius, are taken from Heiter et al. (2015). However, it is expected that SAPP will provide bolometric fluxes from the photometric module as an output.
3.8. Stellar evolution models
The SAPP code also includes a detailed grid of GARSTEC stellar evolution models (Weiss & Schlattl 2008), which covers the mass range from 0.6 to 5.0 M⊙ with a step of 0.02 M⊙ and metallicity from −2.50 to 0.60 with a step of 0.05 dex.
Briefly, the models were computed as follows. Stellar atmospheres are based on the T-τ VAL-C model (Vernazza et al. 1981), implemented with the analytic fit given in Sonoi et al. (2019). This relation leads to stellar models that nicely reproduce the Teff scale of RGB stars in the APOKASC sample (Serenelli et al. 2017; Pinsonneault et al. 2018). Convective overshooting is treated in GARSTEC as a diffusion process parametrised with a coefficient f, which is fixed to 0.02 at all convective boundaries. This is roughly equivalent to an overshooting region extending over 0.2 HP, with HP being the pressure scale height at the convective boundary. For small convective cores, f is decreased linearly from 0.02 down to 0 for stellar masses from 1.4 down to 1.1 M⊙. This prescription has been found to accurately describe results from binary stars (Higl et al. 2018) and mid-age open clusters (Semenova et al. 2020). No convective core overshooting in the main sequence is used below 1.1 M⊙. Mass loss is modelled with a Reimers law and η = 0.2. Microscopic diffusion, without taking into account radiative levitation, is included according to Thoul et al. (1994). Its efficiency is suppressed linearly with stellar mass in the range 1.25−1.35 M⊙ and is not included for higher masses. This is because microscopic diffusion and radiative levitation in the presence of very thin convective envelopes lead to theoretically large changes in surface abundances not supported by observations and likely due to the presence of a yet physically unidentified macroscopic mixing process. For lower masses, however, extra mixing below the convective envelope is included following the prescription described in VandenBerg et al. (2012), with a metallicity-dependent efficiency adjusted to reproduce the solar lithium depletion and the depletion of lithium typical of the stars of the Spite plateau (e.g. Spite & Spite 1982; Sbordone et al. 2010).
The relation between the abundances of metals and helium is assumed to follow a linear relation calibrated using the standard big bang nucleosynthesis (SBBN) helium value YP = 0.2485 (Steigman 2007) and a solar model calibration, which lead to a slope on the enrichment law Δ = 1.14 (Serenelli et al. 2017). More recent determinations of YP lead to slightly lower values (YP = 0.2470 ± 0.0002 and YP = 0.2446 ± 0.0041, which are consistent with each other, for SBNN and non-SBBN, respectively Fields et al. 2020). The impact on the slope of the enrichment law is about 7%, which is equivalent to that produced by a [Fe/H] error of 0.025 dex.
In addition, the models include synthetic photometry computed using ATLAS12/SYNTHE bolometric corrections5 for different passbands: UBVRI, 2MASS, Kepler, Gaia, TESS, HIPPARCOS, Tycho, and PanStarrs. Bolometric corrections have so far been implemented corresponding to Av = 0, so extinction has been applied a posteriori. This leads to errors of approximately a few hundredths of a magnitude for Av < 2 mag.
3.9. Numerical approach
The exact procedure is as follows. In this first step, Teff, log g, and [Fe/H] are fixed to the best-fit spectroscopic value determined using the gradient descent method. This is because this method is fast and does not require probing the entire parameter space. In the second step, the SAPP collects stellar evolution tracks which have Teff, log g, and [Fe/H] centred on the first-guess parameters within a certain range defined by the user. For simplicity, we limit the subdomain range to ±300 K in Teff, ±0.5 dex in log g, and ±0.6 dex in [Fe/H]. Alongside these parameters, collected mass, radius, age, and luminosity values are also tabulated.
Second, for each point in the subdomain of the stellar evolution models, i, the spectroscopic probability is calculated using Eqs. (17), and (18). Finally, this spectroscopic PDF defined on the subdomain of stellar evolution models is folded with the PDFs computed from photometric, astrometric, and asteroseismic data. This procedure returns the full posterior PDF.
The final estimates of all output parameters (Teff, log g, [Fe/H], M, age, R, L) are calculated by fitting a Gaussian to the posterior PDF with mean μ and standard deviation σ. In other studies, for example Schönrich & Bergemann (2014), the expectation values and their moments are used. However, our extensive inspection of the posterior PDFs showed that they are rather symmetric and can all be well approximated by a Gaussian.
4. Results
The results of our analysis of the benchmark stars are discussed in detail below. We begin with quantifying the accuracy and precision of our estimates of Teff, log g, and [Fe/H] obtained using different spectroscopic approaches and different types of observational data (Sect. 4.1). We then proceed to the analysis of using IRFM and SBCR to calculate Teff and radius (Sect. 4.2). The influence of seismic priors on log g and so forth on the analysis of other stellar parameters is the subject of Sect. 4.3. The results for masses, radii, and ages of stars obtained using the full Bayesian solution are presented and discussed in Sect. 4.4. The impact of including covariance from spectroscopy is detailed in Sect. 4.5. Finally, the analysis of medium-resolution spectra is shown in Sect. 4.6.
Figure 4 depicts three spectra (black dots) of α Cen B (one of the reference targets) from different telescopes compared to best-fit spectra models from SAPP (magenta lines): a medium resolution spectrum (HR10) with R = 20 000 and two high-resolution spectra (UVES, HARPS) with original R = 47 000 and 118 000, respectively. The high-resolution spectra have been degraded to the resolution of HR10 in order to demonstrate the performance of fitting spectra of different quality for the same star. The original resolutions are annotated above each spectrum, and we show a sample of diagnostic lines that populate the HR10 wavelength range. This is simply for illustration, but the agreement for all other stars in the sample is equally good. The agreement between the observed data and the models is very good, which suggests that the SAPP in combination with available theoretical models can be used with confidence to analyse spectra of FGK-type dwarfs and subgiants.
 |
Fig. 4. Normalised flux versus wavelength in angstroms. The observed spectra of α Cen B (black dots) is overlaid with SAPP’s best-fit model from the spectroscopy module (magenta solid line). This contains HARPS, UVES, and HR10 spectra with original resolving powers R ∼ 118 000, 47 000, and 20 000 respectively. The UVES and HARPS spectra have been convolved down to the resolution of HR10. |
4.1. Constrained versus unconstrained spectroscopic calculations
We begin with the analysis of the influence of the error model (see Sect. 3.5.3) on the spectroscopic calculations. Hereafter, we refer to the results obtained using the error model as ‘constrained’ analysis, and those obtained without the error model as an ‘unconstrained’ analysis.
We find that the accuracy of stellar parameters Teff, log g, and [Fe/H] is significantly improved if the error model is employed with respect to the reference stars. The scatter of the SAPP Teff estimates decreases from 101 K (unconstrained analysis) to 42 K (constrained analysis) and the bias decreases from 109 K (unconstrained analysis) to −1 K (constrained analysis). Even more impressive is the improvement in log g estimates. The systematic log g bias decreases from −0.16 dex (unconstrained analysis) to −0.04 dex (constrained analysis) and the scatter reduces enormously from 0.13 dex to 0.02 dex, which makes our spectroscopic results competitive with other techniques, such as asteroseismology. As shown in Fig. 5, in the unconstrained analysis, the residuals are large and positive. The constrained analysis, in contrast, is much more successful, because it removes all systematic effects and returns metallicities with the precision of 0.02 dex. This is likely due to the error model reducing the impact of features within the spectrum that are consistently causing the [Fe/H] to be initially overestimated. Not surprisingly, the constrained analysis also improves the results for the detailed chemical composition of stars. The abundances of Ti, Mg, and Mn are in excellent agreement with the reference values, with mean differences of 0.02 ± 0.04 dex, 0.04 ± 0.04 dex, and −0.04 ± 0.03 dex, respectively.
 |
Fig. 5. Residuals between SAPP parameters and reference parameters versus the signal-to-noise ratio of four stars: β Vir, η Boo, β Hyi, and α Cen A. Open circles show cases where a purely spectroscopic module (without error model) was used; these have an average and 1σ in the legend named ⟨Δ[Fe/H]⟩. Filled circles show cases where a spectroscopic module was used with the error model; these have an average and 1σ in the legend named ⟨Δ[Fe/H]emodel⟩. |
However, it should be stressed that the literature values of [Fe/H] abundance and any other elemental abundances cannot be treated as ‘reference’ quantities, because there is no model-independent (fundamental) way to determine the detailed chemical composition of a star. All methods depend on models of stellar atmospheres, and atomic and molecular physics, and therefore on the level of physical complexity of the systems. Therefore, most differences between our values and the reference metallicities stem from the different radiative transfer methods and input physics employed in the spectroscopic calculations.
4.2. IRFM and SBCR modules
In this section, we explore whether constraints on Teff from the IRFM and SBCR methods could help to improve the estimations of effective temperatures. Figure 6 (top panel) shows our estimates of Teff obtained using the IRFM and SBCR methods in comparison with the reference Teff measurements. The results based on both methods are sensitive to the quality of photometry and to extinction, and therefore we limit this comparative analysis to stars with the 2MASS flags ‘A’ or ‘B’, which corresponds to photometric errors below 0.05 mag in the J, H, and Ks bands. Generally, we find that both methods provide excellent constraints on the Teff of a star, with an average bias of only ∼ − 32 K and a scatter of ∼73 K around the reference values. The uncertainties of the IRFM estimates are of the order of 70 K. The uncertainty on the effective temperatures provided by SBCR is ∼123 K, but ranges from 98 to 138 K depending on the quality of photometry.
 |
Fig. 6. Comparison of effective temperatures (top panel) and radii (bottom panel) derived using the SBCR (solid circles) and IRFM (open squares) methods to reference measurement values. The dark grey line corresponds to the 1:1 line, and the light grey shaded region represents our adopted threshold of 2%. The average uncertainty on IRFM, SBCR (vertical), and reference values (horizontal) is annotated in the middle right for Teff and bottom right for radii. The annotation in the upper left represents the average difference between SBCR, IRFM, and reference values with 1σ scatter about the average. |
Figure 6 (bottom panel) compares the resulting SBCR and IRFM radii of stars with the reference measurement values. The uncertainties indicated in the figure are the quadratic sum of the individual uncertainties. The SBCR uncertainties, which are of the order ∼0.052 R⊙, are dominated by the RMS error of the method, with a precision of ∼3.1 to 4.5%. The IRFM radii are slightly more precise, with σ ∼ 0.027 R⊙.
We conclude that both methods, SBCR and IRFM, require accurate and precise 2MASS photometry (with errors of less than 0.05 mag) in order to achieve the PLATO space mission requirements. Also extinction may influence the results. Currently, both methods may be used as auxiliary methods to constrain Teff and radii, foremost as priors on spectroscopy. However, their use as stand-alone modules will require an improvement in the parameter coverage and reference parameters of the calibration samples. In particular, we anticipate that with the data from the upcoming CHARA/SPICA facility, the SBCR method will be improved significantly to reach the desired precision of 1−2% on the radii.
4.3. Influence of seismic priors on stellar parameters
In the following analysis, we investigate whether the use of asteroseismic data improves the constraints on stellar parameters compared to the approach when only stellar spectra are used. So far, most studies employing asteroseismic constraints on log g have reported an improvement in the accuracy of results (Bruntt et al. 2012; Buchhave & Latham 2015; Nissen et al. 2017).
We use two asteroseismic quantities: νmax, the frequency of the maximum oscillation power, and Δν, the large frequency separation (e.g. Serenelli et al. 2017). These seismic data are used as a prior in two methods. The first approach is to estimate a log g value from the asteroseismic PDF, which takes into account both νmax and Δν, and then fix it in the spectroscopic analysis. We note that instead of fixing the surface gravity, a prior on log g can be imposed; however, for the benchmark stars this alternative approach yields the same result. This is due to the very small uncertainties on the seismic log g values, namely of the order 0.01 to 0.02 dex. We also explore a different approach in which the final solution is obtained using an iterative algorithm, with log g constrained via the empirical νmax = f(Teff, log g) relationship (e.g. Belkacem et al. 2012). Briefly, using the observed stellar and solar νmax values, we input an initial guess of Teff from spectroscopy, the resulting log g value from the Eq. (14) is then fixed in the spectroscopic analysis. The re-calculated set of parameters give a new estimate of Teff, which is used in the same equation, and the loop continues until the Teff estimate does not change by more than 10 K. The choice of this convergence criterion is not critical at this stage and the convergence is usually very fast (Fig. A.1). Such an approach has been adopted, for instance, by Lund et al. (2019). Figure 7 shows our results obtained without and with a log g prior, using the iterative solution with log g.
 |
Fig. 7. SAPP spectroscopic parameters Teff and log g of the benchmark stars that have interferometric Teff reference values above 5500 K (this includes two KIC stars 16 Cyg A and B). The vertical axis represents the residuals between Teff, log g, and their corresponding reference values. The horizontal axis represents the reference parameters. The red line is a linear regression of the data points. Top panel: results produced by the SAPP constrained spectroscopy module, and bottom panel: results produced by the SAPP constrained spectroscopy module with a νmax prior applied. The grey shaded region is our tolerance of 1% for Teff and 0.05 dex for log g. The average uncertainty in each panel is located at the bottom right. For each star, several spectra were analysed (see Sect. 2). |
Overall, it is clear that the use of seismic prior on νmax improves the accuracy of Teff and log g estimates (compare panels a–d and b–e), resolving the notorious problem of systematically under- or overestimated temperatures and surface gravities (Mortier et al. 2014; Tsantaki et al. 2019). The iterative solution improves not only the accuracy (central values), but also the precision of the results: the scatter of Teff residuals is reduced by a factor of two, from ±42 K to ±21 K. However, the uncertainties on individual values increase slightly when a seismic prior is applied, which is due to the error in νmax being taken into account. Without the seismic prior, the uncertainties are purely statistical in nature. The most obvious improvement concerns the stars with Teff ⪆ 6200 K: Procyon and HD 49933. For these F-type stars, the spectroscopic analysis without any prior returns a very problematic (and well-known) systematic bias in Teff and log g, which manifests itself in the unfortunate correlation between the residuals of both parameters (Fig. 7, panel c). In other words, the fact that Teff is overestimated by 100 K also implies that the log g estimate is ∼ + 0.1 dex too high. The causal connection between the residual of Teff and that of log g cannot be established, as both parameters are highly correlated (Fig. 3). Remarkably, including the seismic priors resolves the problem: the Teff and log g values are now in good agreement with the reference values, with systematic bias on the order of 40 K between the two quantities.
Accurate surface gravity estimates are essential to determine chemical abundances from gravity-sensitive spectral lines, such as Mg triplet lines at 5100 Å, Ca near-infrared (NIR) triplet lines, and the majority of diagnostic lines of singly ionised elements (Gehren et al. 2004; Lind et al. 2012; Bergemann et al. 2017). We therefore conclude that, similar to Teff, the seismic prior offers a clear improvement in surface gravity and helps to break the degeneracy between the influence of log g and Teff for stars hotter than the Sun.
4.4. Bayesian solution
In this section, we describe the results obtained when all stellar parameters are determined consistently using the Bayesian approach (Sect. 3.1), employing photometric (magnitudes), astrometric (parallaxes), spectroscopic, and asteroseismic (Δν, νmax) data. As emphasised in Sect. 1, we want to leverage the exquisite statistical capabilities of Bayesian inference methods and therefore we also include stellar structure models, which enables us to determine radii, masses, and ages of stars in a consistent homogeneous framework. This also allows us to quantify the correlations between various parameters and to explore the influence of uncertainties on the fundamental parameters of stars: their initial mass and detailed chemical composition.
Figure 8 depicts the PDFs for Procyon from different modes of SAPP. Each PDF shows the likelihood landscape sliced in the [Fe/H] dimension with respect to their maximum probability. The colour scale is the logarithm of the corresponding probability, over-plotted is an evolution track with M = 1.5 M⊙ and Z = Z⊙, and the best-fit value is plotted as a white cross. The differences between the PDFs (d), (e), and (f) are subtle. The probability range of 10−50 to 1 allows us to see the detail of the likelihood landscape and how it changes with various combinations.
 |
Fig. 8. Six PDFs calculated for Procyon from different modes of SAPP: (a) asteroseismology, (b) spectroscopy, (c) photometry and parallax, (d) spectroscopy and asteroseismology (this is analogue to our constrained spectroscopy + νmax prior results described in Sect. 4.1), (e) spectroscopy and photometry (with parallax), and (f) combined (Bayesian scheme). The horizontal axis is effective temperature, the vertical axes is surface gravity, and the colour bar is the logarithm of probability. Each PDF is sliced in the [Fe/H] dimension. The grey solid line represents a stellar evolution track with 1.5 M⊙ and Z = Z⊙ (the pre-main sequence is not included). The white cross represents the best-fit value for the given PDF. |
Final estimated parameters of benchmark stars.
Our final results for the Bayesian scheme are provided in Table 2 and are compared with the reference quantities in Fig. 9. The average uncertainty for each panel is located in its bottom right-hand corner. The systematic uncertainties of SAPP are determined from the average differences calculated and shown in the annotations of each panel. Therefore, the final values presented in Table 2 have the statistical and systematic uncertainties combined. For the stars that have multiple observation spectra, the final values are averaged and the uncertainties are propagated thoroughly. Clearly, our results for all stellar parameters are in excellent agreement with other estimates. The Teff estimates are accurate to 27 (syst.) ± 37 (stat.) K (∼0.5%), whereas the error on log g and [Fe/H] does not exceed 0.00 (syst.) ± 0.01 (stat.) dex and 0.02 (syst.) ± 0.02 (stat.) dex, respectively. Also, the estimates of radii, masses, and ages of the benchmark stars are consistent with the reference values. Radii and masses are determined with the highest accuracy, with a statistical uncertainty of only 0.03 R⊙ and 0.05 M⊙ respectively. Ages are determined with a precision of 0.63 Gyr and a small bias of ∼ − 0.14 Gyr. However, we stress that ages are highly model-dependent quantities, and their determination, in turn, relies on the quality of atmospheric parameters (Teff, [Fe/H], α-enhancement). Also, the reference values are highly heterogeneous, and were determined using different methods and models. Therefore, a disagreement (however small) is not surprising and may simply indicate that different types of stellar evolution models (or isochrones) and/or different input values for atmospheric parameters of stars were employed in the literature studies that we use for comparison with our results.
 |
Fig. 9. SAPP stellar parameters from the full Bayesian scheme versus the reference parameters. The annotations represent the average difference between the SAPP parameters with covariance and the reference parameters, respectively. The uncertainty represents the 1σ scatter about this average. The grey shaded region represents the desirable uncertainties on stellar parameters for PLATO: 1% on Teff, 0.05 dex on log g and [Fe/H], 15% on mass, 10% on age, and 2% on radius. The vertical error bars represent the average 1σ uncertainties. |
Comparing our final Bayesian results with the literature estimates (e.g. Sahlholdt et al. 2019; Das & Sanders 2019; Howes et al. 2019), we can conclude that the SAPP code provides robust estimates of fundamental stellar parameters that are comparable or even superior to those produced using other methods. In Das & Sanders (2019), the precision of parameters is 10% on mass and 10%−25% on age. Sahlholdt et al. (2019) find more conservative uncertainties, namely of the order ∼15%−40% on age. Howes et al. (2019) did not use asteroseismic information, and their estimates are strongly dependent on the evolutionary stage of a star, with typical uncertainties of 15% on age at the turn-off and RGB, but reaching up to 50% on the main sequence and subgiant branch (see their Fig. 18). Our results are qualitatively similar to these latter estimates, if we were to limit the input data to observed spectra, photometry, and parallaxes, but the use of asteroseismology greatly improves the precision of M, R, and τ, allowing us to constrain their values to a precision of 1%−5% for masses and radii, and 15% for ages. Whereas in PLATO (see Sect. 5) these quantities will not be determined using the SAPP, our results suggest that the SAPP delivers robust and accurate estimates of atmospheric and fundamental parameter of stars, making the code useful for the characterisation of stars observed within other ongoing and forthcoming programs, such as WEAVE, 4MOST, and SDSS-V.
4.5. Spectroscopy parameter covariance impact on Bayesian scheme
The current formulation of spectroscopy produces a PDF that can reliably be combined with other modules. In this section, we explore the influence of using the spectroscopic covariance (Eq. (7) in Sect. 3.1) in the full Bayesian calculations.
We also compared the results for stellar parameters computed with and without the inclusion of spectroscopic covariance. Figure C.1 confirms that the differences between the results obtained using the two approaches are small. The only somewhat significant deviation can be seen in Teff and τ, which scatter around ∼±40 K and 0.67 Gyr, respectively. We do not detect any significantly large systematic bias associated with the assumption of independent likelihoods.
The inclusion of covariance is formally correct with respect to statistical analysis, as otherwise the assumption is that the core parameters and their errors are independent. It is also not a significant problem in terms of calculation overheads, as the covariance matrix is always available as a by-product of spectroscopic calculations in the SAPP (Sect. 3.5.2). On the other hand, it is clear that the influence of using the covariance is small in the parameter space of FGK-type stars. We can therefore conclude that it is not critical to include the spectroscopic covariance in the full Bayesian analysis, as long as one does not require the precision of better than 1% in the astrophysical characterisation of stars.
4.6. Analysis of medium-resolution spectra
4.6.1. Gaia-ESO benchmark stars
We present our results obtained from the analysis of medium-resolution HR10 spectra of the Gaia-ESO benchmark stars and compare them with the independently determined stellar parameters (see Sect. 2.2). The GIRAFFE HR10 spectra cover a narrow wavelength range from 5300 to 5600 Å at the resolving power of 20 000. The median S/N is in the range from 70 to over 2000. The HR10 spectra have lower sampling than the degraded UVES and HARPS spectra analysed in Sect. 4.4. which allows the different instrumental effects to be explored. These stars also include one FGK subgiant (HD 140283), two red giants (ξ Hya, HD 122563), an F dwarf (HD 84937), and two G dwarfs (μ Ara, τ Cet). These targets are important because red giants highlight the extent of SAPP’s applicability to metal-poor stars outside the PLATO core program. In Fig. 10, a total of 17 benchmark stars are analysed, where the SAPP estimates of Teff, log g, and [Fe/H] are compared to reference values. The average uncertainty values are shown in the bottom right corner. The upper panel depicts SAPP data derived without asteroseismology data, and the lower panel with asteroseismology. The red data points represent stars that have no asteroseismic information, and these are therefore identical in both panels.
 |
Fig. 10. SAPP best-fit parameters of Gaia-ESO HR10 spectra produced using the Bayesian scheme, with resolution R = 20 000 and coverage λ ⊂ [5300, 5600] Å. In total there are 17 benchmark stars depicting a different parameter (Teff log g, [Fe/H] and [Mg/Fe]) derived from SAPP (vertical axes) versus the given reference parameter (horizontal axes). The panels represent data determined using the Bayesian scheme without asteroseismology (upper) and with asteroseismology (lower). The red data points represent stars without any asteroseismic parameters. |
We find that the analysis of medium-resolution stellar spectra with the SAPP also yields reliable results. If asteroseismic constraints are used, we obtain an average Teff bias of about ∼101 K and a dispersion of 76 K, very precise log g estimates on the order of 0.012 dex, and metallicities accurate to ≈0.05 dex. Also the Mg abundances can be determined with the uncertainty of ≈0.01 ± 0.08 dex. Interestingly, the Teff values obtained from the HR10 spectra alone are superior to those obtained using νmax. This could possibly be the consequence of non-trivial relationships between the physics adopted in the spectroscopic module (Sect. 3.5.1), which is based on MAFAGS-OS atmospheric models. The model atmospheres adopt a mixing length that is empirically constrained to reproduce observed Balmer line profiles (given a pre-defined Teff scale), and may therefore, by coincidence, compensate for the deficits in the model atmospheres, albeit at the expense of the accuracy on surface gravity. Nonetheless, our results in both cases reinforce the evidence that medium-resolution optical spectra, with R ≈ 20 000, are well suited for the analysis of fundamental parameters and the composition of PLATO stars. Spectra of such quality will soon be obtained with 4MOST (Bensby et al. 2019; de Jong et al. 2019) and WEAVE medium-resolution spectrographs (Dalton et al. 2014). Therefore, it can be foreseen that the characterisation of PLATO targets can indeed be done at the required level of accuracy and precision if 4MOST and WEAVE medium-resolution spectra are available.
4.6.2. Gaia-ESO open and globular clusters
Figures 11 and 12 present the results from our analysis of six open and globular clusters6, for which Gaia-ESO HR10 spectra are available in the public Gaia-ESO data release7. None of the clusters were processed using the asteroseismic module in SAPP, and therefore only photometric, astrometric, and spectroscopic data are analysed in this section. In Fig. 11, we also show several isochrones (derived from the GARSTEC stellar evolution tracks described in Sect. 3.8) with varying ages and similar metallicity. These isochrones were not fit to the data, and are only displayed to guide the eye. The unique value of clusters is not just because they –to first order– represent mono-age and mono-metallic stellar populations (Magrini et al. 2017; Bastian & Lardo 2018), but also because homogeneous observations of stars at different evolutionary stages are available. For NGC 6253 and NGC 6752, we can directly test the metallicities in red giants against our estimates obtained for main sequence and subgiant stars. Additionally, literature values of metallicity are available for the turnoff or subgiant stars in NGC 104 (Carretta et al. 2004) and NGC 6253 (Maderak et al. 2015), and we use these estimates to validate our results.
 |
Fig. 11. Teff − log g diagram of the Gaia-ESO clusters. Only data analysed in this work with the SAPP are shown. In each panel, the black solid circles are a star with corresponding error bars in Teff and log g. There are three isochrones varying in age (blue youngest, orange median, green oldest) which have a metallicity close to the average [Fe/H] of the cluster. |
 |
Fig. 12. SAPP metallicities [Fe/H] of stars in clusters versus spectral S/N. In each panel, the average (NLTE) [Fe/H] and 1σ scatter is annotated, the former being shown as the green dotted line. The grey dashed line and corresponding blue shaded region represents NLTE [Fe/H] estimates and their errors from Kovalev et al. (2019), respectively. |
Generally, the results for all six Gaia-ESO clusters are very robust (Fig. 11), with the Teff and log g values being in good agreement with the isochrones. Also, the intracluster metallicity variation (Fig. 12) is very small, consistent with expectations from previous literature estimates of metallicity. In particular, three of the clusters with NLTE metallicites were analysed in Kovalev et al. (2019) and their corresponding average [Fe/H] agree very well with our study. Furthermore, our metallicity estimates for NGC 104 and NGC 6253 are consistent with values based on non-RGB stars from Carretta et al. (2004) and Maderak et al. (2015), who obtain [Fe/H] = −0.67 ± 0.01 ± 0.04 dex and [Fe/H] = +0.445 ± 0.014 dex, respectively. However, it should be noted that NLTE effects are particularly large in the atmospheres of red giants at low [Fe/H] –which is typical of globular clusters (Kovalev et al. 2019)–, and most literature estimates use 1D LTE models, which is why a comparison with other studies is not meaningful. There is no systematic bias or correlation of metallicity with stellar parameters (Teff or log g) or the S/N. This suggests that our abundances are robust and do not depend on the quality of the data, at least for stellar spectra with S/N > 20. The typical [Fe/H] dispersion is about 0.03 dex (NGC 362, NGC 104, NGC 6253) to 0.06 dex (NGC 1261). Only for NGC 6752 is the dispersion slightly larger, σ[Fe/H] ≈ 0.09 dex. Whether some of this dispersion is caused by the presence of subgiants is not yet clear (e.g. Geller et al. 2017; Giesers et al. 2019).
5. BO-SAPP and DO-SAPP
In the context of PLATO, the SAPP will operate in two modes: the version that will run During Operations (DO-SAPP) and the version that will be used Before Operations to provide an initial characterisation of all targets (Before Operations, BO-SAPP). Spectroscopy will be activated in both modes. However, because of scientific and runtime considerations, it is the only module that will be activated in DO-SAPP, which overall minimises the complexity of SAPPs. Thus, DO-SAPP will only rely on stellar spectra and log g priors available from the seismic analysis of PLATO light curves or from the granulation signal. Also, PLATO Follow-Up (FU) spectra and PLATO photometry will be used if necessary. Unlike the current implementation of the SAPP, which uses the MAFAGS-OS model atmospheres, PLATO modules will use the MARCS 1D and Stagger 3D models combined with a newly developed NLTE version of the Turbospectrum code (Plez 2012) as inputs.
In BO-SAPP, all modules combine together to form the SAPP Bayesian framework to produce best-fit parameters Teff, log g, and [Fe/H], chemical abundances, Vmic, luminosity, and so on. Currently, the code makes use of photometry, spectra, and parallaxes, whereas IRFM and SBCR techniques are used to constrain Teff independently and to validate the spectro-photometric results. We furthermore plan to include the interferometry data. Stellar evolution models will not be used, in order to minimise overlap with other modules of the PLATO Stellar Analysis System (SAS). Furthermore, we anticipate that once the Gaia RVS spectra are available, these will be used to complement spectra from instrument archives and surveys. The details of combining different observed spectra, such as Gaia RVS, SDSS-V, and 4MOST data, will be presented in a separate study, but the main advantage of the SAPP is that the same physical models and the same statistical approach will be used for the analysis of all different kinds of spectroscopic observations in order to maximise the consistency of the results. Photometric data will be sourced from 2MASS, SPHEREx, and other surveys.
SAPP parameters will be used by different PLATO working groups to determine the radii, mass, and ages of stars, as well as the astrophysical parameters of their orbiting planets. Therefore, very stringent requirements are posed on the accuracy of the atmospheric characterisation. For example, a 2% error on Teff translates into a 3% error on radius and a 5% error on mass for a typical FGK-type un-evolved star (Serenelli et al. 2017). Owing to the complexity of PLATO algorithms and the details of work organisation within different PLATO packages, the exact scope of both branches of the SAPP pipeline may change slightly in the future.
6. Future developments
The future improvements of the code will involve the transition to 3D convective stellar model atmospheres, but also updates to the SBCR relationship, and a module to analyse M-dwarfs based on optical and infrared spectra. Three-dimensional models are needed because they provide a physically realistic description of convective and radiative energy transport in late-type stars (e.g. Vögler et al. 2005; Nordlund et al. 2009; Freytag et al. 2012), and thereby remove the need for ad hoc adjustable parameters (like the mixing length, micro-turbulence, and macro-turbulence), which are used in 1D hydrostatic models. In addition, the most accurate solar photospheric abundances require 3D NLTE modelling from first principles (e.g. Asplund 2005; Asplund et al. 2009; Lind et al. 2017; Bergemann et al. 2019; Amarsi et al. 2019; Gallagher et al. 2020).
In terms of 3D modelling, the Stagger grid (Magic et al. 2013a,b) will be used by the PLATO consortium to obtain the non-seismic stellar parameter determination, asteroseismic surface effect corrections, limb darkening, and stellar convective noise. The existing STAGGER grid has currently about 200 models with Teff from 3500 to 7000 K (step 500 K), log g from 1.5 to 5 dex (step of 0.5 dex), and metallicity from −4 to +0.5 dex. The grid also contains models for specific benchmark stars which are out of the nodes of the grid. The grid is currently being refined to 250 K steps in Teff and the models are run for longer time sequences to have better relaxation and more snapshots per model, that is, more reliable time averaging. These models will be used to compute 3D NLTE synthetic grids using MULTI3D (Bergemann et al. 2021) with NLTE-Turbospectrum (Gerber et al., in prep.), and will supersede the currently used 1D NLTE grids based on the MAFAGS-OS models (Sect. 3.5.1).
Furthermore, we are planning to improve the calibration relationships for the SBCR module (Sect. 3.7). To this end, we will use the data collected with the CHARA/SPICA instrument8 (Mourard et al. 2017; Pannetier et al. 2020). With the 300 m baselines of the CHARA array (ten Brummelaar et al. 2005) and the optical regime of the SPICA instrument (6500–8500 Å), an angular resolution of 0.2 mas could be reached, yielding angular diameters with a precision of about 1% for several hundred FGK-type stars.
7. Conclusions
In this study, we present the SAPP pipeline for the astrophysical characterisation of FGK-type stars. The code is based on the method of Bayesian inference and is capable of combining various sources of observational information, including but not limited to spectroscopy, photometry, parallaxes, and asteroseismology, along with their uncertainties. Thus, the code avoids the assumption of Gaussian uncertainties and uncorrelated variables, which is commonly used in astronomical literature.
We tested the pipeline on a sample of well-studied FGK-type stars, most of them included in the set of Gaia benchmark stars (Jofré et al. 2018), and we complemented them with a metal-poor TESS subgiant ν Ind (Chaplin et al. 2020) and with stars from the Kepler legacy sample (Nissen et al. 2017). High- and medium-resolution spectra (R > 40 000 and R = 20 000 respectively) with high S/N (S/N > 300) for these stars are available from the ESO archives. The combined sample includes 27 FGK-type stars that cover a broad range in Teff, log g, and metallicity. The majority of our benchmarks are main sequence stars, but there are several subgiants. The reference parameters of these targets were adopted from recent literature studies that employed asteroseismology, interferometric angular diameters, and spectro-photometry.
We find that spectroscopic data provide the most reliable information about atmospheric parameters of stars. From spectra alone, we can determine Teff, log g, metallicity, and individual abundances of α- and iron-group elements with a precision of a 50 to 100 K (Teff) and 0.05 to 0.1 dex in other parameters. These parameters can be recovered from the medium-resolution (R = 20 000) spectra with narrow wavelength coverage in the optical. Higher resolution or wide-band spectra would be needed to obtain reliable abundances of carbon, oxygen, or rare chemical elements such as Li or neutron-capture species.
We also find that the asteroseismic prior offers a clear improvement on the accuracy and precision of Teff and log g estimates. This can be achieved by either using the asteroseismic scaling relationships and iterating with the spectroscopic module, or using asteroseismic constraints as an independent likelihood in the PDF. The combined approach allows us to achieve 1% accuracy on the estimate of Teff for all stellar types relevant to PLATO (FGK-type). M-type stars are relevant to the context of PLATO, but these will be tested in future studies. The strictly spectroscopic analysis without a seismic prior yields highly biased parameters for hotter stars, with Teff and log g estimates being severely overestimated. This bias is the consequence of the progressive loss of important lines of neutral species, which makes it difficult to break the degeneracies between log g and Teff. The SBCR and IRFM modules provide useful constraints on Teff, but they are currently not competitive with spectroscopy, as the precision of both methods is not better than 100 K in Teff. On the other hand, both modules deliver robust estimates of stellar radii, with an accuracy of 3% to 5% in our parameter space. With the upcoming CHARA/SPICA data, we expect that the SBCR method can be improved further to reach the precision of 1% to 2% in radii.
Comparing our results computed using the SAPP pipeline with the independent values, we find that Teff and log g estimates are recovered to better than 1%, assuming the validity of the absolute scale of the interferometric Teff and asteroseismic log g estimates. Our NLTE estimates of metallicity ([Fe/H]), Mg, Ti, and Mn abundances agree with the NLTE estimates based on very high-resolution (HARPS, UVES) spectra to better than 0.04 dex. This precision and accuracy will help PLATO to attain its goals of 2% in R, 15% in mass, and 10% in age (Goupil 2017; Serenelli et al. 2017). Analysis of medium-resolution HR10 spectra of stars with asteroseismic data showed that we obtain reliable results within 5% for Teff and within 1% for log g. NLTE [Fe/H] values are accurate to within 0.1 dex with [Mg/Fe] accurate to −0.03 ± 0.07 dex. SAPP was tested on spectra of stars in six open and globular clusters for an independent assessment of the pipeline. Of the six, three were analysed by Kovalev et al. (2019) for the determination of NLTE [Fe/H] and abundances, which agree very well with the findings of our study. Our results for the six clusters in general are robust and present little scatter with respect to stellar atmospheric parameters (Teff, log g, [Fe/H]). Spectra of this resolution and quality are expected from future facilities, such as 4MOST (e.g. Bensby et al. 2019; de Jong et al. 2019) and WEAVE (e.g. Dalton et al. 2014).
Finally, we note that although in this work our focus is on PLATO, the SAPP pipeline is versatile enough to provide astrophysical parameters for other types of stars, such as red giants and M dwarfs. Kovalev et al. (2019) presented comprehensive tests and validation of the NLTE spectroscopic module on high- and medium-resolution spectra of evolved and un-evolved stars across a broad range of metallicities −2.5 ≲ [Fe/H] ≲ +0.3, effective temperatures 4000 ≲ Teff ≲ 7000 K, and surface gravities 1.2 ≲ log g ≲ 4.6 dex. The advantages of combining spectra, photometry, astrometry, and stellar models to derive ages and masses of evolved stars were carefully explored by Serenelli et al. (2013) and Schönrich & Bergemann (2014). We therefore conclude that the SAPP code delivers robust estimates of stellar astrophysical parameters, which makes the code useful for the analysis of low-mass stars observed with different large-scale spectroscopic surveys, such as 4MOST and WEAVE (e.g. Dalton et al. 2014; Bensby et al. 2019).
Acknowledgments
This work presents results from the European Space Agency (ESA) space mission PLATO. The PLATO payload, the PLATO Ground Segment and PLATO data processing are joint developments of ESA and the PLATO Mission Consortium (PMC). Funding for the PMC is provided at national levels, in particular by countries participating in the PLATO Multilateral Agreement (Austria, Belgium, Czech Republic, Denmark, France, Germany, Italy, Netherlands, Portugal, Spain, Sweden, Switzerland, Norway, and United Kingdom) and institutions from Brazil. Members of the PLATO Consortium can be found at https://platomission.com. The ESA PLATO mission website is https://www.cosmos.esa.int/plato. We thank the teams working for PLATO for all their work. We thank P.E. Nissen for providing the reduced spectra of the Kepler legacy stars. M.R.G., M.B., J.G., and M.K. are supported by the Lise Meitner grant from the Max Planck Society. B.P. is partially supported by CNES, the Centre National d’Études Spatiales. We acknowledge support by the Collaborative Research centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation). We thank C. Aerts for providing helpful comments to this study. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. A.S. acknowledges support from MICINN grant PID2019-108709GB-I00. T.M. acknowledges financial support from Belspo for contract PRODEX PLATO mission development. U.H. acknowledges support from the Swedish National Space Agency (SNSA/Rymdstyrelsen). S.M. has been supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, and by the ÚNKP-20-5 New National Excellence Program of the Ministry for Innovation and Technology. N.N. acknowledges Anthony Salsi for useful discussions. V.A. is supported by FCT – Fundação para a Ciência e Tecnologia (FCT) through national grants: UID/FIS/04434/2019; UIDB/04434/2020; UIDP/04434/2020. V.A. also acknowledges the support from FCT through Investigador FCT contract nr. IF/00650/2015/CP1273/CT0001. M.T. acknowledges the funding from MIUR Premiale 2016: MITIC. L.C. is the recipient of the ARC Future Fellowship FT160100402. M.B. is supported through the Lise Meitner grant from the Max Planck Society. We acknowledge support by the Collaborative Research centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 949173).
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1994, A&A, 282, 684 [NASA ADS] [Google Scholar]
- Amarsi, A. M., Nissen, P. E., & Skúladóttir, Á. 2019, A&A, 630, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arribas, S., & Martinez Roger, C. 1989, A&A, 215, 305 [NASA ADS] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [Google Scholar]
- Asplund, M., & García Pérez, A. E. 2001, A&A, 372, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aumann, H. H., & Probst, R. G. 1991, ApJ, 368, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [Google Scholar]
- Bazot, M., Bourguignon, S., & Christensen-Dalsgaard, J. 2012, MNRAS, 427, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Bazot, M., Creevey, O., Christensen-Dalsgaard, J., & Meléndez, J. 2018, A&A, 619, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Dupret, M. A., Baudin, F., et al. 2012, A&A, 540, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K., & Voronov, Y. V. 2020, ApJ, 893, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Bergemann, M., Rybizki, J., et al. 2019, The Messenger, 175, 35 [NASA ADS] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Collet, R., Amarsi, A. M., et al. 2017, ApJ, 847, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Gallagher, A. J., Eitner, P., et al. 2019, A&A, 631, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Hoppe, R., Semenova, E., et al. 2021, MNRAS, 508, 2236 [NASA ADS] [CrossRef] [Google Scholar]
- Bialek, S., Fabbro, S., Venn, K. A., et al. 2020, MNRAS, 498, 3817 [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Shallis, M. J., & Selby, M. J. 1979, MNRAS, 188, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [Google Scholar]
- Brandão, I. M., Doğan, G., Christensen-Dalsgaard, J., et al. 2011, A&A, 527, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P. O., et al. 2010, MNRAS, 405, 1907 [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [Google Scholar]
- Buchhave, L. A., & Latham, D. W. 2015, ApJ, 808, 187 [Google Scholar]
- Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [Google Scholar]
- Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrier, F., Eggenberger, P., & Bouchy, F. 2005, A&A, 434, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, B. S. 1990, MNRAS, 242, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Portinari, L., & Flynn, C. 2006, MNRAS, 373, 13 [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Lin, J., Rains, A. D., et al. 2021, MNRAS, 507, 2684 [NASA ADS] [CrossRef] [Google Scholar]
- Challouf, M., Nardetto, N., Mourard, D., et al. 2014, A&A, 570, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Challouf, M., Nardetto, N., Domiciano de Souza, A., et al. 2015, A&A, 579, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
- Chaplin, W. J., Serenelli, A. M., Miglio, A., et al. 2020, Nat. Astron., 4, 382 [Google Scholar]
- Chiavassa, A., Casagrande, L., Collet, R., et al. 2018, A&A, 611, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J. 2002, Rev. Mod. Phys., 74, 1073 [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Creevey, O. L., Metcalfe, T. S., Schultheis, M., et al. 2017, A&A, 601, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Czesla, S., Schröter, S., Schneider, C. P., et al. 2019, Astrophysics Source Code Library [record ascl:1906.010] [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, eds. S. K. Ramsay, I. S. McLean, & H. Takami, SPIE Conf. Ser., 9147, 91470L [Google Scholar]
- Das, P., & Sanders, J. L. 2019, MNRAS, 484, 294 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 534 [Google Scholar]
- del Burgo, C., & Allende Prieto, C. 2018, MNRAS, 479, 1953 [Google Scholar]
- Den Hartog, E. A., Lawler, J. E., Sneden, C., et al. 2021, ApJS, 255, 27 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., & Carrier, F. 2006, A&A, 449, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engels, D., Sherwood, W. A., Wamsteker, W., & Schultz, G. V. 1981, A&AS, 45, 5 [NASA ADS] [Google Scholar]
- Evans, N. J., II, Levreault, R. M., Beckwith, S., & Skrutskie, M. 1987, ApJ, 320, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, B. D., Olive, K. A., Yeh, T.-H., & Young, C. 2020, JCAP, 2020, 010 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Gaia Collaboration 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, A. J., Bergemann, M., Collet, R., et al. 2020, A&A, 634, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Pietrzyński, G., Graczyk, D., et al. 2018, A&A, 616, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehren, T., Liang, Y. C., Shi, J. R., Zhang, H. W., & Zhao, G. 2004, A&A, 413, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geller, A. M., Leiner, E. M., Bellini, A., et al. 2017, ApJ, 840, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, S. K., Iyengar, K. V. K., Rengarajan, T. N., et al. 1984, MNRAS, 206, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Giesers, B., Kamann, S., Dreizler, S., et al. 2019, A&A, 632, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Glass, I. S. 1974, Mon. Notes Astron. Soc. S. Afr., 33, 53 [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [Google Scholar]
- Goupil, M. 2017, Eur. Phys. J. Web Conf., 160, 01003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graczyk, D., Konorski, P., Pietrzyński, G., et al. 2017, ApJ, 837, 7 [Google Scholar]
- Graczyk, D., Pietrzyński, G., Gieren, W., et al. 2019, ApJ, 872, 85 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Gruberbauer, M., Guenther, D. B., & Kallinger, T. 2012, ApJ, 749, 109 [CrossRef] [Google Scholar]
- Grupp, F. 2004a, A&A, 420, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupp, F. 2004b, A&A, 426, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Higl, J., Siess, L., Weiss, A., & Ritter, H. 2018, A&A, 617, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howes, L. M., Lindegren, L., Feltzing, S., Church, R. P., & Bensby, T. 2019, A&A, 622, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
- Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., et al. 2013, ApJ, 767, 127 [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P., Heiter, U., Tucci Maia, M., et al. 2018, Res. Notes Am. Astron. Soc., 2, 152 [Google Scholar]
- Jofré, P., Heiter, U., & Soubiran, C. 2019, ARA&A, 57, 571 [Google Scholar]
- Johnson, H. L. 1967, ApJ, 149, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Mitchell, R. I., Iriarte, B., & Wisniewski, W. Z. 1966, Commun. Lunar Planet. Lab., 4, 99 [NASA ADS] [Google Scholar]
- Johnson, H. L., Mcarthur, J. W., & Mitchell, R. I. 1968, ApJ, 152, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [Google Scholar]
- Joyce, M., & Chaboyer, B. 2018, ApJ, 864, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Morel, P., et al. 2004, A&A, 413, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., & Lovis, C. 2017, A&A, 598, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalev, M., Bergemann, M., Ting, Y.-S., & Rix, H.-W. 2019, A&A, 628, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liebert, J., Fontaine, G., Young, P. A., Williams, K. A., & Arnett, D. 2013, ApJ, 769, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [Google Scholar]
- Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z., Yang, W., Bi, S., et al. 2013, ApJ, 780, 152 [CrossRef] [Google Scholar]
- Low, F. J., & Johnson, H. L. 1964, ApJ, 139, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Knudstrup, E., Silva Aguirre, V., et al. 2019, AJ, 158, 248 [CrossRef] [Google Scholar]
- Maderak, R. M., Deliyannis, C. P., Anthony-Twarog, B. J., et al. 2015, AJ, 149, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A&A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Sitnova, T., & Belyaev, A. K. 2017, A&A, 605, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McMillan, P. J., Kordopatis, G., Kunder, A., et al. 2018, MNRAS, 477, 5279 [NASA ADS] [CrossRef] [Google Scholar]
- Monroe, T. R., Meléndez, J., Ramírez, I., et al. 2013, ApJ, 774, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M., Piotto, G., Marrese, P. M., et al. 2021, A&A, 653, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Bério, P., Perraut, K., et al. 2017, J. Opt. Soc. Am. A, 34, A37 [NASA ADS] [CrossRef] [Google Scholar]
- Nardetto, N. 2018, PhD Thesis [arXiv:1801.04158] [Google Scholar]
- Ness, M., Hogg, D. W., Rix, H. W., Ho, A. Y. Q., & Zasowski, G. 2015, ApJ, 808, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., Silva Aguirre, V., Christensen-Dalsgaard, J., et al. 2017, A&A, 608, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Nordström, B., Andersen, J., Holmberg, J., et al. 2004, PASA, 21, 129 [CrossRef] [Google Scholar]
- Pannetier, C., Mourard, D., Berio, P., et al. 2020, SPIE Conf. Ser., 11446, 114460T [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 500, 501 [NASA ADS] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., et al. 2018, ApJS, 239, 32 [Google Scholar]
- Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
- Pont, F., & Eyer, L. 2004, MNRAS, 351, 487 [Google Scholar]
- Pourbaix, D., & Boffin, H. M. J. 2016, A&A, 586, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Rains, A. D., Ireland, M. J., White, T. R., Casagrande, L., & Karovicova, I. 2020, MNRAS, 493, 2377 [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rix, H.-W., Ting, Y.-S., Conroy, C., & Hogg, D. W. 2016, ApJ, 826, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M., Echevarria, J., Tapia, M., et al. 1984, A&A, 137, L9 [NASA ADS] [Google Scholar]
- Ruchti, G. R., Bergemann, M., Serenelli, A., Casagrande, L., & Lind, K. 2013, MNRAS, 429, 126 [CrossRef] [Google Scholar]
- Sahlholdt, C. L., Feltzing, S., Lindegren, L., & Church, R. P. 2019, MNRAS, 482, 895 [Google Scholar]
- Salsi, A., Nardetto, N., Mourard, D., et al. 2020, A&A, 640, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salsi, A., Nardetto, N., Mourard, D., et al. 2021, A&A, 652, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., & Bergemann, M. 2014, MNRAS, 443, 698 [CrossRef] [Google Scholar]
- Selby, M. J., Hepburn, I., Blackwell, D. E., et al. 1988, A&AS, 74, 127 [NASA ADS] [Google Scholar]
- Semenova, E., Bergemann, M., Deal, M., et al. 2020, A&A, 643, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A. M., Bergemann, M., Ruchti, G., & Casagrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A., Johnson, J., Huber, D., et al. 2017, ApJS, 233, 23 [Google Scholar]
- Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sonoi, T., Ludwig, H. G., Dupret, M. A., et al. 2019, A&A, 621, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
- Steigman, G. 2007, Annu. Rev. Nucl. Part. Sci., 57, 463 [CrossRef] [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Tapia, M., Roth, M., Costero, R., & Navarro, S. 1984, Rev. Mex. Astron. Astrofis., 9, 65 [NASA ADS] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [Google Scholar]
- Thévenin, F., Kervella, P., Pichon, B., et al. 2005, A&A, 436, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [Google Scholar]
- Ting, Y.-S., Conroy, C., & Rix, H.-W. 2016, ApJ, 826, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ting, Y.-S., Conroy, C., Rix, H.-W., & Cargile, P. 2019, ApJ, 879, 69 [Google Scholar]
- Tsantaki, M., Santos, N. C., Sousa, S. G., et al. 2019, MNRAS, 485, 2772 [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Belle, G. T., Ciardi, D. R., & Boden, A. F. 2007, ApJ, 657, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Bergbusch, P. A., Dotter, A., et al. 2012, ApJ, 755, 15 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- Veeder, G. J., Matson, D. L., & Smith, J. C. 1978, AJ, 83, 651 [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 161 [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
- Wu, T., & Li, Y. 2017, ApJ, 846, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [Google Scholar]
Appendix A: Iterative seismic prior - ceres
Figure A.1 shows the iterative process described in Sect. 4.3 for a spectra of the Sun from Ceres taken by HARPS, whereby the process determines a new log g given a spectral Teff and asteroseismic νmax using equation 14. Once a log g is calculated, it is fixed and the spectroscopy module is re-run, therefore determining a new Teff which is used in the same equation. The change in effective temperature is tracked and represents the vertical axis, and the number of iterations represents the horizontal axis.
 |
Fig. A.1. Difference between effective temperature estimations per iteration versus number of iterations. This is the iterative method described in section 4.3 for the Sun, specifically Ceres HARPS spectra. |
Appendix B: Pre-processing of spectra
B.1. Continuum normalisation
Typically when spectra are taken, depending on the facility, the data are run through a reduction pipeline which cleans the data of atmospheric interference such as tellurics (these are not always caught), blaze functions, cosmic rays, and other features. Some pipelines also perform continuum normalisation on the spectra, but these are not always fully successful, meaning the spectra collected are not ready for science and must be further processed by authors intending to analyse the data. We found a plethora of such issues for different collected spectra. The Gaia-ESO iDr5 fit files were somewhat continuum normalised but not fully; the given continuum was closer to 5% above unity. HARPS and UVES spectra were not continuum normalised at all and also suffered from different contaminants; they both had to be corrected for tellurics and treated for cosmic rays.
B.2. Contaminant treatment
We masked the pixel location of the tellurics by inspecting the solar spectra for each given facility and then used those masks for any spectra taken by those telescopes. The masks were made by by ‘noising-up’ the errors, i.e. we increased the error at the telluric pixel and 1.7 Å around it such that the fitting routine does not mistake it for a line. The cosmic ray treatment is simple, we apply a sigma clipping routine to the spectra pre-normalisation. The spectra are clipped to 2.5 sigma and no less, otherwise vital information is lost. This is very important to treat as the cosmic ray contamination appears as an emission line, and will therefore affect the continuum normalisation routine, especially ours, as we use linear fitting.
B.3. Normalisation routine
-
Search through spectra for negative fluxes, zero value or NaN pixels (this can happen due to reduction pipelines/bad pixels on CCD). If any bad pixels are found, remove said pixels from spectra.
-
Sigma clip the data to remove cosmic ray emissions. See fig. B.1
-
Search through the spectra for any significant gaps (lost data)
-
Split spectra into individual segments. We developed our own list of zones to split the data in by carefully inspecting the wings of strong lines that appear in the spectra. See fig. B.2
-
Divide the entire spectra by its median value. We found this aids in the normalisation routine by bringing the overall spectra closer to unity. For example if most of the points are above 1, dividing by the median will reduce the spectra down; if most of the points are below 1, dividing by the median will increase the spectra towards 1.
-
Find a linear regression fit for each segment and divide the segment by the fit.
-
For each segment, split data in half (the split point is the pixel closest to unity within 2.5 Å of the middle pixel), divide by the median, and find a linear fit for each half. Divide each half by its given linear fit.
-
Ignore the previous step if the lines are deemed as broad. For example, Hα line would be too broad for this secondary normalisation to work.
-
Stitch each normalised segment together and output the continuum normalised spectra.
 |
Fig. B.1. Comparing UVES spectra of the star δ Eri before and after sigma clipping with σ = 2.5. |
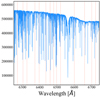 |
Fig. B.2. 18 Sco HARPS-North spectra (blue solid line) from 6250 Å to 6745 Å. The red-dashed lines over-plotted represent wavelength segments defined within the continuum normalisation routine. |
B.4. Radial-velocity correction
After continuum-normalising spectral data and treating contaminants, a further reduction step is required: radial velocity correction. The radial velocity of a star represents the relative motion of the star with respect to the observer at the time of observation. The motions doppler shift the light and either blue shift or red shifts it. What we observe is that the spectra are shifted along the wavelength scale by some amount. This greatly affects analysis of the spectra of the star; specifically, the line profiles of the models will not match the lines from the observations. This will result in a high χ2 value for many pixels and thus produce an erroneous “best-fit” model with incorrect parameters. We decided to write our own RV correction procedure as it is relatively simple and allows us to verify the RV value given typically with the spectral data (sometimes it is not given). To shift the spectra to rest frame with a RV value known, the following equation is required,
Our procedure took direct inspiration from PyAstronomy RV correction module, PyAstronomy.pyasl.crosscorrRV, which is a collection of astronomy packages (Czesla et al. 2019). The procedure we follow involves testing a range of RV values, doppler shifting the observed spectrum, and comparing it to a model which is in the rest frame. As all the stars in our benchmark sample are on the main sequence and are therefore subgiant or dwarfs, we only require one model for RV correcting our spectra: a main sequence star such as our Sun. A spectral model of R ≈ 500,000 was created using Turbospectrum (Plez 2012) with the classical parameters of the Sun (see Table 1). This model works as a template because despite some changes in the HR diagram, all the stars’ line profiles should approximately match the location of the solar line profiles. Therefore, we linearly shift the observed spectrum and see how well the lines match. This is done via Cross-Correlation, a method whereby we measure the similarity of two spectra (observed and model) as a function of the displacement of one relative to the other. To calculate the Cross-Correlation exactly, the procedure follows the subsequent steps:
-
Create a list of plausible ΔRV values, for example -50 to 50 kms−1 with a resolution of 0.05 kms−1.
-
For each ΔRV value, interpolate the model template spectra onto the observation spectra wavelength frame. This can be done by making λobs the subject of equation B.1, thus λ0, shift = λ0 × (RV/c + 1) where λ0 in this case is the original model wavelength (i.e. rest frame). Interpolating ensures the model wavelength scale sampling matches the observation scale exactly.
-
Calculate the Cross-Correlation value using the following equation,
where i represents the wavelength pixel. This total number is the CC value given the ΔRV value used.
-
Calculate CC for all ΔRV values and locate where the maxima occurs. This will indicate the ΔRV value required for radial-velocity correction.
Figure B.3 shows the results of calculating the RV correction of UVES α Centauri A spectra. The first panel shows a variable called “CC” (Cross-Correlation) versus RV correction in kms−1. Here we see the peak of the CC is at ΔRV = -36.2 kms−1. The second panel shows three spectra, the black solid line is the observed spectra pre-shifted, the black dashed line is the observed spectra RV shifted, and the grey solid line is the solar model.
 |
Fig. B.3. Radial-velocity correction process for a UVES spectra of Alpha Cen A convolved to HR10 resolution. The left panel depicts the Cross-Correlation value versus the doppler RV shift for a given model and observation comparison. The right panel shows the RV-corrected spectra (black solid line) and the uncorrected spectra (black dashed line) versus the high-resolution solar model from Turbospectrum (grey solid line). |
Appendix C: Impact of spectroscopic covariance on Bayesian scheme
Figure C.1 explores the difference between using the covariance matrix from spectroscopy and assuming independence between spectroscopic parameters in the Bayesian scheme. For each parameter, the difference is plotted against the reference value of each star with the average uncertainties annotated in the bottom right corner. The grey shaded region represents the desired tolerance of the final results.
 |
Fig. C.1. Differences between SAPP best-fit parameters from Bayesian scheme calculated with and without covariance matrix from spectroscopy (vertical axes) versus the reference parameters presented in Table 1 (horizontal axes). The uncertainty represents the 1 σ deviation. The grey shaded region represents the desired errors: 1% for Teff, 0.05 dex for log g and [Fe/H], 15% for mass, 10% for age, and 2% for radius. |
All Tables
All Figures
 |
Fig. 1. Teff − log g relation of the benchmark targets. The colour scale represents metallicity (the blue end is metal poor and the red end is just above solar metallicity). Each star is plotted with its reference values (Table 1) on top of a solar isochrone. |
| In the text | |
 |
Fig. 2. Percentage difference between Gaia EDR3 parallax and HIPPARCOS parallax (van Leeuwen 2007) with respect to Gaia EDR3 in mas. The error represents the uncertainty of EDR3 parallaxes and HIPPARCOS parallaxes propagated through the percentage difference. The open circles represent the Kepler legacy stars, the solid black circles represent Gaia-ESO stars, and the single open square represents our metal-poor star ν Ind. The average uncertainties for the Kepler legacy and Gaia ESO stars are shown in the bottom right corner. |
| In the text | |
 |
Fig. 3. Correlation coefficient tables. Each table has a colour scale that represents the correlation coefficient, which ranges from −1 (negatively correlated) through 0 (no correlation) to 1 (positively correlated). This number informs how each spectroscopic parameter is correlated with the others. The top table shows the coefficients for a K-type star (δ Eri) and the bottom table for a F-type star (HD 49933). The vertical and horizontal axes for both depict the eight spectroscopic parameters from the SAPP spectroscopy module. |
| In the text | |
 |
Fig. 4. Normalised flux versus wavelength in angstroms. The observed spectra of α Cen B (black dots) is overlaid with SAPP’s best-fit model from the spectroscopy module (magenta solid line). This contains HARPS, UVES, and HR10 spectra with original resolving powers R ∼ 118 000, 47 000, and 20 000 respectively. The UVES and HARPS spectra have been convolved down to the resolution of HR10. |
| In the text | |
 |
Fig. 5. Residuals between SAPP parameters and reference parameters versus the signal-to-noise ratio of four stars: β Vir, η Boo, β Hyi, and α Cen A. Open circles show cases where a purely spectroscopic module (without error model) was used; these have an average and 1σ in the legend named ⟨Δ[Fe/H]⟩. Filled circles show cases where a spectroscopic module was used with the error model; these have an average and 1σ in the legend named ⟨Δ[Fe/H]emodel⟩. |
| In the text | |
 |
Fig. 6. Comparison of effective temperatures (top panel) and radii (bottom panel) derived using the SBCR (solid circles) and IRFM (open squares) methods to reference measurement values. The dark grey line corresponds to the 1:1 line, and the light grey shaded region represents our adopted threshold of 2%. The average uncertainty on IRFM, SBCR (vertical), and reference values (horizontal) is annotated in the middle right for Teff and bottom right for radii. The annotation in the upper left represents the average difference between SBCR, IRFM, and reference values with 1σ scatter about the average. |
| In the text | |
 |
Fig. 7. SAPP spectroscopic parameters Teff and log g of the benchmark stars that have interferometric Teff reference values above 5500 K (this includes two KIC stars 16 Cyg A and B). The vertical axis represents the residuals between Teff, log g, and their corresponding reference values. The horizontal axis represents the reference parameters. The red line is a linear regression of the data points. Top panel: results produced by the SAPP constrained spectroscopy module, and bottom panel: results produced by the SAPP constrained spectroscopy module with a νmax prior applied. The grey shaded region is our tolerance of 1% for Teff and 0.05 dex for log g. The average uncertainty in each panel is located at the bottom right. For each star, several spectra were analysed (see Sect. 2). |
| In the text | |
 |
Fig. 8. Six PDFs calculated for Procyon from different modes of SAPP: (a) asteroseismology, (b) spectroscopy, (c) photometry and parallax, (d) spectroscopy and asteroseismology (this is analogue to our constrained spectroscopy + νmax prior results described in Sect. 4.1), (e) spectroscopy and photometry (with parallax), and (f) combined (Bayesian scheme). The horizontal axis is effective temperature, the vertical axes is surface gravity, and the colour bar is the logarithm of probability. Each PDF is sliced in the [Fe/H] dimension. The grey solid line represents a stellar evolution track with 1.5 M⊙ and Z = Z⊙ (the pre-main sequence is not included). The white cross represents the best-fit value for the given PDF. |
| In the text | |
 |
Fig. 9. SAPP stellar parameters from the full Bayesian scheme versus the reference parameters. The annotations represent the average difference between the SAPP parameters with covariance and the reference parameters, respectively. The uncertainty represents the 1σ scatter about this average. The grey shaded region represents the desirable uncertainties on stellar parameters for PLATO: 1% on Teff, 0.05 dex on log g and [Fe/H], 15% on mass, 10% on age, and 2% on radius. The vertical error bars represent the average 1σ uncertainties. |
| In the text | |
 |
Fig. 10. SAPP best-fit parameters of Gaia-ESO HR10 spectra produced using the Bayesian scheme, with resolution R = 20 000 and coverage λ ⊂ [5300, 5600] Å. In total there are 17 benchmark stars depicting a different parameter (Teff log g, [Fe/H] and [Mg/Fe]) derived from SAPP (vertical axes) versus the given reference parameter (horizontal axes). The panels represent data determined using the Bayesian scheme without asteroseismology (upper) and with asteroseismology (lower). The red data points represent stars without any asteroseismic parameters. |
| In the text | |
 |
Fig. 11. Teff − log g diagram of the Gaia-ESO clusters. Only data analysed in this work with the SAPP are shown. In each panel, the black solid circles are a star with corresponding error bars in Teff and log g. There are three isochrones varying in age (blue youngest, orange median, green oldest) which have a metallicity close to the average [Fe/H] of the cluster. |
| In the text | |
 |
Fig. 12. SAPP metallicities [Fe/H] of stars in clusters versus spectral S/N. In each panel, the average (NLTE) [Fe/H] and 1σ scatter is annotated, the former being shown as the green dotted line. The grey dashed line and corresponding blue shaded region represents NLTE [Fe/H] estimates and their errors from Kovalev et al. (2019), respectively. |
| In the text | |
 |
Fig. A.1. Difference between effective temperature estimations per iteration versus number of iterations. This is the iterative method described in section 4.3 for the Sun, specifically Ceres HARPS spectra. |
| In the text | |
 |
Fig. B.1. Comparing UVES spectra of the star δ Eri before and after sigma clipping with σ = 2.5. |
| In the text | |
 |
Fig. B.2. 18 Sco HARPS-North spectra (blue solid line) from 6250 Å to 6745 Å. The red-dashed lines over-plotted represent wavelength segments defined within the continuum normalisation routine. |
| In the text | |
 |
Fig. B.3. Radial-velocity correction process for a UVES spectra of Alpha Cen A convolved to HR10 resolution. The left panel depicts the Cross-Correlation value versus the doppler RV shift for a given model and observation comparison. The right panel shows the RV-corrected spectra (black solid line) and the uncorrected spectra (black dashed line) versus the high-resolution solar model from Turbospectrum (grey solid line). |
| In the text | |
 |
Fig. C.1. Differences between SAPP best-fit parameters from Bayesian scheme calculated with and without covariance matrix from spectroscopy (vertical axes) versus the reference parameters presented in Table 1 (horizontal axes). The uncertainty represents the 1 σ deviation. The grey shaded region represents the desired errors: 1% for Teff, 0.05 dex for log g and [Fe/H], 15% for mass, 10% for age, and 2% for radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



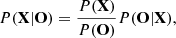
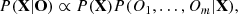
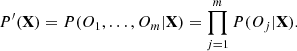
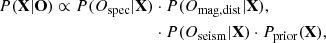
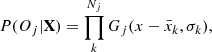
![$$ \begin{aligned} G_j(x-\bar{x}_k,\sigma _k) =\frac{1}{(\sigma _k^{N_j}2\pi )^{\frac{1}{N_j}}} \exp \left[-\frac{(x-\bar{x}_k)^2}{2\sigma _k^2}\right]. \end{aligned} $$](/articles/aa/full_html/2022/02/aa40863-21/aa40863-21-eq6.gif)
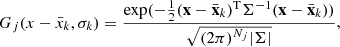
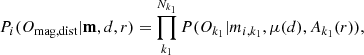
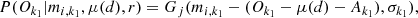
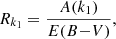
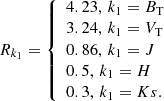
![$$ \begin{aligned} P_{i,\alpha ,\beta } =&P_i(O_{\mathrm{mag,dist}}|\mathbf m ,d,r) \times \exp \left[-\frac{(\mu _\alpha - \mu (d))^2}{2\delta \mu (d)^2}\right]\nonumber \\&\times \exp \left[-\frac{(A_{k_1,\beta } - A_{k_1}(r))^2}{2\delta A_{k_1}(r)^2}\right], \end{aligned} $$](/articles/aa/full_html/2022/02/aa40863-21/aa40863-21-eq12.gif)
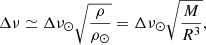
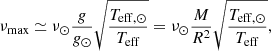
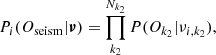
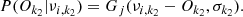
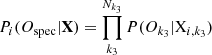
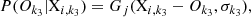
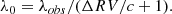
![$$ \begin{aligned} \mathrm{CC} = \sum \limits _{i} \mathrm{flux}[i]_{\mathrm{obs}} \times \mathrm{flux}[i]_{0,\mathrm{shift}}, \end{aligned} $$](/articles/aa/full_html/2022/02/aa40863-21/aa40863-21-eq23.gif)