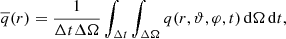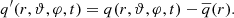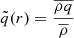| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 24 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202140825 | |
| Published online | 07 September 2021 | |
Multidimensional low-Mach number time-implicit hydrodynamic simulations of convective helium shell burning in a massive star
1
Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
e-mail: leonhard.horst@posteo.de
2
Astrophysics Group, Keele University, Keele, Staffordshire ST5 5BG, UK
3
Kavli Institute for the Physics and Mathematics of the Universe (WPI), University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8583, Japan
4
X Computational Physics (XCP) Division and Center for Theoretical Astrophysics (CTA), Los Alamos National Laboratory, Los Alamos, NM 87545, USA
5
Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Philosophenweg 12, 69120 Heidelberg, Germany
Received:
17
March
2021
Accepted:
30
June
2021
Context. A realistic parametrization of convection and convective boundary mixing in conventional stellar evolution codes is still the subject of ongoing research. To improve the current situation, multidimensional hydrodynamic simulations are used to study convection in stellar interiors. Such simulations are numerically challenging, especially for flows at low Mach numbers which are typical for convection during early evolutionary stages.
Aims. We explore the benefits of using a low-Mach hydrodynamic flux solver and demonstrate its usability for simulations in the astrophysical context. Simulations of convection for a realistic stellar profile are analyzed regarding the properties of convective boundary mixing.
Methods. The time-implicit Seven-League Hydro (SLH) code was used to perform multidimensional simulations of convective helium shell burning based on a 25 M⊙ star model. The results obtained with the low-Mach AUSM+-up solver were compared to results when using its non low-Mach variant AUSMB+-up. We applied well-balancing of the gravitational source term to maintain the initial hydrostatic background stratification. The computational grids have resolutions ranging from 180 × 902 to 810 × 5402 cells and the nuclear energy release was boosted by factors of 3 × 103, 1 × 104, and 3 × 104 to study the dependence of the results on these parameters.
Results. The boosted energy input results in convection at Mach numbers in the range of 10−3–10−2. Standard mixing-length theory predicts convective velocities of about 1.6 × 10−4 if no boosting is applied. The simulations with AUSM+-up show a Kolmogorov-like inertial range in the kinetic energy spectrum that extends further toward smaller scales compared with its non low-Mach variant. The kinetic energy dissipation of the AUSM+-up solver already converges at a lower resolution compared to AUSMB+-up. The extracted entrainment rates at the boundaries of the convection zone are well represented by the bulk Richardson entrainment law and the corresponding fitting parameters are in agreement with published results for carbon shell burning. However, our study needs to be validated by simulations at higher resolution. Further, we find that a general increase in the entropy in the convection zone may significantly contribute to the measured entrainment of the top boundary.
Conclusion. This study demonstrates the successful application of the AUSM+-up solver to a realistic astrophysical setup. Compressible simulations of convection in early phases at nominal stellar luminosity will benefit from its low-Mach capabilities. Similar to other studies, our extrapolated entrainment rate for the helium-burning shell would lead to an unrealistic growth of the convection zone if it is applied over the lifetime of the zone. Studies at nominal stellar luminosities and different phases of the same convection zone are needed to detect a possible evolution of the entrainment rate and the impact of radiation on convective boundary mixing.
Key words: stars: massive / stars: interiors / convection / methods: numerical / hydrodynamics
© ESO 2021
1. Introduction
Mixing induced by convection in the stellar interior plays an essential role in the evolution of stars. Parametrizing its complex multidimensional nature in one-dimensional (1D) stellar evolution codes is, however, particularly difficult. A reliable prescription of convective effects in 1D codes is still lacking today and the resulting stellar evolution models depend on the specific choice of the employed paramterization and the particular parameter values. This is, for example, demonstrated in recent studies by Kaiser et al. (2020) and Davis et al. (2019) on uncertainties in core properties and nucleosynthesis for massive stars.
With asteroseismic data of observed stars, it is possible to determine properties of the stellar interiors (see Aerts 2021 for a detailed review). They can be utilized to narrow down the range of possible parameters. It is now possible to determine that some convective boundary mixing models provide a better fit to certain asteroseismic observations than others (e.g., Viani & Basu 2020; Angelou et al. 2020; Michielsen et al. 2019; Pedersen et al. 2018, 2021), but probing the small-scale physics of the mixing is beyond the reach of even state-of-the-art asteroseismology.
A complimentary approach to improve the current situation is to perform multidimensional simulations by numerically solving the equations of fluid dynamics for realistic stellar models. In such simulations, convection develops self-consistently and their detailed analysis provides insights into the fundamental processes at play. This way, currently used parametrizations of convection in 1D codes can be constrained or discarded and new prescriptions may be developed.
The complex problem of convection and associated mixing of material across the interfaces into stable zones in the stellar context is subject of active, ongoing research. Numerical simulations become particularly challenging when the flow of interest is slow compared to the speed of sound, that is for small values of the Mach number
where v is the flow velocity and csound is the local speed of sound. One challenge is the restricted step size of conventional explicit time stepping schemes which must be smaller than the sound crossing time of a single grid cell for numerical stability. Thus, at low Mach numbers, an excessively large number of time steps is needed to evolve the slow flow and explicit schemes become inefficient. Additionally, artifacts of the numerical discretization must be kept at a very low level because inaccuracies can quickly lead to spurious velocities at the same order as the flow of interest. Hence, appropriate numerical techniques must be chosen carefully.
For massive stars, low-Mach number flows typically arise in convection during the early phases of stellar evolution, see for example the evolution of the 25 M⊙ star depicted in Fig. 1. Inaccuracies in the 1D prescription of convection in these phases propagate to all subsequent evolutionary phases and also enter predictions for the final stages of stars and observables. We therefore believe that successful simulations of these challenging settings are crucial to further improve the agreement between stellar modeling and observations.
 |
Fig. 1. Convective regions during the evolution of an 1D 25 M⊙ star model simulated with the MESA code. Shaded regions correspond to convection zones. The color-shading represents the mixing-length theory (MLT)-predicted Mach number. The black solid line denotes the total mass of the model. The red vertical line indicates the point in the evolution at which the SLH simulations start and the mass extent of the initial model. The green lines indicate the mass entrainment at the upper and lower boundaries as extracted from the 3D hydrodynamic simulations. See discussion in Sect. 5.4. |
One approach to meet the challenges of low-Mach flows is to modify the underlying hydrodynamic equations. This is, for example, done in the MAESTRO code (Almgren et al. 2007; Nonaka et al. 2010; Fan et al. 2019), where the Euler equations are modified to exclude the physics of sound waves and to ensure the correct scaling of leading-order terms in the low-Mach limit. This permits larger time steps and increases the efficiency for slow flows. An example for low-Mach simulations with the MAESTRO code are the three-dimensional (3D) simulations of core hydrogen burning by Gilet et al. (2013). Another approach is to perform implicit time stepping while solving the unmodified Euler equations, including sound waves. The time step size is then only restricted by the desired accuracy at which the flow is to be followed. This is for example employed by the MUSIC code in combination with a staggered spatial grid. Benchmark tests have shown that the code is able to evolve flows at Mach numbers down to Ma ≈ 10−6 (Viallet et al. 2016) and that a hydrostatic atmosphere remains stable (Goffrey et al. 2017).
The Seven-League (SLH) hydro code, which is used for the simulation presented here, is designed to tackle the numerical difficulties of low-Mach flows. It uses implicit time stepping and solves the fully compressible Euler equations. Furthermore, it applies special numerical flux functions with enhanced low-Mach capabilities in combination with well-balancing techniques to improve the representation of slow flows. This way, the SLH code is able to capture flows at low and moderate Mach numbers on the same grid.
The work we present in this paper aims at contributing to the recent effort to improve the understanding of the complex behavior of convection by means of hydrodynamic simulations. We demonstrate the benefits from using the low-Mach-number flux AUSM+-up even at moderate Mach numbers. For this, 3D simulations of convective He-shell burning in a 25 M⊙ star are presented and analyzed regarding general properties of the turbulent convection. In addition, we complement recent efforts to characterize convective boundary mixing by means of multidimensional simulations (e.g., Meakin & Arnett 2007; Woodward et al. 2015; Jones et al. 2017; Cristini et al. 2017, 2019; Pratt et al. 2017, 2020; Higl et al. 2021).
The paper is structured as follows: In Sect. 2 we briefly describe the basic properties of the SLH code. In Sect. 3 the initial conditions for the simulations are presented along with a detailed description of mapping the 1D model to the SLH grid and the applied energy boosting. In the 1D and two-dimensional (2D) test simulations presented in Sect. 4 we assess the hydrostatic stability of the initial profile using the Cargo–LeRoux well-balancing method and determine the required amount of artificial energy boosting. The corresponding 3D simulations are analyzed in Sect. 5 regarding properties of the turbulent convective flow and boundary mixing. Section 6 summarizes the results.
2. The Seven-League Hydro (SLH) code
The hydrodynamic simulations presented in this paper are performed with the SLH code (Miczek 2013; Edelmann 2014). It solves the fully compressible Euler equations in a finite volume approach. The underlying equations are formulated in general, curvilinear coordinates and mapped onto a logically rectangular computational grid, following the method of Kifonidis & Müller (2012). This allows one to construct almost arbitrary grid geometries that can be adapted to the physical setup that is investigated (Miczek 2013). The Helmholtz equation of state (EoS) (Timmes & Swesty 2000) is implemented and accounts for radiation pressure and degeneracy effects. The hydrodynamic equations are coupled to a nuclear reaction network (Edelmann 2014).
The SLH code is designed to simulate hydrodynamic phenomena in the context of stellar astrophysics for flows at low and intermediate Mach numbers. The following discussion briefly summarizes how the numerical challenges, especially for low-Mach flows, are approached in SLH. For a more in-depth description of the applied methods we refer the reader to Edelmann et al. (2021), Edelmann (2014), and Miczek (2013).
2.1. Flux Solver
Miczek et al. (2015) and Barsukow et al. (2017) demonstrated that low-Mach flows require special numerical flux functions because common schemes, as for example the popular Roe solver (Roe 1981), suffer from excessive numerical dissipation. A variety of flux functions with improved low-Mach capabilities can be found in the literature. One promising method that seems to be applicable to problems in stellar astrophysics is the AUSM+-up scheme (Liou 2006) which is implemented into SLH with a slight modification. As described in Edelmann et al. (2021), the SLH implementation uses two independent parameters to control the velocity diffusion (fa) and pressure diffusion (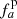 ), respectively. The original AUSM+-up scheme only uses a single parameter. It has been demonstrated by Horst et al. (2020) that compared to the classical Roe scheme the AUSM+-up solver significantly improves the accuracy at which internal gravity waves can be followed for group velocities at low Mach numbers. For all simulations with the AUSM+-up solver presented in this paper, we set the parameters to the values
), respectively. The original AUSM+-up scheme only uses a single parameter. It has been demonstrated by Horst et al. (2020) that compared to the classical Roe scheme the AUSM+-up solver significantly improves the accuracy at which internal gravity waves can be followed for group velocities at low Mach numbers. For all simulations with the AUSM+-up solver presented in this paper, we set the parameters to the values 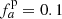 and fa = 10−10, which has proven to yield robust results in previous test simulations.
and fa = 10−10, which has proven to yield robust results in previous test simulations.
In Sect. 5 we compare simulations with the AUSM+-up solver with its basic variant 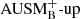 in order to demonstrate the improved results when using AUSM+-up. The
in order to demonstrate the improved results when using AUSM+-up. The 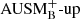 scheme is a subclass of the AUSM+-up scheme and is obtained by disabling the scaling of the incorporated velocity and pressure diffusion with Mach number. This scaling ensures the correct behavior of leading terms of the pressure field in the limit of Ma → 0 (see Liou 2006, Sec. 3.2 for details). Hence,
scheme is a subclass of the AUSM+-up scheme and is obtained by disabling the scaling of the incorporated velocity and pressure diffusion with Mach number. This scaling ensures the correct behavior of leading terms of the pressure field in the limit of Ma → 0 (see Liou 2006, Sec. 3.2 for details). Hence, 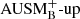 does not have enhanced low-Mach capabilities. In SLH, the
does not have enhanced low-Mach capabilities. In SLH, the 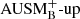 solver option is obtained by setting
solver option is obtained by setting 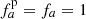 .
.
2.2. Well-balancing
Maintaining hydrostatic equilibrium is not trivial in finite volume codes because commonly gravity is discretized differently than the conserved variables and enters the equations in an operator-split approach. Hence, even if the initial data on the computational grid is formally in perfect hydrostatic equilibrium, a residual source term in the momentum and energy parts of the Euler-equations will remain (see, e.g., Käppeli & Mishra 2016; Popov et al. 2019; Berberich et al. 2021; Edelmann et al. 2021). For the SLH code, Edelmann et al. (2021) demonstrate that proper well-balancing techniques allow to simulate convection at Ma ∼ 10−4. However, this requires methods that have become available only after the simulations of helium shell burning were carried out. In the simulations presented here, we use the multidimensional extension (Edelmann et al. 2021) of the 1D Cargo–LeRoux well-balancing scheme (Cargo & Le Roux 1994). Edelmann et al. (2021) show that it is not possible to perform simulations at Mach numbers considerably smaller than Ma ∼ 10−3. At Mach numbers below this threshold the flow is deteriorated by discretization errors. Thus, for our study, the energy generation from helium burning that drives the convection has to be boosted by three orders of magnitude to increase the convective velocities, see Sects. 3.2 and 4.2. Still, Cargo–LeRoux well-balancing is crucial to maintain the background stratification, as demonstrated in Sect. 4.1.
2.3. Time stepping
To circumvent the small time step sizes of explicit time marching schemes, the SLH code applies implicit time stepping. Here, the time step size is not restricted by numerical stability requirements but only by the desired accuracy at which the flow is to be followed. At low Mach numbers, the large time steps and hence smaller number of total steps overcompensates the higher computational costs of a single step compared with explicit schemes. For the simulations presented in this paper the ESDIRK23 scheme (Hosea & Shampine 1996) is used, which is second order accurate in time. The resulting system of nonlinear equations is solved with the Newton-Raphson method.
For all simulations presented here, linear reconstruction is used. Slope limiter are usually required to diminish oscillations at steep gradients. However, the partially discontinuous spatial derivatives of common limiters deteriorate the convergence rate of the Newton-Raphson method. Further tests are needed to explore their possible applications in implicit SLH simulations.
3. Model setup
3.1. Construction of the initial model
The initial conditions for the hydrodynamic SLH simulation are based on an 1D model obtained with the open-source stellar evolution code MESA (Paxton et al. 2011, 2013, 2015, 2019),
The model corresponds to a 25 M⊙ star at solar metallicity (Z = 0.014) evolved until the exhaustion of core oxygen burning. The model develops a convective helium burning shell (at log10(time left) ≲ 4 in Fig. 1) following core helium burning. The numerical settings are similar to Kaiser et al. (2020) (see their Sect. 3) and briefly summarized here. Convective zones are determined using the Schwarzschild criterion, which neglects chemical gradients. It states that regions are convective if the superadiabaticity Δ∇ is positive, that is
where ∇ad denotes the adiabatic temperature gradient while the actual temperature gradient of the gas is given by ∇ = dlnT/dlnP.
Convection is parametrized using MLT and a mixing length of ℓMLT = 1.6 HP, where HP denotes the pressure scale height
To model convective boundary mixing (CBM), the exponentially-decaying diffusion approach of Freytag et al. (1996) and Herwig et al. (1997) is used. The corresponding diffusion coefficient is (Herwig et al. 1997):
where the free parameter fCBM determines the extent of the CBM in terms of the pressure scale height at the boundary of the convection zone 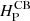 . For the top boundary of convective regions, D0(f0) is the MLT diffusion coefficient evaluated at r0(f0) = rCB − (f0 Hp) where rCB is the radius of the boundary as given by Eq. (2). The free parameter f0 ensures that the diffusion coefficient is calculated inside the convection zone to avoid the sharp drop in D in the immediate vicinity of the boundary. The diffusion coefficient DCBM is applied for radii larger than r0(f0) until it drops below 102 cm s−1. For the bottom boundary of convective regions, the scheme is adapted to apply CBM below the convective boundary. The initial 1D model was obtained with the parameters fCBM = 0.022 and 0.0044 for the top and bottom boundaries, respectively. At both boundaries, f0 = 0.025 was used. We refer to Kaiser et al. (2020) for a discussion of these parameters and the related uncertainties.
. For the top boundary of convective regions, D0(f0) is the MLT diffusion coefficient evaluated at r0(f0) = rCB − (f0 Hp) where rCB is the radius of the boundary as given by Eq. (2). The free parameter f0 ensures that the diffusion coefficient is calculated inside the convection zone to avoid the sharp drop in D in the immediate vicinity of the boundary. The diffusion coefficient DCBM is applied for radii larger than r0(f0) until it drops below 102 cm s−1. For the bottom boundary of convective regions, the scheme is adapted to apply CBM below the convective boundary. The initial 1D model was obtained with the parameters fCBM = 0.022 and 0.0044 for the top and bottom boundaries, respectively. At both boundaries, f0 = 0.025 was used. We refer to Kaiser et al. (2020) for a discussion of these parameters and the related uncertainties.
Our simulations focus on convection in the helium-burning shell. The red vertical line in Fig. 1 indicates the evolutionary point at which the SLH simulations start and the extent in mass coordinates of the simulation domain. It corresponds to the early phase of helium-shell burning when the radial extent of the shell is still relatively small. Compared with later phases, this enables a better resolution at convective boundaries for a fixed computing budget. Choosing the convective shell also allows us to study two boundaries rather than only one for convective cores.
Models from stellar evolution codes typically exhibit step-like transitions in the 1D profiles, for example in the profiles of species abundances or thermodynamic quantities such as entropy. Even with moderate CBM parameters, such as used in the 1D input models, convective boundaries are very narrow. This is problematic for conventional hydrodynamic simulations because, if possible at all, a high number of grid cells is necessary to spatially resolve such transitions. Furthermore, we found in preliminary 2D test simulation that the steep gradients lead to strong initial flows in the convection zone. This effect was diminished, yet not fully resolved, for low resolution runs by applying rather strong smoothing to the initial profiles.
SLH simulations require the initial conditions to accurately fulfill the equation of hydrostatic equilibrium. This is not guaranteed for the 1D input profiles after they have been smoothed. Therefore, the equation of hydrostatic equilibrium needs to be integrated again while prescribing the profile of one thermodynamic quantity from the 1D MESA profiles. It is important that in this process the convection zone, characterized by a negative Brunt-Väisälä frequency (BVF), is maintained. For a nonrotating star, the BVF is given by (e.g., see Maeder 2009, Sect. 6.4.1)
where g is the magnitude of the gravitational acceleration, δ = −(∂lnρ/∂lnT)P, μ, φ = (∂lnρ/∂lnμ)P, T, and the gradient in mean molecular weight μ reads ∇μ = dlnμ/dlnP. These quantities are determined by the EoS. For the simulations presented here, we follow the approach of Edelmann et al. (2017) to reproduce a given 1D profile of the superadiabaticity Δ∇. This allows one to directly control the extent of the convective region in the initial condition if the chemical gradient can be neglected in the convection zone, as is the case for our model. It also ensures that the value of Δ∇ is reasonably close to zero and does not lead to an initial convective flow that is mainly driven by an excess in superadiabaticity. We construct the initial model on a radial grid that is much finer than the actual computational grid in SLH. For the computational grid, the initial state is obtained by interpolating from the fine grid to the positions of the respective cell centers. Because of the fine input grid, interpolation errors are negligibly small.
Preliminary SLH simulations revealed that setting the superadiabaticity on the SLH grid to a value of −1.5 × 10−5 whenever Δ∇MESA > −10−3 leads to a gentle transition from the initial hydrostatic stratification to fully developed convection and avoids a large initial peak in kinetic energy at the onset of convection. The slightly stable stratification would considerably hinder convection if the nominal luminosity was used. Because we have to increase the energy input anyway, this is not an issue for the simulations presented here.
In addition to the convective shell, parts of the radiative zones which lie above and below the convection zone are included in the computational domain. Their respective radial extent is chosen to be one half of the extent of the convection zone itself. This way, the impact of the top and bottom boundary conditions will be reduced while keeping the computational cost at a moderate level.
The resulting profiles after smoothing and mapping the region of interest from the 1D stellar model to the computational grid are shown in Fig. 2. The density closely follows the profiles as given by the 1D MESA input model. However, smoothing changes the profile of the BVF and alters the size of the convection zone (shaded areas in Fig. 2). Especially the position of the bottom boundary changes and the convection zone starts at a somewhat larger radius in the mapped model.
 |
Fig. 2. Initial profiles for the underlying 1D MESA model (dashed) and the mapped SLH model (solid lines). The shaded areas mark the convection zone for mapped profiles (blue) and MESA profiles (orange). The oscillatory behavior of the energy generation is a numerical artifact at negligible amplitudes. |
In Sect. 5.4 we measure the mass entrainment across the boundaries of the convective zone. An often employed quantity to characterize the resistance to such a mixing (also called stiffness) is the bulk Richardson number RiB. For comparability, we follow the notation of Cristini et al. (2017, 2019) (C+17 and C+19 hereafter) and write
where vrms is the rms velocity of the convection and the integral length scale l of the convection is set to one half of the pressure scale height at the boundary. The buoyancy jump ΔB is given by
where rc is the radial position of the respective boundary. The integration width Δr is a somewhat arbitrary parameter but should be chosen such that it includes the full region of the evanescent convective flow at the boundaries. Following C+19, we set Δr to a quarter of the local pressure scale height. Compared to our measurements of the boundary widths given in Sect. 5.6 (see Table 5), this seems to be an appropriate value for the top boundary but might overestimate the bottom boundary.
The definition of C+17 for l and Δr is not applicable for convection zones that are thinner than a pressure scale height and some form of correlation function of the turbulent flow field might be more appropriate. This, however, is not easily obtained in 1D stellar evolution codes. Generally, the definition of l and Δr is ambiguous in the astrophysical literature which makes it difficult to directly compare the values of the bulk Richardson number in simulations carried out by different groups (see for example Meakin & Arnett 2007; Arnett et al. 2009; Salaris & Cassisi 2017; Cristini et al. 2017; Collins et al. 2018; Higl et al. 2021).
To assess the impact of the applied smoothing on the stiffness, we compare the numerator of Eq. (6) for the original 1D MESA input model and the mapped SLH model at the respective top and bottom boundary. We find
which indicates that the mapping only has a moderate impact on the stiffness of the boundary.
Due to the computational costs involved, not all nuclear species of the MESA nuclear network can be included to the SLH simulation. Instead, we only account for 4He, 12C, 16O, 20Ne, and 22Ne. The abundance profile of each species, except for 22Ne, is taken directly from the MESA model and smoothed in the same way as the other input profiles. The abundance of 22Ne follows from the condition ∑iXi = 1 in every cell, where Xi is the mass fraction of species i. The resulting profiles are shown in the middle panel of Fig. 2.
Although the smoothing procedure causes the SLH model to slightly deviate from the original 1D MESA model, the MESA model involves uncertainties of its own. Therefore, we still consider the SLH model to be representative of typical conditions expected in He-burning shells of massive stars.
3.2. Energy generation and boosting
The energy release is calculated using the JINA REACLIB reaction files (Cyburt et al. 2010) and displayed in the lowest panel of Fig. 2. From the profile of the energy generation rate as given directly by the MESA model (dashed line) it is apparent that the peak of nuclear burning does not coincide with the convection zone (orange shade) but instead is located somewhat beneath. This is common for burning shells, which develop convection above the energy peak where the temperature gradient becomes steeper than the adiabatic one.
To ensure that convection is driven by the actual energy input and not by numerical artifacts, the nominal energy input must be boosted. The strength of the required boosting is determined in Sect. 4.2. We couple the boosting of the energy generation to the abundance of 4He such that only regions are boosted where the mass fraction of 4He is higher than 90% of the initial abundance in the convection zone, that is for abundances higher than 0.87. The energy input is turned off everywhere else.
3.3. Thermal diffusion
Thermal radiation is treated in the diffusion limit in SLH. This is justified by the high optical depth in the interior regions of stars. While the 1D input profile from the MESA code is in thermal balance, that is the energy flux equals the integrated energy generation, this is not true anymore within the convection zone of the SLH simulations with boosted energy generation. Radiative effects certainly are crucial over the long timescales covered in simulations of stellar evolution. However, for the much shorter dynamical timescales we expect the imbalance to be of minor importance: Following the same arguments as Horst et al. (2020), we calculate the thermal adjustment timescale (e.g., Maeder 2009, Sect. 3.2.) via
where Δxdiff is a typical diffusion length scale, the radiation constant a = 7.57 × 1015 erg cm−3 K−4 and CP denotes the specific heat of the gas at constant pressure. All other values have their usual meanings. The opacity κ that enters the thermal diffusivity K is taken from the 1D MESA profile. Because advective and diffusive processes have a different temporal and spatial scaling, it is not clear how to scale the opacity with our energy boosting. Therefore, we keep the opacity at its stellar value in this study.
Assuming as typical length scale the radial grid spacing of the finest resolution that will be used (810 radial cells, see Sect. 5), we find a mean adjustment timescale of 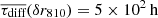 . The timescale is shortest at the outermost regions where the opacity is the smallest, but is always larger than 102 h (see Fig. B.1). This is at the order of our longest runs, which, however, have lower radial resolution than what is assumed in this estimate. Taking the convection zone as typical length scale we obtain
. The timescale is shortest at the outermost regions where the opacity is the smallest, but is always larger than 102 h (see Fig. B.1). This is at the order of our longest runs, which, however, have lower radial resolution than what is assumed in this estimate. Taking the convection zone as typical length scale we obtain 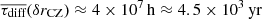 which is orders of magnitude longer than all of our simulations. We therefore conclude that for the particular simulations presented here the effect of thermal diffusion is negligible and that the thermal imbalance due to our increased energy input does not impact the global structure of the star over the duration of our simulations.
which is orders of magnitude longer than all of our simulations. We therefore conclude that for the particular simulations presented here the effect of thermal diffusion is negligible and that the thermal imbalance due to our increased energy input does not impact the global structure of the star over the duration of our simulations.
3.4. Discretizing the computational domain
To reduce the computational costs, we have to use a spherical-wedge grid geometry, although this choice eliminates the large-scale flows seen in comparable 4π simulations of Woodward et al. (2015), Jones et al. (2017), Andrassy et al. (2020), and Gilet et al. (2013). The chosen wedge geometry reduces the computational cost by a factor of 32 compared to a full 4π simulation at the same vertical and horizontal resolution.
For the 4π simulations mentioned above, we calculate the aspect ratios (we adopt here the formulation of Jones et al. 2017) as (rtop − rbot)/rtop, where rtop, rbot denote the radial position of the bottom and top boundary of the convection zone. The aspect ratio for the He-flash simulation of Woodward et al. (2015) is about 0.67, for the O-shell simulation of Jones et al. (2017), Andrassy et al. (2020) it is about 0.5 and for the H-core burning of Gilet et al. (2013) it is 1. With decreasing aspect ratio, the maximum possible size of convection cells decreases and so does the impact of restricting the flow to a spherical wedge. The He-shell simulation presented here has an aspect ratio of only 0.32. Furthermore, the study by Gilet et al. (2013) indicates that, while the flow morphology differs distinctly between their hydrogen core simulations for full 4π and single octant domains, basic turbulent properties and mixing rates are in a reasonable agreement. From this, we expect that the imprint of the restricted geometry on our results is sufficiently small. However, the influence of the domain size should be assessed in more detail in future studies.
We set the horizontal extent of the computational domain to be as twice as large as the vertical extent of the convection zone. This enables the formation of two large vortices, a typical phenomenon we observe in 2D and 3D simulations. The corresponding opening angle is about 45°. The constant grid spacing giving cell aspect ratios ranging from roughly unity at the bottom to one half at the top of the domain.
The lowest resolution that will be used in this study has 180 vertical cells and 90 horizontal cells. This ensures that the pressure scale height is resolved by at least 25 cells and that the initial transitions from radiative to convective regions as given by the profile of the BVF are resolved by at least 20 cells.
Periodic boundary conditions are employed in horizontal direction. In both radial directions, layers of two cells are added (ghost cells). They are initialized with the mapped hydrostatic state but are not evolved in time.
4. 1D and 2D test simulations
While proper turbulent behavior of convection can only be followed in 3D simulations, much cheaper 1D and 2D simulations are well suited to test stability and basic properties of the initial hydrostatic stratification. Such low-dimensional simulations are utilized in this section to demonstrate that applying the Cargo–LeRoux well-balancing method successfully stabilizes the hydrostatic stratification described in Sect. 3, even at low resolution. Furthermore, a series of 2D simulations is presented to estimate the required strength of the artificial boost of the nuclear energy release.
4.1. Testing the impact of the Cargo–LeRoux well-balancing in 1D and 2D
To demonstrate the capabilities of well-balancing, we performed 1D simulations with and without the Cargo–LeRoux method. For these simulations, the energy input was switched off.
In Fig. 3, the change in the BVF and the pressure are shown after simulating 10 h of physical time (about 500 sound crossing times) in 1D. If the hydrostatic stratification was perfectly maintained, the initial profiles would stay constant in time. However, for a grid with 180 radial cells, it is obvious that the formally static setup changes considerably if no well-balancing is applied. The BVF has increased its value in the convection zone and the top boundary of the convection zone has moved inward. The relative pressure change is on the order of 10−3 throughout the domain. In contrast, the BVF profile does not visibly change in the run with Cargo–LeRoux well-balancing. The relative pressure changes are about 10−8 which is 4 orders of magnitude smaller. The simulations shown in Fig. 3 apply the lowest radial resolution that is used for the 3D simulations in Sect. 5. The spurious change of the background stratification is expected to decrease at higher resolutions even if no well-balancing is applied. Indeed, for 540 radial cells, the overall changes decrease considerably. Yet, deviations from the initial stratification are still visible and the change in pressure is significant.
 |
Fig. 3. Profiles of the BVF (upper panel) and relative change in pressure (lower panel) after simulating 10 h of physical time with and without well-balancing. Nr denotes the number of radial cells that are used for the discretization. |
Hence, the 1D simulations indicate that, especially at low resolution, well-balancing is necessary to maintain hydrostatic equilibrium at a sufficient accuracy. This is further confirmed in the heated 2D counterparts of the 1D simulations. For a moderate energy input the setup is evolved for 10 h of physical time in 2D wedge geometry. The resulting flow is depicted in Fig. 4. The simulation with Cargo–LeRoux well-balancing has developed the typical large coherent convective eddies inside the convection zone that are driven by the energy input. This is clearly different from the flow that develops if no well-balancing is applied. Because of the changing background, the BVF has become too large, such that the energy input is not sufficient to establish convection. Instead, only at the base of the convection zone where the heating has its maximum a narrow band of small-scale eddies emerges.
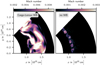 |
Fig. 4. Flow morphology in terms of Mach number in a 2D wedge after simulating 10 h of physical time. The nuclear energy release has been boosted by a factor of 1 × 104. The left panel corresponds to a simulation that applies Cargo–LeRoux well-balancing while well-balancing is absent in the simulation shown on the right. The domain is discretized by 180 × 90 cells. |
4.2. Testing artificial boosting of nuclear burning in 2D simulations
Boosting the physical energy generation from nuclear burning is a common technique in multidimensional simulations of steady convection, especially in early stellar evolutionary phases. As predicted by mixing-length theory and confirmed in numerical studies (see, e.g., C+19 or Andrassy et al. 2020) the convective velocity vconv scales as
where L is the luminosity in the convection zone. Thus, increasing the energy input leads to larger velocities.
Higher velocities can be beneficial for several reasons. As discussed in Sect. 2, convectional finite-volume schemes based on Riemann solvers have difficulties to resolve flows at low Mach numbers. Therefore, artificial boosting can be used to move the flow-velocities to regimes that are more suitable for the applied numerical scheme. Furthermore, if explicit time stepping is used, higher velocities improve the ratio of permitted time step size to the timescale of the flow. This reduces the computational costs.
Another purpose of applying energy boosting is to run simulations with the same setup but different boosting strengths. This allows one to investigate the properties of mixing at the boundaries and the entrainment rate as functions of convective velocities for a single stratification. This has been done in later phases of stellar evolution for example by C+19 or Andrassy et al. (2020) and is also utilized in Sect. 5.
The obvious downside of the artificial energy boosting is that the simulations do not represent the physical situation in the original stellar model anymore. In 1D stellar evolution codes, the structure of a star critically depends on the balance between energy generation (e.g., by nuclear burning), cooling processes (e.g., by escaping neutrinos) and energy transport within the star (e.g., by radiation or convection). This balance is disturbed if the energy input is changed. While we think it is still possible with such simulations to assess the effect of dynamical phenomena such as turbulent mixing and excitation of waves, they are probably not suitable to study the long-term behavior of convection where the interplay between turbulence and thermal diffusion might become important.
Apart from the reasons mentioned above, a sufficient energy boosting is also necessary to increase the velocity above the numerical threshold at about Ma ≈ 10−3 for SLH simulations with the Cargo–LeRoux well-balancing method. To assess by how much the energy generation has to be increased for the 3D simulations, a set of 2D wedge simulations is performed with varying strengths of the energy boosting. The resolution is set to 180 × 90 cells (lowest resolution in the 3D runs) and the simulations are performed for boosting factors ranging from 1 (no boosting) to 3 × 104. The resulting temporal mean of the root-mean square (rms) Mach number Marms as a function of energy input is then compared to the scaling law in Eq. (10). In order to determine the region for which the rms value of the Mach number is calculated, the convection zone is identified by means of the gradient of the advected passive scalar, as will be explained in Sect. 5.1. For the size of the time frame, we consider the convective turnover time
where ΔCZ is the radial extent of the convection zone and vrms the rms velocity within the area spanned by ΔCZ and the horizontal extent of the domain. By taking τconv as the underlying unit of time, we account for the different speed at which the hydrodynamical processes evolve for different driving strengths. To finally determine the time frame for which vrms is determined, we calculate the number of covered turnover times Nτconv as
Using Eq. (12) automatically accounts for different lengths and characteristics that may arise for initial transients for different luminosity boosting and resolutions. Therefore, we find it more convenient to define a time frame in terms of Nτconv instead of finding a suitable physical time interval by hand.
To account for the fact that the boosted region may change during a simulation, the energy release is integrated over the domain and averaged for the considered time frame of t ∈ [t(Nτconv = 10), t(Nτconv = 20)].
As shown in Fig. 5, the data points of the three highest boostings (3 × 103, 1 × 104, and 3 × 104) closely follow the expectation of Eq. (10). For lower energy boosting, we find deviations from the scaling. The corresponding flow patterns along with the detected boundaries are shown in Fig. B.2. The flow of the 2D simulation with the lowest boosting clearly differs from the other 2D simulations. The appearance of incoherent, small-scale patterns in SLH simulations of convection is likely an indication that the flow is driven by numerical artifacts (see also Edelmann et al. 2021). Based on these results, we conclude that the set of boosting factors b ∈ [3×103,1×104,3×104] is suitable for the subsequent 3D simulations.
 |
Fig. 5. Measured rms Mach number as function of the input energy rate ė in 2D (blue) and 3D simulations (orange). Vertical error bars correspond to the standard deviation of the average over the time frame of ΔNτconv = 10. The dashed lines reflect the scaling law in Eq. (10). Numbers given in the boxes correspond to energy boosting factors for the lowest and the three highest boostings. The green cross marks the Mach number of Ma ≈ 1.6 × 10−4 as predicted by MLT at the nominal energy generation rate in the original MESA model. |
5. 3D SLH results
After the basic properties of the stellar model have been tested in 1D and 2D hydrodynamic simulations, this section presents the results regarding turbulent flow properties and entrainment obtained from 3D simulations. We analyze the results for varying resolution and convective driving. To demonstrate that the low-Mach AUSM+-up flux scheme is beneficial even for moderate Mach numbers, the respective results are compared to its basic version 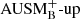 that is not expected to show enhanced low-Mach capabilities. A comparison to more commonly used flux functions, such as the Roe solver, would have been a more obvious choice. This was not possible as the applied Cargo–LeRoux well-balancing method is not fully compatible with the Roe scheme. However, in Sect. 5.2, we show for a reduced domain that the numerical diffusivity is similar for
that is not expected to show enhanced low-Mach capabilities. A comparison to more commonly used flux functions, such as the Roe solver, would have been a more obvious choice. This was not possible as the applied Cargo–LeRoux well-balancing method is not fully compatible with the Roe scheme. However, in Sect. 5.2, we show for a reduced domain that the numerical diffusivity is similar for 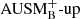 and the Roe scheme.
and the Roe scheme.
A major restriction for our 3D simulations is posed by the available computational resources. While a higher resolution is certainly desirable, it considerably reduces the physical time for which we could follow convection. However, convection has to be covered for several turnover times τconv in order to analyze mixing processes at the boundaries of the convection zone. We therefore can only investigate the effect of boundary mixing at the lowest resolution of 180 × 902. At higher resolution, our simulations only cover a few multiples of τconv which is too short to track mixing at the boundaries but is sufficient to extract properties of turbulence. In this section we present simulations with resolutions ranging from 180 × 902 to 810 × 5402. The basic properties of the simulations are summarized in Tablea 1–3. We note that the radial resolution from 360 × 1802 to 540 × 3602 cells changes by a factor of 1.5, while the corresponding number of horizontal cells changes by a factor of 2. This was done inadvertently, but we are confident that it does not prevent the comparison of the results between the different resolutions. The simulations at a resolution of 810 × 5402 cells are restarted from the corresponding simulations at 540 × 3602 at a stage of fully developed convection. This avoids the slow initial transients and hence reduces computational costs.
Properties of the 3D simulations with a boosting factor of 3 × 104.
Properties of the 3D simulations with a grid size of 180 × 902 cells.
Properties of the 3D simulations with a grid size of 360 × 2402 cells.
To conclude the 2D scaling test of the previous section, the scaling relation Eq. (10) is shown for the lowest resolution and the AUSM+-up solver in Fig. 5 (orange crosses). The 3D data is in good agreement with the expected scaling. The corresponding flow patterns are found in Fig. B.2 at a resolution of 180 × 902. From MLT, a convective velocity of MaMLT ≈ 1.6 × 10−4 is predicted. If we extrapolate from the 3D results to stellar luminosity we find a value of Maext ≈ 4.0 × 10−4. The ratio Maext/MaMLT ≈ 2.5 is similar to what has been obtained by Jones et al. (2017). This ratio indicates a reasonable agreement, taking into account that MLT only provides an order-of-magnitude estimate and that the results from our simulations need to be extrapolated to nominal luminosity.
5.1. Tracing the boundaries of the convection zone
For the analysis that is presented in the subsequent sections, the top and bottom radii of the convection zone, rCZ,0 and rCZ,1, have to be extracted from the simulations. This can be done in different ways, for example by considering the radii where the decline in the horizontal velocity is steepest (Jones et al. 2017), where the species abundance gradient is steepest (Meakin & Arnett 2007), or where the mean atomic weight is equal to its averaged value within the convective and adjacent stable zone (C+17). Furthermore, to avoid the use of averages which might underestimate the effect of strong but rare mixing events, extreme value statistics could be used (Pratt et al. 2017) or the standard deviation of a dynamical quantity like the kinetic energy (Higl et al. 2021).
Our approach is to advect ρX with the fluid flow where X is a passive scalar. Its initial distribution increases at a constant slope from −1 at the bottom boundary of the computational domain to 1 at the top (dashed line in Fig. 6). The passive scalar will quickly be mixed within the convection zone while forming a transition between the initially linear decrease and a flat region. The position of the boundaries is then defined as the radius where the spatial gradient of the horizontally averaged passive scalar is largest. We find that after an initial redistribution of the scalar by the onset of convection our method gives robust results.
 |
Fig. 6. Horizontal mean of the advected passive scalar for a simulation with a resolution of 180 × 902. The initial distribution of the scalar is shown as dashed line, the solid line represents the time-averaged profile for t ∈ [t(Nτconv = 9.9),t(Nτconv = 10.1)]. The blue shaded area corresponds to the minimal and maximal value of the passive scalar at the corresponding radius for the latest considered snapshot. The radii at which the absolute value of the radial derivative is largest are indicated by dots. They define the position of the top and bottom boundaries. The shaded orange area marks the convective region according to the stability criterion N2 < 0. Vertical dashed lines denote the respective boundary widths which are defined in Sect. 5.6. |
This definition of the boundary position is similar to using the abundance gradient. However, it does not depend on the initial 1D structure in terms of strength and position of the gradients. Furthermore, the abundance and passive scalar profiles are immediate measurements of the mixing compared to measuring for example overshooting events or standard deviations, which are linked to mixing only indirectly.
For an exemplary simulation, Fig. 6 shows the profile of the advected passive scalar at the start of the simulation and around t(Nτconv = 10). The efficient mixing by convection has homogenized the passive scalar within the convection zone. At the top and bottom boundary of the computational domain, the profile of the passive scalar is almost not distinguishable from the initial distribution. The orange shaded area denotes the convection zone according to the criterion N2 < 0 and it is clearly visible that this definition underestimates the extent of the convection zone. The bottom and top boundaries of the convection zone as given by the maximum absolute value of the radial gradient of the passive scalar are shown as blue dots. There are small amounts of numerical under- and overshoots in the profile of the passive scalar. This is due to a lack of slope-limiter for reconstruction for the implicit time stepping.
5.2. Kinetic energy spectra and comparison with turbulence theory
Kolmogorov (1941) (see also Landau & Lifshitz 1987) predicts that the spectrum of kinetic energy εkin in 3D isotropic turbulence follows
where ℓ is the angular order. Although stellar convection is not isotropic on large scales, many numerical experiments reveal spectra similar to this prediction on sufficiently small scales (Porter & Woodward 2000; Gilet et al. 2013; Verma et al. 2017, C+17). The spectra of turbulent convection in 3D typically divide into three regions (see Arnett et al. 2015 for a more detailed discussion): At large spatial scales, that is at small values of the angular order ℓ, the energy from heating is injected into the flow, forming the integral range. At somewhat smaller scales, or equivalently for larger ℓ, the inertial range forms that follows the scaling of Eq. (13). The inertial range extends down to the small scales where dissipating effects such as viscosity become relevant and turbulent kinetic energy is transformed into internal energy. This leads to a steeper drop in εkin(ℓ) for larger ℓ and marks the dissipation range. In the stellar context, it is impossible to resolve the spatial scales where physical viscosity takes place. Thus, in implicit large eddy simulations (ILES), the effect of viscosity is not modeled explicitly but follows from the numerical viscosity inherent in the applied numerical scheme at small scales (see, e.g., Arnett et al. 2015, 2018). This is the case for the SLH code that solves the Euler equations which follow from the Navier-Stokes equations for vanishing viscosity but does not apply any subgrid scale model for turbulent dissipation. It therefore is desirable to resolve the scaling Eq. (13) to the smallest scales possible while still having a numerically stable scheme. Hence, one way to compare the quality of numerical schemes is to compare their respective range in ℓ for which they reproduce an inertial range with a scaling according to Eq. (13).
In the following, we present the spectra for the 3D SLH simulations and compare the low-Mach AUSM+-up solver to the 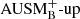 scheme. In setups with an approximate spherical symmetry, the spatial spectra of turbulent flows are typically given in terms of power spectra for spherical harmonics. This makes use of the fact that a given function F(ϑ, φ) on the spherical surface can be decomposed into spherical harmonics as
scheme. In setups with an approximate spherical symmetry, the spatial spectra of turbulent flows are typically given in terms of power spectra for spherical harmonics. This makes use of the fact that a given function F(ϑ, φ) on the spherical surface can be decomposed into spherical harmonics as
where fℓm is the amplitude for the corresponding spherical harmonic Ylm of angular degree ℓ and angular order m. For our analysis we apply the open-source shtools1 (Wieczorek & Meschede 2018), a collection of Fortran90 and Python libraries for spherical harmonics data analysis. To decompose the velocity fields that result from our simulations, we proceed as follows:
The shtools assume that the input data is provided for the whole spherical surface. The computational domain in our simulations, however, is a spherical wedge. We therefore expand the φ − ϑ plane covered by our simulations to the full spherical surface. For this, the data from our simulation is repeated periodically to fill the regions that are not covered by the computational domain, see Fig. 7. This gives slightly weaker artifacts than zero-padding.
 |
Fig. 7. Expansion of the velocity data for one exemplary 3D wedge simulation. Color coded is the velocity component in φ-direction. The red square marks the actual computational domain. The rest of the plane is filled by periodically repeating the simulation data in ϑ and φ direction. |
To further reduce the artifacts introduced by our limited domain, we make use of the ability of shtools to apply an arbitrary window function to extract localized spectra. The shtools construct the windows automatically and provide the user the option to restrict the bandwidth of the created windows by an upper limit ℓmax. The necessary bandwidth of the window function increases with smaller localized areas. The shtools then calculate different realizations of window functions that have their power concentrated in the considered region within the ϑ − φ plane. The spectra of all windows are averaged (multitaper, see also Wieczorek & Simons 2005). For the input of the multitaper spectrum, we set ℓmax to a sufficiently high value to obtain at least 10 window realizations from shtools which have 99% of their power localized in the computational domain.
The spectra that are presented in the following are taken at a constant radius in the middle of the convection zone. This is justified if the flow is isotropic, which is not the case at large scales (small ℓ) but a reasonable assumption at small scales. Isotropy is also a necessary condition for the Kolmogorov-scaling Eq. (13) to form. The extracted spectra are averaged over roughly one convective turnover time.
In order to demonstrate the improved performance of the low-Mach AUSM+-up solver, we compare it to its basic variant 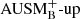 . The AUSM solver family is not yet widely used in the astrophysical community. To get an idea how
. The AUSM solver family is not yet widely used in the astrophysical community. To get an idea how 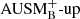 compares to the well-known Roe scheme, we compare their spectra for a reduced domain, which only contains a subset of the convection zone. This is necessary because we find numerical artifacts for Roe in combination with Cargo–LeRoux well-balancing that lead to spurious flows in the stable regions at radii where abundances change.
compares to the well-known Roe scheme, we compare their spectra for a reduced domain, which only contains a subset of the convection zone. This is necessary because we find numerical artifacts for Roe in combination with Cargo–LeRoux well-balancing that lead to spurious flows in the stable regions at radii where abundances change.
Their spatial resolutions are the same as for the 540 × 3602 simulations of the full domain. The result is shown in Fig. 8. The spectra demonstrate that, at least within the convection zone, the 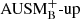 and the Roe solver are both dissipative and do not show an inertial range. For comparison, the spectrum of a simulation which has the same spatial resolution but using the
and the Roe solver are both dissipative and do not show an inertial range. For comparison, the spectrum of a simulation which has the same spatial resolution but using the 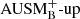 scheme is added to the figure along with the Kolmogorov-law Eq. (13). The similarity between the Roe and
scheme is added to the figure along with the Kolmogorov-law Eq. (13). The similarity between the Roe and  solver is also evident in the flow pattern, Fig. B.3.
solver is also evident in the flow pattern, Fig. B.3.
 |
Fig. 8. Spectra of the radial kinetic energy component. The blue and orange line correspond to simulations with the Roe and |
The spectra for the highest available resolution and the full domain are shown in Fig. 9. We find that the  and AUSM+-up solver both show a well-defined inertial range where the slope closely follows the prediction of a Kolmogorov spectrum. The vertical dotted lines in Fig. 9 mark the scale at which there is a significant deviation from the Kolmogorov-law. From this measure we find that the inertial range of the AUSM+-up solver extends toward scales that are about a factor two smaller compared to the
and AUSM+-up solver both show a well-defined inertial range where the slope closely follows the prediction of a Kolmogorov spectrum. The vertical dotted lines in Fig. 9 mark the scale at which there is a significant deviation from the Kolmogorov-law. From this measure we find that the inertial range of the AUSM+-up solver extends toward scales that are about a factor two smaller compared to the  solver.
solver.
 |
Fig. 9. Spectra of the radial kinetic energy component for the |
In Fig. 10 the turbulent convective velocity field is depicted for a slice through the three-dimensional domain for a single snapshot. The AUSM+-up scheme clearly shows smaller structures in the flow field as compared with  on the same computational grid. This is also apparent in Fig. 11 which shows the magnitude of vorticity |∇×u|, where u is the velocity vector. To further illustrate the advantages of the low-Mach flux AUSM+-up over
on the same computational grid. This is also apparent in Fig. 11 which shows the magnitude of vorticity |∇×u|, where u is the velocity vector. To further illustrate the advantages of the low-Mach flux AUSM+-up over 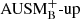 , we compare in Fig. 12 the spectra at different resolutions. We find that for the AUSM+-up solver, a grid resolution of 360 × 1802 gives an inertial range that is comparable to the 810 × 5402 resolution of simulations with
, we compare in Fig. 12 the spectra at different resolutions. We find that for the AUSM+-up solver, a grid resolution of 360 × 1802 gives an inertial range that is comparable to the 810 × 5402 resolution of simulations with 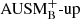 .
.
 |
Fig. 10. Mach number for a slice through the domain for simulations at a resolution of 810 × 5402 cells with the |
 |
Fig. 12. Spectra of the radial kinetic energy component for the |
5.3. Comparing numerical dissipation from RA-ILES results
The comparison of the kinetic energy spectra is complemented by analyzing the different simulations in the terms of Reynolds averaged implicit large eddy simulations (RA-ILES) (Mocák et al. 2014; Arnett et al. 2019). The fundamental idea is to separate the different components of the Navier-Stokes equations into mean and fluctuating parts and to determine them by analyzing numerical simulations. The physical interpretation of these parts then gives useful insight into the complex interplay between different processes that act in turbulent convection and at the boundaries of the convection zone.
While the RA-ILES framework provides a wealth of equations (see Mocák et al. 2014 for an extensive overview), we focus on analyzing the equation for turbulent kinetic energy. It allows one to quantify the effect of implicit numerical dissipation of kinetic energy that is inherent in all ILES. This equation has been used in several publications in the past (see, e.g., Arnett et al. 2009; Mocák et al. 2014, 2018), and aided the analysis of the effects of resolution and convective driving (C+17, C+19) or different strengths of stratification (Viallet et al. 2013). Following the formulation of Mocák et al. (2014), the time evolution for the kinetic energy of an inviscid fluid can be written as
where ϵk is the specific kinetic energy, 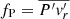 the acoustic flux,
the acoustic flux, 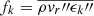 the turbulent kinetic energy flux,
the turbulent kinetic energy flux, 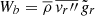 the buoyancy work,
the buoyancy work, 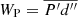 the turbulent pressure dilatation, and d = ∇ ⋅ v. The radial component of the gravitational acceleration is denoted by gr. The definition of the Reynolds average
the turbulent pressure dilatation, and d = ∇ ⋅ v. The radial component of the gravitational acceleration is denoted by gr. The definition of the Reynolds average 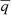 , Favre average
, Favre average 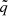 , and the corresponding fluctuations q′, q″ for a quantity q are given in Appendix A. For a more detailed discussion of the individual terms, see for example Meakin & Arnett (2007), Viallet et al. (2013), or Mocák et al. (2014).
, and the corresponding fluctuations q′, q″ for a quantity q are given in Appendix A. For a more detailed discussion of the individual terms, see for example Meakin & Arnett (2007), Viallet et al. (2013), or Mocák et al. (2014).
Because numerical solutions are only approximations to the true solution, Eq. (15) will in general not be fulfilled exactly in hydrodynamic simulations. Instead, there will be a residual 𝒩ϵk between the left-hand and right-hand side. In energy conserving methods like finite volume schemes, 𝒩ϵk then measures the numerical dissipation of kinetic energy into internal energy, the fundamental property of ILES. The exact value of 𝒩ϵk depends on the details of the numerical scheme, the resolution, but also on the specific physical problem at hand. Generally, the value of 𝒩ϵk cannot be controlled in ILES. However, extracting the terms in Eq. (15) from a hydrodynamic simulation, the strength of numerical dissipation that acted for the considered time in a specific simulation can be determined from the average value of 𝒩ϵk.
We calculate all the terms in Eq. (15) for the 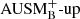 and AUSM+-up solver at different resolutions. Third-order central differences are used to evaluate the gradients. Except for the highest resolution, the results are averaged over the time interval of t ∈ [t(Nτconv = 2),t(Nτconv = 3)] which is the maximum overlapping time frame. For the highest resolution, the simulations are averaged over only ΔNτconv = 0.6. Ideally, the averages would be performed over several turnover times to improve the statistics. While our short time frames probably make a quantitative comparison of the components less robust, we think that a qualitative comparison is still meaningful and that the main characteristics of Eq. (15) are captured.
and AUSM+-up solver at different resolutions. Third-order central differences are used to evaluate the gradients. Except for the highest resolution, the results are averaged over the time interval of t ∈ [t(Nτconv = 2),t(Nτconv = 3)] which is the maximum overlapping time frame. For the highest resolution, the simulations are averaged over only ΔNτconv = 0.6. Ideally, the averages would be performed over several turnover times to improve the statistics. While our short time frames probably make a quantitative comparison of the components less robust, we think that a qualitative comparison is still meaningful and that the main characteristics of Eq. (15) are captured.
In Fig. 13 the profiles of the individual terms of Eq. (15) are depicted for successively increasing resolutions2. We find our results in qualitative agreement with simulations of oxygen burning (Viallet et al. 2013, Fig. 8) and carbon burning (Fig. 9 of C+17, see also C+19). The small but noticeable nonzero values for the left-hand side of Eq. (15) (dashed lines in Fig. 13) are due to the short time interval considered. For comparison, we recalculated in Fig. 14 the results for the lowest resolution but a time interval that covers ΔNτconv = 10. Here, the time evolution of the kinetic energy is close to zero.
 |
Fig. 13. Profiles of the different components of kinetic energy equation in the RA-ILES framework, Eq. (15). The resolution increases from top to bottom. The left column corresponds to results using the |
 |
Fig. 14. Same quantities as in Fig. 13, but for a time interval of t ∈ [t(Nτconv = 10),t(Nτconv = 20)]. |
The dominant part on the right-hand side is the buoyancy work Wb that is positive in the convection zone and changes sign at the boundaries to the stable layers. The acoustic and turbulent kinetic energy fluxes show a more complex behavior and change signs several times in the convection zone. The pressure dilatation term WP takes a rather low value for all simulations owing to the fact that the density stratification within the convection zone is small. As shown by Viallet et al. (2013), the situation can be different in other setups. They find that in the convective envelope of a 5 M⊙ red giant star, pressure dilatation contributes a significant part to the overall budget of Eq. (15) as the convection zone spans several pressure scale-heights. In general, we do not find significant qualitative differences between different resolutions and between the 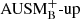 and AUSM+-up solver. At the lowest resolution with AUSM+-up, small oscillations on the grid level are visible for the acoustic flux fP within the convection zone. However, they vanish for increasing resolution. At high resolution, we find oscillations in fP at the domain boundaries, the origin of which is not completely clear. We suspect an interplay of better resolved internal gravity waves with the constant ghost cell boundaries. This inevitably leads to shear because velocities are set to zero in the boundary cells.
and AUSM+-up solver. At the lowest resolution with AUSM+-up, small oscillations on the grid level are visible for the acoustic flux fP within the convection zone. However, they vanish for increasing resolution. At high resolution, we find oscillations in fP at the domain boundaries, the origin of which is not completely clear. We suspect an interplay of better resolved internal gravity waves with the constant ghost cell boundaries. This inevitably leads to shear because velocities are set to zero in the boundary cells.
The dotted lines in Fig. 13 correspond to the numerical dissipation of kinetic energy 𝒩ϵk acting in the respective simulation. In general, the dissipation is distributed over the whole convection zone and vanishes in the stable layers. For the AUSM+-up solver, some smaller oscillations are visible near the boundaries which stem from the oscillations in fP. Comparing the results of the 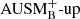 and AUSM+-up solver at each resolution, the profiles of 𝒩ϵk have similar amplitudes in the main part of the convection zone. However, for the simulations using the
and AUSM+-up solver at each resolution, the profiles of 𝒩ϵk have similar amplitudes in the main part of the convection zone. However, for the simulations using the 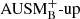 solver, the numerical dissipation shows a distinct peak at the bottom boundary. The peak height and width decreases with increasing resolution. The same behavior was found by C+17 for carbon-shell burning and by Viallet et al. (2013) for oxygen-shell burning. However, this peak is absent in the simulations using the AUSM+-up solver. From the shape and position of the peak of 𝒩ϵk in the plots for the
solver, the numerical dissipation shows a distinct peak at the bottom boundary. The peak height and width decreases with increasing resolution. The same behavior was found by C+17 for carbon-shell burning and by Viallet et al. (2013) for oxygen-shell burning. However, this peak is absent in the simulations using the AUSM+-up solver. From the shape and position of the peak of 𝒩ϵk in the plots for the 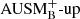 solver it seems that the peak is due to an imbalance between the acoustic flux fp and Wb. Although the peak in fp appears to be similar in shape and amplitude for the two solvers, a more pronounced opposed peak in Wb seems to counteract the gradient of fp in the AUSM+-up runs.
solver it seems that the peak is due to an imbalance between the acoustic flux fp and Wb. Although the peak in fp appears to be similar in shape and amplitude for the two solvers, a more pronounced opposed peak in Wb seems to counteract the gradient of fp in the AUSM+-up runs.
We directly compare the numerical dissipation 𝒩ϵk for the different simulations in Fig. 15. For AUSM+-up, the amplitudes seem to be converged already for the lowest resolution, although low-resolution runs show oscillations in the numerical dissipation. Also for the 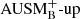 solver, the dissipation in the bulk of the convection zone seems not to depend strongly on the resolution. This is consistent with the expected independence of the turbulent dissipation rate from the effective viscosity, which is set by the grid scale. However, at the bottom boundary, the peak decreases with increasing resolution and seems to converge toward a value that is similar to the dissipation of the AUSM+-up solver. These results are fully in line with the simulations shown in Figs. 1 and 2 of Arnett et al. (2018) which summarize the numerical dissipation in oxygen- and carbon-shell burning simulations with the PROMPI code. For their highest-resolution run, they find that the peak at the bottom boundary seems to merge with the bulk dissipation. This indicates that the low-Mach AUSM+-up solver improves the behavior at the bottom boundary, even at moderate Mach numbers and moderate resolution.
solver, the dissipation in the bulk of the convection zone seems not to depend strongly on the resolution. This is consistent with the expected independence of the turbulent dissipation rate from the effective viscosity, which is set by the grid scale. However, at the bottom boundary, the peak decreases with increasing resolution and seems to converge toward a value that is similar to the dissipation of the AUSM+-up solver. These results are fully in line with the simulations shown in Figs. 1 and 2 of Arnett et al. (2018) which summarize the numerical dissipation in oxygen- and carbon-shell burning simulations with the PROMPI code. For their highest-resolution run, they find that the peak at the bottom boundary seems to merge with the bulk dissipation. This indicates that the low-Mach AUSM+-up solver improves the behavior at the bottom boundary, even at moderate Mach numbers and moderate resolution.
 |
Fig. 15. Residual 𝒩ϵk for the runs shown in Fig. 13. For comparison, the profile of 𝒩ϵk for the 810 × 5402 AUSM+-up simulation is included as a red dashed line in the upper panel. |
5.4. Convective boundary mixing
An important process in stellar interiors is the entrainment of material from stable layers at the boundaries of a convection zone into the convective region. This has implications for the star’s further evolution because the entrained material serves as fuel for the burning region. Despite its importance, it needs to be parametrized in conventional 1D stellar evolution simulations due to its inherently multidimensional nature. For the various types of convection, for example in shallow zones in the stellar interior or extended regions in the envelope of solar-like stars, different physical mechanisms are dominant. It is therefore of interest to develop and validate different possible parametrizations with the help of multidimensional simulations.
Viallet et al. (2015) suggest to use the local Pécletnumber, the ratio of advective and diffusive timescales, in the boundary region to distinguish between different types of convective boundary mixing. Estimating the typical velocity v and length scale l of convection through MLT, we find a minimum Pécletnumber within the convection zone of
where K is the thermal diffusivity (see Eq. (9)) and DMLT = 1/3 uMLT lMLT is the diffusion coefficient obtained from MLT. The large Pécletnumber implies minor importance of radiation for the mixing, in accordance with our estimates in Sect. 3.3. The artificial boosting will increase the Pécletnumber even further in the hydrodynamic simulations. Following Viallet et al. (2015), at Pe ≫ 1 mixing can be thought to occur via turbulent entrainment, where small-scale instabilities are caused by the shear created by overturning convective cells at the boundaries (see Viallet et al. 2013 for a detailed description). As demonstrated by Meakin & Arnett (2007) for stellar convection, turbulent entrainment can be characterized in terms of the bulk Richardson entrainment law
where ve is the entrainment velocity of the top or bottom convective boundary, vrms the rms velocity in the convection zone, and RiB the bulk Richardson number (see Eq. (6)). For the results presented in the following, we have checked by visually inspecting the time evolution of the density and boundary profiles that ve is dominated by mass entrainment and the impact of thermal expansion is negligible. The analysis with respect to Eq. (17) is reported in various other studies which generally find an agreement with the measured entrainment (e.g., Gilet et al. 2013, Müller et al. 2016, C+17, C+19, Higl et al. 2021). In the following, we extend these studies for the case of helium shell burning.
By fitting Eq. (17) to simulations of mixing across boundaries at different RiB, the value of A and n can be determined. In shell simulations, this is possible either by measuring the entrainment at the bottom and top boundary in a single simulation (different RiB because of different BVF profiles, e.g., C+17), by measuring entrainment in simulations with different convective driving (different RiB because of varying vrms), or both (e.g., C+19).
To extract meaningful results, such simulations need to be run for multiple convective turnover times. Furthermore, as pointed out by Woodward et al. (2015), the resolution must be sufficiently high for obtaining converged entrainment rates across the boundaries. To relate the different grid sizes that have been used in the aforementioned studies, we compare the number of vertical grid cells (#CZ) that are located within the convection zones. Only grids that have been used to derive an entrainment rate are considered here. This simple comparison neglects the impact of restricted domains and does not consider the different stiffness of transitions from stable to convection zones. However, it still gives an estimate of the scales that are resolved by the grid compared to the global scale of the convection zone. Woodward et al. (2015) find entrainment rates that are in reasonable agreement for simulations with #CZ = 219 (grid sizes of 7683) and more cells. Most of the simulations presented by Jones et al. (2017) have #CZ = 170, while they show for one particular case that entrainment agrees with the results of a simulation with #CZ = 341 (grid sizes of 7683 and 15363, respectively). The highest resolution used by C+17 to determine the entrainment rate has #CZ = 256 (for a grid of 5123). Our computational resources only allow to run simulations long enough on grids with 180 × 902 cells which corresponds to #CZ = 105. This resolution might not be sufficient and we cannot test whether the results presented in this section are converged. However, our analysis still provides a first glimpse on what coefficients might be expected for the He-shell burning. Moreover, we are able to compare the results from the low-Mach AUSM+-up solver to 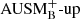 and assess whether the bulk Richardson scaling can be reproduced even at low resolution.
and assess whether the bulk Richardson scaling can be reproduced even at low resolution.
We determine the entrainment rate ve in Eq. (17) from the mean radial position over time of the top and bottom boundary, respectively. The positions of the boundaries are extracted as described in Sect. 5.1, the values for vrms consider the entire convection zone.
The plots on the left of Fig. 16 show the evolution of the boundary positions for the boosting factors 3 × 103, 1 × 104, and 3 × 104 when using the AUSM+-up solver. Qualitatively, the behavior is as expected: A higher boosting factor leads to stronger convection, faster entrainment of the passive scalar, and thus to a faster moving boundary. The entrainment velocity at the bottom boundary is considerably smaller than at the top boundary. According to Eq. (17) this is expected for a larger value of RiB which is indeed confirmed in the right panel, where the data for the bottom boundary reside at RiB > 103. A similar situation is observed for simulations with the 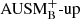 solver, shown in Fig. 17.
solver, shown in Fig. 17.
 |
Fig. 16. Left plots: radial positions of the top and bottom boundaries as functions of multiples of the respective convective turnover times. The radial position is the average position over all angles, the shading marks the corresponding spatial standard deviation of the boundary position. The white dashed lines indicate the time frame considered to obtain the data for the right column. Thick red lines show the evolution of simulations with a grid size of 360 × 2402 cells for comparison. The scales of the y-axis for the top and bottom boundary have been adapted for better visibility. All simulations apply the AUSM+-up scheme while the nuclear energy release is boosted by factors of 3 × 103, 1 × 104, and 3 × 104. Right plot: ratio of entrainment velocity ve and rms velocity vrms as a function of the bulk Richardson number RiB for the simulations shown in the left column. The horizontal error bars indicate the standard deviations of the temporal means of RiB. Vertical error bars correspond to the standard deviations of the entrainment velocities for a sliding window of size ΔNτconv = 1. The time frame is large enough to filter out sound waves but it is somewhat arbitrary. However, the error bars give an idea of the spread in the entrainment velocity. Markers that are crossed are not considered for fitting Eq. (17) to the data. The fit is shown as solid blue line. The dashed line at high RiB marks the regime of extrapolation. |
In order to fit Eq. (17) to the data, we consider the time frame of t ∈ [t(Nτconv = 10),t(Nτconv = 20)]. The lower limit is given by the end of the initial transient in the evolution of the passive scalar. The length of the shortest simulations constitutes the upper limit, such that the same time frame can be used for both sets of simulations. The extracted values listed in Table 4 reveal that the bottom boundaries move only by about one cell during the entire considered time frame of ΔNτconv = 10.0. This indicates that our grid is not fine enough to properly track this subtle shift, which is also suggested from the thin boundary widths measured for the bottom boundary, see Sect. 5.6. An additional complication arises by the profile of energy generation (Fig. 2) which has its peak beneath the convection zone. Because we do not increase the efficiency of radiative diffusion in accordance with the artificial boosting, internal energy will accumulate below the convection zone. This leads to a local increase in the BVF and the boundary gets stiffer. Hence, the entrainment velocity decreases when the bottom boundary approaches the peak of the energy generation. Because of this artificial phenomenon and the unresolved boundary motion we exclude the data points of the bottom boundaries from the analysis.
Using a least-square fit of Eq. (17) to the extracted data, we find
where the errors correspond to the standard deviation of the fitting parameters. We note that the errors are obtained without taking the individual error bars shown in Figs. 16 and 17 into account. The standard deviation in RiB and the spread in the entrainment velocity are likely correlated between some of the data points and subject to systematic shifts. Therefore, we think a treatment in terms of proper error propagation could be misleading. The error bars are shown nonetheless in the figures to give an idea of the general variability of the data points. The small uncertainties given in Eq. (18) thus indicate only that our data is well represented by Eq. (17) but should not be taken as a measure of the overall accuracy of our analysis.
The results with the AUSM+-up and 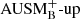 schemes are similar, but the dependence of the entrainment on the bulk Richardson number is somewhat steeper for AUSM+-up. As a rough test for convergence, the set of simulations with the AUSM+-up solver has been restarted after the initial transient on grids with a resolution of 360 × 2402. The flow state is interpolated to the finer grids using constant interpolation. The corresponding tracks of the radial boundary positions are shown as thick red lines in Fig. 16. For the top boundary, the entrainment rate is similar to the low resolution runs. At the bottom boundaries, entrainment appears to be slightly faster. Generally, the better resolved simulations follow a similar trend as the low resolution runs. However, more data is needed for a stronger statement on convergence and to extract meaningful estimates for A and n also from the better resolved simulations. Another parameter that impacts the results is the considered time interval. Using the full data of the AUSM+-up runs shown in Fig. 16, we extract the parameters A and n for a fixed length of ΔNτconv = 5 but for a changing central time (Fig. 18). We find that the value of the exponent n increases from n ≈ 0.4 and settles to a value of n ≈ 0.75 for central times later than t(Nτconv = 20). The value of lnA changes in a very similar way from lnA ≈ −3.5 to lnA ≈ −2.5. Figure 18 reveals that the values settle after central Nτconv ≈ 20. Therefore, it seems more appropriate to consider the time interval of t ∈ [t(Nτconv = 17.5),t(Nτconv = 25)] to determine best-fitting values of A and n. The upper limit is given by the time the top boundary reaches the top of the computational domain and boundary conditions will start to affect the results. We obtain
schemes are similar, but the dependence of the entrainment on the bulk Richardson number is somewhat steeper for AUSM+-up. As a rough test for convergence, the set of simulations with the AUSM+-up solver has been restarted after the initial transient on grids with a resolution of 360 × 2402. The flow state is interpolated to the finer grids using constant interpolation. The corresponding tracks of the radial boundary positions are shown as thick red lines in Fig. 16. For the top boundary, the entrainment rate is similar to the low resolution runs. At the bottom boundaries, entrainment appears to be slightly faster. Generally, the better resolved simulations follow a similar trend as the low resolution runs. However, more data is needed for a stronger statement on convergence and to extract meaningful estimates for A and n also from the better resolved simulations. Another parameter that impacts the results is the considered time interval. Using the full data of the AUSM+-up runs shown in Fig. 16, we extract the parameters A and n for a fixed length of ΔNτconv = 5 but for a changing central time (Fig. 18). We find that the value of the exponent n increases from n ≈ 0.4 and settles to a value of n ≈ 0.75 for central times later than t(Nτconv = 20). The value of lnA changes in a very similar way from lnA ≈ −3.5 to lnA ≈ −2.5. Figure 18 reveals that the values settle after central Nτconv ≈ 20. Therefore, it seems more appropriate to consider the time interval of t ∈ [t(Nτconv = 17.5),t(Nτconv = 25)] to determine best-fitting values of A and n. The upper limit is given by the time the top boundary reaches the top of the computational domain and boundary conditions will start to affect the results. We obtain
 |
Fig. 18. Time evolution of the fit parameters A (blue solid line) and n (orange dashed line) for a fixed time frame of ΔNτconv = 5 and moving central time. |
see also Fig. B.4. These values are similar to the previous result. However, considering the peak in the evolution in Fig. 18 between Nτconv = 10 and Nτconv = 20, this might be a coincidence. There is not sufficient data for the simulations with the 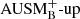 solver to repeat this calculation but we expect it to show a similar trend.
solver to repeat this calculation but we expect it to show a similar trend.
The results given in Eqs. (18) and (19) are within the regime 0.5 ≤ n ≤ 1, which is compatible with values reported in laboratory and numerical experiments (see, e.g., Meakin & Arnett 2007 and C+17 for a discussion and corresponding references). Our fitting parameters are similar to the findings of C+19 for the carbon shell. They obtain parameters3 of lnAC19 = −2.98 ± 0.13 and nC19 = 0.74 ± 0.04. In contrast, Meakin & Arnett (2007) report lnAM07 = 0.062 ± 0.87 and nM07 = 1.05 ± 0.21 and also the results of Jones et al. (2017) and Andrassy et al. (2020) agree with an exponent of n ≈ 1, as pointed out by Müller (2020). Further simulations are needed to scrutinize the values of A and n, also keeping in mind that different values may exist for different stellar convection zones.
Combining the results of Eq. (19) with the MLT prediction of MaMLT ≈ 10−4 and RiB = 7 × 104 for the 1D MESA model, we find a mass entrainment rate of
for the top boundary. The value for the bottom boundary is about a factor ten smaller. This confirms the finding of previous 3D hydro simulations (e.g., C+17) that lower boundaries of convective shells are stiffer and thus have less entrainment than the top boundaries. The associated growth of the convective region at the upper and lower boundaries using these rates until the end of the evolution is indicated by green lines in Fig. 1. This illustrates that, while the much stiffer lower boundary only slightly changes, the upper boundary considerably moves outward. At the rate of the mass entrainment of Eq. (20), the total mass of the initial convection zone of 1.1 M⊙ is doubled within 350 yr. However, a substantial growth of the convection zone leads to different bulk Richardson numbers at the boundaries and thus change the mass entrainment rate. Moreover, as seen in Fig. 1, the convection zone is growing also in the 1D evolution calculation. The mass entrainment rate given in Eq. (20) is therefore only representative for a short fraction of the shell’s lifetime at the evolutionary time the simulation was calculated. It is also a warning that one cannot simply use numerical values like entrainment rates extracted from single 3D simulations and apply them at different phases of stellar evolution. Instead, it is best to use theoretical prescriptions like the entrainment law. Recently, 1D stellar evolution models using the entrainment law on the main-sequence have been computed by Scott et al. (2021) and better reproduce the mass dependence of the main-sequence width. New 1D models during other phases of stellar evolution will be needed to assess the ability of the entrainment law to represent convective boundary mixing in 1D models throughout stellar evolution.
The expansion of the convection zone seen in the 1D evolution is part of a global restructuring of the star after core helium burning. Turbulent entrainment does not contribute as it is not included in our 1D calculation. However, the growth may be attributed to a process that is likely also present in our hydrodynamic simulations: In a simplified picture, the heating through nuclear burning successively increases the entropy within the convection zone. This leads to a small region at the top boundary where it exceeds the entropy at the immediate beginning of the radiation zone. This region is unstable and will merge with the convection zone. We estimate the speed vΔs at which this process would move the outer boundary by
where ΔsCZ/Δt is the ratio of the mean temporal increase in entropy inside the convection zone and sRZ/Δr corresponds to the mean entropy gradient at t = 0 for a region above the top boundary. For the simulation with the highest boosting that was used to obtain the results in Eq. (19) we find a ratio of
where 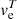 is the entrainment velocity at the top boundary as measured from the advected passive scalar. The considered profiles to calculate vΔs are plotted in Fig. 19, the spatial entropy gradient is calculated considering the initial model. The ratios of our other simulations range between 30% to 50% and are listed in Table 4. This is similar to the value of 49% found by Andrassy et al. (2020) for carbon-shell burning while Meakin & Arnett (2007) find a maximum ratio of 17% for oxygen shell burning4. These values suggest that a considerable fraction of the entrainment speed could be contributed through increasing entropy. Consequently, this process needs to be disentangled from the growth through turbulent entrainment before the entrainment according to Eq. (17) is used in stellar evolution codes or compared between simulations of different convection zones.
is the entrainment velocity at the top boundary as measured from the advected passive scalar. The considered profiles to calculate vΔs are plotted in Fig. 19, the spatial entropy gradient is calculated considering the initial model. The ratios of our other simulations range between 30% to 50% and are listed in Table 4. This is similar to the value of 49% found by Andrassy et al. (2020) for carbon-shell burning while Meakin & Arnett (2007) find a maximum ratio of 17% for oxygen shell burning4. These values suggest that a considerable fraction of the entrainment speed could be contributed through increasing entropy. Consequently, this process needs to be disentangled from the growth through turbulent entrainment before the entrainment according to Eq. (17) is used in stellar evolution codes or compared between simulations of different convection zones.
 |
Fig. 19. Initial entropy profile and profiles after 17.5 and 25 convective turnover times for the 3D simulation with a grid of 180 × 902 cells, the AUSM+-up solver, and an energy boosting of b = 3 × 104. Vertical dotted lines mark the region that is considered to calculate the mean entropy gradient in the radiation zone ΔsRZ/Δr from the initial entropy profile. |
5.5. Characterizing the mixing
It is not trivial to determine the details of the – possibly small-scale – events that lead to turbulent mixing. In their PPMstar simulations, Woodward et al. (2015), Jones et al. (2017), and Andrassy et al. (2020) find that trains of small Kelvin-Helmholtz rolls emerge at the boundary. However, they do not appear in regions of largest shear but rather at the point where two convective cells turn and move back into the convection zone.
From our 2D visualizations we are not able to easily find large scale, coherent modes. In order to identify possible correlations between the strength of shear and the amount of mixing in our simulations, we use a simple analysis of the velocity field at the top boundary: For a narrow region below the top boundary, we measure along radial rays the volume-weighted deviation of the passive scalar from its mean in the convection zone
where PS denotes the value of the passive scalar, 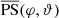 is the average over the middle third of the convection zone, and V the volume of the grid cell. The radii rPS, rP define the considered radial domain, where rP corresponds to the beginning of the transition to the stable zone at the top of the convection zone, as defined in Sect. 5.6 and rPS = 0.95 rP. The value of the passive scalar is larger above the top boundary compared to its mean (see Fig. 6). Hence, a positive deviation from the mean corresponds to an entrainment event. The considered domain does not include mixing directly at the boundary because there, deviations are usually large but do not necessarily descend into the convection zone.
is the average over the middle third of the convection zone, and V the volume of the grid cell. The radii rPS, rP define the considered radial domain, where rP corresponds to the beginning of the transition to the stable zone at the top of the convection zone, as defined in Sect. 5.6 and rPS = 0.95 rP. The value of the passive scalar is larger above the top boundary compared to its mean (see Fig. 6). Hence, a positive deviation from the mean corresponds to an entrainment event. The considered domain does not include mixing directly at the boundary because there, deviations are usually large but do not necessarily descend into the convection zone.
In addition, we estimate the strength of shear by
where vϑ, vφ denotes the ϑ, φ-velocity components. Because the shear at the boundary matters here, we extend the considered zone to rS which coincides with the end of the transition to the radiation zone as defined in Sect. 5.6. The different regions are indicated in Fig. 20. With the described procedure we obtain data pairs that correlate shear strength to mixing strength. Our simple approach does not consider that the mixing events will also depend on the history of the velocity field and its gradient along the individual downflows. However, it still gives some measure of the correlation between shear and mixing: The characteristic time scale for global changes of the flow field is given by the turn over time. The animated versions5 of Fig. 20 illustrate that the mixing events detected between the dashed-dotted line and the dashed line happen on time scales which are much shorter. If the mixing were caused by Kelvin-Helmholz instabilities overturning the whole boundary layer one may assume that they grow fastest in regions of strongest shear. We then would expect the rapidly-growing Kelvin-Helmholz rolls to become detectable in the layer where we measure 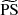 after a fraction of the global turnover time scale. However, the shear layers caused by the overturning of the large scale flows at the convective boundary should be present for as long as the global turnover time scale. The extracted data pairs can therefore be used to investigate a possible correlation between shear strength and mixing.
after a fraction of the global turnover time scale. However, the shear layers caused by the overturning of the large scale flows at the convective boundary should be present for as long as the global turnover time scale. The extracted data pairs can therefore be used to investigate a possible correlation between shear strength and mixing.
 |
Fig. 20. Fluctuations of the passive scalar PS from its mean value |
The result for the AUSM+-up solver at a resolution of 180 × 902 is shown in Fig. 21 for increasing energy boostings. In all simulations, the counts of positive passive scalar fluctuations cluster at the lower end of the measured shear strength range. At slightly negative deviations, a narrow band with a high number of counts forms which stretches over a larger range of shear strengths. As indicated by the blue lines, at smaller shear strengths mixing events dominate over “no mixing” events. The noisy profile at the strongest shear can be attributed to the small number of total counts (thin line) and corresponding poor statistics.
 |
Fig. 21. Histogram of fluctuations of the passive scalar |
The evidence of mixing at the lower end of the range is in line with the fact that the horizontal velocity naturally has to decrease where strong downflows form because the velocity is redirected inward there. The narrow band corresponds to rays with no mixing events such that the contained passive scalar is slightly below but very close to the average within the convection zone. If the energy boosting is increased, convection gets more vigorous and hence the narrow band extends toward larger shear strengths. Mixing follows this trend, but still dominantly appears at lower shear strengths. By visually inspecting the flow morphology of their 3D simulations, Woodward et al. (2015) find that mixing predominately occurs in regions where two large convective cells meet and overturn. The premixed material that accumulates in the wedge between two cells somewhat beneath the boundary has a sufficiently small buoyancy force with respect to the bulk of the convection zone such that the downflows are strong enough to bring the material inward. Because of the decreasing horizontal velocity of the turning cells, this premixed region will necessarily have weaker shear (as measured by Eq. (24)) compared to the region where the fluid moves almost horizontally. The results of our analysis seem to support this picture.
In Fig. 22 we compare in a similar histogram the results of the AUSM+-up and 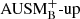 solver at the runs with highest resolution. The direct comparison shows that shear values spread over a larger range for the AUSM+-up solver, which can be attributed to its better-resolved turbulent flow (see Figs. 9 and 10). The
solver at the runs with highest resolution. The direct comparison shows that shear values spread over a larger range for the AUSM+-up solver, which can be attributed to its better-resolved turbulent flow (see Figs. 9 and 10). The 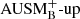 solver shows slightly stronger mixing events. The apparent return toward positive deviations at large shear is insignificant due to the small number of total counts at larger shear, as indicated by the thin line.
solver shows slightly stronger mixing events. The apparent return toward positive deviations at large shear is insignificant due to the small number of total counts at larger shear, as indicated by the thin line.
 |
Fig. 22. Same as Fig. 21, but here for the |
5.6. Boundary width
Another characteristic of convection is the shape of the boundary layers between the convection zone and the convectively stable zones. While the boundary width has to be parametrized in 1D stellar evolution codes, it develops self-consistently in hydrodynamic simulations. As can be seen in Fig. 6, the transition that forms during the simulation is not sharp but rather changes gradually across a certain vertical width. This is due to at least two processes. The first, and most important, is partial mixing across the boundary layer by turbulent entrainment. The second, which is less important in the simulations presented in this study, is the deformation of the boundary layer producing an undulated surface rather than a perfectly spherical surface. Neither of these processes exist in most 1D models, which generally assume a sharp step-like boundary. The exception is 1D models using partial mixing beyond the convective boundary such as the prescriptions of exponentially decaying mixing by Freytag et al. (1996) and Herwig et al. (1997).
Comparisons to asteroseismology (e.g., Moravveji et al. 2016; Arnett & Moravveji 2017; Michielsen et al. 2019; Pedersen et al. 2021) also support smoother over step-like boundaries. More work is needed to better understand the shape boundaries since they can have a decisive impact on the evolution and nucleosynthesis (e.g., Battino et al. 2016).
In this section we compare the transition layer widths for simulations with different resolutions, flux solvers and boostings. Our approach to extract the widths is similar to the procedure described by C+17 but instead of abundance profiles we use the passive scalar as tracer. We define the inner radii of the transitions at the bottom (top) of the convection zone as the radii at which the horizontal mean of the passive scalar is larger than its initial value at this radius plus (minus) 0.05. The outer radius of the transitions at the bottom (top) is taken to be the radius at which the horizontal mean of the passive scalar is below (above) the spatial mean over the inner third by 0.05. To determine the corresponding radii, the profile of the passive scalar is interpolated. The resulting widths are shown exemplarily in Fig. 6, marked by vertical dashed lines. The absolute value of the width depends on the particular choice of the thresholds for the deviations from the initial profile. However, it still gives a measure for the relative dependence on resolution, boosting strength and numerical flux solver. We have verified that the trends found for the boundary widths do not depend on the specific choice of the threshold value.
In Table 5 the resulting widths are listed for simulations applying the 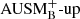 and AUSM+-up solver at a fixed resolution of 180 × 902 for varying boosting strength. We find that generally the top boundary width is larger than the bottom boundary. This is in line with the much higher bulk Richardson number at the bottom boundary (Table 4). The top boundary broadens with increasing energy input because stronger driving leads to stronger convection and eventually to enhanced mixing that reaches further into the stable zone. In addition, the interface gets more deformed. This is in accordance with the results reported by C+17. Also the transition of the bottom boundary widens with increasing driving and is generally narrower for runs with the
and AUSM+-up solver at a fixed resolution of 180 × 902 for varying boosting strength. We find that generally the top boundary width is larger than the bottom boundary. This is in line with the much higher bulk Richardson number at the bottom boundary (Table 4). The top boundary broadens with increasing energy input because stronger driving leads to stronger convection and eventually to enhanced mixing that reaches further into the stable zone. In addition, the interface gets more deformed. This is in accordance with the results reported by C+17. Also the transition of the bottom boundary widens with increasing driving and is generally narrower for runs with the  solver. However, because of the stiffness of the bottom boundary, changes are only subtle. With a radial grid spacing of about 0.6 × 108 cm, the bottom boundaries are resolved by a few cells only. The relative changes are even on the subgrid level and can only be followed by interpolation. Hence, the robustness of these results is difficult to assess.
solver. However, because of the stiffness of the bottom boundary, changes are only subtle. With a radial grid spacing of about 0.6 × 108 cm, the bottom boundaries are resolved by a few cells only. The relative changes are even on the subgrid level and can only be followed by interpolation. Hence, the robustness of these results is difficult to assess.
Boundary widths of the bottom and top boundaries for different energy boosting factors at a resolution of 180 × 902 cells.
Figure 23 illustrates the boundary widths for one particular point in time. This is similar to Fig. 12 of C+17 for the carbon-burning shell simulations: For the top boundary, the broadening with increasing energy input is clearly visible but it is less obvious at the bottom boundary.
 |
Fig. 23. Profiles of the advected passive scalar for different energy input boostings. All simulations use the AUSM+-up solver. The profiles are taken at t(Nτconv = 15), crosses denote the beginning and end of the boundary transition zone, as defined in the text. Following the approach of C+17, the profiles are shifted by the radial position of the bottom (rb, bot) and top (rb, top) boundary, respectively. The different amplitudes of the passive scalar below the bottom and above the top boundary are due to the fact that the initial profile is linear, see Fig. 6. Larger boosting leads to faster entrainment and the top boundary will have already moved toward larger radii, that is larger values of the passive scalar, for the snapshot shown in Fig. 23. |
The time evolution of the boundary widths is shown in Fig. 24. The upper transition exhibits some variability over time with an amplitude that increases with the driving strength. Almost no fluctuations are visible for the bottom boundary. A slight trend toward shallower transitions is noticeable. These results confirm the general dependence of the boundary width on the stiffness and driving strength.
 |
Fig. 24. Widths of the upper (dashed lines) and lower (solid lines) boundary for different strengths of the energy generation boosting as a function of convective turnover times τconv. All simulations use the AUSM+-up flux. |
To assess the impact of resolution, we compare the widths at a boosting factor of 3 × 104 for simulations on successively finer grids in Table 6. Because the finer resolved simulations cover less convective turn over times, the averages are taken at earlier times compared to the data listed in Table 5.
Boundary widths of the bottom and top boundaries for different resolutions and a boosting factor of 3 × 104.
For both flux functions we find that the widths of the upper boundary noticeably decrease when the grid is refined from a resolution of 180 × 902 to 360 × 1802. For even finer grids, the width changes only slightly, which is confirmed in the boundary profiles shown in Fig. 25. While the results seem to be converged for the respective flux functions, there is still a discrepancy between the solvers at the bottom boundary which persists even for the highest resolution. This offset is much larger than the small fluctuations of the width for the lower boundary (Fig. 26). However, we note that the boundaries for the highest resolution runs need some time to adapt to the increased grid resolution and that boundary widths at early times may still change, as indicated in Fig. 24. Therefore, larger time intervals are needed for a stronger statement on the convergence.
 |
Fig. 25. Similar to Fig. 23 but for a fixed energy boosting factor of 3 × 104 and varying resolution. All simulations use the AUSM+-up solver. The profiles are taken at Nτconv = 4.5, except for the run with a grid of 540 × 3602 cells. Here, the profile is taken at Nτconv = 3.1, the latest available snapshot. |
6. Conclusion
Our study complements the exploration of convective boundary mixing in stellar interiors with multidimensional hydrodynamic simulations of convective helium-shell burning. The initial stratification is based on an 1D MESA model of a 25 M⊙ star. Gilkis & Soker (2016) use the MAESTRO code to perform hydrodynamic simulations of convective helium-shell burning in a 15 M⊙ star. Their study, however, focuses on the angular momentum distribution within the convection zone and the boundaries to stable layers above and below the convective shell are not analyzed in detail.
Our 2D and 3D hydrodynamic simulations in spherical-wedge geometry are performed with the time-implicit, finite-volume Seven-League Hydro (SLH) code. We calculate the hydrodynamic fluxes with the low-Mach AUSM+-up scheme in combination with Cargo–LeRoux well-balancing. Because previous SLH simulations with this combination had shown that convection is represented properly only for Mach numbers above 10−3, the energy input had to be boosted to increase the velocities. We applied boosting factors ranging from 3 × 103 to 3 × 104. This results in Mach numbers ranging from ∼5 × 10−3 to ∼1 × 10−2. The employed grid resolutions range from 180 × 902 cells up to 810 × 5402 cells.
In order to assess the performance of the AUSM+-up solver, we compare different diagnostic values to a variant of this scheme, denoted as  , that does not employ the improved low-Mach capabilities. The flow morphology of fully developed convection at a resolution of 810 × 5402 reveals that AUSM+-up reproduces significantly more small-scale structures than the
, that does not employ the improved low-Mach capabilities. The flow morphology of fully developed convection at a resolution of 810 × 5402 reveals that AUSM+-up reproduces significantly more small-scale structures than the  scheme (Fig. 10). This is confirmed by the corresponding kinetic energy spectrum (Fig. 9). The spectrum obtained with the AUSM+-up scheme has an inertial range that reaches down to scales a factor of two smaller than in the spectrum for the
scheme (Fig. 10). This is confirmed by the corresponding kinetic energy spectrum (Fig. 9). The spectrum obtained with the AUSM+-up scheme has an inertial range that reaches down to scales a factor of two smaller than in the spectrum for the  scheme. The numerical dissipation as obtained from the RA-ILES kinetic energy equation shows an improved behavior at the bottom boundary and indicates that the dissipation is converged already at rather low resolution (Fig. 13). For the
scheme. The numerical dissipation as obtained from the RA-ILES kinetic energy equation shows an improved behavior at the bottom boundary and indicates that the dissipation is converged already at rather low resolution (Fig. 13). For the 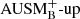 solver, convergence is found only at the highest resolution of 810 × 5402 cells. These results indicate that a low-Mach method is beneficial already at moderate Mach numbers. In a future study, simulations of convection with the AUSM+-up solver will be compared in detail to more widely used approaches, as, for example, to the PPM method.
solver, convergence is found only at the highest resolution of 810 × 5402 cells. These results indicate that a low-Mach method is beneficial already at moderate Mach numbers. In a future study, simulations of convection with the AUSM+-up solver will be compared in detail to more widely used approaches, as, for example, to the PPM method.
We analyzed the entrainment rate at the boundaries of the convection zone in terms of the bulk Richardson number (Eq. (6)). For this, a series of simulations with varying boosting strength has been carried out on grids with 180 × 902 cells. We found an exponent of n = 0.76 (Fig. 16) which is compatible with C+17 and C+19 but smaller than results reported for example by Meakin & Arnett (2007) or Andrassy et al. (2020) who find n ≈ 1. Furthermore, in our simulations a considerable fraction of the measured entrainment velocity may be attributed to entropy increase in the convection zone due to the energy release. This is an important aspect if the results of entrainment studies from hydrodynamic simulations are to be used in 1D calculations. Recently, the Bulk-Richardson entrainment scaling was applied to stellar evolution calculations (Staritsin 2013; Scott et al. 2021). Scott et al. (2021) show that it naturally leads to a mass-dependent efficiency of CBM, which is suggested by observations. However, their study indicates that values of n < 1 result in a too efficient mixing and that the values for A that are commonly found in hydrodynamic simulations are too large. Future simulations, especially at nominal luminosity, may help to identify the origins of this discrepancy, also regarding the question whether it is applicable only to a subset of convection zones during stellar evolution as suggested by Viallet et al. (2015).
Measuring the widths of the transitions from the convection zone to the adjacent stable zones showed that the transition is wider for the 180 × 902 resolution compared with simulations on finer grids. This indicates that our results may not be numerically converged and that our higher-resolution simulations need to be continued to verify the robustness of our result for the entrainment rate. We further assessed the relation between shear strength and mixing events in our simulations and found that mixing occurs not in the regions of strongest shear but rather at lower values in the range of measured shear strengths (Fig. 21). This is consistent with the findings of Woodward et al. (2015).
Our study has demonstrated that the low-Mach AUSM+-up solver is suitable to address setups that base on realistic stellar models if well-balancing is used. Recently, the Deviation well-balancing scheme of Berberich et al. (2021) was added to the SLH code. In simplified convective test simulations presented by Edelmann et al. (2021), the achieved Mach numbers reach Ma ≈ 10−4. These velocities are in the regime of convective velocities predicted by MLT in early evolutionary phases of stars. The combination of the new Deviation well-balancing method and the AUSM+-up solver is a promising approach for future SLH simulations of stellar convection in the low-Mach regime without the need of artificially boosted energy generation.
In the RA-ILES analysis framework of SLH, all required fluctuations are calculated and stored already during the simulation, such that we have data for every single time step. However, there was a flaw in the calculation of the velocity divergence for the simulations presented here. Therefore, the velocity divergence had to be re-calculated in a post-processing step, for which the 3D velocity data is only available for the stored grid files but not for every time step. Fortunately, only the value of WP is affected which is, however, small in general and the impact of the post-processing is negligible.
It is not clear to us whether Meakin & Arnett (2007) calculated the spatial entropy gradient in the radiation zone or at the transition from convection to radiation zone. In the latter case, the gradient is much steeper, the estimated velocity will be smaller, and we would obtain a ratio similar to that of Meakin & Arnett (2007). However, we think that only the gradient above the boundary transition is relevant.
Acknowledgments
L. H., F. K. R., and R. A. acknowledge support by the Klaus Tschira Foundation. The work of F. K. R. is supported by the German Research Foundation (DFG) through grants KL 566/22-1 and RO 3676/3-1, respectively. PVFE was supported by the US Department of Energy through the Los Alamos National Laboratory (LANL). LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the US Department of Energy (Contract No. 89233218CNA000001). The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputers JUQUEEN (Jülich Supercomputing Centre 2015) and JUWELS (Jülich Supercomputing Centre 2019) at Jülich Supercomputing Centre (JSC). This work also used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/P002293/1, ST/R002371/1 and ST/S002502/1, Durham University and STFC operations grant ST/R000832/1. DiRAC is part of the National e-Infrastructure. Furthermore, this article is based upon work from the “ChETEC” COST Action (CA16117), supported by COST (European Cooperation in Science and Technology). R. H. acknowledges support from the IReNA AccelNet Network of Networks, supported by the National Science Foundation under Grant No. OISE-1927130 and from the World Premier International Research Centre Initiative (WPI Initiative), MEXT, Japan. This work has been assigned a document release number LA-UR-21-22119. The authors thank Cyril Georgy for useful discussion in the early stages of this project and in particular for organizing the ISSI Team 367 meeting in 2018.
References
- Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
- Almgren, A. S., Bell, J. B., & Zingale, M. 2007, J. Phys. Conf. Ser., 78, 012085 [NASA ADS] [CrossRef] [Google Scholar]
- Andrassy, R., Herwig, F., Woodward, P., & Ritter, C. 2020, MNRAS, 491, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Angelou, G. C., Bellinger, E. P., Hekker, S., et al. 2020, MNRAS, 493, 4987 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D., & Moravveji, E. 2017, ApJ, 836, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, D., Meakin, C., & Young, P. A. 2009, ApJ, 690, 1715 [CrossRef] [Google Scholar]
- Arnett, W. D., Meakin, C., Viallet, M., et al. 2015, ApJ, 809, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D., Meakin, C., Hirschi, R., et al. 2018, ArXiv e-prints [arXiv:1810.04659] [Google Scholar]
- Arnett, W. D., Meakin, C., Hirschi, R., et al. 2019, ApJ, 882, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Barsukow, W., Edelmann, P. V. F., Klingenberg, C., Miczek, F., & Röpke, F. K. 2017, J. Sci. Comput., 72, 623 [CrossRef] [Google Scholar]
- Battino, U., Pignatari, M., Ritter, C., et al. 2016, ApJ, 827, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Berberich, J. P., Chandrashekar, P., & Klingenberg, C. 2021, Comput. Fluids, 104858 [Google Scholar]
- Cargo, P., & Le Roux, A. 1994, C.R. Acad. Sci., Ser 1, Math., 318, 73 [Google Scholar]
- Collins, C., Müller, B., & Heger, A. 2018, MNRAS, 473, 1695 [NASA ADS] [Google Scholar]
- Cristini, A., Meakin, C., Hirschi, R., et al. 2017, MNRAS, 471, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Cristini, A., Hirschi, R., Meakin, C., et al. 2019, MNRAS, 484, 4645 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, A., Jones, S., & Herwig, F. 2019, MNRAS, 484, 3921 [NASA ADS] [CrossRef] [Google Scholar]
- Edelmann, P. V. F. 2014, Dissertation (Technische Universität München) [Google Scholar]
- Edelmann, P. V. F., Röpke, F. K., Hirschi, R., Georgy, C., & Jones, S. 2017, A&A, 604, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edelmann, P. V. F., Horst, L., Berberich, J. P., et al. 2021, A&A, 652, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, D., Nonaka, A., Almgren, A. S., Harpole, A., & Zingale, M. 2019, ApJ, 887, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Gilet, C., Almgren, A. S., Bell, J. B., et al. 2013, ApJ, 773, 137 [Google Scholar]
- Gilkis, A., & Soker, N. 2016, ApJ, 827, 40 [CrossRef] [Google Scholar]
- Goffrey, T., Pratt, J., Viallet, M., et al. 2017, A&A, 600, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Higl, J., Müller, E., & Weiss, A. 2021, A&A, 646, A133 [CrossRef] [EDP Sciences] [Google Scholar]
- Horst, L., Edelmann, P. V. F., Andrássy, R., et al. 2020, A&A, 641, A18 [CrossRef] [EDP Sciences] [Google Scholar]
- Hosea, M., & Shampine, L. 1996, Appl. Numer. Math., 20, 21 [CrossRef] [Google Scholar]
- Jones, S., Andrassy, R., Sandalski, S., et al. 2017, MNRAS, 465, 2991 [NASA ADS] [CrossRef] [Google Scholar]
- Jülich Supercomputing Centre, 2015, J. Large-scale Res. Facil., 1 [Google Scholar]
- Jülich Supercomputing Centre, 2019, J. Large-scale Res. Facil., 5 [Google Scholar]
- Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
- Käppeli, R., & Mishra, S. 2016, A&A, 587, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kifonidis, K., & Müller, E. 2012, A&A, 544, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolmogorov, A. N. 1941, Dokl. Akad. Nauk SSSR, 30, 299 . in Russian [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics (Course of Theoretical Physics: Volume 6), 2nd edn. (Oxford: Butterworth-Heinemann) [Google Scholar]
- Liou, M.-S. 2006, J. Comput. Phys., 214, 137 [CrossRef] [MathSciNet] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Astronomy and Astrophysics Library (Berlin Heidelberg: Springer) [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Michielsen, M., Pedersen, M. G., Augustson, K. C., Mathis, S., & Aerts, C. 2019, A&A, 628, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miczek, F. 2013, Dissertation, Technische Universität München, Germany [Google Scholar]
- Miczek, F., Röpke, F. K., & Edelmann, P. V. F. 2015, A&A, 576, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Meakin, C., Viallet, M., & Arnett, D. 2014, ArXiv e-prints [arXiv:1401.5176] [Google Scholar]
- Mocák, M., Meakin, C., Campbell, S. W., & Arnett, W. D. 2018, MNRAS, 481, 2918 [NASA ADS] [CrossRef] [Google Scholar]
- Moravveji, E., Townsend, R. H. D., Aerts, C., & Mathis, S. 2016, ApJ, 823, 130 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Müller, B. 2020, Liv. Rev. Comput. Astrophys., 6, 3 [Google Scholar]
- Müller, B., Viallet, M., Heger, A., & Janka, H.-T. 2016, ApJ, 833, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Nonaka, A., Almgren, A. S., Bell, J. B., et al. 2010, ApJS, 188, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., 5, 715 [CrossRef] [Google Scholar]
- Popov, M. V., Walder, R., Folini, D., et al. 2019, A&A, 630, A129 [CrossRef] [EDP Sciences] [Google Scholar]
- Porter, D. H., & Woodward, P. R. 2000, ApJS, 127, 159 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pratt, J., Baraffe, I., Goffrey, T., et al. 2017, A&A, 604, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, J., Baraffe, I., Goffrey, T., et al. 2020, A&A, 638, A15 [CrossRef] [EDP Sciences] [Google Scholar]
- Roe, P. L. 1981, J. Comput. Phys., 43, 357 [Google Scholar]
- Salaris, M., & Cassisi, S. 2017, Roy. Soc. Open Sci., 4, 170192 [Google Scholar]
- Scott, L. J. A., Hirschi, R., Georgy, C., et al. 2021, MNRAS, 503, 4208 [CrossRef] [Google Scholar]
- Staritsin, E. I. 2013, Astron. Rep., 57, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, M. K., Kumar, A., & Pandey, A. 2017, New J. Phys., 19, 025012 [CrossRef] [Google Scholar]
- Viallet, M., Baraffe, I., & Walder, R. 2013, A&A, 555, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., Meakin, C., Prat, V., & Arnett, D. 2015, A&A, 580, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., Goffrey, T., Baraffe, I., et al. 2016, A&A, 586, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viani, L. S., & Basu, S. 2020, ApJ, 904, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Wieczorek, M. A., & Meschede, M. 2018, Geochem. Geophys. Geosyst., 19, 2574 [Google Scholar]
- Wieczorek, M. A., & Simons, F. J. 2005, Geophys. J. Int., 162, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Woodward, P. R., Herwig, F., & Lin, P.-H. 2015, ApJ, 798, 49 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Reynolds and Favre decomposition
The Reynolds decomposition splits a quantity q(r, ϑ, φ, t) in its mean value 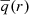 averaged over space and time
averaged over space and time
where dΩ = sin ϑ dφ dϑ and the fluctuation q′ is defined as
The Favre decomposition separates a quantity q into the density-weighted average
and the corresponding fluctuation q″ defined via
Appendix B: Supplementary plots
 |
Fig. B.1. Thermal adjustment timescale τdiff according to Eq. (9). The typical length scale is taken to be the radial grid spacing of the 3D simulation run with the highest resolution presented in Section 5. |
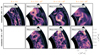 |
Fig. B.2. Flow patterns for 2D (upper row) and 3D (lower row) simulations at different boosting strengths. The Mach number is color-coded; the color-scale is adjusted to every subplot individually. Plots for the 3D simulations show the equatorial plane. White dashed lines denote the detected boundaries as described in Section 5.1. For all simulations, the AUSM+-up solver was used. No 3D data is available for b = 1.0. |
 |
Fig. B.3. Fluid flow in terms of Mach number for the |
 |
Fig. B.4. Same as Fig. 16 but for the time interval t ∈ [t(Nτconv = 17.5),t(Nτconv = 25)]. |
All Tables
Boundary widths of the bottom and top boundaries for different energy boosting factors at a resolution of 180 × 902 cells.
Boundary widths of the bottom and top boundaries for different resolutions and a boosting factor of 3 × 104.
All Figures
 |
Fig. 1. Convective regions during the evolution of an 1D 25 M⊙ star model simulated with the MESA code. Shaded regions correspond to convection zones. The color-shading represents the mixing-length theory (MLT)-predicted Mach number. The black solid line denotes the total mass of the model. The red vertical line indicates the point in the evolution at which the SLH simulations start and the mass extent of the initial model. The green lines indicate the mass entrainment at the upper and lower boundaries as extracted from the 3D hydrodynamic simulations. See discussion in Sect. 5.4. |
| In the text | |
 |
Fig. 2. Initial profiles for the underlying 1D MESA model (dashed) and the mapped SLH model (solid lines). The shaded areas mark the convection zone for mapped profiles (blue) and MESA profiles (orange). The oscillatory behavior of the energy generation is a numerical artifact at negligible amplitudes. |
| In the text | |
 |
Fig. 3. Profiles of the BVF (upper panel) and relative change in pressure (lower panel) after simulating 10 h of physical time with and without well-balancing. Nr denotes the number of radial cells that are used for the discretization. |
| In the text | |
 |
Fig. 4. Flow morphology in terms of Mach number in a 2D wedge after simulating 10 h of physical time. The nuclear energy release has been boosted by a factor of 1 × 104. The left panel corresponds to a simulation that applies Cargo–LeRoux well-balancing while well-balancing is absent in the simulation shown on the right. The domain is discretized by 180 × 90 cells. |
| In the text | |
 |
Fig. 5. Measured rms Mach number as function of the input energy rate ė in 2D (blue) and 3D simulations (orange). Vertical error bars correspond to the standard deviation of the average over the time frame of ΔNτconv = 10. The dashed lines reflect the scaling law in Eq. (10). Numbers given in the boxes correspond to energy boosting factors for the lowest and the three highest boostings. The green cross marks the Mach number of Ma ≈ 1.6 × 10−4 as predicted by MLT at the nominal energy generation rate in the original MESA model. |
| In the text | |
 |
Fig. 6. Horizontal mean of the advected passive scalar for a simulation with a resolution of 180 × 902. The initial distribution of the scalar is shown as dashed line, the solid line represents the time-averaged profile for t ∈ [t(Nτconv = 9.9),t(Nτconv = 10.1)]. The blue shaded area corresponds to the minimal and maximal value of the passive scalar at the corresponding radius for the latest considered snapshot. The radii at which the absolute value of the radial derivative is largest are indicated by dots. They define the position of the top and bottom boundaries. The shaded orange area marks the convective region according to the stability criterion N2 < 0. Vertical dashed lines denote the respective boundary widths which are defined in Sect. 5.6. |
| In the text | |
 |
Fig. 7. Expansion of the velocity data for one exemplary 3D wedge simulation. Color coded is the velocity component in φ-direction. The red square marks the actual computational domain. The rest of the plane is filled by periodically repeating the simulation data in ϑ and φ direction. |
| In the text | |
 |
Fig. 8. Spectra of the radial kinetic energy component. The blue and orange line correspond to simulations with the Roe and |
| In the text | |
 |
Fig. 9. Spectra of the radial kinetic energy component for the |
| In the text | |
 |
Fig. 10. Mach number for a slice through the domain for simulations at a resolution of 810 × 5402 cells with the |
| In the text | |
 |
Fig. 11. Similar to Fig. 10, but for the magnitude of the vorticity. |
| In the text | |
 |
Fig. 12. Spectra of the radial kinetic energy component for the |
| In the text | |
 |
Fig. 13. Profiles of the different components of kinetic energy equation in the RA-ILES framework, Eq. (15). The resolution increases from top to bottom. The left column corresponds to results using the |
| In the text | |
 |
Fig. 14. Same quantities as in Fig. 13, but for a time interval of t ∈ [t(Nτconv = 10),t(Nτconv = 20)]. |
| In the text | |
 |
Fig. 15. Residual 𝒩ϵk for the runs shown in Fig. 13. For comparison, the profile of 𝒩ϵk for the 810 × 5402 AUSM+-up simulation is included as a red dashed line in the upper panel. |
| In the text | |
 |
Fig. 16. Left plots: radial positions of the top and bottom boundaries as functions of multiples of the respective convective turnover times. The radial position is the average position over all angles, the shading marks the corresponding spatial standard deviation of the boundary position. The white dashed lines indicate the time frame considered to obtain the data for the right column. Thick red lines show the evolution of simulations with a grid size of 360 × 2402 cells for comparison. The scales of the y-axis for the top and bottom boundary have been adapted for better visibility. All simulations apply the AUSM+-up scheme while the nuclear energy release is boosted by factors of 3 × 103, 1 × 104, and 3 × 104. Right plot: ratio of entrainment velocity ve and rms velocity vrms as a function of the bulk Richardson number RiB for the simulations shown in the left column. The horizontal error bars indicate the standard deviations of the temporal means of RiB. Vertical error bars correspond to the standard deviations of the entrainment velocities for a sliding window of size ΔNτconv = 1. The time frame is large enough to filter out sound waves but it is somewhat arbitrary. However, the error bars give an idea of the spread in the entrainment velocity. Markers that are crossed are not considered for fitting Eq. (17) to the data. The fit is shown as solid blue line. The dashed line at high RiB marks the regime of extrapolation. |
| In the text | |
 |
Fig. 17. Same as Fig. 16 but for simulations using the |
| In the text | |
 |
Fig. 18. Time evolution of the fit parameters A (blue solid line) and n (orange dashed line) for a fixed time frame of ΔNτconv = 5 and moving central time. |
| In the text | |
 |
Fig. 19. Initial entropy profile and profiles after 17.5 and 25 convective turnover times for the 3D simulation with a grid of 180 × 902 cells, the AUSM+-up solver, and an energy boosting of b = 3 × 104. Vertical dotted lines mark the region that is considered to calculate the mean entropy gradient in the radiation zone ΔsRZ/Δr from the initial entropy profile. |
| In the text | |
 |
Fig. 20. Fluctuations of the passive scalar PS from its mean value |
| In the text | |
 |
Fig. 21. Histogram of fluctuations of the passive scalar |
| In the text | |
 |
Fig. 22. Same as Fig. 21, but here for the |
| In the text | |
 |
Fig. 23. Profiles of the advected passive scalar for different energy input boostings. All simulations use the AUSM+-up solver. The profiles are taken at t(Nτconv = 15), crosses denote the beginning and end of the boundary transition zone, as defined in the text. Following the approach of C+17, the profiles are shifted by the radial position of the bottom (rb, bot) and top (rb, top) boundary, respectively. The different amplitudes of the passive scalar below the bottom and above the top boundary are due to the fact that the initial profile is linear, see Fig. 6. Larger boosting leads to faster entrainment and the top boundary will have already moved toward larger radii, that is larger values of the passive scalar, for the snapshot shown in Fig. 23. |
| In the text | |
 |
Fig. 24. Widths of the upper (dashed lines) and lower (solid lines) boundary for different strengths of the energy generation boosting as a function of convective turnover times τconv. All simulations use the AUSM+-up flux. |
| In the text | |
 |
Fig. 25. Similar to Fig. 23 but for a fixed energy boosting factor of 3 × 104 and varying resolution. All simulations use the AUSM+-up solver. The profiles are taken at Nτconv = 4.5, except for the run with a grid of 540 × 3602 cells. Here, the profile is taken at Nτconv = 3.1, the latest available snapshot. |
| In the text | |
 |
Fig. 26. Same as Fig. 24 but for a resolution of 810 × 5402 and a fixed energy boosting of 3 × 104. |
| In the text | |
 |
Fig. B.1. Thermal adjustment timescale τdiff according to Eq. (9). The typical length scale is taken to be the radial grid spacing of the 3D simulation run with the highest resolution presented in Section 5. |
| In the text | |
 |
Fig. B.2. Flow patterns for 2D (upper row) and 3D (lower row) simulations at different boosting strengths. The Mach number is color-coded; the color-scale is adjusted to every subplot individually. Plots for the 3D simulations show the equatorial plane. White dashed lines denote the detected boundaries as described in Section 5.1. For all simulations, the AUSM+-up solver was used. No 3D data is available for b = 1.0. |
| In the text | |
 |
Fig. B.3. Fluid flow in terms of Mach number for the |
| In the text | |
 |
Fig. B.4. Same as Fig. 16 but for the time interval t ∈ [t(Nτconv = 17.5),t(Nτconv = 25)]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



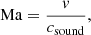
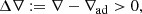
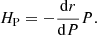
![$$ \begin{aligned} D_{{\mathrm{CBM}}} = D_0(f_0) \, \exp \left( \frac{-2 \left[r-r_0(f_0)\right]}{f_{{\mathrm{CBM}}}\, H^\mathrm{{CB}}_{\rm P}} \right), \end{aligned} $$](/articles/aa/full_html/2021/09/aa40825-21/aa40825-21-eq13.gif)
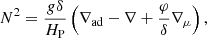
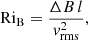
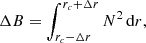
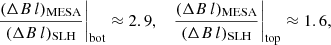
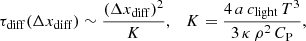
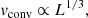
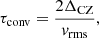
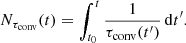

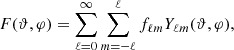
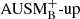
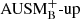
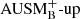
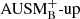
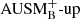
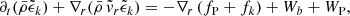
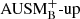
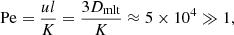
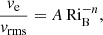
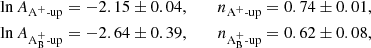
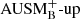
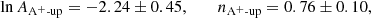
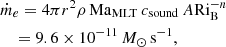
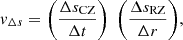
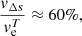
![$$ \begin{aligned} \widetilde{\mathrm{PS}}(\vartheta ,\varphi ) = \frac{\sum _{r\in \left[r_{\mathrm{PS}},r_{\mathrm{P}}\right]} V(r,\vartheta ,\varphi )\left[\mathrm{PS}(r,\vartheta ,\varphi )-\overline{\mathrm{PS}}(\vartheta ,\varphi )\right]}{\sum _{r\in \left[r_{\mathrm{PS}},r_{\mathrm{P}}\right]} V(r,\vartheta ,\varphi )}, \end{aligned} $$](/articles/aa/full_html/2021/09/aa40825-21/aa40825-21-eq100.gif)