| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202038914 | |
| Published online | 13 April 2021 | |
Medium-resolution spectrum of the exoplanet HIP 65426 b★
1
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
e-mail: simon.petrus@univ-grenoble-alpes.fr
2
Unidad Mixta Internacional Franco-Chilena de Astronomía, CNRS/INSU UMI 3386 and Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
3
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
4
Institut fur Astronomie und Astrophysik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
5
Physikalisches Institut, University of Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
6
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
7
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
8
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
9
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
10
Univ Lyon, Ens de Lyon, Univ Lyon 1, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69007 Lyon, France
11
Observatoire de Genève, University of Geneva, Chemin des Maillettes, 1290, Sauverny, Switzerland
12
Center for Space and Habitability, Universität Bern, Gesellschaftsstrasse 6, 3012, Bern, Switzerland
Received:
13
July
2020
Accepted:
3
December
2020
Medium-resolution integral-field spectrographs (IFS) coupled with adaptive-optics such as Keck/OSIRIS, VLT/MUSE, or SINFONI are appearing as a new avenue for enhancing the detection and characterization capabilities of young, gas giant exoplanets at large heliocentric distances (>5 au). We analyzed K-band VLT/SINFONI medium-resolution (Rλ ~5577) observations of the young giant exoplanet HIP 65426 b. Our dedicated IFS data analysis toolkit (TExTRIS) optimized the cube building, star registration, and allowed for the extraction of the planet spectrum. A Bayesian inference with the nested sampling algorithm coupled with the self-consistent forward atmospheric models BT-SETTL15 and Exo-REM using the ForMoSA tool yields Teff = 1560 ± 100 K, log(g) ≤ 4.40 dex, [M/H] = 0.05−0.22+0.24 dex, and an upper limit on the C/O (≤0.55). The object is also re-detected with the so-called “molecular mapping” technique. The technique yields consistent atmospheric parameters, but the loss of the planet pseudo-continuum in the process degrades or modifies the constraints on these parameters. The solar to sub-solar C/O ratio suggests an enrichment by solids at formation if the planet was formed beyond the water snowline (≥20 au) by core accretion (CA hereafter). However, a formation by gravitational instability (GI hereafter) cannot be ruled out. The metallicity is compatible with the bulk enrichment of massive Jovian planets from the Bern planet population models. Finally, we measure a radial velocity of 26 ± 15 km s−1 compatible with our revised measurement on the star. This is the fourth imaged exoplanet for which a radial velocity can be evaluated, illustrating the potential of such observations for assessing the coevolution of imaged systems belonging to star forming regions, such as HIP 65426.
Key words: infrared: planetary systems / methods: data analysis / planets and satellites: atmospheres / techniques: imaging spectroscopy
© S. Petrus et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Direct imaging can provide high-fidelity spectra of young (age <150 Myr) self-luminous giant exoplanets. These spectra are typically made of tens to thousands of data points over a broad wavelength range (0.5–5 μm) and can be acquired in a few hours of telescope time. The set of spectro-photometric data collected thus far on the few dozen imaged planetary-mass companions (e.g., Chauvin et al. 2005; Mohanty et al. 2007; Lafrenière et al. 2008; Patience et al. 2010; Janson et al. 2010; Konopacky et al. 2013; Bonnefoy et al. 2014; Bailey et al. 2014; Chilcote et al. 2017; Samland et al. 2017) exhibits numerous molecular and atomic lines (e.g., H2O, 12CO, and K I). They enable us to probe the chemical and physical phenomena at play in exoplanetary atmospheres with effective temperature (Teff) in the range ~600–2300 K, similar to those of mature brown dwarfs (hereafter BDs, Becklin & Zuckerman 1988; Nakajima et al. 1995), but with surface gravities 100 to 1000 times lower because the radii at the very early evolution stages are larger. Planetary formation models indicate that the gaseous envelope of these young Jupiters that formed in circumstellar disks should undergo a differential chemical enrichment depending on the detailed formation history (e.g., Boley et al. 2011; Öberg et al. 2011; Barman et al. 2011; Helling et al. 2014; Öberg & Bergin 2016; Mordasini et al. 2016; Valletta & Helled 2018).
Exoplanet spectra obtained in direct imaging therefore offer the opportunity to determine the physical characteristics of the studied objects (age, mass, radius, Teff, and log(g)), explore the impact of surface gravity on the atmospheres (e.g., Patience et al. 2010; Bonnefoy et al. 2014), reveal any deviation from the host-star chemical composition (e.g. C/O, and [M/H]; Konopacky et al. 2013; Lavie et al. 2017; Nowak et al. 2019), and ultimately trace their formation mechanism. Atmospheric models, that include the formation of clouds of different compositions (silicates, iron, and sulfites) have been used for more than a decade to reproduce the spectral features, colors, and luminosity of directly imaged planets (Allard et al. 2001, 2012; Ackerman & Marley 2001; Helling et al. 2008; Barman et al. 2011; Madhusudhan et al. 2011; Morley et al. 2012; Charnay et al. 2018; Mollière et al. 2019). They are now widely used to derive the physical properties of the atmosphere of imaged exoplanets.
With the direct-imaging technique, the challenge of accurately removing the dominant stellar flux on broad wavelength intervals represents the main hurdle for extracting unbiased exoplanet spectra. Since 2013, the high-contrast imagers and spectrographs such as GPI (Macintosh et al. 2006), SPHERE (Beuzit et al. 2019)or SCExAO/CHARIS (Groff et al. 2015; Jovanovic et al. 2015) have gathered low-resolution (Rλ = 30–350) near-infrared (0.95–2.45 μm) spectra of exoplanets down to 100 mas from their host star. The spectra confirmed some of the results inferred earlier from photometric spectral energy distributions (e.g., Marois et al. 2008; Bonnefoy et al. 2013): the reduced surface gravity affects the vertical mixing and the gravitational settling of condensates, which leads to thicker cloud layers, upper atmosphere submicron hazes, and causes cloud opacities to remain down to Teff = 600 K at early ages (Bonnefoy et al. 2016; Rajan et al. 2017; Chauvin et al. 2017, 2018; Samland et al. 2017; Greenbaum et al. 2018; Uyama et al. 2020; Delorme et al. 2017; Mesa et al. 2020). These spectra, however had led to contradicting conclusions on the derivation of the atmospheric composition (Samland et al. 2017; Rajan et al. 2017), possibly owing to the limited resolution of the observations and uncertainties in the atmospheric models. Spectroscopy at medium resolving powers (R of a few 1000s) is warranted to access this information (see Lavie et al. 2017) and test the models further.
Adaptive-optics-fed integral-field spectrographs (IFS) operating at medium spectral resolving power (Rλ = 2000−5000) in the near-infrared such as SINFONI at the VLT, NIFS at Gemini-North, or OSIRIS at the Keck Observatory offer to partly deblend the rich set of molecular absorption that is contained in the exoplanet spectra. They have been used to gather the spectra of young low-mass companions at large distance from their host stars (> 1”) or in systems with moderate contrasts in the near-infrared (McElwain et al. 2007; Seifahrt et al. 2007; Schmidt et al. 2008, 2014; Lavigne et al. 2009; Bowler et al. 2011, 2017; Bonnefoy et al. 2014; Bowler & Hillenbrand 2015; Daemgen et al. 2017). More recently, high-contrast imaging techniques such as the angular differential imaging (e.g. ADI, Marois et al. 2006) have been implemented on these instruments and allowed characterizing companions at shorter separations (ρ <1"; Bowler et al. 2010; Meshkat et al. 2015; Hoeijmakers et al. 2018; Mesa et al. 2019; Christiaens et al. 2019). Using OSIRIS, Konopacky et al. (2013) and Barman et al. (2015) detected carbon monoxide and water in the spectrum of HR 8799 b and c, which they confirmed using the cross correlation of the spectra with templates of pure H2O, CO, and CH4 absorption. The cross-correlation approach has been generalized to all spaxel contained in IFS datacubes by Hoeijmakers et al. (2018) following a modified prescription of the algorithm described in Sparks & Ford (2002). This molecular mapping method allows removing the remaining stellar flux residuals, including the quasi-static noise created by the IFS optical elements (Janson et al. 2008), while providing an interesting mean to unambiguously identify cool companions and characterize their properties (Teff, log(g), [M/H], composition, and radial velocity). The approach has thus far been used on a limited set of data (β Pictoris b, HR8799 b; Hoeijmakers et al. 2018; Petit dit de la Roche et al. 2018), and its performances and limitations are yet to be investigated on additional data and against alternative methods exploiting the IFS data diversity (e.g., Marois et al. 2006; Thatte et al. 2007; Ruffio et al. 2019).
HIP 65426 b (Chauvin et al. 2017) is the first exoplanet discovered with the VLT/SPHERE instrument at a projected separation of 92 au from the young (14 ± 4 Myr) intermediate-mass star HIP 65426 (A2V, M = 1.96 ± 0.04 M⊙). The star is located at a distance of 111.4 ± 3.8 pc (Gaia Collaboration 2016) and belongs to the Lower Centautus-Crux (hereafter LCC) association (de Zeeuw et al. 1999; Rizzuto et al. 2011). The low-resolution Y - to H-band photometry and spectra of HIP 65426 b indicate that the object has a L6 ± 1 spectral type with clear signatures of reduced surface gravity (Chauvin et al. 2017). The hot-start evolutionary models (Baraffe et al. 2003; Chabrier et al. 2000; Mordasini 2013) predict Mb = 6−12 MJup in the planetary-mass range. Atmospheric models estimate Teff in the range 1100–1700 K, a surface gravity log(g) lower than 5 dex, and a radius from 1 to 1.8 RJup. These physical properties were confirmed by Cheetham et al. (2019), who analysed the SPHERE data together with new VLT/NaCo L- and M-bands (3.49–4.11 μm and 4.48–5.07 μm) observations. They found Teff = 1618 ± 7 K, 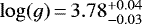 dex and R = 1.17 ± 0.04 RJup and estimated a new mass M = 8 ± 1MJup (statistical errors). The relatively low mass ratio of HIP 65426 b with A (Mb ∕MA ~ 0.004), its intermediate semimajor axis (
dex and R = 1.17 ± 0.04 RJup and estimated a new mass M = 8 ± 1MJup (statistical errors). The relatively low mass ratio of HIP 65426 b with A (Mb ∕MA ~ 0.004), its intermediate semimajor axis (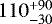 au, Cheetham et al. 2019), and the nondetection of a debris disk in the system (Chauvin et al. 2017) question the origin of HIP 65426 b and make the system an interesting test for planet formation theories. Marleau et al. (2019) explored formation scenarios for HIP 65426 b, including the evolution of the protoplanetary disk and the gravitational interaction with possible further companions in the system.
au, Cheetham et al. 2019), and the nondetection of a debris disk in the system (Chauvin et al. 2017) question the origin of HIP 65426 b and make the system an interesting test for planet formation theories. Marleau et al. (2019) explored formation scenarios for HIP 65426 b, including the evolution of the protoplanetary disk and the gravitational interaction with possible further companions in the system.
In this paper, we analyze medium-resolution (Rλ ~ 5500) K-band data of HIP 65426 b collected with the VLT/SINFONI IFS to characterize the exoplanet and evaluate the potential of the molecular mapping technique. We describe in Sect. 1 the observations and data reduction based on the molecular mapping and classical ADI extraction techniques. We characterize the planet in Sect. 3 using the new spectroscopic data, and discuss our results in the Sect. 4.
2 Observations and data reduction
2.1 Observations
HIP 65426 was observed on May 25 and May 26, 2018 with the VLT/SINFONI instrument (program 0101.C-0840; PI Hoeijmakers) mounted at the Cassegrain focus of VLT/UT41 (see Table 1). SINFONI is made of a custom adaptive optics module (MACAO) and of an IFS (SPIFFI). SPIFFI cuts the field of view into 32 horizontal slices (slitlets) that are realigned to form a pseudo-slit and are dispersed by a grating on a Hawaii 2RG (2k × 2k) detector (Eisenhauer et al. 2003; Bonnet et al. 2004).
The instrument was operated with pre-optics and a grating sampling a 0.8′′ × 0.8′′ field of view with rectangular spaxels of 12.5 × 25 mas size, from 1.928 to 2.471 μm, at a spectral resolution Rλ = λ∕Δλ ~ 5577 (from the width of the line-spread function). MACAO was used at all times during the observations with the primary star as a reference forthe wave-front sensing. The derotator at the telescope focus was in addition turned off to allow pupil-tracking observations.
At each night, the star was first placed inside the field of view, and two 10 s integrations were obtained. The core of the stellar point-spread function (PSF) was then moved outside of the field of view with the instrument field selector, and a sequence of 100 s integrations centered on the expected position of the planet was performed. This strategy is similar to the one adopted on β Pictoris (Hoeijmakers et al. 2018, Bonnefoy et al., in prep.). It reduces the effect of the read-out in the noise budget while avoiding any persistence on the detector of SPIFFI.
Observing log.
2.2 Cube building and registration
The data were initially reduced with the SINFONI data handling pipeline v3.2.3 (Abuter et al. 2006) through the EsoReflex environment (Freudling et al. 2013). The pipeline used a set of calibration frames obtained at day time to perform basic cosmetic steps on the raw bidimensional science frames and correct them for the distortion. The pipeline also identified the position of slitlets on the frames and the wavelength associated with each pixel before building a series of datacubes corresponding to each exposure. The sky emission was evaluated and removed through the field of view using the methods from Davies (2007).
We used the Toolkit for Exoplanet deTection and chaRacterization with IfS (hereafter TExTRIS) in addition to the ESO recipes to optimize our cubes for the high-contrast science (the main steps are described below; see Bonnefoy et al., in prep. for another application of this tool). The toolkit first corrected the raw SINFONI data for various noises occurring on the detector, as described in Bonnefoy et al. (2014).
TExTRIS also mitigated two different effects on the cubes. First, we corrected an incorrect estimate of the slitlet positions on the raw science frame and masked the first and last two columns of spaxels in the cubes that were affected by crosstalk at the slitlet edges. This step is critical to remove strong stellar flux residuals at the edges of the field of view and to obtain an accurate knowledge of the star position outside the field of view. Then, we reexamined the wavelength calibration performed by the ESO pipeline by comparing the many telluric absorption lines contained in each spaxel to a model generated for the observing conditions with the python module skycalc_ipy2 and based on the ESO Skycalc tool (Noll et al. 2012; Jones et al. 2013). The method was shown to be critical to derive a robust radial velocity measurement of β Pictoris b (Bonnefoy et al., in prep.) and improve the capabilities of the molecular mapping technique (see Sect. 2.4). It is applicable whenever the spaxels contain enough stellar light to show the telluric absorptions. The shifts were evaluated in each input cube across the field of view. A master median-combined map of the velocity shift was then created, and each individual cube was corrected for the effect. We find that spaxels are redshifted by 21.6 and 16.4 km s−1 on average (0.6 and 4.2 km s−1 dispersion along the sequences) on the first and second observation night, respectively. We found and corrected additional relative shifts of ~ km s−1 from spaxel to spaxel across the field. These smaller shifts are visible at the same position for all cubes throughout the sequence and indicate differential errors on the wavelength solutions between the slitlets. We validate this recalibration on the final products in Appendix A using an independent method that relies on OH sky emission lines.
We used TExTRIS to recompute the parallactic angles and rotator angular offsets following the method we described in Meshkat et al. (2015) to allow realigning the cubes to north.
To conclude, the software retrieved the position of the star outside the field of view. SINFONI lacks an atmospheric dispersion corrector, which makes the registration more complex. We followed a three-step strategy. First, the position of the star was evaluated ateach wavelength in the last cube, corresponding to the 10 s exposure using a Moffat function. The drift was fit with a low-order polynomial. Second, we accounted for the field selector offsets, the field rotation, and the change in atmospheric refraction tomeasure the star position outside the field of view in the first 100 s exposure. The theoretical change of the star position dueto atmospheric refraction was computed using empirical formulas reported in the source code of the SINFONI data-handling pipeline recipes and adapted to the case of the pupil-tracking mode (see the pipeline user manual3). Lastly, we iterated over the next 100 s exposures using our computed change of theoretical atmospheric refraction and the evolution of the parallactic angle.
We assumed a pivot point located at the center of the field of view (X = 32, Y = 32; see the ESO manual4) for this purpose. The accuracy on the position of that pivot point is tied to the proper correction of the slitlet edges, however, which we evaluate to be accurate to ~1 pixel. We therefore explored different pivot point locations within a 3-pixel-wide box centered on the theoretical ones, with 0.5 pixel increments. We conclude that the theoretical value offers the strongest cross-correlation signal (see Sect. 3) on the planet on both nights in our data. The strategy was vetted on similar data obtained on β Pictoris b (Bonnefoy et al., in prep.), and provides a centering with an accuracy better than a spaxel (~12.5 mas) throughout the sequence.
 |
Fig. 1 Detection of HIP 65426 b with SINFONI using (from left to right) a simple derotation and stacking of the individual cubes (nADI), a removal of the halo at each wavelength using a circular profile and a local fit with a 2D polynomials, the PCA algorithm (three modes), and the molecular mapping with an Exo-REM model at Teff = 1600 K, log(g) = 4.0 dex, [M/H] = 0 dex, and C/O = 0.35 (at 20 km s−1). |
2.3 Extraction of emission spectra using the ADI
We applied the angular differential imaging technique (Marois et al. 2006) on each cube slice to evaluate and remove the halo. Both the classic ADI approach and the PCA5 (five modes)allow retrieving the planet at each epoch with a shape and size compatible with the PSF (Fig. 1). This furthervalidates the star registration process. The post-ADI cubes are affected by residuals from the diffraction pattern that is created by the telescope spiders (the negative and positive lines near the edges of the field of view). The PCA appears to mitigate some of these residuals. We also used the nADI approach considering a simple realignment of the individual cubes to north and a stack. The nADI reveals the planet on top of the stellar halo. We found that the halo could be subtracted on data from May 25, 2018 with the nADI approach removing a circular profile at first and fitting the residuals in a 20-pixel square box around the planet with a 2D polynomial. The box size was chosen to avoid introducing artifacts at the edges of the field of view that could bias the fit while allowing for having a stable (converged) fit of the halo at each wavelength (Appendix B). This method fails to provide an accurate removal of the halo in the data from May 26, 2018, which were obtained in poorer conditions. The companion spectrum was extracted within a 75 mas circular aperture in the PCA and the halo-subtracted nADI cubes. We used the average fluxof the residuals in the halo-subtracted nADI cubes in an annulus of radius 50–113 mas to estimate the error bars on the planet flux. A spectrum of the star was obtained from the short-exposure datacubes (see Table 1) within the same aperture, which allowed us to compute the flux ratio with the planet at each wavelength. This ratio was multiplied by a BT-NEXTGEN synthetic spectrum (Allard et al. 2012) at Teff = 8400 K, log(g) = 3.5 dex, and M/H = 0 dex degraded to the resolution of SINFONI and flux-calibrated on the TYCHO (B, V), 2MASS (J, H, K), DENIS (K),WISE (W1 to W4) and AKARI (S9W) photometry (Høg et al. 2000; Cutri et al. 2003, 2012; DENIS Consortium 2005) of the star extracted from the VOSA (Bayo et al. 2008) spectral energy distribution analyzer6. This allowed us to obtain final telluric-free spectra of the planet. The spectra of HIP 65426 b extracted from the PCA on both nights have an identical shape but are noisier than the spectrum extracted from the nADI-processed datacubes obtained at one epoch (see Appendix B). The absolute flux of the later spectrum is in excellent agreement with the K1 and K2 photometry reported in Cheetham et al. (2019). We chose to use it for the analysis presented in Sect. 3.
2.4 Molecular mapping
We implemented the molecular mapping technique in TExTRIS following the main steps described in Hoeijmakers et al. (2018). A reference spectrum of the star was first extracted from each cube from the median-combination of the 1% most illuminated spaxels in the field of view. This reference spectrum contains a representative set of telluric and stellar features (here Brackett γ), but does not model the changing slope of the spectra of each individual spaxel across the field of view because the SINFONI PSF evolves with wavelength. A model of the stellar emission was then created for each spaxel (i, j) by computing the ratio between the spaxel (i, j) and the referenced spectrum. The ratio was smoothed with a Gaussian boxcar of width 22 Å (ten spectral elements) and used to compute a slope-corrected model of each spaxel (i, j). The model was then subtracted from the spaxels to create a cube of residuals from which both the continuum emission of the star and of any companion was removed. This step was repeated once for each datacube for the sequence.
We then cross-correlated each spaxel with a template spectrum (see Sect. 3.1) smoothed to the spectral resolution of SINFONI and for which the continuum had been removed before using a Gaussian boxcar of 20 Å too. The cross-correlation function (CCF) was performed with the Python module crosscorrRV from the PyAstronomy package7 customized to include a normalization of the CCF following Briechle & Hanebeck (2001). The CCF explores velocities from −100 to +100 km s−1 in steps of 8 km s−1 (about four times the original sampling of the data in velocity). The individual cubes of the CCF were then corrected for the barycentric velocity using the Python module barycorrpy8 (Kanodia & Wright 2018a,b) and combined after they were phased in velocity. The planet was redetected at a separation ρ = 812 ± 18 mas and PA = 150.2 ± 1.2°, and ρ = 796 ± 18 mas and PA = 150.6 ± 1.2° on May 25 and 26, 2018, respectively (the error bars correspond to 1 pixel in the SINFONI field). The SINFONI astrometry is compatible within 2σ with the one measured on VLT/SPHERE data on May 12, 2018 (ρ = 822.9 ± 2.0 mas, PA = 149.85 ± 0.15°), by Cheetham et al. (2019), while it does not rely on a proper calibration of the spaxel size and absolute orientation of the instrument. We present an analysis of the correlation signals in Sect. 3.3.
3 Physical properties
We adopted two independent methods for deriving the physical properties of the HIP 65426 b atmosphere. We used a classical forward-modeling approach that compares observed spectra with grids of precomputed synthetic spectra using Bayesian inference methods to estimate posteriors on a set of parameters. We also applied the molecular mapping technique to study the evolution of the cross-correlation signal at the planet location for different molecular templates or grids of atmospheric models used as input. For both methods, we considered grids of BT-SETTL15 and Exo-REM (Allard et al. 2012; Charnay et al. 2018) synthetic spectra. The corresponding models are described below.
3.1 Atmospheric models
3.1.1 BT-SETTL15
BT-SETTL15 includes a 1D cloud model where the abundance and size distribution of 55 types of grain are determined by comparing the timescale of the condensation, the coalescence, the gravitational settling, and the mixing of these solids that are assumed to be spherical. The details of each solid and chemical element included in the model are described in Rajpurohit et al. (2018). The opacities in the spectral energy distribution were calculated line by line, and the overall radiative transfer was carried out with the PHOENIX code (Hauschildt et al. 1997; Allard et al. 2001). Convection was handled following the mixing-length theory, and works at hydrostatic and chemical equilibrium. The model also accounts for nonequilibrium chemistry between CO, CH4, CO2, N2, and NH3. The grid we used (CIFIST2011c9) considers a Teff from 300 to 7000 K in steps of 100 K, a surface gravity (hereafter log(g)) from 2.5 to 5.5 dex in steps of 0.5 dex. For computing efficiency, we used models with Teff in the range of 1200–2000 K, which is a conservative prior considering the previous spectral characterization of HIP 65426 b. The grid does not allow an exploration of nonsolar metallicities in this temperature range.
3.1.2 Exo-REM
Exo-REM is an atmospheric radiative-convective equilibrium model that also includes a cloud description that is well suited to reproduce the spectra of brown dwarfs and exoplanets where dust dominates, especially at the L-T transition. Much like the BT-SETTL15 models, the atmosphere is cut into 64 pressure levels. The flux over these layers is calculated iteratively using a constrained linear inversion method for a radiative-convective equilibrium. The initial abundances of each chemical element are first established using the values tabulated in Lodders (2010). The model includes the collision-induced absorptions of H2 –H2 and H2–He, ro-vibrational bands from nine molecules (H2O, CH4, CO, CO2, NH3, PH3, TiO, VO, and FeH), and resonant lines from Na and K. As BT-SETTL15, Exo-REM accounts for nonequilibrium chemistry between CO, CH4, CO2, and NH3 that is due to vertical mixing. The abundances of the other species are computed at thermochemical equilibrium. The vertical mixing is parameterized by an eddy-mixing coefficient from cloud-free simulations. The cloud model includes the formation of iron, silicate, Na2 S, KCl, and water clouds. This grid was generated exclusively for this study and provides spectra from 1.887 μm to 2.500 μm and includes four free parameters: the Teff from 300 to 1800 K in steps of 50 K, the log(g) from 3.5 to 5.0 dex in steps of 0.5 dex, the [M/H] for −0.5 to 0.5 in steps of 0.5 dex, and the [C/O] from 0.35 to 0.8, in steps of 0.05. We note that synthetic spectra are available at higher Teff but we chose not to include them because these models do not converge beyond Teff = 1800 K.
3.2 Bayesian inference of the spectrophotometry
We used the ForMoSA code presented in Petrus et al. (2020) to compare the synthetic spectra to the data following the forward-modeling approach. ForMoSA relies on the nested sampling algorithm (Skilling 2006) to determine the posterior distribution function of a set of free parameters in the models. This method performs a global exploration of the model parameter space to search for local maxima of likelihoods following an iterative method that isolates a progressively restrained area of iso-likelihood while converging toward the maximum values. This avoids missing local maxima of likelihood and allows us to evaluate the Bayesian evidence that can be used for the model selection (Trotta 2008).
Because the Bayesian inference implies that random points with a continuous distribution inside the parameter space are generated, we chose to reduce the step of each model grid by interpolating them with the N-dimensional linear interpolation python package griddata, which triangulates the input data with Qhull10 before applying barycentric interpolation. The interpolated steps of the BT-SETTL15 grids are 10 K for the Teff and 0.1 dex for the log(g) while the interpolated steps of the Exo-REM grids are 10 K for the Teff, 0.1 dex for the log(g), 0.1 for the metallicity and 0.05 for the C/O ratio. It increases the accuracy of the second interpolation step which occurs over the course of the nested sampling process when a new random point is generated in the parameter space. This interpolation is based on the N-dimensional weighted mean of the closest neighboring spectra inside the interpolated grid. The physical parameters derived by ForMoSA are summarized in Table 2. We stress that the errors given by ForMoSA are statistical and have been determined for each parameter as the range that encompasses 68% of the solutions in each posterior, they do not include possible systematical errors in models, which are difficult to quantify (see Petrus et al. 2020). Whenever the posterior distribution did not show a maximum (e.g., C/O ratio), we defined an upper limit on the given parameter encompassing 68% of the posterior distribution starting from the posterior maximum. Extended grids would be needed to constrain these parameters, but this analysisis left for future work. The best fits to the data, obtained using 20 000 living points in the nested sampling algorithm, are presented in Figs. 2 and 3 for the two families of atmospheric models.
When the 1.0–4.7 μm spectral energy distribution is compared to the BT-SETTL15 models (Fig. 2), two distinct groups of solutions emerge: at low Teff (Teff = 1464 ± 3 K), and at high Teff (Teff = 1645 ± 10 K). Both sets of solutions were explored within separate runs using flat priors between 1200–1500 K and 1500–2000 K. The results are shown in Table 2 together with the data and the distribution of 50 synthetic spectra corresponding to draws within the 1σ interval of each posterior. The residuals between the observations and the best solutions are also shown, and compared with the data error bars.
The L’ and M’ photometry is up to 1.5σ above the predictions. This may be due to the lack of exploration of nonsolar atmospheric composition by the BT-SETTL models, to an imperfect handling of the nonequilibrium chemistry that tends to enhance the L’ and M’ band fluxes in young L–T transition objects (Hubeny & Burrows 2007; Skemer et al. 2014; Moses et al. 2016; Stone et al. 2016) or cloud properties (e.g., Skemer et al. 2014), or even to excess emission from a putative circumstellar disk (Christiaens et al. 2019). Similar deviations beyond 2.5 μm are also seen in the spectral energy distribution fit of mid- and late-L type brown dwarfs from Upper Scorpius (Lodieu et al. 2018) using the same models. We also note that the H-band fluxes (SPHERE) are not reproduced well in the case of the low-Teff solution, while the L’- and M’-band fluxes and the water-band absorption from 1.35 to 1.45 μm are better represented. Previous version of the BT-SETTL models also failed to represent the shape of the H-band of young L dwarfs sampled by the SPHERE H-band filters (Manjavacas et al. 2014). Removing these points does not remove the bimodal posterior distribution.
Conversely, one unique set of solutions at intermediate Teff is found with the Exo-REM models (Fig. 3), which allow an exploration of nonsolar abundances. Conversely, both models tend to predict close monomodal solutions when the continuum is removed that are in better agreement with the ones found by Cheetham et al. (2019) made without the SINFONI data, but with much larger uncertainties.
A consistent radial velocity of 22 ± 6 km s−1 and 20 ± 6 km s−1 is found for HIP 65426 b using the BT-SETTL15 and Exo-REM models at K-band, respectively.
We used the Teff inferred from ForMoSA and the DUSTY evolutionary model (Chabrier et al. 2000) to derive a planet mass between 8.1 and 10.0 MJup consistent with the values from Marleau et al. (2019), and a radius between 1.48 and 1.53RJup. The radii obtained with ForMoSA and the BT-SETTL models for the cold-Teff solution agree better with the tracks, while those obtained for the high-Teff prediction are clearly at odds with the expected evolution of a young Jupiter such as HIP 65426b. The Exo-REM models also tend to underpredict the radii, but less strongly. These differences have also been well documented for young L-type planets such as HIP 65426b (e.g., Marley et al. 2012; De Rosa et al. 2016) and could be explained by the imperfect description of the cloud physics and opacity.
Estimates of the atmospheric parameters of HIP 65426 b for each grid of synthetic precomputed spectra and for each method.
 |
Fig. 2 Application of ForMoSA using the BT-SETTL15 models. Top: bimodal posterior distribution. Bottom left and right: comparison of the best fit and the observed data for the low Teff and high Teff modes. The data points were obtained using the low-resolution SPHERE-IFS spectrum (R ≃ 30–50; blue points, Chauvin et al. 2017), the SPHERE-IRDIS H-band photometry (green and red points; Cheetham et al. 2019), our medium-resolution SINFONI spectrum (R ≃ 5500); orange points, this work), and the NaCo L’ and M’-band photometry (purple and brown points, respectively; Cheetham et al. 2019). We overlaid 50 synthetic spectra picked randomly within the 1σ envelop of each posterior in gray. |
 |
Fig. 3 Same as Fig. 2, but with the grid of Exo-REM spectra and applicable to the K-band SINFONI data. |
3.3 Characterization with the molecular mapping
In this section we will define our method to estimate the correlation signal of each spaxel. Then, we will present our results that we obtained cross-correlating our data cubes with entire grids of synthetic spectra.
3.3.1 Extraction of the planet’s correlation signal
We ran the molecular mapping steps with the TExTRIS package (Sect. 2.4) on the molecular templates (see Sect. 3.3.2) and the grids of Exo-REM and BT-SETTL15 model spectra (see Sect. 3.3.3). The tool was parallelized to gain computation time and produced as many cross-correlation maps as input model spectra. The planet is detected with a radial velocity of 20 ± 8 km s−1 (see Fig. 1). We extracted the cross-correlation signal in the correlation maps by averaging the CCF over the full width at half maximum (FWHM) of the autocorrelation, centered on the radial velocity of the planet to produce averaged correlation maps and within a circular aperture centered on the planet position of 4 pixels radius (~FWHM of the PSF) to extract the correlation signal of the planet. We detail our exploitation of the correlation signal to characterize the properties of the planet below.
3.3.2 Molecular template analysis
We used precomputed templates of individual molecules (13CO, 12CO, CO2, CH4, FeH, H2O, HDO, K, NH3, Na, PH3, TiO, and VO) as input of TExTRIS to evaluate whether these species produce a strong set of absorption in the planet spectrum. The templates were computed with the Exo-REM model assuming the pressure-temperature profile of a solar-metallicity atmosphere with Teff = 1700 K and log(g) = 4.0 dex (e.g., a generic model close to the physical properties of HIP 65426 b). We show in Fig. 4 (left column) the averaged correlation maps for the CO, H2O, CH4 and NH3 templates, and with the full molecule template (Teff = 1700 K, log(g) = 4.0 dex, [M/H] = 0.0, and C/O = 0.50). The planet is detected with the full molecule template, the H2O template, and marginally with the 12CO template. The distribution of correlation signals (see Fig. 4, right column) shows a Gaussian distribution and indicates a detection at a signal-to-noise ratio (S/N) of 2.5, 2.2, and 1.2 for the full molecule template, and the H2O and 12CO templates, respectively. This is consistent with the mid-L spectral type of the object.
The lack of a clear detection of the 12CO is unexpected for an L6 object. We discuss this in Sect. 4.1.1.
3.3.3 Exploring the grids of synthetic spectra
As a following step, we explored the evolution of the cross-correlation signal over the synthetic grid of spectra from the BT-SETTL15 and Exo-REM models. Synthetic spectra with anomalous spectral slopes indicative of nonconverged cloud models were excluded and are reported as white rectangles. The application with the BT-SETTL15 grid is shown in Fig. 5, giving the correlation signal evolution with the effective temperature and the surface gravity. The 2D posterior distribution obtained with the ForMoSAcode on the continuum-removed SINFONI spectrum (see Sect. 3.2) is overlaid. We also show the corresponding 1D posteriors along with the averaged χ2 and mean correlation signals (“pseudo-1D posteriors”). The χ2 pseudo-1D posteriors start from the original grid of models. We note that this alternative approach to the forward-modeling also identifies two distinct modes of physical parameters for HIP 65426 b at low Teff (Teff ≃ 1400 K) and high Teff (Teff ≃ 1800 K).
A similar analysis with the Exo-REM model grid is shown in Fig. 6 considering different layouts in the parameter space. Their exploitation also shows a similar behavior as previously and favors one family of solutions with Teff = 1700 K, log(g) = 3.5, [M/H] = 0.0,and C/O = 0.40. For both models, the detailed set of physical parameters maximizing the correlation signal is reported in Table 2 for the BT-SETTL15 and Exo-REM models. We note that the maximum of the CCF value obtained with both models is similar (~0.011). The CCF signal using the Exo-REM models is maximized at solar metallicity, which corresponds de facto to the one of the BT-SETTL15 models.
The comparison of the two approaches (forward-modeling versus molecular mapping) for the characterization of planetary signals is discussed below, together with the physical properties and possible origin of HIP 65426 b.
4 Discussion
4.1 Performances and limitations of our data analysis
In this section we will discuss the potential of the molecular mapping to detect companion and characterize them. We will also present the first comparison between the atmospheric characterization using the molecular mapping and the Bayesian inference which are two independent methods.
4.1.1 The molecular mapping on noisy data
The exposure time calculator (ETC- of SINFONI estimates a theoretical maximum S∕N = 15.2 from 2.1 to 2.15 μm for the first night of observations. We measure a S/N of 9.7 on the extracted spectrum over a similar wavelength interval (see Appendix B). The difference may be due to wavelength-to-wavelength noise introduced by the extraction process. The data are read-out noise limited because of the short integration time used to avoid the persistence on the detector. This advocates the use of specific high-contrast modes on such medium-resolution IFUs (e.g., GTC/FRIDA, ELT/HARMONI; N’Diaye et al. 2018; Carlotti et al. 2018).
The observations of HIP 65426 b offer an interesting test-case of the molecular mapping method when applied in the low S/N regime. In this case, only the strongest molecular absorptions contribute to the correlation signal. The H2O tend to produce a larger number of strong lines than 12CO. The 12CO lines are spread in a narrow range of wavelength where the theoretical S/N predicted by the ETC is lower (10.5 for wavelengths longward of 2.29 μm) because of the numerous telluric lines and the lower transmission of the K-band filter of the instrument. Conversely, the set of narrow water absorption is found as a set of partly blended features at the resolution of SINFONI and spread over the entire K band (Fig. 4). This explains why 12CO does not produce a strong correlation signal, as would naively be expected for a mid-L type exoplanet. We investigate the detection capability of the molecular mapping using the CO template further in Appendix C by injecting simulated planets at different C/O ratio into our datacube. The tests reveal the ability of the method to recover a planet with a noiseless spectral signature close to that of HIP 65426b at a low S/N. We show in addition that the significance of the detection drops for synthetic planets with a low C/O ratio for which the strongest CO overtone is shallower.
We show in Fig. 7 the correlation signal between the extracted SINFONI spectrum of the planet (continuum subtracted) and the molecular templates. We confirm the conclusions from Fig. 4 and in particular the faintness of the correlation signal of 12CO with respect to H2O. To conclude, the figure also reveals additional correlation and anticorrelation peaks over the velocity span. As noted by Hoeijmakers et al. (2018), some of these peaks are likely to be caused by the regular spacing of molecular absorption both in the template and exoplanet spectra (overtones). This was confirmed by computing the autocorrelation of the templates and justifies the use of the spatial distribution of CCF values for computing an S/N rather than the velocity dimension. The overtones appear at different velocities in the various molecules, and therefore the correlation of full synthetic spectra that combine all the molecular absorption offers to reduce these parasitic signals with respect to the main correlation peak in the velocity space.
These features are slightly reduced and the central correlation peak is enhanced when a full synthetic spectrum corresponding to the Teff log(g), and composition assumed for the templates of individual molecules is used. For all these reasons, full synthetic spectra offer a more robust way of characterizing any object and achieving a convincing detection of new ones than templates of individual molecules.
 |
Fig. 4 Application of TExTRIS on SINFONI data of HIP 65426 b using templates of molecules 12CO, H2O, CH4, and NH3 and the full molecule template (top to bottom, respectively) at a velocity of 20 km s−1. Left: cross-correlation maps. The star represents the position of the host star, which lies out of the field. We detect the companion with the full molecule template (S∕N = 2.5), H2O (S∕N = 2.2) and possibly with the 12CO (S∕N = 1.1). Center: distribution of cross-correlation values in the integrated cross-correlation cube for each position. The correlation signal is significant for the full molecule template, H2O, and 12CO, but not for CH4 and NH3. Right: molecular template. |
 |
Fig. 5 Comparison of the correlation signal of each spectrum of the grid BT-SETTL15 obtained with TExTRIS (color map) and the 2D posterior obtained with ForMoSA (gray contours). We also compare the normalized 1D posterior obtained with ForMoSA on the K band without the continuum (black line) with the normalized 1D pseudo-posteriors extracted from the correlation signal map (blue cross) and a χ2 map (green cross) for the Teff and the log(g) (top and right panel, respectively). The white rectangle corresponds to a nonconverged synthetic spectra. |
4.1.2 Comparison of the characterization approaches
We compare three different approaches to determine the physical parameters of HIP 65426 b: a standard χ2 minimization, a Bayesian inference with the code ForMoSA, and the molecular mapping with the code TExTRIS. We show in the Figs. 5 and 6, and Table 2 that all three methods yield consistent results.
The coherency between the χ2 minimization and the Bayesian inference stems from our assumption that the uncertainties on the observed spectra are Gaussian distributed and that the data-points are nor correlated. The likelihood and the CCF are related assuming the same underlying hypothesis on the data (Brogi & Line 2019; Ruffio et al. 2019). This can explain the overall similar trends in the results from the Bayesian inference (and the χ2 minimization) and the molecular mapping. The remaining differences, shown in Figs. 5 and 6, may have several origins. The likelihood and the CCF are related by the model variance and data variance. The model variances vary accros the grid. The data variance is expected to be constant for a given spaxel, which might not be the case because the planet signal is sampled by different spaxels (with their own noise distribution) throughout the sequence because of the field rotation. The removal of the halo and the continuum-subtraction method is not performed at the same stage in TExTRIS and ForMoSA, which may introduce different correlated noises. The remaining differences may arise from correlations in the CCF signals. This can render molecular mapping for the characterization unsuitable. It further advocates the direct extraction of spectra of companions whenever they are detected or more robust approaches such as the forward-modeling of the joint speckles and planetary signals for objects blurred into the stellar halo (e.g., Ruffio et al. 2019).
The evolution of the CCF across the grids remains very similar to the one of the χ2 values, however, and the main differences with the posteriors (ForMoSA) appear at the grid edges. This may stem from the interpolation steps performed by ForMoSA. The grid generation can originally produce nonconverged synthetic spectra that will propagate at the interpolation steps and affect the posterior shape. Figure 8 shows the difference between the posteriors obtained with the original grid Exo-REM spectra and with a grid from which we removed all the obvious nonconverged models. When no cleaning of the grid is performed beforehand, local maxima of likelihood appear due to the non-converged models and produce patterns in the posteriors. We took particular care and removed any nonconverged models before running the code. However, it is still possible that some models may be slightly nonconverged at the edges of the grids, especially in the low-gravity range where dust is expected to play a prominent role in the atmospheric balance, or at high Teff, where the Exo-REM models are less suitable.
These appear as inherent limitations of Bayesian inference with precomputed grids of forward models. These biases might be lifted when a fully integrated Bayesian scheme coupled to Exo-REM (retrieval) becomes available or when extended and input grids of models with a refined meshing are used.
4.1.3 Losing the pseudo-continuum information
The molecular mapping implies that information contained in the planet spectral continuum is removed. Figure 8 compares Bayesian posteriors obtained using the grid Exo-REM on the band K with and without the continuum (solid and dashed green lines, respectively), and Table 2 summarizes the values of the parameters extracted with error bars. The results of both approaches agree within the error bars (1σ). Nevertheless, the subtraction of the continuum shifts and flattens the Teff posterior (factor of ≃2.0 between the error bars). The constraint on the other physical parameters is less affected by the continuum removal, which indicates that the related information is encoded in the line intensities.
These differences clearly indicate the limitations of the molecular mapping in constraining the Teff of objects in the L-type regime from observations at K band. We still need to investigate whether the method, when it is applied to a different band (J or H band) or at higher spectral resolution (VLT/ERIS K-band mode at R ~ 8000, ELT/HARMONI), could retrieve this information.
 |
Fig. 6 Same as Fig. 5, but with the grid Exo-REM. We considered different layouts around the set of parameters that maximize the CCF in each direction of the parameter space. Models at Teff = 1800 K are unconverged at the given [M/H] and/or C/O, and/or log(g) so that the corresponding CCF values and posteriors stop at Teff = 1700 K. |
 |
Fig. 7 Cross-correlation signals obtained when using the continuum-subtracted spectrum of HIP 65426 b and the molecular templates (color) or a full Exo-REM spectrum at Teff = 1700 K, log(g) = 4.0 and solar abundances (black). |
 |
Fig. 8 Comparison of posteriors from ForMoSA with different data and model configurations with the grid Exo-REM. We show in blue that the grid has been taken on the shelf and the continuum has been kept. In red (solid line) we show that the grid has been cleaned of its nonconverged models and the continuum has been kept. In red (dashed line) we plot the grid that has been cleaned of its nonconverged models and the continuum has been removed. We show in grey the grid steps for each parameter. |
4.2 Interpreting the radial velocity of HIP 65426 b
An interesting result from the SINFONI K-band spectrum of HIP 65426 b is the determination of the radial velocity of the planet itself. As described in Sect. 2, great care has been taken to calibrate the wavelength dispersion of the cubes using the various telluric absorption lines, and we cross-checked it at the end with the solution found for the OH lines in the data (centered on zero km s−1, see Fig. A.1). When the two independent approaches, the Bayesian inference and the molecular mapping, are used to measure the radial velocity of HIP 65426 b in the SINFONI datacubes, we find compatible values that give a radial velocity estimate of 21 ± 7 km s−1. Similar results are obtained with the molecular mapping approach using the observation acquired on May 25, 2018 (20 ± 8 km s−1). We used the molecular mapping technique to estimate the radial velocity on the set of observations acquired on May 26 2018, and we found 31 ± 8 km s−1. The radial velocity in both nights is consistent at 2σ and we chose to define our final estimate of the radial velocity as 26 ± 15 km s−1 to be the most conservative.
A direct application of this result is to verify the consistency with the expected Keplerian motion of a bound companion orbiting HIP 65426 A. Considering the orbital solution found for HIP 65426 b by Cheetham et al. (2019), we might expect a maximum difference of ± 4.4 km s−1 relative to the primary star absolute radial velocity. In the discovery paper of HIP 65426 b, Chauvin et al. (2017) reported for HIP 65426 A a value of 5.2 ± 1.3 km s−1, and a very high projected rotational velocity of vsini = 299 ± 9 km s−1. They considered for this analysis a set of 14 HARPS spectra acquired during the nights of January 16, 17, and 18 2017, and a two sets of lines: (i) Six strong lines (Ca II K and five H lines from Hβ to H9, excluding Hϵ; using the rotationally broadened core of the lines), and (ii) 35 atomic metallic lines. More details can be found in Appendix B of Chauvin et al. (2017). Because of the primary spectral type and its rotational velocity, a precise measurement of the absolute radial velocity is challenging. This motivates us to revisit this first analysis, which mainly focused on the extraction of the stellar rotational velocity. This time, we used 78 HARPS spectra11 obtained during ten nights between January 2017 to March 2018. We first followed a similar analysis to extract the radial and rotational velocities using the two line sets (i) and (ii). Although H lines are adapted for the extraction of rotational velocities and the search for variability given their strength, their extended wings makes them less reliable to derive absolute radial velocity as they are more sensitive on the continuum tracing. The revisited absolute radial velocity of HIP 65426 was therefore extracted using only the second set of lines (ii), that is, the weak metallic lines that are essentially only broadened by the atmospheric velocity field. The resulting radial velocity measurements are shown in Fig. 9. A mean radial velocity of 12.2 ± 0.3 km s−1 (2.9 km s−1 for the standard deviation of the radial velocity measurements) is derived, which is significantly different from the value derived by Chauvin et al. (2017), but more reliable because more spectra where used, because of the temporal baseline, and because the selection of metallic lines is more adapted for absolute radial velocity measurements. Moreover, high-frequency variation probably caused by pulsation are clearly identified. The average value of vsini is lower than originally derived with a value of 261 ± 2 km s−1 (16 km s−1 for the standard deviation of the radial velocity measurements) and no sign of a spectral binary 1 (SB1) or spectral binary 2 (SB2) binary is detected.
From this, we conclude that the difference of radial velocities between HIP 65426 b and A is compatible with a physical object in Keplerian motion (considering the uncertainties on the radial velocities of A and b, and the predicted Keplerian motion for b). We note that the new value for the radial velocity measurement of HIP 65426 A agrees better with a membership to the LCC subgroup considering the probability predictions of the BANYAN Σ code by Gagné et al. (2018). Finally, the direct determination of the radial velocity of imaged exoplanets with medium-resolution (to high-resolution) spectrographs, as already obtained for β Pic b (Snellen et al. 2014), HR 8799 b and c (Ruffio et al. 2019) and now HIP 65426 b, highlights the rich perspective of this technique when combined with astrometric monitoring to (i) test the companionship of the newly imaged exoplanetary candidates, (ii) refine their orbital parameters when confirmed, and (iii) measure their projected rotational velocity and potentially their spin with very high-resolution spectra.
 |
Fig. 9 Radial velocity measurements of HIP 65426 using a total of 78 HARPS spectra obtained between 2017 and 2018 at the La Sill /3.6m telescope and weak metallic lines that are less sensitive to the continuum tracing. |
4.3 HIP 65426 b formation pathway
The broad constraints on the C/O ratio and metallicity of HIP 65426 b derived in Sect. 3 give the opportunity of discussing the planet formation mode. We caution that the C/O ratio estimate depends on the correct assumptions on the cloud prescriptions where grains are efficient oxygen carriers and can affect the composition of the gas phase from which the molecular lines arise (e.g., Helling et al. 2014).
The interpretation relies on several additional hypotheses. The original composition of the putative circumstellar disk where HIP 65426 b may have formed is obviously unknown and the C/O and metallicity of HIP 65426 A, which is a fast rotator (Chauvin et al. 2017), have not been determined either, to our knowledge. Kane et al. (1980) reported the C/O ratio of six bona fide members of LCC and UCL but these estimates show a strong dispersion and would need to be revised with the help of recent stellar model atmospheres. Bubar et al. (2011) reported a subsolar metallicity on average ([Fe/H] = −0.12 dex, 0.10 dex rms) for a sample of UCL and LCC solar-type stars. Viana Almeida et al. (2009) reported metallicities of 0.02 ± 0.05 dex and −0.02 ± 0.09 dex for six and ten stars from UCL and Upper Scorpius, respectively. Nissen (2013) reported a correlation between the C/O ratio and the Fe/H of stars with planets with a mean C/O = 0.58 at Fe/H = 0 (0.06 rms scatter). Therefore we can expect that the HIP 65426A metallicity and C/O are close to solar values. Knowing the host star composition would be important to strengthen the conclusions on the formation pathway based on the atmospheric composition of the exoplanet, however.
The Gravity Collaboration (2020) have proposed a simple analytical method for interpreting the C/O ratio measured for imaged exoplanets. From the relative abundances of CO, CO2, H2O, C (grains) and O (silicates) given in Öberg et al. (2011), they estimated the relative abundance of the C and O in the solid (nC, s, nO, s) and gaseous phases (nC, g, nO, g) and for two possible planet birth locations: within the water-ice line and between the water and CO2 ice lines. We additionally considered the case of a formation between the CO2 and CO ice lines given the projected physical separation of 92 au for HIP 65426 b. To calculate the C/O, we assumed Msolid and Mgas as the amount of solid and gas in the atmosphere of the planet and fs/g the solid-to-gas ratio in the initial disk.
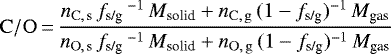 (1)
(1)
In the case of Msolid = fs/g Mplanet and Mgas = (1–fs/g) Mplanet where Mplanet is the total mass of the planet and fs/g is assumed to be equal to the standard solid-to-gas ratio of circumstellar disks (0.01), Eq. (1) gives a C/O ~ 0.55 corresponding to the solar value. During planet formation, this C/O ratio is modified by the accretion of solids and gas. In the case of the GI scenario, solids are accreted during the sudden collapse (Msolid ini) and later through planetesimal accretion (Maccreted). When we assume that the total mass accreted during the collapse is Mini ≫ Maccreted, the total mass of solids in the planet is:
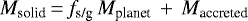 (2)
(2)
When a formation follows CA, Msolid is collected through the slower CA process, while the gas is added mostly at the runaway accretion step (Msolid = Maccreted). For both scenarii, the fraction of the gas mass in the planet is Mgas = (1–fs/g) Mplanet. This mix is assumed to be representative of the atmospheric composition.
We show in Fig. 10 (left) the predictions of the C/O ratio for different values of Msolid and the two formation paradigms for a Mplanet = 10 MJup (Marleau et al. 2019) planet and birthsites within the water-ice line, between the water and CO2 ice lines, and between CO2 and CO ice lines. The predictions are compared with the estimate of HIP 65426 b C/O ratio. The two scenarii are consistent with our estimate of the C/O.
Kennedy & Kenyon (2008) estimated the water-ice line to be originally at ~7 au around a ~ 2M⊙ star before it moves inward to ~2.5 au at 3 Myr. van der Marel et al. (2019) located the CO2 ice line at ~ 10 au in the midplane of the disks around the ~2 M⊙ young stars V1247 Ori and HD 163296. They also predicted CO ice lines at ~70 au and ~140 au for these two stars. Qi et al. (2015) reported observations of the CO snow line at 75 au around HD 163296 (we revised the published value using the Gaia-DR2 distance of the star), that is, at shorter separation than the projected physical separation of HIP 65426 b. Therefore, if it formed in situ, possibly beyond the CO snow line, the planet must have accreted a substantial amount of solids to lower its C/O ratio.
We caution that these conclusions remain based on a simple approach of planet formation processes and snow lines in disks. The fs/g might be different than the interstellar value adopted here and is expected to decrease with age due to the growth from micron-sized particles to planetesimals and planets. The ionization process in the disk can drastically modify the chemical abundances of elements in the region between the H2O and CO2 ice lines (Eistrup et al. 2018). Furthermore, our 1D approach neglects the variation in snow-line radii at different scale heights in the disk (e.g., Dullemond et al. 2020) and their complex evolution in time that is due to episodic accretion (e.g., Cieza et al. 2016).
The population synthesis approach offers to follow the subtle effects involved in planet formation. The new-generation planetary population synthesis (hereafter NGPPS) from the Bern group (Marleau et al. 2019; Schlecker et al. 2021) predicts that the bulk enrichment of planets is by CA. Marleau et al. (2019) account for type I and II migration and for the formation and dynamical interactions of multiple planet embryos per disk. The population has not yet been computed for a host star more massive than 1.5 M⊙. However, the predictions of bulk enrichment for the populations of planets around 1.0 and 1.5 M⊙ show not significant change and we therefore assume here that it remains valid for a 2 M⊙ star such as HIP 65426 A.
At an age of 10 Myr, the simulation contains ~24500 bodies with masses up to 65.9 MJup and semimajor axes out to ~800 au. The solar metallicity of HIP 65426 b is well compatible with the bulk metallicity of the NGPPS planets in the same mass range (Fig. 10), but the simulated planets are found on much tighter orbits (semimajor axes from 0.57 to 11.16 au for planets in the same ranges of mass and metallicity as HIP 65426 b) than the projected separation of HIP 65426 b (92 au). The conclusions remain unchanged at 20 Myr. This comparison of the atmospheric metallicity and bulk enrichment assumes that the metals acquired at formation become diluted in the planet envelope.
To conclude, the abundances of HIP 65426 b can be compared to those of imaged companions around intermediate-mass stars with similar measurements (Table 3)12. The C/O and mass of HIP 65426 b are reminiscent of those of β Pictoris b, which is located much closer to its host star at 11 au. This supports the above hypothesis that the planet is formed closer in and is then scattered at larger separation through planet-planet interactions (see Marleau et al. 2019). This hypothesis could also explain the different separations observed between HIP 65426 b and the NGPPS population at the same mass, age, and metallicity ranges. A future refinement of the orbital parameters with GRAVITY will help clarify the dynamical history of the planet and the interpretation of the planet composition derived here.
 |
Fig. 10 Exploitation of our C/O and [M/H] to constrain the formation pathway. Left: comparison of the posterior of the C/O ratio given by ForMoSA (gradient; black: high likelihood) and different scenario of formation as a function of the accreted solid mass. The solid lines correspond to the GI scenario, and the dashed lines correspond to the CA scenario. The blue, green, and purple curves represent a formation within the water-ice line, between the water and CO2 ice lines, andbetween CO2 and CO ice lines, respectively. Right: comparison of the bulk enrichment of the NGPPS (red dots) and the estimated properties of HIP 65426 b (blue dot). We show here the NGPPS with a mass higher than 0.05 MJup (approximately the mass of Neptune). |
Imaged planets around intermediate-mass stars with reported abundance measurements.
5 Summary and conclusions
We analyzed new K-band medium-resolution IFS data obtained with SINFONI at the VLT of the HIP 65426 b exoplanet, discovered by SPHERE, to further characterize its atmosphere. Our TExTRIS python analysis toolkit for IFS data was able to retrieve the star position outside the field of view and to optimize the data processing, which allowed us to extract the planet emission spectrum. We interpreted this spectrum following a Bayesian inference with self-consistent atmospheric forward models with the ForMoSA code (Petrus et al. 2020) and compared the inferred atmospheric properties of the planet to those obtained from the recent molecular mapping technique based on cross correlation between the IFS data elements and grid of models. We summarize the main results as follows:
- 1.
We find a Teff = 1560 ± 100 K, log(g) ≤ 4.40 dex, [M/H] =
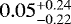 dex, and C/O ≤ 0.55 from ForMoSA. The accuracy is limited by the systematic uncertainties induced by the use of different models and by the bimodal distribution of solutions found with the BT-SETTL15 models. This composition is consistent with a formation of HIP 65426 b closer to the host star by CA. We cannot exclude a formation by GI at large separation, but this would imply the accretion of a substantial amount of solids.
dex, and C/O ≤ 0.55 from ForMoSA. The accuracy is limited by the systematic uncertainties induced by the use of different models and by the bimodal distribution of solutions found with the BT-SETTL15 models. This composition is consistent with a formation of HIP 65426 b closer to the host star by CA. We cannot exclude a formation by GI at large separation, but this would imply the accretion of a substantial amount of solids. - 2.
The molecular mapping as performed with TExTRIS yields results that are consistent with those from ForMoSA, which validates the ability of the molecular mapping to characterize atmospheres. Nevertheless, this alternative method is limited by the loss of the spectral continuum information in the data that can shift the estimates of Teff, and it degrades the constraints on the other parameters (log(g), [M/H], and C/O).
- 3.
We estimated a radial velocity of 26 ± 15 km s−1 for the planet, which is compatible with the revised radial velocity of the host star. This highlights the usefulness of medium-resolution (to high-resolution) spectrographs to test companionship.
GRAVITY observations could soon drastically improve the knowledge of the orbital parameter of the planet and potentially draw a consistent picture of its formation. Observations with ERIS and CRIRES+ would also allow us to improve the knowledge of the radial velocity and consolidate the constraints on the atmospheric parameters derived from our K-band data.
A new generation of integral field spectrographs that succeed SINFONI (VLT-ERIS, GTC-FRIDA, JWST-NIRSpec and MIRI, ELT-HARMONI and METIS) will soon observe at high-Strehl ratios, higher spectral resolution (up to Rλ ~ 100 000 for METIS), and high contrast (GTC-FRIDA, HARMONI high-contrast arm; METIS). All these instruments belong to the same class of slicer-based IFS and present similar challenges in terms of data analysis. The techniques developed and explored as part of this study could be adapted to process these observations.
Acknowledgements
We dedicate this work to the memory of Dr. France Allard, a great source of inspiration for our community. We hope that this paper will honor her career, her research and her huge contribution in the domain of the physics of atmospheres of stars, brown dwarfs and exoplanets. S.Pe, M.Bo, G.Ch, B.Ch., A.-M.La, P.De and A.Bo, acknowledge support of the Programme National de Planétologie through project grants “ISEP” and “EXO-SPEC” and the Agence Nationale de la Recherche through grant ANR-14-CE33-0018. This research has benefited from the support of the IDEX cross-disciplinary project Origin of Life, and the visiting program of the French Chilean Lab for Astronomy (FCLA, UMI-3886). A.Vi and M.Ho acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 757561). A.Wy acknowledges the financial support of the SNSF by grant number P400P2_186765. G.-D. Ma acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (KU 2849/7-1) and from the Swiss National Science Foundation under grant BSSGI0_155816 “PlanetsInTime”. Part of this work has been carriedout within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation. F. Al acknowledges financial support from the “Programme National de PhysiqueStellaire” (PNPS) and the “Programme National de Planétologie” of CNRS/INSU, France. The computations of brown dwarf and exoplanet models were performed at the Pôle Scientifique de Modélisation Numérique(PSMN) at the École Normale Supérieure (ENS) in Lyon. The results presented in this research paper were obtained using the matplotlib and astropy libraries (Hunter 2007; Astropy Collaboration 2018).
Appendix A Robustness of the wavelength solution at the location of the companion
We confirmed the accuracy of the correction we applied on the wavelength solution of the instrument using OH− emission lines. Seventeen lines from 1.977 to 2.23 μm are well detected in the stacked cubes (e.g., Fig. 1) on both nights. We were therefore able to determine the central wavelength at the location of the companion with an average accuracy of 3.5 km s−1 using a Gaussian fit, and we compared it to reference values from Rousselot et al. (2000). The residual shifts are reported in Fig. A.1 and oscillate around means of 2.3 and 2.8 km s−1 for the May 25 and 26 data, respectively. These values and the measurement accuracy indicate no significant residual wavelength shift and locally validate our recalibration based on telluric absorption.
 |
Fig. A.1 Velocity shifts between the measured and tabulated positions (vacuum) of OH lines at the position of the companion in the stacked datacubes. |
Appendix B Validating the extraction procedure
We tested the different extraction methods described in Sect. 2 by injecting a simulated planet with a K-band contrast of 10 magnitudes (corresponding to the values reported in Cheetham et al. 2019) and a position angle of 165.2°. The simulated planet spectrum was extracted within a 75 mas wide circular aperture and compared to the injected signal. The results are shown for both nights in Fig. B.1.
The test confirms the ability of the PCA to conserve the continuum shape. Conversely, the removal of the circular profile in the nADI cubes leaves large-scale flux halo residuals that introduce a bias of the continuum at the location of the simulated planet. The 2D polynomials applied on these cubes remove these residuals efficiently at shorter wavelengths, but bias the pseudo-continuum longward of 2.3 μm. We estimated the S/N from the difference of the normalized extracted and injected spectra. The S/N is systematically lower when the PCA is used. We therefore conclude that the PCA conserves the planet continuum information, but is not optimized for accessing the molecular lines.
We show in Fig. B.2 the flux-calibrated spectrum of HIP 65426b. The PCA-extracted spectra obtained from the May 25 and 26 datacubes and the spectrum extracted from the May 25 nADI cubes show identical continua. This confirms that the latter method works better at the planet position. The PCA spectrum is noisier than the nADI spectrum, in agreement with the conclusions based on simulated planets. The combination of the two PCA-extracted spectra of HIP 65426b does not reach the S/N obtained from the nADI/polynomial fit from the May 25 data. We therefore adopted the spectrum extracted from the nADI and polynomial fit. The final flux-calibrated spectrum of HIP 65426b appears to be consistent with the SPHERE K-band photometry.
To conclude, we tested different square box sizes (widths of 10, 15, 20, and 25 pixels) as well as different degrees (1 to 5) of polynomials when we applied the background correction to the nADI cubes. The results are shown in Fig. B.3 for the May 25, 2018 observations. Boxes smaller than 15 pixels do not contain enough spaxels to evaluate the background and lead to noisier spectra. Boxes larger than 20 pixels encompass artifacts at the edges of the field of view of SINFONI and were discarded. Square boxes with a width of 15 and 20 pixels yield similar results. We chose the latter to be able to estimate the level of residuals within an annulus of 53mas width (e.g., a resolution element) centered on the planet. Polynomials of degree 2 to 5 produce spectra with identical continua. The S/N decreases when higher degrees are considered. Polynomials of degree 1 seem to optimize the S/N. However, it leaves a higher level of residuals around the planet and does not subtract the continuum properly at shorter wavelengths. We therefore conclude that a box size of 20 pixels and a polynomial of degree 2 is the best trade-off on these data.
 |
Fig. B.1 Comparison of the injected (black lines) and extracted simulated planet spectra (color lines) using the methods described in Sect. 2: PCA (blue), the removal of a circular profile at each wavelength (orange), and the removal of a 2D polynomial at each wavelength at the position of the simulated planet (green). The S/N of the recovered spectra is computed from 2.1 to 2.25 μm (dashed vertical lines) and given in parentheses. |
 |
Fig. B.2 Flux-calibrated spectra of HIP 65426 b obtained with the PCA on both nights and compared to the spectrum extracted from the nADI reduction of the May 25 2018, data followed by a subtraction of a 2D polynomials. The S/N estimated from 2.1 to 2.25 μm is given in parentheses. The red datapoints correspond to the SPHERE K1 and K2 photometry from Cheetham et al. (2019). |
 |
Fig. B.3 Extracted spectra (with telluric features) of HIP 65426 b for different box sizes (left) and degree (right) of the polynomial fit applied to the nADI data. The S/N of the spectra estimated from 2.1 to 2.25 μm is given in parentheses. |
Appendix C Detection of planets with different C/O ratio with the CO molecular template
We investigate below the faint detection of HIP 65426b using the CO molecular template. We injected simulated planets into our datacube and compared the detection S/N in the CCF signal maps generated for each cases. The simulated planets were injected at ρ = 812 mas, PA = 165.2°, a broadband contrast ΔK = 10 mag, and a radial velocity of 30 km s−1. We used a noiseless synthetic spectrum generated with the Exo-REM model corresponding to a Teff = 1650 K, a log(g) = 4.0 dex, an [M/H] = 0.0, and a C/O = 0.35 and 0.70 for each simulated planet. Figure C.1 shows the CCF for each simulated planet obtained following the method described in Sect. 3.3.1. The signal is detected at a higher S/N than for the real planet which might be due to the lack of noise in the injected spectral signature. The comparison shows that planets with low C/O such as HIP 65426b are detected at a lower S/N than planets with supersolar C/O, however. The Exo-REM models predict a less pronounced ν = 2–0 overtone, which is the strongest spectroscopic signature of 12CO in the spectrum (see also Fig. 4). This translates into a reduced cross-correlation signal (Fig. C.2). This may therefore in part explain the marginal detection of HIP 65426b with the CO molecular template.
 |
Fig. C.1 Investigations of the detection performances using the molecular mapping. Upper left and right: CO molecular maps obtained following the injection of a simulated planet at ρ = 812 mas and PA = 165.2° in the original datacubes using Exo-REM models at Teff = 1650 K, log(g) = 4.0 dex, [M/H] = 0.0,and C/O = 0.35 and 0.70 at a velocity of 30 km s−1. Bottom left: histograms of CCF values at a velocity of 30 km s−1. Bottom right: CCF obtained at the position of the simulated planet. |
 |
Fig. C.2 Investigations of the characterization performances using the molecular mapping. Left: zoom into the ν = 2–0 CO overtoneat 2.29 μm of normalized continuum-subtracted Exo-REM models at different C/O ratios (Teff = 1650 K, log(g) = 0.40 dex, [M/H] = 0.0 and C/O = 0.35–0.70). Right: CCF between the Exo-REM models and the CO template shown in Fig. 4. |
References
- Abuter, R., Schreiber, J., Eisenhauer, F., et al. 2006, New Astron. Rev., 50, 398 [Google Scholar]
- Ackerman, A. S., & Marley, M. S. 2001, ApJ, 556, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, Philos. Trans. Roy. Soc. London Ser. A, 370, 2765 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bailey, V., Meshkat, T., Reiter, M., et al. 2014, ApJ, 780, L4 [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Konopacky, Q. M., Macintosh, B., & Marois, C. 2015, ApJ, 804, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becklin, E. E., & Zuckerman, B. 1988, Nature, 336, 656 [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boley, A. C., Helled, R., & Payne, M. J. 2011, ApJ, 735, 30 [Google Scholar]
- Bonnefoy, M., Boccaletti, A., Lagrange, A. M., et al. 2013, A&A, 555, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Lagrange, A. M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Zurlo, A., Baudino, J. L., et al. 2016, A&A, 587, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, Messenger, 117, 17 [Google Scholar]
- Bowler, B. P., & Hillenbrand, L. A. 2015, ApJ, 811, L30 [Google Scholar]
- Bowler, B. P., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 723, 850 [Google Scholar]
- Bowler, B. P., Liu, M. C., Kraus, A. L., Mann, A. W., & Ireland, M. J. 2011, ApJ, 743, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P., Kraus, A. L., Bryan, M. L., et al. 2017, AJ, 154, 165 [Google Scholar]
- Briechle, K., & Hanebeck, U. D. 2001, in Optical Pattern Recognition XII, eds. D. P. Casasent, & T.-H. Chao, 4387, International Society for Optics and Photonics (SPIE), 95, 102 [Google Scholar]
- Brogi, M., & Line, M. R. 2019, AJ, 157, 114 [Google Scholar]
- Bubar, E. J., Schaeuble, M., King, J. R., Mamajek, E. E., & Stauffer, J. R. 2011, AJ, 142, 180 [Google Scholar]
- Carlotti, A., Hénault, F., Dohlen, K., et al. 2018, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 10702, Proc. SPIE, 107029N [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [Google Scholar]
- Charnay, B., Bézard, B., Baudino, J. L., et al. 2018, ApJ, 854, 172 [Google Scholar]
- Chauvin, G., Lagrange, A. M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Desidera, S., Lagrange, A. M., et al. 2017, A&A, 605, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Gratton, R., Bonnefoy, M., et al. 2018, A&A, 617, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheetham, A. C., Samland, M., Brems, S. S., et al. 2019, A&A, 622, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chilcote, J., Pueyo, L., De Rosa, R. J., et al. 2017, AJ, 153, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Christiaens, V., Cantalloube, F., Casassus, S., et al. 2019, ApJ, 877, L33 [Google Scholar]
- Cieza, L. A., Casassus, S., Tobin, J., et al. 2016, Nature, 535, 258 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Cutri, R. M., et al. 2012, VizieR Online Data Catalog, II/311 [Google Scholar]
- Daemgen, S., Todorov, K., Quanz, S. P., et al. 2017, A&A, 608, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. I. 2007, MNRAS, 375, 1099 [Google Scholar]
- De Rosa, R. J., Rameau, J., Patience, J., et al. 2016, ApJ, 824, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Schmidt, T., Bonnefoy, M., et al. 2017, A&A, 608, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DENIS Consortium 2005, VizieR Online Data Catalog: II/263 [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Isella, A., Andrews, S. M., Skobleva, I., & Dzyurkevich, N. 2020, A&A, 633, A137 [EDP Sciences] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, Proc. SPIE, 4841, 1548 [Google Scholar]
- Eistrup, C., Walsh, C., & van Dishoeck, E. F. 2018, A&A, 613, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gagné, J., Mamajek, E. E., Malo, L., et al. 2018, ApJ, 856, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, C. A. G., Wertz, O., Absil, O., et al. 2017, AJ, 154, 7 [Google Scholar]
- Gravity Collaboration (Nowak, M., et al.) 2020, A&A, 633, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenbaum, A. Z., Pueyo, L., Ruffio, J.-B., et al. 2018, AJ, 155, 226 [Google Scholar]
- Groff, T. D., Kasdin, N. J., Limbach, M. A., et al. 2015, Proc. SPIE., 9605, 96051C [Google Scholar]
- Hauschildt, P. H., Baron, E., & Allard, F. 1997, ApJ, 483, 390 [Google Scholar]
- Helling, C., Ackerman, A., Allard, F., et al. 2008, MNRAS, 391, 1854 [Google Scholar]
- Helling, C., Woitke, P., Rimmer, P. B., et al. 2014, Life, 4, 142 [Google Scholar]
- Hoeijmakers, H. J., Schwarz, H., Snellen, I. A. G., et al. 2018, A&A, 617, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Hubeny, I., & Burrows, A. 2007, ApJ, 669, 1248 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Brandner, W., & Henning, T. 2008, A&A, 478, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Bergfors, C., Goto, M., Brandner, W., & Lafrenière, D. 2010, ApJ, 710, L35 [Google Scholar]
- Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jovanovic, N., Martinache, F., Guyon, O., et al. 2015, PASP, 127, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, L., McKeith, C. D., & Dufton, P. L. 1980, A&A, 84, 115 [NASA ADS] [Google Scholar]
- Kanodia, S., & Wright, J. 2018a, Res. Notes Am. Astron. Soc., 2, 4 [Google Scholar]
- Kanodia, S., & Wright, J. T. 2018b, Barycorrpy: Barycentric Velocity Calculation and Leap Second Management [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q. M., Barman, T. S., Macintosh, B. A., & Marois, C. 2013, Science, 339, 1398 [Google Scholar]
- Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2008, ApJ, 689, L153 [Google Scholar]
- Lavie, B., Mendonça, J. M., Mordasini, C., et al. 2017, AJ, 154, 91 [Google Scholar]
- Lavigne, J.-F., Doyon, R., Lafrenière, D., Marois, C., & Barman, T. 2009, ApJ, 704, 1098 [Google Scholar]
- Lodders, K. 2010, Astrophys. Space Sci. Proc., 16, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Lodieu, N., Zapatero Osorio, M. R., Béjar, V. J. S., & Peña Ramírez, K. 2018, MNRAS, 473, 2020 [Google Scholar]
- Macintosh, B., Graham, J., Palmer, D., et al. 2006, Proc. SPIE, 6272, 62720L [Google Scholar]
- Madhusudhan, N., Burrows, A., & Currie, T. 2011, ApJ, 737, 34 [Google Scholar]
- Manjavacas, E., Bonnefoy, M., Schlieder, J. E., et al. 2014, A&A, 564, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marleau, G.-D., Coleman, G. A. L., Leleu, A., & Mordasini, C. 2019, A&A, 624, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marley, M. S., Saumon, D., Cushing, M., et al. 2012, ApJ, 754, 135 [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McElwain, M. W., Metchev, S. A., Larkin, J. E., et al. 2007, ApJ, 656, 505 [Google Scholar]
- Mesa, D., Bonnefoy, M., Gratton, R., et al. 2019, A&A, 624, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mesa, D., D’Orazi, V., Vigan, A., et al. 2020, MNRAS, 495, 4279 [Google Scholar]
- Meshkat, T., Bonnefoy, M., Mamajek, E. E., et al. 2015, MNRAS, 453, 2378 [NASA ADS] [Google Scholar]
- Mohanty, S., Jayawardhana, R., Huélamo, N., & Mamajek, E. 2007, ApJ, 657, 1064 [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A&A, 627, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., Stolker, T., Lacour, S., et al. 2020, A&A, 640, A131 [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C. 2013, A&A, 558, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., van Boekel, R., Mollière, P., Henning, T., & Benneke, B. 2016, ApJ, 832, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Fortney, J. J., Marley, M. S., et al. 2012, ApJ, 756, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Marley, M. S., Zahnle, K., et al. 2016, ApJ, 829, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, T., Oppenheimer, B. R., Kulkarni, S. R., et al. 1995, Nature, 378, 463 [Google Scholar]
- N’Diaye, M., Cuevas, S., Sánchez, B., et al. 2018, Proc. SPIE, 10703, 107033E [Google Scholar]
- Nissen, P. E. 2013, A&A, 552, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowak, M., Lacour, S., Mollière, P., Wang, J., & Charnay, B. 2019, in AAS/Division for Extreme Solar Systems Abstracts, 51, AAS/Division for Extreme Solar Systems Abstracts, 404.07 [Google Scholar]
- Öberg, K. I., & Bergin, E. A. 2016, ApJ, 831, L19 [Google Scholar]
- Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Patience, J., King, R. R., de Rosa, R. J., & Marois, C. 2010, A&A, 517, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit dit de la Roche, D. J. M., Hoeijmakers, H. J., & Snellen, I. A. G. 2018, A&A, 616, A146 [EDP Sciences] [Google Scholar]
- Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2020, A&A, 633, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qi, C., Öberg, K. I., Andrews, S. M., et al. 2015, ApJ, 813, 128 [Google Scholar]
- Rajan, A., Rameau, J., De Rosa, R. J., et al. 2017, AJ, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Rajpurohit, A. S., Allard, F., Rajpurohit, S., et al. 2018, A&A, 620, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rizzuto, A. C., Ireland, M. J., & Robertson, J. G. 2011, MNRAS, 416, 3108 [Google Scholar]
- Rousselot, P., Lidman, C., Cuby, J. G., Moreels, G., & Monnet, G. 2000, A&A, 354, 1134 [Google Scholar]
- Ruffio, J.-B., Macintosh, B., Konopacky, Q. M., et al. 2019, AJ, 158, 200 [Google Scholar]
- Samland, M., Mollière, P., Bonnefoy, M., et al. 2017, A&A, 603, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlecker, M., Mordasini, C., Emsenhuber, A., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202038554 [Google Scholar]
- Schmidt, T. O. B., Neuhäuser, R., Seifahrt, A., et al. 2008, A&A, 491, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, T. O. B., Mugrauer, M., Neuhäuser, R., et al. 2014, A&A, 566, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skemer, A. J., Marley, M. S., Hinz, P. M., et al. 2014, ApJ, 792, 17 [Google Scholar]
- Skilling, J. 2006, Bayesian Anal., 1, 833 [Google Scholar]
- Snellen, I. A. G., Brandl, B. R., de Kok, R. J., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Eisner, J., Skemer, A., et al. 2016, ApJ, 829, 39 [Google Scholar]
- Thatte, N., Abuter, R., Tecza, M., et al. 2007, MNRAS, 378, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Uyama, T., Currie, T., Hori, Y., et al. 2020, AJ, 159, 40 [Google Scholar]
- Valletta, C., & Helled, R. 2018, ArXiv e-prints [arXiv:1811.10904] [Google Scholar]
- van der Marel, N., Dong, R., di Francesco, J., Williams, J. P., & Tobin, J. 2019, ApJ, 872, 112 [Google Scholar]
- Viana Almeida, P., Santos, N. C., Melo, C., et al. 2009, A&A, 501, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J. J., Graham, J. R., Dawson, R., et al. 2018, AJ, 156, 192 [Google Scholar]
We used the numpy-LAPACK implementation of the PCA that is implemented as part of the VIP_HCI package (Gonzalez et al. 2017).
All Tables
Estimates of the atmospheric parameters of HIP 65426 b for each grid of synthetic precomputed spectra and for each method.
Imaged planets around intermediate-mass stars with reported abundance measurements.
All Figures
 |
Fig. 1 Detection of HIP 65426 b with SINFONI using (from left to right) a simple derotation and stacking of the individual cubes (nADI), a removal of the halo at each wavelength using a circular profile and a local fit with a 2D polynomials, the PCA algorithm (three modes), and the molecular mapping with an Exo-REM model at Teff = 1600 K, log(g) = 4.0 dex, [M/H] = 0 dex, and C/O = 0.35 (at 20 km s−1). |
| In the text | |
 |
Fig. 2 Application of ForMoSA using the BT-SETTL15 models. Top: bimodal posterior distribution. Bottom left and right: comparison of the best fit and the observed data for the low Teff and high Teff modes. The data points were obtained using the low-resolution SPHERE-IFS spectrum (R ≃ 30–50; blue points, Chauvin et al. 2017), the SPHERE-IRDIS H-band photometry (green and red points; Cheetham et al. 2019), our medium-resolution SINFONI spectrum (R ≃ 5500); orange points, this work), and the NaCo L’ and M’-band photometry (purple and brown points, respectively; Cheetham et al. 2019). We overlaid 50 synthetic spectra picked randomly within the 1σ envelop of each posterior in gray. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but with the grid of Exo-REM spectra and applicable to the K-band SINFONI data. |
| In the text | |
 |
Fig. 4 Application of TExTRIS on SINFONI data of HIP 65426 b using templates of molecules 12CO, H2O, CH4, and NH3 and the full molecule template (top to bottom, respectively) at a velocity of 20 km s−1. Left: cross-correlation maps. The star represents the position of the host star, which lies out of the field. We detect the companion with the full molecule template (S∕N = 2.5), H2O (S∕N = 2.2) and possibly with the 12CO (S∕N = 1.1). Center: distribution of cross-correlation values in the integrated cross-correlation cube for each position. The correlation signal is significant for the full molecule template, H2O, and 12CO, but not for CH4 and NH3. Right: molecular template. |
| In the text | |
 |
Fig. 5 Comparison of the correlation signal of each spectrum of the grid BT-SETTL15 obtained with TExTRIS (color map) and the 2D posterior obtained with ForMoSA (gray contours). We also compare the normalized 1D posterior obtained with ForMoSA on the K band without the continuum (black line) with the normalized 1D pseudo-posteriors extracted from the correlation signal map (blue cross) and a χ2 map (green cross) for the Teff and the log(g) (top and right panel, respectively). The white rectangle corresponds to a nonconverged synthetic spectra. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but with the grid Exo-REM. We considered different layouts around the set of parameters that maximize the CCF in each direction of the parameter space. Models at Teff = 1800 K are unconverged at the given [M/H] and/or C/O, and/or log(g) so that the corresponding CCF values and posteriors stop at Teff = 1700 K. |
| In the text | |
 |
Fig. 7 Cross-correlation signals obtained when using the continuum-subtracted spectrum of HIP 65426 b and the molecular templates (color) or a full Exo-REM spectrum at Teff = 1700 K, log(g) = 4.0 and solar abundances (black). |
| In the text | |
 |
Fig. 8 Comparison of posteriors from ForMoSA with different data and model configurations with the grid Exo-REM. We show in blue that the grid has been taken on the shelf and the continuum has been kept. In red (solid line) we show that the grid has been cleaned of its nonconverged models and the continuum has been kept. In red (dashed line) we plot the grid that has been cleaned of its nonconverged models and the continuum has been removed. We show in grey the grid steps for each parameter. |
| In the text | |
 |
Fig. 9 Radial velocity measurements of HIP 65426 using a total of 78 HARPS spectra obtained between 2017 and 2018 at the La Sill /3.6m telescope and weak metallic lines that are less sensitive to the continuum tracing. |
| In the text | |
 |
Fig. 10 Exploitation of our C/O and [M/H] to constrain the formation pathway. Left: comparison of the posterior of the C/O ratio given by ForMoSA (gradient; black: high likelihood) and different scenario of formation as a function of the accreted solid mass. The solid lines correspond to the GI scenario, and the dashed lines correspond to the CA scenario. The blue, green, and purple curves represent a formation within the water-ice line, between the water and CO2 ice lines, andbetween CO2 and CO ice lines, respectively. Right: comparison of the bulk enrichment of the NGPPS (red dots) and the estimated properties of HIP 65426 b (blue dot). We show here the NGPPS with a mass higher than 0.05 MJup (approximately the mass of Neptune). |
| In the text | |
 |
Fig. A.1 Velocity shifts between the measured and tabulated positions (vacuum) of OH lines at the position of the companion in the stacked datacubes. |
| In the text | |
 |
Fig. B.1 Comparison of the injected (black lines) and extracted simulated planet spectra (color lines) using the methods described in Sect. 2: PCA (blue), the removal of a circular profile at each wavelength (orange), and the removal of a 2D polynomial at each wavelength at the position of the simulated planet (green). The S/N of the recovered spectra is computed from 2.1 to 2.25 μm (dashed vertical lines) and given in parentheses. |
| In the text | |
 |
Fig. B.2 Flux-calibrated spectra of HIP 65426 b obtained with the PCA on both nights and compared to the spectrum extracted from the nADI reduction of the May 25 2018, data followed by a subtraction of a 2D polynomials. The S/N estimated from 2.1 to 2.25 μm is given in parentheses. The red datapoints correspond to the SPHERE K1 and K2 photometry from Cheetham et al. (2019). |
| In the text | |
 |
Fig. B.3 Extracted spectra (with telluric features) of HIP 65426 b for different box sizes (left) and degree (right) of the polynomial fit applied to the nADI data. The S/N of the spectra estimated from 2.1 to 2.25 μm is given in parentheses. |
| In the text | |
 |
Fig. C.1 Investigations of the detection performances using the molecular mapping. Upper left and right: CO molecular maps obtained following the injection of a simulated planet at ρ = 812 mas and PA = 165.2° in the original datacubes using Exo-REM models at Teff = 1650 K, log(g) = 4.0 dex, [M/H] = 0.0,and C/O = 0.35 and 0.70 at a velocity of 30 km s−1. Bottom left: histograms of CCF values at a velocity of 30 km s−1. Bottom right: CCF obtained at the position of the simulated planet. |
| In the text | |
 |
Fig. C.2 Investigations of the characterization performances using the molecular mapping. Left: zoom into the ν = 2–0 CO overtoneat 2.29 μm of normalized continuum-subtracted Exo-REM models at different C/O ratios (Teff = 1650 K, log(g) = 0.40 dex, [M/H] = 0.0 and C/O = 0.35–0.70). Right: CCF between the Exo-REM models and the CO template shown in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


