| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A214 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347653 | |
| Published online | 25 March 2024 | |
Atmospheric properties of AF Lep b with forward modeling
1
Laboratoire Lagrange, Université Côte d’Azur, CNRS,
Observatoire de la Côte d’Azur,
06304
Nice,
France
e-mail: paulina.palma-bifani@oca.eu
2
LESIA, Observatoire de Paris, Univ PSL, CNRS, Sorbonne Univ, Univ de Paris,
5 place Jules Janssen,
92195
Meudon,
France
3
Université Grenoble-Alpes, CNRS, IPAG,
38000
Grenoble,
France
4
Núcleo Milenio Formación Planetaria - NPF, Universidad de Valparaiso,
Av. Gran Bretaña 1111,
Valparaiso,
Chile
5
INAF – Osservatorio Astronomico di Padova,
Vicolo dell'Osservatorio 5,
35122
Padova,
Italy
6
European Southern Observatory,
Alonso de Córdova 3107,
Vitacura,
Santiago,
Chile
7
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
8
Université Paris-Saclay, UVSQ, CNRS, CEA,
Maison de la Simulation,
91191
Gif-sur-Yvette,
France
9
Aix-Marseille Université, CNRS, CNES, LAM,
Marseille,
France
Received:
4
August
2023
Accepted:
9
January
2024
Context. About a year ago, a super-Jovian planet was directly imaged around the nearby young solar-type star AF Lep. The 2.8 MJup planet orbiting at a semimajor axis of 8.2 au matches the predicted location based on the HIPPARCOS-Gaia astrometric acceleration.
Aims. Our aim is to expand the atmospheric exploration of AF Lep b by modeling all available observations obtained with SPHERE at VLT (in the range 0.95–1.65, at 2.105, and at 2.253 µm), and NIRC2 at Keck (at 3.8 µm) with self-consistent atmospheric models.
Methods. To understand the physical properties of this exoplanet, we used ForMoSA. This forward-modeling code compares observations with grids of pre-computed synthetic atmospheric spectra using Bayesian inference methods. We used Exo-REM, an atmospheric radiative-convective equilibrium model, including the effects of nonequilibrium processes and clouds.
Results. From the atmospheric modeling we derived solutions at the low Teff of ~750 K. Our analysis also favors a metal-rich atmosphere (>0.4) and solar to super-solar carbon-to-oxygen ratio (~0.6). We tested the robustness of the estimated values for each parameter by cross-validating our models using the leave-one-out strategy, where all points are used iteratively as validation points. Our results indicate that the photometry point at 3.8 µm strongly drives the metal-rich and super-solar carbon-to-oxygen solutions.
Conclusions. Our atmospheric forward-modeling analysis strongly supports the planetary nature of AF Lep b. Its spectral energy distribution is consistent with that of a young, cold, early-T super-Jovian planet. We recover physically consistent solutions for the surface gravity and radius, which allows us to reconcile atmospheric forward modeling with evolutionary models, in agreement with the previously published complementary analysis done by retrievals. Finally, we identified that future data at longer wavelengths are necessary before we can conclude about the metal-rich nature of AF Lep b.
Key words: planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: formation / planets and satellites: gaseous planets
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The era of exoplanet characterization started two decades ago with atmospheric studies of hot and highly irradiated Jupiters using transmission and emission spectroscopy (Charbonneau et al. 2002). Such observations have been reported for more than 30 exoplanets, including mature hot Jupiters (0.5–10 Gyr), hot Neptunes, and even super-Earths, and have allowed us to access information regarding the composition, spatial structures, and dynamics of exoplanetary atmospheres (Guillot et al. 2022). For young exoplanets (1–100 Myr) that can be spatially resolved, high-contrast imaging techniques (i.e., extreme adaptive optics, coronagraphy, and integral-field spectrographs) currently provide high-fidelity spectra at predominantly low resolution, consisting of tens to thousands of data points over a wide range of wavelengths (0.5–5 µm), and can be acquired in a few telescope hours. These observations have allowed the community to explore the physical properties, composition, and clouds of a few young super-Jovian exoplanets (Currie et al. 2023).
For more than a decade, direct imaging surveys have targeted a broad sample of young nearby stars to search for giant exoplanets beyond typically 10 au with a low discovery rate. The recent results coupling Gaia DR3 and HIPPARCOS proper motions promise to be an efficient target selection tool to narrow down the sample. The proper motion anomaly (PMa) can point toward the presence of companions, potentially planetary-mass ones (Kervella et al. 2022; Brandt et al. 2021), since they grav-itationally impact the proper motion of their host star. AF Lep b is one of these first astrometrically tagged exoplanets confirmed by high-contrast imaging by three different groups nearly simultaneously: Mesa et al. (2023), De Rosa et al. (2023), and Franson et al. (2023).
AF Lep A, also known as HD 35850, HR1817, and HIP 25486, is a 1.09 ± 0.06 M⊙ star of spectral type F8, and slightly sub-solar metallicity ([Fe/H] = –0.27 ± 0.31), located at 26.825 ± 0.014pc (values updated in Zhang et al. 2023). The age of the system is 24 ± 3 Myr (Bell et al. 2015), measured from an absolute isochronal age scale considering its membership to the ß Pictoris moving group. In Zhang et al. (2023) the authors revisit the atmospheric and orbital properties of AF Lep b updating the mass to 2.8 ± 0.5 MJup and the semimajor axis to 8.2 ±1.5 au, using HlPPARCOS-Gaia DR3 PMa and relative astrometry. Their orbital fit is more accurate because they combined the information from the previous three works. The estimated spectral type for this companion is late L (>L6) with a corresponding effective temperature (Teff) first estimated between 1000 and 1700 K by Mesa et al. (2023). Zhang et al. (2023) updated the Teff to be ∽800 K and constrained additional parameters as the surface gravity (log(g)) to be 3.7 dex and a potential metal enrichment on the atmosphere through a retrieval analysis. In addition, the system likely hosts an unresolved debris disk at 46 ± 9 au, as shown by Pearce et al. (2022) who model the red excess of the spectral energy distribution (SED) of AFLepA. In Pearce et al. (2022) they discuss that one additional planetary-mass companion should be present between the orbit of AF Lepb and the inner edge of the debris disk to truncate the disk. However, the existence and location of the disk and planet c remain to be confirmed.
The intriguing combination of the AF Lep b architecture and its unique position on the color-magnitude diagrams (L-T transition), where clouds and disequilibrium chemistry play a prominent role, makes it an exceptional laboratory for gaining insights into the formation and evolution of young planetary systems. Here we study the atmosphere of AF Lepb based on forward modeling, complementary to the retrieval atmospheric study by Zhang et al. (2023). We present an overview of the data in Sect. 2. We describe the atmospheric models in Sect. 3, and explore physically consistent solutions in Sect. 4. We discuss the results and limitations in Sect. 5, and our main takeaway points are in Sect. 6. A detailed view of the model setup and results can be found in Appendices A and B.
Description of the observations.
 |
Fig. 1 Spectroscopic and photometric measurements recovered for AF Lep b from the original publications (Mesa et al. 2023; De Rosa et al. 2023; Franson et al. 2023). The absorption features for H2O, CO, and CH4 are colored, which were computed by Exo-REM (Charnay et al. 2021) at Teff = 800 K, log(g) = 4, [M/H] = 1, and C/O = 0.5. The black solid line represents the total flux for that model. |
2 Available observations
2.1 Published data
The currently available datasets are from the three publications reporting the discovery of AFLepb. The observing conditions and methodology for the three VLT/SPHERE epochs (one from De Rosa et al. 2023 and two from Mesa et al. 2023) and the two Keck/NIRC2 epochs (Franson et al. 2023) are summarized in Table 1. Using the initially published spectroscopic and photometric data points, we reconstructed the SED of AF Lep b (see Fig. 1). Mesa et al. (2023) published observations from two epochs using SPHERE at the VLT at low resolution (Rλ ∽ 30) for the YJH band and photometry points for the K 1 and K2 filters using Angular and Spectral Differential Imaging (ASDI) as their observational technique (see Table 1). De Rosa et al. (2023) observed the target using SPHERE at the VLT with the same filters and a similar spectral resolution, but only one epoch. Their observational technique was reference-star differential imaging (RDI). Franson et al. (2023) observed AF Lep b on two epochs at Keck using the NIRC2 vortex coronagraph in the Ľ -band filter. We constructed two sets of observations, called datasets DR-F and M-F, corresponding to the data published by De Rosa et al. (2023) and Mesa et al. (2023), respectively, and combined with the photometric point from Franson et al. (2023). The K-band flux difference between the K1 and K2 points suggests the potential presence CH4 on the atmosphere of AF Lep b, as visible in Fig. 1 from the slope of the absorption feature. The absorption features are calculated by considering the cross section of the specified molecule together with the collision-induced absorption (CIA) of H2–H2 and H2–He and scattering within Exo-REM (Baudino et al. 2015). We normalized the absorptions by the CIAs and applied an offset for visualization in Fig. 1.
2.2 Flux discrepancies
The two SPHERE datasets do not have the same wavelength coverage because in De Rosa et al. (2023) only upper limits were provided for points below 1.22 µm, which we did not include here. We separated the datasets given that their flux level differs by more than 1 σ between 1.24 and 1.65 µm (see Fig. 1). As shown in Table 1, all SPHERE observations were completed in relatively good conditions in terms of coherence time (>4 ms) and exposure time on the target. Therefore, the flux difference could come from the observing sequence under relatively high-airmass conditions obtained by De Rosa et al. (2023) in RDI that could be more sensitive to the temporal residuals of the extreme adaptive optics correction and of the uncommon path aberrations. Another explanation could come from the data processing itself and the use of two different pipelines (pyKLIP from Pueyo 2016 versus Specal from Galicher et al. 2018). Since the K1 and K2 fluxes look consistent, it is more likely that the difference arises from the data reduction process of the IFS observations. AF Lep b is a faint source in the speckle-limited regime at a close separation that is a challenge for the available data reduction tools to distinguish.
3 Atmospheric forward modeling
We proceeded with forward modeling for the atmospheric study using a self-consistent pre-computed grid. This provided a gain in computation time and a complementary approach with respect to retrievals. We implemented the forward modeling Python package called ForMoSA1, which we have been developing over the past years.
3.1 ForMoSA
ForMoSA is a Bayesian forward-modeling code based on a nested sampling algorithm performing parameter exploration given a likelihood function (Skilling 2006). A full description of the code and applications on planetary-mass companions can be found in Petrus et al. (2021) for HIP 65426 b, in Petrus et al. (2023) for VHS 1256 ABb, and in Palma-Bifani et al. (2023) for AB Pic b. Here we exploit its capabilities for studying the atmosphere of a companion at low spectral resolution (Rλ ~ 30). Several grids with different atmospheric physical descriptions are currently available in the community.
For this work we used Exo-REM, an atmospheric radiative-convective equilibrium model developed and presented in Baudino et al. (2015), Charnay et al. (2018, 2021), and Blain et al. (2021). In this model, the atmosphere is split into pressure levels where the flux is calculated iteratively, assuming radiative-convective equilibrium and initial abundances from Lodders (2010). To calculate the opacities, this model considers the CIA of H2–H2 and H2–He, ro-vibrational bands from nine molecules (H2O, CH4, CO, CO2, NH3, PH3, TiO, VO, and FeH), and resonant lines from Na and K. In addition, Exo-REM includes nonequilibrium chemistry between C-, O-, and N-bearing compounds due to vertical mixing, parameterized by the eddy mixing coefficient, as described in Sect. 2.2.2 from Charnay et al. (2018). The cloud description of the models is specially defined to suit the L/T transition, including iron and silicate clouds. For the grid implemented here, the free parameters are Teff from 400 to 2000 K, log(g) from 3 to 5 dex, [M/H] from -0.5 to 1.0, and C/O from 0.1 to 0.8, at a spectral resolution of ~ 10 000 between 0.7 and 251 µm. In Exo-REM, [M/H] refers to the bulk metallicity, meaning the metal abundance with respect to hydrogen relative to the solar value, where a metal is any element heavier than helium.
In addition to the parameterization of the grids, we explored solutions for the radius (R) and interstellar medium extinction (Av). By default, the re-normalization of the synthetic spectrum is done analytically in ForMoSA. However, when the distance (d) to the target is known, we can include R as a free parameter and re-normalize by (R/d)2. We explored three different combinations of free parameters using uniform priors in the ranges listed in Table A.1. We label the results corresponding to the parameter setup: grid parameters only; grid including R and fixing the distance to AF Lep; grid including R and Av, and fixing the distance. More details regarding the priors and the different setups can be found in Appendix A.
3.2 Results for datasets DR-F and M-F
A convenient feature of nested sampling is that it returns the natural logarithm of the Bayesian evidence (log(z)) together with a measure of the information (h). The information is defined in Skilling (2006) as the logarithm of the fraction of the prior mass that contains the bulk of the posterior mass, also refer to as the “peakiness” of the likelihood function in Nestle2, the nested sampling algorithm implemented in ForMoSA. A log(z) in ForMoSA will always be negative, meaning that the closer to 0, the better the fit. If h is zero, the likelihood function is constant and does not carry any information. The parameter h is used to compute the statistical sampling uncertainty on log(z) as
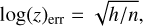 (1)
(1)
with n representing the number of living points.
The derived physical properties for each run are listed in Table A.1. The log(z) has higher values for both datasets when fitting only for the atmospheric model grid parameters. Therefore, we cannot constrain the presence of additional components as interstellar dust causing extinction (Av) or any other additional parameter implemented in ForMoSA.
We show the best-modeled spectra and the posterior parameter distributions in Fig. 2 for both datasets. The errors given by ForMoSA represent 1σ ranges assuming asymmetric Gaussian distributions of the posteriors. They result from the propagation of the data errors through the Bayesian inversion, meaning that they do not account for systematic deviations of the model versus the data, and should be treated as purely statistical. A significant result is that ExoREM favors the tail of the coldest solutions initially found by Mesa et al. (2023). The best fit shows that AF Lep b has a Teff of 900 ± 20 K and 830 ± 90 K respectively for the DR-F and M-F datasets modeled with Exo-REM (see Table 2).
The log(g) best solution for both datasets is high (>4.2 dex). In addition, the derived R is too small and nonphysical (~0.9 Rjup) as often derived with atmospheric models (often referred to as the small radii problem). Regarding the composition, we have some preliminary constraints on [M/H] and the C/O ratio, which must be considered cautiously. The [M/H] is >0.4 for both datasets, consistent with super-solar values. For the C/O ratio, the solutions range between 0.4 and 0.8, compatible with a solar to super-solar value (C/O⊙ = 0.55; Asplund et al. 2009). The bolometric luminosity (log(L/L⊙)) derived by ForMoSA from the models without Av is ∽–5.4 for both datasets, fainter than the estimations of De Rosa et al. (2023).
The Av exploration differs considerably for both datasets. For the M-F dataset, Av is ~0.5 mag, which could be caused by a cir-cumplanetary disk (CPD). The detection of emission lines on the companions 2MASS J0249-0557 c (Chinchilla et al. 2021) from the ß Pictoris moving group suggests that CPDs might surround exoplanets such as AF Lep b. For DR-F, the Av value is unexpectedly high (~7mag). Such high values are expected for a young planet such as PDS 70 c (Wang et al. 2021b), but rather unexpected for older systems such as AFLep. We discuss this high Av result further in Sect. 4.2.
 |
Fig. 2 Best fit for the two datasets using Exo-REM with only grid parameters. The left panel shows the posterior distributions. The upper right panel shows the models, with an offset applied to the DR-F dataset. We extrapolated the models to visualize the complete spectral energy distribution from 0.9 to 4 µm at Rλ = 100. The colored areas represent rough variations on the models when considering 1 σ uncertainties for each parameter. |
ForMoSA initial results for the two datasets.
4 Exploring physically consistent solutions
4.1 Evolutionary models
In Sect. 3.2, we give a preliminary look over the physical properties of this companion and identify high log(g) and small R solutions for the two datasets. Evolutionary models provide an essential extra piece of information to estimate and corroborate parameters such as log(g), radius, and luminosity. We considered the BEX-Hot-COND 03 models (Marleau et al. 2019), which tabulate how the flux varies for different spectral bands as a function of age, radius, luminosity, Teff, and log(g). We report the predictions of these models in terms of iso-mass (red-yellow lines) and iso-temperature (gray lines) curves as a function of R and log(g) for different ages (see Fig. 3), as done previously in Palma-Bifani et al. (2023). A way to interpret the curves in Fig. 3 is by observing that a planet with a fixed mass contracts over time, leading to an increase in log(g).
We extracted from the tabulated variations the predicted log(g) and R values for AFLepb, by using the reported photometry in the H2, K1, and K2 filters from De Rosa et al. (2023) and Mesa et al. (2023), together with the age as input. To avoid interpolations, we used an approximated mass of 3 ±1 Mjup for AF Lep b. We note that the H2 data point predictions from De Rosa et al. (2023) are slightly off, indicating that their spectrum flux level and/or wavelength calibration need to be revisited. Apart from that point, we observe that all other points agree with a lower log(g) of 3.85±0.15 dex, and a larger R of 1.3 ± 0.1 RJup (see Fig. 3). Similar inconsistencies between evolutionary models and forward modeling have already been reported, as for the mid-L-type exoplanet HIP 65426b (Carter et al. 2023). This degeneracy of the atmospheric models seems to resolve when including observations at longer wavelengths for planets at the L-T transition, as explored with JWST/MIRI observations by Boccaletti et al. (2023).
 |
Fig. 3 Evolutionary models from BEX-Hot-COND03. The model curves are a function of R and log(g), which are represented in terms of their age and Teff variations by two different color scales. The red-yellow lines represent iso-mass curves; the gray lines show iso-temperature curves; and the blue-white scale gives the age variations. For AF Lep b the predicted values of Teff range from 950 to 1200 K and of R between 1.2 and 1.4 RJup; log(g) ~ 3.8 dex using the absolute magnitudes from the photometry points published by De Rosa et al. (2023; black) and Mesa et al. (2023; blue). The errors from the magnitude values were propagated onto log(g) and R. |
4.2 DR-F dataset issues
Several issues regarding the DR-F dataset can be identified from the previous sections. In Fig. 2, we observe that the M-F dataset matches the atmospheric models better than the DR-F dataset. The main spectral features are redshifted for the De Rosa et al. (2023) spectrum with respect to the best model. In the corner plot in Fig. 2, we also observe that the DR-F posteriors are much tighter than M-F, but as mentioned before the errors provided by ForMoSA are purely statistical. Therefore, the tighter posteriors do not mean that the DR-F dataset provides tighter constraints, and is instead related to the shifted features observable in Fig. 2 between 1.3 and 1.4 µm together with the different spectral coverage of the two datasets. In addition, the high Av result (~7 mag) from model DR-F E3 with a corresponding Teff of ~ 1870 K is somewhat unrealistic, and tells us that the models do not closely reproduce the flux level of the DR-F observations. Finally, the H2 data point from the De Rosa et al. (2023) evolutionary models prediction is also inaccurate. The overall impact of these discrepancies remains minimal in ForMoSA with ExoREM given that the physical properties are consistent within 3 σ (see Table 2 and right panel of Fig. 2). However, to avoid propagating the wavelength or flux calibration issue onto our solutions, we only use the M-F dataset in the following sections.
Results with and without restrictive log(g) prior for M-F.
 |
Fig. 4 Comparison of the results with and without the restrictive log(g) prior. The colored areas represent 1σ uncertainties, assuming Gaussian distributions of the posteriors. |
4.3 Prior in log(g) and final results
When looking carefully at the log(g) posterior distribution in the corner plot in Fig. 2 we observe a double-peaked solution. The primary solution peaks at 4.8 dex, and a second family of solutions peaks at log(g) around 3.6 dex, albeit with a lower probability. This lower log(g) solution is consistent with the predictions of the evolutionary models, and can be recovered when taking the mass value of 2.8 ± 0.6 Mjup derived by the orbital modeling in Zhang et al. (2023) and the estimated radius from evolutionary models from above into the equation
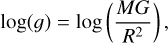 (2)
(2)
where G is the gravitational constant. When replacing the numbers and propagating the errors, log(g) is expected to be 3.7 ± 0.1 dex, in agreement with the lower intensity peak of the posterior distribution and the retrievals solutions by Zhang et al. (2023).
To reconcile the evolutionary models’ predictions with the atmospheric models, we add a restrictive uniform prior over the log(g) (𝒰(3,4)). For the setup of these models, we include the radius as an additional free parameter. In Table 3 and Fig. 4, we compare the final adopted values for the M-F dataset with and without the restrictive prior. We recover the evolutionary model consistent radius and log(g) solutions. In Fig. 4 and the corner plot of Fig. B.1, we show that the updated Teff is about 100 K lower for the low log(g) solution, while the [M/H] and C/O ratio remain consistent within 3 σ. Our results show that it is impossible to favor either of the two model solutions statistically since their Bayesian evidence is equal within the error bars (see last row in Table 3). We note that our restrictive prior does not degrade the error bars on other parameters, which we can interpret as high log(g) solutions (–4.8 dex) being favored from the full range because of degeneration within the model’s parameters. We further explore these degeneracies in Sect. 5.
 |
Fig. 5 Leave-one-out analysis for the model with default priors. This figure consists of six panels where the M-F dataset is plotted and the behavior of the posteriors analyzed for each parameter. A color level is assigned to each point of the spectrum representing the derived values when that point was excluded from the fit. In each panel the posterior value for the case where all points were included is given to guide the comparison. |
5 Discussion
We modeled the atmosphere of AF Lep b with forward modeling, and recovered the atmospheric parameters. We then identified that using a prior is a straightforward solution to reconcile evolutionary and atmospheric models. Our atmospheric physical property solutions are given by the model with the restrictive prior (see Table 3 and model b0 in Table B.2), meaning that the AF Lep b Teff is ∽750K, log(g) is ∽3.7dex, [M/H] is >0.4, C/O is ∽0.6, R is ∽1.2 Rjup, and log(L/L⊙) is ∽–5.36.
The use of a prior allowed our results based on forward-modeling analysis to be consistent for the Teff and log(g) with the previous characterization using atmospheric retrieval by Zhang et al. (2023), where they derived a Teff of 800 K and a log(g) of 3.7 dex, together with an unconstrained C/O ratio and a super-solar metallicity. The metallicity obtained by Zhang et al. (2023) ([Fe/H] > 1) is higher than ours ([M/H]∽0.6). The labels used for the metallicity in the two cases are different, but they both refer to the bulk metallicity. In Zhang et al. (2023), the metallic-ity is explored with a uniform prior between –1 and 2, while in Exo-REM we can only explore values between –0.5 and 1. Both values indicate a metal-enriched atmosphere for AF Lep b, but need to be further investigated given the large uncertainties.
In our approach, the Bayesian evidence does not favor one model over another as the best solution. In other words, the single number hiding behind the Bayesian evidence does not contain enough information to reveal where and how the models fail to perform well. To further address the models’ robustness, we performed a cross-validation test similar to that presented by Welbanks et al. (2022). The leave-one-out strategy is a case of cross-validation tests where we remove a data point from the original set and evaluate the impact of that change on the posterior distribution. The process is repeated for each data point until every point has been used as a testing point. We based the application of this method on the in-progress book called “An Introduction to Bayesian Data Analysis for Cognitive Science” publicly available through GitHub by Bruno Nicenboim, Daniel Schad, and Shravan Vasishth3. We computed the models for the M-F dataset and the Exo-REM grid in the cases with and without the restrictive log(g) prior, leaving one point out iteratively. The 76 model runs with the corresponding best-fit values and uncertainties are listed in Table B.1 for the default prior and in Table B.2 for the restrictive log(g) prior.
The analysis we can extract from these models does not lead us to favor one model or the other, but allows us to visualize the presence of outliers and critical points driving the results. In Figs. 5 and 6, we present the variations for every parameter as a function of leaving one point out iteratively. When the posterior value (color scale) is close to the value obtained when all points were included (first row in Tables B.1 and B.2), the predictive capacity of the models in the specific wavelength is high; conversely, when a point is assigned a very different value, it means that this point is driving the results. In other words, when that point is not included, the results change drastically, meaning that the point is an outlier in the data or carries valuable information on the atmospheric properties of the object.
In the case of AF Lep b, we identified two critical conclusions from this analysis. The first conclusion is that the photometric point from Franson et al. (2023) at 3.8 µm significantly impacts the temperature Teff solution (see Fig. 5). When that point is taken out, the Teff lowers by –100 K. In the same way, this point favors high-metallicity solutions. In Fig. 6 with a log(g) exploration restricted, we find that the same behavior is observed. Although the new solutions for Teff, log(g), and R seem more constrained, the 3.8 µm photometric point still drives and favors high-metallicity and super-solar C/O ratio solutions. We draw attention to these results, as one single photometric point significantly influences current fitting solutions on metallicity and C/O ratios. There can be several explanations for such peculiar behavior regarding this data point. The effect of clouds varies as we transition from near-infrared (IR) to mid-IR since the emission will reach us from different atmospheric layers (Madhusudhan 2019), and we cannot rule out that the models are not able to simultaneously handle these two regimes.
The second conclusion is that, when we focus on the last data point of the SPHERE/IFS spectrum from Mesa et al. (2023) (λ = 1.645 µm), we observe that this value behaves differently with respect to its neighbors. The flux decreases for this last point, which does not seem realistic from the spectral energy distribution for a late-L object (see Fig. 6). This behavior can also be observed in the best model’s extrapolation compared to the data points in Fig. 2. Together, the two things seem to be telling us that this point is probably an outlier that needs to be investigated with further data analysis and new observations.
6 Conclusions
Our atmospheric forward-modeling analysis strongly supports the planetary nature of AF Lep b. Its spectral energy distribution between 0.96 and 3.8 µm is consistent with that of a young, cold, early-T super-Jovian planet. We recover physically consistent solutions for the radius by implementing a restrictive prior on the surface gravity, which allows us to solve the small radius problem for this specific exoplanet. Our final solutions agree with the atmospheric retrieval solutions published by Zhang et al. (2023). We implemented a cross-validation analysis, allowing us to identify the most critical data points driving the solutions, and we conclude that the high-metallicity and super-solar carbon-to-oxygen ratio solutions driven by the photometry point from Franson et al. (2023).
It should be noted that spectroscopic data at longer wavelengths or higher spectral resolution have the potential to solve some of the degeneracies encountered with low-resolution observations. This can be observed, for example, in the works done with VLTI/GRAVITY observations by Nowak et al. (2020) on ß Picb and by Mollière et al. (2020) on HR 8799 e, or with the Keck/KPIC observations published by Wang et al. (2021a) for HR 8799 cde and by Xuan et al. (2022) for HD4747B, or soon with the promising VLT/HiRISE observations performed by Vigan et al. (2024). To close this work, we would like to state that new observations are necessary before a conclusion about AF Lep b’s metal-rich nature and super-solar C/O ratio can be reached.
Acknowledgements
We would like to thank Vivien Parmentier, Andrea Chiavassa, and Mark Hammond for their insightful comments on this analysis. This publication used the SIMBAD and VizieR databases operated at the CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia https://www.cosmos.esa.int/gaia, processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular, the institutions participating in the Gaia Multilateral Agreement. P.P.-B., G.C., and M.B. received funding from the French Programme National de Planétologie (PNP) and de Physique Stellaire (PNPS) of CNRS (INSU). D.B., P.P.-B., and G.C. also received funding from the 2023 EPEx program of Observatoire Côte d'Azur. D.M. acknowledges the PRIN-INAF 2019 “Planetary systems at young ages (PLATEA)” and ASI-INAF agreement no. 2018-16-HH.0. C.D. acknowledges support from the European Research Council under the European Union’s Horizon 2020 research and innovation program under grant agreement no. 832428-Origins and support from Labex OSUG (Investissements d’avenir -ANR10 LABX56). S.P. acknowledges the support of ANID, - Millennium Science Initiative Program - Center Code NCN19_171 and NCN2021_080.
Appendix A Details on the atmospheric modeling with ForMoSA
The posterior best values and 1 σ asymmetric confidence intervals for each free parameter and dataset can be found in Table A.1. We also list the Bayesian evidence used to compare models in the last column of Table A.1.
Posteriors of the atmospheric models performed with ForMoSA.
Appendix B Leave-one-out posteriors
The two tables in this section show the same results as Table A.1, but for the leave-one-out setup. The M-F dataset has 37 points in total. We therefore made 38 models in both cases, where one point was left out iteratively, and the model with index 0 is the validation case with all points included.
 |
Fig. B.1 Cornet plot comparing the posterior distributions for the models a0 and b0 from Table B.1 and B.2 where a 𝒰(3, 4) prior was added to the purple model (b0) to recover solutions in agreement with the evolutionary models. |
Leave-one-out models for the M-F dataset with Exo-REM and default priors.
Leave-one-out models for the M-F dataset with Exo-REM and a restrictive log(g) prior.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baudino, J.-L., Bézard, B., Boccaletti, A., et al. 2015, A&A, 582, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, C. P. M., Mamajek, E. E., & Naylor, T. 2015, MNRAS, 454, 593 [Google Scholar]
- Blain, D., Charnay, B., & Bézard, B. 2021, A&A, 646, A15 [EDP Sciences] [Google Scholar]
- Boccaletti, A., Mâlin, M., Baudoz, P., et al. 2023, A&A, submitted [arXiv: 2310.13414] [Google Scholar]
- Brandt, G. M., Michalik, D., Brandt, T. D., et al. 2021, AJ, 162, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, A. L., Hinkley, S., Kammerer, J., et al. 2023, ApJ, 951, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [Google Scholar]
- Charnay, B., Bézard, B., Baudino, J.-L., et al. 2018, ApJ, 854, 172 [Google Scholar]
- Charnay, B., Blain, D., Bezard, B., et al. 2021, A&A, 646, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chinchilla, P., Béjar, V. J. S., Lodieu, N., Zapatero Osorio, M. R., & Gauza, B. 2021, A&A, 645, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Currie, T., Biller, B., Lagrange, A.-M., et al. 2023, in Protostars and Planets VII, eds. S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, & M. Tamura, ASP Conf. Ser., 534, 799 [NASA ADS] [Google Scholar]
- De Rosa, R. J., Nielsen, E. L., Wahhaj, Z., et al. 2023, A&A, 672, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franson, K., Bowler, B. P., Zhou, Y., et al. 2023, ApJ, 950, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Galicher, R., Boccaletti, A., Mesa, D., et al. 2018, A&A, 615, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Fletcher, L. N., Helled, R., et al. 2022, arXiv e-prints [arXiv: 2205.04100] [Google Scholar]
- Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2010, in Formation and Evolution of Exoplanets (Weinheim: Wiley-VCH Verlag GmbH), 157 [Google Scholar]
- Madhusudhan, N. 2019, ARA&A, 57, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Marleau, G. D., Coleman, G. A., Leleu, A., & Mordasini, C. 2019, A&A, 624, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mesa, D., Gratton, R., Kervella, P., et al. 2023, A&A, 672, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., Stolker, T., Lacour, S., et al. 2020, A&A, 640, A131 [Google Scholar]
- Nowak, G. C. M., Lacour, S., Mollière, P., et al. 2020, A&A, 633, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palma-Bifani, P., Chauvin, G., Bonnefoy, M., et al. 2023, A&A, 670, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearce, T. D., Launhardt, R., Ostermann, R., et al. 2022, A&A, 659, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2021, A&A, 648, A59 [EDP Sciences] [Google Scholar]
- Petrus, S., Chauvin, G., Bonnefoy, M., et al. 2023, A&A, 670, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pueyo, L. 2016, ApJ, 824, 117 [Google Scholar]
- Skilling, J. 2006, Bayesian Analys., 1, 833 [CrossRef] [Google Scholar]
- Vigan, A., El Morsy, M., Lopez, M., et al. 2024, A&A, 682, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J. J., Ruffio, J.-B., Morris, E., et al. 2021a, AJ, 162, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. J., Vigan, A., Lacour, S., et al. 2021b, AJ, 161, 148 [Google Scholar]
- Welbanks, L., McGill, P., Line, M., & Madhusudhan, N. 2022, BAAS, 54, 102.105 [Google Scholar]
- Xuan, J. W., Wang, J., Ruffio, J.-B., et al. 2022, ApJ, 937, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z., Mollière, P., Hawkins, K., et al. 2023, AJ, 166, 198 [NASA ADS] [CrossRef] [Google Scholar]
ForMoSA documentation at https://formosa.readthedocs.io
Nestle documentation at http://kylebarbary.com/nestle/
Access to the online book is available at https://vasishth.github.io/bayescogsci/book/
All Tables
Leave-one-out models for the M-F dataset with Exo-REM and a restrictive log(g) prior.
All Figures
 |
Fig. 1 Spectroscopic and photometric measurements recovered for AF Lep b from the original publications (Mesa et al. 2023; De Rosa et al. 2023; Franson et al. 2023). The absorption features for H2O, CO, and CH4 are colored, which were computed by Exo-REM (Charnay et al. 2021) at Teff = 800 K, log(g) = 4, [M/H] = 1, and C/O = 0.5. The black solid line represents the total flux for that model. |
| In the text | |
 |
Fig. 2 Best fit for the two datasets using Exo-REM with only grid parameters. The left panel shows the posterior distributions. The upper right panel shows the models, with an offset applied to the DR-F dataset. We extrapolated the models to visualize the complete spectral energy distribution from 0.9 to 4 µm at Rλ = 100. The colored areas represent rough variations on the models when considering 1 σ uncertainties for each parameter. |
| In the text | |
 |
Fig. 3 Evolutionary models from BEX-Hot-COND03. The model curves are a function of R and log(g), which are represented in terms of their age and Teff variations by two different color scales. The red-yellow lines represent iso-mass curves; the gray lines show iso-temperature curves; and the blue-white scale gives the age variations. For AF Lep b the predicted values of Teff range from 950 to 1200 K and of R between 1.2 and 1.4 RJup; log(g) ~ 3.8 dex using the absolute magnitudes from the photometry points published by De Rosa et al. (2023; black) and Mesa et al. (2023; blue). The errors from the magnitude values were propagated onto log(g) and R. |
| In the text | |
 |
Fig. 4 Comparison of the results with and without the restrictive log(g) prior. The colored areas represent 1σ uncertainties, assuming Gaussian distributions of the posteriors. |
| In the text | |
 |
Fig. 5 Leave-one-out analysis for the model with default priors. This figure consists of six panels where the M-F dataset is plotted and the behavior of the posteriors analyzed for each parameter. A color level is assigned to each point of the spectrum representing the derived values when that point was excluded from the fit. In each panel the posterior value for the case where all points were included is given to guide the comparison. |
| In the text | |
 |
Fig. 6 Same leave-one-out analysis as in Fig. 5, but for the models with restrictive log(g) prior. |
| In the text | |
 |
Fig. B.1 Cornet plot comparing the posterior distributions for the models a0 and b0 from Table B.1 and B.2 where a 𝒰(3, 4) prior was added to the purple model (b0) to recover solutions in agreement with the evolutionary models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


