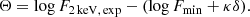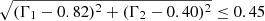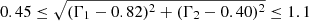| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038899 | |
| Published online | 13 October 2020 | |
Quasars as standard candles
III. Validation of a new sample for cosmological studies⋆
1
Dipartimento di Fisica e Astronomia, Università di Firenze, Via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
e-mail: elisabeta.lusso@unifi.it
2
INAF – Osservatorio Astrofisico di Arcetri, 50125 Florence, Italy
3
Dipartimento di Fisica, Università degli studi di Napoli Federico II, Via Cinthia, 80126 Napoli, Italy
4
INFN – Sezione di Napoli, Via Cinthia 9, 80126 Napoli, Italy
5
Scuola Superiore Meridionale, Università di Napoli Federico II, Largo San Marcellino 10, 80138 Napoli, Italy
6
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Milano, Via Corti 12, 20133 Milano, Italy
7
Gran Sasso Science Institute, Via F. Crispi 7, 67100 L’Aquila, Italy
8
Laboratory for Theoretical Cosmology, Tomsk State University of Control Systems and Radioelectronics (TUSUR), 634050 Tomsk, Russia
9
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
10
Yale University, Department of Computer Science, 51 Prospect St, New Haven, CT 06511, USA
11
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, via Gobetti 93/3, 40129 Bologna, Italy
12
Dipartimento di Astronomia, Università degli Studi di Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
13
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
Received:
12
July
2020
Accepted:
19
August
2020
We present a new catalogue of ∼2400 optically selected quasars with spectroscopic redshifts and X-ray observations from either Chandra or XMM–Newton. The sample can be used to investigate the non-linear relation between the ultraviolet (UV) and X-ray luminosity of quasars as well as to build a Hubble diagram up to a redshift of z ∼ 7.5. We selected sources that are neither reddened by dust in the optical and UV nor obscured by gas in the X-rays, and whose X-ray fluxes are free from flux-limit-related biases. After checking for any possible systematics, we confirm, in agreement with our previous works, that the X-ray to UV relation provides distance estimates matching those from supernovae up to z ∼ 1.5, and its slope shows no redshift evolution up to z ∼ 5. We provide a full description of the methodology for testing cosmological models, further supporting a trend whereby the Hubble diagram of quasars is well reproduced by the standard flat cold dark matter model up to z ∼ 1.5–2, but strong deviations emerge at higher redshifts. Since we have minimised all non-negligible systematic effects and proven the stability of the LX − LUV relation at high redshifts, we conclude that an evolution of the expansion rate of the Universe should be considered as a possible explanation for the observed deviation, rather than some systematic (redshift-dependent) effect associated with high-redshift quasars.
Key words: galaxies: active / quasars: general / quasars: supermassive black holes / methods: statistical
Full Table 3 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/642/A150
© ESO 2020
1. Introduction
Quasars are the most luminous and persistent energy sources in our Universe. As they can be observed up to a redshift of ≃7.5 (Bañados et al. 2018), when the age of the Universe was less than ≃700 million years old, quasars bear an extraordinary potential as cosmological probes. Several techniques making use of empirical correlations between quasar properties have been proposed to determine cosmological parameters such as the dark matter (ΩM) and dark energy (ΩΛ) content of the Universe. Examples include the relation between the continuum luminosity and the emission-line equivalent width (Baldwin 1977), or with the radius of the quasar broad-line region established via reverberation mapping (Watson et al. 2011). Another luminosity distance estimator combines the correlation between the quasar X-ray variability amplitude and its black hole (BH) mass (La Franca et al. 2014). Nonetheless, these correlations are affected by too large a dispersion (up to ≃0.6 dex), and they are typically applicable over a limited redshift range. Other promising methods employ geometric distances through, again, the broad-line region radius via reverberation mapping (Elvis & Karovska 2002), the luminosity of super-Eddington accreting quasars (Wang et al. 2013), the eigenvector formalism in the quasar main sequence (Marziani & Sulentic 2014), or the combination of spectroastrometry and reverberation mapping (Wang et al. 2020). All of these techniques still need some level of refinement, and (or) much higher sample statistics, in order to be competitive as cosmological tools.
Since 2015, our group has been developing a new technique that hinges on the observed non-linear relation between the ultraviolet (UV, at 2500 Å, LUV) and the X-ray (at 2 keV, LX) emission in quasars (e.g. Tananbaum et al. 1979, 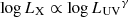 , with γ ≃ 0.6) to provide an independent measurement of their distances, thus turning quasars into standardizable candles and extending the distance modulus–redshift relation (or the so-called Hubble-Lemaître diagram) of supernovae Ia to a redshift range that is still poorly explored (z > 2; Risaliti & Lusso 2015).
, with γ ≃ 0.6) to provide an independent measurement of their distances, thus turning quasars into standardizable candles and extending the distance modulus–redshift relation (or the so-called Hubble-Lemaître diagram) of supernovae Ia to a redshift range that is still poorly explored (z > 2; Risaliti & Lusso 2015).
The applicability of our technique is based on the understanding that most of the observed dispersion in the LX − LUV relation is not intrinsic to the relation itself but due to observational issues, such as X-ray absorption by gas, UV extinction by dust, calibration uncertainties in the X-rays (Lusso 2019), variability, and selection biases associated with the flux limits of the different samples. In fact, with an optimal selection of clean sources (i.e. where we can measure the intrinsic UV and X-ray quasar emission), the dispersion drops from 0.4 to ≃0.2 dex (Lusso & Risaliti 2016, 2017). A key consequence of this technique is that the LX − LUV relation must be the manifestation of a universal mechanism at work in the quasar engines. However, the details on the physical process at the origin of this relation are still unknown (e.g. Haardt & Maraschi 1991, 1993; Haardt et al. 1994; Nicastro 2000; Merloni 2003; Lusso & Risaliti 2017; Arcodia et al. 2019).
The main results of our work are that the distance modulus-redshift relation of quasars at z < 1.4 is in agreement with that of supernovae Ia and with the concordance cold dark matter (ΛCDM) model (Risaliti & Lusso 2015, 2019; Lusso et al. 2019), yet a deviation from ΛCDM emerges at a higher redshift, with a statistical significance of about 4σ. If we interpret the latter result by considering an evolution of the dark energy equation of state in the form w(z) = w0 + wa × z/(1 + z), the data suggest that the dark energy density is increasing with time (Risaliti & Lusso 2019; Lusso et al. 2019).
As our approach may still have shortcomings, we need to demonstrate that the observed deviation from ΛCDM at a redshift > 2 is neither driven by systematics in the quasar sample selection nor by the procedure adopted to fit the quasar Hubble-Lemaître diagram. To build a quasar sample that can be utilised for cosmological purposes, both X-ray and UV data are required to cover the rest-frame 2 keV and 2500 Å. The choice of these monochromatic luminosities is rather arbitrary, and mostly based on historical reasons. It is possible that the LX − LUV relation is tighter with a different choice of the indicators of UV and X-ray emission (see e.g. Young et al. 2010). A careful analysis of this issue may also provide new insights as to the physical process responsible for this relation. In the present analysis, we do not investigate the possible alternatives, but we focus on demonstrating that the commonly used relation is calibrated in a robust way and can be safely used as a tool to determine quasar distances. In this third paper of our series, we thus mainly concentrate on the quasar sample selection, whilst we defer a detailed analysis of the cosmographic fitting technique we adopted to a forthcoming publication.
At the time of writing this paper, the most extended spectroscopic coverage in the UV is given by the Sloan Digital Sky Survey (Pâris et al. 2018), which supplies more than ∼500 000 quasars with spectroscopic redshift up to z ∼ 7. This sample needs to be cross-matched with the current X-ray catalogues, namely the Chandra X-ray Catalogue (CXC2.0, Evans et al. 2010) and the 4XMM Data Release 9 (Webb et al. 2020), which contain all the X-ray sources detected by the Chandra and XMM–Newton observatories that are publicly available in the respective archives. These data need to be complemented by dedicated pointed observations of active galactic nuclei1 (AGN) at both low (z < 0.1) and high (z > 3) redshifts to extend the coverage and increase the sample statistics in the distance modulus–redshift relation.
The main aims of this manuscript are to discuss in detail all the criteria required to select a homogeneous sample of quasars for cosmological purposes from the above archives, and to present the key steps in fitting the Hubble-Lemaître diagram that can be adopted to reproduce our results. Specifically, we examine the effects on the sample selection and on the UV and X-ray flux measurements of dust extinction and host-galaxy contamination, gas absorption in the X-rays, and Eddington bias. We identify the quasars that can be used for testing cosmological models, and investigate in depth all the possible systematics in the quasar Hubble-Lemaître diagram as a function of the contaminants mentioned above.
Since a detailed spectroscopic UV and X-ray analysis can only be carried out only for a relatively small number of sources, our latest quasar sample presented here still relies also on broadband photometry in both UV and X-rays, as most of the parameters currently employed in our works, such as monochromatic UV and X-ray fluxes, UV colours and X-ray slopes, are derived from the photometric spectral energy distribution (SED) of our sources. In the future, we plan to gradually move towards a full spectroscopic analysis, as spectroscopy can deliver cleaner measurements of the relevant parameters.
The paper is constructed as follows. In Sect. 2 we present the different data sets employed to build the main quasar sample and the procedures adopted to measure the UV fluxes and slopes from the photometry. Section 3 discusses how the photometric quasar SEDs are constructed, whilst in Sect. 4 we justify the use of the rest-frame 2500 Å monochromatic fluxes derived from photometry. Section 5 is devoted to the presentation of our technique to compute the monochromatic X-ray emission and the photon index from the catalogued broadband flux values. Section 6 gives reasons for the analysis of the Hubble diagram where non-detections are neglected. In Sect. 7 we discuss the several quality filters employed to select a homogeneous sample of quasars for cosmological purposes, whilst in Sect. 8 we verify that the LX − LUV relation for the final “best” quasar sample does not evolve with redshift. Section 9 presents the main steps adopted to fit the Hubble diagram using a model independent technique (i.e. cosmography), whilst in Sect. 10 we fit the Hubble diagram with the most commonly used ΛCDM extension to test our fitting technique and to verify how different choices regarding the fitting method and the quasar sample selection affect the final results. In Sect. 11 we carry out an in-depth investigation on possible remaining systematics in the residuals of the quasar Hubble diagram, as a function of the parameters involved in the selection of the sample. Finally, we summarise our work and main results in Sect. 12. Although we mainly use fluxes, whenever luminosity values are reported we have assumed a standard flat ΛCDM cosmology with ΩM = 0.3 and H0 = 70 km s−1 Mpc−1.
2. The data set
The broad-line quasar sample we considered for our analysis has been assembled by combining seven different samples from both the literature and the public archives. The former group includes the samples at z ≃ 3.0–3.3 by Nardini et al. (2019), 4 < z < 7 by Salvestrini et al. (2019), z > 6 by Vito et al. (2019), and the XMM–XXL North quasar sample published by Menzel et al. (2016). We then complemented this collection by including quasars from a cross-match of optical (i.e. the Sloan Digital Sky Survey) and X-ray public catalogues (i.e. XMM–Newton and Chandra), which we refer to as SDSS–4XMM and SDSS–Chandra samples hereafter. Finally, we also added a local subset of AGN with UV (i.e. International Ultraviolet Explorer) data and X-ray archival information. The same order in which these samples have been introduced above is adopted as an order of priority to take into account all the possible overlaps. X-ray fluxes coming from pointed observations and medium-deep surveys (i.e. XMM–XXL) have been considered first, as they are generally more reliable. The main parent sample is composed by ∼19 000 objects spanning the redshift range 0.009 < z < 7.52. In Fig. 1 we present the distribution of rest-frame 2500 Å luminosities as a function of redshift for all the different quasar sub-samples. A summary of the sample statistics is provided in Table 1, whilst below we describe in detail of how each sub-sample has been constructed.
 |
Fig. 1. Distribution of luminosities at rest-frame 2500 Å as a function of redshift for the main (grey points) and the selected (cleaned) samples (see Sect. 7.4). Brown and yellow squares: high-z sample (Salvestrini et al. 2019; Vito et al. 2019, see Sect. 2.6), cyan points: SDSS–4XMM (Sect. 2.1), brown triangles: XMM–XXL (Menzel et al. 2016, Sect. 2.3), orange pentagons: the local AGN sample (Sect. 2.7), red stars: z ≃ 3 quasar sample (Nardini et al. 2019, green star: new z ≃ 4 quasar (Sect. 2.5), gold pentagons: SDSS–Chandra (Sect. 2.2). |
Summary of sample statistics.
2.1. The SDSS–4XMM sample
The bulk of the data belongs to the Sloan Digital Sky Survey quasar catalogue, Data Release 14 (hereafter SDSS–DR14; Pâris et al. 2018). The catalogue contains 526 356 optically selected quasars detected over 9376 deg2 with robust identification and spectroscopic redshift. Firstly, we removed from the catalogue all quasars flagged as broad absorption lines (BALs, where sources with the BI_CIV = 0 flag are non-BALs) and kept all the objects with a measurement in all the SDSS magnitudes. This preliminary selection leads to 503 744 quasars.
We note that the BAL classification in the SDSS–DR14 quasar catalogue is based on a fully automated detection procedure on C IV absorption troughs for sources at z > 1.57. Hence, a number of BAL quasars might still be included in this preliminary sample. BAL quasars are often found in galaxies with red optical and UV colours and hard X-ray spectra (e.g. Gallagher et al. 2006), the latter suggesting that their relative X-ray weakness could be primarily due to gas absorption. The selection criteria discussed in Sect. 7 efficiently remove red and X-ray absorbed quasars, possibly excluding most unclassified BALs from the final sample.
The photometric rest-frame spectral energy distribution (SED), whose derivation is discussed in Sect. 3, is then used to define the parameters required to exclude radio-loud, dust-absorbed or host-galaxy contaminated sources. Also the rest-frame monochromatic luminosities at 2500 Å are obtained from the photometric SEDs. For comparison purposes, as in our previous works on this topic, we discard bright radio quasars through the same radio loudness parameter, R, as that used in Shen et al. (2011), which is defined as the ratio of the rest-frame fluxes at 6 cm and 2500 Å (i.e. R = Lν,6 cm/Lν,2500 Å). A quasar is then classified as radio-loud if R > 10. We computed R for the 17 561 objects with a FIRST detection, 16 315 of which are indeed radio-loud and have been therefore excluded from our sample.
To further remove powerful radio-loud quasars we considered the catalogue published by Mingo et al. (2016), which is currently the largest available Mid-Infrared (WISE), X-ray (3XMM) and Radio (FIRST+NVSS) collection (MIXR) of AGN and star-forming galaxies: 2753 sources, 918 of which are considered radio-loud based on multiwavelength diagnostics (we refer to their paper for details). We excluded 349 quasars in our sample flagged as radio-loud in the MIXR catalogue within a matching radius of 3 arcsec. This yields 487 080 SDSS radio-quiet quasars with a LUV measurement.
This SDSS quasar sample is then cross-matched with the latest XMM–Newton source catalogue 4XMM–DR9 (Webb et al. 2020). 4XMM–DR9 is the fourth generation catalogue of serendipitous X-ray sources, which contains 810 795 detections (550 124 unique X-ray sources) made publicly available by 2018 December 182. The net sky area covered (taking into account overlaps between observations) is ∼1152 deg2, for a net exposure time of ≥1 ksec.
To select reliable X-ray detections, we have applied the following quality cuts in the 4XMM–DR9 catalogue: SUM_FLAG < 3 (low level of spurious detections), OBJ_CLASS≤3 (quality classification of the whole observation3) and EP_TIME > 0 (EPIC exposure time available). These filters lead to 692 815 X-ray detections. We have adopted a maximum separation of 3 arcsec to provide optical classification and spectroscopic redshift for all the cross-matched objects. This yields 22 196 XMM–Newton observations: 13 858 unique sources (3976 of which have ≥2 observations) covering the redshift range 0.056 < z < 4.306.
Following the results presented by Lusso & Risaliti (2016, LR16 hereafter; see their Sect. 4), we decided to average all X-ray observations for sources with multiple detections that meet our selection cuts, including that associated with the Eddington bias (see Sect. 7.3 for details). In this way, we reduce the effect of X-ray variability on the dispersion (∼0.12 dex, see Sect. 4 in LR16) by using only unbiased detections.
For each XMM–Newton observation, we have computed the EPIC sensitivity (5σ minimum detectable flux) at 2 keV following a similar approach as in LR16. We first estimated the minimum detectable flux in the soft band for both pn and MOS as a function of the on-time4 exposure following the relations plotted in Fig. 3 by Watson et al. (2001). The total MOS on-time exposure is the one with the largest exposure value between the two individual cameras, MOS1 and MOS2. We then corrected this sensitivity for the pn and MOS, using the same vignetting correction for both cameras at the energy of 1.5 keV, as a function of their respective off-axis angles, where the smaller value between the two individual cameras is again assumed for the MOS. The sensitivity at 2 keV (Fmin) is then estimated for both pn and MOS, assuming a photon index of 1.7, following the same approach as in LR16. Finally, we have prioritised the pn sensitivity flux values over the MOS when available.
2.2. The SDSS–Chandra sample
To further increase the statistics, we also cross-matched the SDSS–DR14 quasar catalogue with the second release of the Chandra Source Catalog (CSC2.0). The CSC2.05 (Evans et al. 2010) contains ∼315 000 X-ray sources observed in 10 382 Chandra ACIS and HRC-I imaging observations publicly released prior to 2015. A cross-match of these two catalogues, with a matching radius of 3 arcsec, leads to 7036 unique objects. The detailed analysis of this sample will be presented in a forthcoming publication (Bisogni et al., in prep.). Briefly, from this sample we excluded radio-loud and BAL quasars following the same approach adopted with the SDSS–4XMM sample. SEDs were also compiled for all the quasars (see Sect. 3), which were then used to estimate both LUV and optical colours and thus select objects with low levels of dust reddening and host-galaxy contamination.
CSC2.0 provides photometric information and data products for each source, already reduced and ready to use for spectroscopic analysis6. We selected all the AGN with at least one measure of the flux in the soft band and with an off-axis angle < 10 arcmin (3569 quasar observations, 2392 single quasars). We performed a full spectral analysis with the XSPEC v.12.10.1b X-ray spectral fitting package (Arnaud 1996). For each observation, we assumed a model consisting of a power law with Galactic absorption, as provided by the CSC 2.0 catalogue at the source location. The spectral analysis provides us with the rest-frame flux at 2 keV and its uncertainty. Overall, the Chandra data have a reasonable signal-to-noise ratio (S/N > 5 in the soft band) that ensures uncertainties on FX of the order of 0.15 dex or better.
Flux limits are estimated for any given Chandra observation by computing the percentage of net counts to deduce the significance of the source detection, and a factor that takes into account the level of background, Pbkg. The 0.5–2 keV and 2–7 keV fluxes are then multiplied by Pbkg to obtain an approximate value of the background flux in these energy bands. The flux limit in each energy band is then estimated from the background flux by assuming a minimum signal-to-noise ratio of 3. The flux limit at 2 keV is finally inferred by interpolation (or extrapolation) of the band flux limits, depending on the redshift of the source.
2.3. The XMM–XXL sample
We also considered the AGN sample published by Menzel et al. (2016) from the equatorial subregion of the XMM–Newton XXL survey (XMM–XXL, PI: Pierre), that is, XMM–XXL North (in the following we refer to this sample as XXL for simplicity), which overlaps with the SDSS–DR8 imaging survey. XMM–XXL North is a medium-depth (10 ks per pointing) X-ray survey distributed around the area of the original 11 deg2 XMM-LSS survey. The total catalogue contains 2570 X-ray AGN with optical counterparts, spectroscopic redshifts and emission lines information. From the main sample, we considered only the AGN classified as (point-like) optically unobscured (flagged as BLAGN1; 1353 sources). To have consistent measurements of optical and UV luminosities and redshifts amongst the different samples, we cross-matched the XXL BLAGN1 with the SDSS–DR14 quasar catalogue (with 3 arcsec matching radius) finding 1067 objects. We have then included only the AGN with available SDSS photometry and classified as non-BAL, leading to 915 AGN. For this sample, we compiled the photometric SEDs following the same approach as in Sect. 3, and computed luminosities at various rest-frame wavelengths (e.g. 2500 Å, 1450 Å, 6 cm), optical and UV colours (Γ1, Γ2, see Sect. 7.1 for details) and radio loudness. The latter parameter further excludes 75 AGN, leading to a final sample of 840 sources.
2.4. The z ∼ 3 quasar sample
We included a sample of 29 bright (Lbol > 1047 erg s−1) quasars at z ≃ 3 with X-ray observations obtained from an extensive campaign performed with XMM–Newton (cycle 16, proposal ID: 080395, PI: Risaliti). This campaign targeted 30 quasars7 in the z = 3.0–3.3 redshift range for a total exposure of 1.13 Ms. This sample, selected in the optical from the SDSS Data Release 7 to be representative of the most luminous, intrinsically blue quasar population, boasts by construction a remarkable degree of homogeneity in terms of optical and UV properties. The X-ray data have been extensively analysed: the interested reader should refer to Nardini et al. (2019) for details.
2.5. New z ∼ 4 quasar
We also included one new optically-selected SDSS quasar at z = 4.109, J074711.14+273903.3, whose X-ray observation was obtained as part of a proposed large programme with XMM–Newton (cycle 18, proposal ID: 084497, PI: Lusso). This is the only target actually observed from its parent sample, which consisted of 19 quasars in the z ≃ 4 redshift range for a total exposure of 1.34 Ms. The sample had been selected in the optical from the SDSS Data Release 14 with the same criteria described in Sect. 2.4. The X-ray spectrum of this quasar has been analysed following the same procedure as presented by Nardini et al. (2019), and we decided to include this source in the current sample as a proof of feasibility for future campaigns.
2.6. The high redshift sample
To improve the coverage at high redshifts, we considered two additional samples of z > 4 quasars with pointed X-ray observations published by Salvestrini et al. (2019) and Vito et al. (2019).
The Salvestrini et al. (2019) quasar sample consists of 53 objects in the redshift range 4.01 < z < 7.08, which benefit from a moderate-quality coverage in the UV and X-ray energy bands. Of the 53 quasars, 47 objects were observed with Chandra and 9 with XMM–Newton. The galaxies ULAS J1120+0641, SDSS J114816.7+525150.4 and SDSS 1030+0524 have been observed by both satellites. The authors performed a full X-ray spectral analysis of the archival data, we thus refer to their paper for details. The majority of the quasars in this sample (33 out of 53) have LUV measurements from the SDSS–DR7 quasar catalogue. For the remaining quasars, the LUV values are computed by extrapolating the UV spectra to longer wavelengths with a fixed continuum slope (see their Sect. 4 and Appendix B for further details).
Vito et al. (2019) published a sample of 25 quasars at z > 6 with either archival data (15 objects) or new Chandra observations (10 sources), which were selected to have virial black-hole mass estimates from Mg II line spectroscopy. All the X-ray data were reprocessed by the authors (see their Sect. 3.1), whilst the LUV values were computed from the 1450 Å magnitude assuming a power-law spectrum (Fν ∝ να) with α = −0.3 (see their Sect. 4.1). We excluded from their sample 3 BAL candidates, 1 weak line quasar, all sources with an upper limit in αox (i.e. X-ray undetected) and all radio-loud sources, for a total of 9 quasars. For the remaining 16 sources, we found five overlaps with the Salvestrini et al. (2019) sample, so the final number of quasars included from Vito et al. (2019) is 11 sources. This sample also contains the highest-redshift quasar observed so far, ULAS J134208.10+092838.61, at z = 7.54 (Bañados et al. 2018).
2.7. The local quasar sample
To anchor the normalisation of the quasar Hubble diagram with supernovae Ia, we need to extend the coverage at very low redshifts (0.009 < z < 0.1). We searched for all the local AGN with ultraviolet data from the International Ultraviolet Explorer (IUE) in the Mikulski Archive for Space Telescopes (MAST). We chose to use the reduced spectra from the long-wavelength prime (LWP) camera of IUE, which spans the wavelength interval 1845–2980 Å, thus always covering the rest-frame 2500 Å at the redshifts of interest. We then considered all AGN with X-ray data available in the XMM–Newton archive or the with X-ray flux values in the literature, finding 17 objects, 11 of which with ≥2 UV spectra (although the majority consists of consecutive observations). In this sample, NGC 1566 and NGC 7603 are well known highly variable and changing look sources, so we excluded them from the starting sample. Multiple UV spectra for the remaining AGN have been stacked, verifying that the inclusion of non consecutive observations does not change the final composite for each AGN.
We then carried out a detailed spectral fitting of all the UV spectra using the publicly available QSFit package (Calderone et al. 2017). We modelled each spectrum as follows: the Mg II emission line is reproduced by a combination of a broad (with a full-width at half-maximum, FWHM, larger than 2000 km s−1) and a narrow (FWHM < 2000 km s−1) profile, whilst the continuum includes the contributions from the host galaxy, the iron complex, the Balmer continuum and the AGN continuum. Spectra are also corrected for Galactic extinction using the parametrisation by Cardelli et al. (1989) and O’Donnell (1994), with a total selective extinction A(V)/E(B − V) = 3.1 (Calderone et al. 2017). The rest-frame 2500 Å luminosity is finally measured from the AGN continuum component only. An example of a UV spectral fit on one of the objects in the local AGN sample is shown in Fig. 2.
 |
Fig. 2. Example of UV spectral fitting. Best-fit model (left panel, orange curve) and residuals (right panel, in units of 1σ uncertainties on the data and cumulative reduced χ2) are presented for Ark 120. Redshift and Galactic extinction at the source location are shown on top of the plot. The main model components are plotted with different colours: the solid red line is the sum of continuum and host galaxy components; the black solid line is the absorption component; the dot-dashed green line is the Balmer component; the solid green line is the UV iron template; the sum of all broad and narrow emission-line components is shown with blue and brown lines, respectively. The red square symbols are the continuum luminosities estimated by QSFit. |
The X-ray information (soft and hard fluxes, photon index) has been taken from the literature. Most of the sources in the local sample have been drawn from the CAIXA catalogue, which consists of radio-quiet, X-ray unobscured (NH < 2 × 1022 cm−2) AGN observed by XMM–Newton in targeted observations (Bianchi et al. 2009). For two AGN, ESO 141-G055 and IRAS 09149−6206, the X-ray fluxes and ΓX values are given by de Marco et al. (2009) and Ricci et al. (2017), respectively. The rest-frame 2 keV monochromatic flux is then estimated following the procedure described in Sect. 5. A summary of the properties of the local AGN sample is provided in Table 2.
Properties of the local AGN sample.
3. The quasar SED compilation
To compile the quasar SEDs, we used all the multicolour information as reported in the SDSS–DR14 catalogue. The catalogue includes multiwavelength data from radio to UV: the FIRST survey in the radio (Becker et al. 1995), the Wide-Field Infrared Survey (WISE, Wright et al. 2010) in the mid-infrared, the Two Micron All Sky Survey (2MASS, Cutri et al. 2003; Skrutskie et al. 2006) and the UKIRT Infrared Deep Sky Survey (UKIDSS; Lawrence et al. 2007) in the near-infrared, and the Galaxy Evolution Explorer (GALEX, Martin et al. 2005) survey in the UV. Galactic reddening has been properly taken into account by utilising the selective attenuation of the stellar continuum k(λ) from Fitzpatrick (1999), whilst Galactic extinction is estimated from Schlegel et al. (1998) for each object in the SDSS catalogue. For each source, we computed the observed flux and the corresponding frequency in all the available bands. The data used in the SED computation were blueshifted to the rest-frame, and no K-correction was applied. All the rest-frame luminosities were then determined from a first-order polynomial between two adjacent points. At wavelengths bluer than about 1400 Å, we expect significant absorption by the intergalactic medium (IGM) in the continuum (∼10% between the Ly[[INLINE189]] and C IV emission lines, see Lusso et al. 2015 for details). Hence, when computing the relevant parameters, we excluded from the SED all the rest-frame data at λ < 1500 Å. The rest-frame monochromatic luminosities are finally obtained by interpolation whenever the reference frequency is covered by the photometric SED. Otherwise, the value is extrapolated by considering the slope between the luminosity values at the closest frequencies. Thanks to this broad photometric coverage, we can compute the rest-frame luminosity at 2500 Å (LUV) via interpolation for the majority of the SDSS quasars. Indeed, we were not able to estimate LUV due to a sparse photometric SED coverage (i.e. when the SED is composed by a single rest-frame data point) for only 130 quasars.
Uncertainties on monochromatic luminosities (Lν ∝ ν−γ) from the interpolation (extrapolation) between two values L1 and L2 are computed as:
Examples of photometric SEDs for two quasars at different redshifts in the SDSS–4XMM sample are shown in Fig. 3. The red circles in the figure mark all the available photometry from the SDSS–DR14 catalogue, whilst the ones used to construct the SEDs are highlighted with black circles. The magenta squares represent the luminosities at 2500 Å and 1450 Å. The cyan and blue solid lines are the composite SDSS quasar spectum from Vanden Berk (2001) and the average SDSS quasar SED from Krawczyk et al. (2013), respectively. Both composites are shown for reference, for the AGN continuum plus line emission and continuum only, and are normalised to 2500 Å. The AGN SED in the left panel shows a case of both host-galaxy contamination and dust absorption. This source, indeed, does not fulfil our selection criteria (described in detail in Sect. 7), as opposed to the object in the right panel, which represents an object with low levels of contaminants.
 |
Fig. 3. Examples of AGN SEDs. The red circles mark all the available photometry from the SDSS catalogue, whilst the ones used to construct the SEDs are highlighted with black circles. The magenta squares represent the luminosities at 2500 Å and 1450 Å. The cyan line is the composite SDSS quasar spectrum from Vanden Berk (2001), whilst the blue solid line is the average SDSS quasar SED from Krawczyk et al. (2013). Both composites are normalised to 2500 Å. The green dashed and dot-dashed lines represent the two near-infrared and optical slopes Γ1 and Γ2 in the 0.3–1 μm and 1450–3000 Å range (rest frame), respectively. The SED in the left panel is representative of an AGN that does not fulfil our selection criteria (see Sect. 7), as it is affected by both host-galaxy contamination and dust absorption in the UV. The SED in the right panel, instead, is characteristic of an object with low levels of contaminants, which therefore belongs to the clean AGN sample. |
4. On the use of photometric rest-frame 2500 Å fluxes
In this work, we focus on rest-frame 2500 Å monochromatic fluxes as derived from photometry for two main reasons. The first one is based on the physics of the LX − LUV relation, whilst the other on the fact that broadband photometry allows us to build much bigger samples over a larger redshift and luminosity range than spectroscopy alone.
Concerning the former, the 2500 Å monochromatic flux has been adopted since the first studies on the topic, yet its choice was mainly based upon observational considerations. Indeed, the rest-frame 2500 Å at z ≃ 1 corresponds to the observed V band, which was available for a significant number of sources. Additionally, this rest-frame UV wavelength is less affected by host-galaxy contamination (dominant at low luminosity for λ > 4000 Å) and intergalactic absorption (λ < 1450 Å) than other regions of the AGN SED, thus representing the ideal proxy of the intrinsic disc emission. This notwithstanding, the photometric 2500 Å flux might be contaminated by strong Fe II line emission (see Fig. 2), which can introduce systematic uncertainties on the photometrically derived FUV values (e.g. Netzer 2019).
Rakshit et al. (2020) recently published spectroscopic measurements for more than 500 000 quasars selected from the SDSS–DR14 quasar catalogue. They performed a homogeneous analysis of the SDSS spectra to estimate the continuum and line properties (e.g. H[[INLINE212]], H[[INLINE213]], Mg II, C IV, and Ly[[INLINE214]]) of these sources. This catalogue also provides a measurement of the 3000 Å luminosity, which is the closet wavelength to the one of our interest. We have therefore estimated the 3000 Å monochromatic luminosities from the photometric SEDs for all the SDSS–4XMM quasars in the initial sample of 13 800 quasars, similarly to what we have done at 2500 Å. Figure 4 shows the comparison between the photometric and the spectroscopic SDSS luminosity values (i.e. Δ log L3000 = log L3000, photo − log L3000, spectro) as a function of redshift for the objects within the SDSS–4XMM sample with a good quality 3000 Å monochromatic luminosity value (QUALITY_L3000 = 0) available from spectroscopy, ≃12 000 quasars (where z ≃ 2.5 represents the higher redshift for which the rest-frame 3000 Å is covered by the BOSS spectrograph). The Δ log L3000 distribution shows a mean at 0.1 dex, a dispersion around the mean of 0.18 dex, and no trend with redshift. Although a systematic offset in the Δ log L3000 measurements is expected, as our L3000 could be contaminated by the Fe II emission, this is reassuringly small (only a flux factor of ∼1.3). We also note that, any redshift independent offset in the UV fluxes would not be an issue, since it is balanced out in the cross-calibration between the Hubble diagram of supernovae and quasars.
 |
Fig. 4. Comparison between the photometric SDSS luminosity values at 3000 Å and the spectroscopic ones (i.e. Δ log L3000 = log L3000, photo − log L3000, spectro) as a function of redshift for all the quasars in our sample with available 3000 Å monochromatic luminosities from Rakshit et al. (2020). Grey and cyan points represent the initial (∼12 000) and selected (∼1500) quasar samples from SDSS–4XMM, respectively. The black and blue lines mark the mean (solid) and 1σ dispersion (dashed and dot-dashed) of Δ log L3000 for the initial and selected samples, respectively (black and blue solid lines overlap at ⟨Δ log L3000⟩ = 0.11). The red solid line is the Δ log L3000 = 0. |
Figure 4 also shows the Δ log L3000 distribution as a function of redshift for the 1473 quasars in the clean SDSS–4XMM sample (1644 total sources, see Sect. 7 for details) with a measurement of L3000. The average Δ log L3000 is perfectly consistent with the initial sample, the dispersion around the mean is 0.13 dex, and again there is no trend with redshift, implying that our selection criteria have the only effect of singling out the most reliable luminosity measurements as proxy of the nuclear emission.
We finally note that, regardless of the details of the physical mechanism driving the LX − LUV relation, the characteristic UV flux wavelength should be the one most closely related to the global emission of accretion disc, and might not be precisely the rest-frame 2500 Å (see Sect. 6 in Risaliti & Lusso 2019). It is even possible that nuclear emission should be combined with other AGN spectral properties (e.g. emission-line FWHM, continuum slope; see Lusso & Risaliti 2017). We are currently exploring these possibilities, and results will be published in a forthcoming work.
Since we are still far from grasping the nature of the LX − LUV relation, our photometric fluxes are seen as a more conservative representation of the broadband disc emission, capturing the “true” dependence between disc and X-ray corona in AGN in a statistical sense.
5. The rest-frame 2 keV monochromatic flux
Given the large source statistics in the SDSS–4XMM and XXL samples, a detailed X-ray spectral analysis of all the quasars is impractical. Therefore, to compute the rest-frame 2 keV monochromatic flux (FX), we follow the same approach as described in Risaliti & Lusso (2019). For the SDSS–4XMM sample, we derived the rest-frame 2 keV fluxes and the relative (photometric) photon indices, ΓX (along with their 1σ uncertainties), from the tabulated 0.5–2 keV (soft, FS) and 2–12 keV (hard, FH) fluxes reported in the 4XMM–DR9 serendipitous source catalogue. These band-integrated fluxes are blueshifted to the rest-frame by considering a pivot energy value of 1 keV (ES) and 3.45 keV (EH), respectively, and by assuming the same photon index used to derive the fluxes in the 4XMM catalogue (i.e. ΓX = 1.42). For the soft band, the monochromatic flux at ES is then:
in units of erg s−1 cm−2 keV−1. An equivalent expression holds for the hard band, with the obvious modifications. Flux values are corrected for Galactic absorption.
The photometric photon index is then estimated from the slope of the power law connecting the two soft and hard monochromatic fluxes at the rest-frame energies corresponding to the observed pivot points. The rest-frame photometric 2 keV flux (and its uncertainty) is interpolated (or extrapolated) based on such a power law.
To justify the employed soft and hard pivot energy values and to ensure that our photometric FX values are accurate, we performed on the one hand several simulations, and on the other hand full X-ray spectral fitting of a number of random objects at different redshifts.
Regarding the former approach, we simulated a high-quality power-law spectrum, assuming both a typical average background and calibrations for XMM–Newton, with the same photon index assumed by the 4XMM–DR9 catalogue. We fitted the data in the soft band with a power law parametrised as F(E) = F(E0)(E/E0)−ΓX, with F(E0) and ΓX as free parameters, with E0 ranging from 0.5 to 1.5 keV in steps of 0.05 keV. In each case, we derived the F(E0)−ΓX confidence contours. In general, the covariance between these two parameters is non-zero (i.e. the contours are elongated and tilted), so we explored which value of energy ES returns covariance zero between F(ES) and ΓX (i.e. the contours become 2D Gaussians). This pivot energy represents the energy value dividing the soft band in two regions having the same statistical weight. As such, this value is not located at exactly the centre of the energy band because of the dependence of the effective area on energy.
As a result of the F(ES)−ΓX zero-covariance, our photometric FX values are independent of the specific ΓX assumed in the 4XMM–DR9 catalogue. This also implies that, even if our photometric ΓX deviates from the true intrinsic value, the resulting FX will be accurate in any case. Finally, the relative error on the monochromatic flux, ΔF(E)/F(E), at the pivot energy is the same as the one of the band flux, whereby the absolute value of ΔF(E) at the pivot energy is the smallest possible. The same procedure is also applied to the XXL sample using their catalogued soft and hard band fluxes.
In parallel, we performed a full spectral analysis on a number of random objects. The top panels in Figs. 5 and 6 present the comparison between the inferred spectroscopic and photometric FX and ΓX values, respectively, for 30 random quasars in the SDSS–4XMM sample. We also considered for this comparison the 27 sources in the z ≃ 3 quasar sample (Nardini et al. 2019) that have an entry in the 4XMM–DR9 catalogue8. The points are colour-coded by their number of net counts. Whilst the values of ΓX display a large scatter (up to ∼0.46 dex), our photometric FX values are in remarkable agreement with the spectroscopic ones (with a scatter of just ∼0.15 dex). The most obvious outlier in the bottom panel of Fig. 6 is J1425+54, a marginally detected z ≃ 3 quasar with 22 ± 13 net counts in the pn (see Table 1 in Nardini et al. 2019; for the same camera, 4XMM–DR9 gives a consistent number of counts). The observed soft flux reported in the 4XMM–DR9 catalogue for this object is (2.0 ± 0.5)×10−15 erg s−1 cm−2, whilst it is virtually undetected in the observed hard band, with a S/N of ∼0.5 and FH = (9 ± 20)×10−16 erg s−1 cm−2. Nonetheless, even with a nominally large discrepancy between the spectroscopic and photometric ΓX values9, the FX estimates are well within a factor of 1.2. Overall, we have a consistency within a flux factor of 1.6 for about 80% of the sample (only 12/57 quasars lie outside |Δ log FX| = 0.2) and, as expected, the higher the number of counts, the better the agreement, with the most deviant points having less than 100 counts10.
 |
Fig. 5. Top panel: comparison between the spectroscopic and photometric 2 keV monochromatic fluxes for 30 quasars randomly extracted from the SDSS–4XMM sample and the quasars of the z ≃ 3 sample (Nardini et al. 2019, marked with open star symbols). Bottom panel: difference between the spectroscopic and photometric 2 keV monochromatic fluxes as a function of redshift. The mean Δ log FX = log FX, spectro − log FX, photo value and its 1σ dispersion are shown with the red and dashed lines, respectively. Points are colour-coded by the number of net counts. The Δ log FX distribution is scattered around Δ log FX ∼ 0 with no clear trend with redshift. |
 |
Fig. 6. Top panel: comparison between the spectroscopic and photometric photon indices for 30 quasars randomly extracted from the SDSS–4XMM sample and the quasars of the z ≃ 3 sample (Nardini et al. 2019, marked with open star symbols). Bottom panel: difference between the spectroscopic and photometric photon index values as a function of redshift. The mean ΔΓX = ΓX, spectro − ΓX, photo value and its 1σ dispersion are shown with the red and dashed lines, respectively. Points are colour-coded by the number of net counts. Although the ΓX distribution along the one-to-one relation is rather scattered, the ΔΓX does not seem to show a clear trend with redshift. |
We have also investigated whether the difference between spectroscopic and photometric fluxes (ΔFX = FX, spectro − FX, photo) and photon indices (ΔΓX = ΓX, spectro − ΓX, photo) displays any trend with redshift. The bottom panels of Figs. 5 and 6 show such distributions and, despite the limited statistics, both ΔFX and ΔΓX are scattered around zero with no clear trend.
The rather poor comparison between ΓX, spectro and ΓX, photo shown in Fig. 6 might cast some doubts on the reliability of the photon indices derived from the broadband (soft and hard) fluxes. However, we believe that our technique of computing photometric ΓX values can be safely employed for large sample of quasars and that it provides robust results, for the following reasons: firstly, the spectroscopic and photometric X-ray fluxes are in very good agreement, meaning that our distance measures are not strongly affected by the use of photometric ΓX values; and secondly, we performed a series of checks by varying the photometric ΓX range employed to select the final sample, finding that our main results are not significantly modified (see Sect. 7.2 for further details). In summary, our ΓX, photo may not be correct on an object-by-object basis, but they are reliable in a statistical sense for large enough samples.
6. X-ray non-detected quasars
Quasar samples that include X-ray non-detections are likely to be unbiased, but the analysis of both the LUV − LX and the distance modulus–redshift relations is far from straightforward, since it strongly depends on the weights assumed in the fitting algorithm. In the case of flux-limited surveys, objects with an expected emission (based on the observed LUV − LX relation) close to the flux limit will be observed only in case of positive fluctuations, and this effect is likely redshift-dependent (see Sect. 7.3). Considering only detections might thus introduce some bias in the LUV − LX relation, and this should be more relevant to the X-rays, since the relative observed flux interval is narrower than in the UV.
Lusso & Risaliti (2016) investigated the effect of the inclusion of X-ray non-detections in the study of the LX − LUV relation for an optically selected sample of quasars, whose selection was very similar to the one employed in the present analysis. Their main conclusion was that there were no statistically significant variations on slope, intercept and dispersion (within their uncertainties) between X-ray detected and censored quasar samples across the different selection steps, with the slope being rather constant around 0.6. Further analysis was performed in Risaliti & Lusso (2019, see Sect. 3 of their supplementary material), where the fraction of X-ray non-detected quasars was of the order of 2% in their final cleaned sample. Such a fraction of censored data has negligible statistical weight in the fitting procedure, so their inclusion does not change the results of the statistical analysis.
Here, we have adopted a similar strategy as the one presented by Risaliti & Lusso (2019) to obtain a sample where biases are minimised even without the inclusion of non-detections, which is discussed at length in Sect. 7.3. Additionally, we explored whether any possible remaining bias in our X-ray detected quasar sample is present in the residuals of the quasar Hubble diagram (see Sect. 11.1). All these checks motivated us to analyse the Hubble diagram where non-detections are neglected.
7. Selection of a clean quasar sample
Our aim is to select a sub-sample with accurate estimates of LUV and LX, covering a redshift range as wide as possible, by removing systematic effects and low-quality measurements. For the latter, we applied a couple of preliminary filters that ensure good measurement quality. These filters mainly involve the X-ray data, since these affected by larger uncertainties. Specifically, we considered only soft and hard flux measurements with a relative error smaller than 1 (i.e. a minimum S/N of 1 on both band fluxes): ΔFS/FS < 1 and ΔFH/FH < 1. A similar filter is currently not applied to UV fluxes since the S/N at these wavelengths is typically much higher than 1. Overall, these two filters exclude about 30% of the X-ray detections in the initial sample.
The main possible sources of contamination and systematic error are: dust reddening and host-galaxy contamination in the optical and UV, gas absorption in the X-rays, and Eddington bias associated with the flux limit of the X-ray observations. Here we briefly discuss each of these effects, and describe the filters we applied to obtain the final “best” sample for a cosmological analysis.
7.1. Dust reddening and host-galaxy contamination
To retain the quasars with minimum levels of dust reddening and host galaxy contamination, we follow a similar approach to the one presented in our previous works (Risaliti & Lusso 2015, 2019; Lusso & Risaliti 2016). We used the rest-frame photometric SEDs discussed in Sect. 3 to compute, for each object, the slope Γ1 of a log(ν)−log(νLν) power law in the rest frame 0.3–1 μm range, and the analogous slope Γ2 in the 1450–3000 Å range (see also Hao et al. 2013). Figure 3 shows two examples, where the green dashed and dot-dashed lines represent the 0.3–1 μm and 1450–3000 Å(rest frame) slopes Γ1 and Γ2, respectively. The wavelength intervals for these slopes are chosen based on the fact that the SED of an intrinsically blue quasar is very different from the one of an inactive galaxy or a dust-reddened source. The intrinsic SED of a quasar presents a dip around 1 μm, where the galaxy has the peak of the emission from the passive stellar population (e.g. Elvis et al. 1994, 2012; Richards et al. 2006; Krawczyk et al. 2013). Dust reddening is wavelength dependent and the UV portion of the quasar SED will be attenuated differentially. These two concurrent factors impact on the quasar SED shape, allowing us to define a set of slopes that single out the majority of quasars with minimum levels of both host-galaxy emission and dust reddening (see Fig. 1 in Hao et al. 2013).
The Γ1 − Γ2 distribution for the XXL subset of quasars is shown, as an example, in Fig. 7. We assumed a standard SMC extinction law k(λ) after Prevot et al. (1984), with RV = 3.1 (as appropriate for unobscured AGN; Hopkins et al. 2004; Salvato et al. 2009), to estimate the Γ1 − Γ2 correlation as a function of extinction, parametrised by the colour excess E(B − V). We obtained the red dashed line shown in Fig. 7, where the starting point corresponds to the SED of Richards et al. (2006, i.e. Γ1 = 0.82, Γ2 = 0.40) with zero extinction. The distribution of Γ1 − Γ2 towards low values along the red dashed line is indicative of possible dust reddening, whilst sources towards more negative Γ1 values are objects with possible host-galaxy contamination. The Γ1 − Γ2 plane is also very useful to identify unusual SEDs or SEDs characterised by bad photometry, which are then excluded from the sample. We selected all the sources in the (Γ1, Γ2) plane within a circle centred at the reference values for a standard quasar SED (see Risaliti & Lusso 2015, 2019; Lusso & Risaliti 2016 for further details), with a radius corresponding to a reddening E(B − V) ≃ 0.1.
 |
Fig. 7. Example of the Γ1 − Γ2 distribution for the XXL quasar sample, where Γ1 and Γ2 are the slopes of a power law in the log(ν)−log(νLν) plane in the 0.3–1 μm and 1450–3000 Å intervals, respectively (see Sect. 7.1). The stars represent the Γ1 − Γ2 values of the quasar SED by Richards et al. (2006) with increasing dust reddening (following the extinction law of Prevot et al. 1984), with E(B − V) in the range 0–0.3. We selected all the quasars inside the blue circle (i.e. with minimum host-galaxy and dust reddening contamination). |
We note that our quasar selection based on photometry could still be affected by some contamination from the light of the host, especially in low redshift (z ≲ 0.7) AGN, whose flux values at 2500 Å are located at the edge of the SDSS photometric coverage. Hence, any uncertainties in the estimate of the quasar UV continuum from the optical can make the 2500 Å monochromatic fluxes less reliable and possibly overestimated. Low-redshift AGN are on average less luminous in the optical and UV, with Lbol ≲ 1044 erg s−1, thus the contrast between nuclear continuum and host-galaxy emission is smaller with respect to higher luminosity objects. Moreover, the data quality of low-redshift and low-luminosity AGN is, on average, lower. Host-galaxy contamination can be minimised through a source-by-source spectral fitting, as we did for the local AGN sample, but this procedure is rather time consuming for samples of several hundred thousands of objects. We further discuss possible issues for cosmology related to our selection in Sect. 10.
7.2. X-ray absorption
Since X-ray fluxes may contain some level of absorption, which is naturally heavier in the soft band, we included only X-ray detections with a photon index ΓX that falls within a range representative of unobscured quasars. For the majority of the sample, we adopted the following selection criterion, which also takes into account the uncertainties on ΓX: ΓX − δΓX ≥ ΓX, min and ΓX ≤ ΓX, max. The values of ΓX, min and ΓX, max are chosen based on two considerations: the average ΓX within that interval should roughly correspond to ΓX ∼ 2 with a dispersion of 0.2–0.3 (consistent with e.g. Young et al. 2009a), and the LX − LUV relation should not present any systematic deviation from the assumed true slope of 0.6 (within uncertainties).
We thus proceeded as follows. We evaluated the FX − FUV relation in narrow redshift bins (so the effect of cosmology is negligible) for different choices of ΓX, min and ΓX, max. For the SDSS–4XMM sample, we started by assuming a reasonable ΓX, max of 2.8 and a varying ΓX, min in the interval 1.4–1.9 with steps of 0.1, and converged to a ΓX, min = 1.7. We checked that a smaller value of ΓX, min (i.e. 1.6) would not change the results of our analysis, but we prefer to be conservative, even at the expenses of sample statistics. For the SDSS-4XMM sample, we selected only X-ray observations with a photon index satisfying the condition ΓX − δΓX > 1.7, and excluded the (few) objects with ΓX > 2.8. The latter filter on ΓX is needed to avoid strong outliers (∼5%) which may be due to observational issues such as incorrect background subtraction in one of the two bands. This ΓX interval roughly corresponds to an average ΓX ∼ 2.1 − 2.2 and a dispersion of 0.3. The same selection is applied to all the other sub-samples at z < 4. For the higher redshift (z > 4) sample, such a stringent criterion on ΓX would exclude the majority of the objects, given their higher uncertainties. We thus decided to simply select all the objects with ΓX ≥ 1.7.
Given the observed ΓX range (up to 2.8), some soft-excess (e.g. Sobolewska & Done 2007; Gliozzi & Williams 2020) contribution for low-z quasars might be still present. We have thus repeated the analysis further imposing an upper limit to the ΓX range of 2.5, but, besides losing statistics, our results are not affected.
7.3. Eddington bias
Owing to X-ray variability, AGN with an average X-ray intensity close to the flux limit of the observation will be observed only in case of a positive fluctuation. This introduces a systematic, redshift-dependent bias towards high fluxes, known as Eddington bias, which has the effect to flatten the LX − LUV relation.
To reduce this bias, we excluded all X-ray detections below a threshold defined as κ times the intrinsic dispersion of the LX − LUV relation (LR16; Risaliti & Lusso 2019), specifically:
where F2 keV, exp is the monochromatic flux at 2 keV expected from the observed rest-frame quasar flux at 2500 Å with the assumption of a true γ of 0.6, and it is calculated as follows:
where dL is the luminosity distance calculated for each redshift with a fixed cosmology, and the parameter β represents the pivot point of the non-linear relation in luminosities, β = 26.5 − 30.5γ ≃ 8.211. Fmin in Eq. (3) is obtained as detailed in Sects. 2.1 and 2.2, whilst the product κδ is a value estimated for all the sub-samples that we constructed from archives (SDSS–4XMM, SDSS–Chandra) or surveys (XXL).
In particular, we first computed the flux limit of each X-ray observation, for both the SDSS–4XMM and SDSS–Chandra samples (see Sects. 2.1 and 2.2). We minimised the Eddington bias by including only X-ray detections for which the minimum detectable flux Fmin in that given observation is lower than the expected X-ray flux F2 keV, exp by a factor that is proportional to the intrinsic dispersion in the LX − LUV relation (we refer to Appendix A in LR16 and Risaliti & Lusso 2019). On average, the minimum detectable monochromatic fluxes at 2 keV are approximately 4.6 × 10−32 erg s−1 cm−2 Hz−1 and 3 × 10−32 erg s−1 cm−2 Hz−1 for the SDSS–4XMM and SDSS–Chandra samples, respectively. However, we caution that these values should not be considered as the “survey limiting fluxes”, since both the 4XMM and CSC2.0 catalogues are not proper flux-limited samples, but rather a collection of all X-ray observations performed over a certain period. It is thus not trivial to estimate the expected minimum flux for these catalogues. The XXL sample is, instead, a “standard” flux-limited sample, so we applied a soft-band flux threshold to the data (FS > 10−15 erg s−1 cm−2), which corresponds to a flux limit at 2 keV of 5 × 10−32 erg s−1 cm−2 Hz−1. We considered κδ = 0.9 for SDSS–4XMM and XXL, whilst we used κδ = 0.5 for the SDSS–Chandra sample. All the other sub-samples rely on pointed observations, so we did not apply any flux threshold to the data.
In principle, the effects of this bias could be further reduced if also non-detections were considered. Yet, this would not only complicate the statistical analysis, but also make the estimate of the intrinsic dispersion of the observed relations (e.g. LUV − LX, Hubble diagram) much more uncertain. Moreover, we have shown that there is no significant variation in both the slope and the intercept of the LUV − LX correlation (within their uncertainties) among censored and detected samples once the Eddington bias is taken into account (see Appendix A in LR16). We therefore decided to include only detections in this work. This choice implies that we have to be very conservative in the correction for the Eddington bias, at the expense of sample statistics.
It is worth noting that our procedure to minimise the Eddington bias is slightly circular: we need the LX − LUV relation (i.e. we assumed γ = 0.6) in order to estimate the “expected” X-ray flux. Yet, our simulations show that we are able to retrieve the assumed cosmology (using different input values for ΩM and ΩΛ), when the selection criteria are applied to mock quasar samples.
7.4. The final cleaned sample
In summary, we applied a series of selection criteria to filter all the data that are likely contaminated by dust reddening, host-galaxy contamination, and X-ray absorption, or affected by the Eddington bias. We first selected all quasars within a circle centred at (Γ1, Γ2) = (0.82, 0.4), that is E(B − V) = 0, and with a radius such as:
which corresponds to an E(B − V) ≲ 0.1. The equation above filters out all quasar SEDs that show reddening in the UV, significant host-galaxy contamination in the near-infrared, as well as bad photometry (see Sect. 7.1). We then applied an additional cut to keep only the X-ray observations where photon indices are indicative of low levels of X-ray absorption, and to exclude the X-ray data characterised by peculiar photon indices, especially at low and moderate redshifts (see Sect. 7.2). Specifically, we required that:
To correct for the Eddington bias, we further selected all observations that satisfy Eq. (3) where the product κδ is 0.9 for the SDSS–4XMM and XXL sub-samples, and 0.5 for SDSS–Chandra. Pointed observations are available for the local, z ≃ 3, and high-redshift samples (see Sect. 7.3). For any quasar, all the multiple X-ray observations that survive the filters above are finally averaged to minimise the effects of X-ray variability (e.g. LR16, see also Lusso 2019).
The final cleaned sample is composed by 2421 quasars spanning a redshift interval 0.009 ≤ z ≤ 7.52, with a mean (median) redshift of 1.442 (1.295). Table 1 summarises the statistics of each sub-sample, whilst a more detailed summary of the various sub-samples after a given selection is provided in Table A.1. The main UV and X-ray properties of the final sample are presented in Table 3.
Properties of the final quasar sample.
8. Analysis of the FX − FUV relation with redshift
Before building the Hubble diagram, we need to check whether the FX − FUV relation for the clean quasar sample shows any trend with redshift. We thus divided the sample in narrow redshift bins, with a variable step Δz = 0.06 − 0.45 within the redshift range 0.45–4 to have enough statistics. The redshift step is chosen to ensure that the dispersion in distances over each interval is smaller than the one of the relation in luminosities. In this way, we can consider fluxes as proxies of luminosities.
The best-fit parameters (slope, intercept and dispersion) of the FX − FUV relation and their uncertainties are shown in Fig. 8, whilst all the fits of the FX − FUV relation in the chosen redshift bins are presented in Fig. B.1. They are obtained through the Python package EMCEE (Foreman-Mackey et al. 2013), which is a pure-Python implementation of Goodman & Weare’s affine invariant Markov chain Monte Carlo (MCMC) ensemble sampler. To perform the regression fit, X-ray and UV fluxes were normalised to 10−28 and 10−30 erg s−1 cm−2 Hz−1, respectively. On average, the FX − FUV slope does not show any clear trend with redshift within the analysed interval. Conversely, the trend of the intercept 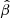 of the normalised FX − FUV relation observed in the middle panel of Fig. 8 just reflects the overall shape of the quasar Hubble diagram (see Sect. 9). We note that, the trend of
of the normalised FX − FUV relation observed in the middle panel of Fig. 8 just reflects the overall shape of the quasar Hubble diagram (see Sect. 9). We note that, the trend of 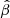 with redshift, is not exactly the same as the one in Fig. 9 since such a parameter does not have a simple direct proportional dependence on the distance modulus (Eq. (7)) because of the different dependence between slope and normalisation in each redshift bin.
with redshift, is not exactly the same as the one in Fig. 9 since such a parameter does not have a simple direct proportional dependence on the distance modulus (Eq. (7)) because of the different dependence between slope and normalisation in each redshift bin.
 |
Fig. 8. Redshift evolution of the slope γ, the intercept |
The sample statistics is so sparse at a redshift higher than 4 that we cannot provide a meaningful fit of the relation. Nonetheless, we have checked that the data points at z > 4 do not show any trend with redshift in the residuals of the Hubble diagram (see Sect. 11). In fact, these data points are extremely useful to set the shape of the Hubble diagram, thus providing better constraints on the measurements of the expansion rate of the Universe. We thus confirm that the slope of the X-ray to UV relation shows no redshift evolution up to z ∼ 4, in agreement with our previous works (e.g. Risaliti & Lusso 2015, 2019; Lusso & Risaliti 2016, 2017; Lusso et al. 2019; see also Salvestrini et al. 2019 for a high redshift analysis).
9. The quasar Hubble diagram
To fit the Hubble diagram we first need to derive the distance modulus for each object. We start by computing the luminosity distance (e.g. see Risaliti & Lusso 2015, 2019) as:
where FX and FUV are the flux densities (in erg s−1 cm−2 Hz−1). FUV is normalised to the (logarithmic) value of 27.5 in the equation above, whilst dL is in units of cm and is normalised to 28.5 (in logarithm). The slope of the FX − FUV relation, γ, is a free parameter, and so is the intercept β12. The distance modulus, DM, is thus:
and the uncertainty on DM, dDM, is:
where d log FX and d log FUV are the logarithmic uncertainties on FX and FUV, respectively. Equation (9) assumes that all the parameters are independent, and takes into account also the uncertainties on β and γ. The fitted likelihood function, LF, is then defined as:
where N is the number of sources, 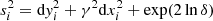 takes into account the uncertainties on both the xi (log FUV) and yi (log FX) parameters of the fitted relation, whilst δ represents its intrinsic dispersion. The variable ψ is the modelled X-ray monochromatic flux, defined as:
takes into account the uncertainties on both the xi (log FUV) and yi (log FX) parameters of the fitted relation, whilst δ represents its intrinsic dispersion. The variable ψ is the modelled X-ray monochromatic flux, defined as:
and is dependent upon the data, the redshift and the cosmological model assumed for the distances (e.g. ΛCDM, wCDM or a polynomial function). We fitted the data with a luminosity distance described by a fifth-grade polynomial of log(1 + z), where the cosmographic function is:
where k, a2, a3, a4, and a5 are free parameters.
For any analysis that involves a detailed test of cosmological models, we should cross-calibrate quasar distances making use of the distance ladder through supernove Ia. In fact, the DM values of quasars are not absolute, thus a cross-calibration parameter (k) is needed. The parameter k should be fit separately for supernovae Ia and quasars (i.e. k is a rigid shift of the quasar Hubble diagram to match the one of supernovae).
Whilst in our previous works we kept γ fixed, in this analysis we have marginalised over the slope γ of the LX − LUV relation. The latter approach is preferred to check whether any degeneracy of the slope with the other parameters is present, and whether the statistical significance of the deviation from the ΛCDM model can be affected by the assumption of a γ value that slightly deviates from the true one. The marginalisation on γ is a more conservative procedure, hence it might reduce the significance of the deviation with respect to the same MCMC analysis with γ fixed. Therefore, if a statistical deviation persists even allowing for a variable γ, its significance should be considered as an indicative lower limit with respect to the case where γ is fixed.
We finally note that the Hubble constant H0 in Eq. (12) is degenerate with the k parameter, so it can assume any arbitrary value and was fixed to H0 = 70 km s−1 Mpc−1 (see also Lusso et al. 2019).
Figure 9 shows the Hubble diagram for the clean quasar sample, combined with the most updated compilation of supernovae Ia from the Pantheon survey (Scolnic et al. 2018). The best MCMC cosmographic fit is shown with the red line, whilst black points are the averages (along with their uncertainties) of the distance modulus in narrow (logarithmic) redshift intervals, plotted for clarity purposes only. The residuals are displayed in the middle panel with the same symbols, and do not reveal any apparent trend with redshift. The MCMC fit assumes uniform priors on the parameters. More details on our cosmographic technique will be provided in a companion publication (Bargiacchi et al., in prep.).
 |
Fig. 9. Top panel: distance modulus–redshift relation (Hubble diagram) for the clean quasar sample and supernovae Ia (Pantheon, magenta points). Symbol keys are the same as in Fig. 1. The red line represents a fifth order cosmographic fit of the data, whilst the black points are averages (along with their uncertainties) of the distance moduli in narrow (logarithmic) redshift intervals. The dashed black line shows a flat ΛCDM model fit with ΩM = 0.3. Middle panel: residuals with respect to the cosmographic fit and the black points are the averages of the residuals over the same redshift intervals. Bottom panel: distance modulus–redshift relation plotted with a logarithmic horizontal axis scale to better visualise the agreement between supernovae Ia and quasars in the low-redshift range. |
We confirm that, whilst the Hubble diagram of quasars is well reproduced by a standard flat ΛCDM model (with ΩM = 0.3) up to z ∼ 1.5, as shown in the top panel of Fig. 9, a statistically significant deviation emerges at higher redshifts, in agreement with our previous works (e.g. Risaliti & Lusso 2015, 2019; Lusso et al. 2019) and other works on the same topic (e.g. Di Valentino et al. 2020).
The detailed discussion of the cosmological implications of this deviation and its statistical significance is not the main aim of this analysis. Here we want to focus on the study of possible systematic effects that could drive this deviation instead.
10. Cosmological fits of the Hubble diagram
In this section we want to test our quasar sample and our method by fitting a “physical” cosmological model. Our aim is not to fully explore the consequences of our new Hubble diagram for the determination of cosmological parameters, or for the tests of different cosmological models, which will be presented in subsequent papers. Here we only intend to verify how different choices regarding the fitting method and the quasar sub-sample affect the final results. We choose to perform these tests with a flat w0waCDM model, which is the simplest and most commonly used extension of the standard ΛCDM model, where the parameter w of the equation of state of the dark energy is assumed to vary with redshift according to the parametrisation w(z) = w0 + wa × (1 − a), where a = 1/(1 + z). Based on the analysis presented in the previous sections, three points deserve further consideration regarding cosmological fits.
Firstly, we can use the full quasar sample or add a filter of z > 0.7 for the sources with photometric determination of the UV flux. As discussed in Sect. 7.1, the possible uncertainties in the extrapolation from the optical of the quasar UV continuum at low redshift, where the host-galaxy contamination can be important, make the 2500 Å monochromatic luminosities less reliable at z < 0.7. In particular, this effect is likely to be more severe at lower fluxes (or luminosities), where the data quality is also lower. If the continuum slope at UV wavelengths becomes steeper than in the optical, the actual 2500 Å flux would be underestimated and this could explain the higher average values of the slope of the LX − LUV relation at z < 0.7 (see Fig. 8). This point deserves further investigation, which is deferred to a subsequent paper. To define the optical sample for cosmological applications in a conservative way, we thus prefer to cut the quasar sample at z > 0.7, with the exception of the local sources discussed in Sect. 2.7, whose 2500 Å flux is determined from the UV spectra without extrapolations. The results of the fit of this best quasar sample with the flat w0waCDM model are shown in Fig. 10. We can see that considering our data significantly reduces the w0 − wa parametric space with respect to the CMB analysis only (Planck Collaboration VI 2020)13, still being compatible with the latter data at 1σ. At the same time, the ΛCDM model (recovered for values w0 = −1 and wa = 0) is in tension with our data at more than 3σ, in agreement with RL19. We finally note that the role of quasars at z < 1–1.3 is mainly to set the absolute calibration with supernovae in cosmological fits, with only a small contribution to the determination of the values and uncertainties of the cosmological parameters, given the much higher statistical weight of the supernovae. Removing quasars at z < 0.7 should not affect the final results significantly, and the number of quasars at redshifts overlapping with supernovae remains high enough for a precise calibration. In order to test these expectations, we repeated the fit with the whole sample, obtaining the results shown in the first panel of Fig. C.1, where the contours are nearly indistinguishable from those of Fig. 10.
 |
Fig. 10. Results from a fit of a w0waCDM model to the combined Hubble diagram of supernovae and the ‘best’ quasar sample, that is removing objects at z < 0.7 with a photometric determination of the UV flux (see the text for details). The green contours refer to the CMB results from Planck (Planck Collaboration VI 2020). The orange (3σ), red (2σ), and brown (1σ) contours are obtained by adding the constraints from the Hubble diagram of supernovae and quasars. |
Secondly, to fit the Hubble diagram, we can either adopt a fixed value of the slope of the relation (with its uncertainty), γ = 0.59 ± 0.06, as determined in Sect. 8, or marginalise on γ as a free parameter, as discussed in Sect. 9. In general, the latter choice is more conservative and should be preferred. This is what we did for our reference fit, and also for the cosmographic fit used to analyse the residuals. Yet, it is worth noting that, in case of a mismatch in the shape of the Hubble diagrams of quasars and supernovae in the common redshift interval, leaving γ as a free parameter allows us to partly alleviate this problem by slightly “bending” the LX − LUV relation in order to obtain a better agreement. In our case, the fit of the best sample gives γ = 0.600 ± 0.015, consistent within 1.5σ with the value found from the fits of the relation in narrow redshift bins. In order to check the possible effects of this choice, we repeated the fit with the w0waCDM model, again obtaining a contour plot totally consistent with the reference case (second panel in Fig. C.1).
Third and last consideration, the residuals in the Hubble diagram show a moderate, but statistically significant, redshift dependence on the X-ray slope, ΓX. It is important to understand whether this introduces a bias in the fits of the Hubble diagram. We checked this possibility by splitting the sample in two parts, with ΓX < 2.2 and ΓX > 2.2, respectively, and repeating the fit with the w0waCDM model. The results are shown in the last two panels of Fig. C.1. These contours are slightly larger than in the previous cases, as expected given the lower statistics, but no systematic trend is observed.
We conclude that, whilst the possible dependence on ΓX deserves further analysis in order to understand its physical and observational origin and to reduce the dispersion of the LX − LUV relation (Signorini et al., in prep.), no systematic effect related to ΓX is introduced in the Hubble diagram of quasars.
11. Study of systematics in the Hubble diagram
Since the main aim of our analysis is to check whether any systematic is present in the residuals of the quasar Hubble diagram, at this stage we avoid the inclusion of supernovae Ia. As noted above, when only quasars are involved the DM values should not be considered as proper absolute distances. In this Section we thus present an in-depth investigation of possible systematics in the residuals of the quasar Hubble diagram, unaccounted for in the selection of the sample. In particular, we explored whether our procedure to correct for the Eddington bias (Sect. 7.3), to neglect quasars with possible gas absorptions (Sect. 7.2), and to select blue quasars based on their SED shape, where dust absorption and host-galaxy contamination are minimised (Sect. 7.1), introduces spurious trends in the Hubble diagram residuals as a function of redshift and for different intervals of the relevant parameters. For each variable, we divided the sample between the sources that fall below and above the average value of the variable itself, and examined each subset separately as any hidden dependence should lead to a systematic difference between the two.
11.1. Residuals as a function of the Eddington bias
To verify whether our adopted technique to correct for the Eddington bias, based on the assumption that the true slope of the LX − LUV is γ = 0.6, leaves some hidden trends in the residuals of the Hubble diagram as a function of redshift, we defined an Eddington bias parameter, Θ, as the difference between the expected X-ray monochromatic flux at 2 keV and the sum of the flux sensitivity value at 2 keV (Fmin) and the product κδ (see Eq. (3)):
Given the fact that the source has survived the Eddington bias filter (see Eq. (3), where κδ = 0.5 for SDSS–Chandra and 0.9 for XXL and SDSS–4XMM, respectively), Θ is always positive: the higher its value, the lower the bias due to the flux limit of the specific X-ray observation. The other samples benefit from pointed observations, for which the bias due to the X-ray flux sensitivity is fully negligible.
We then defined two subsets, above (1069 objects) and below (1289) the mean of this distribution, ⟨Θ⟩ = 1.17 ± 0.01 (with a 1σ dispersion of 0.33), and plotted the residuals of the Hubble diagram as a function of redshift in Fig. 11. The three quasar samples span a rather large redshift interval, showing no clear trend of the residuals with a distance and a similar dispersion around zero (≃1), with an average residual value of about −0.07 (0.04) for Θ > 1.2 (Θ < 1.2). These results imply that our selection of X-ray observations discussed in Sect. 7.3 does not introduce any systematic trends, at least up to z ≃ 4.
 |
Fig. 11. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with Θ lower (higher) than the average (i.e. ⟨Θ⟩ = 1.2). The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
11.2. Residuals as a function of the photon index
Gas absorption in the X-ray band and strong outliers with extremely steep ΓX are minimised by neglecting all quasars outside a given interval of photon index values (1.7 ≤ ΓX ≤ 2.8, see Sect. 7.2). In Fig. 12 we present the distribution of the ΓX values for the clean quasar sample. The mean (median) value for the sample is ⟨ΓX⟩≃2.202 ± 0.005 (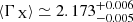 ), with a dispersion of about 0.23 (0.30). Statistical errors are quoted.
), with a dispersion of about 0.23 (0.30). Statistical errors are quoted.
 |
Fig. 12. Distribution of the photon index ΓX for the clean final sample. The mean and the statistical error on the mean are also quoted. The red (blue) solid line represents the mean (median) of ΓX, with its 1σ dispersion around the average marked with the dashed (dot-dashed, 16% and 84%) lines. |
The average ΓX is biased towards slightly steeper values with respect to the more typical ΓX ∼ 1.9–2 (e.g. ΓX = 1.99 ± 0.01 with a dispersion of 0.3, Scott et al. 2011; see also Young et al. 2009b; Mateos et al. 2010), which is likely due to our conservative cut at ΓX = 1.7 and to the presence of a tail of sources with power laws softer than ΓX = 2.6. The residuals of the Hubble diagram do not show a significant trend as a function of redshift when the sample is split in two subsets with ΓX higher and lower than 2.2 (Fig. 13). Nonetheless, the marginalised distribution of residuals shown in Fig. 14 presents an offset with respect to zero, with an average value for the two sub-samples of −0.32 ± 0.03 and 0.24 ± 0.03 for ΓX higher and lower than 2.2, respectively. The dispersion around the average values is 0.82 (1.05) for ΓX > 2.2 (ΓX < 2.2).
 |
Fig. 13. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with ΓX lower (higher) than the average (i.e. ⟨ΓX⟩ = 2.2, see Fig. 12). The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
 |
Fig. 14. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) for the quasars with ΓX higher (blue) and lower (red) than the average (i.e. ⟨ΓX⟩ = 2.2, see Fig. 12). The blue and red solid lines represent the mean of the residuals in each ΓX distribution, respectively (averages are reported on top). |
As we pointed out in Sect. 7.2, our photometric ΓX values may not be always accurate for individual objects, but they are reliable in a statistical sense over a large sample of quasars. Consequently, the main drawback of not using the spectroscopic values is likely to increase the dispersion, rather than to introduce a strong systematic with redshift that may affect the cosmological analysis. Moreover, even considering the presence of a small redshift trend in Fig. 13 for z < 2, this is counterbalanced by the use of supernove Ia in the same redshift interval. In fact, the statistical significance of the deviation of the quasar Hubble diagram from the standard ΛCDM reported in our previous works starts to be important for z > 2, where all the residuals do not present any obvious systematic with redshift.
11.3. Residuals as a function of SED colours
As a further check, we have explored whether the SED colours produce some systematic trends with redshift in the residuals of the Hubble diagram. We have selected two sub-samples in different regions of the (Γ1, Γ2) plane (see Fig. 7). The first one considers all the quasars within the circle having a radius of 0.45 (i.e. 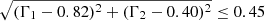 ; 1271 quasars), which corresponds to a colour excess E(B − V) of 0.04 (using an SMC-like reddening law). The second is the contiguous annulus with outer radius of 1.1 (1087 quasars) corresponding to an E(B − V) ≃ 0.1. As the majority of the quasars in the final sample are drawn from the SDSS–DR14 catalogue, the sub-sample with a colour excess lower than 0.04 should represents the bluest objects, whilst the sample in the outer annulus with 0.04 ≤ E(B − V) ≤ 0.1 could show some pattern in the residuals in case of a colour-related systematic with redshift.
; 1271 quasars), which corresponds to a colour excess E(B − V) of 0.04 (using an SMC-like reddening law). The second is the contiguous annulus with outer radius of 1.1 (1087 quasars) corresponding to an E(B − V) ≃ 0.1. As the majority of the quasars in the final sample are drawn from the SDSS–DR14 catalogue, the sub-sample with a colour excess lower than 0.04 should represents the bluest objects, whilst the sample in the outer annulus with 0.04 ≤ E(B − V) ≤ 0.1 could show some pattern in the residuals in case of a colour-related systematic with redshift.
Figure 15 presents the distribution of the residuals as a function of redshift for the two sub-samples defined as above for the clean SDSS–4XMM, XXL and SDSS–Chandra samples, since we can construct homogeneous SEDs (and thus retrieve Γ1 and Γ2 slopes) for them all using the SDSS photometry from the DR14 quasar catalogue. It is clear that there is no obvious trend of the residuals with redshift in either sub-sample, implying that our colour selection does not introduce any redshift-dependent bias in the Hubble diagram. Moreover, in both cases there is no difference in the dispersion of the residuals around zero (≃1), with average values of about −0.04 for E(B − V) ≤ 0.04 and 0.03 for 0.04 ≤ E(B − V) ≤ 0.1). This further proves that even the inclusion of sources with possible (yet modest) contamination from dust and (or) host galaxy does not lead to any systematics with redshift up to z ≃ 4.
 |
Fig. 15. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with |
11.4. Determining whether dust and gas absorption drives the deviation in the quasar Hubble diagram
Among the possible residual (and redshift-dependent) observational systematics in the Hubble diagram, we must also consider the presence of an additional contribution of dust reddening in the UV band. As we move to higher redshifts, the rest-frame optical and UV spectra shift to higher (shorter) frequencies (wavelengths), where the dust absorption cross-section is higher. This might lead to an underestimate of FUV, which would imply an intrinsically larger value of the luminosity distance (and thus DM) than the one we measured.
We thus evaluated the amount of dust extinction required to make the cosmographic fit shown in Fig. 9 coincide with a standard flat ΛCDM model with ΩM = 0.3 (i.e. the black dashed line in Fig. 9). We defined five redshift intervals with increasing values of E(B − V), specifically, E(B − V) = 0, 0.1, 0.15, 0.2, and 0.25 at z = 0–1, z = 1–2, z = 2–3, z = 3–4, and z > 4. We then assumed the standard extinction law by Prevot et al. (1984) with RV = 3.1 and corrected FUV by the amount dictated by the chosen E(B − V) in each redshift interval, and we finally fitted the “reddening corrected” distance modulus (DMred)–redshift relation.
Figure 16 shows the resulting distribution of the difference of the distance moduli, ΔDM (red points) between the DMred values computed above and the observed DM in Fig. 9 (see Sect. 9), as a function of redshift. The cosmographic fit obtained from the DMred − z relation perfectly matches the ΛCDM curve (bottom panel). We also report the values of optical depth, τ, at the rest-frame 2500 Å that would be needed to entirely ascribe the discrepancy to underestimated dust extinction on the 2500 Å quasar fluxes.
 |
Fig. 16. Analysis of the possible contribution of dust at 2500 Å. Top: distribution of the difference of the distance moduli (ΔDM, red points; ΔDM = 0 represents the ΛCDM) as a function of redshift. The parameter ΔDM is defined as DMred − DM, where DM is computed from the quasar data as described in Sect. 9. The DMred values are estimated by correcting the observed FUV for an additional intrinsic (and redshift-dependent) extinction. τ is the optical depth at the rest-frame 2500 Å that would be needed to ascribe the discrepancy to an underestimated dust extinction in the UV flux. The black points represent the average (and 1σ uncertainties) of ΔDM in the same narrow redshift intervals used in Figs. 8 and 9. Middle: deviation in σ of the average points with respect to ΛCDM. Bottom: ratio between the cosmographic fit obtained from the data, where FUV is corrected for additional extinction, and the ΛCDM. The cosmographic fit perfectly matches ΛCDM for the chosen values of dust reddening (see Sect. 11.4). |
We note that the negative ΔDM values at z < 1 (where no dust extinction correction is applied) are simply caused by the different overall cosmographic fit obtained for the DMred − z relation with respect to the observed one. Therefore, the ΔDM values in this redshift range should not be taken at face value.
At 2500 Å, it is k(λ)≃7, which corresponds to an increase in flux by a factor of ≃2.6 − 5 for E(B − V) = 0.15 − 0.25 at z ≥ 2. The bolometric luminosities of the z > 4 quasars in the clean sample are in the range 1046.5 − 48.1 erg s−1, assuming a bolometric correction of 2.75 at 2500 Å (Krawczyk et al. 2013). If the extra correction were effectively required, this would imply an intrinsic bolometric luminosity for these sources of the order of 1047.3 − 49 erg s−1. For example, the highest redshift quasar in the sample, ULAS J134208.10+092838.61, would have a bolometric luminosity by at least a factor of 4 higher than reported the literature (i.e. 1.6 × 1047 erg s−1, Bañados et al. 2018). This would also imply a larger black-hole mass, thus a heavier seed, which needs to be interpreted within current models of black-hole growth (e.g. Latif et al. 2013; Dijkstra et al. 2014; Pacucci et al. 2015).
For the spectroscopic XMM–Newtonz ≃ 3 sample, the FUV values would increase by a factor of at least 3.5, thus shifting Lbol into the range 1048 − 48.8 erg s−1. We note that the average stack of their SDSS spectra does not suggest any significant levels of dust absorption when compared to other composites obtained from bright, blue quasar spectra (see Fig. 2 in Nardini et al. 2019). As a result, the presence of any additional dust component does not seem to be justified.
For completeness, we have also employed a different reddening law (i.e. Fitzpatrick 1999), and modified both the E(B − V) values and the redshift intervals (always verifying that the cosmographic fit of the modified Hubble diagram is consistent with the standard ΛCDM), finding equivalent results.
In conclusion, the intrinsic UV fluxes required to offset the observed tension between the cosmographic fit of the Hubble diagram and the ΛCDM through redshift-dependent dust absorption should be, on average, brighter by 0.4–0.8 mag. This would imply a steeper extrapolated slope than observed at longer wavelengths, which would be hard to reconcile with a standard α−disc model (Shakura & Sunyaev 1976).
We note that concurrent, and redshift-dependent, absorption is found at X-ray energies. The observed 0.5–2 keV energy band moves towards higher rest-frame energies as the redshift increases, where the effect of any gas absorption should become progressively negligible. Spectra with flat photon indices (ΓX < 1.7) are removed from the sample, so we expect a minimal degree of residual gas absorption in the X-rays. In the high-redshift (z > 6) quasars for which a spectral analysis was carried out (see e.g. Vito et al. 2019), the level of intrinsic gas absorption is always suggested to be rather low (of the order of ×1023 cm−2 or less). Assuming the presence of a local column density with NH = 1023 cm−2 at z = 6, the exact correction to the inferred rest-frame 2 keV flux density depends on the details (flux, observed slope, data quality) of the single observation, but it is expected to be within a factor of 2, thus comparable to the typical measurement uncertainty. Such high NH values are not required in any of the X-ray spectral fits for the high-redshift quasars that belong to the clean sample. By shifting the data to higher DM values, this correction would have the effect of increasing the departure from the ΛCDM (i.e. opposite to the one for the dust absorption in the UV).
11.5. On the possible dependence of the LX − LUV relation on black-hole mass and accretion rate
One can argue that the observed LX − LUV relation might be a secondary manifestation of some other, more fundamental relations, involving, for instance, a possible dependence on black-hole mass and accretion rate (usually parametrised by the Eddington ratio, λedd, defined as the ratio of the bolometric and the Eddington luminosity). Yet, when estimated from single-epoch spectroscopy, both parameters are derived quantities, that is a combination of continuum luminosity and emission-line FWHM. Therefore, the presence or absence of a correlation between the residuals of the Hubble diagram and MBH and (or) the Eddington ratio could be misleading and potentially hide systematics.
Since the LX − LUV relation already has a dependence on the nuclear luminosity (which we have discussed in detail in Sect. 4), we can explore possible additional correlations with the FWHM of a given emission line. This issue was already investigated in Lusso & Risaliti (2017), who found that not only is the dependence of the LX − LUV relation on the FWHM (of Mg II) statistically significant, but also that such a dependence has the effect of further reducing the dispersion of the LX − LUV correlation. However, building a statistically significant quasar sample that both covers a wide redshift range (as the one presented here) and relies on a measurement of FWHM from a single line (to ensure homogeneity in the estimate of the line parameters, see Sect. 2.1 in Lusso & Risaliti 2017) is impractical, as it would require a series of dedicated spectroscopic near-infrared campaigns to probe the same line (e.g. Mg II) at high redshifts (z > 2.5). The statistical relevance of the supplementary dependence of the LX − LUV relation on the FWHM, as well as on other parameters inferred from spectroscopy (e.g. continuum slope, iron content, line strength) will be further investigated in a forthcoming publication, entirely dedicated to the physics of the relation.
Whilst here we prefer to consider the simple LX − LUV relation for cosmological purposes, as the present analysis aims at verifying that our selection criteria do not introduce systematics in the quasar Hubble diagram, we can still check whether the sources in the clean sample with a measurement of the FWHM from Mg II (which provides the widest possible redshift coverage in BOSS) show any systematic trend and (or) a reduced scatter in the residuals. We thus cross-matched the clean sample with the catalogue of spectral quasar properties of Rakshit et al. (2020), and selected the quasars with a broad (FWHM > 2000 km s−1) component of the Mg II emission line, finding 1858 quasars (77% of the clean sample).
The distribution of the residuals as function redshift for this sample is shown in Fig. 17. The amplitude of the scatter of the residuals is similar to the other cases discussed in Sects. 11.1–11.3. Moreover, there is no trend with redshift up to z ≃ 2.5. These results further prove that our selection criteria are already effective in selecting an optimal sample for cosmology, without introducing strong systematics.
 |
Fig. 17. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with a broad (FWHM > 2000 km s−1) component of the Mg II emission line in the clean sample. The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
12. Discussion and conclusions
Our group has presented a new technique that makes use of the observed non-linear relation between the 2500 Å and the 2 keV emission in quasars to provide an independent measurement of their distances, thus turning quasars into standardizable candles. Our method extends the distance modulus–redshift relation (or the so-called Hubble-Lemaître diagram) of supernovae Ia to a redshift range still poorly explored (z > 2; e.g. Risaliti & Lusso 2015, 2019; Lusso et al. 2019), and it relies upon the evidence that most of the observed dispersion in the LX − LUV relation is not intrinsic to the relation itself but due to observational issues. When an optimal selection of clean sources (i.e. for which we can measure the intrinsic UV and X-ray quasar emission) is possible, the dispersion in the LX − LUV relation drops to ≃0.2 dex (Lusso & Risaliti 2016, 2017).
We have previously demonstrated that the distance modulus–redshift relation of quasars at z < 1.4 is in agreement with that of supernovae Ia and with the concordance ΛCDM model (Risaliti & Lusso 2015, 2019; Lusso et al. 2019), yet a deviation from the ΛCDM emerges at higher redshift, with a statistical significance of about 4σ. If we interpret the latter result by considering an evolution of the dark energy equation of state in the form w(z) = w0 + wa × z/(1 + z), the data suggest that the dark energy density is increasing with time (Risaliti & Lusso 2019; Lusso et al. 2019). However, our technique may still have some limitations, and we need to verify that the observed deviation from the ΛCDM at a redshift > 2 is not driven by either systematics in the quasar sample selection or the cosmological procedure adopted to fit the distance modulus–redshift relation.
The aim of this manuscript is thus to discuss, on the one hand, all the criteria required to select a homogeneous sample of quasars for cosmological purposes and, on the other hand, the specific procedures adopted to compute the UV and X-ray fluxes and spectral slopes from the available photometry. We identified the quasars that can be used for a cosmological analysis, examined the key steps in fitting the distance modulus–redshift relation, and considered the possible systematics in the quasar Hubble-Lemaître diagram. In particular, we investigated in depth the residuals of the quasar Hubble diagram, in order to unveil any systematics unaccounted for in the selection of the sample. We explored whether our procedure to correct for the Eddington bias, to neglect quasars with possible gas absorption, and to select blue quasars based on their SED shape, where dust absorption and host-galaxy contamination are minimised, introduces spurious trends in the Hubble diagram residuals as a function of redshift and for different intervals of the relevant parameters.
Our main results are the following:
-
We verified that the LX − LUV relation (i.e. slope and dispersion) for the final best quasar sample does not evolve with redshift.
-
We confirmed that, whilst the quasar Hubble diagram is well reproduced by a standard flat ΛCDM model (with ΩM = 0.3) up to z ∼ 1.5, a statistically significant deviation emerges at higher redshifts, in agreement with our previous works (e.g. Risaliti & Lusso 2015, 2019; Lusso et al. 2019).
-
We found that none of the adopted filters introduce strong systematics in the Hubble diagram residuals, and specifically where the quasars become the only contributors and the deviation from the standard ΛCDM is more significant (i.e. at z > 1.5).
Even if our analysis shows that both the quasar selection criteria and the cosmological fitting technique are robust, we can already envisage several further improvements, especially in the quasar sample selection (e.g. by using spectra instead of photometry in both X-rays and UV to better measure the X-ray and UV fluxes and slopes). Nonetheless, given the remarkable absence of systematics in the residuals, the main effect of these refinements will be on the reduction of the dispersion, thus allowing a better estimate of the cosmological parameters.
With currently operating facilities, dedicated observations of well-selected high-z quasars (similarly to what our group has done at z ≃ 3) will greatly improve the test of the cosmological model and the study of the dispersion of the LX − LUV relation, especially at z ≃ 4. The extended Roentgen Survey with an Imaging Telescope Array (eROSITA, Predehl 2012; Merloni et al. 2012), flagship instrument of the ongoing Russian Spektrum-Roentgen-Gamma (SRG) mission, will represent an extremely powerful and versatile X-ray observatory in the next decade. The sky of eROSITA will be dominated by the AGN population, with ∼3 million AGN with a median redshift of z ∼ 1 expected by the end of the nominal 4-year all-sky survey at the sensitivity of F0.5 − 2 keV ≃ 10−14 erg s−1 cm−2, for which extensive multiwavelength follow-up is already planned. Concerning the constraints on the cosmological parameters (such as ΩM, ΩΛ, and w) through the Hubble diagram of quasars, we predict that the 4-year eROSITA all-sky survey alone, complemented by redshift and broadband photometric information, will supply the largest quasar sample at z < 2 (average redshift z ≃ 1), but a relatively small population should survive the Eddington bias cut at higher redshifts (see e.g. Medvedev et al. 2020), thus being available for cosmology. Indeed, eROSITA will sample the brighter end of the X-ray luminosity function (Lusso 2020, but see also Sect. 6.2 in Comparat et al. 2020). Nonetheless, the large number of eROSITA quasars at z ≃ 1 will be pivotal for both a better cross-calibration of the quasar Hubble diagram with supernovae and a more robust determination of ΩΛ, which is sensitive to the shape of the low redshift part of the distance modulus–redshift relation.
In the mid and long term, surveys from Euclid and LSST in the optical and UV, and Athena in the X-rays, will also provide samples of millions of quasars. With these samples it will be possible to obtain constraints on the observed deviations from the standard cosmological model, which will rival and complement those available from the other cosmological probes.
All the X-ray info can be downloaded from the CSCview application http://cda.harvard.edu/cscview/
Out of the 30 objects in the z ≃ 3 sample, one had no public data on 2018 December 18, and two (J0945+23 and J1159+31; see Sect. 4.3 in Nardini et al. 2019) are not detected in 4XMM–DR9.
Interestingly, J1425+54 would not have met the selection criterion on ΓX in either case (see Sect. 7.2).
We note that this is the typical threshold for spectral analysis to return reasonably accurate results (see e.g. Nardini et al. 2019).
The intercept β of the LX − LUV relation is related to the one of the FX − FUV, 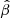 (see Sect. 8), as
(see Sect. 8), as 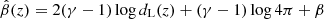 .
.
Baseline ΛCDM chains with baseline likelihoods: https://wiki.cosmos.esa.int/planck-legacy-archive/index.php/Cosmological_Parameters
Acknowledgments
We thank the referee for their constructive comments and suggestions which have significantly improved the clarity of the paper. We also thank M. Millon and F. Courbin for reading the manuscript and providing useful comments. We acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.O.
References
- Arcodia, R., Merloni, A., Nandra, K., & Ponti, G. 2019, A&A, 628, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Fonseca Bonilla, N., Guainazzi, M., Matt, G., & Ponti, G. 2009, A&A, 501, A915 [Google Scholar]
- Calderone, G., Nicastro, L., Ghisellini, G., et al. 2017, MNRAS, 472, 4051 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Comparat, J., Merloni, A., Dwelly, T., et al. 2020, A&A, 636, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- de Marco, B., Iwasawa, K., Cappi, M., et al. 2009, A&A, 507, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dijkstra, M., Ferrara, A., & Mesinger, A. 2014, MNRAS, 442, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Di Valentino, E., Melchiorri, A., & Silk, J. 2020, ArXiv e-prints [arXiv:2003.04935] [Google Scholar]
- Elvis, M., & Karovska, M. 2002, ApJ, 581, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Hao, H., Civano, F., et al. 2012, ApJ, 759, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I. N., Primini, F. A., Glotfelty, K. J., et al. 2010, ApJS, 189, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Chartas, G., et al. 2006, ApJ, 644, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Gliozzi, M., & Williams, J. K. 2020, MNRAS, 491, 532 [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, H., Elvis, M., Bongiorno, A., et al. 2013, MNRAS, 434, 3104 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Strauss, M. A., Hall, P. B., et al. 2004, AJ, 128, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczyk, C. M., Richards, G. T., Mehta, S. S., et al. 2013, ApJS, 206, 4 [NASA ADS] [CrossRef] [Google Scholar]
- La Franca, F., Bianchi, S., Ponti, G., Branchini, E., & Matt, G. 2014, ApJ, 787, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013, MNRAS, 436, 2989 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lusso, E. 2019, Astron. Nachr., 340, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E. 2020, Front. Astron. Space Sci., 7, 8 [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2017, A&A, 602, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Piedipalumbo, E., Risaliti, G., et al. 2019, A&A, 628, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Marziani, P., & Sulentic, J. W. 2014, Adv. Space Res., 54, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Mateos, S., Carrera, F. J., Page, M. J., et al. 2010, A&A, 510, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Medvedev, P., Sazonov, S., Gilfanov, M., et al. 2020, MNRAS, 497, 1842 [CrossRef] [Google Scholar]
- Menzel, M.-L., Merloni, A., Georgakakis, A., et al. 2016, MNRAS, 457, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A. 2003, MNRAS, 341, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Mingo, B., Watson, M. G., Rosen, S. R., et al. 2016, MNRAS, 462, 2631 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Lusso, E., Risaliti, G., et al. 2019, A&A, 632, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H. 2019, MNRAS, 488, 5185 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F. 2000, ApJ, 530, L65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Pacucci, F., Volonteri, M., & Ferrara, A. 2015, MNRAS, 452, 1922 [CrossRef] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2018, A&A, 613, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P. 2012, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proc. SPIE, 8443, 84431R [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [Google Scholar]
- Rakshit, S., Stalin, C. S., & Kotilainen, J. 2020, ApJS, 249, 17 [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Strauss, M. A., Fan, X., et al. 2006, AJ, 131, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2015, ApJ, 815, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2019, Nat. Astron., 195 [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Salvestrini, F., Risaliti, G., Bisogni, S., Lusso, E., & Vignali, C. 2019, A&A, 631, A120 [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A. E., Stewart, G. C., Mateos, S., et al. 2011, MNRAS, 417, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1976, MNRAS, 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Done, C. 2007, MNRAS, 374, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Tananbaum, H., Avni, Y., Branduardi, G., et al. 1979, ApJ, 234, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vito, F., Brandt, W. N., Bauer, F. E., et al. 2019, A&A, 630, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J.-M., Du, P., Valls-Gabaud, D., Hu, C., & Netzer, H. 2013, Phys. Rev. Lett., 110, 081301 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-M., Songsheng, Y.-Y., Li, Y.-R., Du, P., & Zhang, Z.-X. 2020, Nat. Astron., 4, 517 [CrossRef] [Google Scholar]
- Watson, D., Denney, K. D., Vestergaard, M., & Davis, T. M. 2011, ApJ, 740, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., Auguéres, J.-L., Ballet, J., et al. 2001, A&A, 365, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webb, N. A., Coriat, M., Traulsen, I., et al. 2020, A&A, 641, A136 [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009a, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., Risaliti, G., & Marscher, A. 2009b, Bull. Am. Astron. Soc., 41, 454 [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2010, ApJ, 708, 1388 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Detailed sample selection summary
Table A.1 provides a detailed summary of the statistics of the various sub-samples for a given selection.
Sample statistics of the various sub-samples in each give selection.
Appendix B: Fit of the relation FX − FUV in redshift intervals
Figure B.1 presents the fits of the FX − FUV relation in narrow redshift bins as discussed in Sect. 8. The best-fit parameters (slope and dispersion) of the FX − FUV relation and their uncertainties, the number of objects in each bin and the average redshift are also shown.
 |
Fig. B.1. FX − FUV relation in narrow redshift bins as discussed in Sect. 8. The best-fit parameters (slope and dispersion) of the FX − FUV relation and their uncertainties, the number of objects in each bin, and the average redshift are also reported. Symbol keys as in Fig. 1. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
Appendix C: Additional cosmological fits of the Hubble diagram
Figure C.1 presents the results of the fit with the flat w0waCDM model of the quasar sample in four different cases: (1) the full sample of ∼2400 quasars where the slope, γ, of the FX − FUV relation is a variable parameter, (2) the best z > 0.7 quasar sample with γ fixed to the average value of the entire sample estimated in narrow redshift bins (i.e. γ = 0.59, see Sect. 8), (3) the best z > 0.7 quasar sample with ΓX lower than the average photon index as discussed in Sect. 11.2 (see Fig. 12) and finally (4) the best z > 0.7 quasar sample with ΓX higher than the average photon index. In both fits with the (3) and (4) samples γ is left free. This analysis confirms that the ΛCDM model is in tension with our data at more than 3σ, in agreement with the results in RL19, irrespectively of the sample selection.
 |
Fig. C.1. Results from a fit of a w0waCDM model to our Hubble diagram of supernovae and quasars in four different cases. Top left: whole quasar sample, with the slope of the LX − LUV relation as a free parameter; top right: quasars at z > 0.7 with a fixed LX − LUV slope, γ = 0.59, that is the average value from the fit of the relation in narrow redshift intervals, as shown in Sect. 8; bottom panels: results for two sub-samples with ΓX < 2.2 and ΓX > 2.2. Contours are at the 1σ, 2σ, and 3σ confidence levels. The green contours refer to the CMB results from Planck (Planck Collaboration VI 2020). The orange, red, and brown contours are obtained by adding the constraints from the Hubble diagram of supernovae and quasars. |
All Tables
All Figures
 |
Fig. 1. Distribution of luminosities at rest-frame 2500 Å as a function of redshift for the main (grey points) and the selected (cleaned) samples (see Sect. 7.4). Brown and yellow squares: high-z sample (Salvestrini et al. 2019; Vito et al. 2019, see Sect. 2.6), cyan points: SDSS–4XMM (Sect. 2.1), brown triangles: XMM–XXL (Menzel et al. 2016, Sect. 2.3), orange pentagons: the local AGN sample (Sect. 2.7), red stars: z ≃ 3 quasar sample (Nardini et al. 2019, green star: new z ≃ 4 quasar (Sect. 2.5), gold pentagons: SDSS–Chandra (Sect. 2.2). |
| In the text | |
 |
Fig. 2. Example of UV spectral fitting. Best-fit model (left panel, orange curve) and residuals (right panel, in units of 1σ uncertainties on the data and cumulative reduced χ2) are presented for Ark 120. Redshift and Galactic extinction at the source location are shown on top of the plot. The main model components are plotted with different colours: the solid red line is the sum of continuum and host galaxy components; the black solid line is the absorption component; the dot-dashed green line is the Balmer component; the solid green line is the UV iron template; the sum of all broad and narrow emission-line components is shown with blue and brown lines, respectively. The red square symbols are the continuum luminosities estimated by QSFit. |
| In the text | |
 |
Fig. 3. Examples of AGN SEDs. The red circles mark all the available photometry from the SDSS catalogue, whilst the ones used to construct the SEDs are highlighted with black circles. The magenta squares represent the luminosities at 2500 Å and 1450 Å. The cyan line is the composite SDSS quasar spectrum from Vanden Berk (2001), whilst the blue solid line is the average SDSS quasar SED from Krawczyk et al. (2013). Both composites are normalised to 2500 Å. The green dashed and dot-dashed lines represent the two near-infrared and optical slopes Γ1 and Γ2 in the 0.3–1 μm and 1450–3000 Å range (rest frame), respectively. The SED in the left panel is representative of an AGN that does not fulfil our selection criteria (see Sect. 7), as it is affected by both host-galaxy contamination and dust absorption in the UV. The SED in the right panel, instead, is characteristic of an object with low levels of contaminants, which therefore belongs to the clean AGN sample. |
| In the text | |
 |
Fig. 4. Comparison between the photometric SDSS luminosity values at 3000 Å and the spectroscopic ones (i.e. Δ log L3000 = log L3000, photo − log L3000, spectro) as a function of redshift for all the quasars in our sample with available 3000 Å monochromatic luminosities from Rakshit et al. (2020). Grey and cyan points represent the initial (∼12 000) and selected (∼1500) quasar samples from SDSS–4XMM, respectively. The black and blue lines mark the mean (solid) and 1σ dispersion (dashed and dot-dashed) of Δ log L3000 for the initial and selected samples, respectively (black and blue solid lines overlap at ⟨Δ log L3000⟩ = 0.11). The red solid line is the Δ log L3000 = 0. |
| In the text | |
 |
Fig. 5. Top panel: comparison between the spectroscopic and photometric 2 keV monochromatic fluxes for 30 quasars randomly extracted from the SDSS–4XMM sample and the quasars of the z ≃ 3 sample (Nardini et al. 2019, marked with open star symbols). Bottom panel: difference between the spectroscopic and photometric 2 keV monochromatic fluxes as a function of redshift. The mean Δ log FX = log FX, spectro − log FX, photo value and its 1σ dispersion are shown with the red and dashed lines, respectively. Points are colour-coded by the number of net counts. The Δ log FX distribution is scattered around Δ log FX ∼ 0 with no clear trend with redshift. |
| In the text | |
 |
Fig. 6. Top panel: comparison between the spectroscopic and photometric photon indices for 30 quasars randomly extracted from the SDSS–4XMM sample and the quasars of the z ≃ 3 sample (Nardini et al. 2019, marked with open star symbols). Bottom panel: difference between the spectroscopic and photometric photon index values as a function of redshift. The mean ΔΓX = ΓX, spectro − ΓX, photo value and its 1σ dispersion are shown with the red and dashed lines, respectively. Points are colour-coded by the number of net counts. Although the ΓX distribution along the one-to-one relation is rather scattered, the ΔΓX does not seem to show a clear trend with redshift. |
| In the text | |
 |
Fig. 7. Example of the Γ1 − Γ2 distribution for the XXL quasar sample, where Γ1 and Γ2 are the slopes of a power law in the log(ν)−log(νLν) plane in the 0.3–1 μm and 1450–3000 Å intervals, respectively (see Sect. 7.1). The stars represent the Γ1 − Γ2 values of the quasar SED by Richards et al. (2006) with increasing dust reddening (following the extinction law of Prevot et al. 1984), with E(B − V) in the range 0–0.3. We selected all the quasars inside the blue circle (i.e. with minimum host-galaxy and dust reddening contamination). |
| In the text | |
 |
Fig. 8. Redshift evolution of the slope γ, the intercept |
| In the text | |
 |
Fig. 9. Top panel: distance modulus–redshift relation (Hubble diagram) for the clean quasar sample and supernovae Ia (Pantheon, magenta points). Symbol keys are the same as in Fig. 1. The red line represents a fifth order cosmographic fit of the data, whilst the black points are averages (along with their uncertainties) of the distance moduli in narrow (logarithmic) redshift intervals. The dashed black line shows a flat ΛCDM model fit with ΩM = 0.3. Middle panel: residuals with respect to the cosmographic fit and the black points are the averages of the residuals over the same redshift intervals. Bottom panel: distance modulus–redshift relation plotted with a logarithmic horizontal axis scale to better visualise the agreement between supernovae Ia and quasars in the low-redshift range. |
| In the text | |
 |
Fig. 10. Results from a fit of a w0waCDM model to the combined Hubble diagram of supernovae and the ‘best’ quasar sample, that is removing objects at z < 0.7 with a photometric determination of the UV flux (see the text for details). The green contours refer to the CMB results from Planck (Planck Collaboration VI 2020). The orange (3σ), red (2σ), and brown (1σ) contours are obtained by adding the constraints from the Hubble diagram of supernovae and quasars. |
| In the text | |
 |
Fig. 11. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with Θ lower (higher) than the average (i.e. ⟨Θ⟩ = 1.2). The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
| In the text | |
 |
Fig. 12. Distribution of the photon index ΓX for the clean final sample. The mean and the statistical error on the mean are also quoted. The red (blue) solid line represents the mean (median) of ΓX, with its 1σ dispersion around the average marked with the dashed (dot-dashed, 16% and 84%) lines. |
| In the text | |
 |
Fig. 13. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with ΓX lower (higher) than the average (i.e. ⟨ΓX⟩ = 2.2, see Fig. 12). The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
| In the text | |
 |
Fig. 14. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) for the quasars with ΓX higher (blue) and lower (red) than the average (i.e. ⟨ΓX⟩ = 2.2, see Fig. 12). The blue and red solid lines represent the mean of the residuals in each ΓX distribution, respectively (averages are reported on top). |
| In the text | |
 |
Fig. 15. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with |
| In the text | |
 |
Fig. 16. Analysis of the possible contribution of dust at 2500 Å. Top: distribution of the difference of the distance moduli (ΔDM, red points; ΔDM = 0 represents the ΛCDM) as a function of redshift. The parameter ΔDM is defined as DMred − DM, where DM is computed from the quasar data as described in Sect. 9. The DMred values are estimated by correcting the observed FUV for an additional intrinsic (and redshift-dependent) extinction. τ is the optical depth at the rest-frame 2500 Å that would be needed to ascribe the discrepancy to an underestimated dust extinction in the UV flux. The black points represent the average (and 1σ uncertainties) of ΔDM in the same narrow redshift intervals used in Figs. 8 and 9. Middle: deviation in σ of the average points with respect to ΛCDM. Bottom: ratio between the cosmographic fit obtained from the data, where FUV is corrected for additional extinction, and the ΛCDM. The cosmographic fit perfectly matches ΛCDM for the chosen values of dust reddening (see Sect. 11.4). |
| In the text | |
 |
Fig. 17. Distribution of the Hubble diagram residuals (middle panel of Fig. 9) as a function of redshift for the quasars with a broad (FWHM > 2000 km s−1) component of the Mg II emission line in the clean sample. The black and red points represent the mean and median of the residuals in narrow redshift intervals, respectively. Symbol keys as in Fig. 1. |
| In the text | |
 |
Fig. B.1. FX − FUV relation in narrow redshift bins as discussed in Sect. 8. The best-fit parameters (slope and dispersion) of the FX − FUV relation and their uncertainties, the number of objects in each bin, and the average redshift are also reported. Symbol keys as in Fig. 1. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. C.1. Results from a fit of a w0waCDM model to our Hubble diagram of supernovae and quasars in four different cases. Top left: whole quasar sample, with the slope of the LX − LUV relation as a free parameter; top right: quasars at z > 0.7 with a fixed LX − LUV slope, γ = 0.59, that is the average value from the fit of the relation in narrow redshift intervals, as shown in Sect. 8; bottom panels: results for two sub-samples with ΓX < 2.2 and ΓX > 2.2. Contours are at the 1σ, 2σ, and 3σ confidence levels. The green contours refer to the CMB results from Planck (Planck Collaboration VI 2020). The orange, red, and brown contours are obtained by adding the constraints from the Hubble diagram of supernovae and quasars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



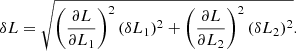
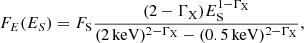
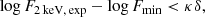
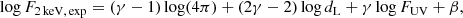

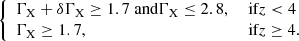
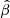
![$$ \begin{aligned} \log d_{\rm L}&= \frac{\left[\log F_{\rm X}-\beta -\gamma (\log F_{\rm UV}+27.5) \right]}{2(\gamma -1)} +\nonumber \\&\quad -\frac{1}{2}\log (4\pi ) + 28.5, \end{aligned} $$](/articles/aa/full_html/2020/10/aa38899-20/aa38899-20-eq11.gif)
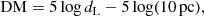
![$$ \begin{aligned} \mathrm{d}\mathrm{DM}&= \frac{5}{2(\gamma -1)} \left[ \left(\mathrm{d}\log F_{\rm X}\right)^2 + \left(\gamma \mathrm{d}\log F_{\rm UV}\right)^2 + \left(\mathrm{d}\beta \right)^2 + \right. \nonumber \\&\quad \left. + \left( \frac{\mathrm{d}\gamma \left[\beta +\log F_{\rm UV}+27.5-\log F_{\rm X}\right]}{\gamma -1} \right)^2\right]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2020/10/aa38899-20/aa38899-20-eq13.gif)
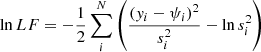
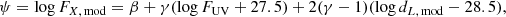
![$$ \begin{aligned} \begin{aligned} d(z)_{\rm L,\,mod}&=k \ln (10)\frac{c}{H_0}[\log (1+z)+a_2\log ^2(1+z)+\\&\quad +a_3\log ^3(1+z)+a_4\log ^4(1+z)+a_5\log ^5(1+z)] +\\&\quad +O [\log ^6(1+z)], \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/10/aa38899-20/aa38899-20-eq17.gif)