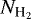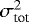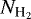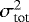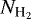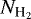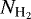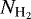| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936625 | |
| Published online | 15 May 2020 | |
Edge collapse and subsequent longitudinal accretion in filament S242
1
National Astronomical Observatories, Chinese Academy of Sciences,
20A Datun Road, Chaoyang District,
Beijing
100012,
PR China
e-mail: lxyuan@bao.ac.cn; mz@nao.cas.cn
2
University of Chinese Academy of Sciences,
100049
Beijing, PR China
3
Key Laboratory of FAST, NAOC, Chinese Academy of Sciences,
Beijing
100012,
PR China
4
South-Western Institute for Astronomy Research, Yunnan University,
Kunming,
650500
Yunnan,
PR China
e-mail: gxli@ynu.edu.cn
5
Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, Chinese Academy of Sciences,
80 Nandan Road,
Shanghai
200030,
PR China
6
Kavli Institute for Astronomy and Astrophysics, Peking University,
5 Yiheyuan Road, Haidian District,
Beijing
100871,
PR China
7
Department of Astronomy, Peking University,
100871
Beijing,
PR China
8
Korea Astronomy and Space Science Institute,
776 Daedeokdae-ro,
Yuseong-gu,
Daejeon
34055,
Republic of Korea
9
University of Science and Technology, Korea (UST),
217 Gajeong-ro,
Yuseong-gu,
Daejeon
34113,
Republic of Korea
10
Nobeyama Radio Observatory, National Astronomical Observatory of Japan, National Institutes of Natural Sciences,
462-2 Nobeyama, Minamimaki, Minamisaku,
Nagano
384-1305,
Japan
11
Department of Astronomical Science, SOKENDAI (The Graduate University for Advanced Studies),
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588,
Japan
Received:
3
September
2019
Accepted:
31
March
2020
Filament S242 is 25 pc long with massive clumps and YSO clusters concentrated in its end regions; it is considered a good example of edge collapse. We mapped this filament in the 12CO(1–0) and 13CO(1–0) lines. A large-scale velocity gradient along filament S242 has been detected; the relative velocity between the two end-clumps is ~3 km s−1, indicating an approaching motion between them. These signatures are consistent with the filament S242 being formed through the collapse of a single elongated entity, where an effect known as “gravitational focusing” drives the ends of the filament to collapse (edge collapse). Based on this picture, we estimate a collapse timescale of ~4.2 Myr, which is the time needed for a finite and elongated entity evolving to the observed filament S242. For the whole filament, we find that increases in surface densities lead to increases in velocity dispersion, which can be consistently explained as the result of self-gravity. We also calculated the contribution of longitudinal collapse to the observed velocity dispersion and found it to be the dominant effect in driving the gas motion near the end-clumps. We propose that our filament S242 is formed through a two-stage collapse model, where the edge collapse of a truncated filament is followed by a stage of longitudinal accretion toward the dense end-clumps.
Key words: stars: formation / ISM: kinematics and dynamics / ISM: structure
© ESO 2020
1 Introduction
Molecular clouds exhibit a complex, irregular, and filamentary morphology (Bally et al. 1987; Wiseman & Ho 1998; Goldsmith et al. 2008; Busquet et al. 2013; André et al. 2016). Recent dust continuum surveys, including the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL; Schuller et al. 2009) and the Herschel infrared Galactic Plane Survey (Hi-GAL; Molinari et al. 2010), have revealed that filaments are ubiquitous along the Galactic plane. These filamentary structures have wide ranges of masses (~1–105 M⊙) and lengths (~0.1–100 pc) (Kirk et al. 2013; Hacar et al. 2013; Wang et al. 2015, 2016; Li et al. 2013, 2016a; Mattern et al. 2018; Kainulainen et al. 2013, 2017). Moreover, a significant fraction of gravitationally bound dense cores and protostars are embedded in filaments, which implies that filaments play an important role in the process of star formation (André et al. 2013, 2014; André 2017; Schneider et al. 2012; Contreras et al. 2016; Li et al. 2016b; Liu et al. 2018a,b; Lu et al. 2018; Yuan et al. 2019).
The process of filament formation and the roles of filaments in star formation are not yet well understood. It is hypothesized that a star-forming cloud prior collapses to lower dimensionality structures, such as sheets and filaments, the resulting layers or filaments will further fragment as a result of the gravitational instability (Schneider & Elmegreen 1979; Larson 1985). Infinite isothermal sheets are perturbed to form successive and parallel filaments; furthermore, infinite isothermal filaments tend to fragment into the strings of dense cores (Inutsuka & Miyama 1992; Curry 2000; Myers 2009). For finite sheets and filaments, simulations show that gravitational focusing can result in strong density enhancements of dense gas in their edge-regions (Burkert & Hartmann 2004; Hartmann & Burkert 2007; Heitsch & Hartmann 2008; Pon et al. 2011, 2012). Meanwhile, far-infrared and submillimeter observations reveal that the dense gas-clumps are mainly concentrated at the ends of filamentary clouds (Hacar et al. 2013; Dewangan et al. 2017; Johnstone et al. 2017; Kainulainen et al. 2017; Ohashi et al. 2018).
Burkert & Hartmann (2004) suggested that non-spherical substructures collapse on timescales longer than equal-density spherical objects. Uniform-density spheres collapse homologously (Binney & Tremaine 1987); instead, for structures like sheets and filaments the edge effect causes their edges to be preferentially accelerated, and then an infalling edge would sweep up the interior material (Burkert & Hartmann 2004; Pon et al. 2011, 2012; Clarke & Whitworth 2015).
The molecular cloud S242 is a spatially elongated filamentary structure with a length of ~25 pc at the distance of 2 kpc (Yuan et al. 2019; Dewangan et al. 2017, 2019). The northern end regions of S242 include two Planck Galactic cold clumps (PGCCs) G181.84+0.31 (hereafter G181) and G182.04+0.41 (hereafter G182), as presented in Fig. 1 (Planck Collaboration XXVIII 2016). The southern end region (hereafter S242-S) is associated with an HII region, which is ionized by the star BD+26 980 (Hunter & Massey 1990). Recently, Dewangan et al. (2017, 2019) found that most massive clumps and YSOs clusters are located at the ends of S242 and concluded that filament S242 is a good example to study the end-dominated collapse. Some candidates, such as the Serpens filament, are velocity-coherent (trans)sonic structures and at the onset of slightly supercritical collapse (Gong et al. 2018). Our filament S242 with larger Mach number of ~2.7–4.0 is indicative of supersonic turbulent motion (Dewangan et al. 2019). In addition, clear evidence of sequential star formation in G181 are revealed, which is supposed to be caused by the edge effect in the collapse of S242 (Yuan et al. 2019).
In this paper we analyze the edge collapse and subsequent longitudinal accretion in filament S242. This paper is organized as follows. Section 2 presents the TRAO observation and data reduction. Section 3 presents the results, including the basic physical and kinematical information of filament S242. In Sect. 4 we discuss the kinematics of end-dominated collapse and the relation between self-gravity and turbulence motion. Section 5 presents the conclusions of this study.
 |
Fig. 1 Panels a and d: color-scale images represent the distributions of the integrated intensity for 12CO(1–0) and 13CO(1–0) lines in the velocity range of −5 to 10 km s−1. The red circles denote the IRAS sources in the filament S242. The orange star represents the star BD+26 980, which triggers the HII region associated with the S242-S region. The white dashed circles indicate the Planck Galactic cold clumps G181.84+0.31 and G182.04+0.41. The black and white contours in all the panels, except for panel b, display the H2 column density distribution of S242, which derived as Dewangan et al. (2017), ranging from 25 to 90% stepped by 15% of the value (2.0 × 1022 cm−2). Panel b: excitation temperature map derived from 12CO(1–0) line. The white contours display 13CO column density distribution of S242, ranging from 10 to 90% stepped by 15% of the value (2.0 × 1016 cm−2). Panel c: 13CO column density map. Panel e: centroid velocity field of S242, which derived from the Gaussian fitting of 13CO(1–0) line. Panel f: distribution of FWHM velocity width for S242, which derived from the Gaussian fitting of 13CO(1–0) line. The orange circle in panel f shows the effective beam size of TRAO. |
2 Observations and data reduction
We performed the on-the-fly (OTF) mapping observations at the J = 1–0 transition lines of 12CO and 13CO for the whole molecular cloud S242 using the 14-meter Radio Telescope1 of Taeduk Radio Astronomy Observatory (TRAO)2. We divided the molecular cloud S242 into two OTF maps (32 arcmin × 32 arcmin for each map). The FWHM-width beam sizes (θB) for the 12CO(1–0) and 13CO(1–0) lines are 45 arcsec and 47 arcsec, respectively. The main beam efficiencies (ηB) for 12CO(1–0) and 13CO(1–0) lines are 0.54 and 0.51, respectively. An RMS noise level of ~0.8 K in TA* for the 12CO(1–0) line and ~0.4 K for the 13CO(1–0) line are achieved with a spectral resolution of ~0.04 km s−1. The OTF data are gridded into the Class format files with a pixel size of 24 arcsec using the OTF tool at TRAO.
3 Results
3.1 The integrated intensity of CO lines
Figure 1 shows the integrated intensity distributions of 12CO(1–0) line in Panel a and 13CO(1–0) line in panel d in the S242 field. Only the region with CO peak intensity higher than 2 K (5σ, an RMS noise of 0.4 K at 0.2 km s−1 for Tmb) is considered. We find that 13CO emission mainly distributes along the extended S242 and agree well with the dust emission. The CO intensity values are higher in both end regions of the S242, especially for S242-S. While the 12CO line is optically thick and could trace relatively diffuse molecular gas. We find that there is diffuse molecular gas in the gap between G181 and G182. Dewangan et al. (2019) have presented the integrated intensity maps of 13CO(1–0), C18O(1–0), and CS(2–1) emission, the dense gas traced by C18O(1–0) and CS(2–1) lines are also mainly located in northern G181, G182, and S242-S regions.
3.2 Excitation temperature map and 13CO column densities of S242
We estimated the excitation temperature and 13CO column density using the 12CO and 13CO line data with Eqs. (4)–(13) in Qian et al. (2012). The resultant gas excitation temperature map of S242 is presented in panel b of Fig. 1, where most of the gas is in the range between 8 and 25 K. Prior dust temperature estimated for S242 ranges from 10 to 27 K (Dewangan et al. 2017), which seems to be in a good agreement with gas excitation temperature. In S242, the higher temperatures (~15–25 K) in the S242-S region may be caused by the warm gas associated with the S242 HII region or the active star formation activities revealed in Dewangan et al. (2017), while molecular gas away from the S242-S region is in the temperature range of about 10–14 K.
As presented in the panel c of Fig. 1, 13CO column density(N(CO)) distributes in the range of 0.2 × 1016 cm−2 –2 × 1016 cm−2. N(CO) is influenced by chemical processes, such as CO depletion at high column densities (Kramer et al. 1999; Caselli et al. 1999; Tafalla et al. 2002) and the CO formation and destruction at low column densities (van Dishoeck & Black 1988; Visser et al. 2009). Moreover, temperature gradients in the molecular clouds also affect N(CO) by ~30–70% (Evans et al. 2001; Pineda et al. 2010). We find the gas distribution is very consistent with the H2 column density estimated from the Herschel dust continuum emission. In addition, the densest gas-clumps are mainly concentrated on S242-S.
3.3 Centroid velocity and velocity-width of 13CO(1–0) molecular lines
Panels e and f of Fig. 1 display the distribution of the line-of-sight centroid velocity (Vlsr) and FWHM velocity-width (ΔV), both of which are derived by fitting a single Gaussian to the 13CO(1–0) line profile. We limited the available 13CO(1–0) line emission to regions where the intensity value are higher than ~8 σ (3.0 K, Tmb). The fitted 13CO emission is within the velocity range of −5 to 10 km s−1. The value of Vlsr map ranges from 0.5 to 3.5 km s−1 ; we find that the northern end is red-shifted (2.5–3.5 km s−1), while the southern S242-S is mainly blue-shifted (0.5–1.0 km s−1). Furthermore, the large-scale centroid velocity gradients, from bluer clump at the southern end to the redder one at the northern end, may represent the gas flow along the filament or the approaching movement between the two end-clumps. However, such a gradual change in velocity is disturbed in the gas near end-clumps, which show larger local velocity-gradients of ~1 km s−1 pc−1 against S242-S and ~0.5 km s−1 pc−1 against the northern clump. The FWHM velocity-width distribute in a range of 0.5–2.5 km s−1. We find that there is an increasing velocity width (FWHM) toward the two end-clumps, especially for that in S242-S with a peak value of 2.5 km s−1.
3.4 Channel maps of CO molecular lines for S242
Figure 2 presents the channel maps of 13CO(1–0) and 12CO(1–0) lines emission in the increment of 0.6 km s−1 ranging from −0.1 to 4.8 km s−1. In the low-velocity range of −0.1 to 1.1 km s−1, the molecular gas mainly locates in the S242-S region. As the velocity increases from 1.1 to 2.4 km s−1, the CO emission gradually extends from S242-S to the northern end (G181 and G182). The gas in the northern end is mainly in the red-shifted velocity range of 2.4–3.6 km s−1. Our 12CO observationsreveal much more diffuse molecular gas, which was missed by Dewangan et al. (2019). In the red-shifted velocity range of 2.4 km s−1– 3.6 km s−1, both G181 and G182 are included in the diffuse structure of S242.
3.5 Filamentary structures in molecular cloud S242
3.5.1 Skeleton structures of filament S242
We used the FILFINDER algorithm (Koch & Rosolowsky 2015) to detect the filamentary structures in H2 column density map, which is derived by Herschel dust continuum emission (160–500 μm) in the same way as in Dewangan et al. (2017). The FILFINDER procedure has been successfully applied in Yuan et al. (2019). In Fig. 3, we plot the skeletons of the filament S242, color-coded by the centroid velocities of 13CO(1–0) line. Combing this data with panel e of Fig. 1, it is evident that the extended skeletons along the whole S242 filament present global velocity gradients, especially for the substructures in both end regions of S242.
In addition, the width of filament S242 can be calculated by building a radial profile of H2 column density with respect to the skeleton. As presented in Fig. A.1, we use RadFil, a publicly available Python package to build and fit a radial profile for filament S242 (Zucker & Chen 2018). The radial profiles are built by taking radial cuts across the above skeletons extracted by FILFINDER, thereby presenting the radial structure of the filament across its entire length. In panel a of Fig. A.1 we present the distribution of cuts across the spine, where we determine an approximate distance between cuts of ~0.7 pc (the parameter of samp_int = 5 in the RadFil procedure means the cuts are ~5 pixels apart, corresponding to ~0.7 pc at a pixel scale of 14 arcsec and distance of 2 kpc). In panels b and c of Fig. A.1, Plummer and Gaussian functions are used to fit the entire ensemble of radial cuts, respectively. We get a best-fit flattening radius of 0.5 ± 0.16 pc using Plummer fitting function, a non-deconvolved FWHM-width of 0.93 pc and a deconvolved FWHW-width of 0.86 pc with the Gaussian fitting function.
 |
Fig. 2 Channel maps of 12CO(1–0) and 13CO(1–0) lines. The green and magenta contours display the distribution of the integrated intensity 12CO(1–0) and 13CO(1–0) lines, respectively, in the interval velocity range of 0.6 km s−1. The levels of green contours are from 6σ (~1.2 K km s−1) to the peak value by intervals of 6σ. The levels of magenta contours are from 3σ (~0.6 K km s−1) to the peak value by intervals of 3σ. |
3.5.2 Main velocity component of filament S242
In panel a of Fig. 4, we present the position-velocity diagram produced along the spine of the filament S242, as well as the centroid velocity and FWHM velocity-width obtained by fitting a single Gaussian along the spine, as shown by the dark blue curve and vertical white lines, respectively. In some regions, which are indicated as black rectangles, they cannot be fitted by a single Gaussian. The spectra of 13CO(1–0) lines and their associated fits along the spine are also shown in Fig. A.3; each profile is the averaged spectrum in each magenta circle (Fig. A.2) with a radius of 0.5 pc. The profiles of 13CO(1–0) lines are fitted by either one or two Gaussians. We find that the average 13CO(1–0) lines in the magentacircle of No. 6 – No. 8 and No. 13 – No. 15 show two peaks. The existence of multiple components is validated with the optical thin line C18O(1–0). As presented in Fig. A.3, we findthe C18O spectra are also double peaked at the locations where 13CO double peaked. These C18O line data are from the Milky Way Imaging Scroll Painting project (MWISP), which is an unbiased Galactic plane CO survey with the 13.7 m telescope of the Purple Mountain Observatory (Su et al. 2019).
Except for the noted structures in the length ranges of ~6.5 pc–8.5 pc and ~13.5–15.5 pc, which show two velocity components, most regions are mainly dominated by one velocity component. Therefore, the spines are fitted with a single Gaussian or double Gaussians accordingly. Then we pick one component as the main component along filament S242. The main component is defined as the velocity component, which accounts for a larger fraction and is coherent with adjacent structures. In panel b of Fig. 4, we present the fractional intensity (fG) of the mainvelocity component taken in the total observed velocity components, the fG is calculated as the ratio of the velocity-integrated intensity of the fitting Gaussian for each main velocity component to that of the observed spectrum. As presented, the values of fG in the length range of ~6.5–8.5 pc and ~13.5–15.5 pc are from 0.5 to 0.7, the values in other regions are close to 1. In addition, at each location with two velocitycomponents, the fitted centroid velocity for the main velocity component in the 13CO(1–0) line is nearly consistent with that traced by C18O line, as presented in Fig. A.3.
 |
Fig. 3 Skeletons of the filamentary network extracted with the FilFinder, color-coded by the centroid velocities of the 13CO spectral line.The gray map is the H2 column density map derived from Herschel continuum map (160–500 μm) in Dewangan et al. (2017). The overlaid green contours display 13CO column density distribution of filament S242, ranging from 15 to 90% stepped by 15% of the value (1.5 × 1016 cm−2). |
3.5.3 Longitudinal profiles of the main skeleton in filament S242
Panel b of Fig. 4 presents the profiles of fitted centroid velocity, velocity dispersion (σtot), H2 column density (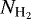 ), and excitation temperature (Tex) for the mainskeleton from the southern to northern end-point (only the eastern skeleton in G181 is included). The southern end-point is defined as the zero point of the x-axis. The x-axis value of a pixel on the skeleton represents its distance from the zero point integrated along the spine line in Fig. 3. The vertical dashed black lines denote the peaks of H2 column densities (
), and excitation temperature (Tex) for the mainskeleton from the southern to northern end-point (only the eastern skeleton in G181 is included). The southern end-point is defined as the zero point of the x-axis. The x-axis value of a pixel on the skeleton represents its distance from the zero point integrated along the spine line in Fig. 3. The vertical dashed black lines denote the peaks of H2 column densities (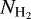 ) along the skeleton.
) along the skeleton.
The total 1D velocity dispersion (σtot) for the mean molecules is calculated using (Fuller & Myers 1992)
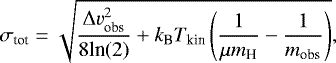 (1)
(1)
where Δvobs is the observed line width (FWHM) derived by the Gaussian fitting of the C13O lines; kB is the Boltzmann constant; μ =2.33, the atomic weight of the mean molecule; mH is the mass of a hydrogen atom; and mobs is the mass of the observed molecule (29 a.m.u for C13O), Tkin is the kinetic temperature of gas, which is assumed to be the value of excitation temperature. The uncertainties for σtot are mainly contributed from the measured FWHM of ~5%, an estimated excitation temperature of ~10% and optical depth of ~20% (Hacar et al. 2016). In addition, Dewangan et al. (2019) derived the Mach number of ~2.7–4.0 for the subregions in filament S242 based on the C18O spectra, suggesting that all the subregions are supersonic. These subregions are marked in Fig. 6 of Dewangan et al. (2019) and cover our skeleton structures for the filament S242.
4 Discussion
4.1 Edge collapse of molecular cloud S242
4.1.1 The case of the edge collapse in molecular cloud S242
Burkert & Hartmann (2004) simulated the collapse and fragmentation in the finite self-gravitating sheets. This simulation shows that the gravitational acceleration has a steep increase at the edges of finite sheets or filaments that causes these structures to collapse immediately with material piling up most rapidly at the outer edges. In addition, the edge-clumps are given more momentum and may further approach the center of filaments (Pon et al. 2011, 2012). Moreover, Clarke & Whitworth (2015) suggested that due to the gravitational attraction of the massive end-clumps, the gas ahead of the end-clumps can also be accelerated toward the end-clumps.
In Fig. 5, we sketch the edge-collapse process of a finite entity. In the time slice of “Before collapse”, its geometry is a longer filament. Due to the gravitational focusing near the closed end of the structure, materials are rapidly accelerated into both end regions, which results in the formation of gas clumps and star clusters near the ends of structures, as presented in the time slice of “After collapse” (Burkert & Hartmann 2004; Pon et al. 2011, 2012). For the filament S242, the massive clumps and YSOs clusters are mainly located in the end regions (Dewangan et al. 2017; Yuan et al. 2019). Moreover, as presented in panel e of Fig. 1, the large-scale velocity gradients distribute along S242; the blue-shift in the southern end and the red-shift in the northern end may indicate the approaching movement between the two end-clumps. These all suggest that S242 is formed as a result of theglobal gravity acting on a finite cloud with non-spherical geometry, such as filaments.
 |
Fig. 4 Panel a: position-velocity distribution along the spine of filament S242 from the southern to northern end. The dark blue curve and vertical white lines represent the fitted centroid velocity and FWHM velocity width by a single Gaussian, respectively. Panel b: centroid velocity (Vlsr), total 1D velocity dispersion (σtot), H2 column density ( |
4.1.2 Collapse timescale for the molecular cloud S242
We illustrate an evolutionary scenario for filament S242 in Fig. 5. The initial filament S242 has a length of Lbefore. After the edge collapse, its length becomes Lafter. Considering all the subregions of S242 listed in Table 1 of Dewangan et al. (2019), the total mass of filament S242 (M) derived from the C18O line, is estimated to be about 9700 M⊙. Before collapsing, the line mass of filament S242 (Mline) is thought to be 209 M⊙ pc−1, the observed line mass of a subregion between two end regions (Dewangan et al. 2019). Therefore, Lbefore = M∕Mline ≃ 46 pc. The observed filament S242 has a length of ~25 pc, and therefore Lafter ≃ 25 pc.
To estimate the age of filament S242, we consider a filament of length L and width d; the gravitational acceleration at one end of the filament can be calculated approximately as
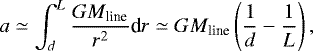 (2)
(2)
where G is the gravitational constant, Mline is the line mass, and Mline= dM/dL ≃ 209 M⊙ pc−1. For filament S242, the length L ≃ 25 pc, the width d ≃ 0.86 pc, and the derived gravitational acceleration is about 1.1 pc Myr−2. Under the gravitational acceleration at the end regions, the length of filament S242 becomes Lafter; therefore,
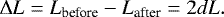 (3)
(3)
We further estimate the collapse time as
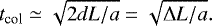 (4)
(4)
The collapse time of filament S242 is about 4.2 Myr; if we take the projection effect into account and assume an inclination (θ) of 30 degrees, the value is about 4.2/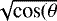 ) Myr ≃ 4.5 Myr. Dewangan et al. (2019) have estimated a collapse timescale of ~3.5 Myr for filament S242, which is derived as tcol = (0.49+0.26A)/(Gρ)1∕2 for the filamentary structures in Clarke & Whitworth (2015), where A is the initial aspect ratio of filament. They took the observed aspect ratio (A) and a mean density (ρ) of the observed S242 filament to calculate the collapse timescale. Their value is the time for the observed filament S242 to collapse into a singledense core and different from the collapse time we estimated; our value is the timescale from the “Before collapse” to “After collapse” in Fig. 5. During our timescale, the S242 cloud undergoes the process of edge collapse from its initial structure to the current observed filament.
) Myr ≃ 4.5 Myr. Dewangan et al. (2019) have estimated a collapse timescale of ~3.5 Myr for filament S242, which is derived as tcol = (0.49+0.26A)/(Gρ)1∕2 for the filamentary structures in Clarke & Whitworth (2015), where A is the initial aspect ratio of filament. They took the observed aspect ratio (A) and a mean density (ρ) of the observed S242 filament to calculate the collapse timescale. Their value is the time for the observed filament S242 to collapse into a singledense core and different from the collapse time we estimated; our value is the timescale from the “Before collapse” to “After collapse” in Fig. 5. During our timescale, the S242 cloud undergoes the process of edge collapse from its initial structure to the current observed filament.
In addition, Yuan et al. (2019) and Dewangan et al. (2019) reveal a number of YSO clusters (including Class I and Class II) concentrated mainly in the end clumps. Their average lifetime should be in the range of ~0.5–2 Myr (Evans et al. 2009). As shown in panel e of Fig. 1, the relative velocity of the two end-clumps is about 3 km s−1 ; we take the average velocity (vaver) of 1.5 km s−1 for the two end-clumps. During the lifetime of Class II YSOs, we estimate that the moving distance for the end-clumps is about 2 Myr × 1.5 km s−1 ~3.0 pc. This distance is longer than the size of the dense clumps (~1 pc for substructures in G181) that harbor the YSOs clusters. Therefore, we suggest that the old YSOs previously formed may also be moving toward the center of the filament, together with the end-clumps.
 |
Fig. 5 Sketch of the edge-collapse process of the filament S242. |
4.2 Gravitational stability and gravity-driven longitudinal accretion in filament S242
4.2.1 Self-gravity as the cause of increased velocity dispersion?
In panel b of Fig. 4, we find a similarity between the σtot profile and that of 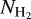 , where the peaks of
, where the peaks of 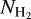 coincide with the peaks of σtol. Furthermore, the peaks of
coincide with the peaks of σtol. Furthermore, the peaks of 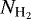 also match the maximum or minimum values of the centroid-velocity profile. Therefore, the local velocity perturbations may be related to the gravitational perturbation caused by the varying line mass. In the upper panel of Fig. 6, we plot the velocity dispersion (
also match the maximum or minimum values of the centroid-velocity profile. Therefore, the local velocity perturbations may be related to the gravitational perturbation caused by the varying line mass. In the upper panel of Fig. 6, we plot the velocity dispersion (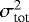 ) against the H2 column density (
) against the H2 column density (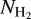 ) for the main skeleton; we calculate that their Spearman’s correlation coefficient is about 0.55, indicating a roughly positive correlation between the H2 column density (
) for the main skeleton; we calculate that their Spearman’s correlation coefficient is about 0.55, indicating a roughly positive correlation between the H2 column density (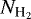 ) and velocity dispersion (
) and velocity dispersion (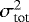 ). The best-fit slope for the linear relationship between log(
). The best-fit slope for the linear relationship between log(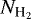 ) and log(
) and log(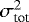 ) is 0.62 ± 0.07. This may imply that the increased velocity dispersion is caused by the matter concentration under self-gravity. Other studies also mentioned that gravitational collapse could generate additional turbulence motion (Klessen & Hennebelle 2010; Peretto et al. 2014; Hacar et al. 2017).
) is 0.62 ± 0.07. This may imply that the increased velocity dispersion is caused by the matter concentration under self-gravity. Other studies also mentioned that gravitational collapse could generate additional turbulence motion (Klessen & Hennebelle 2010; Peretto et al. 2014; Hacar et al. 2017).
Can the self-gravity account for the increased velocity dispersion? We further estimate the self-gravity induced velocities as
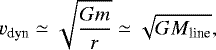 (5)
(5)
where G is the gravitational constant; Mline is the line mass estimated as Mline= μ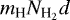 , where the
, where the 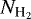 is the H2 column density along the skeleton and d is defined as half of the S242 filament width (~0.4 pc). Furthermore, for a filament the virial parameters could be calculated as (Ostriker 1964; Watkins et al. 2019)
is the H2 column density along the skeleton and d is defined as half of the S242 filament width (~0.4 pc). Furthermore, for a filament the virial parameters could be calculated as (Ostriker 1964; Watkins et al. 2019)
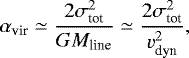 (6)
(6)
where the prefactor of 2 depends on the equation of state and the density profile in filament S242 (Chandrasekhar & Fermi 1953), which is consistent with the value in Watkins et al. (2019).
In the upper panel of Fig. 6, the cyan line shows the limit for the parameter αvir = 2. The log-scale of αvir histograms for the S242 skeletons are presented in the lower panel of Fig. 6, which is weighted by the value of H2 column density. We find that the distribution of the log(αvir) concentratesin the range of ~0.2–0.5 (1.6–3.1 for αvir). In addition, we also present the distribution of log(αvir) for the skeleton gas with 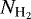 ≥ 1 × 1022 and
≥ 1 × 1022 and 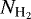 < 1 × 1022, respectively. The log(αvir) in the gas associated with
< 1 × 1022, respectively. The log(αvir) in the gas associated with 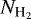 ≥ 1 × 1022 mainly distributes in the range of ~0.2–0.3 (1.6–2.0 for αvir), which is lower than the value of ~0.3–0.5 (2.0–3.1 for αvir) for the log(αvir) in gas corresponding to
≥ 1 × 1022 mainly distributes in the range of ~0.2–0.3 (1.6–2.0 for αvir), which is lower than the value of ~0.3–0.5 (2.0–3.1 for αvir) for the log(αvir) in gas corresponding to 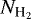 < 1 × 1022. Overall, self-gravity accounts for a higher fraction of velocity dispersion in the regions with high surface mass than that with low surface mass.
< 1 × 1022. Overall, self-gravity accounts for a higher fraction of velocity dispersion in the regions with high surface mass than that with low surface mass.
It should be noted that the importance of gravity can only be partially reflected by the virial parameter. This is because gravity is balanced by a combination of turbulence motion, radial collapse, and longitudinal collapse. When we evaluate the virial parameters, the velocity dispersion contrails are caused by turbulence, radial collapse, and longitudinal collapse. However, due to the projection, only a small fraction of σlongi is contained in our velocity dispersion
 |
Fig. 6 Upper panel: velocity dispersion ( |
4.2.2 Contribution of velocity dispersions from the longitudinal collapse
The longitudinal velocity profile for the main skeleton is shown in panel b of Fig. 4. There are large-scale velocity gradients distributed along filament S242 from the blue-shifted S242-S to red-shifted northern end. How much does the longitudinal collapse contribute to the velocity dispersion? We propose the following equation through which the velocity dispersion of the filament can be decomposed:
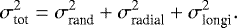 (7)
(7)
Here 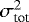 is the total turbulent motion of gas, which includes
is the total turbulent motion of gas, which includes 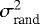 ,
, 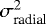 , and
, and 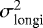 , representing the random, radial, and longitudinal gas motion, respectively.
, representing the random, radial, and longitudinal gas motion, respectively.
To estimate the contribution of longitudinal collapse, the profiles of longitudinal velocity (Vlsr), velocity gradients (dV/dl), velocity dispersion (σtot), and H2 column density (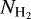 ) are convolved to the spatial resolution of the average filament width of 0.86 pc, using a Gaussian kernel and weighting by the value of H2 column density. The resultant profiles are presented in Fig. 7. We further calculate the contribution of longitudinal velocity gradients to the overall velocity dispersion in a width (d) of 0.86 pc, which is defined as longitudinal factor fL = (dV/dl) × d/σtot = σlongi/σtot. The distribution of longitudinal factor fL along the main skeleton is presented in Fig. 7; we find that values of fL greater than 0.5 are mainly located in the structures near the end-clumps, which may be caused by the longitudinal collapse of end-clumps or gravitational attraction by the massive end-clumps. However, the origin of the observed velocity dispersion in substructures with the factor of fL smaller than 0.5 is likely due to the radial collapse or random motion of the cloud.
) are convolved to the spatial resolution of the average filament width of 0.86 pc, using a Gaussian kernel and weighting by the value of H2 column density. The resultant profiles are presented in Fig. 7. We further calculate the contribution of longitudinal velocity gradients to the overall velocity dispersion in a width (d) of 0.86 pc, which is defined as longitudinal factor fL = (dV/dl) × d/σtot = σlongi/σtot. The distribution of longitudinal factor fL along the main skeleton is presented in Fig. 7; we find that values of fL greater than 0.5 are mainly located in the structures near the end-clumps, which may be caused by the longitudinal collapse of end-clumps or gravitational attraction by the massive end-clumps. However, the origin of the observed velocity dispersion in substructures with the factor of fL smaller than 0.5 is likely due to the radial collapse or random motion of the cloud.
We note that the value of σlongi and fL are affected by the inclination of filament S242. If an inclination (θ) of 30 degrees is assumed, the value of σlongi could be underestimated by a factor of 1/sin(θ) ~ 2. For the structures near the end-clumps, the longitudinal accretion becomes the dominant factor.
4.2.3 Subsequent longitudinal-accretion caused by the massive end-clumps
The regions where the fraction of velocity dispersion from the longitudinal collapse is high are mainly located in the structures near end-clumps. These structures present the higher velocity-gradients (up to ~2 km s−1 pc−1). What is the origin of the longitudinal velocity gradients? The blue-shifted S242-S and red-shifted northern end-clumps imply the approaching movement between the two end-clumps in the edge collapse of filament S242 (Burkert & Hartmann 2004; Pon et al. 2011, 2012). However, the larger velocity-gradients of ~1 km s−1 pc−1 against the end-clumps may be due to the accretion flows driven by the gravitational attraction of massive end-clumps, as suggested in Clarke & Whitworth (2015). As shown in Fig. 8, we sketch the gas motion in the collapse process of filament S242. The magenta sub-skeletons represent the substructures with the value of factor (fL) larger than 0.5, which means the longitudinal collapse–accretion dominates the increasing velocity dispersion. The blue regions with the fL smaller than 0.5, which are mainly located in substructures between the two end-clumps, are either under the radial collapse or turbulence motion. Combining with the velocity field for filament S242, we propose the following pictures in Fig. 8, which indicate the directions of gas motion in the collapse of filament S242.
We suggest that there are two stages in the formation of filament S242. First, the collapse of a finite and elongated filament is affected by edge-effect and the end-clumps acquire a significant amount of mass. Second, the longitudinal accretion becomes dominated toward massive end-clumps, due to their local gravitational attraction.
 |
Fig. 7 Convolved profiles of centroid velocity (Vlsr), velocity gradients (dV/dl), total 1D velocity dispersion (σtot), the contribution of longitudinal collapse in the total velocity dispersion (fL), and the H2 column density. The vertical black dashed lines indicate the peaks of the H2 column density profile; the horizontal green dashed line represents fL = 0.5. |
 |
Fig. 8 Sketch of the subsequent longitudinal accretion of the filament S242. The overlaid green contours display 13CO column density distribution of filament S242, ranging from 15 to 90% stepped by 15% of the value (1.5 × 1016 cm−2). The skeleton structures of the filament S242 are color-coded by the longitudinal factor fL, which is the contribution of longitudinal collapse for the observed velocity dispersion. The magenta arrows indicate the direction of gas motion in longitudinal collapse and accretion, the blue arrows in radial collapse. The right subpanel presents the profile of longitudinal factor fL along the spine of filament S242. |
5 Conclusions
The main results of this study are summarized as follows:
-
Filament S242 is regarded as a candidate for edge collapse, a mechanism proposed by Burkert & Hartmann (2004). The massive clumps and YSOs clusters are mainly located in its end regions (Dewangan et al. 2017; Yuan et al. 2019). We report the TRAO observations of 12CO and 13CO lines for filament S242. In addition, its distributions of the excitation temperature (8–25 K), 13CO column density (0.2 × 1016 cm−2–2 × 1016 cm−2), line width, and centroid velocity are also presented. We extract the main and coherent velocity component from the skeleton structures and derive a FWHM of ~0.86 pc for filament S242.
-
We find a gradual change in velocity along the filament S242. The relative velocity between northern and southern massive end-clumps is about 3 km s−1, which may represent the approaching movement between them. These signatures indicate that the filament S242 may start as a finite, truncated filament, where the material is concentrated on the end regions through the edge-collapse mechanism proposed by Burkert & Hartmann (2004). Moreover, the end-clumps may have acquired more momentum, which causes both end-clumps to approach the center of the filaments. In addition, we estimate the collapse timescale of filament S242 to be ~4.2 Myr, which is the time from the elongated initial structure to the currently observed filament. Compared with the lifetime of YSOs(0.5–2 Myr) and the relative movement of end-clumps, we suggest that the old YSOs are moving toward the center of filament, together with the end-clumps.
-
We find that the total velocity dispersion σtot increases correlatively with the H2 column density. In addition, the viral parameters αvir (2
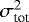 /v
/v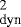 ) in regions with high surface mass tend to be lower than those with low surface mass. Thus, the increased turbulence motion in filament S242 might be gravitationally generated. In addition, we also reveal that the origin of the observed velocity dispersion may be dominated by the longitudinal collapse in the structures in the vicinity of end-clumps; however, for the subfilament between two end-clumps, the velocity dispersion mainly comes from the radial and random motion of the cloud.
) in regions with high surface mass tend to be lower than those with low surface mass. Thus, the increased turbulence motion in filament S242 might be gravitationally generated. In addition, we also reveal that the origin of the observed velocity dispersion may be dominated by the longitudinal collapse in the structures in the vicinity of end-clumps; however, for the subfilament between two end-clumps, the velocity dispersion mainly comes from the radial and random motion of the cloud. -
We propose a two-stage fragmentation scenario for filament S242. First, due to gravitational focusing, the material in the finite filament is preferentially concentrated at the end regions, and the end-clumps acquire a significant amount of mass. Second, the longitudinal accretion becomes dominant in the vicinity of the high-mass clumps.
Acknowledgements
We are grateful to the anonymous referee for a critical reading of the manuscript and constructive suggestions that greatly improved the quality of this paper. Lixia Yuan, Ming Zhu are supported by the National Key R&D Program of China No.2017YFA0402600, the NSFC grant No.U1531246 and also supported by the Open Project Program of the Key Laboratory of FAST, NAOC, Chinese Academy of Sciences. Ke Wang acknowledges support by the National Key Research and Development Program of China (2017YFA0402702, 2019YFA0405100), the National Science Foundation of China (11973013, 11721303), and the starting grant at the Kavli Institute for Astronomy and Astrophysics, Peking University (7101502016). Jinghua Yuan is supported by the NSFC funding No.11503035 and No.11573036.
Appendix A
 |
Fig. A.1 Radial profile for H2
column density for the filament S242. Panel a: distribution of radial cuts along the spine of filament S242. The red curve represents the spine across the entire filament S242, extractedby FilFinder. The blue dots show the sampling points with an interval of
~0.7 pc. The red radial lines, perpendicular to the tangent of the spine, are the cuts used to calculated the radial distances from the spine. Panels b and c: Plummer and Gaussian fitting for the radial profiles. The black dots represent the value of
|
 |
Fig. A.2 As in Fig. 3, but the magenta circles show the subregions for the average spectra from No.1 to No.24 displayed in Fig. A.3. |
 |
Fig. A.3 Average spectral profiles for 13CO lines in thecorresponding subregions from No.1 to No.24, displayed in Fig. A.2. The black profiles represent the observed spectra, the magenta dashed profiles are our fitted results by one or two Gaussians. The fitted parameters for the main velocity components (including peak intensity, centroid velocity, and velocity dispersion) are given at the top of every subpanel. The blue profiles in No. 6 – No. 8 and No. 13 – No. 15 are the average C18O line spectra, which are amplified by a factor of 3. These C18O data are from MWISP CO surveys (Su et al. 2019). In each of those panels, the vertical green dashed line shows the centroid velocity of the main velocity component. |
References
- André, P. 2017, C. R. Geosci., 349, 187 [Google Scholar]
- André, P., Könyves, V., Arzoumanian, D., Palmeirim, P., & Peretto, N. 2013, ASP Conf. Ser., 476, 95 [NASA ADS] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 27 [Google Scholar]
- André, P., Revéret, V., Könyves, V., et al. 2016, A&A, 592, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bally, J., Langer, W. D., Stark, A. A., & Wilson, R. W. 1987, ApJ, 312, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton: Princeton University Press) [Google Scholar]
- Burkert, A., & Hartmann, L. 2004, ApJ, 616, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Busquet, G., Zhang, Q., Palau, A., et al. 2013, ApJ, 764, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Clarke, S. D., & Whitworth, A. P. 2015, MNRAS, 449, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, Y., Garay, G., Rathborne, J. M., & Sanhueza, P. 2016, MNRAS, 456, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C. L. 2000, ApJ, 541, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Dewangan, L. K., Baug, T., Ojha, D. K., et al. 2017, ApJ, 845, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Dewangan, L. K., Pirogov, L. E., Ryabukhina, O. L., Ojha, D. K., & Zinchenko, I. 2019, ApJ, 877, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., I., Allen, L. E., Blake, G. A., et al. 2001, AAS Meeting Abstracts, 198, 25.05 [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, G. A., & Myers, P. C. 1992, ApJ, 384, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, Y., Li, G. X., Mao, R. Q., et al. 2018, A&A, 620, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Alves, J., Burkert, A., & Goldsmith, P. 2016, A&A, 591, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Alves, J., Tafalla, M., & Goicoechea, J. R. 2017, A&A, 602, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., & Burkert, A. 2007, ApJ, 654, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., & Hartmann, L. 2008, ApJ, 689, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., & Massey, P. 1990, AJ, 99, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Ciccone, S., Kirk, H., et al. 2017, ApJ, 836, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Ragan, S. E., Henning, T., & Stutz, A. 2013, A&A, 557, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Stutz, A. M., Stanke, T., et al. 2017, A&A, 600, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, E. W., & Rosolowsky, E. W. 2015, MNRAS, 452, 3435 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, C., Alves, J., Lada, C. J., et al. 1999, A&A, 342, 257 [NASA ADS] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Li, G.-X., Wyrowski, F., Menten, K., & Belloche, A. 2013, A&A, 559, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G.-X., Urquhart, J. S., Leurini, S., et al. 2016a, A&A, 591, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, P. S., Klein, R. I., & McKee, C. F. 2016b, IAU Symp., 315, 103 [NASA ADS] [Google Scholar]
- Liu, T., Kim, K.-T., Juvela, M., et al. 2018a, ApJS, 234, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Li, P. S., Juvela, M., et al. 2018b, ApJ, 859, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, X., Zhang, Q., Liu, H. B., et al. 2018, ApJ, 855, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Mattern, M., Kauffmann, J., Csengeri, T., et al. 2018, A&A, 619, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, S., Sanhueza, P., Sakai, N., et al. 2018, ApJ, 856, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peretto, N., Fuller, G. A., André, P., et al. 2014, A&A, 561, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2010, ApJ, 712, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XXVIII. 2016, A&A, 594, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pon, A., Johnstone, D., & Heitsch, F. 2011, ApJ, 740, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Toalá, J. A., Johnstone, D., et al. 2012, ApJ, 756, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, L., Li, D., & Goldsmith, P. F. 2012, ApJ, 760, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Su, Y., Yang, J., Zhang, S., et al. 2019, ApJS, 240, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, K., Testi, L., Ginsburg, A., et al. 2015, MNRAS, 450, 4043 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wang, K., Testi, L., Burkert, A., et al. 2016, ApJS, 226, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, E. J., Peretto, N., Marsh, K., & Fuller, G. A. 2019, A&A, 628, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiseman, J. J., & Ho, P. T. P. 1998, ApJ, 502, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, L., Zhu,M., Liu, T., et al. 2019, MNRAS, 487, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., & Chen, H. H.-H. 2018, ApJ, 864, 152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
The new receiver system, SEQUOIA-TRAO, is equipped with high-performance 16-pixel MMIC preamplifiers in a 4 × 4 array, operating within the 85–115 GHz frequency range. The backend system (an FFT spectrometer) provides 4096 × 2 channels with fine velocity resolution of ~0.04 km s−1(15 kHz) per channel, and full spectral bandwidth of 62.5 MHz (~160 km s −1 for 12CO).
All Figures
 |
Fig. 1 Panels a and d: color-scale images represent the distributions of the integrated intensity for 12CO(1–0) and 13CO(1–0) lines in the velocity range of −5 to 10 km s−1. The red circles denote the IRAS sources in the filament S242. The orange star represents the star BD+26 980, which triggers the HII region associated with the S242-S region. The white dashed circles indicate the Planck Galactic cold clumps G181.84+0.31 and G182.04+0.41. The black and white contours in all the panels, except for panel b, display the H2 column density distribution of S242, which derived as Dewangan et al. (2017), ranging from 25 to 90% stepped by 15% of the value (2.0 × 1022 cm−2). Panel b: excitation temperature map derived from 12CO(1–0) line. The white contours display 13CO column density distribution of S242, ranging from 10 to 90% stepped by 15% of the value (2.0 × 1016 cm−2). Panel c: 13CO column density map. Panel e: centroid velocity field of S242, which derived from the Gaussian fitting of 13CO(1–0) line. Panel f: distribution of FWHM velocity width for S242, which derived from the Gaussian fitting of 13CO(1–0) line. The orange circle in panel f shows the effective beam size of TRAO. |
| In the text | |
 |
Fig. 2 Channel maps of 12CO(1–0) and 13CO(1–0) lines. The green and magenta contours display the distribution of the integrated intensity 12CO(1–0) and 13CO(1–0) lines, respectively, in the interval velocity range of 0.6 km s−1. The levels of green contours are from 6σ (~1.2 K km s−1) to the peak value by intervals of 6σ. The levels of magenta contours are from 3σ (~0.6 K km s−1) to the peak value by intervals of 3σ. |
| In the text | |
 |
Fig. 3 Skeletons of the filamentary network extracted with the FilFinder, color-coded by the centroid velocities of the 13CO spectral line.The gray map is the H2 column density map derived from Herschel continuum map (160–500 μm) in Dewangan et al. (2017). The overlaid green contours display 13CO column density distribution of filament S242, ranging from 15 to 90% stepped by 15% of the value (1.5 × 1016 cm−2). |
| In the text | |
 |
Fig. 4 Panel a: position-velocity distribution along the spine of filament S242 from the southern to northern end. The dark blue curve and vertical white lines represent the fitted centroid velocity and FWHM velocity width by a single Gaussian, respectively. Panel b: centroid velocity (Vlsr), total 1D velocity dispersion (σtot), H2 column density ( |
| In the text | |
 |
Fig. 5 Sketch of the edge-collapse process of the filament S242. |
| In the text | |
 |
Fig. 6 Upper panel: velocity dispersion ( |
| In the text | |
 |
Fig. 7 Convolved profiles of centroid velocity (Vlsr), velocity gradients (dV/dl), total 1D velocity dispersion (σtot), the contribution of longitudinal collapse in the total velocity dispersion (fL), and the H2 column density. The vertical black dashed lines indicate the peaks of the H2 column density profile; the horizontal green dashed line represents fL = 0.5. |
| In the text | |
 |
Fig. 8 Sketch of the subsequent longitudinal accretion of the filament S242. The overlaid green contours display 13CO column density distribution of filament S242, ranging from 15 to 90% stepped by 15% of the value (1.5 × 1016 cm−2). The skeleton structures of the filament S242 are color-coded by the longitudinal factor fL, which is the contribution of longitudinal collapse for the observed velocity dispersion. The magenta arrows indicate the direction of gas motion in longitudinal collapse and accretion, the blue arrows in radial collapse. The right subpanel presents the profile of longitudinal factor fL along the spine of filament S242. |
| In the text | |
 |
Fig. A.1 Radial profile for H2
column density for the filament S242. Panel a: distribution of radial cuts along the spine of filament S242. The red curve represents the spine across the entire filament S242, extractedby FilFinder. The blue dots show the sampling points with an interval of
~0.7 pc. The red radial lines, perpendicular to the tangent of the spine, are the cuts used to calculated the radial distances from the spine. Panels b and c: Plummer and Gaussian fitting for the radial profiles. The black dots represent the value of
|
| In the text | |
 |
Fig. A.2 As in Fig. 3, but the magenta circles show the subregions for the average spectra from No.1 to No.24 displayed in Fig. A.3. |
| In the text | |
 |
Fig. A.3 Average spectral profiles for 13CO lines in thecorresponding subregions from No.1 to No.24, displayed in Fig. A.2. The black profiles represent the observed spectra, the magenta dashed profiles are our fitted results by one or two Gaussians. The fitted parameters for the main velocity components (including peak intensity, centroid velocity, and velocity dispersion) are given at the top of every subpanel. The blue profiles in No. 6 – No. 8 and No. 13 – No. 15 are the average C18O line spectra, which are amplified by a factor of 3. These C18O data are from MWISP CO surveys (Su et al. 2019). In each of those panels, the vertical green dashed line shows the centroid velocity of the main velocity component. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.