| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 16 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201834425 | |
| Published online | 13 December 2019 | |
Polar flux imbalance at the sunspot cycle minimum governs hemispheric asymmetry in the following cycle
1
Department of Mathematical Sciences, Durham University, Durham DH1 3LE, UK
e-mail: prantika.bhowmik@durham.ac.uk, prantika.bh@gmail.com
2
Center of Excellence in Space Sciences India, Indian Institute of Science Education and Research Kolkata, Mohanpur 741246, West Bengal, India
Received:
14
October
2018
Accepted:
22
October
2019
Aims. Hemispheric irregularities of solar magnetic activity is a well-observed phenomenon, the origin of which has been studied through numerical simulations and data analysis techniques. In this work we explore possible causes generating north-south asymmetry in the reversal timing and amplitude of the polar field during cycle minimum. Additionally, we investigate how hemispheric asymmetry is translated from cycle to cycle.
Methods. We pursued a three-step approach. Firstly, we explored the asymmetry present in the observed polar flux and sunspot area by analysing observational data of the last 110 years. Secondly, we investigated the contribution from various factors involved in the Babcock–Leighton mechanism to the evolution and generation of polar flux by performing numerical simulations with a surface flux transport model and synthetic sunspot input profiles. Thirdly, translation of hemispheric asymmetry in the following cycle was estimated by assimilating simulation-generated surface magnetic field maps at cycle minimum in a dynamo simulation. Finally, we assessed our understanding of hemispheric asymmetry in the context of observations by performing additional observational data-driven simulations.
Results. Analysis of observational data shows a profound connection between the hemispheric asymmetry in the polar flux at cycle minimum and the total hemispheric activity during the following cycle. We find that the randomness associated with the tilt angle of sunspots is the most crucial element among diverse components of the Babcock–Leighton mechanism in resulting hemispheric irregularities in the evolution of polar field. Our analyses with dynamo simulations indicate that an asymmetric poloidal field at the solar minimum can introduce significant north-south asymmetry in the amplitude and timing of peak activity during the following cycle. While observational data-driven simulations reproduce salient features of the observed asymmetry in the solar cycles during the last 100 years, we speculate that fluctuations in the mean-field α-effect and meridional circulation can have finite contributions in this regard.
Key words: Sun: magnetic fields / Sun: activity / Sun: photosphere / dynamo / magnetohydrodynamics (MHD)
© ESO 2019
1. Introduction
Characteristics of the 11-year solar cycle are not manifested identically in the two hemispheres of the Sun. Diversity of the asymmetry between the northern and southern hemispheres can be perceived in various observables of solar magnetic activity, among which sunspots are the most widely studied. The detection of hemispheric asymmetry in sunspot number goes way back to the beginning of the 20th century (Maunder 1904). Utilizing long-term sunspot data series, several groups have explored various aspects of the asymmetry present in sunspot number and their associated area (Newton & Milsom 1955; Waldmeier 1961; White & Trotter 1977; Swinson et al. 1986; Li et al. 2001, 2002; Ballester et al. 2005; Temmer et al. 2006; Hathaway 2015; Deng et al. 2016, and references therein) and have established that the observed irregularities are statistically significant and cannot be achieved from a random distribution of sunspots (Carbonell et al. 1993; Oliver & Ballester 1994; Temmer et al. 2006). Using historical records of sunspot data of last 300 years, Zolotova et al. (2010) showed that a hemispheric phase difference exists in the rising, peak, and declining epochs associated with each cycle and that hemispheric dominance roughly changes in every 8 solar cycles. The phase lag can become as high as 19 months (Norton & Gallagher 2010). In a review, Norton et al. (2014) provided an observed upper limit of 20% of asymmetry both in the cycle amplitude and timing of peak activity. The north-south asymmetry of solar magnetic activity is also reflected in high energetic events such as flares, coronal mass ejections (CMEs), gamma-ray, and Type II radio bursts (Verma 1987; Ataç & Özgüç 1996; Gao et al. 2009; Waldmeier 1971; McIntosh et al. 2015 and references therein).
Apart from the extensive observational studies on hemispheric variability of solar magnetic activity, many groups have also explored the origin of asymmetry by utilizing solar dynamo models (see reviews by Norton et al. 2014 and Brun et al. 2015). The solar magnetic field is believed to be originated and sustained by a dynamo mechanism acting in the solar convection zone governed by the laws of magnetohydrodynamics (MHD; Charbonneau 2010). In the framework of a solar dynamo, two components of the magnetic field, known as toroidal and poloidal components, interchange between themselves in the presence of large-scale plasma flows. While the differential rotation converts the poloidal component to the toroidal component by stretching it along the azimuthal direction (Parker 1955), diverse conjectures exist to explain the generation of the poloidal component from the toroidal component, such as mean-field α-effect, MHD instabilities, hydrodynamical shear instabilities, and Babcock–Leighton (B–L) mechanism (see review by Charbonneau 2010).
The variation of the toroidal component is manifested in the modulation of sunspot number as the toroidal flux tubes satisfying the magnetic buoyancy criterion rise through the solar convection zone (Fan 2009) and emerge on the photosphere as sunspots (also known as active regions) with certain latitude-dependent tilt induced by the Coriolis force (Joy’s law; Hale et al. 1919). Most of the sunspots emerge on the surface in pairs as bipolar magnetic regions (BMRs) with a “leading” and a “following” spot (according to rotating direction) of opposite magnetic polarities in which the leading spot predominantly appears at a lower latitude compared to the following spot. For a particular cycle, if the preceding (and succeeding) spots of the BMRs in the northern hemisphere have a positive (and negative) polarity, the leading and following spots in the southern hemisphere are of negative and positive polarity, respectively. But this polarity distribution reverses during the next solar cycle, thereby creating a 22-year-long magnetic cycle. This polarity rule is known as Hale’s polarity law (Hale & Nicholson 1925).
Modulation of the poloidal component is captured in the intensity of the magnetic field near to the polar regions of the Sun such that polar field can serve as a proxy for quantifying the poloidal component. The importance of the solar polar field, which is also a measure of the global magnetic dipole of the Sun, is manifold. On the one hand, this polar field controls magnetic environment of the heliosphere by regulating the radiative and particulate output of the Sun primarily during cycle minimum. On the other hand, the amplitude of the polar field at cycle minimum is one of the best precursors used to predict the strength of the following solar cycle (Petrovay 2010; Cameron et al. 2016; Hathaway & Upton 2016). Generation and evolution of polar field can be explained in the framework of the B–L mechanism (Babcock 1961; Leighton 1969; Wang et al. 1989; Dasi-Espuig et al. 2010; Cameron et al. 2010; Jiang et al. 2014), where the magnetic flux associated with tilted sunspots get diffused owing to turbulent diffusion, caused by turbulent motion of super-granular convective cells, and drift towards the pole aided by meridional circulation. The advected flux (primarily from the following polarities in both the hemispheres) accumulate at the poles and alter the polarity of the global solar magnetic field. This polarity reversal occurs during cycle maximum and the polar field attains its peak value during cycle minimum. Since any significant hemispheric irregularities associated with the emerging sunspots and transport parameters involved in the B–L mechanism can influence the polar field evolution, we observe profound north-south asymmetry both in the timing of reversal as well as the final strength of polar field during cycle minimum.
In this study, we primarily explore the origin of hemispheric asymmetry prevailed in the development and evolution of polar field via a surface flux transport (SFT) model which mimics the B–L mechanism on the solar surface. In addition, we investigate the interdependency between the polar field during the solar minimum and the amplitude of the following solar cycle in the context of hemispheric asymmetry by analysing the observational data. Lastly, we study how any asymmetry present in the polar field can impact the following solar cycle with a dynamo model while employing a hemispherically asymmetric poloidal field source at cycle minimum. We perform this analysis by assimilating surface magnetic field maps obtained from SFT simulations driven by both synthetic and observed sunspot input profiles in a continuous dynamo run and finally comparing the simulation results with actual observations.
The paper is organized as follows: in Sect. 2, we present an analysis of the observational data followed by a brief description of the computational models used in our study (in Sect. 3). In Sect. 4, we delineate the results obtained from SFT simulations with synthetic sunspot data along with corresponding analyses. Investigation of hemispheric asymmetry with the dynamo model is detailed in Sect. 5. Finally, we evaluate our understanding of hemispheric asymmetry in the context of solar observations in Sect. 6. The last section (Sect. 7) is assigned for discussions and conclusions.
2. Hemispheric asymmetry as observed in the solar magnetic field
The presence of north-south asymmetry in the monthly and yearly averaged sunspot area has been reported in various studies (Vizoso & Ballester 1990; Verma 1993; Carbonell et al. 1993; Li et al. 2002). We used the sunspot area data from the Royal Greenwich Observatory (RGO) and United States Air Force (USAF)/National Oceanic and Atmospheric Administration (NOAA) databases for a period spanning over 1900–2016.5 to investigate hemispheric asymmetry (see Fig. 1a).
 |
Fig. 1. Panel a: time variation of averaged monthly (total) sunspot area during solar cycles 14–24 after performing 13-month running average. Panel b: same in the northern (blue curve) and southern (red curve) hemispheres, respectively, during that period. Panel c: hemisphere-wise excess activity: the blue-filled colour indicates the total area associated with the north hemispheric sunspots to be higher than the southern hemispheric total sunspot area and the red-filled colour depicts the opposite scenario. Panel d: variation of unsigned polar flux with error bars in two hemispheres. The rectangular grey bars depict episodes of solar minimum during 1906–2016.5. |
In Fig. 1b, we depict the 13-month running average of the monthly sunspot area associated with the northern and southern hemispheres during cycles 14–24. The figure reveals two aspects of hemispheric asymmetries which exist in each solar cycle: a difference in the peak amplitude and total sunspot area and a profound gap between the epochs of peak activity in two hemispheres. We expect this asymmetry to be similarly reflected in magnetic flux associated with sunspots as the flux is linearly proportional to the spot area (Dikpati et al. 2006). Figure 1c depicts the excess of the monthly averaged hemispheric sunspot area for the same set of cycles, thereby demonstrating the relative change in cycle phase in two hemispheres. The last panel in Fig. 1 represents the time evolution of polar flux (in terms of absolute value) in the northern and southern hemispheres during 1907–2015; the associated data for polar flux is obtained from MWO calibrated polar faculae data (Muñoz-Jaramillo et al. 2012). We indicate the sunspot minima by grey rectangular patches (as shown in Fig. 1d), while each has a width of two years. A study by Muñoz-Jaramillo et al. (2013), using the same database, found polar flux at cycle minimum to be strongly correlated with the peak activity of the following sunspot cycle.
We performed a correlation analysis between the polar flux during cycle minima (averaged over two years) and the peak sunspot area of the succeeding cycle considering two hemispheres separately. For the northern hemisphere, Pearson’s linear correlation coefficient (rN) is 0.62 with a p-value of 0.07, while in case of the southern hemisphere the coefficient (rS) is 0.71 with a p-value of 0.03. The corresponding Spearman’s rank correlation coefficients are lesser compared to the linear correlation coefficients for all data sets, indicating the underlying mechanism connecting these two quantities to be linear in nature. While the polar flux at cycle minimum is comparable to the poloidal component of magnetic field, the sunspots and their associated area as observed on the solar surface is a manifestation of the toroidal magnetic field stored in the solar convection zone. Therefore, a high degree of linear correlation supports the theory used in various dynamo models (Dikpati & Charbonneau 1999; Nandy & Choudhuri 2002; Chatterjee et al. 2004; Yeates et al. 2008; Passos et al. 2014; Hazra et al. 2014; Hazra & Nandy 2016), where the generation of the toroidal component from the poloidal component occurs through a linear process through differential rotation.
We would expect north-south asymmetry present in the polar flux during cycle minimum (see Fig. 1d) to be similarly reflected in hemispheric asymmetry in the peak sunspot activity of the following cycle, such that a positive correlation should exist between them with the same hemispheric dominance (Goel & Choudhuri 2009). In Figs. 2a and b, we compare the asymmetry in polar flux (with error bars) during nth cycle minimum with the asymmetry present in both the peak sunspot area and total sunspot area during (n + 1)th cycle. Considering every possible position, all points should lie either in the first or third quadrants to satisfy the primary requirement for positive correlation. Although this requirement is not fulfilled in the case of peak sunspot area (see Fig. 2a); we find all data points satisfying the essential condition of positive correlation while considering the total sunspot area of different cycles (Fig. 2b).
 |
Fig. 2. Panel a: hemispheric asymmetry in polar flux (maxwells) during minimum of the nth cycle (“n” varying from 15 to 22) vs. the asymmetry in sunspot area (in micro-hemispheres) during the following cycle maximum. Panel b: asymmetry in polar flux is compared with the asymmetry in total sunspot area of the following cycle. The numbers 1–4 represent the first, second, third, and fourth quadrants, respectively. The uncertainties present in polar flux observation are also depicted by error bars in both panels. The Spearman’s rank correlation coefficient between the absolute amplitude of the asymmetry associated with the polar flux and total hemispheric sunspot area is 0.73 with p-value 0.04. |
A correlation analysis between the absolute values of hemispheric asymmetry in polar flux amplitude during cycle minima and the total sunspot area of the following cycle gives a Pearson linear correlation coefficient of 0.73 (with a p-value 0.04) and a Spearman rank correlation coefficient of 0.81 (with p-value 0.02). This particular result distinctly indicates that the north-south asymmetry present in polar flux (during cycle minimum) is transmitted in a non-linear manner to the asymmetry in the total sunspot area (or flux) of the following cycle.
A careful inspection of Fig. 1d reveals that hemispheric polar flux can acquire its maximum amplitude during the descending phase of a cycle and eventually settles at a comparatively lower amplitude at solar minimum. For example, during the descending phase of cycle 19, we observe that the amplitude of both the northern and southern hemispheric polar flux becomes maximum at 1962 and 1959, respectively, much earlier than the cycle 19 minimum (1964). We denote such time instances as 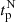 and
and 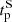 for the northern and southern hemispheres, respectively. We performed a thorough correlation analysis to explore how this feature of polar flux is connected with the activity in the following cycle. We find no correlation between (
for the northern and southern hemispheres, respectively. We performed a thorough correlation analysis to explore how this feature of polar flux is connected with the activity in the following cycle. We find no correlation between (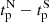 ) during the nth cycle and the phase lag in the hemispheric peak activity during the (n + 1)th cycle. This result implies that a scenario in which the northern hemispheric polar flux attains its maximum amplitude earlier than the south during a solar cycle (i.e.
) during the nth cycle and the phase lag in the hemispheric peak activity during the (n + 1)th cycle. This result implies that a scenario in which the northern hemispheric polar flux attains its maximum amplitude earlier than the south during a solar cycle (i.e. 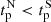 ) does not lead to a faster rise of the northern hemispheric activity compared to the south in the following cycle. Moreover, we carried out another correlation analysis between the amplitude of the polar flux at
) does not lead to a faster rise of the northern hemispheric activity compared to the south in the following cycle. Moreover, we carried out another correlation analysis between the amplitude of the polar flux at 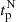 and
and 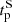 and the corresponding hemispheric peak activity in the (n + 1)th cycle. We found the degree of correlation associated with both the hemispheres to be poorer (r ≈ 0.3 on average) in contrast to the results we obtained while using the amplitude of the polar flux at cycle minimum (r ≈ 0.66 on average).
and the corresponding hemispheric peak activity in the (n + 1)th cycle. We found the degree of correlation associated with both the hemispheres to be poorer (r ≈ 0.3 on average) in contrast to the results we obtained while using the amplitude of the polar flux at cycle minimum (r ≈ 0.66 on average).
We additionally performed every correlation analysis discussed above while considering sunspot numbers instead of sunspot area. We found a similar positive linear correlation exists between the hemispheric polar flux at the cycle minimum and peak amplitude of the sunspot number in the following cycle, which is expected as the peak sunspot number and peak sunspot area (or flux) are well correlated; Pearson’s correlation coefficient is 0.76 with a p-value of 0.01 based on last 110 years of data. The Pearson correlation coefficients associated with the northern and southern hemispheres are rN = 0.66 (with a p-value of 0.053) and rS = 0.66 (with a p-value of 0.054), respectively. We note that the overall degree of positive linear correlation is higher in case of sunspot area compared to sunspot numbers, as the latter is a better representative of magnetic activity of the Sun. In the following sections, we perform multiple computational simulations to explore probable causes instigating hemispheric asymmetry.
3. Computational models
In this work we use two disparate 2D numerical models. First, we use an SFT model to study the dissipation and advection of magnetic field associated with the tilted BMRs on the solar surface in the presence of magnetic diffusion and large-scale velocity fields, which is the mechanism responsible for generating the polar field. Second, we use a dynamo model to study the generation of the toroidal field from poloidal field in the solar convection zone. In the following section, we briefly outline these two computational models.
3.1. Surface flux transport model
3.1.1. Basic equation
We developed an SFT model to study the evolution of photospheric magnetic field on the solar surface, which is governed by magnetic induction equation,
where v represents the large-scale velocities, i.e. meridional circulation and differential rotation present on the solar surface, and the parameter η is the magnetic diffusivity. As observations (Solanki 1993) have shown that the surface magnetic field is predominantly along the radial direction, we numerically solve only the radial component of the induction equation, which is expressed in spherical polar coordinates as
where Br(θ, ϕ, t) is the radial component of magnetic field as a function of co-latitude (θ) and longitude (ϕ), and R⊙ is the solar radius. The axisymmetric differential rotation and meridional circulation are incorporated through ω(θ) and v(θ), respectively. The parameter ηh is the effective diffusion coefficient and S(θ, ϕ, t) is the source term representing the emergence of new sunspots. Since we are studying the evolution of Br on the surface of a sphere, we developed the model using spherical harmonics. The same model was utilized earlier by Nandy et al. (2018) to extrapolate coronal magnetic fields from surface magnetic field maps generated by SFT simulations.
3.1.2. Transport parameters
The Sun has a large-scale axisymmetric rotational velocity of differential nature, i.e. plasma at different layers rotate with different speeds. This variation in velocity is observed both in radial and latitudinal directions. On the surface, the equator rotates faster than the poles. An empirical profile (Snodgrass 1983) can express the surface differential rotation as a function of co-latitudes,
wherein ω(θ) has units in degrees per day. This profile has also been validated by helioseismic observations (Schou et al. 1998). Another significant large-scale flow active on the solar surface is the meridional circulation which carries magnetized plasma from the equatorial region to the polar regions in both the hemispheres. The flow speed becomes zero at the equator and the poles and attains its peak amplitude near mid-latitudes. To replicate this flow in our model, we used a velocity profile prescribed by van Ballegooijen (van Ballegooijen et al. 1998),
where λ is latitude in degrees (λ = π/2 − θ) and λ0 is the latitude beyond which circulation speed becomes zero, which in our model is set at ±75°. The parameter, v0, represents the maximum speed attained by the meridional circulation near mid-latitudes, which varies within the range 10–20 ms−1. For the standard simulation, we considered the anti-symmetric (about the equator) meridional circulation profile to be identical in two hemispheres with v0 = 15 ms−1. The last transport parameter present in our model is magnetic diffusivity. It arises as a result of the random motions of super-granular convective cells present in the solar convection zone. We used a constant diffusion coefficient of 250 km2 s−1, which lies within the range inferred from observations (Schrijver & Zwaan 2000).
3.1.3. Synthetic input profiles: emergence of sunspots
The number of sunspots appearing on the solar surface roughly follows an 11-year cycle. At the beginning of the cycle, in general sunspots emerge at higher latitudes (near ±400), and as the cycle advances in time, sunspots appear closer to the equator. This equator-ward propagation of the spots forms a structure similar to the wings of a butterfly about the equator. We considered each active region (or sunspot) associated with the synthetic input profiles as ideal BMRs with their latitudinal distribution motivated by actual observation (Jiang et al. 2011). All active regions follow Hale’s polarity law (Hale & Nicholson 1925) and have latitude-dependent tilt angles determined by Joy’s law (Hale et al. 1919) such that tilt angles increase with increasing latitudes. We implemented Joy’s law in our model with the relation, 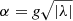 , where α is the tilt angle and λ is the latitudinal position of the centroid of the whole BMR (Jiang et al. 2011). Apart from the large-scale flows, there exist localized inflows towards active regions which reduce the latitudinal separation between opposite polarities and allow a lesser amount of flux to reach the polar regions. To mimic these inflows, we introduced an additional factor, g in the tilt angle calculation (Cameron et al. 2010). We chose g to be 0.7.
, where α is the tilt angle and λ is the latitudinal position of the centroid of the whole BMR (Jiang et al. 2011). Apart from the large-scale flows, there exist localized inflows towards active regions which reduce the latitudinal separation between opposite polarities and allow a lesser amount of flux to reach the polar regions. To mimic these inflows, we introduced an additional factor, g in the tilt angle calculation (Cameron et al. 2010). We chose g to be 0.7.
The active regions are randomly distributed over the full 360° range of longitude. Typically, the number of sunspots and their corresponding area in a certain solar cycle follow a power-law distribution (Jiang et al. 2011), which ensures the presence of very few sunspots with a large area. The magnetic flux associated with an active region is decided based on an empirical relation (Dikpati et al. 2006), Φ(A) = 7.0 × 1019A maxwells, where A is the area of the whole sunspot in units of micro-hemispheres. We assumed the flux was equally distributed among the two polarities of the BMR. The separation between the centroids of two polarities was taken proportional to the spot radius obtained from its associated area. The magnetic field within a single polarity was distributed following a Gaussian distribution where the peak of the Gaussian was determined according to the prescription by van Ballegooijen et al. (1998). The total amount of magnetic flux associated with the sunspots of a particular synthetic input profile was about 5.4 × 1024 maxwells with 3100 active regions equally distributed between two hemispheres.
3.1.4. Initial field configuration
We initialised our simulations with an ideal dipole with magnetic field primarily concentrated near to the polar cap region (±70 ° −90°) in each hemisphere. The strength (absolute value) of the polar field in each hemisphere is about 4.2 gauss.
3.1.5. Numerical modelling parameters
Ideally, one should consider all possible values of degree (l) associated with spherical harmonics. Instead of taking the whole range of values of l from 0 to ∞, we considered l values varying from 0 to 63, which can spatially resolve elements with an equivalent size of super-granular cells (roughly 30 Mm) on the solar photosphere. Our SFT model is accurate up to second order in space and first order in time.
3.2. Solar dynamo model
Recent 2D kinematic solar dynamo models consider different mechanisms for the generation of the poloidal component (BP) from the toroidal component (Bϕ) of magnetic field. While the majority of dynamo models (Dikpati & Charbonneau 1999; Nandy & Choudhuri 2002; Chatterjee et al. 2004; Yeates et al. 2008) identify B–L mechanism as the sole process, others (Passos et al. 2014; Hazra et al. 2014) found that an additional mean-field α-effect is also essential for sustenance of the solar dynamo. In our study, we primarily focussed on the generation of the toroidal component from a given poloidal component and used an existing 2D dynamo model in which the poloidal field source term depends on both the above processes (Passos et al. 2014). The same model has provided satisfactory results previously (Passos et al. 2014). Additionally, assimilating output from the observational data-driven SFT simulations in the same dynamo model was successful in reproducing solar activities during the past eight solar cycles (Bhowmik & Nandy 2018). The basic equations used in our axisymmetric kinematic dynamo model are as follows:
where B(r, θ) (i.e. Bϕ) and A(r, θ) are the toroidal and poloidal (in the form of vector potential) components of magnetic field, respectively. The symbols vp and Ω are the meridional circulation and differential rotation in the solar convection zone and s = r sin(θ). Two different diffusivity profiles, ηt and ηp, are used for the toroidal and poloidal components of the magnetic field, respectively. In Eq. (5), “αB” is the source term for generating the poloidal field, which considers contributions from both the B–L mechanism and mean-field α-effect. The details of every profile and parameter used in this dynamo model are described in an already published work by Passos et al. (2014).
In addition to the large-scale meridional circulation, in our dynamo model, we considered advection due to turbulent pumping, which is only effective on the poloidal component. The presence of downward magnetic pumping was suggested by several theoretical studies and simulations of local magneto-convection (Petrovay & Szakaly 1993; Tobias et al. 1998; Käpylä et al. 2009; Brandenburg et al. 1996). We assumed that the much stronger component of magnetic field remains unaffected by this downward pumping (Käpylä et al. 2006; Ossendrijver et al. 2002). In addition, Cameron et al. (2012) and Karak & Cameron (2016) demonstrated the importance of turbulent pumping in flux transport dynamo models in the context of compatibility with surface observations as well as SFT simulations. Thus, we added a downward radial pumping velocity with the meridional circulation (vp) in Eq. (5) such that the radial component of velocity (vr) is changed to vr + γr. The profile of the radial magnetic pumping (γr) is the same as that used in Karak & Nandy (2012) and given by
The amplitude of the pumping speed is controlled by the value of fγ0r and is taken as 3.6 ms−1. This amplitude ensures a magnetic Reynolds number of approximately 5 (Cameron et al. 2012) and a positive dynamo growth rate in which advection time due to pumping is at least five times the diffusion time. Considering the average (over the convection zone) magnetic diffusivity associated with the poloidal magnetic field to be 1.5 km2 s−1 and the width of the layer throughout which the pumping is functioning as 0.3 R⊙, fγ0r = 3.6 ms−1 satisfies the mentioned conditions.
The magnetic buoyancy algorithm (Nandy & Choudhuri 2002; Chatterjee et al. 2004; Passos et al. 2014) in the dynamo simulation produces a quantity (say BDyn) proportional to the strength of the toroidal field at the base of the convection zone and represents the sunspots which emerge on the solar surface after satisfying the magnetic buoyancy criterion. We used this proxy as a representative of the sunspot cycle to study the asymmetry translated into the hemispheric activity in the following cycle from the previous cycle poloidal field.
4. Factors inducing hemispheric asymmetry in the polar field: An SFT perspective
Utilizing the SFT model described in the previous section, we investigated various sources that contribute to the north-south asymmetry in the final strength of polar field at cycle minimum. Two aspects of the B–L mechanism govern the evolution of the photospheric magnetic field and the polar field: firstly, the transport parameters on the solar surface and secondly, diverse characteristics of the emerged sunspots. Therefore, variation of these factors can originate hemispheric asymmetry in the final polar field strength, assuming the initial strength of the polar field at the beginning of cycle in two hemispheres to be precisely equal. We identified five possible sources and thoroughly investigated their effects on the final amplitude of polar field in both the hemispheres. The same analysis also sheds light into the causes of relative time differences in the reversal of the hemispheric polar field.
From the time series data of observed sunspot area during the last 110 years (see Figs. 1b and c), we can perceive three distinguishable characteristics of north-south asymmetry: differences in (1) amplitude of peak activity, (2) timing of peak activity, and (3) the total sunspot area associated with two hemispheres in a particular cycle. Following the understanding gleaned from the analysis of observational data (as described in Sect. 2), in our current study we give more importance to hemispheric asymmetry present in the total sunspot-associated area (or flux) rather than the amplitude of peak activity. (4) Another significant source of hemispheric irregularities related to sunspot data is the presence of randomness in the tilt angle of individual sunspots in addition to their systematic tilts determined by Joy’s law (Dasi-Espuig et al. 2010; Sivaraman et al. 1999; McClintock & Norton 2013). (5) The last hemispheric inequality incorporated in our analysis regards the transport parameters involved in the B–L mechanism. We applied different meridional circulation and differential rotation profiles in the northern and southern hemispheres. However, magnetic diffusivity can be assumed as homogeneous and isotropic since this diffusivity originates from the random motion of granules and super-granules on the solar surface, which does not possess any directional preferences (Nandy 2006). Thus this allows us to use a constant diffusion coefficient (ηh) in the SFT simulations.
We explored the effect of these factors on the final amplitude of the polar field through studying the time evolution of polar flux that is calculated by integrating the radial magnetic field within the polar cap regions (extended from ±70° to ±90° latitudes in both the hemispheres) as follows:
where λ is latitude and ϕ is longitude. Aside from polar flux, we also calculated the unsigned magnetic flux associated with sunspots emerging in the northern and southern hemispheres separately. Assuming, 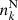 number of individual spots with the corresponding area,
number of individual spots with the corresponding area, 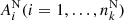 appeared on the northern hemisphere during the kth month, then the total sunspot-associated unsigned flux in that hemisphere during that month would be written as
appeared on the northern hemisphere during the kth month, then the total sunspot-associated unsigned flux in that hemisphere during that month would be written as
wherein, 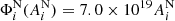 maxwells, while
maxwells, while 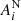 is in micro-hemispheres. Unsigned magnetic flux in the southern hemisphere is calculated following the same method. We measured the difference between
is in micro-hemispheres. Unsigned magnetic flux in the southern hemisphere is calculated following the same method. We measured the difference between 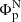 and
and 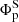 to quantify the asymmetry in the amplitude of hemispheric polar flux, while the difference between
to quantify the asymmetry in the amplitude of hemispheric polar flux, while the difference between 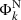 and
and 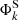 estimates the asymmetry in hemispheric activity regarding sunspot area.
estimates the asymmetry in hemispheric activity regarding sunspot area.
In the following section, we separately consider each factor associated with the B–L mechanism through which hemispheric asymmetry can be introduced while keeping the other factors unaltered. We then investigate their individual effect on the final strength of the polar flux.
4.1. Time difference in peak activity
For a particular cycle, one hemisphere may reach peak activity before the other, thus introducing an asymmetry. As perceived from Fig. 1, in case of 80% cycles, two hemispheres were out of phase at cycle maximum during the last 110 years. For example, during solar cycle 18, the southern hemisphere reached its peak activity almost two years before the northern hemisphere reached its maximum. A similar instance was observed during cycle 19. In case of solar cycles 22 and 23, the northern hemisphere peaked earlier than the southern hemisphere. Overall, the observational data series (of last 110 years) of sunspot area shows a time gap of 6–24 months between the occurrence timing of peak activity in the northern and southern hemispheres.
We explored the effect of hemispheric asymmetry on the reversal timing of polar flux as well as its final amplitude at the solar minimum utilizing multiple synthetic sunspot profiles with different time lags. During a specific cycle, the total amount of unsigned magnetic flux associated with the set of emerging sunspots is equal in both the hemispheres. The only asymmetry is introduced through a phase lag between the epochs of peak activity in two hemispheres which varies over a range of 6–30 months. We note that the phase-dependent mean latitudinal positions of sunspots are roughly similar in two hemispheres such that we can ignore the hemispheric asymmetry regarding the emergence latitudes of sunspots. In Fig. 3a, time evolution of unsigned flux (ΦN/S) associated with the multiple sunspot profiles are depicted separately with different coloured curves for the northern and southern hemispheres. The corresponding time evolution of hemispheric polar flux (see Fig. 3b) demonstrates a spread in the reversal timing of hemispheric polar flux; however, leaving the final amplitude at cycle minimum unaffected. We note that all other model parameters used in the SFT simulations were kept fixed throughout these analyses.
 |
Fig. 3. Panel a: time evolution of the unsigned magnetic flux associated with the synthetic sunspot input profiles in the northern and southern hemispheres with time difference in their respective peak activity. Panel b: evolution of corresponding polar flux in two hemispheres is depicted. Panel c: time lag in peak hemispheric activity is compared with the corresponding time difference in the reversal of polar flux, where the blue curve depicts a polynomial (of degree 2) fit to the data points. The associated Spearman’s rank correlation coefficient is given with p-value. |
We find a strong correlation between the phase lag in the peak of sunspot flux and the corresponding time difference of polar flux reversal, such that Pearson correlation coefficient (rp) is 0.9507 (with a p-value 4.46e−4), and Spearman rank correlation coefficient (rs) is 1 (with a p-value 3.96e−4). The same is represented in Fig. 3c in which the time difference in polar flux reversal is plotted as a function of the phase lag.
4.2. Hemispheric asymmetry in total sunspot flux
In the second scenario of our study, the emergence timing and position of individual sunspot appearing in the northern and southern hemispheres are identical to each other. The only difference is that the southern hemispheric spots are larger in areal coverage (thus, have higher magnetic flux) compared to the northern hemispheric spots; this results in a surplus of the total flux in the southern hemisphere. For simplicity of analysis, we multiplied the area (and also the flux) of each active region in the southern hemisphere by a constant factor “m”, where m varies over the range of 1.05–1.70, such that the total, as well as the peak amplitude of southern hemispheric flux, becomes 5–70% more compared to the northern hemispheric flux (see Fig. 4a). Although 70% asymmetry may seem unusually high given that observational studies (Norton et al. 2014) have suggested the maximum asymmetry regarding the peak hemispheric activity to be about 20%, we find that in case of solar cycle 20, the total sunspot-associated area (and also the flux) in the northern hemisphere was 45% more compared to that in the southern hemisphere. Additionally, we considered a certain reduction in the mean tilt angle of spots associated with the hemisphere with higher activity, although the latitudinal positions of sunspots in two hemispheres are the mirror image of each other. Such modification of mean tilt angle based on cycle amplitude has been observationally reported (Dasi-Espuig et al. 2010) and used in data-driven SFT simulations (Cameron et al. 2010; Jiang et al. 2011, 2014).
 |
Fig. 4. Panel a: time evolution of unsigned magnetic flux in the northern by a blue curve and in the southern hemispheres by red curves with different shades corresponding to increasing strength (5%–70% compared to the northern hemisphere). Panel b: corresponding polar flux evolution in two hemispheres. The time evolution of the longitudinally averaged magnetic field (radial component) as a function of latitude is depicted for two cases; in panel c the input sunspot profile is identical in two hemispheres and in panel d the southern hemispheric sunspot flux is 70% higher compared to that in the northern hemisphere. The red and yellow arrows indicate two prominent distinct patterns in the time latitude distribution of the magnetic field present corresponding to the hemispheric asymmetric case. The red (and the black in (b)) dashed vertical lines refer to the timing of sunspot cycle maximum. |
Based on analyses of observational data of sunspot tilt angles, Jiang et al. (2011) described how a factor (Tn; see Eq. (15) in their paper) dependent on the cycle amplitude (in terms of sunspot number) can be introduced to calculate tilt angle of BMRs. Since peak sunspot number and sunspot flux (or area) are well correlated, we used this concept to establish a similar relation between the average tilt angle and peak amplitude of unsigned hemispheric magnetic flux (monthly averaged), TN/S = 1.71 − 0.12mFN/S. In this work, FN/S represents the peak amplitude of unsigned magnetic flux (ΦN/S) associated with sunspots appearing in the northern and southern hemispheres, respectively. The factor TN/S is incorporated in determining the tilt angle of an individual active region through the relation 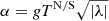 , where α, g, and λ represent the same quantities as described in Sect. 3.1.3.
, where α, g, and λ represent the same quantities as described in Sect. 3.1.3.
The corresponding time evolution of polar flux shows that an increase in sunspot-associated magnetic flux in the southern hemisphere results in an early reversal and an increment in the final strength (at cycle minimum) of the southern hemispheric polar flux (as shown in Fig. 4b). Additionally, the final polar flux in the northern hemisphere also increases (as shown in Fig. 4b), although the sunspot-associated flux does not change in the northern hemisphere while considering different synthetic sunspot profiles. In Fig. 4c, we represent the time-latitude distribution of a longitudinally averaged radial component of the surface magnetic field (also known as the magnetic butterfly diagram) corresponding to the symmetric case where the emergence profile of sunspots are identical in two hemispheres. In Fig. 4d, we depict the magnetic butterfly diagram corresponding to an input profile with the southern hemisphere being 70% more active compared to the north. With increased input sunspot flux, a proportionate increment in the southern hemispheric polar flux is expected. But the cause of enhancement in the northern hemispheric polar flux lies in the complexity of the B–L mechanism. We speculate that the high magnetic flux content of leading polarity spots in the southern hemisphere facilitate higher cross-equatorial flux cancellation with leading polarities belonging to the northern hemisphere. This eventually reduces the scope of intra-hemispheric flux cancellation among leading and following polarities of BMRs in the northern hemisphere and increases the amount of resultant unipolar flux that is accumulated from the following polarity spots and subsequently is advected towards the north pole. The magnetic field distribution of negative polarity in the northern hemisphere (shown in Figs. 4c and d) reveals a significant contrast between the symmetric and asymmetric cases and indicates larger transportation of magnetic flux (of negative polarity) towards the pole in the asymmetric case. One of these contrasting features can be seen during years 9−10 in the northern hemisphere (pointed by the red arrow). We note that the effect of cross-equatorial flux cancellation among leading spots (of opposite magnetic polarity) becomes more pronounced after cycle maximum has occurred.
Interestingly, an imbalance in activities between two hemispheres can result in the advection of magnetic flux from both the leading and following polarities towards the polar region – effectively reducing the net polar flux in the dominant hemisphere. A manifestation of this phenomenon can be observed in the southern hemisphere, where negative polarity flux from the leading polarity spots reach beyond −55° latitude (Fig. 4d).
As the polar field is generated through a complex process of flux cancellation and advection, we find the nature of positive correlation that exists between the cycle amplitude and the final strength of the polar flux at cycle minimum to be non-linear in the southern hemisphere. The corresponding Spearman rank correlation coefficient is 1.0 and has a p-value of 99.99%. A quantitative analysis shows that a 70% increment of magnetic flux associated with the sunspots in the southern hemisphere (compared to the north) results in only 14% hemispheric asymmetry in the final amplitude of polar flux during cycle minimum.
4.3. Scatter in active region tilt angle
Another factor capable of introducing hemispheric irregularities is the randomness present in the tilt angle distribution of active regions emerging on the photosphere and participating in the B–L mechanism. Several observational studies (Dasi-Espuig et al. 2010; Sivaraman et al. 1999; McClintock & Norton 2013) have found a significant scatter in the tilt angles of BMRs, in addition to deterministic latitude-dependent tilt angles. Within the solar convection zone, the Coriolis force acts on a diverging flow field in a buoyantly rising flux tube. This results in a systematic latitudinal tilt of active region as delineated by Joy’s law (D’Silva & Choudhuri 1993; Fan et al. 1993; Fisher et al. 1995; Fan 2009; Weber et al. 2013). The turbulent convective flows on the rising flux tube introduces randomness which is inversely proportional to its magnetic field strength (Fisher et al. 1995; Longcope & Fisher 1996; Weber et al. 2011, 2013). In this section, we explore the impact of scatter present in the tilt angle of active regions on the final hemispheric polar flux amplitude and the associated asymmetry during cycle minimum.
A study using SFT simulations (Baumann et al. 2004) has shown the final polar flux to be proportional to the tilt angle of active regions. Jiang et al. (2014) and Nagy et al. (2017) demonstrated that large sunspots with large scatter in their tilt angles can significantly affect polar field amplitude during solar minimum. Moreover, a large individual sunspot of non-Hale nature appearing at lower latitude can potentially reduce the polar field strength (Yeates et al. 2015). To find the possible scatter in the tilt angle of a particular active region, we followed the prescription given by Jiang et al. (2014), where they established an empirical (linear logarithmic) relation between the variance of tilt angle distribution and the associated active region area (see Eq. (1) in their paper) by analysing observational data. We considered a sunspot input profile with the emergence timing and position on the solar surface to be identical in the northern and southern hemispheres; the only difference is introduced through the randomness of tilt angles. The tilt angle of every single active region is determined by the relation, 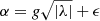 , where the latitude-dependent Joy’s law decides the first part in the right-hand side and the second part, ϵ, represents the randomness (Jiang et al. 2014). The value of ϵ is chosen through random selection from a Gaussian distribution with zero mean and a standard deviation decided by the area of the active region in consideration. The tilt angle of every active region in the symmetric input profile is modified by adding individual ϵ selected through the above process; this eventually generates a sunspot input profile with hemispheric asymmetry. We studied the evolution of polar flux in both the hemispheres while considering 50 such distinct input profiles.
, where the latitude-dependent Joy’s law decides the first part in the right-hand side and the second part, ϵ, represents the randomness (Jiang et al. 2014). The value of ϵ is chosen through random selection from a Gaussian distribution with zero mean and a standard deviation decided by the area of the active region in consideration. The tilt angle of every active region in the symmetric input profile is modified by adding individual ϵ selected through the above process; this eventually generates a sunspot input profile with hemispheric asymmetry. We studied the evolution of polar flux in both the hemispheres while considering 50 such distinct input profiles.
Scatter in the tilt angles of the active regions results in significant uncertainties in the final polar field strength during solar minimum in both the hemispheres (see Fig. 5). While the timing of polarity reversal and the final amplitude of the hemispheric polar flux are identical for the symmetric profile, we see a spread of ±45% and ±35% in the northern and southern hemispheric polar flux at cycle minimum, respectively, corresponding to the 50 asymmetric sunspot input profiles. Furthermore, the randomness in tilt angle affects the reversal timing of the polar flux, thereby resulting in uncertainty of approximately eight months in both the hemispheres (on average) with respect to the timing related to the standard symmetric profile. Among these 50 realizations, hemispheric asymmetry in the final polar flux strength becomes as high as 4.2 × 1021 maxwells, which is 36% of the polar flux amplitude obtained using the standard symmetric profile.
 |
Fig. 5. Time evolution of polar flux in the northern and southern hemispheres associated with 50 individual input profiles depicted by set of light blue and light red curves, respectively. The dark blue and dark red curves represent the same corresponding to the standard symmetric profile. |
4.4. Hemispheric asymmetry in transport parameters
Transport parameters involved in the B–L mechanism are magnetic diffusivity and two large-scale velocities: meridional circulation and differential rotation. Among these three parameters, hemispheric asymmetry can exist only in the velocity fields because diffusion originated from the turbulent motion of the convective cells within the solar convection zone are homogeneous and isotropic (Nandy 2006). Observational studies (Zhang et al. 2013, and the references therein) have found the rotation rates to vary around the mean profile (see Eq. (3)) about 3–4% in two hemispheres, such that the maximum hemispheric asymmetry that can exist in the differential rotation is about 8%. However, the inclusion of such small variation of differential rotation in the SFT simulations does not induce any significant hemispheric asymmetry (less than 1%) in the reversal timing and the final amplitude of polar field (during cycle minimum).
Helioseismology (Haber et al. 2002; Zaatri et al. 2006; Komm et al. 2015) and feature tracking techniques (Hathaway & Rightmire 2010, 2011) have revealed that the observationally deduced meridional circulation profile on the solar surface occasionally differs from its time invariant and simplistic anti-symmetric (about the equator) form (as expressed by Eq. (4)) and exhibits variation over time along with hemispheric asymmetry. In this study, we primarily explored the consequences of various peak flow speeds in two hemispheres on the evolution of polar field without introducing any time-varying component in the meridional circulation profile. We varied the peak speed of meridional flow in the southern hemisphere (i.e. the amplitude of v0 in Eq. (4)) within the range 7.5–22.5 ms−1, while keeping the peak flow speed fixed at 15 ms−1 in the northern hemisphere; this effectively introduces a ±50% north-south asymmetry in the amplitude of the flow (see Fig. 6a).
 |
Fig. 6. Panel a: meridional circulation profiles as functions of latitude where the peak speed varies from 7.5 ms−1 to 22.5 ms−1 (denoted by different colours) in southern hemisphere. Positive (and negative) velocities indicate the flow is towards the south (and north) pole. Each flow profile is labelled alphabetically starting from “A” to “F”, while “S” represents the symmetric profile. Panel b: time evolution of the corresponding hemispheric polar flux. Panels c and d: magnetic butterfly diagram corresponding to the case A (with peak flow speed 7.5 ms−1) and the case F (peak speed 22.5 ms−1). The red dashed vertical lines depict the time of sunspot maximum. |
We considered six different meridional flow profiles (case A to F; see Fig. 6) and studied the time evolution of polar flux by running SFT simulations with a hemispherically symmetric sunspot input profile. From Fig. 6b, we observe that with decreasing flow speed in the southern hemisphere, polarity reversal occurs earlier and also results in stronger final polar flux during cycle minimum in the same hemisphere. Surprisingly, the change in peak flow speed in the southern hemisphere profoundly affects the final amplitude of the northern hemispheric polar flux. In order to explain these features we analysed the magnetic butterfly diagram associated with two extreme cases, A and F, in which the peak flow speed in the southern hemisphere is 50% lesser (i.e. 7.5 ms−1) and 50% higher (22.5 ms−1), respectively, compared to the peak flow speed in the northern hemisphere (see Figs. 6c and d).
Evolution of the surface magnetic field is governed by the interplay between velocity fields and magnetic diffusivity. While the primary role played by meridional circulation is to carry magnetic flux from the equator to the polar region, magnetic diffusion promotes cancellation of magnetic flux among opposite polarities along with participating in the process of advection of flux. During the initial phase of a sunspot cycle, active regions primarily appear at higher latitudes in both the hemispheres and intra-hemispheric interaction occurs between the leading and following spots. Thus, magnetic flux cancellation remains restricted within individual hemispheres during this phase. As sunspot activity belts in two hemispheres approach towards the equator (predominantly visible after sunspot maximum), cross-equatorial flux cancellation among the leading spots belonging to the northern and southern hemispheres becomes important. Throughout the cycle, the residual flux from the following polarity spots is transported to the poles aided by meridional circulation.
Therefore, a slower flow in the southern hemisphere (case A) provides sufficient time for a substantial flux cancellation of opposite magnetic polarities, thus effectively allowing more unipolar flux to travel towards south pole as observed in Fig. 6c. This results in an early reversal and a higher final strength of the southern hemispheric polar flux. The same mechanism of flux cancellation across the equator also instigates a change in the northern hemispheric polar flux. Slower southern hemispheric meridional circulation facilitates a higher amount of unipolar magnetic flux (from the following spots) in the northern hemisphere to advect towards the north pole – eventually resulting in higher amplitude. On the contrary, a faster meridional flow in the southern hemisphere (case F) drags magnetic flux from both the leading and the following spots in such a way that both polarities can reach near to the polar region, thereby effectively delaying the process of polarity reversal and building up of new polar field in that hemisphere. In Fig. 6d, we observe such events to occur in the southern hemisphere during the 2nd and the 4th year, where flux from the leading spots reach beyond −60° latitudes. The same fast flow hinders cross-equatorial flux cancellation; this eventually reduce the final strength of the north hemispheric polar flux. We note that the distinction between the magnetic field distribution in the northern hemisphere corresponding to cases A and F enhances after cycle maximum is reached, beyond which cross-equatorial flux cancellation becomes profound. In all cases (A to F), the southern hemispheric polar flux is slightly stronger compared to the northern hemisphere. In summary, a hemispheric asymmetry as high as ±50% in the peak flow speed eventually introduces only about 3% asymmetry in the final polar field strength associated with two hemispheres.
So far, we have explored different aspects of the B–L mechanism responsible for north-south asymmetry in the hemispheric polar field evolution and have investigated their individual potential. We summarize our findings in Table 1. Our next aim is to study how the asymmetry present in polar flux during cycle minimum is translated and reflected in hemispheric activity of the following cycle in the context of dynamo mechanism.
Hemispheric asymmetry.
5. Translation of hemispheric asymmetry in the succeeding solar cycle: a dynamo perspective
Several numerical studies using dynamo simulations have investigated the origin of hemispheric asymmetry and identified two sources: stochastic fluctuation and non-linear effects (discussed in detail in recent reviews by Norton et al. 2014 and Brun et al. 2015). While non-linearity is embedded in the dynamo equations, stochastic fluctuations can be infused in the source of poloidal field. Randomness in the flows associated with the convective cells in the turbulent solar convection zone can lead to fluctuations in the mean field-α effect, which is considered as a potential source for poloidal field generation from the toroidal component (in azimuthal direction). Moreover, recent observational (Muñoz-Jaramillo et al. 2013) and numerical works (Nandy & Choudhuri 2002; Chatterjee et al. 2004; Yeates et al. 2008; Cameron & Schüssler 2015; Bhowmik & Nandy 2018) have established the B–L mechanism as the prime candidate for poloidal field generation, which acts through a combination of diffusion, cancellation, and advection of the magnetic field associated with the tilted active regions emerging on the solar surface. Thus, any sudden variation in the transport parameters associated with the B–L mechanism and significant scatter in the active region tilt angle can cause fluctuation in the poloidal field source term. To explore how the hemispheric asymmetry obtained from the SFT simulations is translated in the succeeding cycle, we considered a dynamo model with both the B–L mechanism and mean-field α-effect as two sources for poloidal field generation (as described in Sect. 3.2), where the irregularities and fluctuations are introduced only through the B–L source. The origin of hemispheric asymmetry using a dynamo model has been explored recently by Schüssler & Cameron (2018).
We followed the same approach as Bhowmik & Nandy (2018) (similar to the method used by Jiang et al. 2007) to include the SFT-generated surface magnetic field during sunspot minimum in the poloidal field source term of the dynamo model. We calculated the vector potential on the solar surface (say, ASFT(R⊙, θ, tmin)) by integrating BSFT(R⊙, θ, tmin), which is obtained by averaging the radial component of the surface magnetic field over longitude(ϕ). The relation between these two quantities is described as (Jiang et al. 2007)
We used the following relations to calculate ASFT on the solar surface at the cycle minimum (tmin) as a function of co latitude (θ),
The task of comprising the ASFT(R⊙, θ, tmin) in the magnetic vector potential (i.e. the poloidal field source, ADyn) associated with the dynamo simulation is conducted through the following process. We first evaluated a function γ(θ) by taking a ratio of ASFT(R⊙, θ, tmin) to ADyn(R⊙, θ, tmin) (as shown in Fig. 7b). The imprint of the B–L mechanism as simulated by the SFT model is infused in this γ(θ) function. The quantity γ(θ) is comprised of two parts: a constant factor “c” and a latitude-dependent function ζ(θ). The constant “c” arises as a consequence of the difference in amplitude of ASFT and ADyn obtained from two disparate numerical models. The value of “c” remains unaltered while incorporating individual ASFTs in dynamo simulation. The other function, ζ(θ), takes care of the distinct latitudinal distribution of ASFT and ADyn on the solar surface. Thus, the latitudinal variation of ζ(θ) is subjected to the particular ASFT in consideration. Assuming the B–L mechanism as a near-surface process, we modified ADyn by multiplying it with γ(θ) within a restricted region spanning from 0.8 R⊙ to R⊙ (over the full range of latitude). Finally, the modified ADyn is used as an initial condition at cycle minimum to perform the dynamo simulation. We compared the quantity BDyn (as described in Sect. 3.2) associated with the northern and southern hemispheres to explore hemispheric asymmetry.
 |
Fig. 7. Panel a: vector potentials at cycle minimum on the solar surface as obtained from SFT and dynamo simulations. Panel b: two distribution of vector potentials associated with the symmetric and asymmetric cases on the meridional plane. Panels c and d: evolution of BDyn for the symmetric and asymmetric cases, while the green arrows indicate the timing when outputs obtained from the SFT simulations are assimilated in the dynamo model. |
Among the four categories discussed in Sect. 4, introducing randomness in tilt angles of active regions results in the maximum hemispheric asymmetry (about 36%). We assimilated the SFT-generated surface magnetic field associated with this case in a dynamo simulation at the solar minimum by employing the method outlined above. We represented the vector potentials on the solar surface originated from the SFT (both the symmetric and asymmetric cases) and dynamo simulations as a function of latitude in Fig. 7a; these vector potentials are further used to obtain the associated γ(θ) functions. From the SFT generated profiles, it is apparent that the northern hemispheric poloidal field (on the surface) for the asymmetric case is slightly stronger than the symmetric case. However, the southern hemisphere is significantly weak in the asymmetric case, which is also apparent in the corresponding distribution of vector potentials within the solar convection zone (as depicted in Fig. 7b). Each of these vector potentials is used as an initial condition at the solar minimum in a continuous dynamo simulation.
Figures 7c and d depict the time evolution of BDyn (as described in Sect. 3.2) associated with the northern and southern hemispheres. Following the assimilation of the symmetric vector potential, we find the hemispheric solar activity to be reasonably similar (see Fig. 7a) with an overall increase in strength in both hemispheres. However, inclusion of the SFT-originated asymmetric vector potential in the dynamo simulation severely affects the solar activity in the southern hemisphere, keeping the northern hemispheric activity almost unaltered (see Fig. 7d). A detailed analysis of the observational data (in Sect. 2) indicated that the translation of hemispheric asymmetry is better reflected in the total activity associated with a specific hemisphere. We obtained an asymmetry of 21% (with respect to the symmetric case) by considering the difference between the sum of BDyn associated with the northern and southern hemispheres. A thorough comparison between hemispheric activity profiles associated with the symmetric and asymmetric cases reveals two aspects: firstly, a reduced amplitude of the poloidal field source originated from the B–L mechanism in the southern hemisphere is able to decrease the peak activity during the following cycle in the same hemisphere; and secondly, the timing of peak activity in the corresponding hemisphere can also be shifted. Thus, hemispheric asymmetry is effectively introduced both in the amplitude, and in the timing of peak activity during the next cycle, which can eventually result in double peak activity during the following cycle.
We intriguingly find that the summation BDyn in the northern hemisphere associated with the asymmetric case decreases by 1% even if corresponding polar flux increased by 8% compared to the symmetric case. We speculate this decrement is caused by the coupling between two hemispheres, where a weak poloidal field source in the southern hemisphere can effectively reduce the overall activity in the northern hemisphere.
6. Reproducing observed asymmetry by data-driven SFT and dynamo simulations
With the understanding gleaned from the previous sections, we now explore the basis of hemispheric asymmetry present in the observed sunspot cycles by conducting numerical simulations with actual observation. We performed a century-scale (1913–2016.75), data-driven SFT simulation starting from solar cycle 15 with a dipolar magnetic field as an initial condition while using the RGO-NOAA/USAF sunspot database which provides information on emergence timing, position and area (thus also the flux) of active regions appearing on the solar surface (Bhowmik & Nandy 2018). We note that no hemispheric asymmetry is introduced in this data-driven simulation through transport parameters other than the hemispheric irregularities embedded in the observed sunspot input profile itself. All active regions incorporated in the SFT simulations are assumed to emerge as BMRs, and their associated tilt angles are determined by Joy’s law with a systematic modification based on cycle amplitude (see Eq. (15) of Jiang et al. 2011). We do not introduce any additional randomness in assigning tilt angles to the active regions.
A comparison between the polar flux obtained from SFT simulation and those derived from the MWO polar faculae observation (Muñoz-Jaramillo et al. 2012) reveals an overall agreement (see Fig. 8a). The simulated polar flux shows a strong correlation (Pearson’s correlation coefficient 0.84 with p-value 0.0001) with the observed polar flux at cycle minima. Excluding the northern and southern polar flux data corresponding to cycle 18/19 minimum from our analysis improves the degree of correlation further such that Pearson’s correlation coefficient becomes 0.94 with p-value 7.5e−7. Moreover, the north-south asymmetry in polar flux at cycle minimum obtained from the SFT simulations and observations are highly correlated; Pearson’s correlation coefficient is 0.91 with p-value 0.0016. In earlier work, Goel & Choudhuri (2009) investigated hemispheric asymmetry by first modelling the poloidal fields at the beginning of solar cycles with the polar faculae data of the last century and then assimilating these data in a dynamo simulation. However, in certain occasions their results were unable to maintain the basic requirement of one-to-one correspondence between the hemispheric asymmetry present in polar flux at cycle minimum and the activity of the following cycle (i.e. few data points fall in the 2nd and 4th quadrants; see Figs. 5 and 6 in their paper). In contrast, we incorporated the SFT-generated poloidal fields (in terms of vector potential) at every cycle minimum in a continuous dynamo simulation for cycles 17–24 by following a similar method described in Sect. 5. As BDyn generated by the magnetic buoyancy algorithm serves as a proxy for emerging sunspot flux, we performed a calibration between the peak amplitudes of BDyn and the associated peak in sunspot area for cycle 17–24 to evaluate a constant multiplicative factor. This scaling factor is further used to capture the modulation of solar activity (in units of micro-hemispheres) obtained from “SFT-assimilated” dynamo simulations for both the hemispheres (see Fig. 8b). A correlation analysis between the amplitudes of peak sunspot area obtained from dynamo simulation and observation gives a Pearson’s correlation coefficient of 0.74 with p-value 0.0023 (excluding the data points corresponding to cycle 19).
 |
Fig. 8. Panel a: time variation of simulated polar flux in northern (blue) and southern (red) hemispheres compared with observed polar flux (north: light blue; south: light red) with error bars. Panel b: time evolution of hemispheric activities in terms of sunspot area (13 months running averaged) obtained from dynamo simulation. Panels c and d: relative activity (in terms of sunspot area in unit micro-hemispheres) between two hemispheres as obtained from dynamo simulation and observation for solar cycles 17–24, respectively. |
A close inspection of Fig. 8b reveals that north-south asymmetry exists both in the maximum amplitude and epochs of peak magnetic activity in the two hemispheres during solar cycles 17–24. Figure 8c highlights the relative dominance between the northern and southern hemispheric sunspot areas by depicting the time lags present in the rising, peak, and declining phases. While comparing with the observed hemispheric asymmetry in sunspot area (see Fig. 8d), we find that the SFT-assimilated dynamo simulations can reproduce the relative dominance and the phase difference (primarily for cycles 20–24), thereby indicating that asymmetry in polar flux at cycle minimum can indeed introduce asymmetry in the following cycle. In Fig. 9a, asymmetry in polar flux at cycle minimum obtained from SFT simulation is plotted against the asymmetry in the total hemispheric sunspot area in the following cycle obtained from dynamo simulations. This figure shows all data points falling in the 1st and 3rd quadrants; this satisfies the essential condition of the positive correlation between these two quantities. We find Pearson’s correlation coefficient to be 0.88 with p-value 0.0072. A comparison between the observation and the north-south asymmetry calculated from total sunspot area derived from dynamo simulation (see Fig. 9b) shows that our simulations are successful in preserving the relative hemispheric dominance, while the degree of correlation is substantial; Spearman’s rank correlation coefficient is 0.79 with p-value 0.048, excluding cycle 19 from our analysis. We note that even though results generated from simulations capture the nature of relative time difference in the epochs of peak activity for cycles 20–24 (i.e. which hemisphere peaks earlier in a cycle), the amplitude of phase lag is not same as the seen in observation.
 |
Fig. 9. Panel a: hemispheric asymmetry in simulated polar flux (maxwells) during beginning of the nth cycle (“n” varying from 17 to 24) vs. asymmetry (obtained from dynamo simulation) in total sunspot area (in micro-hemispheres) during that cycle. Panel b: asymmetry in the total sunspot area during nth cycle as obtained from dynamo simulation is compared with observation. The associated Pearson’s correlation coefficients, along with the p-values, are mentioned. |
We attribute the discrepancies between the simulated results and observations (see Figs. 8a and b) to different aspects of our assumptions used in dynamo simulations. In this work, we assume the origin of hemispheric asymmetry in the poloidal field source to be solely the B–L mechanism, while considering the amplitude of the mean-field α-effect to remain constant throughout the simulations (i.e. free from any hemispheric irregularities). Additionally, earlier studies (Hathaway et al. 2003; Nandy 2004; Yeates et al. 2008) have found that the speed of equator-ward meridional flow controls the duration of the solar cycle along with the timing of peak activity to some extent; we have not accounted for this effect in this current work. Thus, any profound hemispheric irregularities in meridional circulation speed can induce a relative phase difference in the rising, peak, and declining epochs of the northern and southern hemispheric magnetic activities.
7. Discussions and conclusions
A detailed analysis of the observational data shows a strong positive correlation between the polar flux during cycle minimum and the peak activity of the following cycle in both the northern and southern hemispheres, which is in agreement with earlier studies. Moreover, the north-south asymmetry in polar flux at cycle minimum is strongly correlated, because the relation is non-linear, with the asymmetry in the overall hemispheric activity during the following cycle. Additionally, we observe that the polar flux can attain its maximum amplitude much before the solar minimum. However, the maximum amplitude of the hemispheric polar flux and the associated timing (tN or tS) have no impact on the following cycle regarding the timing and magnitude of peak activity in the corresponding hemisphere. This observational feature establishes the amplitude of the polar flux at the solar minimum as a better precursor for forecasting the strength of the following cycle, thereby strongly supporting the concept used in various studies of solar cycle prediction (Cameron et al. 2016; Hathaway & Upton 2016).
We have performed multiple SFT simulations by incorporating diverse irregularities associated with the B–L mechanism in the northern and southern hemispheres. We consider three aspects of hemispheric asymmetry associated with the sunspots emerging on the solar surface. A time-gap of 2.5 years between the peak hemispheric activity results in a time difference of approximately one year in the reversal timing of the polar flux in two hemispheres. Given the initial polar field strength (at the beginning of the cycle) and the total flux associated with the sunspots are equal in both the hemispheres, the final polar field strength during cycle minimum remains unaffected by the imposed time gap. Since the cancellation of the older polar field and development of the new field materialize through a slow process, a temporal discrepancy in the peak hemispheric activity does not induce any asymmetry in the final polar field strength.
An imbalance in the total magnetic flux associated with sunspots in the northern and southern hemispheres modifies the final polar flux in both the hemispheres such that a 70% asymmetry in sunspot-associated flux induces only 14% hemispheric asymmetry in the final polar flux strength. In the absence of sufficient leading polarity spots in the northern hemisphere, magnetic flux from both the leading and following polarities advects towards the south pole, effectively weakening the polar flux in the more active hemisphere. Moreover, magnetic flux from the leading polarity may cross the equator and traverse towards the pole of the other hemisphere in the case of an extreme asymmetry, where almost no spot appears on the other hemisphere. Incorporating randomness in the tilt angles of active regions produces the maximum asymmetry in the final amplitude of the polar flux (as high as 36%). The only significant transport parameter through which hemispheric irregularities can be introduced in the B–L mechanism is the meridional circulation. However, we find that a north-south asymmetry of ±50% in the peak amplitude of meridional flow generates only 3% asymmetry in the polar field strength at cycle minimum; the reason for this has been explained in the context of cross-equatorial flux cancellation between the leading polarity spots in the two hemispheres. In summary (refer to Table 1), irregularities present in tilt angle and areal coverage of sunspots emerged on the solar surface during a cycle can induce significant hemispheric asymmetry in both the timing of reversal and final amplitude of the polar field. In contrast, we can neglect the contribution from a relative discrepancy in the peak flow speed of meridional circulation between two hemispheres.
We explore the extent to which the north-south asymmetry present in the polar field at solar minimum is translated to the hemispheric activity in the succeeding cycle. We find that a critically weak poloidal field source in the southern hemisphere, where 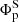 is 36% weaker than
is 36% weaker than 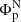 , strongly modulates the amplitude and timing of peak activity in the same hemisphere during the following magnetic cycle. This eventually introduces an asymmetry in the overall hemispheric activity (i.e. a summation of BDyn) and a profound time gap between the occurrence of peak activity in two hemispheres. Additionally, a hemispheric coupling reduces the overall strength in the northern hemisphere, effectively, decreasing the magnitude of asymmetry. However, we surmise that the degree of this coupling is subjected to the profiles associated with the parameters used in dynamo simulations.
, strongly modulates the amplitude and timing of peak activity in the same hemisphere during the following magnetic cycle. This eventually introduces an asymmetry in the overall hemispheric activity (i.e. a summation of BDyn) and a profound time gap between the occurrence of peak activity in two hemispheres. Additionally, a hemispheric coupling reduces the overall strength in the northern hemisphere, effectively, decreasing the magnitude of asymmetry. However, we surmise that the degree of this coupling is subjected to the profiles associated with the parameters used in dynamo simulations.
Analysing the results obtained from the century-scale, data-driven SFT and dynamo simulations we establish that hemispheric asymmetry present in the poloidal field source at cycle minimum originated from the B–L mechanism is capable of inducing significant asymmetry in hemispheric sunspot activity in the following solar cycle. However, other factors, such as fluctuations in mean-field α-effect and hemispheric irregularities in the meridional circulation flow speed, can also play a crucial role in reproducing the exact hemispheric asymmetry as observed in the past sunspot cycles. We speculate that a detailed analysis with diverse configurations of the initial poloidal field source and an extended parameter space study along with different levels of fluctuations can reveal essential aspects of the underlying physics involved in the dynamo mechanism. We plan to address these aspects of the analyses in follow-up work.
In summary, our analyses elaborate intricate characteristics of the B–L mechanism with a primary focus on the key elements causing hemispheric asymmetry in the large-scale polar field of the Sun. We demonstrate the importance of cross-equatorial cancellation of magnetic flux among the leading polarity spots associated with two hemispheres for the development of the new polar field following a polarity reversal at solar maximum. Lastly, by assimilating synthetic and observed data-driven SFT results in dynamo simulations, we illustrated that an asymmetric poloidal field at the solar minimum is capable of introducing notable asymmetry in both the amplitude and phase of hemispheric activities in the succeeding cycle. This result indicates that such asymmetry can be a potential basis for the generation of double peak cycles.
Acknowledgments
The author acknowledges the utilization of data from the Royal Greenwich Observatory/USAF-NOAA active region database compiled by David H. Hathaway (https://solarscience.msfc.nasa.gov/greenwch.shtml). MWO calibrated polar faculae data were downloaded from the solar dynamo database maintained by Andrés Muñoz-Jaramillo (https://dataverse.harvard.edu/dataverse/solardynamo). The author acknowledges funding by CEFIPRA/IFCPAR through grant 5004-1. The project is also partially supported by UK-STFC research grant. The author is thankful to Prof. Dibyendu Nandy for fruitful discussions and suggestions, which helped to improve the quality of this work. The author also thank the anonymous referee for the constructive suggestions which have improved the work further.
References
- Ataç, T., & Özgüç, A. 1996, Sol. Phys., 166, 201 [NASA ADS] [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Ballester, J. L., Oliver, R., & Carbonell, M. 2005, A&A, 431, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhowmik, P., & Nandy, D. 2018, Nat. Commun., 9, 5209 [Google Scholar]
- Brandenburg, A., Jennings, R. L., Nordlund, Å., et al. 1996, J. Fluid Mech., 306, 325 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Brun, A. S., Browning, M. K., Dikpati, M., Hotta, H., & Strugarek, A. 2015, Space Sci. Rev., 196, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., & Schüssler, M. 2015, Science, 347, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Schmitt, D., Jiang, J., & Işık, E. 2012, A&A, 542, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H., Jiang, J., & Schüssler, M. 2016, ApJ, 823, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. L. 1993, A&A, 274, 497 [NASA ADS] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Solar Phys., 7, 3 [Google Scholar]
- Chatterjee, P., Nandy, D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R., & Peñuela, T. 2010, A&A, 518, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deng, L. H., Xiang, Y. Y., Qu, Z. N., & An, J. M. 2016, AJ, 151, 70 [CrossRef] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., de Toma, G., & Gilman, P. A. 2006, Geophys. Res. Lett., 33, L05102 [NASA ADS] [CrossRef] [Google Scholar]
- D’Silva, S., & Choudhuri, A. R. 1993, A&A, 272, 621 [NASA ADS] [Google Scholar]
- Fan, Y. 2009, Liv. Rev. Sol. Phys., 6, 4 [Google Scholar]
- Fan, Y., Fisher, G. H., & Deluca, E. E. 1993, ApJ, 405, 390 [Google Scholar]
- Fisher, G. H., Fan, Y., & Howard, R. F. 1995, ApJ, 438, 463 [Google Scholar]
- Gao, P.-X., Li, K.-J., & Shi, X.-J. 2009, MNRAS, 400, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Goel, A., & Choudhuri, A. R. 2009, Res. Astron. Astrophys., 9, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Haber, D. A., Hindman, B. W., Toomre, J., et al. 2002, ApJ, 570, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E., & Nicholson, S. B. 1925, ApJ, 62, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E., Ellerman, F., Nicholson, S. B., & Joy, A. H. 1919, ApJ, 49, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Hathaway, D. H., & Rightmire, L. 2010, Science, 327, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., & Rightmire, L. 2011, ApJ, 729, 80 [Google Scholar]
- Hathaway, D. H., & Upton, L. A. 2016, J. Geophys. Res. (Space Physics), 121, 10 [Google Scholar]
- Hathaway, D. H., Nandy, D., Wilson, R. M., & Reichmann, E. J. 2003, ApJ, 589, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, S., & Nandy, D. 2016, ApJ, 832, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, S., Passos, D., & Nandy, D. 2014, ApJ, 789, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Chatterjee, P., & Choudhuri, A. R. 2007, MNRAS, 381, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Cameron, R. H., & Schüssler, M. 2014, ApJ, 791, 5 [Google Scholar]
- Käpylä, P. J., Korpi, M. J., Ossendrijver, M., & Stix, M. 2006, A&A, 455, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009, A&A, 500, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karak, B. B., & Cameron, R. 2016, ApJ, 832, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B., & Nandy, D. 2012, ApJ, 761, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Komm, R., González Hernández, I., Howe, R., & Hill, F. 2015, Sol. Phys., 290, 3113 [NASA ADS] [CrossRef] [Google Scholar]
- Leighton, R. B. 1969, ApJ, 156, 1 [Google Scholar]
- Li, K. J., Yun, H. S., & Gu, X. M. 2001, ApJ, 554, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Li, K. J., Wang, J. X., Xiong, S. Y., et al. 2002, A&A, 383, 648 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longcope, D. W., & Fisher, G. H. 1996, ApJ, 458, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Maunder, E. W. 1904, MNRAS, 64, 747 [NASA ADS] [Google Scholar]
- McClintock, B. H., & Norton, A. A. 2013, Sol. Phys., 287, 215 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., Leamon, R. J., Krista, L. D., et al. 2015, Nat. Commun., 6, 6491 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Sheeley, N. R., Zhang, J., & DeLuca, E. E. 2012, ApJ, 753, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Dasi-Espuig, M., Balmaceda, L. A., & DeLuca, E. E. 2013, ApJ, 767, L25 [Google Scholar]
- Nagy, M., Lemerle, A., Labonville, F., Petrovay, K., & Charbonneau, P. 2017, Sol. Phys., 292, 167 [Google Scholar]
- Nandy, D. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA Spec. Publ., 559, 241 [NASA ADS] [Google Scholar]
- Nandy, D. 2006, J. Geophys. Res. (Space Physics), 111, A12S01 [NASA ADS] [CrossRef] [Google Scholar]
- Nandy, D., & Choudhuri, A. R. 2002, Science, 296, 1671 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nandy, D., Bhowmik, P., Yeates, A. R., et al. 2018, ApJ, 853, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, H. W., & Milsom, A. S. 1955, MNRAS, 115, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., & Gallagher, J. C. 2010, Sol. Phys., 261, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., Charbonneau, P., & Passos, D. 2014, Space Sci. Rev., 186, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., & Ballester, J. L. 1994, Sol. Phys., 152, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ossendrijver, M., Stix, M., Brandenburg, A., & Rüdiger, G. 2002, A&A, 394, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Passos, D., Nandy, D., Hazra, S., & Lopes, I. 2014, A&A, 563, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovay, K. 2010, Liv. Rev. Solar Phys., 7, 6 [NASA ADS] [Google Scholar]
- Petrovay, K., & Szakaly, G. 1993, A&A., 274, 543 [NASA ADS] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, in Solar and Stellar Magnetic Activity (New York: Cambridge University Press), Cambridge Astrophysics Series, 34 [CrossRef] [Google Scholar]
- Schüssler, M., & Cameron, R. H. 2018, A&A, 618, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sivaraman, K. R., Gupta, S. S., & Howard, R. F. 1999, Sol. Phys., 189, 69 [Google Scholar]
- Snodgrass, H. B. 1983, ApJ, 270, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Swinson, D. B., Koyama, H., & Saito, T. 1986, Sol. Phys., 106, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Temmer, M., Rybák, J., Bendík, P., et al. 2006, A&A, 447, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobias, S. M., Brummell, N. H., Clune, T. L., & Toomre, J. 1998, ApJ, 502, L177 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., Cartledge, N. P., & Priest, E. R. 1998, ApJ, 501, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, V. K. 1987, Sol. Phys., 114, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, V. K. 1993, ApJ, 403, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Vizoso, G., & Ballester, J. L. 1990, A&A, 229, 540 [NASA ADS] [Google Scholar]
- Waldmeier, M. 1961, The Sunspot-activity in the Years 1610–1960 (Zurich: Schulthess) [Google Scholar]
- Waldmeier, M. 1971, Sol. Phys., 20, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., Nash, A. G., & Sheeley, Jr., N. R. 1989, Science, 245, 712 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2011, ApJ, 741, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2013, Sol. Phys., 287, 239 [NASA ADS] [CrossRef] [Google Scholar]
- White, O. R., & Trotter, D. E. 1977, ApJS, 33, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., Nandy, D., & Mackay, D. H. 2008, ApJ, 673, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., Baker, D., & van Driel-Gesztelyi, L. 2015, Sol. Phys., 290, 3189 [NASA ADS] [CrossRef] [Google Scholar]
- Zaatri, A., Komm, R., González Hernández, I., Howe, R., & Corbard, T. 2006, Sol. Phys., 236, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Mursula, K., & Usoskin, I. 2013, A&A, 552, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zolotova, N. V., Ponyavin, D. I., Arlt, R., & Tuominen, I. 2010, Astron. Nachr., 331, 765 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Panel a: time variation of averaged monthly (total) sunspot area during solar cycles 14–24 after performing 13-month running average. Panel b: same in the northern (blue curve) and southern (red curve) hemispheres, respectively, during that period. Panel c: hemisphere-wise excess activity: the blue-filled colour indicates the total area associated with the north hemispheric sunspots to be higher than the southern hemispheric total sunspot area and the red-filled colour depicts the opposite scenario. Panel d: variation of unsigned polar flux with error bars in two hemispheres. The rectangular grey bars depict episodes of solar minimum during 1906–2016.5. |
| In the text | |
 |
Fig. 2. Panel a: hemispheric asymmetry in polar flux (maxwells) during minimum of the nth cycle (“n” varying from 15 to 22) vs. the asymmetry in sunspot area (in micro-hemispheres) during the following cycle maximum. Panel b: asymmetry in polar flux is compared with the asymmetry in total sunspot area of the following cycle. The numbers 1–4 represent the first, second, third, and fourth quadrants, respectively. The uncertainties present in polar flux observation are also depicted by error bars in both panels. The Spearman’s rank correlation coefficient between the absolute amplitude of the asymmetry associated with the polar flux and total hemispheric sunspot area is 0.73 with p-value 0.04. |
| In the text | |
 |
Fig. 3. Panel a: time evolution of the unsigned magnetic flux associated with the synthetic sunspot input profiles in the northern and southern hemispheres with time difference in their respective peak activity. Panel b: evolution of corresponding polar flux in two hemispheres is depicted. Panel c: time lag in peak hemispheric activity is compared with the corresponding time difference in the reversal of polar flux, where the blue curve depicts a polynomial (of degree 2) fit to the data points. The associated Spearman’s rank correlation coefficient is given with p-value. |
| In the text | |
 |
Fig. 4. Panel a: time evolution of unsigned magnetic flux in the northern by a blue curve and in the southern hemispheres by red curves with different shades corresponding to increasing strength (5%–70% compared to the northern hemisphere). Panel b: corresponding polar flux evolution in two hemispheres. The time evolution of the longitudinally averaged magnetic field (radial component) as a function of latitude is depicted for two cases; in panel c the input sunspot profile is identical in two hemispheres and in panel d the southern hemispheric sunspot flux is 70% higher compared to that in the northern hemisphere. The red and yellow arrows indicate two prominent distinct patterns in the time latitude distribution of the magnetic field present corresponding to the hemispheric asymmetric case. The red (and the black in (b)) dashed vertical lines refer to the timing of sunspot cycle maximum. |
| In the text | |
 |
Fig. 5. Time evolution of polar flux in the northern and southern hemispheres associated with 50 individual input profiles depicted by set of light blue and light red curves, respectively. The dark blue and dark red curves represent the same corresponding to the standard symmetric profile. |
| In the text | |
 |
Fig. 6. Panel a: meridional circulation profiles as functions of latitude where the peak speed varies from 7.5 ms−1 to 22.5 ms−1 (denoted by different colours) in southern hemisphere. Positive (and negative) velocities indicate the flow is towards the south (and north) pole. Each flow profile is labelled alphabetically starting from “A” to “F”, while “S” represents the symmetric profile. Panel b: time evolution of the corresponding hemispheric polar flux. Panels c and d: magnetic butterfly diagram corresponding to the case A (with peak flow speed 7.5 ms−1) and the case F (peak speed 22.5 ms−1). The red dashed vertical lines depict the time of sunspot maximum. |
| In the text | |
 |
Fig. 7. Panel a: vector potentials at cycle minimum on the solar surface as obtained from SFT and dynamo simulations. Panel b: two distribution of vector potentials associated with the symmetric and asymmetric cases on the meridional plane. Panels c and d: evolution of BDyn for the symmetric and asymmetric cases, while the green arrows indicate the timing when outputs obtained from the SFT simulations are assimilated in the dynamo model. |
| In the text | |
 |
Fig. 8. Panel a: time variation of simulated polar flux in northern (blue) and southern (red) hemispheres compared with observed polar flux (north: light blue; south: light red) with error bars. Panel b: time evolution of hemispheric activities in terms of sunspot area (13 months running averaged) obtained from dynamo simulation. Panels c and d: relative activity (in terms of sunspot area in unit micro-hemispheres) between two hemispheres as obtained from dynamo simulation and observation for solar cycles 17–24, respectively. |
| In the text | |
 |
Fig. 9. Panel a: hemispheric asymmetry in simulated polar flux (maxwells) during beginning of the nth cycle (“n” varying from 17 to 24) vs. asymmetry (obtained from dynamo simulation) in total sunspot area (in micro-hemispheres) during that cycle. Panel b: asymmetry in the total sunspot area during nth cycle as obtained from dynamo simulation is compared with observation. The associated Pearson’s correlation coefficients, along with the p-values, are mentioned. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



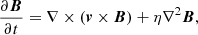
![$$ \begin{aligned} \frac{\partial B_{\rm r}}{\partial t}&= - \omega (\theta )\frac{\partial B_{\rm r}}{\partial \phi } - \frac{1}{R_\odot \sin \theta } \frac{\partial }{\partial \theta }\bigg ({ v}(\theta )B_{\rm r} \sin \theta \bigg ) \nonumber \\&\quad +\frac{\eta _h}{R_\odot ^2}\bigg [\frac{1}{\sin \theta } \frac{\partial }{\partial \theta }\bigg (\sin \theta \frac{\partial B_{\rm r}}{\partial \theta }\bigg ) + \frac{1}{\sin \theta ^2}\frac{\partial ^ 2 B_{\rm r}}{\partial \phi ^2}\bigg ] + S(\theta , \phi , t), \end{aligned} $$](/articles/aa/full_html/2019/12/aa34425-18/aa34425-18-eq8.gif)
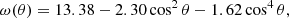
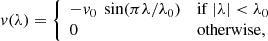
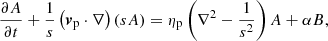
![$$ \begin{aligned}&\frac{\partial B}{\partial t} + s\left[ \boldsymbol{v}_{\rm p} \cdot \nabla \left(\frac{B}{s} \right) \right] + (\nabla \cdot \boldsymbol{v}_{\rm p})B = \eta _t\left( \nabla ^2 - \frac{1}{s^2} \right)B \nonumber \\&\quad \; + s\left(\left[ \nabla \times (A (r,\theta ) {\boldsymbol{\hat{e}}}_\phi ) \right]\cdot \nabla \Omega \right) + \frac{1}{s}\frac{\partial (sB)}{\partial r}\frac{\partial \eta _t}{\partial r}, \end{aligned} $$](/articles/aa/full_html/2019/12/aa34425-18/aa34425-18-eq13.gif)
![$$ \begin{aligned} \gamma _{\rm r}&= -f \gamma _{0r} \Bigg [1 + \mathrm{erf} \bigg ( \frac{r - 0.715}{0.015}\bigg )\Bigg ] \Bigg [1 - \mathrm{erf} \bigg ( \frac{r - 0.97}{0.1}\bigg )\Bigg ] \nonumber \\&\quad \times \Bigg [\exp \bigg ( \frac{r - 0.715}{0.25}\bigg )^2 \cos \theta + 1 \Bigg ]. \end{aligned} $$](/articles/aa/full_html/2019/12/aa34425-18/aa34425-18-eq14.gif)
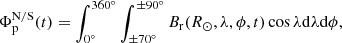
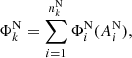
![$$ \begin{aligned} B^\mathrm{SFT}_{\rm r}(R_{\odot },\theta ,t_{\rm min})=\dfrac{1}{R_{\odot } \sin \theta } \dfrac{\partial }{\partial \theta } [\sin \theta A^\mathrm{SFT}(R_{\odot },\theta ,t_{\rm min})] . \end{aligned} $$](/articles/aa/full_html/2019/12/aa34425-18/aa34425-18-eq27.gif)