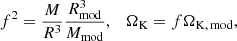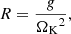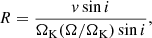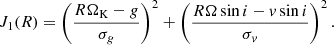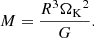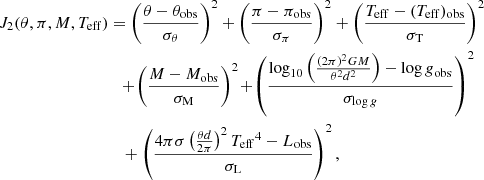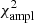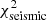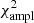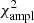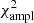| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 25 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834744 | |
| Published online | 27 June 2019 | |
Revisiting the pulsational characteristics of the exoplanet host star β Pictoris⋆,⋆⋆,⋆⋆⋆
1
Institut für Astro- und Teilchenphysik, Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria
e-mail: konstanze.zwintz@uibk.ac.at
2
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
3
Instytut Astronomiczny, Uniwersytet Wroclawski, Kopernika 11, 51-622 Wroclaw, Poland
4
Institut für Kommunikationsnetze und Satellitenkommunikation, Technical University Graz, Inffeldgasse 12, 8010 Graz, Austria
5
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, CS 34229, 06304 Nice Cedex 4, France
6
Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716 Warsaw, Poland
7
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
8
Département de physique, Université de Montréal, CP 6128, Succursale Centre-Ville, Montréal, Québec H3C 3J7, Canada
9
Centre de Recherche en Astrophysique du Québec (CRAQ), Montréal, Québec H3C 3J7, Canada
10
Institute of Automatic Control, Silesian University of Technology, Akademicka 16, Gliwice, Poland
11
Department of Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, Ontario M5S 3H4, Canada
12
Department of Physics and Space Science, Royal Military College of Canada, PO Box 17000, Stn Forces, Kingston K7K 7B4 Ontario, Canada
13
Universität Wien, Institut für Astrophysik, Türkenschanzstrasse 17, 1180 Wien, Austria
14
Department of Physics, University of California at Santa Barbara, Santa Barbara, CA 93111, USA
15
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
16
South African Astronomical Observatory, Observatory Rd, Observatory Cape Town, 7700 Cape Town, South Africa
17
Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia
18
Department of Astronomy, University of Cape Town, Rondebosch, 7700 Cape Town, South Africa
19
Jet Propulsion Laboratory, California Institute of Technology, M/S 321-100, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
20
Department of Physics & Astronomy, University of Rochester, 500 Wilson Blvd., Rochester, NY 14627, USA
21
Institut de Recherche sur les Exoplanètes, Département de Physique, Université de Montréal, Montréal, QC H3C 3J7, Canada
Received:
29
November
2018
Accepted:
14
May
2019
Context. Exoplanet properties crucially depend on the parameters of their host stars: more accurate stellar parameters yield more accurate exoplanet characteristics. When the exoplanet host star shows pulsations, asteroseismology can be used for an improved description of the stellar parameters.
Aims. We aim to revisit the pulsational properties of β Pic and identify its pulsation modes from normalized amplitudes in five different passbands. We also investigate the potential presence of a magnetic field.
Methods. We conducted a frequency analysis using three seasons of BRITE-Constellation observations in the two BRITE filters, the about 620-day-long bRing light curve, and the nearly 8-year-long SMEI photometric time series. We calculated normalized amplitudes using all passbands and including previously published values obtained from ASTEP observations. We investigated the magnetic properties of β Pic using spectropolarimetric observations conducted with the HARPSpol instrument. Using 2D rotating models, we fit the normalized amplitudes and frequencies through Monte Carlo Markov chains.
Results. We identify 15 pulsation frequencies in the range from 34 to 55 d−1, where two, F13 at 53.6917 d−1 and F11 at 50.4921 d−1, display clear amplitude variability. We use the normalized amplitudes in up to five passbands to identify the modes as three ℓ = 1, six ℓ = 2, and six ℓ = 3 modes. β Pic is shown to be non-magnetic with an upper limit of the possible undetected dipolar field of 300 Gauss.
Conclusions. Multiple fits to the frequencies and normalized amplitudes are obtained, including one with a near equator-on inclination for β Pic, which corresponds to our expectations based on the orbital inclination of β Pic b and the orientation of the circumstellar disk. This solution leads to a rotation rate of 27% of the Keplerian breakup velocity, a radius of 1.497 ± 0.025 R⊙, and a mass of 1.797 ± 0.035 M⊙. The ∼2% errors in radius and mass do not account for uncertainties in the models and a potentially erroneous mode-identification.
Key words: asteroseismology / stars: individual: β Pictoris / stars: interiors / stars: variables: δ Scuti / stars: magnetic field
Based on data collected by the BRITE Constellation satellite mission, designed, built, launched, operated and supported by the Austrian Research Promotion Agency (FFG), the University of Vienna, the Technical University of Graz, the University of Innsbruck, the Canadian Space Agency (CSA), the University of Toronto Institute for Aerospace Studies (UTIAS), the Foundation for Polish Science & Technology (FNiTP MNiSW), and National Science Centre (NCN).
Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 094.D-0274A.
Light-curve data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/627/A28
© ESO 2019
1. Introduction
The description of the formation, structure, and evolution of young stars is one of the great challenges in stellar astrophysics. Early stellar evolution plays a crucial role in our understanding of the formation and evolution of exoplanets, whose properties depend on the accuracy of the inferred stellar parameters. In many cases, stellar activity (star spots, magnetic fields, pulsations, circumstellar material, etc.) complicates the reliable determination of the physical properties of stars from the combination of spectroscopic observations and theoretical models and affects the investigation of the exoplanet properties. However, the presence of pulsations might also be beneficial because asteroseismic methods can be used to constrain the interior structure of exoplanet host stars. With it, more reliable results for the fundamental stellar parameters can be inferred, which in turn affects the precision of the derived exoplanet properties. In this context, the β Pictoris system is a quite interesting object.
β Pictoris (HD 39060, spectral type A6 V) is a bright star (V = 3.86 mag) located relatively close to us at a distance of 19.76 pc (calculated using a parallax of 50.623 ± 0.334 mas as given in the Gaia DR2 catalog; Brown et al. 2018). It is a member of the β Pic moving group (Mamajek & Bell 2014). The star β Pic is surrounded by a gas and dust debris disk that is seen nearly edge-on; its outer extent varies from 1450 to 1835 Astronomical Units (AU) (Larwood & Kalas 2001). The observed warp of its inner disk suggested the presence of a planet in the system. Using observations with the Very Large Telescope (VLT) at Paranal and the NACO camera, Lagrange et al. (2009, 2010) directly imaged the giant gas planet β Pic b for the first time. Although its orbital inclination is close to equator-on, that is, 88.81 ± 0.12° as seen from Earth, it is sufficiently inclined for β Pic b to not transit its host star (Wang et al. 2016). The reported four distinct belts around the star kinematically indicate the presence of other planets (Wahhaj et al. 2003). So far, no additional planet has been detected (e.g., Lous et al. 2018).
The age of the β Pic system was investigated by several authors using many different methods (for a review, see Mamajek & Bell 2014). The current agreement appears to be that the age of the β Pic system is ∼23 Myr (Mamajek & Bell 2014). From both spectroscopic observations and the derived age, it is evident that the star is in its early main-sequence stage of evolution (e.g., Zwintz et al. 2014).
δ Scuti pulsations in β Pic were first discovered 2003 through ground-based photometric time series (Koen 2003) where three low-amplitude modes were identified. Subsequent spectroscopic time-series observations obtained with the 1.9 m telescope at the South African Astronomical Observatory (SAAO) revealed 18 δ Scuti pulsation frequencies in the range from 24 to 71 d−1 from line profile variations (Koen et al. 2003). Recently, Mékarnia et al. (2017) reported 31 pulsation frequencies between 34.76 and 75.68 d−1 derived from photometric time series obtained between March and September 2017 using the 40cm Antarctic Search for Transiting ExoPlanets (ASTEP) telescope at Concordia Station in Antarctica.
Asteroseismology has been successfully used to study different types of pulsating stars from the pre-main sequence (pre-MS) to the final stages of evolution (e.g., in white dwarfs) in a mass range from ∼0.5 to 40 M⊙ with effective temperatures between ∼3000 K and 100 000 K. δ Scuti stars are located in the lower part of the so-called classical instability strip where it intersects with the main sequence. They have spectral types from A2 to F2 (Rodríguez & Breger 2001) and masses between 1.5 and 4 M⊙ (e.g., Aerts et al. 2010) and lie in the effective temperature range between 6300 and 8600 K (Uytterhoeven et al. 2011). δ Scuti pulsations can be found in the pre-MS, main-sequence, and post-main-sequence evolutionary stages and are driven by the heat-engine (κ-) mechanism acting in the second helium ionization zone (e.g., Aerts et al. 2010). The pulsation modes are radial and nonradial pressure (p) modes with periods in the range from ∼18 min to 0.3 days.
Although δ Scuti stars were one of the first types of stars discovered to pulsate, little progress has been made in interpreting their pulsation spectra because they are so complex. δ Scuti stars are mostly multiperiodic and can show very rich pulsation frequency spectra (e.g., Poretti et al. 2009). As they are moderate to fast rotators (Breger et al. 2000), the influence of rotation on the pulsation frequencies cannot be neglected in theoretical models. One of the first effects of rotation is to split the frequencies of modes with the same n and ℓ values but different m values, thus removing their degeneracy. At slow rotation rates for uniform rotation profiles, these rotationally split modes should be observed as multiplets with nearly equidistant frequency spacings, but in fact, only a few cases are known where such clear rotational splittings were found (e.g., Kurtz et al. 2014). At faster rotation rates, the multiplets become non-equidistant as higher-order effects of rotation intervene (e.g., Saio 1981; Espinosa et al. 2004), and they start to overlap, which makes the spectrum more complicated to interpret (Reese et al. 2006). Eventually, the frequency spectrum of acoustic modes takes on a new structure that is composed of overlapping independently organized subspectra that are associated with different classes of modes (Lignières & Georgeot 2008, 2009).
Furthermore, the pulsation amplitudes of δ Scuti stars can be variable for different reasons. A good overview of this topic can be found in Bowman et al. (2016), where the authors explain the two intrinsic causes, (i) beating of a pair of close unresolved pulsation frequencies and (ii) nonlinearity and coupling of modes. They also cover one extrinsic cause of amplitude modulations, that is, binary or multiple systems. In the same study, the authors reveal that 61.3% of their sample of 983 δ Scuti stars include at least one pulsation mode that shows an amplitude modulation, which illustrates that this is a quite common effect in this group of stars.
Another complicating factor in the interpretation of δ Scuti type pulsations can be the presence of a magnetic field. δ Scuti and rapidly oscillating, chemically peculiar A (roAp) stars are located in the same region of the Hertzsprung–Russel (HR) diagram. The roAp stars (Kurtz et al. 2006) show pulsation periods between 6 and 24 min (e.g., Smalley et al. 2015) and possess global magnetic fields, inhomogeneous surface distributions of some chemical elements, and strong overabundances, including the rare-earth elements (Ryabchikova et al. 2004). While the presence of sometimes quite strong magnetic fields are typical for roAp stars, magnetic fields have been measured for only very few δ Scuti stars (e.g., Kurtz et al. 2008; Neiner & Lampens 2015) or were suggested based on the presence of the aforementioned rare-earth anomaly (Escorza et al. 2016).
We here use photometric time series obtained by the Bright-star Target Explorer (BRITE) Constellation satellites in two filters in three observing seasons in combination with photometric time series observed with the Solar Mass Ejection Imager (SMEI) satellite (Jackson et al. 2004; Howard et al. 2013), the β Pictoris b Ring project (bRing) instrument (Stuik et al. 2017) and the previously published results by Mékarnia et al. (2017) based on data from the ASTEP telescope in Antarctica (Abe et al. 2013; Guillot et al. 2015; Mékarnia et al. 2016) to constrain the pulsational properties of β Pic, identify its pulsation modes from the multiband photometry, and investigate the presence of amplitude modulation. Additionally, we use spectromolarimetric data obtained with the polarimetric unit HARPSpol on the High Accuracy Radial velocity Planet Searcher (HARPS; Piskunov et al. 2011) to investigate the presence of a magnetic field.
2. Observations
2.1. BRITE-Constellation
BRITE-Constellation1 consists of five 20 cm cube nanosatellites each carrying a 3 cm telescope and feeding an uncooled CCD (Weiss et al. 2014). The three BRITE satellites BRITE-Toronto (BTr), Uni-BRITE (UBr), and BRITE-Heweliusz (BHr), carry a customized red filter (550–700 nm), and the two satellites BRITE-Austria (BAb) and BRITE-Lem (BLb) carry a customized blue filter (390–460 nm). More details on the detectors, pre-launch, and in-orbit tests are described by Pablo et al. (2016). Popowicz et al. (2017) described the pipeline that processes the observed images that yield the instrumental magnitudes that are delivered to the users.
BRITE-Constellation observes large fields with typically 15–20 stars brighter than V = 6 mag that include at least three targets brighter than V = 3 mag. Each field is observed at least 15 min in each ∼100-min orbit for up to half a year (Weiss et al. 2014).
BRITE-Constellation first obtained observations of β Pic from 16 March–2 June 2015 (BRITE Run ID: 08-VelPic-I-2015), yielding a total time base of 78.323 days using BHr in stare mode (Popowicz et al. 2017). Hence, the corresponding frequency resolution, 1/T, is 0.013 d−1. After the success of this first observing season, a longer observing run was conducted using BTr from 4 November 2016 to 17 June 2017 for a total of 224.573 days and BLb from 15 December 2016 to 21 June 2017 for 187.923 days (BRITE Run ID: 23-VelPic-II-2016). BHr was used from 7 January 2017 to 30 January 2017 for 24 days to cover a gap in the BTr observations. Recently, the BRITE-Constellation observations of the third season for β Pic were completed. The red BHr satellite obtained time series of β Pic between 9 November 2017 and 25 April 2018 for 167.335 days (BRITE Run ID: 33-VelPicIII-2017). The 2016/2017 and 2017/2018 observations were made using the chopping mode, where the position of the target star within the CCD plane is constantly alternated between two positions about 20 pixels apart on the CCD (Popowicz et al. 2017). An overview of the BRITE-Constellation observations is given in Table 1. Publicly available BRITE-Constellation data can be retrieved from the BRITE Public Data Archive2.
Properties of the multicolor observations for β Pictoris.
2.2. bRing
The “β Pictoris b Ring project”, bRing, consists of two ground-based observatories that monitored β Pic photometrically in particular during the expected transit of the Hill sphere of its giant exoplanet β Pic b in 2017–2018 (Stuik et al. 2017). One bRing instrument is located in the Sutherland observing station of the SAAO, the second bRing site is at the Siding Spring Observatory in Australia. Both telescopes take observations in the wavelength range from 463 to 639 nm. A detailed description of the design, operations, and observing strategy of bRing is provided by Stuik et al. (2017). Both bRing instruments will continue the observations of β Pic for as long as possible in the future.
The data set used here was taken between 2 February 2017 and 16 October 2018 with a cadence of ∼5 min. It used a combination of the data obtained by the two bRing instruments.
2.3. Solar Mass Ejection Imager
The Solar Mass Ejection Imager (SMEI; Eyles et al. 2003; Jackson et al. 2004; Howard et al. 2013) was launched as a secondary payload on board the Coriolis spacecraft in January 2003. Its main purpose was to monitor and predict space weather in the inner solar system. The orbital period of SMEI is ∼101.5 min (e.g., Eyles et al. 2003). The mission was terminated due to budgetary reasons in September 2011. However, the SMEI images have also been shown to yield high-quality long-duration stellar photometry. SMEI obtained brightness measurements of nearly the full sky using three cameras with a field of view of 3 × 60 deg2 each. The photometric passband ranges from 450 to 950 nm. The data rate for the SMEI photometric time series for a single star is one measurement in each ∼101.5-min orbit. Consequently, the Nyquist frequency of the SMEI data lies at 7.08 d−1.
Stellar time series obtained by SMEI can be extracted from the SMEI website3. They have been used several times in the past for a common interpretation with BRITE-Constellation data (e.g., Baade et al. 2018a; Kallinger et al. 2017). In the case of β Pic, only times and magnitudes were available from the SMEI website, with no additional information about the instrumental settings.
The SMEI data for β Pic comprise 28 623 data points obtained between 6 February 2003 and 30 December 2010 for about eight years in total. This corresponds to a classical Rayleigh frequency resolution of 0.0003 d−1 (see Table 1).
2.4. Spectropolarimetry
β Pic was observed in conjunction with the BRITE spectropolarimetric survey (Neiner & Lébre 2014) with the HARPSpol spectropolarimeter (Piskunov et al. 2011) installed on the ESO 3.6 m telescope in La Silla (Chile). Observations were acquired on 7 November 2014 and are available through the ESO archive4. A series of seven consecutive Stokes V sequences were obtained to increase the signal-to-noise ratio (S/N) of the coadded spectrum while avoiding saturation of the detector. Each sequence consisted of four subexposures of 246 s, each subexposure was made in a different configuration of the polarimeter. This led to a total of almost 2 h of exposure for the seven sequences.
The usual bias, flat-field, and ThAr calibrations were obtained on the same night and were applied to the data. The data were reduced using a modified version of the REDUCE software (Piskunov & Valenti 2002; Makaganiuk et al. 2011). This included automatic normalization of the spectra to the intensity continuum level.
3. Photometric data reduction and frequency analysis
The frequency analysis of the BRITE, SMEI, and bRing photometric time series was performed independently of each other using the software package Period04 (Lenz & Breger 2005), which combines Fourier and least-squares algorithms. Frequencies were then prewhitened and considered to be significant if their amplitudes exceeded 3.8 times the local noise level in the amplitude spectrum (Breger et al. 1993; Kuschnig et al. 1997). Frequency, amplitude, and phase errors were calculated using the formulae given by Montgomery & Odonoghue (1999). We verified the analysis using the iterative prewhitening method based on the Lomb-Scargle periodogram that is described by Van Reeth et al. (2015).
3.1. Analysis of the BRITE photometry
The raw BRITE photometry was corrected for instrumental effects. The corrections included outlier rejection, and both 1D and 2D decorrelations with all available parameters, in accordance with the procedure described by Pigulski (2018).
The data obtained in 2016/17 by BTr and BHr were combined to a single red-filter data set. An overview of their properties is given in Table 1. Figure 1 shows the light curves obtained by BHr in 2015 (panel a), by BTr and BHr in 2016/2017 (panel b), by BLb in 2016/2017 (panel c), and by BHr in 2017/2018 (panel d) to the same Y-axis scale. For β Pic with a B magnitude of 4.03 and a V magnitude of 3.86, significantly less flux is measured through the blue than through the red filter, which is reflected by the scatter, which is more than a factor of four higher. This causes a residual noise level in the frequency analysis that is also a factor four higher (Table 1).
 |
Fig. 1. Final reduced light curves of β Pic from BRITE-Constellation, bRing and SMEI: BHr data 2015 (panel a, gray points), combined BTr (panel b, red points) and BHr (panel b, gray points) data 2016/17, BLb data 2016/17 (panel c, blue points), BHr data 2017/18 (panel d, gray points) where black dots show binning of the light curves in three-minute intervals; the bRing and SMEI time series are shown in panels e and f. |
3.1.1. 2015 data
The frequency analysis of the BHr 2015 data yielded eight intrinsic frequencies with an S/N higher than 3.8. A comparison to the frequencies reported by Mékarnia et al. (2017) shows that there is agreement for six frequencies (F1, F8, F11, F13, F14, and F15; see Table 2 and gray triangles in Fig. A.1). Additionally, we find two frequencies at 32.456 d−1 with an amplitude of 0.47 ± 0.05 mmag and at 61.367 d−1 with an amplitude of 0.49 ± 0.05 mmag to be statistically significant with an S/N of 4.66 and 4.92. As these frequencies do not appear in any of our other data sets, including those obtained by bRing, SMEI, and ASTEP (Mékarnia et al. 2017), their origin is currently unclear, and we therefore treat them with caution and discard them from our further analysis.
Pulsation frequencies, amplitudes, phases, and S/N values derived from the BRITE-Constellation data sorted by increasing frequency and comparison to the literature.
The residual noise level after prewhitening of the eight frequencies is 100 ppm. The spectral window function and amplitude spectra are shown in Fig. A.1 in Appendix A.
3.1.2. 2016/2017 data
The analysis of the combined 2016/2017 BRITE red-filter data set yielded 13 significant pulsation frequencies (Table 2). Only frequency F10 at 49.4161 d−1 was not reported by Mékarnia et al. (2017). Although frequency F4 at 43.5268 d−1 is close to three times the BRITE orbital frequency and we would normally have to omit it, we identify it as pulsational because it was previously reported by Mékarnia et al. (2017).
Because the noise level of the blue filter data set is significantly higher, only four pulsation frequencies were identified from the BLb observations (Table 2). These four frequencies (F3, F4, F8, and F11) are also found in the 2015, 2016/2017, and 2017/2018 red-filter data sets and have also been reported by Mékarnia et al. (2017).
The residual noise level after prewhitening all frequencies is 40 ppm for the combined red-filter and 170 ppm for the blue-filter data. Figure 2 shows the amplitude spectra using the combined BTr and BHr data set (left) and the BLb data (right).
 |
Fig. 2. Frequency analysis of the BRITE 2016/17 data in the red (left) and the blue filter (right). Spectral window (panels a and e), original amplitude spectrum from 0 to 100 d−1 (panels b and f), zoom into the original amplitude spectrum (panels c and g), and residual amplitude spectrum after prewhitening the corresponding pulsation frequencies (panels d and h) with the residual noise level marked as horizontal dashed lines. The identified pulsation frequencies (as listed in Table 2) are marked in panels b and c as red (for the BRITE red filter) and in panels f and g as blue (for the BRITE blue filter) lines. The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the respective satellite’s orbital frequency (i.e., BTr on the left and BLb on the right) and its multiples. |
3.1.3. 2017/2018 data
With the 2017/18 BHr data set we confirmed seven of the pulsation frequencies that were previously identified from the BRITE-Constellation 2016/2017 data and Mékarnia et al. (2017). Additionally, two frequencies at 34.085 d−1 and 52.960 d−1 with amplitudes of 0.27 ± 0.03 mmag and 0.20 ± 0.03 mmag that were not found in the 2015 and 2016/17 data sets before are statistically significant with S/N values of 6.34 and 4.77, respectively. As these frequencies do not appear in any of the other observations, we discard them from any further investigation. The residual noise level after prewhitening all pulsation frequencies is 43 ppm. The corresponding amplitude spectrum is shown in Fig. A.2 in Appendix A.
3.1.4. Combined BRITE red-filter data
Combining the three seasons of BRITE-Constellation red filter data yields a total time base of 1135 days, corresponding to a Rayleigh frequency resolution, 1/T, of 0.0009 d−1. All frequencies listed in Table 2 can be found in the combined BRITE red-filter data set; no additional peaks are statistically significant. The residual noise level calculated from 0 to 100 d−1 after prewhitening all significant frequencies lies at 36 ppm.
Although BRITE-Constellation observations are sensitive in the low-frequency domain, as was illustrated by Baade et al. (2018b) or Ramiaramanantsoa et al. (2018), for instance, there is no evidence for the presence of g-modes.
3.2. Analysis of the bRing photometry
The complete bRing light curve used for the present analysis has a total time base of more than 620 days (panel e in Fig. 1). The Nyquist frequency lies at 135.37 d−1. We were able to identify six of the previously reported pulsation frequencies (i.e., F2, F6, F8, F11, F13, and F15) from this data set (left side in Fig. 3). The residual noise level after subtracting all formally significant frequencies is at 110 ppm (Table 1 and panel c in Fig. 3). Panel a in Fig. 3 shows the bRing spectral window.
 |
Fig. 3. Frequency analysis using the bRing and SMEI photometric time series. Spectral windows (panels a and d), original amplitude spectrum from 30 to 60 d−1 (panel b) for bRing and from 0 to 100 d−1 (panel e) for SMEI, the residual bRing amplitude spectrum after subtraction of the six identified pulsation frequencies (panel c), and zoom into the frequency range from 30 to 60 d−1 for SMEI (panel f). The identified pulsation frequencies are marked as thick black lines and labeled according to their numbers in Table 3. Frequency f13 was identified in the SMEI data due to its presence in DM17, but it is not present in the BRITE data. The red dashed vertical lines mark the position of the Nyquist frequency for SMEI and its multiples. The occurrence of the orbital frequency of SMEI at 14.16 d−1 (i.e., twice fNyquist) and its multiples can be seen as the regular structure in the spectral window (panel d) and in the amplitude spectrum (panels e and f) as the points where the noise decreases steeply to very low levels. |
3.3. Analysis of the SMEI photometry
The SMEI light curves are affected by strong instrumental effects, such as large yearly flux fluctuations. We corrected for this one-year periodicity of instrumental origin by phasing the raw data with a one-year period, calculating median values in 200 phase intervals, interpolating between these points, and subtracting the interpolated light curve. In the next step we detrended the data repeatedly with simultaneous sigma clipping to remove outliers and suppress any instrumental signal at low frequencies. The detrending was repeated 30 times starting with a time interval to calculate the mean, T, of 100 days and a sigma of 5, and ending the procedure with T = 0.7 days and a sigma of 4. As a consequence of this method, frequencies lower than 0.5 d−1 are suppressed. The annual light curves of β Pic show very similar behavior, hence the corresponding minor differences were subtracted by detrending. Panel f in Fig. 1 shows the complete reduced SMEI light curve.
The sampling of the SMEI data is only about one data point per 1.7 h (i.e., the orbital period of the satellite), which results in a Nyquist frequency of only 7.08 d−1. Hence, investigating SMEI data for the presence of δ Scuti-type pulsations in the range from about 30 to 70 d−1 as expected for β Pic goes already beyond the Nyquist frequency, fNyquist. As was shown for Kepler data by Murphy et al. (2013), for example, it is similarly possible to perform super-Nyquist asteroseismology using the SMEI data because real peaks remain as singlets even if they are above fNyquist. Panel e in Fig. 3 shows the complete amplitude spectrum of the SMEI data ranging up to 100 d−1. The pulsation frequencies between 30 and 60 d−1 clearly remain single peaks that can be easily distinguished from aliases caused by fNyquist. The dips in the noise around 42.5 and 52 d−1 are caused by the strong detrending. The frequency analysis of the SMEI data yielded seven pulsation frequencies that are either present in the BRITE data or were reported by Mékarnia et al. (2017) or both (Table 3, panels d to f in Fig. 3).
Pulsation frequencies, amplitudes, phases, and S/N values derived from the SMEI and bRing data sorted by increasing frequency and comparison to the literature.
4. Spectropolarimetric analysis
4.1. Stokes profiles
We applied the least-squares deconvolution (LSD) method (Donati et al. 1997) to the HARPSpol data to produce seven mean LSD Stokes I, Stokes V, and N profiles. The seven sequences were then coadded to produce one final set of LSD profiles, shown in Fig. 4.
 |
Fig. 4. LSD Stokes V (top), N (middle), and Stokes I (bottom) profiles of β Pic. Data are shown in black, while red lines show a smoothed profile. Vertical dashed lines indicate the range of integration for calculating the longitudinal magnetic field and estimating the FAP. |
Performing LSD requires the use of a mask indicating the list of lines present in the spectrum and to be used in the averaging, their wavelengths, depths, and Landé factors. To produce this mask, we started from a line list extracted from the VALD3 atomic database (Piskunov et al. 1995; Kupka et al. 1999) for a star with Teff = 8200 K and log g = 4.0 (i.e., the stellar parameters of β Pic taken from (Lanz et al. 1995). We retained only the lines with a predicted depth larger than 0.01. In addition, we rejected hydrogen lines, lines blended with H lines or interstellar lines, and regions affected by telluric absorption. Finally, we adapted the depth of the lines in the mask to the actual depth of the lines observed in the spectra with an automatic fitting routine. In total, we used 6391 spectral lines, with a mean wavelength of 503.8 nm and a mean Landé factor of 1.202.
The LSD N profile represents the null polarization and is used as a sanity check for the spectropolarimetric measurement. The fact that the N profile shows only noise (see Fig. 4, middle panel) indicates that the spectropolarimetric measurement has not been polluted by instrumental effects or stellar variability of nonmagnetic origin.
The LSD Stokes V profile will indicate a Zeeman signature if a magnetic field is present in β Pic. This profile also shows only noise (see Fig. 4, top panel), which indicates that β Pic is not magnetic at the precision level of our measurement.
We can statistically evaluate the detection of a magnetic field with the false-alarm probability (FAP). We checked the presence of a signature in the LSD Stokes V profile inside the velocity range [−110:152] km s−1, compared to the mean noise level in the LSD Stokes V profile outside the line. We adopted the convention defined by Donati et al. (1997) that there is a definite or marginal magnetic detection if FAP < 0.1%.
The FAP analysis of the LSD Stokes V profile leads to no magnetic detection (with a FAP = 99.99%). A similar analysis of the N profile also indicates no detection in N (as expected).
4.2. Longitudinal magnetic field measurement
A first quantitative estimate of the nondetection of a magnetic field in β Pic can be obtained through measuring the (undetected) longitudinal magnetic field Bl. To this aim, we used a center-of-gravity method (Rees & Semel 1979; Wade et al. 2000) and applied it to the Stokes V and N profiles. We integrated the profiles over the same velocity range as for the FAP analysis, that is, [−110:152] km s−1. We obtained Bl = −14 ± 20 G. We applied the same method to the N profile and obtained Nl = 11 ± 20 G. Both values are compatible with 0, indicating that no field is detected in β Pic. The error of 20 G shows that our measurement has a good precision.
4.3. Upper limit of the undetected magnetic field
Another quantitative estimate of the nondetection of a magnetic field in β Pic can be obtained by determining the maximum strength of a magnetic field that could have remained hidden in the noise of our data. Because β Pic is an A6 V star, its envelope is radiative, which means that if it hosts a magnetic field, it must be of fossil origin (Neiner et al. 2015a). Fossil fields are usually dipolar and tilted with respect to the rotation axis of the star (Grunhut & Neiner 2015). To estimate the upper limit of a possibly undetected magnetic field, we therefore assumed an oblique dipolar field.
We followed the method described in Neiner et al. (2015b): for various values of the polar magnetic field strength Bpol, we calculated 1000 models of the LSD Stokes V profile with random inclination angle i, obliquity angle β, and rotational phase, and a white Gaussian noise with a null average and a variance corresponding to the S/N of the observed profile. We first fit the LSD I profile, we then calculated local Stokes V profiles assuming the weak-field case, and we integrated over the visible hemisphere of the star. We used a projected rotational velocity of v sin i = 124 km s−1 taken from (Lanz et al. 1995) and a limb-darkening coefficient of 0.6. In this way, we obtained a synthetic Stokes V profile for each model, which we normalized to the intensity continuum. We used the same Landé factors and wavelengths as in the LSD calculation.
We then computed the probability of detection of a field in these 1000 models by applying the Neyman–Pearson likelihood ratio test. We further calculated the rate of detections among the 1000 models depending on the field strength (see Fig. 5). We required a 90% detection rate to consider that the field should have statistically been detected. This translates into an upper limit for the possible undetected dipolar field strength for β Pic of Bpol = 300 G. Using a 50% detection rate would bring the limit of the possible undetected dipolar field strength down to Bpol = 120 G.
 |
Fig. 5. Detection probability of a magnetic field in the observation of β Pic as a function of the magnetic polar field strength. The horizontal dashed line indicates the 90% detection probability. A dipole field stronger than Bpol = 300 G would have statistically been detected. |
5. Amplitude variability
δ Scuti stars can show variable pulsation amplitudes that are either of intrinsic (beating of unresolved frequencies, nonlinearity, or mode-coupling) or extrinsic (binarity and multiple systems) origin (for a detailed overview see Bowman et al. 2016). We examined the amplitude variability of β Pic using the three seasons of BRITE-Constellation red-filter data and the bRing observations.
5.1. Annual changes in the amplitudes
Using the three BRITE R-filter data sets obtained in consecutive years and the bRing light curve, we can study the annual amplitude variability in the pulsation frequencies of β Pic from 2015 to 2018. Only four of the 15 identified pulsation frequencies appear in the BRITE data sets of all three years: F8, F11, F13, and F15. Frequencies F1, F3, F4, and F6 are detectable in two of the three BRITE observing seasons, and the other seven frequencies only appear in one year of BRITE data. The top panel in Fig. 6 illustrates that the amplitudes of six of these frequencies remain rather stable or change only slightly from year to year (i.e., F1, F3, F4, F6, F8, and F15), while F11 shows a strong increase in amplitude, and the amplitude of F13 decreases significantly in the 2016/2017 observations and increases again in the 2017/2018 data set. A zoom into the BRITE R-filter amplitude spectra around F11 and F13 illustrates this behavior in the Fourier domain within the three seasons of BRITE-Constellation observations (Fig. 7).
 |
Fig. 6. Top panel: annual behavior of the amplitudes of the four pulsation frequencies F8, F11, F13, and F15 in all three BRITE red-filter data sets (filled symbols) and of the four pulsation frequencies F1, F3, F4, and F6 that appear in two of the three BRITE R epochs (open symbols). Bottom panel: annual behavior of the five pulsation frequencies F3, F6, F8, F11, and F13 in the bRing data. |
 |
Fig. 7. Zoom around F13 (left side, seen alongside with F14 in the 2015 data to the right of F13) and F11 (right side) into the original amplitude spectra of the BRITE red-filter data obtained in 2015 (top), 2016/2017 (middle), and 2017/2018 (bottom). The peak next to F13 in the bottom left panel showing the 2017/18 data is an alias frequency to F3 with the orbital frequency of BHr (i.e., 14.83053 d−1) that only appears quite close to the location of F14, which itself is not found in the 2017/18 data. |
In a next step, we divided the 620-day-long bRing light curve into two parts of equal length and studied the resulting behavior of the amplitudes with respect to the center points in time, that is, mid-2017 and mid-2018. Despite the higher noise level in the bRing data, which translates into larger errors on the amplitudes, it is obvious that the amplitude for F13 increases during this period of time. As the errors of the other four pulsation amplitudes (i.e., F3, F6, F8, and F11) are quite large, no clear conclusion on variability or stability can be drawn from these data.
5.2. Amplitude variability within observing seasons
Mékarnia et al. (2017) investigated the presence of amplitude and phase changes for the first ten of their frequencies during their seven-month-long observations by dividing their data set into seven parts, each 30 days in length. They showed that only their frequency f3 (corresponding to our frequency F13) at 53.69138 d−1 changes amplitude from 403 to 826 ± 66 ppm (i.e., 0.403–0.826 ± 0.066 mmag).
For the purposes of comparison, we conducted the same analysis as Mékarnia et al. (2017), that is, calculating the amplitude behavior using 30-day subsets. As the overall amplitude of our frequency F13 is significantly lower during the longest BRITE observing run in 2016/17 (see Fig. 6) and is therefore buried in the noise (i.e., not significant) when the 30-day subsets are calculated, we chose the 2017/18 BHr data set for this comparative analysis. Using subsets of 30-day lengths with 20 days of overlap, we find that the amplitude of F13 increased from 965 ppm (i.e., 0.965 mmag) to a maximum of 1489 ppm (i.e., 1.489 mmag); see blue symbols and line in the top panel of Fig. 8).
 |
Fig. 8. Amplitude (top panel) and phase (middle panel) behavior of the five pulsation frequencies with the highest amplitudes during the 2017/18 BHr observations calculated from 30-day subsets with 20-day overlaps, and amplitude-phase relation (bottom panel). The errors in phases are often smaller than the symbol size. |
As the ASTEP observations were conducted from March to September 2017 (Mékarnia et al. 2017), they overlap by about four months with the second BRITE data set from 2016/17, which was taken slightly earlier, starting in November 2016 and running until June 2017. The overall amplitude of our F13 at 53.6917 d−1 in this data set is only 396 ppm (i.e., 0.396 mmag), which is the lowest in our analysis. During the subsequent observations with ASTEP, the amplitude seems to have already increased. When BRITE-Constellation picked up β Pic again in November 2017 for the third season, the amplitude continued to increase. This effect is evident even though ASTEP and BHr are different instruments that carry different filters.
The other four frequencies with the highest amplitudes (F3, F8, F11, and F15) vary to a much smaller extent or remain basically at a constant level during this season (top panel in Fig. 8). These four frequencies have also been identified in Mékarnia et al. (2017), but were not marked as showing variable amplitudes.
The pulsation phases for the five selected frequencies during the BRITE 2017/18 observations can clearly be regarded as stable (middle panel in Fig. 8). As the changes in the amplitudes of β Pic are not correlated with changes in phases (bottom panel in Fig. 8), we interpret the variability of the amplitudes as being intrinsic and not caused by beating of two or more unresolved modes.
In a final test, we used the bRing data set for a comparable investigation of amplitude variability. Because the data have higher S/N than the BRITE observations, we had to choose 100-day subsets with 50-day overlaps to detect frequencies F8, F11, and F13. Unfortunately, the uncertainties of the amplitudes derived in the 100-day subsets are too high for an analogous interpretation of amplitude variability, which can be seen in Fig. B.1.
6. Asteroseismic interpretation
We used the pulsation frequencies and amplitudes derived from up to five passbands to identify the pulsation modes from comparing the observed and theoretical normalized amplitudes. The five filters are BRITE B, BRITE R, SMEI, and bRing (filter information is given in Table 1) together with the previously published 31 frequencies using the ASTEP instrument (Mékarnia et al. 2017), which uses a Sloan i′ filter (passband from 695 to 844 nm). The transmission curves of the filters of all five instruments we used in our analysis are illustrated in Fig. 9.
 |
Fig. 9. Transmission curves of the five instruments: BRITE B (blue solid line), BRITE R (red solid line), bRing (orange dashed line), ASTEP i′ (dark red dash-dotted line), and SMEI (black dotted line). |
In order to carry out mode identification, we used a sequence of seven 1.8 M⊙ models from the self-consistent field method (Jackson et al. 2005; MacGregor et al. 2007) with rotation rates ranging from 0 to 0.6 ΩK in increments of 0.1 ΩK, where 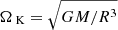 is the Keplerian breakup rotation rate. The initial mass for the models was chosen based on the value of 1.8 M⊙ given by Wang et al. (2016). The models are zero-age main-sequence (ZAMS) models, which is fairly realistic in the case of β Pic, which was identified as a 23 Myr old ZAMS star (Mamajek & Bell 2014). We then calculated their low-degree acoustic mode pulsations for n ranging from 1 or 2 to 10, ℓ from 0 to 3, and m from −3 to 3, using the adiabatic version of the two-dimension oscillation program (TOP, see Reese et al. 2006, 2009). Pseudo-nonadiabatic mode visibilities (i.e., disk-integrated geometric factors) were derived using the approach described by Reese et al. (2013, 2017), where the nonadiabatic pulsation amplitudes and phases came from 1D pulsation calculations using the MAD code (Dupret 2001) in nonrotating stellar models that span the relevant range in effective temperature and gravity. These mode visibilities were calculated for all inclinations between 0° and 90° in increments of 1°. The intensities in different photometric bands at each point of the stellar surface were obtained by integrating a blackbody spectrum at the latitude-dependent effective temperature multiplied by the filter transmission curve, thus taking gravity darkening into account. Limb darkening was included by multiplying these intensities by the Claret law (Claret 2000) for the filter5 that was the closest match to the photometric bands used here, as listed in Table 4. The correlations given in the third column of Table 4 are defined as
is the Keplerian breakup rotation rate. The initial mass for the models was chosen based on the value of 1.8 M⊙ given by Wang et al. (2016). The models are zero-age main-sequence (ZAMS) models, which is fairly realistic in the case of β Pic, which was identified as a 23 Myr old ZAMS star (Mamajek & Bell 2014). We then calculated their low-degree acoustic mode pulsations for n ranging from 1 or 2 to 10, ℓ from 0 to 3, and m from −3 to 3, using the adiabatic version of the two-dimension oscillation program (TOP, see Reese et al. 2006, 2009). Pseudo-nonadiabatic mode visibilities (i.e., disk-integrated geometric factors) were derived using the approach described by Reese et al. (2013, 2017), where the nonadiabatic pulsation amplitudes and phases came from 1D pulsation calculations using the MAD code (Dupret 2001) in nonrotating stellar models that span the relevant range in effective temperature and gravity. These mode visibilities were calculated for all inclinations between 0° and 90° in increments of 1°. The intensities in different photometric bands at each point of the stellar surface were obtained by integrating a blackbody spectrum at the latitude-dependent effective temperature multiplied by the filter transmission curve, thus taking gravity darkening into account. Limb darkening was included by multiplying these intensities by the Claret law (Claret 2000) for the filter5 that was the closest match to the photometric bands used here, as listed in Table 4. The correlations given in the third column of Table 4 are defined as 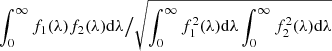 , where λ is the wavelength.
, where λ is the wavelength.
Correspondence between photometric bands used to observe β Pic (“This study”) and those used to implement the limb-darkening law (“Claret (2000)”).
As a first step, we searched for the low-degree modes that individually provide the best match to the observed amplitudes. We did not attempt to match observed phase differences as the pseudo-nonadiabatic calculations were not considered to be sufficiently reliable to provide accurate theoretical phase differences. We chose not to compare normalized amplitudes directly because this amounts to choosing one of the photometric bands as a reference band and normalizing the amplitudes in the other bands with respect to the amplitude in this reference band. This can lead to difficulties if the amplitude in the chosen reference band is close to zero. Instead, we normalized the observed amplitudes so that the sum of their squares equaled one. For the sake of consistency, the errors on the amplitudes were also normalized by the same factor. The theoretical amplitudes were then normalized so as to optimize the χ2 fit to the observations taking the errors into account. Moreover, given the relatively large increment on the rotation rate, the normalized amplitudes and frequencies were interpolated to intermediate rotation rates in increments of 0.01 ΩK.
Figure 10 shows a comparison between the observed and best-fitting normalized amplitudes. A good match can be observed for most of the modes, and a relatively low χ2 value is obtained. However, because the modes were fit individually, the inclinations and rotation rates obtained for the different modes do not match. Figure 11 illustrates these results: dark blue symbols represent the best solutions (i.e., those illustrated in Fig. 10). The small light blue dots are other solutions that satisfy the criterion χ2 ≤ (Nbands − 1), where χ2 is the χ2-value on the amplitudes for that particular mode and Nbands is the number of bands in which that mode is detected. On the right side of the latter relation, (Nbands − 1) was chosen and not Nbands because the intrinsic amplitude of theoretical mode is a free parameter. If none of the solutions (including the best solution) satisfied the above criterion, then the best solution is plotted using a square rather than a star. The light blue solutions thus give an idea of the uncertainties on these solutions. In order to obtain a more coherent result, it is therefore necessary to fit the modes simultaneously using a fixed value of the inclination and rotation rate. The fits to the normalized amplitudes shown here are nonetheless useful as they represent the best fit that can be hoped to be achieved using our set of theoretical mode visibilities.
 |
Fig. 10. Observed (blue) and best-fitting theoretical (red) normalized amplitudes using individual fits. fo represents the observed frequencies. In several cases, the match between observed and theoretical normalized amplitudes is sufficiently good for the latter to be hidden in the plots. Finally, the total χ2 value is 68.9. |
 |
Fig. 11. Inclinations (upper panel) and rotation rates (lower panel) obtained for each mode fit individually. The dark blue symbols represent the best solutions (i.e., those illustrated in Fig. 10). The small light blue dots are other solutions that satisfy the criterion χ2 ≤ (Nbands − 1), where χ2 is the χ2-value on the amplitudes for that particular mode and Nbands is the number of bands in which that mode is detected. The light blue solutions thus give an idea of the uncertainties on the above results. |
We then fit the frequencies and normalized amplitudes simultaneously. In order to achieve this, we carried out Monte Carlo Markov chains (MCMC) runs using the python emcee package (Foreman-Mackey et al. 2013) and using the rotation rate, Ω/ΩK, the inclination, i, and a dimensionless scale factor, f, on the frequencies as free parameters together with the free amplitudes of the 15 pulsation frequencies. These 18 free parameters were then used to fit 46 amplitudes in five passbands, 15 pulsation frequencies, and four classic constraints (mass, radius, log g, and v sin i) corresponding to 65 observables in total. We assumed a uniform prior on Ω/ΩK over the interval [0.0, 0.6] and on f over the interval [0.5, 2]. The prior on i was proportional to sin i in accordance with what is expected for random orientations of the rotation axis, although as we explain below, we sometimes restricted the range of i values. The scale factor was introduced to compensate for the fact that the set of stellar models was limited to a single mass. Multiplying the frequencies by a dimensionless scale factor f amounts to carrying out a homologous transformation in which the mean density of the model is multiplied by f2, thus providing a poor substitute for modifying the mass. This leads to the following relations:
where quantities with the subscript “mod” refer to the model prior to scaling, and those without this subscript to the scaled model (which should hopefully be close to the actual properties of β Pic). We note that because our models only depend on Ω/ΩK, this parameter also uniquely determines ΩK, mod. Finally, when the theoretical modes were matched to the observed ones, we were careful to avoid assigning the same identification to two different observed modes.
After we fixed the values of Ω/ΩK, f, and i, we were able to deduce the radius of the scaled model using the observational constraints on log g and v sin i (recalled in Table 5 below) using two different methods. The following relations are obtained:
List of classical constraints and least-squares fit.
where we recall that ΩK = fΩK, mod. We note that we have neglected possible differences between the polar and equatorial radius in the above expressions. Given that the values of Ω/ΩK, f, and i are selected by the MCMC algorithm, there is no reason to assume that the two above expressions give a priori the same values of R. One of the free parameters in the MCMC calculations might therefore be eliminated. We opted for a different approach, however, which consisted of keeping all of the free parameters, calculating R using both of the above equations, and rejecting solutions for which the two values of R differed by more than 20%. The final value of R was then obtained by minimizing the following least-squares cost function:
The mass was subsequently obtained through the Keplerian breakup rotation rate and the above radius:
At this point, it is useful to discuss the classical constraints on the fundamental atmospheric parameters of β Pic. In Table 5 we list various constraints found in the literature. We note that other values have been obtained for some of these parameters: log g = 4.15 dex according to Gray et al. (2006), the angular diameter θ = 0.84 ± 0.12 ± 0.10 mas including limb darkening according to Di Folco et al. (2004), θ = 0.712 ± 0.010 mas based on surface-brightness relations from Kervella et al. (2004) (see Defrère et al. 2012) and v sin i = 130 ± 4 km s−1 according to Royer et al. (2002). It is then interesting to investigate to what extent these values are self-consistent. For this, we minimized the following cost function in order to obtain a coherent set of parameters:
where d is one AU that is used to convert parallax into distance, quantities with the subscript “obs” are the observed values from Table 5, σx, x representing any one of these quantities and the associated uncertainties, and σM the average of the two errors on mass from the table. The above cost function makes use of the relations:
where π represents the parallax in the third equation. The best fit is provided in the fourth column of Table 5. The observational constraints are mostly consistent. This would have been less true if some of the alternate values such as log g = 4.15 dex (Gray et al. 2006) or θ = 0.84 ± 0.12 ± 0.10 (Di Folco et al. 2004) had been used. The errors were estimated by carrying out 10 000 Monte Carlo realizations of the observed errors before carrying out the above minimization and taking the standard deviation of the resultant parameters. In some cases, these are very similar to the observed errors (e.g., the mass), whereas in other cases, they are considerably smaller (e.g., log g).
In the MCMC runs that follow, we used the observational constraints directly rather than using the results from the fit, but ensured that the observational constraints encompassed the results from the fit. The error on the mass was increased by 50% to account for possible uncertainties resulting from the limited time span over which β Pic b has been observed compared to the estimated orbital period (thus affecting the stellar mass estimate). We excluded solutions with masses or radii more than 3σ away from the estimated values in order to avoid that the classic constraints were drowned out by the seismic ones. We also preferred the v sin i value from Koen et al. (2003) over that of Royer et al. (2002) because the resolution and S/N in the spectroscopic observations are slightly higher, although we do note that the two values are within 2σ of each other. We recall that the values and errors of v sin i and log g intervene when the radius is calculated during the MCMC runs (see Eq. (4)). These constraints are summarized in the last column of Table 5.
We started with an MCMC run using the observational errors on the frequencies and on the amplitudes. Figure 12 shows the best solution6 found from the run. The upper panel compares observed and theoretical amplitude in different photometric bands, whereas the lower panel compares the resultant spectra. A fairly good fit to the spectrum is achieved, but at the expense of the normalized amplitudes. The extremely small errors on the frequencies mean that the normalized amplitudes are hardly taken into account. The parameters of this fit are given in the first row of Table 6 and the corresponding mode identifications are provided both in Fig. 12 and in the second column of Table 7.
 |
Fig. 12. Upper panel: observed and best-fitting mode-normalized amplitudes in different photometric bands using the true errors and σF = 0.1 on the frequencies. In the latter case, only even modes are retained and the inclination search interval is [70 ° ,90 ° ] rather than [0 ° ,90 ° ]. The (n, ℓ, m) mode identifications are provided in each panel. Lower panel: observed vs. theoretical pulsation spectra for the two above cases. The observed frequencies are represented by the continuous vertical lines that span the plot. In both panels, the observations are shown in blue and the theoretical results and annotations are color-coded. χ2 calculations have 18 degrees of freedom, i.e., Ω/ΩK, i, f, and the 15 free amplitudes. In the upper panel, |
Best solutions obtained for different MCMC runs.
Mode identifications in the form (n, ℓ, m) for best and alternate configurations.
In order to obtain a more complete picture of the posterior probability distribution resulting from the above constraints, we show a triangle plot of the distribution of solutions obtained through the MCMC run in Fig. 13. This figure contains scatter plots for pairs of variables and histograms for single variables. These are color-coded according to the mode identification in the solution. The MCMC run produced several isolated groups of solutions in the parameter space, associated with different mode identifications. Accordingly, providing errors that cover all of these solutions is not meaningful; instead, we provide below errors along with the statistical averages for the group of solutions with the same identification as the best solution, that is, the solution that minimizes our cost function. These are provided on the line below the best solution in Table 6 for each configuration. Nonetheless, some of the other groups of solutions can also be quite important. For instance, the turquoise group contains a number of solutions with inclinations ranging from 83 to 90°, which seems more realistic given the orientation of the orbit of β Pic b and the disk around the star. The statistical averages and standard deviations are provided in the third line of Table 7 (excluding the line with the headers). The corresponding mode identifications are provided in the third column of Table 7.
 |
Fig. 13. Distribution of solutions resulting from the seismic contraints (with the true observational errors), normalized amplitudes, and observed values of log g and v sin i. The plots along the diagonal are histograms for single variables, whereas the remaining plots are scatter plots for pairs of variables. The plots are color-coded according to the mode identification. The solutions shown in red have the same n, ℓ, m identification as the best solution. |
In order to increase the weight of the observed amplitudes in the fit, we carried out other MCMC runs using a uniform frequency tolerance, denoted σF. This frequency tolerance acts as a trade-off parameter between fitting the spectrum and matching the amplitudes. If a low value is chosen for σF, the MCMC algorithm will favor solutions where the frequencies are a good match to the observations, but the amplitudes will be a poor fit. Conversely, high values of σF lead to the opposite behavior. Fig. C.1 in Appendix C shows the solutions obtained for σF = 0.01 d−1 and 0.05 d−1 respectively. The corresponding identifications are provided in these figures as well as in Table 7. The resultant parameters are given in lines 4–7 of Table 6 (excluding the header line). The different choices of σF have led to rather different solutions that both match the observations fairly well, however. Moreover, the solution for σF = 0.05 d−1 is fairly close to equator-on. This may be realistic for β Pic because of the nearly edge-on configuration of its disk and the planetary orbit, and because plausible mechanisms that might misalign the system are lacking. Nonetheless, this solution includes a few odd modes, that is, modes that are antisymmetric with respect to the equator, as we show in Table 7 (by calculating the parity of ℓ + m). This seems somewhat unrealistic because such modes should cancel out for an equator-on configuration and thus not be visible. Accordingly, we carried out an MCMC run for σF = 0.05 d−1 including only even modes and restricting the inclination to values between 70° and 90° (rather than 0° to 90°). The corresponding solution is also shown in Fig. C.1, and the resultant parameters given in Table 6. Although this solution has fairly similar parameter values for Ω/ΩK and i as the previous solution including even and odd modes, this solution corresponds to a completely different set of mode identifications. Furthermore, the inclination i = 76.8° is not entirely satisfactory as it is sufficiently far from equator-on to invalidate the exclusion of odd modes.
Another MCMC run was carried out using σF = 0.1 d−1 in search of solutions that were closer to equator-on. The best solution is shown in Fig. 12 and the corresponding parameters are given in Table 6. This solution is much closer to equator-on. The statistical average value for the inclination provided in Table 6 is biased because the inclination range is bounded by 90°, which artificially leads to a lower average. This best solution contains several modes with a similar identification as was obtained for σF = 0.05 d−1 with even and odd modes, except for an offset of 1 on the radial order. Finally, Fig. 14 provides a color-coded triangle plot showing the distribution of solutions in parameter space. A diversity of identifications is obtained. Furthermore, the group associated with the best solution (light green-yellow) clearly peaks at 90°, thus favoring an equator-on configuration.
 |
Fig. 14. Same as Fig. 13 except σF = 0.1 d−1 has been used as a frequency tolerance, the inclination has been restricted to the [70 ° ,90 ° ] interval and odd modes have been excluded. |
Another factor to be taken into account is that some of the amplitudes change significantly in the BRITE R band between two observational runs. The amplitude of the F11 mode at 50.49 d−1 is 0.84 mmag in 2016/17 and increases to 1.06 mmag in 2017/18. Likewise, the amplitude of the F13 mode at 53.69 d−1 is 0.40 mmag in 2016/17 in BRITE R and increases to 1.27 mmag in 2017/18. The fits carried out so far were primarily based on the 2016/17 data. We therefore carried out a few more MCMC runs using the 2017/18 data instead. The resultant best solutions as well as relevant statistical averages and standard deviations are listed in Table 6. The corresponding mode identifications are provided in Table 7. The choice of observing season does have some effect on the values of Ω/ΩK, i, and f, especially for σF = 0.05 d−1 using only even modes. The mode identification is completely modified for this particular case, but is hardly affected for σF = 0.1 d−1 with even modes.
It is expected that modifying the amplitudes of two modes can affect the entire mode identification because the MCMC algorithm optimizes the fit to all of the modes simultaneously. Furthermore, the seismic and amplitude-related values of χ2 are degraded in almost all cases. This shows that the models clearly provide a better match to the 2016/17 run than to that in 2017/18. One possible explanation for this poorer fit is the fact that the observations in the various photometric bands are not simultaneous and are for the most part more representative of the 2016/17 time period. Ideally, amplitude changes should proportionally be the same in the different bands over similar time periods and should therefore cancel out when normalized amplitudes are calculated because these only depend on mode geometry.
Overall, our favored solution is obtained for σF = 0.1 d−1, using only even modes. This solution seems to be the most coherent in terms of stellar inclination, given the measured inclination of the planetary orbit and the circumstellar disk of 88.81 ± 0.12° (Wang et al. 2016). It also leads to the best fit with the normalized amplitudes. However, the price to pay is a relatively high χ2 value for the seismic component (although the theoretical frequencies come in the same order as the observed ones). Possible causes for this significant difference in the frequencies include shortcomings in the stellar models. In particular, the models are uniformly rotating. This does not seem very realistic because baroclinic effects are expected to lead to differential rotation as shown in more realistic models based on the ESTER code (Espinosa Lara & Rieutord 2013; Rieutord et al. 2016). This in turn will affect rotational splittings (Reese et al. 2009), thus modifying the frequencies of non-axisymmetric modes. The differences between the fitted and observed mode amplitudes also still remain relatively high even for the most favorable solution. Possible causes for this include the use of pseudo-nonadiabatic mode visibilities rather than visibilities based on fully nonadiabatic calculations.
However, at this point it is not possible to obtain reliable fully nonadiabatic calculations. Rapidly rotating models that solve the energy conservation equation in a consistent way would be required, which is currently only achieved in the ESTER code. However, the ESTER code does not currently model subsurface convective envelopes, which is expected to be relevant in a star of this mass. Another limitation in the visibility calculations is the fact that they do not rely on realistic model atmospheres but rather on blackbody spectra, as was pointed out earlier. Finally, another factor that needs to be considered is the set of modes used in the identification. We restricted ourselves to modes with ℓ between 0 and 3. However, visibility calculations at rapid rotation rates suggest that higher ℓ modes may become more visible (e.g., Lignières & Georgeot 2009). Carrying out fits with higher ℓ values does lead to better fits with 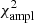 below 400 and/or
below 400 and/or 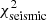 below 1000 in some cases, as expected. An alternative approach may therefore be to select modes based on their visibilities at the relevant rotation rate, rather than using a predefined set of modes, as was done above. Nonetheless, nonlinear mode coupling and saturation mechanisms may lead to intrinsic mode amplitudes that alter which modes are actually observed compared to what would be expected from geometric visibility factors.
below 1000 in some cases, as expected. An alternative approach may therefore be to select modes based on their visibilities at the relevant rotation rate, rather than using a predefined set of modes, as was done above. Nonetheless, nonlinear mode coupling and saturation mechanisms may lead to intrinsic mode amplitudes that alter which modes are actually observed compared to what would be expected from geometric visibility factors.
7. Discussion and conclusion
The exoplanet host star β Pic was already known to show p-mode pulsations of δ Scuti-type (Koen 2003; Koen et al. 2003; Mékarnia et al. 2017). Because observations with the Kepler space telescope (Borucki et al. 2010) revealed that many δ Scuti stars show both p- and g-modes (Uytterhoeven et al. 2011), we also investigated the presence of g-modes in our β Pic data sets. The modes would be expected to lie in the frequency range between 0.3 and 3 d−1 (Aerts et al. 2010). BRITE-Constellation observations are known to be in particular sensitive to frequencies in this range (e.g., Baade et al. 2018b; Ramiaramanantsoa et al. 2018) because of the observing strategy of the satellites (Weiss et al. 2014).
Using our best data set alone (i.e., the BRITE R-filter observations of 2016/17, which reach the lowest residual noise level) and a combination of three seasons of BRITE R-filter observations, we did not find evidence for the presence of g-modes down to a residual noise level of 36 ppm. It is therefore evident that if g-modes exist in β Pic, they must possess even lower amplitudes that remain undetected in the data sets analyzed here.
Our 15 identified pulsation frequencies correspond to the 14 highest amplitude frequencies in Mékarnia et al. (2017), which are numbered f1 to f14 and their frequency f23. Because the residual noise level of 9.45 ppm is significantly lower in Mékarnia et al. (2017) than our best data set (i.e., the BRITE R-filter observations obtained in 2016/17) with a residual noise level of 40 ppm, not all the pulsation frequencies reported earlier are identified to be significant in our analysis.
We used the amplitudes of 15 δ Scuti-type p-mode frequencies detected in up to five different passbands, BRITE B and R, SMEI, bRing and ASTEP i′, to calculate normalized amplitudes for an asteroseismic study of β Pic and an identification of its pulsation modes. This analysis was complicated by the fact that two pulsation frequencies show a clear variability in our time-series observations: The frequency F13 at 53.6917 d−1 first decreases between the 2015 and 2016/17 observations and then increases again between 2016/17 and 2018; the amplitude of frequency F11 at 50.4921 d−1 constantly increases in the observations obtained between 2015 and 2018. This behavior was consistently found in the BRITE-Constellation and the bRing data and confirms earlier reports by Mékarnia et al. (2017). All other pulsation modes have stable amplitudes within the observational errors.
In general, the variability of certain amplitudes should proportionally be the same in different bands over similar periods of time; thus amplitude variability should not affect the calculations of normalized amplitudes given that these only depend on mode geometry. In the present case, the observations obtained by BRITE-Constellation, bRing, and ASTEP were not taken exactly simultaneously, but with overlapping periods of time, and the SMEI photometry was obtained years before. The variable amplitudes of the two modes therefore affect the observed normalized amplitudes and thus the identification of the pulsation modes.
For our asteroseismic interpretation of the normalized amplitudes, we used the most precise BRITE R-filter data set (i.e., the ∼224-day-long BRITE R-filter observations obtained in 2016/17 with a residual noise level of 40 ppm), the simultaneous BRITE B-filter observations of 2016/17, the overall amplitudes obtained from the bRing and SMEI data, and the previously published ASTEP i′ amplitudes. From this, our favored solution of the asteroseismic models was obtained for a relatively high value for the frequency tolerance σF = 0.1 d−1 on the frequencies, only including even modes. This leads to the best fit to the normalized amplitudes, while at the same time we obtain a near equator-on inclination of i = 89.1°, which is in agreement with our expectations based on the orbital inclination of β Pic b as well as that of the circumstellar disk. Correspondingly, the pulsation modes were identified as three ℓ = 1, six ℓ = 2, and six ℓ = 3 modes. Our preferred model also yields a rotation rate of ∼27% of Keplerian breakup velocity, a radius of 1.497 ± 0.025 R⊙ and a mass of 1.797 ± 0.035 M⊙ corresponding to an error of ∼2% in stellar mass and less than 2% in stellar radius. These errors do not account for uncertainties in the models and for errors resulting from an erroneous mode identification. The difference between the observations and the theory remains high, which implies that the model errors could be quite significant. Although the errors on mass and radius of β Pic are quite small, they therefore only account for a small part of the true error. The choice of observing season has only a limited effect on the values of Ω/ΩK, i, and f when a relatively large observational frequency tolerance σF = 0.1 d−1 on the frequencies is assumed. Finally, the choice of what set of theoretical modes should be considered when fitting the observations remains an open question.
Our analysis yields an independent and more accurate determination of the stellar parameters based on the combination of classic constraints with the pulsational properties of β Pictoris derived in multiple passbands. We illustrated that adding seismic constraints considerably reduces the set of acceptable theoretical models and therefore results in higher precision.
Mode identification in rapidly rotating δ Scuti stars is one of the outstanding problems in stellar physics (e.g., Goupil et al. 2005; Deupree 2011). Our work constitutes an important step in addressing this, and it therefore illustrates the importance of good priors on the classic quantities. However, the seismic analysis can still further restrict the acceptable values for the mass and radius. Additionally, β Pictoris is a δ Scuti-type star where most pulsation amplitudes remain stable over many years, while a few change sometimes even significantly. This makes it another candidate for future studies of the physical reasons of amplitude variability versus stability in δ Scuti stars. Our search for g-modes in our data sets was motivated by the idea to use them to probe the near-core region of β Pictoris; the detection of g-modes would allow us to investigate differential rotation in the stellar interiors using prograde and retrograde pulsation modes (e.g., Zwintz et al. 2017) and study the angular momentum distribution (e.g., Aerts et al. 2017). The absence of a magnetic field (i.e., if there is a magnetic field, its strength has to be lower than 300 G) might also be a crucial factor to be considered when the exoplanetary system and circumstellar disk around β Pictoris are studied.
The relevant transmission curves were downloaded from http://www.aip.de/en/research/facilities/stella/instruments/data/johnson-ubvri-filter-curves
Acknowledgments
The authors thank Marc-Antoine Dupret for results from the MAD code that allowed us to calculate pseudo-nonadiabatic mode visibilities. We thank P. Kervella and F. Royer for helpful discussions and clarifications concerning some of the constraints on β Pictoris. We also express our gratitude to our referee, Dietrich Baade, for his very constructive comments. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. K.Z. acknowledges support by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF, project V431-NBL) and the Austrian Space Application Programme (ASAP) of the Austrian Research Promotion Agency (FFG). D.R.R. acknowledges the support of the French Agence Nationale de la Recherche (ANR) to the ESRR project under grant ANR-16-CE31-0007 as well as financial support from the Programme National de Physique Stellaire (PNPS) of the CNRS/INSU co-funded by the CEA and the CNES. A.Pi. acknowledges support from the NCN grant 2016/21/B/ST9/01126. APo was responsible for image processing and automation of photometric routines for the data registered by the BRITE nano-satellite constellation, and was supported by the statutory activities grant BK/200/RAU1/2018 t.3. GH thanks the Polish National Center for Science (NCN) for support through grant 2015/18/A/ST9/00578. The research of S.M.R. and A.F.J.M. has been supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada. GAW acknowledges Discovery Grant support from the Natural Science and Engineering Research Council (NSERC) of Canada. MI was the recipient of an Australian Research Council Future Fellowship (FT130100235) funded by the Australian Government. SNM is a U.S. Department of Defense SMART scholar sponsored by the U.S. Navy through SSC-LANT. Part of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. E.E.M. and S.N.M. acknowledge support from the NASA NExSS program. The bRing observatory at Siding Springs, Australia was supported by a University of Rochester University Research Award.
References
- Abe, L., Gonçalves, I., Agabi, A., et al. 2013, A&A, 553, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Berlin: Springer Science & Business Media) [Google Scholar]
- Aerts, C., Van Reeth, T., & Tkachenko, A. 2017, ApJ, 847, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., & Lambert, D. L. 1999, A&A, 352, 555 [NASA ADS] [Google Scholar]
- Baade, D., Pigulski, A., Rivinius, T., et al. 2018a, A&A, 610, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baade, D., Pigulski, A., Rivinius, T., et al. 2018b, A&A, 620, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackwell, D. E., & Lynas-Gray, A. E. 1998, A&AS, 129, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 3 [NASA ADS] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Brown, A. G. A., Vallenari, A., Prusti, T., et al. 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Crifo, F., Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M. 1997, A&A, 320, L29 [NASA ADS] [Google Scholar]
- da Silva, L., Torres, C. A. O., de La Reza, R., et al. 2009, A&A, 508, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, T. J., & Hillenbrand, L. A. 2015, ApJ, 804, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Defrère, D., Lebreton, J., Le Bouquin, J.-B., et al. 2012, A&A, 546, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deupree, R. G. 2011, ApJ, 742, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A&A, 426, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dupret, M. A. 2001, A&A, 366, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Escorza, A., Zwintz, K., Tkachenko, A., et al. 2016, A&A, 588, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa, F., Pérez Hernández, F., & Roca Cortés, T. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 424 [NASA ADS] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eyles, C. J., Simnett, G. M., Cooke, M. P., et al. 2003, Sol. Phys., 217, 319 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Goupil, M.-J., Dupret, M. A., Samadi, R., et al. 2005, A&A, 26, 249 [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grunhut, J. H., & Neiner, C. 2015, in Polarimetry, eds. K. N. Nagendra, S. Bagnulo, R. Centeno, & M. Jesús Martínez González, IAU Symp., 305, 53 [NASA ADS] [Google Scholar]
- Guillot, T., Abe, L., Agabi, A., et al. 2015, Astron. Nachr., 336, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H., & Rentzsch-Holm, I. 1995, A&A, 303, 819 [NASA ADS] [Google Scholar]
- Howard, T. A., Bisi, M. M., Buffington, A., et al. 2013, Space Sci. Rev., 180, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B. V., Buffington, A., Hick, P. P., et al. 2004, Sol. Phys., 225, 177 [Google Scholar]
- Jackson, S., MacGregor, K. B., & Skumanich, A. 2005, ApJS, 156, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Weiss, W. W., Beck, P. G., et al. 2017, A&A, 603, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koen, C. 2003, MNRAS, 341, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Balona, L. A., Khadaroo, K., et al. 2003, MNRAS, 344, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurtz, D. W., Elkin, V. G., & Mathys, G. 2006, MNRAS, 370, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Hubrig, S., González, J. F., van Wyk, F., & Martinez, P. 2008, MNRAS, 386, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kuschnig, R., Weiss, W. W., Gruber, R., Bely, P. Y., & Jenkner, H. 1997, A&A, 328, 544 [NASA ADS] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A.-M., Gratadour, D., Chauvin, G., et al. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., Heap, S. R., & Hubeny, I. 1995, ApJ, 447, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Larwood, J. D., & Kalas, P. G. 2001, MNRAS, 323, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., & Georgeot, B. 2008, Phys. Rev. E, 78, 016215 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., & Georgeot, B. 2009, A&A, 500, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lous, M. M., Weenk, E., Kenworthy, M. A., Zwintz, K., & Kuschnig, R. 2018, A&A, 615, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., Jackson, S., Skumanich, A., & Metcalfe, T. S. 2007, ApJ, 663, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Makaganiuk, V., Kochukhov, O., Piskunov, N., et al. 2011, A&A, 525, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., & Bell, C. P. M. 2014, MNRAS, 445, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Mékarnia, D., Guillot, T., Rivet, J.-P., et al. 2016, MNRAS, 463, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Mékarnia, D., Chapellier, E., Guillot, T., et al. 2017, A&A, 608, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mittal, T., Chen, C. H., Jang-Condell, H., et al. 2015, ApJ, 798, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, M. H., & Odonoghue, D. 1999, Delta Scuti Star Newslett., 13, 28 [Google Scholar]
- Murphy, S. J., Shibahashi, H., & Kurtz, D. W. 2013, MNRAS, 430, 2986 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653 [Google Scholar]
- Neiner, C., & Lampens, P. 2015, MNRAS, 454, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., & Lèbre, A. 2014, in SF2A-2014: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 505 [Google Scholar]
- Neiner, C., Mathis, S., Alecian, E., et al. 2015a, in Polarimetry, eds. K. N. Nagendra, S. Bagnulo, R. Centeno, & M. Jesús Martínez González, IAU Symp., 305, 61 [NASA ADS] [Google Scholar]
- Neiner, C., Grunhut, J., Leroy, B., De Becker, M., & Rauw, G. 2015b, A&A, 575, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pablo, H., Whittaker, G. N., Popowicz, A., et al. 2016, PASP, 128, 125001 [NASA ADS] [CrossRef] [Google Scholar]
- Pigulski, A. 2018, ArXiv e-prints [arXiv:1801.08496] [Google Scholar]
- Piskunov, N. E., & Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Piskunov, N., Snik, F., Dolgopolov, A., et al. 2011, The Messenger, 143, 7 [NASA ADS] [Google Scholar]
- Popowicz, A., Pigulski, A., Bernacki, K., et al. 2017, A&A, 605, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramiaramanantsoa, T., Ratnasingam, R., Shenar, T., et al. 2018, MNRAS, 480, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1 [NASA ADS] [Google Scholar]
- Reese, D., Lignières, F., & Rieutord, M. 2006, A&A, 455, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., MacGregor, K. B., Jackson, S., Skumanich, A., & Metcalfe, T. S. 2009, A&A, 506, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., Prat, V., Barban, C., van’t Veer-Menneret, C., & MacGregor, K. B. 2013, A&A, 550, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., Lignières, F., Ballot, J., et al. 2017, A&A, 601, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comput. Phys., 318, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, E., & Breger, M. 2001, A&A, 366, 178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Royer, F., Gerbaldi, M., Faraggiana, R., & Gómez, A. E. 2002, A&A, 381, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T., Nesvacil, N., Weiss, W. W., Kochukhov, O., & Stütz, C. 2004, A&A, 423, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffe, C., Gómez, M., Pintado, O., & González, E. 2008, A&A, 490, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saio, H. 1981, ApJ, 244, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, C., Reiners, A., & Schmitt, J. H. M. M. 2009, A&A, 493, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smalley, B., Niemczura, E., Murphy, S. J., et al. 2015, MNRAS, 452, 3334 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolov, N. A. 1995, A&AS, 110, 553 [NASA ADS] [Google Scholar]
- Stuik, R., Bailey, J. I., Dorval, P., et al. 2017, A&A, 607, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, in Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib., 350 [Google Scholar]
- Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, A&A, 574, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Donati, J.-F., Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Koerner, D. W., Ressler, M. E., et al. 2003, ApJ, 584, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. J., Graham, J. R., Pueyo, L., et al. 2016, AJ, 152, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., et al. 2014, PASP, 126, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., & Royer, F. 2012, A&A, 537, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwintz, K., Fossati, L., Ryabchikova, T., et al. 2014, Science, 345, 550 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zwintz, K., Van Reeth, T., Tkachenko, A., et al. 2017, A&A, 608, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Supplementary figures for the frequency analysis of BRITE data
Figure A.1 shows the amplitude spectrum of the original BHr data (gray) with the eight identified frequencies (red). The orbital frequency of BHr at 14.831 d−1 and its multiples are given as dashed dark red lines. Some of the peaks with high amplitude are alias frequencies to one of the pulsation frequencies with the orbital frequency and disappear after prewhitening.
 |
Fig. A.1. Frequency analysis of the BHr 2015 data. Spectral window (panel a), original amplitude spectrum from 0 to 100 d−1 (panel b), zoom into the original amplitude spectrum (panel c), and residual amplitude spectrum after prewhitening of the eight frequencies (panel d) with the residual noise level marked as horizontal dashed line. The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the orbital frequencies of the BHr satellite and its multiples. |
The amplitude spectrum using the BHr 2017/18 data is shown in Fig. A.2, where again the frequencies reported by Mékarnia et al. (2017) are marked as gray triangles, the orbital frequency of BHr and its multiples are identified as dark red dashed lines, and the spectral window is given in the top panel.
 |
Fig. A.2. Frequency analysis of the BHr 2017/2018 data: spectral window (panel a), original amplitude spectrum from 0 to 100 d−1 (panel b), zoom into the original amplitude spectrum (panel c), and residual amplitude spectrum after prewhitening of the eight frequencies (panel d). The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the orbital frequency of the respective satellite and its multiples. |
The frequency analysis of the combined BRITE R-filter data yielded the same pulsation frequencies as given in Table 2. The corresponding amplitude spectrum with the identified frequencies marked in red is shown in Fig. A.3.
 |
Fig. A.3. Frequency analysis of the combined BRITE R-filter data. Spectral window (top) and original amplitude spectrum from 30 to 60 d−1 (bottom) with the identified pulsation frequencies marked in red. |
Appendix B: Supplementary material for amplitude variability using bRing data
 |
Fig. B.1. Amplitude behavior of the pulsation frequencies with the three highest amplitudes during the bRing observations calculated from 100-day subsets. |
Investigation of the amplitude variability using the bRing time series, which consists of observations taken in South Africa and Australia. Because the Australian bRing instrument had first light on 1 December 2017, corresponding to a JD of ∼2458091.0, we did not detect the three frequencies F8, F11, and F13 in the subsets using the first about 200 days of the bRing light curve. Unfortunately, the errors on the amplitudes calculated from the individual subsets are mostly too high for a reliable study of amplitude variability from this data set.
Appendix C: Supplementary material for the asteroseismic interpretation
Figure C.1 shows the best matches from the MCMC runs between observed and theoretical multicolor amplitudes and spectra using σF = 0.01 and σF = 0.05 d−1 as tolerances on the frequencies and restricting the theoretical spectrum to even modes and the inclination to the [70 ° ,90 ° ] interval in the last case.
 |
Fig. C.1. Same as Fig. 12 except that σF = 0.01 (all modes and inclinations), σF = 0.05 (all modes and inclinations), and σF = 0.05 (even modes and inclination between 70° and 90°) have been used during the MCMC runs. The |
Table C.1 lists the complete theoretical model frequency spectra from our best-fitting solutions. The frequencies in boldface are those that matched the pulsations of β Pic. Those in italics were filtered out before the fitting process because they correspond to modes that are antisymmetric with respect to the equator, and only near equator-on solutions were being searched for in these particular MCMC runs. We note that these predicted frequencies are subject to large uncertainties in the models, and will change significantly when the input physics are improved.
Complete spectra from best fitting solutions.
All Tables
Pulsation frequencies, amplitudes, phases, and S/N values derived from the BRITE-Constellation data sorted by increasing frequency and comparison to the literature.
Pulsation frequencies, amplitudes, phases, and S/N values derived from the SMEI and bRing data sorted by increasing frequency and comparison to the literature.
Correspondence between photometric bands used to observe β Pic (“This study”) and those used to implement the limb-darkening law (“Claret (2000)”).
Mode identifications in the form (n, ℓ, m) for best and alternate configurations.
All Figures
 |
Fig. 1. Final reduced light curves of β Pic from BRITE-Constellation, bRing and SMEI: BHr data 2015 (panel a, gray points), combined BTr (panel b, red points) and BHr (panel b, gray points) data 2016/17, BLb data 2016/17 (panel c, blue points), BHr data 2017/18 (panel d, gray points) where black dots show binning of the light curves in three-minute intervals; the bRing and SMEI time series are shown in panels e and f. |
| In the text | |
 |
Fig. 2. Frequency analysis of the BRITE 2016/17 data in the red (left) and the blue filter (right). Spectral window (panels a and e), original amplitude spectrum from 0 to 100 d−1 (panels b and f), zoom into the original amplitude spectrum (panels c and g), and residual amplitude spectrum after prewhitening the corresponding pulsation frequencies (panels d and h) with the residual noise level marked as horizontal dashed lines. The identified pulsation frequencies (as listed in Table 2) are marked in panels b and c as red (for the BRITE red filter) and in panels f and g as blue (for the BRITE blue filter) lines. The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the respective satellite’s orbital frequency (i.e., BTr on the left and BLb on the right) and its multiples. |
| In the text | |
 |
Fig. 3. Frequency analysis using the bRing and SMEI photometric time series. Spectral windows (panels a and d), original amplitude spectrum from 30 to 60 d−1 (panel b) for bRing and from 0 to 100 d−1 (panel e) for SMEI, the residual bRing amplitude spectrum after subtraction of the six identified pulsation frequencies (panel c), and zoom into the frequency range from 30 to 60 d−1 for SMEI (panel f). The identified pulsation frequencies are marked as thick black lines and labeled according to their numbers in Table 3. Frequency f13 was identified in the SMEI data due to its presence in DM17, but it is not present in the BRITE data. The red dashed vertical lines mark the position of the Nyquist frequency for SMEI and its multiples. The occurrence of the orbital frequency of SMEI at 14.16 d−1 (i.e., twice fNyquist) and its multiples can be seen as the regular structure in the spectral window (panel d) and in the amplitude spectrum (panels e and f) as the points where the noise decreases steeply to very low levels. |
| In the text | |
 |
Fig. 4. LSD Stokes V (top), N (middle), and Stokes I (bottom) profiles of β Pic. Data are shown in black, while red lines show a smoothed profile. Vertical dashed lines indicate the range of integration for calculating the longitudinal magnetic field and estimating the FAP. |
| In the text | |
 |
Fig. 5. Detection probability of a magnetic field in the observation of β Pic as a function of the magnetic polar field strength. The horizontal dashed line indicates the 90% detection probability. A dipole field stronger than Bpol = 300 G would have statistically been detected. |
| In the text | |
 |
Fig. 6. Top panel: annual behavior of the amplitudes of the four pulsation frequencies F8, F11, F13, and F15 in all three BRITE red-filter data sets (filled symbols) and of the four pulsation frequencies F1, F3, F4, and F6 that appear in two of the three BRITE R epochs (open symbols). Bottom panel: annual behavior of the five pulsation frequencies F3, F6, F8, F11, and F13 in the bRing data. |
| In the text | |
 |
Fig. 7. Zoom around F13 (left side, seen alongside with F14 in the 2015 data to the right of F13) and F11 (right side) into the original amplitude spectra of the BRITE red-filter data obtained in 2015 (top), 2016/2017 (middle), and 2017/2018 (bottom). The peak next to F13 in the bottom left panel showing the 2017/18 data is an alias frequency to F3 with the orbital frequency of BHr (i.e., 14.83053 d−1) that only appears quite close to the location of F14, which itself is not found in the 2017/18 data. |
| In the text | |
 |
Fig. 8. Amplitude (top panel) and phase (middle panel) behavior of the five pulsation frequencies with the highest amplitudes during the 2017/18 BHr observations calculated from 30-day subsets with 20-day overlaps, and amplitude-phase relation (bottom panel). The errors in phases are often smaller than the symbol size. |
| In the text | |
 |
Fig. 9. Transmission curves of the five instruments: BRITE B (blue solid line), BRITE R (red solid line), bRing (orange dashed line), ASTEP i′ (dark red dash-dotted line), and SMEI (black dotted line). |
| In the text | |
 |
Fig. 10. Observed (blue) and best-fitting theoretical (red) normalized amplitudes using individual fits. fo represents the observed frequencies. In several cases, the match between observed and theoretical normalized amplitudes is sufficiently good for the latter to be hidden in the plots. Finally, the total χ2 value is 68.9. |
| In the text | |
 |
Fig. 11. Inclinations (upper panel) and rotation rates (lower panel) obtained for each mode fit individually. The dark blue symbols represent the best solutions (i.e., those illustrated in Fig. 10). The small light blue dots are other solutions that satisfy the criterion χ2 ≤ (Nbands − 1), where χ2 is the χ2-value on the amplitudes for that particular mode and Nbands is the number of bands in which that mode is detected. The light blue solutions thus give an idea of the uncertainties on the above results. |
| In the text | |
 |
Fig. 12. Upper panel: observed and best-fitting mode-normalized amplitudes in different photometric bands using the true errors and σF = 0.1 on the frequencies. In the latter case, only even modes are retained and the inclination search interval is [70 ° ,90 ° ] rather than [0 ° ,90 ° ]. The (n, ℓ, m) mode identifications are provided in each panel. Lower panel: observed vs. theoretical pulsation spectra for the two above cases. The observed frequencies are represented by the continuous vertical lines that span the plot. In both panels, the observations are shown in blue and the theoretical results and annotations are color-coded. χ2 calculations have 18 degrees of freedom, i.e., Ω/ΩK, i, f, and the 15 free amplitudes. In the upper panel, |
| In the text | |
 |
Fig. 13. Distribution of solutions resulting from the seismic contraints (with the true observational errors), normalized amplitudes, and observed values of log g and v sin i. The plots along the diagonal are histograms for single variables, whereas the remaining plots are scatter plots for pairs of variables. The plots are color-coded according to the mode identification. The solutions shown in red have the same n, ℓ, m identification as the best solution. |
| In the text | |
 |
Fig. 14. Same as Fig. 13 except σF = 0.1 d−1 has been used as a frequency tolerance, the inclination has been restricted to the [70 ° ,90 ° ] interval and odd modes have been excluded. |
| In the text | |
 |
Fig. A.1. Frequency analysis of the BHr 2015 data. Spectral window (panel a), original amplitude spectrum from 0 to 100 d−1 (panel b), zoom into the original amplitude spectrum (panel c), and residual amplitude spectrum after prewhitening of the eight frequencies (panel d) with the residual noise level marked as horizontal dashed line. The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the orbital frequencies of the BHr satellite and its multiples. |
| In the text | |
 |
Fig. A.2. Frequency analysis of the BHr 2017/2018 data: spectral window (panel a), original amplitude spectrum from 0 to 100 d−1 (panel b), zoom into the original amplitude spectrum (panel c), and residual amplitude spectrum after prewhitening of the eight frequencies (panel d). The triangles mark the frequencies found in the ASTEP data by Mékarnia et al. (2017). Vertical dashed lines mark the positions of the orbital frequency of the respective satellite and its multiples. |
| In the text | |
 |
Fig. A.3. Frequency analysis of the combined BRITE R-filter data. Spectral window (top) and original amplitude spectrum from 30 to 60 d−1 (bottom) with the identified pulsation frequencies marked in red. |
| In the text | |
 |
Fig. B.1. Amplitude behavior of the pulsation frequencies with the three highest amplitudes during the bRing observations calculated from 100-day subsets. |
| In the text | |
 |
Fig. C.1. Same as Fig. 12 except that σF = 0.01 (all modes and inclinations), σF = 0.05 (all modes and inclinations), and σF = 0.05 (even modes and inclination between 70° and 90°) have been used during the MCMC runs. The |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.