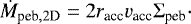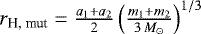| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834229 | |
| Published online | 04 July 2019 | |
Formation of planetary systems by pebble accretion and migration
How the radial pebble flux determines a terrestrial-planet or super-Earth growth mode
1
Department of Astronomy and Theoretical Physics, Lund Observatory, Lund University,
Box 43,
22100
Lund, Sweden
e-mail: michiel@astro.lu.se
2
Laboratoire Lagrange, UMR7293, CNRS, Observatoire de la Côte d’Azur, Université Côte d’Azur, Boulevard de l’Observatoire,
06304
Nice Cedex 4,
France
3
Department of Earth and Planetary Sciences, Technological Institute, Northwestern University,
F293/4, 2145 Sheridan Road,
Evanston,
IL
60208-3130, USA
4
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
5
UNESP, Universidade Estadual Paulista – Grupo de Dinàmica Orbital Planetologia,Guaratinguetà,
CEP 12.516-410
São Paulo, Brazil
6
Laboratoire d’Astrophysique de Bordeaux, CNRS and Université de Bordeaux, Allée Geoffroy St. Hilaire,
33165
Pessac, France
Received:
12
September
2018
Accepted:
22
February
2019
Super-Earths – planets with sizes between the Earth and Neptune – are found in tighter orbits than that of the Earth around more than one third of main sequence stars. It has been proposed that super-Earths are scaled-up terrestrial planets that also formed similarly, through mutual accretion of planetary embryos, but in discs much denser than the solar protoplanetary disc. We argue instead that terrestrial planets and super-Earths have two clearly distinct formation pathways that are regulated by the pebble reservoir of the disc. Through numerical integrations, which combine pebble accretion and N-body gravity between embryos, we show that a difference of a factor of two in the pebble mass flux is enough to change the evolution from the terrestrial to the super-Earth growth mode. If the pebble mass flux is small, then the initial embryos within the ice line grow slowly and do not migrate substantially, resulting in a widely spaced population of approximately Mars-mass embryos when the gas disc dissipates. Subsequently, without gas being present, the embryos become unstable due to mutual gravitational interactions and a small number of terrestrial planets are formed by mutual collisions. The final terrestrial planets are at most five Earth masses. Instead, if the pebble mass flux is high, then the initial embryos within the ice line rapidly become sufficiently massive to migrate through the gas disc. Embryos concentrate at the inner edge of the disc and growth accelerates through mutual merging. This leads to the formation of a system of closely spaced super-Earths in the five to twenty Earth-mass range, bounded by the pebble isolation mass. Generally, instabilities of these super-Earth systems after the disappearance of the gas disc trigger additional merging events and dislodge the system from resonant chains. Therefore, the key difference between the two growth modes is whether embryos grow fast enough to undergo significant migration. The terrestrial growth mode produces small rocky planets on wider orbits like those in the solar system whereas the super-Earth growth mode produces planets in short-period orbits inside 1 AU, with masses larger than the Earth that should be surrounded by a primordial H/He atmosphere, unless subsequently lost by stellar irradiation. The pebble flux – which controls the transition between the two growth modes – may be regulated by the initial reservoir of solids in the disc or the presence of more distant giant planets that can halt the radial flow of pebbles.
Key words: planets and satellites: formation / planets and satellites: dynamical evolution and stability / protoplanetary discs / planets and satellites: composition / planets and satellites: terrestrial planets
© ESO 2019
1 Introduction
Super-Earths are, broadly speaking, exoplanets with masses or radii intermediate to those of the Earth and Neptune. The occurrence rate of such exoplanets is high: more than 30% of sun-like stars harbour super-Earth planets within 100-day orbits (Mayor et al. 2011; Petigura et al. 2013; Zhu et al. 2018). Occurrence rates are even higher, by approximately a factor of three, around lower-mass M-dwarf stars (Mulders et al. 2015). Systems of multiple super-Earths are common and typically have low eccentricities (e < 0.05, Xie et al. 2016) and low mutual inclinations (i ≲ 10°, Lissauer et al. 2011; Johansen et al. 2012; Zhu et al. 2018).
The composition of these super-Earths are observationally difficult to determine, but their mass budget appears to be dominated by a rocky interior. From the subset of well-characterised planets, it is inferred that planets with radii below 1.8 Earth radii (RE) are mainly rocky in composition, based on planetary structure models (Rogers 2015; Lopez & Fortney 2014). Larger planets – above 2 RE and mass of about five Earth mass (ME) – are consistent with having primordial H/He envelopes that make up between 1 and 20% of the total mass (Hadden & Lithwick 2017). The composition of the core of these planets with gas envelopes is not well known, but can be probed around close-in planets that likely lost their envelope through irradiation from the host star. Models of envelope loss favour rocky interiors to explain the lack of planets with radii between 2 and 4 RE on highly irradiated orbits (Lundkvist et al. 2016). Similarly, the lack of planets with radii around 1.8 RE within 100-day orbits (Fulton et al. 2017) may be best explained when envelope loss occurs around cores with a rocky, as opposed to water-rich, composition (Owen & Wu 2017; Jin & Mordasini 2018).
It is not obvious that super-Earths, even when rock-dominated, could have formed in a way similar to the Earth. This is because the Earth is characterized not only by its rocky composition of 67.5% silicates and 32.5% iron, but also by its slow formation. The growth of the Earth likely took place over a timescale of several tens of millions of years based on the age constraints on the Moon-forming impact (Touboul et al. 2007; Kleine et al. 2009; Jacobson et al. 2014; Barboni et al. 2017). In contrast, Mars formed within 3–5 Myr, according to radiogenic dating (Nimmo & Kleine 2007; Dauphas & Pourmand 2011). Thus, the formation timescale of the Earth greatly exceeds the average gas-rich phase of protoplanetary discs of 3 to 5 Myr (Haisch et al. 2001), while Mars could have formed within the gas phase. Terrestrial planet formation beyond the mass of Mars is therefore believed to have taken place in a gas-free environment, where the Earth is the product of mutual collisions of planetary embryos which were roughly Mars-sized at the time the gas disc dissipated (see Morbidelli et al. 2012 and Raymond et al. 2014 for a review). The last of these collisions corresponds to the Moon-forming event (Hartmann & Davis 1975; Cameron & Ward 1976).
This gas-free growth mode of the Earth from Mars-sized embryos had several implications for its final properties. For instance, Mars-mass protoplanets do not migrate significantly in the proto-planetary disc (Tanaka et al. 2002), which explains why the Earth could remain relatively far from the Sun. Similarly, Mars-mass protoplanets cannot capture substantial H and He envelopes directly from the gas disc (Mizuno et al. 1978) and such tenuous envelopes erode easily during the subsequent series of impacts (Schlichting et al. 2015). This explains why the Earth does not have a primitive atmosphere, but instead one outgassed from its interior, dominated by much heavier gases than hydrogen (Schaefer & Fegley 2010).
Super-Earths must have experienced a different, more rapid growth process. Their larger rocky cores argue for an increased mass reservoir resulting in faster embryo growth. This leads to larger embryos before disc dissipation, which necessarily introduces significant inward migration (Ogihara et al. 2015). In turn, the resulting concentration of embryos can speed up further growth by collisions. Also, these larger embryos can capture significant primitive H/He atmospheres, like those inferred around large super-Earths.
The goal of this paper is to develop a unified model for the formation of, on the one hand, Earth-like planets with temperate orbits, and on the other hand, close-in super-Earths. In order to do so, we consider embryo growth that is mainly driven by the accretion of inward-drifting pebbles. The accretion cross section of an embryo for pebbles that feel gas drag can greatly exceed the cross section for gravitationally focused planetesimals (Ormel & Klahr 2010; Lambrechts & Johansen 2012). Therefore, core growth by pebble accretion from the radial mass flux of pebbles that settle to the midplane and drift inward through the disc can exceed classical planetesimal accretion rates (Lambrechts & Johansen 2014; Levison et al. 2015a,b; Lin et al. 2018). Specifically, in this work, we only consider embryos that are located within the ice line. This also implies that the pebbles are ice-free. Thus, the focus is on the growth of rocky embryos.
We find that the critical parameter dividing Earth-like formation from migration-assisted formation of super-Earths is the integrated pebble-mass flux through the inner protoplanetary disc. The available mass in pebbles depends on many parameters, the initial total disc mass, the initial dust-to-gas ratio, the radial extent of the disc, and also the possible presence of planets larger than approximately 10 ME that block the flow of pebbles to the inner disc (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014). In this work, we assume the integrated pebble-mass flux to be a unique free parameter, for simplicity.
This paper is structured as follows. Section 2 describes the setup of the simulations and explains how we take into account the presence of the gas disc, planetary migration, and pebble accretion. Validation tests and a more detailed description of the pebble-accretion formulae can be found in Appendix A.
Section 3 shows that the divergent evolution of a system of growing embryos depends on the mass carried by the integrated pebble flux. We find that a low pebble flux leads to the slow formation of small planetary embryos that do not migrate significantly in the disc. At most these embryos grow to about three Mars-masses. The increase in the pebble flux, by less than a factor of two with respect to this case, drastically bifurcates the evolution of the system. As expected, the embryos grow faster and become more massive as they start to migrate towards the star. This migration-assisted growth mode leads to planets of several Earth masses near the inner edge of the disc within the lifetime of the gas disc.
Section 4 follows the systems in their evolution after the removal of the gas disc. All the extended systems of numerous, small planetary embryos become unstable and lead to the formation of Earth-like planets on a timescale of tens of millions of years, with a sequence of giant impacts analogous to that characterising the formation of our planet. We find that the most massive Earth-like planets generated in this way are between 2 and 5 ME. For the super-Earth systems we find that they can undergo a dynamical instability shortly after disc dissipation, typically within 10 Myr, similar to Terquem & Papaloizou (2007), Ogihara & Ida (2009), Ida & Lin (2010), Cossou et al. (2014), Izidoro et al. (2017), Carrera et al. (2018), and Ogihara et al. (2018a).
This leads to the reduction of the final number of planets, a few merging events, and the acquisition of non-resonant orbits with mutual spacings that are more consistent with observations. We note however that the fraction of our super-Earth systems that become unstable after gas removal is much larger than in Izidoro et al. (2017) who find that only half of the super-Earth chains become unstable. We find instead that over 90% of cases are unstable, which appears to be in better agreement with the observations. This is due to our super-Earth systems forming more compactly during the gas disc phase due to the combined effects of migration and pebble accretion, the latter of which is neglected in Izidoro et al. (2017).
Wrapping up these results, we argue in Sect. 5 for a differentiation between Earth-like planets and super-Earths, not based on a simplistic mass-threshold or difference in bulk composition, but instead based on the growth history of the planet. Because the growth history of a given body cannot be observed, we suggest a number of combined observational criteria to distinguish between these two categories of planets: the mass, the orbital architecture, and the presence of a primitive atmosphere, if the planet is not strongly irradiated by the host star. In Sect. 6 we discuss the available mass reservoir of pebbles in the inner disc and summarise the assumptions made in this work. We conclude with our main findings in Sect. 7.
This paper comes as part of a set of three papers on the formation of planets by N-body simulations that take pebble accretion and planetary migration into account. The other two papers differ from this work in that they also consider embryo growth outside of the ice line. Izidoro et al. (2019) show that the inclusion of icy embryos leads to super-Earth systems that can quantitatively reproduce the observed orbital distribution of Kepler systems. However, the predominantly icy composition of these planets is in apparent contrast with the inferred rocky composition of Kepler planets (Owen & Wu 2017; Jin & Mordasini 2018). Finally, Bitsch et al. (2019) discuss the case where the pebble mass flux is large enough such that some of the icy embryos can turn into giant planets in wide orbits, as has occurred in the solar system. These latter authors build on the work by Levison et al. (2015a) and Bitsch et al. (2015a), but uses a self-consistent modelling for the growth of both giant planets and super-Earths. This work by Bitsch et al. (2019) shows that the migration of giant planets into the region interior to 1 AU can be prevented if embryos form sufficiently far from the ice line, outside 30 AU. Embryos closer to the ice line, between 5 and 10 AU, migrate into the inner disc, unless type-II migration rates are reduced compared to nominal values, as expected in discs with comparable mass but lower viscosity (Kanagawa et al. 2018; Robert et al. 2018).
Taken together, this trilogy of papers should provide a quite comprehensive view of planet formation and evolution revealing a broad spectrum of possibilities. They have in common that pebble accretion is the main process fueling the initial growth of proto-planets and that the formation of the final planetary systems is the result of a complex interplay between mass growth and dynamical evolution.
2 Methods
2.1 N-body code
We used a modified version of the N-body code SyMBA, which uses a symplectic algorithm that allows adaptive time-steps for close encounters (Duncan et al. 1998; Levison et al. 2012). Collisions are modelled as events that always lead to perfect merging. We have added prescriptions to the N-body code for the protoplanetary gas disc, planet–disc interaction and the presence and accretion of pebbles. We describe these in turn below.
2.2 Disc model
Here, we use a simple model to describe the gaseous component of the protoplanetary disc. The aspect ratio of the gaseous disc, which is equivalent to the ratio of the sound speed cs to Keplerian velocity rΩK, is given by
 (1)
(1)
We thushave a flat aspect ratio with orbital distance (zero flaring), which is approximately realised in the inner disc, where viscous heating dominates over irradiation (Bitsch et al. 2015b; Ida et al. 2016). The gas surface density is given by
![\begin{equation*} \Sigma_{\textrm{g}} = 610\,\left(\frac{r}\textrm{AU} \right)^{-1/2} \times \exp \left[-\frac{t}{t_{\textrm{disc}}} \right] \, {\textrm{g}\,\textrm{cm}}^{-2}. \end{equation*}](/articles/aa/full_html/2019/07/aa34229-18/aa34229-18-eq2.png) (2)
(2)
The slope of the surface density is chosen such that the disc has a constant viscously driven gas accretion rate through the disc with Ṁ gas = 3πΣgν, assuming a constant α value for the viscosity 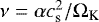 . Our disc mass is thus less centrally concentrated than in the more crude disc estimate based on the minimum mass solar nebula (MMSN), which has
. Our disc mass is thus less centrally concentrated than in the more crude disc estimate based on the minimum mass solar nebula (MMSN), which has 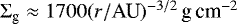 (Weidenschilling 1977; Hayashi 1981). We consider here a low-viscosity disc with α = 10−4. If one were to only consider viscously driven gas accretion, the initial accretion rate would be Ṁ gas = 7 × 10−10 M⊙ yr−1, which would be in a lower range of observed gas accretion rates around young stars (Manara et al. 2016). However, current magnetohydrodynamical disc modelling efforts argue that gas accretion is mainly wind-driven, regulated by active layers above the midplane. This supports the use of low values of α for the midplane turbulence, without increasing the surface density of the disc Σ as 1∕α (Suzuki & Inutsuka 2009; Bai 2014, 2017; Lesur et al. 2014; Gressel et al. 2015). This modern view of discs appears to be observationally supported by measurements of particle settling (Pinte et al. 2016). Because our aim here is to focus on the dynamic interplay between migration and accretion, we have not used complex time-dependent disc models (Bitsch et al. 2015b; Suzuki et al. 2016; Ogihara et al. 2018a,b). Instead, we mimic the dissipation of the gas disc with a simple exponential decay of the gas surface density on a timescale of tdisc = 1 Myr and we consider the gas disc phase to last 3 Myr in our simulations (Haisch et al. 2001). Importantly, we note our assumption that the temperature in the disc does not decrease with time. Therefore, here we do not consider a drifting snow line that can cross the growing protoplanets (see however companion papers Izidoro et al. 2019; Bitsch et al. 2019).
(Weidenschilling 1977; Hayashi 1981). We consider here a low-viscosity disc with α = 10−4. If one were to only consider viscously driven gas accretion, the initial accretion rate would be Ṁ gas = 7 × 10−10 M⊙ yr−1, which would be in a lower range of observed gas accretion rates around young stars (Manara et al. 2016). However, current magnetohydrodynamical disc modelling efforts argue that gas accretion is mainly wind-driven, regulated by active layers above the midplane. This supports the use of low values of α for the midplane turbulence, without increasing the surface density of the disc Σ as 1∕α (Suzuki & Inutsuka 2009; Bai 2014, 2017; Lesur et al. 2014; Gressel et al. 2015). This modern view of discs appears to be observationally supported by measurements of particle settling (Pinte et al. 2016). Because our aim here is to focus on the dynamic interplay between migration and accretion, we have not used complex time-dependent disc models (Bitsch et al. 2015b; Suzuki et al. 2016; Ogihara et al. 2018a,b). Instead, we mimic the dissipation of the gas disc with a simple exponential decay of the gas surface density on a timescale of tdisc = 1 Myr and we consider the gas disc phase to last 3 Myr in our simulations (Haisch et al. 2001). Importantly, we note our assumption that the temperature in the disc does not decrease with time. Therefore, here we do not consider a drifting snow line that can cross the growing protoplanets (see however companion papers Izidoro et al. 2019; Bitsch et al. 2019).
2.3 Type-I migration and e/i-damping
In order to model planet–disc interaction, we make use of prescriptions that model how gas affects embryos in the disc. Because we do not consider planets that grow significantly beyond ≈10 ME we limit ourselves to considering type-I migration as well as inclination and eccentricity damping. We use the formulation by Papaloizou & Larwood (2000) for the acceleration due to the interaction with the gaseous disc,
 (3)
(3)
Here, k is the unit vector in the vertical direction, r, v, and atidal are the radial position, velocity, and acceleration. The first term represents the migration, with tm the migration timescale. The second term damps the eccentricity on a timescale te and the third term corresponds to inclination damping on a timescale ti. All three timescales are proportional to the wave-damping timescale (Tanaka et al. 2002),
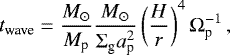 (4)
(4)
but are modified in a complex fashion by their dependency on the eccentricity and inclination of the body (Bitsch & Kley 2010; Cossou et al. 2013; Fendyke & Nelson 2014). Here, Mp and M⊙ are the planet and star mass, respectively. The e, i-dependent formulation for these timescales were taken from fits to hydrodynamical simulations by Cresswell & Nelson (2008)1. The migration timescale we used includes the contribution of the differential Lindblad torque and the co-rotation torque, under the approximation of an isothermal disc (Tanaka et al. 2002). Because we use a simple power-law disc model, there are no corotation torque traps and migration isalways directed inwards. More precisely, for our choice of disc model, the wave-damping timescale (twave) and migration timescale (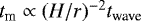 ) do not depend on the orbital radius r. This impliesthat embryos of equal mass would migrate in sync, until they approach the inner disc edge. Companion papers Izidoro et al. (2019) and Bitsch et al. (2019) include the entropy-related corotation torque and consider more complex disc models withtrapping regions. Future work could also explore in more detail the role of embryo heating (Benítez-Llambay et al. 2015), dynamical corotation torques (Paardekooper 2014; McNally et al. 2017, 2018; Fung & Lee 2018), and surrounding pebbles (Benítez-Llambay & Pessah 2018) onto the migration rates of embryos.
) do not depend on the orbital radius r. This impliesthat embryos of equal mass would migrate in sync, until they approach the inner disc edge. Companion papers Izidoro et al. (2019) and Bitsch et al. (2019) include the entropy-related corotation torque and consider more complex disc models withtrapping regions. Future work could also explore in more detail the role of embryo heating (Benítez-Llambay et al. 2015), dynamical corotation torques (Paardekooper 2014; McNally et al. 2017, 2018; Fung & Lee 2018), and surrounding pebbles (Benítez-Llambay & Pessah 2018) onto the migration rates of embryos.
To mimic the edge of the gas disc, we reduce migration rates close to a trap radius of rtrap = 0.1 AU. In practice, when embryos approach within 2 × rtrap the migration rate is reduced by a factor
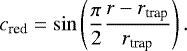 (5)
(5)
In this way, without reducing the eccentricity and inclination damping rates, we smoothly bring the migration of the embryos to a halt. We do not aim to model the complex (non-ideal) magnetohydrodynamics that sculpts the inner edge of the disc (Romanova & Lovelace 2006; Flock et al. 2017). Another trapping radius may be related to the transition to the inner MRI active region (Chatterjee & Tan 2014). Thus, our choice of rtrap is somewhat arbitrary and therefore our final results in terms of semi-major axis distribution can be crudely rescaled by rtrap∕(0.1 AU). Moreover, the disc edge likely moves outwards as the disc evolves, further complicating the picture (Liu & Ormel 2017).
Finally, we note that we do not stop the drift of pebbles at the trap radius, and therefore there is no pebble pile-up. Pebbles keep drifting until they reach the edge of the simulation where they are lost to the sun.
2.4 Embryo distribution
To avoid the numerical cost of simulating too many bodies, we start simulations with Moon-mass embryos (Membr,0 = 0.01 ME). In this way we also avoid the complications related to where, how, and with which size distribution planetesimals form (Johansen et al. 2015; Simon et al. 2016) and how the first Moon-mass embryos emerge from these planetesimal seeds. Planetesimals have to be sufficiently massive, exceeding approximately the mass of the dwarf planet Ceres, to be efficient in accreting pebbles (Lambrechts & Johansen 2012; Visser & Ormel 2016). Therefore, planetesimal collisions may aid in driving initial embryo growth (Johansen et al. 2015; Johansen & Lambrechts 2017). In total, we start out with 25 Embryos, which represents 0.25 ME in total.
We distribute the embryos radially from 0.5 to 3 AU, in a logarithmic fashion. Because the ratio between neighbouring orbital radii ai+1 ∕ai is constant, the initial embryo surface density is relatively steep (Σemb ∝ r −2). The outer boundary is chosen pragmatically such that the initial embryos represent bodies that are not icy. In the solar system this edge approximately corresponds to the position of the asteroid belt. The location of the inner boundary of the embryo population was based on the assumption that the initial embryo seeds emerged early in the disc lifetime outside of the silicate sublimation front, which could have been as far out as 0.5 AU away from the host star, when gas accretion rates onto the star were of the order of 10−7 M⊙ yr−1 (Morbidelli et al. 2016). This choice of the inner edge is also similar to the pragmatically chosen inner edge in terrestrial planet simulations (Hansen 2009). Thereafter, gas accretion rates diminish and the silicate sublimation line moves towards the inner disc edge (Bitsch et al. 2015b). For simplicity, as our disc has no temperature evolution, we assume thatthe silicate sublimation front is sufficiently close so that we can ignore the sublimation of pebbles.
2.5 Pebble accretion
Pebbles are not modelled as individual N-body particle tracers, as done in some works (Kretke & Levison 2014; Levison et al. 2015a,b), because this is numerically expensive. Instead the pebble surface density is calculated as a background field, based on the given gas disc and pebble accretion flux. For each body, we then calculate how much of the passing pebbles are accreted. A similar approach can be found in Coleman et al. (2017) and Matsumura et al. (2017), but here we present a more detailed pebble-accretion model.
Pebble flux
In this work we use a prescription for the global flux of pebbles as function of time described by
![\begin{equation*} F_{\textrm{peb}} = F_{\textrm{peb,0}} \times \exp \left[-\frac{t}{t_{\textrm{peb}}} \right]. \vspace*{-1pt}\end{equation*}](/articles/aa/full_html/2019/07/aa34229-18/aa34229-18-eq9.png) (6)
(6)
We choose to set the decay timescale of the pebble flux equal to the disc dissipation timescale tpeb = tdisc. This is inspired by the observed high occurrence rate of pebbles in discs in the 3 to 5 Myr age range (Ansdell et al. 2017). For our nominal mass flux, we set Fpeb,nom = 120 ME Myr−1 which is on the order of the expected pebble fluxes in discs (Lambrechts & Johansen 2014). However, we expect that the flux of pebbles into the inner disc may change significantly from one protoplanetary disc to the next. Importantly, the available dust mass in solids may vary depending on the initial disc mass and initial dust-to-gas ratio. Moreover, the evolution of the pebble flux may change depending the radial extent of the dust and the sticking efficiency of colliding particles (Brauer et al. 2008). Additionally, pebbles are likely reprocessed around ice lines, where the volatile species sublimate (Ros & Johansen 2013; Morbidelli et al. 2015; Schoonenberg & Ormel 2017). Also the presence of giant planets in the outer disc, not directly modelled in this work, can reduce or even completely halt the pebble flux. Therefore, we simply consider the pebble flux into the inner disc to be a free parameter and explore different values of Fpeb,0 across different simulations. We present results from four different suites of nominally ten simulations.
- 1.
Suite (runf1) has Fpeb,0 = (1 ∕ 3) × Fpeb,nom = 40 ME Myr−1, or a time-integrated pebble flux of 38 ME.
- 2.
Suite (runf3) has Fpeb,0 = Fpeb,nom = 120 ME Myr−1, or an integrated pebble flux of 114 ME.
- 3.
Suite (runf5) has Fpeb,0 = (5 ∕ 3) × Fpeb,nom = 200 ME Myr−1, or an integrated pebble flux of 190 ME.
- 4.
And finally suite 4 (runf9) has Fpeb,0 = 3 × Fpeb,nom = 360 ME Myr−1, or an integrated pebble flux of 340 ME.
We use the suffix “-1” to identify run number 1, and use the suffix “C” to indicate the continuation of the run after disc dissipation.
To facilitate the interpretation of our results, we also choose to simulate a single particle population, characterised by a unique Stokes number. The stokes number is a non-dimensional number which expresses gas drag friction timescale with respect to the orbital period,
 (7)
(7)
Here, we have considered the relevant Epstein drag regime with ρ∙ and R corresponding to, respectively, the solid density and particle radius of the pebble. We consider a constant Stokes number of τf = 3 × 10−3. This is inspired by the small sizes of chondrules which make up a large mass fraction of primitive meteorites (Johansen et al. 2015). Furthermore, a constant Stokes number with orbital radius was chosen, as opposed to pebbles with a fixed particle radius, because it appears to be a better approximation to results of numerical simulations of pebble growth and drift, where pebble sizes are limited by either drift or fragmentation (Brauer et al. 2008). Similarly, when considering the balance between particle growth and drift/fragmentation in evolving discs, the Stokes number of the dominating particles tends to only weakly change as the gas density decreases with time (Birnstiel et al. 2012; Lambrechts & Johansen 2014). Therefore, we also keep the Stokes number constant in time, for simplicity. Alternatively, one should consider a global pebble growth and evolution model, like in Ormel et al. (2017), Izidoro et al. (2019), and Bitsch et al. (2019), but this is outside of the scope of this study.
Finally, the choice of a constant mass flux and Stokes number for the pebbles uniquely defines the pebble surface density,
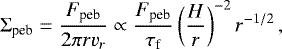 (8)
(8)
where vr ≈−2τfηvK is the radial velocity of the pebbles, assuming the Epstein drag regime with τf ≲ 1. Here, η is a pressure-gradient parameter defined as  . The choice of a constant stokes number thus also has the desirable property that the dust(pebble)-to-gas ratio (Σpeb∕Σg) is constant with orbital radius and constant in time. Therefore, there is no forced pile-up of pebbles anywhere in the disc.
. The choice of a constant stokes number thus also has the desirable property that the dust(pebble)-to-gas ratio (Σpeb∕Σg) is constant with orbital radius and constant in time. Therefore, there is no forced pile-up of pebbles anywhere in the disc.
Pebble accretion
For each body we determine the pebble accretion rate, with a prescription that is described in detail in Appendices sectionlinking A.1, A.2, and A.4. Therefore, the growth of the embryos we model is well-covered by a prescription that spans the Bondi (drift-dominated) to Hill (shear-dominated) accretion regimes (Lambrechts & Johansen 2012). Importantly, we take the dependency of the eccentricity and inclination on the pebble accretion rate into account (Appendix A.1).
Filteringand pebble isolation mass
We reduce the radial flux of pebbles inwards of a body by the fraction the body accreted. Due to this “pebble filtering”, the inner bodies see a reduced pebble flux (Lambrechts & Johansen 2014; Guillot et al. 2014; Morbidelli et al. 2015).
When sufficiently massive, planets can become isolated from pebbles (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014). The gravitational perturbation of the gas by the embryo creates a pressure bump outside of the orbit of the body trapping the inward-drifting pebbles. This isolation mass can be expressed as
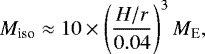 (9)
(9)
which is a reasonable approximation in low-viscosity discs (Lambrechts et al. 2014). More detailed prescriptions that more-or-less agree have recently become available (Bitsch et al. 2018; Picogna et al. 2018; Ataiee et al. 2018). When a body reaches this mass we halt pebble accretion Ṁpeb = 0 and stop the flux of pebbles to bodies in interior orbits.
 |
Fig. 1 Embryo mass and semi-major axis for each embryo as a function of time, for two different global pebble mass fluxes. Growth tracks resulting in the final system indicated with blue circles correspond to runf3-1. The system indicated by orange circles corresponds to runf5-1, which experienced a higher pebble flux by a factor of 1.7. |
3 Simulation results: before gas dissipation
3.1 Terrestrial systems
When the pebble flux is low, such that the total mass in pebbles entering the inner disc is less than ≈110 ME, the initial embryo population does not grow beyond approximately five Mars masses (blue circles in Fig. 1). Mass growth is driven by pebble accretion. Collisions between embryos are rare, because the type-I torques on the planet damp eccentricities and inclinations. The embryos only experience a moderate amount of migration. After 3 Myr of evolution the inner embryo resides around 0.1 AU, slightly inwards of the current orbit of Mercury. Because all embryos increase in mass at relatively similar rates, with only slightly higher accretion rates for the outer embryos, there is no substantial convergent migration. As a result, embryos grow orderly by smooth pebble accretion up to a few Mars masses, with little migration. This changes when we consider higher pebble mass fluxes.
3.2 Super-Earth systems
A larger pebble mass flux that deposits more than 190 ME in the inner disc drastically changes the final masses and orbits of the embryos. When the disc dissipates after 3 Myr, embryos are located in short-period orbits within approximately 0.1 AU, some having been pushed inward of the trap by larger exterior embryos which filtered the pebble flux. The embryos now reach super-Earth-like sizes (Fig. 1). We illustrate the evolution of the embryos in the gas disc phase in more detail in Fig. 2, for a nominal simulation (runf5-1). In the first million years of disc evolution, embryo growth proceeds orderly by sweeping up pebbles. The embryos develop a small mass spread, which is caused by pebble accretion rates being higher on the slightly more massive embryos. However, this picture of smooth growth changes when embryos reach Earth-like sizes. Then, embryos rapidly migrate to the disc edge where their inwards drift comes to a halt. There the piled-up embryos become dynamically excited. The lower-mass embryos generally see the largest eccentricity increase, which results in reduced pebble accretion rates and the suppression of their growth (Fig. A.2). Larger embryos can accrete more efficiently and see their growth boosted by mutual merging events. When embryos grow larger than approximately 5 ME, pebble filtering becomes important: the outer embryos accrete at high rates, which reduces the flux of pebbles to the inner embryos. Consequently, the outer embryos can migrate inward faster than the less massive inner embryos and overtake them. Then,towards final times, the outer embryos accrete the remaining pebble flux while remaining close to the trapping radius, as can be observed by the final steep growth curves in Fig. 1. Even larger embryos reach the pebble isolation mass of 10 ME, which then shuts down the pebble flux to inner embryos. The embryo system typically does not evolve significantly in the last million years before disc dissipation. Besides the dynamical excitation of the embryos, this is mainly the result of the diminished pebble flux, because of mutual pebble filtering and the general time decay of the global pebble flux.
For the formation of super-Earths the gravitational interactions between embryos are important. Therefore we ran ten simulations (suite runf5) to capture the nominal outcome. The final systems, after 3 Myr of evolution in the gas disc, are shown in orange in Fig. 3. Embryos are larger than 1 ME in size, and typically do not grow larger than about 10 ME. We find that the super-Earth cores are located between the inner edge and approximately 0.1 AU. The embryos are found to be in relatively compact configurations, which is characteristic for systems that evolved through orbital migration and experience tidal damping of the eccentricity and inclination (Ogihara et al. 2015). Most neighbouring planet pairs are separated within 13 mutual Hill radii2 from each other, as can be seen in Fig. 4. Also, as expected, orbital migration caused many planet pairs to fall close to first-order mean-motion resonances (Fig. 5). A significant fraction turn out to appear to be near the 4: 3 mean-motion resonance.
For completeness, we also explored simulations with higher pebble flux (suite runf9). Predictably, we find the embryos grow to larger sizes, in the 5–10 ME regime (red circles in Fig. 3). Faster growth leads to an earlier migration of the embryos towards the inner edge. Generally, we observe a more violent dynamical evolution, where embryos can even be excited to orbits with inclinations above the pebble midplane, which strongly reduces pebble-accretion rates. The final systems show a wider orbital spread, out to approximately 1 AU. The majority of planet pairs are now close to first-order j ∕ (j + 1) mean-motion resonances with low j (j = 1, j = 2). This is because more massive embryos are more likely to get trapped in more distant first-order resonances (Ogihara & Kobayashi 2013). This causes the systems to be more extended compared to the systems with lower pebble flux of runf5.
 |
Fig. 2 Example of the time evolution in the gas phase of the disc (runf5-1). Top panel: evolution of the mass of the embryos. Next panel down: decay of their orbits through type-1 migration, which only comes to a halt as embryos approach the inner edge. Bottom two panels: evolution of the eccentricity and inclination, respectively. In the last panel, the blue line corresponds to the opening angle of the gas scale height with respect to the midplane, and similarly the red curve shows the opening angle of the particle layer. |
 |
Fig. 3 Final system architecture, given as the embryo mass vs. orbital distance, at disc dissipation (3 Myr). Different colours represent different pebble mass fluxes: blue, orange, and red experienced, respectively, 3, 5, and 9 times higher mass flux than the grey systems. |
 |
Fig. 4 Planet separation, expressed in mutual Hill radii, between neighbouring planet pairs for runs runf5, after 3 Myr of evolution in the gas disc (yellow) and after 100 Myr of subsequent evolution (red). The most closely spaced planet pairs do not survive. |
 |
Fig. 5 Cumulative distribution of neighbouring planet pairs. Dashed curves show the situation after the end of the gas disc phase (t = 3 Myr), for both simulations suites runf3 (blue) and runf5 (orange). The full lines show the situation after 100 Myr of additional evolution. For the super-Earth systems most resonant pairs do not survive the post-gas phase. The vertical grey thin lines show the period ratios corresponding to, from left to right, the 5: 4, 4: 3, 3:2, 2:1 first-order mean-motion resonances. For comparison, the green short-dashed curve shows the observed period ratio distribution of the Kepler multi-planet systems, limited to a maximal period ratio of Pout ∕Pin = 4. |
 |
Fig. 6 Final planet mass as a function of the integrated pebble flux. Circles, connected with the full black curve, give the mean planet mass across a suite of runs with the same pebble flux, while triangles represent the minimal and maximal embryo mass across all runs with the same pebble flux. The squares, connected by the grey dashed line, give the mean embryo mass at the time of disc dissipation. |
3.3 Understanding the dependency on the pebble flux
The steeper-than-linear relation between the pebble flux and final embryo mass is driven by pebble accretion, and steepened further by growth through embryo mergers. Indeed, in our disc model embryos typically accrete in the 3D regime, where the accretion radius is smaller than the pebble scale height racc ≲ Hp. In the so-calledstrong-coupling limit of the Bondi and Hill branch (Lambrechts & Johansen 2012, see also Apppendix sectionlinking A.1), one then finds embryo growth rates of the form
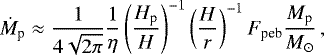 (10)
(10)
which implies that the embryo mass Mp has an exponential dependency on the mass flux Fpeb (Ormel & Klahr 2010; Lambrechts & Johansen 2012; Ida et al. 2016; Ormel 2017; Ormel & Liu 2018; Lin et al. 2018, see Apppendix A.3 for a derivation) Therefore, a change of a factor two in pebble mass flux can lead to almost an order-of-magnitude change in final embryo mass. This steep dependency breaks down when embryo masses become large, get more excited, and mutual filtering and isolation become important.
Figure 3 summarises the final systems at the time of disc dissipation for different pebble fluxes, including a control simulation with a low pebble flux (runf1-1). Combining the results obtained in the gas disc phase also allows us to express the mean embryo mass as a function of the cumulative pebble flux through the disc in Fig. 6.
4 Simulation results: after gas dissipation
4.1 Terrestrial systems
We now follow up on the evolution of the terrestrial embryos after the gas disc has dissipated for an additional 100 Myr. First, we consider the evolution of the set of our terrestrial embryos that grew to approximately a few Mars masses, while in the gas disc (suite runf3). After the disc dissipates, all the small embryo chains become unstable. Bodies grow substantially over the next few tens of millions of years through mutual mergers, just as expected from classical terrestrial planet simulations as reviewed in Morbidelli et al. (2012). Their formation history is thus similar to the formation of the Earth through giant impacts (Chambers 2001; O’Brien et al. 2006; Raymond et al. 2009; Izidoro et al. 2014; Jacobson & Morbidelli 2014).
The final systems are shown in blue in Fig. 7 (suite runf3-C). Planets grow up to approximately 4 ME. This can therefore be considered to be the upper mass limit for what we would classify as a terrestrial planet. Most of the planets are spread between 0.1 and a few AU, corresponding to the outer edge of the original embryo disc. Some get placed in wider orbits of up to 10 AU. On average about five planets remain in the system. The mean eccentricities are relatively high, around e = 0.1, but we do not include dynamical friction by planetesimals.
These simulated planetary systems share some similarities with the terrestrial planets in the solar system. Generally, the most massive planets are found between 0.5 and 1 AU and less massive planets are present in the interior and exterior of that zone. These are the outcome of unfortunate embryos that get kicked out of this central region, after which their growth comes to a halt. This is a generic outcome of terrestrial planet simulations where embryos are initially confined in a narrow annulus. Such an embryo configuration has previously been proposed to explain the origin of Mars as a stranded embryo (Hansen 2009; Raymond et al. 2009; Walsh et al. 2011; Morbidelli et al. 2012; Jacobson & Morbidelli 2014; Walsh & Levison 2016).
The aim here is not to recreate the exact configuration of the terrestrial planets in the solar system. However, we did experiment and found that a moderately reduced integrated mass flux of about 60 ME leads to planets with masses in the Venus to Earth-mass regime. Finally, in our control simulation with the lowest pebble flux that we considered (runf1-1), the embryos are sufficiently small at disc dissipation that they can avoid mergers at later times (Iwasaki & Ohtsuki 2006). These sub-Mars embryos therefore remain small (grey points in Fig. 7).
 |
Fig. 7 Final system architecture, given as planet mass vs. orbital distance, after 100 Myr of evolution. Colour coding is similar to that of Fig. 3. Scattering, collisions, and ejections generally reduce the number of planets per system and set the final orbital architecture of the system. |
4.2 Super-Earth systems
The larger super-Earth-like embryos with shorter periods (suite runf5) undergo a different evolution after the disc dissipates compared to the terrestrial embryos. Typically, we find that the removal of the gas disc renders the embryo chain unstable. Subsequently, within usually the first few tens of millions of years of evolution, embryos merge or collide with the central star and settle in their final configuration. These systems, after 100 Myr of additional evolution after disc dissipation (suite runf5-C), can be inspected in Fig. 7 (orange points). The final planetary masses have increased and range from about 1 to 20 ME. In those systems that undergo a post-gas instability, growth is more efficient for the inner embryos. This can be seen in Fig. 8, where the mass and orbital location of each system at disc dissipation can be compared with respect to the final system. Thus, instabilities after disc dissipation can erase the trend of larger-mass objects in wider orbits that build up through pebble accretion in the gas disc phase (Izidoro et al. 2017; Ogihara et al. 2018a). On average there are about four planets left in the system. The final inclinations are within 10° and most eccentricities fall between e = 10−2 and e = 0.2 (Fig. 9).
Not all systems become unstable, as the green system in Fig. 8 shows (runf5-3). Compared to the unstable systems, it keeps its six planets, which have period ratios between neighbouring planet pairs that are close to mean-motion resonance (3: 2, 4:3, 3:2, 4:3, 3:2). It also maintains low eccentricities (e < 0.04) and inclinations (i <1°). This one system is however the exception. We estimate that more than 90% of all systems experience a post-gas instability, based on a suite of 19 simulations where only one system remained stable. Unstable systems were re-simulated with a longer gas removal timescale of tdisc = 5 Myr. In this way we generate nine additional systems for the post-gas integrations, which revealed all these systems to become unstable. Thus, this experiment also indicates our results are not very sensitive to the choice or tdisc.
The tendency for these systems to become unstable is not surprising. We find that when embryos grow by pebble accretion, many of the super-Earth pairs become too closely spaced when they leave the gas disc phase. Nearly all pairs with mutual Hill spacing within 13 rH,mut merge after the removal of gas (Matsumoto et al. 2012). This can be seen in Fig. 4, by comparing the yellow vs. red histograms. Unsurprisingly, post-gas instabilities also destroy most of the resonant period pairs (orange dashed curve in Fig. 5). The high occurrence of post-gas instabilities is thus different from the earlier results by Izidoro et al. (2017). These latter authors found that only half of the super-Earth systems become unstable after disc dissipation, because in their model, which treats migration but not pebble accretion, embryos are generally more widely spaced. Mass growth by pebbles does not directly change the physical separation between embryos, but it does change the mutual Hill spacing. In the new work by Izidoro et al. (2019), which treats pebble accretion, a similar high probability is found for the break up of resonant chains of planets with similar masses at disc dissipation.
The super-Earth systems we find seem to be in qualitative agreement with the observed population of super-Earths detected by the Kepler survey. Previously, Pu & Wu (2015) noted that the Kepler planets typically have mutual Hill separations around 12 rH,mut, close to the minimal separation required to survive over gigayear-timescales. Therefore, these latter authors argued that most super-Earth systems of greater than or approximately equal to four planets formed in an initially more planet-dense configuration. The formation scenario presented here supports this picture. Moreover, we find that super-Earth pairs are typically not in mean-motion resonance, in agreement with Kepler observations (Lissauer et al. 2011). The period ratio distribution we find for the simulated super-Earth systems is qualitatively similar to the one for the observed Kepler-planet pairs (green dashed line in Fig. 5; see also the companion paper by Izidoro et al. 2019). Eccentricities and inclinations appear also to be broadly consistent, with Kepler systems having (e < 0.05, Xie et al. 2016) and low mutual inclinations (i ≲ 10°, Lissauer et al. 2011; Johansen et al. 2012; Zhu et al. 2018). Furthermore, the inherent multiplicity of a typical Kepler super-Earth system has been inferred to be about four (although this is dependent on the inclination model used; Johansen et al. 2012; Izidoro et al. 2017; Zhu et al. 2018). This would agree with our simulations which have, on average, four surviving planets. Also, recently, Wu (2018) argued, based on modelling the planetary radius distribution, that the Kepler systems are composed of planets with a characteristic rocky mass of about 8 ME, with weak orbital radius dependency. This appears to be roughly consistent with our simulations showing planetary masses do not display a strong dependency on orbital radius and that planets have a mean mass of ~ 10 ME. We refer to Izidoro et al. (2019) for a more quantitative discussion on observational implications.
We now briefly discuss the evolution of the embryos that formed from the largest pebble mass flux we considered (suite runf9-C). Their post-gas growth evolution is largely equivalent to the other super-Earth simulations, where disc dissipation generally triggers a post-gas instability. The final masses and orbits of the planets in these systems are shown in Fig. 7 (red circles). Given that these runs use a large cumulative pebble mass flux of 350 ME and a disc aspect ratio resulting in a relatively large pebble isolation mass of 10 ME, these simulations probe the most massive super-Earth systems we can conceivably form. From these results it thus seems implausible that the rocky cores of super-Earths grow beyond 30 ME in mass.
To summarise, the strong dependency of the embryo mass on the pebble flux at disc dissipation remains reflected in the final planetary masses. The relation between the cumulative pebble mass flux and the mean planetary mass is illustrated in Fig. 6 (black curve). A small increase in the pebble mass flux by a factor of two leads to the formation of super-Earths larger than 10 ME in mass, instead of terrestrial planets in the Earth-mass regime.
 |
Fig. 8 Left panel: ten systems after 3 Myr of evoluton in the protoplanetary disc (runf5). Right panel: same systems, after 100 Myr of evolution(runf5-C). Only one remained stable, here shown as the light-green system, while the other systems all underwent a post-gas instability. These latter systems contain fewer but more massive planets and are less strongly size-sorted with orbital distance. |
 |
Fig. 9 Eccentricity and inclination for the final systems, after 100 Myr of evolution (runf5-C). Lowest values for eccentricity and inclination are found for the stable resonant system. Generally, systems with fewer members have higher eccentricities and inclinations. |
5 Identifying super-Earths and true terrestrial planets
We have argued that systems of terrestrial planets and systems of super-Earth are distinct in the way they form. However, since their growth histories cannot be observed, we here summarise and attempt to quantify where possible the observable differences between these two different types of planetary systems. We believe these two classes of systems should be distinct because our simulations do not argue for planetary systems which could consist of planets with both terrestrial and super-Earth growth histories. A caveat here is that we consider here a growth channel based on a single population of initially similar-sized rocky embryos. Super-Earths may form outside the ice line and migrate inwards, which could leave behind mixed systems (Cossou et al. 2014; Raymond et al. 2018; Izidoro et al. 2019).
Systemsof super-Earths contain planets more massive than the terrestrial planets. However, a simple mass threshold is not sufficient to distinguish between a terrestrial or super-Earth growth history. A system with planets in the approximately 1–5 ME regime can have formed in either growth mode (Fig. 6). Only when planets more massive than approximately 5 ME are present is the system likely to be composed of true super-Earths. We also note that we do not find a strong relation of the planetary mass with orbital radius for the super-Earth systems, while there is a tendency for the outer terrestrial planets to decrease in mass with orbital radius (Fig. 7). These findings are also sensitive to the pebble isolation mass, which in our disc model is about 10 ME. Discs with smaller isolation masses would further limit growth by pebble accretion (Bitsch et al. 2018).
We can also consider the difference in the orbital architecture (Raymond et al. 2008). Our super-Earth systems are typically more concentrated towards the disc edge, around 0.1 AU. The terrestrial systems on the other hand trace their origin location better and stretch out beyond distances of 1 AU. Also, systems found to be in a resonant chain point to a super-Earth-like formation history.
When the composition of a planet can be determined, it can also be used to help distinguish terrestrial from super-Earth systems. Because our terrestrial planets from small Mars-sized embryos, the final planets cannot have significant gaseous envelopes. The envelope mass fraction that could be expected from outgassing alone is in the range of at most a few percent (Rogers et al. 2011). Conversely, the super-Earth planets can have significant gaseous envelopes, but not necessarily so. In this work we have not explored gas accretion onto embryos. Isolated planets exceeding approximately 1 ME can accrete about 10% of their total mass in gas during the disc phase (Lee et al. 2014; Ormel et al. 2015; Lambrechts & Lega 2017). However, our simulations also reveal that planets can experience mutual collisions, both during and after the gas phase. Therefore, it may be possible that part of the original envelopes are lost (Liu et al. 2015; Schlichting et al. 2015). Moreover, close-in planets may loose their envelopes through stellar irradiation (Baraffe et al. 2006; Owen & Wu 2017; Carrera et al. 2018). Finally, some of the largest cores could even undergo runaway gas accretion and in this way escape the super-Earth class by becoming gas giants (Bitsch et al. 2019). Clearly, the role of gas accretion is an area for further study. Nevertheless, we can conclude that when a significant gas envelope is present around a planet, the accretional history must have been super-Earth-like.
Taken together, we argue here that one should ideally consider the mass, orbital architecture, and composition of the planets in a system as a whole in order to observationally distinguish terrestrial from super-Earth systems. In this way we can conclude that a good terrestrial planet candidate is smaller than 5 ME and is part of an extended non-resonant multiple planet system of similarly small planets. Moreover, these planets should have no gaseous envelopes, or small envelopes that do not exceed a few percent of the total planetary mass. Therefore, it is at this point in time not yet clear if a true terrestrial planet has been observed outside of the solar system.
6 Discussion
6.1 Pebble mass reservoir
In this work, we consider the integrated mass flux of pebbles through the inner disc as a free parameter. The distribution of the total mass available in pebbles in protoplanetary discs around solar-like stars is observationally poorly constrained. ALMA surveys of million-year-old star-forming regions argue for dust masses between crudely ~1 and ~100 ME, as inferred from (sub-) millimetre emission around Class II sources (Ansdell et al. 2017; Dullemond et al. 2018). However, such measurements assume that the emission is optically thin, which may not be the case at mm wavelengths. For example, longer-wavelength measurements of the young HL Tau system argue for a total dust reservoir of 300–1000 ME (Carrasco-González et al. 2016), a factor of three larger than inferred from ALMA measurements (Pinte et al. 2016). Additionally, these observations miss all mass located in larger sizes. Indeed, given the uncertain ages of stars in starforming regions, it is plausible that a large fraction of the mass reservoir is already locked up in growing planets (Najita & Kenyon 2014; Manara et al. 2018; Johansen et al. 2019). In our simulations, for example, the embryos grow rapidly in a short time interval of approximately 1.5 Myr. This may then also explain why the dust masses inferred around even younger Class 0 sources are substantially higher, with median dust masses around 250 ME, compared to the above-mentioned Class II sources (Tychoniec et al. 2018).
Becausesuper-Earths appear around approximately a third of solar-like stars (Zhu et al. 2018), without being strongly dependent on stellar metallicity (Buchhave et al. 2012), it appears that the pebble flux for super-Earths systems is commonly available. The exact value of the required pebble mass (we find here approximately 190 ME) depends on the filtering efficiency Ṁp∕Fpeb (Eq. (10)). The latter needs to be numerically determined (Appendix A.1). Recent numerical efforts argue for filtering efficiencies that are higher by approximately a factor of four, which would reduce the required mass in pebbles, but efficiencies decrease again with increasing turbulence (Xu et al. 2017; Ormel & Liu 2018). We also note that filtering factors are higher around low-mass stars (Eq. (10), Ormel et al. 2017)possibly explaining why super-Earth occurrence rates remain high around such small stars (Mulders et al. 2015).
To form the terrestrial planets, a pebble mass reservoir of about 110 ME, within less than a factor of two, is required. This relatively narrow range in the pebble flux appears to indicate that the formation of terrestrialplanets may be less common than the formation of super-Earth systems. However, as we argued above, we do not know the true distribution of the total pebble masses in protoplanetary discs, which may often fall in the range that produces terrestrial planets. An additional complication is that the mass flux past the ice line would be modified when outer giant planets are present that can filter and even halt the flux of pebbles (Lambrechts et al. 2014). For example, in the context of the solar system, when the core of Jupiter reached pebble isolation in the outer disc it should have halted the mass flux of pebbles to the inner disc, which could then have limited the growth of inner planetary embryos to the mass of Mars (Morbidelli et al. 2015).
In general, the early formation of pebble-filtering giant planets in wide orbits could suppress the formation of close-in super-Earths. However, Zhu & Wu (2018) argue, based on statistical grounds, that there appears to be a correlation between close-in super-Earths and wide-orbit giant planets, although radial-velocity surveys show this line of evidence may not yet be conclusive (Barbato et al. 2018). If this correlation indeed holds, it implies that the solar system configuration with terrestrial planets and wide-orbit gas giants is rare. It could then mean that typically gas giants form late, close to disc dissipation, which would minimise their effect on the pebble flux. Alternatively, this may suggest that these super-Earths do not follow the growth path investigated in this study where rocky cores are grown inside the ice line. Indeed, the companion paper by Bitsch et al. (2019) shows that the formation of giant planets outside the ice line does not appear to generally prevent smaller icy super-Earth-sized planets from migrating inwards.
In summary, we believe that we have invoked plausible pebble mass reservoirs. Future work is needed to more precisely quantify the mass required to form observed planetary systems and the role of planets in the outer disc in shaping the pebble flux. Nevertheless, the strong dependency that we have highlighted between the pebble flux and the type of planetary system that is formed should be robust.
6.2 Summary of simplifying assumptions
In order to model the growth of the planetary embryos, we took into account pebble accretion, planetary migration and gravitational interactions with the help of an N-body code. We found that, together these three processes shape the final planetary systems. However, in this study we made several simplifying assumptions that deserve to be studied in more detail.
We considered a simple model for the gas disc and its inner edge, which only allows for inwards type-I migration of embryos. In our particular disc model, embryos of equal mass migrate with the same migration timescale independent of orbital radius, which does not necessarily hold in disc models with steeper density gradients. However, for the low-pebble-flux cases migration is not particularly relevant, while for the high-pebble-flux cases migration is convergent as the outer embryos tend to grow larger than the inner ones and because there is a planet trap at the inner edge of the disc.
We used a simplified prescription of the disc edge, which also ignored the role of the exterior silicate sublimation line. However, the inner edge is critical to prevent the super-Earth embryos from migrating into the star. Therefore, our work would benefit from an improved physical description of the disc edge (Flock et al. 2017), while also treating the particle size evolution through coagulation and sublimation (Ros & Johansen 2013; Schoonenberg & Ormel 2017).
We also considered a single population of close-in embryo seeds located inside of the ice line. The initial embryo masses matter because, for a single embryo grown by pebble accretion, the final mass after exponential growth is linearly dependent on the initial embryo mass (Eq. (10)). This remains approximately true for multiple embryos when they are small enough to ignore pebble filtering. However, this breaks down around larger embryos or when systems become sufficiently dense to cause dynamical excitation. Ultimately, where and when the first embryos emerge is uncertain (e.g. a different time-dependent embryo emergence is explored in Ormel et al. 2017). We did not further explore the initial embryo distribution here.
While we assumed the embryo seeds to exist only within the ice line, the companion papers Izidoro et al. (2019) and Bitsch et al. (2019) consider embryo seeds also located beyond the snow line, as well as the effects of a migrating snow line, in more detailed disc models with migration traps (Bitsch et al. 2015b). They find that icy embryos growing beyond the snow line generally migrate inwards. This would disrupt the formation of systems of rock-dominated cores as outlined in this work. If super-Earth cores are indeed dominantly rocky in composition (Owen & Wu 2017; Lopez 2017), this remains an open problem.
7 Conclusions
We studied the migration and growth of rocky embryos within the ice line around a solar-like star. Additionally, we followed their subsequent post-gas disc evolution. In the gas phase, we find the pebble mass flux strongly regulates the final masses of the embryo. A factor of two difference in the pebble mass flux can result in a change from Mars-sized embryos to larger-than-Earth-mass ones. This strong difference is caused by the fact that if embryos become Earth-sized they start rapidly migrating and become highly efficient in accreting pebbles. These planets pile up close to the disc edge and their growth by pebble accretion is limited by the pebble isolation mass. After the gas disc dissipates, the smaller Mars-sized embryos grow through mutual mergers to planets in the Earth-mass regime, forming terrestrial planets, like those in the solar system. The larger super-Earth planets typically experience instabilities in the post-gas evolution, because the combination of pebble accretion and migration left behind compact systems with planets in closely spaced resonances, with small separations as measured in their mutual Hill radii. In this way the systems are typically dislodged from their resonant chains.
The largest planets that form in the terrestrial mode can become as massive as approximately 5 ME. However, to discriminate between terrestrial and super-Earth systems from an observational viewpoint, we argue a mass threshold is not sufficient. Fortunately, the orbital architecture and the presence of gaseous envelopes can be used to separate the two classes of planetary systems.
The pebble mass flux was chosen to be a free parameter in this study. Further observational constraints on the distribution of initial dust disc masses are needed in order to asses if this formation model is in agreement with observed exoplanet occurrence rates. This also requires continued work on the precise determination of the pebble accretion efficiency (Liu & Ormel 2018; Ormel & Liu 2018). The complete evolution of the gas disc, pebble component, and the embryos across the disc remains a key point for further exploration. Companion papers Izidoro et al. (2019) and Bitsch et al. (2019) expand this study beyond the ice line. There, outer planets can reduce and halt the pebble flux. Moreover, icy cores can migrate across the ice line.
To conclude, we have shown here two growth modes, regulated by only the radial pebble mass flux. When the pebble flux is sufficiently high, we no longer form terrestrial systems from rocky embryos, but instead resonant chains of super-Earths by migration-assisted growth. These compact systems typically become unstable after disc dissipation, leaving behind non-resonant systems of approximately four super-Earths with eccentricities and inclinations consistent with observed values.
Acknowledgements
M.L. thanks Masahiro Ogihara, Yasunori Hori and Eiichiro Kokubo for stimulating discussions at DTA symposium VIII. The authors are grateful for the constructive feedback by an anonymous referee. M.L., A.M. and S.R. were supported by ANR through project MOJO (Modeling the Origin of JOvian planets, ANR-13-BS05-0003-01). S.J. and A.M. were supported by the European Research Council (ERC) Advanced grant ACCRETE (contract number 290568). A.J. is grateful for support from the KAW Foundation (grant 2012.0150), the European Research Council (ERC Consolidator Grant 724687-PLANETESYS) and the Swedish Research Council (grant 2014-5775). B.B. thanks the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support. A.I. gratefully acknowledges financial support from FAPESP via grants #16/19556-7 and #16/12686-2.
Appendix A Pebble accretion prescription
A.1 Accretion radius
The pebble accretion radius is calculated as a function of the relative velocity between pebbles and the embryo, and the drag force the particle feels. We verified the prescription described below against our two-body integrations performed in the shearing sheet, whichinclude drag (Ormel & Klahr 2010; Lambrechts & Johansen 2012; Johansen et al. 2015; Liu & Ormel 2018). Below, we follow the terminology of Lambrechts & Johansen (2012).
Massive bodies accrete in the Hill regime, where Keplerian shear largely determines the accretion rate. Lower-mass bodies typically accrete in the so-called strong Bondi branch, where particles are well-coupled to the gas, but approach velocities are now dominated by the sub-Keplerian velocity of the gas with respect to the embryo.
In thesetwo regimes, accretion relies on the friction time across the accretion radius to be shorter than the deflection time. This then sets an effective accretion radius. The friction time is given by
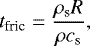 (A.1)
(A.1)
where R and ρs are respectively the radius and density of the particle. The deflection time is expressed as
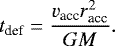 (A.2)
(A.2)
Here, M is the mass of the embryo and vacc is the accretion velocity. The latter is dependent on the accretion radius through
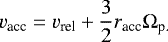 (A.3)
(A.3)
The relativevelocity of the embryo with respect to the pebbles orbiting in a sub-Keplerian gas disc is given by
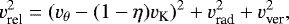 (A.4)
(A.4)
where vtheta, vrad, vver are respectively the azimuthal, radial, and vertical velocity components of the embryo, and (1 − η)vK is the velocity of the gas. By using this formulation of the relative velocity, we automatically take the eccentricity and inclination dependency of the pebble accretion rate into account. Finally, the accretion radius is determined from the requirement that tfric = tdef, which we do numerically by iteration.
In the above regimes, the crossing time past the embryo was always longer than the deflection time. Around lower mass bodies, this may no longer be true. Therefore, in this so-called weak-coupling Bondi regime, we need the crossing time
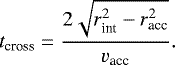 (A.5)
(A.5)
Here, the nominator gives the length of the path of an unperturbed particle, the chord, through the circle around the accretor with interaction radius rint. In practice, we take rint to be the smallest of the Bondi or Hill radius 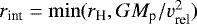 . Therefore, when tcross < tdef, we limit the accretion radius by requiring tfric = tcross. The latter expression can simply be solved analytically. We illustrate in Fig. A.1 the accretion prescription (dashed lines) against 2D integrations performed in the shearing sheet, showing good agreement including the transition to weak coupling, for example for τf = 0.1-pebbles from Pluto to Ceres mass, into the regime for a purely gravitational cross section around even smaller masses.
. Therefore, when tcross < tdef, we limit the accretion radius by requiring tfric = tcross. The latter expression can simply be solved analytically. We illustrate in Fig. A.1 the accretion prescription (dashed lines) against 2D integrations performed in the shearing sheet, showing good agreement including the transition to weak coupling, for example for τf = 0.1-pebbles from Pluto to Ceres mass, into the regime for a purely gravitational cross section around even smaller masses.
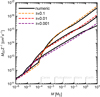 |
Fig. A.1 Product 2raccvacc, or equivalently Ṁpeb,2D∕Σpeb, as function of embryo mass. Dark lines represent the results of two-body embryo–pebble integrations in 2D, for particles with different Stokes number. The coloured dashed lines correspond to the results from our accretion prescription, covering strong coupling, the decrease to weak coupling, and finally, around the smallest masses, the accretion purely following gravitational deflection. Values shown here are for an embryo at 2.5 AU with headwind velocity ηvK = 7 × 103 cm s−1. The simulations presented in this paper start with embyos with a mass of 0.01 ME. |
A.2 Pebble midplane
In order to determine the accretion rate, we have to determine how much of the pebble flow falls within the accretion radius. Pebbles settle towards the disc midplane (Youdin & Lithwick 2007). The pebble scale height is given by
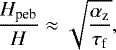 (A.6)
(A.6)
where we have taken the vertical stirring parameter αz to be equal to the viscous α. This represents a well-settled particle layer in a nearly laminar midplane.
If the accretion radius starts exceeding the pebble scale height, we switch from 3D pebble accretion,
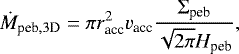 (A.7)
(A.7)
Because of the low pebble scale height, it is possible for bodies with inclinations i ≳ Hp∕r to escape from the pebble midplane and to stop accreting pebbles. We therefore simply cut the accretion rate Ṁ peb = 0, when the vertical position of the body exceeds the pebble scale height z > Hpeb.
A.3 Pebble accretion in the 3D strong-coupling regime
We briefly derive the expression of Eq. (10). Setting tfric equal to tdef, one obtains
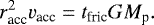 (A.9)
(A.9)
In the 3D accretion regime the accretion rate becomes
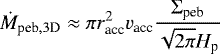 (A.10)
(A.10)
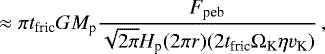 (A.11)
(A.11)
where in the last line we expressed the surface density through the pebble flux Fpeb. Here, the product 2tfricΩKηvKis the radial drift speed of the pebbles. One finally obtains
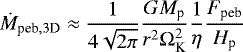 (A.12)
(A.12)
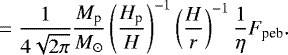 (A.13)
(A.13)
Therefore, when embryos are sufficiently large that tdef > tcross and accretion proceeds in the 3D regime, growth is exponential in nature. Moreover, the expression has no orbital dependency in the viscously heated inner discs where we took the aspect ratio H∕r to be constant. Because there is no longer an explicit dependency on the relative velocity the expression does not depend on the eccentricity, as long the strong coupling criterion is satisfied. This is not true in the 2D accretion regime (Liu & Ormel 2018). The accretion rate only depends on the particle size through the level of pebbles settling to the midplane  .
.
Recently, Ormel & Liu (2018) numerically derived 3D accretion rates, which differ from the 2D integrations discussed in Appendix A.1. These latter authors find a similar scaling relation to Eq. (10), but measure accretion rates larger by approximately a factor four. Therefore, following Ormel & Liu (2018), we have moderately underestimated the filtering fraction in 3D for our choice of αz and τf. This implies similar growth rates as in this work could be obtained with, crudely, a factor four smaller pebble flux or a factor four larger pebble scale height. However, we do note that filtering efficiencies are also changed and higher scale heights alter the accretion rates of inclined embryos, so this may lead to differences. Therefore, follow-up work will benefit from accurate prescriptions as in Ormel & Liu (2018) and the future inclusion of the effect of the complex gas flows around planetary bodies (Ormel 2013; Ormel et al. 2015; Lambrechts & Lega 2017; Popovas et al. 2018).
A.4 Pebble accretion-driven drift
Because of our prescribed accretion rates we do not automatically take into account the angular momentum exchange between embryos and the population of planetesimals and pebbles. For embryos on the short orbits that we consider, type-I migration and damping dominates pebble-related effects. And, in this study, we choose to ignore the planetesimal population.
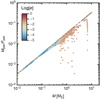 |
Fig. A.2 Accretion rate with respect to the total outer pebble flux, as function of embryo mass. The points show the embryos with their evolution shown in steps of 104 yr, for the 3 Myr duration of the gas disc phase (runf5-1). The colours correspond to the eccentricities of the bodies, as indicated by the colour bar. The grey dashed line is the analytical expression Eq. (10), which represents 3D accretion in the strong coupling limit. The strong reduction in accretion rate at late time is mainly due to pebble filtering by the outer embryos. |
Nevertheless, we want to avoid the unphysical limit of accreting zero angular momentum material. Therefore, we have implement a correction for pebble accretion-driven drift. Consider the angular momentum balance as a body grows by a mass dM,
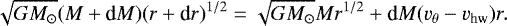 (A.14)
(A.14)
Here, the first term on the right-hand side is the initial angular momentum and the second term is accreted angular momentum of the inwards drifting pebbles. For simplicity we assume that the relative velocity is dominated by the headwind and ignore the dependency on the Stokes number. This can be rewritten to give
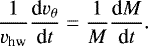 (A.15)
(A.15)
This drag force would result in inwards drift. In our code, we have balanced this force against the artificial drift driven by adding mass without angular momentum transport. In this way we find an expression for a correction force along the azimuthal direction of the form
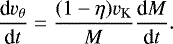 (A.16)
(A.16)
We note that we have made several assumptions here (low e, i, no angular momentum transfer to spin, surrounding gas or a pebble accretion disc). However, as mentioned, this procedure is mainly here to avoid the unphysical limit of mass growth without any angular momentum exchange.
References
- Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bai, X.-N. 2014, ApJ, 791, 137 [Google Scholar]
- Bai, X.-N. 2017, ApJ, 845, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Alibert, Y., Chabrier, G., & Benz, W. 2006, A&A, 450, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbato, D., Sozzetti, A., Desidera, S., et al. 2018, A&A, 615, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barboni, M., Boehnke, P., Keller, B., et al. 2017, Sci. Adv., 3, e1602365 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., & Pessah, M. E. 2018, ApJ, 855, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., Masset, F., Koenigsberger, G., & Szulágyi, J. 2015, Nature, 520, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015a, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015b, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Cameron, A. G. W., & Ward, W. R. 1976, Lunar Planet. Sci. Conf., 7, 120 [NASA ADS] [Google Scholar]
- Carrasco-González, C., Henning, T., Chandler, C. J., et al. 2016, ApJ, 821, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Ford, E. B., Izidoro, A., et al. 2018, ApJ, 866, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2001, Icarus, 152, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2014, ApJ, 780, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. A. L., Nelson, R. P., Paardekooper, S. J., et al. 2017, MNRAS, 467, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Cossou, C., Raymond, S. N., & Pierens, A. 2013, A&A, 553, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cossou, C., Raymond, S. N., Hersant, F., & Pierens, A. 2014, A&A, 569, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauphas, N., & Pourmand, A. 2011, Nature, 473, 489 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fendyke, S. M., & Nelson, R. P. 2014, MNRAS, 437, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., Turner, N. J., & Benisty, M. 2017, ApJ, 835, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., & Lee, E. J. 2018, ApJ, 859, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Turner, N. J., Nelson, R. P., & McNally, C. P. 2015, ApJ, 801, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadden, S., & Lithwick, Y. 2017, AJ, 154, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr. K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 2009, ApJ, 703, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, W. K., & Davis, D. R. 1975, Icarus, 24, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ida, S., & Lin,D. N. C. 2010, ApJ, 719, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwasaki, K., & Ohtsuki, K. 2006, AJ, 131, 3093 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Morbidelli, A., & Raymond, S. N. 2014, ApJ, 794, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Bitsch, B., Raymond, S., et al. 2019, A&A, submitted [Google Scholar]
- Jacobson, S. A., & Morbidelli, A. 2014, Phil. Trans. R. Soc. London, Ser. A, 372, 0174 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, S. A., Morbidelli, A., Raymond, S. N., et al. 2014, Nature, 508, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., & Mordasini, C. 2018, ApJ, 853, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lambrechts, M. 2017, Ann. Rev. Earth Planet. Sci., 45, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Davies, M. B., Church, R. P., & Holmelin, V. 2012, ApJ, 758, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 1500109 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Touboul, M., Bourdon, B., et al. 2009, Geochim. Cosmochim. Acta, 73, 5150 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Levison, H. F. 2014, AJ, 148, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Lega, E. 2017, A&A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., Duncan, M. J., & Thommes, E. 2012, AJ, 144, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015a, Nature, 524, 322 [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., Walsh, K. J., & Bottke, W. F. 2015b, Proc. Natl. Acad. Sci., 112, 14180 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J. W., Lee, E. J., & Chiang, E. 2018, MNRAS, 480, 4338 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., & Ormel, C. W. 2017, A&A, 606, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, B., & Ormel, C. W. 2018, A&A, 615, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, S.-F., Hori, Y., Lin, D. N. C., & Asphaug, E. 2015, ApJ, 812, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D. 2017, MNRAS, 472, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lundkvist, M. S., Kjeldsen, H., Albrecht, S., et al. 2016, Nat. Commun., 7, 11201 [Google Scholar]
- Manara, C. F., Rosotti, G., Testi, L., et al. 2016, A&A, 591, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsumoto, Y., Nagasawa, M., & Ida, S. 2012, Icarus, 221, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, S., Brasser, R., & Ida, S. 2017, A&A, 607, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- McNally, C. P., Nelson, R. P., Paardekooper, S.-J., Gressel, O., & Lyra, W. 2017, MNRAS, 472, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- McNally, C. P., Nelson, R. P., & Paardekooper, S.-J. 2018, MNRAS, 477, 4596 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, H., Nakazawa, K., & Hayashi, C. 1978, Progr. Theor. Phys., 60, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A.,& Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Lunine, J. I., O’Brien, D. P., Raymond, S. N., & Walsh, K. J. 2012, Ann. Rev. Earth Planet. Sci., 40, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bitsch, B., Crida, A., et al. 2016, Icarus, 267, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., Pascucci, I., & Apai, D. 2015, ApJ, 814, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., & Kenyon, S. J. 2014, MNRAS, 445, 3315 [NASA ADS] [CrossRef] [Google Scholar]
- Nimmo, F., & Kleine, T. 2007, Icarus, 191, 497 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, D. P., Morbidelli, A., & Levison, H. F. 2006, Icarus, 184, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Kobayashi, H. 2013, ApJ, 775, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., Morbidelli, A., & Guillot, T. 2015, A&A, 578, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogihara, M., Kokubo, E., Suzuki, T. K., & Morbidelli, A. 2018a, A&A, 615, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogihara, M., Kokubo, E., Suzuki, T. K., & Morbidelli, A. 2018b, A&A, 612, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W. 2013, MNRAS, 428, 3526 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2017, Astrophys. Space Sci. Lib., 445, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Liu, B. 2018, A&A, 615, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R. 2015, MNRAS, 447, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Liu, B., & Schoonenberg, D. 2017, A&A, 604, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J. 2014, MNRAS, 444, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Larwood, J. D. 2000, MNRAS, 315, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Petigura, E. A., Howard, A. W., & Marcy, G. W. 2013, Proc. Natl. Acad. Sci., 110, 19273 [Google Scholar]
- Picogna, G., Stoll, M. H. R., & Kley, W. 2018, A&A, 616, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Popovas, A., Nordlund, Å., Ramsey, J. P., & Ormel, C. W. 2018, MNRAS, 479, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- Pu, B., & Wu, Y. 2015, ApJ, 807, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Barnes, R., & Mandell, A. M. 2008, MNRAS, 384, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., O’Brien, D. P., Morbidelli, A., & Kaib, N. A. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Kokubo, E., Morbidelli, A., Morishima, R., & Walsh, K. J. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 595 [Google Scholar]
- Raymond, S. N., Boulet, T., Izidoro, A., Esteves, L., & Bitsch, B. 2018, MNRAS, 479, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Robert, C. M. T., Crida, A., Lega, E., Méheut, H., & Morbidelli, A. 2018, A&A, 617, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, L. A. 2015, ApJ, 801, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., Bodenheimer, P., Lissauer, J. J., & Seager, S. 2011, ApJ, 738, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., & Lovelace, R. V. E. 2006, ApJ, 645, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaefer, L., & Fegley, B. 2010, Icarus, 208, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. E., Sari, R., & Yalinewich, A. 2015, Icarus, 247, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Schoonenberg,D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, J. B., Armitage, P. J., Li, R., & Youdin, A. N. 2016, ApJ, 822, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K.,& Inutsuka, S.-i. 2009, ApJ, 691, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., Ogihara, M., Morbidelli, A., Crida, A., & Guillot, T. 2016, A&A, 596, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2007, ApJ, 654, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Touboul, M., Kleine, T., Bourdon, B., Palme, H., & Wieler, R. 2007, Nature, 450, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tychoniec, Ł., Tobin, J. J., Karska, A., et al. 2018, ApJS, 238, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R. G., & Ormel, C. W. 2016, A&A, 586, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, K. J., & Levison, H. F. 2016, AJ, 152, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
- Wu, Y. 2018, ApJ, 874, 91 [Google Scholar]
- Xie, J.-W., Dong, S., Zhu, Z., et al. 2016, Proc. Natl. Acad. Sci., 113, 11431 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Z., Bai, X.-N., & Murray-Clay, R. A. 2017, ApJ, 847, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., & Wu, Y. 2018, AJ, 156, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., Petrovich, C., Wu, Y., Dong, S., & Xie, J. 2018, ApJ, 860, 101 [NASA ADS] [CrossRef] [Google Scholar]
We found it important to use the formulation by Cresswell & Nelson (2008), because it also covers the cases of high eccentricity and inclination (e > h∕r). Additionally, we also noted that the eccentricity and inclination damping timescale fits of Cresswell & Nelson (2008) are best used joined with the Papaloizou & Larwood (2000) force approach. Applying the Cresswell & Nelson (2008) damping formula to the type-I force formulation by Tanaka et al. (2002) and Tanaka & Ward (2004) can lead to unexpected results for case of high-e, i.
All Figures
 |
Fig. 1 Embryo mass and semi-major axis for each embryo as a function of time, for two different global pebble mass fluxes. Growth tracks resulting in the final system indicated with blue circles correspond to runf3-1. The system indicated by orange circles corresponds to runf5-1, which experienced a higher pebble flux by a factor of 1.7. |
| In the text | |
 |
Fig. 2 Example of the time evolution in the gas phase of the disc (runf5-1). Top panel: evolution of the mass of the embryos. Next panel down: decay of their orbits through type-1 migration, which only comes to a halt as embryos approach the inner edge. Bottom two panels: evolution of the eccentricity and inclination, respectively. In the last panel, the blue line corresponds to the opening angle of the gas scale height with respect to the midplane, and similarly the red curve shows the opening angle of the particle layer. |
| In the text | |
 |
Fig. 3 Final system architecture, given as the embryo mass vs. orbital distance, at disc dissipation (3 Myr). Different colours represent different pebble mass fluxes: blue, orange, and red experienced, respectively, 3, 5, and 9 times higher mass flux than the grey systems. |
| In the text | |
 |
Fig. 4 Planet separation, expressed in mutual Hill radii, between neighbouring planet pairs for runs runf5, after 3 Myr of evolution in the gas disc (yellow) and after 100 Myr of subsequent evolution (red). The most closely spaced planet pairs do not survive. |
| In the text | |
 |
Fig. 5 Cumulative distribution of neighbouring planet pairs. Dashed curves show the situation after the end of the gas disc phase (t = 3 Myr), for both simulations suites runf3 (blue) and runf5 (orange). The full lines show the situation after 100 Myr of additional evolution. For the super-Earth systems most resonant pairs do not survive the post-gas phase. The vertical grey thin lines show the period ratios corresponding to, from left to right, the 5: 4, 4: 3, 3:2, 2:1 first-order mean-motion resonances. For comparison, the green short-dashed curve shows the observed period ratio distribution of the Kepler multi-planet systems, limited to a maximal period ratio of Pout ∕Pin = 4. |
| In the text | |
 |
Fig. 6 Final planet mass as a function of the integrated pebble flux. Circles, connected with the full black curve, give the mean planet mass across a suite of runs with the same pebble flux, while triangles represent the minimal and maximal embryo mass across all runs with the same pebble flux. The squares, connected by the grey dashed line, give the mean embryo mass at the time of disc dissipation. |
| In the text | |
 |
Fig. 7 Final system architecture, given as planet mass vs. orbital distance, after 100 Myr of evolution. Colour coding is similar to that of Fig. 3. Scattering, collisions, and ejections generally reduce the number of planets per system and set the final orbital architecture of the system. |
| In the text | |
 |
Fig. 8 Left panel: ten systems after 3 Myr of evoluton in the protoplanetary disc (runf5). Right panel: same systems, after 100 Myr of evolution(runf5-C). Only one remained stable, here shown as the light-green system, while the other systems all underwent a post-gas instability. These latter systems contain fewer but more massive planets and are less strongly size-sorted with orbital distance. |
| In the text | |
 |
Fig. 9 Eccentricity and inclination for the final systems, after 100 Myr of evolution (runf5-C). Lowest values for eccentricity and inclination are found for the stable resonant system. Generally, systems with fewer members have higher eccentricities and inclinations. |
| In the text | |
 |
Fig. A.1 Product 2raccvacc, or equivalently Ṁpeb,2D∕Σpeb, as function of embryo mass. Dark lines represent the results of two-body embryo–pebble integrations in 2D, for particles with different Stokes number. The coloured dashed lines correspond to the results from our accretion prescription, covering strong coupling, the decrease to weak coupling, and finally, around the smallest masses, the accretion purely following gravitational deflection. Values shown here are for an embryo at 2.5 AU with headwind velocity ηvK = 7 × 103 cm s−1. The simulations presented in this paper start with embyos with a mass of 0.01 ME. |
| In the text | |
 |
Fig. A.2 Accretion rate with respect to the total outer pebble flux, as function of embryo mass. The points show the embryos with their evolution shown in steps of 104 yr, for the 3 Myr duration of the gas disc phase (runf5-1). The colours correspond to the eccentricities of the bodies, as indicated by the colour bar. The grey dashed line is the analytical expression Eq. (10), which represents 3D accretion in the strong coupling limit. The strong reduction in accretion rate at late time is mainly due to pebble filtering by the outer embryos. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.