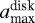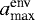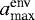| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833666 | |
| Published online | 25 March 2019 | |
Revealing the dust grain size in the inner envelope of the Class I protostar Per-emb-50★
1
Max-Planck-Institute for Extraterrestrial Physics (MPE),
Giessenbachstr. 1,
85748
Garching,
Germany
e-mail: cagurto@mpe.mpg.de
2
ESO,
Karl Schwarzschild str. 2,
85748
Garching, Germany
3
INAF – Osservatorio Astrofisico di Arcetri,
L.go E. Fermi 5,
50125
Firenze, Italy
4
Excellence Cluster Universe,
Boltzmannstr. 2,
85748
Garching, Germany
5
Institute of Astronomy, University of Cambridge,
Madingley Road,
CB3 0HA
Cambridge, UK
6
Department of Physics, State University of New York at Fredonia,
280 Central Ave,
Fredonia,
NY
14063, USA
7
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA
02138, USA
8
SKA Organisation, Jodrell Bank Observatory,
Cheshire
SK11 9DL, UK
Received:
18
June
2018
Accepted:
14
January
2019
Context. A good constraint of when the growth of dust grains from sub-micrometer to millimeter sizes occurs, is crucial for planet formation models. This provides the first step towards the production of pebbles and planetesimals in protoplanetary disks. Currently, it is well established that Class II objects have large dust grains. However, it is not clear when in the star formation process this grain growth occurs.
Aims. We use multi-wavelength millimeter observations of a Class I protostar to obtain the spectral index of the observed flux densities αmm of the unresolved disk and the surrounding envelope. Our goal is to compare our observational results with visibility modeling at both, 1.3 and 2.7 mm simultaneously.
Methods. We present data from NOEMA at 2.7 mm and SMA at 1.3 mm of the Class I protostar, Per-emb-50. We model the dust emission with a variety of parametric and radiative-transfer models to deduce the grain size from the observed emission spectral index.
Results. We find a spectral index in the envelope of Per-emb-50 of αenv = 3.3 ± 0.3, similar to the typical ISM values. The radiative-transfer modeling of the source confirms this value of αenv with the presence of dust with a amax ≤ 100 μm. Additionally, we explore the backwarming effect, where we find that the envelope structure affects the millimeter emission of the disk.
Conclusions. Our results reveal grains with a maximum size no larger than 100 μm in the inner envelope of the Class I protostar Per-emb-50, providing an interesting case to test the universality of millimeter grain growth expected in these sources.
Key words: stars: formation / stars: protostars / circumstellar matter / techniques: interferometric
© C. Agurto-Gangas et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Disks and envelopes around protostars play a fundamental role in the process of planet formation since they contain the ingredients out of which planets are formed (Testi et al. 2014).
Thanks to detailed studies of protoplanetary disks at several sub-millimeter and millimeter wavelengths such as HL Tau (Carrasco-González et al. 2016), CY Tau, DoAr 25, and FT Tau (Pérez et al. 2015; Tazzari et al. 2016) it is now well established that the radial profiles of their grain-size distributions are compatible with millimeter-sized grains. However, it is not yet clear at which stage of the star and planet formation process dust grains start to efficiently coagulate and evolve from micrometer-sized particles to macroscopic dimensions.
Ormel et al. (2009) studied in detail the possibility of grain growth in pre-stellar cores and found that while it is easy to grow to micron-sized particles, the growth to millimeter- or centimeter-sized pebbles requires high densities and relatively long timescales of ~ 107 yr, much longer than the lifetimes of dense cores. This is also explored recently in Chacón-Tanarro et al. (2017), where they calculate the grain size in the center of the pre-stellar core L1544, finding that only in the central 300 AU, can grain size grow to about 200μm.
In the earliest protostellar phases, for example during the Class 0 stage, the protostar is fully embedded in the parent envelope, while in the Class I phase, the envelope is partially dissipated and the disk emission can be better separated from the envelope. Therefore, Class I protostars can more easily address the start of planetesimal formation and constrain the initial conditions of the evolution of protoplanetary disks.
The possibility for the first large solids to assemble during the early phases of disk evolution would have important implications. If the process starts already in the Class I stage, this would imply a much more effective and rapid planetesimal formation phase in the disks. In fact, if large (mm to cm-size) dust particles from the inner envelope (Chiang et al. 2012; Tobin et al. 2013; Miotello et al. 2014) are deposited in the disk at large radii during the disk-formation stage, they would be much less affected by the radial transport and fragmentation processes, which adversely affect the growth from sub-micron particles, and large dust aggregates could form (Birnstiel et al. 2010).
The advantage of studying protostars at millimeter wavelengths is that the dust emission from the envelope and the disk is mostly optically thin. In this wavelength range, the dust opacity coefficient κν, can be approximated by a power law κν ∝ νβmm, where βmm is the millimeter dust opacity spectral index, and is directly related to the maximum size of the grain (Natta et al. 2007). In the presence of very large grains, much larger than the observing wavelength, the opacity becomes gray (only the geometrical cross section of the grains is relevant) and βmm = 0. Values of βmm can be estimated by measuring the slope αmm of the sub-millimeter spectral energy distribution (SED), Fν ∝ ναmm. When the Rayleigh–Jeans approximation is applicable, the spectral index of the observed flux densities, αmm, would translate to a power-law index of the dust opacity βmm = αmm − 2. While values around αmm ~ 3.7 represent size distribution similar to interstellar medium (ISM) particles (Natta et al. 2007; Testi et al. 2014). Classical protoplanetary disks around Class II objects, present clear signs of dust coagulation, with αmm ≤ 3 (Testi et al. 2014, and references therein).
Previous observations of Class 0 protostars by Chiang et al. (2012), Jørgensen et al. (2007) and Kwon et al. (2009) indicate spectral indexes αmm ~ 3, which is shallower than the ISM, but not quite as steep as Class II disks. However, Class 0 objects, are affected by the presence of powerful accretion of material from the envelope and jets (e.g. Tobin et al. 2013), making them difficult to observe and model. In contrast, Class I protostars have less-massive envelopes, which provides a cleaner analysis of the dust properties since the envelope and disk emission can be separated.
Here, we present a dual-wavelength analysis and modeling on the Class I protostar Per-emb-50, in the Perseus star-forming region. Observations and data reduction are described in Sect. 2. In Sect. 3 we present our observational analysis. The modeling and discussion are presented in Sects. 4 and 5, respectively. Conclusions and future work are in Sect. 6.
 |
Fig. 1 Left panel: continuum map of the NGC1333 complex at 1.1 mm wavelength. Right panel: zoom-in to the direct environment of Per-emb-50. The map is adapted from the Bolocam survey at the Caltech Submillimeter Observatory (CSO) by Enoch et al. (2006). |
2 Observations and data reduction
2.1 The source
Per-emb-50 is a protostar located in the active cluster forming region NGC 1333 in the Perseus cloud (see Figure 1), at a recently revised distance of 293 pc (Ortiz-León et al. 2018; Zucker et al. 2018). It is classified as a Class I protostar from the slope of its SED in the near- and mid-infrared (“Cores to Disks” or c2d Spitzer Legacy project from, Evans et al. 2003). Based on Bolocam 1.1 mm data, the bolometric temperature is Tbol = 254 ± 23 K. The rescaled bolometric luminosity is Lbol = 13.7 ± 3 L⊙, making it one of the brightest Class I sources in Perseus.
High-angular-resolution observations conducted at 8 mm in the VLA Nascent Disk and Multiplicity (VANDAM) survey, provide a lower limit for the disk mass and outer disk radius. The rescaled values from Segura-Cox et al. (2016) for mass and radius are: Mdisk = 0.28–0.58 M⊙ and rout = 27–32 AU, respectively.
Literature values for envelope mass, disk mass, disk inclination, and other parameters are presented in Table 1. We note that some of these physical parameters were calculated using the 230 pc from Hirota et al. (2008) or 250 pc in the case of Bolocam observations. Therefore, we rescale the limits taking into account the different distance adopted.
Even though Per-emb-50 presents a small disk at 8 mm, it is the perfect candidate for studying the growth in the inner envelope and their dust properties.
Parameters from literature.
2.2 Submillimeter Array observations
The Submillimeter Array (SMA) data shown in this paper are from the MASSES legacy program (Mass Assembly of Stellar Systems and their Evolution with the SMA, PI: I.W. Stephens, M. Dunham; e.g., Stephens et al. 2018).
Per-emb-50 was observed at 1.3 mm with the receiver centered at 220.69 GHz, in the Extended (eight antennas) and Subcompact (seven antennas) configuration with the ASIC (Application Specific Integrated Circuit) correlator during September 2015 and November 2014, respectively. Additionally, Per-emb-50 was observed during October 2015 with the SWARM (SMA Wideband Astronomical ROACH2 Machine) correlator at 1.3 mm in extended configuration (see Table 2 for more details). Weather conditions were good, with zenith optical depths at 220 GHz of τ220 = 0.07–0.15.
Calibration was done in MIR software package1, while imaging was done in MIRIAD software package (Sault et al. 1995), using the standard calibration procedure. We inspected the amplitudes and phases of the calibrators on each baseline in order to look for variations or noisy data, which were manually flagged. Corrections for system temperatures were applied in order to calibrate the atmosphere attenuation in the visibility amplitudes. Detailed information of the calibration can be found in Stephens et al. (2018).
The quasars 3C454.3 and 3C84 were used as bandpass and phase calibrators. The absolute flux was calibrated on Uranus, with ~20% flux calibration uncertainty. For the purpose of this work, we use the 1.3 mm data in the Subcompact and Extended array configurations, with projected baselines in the range of 23–119 kλ. The resulting combined beam was 1.′′72 × 1.′′ 40 at PA 50.80°.
Summary of observations.
2.3 NOEMA observations
The 2.7 mm data presented in this work were obtained with NOEMA, the IRAM2 NOrthern Extended Millimeter Array. The observations were performed on November 6 and 12, 2016. The array was in the C compact configuration, with eight antennas (8C) in operation during the first track, and six antennas (6C) in operation for the second. Antennas were based on stations E10, W20, W10, N20*, E18, N11*3, N17 and E04. The projected baselines were from 7.8 and 102 kλ.
Per-emb-50 was observed for hour angles from −5.8 to 1.5 h for 8C, and from −5.3 to 1.4 h for 6C. In total we spent 9 h on source. The source 0333+321 was used as phase/amplitude calibrator. The sources LkHa101 and MWC349 were used for the flux calibration, while the quasars 3C84 and 3C454.3 were used for the bandpass calibration. We consider an absolute flux uncertainty of 10%. The total bandpass for the 110 GHz continuum measurement was 2 GHz. Data reduction and image synthesis were carried out using the GILDAS software (Guilloteau & Lucas 2000) with the procedure of MAPPING> Selfcal. The continuum map (Fig. 2) was produced using natural weighting and the resulting beam size is 2.′′1 × 1.′′ 6 at P.A. 34.84°. The clean map has a rms noise level of2.1 mJy beam−1.
 |
Fig. 2 Real and imaginary parts of the measured visibilities of Per-emb-50 as a function of the deprojected baseline, assuming the PA and i from Table 1. The data are averaged in 8 kλ bins. The error bars in the real parts show the statistical standard errors of visibilities in each bin. Red and blue shaded areas show the 20 and 10% flux calibration uncertainties of the SMA and NOEMA data, respectively. Red and blue dashed lines are the disk average fluxes using baselines larger than 47 kλ. |
3 Observational analysis
Since we are working with interferometric data, the best way to analyze our source is by working on the visibility domain. This is to avoid biases in the model–data comparison that are introduced by the CLEAN algorithm, uv sampling, and the imaging process.
In Fig. 2 we plot the real visibility as a function of the deprojected baseline length (uv -distance). The deprojected uv-distances are given by ![$R\;{=}\;\sqrt{\smash[b]{d_{a}^{2} + d_{b}^{2}}}$](/articles/aa/full_html/2019/03/aa33666-18/aa33666-18-eq1.png) , where
, where 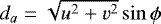 and
and 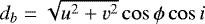 , ϕ = arctan (v∕u) −PA (Lay et al. 1997). The values for inclination i, and positionangle, PA, are presented in Table 1.
, ϕ = arctan (v∕u) −PA (Lay et al. 1997). The values for inclination i, and positionangle, PA, are presented in Table 1.
In Fig. 3, we show images of the SMA and NOEMA observations. Per-emb-50 appears as a point source in these two images, so we do not resolve the embedded disk. Consequently, since the disk is unresolved, then it contributes as a constant component at all baselines. At long baselines, we expect that the amplitude of the visibility is dominated by the disk component, while in shorter baselines the resolved envelope dominates.
For Per-emb-50, the value of the amplitudes start becoming constant above 47 kλ (see Fig. 2) for both wavelengths. We assume that the emission from those baselines belongs to the embedded disk, where the average values at 2.7 and 1.3 mm are: 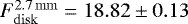 mJy and
mJy and 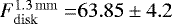 mJy.
mJy.
The spectral index αmm can be calculated through the flux ratio between two wavelengths,
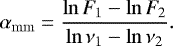 (1)
(1)
Using the fluxes between the uv ranges 47–80 kλ at 1.3 and 2.7 mm, we obtain the average value αmm in the unresolved disk, which is αdisk = 1.71 ± 0.3.
As shown in the Fig. 2, an excess of emission is present at short baselines (<47 kλ) at 2.7 and 1.3 mm, which correspond to physical scales of 1500–3000 AU. The excess values at these baselines, after subtracting the disk visibilities, are 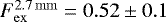 mJy and
mJy and 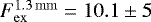 mJy. The excess, even if not very pronounced at 2.7 mm, is detected at 1.3 mm, therefore this indicates the presence of extended emission related to the inner envelope. Considering the average fluxes at these very short baselines, and using the same uv distances ranges at both wavelengths, we recover a greater average value for αenv than the typical ISM values, αenv = 4.0 ± 0.8.
mJy. The excess, even if not very pronounced at 2.7 mm, is detected at 1.3 mm, therefore this indicates the presence of extended emission related to the inner envelope. Considering the average fluxes at these very short baselines, and using the same uv distances ranges at both wavelengths, we recover a greater average value for αenv than the typical ISM values, αenv = 4.0 ± 0.8.
The uncertainties in αdisk and αenv are estimated following the procedure shown in Appendix A, with the absolute flux uncertainty of 10% for 2.7 mm data and 20% for 1.3 mm data added in quadrature. We present αenv and its change as a function of deprojected baseline in Fig. 4. If we translate this value to the spectral index of the dust opacity, we obtain βenv ~ 2.0, which is similar to the values found in the ISM.
These preliminary results are showing a discrepancy with previous studies on spectral indexes in Class I protostar or even younger sources with dust opacityindexes αmm < 3 (Miotello et al. 2014; Kwon et al. 2009; Chiang et al. 2012). To investigate possible explanations, we performed a partial and full radiative-transfer modeling on envelope and disk to take into account possible deviations from the optically thin and Rayleigh Jeans regimes, which can affect the values of αmm.
 |
Fig. 3 Continuum map of Per-emb-50 at 1.3 mm (SMA) and 2.7 mm (NOEMA) wavelengths. The synthesized beam FWHM is represented as a white ellipse in the bottom-left corner of each map. For SMA and NOEMA data, the contours start at 76 and 20 mJy beam−1, respectively, and both increase in 25% intervals. |
 |
Fig. 4 Spectral index of the envelope as a function of deprojected baseline. The black dashed line represents the typical value of α ~ 3.7 related to grain properties in the diffuse interstellar medium. |
4 Modeling
In order to model the Class I protostar and compare with the observations, we consider appropriate physical structure and conditions of the source, including the envelope structure, density, properties of the dust grains, and we predict the 1.3 and 2.7 mm emission with a uv modeling described below.
In the first step, we fit the Per-emb-50 data with a parametric modeling in uv space (Sect. 4.1) in order to address the α values, as well as visibility comparisons. Afterward, we use the radiative-transfer tool RADMC-3D (Dullemond et al. 2012) in two ways: (a) to apply the modeling approach of Miotello et al. (2014), where the disk and envelope are modeled separately (Sect. 4.2) and (b) to compute the emission for the new modeling presented in this work, including a self-consistent radiative-transfer model for the disk and the envelope (Sect. 4.3). In the following sections, we discuss and compare thedetails of the results of each modeling case.
4.1 Parametric model
4.1.1 Disk and envelope modeling
We implement a model that consists of an extended envelope described by a Gaussian, and an unresolved disk (point source) that has constant flux at all baselines. Therefore, the combined amplitude profile, which depends on the uv distance, defined as 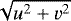 , and frequency, ν, is described by:
, and frequency, ν, is described by:
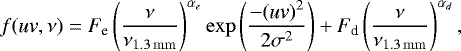 (2)
(2)
where Fe and Fd are the flux density from the Gaussian emission (extended envelope) and point source emission (unresolved disk) respectively, αe and αd are the spectral indexes of the two components, and σ is the width of the Gaussian given by σ ≈FWHM∕2.355.
In this simple model, we first set the flux from the disk at 1.3 mm based on the average value reported in Sect. 3, Fd = 63 mJy. Then, four parameters are explored: Fe, αe, αd and σ. The Markov chain Monte Carlo (MCMC) method, implemented as a python package emcee (Foreman-Mackey et al. 2013), is used to calculate the posterior probability distributions of each of these parameters. For each model we used the 750 steps after the burn-in and 400 walkers (see Appendix B for more details). The results from this simple model are discussed in the following section.
4.1.2 Parametric model results
In Fig. 5, model visibilities are compared with observational data at each uv sample and wavelength. In Table 3 we present the best-fit parameters found for this parametric model. The values of the flux spectral index in the disk and envelope are consistent with the observational analysis (see Sect. 3), but their errors are highly dominated by the systematic error of absolute fluxes and the statistical error of the data. We estimate that the uncertainty on αmm for the envelope and disk using a simplistic approximation for noncorrelated errors is ± 0.3.
Additionally, from this simple model we can constrain the size of the region where the envelope emission arises, which has a 1-σ width (from Table 3) of 43 kλ (1405 AU). From the model we can derive the flux from the disk at 2.7 mm and the prediction of the total flux at baseline = 0 kλ or zero spacing flux, 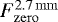 and
and 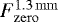 . The results are shown in Table 4.
. The results are shown in Table 4.
We use the derived parameters from our parametric model (Table 4) to estimate the zero-spacing flux at 1.1 mm, 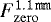 . We find the flux is only 127.4 mJy beam−1 which is much lower than the single dish flux of 612 ± 18 mJy reported by Enoch et al. (2006). This discrepancy is related to the resolution of the observations. While our interferometric data are sensitive to the inner envelope of this source, the 31′′ beam size of Bolocam recovers the extended emission, which is affected by blending effects, especially in a crowded region such as NGC 1333 (see Fig. 1).
. We find the flux is only 127.4 mJy beam−1 which is much lower than the single dish flux of 612 ± 18 mJy reported by Enoch et al. (2006). This discrepancy is related to the resolution of the observations. While our interferometric data are sensitive to the inner envelope of this source, the 31′′ beam size of Bolocam recovers the extended emission, which is affected by blending effects, especially in a crowded region such as NGC 1333 (see Fig. 1).
Since this simple model is not taking into account properties of the dust grains and density profiles for both the envelope and disk, we also analyze Per-emb-50 with more detailed dust radiative-transfer models.
 |
Fig. 5 Black points are the real part of the visibilities as a function of the baseline length. Red curves show the best-fit model, whilethe dashed and dotted lines indicate its point source and Gaussian components, respectively. Bottom panels: residual between the model and data. |
Best parametric model.
4.2 Two-step model
For this model, we adopted the procedure described by Miotello et al. (2014), where they analyzed two Class I protostars with a two-step model. The disk is modeled adopting the two-layer model by Dullemond et al. (2001), whose output spectrum is taken as the central source of illumination in the envelope model. The envelope, on the other hand, is modeled using RADMC-3D (Dullemond et al. 2012).
4.2.1 Modeling protostar and disk
We adopt a simple disk model heated by protostellar radiation. We calculate the properties of the central protostar, assuming that it emits black body radiation, characterized by a radius R⋆, effective temperatureTeff, and mass M⋆. To obtain Teff we assume that Per-emb-50 lies along the birthline for intermediate mass stars by Palla & Stahler (1990). Given the rescaled bolometric luminosity Lbol reported in Table 1, we estimate Teff = 5011 K. With Lbol and Teff, we can estimate Reff using the Stefan-Boltzmann law:
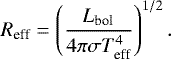 (3)
(3)
Subsequently, with Reff = 5.01 R⊙, we use the mass-versus-radius relation for a spherical protostar accreting at a rate of 10−5 M⊙ yr−1 from Palla & Stahler (1991), to deduce an effective mass of Meff = 2.9 M⊙ (Table 5). Additionally, we add a disk structure defined by an inner and outer radius, rin and rout, an inclination angle i, and a dust surface density profile that follows a simple power law,
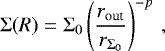 (4)
(4)
where Σ0 is the surface dust density fixedat 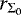 = 1 AU from the central protostar, and where p = 1 since the quality of the data is not sensitive enough to discriminate between different values of p. The disk inclination i is fixed to 67° as found bySegura-Cox et al. (2016). Since the millimeter-SED is not sensitive to rin, we set rin = 0.1 AU. rout and Mdisk can be constrained by our observations assuming a dust opacity (see Sect. 4.2.3) and gas-to-dust mass ratio of 100.
= 1 AU from the central protostar, and where p = 1 since the quality of the data is not sensitive enough to discriminate between different values of p. The disk inclination i is fixed to 67° as found bySegura-Cox et al. (2016). Since the millimeter-SED is not sensitive to rin, we set rin = 0.1 AU. rout and Mdisk can be constrained by our observations assuming a dust opacity (see Sect. 4.2.3) and gas-to-dust mass ratio of 100.
Derived parameters from parametric model.
4.2.2 Modeling the envelope
We adopted the rotating and collapsing spheroid structure by Ulrich (1976) to model the envelope. The density of this envelope structure is given by,
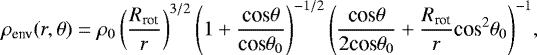 (5)
(5)
where ρ0 is the density in the equatorial plane at the centrifugal radius Rrot of the envelope, and θ0 is the solution of the parabolic motion of an infalling particle given by:
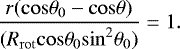 (6)
(6)
The outer radius of the envelope is fixed at 8800 AU, which is equivalent to the 30′′ aperture of Bolocam. In this case we use the envelope mass derived by Bolocam to compare with the models. We computed ρ0 by imposing a total envelope mass Menv, and Rrot, which can have a significant influence on the amplitude as a function of baseline, it was left free to vary. Outflow cavities are not included in this model.
RADMC-3D is used to compute the temperature of the envelope, with the implementation of Eq. (5) to describe the density structure. The protostar and disk system presented in the previoussubsections are used as the heating source of the envelope, whose emission is calculated using the two-layer model by Dullemond et al. (2001), and then the output spectrum is used in the 2D radiative-transfer calculation for the envelope structure.
4.2.3 Dust opacity
We adopt the dust opacity model used in Ricci et al. (2010). A dust population characterized by a distribution of grains with different sizes was implemented. We used a truncated power-law distribution n(a) ∝ a−q, between a minimum and a maximum grain size, amin and amax respectively. We fixed the chemical composition to a silicate, carbonaceous material and water ice in a 1:2:3 volume fractional ratio. Additionally, we set amin = 0.01 μm and we use q = 3.0. We varied 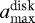 and
and 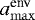 according tothe range presented in Table 5.
according tothe range presented in Table 5.
4.2.4 Model fitting
To compare the model with the interferometric observations, we have to create images at the exact wavelengths of our observations. Subsequently, those model images have to be transformed to model visibilities. For that we used the computational library GALARIO (Tazzari et al. 2018). The model image is convolved with the primary beam patterns of the antennas and then Fourier transformed into visibilities.
The first step in this modeling is to fit the disk emission. We created a grid of parameters varying Mdisk, Rout and amax to reproduce together 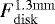 and
and 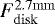 . Once we found the three parameters that match F
. Once we found the three parameters that match F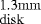 = 63.97 mJy and F
= 63.97 mJy and F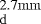 = 18.8 mJy, we implement these output fluxes (output spectrum) as the heating central source of the envelope.
= 18.8 mJy, we implement these output fluxes (output spectrum) as the heating central source of the envelope.
Using RADMC-3D (Dullemond et al. 2012), we then vary Menv and 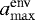 in order to reproduce the interferometric fluxes at 1.3 and 2.7 mm. Table 5 gives a complete list of model parameters and indicates whether they are fixed or varied. In Fig. 6 we present the best fit for the observed visibilities at both wavelengths. The set of parameters that provided the best match with the observations is presented in Table 6. The two best fits are discussed in the following section.
in order to reproduce the interferometric fluxes at 1.3 and 2.7 mm. Table 5 gives a complete list of model parameters and indicates whether they are fixed or varied. In Fig. 6 we present the best fit for the observed visibilities at both wavelengths. The set of parameters that provided the best match with the observations is presented in Table 6. The two best fits are discussed in the following section.
4.2.5 Results from the two step model
The parameters that provide a good fit respect to the disk emission at both wavelengths are reported in Table 6. The model M1 with a 32 AU disk radius and Mdisk = 0.4M⊙ is consistentwith the rescaled values reported by Segura-Cox et al. (2016). While all the disk models match the long baseline 1.3 mm data, the disk emission at 2.7 mm is 15% lower than the data. On the other hand, the disk model M2, with a 34 AU disk radius and Mdisk = 0.2M⊙ matches very well the observations at both wavelengths, but compared with values of Table 1, the disk radius is slightly larger.
The differences in the disk models may be due to the assumed values of κν = 0.00146 cm2 g −1 and disk temperatures of 20 and 40 K in Segura-Cox et al. (2016). Therefore, higher resolution millimeter observations that resolve the disk are needed to put much stronger constraints on Per-emb-50.
For the envelope, we explore the effects of changing Rrot, amax and ρ0. The envelope inner radius is fixed at the outer radius of the disk model. We tested different Rrot between 100 and 1000 AU to accommodate the total enclosed envelope mass. As mentioned in Crapsi et al. (2008), decreasing the centrifugal radius results in more peaked and spherical envelopes. Using a small centrifugal radius has a significant influence on the amplitude at short baseline length. For example varying the centrifugal radius by a factor of two changes the first amplitude point of the model by 20%. We found that a Rrot of 600 AU is consistent with the slope at short baselines in both wavelengths.
We can constrain the level of grain sizes in the envelope within the framework of the collapsing rotating envelope model. For example, in Fig. 6, if we consider a dust grain size distribution in the envelope with a maximum size of 1 mm, we can reproduce the 1.3 mm observations, but we underestimate the total envelope mass by a factor of six. In the case of models with 0.1 μm < amax < 100μm, the flux at 1.3 and 2.7 mm matches the observations very well, but the derived envelope masses differ from those derived from observations. The best match with the 2.2 M⊙ envelope mass derived by Enoch et al. (2009) are those derived from models with dust grain sizes of amax ≤ 50 μm (see Table 6). The models with amax = 100 μm recover almost 60% of the envelope mass. Table 7 presents the derived masses for the envelope using different amax in M1 and M2.
A distribution of grains with amax ≤ 50 μm provides a good match with the observations since the flat emission at 2.7 mm matches the observations well and is consistent with the systematic errors due the flux calibration.
Based on this model, the maximum grain sizes in the envelope are unlikely to be larger than a hundred microns. This would imply that the envelope may have gone through a process of grain growth, but there is no evidence that a substantial fraction of grains are large millimeter-sized dust aggregates.
As we mention before, the observed flux and spectral index of Per-emb-50 are consistent with a small optically thick disk, in which case, we cannot constrain the spectral index α.
For the envelope we can use our dust model to infer the value of β, which is βenv = 1.46 and βenv = 1.63 for amax = 10 and amax = 50 μm, respectively. In Fig. 7 we compare the different β values for each amax with the value obtained from the parametric model. The β values for 0.1 μm < amax < 100 μm are consistent, within the uncertainties, with the β calculated using the parametric model. In the case of grains larger than 100 μm, the total envelope mass is underestimated.
Two-step model grid parameters.
Two-step model best-fit parameters.
 |
Fig. 6 Realpart of the visibilities as a function of baseline. Left panels: 1.3 mm data. Right panels: 2.7 mm data. Upper panels: models with the disk model M1. Bottom panels: models using disk model M2 (see Table 6). In solid lines we present models with grain sizes of amax ≤ 100 μm. In dashed lines are models with grain sizes of amax = 300, 1000 μm. The best fits are the models with a distribution of grain sizes with amax ≤ 100μm. The red shaded region is the uncertainty on the data due to flux calibration. The bottom of each panel shows the residuals between the data and the model with different amax. |
4.3 Full radiative-transfer model
In this model we used a system that consists of disk, protostar, envelope and outflow cavity. We used the radiative-transfer tool RADMC-3D from Dullemond et al. (2012) to compute the emission from all the contributions. The details of each contribution will be discussed in the following sections.
4.3.1 Disk model
We adopt adisk model heated by its protostellar radiation. The surface density profile Σ(R) was modeled as a truncated power law as in Eq. (4), with a power exponent of the surface density distribution p = 1; Σ0 is scaled to accommodate the total mass of the disk Mdisk. The 2D volume density with an exponential vertical profile is defined by
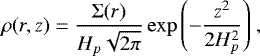 (7)
(7)
where Hp is the pressure scale height and is defined as Hp ∕r = 0.1(r/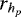 )ϕ,
)ϕ, 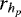 is the reference radius set at 25 AU, and ϕ is the flaring index of the disk, which in this case is set to 1.14, as an average value according to previous studies on young sources (Pineda et al. 2011; Tobin et al. 2013). We used the disk inclination angle, disk radius, and disk mass presented in Table 1.
is the reference radius set at 25 AU, and ϕ is the flaring index of the disk, which in this case is set to 1.14, as an average value according to previous studies on young sources (Pineda et al. 2011; Tobin et al. 2013). We used the disk inclination angle, disk radius, and disk mass presented in Table 1.
4.3.2 Envelope model
For the envelope model we adopted a density profile by Tafalla et al. (2002), which combines a power-law behavior for large radius and a central flattening profile at small radius, that is,
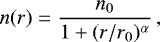 (8)
(8)
where n0 is the central density, r0 is the radius of the flat region or truncation radius, and α is the asymptotic power index. The outer radius of the envelope is fixed at 8800 AU to match the beam of Enoch et al. (2009) observations, in which the rescaled envelope mass is 2.2 M⊙. Additionally, since we have evidence of an outflow in this source (Stephens et al. 2017), we included an outflow cavity with an opening angle of 30° (M. Dunham, priv. comm.) and a lower density of 1.0 × 10−30 g cm −3 for the region inside the cavity and the background.
 |
Fig. 7 Left panel: dust absorption opacity as a function of wavelength for grain size distributions characterized by (a) ∝ a−3.0 and increasing maximum grain size (amax). Right panel: dust opacity spectral index (β) calculated between 1.3 and 2.7 mm wavelengths as a function of the maximum grain size. Black solid line is the βenv value from the parametric model and the black dashed lines are the uncertainties. Green region shows an upper limit for amax in the envelope of Per-emb-50. |
Derived envelope masses.
4.3.3 Backwarming effect
The effects of the envelope thermal emission on disk (i.e., backwarming) have been studied in different environment, as in the case of the heavily embedded source L1551 IRS 5 (Butner et al. 1994).
In the case of an envelope around a disk, the millimeter emission of the disk increases. This is because the envelope acts as a thermal cavity, preventing the temperature within the cavity from falling below the temperature of the envelope wall. Therefore, a substantial backwarming effect on the disk can be present depending on the optical depth and geometry of the cavity.
In the previous envelope modeling following Miotello et al. (2014), this effect was ignored due the geometry of the envelope. Different profiles might heat the disk to a different degree. To explore the effects of backwarming we have computed new models which attempt to take it into account. The net effect of the envelope on the disk temperature is discussed in the Appendix D.
4.3.4 Dust opacity
We used two kinds of dust opacities in order to test the model. Firstly, we used the opacity computed in Ossenkopf & Henning (1994) based on a coagulated grain size distribution. In this model, a truncated power law is adopted for the initial dust distribution, n(a) ∝ a−q, where the minimum size of the grain is amin = 5 nm, the maximum size is amax = 250 nm and the power index q is set to 3.5. The dust distribution is calculated after 105 yr of coagulation with a gas density of nH = 105 cm−3 expected in a prestellar core. Secondly, we used the previous dust opacities presented in Sect. 4.2.3.
Since the second dust opacity approach covers maximum grain sizes from small grains of 0.1 μm, to big grains of1 cm, we decided to present here the results with those opacities to compare consistently with the previous modeling.
4.3.5 Model fitting
The free parameters for the disk are the outer radius, rout and the disk surface density Σ0. The free parameters for the envelope are its mass Menv, its power-law density profile α, its flattening envelope radius r0, and its dust opacity, characterized by 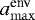 . The truncation radius of the envelope is set at the outer radius of the disk parameter.
. The truncation radius of the envelope is set at the outer radius of the disk parameter.
Since the disk parameters estimated by Segura-Cox et al. (2016) are not solid constraints, we test our model using their mass and outer radius values as an upper and lower limit on Σ0. The grid of parameters that we test and set are presented in Table 8. Once the dust temperature of the system is calculated from the input parameters of Table 8, we compute the synthetic images, for 1.3 and 2.7 mm, following the same procedure reported in Sect. 4.2.4. We simultaneously fit the 1.3 and 2.7 mm visibilities by calculating χ2 values for each model using the equation
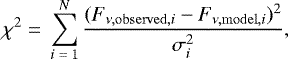 (9)
(9)
for the entire set of visibility points between 20 and 110 kλ. The uncertainty in the data, σi, includes the statistical uncertainty and the absolute flux uncertainty of 10% for 2.7 mm data and 20% for 1.3 mm data, both added in quadrature. Since our observational constraints are dominated by the errors of the data sets, it is possible that the disk and/or envelope structure could be inaccurate at some level. Therefore, our χ2 value is simply an indicator of an acceptable model, not a best fit. After performing a visual inspection of the models, we report the best match with the observations in the following paragraph and in Table 9.
A sample of models with different amax and derived envelope masses is presented in the Appendix C.1.
Full radiative-transfer model grid parameters.
4.3.6 Results from the full radiative-transfer model
From our interferometric observations, we are limited to studying the inner regions of the envelope, from 4000 to 600 AU. Therefore, we examine a power-law density profile following Tafalla et al. (2002). An unresolved component is included to represent a compact disk structure. In the envelope we used a constant dust grain population, in which we vary the maximum grain size from 0.1 to 1000 μm. To study the impact of the maximum grain size in the envelope, 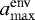 , the central density, n0, and the density power law index, α, we used the range of parameters reported in Table 8.
, the central density, n0, and the density power law index, α, we used the range of parameters reported in Table 8.
Table 9 shows the model parameters that provides the best fits to the observations. For the disk properties, we compare our results with the values reported in Table 1. Our disk mass and radius are consistent with the rescaled values reported by Segura-Cox et al. (2016). Both disk models in Per-emb-50 are consistent with a small optically thick disk, but do not allow us to probe if there is grain growth throughout the disk since we are missing very long baselines to resolve the disk.
Similar to the results of the two-step model, the full radiative-transfer models suggest a distribution of dust grains in the envelope with maximum size 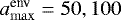 μm and a resulting envelope mass within 8800 AU radius of Menv ~ 2.24, 1.54 M⊙, respectively.In Fig. 8, we present a variety of models with different amax in the envelopethat match the visibility data. While all the models match the 1.3 mm data within the flux uncertainty (red region), the 2.7 mm data allow us to determine a good model because of the shape of the short-baseline emission.
μm and a resulting envelope mass within 8800 AU radius of Menv ~ 2.24, 1.54 M⊙, respectively.In Fig. 8, we present a variety of models with different amax in the envelopethat match the visibility data. While all the models match the 1.3 mm data within the flux uncertainty (red region), the 2.7 mm data allow us to determine a good model because of the shape of the short-baseline emission.
Models with 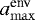 < 100 μm follow the flat emission of the 2.7 mm data, while models with
< 100 μm follow the flat emission of the 2.7 mm data, while models with 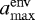 > 300 μm overestimate the short baseline emission at 2.7mm and underestimate the envelope mass of Table 1. These results are consistent with our previous modeling and in agreement with the spectral index β that we calculated in Fig. 7. We also reported the 1.1 mm single dish flux (see Table 10) for each model.
> 300 μm overestimate the short baseline emission at 2.7mm and underestimate the envelope mass of Table 1. These results are consistent with our previous modeling and in agreement with the spectral index β that we calculated in Fig. 7. We also reported the 1.1 mm single dish flux (see Table 10) for each model.
As discussed by many authors (Draine 2006; Banzatti et al. 2011; Testi et al. 2014), it is quite difficult to explain values of β of less than 1 without invoking the presence of millimeter size grains, regardless of the chemical composition, porosity, or grain geometry. In the case of Per-emb-50, the high value of β is compatible with grains no larger than 100 μm, and with values found in Class 0 sources by I-Hsiu Li et al. (2017). The fact that we find grains that have not reached millimeter sizes in the envelope of Per-emb-50 is discussed in the following section.
5 Discussion
5.1 Grain sizes in Class I protostellar envelopes
The presence of millimeter-sized grains in envelopes of young protostars as Class 0/I, has been studied and modeled by many authors (e.g., Kwon et al. 2009; Chiang et al. 2012; Tobin et al. 2013; Miotello et al. 2014), but current models cannot easily explain growth at that level (Ormel et al. 2009). This is because the models require high number densities, nH > 106 cm−3, to form such large grains on timescales of 1 Myr.
Miotello et al. (2014) found that dust grains start to aggregate up to millimeter sizes already in the envelope of two Class I protostars, producing a change in the spectral index with values of βenv = 0.6 ± 0.3 for Elias 29 and βenv = 0.8 ± 0.7 for WL 12. Those values are smaller than the spectral index for the envelope of Per-emb-50, βenv = 1.4 ± 0.3, by a factor of two. The differences between these studies may be associated with the properties of the star-formingregion. In our case, Per-emb-50 is in the NGC1333 region in Perseus, which is a very crowded region with young stellar objects, while the sources of Miotello et al. (2014) are isolated and embedded in L1688 in Ophiuchus. With this study on Per-emb-50, we suggest the possibility that: (a) millimeter grains in envelopes of young protostars may not be a common result, or (b) the dust grain growth is not a homogeneous process. Finally, the environment within which a protostar forms could also play a role in the amount of dust coagulation, which significantly affects the future formation and structure of the protoplanetary disk, as shown by Zhao et al. (2016, 2018).
The possibility that grains can grow up to millimeter sizes in the envelope of Class 0/I protostars was studied by Wong et al. (2016). They proposed another mechanism to explain the existence of millimeter-sized grains in the envelopes of young protostellar sources that consists of transport of millimeter-sized grains from dense regions close to the protostar to the envelope via the outflow. This scenario is quite plausible before the central mass of the protostar reaches a mass of 0.1 M⊙ with a mass-loss rate of 10−6 M⊙ yr−1. This could be the case for Per-emb-50, but high-resolution data are needed to model the inner regions of this source.
The results of our analysis show that dust grains may have grown as large as ~100 μm in size in the envelope of Per-emb-50 at scales of 4000–2000 AU. This implies that there is a degree of grain growth with respect to the ISM sizes, but not significant enough to lower the value of α. This is also in agreement with the work of Chacón-Tanarro et al. (2017), where they predict grain sizes of a few hundred μm in the central 300 AU of the prestellar core L1544.
Taking this into account, it is crucial to perform surveys for Class I protostars embedded in different environments and at different physical scales to determine the variation of α spectral index and the corresponding amount of grain growth.
Full radiative-transfer best fit models
Derived 1.1 mm fluxes and envelope mass.
 |
Fig. 8 Real part of the visibilities as a function of the deprojected baseline. Left panel: 1.3 mm data. Right panel: 2.7 mm data. Red shaded regions are the uncertainties due the flux calibration. We show a variety of models with a maximum grain size in the envelope of amax = 0.1, 50, 100, 300, 1000 μm. At the bottom of each panel are the residuals between the data and the best model. |
5.2 The effects of backwarming
We find that backwarming is important for modeling Per-emb-50. From the previous analysis, using the two-step modeling, it was straightforward to fit the nearly constant emission at long baselines with an unresolved disk. For the full radiative-transfer modeling, however, this was not the case. Considering the full radiative-transfer model, the use of a Tafalla et al. (2002) density profile combined with a power-law behavior for large radius and a central flattening profile at small radius shows that backwarming is important since the disk emission is completely affected by the addition of the envelope. This change in emission is discussed in Butner et al. (1994) and in the Appendix D.1. To study the effects of different envelope geometries on disk emission is beyond the scope of this work.
However, backwarming can have other consequences. The change of temperature between a backwarmed disk (~100 K) and a nonbackwarmed disk with ~20 K, would significantly affect the gas phase chemistry and the dust mantle chemistry in young disks and envelopes (Butner et al. 1994). Finally, the backwarming in Class I protostars could have an important effect on the thermal history of the outer disks of planetary systems. Detailed studies using proper physical structures and radiative-transfer models are necessary to address the backwarming effect present in most young embedded sources.
6 Conclusions
We present new 1.3 mm data from SMA and 2.7 mm data from NOEMA of the brightest Class I protostar Per-emb-50 in the NGC 1333 cluster in the Perseus star-forming region. In the uv plane it is possible to distinguish the presence of a large-scale envelope at short baselines and an unresolved and optically thick disk at longer uv distances. From the data analysis and the different modeling approaches on this source we can make the following conclusions:
-
For the envelope uv analysis we find a spectral index similar to the typical ISM values, αmm = 3.3 ± 0.3.
-
The current observations on Per-emb-50 and the radiative-transfer modeling reveal a Class I envelope consistent with maximum sized grains of <100 μm. This suggests that grain growth has proceeded within the envelope, but not far enough to produce changes in α as the presence of millimeter-sized grains does.
-
The presence of grains with a size range of <100 μm in envelopes of Class I protostars may have an impact on our understanding of protostellar evolution. Following the prediction from Chacón-Tanarro et al. (2017), who find that dust grains are expected to grow to sizes of a few hundred micrometers in the central 300 AU of a pre-stellar core, we could suggest that the larger grains found in the envelopeof Per-emb-50 may be inherited from the prestellar phase.
-
These results show for the first time no evidence of grain growth to millimeter sizes in the inner regions of the envelope of a Class I protostar, providing an interesting case for future studies of the efficiency of the grain-growth process in these stages.
-
We also explore the effects of backwarming. The analysis shows that the envelope geometry highly affects the disk temperature. In the collapsing envelope model, the effect is weak, but if a power-law envelope is used, the effect is more obvious.
Future high-sensitivity data will be needed to allow us to conclude on whether or not there are spectral index variations between the disk and the envelope. Moreover, the study of a larger sample of Class I sources in different star-forming regions is important to understand how general this process is for grain growth.
Acknowledgements
C.A.G. acknowledges support from CONICYT-Becas Chile (grant 72160297). P.C, J.P and L.S acknowledge the financial support of the European Research Council (ERC; project 320620). L.T. acknowledges the financial support of the Italian Ministero dell’Istruzione, Universitá e Ricerca through the grant Progetti Premiali 2012 – iALMA (CUP C52I13000140001), and by the Deutsche Forschungs-gemeinschaft (DFG, German Research Foundation) – Ref no. FOR 2634/1 TE 1024/1–1. M.T. has been supported by the DISCSIM project, grant agreement 341137 funded by the European Research Council under ERC-2013-ADG. A.M. acknowledges an ESO Fellowship.
Appendix A Error estimate of the spectral index of the observed flux densities
The spectralindex of the observed flux densities αmm can be approximated using the flux density at two wavelengths. In this appendix, we discuss the error propagation from the observational uncertainty to the deduced αmm value. Let F1 and F2 be the flux density at frequencies ν1 and ν2, αmm can be expressed as in Eq. (1):
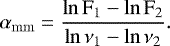 (A.1)
(A.1)
We assume that the fluxes F1 and F2 are independent and that 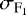 and
and 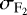 are their standard deviations; using the error propagation we obtain
are their standard deviations; using the error propagation we obtain
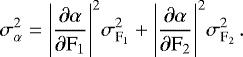 (A.2)
(A.2)
Taking the partial derivative of Eq. (A.1), we obtain
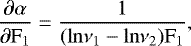 (A.3)
(A.3)
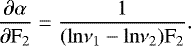 (A.4)
(A.4)
SubstitutingEqs. (A.3) and (A.4) in Eq. (A.2), the uncertainty of the derived αmm is then:
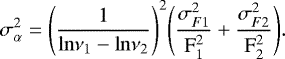 (A.5)
(A.5)
Appendix B emcee implementation
To compute the posterior distribution for all the free parameters, we use a variant of the Markov chain Monte Carlo (MCMC;
Mackay 2003; Press et al. 2007) algorithm, which is widely known and efficient in finding a global maximum for a range of posteriors. We follow the affine-invariant ensemble sampler for MCMC by Goodman & Weare (2010), which basically transforms highly anisotropic and difficult-to-be-sampled multivariate posterior probability distribution function (PDFs) into isotropic Gaussians. The immediate advantage is that it is possible to simultaneously run many Markow chains (walkers) that will interact in order to converge to the maximum of the posterior.
This algorithm involves an ensemble 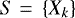 of simultaneously evolving K walkers, where the transition distribution for each walker is based on the current position of the other K − 1 walkers belonging to the complementary ensemble
of simultaneously evolving K walkers, where the transition distribution for each walker is based on the current position of the other K − 1 walkers belonging to the complementary ensemble 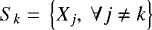 . The position of a walker Xk(t) is updated as follows:
. The position of a walker Xk(t) is updated as follows:
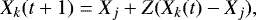 (B.1)
(B.1)
where Xj ∈ Sk and Z is a random variable drawn from a distribution that does not depend on the covariances between the parameters.
In this study we adopted an ensemble of 400 walkers, and let MCMC evolve for an initial burn-in phase. The burn-inphase is needed to allow MCMC to perform a consistent sampling of the space of parameters and to find the posterior maximum. To achieve the posterior maximum is needed to introduce the term: autocorrelation-time4, which is a direct measurement of the number of the posterior PDF evaluations needed to produce independent samples of the target density. For the analysis of Per-emb-50, 750 burn-in steps were performed to achieve convergence. Figure D.1 presents a staircase plot, using the Python module corner by Foreman-Mackey (2016), showing the marginalized and bi-variate probability distributions resulting from the fit for Per-emb-50.
 |
Fig. B.1 Representation of the MCMC results for Per-emb-50. On the top diagonal, the 1D histograms are the marginalized distributions of the fitted parameters; the vertical dashed lines represent (from left to right panels) the 16th, the 50th, and the 84th percentiles. The 2D density plots represent the bi-variate distributions for each pair of parameters, with one dot representing one sample. The plot shows the posterior sampling provided by 1000 steps of the 400-walkers chain (750 burn-in steps were performed to achieve convergence). |
Appendix C Full radiative transfer models
The models presented in this appendix were created using a simple python module to set up RADMC-3D for disk plus envelope systems, SimpleDiskEnv5. Figure C.1. shows the best 36 models from a total of 288 for each maximum grain size (0.1, 50, 100, 300, 1000 μm).
 |
Fig. C.1 Fullradiative-transfer models for different amax. The name of the model and derived envelope mass are in the right panels. The color gradient represents the χ2 from low (blue) to high values (yellow), that were used only as reference. After visual inspection, we chose the best models fromthe green area. |
 |
Fig. C.1 continued. |
Appendix D Backwarming effect
We studied the net effect of the envelope on the disk temperature using a RADMC-3D toy model of a Class I protostar. As mentioned in Butner et al. (1994), the envelope can have an important backwarming effect on the disk, affecting the outer edges of the disk with a flat temperature distribution.
To probe this effect, we first modeled a disk of 25 AU without an envelope and with a distribution of dust grains in the disk with a maximum size 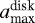 = 1 cm. Then we add a 1.3M⊙ envelope, with a Tafalla et al. (2002) density profile and grain sizes with
= 1 cm. Then we add a 1.3M⊙ envelope, with a Tafalla et al. (2002) density profile and grain sizes with
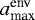 = 100 μm. The inner edge of the envelope and the outer radius of the disk are the same. To compare and quantify the effect, we model a disk with the same characteristics but with a density profile of a collapsing envelope defined by Ulrich (1976). Figure D.1. shows the temperature structure (in cylindrical coordinates) for both of these cases. In the left panels (diskonly) we can see that the outer regions of the disk are around 20–30 K. In the right upper panel (disk+envelope) using the Ulrich (1976) envelope structure, the temperature increases to 40–60 K. In the case of the model with a Tafalla et al. (2002) envelope structure the effect is quite strong, reaching disk outer temperatures of 120–140 K.
= 100 μm. The inner edge of the envelope and the outer radius of the disk are the same. To compare and quantify the effect, we model a disk with the same characteristics but with a density profile of a collapsing envelope defined by Ulrich (1976). Figure D.1. shows the temperature structure (in cylindrical coordinates) for both of these cases. In the left panels (diskonly) we can see that the outer regions of the disk are around 20–30 K. In the right upper panel (disk+envelope) using the Ulrich (1976) envelope structure, the temperature increases to 40–60 K. In the case of the model with a Tafalla et al. (2002) envelope structure the effect is quite strong, reaching disk outer temperatures of 120–140 K.
 |
Fig. D.1 Temperature structure in cylindrical coordinates of two cases. Top left panel: 25 AU disk with
|
References
- Banzatti, A., Testi, L., Isella, A., et al. 2011, A&A, 525, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Ricci, L., Trotta, F., et al. 2010, A&A, 516, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butner, H. M., Natta, A., & Evans, II, N. J. 1994, ApJ, 420, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Henning, T., Chandler, C. J., et al. 2016, ApJ, 821, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Chacón-Tanarro, A., Caselli, P., Bizzocchi, L., et al. 2017, A&A, 606, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, H.-F., Looney, L. W., & Tobin, J. J. 2012, ApJ, 756, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., van Dishoeck, E. F., Hogerheijde, M. R., Pontoppidan, K. M., & Dullemond, C. P. 2008, A&A, 486, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. App. Math. Comp. Sci., 5, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., & Lucas, R. 2000, in Imaging at Radio through Submillimeter Wavelengths, eds. J. G. Mangum & S. J. E. Radford, ASP Conf. Ser, 217, 299 [NASA ADS] [Google Scholar]
- Hirota, T., Bushimata, T., Choi, Y. K., et al. 2008, PASJ, 60, 37 [NASA ADS] [CrossRef] [Google Scholar]
- I-Hsiu Li, J., Liu, H. B., Hasegawa, Y., & Hirano, N. 2017, ApJ, 840, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2007, ApJ, 659, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., Chiang, H.-F., & Kemball, A. J. 2009, ApJ, 696, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lay, O. P., Carlstrom, J. E., & Hills, R. E. 1997, ApJ, 489, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. J. C. 2003, Information Theory, Inference and Learning Algorithms (Cambridge: Cambridge University Press), 640 [Google Scholar]
- Miotello, A., Testi, L., Lodato, G., et al. 2014, A&A, 567, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, Protostars and Planets V, (Tucson, AZ: University of Arizona Press), 767 [Google Scholar]
- Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, 502, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 865, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palla, F., & Stahler, S. W. 1990, ApJ, 360, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1991, ApJ, 375, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Chandler, C. J., Isella, A., et al. 2015, ApJ, 813, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Arce, H. G., Schnee, S., et al. 2011, ApJ, 743, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 2007, Numerical Recipes: The Art of Scientific Computing, 3rd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [NASA ADS] [Google Scholar]
- Segura-Cox, D. M., Harris, R. J., Tobin, J. J., et al. 2016, ApJ, 817, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Dunham, M. M., Myers, P. C., et al. 2017, ApJ, 846, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Dunham, M. M., Myers, P. C., et al. 2018, ApJS, 237, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A&A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tazzari, M., Beaujean, F., & Testi, L. 2018, MNRAS, 476, 4527 [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 339 [Google Scholar]
- Tobin, J. J., Hartmann, L., Chiang, H.-F., et al. 2013, ApJ, 771, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 1976, ApJ, 210, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, Y. H. V., Hirashita, H., & Li, Z.-Y. 2016, PASJ, 68, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., et al. 2016, MNRAS, 460, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., & Krasnopolsky, R. 2018, MNRAS, 473, 4868 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Schlafly, E. F., Speagle, J. S., et al. 2018, ApJ, 869, 83 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panel: continuum map of the NGC1333 complex at 1.1 mm wavelength. Right panel: zoom-in to the direct environment of Per-emb-50. The map is adapted from the Bolocam survey at the Caltech Submillimeter Observatory (CSO) by Enoch et al. (2006). |
| In the text | |
 |
Fig. 2 Real and imaginary parts of the measured visibilities of Per-emb-50 as a function of the deprojected baseline, assuming the PA and i from Table 1. The data are averaged in 8 kλ bins. The error bars in the real parts show the statistical standard errors of visibilities in each bin. Red and blue shaded areas show the 20 and 10% flux calibration uncertainties of the SMA and NOEMA data, respectively. Red and blue dashed lines are the disk average fluxes using baselines larger than 47 kλ. |
| In the text | |
 |
Fig. 3 Continuum map of Per-emb-50 at 1.3 mm (SMA) and 2.7 mm (NOEMA) wavelengths. The synthesized beam FWHM is represented as a white ellipse in the bottom-left corner of each map. For SMA and NOEMA data, the contours start at 76 and 20 mJy beam−1, respectively, and both increase in 25% intervals. |
| In the text | |
 |
Fig. 4 Spectral index of the envelope as a function of deprojected baseline. The black dashed line represents the typical value of α ~ 3.7 related to grain properties in the diffuse interstellar medium. |
| In the text | |
 |
Fig. 5 Black points are the real part of the visibilities as a function of the baseline length. Red curves show the best-fit model, whilethe dashed and dotted lines indicate its point source and Gaussian components, respectively. Bottom panels: residual between the model and data. |
| In the text | |
 |
Fig. 6 Realpart of the visibilities as a function of baseline. Left panels: 1.3 mm data. Right panels: 2.7 mm data. Upper panels: models with the disk model M1. Bottom panels: models using disk model M2 (see Table 6). In solid lines we present models with grain sizes of amax ≤ 100 μm. In dashed lines are models with grain sizes of amax = 300, 1000 μm. The best fits are the models with a distribution of grain sizes with amax ≤ 100μm. The red shaded region is the uncertainty on the data due to flux calibration. The bottom of each panel shows the residuals between the data and the model with different amax. |
| In the text | |
 |
Fig. 7 Left panel: dust absorption opacity as a function of wavelength for grain size distributions characterized by (a) ∝ a−3.0 and increasing maximum grain size (amax). Right panel: dust opacity spectral index (β) calculated between 1.3 and 2.7 mm wavelengths as a function of the maximum grain size. Black solid line is the βenv value from the parametric model and the black dashed lines are the uncertainties. Green region shows an upper limit for amax in the envelope of Per-emb-50. |
| In the text | |
 |
Fig. 8 Real part of the visibilities as a function of the deprojected baseline. Left panel: 1.3 mm data. Right panel: 2.7 mm data. Red shaded regions are the uncertainties due the flux calibration. We show a variety of models with a maximum grain size in the envelope of amax = 0.1, 50, 100, 300, 1000 μm. At the bottom of each panel are the residuals between the data and the best model. |
| In the text | |
 |
Fig. B.1 Representation of the MCMC results for Per-emb-50. On the top diagonal, the 1D histograms are the marginalized distributions of the fitted parameters; the vertical dashed lines represent (from left to right panels) the 16th, the 50th, and the 84th percentiles. The 2D density plots represent the bi-variate distributions for each pair of parameters, with one dot representing one sample. The plot shows the posterior sampling provided by 1000 steps of the 400-walkers chain (750 burn-in steps were performed to achieve convergence). |
| In the text | |
 |
Fig. C.1 Fullradiative-transfer models for different amax. The name of the model and derived envelope mass are in the right panels. The color gradient represents the χ2 from low (blue) to high values (yellow), that were used only as reference. After visual inspection, we chose the best models fromthe green area. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. D.1 Temperature structure in cylindrical coordinates of two cases. Top left panel: 25 AU disk with
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.