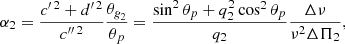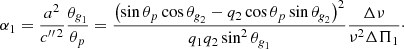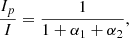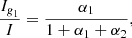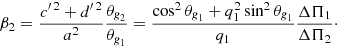| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 23 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833409 | |
| Published online | 03 December 2018 | |
Seismic characterization of red giants going through the helium-core flash
1 IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse, France
e-mail: sebastien.deheuvels@irap.omp.eu
2 LESIA, Observatoire de Paris, PSL Research University, CNRS, Université Pierre et Marie Curie, Université Denis Diderot, 92195 Meudon, France
Received:
11
May
2018
Accepted:
31
August
2018
Context. First-ascent red giants in the approximate mass range 0.7 ≲ M/M⊙ ≲ 2 ignite helium in their degenerate core as a flash. Stellar evolution codes predict that the He flash consists of a series of consecutive subflashes. Observational evidence of the existence of the He flash and subflashes is lacking. The detection of mixed modes in red giants from space missions CoRoT and Kepler has opened new opportunities to search for such evidence.
Aims. During a subflash, the He-burning shell is convective, which splits the cavity of gravity modes in two. We here investigate how this additional cavity modifies the oscillation spectrum of the star. We also address the question of the detectability of the modes, to determine whether they could be used to seismically identify red giants passing through the He flash.
Methods. We calculate the asymptotic mode frequencies of stellar models going through a He subflash using the Jeffreys-Wentzel-Kramers-Brillouin (JWKB) approximation. To predict the detectability of the modes, we estimate their expected heights, taking into account the effects of radiative damping in the core. Our results are then compared to the oscillation spectra obtained by numerically calculating the mode frequencies during a He subflash.
Results. We show that during a He subflash, the detectable oscillation spectrum mainly consists of modes trapped in the acoustic cavity and in the outer g-mode cavity. The spectrum should thus at first sight resemble that of a core-helium-burning giant. However, we find a list of clear, detectable features that could enable us to identify red giants passing through a He subflash. In particular, during a He subflash, several modes that are trapped in the innermost g-mode cavity are expected to be detectable. We show that these modes could be identified by their frequencies or by their rotational splittings. Other features, such as the measured period spacing of gravity modes or the location of the H-burning shell within the g-mode cavity could also be used to identify stars going through a He subflash.
Conclusions. The features derived in this study can now be searched for in the large datasets provided by the CoRoT and Kepler missions.
Key words: stars: evolution / stars: oscillations (including pulsations)
© ESO 2018
1. Introduction
Stars in the mass range 0.7 ≲ M/M⊙ ≲ 2 ignite He in their core under conditions of strong electron degeneracy, which results in a thermal runaway known as the He core flash. The basic features of the He core flash have been known since numerical models of stellar evolution were followed from the tip of the red giant branch (RGB) to the core He-burning phase (Härm & Schwarzschild 1964; Thomas 1967). It is well established that He is ignited off-center, in the layers of maximal temperature, because of the energy carried away by neutrinos in the center of the star. Instead of expanding and cooling, these layers are further heated owing to the degeneracy of electrons, which results in a thermal runaway. The localized heating leads to superadiabatic gradients and to the onset of convection in the He-burning layers. The rapid increase in temperature eventually removes the electron degeneracy. Initial hydrodynamic calculations of the He core flash found that it should induce a disruption of the star (Edwards 1969; Deupree 1984), while more modern two- (2D) and three-dimensional (3D) simulations have shown that the flash does not produce a hydrodynamical event (Deupree 1996; Mocák et al. 2008, 2009).
One critical question is the time it takes for He burning to reach the center of the star. One-dimensional (1D) evolutionary models predict that after the peak of the He flash, electron degeneracy is locally removed in the shell where He was ignited. The layers below remain inert and degenerate until the heat produced by the first He flash diffuses inward. Electron degeneracy is then removed in the inner layers through a series of weaker secondary He flashes occurring closer and closer to the stellar center (Thomas 1967; Iben & Renzini 1984; Bildsten et al. 2012). The duration of the phase of successive He subflashes is determined by the timescale over which thermal diffusion operates inward after each subflash. It was found to be of the order of 2 Myr (Bildsten et al. 2012), which represents a non-negligible fraction of the duration of the phase of quiet He core burning (∼100 Myr). The existence of these subflashes has been questioned by 2D and 3D simulations of the He core flash (Mocák et al. 2008, 2009). These studies suggest that the convective region that develops as a result of He burning rapidly extends inward, potentially reaching the center of the star on a timescale of about a month. Degeneracy would then be lifted in the core without the occurrence of He subflashes. So far, no observational evidence has been obtained of any star going through the He-flash or the subsequent subflashes.
If the He flash consists in a series of subflashes, the odds of observing a star in this phase are much higher than if it is a single event, as suggested by 2D and 3D simulations. Asteroseismology could then be very helpful to identify stars during the He flash. Indeed, red giants are known to stochastically excite nonradial mixed modes in their convective envelopes. These modes behave as gravity (g) modes in the core, and as pressure (p) modes in the envelope. The exceptional diagnostic potential of these modes has been known since they were found in stellar models (Dziembowski 1971; Scuflaire 1974; Osaki 1975). With the advent of space missions CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010), mixed modes have been detected in thousands of subgiants (Deheuvels et al. 2010; Deheuvels & Michel 2011; Campante et al. 2011) and red giants (Bedding et al. 2011; Mosser et al. 2011). Among other applications, mixed modes can be used to measure the nearly constant period spacing ΔΠ of high-radial-order dipolar g modes (Bedding et al. 2011; Mosser et al. 2011; Vrard et al. 2016), which depends on the fine structure of the deep core. It has been shown that He-core-burning giants (belonging to the so-called red clump), which have convective cores, have distinctly larger ΔΠ than H-shell burning giants (first-ascent red giants), whose cores are radiative. This has been used as a powerful tool to distinguish the two populations (Bedding et al. 2011; Mosser et al. 2011). Bildsten et al. (2012) argued that the period spacings of g modes could also be used to identify red giants in the phases between He subflashes. Indeed, in the aftermath of a He subflash, the core structure is close to that of a star on the RGB, but the subflash leaves an imprint that significantly modifies the period spacing of g modes. Bildsten et al. (2012) thus found that stars between two subflashes have values of ΔΠ intermediate between those of RGB stars and those of He core burning giants.
In this paper, we investigate the oscillation spectrum of red giants during the He subflashes. As mentioned above, during a subflash, the layers in which He is ignited become convective, owing to the heating that the nuclear reactions produce. Consequently, gravity waves become evanescent in the He-burning layers. The g-mode cavity is thus split into two distinct cavities that are separated by the He-burning shell. During a subflash, the star has three different cavities: two internal g-mode cavities and the external p-mode cavity. The oscillation spectrum is thus expected to be altered compared to other phases (i) because the shape of the cavities is modified, and (ii) because of the additional g-mode cavity. We here investigate whether this can be used to identify red giants undergoing a He subflash. Detecting a star in this phase would provide direct evidence of the existence of He subflashes and provide valuable insight into this poorly understood event of stellar evolution.
In Sect. 2, we show that if He subflashes exist, several tens of red giants are expected to be in the process of a subflash among the ∼15 000 red giants for which the Kepler satellite (Borucki et al. 2010) has detected oscillations. The special case of three mode cavities inside a star has not been addressed so far. One can expect that it leads to complex oscillation spectra, whose interpretation can be complicated. In Sect. 3, we calculate the asymptotic mode frequencies in the case of three cavities using the Jeffreys-Wentzel-Kramers-Brillouin (JWKB) approximation. We use these analytic calculations to predict the oscillation spectrum of red giants undergoing a He subflash. In Sect. 4, we numerically calculate the oscillation spectra of stellar models during a He subflash and we compare the results to the predictions of the asymptotic mode frequencies. This leads us to propose ways of seismically identifying red giants going through a He subflash in Sect. 5.
2. He subflashes in 1D stellar evolution models
2.1. Computation of stellar models during He subflashes
We used the stellar evolution code MESA (Paxton et al. 2011, version 10108) to evolve models of different masses ranging from 0.7 to 2 M⊙ until the triggering of He-burning. We considered initial mass fractions of hydrogen of X = 0.70 and helium Y = 0.28, which corresponds to Z = 0.02, and assumed the mixture of heavy elements of Grevesse & Sauval (1998). We used the OPAL equation of state (Rogers & Nayfonov 2002), complemented by the HELM equation of state (Timmes & Swesty 2000) where necessary, as described by Paxton et al. (2011). The opacity tables were taken from OPAL (Iglesias & Rogers 1996), complemented by those of Ferguson et al. (2005) at low temperatures. We used the nuclear reaction rates from the NACRE compilation (Angulo et al. 1999). We neglected the effects of rotation and mass loss. Convection was treated using the classical mixing-length-theory with αMLT = 2.0.
During He subflashes, sharp gradients of the mean molecular weight develop near the edges of the convective shell where He is burnt. Consequently, the extent and the evolution of the convective region depends on the criterion chosen for the onset of convection. We computed models using three different prescriptions: (i) the Schwarzschild criterion, (ii) the Ledoux criterion, including the effects of thermohaline mixing following the prescription of Brown et al. (2013)1, and (iii) the Schwarzschild criterion with a mild exponential diffusive overshooting following the prescription of Herwig (2000), extending over a distance of 0.01 pressure scale height. It is important to note that at the beginning of the subflash, convection starts in a region where the mean molecular weight is increasing outwards. Indeed, below the convective shell the core is comprised of nearly pure helium and above this shell, the matter has been enriched in carbon by previous subflashes. At both edges of the convective shell, the gradient of chemical composition, defined as ∇μ ≡ dlnμ/dlnP, is thus negative during the first part of the subflash, which is known to have a destabilizing effect. For this reason, we chose to consider models that include the Brown et al. (2013) prescription for thermohaline mixing, keeping in mind that the efficiency of this mixing remains uncertain. Unless mentioned otherwise, the results presented use the bare Schwarzschild criterion.
2.2. Expected prevalence of helium-flashing giants among Kepler data
Before seismically characterizing red giants undergoing a He-subflash, we addressed the question of the expected number of Kepler targets that are in this short-lived period of their evolution. Figure 1 shows the variations in the luminosity produced by helium-burning as a function of time for a 1.7 M⊙ model. The shaded areas indicate the periods during which He-burning off-center causes the apparition of an intermediate convective region, which splits the g-mode cavity in two. The cumulative time of these subflashes corresponds to about 0.3 Myr. This represents roughly 0.4% of the total duration of the He core burning phase (which lasts about 80 Myr). This ratio is weakly dependent on the stellar mass. This number shows that only a small fraction of primary clump red giants are in this stage of evolution. However, the Kepler data have led to the detection of oscillations in about 15 000 red giants.
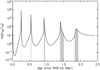 |
Fig. 1. Variations in the luminosity produced by He-burning during the He-subflashes of a 1.7 M⊙ model computed with MESA. The shaded areas indicate periods during which the (convective) He-burning region splits the g-mode cavity in two. |
To estimate the expected number of helium-flashing giants, we used the catalog of Vrard et al. (2016), who extracted global seismic parameters for 6111 red giants observed with the Kepler satellite. About 67% of these targets are in the He core burning phase. Among this group, about 89% have stellar masses below 2 M⊙, meaning that they have gone through the He flash and thus belong to the so-called primary clump. We thus estimate the proportion of Kepler red giants that are in the primary clump to be equal to about 60%. Among those, a proportion of 0.4% is expected to be going through a subflash. This corresponds to about 35 targets among the whole Kepler dataset. This demonstrates that, provided the He-flash occurs as a series of subflashes as predicted by 1D stellar evolution models, the Kepler sample should contain several tens of giants that are in the process of a subflash.
2.3. Preliminary considerations on the oscillation spectra of He-flashing giants
A propagation diagram of the 1.7 M⊙ model during a helium subflash is shown in Fig. 2. The regions of propagation of a wave with a frequency corresponding to the expected maximum power of excited oscillation (νmax) is overplotted. As mentioned in Sect. 1, the g-mode cavity is split in two propagating regions. We further refer to the deeper and shallower g-mode cavities as the g1 and g2 cavities, respectively. We refer to the inner and outer turning points of the g1 cavity as ra and rb. Similarly, rc and rd are the turning points of the g2 cavity, and re and rf are the turning points of the p-mode cavity.
 |
Fig. 2. Propagation diagram for a 1.7 M⊙ model during a He-burning subflash. The Brunt–Väisälä frequency is represented by the full red curve, and the l = 1 Lamb frequency S1 corresponds to the long-dashed blue curve. The horizontal line corresponds to the angular frequency ω = 2πνmax. A wave with pulsation ω propagates where the line is solid, and it is evanescent where the line is dotted. Turning points for the cavities are also depicted by the filled circles. The gray vertical arrow indicates the position of the H-burning shell. |
During a helium subflash, the oscillation spectrum is expected to be more complex than for regular red giants, since it is a collection of the spectra of the three cavities. We also expect the frequencies of the eigenmodes of each cavity to be modified because of the coupling produced by the evanescent zones [rb, rc] and [rd, re]. The strength of the coupling generated by the latter evanescent region, which separates the g2 cavity from the p-mode cavity, is expected to be similar to the coupling between the two cavities of regular red giants (see Mosser et al. 2017b). We thus expect to detect most of the modes that are trapped mainly in the g2 cavity. The intensity of the coupling between the two g-mode cavities during a helium subflash is much more uncertain. It is also critical because if this coupling is too weak, then the g2 and p-mode cavities are essentially disconnected from the inner g1 cavity, and we can expect to detect only mixed modes from the g2 and p cavities. This would thus yield oscillation spectra qualitatively similar to those of regular red giants.
The numerical computation of mode frequencies in the red-giant phase is notoriously complex. Efforts are currently under way to compare the results of different oscillation codes for first-ascent red giants (Silva Aguirre et al., in prep.) and they are planned to be extended to clump stars. The main issues are (i) the small meshing that is needed to adequately sample the wavelengths of high-order gravity modes in the core (this usually requires to perform a re-interpolation of equilibrium quantities before calculating oscillation frequencies), and (ii) the sharp variations in the equilibrium quantities that can arise owing to the many structural changes. One can expect these issues to be magnified during the complex phase of helium subflashes. For this reason, we chose to first study the general properties of oscillations during subflashes analytically by using an asymptotic method, before attempting to numerically compute the mode frequencies in these stars. We also note that in regular red giants, asymptotic expressions of mode frequencies were extremely useful to identify the observed mixed modes and interpret the oscillation spectra (e.g., Mosser et al. 2012b). If red giants undergoing a helium subflash are ever discovered, the asymptotic expressions that are developed below in the case of three propagating cavities will be crucial to identifying the observed modes.
3. Asymptotic mode frequencies during a subflash
In this section, we extend the asymptotic method that Shibahashi (1979) developed using the JWKB approximation to the case of three cavities, as occurs during He-burning subflashes.
3.1. JWKB approximation with three propagation cavities
We start by briefly recalling how the JWKB approximation can be applied to nonradial adiabatic oscillations, following the development proposed by Shibahashi (1979), see also Unno et al. 1989). We introduce the variables υ and w defined as
where ξr is the radial component of the mode displacement, p′ is the Eulerian pressure perturbation, cs is the sound speed in the medium, N is the Brunt–Väisälä frequency, and the Lamb frequency for modes of degree l is expressed as 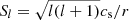 . Under the Cowling approximation, which consists in neglecting the perturbation to the gravitational potential (Cowling 1941), the radial part of the equations of adiabatic stellar oscillations can be reduced to the following pair of turning-point equations (Shibahashi 1979):
. Under the Cowling approximation, which consists in neglecting the perturbation to the gravitational potential (Cowling 1941), the radial part of the equations of adiabatic stellar oscillations can be reduced to the following pair of turning-point equations (Shibahashi 1979):
where kr depends on the angular frequency ω of the wave and can be approximated as
This approximate expression neglects terms that involve derivatives of structural quantities, which are negligibly small compared to the terms in the right-hand side of Eq. (5) everywhere except near the turning points and the stellar surface. We also note that Eqs. (3) and (4) were obtained by neglecting terms involving spatial derivatives of equilibrium quantities, which are negligibly small compared to 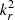 everywhere, except in the neighborhood of the turning points and near the surface. This approximation is especially valid for modes with short wavelength in the radial direction, which is the case for the modes that we are interested in.
everywhere, except in the neighborhood of the turning points and near the surface. This approximation is especially valid for modes with short wavelength in the radial direction, which is the case for the modes that we are interested in.
Equations (3) and (4) can then be solved using the JWKB approximation, that is, assuming that the local wavelength of the wave is small compared to the scale height of variations of the medium. Using the approximate expression for kr given by Eq. (5), it is clear that turning points occur either where ω2 = N2 or where 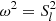 . The interior of the star is thus divided in regions surrounding each turning point, and the turning-point equations are solved in each of these regions. For the turning points where ω2 = N2, Eq. (4) is singular (as shown by Eq. (2)), and we therefore solve Eq. (3). Conversely, for the turning points where
. The interior of the star is thus divided in regions surrounding each turning point, and the turning-point equations are solved in each of these regions. For the turning points where ω2 = N2, Eq. (4) is singular (as shown by Eq. (2)), and we therefore solve Eq. (3). Conversely, for the turning points where 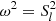 , Eq. (3) is singular, and we solve Eq. (4). The solutions of the turning-point equations can be expressed in terms of Airy functions. The eigenfunctions of each region are then matched together, using the asymptotic forms of Airy functions. This provides a quantization condition for the eigenmodes.
, Eq. (3) is singular, and we solve Eq. (4). The solutions of the turning-point equations can be expressed in terms of Airy functions. The eigenfunctions of each region are then matched together, using the asymptotic forms of Airy functions. This provides a quantization condition for the eigenmodes.
Before applying the procedure described above to the case of three propagation cavities, we recall the results obtained by Shibahashi (1979) in the cases of single cavities and double cavities.
3.1.1. Case of a single cavity
In the case of a single g-mode cavity, for instance assuming that the waves propagate only between ra and rb in Fig. 2, the eigenfunctions must decay exponentially for r ≪ ra and for r ≫ rb. Equation (3) is solved around the turning points ra and rb. The matching of the eigenfunctions υ and w at an intermediate radius r such that ra ≪ r ≪ rb requires that
thus yielding 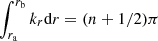 , where n corresponds to the radial order. This expression can then be used to obtain approximate expressions for the frequencies of g modes (Tassoul 1980).
, where n corresponds to the radial order. This expression can then be used to obtain approximate expressions for the frequencies of g modes (Tassoul 1980).
To obtain an analogous expression for a single p-mode cavity, we assume that the wave propagates only between re and rf in Fig. 2. This time, Eq. (4) is used around the turning point re and Eq. (3) around rf. The matching of eigenfunctions inside the cavity provides the condition
that is, 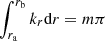 , where m corresponds to the radial order. This expression is the basis for asymptotic expressions of the frequencies of p modes (Tassoul 1980).
, where m corresponds to the radial order. This expression is the basis for asymptotic expressions of the frequencies of p modes (Tassoul 1980).
3.1.2. Case of two cavities
The case of a g-mode cavity and a p-mode cavity coupled through an evanescent region has been considered by Shibahashi (1979) and later studied extensively owing to the detection of mixed modes in red giants (e.g., Mosser et al. 2012b; Goupil et al. 2013; Jiang & Christensen-Dalsgaard 2014; Deheuvels et al. 2015). If we assume that the waves propagate only in the regions [rc, rd] and [re, rf] in Fig. 2 (i.e., disregarding the additional most internal g-mode cavity), one has to solve the turning-point equations in both cavities and then to match the eigenfunctions in the evanescent region in between. This matching yields the condition
where 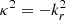 in the evanescent region. The right-hand-side term corresponds to the coupling strength between the two cavities. If this terms vanishes, we recover the conditions found for pure g and p modes given in Eqs. (6) and (7). The use of this expression was paramount to deciphering the oscillation spectra of red giants (Mosser et al. 2012b; Goupil et al. 2013). We note that Eq. (8) is valid only in the case of a weak coupling between the two cavities. Takata (2016) derived a more general expression which extends to the case of a strong coupling and accounts for the perturbation of the gravitational potential.
in the evanescent region. The right-hand-side term corresponds to the coupling strength between the two cavities. If this terms vanishes, we recover the conditions found for pure g and p modes given in Eqs. (6) and (7). The use of this expression was paramount to deciphering the oscillation spectra of red giants (Mosser et al. 2012b; Goupil et al. 2013). We note that Eq. (8) is valid only in the case of a weak coupling between the two cavities. Takata (2016) derived a more general expression which extends to the case of a strong coupling and accounts for the perturbation of the gravitational potential.
3.1.3. Case of three cavities
We extended the derivations of Shibahashi (1979) to the case of three cavities, as shown in Fig. 2. The turning-point equations needed to be solved separately in each of the three cavities, and then matched in the two evanescent regions. Details of the calculation are given in Appendix A. We eventually obtained the following matching condition
where we have defined
and
The term q1 represents the coupling strength between the two g-mode cavities. Similarly, q2 measures the intensity of the coupling between the outer g-mode cavity of the p-mode cavity.
One can check from Eq. (9) that the results of Shibahashi (1979) are recovered in the cases where the coupling is negligible between the propagation cavities. For instance, if we assume that q1 = 0, that is, that the external g-mode cavity is uncoupled to the inner g-mode cavity, the solutions of Eq. (9) correspond to

The first case corresponds to the condition for pure g modes trapped in the inner cavity. The second case is identical to the condition for mixed modes given in Eq. (8), and to the one obtained by Shibahashi (1979, their Eq. (31)). If q1 is indeed negligibly small for red giants undergoing a He subflash, then their oscillation spectrum is expected to be identical to that of regular clump giants, except for the observed period spacing (ΔΠ2), which can be different. However, if the coupling strength q1 is large enough (this is quantified in the following), the observed oscillation spectrum can become much denser because it also includes the eigenfrequencies of the inner g1 cavity (modified, owing to the coupling).
Similarly, if q2 = 0, that is, if no coupling exists between the internal g-mode cavities and the acoustic cavity, then Eq. (9) reduces to

One thus recovers both the frequencies of pure p modes, and the frequencies of mixed modes between the g1 and g2 cavities.
3.2. Expressions of phase terms θg1, θg2, θp
Equation (9) can be used to obtain asymptotic frequencies of oscillation modes, provided the expressions of the terms θp, θg1, θg2, q1, and q2 are specified. For this purpose, we followed Mosser et al. (2012b), who inserted asymptotic expressions for the frequencies of pure p and g modes inside the phase terms θp and θg. We therefore approximate the phase θp for pure l = 1 p modes by the expression
where Δν is the asymptotic frequency separation of consecutive p modes (the so-called “large separation”) and εp is a phase offset. This ensures that when Eq. (7) is satisfied, we recover νn, l = 1 = (n+1/2+εp)Δν, which is the first-order asymptotic expression for high-order l = 1 p modes. We note that this expression can be extended to include higher-order terms of the asymptotic development (Mosser et al. 2012b). However, in our case, there is no need to add this complexity to our development.
Similarly, the phases θg1 and θg2 can be approximated by
These expressions ensure that theoretical pure g1 and g2 modes of degree l = 1 are regularly spaced in period, with period spacings ΔΠ1 and ΔΠ2, respectively. The quantities εg1 and εg2 are phase shifts.
3.3. Estimates of oscillation mode parameters
The pattern of the oscillation modes depends most critically on five parameters: the large separation of pure acoustic modes Δν, the period spacings of pure l = 1 gravity modes in the g1 and g2 cavities (ΔΠ1 and ΔΠ2), and the coupling intensities q1 and q2. To estimate the mode pattern that can be expected in giants experiencing a He-core subflash, we hereafter describe the variations in these seismic parameters during the second subflash of the 1.7 M⊙ MESA model that was introduced in Sect. 2. The evolution is similar for other He subflashes and for other stellar masses (within the mass range where stars undergo a He flash). Values of the seismic parameters are given in Table 1 for three different stages of the He subflash: at the beginning of the subflash (model 1), at an intermediate point (model 2) and at the end of the subflash (model 3). When relevant, we describe the way the global seismic parameters are modified when different prescriptions are used to model the boundaries of the convective regions associated to He-burning.
Seismic parameters of the reference model (1.7 M⊙ model during the second He-core subflash) calculated using their asymptotic expressions (see text).
3.3.1. Large separation of acoustic modes
We obtained first estimates of the mean large separation of p modes Δν for our models by using the asymptotic relation
The large separation was found to vary between 4.5 μHz during the subflash and 5.6 μHz between consecutive subflashes. We also estimated the expected frequency of maximum power of the oscillations νmax by assuming that it scales as the acoustic cut-off frequency, that is, that 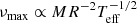 (see Table 1). This assumption is supported by observations (e.g., Kjeldsen & Bedding 1995; Stello et al. 2008) and has received theoretical justification (Belkacem et al. 2011).
(see Table 1). This assumption is supported by observations (e.g., Kjeldsen & Bedding 1995; Stello et al. 2008) and has received theoretical justification (Belkacem et al. 2011).
To first-order the asymptotic frequencies of radial modes can be written as νn, l = 0 ≈ (n + εp)Δν. We refined our estimates of the asymptotic large separation of p modes Δν by fitting this expression to the frequencies of the radial modes of each model, which were numerically computed for each model using the oscillation code ADIPLS. The fits were performed over the interval νmax ± 3Δν, using our preliminary estimates of Δν and νmax. This interval corresponds to the frequency range over which modes are detected in core-He-burning giants (Deheuvels et al. 2015). For red giants going through He subflashes, the frequency range of detected modes should be similar because the envelope properties of these stars are close to those of red clump stars. We give in Table 1 the asymptotic large separations of acoustic modes that we obtained for models 1, 2, and 3 from our fits.
3.3.2. Period spacing of gravity modes
Estimates of ΔΠ1 and ΔΠ2 were obtained from their asymptotic expressions
where the turning points ra, rb, rc, and rd were taken as those of a wave with a frequency of νmax. The variations in the asymptotic period spacings ΔΠ1 and ΔΠ2 during a He subflash are shown in the top panel of Fig. 3. When using the bare Schwarzschild criterion, the splitting of the g-mode cavity occurs earlier (about 0.518 Myr after the tip of the RGB, compared to about 0.541 for other prescriptions). This preliminary phase corresponds to the development of an evanescent zone (N2 < 0) induced by the negative μ-gradient, but stable according to the Schwarzschild criterion. This situation is known to be unstable and thermohaline mixing, if efficient enough, is expected to smooth out the μ-gradient. When it is included following the prescription of Brown et al. (2013), this first phase of the subflash is suppressed (see Fig. 3). Values of ΔΠ1 and ΔΠ2 for models 1, 2, and 3 (whose ages are indicated by vertical dotted lines in Fig. 3) are given in Table 1. They are almost insensitive to the choice of the criterion for the onset of convection.
 |
Fig. 3. Variations in global seismic parameters during the second subflash of a 1.7 M⊙ model. The vertical gray dotted lines indicate the three evolutionary stages at which global seismic parameters are provided in Table 1. Top panel: asymptotic period spacing of dipolar modes in the g1 cavity (ΔΠ1, red solid line) and in the g2 cavity (ΔΠ2, blue dot-dashed line) as a function of time elapsed since the tip of the RGB. The black curve shows the period spacing of the single g-mode cavity outside of the He subflash. Bottom panel: variations in the coupling strength between the g1 and g2 cavities (q1, red solid line for Schwarzschild criterion, purple line for Ledoux criterion with thermohaline mixing, and black dashed line for Schwarzschild criterion with overshooting; see text for more details) and between the g2 and the p-mode cavities (q2, blue dot-dashed line). |
As mentioned in Sect. 2, most of the g2-dominated modes should be detectable, meaning that the period spacing ΔΠ2 should be measurable, provided the oscillation spectrum of the star can be deciphered. If thermohaline mixing is efficient, ΔΠ2 lies between 200 and 300 s during most of the subflash, and is thus comparable to the period spacing of regular clump stars. For inefficient mixing, ΔΠ2 is significantly smaller than the period spacings of clump stars (as shown by Vrard et al. 2016, very few red clump giants have measured period spacings below 200 s) during the first half of the subflash.
The period spacing of the g1 cavity is systematically smaller than ΔΠ2 but it is of the same order of magnitude. This already suggests that the oscillation spectra generated by both g-mode cavities taken separately should have a similar density.
3.3.3. Coupling strength
One critical point was to estimate the coupling strength between the cavities. The expressions of the coupling strength given by Eqs. (11) and (12) have been shown to be valid only in the case of a weak coupling, that is, when the evanescent zone that separates the cavities is thick enough (Takata 2016). For thin evanescent zones, these expressions tend to underestimate the coupling strength (Takata 2016) Calculating coupling strength for He-flashing giants in the general case would require adaptation of the formalism of Takata (2016) to the special case of three mode cavities, which represents a considerable amount of work. Here, we chose to use Eqs. (11) and (12) to obtain first estimates of the coupling strength between the cavities, which provide information about the main contributors to the coupling intensities.
We plugged the expression of κ (Eq. (5)) into Eqs. (11) and (12) to estimate q1 and q2, whose variations during the subflash are shown in Fig. 3. For the coupling intensity between the outer g-mode cavity and the p-mode cavity, we found values of q2 varying between 0.11 and 0.15, with minimal values reached during the subflashes and maximal values between subflashes. The coupling strength q1 between the two g-mode cavities depends on the modeling of the boundaries of the convective region in which He is burnt.
-
When using the bare Schwarzschild criterion, a thin evanescent zone develops at the beginning of the subflash, owing to the negative ∇μ, as mentioned in Sect. 3.3.2. As this zone extends, the coupling q1 decreases by several orders of magnitude. The existence of this preliminary phase is uncertain since it is prone to thermohaline mixing, which could smooth out μ-gradients. About 0.542 Myr after the RGB tip, a part of the evanescent zone becomes convectively unstable according to the Schwarzschild criterion and mixing occurs in this region. The coupling strength q1 becomes dominated by the contribution of the narrow regions adjacent to the convective shell in which sharp negative μ-gradients develop. This is clearly seen in the profile of κ for Model 1 shown in Fig. 4. Since the turning points rb and rc, which delimit the evanescent zone, coincide with the regions of sharp μ-gradients, small variations in rb and rc can induce large changes in the value of q1. This explains at least partly the spiky features of the curve showing the variations in q1 during the first half of the subflash (Fig. 3). Small numerical errors in the computation of the Brunt–Väisälä frequency within the MESA code could also contribute to this spiky behavior. The μ-gradients are progressively smoothed out at both edges, causing q1 to increase, as can be seen in Fig. 3. Indeed, the carbon abundance in the convective shell increases, which reduces the jump in the mean molecular weight at the outer edge of the shell. Also, the layers below the convective shell are progressively heated and they start burning helium into carbon, which increases their mean molecular weight (see top panel of Fig. 4). About 0.549 Myr after the RGB tip, the μ-gradients beyond both edges of the convective shell become positive. The regions of varying chemical composition outside the convective shell no longer contribute to the coupling intensity q1 (see Fig. 4), which slowly increases as the shell shrinks toward the end of the subflash.

Fig. 4. Profiles of the mean molecular weight μ (top panel) and the function κ (bottom panel) in the core of Model 1 (blue curves) and Model 2 (red curves). In the top panel, thick lines indicate the evanescent zone separating the g1- and g2-cavities.
-
Using the Ledoux criterion with thermohaline mixing following the prescription of Brown et al. (2013), the beginning of the subflash is delayed, as explained above. When convection is triggered (around 0.542 Myr after the RGB tip), the regions with negative μ-gradients on both sides of the convective shell are part of the evanescent zone. However, thermohaline mixing smoothes out these gradients and q1 is much higher than with the Schwarzschild criterion. When the μ-gradients become positive outside the convective shell, q1 no longer depends on them and becomes indistinguishable from the bare-Schwarzschild case.
-
When a mild amount of overshooting is added, the regions of sharp μ-gradients are pushed away to the boundaries of the overshooting layers. In these regions, the temperature gradient is equal to the radiative temperature gradient, which is significantly below the adiabatic temperature gradient. As a result, N2 > 0 even when ∇μ is negative. The coupling strength q1 thus remains independent of the μ-gradients outside the convective region throughout the subflash and depends only on the thickness of the shell.
The largest differences between the values of q1 obtained with the different prescriptions occur when convection starts in the He-burning shell (model 1). In the following sections, we refer to the model computed with the Schwarzschild criterion as “model 1”, the model computed with the Ledoux criterion and thermohaline mixing as “model 1th”, and the model computed with overshooting as “model 1ov”. For models 2 and 3, q1 is independent of the adopted criterion.
Our asymptotic calculations predict that the coupling strength q1 should be above 10−2 at least during the largest part of the subflash, and potentially throughout the subflash if mixing is included (thermohaline mixing or overshooting). However, these conclusions should be taken with care. Indeed, at the beginning and in the end of the subflash, the evanescent region is very thin and the formalism of Takata (2016) should be used. Also, around the edges of the evanescent zone, the mean molecular weight varies over length scales that can be smaller than the wavelengths of the modes, which violates the main assumption behind the JWKB approximation. The intensity of the coupling q1 between the two g-mode cavities thus remains uncertain. To address the question of the mode visibilities in Sect. 3.6, we considered three scenarios: a weak coupling (q1 = 10−3), an intermediate coupling (q1 = 10−2) and a strong coupling (q1 = 10−1). The asymptotic values of q1 are compared to the results of full numerical calculations of oscillation frequencies in Sect. 4.
3.4. Synthetic spectrum
Following the steps outlined above, we obtained all the ingredients to build asymptotic oscillation spectra for our reference models. For this purpose, we solved Eq. (9) using a Newton–Raphson algorithm for frequencies in the frequency range νmax ± 3Δν, which corresponds to the expected frequency of maximum power of the oscillations. The oscillation spectra were calculated following this procedure for the three different stages of the He subflash that are represented by vertical dotted lines in Fig. 3. As already suggested above, we found that the coupling strength q1 between the g-mode cavities plays a key role in shaping the oscillation spectra of models in the He subflash. The remaining seismic global parameters do not qualitatively alter the pattern of the oscillation spectra. Consequently, we found it more instructive to show in this section the results corresponding to the seismic parameters of a single model (we chose those of model 1) and to study the influence of varying q1 on this particular model.
As expected, the obtained oscillation spectrum is quite dense. It should be comprised essentially of modes trapped in the g1 or g2 cavities, with a few p-dominated modes. As a first step to separate these modes, we used the obtained mode periods to build period échelle diagrams2 folded using either ΔΠ1 (Figs. 5–7, left panels) or ΔΠ2 (Figs. 5–7, right panels). These échelle diagrams correspond to three different scenarios concerning the coupling strength between the g-mode cavities: a weak (q1 = 10−3, Fig. 5), an intermediate (q1 = 10−2, Fig. 6), and a strong (q1 = 10−1, Fig. 7) coupling . Decreasing the coupling intensity q1 below 10−3 does not significantly modify the oscillation spectrum.
 |
Fig. 5. Period échelle diagrams of asymptotic oscillation modes obtained by solving Eq. (9) using the parameters given in Table 1 and considering a weak coupling between the g-mode cavities (q1 = 10−3). These diagrams were obtained by folding the mode periods using either ΔΠ1 (left panel) or ΔΠ2 (right panel). The horizontal dashed lines indicate the location of theoretical pure l = 1 p modes. Modes trapped predominantly in the g1 cavity (Ig1/I > 0.5) are filled in red, and modes trapped mainly in the g2 cavity (Ig2/I > 0.5) are filled in blue (mode trapping is estimated based on ratios of inertia, see Sect. 3.5). Other modes are left blank. |
The échelle diagrams folded with ΔΠ1 show a clear straight vertical ridge, which corresponds to modes trapped predominantly in the inner g1 cavity. The departures from verticality in the case of a strong coupling q1 are caused by avoided crossings with g2 modes. The remaining modes are mainly trapped either in the g2 cavity or in the acoustic-mode cavity. These modes are clearly identified in the échelle diagrams folded with ΔΠ2 (right panels of Figs. 5–7) because they regroup along S-shaped ridges, which are the result of avoided crossings between modes trapped in the g2 cavity and acoustic modes that are regularly spaced in frequency (horizontal dashed lines in Figs. 5– 7). These features are reminiscent of the period échelle diagrams that are obtained for regular red giants (see e.g., Mosser et al. 2012b). The widening of the S-shaped ridges that is observed in the strong coupling case (q1 = 0.1) is caused by the avoided crossings between modes trapped in the g1-cavity and modes trapped in the g2-cavity.
3.5. Mode trapping
To study this issue further, one needs to know where the different modes are trapped inside the star. For this purpose, it is necessary to estimate the mode inertias I (which are directly related to the kinetic energy of the modes) inside each of the three cavities. We denote the inertias in each cavity Ig1, Ig2, and Ip. Goupil et al. (2013) proposed an approximate expression for the mode inertias based on JWKB analysis in the case of two cavities. We extended their work to the case of three cavities using the asymptotic development presented in Appendix A. The details of the calculation are provided in Appendix B. We were able to estimate the fraction of the total energy of the mode that is trapped in each of the three cavities, which is given by Ig1/I, Ig2/I, and Ip/I. The expressions for these quantities are given by Eqs. (B.10)–(B.12) (or alternatively by Eqs. (B.13)–(B.15) when the former equations are singular; see Appendix B for more details).
We calculated these quantities for each of the asymptotic oscillation modes of our reference model. To illustrate the results, we highlighted the modes for which at least 50% of the mode kinetic energy is trapped within the g1 cavity (Ig1/I > 0.5) as filled red circles in Figs. 5–7. They indeed correspond to the modes that form the vertical ridges in the period échelle diagrams folded with ΔΠ1. Similarly, the modes that are trapped mainly in the g2 cavity (Ig2/I > 0.5) are shown as filled blue circles in Figs. 5– 7. They correspond to the S-shaped ridges in the period échelle diagrams folded with ΔΠ2.
The ratios of inertia Ip/I correspond to the fractional contribution of the acoustic cavity to the kinetic energy of the modes. They are often used as a proxy for mode visibilities. Indeed, for modes with large inertias, this quantity approximately corresponds to the ratio between the height of the considered l = 1 mode in the power spectrum and the height of a pure p mode, provided the effects of radiative damping are neglected (e.g., Grosjean et al. 2014). This statement is justified in Sect. 3.6, where the effects of radiative damping are also addressed. Figure 8 shows the ratios of inertia Ip/I for the modes computed using Eq. (B.10) in the case of an intermediate coupling strength between the two g-mode cavities (q1 = 10−2). For comparison, we overplotted the ratios of inertia Ip/I that would be obtained if the modes were trapped only in the g2- and p-mode cavities (blue dashed curve). The regularly spaced maxima of this curve correspond to the location of theoretical pure p modes. The shape of this curve has been extensively studied (e.g., Mosser et al. 2012b, 2015; Goupil et al. 2013). The modes that lie along this blue dashed curve correspond to modes that are g2-p-dominated, while those that lie outside of it have a non-negligible part of their energy trapped within the innermost g1 cavity. For most of the latter modes, the acoustic cavity contributes very little to the mode energy, which makes them unlikely to be observed. However, Fig. 8 shows the existence of modes that are trapped mainly in the g1 cavity (Ig1/I > 0.5) and yet have non-negligible contribution of the acoustic cavity to the mode energy. The number of such modes naturally increases with the intensity of the coupling q1 between the two g-mode cavities. These modes, which are located in the neighborhood of theoretical pure l = 1 p modes have better chances of being detected. To estimate this quantitatively, we evaluated their damping rate in Sect. 3.6.
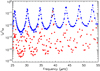 |
Fig. 8. Fractional contribution of the acoustic cavity to the mode inertia (and thus to the mode kinetic energy) using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). Modes that have more than 50% of the energy trapped in the g1 (resp. g2) cavity are shown as filled red circles (resp. blue squares). Other modes are shown as filled black triangles. The dashed blue curve indicates the ratios of inertia Ip/Itot that would be obtained for mixed modes trapped only in the g2 and p mode cavities. |
We note that the variations in the ratios of inertia obtained for g1-dominated modes (filled red circles in Fig. 8) seem quite erratic. The reason for this is the similarity of the period spacings in the two g-mode cavities. This causes the oscillation spectra of both g-mode cavities to have roughly the same density. As a consequence, consecutive modes are trapped alternately in the g1 and g2 cavities and the curve representing the ratios of inertia has a sawtooth behavior. To make this point clearer, we also calculated mode frequencies and ratios of inertia by artificially changing the period spacing in the g1 cavity to either a much lower value than the period spacing in the g1 cavity (we took ΔΠ1 = 30 s) or a much larger value (ΔΠ1 = 800 s). The obtained ratios of inertia Ip/I are shown in Fig. 9. In the former case, the oscillation spectrum of the g1 cavity is much denser than that of the g2 cavity. As a result, between each pair of g2-dominated mode, Ip/I shows a dip, reminiscent of what is obtained in the case of the trapping between an acoustic cavity and a single g-mode cavity. In the latter case (ΔΠ1 = 800 s), the spectrum of the g1 cavity is much sparser. Ip/I closely follows the curve corresponding to the case where modes are trapped only in the g2- and p-mode cavities (blue dashed curve) with sharp dips corresponding to modes trapped in the g1 cavity.
 |
Fig. 9. As in Fig. 8 but assuming values of the asymptotic period spacing ΔΠ1 ranging from 30 to 800 s. To guide the eye, the ratios Ip/I for consecutive modes have been linked by the black dashed curve. |
3.6. Mode heights
One critical point in our study is to predict which modes are likely to be observed among the rich oscillation spectrum obtained from the JWKB analysis. The relevant quantity to study this important question is the expected height of the modes in the power spectrum. This quantity depends on the damping rates of the modes and on the duration of the observations. The damping rate η of a mode is given by the expression
where ∫dW is the work performed by the gas during one oscillation cycle, ω is the mode angular frequency, and 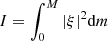 is the mode inertia. As proposed by Grosjean et al. (2014), the work integral can be separated into two contributions: the radiative damping in regions corresponding to both g-mode cavities (Wg1 and Wg2, respectively) and the outer non-adiabatic part of the convective envelope (We), meaning that
is the mode inertia. As proposed by Grosjean et al. (2014), the work integral can be separated into two contributions: the radiative damping in regions corresponding to both g-mode cavities (Wg1 and Wg2, respectively) and the outer non-adiabatic part of the convective envelope (We), meaning that
We examine both contributions in the following.
3.6.1. Surface damping rates
For low-degree modes, the displacement is nearly radial in the outer convective region, where the modes are excited. As a consequence, we can assume that the work We is identical for l = 1 mixed modes and for radial modes. For radial modes, radiative damping in the interior can be safely neglected, and the damping rate is thus given by:
The damping rates of radial modes due to non-adiabatic effects can be estimated observationally using the line widths of these modes (the mode line width Γ is related to the damping rate through the relation η = πΓ). The radial modes of red clump stars have a typical width of the order of 0.1–0.2 μHz (Deheuvels et al. 2015; Mosser et al. 2017a). This provides a damping rate of about ηp ≈ 5 × 10−7 s−1. This value is in broad agreement with the scaling law 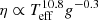 prescribed by Belkacem et al. (2012) on the basis of numerical simulations that include time-dependent convection. We therefore adopted the quoted value of ηp as an estimate of the damping rate undergone by the modes in the outer convective region. Equation (25) was then used to estimate the work We induced by non-adiabatic effects, which we assumed to hold also for l = 1 modes, as mentioned above.
prescribed by Belkacem et al. (2012) on the basis of numerical simulations that include time-dependent convection. We therefore adopted the quoted value of ηp as an estimate of the damping rate undergone by the modes in the outer convective region. Equation (25) was then used to estimate the work We induced by non-adiabatic effects, which we assumed to hold also for l = 1 modes, as mentioned above.
3.6.2. Radiative damping
In the g-mode cavities, the high density induces a very high Brunt–Väisälä frequency, which can produce radiative damping. It is important to quantify this effect in our case, because if the modes that are trapped significantly in the innermost g1 cavity are too severely damped, they might have very low visibilities, leaving us little chance to detect them. Simple expressions for radiative damping have been obtained in the asymptotic limit (Dziembowski 1977; Godart et al. 2009), which we have used here. In our case, we must separate the contributions from both g-mode cavities. In the innermost g1 cavity, the radial displacement can be expressed as
where we have used Eq. (A.2). Following the development of Godart et al. (2009), we found that the contribution of the g1 cavity to the work integral is given by
where
where ∇ad and ∇ are the adiabatic and real temperature gradients, g is the local gravity, L the local luminosity, and p is the pressure. Similarly, using the asymptotic expression of ξr in the g2 cavity (see Appendix A), we can obtain the following expression for the contribution of the g2 cavity to the radiative damping:
The integrals 𝒥(ra, rb) and 𝒥(rc, rd) were calculated using our reference model.
3.6.3. Total damping rates
By plugging Eqs. (25), (27), and (29) into Eq. (23), we obtain the total damping rate of g modes ηmix, which can be expressed as follows
where Eqs. (B.6) and (B.7) have been used. The ratios of inertia can be estimated using Eqs. (B.10)–(B.12) and the phases θgi are approximated by π/(νΔΠi), as explained in Appendix B. Figure 10 shows the damping rates obtained for the modes of a model undergoing a He-subflash.
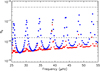 |
Fig. 10. Damping rates ηmix of mixed modes obtained from a JWKB analysis using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). The symbols are the same as in Fig. 8. The horizontal dash-dotted line indicates the damping rates of p modes inferred from seismic observations of typical clump stars (see text). The threshold ηlim = 2/Tobs below which modes are unresolved is represented by the horizontal dashed line (we assumed a duration of Tobs = 4 yr, corresponding to the longest datasets of Kepler). |
3.6.4. Height ratios
The height of a mixed mode in the power spectrum depends on whether or not the mode is resolved (e.g., Dupret et al. 2009). A mode is resolved if its lifetime τ is shorter than Tobs/2, where Tobs is the duration of observations, which is approximately 4 years for the longest datasets available with Kepler data. Since the mode lifetime corresponds to the inverse of the damping rate, we can deduce a limit damping rate ηlim = 2/Tobs, below which the modes are unresolved. This limit has been overplotted in Fig. 10 in the case of the full Kepler datasets. We can see that a large fraction of the modes that are mainly trapped in the g2 and p-cavities are expected to be resolved when using Kepler data. On the contrary, most of the modes trapped in the g1 cavity are expected to be unresolved, with the exception of a few modes in the vicinity of theoretical pure l = 1 p modes.
In the case of resolved mixed modes, Grosjean et al. (2014) have shown that the ratio between their height and that of a p-type mode is given by
This expression involves the ratio between the radiative damping in the g-mode cavities and the damping due to non-adiabatic effects in the outer convective envelope, which can be deduced from Eqs. (25), (27), and (29):
For unresolved modes, the height ratio is given by
as shown by Grosjean et al. (2014). We note that if the effects of radiative damping are neglected, the height ratio between an l = 1 mixed mode and a pure p mode is inversely proportional to the ratio of inertia of the two modes, as was stated in Sect. 3.5.
For each mode, we used Eq. (32) to determine whether the mode is resolved or not. We then estimated the height ratio using either Eq. (31) (if the mode is resolved) or Eq. (35) (otherwise). The results are plotted in Fig. 11. This figure shows that for intermediate coupling intensities between the two g-mode cavities (q1 = 10−2 in Fig. 11), several modes that are mainly trapped in the g1 cavity are expected to have heights comparable to those of radial modes in the power spectrum, which means that they should be detectable.
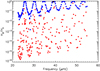 |
Fig. 11. Height ratios between l = 1 mixed modes and theoretical l = 1 pure p mode obtained from a JWKB analysis using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). These ratios were calculated using either Eq. (33) (if the mode is resolved) or Eq. (35) (otherwise). |
3.7. What would the spectrum of a giant in a He-core subflash look like?
We can now address the main question of interest: what would the oscillation spectrum of a red giant undergoing a He subflash look like? To answer this question, we represented the oscillation spectrum obtained from our JWKB analysis by weighting the modes according to their expected heights, based on the results of Sect. 3.6.
We used two types of representation. First, we showed the oscillation spectrum by building a classical échelle diagram folded using the large separation of acoustic modes, Δν = 4.7 μHz in our case (left panels of Fig. 12). For clarity, we plotted only the modes whose expected heights correspond to at least 10% of the height of a pure p mode. For a weak coupling between the two g-mode cavities (q1 < 10−2), only a few modes that are trapped in the g1 cavity have significant predicted heights and the spectrum is indistinguishable from the one that we would obtain if we ignored the g1 cavity altogether. For stronger coupling intensities (q1 ≳ 10−2), the oscillation spectrum corresponds to the spectrum of g2- and p-dominated modes, complemented with additional modes that are trapped mainly in the g1 cavity and have expected heights comparable to those of pure p modes. Quite expectedly, these additional modes are located in the neighborhood of theoretical pure acoustic l = 1 modes (see Fig. 12).
 |
Fig. 12. Échelle diagrams of the oscillation spectrum of model 1 obtained using the JWKB approximation, and assuming different coupling intensities between the g-mode cavities (q1 = 10−3, 10−2, 10−1from left to right panels). The size of the symbols indicates the expected height of each mode. For clarity, only the modes with a height corresponding to at least 10% of the height of a pure p mode are shown. Modes colored in red have at least 50% of their total energy trapped in the innermost g1 cavity (i.e., Ig1/I > 0.5). Top panels: frequency échelle diagrams folded with the large separation of acoustic modes Δν. Bottom panels: stretched period échelle diagrams built following Mosser et al. (2015, see text). |
In order to identify these additional modes, the so-called “stretched” period échelle diagram that was proposed by Mosser et al. (2015) is a particularly helpful representation. We here briefly describe the construction of these diagrams, referring the reader to their paper for more details. In the usual case of two cavities, the period spacings of l = 1 mixed modes vary, which results in S-shaped ridges in the period échelle diagrams (see for instance blue circles in Figs. 5–7). Mosser et al. (2015) showed that the period spacings between l = 1 mixed modes can be related to the ζ function, which is defined as the ratio of the kinetic energy of modes in the g-mode cavity versus their total kinetic energy. Conveniently, theoretical expressions for the ζ function have been obtained from JWKB analyses (Goupil et al. 2013; Deheuvels et al. 2015). Mosser et al. (2015) proposed to express the oscillation spectrum as a function of a modified (“stretched”) period τ instead of the regular mode period P, where τ is defined by the differential equation dτ = dP/ζ. This has the consequence of forcing the oscillation modes to be regularly spaced when using the modified period τ. In other words, this approach straightens the ridge of l = 1 modes in the period échelle diagram. In our case, we expect the oscillation spectrum to be comprised essentially of the modes that are trapped mainly in the g2 and p cavities, along with additional modes trapped in the g1 cavity, whose number depends on the value of q1. We can thus build stretched échelle diagrams taking into account only the g2 and p cavities. The modes that are trapped in these cavities should then regroup along a single vertical ridge. Additional modes, which are trapped mainly in the g1 cavity, are not expected to lie on this ridge and can therefore easily be spotted in this type of diagram. Figure 12 (right column) shows the results obtained for the three coupling intensities that were tested. For q1 ≳ 10−2, additional modes are clearly identified outside of the vertical ridge. We also note that as q1 increases, the vertical ridge widens. This is caused by the avoided crossings between g1 and g2 modes which significantly modify the frequencies of modes trapped in the g2 and p cavities.
To summarize, we found that if the coupling between the two g-mode cavities is large enough (q1 ≳ 10−2) during He subflashes, the observed oscillation spectrum should be comprised mostly of modes trapped in the g2 and p cavities, but it should also include additional modes with detectable heights, which are trapped mainly in the g1 cavity. In this case, these additional modes could be efficiently identified by plotting a stretched period échelle diagram. If the coupling is weaker (q1 < 10−2), the oscillation spectrum during the subflash is expected to be very similar to that of regular clump stars (except for the value of the period spacing, which could differ). But even in this case, some modes would be g1-dominated and could be used to seismically identify stars undergoing a He subflash (see Sect. 5).
4. Numerical calculation of mode frequencies during a He subflash
To complement the asymptotic analysis performed in Sect. 3, we numerically solved the full equations of stellar oscillations for the MESA model that was introduced in Sect. 2. Since oscillation codes have never been thoroughly tested in this evolution stage, we chose to use two different codes: the Aarhus adiabatic oscillation package ADIPLS (Christensen-Dalsgaard 2008) and the oscillation code GYRE (Townsend & Teitler 2013). Both codes have already been adapted to calculate oscillation modes for evolved red giants. We have used the option available for both oscillation codes to reset the mesh grid in order to ensure that the eigenfunctions of the modes are correctly resolved. This requires a fine meshing in the core of the star. A comparison between the results of the two codes is presented in Appendix C. Despite mode-to-mode differences that will need to be looked into in future works, the agreement between ADIPLS and GYRE is sufficient to validate the numerical calculation of mode frequencies and mode trapping during He subflashes, to the level of precision required in this study. We therefore present only the results obtained using ADIPLS in this section.
4.1. Oscillation spectrum during a He subflash
We calculated the oscillation mode frequencies for models 1, 1th, 1ov, 2, and 3, which were presented in Sect. 2. For each model, we built period échelle diagrams that were folded using alternately the period spacing of the g1 cavity and that of the g2 cavity (Fig. 13). The values of ΔΠ1 and ΔΠ2 were slightly adjusted compared to the asymptotic values obtained from Eqs. (21) and (22) in order to obtain vertical ridges in the period échelle diagrams. For models 1, 1th, 1ov, and 2, this adjustment was of the order of 1 s or below. For model 3, which corresponds to the very end of the He subflash, the adjustment reached 8 s for ΔΠ2.
 |
Fig. 13. As in Fig. 5 but using the oscillation modes that were computed with ADIPLS for a 1.7 M⊙ MESA model at several stages during the second He subflash (top-left panels: model 1, top-right panels: model 1ov, bottom-left panels: model 2, bottom-right panels: model 3; see text for description). For each model, period échelle diagrams were constructed using the period spacings of the g1 cavity (left plots) and the g2 cavity (right plots). |
For full numerical solutions of the oscillation equations, estimating the trapping of the modes is straightforward because the energy of the modes in each of the three cavities can be estimated directly using the mode eigenfunctions. We could thus directly determine in which region each mode is predominantly trapped. Modes for which the g1 (resp. g2) cavity was found to contribute to more than half of the mode kinetic energy were highlighted as red (resp. blue) filled circles in Fig. 13.
4.2. Comparison with calculations using the JWKB approximation
The period échelle diagrams of models 1, 1th, and 1ov can be directly compared to those of Figs. 5–7, which were obtained using the JWKB approximation and assuming period spacings corresponding to those of models 1 and 1ov. The first observation is that there seems to be a fairly good qualitative agreement between the predictions obtained with the JWKB approximation and the numerical results. Similarly to the results of Sect. 3, the échelle diagrams folded with ΔΠ1 exhibit a clear vertical line and those folded with ΔΠ2 show the typical S-shaped ridges, whose branches correspond to avoided crossings with acoustic modes. There are however, differences between the numerically computed mode frequencies and those predicted using the JWKB approximation, which are described below.
4.2.1. Coupling between the g-mode cavities
For model 1ov, the large value of q1 (0.10, see Table 1) led us to expect a period échelle diagram similar to that of Fig. 7. Instead, the oscillation spectrum of model 1ov is very similar to that of model 1, for which q1 ∼ 10−3. In particular, for model 1ov, the ridge formed by the g1-dominated modes in the échelle diagram folded using ΔΠ1 is remarkably straight. This suggests a much weaker coupling than predicted by the JWKB approximation. This discrepancy is further studied when we address the question of mode trapping in Sect. 4.3.
By contrast, for model 3, the ridge of g1-dominated modes in the period échelle diagram appears significantly scattered, which is consistent with the large coupling strength that is predicted by the JWKB approximation (q1 = 0.10, see Table 1).
4.2.2. Effects of buoyancy glitches
We also observe that the S-shaped ridges formed by g2-dominated modes in the échelle diagrams folded using ΔΠ2 exhibit oscillations that were not present in the échelle diagrams built using the JWKB approximation. These oscillations are most easily identified in the échelle diagrams of models 1 and 1ov for frequencies above ∼40 μHz. For these two models, each period of the oscillation contains approximately six g2-dominated modes.
These oscillations are caused by glitches in the Brunt–Väisälä frequency (commonly referred to as a buoyancy glitch), which are known to have such an effect on the period spacings (see e.g., Miglio et al. 2008; Cunha et al. 2015). Figure 2 shows that the Brunt–Väisälä frequency indeed features a sharp peak in the g2-cavity, which is produced by the H-burning shell. The apparent increase of the amplitude of these oscillations with mode frequency (see Fig. 13) supports the hypothesis that the observed oscillation is the result of a buoyancy glitch. This behavior is expected for glitch-related oscillations, which arise when the equilibrium quantities vary on a length-scale comparable to or shorter than the mode wavelength. For gravity modes, the wavelength increases with increasing frequency. Thus, if we consider a sharp variation in the Brunt–Väisälä frequency over a length-scale ℓ, high-frequency gmodes with a wavelength larger than ℓ feel this perturbation as a glitch, contrary to low-frequency modes with a wavelength shorter than ℓ. This explains the increasing amplitude of the observed oscillations.
We also calculated the oscillation period that the H-burning shell is expected to produce. Its expression in terms of the radial order n is given by
where xHshell is the normalized buoyancy radius H-burning shell in the g2-cavity, defined as
For models 1 and 1ov, we found a normalized buoyancy radius of xHshell ≈ 0.82 for the H-burning shell, which should give Δn ≈ 1.22 according to Eq. (36). In practice, periodicities such that Δn < 2 cannot be directly observed, as stated by the Nyquist–Shannon sampling theorem. In this case, the signature of the glitch is aliased to a signal whose source would be located at a normalized buoyancy radius of 1 − xHshell (see Montgomery et al. 2003; Miglio et al. 2008). This gives an expected period of Δn ≈ 5.6 for the H-burning-shell-glitch, which is in very good agreement with the visual estimate of six radial orders per period that was obtained from Fig. 13. This confirms that the observed oscillations are indeed produced by the H-burning shell. We further discuss the implications of this oscillation in Sect. 5.
4.3. Mode trapping
The ratios of inertia Ip/I, giving the fractional contribution of the acoustic cavity to the total mode inertia, can be directly estimated using the mode eigenfunctions. They are shown for models 1, 1th, 1ov, 2, and 3 in Fig. 14. For each model, the range of values of Ip/I taken by g1-dominated modes is indicative of the intensity of the coupling between the g1-cavity and the rest of the star. The top panel of Fig. 14 confirms that this coupling is very weak for model 1. The coupling appears to be stronger for model 1th, in which the gradients of mean molecular weight at the boundaries of the He-burning shell are smoothed by thermohaline mixing. For model 1ov, in which the μ-gradients are pushed away from the evanescent zone (see Sect. 3.3.3), the coupling is several orders-of-magnitude stronger than in model 1. This confirms that the sharp μ-gradients play an important role in the intensity of the coupling between the g-mode cavities.
 |
Fig. 14. Fractional contribution of the acoustic cavity to the mode inertia for models 1, 2, and 3. Modes that have more than half of their energy trapped in the g1 (resp. g2) cavity are shown as filled red circles (resp. blue squares). Other modes are shown as filled black triangles. In the top panel, we also show Ip/I for the g1-dominated modes of models 1th (purple downward triangles) and 1ov (green stars). |
The plots shown in Fig. 14 are qualitatively similar to those obtained with the JWKB approximation (Fig. 8). However, they confirm that the coupling strength between the two g-mode cavities is much weaker in numerical calculations than predicted by Eq. (11) during most of the He subflash. For instance, for models 1ov and 2, Fig. 14 shows that the most g1-like modes have a ratio Ip/I between 10−7 and 10−6. To reproduce this using the JWKB approximation, one needs q1 ∼ 10−4, which is much weaker than the values of q1 given by Eq. (11) for these models (q1 = 0.10 for model 1ov and q1 = 0.03 for model 2). These discrepancies show that the asymptotic expression of q1 given by Eq. (11) is inappropriate. This is likely at least partly caused by the sharp μ-gradients located near the edges of the evanescent zone, which produce non-negligible contributions of the derivatives of equilibrium quantities. The coupling strength would likely be better estimated by asymptotic calculations if the μ-gradients were treated as glitch-like perturbations of the equilibrium quantities using a variational principle (e.g., Monteiro et al. 1994). This is however out of the scope of the present paper.
By contrast, for model 3, the g1-dominated modes can reach large values of the ratio Ip/I, which are comparable to those of g2-dominated modes. This is consistent with a coupling strength q1 = 0.1, as given by Eq. (11).
4.4. Mode heights
As was done in the framework of the JWKB approximation, we estimated the expected heights of the oscillation modes in the observed power spectrum based on our numerical calculations. For this purpose, we began by estimating the damping rates of the modes, taking into account non-adiabatic effects in the envelope and the contribution from radiative damping in the core. We used Eq. (32), in which the ratios of inertia Ig1/I and Ig2/I were obtained using the numerically computed mode eigenfunctions. The modes for which the damping rate exceeds the threshold ηlim = 2/Tobs are expected to be resolved.
To estimate the mode heights, we needed to calculate the ratio between the work integral in the g-mode cavities (Wg1 + Wg2) and the work integral in the p-mode cavity We. For this purpose, Eq. (34) was rewritten as
where the ratios of inertia Ig1/Ip and Ig2/Ip were calculated using the mode eigenfunctions. We then used Eqs. (33) and (35) to estimate the heights of resolved and unresolved modes, respectively. The value of ηp obtained in Sect. 3.6.1 was also used here.
Figure 15 shows the ratio between the predicted heights of mixed modes and those of pure p modes for models 1, 1th, 1ov, 2, and 3. For model 1 and 1th, owing to the very weak coupling between the two g-mode cavities, all the modes that are trapped mostly in the g1-cavity are expected to have negligible heights in the power spectrum. On the contrary, for models 1ov, 2, and 3, we find that several g1-dominated modes should have detectable heights in the power spectrum. For model 3, the coupling between the g-mode cavities is so large that all the modes have non-negligible contribution from the g1-cavity (Ig1/I > 0.2 for all the modes). Consequently, we expect to have numerous g1-dominated modes with detectable heights in the vicinity of pure p modes, as shown by the bottom-right panel of Fig. 11. Another consequence of the strong coupling between the two g-mode cavities in model 3 is that the g2-dominated modes have a larger contribution from the g1-cavity than in other models. This induces a decrease in their expected heights, compared to other models. As a result, in the case of a strong coupling between the g-mode cavities, we expect to detect modes almost exclusively in the neighborhood of pure p modes.
 |
Fig. 15. Height ratios between l = 1 mixed modes and theoretical l = 1 pure p modes for models 1, 1th, 1ov, 2, and 3. The symbols are the same as in Fig. 14. |
4.5. Stretched échelle diagrams
As was already mentioned in Sect. 3.7, stretched period échelle diagrams are a very convenient representation of the oscillation spectrum in order to identify g1-dominated mixed modes. To build such diagrams for each of the considered models, we used the g2-dominated modes to estimate the ζ function, following the procedure described by Mosser et al. (2015). We therefore obtained stretched periods τ for all the modes, which we represented in an échelle diagram folded with ΔΠ2. The stretched échelle diagrams for models 1, 1th, 1ov, 2, and 3 are shown in Fig. 16, where we plotted only the modes that have potentially detectable heights. As expected, most of the detectable modes regroup along a vertical ridge. This vertical ridge is not as straight as it was in our asymptotic calculations (see Fig. 12). The oscillation that is clearly seen in the vertical ridge of models 1, 1ov, and 2 is caused by the buoyancy glitch produced by the H-burning shell in the g2-cavity (see Sect. 4.2.2).
 |
Fig. 16. Stretched échelle diagrams for models 1, 1th, 1ov, 2, and 3. The symbols have the same meaning as in Fig. 12. |
Only at the end of the subflash (model 3) does the coupling between the g-mode cavities become large enough to produce additional detectable modes that significantly deviate from the asymptotic pattern of the g2- and p-dominated modes, and thus lie clearly outside of the vertical ridge in the stretched échelle diagram. During the other stages of the subflash, the coupling between the g-mode cavities is weaker, so that the stretched échelle diagram alone cannot yield direct detections of g1-dominated modes. However, for models 1ov and 2, several modes that are mainly trapped in the g1-cavity have detectable heights. We explain how this might be used to identify red giants going through a He subflash in the following section.
5. Discussion and conclusion
In this paper, we show that red giants undergoing He core subflashes could be identified using the properties of their oscillation mode frequencies. During a He subflash, red giants have three propagating cavities because the convective He-burning shell splits the g-mode cavity in two. We calculate the expected mode frequencies in this case using both an asymptotic analysis and full numerical computations. We further estimate the expected mode heights taking into account the effects of radiative damping in order to determine which oscillation modes could be detected in Kepler seismic data.
If the Kepler sample does contain red giants that are undergoing a He subflash, these stars must have been so far identified as core-helium burning giants, considering the resemblance of their oscillation spectra. However, in this study we obtain a list of clear, detectable features that could enable us to identify red giants passing through a He subflash. These features can be summarized as follows.
Asymptotic period spacing between He subflashes. Bildsten et al. (2012) showed that the asymptotic period spacings of g modes in the aftermath of a He subflash are significantly larger than those of RGB stars and much smaller than those of red clump stars (see also Fig. 3, top panel).
Asymptotic period spacing of the g2-cavity during a He subflash. We show in Sect. 3.3.2 that during the first part of a He subflash, the asymptotic period spacing of the g2-cavity also lies in the “period spacing desert” between RGB and red clump stars. As we have shown, most of the g2-dominated modes should have detectable heights in the oscillation spectra of red giants going through a subflash, meaning that the asymptotic period spacing ΔΠ2 should be easy to measure observationally. This could therefore constitute a way of identifying red giants undergoing a He subflash. However, the shortness of the period during which ΔΠ2 is significantly below the lowest period spacings of red clump stars makes this type of detection rather unlikely.
Buoyancy radius of the H-burning shell. We have shown that the signature of the glitch produced by the H-burning shell in the g2-cavity should be clearly detectable in the oscillation spectrum of red giants undergoing a He subflash (see Sect. 4.2.2). It causes the periods of g2-dominated modes to oscillate as a function of the radial order (see Figs. 13 and 16), and the period of this oscillation can be used to estimate the buoyancy radius of the H-burning shell in the g2-cavity (see Eq. (36)). During the He subflash, we found that the buoyancy radius of the H-burning shell corresponds to 82% of the total buoyancy radius of the g2-cavity, which results in an oscillation with a period of Δn ∼ 6. By contrast, during the clump phase, the buoyancy radius of the H-burning shell amounts to about 70% of the buoyancy radius of the g-mode cavity. This corresponds to an oscillation with a period of Δn ∼ 3 for the gmodes, which is significantly different from what was obtained during a He subflash. We therefore conclude that the period of the oscillation produced by the H-burning shell could be used as a means to separate red giants undergoing a He subflash from regular clump stars.
Detection of additional modes trapped in the g1-cavity. Based on our study, we expect to detect mostly g2- and p-dominated modes during a He subflash. Consequently, the oscillation spectrum of a red giant going through a He subflash should be quite similar to that of a regular clump star with an asymptotic period spacing corresponding to ΔΠ2. However, during the most part of the subflash, several g1-dominated mixed modes are also expected to have detectable heights in the power spectrum. These modes could appear as anomalies in the oscillation spectrum of red giants identified as belonging to the red clump. If the coupling q1 between the g-mode cavities is large enough, the frequencies of the detectable g1-dominated modes significantly deviate from the pattern of the g2- and p-dominated modes. In this case, representing the oscillation modes in a stretched échelle diagram would enable us to directly spot these additional modes (see bottom-right panel of Fig. 12 and right panel of Fig. 16). This seems to be an efficient way of identifying stars in a He subflash. However, we find that q1 becomes strong enough to make this type of detection possible only at the end of a He subflash. The probability of detecting a red giant in this specific phase remains low. We should also mention the caveat that additional modes can also be produced by structural glitches in certain conditions (Cunha et al. 2015). Although we did not find such effects in the stellar models that were computed in this study, this should be kept in mind when searching for red giants going through the He flash using seismology.
Detection of anomalous rotational splittings. In the case of weaker coupling intensities q1, the detectable g1-dominated modes are not expected to show significant deviations from the pattern of the g2- and p-dominated modes (see middle panels of Fig. 16). However, for several of the detectable mixed modes, the g1-cavity contributes to more than half of the inertia. One important consequence is that these modes are predominantly sensitive to the rotation in the g1-cavity. Predicting the rotation profile of red giants during the He-core flash would require the determination of (i) the internal rotation profile of red giants at the tip of the RGB (which is unknown because seismology has brought measurements of the rotation of RGB stars no further than the luminosity bump), (ii) the structural changes during the He-flash (expansion of the layers below the H-burning shell by about a factor of 10 and contraction of the layers above), and (iii) the internal transport of angular momentum during this phase, which is completely unknown. The structural changes during the flash induce a strong forcing of radial differential rotation between the layers below the H-burning shell and those above. Unless the redistribution of angular momentum is efficient enough to enforce a solid-body rotation during the flash despite the shortness of this phase, one would expect to find a different rotation rate below and above the H-burning shell. If this is indeed the case, then the average rotation in the g2-mode cavity (which includes the H-burning shell) is expected to be different from the rotation in the g1-cavity, which lies well below the H-burning shell. It is therefore plausible that g1-dominated modes have rotational splittings that differ from those of the g2-dominated modes. This could be used to identify g1-dominated modes in the oscillation spectra.
As mentioned above, the internal rotation profiles of red giants during the He flash are completely unknown. We only know from Mosser et al. (2012a) that the core of primary clump stars spins with an average frequency of about 100 nHz. In order to roughly assess the sensitivity of the diagnostic that we propose here, we considered a piecewise-constant rotation profile with the g2-cavity spinning at a rotation rate Ωg2 = 100 nHz, the p-mode cavity rotating at Ωp = 10 nHz (this value is completely arbitrary, but it does not impact our conclusions), and the g1-cavity rotating only 50% faster than the g2-cavity, that is, Ωg1 = 150 nHz. We calculated the rotational kernels of model 1ov and combined them with the chosen rotation profile to calculate theoretical rotational splittings, which are shown in Fig. 17. As can be seen in Fig. 17, the splittings of g2- and p-dominated modes vary smoothly with frequency3, while modes that have a non-negligible contribution from the g1-cavity to their inertia have rotational splittings that clearly deviate from this relation. With the chosen rotation profile, the splittings of pure g1 modes would be approximately Ωg1/2 = 75 nHz (see e.g., Goupil et al. 2013), a value which is almost reached by the most g1-dominated modes (see Fig. 17). This represents a 25 nHz difference with the splittings of g2-dominated modes. With four years of Kepler data, the expected precision on the measured splittings is about 10 nHz, meaning that g1-dominated would have significantly larger rotational splittings in the observed spectrum. Red giants going through a He subflash could therefore be characterized by the detection of mixed dipolar modes with rotational splittings that are significantly different from those of the g2- and p-dominated modes, which follow a well-understood pattern (Mosser et al. 2015).
 |
Fig. 17. Rotational splittings obtained for model 1ov, assuming a piecewise-constant rotation profile with Ωg1 = 150 nHz, Ωg2 = 100 nHz, and Ωp = 10 nHz (see text). Modes that are trapped mainly in the g1 and g2 cavities are shown as red and blue filled circles, respectively. The size of the circles indicates the expected height of each mode in the observed spectrum. Only the modes with a height corresponding to at least 10% of the height of a pure p mode are shown. The vertical dashed lines indicate the location of theoretical pure p modes. |
These features can already be searched for within the catalog of about 15 000 Kepler red giants for which oscillations have been detected. The seismic detection of He flashing giants would nicely confirm the existence of the He-core subflashes predicted by 1D evolutionary models and exclude the picture based on 2D and 3D simulations claiming no occurrence of a series of subflashes (Mocák et al. 2008, 2009). If rotational splittings can be detected for mixed modes trapped mainly in the inner g-mode cavity during a He-subflash, we could also measure the differential rotation within the core of the star. This would place precious constraints on the transport of angular momentum in red giants. Finally, we stress that the detection of the seismic features of the He subflashes greatly depends on the intensity of the coupling between the two g-mode cavities, which remains uncertain. Consequently, even if these features fail to be detected with Kepler data, it would not necessarily exclude the picture of the He flash based on 1D evolutionary models.
In the case of two mode cavities, it has been shown that the variations in the rotational splittings with frequency correspond to the so-called ζ function (see Mosser et al. 2015 for more details).
Acknowledgments
We wish to thank the referee, H. Shibahashi, for comments and suggestions that significantly improved the clarity of the manuscript. We are very thankful to B. Mosser, J. Christensen-Dalsgaard, M. J. Goupil, and M. Vrard for fruitful discussions about the paper. S.D. acknowledges support from the PNPS under the grant “Rotation interne et magnétisme des sous-géantes et géantes Kepler” and from the Centre National d’Etudes Spatiales (CNES).
References
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., & Barge, P. 2006, ESA SP, 1306, 33 [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Dupret, M. A., Baudin, F., et al. 2012, A&A, 540, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bildsten, L., Paxton, B., Moore, K., & Macias, P. J. 2012, ApJ, 744, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, J. M., Garaud, P., & Stellmach, S. 2013, ApJ, 768, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Cunha, M. S., Stello, D., Avelino, P. P., Christensen-Dalsgaard, J., & Townsend, R. H. D. 2015, ApJ, 805, 127 [Google Scholar]
- Deheuvels, S., & Michel, E. 2011, A&A, 535, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Michel, E., Goupil, M. J., et al. 2010, A&A, 514, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deupree, R. G. 1984, ApJ, 282, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Deupree, R. G. 1996, ApJ, 471, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. 1977, Acta Astron., 27, 203 [NASA ADS] [Google Scholar]
- Dziembowski, W. A. 1971, Acta Astron., 21, 289 [NASA ADS] [Google Scholar]
- Edwards, A. C. 1969, MNRAS, 146, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Godart, M., Noels, A., Dupret, M.-A., & Lebreton, Y. 2009, MNRAS, 396, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J., Mosser, B., Marques, J. P., et al. 2013, A&A, 549, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, ApJ, 85, 161 [Google Scholar]
- Grosjean, M., Dupret, M.-A., Belkacem, K., et al. 2014, A&A, 572, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Härm, H., & Schwarzschild, M. 1964, ApJ, 139, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Iben, I., & Renzini, A. 1984, Phys. Rep., 105, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C., & Christensen-Dalsgaard, J. 2014, MNRAS, 444, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2008, A&A, 490, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2009, A&A, 501, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, A&A, 283, 247 [NASA ADS] [Google Scholar]
- Montgomery, M. H., Metcalfe, T. S., & Winget, D. E. 2003, MNRAS, 344, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012a, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Vrard, M., Belkacem, K., Deheuvels, S., & Goupil, M. J. 2015, A&A, 584, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Belkacem, K., Pinçon, C., et al. 2017a, A&A, 598, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Pinçon, C., Belkacem, K., Takata, M., & Vrard, M. 2017b, A&A, 600, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osaki, J. 1975, PASJ, 27, 237 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Scuflaire, R. 1974, A&A, 36, 107 [NASA ADS] [Google Scholar]
- Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
- Stello, D., Bruntt, H., Preston, H., & Buzasi, D. 2008, ApJ, 674, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, M. 2016, PASJ, 68, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, H.-C. 1967, Z. Astrophys., 67, 420 [NASA ADS] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Vrard, M., Mosser, B., & Samadi, R. 2016, A&A, 588, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Asymptotic analysis for three propagation cavities
Equations (3) and (4) are solved around each turning point, and the solutions are then matched at an intermediate radius between each pair of turning points. We first write the expressions of υ and w in the vicinity of the inner g-mode cavity (g1), which extends between rarb. Since ω = N in ra and rb, Eq. (4) is singular at these radii, and we thus solve Eq. (3). The solutions are given by:
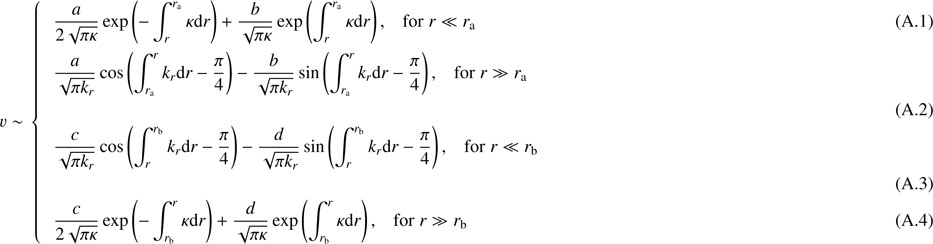
To ensure the regularity of v in the center, the coefficient b must be equal to zero. The expression of w in the vicinity of the g1 cavity can be obtained from the relation (cf. Shibahashi 1979)
which yields
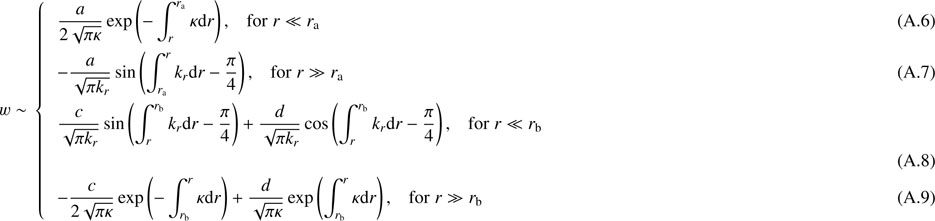
The matching of υ and w inside the first g-mode cavity imposes the relations
which yields
where 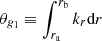 . In the case of a single g-mode cavity, one would need to impose d = 0 for regularity at the surface, and we would thus obtain the eigenvalue condition cosθg1 = 0, which corresponds to pure g modes.
. In the case of a single g-mode cavity, one would need to impose d = 0 for regularity at the surface, and we would thus obtain the eigenvalue condition cosθg1 = 0, which corresponds to pure g modes.
The expressions of the eigenfunctions in the shallower g-mode cavity (g2) are similar to those of the g1-cavity. We introduce the coefficients (a′, b′, c′, d′) analogous to the coefficients (a, b, c, d) corresponding to the g1-cavity. The only difference with the g1-cavity is that the coefficient b′ of the term exp(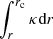 ) in the evanescent zone does not vanish. The matching of v and w in the g2-cavity eventually requires that:
) in the evanescent zone does not vanish. The matching of v and w in the g2-cavity eventually requires that:
where we have introduced 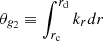 .
.
In the p-mode cavity, we first solve Eq. (4) for w around re and we obtain v from the relation
We then solve Eq. (3) for v around rf and deduce w from Eq. (A.5). Introducing coefficients (a′′, b′′, c′′, d′′) analogous to the coefficients of the g-mode cavities, we obtain
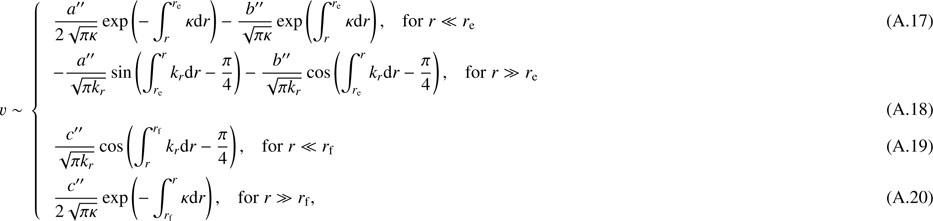
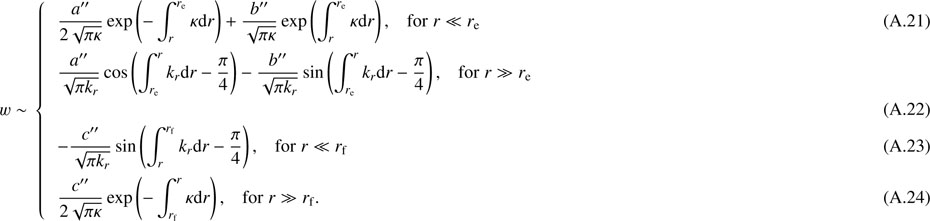
The matching of v and w in the p-mode cavity imposes that
which eventually yields
where 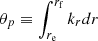 .
.
We then join the three regions by imposing that v and w match in the evanescent zones [rb, rc] and [rd, re]. This gives four more relations:
which eventually yields the eigenvalue relation:
where 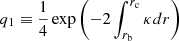 and
and 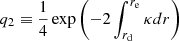 . We also obtain the following relations between a, c′, d′ and c′′:
. We also obtain the following relations between a, c′, d′ and c′′:
Appendix B: Ratios of inertia
Analogously to the approach of Goupil et al. (2013), we seek to estimate the ratios α1 ≡ Ig1/Ip and α2 ≡ Ig2/Ip. We follow the same procedure as these authors, and refer the reader to their paper for more details.
We first estimate the inertia in the p-mode cavity by making the assumption that the radial motion is dominant over the horizontal motion in this region, so that
The second equality has been obtained using Eq. (3). We then use the expression of v in the p-mode cavity given by Eq. (A.11), where we define 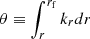 . Assuming that
. Assuming that 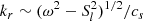 in the p-mode cavity and changing the integration variable to θ in Eq. (B.1), we obtain
in the p-mode cavity and changing the integration variable to θ in Eq. (B.1), we obtain
In the last equality, we have neglected factors of order unity compared to θp, which is valid because we consider modes with large radial order n. We recover the expression obtained by Goupil et al. (2013) for the inertia in the p-mode cavity.
In the external g-mode cavity (delimited by rc and rd), the inertia can be estimated by assuming that the horizontal motion is dominant over the radial motion, so that
where we have used Eq. (2). We use the expression of w in the g2 cavity given in Appendix A and we define 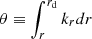 . By assuming that
. By assuming that
in this g-propagative region, and using θ as an integration variable, we obtain
As was done in the p-mode cavity, we have assumed that θg2 ≫ 1.
We proceed similarly to estimate the inertia in the inner g-mode cavity (delimited by ra and rb), and obtain
The ratios of inertias α1 and α2 are thus given by
We have used the ratios between the amplitude of the eigenfunctions as obtained from JWKB analysis (Eqs. (A.33)–(A.35)). We have also used the approximate expressions θp ∼ πν/Δν and θgi ∼ π/(νΔΠi) (i = 1, 2), as advocated by Goupil et al. (2013). We note that these approximations are not valid when these quantities are in the phase of a sine function.
Using these expressions, we were able to calculate the fraction of the total energy of the mode that is trapped in each of the three cavities:
We note that the expression of α1 given by Eq. (B.9) becomes singular when sinθg1 vanishes. Whenever this is the case, one can always rewrite Eq. (B.10) through (B.12) as
where β1 ≡ Ip/Ig1 and β2 ≡ Ig2/Ig1. We have β1 = 1/α1, which is no longer singular, and using the expressions from Appendix A, one obtains:
Appendix C: Comparison between ADIPLS and GYRE
As we have mentioned in Sect. 2, numerically calculating the properties of oscillation modes during a He subflash is tricky. Oscillation codes have never been tested in this special case, and one must therefore treat the results with care. In order to validate the numerical frequencies and eigenfunctions of the modes obtained with the code ADIPLS, we also calculated the numerical frequencies and eigenfunctions of the modes using the code GYRE (Townsend & Teitler 2013), which has been adapted to treat RGB stars. In particular, GYRE performs an interpolation of equilibrium quantities to ensure a certain number of points per mode wavelength in the propagation regions.
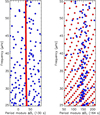 |
Fig. C.1. Period échelle diagrams of model 1 using oscillation modes computed with the code GYRE. These diagrams were obtained by folding the mode periods using alternately ΔΠ1 (left panel) and ΔΠ2 (right panel). Mode that have more the 50% of the energy in the g1-cavity (resp. g2-cavity) are shown as filled red (resp. blue) circles. |
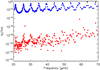 |
Fig. C.2. Fractional contribution of the acoustic cavity to the mode inertia for model 1, computed with GYRE. |
We show in Fig. C.1 the period échelle diagrams calculated with the code GYRE for model 1. As is done in Sect. 4 with oscillation modes computed with ADIPLS, the period échelle diagrams were obtained by folding the mode periods with the asymptotic period spacing of the g1-cavity ΔΠ1 (left panel) and with the asymptotic period spacing of the g2-cavity ΔΠ2 (right panel). This figure is to be compared to the two top-left panels of Fig. 13, which show period échelle diagrams calculated with ADIPLS for model 1. The échelle diagrams are very similar, showing a quite good overall agreement between the two codes concerning the pattern of the oscillation spectrum. A closer inspection shows slight mode-to-mode differences that will need to be looked into, but do not influence the conclusions of the present paper.
A critical point in this study is the intensity of the coupling between the two g-mode cavities, which is reflected by the ratios of inertias of the modes in the different resonant cavities. In order to check the results of the code ADIPLS, we also calculated the ratio Ip/I for the modes of model 1 computed with GYRE. The results are shown in Fig. C.2. This figure is to be compared to the top left panel of Fig. 14, which shows the same quantity for modes computed with ADIPLS. Once again, the overall agreement between the two codes is excellent. For both codes, the fractional contribution of the acoustic cavity to the total mode inertia is between 10−12 and 10−4 for g1-dominated modes, and for g2- and p-dominated modes, the output of the two codes are nearly identical. We do notice some mode-to-mode differences, whereby the contribution of the g1-cavity to the mode inertia differs from one code to the other. We show in Fig. C.3 the integrand of the inertia for two g1-dominated mixed modes of model 1 computed with ADIPLS (in red) and GYRE (in black). For one of the modes, the two codes agree very well, while for the other, the contribution of the g1-cavity to the mode inertia differs by a factor of 10 between the codes. These mode-to-mode differences will need to be investigated more thoroughly. However, the oscillation codes give an identical general pattern for the oscillations spectra and they yield similar order-of-magnitude values for the ratios of the mode inertia in the different propagating cavities. This shows that the results of the oscillation code ADIPLS are reasonably trustworthy, to the level of precision required in this study.
 |
Fig. C.3. Integrand of the inertia of two g1-dominated dipolar mixed modes of model 1 computed with ADIPLS (red curves) and GYRE (black curves). |
All Tables
Seismic parameters of the reference model (1.7 M⊙ model during the second He-core subflash) calculated using their asymptotic expressions (see text).
All Figures
 |
Fig. 1. Variations in the luminosity produced by He-burning during the He-subflashes of a 1.7 M⊙ model computed with MESA. The shaded areas indicate periods during which the (convective) He-burning region splits the g-mode cavity in two. |
| In the text | |
 |
Fig. 2. Propagation diagram for a 1.7 M⊙ model during a He-burning subflash. The Brunt–Väisälä frequency is represented by the full red curve, and the l = 1 Lamb frequency S1 corresponds to the long-dashed blue curve. The horizontal line corresponds to the angular frequency ω = 2πνmax. A wave with pulsation ω propagates where the line is solid, and it is evanescent where the line is dotted. Turning points for the cavities are also depicted by the filled circles. The gray vertical arrow indicates the position of the H-burning shell. |
| In the text | |
 |
Fig. 3. Variations in global seismic parameters during the second subflash of a 1.7 M⊙ model. The vertical gray dotted lines indicate the three evolutionary stages at which global seismic parameters are provided in Table 1. Top panel: asymptotic period spacing of dipolar modes in the g1 cavity (ΔΠ1, red solid line) and in the g2 cavity (ΔΠ2, blue dot-dashed line) as a function of time elapsed since the tip of the RGB. The black curve shows the period spacing of the single g-mode cavity outside of the He subflash. Bottom panel: variations in the coupling strength between the g1 and g2 cavities (q1, red solid line for Schwarzschild criterion, purple line for Ledoux criterion with thermohaline mixing, and black dashed line for Schwarzschild criterion with overshooting; see text for more details) and between the g2 and the p-mode cavities (q2, blue dot-dashed line). |
| In the text | |
 |
Fig. 4. Profiles of the mean molecular weight μ (top panel) and the function κ (bottom panel) in the core of Model 1 (blue curves) and Model 2 (red curves). In the top panel, thick lines indicate the evanescent zone separating the g1- and g2-cavities. |
| In the text | |
 |
Fig. 5. Period échelle diagrams of asymptotic oscillation modes obtained by solving Eq. (9) using the parameters given in Table 1 and considering a weak coupling between the g-mode cavities (q1 = 10−3). These diagrams were obtained by folding the mode periods using either ΔΠ1 (left panel) or ΔΠ2 (right panel). The horizontal dashed lines indicate the location of theoretical pure l = 1 p modes. Modes trapped predominantly in the g1 cavity (Ig1/I > 0.5) are filled in red, and modes trapped mainly in the g2 cavity (Ig2/I > 0.5) are filled in blue (mode trapping is estimated based on ratios of inertia, see Sect. 3.5). Other modes are left blank. |
| In the text | |
 |
Fig. 6. As in Fig. 5 but for an intermediate coupling between the g-mode cavities (q1 = 10−2). |
| In the text | |
 |
Fig. 7. As in Fig. 5 but for a strong coupling between the g-mode cavities (q1 = 10−1). |
| In the text | |
 |
Fig. 8. Fractional contribution of the acoustic cavity to the mode inertia (and thus to the mode kinetic energy) using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). Modes that have more than 50% of the energy trapped in the g1 (resp. g2) cavity are shown as filled red circles (resp. blue squares). Other modes are shown as filled black triangles. The dashed blue curve indicates the ratios of inertia Ip/Itot that would be obtained for mixed modes trapped only in the g2 and p mode cavities. |
| In the text | |
 |
Fig. 9. As in Fig. 8 but assuming values of the asymptotic period spacing ΔΠ1 ranging from 30 to 800 s. To guide the eye, the ratios Ip/I for consecutive modes have been linked by the black dashed curve. |
| In the text | |
 |
Fig. 10. Damping rates ηmix of mixed modes obtained from a JWKB analysis using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). The symbols are the same as in Fig. 8. The horizontal dash-dotted line indicates the damping rates of p modes inferred from seismic observations of typical clump stars (see text). The threshold ηlim = 2/Tobs below which modes are unresolved is represented by the horizontal dashed line (we assumed a duration of Tobs = 4 yr, corresponding to the longest datasets of Kepler). |
| In the text | |
 |
Fig. 11. Height ratios between l = 1 mixed modes and theoretical l = 1 pure p mode obtained from a JWKB analysis using the global seismic parameters of model 1 and assuming an intermediate coupling between the two g-mode cavities (q1 = 10−2). These ratios were calculated using either Eq. (33) (if the mode is resolved) or Eq. (35) (otherwise). |
| In the text | |
 |
Fig. 12. Échelle diagrams of the oscillation spectrum of model 1 obtained using the JWKB approximation, and assuming different coupling intensities between the g-mode cavities (q1 = 10−3, 10−2, 10−1from left to right panels). The size of the symbols indicates the expected height of each mode. For clarity, only the modes with a height corresponding to at least 10% of the height of a pure p mode are shown. Modes colored in red have at least 50% of their total energy trapped in the innermost g1 cavity (i.e., Ig1/I > 0.5). Top panels: frequency échelle diagrams folded with the large separation of acoustic modes Δν. Bottom panels: stretched period échelle diagrams built following Mosser et al. (2015, see text). |
| In the text | |
 |
Fig. 13. As in Fig. 5 but using the oscillation modes that were computed with ADIPLS for a 1.7 M⊙ MESA model at several stages during the second He subflash (top-left panels: model 1, top-right panels: model 1ov, bottom-left panels: model 2, bottom-right panels: model 3; see text for description). For each model, period échelle diagrams were constructed using the period spacings of the g1 cavity (left plots) and the g2 cavity (right plots). |
| In the text | |
 |
Fig. 14. Fractional contribution of the acoustic cavity to the mode inertia for models 1, 2, and 3. Modes that have more than half of their energy trapped in the g1 (resp. g2) cavity are shown as filled red circles (resp. blue squares). Other modes are shown as filled black triangles. In the top panel, we also show Ip/I for the g1-dominated modes of models 1th (purple downward triangles) and 1ov (green stars). |
| In the text | |
 |
Fig. 15. Height ratios between l = 1 mixed modes and theoretical l = 1 pure p modes for models 1, 1th, 1ov, 2, and 3. The symbols are the same as in Fig. 14. |
| In the text | |
 |
Fig. 16. Stretched échelle diagrams for models 1, 1th, 1ov, 2, and 3. The symbols have the same meaning as in Fig. 12. |
| In the text | |
 |
Fig. 17. Rotational splittings obtained for model 1ov, assuming a piecewise-constant rotation profile with Ωg1 = 150 nHz, Ωg2 = 100 nHz, and Ωp = 10 nHz (see text). Modes that are trapped mainly in the g1 and g2 cavities are shown as red and blue filled circles, respectively. The size of the circles indicates the expected height of each mode in the observed spectrum. Only the modes with a height corresponding to at least 10% of the height of a pure p mode are shown. The vertical dashed lines indicate the location of theoretical pure p modes. |
| In the text | |
 |
Fig. C.1. Period échelle diagrams of model 1 using oscillation modes computed with the code GYRE. These diagrams were obtained by folding the mode periods using alternately ΔΠ1 (left panel) and ΔΠ2 (right panel). Mode that have more the 50% of the energy in the g1-cavity (resp. g2-cavity) are shown as filled red (resp. blue) circles. |
| In the text | |
 |
Fig. C.2. Fractional contribution of the acoustic cavity to the mode inertia for model 1, computed with GYRE. |
| In the text | |
 |
Fig. C.3. Integrand of the inertia of two g1-dominated dipolar mixed modes of model 1 computed with ADIPLS (red curves) and GYRE (black curves). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



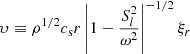
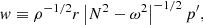
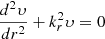
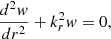
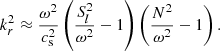
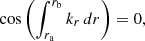
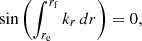
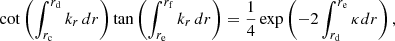
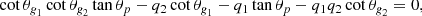
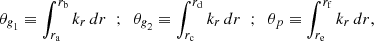
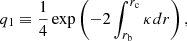
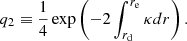
![$$ \begin{aligned} \theta _{p}\approx \pi \left[ \frac{\nu }{\Delta \nu } -\frac{1}{2} - \varepsilon _{p} \right], \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq20.gif)
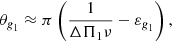
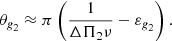
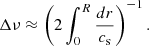
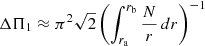
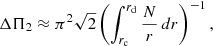
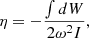
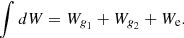
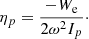
![$$ \begin{aligned} \frac{\xi _r}{r} \sim \frac{a}{\sqrt{\pi }} \frac{\left[l(l+1)\right]^{1/4}}{\sqrt{\rho \omega r^5 N}} \cos \left( \int _{r_{\mathrm{a}}}^r k_{r} {d}r- \frac{\pi }{4} \right) , \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq32.gif)
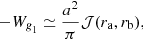
![$$ \begin{aligned} {\mathcal{J} } (r_{\mathrm{a}},r_{\mathrm{b}}) \equiv \frac{\left[l(l+1)\right]^{3/2}}{2\omega ^3} \int _{r_{\mathrm{a}}}^{r_{\mathrm{b}}} \frac{\nabla _{\mathrm{ad}}-\nabla }{\nabla }\frac{\nabla _{\mathrm{ad}}NgL}{p r^5}\,{d}r, \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq34.gif)
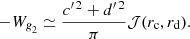
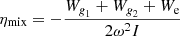
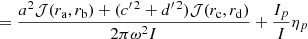
![$$ \begin{aligned}&= \frac{1}{4\pi } \left[ \frac{I_{\textit{g}_1}}{I} \frac{{\mathcal{J} }(r_{\mathrm{a}},r_{\mathrm{b}})}{\theta _{\textit{g}_1}} + \frac{I_{\textit{g}_2}}{I} \frac{{\mathcal{J} }(r_{\mathrm{c}},r_{\mathrm{d}})}{\theta _{\textit{g}_2}} \right] + \frac{I_{p}}{I} \eta _{\mathrm{p,}} \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq38.gif)
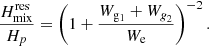
![$$ \begin{aligned} \frac{W_{\textit{g}_1}+W_{\textit{g}_2}}{W_{\mathrm{e}}} = \frac{1}{4\pi \eta _{\mathrm{p}}\theta _{p}} \left[ \frac{a^2}{c{^{\prime \prime \,2}}}{\mathcal{J} }(r_{\mathrm{a}},r_{\mathrm{b}}) + \frac{{c{^{\prime \,2}}}+{d{^{\prime \,2}}}}{c{^{\prime \prime \,2}}}{\mathcal{J} }(r_{\mathrm{c}},r_{\mathrm{d}}) \right]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq40.gif)
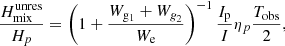
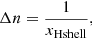
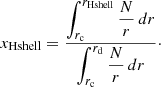
![$$ \begin{aligned} \frac{W_{\textit{g}_1}+W_{\textit{g}_2}}{W_{\mathrm{e}}} = \frac{1}{4\pi \eta _{p}} \left[ \frac{I_{\mathrm{g1}}}{I_{p}}\frac{{\mathcal{J} }(r_{\mathrm{a}},r_{\mathrm{b}})}{\theta _{\mathrm{g1}}} + \frac{I_{\mathrm{g2}}}{I_{p}}\frac{{\mathcal{J} }(r_{\mathrm{c}},r_{\mathrm{d}})}{\theta _{\mathrm{g2}}} \right], \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq44.gif)
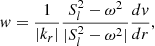
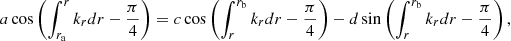
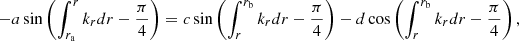
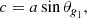
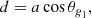
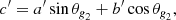
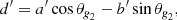
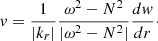
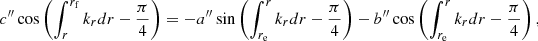
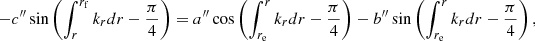
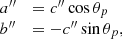
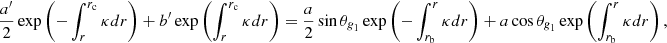
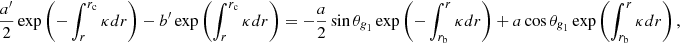
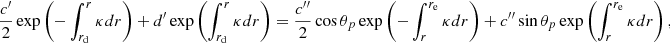
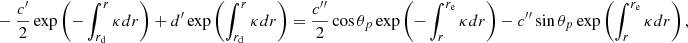
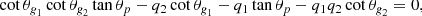
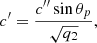
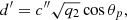
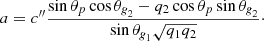
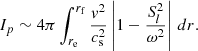
![$$ \begin{aligned} I_{p}&\sim \frac{2 {c{^{\prime \prime \,2}}}}{\omega ^2} \int _0^{\theta _{p}} \left[ 1 + \sin (2\theta ) \right] \,{d}\theta , \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq73.gif)
![$$ \begin{aligned}&\sim \frac{2 {c{^{\prime \prime \,2}}}}{\omega ^2} \left[ \theta _{p}+ \frac{1-\cos (2\theta _{p})}{2} \right] \approx \frac{2 c{^{\prime \prime \,2}}\theta _{p}}{\omega ^2} \cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq74.gif)
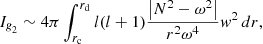
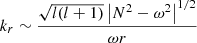
![$$ \begin{aligned} I_{\textit{g}_2}&\sim \frac{2}{\omega ^2} \left[ ({c{^{\prime \,2}}}+{d{^{\prime \,2}}}) \theta _{\textit{g}_2}+ ({c{^{\prime \,2}}}-{d{^{\prime \,2}}})\frac{\cos (2\theta _{\textit{g}_2})-1}{2} -{c^{\prime }}{d^{\prime }}\sin (2\theta _{\textit{g}_2}) \right]\nonumber \\&\approx \frac{2 ({c{^{\prime \,2}}}+{d{^{\prime \,2}}})\theta _{\textit{g}_2}}{\omega ^2} \cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq78.gif)
![$$ \begin{aligned} I_{\textit{g}_1} \sim \frac{2 a^2}{\omega ^2} \left[ \theta _{\textit{g}_1}+ \frac{\cos (2\theta _{\textit{g}_1})-1}{2} \right] \approx \frac{2 a^2\theta _{\textit{g}_1}}{\omega ^2} \cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33409-18/aa33409-18-eq79.gif)