| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201832872 | |
| Published online | 18 October 2018 | |
Mass determination of the 1:3:5 near-resonant planets transiting GJ 9827 (K2-135)★
1
Instituto de Astrofísica de Canarias (IAC),
38205 La Laguna,
Tenerife,
Spain
e-mail: jparranz@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna (ULL),
38206,
La Laguna,
Tenerife,
Spain
3
Dipartimento di Fisica, Universitá di Torino,
Via P. Giuria 1,
10125,
Torino,
Italy
4
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg,
Germany
5
Department of Astrophysical Sciences, Princeton University,
4 Ivy Lane,
Princeto,
NJ
08544,
USA
6
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge,
MA
02139,
USA
7
Leiden Observatory, Leiden University,
2333
CA Leiden,
The Netherlands
8
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala,
Sweden
9
Department of Earth and Planetary Sciences, Tokyo Institute of Technology,
2-12-1 Ookayama,
Meguro-ku,
Tokyo
152-8551,
Japan
10
Department of Astronomy, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo
113-0033,
Japan
11
Astronomy Department and Van Vleck Observatory, Wesleyan University,
Middletown,
CT 06459,
USA
12
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
DK-8000
Aarhus C,
Denmark
13
Institute of Planetary Research,
German Aerospace Center, Rutherfordstrasse 2,
12489
Berlin,
Germany
14
Department of Astronomy and McDonald Observatory, University of Texas at Austin,
2515 Speedway, Stop C1400, Austin,
TX
78712,
USA
15
National Optical Astronomy Observatory,
950 North Cherry Avenue,
Tucson,
AZ
85719,
USA
16
Okayama Astrophysical Observatory,
National Astronomical Observatory of Japan, NINS, Asakuchi,
Okayama
719-0232,
Japan
17
Rheinisches Institut für Umweltforschung an der Universität zu Köln,
Aachener Strasse 209,
50931 Köln,
Germany
18
Departamento de Astronomia do IAG/USP, Universidade de São Paulo, Rua do Matão 1226, Cidade Universitária,
05508-900
São Paulo,
SP,
Brazil
19
Astrobiology Center, NINS, 2-21-1 Osawa, Mitaka,
Tokyo
181-8588,
Japan
20
National Astronomical Observatory of Japan, NINS, 2-21-1 Osawa, Mitaka,
Tokyo
181-8588,
Japan
21
Center for Astronomy and Astrophysics, TU Berlin,
Hardenbergstr. 36,
10623
Berlin,
Germany
22
Institut de Ciències de l’Espai (IEEC-CSIC),
C/ Can Magrans s/n, Campus UAB,
08193
Bellaterra,
Spain
23
Institut d’Estudis Espacials de Catalunya (IEEC),
08034
Barcelona,
Spain
24
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117,
Heidelberg,
Germany
Received:
22
February
2018
Accepted:
14
July
2018
Context. Multiplanet systems are excellent laboratories to test planet formation models as all planets are formed under the same initial conditions. In this context, systems transiting bright stars can play a key role, since planetary masses, radii, and bulk densities can be measured.
Aims. GJ 9827 (K2-135) has recently been found to host a tightly packed system consisting of three transiting small planets whose orbital periods of 1.2, 3.6, and 6.2 days are near the 1:3:5 ratio. GJ 9827 hosts the nearest planetary system (~30 pc) detected by NASA’s Kepler or K2 space mission. Its brightness (V = 10.35 mag) makes the star an ideal target for detailed studies of the properties of its planets.
Methods. Combining the K2 photometry with high-precision radial-velocity measurements gathered with the FIES, HARPS, and HARPS-N spectrographs we revised the system parameters and derive the masses of the three planets.
Results. We find that GJ 9827 b has a mass of Mb = 3.69−0.46+0.48 M⊕ and a radius of Rb = 1.58−0.13+0.14 R⊕, yielding a mean density of ρb = 5.11−1.27+1.74 g cm−3. GJ 9827 c has a mass of Mc = 1.45−0.57+0.58 M⊕, radius of Rc = 1.24−0.11+0.11 R⊕, and a mean density of ρc = 4.13−1.77+2.31 g cm−3. For GJ 9827 d, we derive Md = 1.45−0.57+0.58 M⊕, Rd = 1.24−0.11+0.11 R⊕, and ρd = 1.51−0.53+0.71 g cm−3.
Conclusions. GJ 9827 is one of the few known transiting planetary systems for which the masses of all planets have been determined with a precision better than 30%. This system is particularly interesting because all three planets are close to the limit between super-Earths and sub-Neptunes. The planetary bulk compositions are compatible with a scenario where all three planets formed with similar core and atmosphere compositions, and we speculate that while GJ 9827 b and GJ 9827 c lost their atmospheric envelopes, GJ 9827 d maintained its primordial atmosphere, owing to the much lower stellarirradiation. This makes GJ 9827 one of the very few systems where the dynamical evolution and the atmosphericescape can be studied in detail for all planets, helping us to understand how compact systems form and evolve.
Key words: planetary systems / techniques: high angular resolution / techniques: photometric / techniques: radial velocities / stars: abundances / stars: individual: GJ 9827
Based on observations made with (a) the ESO-3.6 m telescope at La Silla Observatory under program ID 099.C-0491 and 0100.C-0808; (b) the Italian Telescopio Nazionale Galileo operated on the island of La Palma by the Fundación Galileo Galilei of the Istituto Nazionale di Astrofisica; (c) the Nordic Optical Telescope, operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos.
© ESO 2018
1 Introduction
Systems containing multiple planets have drawn much attention because they have frequently been seen as potential solar system analogues. However, none of the systems discovered so far resemble ours. The vast majority of multiplanet systems identified by the NASA’s Kepler space mission contains super-Earths (1 ≤ Rp ≤ 2R⊕) and sub-Neptunes (2 ≤ Rp ≤ 4 R⊕) in tightly packed configurations, with orbits smaller than the orbit of Mercury (Winn & Fabrycky 2015).
Compact systems containing planets of different sizes and masses are the best test beds to constrain planetary formation mechanisms, since all planets have formed under the same initial conditions. The short orbital period increases the geometric probability to see the planets transiting their host stars, allowing us to measure the planetary radii. The Doppler reflex motion is larger, enabling the mass determination via radial velocity (RV) measurements using state-of-the-art, high-precision spectrographs. However, although more than 200 systems with three or more planets have been discovered so far, many questions remain unanswered.
How do compact planetary systems form? It has been proposed that planets with short orbital periods might have either formed in situ (Chiang & Laughlin 2013), or at much larger distance from their host star and then moved inwards via type I or type II migration mechanisms (for a review see Baruteau et al. 2014). Once the disk has been dispersed, planets could also migrate through planet–planet scattering (see, e.g., Marzari & Weidenschilling 2002). Explaining the formation of compact systems with in situ formation is however not easy because a lot of material in the inner disk is required in order to form planets. Using an in situ formation model, Hansen & Murray (2013) found that there are roughly 50% more single-planet candidates observed than those produced by any model population.
How can we observationally distinguish between different scenarios? In order to gain insights into the formation of compact systems, we have to understand whether the planets formed at large distance (e.g., beyond the snow-line), or close-in to their host star. It is now well accepted that the composition of a pre-main sequence disk – where planet formation takes place – depends on the radial distance from the host star. The chemical abundance of planets can thus be used to trace their formation. Thiabaud et al. (2015) showed that the C/O is a good tracer to assess whether a given planet formed in situ or not. The Mg/Si and Fe/Si bulk composition ratios are also interesting tracers. In this respect, the discovery that the ultra-short period planet K2-106 b (Guenther et al. 2017) has an iron core containing 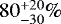 of its mass supports the notion that this planet might have formed in a metal rich environment – typically close to the host star, where photophoresis process can separate iron from silicates in the early phase of planet formation (Wurm et al. 2013). On the contrary, if a close-in planet (a ≾ 0.1 AU) were found to have a high quantity of water, this would imply that the planet formed beyond the snow-line and then migrated inwards to its current position (Raymond et al. 2008; Lopez 2017).
of its mass supports the notion that this planet might have formed in a metal rich environment – typically close to the host star, where photophoresis process can separate iron from silicates in the early phase of planet formation (Wurm et al. 2013). On the contrary, if a close-in planet (a ≾ 0.1 AU) were found to have a high quantity of water, this would imply that the planet formed beyond the snow-line and then migrated inwards to its current position (Raymond et al. 2008; Lopez 2017).
As pointed out by Izidoro et al. (2017), the period ratio distribution of planets in multiplanet systems can also provide some clues about the formation mechanisms involved. Using N-body simulations together with a model of gaseous disk, Izidoro et al. (2017) found that only 50–60% of resonant chains became unstable whereas to match observations at least 75% (and probably 90–95% according to Kepler results) must be expected.
In order to address these questions, a well characterized sample of multiplanet systems transiting relatively bright stars for which planetary radii, masses, and orbital parameters have been determined with high accuracy is needed. The three brightest systems known to host three or more planets for which masses have been determined for all planets, are Kepler-89 (V = 12.2 mag, 4 planets), K2-32 (V = 12.3 mag, 3 planets), and Kepler-138 (V = 12.9 mag, 3 planets). However, for most of the planets in these systems masses are known with a precision of only ~50% due to the faintness of the host stars (Hadden & Lithwick 2017).
To increase the sample of compact systems with planetary masses with a precision at least better than 30%, we need to detect brighter systems (V < 12 mag) for which radial velocity (RV) precisions of 1 m s-1 can be achieved using state-of-the-art spectrographs during a reasonable amount of telescope time.
Using K2 time-series photometry from Campaign 12, we have recently discovered that the star GJ 9827 – also known as K2-135 and EPIC 246389858 (Table 1) – hosts three transiting small planets (Rp ≲ 2R⊕) with orbital periods of 1.2, 3.6, and 6.2 days (Niraula et al. 2017; Rodriguez et al. 2018). With a distance of only ~30 pc, GJ 9827 is the nearest planetary system detected by Kepler or K2, and with V = 10.35 mag (Table 1) is the brightest system known to host three transiting planets.
In this paper, we present the high-precision RV measurements we collected between July and December 2017 to measure the masses of the three small planets transiting GJ 9827. This work is part of the ongoing RV follow-up program of K2 transiting planets successfully carried out by our consortium KESPRINT1 (see, e.g., Nowak et al. 2017; Fridlund et al. 2017; Gandolfi et al. 2017; Barragán et al. 2017; Dai et al. 2017; Guenther et al. 2017).
Teske et al. (2018) recently reported on the mass determinations of the three planets based on a ~7-year-long RV monitoring carried out with the Planet Finder Spectrograph on the Magellan II telescope. We compare their results with ours in Sect. 7.
Equatorial coordinates, optical and near-infrared magnitude, and stellar parameters of GJ 9827.
2 Ground based follow-up observations
2.1 High-spacial resolution
We conducted speckle imaging observations of the host star with the WIYN 3.5-m telescope and the NASA Exoplanet Star and Speckle Imager (NESSI; Scott et al. 2016; Scott et al., in prep.). The observations were conducted at 562 and 832 nm simultaneously, and the data were collected and reduced following the procedures described by Howell et al. (2011). The resulting reconstructed images of the host star are 4.6′′ × 4.6′′, with a resolution close to the diffraction limit of the telescope. We did not detect any secondary sources in the reconstructed images, and we produced 5σ detection limits from the reconstructed images using a series of concentric annuli (Fig. 1).
 |
Fig. 1 Reconstructed images from WIYN/NESSI speckle interferometry and the resulting 5σ contrast curves. The inset panel images are 4.6′′ × 4.6′′ and northeast is up and to the left. |
2.2 FIES
We collected seven RV measurements of GJ 9827 with the FIbre-fed Echelle Spectrograph (FIES; Frandsen & Lindberg 1999; Telting et al. 2014) on the 2.56 m Nordic Optical Telescope (NOT) at the Observatorio del Roque de los Muchachos, La Palma (Spain). The data have already been presented in Niraula et al. (2017). We refer the reader to this work for a description of the observational strategy and data reduction. For the sake of completeness, we report the RV measurements in Table A.1.
2.3 HARPS and HARPS-N
We obtained 35 high-precision RVs with the HARPS spectrograph (Mayor et al. 2003) on the 3.6 m ESO telescope at La Silla Observatory under programs 099.C-0491 and 0100.C-0808, and 23 RV measurements with the HARPS-N spectrograph (Cosentino et al. 2012) on the 3.58 m Telescopio Nazionale Galileo (TNG) at La Palma under programs OPT17A_64 and A36TAC_12. The HARPS spectra were gathered from August 19 to October 24 2017 UT, and the HARPS-N spectra from July 29 to December 9 2017 UT. Both spectrographs have a resolving power of R = λ∕Δaλ ≈ 115 000. HARPS covers the wavelength region from 3830 to 6900 Å, whereas HARPS-N from 3780 to 6910 Å. We used the second fiber of both instruments to monitor the sky background. All calibration frames were taken using the HARPS and HARPS-N standard procedures. The spectra were reduced and extracted using the dedicated data reduction software (DRS). The RVs were measured by cross-correlating the Echelle orders of the observed spectra with a K5 numerical mask (Baranne et al. 1996; Pepe et al. 2002) and by fitting a Gaussian function to the average cross-correlation function (CCF). The DRS also provides the absolute RV, the bisector span (BIS) and full-width at half maximum (FWHM) of the CCF, and the Ca II S-index activity indicator. We list the HARPS and HARPS-N measurements in Tables A.2 and A.3.
3 Properties of the host star
3.1 Spectral analysis
In our previous paper (Niraula et al. 2017), we derived the spe- ctroscopic parameters of GJ 9827 using the co-added FIES spectrum, which has a signal-to-noise ratio (S/N) of ~150 per pixel at 5500 Å. As part of the analysis presented in this work, we refined the spectroscopic properties of the host star using the combined HARPS and HARPS-N spectra, taking advantage of their higher resolving power (R ≈ 115 000) and S/N (~440 and 400, respectively). The spectral analysis was performed following the same methods used in Niraula et al. (2017), which, for the sake of completeness, are briefly described in the next paragraphs.
We used SpecMatch-Emp (Yee et al. 2017), a software suite that utilizes hundreds of Keck/HIRES template spectra of stars whose parameters have been accurately measured via interferometry, asteroseismology, spectral synthesis, and spectrophotometry. The fit is performed in the spectral region 5000–5900 Å. The output parameters of SpecMatch-Emp, namely, the effective temperature Teff, stellar radius R⋆, and iron abundance [Fe/H], are derived by interpolating those of the best matching library stars. Following Hirano et al. (2018), prior to our analysis we reformatted the co-added HARPS and HARPS-N spectra so that they have the same spectral format as Keck/HIRES.
We also analyzed the HARPS and HARPS-N co-added spectra with the spectral analysis package SME (Valenti & Piskunov 1996; Valenti & Fischer 2005). SME calculates synthetic spectra from model atmospheres and fits them to the observed spectrum using a χ2 minimizing procedure. The analysis was carried out with the non-LTE version of the code (5.2.2) and ATLAS12 model atmospheres (Kurucz 2013). Following the calibration equation for Sun-like stars from Bruntt et al. (2010), we fixed the microturbulent velocity to vmic = 0.9 km s−1. The macroturbulent velocity vmac was assumed to be 0.5 km s−1 (Gray 2008). Following Fuhrmann et al. (1993, 1994), the line wings of the Hα and Hβ lines were fitted to determine the effective temperature Teff. The surface gravity log g⋆ was measured from the wings of the Ca I λ 6102, 6122, 6162 Å triplet, and the Ca I λ 6439 Å line. The iron [Fe/H] and calcium [Ca/H] abundance, as well as the projected rotational velocity v sin i⋆ were derived fitting the profile of clean and unblended narrow lines in the spectral region between 6100 and 6500 Å. The analysis was finally checked with the Na doublet λ 5889 and 5896 Å.
We summarize our results in Table 2. The effective temperatures derived by SpecMatch-Emp and SME agree well within the nominal error bars. As for the iron abundance, the two methods provide consistent results within ~2σ. It is worth noting that the error bars calculated by SME are larger than those given by SpecMatch-Emp, owing to the physical uncertainties of model atmospheres of cool stars (Teff < 4500 K). We therefore adopted the effective temperature and iron abundance measured by SpecMatch-Emp and averaged the estimates from the HARPS and HARPS-N spectra. For the projected rotational velocity v sin i⋆, we adopted the value determined with SME. We found Teff = 4219 ± 70 K, [Fe/H] = − 0.29± 0.12 dex, and v sin i⋆ = 1.5 ± 1.0 km s−1 (Table 1). The stellar radius and surface gravity were determined using a different method, as described in the following section.
3.2 Stellar radius and mass
We built the spectral energy distribution of GJ 9827 using the Johnson B and V (Mumford 1956) and 2MASS JHKs (Skrutskie et al. 2006) magnitudes. Following the method described in Gandolfi et al. (2008), we measured the interstellar redding (Av) along the line of sight to the star and found Av = 0.04 ± 0.08 mag (Table 1), which is consistent with zero, as expected given the proximity of GJ 9827. We note that our result agrees with previous findings from McDonald et al. (2017) and Gontcharov & Mosenkov (2018), confirming that the star suffers a negligible reddening.
We derived the stellar radius R⋆ by combining Gaia’s distance d = 29.6864 ± 0.1033 pc (Gaia Collaboration et al. 2018), with the apparent magnitude V = 10.35 ± 0.10 mag (Mumford 1956) and our effective temperature estimate Teff = 4219 ± 70 K (Sect. 3.1). Following Luri et al. (2018), we added 0.1 mas in quadrature to the uncertainty of Gaia’s parallax (33.6855 ± 0.0611 mas) to account for systematic uncertainties of Gaia’s astrometry. The V -band bolometric correction of − 0.847 ± 0.075 was derivedusing the polynomial equations from Flower (1996) combined with the coefficients and the solar bolometric magnitude from Torres (2010). Assuming no reddening (Av = 0 mag), we found a stellar radius of R⋆ = 0.622± 0.051 R⊙, which agrees with the spectroscopic radius derived using SpecMatch-Emp (cf. Table 2).
We finally converted Teff, R⋆, and [Fe/H] into stellar mass M⋆ and surface gravity log g⋆ using the empirical relations of Mann et al. (2015) and Monte Carlo simulations. We found that GJ 9827 has a mass of M⋆ = 0.637 ± 0.051 M⊙ and a surface gravity of log g⋆ = 4.657 ± 0.042 (cgs), which agrees with the spectroscopic gravity derived using SME (cf. Table 2). According to the analysis performed with SpecMatch-Emp, the three stars2 whose spectra best match the HARPS and HARPS-N spectra of GJ 9827 have masses between 0.62 and 0.64 M⊙, confirming our results. The derived stellar mass and radius are are given in Table 1.
3.3 Stellar activity and rotation period
The K2 light curve of GJ 9827 displays a quasi-periodic photometric variability with a peak-to-peak amplitude of about 0.4 % (Fig. 2, left panel). Given the late spectral type of the star (K6 V), the observed photometric variation is very likely caused by active regions (sun-like spots and plages) crossing the visible stellar hemisphere as the star rotates about its axis. This is corroborated by the detection of emission components in the cores of the Ca II H & K lines (Fig. 3), from which we measured an average S-index of 0.677 ± 0.034 and 0.739 ± 0.021 using the HARPS and HARPS-N spectra, respectively.
Applying the auto cross-correlation technique to the K2 light curve, Niraula et al. (2017) and Rodriguez et al. (2018) found that the rotation period Prot of the star is either ~17 or 30 days. A Gaussian process (GP) analysis of the K2 light curve (Sect. 5.2) yields a bimodal posterior distribution with rotational periods peaking at 15.1 ± 1.6 and 30.7 ± 1.4 days, and thus does not provide a conclusive result about the rotation period of the star. However, we note that the ratio between the two measurements is close to 2, suggesting that the first might be the harmonic of the second. A visual inspection of the K2 time series photometry reveals that there are two dips whose minima occur at BJDTBD-2454833 ≈ 2922 and 2971 days, with a duration of ~20 and 16 days, respectively (Fig. 2, left panel). If the observed dips are caused by active regions crossing the visible hemisphere of GJ 9827, the rotation period is likely longer than 15 days, suggesting that Prot might be twice as long. For the analysis presented in the following sections we thus adopted a rotation period of 30.7 ± 1.4 days.
 |
Fig. 2 Left panel: Gaussian process regression model applied to the K2 light curve. The black points are the K2 light curve, and the purple curve and shaded band are the GP model predictive mean and 1-sigma uncertainty. Right panel: K2 light curve folded to the Prot ∕2 stellar rotational period. |
 |
Fig. 3 Cores of the Ca II H and K lines of GJ 9827 as observed with HARPS. |
4 Frequency analysis of the HARPS and HARPS-N data
The presence of active regions coupled to stellar rotation is expected to induce periodic and quasi-periodic RV signals at the stellar rotation frequency and its harmonics (see, e.g., Hatzes et al. 2010; Haywood 2015). Using the code SOAP2 (Dumusque et al. 2014), we estimated the amplitude of the activity-induced RV signal – the so-called activity-induced RV jitter – from the properties of the star, namely, its effective temperature, radius, rotation period, and photometric variability. We found that the predicted semi-amplitude of the RV jitter is ~5 m s-1. Given the precision of most of our measurements (~1 m s-1), RV jitter is expected to be detected in our dataset.
We searched our Doppler time-series data for periodic signals associated with stellar activity by performing a frequency analysis of the RV measurements and activity indicators. For this purpose, we used only the HARPS and HARPS-N data because of the higher precision of the two datasets. On epoch BJD = 2458046, we purposely observed GJ 9827 with both HARPS and HARPS-N nearly simultaneously (within less than 25 min) and used the two sets of measurements to estimate the RV, FWHM, BIS, and S-index offsets between the two instruments. We stress that these offsets have only been used to perform the periodogram analysis of the joint data.
Figure 4 displays the generalized Lomb–Scargle periodograms (GLS; Zechmeister & Kürster 2009) of the combined HARPS andHARPS-N data following the correction for instrument offset. From top to bottom, we show the periodograms of the combined HARPS and HARPS-N RVs, the RV residuals after subtracting the stellar activity signal assumed to be a Fourier component at 2frot (Sect. 5), the RV residuals after subtracting the three planetary signals, the CCF bisector span (BIS), the CCF FWHM, the S-index, and the window function. Periodograms are displayed for two frequencies ranges encompassing the planetary and stellar signals. The vertical dotted lines mark the orbital frequencies of planet b, c, and d, as well as the stellar rotational frequency and its first 2 harmonics. The horizontal dotted lines mark the false alarm probabilities (FAP) of 0.1% derived using the bootstrap method described in Kuerster et al. (1997).
There are several important features to highlight in Fig. 4. The periodogram of the RV data shows peaks at the stellar rotational frequency and its harmonics (first row). The highest peak is found at about twice the rotation frequency with a semi-amplitude of ~3 m s-1, in fairly good agreement with the value predicted by SOAP2 (~5 m s-1). Whereas the signals at the rotation frequency and its harmonics have a FAP > 0.1 in the periodogram of the RV data (first panel), their significances increase with the FAP ≤ 0.1 once the 3 planetary signals are subtracted from the time-series (third row). The periodograms of the CCF, FWHM, and S-index show also significant peaks (FAP ≤ 0.1) whose frequencies are close to the stellar rotation frequency and its first harmonics, confirming that these signals are due to activity.
The presence of two or three active regions separated by ~180/120 degrees in longitude might account for the first and second harmonic of the fundamental rotation frequency. It’s worth noting that the periodogram of the window function (lower row) shows a peak at 0.0342 c/d (~29 days; red arrow), reflecting the fact that our follow-up was carried out around new moon to avoid the contamination from the scattered Sun light. Since the sampling frequency is very close to the rotation frequency of the star, we acknowledge that the peaks associated to the rotation frequency and its harmonics might also arise from aliasing effects.
The periodogram of the RV residuals after subtracting the activity signal at Prot ∕2 (Sect. 5) shows a significant peak (FAP ≤ 0.1) at the orbital frequency of GJ 9827 b (Fig. 4, second row). We conclude that the signal of the inner planet is clearly present in our RV data and that we would have been able to detect GJ 9827 b even in the absence of the K2 transit photometry.
 |
Fig. 4 Generalized Lomb–Scargle periodograms of the combined HARPS and HARPS-N datasets. The right and left columns cover two frequency ranges encompassing the 3 planetary signals (dotted vertical red lines), as well as the stellar rotation frequency and its first 2 harmonics (dotted vertical blue lines). From top to bottom: RV data, RV residuals after subtracting the stellar activity signal, RV residuals after subtracting the signals of the 3 transiting planets, BIS and FWHM of the CCF, S-index, and window function. The dashed horizontal red lines mark the 0.1 % false alarm probabilitiesas derived using the bootstrap technique. The red arrow in the lower panel marks the peak discussed in the main text. |
5 Data analysis
We modeledthe K2 and RV data using two different techniques, as described in the following two sub-sections.
5.1 Pyaneti analysis
We performed the joint analysis to the photometric and RV data with the code pyaneti (Barragán et al. 2017), which explores the parameter space using a Markov chain Monte Carlo (MCMC) algorithm. We fitted Keplerian orbits to the RV data and used the limb-darkened quadratic transit model by Mandel & Agol (2002) for the K2 transit light curves. In order to account for the Kepler long-cadence acquisition, we super-sampled the transit models using 10 subsamples per K2 exposure (Kipping 2010). The fitted parameters and likelihood are similar to those used in previous analyses performed with pyaneti and described, for example, in Barragán et al. (2016); Gandolfi et al. (2017).
We fitted for a transit and a RV signal for each of the three planets. We sampled for 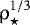 and recovered the scaled semi-major axis (ap /R⋆) of the three planets using Kepler’s third law. We used uniform priors for all the parameters, except for the limb darkening coefficients for which we set Gaussian priors as described in Niraula et al. (2017).
and recovered the scaled semi-major axis (ap /R⋆) of the three planets using Kepler’s third law. We used uniform priors for all the parameters, except for the limb darkening coefficients for which we set Gaussian priors as described in Niraula et al. (2017).
As presented in the previous section, the RV data of GJ 9827 shows activity-induced jitter at the stellar rotation frequency and its harmonics, with a semi-amplitude of ~3 m s-1. The light curve of GJ 9827 (Fig. 2, left panel) suggests that the evolution time scale of active regions is longer than the K2 observations (~80 days). Since our FIES, HARPS, and HARPS-N RV follow-up covers ~140 days, we can model the RV jitter using coherent sinusoidal signals at the stellar rotation frequency and its harmonics, similarly to the work described in, for example, Pepe et al. (2013) and Barragán et al. (2017).
In orderto check which Fourier components at the rotation frequency and its harmonics can better describe the activity signal, we tested different RV models. The first model (3P) includes only the three planetary signals. The second model (3P+Prot) is obtained from 3P by adding a sinusoidal signal at the rotation period of the star (Prot ~ 30 days). The third model called 3P+Prot∕2 includes three Keplerians and a sinusoidal signal at half the rotation period (~15 days). We also tested a model where two sinusoidal signals at both Prot and Prot∕2 were included. Since the stellar rotation period is not well constrained, we set uniform priors in the ranges [Prot − 2: Prot + 2] and [Prot∕2 − 1: Prot∕2 + 1].
Table 3 summarizes out the results of our test, showing the goodness of the fit for each model. With the lowest Bayesian information criteria (BIC), the preferred model is 3P+Prot∕2 (3 planets plus one sinusoidal signal at ~15 days). Table 3 shows also that the semi-amplitudes of the three planetary signals do not change significantly when considering different models, providing evidence that the Doppler motion induced by the three planets is present in our RV dataset and does not depend on the Fourier components used to model the activity-induced RV signal.
We performed a final joint analysis assuming that the RV data are described by the 3P+Prot∕2 model. For the phase, amplitude, and period of the activity signal we adopted uniform priors. We included a jitter term for each spectrograph to account for additional instrumental noise not included in the nominal RV error bars and/or imperfect treatment of the various sources of RV variations. Since GJ 9827 hosts a short-period multiplanetary system, we assumed tidal circularization of the orbits and fixed e = 0 for all three planets (Van Eylen & Albrecht 2015). In Sect. 6.3, we discuss about the correctness of this assumption. We explored the parameter space with 500 Markov chains initialized at random positions in the parameter space. We checked for chain convergence each 250,000 iterations using the Gelman & Rubin (1992) statistics with R = 1.02. Once all chains converged, we ran 5000 iterations more. We used a thin factor of 10 to generate a posterior distribution of 250,000 independentpoints for each parameter. We derived parameter values and uncertainties from the median and the 68.3% credible intervals of their posterior distributions. The final fits are shown in Figs. 5 and 6; parameter estimates are summarized in Table 5.
We emphasize that our approach of treating the RV stellar signal as a coherent signal at the first harmonic of the rotation frequency relies on the fact that the K2 light curve provides evidence that the evolution time-scale of active regions is longer than the duration of our RV follow-up. Unfortunately, the assumption of a coherent stellar signal does not hold for the RV measurements presented by Teske et al. (2018) because their follow-up spans ~7 years with average gaps of ~69 days.
Model comparison.
 |
Fig. 5 From top to bottom and left to right: transit fit and phase-folded RV curve of GJ 9827 b, GJ 9827 c, GJ 9827 d after removing the activity signal from the star and the signals from the other planets. The gray error bars account for additional instrumental noise and/or imperfect treatment of the various sources of RV variations. |
 |
Fig. 6 RV curve of GJ 9827 phase-folded to the first harmonic of the stellar rotation period (Prot ∕2 = 15.1 days) after removing the signals of the three transiting planets. |
Triple transiting systems with measured masses
5.2 Gaussian process
We also experimented with Gaussian Processes (GPs) to model the correlated RV noise associated with stellar activity. GPs model stochastic processes with covariance matrices whose elements are generated by user-chosen kernel functions. GP regression has been successfully used to deal with the correlated stellar noise of the radial velocity datasets of several exoplanetary systems including CoRoT-7, Kepler-78, Kepler-21, and K2-141 (Haywood et al. 2014; Grunblatt et al. 2015; López-Morales et al. 2016; Barragán et al. 2018).
Our GP model was described in detail by Dai et al. (2017). Briefly, we adopted a quasi-periodic kernel with the following hyperparameters: the covariance amplitude h, the correlation timescale τ, the period of the covariance T, and Γ which specifies the relative contribution between the squared exponential and periodic part of the kernel. For each of the transiting planets in GJ 9827, we included a circular Keplerian signal specified by the RV semi-amplitude K, the orbital period Porb, and the time of conjunction tc. For each of spectrographs, we included a jitter parameter σ and a systematic offset γ. We imposed Gaussian priors on Porb and tc with those derived from K2 transit modeling (Sect. 5.1). For the scale parameters h, K, and the jitter parameters we imposed Jeffreys priors. We imposed uniform priors on the systematic offsets γHARPS, γHARPS-N, and γFIES. Finally, for the hyperparameters τ, Γ, and T we imposed priors that were derived from a GP regression of the observed K2 light curve, as described below.
When coupled with stellar rotation, active regions on the host star give rise to quasi-periodic variations in both the measured RV and the flux variation. Given their similar physical origin, one would expect that GP with similar hyperparameters are able to describe the quasi-periodic variations seen in both datasets. Since the K2 light curve was measured with higher precision and sampling rate than our RV dataset, we trained our GP model on the K2 light curve. The resultant constrains on the hyperparameters were then used as priors when we analyzed the RV dataset. We adopted the covariance matrix and the likelihood function described by Dai et al. (2017). We first located the maximum likelihood solution using the Nelder–Mead algorithm implemented in the Python package scipy. We then sampled the posterior distribution using the affine-invariant MCMC implemented in the code emcee (Foreman-Mackey et al. 2013). We started 100 walkers near the maximum likelihood solution. We stopped after running the walkers for 5000 links. We checked for convergence by calculating the Gelman–Rubin statistics which dropped below 1.03 indicating adequate convergence. We report the various parameters using the median and 16–84% percentiles of the posterior distribution. The hyperparameters were constrained to be τ = 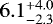 days, T = 15.1 ± 1.6 days, and Γ =
days, T = 15.1 ± 1.6 days, and Γ = 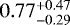 . These served as priors in the subsequent GP analysis of the RV data. The GP model of the K2 light curve is shown in Fig. 2.
. These served as priors in the subsequent GP analysis of the RV data. The GP model of the K2 light curve is shown in Fig. 2.
In the analysis of the RV dataset with GP regression, we first found the maximum likelihood solution and sampled the parameter posterior distribution with MCMC using the same procedure as described above. The RV semi-amplitude for planet b, Kb = 3.41 ± 0.53 m s−1 was detected to a high significance. The RV signal of planet c was not securely detected in the GP model. We therefore report the upper limit of Kc < 1.1 m s−1 at a 95% confidence level. Finally, the RV signal of the outer planet was detected but with less confidence than the inner planet. We report a value of Kd = 1.06 ± 0.52 m s−1. The amplitude of the correlated stellar noise is 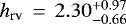 m s−1. All this values are in perfect agreement with the ones derived in previous section. Figure 7 shows the FIES, HARPS, and HARPS-N RVs of GJ 9827 and the GP model. The planet parameter estimates are summarized in Table 5.
m s−1. All this values are in perfect agreement with the ones derived in previous section. Figure 7 shows the FIES, HARPS, and HARPS-N RVs of GJ 9827 and the GP model. The planet parameter estimates are summarized in Table 5.
Given the good agreement between the results provided by the two methods and the fact that GP analysis provides only upper limit to the mass of the second planet, we adopted the values obtained with Pyaneti.
 |
Fig. 7 Measured radial velocity variation of GJ 9827 from FIES (circles) and HARPS (diamonds) and HARPS-N (triangles). The red solid line is the best-fit model including the signal of the planets and the Gaussian Process model of the correlated stellar noise. The colored dashed line shows the signal of the planets. The blue dotted line shows the Gaussian Process model of correlated stellar noise. |
6 Discussion
We determined masses, radii, and densities of the three planets known to transit GJ 9827. We found that GJ 9827 b has a mass of 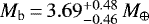 and a radius of
and a radius of 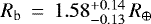 , yielding a mean density of
, yielding a mean density of 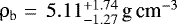 . GJ 9827 c has a mass of
. GJ 9827 c has a mass of 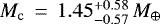 , radius of
, radius of 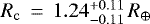 , and a mean density of
, and a mean density of 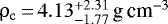 . For GJ 9827 d, we derived
. For GJ 9827 d, we derived 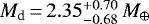 ,
, 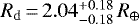 , and
, and 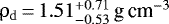 . Figure 8 shows the planetary masses as a function of the host star’s visual magnitudes for systems known to host at least three planets. GJ 9827 is the brightest (V = 10.35 ± 0.10 mag) transiting multiplanet system for which the masses of all planets have been measured.
. Figure 8 shows the planetary masses as a function of the host star’s visual magnitudes for systems known to host at least three planets. GJ 9827 is the brightest (V = 10.35 ± 0.10 mag) transiting multiplanet system for which the masses of all planets have been measured.
In the next sub-sections we will address the following questions. What type of planets are GJ 9827 b, c, and d, and how well can we constrain their evolutionary history?
 |
Fig. 8 Brightness–mass plot of planets with measured mass in multiple systems known to host at least three planets. With three transiting planets and V = 10.35 mag, GJ 9827 is the brightest multiplanet transiting system for which the masses of all planets have been measured. |
6.1 Planets composition
To address these questions we can rely on the recent discovery of the existence of a bimodal distribution of planetary radii described by Fulton et al. (2017) and Van Eylen et al. (2018). According to these works, there is a clear distinction between two different families of planets: super-Earths whose radius distribution peaks at Rp ~ 1.5 R⊕, and sub-Neptunes whose radius distribution peaks at Rp ~ 2.5 R⊕, separated by a gap in the radius distribution. The characteristics of this frontier (negative slope, dependence with period/incident flux) can beexplained with photo-evaporation of planetary atmospheres due to XUV radiation from the host stars.
GJ 9827 hosts a canonical terrestrial planet, GJ 9827 c, and two planets close to the radius valley but from different sides: the super-Earth GJ 9827 b and the sub-Neptune GJ 9827 d. Figure 9 shows the position of the three planets in the mass–radius diagram along with the Zeng et al. (2016)’s theoretical models for different internal compositions. Planets b and c may have rocky nuclei with traces of lighter elements. Given its radius, planet d is likely surrounded by a large gaseous H/He-rich envelope. Since the innermost planets lie on the same isocomposition line of ~80% MgSiO3–20% H2O (Fig. 9), we can speculate that the outer planet might have a nucleus with similar composition too. According to Wolfgang & Lopez (2015), the atmosphere of GJ 9827 d would account for up to only ~1% of the total mass, yielding to a thickness of ~0.6 R⊕, that is, ~30% of the planet’s radius.
 |
Fig. 9 Mass–radius diagram for all rocky planets with masses between 1 and 5 M⊕ and radii between 1 and 2.6 R⊕, as registered in the TEPC at database. The solid circles indicate measurements of the mass and radius of the planets of GJ 9827. The empty circle shows the inferred mass y radius of the nucleus of the third planet under the assumptions made in Sect. 6.1. |
6.2 Planets formation
Based on the low abundance of resonant orbits among Kepler multiplanet systems, Izidoro et al. (2017) found that the instability rate of resonant chains is roughly 95%. This means that GJ 9827 belongs to the exclusive group of only 5% of systems showing resonances. However, how this system came up to this configuration? To place GJ 9827 in context, we show all transiting triple systems with measured masses in Table 4, along with the ratios between the periods of their planets3. For a thorough list of Kepler multiple planets showing resonant or near resonant chains for which masses have been systematically derived see, for example, Hadden & Lithwick (2017). A plethora of these systems have 1:2 or 2:3 period ratios. These resonances have been theoretically predicted by Wang & Ji (2017), where type I migration plays a central role. Remarkably, the triple resonance 1:2:4 appears frequently where close-in terrestrial planets form driven by migration mechanisms (Sun et al. 2017; Wang & Ji 2017). However, the resonant chain of the GJ 9827 planetary system (1:3:5) is far more complex, indicating that possibly formation mechanism other than migration could be at play.
How did GJ 9827 reach the 1:3:5 resonance? According to Izidoro et al. (2017), during planet formation, when the first embryo reaches the inner edge of the disk, its migration is stopped by the planet disk–edge interaction (Masset et al. 2006) and other embryos migrate into a resonant chain. If this formation scenario is correct, several features would still be codified in the orbital eccentricity of the planets. As Van Eylen & Albrecht (2015) demonstrated, the eccentricity of close-in planets can be precisely measured combining short-cadence space-based photometry (as the one that will be gathered during the future K2 Campaign 19 or by the upcoming space-telescope CHEOPS; Broeg et al. 2013) with asteroseismic density measurements (as those from the future PLATO mission; Rauer 2017).
On the other hand, the masses of the three planets amount to a total mass of only 7.5 ± 1.8 M⊕ (less than half the mass of Neptune), a quantity that could be compatible with an in situ formation scenario. Chiang & Laughlin (2013) demonstrated that in situ formation in the minimum-mass extrasolar nebula is fast, efficient, and can reproduce many of the observed properties of close-in super-Earths. Therefore, if we could demonstrate that the three planets orbiting GJ 9827 have formed in situ many information would be inferred about the primordial formation scenario of the system. One observationally testable property of close-in super-Earths mentioned by Chiang & Laughlin (2013) is that they retain their primordial hydrogen envelopes. Additionally, if these planets did not migrate from behindthe snow-line and formed close to the host star they should not show any water features on their atmospheres.
6.3 System stability
To test the long-term dynamical stability of the system, we integrated our MCMC samples using the MVS (Wisdom & Holman 1991) integrator employed by the SWIFT N-body package (Duncan et al. 1998). For realistic integrations of this somewhat compact system we adopted a very small time step of 0.01 days and a maximum integration time of 1 Myr. These numerical constraints ensure high orbital resolution and sufficient number of “close” planetary approaches needed to study the system’s long-term dynamics. During the integrations we simultaneously monitored the planetary semi-major axes and eccentricities for large deviations from their initial values (i.e. potentially unstable configurations), while we assumed as long-term stable those that stay within ±1% of their starting semi-major axes and eccentricities.
Our stability analysis yielded that all the MCMC samples are stable, as shown in Fig. 10. The semi-major axes are constant up to the 0.1% level, while the orbital eccentricities of the planets typically oscillate with very small amplitudes (< 10−3). This was somewhat expected given the relatively small planetary masses and idealistic (but reasonably) small eccentricities fixed at 0. Although with our analysis we cannot obtain further strong constrains on the planetary masses and eccentricities, the stability results are in agreement with the tidal circularization scenario assumed in Sect. 5.1, and thus strengthen the Keplerian planetary hypothesis of the system.
Independently, to check the reliability of our results, we also performed a stability test using mercury6 (Chambers 1999). Assuming that the orbits are coplanar and with an initial zero eccentricity, we evolved the system for 100,000 yr to check its stability. We found changes of the three planets semi-major axis lower than 0.1% and eccentricity amplitudes variations below 2.5 × 10−4, in agreement with the results presented in the previous paragraphs.
 |
Fig. 10 MCMC posterior distributions of the RV semi-amplitudes for each planet fixing the remaining orbital parameters with the values from Table 5 obtained with Pyaneti. Each of the 180,000 independent Keplerian fits have been tested for 1 Myr dynamical stability using the MVS integrator. Stable solutions are shown in light red. The upper panels of the corner plot show the probability density distributions of each fitted parameter and their mean and 1σ uncertainties in vertical dashed lines. |
6.4 Planets atmosphere
The fate of the atmosphere of an exoplanet strongly depends on the incident flux per surface unit due to photo-evaporation processes. For GJ 9827 b, c, and d we calculated an incident flux relative to the Earth’s of 256, 59 and 29, respectively. Interestingly, although there is only a factor two difference between the incident flux of the second and third planet, the later seems to have a much lower density. This third planet lies well above the atmospheric loss frontier described in Fig. 10 of Van Eylen et al. (2018), while the other two are below. Moreover, the ratio between the incident fluxes and the masses of the planets are 70, 41, and 12, respectively. It is clear that the conditions of planet d are remarkably different from the other two.
However, the low density of planet d seems to defy the photo-evaporation models. With a mass of 3M⊕, previous models (Lammer et al. 2003; Owen & Wu 2016; Wang & Ji 2017) would predict that planet d lost its H/He envelope within the first 100 Myr of star’s lifetime. We encourage additional RV follow-up and transmission spectroscopy to pin down the properties of planet d. The results may clarify our understanding of the photo-evaporation process or unveil additional processes such as extreme out-gassing or late migration of planets.
Given the brightness of the host star and small periods of the planets, the three planets transiting GJ 9827 are excellent targets for atmospheric characterization using both space and ground-based facilities. Niraula et al. (2017) calculated the expected S/N of a planetary atmosphere using masses estimated by the mass-radius relationship by Weiss & Marcy (2014) and using a method similar to Gillon et al. (2016). Since we found that the masses are smaller than estimated from that mass–radiusrelation, these planets become even more attractive candidates for atmospheric studies than originally predicted. This is because the low surface gravity leads to a larger scale height, and thereby a larger atmospheric signal. GJ 9827 d ranks as the fifth best candidate overall (behind GJ 1214 b, 55 Cnc e, TRAPPIST-1 b and HD 219134 b), and GJ 9827 b and c rank sixth and seventh, respectively, among the 601 transiting planets with radii <3 R⊕, as shown in Fig. 11. This makes the GJ 9827 system a unique target for atmospheric studies.
 |
Fig. 11 Normalized atmospheric S/N for transiting planets with radii less than 3R⊕ as registered in the NASA Exoplanet Archive. |
7 Conclusions
We have presented the characterization and mass determination of the three planets orbiting GJ 9827 (Niraula et al. 2017; Rodriguez et al. 2018). GJ 9827 is a moderately active K6 V star (S-index ≈ 0.7) with a rotational period of Prot ≈ 30 days transited by three small planets with masses of 3.69, 1.45, and 2.35 M⊕, determined with a precision of 7.7σ, 2.5σ, and 3.4σ, respectively.This system is an ideal laboratory to study planetary formation models and atmospheric photo-evaporation processes. The densities of the three planets and the 1:3:5 orbital period ratio suggest an in situ formation scenario.
Teske et al. (2018) observed this system using the Planet Finder Spectrograph on the Magellan II telescope, from 2010 January to 2016 August. They report a mass of approximately 8.0 M⊕ for the innermost planet and upper limits for the other two, namely, ≤2.5 M⊕ for planet c and ≤6.0 M⊕ for planet d. The discrepancies between their masses and our results may be related to the way stellar activity has been taken into account. The long baseline and low sampling of Teske et al. (2018)’s RV measurements (36 RV points spanning ~7 years vs. our 58 RV spanning only 6 months) makes it difficult to model appropriately the stellar signal, likely affecting the determination of the planetary parameters.
Our findings indicate that the third planet – namely GJ 9827 d – might have an extended primordial atmosphere. The brightness of the host star (V = 10.35 mag, J = 7.984 mag) makes the transiting system around GJ 9827 an ideal target to study the atmosphere of the three planets, using, for instance, JWST and ELT. By measuring the chemical abundances of the planetary atmospheres, it will be possible to further constrain the formation scenario of this system. Combining all this information, we will eventually unveil whether the planets formed roughly where they are found today, or whether they formed at much larger distance and then migrated inwards.
This system presents negligible gravitational perturbations, in agreement with the absence of transit time variations (TTVs) above 5–10 min previously reported by Niraula et al. (2017). However, we cannot rule out completely the existence of a generalized Laplace resonance (Papaloizou 2015), or two-body mean-motion resonance between, for example, the innermost planets. The K2 mission is scheduled to re-observe GJ 9827 during its Campaign 19 using the 2-min short cadence mode. These data will allow us to detect the presence of TTVs and study the dynamical interaction of the planets. Moreover, K2 Campaign 19 will be a forward-facing campaign for which simultaneous observations from the ground will be possible throughout the duration of the campaign. Simultaneous RV follow-up of this system will enable the modeling of the stellar activity and will allow us to further pin down the planetary masses.
Acknowledgements
This work is partly financed by the Spanish Ministry of Economics and Competitiveness through projects ESP2014-57495-C2-1-R, ESP2016-80435-C2-2-R, and ESP2015-65712-C5-4-R of the Spanish Secretary of State for R&D&i (MINECO). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 730890. This material reflects only the authors views and the Commission is not liable for any use that may be made of the information contained therein. D.G. gratefully acknowledges the financial support of the Programma Giovani Ricercatori – Rita Levi Montalcini – Rientro dei Cervelli (2012) awarded by the Italian Ministry of Education, Universities and Research (MIUR). Sz.Cs., A.P.H., M.P., and H.R. acknowledge the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (HA 3279/12-1, PA 525/18-1, RA 714/14-1). I.R. acknowledges support from the Spanish Ministry of Economy and Competitiveness (MINECO) and the Fondo Europeo de Desarrollo Regional (FEDER) through grant ESP2016-80435-C2-1-R, as well as the support of the Generalitat de Catalunya/CERCA programme. NESSI was funded by the NASA Exoplanet Exploration Program and the NASA Ames Research Center. NESSI was built at the Ames Research Center by Steve B. Howell, Nic Scott, Elliott P. Horch, and Emmett Quigley. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Appendix A Radial velocity measurements
FIES RV measurements of GJ 9827
HARPS RV measurements of GJ 9827.
HARPS-N RV measurements of GJ 9827.
References
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barragán, O., Grziwa, S., Gandolfi, D., et al. 2016, AJ, 152, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Barragán, O., Gandolfi, D., & Antoniciello, G. 2017, Astrophysics Source Code Library [record ascl:1707.003] [Google Scholar]
- Barragán, O., Gandolfi, D., Dai, F., et al. 2018, A&A, 612, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S.-J., et al. 2014, Protostars and Planets VI (Tucson, AZ: Arizona University Press), 667 [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, Eur. Phys. J. Web Conf., 47, 03005 [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chiang, E., & Laughlin, G. 2013, MNRAS, 431, 3444 [Google Scholar]
- Cochran, W. D., Fabrycky, D. C., Torres, G., et al. 2011, ApJS, 197, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, Proc. SPIE, 8446, 84461V [CrossRef] [Google Scholar]
- Dai, F., Winn, J. N., Gandolfi, D., et al. 2017, AJ, 154, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Frandsen, S., & Lindberg, B. 1999, Astrophysics with the NOT (Finland: University of Turku), 71 [Google Scholar]
- Fridlund, M., Gaidos, E., Barragán, O., et al. 2017, A&A, 604, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A. et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Alcalá, J. M., Leccia, S., et al. 2008, ApJ, 687, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Barragán, O., Hatzes, A. P., et al. 2017, AJ, 154, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gillon, M., Jehin, E., Lederer, S. M., et al. 2016, Nature, 533, 221 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gontcharov, G. A., & Mosenkov, A. V. 2018, MNRAS, 475, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2008, in The Observation and Analysis of Stellar Photospheres, ed. D. F. Gray (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Grunblatt, S. K., Howard, A. W., & Haywood, R. D. 2015, ApJ, 808, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, E. W., Barragan, O., Dai, F., et al. 2017, A&A, 608, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadden, S., & Lithwick, Y. 2017, AJ, 154, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Murray, N. 2013, ApJ, 775, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., Dvorak, R., Wuchterl, G., et al. 2010, A&A, 520, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D. 2015, PhD Thesis, University of St. Andrews, Scotland [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, T., Dai, F., Gandolfi, D., et al. 2018, AJ, 155, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R., Mullan, D. J., Bercu, B., Paletou, F., & Gebran, M. 2017, ApJ, 837, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Everett, M. E., Sherry, W., Horch, E., & Ciardi, D. R. 2011, AJ, 142, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Jontof-Hutter,D., Rowe, J. F., Lissauer, J. J., Fabrycky, D. C., & Ford, E. B. 2015, Nature, 522, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Jontof-Hutter,D., Ford, E. B., Rowe, J. F., et al. 2016, ApJ, 820, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kuerster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 2013, Astrophysics Source Code Library, [record ascl:1303.024] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D. 2017, MNRAS, 472, 245 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., Haywood, R. D., Coughlin, J. L., et al. 2016, AJ, 152, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Feiden, G. A., Gaidos, E., Boyajian, T., & von Braun, K. 2015, ApJ, 804, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Weidenschilling, S. J. 2002, Icarus, 156, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, K. 2014, ApJ, 783, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McDonald, I., Zijlstra, A. A., & Watson, R. A. 2017, MNRAS, 471, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Mumford, G. S. 1956, AJ, 61, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Niraula, P., Redfield, S., Dai, F., et al. 2017, AJ, 154, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Nowak, G., Palle, E., Gandolfi, D., et al. 2017, AJ, 153, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Wu, Y. 2016, ApJ, 817, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B. 2015, Int. J. Astrobiol., 14, 291 [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2013, The Messenger, 153, 6 [NASA ADS] [Google Scholar]
- Petigura, E. A., Sinukoff, E., Lopez, E. D., et al. 2017, AJ, 153, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H. 2017, EGU General Assembly Conf. Abstracts, 19, 4829 [Google Scholar]
- Raymond, S. N., Barnes, R., & Mandell, A. M. 2008, MNRAS, 384, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J. E., Vanderburg, A., Eastman, J. D., et al. 2018, AJ, 155, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Fabrycky, D. C., Winn, J. N., et al. 2012, Nature, 487, 449 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmitt, J. R., Agol, E., Deck, K. M., et al. 2014, ApJ, 795, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, N. J., Howell, S. B., & Horch, E. P. 2016, Proc. SPIE, 9907, 99072R [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, Z., Ji, J., Wang, S., & Jin, S. 2017, MNRAS, 467, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Teske, J. K., Wang, S., Wolfgang, A., et al. 2018, AJ, 155, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., Leya, I., & Mezger, K. 2015, A&A, 574, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A.,& Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A.,& Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eylen, V., & Albrecht, S. 2015, ApJ, 808, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., & Ji, J. 2017, AJ, 154, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. 2010, in Exoplanets, ed. S. Seager (Tucson, AZ: Arizona University Press) [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfgang, A., & Lopez, E. 2015, ApJ, 806, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Wurm, G., Trieloff, M., & Rauer, H. 2013, ApJ, 769, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, S. W., Petigura, E. A., & von Braun, K. 2017, ApJ, 836, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [NASA ADS] [CrossRef] [Google Scholar]
Source: NASA Exoplanet Archive (https://exoplanetarchive.ipac.caltech.edu/) as of 1 February 2018.
All Tables
Equatorial coordinates, optical and near-infrared magnitude, and stellar parameters of GJ 9827.
All Figures
 |
Fig. 1 Reconstructed images from WIYN/NESSI speckle interferometry and the resulting 5σ contrast curves. The inset panel images are 4.6′′ × 4.6′′ and northeast is up and to the left. |
| In the text | |
 |
Fig. 2 Left panel: Gaussian process regression model applied to the K2 light curve. The black points are the K2 light curve, and the purple curve and shaded band are the GP model predictive mean and 1-sigma uncertainty. Right panel: K2 light curve folded to the Prot ∕2 stellar rotational period. |
| In the text | |
 |
Fig. 3 Cores of the Ca II H and K lines of GJ 9827 as observed with HARPS. |
| In the text | |
 |
Fig. 4 Generalized Lomb–Scargle periodograms of the combined HARPS and HARPS-N datasets. The right and left columns cover two frequency ranges encompassing the 3 planetary signals (dotted vertical red lines), as well as the stellar rotation frequency and its first 2 harmonics (dotted vertical blue lines). From top to bottom: RV data, RV residuals after subtracting the stellar activity signal, RV residuals after subtracting the signals of the 3 transiting planets, BIS and FWHM of the CCF, S-index, and window function. The dashed horizontal red lines mark the 0.1 % false alarm probabilitiesas derived using the bootstrap technique. The red arrow in the lower panel marks the peak discussed in the main text. |
| In the text | |
 |
Fig. 5 From top to bottom and left to right: transit fit and phase-folded RV curve of GJ 9827 b, GJ 9827 c, GJ 9827 d after removing the activity signal from the star and the signals from the other planets. The gray error bars account for additional instrumental noise and/or imperfect treatment of the various sources of RV variations. |
| In the text | |
 |
Fig. 6 RV curve of GJ 9827 phase-folded to the first harmonic of the stellar rotation period (Prot ∕2 = 15.1 days) after removing the signals of the three transiting planets. |
| In the text | |
 |
Fig. 7 Measured radial velocity variation of GJ 9827 from FIES (circles) and HARPS (diamonds) and HARPS-N (triangles). The red solid line is the best-fit model including the signal of the planets and the Gaussian Process model of the correlated stellar noise. The colored dashed line shows the signal of the planets. The blue dotted line shows the Gaussian Process model of correlated stellar noise. |
| In the text | |
 |
Fig. 8 Brightness–mass plot of planets with measured mass in multiple systems known to host at least three planets. With three transiting planets and V = 10.35 mag, GJ 9827 is the brightest multiplanet transiting system for which the masses of all planets have been measured. |
| In the text | |
 |
Fig. 9 Mass–radius diagram for all rocky planets with masses between 1 and 5 M⊕ and radii between 1 and 2.6 R⊕, as registered in the TEPC at database. The solid circles indicate measurements of the mass and radius of the planets of GJ 9827. The empty circle shows the inferred mass y radius of the nucleus of the third planet under the assumptions made in Sect. 6.1. |
| In the text | |
 |
Fig. 10 MCMC posterior distributions of the RV semi-amplitudes for each planet fixing the remaining orbital parameters with the values from Table 5 obtained with Pyaneti. Each of the 180,000 independent Keplerian fits have been tested for 1 Myr dynamical stability using the MVS integrator. Stable solutions are shown in light red. The upper panels of the corner plot show the probability density distributions of each fitted parameter and their mean and 1σ uncertainties in vertical dashed lines. |
| In the text | |
 |
Fig. 11 Normalized atmospheric S/N for transiting planets with radii less than 3R⊕ as registered in the NASA Exoplanet Archive. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


