| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346211 | |
| Published online | 29 August 2023 | |
Cold Jupiters and improved masses in 38 Kepler and K2 small planet systems from 3661 HARPS-N radial velocities
No excess of cold Jupiters in small planet systems★
1
INAF – Osservatorio Astrofisico di Torino,
via Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: aldo.bonomo@inaf.it
2
Département d’astronomie de l’Université de Genève,
Chemin Pegasi 51,
1290
Versoix, Switzerland
3
Dipartimento di Fisica, Università degli Studi di Torino,
via Pietro Giuria 1,
10125
Torino, Italy
4
School of Physics & Astronomy, University of Birmingham,
Edgbaston,
Birmingham,
B15 2TT, UK
5
KICC & Astrophysics Group, Cavendish Laboratory, University of Cambridge,
J.J. Thomson Avenue,
Cambridge
CB3 0HE, UK
6
Dipartimento di Fisica, Università degli Studi di Milano,
Via Celoria 16,
20133
Milano, Italy
7
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
8
INAF – Osservatorio Astronomico di Padova,
vicolo dell’Osservatorio 5,
35122
Padova, Italy
9
DTU Space, National Space Institute, Technical University of Denmark,
Elektrovej 328,
2800 Kgs.
Lyngby, Denmark
10
Astrophysics Group, University of Exeter,
Exeter
EX4 2QL, UK
11
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire,
CS 34229,
06304
Nice cedex 4, France
12
Center for Astrophysics | Harvard & Smithsonian,
60 Garden Street,
Cambridge, MA
02138, USA
13
INAF - Osservatorio Astronomico di Cagliari,
via della Scienza 5,
09047
Selargius, Italy
14
INAF - Osservatorio Astronomico di Brera,
Via E. Bianchi 46,
23807
Merate, Italy
15
Fundación Galileo Galilei - INAF,
Rambla José Ana Fernandez Pérez 7,
38712
Breña Baja, Tenerife, Spain
16
INAF - Osservatorio Astronomico di Palermo,
Piazza del Parlamento, 1,
90134
Palermo, Italy
17
Instituto de Astrofísica de Canarias,
C/Vía Láctea s/n,
38205
La Laguna (Tenerife), Canary Islands, Spain
18
Departamento de Astrofísica, Univ. de La Laguna,
Av. del Astrofísico Francisco Sánchez s/n,
38205
La Laguna (Tenerife), Canary Islands, Spain
19
SUPA, Institute for Astronomy, University of Edinburgh,
Blackford Hill,
Edinburgh
EH9 3HJ, UK
20
Centre for Exoplanet Science, University of Edinburgh,
Edinburgh
EH9 3FD, UK
21
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
Cambridge, MA
02139, USA
Received:
21
February
2023
Accepted:
6
April
2023
The exoplanet population characterized by relatively short orbital periods (P < 100 d) around solar-type stars is dominated by super-Earths and sub-Neptunes. However, these planets are missing in our Solar System and the reason behind this absence is still unknown. Two theoretical scenarios invoke the role of Jupiter as the possible culprit: Jupiter may have acted as a dynamical barrier to the inward migration of sub-Neptunes from beyond the water iceline; alternatively, Jupiter may have considerably reduced the inward flux of material (pebbles) required to form super-Earths inside that iceline. Both scenarios predict an anti-correlation between the presence of small planets and that of cold Jupiters in exoplanetary systems. To test that prediction, we homogeneously analyzed the radial-velocity measurements of 38 Kepler and K2 transiting small planet systems gathered over nearly ten years with the HARPS-N spectrograph, as well as publicly available radial velocities collected with other facilities. We used Bayesian differential evolution Markov chain Monte Carlo techniques, which in some cases were coupled with Gaussian process regression to model non-stationary variations due to stellar magnetic activity phenomena. We detected five cold Jupiters in three systems: two in Kepler-68, two in Kepler-454, and a very eccentric one in K2-312. We also found linear trends caused by bound companions in Kepler-93, Kepler-454, and K2-12, with slopes that are still compatible with a planetary mass for outer bodies in the Kepler-454 and K2-12 systems. By using binomial statistics and accounting for the survey completeness, we derived an occurrence rate of 9.3−2.9+7.7% for cold Jupiters with 0.3–13 MJup and 1–10 AU, which is lower but still compatible at 1.3σ with the value measured from radial-velocity surveys for solar-type stars, regardless of the presence or absence of small planets. The sample is not large enough to draw a firm conclusion about the predicted anti-correlation between small planets and cold Jupiters; nevertheless, we found no evidence of previous claims of an excess of cold Jupiters in small planet systems. As an important byproduct of our analyses, we homogeneously determined the masses of 64 Kepler and K2 small planets, reaching a precision better than 5, 7.5, and 10σ for 25, 13, and 8 planets, respectively. Finally, we release the 3661 HARPS-N radial velocities used in this work to the scientific community. These radial-velocity measurements mainly benefit from an improved data reduction software that corrects for subtle prior systematic effects.
Key words: planetary systems / planets and satellites: detection / planets and satellites: formation / techniques: radial velocities / methods: statistical
Tables 1, A.1 and full Table 2 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A33
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
One of the most striking findings from the detection of almost 4000 transiting planets so far is that the most common type of exoplanets in relatively close orbits (orbital periods P < 100 d) around solar-type stars are small planets (SPs) with radii of 1 < Rp < 4 R⊕. These are hosted by about half of the solar-type stars in the Milky Way (e.g., Winn & Fabrycky 2015 and references therein) and can be subdivided into two main classes: (i) high-density super-Earths with 1.0 ≲ Rp ≲ 1.7 R⊕ and a rocky composition; and (ii) lower-density sub-Neptunes with 1.7 ≲ Rp ≲ 4.0 R⊕, which are thought to be ice-rich and/or have an atmospheric envelope of hydrogen and helium (e.g., Zeng et al. 2019). The rocky and ice-rich compositions, if not considerably altered by post-formation processes such as core-powered mass loss (e.g., Ginzburg et al. 2018; Gupta & Schlichting 2019) or atmospheric photo-evaporation for the hottest planets (e.g., Lopez & Fortney 2014; Owen & Wu 2017), would (in principle) reflect different formation locations, namely, inside or beyond the water iceline (at ~1–3 AU around a solar-type star), respectively. Super-Earths and sub-Neptunes appear to be separated by the so-called radius-valley at Rp ~ 1.7 R⊕ in the distribution of planet radii from the Kepler space mission (Fulton et al. 2017; Van Eylen et al. 2018; Zeng et al. 2021), even though there may be a certain mixing of the two populations that occurs (e.g., Lacedelli et al. 2021, 2022).
Despite being very abundant overall, super-Earths and sub-Neptunes are absent in our Solar System – and the reason for that remains an open question. Some theoretical efforts to explain the lack of SPs in the Solar System have been undertaken, for instance, by Izidoro et al. (2015) and Lambrechts et al. (2019). While relying on different frameworks, both works invoke the influence of Jupiter as the possible culprit and generalize their outcomes to exoplanetary systems, so as to place the Solar System in the exoplanet context.
The scenario proposed by Izidoro et al. (2015) assumes that planet cores form preferentially in the proximity of the different icelines (e.g., Drązkowska & Alibert 2017). The innermost core is expected to grow faster due to the strong dependence of the accretion timescale on orbital radius. If such a core becomes a gas giant, it could then block the migration of the outer cores towards the parent star. Occasionally, one core (or more) could jump over the giant planet and move closer to the star, with a “jumping” probability depending on the gas-disk profiles and the initial number and total mass of the cores. In the simulations carried out by Izidoro et al. (2015), with five cores and a total mass of ~30 M⊕, the jumping probability was found to be ≲ 10–20% (see their Fig. 3).
According to this scenario, the early formation of Jupiter in the Solar System may have prevented the nuclei of Saturn, Uranus, and Neptune from migrating towards the Sun and, hence, from becoming a compact system of short-period sub-Neptunes such as those observed by the Kepler, K2, and TESS space telescopes.
The second framework, described in Lambrechts et al. (2019), is based on the formation of super-Earths inside the water iceline through pebble accretion (e.g., Ogihara et al. 2015). With extensive simulations, Lambrechts et al. (2019) showed that the outcome in the formation of super-Earths is strongly dependent on the amount of pebble flux drifting inwards from the outer regions of the protoplanetary disk. Low pebble fluxes would generate Mars-mass embryos, which may then grow to terrestrial planets at orbital distances a ≳ 0.4 AU through mutual collisions after disk dissipation, as has likely occurred in the Solar System (e.g., Raymond et al. 2014). Conversely, higher fluxes of pebbles would produce more massive embryos in shorter time. These could migrate towards their parent star if gas was still present in the disk, thereby forming a compact system of close-in super-Earths (see their Fig. 3).
When a giant planet forms, it opens a gap in the disk, considerably reducing or even halting the inward flux of pebbles from the regions outside its orbit. The formation of Jupiter might thus explain why the Solar System contains no short-period super-Earths, but terrestrial planets only: Jupiter may have reduced the flux of material required to form bigger planets within the water iceline.
Both scenarios above predict an anti-correlation between the presence of short-period SPs and that of cold Jupiters1 (CJs) in exoplanetary systems, which could be tested observationally. Previous works by Zhu & Wu (2018) and Bryan et al. (2019) seem to contradict this anti-correlation, reporting instead an excess of CJs in SP systems. Specifically, by analyzing 65 transiting and non-transiting systems with low-mass (1 < Mp < 10 M⊕) and short-period (P < 100 d) planets, Bryan et al. (2019) found an occurrence rate of 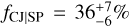 for gaseous giant planets, with masses of Mp = 0.5–13 MJup and semi-major axes of a ~ 1–10 AU. This rate is higher than that found by Wittenmyer et al. (2020), that is,
for gaseous giant planets, with masses of Mp = 0.5–13 MJup and semi-major axes of a ~ 1–10 AU. This rate is higher than that found by Wittenmyer et al. (2020), that is, 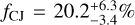 2, for Mp = 0.3–13 MJup and a = 1–10 AU, from the AAT, HARPS/ESO, HIRES/Keck, and CORALIE radial-velocity (RV) data of solar-type stars with time spans longer than eight years, irrespective of the presence or absence of SPs.
2, for Mp = 0.3–13 MJup and a = 1–10 AU, from the AAT, HARPS/ESO, HIRES/Keck, and CORALIE radial-velocity (RV) data of solar-type stars with time spans longer than eight years, irrespective of the presence or absence of SPs.
Other works, based on RV surveys only, have attempted to estimate the frequency of CJs in low-mass planet systems and/or the frequency of low-mass planets in CJ systems, sometimes with apparently conflicting results. For instance, Barbato et al. (2018) reported no low-mass planets with Mp = 10–30 M⊕ and P < 150 d in 20 CJ systems around solar-type stars observed with HARPS. On the contrary, based on the California Legacy Survey conducted with the HIRES/Keck and APF/Lick spectro-graphs, Rosenthal et al. (2022) found that planets with Mp = 2-30 M⊕ and P ≲ 150 d may occur approximately twice as frequently around CJ-host stars. However, the latter authors observed no significant differences in the occurrence of inner low-mass planets with and without CJ siblings, when limiting their range in mass to Mp = 2–20 M⊕.
As also noted by Rosenthal et al. (2022), RV surveys are sensitive to more massive inner planets than transit surveys, besides determining minimum masses only. Moreover, the adopted ranges in semi-major axes by Rosenthal et al. (2022) for both the inner low-mass planets and the outer CJs differ from those in Bryan et al. (2019), and they include, for instance, warm Jupiters with a = 0.23–1 AU. This stands in the way of a straightforward comparison of their results with those in Bryan et al. (2019).
In the present work, we aim to test the theoretical predictions of Izidoro et al. (2015) and Lambrechts et al. (2019) by searching for CJs and determining their occurrence rate in 38 transiting systems: 19 observed by Kepler and 19 by K2; 14 of them are in common with the sample studied by Bryan et al. (2019). For this purpose, we used 3661 high-precision HARPS-N radial velocities, 3471 out of which were collected by the HARPS-N Guaranteed Time of Observations (GTO) consortium, and the remaining 190 RVs by other groups, mainly for the purpose of determining the masses and densities of Kepler and K2 transiting planets. Nonetheless, we monitored these systems over the years specifically to look for outer giant planets. An important byproduct of our RV analyses is the improvement in the precision and/or accuracy of planetary masses and densities, thanks to the use of a significant number of yet unpublished HARPS-N/GTO RVs as well as the first combination of HARPS-N/GTO RVs with literature measurements.
2 Target selection and radial-velocity data
Among the Kepler and K2 systems observed by the HARPS-N/GTO program, we chose those: (i) hosting small (low-mass) planets with a radius of 1 < Rp < 4 R⊕, mass of 1 < Mp < 20 M⊕, and orbital period of P < 100 d; and (ii) having at least 15 HARPS-N RV measurements for a time span longer than ~ 1 yr. This resulted in the selection of the vast majority of Kepler and K2 systems monitored by the HARPS-N/GTO program. As in the work by Zhu & Wu (2018), we adopted a wider range in Mp than Bryan et al. (2019), given that several SPs are known to have Mp > 10 M⊕.
We also included Kepler-22, even though it meets the second criterion only, because the possible presence of CJs may provide valuable information on the architecture of a system with a planet in the habitable zone (Borucki et al. 2012). However, it was not counted in the computation of fCJ|SP in short-period SP systems, because Kepler-22b has an orbital period of 289 d > 100 d.
The HARPS-N radial velocities used in this work were extracted with the original HARPS-N Data Reduction Software version 3.7 from the stellar spectra obtained before the early failure of the red side of the HARPS-N charge-coupled device (CCD) in late September 2012 (e.g., Bonomo et al. 2014), and with the updated DRS version 2.3.5 from the spectra gathered afterwards. This latter version of the pipeline, adapted from the ESPRESSO spectrograph to HARPS-N (Dumusque 2021), computes a more stable wavelength solution through a careful selection of the lines of the Thorium-Argon calibration lamp, by avoiding saturated Thorium and Argon lines. It also corrects for: (i) possible RV long-term variations due to changing levels in the flux of the Thorium-Argon calibration lamp with time; and (ii) an offset in the DRS v3.7 data, occurring at the beginning of June 2020 for the replacement of the Thorium-Argon calibration lamp.
We observed the majority of the stars in our sample in OBJ_AB observing mode, that is, with fiber A on the target and fiber B on the sky to monitor possible contamination by moonlight. For the brightest stars in our sample, namely Kepler-21, Kepler-37, Kepler-68, Kepler-93, Kepler-409, K2-96/HD 3167, K2-167, K2-222, K2-262/Wolf 503, and K2-312/HD 80563, we used simultaneous calibration with fiber A on the target and fiber B on the calibration Thorium-Argon or Fabry-Perot lamp, to achieve higher accuracy on the relative RVs. We extracted the RVs by cross-correlating the spectra with a stellar template close to the stellar spectral type (e.g., Pepe et al. 2002). The only exception is the early-M-late-K-dwarf K2-3, for which we used the TERRA software (Anglada-Escudé & Butler 2012) to overcome the issue of distorted cross-correlation functions (CCFs) for cooler stars (Rainer et al. 2020), thereby achieving a reduced RV scatter (Damasso et al. 2018). For Kepler-10, we performed an additional reduction using the Yarara-v2 tool (Cretignier et al. 2021, 2022), because it proved to slightly enhance the detectabil-ity of the planet-induced Doppler signals (Bonomo et al., in prep.).
Possible contamination of the HARPS-N spectra by moonlight was checked following Malavolta et al. (2017) and corrected by computing the CCF after subtracting the flux of fiber B from the flux of fiber A. This procedure led to a reduced RV scatter in a few systems, the most evident cases being Kepler-19, Kepler-107, and K2-110.
Five systems, namely K2-96/HD 3167, K2-106, K2-111, K2-131, and K2-135/GJ 9827, were also observed with HARPS-N by other groups. To obtain homogeneous HARPS-N datasets across longer time spans and to take advantage of the aforementioned improvements of the HARPS-N pipeline, we recomputed all the HARPS-N RVs with the DRS-v2.3.5 from both the spectra acquired by the GTO and the other publicly available spectra.
For each system, we also collected the published RVs gathered with spectrographs other than HARPS-N, such as HIRES/Keck, HARPS/ESO, ESPRESSO/VLT, PFS/MagellanII, and APF, and analyzed them along with the HARPS-N RVs (see Sect. 3.2). This combination is needed to improve the constraints on the presence or lack of CJs, determine more precise (and accurate) orbital and physical parameters of the detected CJs, and achieve a better precision on the masses and densities of the inner small (low-mass) planets. A few RV datasets with a limited number of RVs and/or considerably lower precision than our HARPS-N RVs were discarded, as they do not yield any improvement in the orbital solution, while requiring additional free parameters (the radial-velocity zero point and the uncorrelated jitter term; cf. Sect. 3.2). We did not use the 71 available HIRES/Keck RVs (Weiss et al. 2016) for the analysis of the Kepler-10 system, because they tend to reduce the RV semi-amplitudes of the long-period SPs Kepler-10c and Kepler-10d (Sect. 4.3) compared to those obtained with the 291 HARPS-N RV measurements only (Bonomo et al., in prep.), even though the simultaneous modeling of both datasets is mainly driven by the much more numerous HARPS-N RVs. In fact, Weiss et al. (2016) also showed that the signal of Kepler-10c is practically undetected in the HIRES data.
We searched for possible outliers in the RV datasets for each system using the Chauvenet’s criterion3 and removed them. For systems with long-period RV signals, such as long-term slopes and/or Keplerians of CJs, we applied the Chauvenet’s criterion after removing those signals. Through visual inspection we checked that this criterion efficiently removes all the clear outliers.
Table 1 lists the 38 systems in our sample, the multiplicity (single planet or multiple planets) of the transiting SPs, the stellar parameters, the number of both total RVs and HARPS-N RVs used in this work after the removal of outliers, and the total time span of the observations. For each target, Table 2 reports the epochs, values, and formal uncertainties of the HARPS-N RVs, the activity indicators of the CCF, namely, the full width at half maximum (FWHM), the contrast and bisector span of the CCF, as well as the spectroscopic activity indexes S index and log 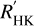 . We warn that correlated variations of the FWHM and contrast may have occurred at certain epochs due to changes in the focus of HARPS-N, but do not affect the RVs because the product [FWHM · contrast] remains constant.
. We warn that correlated variations of the FWHM and contrast may have occurred at certain epochs due to changes in the focus of HARPS-N, but do not affect the RVs because the product [FWHM · contrast] remains constant.
3 Data analysis
3.1 Updated atmospheric and physical stellar parameters
To maintain uniformity with previous studies of the systems published by the HARPS-N/GTO consortium, we derived the atmospheric parameters, that is, effective temperature Teff, metallicity [Fe/H], and surface gravity log g, for the host stars Kepler-22, Kepler-109, Kepler-323, Kepler-409, Kepler-1876, K2-12, K2-38, K2-106, K2-131, and K2-167 from the HARPS-N spectra. To this end, we employed two independent methods, ARES+MOOG (e.g., Mortier et al. 2014) and SPC (Buchhave et al. 2012, 2014), and adopted as final parameters and uncertainties the average values and error bars provided by the two methods (see Mortier et al. 2018 for more details).
To determine the stellar physical parameters, we used the EXOFASTv2 tool (Eastman 2017; Eastman et al. 2019), which adjusts the stellar radius, mass, and age through a Bayesian differential evolution Markov chain Monte Carlo (DE-MCMC) method (Ter Braak 2006), by simultaneously fitting the stellar spectral energy distribution (SED) and employing the MESA Isochrones and Stellar Tracks (MIST; Paxton et al. 2015). To sample the stellar SED, we utilized the WISE W1, W2, W3, and W4 infrared magnitudes (Cutri et al. 2021), the 2-MASS near-infrared J, H, and K magnitudes (Cutri et al. 2003), the optical Tycho BT and VT magnitudes (Hog et al. 2000), and/or the APASS Johnson B, V and Sloan g′, r′, i′ magnitudes (Henden et al. 2016). We imposed Gaussian priors on the Teff and [Fe/H] atmospheric parameters, as derived from the analyses of the HARPS-N spectra, as well as on the Gaia EDR3 parallax (Gaia Collaboration 2021). A uniform prior was instead used for the V-band extinction, AV, with upper limits provided by reddening maps (Schlegel et al. 1998; Schlafly & Finkbeiner 2011).
For the remaining 27 systems, we adopted the previously published stellar parameters, giving preference to those derived using the Gaia parallaxes and/or asteroseismic analyses of the Kepler light curves (e.g., Kepler-10, Kepler-454, and Kepler-107). In one case (Kepler-20), we redetermined the stellar parameters because the prior on the Gaia parallax yields slightly more precise and accurate stellar radius and mass. The atmospheric and physical parameters of all the host stars in our sample are listed in Table 1.
Kepler and K2 systems in our sample.
HARPS-N measurements of radial velocity and activity indicators.
3.2 Orbital fitting
We modeled the RV data of all the 38 systems in our sample with non-interacting Keplerian orbits and a slope by maximizing a Gaussian likelihood function (e.g., Ford 2006) through a DE-MCMC technique. The parameters of the Keplerian model for each planet in a given system are the inferior conjunction time, Tc, which is equivalent to the transit midtime for transiting planets; the orbital period, P; the widely adopted parameterization 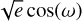 and
and 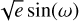 of eccentricity, e, and argument of periastron, ω; and the RV semi-amplitude, K. We included linear slopes to check for significant long-term trends and fit for the RV zero point, γi and jitter term, σjit,i, for the i-th RV dataset gathered with the i-th spectrograph. The jitter terms, σjit, were summed in quadrature to the formal RV uncertainties, σRV, to account for additional white noise of unknown (stellar or instrumental) origin (e.g., Gregory 2005).
of eccentricity, e, and argument of periastron, ω; and the RV semi-amplitude, K. We included linear slopes to check for significant long-term trends and fit for the RV zero point, γi and jitter term, σjit,i, for the i-th RV dataset gathered with the i-th spectrograph. The jitter terms, σjit, were summed in quadrature to the formal RV uncertainties, σRV, to account for additional white noise of unknown (stellar or instrumental) origin (e.g., Gregory 2005).
Correlated noise in the RV time series caused by stellar magnetic activity was modeled through Gaussian process (GP) regression (e.g., Haywood et al. 2014; Haywood 2015; Grunblatt et al. 2015) within the same DE-MCMC tools, using a covariance matrix described by either the quasi-periodic (QP) kernel in the original form of Rasmussen & Williams (2006):
![$k\left( {t,t'} \right) = {h^2} \cdot \exp \,\left[ { - {{{{\left( {t - t'} \right)}^2}} \over {2\lambda _1^2}} - {{2{{\sin }^2}\,\left( {{{\pi \left( {t - t'} \right)} \over {{P_{{\rm{rot}}}}}}} \right)} \over {\lambda _2^2}}} \right] + \left[ {\sigma _{{\rm{RV}}}^2\left( t \right) + \sigma _{{\rm{jit}}}^2} \right] \cdot {\delta _{{\rm{t,t'}}}},$](/articles/aa/full_html/2023/09/aa46211-23/aa46211-23-eq72.png) (1)
(1)
or the simpler squared-exponential (SE) kernel
![$k\left( {t,t'} \right) = {h^2} \cdot \exp \,\left[ { - {{{{\left( {t - t'} \right)}^2}} \over {2\lambda _1^2}}} \right] + \left[ {\sigma _{{\rm{RV}}}^2\left( t \right) + \sigma _{{\rm{jit}}}^2} \right] \cdot {\delta _{{\rm{t,t'}}}},$](/articles/aa/full_html/2023/09/aa46211-23/aa46211-23-eq73.png) (2)
(2)
where h is the semi-amplitude of the correlated noise, λ1 is the correlation decay timescale, Prot is the period of the quasi-periodic variations, and λ2 is the inverse complexity harmonic parameter. The hyper-parameters λ1, Prot, and λ2 can be associated respectively with the decay timescale of the active regions, the stellar rotation period and the complexity of the activity signals (with λ2 ~ 3–5 approaching simpler sinusoidal signals). We point out that the parameter λ2 in Eq. (1) is twice the equivalent parameter w in other implementations of the quasi-periodic kernel (e.g., Grunblatt et al. 2015; Damasso et al. 2018).
The QP kernel was used to model correlated noise with a quasi-periodic behavior, namely, in the presence of stellar rotation signals. The latter were identified when a periodicity in the Generalized Lomb-Scargle (GLS) periodogram of the RVs (Zechmeister & Kürster 2009) with a false alarm probability FAP < 10−3 was also found in the Kepler/K2 light curves and/or in the CCF or S-index activity indicators. This concerns Kepler-21, Kepler-78, Kepler-102, K2-3, K2-36, K2-131, K2-135/GJ 9827, K2-141, and K2-312/HD 80653.
The SE kernel was employed for Kepler-93 and K2-2/ HIP 116454 to account for RV variations on timescales longer than the stellar rotation, which are likely due to magnetic activity cycles and/or shorter Rieger-type cycles (Rieger et al. 1984). The DE-MCMC analysis with the SE kernel proved to model such variations efficiently, producing flat and Gaussian-distributed residuals. The analysis of the same data with the QP kernel yielded very low acceptance rates, which indicates that the GP-QP model is more complex than needed to model long-term variations in both systems, leaving the QP hyper-parameters Prot and λ2 practically unconstrained.
We imposed several priors on the model parameters as well as on the GP hyper-parameters in case GP regression was used (i.e., in the presence of correlated noise). Specifically, we used Gaussian priors on the transit time, Tc, and period, P, of the inner transiting SPs, as provided by the transit ephemerides derived in previous analyses of the Kepler and K2 light curves (see the second and third columns, and references in Table A.1). With regard to orbital eccentricities, we adopted: (i) circular orbits for the closest SPs, whose orbital circularization times are considerably shorter than the stellar age (e.g., Matsumura et al. 2008, 2010). Null eccentricities for these planets are also consistent with the observation of their secondary eclipses at orbital phases Δφ ~ 0.5 from transits (Singh et al. 2022); (ii) half-Gaussian priors with zero mean and σe = 0.098 for the transiting SPs in multiple systems, following the finding of Van Eylen et al. (2019). This prior prevents the fit from converging to spurious eccentricities, a well-known critical effect occurring for low signal-to-noise Doppler signals (e.g., Zakamska et al. 2011; Hara et al. 2019), given that the typical RV semi-amplitudes of the transiting SPs in our sample are usually comparable to the RV scatter. Spurious high eccentricities may also be unphysical, as they would lead to dynamical instabilities (e.g., Giuppone et al. 2013); (iii) uniform priors U[0, 1[ for the single-transiting SPs, except for Kepler-22b, Kepler-454b, Kepler-409b, and Kepler-1876b, for which we used half-Gaussian priors with zero mean and σe = 0.45, 0.35, 0.42, 0.37, respectively, as derived from asteroseismic and transit light-curve analyses (Van Eylen et al. 2019); and (iv) uniform priors for the long-period, non-transiting CJs. We adopted uninformative priors on the RV semi-amplitudes, K, zero points, γ, jitter terms, σjit, and slopes, γ.
As for the GP hyper-parameters, we imposed uniform priors with bounds wide enough to encompass the expected values of λ1, Prot, and λ2, and only a lower bound of 0 m s−1 for h. Table 3 lists the adopted priors on the GP hyper-parameters for the systems that required GP regression to model the non-stationary activity variations along with the Keplerian signals. For three systems, namely Kepler-102, K2-141, and K2-132, we further imposed λ1 > Prot/2, otherwise λ1 converged to very low values, on the order of a couple of days, making the quasi-periodic term practically irrelevant and, hence, unconstrained. Nonetheless, the RV semi-amplitudes obtained with and without this prior (i.e., by also allowing λ1 to converge towards very low values) are fully consistent.
Additional signals attributed to non-transiting planets were searched for in the RV residuals with GLS periodograms and they were included in the DE-MCMC RV analysis if (i) their FAP < 10−3; (ii) their periodicity does not appear in the GLS periodograms of any activity indicator; and (iii) the difference in the Bayesian information criterion (BIC; Burnham & Anderson 2004; Liddle 2007) between the model with the additional planet and the model without it is ABIC > 10 (Kass & Raftery 1995). Similarly, possible RV long-term slopes were considered significant if they were detected at more than 3σ and the ABIC in favor of the model with the slope is greater than 10.
We determined the values and the 1σ uncertainties of the model and derived parameters from the medians and the 15.87–84.14% quantiles of their posterior distributions. For distributions consistent with zero, such as those of eccentricities or RV semi-amplitudes in cases of non-detection of the Doppler signals, we provided only the 1σ upper limits defined as the 0–68.27% quantiles. In Table 4 we report for each system the HARPS-N systemic velocities and jitter terms, the GP hyperparameters in the presence of stellar activity signals, and the linear accelerations. In Tables 6 and 9, we give the parameters of the non-transiting CJs and low-mass planets, respectively. In Table A.1, we give the parameters of the 64 Kepler and K2 transiting SPs in our sample (see Sect. 4).
Priors imposed on the hyper-parameters of the Gaussian process regression for the stars showing significant magnetic activity variations.
3.3 Surveycompleteness
To determine the frequency of CJs in our sample of Kepler and K2 systems, we first need to evaluate the sensitivity of our survey to the presence of such planets. Indeed, CJs might not have been detected in some systems because of limited temporal baselines, poor temporal sampling, and/or relatively low precision of the RV measurements. Therefore, our measure of the occurrence rate of CJs has to take the completeness (or recovery rate) of our survey into account.
The completeness can be estimated with experiments of injection and recovery of planetary signals for each system, by considering the real times of the observations and the RV uncertainty of each measurement at time t, that is, 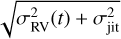 . Following Bryan et al. (2019), we simulated signals of CJs in a logarithmic grid of 30x30 cells of planetary mass, ΔMp, versus semi-major axis, Δa, covering the ranges of 0.3–20 MJup in Mp and 0.5–20 AU in a. For each cell of a given system, we simulated 300 RV signals of CJs at the epochs of our RV observations by randomly varying (i) Mp and a within the cell bounds; (ii) Tc within the orbital period corresponding to a and the stellar mass M* (Table 1) from Kepler’s third law; (iii) cos i from 0 to 1, where i is the orbital inclination; and (iv) the argument of periastron, ω, from 0 to 2π, while drawing the orbital eccentricity, e, from a beta distribution (Kipping 2013). We then shifted every RV point at time t according to a Gaussian distribution with a mean equal to the RV value and a standard deviation σ(t). For simplicity, we did not simulate stellar magnetic activity signals, assuming that those signals would be efficiently modeled with GP regression, as shown in Sect. 4.
. Following Bryan et al. (2019), we simulated signals of CJs in a logarithmic grid of 30x30 cells of planetary mass, ΔMp, versus semi-major axis, Δa, covering the ranges of 0.3–20 MJup in Mp and 0.5–20 AU in a. For each cell of a given system, we simulated 300 RV signals of CJs at the epochs of our RV observations by randomly varying (i) Mp and a within the cell bounds; (ii) Tc within the orbital period corresponding to a and the stellar mass M* (Table 1) from Kepler’s third law; (iii) cos i from 0 to 1, where i is the orbital inclination; and (iv) the argument of periastron, ω, from 0 to 2π, while drawing the orbital eccentricity, e, from a beta distribution (Kipping 2013). We then shifted every RV point at time t according to a Gaussian distribution with a mean equal to the RV value and a standard deviation σ(t). For simplicity, we did not simulate stellar magnetic activity signals, assuming that those signals would be efficiently modeled with GP regression, as shown in Sect. 4.
To establish the recovery rate in every ΔMp-Δa cell, we fit the injected signals with a slope, a quadratic trend and a Keplerian orbit (with input parameters close to the simulated ones) and compared these models with a constant model (i.e., no signal) through the ΔBIC criterion: if ΔBIC > 10 in favor of the model with the planet-induced signal, we recorded a detection of the simulated signal, otherwise its non-detection. Figure 1 shows the completeness of two systems, Kepler-1876 (top panel), and Kepler-93 (middle panel) as one of the worst and best cases in our sample, respectively, and the average completeness of the 37 systems (bottom panel).
HARPS-N systemic radial velocities and jitter terms, Gaussian process hyper-parameters, and linear accelerations from the DE-MCMC radial-velocity modeling.
 |
Fig. 1 Recovery rate (completeness) maps of cold Jupiters. Top panel: completeness of Kepler-1876, one of the systems with the worst completeness mainly due to the relatively short temporal baseline of the HARPS-N radial-velocity observations. Black and white indicate 0% and 100% recovery rates, respectively. Middle panel: completeness of Kepler-93, showing a very high detection rate, given the long time span of observations. Bottom panel: mean survey completeness obtained by averaging out the individual completenesses of the 37 systems. |
 |
Fig. 2 Radial-velocity measurements of K2-110. Top panel: radial velocities as a function of time, showing no long-term trends. The blue and light blue points display the measurements obtained with the HARPS-N and HARPS spectrographs, respectively, and the black line indicates the Keplerian best-fit model. Bottom panel: same radial velocities as in the top panel, but phase folded at the ephemeris of K2-110b (P = 13.86 d). |
4 Results
4.1 Search for and characterization of cold Jupiters
We first present the results of the search for CJs in our survey.
4.1.1 Systems with no long-term trends
Altogether 31 out of 38 systems do not show any significant long-term trend as caused by sufficiently massive outer companions within the completeness limits (Table 4). The RVs of two of these systems, K2-110 (Osborn et al. 2017) and Kepler-78 (Pepe et al. 2013; Howard et al. 2013), are shown in Figs. 2 and 3 as representative cases. Possible extra noise in the K2-110 system was taken into account through the white noise term, σjit, only, because the host star is not magnetically active. On the contrary, GP regression with a quasi-periodic kernel was needed to model the strongly correlated variations of the active star Kepler-78 (Fig. 3; see also Grunblatt et al. 2015).
 |
Fig. 3 Radial-velocity measurements of Kepler-78. Top panel: radial velocities as a function of time, showing variations due to both stellar activity and the ultra-short-period planet Kepler-78b, but no significant long-term trends. The blue and red circles indicate the radial-velocity points gathered with the HARPS-N and HIRES spectrographs, respectively. Middle panel: zoom on the first 100 days, mainly showing the non-stationary stellar activity signal, which was modeled with Gaussian process regression and a quasi-periodic kernel (black solid line). Bottom panel: radial velocities phase-folded at the ephemeris of Kepler-78b (P = 0.35 d), after removing the Gaussian process model for the stellar activity variations. |
Orbital parameters and minimum masses of the companions causing the long-term trends observed in the Kepler-93, Kepler-454, and K2-12 systems.
4.1.2 Systems with long-term linear trends
Five systems show long-term linear trends, namely Kepler-93 (Dressing et al. 2015; Fig. 4), Kepler-454 (Gettel et al. 2016; Fig. 8), K2-12 (Mayo et al. 2018; Fig. 5), K2-96/HD 3167 (Christiansen et al. 2017; Gandolfi et al. 2017; Fig. 6), and K2-262/Wolf 503 (Polanski et al. 2021). The trends in Kepler-93, Kepler-454 and K2-12 are caused by bound companions, while those in K2-96/HD3167 and K2-262/Wolf 503 are due to stellar magnetic activity, because similar trends are also seen in the activity indicators (see Fig. 6 for the case of K2-96/HD 3167; cf. also Bourrier et al. 2022). Gaussian processes with a SE kernel were used to model the RVs of Kepler-93 to account for long-term variations overlapping with the linear trend and the signal of the planet Kepler-93b (Fig. 4). Such variations are likely due to stellar activity, as they seem to follow those of the S-index activity indicator after 7000 BJDTDB – 2 450 000 with a Pearson correlation coefficient of 0.26 ± 0.03 (Fig. 4, right panel).
From the temporal baseline, ΔT, of the RV time series and the amplitude of the trend, 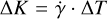 , we could estimate the lower limits of orbital period, P, and minimum mass, Mp sin i, of the companions producing the trends, by assuming circular or quasi-circular orbits, namely: P ≥ 4 · ΔT and Mp sin i ≥ (ΔK/28.4 m s−1) ··(Ms/M⊙)2/3 · (P/yr)1/3. Table 5 reports the lower limits of the orbital parameters and Mp sin i of the outer companions in the Kepler-93, Kepler-454, and K2-12 systems. The companion generating the linear trend in Kepler-93 is a brown dwarf or a low-mass star, having Mp sin i ≥ 21 MJup, while the masses of the companions producing the slopes in the Kepler-454 and K2-12 systems are currently compatible with a planetary companion, but further monitoring is needed to unveil their nature.
, we could estimate the lower limits of orbital period, P, and minimum mass, Mp sin i, of the companions producing the trends, by assuming circular or quasi-circular orbits, namely: P ≥ 4 · ΔT and Mp sin i ≥ (ΔK/28.4 m s−1) ··(Ms/M⊙)2/3 · (P/yr)1/3. Table 5 reports the lower limits of the orbital parameters and Mp sin i of the outer companions in the Kepler-93, Kepler-454, and K2-12 systems. The companion generating the linear trend in Kepler-93 is a brown dwarf or a low-mass star, having Mp sin i ≥ 21 MJup, while the masses of the companions producing the slopes in the Kepler-454 and K2-12 systems are currently compatible with a planetary companion, but further monitoring is needed to unveil their nature.
4.1.3 Systems with Keplerian signals of cold Jupiters
Resolved Keplerian orbits of CJs are observed only in three of the thirty-eight systems, namely: Kepler-68 (Gilliland et al. 2013), Kepler-454 (Gettel et al. 2016), and K2-312/HD 80653 (Frustagli et al. 2020).
The two CJs, Kepler-68d and Kepler-454c, with P = 633 and 524 d and Mp sin i = 0.75 and 4.51 MJup, were previously discovered by Gilliland et al. (2013) and Gettel et al. (2016). Moreover, a long-term quadratic trend in Kepler-68 (Mills et al. 2019) and a slope in Kepler-454 (Gettel et al. 2016) were also found in the RV data, revealing the presence of additional outer companions in both systems, given that no trends were seen in the activity indicators. Our analysis not only allowed us to refine the parameters of the Kepler-68d and Kepler-454c giant planets, but also unveiled two additional CJs, namely: Kepler-68e and Kepler-454d, with P ~ 3450 and 4070 d and minimum masses of 0.27 and 2.31 MJup, respectively (see also Margini et al., in prep., for Kepler-68). The RVs of both systems as a function of time and the phase-folded RV signals of the CJs Kepler-68d, Kepler-68e, Kepler-454c, and Kepler-454d are shown in Figs. 7 and 8.
The RV monitoring of the K2-312 system revealed that the linear trend observed by Frustagli et al. (2020) is due to a very eccentric CJ, namely, K2-312c, with P = 921 d, Mp sin i = 5.41 MJup, and e = 0.85 (Fig. 9; Poretti et al., in prep.). The parameters of the five CJs with resolved Keplerian orbits and their 1σ uncertainties are given in Table 6.
 |
Fig. 4 Radial-velocity and CaII S-index measurements of Kepler-93. Left panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities. The black line shows the best-fit model with a long-term linear slope caused by a non-planetary companion, a Keplerian orbit for the transiting planet Kepler-93b (P = 4.73 d), and Gaussian process regression with a squared exponential kernel to account for long-term stellar activity variations. Right panel: residuals of the HARPS-N radial velocities after subtracting the linear long-term trend and the signal of Kepler-93b (top), and measurements of the stellar activity S index (bottom). The increase in both the RVs and the S index from ~ 7000 to ~ 8300 BJDTDB – 2 450 000 indicates that the small-amplitude long-term variations superposed to the linear slope seen in the left panel are likely due to stellar magnetic activity. |
 |
Fig. 5 Radial-velocity and activity index measurements of K2-12. Left panel: HARPS-N radial velocities showing the long-term linear slope due to a companion of yet unknown nature. The Doppler signal of the transiting planet K2-12b (P = 8.28 d) is undetected, hence, only an upper limit to its mass could be given. Right panel: FWHM of the cross-correlation function (top) and CaII S-index (bottom) time series showing no significant linear trends. This would indicate that the radial-velocity linear trend in the left panel is caused by a physically bound companion. |
Parameters of the long-period non-transiting giant planets with resolved orbit.
 |
Fig. 6 Radial-velocity and CCF FWHM measurements of K2-96/HD 3167. Left panel: radial velocities showing a long-term linear trend: red, green, blue, and light blue points show the measurements obtained with the HIRES, APF, HARPS-N, and HARPS spectrographs, respectively. Right panel: linear trend observed in the FWHM of the HARPS-N cross-correlation functions. A similar behavior is observed in the CaII S index. This implies that the slope observed in the RVs (left panel) is produced by stellar activity, and not by a physical companion. |
Completeness (recovery rate) and fraction of stars hosting both short-period small planets and cold Jupiters for different intervals of orbital separation.
Fraction of stars with cold Jupiters in our sample compared with those from previous works.
4.2 Occurrence rate of cold Jupiters
By considering the three systems with resolved Keplerian orbits (Kepler-68, Kepler-454, and K2-312) and possibly the K2-12 system, which shows a trend that is currently compatible with a planetary companion at orbital distance a < 10 AU, we can derive the occurrence rate of CJs, fCJ|SP, in our sample. From this sample, we have to remove Kepler-22 for the reason explained in Sect. 2, which yields a total of 37 Kepler and K2 systems. We used binomial statistics, namely:
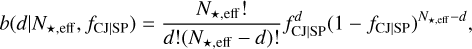 (3)
(3)
where is the number of systems with detected CJs, that is, d = 3 or 4, depending on whether K2-12 is included or not; and N*,eff is not just the number of systems in our sample N* = 37, but the “effective” number of stars N*,eff = N* · C, where C is the average completeness obtained by computing the mean of the completeness maps of the 37 systems (Fig. 1, bottom panel).
To compare our results with those of Wittenmyer et al. (2020), we computed C and fCJ|SP for the range ΔMp = 0.3–13 MJup in planetary mass, and different intervals Δa = 1–2, 2–4, 4–10, and 1–10 AU in semi-major axis (see Table 7). Similarly, we also derived C and fCJ|SP for ΔMp = 0.5–13, 0.5-20 MJup, and Δa = 1–10 and 1–20 AU, for comparison with the fCJ|SP found by Bryan et al. (2019). We report our values and 1σ error bars of the occurrence rates of CJs as well as those obtained by Bryan et al. (2019) and Wittenmyer et al. (2020) in Table 8. In summary, we found 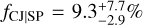 for d =3 and
for d =3 and 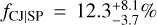 for d = 4, namely, by considering the long-term trend in K2-12 as planetary in origin, for ΔMp = 0.3–13 MJup and Δa = 1–10 AU. The former value is lower than that found by Wittenmyer et al. (2020), namely,
for d = 4, namely, by considering the long-term trend in K2-12 as planetary in origin, for ΔMp = 0.3–13 MJup and Δa = 1–10 AU. The former value is lower than that found by Wittenmyer et al. (2020), namely, 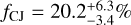 , by a factor of 2; however, given the large uncertainties, the two measurements are compatible at 1.3σ. Our fCJ|SP is four times lower than that derived by Bryan et al. (2019).
, by a factor of 2; however, given the large uncertainties, the two measurements are compatible at 1.3σ. Our fCJ|SP is four times lower than that derived by Bryan et al. (2019).
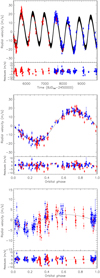 |
Fig. 7 Radial-velocity measurements of Kepler-68. Top panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities and the bestfit model (black line) with four Keplerians corresponding to the two transiting planets Kepler-68b (P = 5.40 d) and Kepler-68c (P = 9.60 d), and the two cold giant planets Kepler-68d (P = 633 d = 1.7 yr) and Kepler-68e (P ~ 3450 d = 9.4 yr). Middle and bottom panels: phase-folded radial-velocity signals of the cold giant planets Kepler-68d and Kepler-68e. Note: orbital phases equal to 0 and 1 correspond to inferior conjunction. |
4.3 Non-transiting low-mass planets
By employing GLS periodograms of the RV residuals and Bayesian model comparison through the BIC criterion (Sect. 2), we confirmed the presence of additional RV signals that can be attributed to the non-transiting planets Kepler-10d (P = 151.0 d, Mp sin i = 12.8 M⊕; Bonomo et al., in prep.), K2-96b/HD 3167b (P = 8.4 d, Mp sin i = 4.3 M⊕; Christiansen et al. 2017), K2-96e/HD3167e (P = 96.6 d, Mp sin i = 8.4 M⊕; Bourrier et al. 2022), and K2-111c (P = 15.7 d, Mp sin i = 11.1 M⊕; Mortier et al. 2020); their orbital parameters and minimum masses are given in Table 9. Concerning K2-96e/HD 3167e, we found a slightly different P than Bourrier et al. (2022), namely, Pe = 102.09 ± 0.52 d, which is likely due to a different treatment of the activity signal: we fit a slope to all the RVs (see Fig. 6), while Bourrier et al. (2022) included in their MCMC analysis two activity-decorrelation terms for the HARPS and HARPS-N spectrographs. In any case, as noted by Bourrier et al. (2022), the observing spectral window allows for different solutions of Pe with multiple peaks in the posterior distribution (see their Fig. 12).
We report a new planet candidate, Kepler-1876c (P = 15.8 d, Mp sin i = 11.0 M⊕), in the single transiting system Kepler-1876 (Fig. 10). The GLS periodogram of the HARPS-N RVs of Kepler-1876 shows a significant periodicity at P = 15.8 d with FAP of 5.6 × 10−5, which does not appear in any of the activity indicators. Nonetheless, the ΔBIC in favor of the two-planet model is currently ΔBIC = 5.3 < 10; thus, more RVs are needed to confirm the planetary nature of this signal, also by checking that its phase and amplitude do not change with time.
We cannot confirm the signals of the non-transiting planet Kepler-20g (Buchhave et al. 2016) or the non-transiting candidate K2-2c (Vanderburg et al. 2015) with respective periods of P = 35 and 45 d and RV semi-amplitudes of K = 4.1 and ~2 m s−2. The former signal is no longer present after the improvement of the DRS software to extract the HARPS-N RVs (Sect. 2). The latter was likely due to a combination of the spectral window of the original RVs in Vanderburg et al. (2015) and an activity signal with periodicity of ~270 d, which is also seen in the GLS periodograms of the S-index and FWHM activity indicators, and was modeled with a GP-SE approach (see Table 4). The fact that the 45 d signal could have originated from stellar activity variations was already discussed and considered by Vanderburg et al. (2015).
As specified in Sect. 3.2, we used non-interacting Keplerians to model RV planetary signals and GLS periodograms to search for non-transiting planets in the RV residuals. This implies that additional planets revealed by transit timing variations (TTVs), with undetectable signal in the RVs only (according to the criteria given in Sect. 3.2), such as Kepler-19c and d (Malavolta et al. 2017), were not modeled in this study for uniformity.
 |
Fig. 8 Radial-velocity measurements of Kepler-454. Top left panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities and the best-fit model (black line) with a long-term linear trend and three Keplerians corresponding to the transiting planet Kepler-454b (P = 10.57 d) and the two cold giant planets Kepler-454c (P = 524 d = 1.4 yr) and Kepler-454d (P ~ 4070 d = 11.1 yr). Top right panel: linear trend after removing the three Keplerian signals, which is caused by an additional fourth companion of yet unknown nature. Bottom panels: phase-folded radial-velocity signals of the cold giant planets Kepler-454c (left) and Kepler-454d (right). Note: orbital phases equal to 0 and 1 correspond to inferior conjunctions. |
Parameters of the non-transiting small planets.
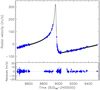 |
Fig. 9 HARPS-N radial velocities of K2-312 / HD 80653 and the best-fit model (black line) with two Keplerians, which correspond to the ultra-short-period transiting planet K2-312b (P = 0.72 d) and the eccentric cold giant planet K2-312c (P ~ 921 d = 2.5 yr; e = 0.85), and Gaussian process regression with a quasi-periodic kernel. |
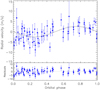 |
Fig. 10 Phase-folded HARPS-N radial velocities (blue dots) of Kepler-1876 at the period P = 15.8 d of the possible planet candidate Kepler-1876c. The black solid line shows the best-fit model. |
4.4 Improved physical and orbital parameters of 64 Kepler and K2 small planets
As mentioned in Sect. 1, the DE-MCMC analyses of new HARPS-N RVs, combined (in some cases for the first time) with the literature RVs obtained with other instruments, allowed us to update the orbital and physical parameters of the 64 transiting planets. In particular, from the stellar parameters given in Table 1, the transit parameters (P, Rp and i) from the liter-ature4, and our updated RV semi-amplitudes K, we re-derived the masses, densities, and surface gravities for all the planets as in Table A.1. We also report in the same table the planet equilibrium temperature, Teq, assuming a null Bond albedo and full redistribution of heat from the dayside to the nightside (e.g., López-Morales & Seager 2007), and the incident flux, Fp. Both Teq and Fp were updated in case the stellar Teff needed to be re-determined from our HARPS-N spectra (Table 1).
Table A.1 also emphasizes the fundamental contribution of HARPS-N in determining precise masses and densities to infer the composition of SPs. Specifically, the masses of 25 planets are determined with a precision higher than 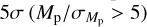 , 13 of which with
, 13 of which with 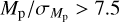 , and 8 with
, and 8 with 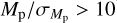 . Only upper limits on Mp are given for 20 planets whose induced Doppler signal was not detected. We note that a discussion of the planetary compositions from the measure of planetary masses and densities is beyond the scope of this work5.
. Only upper limits on Mp are given for 20 planets whose induced Doppler signal was not detected. We note that a discussion of the planetary compositions from the measure of planetary masses and densities is beyond the scope of this work5.
5 Discussion and conclusions
The value of the occurrence rate of CJs from the sample of 37 Kepler and K2 systems monitored by the HARPS-N/GTO consortium over the long term, namely, 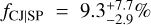 , is lower than the frequency of
, is lower than the frequency of 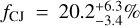 derived by Wittenmyer et al. (2020) for solar-type stars from RV surveys, regardless of the possible presence of inner SPs (Table 8). This might hint at the theoretical anti-correlation between the presence of SPs and CJs predicted by Izidoro et al. (2015) and Lambrechts et al. (2019). However, the large uncertainty on our fCJ|SP associated with the inevitably limited target sample does not allow us to draw a firm conclusion. Moreover, the sample considered by Wittenmyer et al. (2020) likely contains a certain fraction of stars hosting SPs, which went undetected through the Doppler method and, thus, a comparison of cold-Jupiter occurrence rates for stars with and without SPs is not straightforward. Nonetheless, assuming that the aforementioned anti-correlation does hold, the possible “contamination” of the sample of Wittenmyer et al. (2020) by SP systems would tend to make fCJ lower than it really is (in other words, fCJ might be higher than ~20% for solar-type stars hosting no SPs).
derived by Wittenmyer et al. (2020) for solar-type stars from RV surveys, regardless of the possible presence of inner SPs (Table 8). This might hint at the theoretical anti-correlation between the presence of SPs and CJs predicted by Izidoro et al. (2015) and Lambrechts et al. (2019). However, the large uncertainty on our fCJ|SP associated with the inevitably limited target sample does not allow us to draw a firm conclusion. Moreover, the sample considered by Wittenmyer et al. (2020) likely contains a certain fraction of stars hosting SPs, which went undetected through the Doppler method and, thus, a comparison of cold-Jupiter occurrence rates for stars with and without SPs is not straightforward. Nonetheless, assuming that the aforementioned anti-correlation does hold, the possible “contamination” of the sample of Wittenmyer et al. (2020) by SP systems would tend to make fCJ lower than it really is (in other words, fCJ might be higher than ~20% for solar-type stars hosting no SPs).
Our results do not support the claim by Bryan et al. (2019) regarding an excess of CJs in SP systems (see Table 8): according to their fCJ|SP, we should have discovered CJs in 12 ± 2 of our systems, while we only found them in 3 systems. The reason for such a discrepancy lies at least in part in an incorrect interpretation of the planetary origin of some linear trends by Bryan et al. (2019, see their Fig. 3): for instance, the trend in the GJ 273 system is due to secular acceleration, the slope in HD 3167 to stellar activity (Fig. 6), and those in Kepler-93b and Kepler-407b are compatible with being generated by brown dwarfs or low-mass stellar companions. In addition, fCJ|SP was computed by Bryan et al. (2019) in a different way, namely, by assuming a double power law 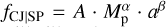 , deriving the coefficients A, α, and β with a likelihood approach, and integrating fCJ|SP over the parameter space. Nonetheless, the exclusion of approximately half of the long-term trends found by Bryan et al. (2019), since they were not due to CJs, would considerably reduce their fCJ|SP and make it more compatible with our estimate.
, deriving the coefficients A, α, and β with a likelihood approach, and integrating fCJ|SP over the parameter space. Nonetheless, the exclusion of approximately half of the long-term trends found by Bryan et al. (2019), since they were not due to CJs, would considerably reduce their fCJ|SP and make it more compatible with our estimate.
The present work will be extended to a larger sample, including the TESS SPs monitored with HARPS-N since 2019 (e.g., Cloutier et al. 2021; Lacedelli et al. 2021; Naponiello et al. 2022), as well as the K2 and TESS SP systems observed from the Southern hemisphere with other spectrographs such as ESPRESSO and HARPS. Performing the same analyses of RV data in Sect. 3.2 on a sample at least three times as large will allow us to:
- (i)
Derive a more precise fCJ|SP in SP systems.
- (ii)
Compute fCJ|SP as a function of the multiplicity of SPs. Indeed, the predicted anti-correlation between CJs and SPs is expected to be more pronounced for systems with a higher level of multiplicity of SPs, because single cores have a higher probability of “jumping” inside the orbit of the cold gas giant during their inward migration (see Fig. 3 in Izidoro et al. 2015). Detecting non-transiting planets with RVs (Sect. 4.3), especially in single transiting systems, is therefore crucial for more detailed studies of the possible dependence of fCJ|SP on the multiplicity of SPs.
- (iii)
Compute fCJ|SP as a function of the cold-Jupiter multiplicity: if multiple CJs were formed, it would be (in principle) even more difficult for the farther icy cores to migrate inward because the multiple CJs would act as a stronger dynamical barrier than a single CJ. The Jupiter-Saturn pair in the Solar System might have prevented the Uranus and Neptune cores from migrating towards the Sun. Nevertheless, the CJ pairs we discovered in the Kepler-68 and Kepler-454 systems did not hinder the formation of the inner SPs Kepler-68b/c and Kepler-454b.
- (iv)
Determine fCJ|SP as a function of the composition of SPs, which would be mainly ice-rich (sub-Neptunes) in the scenario of Izidoro et al. (2015, cf. also Zeng et al. 2019) or rocky (super-Earths) in the scenario of Lambrechts et al. (2019); this is because they are expected to form beyond or inside the water iceline, respectively. Unveiling a possible anti-correlation between CJs and predominantly ice-rich or rocky SPs may thus yield important clues on the mechanisms of formation of short-period SPs. An anti-correlation between rocky super-Earths and CJs would not be expected instead, if the former mainly originate inside rings of silicate-rich planetesimals at approximately 1 AU and then migrate inward (Batygin & Morbidelli 2023). Actually, a positive correlation could exist if the mass initially in the ring of silicate-rich planetesimals, leading to rocky super-Earths, is correlated with the mass of the ice-rich planetesimals, leading to the formation of the cores of outer giant planets. In this regard, the improvement in the mass determination of several of the 64 Kepler and K2 transiting SPs from our RV analyses (Table A.1) is useful to distinguish between rocky and non-rocky compositions.
For these purposes, we recommend continuing to follow up on SP systems, even after achieving the desired precision on planetary masses for the investigation of SP compositions. This can be done at a very low cost, given that just a few RV measurements over the years would, in principle, be sufficient to search for outer giant planets, provided that the spectrograph is stable. For the brightest targets, additional, complementary information on the presence of CJs will also be provided by the Gaia mission (e.g., Holl et al. 2023), starting with the publication of Data Release 4, slated for the end of 2025.
The 3661 HARPS-N RVs and activity indicators used for this work are released to the scientific community via the CDS6 and DACE7 databases to serve as the basis for further studies.
Acknowledgements
This work is based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias (GTO programme). The HARPS-N project was funded by the Prodex Program of the Swiss Space Office (SSO), the Harvard-University Origin of Life Initiative (HUOLI), the Scottish Universities Physics Alliance (SUPA), the University of Geneva, the Smithsonian Astrophysical Observatory (SAO), the Italian National Astrophysical Institute (INAF), the University of St. Andrews, Queen’s University Belfast and the University of Edinburgh. This paper is based on small-size planetary systems discovered by the Kepler mission. Funding for the Kepler mission was provided by the NASA Science Mission directorate. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement SCORE No 851555). This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. The authors acknowledge the financial support of the SNSF. We acknowledge financial contribution from the agreement ASI-INAF n.2018-16-HH.0. F.P.E. would like to acknowledge the Swiss National Science Foundation (SNSF) for supporting research with HARPS-N through the SNSF grants nr. 140649, 152721, 166227 and 184618. R.D.H. is funded by the UK Science and Technology Facilities Council (STFC)’s Ernest Rutherford Fellowship (grant number ST/V004735/1).
Appendix A Orbital and physical parameters of the 64 transiting Kepler and K2 planets
Orbital and physical parameters of the 64 transiting Kepler and K2 planets.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [Google Scholar]
- Ballard, S., Fabrycky, D., Fressin, F., et al. 2011, ApJ, 743, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Ballard, S., Chaplin, W. J., Charbonneau, D., et al. 2014, ApJ, 790, 12 [Google Scholar]
- Barbato, D., Sozzetti, A., Desidera, S., et al. 2018, A&A, 615, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barclay, T., Rowe, J. F., Lissauer, J. J., et al. 2013, Nature, 494, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Barragán, O., Gandolfi, D., Dai, F., et al. 2018, A&A, 612, A95 [Google Scholar]
- Batygin, K., & Morbidelli, A. 2023, Nat. Astron., 7, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Bol’shev, L. N., & Ubaidullaeva, M. 1975, Theory Probab. Appl., 19, 683 [CrossRef] [Google Scholar]
- Bonomo, A. S., Sozzetti, A., Lovis, C., et al. 2014, A&A, 572, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Zeng, L., Damasso, M., et al. 2019, Nat. Astron., 3, 416 [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Deline, A., Krenn, A., et al. 2022, A&A, 668, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkman, C. L., Cadman, J., Weiss, L., et al. 2023, AJ, 165, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, M. L., Knutson, H. A., Lee, E. J., et al. 2019, AJ, 157, 52 [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [Google Scholar]
- Buchhave, L. A., Dressing, C. D., Dumusque, X., et al. 2016, AJ, 152, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Burnham, K. P., & Anderson, D. R. 2004, Sociol. Methods Res., 33, 261 [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 619 [Google Scholar]
- Christiansen, J. L., Vanderburg, A., Burt, J., et al. 2017, AJ, 154, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutier, R., Charbonneau, D., Stassun, K. G., et al. 2021, AJ, 162, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, J. L., Mullally, F., Thompson, S. E., et al. 2016, ApJS, 224, 12 [Google Scholar]
- Cretignier, M., Dumusque, X., Hara, N. C., & Pepe, F. 2021, A&A, 653, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cretignier, M., Dumusque, X., & Pepe, F. 2022, A&A, 659, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR Online Data Catalog: II/328 [Google Scholar]
- Dai, F., Winn, J. N., Gandolfi, D., et al. 2017, AJ, 154, 226 [CrossRef] [Google Scholar]
- Dai, F., Masuda, K., Winn, J. N., & Zeng, L. 2019, ApJ, 883, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Damasso, M., Bonomo, A. S., Astudillo-Defru, N., et al. 2018, A&A, 615, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damasso, M., Zeng, L., Malavolta, L., et al. 2019, A&A, 624, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dressing, C. D., Charbonneau, D., Dumusque, X., et al. 2015, ApJ, 800, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Drązkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Dubber, S. C., Mortier, A., Rice, K., et al. 2019, MNRAS, 490, 5103 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X. 2021, in Plato Mission Conference 2021. Presentations and posters of the online PLATO Mission Conference 2021, 106 [Google Scholar]
- Dumusque, X., Bonomo, A. S., Haywood, R. D., et al. 2014, ApJ, 789, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J. 2017, Astrophysics Source Code Library [record ascl:1710.003] [Google Scholar]
- Eastman, J. D., Rodriguez, J. E., Agol, E., et al. 2019, ArXiv e-prints [arXiv:1907.09480] [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [Google Scholar]
- Fridlund, M., Gaidos, E., Barragán, O., et al. 2017, A&A, 604, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frustagli, G., Poretti, E., Milbourne, T., et al. 2020, A&A, 633, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gajdoš, P., Vaňko, M., & Parimucha, Š. 2019, Res. Astron. Astrophys., 19, 041 [Google Scholar]
- Gandolfi, D., Barragán, O., Hatzes, A. P., et al. 2017, AJ, 154, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gettel, S., Charbonneau, D., Dressing, C. D., et al. 2016, ApJ, 816, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 766, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
- Giuppone, C. A., Morais, M. H. M., & Correia, A. C. M. 2013, MNRAS, 436, 3547 [Google Scholar]
- Gregory, P. C. 2005, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Grunblatt, S. K., Howard, A. W., & Haywood, R. D. 2015, ApJ, 808, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, E. W., Barragán, O., Dai, F., et al. 2017, A&A, 608, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, A., & Schlichting, H. E. 2019, MNRAS, 487, 24 [Google Scholar]
- Hara, N. C., Boué, G., Laskar, J., Delisle, J. B., & Unger, N. 2019, MNRAS, 489, 738 [Google Scholar]
- Haywood, R. D. 2015, Ph.D. Thesis, Saint Andrews University, UK [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
- Haywood, R. D., Vanderburg, A., Mortier, A., et al. 2018, AJ, 155, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalog: II/336 [Google Scholar]
- Hog, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Holczer, T., Mazeh, T., Nachmani, G., et al. 2016, ApJS, 225, 9 [Google Scholar]
- Holl, B., Sozzetti, A., Sahlmann, J., et al. 2023, A&A, 674, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A. W., Sanchis-Ojeda, R., Marcy, G. W., et al. 2013, Nature, 503, 381 [CrossRef] [Google Scholar]
- Howell, S. B., Rowe, J. F., Bryson, S. T., et al. 2012, ApJ, 746, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., Hersant, F., & Pierens, A. 2015, ApJ, 800, L22 [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [Google Scholar]
- Kosiarek, M. R., Crossfield, I. J. M., Hardegree-Ullman, K. K., et al. 2019, AJ, 157, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lacedelli, G., Malavolta, L., Borsato, L., et al. 2021, MNRAS, 501, 4148 [NASA ADS] [CrossRef] [Google Scholar]
- Lacedelli, G., Wilson, T. G., Malavolta, L., et al. 2022, MNRAS, 511, 4551 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liddle, A. R. 2007, MNRAS, 377, L74 [NASA ADS] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
- López-Morales, M., & Seager, S. 2007, ApJ, 667, L191 [CrossRef] [Google Scholar]
- López-Morales, M., Haywood, R. D., Coughlin, J. L., et al. 2016, AJ, 152, 204 [Google Scholar]
- Malavolta, L., Borsato, L., Granata, V., et al. 2017, AJ, 153, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Malavolta, L., Mayo, A. W., Louden, T., et al. 2018, AJ, 155, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Isaacson, H., Howard, A. W., et al. 2014, ApJS, 210, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, S., Takeda, G., & Rasio, F. A. 2008, ApJ, 686, L29 [Google Scholar]
- Matsumura, S., Peale, S. J., & Rasio, F. A. 2010, ApJ, 725, 1995 [Google Scholar]
- Mayo, A. W., Vanderburg, A., Latham, D. W., et al. 2018, AJ, 155, 136 [Google Scholar]
- Mayo, A. W., Rajpaul, V. M., Buchhave, L. A., et al. 2019, AJ, 158, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, S. M., Howard, A. W., Weiss, L. M., et al. 2019, AJ, 157, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Bonomo, A. S., Rajpaul, V. M., et al. 2018, MNRAS, 481, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Zapatero Osorio, M. R., Malavolta, L., et al. 2020, MNRAS, 499, 5004 [Google Scholar]
- Naponiello, L., Mancini, L., Damasso, M., et al. 2022, A&A, 667, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nava, C., López-Morales, M., Mortier, A., et al. 2022, AJ, 163, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., Morbidelli, A., & Guillot, T. 2015, A&A, 578, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osborn, H. P., Santerne, A., Barros, S. C. C., et al. 2017, A&A, 604, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cameron, A. C., Latham, D. W., et al. 2013, Nature, 503, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, M. S., Benneke, B., David, T. J., et al. 2018, AJ, 156, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Polanski, A. S., Crossfield, I. J. M., Burt, J. A., et al. 2021, AJ, 162, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto-Arranz, J., Palle, E., Gandolfi, D., et al. 2018, A&A, 618, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rainer, M., Borsa, F., & Affer, L. 2020, Exp. Astron., 49, 73 [Google Scholar]
- Rajpaul, V. M., Buchhave, L. A., Lacedelli, G., et al. 2021, MNRAS, 507, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning (USA: MIT Press) [Google Scholar]
- Raymond, S. N., Kokubo, E., Morbidelli, A., Morishima, R., & Walsh, K. J. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 595 [Google Scholar]
- Rice, K., Malavolta, L., Mayo, A., et al. 2019, MNRAS, 484, 3731 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, E., Share, G. H., Forrest, D. J., et al. 1984, Nature, 312, 623 [Google Scholar]
- Rosenthal, L. J., Knutson, H. A., Chachan, Y., et al. 2022, ApJS, 262, 1 [Google Scholar]
- Rowe, J. F., Coughlin, J. L., Antoci, V., et al. 2015, ApJS, 217, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Singh, V., Bonomo, A. S., Scandariato, G., et al. 2022, A&A, 658, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sinukoff, E., Howard, A. W., Petigura, E. A., et al. 2016, ApJ, 827, 78 [Google Scholar]
- Sinukoff, E., Howard, A. W., Petigura, E. A., et al. 2017, AJ, 153, 271 [CrossRef] [Google Scholar]
- Ter Braak, C. J. F. 2006, Stat. Comput., 16, 239 [Google Scholar]
- Teske, J. K., Wang, S., Wolfgang, A., et al. 2018, AJ, 155, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Toledo-Padrón, B., Lovis, C., Suárez Mascareño, A., et al. 2020, A&A, 641, A92 [Google Scholar]
- Vanderburg, A., Montet, B. T., Johnson, J. A., et al. 2015, ApJ, 800, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [Google Scholar]
- Van Eylen, V., Albrecht, S., Huang, X., et al. 2019, AJ, 157, 61 [Google Scholar]
- Weiss, L. M., Rogers, L. A., Isaacson, H. T., et al. 2016, ApJ, 819, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [Google Scholar]
- Wittenmyer, R. A., Wang, S., Horner, J., et al. 2020, MNRAS, 492, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Zakamska, N. L., Pan, M., & Ford, E. B. 2011, MNRAS, 410, 1895 [NASA ADS] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, Proc. Natl. Acad. Sci., 116, 9723 [Google Scholar]
- Zeng, L., Jacobsen, S. B., Hyung, E., et al. 2021, ApJ, 923, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., & Wu, Y. 2018, AJ, 156, 92 [Google Scholar]
We define a cold Jupiter as a planet with mass between 0.3 and 13 MJup and semi-major axis between 1 and 10 AU. Even though some studies have shown that giant planets might have masses greater than the deuterium burning limit of 13 MJup (e.g., Chabrier et al. 2014), the above formation models generally refer to cold Jupiters with Mp < 13 MJup.
This value was determined by summing up the occurrence rates of cold Jupiters from 300 to 10 000 d in Table 3 of Wittenmyer et al. (2020).
The Chauvenet’s criterion states that a value from a set of N measurements can be excluded if its deviation from the mean value is so high that the normal distribution probability that one of the N measurements with an equal or greater deviation may occur is less than 1/2N (see, e.g., Bol’shev & Ubaidullaeva 1975).
For the systems with updated R* values in Table 1, we recomputed Rp from the Rp /R* transit parameter and R*. In cases where the impact parameter b only is provided in literature assuming circular orbits, we derived the orbital inclination as i = arccos (b · R*/a).
All Tables
Priors imposed on the hyper-parameters of the Gaussian process regression for the stars showing significant magnetic activity variations.
HARPS-N systemic radial velocities and jitter terms, Gaussian process hyper-parameters, and linear accelerations from the DE-MCMC radial-velocity modeling.
Orbital parameters and minimum masses of the companions causing the long-term trends observed in the Kepler-93, Kepler-454, and K2-12 systems.
Completeness (recovery rate) and fraction of stars hosting both short-period small planets and cold Jupiters for different intervals of orbital separation.
Fraction of stars with cold Jupiters in our sample compared with those from previous works.
All Figures
 |
Fig. 1 Recovery rate (completeness) maps of cold Jupiters. Top panel: completeness of Kepler-1876, one of the systems with the worst completeness mainly due to the relatively short temporal baseline of the HARPS-N radial-velocity observations. Black and white indicate 0% and 100% recovery rates, respectively. Middle panel: completeness of Kepler-93, showing a very high detection rate, given the long time span of observations. Bottom panel: mean survey completeness obtained by averaging out the individual completenesses of the 37 systems. |
| In the text | |
 |
Fig. 2 Radial-velocity measurements of K2-110. Top panel: radial velocities as a function of time, showing no long-term trends. The blue and light blue points display the measurements obtained with the HARPS-N and HARPS spectrographs, respectively, and the black line indicates the Keplerian best-fit model. Bottom panel: same radial velocities as in the top panel, but phase folded at the ephemeris of K2-110b (P = 13.86 d). |
| In the text | |
 |
Fig. 3 Radial-velocity measurements of Kepler-78. Top panel: radial velocities as a function of time, showing variations due to both stellar activity and the ultra-short-period planet Kepler-78b, but no significant long-term trends. The blue and red circles indicate the radial-velocity points gathered with the HARPS-N and HIRES spectrographs, respectively. Middle panel: zoom on the first 100 days, mainly showing the non-stationary stellar activity signal, which was modeled with Gaussian process regression and a quasi-periodic kernel (black solid line). Bottom panel: radial velocities phase-folded at the ephemeris of Kepler-78b (P = 0.35 d), after removing the Gaussian process model for the stellar activity variations. |
| In the text | |
 |
Fig. 4 Radial-velocity and CaII S-index measurements of Kepler-93. Left panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities. The black line shows the best-fit model with a long-term linear slope caused by a non-planetary companion, a Keplerian orbit for the transiting planet Kepler-93b (P = 4.73 d), and Gaussian process regression with a squared exponential kernel to account for long-term stellar activity variations. Right panel: residuals of the HARPS-N radial velocities after subtracting the linear long-term trend and the signal of Kepler-93b (top), and measurements of the stellar activity S index (bottom). The increase in both the RVs and the S index from ~ 7000 to ~ 8300 BJDTDB – 2 450 000 indicates that the small-amplitude long-term variations superposed to the linear slope seen in the left panel are likely due to stellar magnetic activity. |
| In the text | |
 |
Fig. 5 Radial-velocity and activity index measurements of K2-12. Left panel: HARPS-N radial velocities showing the long-term linear slope due to a companion of yet unknown nature. The Doppler signal of the transiting planet K2-12b (P = 8.28 d) is undetected, hence, only an upper limit to its mass could be given. Right panel: FWHM of the cross-correlation function (top) and CaII S-index (bottom) time series showing no significant linear trends. This would indicate that the radial-velocity linear trend in the left panel is caused by a physically bound companion. |
| In the text | |
 |
Fig. 6 Radial-velocity and CCF FWHM measurements of K2-96/HD 3167. Left panel: radial velocities showing a long-term linear trend: red, green, blue, and light blue points show the measurements obtained with the HIRES, APF, HARPS-N, and HARPS spectrographs, respectively. Right panel: linear trend observed in the FWHM of the HARPS-N cross-correlation functions. A similar behavior is observed in the CaII S index. This implies that the slope observed in the RVs (left panel) is produced by stellar activity, and not by a physical companion. |
| In the text | |
 |
Fig. 7 Radial-velocity measurements of Kepler-68. Top panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities and the bestfit model (black line) with four Keplerians corresponding to the two transiting planets Kepler-68b (P = 5.40 d) and Kepler-68c (P = 9.60 d), and the two cold giant planets Kepler-68d (P = 633 d = 1.7 yr) and Kepler-68e (P ~ 3450 d = 9.4 yr). Middle and bottom panels: phase-folded radial-velocity signals of the cold giant planets Kepler-68d and Kepler-68e. Note: orbital phases equal to 0 and 1 correspond to inferior conjunction. |
| In the text | |
 |
Fig. 8 Radial-velocity measurements of Kepler-454. Top left panel: HIRES (red circles) and HARPS-N (blue circles) radial velocities and the best-fit model (black line) with a long-term linear trend and three Keplerians corresponding to the transiting planet Kepler-454b (P = 10.57 d) and the two cold giant planets Kepler-454c (P = 524 d = 1.4 yr) and Kepler-454d (P ~ 4070 d = 11.1 yr). Top right panel: linear trend after removing the three Keplerian signals, which is caused by an additional fourth companion of yet unknown nature. Bottom panels: phase-folded radial-velocity signals of the cold giant planets Kepler-454c (left) and Kepler-454d (right). Note: orbital phases equal to 0 and 1 correspond to inferior conjunctions. |
| In the text | |
 |
Fig. 9 HARPS-N radial velocities of K2-312 / HD 80653 and the best-fit model (black line) with two Keplerians, which correspond to the ultra-short-period transiting planet K2-312b (P = 0.72 d) and the eccentric cold giant planet K2-312c (P ~ 921 d = 2.5 yr; e = 0.85), and Gaussian process regression with a quasi-periodic kernel. |
| In the text | |
 |
Fig. 10 Phase-folded HARPS-N radial velocities (blue dots) of Kepler-1876 at the period P = 15.8 d of the possible planet candidate Kepler-1876c. The black solid line shows the best-fit model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


