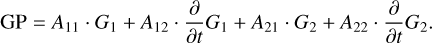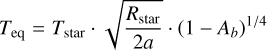EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 684 (April 2024) A&A, 684 (2024) A22 Full HTML
Open Access
Issue
A&A
Volume 684, April 2024
Article Number A22
Number of page(s) 28
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202348592
Published online 03 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

GJ 9827 is a K7V star orbited by two super-Earth planets and one mini-Neptune at periods of 1.209, 3.648, and 6.201 days corresponding to planets b, c, and d, respectively. The orbital periods of planet b and c are near the 3:1 mean motion resonance, and b and d are near a 5:1 resonance. The planets were first discovered by Niraula et al. (2017) and Rodriguez et al. (2018) analysing K2 Campaign 12 data (Howell et al. 2014). The three planets span the radius gap for small close-in planets described by Fulton et al. (2017). They occupy the transition region from rocky to gaseous planets, which makes characterizing their interior structures and atmospheres particularly interesting.

At the time of discovery, the system was the closest planetary system detected by K2, located at a distance of 29.652 pc from the Sun (Gaia Collaboration 2020). The star is relatively bright with a V magnitude of 10.25 mag (Henden et al. 2016), which makes it an excellent target for atmospheric composition studies through transmission spectroscopy with the James Webb Space Telescope (Gardner et al. 2006) and the future ANDES (ArmazoNes high Dispersion Echelle Spectrograph) at the ELT (Extremely Large Telescope, Marconi et al. 2022). However, a robust mass measurement is crucial to retrieve accurate molecular abundances in the planet’s atmosphere. The strength of atmospheric features depends on the scale height of the atmosphere which, in turn, depends on the surface gravity of the planet and, therefore, its mass and radius (Kreidberg 2018). Precise masses and radii are also important for estimations on the interior composition of the planets and the evolution of the planetary system. So far, literature determinations of the planetary masses have shown large variations, ranging from 3.42 M⊕ (Rodriguez et al. 2018) to 8.16 M⊕ (Teske et al. 2018) for planet b, 0.67 M⊕ (Rice et al. 2019) to 2.56 (Teske et al. 2018) for planet c, and 2.35 M⊕ (Prieto-Arranz et al. 2018) to 5.58 M⊕ (Teske et al. 2018) for planet d, with uncertainties as large as 100%. Based on their results, Prieto-Arranz et al. (2018) and Rice et al. (2019) argue that the two inner planets have high densities, whereas the outer planet has a low density, which suggests that during the evolution of the system migration or photoevaporation could have been important factors.

In an attempt to better constrain the masses and other planetary parameters, we used 54 observations obtained by the Échelle Spectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO) through the Guaranteed Time Observation (GTO) consortium (Program ID 1102.C-744, 1104.C-0350, PI: F. Pepe) between October 2018 and December 2019. These observations are part of the GTO subprogram focusing on the radial velocity follow-up of K2 and TESS (Transiting Exoplanet Survey Satellite) transiting candidates (Damasso et al. 2020, 2023; Toledo-Padrón et al. 2020; Sozzetti et al. 2021; Mortier et al. 2020; Demangeon et al. 2021; Lavie et al. 2023; Castro-González et al. 2023). We complement them with published measurements from HARPS (High Accuracy Radial velocity Planet Searcher), HARPS-N, and HIRES (High Resolution Echelle Spectrometer) and carried out a combined analysis with K2 and TESS photometry using Gaussian process (GP) regression to model stellar activity and planetary orbits simultaneously. In the following we provide a description of the data in Sect. 2 and a discussion on previous analyses of the planetary system in the literature in Sect. 3. We also explain our GP method in Sect. 4 and present our results together with a literature comparison in Sect. 5.

thumbnail Fig. 1

Time-series observations of all RV measurements used in this work.
thumbnail Fig. 2

Comparison between S-BART- and CCF-extracted RVs for ESPRESSO DRS.

2 Observations

2.1 Spectroscopic observations

We use radial velocity (RV) measurements from ESPRESSO, HARPS, HARPS-N, and HIRES and present all measurements in Fig. 1. ESPRESSO is a high-resolution fibre-fed echelle spec-trograph mounted at the ESO Very Large Telescope (VLT) array on Paranal, Chile (Pepe et al. 2013, 2021). The instrument operates in a spectral range from 380 to 788 nm with a resolution of R ≈ 140 000. A Fabry Pérot Etalon is used for simultaneous calibrations, allowing an RV precision of down to 10 cm s−1 to be reached (Wildi et al. 2010). The observations of GJ 9827 were collected between October 29, 2018, and December 2, 2019, during the GTO using HR11 observing mode. The data were reduced using the ESPRESSO data reduction pipeline (DRS) version 3.0.0. We compared the RVs extracted by the ESPRESSO DRS, which uses a cross-correlation function (CCF), to RVs extracted with the S-BART (Semi-Bayesian Approach for RVs with Template matching) pipeline (Silva et al. 2022), using the template matching technique within a semi-Bayesian framework. Figure 2 shows a comparison between S-BART RVs and RVs from the ESPRESSO DRS. Although the root mean square (rms) for both sets is very similar (4.042 m s−1 for S-BART and 4.003 m s−1 for CCF), the errors from S-BART are significantly smaller. On average, S-BART provides errors of about 0.426 m s−1, whereas the CCF gives errors of 0.617 m s−1. Therefore, we decided to use the S-BART RVs. After removing three measurements with a low exposure time (<900 s), 54 measurements remained for our analysis.

HARPS (Mayor et al. 2003) is mounted at the ESO 3.6 m telescope at La Silla Observatory, Chile. This high-resolution fiber-fed echelle spectrograph observes in a wavelength range between 380 and 690 nm with a resolution of R ≈ 115 000. The instrument has demonstrated a long-term precision of about 0.8 m s−1 (e.g., Dumusque et al. 2012), and after the installation of a laser-frequency comb in 2018 the precision is expected to improve down to 0.5 m s−1 (Lo Curto et al. 2015; Coffinet et al. 2019). HARPS was involved in the discovery of numerous exoplanets in the southern hemisphere (e.g., Mayor et al. 2011; Astudillo-Defru et al. 2017; Unger et al. 2021). We used data obtained under programs 099.C-0491(A), 0100.C-0808(A) between August 19 and October 24, 2017. We also included out-of-transit measurements from program 0101.C-0788, which were obtained between August 4 and December 19, 2018. These observations were taken with a shorter exposure time than the rest of the HARPS measurements, leading to higher photon noise and larger uncertainties. As for ESPRESSO, we extracted the RVs with S-BART, which leads to an average error of 1.34 m s−1 compared to 2.14 m s−1 from the CCF. To reduce the effect of short-term stellar variability, we binned data points obtained within a time span of three hours using a weighted average. For the ESPRESSO data this step was not necessary, since all measurements lie more than three hours apart. We ended up with 31 measurements from HARPS.

The HARPS-N spectrograph (Cosentino et al. 2012) is located in the northern hemisphere at the 3.6 m Telescopio Nazionale Galileo (TNG) at the Observatorio del Roque de los Muchachos in La Palma, Spain. Having the same instrumental specifications as HARPS, it can also reach an RV stability of better than 1 m s−1. We used data published in literature from Prieto-Arranz et al. (2018) and Rice et al. (2019), which have average errors of 1.63 and 1.87 m s−1, respectively. Both works extracted the RVs using a cross-correlation function with a K5-dwarf mask. Applying the same binning criterion as for HARPS, we had 44 measurements from HARPS-N observed from July 29 to December 15, 2017.

Lastly, we added 92 measurements from Kosiarek et al. (2021) obtained with HIRES (Vogt et al. 1994) mounted at the Keck I telescope on Maunakea, Hawai’i. HIRES is a grating cross-dispersed echelle spectrograph operating between 300 and 1000 nm with an resolution of up to 85 000. The observations were taken between September 22, 2017, and January 8, 2020. The average error of the measurements is 1.17 m s−1.

2.2 Photometric observations

After the failure of two of its four reaction wheels in May 2013, the Kepler spacecraft (Borucki et al. 2010) started its extended K2 mission and observed several fields near the ecliptic to obtain high-precision photometry, each field being observed for about 80 days at a time (Howell et al. 2014). GJ 9827 was monitored during K2 Campaign 12 from December 16, 2016, to March 4, 2017, under the identifier EPIC 246389858. K2 collected 3379 data points with a cadence of about 30 minutes. We used the light curve produced by the EVEREST (EPIC Variability Extraction and Removal for Exoplanet Science Targets) K2 pipeline (Luger et al. 2016, 2018), more specifically, the PDCSAP flux (Pre-search Data Conditioning Simple Aperture Photometry). Each data point has a precision of about 20 ppm. The light curve and corresponding GLS periodogram are presented in Fig. 3. The rotation period of the star clearly shows as highest peak in the periodogram with the second highest peak corresponding to half the rotation period. After subtracting the offset, linear trend, and stellar activity contribution to the light curve using a Gaussian Process with a simple harmonic oscillator (SHO) kernel (see Sect. 4.1), we measured a standard deviation of 15 ppm over the whole light curve. We adopted this value as jitter term in the combined model.

GJ 9827 (TIC 301289516) was observed by TESS (Ricker et al. 2014) in sector 42 from August 21 to September 13, 2021. The sector was processed by the Science Processing Operations Center pipeline (SPOC; Jenkins et al. 2016), which searches for transit-like signatures using an adaptive, wavelet-based transit detection algorithm (Jenkins 2002; Jenkins et al. 2010). In the process, planet b (TOI 4517.01) was identified with an period of 1.2089 ± 0.0001 days, T0 = 2459448.316 ± 0.001 days, and a radius of 1.62 ± 1.39 R⊕. The observations were performed in high-cadence with a data point every 20 s. To reduce high-frequency noise and computing time, which scales linearly to the number of points, we binned the data to 10 min. We measured a standard deviation of 32 ppm in the binned PDCSAP flux, and as for K2, we adopted this value as jitter term for this dataset. Figure 4 presents the TESS light curve, showing SAP and PDC-SAP flux, both in original cadence and binned to 10 minutes, as well as the phasefolds for all three planets according to periods derived from K2 (Rodriguez et al. 2018) for illustrative purposes.

thumbnail Fig. 3

K2 light curve (top) and corresponding GLS periodogram (bottom). The purple area indicates the approximate rotation period of the star, with the gray line presenting the highest period peak found by GLS, which corresponds to the rotation period of the star.

3 Current and previous analyses of system properties

3.1 Stellar parameters from this work

Table 1 summarizes the stellar properties of GJ 9827. We derived stellar parameters Teff, log g, [Fe/H], and the total line-broadening velocity, υbroad, using a high-S/N template generated from the ESPRESSO spectra and the SteParSyn code1 described in Tabernero et al. (2022). The instrumental broadening υins ~ 2.1 km s−1 (R ~ 140 000) was also taken into account as a fixed parameter. From this, we determined Teff = 4236 ± 12 K, log gspec = 4.70 ± 0.10 dex and [Fe/H] = −0.29 ± 0.03 dex, which are in good agreement with stellar parameters determined in previous studies, for example, Niraula et al. (2017; Teff = 4255 ± 110 K, [Fe/H] = −0.28 ± 0.12 dex), Rodriguez et al. (2018; 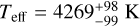), Prieto-Arranz et al. (2018; Teff = 4219 ± 70 K, [Fe/H] = −0.29 ± 0.12 dex), Rice et al. (2019; 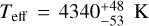, [Fe/H] = −0.26 ± 0.09 dex), and Kosiarek et al. (2021; Teff = 4294 ± 52 K, [Fe/H] = −0.26 ± 0.08 dex). We derived a υbroad = 1.75 ± 0.03 km s−1. All uncertainties reported here are statistical errors coming only from the SteParSyn computation and do not account for any systematic errors. We disentangled the broadening velocity into macroturbulent velocity υmac = 1.418 ± 0.003 km s−1 and projected rotational velocity v sin i = 1.02 ± 0.05 km s−1 using Eq. (2) from Brewer et al. (2016) and the assumption that 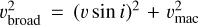. The stated uncertainties are probably underestimated due to the fact that they involve only statistical errors. Additionally, the temperature of GJ 9827 lies outside the calibration range used by Brewer et al. (2016) to derive Eq. (2). However, since υbroad is rather low, we expected υ sin i to be low as well and assumed an upper limit of υ sin i < 1.75 km s−1.

We put our derived Teff and [Fe/H] into PARAM1.32 (da Silva et al. 2006) together with the parallax from Gaia DR3 (Gaia Collaboration 2022) and Vmag from Henden et al. (2016) to compute the stellar age, mass, and radius using PARSEC isochrones version 1.1 (Bressan et al. 2012). Marfil et al. (2021) present a systematic offset in Teff compared to interferometric measurements of 72 K. As done by Murgas et al. (2023), we added this systematic error to our temperature uncertainty of 12 K to obtain a more conservative error estimation, therefore using an uncertainty of 84 K in PARAM1.3. For [Fe/H], we doubled the uncertainty provided by SteParSyn. As a result we got an age of 5.465 ± 4.058 Gyr, a mass of 0.592 ± 0.012 M⊙, and a radius of 0.542 ± 0.012 R⊙. We note that the stellar age is not very well defined. A recent work by Engle & Guinan (2023) presents an age of 2.92 ± 0.60 Gyr using an age-rotation relation, however, Rice et al. (2019) claim 5–10 Gyr from an isochrone analysis, and Kosiarek et al. (2021) derive 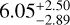Gyr from an MCMC analysis. We used these values of stellar mass and radius together with other literature values summarized in Table A.1 to calculate a weighted average that served as a prior in our GP analysis. The width of the priors is defined by the uncertainties added in quadrature. The posterior values for mass and radius from this analysis are presented in Table 1.

We also derived the stellar age, mass, and radius using the 2-step method of PARAM1.53. Therefore, we input the same values as above for Teff, [Fe/H], and parallax, as well as our spectro-scopically derived log g with twice the uncertainty determined by SteParSyn, and the 2MASS magnitudes J = 7.984 ± 0.02 mag, H = 7.379 ± 0.042 mag, and Ks = 7.193 ± 0.024. The result is very similar to the output of PARAM1.3, with an age of 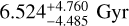, M = 0.586 ± 0.02 M⊙, 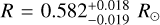, and log .

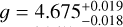We would like to point out here that stellar mass and radius derived with PARAM1.3 significantly depends on the value of Vmag used. On the other hand, these parameters are less sensitive to changes in the parallax. This is demonstrated in Table 2, where we tested two different Vmag (Vmag = 10 101 ± 0 001 mag from UCAC4, Zacharias et al. 2012; and Vmag = 10.250 ± 0.138 mag from APASS DR9, Henden et al. 2016) and two different parallaxes (π = 33.7247 ± 0.00169 mas from Gaia DR3, Gaia Collaboration 2022; and the zero-point corrected value of π = 33.762 ± 0.019 mas from Gaia eDR3, Kervella et al. 2022) with PARAM1.3. We decided to use the magnitude from Henden et al. (2016) and the corresponding stellar parameters because of the more conservative error compared to Zacharias et al. (2012).

thumbnail Fig. 4

TESS light curve SAP (top panel) and PDCSAP flux (middle panel) with original cadence (blue) and binned to 10 minutes (orange). The bottom panel shows phase folds according to planetary periods and mid-transit times derived by Rodriguez et al. (2018) for planet b (left), planet c (middle), and planet d (right). The red line presents a transit model based on parameters from Rodriguez et al. (2018) for illustrative purpose.
Table 1

Summary of stellar properties for GJ 9827.

Table 2

Stellar parameters derived with PARAM1.3 using different input parallaxes and magnitudes.

3.2 Planetary parameters from the literature

Niraula et al. (2017) first detected the transits using a Box Least-Squared (BLS; Kovács et al. 2002) search. Then, they fitted all transits simultaneously with the batman model (Kreidberg 2015) and derived uncertainties on the fitted parameters with the Markov chain Monte Carlo (MCMC) method implemented in emcee (Foreman-Mackey et al. 2013). This results in radii for all three planets of 1.75 ± 0.18 R⊕, 1.36 ± 0.14 R⊕, and 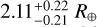, respectively. They also collected 7 high-resolution spectra with the FIbre-fed Échelle Spectrograph (FIES; Frandsen & Lindberg 1999; Telting et al. 2014) at the Nordic Optical Telescope on La Palma, Spain. No significant RV variation is found, but they used the coadded spectrum to derive stellar parameters of the host star.

Almost at the same time, Rodriguez et al. (2018) announced their discovery of the GJ 9827 system, also from K2 data. They modeled the system using EXOFASTv2 (Eastman 2017; Eastman et al. 2019), an MCMC algorithm to simultaneously fit multiple planets. With this, they derived planetary radii of 1.62 ± 0.11 R⊕, 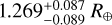, and 2.07 ± 0.14 R⊕, for planets b, c, and d, respectively. 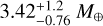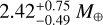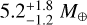Within the global model, EXOFASTv2 can also estimate the planetary masses using the mass-radius relation from Chen & Kipping (2017), resulting in values of , , and , respectively.

The first mass measurement from RV data was done by Teske et al. (2018), using 36 high-resolution spectra from the Carnegie Planet Finder Spectrograph (PFS; Crane et al. 2006, 2008, 2010) on Magellan II at Las Campanas Observatory, Chile, observed between January 2010 and August 2016. They derived planetary masses using two methods, SYSTEMIC (Meschiari et al. 2009) and radvel (Fulton et al. 2018). Both methods model Keplerian orbits using a maximum likelihood function and incorporate an MCMC method to determine median values and errors. For SYSTEMIC, Teske et al. (2018) report a mass of 7.50 ± 1.52 M⊕ for planet b, and upper limits of 2.56 M⊕ and 5.58 M⊕ for planets c and d, respectively. The radvel analysis gives masses of 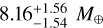for planet b, 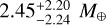for planet c, and 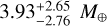for planet d. For both methods the resulting masses are not well constrained with uncertainties up to 100%.

Additionally to the seven FIES spectra presented by Niraula et al. (2017), Prieto-Arranz et al. (2018) obtained 35 highresolution spectra with HARPS and 23 spectra with HARPS-N. They performed a joint analysis of the RV and photometric K2 data with the pyaneti code (Barragán et al. 2017), which incorporates an MCMC algorithm. With this, they determined for planet b 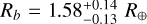and 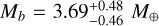, for planet c Rc = 1.24 ± 0.11 R⊕ and 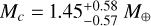, and for planet d Rd = 2.04 ± 0.18 R⊕ and 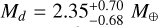. Compared to the previous first mass measurements by Teske et al. (2018), these results are more precise, however, the uncertainties still reach 40% for planet c and about 30% for planet d. Furthermore, the mass of planet b is significantly lower compared to Teske et al. (2018). Prieto-Arranz et al. (2018) also modeled the stellar activity in the RVs with a Gaussian process and obtained similar planetary parameters with this technique.

Rice et al. (2019) added another 43 HARPS-N measurements to the previously published HARPS and HARPS-N data from Prieto-Arranz et al. (2018), PFS data (Teske et al. 2018), and FIES data (Niraula et al. 2017). They simultaneously modeled stellar activity and RVs with the package PyORBIT (Malavolta et al. 2016), which implements a GP quasi-periodic kernel through the GEORGE package (Ambikasaran et al. 2016). As a result, they derived Mb = 4.91 ± 0.49 M⊕, Mc = 0.84 M⊕ with an upper limit of 1.50 M⊕ and 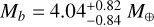. Comparing these results to Prieto-Arranz et al. (2018) shows that the uncertainties do not improve and the mass of planet d is significantly larger.

Kosiarek et al. (2021) collected 92 RV measurements with HIRES with an average uncertainty of 1.17 ms−1. Together with already published RV data, this makes a total of 234 measurements for GJ 9827. They analyzed the RV data using radvel and a Gaussian Process and determined masses of Mb = 4.87 ± 0.37 M⊕, Mc = 1.92 ± 0.49 M⊕, and Md = 3.42 ± 0.62 M⊕. So far, these are the best constrained values with uncertainties better than 25%. A comprehensive collection of all planetary parameters determined in the literature is given in Table A.1.

4 Analysis

In this work, we performed a combined analysis of spectroscopy and photometry within the Gaussian Process regression framework (GP; Rasmussen & Williams 2006; Roberts et al. 2012), following the approach described in Suárez Mascareño et al. (2020, 2023). Within the last decade, GPs have become very successful in characterizing and modeling stellar activity in RV time series (e.g., Haywood et al. 2014). GPs are flexible in modeling quasi-periodic signals, such as stellar rotation signals induces by active regions on the stellar surface. They are able to account for changes in the amplitude, phase, and period of the signal, however, they can also easily overfit the data and erase the planetary signal. One way to overcome this is to simultaneously model activity indicators, which should be independent of the planet-induced periodic signal, and radial velocity with shared hyper parameters (e.g., Suárez Mascareño et al. 2020; Faria et al. 2022). Another possibility is to use multi-dimensional GPs as done by, for example, Rajpaul et al. (2015), Barragán et al. (2022), and Delisle et al. (2022), where the whole time series is joined under a single covariance matrix. This approach is especially useful in cases where there is a good correlation between the activity indicator and the activity-induced RV signal, like in the case of Proxima Centauri (Suárez Mascareño et al. 2020) or GJ 1002 (Suárez Mascareño et al. 2023). We did not see any correlation between RV and full-width at half maximum (FWHM) in our data (see Fig. A.1), however, we followed the approach as described in Suárez Mascareño et al. (2023), because the correlation might still exist with the gradient as in the case of Proxima, and as described in the FF’ formalism (Aigrain et al. 2012). We used the S+LEAF code (Delisle et al. 2022) together with Dynesty (Speagle 2020).

S+LEAF is an open-source software, which is able to simultaneously model several time series with the same Gaussian processes and their derivatives. It provides a flexible noise model to account for instrument calibration errors (Delisle et al. 2020), and offers a number of different GP kernels with different properties.

Dynesty uses nested sampling (Skilling 2004, 2006) to infer the Bayesian evidence of the model. It performs a random walk or random slice sampling strategy (Handley et al. 2015a,b) to explore large parameter spaces. Due to the large dataset, the number of live points was set to 10 × npar and the number of slices was 2 × npar, where npar is the number of free model parameters.

4.1 Stellar activity

We analyzed different activity indicators with the Generalised Lomb-Scargle periodograms (GLS; Zechmeister & Kürster 2009). Figure 5 presents a plot of the spectroscopic data used in this study and their corresponding GLS periodograms. The RV data (top row) shows a significant peak at the period of planet b. We marked the periods of the three planets with orange dashed lines. The following rows present the activity indicators, FWHM, CaII S-index (Vaughan et al. 1978), and Hα. Not all indicators are available for every dataset. The FWHM shows a significant signal around the rotation period of the star (indicated by the purple region), which is determined by Rodriguez et al. (2018) with 31 ± 1 d, Prieto-Arranz et al. (2018) with 30.7 ± 1.4 d, Rice et al. (2019) with 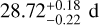, and Kosiarek et al. (2021) with 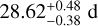. Niraula et al. (2017) also find a signal around 30 days, however, they favor a period at 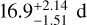. The CaII S-index also shows some signal around 30 days, however, less significant than in FWHM. Therefore, we used FWHM in our following analysis.

We analyzed the stellar activity by fitting a GP to the FWHM and RV data without a planetary model to determine the rotational period of the star. We used a GP with two SHO kernels at Prot and Prot/2 with a normal distributed prior centered around the expected rotation period. The GP amplitudes were the same for all datasets and we used a log uniform jitter term. We found a rotation period of 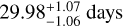. Figure 6 shows the best model fit to the FWHM. We confirmed the rotation period by using the median value of the ESPRESSO S-index (0.66 ± 0.06) to compute log R′Hk, following Suárez Mascareño et al. (2016). We obtained a measurement of log R′HK = −5.28 ± 0.05 and from the rotation-activity relationship of Suárez Mascareño et al. (2016) we estimated a rotation period of 32.9 ± 1.4 d. These values are consistent with the great majority of the stellar rotation period measurements from the literature including the most recent determination by Engle & Guinan (2023), Prot = 28.72 ± 0.19 d.

Using the star’s equatorial radius, R, from Table 1 and , we estimated a υrot of 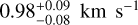. This value is consistent at the 1-σ level with the spectroscopically derived υ sin i = 1.02 ± 0.05 km s−1 in Sect. 3.1 and is compliant with our conservative upper limit of υ sin i < 1.75 km s−1. Due to the small value of υrot, we can assume that GJ 9827 is likely seen near equator on with a spin axis inclination angle close to 90 deg. The knowledge of the star’s spin axis angle is relevant to address the true 3D architecture of the multiple planetary system (e.g., Albrecht et al. 2021).

thumbnail Fig. 5

Left: ESPRESSO, HARPS, HARPS-N, and HIRES spectroscopic data used in this study. We present plots for RV, FWHM, CaII S-index, and Hα. Right: corresponding GLS periodograms. The orange dashed lines mark the periods of the three planets. The purple area indicates the approximate rotation period of the star. The gray line presents the highest period peak found by GLS for each panel.

4.2 Radial velocity

After assessing the stellar activity in the spectroscopic data, we performed a GP analysis with FWHM and RVs including a three-planet model. To do that, we used celerite2, an update of the celerite package by Foreman-Mackey et al. (2017), a fast and scalable 1-D GP regression. With that, stellar rotation is modeled with a SHO kernel at Prot and Prot/2 and a normal distributed prior centered around the expected rotation period of the star, that is, 30 ± 5 d.

We investigated circular and eccentric models and used narrow normal distributed priors for the orbital period and time of periastron T0, as derived by Rodriguez et al. (2018) and presented in Table A.2. The priors for the planet amplitudes were set uniformly between 0 and 5 times the standard deviation (stdev). The priors for the offsets for each instrument were normally distributed, centered around 0 with a sigma of 3× stdev. We did not fit any long-term cycle, but we included a linear trend with normally distributed priors around 0, with a sigma equal to the flux range peak-to peak divided by the observation baseline. The jitter prior is log-uniform ranging from −10 to log(5 × stdev). The log likelihood of the eccentric and circular model are almost indistinguishable with ln Zecc = −1063.89 ± 0.39 compared to ln Zcirc = −1063.93 ± 0.39 and Δ ln Z = 0.04. Therefore, we favored the circular model. The resulting planetary parameters for the circular model are summarized in Table A.3.

thumbnail Fig. 6

FWHM from ESPRESSO, HARPS, and HARPS-N with best GP model. The bottom panel shows a zoom-in on ESPRESSO data.

4.3 Photometry

Before combining radial velocity and transit data, we analyzed the TESS and K2 data separately. For both, we used the PDC-SAP flux and estimated the jitter of the data from the standard deviation as described in Sect. 2.2. This gave a jitter term of 0.15 ppt for K2 and 0.32 ppt for TESS. We defined normal and log-normal distributed priors for the offsets and linear trends of both datasets, respectively. The rotation periods and timescales of evolution got log-normal priors as well, whereas the GP amplitude priors were defined by uniform log-priors.

We tested several kernels, such as the exponential kernel, SHO kernel, quasi-periodic kernel, and the Matérn kernels 1/2 to 5/2 (Genton 2002). We found that the Matérn 3/2 kernel offers the best model for the PDCSAP flux of the TESS light curve without affecting the planetary transits due to overfitting. The kernel has the form

(1)

where σ is the amplitude of the signal and ρ is the scale. The SHO kernels are best suited for modeling the stellar activity signal in the K2 light curve.

As can be seen from Fig. 4, the signal of planet c is very small, even in the binned TESS data; however, it is clearly detectable in K2, which helps to guide the GP. We incorporated the PyTransit algorithm (Parviainen 2015) with the quadratic limb-darkening transit model from Mandel & Agol (2002). The linear and quadratic limb-darkening coefficients were characterized by uniform priors, and the stellar radius by a normal distributed prior centered around 0.592 R⊙ with a width of 0.049, calculated from the weighted average of literature values (see Sect. 3.1). Additionally to the priors of the orbital periods and T0, which were defined in the same way as for the RVs in Sect. 4.2, we set uniform priors for the planetary radius and impact parameter, and, for the eccentric model, normal distributed priors for the values of 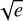• cos ω and 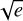• sin ω, where e is the eccentricity of the orbit and ω is the argument of periapsis.

Also here, the log likelihoods for the eccentric and circular case are almost the same, resulting in ln Zecc = 41457.24 ± 0.40 and ln Zcirc = 41457.01 ± 0.45 with Δ ln Z = 0.23. Table A.3 presents the planetary parameters for the circular model. The rotational period is modeled very well from the K2 light curve and gives a rotation period of 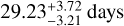, consistent with the value we determined from FWHM.

4.4 Combined fit

Finally, we combined the spectroscopic and photometric datasets and ran a combined fit using S+LEAF and Dynesty. Again, we investigated the circular and eccentric case. As described above, although we combined all RV data into a single dataset, the offsets, trends, and jitter terms were allowed to be different for each instrument, to account for uncorrelated trends and noise. The same applies to FWHM and photometry. All priors and best fit parameters for eccentric and circular cases are collected in Table A.2. The priors for the offsets and trends were normal distributed, whereas for the jitters we used uniform priors. We used three GPs for RV+FWHM, K2, and TESS. All GP amplitudes used uniform priors, where K2 and TESS have one amplitude each, and RV and FWHM have four amplitudes each at Prot, Prot/2, and their corresponding derivatives, according to

(2)

The priors for Prot and the timescale of evolution were normal distributed, centered around 30 and 30 × 2, respectively (see Giles et al. 2017). We sampled the planet mass and radius explicitly, and transformed them into RV amplitude and transit depth within the likelihood function. Both, the Keplerian model for RV and the transit model for photometry shared the same planetary priors. We accounted for the longer exposure time of K2 by using a higher supersampling rate in the K2 time series (see Parviainen 2015). The resulting log likelihoods for the circular and eccentric fit are very similar, with ln Zecc = 40420.0682 ± 0.3856 and ln Zcirc = 40420.0689 ± 0.4039. Although neither the circular nor the eccentric case is favored by the model, and the RV rms is slightly larger for ESPRESSO, HARPS, and HARPS-N for circular orbits (rmsESP = 0.30 ms−1, rmsH–S = 0.83 ms−1, rmsH–N = 1.34 ms−1) compared to eccentric orbits (rmsESP = 0.27 ms−1, rmsH–S = 0.82 ms−1, rmsH–N = 1.31 ms−1), we consider the circular model in the following. It is expected that, due to the small distances between the star and the planets, the orbits have circularized over the lifetime of the system (Van Eylen & Albrecht 2015). Furthermore, the uncertainties of the majority of planetary parameters improve when considering a circular orbit (see Table A.2). 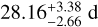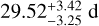For Prot, we derived consistent periods from the radial velocity and K2 data, that is, and , respectively. As a final value, we adopted 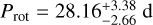(see Table 1).

thumbnail Fig. 7

Best-fit model from combined fit, showing K2 (top) and TESS data (middle). The three planets are illustrated with different colors. The bottom panel presents phase folds of K2 and TESS data with the transit model.

5 Results and discussion

In this section we present our results from the combined GP fit. Figure 7 shows the photometric data with the best model from the combined fit and Fig. 8 shows the same model with the spectroscopic data. The derived parameters for each planet are presented in Table 3 and discussed in more detail in the following.

5.1 Comparison with literature

We compared our results from the combined eccentric fit to previous results in the literature, focusing on radius, mass, period, and T0, because these parameters are most critical for accurate transit spectroscopy and atmospheric characterization. Figure 9 presents the comparison for planetary radius and shows that all measurements are consistent within their uncertainties. We derived 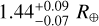for planet b, 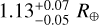for planet c, and 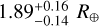for planet d. Niraula et al. (2017) determined tentatively larger radii, which is most likely attributed to the larger stellar radius they assumed (0.651 R⊙). Although our uncertainties in radius for all three planets are less than 10%, Rice et al. (2019) and Kosiarek et al. (2021) derived significantly smaller uncertainties, as is shown in the right column of Fig. 9. Rice et al. (2019) inferred one magnitude smaller uncertainties for the stellar radius 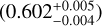, because they used the isochrones Python package (Morton 2015) with Gaia parallaxes as priors, which in turn influences the uncertainty in planetary radius. We let the model find the stellar mass and radius with priors based on the weighted average of all available literature values, which explains the higher, but more realistic uncertainties on the stellar parameters. Tayar et al. (2022) demonstrate that systematic uncertainties can dominate the error of stellar parameters, and errors of ≈4% in stellar radius and ≈5% in stellar mass are a realistic assumption. Kosiarek et al. (2021) analyzed the RV data from HIRES, FIES, PFS, HARPS, and HARPS-N using radvel (Fulton et al. 2018). They determined hyperparameters for stellar activity from the K2 light curve with a quasi-periodic GP kernel, and then used these posteriors as priors to model stellar activity in RV data and derived planetary parameters. The errors were determined from an MCMC analysis. They derived stellar effective temperature and metallicity from HIRES spectra using the SpecMatch-Emp tool (Yee et al. 2017). Together with multi-band stellar photometry (Gaia G and Two Micron All-Sky Survey JHK) and the Gaia DR2 parallax, they input these parameters into the isoclassify tool using the grid-mode option (Huber et al. 2017) to derive stellar mass and radius. Then, they calculated the planetary radii from the radius ratios given in Rodriguez et al. (2018). Therefore, their smaller uncertainties in planetary radii can be attributed to their smaller uncertainties in stellar radius.

To further explore our higher uncertainties in radius, we compared our results from different GP fits involving different datasets, as presented in Fig. A.2. We show results derived from all datasets (i.e., ESPRESSO, HARPS, HARPS-N, HIRES, K2, TESS), from the RV datasets and K2, from K2 and TESS, and from K2 and TESS separately. In general, the values agree very well within their uncertainties, except for planet d, which has some larger spread. The uncertainties (right panel) are mostly comparable as well, however, we find slightly larger uncertainties when using K2 or TESS data separately. Including RVs helps to better constrain parameters such as, for example, orbital period, which in turn better constrains other parameters such as the radius. For planets c and d the uncertainties are smallest when using all datasets, for planet b the smallest uncertainties are found when using K2+RV followed by all datasets. However, these are still slightly higher than those derived by Kosiarek et al. (2021), who provide an uncertainty of 0.058 R⊕ for planet b, whereas we derived 0.062 R⊕ using K2+RV.

For planetary masses we determine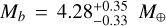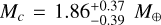d , , and 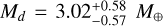. Figure 10 shows the comparison with the literature. The mass of planet b is generally well defined, however, Teske et al. (2018) measured almost twice the mass than other literature studies. Their uncertainties are very large, for planet c and d the values are only upper limits. This is probably due the low number of RV observations available at that time (36 measurements from PFS). For all three planets, we derived the smallest uncertainties compared to literature, which range at 8, 20, and 19% of the derived planetary mass, respectively. Consequently, we also determined the smallest uncertainties in RV amplitude, which are Kb = 3.53 ± 0.22 m s−1, Kc = 1.06 ± 0.21 m s−1, and Kd = 1.44 ± 0.27 m s−1. This is slightly smaller than the uncertainties from Kosiarek et al. (2021), who determined 0.30 m s−1 for planets b and d, and 0.29 m s−1 for planet c.

Looking at the comparison of orbital periods in Fig. 11, we derived a period of 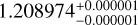days for planet b, 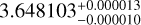days for planet c, and 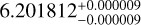days for planet d. It might seem that the periods of planet b do not agree very well in literature, with Niraula et al. (2017) measuring a much smaller period than Rice et al. (2019). However, the difference between these two values is 2.5e-5 d, which are only 2.15 s. For all three planets, we derived the smallest uncertainties, which are less than 0.1 s for planet b and less than 1 second for planets c and d. Therefore, the period of planet b is determined with high accuracy and precision. Our period for planet d is consistent with Kosiarek et al. (2021), but significantly different from the rest of the literature by about 35 s. However, our work and Kosiarek et al. (2021) are the most recent works and include most recent data, including high-precision RV data from ESPRESSO, therefore we believe that our value is more accurate than previous works.

Figure 12 shows the literature comparison for T0. We measure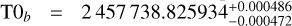d d, 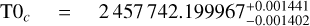d, and ' 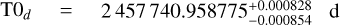. In general, the values agree with each other within their uncertainties. For planet c, T0 from Niraula et al. (2017) and Prieto-Arranz et al. (2018) are significantly different from our result and other literature values, amounting to 2457738.5519 ± 0.0014 d and 2457738.5496 ± 0.0015 d, respectively. Both studies find the first transit of planet c at the very beginning of the K2 light curve and right before the first transit of planet b. This transit is visible in our light curve (see top panel of Fig. 7), but because we used narrow priors based on results from Rodriguez et al. (2018) it was not found. The first transit of planet c is also visible in Fig. 1 of Rodriguez et al. (2018), it is not clear why it was not found. To be able to compare T0 for all three planets, we adjusted T0 from Niraula et al. (2017) and Prieto-Arranz et al. (2018) by adding one orbital period of planet c. For all three planets our uncertainties are larger than other literature uncertainties, except Prieto-Arranz et al. (2018) for planet c, which is even slightly larger. Compared to the smallest uncertainties (Kosiarek et al. 2021 and Rice et al. 2019 for planet b, Rodriguez et al. 2018 for planets c and d), our uncertainties are larger by 19 s, 66 s, and 35 s for each planet, respectively. As for the radius, we compared results from different GP runs (see Fig. A.3) and found that the largest uncertainties arise when using only RV, whereas uncertainties decrease when including K2 and TESS. Therefore, we derive the smallest uncertainties when using the whole dataset.

Overall, our parameters agree very well with those of Kosiarek et al. (2021), also the uncertainties are comparable in most cases. We derive the smallest uncertainties for planetary mass, RV amplitude and orbital period.

thumbnail Fig. 8

Best-fit circular model from combined fit. (a) FWHM with activity model. (b) RV with combined activity and eccentric model. (c) Zoom-in of panel b. (d) RV residuals after subtraction of activity and planet model. (e)–(g) Phase folds of RVs for all three planets.
Table 3

Derived planetary parameters for GJ 9827 for the circular case.

thumbnail Fig. 9

Literature comparison for planetary radius (left column) and error (right column) for each planet.
thumbnail Fig. 10

Literature comparison for planetary mass (left column) and error (right column) for each planet.
thumbnail Fig. 11

Literature comparison for planetary period (left column) and error (right column) for each planet.

5.2 Orbital configuration

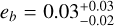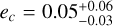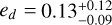As mentioned in Sect. 4.4, we performed GP fits with circular and eccentric orbits. In the eccentric case, the eccentricities of all three planets are essentially consistent with zero within their uncertainties, with , , and . Kosiarek et al. (2021) evaluated if the system is stable over 109 orbits for different values of eccentricity and the argument of periapse, co, using spock (Tamayo et al. 2020). Averaging over the ω grid shows that the orbital configuration is stable if eb ≤ 0.4, ec ≤ 0.2, ed ≤ 0.1, which is consistent with the eccentricity values we derived for the system in the eccentric case. Prieto-Arranz et al. (2018) also performed two types of stability analyses. First, they integrated their MCMC samples using the SWIFT N-body package (Duncan et al. 1998) and the MVS integrator (Wisdom & Holman 1991) with a maximum integration time of 1 Myr. Additionally, they did a stability test using mercury6 (Chambers 1999) over 100000 yr. In both cases, they assumed tidal circularization and find that the semi-major axes are constant within 0.1% and the eccentricity variation is less than 10−3.

All planets have a similar inclination (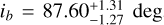, , 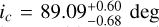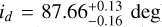), however, they cannot be considered coplanar, because of the unknown angle Ω, the longitude of the ascending node. Concerning the impact factor b, it is notable that planet d (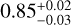) has a significantly higher value than planet b (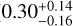) and planet c (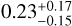). Herewith, we confirm the values published by Niraula et al. (2017, 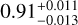), Rodriguez et al. (2018, 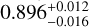), Prieto-Arranz et al. (2018, 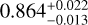), and Rice et al. (2019, 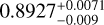). Niraula et al. (2017) first noted the higher impact parameter of planet d and argued that this might suggest additional non-transiting planets in the system. We investigated this possibility in the following section.

No further discussion on the impact parameter is given by the other authors. Prieto-Arranz et al. (2018) discuss how the planets could have reached a near 5:3:1 resonance, which could be either due to inward migration and lining up in a resonant chain (Izidoro et al. 2017), or due to in situ formation as suggested by Chiang & Laughlin (2013), which reproduces many of the observed properties of close-in super-Earths. In the latter case, the planets should have retained their primordial hydrogen envelopes and their atmospheres should not show any water features due to the proximity to the star.

thumbnail Fig. 12

Literature comparison for time of periastron (left column) and error (right column) for each planet. Note that for planet c we added one orbital period to T0 from Niraula et al. (2017) and Prieto-Arranz et al. (2018) to make their values comparable.

5.3 Potential additional planet

We investigated the possibility of an undiscovered additional planetary signal. As suggested by Niraula et al. (2017), this planet is likely to be non-transiting. Figure 13 shows the residuals of the RV and K2 time series after subtracting stellar activity and the three planetary signals. The GLS periodograms of both datasets show no significant signals. However, we performed a GP analysis on the RV data as described in Sect. 4.2, using our results of the three planet model as priors for the three known planets and wide uniform priors for the potential fourth planet. The posterior distributions of the parameters of the fourth planet do not reveal a significant signal, indicating that no other planetary signal can be found in the data. The corresponding corner plot is shown in Fig. A.4.

5.4 Future multi transits

Multiple transits are an interesting phenomenon. Besides the fact that these events are quite rare, they are predicted and observed in several exoplanet systems (Luger et al. 2017; Müller et al. 2022). The great advantage of such events is given by the fact that, if they exist, the observer can study, for instance, transit timing variations (TTVs), and therefore learn something about the orbital dynamics of such systems and find potential undetected planets in the system. Niraula et al. (2017) do not find TTVs greater than three minutes for any of the three planets in the system. Recently, Roy et al. (2023) analyzed data from Wide Field Camera 3 on the Hubble Space Telescope (HST/WFC3) and find TTVs in the order of 5–10 minutes for planet d, which is not surprising for a near-resonant system.

Additionally, these multi transits offer the possibility of the occurrence of extremely rare events called planet-planet occultations (PPOs), where one planet passes in front of another one during its transit passage leaving a well defined imprint to the light curve (e.g., Hirano et al. 2012). If present, such an event allows to pin down the orbital parameters of the planets to a very high precision. Nevertheless, both cases, ordinary multi transits or those with PPOs, are of special interest for planet observers. For the year 2024, we predict double transit events for planets in the GJ 9827 system. We carried out a simulation of transit light curves using the occultquad routine from Mandel & Agol (2002) together with the planetary and orbital parameters of all planets determined in Sect. 4.4, not taking into account uncertainties in P and T0. We found seven double transits of the planets b and c, and six double transits for planets b and d. However, we did not find any double transits of planets c and d until end of March 2051. In Table 4, we list double transit events for planets b+c and b+d, including transit start and end time of the individual planets, duration of the whole event, and duration of the double transit. Due to the smaller size of planet c, the double transits of planet b and c are shallower compared to those of planet b and d. In Fig. 14, we show as an example of simulated light curves of the first and fifth multi transit of planets b and d occurring at BJD 2460 333.25 d and 2460 618.57 d, respectively.

For the sake of completeness, we also tried to find a triple transit where all three planets transit in front of the stellar disk at the same time and which is of course a very rare event. We found that the first triple transit occurs in January 2057. Since the multi transits of planets c+d and b+c+d are far in the future and given the uncertainties of the orbital periods of all planets together with possible periastron drifts, these events might occur earlier or later, or maybe not at all.

thumbnail Fig. 13

Left: residuals of the RV and K2 time series after subtracting stellar activity and the three planetary signals. Right: correpsonding GLS periodograms do not show any remaining significant signals.
Table 4

Future multi transits of GJ 9827 for the year 2024.

thumbnail Fig. 14

Simulated light curves of multi transits of GJ 9827 b and GJ 9827 d starting at BJD 2460333.25 d (top) and 2460618.57 d (bottom). The latter event is the deepest in this series.

5.5 Interior bulk composition

The composition of the planets is discussed extensively in Teske et al. (2018), Rice et al. (2019), Prieto-Arranz et al. (2018), and Kosiarek et al. (2021). Teske et al. (2018) note that planet b is one of the densest and most massive terrestrial planets found so far, which is due to the high mass of 8 M⊕ they derive. Considering our mass measurement of 4.28 M⊕, planet b is not so anomalously dense anymore. Because of its small mass and large errors, planet c is the least constrained in Teske et al. (2018), however, for planet d they find a water mass fraction of 50–100%, maybe indicating an H2/He-dominated envelope.

Rice et al. (2019) also cannot constrain the mass of planet c very well, therefore its composition remains unclear. They speculate that it could be rocky with a substantial water mass fraction. From their mass and radius measurements, they conclude that planet b is Earth-like, and planet d must have a substantial atmosphere and water mass fraction. They explain that planet b and c receive 316 and 73 times more flux than Earth, respectively, therefore these planets could have formed with a similar composition as planet d and then lost their atmospheres due to photoevaporation.

Prieto-Arranz et al. (2018) present better constraints for planet c and conclude that both planet b and c have rocky nuclei with traces of lighter elements, whereas planet d has a large gaseous H/He-rich envelope with a nucleus similar to the other two planets. They also suggest that the inner planets might have lost their envelopes because of photoevaporation.

Kosiarek et al. (2021) used the three-component H2O/MgSiO3/Fe model (Zeng & Sasselov 2013; Zeng et al. 2016) to draw ternary diagrams. They show that planet b and c have a H2O fraction of ≤40% and a wide range of possible MgSiO3 and Fe compositions. Planet d is consistent with a higher H2O fraction of 50–100% and smaller fractions of MgSiO3 (≤50%) and Fe (≤30%). In Table 5, we summarize all planetary densities from literature, including results from this work, which show that planets b and c have a larger density than Earth (ρ⊕ = 5.51 g cm−3 ) and planet d has a density larger than Neptune (ρNeptune = 1.64 g cm−3).

We investigated the inner structure of all three planets and first produced mass-radius and mass-density diagrams, presented in Figs. 15 and 16 with the position of the planets around GJ 9827 clearly marked. We overplotted composition curves taken from Zeng et al. (2019). Earth-like composition corresponds to 32.5% Fe and 67.5% MgSiO3, 100% rock is equal to 100% MgSiO3, and 50% H2O assumes a composition of 50% water and 50% Earth-like. We included other confirmed planets around K dwarfs from the Transiting Extrasolar Planets Catalogue (TEPCat; Southworth 2011), selecting only those planets with host star effective temperatures between 4000 and 5200 K, planetary radius precisions better than 8%, and mass precisions better than 25%. From these plots, we can see that planets b and c have an almost Earth-like composition, while the outer planet d must have a substantial water fraction.

Comparing these plots to Fig. S19 (A-B) of Luque & Pallé (2022), who used TEPCat with the same constraints, we can also see distinct groups of planets, the rocky planets and the waterand gas-rich planets. The density gap proposed by Luque & Pallé (2022) does not appear so clearly in our plots, which could be due to an update of the planet database. However, GJ 9827 b and c can be assigned to the rocky family of planets with Earthlike composition, while GJ 9827 d could be consistent with both a large water mass fraction (water world) and a H/He-rich subNeptune scenarios.

Then, we calculated the equilibrium temperature Teq for each planet following Eq. (3), where a is the semi-major axis of the planet and Ab the albedo. For each planet, we adopted an albedo of 0.3 from Niraula et al. (2017). For error propagation (Eq. (4)), we assumed symmetrical errors for each parameter by calculating the average error:

(3) (4)

We modeled the interior structure of the three planets using ExoMDN (Baumeister & Tosi 2023). ExoMDN is a machine-learning-based exoplanet interior inference model trained on more than 5.6 million synthetic planet interior structures consisting of an iron core, a silicate mantle, a water and high-pressure ice layer, and a H/He atmosphere. It uses Mixture Density Networks (Bishop 1994), which approximate the parameters with a linear combination of Gaussian kernels to predict their probability distributions. ExoMDN provides a full inference of the interior structure of exoplanets below 25 M⊕, given mass, radius, and equilibrium temperature of the planet, in under a second.

Baumeister & Tosi (2023) show that mass, radius, and equilibrium temperature alone are not always sufficient to fully constrain the interior of a planet. Therefore, they provide a second trained model including the second degree fluid Love number k2 (Love 1909). The Love number depends on the density distribution of the planet's interior and describes the shape of a rotating planet in hydrostatic equilibrium (Padovan et al. 2018; Kellermann et al. 2018; Baumeister et al. 2020). For example, k2 = 0 corresponds to a body with all mass concentrated in the center and k2 = 1.5 characterizes a fully homogeneous body.

Although it is possible to measure k2 for exoplanets, it is rather difficult as it requires the measurement of second-order effects in the shape of the transit light curve (Akinsanmi et al. 2019; Hellard et al. 2019; Barros et al. 2022) or the apsidal precession of the orbit (Csizmadia et al. 2019). Therefore, we assumed the Love number of Earth (k2 = 0.933; Lambeck 1980) for planets b and c and the Love number of Neptune (k2 = 0.392; Baumeister & Tosi 2023) for planet d. This imposes an internal structure model similar to Earth and Neptune, respectively, which might not necessarily be true, but is a legitimate assumption, based on the planets’ positions in the mass-radius diagram of Fig. 15.

Together with the planetary masses, radii, and equilibrium temperatures shown in Table 3, we ran ExoMDN. To account for uncertainties in the planetary parameters we drew normal distributions with σ equal to the uncertainties of each parameter. For the Love numbers, we assumed an uncertainty of 10%. Baumeister & Tosi (2023) demonstrate that with a k2 uncertainty of 10%, the core and mantle thickness of Earth can be constrained to about 13% of their actual value. We randomly picked planetary parameters from these distributions and ran 500 predictions with 1000 samples each, amounting to a total of 500 000 predictions. We present the results for the mass fraction in Figs. 17 and 18 and for the radius fraction in Figs. 19 and 20, as ternary diagrams and historgams, respectively.

It can be seen that the radius fraction for core and mantle are very similar for planets b and c, 60% of the radius is attributed to the core and 40% to the mantle for planet b, for planet c it is 65% for the core and 35% for the mantle. Planet b has a core mass fraction (CMF) of 40% and a mantle mass fraction (MMF) of 60%, while planet c has a CMF of 45% and an MMF of 55%. This distribution is similar to Earth, which has a CMF of 32.5% and an MMF of 67%. For planet c, the histograms of the CMF and MMF are two-fold, indicating that a significant amount of models points toward a planet with a higher CMF and smaller MMF. Both planets have no water and no atmosphere. This is consistent with the non-detection of Lya, Ha, and He I transitions by Carleo et al. (2021) using HST and CARMENES transit observations. With an estimated mass-loss rate of 1.9 M⊕ Gyr−1 for planet b and 0.5 M⊕ Gyr−1 for planet c (Carleo et al. 2021), both planets are very likely to have lost their primordial atmospheres.

As expected, planet d is different and consists of a significant amount of water. It has a CMF of 20%, a MMF of 5%, and a water mass fraction (WMF) of 75%. The histograms of the MMF and WMF show a tail toward higher MMF and lower WMF, which is also visible in the ternary diagram. The position of the planet in the mass-radius and mass-density diagrams, on the other hand, supports a large water composition. The radius histograms for planet d are better constrained (Fig. 20, bottom panel), showing a core radius fraction of 30%, a mantle radius fraction of 20%, a water radius fraction of 45%, and an atmosphere radius fraction of 5%. From this, we conclude that planet d has a rocky core surrounded by a significant hydrogen envelope, placing it in the mini-Neptune regime. This is in line with transmission spectroscopy from Roy et al. (2023) using HST/WFC3. They report a hint of an absorption feature at 1.4 µm in its transit spectrum due to water vapor in the atmosphere of planet d. This points toward a water-dominated envelope, although a cloudy H2/He atmosphere with a small amount of water vapor can also explain the observed features (Roy et al. 2023). However, as for planet b, no Hα and He features are found in the atmosphere of GJ 9827 d (Carleo et al. 2021; Krishnamurthy et al. 2023). Due to the planet’s proximity to the host star, its low mass, and an estimated mass-loss rate of >0.2 M⊕ Gyr−1 (Krishnamurthy et al. (2023); 0.3 M⊕ Gyr−1: Carleo et al. 2021) it is unlikely that the planet could retain an H-dominated atmosphere.

Table 5

Planetary densities for GJ 9827 from the literature.

thumbnail Fig. 15

Mass-radius diagram showing the positions of the three planets around GJ 9827 and planets detected around K dwarfs from literature. The different lines present different planetary compositions from 100% iron to 100% H2O.
thumbnail Fig. 16

Mass-density diagram showing the positions of the three planets around GJ 9827 and planets detected around K dwarfs from literature. The different lines present different planetary compositions from 100% iron to 100% H2O.
thumbnail Fig. 17

Ternary diagrams of the mass fractions of GJ 9827 b, c, and d derived with ExoMDN.
thumbnail Fig. 18

Histograms of mass fractions for core, mantle, water, and atmosphere of GJ 9827 b (top), c (middle), and d (bottom) derived with ExoMDN.
thumbnail Fig. 19

Ternary diagrams of the radius fractions of GJ 9827 b, c, and d derived with ExoMDN.
thumbnail Fig. 20

Histograms of radius fractions for core, mantle, water, and atmosphere of GJ 9827 b (top), c (middle), and d (bottom) derived with ExoMDN.

6 Summary and conclusions

GJ 9827 hosts three transiting planets, which have first been detected using K2 data. The system was observed and characterized with different spectrographs in the recent years. Several studies derive planetary masses and radii, however, the results span a wide range of values with large uncertainties. In this study, we used data from ESPRESSO, HARPS, HARPS-N, HIRES, K2, and TESS to improve the accuracy and precision of planetary parameters. To do this, we employed a combined GP analysis using high-precision spectroscopy and photometry.

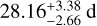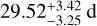With this, we could model the stellar activity signal from the radial velocity and K2 data, and derive a consistent rotation period of and , respectively. We used two SHO kernels at Prot and Prot/2 for the RV and K2 datasets and a Matérn 3/2 kernel for TESS from the S+LEAF code, together with nested sampling using Dynesty. We investigated circular and eccentric orbits and find that both models are indistinguishable with almost the same likelihood. Therefore, we favor the simpler circular model. Due to the proximity of the planets to their host star, circularization of the orbits can be expected over the lifetime of the system. Planet d has a higher impact parameter of 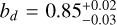compared to planet b with 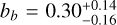and planet c 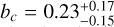, which is also found by previous studies. On the other hand, all planets have very similar orbital inclination between 87 and 89 deg, which could give interesting insights in the evolution of the system.

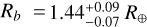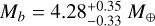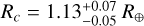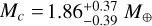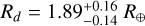Regarding planetary mass and radius, we derive and , and , and and 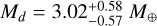. We compared our results to those of Niraula et al. (2017), Rodriguez et al. (2018), Teske et al. (2018), Rice et al. (2019), Prieto-Arranz et al. (2018), and Kosiarek et al. (2021). Our values are mostly consistent with the results of Kosiarek et al. (2021) and we improve uncertainties in RV amplitude, mass, and period. We drew mass-radius and mass-density diagrams and modeled the inner structure of all three planets with ExoMDN. We confirm Article number, page 20 of 28 previous composition studies and find that GJ 9827 b and c have an Earth-like composition, whereas the outer planet d consists of a rocky core with an hydrogen envelope. It can also be seen that the planets lie on both sides of the radius gap.

The planetary system around GJ 9827 is a good candidate for transit spectroscopy. Our improvement on the precision of period and mass will help in an accurate atmospheric characterization. Additionally, we predict times of future multi transit events, which allow further analysis of orbital dynamics and, in case of planet-planet-occultations, the determination of orbital parameters to very high precision.

Acknowledgements

V.M.P., A.S.M., J.I.G.H., and R.R. acknowledge financial support from the Spanish Ministry of Science and Innovation (MICINN) project PID2020-117493GB-I00 and from the Government of the Canary Islands project ProID2020010129. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. R.A. is a Trottier Postdoctoral Fellow and acknowledges support from the Trottier Family Foundation. This work was funded by the Institut Trottier de Recherche sur les Exoplanètes (iREx) and supported in part through a grant from the Fonds de Recherche du Québec – Nature et Technologies (FRQNT). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement SCORE No 851555). F.P. and C.L. would like to acknowledge the Swiss National Science Foundation (SNSF) for supporting research with ESPRESSO through the SNSF grants nr. 140649, 152721, 166227, 184618 and 215190. The ESPRESSO Instrument Project was partially funded through SNSF's FLARE Programme for large infrastructures. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds in the framework of the project 2022.04048.PTDC (Phi in the Sky) and by FEDER through COM-PETE2020 - Programa Operacional Competitividade e Internacionalização by these grants: UIDB/04434/2020; UIDP/04434/2020. A.M.S acknowledges support from the FCT through the Fellowship 2020.05387.BD. C.J.A.P.M. also acknowledges FCT and POCH/FSE (EC) support through Investigador FCT Contract 2021.01214.CEECIND/CP1658/CT0001. A.C.-G. is funded by the Spanish Ministry of Science through MCIN/AEI/10.13039/501100011033 grant PID2019-107061GB-C61. We acknowledge financial support from the Agencia Estatal de Investigación (AEI/10.13039/501100011033) of the Ministerio de Ciencia e Innovación and the ERDF “A way of making Europe” through projects PID2019-109522GB-C51 and PID2019-109522GB-C54. The research leading to these results has received funding from the European Research Council through the grant agreement 101052347 (FIERCE). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The manuscript was written using Overleaf. Main analysis performed in Python3 (Van Rossum & Drake 2009) running on Ubuntu (Sobell 2015) systems. Extensive use of the DACE platform (https://dace.unige.ch/). Extensive usage of Numpy (van der Walt et al. 2011). Extensive usage of Scipy (Virtanen et al. 2020). All figures built with Matplotlib (Hunter 2007) and gnuplot (Williams et al. 2020). The bulk of the analysis was performed on a server hosting 2× Intel(R) Xeon(R) Gold 5218 (2 × 16 cores, 2 threads per core, 2.3–3.9 GHz).

Appendix A Additional tables and plots

Table A.1

Collection of planetary parameters from the literature.

Table A.2

Priors and measured parameters for GP models in the circular and eccentric case.

Table A.3

Derived planetary parameters for GJ 9827 for the circular case.

thumbnail Fig. A.1

Plotting RV vs FWHM for ESPRESSO, HARPS, and HARPS-N shows no correlation.
thumbnail Fig. A.2

Comparison of planetary radius from different GP runs using different combinations of datasets. RV refers to ESPRESSO, HARPS, HARPS-N, and HIRES, and All refers to RV, K2, and TESS combined.
thumbnail Fig. A.3

Comparison of time of periastron from different GP runs using different combinations of datasets. RV refers to ESPRESSO, HARPS, HARPS-N, and HIRES, and All refers to RV, K2, and TESS combined.
thumbnail Fig. A.4

Corner plot of the posterior distributions of Kepler amplitude (K), period (P), and T0/Phase for the three known planets and the potential fourth planet.

References

  1. Aigrain, S., Pont, F., & Zucker, S. 2012, MNRAS, 419, 3147 [NASA ADS] [CrossRef] [Google Scholar]
  2. Akinsanmi, B., Barros, S. C. C., Santos, N. C., et al. 2019, A&A, 621, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Albrecht, S. H., Marcussen, M. L., Winn, J. N., Dawson, R. I., & Knudstrup, E. 2021, ApJ, 916, L1 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2016, IEEE Transac. Pattern Anal. Mach. Intell., 38, 252 [Google Scholar]
  5. Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barragán, O., Gandolfi, D., & Antoniciello, G. 2017, Astrophysics Source Code Library [record ascl:1707.003] [Google Scholar]
  7. Barragán, O., Aigrain, S., Rajpaul, V. M., & Zicher, N. 2022, MNRAS, 509, 866 [Google Scholar]
  8. Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022, A&A, 657, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Baumeister, P., & Tosi, N. 2023, A&A, 676, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Baumeister, P., Padovan, S., Tosi, N., et al. 2020, ApJ, 889, 42 [Google Scholar]
  11. Bishop, C. 1994, Mixture density networks, Workingpaper, Aston University, UK [Google Scholar]
  12. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  13. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  14. Brewer, J. M., Fischer, D. A., Valenti, J. A., & Piskunov, N. 2016, ApJS, 225, 32 [Google Scholar]
  15. Carleo, I., Youngblood, A., Redfield, S., et al. 2021, AJ, 161, 136 [NASA ADS] [CrossRef] [Google Scholar]
  16. Castro-González, A., Demangeon, O. D. S., Lillo-Box, J., et al. 2023, A&A, 675, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Chambers, J. E. 1999, MNRAS, 304, 793 [Google Scholar]
  18. Chen, J., & Kipping, D. 2017, ApJ, 834, 17 [Google Scholar]
  19. Chiang, E., & Laughlin, G. 2013, MNRAS, 431, 3444 [Google Scholar]
  20. Coffinet, A., Lovis, C., Dumusque, X., & Pepe, F. 2019, A&A, 629, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
  22. Crane, J. D., Shectman, S. A., & Butler, R. P. 2006, SPIE Conf. Ser., 6269, 626931 [NASA ADS] [Google Scholar]
  23. Crane, J. D., Shectman, S. A., Butler, R. P., Thompson, I. B., & Burley, G. S. 2008, SPIE Conf. Ser., 7014, 701479 [NASA ADS] [Google Scholar]
  24. Crane, J. D., Shectman, S. A., Butler, R. P., et al. 2010, SPIE Conf. Ser., 7735, 773553 [NASA ADS] [Google Scholar]
  25. Csizmadia, S., Hellard, H., & Smith, A. M. S. 2019, A&A, 623, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  27. Damasso, M., Sozzetti, A., Lovis, C., et al. 2020, A&A, 642, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Damasso, M., Rodrigues, J., Castro-González, A., et al. 2023, A&A, 679, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Delisle, J. B., Hara, N., & Ségransan, D. 2020, A&A, 638, A95 [EDP Sciences] [Google Scholar]
  31. Delisle, J. B., Unger, N., Hara, N. C., & Ségransan, D. 2022, A&A, 659, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Demangeon, O. D. S., Zapatero Osorio, M. R., Alibert, Y., et al. 2021, A&A, 653, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Dressing, C. D., Hardegree-Ullman, K., Schlieder, J. E., et al. 2019, AJ, 158, 87 [NASA ADS] [CrossRef] [Google Scholar]
  34. Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [Google Scholar]
  35. Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [Google Scholar]
  36. Eastman, J. 2017, Astrophysics Source Code Library [record ascl:1710.003] [Google Scholar]
  37. Eastman, J. D., Rodriguez, J. E., Agol, E., et al. 2019, arXiv e-prints [arXiv: 1907.09480] [Google Scholar]
  38. Engle, S. G., & Guinan, E. F. 2023, ApJ, 954, L50 [NASA ADS] [CrossRef] [Google Scholar]
  39. Faria, J. P., Suárez Mascareño, A., Figueira, P., et al. 2022, A&A, 658, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  41. Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, Astrophysics Source Code Library [record ascl:1709.008] [Google Scholar]
  42. Frandsen, S., & Lindberg, B. 1999, in Astrophysics with the NOT, eds. H. Karttunen, & V. Piirola (Berlin: Springer), 71 [Google Scholar]
  43. Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
  44. Fulton, B. J., Petigura, E. A., Blunt, S., & Sinukoff, E. 2018, PASP, 130, 044504 [Google Scholar]
  45. Gaia Collaboration 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
  46. Gaia Collaboration 2022, VizieR Online Data Catalog: I/355 [Google Scholar]
  47. Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [Google Scholar]
  48. Genton, M. G. 2002, J. Mach. Learn. Res., 2, 299 [Google Scholar]
  49. Giles, H. A. C., Collier Cameron, A., & Haywood, R. D. 2017, MNRAS, 472, 1618 [Google Scholar]
  50. Handley, W. J., Hobson, M. P., & Lasenby, A. N. 2015a, MNRAS, 450, L61 [NASA ADS] [CrossRef] [Google Scholar]
  51. Handley, W. J., Hobson, M. P., & Lasenby, A. N. 2015b, MNRAS, 453, 4384 [Google Scholar]
  52. Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
  53. Hellard, H., Csizmadia, S., Padovan, S., et al. 2019, ApJ, 878, 119 [NASA ADS] [CrossRef] [Google Scholar]
  54. Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalog: II/336 [Google Scholar]
  55. Hirano, T., Narita, N., Sato, B., et al. 2012, ApJ, 759, L36 [NASA ADS] [CrossRef] [Google Scholar]
  56. Houdebine, E. R., Mullan, D. J., Paletou, F., & Gebran, M. 2017, VizieR Online Data Catalog: J/ApJ/822/97 [Google Scholar]
  57. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
  58. Huber, D., Zinn, J., Bojsen-Hansen, M., et al. 2017, ApJ, 844, 102 [Google Scholar]
  59. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  60. Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [Google Scholar]
  61. Jenkins, J. M. 2002, ApJ, 575, 493 [Google Scholar]
  62. Jenkins, J. M., Chandrasekaran, H., McCauliff, S. D., et al. 2010, SPIE Conf. Ser., 7740, 77400D [Google Scholar]
  63. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  64. Kellermann, C., Becker, A., & Redmer, R. 2018, A&A, 615, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Kosiarek, M. R., Berardo, D. A., Crossfield, I. J. M., et al. 2021, AJ, 161, 47 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [Google Scholar]
  68. Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
  69. Kreidberg, L. 2018, in Handbook of Exoplanets (Berlin: Springer International Publishing), 2083 [CrossRef] [Google Scholar]
  70. Krishnamurthy, V., Hirano, T., Gaidos, E., et al. 2023, MNRAS, 521, 1210 [NASA ADS] [CrossRef] [Google Scholar]
  71. Lambeck, K. 1980, The Earth’s Variable Rotation: Geophysical Causes and Consequences (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
  72. Lavie, B., Bouchy, F., Lovis, C., et al. 2023, A&A, 673, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
  74. Love, A. E. H. 1909, MNRAS, 69, 476 [NASA ADS] [Google Scholar]
  75. Luger, R., Agol, E., Kruse, E., et al. 2016, AJ, 152, 100 [Google Scholar]
  76. Luger, R., Lustig-Yaeger, J., & Agol, E. 2017, ApJ, 851, 94 [NASA ADS] [CrossRef] [Google Scholar]
  77. Luger, R., Kruse, E., Foreman-Mackey, D., Agol, E., & Saunders, N. 2018, AJ, 156, 99 [Google Scholar]
  78. Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  79. Malavolta, L., Nascimbeni, V., Piotto, G., et al. 2016, A&A, 588, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
  81. Marconi, A., Abreu, M., Adibekyan, V., et al. 2022, SPIE, 12184, 1218424 [NASA ADS] [Google Scholar]
  82. Marfil, E., Tabernero, H. M., Montes, D., et al. 2021, A&A, 656, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  84. Mayor, M., Marmier, M., Lovis, C., et al. 2011, arXiv e-prints [arXiv: 1109.2497] [Google Scholar]
  85. Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [Google Scholar]
  86. Mortier, A., Zapatero Osorio, M. R., Malavolta, L., et al. 2020, MNRAS, 499, 5004 [Google Scholar]
  87. Morton, T. D. 2015, Astrophysics Source Code Library [record ascl:1503.010] [Google Scholar]
  88. Müller, H. M., Ioannidis, P., & Schmitt, J. H. M. M. 2022, A&A, 657, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Murgas, F., Castro-González, A., Pallé, E., et al. 2023, A&A, 677, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Niraula, P., Redfield, S., Dai, F., et al. 2017, AJ, 154, 266 [Google Scholar]
  91. Padovan, S., Spohn, T., Baumeister, P., et al. 2018, A&A, 620, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Parviainen, H. 2015, MNRAS, 450, 3233 [Google Scholar]
  93. Pepe, F., Cristiani, S., Rebolo, R., et al. 2013, The Messenger, 153, 6 [NASA ADS] [Google Scholar]
  94. Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Prieto-Arranz, J., Palle, E., Gandolfi, D., et al. 2018, A&A, 618, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Rajpaul, V., Aigrain, S., Osborne, M. A., Reece, S., & Roberts, S. 2015, MNRAS, 452, 2269 [Google Scholar]
  97. Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning (Massachusetts: MIT Press) [Google Scholar]
  98. Rice, K., Malavolta, L., Mayo, A., et al. 2019, MNRAS, 484, 3731 [NASA ADS] [CrossRef] [Google Scholar]
  99. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
  100. Roberts, S., Osborne, M., Ebden, M., et al. 2012, Philos. Trans. R. Soc. London Ser. A, 371, 20110550 [NASA ADS] [Google Scholar]
  101. Rodriguez, J. E., Vanderburg, A., Eastman, J. D., et al. 2018, AJ, 155, 72 [NASA ADS] [CrossRef] [Google Scholar]
  102. Roy, P.-A., Benneke, B., Piaulet, C., et al. 2023, ApJ, 954, L52 [NASA ADS] [CrossRef] [Google Scholar]
  103. Silva, A. M., Faria, J. P., Santos, N. C., et al. 2022, A&A, 663, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Skilling, J. 2004, AIP Conf. Ser., 735, 395 [Google Scholar]
  105. Skilling, J. 2006, Bayesian Anal., 1, 833 [Google Scholar]
  106. Sobell, M. G. 2015, A Practical Guide to Ubuntu Linux (New Jersey: Pearson Education) [Google Scholar]
  107. Southworth, J. 2011, MNRAS, 417, 2166 [Google Scholar]
  108. Sozzetti, A., Damasso, M., Bonomo, A. S., et al. 2021, A&A, 648, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Speagle, J. S. 2020, MNRAS, 493, 3132 [Google Scholar]
  110. Suárez Mascareño, A., Rebolo, R., & González Hernández, J. I. 2016, A&A, 595, A12 [Google Scholar]
  111. Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2020, A&A, 639, A77 [Google Scholar]
  112. Suárez Mascareño, A., González-Álvarez, E., Zapatero Osorio, M. R., et al. 2023, A&A, 670, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Tabernero, H. M., Marfil, E., Montes, D., & González Hernández, J. I. 2022, A&A, 657, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Tamayo, D., Cranmer, M., Hadden, S., et al. 2020, Proc. Natl. Acad. Sci., 117, 18194 [CrossRef] [Google Scholar]
  115. Tayar, J., Claytor, Z. R., Huber, D., & van Saders, J. 2022, ApJ, 927, 31 [NASA ADS] [CrossRef] [Google Scholar]
  116. Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [Google Scholar]
  117. Teske, J. K., Wang, S., Wolfgang, A., et al. 2018, AJ, 155, 148 [NASA ADS] [CrossRef] [Google Scholar]
  118. Toledo-Padrón, B., Lovis, C., Suárez Mascareño, A., et al. 2020, A&A, 641, A92 [Google Scholar]
  119. Unger, N., Ségransan, D., Queloz, D., et al. 2021, A&A, 654, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  121. Van Eylen, V., & Albrecht, S. 2015, ApJ, 808, 126 [Google Scholar]
  122. Van Rossum, G., & Drake, F. L. 2009, Python 3 Reference Manual (Scotts Valley, CA: CreateSpace) [Google Scholar]
  123. Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [Google Scholar]
  124. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  125. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, SPIE Conf. Ser., 2198, 362 [NASA ADS] [Google Scholar]
  126. Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2010, SPIE Conf. Ser., 7735, 77354X [NASA ADS] [Google Scholar]
  127. Williams, T., Kelley, C., et al. 2020, Gnuplot 5.4: an interactive plotting program, http://gnuplot.sourceforge.net/ [Google Scholar]
  128. Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [Google Scholar]
  129. Yee, S. W., Petigura, E. A., & von Braun, K. 2017, ApJ, 836, 77 [Google Scholar]
  130. Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322A [Google Scholar]
  131. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
  132. Zeng, L., & Sasselov, D. 2013, PASP, 125, 227 [Google Scholar]
  133. Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [Google Scholar]
  134. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, Proc. Natl. Acad. Sci., 116, 9723 [Google Scholar]

All Tables

Table 1

Summary of stellar properties for GJ 9827.

In the text
Table 2

Stellar parameters derived with PARAM1.3 using different input parallaxes and magnitudes.

In the text
Table 3

Derived planetary parameters for GJ 9827 for the circular case.

In the text
Table 4

Future multi transits of GJ 9827 for the year 2024.

In the text
Table 5

Planetary densities for GJ 9827 from the literature.

In the text
Table A.1

Collection of planetary parameters from the literature.

In the text
Table A.2

Priors and measured parameters for GP models in the circular and eccentric case.

In the text
Table A.3

Derived planetary parameters for GJ 9827 for the circular case.

In the text

All Figures

thumbnail Fig. 1

Time-series observations of all RV measurements used in this work.
In the text
thumbnail Fig. 2

Comparison between S-BART- and CCF-extracted RVs for ESPRESSO DRS.
In the text
thumbnail Fig. 3

K2 light curve (top) and corresponding GLS periodogram (bottom). The purple area indicates the approximate rotation period of the star, with the gray line presenting the highest period peak found by GLS, which corresponds to the rotation period of the star.
In the text
thumbnail Fig. 4

TESS light curve SAP (top panel) and PDCSAP flux (middle panel) with original cadence (blue) and binned to 10 minutes (orange). The bottom panel shows phase folds according to planetary periods and mid-transit times derived by Rodriguez et al. (2018) for planet b (left), planet c (middle), and planet d (right). The red line presents a transit model based on parameters from Rodriguez et al. (2018) for illustrative purpose.
In the text
thumbnail Fig. 5

Left: ESPRESSO, HARPS, HARPS-N, and HIRES spectroscopic data used in this study. We present plots for RV, FWHM, CaII S-index, and Hα. Right: corresponding GLS periodograms. The orange dashed lines mark the periods of the three planets. The purple area indicates the approximate rotation period of the star. The gray line presents the highest period peak found by GLS for each panel.
In the text
thumbnail Fig. 6

FWHM from ESPRESSO, HARPS, and HARPS-N with best GP model. The bottom panel shows a zoom-in on ESPRESSO data.
In the text
thumbnail Fig. 7

Best-fit model from combined fit, showing K2 (top) and TESS data (middle). The three planets are illustrated with different colors. The bottom panel presents phase folds of K2 and TESS data with the transit model.
In the text
thumbnail Fig. 8

Best-fit circular model from combined fit. (a) FWHM with activity model. (b) RV with combined activity and eccentric model. (c) Zoom-in of panel b. (d) RV residuals after subtraction of activity and planet model. (e)–(g) Phase folds of RVs for all three planets.
In the text
thumbnail Fig. 9

Literature comparison for planetary radius (left column) and error (right column) for each planet.
In the text
thumbnail Fig. 10

Literature comparison for planetary mass (left column) and error (right column) for each planet.
In the text
thumbnail Fig. 11

Literature comparison for planetary period (left column) and error (right column) for each planet.
In the text
thumbnail Fig. 12

Literature comparison for time of periastron (left column) and error (right column) for each planet. Note that for planet c we added one orbital period to T0 from Niraula et al. (2017) and Prieto-Arranz et al. (2018) to make their values comparable.
In the text
thumbnail Fig. 13

Left: residuals of the RV and K2 time series after subtracting stellar activity and the three planetary signals. Right: correpsonding GLS periodograms do not show any remaining significant signals.
In the text
thumbnail Fig. 14

Simulated light curves of multi transits of GJ 9827 b and GJ 9827 d starting at BJD 2460333.25 d (top) and 2460618.57 d (bottom). The latter event is the deepest in this series.
In the text
thumbnail Fig. 15

Mass-radius diagram showing the positions of the three planets around GJ 9827 and planets detected around K dwarfs from literature. The different lines present different planetary compositions from 100% iron to 100% H2O.
In the text
thumbnail Fig. 16

Mass-density diagram showing the positions of the three planets around GJ 9827 and planets detected around K dwarfs from literature. The different lines present different planetary compositions from 100% iron to 100% H2O.
In the text
thumbnail Fig. 17

Ternary diagrams of the mass fractions of GJ 9827 b, c, and d derived with ExoMDN.
In the text
thumbnail Fig. 18

Histograms of mass fractions for core, mantle, water, and atmosphere of GJ 9827 b (top), c (middle), and d (bottom) derived with ExoMDN.
In the text
thumbnail Fig. 19

Ternary diagrams of the radius fractions of GJ 9827 b, c, and d derived with ExoMDN.
In the text
thumbnail Fig. 20

Histograms of radius fractions for core, mantle, water, and atmosphere of GJ 9827 b (top), c (middle), and d (bottom) derived with ExoMDN.
In the text
thumbnail Fig. A.1

Plotting RV vs FWHM for ESPRESSO, HARPS, and HARPS-N shows no correlation.
In the text
thumbnail Fig. A.2

Comparison of planetary radius from different GP runs using different combinations of datasets. RV refers to ESPRESSO, HARPS, HARPS-N, and HIRES, and All refers to RV, K2, and TESS combined.
In the text
thumbnail Fig. A.3

Comparison of time of periastron from different GP runs using different combinations of datasets. RV refers to ESPRESSO, HARPS, HARPS-N, and HIRES, and All refers to RV, K2, and TESS combined.
In the text
thumbnail Fig. A.4

Corner plot of the posterior distributions of Kepler amplitude (K), period (P), and T0/Phase for the three known planets and the potential fourth planet.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.