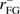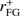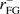| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A166 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201832768 | |
| Published online | 30 October 2018 | |
S–PASS view of polarized Galactic synchrotron at 2.3 GHz as a contaminant to CMB observations
1
SISSA, Via Bonomea 265, Trieste 34136, Italy
e-mail: nkrach@sissa.it
2
INAF Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047 Selargius (CA), Italy
3
CSIRO Astronomy and Space Science, PO Box 76, Epping, NSW 1710, Australia
4
INAF – Istituto di Radioastronomia, Via Gobetti 101, Bologna 40129, Italy
5
INFN, Via Valerio 2, 34127 Trieste, Italy
6
Department of Physics & Electronics, Rhodes University, Grahamstown, South Africa
7
Square Kilometre Array South Africa (SKA SA), Park Road, Pinelands 7405, South Africa
8
Department of Physics & Astronomy, The University of Iowa, Iowa City, Iowa 52245, USA
9
BABL AI Inc., 630 Fairchild St., Iowa City, IA 52245, USA
10
Dunlap Institute for Astronomy and Astrophysics, University of Toronto, 50 St. George St, Toronto, ON M5S 3H4, Canada
11
ARC Centre of Excellence for All-sky Astrophysics (CAASTRO), Sydney, Australia
12
Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500, GL Nijmegen, The Netherlands
13
International Centre for Radio Astronomy Research, University of Western Australia, Crawley, WA 6009, Australia
Received:
4
February
2018
Accepted:
26
July
2018
We have analyzed the southern sky emission in linear polarization at 2.3 GHz as observed by the S -band Polarization All Sky Survey (S-PASS). Our purpose is to study the properties of the diffuse Galactic polarized synchrotron as a contaminant to B-mode observations of the cosmic microwave background (CMB) polarization. We studied the angular distribution of the S-PASS signal at intermediate and high Galactic latitudes by means of the polarization angular power spectra. The power spectra, computed in the multipole interval 20 ≤ ℓ ≤ 1000, show a decay of the spectral amplitude as a function of multipole for ℓ ≲ 200, typical of the diffuse emission. At smaller angular scales, power spectra are dominated by the radio point source radiation. We find that, at low multipoles, spectra can be approximated by a power law CℓEE,BB ∝ ℓα, with α ≃ −3, and characterized by a B-to-E ratio of about 0.5. We measured the polarized synchrotron spectral energy distribution (SED) in harmonic space, by combining S-PASS power spectra with low frequency WMAP and Planck ones, and by fitting their frequency dependence in six multipole bins, in the range 20 ≤ ℓ ≤ 140. Results show that the recovered SED, in the frequency range 2.3–33 GHz, is compatible with a power law with βs = −3.22 ± 0.08, which appears to be constant over the considered multipole range and in the different Galactic cuts. Combining the S-PASS total polarized intensity maps with those coming from WMAP and Planck we derived a map of the synchrotron spectral index βs at angular resolution of 2° on about 30% of the sky. The recovered βs distribution peaks at the value around −3.2. It exibits an angular power spectrum which can be approximated with a power law Cℓ ∝ ℓγ with γ ≃ −2.6. We also measured a significant spatial correlation between synchrotron and thermal dust signals, as traced by the Planck 353 GHz channel. This correlation reaches about 40% on the larger angular scales, decaying considerably at the degree scales. Finally, we used the S-PASS maps to assess the polarized synchrotron contamination to CMB observations of the B-modes at higher frequencies. We divided the sky in small patches (with fsky ≃ 1%) and find that, at 90 GHz, the minimal contamination, in the cleanest regions of the sky, is at the level of an equivalent tensor-to-scalar ratio rsynch ≃ 10−3. Moreover, by combining S-PASS data with Planck 353 GHz observations, we recover a map of the minimum level of total polarized foreground contamination to B-modes, finding that there is no region of the sky, at any frequency, where this contamination lies below equivalent tenor-to-scalar ratio rFG ≃ 10−3. This result confirms the importance of observing both high and low frequency foregrounds in CMB B-mode measurements.
Key words: polarization / methods: data analysis / Galaxy: general / cosmic background radiation / diffuse radiation / radio continuum: ISM
© ESO 2018
1. Introduction
The cosmic microwave background (CMB) anisotropies in linear polarization are sourced by local inhomogeneities at the time of recombination via Thomson scattering (see Hu & White 1997, and references therein). In modern Cosmology, their measurement plays a fundamental role in understanding the physics of the early Universe, the structure formation, as well as the nature of cosmological components.
The Q and U Stokes parameters, describing linear polarization, are usually decomposed in E and B modes, representing a gradient and curl component of the polarized field, respectively (Zaldarriaga & Seljak 1997; Kamionkowski et al. 1997). The B-modes are sourced by non-scalar cosmological perturbations in the early Universe. In particular, primordial gravitational waves (GWs) are produced during inflation, an era of accelerated expansion in the very early Universe, responsible for the generation of all cosmological perturbations (Lyth et al. 2010). The GWs signature on the polarized CMB signal is characterized by a peak in the angular distribution of the observed B-modes power, at degree angular scales. At larger scales, the primordial signal is boosted by a second electromagnetic scattering era, known as reionization, causing a bump in the B-mode power spectrum at ℓ < 20. On the other side, at smaller scales, the gravitational deflection of CMB photons from forming cosmological structures causes a leak of the E into B-modes (Zaldarriaga & Seljak 1998). The latter mechanism contributes to the angular distribution of the B-mode power, causing a broad lensing peak on angular scales of a few arcminutes.
The CMB anisotropies in total intensity (T), E-mode polarization, and their correlation T E, have been observed by many experiments, culminating with the all sky observations at multiple frequencies, and down to arcminute angular resolution, by the Wilkinson Microwave Anisotropy Probe (WMAP; Bennett et al. 2013) and Planck satellites (Planck Collaboration I 2016).
Because of the potential breakthrough which would come from the discovery of cosmological GWs, the observation of B-modes in CMB experiments has progressed substantially in the last few years. Following early evidences obtained through cross-correlation of lensing, E and B modes by the South Pole Telescope (Hanson et al. 2013, SPTpol), the lensing peak has been successfully measured by the PolarBear experiment (The Polarbear Collaboration 2014, 2017), the Atacama Cosmology Telescope (Louis et al. 2017, ACTpol), and others 1.
On degree and larger angular scales, the main goal of the experiments is the detection of the inflationary B-modes, whose amplitude is usually parametrized through the ratio of the tensor and scalar modes, r. Currently, the best upper limit on the tensorto-scalar ratio is r < 0.07 at 95% confidence level obtained from the combination of CMB data with other observational probes (mainly Baryon acoustic oscillations, BAO, of the matter density), while the best constraint coming from CMB only observations is r < 0.09 (BICEP2 and Keck Array Collaborations 2016). The ultimate accuracy of experiments planned for the next decade is expected to reach the level of r ≃ 10−3, from ground-based facilities such as the Simons Array (Takayuki Matsuda & the Polarbear Collaboration 2017), the Simons Observatory2 and Stage IV (Abazajian et al. 2016) as well as from space-borne missions (Delabrouille et al. 2018; Matsumura et al. 2016).
Given the faintness of primordial B-modes, a great challenge for the experiments aiming at observing this signal, is represented by the control and removal of diffuse Galactic foreground contamination. At least two mechanisms are active in our own Galaxy generating linear polarized emission: the synchrotron radiation from cosmic ray electrons accelerating around the Galactic magnetic field, and the thermal dust emission from dust grains also aligned with magnetic field. Synchrotron brightness temperature presents a steep decrease in frequency v (roughly ∝ v−3) and dominates the sky emission in polarization at frequencies ≲100 GHz. Thermal dust emission is important at higher frequencies (≳100 GHz) with a frequency scaling well approximated by a modified blackbody with temperature of ~20 K.
All sky reconstructions of both components have been obtained from the data of the Planck and WMAP satellites, covering a frequency range extending from 23 to 353 GHz with sensitivity to linear polarization (Planck Collaboration X 2016). The analysis of data, targeting explicitly the degree angular scales (Planck Collaboration Int. XXX 2016; Krachmalnicoff et al. 2016) indicate that there is no frequency or region in the sky where the foregrounds are proved to be subdominant with respect to CMB B-modes (at the level of r ≃ 10−3). Also, analyses that reach the limits of instrumental accuracy show evidence of complex behavior in the Galactic dust and synchrotron emission (Planck Collaboration Int. L 2017; Sheehy & Slosar 2018; Planck Collaboration Int. LIV 2018; Choi & Page 2015; Zaroubi et al. 2015). Examples of such potential complexity are represented by the composition and spatial distribution of the dust which, projected along the line of sight, may give rise to decor-relation mechanisms of the polarized emission, in other words, changes in the angular distribution of the signal across frequencies. Line of sight effects, coupled with the spatial distribution of cosmic ray electrons, could in principle affect synchrotron as well. In addition, the energy distribution of cosmic ray electrons could give rise to a curvature in the frequency dependence of the polarized emission, complicating the extrapolation to CMB frequencies. In the near future it might become important to take into account these aspects, implying extra parameters for estimating, fitting, and subtracting the foregrounds in CMB maps.
These considerations motivate two important investigations: firstly the development of robust data analysis techniques, capable of removing the foreground component from the data using multi-frequency observations (component separation, see Stompor et al. 2016; Errard et al. 2016; Planck Collaboration IX 2016, and references therein); and secondly the investigation of available data tracing the foreground themselves, in order to determine their complexity.
This paper is about the latter investigation. While for thermal dust emission, full sky observations carried out by the Planck satellite at 353 GHz are sensitive enough to allow the study of the main characteristics of the signal and to provide indication of the level of contamination to the current CMB experiments (down to the level of r ≃ 3 × 10−3 at 90 GHz as shown by Planck Collaboration Int. XXX 2016), for synchrotron emission the currently available data are less informative. The sensitivity of low frequency observations from Planck and WMAP does not allow the detection of synchrotron signal at intermediate and high Galactic latitudes, where observations for current ground-based experiments are taking place, and therefore the level of contamination to CMB observation at higher frequency is unclear.
To such an aim, radio frequency datasets are being analyzed and will be soon available, specifically at 2.3 GHz from the S band Polarization All Sky Survey (Carretti 2010; Carretti et al. 2013, Carretti et al., in prep., S-PASS), and the C-band All Sky Survey at 5 GHz (Pearson & C-BASS Collaboration 2016; Jones et al. 2018, C-BASS). These data have great potential for characterizing the physics of the Galactic medium and magnetic field, but also to study the synchrotron component as a contaminant to CMB polarization measurements, given the fact that at these frequencies the synchrotron signal is much stronger than at the typical low frequency channels of CMB experiments (≳20 GHz). Moreover, new polarization data will be soon available in the frequency interval 10–40 GHz from the Q and U Joint Experiment at Tenerife (Rubiño-Martín et al. 2017, QUIJOTE) covering about 50% of the sky in the northern hemishpere. The cross-correlation of all of these data sets (S-PASS and C-BASS in the south, C-BASS and QUIJOTE in the north) with Planck and WMAP will be important to gain insight into the polarized synchrotron behavior, specifically investigating a potential frequency dependence of the spectral index.
 |
Fig. 1. S-PASS total polarized intensity map |
In this paper we describe the analysis of the S-PASS data focusing on the study of synchrotron as CMB contaminant; all the survey details are described in a forthcoming paper (Carretti et al., in prep.). The most important goals in this analysis are related to the study of the angular power spectra of S-PASS maps, together with the joint analysis of S-PASS data with those at higher frequencies from the Planck and WMAP, in order to constrain the synchrotron spectral properties, their spatial distribution, and ultimately quantify the level of contamination at CMB frequencies.
The paper is organized as follows. In Sect. 2 we describe the S-PASS survey and the data used for the analysis. In Sect. 3 we characterize the signal by means of the auto angular power spectra on different sky regions. In Sect. 4 we study the synchrotron frequency dependence using also angular power spectra of low frequency Planck and WMAP data. A map of the synchrotron spectral index is described in Sect. 5. In Sect. 6 we constrain the spatial correlation between synchrotron and thermal dust emission as observed by Planck. In Sect. 7 we estimate the level of total foreground contamination to CMB B-mode signal. Our conclusions are summarized in Sect. 8.
2. S-PASS survey at 2.3 GHz
In this section we describe the main characteristics of the S-PASS polarization maps which have been used in our analysis. For a full description of the S-PASS dataset, the observation strategy and the map-making process we refer to (Carretti et al., in prep.).
2.1. S-PASS polarization maps
The S-PASS survey covers the sky at declination < −1° resulting in a sky fraction ~50%. Observations were conducted with the Parkes Radio Telescope, a 64-meter single-dish antenna located in the town of Parkes (NSW, Australia). All details about the survey can be found in Carretti et al. (2013) and Carretti et al., in prep., here we briefly report on the main points relevant to this paper. The signal was detected with a digital correlator with 512 frequency channels, 0.5 MHz each. Flux calibration was performed with the sky sources B1934–638 and B0407–658, used as the primary and secondary flux calibrators, respectively. All frequency channels were calibrated individually, reaching an accuracy of 5%. The sources 3C 138 and B0043–424 were used as polarization calibrators, for an error on the polarization angle of 1°. Channels with RFI (Radio Frequency Interference) contamination were flagged, and only data in the range 2176–2216 MHz and 2272–2400 MHz were used, binned in one band of 168 MHz effective bandwidth and central frequency of 2303 MHz. The residual instrumental polarization after calibration (leakage of Stokes I into Q and U) is better than 0.05%. Total intensity and polarization data are projected on Stokes I, Q, and U maps, according to the Healpix3 pixelization scheme (Gόrski et al. 2005). The final maps have an angular resolution of 8.9 arcminute and Healpix Nside = 1024 parameter (corresponding to a pixel dimension of about 3.4 arcminutes).
In this analysis we made use only of Stokes Q and U maps4, which completely define the linear polarization amplitude of the observed signal. Figure 1 shows the total polarized intensity map obtained from these data 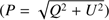 in Galactic coordinates and in thermodynamic Kelvin units. The map shows the presence of a diffuse component, due to synchrotron radiation, which dominates the sky polarized emission at this frequency, together with the detection of several point and diffuse radio sources. A bright compact source sample catalog with polarization information, obtained from S-PASS observations, has been presented in Lamee et al. (2016), while a Stokes
in Galactic coordinates and in thermodynamic Kelvin units. The map shows the presence of a diffuse component, due to synchrotron radiation, which dominates the sky polarized emission at this frequency, together with the detection of several point and diffuse radio sources. A bright compact source sample catalog with polarization information, obtained from S-PASS observations, has been presented in Lamee et al. (2016), while a Stokes
I compact source catalog, complete down to the confusion limit, has been described in Meyers et al. (2017). Close to the Galactic plane (for Galactic latitudes |b| ≲ 20°) the granularity of the emission is indicative of depolarization effects. These are induced by the Faraday rotation of the polarization angle of light propagating through the ionized Galactic medium in the presence of the magnetic field, resulting in different rotations affecting different emission regions across the entire Galactic disk.
It is useful to notice that the amplitude of the diffuse synchrotron radiation at 2.3 GHz is a factor of about 103 larger than at 23 GHz (the lowest of WMAP frequencies) and about 2 × 103 larger than at 30 GHz (the lowest of the Planck frequencies). These numbers make it clear the unique benefit of using very low frequency data to characterize the Galactic synchrotron emission, given the high signal-to-noise ratio which can be reached even in those regions where the emission is faint. On the other hand, as we mentioned, observations at low frequencies are affected by Faraday rotation effects, mainly at low latitudes, which can depolarize the synchrotron emission around the Galactic plane, while being marginal at high latitudes. Faraday rotation effects at low Galactic latitude are expected to become milder at frequencies higher than 5–10 GHz.
The average noise level on S-PASS Q and U maps at Nside = 1024 is about 2.2 mK, leading to a signal-to-noise ratio larger than three on about 94% of the observed pixels.
2.2. Sky masks
To perform the analysis described in this paper, we use two different sets of masks that we briefly describe in this section. To characterize synchrotron emission over large portions of the sky we used a set of six masks obtained as simple isolatitude cuts in Galactic coordinates. We focussed on the sky at intermediate and high Galactic latitudes, where CMB experiments are observing, or plan to observe. In particular, this mask set is composed by cuts at latitudes |b| larger than 20, 25, 30, 35, 40 and 50°. We also masked out those regions of the sky where the polarized signal at 2.3 GHz is contaminated by the emission of bright extended radio sources. We masked out the regions around Centaurus A, the Large Magellanic Cloud, and Fornax A, removing circular patches with radii of 5, 3 and 1° respectively.
In order to compute angular power spectra on these sky regions we applied an apodization to the masks, computed with a simple cos2 function, with apodization length of 3°. The final sky fractions retained for the analysis are of 30, 26, 22, 19, 16, and 10% for this set of six isolatitude masks.
The second mask set is composed by smaller sky regions that we use to assess the level of contamination coming from foreground emission to CMB B-modes (see Sect. 7). In this case we considered 184 regions obtained as circular patches with radius of 15° centered on the pixel centers of the Healpix grid at Nside = 8 with |b| > 20°. We compute power spectra on these smaller regions also applying a cos2 apodization to the masks, with length of 5°. The resulting sky fraction for each of the 184 patches in this set of masks is ~1.2%. This second set of smaller sky regions is similar to the one used in Planck Collaboration Int. XXX (2016) and Krachmalnicoff et al. (2016) (the difference being represented by a larger apodization length here for a better power spectrum estimation, given the angular scales of interest), where the level of contamination to CMB B-modes coming from thermal dust radiation and synchrotron emission has also been studied.
3. S-PASS angular power spectra
In order to statistically characterize the Galactic synchrotron signal, we computed angular power spectra of the S-PASS polarization maps. We computed both EE and BB auto-spectra on the set of six isolatitude masks, in the multipole interval between 20 and 1000. To correct for the incomplete sky coverage, inducing mixing both between multipoles and polarization states, we computed spectra with an implementation of the Xpol5 algorithm (Tristram et al. 2005). This code has already been used and tested in several previous works, also for foreground studies (see Planck Collaboration Int. XXX 2016, and references therein). Spectra were binned considering a top-hat band-power with Δℓ = 20. In the entire multipole range, the noise level lies more than one order of magnitude below the signal power on both EE and BB spectra, and therefore we have not applied any correction for the noise bias.
The EE and BB angular power spectra for the set of six masks are plotted in Fig. 2, showing Dℓ = ℓ(ℓ + 1)Cℓ/2π, where Cℓ are the two point correlation function coefficients of the expansion in Legendre polynomials. As expected, the amplitude depends on the considered sky region, with spectra computed at higher Galactic latitudes showing less power than the ones including also regions closer to the Galactic plane, where the synchrotron emission is stronger. At low multipoles, corresponding to large angular scales, the sky emission is dominated by the diffuse synchrotron radiation, characterized by a typical power law decay. At ℓ ≳ 200, the Dℓ start rising due to the emission of extra-Galactic compact sources in the radio band (here-after, labeled as point or radio sources).
In order to describe the spectral behavior as a function of ℓ we implemented a fitting procedure considering the following model:
The model characterizes the diffuse Galactic synchrotron emission by means of a power law with index α and amplitude As evaluated on a pivot point, corresponding to ℓ = 80. This value corresponds to the angular scale where, for CMB emission, the maximum of the contribution from cosmological gravitational waves is located, and therefore most important for measuring the contamination to CMB from synchrotron. The emission from point sources is assumed to be Poisson noise on maps with a flat Cℓ power spectrum with amplitude Ap.
We fitted the model in Eq. (1), separately for E and B-modes and for the different masks, for the whole range of considered multipoles. In performing the fitting we weighted each point with the corresponding signal variance.
The fitted power spectra are shown in Fig. 2 with the resulting best fit parameters reported in Table 2. Figure 3 shows the recovered values for α and Ap, together with the synchrotron B-to-E ratio 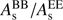 .
.
Results show a steep decay of the amplitude as a function of multipoles for the diffuse component of the signal. For isolatitude cuts with |b| > 30° the values of stabilize around −3.15 (weighted mean) with a slightly steeper value for E than for B-modes. On masks including also low Galactic latitudes the spectrum is flatter, exhibiting a similar behavior for the two polarization states. This is probably due to Faraday rotation of the polarization angle of the signal at mid latitudes, whose effect is to mix E and B-modes and to cause excess power on the small angular scales (Baccigalupi et al. 2001). This consideration is supported also by the behavior of the polarization power spectra computed on the whole sky region observed by S-PASS (with the only exclusion of brightest extended sources as described in Sect. 2.2). As a matter of fact, in this case, where the signal is dominated by Faraday rotation effects on the Galactic plane, spectra are almost flat in the whole considered multipole range with similar amplitude for E and B-modes (gray curves in Fig. 2). Given the strong contamination, we did not apply the fit in this case.
 |
Fig. 2. EE (left panel) and BB (right panel) power spectra of the S-PASS polarization maps computed on the set of isolatitude masks described in Sect. 2.2 (colored curves). Solid lines show the best fit curve obtained by fitting the model in Eq. (1) to the data (we note that in this figure the amplitude of Dℓ = ℓ(ℓ + 1)Cℓ/2π is plotted). Gray curves represent the polarization spectra computed on the whole sky region observed by S-PASS where the signal is strongly contaminated by the Faraday rotation effects on the Galactic plane. |
 |
Fig. 3. Best fit parameters obtained by fitting the model in Eq. (1) to S-PASS polarization spectra. The color of different points refers to the different sky masks described in the text, following the same color scheme as in Fig. 2. |
The EE spectra show more power than BB, especially at high Galactic latitudes, with 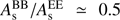 for |b| > 35°. A similar asymmetry has been observed as a characterizing feature of the thermal dust emission, on the basis of Planck observation at 353 GHz (Planck Collaboration Int. XXX 2016; Planck Collaboration Int. LIV 2018). A physical explanation of this feature has been proposed for thermal dust emission (Planck Collaboration Int. XXXII 2016) in terms of filaments constituted by dense structures aligned to the Galactic magnetic field. The question whether this reasoning can explain in part or totally the same asymmetry observed here for synchrotron is open. As for the Ap parameter, representing the power of point sources on the spectra, the resulting amplitude is pretty constant for the considered sky regions.
for |b| > 35°. A similar asymmetry has been observed as a characterizing feature of the thermal dust emission, on the basis of Planck observation at 353 GHz (Planck Collaboration Int. XXX 2016; Planck Collaboration Int. LIV 2018). A physical explanation of this feature has been proposed for thermal dust emission (Planck Collaboration Int. XXXII 2016) in terms of filaments constituted by dense structures aligned to the Galactic magnetic field. The question whether this reasoning can explain in part or totally the same asymmetry observed here for synchrotron is open. As for the Ap parameter, representing the power of point sources on the spectra, the resulting amplitude is pretty constant for the considered sky regions.
It is worth noticing that, in all the considered cases where we fit the model of Eq. (1) to the data, we get high χ2 values, with probability to exceed (PTE) below 5%. Nevertheless, this is not unexpected: we are modeling the data using a simple model (although being a typical one for this kind of studies, see for example Planck Collaboration Int. XXX (2016)), in the high signal-to-noise ratio regime allowed by S-PASS. Given the highly non-stationarity and non-Gaussianity of foreground emissions, the spectra are not a perfect power law in ℓ and vary in shape and amplitude from region to region. Therefore, the fit may result in a poor correspondence between model and data. Gross statistical indicators, such as power law spectra fitting, are important to assess the overall contamination of foregrounds, but are far from constituting a complete knowledge of the signal, which is necessary in order to achieve an effective CMB B-mode cleaning.
4. Synchrotron spectral energy distribution
In this section we describe the results obtained from the analysis of the S-PASS polarization data in combination with other publicly available polarization maps, at higher frequencies, coming from the WMAP and Planck surveys. The goal of this analysis is to characterize the synchrotron spectral energy distribution (SED) on a large interval of frequencies, from 2.3 GHz to 33 GHz. In this section we summarize the results obtained by analyzing data in the harmonic space, through computation of angular power spectra of the different frequency maps, while in Sect. 5 we report the results obtained from a pixel-based study.
4.1. WMAP and Planck data
The angular power spectra of the S-PASS data and WMAP/Planck low frequency polarization maps are evaluated using the set of six isolatitude masks described previously (Sect. 2.2). We include in our analysis the two lowest frequencies of the WMAP dataset, namely the K and Ka bands, centered at 23 and 33 GHz, respectively (Bennett et al. 2013). In order to calculate the cross spectra between different frequency maps, we use the full nine-year WMAP Stokes Q and U parameters6 degraded at the pixel resolution corresponding to Nside = 256. To compute single frequency spectra we cross-correlate the dataset splits, to avoid noise bias. In particular, we split WMAP data by co-adding the single year maps from 1 to 4 on one side, and from 5 to 9 on the other.
We also include the Planck polarizations maps in the 30 GHz band (central frequency 28.4 GHz) obtained from the Low Frequency Instrument (LFI) observations (Planck Collaboration I 2016; Planck Collaboration II 2016). Again, for cross frequency spectra we used the full mission maps, while for the case of single frequency we compute the cross correlation of the splits coming from the co-addition of odd and even years maps7.
Therefore, our dataset includes four frequencies (2.3, 23, 28.4 and 33 GHz) from which we obtain in total ten power spectra, four computed at a single frequency (corresponding to the one of each single map) and six from the cross correlation among different channels.
4.2. Signal and noise simulations
In order to estimate error bars on our set of power spectra we use simulations. In particular, we generate a hundred realizations of signal plus noise maps, as described in the scheme below.
First, we defined the simulated polarized synchrotron and CMB radiations included in the simulations. For synchrotron, we considered the sky model adopted in Planck Full Focal Plane version 8 (FFP8) simulations (Planck Collaboration XII 2016) that we extrapolate, considering a simple power law SED with β = −3.1, at the S-PASS and WMAP K and Ka and LFI-30 frequencies. The obtained polarization maps are smoothed with a Gaussian beam for reproducing the angular resolution of the instrument, in other words full width half maximum (FWHM) of 8.9 arcminutes for S-PASS, 52.8 and 39.6 arcminutes for WMAP K and Ka, respectively, and 33.1 arcminutes for LFI-30. Finally we degraded the maps at Nside = 256.
We simulated the polarized CMB signal using the synfast code of the healpy python package. We simulated 100 different maps of the CMB signal, as Gaussian realization of the best Planck 2015 ΛCDM model (Planck Collaboration XIII 2016) considering a tensor-to-scalar ratio r = 0. Maps are generated at Nside = 256 and convolved with a Gaussian beam corresponding to the angular resolution of each considered frequency channel.
Next, we generated realizations of WMAP and Planck noise maps, estimating the noise level directly from the data. In particular, we computed the difference maps of the WMAP and Planck splits described previously. These difference maps, after being properly rescaled with a multiplication factor (1/2 for the case of LFI splits which both include half of the total time of Planck-LFI observations, and  for WMAP splits which include on one side 4/9 and on the other 5/9 of the total time of WMAP observations), are a good representation of the noise on the full mission maps. To these maps, we applied the iso-latitude mask with |b| > 20° and multiply them by the square root of the corresponding full mission map of hits counts, in order to get uniform levels of noise across the sky. We then computed polarization power spectra of these noise maps and we fit them with a simple Cℓ = A/ℓ + B model, which, in addition to the flat white noise component, also takes into account the contribution ∝ 1/ℓ, coming from the residual 1/f noise component on maps. The fit is done in the multipole interval ranging from ℓ = 10 to 200 which includes the angular scales of interest for this analysis. We generated 100 independent maps of noise at Nside = 256 (for each considered WMAP and Planck frequency, full mission and split maps) as Gaussian realizations of the obtained fitted spectra. We then divided them by the square root of the hits in each pixel, in order to normalize properly the noise level and take into account the sky scanning strategy effect. For S-PASS we computed noise maps as random realizations of the variance map (degraded at Nside = 256) which we assumed to be the same for both Q and U, therefore without including any 1/f noise component. The final signal+noise maps are obtained as the sum of the single synchrotron map at each frequency plus the 100 realizations of CMB and noise maps described previously.
for WMAP splits which include on one side 4/9 and on the other 5/9 of the total time of WMAP observations), are a good representation of the noise on the full mission maps. To these maps, we applied the iso-latitude mask with |b| > 20° and multiply them by the square root of the corresponding full mission map of hits counts, in order to get uniform levels of noise across the sky. We then computed polarization power spectra of these noise maps and we fit them with a simple Cℓ = A/ℓ + B model, which, in addition to the flat white noise component, also takes into account the contribution ∝ 1/ℓ, coming from the residual 1/f noise component on maps. The fit is done in the multipole interval ranging from ℓ = 10 to 200 which includes the angular scales of interest for this analysis. We generated 100 independent maps of noise at Nside = 256 (for each considered WMAP and Planck frequency, full mission and split maps) as Gaussian realizations of the obtained fitted spectra. We then divided them by the square root of the hits in each pixel, in order to normalize properly the noise level and take into account the sky scanning strategy effect. For S-PASS we computed noise maps as random realizations of the variance map (degraded at Nside = 256) which we assumed to be the same for both Q and U, therefore without including any 1/f noise component. The final signal+noise maps are obtained as the sum of the single synchrotron map at each frequency plus the 100 realizations of CMB and noise maps described previously.
Finally, once we have our set of simulated maps, we compute cross spectra on them on our six sky masks. We therefore get 100 realizations of our set of ten spectra. Error bars are then calculated as the standard deviation of these 100 realizations in each considered multiple bin. Since we considered a hundred different realization of the CMB, the final error bars also included cosmic variance.
For S-PASS data, we also included in the error budget the calibration uncertainty. In particular we consider a 5% photo-metric calibration uncertainty (at the map level) that we added in quadrature to the statistical error.
4.3. SED fitting
As mentioned, we computed power spectra on our set of six iso-latitude masks, using the Xpol power spectrum estimator, on multipoles ranging from ℓ = 20 to ℓ ≃ 140. In particular, we consider top-hat band powers in the following multipole bins: [20, 39], [40, 59], [60, 79], [80, 99], [100, 119], [120, 139]. We restricted our analysis to the large angular scales, in order to maximize the signal-to-noise ratio on WMAP and Planck data, and to avoid contamination from point sources in S-PASS data. Power spectra are corrected for the beam window function, considering Gaussian beam profiles at the nominal angular resolution of each channel.
We used the spectra to fit for the synchrotron SED. In particular we performed the fit separately for each sky mask, for each multipole bin and for B and E modes, ending up in doing 72 different fits (six sky masks × six multipole bins × two polarization states).
We fit the following model to data:
where Cℓ(v1 × v2) represents the amplitude of the cross power spectrum between frequency v1 and v2 (in GHz), in a given multipole bin and mask, and it is expressed in terms of squared brightness temperature units. We fixed the pivot frequency at v0 = 9 GHz, close to the geometrical mean of the considered frequency range.
At this stage of our analysis we fit this simple model, whose free parameters are the amplitude As of synchrotron radiation at the pivot frequency of 9 GHz and the spectral index βs, to a subset of the available frequencies. In particular, we restrict the fit to the S-PASS auto spectra, the WMAP and Planck single frequency spectra, and all the possible cross spectra between WMAP and Planck, excluding cross-spectra involving S-PASS. Therefore, we fit our model to data at seven different effective frequencies (where as effective frequency we considered the geometrical mean 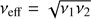 ), being: 2.3, 23, 25.5, 27.5, 28.4, 30.6 and 33 GHz. We restricted to this subset of frequencies in order to avoid possible biases due to frequency decorrelation (Planck Collaboration Int. L 2017) making the model in Eq. (2) not appropriate. This effect is negligible, due to noise, in cross spectra between WMAP and Planck, but could play a role in the case of cross spectra involving S-PASS. We address the problem of decorrelation in Sect. 4.4.
), being: 2.3, 23, 25.5, 27.5, 28.4, 30.6 and 33 GHz. We restricted to this subset of frequencies in order to avoid possible biases due to frequency decorrelation (Planck Collaboration Int. L 2017) making the model in Eq. (2) not appropriate. This effect is negligible, due to noise, in cross spectra between WMAP and Planck, but could play a role in the case of cross spectra involving S-PASS. We address the problem of decorrelation in Sect. 4.4.
Before performing the fit, we corrected our power spectra amplitude by applying the color correction coefficients to WMAP and Planck data, in order to account for the effect introduced by the finite width of the frequency bands. In particular, we used the coefficients listed in Table 2 of Planck Collaboration Int. LIV (2018). For S-PASS data this correction is negligible due to the narrowness of the bandpass. We also subtracted from the Cℓ the polarization amplitude of the CMB in the corresponding multipole bin, for both E and B-modes, taking as reference CMB values the ones coming from the Planck 2015 ΛCDM best fit with r = 0 (Planck Collaboration XIII 2016). As we stressed already, since in the simulation setup described in Sect. 4.2 we included the CMB signal, our error bars on spectra include the contribution of cosmic variance.
4.3.1. Results on data
With the setup described in the previous section we computed the fit of the model in Eq. (2) to the data. The fit is performed using a Marcov chain Monte Carlo (MCMC) algorithm, implemented with the python programming language.
Results of the fit are shown in Figs. 4, 6 and Table 2. In the majority of the considered cases, data are well fitted by the simple power law model adopted, with four of the 72 cases having a PTE value of the fit below 5%. The points with PTE<0.05 are for multipoles ℓ > 100, where the signal to noise ratio for WMAP and Planck data is low and where S-PASS maps may include contamination by point sources.
We were able to constrain the spectral index βs for all the fitted SEDs, recovering an average value βs = −3.22 ± 0.08, corresponding to weighted mean and dispersion of the points. The value of βs appears to be rather constant across the different sky regions, and as a function of the angular scale. Moreover, we do not find any significant difference in the synchrotron behavior for E and B modes.
We stress the remarkable results we are achieving here. First, despite of fitting in an unprecedentedly wide range of frequencies, adding the S-PASS channel at 2.3 GHz to the typical interval of frequencies of CMB experiments, the recovered value of βs is in agreement with what already found in previous studies of synchrotron SED from satellites at frequencies more than a factor of ten higher (Fuskeland et al. 2014; Planck Collaboration Int. LIV 2018). Second, constancy of the SED in angular bins, measurable for the first time, thanks to the high signal-to-noise ratio of the S-PASS data, seems a characteristic feature of synchrotron, stable for all sky fractions we consider.
4.3.2. Validation on simulations
We check the consistency of our fitting procedure on simulations. In particular, we used the set of one hundred realizations of signal + noise maps described in Sect. 4.2.
We fit the model of Eq. (2) to the mean value of the spectra obtained from the simulations. We stress that the synchrotron signal in our simulations is rigidly rescaled at the different frequencies considering a constant spectral index βs = −3.1, and any possible cause of decorrelation among frequencies (other than noise) is excluded. Therefore, unlike what we described previously for data, we fit the SED model on simulations, considering the full set of ten frequencies, including therefore also the cross spectra among S-PASS and WMAP/Planck.
Results of the fits are shown in Fig. 5. We were able to recover the input value of the βs parameter in all the considered cases.
 |
Fig. 4. Best fit values for the synchrotron SED spectral index βs (upper panel) and PTE coefficients (lower panel), obtained by fitting the model of Eq. (2) to S-PASS, WMAP and Planck data. Different point colors and shapes refer to the different sky regions. The black line and gray area in the upper plot show the retrieved average value βs = −3.22 ± 0.08. |
 |
Fig. 5. Retrieved βs parameter obtained by fitting synchrotron SED model on simulated spectra. Point colors and shapes follows the same scheme of Fig. 4. The horizontal line corresponds to βs = −3.1, which represents the input value for our set of simulations. |
4.4. Correlation between S-PASS and WMAP/Planck polarization maps
In the upper panel of Fig. 6 we show the amplitude of EE and BB spectra we get from data (Dℓ), for all the multipole bins and sky masks, together with the best fit curves. The lower panel of the same figure shows the residuals of each fit. In all these plots the points inside the gray shaded area come from the cross correlation between the S-PASS polarization maps and the other three maps at higher frequencies from WMAP and Planck data.
As described in the previous section, we did not consider these points while performing the fit. The reason of excluding them appears clear while looking at the residuals: the majority of them show a lack of power with respect to the best synchrotron SED model. In particular, residuals can be more than 4σ away from the best fit curve for the largest masks. On the other hand, at high latitudes deviations are generally within 2σ, and therefore not statistically significant. This indicates that S-PASS and WMAP/Planck maps do not properly correlate in the sky regions close to the Galactic plane and that, here, some kind of mechanism causing decorrelation is present.
In general, decorrelation may originate either from instrumental effects or physical motivations. In our case, systematics effects can not be the primary source since they would cause stronger decorrelation where the signal is weaker, meaning at high Galactic latitudes, which is opposite to what we find. For WMAP and Planck, residual intensity-to-polarization leakage and 1/f noise contribution can be present. However, the low signal-to-noise ratio makes it difficult to assess the proper level of those signals and estimate their effects on decorrelation. S-PASS has low systematics, unlikely to generate such effects. In particular, the leading spurious signal comes from residual ground emission, but it is too small (less than 3% of the signal in the low emission areas at high latitudes, Carretti et al., in prep.) to cause significant effects on spectra and, in turn, on decorrelation.
A second, more likely, cause for decorrelation is Faraday rotation at 2.3 GHz which is present, as we already noticed, in those sky regions close to the Galactic plane, while its effect is negligible at WMAP and Planck frequencies. The fact that residuals, for the three cross-correlation points, are larger on those sky masks including also lower Galactic latitudes, represents a hint that Faraday rotation plays an important role in causing decorrelation, at least on these large sky regions. Nevertheless, the lack of independent data estimating the level of Faraday rotation does not allow a thorough characterization of the effect.
 |
Fig. 6. Upper panel: amplitude of computed power spectra on data for different multipole bins and sky masks (the color scheme is the same of Fig. 4) as a function of the effective frequency. Filled points refers to EE spectra, empty ones to BB. Curves represent the best model we obtain when fitting Eq. (2) to data (solid and dashed lines for E and B-modes respectively). We note that in this figure the amplitude of Dℓ = ℓ(ℓ +1)Cℓ/2π is plotted. Lower panel: residuals of the fits normalized to the 1σ error, the dashed horizontal lines represent the 2σ level. In both upper and lower panel the points inside the gray shaded area come from the correlation of S-PASS with WMAP/Planck data which, as described in the text, are not considered in the fitting. |
Lastly, it is important to notice that we cross-correlated maps at frequencies which are far away from each other, and we are fitting the data with a simple power-law model, having a single spectral index βs. Any deviation from this approximated model, caused for example by a frequency or a spatial variation of the spectral index can cause large residuals, especially visible in the cross-correlation of data at distant frequencies. The possibility that decorrelation is actually due to the variation of the underlying physical properties of synchrotron would have important implications for B-mode experiments targeting cosmological GWs. It would imply that these experiments need to design focal planes monitoring synchrotron at frequencies close to the one of minimum foreground contamination, for properly mapping the foreground contamination and subtract it out with low residuals on the CMB signal.
A quantitative assessment of decorrelation and its physical properties, though, will have to wait for other independent data at intermediate frequencies. Several observations are ongoing in the northern (Génova-Santos et al. 2017; Jones et al. 2018; Aiola et al. 2012, QUIJOTE, C-BASS, LSPE) and southern (Pearson & C-BASS Collaboration 2016; Essinger-Hileman et al. 2014, C-BASS, CLASS) hemispheres which will allow to further characterize this effect.
4.5. Constraints on synchrotron curvature
As aforementioned, by fitting the data with a simple power law model, in the frequency range 2.3–33 GHz, we retrieve an average value for the spectral index of synchrotron in agreement with constraints obtained considering only higher frequency data. This result, therefore, seems to exclude the possibility of having a strong curvature of the synchrotron SED with frequency, in polarization. In order to better quantify this statement, we fit the same set of data described in Sect. 4.1 with a model that also includes a curvature of the synchrotron spectral index. In particular we fit the Cℓ(v1 × v2) amplitude of power spectra as follows:
allowing, therefore, a logarithmic steepening or flattening of the synchrotron spectrum with frequency, through the srun parameter (Kogut et al. 2007; Kogut 2012).
In performing the fit we applied a Gaussian prior on the βs parameter with βs = −3.13±0.13. This prior is the same adopted in Planck Collaboration Int. LIV (2018) and has been obtained as the mean value of the βs computed from Planck and WAMP data in sky regions with fsky ranging from 24% to 71% and multipole bins from ℓ = 4 to ℓ = 160. The reason for applying this prior is that the βs and srun parameters are highly correlated. Moreover, the constraint on βs from WMAP and Planck data, on our sky masks, is too weak to allow the fit of both parameters simultaneously, without any prior. Since the prior on the βs comes from WMAP and Planck data, in this case we fix the pivot frequency v0 at 23 GHz.
Figure 7 and Table 3 report the resulting constraints on the srun parameter, in each multipole bin and sky maps. In all the cases the srun parameter is compatible with zero at 1.5σ at most, with error bars ranging from 0.07 to 0.14. In Fig. 8 we show the posterior distribution from the MCMC fit, in the particular case at ℓ ≃ 50, isolatitude mask with |b| > 35° and BB spectrum.
5. Polarized synchrotron spectral index map
In the previous section we describe how we used S-PASS, WMAP and Planck data to estimate the synchrotron spectral index in the harmonic domain. In this section we estimate βs by performing a pixel based analysis for deriving the corresponding map.
 |
Fig. 7. Constraint on the srun parameter describing the curvature of the synchrotron spectral index in polarization. |
Mean value and 1σ error of the srun parameter in the different multiple bins and considered sky mask for E and B-modes.
5.1. Procedure
We evaluated the synchrotron spectral index considering again the simple power law model and fitting the data in the pixel domain. As before, we considered the S-PASS, WMAP K, Ka and Planck-LFI 30 GHz polarization maps. Contrary to the procedure followed for power spectra, here we fixed the amplitude of synchrotron at the value measured at 2.3 GHz in the S-PASS data and fit only for the spectral index βs. We performed this analysis on the sky region observed by S-PASS at |b| > 20°.
In the preprocessing, we smoothed all the maps at the same angular resolution of 2°. We fit for βs in each pixel, after degrading the input maps at Nside = 256.
We performed the fit on the polarized intensity maps P (with 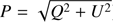 ), in order to avoid effects coming from possible rotation in the polarization angle with frequency. Nevertheless, total polarization maps are positively biased, due to the presence of noise. This bias is negligible for S-PASS which, at the angular resolution of 2°, has S/N > 5 everywhere on both stokes Q and U maps. On the contrary, the bias is important for WMAP and Planck, which have lower signal to noise. If not properly taken into account, the noise bias can therefore cause a shift of the recovered spectral index βs toward higher values (flatter spectra).
), in order to avoid effects coming from possible rotation in the polarization angle with frequency. Nevertheless, total polarization maps are positively biased, due to the presence of noise. This bias is negligible for S-PASS which, at the angular resolution of 2°, has S/N > 5 everywhere on both stokes Q and U maps. On the contrary, the bias is important for WMAP and Planck, which have lower signal to noise. If not properly taken into account, the noise bias can therefore cause a shift of the recovered spectral index βs toward higher values (flatter spectra).
In order to obtain an unbiased estimate, we included the presence of noise while preforming the fit. In particular, in each pixel we minimize the following function:
where vi ∊ [23, 28.4, 33] GHz and Pvi is the total polarization amplitude observed on maps at frequency vi. 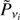 is computed starting from the S-PASS polarization maps as
is computed starting from the S-PASS polarization maps as
where Q2.3 and U2.3 represent the amplitude of S-PASS Stokes Q and U maps respectively, while 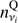 and
and 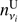 are a random realization of white noise, for Q and U, at the frequency vi. These random realizations are computed from the variance map of the noise at 2°, for each different frequency vi.8
are a random realization of white noise, for Q and U, at the frequency vi. These random realizations are computed from the variance map of the noise at 2°, for each different frequency vi.8 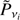 represents, therefore, our model of the total polarization amplitude at the frequency vi, and includes also the noise bias. We stress again that, given our model, the only free parameter in performing the minimization of the function in Eq. (4) is the spectral index βs while the synchrotron amplitude is fixed at the value we observe in S-PASS maps (that we consider to be noiseless). Obviously, in order to take into account properly the effect of noise, we have to perform the fit multiple times, randomizing on the noise realizations
represents, therefore, our model of the total polarization amplitude at the frequency vi, and includes also the noise bias. We stress again that, given our model, the only free parameter in performing the minimization of the function in Eq. (4) is the spectral index βs while the synchrotron amplitude is fixed at the value we observe in S-PASS maps (that we consider to be noiseless). Obviously, in order to take into account properly the effect of noise, we have to perform the fit multiple times, randomizing on the noise realizations  and
and  . In particular, for each pixel, we computed the fit a hundred times getting the final value and the statistical error on βs as mean and standard deviation of these estimated values.
. In particular, for each pixel, we computed the fit a hundred times getting the final value and the statistical error on βs as mean and standard deviation of these estimated values.
 |
Fig. 8. Posterior distribution of the parameters obtained by fitting the model in 3 to BB power spectra of S-PASS, Planck and WMAP in the multiple bin at ℓ ≃ 50 and for the isolatitude mask with |b| > 35°. The fit has been computed by applying a Gaussian prior on the synchrotron spectral index with βs = −3.13 ± 0.13. |
5.2. βs map and errors
Figure 9 shows the recovered spectral index map and corresponding errors (upper and middle panel, respectively). In the error budget we include both the statistical error (obtained as described in the previous section) and the error coming from the uncertainty in the S-PASS calibration, which is 5% on map. The two kinds of uncertainty are added together in quadrature to obtain the final value of σ(βs) in each pixel. In the maps, values of the spectral index vary in the range −4.4 ≤ βs ≤ −2.5, with 0.02 ≤ σ(βs) ≤ 1.06. In about 46% of the analyzed sky the spectral index value is recovered with a total uncertainty below 0.1.
Figure 10 shows the histogram of the recovered βs on map. This distribution peaks around βs ≃ −3.2, with an average value βs = −3.25 ± 0.15. These numbers are in agreement with the value we find fitting for the synchrotron SED in harmonic space (see Sect. 4.3.1), and are also consistent with the result obtained by Carretti et al. (2010) who, using polarization maps at 1.4 and 23 GHz found a spectral slope at high Galactic latitudes that peaked around −3.2. We compared the distribution of the βs with the one obtained from simulations. In particular, in the simulated case, we extrapolate the S-PASS polarization maps to WMAP and Planck frequencies, considering a fixed spectral index 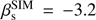 . After properly adding noise on maps at the different frequencies, and smoothing them at the angular resolution of 2°, we perform the fit with the procedure described in Sect. 5.1. The histogram of the recovered values of the spectral index on map is also shown in Fig. 10. We first observe that the histogram peaks at βs ≃ −3.2, showing that our fitting procedure recovers a spectral index map which is unbiased. Moreover, we notice that the βs distribution for the simulated case appears to be narrower when compared to the one from data. This indicates that the spread of βs we find is a real feature of the sky emission and not only due to noise.
. After properly adding noise on maps at the different frequencies, and smoothing them at the angular resolution of 2°, we perform the fit with the procedure described in Sect. 5.1. The histogram of the recovered values of the spectral index on map is also shown in Fig. 10. We first observe that the histogram peaks at βs ≃ −3.2, showing that our fitting procedure recovers a spectral index map which is unbiased. Moreover, we notice that the βs distribution for the simulated case appears to be narrower when compared to the one from data. This indicates that the spread of βs we find is a real feature of the sky emission and not only due to noise.
 |
Fig. 9. Upper panel: synchrotron spectral index map derived as described in the text. Middle panel: 1σ uncertainty on βs. Lower panel: Significance of the spectral index variation with respect to βs = −3.2, corresponding to the value at which the distribution of the βs on map peaks (see Fig. 10). We note that colors are saturated for visualization purposes. The complete range of values is: −4.4 ≤ βs ≤ −2.5, −1.6 ≤ log10[σ(βs)] ≤ 0.03, −6 ≤ S/N ≤ 20 |
In the lower panel of Fig. 9 we also show an estimate of the significance of the recovered variation of the spectral index with respect to the reference value βs = −3.2 in each pixel, computed as S = (βs + 3.2)/σ(βs). We find that |S| > 2 in about 12% of the analyzed sky. We stress here that the synchrotron spectral index map obtained in this work is the first available one computed using only polarized data, and represents, therefore, an important tool to generate realistic simulations of the polarized synchrotron sky9.
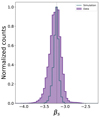 |
Fig. 10. Comparison of the normalized histograms of the synchrotron spectral index map obtained from data (indigo) and simulation (cyan line). The dashed line is at βs = −3.2, where the βs distribution peaks and also represents the reference value of the simulated case. |
 |
Fig. 11. Angular power spectrum of the S-PASS βs map before (blue) and after (purple) correction for the contribution of noise. For a complete description of the figure see text in Sect. 5.3. |
5.3. Angular power spectrum of the βs map
We computed the angular power spectrum of the βs map, in order to get information about the amplitude of the spectral index variations as a function of the angular scale. We computed the 〈βsβs〉 auto-power spectrum on the full sky region covered by our map (about 30% of the sky), in the multipole range 10–80 with Δℓ = 10 and correcting for a Gaussian beam window function with FWHM = 2°. The spectrum is shown in Fig. 11 (cyan curve). We corrected this spectrum for the noise bias, i.e. the the contribution coming from βs fluctuations due the presence of noise on the WMAP and Planck maps. Estimating this contribution is not trivial, since the level of fluctuations on the βs map due to noise depends on the value of the βs itself. We therefore relied on the following procedure:
we started from the S-PASS total polarization map that we extrapolate at WMAP/Planck frequencies using our βs map;
we added a noise realization representative of WMAP/Planck noise to the extrapolated maps (following the procedure described in Sect. 4.2);
on this set of simulated maps we estimated the value of the spectral index
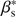 with the procedure used for data;
with the procedure used for data;we computed the power spectrum of the
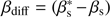 map (thin gray lines in Fig. 11);
map (thin gray lines in Fig. 11);we repeated this procedure a hundred times changing the noise realizations;
we evaluated the noise bias as the mean of the obtained one hundred spectra (black line in Fig. 11);
the unbiased βs spectrum was obtained by subtracting this mean curve to the spectrum of βs;
error bars on the unbiased spectrum were obtained as the standard deviation of the hundred noise spectra.
The unbiased spectrum is shown in Fig. 11 in purple, for the four multiple bins not compatible with zero. In order to extrapolate the amplitude of fluctuations at all angular scales we fit these points with a power law model with Cℓ ∝ ℓγ, finding a value of γ = −2.6 ± 0.2 (dashed purple line). We also compared our results with the power spectrum of the synchrotron spectral index map included in the PySM simulation package (Thorne et al. 2017)) (computed on the same 30% sky region of our analysis and shown in orange in Fig. 11), currently used in the sky modeling for many CMB experiments. We stress that this map was obtained combining the first WMAP polarization data with the Haslam total intensity ones at 408 MHz (Haslam et al. 1981), considering a model for the Galactic magnetic field, and it includes variations of the synchrotron spectral index only on scale larger then ~7° (Miville-Deschênes et al. 2008). The extrapolation of our results to low multipoles leads to fluctuations of the spectral index with amplitude about three times larger (at the spectrum level) than those in the PySM βs map.
6. Spatial correlation with thermal dust emission
Polarized Galactic synchrotron and thermal dust signals are expected to have some degree of correlation, due to the same underlying Galactic magnetic field. This correlation has already been measured on the larger angular scales (ℓ ≲ 100) through the computation of cross angular power spectra between WMAP and Planck low and high frequency channels (see Choi & Page 2015; Planck Collaboration Int. LIV 2018). In these works, the reported values for the correlation coefficient ρ show a progressive decay for increasing multipoles, with ρ ≃ 0.5 at ℓ ≃ 10 and approaching values compatible with zero at the degree angular scales. In this section we summarize the results we obtain by computing the cross correlation between the S-PASS and Planck maps at 353 GHz.
The Planck-HFI (High Frequency Instrument) observations of the full sky at 353 GHz represent the best measurement of the polarized thermal dust emission currently available. They have been intensively used to study the properties of the signal and its contamination to CMB primordial B-modes, and several experiments are currently relying on them to perform component separation and to isolate the CMB signal (BICEP2/Keck and Planck Collaborations 2015) or to put upper limits on foreground emissions in the observed regions of the sky (The Polarbear Collaboration 2017)
Therefore, in order to estimate the ρ coefficient describing the correlation between synchrotron and thermal dust, we use the Planck 353 GHz Q and U polarization maps, and compute the cross spectra with S-PASS data. In particular, the value of ρ is obtained as follows:
 |
Fig. 12. Correlation coefficient for thermal dust and synchrotron computed as in Eq. (6), using S-PASS and Planck 353 GHz polarization maps. |
where the numerator contains the amplitude in a given multipole bin of the cross spectrum between S-PASS and Planck-353 polarization maps divided by the amplitude of the single-frequency spectra (at 2.3 and 353 GHz). In particular, as previously done, the value of Cℓ(2.3) is obtained from the auto spectra of the S-PASS maps (given the low level of noise at the angular scale of interest). On the contrary, we estimate Cℓ(353) by computing cross spectra of independent splits obtained from the Planck dataset at 353 GHz, in order to avoid the presence of noise bias on the spectra. The Planck HFI maps are publicly available through the Planck legacy archive. As independent splits we considered the two half-mission maps.
We evaluated ρℓ by computing the E and B-mode spectra on the set of six isolatitude masks described previously (Sect. 2.2), in the same multipole bins we use in the analysis of the synchrotron SED, ranging from ℓ = 20 to ℓ ≃ 140 (see Sect. 4.3), and considering maps degraded at the Nside = 256 pixelization.
The values for ρ obtained in the different masks and multi-pole bins for E and B-modes are shown in Fig. 12. The error bars are again obtained through simulations; in particular, we generate a set of one hundred signal + noise simulations at 2.3 and 353 GHz, where the signal includes synchrotron and thermal dust emissions (obtained from the Planck FFP8 sky maps), and CMB realizations (from the best Planck 2015 ΛCDM model). We get the S-PASS noise as Gaussian realizations of the variance map. For the Planck-353 GHz channel we obtain the noise from data, following the procedure described in Sect. 4.2, and using the half-mission maps as splits. We computed the cross-frequency and single-frequency spectra from this set of simulations, calculated the value of ρ through Eq. (6), and obtained the error bars as the standard deviations of these simulated values.
The results show a level of correlation as high as 40% at large angular scales, and a general decaying trend at higher multipoles. It is worth noticing that the correlation is positive in particular at high latitudes; for both E and B-modes, indicating that some decorrelating contamination, probably due to Faraday modulation, may be active at low latitudes.
The observed correlation level at intermediate and high latitudes is in agreement with what previously found by Choi & Page (2015) and Planck Collaboration Int. LIV (2018), showing at the same time that S-PASS at intermediate and high latitudes is a good tracer of synchrotron, and that the correlation between the two emissions, especially at low multipoles, persists also when we compare very distant frequencies, such as for S-PASS and Planck-353 GHz channels.
7. Contamination to CMB polarization
As a final aspect of our analysis, we used the S-PASS and Planck data to estimate the level of contamination from foregrounds to the observation of primordial CMB B-modes. We focussed on the degree angular scales, around ℓ ~ 80, where the recombination bump of the CMB B-modes peaks.
We estimated the amplitude of foreground radiation on small sky regions, with fsky ~ 1%, with the goal of obtaining a map of the level of contamination. This approach has already been used in Planck Collaboration Int. XXX (2016) to estimate the contamination coming from Galactic thermal dust emission. Moreover, the analysis we present here represents an update of the work described in Krachmalnicoff et al. (2016), where the synchrotron and thermal dust signals at the degree scales were estimated using Planck and WMAP data.
7.1. Synchrotron contamination to primordial B-modes
As a first step we analyzed S-PASS data alone, with the goal of obtaining a map of the level of contamination coming only from synchrotron radiation to primordial B-modes. As mentioned, in this part of our work, we focussed on small regions of the sky located at intermediate and high Galactic latitudes (|b| > 20°). We constructed a set of 184 circular masks, each of which covers a fraction of the sky of about 1.2%10. The procedure we used to generate these masks is described in Sect. 2.2.
On each mask we computed the B-mode auto angular power spectrum of S-PASS maps, using the Xpol algorithm. Spectra were computed for multipoles ranging from ℓ = 40 to ℓ = 140, considering 5 bins with Δℓ = 20.
Once we have our set of 184 B-mode spectra, we fit each of them considering a power law to describe the power spectrum behavior, i.e. 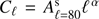 . We used the value α = −3, which represents the average of the values we find by performing the fit on S-PASS power spectra on the set of isolatitude masks (see Sect. 3 and Table 2), and fit only for the spectra amplitude. Withthis procedure we obtained an estimate of the amplitude of
. We used the value α = −3, which represents the average of the values we find by performing the fit on S-PASS power spectra on the set of isolatitude masks (see Sect. 3 and Table 2), and fit only for the spectra amplitude. Withthis procedure we obtained an estimate of the amplitude of 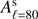 of synchrotron B-mode spectrum at 2.3 GHz and at ℓ = 80, in each region. The error on this amplitude takes into account both the one coming from the power law fit as well as the uncertainty on S-PASS photometric calibration that we considered to be at 5% level on maps.
of synchrotron B-mode spectrum at 2.3 GHz and at ℓ = 80, in each region. The error on this amplitude takes into account both the one coming from the power law fit as well as the uncertainty on S-PASS photometric calibration that we considered to be at 5% level on maps.
 |
Fig. 13. Synchrotron contamination to CMB B-modes at 90 GHz from S-PASS data, expressed in term of equivalent tensor-to-scalar ratio. In the top panels, the larger and smaller maps show the mean estimated value for rsynch and the 1σ lower and upper limit, |
We assessed the level of contamination coming from synchrotron to CMB B-modes at 90 GHz, one of the typical channels at which CMB experiments observe the sky and close to the minimum of foreground emission. To do so, we extrapolated the recovered amplitudes 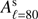 , considering a power law SED, with βs = −3.22 ± 0.08. We divided these amplitudes extrapolated at 90 GHz, by the amplitude of CMB B-modes at ℓ = 80, considering the best Planck 2015 ΛCDM model with tensor-to-scalar ratio r = 1 (
, considering a power law SED, with βs = −3.22 ± 0.08. We divided these amplitudes extrapolated at 90 GHz, by the amplitude of CMB B-modes at ℓ = 80, considering the best Planck 2015 ΛCDM model with tensor-to-scalar ratio r = 1 (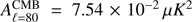 ). In this way we obtain an estimate of the parameter, hereafter called rsynch, whose value describes the contamination to primordial CMB B-modes in term of equivalent tensor-to-scalar ratio.
). In this way we obtain an estimate of the parameter, hereafter called rsynch, whose value describes the contamination to primordial CMB B-modes in term of equivalent tensor-to-scalar ratio.
Figure 13 reports the map, together with the corresponding histogram, of the value of rsynch in the pixels of a map at Nside = 8 on which each of the considered circular sky regions is centered. We also report the 1σ upper and lower limits on the value of rsynch, computed by taking into account both the error on 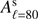 and the uncertainty on βs. Figure 13 shows new remarkable features with respect to what has been found in previous works considering satellite data (Krachmalnicoff et al. 2016). There, only peaks in the synchrotron emission were detectable above noise threshold, while here the regions with lowest emission can also be measured. Results show that, even in the cleanest region of the sky, the synchrotron contamination is at the level of rsynch = 10−3 at 90 GHz.
and the uncertainty on βs. Figure 13 shows new remarkable features with respect to what has been found in previous works considering satellite data (Krachmalnicoff et al. 2016). There, only peaks in the synchrotron emission were detectable above noise threshold, while here the regions with lowest emission can also be measured. Results show that, even in the cleanest region of the sky, the synchrotron contamination is at the level of rsynch = 10−3 at 90 GHz.
7.2. Foreground minimum
Finally, we compared the S-PASS levels of synchrotron measured in this work with those from dust, to assess the relevance and location in frequency of the foreground minimum with respect to cosmologically interesting values of r.
In Fig. 14 we report the synchrotron B-mode power spectra inferred in this work from S-PASS data, evaluated as described in Sect. 7.1 on the 184 sky regions outlined above. For the spectral shape we use the usual power law with βs = − 3.22, to extrapolate the synchrotron amplitude at the frequencies of 30, 40, 90 and 150 GHz. These spectra were compared with those for the thermal dust emission, with amplitude evaluated by fitting the B-modes power spectra. We computed these spectra by cross correlating the Planck 353 GHz half-mission maps on the same circular sky regions, with a power law with αd = − 2.42 (Planck Collaboration Int. XXX 2016), on the multipole interval 40 ≤ ℓ ≤ 140. The extrapolation in frequency for thermal dust emission is done considering a modified black body SED with βd = 1.59 and Td = 19.6 K (Planck Collaboration Int. XXII 2015).
The amplitude of the two signals, in the different sky regions, are compared, at different frequencies, with cosmologically interesting levels of r as well as lensing, again as predicted by the Planck 2015 best fit ΛCDM cosmology. Results shows that there is no region of the sky, nor frequency, where the foreground level lies below the CMB power B-modes power spectrum with r ≃ 10−3.
 |
Fig. 14. Synchrotron (violet areas) and thermal dust (cyan areas) amplitude evaluated in 184 sky regions with fsky ≃ 1% extrapolated at the indicated frequencies and compared with cosmological B-modes with given values of r (solid black lines, dashed for cosmological lensing again as predicted by Planck 2015 best fit CDM cosmologies). |
In Fig. 15 we show the sky distribution of the minimum of foreground emission. This is obtained by summing the amplitude of synchrotron and thermal dust B-modes at ℓ = 80 extrapolated at the different frequencies, using the SEDs described above, and looking for the frequency at which this sum reaches its minimum. By computing the simple sum of the two kinds of emission, here we are neglecting the correlation between the two. Levels of the minimum emission show rFG ≃ 10−2 at high latitudes, while approaching unity at the lowest latitudes considered. As in Fig. 13, uncertainties take into account the contribution of the noise and the extrapolation in frequencies. The best location looks to be the south Galactic cap, which is thus the most opportune place where to observe for experiments aiming at the lowest possible r value.
In Fig. 16, we show the sky distribution and histogram of the frequency rFG corresponding to the rFG shown in Fig. 15. The range of values is concentrated mostly between 60 and 90 GHz, confirming what previously inferred with a much poorer statistics (Krachmalnicoff et al. 2016). The frequency distribution appears to be rather flat, when we consider all the analyzed sky patches, while, if we restrict only to the cleanest regions (with rFG < 0.03) the foreground minimum is preferably reached at frequencies around 80 GHz.
8. Discussion and conclusion
In this work, we have analyzed the southern sky linear polarization at 2.3 GHz as observed by the S-PASS survey. The forthcoming S-PASS survey paper describes in detail the data reduction and production of sky maps which represent the starting point of the present analysis. These measurements represent an important supplement to the observations of the synchrotron radiation carried out by the WMAP and Planck satellites, at higher and more interesting frequencies for CMB purposes, but with poorer angular resolution, and lower signal-to-noise ratio.
The main target of our analysis has been the study of the properties of the diffuse Galactic polarized synchrotron. We have measured the angular distribution of the S-PASS signal at increasingly high Galactic latitudes, computing the auto power spectra of the polarization maps. At large angular scale (ℓ ≲ 200), the Cℓ signal can be described, in first approximation, as a power law ∝ ℓα. The recovered value of the index α changes significantly with respect to the considered sky regions. At Galactic latitudes |b| > 30° the mean value is α ≃ −3.15, with steeper spectra for E than for B-modes. At Galactic latitude including also portion of the sky closer to the Galactic plane, the signal is contaminated by Faraday rotation effects, causing polarization angle modulation, and inducing a mixing between the polarization states and flatter power spectra. Synchrotron signal also shows an asymmetry between B and E-modes emission, with a B-to-E ratio ~0.5 for |b| > 35°.
We have combined S-PASS data with those from WMAP and Planck satellites (at the frequencies of 23, 33 and 28.4 GHz) to obtain information about the synchrotron SED. We have performed this analysis in either harmonic or pixel space.
In the first case we computed power spectra of the polarization maps of the different instruments, and have fit the amplitude of those spectra, as a function of frequency, separately for different multipole bins and sky masks. The recovered mean value for the synchrotron spectral index is βs = −3.22 ± 0.08, which appears to be constant in the entire multipole range we have studied (six bins in the interval 20 ≤ ℓ < 140) and sky regions. Also, we did not observe any significant difference in the spectral behavior of E and B-modes. Although we have fit the data in an unprecedented range of frequency (from 2.3 to 33 GHz), the value we find for the βs index is in agreement with what measured from Planck and WMAP at higher frequencies. We also have fit the data with a model allowing a curvature for the synchrotron spectral index, that we find to be compatible with zero. We however emphasize the need of more data at intermediate frequencies to better constrain this parameter. We have seen evidence of decorrelation at mid latitudes, with a deficit of the power measured in the cross-spectra between S-PASS and WMAP/Planck. This decorrelation is strong close to the Galactic plane, indicating that, in these regions, Faraday rotation in S-PASS data plays an important role. On the other hand, the effect is not statistically significant at high latitudes.
 |
Fig. 15. Sky distribution of the minimum foreground emission at ℓ = 80 expressed in units of the cosmological tensor-to-scalar ratio, rFG, from S-PASS and Planck-353 data. Larger and smaller maps show the mean estimated value for rFG and the 1σ lower and upper limit, |
 |
Fig. 16. Sky distribution (left panel) and histogram (right panel) of the frequency corresponding to rFG in Fig. 15. |
We also analyzed the synchrotron SED in pixel space, constructing a map of the synchrotron spectral index. We have again used the S-PASS/WMAP/Planck data, covering the frequency range 2.3–33 GHz. To obtain the βs map we have fit the data in total polarization at 2° angular resolution. The distribution of βs on the map peaks around the value −3.2, in agreement with what we have found from the SED analysis in the harmonic domain. The angular power spectrum of this map can be approximated with a power law, with 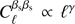 and γ = −2.6 ± 0.2. We stress here that this represents the first available βs map, and associated power spectrum, obtained using only polarization data, and therefore will be useful to build realistic simulations of the synchrotron signal as input for assessing the performance of component separation algorithms.
and γ = −2.6 ± 0.2. We stress here that this represents the first available βs map, and associated power spectrum, obtained using only polarization data, and therefore will be useful to build realistic simulations of the synchrotron signal as input for assessing the performance of component separation algorithms.
By cross-correlating S-PASS data with the high frequency polarization maps coming from the Planck-HFI 353 GHz channel, we have measured the spatial correlation between synchrotron and thermal dust signals. We find evidence for positive correlation, reaching about 40% on large angular scales, gently decaying to smaller values on smaller scales, depending on the latitudes considered. These results confirm the previous ones obtained from joint Planck and WMAP analysis, showing that the correlation among the two different kind of signals, on the large angular scale, persists over a wide interval of frequencies.
Finally, by taking advantage of the high signal-to-noise regime of the S-PASS survey, and our measured synchrotron SED, we have refined the estimation of the synchrotron contamination to CMB B-modes. We have constructed a map reporting the level of contamination at the degree angular scale (ℓ = 80) and at 90 GHz in 184 sky patch, each of which covers a sky fraction of about 1%. Results show that the minimum contamination is at the level of an equivalent tensor-to-scalar ratio rsynch ≃ 10−3. We also combined synchrotron and thermal dust information, getting a map of the estimated total level of contamination coming from foregrounds. Our findings confirm, once again, that there is no region of the sky (among the sky portion covered by the S-PASS survey) nor frequency where the foreground amplitude (at the degree angular scales) lie below a CMB B-mode signal with r ≃ 10−3, and that therefore frequency channel monitoring foreground emission, on both low and high frequency, are mandatory for all the experiments aiming at observing the primordial GWs signal at this level.
We conclude that stressing the importance of radio survey as tracer for synchrotron radiation. Given the brightness of the emission at these frequencies they can reach high signal-to-noise ratio, giving therefore fundamental information about the characteristics of the signal itself, precious to build realistic sky models. Nevertheless, new data at intermediate frequencies are needed, in order to better characterize the synchrotron SED, better constrain the curvature of the spectral index, and possibly identify the presence of frequency decorrelation and its physical nature. Additional data will be fundamental to understanding whether radio observations can also be used as complementary data for CMB experiments to perform component separation and to isolate the cosmological signal.
See https://lambda.gsfc.nasa.gov/product/expt/ for a list of all operating experiments.
We used the publicly available maps downloaded from the Planck Legacy Archive (PLA) website (http://pla.esac.esa.int/pla). We used the nominal LFI-30 GHz polarization maps, without applying the correction for the bandpass mismatch. We did, however, check that our results are not affected by this correction.
Variance maps are obtained from a hundred noise realizations, generated as described in Sect. 4.2, after having smoothed them to get the angular resolution of 2° (FWHM).
We note that given the geometry of the portion of the sky observed by the S-PASS survey, and the latitude cut we consider, some of the sky patches may not be circular and cover a smaller sky fraction. Nevertheless, all the 184 regions we include in the analysis have fsky > 1% (before applying apodization).
Acknowledgments
The Parkes Radio Telescope is part of the Australia Telescope National Facility, which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. This work has been carried out in the framework of the S-band Polarization All Sky Survey (S-PASS) collaboration. This research was supported by the RADIOFOREGROUNDS project, funded by the European Commissions H2020 Research Infrastructures under the Grant Agreement 687312. CB acknowledges support by the INDARK INFN Initiative. We acknowledge support from the ASI-COSMOS Network (cosmosnet.it).
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, Cosmol. Nongalactic Astrophys., [arXiv:1610.02743] [Google Scholar]
- Aiola, S., Amico, G., Battaglia, P., et al. 2012, in Proc. SPIE, 8446, 84467A [NASA ADS] [CrossRef] [Google Scholar]
- Baccigalupi, C., Burigana, C., Perrotta, F., et al. 2001, A&A, 372, 8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- BICEP2 and Keck Array Collaborations 2016, Phys. Rev. Lett., 116, 031302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- BICEP2, Keck and Planck Collaborations 2015, Phys. Rev. Lett., 114, 101301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carretti, E. 2010, in ASP Conf. Ser., 438, 276 [NASA ADS] [Google Scholar]
- Carretti, E., Haverkorn, M., McConnell, D., et al. 2010, MNRAS, 405, 1670 [NASA ADS] [Google Scholar]
- Carretti, E., Crocker, R. M., Staveley-Smith, L., et al. 2013, Nature, 493, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Choi, S. K., & Page, L. A. 2015, JCAP, 12, 020 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., de Bernardis, P., Bouchet, F. R., et al. 2018, JCAP, 04, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Errard, J., Feeney, S. M., Peiris, H. V., & Jaffe, A. H. 2016, JCAP, 3, 052 [Google Scholar]
- Essinger-Hileman, T., Ali, A., Amiri, M., et al. 2014, in SPIE Conf. Ser., 9153, 1 [Google Scholar]
- Fuskeland, U., Wehus, I. K., Eriksen, H. K., & Næss, S. K. 2014, ApJ, 790, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Génova-Santos, R., Rubiño-Martín, J. A., Peláez-Santos, A., et al. 2017, MNRAS, 464, 4107 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, D., Hoover, S., Crites, A., et al. 2013, Phys. Rev. Lett., 111, 141301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&A, 100, 209 [NASA ADS] [Google Scholar]
- Hu, W., & White, M. 1997, New Astron., 2, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. E., Taylor, A. C., Aich, M., et al. 2018, MNRAS, 480, 3224 [NASA ADS] [CrossRef] [Google Scholar]
- Kamionkowski, M., Kosowsky, A., Stebbins, A. 1997, Phys. Rev. D, 55, 7368 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A. 2012, ApJ, 753, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Dunkley, J., Bennett, C. L., et al. 2007, ApJ, 665, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Keisler, R., Hoover, S., Harrington, N., et al. 2015, ApJ, 807, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Krachmalnicoff, N., Baccigalupi, C., Aumont, J., Bersanelli, M., & Mennella, A. 2016, A&A, 588, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamee, M., Rudnick, L., Farnes, J. S., et al. 2016, ApJ, 829, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Louis, T., Grace, E., Hasselfield, M., et et al. 2017, JCAP, 6, 031 [NASA ADS] [CrossRef] [Google Scholar]
- Lyth, D. H., Liddle, A. R., & Ma, C.-P. 2010, Phys. Today, 63, 49 [Google Scholar]
- Matsumura, T., Akiba, Y., Arnold, K., et al. 2016, J. Low Temp. Phys., 184, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Meyers, B. W., Hurley-Walker, N., Hancock, P. J., et al. 2017, PASA, 34, e013 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Ysard, N., Lavabre, A., et al. 2008, A&A, 490, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, T. J., & C-BASS Collaboration. 2016, in AAS Meeting Abstracts, 228, 301.04 [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2016, A&A, 594, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2016, A&A, 594, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2016, A&A, 594, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXII. 2015, A&A, 576, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXX. 2016, A&A, 586, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. L. 2017, A&A, 599, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. LIV. 2018, A&A, in press, DOI: 10.1051/0004-6361/201832888 [Google Scholar]
- Rubiño-Martín, J. A., Génova-Santos, R., Rebolo, R., et al. 2017, in Highlights on Spanish Astrophysics IX, ed. S. Arribas, A. Alonso-Herrero, F. Figueras, et al., 99 [Google Scholar]
- Sheehy, C., & Slosar, A. 2018, Phys. Rev. D, 97, 043522 [NASA ADS] [CrossRef] [Google Scholar]
- Stompor, R., Errard, J., & Poletti, D. 2016, Phys. Rev. D, 94, 083526 [NASA ADS] [CrossRef] [Google Scholar]
- Takayuki Matsuda, F., & The Polarbear Collaboration. 2017, in AAS Meeting Abstracts, 230, 304.01 [Google Scholar]
- The Polarbear Collaboration. 2014, ApJ, 794, 171 [NASA ADS] [CrossRef] [Google Scholar]
- The Polarbear Collaboration. 2017, ApJ, 848, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, B., Dunkley, J., Alonso, D., & Næss, S. 2017, MNRAS, 469, 2821 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J. F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, 55, 1830 [Google Scholar]
- Zaldarriaga, M., & Seljak, U. 1998, Phys. Rev. D, 58, 023003 [NASA ADS] [CrossRef] [Google Scholar]
- Zaroubi, S., Jelić, V., de Bruyn, A. G., et al. 2015, MNRAS, 454, L46 [NASA ADS] [Google Scholar]
All Tables
Mean value and 1σ error of the srun parameter in the different multiple bins and considered sky mask for E and B-modes.
All Figures
 |
Fig. 1. S-PASS total polarized intensity map |
| In the text | |
 |
Fig. 2. EE (left panel) and BB (right panel) power spectra of the S-PASS polarization maps computed on the set of isolatitude masks described in Sect. 2.2 (colored curves). Solid lines show the best fit curve obtained by fitting the model in Eq. (1) to the data (we note that in this figure the amplitude of Dℓ = ℓ(ℓ + 1)Cℓ/2π is plotted). Gray curves represent the polarization spectra computed on the whole sky region observed by S-PASS where the signal is strongly contaminated by the Faraday rotation effects on the Galactic plane. |
| In the text | |
 |
Fig. 3. Best fit parameters obtained by fitting the model in Eq. (1) to S-PASS polarization spectra. The color of different points refers to the different sky masks described in the text, following the same color scheme as in Fig. 2. |
| In the text | |
 |
Fig. 4. Best fit values for the synchrotron SED spectral index βs (upper panel) and PTE coefficients (lower panel), obtained by fitting the model of Eq. (2) to S-PASS, WMAP and Planck data. Different point colors and shapes refer to the different sky regions. The black line and gray area in the upper plot show the retrieved average value βs = −3.22 ± 0.08. |
| In the text | |
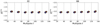 |
Fig. 5. Retrieved βs parameter obtained by fitting synchrotron SED model on simulated spectra. Point colors and shapes follows the same scheme of Fig. 4. The horizontal line corresponds to βs = −3.1, which represents the input value for our set of simulations. |
| In the text | |
 |
Fig. 6. Upper panel: amplitude of computed power spectra on data for different multipole bins and sky masks (the color scheme is the same of Fig. 4) as a function of the effective frequency. Filled points refers to EE spectra, empty ones to BB. Curves represent the best model we obtain when fitting Eq. (2) to data (solid and dashed lines for E and B-modes respectively). We note that in this figure the amplitude of Dℓ = ℓ(ℓ +1)Cℓ/2π is plotted. Lower panel: residuals of the fits normalized to the 1σ error, the dashed horizontal lines represent the 2σ level. In both upper and lower panel the points inside the gray shaded area come from the correlation of S-PASS with WMAP/Planck data which, as described in the text, are not considered in the fitting. |
| In the text | |
 |
Fig. 7. Constraint on the srun parameter describing the curvature of the synchrotron spectral index in polarization. |
| In the text | |
 |
Fig. 8. Posterior distribution of the parameters obtained by fitting the model in 3 to BB power spectra of S-PASS, Planck and WMAP in the multiple bin at ℓ ≃ 50 and for the isolatitude mask with |b| > 35°. The fit has been computed by applying a Gaussian prior on the synchrotron spectral index with βs = −3.13 ± 0.13. |
| In the text | |
 |
Fig. 9. Upper panel: synchrotron spectral index map derived as described in the text. Middle panel: 1σ uncertainty on βs. Lower panel: Significance of the spectral index variation with respect to βs = −3.2, corresponding to the value at which the distribution of the βs on map peaks (see Fig. 10). We note that colors are saturated for visualization purposes. The complete range of values is: −4.4 ≤ βs ≤ −2.5, −1.6 ≤ log10[σ(βs)] ≤ 0.03, −6 ≤ S/N ≤ 20 |
| In the text | |
 |
Fig. 10. Comparison of the normalized histograms of the synchrotron spectral index map obtained from data (indigo) and simulation (cyan line). The dashed line is at βs = −3.2, where the βs distribution peaks and also represents the reference value of the simulated case. |
| In the text | |
 |
Fig. 11. Angular power spectrum of the S-PASS βs map before (blue) and after (purple) correction for the contribution of noise. For a complete description of the figure see text in Sect. 5.3. |
| In the text | |
 |
Fig. 12. Correlation coefficient for thermal dust and synchrotron computed as in Eq. (6), using S-PASS and Planck 353 GHz polarization maps. |
| In the text | |
 |
Fig. 13. Synchrotron contamination to CMB B-modes at 90 GHz from S-PASS data, expressed in term of equivalent tensor-to-scalar ratio. In the top panels, the larger and smaller maps show the mean estimated value for rsynch and the 1σ lower and upper limit, |
| In the text | |
 |
Fig. 14. Synchrotron (violet areas) and thermal dust (cyan areas) amplitude evaluated in 184 sky regions with fsky ≃ 1% extrapolated at the indicated frequencies and compared with cosmological B-modes with given values of r (solid black lines, dashed for cosmological lensing again as predicted by Planck 2015 best fit CDM cosmologies). |
| In the text | |
 |
Fig. 15. Sky distribution of the minimum foreground emission at ℓ = 80 expressed in units of the cosmological tensor-to-scalar ratio, rFG, from S-PASS and Planck-353 data. Larger and smaller maps show the mean estimated value for rFG and the 1σ lower and upper limit, |
| In the text | |
 |
Fig. 16. Sky distribution (left panel) and histogram (right panel) of the frequency corresponding to rFG in Fig. 15. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



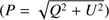
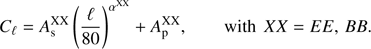
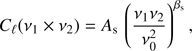
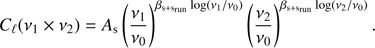
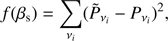
![$ {\tilde P_{{\nu _i}}} = \sqrt {{{\left[ {{Q_{2.3}}{{\left( {\frac{{2.3}}{{{\nu _i}}}} \right)}^{{\beta _{\rm{s}}}}} + n_{{\nu _i}}^{\rm{Q}}} \right]}^2} + {{\left[ {{U_{2.3}}{{\left( {\frac{{2.3}}{{{\nu _i}}}} \right)}^{{\beta _{\rm{s}}}}} + n_{{\nu _i}}^{\rm{U}}} \right]}^2}} , $](/articles/aa/full_html/2018/10/aa32768-18/aa32768-18-eq23.gif)