| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731833 | |
| Published online | 12 February 2018 | |
Clustering the Orion B giant molecular cloud based on its molecular emission⋆
1 ICMM, Consejo Superior de Investigaciones Cientificas (CSIC), 28049 Madrid, Spain
2 LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, 92190 Meudon, France
e-mail: emeric.bron@obspm.fr
3 LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, École normale supérieure, 75005 Paris, France
4 IRAM, 300 rue de la Piscine, 38406 Saint Martin d’Hères, France
5 Laboratoire d’astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, allée Geoffroy Saint-Hilaire, 33615 Pessac, France
6 Univ. Grenoble Alpes, IRAM, 38000 Grenoble, France
7 Joint ALMA Observatory (JAO), Alonso de Cordova 3107 Vitacura, Santiago de Chile, Chile
8 National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
9 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
10 School of Physics and Astronomy, Cardiff University, Queen’s buildings, Cardiff CF24 3AA, UK
11 Maison de la Simulation, CEA-CNRS-INRIA-UPS-UVSQ, USR 3441, Centre d’étude de Saclay, 91191 Gif-Sur-Yvette, France
Received: 25 August 2017
Accepted: 2 October 2017
Context. Previous attempts at segmenting molecular line maps of molecular clouds have focused on using position-position-velocity data cubes of a single molecular line to separate the spatial components of the cloud. In contrast, wide field spectral imaging over a large spectral bandwidth in the (sub)mm domain now allows one to combine multiple molecular tracers to understand the different physical and chemical phases that constitute giant molecular clouds (GMCs).
Aims. We aim at using multiple tracers (sensitive to different physical processes and conditions) to segment a molecular cloud into physically/chemically similar regions (rather than spatially connected components), thus disentangling the different physical/chemical phases present in the cloud.
Methods. We use a machine learning clustering method, namely the Meanshift algorithm, to cluster pixels with similar molecular emission, ignoring spatial information. Clusters are defined around each maximum of the multidimensional probability density function (PDF) of the line integrated intensities. Simple radiative transfer models were used to interpret the astrophysical information uncovered by the clustering analysis.
Results. A clustering analysis based only on the J = 1–0 lines of three isotopologues of CO proves sufficient to reveal distinct density/column density regimes (nH ~ 100 cm-3, ~500 cm-3, and >1000 cm-3), closely related to the usual definitions of diffuse, translucent and high-column-density regions. Adding two UV-sensitive tracers, the J = 1–0 line of HCO+ and the N = 1–0 line of CN, allows us to distinguish two clearly distinct chemical regimes, characteristic of UV-illuminated and UV-shielded gas. The UV-illuminated regime shows overbright HCO+ and CN emission, which we relate to a photochemical enrichment effect. We also find a tail of high CN/HCO+ intensity ratio in UV-illuminated regions. Finer distinctions in density classes (nH ~ 7 × 103 cm-3, ~4 × 104 cm-3) for the densest regions are also identified, likely related to the higher critical density of the CN and HCO+ (1–0) lines. These distinctions are only possible because the high-density regions are spatially resolved.
Conclusions. Molecules are versatile tracers of GMCs because their line intensities bear the signature of the physics and chemistry at play in the gas. The association of simultaneous multi-line, wide-field mapping and powerful machine learning methods such as the Meanshift clustering algorithm reveals how to decode the complex information available in these molecular tracers.
Key words: astrochemistry / ISM: molecules / ISM: clouds / ISM: structure / methods: statistical / ISM: individual objects: Orion B
Data products associated with this paper are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/610/A12 and at http://www.iram.fr/~pety/ORION-B
© ESO, 2018
1. Introduction
The interstellar medium (ISM) is made of several physical/chemical phases: dense vs. diffuse gas, hot vs. cold gas, ionised, atomic, or molecular gas, far-UV (FUV)-illuminated vs. FUV-shielded gas, and gravitationally bound vs. free-floating gas. The ISM molecular composition is particularly sensitive to the changes that affect the gas and dust when they cycle between these different phases. Wide-field mapping of the line emission of many molecules sensitive to different physical processes could thus enable one to segment giant molecular clouds (GMCs) into regions belonging to distinct physical/chemical phases, so that we can then study the physics and chemistry of these regions in detail. Moreover, understanding the prevalence of these different phases inside a given molecular cloud, and learning how to disentangle their relative contributions to each molecular tracer is of interest to interpret the spatially unresolved molecular emission in extragalactic studies.
The advent of wide-band high-spectral-resolution spectrometers associated to future multi-beam receivers in the (sub-)millimetre domain will enable radio-astronomers to easily map the emission of many lines from tens of species over tens of square degrees on the sky. The pioneer ORION-B project (Outstanding Radio-Imaging of OrioN-B, PI: J. Pety and M. Gerin) currently uses the IRAM-30m/EMIR spectrometer to image about 4.5 square degrees of the Southern part of the Orion B molecular cloud at typical spectral resolutions of 0.6 km s-1 and an angular resolution of 26′′ (i.e.~50 mpc or ~104 AU at the distance of Orion B: 400 pc, Menten et al. 2007; Schlafly et al. 2014) and a typical sensitivity of 0.1 K over almost all of the 3 mm atmospheric window.
This paper is part of the first series of papers based on the already acquired dataset that covers about 1 square degree of the Orion B molecular cloud surrounding the Horsehead nebula, NGC 2023, and NGC 2024, in the 84−116 GHz frequency range. Pety et al. (2017) introduce the molecular anatomy of the Orion B GMC, including relationships between line intensities and gas column density or FUV radiation field, and correlations between selected lines and line ratios. They obtain a dust-traced gas mass that is less than approximately one third of the CO-traced mass, using the standard X CO conversion factor. The presence of overluminous CO can be traced back to the dependence of the CO intensity on the gas kinetic temperature, which in turn is affected by the FUV illumination (photo-electric heating). While most lines show some dependence on the UV radiation field, CN and C2H are found to be the most sensitive. Moreover, dense cloud cores are almost exclusively traced by N2H+. Other traditional high-density tracers, such as HCN(1–0) or HCO+(1–0), are also easily detected in extended translucent regions at a typical density of about 500 H cm-3. Gratier et al. (2017) propose a first multi-line approach applying principal component analysis (PCA; Jolliffe 2002) on 12 of the brightest lines (integrated over a narrow velocity range) to reveal the pattern of correlations between the different tracers. This approach emphasises three clear trends: 1) the line intensities are well correlated with the column density, that is, the more matter along the line of sight, the brighter the lines; 2) CCH, CN, HCN are correlated with the FUV (<13.6 eV) irradiation (while N2H+ and the CO isotopologues are anti-correlated); and 3) the PCA method confirms the known anticorrelation between N2H+ and CO in dense cores. Finally, the 13CO position-position-velocity cube has been used by Orkisz et al. (2017) to show that solenoidal motions clearly dominate over the observed field of view, in agreement with the low star formation efficiency measured in Orion B (Lada 1992; Carpenter 2000; Megeath et al. 2016).
In this paper, we take a further step to characterise the different ISM phases from a multi-line wide-field dataset. The basic idea is similar to remote sensing in Earth studies (e.g. Inglada et al. 2017) which tries to classify environments (forests, deserts, mountains, oceans, etc.), based on the dominant colour they emit. In other words, we wish to segment the dataset into a small (yet unknown) number of classes that have a well defined physical or chemical meaning, based on their molecular emission. This goal requires the use of data-mining techniques in order to go beyond a tracer-by-tracer analysis, and take advantage of the full information hidden in the joint variations of the different tracers. Classification techniques are divided into two categories. Supervised ones use known examples of the desired classes to learn how to automatically classify new observations. They thus require a priori independent knowledge of the physical or chemical properties of the different ISM phases. These approaches will be explored in future papers. In contrast, clustering, which is an unsupervised technique, aims to reveal how the data points naturally group themselves into distinct clusters of points with similar properties, hinting at the existence of different physical or chemical regimes. This is the approach that we adopt in this paper.
Traditional segmentation approaches in GMC studies typically segment the map of emission of a single tracer into constitutive clumps (Stutzki & Guesten 1990; Williams et al. 1994; Rosolowsky & Leroy 2006; Colombo et al. 2015). These methods use in one way or another the topology (contiguity) of the emission in the position-position-velocity space, sometimes associated with additional physical properties such as the virial state. Their goal is thus to separate the spatial components of a GMC. In contrast, we here propose to work on multi-dimensional probability density distributions (PDFs) of the line integrated intensities. The PDF shape can indeed show distinct components, which can reveal distinct physical/chemical regimes, and which we want to automatically separate. For instance, in the Hertzprung-Russell (HR) diagram, different branches in the colour vs. magnitude plot correspond to different stages of stellar evolution (main sequence, giant branch, etc.). However, while recognising structure by eye is possible in two-dimensional (2D) datasets, direct visualisation of the data becomes difficult in higher dimension. Simple 2D projections for each pair of line intensities do not necessary reveal all the existing structure, and clustering algorithms become necessary. In the case of the ORION-B dataset, Gratier et al. (2017) show that understanding the physics and chemistry underlying the extended molecular line emission requires a multi-dimensional analysis of the data. To our knowledge, clustering a GMC based on its (multi-molecule) molecular emission similarity rather than spatial (or PPV) contiguity has never been done before.
This paper is organised as follows. In Sect. 2, we present the data used in our analysis. We then explain the clustering algorithm that we chose to use in Sect. 3. This clustering method is first applied to the most widely observed lines in the millimetre wave domain, that is, the J = 1 → 0 lines of three CO isotopologues (12CO, 13CO, and C18O) in Sect. 4. Section 5 then discusses the additional results obtained when adding the ground-state transitions of HCO+ and CN to the analysis, whose intensities are known to be related to the FUV illumination. We discuss the benefits and limits of the method in Sect. 6. We present our conclusions in Sect. 7.
2. Data
2.1. IRAM-30m observations
Pety et al. (2017) present in detail the acquisition and data reduction of the dataset used in this study. In short, the data were acquired at the IRAM-30m telescope by the ORION-B project from August 2013 to November 2014. The frequency range from 84 to 116 GHz was completely sampled at 200 kHz spectral resolution. Such a large bandwidth allowed us to image over 20 chemical species at a median sensitivity of 0.1 K (main-beam temperature) per channel. As opposed to several small bandwidth mappings, the spectral lines in this survey are observed in only two tunings covering 16 GHz each. They are thus well inter-calibrated, which gives an unprecedented spectral accuracy for such a large field of view. The intensity dynamic range reaches ~720.
The field of view presented covers 0.8° × 1.1° towards the Orion B molecular cloud part that contains the Horsehead nebula, and the Hii regions NGC 2023, NGC 2024, IC 434, and IC 435. The angular resolution ranges from 22.5 to 30.5′′. The position-position-velocity cubes of each line were smoothed at a common angular resolution of 31′′ to avoid resolution effects during the comparison. At a distance of 400 pc (Menten et al. 2007), the sampled linear scales range from ~50 mpc to ~8 pc.
The observations provided a position-position-frequency cube of 315 × 420 × 160 000 pixels, each pixel covering 9′′ × 9′′ × 0.5 km s-1 (Nyquist sampling at the highest frequency, i.e.12CO(1–0) at 115.27 GHz).
We here study maps of line integrated intensities. Lines are detected over quite different velocity ranges. Using a large velocity range would artificially increase the noise for most of the lines, while adapting the velocity range to each line could bias the comparisons. We thus focus on a narrow velocity range where the bulk of the gas emits. While Gratier et al. (2017) computed for each line the mean of three 0.5 km s-1 velocity channels around 10.5 km s-1, we use here a more common radioastronomical approach, which is to integrate the line intensity profile. We here integrate over the [9,12 km s-1] velocity interval where the main velocity component of the Orion B cloud sits (see Sect. 2.5 of Pety et al. 2017). To first order, both sets of maps are proportional to one another (the respective velocity ranges differ slightly).
2.2. Herschel observations
 |
Fig. 1 PDFs of the dust visual extinction (top left), the dust temperature (top right), the deduced approximate gas volume density (bottom left), and the deduced FUV illumination (bottom right) in the observed field of view. |
In order to get independent constraints on the physical conditions in the Orion B cloud, we use the dust continuum observations from the Herschel Gould Belt Survey (André et al. 2010; Schneider et al. 2013) and from the Planck satellite (Planck Collaboration 2011). The fit of the spectral energy distribution by Lombardi et al. (2014) gives us access to the spatial distributions of the dust opacity at 850 μm and of the dust temperature. As in Pety et al. (2017), we converted τ850 μm to visual extinctions using AV = 2.7 × 104τ850 mag. The top panels of Fig. 1 show the PDF of the dust visual extinction and temperature.
The AV PDF shows three distinct peaks, indicating that the field of view samples three different regimes: AV = 1−2, 2−6, and ≥ 6. These regimes are consistent with the usual distinction between diffuse, translucent, and high-column-density regions (Snow & McCall 2006). As in Pety et al. (2017), we use NH/AV = 1.8 × 1021 cm-2/ mag as conversion factor between visual extinction and hydrogen column density: NH = NHI + 2NH2. In addition, we propose a conversion from the column density to an approximate volume density map. The procedure is discussed in detail in Appendix A. In summary, we assume a rough isotropy of the cloud (similar dimensions along the line of sight and in the plane of the sky) to deduce an estimate of the average hydrogen density along each line of sight as follows. For a given column density value x, we consider the region where NH ≥ x. We then estimate the line-of-sight depth l of this region from its plane-of-the-sky surface S as 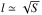 (using our isotropy assumption). We finally assign the approximate volume density nH = x/l to the pixels where NH = x.
(using our isotropy assumption). We finally assign the approximate volume density nH = x/l to the pixels where NH = x.
The resulting approximate volume density PDF is shown in the bottom-left panel of Fig. 1. The three distinct AV regimes correspond to three volume density regimes: one low-density peak close to 102 cm-3 corresponds to diffuse gas, a second peak covering the range 300−800 cm-3 is associated to the translucent gas, and a third smaller peak slightly above 103 cm-3 with a long tail extending up to a few 106 cm-3 corresponds to denser gas. The values found after our conversion are consistent with the usual orders of magnitude for diffuse, translucent, and denser gas. More quantitatively, Appendix A shows that our estimation of the volume density is valid in a statistical way with a bias of a factor of 3 at most and a typical scatter of one order of magnitude, when compared with volume density estimates from the literature that make different hypotheses. The deduced values of nH are rough estimates that should not be trusted beyond order-of-magnitude comparisons. However, this method reproduces the observed range of densities fairly well, indicating that the shape of the PDF is also approximately correct.
The Tdust PDF shows a less marked multi-peak structure with a sharp first peak at ~22 K, a small secondary peak at ~25 K and a shallow third peak at ~27 K. A first steep tail extends up to ~33 K, followed by a second flatter tail (reaching values up to 100 K). These two tails are indicative of highly FUV-illuminated regions. Pety et al. (2017) converted the dust temperature map into an approximate map of the FUV radiation field G0 in units of the Habing interstellar standard radiation field (ISRF; Habing 1968), using the simple approximation of Hollenbach et al. (1991)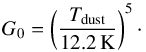 (1)Shimajiri et al. (2017) compared this estimation with another estimation directly using the far infra-red intensities at 70 and 100 μm. Both estimates agree within 30%. The PDF of log (G0) is shown as the bottom right panel of Fig. 1 and is very similar to the dust temperature PDF (as the conversion is a simple power law). As mentioned before, the main peak is close to 20 times the ISRF while the tail extends up to several thousand times the ISRF. As for our estimate of nH, the deduced values of G0 should only be trusted at order-of-magnitude levels.
(1)Shimajiri et al. (2017) compared this estimation with another estimation directly using the far infra-red intensities at 70 and 100 μm. Both estimates agree within 30%. The PDF of log (G0) is shown as the bottom right panel of Fig. 1 and is very similar to the dust temperature PDF (as the conversion is a simple power law). As mentioned before, the main peak is close to 20 times the ISRF while the tail extends up to several thousand times the ISRF. As for our estimate of nH, the deduced values of G0 should only be trusted at order-of-magnitude levels.
3. The Meanshift clustering method
From a mathematical viewpoint, the data are a set of points characterised by their two sky coordinates and the integrated intensities of D molecular lines. The dataset thus lies in a space of D + 2 dimensions. As discussed before, we aim to cluster the datapoints based on their molecular emission only, and not their spatial proximity. For clarity, we thus separate the data space into two parts: 1) the usual position space; and 2) the line space of dimension D spanned by the molecular line intensities. Clustering will only be done in the line space, ignoring the location of the pixels in the position space. After a non-exhaustive discussion of methods that segment the data based on their multi-dimensional PDF, we describe the Meanshift algorithm and the implementation used in this paper.
3.1. The two families of PDF-based clustering methods
We are interested in clustering methods that aim to separate components in the (multi-dimensional) PDF of the data. Two families of such methods can be defined. The first family assumes that the data PDF can naturally be decomposed into components of some given functional form, for example, Gaussian functions, controlled by free parameters. These methods are thus called parametric approaches. The complete dataset is assumed to be a mixture of several components, with the same functional form but different values for the control parameters. These algorithms are thus usually called mixture models (see Bishop 2006, Chap. 9). This approach has two main drawbacks. First, the number of free parameters tends to increase quickly with the dimension of the problem, resulting in a difficult and often degenerate optimisation. To alleviate this problem, restrictions are imposed on the free parameters. For instance, assuming Gaussian components and forcing them to all have the same scalar covariance matrix (thus forcing spherically symmetric clusters of equal size) yields the K-means algorithm, one of the most used clustering algorithms. Second, the assumption of a functional PDF form is a strong a priori that can bias the clustering when this form is inadequate for the studied data. More flexible functional forms reduce this problem but result in more free parameters. In this family, a compromise has to be made between the flexibility of the assumed functional PDF form and the number of free parameters.
The second family takes a data-driven approach, by defining clusters around local maxima of the data PDF. Each cluster is thus a region of high density in the line space, separated from the other clusters by regions of lower density. This definition has two advantages: 1) It allows to capture any shape of the PDF of the clusters (possibly curved and elongated); and 2) The number of clusters is determined automatically from the data. Data clusters must however create a maximum in the PDF to be detected. A small group of datapoints blended in the tail of another more common cluster might thus not be detected. The two most famous algorithms in this family take a different approach to finding the high-density regions in the line space. First, the DBSCAN algorithm (Ester et al. 1996) uses a graph-based approach to find high-density regions, but it assumes a similar density of points inside all clusters. Second, the Meanshift algorithm (Comaniciu & Meer 2002) searches for the maxima of the data PDF using a kernel-based approach. We choose to use the Meanshift approach, as it can detect clusters that have both different sizes and different densities. Moreover, its direct link to the data PDF eases the interpretation of the clusters. The following section describes this algorithm in detail.
3.2. The Meanshift algorithm
3.2.1. General description
The Meanshift algorithm (see Comaniciu & Meer 2002 for more details) associates each data point to the closest local maximum of some empirical estimate of the PDF. The algorithm iteratively climbs up the slope of the PDF starting from each of the datapoints. The set of datapoints converging to the same PDF maximum constitutes a cluster.
The algorithm is based on the same concept as the Kernel Density Estimate method (Rosenblatt 1956; Parzen 1962), which estimates the PDF of a random variable (here, the intensities) from one sample realisation. The kernel density estimator for a given set of ND-dimensional data points { xi } 1 ≤ i ≤ N is 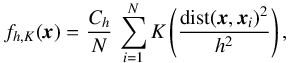 (2)where dist(x,xi) is a distance in the line space between a given vector x and the vector xi associated to the ith datapoint (both are vectors of line intensities), K is the smoothing kernel (a non-negative decreasing function of R+), h is the bandwidth of the smoothing and Ch a normalisation constant. The kernel often has a finite support [0,1], so that the estimation of the PDF at x is only based on the datapoints that are closer to x than the bandwidth h.
(2)where dist(x,xi) is a distance in the line space between a given vector x and the vector xi associated to the ith datapoint (both are vectors of line intensities), K is the smoothing kernel (a non-negative decreasing function of R+), h is the bandwidth of the smoothing and Ch a normalisation constant. The kernel often has a finite support [0,1], so that the estimation of the PDF at x is only based on the datapoints that are closer to x than the bandwidth h.
The Meanshift algorithm avoids the estimation of the PDF itself by directly estimating the PDF gradient with the same kernel smoothing approach. By taking the gradient of Eq. (2) in the case of an Euclidean distance, and noting G(x) = −K′(x), which is a new kernel, we obtain 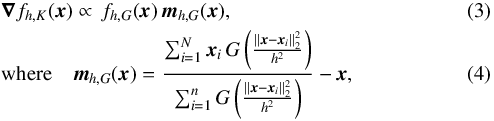 which is called the Mean Shift vector as it gives the shift from the current position x to the mean of the datapoints weighted by the kernel G centered on x. Equation (3) indicates that this Mean Shift vector gives an estimate of the relative gradient (the local PDF gradient divided by the local PDF).
which is called the Mean Shift vector as it gives the shift from the current position x to the mean of the datapoints weighted by the kernel G centered on x. Equation (3) indicates that this Mean Shift vector gives an estimate of the relative gradient (the local PDF gradient divided by the local PDF).
The following iterative algorithm is applied, starting from each of the datapoints:
-
Compute the Mean Shift vectormh,G(x) at the current estimate x of the searched local maxima.
-
Modify the current estimate by shifting it by the Mean Shift vector.
This algorithm converges to points where the PDF gradient estimate is zero, and that usually are local maxima due to its hill climbing nature. Convergence points that are closer to each other than the bandwidth h are then merged, and clusters are defined as the sets of datapoints that have converged to the same extremum. Data points lying close to local minima can sometimes stay stuck due to the associated null gradient, but the resulting unwanted clusters can easily be recognised by the very small number of datapoints they contain, and removed by assigning their datapoints to the closest clusters.
3.2.2. The FAMS implementation
In this article, we used the Fast Adaptive Mean Shift (FAMS) code described in Georgescu et al. (2003), and provided by the authors on their webpage1. This code implements several modifications to the Meanshift principle in order to improve the quality of the gradient estimate in low-density regions.
The quality of the PDF gradient estimate depends on the number of datapoints present inside the smoothing kernel. Consequently, using a fixed bandwidth results in insufficiently sampled gradient estimates in the tails of the data PDF. This leads to many artificial maxima being found in these tails, unless the bandwidth is increased. But the central parts of the PDF then risk being overly smoothed and significant maxima can be lost. To alleviate this problem, Comaniciu et al. (2001) proposed an adaptive-bandwidth Meanshift algorithm, in which a different bandwidth hi is assigned to each data point xi (h is replaced by hi in Eq. (4)). The Adaptive Meanshift Algorithm uses the simplest method to choose the bandwidth for each datapoint: taking the distance to the kth-nearest neighbour to the datapoint as the bandwidth, so that there is always roughly the same number of datapoints inside the kernel. This number of neighbours k becomes a parameter of the method to be adjusted by the user (instead of the bandwidth value in the classical Meanshift algorithm). In other words, there is a trade-off between the sampling variance and the smoothing factor to estimate the PDF: an adaptive smoothing is applied so that low-density regions are smoothed on a larger scale than high-density regions. All estimates of the PDF gradient are then equally well sampled.
Second, the FAMS implementation uses a L1 distance (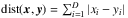 ) instead of the usual Euclidean distance (
) instead of the usual Euclidean distance (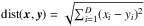 ). This allows for an additional optimisation in high dimension (Georgescu et al. 2003); but it is only an approximation of the Meanshift algorithm, as Eq. (4) assumes a Euclidean distance. Finally, the kernel used in this implementation is G(x) = (1−x)2.
). This allows for an additional optimisation in high dimension (Georgescu et al. 2003); but it is only an approximation of the Meanshift algorithm, as Eq. (4) assumes a Euclidean distance. Finally, the kernel used in this implementation is G(x) = (1−x)2.
3.2.3. In practice
The main control parameter of the Meanshift algorithm is either the bandwidth value h when using the fixed bandwidth implementation or the number of nearest neighbours k when using the adaptative bandwidth version. This parameter controls the scale on which the PDF is smoothed in both cases. We use here the adaptive bandwidth version. In each studied case, k was varied from a few hundred to a few thousand, and adjusted to increase or decrease the number of clusters found. Any cluster that contains a number of pixels that is very small compared to k is merged with the closest cluster. This can happen when the Meanshift algorithm is stuck into a local minimum of the PDF.
The smoothing part uses a spherical kernel, so that the applied smoothing is isotropic, that is, it has the same absolute bandwidth in all directions. It is thus necessary to ensure that the variability of the dataset along the different dimensions (that is the intensity dynamic of each line) is comparable. Without a linear rescaling, either the variations of the faint lines would be smoothed out by a bandwidth adapted to the bright lines or the bright lines would drive the segmentation into many small clusters when using a bandwidth adapted to the faint lines. We thus standardised the dataset (we ensured that the intensity PDF of each line has a unit standard deviation) before applying the Meanshift algorithm. Additional non-linear transformations applied to the dataset before clustering it with Meanshift would in general modify the number and positions of PDF maxima and thus affect the results. As we wish to check the amount of physical/chemical information encoded in the line intensities, we chose to only linearly standardise the data.
The clustering of our ~105 data points with D = 5 and k = 500−2000, typically takes 10 to 20 h of computation on a single standard CPU in 2017. Taking into account that our data has some redundancy (Nyquist sampling), we tested the method on a decimated dataset before getting the final results on the full dataset.
Comaniciu et al. (2001) showed that adding spatial coordinates in addition to intensities when clustering images may smooth the resulting clusters. We did not use the spatial information present in our dataset, as our focus is on grouping pixels where the intensities are similar rather that pixels belonging to the same spatial structure. We will however use the spatial coherence of the clusters found as a consistency check of the results because some amount of physical/chemical similarity is expected between neighbouring pixels.
When discussing the results, we visualise the 2D PDFs of pairs of lines (comparing the contributions of the obtained clusters) using kernel density estimation (Rosenblatt 1956; Parzen 1962) from the scikit-learn Python package (Pedregosa et al. 2011), with an Epanechnikov kernel (∝ 1−x2, optimal in terms of mean squared error, Epanechnikov 1969). This implementation uses a fixed bandwidth. This is however only used as a visualisation tool, and is independent of our Meanshift clustering analysis.
4. The CO isotopologue emission enables us to separate the diffuse, translucent, and denser gas regimes
 |
Fig. 2 Map of the clusters based on the 12CO, 13CO, and C18O (1–0) line integrated intensities. White crosses mark the positions of remarkable regions. Left: raw results. Right: clusters CO-0 and CO-1 are merged into a single cluster named 1. |
 |
Fig. 3 Comparison of the original intensity spatial distribution (top row) with the mean intensity computed for each cluster separately (bottom row). The colour scales are identical for the top and bottom rows, but they differ from one column to another. The levels shown on the bottom colour lookup table represents the mean values of the cluster intensities. The clusters were defined using the 12CO, 13CO, and C18O (1–0) lines. The circles show the typical extensions of the Hii regions and the crosses show the position of the associated exciting stars (see Pety et al. 2017, for details). |
The 12CO, 13CO, and C18OJ = 1–0 lines are amongst the most observed radio lines in molecular clouds. At constant elemental ratios of the carbon isotopes, the naive chemical interpretation suggests that the relative abundances of these three species should be identical in all lines of sight of a GMC. Moreover, the critical densities of these three lines for collisional excitation with H2 are similar (~2 × 103 cm-3), implying similar excitation conditions. Differences in optical depths should therefore be the main factor governing the intensity ratios. In this section, we ask whether or not clustering the intensities of these lines can distinguish physical regimes known to happen in the studied field of view. We thus first apply the Meanshift algorithm to a dataset consisting of the maps of the J = 1–0 lines of 12CO, 13CO, and C18O only (N = 141 050, D = 3).
After several trials for the number of neighbours in the adaptive kernel width, we chose a compromise between avoiding picking up sampling fluctuations in the PDF as artificial maxima and smoothing out physical maxima of interest (see Appendix B for a discussion of this choice). We settled on k = 1900 neighbours. In order to understand and interpret the clustering, we present in the following the spatial distribution of the clusters as well as PDFs of 1D or 2D projections of the data (that is, PDFs of single lines or pairs of lines).
4.1. Spatial distribution
We find nine clusters, whose spatial distribution is shown in Fig. 2. For the following discussion, we name these clusters CO-0 to CO-8. While our use of the Meanshift clustering does not take into account the spatial contiguity, they show very consistent spatial distributions, except for clusters CO-0 and CO-1 which share the outer region of the cloud and display a noise-like pattern. A visual inspection of the CO isotopologue PDFs shows that this distinction most likely comes from noise properties. We thus merge cluster CO-0 with cluster CO-1. We call the new cluster CO-1 and represent it in light blue. The resulting cluster map is shown on the right panel of Fig. 2.
Clusters CO-1 to CO-7 show a nested pattern highlighting successive layers from the surface to the inner parts of the cloud. These clusters are present both on the eastern and western sides that surround the inner region of the imaged field of view. However, an asymmetry between the two sides is visible in the much smaller thickness of the surface layers highlighted by the transition from clusters CO-2 to CO-5 on the western FUV-illuminated side. This is a consequence of the much steeper intensity gradients for all three CO lines on this side of the cloud. In other words, high FUV illumination has a much stronger impact on the CO intensity gradients than on the intensities themselves. Cluster CO-8 differs as it only appears towards the two Hii regions, NGC 2023 and NGC 2024, which are embedded in the south-western part of Orion B.
One way to check the quality of the clustering is to compare the spatial distributions of the original line intensities with the line intensities averaged in each cluster. This is somehow a test of the ability of the clustering method to compress the information contained in the line intensity maps while retaining the most important aspects. Taking the mean of the line intensities for each cluster conserves the total flux in the output images. Figure 3 presents such a comparison. The mean intensities (and other characteristic intensity values) of each line in each cluster are listed in Table C.1. Most of the 12CO and 13COspatial features are preserved in the clustered images, while the representation of the C18O image is not as good: some spatial features appear and others disappear. This comparison also highlights that cluster CO-8 is characterised by an increased 12CO intensity compared to its surrounding. We can note that the Horsehead pillar and the other dense clumps that emerge from the IC 434 Hii region belong to cluster CO-7 which is associated with relatively dense gas (as discussed in the following subsections).
4.2. Projected PDFs
 |
Fig. 4 PDF of the 12CO J = 1–0 line intensity, comparing the PDF of the total dataset (dashed) to the contributions of the different clusters (solid contours coloured according to the colour coding of clusters in Fig. 2). The thin vertical dashed line shows the median 4σ noise level. |
 |
Fig. 5 Contour plot of the 2D PDFs of 13CO vs. 12CO (left), and 13CO vs. C18O (right). The PDFs of the total dataset are shown as black dotted contours, while the PDFs of the individual clusters are shown as solid contours coloured according to the colour coding of clusters in Fig. 2. On the right panel clusters CO-1 to CO-5 have been grouped (grey contours) for better readability. The thin vertical and horizontal dashed lines show the median 4σ noise levels, while the coloured crosses show the positions of the PDF maxima for each cluster. |
Figure 4 shows the 12CO 1D PDF computed for the full dataset and for each individual cluster. The full dataset PDF is clearly multi-peaked with a main peak at low intensities (~2 K km s-1), two other peaks around 37 and 60 K km s-1 separated by a plateau, and several minor peaks, one of them corresponding to very bright 12CO around 90 K km s-1. In contrast, the 1D PDF of 13COand C18O (not shown here) are mostly mono-modal (only one clear peak). A good correspondence between the maxima of the 12CO PDF and most of the clusters can be seen. This indicates that 12CO plays a major role in the definition of the clusters. Cluster CO-1 corresponds to the highest and narrowest, low-intensity peak, clusters CO-3 and CO-4 constitute the 37 K km s-1 peak, cluster CO-5 contributes to the plateau between the 37 and the 60 K km s-1 peaks, cluster CO-6 and CO-7 corresponds to the 60 K km s-1 peak, and cluster CO-8 corresponds to the clear bump in the high-intensity tail of the PDF (around 90 K km s-1).
However, significant overlap between the clusters can be seen, and two clusters share the 60 K km s-1 peak. Both facts highlight the influence of the other two isotopologues on the clustering. To understand the role of 13COand C18O in the clustering, Fig. 5 shows the 2D PDFs of 13COvs. 12CO, and 13COvs. C18O as contour plots. In each case, the PDF of the full dataset is shown as black dotted contours, while the PDFs of the different clusters are coloured according to the cluster colours presented in Fig. 2. All clusters have clear separations in the 13COvs. 12CO plane, so that the overlap seen in Fig. 4 is only a projection effect. Clusters CO-1 to CO-5 clearly follow the ridgeline (the line connecting the cluster maxima, similar to the ridgeline of a mountain ridge connecting the summits) of the 2D PDF. The maxima to which they are associated are small bumps along this ridge. The separations of the basins of attraction of each of these maxima thus lie roughly orthogonally to the direction of this ridge. This is probably why the shape of CO-5 cluster looks like an anti-correlation. Clusters CO-2 to CO-5 are associated to relatively small fluctuations of the PDF along the ridge line. While statistically significant, these fluctuations might be too weak to be each attributed a physical meaning: these four clusters might thus represent a single physical category. In the 13COvs. C18O space, the PDFs of clusters CO-1 to CO-5 are nearly indistinguishable because they lie below the C18O detection limit. We thus grouped them into a single PDF (grey contours) for better readability.
While clusters CO-6 and CO-7 are undistinguishable on the 12CO 1D PDF, they are clearly separated by their 13CO intensities (cluster CO-7 having 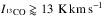 ). Cluster CO-8 is distinguished both by its high 12CO intensity and by higher 13CO/ C18O ratios at similar C18O intensity than lines of sight belonging to cluster CO-7. Clusters CO-7 and CO-8 thus correspond to a separation of the 13COvs. 12CO ridge line into two distinct ones at high intensities. Cluster CO-6 is an intermediate cluster that probably lies around the intersection of these two ridge lines. This explains why it is so extended along the 12CO axis and narrow along the 13COaxis. We discuss these cluster shapes in relation to local thermodynamic equilibrium (LTE) calculations in Sect. 4.4.
). Cluster CO-8 is distinguished both by its high 12CO intensity and by higher 13CO/ C18O ratios at similar C18O intensity than lines of sight belonging to cluster CO-7. Clusters CO-7 and CO-8 thus correspond to a separation of the 13COvs. 12CO ridge line into two distinct ones at high intensities. Cluster CO-6 is an intermediate cluster that probably lies around the intersection of these two ridge lines. This explains why it is so extended along the 12CO axis and narrow along the 13COaxis. We discuss these cluster shapes in relation to local thermodynamic equilibrium (LTE) calculations in Sect. 4.4.
4.3. Relation with volume density and FUV illumination
 |
Fig. 6 Violin plot showing the PDF of the approximate gas volume density nH, comparing the contributions of the three groups of CO clusters discussed in the text (CO-1, CO-2 to 5, and CO-6 to 8) to the PDF of the total data set. |
 |
Fig. 7 Violin plot showing the PDF of log 10(G0) for each CO cluster (blue profiles) and the median value in each cluster (red squares). |
Figure 6 shows how the clusters contribute to the PDF of the approximate volume density (see Sect. 2.2) in the form of a violin plot: for each group of clusters, the blue profiles show the volume density PDF (normalised to an identical width) and the median values are shown as red squares. We find a close correspondance between our clusters and the three peaks of the density PDF discussed in Sect. 2.2: Cluster CO-1 corresponds to diffuse gas (nH ~ 100 cm-3), the group of clusters CO-2 to CO-5 are associated to translucent gas (nH ~ 500 cm-3), while clusters CO-6, 7, and 8 correspond to denser gas (nH ≳ 1000 cm-3). The CO clusters thus reveal underlying density regimes.
Figure 7 compares the distributions of the FUV illumination for the different clusters. Clusters CO-1 to CO-6 have similar median values of G0 ~ 30−35. Moreover, a higher G0 wing is present for all these clusters. In contrast, cluster CO-7 has a significantly lower value of G0 ~ 20. This cluster thus tracks gas relatively shielded from the FUV illumination. In addition, the high-G0 wing is negligible for this cluster. Finally, cluster CO-8 has a much larger median value of G0 ~ 180, and its PDF has two broad components at typical values of G0 ~ 50 and 300, consistent with the presence of the NGC 2023 and NGC 2024 Hii regions.
In summary, clustering of the CO isotopologues allows us: 1) to distinguish three different regimes of column/volume density (diffuse, translucent, and higher density); and 2) to start distinguishing FUV-illuminated from FUV-shielded gas; but only for relatively dense gas.
4.4. Interpretation: nested CO isotopologues and higher [13CO]/[C18O] abundance ratios in FUV-illuminated dense gas
We wish to understand the physical and chemical processes that determine the variations in line intensities detected by the clustering method. We thus make the simplest possible radiative transfer model that will allow us to match the observed line intensities and ratios of the CO isotopologue lines.We then interpret the astrophysical information uncovered by the clustering of the CO isotopologues.
4.4.1. Modeling principles
The typical density over the studied field of view is ~300 H2 cm-3, and the density of at least 25% of the field (Pety et al. 2017) is larger than 2 × 103 H2 cm-3 (the typical critical density of CO J = 1–0). We thus chose to use LTE models, as we are mainly interested by the denser parts of the field of view. The clustering analysis taught us that the CO isotopologue intensities trace different ranges of hydrogen column density, and consequently of approximate volume density (see Sect. 2.2). We have thus chosen to model intensity curves for several fixed values of the CO isotopologue column densities, varying the kinetic temperature.
Figure 3 indicates that the structure of the dense inner parts of the cloud is well delineated by the C18O (1–0) emission, still visible in the 13CO(1–0) emission, and mostly hidden in the 12CO (1–0) emission. The usual interpretation is that the 12CO line is so optically thick that the outer, less dense layers along the line of sight can already produce a saturated 12CO emission. This means that the 13COand C18O (1–0) lines would be sensitive to denser, cooler gas more deeply embedded along the line of sight while the 12CO (1–0) line would to first order be mostly sensitive to the foreground, more FUV-illuminated and thus warmer gas. We thus propose to use two different values for the excitation temperature: a high value for 12CO and a lower value for 13COand C18O. This in turn implies that the model 12CO column density will be a lower limit to the total CO column density as it only represents the warm gas.
The detailed parametrisation of our modelling is described in Appendix D.
 |
Fig. 8 LTE radiative transfer models for the three main CO isotopologues. The four rows show the best match between the observations and the models for, from top to bottom, the full field of view studied here, clusters 1 to 6, and the 7th and 8th clusters. The control parameters of the family of models are written on top of each associated row. The left and middle columns show the joint histogram of the (1–0) lines of 13CO vs. 12CO, and of 13CO vs. C18O. The right column shows the joint histogram of the 13CO/ C18O vs. 12CO /13CO intensity ratios. The colour look-up tables show the number of lines of sight that fall within a given bin of the histogram. The white curves present the LTE intensity variations as a function of the 13CO kinetic temperature for different fixed 13CO opacities (0.03, 0.1, 0.3, 0.5, 0.65, 1.2, 1.75, 2.5). |
4.4.2. Observations and modeled curves
Figure 8 shows the modeled curves over the joint histograms of the 13COvs. 12CO emission (left column), of the 13COvs. C18O emission (middle column), and of the 13CO/ C18O vs. 12CO/13COline ratios (right column). The ratio vs. ratio histograms allow us to check how the models take care of the co-variations of the three studied CO lines.
The first row presents the observations for the full field of view, while the next three rows present the observations for different sets of CO clusters (from 1 to 6, the 7th one, and the 8th one, respectively). The sets of input parameters described above each row were chosen to deliver the best visual match between the modelled curves and the three associated histograms.
In all cases, only the lines of sight where the isotopologue lines considered have intensities above 4σ are used to compute the histogram. For each 13COopacity (i.e. along each white curve), the 13COand C18O excitation temperature increases clockwise and counter-clockwise for the 13COvs. 12CO, and 13COvs. C18O histograms, respectively. On the ratio vs. ratio histograms (right column), the 13COand C18O excitation temperature increases from left to right.
On the line vs. line histograms (left and middle columns), the higher the 13COopacity, the more opened the corresponding model curve. In contrast, the dependency on the column density is reduced in the ratio vs. ratio histograms, as indicated by the fact that all curves for different 13COopacities almost overlap. This is linked to the fact the line intensity is proportional to the column density to lowest order. And therefore, line ratios remove this trend.
4.4.3. Global results
The first row of Fig. 8 shows the best visual match between observations and models for the full field of view. The FWHM of the lines (2 km s-1) is the median value measured over the field of view on the 10.5 km s-1 main component of the 13COand C18O (1–0) lines. The line emission of the modelled curves is integrated over 3 km s-1 as in the observations.
The range of 13CO(1–0) opacities runs from optically thin lines (minimum: 0.03) to moderately saturated lines (maximum: 2.5). The C18O (1–0) line is always optically thin as expected from the fact that C18O (1–0) shows an excellent correlation with the visual extinction (Pety et al. 2017). The 12CO (1–0) line is almost always optically thick.
Kinetic temperatures of up to ~100 K are required to explain the low intensity part of the 13COvs. 12CO histogram. The [ 13CO ] / [ C18O] abundance ratio is larger than the expected elemental ratio value of ~8 (Wilson & Rood 1994). Both inferences can be explained by the significant FUV illumination in the observed field of view, with contributions from external and embedded Hii regions. The joint histogram of 13COvs. 12CO intensities, especially the range of 13COintensities at a given 12CO intensity, can only be explained if 12CO and 13COhave different kinetic temperatures. In contrast, the observation space can be understood with similar kinetic temperatures of the gas that emits the 13COand C18O (1–0) lines.
4.4.4. Results per CO clusters
In order to better understand how the CO clustering can distinguish different regimes of density and FUV illuminations, we now discuss the input parameters that deliver the best visual match between the modelled curves and the three histograms for three different subsets of the CO clusters.
Starting with the histograms computed for clusters CO-1 to CO-6, shown on the second rows, we obtain the same set of parameters as for the entire field of view (first row). There are only two exceptions. First, we need relatively low 13COopacities (from 0.03 to 0.5), confirming that we deal with low-opacity lines of sight. The horizontal edge between clusters CO-6 and CO-7/8 in the 13COvs. 12CO histogram closely follows a constant column density curve, confirming that it separates two column density regimes (the cut corresponds to a 13COopacity of ~0.5). Second, the minimum kinetic temperature is slightly lower than for the global fit as we are less constrained by the lower edge of the 13COvs. C18O histogram. It is unclear whether this fact is significant.
The third and fourth rows show our best matches for clusters CO-7 and CO-8, respectively. In both cases, only the high 13COopacity (0.65 to 2.5) curves are displayed. This confirms that we are in the high-column-density regime. In both cases, we need to restrict the 13COkinetic temperature range from 11–12 to 20 K. The other parameters differentiate the two clusters. First, the 12CO/13COkinetic temperature ratio is higher in cluster CO-8 than in cluster CO-7. This confirms the idea that the outer layers of the CO-8 cluster are more exposed to the FUV illumination than those of the CO-7 cluster. Finally, the [13CO]/[C18O] abundance ratio is much closer to the expected elemental abundance ratios for cluster CO-7 than for cluster CO-8. This is consistent with the idea that most of the gas in cluster CO-7 is well shielded, in complete contrast with the gas in cluster CO-8, as discussed in the following section.
 |
Fig. 9 Comparison of the clusters obtained based on the CO isotopologues alone (left) and the clusters obtained when associating the CO isotopologues to HCO+ and CN (right). In both cases, the clusters have been ordered by increasing 12CO (1–0) mean intensity. White crosses mark the positions of remarkable regions. |
4.4.5. Discussion
In all our models, we need to distinguish the kinetic temperature of the gas that emits the 12CO (1–0) line on the one hand, and the 13COand C18O (1–0) lines on the other. The effect is the most pronounced in cluster CO-8 that is highly FUV illuminated and then in clusters CO-1 to CO-6 that contain diffuse and translucent gas. This implies that the 12CO and 13CO/ C18O emissions have different spatial extents along the line of sight (as 12CO emission quickly saturates and thus only traces a limited surface layer). It is thus impossible to use the flux ratio of these lines to try to infer the [12CO]/[13CO] and [12CO]/[ C18O] abundance ratios.
In the high column/volume density clusters, 12CO is very optically thick (the saturation of the 12CO vs. AV relation is noticeable starting from AV ~ 5 as shown by Pety et al. 2017), and the variations of integrated intensities are largely caused by variations in the CO excitation temperature, which is close to the gas kinetic temperature. Cluster CO-8 shows significantly higher 12CO intensities (~90 K km s-1) than clusters CO-6 and CO-7 (~60 K km s-1) and thus traces a warmer dense gas regime. This is consistent with its location around the NGC 2024 and NGC 2023 star forming regions.
Cluster CO-8 is also distinguished from cluster CO-7 by higher 13CO/C18O intensity ratios: the median ratio is ~18 in cluster CO-8, while it is ~11 in cluster CO-7. This difference is a sign of FUV illumination as the 13CO abundance in PDRs is tightly coupled to 12CO by the isotopic fractionation reaction (Langer et al. 1984) 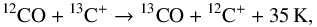 (5)which, at the gas temperatures of PDRs, does not favour any enrichment, but ensures a strong coupling between the abundances of 12CO and 13CO. In contrast, C18O in FUV-illuminated regions is formed separately from pure carbon chemistry followed by reactions of small hydrocarbons such as CH, CH2 or C2H with 18O. As a result, 13CO indirectly benefits from 12CO self-shielding while C18O is easily dissociated. This might explain the large [ 13CO ] / [ C18O] abundance ratio compared to the value expected from elemental abundances.
(5)which, at the gas temperatures of PDRs, does not favour any enrichment, but ensures a strong coupling between the abundances of 12CO and 13CO. In contrast, C18O in FUV-illuminated regions is formed separately from pure carbon chemistry followed by reactions of small hydrocarbons such as CH, CH2 or C2H with 18O. As a result, 13CO indirectly benefits from 12CO self-shielding while C18O is easily dissociated. This might explain the large [ 13CO ] / [ C18O] abundance ratio compared to the value expected from elemental abundances.
Clusters CO-7 and CO-8 thus highlight a separation of the global intensity PDF into two different tails at high column density that correspond to warm illuminated dense regions around massive star forming regions (cluster CO-8) and shielded dense gas (cluster CO-7).
5. Adding HCO+ and CN to get a better clustering of high-density and high-FUV-illumination regimes
Clustering ability is limited by the information contained in the tracers input to the algorithm. Our first application of the Meanshift clustering algorithm to the CO isotopologues proved its ability to reveal several distinct density regimes. It also hinted at a first distinction of FUV illumination regimes. However, using only the three CO isotopologues is insufficient to clearly distinguish FUV illumination effects. We thus now include in the clustering analysis the HCO+ and CN (1–0) maps together with the three CO isotopologues maps. Indeed, Pety et al. (2017) and Gratier et al. (2017) have shown that HCO+ and CN were sensitive to FUV illumination. We chose CN rather than small hydrocarbons (C2H or c-C3H2) as the latter are detected at a lower signal-to-noise ratio (S/N), making the clustering noisier. For simplicity, we only used the brightest hyperfine component of the CN (1–0) transition. In addition, these two lines have significantly higher critical densities (~2 × 105 cm-3 for HCO+ and ~2 × 106 cm-3 for CN).
We used in this case the adaptive bandwidth method with 425 neighbours. This number is a compromise between eliminating artificial clusters coming from sampling fluctuations of the PDF and retaining sufficiently fine cluster subdivisions to find the interesting physical distinctions.
5.1. Resulting spatial distribution
 |
Fig. 10 Same as Fig. 3, except that clusters were defined on the 12CO, 13CO, C18O, CN, and HCO+ (1–0) lines. |
Figure 9 compares the clusters obtained based on the CO isotopologues alone with the clusters obtained by adding CN and HCO+. Several striking facts are visible. First, the CO clustering brought 8 clusters while the new clustering identifies 19 clusters. The increase in number of clusters is related to the finer physics we wish to reveal through the increase of the dimension of the intensity space from 3 to 5 lines, at a constant number of pixels. We name the new clusters FUV-1 to FUV-19. For convenience they have been numbered by order of increasing mean 12CO intensity.
Second, the spatial edges of the FUV clusters that appear from the north-eastern to the south-western corners appear noisier. Indeed, mostly translucent gas is present in these regions, implying that CN and HCO+ are barely detected there. Third, a clear East-West asymmetry is now seen in the distributions of the clusters. Some clusters, such as FUV-2, 3, 4, 7, 8 or 11, appear mostly on regions less exposed to FUV illumination, while cluster FUV-16 is clearly associated with the NGC 2024, NGC 2023, and IC 434 Hii regions. In the previous clustering, cluster CO-8 does not tag the PDRs associated with IC 434 (the Horsehead PDR, for instance). The western edges of the CO-3 to CO-5 clusters are mostly merged now in the cluster FUV-1 that mainly contains diffuse gas. For instance, the envelope of the Horsehead nebula has been merged into FUV-1, only leaving the less familiar silhouette of the denser parts of the Horsehead visible.
Figure 10 compares the spatial distributions of the original line intensities with those of the line intensities averaged per cluster. Comparing with Fig. 3, we see that the FUV clustering reproduces the 12CO (1–0) faint intensity regimes (≤ 5 K km s-1) less well, but it much better samples the 12CO (1–0) high intensity regime (≥ 50 K km s-1) and the 13COand C18O median intensity regimes (between 10 and 50 K km s-1, and between 2 and 6 K km s-1, respectively). The better sampling of the median- to high-intensity regimes of the CO isotopologue (1–0) lines is linked to the detection of several clusters at relatively high HCO+ integrated intensity (≥ 2 K km s-1). This is particularly clear on the C18O and HCO+ compressed maps that emphasise dense regions extending south of NGC 2024 and surrounding NGC 2023. In contrast, the high-CN-integrated-intensity end (≥ 2 K km s-1) is not well sampled by the new clustering.
In summary, this clustering seems to provide most of the FUV illumination contrast between east and west. On the one hand, the FUV clustering thus provides a better data compression in the inner dense parts and in the FUV-illuminated regions; on the other, the shapes of the Horsehead and of the western illuminated edge are less well reproduced.
 |
Fig. 11 Left: 1D PDF of the HCO+ (1–0) line intensity, comparing the full dataset PDF (thick dashed black line), the contribution of each of the groups defined in Sect. 5.2 (coloured thick lines), and the contribution of each individual cluster (thin coloured lines). The cluster contributions are coloured according to the group to which they belong. For readability, we have separated groups HCO+-1 to HCO+-4 and their constitutive clusters (left panels) and groups HCO+-5 to HCO+-7 and their constitutive clusters (right panels). Right: map of the 7 groups resulting from the grouping of consecutive clusters described in the text (Sect. 5.2). |
While the 19 clusters are statistically significant, interpreting all of them is difficult. Indeed, clusters with extreme behaviour have relatively clear physico-chemical interpretations but they are separated in the line space by clusters with intermediate properties that reflect subtler, second-order distinctions. The major physical distinctions brought forward by this clustering are thus best discussed in terms of groups of clusters. Moreover, we wish to understand the first-order roles of the HCO+ and CN (1–0) lines in the classification. We thus group the clusters in two ways. We group together clusters with similar most probable intensities of HCO+ or CN, respectively, ordered by increasing values. Our goal is to keep the minimum number of groups needed to visualise the physico-chemical regimes first brought forward by each line.
5.2. HCO+-based grouping and high-density regimes
We first constitute groups based on the HCO+ intensities in each cluster following the numerical recipe explained in the previous section.
5.2.1. One-dimensional PDFs and spatial distribution
The left panels of Fig. 11 show the HCO+ PDF of each individual cluster, and the way we grouped them: the clusters whose most probable values (1D-PDF peaks) gather at similar integrated intensities are grouped. We end up with seven groups, named HCO+-1 to HCO+-7, whose mean integrated intensities regularly increase from 0.3 to 6.3 K km s-1. Cluster FUV-1 alone constitutes group HCO+-1 as it mostly traces diffuse gas surrounding the molecular cloud. We nevertheless note that it has a wing between 1 and 3 K km s-1 that corresponds, for instance, to the Horsehead envelope. Group HCO+-2 contains clusters FUV-2, 3 and 4, group HCO+-3 clusters FUV-6, 7, 8, and 9, group HCO+-4 clusters FUV-5, 10, 11, 13, and 15, group HCO+-5 clusters FUV-12, 16, and 17, group HCO+-6 clusters FUV-14 and 18, and finally, group HCO+-7 contains only cluster FUV-19. The characteristic intensity values (median, mean, standard deviation) of the lines in each group are listed in Table C.2.
The spatial distribution of these groups is displayed as the right panel of Fig. 11. We see that the resulting groups have a faint mean HCO+ intensity in the outer part of the cloud and that this intensity increases towards the densest parts. In comparison to the CO clustering, the CO-6 to CO-8 bright clusters are now distributed over groups HCO+-3 to HCO+-7, and clusters CO-1 to CO-5 (faint CO intensity) are distributed over the groups HCO+-1 and HCO+-2. This suggests that the HCO+ (1–0) line is better at discriminating higher-density regimes than the CO (1–0) lines, even though about half of the HCO+ flux over the observed field of view is coming from diffuse and translucent regions (Pety et al. 2017). Finally, the boundaries of some groups are close to the CO clustering results, indicating that CO isotopologues still play an important role in defining some of the groups. For instance, the boundary between the HCO+-4 and HCO+-5 groups is similar to the boundary between clusters CO-7/8 and CO-6.
5.2.2. Two-dimensional PDFs
 |
Fig. 12 Contour plot of the 2D PDFs of C18O vs. 13CO (left) and C18O vs. HCO+ (right). The PDFs of the total dataset are shown as black dotted contours. The contributions of the 7 groups resulting from the grouping discussed in the text are shown in contours coloured according to Fig. 11 (right). In addition, the PDF maximum of each group is shown as a cross with the same colour as the group. |
To further understand the relative roles of the CO isotopologues and HCO+, we show in Fig. 12 the 2D-PDFs of 13CO vs. C18O (left) and HCO+ vs. C18O (right), which we found to be the most informative among the possible pairs of lines. The first striking impression is that the groups overlap considerably in both 2D PDFs. However, some groups clearly separate in one of the 2D PDFs but not in the other. For instance, while groups HCO+-4 and 6 strongly overlap in the (HCO+ vs. C18O) PDF, they are cleanly separated in the (13CO vs. C18O) PDF. Finding the right 2D projection to reveal cluster separations quickly becomes impossible. Moreover, this 2D projection might not even exist when the clusters are not linearly separable; for example, when one cluster is completely surrounded by another one. We have to rely on the Meanshift algorithm to reveal information about the morphology of the complete PDFs (maxima and their associated basins of attraction) that we cannot otherwise directly visualise.
The groups form a sequence that mostly follows a single trend with increasing line intensities. This is better visualised when trying to connect the crosses that represent the group mean intensities. Group HCO+-5 only partially follows this trend: a part of it (actually mostly cluster FUV-16) is overluminous in HCO+ at constant C18O intensity. This is linked to the sensitivity of the HCO+ (1–0) line to the FUV illumination (cf. the following section).
5.2.3. Link with volume density and FUV illumination
 |
Fig. 13 Violin plots showing the PDF (blue profiles) and median values (red squares) of the approximate volume density nH for each HCO+-group, and for the full map (label “Total”). |
 |
Fig. 14 Violin plots showing the PDF (blue profiles) and median values (red squares) of the FUV illumination G0 for each HCO+-group. |
 |
Fig. 15 Left: 1D PDF of CN (1–0) line intensity, comparing the full dataset PDF (thick dashed black line), the contribution of each of the groups defined in Sect. 5.3 (coloured thick lines), and the contribution of each individual cluster (thin coloured lines). The contributions of clusters are coloured according to the group to which they belong. For readability, we have separated groups CN-1 and CN-2 and their constitutive clusters (top panel) and groups CN-3 to CN-5 and their constitutive clusters (bottom panel). Right: map of the 5 groups resulting from the grouping of consecutive clusters described in the text (Sect. 5.3). |
As shown in Gratier et al. (2017), the main underlying parameter contributing to intensity variations across our maps is the gas column density. The single trend highlighted here could thus to first order be associated with column density variations and thus approximate volume density variations as discussed in Sect. 2.2. Figure 13 shows the PDF and median value of the volume density in each group (violin plots). We indeed see that the HCO+-groups correspond to increasing ranges of volume densities. On the one hand, the first five HCO+-groups contribute to the three main peaks of the approximate volume density PDF: the HCO+-1 group corresponds to the diffuse gas peak, the HCO+-2 and 3 groups dominate the translucent gas peak, and the HCO+-4 and 5 groups contribute to the denser gas peak. On the other hand, groups HCO+-6 and 7 are located in the high-density tails.
While part of the distinction is linked to the underlying existence of the three density regimes, the distinction between groups HCO+-6 and 7 hints at the existence of higher-density regimes. Their rarity makes them only barely noticeable as bumps in the density PDF. This distinction is probably the result of an excitation effect. Indeed, their typical volume densities (probably underestimated as they are averaged along the line of sight) are 7 × 103, and 4 × 104 cm-3, respectively. These values approach the critical density of HCO+ for collisional excitation with H2 (~105 cm-3). We thus probably experience a transition from a weak excitation regime (Liszt & Pety 2016) towards a regime closer to the usual thermalised excitation.
Figure 14 shows the PDF and median value of the FUV illumination for each group. In contrast to the density, no clear separation of the groups in terms of FUV illumination is visible, except for the fact that HCO+-5 has a much broader G0 distribution than the other groups. The HCO+ grouping thus does not cleanly capture distinctions only related to FUV illumination, even though the complex behaviour of HCO+-5 in the 2D PDFs of the line intensities is likely related to the presence of a mixture of FUV illumination (varying by more than one order of magnitude) in this group. This is not a property of the initial 19 clusters but of the grouping, as is shown in the following section.
5.3. CN-based grouping and FUV illumination regimes
We now present the second grouping of the clusters, based on their CN intensities.
5.3.1. One-dimensional PDFs and spatial distribution
The left panels of Fig. 15 show how the CN PDF of the individual clusters contributes to the PDF of their group. After sorting them by increasing CN mean intensity, we merged the first six clusters into group CN-1 (clusters FUV-1, 2, 3, 4, 7, 8) because they correspond to regions where CN is not detected. We then merged the next seven clusters into group CN-2 (clusters FUV-5, 6, 9, 10, 11, 13, 15). The CN line is barely detected in these clusters. Groups CN-3 and CN-4 gather the next three (FUV-12, 14 and 17) and two clusters (FUV-16 and 18), respectively. The last cluster (FUV-19) is significantly brighter in CN. It thus has its own group CN-5. The characteristic intensity values (median, mean, standard deviation) of the lines in each group are listed in Table C.3.
The most striking distinction revealed by the resulting spatial distribution (see the right panel of Fig. 15) is the separation of the central regions of the cloud between groups CN-3 and CN-4; contrary to the previous cases, this separation does not show a nested pattern. The CN-3 group covers dense regions in the inner parts of the cloud. The CN-4 group appears towards the interfaces between the molecular cloud and the NGC 2024, NGC 2023, and IC 434 Hii regions. This distinction thus seems to separate FUV-shielded dense gas (group CN-3) and FUV-illuminated dense gas (group CN-4). Group CN-5 highlights smaller regions at the interface between groups CN-3 and CN-4. Groups CN-1 and 2 represent outer regions of the cloud.
5.3.2. Two-dimensional PDFs
 |
Fig. 16 Contour plot of the 2D PDFs of CN vs. C18O (left) and CN vs. HCO+ (right). The PDFs of the total dataset are shown as black dotted contours. The contribution of the 5 groups resulting from the grouping discussed in the text are shown coloured according to Fig. 15 (right). In addition, the PDF maximum of each group is shown as a cross with the same colour as the group. |
Figure 16 shows the 2D PDFs of CN vs. C18O (left panel), and CN vs. HCO+ (right panel); it compares the full dataset PDF (dashed line) with the contributions of our five groups (solid lines). Two distinct trends in the tail of the PDF are obvious on the 2D PDF of CN vs. HCO+: a low CN/HCO+ ratio corresponding to group CN-5, and a high CN/HCO+ ratio corresponding to group CN-4. The other groups lie in a low-intensity region where the two trends are blended.
This dual trend is already seen on the CN vs. C18O 2D-PDF: for groups CN-2, CN-3, and CN-5, CN increases very slowly with C18O, in a mostly linear way. In contrast, group CN-4 has higher CN intensities than the other groups, with the CN intensity increasing much faster with the C18O one; although this trend has a larger scatter.
Finally, while there is a large overlap region between groups CN-4 and CN-5 in the PDF of CN vs. HCO+, these two groups are clearly separated in the PDF of CN vs. C18O. Group CN-4 is thus observationally distinguished by an overly bright CN emission.
5.3.3. Link with FUV illumination (and volume density)
 |
Fig. 17 Violin plots showing the PDF (blue profiles) and median values (red squares) of the approximate nH (left panel) and G0 (right panel) in each of the groups CN-1 to 5. |
As a species easily detected in diffuse clouds, CN is a good tracer of FUV-illuminated gas (Snow & McCall 2006). We thus interpret the dual trend as a separation between regions where the photo-chemistry is active and regions of dense FUV-shielded molecular gas. The spatial consistency of groups CN-3 with regions of dense FUV-shielded gas and CN-4 with FUV-illuminated gas strengthens this interpretation, all the more so that spatial information is not used in the clustering analysis.
More quantitatively, Fig. 17 shows the approximate volume densities (left panel) and FUV illuminations (right panel) found for the different groups. Groups CN-3 and CN-4 have very similar volume densities (median densities of ~3 × 103 and ~4 × 103 cm-3, respectively), while the CN-1, CN-2, and CN-5 correspond to distinct ranges of volume densities (respective median densities of ~2 × 102, ~8 × 102, and ~4 × 104 cm-3). In contrast, the G0 distributions show that group CN-4 clearly has higher FUV illumination (median G0 ~ 210) than all other groups (median G0 between 15 and 30), in particular groups CN-3 and CN-5 (median G0 ~ 20 and G0 ~ 15, respectively). This confirms our interpretation that group CN-4 corresponds to FUV-illuminated (relatively) dense gas.
Groups CN-1 and CN-2 have lower approximate volume densities than groups CN-3 and CN-4. However the distribution of Tdust and therefore G0 in groups CN-1 and CN-2 overlaps with that of both groups CN-3 and CN-4. This shows that it is more difficult to separate the influence of the radiation field for low-density regions. This is related to the fact that the envelope of the Horsehead nebula has been merged into group CN-1, leaving only the less familiar silhouette of the denser parts of the Horsehead visible.
The highest-density group (CN-5) is found only in the immediate vicinity of the two star-forming regions NGC 2023 and NGC 2024 and their Hii regions. This might be a signature of compression of the molecular gas by the expansion of the Hii regions: Tremblin et al. (2014) have indeed found this process to cause bimodality in the column density PDF (on spatial scales of a few pc). The gas kinematics in these two regions was in addition found to be dominated by compressive (rather than solenoidal) motions by Orkisz et al. (2017), in contrast to the rest of the field of view.
5.3.4. Interpretation: enrichment of HCO+ and CN with respect to C18O in FUV-illuminated gas
The PDFs of HCO+ vs. C18O and CN vs. C18O show a dual regime at high C18O (1–0) intensity (cf. Fig. 12, right panel, and Fig. 16, left panel), with one regime where HCO+ and CN are overluminous relative to C18O. This latter regime is clearly associated with high FUV illumination at high volume density. We here check whether this is the sign of a chemical enrichment of HCO+ and CN in FUV-illuminated regions, using a non-LTE code (RADEX, van der Tak et al. 2007) to estimate the column densities of these species.
The modeling details and the derived column densities are described in Appendix E. For simplicity, we only model the radiative transfer for typical conditions in each group (median gas volume density, median kinetic temperature, and median line integrated intensities). As an estimate of the kinetic temperature, we take a combination of the dust temperature and the 12CO excitation temperature as in the Appendix A of Orkisz et al. (2017): we take the 12CO excitation temperature when it is above 60 K, and the maximum of the dust temperature and 12CO excitation temperature otherwise.
 |
Fig. 18 Column density ratios N(HCO+) /N(C18O) (top panel) and N(CN)/N(C18O) (middle panel) as a function of the G0/nH ratio for the five CN groups. The lower panel gives fractional abundances for each of the three species. A range of values is given for CN and HCO+ when the ionisation fraction is uncertain (with the limits being xe = 0 and xe = 1.4 × 10-4). |
Figure 18 shows the behaviour of the derived abundance ratios [HCO+]/[C18O], and [CN]/[C18O] as a function of the G0/nH parameter, which is expected to be the dominant controlling parameter of the physics and chemistry in a PDR (Hollenbach & Tielens 1997). An increase by about two orders of magnitude of the HCO+ and CN abundances relative to C18O can be seen when increasing G0/nH. The abundances relative to C18O seem to reach a constant value at high G0/nH values in both cases.
Fractional abundances for each of the three species are also computed relative to the total (dust-derived) column density NH. These abundances are shown in the lower panel of Fig. 18 as a function of G0/nH. Both the HCO+ and CN abundances steeply increase with G0/nH with G0/nH at first (up to G0/nH ~ 10-2), before saturating at a nearly constant value up to G0/nH ~ 10-1. The C18O abundance smoothly decreases with increasing G0/nH over the full range of values. This marked difference of chemical behaviour therefore explains the difference in line intensities identified by the MeanShift algorithm. The abundances of CN and HCO+ remain at a high but nearly constant value in strongly or mildly FUV-illuminated regions, while the C18O abundance decreases with increasing FUV illumination. The overbright HCO+ and CN regime found in FUV-illuminated regions is thus caused by a combination of photochemical enrichment in CN and HCO+ and photodissociation of C18O.
6. The Meanshift algorithm, an interesting clustering method: biases and data requirements
We first present why and how clustering and PCA are complementary. We then discuss the effects (noise, sampling, dimensionality) that can alter our results.
6.1. On the complementarity of clustering and principal component analyses
We chose here to use a clustering approach in order to analyse the structure of the multi-dimensional PDF of several line intensities, based on the idea that this structure can reveal interesting insights into the physics and chemistry at play. As soon as we use a dataset with more than two dimensions, visualising the structure of its PDF becomes difficult, and specific methods must be used. Each of these methods is usually focused on highlighting a particular kind of structure, and applying different methods to the same dataset thus provides complementary results.
For instance, clustering provides a complementary approach to PCA. On the one hand, PCA highlights the non-sphericity of the data by revealing the axes of strong covariance or correlation. However, PCA cannot capture non-linear patterns of co-variations between the intensities. Moreover, PCA highlights variations around a centre of the dataset (usually the mean), which might not be relevant if the data points are gathered in several natural clusters, with different centres (that is, if the PDF is multimodal). On the other hand, clustering algorithms aim at revealing any grouping of the data points in different regions of intensity space, that is, to reveal multimodality in the (multi-dimensional) PDF of the data.
By applying PCA to this dataset, Gratier et al. (2017) showed that column density, volume density, and FUV illumination are some of the underlying parameters controlling the intensity variations. And they listed the tracers that are the most affected by each of these parameters. The clustering analysis we have performed in the present study reveals, in addition, a multimodality of the line intensity PDF with modes related to the density and the FUV illumination. In the case of the CO clustering, the modes of the CO isotopologue PDF are directly related to modes of the column/volume density PDF, thus revealing the existence of distinct density regimes in the Orion B cloud. In our clustering analysis including HCO+ and CN, the transition to a photon-dominated chemistry leads to a separate mode corresponding to dense PDRs. In this case, clustering reveals a transition between two different physical/chemical regimes.
Moreover, both approaches can be used as data compression methods, in order to reduce the volume of data before applying some other very time-consuming data analysis. PCA compresses the dataset by reducing the number of variables characterising each data point, while clustering can be used as a segmentation method, discretising the possible values of each variable. Finally, these two approaches could be combined in future work. One possibility would be to decompose a multi-line PDF into separate components with simpler structure before applying PCA to each of these components. Alternatively, a PCA analysis could be performed first to eliminate irrelevant components of the data (e.g. noise), followed by a clustering analysis restricted to the relevant features deduced by the PCA.
6.2. What is the impact of noise?
The effect of the measurement noise present in our line-intensity maps on the results of the Meanshift algorithm can be understood in two ways: 1) Its effect on the data PDF, used by the Meanshift algorithm to define clusters; and 2) its effect on the attribution of a given pixel to one of the clusters.
Assuming an identical noise rms, σ, on all datapoints (a good approximation for this dataset, see Pety et al. 2017), the addition of Gaussian noise to the true variables replaces the underlying PDF by an observed PDF that is the convolution of the underlying PDF with a Gaussian of standard deviation σ. This is equivalent to a Gaussian smoothing of the PDF. This effect will mostly tend to merge some maxima if their separation is too small compared to the smoothing scale (that is, the noise level), rather than creating artificial maxima. The smoothing effect can also slightly shift the position of the extrema. But the existence of the clusters will be unaffected as long as their PDF maxima are well separated compared to the smoothing scale.
Noise also alters the boundaries between the clusters. If the true intensity values of a given pixel place it close enough to a boundary between clusters in the line space (typically closer than the noise level), adding noise can move this pixel across the border, and thus change the cluster to which it belongs. As a result, noise on the line intensities tends to make the spatial boundaries between clusters appear noisy (not forming a regular curve on the map). This effect is more pronounced in regions of the map where intensity gradients are small. In this case, pixels relatively far away from the cluster spatial boundary can still be close to the cluster boundary in the line space and thus be transferred to another cluster. On the contrary, if intensity gradients are steep at the spatial boundary, even pixels located just one or two pixels away from the spatial boundary can be far enough from the cluster boundary in the line space so that noise is unlikely to transfer them to another cluster. This effect is at play when we include CN and HCO+ which have low S/Ns on significant fractions of the map. Relatively noisy boundaries can be seen on the eastern side of the cloud while the boundaries on the western edge remain sharp (cf. Fig. 9). The intensity gradients are indeed much steeper on the western side of the cloud than on the eastern side.
6.3. What is the impact of limited sampling (field of view)?
The Meanshift algorithm estimates the PDF gradient in the line space in order to find the PDF maxima, and it needs to estimate this gradient from a finite sample (the observed dataset). There are two different aspects here. First, the observed field of view may be biased towards some values of the parameters that control the physics or the chemistry. Pety et al. (2017) showed that this is the case here, as the studied field of view has a large FUV illumination compared to the ISRF because it includes several Hii regions. In the ORION-B project, we will increase the observed field of view towards regions of lower FUV illumination to circumvent this limitation. In the meantime, our clustering analysis must be interpreted with this limitation in mind.
Second, the gradient estimate can be affected by sampling noise: a different dataset drawn from the same underlying PDF (corresponding to this specific field of view) would yield slightly different gradient estimates, and thus converge towards slightly different maxima. We chose to use an adaptive bandwidth (so that the kernel always includes the same number of datapoints), rather than a fixed bandwidth (which would give better sampled gradient estimates close to the major PDF peaks than in the tails) to reduce the impact of this effect. This ensures that the sampling noise is similar for all gradient estimations, and it avoids finding sampling-noise-induced artificial maxima in the tail of the PDF. Having at least a few hundred datapoints in the kernel generally ensures that the sampling noise has negligible effect.
However, implicitly increasing the kernel bandwidth in low-density regions of the PDF means a decreased capacity to resolve small-scale features in the PDF. As a result, PDF maxima corresponding to a small number of pixels (compared to the kernel size) might be smoothed out unless these pixels have intensities widely different from all other pixels. This means that our analysis is likely to miss specific physical or chemical regimes if they occur on too small a region of the map. This was the case in our tests where we found that dense cores are difficult to capture as a cluster with the Meanshift algorithm even when including specific dense core chemical tracers such as N2H+.
6.4. Choice of the number of molecular lines included in the analysis
In contrast to our PCA study (Gratier et al. 2017), we limited the clustering analysis to a moderate number of lines (5 at most). This choice was driven by several considerations.
The first reason is practical. As discussed in Sect. 6.2, while including low S/N line maps may change the total number of clusters, the presence of such low-S/N data always degrades the quality of the cluster boundaries. Well defined clusters with clear interfaces are only obtained in the regions where all lines have high S/N. A consequence of using several lower-brightness lines at relatively constant noise level (our observing case) is therefore a reduction of the usable pixels to the regions where all the lines have high S/N, that is the regions of highest column densities. This requirement of significant S/N for all line maps limits the usefulness of the Meanshift algorithm when applying it to a large set of lines of varying S/N. We thus restricted our study to lines showing extended emission with high S/N on a large fraction of the map.
The second reason is more fundamental. In this paper, we try to understand the physical and chemical processes that regulate the intensities of the lines used in the clustering algorithm. The clustering of the CO isotopologue ground-state line maps, complemented by the HCO+ and CN lines, showed two trends. First, the number of significant clusters increases with the number of lines because we add lines that exhibit different sensitivities to the physical or chemical processes at work. Second, the interpretation of a large number of clusters is difficult because the associated clusters have less data points implying a lower statistical significance of the trends. Moreover, it is difficult to get a good appreciation of the full distribution of the data over which the Meanshift algorithm operates in dimensions larger than two through standard 2D PDFs.
Our experience is thus that it is better to start clustering in low dimension to understand the sensitivity of the different lines to the many underlying physical and chemical processes at play in the ISM. It will then be possible to cluster higher-dimension data to get a finer segmentation that will depend on the underlying properties that need to be emphasised.
7. Conclusions
In this paper, we present a segmentation of the Orion B molecular cloud into regions of similar molecular emission, in order to reveal the different physical and chemical phases constitutive of molecular clouds. We have applied the Meanshift algorithm, a PDF-based (unsupervised) clustering algorithm defining clusters around the maxima of the PDF, to the (high-dimensional) multi-line PDF of our dataset. This is the first application of a clustering analysis based on molecular emission properties only (and not spatial proximity between pixels) to ISM data.
We first applied the clustering analysis to the maps of the three main CO isotopologue lines only. While the clustering did not take the spatial distribution of the CO emission into account, it highlighted a nested pattern from the outer edges to the innermost parts of the Orion B cloud. Comparison with an approximate volume density map showed that the clusters have increasing typical volume densities with significant grouping at densities of 100, 500, >1000 cm-3. The CO isotopologue maps alone were thus found to be sufficient to reveal the existence of the diffuse, translucent and high-column-density regimes. Simple LTE radiative transfer modelling implies that the gas emitting the 12CO (1–0) line is more extended than the gas emitting the 13CO/ C18O (1–0) lines. It is thus impossible to use the flux ratio of these lines to try to infer the [12CO]/[13CO] and [12CO]/[ C18O] abundance ratios.
In the densest regime, an additional separation of the PDF in two distinct tails was found, which we could associate to FUV-illumination effects. Comparison with LTE radiative transfer models shows that this distinction is related to the presence of a warmer 12CO-traced surface layer and higher than usual [13CO]/[ C18O] ratios, which can both be explained by the increased FUV illumination caused by the nearby Hii regions. It however proved insufficient to get a satisfactory separation of the FUV illuminated regions.
We thus added two FUV-sensitive tracers (the (1–0) lines of HCO+ and CN) to the CO isotopologues, and performed a second clustering analysis. This analysis revealed a similar separation into increasing density regimes, but captured finer distinctions at higher density (nH ~ 104 and 5 × 104 cm-3) due to the high critical density of the added tracers. Pety et al. (2017) have however shown that about half of the HCO+ flux over the observed field of view is coming from diffuse and translucent regions, implying that the use of the HCO+ line intensity as a tracer of high density gas (≳ 104 cm-3) in unresolved GMC observations is questionable.
Moreover, the clustering also revealed the existence of another clear separation of the data at high column density. On the one hand, part of the data presents a CN and HCO+ (1–0) emission that is overly bright with respect to the C18O (1–0). This data also shows a high CN/HCO+ intensity ratio. The associated lines of sight form the dense PDR regions around the star forming regions NGC 2023 and NGC 2024, and on the Orion B western edge illuminated by σ Ori (including the Horsehead PDR). On the other hand, other high-column-density lines of sight have low CN/ C18O, HCO+/ C18O, and CN/HCO+ intensity ratios. These lines of sight correspond to the FUV-shielded, dense regions in the inner parts of Orion B. Non-LTE models show that this distinction is related to a clear increase of the [HCO+]/[ C18O] and [CN]/[ C18O] abundance ratios with G0/nH.
Our clustering analysis based on the (1–0) lines of the CO isotopologues, HCO+ and CN, thus managed to both capture finer density categories in the densest regions, and to reveal the existence of two distinct chemical phases (characterised by different abundance ratios) corresponding to FUV-induced photochemistry and shielded-gas chemistry. This exposes the wealth of physical and chemical information that can be inferred from molecular tracers when powerful statistical methods (as the Meanshift algorithm) are applied to large amounts of data. One of the next steps in the ORION-B project is to stack the spectra inside each of the clusters found here, to better characterise the molecular content of each regime using the whole information available in the 3 mm band.
Acknowledgments
The authors thank the referee for his constructive comments, useful suggestions, and his very fast refereeing. E.B. post-doctoral position during this work was funded by the ERC grant ERC-2013-Syg-610256-NANOCOSMOS. This work was in part supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP, and co-funded by CEA and CNES. We thank the CIAS for its hospitality during the three workshops devoted to this project. JRG thanks the Spanish MINECO for funding support through grant AYA2012-32032. NRAO is operated by Associated Universities Inc. under contract with the National Science Foundation. This paper is based on observations carried out at the IRAM-30 m single-dish telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). This research also used data from the Herschel Gould Belt survey (HGBS) project (http://gouldbelt-herschel.cea.fr). The HGBS is a Herschel Key Programme jointly carried out by SPIRE Specialist Astronomy Group 3 (SAG 3), scientists of several institutes in the PACS Consortium (CEA Saclay, INAF-IFSI Rome and INAF-Arcetri, KU Leuven, MPIA Heidelberg), and scientists of the Herschel Science Center (HSC).
References
- Allison, A. C., & Dalgarno, A. 1971, A&A, 13, 331 [NASA ADS] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bishop, C. 2006, Pattern Recognition and Machine Learning (New York: Springer-Verlag) [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1991, ApJ, 369, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2000, AJ, 120, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Rosolowsky, E., Ginsburg, A., Duarte-Cabral, A., & Hughes, A. 2015, MNRAS, 454, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Comaniciu, D., & Meer, P. 2002, IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 603 [Google Scholar]
- Comaniciu, D., Ramesh, V., & Meer, P. 2001, in Proc. 8th Intl. Conf. on Computer Vision, 438 [Google Scholar]
- Epanechnikov, V. A. 1969, Theory of Probability and Its Applications, 14, 153 [Google Scholar]
- Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. 1996, in Knowledge Discovery and Data Mining Conference (AAAI Press), 226 [Google Scholar]
- Faure, A., & Tennyson, J. 2001, MNRAS, 325, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Babu, G. J. 2012, Modern Statistical Methods for Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
- Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., García-Burillo, S., Usero, A., et al. 2008, A&A, 492, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgescu, B., Shimshoni, I., & Meer, P. 2003, in Computer Vision, Proc. Ninth IEEE International Conference, 456 [Google Scholar]
- Goldsmith, P. F., & Kauffmann, J. 2017, ApJ, 841, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Bron, E., Gerin, M., et al. 2017, A&A, 599, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Inglada, J., Vincent, A., Arias, M., et al. 2017, Remote Sensing, 9, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Jolliffe, I. 2002, Principal Component Analysis, Springer Series in Statistics (New York: Springer-Verlag) [Google Scholar]
- Kirk, H., Di Francesco, J., Johnstone, D., et al. 2016, ApJ, 817, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Krčo, M., & Goldsmith, P. F. 2016, ApJ, 822, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, E. A. 1992, ApJ, 393, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., Spielfiedel, A., Feautrier, N., et al. 2010, J. Chem. Phys., 132, 024303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Liszt, H. S. 2012, A&A, 538, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., & Pety, J. 2016, ApJ, 823, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin-Zaïdi, C., Deleuil, M., Le Bourlot, J., et al. 2008, A&A, 484, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCauley, P. I., Mangum, J. G., & Wootten, A. 2011, ApJ, 742, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orkisz, J. H., Pety, J., Gerin, M., et al. 2017, A&A, 599, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parzen, E. 1962, Ann. Math. Statist., 33, 1065 [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Machine Learning Res., 12, 2825 [Google Scholar]
- Pety, J., Guzmán, V. V., Orkisz, J. H., et al. 2017, A&A, 599, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration, Ade, P. A. R., Aghanim, N., et al. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenblatt, M. 1956, Ann. Math. Statist., 27, 832 [CrossRef] [MathSciNet] [Google Scholar]
- Rosolowsky, E., & Leroy, A. 2006, PASP, 118, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Green, G., Finkbeiner, D. P., et al. 2014, ApJ, 786, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Shimajiri, Y., André, P., Braine, J., et al. 2017, A&A, 604, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1960, Soviet Ast., 4, 1 [NASA ADS] [Google Scholar]
- Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward-Thompson, D., Nutter, D., Bontemps, S., Whitworth, A., & Attwood, R. 2006, MNRAS, 369, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Column density and approximate volume density
 |
Fig. A.1 Steps to statistically derive an approximate volume density from the column density under the assumptions of isotropy and of nested distributions of increasing density. Panel a: spatial distribution of the column density of gas as deduced from the spectral energy distribution of the dust continuum emission. Panel b: surface area of the observed field of view that has a column density larger than a lower limit. Panel c: typical depth (square root of the previous surface) associated with a given column density. Panel d: typical volume density associated with a given column density. The contour levels in panel a and the dashed vertical lines in panels b to d take the column density values corresponding to a visual extinction of 2, 6, 18, 54, and 162 mag. |
In this section, we explore whether the assumptions of isotropy and of a nested distribution of volume density (density smoothly increasing from the outer regions to the inner parts of the cloud) can be used to derive an approximate volume density from the spatial distribution of the column density. After a discussion of the spatial and statistical distributions of the column density, we use the above assumptions to derive an approximate volume density. We then compare the derived values to previously published measures of the density in this field of view to understand the limits of the method and to estimate its accuracy.
Figure A.1 shows the spatial (panel a) and statistical (panel b) distributions of the gas column density deduced from the dust continuum emission (see Sect. 2.2). The targeted region exhibits a large range of column densities. There is slightly more than a factor of 100 between the minimum and maximum values. A hypothesis of nearly constant gas volume density would imply that the high-column-density regions should be about one hundred times deeper than the low-column-density ones, which would require an unrealistic cloud geometry. Moreover, the spatial distribution of the column density shows a nested pattern. Indeed the highest-column-density contours are surrounded by the smaller-column-density ones. This is also easily seen on the column density PDF (Fig. 1), which shows a faint tail at high column density. Higher-column-density regions must thus be less extended along the line of sight (according to our isotropy hypothesis), and as a consequence be associated with higher volume densities, at least in the statistical sense.
Assuming the simplest possible hypotheses about the spatial distribution of volume density, that is the hypothesis of no privileged direction and nested increasing volume density, we estimate the typical lengthscale l of regions with a given column density value x as the square root of the projected surface area where NH ≥ x. Pixels with NH are then given the volume density nH = NH/l. This procedure is illustrated in the last three panels of Fig. A.1. This reasoning assumes a one to one correspondence between a column density and the approximate volume density. We only expect this relationship to hold in a statistical
sense: it may not be valid pixel by pixel but we expect it to correctly represent the range of volume densities at a given column density.
In order to estimate the accuracy of this estimate, we gathered volume density estimations from the literature at positions within our field of view, and derived from a variety of different methods. From the catalogue of cores of Kirk et al. (2016) (SCUBA dust emission observations), we derived core masses from their Eq. (3) (using the background-substracted fluxes), and we complemented the mass value with their measured size to yield volume densities. We completed this sample with a few density estimates at particular positions. The volume density of the diffuse foreground gas of HD 38087 was derived by Martin-Zaïdi et al. (2008) from H2 UV absorption lines through the use of PDR models. The volume densities for two positions in NGC2024 was inferred from H2CO emission lines (McCauley et al. 2011). And the volume densities in the B33-SMM1 and B33-SMM2 cores in the Horsehead were derived from dust emission observations (Ward-Thompson et al. 2006). Figure A.2 shows our volume density estimates compared to the ones from the literature. In addition, the red points and their error bars show the average of our density estimate in log-spaced bins of the literature density values.
On average, our density estimate is within a factor of 3 of the densities from the literature, with a typical scatter of one order of magnitude. For the diffuse medium data point of Martin-Zaïdi et al. (2008), we find a density ~10 times larger. This is consistent with the typical scatter, but could also come from a bias of our estimate at low densities, as our lengthscale estimate is limited to the size of our field of view while diffuse medium might span larger scales. We note that our estimate is however qualitatively correct by predicting a diffuse-medium-like density at this position.
As an additional check, we consider a simple analytical example: a spherically symmetrical cloud whose volume density profile is 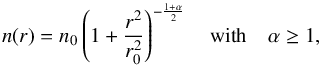 (A.1)
(A.1)
(used for instance in Krčo & Goldsmith 2016). This corresponds to an observed column density profile 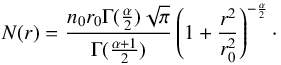 (A.2)Our simple estimate of the volume density would yield at a distance r from the cloud centre
(A.2)Our simple estimate of the volume density would yield at a distance r from the cloud centre 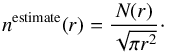 (A.3)The ratio of the two values,
(A.3)The ratio of the two values, 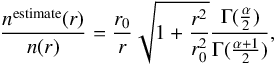 (A.4)is shown on Fig. A.3 for different values of α. Our estimation ranges from 0.8 to 2.5 times the true density value for all estimation scales larger than the typical scale r0 and it diverges when the estimation scale is much smaller than r0. This comes from the fact that the surface estimate describing the scale of the inner region goes to zero close to the centre. However, the spatial resolution of our data (60 mpc) avoids the regime r ≪ r0. Indeed, our comparison to literature values does not show any dramatic overestimation for the high-column-density pixels.
(A.4)is shown on Fig. A.3 for different values of α. Our estimation ranges from 0.8 to 2.5 times the true density value for all estimation scales larger than the typical scale r0 and it diverges when the estimation scale is much smaller than r0. This comes from the fact that the surface estimate describing the scale of the inner region goes to zero close to the centre. However, the spatial resolution of our data (60 mpc) avoids the regime r ≪ r0. Indeed, our comparison to literature values does not show any dramatic overestimation for the high-column-density pixels.
In conclusion, the method proposed here provides a reasonable estimate in a statistical sense with a bias of a factor 3 at most and a typical scatter of one order of magnitude. It can thus be trusted for order-of-magnitude comparisons. Moreover, this estimation of the volume density map is completely independent from the clustering analysis presented in this paper, and is only used to help in the interpretation of the clustering analysis.
 |
Fig. A.2 Approximate estimation of the volume density as a function of independent estimations from the literature. The solid black line shows a perfect one-to-one relationship, while the red points and their error bars show the bin averaged relationship. The horizontal and vertical error bars indicates the bin size and the interquartile interval, respectively. |
 |
Fig. A.3 Approximate density estimate divided by the true density for different analytical spherical density profiles as a function of distance to the centre. |
Appendix B: Impact of the number of neighbours on the number of clusters
 |
Fig. B.1 Variation of the number of clusters found Nclusters with the number of neighbours kneighbors in the adaptive kernel of the Meanshift algorithm, when applied to the three CO isotope lines only. |
In the Adaptive Meanshift algorithm, kneighbors controls the size of the adaptive bandwidth of the smoothing kernel: for each datapoint the bandwidth is automatically adjusted to include its kneighbors nearest neighbours. As a result, this parameter controls the degree of smoothing applied to the PDF gradient estimate, while ensuring equal sampling in the peaks and tails of the PDF.
Most of the time, increasing kneighbors will result in a decrease in the number of clusters found by the algorithm as local maxima are merged by the increased smoothing. As discussed in Sect. 6.3, too low a value of kneighbors results in finding artificial maxima caused by the sampling noise. A very large value will smooth the data PDF to a single peak with the shape of the kernel. When decreasing kneighbors from this large value, the most well separated maxima of the PDF will be distinguished first, then maxima that are weaker or close to the highest maxima.
The first maxima that appear are thus likely to correspond to the strongest physical distinctions, and the following ones to subtler and subtler distinctions (until artificial maxima caused by sampling noise start to appear). As a result, the choice of kneighbors is mostly a choice of the level of detail we want in our analysis, as long as it is large enough to get rid of sampling noise effects.
Figure B.1 shows the variation of the number of clusters found as a function of kneighbors, for the clustering analysis of the three CO isotopologue lines (cf. Sect. 4). We see a flat plateau close to 10 clusters starting from kneighbors> 1200, indicating that these clusters are more strongly separated than the ones appearing at lower values of kneighbors (they do not disappear with increased smoothing until much larger smoothing). We thus chose a value corresponding to this plateau.
Appendix C: Characteristic intensities in the clusters
Characteristic line intensities in each CO cluster: PDF maximum of the cluster, median value, mean value, and standard deviation.
Table C.1 lists characteristic intensity values of the three CO isotopologues for the clusters derived from CO isotopologues only. The values given correspond to the mean, median, standard deviation inside each cluster, as well as the most represented intensity of the cluster (i.e., the PDF local maxima). The cluster’s most represented intensity is generally fainter than the cluster median and mean. This is a natural consequence of the asymmetry of the PDFs that have extended high intensity tails.
Similarly, Table C.2 and C.3 give the characteristic intensity values (median, mean and standard deviation) for the groups of clusters HCO+-1 to 7 and CN-1 to 5.
Characteristic line intensities in each HCO+ group: median value, mean value, and standard deviation.
Characteristic line intensities in each CN group: median value, mean value, and standard deviation.
Appendix D: Details of the CO LTE modeling
Here, we describe the details of the modeling that allows us to derive the physical and chemical conditions discussed in Sect. 4.4.
Appendix D.1: Parametrization
The intensity integrated over the line profile is defined as  (D.1)with ij = 12, 13, and 18 for the 12CO, 13CO, and C18O (1–0) lines, respectively. In this equation,
(D.1)with ij = 12, 13, and 18 for the 12CO, 13CO, and C18O (1–0) lines, respectively. In this equation,  is the LTE intensity that is defined as
is the LTE intensity that is defined as  (D.2)where τij is the opacity at the line center, Tcmb = 2.73 K is the cosmic microwave background temperature, and
(D.2)where τij is the opacity at the line center, Tcmb = 2.73 K is the cosmic microwave background temperature, and 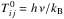 (= 5.53 K for 12CO (1–0), 5.29 K for 13CO, and 5.27 K for C18O).
(= 5.53 K for 12CO (1–0), 5.29 K for 13CO, and 5.27 K for C18O).
Assuming LTE, we will parametrize the modeled curves with increasing kinetic temperature (Tkin) at constant 13COopacity 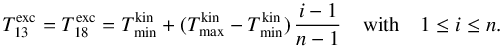 (D.3)Moreover, we will use the additional freedom to have a higher excitation temperature for 12CO, i.e.,
(D.3)Moreover, we will use the additional freedom to have a higher excitation temperature for 12CO, i.e.,  (D.4)The variation of the opacity with the temperature is computed using the opacity at 20 K as reference, i.e.,
(D.4)The variation of the opacity with the temperature is computed using the opacity at 20 K as reference, i.e.,  (D.5)
(D.5) (D.6)
(D.6)![\appendix \setcounter{section}{4} \begin{equation} \mbox{and} \quad \frac{\op{13}}{\op{18}} = \frac{N(\thCO)}{N(\CeiO)} = \frac{[\thCO]}{[\CeiO]}, \end{equation}](/articles/aa/full_html/2018/02/aa31833-17/aa31833-17-eq191.png) (D.7)where N(CO) is the column density of each CO isotopologue (in fact, a lower limit for 12CO), and [CO] is the abundance relative to H2 of each CO isotopologue. Only the I( 13CO) /I( C18O) can be interpreted in terms of relative abundances because the emission of these isotopologues is probably co-spatial, while the 12CO line is mainly sensitive to the foreground part of the emission.
(D.7)where N(CO) is the column density of each CO isotopologue (in fact, a lower limit for 12CO), and [CO] is the abundance relative to H2 of each CO isotopologue. Only the I( 13CO) /I( C18O) can be interpreted in terms of relative abundances because the emission of these isotopologues is probably co-spatial, while the 12CO line is mainly sensitive to the foreground part of the emission.
The second factor on the right-hand side of Eq. (D.1) takes care of the integration over a Gaussian line profile, including the opacity broadening term 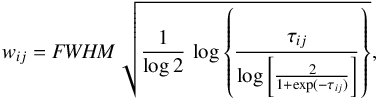 (D.8)where FWHM is the measured linewidth of the Gaussian profile for an optically thin line. As we limited the range of velocity over which we integrate the CO lines to Δv, we saturate wij as follows
(D.8)where FWHM is the measured linewidth of the Gaussian profile for an optically thin line. As we limited the range of velocity over which we integrate the CO lines to Δv, we saturate wij as follows 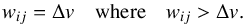 (D.9)
(D.9)
Appendix D.2: Impact of each input parameter
Here, we describe the specific influence that each input parameter has on the curves in the histograms of Fig. 8. At constant 13COopacity, a change of the line FWHM has an homothetic effect on the modeled curves in the intensity vs. intensity histograms: the higher the FWHM, the larger the amplitude of the curve. Limiting the interval of velocity over which we integrate quickly leads to a saturation of the 13COintegrated intensities. This is the reason why the upper edge of the 13COvs. 12CO histogram is relatively sharp. This effect is less obvious for the 12CO line because the opacity is so large that the line is already saturated. Saturation of the 13COemission also explains the range of observed values of CO isotopologue ratios (bottom left panel). When both 12CO and 13COget saturated the intensity ratio is mainly controlled by the ratio of the excitation temperatures, with a modest influence of the opacity broadening term.
The minimum kinetic temperature sets the lower edge of the histogram of 13COvs. C18O. Using a lower temperature would result in curves that go beyond the observed minimum 13COintensity for each given C18O intensity. The maximum kinetic temperature controls the regions of low intensities at low column density for all three isotopologues. In other words, we do not populate correctly the low intensity part of the histogram when the maximum temperature is too low.
The N( 12CO) /N( 13CO) column density ratio controls the observed lower edge of the associated intensity vs. intensity histogram. A too low value underestimates the 13COintensity at constant 12CO intensity and vice versa. In a similar way, the [ 13CO ] / [ C18O] abundance ratio controls the observed upper edge of the associated intensity vs. intensity histogram.
Finally, the ratio of the  excitation temperatures controls the 13CO“width” of the curves. A higher
excitation temperatures controls the 13CO“width” of the curves. A higher  implies both a lower and higher 13COintensity (at low and high
implies both a lower and higher 13COintensity (at low and high 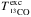 value) for the same 12CO intensity. In other words, a higher
value) for the same 12CO intensity. In other words, a higher 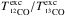 would less well describe both the lower and upper edge of the 13COvs. 12CO histogram if all other parameters stay constant. A higher
would less well describe both the lower and upper edge of the 13COvs. 12CO histogram if all other parameters stay constant. A higher 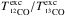 also implies a higher slope of the 13CO/ C18O vs. 12CO/13COcurves.
also implies a higher slope of the 13CO/ C18O vs. 12CO/13COcurves.
Appendix E: Details of the CN, HCO+, and C18O RADEX modeling
Here, we describe the detail of our modeling approach for deriving the HCO+ and CN abundances and abundance ratios discussed in Sect. 5.3.4.
Median gas volume density, gas temperature, C18O, HCO+, and CN integrated intensities and associated column densities derived from RADEX models for each CN group.
Appendix E.1: RADEX non-LTE radiative transfer models
The radiative transfer modeling is subtle for two reasons. First, the critical densities of C18O, HCO+, and CN (for collisional excitation with H2) differ by two to three orders of magnitude (~2 × 103, 2 × 105, and ~2 × 106 cm-3, respectively). The emission of C18O is mostly thermalized in all groups (except CN-1). In contrast, the excitation of HCO+, and CN is subthermal. We thus use a non-LTE radiative transfer approach. Second, collisions with electrons can dominate the excitation of high dipole moment species such as CN and HCO+ in regions where the electronic fraction is high enough (Black & van Dishoeck 1991; Liszt 2012; Goldsmith & Kauffmann 2017). This effect can be important for the regions of low visual extinction, e.g., groups CN-1 and to a lesser extent CN-2, and for the highly FUV-illuminated PDRs of group CN-4.
We used the RADEX code (van der Tak et al. 2007) which uses the escape probability approach of Sobolev (1960) to compute the non-LTE level populations and the emission from a region of given temperature and volume density of collision partners within a given velocity interval. The position-position-velocity data suggest to use a linewidth of 1 km s-1. The cross-section coefficients for collisional excitation are obtained from the LAMDA database2. The coefficient data for collisional excitation of C18O, HCO+, and CN with H2 were computed by Yang et al. (2010), Flower (1999), and Lique et al. (2010), respectively. The data for the excitation by electrons were computed by Faure & Tennyson (2001), Fuente et al. (2008) for HCO+, and Allison & Dalgarno (1971) for CN.
For each CN group, we ran RADEX models for the median values of the volume density and temperature corresponding to each group, and we adjusted the column densities of C18O, HCO+, and CN to best reproduce the median line intensities. As electrons may be important for the collisional excitation of high dipole moment molecules, we used two hypotheses for the electron fraction: (1) The electron fraction xe is 0 and only H2 contributes to the excitation; (2) The electron fraction is set by the ionisation of all carbon atoms and xe = 1.4 × 10-4. Case (2) was computed only for groups where this hypothesis can be relevant : CN-1, 2 and 4. For the diffuse medium of group CN-1, case (2) is a good hypothesis and we take only the corresponding column density values. In group CN-2 and CN-4 however, the electronic fraction is more uncertain, and we give a range of values corresponding to the extreme cases (1) and (2). We assumed a negligible electronic fraction in the other groups.
Appendix E.2: Uncertainties
We estimated the uncertainties on the median line intensities by two different methods. First, we used a perturbative Monte Carlo approach. We produced 1000 perturbed datasets (where Gaussian noise is added to each pixel’s intensities according to the local noise rms). We then computed the median intensities inside each group. And we finally took the standard deviation of these results as the uncertainty on the median intensity. Second, we used a bootstrapping method (Feigelson & Babu 2012). We produced 1000 bootstrapped datasets of the same size as the original one (drawing with replacement from the initial dataset). And we took the standard deviation of the medians of these datasets. Both approaches give similar uncertainties. The relative (1σ) uncertainties are below 2% for all groups and for the three molecular lines considered here.
Due to the large number of pixels in each group, the median values are highly statistically significant, even in group CN-1 where the three lines stay undetected in most pixels. However, potential unknown biases in the integrated intensities (baseline distortion, etc.) are not taken into account. As a result, the median values for group CN-1 are less reliable than for the other groups. Our estimates of the volume density and kinetic temperature are likely to suffer from global biases. We thus did not try to estimate a noise-associated uncertainty for these quantities.
Appendix E.3: Column densities
Figure E.1 illustrates how the column densities were derived from the radiative transfer models. Table E.1 lists the median input data and the output results. For C18O, the curves of all groups are roughly superimposed (thermalized emission) and the derived column densities are mostly proportional to the median intensities of the groups. In contrast, the intensity vs. column density relations are strongly dependent on the median density of the group for HCO+ and CN. For HCO+ and CN, the excitation is subthermal, and closer to the weak excitation regime of Liszt & Pety (2016). As a result, the intensity-column density relations are strongly dependent on the median volume density of the group (in the weak excitation regime, the intensity is proportional to the product of column density and volume density).
 |
Fig. E.1 Line intensity as a function of column density for non-LTE radiative transfer models at the median gas volume density and temperature for each CN group. The full and dotted lines assume a ionisation fraction of 0 and 1.4 × 10-4, respectively. The horizontal dashed lines represent the median observed intensity computed for each group. The symbols show the best column density for each group according to the RADEX models, with full circles for models with xe = 0 and open squares for xe = 1.4 × 10-4. |
All Tables
Characteristic line intensities in each CO cluster: PDF maximum of the cluster, median value, mean value, and standard deviation.
Characteristic line intensities in each HCO+ group: median value, mean value, and standard deviation.
Characteristic line intensities in each CN group: median value, mean value, and standard deviation.
Median gas volume density, gas temperature, C18O, HCO+, and CN integrated intensities and associated column densities derived from RADEX models for each CN group.
All Figures
 |
Fig. 1 PDFs of the dust visual extinction (top left), the dust temperature (top right), the deduced approximate gas volume density (bottom left), and the deduced FUV illumination (bottom right) in the observed field of view. |
| In the text | |
 |
Fig. 2 Map of the clusters based on the 12CO, 13CO, and C18O (1–0) line integrated intensities. White crosses mark the positions of remarkable regions. Left: raw results. Right: clusters CO-0 and CO-1 are merged into a single cluster named 1. |
| In the text | |
 |
Fig. 3 Comparison of the original intensity spatial distribution (top row) with the mean intensity computed for each cluster separately (bottom row). The colour scales are identical for the top and bottom rows, but they differ from one column to another. The levels shown on the bottom colour lookup table represents the mean values of the cluster intensities. The clusters were defined using the 12CO, 13CO, and C18O (1–0) lines. The circles show the typical extensions of the Hii regions and the crosses show the position of the associated exciting stars (see Pety et al. 2017, for details). |
| In the text | |
 |
Fig. 4 PDF of the 12CO J = 1–0 line intensity, comparing the PDF of the total dataset (dashed) to the contributions of the different clusters (solid contours coloured according to the colour coding of clusters in Fig. 2). The thin vertical dashed line shows the median 4σ noise level. |
| In the text | |
 |
Fig. 5 Contour plot of the 2D PDFs of 13CO vs. 12CO (left), and 13CO vs. C18O (right). The PDFs of the total dataset are shown as black dotted contours, while the PDFs of the individual clusters are shown as solid contours coloured according to the colour coding of clusters in Fig. 2. On the right panel clusters CO-1 to CO-5 have been grouped (grey contours) for better readability. The thin vertical and horizontal dashed lines show the median 4σ noise levels, while the coloured crosses show the positions of the PDF maxima for each cluster. |
| In the text | |
 |
Fig. 6 Violin plot showing the PDF of the approximate gas volume density nH, comparing the contributions of the three groups of CO clusters discussed in the text (CO-1, CO-2 to 5, and CO-6 to 8) to the PDF of the total data set. |
| In the text | |
 |
Fig. 7 Violin plot showing the PDF of log 10(G0) for each CO cluster (blue profiles) and the median value in each cluster (red squares). |
| In the text | |
 |
Fig. 8 LTE radiative transfer models for the three main CO isotopologues. The four rows show the best match between the observations and the models for, from top to bottom, the full field of view studied here, clusters 1 to 6, and the 7th and 8th clusters. The control parameters of the family of models are written on top of each associated row. The left and middle columns show the joint histogram of the (1–0) lines of 13CO vs. 12CO, and of 13CO vs. C18O. The right column shows the joint histogram of the 13CO/ C18O vs. 12CO /13CO intensity ratios. The colour look-up tables show the number of lines of sight that fall within a given bin of the histogram. The white curves present the LTE intensity variations as a function of the 13CO kinetic temperature for different fixed 13CO opacities (0.03, 0.1, 0.3, 0.5, 0.65, 1.2, 1.75, 2.5). |
| In the text | |
 |
Fig. 9 Comparison of the clusters obtained based on the CO isotopologues alone (left) and the clusters obtained when associating the CO isotopologues to HCO+ and CN (right). In both cases, the clusters have been ordered by increasing 12CO (1–0) mean intensity. White crosses mark the positions of remarkable regions. |
| In the text | |
 |
Fig. 10 Same as Fig. 3, except that clusters were defined on the 12CO, 13CO, C18O, CN, and HCO+ (1–0) lines. |
| In the text | |
 |
Fig. 11 Left: 1D PDF of the HCO+ (1–0) line intensity, comparing the full dataset PDF (thick dashed black line), the contribution of each of the groups defined in Sect. 5.2 (coloured thick lines), and the contribution of each individual cluster (thin coloured lines). The cluster contributions are coloured according to the group to which they belong. For readability, we have separated groups HCO+-1 to HCO+-4 and their constitutive clusters (left panels) and groups HCO+-5 to HCO+-7 and their constitutive clusters (right panels). Right: map of the 7 groups resulting from the grouping of consecutive clusters described in the text (Sect. 5.2). |
| In the text | |
 |
Fig. 12 Contour plot of the 2D PDFs of C18O vs. 13CO (left) and C18O vs. HCO+ (right). The PDFs of the total dataset are shown as black dotted contours. The contributions of the 7 groups resulting from the grouping discussed in the text are shown in contours coloured according to Fig. 11 (right). In addition, the PDF maximum of each group is shown as a cross with the same colour as the group. |
| In the text | |
 |
Fig. 13 Violin plots showing the PDF (blue profiles) and median values (red squares) of the approximate volume density nH for each HCO+-group, and for the full map (label “Total”). |
| In the text | |
 |
Fig. 14 Violin plots showing the PDF (blue profiles) and median values (red squares) of the FUV illumination G0 for each HCO+-group. |
| In the text | |
 |
Fig. 15 Left: 1D PDF of CN (1–0) line intensity, comparing the full dataset PDF (thick dashed black line), the contribution of each of the groups defined in Sect. 5.3 (coloured thick lines), and the contribution of each individual cluster (thin coloured lines). The contributions of clusters are coloured according to the group to which they belong. For readability, we have separated groups CN-1 and CN-2 and their constitutive clusters (top panel) and groups CN-3 to CN-5 and their constitutive clusters (bottom panel). Right: map of the 5 groups resulting from the grouping of consecutive clusters described in the text (Sect. 5.3). |
| In the text | |
 |
Fig. 16 Contour plot of the 2D PDFs of CN vs. C18O (left) and CN vs. HCO+ (right). The PDFs of the total dataset are shown as black dotted contours. The contribution of the 5 groups resulting from the grouping discussed in the text are shown coloured according to Fig. 15 (right). In addition, the PDF maximum of each group is shown as a cross with the same colour as the group. |
| In the text | |
 |
Fig. 17 Violin plots showing the PDF (blue profiles) and median values (red squares) of the approximate nH (left panel) and G0 (right panel) in each of the groups CN-1 to 5. |
| In the text | |
 |
Fig. 18 Column density ratios N(HCO+) /N(C18O) (top panel) and N(CN)/N(C18O) (middle panel) as a function of the G0/nH ratio for the five CN groups. The lower panel gives fractional abundances for each of the three species. A range of values is given for CN and HCO+ when the ionisation fraction is uncertain (with the limits being xe = 0 and xe = 1.4 × 10-4). |
| In the text | |
 |
Fig. A.1 Steps to statistically derive an approximate volume density from the column density under the assumptions of isotropy and of nested distributions of increasing density. Panel a: spatial distribution of the column density of gas as deduced from the spectral energy distribution of the dust continuum emission. Panel b: surface area of the observed field of view that has a column density larger than a lower limit. Panel c: typical depth (square root of the previous surface) associated with a given column density. Panel d: typical volume density associated with a given column density. The contour levels in panel a and the dashed vertical lines in panels b to d take the column density values corresponding to a visual extinction of 2, 6, 18, 54, and 162 mag. |
| In the text | |
 |
Fig. A.2 Approximate estimation of the volume density as a function of independent estimations from the literature. The solid black line shows a perfect one-to-one relationship, while the red points and their error bars show the bin averaged relationship. The horizontal and vertical error bars indicates the bin size and the interquartile interval, respectively. |
| In the text | |
 |
Fig. A.3 Approximate density estimate divided by the true density for different analytical spherical density profiles as a function of distance to the centre. |
| In the text | |
 |
Fig. B.1 Variation of the number of clusters found Nclusters with the number of neighbours kneighbors in the adaptive kernel of the Meanshift algorithm, when applied to the three CO isotope lines only. |
| In the text | |
 |
Fig. E.1 Line intensity as a function of column density for non-LTE radiative transfer models at the median gas volume density and temperature for each CN group. The full and dotted lines assume a ionisation fraction of 0 and 1.4 × 10-4, respectively. The horizontal dashed lines represent the median observed intensity computed for each group. The symbols show the best column density for each group according to the RADEX models, with full circles for models with xe = 0 and open squares for xe = 1.4 × 10-4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


