| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526012 | |
| Published online | 14 March 2016 | |
The VIMOS Ultra Deep Survey: Lyα emission and stellar populations of star-forming galaxies at 2 < z < 2.5⋆
1 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani,1, 40127 Bologna, Italy
3 INAF–IASF, via Bassini 15, 20133 Milano, Italy
4 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
5 University of Bologna, Department of Physics and Astronomy (DIFA), V.le Berti Pichat, 6/2 – 40127 Bologna, Italy
6 INAF–IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
7 Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre et Marie Curie, 98 bis Boulevard Arago, 75014 Paris, France
8 Institut de Recherche en Astrophysique et Planétologie – IRAP, CNRS, Université de Toulouse, UPS-OMP, 14, avenue E. Belin, 31400 Toulouse, France
9 Department of Astronomy, University of Geneva, ch. d’Écogia 16, 1290 Versoix, Switzerland
10 Geneva Observatory, University of Geneva, ch. des Maillettes 51, 1290 Versoix, Switzerland
11 Centro de Estudios de Física del Cosmos de Aragón, 44001 Teruel, Spain
12 Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., MC 249–17, Pasadena, CA 91125, USA
13 Astronomy Department, University of Massachusetts, Amherst, MA 01003, USA
14 Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching bei München, Germany
15 Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho 2–5, 790-8577 Matsuyama, Japan
16 SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
17 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
18 Instituto de Fisica y Astronomia, Facultad de Ciencias, Universidad de Valparaiso, Av. Gran Bretana 1111, Casilla 5030, Valparaiso, Chile
Received: 3 March 2015
Accepted: 11 December 2015
The aim of this paper is to investigate spectral and photometric properties of 854 faint (iAB ≲ 25 mag) star-forming galaxies (SFGs) at 2 < z < 2.5 using the VIMOS Ultra-Deep Survey (VUDS) spectroscopic data and deep multi-wavelength photometric data in three extensively studied extragalactic fields (ECDFS, VVDS, COSMOS). These SFGs were targeted for spectroscopy as a result of their photometric redshifts. The VUDS spectra are used to measure the UV spectral slopes (β) as well as Lyα equivalent widths (EW). On average, the spectroscopically measured β (–1.36 ± 0.02), is comparable to the photometrically measured β (–1.32 ± 0.02), and has smaller measurement uncertainties. The positive correlation of β with the spectral energy distribution (SED)-based measurement of dust extinction Es(B−V) emphasizes the importance of β as an alternative dust indicator at high redshifts. To make a proper comparison, we divide these SFGs into three subgroups based on their rest-frame Lyα EW: SFGs with no Lyα emission (SFGN; EW ≤ 0 Å), SFGs with Lyα emission (SFGL; EW > 0 Å), and Lyα emitters (LAEs; EW ≥ 20 Å). The fraction of LAEs at these redshifts is ~10%, which is consistent with previous observations. We compared best-fitSED-estimated stellar parameters of the SFGN, SFGL and LAE samples. For the luminosities probed here (~ L∗), we find that galaxies with and without Lyα in emission have small but significant differences in their SED-based properties. We find that LAEs have less dust, and lower star-formation rates (SFR) compared to non-LAEs. We also find that LAEs are less massive compared to non-LAEs, though the difference is smaller and less significant compared to the SFR and Es(B−V). When we divide the LAEs according to their Spitzer/IRAC 3.6 μm fluxes, we find that the fraction of IRAC-detected (m3.6 ≲ 25 mag) LAEs is much higher than the fraction of IRAC-detected narrow band (NB)-selected LAEs at z ≃ 2–3. This could imply that UV-selected LAEs host a more evolved stellar population, which represents a later stage of galaxy evolution, compared to NB-selected LAEs.
Key words: galaxies: evolution / galaxies: formation / galaxies: high-redshift
© ESO, 2016
1. Introduction
In the last decade, large numbers of star-forming galaxies (SFGs) – selected using the Lyman break color technique and/or the photometric redshift technique – were identified and studied at z ≳ 3 using deep photometric surveys (e.g., Bouwens et al. 2007; Hathi et al. 2008a; Ouchi et al. 2009; McLure et al. 2010; Yan et al. 2010; Finkelstein et al. 2010; Hathi et al. 2012; Tilvi et al. 2013; Ellis et al. 2013; Finkelstein et al. 2013). This big reservoir of SFGs spanning a wide redshift range (z ≃ 3–8), and brightnesses (24–29 mag), has tremendous impact on our understanding of the process of galaxy formation and evolution (e.g., Maioline et al. 2008; Ilbert et al. 2013; Speagle et al. 2014; Finkelstein et al. 2015). However, the spectroscopic and photometric studies for most of these galaxies are very challenging because of their faint magnitudes and lack of high resolution multi-wavelength data. Therefore, detailed studies of SFGs at lower redshifts (z < 3) using ground-based spectroscopy and multi-wavelength photometry are vital for understanding physical processes at the peak epoch of star formation as well as to better understand high redshift galaxy formation.
The study of SFGs at z ~ 2 has a significant impact on our understanding of galaxy properties. First, these SFGs are at redshifts corresponding to the peak epoch (z ~ 1–3) of the global star formation rate (SFR) density (e.g., Madau et al. 1998; Cucciati et al. 2012; Madau & Dickinson 2014), where >50% of the stars in the present-day Universe formed, and is a perfect epoch to study star formation processes. Second, this cosmologically interesting redshift is also where we have access to a wealth of multi-wavelength data, and rest-frame optical spectroscopy, to study galaxy properties that we cannot investigate at higher redshifts with current technology. The major advantage of identifying and studying various physical properties – including star formation properties – of these SFGs is that they can be investigated in rest-frame UV as well as rest-frame optical filters. Third, these galaxies are likely lower redshift analogs of the high redshift SFGs, and putting in a context such analysis will help to shed light on the process of reionization in the early Universe (e.g., Labbé et al. 2010; Stark et al. 2010) and how the first galaxies formed. Finally, the redshift z ~ 2 is the lowest redshift where we can identify and study Lyα in emission from ground-based spectroscopy and these galaxies are bright enough for extensive spectroscopic studies on 8−10 m class telescopes.
Spectroscopy is an essential and powerful tool to fully understand galaxy properties but the underlying photometric selection of galaxies can bias the spectroscopic sample properties. The primary techniques to select SFGs by color at z ≃ 2 are: (1) sBzK (using the B, z, K bands, Daddi et al. 2004, 2007); (2) BX/BM (using the U, G, R bands, Steidel et al. 2004; Adelberger et al. 2004); and (3) LBG (using the bands which bracket the redshifted Lyman limit, Hathi et al. 2010; Oesch et al. 2010). The other main approach is based on the magnitude/flux limit and/or photometric redshift selection, as used by many spectroscopic surveys such as, VVDS, GMASS, zCOSMOS (e.g., Le Fèvre et al. 2005, 2013; Lilly et al. 2007; Kurk et al. 2009). On the other hand, SFGs are also selected based on the emission-line/narrow-band (NB) techniques (e.g., Guaita et al. 2010; Berry et al. 2012; Vargas et al. 2014) which bracket strong emission lines at z ≃ 2. All these approaches select star-forming galaxies, and yield insight into the star-forming properties of these galaxies, but they have differing selection biases, and therefore, these samples do not completely overlap (see Ly et al. 2011; Haberzettl et al. 2012, for details). Therefore, it is essential to apply a well defined selection leading to the identification of a population with a broad range of galaxy properties, which can then be compared to similar galaxies at higher redshifts.
The comparison of stellar populations of (strong) Lyα emitting galaxies (LAEs), primarily selected based on the NB imaging technique, and non-LAEs (with weak or no Lyα-emission), primarily selected based on photometric colors that mimic a break (i.e., Lyman break galaxies, LBGs), has yielded diverse and inconclusive results. Gawiser et al. (2006) found that NB-selected LAEs at z ≃ 3.1 are less massive and less dusty compared to continuum selected LBGs suggesting that LAEs represent an early stage of an evolutionary sequence where galaxies gradually become more massive and dusty as a result of mergers and star formation (Gawiser et al. 2007). This conclusion is consistent with high specific star formation rates (SSFR, SFR per unit mass) of NB-selected LAEs found by Lai et al. (2008) relative to LBGs at the same redshift. On the other hand, Finkelstein et al. (2009) found a range of dust extinctions in a sample of 14 NB-selected LAEs at z ≃ 4.5, which is not consistent with LAEs being the first galaxies in the evolutionary sequence. Similarly, Nilsson et al. (2011) used 171 NB-selected LAEs at z ≃ 2.25 and concluded that the stellar properties of LAEs are different from those at higher redshift and that they are diverse. They also believe that Lyα selection could be tracing different galaxies at different redshifts, which is consistent with the findings of Acquaviva et al. (2012). Lai et al. (2008) found that IRAC-detected LAEs are significantly older (age ≳ 1 Gyr) and more massive (mass ~1010M⊙) compared to IRAC-undetected LAEs at z ≃ 3.1, which lead them to suggest that the IRAC-detected LAEs may be a lower-mass extension of the LBG population. These studies show heterogeneity of NB-selected LAEs, and comparison between these objects and continuum selected LBGs continues to be the subject of many new studies.
Various authors have compared stellar population properties of LAEs and non-LAEs in UV flux-limited samples (e.g., Shapley et al. 2001; Erb et al. 2006; Pentericci et al. 2007; Reddy et al. 2008; Kornei et al. 2010). Shapley et al. (2001) generated rest-frame UV composite spectra of LBGs at z ≃ 3 dividing subsamples in “young” (t ≤ 35 Myr) and “old” (t ≥ 1 Gyr) galaxies. They found that younger galaxies have weaker Lyα emission, are more dusty, and less massive compared to older galaxies. On the other hand, the analysis of Erb et al. (2006) of the composite UV spectra for ~60 SFGs at z ≃ 2 concluded that, on average, objects with lower stellar mass had stronger Lyα emission line than more massive objects. Using a sample of 14 UV-selected galaxies at z ≃ 2–3 with Lyα equivalent width (EW) ≥ 20 Å, Reddy et al. (2008) found no significant difference in the stellar populations of strong Lyα-emitters compared to the rest of the sample. At higher redshifts, Pentericci et al. (2007) found that, in general, younger galaxies at z ≃ 4 showed Lyα in emission while older galaxies showed Lyα in absorption. More recently, Kornei et al. (2010) used 321 LBGs at z ≃ 3 to study the relationship between Lyα-emission and stellar populations. Based on their analysis, they concluded that objects with strong Lyα-emission are older, lower in SFR, and less dusty compared to objects with weak or no (Lyα in absorption) Lyα-emission. The results of these studies emphasize that the exact relation between stellar populations and Lyα-emission is still not yet fully understood.
In this paper we use spectroscopic data from the VIMOS Ultra-Deep Survey (VUDS), to study the spectral and photometric properties of a large sample of faint SFGs at 2 < z < 2.5 (zmedian ≃ 2.3). VUDS recently obtained data for ~10 000 galaxies over an area of ~1 deg2 using the 8.2 m Very Large Telescope (VLT). The VUDS observations were performed in the well-studied COSMOS (Scoville et al. 2007; Koekemoer et al. 2007) and ECDFS (Giavalisco et al. 2004; Rix et al. 2004) fields now partly covered with HST/WFC3 by CANDELS (Grogin et al. 2011; Koekemoer et al. 2011), and in the VVDS-02h field (Le Fèvre et al. 2004; McCracken et al. 2003). These fields have extensive multi-wavelength data. We extract a sample of 854 galaxies with confirmed spectroscopic redshifts at 2 < z < 2.5, uniformly selected from their continuum properties with iAB ≲ 25 mag. The goal of this paper is to study the physical properties of these SFGs which include galaxies with and without Lyα emission.
This paper is organized as follows: in Sect. 2, we summarize the VUDS observations, and discuss our sample selection as well as its basic properties. In Sect. 3, we fit observed rest-frame UV VUDS spectra at 2 < z < 2.5 to measure the UV spectral slope, and discuss its correlation with the Es(B−V), stellar mass, and UV absolute magnitude. In Sect. 4, we discuss differences in stellar population properties between galaxies with and without Lyα in emission. In Sect. 5, we investigate correlations between derived physical parameters (UV absolute magnitude, SFRs, Es(B−V), stellar mass, and UV spectral slope) as a function of rest-frame Lyα EW for SFGs and their implications on our understanding of these galaxies. Results are discussed in Sect. 6, and we conclude with a summary in Sect. 7.
Throughout this paper, we assume the standard cosmology with Ωm = 0.3, ΩΛ = 0.7 and H0 = 70 km s-1 Mpc-1. This corresponds to a look-back time of ~10.4 Gyr at z ≃ 2. Magnitudes are given in the AB system (Oke & Gunn 1983).
2. Data and sample selection
The VUDS observations (Le Fèvre et al. 2015) were done using the low-resolution multi-slit mode of VIMOS on the VLT. A total of 15 VIMOS pointings (~224 arcmin2 each, ~1 deg2 total) were observed with both the LRBLUE and LRRED grisms covering the full wavelength range from 3650 Å to 9350 Å in three fields (ECDFS, VVDS-02h, COSMOS). The total exposure time per pointing was 14h in each grism. This paper is based on ~80% of the data, which is the amount processed at the time of writing this paper. Details of these observations and the reduction process are described in Le Fèvre et al. (2015).
2.1. Photometry
VUDS targeted three well-studied extragalactic fields with extensive multi-wavelength photometry. Details are given in Le Fèvre et al. (2015). Here, we briefly summarize the most relevant imaging observations for these three fields.
The COSMOS field was observed with HST/ACS in the F814W filter (Scoville et al. 2007; Koekemoer et al. 2007). Deep ground based imaging includes observations in u∗,B,V,g+,r+,i+,z+ bands from Subaru and CFHT. Details about these and other publicly available multi-wavelength observations are available at COSMOS websites1. The UltraVista survey is acquiring very deep near-infrared imaging in the YJHK bands using the VIRCAM camera on the VISTA telescope (McCracken et al. 2012), while deep Spitzer/IRAC observations are available through the SCOSMOS (Sanders et al. 2007) program. The CANDELS survey (Grogin et al. 2011; Koekemoer et al. 2011) also provided WFC3 NIR photometry in the smaller, central part of the COSMOS field.
The ECDFS field has been the target of many multi-wavelength surveys in the last decade. The central part of the field, covering ~160 arcmin2, has HST/ACS observations (Giavalisco et al. 2004) combined with the recent CANDELS HST/WFC3 observations in the near-infrared bands (Koekemoer et al. 2011). The ECDFS field is covered by deep UBVRIzJHK imaging as part of MUSYC and other surveys in this field (Cardamone et al. 2010, and references therein). The SERVS program obtained medium-deep observations in 3.6 μm and 4.5 μm (Mauduit et al. 2012), which complement those obtained by the GOODS team (PI: M. Dickinson) at 3.6, 4.5, 5.6, and 8.0 μm.
The VVDS-02h field has deep optical imaging from CFHT in the u∗,g′,r′,i′,z′ bands (e.g., Cuillandre et al. 2012) as part of the CFHT Legacy Survey. Deep near-infrared imaging in the JHKs bands has been obtained with WIRCam on CFHT as part of the WIRCam Deep Survey (WIRDS; Bielby et al. 2012). The deep near-infrared imaging data (3.6 μm and 4.5 μm) has been obtained with Spitzer/IRAC as part of the SERVS program (e.g., Mauduit et al. 2012). We refer the reader to Lemaux et al. (2014a) for a detailed description of multi-wavelength imaging data in the VVDS-02h field.
2.2. VUDS target selection
The primary selection criterion for galaxies in the VUDS program was photometric redshifts (zphot + 1σ ≥ 2.4), which are accurate to within 5% errors for these well-studied fields (e.g., Ilbert et al. 2009; Coupon et al. 2009; Dahlen et al. 2010). For high redshift (z ≳ 2.5) targets, this photometric redshift selection was supplemented by color criteria (e.g., LBG/ugr, LBG/gri, LBG/riz), if the objects satisfied these color criteria but were not selected from the primary photometric redshift criterion. The fraction of targets selected for each criterion at different redshifts is shown in Table 2 of Le Fèvre et al. (2015). At 2 < z < 2.5, all spectroscopic targets were selected solely based on the photometric redshift criterion. Therefore, the targets for the VUDS program include a representative sample of all star-forming galaxies at a particular redshift within a given magnitude limit (iAB ≲ 25 mag, with some galaxies as faint as iAB ~ 27 mag). It is important to note that the target selection is not based on any particular emission line of a galaxy but on the continuum magnitude. A detailed discussion on the target selection, reliability of the redshift measurements and corresponding quality flags is presented in Le Fèvre et al. (2015).
2.3. Sample selection
For this paper, the primary selection criterion for the sample of SFGs from the VUDS spectroscopic data is the redshift. All objects between z = 2 and z = 2.5 are selected in the final sample, keeping the best reliability flags (2, 3, 4, 9) – which gives very high probability (75−85%, 95−100%, 100%, 80%, respectively; see Le Fèvre et al. 2015 for details) for these redshifts to be correct. The total number of galaxies selected at 2 < z < 2.5 for the current work is 854. Based on a simple nearest-neighbor matching to the most recent catalogs in each field (e.g., Chiappetti et al. 2005; Elvis et al. 2009; Xue et al. 2011), we find that our sample contains minimal contamination from X-ray AGN (≲1%), which suggests that our sample is comprised almost exclusively of galaxies without powerful X-ray AGN activity. We also checked for obscured AGN using Donley et al. (2012)Spitzer/IRAC criteria, and found that ~3% of galaxies in our sample could host AGN based on this criteria. Some of these IRAC-selected AGN are also X-ray AGN, so after removing these overlapping AGN we end up with ~2% of additional AGN candidates using the Donley et al. IRAC criteria. This confirms that our SFGs sample has minimum contamination (≲3%) from AGN identified based on their X-ray emission and IRAC colors. This does not rule out the presence of other types of AGN or AGN-like activity in our sample (e.g., Cimatti et al. 2013; Lemaux et al. 2010), but such phenomena do not, typically, dominate the UV/optical/NIR light of their host galaxies, which is the important point for our analysis.
The Le PHARE software package (Arnouts et al. 1999; Ilbert et al. 2006) was used to fit the broad-band observed spectral energy distributions (SEDs) with synthetic stellar population models. We use BC03 (Bruzual & Charlot 2003) templates to generate a set of stellar population models assuming a Chabrier initial mass function (IMF; Chabrier 2003), and fixed the spectroscopic redshift, while varying metallicity (Z = 0.4 and 1 Z⊙), age (0.05 Gyr ≤ t ≤ tH), dust extinction (0 ≤ Es(B−V) ≤ 0.7 mag) – using a Calzetti et al. (2000) attenuation law or, in some cases, Calzetti law + 2175 Å bump – and e-folding timescale (τ = 0.1–30 Gyr, i.e., from instantaneous burst to continuous star formation) for a star-formation history (SFH) ∝ exp(−t/τ). We also included two delayed SFH models with peaks at 1 and 3 Gyr. The Le PHARE code assumes the Madau (1995) prescription to estimate inter-galactic medium (IGM) opacity. From the best-fit model, we estimate stellar mass, dust extinction Es(B−V), SFRs, and SSFR for each galaxy. The UV absolute magnitudes are measured using the prescription of Ilbert et al. (2005) and are not corrected for the internal dust extinction.
We emphasize that SFRs and Es(B−V)/dust inferred from fitting BC03 models to the SED of galaxies give a rough estimate of these physical parameters. To understand the effect of medium-band filters as well as other input quantities on the best-fit SED parameters, we compared our SFR and Es(B−V) measurements with two different surveys that use medium band photometry: (1) NEWFIRM Medium Band Survey (NMBS) in the COSMOS field (Whitaker et al. 2012) and (2) COSMOS SED measurements using 30 photometric bands (Ilbert et al. 2009), which includes broad-band as well as intermediate and narrow bands in the optical and NIR. For NMBS data, we have a small number (~20) of galaxies matching both catalogs. For these galaxies, we find that, on average, SFRs differ by ~0.5 dex (factor of ~3), and Av (Es(B−V)) differ by ≲0.2 (≲0.07). For COSMOS 30-band data which has a bigger sample (~300) of galaxies, we find that, on average, SFRs differ by ~0.2 dex (factor of ~2), and Av (Es(B−V)) differ by ≲0.15 (≲0.05). It is crucial to note that NMBS uses slightly different input set-up for SED-fitting e.g., slightly different SFHs, different choice of extinction laws, different metallicity range, use of photometric redshifts, compared to what we use, so these choices of input parameters will also affect SFRs and dust measurements. Therefore, the sizeable difference between NMBS and our SED measurements is not only due to photometric bands. As for COSMOS 30-band, we kept all the input parameters same as in the broad-band photometry SED fitting except the input photometric bands, so other effects do not play any role, and we see much smaller differences. These comparisons show that the uncertainties in SFRs and dust measurements because of the choice of photometric bands and other input SED parameters could be as high as factor of ~3 for SFRs and ~0.2 mag for Av (or ~0.07 for Es(B−V)), which is typically expected for the SED-fitting process (e.g., Muzzin et al. 2010; Mostek et al. 2012). It is important to mention that these uncertainties are inherent in the SED fitting process and are not unique to this study. Moreover, this study is based on the relative measurements of three different galaxy populations and as long as there are no drastic differences in the IMF or SFHs of these populations, these systematic uncertainties does not play a significant role in the conclusions of this paper.
The contribution of major emission lines in different filters has been included in the models of the Le PHARE code. We use these templates with emission lines to carry out SED fitting. Neglecting emission lines during the SED fitting process can overestimate the best-fit stellar ages and stellar masses by up to ~ 0.3 dex (e.g., Schaerer & de Barros 2009; Finkelstein et al. 2011; Atek et al. 2011). The Le PHARE code accounts for the contribution of emission lines with a simple recipe based on the Kennicutt (1998) relations between the SFR and UV luminosity, Hα and [OII] lines. The code includes the Lyα, Hα, Hβ, [OII], OIII[4959] and OIII[5007] lines with different line ratios with respect to the [OII] line, as described in Ilbert et al. (2009).
2.4. Sample properties
Figure 1 shows distributions of spectroscopic redshifts and far-UV (1500 Å) absolute magnitudes (M1500) for the full SFG sample at 2 < z < 2.5. The median M1500 of the sample is –20.22 mag, while the median redshift is 2.320. The figure also shows the evolving characteristic magnitude M∗ as a function of the redshift, as derived from the compilation of Hathi et al. (2010). The M∗ ±1 mag range covers most of our data which implies that we are probing luminosities around L∗ at these redshifts. The shape of the redshift distribution is dictated, in part, by the selection function used to select target galaxies for VUDS. The main selection criteria under which primary targets are selected, is zphot + 1σ ≥ 2.4. Therefore, at lower redshifts (2 < z < 2.4) we are on the tail of the probability distribution of photometric redshifts, and this explains the decreasing number of galaxies at z < 2.4. This bias equally affects all galaxies – galaxies with and without Lyα in emission – so the general results in this paper, making relative comparisons of the two populations, are not affected by this selection bias. The second reason for the small number of galaxies close to the lower limit of our redshift range could be the sensitivity of the VIMOS instrument which starts to decrease dramatically below 3800 Å. This means that we might not be able to properly identify continuum breaks, important features to secure the redshift, below redshift z ≲ 2.15. In this redshift range, we might be biased in favor of strong Lyα emitters as we could still identify those even at z ≲ 2.15. To check this sample selection effect, we cut our sample at redshift z = 2.15. By doing so, we remove ~10% of galaxies from the full sample, which is very small compared to the large sample size of VUDS galaxies. This small change in number of galaxies does not change our final results. Therefore, the results presented in this paper are not affected by this selection bias.
 |
Fig. 1 Redshift versus UV absolute magnitude (M1500) for spectroscopically confirmed SFGs at 2 < z < 2.5 from VUDS. The median M1500 of the sample is –20.22 mag, the median redshift is 2.320. The quoted uncertainties are the errors on the median ( |
 |
Fig. 2 SFR versus stellar mass for SFGs at 2 < z < 2.5 in VUDS. The full sample has median stellar mass of 109.64 ~ 4 × 109M⊙ and median SFR of 101.32 ~ 20 M⊙ per year. The quoted uncertainties are the errors on the median ( |
Figure 2 shows distributions of stellar mass and SFR for the full SFG sample at 2 < z < 2.5. The median stellar mass of the sample is ~ 4 × 109M⊙ and the median SFR is ~20 M⊙ per year. We show the “main sequence” of SFGs as defined by Daddi et al. (2007) at z ≃ 2, and the best-fit relation for our sample with the corresponding scatter (~0.4 dex). We keep the logarithmic slope fixed to the value from Daddi et al. relation because the redshift probed is very similar for both studies. If we fit the observed SFR-stellar mass relation without keeping the slope fixed, then we get the logarithmic slope of ~0.66 which is flatter than the slope of 0.90 obtained by Daddi et al. at similar redshifts. Figure 2 shows that our sample has a large scatter in the stellar mass-SFR plane covering a wide range in SFR and over two orders of magnitude in stellar mass. It is important to note that our best-fit relation (keeping the logarithmic slope fixed at 0.90) between SFR and stellar mass is ~0.2 dex off from the Daddi’s SF main sequence. The average redshift of the Daddi et al. sample is slightly lower compared to our sample, so in Fig. 2 we also show the best-fit main sequence relation from Whitaker et al. (2014) and Schreiber et al. (2015). The redshift probed by these two studies is very similar to ours. We still find a similar offset (~0.2 dex) between our main sequence relation and the relation from these studies, that predicts slightly lower normalization i.e., lower SFR at a given stellar mass. This difference could be because of the fact that we estimate SFRs based on the SED fitting process which has wide variety of SFHs and it gives slightly different SFR compared to SFR(UV) or SFR(UV+IR). When we estimate SFR using UV luminosity (corrected for dust using the UV slope), we find average SFR to be ~0.2 dex lower compared to SFR(SED). This difference might explain the ~0.2 dex offset we see in the main sequence relation compared to other studies, that uses SFR(UV) or SFR(UV+IR) in their relations. By selection, and confirmed by the NUV−r−J plot, our galaxies are not very dusty and hence, not many galaxies have IR/FIR detections. In future studies, we will investigate IR SFRs for these galaxies based on their 24 μm and Herschel observations.
The scatter (total scatter obtained from the fitting process) in the SFR-stellar mass correlation is ~0.4 dex, which is larger than that of Daddi et al. (2007) by ~0.2 dex. We believe that this bigger scatter is caused by the choice of wide range of SFHs in the SED fitting process. Various studies (e.g., McLure et al. 2011; Schaerer et al. 2013) have shown that a broader range in SFHs for the SED fitting process could have strong implications on the scatter of the main sequence relation. Considering that our sample has similar redshift (z ≃ 2) as Daddi et al. and other studies, these differences in the main sequence relation emphasize that the sample properties as well as measurement techniques play a significant role in the determination of the correlation between SFR and stellar masses of galaxies (see, e.g., Pforr et al. 2012, for uncertainties in SED fitting process). To underscore the importances of these differences, we point out few subtleties between the Daddi et al. relation and ours. Our sample was selected based on the photometric redshift technique, while the Daddi et al. (2007) sample was selected based on a single BzK color technique, highlighting that sample selection likely plays a significant role in determining the parameters of the stellar mass-SFR relation. We use different star-formation histories in our SED-fitting technique that estimates SFR and stellar masses, while Daddi et al. (2007) obtain SFRs directly from UV luminosity and their stellar masses are based on a single color technique (Daddi et al. 2004). This difference in method also likely influences the measurements of these stellar parameters and thus the shape & normalization of the stellar mass-SFR relation. The detailed discussion on various aspects of this relation is beyond the scope of this paper, therefore, for in-depth study on this relation and its evolution with redshift, we refer the reader to Tasca et al. (2015), and for more details on the effect of different SFHs on the SFR-stellar mass correlation, we refer the reader to Cassarà et al. (in prep). Both these investigations are based on the same VUDS dataset, but over a wider redshift range.
3. UV spectral slope (β)
The UV spectral slope (β) is determined from a power-law fit to the UV continuum spectrum (Calzetti et al. 1994), fλ ∝ λβ, where fλ is the flux density per unit wavelength (ergs s-1 cm-2 Å-1). We use the VUDS spectra of SFGs at 2 < z < 2.5 to estimate their UV slope by fitting a linear relation to the full wavelength range between rest-frame 1400 and 2400 Å in the observed (Log(λ) versus Log(fλ)) spectrum. The rest-frame wavelength range (1400−2400 Å) includes 7 out of 10 spectral fitting windows identified by Calzetti et al. (1994) to estimate the UV spectral slope for local starburst galaxies, and takes full advantage of the spectral coverage of the VUDS spectra at these redshifts. Figure 3 shows four examples of UV spectral slope fitting on the VUDS spectra. Before fitting, the spectra were cleaned by masking out known lines and removing any spurious noise spikes. The fitting was done using the IDL routine LINFIT, which fits the data to the linear model by minimizing the χ2 statistic. The running dispersion values measured on the clean spectra are used as measured errors, and the routine uses these errors to compute the covariance matrix. In Fig. 3, the solid red line is the best-fit spectroscopic slope while dashed red lines show 1σ uncertainties associated with the best-fit relation. The formal statistical uncertainty in the best-fit βspec, which is measured over a large number of points, is smaller than the uncertainty in βphot measured using few photometric points. For comparison, we also measure the UV spectral slope directly from the broad-band photometry which encompasses a similar rest-frame wavelength range. We used BVRI bands for the ECDFS field, g+Vr+i+ bands for the COSMOS field, and g′r′i′z′ bands for the VVDS field. These photometric bands cover a rest-frame wavelength range from ~1200 Å to ~3000 Å, depending on the redshift. Figure 3 also shows the photometric magnitudes of the broad-band filters which are used to measure the photometric UV slope, and the corresponding best-fit photometric UV slope. Figure 4 shows the UV spectral slope (β) distribution as measured from the VUDS spectra (βspec) and the broad-band photometry (βphot). The median βspec is –1.36 ± 0.02, and the median βphot is –1.32 ± 0.02. The quoted uncertainties are the errors on the median (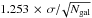 ). It is worth noting that even if we use two or three photometric bands, covering the similar wavelength range as four bands, we get similar median values for the photometric UV slope of the whole sample, which is in the range of –1.40 ± 0.10. We also measured UV slopes by convolving the spectra with the photometric filter curves, and found that the median value is –1.31 ± 0.03, which is very similar to the median photometric and spectroscopic UV slopes.
). It is worth noting that even if we use two or three photometric bands, covering the similar wavelength range as four bands, we get similar median values for the photometric UV slope of the whole sample, which is in the range of –1.40 ± 0.10. We also measured UV slopes by convolving the spectra with the photometric filter curves, and found that the median value is –1.31 ± 0.03, which is very similar to the median photometric and spectroscopic UV slopes.
 |
Fig. 3 Examples of UV spectral slope (β) fitting on the VUDS spectra (shown in gray). The spectra between rest-frame 1400 Å to 2400 Å (between dashed vertical lines) are fitted with a linear relation (solid red lines) between Log(λ) vs. Log(Fλ) after masking out known lines and removing spurious noise spikes. The dashed red lines are 1σ deviations in the best-fit relation. The blue filled circles are the photometric magnitudes from the broad-band filters (gray curves) used to measure the photometric β, while the blue dashed line is a linear fit between these photometric data points to estimate the photometric UV slope. |
 |
Fig. 4 Left: UV spectral slope (β) distribution as measured from the VUDS spectra (red histogram) and the broad-band photometry (blue histogram). The solid curve is the KDE of the distribution. The median β values as well as KS-test probability (PKS) show very small difference in these βs. Middle: βspec versus βphot. The solid red line is the best orthogonal fit relation between these two βs, while the dashed lines show the uncertainties in the best-fit relation. This figure also shows the difference (βspec−βphot) as a function of βspec. The dotted line is for βspec−βphot = 0. The density of points is color-coded as in previous figures. Average uncertainties in these measurements are plotted in the bottom-right corner. Right: the correlation between the UV slope and the SED derived Es(B−V) is such that the redder UV slope implies dustier [higher Es(B−V)] galaxies. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between the 16th and the 84th percentile values within each bin, while the smaller solid error bars are the errors on the median values ( |
In Fig. 4, and in subsequent figures of this paper, we will calculate statistical significance for the distributions and correlations in the following two ways: (a) for histograms, we use KS-statistics on the distributions. The probability of KS-statistics (PKS) measures whether two sets of data are drawn from the same parent distribution or not. Small values (close to zero) of PKS show that the cumulative distribution functions of the two sets of data are significantly different. This is measured using the IDL routine KSTWO; and (b) for correlations, we use the Spearman correlation test. Values of the Spearman correlation coefficient (ρ) close to ±1 imply strong monotonic correlation, while values close to 0 imply no significant correlation between two variables. The significance level is denoted by PSC, where small values of PSC imply significant correlation. It is important to note that for a big sample size, very small differences (or small ρ values) in two sets of data will be detected as highly significant. When a statistic is significant, it simply means that the difference is real. It does not mean the difference is substantial or important. The Spearman correlation coefficient is measured using the IDL routine R_CORRELATE, and is measured from all galaxies as well as from the median-binned values.This routine can also give the value of the sum-squared difference of ranks, and the number of standard deviations (σ) by which it deviates from its null-hypothesis expected value.
In Fig. 4 (left panel), the median values of βspec and βphot are very similar and differ by only ~0.04. This difference is not significant considering that the errors on the median values is ±0.02. However, the full distributions of βspec and βphot are marginally different as confirmed by PKS ~ 0.00057, which implies that a null hypothesis (similar distributions) is rejected at ~3σ level. To investigate the difference between individual βspec and βphot, we look at four examples shown in Fig. 3. Figure 3a shows an extreme example in which the difference between two βs is ~0.5, though βphot is within the 1σ uncertainties of βspec. Figure 3b and c show examples where βphot is just outside the 1σ uncertainties in βspec and we find that both these β values differ by ~0.2−0.3. Figure 3d shows an example where the difference between the two βs is very small (~0.1) and well within the measurement uncertainties.
The middle panel of Fig. 4 shows the direct comparison between individual βspec and βphot, while the bottom plot in the middle panel shows the difference between βspec and βphot as a function of βspec. The best orthogonal fit relation between βspec and βphot is flatter than the one-to-one relation, and is given by βphot = −0.43 + 0.63 × βspec. The total scatter in the βspec vs. βphot relation could be as high as ~0.5. The uncertainties in both β measurements could be the main cause of the flatter slope (<1) and the large scatter. The average measurement error in βspec is ~0.08, while it is ~0.15 for βphot. Depending on the object and its redshift, it is possible to have additional factors affecting β measurements of individual galaxies, as discussed below.
For βspec, there are two potential sources of uncertainties. First, the bluest part of the spectra is sensitive to various atmospheric and galactic corrections made to the spectra (see Le Fèvre et al. 2015; Thomas et al. 2014, for details), and even though these corrections are carefully applied to minimize the flux loss, there are uncertainties in the bluest part of the spectra. The UV slope measurement is sensitive to the changes in the anchor blue region of the spectra and hence, this could affect the UV slope measurements for some objects. Second, as seen in Fig. 3a, the spectroscopic β is fitted in such a way that it avoids the more noisy red part of the spectrum to minimize its effect on the best-fit slope, which could make βspec steeper or bluer compared to βphot. While this fitting effect is kept at the minimum level, any small difference in the fitting of the red part of the spectrum could lead to slightly bluer βspec compared to βphot. These uncertainties in βspec are estimated to be small (≲0.1), but could vary from object to object.
For βphot, the wavelength range over which β is measured has a great influence on the resulting β values. Calzetti et al. (1994) defined the wavelength baseline (1250 Å to 2600 Å) to measure β for galaxies at lower redshifts and this range is widely used for all measurements. But as discussed in Calzetti (2001), the UV slopes fitted with a longer wavelength baseline are always bluer (more negative) compared to the UV slopes from a shorter baseline (see also Meurer et al. 1999; Talia et al. 2015). The main reason is that the slopes fitted with a longer wavelength baseline cover the 2300−2800 Å range, which has a significant decrement because of a large number of closely spaced FeII absorption lines that gives low continuum and steeper/bluer slopes. Our βphot is measured using broad photometric bands, and depending on the exact redshift of a galaxy the wavelength range covered by these bands could be as wide as ~1200 Å to ~3000 Å. This range includes the wavelength range (1400 Å to 2400 Å) used to measure βspec, but βphot has a longer wavelength baseline for many galaxies which could lead to bluer βphot for these galaxies. The other factor affecting the βphot measurement is the contribution of strong Lyα emission to the flux in the bluest band used for measuring βphot. For a small number of strong Lyα emitters, it is likely that the bluest band used in the βphot measurement is affected by the strong Lyα emission line. To check this effect, we compared βs for galaxies with no Lyα emission and for galaxies with strong Lyα emission. We find that the difference between the median values of βphot and βspec is smaller (βspec bluer by ~0.05) for galaxies with no Lyα emission compared to galaxies with strong Lyα emission, where on average βphot is bluer compared to βspec by ~0.13. Hence, strong Lyα line in the bluest photometric band could lead to higher flux in that band which in turn could give steeper/bluer βphot. This is confirmed by our estimation of Lyα contamination to the bluest photometric band by comparing flux densities with and without Lyα line in the broadband. We found that the contamination in the broadband for the strongest Lyα emission lines could be ~0.05–0.1 mag. This difference in the magnitude of the bluest band could cause ~0.1–0.2 difference in the photometrically measured UV slope. These uncertainties in βphot are estimated to be ≲0.2, but could vary from object to object.
In summary, the average βspec and βphot are very similar for the VUDS SFG sample, and the uncertainties discussed above could affect individual measurements, as shown in the middle panel of Fig. 4. The detailed comparison between individual βs, and quantifying various sources of the uncertainties for such a big sample, requires an in-depth study, which is beyond the scope of this paper.
The median βspec value of the whole SFG sample, −1.36 ± 0.02 with the 1σ scatter of ~0.5, is consistent with the UV slope estimates obtained at similar redshifts using ground-based spectra. Talia et al. (2012) obtained βspec of −1.11 ± 0.44 (rms) for 74 SFGs at z ≃ 2 using VLT/FORS2 spectra, while Noll & Pierini (2005) used FORS spectroscopic data of 34 UV-luminous galaxies at 2 < z < 2.5 and found βspec for the sub-sample of galaxies to be –1.01 ± 0.11. Both these β values are roughly consistent with our median βspec when considering the additional uncertainty introduced by the fact that both studies used slightly different wavelength range (~1200−2600 Å, and ~1200−1800 Å, respectively), from each other & our own, to fit the UV slope. In addition, the median photometric UV slope obtained here, –1.32 ± 0.02 with the 1σ scatter of ~0.5, is very similar to the average UV slopes measured at these redshifts (2 < z < 2.5) from HST photometry (e.g., –1.58 ± 0.27 (1σ) from Bouwens et al. 2009 and –1.71 ± 0.34 (1σ) from Hathi et al. 2013). These β values – spectroscopic and photometric – are also in good agreement with the evolution of β with redshift which shows that the average β at 2 < z < 2.5 is redder compared to β at higher redshifts (e.g., Hathi et al. 2008b; Bouwens et al. 2009; Finkelstein et al. 2012).
3.1. β versus Es (B–V)
The UV radiation is absorbed by dust and heated dust particles re-emit absorbed energy in the mid- and far-infrared. The ratio of LIR-to-LUV is the direct measure of dust attenuation in a galaxy. A higher LIR/LUV ratio implies a larger dust content. There is an excellent correlation between LIR/LUV and the UV spectral slope at z ~ 2 (e.g., Seibert et al. 2002; Reddy et al. 2012), which is in good agreement with the local measurements (e.g., Meurer et al. 1997, 1999), in that, an increase in LIR/LUV corresponds to redder UV slopes. For SFGs at 2 < z < 2.5 in the VUDS sample, the correlation between the UV slope and SED derived Es(B−V) is shown in Fig. 4 (right panel). A positive correlation is observed between β and Es(B−V) implying redder UV slope for dustier (higher Es(B−V)) galaxies. We show the correlation of Es(B−V) with both, photometric and spectroscopic, βs. The statistical significance of this correlation is measured by the Spearman correlation test. The Spearman correlation coefficient (ρ) is 0.25 (0.95) for all (binned) βspec values and 0.65 (1.00) for all (binned) βphot values, which implies high significance (PSC ~ 0) for a strong positive correlation. The significance of ρ as measured by the number of standard deviations by which the sum-squared difference of ranks deviates from its null-hypothesis expected value is ~7σ for all βspec values and ~18σ for all βphot values. The correlation between βphot and Es(B−V) is stronger, in part, because they are both estimated from the same photometry. The βspec correlation is flatter compared to the βphot correlation, which means that galaxies with bluer β have lower Es(B−V) for βphot, and galaxies with redder β have higher Es(B−V) for βphot, compared to βspec. Also, we note that within the large 1σ scatter in the Es(B−V) values, the difference between these two βs is small in all UV slope bins. The corresponding A1600 (the dust absorption at 1600 Å) in Fig. 4 (right panel) is estimated from Es(B−V) using the Calzetti law (A1600 ~ 10 × Es(B−V); Calzetti et al. 2000). We have added the best-fit relations from three different studies (Talia et al. 2015; Oteo et al. 2014; Buat et al. 2012). The Oteo et al. (2014) relation is for galaxies at z ~ 2, while the Buat et al. (2012) relation is for galaxies at 1 ≲ z ≲ 2. The Talia et al. (2015) relation covers a wider redshift range, 1 < z < 3. We do not see any trend (with redshift) between these relations and ours. Our relation is flatter compared to their relations and the difference is maximum at redder UV slopes. This difference between our relation and theirs could be due to the sample of SFGs used in these studies. All these studies use UV+FIR selected galaxies which are primarily dusty galaxies with FIR detection in 24 μm and/or Herschel observations, while we do only UV selection and do not require FIR detection for our sample. This means that our sample does not include most of the dusty galaxies at these redshifts, which would make this relation much steeper with higher E(B−V) values and redder UV slopes. Talia et al. (2015) finds that the differences in various samples could also lead to a large dispersion (~0.7) in the dust-UV slope relation. Our future studies will specifically look at IR/FIR detections for these galaxies to investigate their dust properties.
In the remaining sections of this paper we use the spectroscopic UV slope and refer to βspec as β, unless stated otherwise. We are using βspec in this paper because they have smaller measurement uncertainties, and the trends/relations explored in this paper are very similar for both the spectroscopic and photometric UV slopes.
3.2. β versus M1500
A color–magnitude relation has previously been observed at various redshifts. The interpretation of this relation depends on which color is used. If the color is between the rest-frame UV and the rest-frame optical (e.g., Papovich et al. 2004) and spans the 4000 Å/Balmer break, then it is strongly dependent on the stellar population age, while if the color is blue-ward of the 4000 Å break (e.g., Finkelstein et al. 2012) then it is more sensitive to the dust extinction than age. Here we use rest-frame UV colors (i.e., UV spectral slope, β) to infer the color-magnitude relation for SFGs at 2 < z < 2.5. Fig. 5 shows the spectroscopic UV slope versus UV absolute magnitude (M1500). We estimate the slope, dβ/ dM1500, by fitting a linear model to the median-binned values, β = a + dβ/ dM1500 × M1500. We find the best-fitting solution to be dβ/ dM1500 = 0.00 ± 0.04. Essentially no correlation of β with absolute magnitude is observed, which could imply that β does not change with UV luminosity for ~L∗ galaxies. The Spearman correlation coefficient (ρ) is 0.18 (−0.4) for all (binned) M1500–β values, which implies no correlation at a high significance (PSC = 0.60). The ρ for all galaxies shows high significance (PSC < 10-3) for a strong correlation but it is misleading as it is strongly affected by a small number of galaxies with significant redder UV slope.
Various studies have investigated the color-magnitude relation at high redshifts (z ≳ 2), and the results are inconclusive. Reddy et al. (2008) found weak-to-no correlation between dust or UV color (related as shown in Fig. 4) and R mag for UV-selected galaxies at 1.5 ≲ z ≲ 2.6. Similarly, Heinis et al. (2013) through their investigation of far-infrared/dust properties of UV selected galaxies at z ~ 1.5 found that the average UV slope is mostly independent of the UV luminosity. On the other hand, Bouwens et al. (2009) studied the relation between the UV slope and MUV for a sample of U-band dropout galaxies at z ≃ 2.5 and found a positive color-magnitude correlation. At higher redshifts (z > 3), similar disagreements have been observed for samples based on the Lyman break color selection, in the sense that, some studies find no (or very weak) trends between β and UV magnitude (e.g., Ono et al. 2010; Finkelstein et al. 2012; Dunlop et al. 2012; Castellano et al. 2012), while other studies find a strong color-magnitude relation (e.g., Wilkins et al. 2011; Bouwens et al. 2012; Rogers et al. 2014; Bouwens et al. 2014). Bouwens et al. (2014) also argue that this relation could be described by a double power-law with a different slope for fainter magnitudes. The differences in these various studies could be because of many systematic and/or physical reasons, such as selection of galaxy samples (especially at lower redshifts), UV magnitude and/or β measurements, intrinsic scatter in β, dynamic range in UV luminosity. Our study relies on a UV selected sample with spectroscopic redshifts but it lacks a significant dynamic range in UV luminosity as seen in Fig. 5. A detailed study of a uniformly selected spectroscopic sample covering a wider range in UV luminosity is needed to understand the true nature of the color-magnitude relation at high redshifts. At least for ~L∗ (~0.5L∗ – 3.0L∗) galaxies in a uniformly selected VUDS sample at 2 < z < 2.5 there appears to be no correlation between β and M1500.
 |
Fig. 5 Spectroscopic UV slope versus the UV absolute magnitude (left) and the stellar mass (right). The density of points is color-coded as in previous figures, while the red open circles are the median-binned values for these parameters. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between the 16th and the 84th percentile values within each bin, while smaller solid error bars are the errors on the median values ( |
3.3. β versus stellar mass
The relation between β and M1500 could be affected by the biases and/or differences in the way different authors measure and define M1500 (e.g., Finkelstein et al. 2012). On the other hand, there is a well known correlation between M1500 and the stellar mass such that, stellar mass increases as brightness increases (e.g., Stark et al. 2009; Sawicki 2012; Hathi et al. 2013), which we can exploit to better understand the dependence of β on M1500. Therefore, we can compare β to the stellar mass as an alternate way to explore the dependence of β on M1500. Figure 5 shows the correlation between the spectroscopic UV slope and the stellar mass (M∗). We estimate the slope, dβ/ dLog(M∗), by fitting a linear model to the median-binned values, β = a + dβ/ dLog(M∗) × Log(M∗). We find the best-fitting solution to be dβ/ dLog(M∗) = 0.18 ± 0.04. A stronger correlation of β with stellar mass is observed compared to the β–M1500 correlation, which suggests a redder UV slope (more dust) for massive star-forming galaxies. This is not necessarily surprising as star-formation generally increases with stellar mass in star-forming samples and in turn, the dust content generally increases with increasing star-formation (e.g., Lemaux et al. 2014b). The Spearman correlation coefficient (ρ) is 0.11 (1.0) for all (binned) M∗−β values, which implies high significance (PSC ~ 10-3) for a strong positive correlation. A similar trend between β and stellar mass is also observed at z ≳ 4.0 (e.g., Finkelstein et al. 2012).
The VUDS survey targets star-forming galaxies brighter than iAB ~ 25 mag, so there are survey limitation/incompleteness given the limited area of the survey, in the sense that, we do not target many high mass galaxies (Log(M∗) ≳ 10.5), and we miss many fainter star-forming galaxies with lower stellar masses (Log(M∗) ≲ 9.0) because of the magnitude limit. These survey limitations affect the range in stellar mass range probed in our study, and hence, could impact the exact nature of our β-stellar mass correlation. An extensive study covering a wide mass range is required to fully understand this M∗–β correlation.
The M1500–β and M∗–β correlations are similar if we use βphot instead of βspec. For βphot, the linear slope values for the M1500–β and M∗–β relations are 0.01 ± 0.05 and 0.32 ± 0.05, respectively.
4. SFGs with and without Lyα emission
The galaxies selected by their (strong) Lyα-emission are becoming an important probe of galaxy formation, cosmic reionization, and cosmology. Lyα emission is an important diagnostic of physical processes in star forming galaxies, in particular at cosmological distances, since Lyα becomes the strongest emission line in the UV-optical window at redshifts z > 2.0. These galaxies – because of their observed physical properties at higher redshifts – are thought to be the progenitors of present-day Milky Way type galaxies (e.g., Gawiser et al. 2007), though dissimilar results from various Lyα studies at different redshifts amplify the importance to better understand these galaxies. The SFG population in our sample is divided into Lyα emitters and non-emitters based on their rest-frame Lyα EW.
 |
Fig. 6 Left: rest-frame EW distribution for SFGs with Lyα in emission (positive EWs) and Lyα in absorption (negative EWs). The vertical dashed line indicates EW = 20 Å, the adopted lower limit in Lyα EW for LAEs (or strong Lyα emitters). The solid curve is the KDE of the distribution. Middle: distribution of Lyα luminosities for the SFGL (black) and the LAE (red) samples. The KDE of the distribution is shown by a solid curve. Right: fraction of LAEs as a function of redshift for our sample. Approximately 10% of SFGs at these redshifts are strong Lyα emitters, consistent with previous Lyα studies (e.g., Reddy et al. 2008; Cassata et al. 2015) at similar redshifts. |
The Lyα EWs for VUDS SFGs were measured as described in Cassata et al. (2015). To summarize, we measured EWs of the Lyα line manually using the IRAF splot tool, while the uncertainties in EW were estimated using the formalism from Tresse et al. (1999). The median EW uncertainty varies as a function of the EW from ±5 Å (for weak absorbers and emitters) to ±25 Å (for strong absorbers and emitters). We first put each galaxy spectrum in its rest-frame based on the spectroscopic redshift. Then, two continuum points bracketing Lyα are manually marked and the rest-frame EW is measured for emission as well as absorption lines. The line is not fitted with a Gaussian, but the flux in the line is determined by simply summing the pixels in the area covered by the line and the continuum. This method allows the measurement of lines with asymmetric shapes (i.e., with deviations from Gaussian profiles), which is the shape observed for most Lyα lines. The interactive method also allows us to control the level of the continuum, taking into account defects that may be present around the line. This approach produces more reliable and accurate measurements compared to an automated “impartial” measurement because the visual inspection is capable of accounting for the complex nature of the Lyα emission/absorption line.
Figure 6 shows the rest-frame EW distribution for the Lyα line. Here, positive EWs are emission lines, while negative EWs are for absorption lines. We divide the SFG population into three sub-groups based on their Lyα EW. The galaxies that show no Lyα in emission (EW ≤ 0 Å) are defined as SFGN, while the galaxies with Lyα in emission, irrespective of its strength (EW > 0 Å), are defined as SFGL. The third group is for strong Lyα emitters (EW ≥ 20 Å) called LAEs. The number of galaxies with LyαEW ≥ 20 Å is 87 and this number drops to 27 for galaxies with EW ≥ 50 Å. Such a distribution is partially because of the fact that our sample does not select most of the galaxies with very high EW (EW ≳ 50 Å), whose continuum is usually very faint (~27 mag) and which are usually detected in NB imaging/emission-line selected surveys. This selection effect means that we are probing Lyα emitting galaxies with brighter continuum compared to galaxies selected based on NB/emission-line surveys. We also show the distribution of Lyα luminosities, L(Lyα), for SFGL and LAEs in the middle panel of Fig. 6. The median L(Lyα) of the SFGL sample is ~1040 erg/s, while the median L(Lyα) of the LAE sample is ~1041 erg/s. The LAEs discovered in the VUDS survey are significantly less luminous than the Lyα emitters found by most NB/emission-line surveys (~1042 erg/s) at similar redshifts (e.g., Guaita et al. 2010; Hagen et al. 2014). The fraction of LAEs as a function of redshift is shown in the right panel of Fig. 6. Approximately 10% of SFGs at these redshifts are strong Lyα emitters, consistent with previous Lyα studies at z ≃ 2 (e.g., Reddy et al. 2008), and in agreement with the general scenario that the number of LAEs increases as redshift increases reaching ~30−40% at z ≃ 6 (e.g., Stark et al. 2010; Curtis-Lake et al. 2012; Cassata et al. 2015).
 |
Fig. 7 Stacked (median-combined) rest-frame UV spectra for SFGN, SFGL, and LAEs. The strong absorption and emission features are marked by the vertical dotted lines. The SFGN spectrum shows strong absorption lines (Si, C, O, Fe, Al), but these absorption lines get weaker with increasing strength of Lyα-emission. The bottom panel shows similarity in the spectroscopic UV slope for these samples. |
 |
Fig. 8 Comparison between SFGN (black histograms), SFGL (red histograms), and LAEs (blue histograms) as a function of stellar parameters. The total number of galaxies identified as SFGN, SFGL, and LAEs are shown in the legend. The median value of the distribution is indicated by a vertical dashed line. The solid curves are KDE of the distribution. The gray shaded regions cover ±1σ dispersion/scatter, which corresponds to the range between the 16th and the 84th percentile values, of the SFGN distribution. The statistical significance based on the KS test (red for SFGL, and blue for LAEs with respect to SFGN) is shown to confirm any correlation. |
The composite spectra of the SFGN, SFGL, and LAE samples are shown in Fig. 7. They are generated by stacking the rest-frame shifted individual spectra which are rebinned to dispersion of 2 Å per pixel (2 Å ~ 5 Å/(1+z), where ~5 Å is the native pixel scale of the LR Blue grism in the observed frame), and then the entire spectrum is normalized to the mean flux in the wavelength range of 1350−1450 Å before taking the median value of all galaxies in the composite at each wavelength. Figure 7 shows the most prominent emission and absorption lines, whose detailed analysis will be conducted in a future paper. Here, it is worth pointing out that the median UV spectral slope (between 1400−2400 Å) does not show any appreciable difference among these three sub-samples as shown in the bottom panel of Fig. 7.
The galaxies with strong Lyα in emission, usually selected using NB imaging or serendipitous spectroscopy, show different physical properties compared to galaxies with no Lyα in emission or LBGs (e.g., Gawiser et al. 2006, 2007; Lai et al. 2008; Cassata et al. 2011). These two galaxy populations (LAEs and LBGs) are selected differently so the differences seen when comparing the two populations are mainly because of the selection effects. Here, we use a UV-selected sample (selected based on UV continuum/magnitude) to investigate stellar population differences between Lyα emitting galaxies and non-Lyα emitting galaxies. A common selection for Lyα emitters as well as non-emitters could reveal real intrinsic differences between these two classes of objects. Figure 8 shows the comparison between SFGN, SFGLand LAEs. The total number of galaxies identified as SFGL and SFGN is big enough (457 SFGN, 397 SFGL, 87 LAEs) to get robust statistics. On average, SFGL (and LAEs) are less dusty, and have lower SFR compared to SFGN. These differences are small, but they are significant because of the large sample size used in this study. To understand the significance of these differences we use KS-statistics on these distributions. The PKS ~ 10-4 value for Es(B−V) and SFR distributions implies that the null hypothesis (similar distributions) is rejected at >99.9% or >3σ level. The differences in stellar mass, SSFR, M1500, and βspec for SFGN and SFGL/LAEs are not statistically significant (i.e., the null hypothesis is rejected at ≲2.5σ level). It is important to note that the KS-test does not consider errors/uncertainties in two quantities while comparing their distributions. We tested the robustness of these results by constructing 100 bootstrap samples by randomly extracting values from the confidence intervals of the best-fit stellar parameters. We re-ran the KS test on each of these 100 artificial samples with a goal to compare the stellar population parameters of the LAE and non-LAE populations. For Es(B−V) and SFR, a null hypothesis was consistently ruled out at ~3σ level, while for other parameters, the null hypothesis rejection is at much lower significance (≲2σ). We also compare the median values of the best-fit stellar parameters for LAEs and non-LAEs, and we find similar significance (as above) for the median values of the SED parameters in these bootstrap samples. These artificial samples show that even when accounting for the uncertainty in the best-fit parameters, a significant difference exists for Es(B−V) and SFR, such that galaxies with Lyα emission tend to be less dusty, and lower in SFR than galaxies with weak or no Lyα emission.
Table 1 summarizes average spectral and photometric properties of our SFGN, SFGL, and LAE samples. Our results show that SFGL (and LAEs) have – on average – lower dust content than SFGN. The differences in these two samples is statistically significant based on the K-S test results (PKS ~ 10-4), which says that distributions of Es(B−V) are different for SFGN and SFGL. Though the difference in the distributions of these populations is statistically significant, the difference between their median values is small as shown in Table 1. The median Es(B−V) values for SFGL or LAEs and SFGN differ only by ~0.05 or ~0.1 (i.e., by a factor of ~1.3 or 2) which is smaller than or similar to the 1σ scatter in these distributions (~0.1). This small difference in the dust content of SFGN and SFGL or LAE galaxies is consistent, within the large scatter, with the small difference in the median values of βspec, and a small difference in βphot values (~0.1−0.2) between these populations. Such a small difference between the Es(B−V) values for SFGL or LAEs and SFGN is also consistent with the observations at higher redshifts. Pentericci et al. (2010) found small differences between Es(B−V) values for their samples of LBGN and LBGL at z ~ 3. A similar study at z ~ 4 by Pentericci et al. (2007) agrees with this Es(B−V) trend for galaxies with and without Lyα in emission.
Average properties of SFGN, SFGL, and LAEs derived from the SED-fitting.
Figure 8 also shows that SFGL (and LAEs) have – on average – lower SED-based SFRs than SFGN. The KS test results show that distributions of the SFGL and SFGN samples are significantly different i.e., PKS ~ 10-4, which is as significant as the Es(B−V) comparison. The median SFR for the SFGL or LAE sample from the SED-fitting technique is 101.26 ~ 18 M⊙ yr-1 or 101.19 ~ 15 M⊙ yr-1, while the median SFR for the SFGN sample is 101.37 ~ 23 M⊙ yr-1. Therefore, the median SFR values for SFGL or LAEs and SFGN differ only by a factor of ~1.3 or 1.5, which is much smaller in comparison to the 1σ scatter of these distributions (~0.4 dex or a factor of ~2). To assess the effect of SED-fitting parameters on the SFRs (e.g., Kusakabe et al. 2015), we also compute SFR using the UV luminosity (M1500) corrected for the dust using the β–A1600 relation from Meurer et al. (1999). The median values for the UV-based SFRs (SFRUV) are shown in Table 1 and they are very similar to the SED-based SFRs. The median SFRUV for the SFGL or LAE sample is 101.19 ~ 15 M⊙ yr-1 or 100.99 ~ 10 M⊙ yr-1, and for the SFGN sample is 101.23 ~ 17 M⊙ yr-1. Therefore, the difference between SFRUV values of these populations is very small and agrees very well with the difference quoted for the SED-based SFRs. This is consistent with the fact that the UV absolute magnitudes (M1500) of galaxies with and without Lyα in emission are very similar as shown in the Table 1. This result is consistent with similar studies at z ~ 3–4 (e.g., Pentericci et al. 2007, 2010).
Figure 8 does not show any significant difference between the median values of stellar mass (~0.1 dex or a factor of ~1.2). This result is in contrast to higher redshift studies at z ~ 3–4 (e.g., Pentericci et al. 2007, 2010), where they find that galaxies without Lyα in emission are more massive (by a factor of ~2–5) compared to galaxies with Lyα in emission. The difference between these studies could be due to the sample selection, in that the stellar mass probed in those studies by the galaxies at z ~ 3–4 are much lower (down to ~108M⊙) compared to the VUDS sample (down to ~109M⊙). The lowest mass regime at z ~ 3–4 is mostly populated by galaxies with Lyα in emission which results in this significant difference in stellar masses for Lyα emitters and non-emitters at these redshifts. We do not probe this low mass regime between 108 and 109M⊙ at 2 < z < 2.5 because of our continuum magnitude limit of iAB ≲ 25 mag. Therefore, we conclude that, within the luminosities probed by VUDS, we do not see any significant difference between the stellar mass of galaxies with and without Lyα in emission. We will investigate any redshift evolution in these correlation in our future VUDS studies, which will extend these measurements to higher redshifts (z ≳ 3).
5. Lyα EW and stellar population properties
To further investigate properties of SFGN and SFGL, we explore the correlation between the rest-frame Lyα EW and stellar population parameters, such as M1500, UV slope, Es(B−V), SFR, stellar mass, and SSFR. Figure 9 shows the correlation between Lyα EW and best-fit SED/spectral parameters. The Spearman correlation is measured from all galaxies as well as from the median-binned values. The Es(B−V) and SFR show moderate-to-weak monotonic correlation (ρ ~ –0.2 and PSC< 10-4) with Lyα EW. The significance of ρ as measured by the number of standard deviations by which the sum-squared difference of ranks deviates from its null-hypothesis expected value is ~5σ for all Es(B−V) values and ~6σ for all SFR values. The stellar mass, M1500, and β show much weaker correlation with EW (ρ ≲ 0.1). The significance of ρ as defined above is ≲3σ for all values of these parameters. The trends observed between the best-fit stellar parameters and EWs are in general agreement with the median values of the stellar parameters obtained from the distributions of SFGN and SFGL in Fig. 8.
 |
Fig. 9 Correlation between rest-frame Lyα EW and best-fit stellar population parameters. The vertical dashed line indicates EW = 20 Å, the adopted lower limit in Lyα equivalent width for LAEs. The size of the last bin is increased with respect to that of the other bins to increase the number of galaxies in that bin. The light gray points are individual measurements while the black circles are binned medians. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between 16th and the 84th percentile values within each bin, while smaller solid error bars are the errors on the median values ( |
With increasing rest-frame Lyα EW, we see a weak but significant trend in that, galaxies are less dusty, and less star-forming, as indicated by the decrease in SFR by about ~0.2 dex from non-LAEs to LAEs. While the average EW varies from –38.0 Å to 120 Å, the median Es(B−V) decreases from 0.20 to 0.15, the median SFRSED decreases from 28 M⊙ yr-1 to 16 M⊙ yr-1, the median stellar mass decreases from 6.2 × 109M⊙ to 3.9 × 109M⊙, and the median SSFR decreases from 5.9 × 10-9 yr-1 to 6.3 × 10-9 yr-1. All these differences in stellar parameters as a function of Lyα EW are small compared to the scatter observed in each EW bin, as measured by 1σ dispersion (see Fig. 9).
 |
Fig. 10 Comparison between Spitzer/IRAC 3.6 μm-detected (red; brighter than m3.6 ~ 25 mag) and IRAC-undetected (blue; fainter than m3.6 ~ 25 mag) galaxies as function of stellar mass and SFR for SFGN, SFGL, and LAEs. The fraction of galaxies detected/un-detected in IRAC are shown in the legend. The solid curve is the KDE of the distribution. The statistical significance based on the KS test is shown to confirm the observed correlation. |
These results demonstrate that there is a statistically significant correlation between Lyα EW and stellar parameters, such as SFR and Es(B−V), while no significant correlations are found for stellar mass, M1500, and β. The differences we observe are small compared to the large scatter in their distributions. This outcome is true whether or not we focus on all galaxies with Lyα in emission or only strong Lyα emitters (LAEs). This is in contrast with results from NB or emission-line selected LAE studies (e.g., Gawiser et al. 2006, 2007; Lai et al. 2008; Guaita et al. 2011; Hagen et al. 2014). These studies find lower dust, lower stellar mass and higher SSFR for galaxies with strong Lyα in emission. The LAE samples used in these emission-line/NB-selected surveys have Lyα luminosities in the range of ~1042 erg/s, which is an order of magnitude more luminous than VUDS LAEs, as shown in Fig. 6. It is also worth emphasizing that VUDS is a UV continuum selected survey and galaxies are targeted based on their photometric redshifts and not on the strength of the Lyα line. We have 27 galaxies beyond rest-frame Lyα EW = 50 Å, so by selection, our sample does not include extremely low mass (~108M⊙) galaxies usually selected from emission-line/NB techniques. Moreover, among the emission-line/NB-selected LAEs, those that have lower Lyα luminosities, have similar SFR as normal star-forming galaxies but lie on the lower mass end of the star-forming main sequence (e.g., Kusakabe et al. 2015). Hence, the difference in the sample selection could play a significant role in such a comparison as we could be comparing two intrinsically different populations of galaxies.
The comparison of stellar population properties of galaxies with and without Lyα emission has also been done on UV-selected galaxies at z ≃ 2 and higher, and our results are broadly consistent with the literature. Pentericci et al. (2010) found weak/no correlation between SFRs of galaxies with and without Lyα emission at z ≃ 3 but we find a correlation (with a small difference in SFR) possibly because of the ample statistics in the VUDS sample. With a smaller number of galaxies (130) in the Pentericci et al. sample such a detection was difficult to observe. Our finding of a very small decrease in the SED-based dust content (i.e., Es(B−V)) of these two populations agrees well with the Pentericci et al. (2010) study. At z ≃ 3, Kornei et al. (2010) find that LAEs have lower Es(B−V) and SFRs compared to non-LAEs. The difference in these two stellar population parameters for LAEs and non-LAEs, as found by Kornei et al., is much larger than what we observe, but show similar decreasing trends in these two quantities. This trend of lower dust and SFR for strong Lyα emitters has also been observed at z ≃ 2 by Reddy et al. (2006). The study of Kornei et al. (2010) agrees well with our result that there is no significant difference between stellar masses of LAEs and non-LAEs. Therefore, based on the comparison between SFGL/LAEs and SFGN, as well as Lyα EW correlations with stellar parameters, we suggest that our LAE sample shows a small decrease in Es(B−V) and SFR but otherwise their stellar populations are not very different from the galaxies that do not show Lyα in emission.
Lai et al. (2008) studied NB-selected LAEs at z ≃ 3 by dividing them into Spitzer/IRAC-detected (brighter than m3.6 = 25.2 mag) and IRAC-undetected (fainter than m3.6 = 25.2 AB mag) samples. They found that IRAC-undetected LAEs were less massive and younger compared to IRAC-detected LAEs, concluding that IRAC-detected LAEs are a more evolved population similar to brighter/massive UV-selected LAEs (e.g., Shapley et al. 2001, 2003). To investigate this trend for VUDS LAEs, we examined our LAEs as a function of magnitude in the Spitzer/IRAC 3.6 μm band. We find that 74% of SFGN, 66% of SFGL, and 53% of LAEs have detections in the Spitzer/IRAC 3.6 μm band down to ~25 mag. The LAE fraction with IRAC detection in our sample is much larger than the ~30% found in Lai et al. (2008), which is a direct consequence of the difference in the sample selection between the two studies. The NB-selected LAEs typically have a very faint continuum in all optical and NIR bands as they are mostly lower mass/younger galaxies compared to normal star-forming galaxies. The detection of NB-LAEs in the IRAC bands is possible if they host a more evolved population, which makes the continuum brighter in the red bands. We do not expect many NB-selected LAEs to be more evolved/massive and brighter in the IRAC bands, therefore their IRAC-detected fractions are more likely to be smaller compared to other star-forming galaxies. A similar study at z ≃ 2 (Guaita et al. 2011), also found that ~25% of NB-selected LAEs had IRAC detection down to m3.6 ~ 24.5 AB mag. We find a higher detection rate (51%) of IRAC-detected LAEs in our sample using the same limiting magnitude of 24.5 mag as Guaita et al. Figure 10 shows the comparison of IRAC-detected and IRAC-undetected galaxies in all three samples as a function of stellar mass, and SFR. The stellar mass correlations show that, in all three samples, IRAC-detected galaxies are more massive than IRAC-undetected galaxies. These correlations are statistically significant based on their PKS values <10-2. We do not see any significant correlation for SFR in all three samples, both in terms of PKS and their median values.
These comparisons show that the VUDS LAE sample has a larger fraction of galaxies with IRAC detection compared to NB-selected LAEs at z ≃ 2–3, and that IRAC-detected LAEs are more likely to host evolved populations compared to IRAC-undetected LAEs. A substantial fraction of UV-selected LAEs have similar masses as SFGN galaxies, but with lower SFRs, suggesting that these LAEs host more evolved populations. The low fraction of IRAC detection in NB-selected LAEs implies that these galaxies are less evolved compared to UV-selected LAEs.
6. Results and discussion
We use a large spectroscopic sample of 854 SFGs at 2 < z < 2.5 from VUDS to investigate their spectral and photometric properties. The VUDS spectra were used to measure the UV spectral slope and Lyα EW. The SED fitting on multi-wavelength photometric data using Le PHARE provided best-fitting stellar parameters, such as stellar mass, M1500, Es(B−V), SFR, and SSFR. The VUDS observations cover a wide area of ~1 deg2, which implies that our sample spans a sizeable range in SFR (~3−150 M⊙ yr-1) and stellar mass (~5 × 108 to 1011M⊙). The VUDS 2 < z < 2.5 sample covers a substantial range in UV absolute magnitude around M∗ (±1 mag), the characteristic magnitude at these redshifts. We divide SFGs into three sub-groups, SFGN, SFGL and LAEs, based on their rest-frame Lyα EW. We find that the fraction of LAEs is ~10% at these redshifts, which is consistent with previous studies (e.g., Reddy et al. 2008), and is in accordance with the general picture where the Lyα fraction increases with redshift (e.g., Stark et al. 2010; Curtis-Lake et al. 2012; Cassata et al. 2015). The Lyα fraction apparently starts to decrease at higher redshift (z ≳ 6.5; e.g., Pentericci et al. 2011), where great amounts of neutral hydrogen start to affect the visibility of Lyα line indicating the onset of the reionization epoch.
The UV spectral slope β can be used to derive the dust attenuation for local starburst galaxies (e.g., Calzetti et al. 1994; Leitherer et al. 1999) and has been adopted as a dust indicator for high redshifts galaxies (e.g., Noll et al. 2004; Hathi et al. 2008b; Finkelstein et al. 2012; Bouwens et al. 2014). The main reason is that the intrinsic UV slope depends weakly on metallicity and stellar populations for star-forming galaxies (e.g., Heckman et al. 1998; Leitherer et al. 1999). In addition, β shows a strong correlation with the LIR-to-LUV ratio, a standard dust indicator (e.g., Meurer et al. 1999; Reddy et al. 2010). On average, the spectroscopic UV slope for SFGs at 2 < z < 2.5, measured using VUDS spectra, is comparable to the photometric UV slope measured using multiple photometric bands, and has smaller measurement uncertainties. The measured UV slope – spectroscopic and photometric – is in accordance with the evolutionary trend of β with redshift, which shows that lower redshift galaxies have, on average, redder UV slope compared to higher redshift galaxies (e.g., Bouwens et al. 2012; Hathi et al. 2013). With dust being the major factor influencing the UV slope, this implies that lower redshift galaxies have more dust compared to higher redshift galaxies. We use the spectroscopic β measurements to explore its correlation with M1500 and stellar mass. Comparing β to the stellar mass we find a significant correlation, in the sense that massive galaxies are redder, which is in general agreement with the higher redshift measurements of Finkelstein et al. (2012). We find no correlation between M1500 and β. This result is at variance with what is found by some authors at higher redshifts (e.g., Bouwens et al. 2012; Rogers et al. 2014), but it is similar to other studies which do not find any significant correlation between β and M1500 (e.g., Finkelstein et al. 2012; Castellano et al. 2012; Heinis et al. 2013). It is vital to note that this correlation could be affected by the biases and/or differences in the way different authors measure M1500 and/or β but most importantly the dynamic range in M1500 plays a crucial role. Extensive studies exploring a wider range in M1500 and stellar masses, and investigating different biases in these correlations, will shed more light on the true nature of these relations and provide a better physical understanding.
There are several studies investigating the stellar population of UV-selected LAEs at z ≃ 2–3 (e.g., Shapley et al. 2001, 2003; Erb et al. 2006; Reddy et al. 2008; Kornei et al. 2010). We find that LAEs in our sample have lower dust content, lower SFR and lower SSFR compared to non-LAEs. These differences are very small compared to the large scatter in these SED-based parameters, but they are significant because of the big sample size. Shapley et al. (2001) and Kornei et al. (2010) found that LAEs at z ≃ 3 have lower SFRs, lower dust and lower SSFR compared to LBGs, which is consistent with our observed trends, but we find much smaller differences in these stellar parameters for our galaxies. We find weak or no correlation of stellar mass with Lyα EW for a sample with median Log(M∗) = 9.64 and median Log(SFR) = 1.32. Kornei et al. (2010) studied a sample of ~300 UV-selected galaxies, with and without Lyα emission, with a median stellar mass of Log(M∗) = 9.92 and a median SFR of Log(SFR) = 1.57, both slightly higher than for our sample. They found that there is no significant difference in the stellar mass between these two populations in accordance with our weak-to-no correlation of stellar mass with the Lyα EW. The results obtained here show no strong correlation or substantial differences between stellar parameters as a function of the Lyα EW, which is consistent with the small sample study of Reddy et al. (2008) using UV-selected galaxies at z ≃ 2–3. It is clear that the properties of galaxies with and without Lyα in emission are pretty similar suggesting that the two populations, at least for typical (~L∗) galaxies and to the level of detail we are able to probe, are roughly comprised of similar galaxies. Erb et al. (2006) used composite spectra of UV-selected LAEs and non-LAEs at z ≃ 2 and found that galaxies with strong Lyα EW had lower stellar masses. Our results on SFR and dust are broadly consistent with previous studies, but the lack of a strong correlation between stellar mass and EW needs to be explored with a sample that spans a larger dynamic range in stellar mass as lower mass galaxies could strongly impact the stellar mass correlation between Lyα emitters and non-emitters.
In comparison to UV-selected LAEs, LAEs selected based on the emission-line/NB technique at z ≃ 2 and beyond have very low masses ~108M⊙ compared to ~1010M⊙ for non-LAEs (e.g., Gawiser et al. 2007; Finkelstein et al. 2007; Lai et al. 2008; Guaita et al. 2011; Vargas et al. 2014). Also, these LAEs are much more luminous in Lyα (~1042 erg/s) than VUDS LAEs, which are on average an order of magnitude less luminous (~1041 erg/s). We do not find such low mass, high Lyα luminosity LAEs in our sample mainly because these strong emitters have low continuum luminosities and are not selected by the VUDS magnitude selection. In fact, such galaxies would be missed in almost all UV continuum selected samples (e.g., Shapley et al. 2001; Reddy et al. 2008; Kornei et al. 2010), as emission-line/NB LAEs probe a different luminosity range compared to magnitude-limited samples. However, Kornei et al. (2010) have argued that when NB-selected LAEs are restricted to luminosities probed by continuum selected samples, both samples are statistically very similar, which is consistent with the result put forward by the study of Verhamme et al. (2008), where bright NB-selected LAEs represent the same population as continuum selected LAEs. Therefore, UV-selected LAEs and NB-selected LAEs need to probe similar luminosities for proper comparison between these two populations.
In the literature there are two possible scenarios under which galaxies emit Lyα during the evolution process. Studies of faint NB-selected LAEs (e.g., Gawiser et al. 2006, 2007; Lai et al. 2008) have argued that LAEs represent the beginning of an evolutionary sequence of galaxy formation. According to these studies, the main reason behind this argument is that LAEs have lower dust content, lower stellar mass, younger stellar ages, and higher SSFRs compared to non-LAEs which means that LAEs are building up their stellar mass at a faster rate than non-LAEs through mergers and/or star-formation episodes. On the other hand, studies of brighter continuum selected LAEs (e.g., Shapley et al. 2001, 2003; Kornei et al. 2010) have suggested that LAEs represent a later stage in the evolutionary sequence. These studies argue that LAEs have lower dust content, lower SFR, older stellar ages, and lower SSFRs compared to non-LAEs which means that LAEs are more quiescent than non-LAEs. This could be the result of strong outflows from supernovae and massive star winds, which expel both gas and dust from a young, dusty non-LAE. These arguments raise a question: are these two scenarios two different phases of the evolution process or do these two possibilities describe a single phase? Lai et al. (2008) investigated the stellar populations of 162 NB-selected LAEs at z ≃ 3.1 by dividing them in two groups based on their Spitzer/IRAC flux. They find that ~70% of the LAEs are undetected in 3.6 μm down to 25.2 mag. Based on their stacking analysis, they find a clear difference between these two divided samples. The average stellar population of the IRAC-undetected sample had an age of ~200 Myr and a mass of ~3×108M⊙, consistent with the scenario that LAEs are mostly young and low-mass galaxies. On the other hand, the IRAC-detected LAEs were on average significantly older and more massive, with an average age of ~1 Gyr and mass of ~1010M⊙. The stellar populations of the IRAC-detected sample of Lai et al. (2008) are very similar to those of continuum selected brighter LAEs (e.g., Shapley et al. 2001, 2003; Kornei et al. 2010). Similar results are also found in the study of Guaita et al. (2011) at z ≃ 2.1, in that, the fraction of IRAC-detected LAEs is ~25% down to 24.5 mag and these galaxies are more massive/evolved than those that are faint in IRAC. We find larger fraction of IRAC-detected LAEs (~50%) compared to NB-selected LAEs (~30%) at z ≃ 2–3, which could imply that UV-selected LAEs are more evolved compared to NB/emission-line selected LAEs. Also, the IRAC-detected LAEs have higher stellar mass, similar to IRAC-detected non-LAEs, but with lower SFR which is consistent with the more evolved nature of these galaxies. The scenario in which LAEs are more evolved than non-LAEs is plausible if strong outflows in non-LAEs destroy or remove dust and gas from the galaxies, allowing Lyα photons to escape. Our results from direct comparison of galaxies with and without Lyα emission show small differences in stellar populations, such that galaxies with Lyα emission have lower SFR and dust content than non-Lyα emitting galaxies. This result broadly agrees with previous studies involving UV-selected galaxies at z ≃ 3 (e.g., Shapley et al. 2003; Kornei et al. 2010), though we observe small difference between physical parameters of Lyα emitters and non-emitters. Past studies of LAEs (e.g., Verhamme et al. 2008; Nilsson et al. 2011; Acquaviva et al. 2012), suggest that LAEs have a wide range in stellar population properties implying that a strong LAE phase either is a long duration phase (~1 Gyr; Lai et al. 2008) or is recurring in SFGs.
Studies focusing on comparing stellar populations of galaxies with and without Lyα emission have shown that various effects, including the sample selection, continuum and Lyα luminosities, measurements of stellar parameters, and SED fitting assumptions play an important role in how we compare Lyα emitters and non-emitters. It is also essential to understand that these comparisons and correlations are not universal and could change with redshift. Extending these studies to higher redshifts, where the fraction of Lyα emitters increases, is essential to generate a self-consistent picture of how LAEs and non-LAEs form and evolve. In future studies, we will extend such an analysis to z ≃ 3–6 using the VUDS data, to better understand how these LAE properties/trends evolve with redshift from z ~ 6 to z ~ 2.
7. Summary
In this paper, we have investigated the spectro-photometric properties of a large sample of SFGs at 2 < z < 2.5 that were selected from the VIMOS Ultra-Deep Survey in the ECDFS, COSMOS, and VVDS fields. These galaxies were targeted as a result of their photometric redshifts, and are therefore UV continuum-selected galaxies. The VUDS spectra were used to measure the UV spectral slope (β) and Lyα EWs, while we used deep multi-wavelength observations in these extensively observed fields to derive physical parameters (stellar mass, SFR, Es(B−V), M1500, SSFR) from the SED fitting process. We compared Lyα emitters and non-emitters using these parameters and also explored correlations of these parameters with Lyα EW. Our results can be summarized as follows:
-
We obtain reliable measurements ofβspec, which are – on average – similar to βphot, and have smaller measurement uncertainties. The median values of βspec and βphot are consistent with each other and with the general picture in which UV slopes get redder with decreasing redshift, implying higher dust content at lower redshifts. We find a significant correlation between β and SED-based dust indicator Es(B−V). We observe no correlation between β and M1500, while a strong correlation between β and stellar mass is observed. These results are consistent with higher redshift observations.
-
For a proper comparison, we divide these SFGs into three subgroups based on their EWs: SFGN (EW ≤ 0 Å), SFGL (EW > 0 Å), and LAEs (EW ≥ 20 Å). The LAEs make up ~10% of the total SFG sample at 2 < z < 2.5, which is consistent with previous observations.
-
We find that at 2 < z < 2.5, within the luminosities probed, the SFGL (and LAE) sample has slightly lower Es(B−V) and SFRs compared to the SFGN sample. These differences are small but statistically significant. It is important to note that we are able to probe these small differences in the physical parameters because of our large SFG sample. We do not find any or find weaker significant differences in stellar mass, M1500, and β for these two samples. We find similar results when we compare Lyα EW and physical parameters. These results indicate that the properties of galaxies with and without Lyα in emission are remarkably similar which suggests that the two populations, at least for typical (~L∗) galaxies and to the level of detail we are able to probe, are roughly made up of similar galaxies.
-
When we divide the LAEs based on their Spitzer/IRAC 3.6 μm magnitudes, the fraction of IRAC-detected LAEs (~50%) is much greater than the fraction of IRAC-detected NB-selected LAEs (~30%) at z ≃ 2–3. This could imply that UV-selected LAEs host a more evolved stellar population compared to NB/emission line-selected LAEs. Based on differing stellar population results for LAEs at various redshifts, we cannot rule out multiple or recurring Lyα emitting phases for SFGs.
Future studies of higher redshift (z ≃ 3–6) galaxies from VUDS, where the fraction of Lyα-emitting galaxies increases substantially, will help us to better understand the LAE population at these redshifts, as well as to see how these correlation evolve with redshift.
Acknowledgments
We thank the referee for helpful comments and suggestions that significantly improved this paper. This work is supported by funding from the European Research Council Advanced Grant ERC-2010-AdG-268107-EARLY and by INAF Grants PRIN 2010, PRIN 2012 and PICS 2013. A.C., O.C., M.T. and V.S. acknowledge the grant MIUR PRIN 2010–2011. This work is based on data products made available at the CESAM data center, Laboratoire d’Astrophysique de Marseille. This work partly uses observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
References
- Adelberger, K. L., Steidel, C. C., Shapley, A. E., et al. 2004, ApJ, 607, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Acquaviva, V., Vargas, C., Gawiser, E., et al. 2012, ApJ, 751, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Siana, B., Scarlata, C., et al. 2011, ApJ, 743, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Berry, M., Gawiser, E., Guaita, L., et al. 2012, ApJ, 749, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2007, ApJ, 670, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R., Illingworth, G. D., Oesch, P. A., et al. 2014, ApJ, 793, 115 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardamone, C. N., van Dokkum, P. G., Urry, C. M., et al. 2010, ApJS, 189, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Le Fèvre, O., Garilli, B., et al. 2011, A&A, 525, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassata, P., Tasca, L., Le Fèvre, O., et al. 2015, A&A, 573, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Fontana, A., Grazian, A., et al. 2012, A&A, 540, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappetti, L., Tajer, M., Trinchieri, G., et al. 2005, A&A, 439, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimatti, A., Brusa, M., Talia, M., et al. 2013, ApJ, 779, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuillandre, J.-C., Withington, K., Hudelot, P., et al. 2012, Observatory Operations: Strategies, Processes, and Systems IV, Proc. SPIE, 8448, 84480 [Google Scholar]
- Curtis-Lake, E., McLure, R., Pearce, H., et al. 2012, MNRAS, 422, 1425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Cimatti, A., Renzini, A., et al. 2004, ApJ, 617, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Mobasher, B., Dickinson, M., et al. 2010, ApJ, 724, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R., Robertson, B., et al. 2012, MNRAS, 420, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, R. S., McLure, R. J., Dunlop, J. S., et al. 2013, ApJ, 763, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Rhoads, J. E., Malhotra, S., et al. 2007, ApJ, 660, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Rhoads, J. E., Malhotra, S., et al. 2009, ApJ, 691, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Giavalisco, M., et al. 2010, ApJ, 719, 1250 [Google Scholar]
- Finkelstein, S. L., Hill, G. J., Gebhardt, K., et al. 2011, ApJ, 729, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Salmon, B., et al. 2012, ApJ, 756, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Dickinson, M., et al. 2013, Nature, 502, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Ryan, R. E., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gawiser, E., van Dokkum, P., Gronwall, C., et al. 2006, ApJ, 642, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gawiser, E., Francke, H., Lai, K., et al. 2007, ApJ, 671, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guaita, L., Gawiser, E., Padilla, N., et al. 2010, ApJ, 714, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Guaita, L., Acquaviva, V., Padilla, N., et al. 2011, ApJ, 733, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Haberzettl, L., Williger, G., Lehnert, M. D., et al. 2012, ApJ, 745, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Hagen, A., Ciardullo, R., Gronwall, C., et al. 2014, ApJ, 786, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Jansen, R. A., Windhorst, R. A., et al. 2008a, AJ, 135, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Malhotra, S., & Rhoads, J. 2008b, ApJ, 673, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Ryan, R. E., Cohen, S. H., et al. 2010, ApJ, 720, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Mobasher, B., Capak, P., et al. 2012, ApJ, 757, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Cohen, S. H., Ryan, R. E., et al. 2013, ApJ, 765, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Heinis, S., Buat, V., Bethermin, M., et al. 2013, MNRAS, 429, 1113 [Google Scholar]
- Heckman, T. M., Robert, C., Leitherer, C., et al. 1998, ApJ, 503, 646 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K., Shapley, A., Erb, D., et al. 2010, ApJ, 711, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Kurk, J., Cimatti, A., Daddi, E., et al. 2009, Msngr, 135, 40 [NASA ADS] [Google Scholar]
- Kusakabe, H., Shimasaku, K., Nakajima, K., et al. 2015, ApJ, 800, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 708, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, K., Huang, J.-S., Fazio, G., et al. 2008, ApJ, 674, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Mellier, Y., McCracken, H., et al. 2004, A&A, 417, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Guzzo, L., Meneux, B., et al. 2005, A&A, 439, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Tasca, L., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemaux, B. C., Lubin, L., Shapley, A., et al. 2010, ApJ, 716, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaux, B. C., Cucciati, O., Tasca, L. A. M., et al. 2014a, A&A, 572, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemaux, B. C., Le Floc’h, E., Le Fèvre, O., et al. 2014b, A&A, 572, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Malkan, M. A., Hayashi, M., et al. 2011, ApJ, 735, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P. 1995, ApJ, 441, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauduit, J.-C., Lacy, M., Farrah, D., et al. 2012, PASP, 124, 714 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H., Radovich, M., Bertin, E., et al. 2003, A&A, 410, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, H., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, 156 [Google Scholar]
- McLure, R., Dunlop, J. S., Cirasuolo, M., et al. 2010, MNRAS, 403, 960 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R., Dunlop, J. S., de Ravel, L., et al. 2011, MNRAS, 418, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., Lehnert, M. D., et al. 1997, AJ, 114, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Mostek, N., Coil, A., Moustakas, J., et al. 2012, ApJ, 746, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., van Dokkum, P., Kriek, M., et al. 2010, ApJ, 725, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K., Östlin, G., Moller, P., et al. 2011, A&A, 529, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., & Pierini, D. 2005, A&A, 444, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., Mehlert, D., Appenzeller, I., et al. 2004, A&A, 418, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Carollo, C. M., et al. 2010, ApJ, 725, L150 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Masami, O., Kazuhiro, S., et al. 2010, ApJ, 724, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Oteo, I., Bongiovanni, A., Magdis, G., et al. 2014, MNRAS, 439, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ono, Y., Egami, E., et al. 2009, ApJ, 696, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Dickinson, M., Ferguson, H. C., et al. 2004, ApJ, 600, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Grazian, A., Fontana, A., et al. 2007, A&A, 471, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pentericci, L., Grazian, A., Scarlata, C., et al. 2010, A&A, 514, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pentericci, L., Fontana, A., Vanzella, E., et al. 2011, ApJ, 743, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Pforr, J., Maraston, C., & Tonini, C. 2012, MNRAS, 422, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C., Pettini, M., et al. 2008, ApJS, 175, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Erb, D., Pettini, M., et al. 2010, ApJ, 712, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Dickinson, M., Elbaz, D., et al. 2012, ApJ, 744, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, A., McLure, R., Dunlop, J., et al. 2014, MNRAS, 440, 3714 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Sawicki, M. 2012, MNRAS, 421, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., de Barros, S., & Sklias, P. 2013, A&A, 549, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Seibert, M., Heckman, T. M., & Meurer, G. R. 2002, AJ, 124, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A., Steidel, C., Adelberger, K., et al. 2001, ApJ, 562, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A., Steidel, C., Pettini, M., et al. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C., Capak, P., et al. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Chiu, K., et al. 2010, MNRAS, 408, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Shapley, A. E., Pettini, M., et al. 2004, ApJ, 604, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Talia, M., Mignoli, M., Cimatti, A., et al. 2012, A&A, 539, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talia, M., Cimatti, A., Pozzetti, L., et al. 2015, A&A, 582, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Hathi, N. P., et al. 2015, A&A, 581, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, R., Le Fèvre, O., Le Brun, V., et al. 2014, A&A, submitted [arXiv:1411.5692] [Google Scholar]
- Tilvi, V., Papovich, C., Tran, H.-V. H., et al. 2013, ApJ, 768, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Tresse, L., Maddox, S., Loveday, J., & Singleton, C. 1999, MNRAS, 310, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Vargas, C. J., Bish, H., Acquaviva, V., et al. 2014, ApJ, 783, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., et al. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitaker, K. E., Kriek, M., van Dokkum, P. G., et al. 2012, ApJ, 745, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wilkins, S. M., Bunker, A. J., Stanway, E., et al. 2011, MNRAS, 417, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Windhorst, R. A., Hathi, N. P., et al. 2010, RA&A, 10, 867 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Redshift versus UV absolute magnitude (M1500) for spectroscopically confirmed SFGs at 2 < z < 2.5 from VUDS. The median M1500 of the sample is –20.22 mag, the median redshift is 2.320. The quoted uncertainties are the errors on the median ( |
| In the text | |
 |
Fig. 2 SFR versus stellar mass for SFGs at 2 < z < 2.5 in VUDS. The full sample has median stellar mass of 109.64 ~ 4 × 109M⊙ and median SFR of 101.32 ~ 20 M⊙ per year. The quoted uncertainties are the errors on the median ( |
| In the text | |
 |
Fig. 3 Examples of UV spectral slope (β) fitting on the VUDS spectra (shown in gray). The spectra between rest-frame 1400 Å to 2400 Å (between dashed vertical lines) are fitted with a linear relation (solid red lines) between Log(λ) vs. Log(Fλ) after masking out known lines and removing spurious noise spikes. The dashed red lines are 1σ deviations in the best-fit relation. The blue filled circles are the photometric magnitudes from the broad-band filters (gray curves) used to measure the photometric β, while the blue dashed line is a linear fit between these photometric data points to estimate the photometric UV slope. |
| In the text | |
 |
Fig. 4 Left: UV spectral slope (β) distribution as measured from the VUDS spectra (red histogram) and the broad-band photometry (blue histogram). The solid curve is the KDE of the distribution. The median β values as well as KS-test probability (PKS) show very small difference in these βs. Middle: βspec versus βphot. The solid red line is the best orthogonal fit relation between these two βs, while the dashed lines show the uncertainties in the best-fit relation. This figure also shows the difference (βspec−βphot) as a function of βspec. The dotted line is for βspec−βphot = 0. The density of points is color-coded as in previous figures. Average uncertainties in these measurements are plotted in the bottom-right corner. Right: the correlation between the UV slope and the SED derived Es(B−V) is such that the redder UV slope implies dustier [higher Es(B−V)] galaxies. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between the 16th and the 84th percentile values within each bin, while the smaller solid error bars are the errors on the median values ( |
| In the text | |
 |
Fig. 5 Spectroscopic UV slope versus the UV absolute magnitude (left) and the stellar mass (right). The density of points is color-coded as in previous figures, while the red open circles are the median-binned values for these parameters. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between the 16th and the 84th percentile values within each bin, while smaller solid error bars are the errors on the median values ( |
| In the text | |
 |
Fig. 6 Left: rest-frame EW distribution for SFGs with Lyα in emission (positive EWs) and Lyα in absorption (negative EWs). The vertical dashed line indicates EW = 20 Å, the adopted lower limit in Lyα EW for LAEs (or strong Lyα emitters). The solid curve is the KDE of the distribution. Middle: distribution of Lyα luminosities for the SFGL (black) and the LAE (red) samples. The KDE of the distribution is shown by a solid curve. Right: fraction of LAEs as a function of redshift for our sample. Approximately 10% of SFGs at these redshifts are strong Lyα emitters, consistent with previous Lyα studies (e.g., Reddy et al. 2008; Cassata et al. 2015) at similar redshifts. |
| In the text | |
 |
Fig. 7 Stacked (median-combined) rest-frame UV spectra for SFGN, SFGL, and LAEs. The strong absorption and emission features are marked by the vertical dotted lines. The SFGN spectrum shows strong absorption lines (Si, C, O, Fe, Al), but these absorption lines get weaker with increasing strength of Lyα-emission. The bottom panel shows similarity in the spectroscopic UV slope for these samples. |
| In the text | |
 |
Fig. 8 Comparison between SFGN (black histograms), SFGL (red histograms), and LAEs (blue histograms) as a function of stellar parameters. The total number of galaxies identified as SFGN, SFGL, and LAEs are shown in the legend. The median value of the distribution is indicated by a vertical dashed line. The solid curves are KDE of the distribution. The gray shaded regions cover ±1σ dispersion/scatter, which corresponds to the range between the 16th and the 84th percentile values, of the SFGN distribution. The statistical significance based on the KS test (red for SFGL, and blue for LAEs with respect to SFGN) is shown to confirm any correlation. |
| In the text | |
 |
Fig. 9 Correlation between rest-frame Lyα EW and best-fit stellar population parameters. The vertical dashed line indicates EW = 20 Å, the adopted lower limit in Lyα equivalent width for LAEs. The size of the last bin is increased with respect to that of the other bins to increase the number of galaxies in that bin. The light gray points are individual measurements while the black circles are binned medians. The error bars in x illustrate the sizes of the bins, while the errors in y are ±1σ scatter (dashed error bars) corresponding to the range between 16th and the 84th percentile values within each bin, while smaller solid error bars are the errors on the median values ( |
| In the text | |
 |
Fig. 10 Comparison between Spitzer/IRAC 3.6 μm-detected (red; brighter than m3.6 ~ 25 mag) and IRAC-undetected (blue; fainter than m3.6 ~ 25 mag) galaxies as function of stellar mass and SFR for SFGN, SFGL, and LAEs. The fraction of galaxies detected/un-detected in IRAC are shown in the legend. The solid curve is the KDE of the distribution. The statistical significance based on the KS test is shown to confirm the observed correlation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


