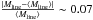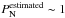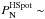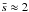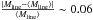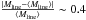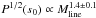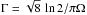| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526431 | |
| Published online | 01 December 2015 | |
Possible link between the power spectrum of interstellar filaments and the origin of the prestellar core mass function⋆
1 Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, C.E. Saclay, Orme des Merisiers, 91191 Gif-sur-Yvette, France
e-mail: Arabindo.Roy@cea.fr; philippe.andre@cea.fr
2 Institut d’Astrophysique Spatiale, CNRS/Université Paris-Sud 11, 91405 Orsay, France
3 School of Physics & Astronomy, Cardiff University, Cardiff, CF29, 3 AA, UK
4 Université de Bordeaux, LAB, CNRS/INSU, UMR 5804, BP 89, 33271 Floirac Cedex, France
5 INAF-Istituto di Astrofisica e Planetologia Spaziali, via Fosso del Cavaliere 100, 00133 Rome, Italy
6 Department of Physics and Astronomy, University of Victoria, PO Box 355, STN CSC, Victoria, BC, V8W 3P6, Canada
7 National Research Council Canada, 5071 West Saanich Road, Victoria, BC, V9E 2E7, Canada
8 Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
9 Departamento de Astronomía, Universidad de Chile, 1058 Santiago, Chile
10 Jeremiah Horrocks Institute, University of Central Lancashire, Preston, Lancashire, PR1 2HE, UK
11 Department of Physics and Astronomy, The Open University, Walton Hall Milton Keynes, MK7 6AA, UK
12 RAL Space, STFC Rutherford Appleton Laboratory, Chilton Didcot, Oxfordshire OX11 0QX, UK
Received: 28 April 2015
Accepted: 8 September 2015
A complete understanding of the origin of the prestellar core mass function (CMF) is crucial. Two major features of the prestellar CMF are 1) a broad peak below 1 M⊙, presumably corresponding to a mean gravitational fragmentation scale, and 2) a characteristic power-law slope, very similar to the Salpeter slope of the stellar initial mass function (IMF) at the high-mass end. While recent Herschel observations have shown that the peak of the prestellar CMF is close to the thermal Jeans mass in marginally supercritical filaments, the origin of the power-law tail of the CMF/IMF at the high-mass end is less clear. In 2001, Inutsuka proposed a theoretical scenario in which the origin of the power-law tail can be understood as resulting from the growth of an initial spectrum of density perturbations seeded along the long axis of star-forming filaments by interstellar turbulence. Here, we report the statistical properties of the line-mass fluctuations of filaments in the Pipe, Taurus, and IC 5146 molecular clouds observed with Herschel for a sample of subcritical or marginally supercritical filaments using a 1D power spectrum analysis. The observed filament power spectra were fitted by a power-law function (Ptrue(s) ∝ sα) after removing the effect of beam convolution at small scales. A Gaussian-like distribution of power-spectrum slopes was found, centered at α̅corr = −1.6 ± 0.3. The characteristic index of the observed power spectra is close to that of the 1D velocity power spectrum generated by subsonic Kolomogorov turbulence (−1.67). Given the errors, the measured power-spectrum slope is also marginally consistent with the power spectrum index of −2 expected for supersonic compressible turbulence. With such a power spectrum of initial line-mass fluctuations, Inutsuka’s model would yield a mass function of collapsed objects along filaments approaching dN/dM ∝ M− 2.3 ± 0.1 at the high-mass end (very close to the Salpeter power law) after a few free-fall times. An empirical correlation, P0.5(s0) ∝ ⟨NH2⟩1.4 ± 0.1, was also found between the amplitude of each filament power spectrum P(s0) and the mean column density along the filament ⟨NH2⟩. Finally, the dispersion of line-mass fluctuations along each filament σMline was found to scale with the physical length L of the filament roughly as σMline ∝ L0.7. Overall, our results are consistent with the suggestion that the bulk of the CMF/IMF results from the gravitational fragmentation of filaments.
Key words: ISM: structure / stars: formation / stars: luminosity function, mass function / evolution
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Understanding the origin of the stellar initial mass function (IMF) is a fundamental open problem in modern astrophysics (see, e.g., Offner et al. 2014 for a recent review). Since the end of the 1990s, several observational studies of prestellar dense cores in nearby molecular clouds have found a strong link between the prestellar core mass function (CMF) and the IMF (e.g., see Motte et al. 1998; Alves et al. 2007; Könyves et al. 2010, 2015), suggesting that the IMF is at least partly the result of the core formation process. Theories of the CMF/IMF based on gravo-turbulent fragmentation (e.g., Padoan & Nordlund 2002; Hennebelle & Chabrier 2008, Hopkins 2012) are consistent with this view, but do not account for the fact that most cores/stars appear to form within interstellar filaments. Indeed, recent Herschel observations (e.g., André et al. 2010; Molinari et al. 2010; Arzoumanian et al. 2011; Hill et al. 2011; Könyves et al. 2015) emphasize the role of interstellar filaments in star-forming clouds and support a paradigm for star formation in which the formation of ~0.1 pc-wide filaments and the subsequent fragmentation of the densest filaments into prestellar cores are two key steps in the star formation process (see André et al. 2014). The results of the Herschel Gould Belt survey (HGBS) further suggest that gravitational fragmentation of marginally supercritical filaments with masses per unit length Mline approaching the critical line mass of nearly isothermal ~10 K gas cylinders 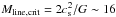 M⊙/pc (Ostriker 1964; Inutsuka & Miyama 1997) may be responsible for the peak of the prestellar CMF at ~0.6 M⊙, as observed in the Aquila cloud complex for example (André et al. 2014; Könyves et al. 2015). This idea is consistent with the view that the peak of the IMF is related to the typical Jeans mass in star-forming clouds (Larson 1985).
M⊙/pc (Ostriker 1964; Inutsuka & Miyama 1997) may be responsible for the peak of the prestellar CMF at ~0.6 M⊙, as observed in the Aquila cloud complex for example (André et al. 2014; Könyves et al. 2015). This idea is consistent with the view that the peak of the IMF is related to the typical Jeans mass in star-forming clouds (Larson 1985).
In gravo-turbulent fragmentation theories of the CMF/IMF, the peak of the IMF results from a combination of thermal physics, setting the mean thermal Jeans mass in the parent cloud, and turbulence effects, through the turbulence Mach number (Hennebelle & Chabrier 2008; Hopkins 2012; Chabrier et al. 2014). In the filamentary picture proposed by André et al. (2014), a characteristic thermal Jeans mass results from the existence of a critical line mass for filaments (which depends only on gas temperature) and from the characteristic filament width ~0.1 pc measured with Herschel (Arzoumanian et al. 2011), which is close to the sonic scale of turbulence (Federrath et al. 2010, and references therein) in low-density molecular gas. Taken together, this sets a density or column density threshold for prestellar cores and star formation as observed in nearby clouds with Herschel (André et al. 2010; Könyves et al. 2015) and Spitzer (Heiderman et al. 2010; Lada et al. 2010), respectively.
 |
Fig. 1 Herschel 250 μm surface brightness image of the Pipe molecular cloud observed as a part of the HGBS key project (cf. Peretto et al. 2012). The image is displayed at the diffraction limited 250 μm beam resolution of 18.̋2. The 43 filaments traced with the DisPerSE algorithm (Sousbie et al. 2011) are highlighted in white. A more detailed view of the filament enclosed by the black dashed rectangle is shown in Fig. 2. (This figure is available in color in electronic form.) |
Although the thermal Jeans mass within marginally supercritical filaments may account for the peak of the prestellar CMF, pure thermal fragmentation of filaments at the threshold of gravitational instability is expected to lead to a sharply peaked CMF (such as a delta function) and can hardly explain the Salpeter power-law regime of the IMF at the high-mass end. Inutsuka (2001) suggested, however, that a Salpeter-like CMF can quickly develop within filaments provided that turbulence has generated the appropriate power spectrum of initial density fluctuations in the first place. More specifically, Inutsuka (2001) found that the hierarchical structural property of the perturbed density field along filaments may statistically produce a population of cores with a power-law mass function. Inutsuka’s approach consisted of counting the distribution of “isolated” collapsed regions of mass scale M above a critical density using the Press-Schechter formalism (Press & Schechter 1974; Jedamzik 1995), where the statistics of such regions depend on the logarithmic slope of the power spectrum characterizing the initial fluctuating density field. Inutsuka (2001) showed that the resulting core mass distribution converges toward a Salpeter-like mass function dN/dM ∝ M-2.5 when the power spectrum of the field of initial line-mass fluctuations approaches P(s) ∝ s-1.5. This value was adopted on a purely ad hoc basis, however, and the true statistical nature of the density fluctuations along filaments remained to be quantified observationally. Another important assumption of Inutsuka’s model was that the initial line-mass fluctuations along filaments could be represented by a Gaussian random distribution.
In this paper, we exploit the unprecedented sensitivity and resolution of Herschel submillimeter continuum images as well as the proximity of the molecular clouds targeted as part of the HGBS key project to characterize, for the first time, the statistical properties of the line-mass fluctuations along interstellar filaments by analyzing their 1D power spectrum. Our main goal is to constrain observationally the validity of the theoretical model outlined by Inutsuka (2001) for the origin of a Salpeter-like prestellar CMF above ~1 M⊙.
2. Herschel observations and column density maps
The three target fields that we used in the present analysis were all observed with the Herschel1 space observatory (Pilbratt et al. 2010) as part of the HGBS key project (André et al. 2010); they cover surface areas of ~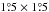 , ~
, ~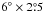 , and ~
, and ~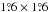 in the IC 5146, Pipe, and Taurus molecular clouds, respectively (Arzoumanian et al. 2011; Peretto et al. 2012; Palmeirim et al. 2013). These three regions were mapped at a scanning speed of 60″s-1 in parallel mode simultaneously at five Herschel wavelengths using the SPIRE (Griffin et al. 2010) and PACS (Poglitsch et al. 2010) photometric cameras. The data were reduced using HIPE version 7.0. For the SPIRE data reduction, we used modified pipeline scripts. Observations during the turnaround of the telescope were included, and a destriper module with a zero-order polynomial baseline was applied. The default naïve mapper was used to produce the final maps. For the PACS data, we applied the standard HIPE data reduction pipeline up to level 1, with improved calibration. Further processing of the data, such as subtraction of thermal and non-thermal low-frequency noise and map projection was performed with Scanamorphos v11 (Roussel 2013). The Scannamorphos map-maker avoids any high-pass filtering, which is crucial for preserving extended emission. We adjusted the zero-point values of individual Herschel images based on cross-correlations of the Herschel data with IRAS and Planck data (cf. Bernard et al. 2010). Figure 1 shows an example of 250 μm surface brightness image of the Pipe Nebula at the native resolution of 18.̋2.
in the IC 5146, Pipe, and Taurus molecular clouds, respectively (Arzoumanian et al. 2011; Peretto et al. 2012; Palmeirim et al. 2013). These three regions were mapped at a scanning speed of 60″s-1 in parallel mode simultaneously at five Herschel wavelengths using the SPIRE (Griffin et al. 2010) and PACS (Poglitsch et al. 2010) photometric cameras. The data were reduced using HIPE version 7.0. For the SPIRE data reduction, we used modified pipeline scripts. Observations during the turnaround of the telescope were included, and a destriper module with a zero-order polynomial baseline was applied. The default naïve mapper was used to produce the final maps. For the PACS data, we applied the standard HIPE data reduction pipeline up to level 1, with improved calibration. Further processing of the data, such as subtraction of thermal and non-thermal low-frequency noise and map projection was performed with Scanamorphos v11 (Roussel 2013). The Scannamorphos map-maker avoids any high-pass filtering, which is crucial for preserving extended emission. We adjusted the zero-point values of individual Herschel images based on cross-correlations of the Herschel data with IRAS and Planck data (cf. Bernard et al. 2010). Figure 1 shows an example of 250 μm surface brightness image of the Pipe Nebula at the native resolution of 18.̋2.
 |
Fig. 2 Close-up view of the sub-region indicated by the black dashed rectangle in Fig. 1 showing a) an example of a nearly critical filament in the Pipe cloud at an adopted distance d = 145 pc and b) the line-mass/column density fluctuations along the long axis of the same filament, both at the 18.̋2 (HPBW) resolution of the SPIRE 250 μm data. The black curve in a) shows the crest of the filament as traced by the DisPerSE algorithm (cf. Sousbie et al. 2011). In b) the right ordinate axis shows the net H2-column density fluctuations along the filament. Equivalent line-mass values (assuming a characteristic filament width of 0.1 pc) are indicated on the left ordinate axis. A constant background column density level was subtracted before deriving the line mass fluctuations. The dotted horizontal line marks the mean line mass of the filament, ⟨Mline⟩ ~ 15 M⊙/pc, which is only slightly lower than critical line mass of 16.3 M⊙/pc for an isothermal cylinder at 10 K. The median relative amplitude of the line-mass fluctuations is |
For the present analysis, we needed high-resolution column density maps to recover small-scale fluctuations which would otherwise be smeared due to beam convolution. We employed two methods for generating such column density maps. First, we generated them at an effective resolution corresponding to the SPIRE 250 μm beam following the method described in Appendix A of Palmeirim et al. (2013). In this method, large-scale information is obtained from a standard Herschel column density map constructed at the SPIRE 500 μm resolution, while finer details are recovered by constructing more approximate column density maps at the resolution of SPIRE 350 μm and SPIRE 250 μm data. Following the steps described in Palmeirim et al., we fitted a single-temperature modified blackbody to the observed data on a pixel-by-pixel basis, adopting a wavelength-dependent dust opacity of the form κλ = 0.1(λ/ 300 μm)− β cm2 per g (of gas + dust) with an emissivity index β = 2 (cf. Hildebrand 1983; Roy et al. 2014). In the second method, we directly converted the surface brightness maps observed at 250 μm I250 into approximate column density maps by using the relation NH2 = I250/ (B250 [ Td,SED ] κ250μH2mH), where μH2 = 2.8 is the mean molecular weight and Td,SED is the spectral energy distribution (SED) dust temperature obtained by fitting a modified blackbody to the SED observed between 160 μm and 500 μm with Herschel data toward each line of sight. For the Pipe Nebula filament shown in Fig. 2, for instance, the median dust temperature along the filament crest is 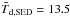 K. The advantage of the first method is that it produces a more accurate column density map at the 18.2″ resolution of the SPIRE 250 μm data. The disadvantage, however, is that the resulting map is significantly noisier than the SPIRE 250 μm map and the point spread function (PSF) is more difficult to characterize because of the various steps involved in the processing. In contrast, in the second method (which simply produces modified 250 μm maps), the effective PSF is exactly the same as that of the SPIRE 250 μm photometer. Since an accurate knowledge of the beam is important in the present power-spectrum study, we report results based on the second method in the body of the paper. The results of a power-spectrum analysis performed using high-resolution column density maps produced with the first method are given in Appendix B. They confirm the robustness of our conclusions.
K. The advantage of the first method is that it produces a more accurate column density map at the 18.2″ resolution of the SPIRE 250 μm data. The disadvantage, however, is that the resulting map is significantly noisier than the SPIRE 250 μm map and the point spread function (PSF) is more difficult to characterize because of the various steps involved in the processing. In contrast, in the second method (which simply produces modified 250 μm maps), the effective PSF is exactly the same as that of the SPIRE 250 μm photometer. Since an accurate knowledge of the beam is important in the present power-spectrum study, we report results based on the second method in the body of the paper. The results of a power-spectrum analysis performed using high-resolution column density maps produced with the first method are given in Appendix B. They confirm the robustness of our conclusions.
3. Filament identification
For the purpose of detecting coherently elongated filamentary structures in the column density maps as well as the modified 250 μm images, we employed the DisPerSE algorithm which traces the crests of segments of topological filaments by connecting saddle points to maxima following the gradient in an image (Sousbie et al. 2011; see also Arzoumanian et al. 2011; Hill et al. 2011 for details on practical applications of DisPerSE on Herschel images). It is important to point out here that DisPerSE was used solely for tracing the filament crests, while the filament longitudinal profiles were measured directly on the original images. Our filament sample consists of 28 filaments in the Taurus cloud (adopted distance d = 140 pc; Elias 1978), 42 filaments in the Pipe nebula region (d = 145 pc; Alves et al. 2007), and 36 filaments in the IC 5146 cloud (d = 460 pc; Lada et al. 1999). Combining the three regions, we identified a total of 106 filaments of various lengths above a 5σ persistence level of ~1021 cm-2; however, for a proper power-spectrum analysis, which was our ultimate goal, we had to select moderately long filaments to have an adequate number of Fourier modes at small spatial frequencies (see Sect. 5 below). Our final analysis was thus based on the subset of 80 filaments that are longer than 5.́5 (~18 beams).
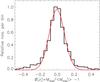 |
Fig. 3 Normalized histogram showing the probability distribution of relative line-mass fluctuations along the long axes of the subset of 67 filaments, which are entirely subcritical. The red curve shows the Gaussian best fit to the observed distribution, which has a mean of ~0 and a standard deviation of ~0.09. (This figure is available in color in electronic form.) |
 |
Fig. 4 Power spectrum of the line-mass fluctuations observed along the Pipe filament shown in Fig. 2 as a function of spatial frequency s (bottom x-axis) or angular frequency |
 |
Fig. 5 Panels a) and b) are similar to Figs. 2a and b, but for an example of a thermally subcritical filament in the IC 5146 molecular cloud (d ~ 460 pc). The mean line mass of the filament is ⟨Mline⟩ ~ 3M⊙/pc ≪Mline,crit, as shown by the dotted horizontal line in panel (b). The median relative amplitude of the line-mass fluctuations is |
 |
Fig. 6 Similar to Fig. 5, but for the thermally supercritical filament B211/B213 in the Taurus cloud at d ~ 140 pc (cf. Palmeirim et al. 2013). The mean line mass of the filament is ⟨Mline⟩ ~ 30M⊙/pc ≫Mline,crit, as shown by the dotted horizontal line in panel b). The median relative amplitude of the line-mass fluctuations is |
4. Column density/line mass fluctuations along selected filaments
Figure 2 shows an example of a longitudinal profile of column density or line-mass fluctuations along a marginally critical filament in the Pipe molecular cloud. As the mass per unit length or line mass is a fundamental variable in cylindrical geometry (cf. Inutsuka 2001), we converted the observed column density fluctuations to line-mass fluctuations by making use of the quasi-universal filament width ~0.1 pc found by Arzoumanian et al. (2011). The line-mass fluctuations corresponding to the example filament in Fig. 2a are shown in Fig. 2b, while the equivalent column density fluctuations are quantified on the right ordinate axis of Fig. 2b. To estimate fluctuations intrinsic to the selected filaments themselves, a mean line-of-sight background column density was subtracted from the observed data for each field. The dotted horizontal line in Fig. 2b shows the mean line-mass of the filament (~15.5 M⊙/pc), and allows the relative strength of the line-mass fluctuations about the mean to be evaluated. In this example, and for all other subcritical filaments in our sample, the line-mass fluctuations are small in relative amplitude, i.e., 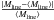 < 0.1, implying that the perturbation modes are in the linear regime (see also Sect. 6 below).
< 0.1, implying that the perturbation modes are in the linear regime (see also Sect. 6 below).
Figure 3 shows the distribution of normalized line-mass fluctuations, 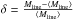 , along the 67 filaments in our sample that are subcritical over their entire length. It can be seen in Fig. 3 that the distribution of line-mass fluctuations for subcritical filaments is nearly Gaussian, which is an important assumption of the CMF/IMF model calculations presented by Inutsuka (2001). It can also be seen that the density/line-mass fluctuations along subcritical filaments are typically less than 10%, i.e., in the linear regime.
, along the 67 filaments in our sample that are subcritical over their entire length. It can be seen in Fig. 3 that the distribution of line-mass fluctuations for subcritical filaments is nearly Gaussian, which is an important assumption of the CMF/IMF model calculations presented by Inutsuka (2001). It can also be seen that the density/line-mass fluctuations along subcritical filaments are typically less than 10%, i.e., in the linear regime.
The power spectrum of the fluctuations observed along the filament in Fig. 2 is shown in Fig. 4 and discussed in Sect. 5 below. Panels a and b of Figs. 5 and 6 are similar to Fig. 2, but show two extreme examples of a subcritical filament (with ⟨Mline⟩ ~ 3M⊙/pc ≪ Mline,crit) and a supercritical filament (with ⟨Mline⟩ ~ 30M⊙/pc >Mline,crit) in the IC 5146 and Taurus2 clouds, respectively.
The column density/line mass longitudinal profiles used in this paper (see Figs. 2b, 5b, and 6b) have an effective 18.̋2-beam resolution. The pixel resolution of the corresponding data is 6.̋0, close to the Nyquist sampling limit (λ/ 2D ~ 7.̋4) of SPIRE 250 μm observations where D = 3.5 m is the diameter of the primary mirror of the Herschel telescope. When deriving physical properties from the power spectra of individual filaments, we took special care to exclude angular frequencies higher than the Nyquist critical frequency D/λ ~ 1/(2 × 7.4″) ~ 0.068 arcsec-1 ~ 4.0 arcmin-1.
5. Power spectrum analysis of the filaments
The normalized power spectrum P(s) of a 1D spatially-varying field I(l) is proportional to the square of the Fourier amplitude of the signal, and mathematically the relationship in the 1D case is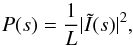 (1)where s denotes spatial frequency (and
(1)where s denotes spatial frequency (and 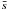 denotes angular frequency),
denotes angular frequency), 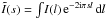 is the Fourier transform of I(l), and L = ∫dl is the total length over which the signal is measured. In the present case, it is convenient to take I(l) as the field of line-mass fluctuations (in M⊙/pc) along a given filament and to express the offset along the filament crest, l, in units of pc. Then, the normalized power spectrum P(s) has units of
is the Fourier transform of I(l), and L = ∫dl is the total length over which the signal is measured. In the present case, it is convenient to take I(l) as the field of line-mass fluctuations (in M⊙/pc) along a given filament and to express the offset along the filament crest, l, in units of pc. Then, the normalized power spectrum P(s) has units of 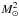 /pc.
/pc.
The observed signal after convolution with the telescope beam, B, is given by Iobs(l) = Itrue(l) ∗ B + N(l), where N(l) is a noise term arising from small-scale fluctuations primarily due to instrument noise. The Fourier transform of Iobs(l) is 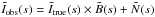 . Using Eq. (1) and the previous relation, it can be seen that the total power spectrum observed along the filament axis is composed of the true power spectrum, Ptrue(s), due to line-mass variations along the filament modified by the power spectrum of the beam, γbeam(s), plus a white noise power spectrum3 term, PN(s), and can be expressed as
. Using Eq. (1) and the previous relation, it can be seen that the total power spectrum observed along the filament axis is composed of the true power spectrum, Ptrue(s), due to line-mass variations along the filament modified by the power spectrum of the beam, γbeam(s), plus a white noise power spectrum3 term, PN(s), and can be expressed as 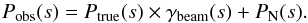 (2)In deriving Eq. (2), we assumed that the noise and the filament line-mass fluctuations are completely uncorrelated, resulting in a vanishing cross-power spectrum term. To estimate the amplitude of PN(s), we computed the median of the power spectrum in a narrow band of angular frequencies, 3.9 arcmin
(2)In deriving Eq. (2), we assumed that the noise and the filament line-mass fluctuations are completely uncorrelated, resulting in a vanishing cross-power spectrum term. To estimate the amplitude of PN(s), we computed the median of the power spectrum in a narrow band of angular frequencies, 3.9 arcmin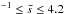 arcmin-1, centered about the Nyquist angular frequency of 4.0 arcmin-1.
arcmin-1, centered about the Nyquist angular frequency of 4.0 arcmin-1.
In practice, to recover Ptrue(s), we first computed Pobs(s) directly from the data, then subtracted a constant noise power level, and finally corrected the result for the beam convolution effect by dividing by γbeam(s). Within the relevant range of angular frequencies (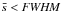 of the beam power spectrum ~2 arcmin-1), both Pobs(s) and Ptrue(s) can be approximated and fitted by a power-law function,
of the beam power spectrum ~2 arcmin-1), both Pobs(s) and Ptrue(s) can be approximated and fitted by a power-law function, 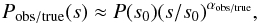 (3)where P(s0) is the normalizing amplitude of the power spectrum at spatial frequency s0 and α is the power-law index of the fitted power spectrum.
(3)where P(s0) is the normalizing amplitude of the power spectrum at spatial frequency s0 and α is the power-law index of the fitted power spectrum.
The results of such a power spectrum analysis are shown in Fig. 4 for the marginally critical filament of Fig. 2. The plus symbols in Fig. 4 correspond to the observed power spectrum of the example filament, Pobs(s), prior to noise subtraction and beam correction. The upper panel of Fig. 4 explicitly shows the effect of noise level subtraction. The horizontal red line marks the estimated power level due to instrument noise, 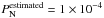 M⊙2/pc, derived following the above recipe. For comparison, the blue horizontal line shows the noise power spectrum level (
M⊙2/pc, derived following the above recipe. For comparison, the blue horizontal line shows the noise power spectrum level (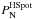 ) corresponding to the root mean square (rms) instrument noise level (i.e., 1σ ~ 1 MJy/sr or ~10 mJy/beam) expected for SPIRE 250 μm data corresponding to two orthogonal scans taken at 60″s-1 in parallel-mode observations according to the Herschel Observation Planning Tool (HSpot)4. The noise power spectrum level
) corresponding to the root mean square (rms) instrument noise level (i.e., 1σ ~ 1 MJy/sr or ~10 mJy/beam) expected for SPIRE 250 μm data corresponding to two orthogonal scans taken at 60″s-1 in parallel-mode observations according to the Herschel Observation Planning Tool (HSpot)4. The noise power spectrum level 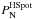 was determined using Parseval’s theorem which relates the variance of the instrumental noise to the integral of its power spectrum:
was determined using Parseval’s theorem which relates the variance of the instrumental noise to the integral of its power spectrum: 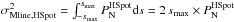 , where the integral is taken over the relevant spatial frequency range given the maximum angular frequency
, where the integral is taken over the relevant spatial frequency range given the maximum angular frequency 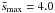 arcmin-1 sampled by our SPIRE 250 μm data. For a 0.1 pc wide filament with a median dust temperature of 13.5 K as measured along the filament crest in Fig. 2, a 1σ rms level of ~1 MJy/sr at 250 μm corresponds to a standard deviation σMline,HSpot ~ 0.09 M⊙/pc in line-mass units. Given the distance d = 145 pc to the filament of Fig. 2, this yields
arcmin-1 sampled by our SPIRE 250 μm data. For a 0.1 pc wide filament with a median dust temperature of 13.5 K as measured along the filament crest in Fig. 2, a 1σ rms level of ~1 MJy/sr at 250 μm corresponds to a standard deviation σMline,HSpot ~ 0.09 M⊙/pc in line-mass units. Given the distance d = 145 pc to the filament of Fig. 2, this yields 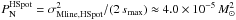 /pc in the same unit as that used on the y-axis of Fig. 4.
/pc in the same unit as that used on the y-axis of Fig. 4.
The red dots and overplotted blue triangles in Fig. 4a show the power spectrum data points after subtracting the estimated noise spectrum level 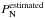 and the expected instrument noise spectrum level
and the expected instrument noise spectrum level 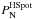 , respectively. It is apparent from Fig. 4a that the departure of the noise-subtracted data points from the observed filament power spectrum is negligible in the angular frequency range
, respectively. It is apparent from Fig. 4a that the departure of the noise-subtracted data points from the observed filament power spectrum is negligible in the angular frequency range 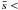 2 arcmin-1 where we fit a power-law slope. Therefore, even though our estimated noise spectrum level,
2 arcmin-1 where we fit a power-law slope. Therefore, even though our estimated noise spectrum level, 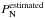 , likely overestimates the actual noise spectrum level, the step of noise subtraction has effectively no influence on the estimated power-law slope of the observed power spectrum.
, likely overestimates the actual noise spectrum level, the step of noise subtraction has effectively no influence on the estimated power-law slope of the observed power spectrum.
The beam-corrected power spectrum, Ptrue(s), shown by the cyan solid dots in Fig. 4b was obtained by dividing the noise-subtracted power spectrum by the 250 μm SPIRE beam power spectrum (γbeam). The derivation of the SPIRE beam power spectrum is described in Appendix A. The Pobs(s) spectrum has more power at low spatial frequencies s (large scales) and decreases roughly as a power law toward high spatial frequencies until it merges with the noise power spectum level at a spatial frequency close to s ~ 100 pc-1 (i.e., angular frequency ~4.0 arcmin-1). The beam-corrected power spectrum, Ptrue(s), has a slightly shallower slope than Pobs(s). At spatial frequencies higher than the FWHM of the beam power spectrum shown by the dotted vertical line at s ~ 50 pc-1 (angular frequency 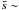 2 arcmin-1) in Fig. 4, Ptrue(s) is overcorrected owing to amplification of residual noise when dividing by the beam power spectrum. This unphysical rise of Ptrue(s) (see Fig. 4b) at very small angular frequencies is a generic feature of beam-corrected power spectra and is well documented in earlier Herschel studies of cirrus noise (e.g., Martin et al. 2010; Miville-Deschênes et al. 2010). To get around this problem, it is customary to avoid angular frequencies greater than the FWHM of the beam power spectrum, i.e.,
2 arcmin-1) in Fig. 4, Ptrue(s) is overcorrected owing to amplification of residual noise when dividing by the beam power spectrum. This unphysical rise of Ptrue(s) (see Fig. 4b) at very small angular frequencies is a generic feature of beam-corrected power spectra and is well documented in earlier Herschel studies of cirrus noise (e.g., Martin et al. 2010; Miville-Deschênes et al. 2010). To get around this problem, it is customary to avoid angular frequencies greater than the FWHM of the beam power spectrum, i.e., 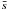 > 2 arcmin-1 at 250 μm (cf. Miville-Deschênes et al. 2010), a compromise that we also adopt in this paper. Upon visually inspecting Fig. 4b, there may still be an indication of a slight overcorrection of Ptrue(s) in the frequency range 1.5 arcmin-1
> 2 arcmin-1 at 250 μm (cf. Miville-Deschênes et al. 2010), a compromise that we also adopt in this paper. Upon visually inspecting Fig. 4b, there may still be an indication of a slight overcorrection of Ptrue(s) in the frequency range 1.5 arcmin-1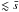 ≤ 2 arcmin-1. Therefore, we also report the results of more conservative power-law fits obtained by fitting Ptrue(s) only up to
≤ 2 arcmin-1. Therefore, we also report the results of more conservative power-law fits obtained by fitting Ptrue(s) only up to 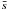 = 1.5 arcmin-1. Finally, it is common practice to avoid very small spatial frequencies when fitting power spectrum slopes in the case of 2D images because of edge effects or large scanning lengths, for example. In principle, in the case of a filament much smaller than the size of the mapped region, there should be no technical difficulty in reconstructing features at all angular scales with Fourier modes. To be on the safe side, we nevertheless excluded the smallest non-zero angular frequency data point when fitting a power law to the power spectrum of each filament5.
= 1.5 arcmin-1. Finally, it is common practice to avoid very small spatial frequencies when fitting power spectrum slopes in the case of 2D images because of edge effects or large scanning lengths, for example. In principle, in the case of a filament much smaller than the size of the mapped region, there should be no technical difficulty in reconstructing features at all angular scales with Fourier modes. To be on the safe side, we nevertheless excluded the smallest non-zero angular frequency data point when fitting a power law to the power spectrum of each filament5.
For the Pipe filament shown in Fig. 4, the beam-corrected power spectrum has a best-fit slope αtrue=−1.6 ± 0.2 and an amplitude P(s0 = 10 pc-1) = 9.5 × 10-2M⊙2/pc. For comparison, the observed power spectrum has a somewhat steeper best-fit slope αobs = −2.1 ± 0.2 and an amplitude P(s0 = 10 pc-1) = 6 × 10-2M⊙2/pc. Two other examples of filament power spectra are shown in Fig. 5c and Fig. 6c for the IC 5146 subcritical filament of Fig. 5a and the Taurus supercritical filament of Fig. 6a, respectively.
 |
Fig. 7 Distributions of power spectrum slopes measured before beam correction (dashed histogram) and after beam correction (solid histogram) for our selected sample of 80 filaments. Best-fit Gaussian curves to the two observed distributions are overplotted. The two distributions are centered on |
5.1. Characteristic power spectrum slope for filaments
To reach statistically significant conclusions on the typical power spectrum slope, we considered a sample of 80 subcritical (or marginally supercritical) filaments belonging to three distinct nearby molecular clouds (see Sect. 3). Since the reliability of the derived power spectrum properties also depends on the dynamic range covered in spatial frequency space, we excluded from our present analysis filaments that were smaller than 5.́5 in the plane of sky. The resulting distribution of power spectrum slopes is shown in Fig. 7. The two histograms shown by the dashed and solid lines represent the distributions obtained for the observed [Pobs(s)] and beam-corrected [Ptrue(s)] filament power spectra, respectively. Both histograms are well fitted by Gaussian distributions (see Fig. 7).
The mean power-law index 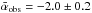 measured for the observed power spectra is slightly steeper than the mean power-law index
measured for the observed power spectra is slightly steeper than the mean power-law index 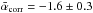 obtained at
obtained at  < 2 arcmin-1 after correcting for the beam convolution effect. Fitting Ptrue(s) with a power law over the more conservative range of angular frequencies
< 2 arcmin-1 after correcting for the beam convolution effect. Fitting Ptrue(s) with a power law over the more conservative range of angular frequencies  ≤ 1.5 arcmin-1 yields essentially the same index within errors,
≤ 1.5 arcmin-1 yields essentially the same index within errors, 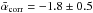 . The distribution of beam-corrected power spectrum slopes has a larger dispersion than the distribution of uncorrected slopes, due to the propagation of uncertainties resulting from the amplification of residual noise at small scales.
. The distribution of beam-corrected power spectrum slopes has a larger dispersion than the distribution of uncorrected slopes, due to the propagation of uncertainties resulting from the amplification of residual noise at small scales.
5.2. Correlation between P(s0) and mean column density
Figure 8 shows a positive correlation between the amplitude of the line-mass fluctuations, expressed by P1/2(s0), and the mean column density of the filaments. In other words, filaments with higher mean column densities tend to have higher power spectrum amplitudes, i.e., stronger column density fluctuations. The red straight line in Fig. 8 shows the best-fit power law to the data points, which has an index of 1.4 ± 0.1. Physically, this empirical relation means that the rms fluctuations of the perturbative modes inside a filament increase with the mean line mass of the filament. A similar empirical correlation with a somewhat different power-law index (Pcirrus ∝ ⟨Sν⟩3) exists between the 2D power spectrum amplitude of far-infrared cirrus (Pcirrus) and the average surface brightness ⟨Sν⟩ in far-infrared images of the sky (Gautier et al. 1992).
 |
Fig. 8 Square root of filament power spectrum amplitude at s0 = 10 pc-1 versus mean line mass of each filament. The solid line shows the best-fit power-law |
5.3. Line-mass dispersion versus filament length
Figure 9 shows that the dispersion of line-mass fluctuations along the long axis of each filament, σMline, is correlated with the physical length L of the filament. The best-fit power-law relation between σMline and L is σMline ∝ L0.7, which is reminiscent of the well-known power-law scaling between internal velocity dispersion and region size in molecular clouds (σv ∝ L0.5) originally found by Larson (1981). Such a similarity is not surprising since, in the subsonic turbulence regime which approximately holds for subcritical or marginally subcritical filaments (Arzoumanian et al. 2013), density fluctuations are expected to be directly proportional to velocity fluctuations.
 |
Fig. 9 Dispersion of line-mass fluctuations σMline versus projected length L for the filaments in our sample. The solid line shows the best-fit power-law σMline ∝ L0.7 to the data points. For comparison, the dashed line shows a power-law scaling equivalent to the well-known linewidth–size relation in molecular clouds σv ∝ L0.5 (cf. Larson 1981), with an arbitrary normalization. |
6. Concluding remarks
Our 1D power spectrum analysis along the axis of 80 nearby Herschel filaments shows that the longitudinal line-mass fluctuations along these filaments have a characteristic 1D power spectrum slope 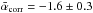 . This result is the first observational confirmation that the density/line-mass fluctuations along interstellar filaments have a characteristic power spectrum slope. The slope we find is remarkably close to the fiducial value αtheory = −1.5 adopted by Inutsuka (2001) in his attempt to explain the origin of Salpeter-like power-law tail of the CMF/IMF at the high-mass end (dN/dM ∝ M-2.5). Repeating Inutsuka’s analysis with the observationally derived power spectrum slope
. This result is the first observational confirmation that the density/line-mass fluctuations along interstellar filaments have a characteristic power spectrum slope. The slope we find is remarkably close to the fiducial value αtheory = −1.5 adopted by Inutsuka (2001) in his attempt to explain the origin of Salpeter-like power-law tail of the CMF/IMF at the high-mass end (dN/dM ∝ M-2.5). Repeating Inutsuka’s analysis with the observationally derived power spectrum slope 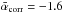 found in the present study6 would lead to a CMF approaching dN/dM ∝ M-2.4 at the high-mass end after a few free-fall times, which is even closer to a Salpeter mass function (dN/dM ∝ M-2.35).
found in the present study6 would lead to a CMF approaching dN/dM ∝ M-2.4 at the high-mass end after a few free-fall times, which is even closer to a Salpeter mass function (dN/dM ∝ M-2.35).
Interestingly, the measured power spectrum of density fluctuations along interstellar filaments shows a striking similarity to the energy spectrum or velocity power spectrum of incompressible hydrodynamical turbulence in 1D, i.e., 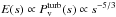 (Kolmogorov 1941)7. For a weakly compressible flow, as long as self-gravity does not dominate, the continuity equation implies a direct proportionality between the Fourier modes of small density fluctuations and the modes of subsonic velocity perturbations. Our measured power spectrum slope for the density fluctuations (
(Kolmogorov 1941)7. For a weakly compressible flow, as long as self-gravity does not dominate, the continuity equation implies a direct proportionality between the Fourier modes of small density fluctuations and the modes of subsonic velocity perturbations. Our measured power spectrum slope for the density fluctuations (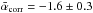 ) is thus consistent with the fact that subcritical and marginally supercritical filaments – like the filaments considered in the present study – are observed to have subsonic or at most transonic turbulent velocity dispersions (Hacar & Tafalla 2011; Arzoumanian et al. 2013).
) is thus consistent with the fact that subcritical and marginally supercritical filaments – like the filaments considered in the present study – are observed to have subsonic or at most transonic turbulent velocity dispersions (Hacar & Tafalla 2011; Arzoumanian et al. 2013).
The origin of the characteristic power spectrum slope of filaments may have a close connection with the process generating cirrus fluctuations of far-infrared surface brightness in the interstellar medium. The statistical analysis of Galactic cirrus fluctuations in IRAS 2D images by Gautier et al. (1992) has suggested a plausible role of interstellar turbulence in shaping these fluctuations. The power spectrum of cirrus fluctuations obtained from Roy et al. (2010) and recent Herschel images (Martin et al. 2010; Miville-Deschênes et al. 2010) has a power-law slope of −2.7, very similar to the slope of −8/3 ≈ −2.67 expected for the velocity power spectrum of Kolmogorov turbulence in 2D. This 2D slope translates to a power spectrum slope of −5/3 ≈ −1.67 in 1D8.
Our Herschel results support the following speculative picture. Filamentary structures form in the cold interstellar medium as a result of a combination of compression and shear in large-scale magneto-hydrodynamic flows (Padoan et al. 2001; Balsara et al. 2001; Hennebelle 2013; Inutsuka et al. 2015). Supersonic turbulent motions dissipate quickly within dense filaments, forming more stable and coherent structures, and leaving an imprint of subsonic fluctuations along the filaments. Molecular line observations of the inner parts of subcritical or marginally supercritical filaments do show subsonic or transonic velocity dispersions (Hacar & Tafalla 2011; Arzoumanian et al. 2013), supporting the view that the dissipation of turbulence may play a role in the formation and evolution of these structures. The density fluctuations along supercritical filaments are Jeans-unstable and grow by local gravitational instability, generating a distribution of prestellar cores.
The observational verification of the existence of a characteristic power spectrum slope for line-mass fluctuations along interstellar filaments has therefore opened an interesting avenue for understanding an important aspect of the origin of the prestellar CMF. Our findings suggest that an initial spectrum of density perturbations seeded by interstellar turbulence may be a prerequisite for generating a Salpeter-like CMF at the high-mass end. The present study combined with previous Herschel results therefore provides insight into the possible origin of two distinct features of the CMF: the thermal gravitational fragmentation scale of filaments may set the peak of the lognormal base of the prestellar CMF (e.g., André et al. 2014), while the evolutionary characteristics of the underlying line-mass perturbations may help to set the power-law slope of the CMF/IMF at the high mass end (Inutsuka 2001 and this paper). A final caveat should be mentioned, however. There is mounting evidence that true high-mass analogs to low-mass prestellar cores may not exist (e.g., Motte et al. 2007) and that massive protostars may acquire the bulk of their final mass from much larger scales than a single prestellar core (e.g., Peretto et al. 2013). Further work will be needed to evaluate the relative importance of initial density fluctuations and large-scale accretion in generating the high-mass end of the IMF9.
Online material
Appendix A: Deriving the power spectrum of the SPIRE 250 μm beam
The power spectrum of the SPIRE 250 μm beam was derived from an empirical PSF image obtained by the SPIRE ICC from scan map data10 of Neptune in four directions. There are two sets of empirical PSFs available, one gridded at the nominal pixel size for each SPIRE passband and the other at a higher pixel resolution of 0.̋6. We used the latter product, but the angular extent of the footprint was only about 6.́0, corresponding to an angular frequency scale of ~0.3 arcmin-1, insufficient to correct for the beam convolution effect on large scales (i.e., small 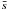 ). Therefore, to extend the angular frequency range of the beam power spectrum to lower
). Therefore, to extend the angular frequency range of the beam power spectrum to lower 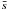 values, we embedded the beam map of Neptune inside a larger map 25.́0 on a side, and then padded the pixels outside the central Neptune insert using the best-fit 2D Gaussian approximation to the beam.
values, we embedded the beam map of Neptune inside a larger map 25.́0 on a side, and then padded the pixels outside the central Neptune insert using the best-fit 2D Gaussian approximation to the beam.
The power spectrum of the SPIRE 250 μm beam as a function of angular frequency, 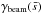 , is shown in Fig. A.1. The power spectrum asymptotically converges to unity at small angular frequencies, but rapidly declines toward high angular frequencies (small angular scales). We caution that the SPIRE beam spectrum has a slight suppression of power around 0.2 arcmin-1<
, is shown in Fig. A.1. The power spectrum asymptotically converges to unity at small angular frequencies, but rapidly declines toward high angular frequencies (small angular scales). We caution that the SPIRE beam spectrum has a slight suppression of power around 0.2 arcmin-1<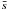 < 1.5 arcmin-1 compared to a pure Gaussian shape. This problem led Martin et al. (2010) and Miville-Deschênes et al. (2010) to approximate the beam power spectrum using higher-order polynomial corrections to the Gaussian fit. The effective full width at half maximum (FWHM) of the SPIRE 250 μm beam power spectrum11 is about 2 arcmin-1, as shown by the dashed curve in Fig. A.1.
< 1.5 arcmin-1 compared to a pure Gaussian shape. This problem led Martin et al. (2010) and Miville-Deschênes et al. (2010) to approximate the beam power spectrum using higher-order polynomial corrections to the Gaussian fit. The effective full width at half maximum (FWHM) of the SPIRE 250 μm beam power spectrum11 is about 2 arcmin-1, as shown by the dashed curve in Fig. A.1.
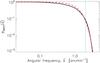 |
Fig. A.1 Power spectrum of the SPIRE 250 μm beam, |
Appendix B: Results from high-resolution column density maps
Figure B.1 shows the power spectrum of the same filament already displayed in Fig. 2, but here derived from a high-resolution column density map obtained using the multi-scale decomposition scheme of Palmeirim et al. (2013). The power spectrum values at high spatial frequencies has more scatter than the one derived by converting I250 to H2-column density (see Fig. 4). This is primarily because the multi-scale decomposition technique introduces fluctuations at small spatial scales which manifest themselves through enhanced scatter in the Fourier modes at high spatial frequencies. The distribution of power spectrum slopes derived from high-resolution column density maps for the whole sample of filaments is shown in Fig. B.2. The mean power spectrum slopes before and after correcting for the beam effect are 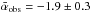 and
and 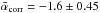 , respectively. Within the quoted errors, these results are indistinguishable from those found in Sect. 5.1 using modified 250 μm maps.
, respectively. Within the quoted errors, these results are indistinguishable from those found in Sect. 5.1 using modified 250 μm maps.
 |
Fig. B.1 Power spectrum of the line-mass fluctuations along the Pipe filament shown in Fig. 2 as measured in the high-resolution H2-column density map resulting from the multi-scale decomposition technique of Palmeirim et al. (2013) Fig. 4. The power-law fits to the power spectra Pobs(s) (black plus symbols) and Ptrue(s) (cyan filled circles) have logarithmic slopes αobs = −2.3 ± 0.2 and αcorr = −1.7 ± 0.3, respectively. |
 |
Fig. B.2 Distributions of power spectrum slopes measured in the high-resolution H2-column density maps before beam correction (dashed histogram) and after beam correction (solid histogram). Similar to Fig. 7 but based on data from the high-resolution column density maps instead of the modified 250 μm maps. Best-fit Gaussian curves to the two observed distributions are overplotted. The two distributions are centered on αobs = −1.9 ± 0.3 and αcorr = −1.6 ± 0.45 for the uncorrected and beam-corrected power spectra, respectively. |
Here ⟨Mline⟩ was obtained by multiplying the mean background-subtracted column density by a characteristic 0.1 pc width, whereas Palmeirim et al. (2013) obtained a value of 54 M⊙/pc by integration over the full radial column density profile of the filament.
The SPIRE bolometers have a measured temporal stability ≳250 s, which for Herschel parallel-mode observations taken at a scanning speed of 60′′ s-1 translates to a 1 /f noise “knee” at spatial frequencies corresponding to angular scales larger than ~4° (see Fig. 2 of Pascale et al. 2011). The angular scale of the longest filament considered here (~2°) is significantly smaller than both the angular scale of the 1 /f knee and the maximum scan length of the corresponding scan-map observations. We can therefore safely assume that the instrumental noise behaves as white noise over the entire range of spatial frequencies considered in the paper.
Including the lowest s data point when fitting the power spectrum slope would change the overall distribution of slopes in Fig. 7 by less than one standard deviation.
Here we adopt the mean beam-corrected value 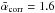 derived in Sect. 5.1 as our best estimate of the power spectrum slope. Using the prescription of Inutsuka (2001) with the mean power-law index
derived in Sect. 5.1 as our best estimate of the power spectrum slope. Using the prescription of Inutsuka (2001) with the mean power-law index 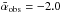 measured before beam correction (see Fig. 7) instead would lead to a CMF approaching dN/dM ∝ M-2.2 after a few free-fall times.
measured before beam correction (see Fig. 7) instead would lead to a CMF approaching dN/dM ∝ M-2.2 after a few free-fall times.
Given the uncertainties associated with beam correction (see Sect. 5), the mean beam-corrected index 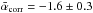 is marginally consistent with both the energy spectrum
is marginally consistent with both the energy spectrum 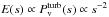 (cf. Kritsuk et al. 2007) and the 1D density power spectrum (cf. Federrath et al. 2009) expected for supersonic compressible turbulence.
(cf. Kritsuk et al. 2007) and the 1D density power spectrum (cf. Federrath et al. 2009) expected for supersonic compressible turbulence.
Another, more theoretical issue is that, for technical reasons related to the Press-Schechter formalism, the model discussed by Inutsuka (2001) may, strictly speaking, not be a model for the mass function of (prestellar) cores, but a model for the mass function of groups of cores (P. Hennebelle, priv. comm.).
The reduction of the beam map from scan-map data of Neptune is described at http://herschel.esac.esa.int/Docs/SPIRE/html/spire_om.html
Acknowledgments
We are thankful to Prof. Shu-Ichiro Inutsuka for stimulating and enlightening discussions on filaments. We also acknowledge insightful discussions with Patrick Hennebelle and Gilles Chabrier about the origin of the CMF/IMF and the Press-Schechter formalism. This work has received support from the European Research Council under the European Union’s Seventh Framework Programme (ERC Advanced Grant Agreement No. 291294 – “ORISTARS”) and from the French National Research Agency (Grant No. ANR–11–BS56–0010 – “STARFICH”). SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/AOT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICT/MCT (Spain).
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, ed. H. Beuther (Tuscon, AZ: Univ. of Arizona press), 27 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Könyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balsara, D., Ward-Thompson, D., & Crutcher, R. M. 2001, MNRAS, 327, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Hennebelle, P., & Charlot, S. 2014, ApJ, 796, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Elias, J. H. 1978, ApJ, 224, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2009, ApJ, 692, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gautier, III, T. N., Boulanger, F., Perault, M., & Puget, J. L. 1992, AJ, 103, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiderman, A., Evans, II, N. J., Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F. 2012, MNRAS, 423, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I. 2001, ApJ, 559, L149 [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., Inoue, T., Iwasaki, K., & Hosokawa, T. 2015, A&A, 580, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jedamzik, K. 1995, ApJ, 448, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., Padoan, P., & Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Alves, J., & Lada, E. A. 1999, ApJ, 512, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Martin, P. G., Miville-Deschênes, M.-A., Roy, A., et al. 2010, A&A, 518, L105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offner, S. S. R., Clark, P. C., Hennebelle, P., et al. 2014, in Protostars and Planets VI, ed. H. Beuther (Tuscon, AZ: Univ. of Arizona press), 53 [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Padoan, P., Juvela, M., Goodman, A. A., & Nordlund, Å. 2001, ApJ, 553, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascale, E., Auld, R., Dariush, A., et al. 2011, MNRAS, 415, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roy, A., Ade, P. A. R., Bock, J. J., et al. 2010, ApJ, 708, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., André, P., Palmeirim, P., et al. 2014, A&A, 562, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousbie, T., Pichon, C., & Kawahara, H. 2011, MNRAS, 414, 384 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Herschel 250 μm surface brightness image of the Pipe molecular cloud observed as a part of the HGBS key project (cf. Peretto et al. 2012). The image is displayed at the diffraction limited 250 μm beam resolution of 18.̋2. The 43 filaments traced with the DisPerSE algorithm (Sousbie et al. 2011) are highlighted in white. A more detailed view of the filament enclosed by the black dashed rectangle is shown in Fig. 2. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 2 Close-up view of the sub-region indicated by the black dashed rectangle in Fig. 1 showing a) an example of a nearly critical filament in the Pipe cloud at an adopted distance d = 145 pc and b) the line-mass/column density fluctuations along the long axis of the same filament, both at the 18.̋2 (HPBW) resolution of the SPIRE 250 μm data. The black curve in a) shows the crest of the filament as traced by the DisPerSE algorithm (cf. Sousbie et al. 2011). In b) the right ordinate axis shows the net H2-column density fluctuations along the filament. Equivalent line-mass values (assuming a characteristic filament width of 0.1 pc) are indicated on the left ordinate axis. A constant background column density level was subtracted before deriving the line mass fluctuations. The dotted horizontal line marks the mean line mass of the filament, ⟨Mline⟩ ~ 15 M⊙/pc, which is only slightly lower than critical line mass of 16.3 M⊙/pc for an isothermal cylinder at 10 K. The median relative amplitude of the line-mass fluctuations is |
| In the text | |
 |
Fig. 3 Normalized histogram showing the probability distribution of relative line-mass fluctuations along the long axes of the subset of 67 filaments, which are entirely subcritical. The red curve shows the Gaussian best fit to the observed distribution, which has a mean of ~0 and a standard deviation of ~0.09. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 4 Power spectrum of the line-mass fluctuations observed along the Pipe filament shown in Fig. 2 as a function of spatial frequency s (bottom x-axis) or angular frequency |
| In the text | |
 |
Fig. 5 Panels a) and b) are similar to Figs. 2a and b, but for an example of a thermally subcritical filament in the IC 5146 molecular cloud (d ~ 460 pc). The mean line mass of the filament is ⟨Mline⟩ ~ 3M⊙/pc ≪Mline,crit, as shown by the dotted horizontal line in panel (b). The median relative amplitude of the line-mass fluctuations is |
| In the text | |
 |
Fig. 6 Similar to Fig. 5, but for the thermally supercritical filament B211/B213 in the Taurus cloud at d ~ 140 pc (cf. Palmeirim et al. 2013). The mean line mass of the filament is ⟨Mline⟩ ~ 30M⊙/pc ≫Mline,crit, as shown by the dotted horizontal line in panel b). The median relative amplitude of the line-mass fluctuations is |
| In the text | |
 |
Fig. 7 Distributions of power spectrum slopes measured before beam correction (dashed histogram) and after beam correction (solid histogram) for our selected sample of 80 filaments. Best-fit Gaussian curves to the two observed distributions are overplotted. The two distributions are centered on |
| In the text | |
 |
Fig. 8 Square root of filament power spectrum amplitude at s0 = 10 pc-1 versus mean line mass of each filament. The solid line shows the best-fit power-law |
| In the text | |
 |
Fig. 9 Dispersion of line-mass fluctuations σMline versus projected length L for the filaments in our sample. The solid line shows the best-fit power-law σMline ∝ L0.7 to the data points. For comparison, the dashed line shows a power-law scaling equivalent to the well-known linewidth–size relation in molecular clouds σv ∝ L0.5 (cf. Larson 1981), with an arbitrary normalization. |
| In the text | |
 |
Fig. A.1 Power spectrum of the SPIRE 250 μm beam, |
| In the text | |
 |
Fig. B.1 Power spectrum of the line-mass fluctuations along the Pipe filament shown in Fig. 2 as measured in the high-resolution H2-column density map resulting from the multi-scale decomposition technique of Palmeirim et al. (2013) Fig. 4. The power-law fits to the power spectra Pobs(s) (black plus symbols) and Ptrue(s) (cyan filled circles) have logarithmic slopes αobs = −2.3 ± 0.2 and αcorr = −1.7 ± 0.3, respectively. |
| In the text | |
 |
Fig. B.2 Distributions of power spectrum slopes measured in the high-resolution H2-column density maps before beam correction (dashed histogram) and after beam correction (solid histogram). Similar to Fig. 7 but based on data from the high-resolution column density maps instead of the modified 250 μm maps. Best-fit Gaussian curves to the two observed distributions are overplotted. The two distributions are centered on αobs = −1.9 ± 0.3 and αcorr = −1.6 ± 0.45 for the uncorrected and beam-corrected power spectra, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.