| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425178 | |
| Published online | 01 June 2015 | |
Short-period X-ray oscillations in super-soft novae and persistent super-soft sources
1
Science Operations Division, Science Operations Department of ESA,
ESAC, Villanueva de la
Cañada ( Madrid),
Spain
e-mail:
juness@sciops.esa.int
2
Department of Physics & Astronomy, University of
Leicester, Leicester,
LE1 7RH,
UK
3
Theoretical Astrophysics, California Institute of
Technology, 1200 E California Blvd,
M/C 350-17, Pasadena, CA
91125,
USA
4
Observatories of the Carnegie Institution of
Science, 813 Santa Barbara
Street, Pasadena,
CA
91101,
USA
5
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
6
Advanced Technologies Research Institute, Slovak University of
Technology in Bratislava, Paulinska
16, 91724
Trnava, Slovak
Republic
7 American Astronomical Society, 2000 Florida Ave., NW, Suite
400, DC 20009-1231, USA
8
School of Earth and Space Exploration, Arizona State
University, Tempe,
AZ
85287-1404,
USA
9
Remeis Sternwarte & Erlangen Centre for Astroparticle
Physics, Sternwartstr. 7, 96049
Bamberg,
Germany
Received: 19 October 2014
Accepted: 25 February 2015
Context. Transient short-period (<100 s) oscillations have been found in the X-ray light curves of three novae during their super-soft source (SSS) phase and in one persistent SSS.
Aims. We pursue an observational approach to determine possible driving mechanisms and relations to fundamental system parameters such as the white dwarf mass.
Methods. We performed a systematic search for short-period oscillations in all available XMM-Newton and Chandra X-ray light curves of persistent SSS and novae during their SSS phase. To study time evolution, we divided each light curve into short time-segments and computed power spectra. We then constructed a dynamic power spectrum from which we identified transient periodic signals even when only present for a short time. We base our confidence levels on simulations of false-alarm probability for the chosen oversampling rate of 16, corrected for multiple testing based on the number of time segments. From all time segments of each system, we computed fractions of time when periodic signals were detected.
Results. In addition to the previously known systems with short-period oscillations, RS Oph (35 s), KT Eri (35 s), V339 Del (54 s), and Cal 83 (67 s), we found one additional system, LMC 2009a (33 s), and also confirm the 35 s period from Chandra data of KT Eri. The oscillation amplitudes are of about <15% of the respective count rates and vary without any clear dependence on the X-ray count rate. The fractions of the time when the respective periods were detected at 2σ significance (duty cycle) are 11.3%, 38.8%, 16.9%, 49.2%, and 18.7% for LMC 2009a, RS Oph, KT Eri, V339 Del, and Cal 83, respectively. The respective highest duty cycles found in a single observation are 38.1%, 74.5%, 61.4%, 67.8%, and 61.8%.
Conclusions. Since fast rotation periods of the white dwarfs as origin of these transient oscillations are speculative, we concentrate on pulsation mechanisms. We present initial considerations predicting the oscillation period to scale linearly with the white dwarf radius (and thus mass), weakly with the pressure at the base, and luminosity. Estimates of the size of the white dwarf could be useful for determining whether these systems are more massive than typical white dwarfs, and thus whether they are growing from accretion over time. Signs of such mass growth may have implications for whether some of these systems are attractive as Type Ia supernova progenitors.
Key words: novae, cataclysmic variables / stars: oscillations / white dwarfs / X-rays: stars
© ESO, 2015
1. Introduction
The class of super-soft sources (SSS) was empirically defined as X-ray sources emitting a blackbody-like spectrum yielding temperatures between 20−100 eV (3−7 × 105 K) and luminosities above 1035 erg s-1 (Greiner 1996). The first such sources were found with the Einstein Observatory by Long et al. (1981) and were later defined as a class after more were discovered with ROSAT (Truemper 1992; Kahabka et al. 1994; Greiner et al. 1991). It is now commonly accepted that SSS emission originates in binary systems containing a white dwarf primary that hosts nuclear burning of material that is accreted from a secondary star; see van den Heuvel et al. (1992) and Kahabka & van den Heuvel (1997). Based on this interpretation, the term super-soft X-ray binary (SSB) is sometimes used. In high spectral resolution data that can be achieved with the gratings on board XMM-Newton1 and Chandra2, details can be seen that clearly confirm theoretical expectations that the X-ray spectra are not a blackbody (as e.g. several neutron stars), but an atmospheric continuum spectrum with absorption lines and edges. Important system parameters can be derived using atmsophere models, which was, for example, demonstrated for the famous persistent SSS Cal 83 by Lanz et al. (2005).
In addition to the persistent SSS, classical and recurrent novae (CNe, RNe) pass through a phase during which they emit an SSS spectrum in X-rays that is thought to originate from the hottest layers closest to the surface of the white dwarf. The SSS phase lasts until the hydrogen content of the accreted material is consumed or ejected. The X-ray and UV evolution of novae during their outbursts has been determined using Swift monitoring observations. Deeper, continuous XMM-Newton and Chandra observations have been obtained, guided by the long-term evolution of UV/X-ray emission determined by the Swift UVOT and XRT instruments. The turn-on time of the SSS phase, when bright SSS emission becomes visible, depends on the evolution of the nova ejecta. Accurate predictions are currently not possible from evolutionary models, but empirical scaling relations have recently been derived from population studies (Henze et al. 2014; Schwarz et al. 2011). Their predictive power is not yet well established, and Swift is still needed to study the X-ray evolution of individual novae and to guide deeper X-ray observations.
The first Swift X-ray monitoring campaign of a nova was performed during the 2006 outburst of the recurrent nova RS Oph, and Osborne et al. (2006) found short-period oscillations of about 35 s in some but not all X-ray observations taken during the SSS phase. This transient signal in RS Oph was studied in more detail by Osborne et al. (2011). The period was first seen on day 32.9 after outburst and last detected on day 58.8, consistent with the start of the SSS phase and the onset of the decline, respectively. Independent evidence for this period was reported by Ness et al. (2007) in an XMM-Newton observation taken on day 54 after outburst. They confirmed that the signal came from the SSS component and not from the shock emission that was present in the same observation at higher energies. Nelson et al. (2008) also reported having seen this signal for a short time in an XMM-Newton observation taken on day 26.1.
Surprisingly, a transient 35 s period was also seen in Swift/XRT data obtained for KT Eri (Beardmore et al. 2010). Most recently, a 54 s transient period was found for the nova V339 Del in Swift/XRT (Beardmore et al. 2013) and XMM-Newton observations (Ness et al. 2013b), both taken during the SSS phase. Two Chandra observations taken on 2013 November 9 (day 87.2) and 2013 December 6 (day 114) also contain the 54 s period (Nelson, priv. comm., publication in prep.).
Similar X-ray periods were found in probably non-burning white dwarfs, for instance, a 33 s spin of AE Aqr (Patterson et al. 1980), ~29 s in WZ Sge (Nucita et al. 2014, and references therein), or few-second quasi-periodic oscillations (QPOs) in a number of dwarf novae, e.g., SS Cyg, U Gem, (Cordova et al. 1984); referred to as dwarf nova oscillations (DNOs), see for example, Mauche (2002), Warner et al. (2003a) and references therein. Since the X-ray spectra of these systems reflect distinctly different production mechanisms from SSS spectra (e.g., accretion disc or the boundary layer), we do not include these CV systems in our study.
In addition to novae, a period of ~67 s has been seen by Odendaal et al. (2014) in the prominent persistent SSS Cal 83, which they interpreted as driven by the rotation period of the white dwarf. While this is close to the break-up period, they argued that the white dwarf may be spun up by accretion disc torques. A ±3 s drift from the median value in this scenario would be more difficult to explain (see the discussion in Sect. 5.2).
All indicators suggest that the short-period oscillations originate in the SSS component. This type of short-period oscillation may thus originate from the surface of the white dwarf while undergoing nuclear burning. It will be of interest to determine whether the 35−54 s periods in the novae are related to the 67 s period in the persistent SSS Cal 83. If the origin is not the spin period of the white dwarf, it might be related to the interiors or the nuclear burning regions, and understanding these processes would give a new diagnostic method to determine fundamental parameters such as the mass of the underlying white dwarf. It is therefore important to find as many systems as possible that host short-period oscillations, ideally covering a wide range of system parameters, to identify those properties that drive them.
We have searched for short-period variations in all systems showing bright SSS emission, focusing here on XMM-Newton and Chandra observations, while a similar project based on all Swift/XRT data will be presented by Beardmore et al. For systems with short-period oscillations, we study the evolution of the power and the period.
We briefly describe the techniques and the observations used in this article in Sect. 2. We then describe the timing analysis in Sect. 3 and the results of it in Sect. 4. We discuss our results in Sect. 5 and summarise our findings and conclusions in Sect. 6.
2. Observations
XMM-Newton and Chandra observe from highly elliptical orbits allowing long uninterrupted observations for up to two days. The instrumentation on board provides high resolution in time and energy using various combinations of CCD detectors and dispersive gratings. For more details, we refer to the corresponding papers about the XMM-Newton satellite (Jansen et al. 2001) hosting the European Photon Imaging Camera (EPIC), consisting of the pn detector (Strüder et al. 2001) and the Metal Oxide Semi-conductor (MOS, Turner et al. 2001), and the Reflection Grating Spectrometers (RGS, den Herder et al. 2001). The Chandra satellite is described by Weisskopf et al. (2002) with the High Resolution Camera (HRC, Murray et al. 2000), the Low Energy Transmission Grating (LETG, Brinkman et al. 2000), and the Advanced CCD Imaging Spectrometer (ACIS, Nousek et al. 1987).
A large sample of high-resolution X-ray grating spectra of SSS was presented by Ness et al. (2013a), where a list of observations is given in their Table 2, from which we selected the observations in this work. We used the light curves from the contemporaneous XMM-Newton/EPIC detectors or zero order for Chandra transmission grating observations. In Table 1 we list the target names, day after outburst for novae (reference day given in Table 1 of Ness et al. 2013a), observation identifier, detector from which light curves were extracted (see table footnotes and text below), start date, exposure time, and the bin size used for the period analysis. The following five columns give the larger bin size used to determine count rates given in the following four columns, minimum and maximum count rates (thus the range of variability) supplemented by median and mean count rates. These numbers give an idea of the brightness and the degree of variability. In the last column we list a code that indicates the detrending method (see Sect. 3).
Journal of X-ray observations of super-soft X-ray sources.
For XMM-Newton observations, we extracted light curves from the EPIC detectors pn in 1s time bins. V4743 Sgr, RS Oph, and V339 Del were too bright for the EPIC pn camera, which suffered excessive event losses from buffer overflow. For these novae, we used the light curves from either the less sensitive MOS cameras (V339 Del) or from the Reflection Grating Spectrometers (RGS). The instrument with mode and filter used is given in the fourth column of Table 1. Some details of the instruments are also included in the corresponding graphical representations of the results.
The raw data were processed with standard SAS tools of version 13.5. We started with a standard run using the general SAS tool xmmextractor, which delivers a full set of event files and science products using standard parameter settings, some of them optimised to the specific observation. We then inspected the science products and re-generated the EPIC and RGS light curves over the 0.1−10-keV range using evselect and epiclccorr or rgslccorr. We furthermore extracted all available light curves that were taken with the optical monitor in fast mode in time binnings of 0.5 s.
All Chandra observations in our sample used the LETG. We extracted the light curves from the zero-order photons of the HRC or the ACIS (Cal 87) using the regions of zero order that are automatically created during extraction of grating spectra. The extraction was made with the task Ciao v. 4.6 dmextract in binning of 1 s (for HRC) and 2 s for ACIS, without energy filtering.
3. Analysis
Before searching for periodic oscillations, we detrended the light curves. We first fitted either a high-order polynomial to the light curve or smoothed it with a Gaussian kernel. The polynomial or smoothed curves were then subtracted from the light curve and the difference used for further analysis. In the last column of Table 1 we list the detrending mode as Pn when using an nth order polynomial and Gn when using a Gaussian-smoothed light curve, with n reporting the full width at half maximum (in seconds).
The period searches were performed using power spectra calculated with the method of Horne & Baliunas (1986). The details are described in the appendix. Since past observations imply that we here investigate a transient signal, we have to consider the possibility that a signal might not be detectable in a full light-curve. To detect any sporadic appearance within an observation, we therefore computed power spectra from overlapping t = 1000 s time segments in adjacent steps of 500 s. In all cases we tested Nf = 500 frequencies within a range of periods between 25 s and 100 s. This range covers all periods so far reported and avoids contamination by low-frequency noise.
In the Appendix we present simulations supporting the way we interpret the resulting powers from the power spectra as likelihood of detecting a periodic signal. We also discuss corrections for multiple testing when studying various time intervals from a single light-curve based on the conservative Bonferroni correction (Bonferroni 1936; Dunn 1959, 1961).
 |
Fig. 1 RS Oph on day 26.1: spectral (left) and period (right) time-maps on the same time scales in vertical direction. Left: spectral time-map showing the evolution of the RGS spectrum; taken from Ness et al. (2013a), adding unidentified emission features with their wavelengths in Å. The simultaneous EPIC/pn and MOS2 light curves are shown in the right panel, rotated clockwise by 90°. The pn has a longer initial overhead such that the exposure started ~1170 s later than the RGS and the MOS exposures, thus the black curve (pn) starts at 0.33 h, while the red curve (MOS) starts at 0 h. Right: dynamic power spectrum consisting of the power spectra computed from 24 overlapping 1000 s time segments from the pn light curve. To map them into the 11 ks time frame of the observation, the width of each row in the central panel is reduced to 500 s. The horizontal orange/blue dashed lines running across the main panel border two adjacent 500 s time intervals that correspond to the (wider) coloured bars in the right panel. They mark the overlapping 1000 s time intervals from which the individual power spectra were computed that are shown with the same colours in the top panel. The colour scheme for the main panel is decoded in the top right part; blue colours were chosen to mark periods with >90% confidence and red for 30−80%, while yellow/light green reflect noise. Colour-coding and thresholds have been corrected for oversampling and multiple testing (see text). The short horizontal black line in the main panel at 35 s represents the 90% uncertainty range in period of a significant (> 2σ) signal. In the top panel, in addition to the two power spectra from partial light-curves, the power spectrum from the full light-curve is shown in black; the same oversampling factor of 16.67 has been applied and contains no significant signal. The widths of the peaks in the respective power spectra are consistent with the intrinsic period resolution imposed by windowing. At the right, we show the evolution of the modulation amplitude, most of them are upper limits. |
To illustrate the evolution of a periodic signal, we display the series of power spectra with the concept of a dynamic power spectrum, similar to the dynamic spectra that were used for X-ray spectra by Ness (2012), for example. A comparison is shown in Fig. 1 (discussed in Sect. 4.1), where time evolution maps of the X-ray spectrum (left panel) and of the power spectrum (right panel) are shown. The light curve is shown with time running down in the right part of the left panel, turned around by 90° clockwise, where in this case both EPIC/pn and EPIC/MOS light curves of RS Oph are shown in units of count rates. In the right plot, the modulation amplitudes are shown in units of counts per second for each 500 s time bin along the same vertical time axis. The horizontal period axis in the right plot is centred on the 35 s period found in the later Swift and XMM-Newton observations. While we always searched for periods over 25−100 s, we here show only the period range around the significant signal. We defined the colour scheme based on detection likelihood using red at ~30−80% and blue at >90%. The colour scheme and the marked confidence levels are based on the thresholds after correcting for multiple testing and oversampling. The colour-encoding can be identified from the colour bar and the corresponding horizontal lines in the upper right corner.
We first searched for significant signals within the entire 25−100 s period interval in each time segment. For the strongest peak, we focused on a narrow period interval ±2 s to determine the period from a spline fit. We then determined the amplitude from a sine fit to the folded light curve. Rough uncertainties in amplitude were estimated by observing the increases in χ2 when varying the amplitude from the best-fit value while keeping the other two parameters (period and phase) fixed at their respective best-fit values.
We then calculated the uncertainty of the pulse period in two different ways. In the first approach, we computed the standard deviation using Eq. (4) in Larsson (1996), using the standard deviation of count rates in the corresponding time segment, σtot, and the amplitude of the best-fit sinusoid fitted to the folded light curve; see also Eq. (14) in Horne & Baliunas (1986) and Kovacs (1981). Here we neglected the uncertainties in the amplitude. In the second approach, we determined the standard deviation of the pulse periods obtained from Monte Carlo simulated light curves. These light curves were obtained by replicating the folded light curve using the same sampling as the original light curve and adding the appropriate Poisson noise. We then calculated the standard deviation of the periods measured from 10 000 such realizations and assigned this number to the uncertainty of the period. In general, both approaches yield comparable results. In this work we use twice the standard deviation as estimates of uncertainties in period. Assuming Gaussian statistics, this would correspond to 95% confidence ranges. The respective results are illustrated with the short horizontal black lines in the dynamic power spectra plots such as Fig. 1, centred around the respective strongest signal.
We determined the widths of the peaks in the power spectra from a Gaussian fit to the peak in the power spectrum in frequency space to compare them to the frequency resolution imposed by windowing, determined by the duration of the time segments: df = 1 /T. The corresponding width in period space depends on the period p, yielding p2/T, thus a narrower peak for shorter periods. If the measured width of a significant peak at period p is broader than p2/T, then the period is not constant.
Finally, we computed the fraction of the total time that a period is detected above a given detection threshold, similar to a duty cycle, where we determined these fractions for a range of thresholds. For each source, we computed new time series of power spectra that do not overlap, and in this sample, we summed the integration time of all time segments that contain a signal above a given threshold. We computed the fractions for each observation separately and for all time segments from all observations combined. The results are described in Sect. 4.7.
4. Results
We performed the analysis described in Sect. 3 for the observations listed in Table 1 and discuss the results for some of the individual systems in the following subsections.
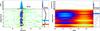 |
Fig. 2 RS Oph on day 54. Left: time map of the 35 s period in the XMM-Newton RGS2 light curve, see description of right panel in Fig. 1. Right: time map of folded light curves, where each curve was artificially moved in phase for the peak to occur at phase 0.25. In the top panel, an example is shown with the sine curve fit from which the modulation amplitudes with uncertainties were determined. In the right panel, the evolution of amplitudes is shown. |
4.1. RS Oph
We searched for the 35 s period found from Swift observations by Osborne et al. (2006) in three XMM-Newton and two Chandra observations of RS Oph. We first analysed the XMM-Newton observation taken on day 14 (ObsID 0410180101), which is not listed in Table 1 because it was not taken during the SSS phase; (Ness et al. 2009). We divided the 23 ks observation into 46 overlapping 1000 s time segments but found no significant detection. While a 35 s signal with a false-alarm probability of 10% is found in one time interval, the correction for multiple testing reduces the detection probability to <1%. Thus, repeating a search 46 times in a light curve without a signal could produce such a peak and it may thus be a random occurrence. The XMM-Newton observation taken on day 26.1 is also dominated by the early shock emission, but has an additional soft component that appeared during the observation. Nelson et al. (2008) reported that a 35 s period was present during a short time when the soft count rate rapidly increased by a factor 3, and in Fig. 1, we give a graphical illustration of the spectral (left) and period (right) evolution on the same vertical time axis. Numerous short-lived unidentified soft spectral emission features, noted by Ness et al. (2013a), are included with the values of wavelengths of unidentified features in the top left panel. So far, no convincing identifications were found after investigating possibilities of extreme line shifts (Nelson et al. 2008) or exotic elemental abundances (Orio et al. 2010).
In two time segments around the same time, a periodic signal appeared at 35 s above 90% detection probability, which can be seen in the right panel. The black line in the top panel is the power spectrum from the full light-curve and contains no significant signal at 35 s. While this might seem like a marginal result, we emphasise that the confidence levels and colour scheme have been conservatively corrected for the effects of oversampling and multiple testing with 24 trials. Moreover, a similar period value was obtained with high confidence from later Swift and XMM-Newton observations, and it also coincides with the rise in brightness and the appearance of an apparent emission line spectrum with many unknown line features.
 |
Fig. 3 RS Oph on day 54: relations between power (top row) and period (middle row) versus mean RGS2 count rate (left column) and modulation amplitude (right column). The amplitude is mean to peak in units of RGS2 counts per second. A typical uncertainty range in amplitude, derived while fitting sine curves to the phased light curves, is shown with the grey horizontal line in the left corner. The 95% (2σ) detection level (corrected for oversampling) is marked by the horizontal line in the top panels. In the middle panels, the error-weighted median period with standard deviation of the periods is marked with the horizontal solid and dotted lines, respectively. The 95% error bars on periods were calculated with Eq. (4) in Larsson (1996; see text). We show 30 out of 38 data points for which the signal power exceeds a 95% detection and a sine fit yields a positive amplitude. The distribution of periods is shown in the small inset where a Gaussian is added for comparison. Middle right panel: period versus amplitudes are shown, suggesting that larger variations in period occur with smaller amplitudes. Bottom left panel: amplitudes are shown versus count rate, demonstrating that there is no correlation. Ranges of amplitudes relative to count rate are marked by the dashed and dotted lines. Bottom right panel: periods versus power are shown, which also seem to show that larger variations in period occur at lower values of power. |
Since after day ~29, the 35 s period was always associated with SSS emission, this coincidence may indicate that the strange soft component with emission lines (Fig. 1) is also associated with SSS emission, even though the spectrum does not appear to be a typical SSS continuum spectrum. In this context, it is noteworthy that the low-resolution simultaneous EPIC spectrum can be reproduced by a blackbody (Ness 2013).
A Chandra observation taken on day 39.7 after outburst (top panel of Fig. 4) contains a peak at 37.5 s that proved to be insignificant. This observation was taken during an episode of low count rate during an early variability phase (Osborne et al. 2011).
During the XMM-Newton observation taken on day 54, the peak of the overall X-ray brightness evolution (Osborne et al. 2011), the 35 s period was detected at a significance >99.9%. The extreme brightness of RS Oph at this time led to difficulties in telemetering the data to the ground, and the EPIC data can only be used for spectroscopy. The RGS1 light curve could not be used for the same reason; only the RGS2, which had a lower count rate owing to a failure of a CCD chip (that would have recorded the dispersed photons from the peak of the SSS spectrum), contained a controllable number of telemetry drop outs. In Fig. 2 we show the time evolution of the period (left) and of the amplitude (right) from the RGS2 data. The signal power varies considerably, as shown by the two power spectra in the top panel, extracted from the time intervals marked in the right panel of the left plot. The orange open histogram contains two much weaker signals at ~34 s and ~36 s. In the right panel, the evolution of the phase-folded light curves is shown on the same (vertical) time axis as the left plot. Since the start and stop of the time segments do not coincide with the same epochs, we have artificially moved each curve such that the peak is always at phase 0.25. The right plot in the right panel shows the evolution of the amplitude.
We studied the relations between the period, power, amplitude, and the mean count rate in 38 time segments of the full light-curve, excluding six segments in which the amplitude only yields an upper limit. In Fig. 3 the values of these parameters are plotted against each other. In the left column, the three period parameters are plotted against the mean count rate. In the top row, the 95% (2σ) detection threshold (corrected for oversampling) is indicated by the horizontal line. The signal power does not seem to depend on the count rate. Out of the 32 time segments with positive amplitudes, 30 yield >2σ detections of the 35 s period, and these are used in the two panels below. The 95% error bars included for the periods in the middle left panel are twice the standard deviation, calculated with Eq. (4) in Larsson (1996). The error-weighted mean period is given with the horizontal line with the value and standard deviation given above this line. The errors are smaller than the widths of the peaks, which are driven by windowing and thus the duration of the time segments T. The frequency resolution scales with 1 /T2, and at the period of 35 s, the expected width of the peak is dp = p2/T ~ 1 s. The variations of the period are slightly larger than the 95% error bars and thus may be real, although we note that the large uncertainties in amplitudes have not been accounted for when calculating the period errors. Furthermore, the distribution of periods, shown in the small inset, indicates that the variations are normally distributed, because the distribution can be fit by a Gaussian. The distribution and formal errors do not provide information to conclude whether or not the period varies with time, as concluded by Odendaal et al. (2014) for the 67 s period in Cal 83. In the top panel of Fig. 2, the power spectrum derived from the complete light curve is shown by the thin black line, and the higher period resolution achieved by the longer baseline of the total light curve reveals multiple peaks. This would support that the period is not constant in time.
In the bottom left panel of Fig. 3, the amplitudes in units of RGS2 count rate are shown against the average count rates for each time segment. The dashed and dotted lines indicate the lowest and highest amplitudes relative to the respective count rate in per cent. The amplitudes range between 2.3−11 counts per second (1.7−7% of the total count rate) without any systematic trend with count rate. Uncertainties in amplitude range between 30% and 90%.
In the right column of Fig. 3, relations between the amplitude, power, and period can be studied. Obviously, small amplitudes are more difficult to detect because they yield low detection powers. Some outliers with low signal power but high amplitude can be caused by a high degree of additional non-periodic variability, which in a folded light curve could result in a large amplitude. The uncertainty in amplitude is marked with the horizonal grey line in the top left panel and is larger than the deviations from the main trend. In the middle right panel, the variations of period with amplitude are shown and it seems that the larger variations in period coincide with low amplitudes. This trend seems even stronger in the bottom right panel, which plots power versus period. Osborne et al. (2011) showed that the period stability increased with time through the SSS phase.
 |
Fig. 4 RS Oph on day 67: time map around the 35 s period in the Chandra HRC light curve, see description in the right panel of Fig. 1. The strongest peak coincides with the 35 s period seen in earlier Swift and XMM-Newton observations (see Fig. 2). The power (conservatively corrected for multiple testing and oversampling, see Appendix) only yields a 1σ detection. |
Another Chandra observation taken on day 67 after outburst may present some evidence for the 35 s period at the 1σ level (see Fig. 4). The colour scheme and thresholds for testing include the correction for oversampling and for multiple testing, although the latter is conservative and does not recognise that this particular period was clearly detected in other observations. Osborne et al. (2011) reported that the 35 s period disappeared on day 58.8, about a week before this observation was taken. If the period is real, then it might be related to a short re-brightening that seems evident from the Swift light curve shown in Fig. 2 in Osborne et al. (2011). On the other hand, the Chandra observation contains no re-brightening, in particular not around the time of this marginal detection.
Only one 4400-s exposure was taken with the XMM-Newton optical monitor on day 54 with the UVW2 filter. While the exposure was taken in fast mode, the source was not centred within the small readout window, leaving most of the PSF outside of it. The light curve extracted from the remaining part of the source contains no significant periodic signal.
 |
Fig. 5 KT Eri on day 159: time map around the 35 s period in the Chandra HRC light curve, see description in the right panel of Fig. 1. The thin solid line in the top panel is the power spectrum from the entire observation and shows two >99.9% significant peaks. This indicates that the period is not constant in time. |
4.2. KT Eri
KT Eri was the second nova in which a transient 35 s period was seen in Swift monitoring observations during the SSS phase (Beardmore et al. 2010). Four Chandra observations were taken during the eruption on days 71.3, 79.3, 84.6, and 158.8, and we searched the light curves for periodic oscillations. Owing to the high brightness of the source and with the main goal being to obtain high-resolution grating spectra, the observing times were rather short. In such short exposures, transient periodicities can be missed easily.
We detected the 35 s period only during the early and late parts of the observation on day 159 (see Fig. 5). The width of the peak is consistent with the highest possible resolution power in period, associated with the selected duration of each time segment. Extracting the power spectrum from the total light curve yields a higher resolution in period, as can be seen from the thin black line in the top panel. The double nature of the peak suggests that the period was variable.
4.3. V339 Del
The third time a transient short-period signal was seen in Swift observations of a nova was V339 Del (on days 77.5 to 88.6), in which Beardmore et al. (2013) reported a 54 s period; this was confirmed to have also been present in an XMM-Newton observation taken on day 99 (Ness et al. 2013b). While the XMM-Newton EPIC-pn camera suffered a full scientific buffer at almost all times and could be used only for spectroscopy, simultaneous light curves from the MOS and RGS instruments provide independent evidence. The time evolution of power spectra derived from the MOS2 data is illustrated in Fig. 6, where we can see that the signal was not constant in power, similar to RS Oph. We also analysed the two Chandra observations taken on days 87.2 and 114 and found similar results. We performed the same parameter studies as for RS Oph for all time segments from all three observations and show the results in Fig. 7. The XMM-Newton and Chandra data can clearly be distinguished by the lower Chandra count rates − owing to the smaller effective areas − and consequently smaller amplitudes, which are given in units of count rate. The minimum and maximum ratios of amplitudes versus count rates are indicated in the bottom left panel with dashed and dotted lines, respectively. The relative amplitudes are consistent for Chandra and XMM-Newton data. In V339 Del, as in RS Oph, no clear relation between the power and the brightness of the source can be found. The variations in period are slightly larger than the 95% uncertainties in period and thus may likewise be real. The modulation amplitude of signals detected with more than 95% confidence varies between 3.1−10% of the count rate, clearly yielding more significant detections (higher powers) with higher amplitudes (top right panel of Fig. 7). The slope in the top right panel is steeper for the Chandra than the XMM-Newton data owing to the difference in sensitivity and background. Again, like RS Oph, the amplitude variations are not related to the brightness of the source (bottom left panel). The bottom right panel suggests that the largest scatter in period is found for the lowest power.
The XMM-Newton optical monitor was operated in fast mode, taking ten exposures with the UVW2 filter. The count rate ranged around 140 ± 10 s-1, consistent with Poissonian noise, and we found no periodic oscillations.
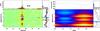 |
Fig. 6 V339 Del on day 99: Same as Fig. 2, focusing on the 54 s period in V339 Del based on the XMM-Newton MOS2 light curve. The simultaneous combined RGS1 and RGS2 light curve yields a consistent result. |
 |
Fig. 7 Same as Fig. 3 for the Chandra and XMM-Newton/MOS2 observations of V339 Del. We show 94 out 266 data points in the middle and bottom rows that yield >2σ detections and positive amplitudes. As in RS Oph (Fig. 3), no relation between period properties and count rate is apparent, and the period seems to be variable. The modulation amplitude clearly correlates with the power of the period because modulations with a larger amplitude are easier to detect. The Chandra and XMM-Newton data yield different slopes for amplitudes in unit counts per second, while for count rates, a single slope is encountered. In the bottom left panel, we show that the data from both telescopes yield similar ranges of relative amplitudes. The bottom right panels appear similar to RS Oph (Fig. 3), with largest variations in period occurring with low values of power. |
 |
Fig. 8 LMC 2009a on days 90, 165, 197, and 230: time maps around the 33 s period in four XMM-Newton/pn light curves, see description in the right panel of Fig. 1. The vertical (time) axes are different in each plot; they only cover the respective exposure times. |
4.4. LMC 2009a
We found a new system with a 33 s period in two out of four XMM-Newton observations of nova LMC 2009a (Ness et al. 2014). In Fig. 8 the time maps are shown for all four observations. In the first observation, taken on day 90 after outburst (top left panel), no periodic signal is seen. In the second observation, taken on day 165 after outburst (top right panel), a significant signal with a period of 33 s can be seen at ~8 h of elapsed time. The same period is more clearly detected in the third observation taken on day 197 (bottom left panel). In the last observation, none of the time segments contains a significant signal. We note the single peak in the power spectra derived from the respective full light-curves. While a peak at 33 s is apparent, it is not statistically significant. In the bottom left panel, the total power spectrum contains multiple peaks around 33 s, clearly indicating strong variability of the period. We performed the same studies on correlations as those shown in Figs. 3 and 7 using 22 data points with >2σ detections and positive amplitudes and find similar results of significant variability in the period, while variations in power and amplitude do not correlate with the count rate.
As can be seen from Fig. 8, the fraction of time that the 33 s period is detectable in LMC 2009a is much lower than for the periods in RS Oph, KT Eri, and V339 Del (see Sect. 4.7). Perhaps this explains why it is not found in the Swift/XRT data (Beardmore in prep); Swift might have observed only during the times when the period was absent.
Each observation was accompanied by 20−30 fast mode exposures with the optical monitor, all using the UVW1 filter. The count rates decreased with time starting from 6.3 ± 1.3 s-1 on day 90.4 through 2.4 ± 0.7 s-1 on days 165 and 196 to 2.1±0.6 s-1 on day 230. From each light curve we constructed the power spectrum, but found no significant signal, even when combining all exposures into a single light-curve.
4.5. Cal 83
For the persistent SSS Cal 83, Odendaal et al. (2014) have recently reported a 67 s periodic modulation. We have produced our period time maps for 19 XMM-Newton observations, for which Odendaal et al. (2014) report that the source was not in the off state, and present an example in Fig. 9 for ObsID 0506531701 that yields the same result as that shown in Fig. 8 of Odendaal et al. (2014).
 |
Fig. 9 Cal 83 on 2009-05-30.4: time map around the 67 s period in one of 19 XMM-Newton/pn light curves, see description in the right panel of Fig. 1. The time evolution is consistent with that shown in a different format in Fig. 8 in Odendaal et al. (2014). |
 |
Fig. 10 Same as Fig. 3, with data collected from 20 observations of Cal 83, divided into a total of 578 1000 s time segments. 17 of these intervals yield zero count rate and were excluded. Furthermore, all data points yielding only upper limits in amplitude were excluded, which left 202 data points, of which 34 time intervals yield a >95% detection of a periodic signal. The expected correlation between modulation amplitude and signal power (top right) is contaminated by a large number of overestimated amplitudes that are most likely caused by additional, non-periodic variability. These deviations are consistent with the large uncertainties in amplitude. The 95% threshold is corrected for oversampling, but not for multiple testing. 31 of 34 data points that are found above this threshold and yield a successful sine fit are used in the lower two rows. The variations in period of about ±3 s reported by Odendaal et al. (2014) can be recognised in the middle row and bottom right, but do not seem to correlate with count rate, amplitude, or signal power. |
We repeated the same correlation studies of the power of the period and period with count rate that we have presented for RS Oph and V339 Del. For Cal 83, we have a much larger sample, which is shown in Fig. 10. In the top panel, we include the results from all time segments. The variations in period are again slightly larger than the 95% errors and thus might be real. At intermediate count rates, the period seems to be anti-correlated, but this would be based on too few data points (middle row). We also searched for periodic variations of the power on amplitude on longer time scales, but found no clear patterns in the power spectra of signal powers and amplitudes.
We checked all available XMM-Newton observations with the optical monitor, which contain exposures in U, B, UVW1, UVM2, and UVW2 filters, but found no periodic signal in any of these exposures nor in combined light curves for each filter.
4.6. Search for other candidates
We screened all power spectra from the datasets listed in Table 1 for any significant signals that might account for multiple testing and oversampling. With these corrections any peak at any period that rises above a given threshold is a strong candidate. We searched for signals that rise above the 95% threshold, but found only the five sources already discussed above, thus no other candidate can be identified.
4.7. Fraction of observing time for which short-period oscillations are detectable
To compute the fraction of time for which the signals are detectable above a given threshold, we recomputed power spectra for adjacent, non-overlapping time segments of 1000 s duration. We first defined a detection threshold and summed the exposure times of all time segments in which a period is detected above the given threshold. We then computed the ratio of the summed exposure time by the total available exposure time. The resulting fractions depend on the chosen significance level, yielding higher fractions for lower detection thresholds.
For each target, we probed a range of detection levels, and in Fig. 11 we show fractions of times as a function of detection threshold for the five sources with detected periodic signals. Since the period was not necessarily present in all observations, the global ratio strongly depends on the coverage of the total evolution, which is generally much better determined with Swift. To study the short-term behaviour, we also include in Fig. 11 the ratio for the observation with the highest fraction with dotted lines and labels in italics for each source. For all sources, solid lines indicate that the transient signal is episodic. These estimates can be refined with the Swift data, which will be presented by Beardmore et al. (in prep.).
 |
Fig. 11 Fractions of observing time for which the strongest periods are detectable as a function of detection threshold. The solid lines are the average fractions of time derived from all available observations, while the dotted lines (with labels in italics) are the fractions of time derived from the single observation in which the period is seen most frequently. For this plot, power spectra from directly adjacent, non-overlapping time intervals have been used. For no system, the period was detected 100% of the time, showing the transient nature. Furthermore, the signal is episodic because the fractions are not the same in all observations. |
Properties of systems with known periodic signals.
4.8. Search for patterns in the transient signal
The short-period oscillations are clearly transient in all five systems with detected periods, and we investigated whether there are any patterns in the power of the signal. For example, periodic variations could be caused by the rotation of the white dwarf if the oscillations originated in an accretion spot. For each source, we created a time series of the signal power and period value from all time segments. We computed a power spectrum based on the central times of each time segment and the associated parameters. None of the resulting power spectra reveal any significant signatures.
5. Discussion
We have four confirmed novae with periodic or quasi-periodic transient signals ranging between 33 and 54 s and one persistent SSS with a periodic signal of 67 s. For these five systems, we list in Table 2 the periods, limiting count rates, and relative amplitudes of the modulation for 2σ detections, the optical speed class parameters t2 and t3, and fractions of time when detected. The limiting count rates and amplitudes are the lowest value from the sample of time intervals when a period was detected with more than 2σ significance. Although this sample is too small for searches of systematic trends, it covers a wider range of parameters than the time series of individual systems illustrated in Figs. 3, 7, and 10. No systematic trends can be seen between the period and the count rate or amplitude, but the nova speed class seems to scale with the period, yielding longer periods for slower novae. The speed class is known to scale with the mass of the underlying white dwarf, yielding higher masses for shorter speed class (Livio 1992), and shorter periods thus may be present in systems with more massive white dwarfs.
5.1. Detectability of the period during Thomson scattering?
In this section we show that Thomson scattering does not reduce the detectability of the period. Recent studies of the eclipsing recurrent nova U Sco have revealed that about 50% of the continuum emission from the white dwarf is still visible during total eclipse. The shape of the continuum spectrum seems to have been preserved, while emission lines dominate the spectrum. This indicates substantial effects of Thomson scattering of the continuum while the emission lines are not eclipsed (Ness et al. 2012). A few other SSS spectra show similar characteristics of reduced but detectable continuum emission with emission lines on top, and Ness et al. (2013a) have classified this type of SSS spectrum as the SSe subclass: “e” for emission lines as opposed to SSa with continuum-dominated spectra in which deep absorption lines can be seen.
Chang & Kylafis (1983) have studied the effects of scattering of photons on the spectra and variability patterns of X-ray sources. Since Thomson scattering is an energy-independent process, their calculations of spectral changes are not of interest to us, and we focus on their predictions of reductions of the amplitude of oscillations caused by scattering. These reductions are shown in their Figs. 7 and 8 and depend on the ratio of the period p to the light travel-time, pc/r0 and the optical depth, 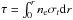 with σt = 0.6652457 × 10-24 cm2 the cross-section for Thomson scattering by electrons, and ne the electron density. For our purposes, we focus on the models for a uniform sphere because we most likely examine a continuous outflow and not an abrupt ejection event that would produce a thin shell. We have observed amplitudes of about 10% of the count rate and can thus concentrate on the range of amplitudes viewed from infinity log(A∞) > −1 in Fig. 8 in Chang & Kylafis (1983) and thus log(p/t) > 0.5 with t = r0/c the light travel-time. While this applies only to the case τ = 10, lower values of τ yield some 0.2 dex lower values of log(p/t) for log(A∞) > −1, which can be seen from Fig. 7 in Chang & Kylafis (1983). We thus focus on the range log (p/t) > 0 and thus r0<cp. For the period range 33−67 s, this constrains the size of the scattering region to r0< (14−29) R⊙.
with σt = 0.6652457 × 10-24 cm2 the cross-section for Thomson scattering by electrons, and ne the electron density. For our purposes, we focus on the models for a uniform sphere because we most likely examine a continuous outflow and not an abrupt ejection event that would produce a thin shell. We have observed amplitudes of about 10% of the count rate and can thus concentrate on the range of amplitudes viewed from infinity log(A∞) > −1 in Fig. 8 in Chang & Kylafis (1983) and thus log(p/t) > 0.5 with t = r0/c the light travel-time. While this applies only to the case τ = 10, lower values of τ yield some 0.2 dex lower values of log(p/t) for log(A∞) > −1, which can be seen from Fig. 7 in Chang & Kylafis (1983). We thus focus on the range log (p/t) > 0 and thus r0<cp. For the period range 33−67 s, this constrains the size of the scattering region to r0< (14−29) R⊙.
 |
Fig. 12 In the presence of Thomson scattering, the observable amplitude of a signal will be lower than the original modulation amplitude, depending on optical depth, τ, and density, n. We show estimated densities below which periodic oscillations would lead to reductions of the amplitude (and thus detectability) by 64−99%, depending on three values of optical depth τ = 5−1 that would lead to 1−37% of photons escaping unscattered; see Sect. 5.1. |
Depending on the assumed optical depth τ, this allows us to place a constraint on the electron density ne of this plasma. With τ = neσtr for a uniform sphere and r<cp, the constraint on density is thus ne>τ/ (σtcp).
In Fig. 12, the derived densities for a range of optical depths τ = 1−5 (assuming that 1−37% of photons escape unscattered) are illustrated for a period range of 25−85 s. In the extreme case of an intrinsic amplitude of 100%, Thomson scattering can reduce the amplitude to 10% of the count rate only if the electron density of the scattering medium exceeds 1013 cm-3. If the intrinsic amplitude is much below 100%, then the required densities would have to be even higher. A known intrinsic pulsed fraction and optical depth τ would allow us to work out both the size and density of the scattering region by the signal contrast degradation, but the intrinsic amplitude is probably not much higher than the observed one.
We thus conclude that Thomson scattering does not effectively reduce the detectability of the periodic signal, and in fact we also found a periodic signal in the SSe LMC 2009a, even though it is the system with the smallest fraction of total observed time with significant detections and the smallest amplitude.
5.2. Rotation period of the white dwarf
The long-term presence of the 67 s X-ray period in Cal 83 has led Odendaal et al. (2014) to consider the possibility that the rotation period of the white dwarf is the main driver of the oscillations. While typical rotation periods of white dwarfs are much longer, the fastest rotation period in a white dwarf binary, RXJ 0648.0-4418/HD 49798, was observed to be 13.2 s (Warner et al. 2003b), and a rotation period of 67 s is thus possible. Odendaal et al. (2014) argued that a long mass accretion history allows the white dwarf to be sufficiently spun up. The greater challenge would be to explain the observed changes in period by ±3 s. Because of the large amount of inertia of a white dwarf, this drift cannot be the result of accretion-induced spin-up or -down. In addition, there is no relation with the orbital period of 1.0475 ± 0.00004 days (Schmidtke et al. 2004; Odendaal et al. 2014), which excludes Doppler shifts imposed by the orbital motion of the X-ray emitting plasma, for example. Furthermore, the possibility was discussed that the observed period is the beat between the rotation period of the white dwarf and the Keplerian period of the denser X-ray emitting plasma, but the required rotation period of the white dwarf would then have to be even shorter, with an estimated value of 4–12 s, which would set a new record, although this is still longer than the break-up period of 3.4 s. Finally, Odendaal et al. (2014) argued that the X-ray emitting plasma must originate from an extended envelope, some two to three times the radius of the white dwarf, and if that envelope does not rotate synchronously, the spread in the 67 s oscillations can result. However, this is not quantified, and the cause of the modulation within this gas remains unclear.
Within the sample of detected periods, the 67 s period in Cal 83 is the longest one, and interpretating this as the rotation period would imply that the white dwarfs in the Galactic novae in our sample would be even shorter. Spinning up to such short rotation rates implies even longer mass-accretion histories. Osborne et al. (2011) also argued that the period changes are not consistent with realistic torques on the white dwarf. The changes in period by ±3 s argue against rotation of the white dwarf, although the argument about non-synchronous modulation within a hydrogen gas envelope presented by Odendaal et al. (2014) cannot be fully discarded. This non-synchronous region may be similar to that proposed by Warner (2004), who explained “dwarf nova oscillations” by appealing to weak magnetic fields that incompletely enforce co-rotation; see also Woudt et al. (2010). However, it remains unclear how the rotation period would manifest itself as an observable period, for instance, whether it might be caused by periodic absorption patterns.
Beardmore et al. (2010) noted that the presence of the same periods in KT Eri and RS Oph would appear to argue against a rotation-based origin for this modulation. Meanwhile, a possible residual nuclear-burning white dwarf pulsation might be more constrained in frequency, which would also explain the small range of detected periods in our sample.
The rotation of the white dwarf might be an interpretation for the observed oscillations if some speculative arguments were accepted, but we cannot identify under which circumstances this period can be seen in X-ray observations. In particular we cannot explain why the signal is transient and why it is seen in such a small fraction of systems observed. If magnetic fields are needed, as in intermediate polars, the question arises why these oscillations are seen only during the SSS phase, while intermediate polars show the rotation period in optical and X-ray light curves in quiescence, for example, V4743 Sgr (Dobrotka & Ness 2010). An independent measurement of the rotation period for one of our five systems with short-period oscillations would robustly confirm or reject the possibility that the rotation period is the main driver for these oscillations. Meanwhile, other possibilities such as pulsations exist.
5.3. Pulsation modes
An attractive explanation for the observed oscillations is that it is a surface g-mode that is triggered by the ϵ-mechanism. This possibility gains some favour from considering the dynamical time-scale of the white dwarf atmosphere. In the ϵ-mechanism, the contraction and compression of a mode leads to changes in the nuclear burning rate. If this energy input exceeds the cooling during the subsequent rarefaction of the mode, it will be unstably excited. Since the oscillations are preferentially observed in the SSS following nova outbursts, when nuclear burning may be occurring at the surface, the conditions may be met for this to occur.
The ϵ-mechanism has been considered for g-modes in the context of white dwarfs following the production of planetary nebulae (Kawaler 1988), as well as for neutron stars that are stably burning their accreted fuel similarly to the way this occurs in an SSS (Piro & Bildsten 2004). Since this scenario is for physical conditions somewhat different from the nova systems studied here, it is helpful to provide some basic arguments about what types of periods we expect for surface g-modes. This also demonstrates that the mode periods roughly depend on the properties of the white dwarfs and thus indicates that these modes may be useful probes of their structure.
When the white dwarf is in an SSS state, there is an abrupt change in the internal profile (in composition, temperature, and density) where hydrogen is being burned. There is an associated strong buoyant force at this depth, so that we can consider modes that are riding along, unable to penetrate this region. If the burning occurs at a depth H, which is much much lower than the radius of the white dwarf R, this mode’s dispersion relation will be similar to that of a shallow water wave (Faber 1995) 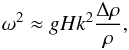 (1)where ω is the mode frequency, g is the local gravitational acceleration, g ≈ GM/R2 when H ≪ R, k2 = l(l + 1) /R2 is the transverse wave number squared, where l is the spherical harmonics quantum number, and Δρ/ρ is the fractional change in density at the burning depth. For simplicity, we assume Δρ/ρ ~ 1 in our discussion below, which corresponds to a maximally discontinuous jump.
(1)where ω is the mode frequency, g is the local gravitational acceleration, g ≈ GM/R2 when H ≪ R, k2 = l(l + 1) /R2 is the transverse wave number squared, where l is the spherical harmonics quantum number, and Δρ/ρ is the fractional change in density at the burning depth. For simplicity, we assume Δρ/ρ ~ 1 in our discussion below, which corresponds to a maximally discontinuous jump.
While g and k depend on the mass and radius of the white dwarf, H depends on the thermal profile of the surface layers. The thermal profile of the white dwarf is set via flux-limited diffusion, which obeys the equation 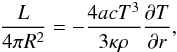 (2)where L is the luminosity, a is the radiation constant, κ is the opacity, T is the temperature, and ρ is the density. We assume κ = 0.34 cm2 g-1 is a constant as set by electron scattering for solar composition material, which is roughly correct for the hot SSS state. Using hydrostatic balance, dP/ dr = −ρg, this expression can be rewritten as
(2)where L is the luminosity, a is the radiation constant, κ is the opacity, T is the temperature, and ρ is the density. We assume κ = 0.34 cm2 g-1 is a constant as set by electron scattering for solar composition material, which is roughly correct for the hot SSS state. Using hydrostatic balance, dP/ dr = −ρg, this expression can be rewritten as 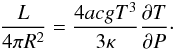 (3)Assuming that L is constant with depth (which is a good approximation above the burning depth in the SSS), this can be integrated to yield
(3)Assuming that L is constant with depth (which is a good approximation above the burning depth in the SSS), this can be integrated to yield 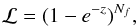 (4)where LEdd = 4πGMc/κ is the Eddington luminosity. The layer thickness is then given by
(4)where LEdd = 4πGMc/κ is the Eddington luminosity. The layer thickness is then given by 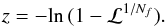 (5)where kB is the Boltzmann constant, μ is the mean molecular weight, mp is the proton mass, and we assume an ideal gas equation of state.
(5)where kB is the Boltzmann constant, μ is the mean molecular weight, mp is the proton mass, and we assume an ideal gas equation of state.
The thickness H therefore depends on the luminosity L, which can be inferred from observations, and the pressure P at the burning depth. This pressure should be related to L and the requirement of steady burning. This therefore can be addressed via theoretical calculations. For now, we know that the pressure must be lower than the pressure at ignition of the layer (for example, see the calculations of Truran & Livio 1986), so for demonstrational purposes we set P ≈ 1018 dyn cm-2, so that 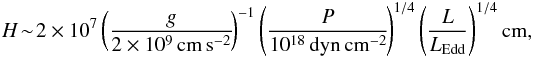 (6)where we use g as appropriate for a roughly ≈ 1.3 M⊙, similar to the kinds of masses inferred for these systems. Substituting this into the shallow water wave dispersion relation, the estimated period is
(6)where we use g as appropriate for a roughly ≈ 1.3 M⊙, similar to the kinds of masses inferred for these systems. Substituting this into the shallow water wave dispersion relation, the estimated period is 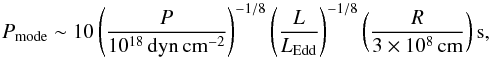 (7)where we take l = 1 since this is the lowest order (and thus easiest to observe) angular mode, and Δρ/ρ ~ 1 due to the strong compositional stratification following the burst. This result highlights that the strongest dependency of Pmode is on R and that for typical parameters associated with recurrent novae the period is too low. The two possible solutions that could reconcile this period with the observed periods are (1) the white dwarfs are much less massive and have a larger radius; or (2) the higher order radial modes are excited instead of the lowest order mode we consider here. The first possibility is unlikely given the constraints on the white dwarf masses from the recurrence times and nova durations (Wolf et al. 2013). The second possibility would give a better match in period since the higher order radial modes increase with the number of radial nodes. This would then require some explanation for why the higher order mode is excited, which requires a more detailed theoretical investigation.
(7)where we take l = 1 since this is the lowest order (and thus easiest to observe) angular mode, and Δρ/ρ ~ 1 due to the strong compositional stratification following the burst. This result highlights that the strongest dependency of Pmode is on R and that for typical parameters associated with recurrent novae the period is too low. The two possible solutions that could reconcile this period with the observed periods are (1) the white dwarfs are much less massive and have a larger radius; or (2) the higher order radial modes are excited instead of the lowest order mode we consider here. The first possibility is unlikely given the constraints on the white dwarf masses from the recurrence times and nova durations (Wolf et al. 2013). The second possibility would give a better match in period since the higher order radial modes increase with the number of radial nodes. This would then require some explanation for why the higher order mode is excited, which requires a more detailed theoretical investigation.
If this mode explanation for the oscillations is confirmed, then the period of these modes provides a constraint on the mass of the white dwarf. This could be useful for determining whether these nova systems are more massive than typical white dwarfs, which may indicate that they are growing from accretion over time. Signs of such mass growth may have implications for whether some of these systems are attractive as Type Ia supernova progenitors.
6. Summary and conclusions
We focused on analysing continuous light curves obtained with XMM-Newton and Chandra. We constructed power spectra that probe the period interval 25−100 s and tested 500 frequencies on an equidistant frequency grid, which corresponds to an oversampling of 16. We estimated detection probabilities (Appendix) based on simulations of 10 000 synthetic light curves with random Poisson noise. We furthermore broke each light curve into 1000 s time segments to study time variability of any periodic signal. We corrected the detection probabilities for multiple testing by the conservative Bonferroni correction.
We confirm the transient nature of the 35 s periods in RS Oph and KT Eri and the 54 s period in V339 Del and determined the fractions of time that the respective periods are detected at 2σ significance as listed in Table 2. The 67 s period in Cal 83 and the 33 s period in LMC 2009a are detected less frequently.
Our dynamic power spectra illustrate variations in power and amplitude on time scales of fractions of an hour. We also found multiple peaks in the global power spectra for each observation, suggesting variations of the period, although the uncertainties in periods are too large to confirm that. None of these variations correlate with the X-ray brightness.
The amplitudes are variable with values up to 15%. We checked the possibility that the amplitudes (and thus detectability) may be degraded by Thomson scattering, which could explain why so few sources are found with a period and why it is transient. We found that the density of the scattering medium would have to exceed 1013 cm-3. It depends on the unknown optical depth and the intrinsic amplitude. The intrinsic amplitude is probably much lower than 100%, thus requiring even higher densities, so we conclude that Thomson scattering has no significant effect.
Potential origins of the observed oscillations are the rotation of the white dwarf or intrinsic pulsations. Only speculative arguments might explain the observations with rotation of the white dwarf, and we thus focused on pulsations. While periods in the 10−100 s range are predicted by nonradial oscillator modes or pulsations in isolated white dwarfs, the validity of these models under conditions of active nuclear burning during a nova outburst is difficult to estimate, and new models need to be calculated to account for the higher luminosity and the physical conditions of nuclear burning near the surface.
Acknowledgments
A. P. Beardmore and J. P. Osborne acknowledge support from the UK Space Agency. M. H. acknowledges support from an ESA fellowship. A. L. Piro is supported through NSF grants AST-1205732, PHY-1151197, PHY-1404569, and the Sherman Fairchild Foundation. A. Dobrotka was supported by the Slovak grant VEGA 1/0511/13. S. Starrfield gratefully acknowledges partial support from NSF and NASA grants to ASU.
References
- Beardmore, A. P., Balman, S., Osborne, J. P., et al. 2010, ATel, 2423, 1 [NASA ADS] [Google Scholar]
- Beardmore, A. P., Osborne, J. P., & Page, K. L. 2013, ATel, 5573, 1 [NASA ADS] [Google Scholar]
- Bonferroni, C. E. 1936, Pubblicazzioni del R Istituto Superiore di Scienze Economoiche e Commerciali di Firenze (High R Institute of Economic and Commercial Sciences of Florence) [Google Scholar]
- Brinkman, B. C., Gunsing, T., Kaastra, J. S., et al. 2000, SPIE, 4012, 81 [Google Scholar]
- Chang, K. M., & Kylafis, N. D. 1983, ApJ, 265, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Chester, T. J., Mason, K. O., Kahn, S. M., & Garmire, G. P. 1984, ApJ, 278, 739 [NASA ADS] [CrossRef] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrotka, A., & Ness, J. 2010, MNRAS, 405, 2668 [NASA ADS] [Google Scholar]
- Dunn, O. J. 1959, Ann. Math. Stat., 30, 192 [CrossRef] [Google Scholar]
- Dunn, O. J. 1961, J. Am. Stat. Association, 56, 52 [CrossRef] [Google Scholar]
- Faber, T. E. 1995, Fluid Dynamics for Physicists (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Greiner, J., 1996, Lect. Not. Phys. 472, Supersoft X-Ray Sources, (Berlin Springer Verlag) [Google Scholar]
- Greiner, J., Hasinger, G., & Kahabka, P. 1991, A&A, 246, L17 [NASA ADS] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2014, A&A, 563, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Hounsell, R., Bode, M. F., Hick, P. P., et al. 2010, ApJ, 724, 480 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Imamura, K., & Tanabe, K. 2012, PASJ, 64, 120 [NASA ADS] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahabka, P., Pietsch, W., & Hasinger, G. 1994, A&A, 288, 538 [Google Scholar]
- Kahabka, P., & van den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 334, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Kovacs, G. 1981, Ap&SS, 78, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., Telis, G. A., Audard, M., et al. 2005, ApJ, 619, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Larsson, S. 1996, A&AS, 117, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livio, M. 1992, ApJ, 393, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., Helfand, D. J., & Grabelsky, D. A. 1981, ApJ, 248, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, E., & Walter, F. M. 2014, 490, 199 [Google Scholar]
- Mauche, C. W. 2002, ApJ, 580, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Siviero, A., Sostero, G., et al. 2007, Baltic Astron., 16, 46 [NASA ADS] [Google Scholar]
- Munari, U., Henden, A., Dallaporta, S., & Cherini, G. 2013, Inform. Bull. Variable Stars, 6080, 1 [NASA ADS] [Google Scholar]
- Murray, S. S., Austin, G. K., Chappell, J. H., et al. 2000, SPIE, 4012, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, T., Orio, M., Cassinelli, J. P., et al. 2008, ApJ, 673, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J. U. 2012, BASI, 40, 353 [Google Scholar]
- Ness, J.-U. 2013, in online presentation given during meeting Spanish X-ray Astronomy, Barcelona, June 17–19 http://www.ice.csic.es/personal/rea/sxa/2013/Entries/2013/6/17_Final_program_files/ness.pdf [Google Scholar]
- Ness, J., Starrfield, S., Beardmore, A., et al. 2007, ApJ, 665, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J. U., Drake, J. J., Starrfield, S., et al. 2009, AJ, 137, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J., Schaefer, B. E., Dobrotka, A., et al. 2012, ApJ, 745, 43 [Google Scholar]
- Ness, J.-U., Osborne, J. P., Henze, M., et al. 2013a, A&A, 559, A50 [Google Scholar]
- Ness, J. U., Schwarz, G. J., Page, K. L., et al. 2013b, ATel, 5626, 1 [NASA ADS] [Google Scholar]
- Ness, J.-U., Kuulkers, E., Henze, M., et al. 2014, ATel, 6147, 1 [NASA ADS] [Google Scholar]
- Nousek, J. A., Garmire, G. P., Ricker, G. R., Collins, S. A., & Reigler, G. R. 1987, Astrophys. Lett. Comm., 26, 35 [NASA ADS] [Google Scholar]
- Nucita, A. A., Kuulkers, E., De Paolis, F., et al. 2014, A&A, 566, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Odendaal, A., Meintjes, P. J., Charles, P. A., & Rajoelimanana, A. F. 2014, MNRAS, 437, 2948 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Behar, E., Rauch, T., & Nelson, T. 2010, in poster presentation #2.03, during the meeting High-resolution X-ray spectroscopy: Past, Present, and Future, March 15–17, in Utrecht, The Netherlands, www.sron.nl/xray2010 [Google Scholar]
- Osborne, J., Page, K., Goad, A. B. M., et al. 2006, ATel, 770, 1 [NASA ADS] [Google Scholar]
- Osborne, J. P., Page, K. L., Beardmore, A. P., et al. 2011, ApJ, 727, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Branch, D., Chincarini, G., & Robinson, E. L. 1980, ApJ, 240, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2004, ApJ, 603, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, P. C., Cowley, A. P., Hutchings, J. B., Winter, K., & Crampton, D. 2004, AJ, 127, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. J., Ness, J., Osborne, J. P., et al. 2011, ApJS, 197, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Truemper, J. 1992, Roy. Astron. Soc. Quarterly J. 33, 165 [Google Scholar]
- Truran, J. W., & Livio, M. 1986, ApJ, 308, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Heuvel, E. P. J., Bhattacharya, D., Nomoto, K., & Rappaport, S. A. 1992, A&A, 262, 97 [NASA ADS] [Google Scholar]
- Warner, B. 2004, PASP, 116, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B., Woudt, P. A., & Pretorius, M. L. 2003a, MNRAS, 344, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B., Woudt, P. A., & Pretorius, M. L. 2003b, MNRAS, 344, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, W. M., Bildsten, L., Brooks, J., & Paxton, B. 2013, ApJ, 777, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Warner, B., O’Donoghue, D., et al. 2010, MNRAS, 401, 500 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A:
The period searches were performed using power spectra calculated with the method of Horne & Baliunas (1986), where the power is normalised to the total variance of the entire data set. Scargle (1982) emphasised that surprisingly large spurious peaks can occur in a power spectrum and investigated the probability that a signal with a given power z is a spurious signal (false-alarm probability). His Eq. (14) computes the probability for a given power peak to be due to a chance noise fluctuation, including the statistical penalty for inspecting a large number of frequencies, Nf. Based on this definition of the false-alarm probability, Pfap, we define the reverse, a detection likelihood ℒ = 1−Pfap, thus: 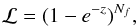 (A.1)from which the power z that yields a given detection likelihood ℒ can then be inferred from
(A.1)from which the power z that yields a given detection likelihood ℒ can then be inferred from 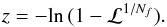 (A.2)For example, in a power spectrum consisting of Nf = 500 tested frequencies, the required normalised power that yields a 99.9% detection probability is z = 13.2. However, in the discussion that follows we determine the most appropriate choice for Nf, and hence the detection threshold, in an oversampled periodogram.
(A.2)For example, in a power spectrum consisting of Nf = 500 tested frequencies, the required normalised power that yields a 99.9% detection probability is z = 13.2. However, in the discussion that follows we determine the most appropriate choice for Nf, and hence the detection threshold, in an oversampled periodogram.
 |
Fig. A.1 Simulations based on N = 10 000 synthetic light curves of 1000 s duration with Poisson noise around various given mean count rates to estimate the likelihood of random detections at four levels of confidence. Power spectra of the random light curves were calculated over the period range 25−100 s, testing 500 frequencies. Left panel: Example of 20 counts per second as mean count rate. We show the maximum powers in the order of trial number in grey and sorted by power value with the thick black line. The sorted curve was used to extract the power thresholds given in the legend. Right panel: results for the four confidence levels as a function of mean count rate with connected black bullet points in comparison to the theoretical thresholds according to Eq. (A.2), with Nf = 500, included with the dotted blue lines. |
In each 1000 s time segment studied in this article, the period range 25−100 s is probed, corresponding to the frequency interval 0.01−0.04 Hz and thus a frequency range df = 0.03 Hz. The sampling above from which no further information can be gained is to test at the Fourier frequencies, thus with a frequency bin size of 1 /t, df × t = 30, within the 0.03 Hz frequency range. Meanwhile, with Nf = 500 frequencies, we oversample with a factor 16. By oversampling, we are more sensitive to periodicities that might fall midway between the Fourier frequencies.
As a test of the detection thresholds defined above, we performed simulations by generating synthetic light curves with random Poisson noise around a range of given mean count rates. For each given mean count rate, we generated a sample of 10 000 synthetic light curves of 1000 s duration, the same duration as was chosen for the time segments into which we split the observations. We then computed power spectra under the same conditions as for the data, thus probing a period range of 25−100 s with Nf = 500 tested frequencies. Next, we determined the maximum peak in each power spectrum and show the results in Fig. A.1. In the left panel, the results are shown for the case of a mean count rate of 20 counts per second. The light grey line indicates the evolution of random maximum peak powers with trial number, while the thick black line shows the same data sorted by peak powers. To estimate the probability of a random encounter at a given confidence level, the sorted curve can be interpolated. For example, for a detection at 99% we determined the power value that corresponds to the sorted curve at trial number 9000 of the black line, in this case, yielding z = 9.19. We extracted the thresholds for four confidence levels and included the results in the right legend of the left panel for synthetic light curves with a mean count rate of 20 counts per second. We performed the same simulations for mean count rates ranging from 0.1−350 counts per second and show the results in the right panel of Fig. A.1. The simulation results are shown with the black bullet points, and the predictions by Scargle (1982), reformulated with Eq. (A.2), are included for the same confidence levels as the blue dotted lines. No systematic trend with count rate can be identified, but all simulated results are well below the corresponding theoretically predicted thresholds.
 |
Fig. A.2 Top: comparison of 99% detection thresholds obtained with simulations as in Fig. A.1 using different oversampling factors 16 (Nf = 500), 3 (Nf = 90), and 1 (Nf = 30) with the number of tested frequencies Nf given in the legend. The dotted lines are the thresholds obtained from Eq. (A.2), and they agree best with the simulation results without oversampling, while for higher oversampling rates, the required power for a 99% detection is much lower. Bottom: shift in power as a function of detection probability, illustrating that it is not constant. When determining detection probabilities, we correct for oversampling by interpolating these simulations. |
To understand the discrepancy, we repeated the simulations with two additional oversampling factors, thus testing 90 frequencies (oversampling by 3) and 30 frequencies (no oversampling). In Fig. A.2 we show the results only for the 99% detection thresholds for these three oversampling factors with black, red, and blue as labelled in the upper right panel. In our case, using a period range 25−100 s (df = 0.03 Hz) and light curve duration 1000 s, the given values Nf need to be divided by 30 to derive the oversampling factor. The dotted lines are the thresholds calculated from Nf using Eq. (A.2), and the dotted and solid lines agree if no oversampling is applied. The discrepancies can therefore solely be attributed to the oversampling. In the bottom panel of Fig. A.2, the difference between powers with and without oversampling is shown for the same three oversampling factors as a function of detection probability, from which it can be seen that the discrepancy depends on the confidence level. Therefore, for this work, we converted observed power values by interpolating look-up tables computed from the simulations instead of using Eq. (A.2) to account for the oversampling effects.
An additional effect that needs to be taken into account is multiple testing when probing a series of time segments. We applied the conservative Bonferroni correction (Bonferroni 1936; Dunn 1959, 1961) to the detection thresholds by dividing the p value by the number of time segments. For example, if we find a single peak in a series of 50 power spectra and wish to know whether this is significant at 99% confidence, we divide the p-value of 0.01 by 50 for the test. A 99% detection is thus only achieved if the power value exceeds a value that corresponds to ℒ = (1 − 0.01 / 50) = 99.98%.
All Tables
All Figures
 |
Fig. 1 RS Oph on day 26.1: spectral (left) and period (right) time-maps on the same time scales in vertical direction. Left: spectral time-map showing the evolution of the RGS spectrum; taken from Ness et al. (2013a), adding unidentified emission features with their wavelengths in Å. The simultaneous EPIC/pn and MOS2 light curves are shown in the right panel, rotated clockwise by 90°. The pn has a longer initial overhead such that the exposure started ~1170 s later than the RGS and the MOS exposures, thus the black curve (pn) starts at 0.33 h, while the red curve (MOS) starts at 0 h. Right: dynamic power spectrum consisting of the power spectra computed from 24 overlapping 1000 s time segments from the pn light curve. To map them into the 11 ks time frame of the observation, the width of each row in the central panel is reduced to 500 s. The horizontal orange/blue dashed lines running across the main panel border two adjacent 500 s time intervals that correspond to the (wider) coloured bars in the right panel. They mark the overlapping 1000 s time intervals from which the individual power spectra were computed that are shown with the same colours in the top panel. The colour scheme for the main panel is decoded in the top right part; blue colours were chosen to mark periods with >90% confidence and red for 30−80%, while yellow/light green reflect noise. Colour-coding and thresholds have been corrected for oversampling and multiple testing (see text). The short horizontal black line in the main panel at 35 s represents the 90% uncertainty range in period of a significant (> 2σ) signal. In the top panel, in addition to the two power spectra from partial light-curves, the power spectrum from the full light-curve is shown in black; the same oversampling factor of 16.67 has been applied and contains no significant signal. The widths of the peaks in the respective power spectra are consistent with the intrinsic period resolution imposed by windowing. At the right, we show the evolution of the modulation amplitude, most of them are upper limits. |
| In the text | |
 |
Fig. 2 RS Oph on day 54. Left: time map of the 35 s period in the XMM-Newton RGS2 light curve, see description of right panel in Fig. 1. Right: time map of folded light curves, where each curve was artificially moved in phase for the peak to occur at phase 0.25. In the top panel, an example is shown with the sine curve fit from which the modulation amplitudes with uncertainties were determined. In the right panel, the evolution of amplitudes is shown. |
| In the text | |
 |
Fig. 3 RS Oph on day 54: relations between power (top row) and period (middle row) versus mean RGS2 count rate (left column) and modulation amplitude (right column). The amplitude is mean to peak in units of RGS2 counts per second. A typical uncertainty range in amplitude, derived while fitting sine curves to the phased light curves, is shown with the grey horizontal line in the left corner. The 95% (2σ) detection level (corrected for oversampling) is marked by the horizontal line in the top panels. In the middle panels, the error-weighted median period with standard deviation of the periods is marked with the horizontal solid and dotted lines, respectively. The 95% error bars on periods were calculated with Eq. (4) in Larsson (1996; see text). We show 30 out of 38 data points for which the signal power exceeds a 95% detection and a sine fit yields a positive amplitude. The distribution of periods is shown in the small inset where a Gaussian is added for comparison. Middle right panel: period versus amplitudes are shown, suggesting that larger variations in period occur with smaller amplitudes. Bottom left panel: amplitudes are shown versus count rate, demonstrating that there is no correlation. Ranges of amplitudes relative to count rate are marked by the dashed and dotted lines. Bottom right panel: periods versus power are shown, which also seem to show that larger variations in period occur at lower values of power. |
| In the text | |
 |
Fig. 4 RS Oph on day 67: time map around the 35 s period in the Chandra HRC light curve, see description in the right panel of Fig. 1. The strongest peak coincides with the 35 s period seen in earlier Swift and XMM-Newton observations (see Fig. 2). The power (conservatively corrected for multiple testing and oversampling, see Appendix) only yields a 1σ detection. |
| In the text | |
 |
Fig. 5 KT Eri on day 159: time map around the 35 s period in the Chandra HRC light curve, see description in the right panel of Fig. 1. The thin solid line in the top panel is the power spectrum from the entire observation and shows two >99.9% significant peaks. This indicates that the period is not constant in time. |
| In the text | |
 |
Fig. 6 V339 Del on day 99: Same as Fig. 2, focusing on the 54 s period in V339 Del based on the XMM-Newton MOS2 light curve. The simultaneous combined RGS1 and RGS2 light curve yields a consistent result. |
| In the text | |
 |
Fig. 7 Same as Fig. 3 for the Chandra and XMM-Newton/MOS2 observations of V339 Del. We show 94 out 266 data points in the middle and bottom rows that yield >2σ detections and positive amplitudes. As in RS Oph (Fig. 3), no relation between period properties and count rate is apparent, and the period seems to be variable. The modulation amplitude clearly correlates with the power of the period because modulations with a larger amplitude are easier to detect. The Chandra and XMM-Newton data yield different slopes for amplitudes in unit counts per second, while for count rates, a single slope is encountered. In the bottom left panel, we show that the data from both telescopes yield similar ranges of relative amplitudes. The bottom right panels appear similar to RS Oph (Fig. 3), with largest variations in period occurring with low values of power. |
| In the text | |
 |
Fig. 8 LMC 2009a on days 90, 165, 197, and 230: time maps around the 33 s period in four XMM-Newton/pn light curves, see description in the right panel of Fig. 1. The vertical (time) axes are different in each plot; they only cover the respective exposure times. |
| In the text | |
 |
Fig. 9 Cal 83 on 2009-05-30.4: time map around the 67 s period in one of 19 XMM-Newton/pn light curves, see description in the right panel of Fig. 1. The time evolution is consistent with that shown in a different format in Fig. 8 in Odendaal et al. (2014). |
| In the text | |
 |
Fig. 10 Same as Fig. 3, with data collected from 20 observations of Cal 83, divided into a total of 578 1000 s time segments. 17 of these intervals yield zero count rate and were excluded. Furthermore, all data points yielding only upper limits in amplitude were excluded, which left 202 data points, of which 34 time intervals yield a >95% detection of a periodic signal. The expected correlation between modulation amplitude and signal power (top right) is contaminated by a large number of overestimated amplitudes that are most likely caused by additional, non-periodic variability. These deviations are consistent with the large uncertainties in amplitude. The 95% threshold is corrected for oversampling, but not for multiple testing. 31 of 34 data points that are found above this threshold and yield a successful sine fit are used in the lower two rows. The variations in period of about ±3 s reported by Odendaal et al. (2014) can be recognised in the middle row and bottom right, but do not seem to correlate with count rate, amplitude, or signal power. |
| In the text | |
 |
Fig. 11 Fractions of observing time for which the strongest periods are detectable as a function of detection threshold. The solid lines are the average fractions of time derived from all available observations, while the dotted lines (with labels in italics) are the fractions of time derived from the single observation in which the period is seen most frequently. For this plot, power spectra from directly adjacent, non-overlapping time intervals have been used. For no system, the period was detected 100% of the time, showing the transient nature. Furthermore, the signal is episodic because the fractions are not the same in all observations. |
| In the text | |
 |
Fig. 12 In the presence of Thomson scattering, the observable amplitude of a signal will be lower than the original modulation amplitude, depending on optical depth, τ, and density, n. We show estimated densities below which periodic oscillations would lead to reductions of the amplitude (and thus detectability) by 64−99%, depending on three values of optical depth τ = 5−1 that would lead to 1−37% of photons escaping unscattered; see Sect. 5.1. |
| In the text | |
 |
Fig. A.1 Simulations based on N = 10 000 synthetic light curves of 1000 s duration with Poisson noise around various given mean count rates to estimate the likelihood of random detections at four levels of confidence. Power spectra of the random light curves were calculated over the period range 25−100 s, testing 500 frequencies. Left panel: Example of 20 counts per second as mean count rate. We show the maximum powers in the order of trial number in grey and sorted by power value with the thick black line. The sorted curve was used to extract the power thresholds given in the legend. Right panel: results for the four confidence levels as a function of mean count rate with connected black bullet points in comparison to the theoretical thresholds according to Eq. (A.2), with Nf = 500, included with the dotted blue lines. |
| In the text | |
 |
Fig. A.2 Top: comparison of 99% detection thresholds obtained with simulations as in Fig. A.1 using different oversampling factors 16 (Nf = 500), 3 (Nf = 90), and 1 (Nf = 30) with the number of tested frequencies Nf given in the legend. The dotted lines are the thresholds obtained from Eq. (A.2), and they agree best with the simulation results without oversampling, while for higher oversampling rates, the required power for a 99% detection is much lower. Bottom: shift in power as a function of detection probability, illustrating that it is not constant. When determining detection probabilities, we correct for oversampling by interpolating these simulations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


