| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424750 | |
| Published online | 03 March 2015 | |
The galaxy stellar mass function at 3.5 ≤z ≤ 7.5 in the CANDELS/UDS, GOODS-South, and HUDF fields⋆
1 INAF–Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio, Italy
e-mail: andrea.grazian@oa-roma.inaf.it
2 SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh EH9 3HJ, UK
3 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
4 Harvard-Smithsonian Center for Astrophysics 60 Garden Street, Cambridge, MA 02138, USA
5 UCO/Lick Observatory, University of California, 1156 High Street, Santa Cruz, CA 95064, USA
6 Kapteyn Astronomical Institute, University of Groningen, 9700 AV Groningen, The Netherlands
7 California Institute of Technology, Pasadena, CA 91125, USA
8 Center for Astrophysics and Planetary Science, Racah Institute of Physics, The Hebrew University, 91904 Jerusalem, Israel
9 NOAO, 950 N. Cherry Avenue, Tucson, AZ 85719, USA
10 Department of Astronomy, The University of Texas at Austin, Austin, TX 78712, USA
11 Max Planck Institute for extraterrestrial Physics, Giessenbachstrasse 1, 85748 Garching bei Munchen, Germany
12 Department of Astronomy, University of Massachusetts, 710 North Pleasant Street, Amherst, MA 01003, USA
13 Department of Physics and Astronomy, University of Kentucky, Lexington, KY 40506, USA
14 Physics Department Purdue University, 525 Northwestern Avenue West Lafayette, IN 47907, USA
15 Kavli Institute for Particle Astrophysics & Cosmology, Physics Department, and SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94305, USA
16 Department of Physics and Astronomy, UC Riverside, 900 University Ave, Riverside, CA 92521, USA
17 INAF–Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
18 George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, and Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
19 INAF–Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
20 University of Bologna, Department of Physics and Astronomy (DIFA), V.le Berti Pichat 6/2, 40127 Bologna, Italy
21 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
Received: 4 August 2014
Accepted: 25 November 2014
Context. The form and evolution of the galaxy stellar mass function (GSMF) at high redshifts provide crucial information on star formation history and mass assembly in the young Universe, close or even prior to the epoch of reionization.
Aims. We used the unique combination of deep optical/near-infrared/mid-infrared imaging provided by HST, Spitzer, and the VLT in the CANDELS-UDS, GOODS-South, and HUDF fields to determine the GSMF over the redshift range 3.5 ≤ z ≤ 7.5.
Methods. We used the HST WFC3/IR near-infrared imaging from CANDELS and HUDF09, reaching H ≃ 27 − 28.5 over a total area of 369 arcmin2, in combination with associated deep HST ACS optical data, deep Spitzer IRAC imaging from the SEDS programme, and deep Y and K-band VLT Hawk-I images from the HUGS programme, to select a galaxy sample with high-quality photometric redshifts. These have been calibrated with more than 150 spectroscopic redshifts in the range 3.5 ≤ z ≤ 7.5, resulting in an overall precision of σz/ (1 + z) ~ 0.037. With this database we have determined the low-mass end of the high-redshift GSMF with unprecedented precision, reaching down to masses as low as M∗ ~ 109 M⊙ at z = 4 and ~6 × 109 M⊙ at z = 7.
Results. We find that the GSMF at 3.5 ≤ z ≤ 7.5 depends only slightly on the recipes adopted to measure the stellar masses, namely the photometric redshifts, the star formation histories, the nebular contribution, or the presence of AGN in the parent sample. The low-mass end of the GSMF is steeper than has been found at lower redshifts, but appears to be unchanged over the redshift range probed here. Meanwhile the high-mass end of the GSMF appears to evolve primarily in density, although there is also some evidence of evolution in characteristic mass. Our results are very different from previous mass function estimates based on converting UV galaxy luminosity functions into mass functions via tight mass-to-light relations. Integrating our evolving GSMF over mass, we find that the growth of stellar mass density is barely consistent with the time-integral of the star formation rate density over cosmic time at z> 4.
Conclusions. These results confirm the unique synergy of the CANDELS+HUDF, HUGS, and SEDS surveys for the discovery and study of moderate/low-mass galaxies at high redshifts, and reaffirm the importance of space-based infrared selection for the unbiased measurement of the evolving GSMF in the young Universe.
Key words: galaxies: luminosity function, mass function / galaxies: distances and redshifts / galaxies: evolution / galaxies: high-redshift
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Deep multi-wavelength surveys have rapidly expanded our knowledge of the young Universe, with the most recent deep near-infrared imaging pushing back the redshift frontier of photometrically selected galaxies out to z ≃ 7 − 12 (Dunlop 2013; Coe et al. 2013; Ellis et al. 2013; Oesch et al. 2013b). Moreover, the physical properties of high-redshift galaxies, such as their star formation rates (SFR) and stellar masses, can now be determined with meaningful accuracy up to z ≃ 7 − 8 (Labbé et al. 2010, 2013), thanks to the combined power of deep space-based (HST, Spitzer) and ground-based (VLT) near-mid infrared imaging (Retzlaff et al. 2010; Fontana et al. 2014; Ashby et al. 2013).
The evolution of star formation activity in galaxies over cosmic history, and the physical processes which may drive and limit such activity, have been the subject of intensive observational and theoretical study in recent years (for a review see Madau & Dickinson 2014). The ultimate goal of the latest generation of galaxy-formation models is to represent, with fully developed cosmological simulations in the Lambda-cold dark matter (Λ-CDM) framework, the baryonic assembly of structures at different mass scales in the Universe as a function of cosmic time. While dark matter evolution is rather simple and clear, the physics regulating the baryonic processes is complex to model, and non-trivial to understand: star formation mechanisms, gaseous dissipation, feedback from stars and active galactic nuclei (AGN), turbulence, and the role of mergers, are only some of the many problems encountered when trying to build a fully realistic simulation of galaxy formation and evolution (Springel 2010).
Stellar mass is a physical parameter that provides a useful and complementary view of galaxy evolution from the measurement of SFR. From an observational perspective, given infrared data of sufficient quality and depth, stellar mass is a more straightforward and robust quantity to measure, being less subject to degenerate uncertainties in age, metallicity, and dust extinction. From the theoretical point of view, since stellar mass is a time-integrated quantity, it is less sensitive to the details of the star formation history (i.e. bursts of star formation, SF quenching). The detailed measurement of the growth of the stellar mass content in galaxies thus offers an important observational probe of the underlying physical processes driving and limiting star formation activity throughout cosmic time. Two statistical descriptions are often used to quantify the growth/distribution of stellar mass as a function of redshift: the galaxy stellar mass function (GSMF) and its integral over mass, namely the stellar mass density (SMD).
Recently, ground-based optical and near-infrared surveys (e.g. SDSS, UKIDSS, UltraVISTA), have been successfully used to explore the physical properties of galaxies at low redshift and to extend such studies out to high-redshift for the high-mass/high-luminosity tail of the galaxy distribution. For example, in the local Universe, Baldry et al. (2012) and Moustakas et al. (2013) have studied the GSMF down to M ~ 108 M⊙, while Ilbert et al. (2013) and Muzzin et al. (2013) have extended the GSMF studies to z ≃ 4, although inevitably limited to progressively higher stellar masses (M> 1010 M⊙).
While the recent ground-based progress is impressive, it remains the case that the analysis of the low-mass tail of the GSMF, especially at high redshifts, requires very deep infrared imaging, which is only really possible with space-based instrumentation (i.e. HST and Spitzer). Accordingly, several studies have used deep HST and Spitzer data to begin to investigate the GSMF at z ≥ 4 (Stark et al. 2009; Labbé et al. 2010; González et al. 2011; Caputi et al. 2011; Lee et al. 2012; Duncan et al. 2014) or down to very small masses but at z ≤ 4 (Tomczak et al. 2014).
Despite this important progress, the robust study of the GSMF at early cosmological epochs has been seriously hampered by a lack of appropriately deep near–mid-infrared imaging over sufficiently large areas of sky. Consequently, there remain many important outstanding questions to be resolved concerning the assembly history of Universe, as quantified through the form and evolution of the the GSMF. Examples of current key issues, where there remains considerable controversy and confusion, are given below:
-
Is the high-mass end of the GSMF evolvingat 0 <z< 3? Both Pérez-González et al. (2008) and Ilbert et al. (2013) found that the GSMF at M> 1011.7 M⊙ did not evolve strongly from z ≃ 2 to z ≃ 0.3, while Marchesini et al. (2009) showed that the SMD of these galaxies evolved by a factor of ~50 in the last 10 Gyr.
-
Does the low-mass end of the GSMF steepen at high-redshift? Recent attempts to extend the study of the GSMF to high redshifts and low masses have produced contrasting results. For example, Santini et al. (2012a) found a steepening towards high-redshift, while Ilbert et al. (2013) found no evidence that the low-mass end of the GSMF was evolving in shape. Uncertainty over the faint-end slope of the GSMF is crucial to the next open problem, the measurement of the growth of SMD.
-
Is the integral of the SFRD consistent with the observed SMD? The time integral of the SFRD, corrected for gas recycling fraction (i.e. gas lost by aging stars), has been claimed to exceed the measured SMD (Wilkins et al. 2008; Reddy & Steidel 2009; Santini et al. 2012a). As shown by Reddy & Steidel (2009), this apparent conflict could possibly be resolved by properly matching the integration limits in the UV galaxy luminosity function and in the GSMF. Subsequently, Santini et al. (2012a) proposed that a steepening of the GSMF with increasing redshift might remove any discrepancy at 2 <z< 4, but at z< 2 found that the steepening was insufficient to bridge the apparent gap. More recently still, Behroozi et al. (2013) pointed out that the previous estimates of SFR density over cosmic time by Hopkins & Beacom (2006) may have been overestimated, due to potentially excessive corrections for dust extinction when inferring SFR, but as discussed by Madau & Dickinson (2014), some tension still remains at z< 2.
-
Do colour and photo-z galaxy selection methods provide a consistent sampling of the GSMF? Reddy & Steidel (2009) suggested that up to ≃50% of the total stellar mass in the redshift range 1.9 <z< 3.4 is in faint galaxies with stellar masses smaller than ~1010 M⊙, as compared to ≃10–20% as obtained from an extrapolation of the Schechter fit to the observed MF obtained by Marchesini et al. (2009). It is worth noticing that Reddy & Steidel (2009) converted UV luminosity directly into stellar mass. At higher redshifts, González et al. (2011) converted the observed UV luminosity function of Lyman-break galaxies (LBGs) at z> 3 into a GSMF using similar assumptions on the mass-to-light ratio. Using a somewhat different approach, Lee et al. (2012) derived the mass function of UV-selected LBGs at z ~ 4 − 5, finding a flatter (α ~ − 1.3) slope with respect to the UV luminosity function of star-forming galaxies at the same redshifts. Their results do not fully agree with the GSMFs derived from near- or mid-infrared selected samples (Pérez-González et al. 2008; Marchesini et al. 2009, 2010; Caputi et al. 2011; Santini et al. 2012a). Recently, Duncan et al. (2014) addressed the issue of photo-z selection vs. Lyman-break selection, showing that the two methods are almost equivalent, once the photometric scatter is properly treated.
-
Which are the most appropriate stellar libraries to use when computing the stellar mass in galaxies, especially at high-redshift? Maraston (2005) and Bruzual (2007; M05, BC07 hereafter) showed that the thermally pulsing asymptotic giant branch (TP-AGB) phase could have a strong impact on the stellar mass derivation from infrared light, especially in the redshift range 0.5 <z< 2.0. This problem has also been investigated by Henriques et al. (2011) and recently this topic has been the subject of a number of papers (Tonini et al. 2010; Courteau et al. 2014; Mobasher et al. 2015), indicating that this is an important issue in the GSMF field.
-
What is the impact of AGNs on the high-mass end of the GSMF? Fontana et al. (2006) excluded all AGNs from their sample, while Marchesini et al. (2009) included AGNs in their sample, obtaining slightly different results, especially at the massive tail of the GSMF. Santini et al. (2012a) included only type 2 AGNs in the ERS field. As shown by Santini et al. (2012b), both for type-1 and type-2 AGN at z ≤ 2.5, the stellar mass derived by adopting only stellar libraries showed no systematic offset from the one coming from a two-component fit (stars+AGN), but presented a large spread (RMS of 0.34 dex for type 1 AGN). This has been explained by the fact that the AGN (especially type 1) is providing additional non-stellar light but it is also making the SED bluer than the pure stellar one. In this case the additional light by the AGN is compensated by the lower M/L ratio.
-
What are the contributions of the nebular lines and continuum to the SED of high-redshift galaxies and hence on the derived stellar masses? Recently, several studies have endeavored to include the contribution of nebular lines and continuum in the fitting of high-redshift galaxy SEDs. In particular, Schaerer & de Barros (2009) showed that the model fit to the SEDs of z> 3 galaxies can be significantly improved by the inclusion of the nebular lines and continuum, and inclusion of this contribution also helps to yield more reasonable ages for galaxies at very high redshifts. More recently, the importance of including the nebular contribution has been inferred more directly from observations via analysis of the Spitzer-IRAC photometry of high-redshift galaxies. Shim et al. (2011) reported a strong Hα line contribution to the Spitzer IRAC 3.6 μm and 4.5 μm bands for a small sample of galaxies with spectroscopic redshifts at z ≃ 4. Further studies (e.g. Stark et al. 2013; Labbé et al. 2013; Oesch et al. 2013a; Schenker et al. 2013) have shown that the nebular contribution can also be important at z > 3−4, when the [OIII] and Hβ lines enter the IRAC 3.6 μm filter. Thus, the inclusion of the nebular contribution (both lines and continuum) is becoming progressively more common in the SED fitting of the photometry of high-redshift galaxies (e.g. Salmon et al. 2014), although how best to estimate the appropriate level of nebular contribution remains a matter of debate.
-
Are theoretical models able to reproduce the observed GSMF? A common feature of predictions from Λ-CDM models has been an over-production of low-mass galaxies, especially at high redshifts (Wang et al. 2008; Bielby et al. 2012; Bower et al. 2012; Guo et al. 2011). Recently, Lu et al. (2013) claimed a better agreement of the recent renditions of SAMs with the observed GSMF at all redshifts (z = 0 − 6). However, as pointed out by Ilbert et al. (2013), the theoretical predictions are still far from reproducing the GSMF of the old/evolved population and the disagreement is larger for the higher redshifts. Using simulations, Wilkins et al. (2013) recently predicted the properties of high-redshift galaxies, but were unable to fully reproduce the observed GSMF of González et al. (2011), both for the low-mass galaxies at z ≃ 5 and for the higher-mass galaxies at z ≃ 7.
The CANDELS project (Koekemoer et al. 2011; Grogin et al. 2011), with its particular combination of survey volume, depth and wavelength coverage (0.5–1 μm rest-frame), provides an ideal data set with which to attempt to resolve some of these issues. In this paper we use the CANDELS data to investigate a number of the outstanding issues mentioned above, exploring carefully how stellar mass derivation depends on the recipes used to derive photometric redshifts, the assumed galaxy star formation histories, the nebular contribution, the AGN content of galaxy samples, and field-to-field variations in the galaxy samples. We then derive and present a new robust analysis of the form and evolution of the GSMF at high-redshift (z ≥ 3.5).
This paper is organized as follows: after introducing the photometric and spectroscopic data set in Sect. 2, we present the stellar mass estimates in Sect. 3.1. The derivation of the stellar mass function is discussed in detail in Sects. 3.2, and 4 is devoted to determining the uncertainties on the GSMF estimate. We present our results in Sect. 5, and include an analysis of the shape of the GSMF, a comparison with recent results in the literature, a discussion of the mass-to-light ratio of galaxies at z ≃ 4 and an investigation of the inferred physical properties of massive galaxies at high redshift. Section 6 describes the redshift evolution of the GSMF, while the stellar mass density and its comparison with the integrated SFRD is discussed in Sect. 7. Finally, we summarize our results in Sect. 8. In Appendix A we compare different recipes for the calculation of the GSMF, in Appendix B we describe the correction of the Eddington bias, and in Appendix C for completeness we provide the results obtained by neglecting the Eddington bias correction. Throughout we adopt the Λ-CDM concordance cosmological model (H0 = 70 km s-1 Mpc-1, ΩM = 0.3 and ΩΛ = 0.7). All magnitudes are in the AB system, and a Salpeter (1955) stellar initial mass function (IMF) is assumed in the derivation of all galaxy masses.
Area and magnitude limits of the CANDELS GOODS-South, HUDF, and UDS fields.
2. Data
2.1. The photometric data set
The CANDELS survey (Grogin et al. 2011; Koekemoer et al. 2011) is an ideal data set with which to study the stellar masses of high-redshift galaxies, thanks to its combination of deep photometry and reasonably wide areal coverage, with superb image quality obtained with the near-infrared camera on HST, the Wide Field Camera 3 (WFC31). We have used the first two CANDELS fields, namely the CANDELS-Wide imaging within the UKIDSS Ultra Deep Survey (UDS) (covering ≃200 arcmin2 to a 5σ depth of H160 = 26.7) and the maximum depth/area CANDELS imaging of the GOODS-South field (covering ≃170 arcmin2 to a mean 5σ depth of H160 = 27.5), combining data from the ERS, CANDELS-Wide, CANDELS-Deep, and the main pointing of the HUDF09 programme (≃5 arcmin2 down to 5σH160 = 28.5). This data set does not include the two parallel fields of the HUDF09 programme, nor the HUDF12 data (Koekemoer et al. 2013). The CANDELS-UDS and GOODS-South+HUDF09 fields with their associated multi-wavelength catalogues are fully described in Galametz et al. (2013) and Guo et al. (2013), respectively.
These imaging data, of unprecedented quality and depth, provide a powerful data set for stellar mass function investigations, especially at low masses and at high redshifts. In particular, they include very deep imaging with the IRAC instrument aboard the Spitzer Space Telescope from the Spitzer Extended Deep Survey (SEDS; Ashby et al. 2013), covering the CANDELS fields to a 3σ depth of 26 AB mag at both 3.6 and 4.5 μm, that are crucial for sampling the rest-frame optical bands at z> 4.
Another crucial data set that is unique to these two fields is the deep Hawk-I imaging obtained through the HUGS (Hawk-I UDS and GOODS Survey) VLT programme (Fontana et al. 2014). This has delivered deep ground-based Y and K-band images of a depth well matched to the H-band magnitude limits of the CANDELS survey, with exposure times ranging from ≃12 h over the shallower CANDELS images to about 85 h of integration in the deepest region of the HUGS/GOODS-South field (which includes most of the Hubble Ultra Deep Field). In the deepest area of GOODS-South, the HUGS data reach a 1σ magnitude limit per square arcsec of ≃28.0 mag in the K band. The Y and K-band imaging of the UDS field reaches a 1σ magnitude limit per square arcsec of ≃28.3 and 27.3, respectively. The image quality of the HUGS images is extremely good, with a seeing of 0.37–0.43 arcsec in the K band, and only slightly poorer in the Y band (0.45–0.50 arcsec). This makes the HUGS survey the deepest K-band image over a significant area (>340 arcmin2), the only deeper K-band imaging being the Super Subaru Deep Field (Minowa et al. 2005), which covers only a very small area (≃1 arcmin2) with the aid of adaptive optics. In Fontana et al. (2014) we show that in the HUGS K-band data we can detect, at 1σ, more than 90% of the H160-band detected galaxies in CANDELS.
The final HUGS data have already been included in the official CANDELS catalogue produced by Galametz et al. (2013), but in the GOODS-South catalogue produced by Guo et al. (2013), only a fraction of the deep K-band imaging from HUGS was included. In this work we use instead the final version of the HUGS K-band image in the GOODS-South field, analysed with the same TFIT code for deep blended photometry. This resulting catalogue is fully described in Fontana et al. (2014).
In addition, we further enhanced the official CANDELS GOODS-South catalogue presented by Guo et al. (2013) by adding the deep VIMOS B-band imaging in the field (Sommariva et al. 2014; Nonino et al., in prep.). This imaging has an effective wavelength of 4310 Å, slightly bluer than the B435W ACS filter on-board HST (4350 Å). The mean seeing of the ground-based image is 0.8 arcsec, but the combination of exposure time (28 h) and collecting area of the 8.2 m VLT telescope yields a magnitude limit of 30.5 mag, (1σ) which is much deeper than that reached by the HST-ACS B435 imaging (Giavalisco et al. 2004), which is 29.2 mag (1σ). The B-band VIMOS photometry has been computed with the TFIT software with the same technique adopted for the other ground-based bands, as described by Guo et al. (2013).
Both the deep B and K-band ground-based images in GOODS-South have been included with the aim of better constraining the galaxy SEDs and the stellar masses, but they have not been used for refining the photometric redshift solutions. For the latter, we adopt the results presented by Dahlen el al. (2013), as described further below.
2.2. Photometric catalogue
We have used the official CANDELS catalogues in the GOODS-South and UDS fields, where object selection has been performed in the H160 band of WFC3. The total number of sources detected in the CANDELS UDS and GOODS-South fields are 35 932 and 34 930, respectively.
Because of the complexity of the GOODS-South and UDS exposure maps in the H160 band, the magnitude limit varies over the field, such that it is impossible to assign a single completeness limit to the whole survey. To overcome this limitation we divided the survey in five areas with relatively homogeneous magnitude limits. To achieve this, we converted the absolute rms maps associated with the H160 science frames into magnitude limit maps at 1σ and in a given area of the sky (1 arcsec2). This value is used as a conventional reference limit to define the various regions of different depths for each galaxy in the two fields. For the UDS, details can be found in Fig. 3 of Galametz et al. (2013), while for GOODS-South the reference plot is Fig. 1 of Guo et al. (2013).
To associate a proper completeness magnitude with each area of the survey (defined by a range of magnitude limits at 1σ in an area of 1 arcsec2), we ran simulations adding artificial sources (point-like) to the H160 band images and recovered them using the same SExtractor configuration adopted in Galametz et al. (2013) and Guo et al. (2013). Then, we computed the completeness in magnitude and derived, at a given flux limit (at 1σ in an area of 1 arcsec2), the magnitude at which the completeness is above 90%. This allows us to simply associate with each galaxy, given its magnitude limit computed locally, a proper completeness limit.
We consider here primarily the detection completeness, although there are also systematic effects on the magnitude estimate, especially for fainter objects. If we restrict the analysis to sources which are 0.5 mag brighter than the completeness limit, we find that 90% of them are within 0.2 mag of the input flux value in our simulations. This fraction then goes to ≃75% approaching the completeness limit. We have verified that this limit is comparable with the independent results of Duncan et al. (2014) for the GOODS-South field. In the following, we will restrict our analysis to brighter than this value, hereafter called photometric limit, to distinguish it from the mass completeness limit that will be discussed later. In any case the cut that will be applied to ensure a robust completeness in mass, as we discuss later, is brighter than the photometric completeness limit due to the detection of objects, described here. Table 1 provides the depth and the area covered by different sub-regions. It also summarizes the number of galaxies available in each region and the total number, which is ≃55 000.
A more general treatment of the completeness would require repetition of the sample selection, simulating all the photometric bands, and redoing the analysis with TFIT on the low-resolution images, verifying the effects on the photometric redshifts and mass estimation. This is however beyond the scope of this paper, and we refer to Lee et al. (2012) for a demonstration of the robustness of our photometric approach.
2.3. Spectroscopic and photometric redshifts
The two catalogues (GOODS-South and UDS) were cross-correlated to existing spectroscopic samples, as described in Galametz et al. (2013) and Guo et al. (2013). Additional spectroscopic redshifts were added to the present sample by a collection of high-redshift LBGs from Fontana et al. (2010), Vanzella et al. (2011), Pentericci et al. (2011) and preliminary results of the ESO Large Programme (PI L. Pentericci) with 140 expected hours of FORS2 spectroscopy on 3 CANDELS fields (UDS, COSMOS, GOODS-South). Currently, we have 31z> 5.5 spectroscopic redshifts in the GOODS-South field, a number which is 3 times larger than the public spectroscopic redshifts currently available on this field (9 galaxies only). In total, there are 2272 spectroscopic redshifts of good quality in the GOODS-South field, and 308 in the CANDELS-UDS in the 0 <z< 7 interval. Restricting the sample to 3.5 <z< 7.5, there are in total 152 galaxies with robust spectroscopic redshifts. As shown later in Sect. 3, these objects sample the redshift-mass plane with reasonable completeness up to z ≃ 6, and become rare at z> 6.
For sources lacking spectroscopic information, photometric redshifts were computed by optimally combining six different photometric redshifts, as described in Dahlen el al. (2013). All these photometric redshifts were computed by fitting the observed spectral energy distribution (SED) of the objects from the U band to the 8.0 μm band of Spitzer using different codes and synthetic libraries. Using a training sample of 1193 spectroscopic redshifts, the optimal photometric redshift solution has been derived by taking into account small zero-point offsets and adding extra smoothing errors to the individual probability distribution function (PDF) in redshift. Then a unique PDF as a function of redshift was derived by optimally combining the 6 individual PDFs using a hierarchical Bayesian approach as explained in Dahlen el al. (2013). This method significantly improves the final accuracy compared to the individual recipes. The absolute scatter of | Δz | /(1 + zspec) is equal to 0.03, with only 3.4% of catastrophic outliers (defined as objects with | Δz | /(1 + zspec) > 0.15), when the comparison is made with the spectroscopic training set, at relatively bright magnitudes (H160 ≤ 24). Comparing the spectroscopic redshifts at 3.5 <z< 7.5 with the Bayesian photometric redshifts we find a scatter of σz/ (1 + z) = 0.037 and an outlier fraction of 11 out of 152 objects (7.2%). The tests with the galaxy pairs show that the uncertainty increases to about 0.06 at H160 ≃ 26 (Dahlen el al. 2013). This method also delivers the redshift probability distribution PDF(z) for each galaxy, that is then used to estimate the relevant uncertainties in the stellar mass functions, as explained in the following sections.
In total, there are 2034 galaxies in the GOODS-South field and 1273 galaxies in UDS with a robust spectroscopic redshift or, alternatively, with a photometric redshift in the range 3.5 <z< 7.5. This defines the sample which will be analysed in this paper with the aim of deriving the GSMF over this redshift range. We note that this sample represents a small sub-sample of the total CANDELS GOODS-South and UDS galaxy catalogues (7% and 5% respectively).
3. The derivation of the GSMF in the CANDELS fields
3.1. Stellar masses
We have derived the stellar masses using a spectral-fitting technique similar to that used in previous studies (Fontana et al. 2004, 2006; Grazian et al. 2006; Maiolino et al. 2008; and Santini et al. 2012a), and similar to those adopted by other groups in the literature (e.g. Dickinson et al. 2003; Drory et al. 2004; Ilbert et al. 2013; Muzzin et al. 2013; Tomczak et al. 2014).
More precisely, to derive the stellar mass of each galaxy, we have fitted the observed SED after fixing the redshift to the high-quality spectroscopic value, or to the photometric one when the former is not available or is not robust. The SED fitting method is based on the χ2 minimization of the differences between the observed multi-colour distribution of each object and a set of templates, computed with standard spectral synthesis models (Bruzual & Charlot 2003, in our case, hereafter BC03). The adopted synthetic library broadly encompasses the variety of star formation histories, metallicities and extinctions displayed by real galaxies. To facilitate the comparison with previous studies, we have used the Salpeter IMF, ranging over a set of metallicities (from Z = 0.02 Z⊙ to Z = 2.5 Z⊙) and dust extinction (0 <E(B − V) < 1.1), with a Calzetti et al. (2000) or a Small Magellanic Cloud (Hutchings 1982) extinction curve left as a free parameter. Different star formation histories (SFH) have been adopted, as described below. In all cases the age is defined as the time elapsed since the onset of star formation, and at each redshift this is varied within a fine grid, the only constraint being that it must be lower than the age of the Universe at that redshift. As in previous analyses, the derived stellar masses are corrected for the gas recycling fraction, (i.e. the fraction of baryons that are returned to the ISM because of stellar winds and SN explosions) taking into account the recipes of BC03. We thus do not use the total integral of gas turned into stars, but only the mass which is actually in the form of stars. For each model in the adopted library, we have computed the synthetic magnitudes in our filter set, and found the best-fitting template with a standard χ2 minimization, leaving the normalization of the model magnitudes as a free parameter.
Within this general framework, we introduce two improvements in the SED-fitting procedure, compared to our previous papers:
-
1)
We adopt three different parametrizations forthe star formation history (SFH):
-
Exponentially declining laws(SFH ∝ exp( − t/τ)) with timescale τ = 0.1,0.3,0.6,1.0,2.0,3.0,5.0,9.0,15.0 Gyr (“τ-models”); we note that, at the redshifts of interest here, the models with large τ (9,15 Gyr) are in practice equivalent to models with constant star formation rate, since the age of the Universe is much smaller than the τ-folding timescale.
-
“Inverted-τ” law (SFH ∝ exp(+t/τ)) with the same range of timescales as above.
-
“Delayed” star formation history (SFH ∝ t2/τ × exp( − t/τ)) with τ going from 0.1 to 2.0 Gyr with a step of 0.1 Gyr. This SFH law rises up to t = 2τ and declines thereafter.
-
-
2)
We include the contribution from nebular emission com-puted following Schaerer & de Barros (2009). Briefly, in this model nebular emission is linked to the amountof hydrogen-ionizing photons in the stellar SED (Schaerer& Vacca 1998) assuming an escape frac-tion fesc = 0.0 (Case B recombination). The ionizing radiation is converted into nebular continuum emission considering free-free, free-bound, and hydrogen two-photon continuum emission, assuming an electron temperature Te = 10 000 K, an electron density Ne = 100 cm-3, and a 10% helium numerical abundance relative to hydrogen. Hydrogen lines from the Lyman to the Brackett series are included considering Case-B recombination, while the relative line intensities of He and metals are taken, as a function of metallicity, from Anders & Fritze (2003).
The SED-fitting has been performed separately for each of the analytical SFHs listed above, both including and excluding nebular emission: in the following we will refer to the masses obtained with exponentially declining models and no emission lines as the “reference” masses, for comparisons with previous studies.
Different spectral libraries could be adopted to derive stellar masses for high-redshift galaxies. For example the libraries provided by Maraston (2005) and Bruzual (2007) both attempt to take into account, in slightly different ways, the contributions of evolved stars (in particular during the TP-AGB phases), to the near-infrared emission from galaxies. The main contribution of TP-AGB stars occurs ~0.5–2 Gyr after an episode of star formation (Maraston 2005). Since the age of the Universe at z = 3.5 is 1.77 Gyr, we cannot neglect a priori the contribution of these peculiar stars. However, recent estimates (Santini et al. 2012a) of the differences between the masses derived through the BC03 and the M05 or BC07 libraries indicate that there are only small dissimilarities between the results from these stellar evolution codes at z< 4, with the largest differences found at z ~ 2. Considering also that these models are undergoing revisions from their authors, we decided to use only the BC03 library in this paper.
The derived galaxy masses for the whole GOODS-South+HUDF field are shown as a function of redshift in Fig. 1. We also indicate (purple big squares) galaxies with robust spectroscopic redshifts in the range 3.5 ≤ z ≤ 7.5. Their positions in the mass vs. redshift diagram show that they are representative of the overall distribution of galaxies in this redshift range. In the interval 6.5 ≤ z ≤ 7.5 very few spectroscopic redshifts are available, and our results rely mainly on the photometric redshifts.
3.2. The GSMF estimate
To compute the GSMF, we adopt two standard methods described in Fontana et al. (2004, 2006), and Santini et al. (2012a). The first is based on the non-parametric 1 /Vmax method by Schmidt (1968) and Avni & Bahcall (1980). For each redshift and stellar mass bin, the total volume Vmax is derived taking into account the magnitude limits in the different areas of the survey, adopting the same technique normally used to compute the luminosity functions.
 |
Fig. 1 Black dots: all the galaxies in the CANDELS GOODS-South field; red dots: galaxies in the deepest region (HUDF). The purple big squares indicate galaxies with robust spectroscopic redshift in the range 3.5 ≤ z ≤ 7.5. The strict completeness mass vs. redshift for a magnitude limit of H160 = 26.0 (dark green). This curve has been derived from the maximally old galaxies in our synthetic library, corresponding to a formation redshift zform = 20, an E(B − V) = 0.1, metallicity of 0.2 Z⊙ and a declining SFH with timescale τ = 0.1 Gyr. The light-green curve shows the completeness-corrected limit corresponding to the shallower pointings in the GOODS-South and UDS fields (H160 = 26.0), while the blue curve represents the corresponding limit for our deepest area, the HUDF field (H160 = 28.0), once the mass limit has been extended taking into account the suitable correction for the M∗/L distribution. For comparison, the magenta curve (dashed) is the completeness limit in mass in the ERS field derived by Santini et al. (2012a) which corresponds to K = 25.5. |
The second method is the STY (Sandage et al. 1979) maximum likelihood analysis assuming a Schechter (1976) parametric form. For each magnitude range considered, we compute the likelihood to find the observed galaxies given the survey characteristics, the various sources of incompleteness and the three parameters describing the Schechter function. We then maximize the global likelihood for the whole survey and find the best fit parameters for the mass function.
The major difference that needs to be introduced in computing a GSMF, compared to a standard luminosity function, is an adequate handling of the distribution of M∗/L ratio of the galaxies in the sample. At a given mass, some galaxies can be characterized, for example, by very high mass-to-light ratios (due to large ages or high dust extinction – e.g. Dunlop et al. 2007) and thus can be much fainter than a more typical blue star-forming and moderately obscured galaxy. To deal with this, we adopt the technique, described in Fontana et al. (2004), that allows us to compute the fraction of objects lost because of their large M∗/L, by measuring the actual distribution of M∗/L immediately above the completeness limit in flux, and assuming that this holds at slightly lower masses/fluxes.
The derived galaxy masses, and the relevant mass completeness limits as a function of redshift are plotted in Fig. 1. This plot shows the strict completeness limit for H = 26 (dark green line), but also shows that the minimum mass, at which the GSMF is computed, is in practice lower than this, because it takes into account the appropriate correction factor for incompleteness. This limit is shown as a light green curve in Fig. 1 for the shallowest areas in GOODS-South and UDS, and by a blue line for the deepest HUDF pointing. The black dots in Fig. 1 show all the galaxies in the CANDELS GOODS-South field while the red dots show those galaxies in the deepest region (HUDF). The minimum mass above which the GSMF is computed is well above the lowest mass galaxies detected in our survey, indicating that this approach of extending the completeness mass is nonetheless robust. The reader interested in the technical issues on the calculation of completeness of the GSMF is referred to Fontana et al. (2004) for all the details.
Based on an extrapolation of the mass-to-light distributions at slightly brighter luminosities, our survey, in the small but very deep HUDF field, can detect a galaxy with mass M = 109 M⊙ at z = 4, M = 2 × 109 M⊙ at z = 5, M = 3 × 109 M⊙ at z = 6 and M = 6 × 109 M⊙ at z = 7. Thus, with the CANDELS+HUDF survey, we can probe the GSMF at masses well below the knee of the GSMF at z = 5 − 6, with an acceptable precision, even at relatively low stellar masses. We cannot exclude however the presence of a rare population of very red dusty galaxies with large masses at high-z. They would be characterized by extreme M/L ratios, and consequently be too faint to be detected by the present CANDELS survey.
4. The uncertainties on the derivation of the GSMF
The uncertainties involved in the computation of the GSMF are numerous and, unfortunately, difficult to estimate. Many of them, of course, stem from the uncertainties involved in the evaluation of the stellar masses of individual galaxies, and are hence larger than those involved in the estimate of the luminosity function. To some extent, they depend on conceptual aspects that have not been fully quantified yet, such as the uncertainties on the actual star formation histories of galaxies, or the metallicity evolution. The impacts of other effects, instead, like the intrinsic degeneracies of input models, depends on the characteristics of the observations adopted and need to be estimated carefully for any data set. We explore in this section such uncertainties, focusing directly on the impact that they have on the estimate of the GSMF. An analysis of the uncertainties of the stellar masses estimated for individual galaxies in CANDELS is presented with more details in two related papers (Mobasher et al. 2015; Santini et al. 2014). These papers explore the systematic and random uncertainties on a galaxy-by-galaxy basis. We anticipate and use here some of their results, deferring to such papers for a more detailed discussion, to show the effect that such uncertainties have on the global GSMF.
We divide such uncertainties into two main categories: random errors, i.e. those arising from photometric uncertainties, from the errors on the redshift determination (quantified via the probability distribution functions of photometric redshifts), and systematic effects, such as the photometric redshift recipes (e.g. libraries, obscuration law, IMF), the adoption of various SFHs, the inclusion of nebular contributions in the SED fitting and from the field-to-field variation, also known as cosmic variance. Last, we consider also the effect of the AGN population on the high-redshift GSMF.
We anticipate here that the differences in the stellar mass estimates using the different systematic variants mentioned above are small (ΔM/M< 0.1 dex), comparable to or lower than the statistical uncertainties. We have also demonstrated that there are no strong trend of these systematic effects with either redshift or stellar mass M, the only notable exception being the contribution of nebular lines and continuum at z> 4. Masses computed assuming strong emission lines are smaller than the fiducial masses by 0.05–0.20 dex and depend on the redshift intervals where strong lines enter the near-infared or IRAC filters (see Fig. 8 of Salmon et al. 2014). All these results will be shown in detail in Santini et al. (2014) both for the UDS and GOODS-South fields.
4.1. Sources of random errors
We consider here the impact of different random effects (photometric uncertainties and model degeneracies) on the GSMF estimation.
4.1.1. The impact of photometric uncertainties and model degeneracies on the stellar mass computation
The derivation of the stellar mass for a galaxy is based on knowledge of its physical parameters (age, dust extinction, metallicity). Since a given SED (even with the small photometric errors that we have in CANDELS) can be fitted with some combination of these parameters, the stellar mass is inevitably uncertain due to unavoidable degeneracies between them. This effect still exists even when the spectroscopic redshift is known with high accuracy, and the uncertainties are obviously larger when a galaxy has only a photometric redshift.
 |
Fig. 2 Relative mass uncertainty, ΔM/M, as a function of stellar mass for different redshift bins from z = 4 to z = 7. Black points are for galaxies in the GOODS-South field, while blue ones are for objects in the CANDELS UDS region. The mass uncertainty is a strong function of the mass of the galaxies, and as expected it is significantly poorer at higher redshifts. |
To estimate the impact of these errors on the GSMF, we have carried out a Monte Carlo simulation, specific to our data set. For each galaxy with a secure spectroscopic redshift we simply adopt it, while for any galaxy without a secure spectroscopic redshift, we extracted a random redshift following the Bayesian probability distribution function PDF(z) computed as described in Dahlen el al. (2013). These probability distribution functions have been derived by combining the PDF(z) computed by six different groups within the CANDELS collaboration. Before the bayesian combination, all the individual PDFs have been slightly modified in order to recover the correct number of spectroscopic redshifts within the errors, as discussed in detail by Dahlen el al. (2013). We then scan all the models in the BC03 synthetic library at that redshift z and compute the probability distribution function of the stellar mass PDF(M | z). Following this distribution, we eventually extract a mass M(z) which is compliant with the observed SED of the specific object both in terms of allowable input parameters and its CANDELS Bayesian photometric redshift probability PDF(z). For each object, the same procedure has been repeated 1000 times, and used to estimate the 1σ uncertainty on its stellar mass by computing ΔM = (M84 − M16)/2, where M16 and M84 are the 16th and 84th percentiles of the mass distribution, respectively.
These values provide us with a clear indication of the level of accuracy on stellar masses of individual galaxies, and are plotted in Fig. 2 as a function of the stellar mass in different redshift bins from z = 4 to z = 7. At z = 4 and for masses of the order of 1010 M⊙ the typical errors are of the order of 0.4 dex, and increase, as expected, towards higher redshifts and/or smaller masses due to the increased photometric uncertainties and model degeneracies. We do not find significant differences between the ΔM/M computed for the GOODS-South or the UDS field. As we will show in Appendix B, the uncertainties in mass we have derived are not Gaussian and, especially at high redshifts and low masses, they are asymmetric, with a trend towards lower masses in general.
It is important to note that this level of accuracy represents a distinct improvement over previous surveys. We can make a direct comparison with our previous data, where we used a comparable approach to estimate the uncertainties. For comparison, a similar accuracy (0.4 dex) was reached at lower redshift (z< 3) and brighter magnitudes (K ≤ 23.5) in the original GOODS-MUSIC data set (Fontana et al. 2006), that used shallower ground-based near-infrared imaging in the J,H,K bands and the first maps by Spitzer on the GOODS-South field (Grazian et al. 2006). In Santini et al. (2012a), using data from the ERS survey by HST, we reached a ΔM/M ~ 0.2 − 0.3 but only at z ≤ 4.
This Monte Carlo simulation has been used to estimate the resulting uncertainty in the GSMF. Using the simulations described above we have obtained 1000 different realizations of the GSMF, and used them to evaluate the scatter in the number density of each bin in mass. This source of error will be labelled MCsim and it will be compared with other systematic errors in below.
 |
Fig. 3 Top left: comparison of the GSMF obtained with different photometric redshift recipes. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields derived using the Bayesian photometric redshifts is shown by the black triangles (non parametric 1/Vmax) and the solid continuous curve (parametric STY maximum likelihood). The error bars show the Poissonian uncertainties of each point. The red triangles, green stars, cyan triangles, magenta and pink asterisks show the GSMFs obtained using the individual photometric redshifts of different realizations that have been used to derive the Bayesian photo-z described in Dahlen el al. (2013). Top right: comparison of the GSMF obtained with different star formation histories. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields assuming BC03 exponentially declining SFHs is shown by the black triangles and the solid continuous curve. The red squares and the blue stars show the GSMFs derived using exponentially increasing and a delayed SFH, respectively. All these star formation histories have been tested without the nebular contribution. Bottom left: comparison of the GSMF with and without a nebular contribution. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields with BC03 exponentially declining SFHs and no nebular contribution is shown by the black triangles and the solid continuous curve. The blue asterisks show the GSMF derived using BC03 and exponentially declining SFHs but this time including allowance for the contribution of nebular lines and nebular continuum (NEB label). Bottom right: comparison of the GSMF in individual fields. The stellar mass function derived for galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS UDS field (empty blue squares) as compared with that derived from GOODS-South (filled black circles). |
4.2. Systematic errors
We consider here the impact of different systematic effects (photometric redshifts, star formation history, nebular contribution, cosmic variance, AGN contamination) on the GSMF estimation. For simplicity, we do not mention here the results for individual galaxies (we refer the reader to Mobasher et al. 2015; Santini et al. 2014, for full details) but only the effect on the GSMF. We therefore compute different GSMFs with the various assumptions, and present the scatter measured directly on their values.
4.2.1. Photometric redshifts
We re-emphasize that the photometric redshifts available for our catalogues have been produced with a Bayesian average of six different photometric-redshift solutions obtained with different codes and techniques. The availability of completely independent photometric redshift solutions gives us a unique opportunity to verify how different recipes for photo-z yield systematic differences in the final estimate of the GSMF. We note that this effect is different from what we have presented in the previous section, where we have included the effect of the uncertainty in the redshift as estimated internally to a given technique (in this case our Bayesian average). The analysis that we describe here is useful for estimating the extent to which the existing differences between published determinations of the GSMF can be ascribed to a scatter induced by the various photo-z techniques.
To achieve this, we have computed the GSMF with the individual recipes for photometric redshift used to assemble the average photo-z used here (Dahlen el al. 2013). To simplify the comparison, we have estimated stellar masses simply using BC03 models with no emission lines and standard exponentially declining histories as a baseline. The results are shown in Fig. 3 (top-left) for the redshift range 3.5 <z< 4.5; the GSMFs for the other redshift intervals are shown in the Appendix A.
Comparing the individual mass functions, it is possible to notice systematic differences, which at low redshift (3.5 <z< 4.5) and at intermediate stellar masses (M ~ 1010 M⊙) are comparable to or slightly larger than the Poissonian errors (represented by the error bars in the plot). The scatter between individual GSMFs is enhanced at the high-mass end, where the photo-z leakage of even a few galaxies into the highest redshift bins may cause a significant increase in the estimated number density. The Bayesian photo-z are less subject to this redshift leakage by construction. In addition, the large scatter between different photometric redshift realizations in the exponential tail can be due also to the low number statistics, since at the massive end only a few galaxies contribute to the GSMF. Galaxies with high stellar masses, indeed, could be highly obscured by dust or characterized by an old stellar population, and in this case the UV optical magnitudes are expected to be faint, with a consequent relatively low accuracy of the photometric redshift solutions.
The low-mass-end slope of the GSMF, instead, is less sensitive to the photo-z recipes adopted, and all the different photometric redshift methods confirm that the GSMF is apparently steepening from z = 4 to z = 7, as shown in Fig. A.1.
4.2.2. Star formation histories
We have investigated also the effect of different parametrizations of the Star Formation History (SFH) on the mass function analysis. As described in Sect. 3.1, we have considered separately the classical exponential declining model, the exponentially increasing SFH (Maraston et al. 2010; Pforr et al. 2012) and the “delayed” SFH that increases at early ages and then shows a declining phase at later epochs. The effect of all these star formation histories on the GSMF has been tested without the nebular contribution at this stage.
Figure 3 (top-right) shows the different mass function estimates assuming different star formation histories at 3.5 <z< 4.5. A similar plot for the other redshift range is shown in the Appendix A. Small differences can be noticed at the massive tail of the distribution (M ≥ M∗), while the slope of the low-mass end of the GSMF is stable against the adoption of different SFHs. This is consistent with the results of Mobasher et al. (2015) and Santini et al. (2014), where it is shown that the stellar mass parameter is practically insensitive to the choice of the adopted SFHs, due to degeneracies with both age and dust extinction. We thus confirm that the choice of the SFH does not strongly influence the form of the inferred GSMF at high redshift.
4.2.3. The impact of nebular lines and nebular continuum
We have considered also the impact of nebular emission (both lines and continuum) on the stellar mass and GSMF derivation. To explore this we have adopted here the approach taken by Schaerer & de Barros (2009), followed also by Duncan et al. (2014). This involves deriving the production rate of ionizing photons by integrating the intrinsic BC03 template at λ< 912 Å rest frame, and then converting ionizing flux into both nebular lines and continuum. These models assume a constant temperature and electron density, which is probably a somewhat rough approximation, but nonetheless gives realistic results, as shown in Castellano et al. (2014) for a sample of galaxies at z = 3 − 4 (taken mainly from the AMAZE sample of Maiolino et al. 2008; and Troncoso et al. 2014).
Figure 3 (bottom-left) shows the impact of the nebular contribution to the GSMF estimate at 3.5 <z< 4.5. A similar plot for the other redshift ranges is shown in the Appendix A. At z ≃ 4 we find agreement with the results of Stark et al. (2013) and Salmon et al. (2014), indicating that the differences in the stellar masses computed with and without the nebular contribution are less than 0.1–0.2 dex. The relatively low contribution of nebular emission on the mass determination at high redshift can be due to the large FWHM in wavelength of the IRAC filters (~0.8–1.0 μm). At higher redshifts (z> 4.5) the differences increases slightly, since stellar masses are systematically shifted lower, due to the larger relative contribution of emission lines in the Spitzer bands, but is in any case within 0.2 dex. This result is consistent with similar results obtained by Duncan et al. (2014) and Salmon et al. (2014), who have also attempted to take into account the potential nebular contribution.
Our results are also consistent with those obtained by Stark et al. (2013) at 3.5 <z< 6.5. At 6.5 <z< 7.5 they find a larger offset in stellar masses of 0.3 dex; this difference could be due to the different method adopted, since their estimate at these large redshifts has been derived assuming the same EW distribution of the Hα line emission inferred at 3.8 <z< 5.0.
In summary, we find that the nebular contribution does not alter dramatically the shape of the GSMF, even at very high redshift (z = 6 − 7). There is, as expected, possibly a slight systematic effect towards lower number densities at a given mass when the nebular contribution is allowed in the fitting, but this trend is within the uncertainties of the GSMF and always less than 0.1–0.2 dex in log (Φ). The difference in the faint end slope Δα computed on the Mass Functions with and without nebular contribution at z ~ 7 is ~0.04, confirming the robustness of the GSMF against this systematic effect.
4.2.4. The cosmic variance
Another source of uncertainty in the GSMF estimation is the field-to-field variation, also known as cosmic variance. Despite the relatively large area covered by the CANDELS survey at an unprecedented depth, the volume sampled by deep HST observations is not larger than the possible scales of over-densities and under-densities at those redshifts (Ouchi et al. 2009). For example, Lee et al. (2012) found strong cosmic variance between the number counts of LBGs at z = 4 and z = 5 between the GOODS-South and GOODS-North fields. Cosmic variance can also be an important source of the scatter observed so far in the various estimates of the GSMF at high redshift, especially at the high-mass end.
To make a first-order estimate of the amplitude of the cosmic variance, we compare the GSMF for the two fields (GOODS-South and UDS) separately in Fig. 3 (bottom-right) for the redshift interval 3.5 <z< 4.5. The same plot for the higher redshift bins is shown in the Appendix A. As expected, the biggest uncertainties/differences are at large masses (M ≥ 1010.6 M⊙ at z = 4). We find a similar trend at higher redshifts, as shown also in the Appendix A. At z = 7 the difference between the best fit of the GSMF in the UDS and GOODS-South field is Δα ~ 0.037, but the value of M∗ is significantly different for the two fields, 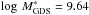 against
against 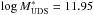 . This indicates that we need larger areas to beat down the cosmic variance: the completion of the CANDELS survey and the availability of other deep fields being observed with HST will probably provide the necessary combination of depth and area to overcome this limitation.
. This indicates that we need larger areas to beat down the cosmic variance: the completion of the CANDELS survey and the availability of other deep fields being observed with HST will probably provide the necessary combination of depth and area to overcome this limitation.
4.2.5. The presence of AGN in the input CANDELS sample
The presence of AGN in principle can alter the stellar mass derivation since the radiation from the active super-massive black holes, if ignored, is usually converted into stellar masses adopting pure stellar libraries.
Adopting the same technique of Fontana et al. (2006), we exclude here all the spectroscopically confirmed AGN (both type 1 and 2) and the luminous hard X-ray detected objects from the parent CANDELS sample (Xue et al. 2011). It is worth noting that in the GOODS-South field the identification of additional high-redshift AGN is also possible thanks to the variability studies and the wealth of multi-wavelength data available (Trevese et al. 1994; Villforth et al. 2010), from ultra-deep X-ray imaging by Chandra to the mid- and far-IR (Spitzer, Herschel). In the GOODS-South field we thus exclude 22 AGN at 3.5 ≤ z ≤ 7.5 from the parent sample (~1%). The removal of AGN in the UDS field is not as trivial as in the GOODS-South case, since such a photometric database is not available or is shallower, at the moment. Moreover, at z> 6 the identification of AGN is made more difficult due to flux limits on the X-ray and on optical spectroscopic identification. For this reason, investigating the contribution of AGNs to the GSMF estimation is important.
 |
Fig. 4 Comparison of the GSMF with and without AGN. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South field without AGN (filled black triangles) and with the AGN included (red asterisks). The error bars show the Poissonian uncertainties of each point. The stellar masses for the AGN have been derived using the same technique adopted for normal galaxies. The solid continuous curve shows the Schechter function derived through a parametric STY maximum likelihood fit of the GSMF without AGN. |
 |
Fig. 5 Various uncertainties in Log (Φ) as a function of stellar mass for different redshift bins from z = 4 to z = 7. Blue curves (SFH) indicate the uncertainties due to the different SFHs adopted in this work. Green curves (MCsim) are related to the Monte Carlo simulations described in paragraph 4.1. The red lines (Zphot) indicate the error introduced by different photometric-redshift solutions. Finally, the dark-green lines (CVar) indicate the error due to cosmic variance. |
In Fig. 4 we compare the galaxy-only GSMF with that which is derived deliberately retaining all known AGN in the sample (but estimating their stellar masses using pure stellar libraries). We find that at 3.5 <z< 4.5 the two are almost identical at M ≤ 1011 M⊙, and within the uncertainties for higher masses. The plot which summarizes the comparison at all redshifts can be found in the Appendix A. From these checks, we can conclude that at masses lower than 1011 M⊙ the role of AGN is negligible, and at the massive tail they are introducing changes that are within the uncertainties. This is as expected, since bright AGN tend to populate the centre of massive galaxies.
4.3. Comparison of different sources of uncertainties
Armed with a full characterization of the random and systematic effects, we are now in a position to compare them and assess the overall reliability of the GSMF. For all the random and systematic effects described above, we have estimated the rms of the different measured densities Φ(M) of the GSMF in each mass bin.
As far as the random errors are concerned, we compute the uncertainties on the GSMF due to the combined probability distribution functions in photometric redshift and stellar mass PDF(z,M) using the 1000 Monte Carlo simulations described in the previous paragraph. The uncertainties are then derived measuring the rms of these GSMFs and are indicated in Fig. 5 with the label “MCsim” (Monte Carlo simulations). For the cosmic variance effect we do not rely on the rms computed only on two fields, but we used the “cosmic variance” tool2 provided by Trenti & Stiavelli (2008) using as input parameters the number of galaxies observed in our two fields.
Similarly, we have computed the GSMF that results from the adoption of different methodologies, such as photometric-redshift recipes, star formation histories (exponentially declining, exponentially rising, delayed) and the nebular model.
These errors are compared in Fig. 5, that shows the different uncertainties in Log (Φ) as a function of stellar mass for different redshift bins from z = 4 to z = 7. Table 2 summarizes the median uncertainties in all the mass bins for 3.5 <z< 7.5, due to the photometric redshifts, the star formation histories and the nebular contribution (SFH+NEB), the Monte Carlo simulations and the field-to-field uncertainties (CVar).
Median uncertainties on the GSMF due to photometric redshifts, Monte Carlo simulations or SFH+NEB.
This comparison shows that the errors in the GSMF are relatively small, 10–20% in most of the bins, when the different sources of uncertainties are individually taken into account (photometric redshift recipes, star formation histories, nebular contribution). In general, we note that errors tend to be larger at the high-mass end (where the number of objects is small) and at small masses (where objects are faint and hence more susceptible to errors), and smaller at intermediate masses, where the statistics are better and photometry is still highly reliable.
It is also clear that the leading source of errors is the adoption of a specific recipe for the computation of the photometric redshifts. This effect dominates over those due to the different parametrizations of the SFH or the adoption of the nebular contribution. We remark that this test has been performed here for the first time, to our knowledge, thanks to the various recipes developed and compared within the CANDELS collaboration. This test is different from the evaluation of the effects of noise in the redshift estimate internal to a given technique, that we have also performed and that is labelled MCsim (and which was already included in previous analyses; e.g. Fontana et al. 2006; Marchesini et al. 2009), but it is instead related to the systematic differences that may arise when different techniques are adopted.
Our check suggests that a significant contribution to the observed scatter among the various GSMF presented in the literature, at least at high redshift, can be ascribed to the different photometric redshift techniques adopted.
We also note that the typical error due to the uncertainties in photo-z (MCsim) in our survey is somewhat lower than in previous surveys thanks to the improved quality of the photometry and to the adoption of a Bayesian approach that improves the accuracy and leads to narrower PDF(M | z) distributions. Our decision to use the Bayesian photo-z by Dahlen el al. (2013) allows us to reduce the uncertainties in the GSMF at high redshift by ≃0.1–0.3 dex.
The other fundamental ingredient to constrain the uncertainties of the GSMF is the limitation of the cosmic variance effect, and this is possible adopting observational strategies tailored to maximize the efficiency of the surveys. From Table 2 it is clear that the uncertainty on the photometric redshifts and the cosmic variance effect of the CANDELS GOODS-South+UDS fields are comparable. Larger areas or multiple fields would be essential in the future to further beat down the field-to-field variations.
The previous tests have allowed us to quantify the effects of different “ingredients” on the mass function, namely photometric redshifts, star formation histories and nebular contribution. However, these have been considered separately, i.e. varying only one parameter at time and checking for its effects on the GSMF, as shown in Table 2 and in Fig. 5. To quantify the co-variance between these three main ingredients, we have considered all their possible combinations, varying simultaneously the five recipes for photo-z including the bayesian solution, the three SFHs and adding or neglecting the nebular contribution. We have thus produced 36 different GSMFs. As a consequence, the total variance of these determinations gives a quantitative estimate for the co-variance between these three ingredients. We find that the scatter of Log (Φ), obtained from the 36 different mass function realizations, is very similar to the square-root combination of the individual variances due to photo-z, SFHs and nebular emissions. We can thus conclude that the co-variance terms between photo-z, SFHs and nebular contribution are negligible and that they can be effectively factorized in different independent variances.
Here we did not consider other sources of variance on the mass function determinations, i.e. mass-variable IMF, different libraries for simple stellar population synthesis, non-uniform dust screen models, different dust laws, and other parameters influencing the stellar mass derivation through SED fitting. Taking into account all these parameters the variance on GSMF can be even larger than what we find here. We thus advertise the reader that the uncertainties summarized in Table 2 and in Fig. 5 are only an underestimation of the true total error budget on the GSMF at high-z.
5. The constituents of the GSMF at high redshift
 |
Fig. 6 Stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS UDS and GOODS-South fields (blue filled and open circles). The error bars show the Poissonian uncertainties of each point with the errors derived through the Monte Carlo simulations added in quadrature. The masses are derived using the BC03 libraries with exponentially declining star formation histories, and without any contribution from nebular lines or continuum. AGN were not included in the present sample. The dotted lines indicate the GSMF at z = 0.6 in the UDS and GOODS-South fields. The dark-green pentagons show the mass function derived by González et al. (2011; G11), while the cyan stars indicate the result of Caputi et al. (2011; C11), which was obtained with a different stellar library (Bruzual 2007) that includes a stronger contribution from TP-AGB stars. The black triangles are from Pérez-González et al. (2008; PG08), the red (empty and filled) squares from Marchesini et al. (2009; M09) and Marchesini et al. (2010; M10), respectively. The magenta points are the GSMF of Santini et al. (2012a; S12). The grey circles come from Fontana et al. (2006; F06) while the magenta triangles are from Stark et al. (2009; S09). The red, orange, dark-yellow and green dashed lines show the best fit GSMFs of Lee et al. (2012; L12), Ilbert et al. (2013; I13), Muzzin et al. (2013; M13) and Duncan et al. (2014; D14), respectively. All the mass functions have been converted to a Salpeter IMF for comparison. The solid continuous curves show the Schechter function derived through a parametric STY maximum likelihood fit. |
5.1. The CANDELS GSMF at z = 4–7
Figure 6 shows the GSMF at 3.5 ≤ z ≤ 7.5 derived by combining the CANDELS GOODS-South and UDS fields (filled and open blue circles). Most of these GSMFs (i.e. those represented by filled circles) have been derived adopting our “baseline” mass estimation; i.e. SED fitting to the whole photometry using BC03 models with exponentially declining SFHs, no nebular contribution, excluding AGN from the parent sample, and adopting the Bayesian photometric redshifts. We extend the GSMF at the very low mass end (as shown by open circles) by converting UV luminosity into stellar mass adopting a constant M/L ratio. The procedure will be described in detail in Sects. 5.2 and 6, where we will present the consequences and lessons learned from our new estimate of the GSMF. We first compare our new determination of the GSMF with results from previous studies, and discuss plausible origins for the discrepancies that we find.
As can be clearly seen from Fig. 6, the various estimates of the GSMF at z = 4, and in particular at M ≥ 1011 M⊙ differ quite dramatically. For example, if we compare our results with the GSMF derived by Stark et al. (2009), Lee et al. (2012) or González et al. (2011), we find an excess of galaxies at the high-mass end and a steeper slope at low masses. The high mass range is particularly sensitive to the systematics that we described above, such as cosmic variance and different recipes for photometric redshifts. In addition, the photometric quality of the various data sets used in different studies varies significantly, and can further contribute to the observed scatter. Indeed, the basic selection wavelength used can be very different. For instance, Caputi et al. (2011) adopted a catalogue selected directly from the Spitzer images at 4.5 μm, rather than utilising an H-band selected catalogue as adopted here or in Santini et al. (2012a). Meanwhile, bluer selection bands were used by Stark et al. (2009) and Lee et al. (2012) who undertook their primary galaxy selection in the i775 and z850 ACS bands respectively (sampling the UV rest-frame wavelengths at z ≥ 4). A more detailed discussion on these differences, especially on the massive side of the GSMFs, has been carried out in Sect. 5.3.
Although we are using deeper WFC3/IR data, the González et al. (2011) GSMFs extend to lower masses than our mass function determinations. This is because the González et al. (2011) GSMF estimate is based on the UV luminosity function, rather than on a directly mass-selected sample. In the next section we will discuss these differences in more detail, and will also investigate the nature of the galaxies at the high-mass end and the relation between mass and UV light.
At z ≥ 5 the number of available GSMF is much smaller, and the general agreement improves. We suspect that, in general, the surveys adopted to estimate the GSMF at extreme redshifts are of superior quality, and that the strong signature provided by the IGM absorption makes the photo-z more robust in this redshift range. The main discrepancy is found again with the Caputi et al. (2011) GSMF at z ≃ 5, and again we suspect that the different selection criterion may have played a role. At z ≃ 7 our GSMF slightly differs from the Duncan et al. (2014) one at M ~ 3 × 1010 M⊙, but this can be due to the low number statistics of the adopted samples. Nonetheless, it is worth noting that the GSMFs at z ≥ 5 shown in Fig. 6 (by Stark et al. 2009; González et al. 2011; Lee et al. 2012; Duncan et al. 2014) have been derived from similar photometric databases (including the GOODS-South field), so the cosmic variance scatter may not be a dominant effect in this case.
5.2. The Mass-to-light ratio of galaxies at z ≥ 3.5
As already mentioned, most previous attempts to derive the GSMF at very high redshift (z> 3) have been carried out through the conversion of rest-frame UV light into masses (González et al. 2011), assuming a tight correlation between SFR and the stellar masses of galaxies observed at z = 4. Our SED fitting procedure is not only providing the stellar masses of the analysed sample, but it also gives the absolute magnitudes at different rest-frame wavelengths. We have therefore derived the mass-to-light ratio at 1400 Å rest frame for galaxies at 3.5 <z< 4.5 in order to compare it with previously derived relations from other studies.
Figure 7 shows the resulting relation between the stellar mass M and the UV-rest frame luminosity L1400 for galaxies at 3.5 <z< 4.5 in the CANDELS GOODS-South field. Green points represent the objects that, although too faint to be detected in the 3.6 μm and 4.5 μm Spitzer bands, are instead detected in the deep K-band HUGS observations. At z ~ 4 the K-band enables a direct measurement of the rest-frame luminosity beyond the Balmer break, where the bulk of the light from ordinary stars is manifest. This is crucial for a robust estimate of stellar mass, and so there is no doubt that the availability of these deep K-band images represents a major improvement of the data now available in the CANDELS fields for high-redshift mass determinations.
At 3.5 <z< 4.5 a linear regression to the observed data yields the relation log M = −0.4 × MUV + 1.6, shown by a thick green line in Fig. 7. This relation implies that, although with large scatter, our data are consistent with a constant M/L ratio. This equation is similar to the one deduced by Duncan et al. (2014), but with a slightly higher normalization. The trend of constant mass-to-light ratio is valid also at higher redshifts, corroborating the results of similar works on the CANDELS survey (Salmon et al. 2014; Duncan et al. 2014). The large scatter that we observe is partly due to noise (in the photometry and in the derived rest-frame quantities) and partly to a genuine scatter of the M/L ratio in high redshift galaxies, but the relative weight of the two aspects is however difficult to quantify. We will discuss below how this affects the resulting GSMF.
When compared with previous surveys, our results are in agreement at bright UV magnitudes, but become progressively more different at fainter UV luminosities. As we show in Fig. 7, the relations found by Lee et al. (2012) and González et al. (2011) do not reproduce the slope of the M/L relation derived here.
 |
Fig. 7 Stellar mass vs. UV absolute magnitude M1400 for galaxies at 3.5 <z< 4.5 in the GOODS-South field. The blue solid line is the relation (at 1700 Å rest frame) found by Lee et al. (2012) for LBGs selected with the B − V vs. V − z colour criterion and a S/N in the z850 band greater than 6. The red solid line represents the relation as derived by González et al. (2011) at z = 4, for a similar rest-frame wavelength of 1500 Å. The grey triangles show the M/L relation derived by Stark et al. (2013). The dark-green line is the best fit to our own results assuming a constant mass-to-light ratio, or equivalently a slope −0.4 between stellar mass and absolute magnitude. The orange line is the best fit of Duncan et al. (2014). All the relations have been converted to a Salpeter IMF for comparison. Magenta points show galaxies undetected in the deep K-band Hawk-I imaging, while green dots represent objects not detected in 3.6 and 4.5 μm in the Spitzer SEDS imaging. |
In particular, the blue solid line in Fig. 7 is the relation at 1700 Å rest-frame found by Lee et al. (2012) for LBGs selected with the B − V vs. V − z colour criterion and signal-to-noise ratio (S/N) in the z850 band greater than 6, and this can be seen to be more consistent with the lower envelope of our data than with our own average M/L relationship. This also appears to be the case for the relation derived by González et al. (2011; red solid line) who also used samples of LBGs selected at z = 4 (i.e. at a rest-frame wavelength of 1500 Å).
 |
Fig. 8 Comparison between the mass function derived by assuming a constant mass-to-light ratio (red squares), relation between mass and L1400 light derived by González et al. (2011; green stars), and the one derived in this work for the GOODS-South and UDS fields (blue circles). The error bars show only the Poissonian uncertainties of each point. The original GSMF presented González et al. (2011) is shown by dark-green symbols. |
We first tried to reproduce the trend observed by González et al. (2011) using only LBGs selected via the B − V vs. V − z colour–colour criterion, or fitting the masses with models of constant star formation histories and/or solar metallicity, but we find that our data points are always best fitted by a constant M/L relation. Following the example of McLure et al. (2011), we explored also synthetic libraries with constant star formation histories and no extinction, but the results are similar to our baseline model, indicating (on average) a constant mass-to-light ratio.
A possible explanation for the differences could be that the relation between mass and light deduced by González et al. (2011; their Fig. 1) appears to be driven – and possibly tilted – by the points at lower masses that are derived from galaxies that are essentially undetected (S/N ≤ 2) in the IRAC 3.6 μm band. In our case, instead, the estimates at low luminosity benefit from the combination of the new deep HUGS Hawk-I K-band photometry (Fontana et al. 2014) and the deeper IRAC imaging provided by the SEDS programme (Ashby et al. 2013), allowing us to improve the mass estimates for faint (M1400 ~ −18) galaxies (green and magenta points in Fig. 7).
These differences have obvious consequences for the form of any GSMF derived from the UV light. Since González et al. (2011) adopted a M/L relations significantly steeper than log M ∝ −0.4 × MUV (they adopted log M ∝ −0.68 × MUV), their inferred stellar masses at very faint UV luminosities are underestimated by an order-of-magnitude with respect to the typical values derived from a constant M/L ratio relation as found here. The resulting GSMFs computed with the steeper M/L relation are thus inevitably flatter at the faint end than the ones derived in the present study.
This effect is clearly shown in Fig. 8, where our derived GSMFs are compared with those obtained by converting the UV luminosity function adopting a non-linear functional form for the M∗/LUV ratio. In addition to a GSMF taken from the literature (González et al. 2011, green pentagons) we show also those obtained from our CANDELS data adopting either the same M∗/LUV relation as used by González et al. (2011; green starred points) or those obtained adopting our own M∗/LUV (red dots). We note that the González et al. (2011) GSMF has been corrected for incompleteness and for the estimated scatter in the M/L relation, and is based on a smaller field, hence its normalization cannot be immediately compared to that of our GSMF computed using their M∗/LUV relation.
A few results are immediately evident. First, comparing the GSMF derived using our M∗/LUV relation with the one derived (from the same data) using the González et al. (2011) relation, it is clear that the latter yields a GSMF that is flatter and appears to extend to lower masses, since the relation between UV light and mass is steeper than the one observed in the CANDELS data, as shown in Fig. 7. At faint magnitudes, the GSMF derived using our average M∗/LUV relation agrees very well with the GSMF that we derive from the full sample. We use this agreement to extend our fiducial GSMF towards even lower masses, namely to M = 6 × 108 M⊙ at z = 4 and M = 2 × 109 M⊙ at z = 7, assuming that losses due to incompleteness are minimal. These additional points have been marked with blue empty circles in Fig. 6.
Another major discrepancy that emerges from Fig. 8 concerns the high-mass end of the GSMF: especially at z ≃ 4, the GSMF derived from our reference sample extends clearly to much higher masses than all GSMFs computed with some average M∗/LUV: our GSMF (blue circles) extends towards M ~ 5 × 1011 M⊙ while the mass functions derived from the UV luminosities are limited to M ≤ 1011 M⊙. In the next sub-section we will explore the reasons for this discrepancy.
We note that all these differences tend to disappear at higher redshifts. Indeed, at z = 6 and z = 7, our GSMFs (blue circles in Fig. 8) are consistent with the mass function derived through the UV luminosity, assuming a constant M∗/LUV ratio (red squares). There are two possible explanations for this behaviour: either all the galaxies at high-z have relatively low dust content and are relatively young or, alternatively, the H160-band selection adopted in this work is missing the more obscured and/or evolved galaxies at z> 6. These alternatives can be distinguished by using a deep mid-infrared selection. Considering the current limitations of IRAC-selected samples, such as the Caputi et al. (2011) one, that are significantly plagued by limited depth and confusion due to poor image resolution, this issue may not be fully resolved until future JWST observations.
5.3. The physical properties of massive galaxies at high redshift
As shown in Fig. 7, there are a number of relatively faint objects (M1400 ~ −18) which are nevertheless very massive, with M ~ 1011 M⊙ (see also Madau & Dickinson 2014). While their absolute number is not very large, it is similar to the number of UV-bright galaxies of comparable masses, and therefore these objects can make an important contribution to the massive end of the GSMF. This is clearly shown in Fig. 8, which illustrates a clear discrepancy, at z ≤ 5.5, between the high-mass end of the GSMF derived from the UV-selected star-forming galaxies (i.e. Stark et al. 2009; González et al. 2011; Lee et al. 2012) and the one derived in this paper, which has been obtained with a complete near-infrared sample without the application of colour pre-selection.
To understand the nature of these galaxies with (relatively) low UV luminosity but high masses we plot in Fig. 9 the SEDs of the four most massive (M ≥ 1010.5 M⊙) but faint (M1400> −18.5) galaxies in the GOODS-South field (see also Fig. 7). The fits to their observed SEDs indicates clearly that is these objects do indeed lie at z> 3.5, but their observed colours are clearly very different from those used to select LBGs at comparable redshifts. Such objects are in fact well fitted with dusty star-forming models or alternatively with passively evolved SEDs. We have checked that they are not type-1 AGN based on the 4 Ms Chandra observations, but we cannot exclude that they are X-ray absorbed (Compton thick) AGN (although they do not show any sign of an unusually steep SED slope in the IRAC bands). In a separate paper (Merlin et al., in prep.), we describe in more details the most interesting objects. Although they are quite rare, these red galaxies are unambiguously very massive and represent a major contribution to the high-mass end of the mass function at z ≃ 4.
6. The evolution of the mass function at high redshift
 |
Fig. 9 Example SEDs of galaxies at 3.5 < z < 4.5 with M > 1010.5 M⊙ and M1400 > −18.5. Their SEDs, especially in the IRAC bands, indicate that they are really massive objects at high redshift and that the nebular contribution is not dominant. The objects ID = 8785 and 17 749 are quite old (age /τ ≥ 8), while ID = 4466 and 13299 have E(B − V) ≥ 0.4. All these galaxies are characterized by very red colours, and thus cannot be selected by standard LBG selection criteria based on UV rest-frame colours. Because of their large masses, however, they represent a relatively rare population, which can contribute significantly to the high-mass tail of the mass function at z = 4. |
We can finally obtain a full description of the shape and redshift evolution of the GSMF by fitting a Schechter function to our data. Before doing so, it is important to carefully consider how the uncertainties on the estimate of the stellar mass for each galaxy may affect the observed shape of the GSMF.
Since the measured masses are randomly perturbed by different noise sources, the net effect on the observed GSMF is a preferential transfer of galaxies from the faintest bins toward the more massive ones, since low mass galaxies are more numerous than brighter ones. This effect is commonly referred to as “Eddington bias”, following Eddington (1913). It is usually believed to affect mostly the massive side of the GSMF, where the slope is steeper than at the faint end, but we show below that this does not necessarily happen in our data set.
For this purpose we use the probability distribution functions PDF(M | z) (i.e. the probability that a given galaxy in our sample has a mass M at a redshift z) derived from the Monte Carlo simulations described in Sect. 4.1.1. We use the individual PDF(M | z)s to build the average PDF(M | z) for each mass bin of the GSMF, at the various redshifts. While this has already been done in previous analyses (Ilbert et al. 2013) as a function of redshift, the novelty of our approach is that we explicitly derive the PDF(M | z) as a function of both redshift and stellar mass. Unsurprisingly, the PDF(M | z)s become wider (implying that masses become less constrained) when redshift increases and when galaxies become fainter (i.e. less massive).
The procedure adopted is fully described in Appendix B, while we report here the major results. The first is that the distortions induced in the shape of the GSMF are progressively larger with increasing redshift, and become particularly severe at z ≃ 7, because, as naively expected, the intrinsic errors on the estimate of individual galaxy stellar masses increase with increasing redshift (Fig. B.1).
The second effect is that, contrary to what was found in previous analyses (e.g. Ilbert et al. 2013), especially at z = 4, the accuracy at the bright end is here good enough to keep the overall shape essentially unaffected. On the contrary, the increase in the noise at the faint end (that was never taken into account in previous estimates) induces a non-negligible steepening of the observed faint end. Both effects are clearly visible in Fig. B.2. At z ≥ 6, instead, the large errors in mass can affect also the shape of the GSMF at the massive side (see Fig. B.3). It is worth noting that the Eddington bias corrections described here depend critically on the shape of the adopted PDFs in mass. As a cautionary note, we warn the reader that the unambiguous estimation of the best fitting GSMF is subject to the correct derivation of the PDF(M).
We include these effects in our fit of the GSMF. We adopt for the GSMF a standard parametrization with a single Schechter function with free parameters α, M∗ and Φ∗. We have performed a best-fit on the data points obtained with the V/Vmax approach. Although this is statistically less rigorous than other approaches (like the STY method), it has two advantages in our case. The first is that we can fit both the GSMF and its extension to lower masses which we derived by assuming a constant M/L ratio (as described in the previous section). The second advantage is that we can correct the observed data points for the Eddington bias. The fit is performed as follows: for any possible combination of the Schechter parameters α, M∗, and Φ∗, we compute the convolved GSMF using the estimated average PDF(M | z)s and we compare it with the observed mass function. We scan the three-dimensional space of the free parameters of the Schechter function to find the best fit solution by a χ2 minimization. The error bars of the GSMF considered here include both the Poissonian error bars from the 1 /Vmax procedure as well as the uncertainties due to the other effects (photometric redshifts, photometric scatter) that are estimated with our Monte Carlo simulations described before. We include also the errors due to cosmic variance.
Figure 10 shows the resulting GSMFs from z = 4 to z = 7 in the combined UDS and GOODS-South fields. Our GSMFs extend toward low masses: 109 M⊙ at z = 4 and 6 × 109 M⊙ at z = 7 (even lower, converting UV light to stellar masses). Since we explicitly correct for the Eddington bias, the best-fit GSMFs do not follow the raw binned data; as mentioned above, the recovered slope is less steep in all cases, and the massive side at high redshift is shifted toward lower masses, though the latter trend is not particularly significant. We also note that in Appendix C we provide for comparison the results of the fitting procedure neglecting any effect from the Eddington bias.
 |
Fig. 10 GSMFs from z = 4 to z = 7 in the CANDELS UDS and GOODS-South fields. The error bars take into account the Poissonian statistics, the cosmic variance and the uncertainties derived through the Monte Carlo simulations. The solid continuous curves show the Schechter function derived through a best-fit approach which corrects the observed data points for the Eddington bias. |
Table 3 summarizes the χ2 best fit values of the free parameter of the GSMF, again corrected for the Eddington bias. We have also been able to compute the errors on such parameters, at the 1σ confidence level, by scanning the three-dimensional volume of the three parameters. The same results are also shown in Fig. 11, that reports the evolution of α, M∗ and Φ∗ with redshift, along with their uncertainties.
We find that the best-fit parameters are reasonably well constrained up to z = 6, such that meaningful conclusions on the evolution of the various parameters can be derived. In the last redshift bin, the uncertainties (that are due to both the intrinsic errors on the stellar masses as well as to the small size of the sample) are much larger, and results are only tentative.
We find that the slope of the low-mass side of the GSMF is almost constant, with α ≃ − 1.6 from z = 4 to z = 6, showing no evidence of a steepening with redshifts. This slope however is significantly steeper than the GSMF slope up to z ≃ 1, indicating that a progressive steepening must occur in between. Santini et al. (2012a) presented the first evidence for such a trend, but this will clearly need to be verified with much deeper and wider surveys like CANDELS.
Most of the evolution of the GSMF appears to be due to a combination of density evolution (Φ∗ grows at lower-z) and mass evolution (M∗ increases with cosmic time).
In the last redshift bin, at z = 7, the large errors reflect strong degeneracies between the Schechter parameters, and the best fit values are much less constrained, so that any conclusion is preliminary. The only robust result is a further decline in the total stellar mass density ρM, that is steadily decreasing as redshift increases, at several σ of significance (Fig. 11, bottom right panel).
Mass function best fit parameters.
Overall, the mild evolution in both log (M∗) and log (Φ∗), together with an almost constant α, seems to indicate that the mass assembly rate was somewhat similar for massive galaxies and for the less massive ones. This behaviour can be linked to the apparently slow (or negligible) redshift evolution of the apparent SF quenching mass as has been found at lower redshifts in the COSMOS data by Peng et al. (2010, 2012) and Ilbert et al. (2013), although clearly the physical processes ongoing in high-redshift galaxies may be very different.
 |
Fig. 11 Evolution of the three parameters (α, M∗, Φ∗) of the GSMF with redshift. The bottom-right panel shows the dependencies of the Stellar Mass Density (ρM in unit of M⊙ Mpc-3) from the parameter α. The stars mark the position of the best fit of the observed GSMF with a Schechter function, obtained by correcting for the Eddington bias as explained in detail in Appendix B. A clear trend with redshift is evident up to z = 6, while at z = 7 the parameters are basically unconstrained. |
7. The stellar mass density at 3.5 ≤z ≤ 7.5
Starting from the best fit of the GSMF and from its uncertainties, we derive the stellar mass density (SMD) by integrating the best-fit GSMF from M = 108 M⊙ to M = 1013 M⊙. These limits have been chosen to facilitate the comparison with previous SMD estimate in the literature. To compute the associated error, we consider all the possible combinations of the parameters α, M∗, and Φ∗ which are still compatible with the observed GSMFs at 68% c.l. and for each of them we compute the integral in mass, thus finding the minimum and maximum range of the SMD at the 1σ level. The results are shown in Fig. 12, that shows the SMD, log (ρM), at 3.5 <z< 7.5 obtained in the CANDELS-UDS and GOODS-South fields (black points). Table 4 summarizes the values of the SMD at 3.5 <z< 7.5 with its uncertainties.
 |
Fig. 12 Redshift evolution of the stellar mass density (SMD) at 3.5 <z< 7.5 obtained by integrating the GSMFs presented in this paper (black points). The evolving SMD at high redshift is compared to the lower redshift results from different surveys. ρM is in units of M⊙ Mpc-3 and has been obtained by integrating the best-fitting mass functions from Mmin = 108 M⊙ to Mmax = 1013 M⊙. All the SMDs have been converted to a Salpeter IMF for comparison. The error bars of the CANDELS data have been computed using the same Monte Carlo simulations developed to derive the uncertainties on the Schechter function parameters. The short-dashed line is the stellar mass density obtained integrating over cosmic time the star formation rate density (SFRD) of Hopkins & Beacom (2006). The long-dashed line is the SMD inferred from the SFRD of Reddy & Steidel (2009). The solid line is the SMD obtained from the SFRD of Behroozi et al. (2013), while the dotted line is the SMD derived by the new fit of the Hopkins & Beacom (2006) carried out by Behroozi et al. (2013). The dotted-dashed line shows the SMD derived from the SFRD of Madau & Dickinson (2014). All the stellar mass densities obtained by integrating the different SFRDs assume a constant recycling fraction of 28%. |
In Fig. 12 we also compare our evolving SMD with those derived by different surveys in various redshift ranges. We translate all the SMDs to the Salpeter one adopted in this paper. At intermediate redshift (2 <z< 4) the scatter is of the order of 0.3–0.5 dex and can be due to cosmic variance or photometric redshift uncertainties. At low redshift (z< 2) the scatter is reduced, and it is probably driven by statistical uncertainties. At z> 4 the different SMDs are in agreement with each other, with a few exceptions.
The redshift evolution of the GSMF derived above results in a rapidly evolving SMD at early cosmic epochs. Our results are in agreement with those of Duncan et al. (2014), which are based on a similar analysis of earlier CANDELS data, and indicate a faster evolution than those of González et al. (2011), whose SMD is instead evolving slowly with redshifts, probably due to the different method adopted (see Sect. 5.2).
Stellar mass density at 3.5 <z< 7.5.
In Fig. 12 we compare the SMD evolution in redshift with the integrated value of the star formation rate density (SFRD) over the cosmic time. We assume a Salpeter IMF and a constant gas recycling fraction of 28% (Nagamine et al. 2006; Santini et al. 2012a; Madau & Dickinson 2014). Different renditions of SMD can be obtained depending on the assumed scenario for the global SFRD. The short-dashed line is the SMD obtained using the SFRD of Hopkins & Beacom (2006). The long-dashed line is the analogous curve for the SFRD by Reddy & Steidel (2009). The solid line is the SMD obtained by the SFRD of Behroozi et al. (2013), while the dotted line is the SMD derived by the new fit of the Hopkins & Beacom (2006) data points carried out by Behroozi et al. (2013). The dot-dashed line shows the SMD obtained integrating the SFRD of Madau & Dickinson (2014). The SFRDs of Hopkins & Beacom (2006) and Reddy & Steidel (2009) show a peak around z ≃ 2, while the one of Behroozi et al. (2013) and their new fit to the data points of Hopkins & Beacom (2006) have a maximum at lower redshift (z ~ 1), similar to the Madau & Dickinson (2014) SFRD. The latter has a slightly lower normalization at z ~ 1 than the other parametrizations and shows a milder evolution towards high redshifts. The typical errors on the SFRD determination are ~0.1 dex at z ≤ 0.9 and ~0.2–0.3 dex at z ≥ 1.7 (see Table 7 of Behroozi et al. 2013).
At face value, the results shown in Fig. 12 indicate that the growth in SMD derived here at high redshifts (z> 4) is in agreement with that inferred from integrating the SFRD histories presented Behroozi et al. (2013) or Madau & Dickinson (2014), and lower than the one derived in the new fit of the Hopkins & Beacom (2006) data set by Behroozi et al. (2013). Indeed, our SMD can be reproduced by a SFRD which is evolving at high redshifts at the same rate of the parametrizations of Hopkins & Beacom (2006), Reddy & Steidel (2009), Behroozi et al. (2013) or Madau & Dickinson (2014). In addition, the normalization of our measurements is slightly lower than the one of Hopkins & Beacom (2006) and Reddy & Steidel (2009). This indicates that at z ≥ 4 the SMD and SFRD are in very good agreement. We must stress however that this is true when the GSMF and the SFRD are integrating till low level of stellar masses and star formation rate – if we restrict the comparison to specific ranges of stellar masses (or, more accurately, of parent halo mass) the results could well be discrepant.
Of course, our analysis cannot say anything new about the puzzling disagreement between the growth of SMD and the time integral of SFRD at z< 2, as noticed also by Santini et al. (2012a) and Madau & Dickinson (2014). In this redshift range we expect that both the SFRD and the SMD estimates are robust and not affected by incompleteness.
The exact size of this discrepancy, and whether it represents a major problem is still matter of considerable debate. Many explanations have been proposed, including an underestimate of the mass density in local galaxies (Bernardi et al. 2013), an effect of “outshining” due to recent stellar populations that lead to an underestimate in stellar masses (Maraston et al. 2010; Courteau et al. 2014), the scattering of stars in the intracluster light (ICL) during galaxy mergers in group or clusters, or even time-varying IMFs. At face value, the agreement that we find at z> 4 is apparently in contrast with a strong evolution of the IMF at high redshift, especially at z> 6 as advocated for example by Chary (2008). They argued that the IMF at z ≥ 6 could be different from the Salpeter one in order to have the Universe reionized by these redshifts and to obtain an agreement with the WMAP measurement of the optical depth τes (Spergel et al. 2007). Clearly, we need more accurate estimates of both the SFRD and SMD to definitely address this issue.
8. Summary and conclusions
We have combined wide and deep HST Spitzer and VLT observations in the CANDELS UDS (Galametz et al. 2013), GOODS-South (Guo et al. 2013), and HUDF (Beckwith et al. 2006; Bouwens et al. 2010) fields to study the evolution of the GSMF in four redshift bins between 3.5 ≤ z ≤ 7.5. The HST data cover 369 arcmin2 down to a magnitude limit (at 5σ in apertures of 2 times the FWHM) of H160 = 26.7 and 27.5 for the UDS and GOODS-South field, respectively, reaching a depth of H160 = 28.5 in a limited area of 5 arcmin2 covered by the HUDF region.
In addition to the imaging data already adopted by Galametz et al. (2013) and Guo et al. (2013), we have included the deep K-band images obtained from the VLT Hawk-I survey HUGS (Fontana et al. 2014), reaching K ≃ 26.5 at 5σ over the GOODS-South and HUDF fields. The deep IRAC images from the SEDS survey (Ashby et al. 2013) are also a crucial ingredient of our data base. Finally, we have also added deep B-band imaging from VIMOS at VLT (Nonino et al., in prep.). The photometric technique adopted to de-confuse the ground-based and Spitzer images at the faintest limits is described in Galametz et al. (2013) and Guo et al. (2013).
The high-quality photometry from the near-UV to 8 μm, has been used to derive accurate estimates of photometric redshifts and stellar masses. For the photometric redshifts we have adopted the innovative technique explored in Dahlen el al. (2013), which combines different photometric redshift solutions with a Bayesian technique to provide probability distribution functions in redshift, taking into account the biases and the scatter of each individual solution. This approach allows us to obtain photometric redshifts that are significantly more accurate than each individual method, as demonstrated by the comparison with a sample of >2500 galaxies with robust spectroscopic redshifts. We find an absolute scatter of ~0.03 and an outlier fraction of 3.4%. At 3.5 ≤ z ≤ 7.5 the photometric redshifts have similar precision, with an absolute scatter of 0.037 and 7% outliers, based on a sample of 152 robust spectroscopic redshifts.
With this exquisite data set at hand, we have explored different recipes to derive the stellar masses, focusing on the redshift range 3.5 <z< 7.5. Following a standard approach, we have used the BC03 spectral synthesis code to predict galaxy colours for a wide range of galaxy properties, including different star formation histories, ages, metallicities and dust content, and derived galaxy stellar mass from the best-fitting spectral template at the photometric redshift. With respect to previous studies, we have significantly increased the breadth of the parameter space spanned by the models. First, we have tested different parametrizations of the star formation histories allowed for galaxies: in addition to the standard exponentially declining models, we have allowed for “Inverted-τ” models (SFH ∝ exp( + t/τ)) as well as for “Delayed” star formation histories (SFH ∝ t2/τ × exp( − t/τ)). For all these models, we have also tested how stellar masses change when full nebular emission (both lines and continuum) is included using the prescription of Schaerer & de Barros (2009).
We have carefully explored the impact of these different assumptions on the derived GSMF, as well as of other systematics, such as cosmic variance (field-to-field variation) and the contribution of AGN (selected via X-ray emission, spectral identification or variability). We show that, quite reassuringly, the stellar masses and the derived stellar mass functions turn out to be quite stable against different choices of the adopted SFH. The inclusion of the contribution of nebular lines and continuum in the SED of the galaxies is also not dramatic, as it systematically lowers the stellar mass estimates by 0.05–0.20 dex at z ≥ 4.
We have found that photo-z errors are the largest sources of uncertainty in the derived GSMF, even larger than cosmic variance. In particular, we have shown that the adoption of different recipes for the computation of photometric redshift (on the same photometric sample) can be the largest source of uncertainty – an important lesson to keep in mind when one compares results from different surveys, where different recipes for photo-z are used. These two error terms increase towards large redshift, from 0.1 dex at z = 4 to slightly less than 0.3 dex at z = 7.
We then used our sample of 3307 galaxies at 3.5 <z< 7.5 selected via photometric redshifts (or spectroscopic when available) to compute the GSMF of galaxies down to low mass limits. For consistency with previous works, we have adopted as reference masses those derived adopting only exponential declining star formation histories, without the contribution of nebular lines nor continuum. At z = 4 we reach a completeness mass limit of M = 109 M⊙, which increases progressively with increasing redshift to M = 6 × 109 M⊙ at z = 7.
A crucial ingredient in our analysis is a careful estimate of how the uncertainties on the measurement of the galaxy stellar mass affect the derived GSMF – the so called Eddington bias. For this purpose we use the probability distribution functions PDF(M | z)s (i.e. the probability that a given galaxy in our sample has a mass M at a redshift z) derived from the Monte Carlo simulations as described in Sect. 4.1.1. At variance with previous analyses (Ilbert et al. 2013), our approach is novel in that we explicitly let the PDF(M | z) vary as a function of redshift and stellar mass. Unsurprisingly, the PDF(M | z)s become wider (implying that masses become less constrained) when redshift increases and when galaxies become fainter. When these effects are properly taken into account, we show that Eddington bias not only flattens and boosts the apparent GSMF at high masses (albeit much less severely than in other surveys, especially at z = 4, because of the excellent quality of our data) but also induces an apparent steepening of the GSMF at the faint side.
A first main result of our analysis is the evidence that, at least at z ≃ 4, the massive side of the GSMF is dominated by galaxies that are not ordinary LBGs. We have shown that there exists a significant population of zphot ≃ 4 galaxies that are intrinsically redder than LBGs, i.e. that are faint in the UV rest-frame but are bright in the IR bands, indicating that they are either highly obscured by dust or old/evolved objects, and thus they have large stellar masses. While the existence of passively evolved galaxies at z = 4 has also been shown recently by Straatman et al. (2014) using the ZFOURGE data set and deep Herschel observations, in agreement with early results by Fontana et al. (2009) in the GOODS-South field, we show here that they do contribute significantly to the high-mass end of the GSMF, certainly at z ≃ 4.
We were led to this evidence by looking at the difference between our GSMF and the previous ones that were computed from LUV luminosity functions, scaled to mass functions by adopting average relations for the M∗/L1400 ratio. The biggest difference is found with respect to the GSMF derived by González et al. (2011) at z ≃ 4. This is clearly shown by a comparison between our GSMF and the one that we derive by assuming that all galaxies have a constant M∗/L1400. In our sample, that is mostly composed of star-forming galaxies with modest dust obscuration, we find that the relation between M∗ and M1400 can be fitted with a linear slope −0.4, although with large scatter, that is equivalent to a constant M∗/L1400. This result is in agreement with recent results on smaller CANDELS data sets (Salmon et al. 2014 and Duncan et al. 2014), and is at variance with González et al. (2011), who found a decreasing trend of the M∗/L1400 with decreasing luminosity. We ascribe this difference to the superior quality of our data, that at z ≃ 4 benefits from the ultra-deep HUGS data in GOODS-South for measuring the rest-frame optical luminosity of even the faintest galaxies.
At higher redshifts (z = 6 − 7) the GSMF inferred by González et al. (2011) is in better agreement with our estimates. At first glance this agreement can indicate that, at very high redshift, the majority of the galaxy population comprises star-forming galaxies with negligible dust extinction and that the population of dusty and/or evolved galaxies has virtually disappeared at very early cosmological epochs. However, an alternative explanation could be that we are not sensitive to those red galaxies at extreme redshift, since our study is based on H-band selected catalogues, which at z = 7 are sampling purely the far UV (λ ~ 2000 Å) rest-frame emission from young stars. Thus the disappearance of dusty or old galaxies could simply be a selection effect. In the future, deep infrared selected samples at longer wavelengths will be fundamental to answering this question.
The central result of our paper is related to the evolution of the GSMF as a function of redshift, in which we detect a clear decrease with increasing redshift, at both high and low masses. Adopting a Schechter parametrization at all redshift, and including the effects due to the Eddington bias, we quantify this evolution by looking at the best fit parameters α, M∗ and Φ∗ along with their errors. We find that these parameters are well constrained up to z = 6, while at z = 7 the increasing uncertainty in the estimate of stellar masses and the small size of our sample prevent us from deriving robust constraints on these parameters, and only the total mass density ρM is robustly derived. We find that the slope of the low mass side of the GSMF is relatively constant at about α = −1.6 at 4 <z< 6. This slope is, however, significantly steeper than the slope up to z ≃ 1, indicating that a progressive steepening must occur at intermediate redshifts. We also find that most of the evolution of the GSMF results from a combination of density evolution and mass evolution (both Φ∗ and M∗ increase with cosmic time). In particular, M∗ shifts from log (M∗/M⊙) = 11 (a value close to M∗ at lower redshift) to log (M∗/M⊙) ≃ 10.4 at z = 6. We caution however that both trends are only marginally significant.
Adopting our parametrization of the GSMF, we computed the stellar mass density (SMD) of galaxies at z = 4 − 7 by integrating the observed GSMF down to 108 M⊙ and compared it with the integrated value of the star formation rate density (SFRD) over cosmic time, assuming a constant recycling fraction of 28%. We found that the time integral of the SFRD is in overall agreement with our measurements at z> 4 when we adopt the estimated parametrization by Behroozi et al. (2013) or Madau & Dickinson (2014), although other parametrizations can be quite discrepant.
The observed evolution of the GSMF with redshift can also provide indications on the expected growth-rate of galaxies at the high-mass end. Using a simple argument based on object number conservation, without taking into account the correction for merging as done in Papovich et al. (2011) and in Behroozi et al. (2013), from Fig. 10 we can derive for galaxies at a fixed density of 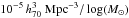 a mean SFR of ~290 M⊙ yr-1 from z = 6 to z = 4. To compute this quantity, we have adopted the best fit of the GSMFs with the Eddington bias correction, as detailed in Sect. 6.
a mean SFR of ~290 M⊙ yr-1 from z = 6 to z = 4. To compute this quantity, we have adopted the best fit of the GSMFs with the Eddington bias correction, as detailed in Sect. 6.
If we compare this star formation rate with the SFR Function of Smit et al. (2012) at 4 ≤ z ≤ 6, it is clear that the massive galaxies we have found at the massive tail of the GSMF at z ≥ 4 are probably not represented by the typical UV bright (and characterized by low dust extinction) population found by HST, but represent plausibly a dusty starburst phase in the life of these galaxies. Thus, the massive galaxies we find in the exponential tail of the GSMF at z ≥ 4 can plausibly be the results of very active phases, which have been detected in the sub-mm regime and that will represent an exploratory field for ALMA in the near future. Alternatively, the SFR derived by UV light using LBGs at high-z can be underestimated by a factor of 2–3, as recently suggested by Castellano et al. (2014). An important aspect here is related to the intrinsic uncertainties of the simple number conservation approach adopted, which does not take into account the effects of merging and the one-to-one correspondence between mass and UV light/SFR. A detail comparison with theoretical predictions can partially alleviate this issue.
We have demonstrated the unique synergy of CANDELS, HUGS, and SEDS in the analysis of the GSMF at high redshifts extending to low stellar masses. In particular these surveys take advantage of a combination of wide and deep data, which allows us to reduce the impact of cosmic variance and the degeneracies between the parameters of the Schechter function, used to fit the observed GSMF. The final CANDELS survey will more than double the present area available, adding data from the COSMOS, EGS, and GOODS-North fields. It will be complemented by the deep HUDF12 data and also by HST images of the Hubble Frontier Fields initiative, offering a further a step forward in our understanding of the high-redshift GSMF before the advent of the JWST and the ELTs.
Online material
Appendix A: Comparison of the GSMFs obtained with different recipes
 |
Fig. A.1 Comparison of the GSMF obtained with different photometric redshift recipes. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South and UDS fields with the Bayesian photometric redshifts is shown by the black triangles and the solid continuous curves. The red triangles, green circles, cyan triangles, magenta and pink asterisks show the GSMFs obtained using the individual photometric redshifts of five different groups that have been used to derive the Bayesian photo-z described in Dahlen el al. (2013). |
 |
Fig. A.2 Comparison of the GSMF obtained with different star formation histories. The stellar mass function of galaxies at z ≥ 3.5 in the CANDELS GOODS-South and UDS fields with our standard BC03 fit (exponentially declining SFHs) is shown by the black triangles and the solid continuous curves. The red squares and the blue stars show the GSMFs derived using exponentially increasing and a t2/τ × exp( − t/τ) SFH, respectively. All these star formation histories have been tested without the nebular contribution. |
 |
Fig. A.3 Comparison of the GSMF with and without an allowed nebular contribution. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South and UDS fields with our standard BC03 fit (exponentially declining SFHs and no nebular contribution) is shown by the black triangles and the solid continuous curves. The blue asterisks show the GSMF derived using BC03 models and exponentially declining SFHs, but this time including the contribution of nebular lines and nebular continuum. |
 |
Fig. A.4 Stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS UDS field (blue squares) is compared with the one derived from the GOODS-South data (black circles). At 6.5 <z< 7.5 the fit to the data point was not derived due to the small range in mass of the observed data in the individual fields. |
 |
Fig. A.5 Comparison of the GSMF with and without AGN. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South field considering only normal galaxies is shown by the black triangles. The red asterisks show the derived GSMF including AGN. |
In this section we show the comparison of the GSMF derived with our standard approach (GOODS-South and UDS fields, Bayesian photometric redshifts, BC03 library (Bruzual & Charlot 2003), exponential declining SFHs, no nebular contribution, no AGN) against the different GSMFs obtained varying only one ingredient at a time. Figure A.1 shows the GSMF at 3.5 <z< 7.5 obtained with different photometric redshift recipes available within the CANDELS team (Dahlen el al. 2013). Figure A.2 investigates the impact of different SFHs, Fig. A.3 shows the effect of the nebular contribution on the mass estimates. Finally, Figs. A.4 and A.5 illustrate the cosmic variance effect (or field-to-field variation) and the contribution of AGN to the GSMF. In this case we must point out that the information available for the UDS field (X-ray coverage, deep spectroscopy, variability) is not equivalent to the rich data set in GOODS-South, so at the present stage only some type-1 AGN can be found in the current UDS galaxy sample adopted in this paper. For this reason only the GOODS-South field has been used to carry out the comparison in Fig. A.5.
Appendix B: The correction of the Eddington bias
As already discussed in the main text, the stellar mass of a single galaxy is not unequivocally determined due to the uncertainties on the photometric redshift determination and on the mass-to-light conversion adopted to derive the stellar mass from the observed SED. These uncertainties must be properly taken into account when the observed data points of the mass function are fitted with a parametric function. This is the so-called Eddington bias (Eddington 1913), and as we will show here it could systematically affect the derivation of the Schechter parameters for the observed mass function.
To correct for this effect we used the probability distribution function in mass PDF(M | z) that we derived for each individual galaxy during our SED fitting procedure, as described in Sect. 4.1.1. For each galaxy in a given redshift and mass bin (i.e. 3.5 ≤ z ≤ 4.5 and M1 ≤ M ≤ M2), we summed up all the individual PDF(M | z) in the given redshift interval, after normalizing them to unit probability. This procedure gives the probability P(Mj,Mi) for a galaxy with an observed mass Mj (resulting from the best fit of its SED) to have a mass Mi still compatible with its photometry and photometric redshifts PDF(z) derived from the Bayesian analysis, as described in Sect. 2.3.
Figure B.1 shows the probability distribution functions for the GOODS-South and UDS fields in different mass bins, both at 3.5 ≤ z ≤ 4.5 (top) and at 5.5 ≤ z ≤ 6.5 (bottom). The dark-green curves are associated with galaxies in the bin centred at log (M/M⊙) = 8.9, while red, blue, green, cyan and black curves are associated with galaxies with masses log (M/M⊙) of 9.3, 9.7, 10.1, 10.7 and 11.1 respectively. For comparison, we plot on the same figure also the PDF(M) adopted by Ilbert et al. (2013) at z = 4, which is the product of a Gaussian with σ = 0.5 and a Lorentzian distribution 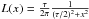 with τ = 0.04 ∗ (1 + z). The CANDELS PDFs shown in Fig. B.1 are based on the BC03 stellar library and on the choice of physical parameters (star formation histories, age, metallicity, dust extinction, IMF) adopted in this paper. The PDFs could vary slightly by adopting different ingredients. However, as shown in the main text, the uncertainties due to photometric scatter and photometric redshift uncertainties are much larger than those due to different choices of the physical ingredients.
with τ = 0.04 ∗ (1 + z). The CANDELS PDFs shown in Fig. B.1 are based on the BC03 stellar library and on the choice of physical parameters (star formation histories, age, metallicity, dust extinction, IMF) adopted in this paper. The PDFs could vary slightly by adopting different ingredients. However, as shown in the main text, the uncertainties due to photometric scatter and photometric redshift uncertainties are much larger than those due to different choices of the physical ingredients.
 |
Fig. B.1 Probability distribution functions (PDFs) of stellar mass for galaxies with measured stellar mass M at different masses and redshifts, resulting from the Monte Carlo simulations described in the text. The PDFs were averaged over all galaxies contained in contiguous bins with separation in mass of 0.2 in log (M), although we plot here only a few examples. The upper panel presents the PDFs at z = 4 ± 0.5, the lower panel at z = 6 ± 0.5. In both panels the dark-green curves are associated with galaxies in the bin centred at log (M/M⊙) = 8.9, while red, blue, green, cyan, and black curves are associated with galaxies with masses log (M/M⊙) of 9.3, 9.7, 10.1, 10.7 and 11.1 respectively. Solid lines refer to GOODS-South, dashed to UDS. The dotted green line shows for comparison the PDF adopted at all masses by Ilbert et al. (2013) at z = 4. |
From this plot we can draw some conclusions. First, and most important, the error in the mass estimation is not constant at all masses, as usually assumed (e.g. Ilbert et al. 2013): it is indeed smaller for higher-mass galaxies than for lower ones. This is expected since larger photometric errors lead to wider ranges of acceptable photometric redshifts and spectral models. We also note that the error is not symmetric and, especially at M ≥ 109 − 10 M⊙ starts to show a tail towards lower masses. The second important aspect is that at higher redshifts the combined PDFs are wider and the asymmetry is more pronounced than at z = 4, due to a combination of larger photometric uncertainties and progressive dimming of the galaxies for a given stellar mass. Thus, this plot shows the relative enhancement of the uncertainties in PDFs towards low-mass objects, independent of the adopted method for the stellar mass derivation. We finally note that the PDF(M | z) adopted by Ilbert et al. (2013) is smaller than our own, at the same mass and redshift, and substantially smaller than our own for faint galaxies. Given the higher S/N and quality of our photometric data, this may likely reflect a more conservative estimate of the implied errors in our computation, which have been derived adopting a different technique w.r.t. Ilbert et al. (2013).
Armed with this full characterization of the error on the estimated mass, we can evaluate the impact of such errors on the estimate of the (binned) GSMF. This is accomplished by convolving any input GSMF with the error distribution of Fig. B.1, at the corresponding redshift. For any given input GSMF we compute its expected values Φ(Mj) in the same mass bins (with a step of 0.2 in log (M)) used to derive the various PDF(M | z). The expected mass function in output is 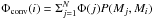 , where N is the number of bins adopted to compute the PDF(M | z).
, where N is the number of bins adopted to compute the PDF(M | z).
To illustrate the effect of this procedure, and the differences with respect to the previous analysis, we first take a representative input mass function (with α ≃ − 1.6 and M∗ ≃ 11) and convolve it with the PDF of Ilbert et al. (2013) at z = 4, namely a constant function at all masses. Figure B.2 shows the convolved mass function (empty blue squares) resulting from the intrinsic mass function (solid line) after applying the convolution process described above. We obtain a behaviour for the convolved GSMF similar to what has been found by Ilbert et al. (2013; their Fig. A.2), namely that the low-mass side is unaffected by the Eddington bias while the density at the high-mass end is enhanced.
 |
Fig. B.2 Effect of different prescription of the Eddington bias on the observed GSMF. The black line shows a Schechter function representing a GSMF with α ≃ − 1.6 and M∗ ≃ 11. The open blue squares show the resulting GSMF in bins of 0.2 in log M after convolution with a constant PDF at all masses, as adopted by Ilbert et al. (2013) at z = 4. The green filled squares represent the GSMF after convolution with the more realistic mass-dependent PDF that widens when mass decreases as we find in CANDELS (Fig. B.1). |
Then, we consider an error distribution similar to that found in CANDELS, i.e. with larger uncertainties at lower masses (Fig. B.1). We adopt the same functional form of Ilbert et al. (2013), namely the product of a Gaussian and a Lorentzian distributions, but we let the σ of the Gaussian change as a function of mass in order to coarsely reproduce the observed PDFs at z = 4 (hence smaller than the Ilbert et al. (2013) one at log (M/M⊙) > 10.3 and larger at smaller masses). Figure B.2 shows with filled green squares the GSMF resulting from the same intrinsic mass function (solid line) adopted in Fig. B.2 after the convolution process with a variable PDF in mass.
The combination of wider PDFs at lower masses and asymmetric distributions has an interesting behaviour on the GSMF shape: in the low-mass regime, M ≤ 109 M⊙, the error is symmetric and contributes to a slight enhancement in the number density of galaxies at the low-mass end, typically fitted with a power law. This results into a steepening of the GSMF. According to Eddington (1913), the effect is higher for steeper distributions and for larger errors. At the high-mass side, instead, the errors in mass are smaller and show an asymmetry towards lower masses. As a consequence, the exponential tail of the mass function is less affected by this scatter, and the observed data points are a good representation of the intrinsic GSMF, at least at z = 4 for the CANDELS GOODS-South and UDS fields. This behaviour is markedly different from what is derived assuming instead a constant error on PDF(M | z), even if the average error is adopted.
Moving to higher redshift, we find that at z = 5 the situation is similar to z = 4, while at z = 6 the effect of noise in the mass estimate becomes more severe and hence the correction for the Eddington bias is larger and more uncertain, as shown in Fig. B.1 (lower panel). Figure B.3 shows the effect of the Eddington bias correction at z = 6. The wide uncertainties in mass, both for faint and for bright objects, affect the GSMF at all scales, producing a steepening of the low-mass side and a pronounced increase of the exponential tail at high masses.
 |
Fig. B.3 Effect of the Eddington bias on the observed GSMF at z = 6 (black dots). The black line shows a Schechter function representing the resulting best fit GSMF at z = 6. The open blue squares show the resulting GSMF after convolution with the observed PDFs at z = 6 (Fig. B.1, bottom panel). |
For instance, we find that there is a small but non-negligible probability (~10-3) for a galaxy at z = 6 to be scattered from a mass of 109.3 M⊙ to 1010.5 M⊙, while it is ~10-6 at z = 4.
At z ≃ 7 these effects become so large that a proper treatment of the Eddington bias is simply impossible with the present data. For instance, the probability that the same galaxy at a mass of 109.3 M⊙ is scattered to 1010.5 M⊙ is as large as ~10-2. Thus if we observe a density of galaxies of Φ = 10-5 Mpc-3 Mag-1 at M = 1010.5 M⊙, this can be entirely due to galaxies at M = 109.3 M⊙ (with Φ = 10-3 Mpc-3 Mag-1) that are scattered to higher masses due to uncertainties in their stellar mass estimation. Since this correction is so important at the high-mass end of the z> 6 GSMF and the derivation of the PDFs at such low levels of probability depends critically on the details (photometric redshifts, stellar libraries adopted, star formation histories, grid of age, dust, metallicity), we can conclude that at the present stage the Eddington bias correction at z = 7 is highly uncertain. Moreover, at z = 7 the PDFs are very noisy due also to the low number statistics (at mass greater than 1010.3 M⊙ we have only 4 galaxies in the whole GOODS-South and UDS fields).
The derivation of the best-fitting Schechter functions have been carried out using the formalism described above. For any possible combination of the Schechter parameters α, M∗, and Φ∗, we compute the convolved GSMF using the observed PDFs in mass and we compare it with the observed mass function. We scan the three parameters of the Schechter function to find the best fit solution by a χ2 minimization. The GSMFs presented in the main text have been computed accordingly.
We note that, for the reasons described above, we decided not to apply the proper correction for the Eddington bias in the z = 7 GSMF. We adopt at z = 7 the same PDFs derived at z = 6, which are less noisy, as a conservative assumption. The small range in masses sampled by our GSMF at z = 7 results in large uncertainties in the best fit Schechter function parameters due to degeneracies between α, M∗, and Φ∗, as shown in Fig. 11. We have verified that due to these degeneracies the parameter space allowed at 1σ by the present data is wide and it does not depend strongly on whether we adopt the PDFs at z = 6 or the ones determined at z = 7 to correct the Eddington bias in the redshift range 6.5 <z< 7.5.
Appendix C: The impact of neglecting to correct for Eddington bias at high redshift
In Sect. 6 we have shown that the uncertainties in the measurement of the galaxy stellar mass do produce a systematic effect in the output GSMF, that must be taken into account when one derives the best-fitting Schechter parameters. However, we have also shown that accurate corrections for this effect are difficult to estimate, partly because they are model-dependent and partly because of the limited statistics available, especially at the highest redshifts.
For the sake of completeness, we report here the results on the GSMF fitting without the corrections for the Eddington bias. This is useful to understand what are the uncertainties at work when one is dealing with the mass function, and to warn the reader about the consequences of neglecting or underestimating this correction. We would like to stress that, given the very high quality of the data used here, other surveys with data of lower S/N or narrower wavelength range are even more affected.
Following the technique described in the previous sections, but removing any correction for the Eddington bias, we have obtained the GSMF that is shown in Fig. C.1. The derived uncertainties on the Schechter function parameters α, M∗ and Φ∗, are also shown in Fig. C.2.
 |
Fig. C.1 GSMFs from z = 4 to z = 7 in the CANDELS UDS and GOODS-South fields. At variance with the main paper, we have neglected here the effects of the uncertainties in the stellar mass (the so-called Eddington bias). The error bars take into account the Poissonian statistics and the uncertainties derived through the Monte Carlo simulations. The solid continuous curves show the best-fitting Schechter function. |
Mass function best fit parameters.
Stellar mass density at 3.5 <z< 7.5.
It is immediately clear that the results are significantly different from our main analysis. The slope α is steeper than our best fit and further steepens with redshift moving from α = −1.8 at z = 4 to α ≃ − 2 at z = 6. The characteristic mass log (M∗), on the contrary, evolves only marginally from z = 4 to z = 6. This is exactly what is predicted by our analysis of the Eddington bias, that is expected to artificially steepen the slope (at all redshifts) and progressively increase the GSMF in our higher redshift bins.
These changes are also reflected in the derived evolution of the stellar mass density that is reported in Fig. C.3. As a result of the steeper slope and higher M∗, the resulting ρM is significantly above the integrated evolution of the star formation rate density.
These results underline the importance of a careful description of the Eddington bias in the estimate of the GSMF.
 |
Fig. C.2 Evolution of the three parameters (α, M∗, Φ∗) of the GSMF with redshift, neglecting the effect of the Eddington bias. The bottom-right panel shows the dependencies of the Stellar Mass Density (ρM in unit of M⊙ Mpc-3) from the parameter α. The stars mark the position of the best fit of the observed GSMF with a Schechter function, while the triangles indicate the position of the best fit from the maximum likelihood procedure. |
 |
Fig. C.3 Redshift evolution of the stellar mass density (SMD) at 3.5 <z< 7.5 obtained in the CANDELS UDS and GOODS-South fields presented in this paper (black points), when the effect of uncertainties in the stellar mass (the so-called Eddington bias) are not taken into account. The SMD is compared to the lower redshift data from different surveys. ρM is in units of M⊙ Mpc-3 and has been obtained by integrating the best fit mass functions from Mmin = 108 M⊙ to Mmax = 1013 M⊙. All the SMDs have been converted to a Salpeter IMF for comparison. The error bars of the CANDELS data have been computed using the same Monte Carlo simulations developed to derive the uncertainties on the Schechter function parameters. The short-dashed line is the stellar mass density obtained integrating over cosmic time the star formation rate density (SFRD) of Hopkins & Beacom (2006). The long-dashed line is the SMD from the SFRD of Reddy & Steidel (2009). The solid line is the SMD obtained by integrating the SFRD of Behroozi et al. (2013), while the dotted line is the SMD derived by integrating the new fit of the Hopkins & Beacom (2006) carried out by Behroozi et al. (2013). The dotted-dashed line shows the SMD derived from the SFRD given by of Madau & Dickinson (2014). All the stellar mass densities obtained by integrating the different SFRDs assume a constant recycling fraction of 28%. |
Acknowledgments
We warmly thank the referee for her/his constructive report. We acknowledge financial contribution from the agreement ASI-INAF I/009/10/0. This work is based on observations taken by the CANDELS Multi-Cycle Treasury Program with the NASA/ESA HST, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Observations were also carried out using the Very Large Telescope at the ESO Paranal Observatory under Programme IDs LP186.A-0898, LP181.A-0717, LP168.A-0485, ID 170.A-0788, ID 181.A-0485, ID 283.A-5052 and the ESO Science Archive under Programme IDs 60.A-9284, 67.A-0249, 71.A-0584, 73.A-0564, 68.A-0563, 69.A-0539, 70.A-0048, 64.O-0643, 66.A-0572, 68.A-0544, 164.O-0561, 163.N-0210, 85.A-0961 and 60.A-9120. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech. A.F. and J.S.D. acknowledge the contribution of the EC FP7 SPACE project ASTRODEEP (Ref. No: 312725). J.S.D. also acknowledges the support of the Royal Society via a Wolfson Research Merit Award, and the support of the ERC through an Advanced Grant.
References
- Anders, P., & Fritze-v., Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashby, M. L. N., Willner, S. P., Fazio, G. G., et al. 2013, ApJ, 769, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Bahcall, J. N. 1980, ApJ, 235, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Meert, A., Sheth, R. K., et al. 2013, MNRAS, 436, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010, ApJ, 709, 133 [Google Scholar]
- Bower, R. G., Benson, A. J., & Crain, R. A. 2012, MNRAS, 422, 2816 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G. 2007, in Stellar populations as building blocks of galaxies, Proc. IAU Symp. 241, eds. A. Vazdekis, & R. Peletier (Cambridge: Cambridge University Press) [arXiv:astro-ph/0703052] [Google Scholar]
- Bruzual, A. G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Cirasuolo, M., Dunlop, J. S., et al. 2011, MNRAS, 413, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Sommariva, V., Fontana, A., et al. 2014, A&A, 566, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chary, R.-R. 2008, ApJ, 680, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Zitrin, A., Carrasco, M., et al. 2013, ApJ, 762, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R. S., et al. 2014, Rev. Mod. Phys., 86, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Mobasher, B., Faber, S. M., et al. 2013, ApJ, 775, 93 [Google Scholar]
- Dickinson, M., Papovich, C., Ferguson, H. C., & Budavári, T. 2003, ApJ, 587, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Drory, N., Bender, R., Feulner, G., et al. 2004, ApJ, 608, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K., Conselice, C. J., Mortlock, A., et al. 2014, MNRAS, 444, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S. 2013, ASSL, 396, 223 [Google Scholar]
- Dunlop, J. S., Cirasuolo, M., & McLure, R. J. 2007, MNRAS, 376, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Ellis, R. S., McLure, R. J., Dunlop, J. S., et al. 2013, ApJ, 763, 7 [Google Scholar]
- Fontana, A., Pozzetti, L., Donnarumma, I., et al. 2004, A&A, 424, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontana, A., Salimbeni, S., Grazian, A., et al. 2006, A&A, 459, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontana, A., Santini, P., Grazian, A., et al. 2009, A&A, 501, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontana, A., Vanzella, E., Pentericci, L., et al. 2010, ApJ, 725, 205 [Google Scholar]
- Fontana, A., Dunlop, J. S., Paris, D., et al. 2014, A&A, 570, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, A., Grazian, A., Fontana, A., et al. 2013, ApJS, 206, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- González, V., Labbé, I., Bouwens, R. J., et al. 2011, ApJ, 735, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., De Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B., Maraston, C., Monaco, P., et al. 2011, MNRAS, 415, 3571 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hutchings, J. B. 1982, ApJ, 255, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Ellis, R. S., McLure, R. J., et al. 2013, ApJS, 209, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fevre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 716, 103 [Google Scholar]
- Labbé, I., Oesch, P. A., Bouwens, R. J., et al. 2013, ApJ, 777, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K.-S., Ferguson, C. H., Wiklind, T., et al. 2012, ApJ, 752, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, Y., Wechsler, R. H., Somerville, R. S., et al. 2014, ApJ, 795, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C., Pforr, J., Renzini, A., et al. 2010, MNRAS, 407, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., van Dokkum, P. G., Forster Schreiber, N. M., et al. 2009, ApJ, 701, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., Whitaker, K. E., & Brammer, G. 2010, ApJ, 725, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Dunlop, J. S., de Ravel, L., et al. 2011, MNRAS, 418, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- Minowa, Y., Kobayashi, N., Yoshii, Y., et al. 2005, ApJ, 629, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Coil, A. L., Aird, J., et al. 2013, ApJ, 767, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Mobasher, B., Dahlen, T., Ferguson, H. C., et al. 2015, ApJS, submitted [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nagamine, K., Ostriker, J. P., Fukugita, M., & Cen, R. 2006, ApJ, 653, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Labbé, I., Bouwens, R. J., et al. 2013a, ApJ, 772, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2013b, ApJ, 773, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Finkelstein, S. L., Ferguson, H. C., Lotz, J. M., & Giavalisco, M. 2011, MNRAS, 412, 1123 [NASA ADS] [Google Scholar]
- Peng, Y., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Lilly, S. J., Renzini, A., & Carollo, M. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Fontana, A., Vanzella, E., et al. 2011, ApJ, 743, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., & Villar, V. 2008, ApJ, 675, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Pforr, J., Maraston, C., & Tonini, C. 2012, MNRAS, 422, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Retzlaff, J., Rosati, P., Dickinson, M., et al. 2010, A&A, 511, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandage, A., Tammann, G. A., & Yahil, A. 1979, ApJ, 232, 352 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2012a, A&A, 538, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Rosario, D. J., Shao, L., et al. 2012b, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Ferguson, H. C., Fontana, A., et al. 2014, ApJ, submitted [arXiv:1412.5180] [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & Vacca, W. D. 1998, ApJ, 497, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2013, ApJ, 777, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Shim, H., Chary, R.-R., Dickinson, M., et al. 2011, ApJ, 738, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Smit, R., Bouwens, R. J., Franx, M., et al. 2012, ApJ, 756, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Fontana, A., Lamastra, A., et al. 2014, A&A, 571, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, ARA&A, 48, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Schenker, M. A., Ellis, R. S., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Straatman, C. M. S., Labbé, I., Spitler, L. R., et al. 2014, ApJ, 783, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2014, ApJ, 783, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tonini, C., Maraston, C., Thomas, D., et al. 2010, MNRAS, 403, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Trevese, D., Kron, R. G., Majewski, S. R., Bershady, M. A., & Koo, D. C. 1994, ApJ, 433, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Villforth, C., Koekemoer, A. M., & Grogin, N. A. 2010, ApJ, 723, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., De Lucia, G., Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 384, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Trentham, N., & Hopkins, A. M. 2008, MNRAS, 385, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Di Matteo, T., & Croft, R. 2013, MNRAS, 429, 2098 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Median uncertainties on the GSMF due to photometric redshifts, Monte Carlo simulations or SFH+NEB.
All Figures
 |
Fig. 1 Black dots: all the galaxies in the CANDELS GOODS-South field; red dots: galaxies in the deepest region (HUDF). The purple big squares indicate galaxies with robust spectroscopic redshift in the range 3.5 ≤ z ≤ 7.5. The strict completeness mass vs. redshift for a magnitude limit of H160 = 26.0 (dark green). This curve has been derived from the maximally old galaxies in our synthetic library, corresponding to a formation redshift zform = 20, an E(B − V) = 0.1, metallicity of 0.2 Z⊙ and a declining SFH with timescale τ = 0.1 Gyr. The light-green curve shows the completeness-corrected limit corresponding to the shallower pointings in the GOODS-South and UDS fields (H160 = 26.0), while the blue curve represents the corresponding limit for our deepest area, the HUDF field (H160 = 28.0), once the mass limit has been extended taking into account the suitable correction for the M∗/L distribution. For comparison, the magenta curve (dashed) is the completeness limit in mass in the ERS field derived by Santini et al. (2012a) which corresponds to K = 25.5. |
| In the text | |
 |
Fig. 2 Relative mass uncertainty, ΔM/M, as a function of stellar mass for different redshift bins from z = 4 to z = 7. Black points are for galaxies in the GOODS-South field, while blue ones are for objects in the CANDELS UDS region. The mass uncertainty is a strong function of the mass of the galaxies, and as expected it is significantly poorer at higher redshifts. |
| In the text | |
 |
Fig. 3 Top left: comparison of the GSMF obtained with different photometric redshift recipes. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields derived using the Bayesian photometric redshifts is shown by the black triangles (non parametric 1/Vmax) and the solid continuous curve (parametric STY maximum likelihood). The error bars show the Poissonian uncertainties of each point. The red triangles, green stars, cyan triangles, magenta and pink asterisks show the GSMFs obtained using the individual photometric redshifts of different realizations that have been used to derive the Bayesian photo-z described in Dahlen el al. (2013). Top right: comparison of the GSMF obtained with different star formation histories. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields assuming BC03 exponentially declining SFHs is shown by the black triangles and the solid continuous curve. The red squares and the blue stars show the GSMFs derived using exponentially increasing and a delayed SFH, respectively. All these star formation histories have been tested without the nebular contribution. Bottom left: comparison of the GSMF with and without a nebular contribution. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South and UDS fields with BC03 exponentially declining SFHs and no nebular contribution is shown by the black triangles and the solid continuous curve. The blue asterisks show the GSMF derived using BC03 and exponentially declining SFHs but this time including allowance for the contribution of nebular lines and nebular continuum (NEB label). Bottom right: comparison of the GSMF in individual fields. The stellar mass function derived for galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS UDS field (empty blue squares) as compared with that derived from GOODS-South (filled black circles). |
| In the text | |
 |
Fig. 4 Comparison of the GSMF with and without AGN. The stellar mass function of galaxies at 3.5 ≤ z ≤ 4.5 in the CANDELS GOODS-South field without AGN (filled black triangles) and with the AGN included (red asterisks). The error bars show the Poissonian uncertainties of each point. The stellar masses for the AGN have been derived using the same technique adopted for normal galaxies. The solid continuous curve shows the Schechter function derived through a parametric STY maximum likelihood fit of the GSMF without AGN. |
| In the text | |
 |
Fig. 5 Various uncertainties in Log (Φ) as a function of stellar mass for different redshift bins from z = 4 to z = 7. Blue curves (SFH) indicate the uncertainties due to the different SFHs adopted in this work. Green curves (MCsim) are related to the Monte Carlo simulations described in paragraph 4.1. The red lines (Zphot) indicate the error introduced by different photometric-redshift solutions. Finally, the dark-green lines (CVar) indicate the error due to cosmic variance. |
| In the text | |
 |
Fig. 6 Stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS UDS and GOODS-South fields (blue filled and open circles). The error bars show the Poissonian uncertainties of each point with the errors derived through the Monte Carlo simulations added in quadrature. The masses are derived using the BC03 libraries with exponentially declining star formation histories, and without any contribution from nebular lines or continuum. AGN were not included in the present sample. The dotted lines indicate the GSMF at z = 0.6 in the UDS and GOODS-South fields. The dark-green pentagons show the mass function derived by González et al. (2011; G11), while the cyan stars indicate the result of Caputi et al. (2011; C11), which was obtained with a different stellar library (Bruzual 2007) that includes a stronger contribution from TP-AGB stars. The black triangles are from Pérez-González et al. (2008; PG08), the red (empty and filled) squares from Marchesini et al. (2009; M09) and Marchesini et al. (2010; M10), respectively. The magenta points are the GSMF of Santini et al. (2012a; S12). The grey circles come from Fontana et al. (2006; F06) while the magenta triangles are from Stark et al. (2009; S09). The red, orange, dark-yellow and green dashed lines show the best fit GSMFs of Lee et al. (2012; L12), Ilbert et al. (2013; I13), Muzzin et al. (2013; M13) and Duncan et al. (2014; D14), respectively. All the mass functions have been converted to a Salpeter IMF for comparison. The solid continuous curves show the Schechter function derived through a parametric STY maximum likelihood fit. |
| In the text | |
 |
Fig. 7 Stellar mass vs. UV absolute magnitude M1400 for galaxies at 3.5 <z< 4.5 in the GOODS-South field. The blue solid line is the relation (at 1700 Å rest frame) found by Lee et al. (2012) for LBGs selected with the B − V vs. V − z colour criterion and a S/N in the z850 band greater than 6. The red solid line represents the relation as derived by González et al. (2011) at z = 4, for a similar rest-frame wavelength of 1500 Å. The grey triangles show the M/L relation derived by Stark et al. (2013). The dark-green line is the best fit to our own results assuming a constant mass-to-light ratio, or equivalently a slope −0.4 between stellar mass and absolute magnitude. The orange line is the best fit of Duncan et al. (2014). All the relations have been converted to a Salpeter IMF for comparison. Magenta points show galaxies undetected in the deep K-band Hawk-I imaging, while green dots represent objects not detected in 3.6 and 4.5 μm in the Spitzer SEDS imaging. |
| In the text | |
 |
Fig. 8 Comparison between the mass function derived by assuming a constant mass-to-light ratio (red squares), relation between mass and L1400 light derived by González et al. (2011; green stars), and the one derived in this work for the GOODS-South and UDS fields (blue circles). The error bars show only the Poissonian uncertainties of each point. The original GSMF presented González et al. (2011) is shown by dark-green symbols. |
| In the text | |
 |
Fig. 9 Example SEDs of galaxies at 3.5 < z < 4.5 with M > 1010.5 M⊙ and M1400 > −18.5. Their SEDs, especially in the IRAC bands, indicate that they are really massive objects at high redshift and that the nebular contribution is not dominant. The objects ID = 8785 and 17 749 are quite old (age /τ ≥ 8), while ID = 4466 and 13299 have E(B − V) ≥ 0.4. All these galaxies are characterized by very red colours, and thus cannot be selected by standard LBG selection criteria based on UV rest-frame colours. Because of their large masses, however, they represent a relatively rare population, which can contribute significantly to the high-mass tail of the mass function at z = 4. |
| In the text | |
 |
Fig. 10 GSMFs from z = 4 to z = 7 in the CANDELS UDS and GOODS-South fields. The error bars take into account the Poissonian statistics, the cosmic variance and the uncertainties derived through the Monte Carlo simulations. The solid continuous curves show the Schechter function derived through a best-fit approach which corrects the observed data points for the Eddington bias. |
| In the text | |
 |
Fig. 11 Evolution of the three parameters (α, M∗, Φ∗) of the GSMF with redshift. The bottom-right panel shows the dependencies of the Stellar Mass Density (ρM in unit of M⊙ Mpc-3) from the parameter α. The stars mark the position of the best fit of the observed GSMF with a Schechter function, obtained by correcting for the Eddington bias as explained in detail in Appendix B. A clear trend with redshift is evident up to z = 6, while at z = 7 the parameters are basically unconstrained. |
| In the text | |
 |
Fig. 12 Redshift evolution of the stellar mass density (SMD) at 3.5 <z< 7.5 obtained by integrating the GSMFs presented in this paper (black points). The evolving SMD at high redshift is compared to the lower redshift results from different surveys. ρM is in units of M⊙ Mpc-3 and has been obtained by integrating the best-fitting mass functions from Mmin = 108 M⊙ to Mmax = 1013 M⊙. All the SMDs have been converted to a Salpeter IMF for comparison. The error bars of the CANDELS data have been computed using the same Monte Carlo simulations developed to derive the uncertainties on the Schechter function parameters. The short-dashed line is the stellar mass density obtained integrating over cosmic time the star formation rate density (SFRD) of Hopkins & Beacom (2006). The long-dashed line is the SMD inferred from the SFRD of Reddy & Steidel (2009). The solid line is the SMD obtained from the SFRD of Behroozi et al. (2013), while the dotted line is the SMD derived by the new fit of the Hopkins & Beacom (2006) carried out by Behroozi et al. (2013). The dotted-dashed line shows the SMD derived from the SFRD of Madau & Dickinson (2014). All the stellar mass densities obtained by integrating the different SFRDs assume a constant recycling fraction of 28%. |
| In the text | |
 |
Fig. A.1 Comparison of the GSMF obtained with different photometric redshift recipes. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South and UDS fields with the Bayesian photometric redshifts is shown by the black triangles and the solid continuous curves. The red triangles, green circles, cyan triangles, magenta and pink asterisks show the GSMFs obtained using the individual photometric redshifts of five different groups that have been used to derive the Bayesian photo-z described in Dahlen el al. (2013). |
| In the text | |
 |
Fig. A.2 Comparison of the GSMF obtained with different star formation histories. The stellar mass function of galaxies at z ≥ 3.5 in the CANDELS GOODS-South and UDS fields with our standard BC03 fit (exponentially declining SFHs) is shown by the black triangles and the solid continuous curves. The red squares and the blue stars show the GSMFs derived using exponentially increasing and a t2/τ × exp( − t/τ) SFH, respectively. All these star formation histories have been tested without the nebular contribution. |
| In the text | |
 |
Fig. A.3 Comparison of the GSMF with and without an allowed nebular contribution. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South and UDS fields with our standard BC03 fit (exponentially declining SFHs and no nebular contribution) is shown by the black triangles and the solid continuous curves. The blue asterisks show the GSMF derived using BC03 models and exponentially declining SFHs, but this time including the contribution of nebular lines and nebular continuum. |
| In the text | |
 |
Fig. A.4 Stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS UDS field (blue squares) is compared with the one derived from the GOODS-South data (black circles). At 6.5 <z< 7.5 the fit to the data point was not derived due to the small range in mass of the observed data in the individual fields. |
| In the text | |
 |
Fig. A.5 Comparison of the GSMF with and without AGN. The stellar mass function of galaxies at 3.5 ≤ z ≤ 7.5 in the CANDELS GOODS-South field considering only normal galaxies is shown by the black triangles. The red asterisks show the derived GSMF including AGN. |
| In the text | |
 |
Fig. B.1 Probability distribution functions (PDFs) of stellar mass for galaxies with measured stellar mass M at different masses and redshifts, resulting from the Monte Carlo simulations described in the text. The PDFs were averaged over all galaxies contained in contiguous bins with separation in mass of 0.2 in log (M), although we plot here only a few examples. The upper panel presents the PDFs at z = 4 ± 0.5, the lower panel at z = 6 ± 0.5. In both panels the dark-green curves are associated with galaxies in the bin centred at log (M/M⊙) = 8.9, while red, blue, green, cyan, and black curves are associated with galaxies with masses log (M/M⊙) of 9.3, 9.7, 10.1, 10.7 and 11.1 respectively. Solid lines refer to GOODS-South, dashed to UDS. The dotted green line shows for comparison the PDF adopted at all masses by Ilbert et al. (2013) at z = 4. |
| In the text | |
 |
Fig. B.2 Effect of different prescription of the Eddington bias on the observed GSMF. The black line shows a Schechter function representing a GSMF with α ≃ − 1.6 and M∗ ≃ 11. The open blue squares show the resulting GSMF in bins of 0.2 in log M after convolution with a constant PDF at all masses, as adopted by Ilbert et al. (2013) at z = 4. The green filled squares represent the GSMF after convolution with the more realistic mass-dependent PDF that widens when mass decreases as we find in CANDELS (Fig. B.1). |
| In the text | |
 |
Fig. B.3 Effect of the Eddington bias on the observed GSMF at z = 6 (black dots). The black line shows a Schechter function representing the resulting best fit GSMF at z = 6. The open blue squares show the resulting GSMF after convolution with the observed PDFs at z = 6 (Fig. B.1, bottom panel). |
| In the text | |
 |
Fig. C.1 GSMFs from z = 4 to z = 7 in the CANDELS UDS and GOODS-South fields. At variance with the main paper, we have neglected here the effects of the uncertainties in the stellar mass (the so-called Eddington bias). The error bars take into account the Poissonian statistics and the uncertainties derived through the Monte Carlo simulations. The solid continuous curves show the best-fitting Schechter function. |
| In the text | |
 |
Fig. C.2 Evolution of the three parameters (α, M∗, Φ∗) of the GSMF with redshift, neglecting the effect of the Eddington bias. The bottom-right panel shows the dependencies of the Stellar Mass Density (ρM in unit of M⊙ Mpc-3) from the parameter α. The stars mark the position of the best fit of the observed GSMF with a Schechter function, while the triangles indicate the position of the best fit from the maximum likelihood procedure. |
| In the text | |
 |
Fig. C.3 Redshift evolution of the stellar mass density (SMD) at 3.5 <z< 7.5 obtained in the CANDELS UDS and GOODS-South fields presented in this paper (black points), when the effect of uncertainties in the stellar mass (the so-called Eddington bias) are not taken into account. The SMD is compared to the lower redshift data from different surveys. ρM is in units of M⊙ Mpc-3 and has been obtained by integrating the best fit mass functions from Mmin = 108 M⊙ to Mmax = 1013 M⊙. All the SMDs have been converted to a Salpeter IMF for comparison. The error bars of the CANDELS data have been computed using the same Monte Carlo simulations developed to derive the uncertainties on the Schechter function parameters. The short-dashed line is the stellar mass density obtained integrating over cosmic time the star formation rate density (SFRD) of Hopkins & Beacom (2006). The long-dashed line is the SMD from the SFRD of Reddy & Steidel (2009). The solid line is the SMD obtained by integrating the SFRD of Behroozi et al. (2013), while the dotted line is the SMD derived by integrating the new fit of the Hopkins & Beacom (2006) carried out by Behroozi et al. (2013). The dotted-dashed line shows the SMD derived from the SFRD given by of Madau & Dickinson (2014). All the stellar mass densities obtained by integrating the different SFRDs assume a constant recycling fraction of 28%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


