| Issue |
A&A
Volume 571, November 2014
Planck 2013 results
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321553 | |
| Published online | 29 October 2014 | |
Planck 2013 results. XIII. Galactic CO emission
1
APC, AstroParticule et Cosmologie, Université Paris Diderot,
CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, SorbonneParis Cité, 10 rue Alice Domon et Léonie
Duquet, 75205
Paris Cedex 13,
France
2
Aalto University Metsähovi Radio Observatory,
Metsähovintie 114, 02540
Kylmälä,
Finland
3
African Institute for Mathematical Sciences,
6-8 Melrose Road, Muizenberg, Cape
Town, 7701
Rondebosch, South
Africa
4
Agenzia Spaziale Italiana Science Data Center,
via del Politecnico snc,
00133
Roma,
Italy
5
Agenzia Spaziale Italiana, Viale Liegi 26, Roma, Italy
6
Astrophysics Group, Cavendish Laboratory, University of
Cambridge, J J Thomson
Avenue, Cambridge
CB3 0HE,
UK
7
Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House,
Egerton Wharf, Birkenhead
CH41 1LD,
UK
8
Astrophysics & Cosmology Research Unit, School of Mathematics,
Statistics & Computer Science, University of KwaZulu-Natal,
Westville Campus, Private Bag
X54001, 4000
Durban, South
Africa
9
CITA, University of Toronto, 60 St. George St., Toronto, ON
M5S 3H8,
Canada
10
CNRS, IRAP, 9 Av.
colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
11
California Institute of Technology, Pasadena, California, USA
12
Centre for Theoretical Cosmology, DAMTP, University of
Cambridge, Wilberforce
Road, Cambridge
CB3 0WA,
UK
13
Centro de Estudios de Física del Cosmos de Aragón
(CEFCA), Plaza San Juan, 1, planta
2,
44001
Teruel,
Spain
14
Computational Cosmology Center, Lawrence Berkeley National
Laboratory, Berkeley,
California,
USA
15
Consejo Superior de Investigaciones Científicas
(CSIC), Madrid,
Spain
16
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
17
DTU Space, National Space Institute, Technical University of
Denmark, Elektrovej
327, 2800
Kgs. Lyngby,
Denmark
18
Département de Physique Théorique, Université de
Genève, 24 quai E.
Ansermet, 1211
Genève 4,
Switzerland
19
Departamento de Física Fundamental, Facultad de Ciencias,
Universidad de Salamanca, 37008
Salamanca,
Spain
20
Departamento de Física, Universidad de Oviedo, ,
Avda. Calvo Sotelo s/n,
33007
Oviedo,
Spain
21
Department of Astronomy and Astrophysics, University of
Toronto, 50 Saint George Street,
Toronto, Ontario,
Canada
22
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
23
Department of Electrical Engineering and Computer Sciences,
University of California, Berkeley, California, USA
24
Department of Physics & Astronomy, University of British
Columbia, 6224 Agricultural Road,
Vancouver, British
Columbia, Canada
25
Department of Physics and Astronomy, Dana and David Dornsife College
of Letter, Arts and Sciences, University of Southern California, ,
Los Angeles, CA
90089,
USA
26
Department of Physics and Astronomy, University College
London, London
WC1E 6BT,
UK
27
Department of Physics, Florida State University, ,
Keen Physics Building, 77 Chieftan
Way, Tallahassee,
Florida,
USA
28
Department of Physics, Gustaf Hällströmin katu 2a, University of
Helsinki, 00014
Helsinki,
Finland
29
Department of Physics, Nagoya University, ,
Chikusa-ku, 464-8602
Nagoya,
Japan
30
Department of Physics, Princeton University, ,
Princeton, New Jersey, USA
31
Department of Physics, University of California, ,
One Shields Avenue, Davis, California, USA
32
Department of Physics, University of California, ,
Santa Barbara, California, USA
33
Department of Physics, University of Illinois at
Urbana-Champaign, 1110 West Green
Street, Urbana,
Illinois,
USA
34
Dipartimento di Fisica e Astronomia G. Galilei, Università degli
Studi di Padova, via Marzolo
8, 35131
Padova,
Italy
35
Dipartimento di Fisica e Scienze della Terra, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
36
Dipartimento di Fisica, Università La Sapienza, ,
P. le A. Moro 2, 00185
Roma,
Italy
37
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria,
16, 20133
Milano,
Italy
38
Dipartimento di Fisica, Università degli Studi di
Trieste, via A. Valerio
2, 34127
Trieste,
Italy
39
Dipartimento di Fisica, Università di Roma Tor
Vergata, via della Ricerca
Scientifica, 1, 00139
Roma,
Italy
40
Discovery Center, Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen,
Denmark
41
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206, La Laguna, Tenerife,
Spain
42
European Space Agency, ESAC, Planck Science Office, Camino bajo del
Castillo, s/n,Urbanización
Villafranca del Castillo, Villanueva de la Cañada, 28691
Madrid,
Spain
43
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ
Noordwijk, The
Netherlands
44
Finnish Centre for Astronomy with ESO (FINCA), University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
45
Graduate School of Science and Engineering, Kagoshima
University, 1-21-35 Korimoto,
Kagoshima, 890-0065
Kagoshima,
Japan
46
Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University
of Helsinki, Helsinki,
Finland
47
INAF – Osservatorio Astrofisico di Catania,
via S. Sofia 78, 95123
Catania,
Italy
48
INAF – Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
49
INAF – Osservatorio Astronomico di Roma,
via di Frascati 33, 00040
Monte Porzio Catone,
Italy
50
INAF – Osservatorio Astronomico di Trieste,
via G.B. Tiepolo 11, 34131
Trieste,
Italy
51
INAF Istituto di Radioastronomia, via P. Gobetti 101, 40129
Bologna,
Italy
52
INAF/IASF Bologna, via Gobetti 101, 40129
Bologna,
Italy
53
INAF/IASF Milano, via E. Bassini 15, 20133
Milano,
Italy
54
INFN, Sezione di Bologna, via Irnerio 46, 40126
Bologna,
Italy
55
INFN, Sezione di Roma 1, Università di Roma Sapienza,
Piazzale Aldo Moro 2,
00185
Roma,
Italy
56
IPAG: Institut de Planétologie et d’Astrophysique de Grenoble,
Université Joseph Fourier, Grenoble 1/CNRS-INSU, UMR 5274, 38041
Grenoble,
France
57
IUCAA, Post Bag 4, Ganeshkhind, Pune University
Campus, 411 007
Pune,
India
58
Imperial College London, Astrophysics group, Blackett
Laboratory, Prince Consort
Road, London,
SW7 2AZ,
UK
59
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena,
CA
91125,
USA
60
Institut Néel, CNRS, Université Joseph Fourier Grenoble
I, 25 rue des
Martyrs, 38042
Grenoble,
France
61
Institut Universitaire de France, 103 bd Saint-Michel, 75005
Paris,
France
62
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
63
Institut d’Astrophysique de Paris, CNRS (UMR 7095),
98bis boulevard Arago,
75014
Paris,
France
64
Institute for Space Sciences, 077125
Bucharest-Magurale,
Romania
65
Institute of Astronomy and Astrophysics, Academia
Sinica, Taipei,
Taiwan
66
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
67
Institute of Astronomy, University of Tokyo,
2-21-1 Osawa, Mitaka,
Tokyo,
Japan
68
Institute of Theoretical Astrophysics, University of
Oslo, Blindern,
0315
Oslo,
Norway
69
Instituto de Astrofísica de Canarias, C/vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
70
Instituto de Física de Cantabria (CSIC-Universidad de
Cantabria), Avda. de los Castros
s/n, 39005
Santander,
Spain
71
Jet Propulsion Laboratory, California Institute of
Technology, 4800 Oak Grove
Drive, Pasadena,
California,
USA
72
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13
9PL, UK
73
Joint Astronomy Centre, 660 N. Aohoku Place, University
Park, Hilo,
Hawaii
96720,
USA
74
Kavli Institute for Cosmology Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
75
LAL, Université Paris-Sud, CNRS/IN2P3, 91898
Orsay,
France
76
LERMA, CNRS, Observatoire de Paris, 61 avenue de l’Observatoire, 75014
Paris,
France
77
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709,
CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
78
Laboratoire Traitement et Communication de l’Information, CNRS (UMR
5141) and Télécom ParisTech, 46 rue
Barrault, 75634
Paris, Cedex 13,
France
79
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble Cedex,
France
80
Laboratoire de Physique Théorique, Université Paris-Sud 11 &
CNRS, Bâtiment 210,
91405
Orsay,
France
81
Lawrence Berkeley National Laboratory, Berkeley, California, USA
82
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
83
McGill Physics, Ernest Rutherford Physics Building, McGill
University, 3600 rue
University, Montréal,
QC, H3A 2T8, Canada
84
MilliLab, VTT Technical Research Centre of Finland,
Tietotie 3, 02044
Espoo,
Finland
85
National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka, 181-8588
Tokyo,
Japan
86
National University of Ireland, Department of Experimental
Physics, Maynooth,
Co. Kildare,
Ireland
87
Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen,
Denmark
88
Nobeyama Radio Observatory, National Astronomical Observatory of
Japan, 462-2 Nobeyama, Minamimaki,
Minamisaku, 384-1305
Nagano,
Japan
89
Observational Cosmology, Mail Stop 367-17, California Institute of
Technology, Pasadena,
CA, 91125, USA
90
Optical Science Laboratory, University College London,
Gower Street, London, UK
91
SB-ITP-LPPC, EPFL, 1015
Lausanne,
Switzerland
92
SISSA, Astrophysics Sector, via Bonomea 265, 34136
Trieste,
Italy
93
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The Parade,
Cardiff, CF24 3AA, UK
94
Space Research Institute (IKI), Russian Academy of
Sciences, Profsoyuznaya Str,
84/32, 117997
Moscow,
Russia
95
Space Sciences Laboratory, University of California,
Berkeley, California, USA
96
Special Astrophysical Observatory, Russian Academy of
Sciences, Nizhnij Arkhyz,
Zelenchukskiy region, 369167
Karachai-Cherkessian Republic,
Russia
97
Stanford University, Dept of Physics, Varian Physics Bldg, 382 via Pueblo
Mall, Stanford,
California,
USA
98
Sub-Department of Astrophysics, University of Oxford,
, Keble Road, Oxford
OX1 3RH,
UK
99
Theory Division, PH-TH, CERN, 1211, Geneva 23, Switzerland
100
UPMC Univ Paris 06, UMR 7095, 98bis boulevard Arago, 75014
Paris,
France
101
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse, Cedex 4,
France
102
Universities Space Research Association, Stratospheric Observatory
for Infrared Astronomy, MS
232-11, Moffett
Field, CA
94035,
USA
103
University of Granada, Departamento de Física Teórica y del Cosmos,
Facultad de Ciencias, 18071
Granada,
Spain
104
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478
Warszawa,
Poland
Received:
22
March
2013
Accepted:
21
March
2014
Rotational transition lines of CO play a major role in molecular radio astronomy as a mass tracer and in particular in the study of star formation and Galactic structure. Although a wealth of data exists for the Galactic plane and some well-known molecular clouds, there is no available high sensitivity all-sky survey of CO emission to date. Such all-sky surveys can be constructed using the Planck HFI data because the three lowest CO rotational transition lines at 115, 230 and 345 GHz significantly contribute to the signal of the 100, 217 and 353 GHz HFI channels, respectively. Two different component separation methods are used to extract the CO maps from Planck HFI data. The maps obtained are then compared to one another and to existing external CO surveys. From these quality checks the best CO maps, in terms of signal to noise ratio and/or residual contamination by other emission, are selected. Three different sets of velocity-integrated CO emission maps are produced with different trade-offs between signal-to-noise, angular resolution, and reliability. Maps for the CO J = 1 → 0, J = 2 → 1, and J = 3 → 2 rotational transitions are presented and described in detail. They are shown to be fully compatible with previous surveys of parts of the Galactic plane as well as with undersampled surveys of the high latitude sky. The Planck HFI velocity-integrated CO maps for the J = 1 → 0, J = 2 → 1, and J = 3 →2 rotational transitions provide an unprecedented all-sky CO view of the Galaxy. These maps are also of great interest to monitor potential CO contamination of the Planck studies of the cosmological microwave background.
Key words: ISM: molecules
© ESO, 2014
1. Introduction
This paper, one of a set associated with the 2013 release of data from the Planck1 mission (Planck Collaboration I 2014), describes the construction and validation of full-sky carbon monoxide (CO) maps from Planck data.
The interstellar medium (ISM) represents about 10–15% of the total mass of the Milky Way. The neutral part of the ISM is a mixture of atomic and molecular gas, the latter containing around 50% of its mass whilst filling only a tiny fraction of the volume (see Ferrière 2001; Cox 2005, for a general introduction and review). The cold neutral gas is confined close to the Galactic disk mid-plane (about 100 pc scale height), in clouds with varying molecular-to-atomic ratios. Molecular clouds are the sites of star formation, and as such, play a pivotal role in the interstellar matter cycle. Giant molecular clouds (GMCs) are the largest self-gravitating structures in spiral galaxies such as the Milky Way, and are also the most massive entities, reaching several times 106 M⊙. Molecular clouds were discovered via the rotational emission line J = 1 → 0 of carbon monoxide in its fundamental electronic and vibrational levels (Wilson et al. 1970; Penzias et al. 1972). Contrary to the atomic component of the neutral ISM, which is directly observable via the spin-flip HI λ21 cm line, the bulk of molecular hydrogen is not directly observable in molecular clouds. Because CO is abundant, easily excited by collisions with H2, and easily observable from the ground, it is considered a good tracer of the cold molecular component of the ISM. It is also a dominant coolant of molecular gas. The ability to detect the CO J = 1 → 0 line from the ground allows large surveys to be performed (Dame et al. 2001; Dame & Thaddeus 2004; Wilson 2005), leading to observational evidence that the molecular gas is structured in clouds that are turbulent and harbour the formation of all stars in the Galaxy. The astrophysical importance of carbon monoxide can hardly be over-emphasized.
Large-scale surveys the J = 1 → 0 line of 12CO, but also of 13CO and C18O isotopologues, have been carried out with meter-sized radio telescopes, mostly through the fundamental rotational transition. The most complete CO(1 → 0) survey is that of Dame et al. (2001), which covers the Milky Way at Galactic latitudes | b | ≤ 30°, with an effective spatial resolution of 0.14° in most regions. CO and isotopologues were observed with the 4 m NANTEN telescope providing spectral maps at slightly higher spatial resolution, towards specific GMCs (Mizuno & Fukui 2004). In addition, there exist a wealth of smaller CO(1 → 0) line surveys, such as for example in Orion and Monoceros (Wilson et al. 2005). Magnani et al. (1985); Hartmann et al. (1998); Magnani et al. (2000) have revealed the existence of CO emission at Galactic latitudes up to 55°. However, these high-latitude observations provide only a limited view of the | b | > 30° sky.
High-resolution full-sky surveys of higher J CO transitions have never been carried out, essentially because these are much more time consuming than J = 1 → 0 observations (atmospheric transmission is poorer, and higher-spatial resolution requires finer spatial sampling). High-J lines are expected to probe molecular gas with stronger excitation conditions (high density and/or warmer) better than the J = 1 → 0 line. Combined with CO(1 → 0), observations of J ≥ 2 lines therefore provide constraints on the physical conditions in the molecular ISM. Only specific regions have been mapped in the J = 2 → 1 CO line, e.g., the Galactic Centre region has been observed by Sawada et al. (2001). Maps of W3 and W5 (Bieging et al. 2010; Bieging & Peters 2011) are also available. For the J = 3 → 2 line, the Galactic centre has been observed by Oka et al. (2012), Orion by Ikeda et al. (1999) and W3 by Bieging et al. (2010).
The ESA Planck satellite was launched on 14 May 2009 in order to (primarily) measure with unprecedented precision the temperature and polarization anisotropies of the cosmological microwave background (CMB). It observed the sky in nine frequency bands covering 30–857 GHz with high sensitivity and angular resolution from 31′ to 5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled down to 0.1 K. Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for Galactic and extragalactic astrophysics as well as cosmology (Planck Collaboration I 2014).
The first nine CO rotational transition lines lie within the spectral bands of the HFI instrument. Of these, the first three, J = 1 → 0, J = 2 → 1, and J = 3 → 2 at 115, 230 and 345 GHz, respectively, present the largest transmission coefficients making them a significant component in the Planck intensity maps. In this paper, we extract full-sky CO maps for these three lines from the LFI and HFI data using component separation methods. The Planck intensity maps are presented in Sect. 2. In Sect. 3, we provide a brief description of HFI bandpasses and estimate the CO transmission coefficients for the most important rotational lines. Specifically tailored component separation methods for CO extraction in the Planck maps are detailed in Sect. 4. The Planck CO maps obtained using the above methods are presented in Sect. 5. Uncertainties and contamination from other astrophysical emission on those maps are discussed in Sect. 6. The internal validation of the Planck CO maps is presented in Sect. 7. Detailed comparisons to existing external CO surveys are presented in Sect. 8. Finally, we discuss the results and draw conclusions in Sect. 9.
 |
Fig. 1 The average spectral response for each of the HFI frequency bands. The vertical dashed lines represent the first nine 12CO rotational transitions assuming zero velocity. |
2. Planck data
This paper is based on the first 15.5 months of Planck survey mission (two full-sky surveys) and uses the full-sky maps of the nine Planck frequency bands, and also the 100, 217 and 353 GHz full-sky maps made of individual bolometer data. These maps are provided in HEALPix2 pixelization (Górski et al. 2005) with Nside = 2048 at full resolution. We refer to Planck Collaboration II (2014), Planck Collaboration V (2014), Planck Collaboration VI (2014), Planck Collaboration X (2014), Planck Collaboration VIII (2014) for the generic scheme of TOI processing and map-making, as well as for calibration. These Planck maps are given in KCMB units, i.e., in temperature units referred to the CMB blackbody spectrum. The scanning strategy of Planck consists of circles on the sky, with radius of about 85°, corresponding to different positions of the satellite spin axis. The latter is changed by 2.́5 every 40 to 60 min in order to cover the full sky in about seven months. The data set acquired for each position of the satellite spin axis is called a ring and consist of 40 to 60 observations of the same circle on the sky. Thus, a noise map can be obtained for each frequency band or bolometer map from the half difference of the maps of the first and second half of the rings. The resulting noise maps are basically free from astrophysical emission and thus a good representation of the statistical instrumental noise and systematic errors. In the following we assume that the beam pattern of the maps can be well represented by effective circular Gaussians with FWHM of 32.́24, 27.́01, 13.́25, 9.́65, 7.́25, 4.́99, 4.́82, 4.́68, and 4.́33 at 30, 44, 70, 100, 143, 217, 353, 545, and 857 GHz, respectively (Planck Collaboration IV 2014; Planck Collaboration VII 2014).
3. CO contribution in the Planck HFI channels
3.1. HFI spectral response and CO emission
In order to isolate the narrow CO features from the other sources of sky emission (e.g., CMB, dust, free-free, etc.), precise knowledge of the instrument spectral response as a function of frequency is required. The original spectral resolution requirement for the response of a given HFI detector was about 3 GHz; this corresponds to a velocity resolution of around 8000 km s-1 for the CO(1 → 0) line. As HFI does not have the ability to measure spectral response within a frequency band during flight, ground-based Fourier Transform Spectrometer (FTS) measurements provide the authoritative data on the HFI spectral transmission. With good S/N, spectral information can be inferred to a fraction (i.e., approximately 1/10th) of a spectral resolution element (Spencer et al. 2010). Thus, the pre-flight calibration FTS measurements (Pajot et al. 2010), which were carried out at a spectral resolution of about 0.6 GHz (better by a factor of 5 than the requirement), may be used to estimate the spectral response at a resolution equivalent to 150 km s-1 for the CO(1 → 0) line. For spectral regions near CO rotational transitions, therefore, the spectral response was oversampled by a factor of around 10 using an interpolation based on the instrument line shape of the FTS. Table 1 lists the relevant CO transitions, and the frequency ranges over which the HFI spectral response was oversampled (Planck Collaboration IX 2014). The oversampling ranges were extended to include all of the common CO isotopologues.
Rotational 12CO transitions within the HFI bands and over-sampled regions.
3.2. Spectral band CO conversion coefficients
The Planck sky maps are calibrated in CMB temperature units
KCMB so that CMB
anisotropies have a constant spectrum across frequencies. The CO velocity-integrated
emission (VIE) is in general expressed as the product of Rayleigh-Jeans temperature and
spectral line width in velocity units, i.e., K km s-1. In practice, to evaluate the
contribution of the CO emission to the Planck maps we need to convert
from the latter CO-based units to the former CMB-based ones accounting for the spectral
bandpass of each of the Planck detectors. We can write the CO emission contribution to the
map of detector b as
![\begin{eqnarray} M_{\mathrm{CO} ,b} [\mathrm{K}_{\rm CMB}]= F_{\mathrm{CO},b} \times M_{\mathrm{CO}}\left[\mathrm{K\,km\,s}^{-1}\right], \end{eqnarray}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq36.png) (1)where FCO,b is the CO
conversion coefficient. These CO conversion coefficients between CO brightness temperature
and CMB temperature can be determined using the measured spectral bandpass of the
detectors following Planck Collaboration IX (2014):
(1)where FCO,b is the CO
conversion coefficient. These CO conversion coefficients between CO brightness temperature
and CMB temperature can be determined using the measured spectral bandpass of the
detectors following Planck Collaboration IX (2014):
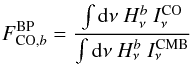 (2)where
(2)where 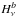 is the spectral transmission of bolometer
b at
frequency ν,
and
is the spectral transmission of bolometer
b at
frequency ν,
and 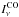 and
and
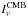 are the CO and CMB intensities,
respectively. The integral is performed across the extension of the spectral band.
are the CO and CMB intensities,
respectively. The integral is performed across the extension of the spectral band.
For the lowest rotational CO transitions a Doppler shifted line profile may be assumed with ν = νCO(1 + v/c)-1 ≈ νCO(1 − v/c) for v ≪ c. As the CO transitions occur at discrete frequencies, with a Doppler line-width much less than the transition frequency (about 103Hz cf. 1011Hz), and much narrower than the available knowledge of the HFI detector spectral response (about 108Hz), the velocity integration may be approximated by approximately a delta-function distribution at νCO, i.e. δνCO.
Bandpass CO conversion coefficients for the first three CO transitions were determined using the above relation (see Planck Collaboration IX 2014); similar data are available for the individual HFI detectors and for the other transitions within HFI bands. Table 2 (first column) lists the relative values of these CO conversion coefficients for the 12CO isotopologue (averaged for each a and b pair of polarized bolometers) normalized to the average transmission of all bolometers in the band (this format is chosen to ease comparison to the sky-calibrated CO conversion coefficients; see next section). To recover the physical CO conversion coefficients, values in the table must be multiplied by the average of 12CO conversion coefficients, namely, 1.42 × 10-5 KCMB/(K km s-1) at 100 GHz, 4.50 × 10-5 KCMB/(K km s-1) at 217 GHz and 17.37 × 10-5 KCMB/(K km s-1) at 353 GHz.
As will be described in Sect. 6.2.2, the
13CO isotopologue
may contribute to the Planck CO maps. The CO conversion coefficients of
13CO are computed
in the same way as described for 12CO, but for the 13CO transitions at
![\hbox{$\nu_0^{[1-0]}=110.2$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq54.png) GHz,
GHz,
![\hbox{$\nu_0^{[2{-}1]}=220.40$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq55.png) GHz, and
GHz, and
![\hbox{$\nu_0^{[3-2]}=330.6$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq56.png) GHz. The average CO conversion
coefficients over all bolometers in the 100, 217, and 353 GHz channel are 1.62 × 10-5 KCMB/(K km s-1), 3.63 × 10-5 KCMB/(K km s-1), and 13.0 × 10-5 KCMB/(K km s-1), respectively.
GHz. The average CO conversion
coefficients over all bolometers in the 100, 217, and 353 GHz channel are 1.62 × 10-5 KCMB/(K km s-1), 3.63 × 10-5 KCMB/(K km s-1), and 13.0 × 10-5 KCMB/(K km s-1), respectively.
3.3. Sky-calibrated CO conversion coefficients
Relative CO conversion coefficients of HFI bolometers (bolometer pairs) in the 100, 217 and 353 GHz channels normalized to the average CO conversion coefficient for each channel.
In the following sections we will use CO conversion coefficients to extract maps of the CO emission from the Planck frequency maps. For this purpose, we need an accurate estimates of the relative CO conversion coefficients between bolometers (see Appendix B for further discussions). The bandpass CO conversion coefficients present two main problems. First, the estimation of the spectral band transmissions of each of the bolometers may be affected by systematic errors as we are dealing with narrow lines. Indeed, HFI bandpasses are not sampled to a sufficient resolution to allow for a satisfactory CO extraction using these coefficients and then need to be interpolated as discussed above. Second, both 12CO and 13CO (and other isotopologues) are present in the Planck maps. The emission from 12CO is spatially correlated to that of 13CO with a varying ratio across the sky and we can not discriminate between the two. Thus, an accurate determination of the relative CO conversion coefficients between bolometers of the same Planck channel is difficult when using bandpass information only.
A way around these issues has been found in estimating the CO conversion coefficients
directly from sky measurements of well-known molecular clouds. For these regions, we can
assume – to first order – that the map of the sky emission for a detector is a linear
combination of CO and thermal dust emissions weighted by the CO and thermal dust
conversion coefficients of the detector. Thus, using an external CO emission template,
PCO, obtained from the Dame et al. (2001)12CO J = 1 → 0 survey and a dust
emission template, the 545 GHz Planck-HFI channel map (in
KCMB units),
Pd, it is possible to determine
sky-calibrated CO and dust transmission coefficients
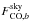 and
and
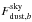 of bolometer b. Notice that we
implicitly assume here perfect spatial correlation between the 12CO and 13CO components.
of bolometer b. Notice that we
implicitly assume here perfect spatial correlation between the 12CO and 13CO components.
 |
Fig. 2 Comparison of normalised CO conversion coefficients computed from the bandpass measurements (black) or estimated on the sky (blue) for the 100 (top), 217 (middle) and 353 GHz (bottom) channels. See Table 2. |
Neglecting other astrophysical components (i.e., CMB, free-free, synchrotron, anomalous
microwave emission and point sources), we perform a simple linear fit between each
bolometer map Mb in the native
units (KCMB) and
the CO and dust templates: 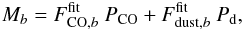 (3)where
(3)where 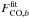 and
and
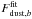 are the results of the linear regression.
To avoid contamination from dust polarization emission we combine the maps of pairs of
polarized bolometers into a single map and a single CO conversion coefficient is computed
for the pair of detectors.
are the results of the linear regression.
To avoid contamination from dust polarization emission we combine the maps of pairs of
polarized bolometers into a single map and a single CO conversion coefficient is computed
for the pair of detectors.
Due to the spatial correlation between the CO and dust emission, we expect the CO
conversion coefficients, 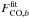 , to be affected by dust contamination and
so biased. We simply assume here that the estimated CO conversion coefficient can be
expressed as
, to be affected by dust contamination and
so biased. We simply assume here that the estimated CO conversion coefficient can be
expressed as 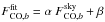 corresponding to an offset and a shift in
total amplitude. However, we will assume that thermal dust conversion coefficientsL are
not affected by CO contamination significantly and thus
corresponding to an offset and a shift in
total amplitude. However, we will assume that thermal dust conversion coefficientsL are
not affected by CO contamination significantly and thus
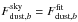 .
.
To compute α
and β we
solve the following system of equations. First, we construct dust-weighted bolometer (or
bolometer pair) maps. Then, we obtain a first set equations by imposing that the
difference of two dust-weighted bolometer (or bolometer pair) maps,
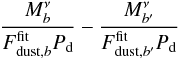 must be correlated with the CO template
(weighted by the dust map). A second set of equations is obtained by searching for the
factor γ that
minimizes the correlation of the difference
must be correlated with the CO template
(weighted by the dust map). A second set of equations is obtained by searching for the
factor γ that
minimizes the correlation of the difference 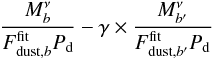 with the CO dust-weighted template,
PCO/Pd.
Uncertainties in the final CO conversion coefficients are obtained from the dispersion of
the coefficients found for different sky regions. For the CO(1 → 0) line we use sky regions for which the
Dame et al. (2001) map is above 2
K km s-1. For the
J = 2 → 1
and J = 3 → 2
lines we consider only the nine brightest CO clouds in the Dame et al. (2001) map.
with the CO dust-weighted template,
PCO/Pd.
Uncertainties in the final CO conversion coefficients are obtained from the dispersion of
the coefficients found for different sky regions. For the CO(1 → 0) line we use sky regions for which the
Dame et al. (2001) map is above 2
K km s-1. For the
J = 2 → 1
and J = 3 → 2
lines we consider only the nine brightest CO clouds in the Dame et al. (2001) map.
The sky CO conversion coefficients3 (normalized to their mean value) obtained from this analysis are presented in the right column of Table 2 and compared to 12CO bandpass conversion coefficients in Fig. 2. The discrepancy between the relative values of the bandpass and sky-calibrated CO conversion can be explained from the quoted uncertainties. A more detailed comparison of sky-calibrated and bandpass computed CO conversion coefficients, and a description of the systematic uncertainties is given in the Planck Collaboration IX (2014) companion paper. However, it is important to notice that they are not expected to be equal as the sky-calibrated CO conversion coefficients account also for the contribution of other spatially correlated CO isotopologues, mainly 13CO and other molecular lines. This is extensively discussed in Sect. 6.2.2.
Finally, note that for the J = 2 → 1 and J = 3 → 2 lines the maps obtained from the sky-calibrated CO conversion coefficients are calibrated in the Dame et al. CO(1 → 0) line units and need to be re-calibrated to their actual frequencies; this is the purpose of the next section.
3.4. Unit convention
In the following the Planck CO maps are extracted using the
sky-calibrated CO conversion coefficients. As discussed above these coefficients convert
from the units of the Dame et al. (2001) survey,
used as a CO template, to the original KCMB units of the
Planck HFI maps. To be useful for scientific purposes these maps must
be converted into the emission of the transition line. This is done by recalibrating the
Planck CO maps so that they are in units of the expected
12CO contribution
at the transition frequency: 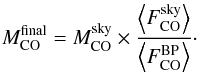 (4)Here
(4)Here 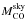 is the CO map of any transition calibrated
on the Dame et al. (2001) data, using the
sky-calibrated CO conversion coefficients. The quantities
is the CO map of any transition calibrated
on the Dame et al. (2001) data, using the
sky-calibrated CO conversion coefficients. The quantities
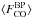 and
and
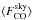 are the average across detectors of the
bandpass-determined and sky-calibrated 12CO conversion coefficients.
are the average across detectors of the
bandpass-determined and sky-calibrated 12CO conversion coefficients.
4. Extracting CO from Planck data
To extract the CO emission from the Planck maps, three main approaches have been considered: i) a single channel analysis (Sect. 4.2.1); ii) a multi-channel approach (Sect. 4.2.2); and finally iii) a multi-line approach (Sect. 4.2.3) using fixed CO line ratios. While the two first methods allow us to reconstruct specific CO transition lines, the third one does not discriminate between CO transitions, but formally yields the best signal-to-noise ratio. Before detailing the specifics of these approaches, we present in Sect. 4.1 the various component separation methods that have been used and adapted to the specifics of CO observations with the Planck satellite.
Main characteristics of the Planck CO products.
4.1. Component separation methods
Component separation algorithms as presented in Planck Collaboration XII (2014) are specifically tailored for CMB extraction and its statistical analysis. Thus, for this paper we have adapted and tested several of these algorithms for CO extraction from which we have selected three. Here we give a brief overview of them and of their main characteristics, while a more detailed description can be found in the references given below.
4.1.1. MILCA
The MILCA (Modified Internal Linear Combination Algorithm) method (Hurier 2012) was specifically developed within the Planck collaboration for the reconstruction of thermal Sunyaev-Zeldovich effect and CO contributions on the Planck maps. MILCA is an extension of the standard Internal Linear Combination (ILC) algorithm originally developed for CMB extraction (Bennett et al. 2003; Eriksen et al. 2004). ILC algorithms assume that the desired physical component can be obtained as a weighted linear combination of the input maps (bolometer or channel maps). They search for the weights of such a linear combination of maps that minimise the variance of the solution with given constraints, which are designed to project out the desired physical component. MILCA provides a flexible way of selecting wanted and unwanted spectral components (Hurier et al. 2013; Hurier 2012) and corrects for the noise bias in standard ILC algorithms. Furthermore, the weights of the internal linear combination can be computed both in real and harmonic space to improve the component separation efficiency. MILCA was tested against CO-oriented simulations, showing no bias in the reconstruction when the CO conversion coefficients are perfectly known (see Appendix B).
4.1.2. Ruler
Ruler is an inversion algorithm, which provides the generalized least squares solution, given a parametric model of Galactic emission. Input data, either bolometer maps or frequency maps, are linearly combined, on a pixel-by-pixel basis, according to weights that account for both the spectral properties of the different emissions and the Planck channel specifications, namely instrumental noise and bandpass. A comprehensive description of the method is given in Planck Collaboration XII (2014). Validation on simulations are presented in Appendix B.
Note that Ruler and MILCA have both been tested in the single- and multi-channel configurations described in Sect. 4.2 and were found to produce compatible results. This brings confidence in the robustness of these independent algorithms.
4.1.3. Commander-Ruler
The Commander-Ruler component separation pipeline consists of two steps: i) the Planck frequency channel maps are brought to a common resolution and the likelihoods of the non linear degrees of freedom of a chosen parametric sky-emissions model are jointly sampled, through a Gibbs sampling Monte-Carlo algorithm (Commander, Eriksen et al. 2008); ii) for each sample of the derived distribution, the linear degrees of freedom, namely the amplitude maps of the components, are computed at the full Planck resolution via a generalized least squared solution (Ruler, described above). The first and second moments of the posterior distribution of a parameter define its mean value and uncertainty, which accounts for both the instrumental and unwanted components modelling error.
A comprehensive description of the Commander-Ruler method is given in Planck Collaboration XII (2014) where it is used to extract simultaneously several sources of sky emission and in particular the CO emission. The CO map obtained in this way is presented in this paper. Commander-Ruler has been extensively tested using the FFP6 simulations (see Planck Collaboration 2013) as part of Planck component separation, a thorough description of which is provided in Planck Collaboration XII (2014).
4.2. CO extraction strategies
4.2.1. Single-channel approach – Type 1 maps
In the single-channel approach we exploit differences in the spectral transmission of a
given CO line among the bolometers (bolometer pairs) of the same frequency channel. As
discussed in Sect. 3 the spectral bandpasses of the
bolometers within a frequency channel are different. This means that the fraction of CO
emission with respect to the total emission will be also different. We can construct
maps of the sky for each of the bolometers, b, in a given frequency channel, ν. These maps,
 , can be considered as a linear
combination of the different sources of sky emission including CMB, Galactic thermal
dust and CO emissions at frequencies between 100 and 353 GHz:
, can be considered as a linear
combination of the different sources of sky emission including CMB, Galactic thermal
dust and CO emissions at frequencies between 100 and 353 GHz:
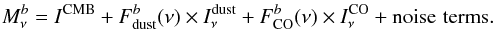 (5)As these bolometer maps are calibrated in
CMB temperature units and assuming that the dust emission does not vary across
bolometers (i.e.,
(5)As these bolometer maps are calibrated in
CMB temperature units and assuming that the dust emission does not vary across
bolometers (i.e., 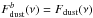 ), the difference between two bolometer
maps gives directly an estimate of the CO emission. Using all differences between
bolometer maps we should be able to extract the CO emission by a simple linear system.
In practice we need to use component separation techniques to regularize the system and
account for uncertainties.
), the difference between two bolometer
maps gives directly an estimate of the CO emission. Using all differences between
bolometer maps we should be able to extract the CO emission by a simple linear system.
In practice we need to use component separation techniques to regularize the system and
account for uncertainties.
The main advantages of this solution are to give access to the first three transitions of CO at the native resolution of the Planck maps and to avoid contamination from other channels. However, this type of CO extraction results in a lower signal-to-noise ratio due to the use of individual bolometer (bolometer pair) maps.
The CO J = 1 → 0, J = 2 → 1 and J = 3 → 2 maps are obtained with MILCA, using all bolometers in the 100, 217 and 353 GHz channel, respectively, and are denoted the Planck Type 1 CO product. Differe denoted the Planck Type 1nding on the line under scrutiny:
-
The J = 1 → 0 map is obtained by requesting cancellation of a flat spectrum(i.e., the CMB) while preserving CO (using thesky-calibrated conversion coefficients given inTable 1). Notice that in this case the diffuseGalactic contamination, mainly dust, can be well approximatedby a flat spectrum within the band and there is no need for extraconstraints.
-
At 217 GHz, dust becomes more of a major contaminant and should be dealt with. The J = 2 → 1 map is therefore extracted using an extra constraint on the dust transmission in the different bolometers, computed from a grey-body spectrum defined as
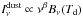 where T = 17 K,
β =
1.6 and Bν(T)
is the Planck function. The choice of this dust spectrum is
discussed in Sect. 6.2.1.
where T = 17 K,
β =
1.6 and Bν(T)
is the Planck function. The choice of this dust spectrum is
discussed in Sect. 6.2.1. -
At 353 GHz, the CMB becomes sub-dominant compared to the dust and we require an estimate of the CO, only removing the dust. We also found that the dust spectrum model used for the J = 2 → 1 line is not optimal at 353 GHz and thus we used the sky-calibrated dust conversion coefficients
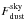 which were also fitted in the
linear regression of Eq. (3) and
for which we obtained better results.
which were also fitted in the
linear regression of Eq. (3) and
for which we obtained better results.
4.2.2. Multi-channel approach – TYPE 2 maps
The multi-channel approach makes use of the intensity maps in several channels to
isolate the CO contribution from other astrophysical sources of emission. As discussed
above, the Planck intensity map for a given frequency channel,
ν, is the
linear combination of different sources of emission including mainly CMB, Galactic
thermal dust, free-free and CO: 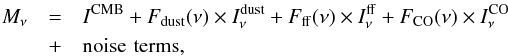 (6)where
(6)where
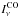 corresponds to the emission of the
J = 1 →
0, J = 2 →
1 or J =
3 → 2 lines. The relative contribution of these emissions changes
between channels. For example the 100 GHz channel shows CO emission while this is not
the case for the 70 and the 143 GHz channels and it can be considered negligible at 353
GHz. Thus, combining the maps of these four channels we should be able to reconstruct
the CO emission using component separation techniques as above.
corresponds to the emission of the
J = 1 →
0, J = 2 →
1 or J =
3 → 2 lines. The relative contribution of these emissions changes
between channels. For example the 100 GHz channel shows CO emission while this is not
the case for the 70 and the 143 GHz channels and it can be considered negligible at 353
GHz. Thus, combining the maps of these four channels we should be able to reconstruct
the CO emission using component separation techniques as above.
The Ruler method was selected to be used in this configuration, to extract the J = 1 → 0 and J = 2 → 1 lines. In order to construct the CO(1 → 0) line, we use LFI 70 GHz, HFI-100, 143 and 353 GHz channels, while CO(2 → 1) is obtained using LFI 70 GHz, 143, 217 and 353 GHz channels. All maps are smoothed to 15′. To solve for the two CO transitions, we assume that the CO contribution to the 353 GHz channel is negligible4. The CO(1 → 0) and CO(2 → 1) maps obtained using the multi-channel method constitute the Planck Type 2 CO product.
For both lines, the requirement is to extract CO while at the same time fitting for CMB, dust and free-free emission. By construction, the CMB spectrum is flat across channels. For the dust, the same grey-body spectrum as for the single-channel J = 2 → 1 line is assumed. Free-free emission is modelled as a power-law spectrum proportional to ν-2.15. The dust and free-free transmission coefficients are obtained by integrating their spectra over Planck’s bandpasses.
4.2.3. Multi-line approach – TYPE 3 map
While the multi-channel approach provides single line maps at relatively high
signal-to-noise ratio, it is possible to use a multi-line approach to further increase
the S/N ratio, potentially allowing the discovery of new faint molecular clouds at high
Galactic latitudes. For this, we need to assume that the line ratios, CO(2 → 1)/CO(1 → 0) and CO(3 → 2)/CO(1 → 0), are constant across the sky. This
is equivalent to considering the CO emission to be the same at 100, 217 and 353 GHz up
to a multiplicative factor that is assumed to be known. Under these assumptions Eq.
(6) reads
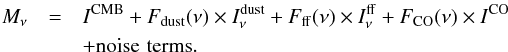 (7)This approach is used as part of the
Commander-Ruler pipeline employed for CMB component separation (Planck Collaboration XII 2014).
(7)This approach is used as part of the
Commander-Ruler pipeline employed for CMB component separation (Planck Collaboration XII 2014).
The Type 3 CO map results from a seven-band run of this pipeline, including 30 to 353 GHz channel maps, with the sky modelled as a superposition of CMB, CO, dust – treated as a modified blackbody – and a power law to describe the low-frequency Galactic emission. The dust optical depth and the dust temperature, as well as the low-frequency component spectral index are fitted at every pixel. Since the total number of parameters would exceed the number of frequencies considered, the three CO lines are assumed to be perfectly correlated. A single CO map is solved for, the so-called Type 3 map, using the average CO bandpass transmission (see Sect. 3.2) in each channel, whereas the CO line ratios are given by the posterior average of the distribution obtained from a dedicated Commander run on small bright CO regions (Taurus, Orion, Polaris, etc.). The line ratios found for CO(2 → 1)/CO(1 → 0) and CO(3 → 2)/CO(1 → 0) are 0.595 and 0.297, respectively. Notice that there are significant spatial variations of these ratios as discussed in Sect. 6.2.2. For further analysis we have selected bright CO regions with large ratios.
5. Planck CO maps
 |
Fig. 3 Full-sky CO J = 1 → 0 maps (left) and their respective statistical error maps (right) in K km s-1 units for the three types of Planck CO products. For display purposes only, the Type 1 and Type 3 maps are smoothed to 15′ to ease the comparison to the Type 2 maps. The error maps correspond to the non-smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
 |
Fig. 4 Full-sky CO J = 2 → 1 maps (left) and their respective statistical error maps (right) in K km s-1 units for Type 1 (top) and Type 2 (bottom) Planck CO products. The Type 1 map has been smoothed to 15′ for display purposes but the error map corresponds to the non smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
 |
Fig. 5 Type 1 full-sky CO J = 3 → 2 maps (left) and its statistical error map (right) in K km s-1 units. The map has been smoothed to 15′ for display purpose but the error map corresponds to the non smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
The Planck CO delivery consists of three types of products, corresponding to the three extraction methods described above:
-
Type 1 maps are extracted using thesingle-channel approach described in Sect. 4.2.1and come at the native resolution of the correspondingPlanck-HFI channel;
-
Type 2 maps come from the multi-channel method given in Sect. 4.2.2 and have a resolution of 15′;
-
The Type 3 map comes from the multi-line approach described in Sect. 4.2.3, assuming fixed CO line ratios in order to obtain the highest possible signal-to-noise ratio, and is delivery at a resolution of ~
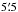 .
.
The main characteristics of all Planck CO maps are shown in in Table 3 while details of the Planck CO product is given in Appendix A. The Type 1, Type 2 and Type 3 terminology will be used throughout the paper. All maps discussed below are in units of K km s-1 at the transition line they represent.
5.1. The CO J = 1 → 0 line at 115 GHz
The Type 1 (top), Type 2 (middle) and Type 3 (bottom) Planck CO(1 → 0) maps are given in the left column of Fig. 3. The right column corresponds to their statistical error and will be discussed further in Sect. 6.
The resolution of the Type 1 product is 9.́65, i.e., the native resolution of the Planck-HFI 100 GHz channel. The Type 2 product has a 15′ beam due to the additional smoothing required to combine several Planck channels: in particular the use of Planck-LFI 70 GHz channel is essential to remove the free-free emission (see Sect. 6.2). Finally, the Type 3 has varying resolution across the sky, resulting from the Ruler solution, and a beam profile is computed from FFP6 simulations. A good Gaussian approximation can be achieved with a FWHM of 5.́5. A simple eye inspection finds a good overall agreement between the maps; an in-depth comparison is conducted in Sect. 7.
5.2. The CO J = 2 → 1 line at 230 GHz
The CO(2 → 1) line can only be extracted using the single-channel or the multi-channel approach. Therefore the 230 GHz Planck CO product consists of Type 1 (5′ resolution) and Type 2 (15′ resolution) maps only, which are displayed in the left column of Fig. 4. The dust emission increases with frequency and becomes more of an issue for the J = 2 → 1 line extraction. This will be discussed at length in Sect. 6.2, but this issue is already clearly visible when comparing the two products: the Type 2 CO presents diffuse dust emission throughout the Galactic plane that is not present in the Type 1 map.
5.3. The CO J = 3 → 2 line at 345 GHz
As mentioned previously, the single-channel approach is the only way to extract this higher J CO line and the corresponding Type 1 CO map is shown in Fig. 5. This map has a resolution of 4.́82.
We compare the reconstructed CO intensity for the different rotational transition lines to the total emission in the Planck original channel maps. For the J = 1 → 0 line the CO intensity in well-known molecular clouds and in the Galactic plane corresponds on average to about 50% of the total emission in the 100 GHz channel map. The J = 2 → 1 line is about 15% of the 217 GHz channel map and the J = 3 → 2 is about 1% of the 353 GHz map. At high Galactic latitudes the CO contribution is negligible on average for the three lines.
6. Uncertainties and contaminants
6.1. Statistical errors
Statistical uncertainties in the CO maps may be obtained using so-called half-ring half
differences5 (Planck HFI Core Team 2011b). For the Type 1 product, standard deviation
(σ-)maps
are generated at the level of individual bolometer maps, starting from the half-ring half
difference noise map whitened using the number of hits in each pixel. A given bolometer
σ-map,
σb, is then obtained by
dividing the standard deviation of the noise map by the square root of the number of hits
in each pixel, namely ![\begin{eqnarray} \sigma_b=\frac{1}{\sqrt{N_b}}{\rm stddev}\left[\frac{\left(M_b^F - M_b^L\right)\sqrt{N_b}}{2}\right], \end{eqnarray}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq110.png) (8)where Nb is the hit number map
and
(8)where Nb is the hit number map
and 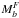 and
and
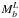 are the first and last half-ring bolometer
maps respectively. This standard deviation of each bolometer map σb is then propagated
quadratically to the CO map level using the weights found by MILCA for the linear
combination.
are the first and last half-ring bolometer
maps respectively. This standard deviation of each bolometer map σb is then propagated
quadratically to the CO map level using the weights found by MILCA for the linear
combination.
This cannot be achieved in such a straightforward fashion for the Type 2 maps smoothed to 15′, resulting in correlated noise. Given the size of the maps, a fully dense matrix description of the noise is not feasible. However, a set of 1000 realistic noise simulations has been processed through the pipeline (first smoothed and then linearly combined), and used to compute a σ-map, which is a good pixel noise approximation. The Type 3 standard deviation map is obtained in a similar fashion.
The σ-maps of all Planck CO maps are plotted in the right columns of Figs. 3–5. For the Type 1 and Type 3 CO(1 → 0) maps, the σ-maps correspond to the maps at their native resolutions, while the CO maps have been smoothed to 15′ for display purpose. These standard deviation maps have all been validated by checking that their mean at high latitude was in agreement with standard deviation measured directly in the CO map at these locations (where no signal is expected; see lower panel of Fig. 17).
Using a common resolution of 15′ to compare the high-latitude noise level in the maps, we find the standard deviation of the CO(1 → 0) maps to be typically 1.77 K km s-1 for the Type 1 map, 0.45 K km s-1 for the Type 2 map and 0.16 K km s-1 for the Type 3 map. These uncertainties can be compared with typical uncertainties on ground-based surveys for CO(1 → 0) for example 0.6 K km s-1 for the and 1.2 K km s-1 for the Dame et al. (2001) and NANTEN (Mizuno & Fukui 2004) surveys. At the same resolution, the Type 1 and Type 2 CO(2 → 1) maps have standard deviations of 0.74 K km s-1 and 0.12 K km s-1, respectively, while it is 0.73 K km s-1 Type 1 CO(3 → 2) map.
 |
Fig. 6 Comparison of the 3 types of CO products with a dust template map for the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. |
6.2. Contaminants
All Planck CO products suffer from systematic effects and contamination from other emission that needs to be characterized; point sources or emission from other CO lines affect all Planck CO products while dust, free-free emission and the Sunyaev Zeldovich effect (SZ) are important for Type 2 and Type 3 maps only (the Type 1 product is the most immune to contamination as it relies on single-channel information). Some of these contaminants (e.g., CMB, dust, free-free), need to be dealt with at the stage of component separation. Others, like point sources and the thermal SZ effect in clusters of galaxies, may simply be masked afterwards. We discuss each of these contaminants in detail below apart from CMB emission for which the electromagnetic spectrum is well-known and can be explicitly nullified within calibration errors in the Planck frequency maps, as discussed in Sect. 4.1.
6.2.1. Dust
Dust emission is the main contaminant as far as CO is concerned and is often strong in the same regions, e.g., star forming regions. The multi-channel approach (i.e., Type 2 products) is particularly sensitive to the choice of the dust spectrum. One assumption we make in these maps is that the dust spectrum is constant over the sky and described by a grey-body with Tdust = 17 K and βdust = 1.6. This assumption is not correct since both the spectral index and temperature of the dust are known to vary across the sky (see, for example, Planck Collaboration XIX 2011; Fauvet et al. 2013). These values are, however, a good representation of the dust found in CO-rich regions as can be seen on the βdust and Tdust maps of Planck Collaboration XI (2014); Planck Collaboration XII (2014).
As far as the dust transmission in HFI is concerned, βdust and Tdust are degenerate quantities. Testing different values of the βdust index6, we find this dust model to be the best compromise for the multi-channel CO extraction. At Tdust = 17 K, choosing βdust = 1.5 results in too much dust removal and a negative residual in the Galactic plane. Conversely, βdust = 1.7 generates much larger remaining dust emission. In the outer regions of the Type 2 maps (l> 90° and l< 270°), changing βdust by ±0.1 yields an increase/decrease of less than about 1 K km s-1 at 115 GHz and less than about 2 K km s-1 at 230 GHz. Still, these are larger than statistical errors. The inner regions of the Galactic plane are far more sensitive to the change of the dust spectrum, with a shift of about 10 K km s-1 at 115 GHz and 15 K km s-1 at 230 GHz, but the signal is much larger.
Given our chosen dust model, Fig. 6 shows the correlation between the types of J = 1 → 0 CO maps discussed above and Planck’s 545 GHz map used here as dust template. All maps were smoothed to 30′. The comparison has been done in three molecular clouds hosting different environments: i) Orion, a very active massive star forming region; ii) Taurus, that hosts low-mass star formation (Kenyon et al. 2008); and iii) Polaris, a high-Galactic latitude translucent cloud with little to no star formation and presenting both atomic and molecular gas (Miville-Deschênes et al. 2010). Figure 7 presents smoothed images of the three regions for the Type 1 and Type 2 Planck CO maps and for Planck’s 545 GHz channel. Snapshots of the Dame et al. (2001)J = 1 → 0 data are also shown in Fig. 7 but will be discussed in Sect. 8.1.
Dust emission is quite intense in both Orion and Taurus (Fig. 7, right column) and, as can be seen in Fig. 6, some correlation is not unexpectedly found between the Planck CO maps and the dust template in these locations. This is particularly true in Orion where the images show very similar patterns of CO and dust. In the Polaris region the correlation loosens significantly; dust is far less intense and shows a different distribution than CO. For the weakest dust emission, probably in atomic gas, there is no CO signal. These correlation plots against dust should be compared with those performed against ground-based CO measurements, where the correlation is this time much tighter (this is discussed in Sect. 8.1; see Fig. 10). Looking at several other molecular clouds (e.g., Ophiucus, Chameleon), we find that whatever the method, the correlation with CO is always much tighter than the one with dust, making us confident that dust is not a major issue for CO-rich regions.
Nonetheless, Type 2 and Type 3 maps do suffer some level of dust contamination. This can be seen by eye in the CO(1 → 0) images of the Taurus regions in Fig. 7 (top) where the Type 2 map shows more flux than the Type 1 CO at the locations where the dust is the brightest. However, contamination is the most important in the Galactic plane of the CO(2 → 1) Type 2 map. This is particularly visible in Fig. 4.
 |
Fig. 7 Images ( |
6.2.2. Other CO lines
For all of the Planck reconstructed CO maps we expect contamination from other CO isotopologue transition lines. Lines from the 13CO isotopologue are the main contaminants in the Type 1 maps, while 13CO and the 12CO(3 → 2) both contribute to the Type 2 maps. The contribution of each contaminant line can be estimated to first order as follows;
Type 1:
forgetting about other contaminants, the CO content of the Type 1
Planck map can be written as 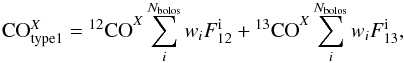 (9)where X represents the
J = 1 →
0, J =
2 → 1 or J = 3 → 2 transition, wi are the weights of
the linear combination and
(9)where X represents the
J = 1 →
0, J =
2 → 1 or J = 3 → 2 transition, wi are the weights of
the linear combination and 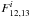 is the 12,13CO transmission in
bolometer i. Using the weights of the Type 1
linear combination and using the bandpass coefficients for 13CO, we find the quantity
is the 12,13CO transmission in
bolometer i. Using the weights of the Type 1
linear combination and using the bandpass coefficients for 13CO, we find the quantity
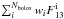 to be equal to 0.53 at 115 GHz, 0.01
at 230 GHz and 0.36 at 353 GHz. Assuming a 13CO to 12CO ratio of 0.2, this translates in
to be equal to 0.53 at 115 GHz, 0.01
at 230 GHz and 0.36 at 353 GHz. Assuming a 13CO to 12CO ratio of 0.2, this translates in
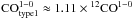 and
and
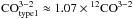 , i.e., an overestimation of about 10%
of the Type 1 J =
1 → 0 and J = 3 → 2 maps. The effect on the
J = 2 →
1 transition is negligible.
, i.e., an overestimation of about 10%
of the Type 1 J =
1 → 0 and J = 3 → 2 maps. The effect on the
J = 2 →
1 transition is negligible.
Type 2:
the Type 2 maps are constructed as 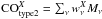 , where X stands for
J = 1 →
0 or J
= 2 → 1, Mν is the
Planck map at the channel frequency ν and wν is a weighting
factor. Using the average CO transmissions in each channel, the CO content of the
Type 2 maps formally reads
, where X stands for
J = 1 →
0 or J
= 2 → 1, Mν is the
Planck map at the channel frequency ν and wν is a weighting
factor. Using the average CO transmissions in each channel, the CO content of the
Type 2 maps formally reads ![\begin{eqnarray} \nonumber {\rm CO}_{\rm type2}^X &=& {^{12}{\rm CO}}^X+ \frac{\langle F_{13}\rangle}{\langle F_{12}\rangle }\; {^{13}{\rm CO}^X} +w_{353} \langle F_{12}\rangle_{353}{^{12}{\rm CO}}^{[3-2]}\\\nonumber & = & {^{12}{\rm CO}}^X\left(1+w_{353}\langle F_{12}\rangle_{353}\frac{{^{12}{\rm CO}}^{[3-2]}}{{^{12}{\rm CO}}^{X}}\right) \\ &&+ \frac{\langle F_{13}\rangle}{\langle F_{12}\rangle }\; {^{13}{\rm CO}^X}\;, \label{eq:13co_type2} \end{eqnarray}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq140.png) (10)where ⟨ F12,13 ⟩
are the average (among bolometers) conversion coefficients of
(10)where ⟨ F12,13 ⟩
are the average (among bolometers) conversion coefficients of
 and
and
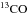 at 100 or 217 GHz, depending on the
transition under scrutiny and ⟨
F12 ⟩ 353 is that of
at 100 or 217 GHz, depending on the
transition under scrutiny and ⟨
F12 ⟩ 353 is that of
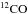 in the 353 GHz channel. In the
following, we assume the the line ratios to be 12CO(3 → 2) / 12CO(1 → 0) = 0.2 and 12CO(3 → 2) / 12CO(2 → 1) = 0.4 as obtained from the median
of the line ratio distributions computed from the Type 1 maps, (see Planck
Collaboration PIP, in prep.). The widths of the distributions are large and thus we
consider uncertainties of ±0.1 in the two ratios. Notice that within these uncertainties the
values considered here are consistent with those derived from the Ruler analysis in
Sect. 4.2.3. Using these values we find
in the 353 GHz channel. In the
following, we assume the the line ratios to be 12CO(3 → 2) / 12CO(1 → 0) = 0.2 and 12CO(3 → 2) / 12CO(2 → 1) = 0.4 as obtained from the median
of the line ratio distributions computed from the Type 1 maps, (see Planck
Collaboration PIP, in prep.). The widths of the distributions are large and thus we
consider uncertainties of ±0.1 in the two ratios. Notice that within these uncertainties the
values considered here are consistent with those derived from the Ruler analysis in
Sect. 4.2.3. Using these values we find
![\hbox{${\rm CO}_{\rm type2}^{[1{-}0]} \approx 1.02 \times {^{12}{\rm CO}}^{[1-0]}$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq145.png) and
and
![\hbox{${\rm CO}_{\rm type2}^{[2{-}1]} \approx 0.75 \times {^{12}{\rm CO}}^{[2{-}1]}$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq146.png) . From this, we see that contamination
by the J = 3 →
2 line can be neglected in the J = 1 → 0 Type
2 map, but reduces by ~25% the
. From this, we see that contamination
by the J = 3 →
2 line can be neglected in the J = 1 → 0 Type
2 map, but reduces by ~25% the 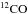 signal in the J = 2 → 1 map. For this
reason, we decided to correct the Type 2 map from this effect by dividing the
output Type 2 (J
= 2 → 1) map by 0.75. With this correction, the overall calibration
of the Type 1 and Type 2 (J = 2 → 1) maps are in agreement (see Sect.
7).
signal in the J = 2 → 1 map. For this
reason, we decided to correct the Type 2 map from this effect by dividing the
output Type 2 (J
= 2 → 1) map by 0.75. With this correction, the overall calibration
of the Type 1 and Type 2 (J = 2 → 1) maps are in agreement (see Sect.
7).
The second term of the contamination due to 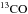 can now be estimated. Using the
bandpass estimate of the coefficients, ⟨
F13CO ⟩ / ⟨
F12CO ⟩ is equal to 1.14
at 115 GHz and 0.82 at 230 GHz, which translate into
can now be estimated. Using the
bandpass estimate of the coefficients, ⟨
F13CO ⟩ / ⟨
F12CO ⟩ is equal to 1.14
at 115 GHz and 0.82 at 230 GHz, which translate into
![\hbox{${\rm CO}_{\rm type2}^{[1{-}0]} \approx 1.2 \times {^{12}{\rm CO^{[1-0]}}}$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq150.png) and
and
![\hbox{${\rm CO}_{\rm type2}^{[2{-}1]} \approx 1.2 \times {^{12}{\rm CO^{[2{-}1]}}}$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq151.png) when assuming a ratio of 0.2 between
when assuming a ratio of 0.2 between
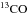 and
and
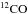 and the 0.75 correction factor for the
J = 2 →
1 line.
and the 0.75 correction factor for the
J = 2 →
1 line.
The values above are given as a rough estimate of the
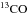 contamination. The latter depends on
the isotopic ratio and relative optical depth, and will, in practice, vary across the
sky.
contamination. The latter depends on
the isotopic ratio and relative optical depth, and will, in practice, vary across the
sky.
6.2.3. Masking SZ clusters and point sources
Planck CO maps are also contaminated by other localized non-CMB signals that have not been included in the component separation. This is the case of radio point sources, which are present in all three types of maps. Also present in the maps is the Sunyaev-Zeldovich (SZ) effect, a secondary anisotropy of the CMB coming from the interaction of CMB photons with the hot electron population of galaxy clusters. The Planck mission has shown the potential of galaxy cluster detection via the SZ effect with the publication of a catalogue of a few thousands clusters (Planck Collaboration XXIX 2014). As far as CO extraction is concerned, SZ is yet another contaminant foreground in the Type 2 and Type 3 maps, as these rely on multi-channel information. On the other hand, Type 1 maps are not affected.
For this first release of the Planck CO maps, a point source mask is provided with the Type 1 and a point source + SZ mask for the Type 2 and Type 3 maps. The point source mask used here was constructed from the Planck-HFI official 100 GHz point source mask by unmasking any pixels located within | b | < 1.5°. This manipulation was necessary given that many point sources in the mask are molecular cold cores located in the Galactic disk, so that using the original mask hides most of the Galactic CO. For the SZ mask we start from a simulated Compton parameter map of the Planck cluster sample (Planck Collaboration XXIX 2014; Planck Collaboration XII 2014) where a universal generalized pressure profile (Arnaud et al. 2010) was assumed. The mask is then generated by imposing a threshold of 4 × 10-6 in Compton parameter units to this map.
6.3. Absolute calibration uncertainties
Three main contributors to the absolute calibration uncertainties of the Planck CO maps have been identified: i) the Planck-HFI calibration uncertainties of the temperature maps; ii) the uncertainty on the CO bandpass conversion coefficients; and iii) the uncertainty on the 13CO contribution. We do not include the effect of dust in this absolute calibration given that, contrary to 13CO, dust is not always spatially correlated to CO and is therefore considered as a systematic effect (see Sect. 6.2.1).
As described in Planck Collaboration VIII (2014), the absolute calibration of the Planck maps is about 0.55% from 100 GHz to 217 GHz, 1.25% at 353 GHz, and 10% at 545 and 857 GHz. Uncertainties on the averaged bandpass CO conversion coefficients are at the 5% level at 100 GHz and 1% at 217 and 353 GHz (Planck Collaboration IX 2014). We described how 13CO affected the Planck CO maps in Sect. 6.2.2; using the results obtained with 13CO/12CO = 0.2 (Solomon et al. 1979), and assuming a conservative uncertainty of ±0.1 on this ratio, we can estimate the 13CO contribution to the absolute uncertainty in each CO map.
Final calibration uncertainties are summarized in Table 4. A conservative estimate of the total absolute calibration uncertainties of each map is given in the last column of the table. For most maps, the calibration uncertainties are of the order of 10% and are dominated by the 13CO contribution. Notice that for Type 1 CO(2 → 1) and CO(3 → 2) the uncertainties are significantly smaller as they are less contaminated by 13CO.
Absolute calibration uncertainties of Planck CO maps.
 |
Fig. 8 Correlation between the Type 1 and Type 2 (top) and Type 1 and Type 3 (middle) J = 1 → 0 CO maps at high Galactic latitudes 25°< | b | < 90°. Correlation between the Type 1 and Type 2 J = 2 → 1 CO maps is shown on the bottom plot. The solid line corresponds to perfect correlation (y = x). Below the dashed horizontal line the colour scale gives the logarithm of the number of pixels in a given bin. The best linear fits (solid red line) are computed from the individual pixels plotted above the dashed line. The best-fit slopes and uncertainties are: a) 0.93 ± 0.17; b) 0.87 ± 0.20; and c) 0.96 ± 0.12. The intercepts are compatible with zero within the error bars. |
7. Internal validation of the CO maps
Before validating these maps on external data, it is possible to perform some internal checks by comparing the CO maps of different types. As mentioned previously, the Type 1 and Type 2 CO products can differ in the Galactic plane because of the higher level of contamination affecting the Type 2 products. However, at high Galactic latitudes, where no significant free-free or dust emission is expected, the products may be compared in order to assess the overall inter-calibration of the Type 1, 2 and 3 CO maps. To perform this comparison, the maps are first smoothed to a common resolution of 30′ and degraded to Nside = 128 to avoid noise correlation between samples. After masking point sources, correlation plots are produced for all remaining pixels located at Galactic latitudes | b | ≥ 25°.
Figure 8 compares both Type 1−Type 2 and Type 1−Type 3 maps. At high latitudes, CO emission is very sparse so that most pixels have very low emission. Therefore, below an empirical threshold, shown as the dashed line in each figure, the number of points is such that a contour representation of binning suffices. Above the dashed line, individual pixels are plotted directly and used to compute the best fit. The orange line gives the best-fit values and is compatible within errors with perfect correlation (y = x). This indicates that the different types of product share the same overall calibration, both for the J = 1 → 0 maps (Fig. 8, left and middle panel) and J = 2 → 1 maps (Fig. 8, right panel).
The different types of product may also be compared in specific molecular clouds, as shown in the top and bottom panels of Fig. 9 for the J = 1 → 0 (top) and J = 2 → 1 (bottom) lines, respectively. As for the comparison to dust, the Taurus (left), Orion (middle) and Polaris (right) molecular clouds have been chosen because of the three very different molecular environments they host. Figure 9 shows tight correlations between the Type 1 and Type 2 CO(1 → 0) products in these three molecular clouds. The best fits are computed for all points in the range [2–15] K km s-1, where the bulk of the emission lies. The fit uncertainties are dominated by the errors bars (not shown in the figure) of the Type 1 points. The Type 2 CO(1 → 0) map shows more flux than the Type 1 with best-fit slopes of about 1.1 for Taurus, Orion and Polaris. Such behavior is nonetheless expected, given that the Type 2 CO(1 → 0) map suffers from more 13CO and dust contamination than the Type 1 CO(1 → 0) map as described in Sects. 6.2.2 and 6.2.1. Similar trends are observed for the CO(2 → 1) maps (bottom panel), but here we also give as dashed lines the best-fits that would have been obtained for a change of ±0.1 in the 12CO(3 → 2)/12CO(2 → 1) ratio assumed to correct the Type 2 map from the 12CO(3 → 2) contamination (see Sect. 6.2.2). Given the absolute calibration and statistical uncertainties quoted above for each of the maps, the residuals between the Type 1 and Type 2 maps are consistent within the errors.
8. Comparison with external data
In this section, we validate the Planck CO products described in Sect. 5 using existing ground-based CO data for the first three transition lines.
8.1. Comparison with the Dame et al. (2001) CO J = 1 → 0 survey
 |
Fig. 9 Correlation between Type 1 and Type 2 CO maps at 115 GHz (left column) and 230 GHz (right column) in the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. The best linear fits (orange solid line) have been computed between 2 and 15 K km s-1 at 115 GHz and between 1 and 15 K km s-1 at 230 GHz, where bulk of the data lie and avoiding the noise around zero. The best-fit slopes and uncertainties are: a)1.12 ± 0.03; b) 1.14 ± 0.01; c) 1.10 ± 0.04; d) 1.07 ± 0.01; e) 1.07 ± 0.06; and f) 1.17 ± 0.04. The intercepts are compatible with zero within error bars. The orange dot-dashed lines in the bottom panels correspond to the recalibration uncertainty due to the contribution of the J = 3 → 2 line in the Type 2 J = 2 → 1 product. See text for detail. |
The publicly available data of Dame et al. (2001) represent the most complete survey of Galactic 12CO J = 1 → 0 emission to date. The original data consist of a composite map constructed from a set of 37 independent surveys taken by the 1.2 m Millimetre-Wave Telescope at the CfA7. In order to compare the Planck CO maps to the Dame et al. (2001) data, we use the velocity-integrated HEALPix rendition of the survey which is available on the Lambda website8.
8.1.1. Molecular clouds
We focus again on the three molecular clouds, Taurus, Orion and, Polaris. Images of the Dame et al. (2001) and Planck data in these fields are shown in Fig. 7. The maps were smoothed to a common resolution of 30′ and degraded to Nside = 128 (to avoid noise correlation between samples) before plotting the correlations shown in Fig. 10. In each panel of this figure, the three types of Planck CO (1 → 0) maps (shown in different colours) are correlated with the Dame et al. (2001) data. The slopes of the best-fit linear regressions for the three products are given in the legend of each panel (with a 1-σ statistical error smaller than 1%). The spread in the data points is reminiscent of the level of noise in the maps, showing once again that the Type 1 map is the noisiest while the Type 3 map has the best signal-to-noise ratio.
The Type 1 CO is in good agreement with the Dame et al. (2001) data, with a slope of about 1.05 in both Taurus and Orion. The excess with respect to the one-to-one correlation is at the level expected from 13CO contamination (see Sect. 6.2.2). For Polaris the slope is about 1.1, but in such faint regions, the level of noise of the Type 1 map makes the comparison more difficult. For all clouds, the Type 2 CO show roughly 20% excess compared to the Dame et al. (2001) data due to a combination of both dust and 13CO contamination. It performs particularly poorly in Orion where the dust is significantly correlated with CO emission. Finally, the Type 3 CO does as well as the Type 1 product in Taurus, but also suffers from some contamination in Orion with a correlation of 1.16. This test was conducted in other molecular regions (not shown here) and similar trends were found. The level of the residuals is always compatible with the calibration uncertainty of the maps.
From these, we conclude that the Type 1map is the most robust J = 1 → 0 map in terms of CO extraction, but its low S/N ratio makes it unsuitable for the study of faint CO regions. The Type 2 and Type 3 maps both suffer from some level of dust contamination but allow us to probe fainter regions and to perform discovery studies.
8.1.2. Velocity effect in the Type J = 1→ 0 map
After checking the behaviour of our maps in these specific locations, we focus here on
the Galactic plane as a whole. Still working at 30′, the Planck map has
been degraded to Nside = 512 in order to match the
HEALPix resolution of the Dame et al. (2001). The
Planck map has been recalibrated to the Dame et al. data by
performing a linear regression on all pixels (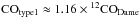 ), after which operation the difference
was taken. Figure 11 shows the residual between
the Type 1 CO(1 →
0) map and Dame et al. (2001)
Galactic plane composite survey. We observe a clear modulation pattern in the Galactic
disk, producing a positive residual at longitude l< 90° and a negative
residuals at l>
270°. This residual can reach 5% of the total intensity of CO and it
is interpreted as the signature of the rotation of the Galactic disk. Because the CO
line frequency is shifted due to the Doppler effect, the emission along different
lines-of-sight with different velocities produces a different CO response in a given
bolometer. The effect is then averaged over all bolometers in the final reconstructed CO
map. Using the mean velocity of CO emission in the Dame
et al. (2001) survey, we can fit the residuals as a linear function of the
velocity. We find that this effect at the J = 1 → 0 transition is well represented by
), after which operation the difference
was taken. Figure 11 shows the residual between
the Type 1 CO(1 →
0) map and Dame et al. (2001)
Galactic plane composite survey. We observe a clear modulation pattern in the Galactic
disk, producing a positive residual at longitude l< 90° and a negative
residuals at l>
270°. This residual can reach 5% of the total intensity of CO and it
is interpreted as the signature of the rotation of the Galactic disk. Because the CO
line frequency is shifted due to the Doppler effect, the emission along different
lines-of-sight with different velocities produces a different CO response in a given
bolometer. The effect is then averaged over all bolometers in the final reconstructed CO
map. Using the mean velocity of CO emission in the Dame
et al. (2001) survey, we can fit the residuals as a linear function of the
velocity. We find that this effect at the J = 1 → 0 transition is well represented by
![\hbox{${\rm CO}_{\rm type1}^{[1-0]} = \left( 1 + v/800~\rm km\;s^{-1} \right) \ {\rm CO}_{\rm true}^{[1-0]}$}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq174.png) , where v is the radial velocity
of the gas. This formula was also found consistent with the difference observed between
survey maps (for which the Planck satellite velocity is modulated by
the satellite revolution around the Sun) and may be used to correct the
Planck map for this velocity effect. Note that this effect is not
seen when performing the residuals in the same way for the Type 2 and
Type 3 producta as it is i) somewhat averaged out by the use of channel maps
instead of bolometer maps; and ii) hidden by the higher Galactic plane contamination of
these maps.
, where v is the radial velocity
of the gas. This formula was also found consistent with the difference observed between
survey maps (for which the Planck satellite velocity is modulated by
the satellite revolution around the Sun) and may be used to correct the
Planck map for this velocity effect. Note that this effect is not
seen when performing the residuals in the same way for the Type 2 and
Type 3 producta as it is i) somewhat averaged out by the use of channel maps
instead of bolometer maps; and ii) hidden by the higher Galactic plane contamination of
these maps.
8.2. Comparison with NANTEN II 12CO and 13CO J = 1 → 0 data
Observations in both 12CO and 13CO have been carried out with the NANTEN II millimetre-submillimetre telescope at Atacama, between February 2010 and October 2012. The dish provides a half-power beam width (HPBW) of 2.́6 in 12CO J = 1 → 0. The spectrometer is a digital Fourier spectrometer with a frequency resolution of 61 kHz and a bandwidth of 1 GHz. A Hanning window function is applied when the FFT is performed in the spectrometer, which results in a final frequency resolution of 79.3 kHz. The velocity coverage and resolution are 2600 km s-1 and 0.21 km s-1 for 12CO, and 2720 km s-1 and 0.22 km s-1 for 13CO respectively. All observations have been carried out in on-the-fly (OTF) mode, where the telescope constantly drives across the sky, with an output grid of 60′′. The standard size of an OTF block is 1° × 1° and at least one scan of longitudinal direction and lateral direction have been done for each OTF block. Each scanning data set was combined by the basket weaving method (Emerson & Graeve 1988) to reduce scanning noise in each OTF direction. The intensity calibration was made with the chopper-wheel method (Kutner & Ulich 1981) and absolute intensity calibration performed on ρ-Oph, Ori-KL, M17SW, and Perseus.
The soon-to-be-published data we use here consist of a 9° × 2° Galactic plane patch around Galactic
coordinates (315°,
0°). We smoothed the NANTEN
and Planck maps to a 15′ resolution before carrying out the comparison. This resolution is
chosen as it corresponds to that of the Type 2 CO map and allows a significant
noise reduction in the Type 1 map (which comes with a 9.́65 native resolution).
Recalling that we expect a 0.53×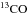 contribution to the Type 1 map
(see Sect. 6.2.2), we show in Fig. 12 the combined NANTEN II 12CO + 0.53 × 13CO on
the top panel, the Type 1 map in the middle and the correlation plot in the
bottom panel. The agreement between the two sets of data is good with a correlation of
0.95. While not shown here, we perform this test for the Type 2 CO map as well,
using this time 1.14×
contribution to the Type 1 map
(see Sect. 6.2.2), we show in Fig. 12 the combined NANTEN II 12CO + 0.53 × 13CO on
the top panel, the Type 1 map in the middle and the correlation plot in the
bottom panel. The agreement between the two sets of data is good with a correlation of
0.95. While not shown here, we perform this test for the Type 2 CO map as well,
using this time 1.14×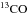 as is estimated in Sect. 6.2.2. The agreement is once again satisfactory with a
best-fit slope of 1.00. In both cases, the level of the residuals between the best-fit and
the combination of NANTEN data is found to be less than about 10% and thus compatible with
the calibration uncertainties.
as is estimated in Sect. 6.2.2. The agreement is once again satisfactory with a
best-fit slope of 1.00. In both cases, the level of the residuals between the best-fit and
the combination of NANTEN data is found to be less than about 10% and thus compatible with
the calibration uncertainties.
 |
Fig. 10 Correlation between the three types of CO products with the Dame et al. (2001) data in the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. The best-fit slope and intercept are given in Table 5. Notice that the intercepts are in all cases below 0.7 K km s-1. |
This test is important, as it validates our understanding of the
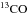 contamination in the
Planck CO(1 →
0) maps. It also highlights that the Type 2 CO(1 → 0) map does not suffer from major dust
contamination in the Galactic plane since, had this been the case, the correlation with
NANTEN would have presented a slope greater than one. We also performed an independent
check of the 13CO
contamination based on FCRAO data (Jackson et al.
2006), which corroborates the results obtained with NANTEN. This is the purpose
of the next section.
contamination in the
Planck CO(1 →
0) maps. It also highlights that the Type 2 CO(1 → 0) map does not suffer from major dust
contamination in the Galactic plane since, had this been the case, the correlation with
NANTEN would have presented a slope greater than one. We also performed an independent
check of the 13CO
contamination based on FCRAO data (Jackson et al.
2006), which corroborates the results obtained with NANTEN. This is the purpose
of the next section.
 |
Fig. 11 Residual map with respect to the Dame et al. (2001) map in K km s-1 for the Type 1 J = 1 → 0Planck CO map. The Planck maps have been recalibrated to Dame before performing the subtraction. |
8.3. Comparison with FCRAO 13CO J = 1 → 0 data
Along the same lines as the comparison performed with NANTEN II data, it is possible to
gain further confidence in our estimation of the 13CO contamination using FCRAO
13CO(1 →
0) data along with the 12CO(1 →
0) data of Dame et al. (2001). In
this analysis, we use the publicly available Boston University FCRAO Galactic Ring
Survey9 (FCRAO-GRS) described in Jackson et al. (2006). It consists of a 75.4
deg2 survey of
the Galactic plane, between 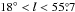 and | b | < 1° at
46′′ resolution.
and | b | < 1° at
46′′ resolution.
We first re-project the FCRAO-GRS data into the HEALPix pixelization scheme (Nside = 2048) using a nearest grid-point approach and correct for the 0.48 beam efficiency given in Jackson et al. (2006). Binning over the ratio 13COFCRAO/12CODame, we compute the average ratio ⟨ COtype1 ⟩ / ⟨ 12CODame ⟩ in each bin and plot the correlation in Fig. 13. Error bars are obtained assuming white noise, the amplitude of which is estimated at high Galactic latitude (| b | > 60°). The standard deviation in each bin is then simply estimated using the number of pixels in the bin. We assume the noise in the Dame et al. (2001) map to be negligible.
The correlation between the two ratios is good and from the best-fit of the linear
regression we see that the Planck Type 1 map can be written as
![\begin{eqnarray*} {\rm CO}_{\rm {\sc TYPE 1}}^{[1-0]} = 0.53 \times {^{13}{\rm CO_{\rm FCRAO}}} + 1.07 \times{^{12}{\rm CO_{\rm Dame}}} , \end{eqnarray*}](/articles/aa/full_html/2014/11/aa21553-13/aa21553-13-eq212.png) which is agreement with the 0.53 × 13CO contamination
estimate we made from the bandpass coefficients (see Sect. 6.2.2). This test shows, in a completely independent manner to that of the
NANTEN comparison, that we have an excellent grasp on the CO content of the Type
1 map.
which is agreement with the 0.53 × 13CO contamination
estimate we made from the bandpass coefficients (see Sect. 6.2.2). This test shows, in a completely independent manner to that of the
NANTEN comparison, that we have an excellent grasp on the CO content of the Type
1 map.
8.4. Comparison with the AMANOGAWA-2SB CO J = 2 → 1 survey
The AMANOGAWA-2SB survey (Handa et al. 2012; Yoda et al. 2010) carried out simultaneous Galactic plane (l = 10° − 245°) observations of the 12CO and 13CO(2 → 1) transitions with the Tokyo-NRO 60-cm telescope, with a resolution and grid-spacing of 9 and 3.́75 respectively. Here, we use a 35° × 8° section of the AMANOGAWA-2SB 12CO Galactic plane survey for comparison to the Planck CO(2 → 1) maps.
The area under scrutiny is shown in Fig. 14 for the AMANOGAWA data set (top) and the Planck Type 1 CO [2–1] map (middle) at the working resolution of 15′. The correlation between the two data sets in given in the bottom panel and shows remarkable agreement with a best-fit value for the correlation of 0.95. Conversely to the CO(1 → 0) map, no 13CO contribution was required to match the two data sets. This is once again in agreement to what was predicted in Sect. 6.2.2 where we found that the 13CO contribution to the Type 1 J = 1 → 0 line should be negligible, given the weighted bandpass transmission of the isotopologue in the 217 GHz channel. The residuals between the best-fit and the AMANOGAWA data are found to be about 5%, which is compatible with the combined calibration uncertainties of Planck and AMANOGAWA.
 |
Fig. 12 Comparison of the Planck (J = 1 → 0) Type 1 map to the NANTEN II survey in a 9° × 2° section of the Galactic plane. Top: combined NANTEN II map as 12CO + 0.53 × 13CO, where the factor applied to 13CO corresponds to the bandpass estimate of the 13CO contamination in the Type 1 map (see Sect. 6.2.2). Middle: Planck Type 1 J = 1 → 0 map. Bottom: correlation plot between the two maps. The colour scale represents the logarithm of the number of pixels in a given intensity bin. The solid and dashed lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slope and intercept are 1.007 ± 0.001 and 5.243 ± 0.032, respectively. |
 |
Fig. 13 Average ratio ⟨ COtype1 ⟩ / ⟨ 12CODame ⟩ in bins of the 13COFCRAO/12CODame ratio. The best linear fit is represented by the orange solid line. The best-fit slope and intercept are 0.53 ± 0.03 and − 1.07 ± 0.01, respectively. |
 |
Fig. 14 Comparison of the PlanckJ = 2–1 Type 1 CO map to the AMANOGAWA-2SB Galactic plane survey. From top to bottom we display the AMANOGAWA data, the Type 1data in the same region and the correlation between the two maps. The log colour scale represents the number of pixels in a given intensity bin. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slope and intercept are 0.941 ± 0.001 and 0.792 ± 0.009, respectively. |
8.5. Comparison with the FIRAS CO J = 1 → 0, J = 2 → 1 and J = 3 → 2 surveys
 |
Fig. 15 Comparison of the Type 1 Planck CO maps with the FIRAS J = 1 → 0 (top), J = 2 → 1 (middle) and J = 3 → 2 (bottom) data. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slopes and intercepts are: a) 0.98 ± 0.17 and 0.33 ± 0.65; b) 1.12 ± 0.02 and − 0.01 ± 0.04; and c) 1.13 ± 0.03 and 0.04 ± 0.02. |
Fixsen et al. (1999) have analyzed a by-product of
the Far Infrared Absolute Spectrophotometer (FIRAS on COBE launched in
1989) sky maps, namely integrated velocity maps of well-known Galactic lines. These
include carbon, nitrogen and water lines, but, more importantly for the present study, the
complete 12CO
rotation ladder. These are absolutely calibrated all-sky measurements. FIRAS has a better
spectral resolution (13.5 GHz) than Planck-HFI but a much lower angular
resolution. FIRAS integrated CO lines are retrieved from the Lambda website10. The first three transitions at 115.27, 230.54 and
345.80 GHz come from the low frequency emission line maps. They are converted from
nW m-2
sr-1 to K km
s-1 with the coefficient
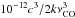 . Error maps are processed in the same way
and we neglect gain uncertainties.
. Error maps are processed in the same way
and we neglect gain uncertainties.
Planck CO maps are convolved with the FIRAS beam in the same way as described in Appendix A of Planck Collaboration VIII (2014) and compared to FIRAS line maps within the FIRAS pixelization scheme. This is simply done by taking the Planck value at the grid point nearest to the FIRAS pixel within 15′. Uncertainties are much larger for FIRAS than Planck; the noisiest FIRAS values are not kept in the comparison. The cut-off is chosen as 160, 11 and 7 K km s-1 for the CO(1 → 0), CO(2 → 1), and CO(3 → 2) lines, respectively. The FIRAS Galactic centre values may not be reliable because of the large velocity spread and we therefore discard any pixels within 4° of the Galactic centre. There is no possible tuning in this straightforward comparison.
Figure 15 shows the correlation plot between the Type 1 Planck CO data and the FIRAS J = 1 → 0 (top), J = 2 → 1 (middle) and J = 3 → 2 (bottom) data. In each panel, the dashed blue line corresponds to perfect correlation (y = x), while the orange line gives the best fit. We find that FIRAS and Planck all-sky CO data are consistent with a linear relationship. For the CO(1 → 0) line, Fixsen et al. (1999) claim a detection only in the Galactic centre. With Planck we obtain a statistical detection of CO(1 → 0) with FIRAS outside the Galactic centre at the 7σ level. For the two other lines, FIRAS measurements tend to overestimate the CO emission with respect to Planck by at most 10%. This is well within the absolute calibration error for Planck and beam uncertainties for FIRAS.
8.6. Comparison with HARP/ACSIS CO J = 3 → 2 data
Surveys in of the CO(3 → 2) transition are not as numerous as those of lower transitions, which makes assessing the quality of the Type 1 J = 3 → 2 map more difficult. We used part of the JCMT HARP/ACSIS 12CO(3 → 2) Galactic plane data (soon to be published). Details on the HARP/ACSIS system and calibration can be found in Buckle et al. (2009); Polychroni et al. (2012).
We use a 2° long section of the Galactic plane from l = 12.5 to l = 14.5 where the survey has latitude range ± 0.5°. The original HARP data were not clipped at some nσ threshold but collapsed over the whole spectral range, after performing a heavy smooth on all regions with signal less than 3σ. This ensures there is no significant emission missing, while minimizing the addition of noise. The data were then smoothed to about the 4.́5 resolution, to mimic the Planck resolution but with pixels of around 5′′. The two maps were then brought down to the same pixelization, the least constraining rebinning resulting in a 43 × 23 pixels patch, with about 2.́7 pixels. Because of the noise level inherent to the Type 1 map, a large dispersion is seen when simply performing the correlation between all pixels of these two patches. Therefore, we perform another rebinning, collapsing the latitude dimension to get a 43-point “average” longitudinal profile of the two maps. The correlation of these two profiles is plotted in Fig. 16.
Despite our rebinning, the correlation remains quite noisy, but the figure shows that the perfect correlation (y = x) line is a fair representation of the data when ignoring the two outliers. More data would be required to perform a thorough characterisation of the Type 1 J = 3 → 2 map.
8.7. High Galactic latitude structures
 |
Fig. 16 Correlation plot between the latitude-collapsed longitudinal profiles (see text for details) of Type 1 J = 3 → 2 HFI CO map and the HARP J = 3 → 2 survey. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best-fit, respectively. |
 |
Fig. 17 Comparison of the Planck CO(1 → 0) maps with the high Galactic latitudes CO detections and non detections from MHHST00. Top: correlation between the CO detections in MHHST00 and the Planck Type 2 and Type 3 maps. The latter was first smoothed to 15′. Bottom: distribution of all Planck CO(1 → 0) maps (at 15′ resolution) at the non-detection positions of MHHST00. The width of the distribution is compatible with the noise in the maps. Differences with respect to the values in Table 3 can be explained by the inhomogeneities of the noise in the Planck maps. |
In order to achieve a deep, high-Galactic-latitude statistical comparison of the Planck CO maps with ground-based observations, we use the observations performed at CfA and described in Hartmann et al. (1998) (HMT98) and Magnani et al. (2000) (MHHST00) for the North and South Galactic hemisphere respectively. These data consist of 8′ beam observations of the | b | > 30° sky, on a regularly-spaced grid, observable from Cambridge (MA). In total, 10 443 points in the north Galactic hemisphere and 4934 in the south were observed. A detection threshold of 0.3 K km s-1 (3σ) was considered. In total 26 detections were reported in the North and 133 in the South.
First, for each of these detection points, we compute the corresponding Planck Type 2 and Type 3 CO [1–0] fluxes (in a 10′ diameter disc). The Type 1 map was not selected for this analysis as its noise level makes it unsuitable for high Galactic latitudes. The top panel in Fig. 17 shows the correlation of the Planck Type 2 and Type 3 fluxes as a function of the 159 HMT98 and MHHST00 fluxes. A reasonable agreement and compatible absolute calibration is reached in these faint CO-emitting regions. The bottom panel presents the histogram of all three types of Planck CO maps fluxes at the 15 218 locations where no detection is expected from the CfA surveys. The Gaussian distributions obtained are all centred on zero and have a standard deviation compatible with the noise level of the map. Discrepancies with respect to the values in Table 3 can be explained the inhomogeneities of the noise in the Planck maps. This comparison to the HMT98 and MHHST00 highlights the high quality of the Planck CO maps in the faintest CO regions.
9. Conclusions
The Planck-HFI maps contain a non-negligible component that is attributed to the emission, in the HFI spectral bands, of the three first CO rotation transitions coming from the interstellar medium. Several component separation methods are used to isolate this component from the others (CMB and diffuse Galactic emission, mainly thermal dust), by using the spectral diversity and large coverage of Planck-HFI.
This paper presents all-sky maps of the velocity-integrated emission of CO in the J = 1 → 0, J = 2 → 1, and J = 3 → 2 transitions. Three different types of maps are produced: i) Type 1 maps obtained from a single-channel analysis for the three transitions; ii) Type 2 maps available for the first two transitions only and coming from a multi-channel analysis; and iii) a single Type 3 map relying on a multi-line approach.
We have characterized the maps in terms of resolution, noise and systematic effects by cross-comparison and internal validation of the maps. Comparison to external CO data was also performed and general agreement found, always within the estimated calibration uncertainties of the data. Note however that the Type 1 J = 3 → 2 map could not be as thoroughly tested as the others because of the few external CO(3 → 2) data sets available.
In summary, Type 1 maps are the noisiest but suffer from the least systematic errors and other sky emission contamination. The Type 2 CO products provide high S/N single-line maps at the price of larger systematics and other sky emissions contamination, and are of lower resolution. Finally, the Type 3 map gives a high S/N and high resolution CO map but relies on the assumption of constant line ratios across the sky. Both Type 2 and Type 3 maps are more suitable for a use at intermediate and high-Galactic latitudes. The Type 1 maps are, by contrast, more reliable in terms of contamination by other sources of emission in the Galactic plane and on high CO intensity regions. In all these maps the 13CO contribution is not corrected and needs to be accounted for in any further scientific analysis.
The Planck CO maps are used within the Planck collaboration for the definition of regions of the sky where CMB, thermal SZ and cosmic infrared background cosmological studies can safely be performed. The Planck CO maps presented in this paper are delivered as part of the Planck nominal mission public archive.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Compatible results within statistical errors are obtained when performing a similar, but independent, analysis using the Commander component separation method (Eriksen et al. 2008) described in Sect. 4.1.3. These results show that these CO conversion coefficients are robust against some possible systematic effects on the method.
While this assumption eases the CO extraction, it also leads to an overall systematic calibration error that can be corrected for afterwards (see Sect. 6.2).
First and last ring sets are independent data sets built using the first and second half of the stable pointing periods (see Sect. 2).
The complete data set can be retrieved from http://www.cfa.harvard.edu/rtdc/CO/
The data of the BU-FCRAO-GRS may be retrieved at http://www.bu.edu/Galacticring/
Acknowledgments
The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php?project=Planck&page=Planck_Collaboration. We acknowledge the use of the HEALPix software.
References
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bieging, J. H., & Peters, W. L. 2011, ApJS, 196, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bieging, J. H., Peters, W. L., & Kang, M. 2010, ApJS, 191, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Buckle, J. V., Hills, R. E., Smith, H., et al. 2009, MNRAS, 399, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 2004, in Milky Way Surveys: The Structure and Evolution of our Galaxy, eds. D. Clemens, R. Shah, & T. Brainerd, ASP Conf. Ser., 317, 66 [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emerson, D. T., & Graeve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
- Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004, ApJ, 612, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Jewell, J. B., Dickinson, C., et al. 2008, ApJ, 676, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fauvet, L., Macías-Pérez, J. F., Hildebrandt, S. R., & Désert, F.-X. 2013, Adv. Astron., 26, 2013 [arXiv:1212.6854] [Google Scholar]
- Ferrière, K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J., Bennett, C. L., & Mather, J. C. 1999, ApJ, 526, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Handa, T., Yoda, T., Kohno, K., et al. 2012, in Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, eds. W. Aoki, M. Ishigaki, T. Suda, T. Tsujimoto, & N. Arimoto, ASP Conf. Ser., 458, 221 [Google Scholar]
- Hartmann, D., Magnani, L., & Thaddeus, P. 1998, ApJ, 492, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G. 2012, Ph.D. Thesis, Université Joseph Fourier [Google Scholar]
- Hurier, G., Hildebrandt, S. R., & Macias-Perez, J. F. 2013, A&A [arXiv:1007.1149] [Google Scholar]
- Ikeda, M., Maezawa, H., Ito, T., et al. 1999, ApJ, 527, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., Gómez, M., & Whitney, B. A. 2008, Low Mass Star Formation in the Taurus-Auriga Clouds, ed. B. Reipurth, 405 [Google Scholar]
- Kutner, M. L., & Ulich, B. L. 1981, ApJ, 250, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnani, L., Blitz, L., & Mundy, L. 1985, ApJ, 295, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., Hartmann, D., Holcomb, S. L., Smith, L. E., & Thaddeus, P. 2000, ApJ, 535, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, A., & Fukui, Y. 2004, in Milky Way Surveys: The Structure and Evolution of our Galaxy, eds. D. Clemens, R. Shah, & T. Brainerd, ASP Conf. Ser. 317, 59 [Google Scholar]
- Oka, T., Onodera, Y., Nagai, M., et al. 2012, ApJS, 201, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Pajot, F., Ade, P. A. R., Beney, J.-L., et al. 2010, A&A, 520, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penzias, A. A., Solomon, P. M., Jefferts, K. B., & Wilson, R. W. 1972, ApJ, 174, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013, The Explanatory Supplement to the Planck 2013 results, http://www.sciops.esa.int/wikiSI/planckpla/index.php?title=Main_Page (ESA) [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2014, A&A, 571, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration III. 2014, A&A, 571, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2014, A&A, 571, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration V. 2014, A&A, 571, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2014, A&A, 571, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2014, A&A, 571, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2014, A&A, 571, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2014, A&A, 571, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, 571, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2014, A&A, 571, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2014, A&A, 571, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, 571, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2014, A&A, 571, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2014, A&A, 571, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2014, A&A, 571, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2014, A&A, 571, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2014, A&A, 571, A23 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Planck Collaboration XXIV. 2014, A&A, 571, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXV. 2014, A&A, 571, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2014, A&A, 571, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2014, A&A, 571, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVIII. 2014, A&A, 571, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXXI. 2014, A&A, 571, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polychroni, D., Moore, T. J. T., & Allsopp, J. 2012, MNRAS, 422, 2992 [NASA ADS] [CrossRef] [Google Scholar]
- Sawada, T., Hasegawa, T., Handa, T., et al. 2001, ApJS, 136, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Sanders, D. B., & Scoville, N. Z. 1979, ApJ, 232, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, L. D., Naylor, D. A., & Swinyard, B. M. 2010, Measurement Science and Technology, 21, 065601 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D. 2005, in Astrochemistry: Recent Successes and Current Challenges, eds. D. C. Lis, G. A. Blake, & E. Herbst, IAU Symp., 231, 271 [Google Scholar]
- Wilson, B. A., Dame, T. M., Masheder, M. R. W., & Thaddeus, P. 2005, A&A, 430, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R. W., Jefferts, K. B., & Penzias, A. A. 1970, ApJ, 161, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Yoda, T., Handa, T., Kohno, K., et al. 2010, PASJ, 62, 1277 [NASA ADS] [Google Scholar]
Appendix A: Description of the Planck CO products
The characteristics of the released maps are the following. We provide HEALPix pixelization all-sky maps with Nside = 2048. For one transition, the CO velocity-integrated line signal map is given in Kkms-1 units at the CO transition frequency. A conversion factor from this unit to the native unit of HFI maps (KCMB) is provided in the header. Four maps are given in a single file per transition (1–0), (2–1) and (3–2) and per Type 1, Type 2, and Type 3,
-
a CO signal map;
-
a CO null test map;
-
a standard deviation map; and
-
a mask for which a value of 1 corresponds to a valid pixel.
Type 1 products have the native HFI resolution 9.́65, 4.́99 and 4.́82 for the CO [1 → 0], [2 → 1] and [3 → 2] transitions respectively. Type 2 products have 15′ resolution and are given for the two first transitions. The Type 3 product has a 5.́5 effective resolution and corresponds to a combined map of the three CO transitions normalized at the (J = 1 → 0) transition frequency. These maps are shown in the left column of Figs. 3–5. The corresponding standard deviation maps are displayed in the right column.
Appendix B: Validation of CO extraction methods on simulations
Planck component separation methods (see Planck Collaboration XII 2014) are generally validated using the FFP6 set of simulations (Planck Collaboration 2013), which aim at providing a complete realization of the Planck mission. They rely on the Planck Sky Model (PSM) fully described in Delabrouille et al. (2013). FFP6 maps can be used for the multi-channel and multi-line approaches, but they do not provide the individual bolometer maps required to validate the single-channel CO extraction method. For the latter, CO-tailored simulations are needed, as described below.
Appendix B.1: Single-channel approach: Type 1 maps
We use here specific simulations of the Planck bolometer maps at 100 GHz. For each bolometer in the Planck 100 GHz channel, we construct a map of the sky emission considering CMB and other sources of sky emission (Galactic diffuse emission from synchrotron, thermal dust and free-free, and Galactic and extragalactic point sources). We use the same PSM model as for the FFP6 simulations (see below for a detailed description). For the CO emission we just use the Dame et al. (2001) map as a template and applied the CO bandpass conversion coefficients from Table 2 to convert to KCMB units. The per bolometer null maps were added to account for the noise contribution. The MILCA algorithm was then applied to these maps to reconstruct the CO signal using the single channel approach discussed in Sect. 4.2.1. We found that when the 12CO conversion coefficients are perfectly known the CO emission is well reconstructed. The contribution from contaminants was estimated to be less than 0.5% of the CO signal overall and the rms of the residuals consistent with the noise at about the 1σ level.
We also tested the sensitivity of the MILCA algorithm to uncertainties on the CO conversion coefficients. These uncertainties translate into noisier final CO maps and an overall calibration bias. For 1% and 5% uncertainties on the CO conversion coefficients we observe a combined signal to-noise-reduction of 6% and 60%, respectively.
Appendix B.2: Multi-channel approach: Type 2 maps
The multi-channel approach may be validated using PlanckFFP6 channel intensity maps. Relevant to our purpose here, includes in particular a ν-2.14 free-free emission component, a two-component dust emission from model 7 of Finkbeiner et al. (1999), and CO emission using the CO map of Dame et al. (2001) as the template.
We apply the multi-channel CO extraction method described in Sect. 4.2.2 to the set of FFP6 intensity maps and characterize the reconstructed CO(1 → 0) map with the input map of the FFP6 simulations. As for some of the other tests done throughout this paper, the comparison is performed in the Orion, Taurus, and Polaris molecular clouds.
A linear correlation (COtype2 = a COFFP6 + b) between the two maps is found in the three regions, with slopes of 0.99 ± 0.01, 1.013 ± 0.001, 0.999 ± 0.002 for Taurus, Orion, and Polaris respectively. We also checked the standard deviation of the residual maps COFFP6 − COtype2 against the average σ in each region obtained from the Type 2 CO(1 → 0) standard deviation map (see Fig. 3). In Polaris, the residual is within the ±1σ level, while it is at about 1.5σ for Taurus and Orion. In these two latter regions, the slightly poorer behaviour of the residual is attributed to the simple modified blackbody dust modelling of the multi-channel approach that cannot properly capture the dust of the FPP6 simulations. With these caveats, the multi-channel approach is successfully validated on FFP6 simulations.
Appendix B.3: Multi-line approach: Type 3 map
The quality of the reconstruction of the Type 3 CO map was also validated using the FFP6 simulations. As described in Sect. 4.2.3, the Type 3 CO map is a byproduct of the CMB oriented component separation procedure and therefore, validation on simulations is presented in the companion CMB-oriented component separation paper Planck Collaboration XII (2014).
All Tables
Relative CO conversion coefficients of HFI bolometers (bolometer pairs) in the 100, 217 and 353 GHz channels normalized to the average CO conversion coefficient for each channel.
All Figures
 |
Fig. 1 The average spectral response for each of the HFI frequency bands. The vertical dashed lines represent the first nine 12CO rotational transitions assuming zero velocity. |
| In the text | |
 |
Fig. 2 Comparison of normalised CO conversion coefficients computed from the bandpass measurements (black) or estimated on the sky (blue) for the 100 (top), 217 (middle) and 353 GHz (bottom) channels. See Table 2. |
| In the text | |
 |
Fig. 3 Full-sky CO J = 1 → 0 maps (left) and their respective statistical error maps (right) in K km s-1 units for the three types of Planck CO products. For display purposes only, the Type 1 and Type 3 maps are smoothed to 15′ to ease the comparison to the Type 2 maps. The error maps correspond to the non-smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
| In the text | |
 |
Fig. 4 Full-sky CO J = 2 → 1 maps (left) and their respective statistical error maps (right) in K km s-1 units for Type 1 (top) and Type 2 (bottom) Planck CO products. The Type 1 map has been smoothed to 15′ for display purposes but the error map corresponds to the non smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
| In the text | |
 |
Fig. 5 Type 1 full-sky CO J = 3 → 2 maps (left) and its statistical error map (right) in K km s-1 units. The map has been smoothed to 15′ for display purpose but the error map corresponds to the non smoothed product. The maps are in Galactic coordinates and follow the HEALPix pixelization scheme for Nside = 2048. |
| In the text | |
 |
Fig. 6 Comparison of the 3 types of CO products with a dust template map for the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. |
| In the text | |
 |
Fig. 7 Images ( |
| In the text | |
 |
Fig. 8 Correlation between the Type 1 and Type 2 (top) and Type 1 and Type 3 (middle) J = 1 → 0 CO maps at high Galactic latitudes 25°< | b | < 90°. Correlation between the Type 1 and Type 2 J = 2 → 1 CO maps is shown on the bottom plot. The solid line corresponds to perfect correlation (y = x). Below the dashed horizontal line the colour scale gives the logarithm of the number of pixels in a given bin. The best linear fits (solid red line) are computed from the individual pixels plotted above the dashed line. The best-fit slopes and uncertainties are: a) 0.93 ± 0.17; b) 0.87 ± 0.20; and c) 0.96 ± 0.12. The intercepts are compatible with zero within the error bars. |
| In the text | |
 |
Fig. 9 Correlation between Type 1 and Type 2 CO maps at 115 GHz (left column) and 230 GHz (right column) in the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. The best linear fits (orange solid line) have been computed between 2 and 15 K km s-1 at 115 GHz and between 1 and 15 K km s-1 at 230 GHz, where bulk of the data lie and avoiding the noise around zero. The best-fit slopes and uncertainties are: a)1.12 ± 0.03; b) 1.14 ± 0.01; c) 1.10 ± 0.04; d) 1.07 ± 0.01; e) 1.07 ± 0.06; and f) 1.17 ± 0.04. The intercepts are compatible with zero within error bars. The orange dot-dashed lines in the bottom panels correspond to the recalibration uncertainty due to the contribution of the J = 3 → 2 line in the Type 2 J = 2 → 1 product. See text for detail. |
| In the text | |
 |
Fig. 10 Correlation between the three types of CO products with the Dame et al. (2001) data in the Taurus (top), Orion (middle) and Polaris (bottom) molecular clouds. The best-fit slope and intercept are given in Table 5. Notice that the intercepts are in all cases below 0.7 K km s-1. |
| In the text | |
 |
Fig. 11 Residual map with respect to the Dame et al. (2001) map in K km s-1 for the Type 1 J = 1 → 0Planck CO map. The Planck maps have been recalibrated to Dame before performing the subtraction. |
| In the text | |
 |
Fig. 12 Comparison of the Planck (J = 1 → 0) Type 1 map to the NANTEN II survey in a 9° × 2° section of the Galactic plane. Top: combined NANTEN II map as 12CO + 0.53 × 13CO, where the factor applied to 13CO corresponds to the bandpass estimate of the 13CO contamination in the Type 1 map (see Sect. 6.2.2). Middle: Planck Type 1 J = 1 → 0 map. Bottom: correlation plot between the two maps. The colour scale represents the logarithm of the number of pixels in a given intensity bin. The solid and dashed lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slope and intercept are 1.007 ± 0.001 and 5.243 ± 0.032, respectively. |
| In the text | |
 |
Fig. 13 Average ratio ⟨ COtype1 ⟩ / ⟨ 12CODame ⟩ in bins of the 13COFCRAO/12CODame ratio. The best linear fit is represented by the orange solid line. The best-fit slope and intercept are 0.53 ± 0.03 and − 1.07 ± 0.01, respectively. |
| In the text | |
 |
Fig. 14 Comparison of the PlanckJ = 2–1 Type 1 CO map to the AMANOGAWA-2SB Galactic plane survey. From top to bottom we display the AMANOGAWA data, the Type 1data in the same region and the correlation between the two maps. The log colour scale represents the number of pixels in a given intensity bin. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slope and intercept are 0.941 ± 0.001 and 0.792 ± 0.009, respectively. |
| In the text | |
 |
Fig. 15 Comparison of the Type 1 Planck CO maps with the FIRAS J = 1 → 0 (top), J = 2 → 1 (middle) and J = 3 → 2 (bottom) data. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best linear fit, respectively. The best-fit slopes and intercepts are: a) 0.98 ± 0.17 and 0.33 ± 0.65; b) 1.12 ± 0.02 and − 0.01 ± 0.04; and c) 1.13 ± 0.03 and 0.04 ± 0.02. |
| In the text | |
 |
Fig. 16 Correlation plot between the latitude-collapsed longitudinal profiles (see text for details) of Type 1 J = 3 → 2 HFI CO map and the HARP J = 3 → 2 survey. The solid orange and dashed blue lines represent perfect correlation (y = x) and the best-fit, respectively. |
| In the text | |
 |
Fig. 17 Comparison of the Planck CO(1 → 0) maps with the high Galactic latitudes CO detections and non detections from MHHST00. Top: correlation between the CO detections in MHHST00 and the Planck Type 2 and Type 3 maps. The latter was first smoothed to 15′. Bottom: distribution of all Planck CO(1 → 0) maps (at 15′ resolution) at the non-detection positions of MHHST00. The width of the distribution is compatible with the noise in the maps. Differences with respect to the values in Table 3 can be explained by the inhomogeneities of the noise in the Planck maps. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.