| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 28 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322612 | |
| Published online | 20 May 2014 | |
Planck intermediate results. XV. A study of anomalous microwave emission in Galactic clouds
Received:
5
September
2013
Accepted:
19
February
2014
Anomalous microwave emission (AME) is believed to be due to electric dipole radiation from small spinning dust grains. The aim of this paper is a statistical study of the basic properties of AME regions and the environment in which they emit. We used WMAP and Planck maps, combined with ancillary radio and IR data, to construct a sample of 98 candidate AME sources, assembling SEDs for each source using aperture photometry on 1°-smoothed maps from 0.408 GHz up to 3000 GHz. Each spectrum is fitted with a simple model of free-free, synchrotron (where necessary), cosmic microwave background (CMB), thermal dust, and spinning dust components. We find that 42 of the 98 sources have significant (>5σ) excess emission at frequencies between 20 and 60 GHz. An analysis of the potential contribution of optically thick free-free emission from ultra-compact H ii regions, using IR colour criteria, reduces the significant AME sample to 27 regions. The spectrum of the AME is consistent with model spectra of spinning dust. Peak frequencies are in the range 20−35 GHz except for the California nebula (NGC 1499), which appears to have a high spinning dust peak frequency of (50 ± 17) GHz. The AME regions tend to be more spatially extended than regions with little or no AME. The AME intensity is strongly correlated with the sub-millimetre/IR flux densities and comparable to previous AME detections in the literature. AME emissivity, defined as the ratio of AME to dust optical depth, varies by an order of magnitude for the AME regions. The AME regions tend to be associated with cooler dust in the range 14−20 K and an average emissivity index, βd, of +1.8, while the non-AME regions are typically warmer, at 20−27 K. In agreement with previous studies, the AME emissivity appears to decrease with increasing column density. This supports the idea of AME originating from small grains that are known to be depleted in dense regions, probably due to coagulation onto larger grains. We also find a correlation between the AME emissivity (and to a lesser degree the spinning dust peak frequency) and the intensity of the interstellar radiation field, G0. Modelling of this trend suggests that both radiative and collisional excitation are important for the spinning dust emission. The most significant AME regions tend to have relatively less ionized gas (free-free emission), although this could be a selection effect. The infrared excess, a measure of the heating of dust associated with H ii regions, is typically >4 for AME sources, indicating that the dust is not primarily heated by hot OB stars. The AME regions are associated with known dark nebulae and have higher 12 μm/25 μm ratios. The emerging picture is that the bulk of the AME is coming from the polycyclic aromatic hydrocarbons and small dust grains from the colder neutral interstellar medium phase.
Key words: HII regions / radiation mechanisms: general / radio continuum: ISM / submillimeter: ISM
© ESO, 2014
1. Introduction
Anomalous microwave emission (AME) has been observed in a few directions of the Galaxy and is an important foreground for the cosmic microwave background (CMB) (Kogut et al. 1996; Leitch et al. 1997; Finkbeiner et al. 2002; Finkbeiner 2004; de Oliveira-Costa et al. 2004; Dobler & Finkbeiner 2008; Miville-Deschênes et al. 2008; Gold et al. 2011). There is strong evidence, particularly in the Perseus and ρ Ophiuchi clouds (Watson et al. 2005; Casassus et al. 2008; Planck Collaboration XX 2011), that AME is due to electric dipole radiation from small spinning dust grains. Along these sight lines, there is highly significant excess emission above free-free, synchrotron, CMB, and thermal dust in the frequency range 10−100 GHz. The spectral energy distributions (SEDs) are peaked at about 30 GHz, and can be fitted by physically-motivated theoretical models of spinning dust (Draine & Lazarian 1998; Ali-Haïmoud et al. 2009; Hoang et al. 2010, 2011). AME has been detected in H ii regions (Dickinson et al. 2006, 2007, 2009; Todorović et al. 2010), dust clouds (Casassus et al. 2006, 2008; Scaife et al. 2009), a supernova remnant (Scaife et al. 2007), and in one external galaxy (Murphy et al. 2010a; Scaife et al. 2010b). There is also evidence for AME in the diffuse emission at high Galactic latitudes (Peel et al. 2012; Macellari et al. 2011; Ghosh et al. 2012).
Definitive evidence for spinning dust was provided by Planck Collaboration XX (2011). Accurate SEDs of the Perseus and ρ Ophiuchi clouds were easily fitted by a physically motivated model for the clouds, including spinning dust components associated with the atomic and molecular phases of the interstellar medium (ISM). The model was found to be an excellent fit with physical parameters that were reasonable for these regions. Planck Collaboration XXI (2011) applied an inversion technique to separate the various contributions of the ISM in Galactocentric rings along the Galactic plane and found that 25 ± 5% of the 30 GHz emission comes from AME and was consistent with spinning dust associated with atomic and molecular gas but not with the ionized phase. Component separation of the diffuse emission at intermediate latitudes in the southern Gould Belt region (Planck Collaboration Int. XII 2013) revealed an AME component consistent with spinning dust emitting at a peak frequency of (25.5 ± 1.5) GHz (in flux density units), compatible with plausible values for the local density and radiation field.
To date there has been no detailed study of AME in a reasonable sample of sources. Dickinson et al. (2007) observed six southern H ii regions with the Cosmic Background Imager at 31 GHz and found tentative evidence for excess emission from the RCW49 complex. Scaife et al. (2008) observed a sample of 16 compact H ii regions at 15 GHz with the Arcminute Microkelvin Imager (AMI) and found no evidence for excess emission; the spectrum was consistent with optically thin free-free emission from warm ionized gas. Todorović et al. (2010) surveyed the Galactic plane at longitudes 27° ≤ l ≤ 46° with the Very Small Array (VSA) at 33 GHz and found statistical evidence for AME in nine regions, but with an emissivity relative to 100 μm brightness that was 30−50% of the average high latitude value.
In this paper, we have assembled a sample of 98 Galactic clouds selected at PlanckfootnotePlanck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark. frequencies to investigate their SEDs and constrain the contribution of AME. Due to the large beam size of the lowest WMAP/Planck channels and the low frequency radio data, there is sometimes a mix of sources within the beam. Many of the sources can be classed as diffuse H ii regions, although we have found a few AME sources with no obvious associated H ii region and very weak free-free emission. Many of the regions are in large star-forming complexes, which at 1° resolution contain many individual sources. These are often located in the vicinity of molecular clouds, which produce strong thermal dust emission. Nevertheless, combining Planck data with ancillary radio and far-infrared data we assemble their SEDs from 0.408 GHz to 5000 GHz. We fit the SEDs with a simple model of free-free, synchrotron (where appropriate), thermal dust, CMB, and AME (spinning dust) components to determine whether there is evidence for AME at frequencies 20−60 GHz and if so, if it agrees with spinning dust models. For the most significant (≥5σ) AME detections, we investigate the observational properties of these regions and compare them with each other and with regions that do not show strong AME. In particular, we would like to distinguish AME and “non-AME” regions using observational and physical properties. This is the first statistical study of AME regions to date.
In Sect. 2 we describe the Planck and ancillary data used in our analysis. Section 3 describes the sample selection, aperture photometry, and model-fitting. Section 4 presents the results of the quantification of AME in these sources. Section 5 investigates the correlation of AME with source properties. Section 6 gives a brief discussion and conclusions.
Sources of the datasets used in this paper, as well as centre frequencies, angular resolutions, and references.
2. Data
2.1. Planck data
Planck (Tauber et al. 2010; Planck Collaboration I 2011) is the third generation space mission to measure the anisotropy of the CMB. It observes the sky in nine frequency bands covering 30−857 GHz with high sensitivity and angular resolution from 31′ to 5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. Polarization is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration II 2011). Two data processing centers (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for Galactic and extragalactic astrophysics as well as cosmology. Early astrophysics results are given in Planck Collaboration VIII−XXVI 2011, based on data taken between 13 August 2009 and 7 June 2010. Intermediate astrophysics results are now being presented in a series of papers based on data taken between 13 August 2009 and 27 November 2010.
In this paper we use Planck data from the 2013 distribution of released products (Planck Collaboration I 2014), based on data acquired during the “nominal” operations period from 13 August 2009 to 27 November 2010, and available from the Planck Legacy Archive1. Specifically, we use the nine temperature maps summarized in Table 1. We also use a CMB-subtracted version for testing the robustness of the detections, using the SMICA CMB map (Planck Collaboration XII 2014). We use the standard conversion factors from CMB to Rayleigh-Jeans (RJ) units and updated colour corrections described in Planck Collaboration I (2014). The Planck bands centred at 100 and 217 GHz are known to be contaminated by CO lines. We corrected these channels using the Dame et al. (2001) integrated CO map smoothed to 1° resolution and scaled with the conversion factors described in Planck Collaboration XIII (2014); however, for some sources, we still see discrepancies with the spectral model at the >10% level. We therefore did not include these two channels in our fitting of the spectral model. The CO contamination in the 353 GHz channel is small, typically <1% (Planck Collaboration XIII 2014), and we do not see significant deviations in our SEDs. Therefore, no correction was made for CO lines in the 353 GHz band.
Although we limit ourselves to bright Galactic regions with typical flux densities at 30 GHz far greater than 10 Jy, at 1° angular scales the integrated flux density of CMB fluctuations can be 10 Jy or more at 100 GHz, a significant fraction of the total flux density of some of the sources in our sample. CMB-subtracted maps would, in principle, be most appropriate for our analysis. However, in bright regions near the Galactic plane, significant foreground residuals remain in the CMB maps produced by the Planck component separation codes in 2013 (Planck Collaboration XII 2014), which used only Planck data and frequencies for separation. These regions can be masked for cosmological work, but they are precisely the regions that we need here. Investigations comparing CMB-subtracted with non-CMB-subtracted maps revealed biases in the plane at the level of 10−15%. Furthermore, incorrect subtraction, particularly at frequencies near 100 GHz, resulted in high χ2 values for some SEDs, and poorly fitted thermal dust components. We therefore use the CMB-subtracted maps only for finding regions of AME, and use non-CMB-subtracted maps for the photometric analysis, where we fit for a CMB component in the spectrum of each source, using the full data available in Table 1 (see Sect. 2.2). In this way we do not bias the flux densities (due to the component separation process), and more importantly, we can characterize and propagate the uncertainty due to the CMB fluctuation. The AME amplitudes from both datasets agree within a fraction of the uncertainty for the majority of sources. In the future, Planck component separation will also make use of many of the external datasets listed in Table 1, and it may be possible to subtract the CMB directly.
2.2. Ancillary data
We use a range of ancillary data to allow the SEDs to be determined from radio (around 1 GHz) to far-infrared (around 3000 GHz). All ancillary data are summarized, along with the Planck data, in Table 1. These data have been smoothed to a common resolution of 1° since some of the maps have only slightly higher resolution than this. The smoothing also reduces the effects of any residual beam asymmetry in some cases, e.g., WMAP and Planck, where non-circular beams vary across the map.
We analysed the northern sky survey at 12–18 GHz from the COSMOSOMAS experiments (Gallegos et al. 2001); however, due to the filtering of emission on large angular scales and large intrinsic beam width, the majority of the sources were strongly affected by negative filtering artefacts from neighbouring bright sources. The exceptions were G160.26−18.62 and G173.6+2.8, which were previously reported by Planck Collaboration XX (2011). We therefore did not consider further the COSMOSOMAS data in our analysis.
In the following sections, we describe the ancillary data in more detail.
2.2.1. Radio surveys
Data at low frequencies (around 1 GHz) are important for excluding regions with synchrotron emission, and for estimating the level of free-free emission. Ideally, we would have several frequency channels in the range 1−10 GHz; however, no large area surveys exist above 2.3 GHz, except for higher resolution surveys that do not retain large-angular-scale information. We therefore use the three well-known surveys at 0.408, 1.42, and 2.326 GHz.
The all-sky survey of Haslam et al. (1982) at 0.408 GHz is widely used as a tracer of synchrotron emission at high Galactic latitudes; however, it also contains strong free-free radiation from the Galactic plane and from H ii regions, where the free-free typically dominates over synchrotron emission even at these lower frequencies.
A number of different versions of the 0.408 GHz map are available. The most widely used
is the NCSA2 destriped and desourced version
available on the LAMBDA website3 at an angular
resolution of 1°. This map
has been Fourier filtered to remove large-scale striations, and bright sources have been
subtracted, including many of the bright H ii regions. Since we want to retain
all the sources for this work, we use a less-processed version of the map4 at 51′ resolution that was originally sampled in a 2D Cartesian
projection with 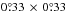 square pixels and B1950 coordinate
frame. This version retains all the bright compact sources, although striations are much
more visible by eye. However, at low latitudes and in bright regions, the striations are
negligible compared to the sky signal. This map was regridded into the HEALPix format
(Górski et al. 2005) using a procedure that
computes the surface intersection between individual pixels of the survey with the
intersecting HEALPix pixels (see Appendix A of Paradis
et al. 2012a). After smoothing the resulting map with a
square pixels and B1950 coordinate
frame. This version retains all the bright compact sources, although striations are much
more visible by eye. However, at low latitudes and in bright regions, the striations are
negligible compared to the sky signal. This map was regridded into the HEALPix format
(Górski et al. 2005) using a procedure that
computes the surface intersection between individual pixels of the survey with the
intersecting HEALPix pixels (see Appendix A of Paradis
et al. 2012a). After smoothing the resulting map with a
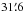 FWHM Gaussian kernel to bring it to
1° resolution, this new
map gave results more consistent with the 1.42 and 2.326 GHz maps.
FWHM Gaussian kernel to bring it to
1° resolution, this new
map gave results more consistent with the 1.42 and 2.326 GHz maps.
The Reich et al. full-sky 1.42 GHz map (Reich 1982; Reich & Reich 1986; Reich et al. 2001) has 36′ resolution, and the Jonas et al. (1998) 2.326 GHz map of the southern hemisphere has 20′ resolution. These have been destriped but not source-subtracted. Although the 2.326 GHz map covers up to +15°, we do not use declinations >+10° because the smoothing operation affects the edges of the map.
The 0.408 GHz map is formally calibrated on angular scales of 5° by comparison with the 404 MHz survey of Pauliny-Toth & Shakeshaft (1962), while the 1.42 GHz and 2.326 GHz maps are tied to absolute sky horn measurements by Webster (1974) and Bersanelli et al. (1994), respectively. Our study is at 1° resolution, with some regions being extended to 2–3°. Therefore one would expect the brightness temperature (and thus flux density) to be under-estimated for many of our sources. The maximum correction factor is given by the full-beam to main-beam ratio, which quantifies the power in the full beam (including sidelobes) compared to the main beam. The largest correction factor we applied is 1.55 for the Reich et al. 1.42 GHz survey, based on comparisons with bright calibrator sources. We did not make any corrections to the 0.408 and 2.326 GHz maps, since they were found to be consistent to within 10% of the 1.4 GHz data for the majority of the sources in our sample and for bright extragalactic sources. We also note that the positional accuracy of these maps, particularly the 0.408 GHz map, is not particularly good. Visual inspection of the maps suggests inconsistencies of bright sources at the level of up to 15′ at 0.408 GHz. For our analysis, however, this is not likely to be a major source of error, since our integration aperture has a diameter of 2°.
We assumed a 10% uncertainty in the radio data at all three frequencies. For the 408 MHz map, which has striations, we added an additional 3.8 Jy uncertainty corresponding to the baseline uncertainty of ±3 K (Haslam et al. 1982) at 1° angular scales. This is required to bring the χ2 value to within acceptable levels for some sources. This additional uncertainty is not always required for sources in our sample, and we find, in fact, that we overestimated our uncertainties in many cases (see Sect. 4.4).
2.2.2. WMAP
WMAP 9-year data are included in our analysis (Bennett et al. 2013). The data span 23 to 94 GHz and thus complement Planck data, particularly the K-band (22.8 GHz) channel. The 1°-smoothed maps available from the LAMBDA website are used. We apply colour corrections to the central frequencies using the recipe described by Bennett et al. (2013); the local spectral index across each band is calculated using the best-fitting model (see Sect. 3.5). This does not exactly take into account curvature of the spectrum, but is a good approximation given that the colour corrections are typically a few percent. For the majority of sources studied in this paper we are not limited by instrumental noise and we assume a 3% overall calibration uncertainty.
2.2.3. Submm/infrared data
To sample the peak of the blackbody curve for temperatures greater than 15 K, we include the COBE-DIRBE data at 240 μm (1249 GHz), 140 μm (2141 GHz), and 100 μm (2997 GHz). The DIRBE data are the Zodi-Subtracted Mission Average (ZSMA) maps (Hauser et al. 1998) regridded into the HEALPix format using the same procedure as used for the 408 MHz map described in Sect. 2.2.1. Colour corrections are applied as described in the DIRBE explanatory supplement version 2.3. Data at higher frequencies are not included in the spectral fits, since they are dominated by transiently heated grains not in thermal equilibrium with the interstellar radiation field and therefore not easily modelled by a single modified blackbody curve. Furthermore, at wavelengths ≲40 μm the spectrum contains many emission/absorption lines, which complicates the modelling. For the statistical comparison, we also include the shorter wavelengths of DIRBE band 7 (4995 GHz) and the IRAS 12 μm (25 000 GHz) and 25 μm (12 000 GHz) bands. We use the IRIS maps of Miville-Deschênes & Lagache (2005), which have had bright sources and a model of zodiacal light removed. Residuals from zodiacal-light subtraction are known to be an issue at wavelengths shorter than about 25 μm, but are not expected to be significant for the bright regions in this study because the zodiacal light is relatively smooth spatially except for a narrow band at low ecliptic latitudes. We test this assumption by comparing the flux densities from improved zodiacal-light-subtracted maps (Marc-Antoine Miville-Deschênes, priv. comm.) where the residuals are clearly much smaller. We obtained consistent results within a fraction of the errors; the scatter is less than 5% at the worst band (12 μm). Sources were not removed for |b| > 5° and therefore do not affect the majority of the sources in our sample.
We use Spitzer data where available at 8 and 24 μm as a dust diagnostic for the polycyclic aromatic hydrocarbons (PAHs) and very small grains (VSGs), respectively. The Spitzer data are obtained from the Spitzer data archive5, and are reprocessed for the purposes of this paper in order to mitigate possible systematics. An extended emission correction is applied to the 8 μm data, and the zodiacal light contribution is subtracted from both the 8 and 24 μm data. Bright point sources are extracted from both bands to enable us to investigate the extended emission, and an overlap correction is applied to ensure a consistent background level. Finally, all the reprocessed data are combined to produce the final maps used in this analysis; see Tibbs et al. (2011) for more details. We are able to measure flux densities for 24 regions.
3. Sample selection and SED fitting
In this section we cover the methods we use to create the sample of sources. Section 3.1 describes the source detection method that forms the main sample. Section 3.2 describes the component subtraction method for detecting potential AME regions. Section 3.3 summarizes the final sample of 98 sources. Section 3.4 describes the aperture photometry method used to extract the flux densities of the sources. Section 3.5 describes the model-fitting that is adopted to quantify the various components and to assess the contribution of AME. Section 3.6 presents example SEDs6 and a summary of what is observed in our sample.
3.1. Detection of bright sources
At high radio frequencies (30–70 GHz), synchrotron and thermal dust emission are expected to be relatively faint. The dominant emission mechanism is thought to be optically thin free-free emission (α ≈ −0.14, where S ∝ να), with a possible contribution from AME. Free-free emission is expected to be particularly strong near the Galactic plane due to the presence of H ii regions and ionized gas near OB stars. This allows H ii regions to be detected by simply searching for bright sources in individual frequency maps. However, in this paper we are mainly interested in constructing accurate SEDs across the radio/submillimetre/far-infrared wavelength range, which requires the detection of the brightest clouds at all WMAP/Planck frequencies. We used the SExtractor software (Bertin & Arnouts 1996), which was used in the “Sextra” pipeline for the Planck Early Release Compact Source Catalogue (Planck Collaboration VII 2011), to detect bright sources at each Planck frequency of the CMB-subtracted maps.
We begin with a SExtractor catalogue of 1194 sources detected at 70 GHz. To increase reliability and to
ensure the region is bright at all Planck frequencies, this catalogue is
further cross-matched with the 28.4 and 100
GHz catalogues, using a matching radius of the largest beam FWHM
(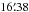 ). This results in 462 sources that are
well-detected across the 30−100 GHz range. We remove extragalactic sources by searching the
NASA Extragalactic Database (NED7) for radio
galaxies. Approximately half of all detected sources, and a majority at |b| ≳ 5°, are found to be
extragalactic, most of which are likely blazars. We also remove a small number of sources
associated with known bright supernova remnants (Green
2009) and planetary nebulae (Acker et al.
1992). The SIMBAD8 database is found to be
useful for confirming that a region is dominated by Galactic emission and that many of our
sources are in fact large H ii complexes or parts of molecular clouds. These
regions often contain several individual sources.
). This results in 462 sources that are
well-detected across the 30−100 GHz range. We remove extragalactic sources by searching the
NASA Extragalactic Database (NED7) for radio
galaxies. Approximately half of all detected sources, and a majority at |b| ≳ 5°, are found to be
extragalactic, most of which are likely blazars. We also remove a small number of sources
associated with known bright supernova remnants (Green
2009) and planetary nebulae (Acker et al.
1992). The SIMBAD8 database is found to be
useful for confirming that a region is dominated by Galactic emission and that many of our
sources are in fact large H ii complexes or parts of molecular clouds. These
regions often contain several individual sources.
The final stage of catalogue trimming is made by visual inspection of the maps and preliminary SEDs made by aperture photometry (Sects. 3.4, 3.5, and 3.6). We make visual inspection at this resolution, since the final SEDs are to be constructed using 1°-smoothed maps (to ensure that the response to diffuse emission is the same at all frequencies). To ensure a robust sample, sources that are not well-defined after smoothing to 1° (i.e., do not show a definite peak of emission on scales of ≲2°), or are relatively faint (≪10 Jy at a frequency of 30 GHz), are discarded, except for a few cases at several degrees distance from the Galactic plane. We find a few sources whose positions are not exactly centred on the peak of the emission at frequencies of 20−60 GHz, with offsets as large as 10−20′. This can occur because of the complexity of the Galactic plane, which after filtering can produce multiple peaks in close proximity to each other. In these cases, we manually shift the position to the approximate centre of the hotspot. Since we are using a large 1° radius aperture (see Sect. 3.4), this makes little difference to the SEDs. We identify 94 candidate AME sources using this technique.
3.2. Detection of AME regions by component subtraction
We use a simple CMB/foreground subtraction method to isolate AME from the other diffuse components. This method is essentially the same as was used by Planck Collaboration XX (2011), where potential AME regions were located by a simple subtraction of the non-AME components from the 28.4 GHz Planck CMB-subtracted map. The one difference is that here we only use the 0.408 GHz map to trace the synchrotron emission, which is extrapolated with a single power law and a spectral index β = −3.0 (T ∝ νβ). This is a typical value of the slope between 408 MHz and WMAP/Planck frequencies (Davies et al. 2006; Gold et al. 2011). The combination of the 1.4 GHz and 2.3 GHz maps is not used, as it creates large-scale artefacts. Although there is some evidence of flattening (β ≈ −2.7) of the synchrotron index at low Galactic latitudes (e.g., Gold et al. 2009), we use the typical high latitude value. For most sources on the Galactic plane, the synchrotron emission is a minor component at frequencies above 23 GHz. For the free-free component we use the dust-corrected Hα map of Dickinson et al. (2003). For thermal dust, we use model 8 of Finkbeiner et al. (1999). Both are calculated at a frequency of 28.4 GHz.
We smooth the Planck CMB-subtracted maps to a resolution of 1° and subtract the non-AME components from the Planck 28.4 GHz map to create a map of residuals. A 5°-smoothed version is also created and subtracted from the 1° map to remove large-scale emission and highlight the compact regions most suited for this analysis. The diffuse emission removed here will be the focus of future papers.
The resulting map of residuals at 28.4 GHz is shown in Fig. 1. The large-scale features, including negative artefacts, are not of concern here. Instead, we used this map as a “finding chart” to identify new regions that emit detectable levels of AME. Approximately 100 bright well-defined sources are located by eye and a spectrum is produced for each one using aperture photometry (see Sect. 3.4). The well-known AME regions in Ophiuchus and Perseus stand out in this map. Lots of free-free emission (usually because it can be self-absorbed at lower frequencies) and synchrotron point sources (with a flatter spectral index than β = −3.0, and hence not removed completely by extrapolating the synchrotron map assuming a steep spectrum) can be found in this residual map. Most of the 100 AME candidates are H ii regions; 20 sources show evidence for excess emission at 30 GHz based on an initial spectral fit, out of which 16 have already been identified using the source-detection method (Sect. 3.1). The four additional sources found using this technique are G037.79−00.11, G293.35−24.47, G317.51−00.11, and G344.75+23.97.
 |
Fig. 1 Map of residuals at 28.4 GHz after subtracting off synchrotron, free-free, thermal dust, and CMB components (see text), in mK (R-J) units. A 5°-smoothed version of the map is subtracted to remove extended diffuse emission to more easily identify bright, relatively compact sources. This map is shown in the Mollweide projection, with l = 0° in the centre and increasing to the left. |
 |
Fig. 2 CMB-subtracted Planck 28.4 GHz map covering the entire Galactic
plane and latitudes | b
| < 30°. The colour scale has a logarithmic stretch. Regions
with the most significant AME are highlighted as thick squares while the rest of the
sample are shown as circles. Regions with significant excess emission but with a
potential UCH ii contribution ( |
3.3. Final sample
The final sample contains 98 sources, listed in Table 3. The superscript letter after the name indicates which method the source is chosen from. Most of the sources are located using the SExtractor detection technique, with a few of the AME-dominated sources being detected using the component subtraction method. We also indicate if a source is already known from previous AME studies. A few previously identified AME candidates are not on this list because they are not detected at high significance in the Planck data, mostly due to the limited angular resolution of this study. These include RCW175 (Dickinson et al. 2009), LDN1621 (Dickinson et al. 2010), M78 (Castellanos et al. 2011), LDN1780 (Vidal et al. 2011), and LDN1111/675/1246 (Scaife et al. 2009, 2010a). Associations with known objects are listed in the notes column of Table 3.
The Planck CMB-subtracted map with the locations of the sources is shown
in Fig. 2. Most of the sources lie within a few
degrees of the Galactic plane. A few sources are in the well-known regions of Ophiuchus
(l = 0°),
Perseus (l =
160°), Orion (l = 200°), and the Gum nebula (l = 260°). The most
significant (σAME
> 5 and 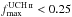 ; see Sect. 4) AME sources are shown as thick squares; sources that have excess emission
(σAME >
5) but have a potentially large contribution of optically thick
free-free emission from ultra-compact H ii (UCH ii) regions
(
; see Sect. 4) AME sources are shown as thick squares; sources that have excess emission
(σAME >
5) but have a potentially large contribution of optically thick
free-free emission from ultra-compact H ii (UCH ii) regions
(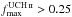 ) are shown as stars. It is interesting to
see that these AME-bright sources appear to cluster in certain regions, particularly along
the local Gould Belt region (Planck Collaboration Int.
XII 2013). There seem to be no bright AME regions along the lines-of-sight to the
local spiral arm at l =
90° and l =
270°. In general, few of the most significant AME sources lie on the
plane. This is partly explained by the removal of AME sources that have a potential
UCH ii contribution, based on infrared sources (see Sect. 4.2), which preferentially lie in the Galactic plane. In addition,
there is a selection effect, since the high free-free brightness temperatures and overall
confusion in the plane make it more difficult to identify individual AME-bright objects.
It may also be that these sight-lines contain a strong component of free-free emission
from warm ionized gas, which is thought to exhibit less AME than cold neutral medium (CNM)
or molecular clouds (Planck Collaboration XXI
2011). With our incomplete sample, such claims cannot be confirmed in this study.
) are shown as stars. It is interesting to
see that these AME-bright sources appear to cluster in certain regions, particularly along
the local Gould Belt region (Planck Collaboration Int.
XII 2013). There seem to be no bright AME regions along the lines-of-sight to the
local spiral arm at l =
90° and l =
270°. In general, few of the most significant AME sources lie on the
plane. This is partly explained by the removal of AME sources that have a potential
UCH ii contribution, based on infrared sources (see Sect. 4.2), which preferentially lie in the Galactic plane. In addition,
there is a selection effect, since the high free-free brightness temperatures and overall
confusion in the plane make it more difficult to identify individual AME-bright objects.
It may also be that these sight-lines contain a strong component of free-free emission
from warm ionized gas, which is thought to exhibit less AME than cold neutral medium (CNM)
or molecular clouds (Planck Collaboration XXI
2011). With our incomplete sample, such claims cannot be confirmed in this study.
3.4. Aperture photometry
We use the HEALPix aperture photometry code developed for Planck Collaboration XX (2011) to extract the flux densities of the regions from the maps. This software has also been used to investigate at the polarization of AME from ρ Ophiuchi in Dickinson et al. (2011). After converting from CMB thermodynamic units (KCMB) to RJ units (KRJ) at the central frequency, the maps are converted to units of Jy pixel-1 using S = 2kTRJΩν2/c2, where Ω is the HEALPix pixel solid angle. The pixels are then summed in a circular aperture of 60′ to obtain an integrated flux density. An estimate of the background is subtracted using a median estimator of pixels lying at radii between 80′ and 100′. By using Monte Carlo injection of sources, we find that this choice of aperture and annulus size provides the least scatter in recovered flux densities, and is a reasonable balance for obtaining an appropriate background level without subtracting appreciable flux density from the source itself.
The flux density uncertainties are estimated from the rms of the values in the background annulus and added in quadrature to the absolute calibration uncertainties for each map (see Sect. 2.2). Simulations of injected point-like sources show that the flux density estimates are unbiased and that the uncertainties are reasonable; however, the exact value of flux density uncertainty for each source is difficult to quantify, since it depends very strongly not only on the brightness of the source and background, but also on the morphology of the emission in the vicinity of the source. This will be discussed further in Sect. 4.4. Colour corrections, based on the local spectral index across each band, are applied during the model-fitting, as described in the next section.
3.5. Model fitting
We take the flux density S for each source from the aperture photometry and
fit a simple model of free-free, synchrotron (where appropriate), CMB, thermal dust, and
spinning dust components: 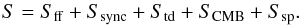 (1)The free-free flux density Sff is
calculated from the brightness temperature Tff, based on the optical depth
τff, using the standard formula
(1)The free-free flux density Sff is
calculated from the brightness temperature Tff, based on the optical depth
τff, using the standard formula
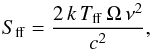 (2)where k is the Boltzmann
constant, Ω is the solid angle
of the aperture, and ν is the frequency, with
(2)where k is the Boltzmann
constant, Ω is the solid angle
of the aperture, and ν is the frequency, with 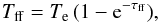 (3)and the optical depth τff is given by
(3)and the optical depth τff is given by
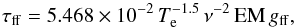 (4)in which the Gaunt factor can be
approximated9 by
(4)in which the Gaunt factor can be
approximated9 by ![\begin{equation} \label{eq:gaunt} g_{\rm ff} = {\rm ln} \left( {\rm exp} \left[5.960 - \frac{\sqrt{3}}{\pi} {\rm ln} (Z_i \,\nu_9 \,T_4^{-3/2}) \right] + 2.71828 \right). \end{equation}](/articles/aa/full_html/2014/05/aa22612-13/aa22612-13-eq98.png) (5)For the analysis of AME, we assume a fixed
electron temperature of 8000 K for Te for all regions, fitting only for the
emission measure (EM). Note that this is not the true EM, but an effective EM over the
1° radius aperture. For
compact sources, the quoted EM will be underestimated.
(5)For the analysis of AME, we assume a fixed
electron temperature of 8000 K for Te for all regions, fitting only for the
emission measure (EM). Note that this is not the true EM, but an effective EM over the
1° radius aperture. For
compact sources, the quoted EM will be underestimated.
For six sources, we also include a synchrotron component modelled as a power law with
amplitude Async and variable flux density spectral
index α,
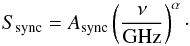 (6)The thermal dust is fitted using a modified
blackbody model,
(6)The thermal dust is fitted using a modified
blackbody model,  (7)fitting for the optical depth τ250, the dust
temperature Td, and the emissivity index
βd. The CMB is fitted using the
differential of a blackbody at TCMB = 2.7255 K (Fixsen 2009)
(7)fitting for the optical depth τ250, the dust
temperature Td, and the emissivity index
βd. The CMB is fitted using the
differential of a blackbody at TCMB = 2.7255 K (Fixsen 2009) 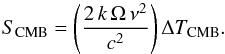 (8)Here ΔTCMB is the CMB
fluctuation temperature in thermodynamic units. The spinning dust is fitted using
(8)Here ΔTCMB is the CMB
fluctuation temperature in thermodynamic units. The spinning dust is fitted using
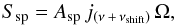 (9)where we use a model for jν calculated using the
SPDUST (v2) code (Ali-Haïmoud et al. 2009; Silsbee et al. 2011). We choose a model corresponding
to the warm ionized medium (WIM) with a peak at 28.1 GHz to give the generic shape, and
allow for a shift of this model with frequency. We therefore fit for two parameters
corresponding to the AME amplitude Asp, and a frequency shift
νshift. Note that the units of
Asp are formally of column density
(cm-2). If the
spinning dust model was appropriate for the line-of-sight, and no frequency shift was
applied, then this would indeed be the column density NH; however,
since this quantity is model-dependent and there is potentially a shift in frequency, we
do not take this to be a reliable estimate of NH. Similarly, in this paper we do not
attempt to fit specific spinning dust models to each source, hence the derived column
density is not necessarily physical; Asp is essentially the flux density at
the peak normalized to the spinning dust model. Given the large uncertainties and
difficulty in separating the various spectral components, we have not attempted to look
for deviations from the basic spinning dust model (Hoang
et al. 2011).
(9)where we use a model for jν calculated using the
SPDUST (v2) code (Ali-Haïmoud et al. 2009; Silsbee et al. 2011). We choose a model corresponding
to the warm ionized medium (WIM) with a peak at 28.1 GHz to give the generic shape, and
allow for a shift of this model with frequency. We therefore fit for two parameters
corresponding to the AME amplitude Asp, and a frequency shift
νshift. Note that the units of
Asp are formally of column density
(cm-2). If the
spinning dust model was appropriate for the line-of-sight, and no frequency shift was
applied, then this would indeed be the column density NH; however,
since this quantity is model-dependent and there is potentially a shift in frequency, we
do not take this to be a reliable estimate of NH. Similarly, in this paper we do not
attempt to fit specific spinning dust models to each source, hence the derived column
density is not necessarily physical; Asp is essentially the flux density at
the peak normalized to the spinning dust model. Given the large uncertainties and
difficulty in separating the various spectral components, we have not attempted to look
for deviations from the basic spinning dust model (Hoang
et al. 2011).
The least-squares fit is calculated using the MPFIT 10 (Markwardt 2009) package written in IDL, with starting values estimated from the data and with amplitude parameters constrained to be positive except for the CMB, which is allowed to go negative. MPFIT also provides estimates of the 1σ uncertainties for each parameter, taken as the square root of the diagonal elements of the parameter covariance matrix. We note four special cases in Table 3 (G068.16+01.02, G076.38–00.62, G118.09+04.96 and G289.80–01.15) where the fitting returned Asp = 0.0 ± 0.0. These could be mitigated by removing the positivity prior, with best-fitting negative values still being consistent with zero. Instead, for these special cases, we fixed Asp to zero to make the fits more physically meaningful, since the spinning dust spectrum should not go negative.
 |
Fig. 3 Example SEDs (see text for description of individual SEDs) of sources with little or no AME (see Fig. 8 for SEDs with significant AME). Data points are shown as circles with errors and are colour-coded for radio data (cyan), WMAP (red), Planck (blue), and DIRBE/ IRAS (black). The best-fitting model of free-free (dotted line), synchrotron (long-dashed line), thermal dust (short-dashed line), CMB (triple-dot-dashed line), and spinning dust (dot-dashed line) are shown. Data included in the fit are shown as filled circles, while the other data are unfilled. The residual spectrum, after subtraction of free-free, synchrotron, CMB and thermal dust components, is shown as an insert. |
3.6. Example SEDs
Some example SEDs for regions with weak AME are shown in Fig. 3; see Sect. 4.3 and Fig. 8 for SEDs with significant AME. Filled circles are used
for data included in the fit, and unfilled circles are for display purposes only. We begin
by including data from 0.408 GHz up to 3000 GHz and make a least-squares fit to the data.
In general, the SEDs are well-fitted by our simple model, although the uncertainties
appear to be over-estimated. This can be seen in some of the example SEDs in Fig. 3 and in the reduced χ2 values in
Table 3; the mean value for the entire sample is
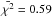 . However, our uncertainties are justified
for some sources where the scatter is consistent with our assigned uncertainties. An
example of this is G017.00+00.85, where there is considerable scatter at low frequencies.
. However, our uncertainties are justified
for some sources where the scatter is consistent with our assigned uncertainties. An
example of this is G017.00+00.85, where there is considerable scatter at low frequencies.
All sources show a strong thermal dust component peaking at about 2000–3000 GHz, indicative of dust grains at Td ≈ 20 K. The one-component modified blackbody function reproduces the spectrum above 100 GHz remarkably well for the majority of our sources; however, the 100/217 GHz data points are often inconsistent with the model due to the CO line contamination within the Planck bands. For this reason, as previously explained, we exclude the 100/217 GHz data from all our fits.
Another effect seen in our SEDs is that of the fluctuations in the CMB. Although the CMB fluctuations are faint (with an rms of 70 μK at 1° scales), the large aperture that we integrate over results in a typical integrated CMB flux density of 7 Jy at 100 GHz, based on the standard deviation of flux densities from Monte Carlo simulations of a CMB-only sky, assuming the WMAP 7-year power spectrum (Larson et al. 2011). It is important to note that these fluctuations are about the mean CMB temperature, and thus can be negative or positive. Figure 3 shows examples of both; G209.01−19.38 contains a large positive CMB fluctuation (ΔTCMB = 371 ± 102 μK), and G274.01−01.15, showing a strong negative fluctuation (ΔTCMB = −37 ± 10 μK). The negative CMB flux densities cause a dip in the spectrum at frequencies near 100 GHz, which could be misinterpreted as spinning dust at lower frequencies.
Similarly, over-fitting by a strong positive CMB fluctuation could affect the AME intensity. This could happen when there is a flattening of the thermal dust spectral index at frequencies below 353 GHz (Planck Collaboration, in prep.), which can be accounted for by the CMB component. A clear example of this is G015.06−00.69, shown in Fig. 3. There is an apparent flattening of the thermal dust spectral index, which appears as an excess at frequencies ≈100−353 GHz relative to the one component dust model, an effect that has been observed before (Paradis et al. 2009, 2012b). In this case, the fitted CMB temperature, ΔTCMB = (533 ± 251) μK, is larger than what could realistically be attributed to a pure CMB fluctuation (≳150 μK). Fortunately, because the uncertainties are large and the CMB does not contribute strongly at frequencies where AME is dominant (10−60 GHz), this does not have a major impact on the AME results. This will be discussed further in Sect. 4.4.
At frequencies below 100 GHz, optically thin free-free emission is seen in many sources and is sometimes consistent with the low frequency radio data at ≈1 GHz and WMAP/Planck data at 20−100 GHz (e.g., G265.15+01.45 and G289.80−01.15 in Fig. 3). These sources justify our use of the 0.408, 1.42, and 2.326 GHz data, and show that the overall calibration factors are within the uncertainties assumed in this study. Where there is evidence of absorption at low frequencies, or if there is a discrepancy between 0.408 GHz and the other low frequency data at 1.4/2.3 GHz, we omit the 0.408 GHz data point (and occasionally the 1.42 GHz data point) in the fit (e.g., G123.13−06.27, G209.01−19.38, and G274.01−01.15 in Fig. 3). For some sources (e.g., G015.06−00.69), we choose not to include the 0.408 and 1.42 GHz data, since they both show evidence of absorption. At 2.3 GHz, the data are consistent with optically thin free-free emission and are a good match to the WMAP/Planck data. This is acceptable since the free-free component usually contains only one free parameter (i.e., EM). Sometimes this is necessary because the maps show considerably higher background relative to the source itself, due to the high levels of synchrotron emission at frequencies ≲1 GHz. This can affect the estimated flux density both inside the aperture and also in the background annulus, resulting in a bias that can be either high or low and may account for data points that are discrepant with the other low frequency data, particularly at 0.408 GHz.
Figure 3 shows examples of other situations. Synchrotron-dominated sources are omitted in our sample except for six sources where the low frequency data are seen to be a good fit to a power-law (amplitude and spectral index) by visual inspection. These sources are G010.19−00.32 (Fig. 3), G008.51−00.31, G012.80−00.19, G037.79−0.11, G344.75+23.97, and G355.44+0.11. No strong supernova remnants are included in our sample; however, weak supernova remnants (SNR) are identified (see the Notes column of Table 3) in some regions. We obtain flux density spectral indices that are in the expected range (− 0.7 to − 1.2) for supernova remnants, with a mean value of −0.9.
4. Regions of AME
4.1. Significance of AME detections
Visual inspection of the SEDs suggests that a large fraction (at least half) of the regions chosen for this study may exhibit excess emission at frequencies in the range 20−60 GHz. All sources have a bright thermal dust component that peaks at 2000–3000 GHz and becomes subdominant at frequencies below 100 GHz; most have a contribution of free-free emission. Approximately half of the 98 sources appear to contain more emission at 20−60 GHz compared to a simple extrapolation of optically thin free-free and thermal dust components.
To quantify the level of AME and its significance, we use the spinning dust amplitude Asp and its uncertainty σAsp, directly from the SED fitting. These are listed in Table 3, along with the significance level of the AME detection, σAME ≡ Asp/σAsp. We also tried subtracting the non-AME components in the SED, thus leaving the AME residual, which gave similar results.
We focus on the AME detections that are at >5σ. Of the 98 sources, 42 initially show highly significant (σAME > 5) evidence for AME while 29 do not exhibit strong AME (σAME< 2). Hereafter, we will refer to these as “AME regions” (shown in boldface in Table 3) and “non-AME regions”, respectively. This leaves 42 sources that show some evidence (σAME = 2−5) of excess emission attributable to AME, which will be referred to as “semi-significant AME regions”. Note that we reclassify 15 of the AME sources into the semi-significant category due to the potential contamination from UCH ii regions and this will be discussed in Sect. 4.2. This leaves 27 that we classify as strong AME detections.
Figure 4 shows a histogram of the AME significances, σAME. As discussed in Sect. 4.4, although there are some concerns for a few sources regarding possible modelling and systematic errors that could be contaminating our results, there is strong evidence for AME in a number of sources.
 |
Fig. 4 Histogram of the AME significance values, σAME, for
the sample of 98 sources. The 5σ limit is shown as a dashed line. Sources
that are significant and have a maximum contribution from UCH ii regions
( |
Two of the strongest detections are the well-known sources within the Perseus (G160.26−18.62) and ρ Ophiuchi (G353.05+16.90) clouds, studied by Planck Collaboration XX (2011). These are the most easily detectable AME-dominated sources in the sky, exhibiting 70−80% of AME at 30 GHz, and are detected at a level of 30σ and 17σ, respectively. We detect them at higher significance in this paper due to using the spinning dust fit amplitude directly (rather than subtracting the best-fitting model and determining the significance from the residuals over a restricted frequency range). For ρ Ophiuchi the best-fitting dust temperature and spectral index are consistent with the values from Planck Collaboration XX (2011), while for Perseus the spectral index is somewhat different; we attribute this to the filtering that was applied in that paper to allow the inclusion of the COSMOSOMAS data. The thermal dust optical depth τ250 was higher in the analysis from the early paper. In the early paper, the quoted optical depth was the value calculated from the modelling of the spinning dust, assuming a given PAH abundance, rather than from the thermal dust component of the SED. For these sources, the bulk of the AME was modelled as originating from the denser molecular component, which has a higher optical depth associated with it.
The two new sources detected by Planck Collaboration XX (2011), G107.20+05.20 and G173.62+02.79, are also high in the significance list at 9.9σ and 5.6σ, respectively. Note that the details of the SEDs are not identical to those presented in Planck Collaboration XX (2011) because the size of the background annulus has changed and the Planck maps have been updated; however, the differences are small and within the stated uncertainties.
4.2. Ultra-compact HII regions (UCHII)
 |
Fig. 5 Colour−colour plot of IRAS PSC sources (grey plus symbols) that lie within the apertures of all 98 sources in our sample. UCH ii candidates (solid black squares) tend to have ratios log 10(S60/S12) ≥ 1.30 and log 10(S25/S12) ≥ 0.57, corresponding to the top-right hand corner of this plot (marked with a dashed line). |
Optically thick free-free emission at frequencies above a few GHz can come from UCH ii regions with EM ≳ 107 cm-6 pc, which can be optically thick up to 10 GHz or higher (Kurtz 2002, 2005). A nearby UCH ii region with typical parameters (Te = 8000 K, angular size 1″) could have a flux density of up to 10 Jy at LFI frequencies, while most are at ≪1 Jy (Wood & Churchwell 1989b). However, in our low resolution analysis there could be numerous sources within the aperture that may be contributing at frequencies ≳10 GHz. Since no high resolution radio surveys exist at frequencies above a few gigahertz11, we use the IRAS Point Source Catalogue (PSC; Beichman et al. 1988) to identify UCH ii candidates within each aperture. Wood & Churchwell (1989a) found that due to the warmer dust temperatures in the vicinity of OB stars, UCH ii regions tend to have IRAS colour ratios of log 10(S60/S12) ≥ 1.30 and log 10(S25/S12) ≥ 0.57.
Figure 5 shows the distribution of these colour ratios for all sources that lie within the apertures of our sample. It can be seen that about 20% of sources lie in this region of colour−colour space. To identify UCH ii regions we choose sources that lie within this colour-colour range, but exclude sources that are identified as extragalactic (IRAS IDFLAG =0) or are upper limits at either 25 μm or 60 μm. Candidate UCH ii regions are marked as solid black squares in Fig. 5. For each of our 98 sources, we typically find 10−50 matched IRAS PSC sources and a few UCH ii candidates within the aperture. Some apertures contain no apparent UCH ii regions, while a few have 10−20; the median value is three UCH ii candidates for each aperture.
To quantify how much of the radio flux density at frequencies ≳10 GHz could be attributed to
UCH ii, we use the 100
μm flux densities of UCH ii candidates to
predict the maximum flux density at a wavelength of 2 cm (15 GHz). Kurtz et al. (1994) measured the ratio of
100 μm to
2 cm flux densities, and found it to lie in the range of 1000 to 400 000, with no
UCH ii regions having S100/S2 <
1000. We can therefore sum up S100 for all
UCH ii candidates within each aperture and use the factor of 1000 to give a
maximum 15 GHz flux density from UCH ii regions,
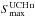 (Dickinson
2013). Strictly speaking, this is an estimate at 15 GHz, but most H ii
regions are in the optically thin regime (i.e., have turned over) at frequencies
≳15 GHz (Kurtz et al. 1994). This is therefore very likely to be
an over-estimate in many cases. First, some of the IRAS PSC sources will not be
UCH ii, as discussed by Wood & Churchwell
(1989a). Ramesh & Sridharan (1997)
suggested that only about one quarter of these candidates were indeed UCH ii
regions, due to contamination by cloud cores with lower mass stars, while Bourke et al. (2005) showed that the contamination by
low-mass (i.e., non-ionizing) protostars is at the 10% level or greater. On the other hand,
such sources are typically weak and will therefore limit such a bias. Second, the average
value of S100 is ≳3000, with a tail to higher values (Kurtz et al. 1994). Therefore, our maximum
UCH ii flux density determination is very conservative and is likely to be a
factor of a few above the true value.
(Dickinson
2013). Strictly speaking, this is an estimate at 15 GHz, but most H ii
regions are in the optically thin regime (i.e., have turned over) at frequencies
≳15 GHz (Kurtz et al. 1994). This is therefore very likely to be
an over-estimate in many cases. First, some of the IRAS PSC sources will not be
UCH ii, as discussed by Wood & Churchwell
(1989a). Ramesh & Sridharan (1997)
suggested that only about one quarter of these candidates were indeed UCH ii
regions, due to contamination by cloud cores with lower mass stars, while Bourke et al. (2005) showed that the contamination by
low-mass (i.e., non-ionizing) protostars is at the 10% level or greater. On the other hand,
such sources are typically weak and will therefore limit such a bias. Second, the average
value of S100 is ≳3000, with a tail to higher values (Kurtz et al. 1994). Therefore, our maximum
UCH ii flux density determination is very conservative and is likely to be a
factor of a few above the true value.
 |
Fig. 6 Estimated maximum contribution from UCH ii regions plotted against
28.4 GHz AME residual flux density. The most significant AME sources
(σAME >
5 and |
We define the maximum fractional contribution at 28.4 GHz,
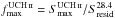 , where 1.0 represents a possible 100%
contribution of UCH ii to the AME amplitude. Figure 6 plots
, where 1.0 represents a possible 100%
contribution of UCH ii to the AME amplitude. Figure 6 plots 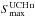 against the 28.4 GHz AME residual flux
density; the values of
against the 28.4 GHz AME residual flux
density; the values of 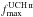 for 1,10, 25, and 100% are shown as
straight lines. A wide range of values is seen, with some regions having no
UCH ii matches and therefore no contribution (they are set to 0.01 Jy in Fig.
6), while many other sources have a potentially
significant contribution from UCH ii. Out of the 42 regions that have
σAME >
5, four sources have
for 1,10, 25, and 100% are shown as
straight lines. A wide range of values is seen, with some regions having no
UCH ii matches and therefore no contribution (they are set to 0.01 Jy in Fig.
6), while many other sources have a potentially
significant contribution from UCH ii. Out of the 42 regions that have
σAME >
5, four sources have 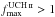 , nine have
, nine have
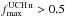 , fifteen have
, fifteen have
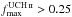 , and eighteen have
, and eighteen have
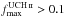 (Table 3).
(Table 3).
We choose to remove the fifteen sources with 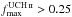 from the significant AME list and
re-classify them as semi-significant hereafter. Therefore they appear as grey circles in
subsequent plots, and in Fig. 6 highlighted with star
symbols. This cut-off value is chosen to keep G353.05+16.90 (ρ Ophiuchi) in the
significant AME sample, since there is good evidence for it not to harbour UCH ii
regions (Casassus et al. 2008). Inspection of the
SEDs of those sources with high
from the significant AME list and
re-classify them as semi-significant hereafter. Therefore they appear as grey circles in
subsequent plots, and in Fig. 6 highlighted with star
symbols. This cut-off value is chosen to keep G353.05+16.90 (ρ Ophiuchi) in the
significant AME sample, since there is good evidence for it not to harbour UCH ii
regions (Casassus et al. 2008). Inspection of the
SEDs of those sources with high 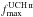 reveals cases where the spectrum at
frequencies between 20 and 60 GHz is indeed very flat (as expected from optically thin
free-free emission from H ii regions). The most prominent example of this is the
source G213.71−12.60, which
has the highest
reveals cases where the spectrum at
frequencies between 20 and 60 GHz is indeed very flat (as expected from optically thin
free-free emission from H ii regions). The most prominent example of this is the
source G213.71−12.60, which
has the highest 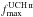 value of 3.9, and a high apparent excess
significance of 15σ. This is likely to be mostly dominated by
UCH ii at these frequencies.
value of 3.9, and a high apparent excess
significance of 15σ. This is likely to be mostly dominated by
UCH ii at these frequencies.
We note in this section that the two new AME regions reported by Planck Collaboration XX (2011), G107.20+05.20 and G173.62+02.79, have
among the highest values of 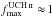 (Table 3). A preliminary analysis of high resolution (2′) follow-up observations at 15 GHz with the
AMI (Perrott et al. 2013) indicates that for both
these sources, the bulk of the Planck flux density is diffuse (on scales
larger than 10 arcmin), making it unlikely for UCH ii to explain the excess. They
found that while G107.2+5.2 may harbour a hyper-compact H ii (HCH ii)
region with a rising spectrum at 15 GHz, but with a flux density ≪1 Jy, a spinning dust model is preferred.
(Table 3). A preliminary analysis of high resolution (2′) follow-up observations at 15 GHz with the
AMI (Perrott et al. 2013) indicates that for both
these sources, the bulk of the Planck flux density is diffuse (on scales
larger than 10 arcmin), making it unlikely for UCH ii to explain the excess. They
found that while G107.2+5.2 may harbour a hyper-compact H ii (HCH ii)
region with a rising spectrum at 15 GHz, but with a flux density ≪1 Jy, a spinning dust model is preferred.
To quantify possible UCH ii regions (or other compact sources) at high latitudes, we searched the NED to look for compact radio sources and, where available, the GB6/PMN 4.85 GHz maps12 (Condon et al. 1991, 1993, 1994). Within 1° of the central position there are typically two to five compact sources with flux densities in the range 0.03 to 0.1 Jy. Most of these are already identified as extragalactic sources (therefore not UCH ii regions) and typically have flat or falling spectra. For example, near G023.47+8.19 lies the radio source PMN J0805−0438 with a flux density 0.193 Jy at 4.85 GHz. Comparison with measurements at 1.4 GHz yields a spectral index of −0.8 ± 0.2 for this source, implying a negligible contribution to the flux density at 23 GHz. The most significant case is the flat-spectrum radio source PKS 1552−033 near G005.4+36.50, which has a flux density of 0.26 Jy at 20 GHz (Murphy et al. 2010b). This source contributes 15% of the AME flux density of 1.7 ± 0.3 Jy, but is within the uncertainty of the residual AME.
 |
Fig. 7 Maps of example sources with significant (σAME > 5) excess emission. Each row is a gnomic map in Galactic coordinates, 5° on a side, and centred on each source, labelled in the 0.408 GHz map. The maps from left to right are 0.408, 1.42, 22.7, 28.4, 44.1, and 143 GHz. The WMAP/Planck maps have been CMB-subtracted. The colour-scale is linear, and ranges from the minimum to maximum value within each map. The aperture is shown as a solid line; the background annulus as dashed lines. The strong AME at frequencies around 30 GHz is evident. |
 |
Fig. 8 SEDs for the sources with very significant AME and
|
4.3. Maps and SEDs of most significant AME detections
Figure 7 presents maps of some of the most statistically significant AME regions, excluding the previously known sources in Perseus and ρ Ophiuchus. The Planck maps have been CMB-subtracted. The brighter emission at 20–60 GHz can sometimes be seen visually. In the most significant AME sources there is little or no discernible emission at low radio frequencies (<2.3 GHz), but there is almost always strong thermal dust emission at high frequencies (≳143 GHz). Good examples of this include G005.40+36.50, G023.47+08.19, G192.34−11.37, and G219.18−8.93. In other sources the picture is not so clear, due to strong backgrounds (e.g., in G355.63+20.52) or because the source is not so well-defined. For example, G004.24+18.09 appears as a spur emanating from a diffuse region. The images show that many of the AME sources are not compact, but rather diffuse and extended. This will be quantified in Sect. 5.1.1.
Figure 8 shows SEDs for some of the most significant AME regions found in this study, excluding the previously known sources. The inset is the residual spectrum after subtraction of free-free, thermal dust, and CMB components. The error bars in the residual spectrum include the additional uncertainty in the model by simple propagation of errors. For these regions the residual spectrum shows significant flux density, although the uncertainties are larger than in the raw spectrum due to subtraction of the model. Nevertheless, the best-fitting spinning dust spectrum is seen to be a remarkably good fit to these residuals.
Similar to the example SEDs of the whole sample (Fig. 3), the SEDs of the AME regions exhibit a wide range of phenomena. In some regions (e.g., G004.24+18.09, G023.47+08.19, G192.34−11.37, and G219.18−08.93), there is little radio emission at frequencies near 1 GHz, resulting in the majority of the flux density at 30 GHz being assigned to spinning dust, and possibly a contribution from the CMB above about 70 GHz. Other regions have a reasonably well-defined level of free-free emission, but the 20–100 GHz flux density is much higher than the extrapolation of the free-free and thermal dust models (e.g., G204.70−11.80 and G234.20−00.20).
4.4. Robustness and validation
Throughout the analysis we have taken a conservative approach to the estimation of uncertainties. A critical part of the analysis is the extrapolation of synchrotron and free-free emission from low radio frequencies (≈1 GHz) to WMAP/Planck frequencies. We believe that our simple models of the synchrotron and free-free emission spectral laws are appropriate based on many other studies, both experimental and theoretical; see Bennett et al. (2003) for an overview. The contribution from UCH ii regions at WMAP/Planck frequencies could be important for a fraction of the sample, but is not thought to be a major contribution in general (see Sect. 4.2).
We find that for the majority of the sources in this study, χ2/d.o.f.<
1 (see Table 3), with a mean
value 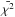 /d.o.f. = 0.59.
For a number of sources it is clear that the uncertainties are overestimated, as the
scatter in the flux densities relative to our model is much smaller than the error bars
would suggest. In many cases this can be attributed to bright backgrounds near the region
of interest. Also, the calculation of χ2 assumes that the errors are
uncorrelated, while the errors will certainly be correlated to some degree due to similar
backgrounds and also similar absolute calibration values from frequency to frequency. The
contribution to the χ2 from various frequency ranges is
found to be approximately equal (e.g., by comparing the χ2 values for
data between 0.4 and 2.3 GHz and between 353 to 857 GHz). Therefore, we do not appear to be systematically
over-estimating (or under-estimating) the errors in any particular range of frequencies.
/d.o.f. = 0.59.
For a number of sources it is clear that the uncertainties are overestimated, as the
scatter in the flux densities relative to our model is much smaller than the error bars
would suggest. In many cases this can be attributed to bright backgrounds near the region
of interest. Also, the calculation of χ2 assumes that the errors are
uncorrelated, while the errors will certainly be correlated to some degree due to similar
backgrounds and also similar absolute calibration values from frequency to frequency. The
contribution to the χ2 from various frequency ranges is
found to be approximately equal (e.g., by comparing the χ2 values for
data between 0.4 and 2.3 GHz and between 353 to 857 GHz). Therefore, we do not appear to be systematically
over-estimating (or under-estimating) the errors in any particular range of frequencies.
We made a number of tests to check that our main results are not grossly affected by our assumptions and fitting methods. These include changing our assumed calibration uncertainties, aperture radii, background annulus radii, spinning dust model, and starting values for the fitting algorithm. In all cases, we find that the general trends presented here are unchanged and the SEDs do not change appreciably; however, we note that in a few individual cases, the spectral model does vary depending on some details of the analysis. These cases are mostly related to the low frequency components, specifically the free-free level, which is not always well-constrained by the data. The uncertainties reflect this, and we are confident in most of the AME detections presented here. Nevertheless, we recommend caution when examining individual sources in detail. Follow-up observations should be made for all our high significance regions.
For most sources, we find the CMB fluctuation temperatures are within the expected range
−150 <
ΔTCMB < 150 μK. From
Monte Carlo simulations, one would expect a fluctuation outside this range only 0.7% of
the time; however, in some cases the fitted CMB temperatures (see Table 3) are found to be larger than expected. Furthermore, a
correlation between the AME amplitude and CMB is observed. Figure 9 shows the correlation between the AME amplitude and CMB fluctuation
temperature for the entire sample. The AME regions (solid filled circles) are mostly
within the expected range, with relatively small uncertainties; however, the highest AME
amplitudes (Asp
> 20 × 1020cm-2) also have the highest CMB temperatures, which are
well above what can be reasonably expected from the CMB alone (ΔTCMB > 150
μK). As discussed in Sect. 3.6, some regions exhibit a flattening of the thermal dust spectral
index at frequencies in the range 100 −
353 GHz (Planck Collaboration, in prep.) that can be artificially
accounted for by a stronger positive CMB fluctuation. This then results in a positive bias
at frequencies <100 GHz,
which increases the AME amplitude. Some of the sources with high CMB temperatures also
have high 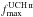 ; these are shown as star symbols in Fig.
9. We do not believe this is a major effect on our
most significant AME sample (i.e., σAME> 5 and
; these are shown as star symbols in Fig.
9. We do not believe this is a major effect on our
most significant AME sample (i.e., σAME> 5 and
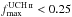 ), since none of the AME sources has an
anomalously high CMB temperature. Although the CMB has a stronger effect on the
semi-significant AME regions, the uncertainties associated with it are larger than for the
rest of the sample, as can be seen in Fig. 9.
), since none of the AME sources has an
anomalously high CMB temperature. Although the CMB has a stronger effect on the
semi-significant AME regions, the uncertainties associated with it are larger than for the
rest of the sample, as can be seen in Fig. 9.
 |
Fig. 9 Correlation plot between the AME amplitude, Asp, and the fitted CMB fluctuation temperature. Symbols are as in Fig. 6. For most sources, the fitted CMB temperatures are within the expected range shown as dashed lines (| ΔTCMB | < 150 μK) and are not strongly correlated with the AME flux density. However, for some sources, there is a strong positive correlation with CMB temperatures that are higher than expected, but associated with larger uncertainties. |
To test robustness, the entire analysis was repeated without fitting for a CMB component (ΔTCMB = 0 μK); the results do not change substantially. We do find an additional source in G102.88−00.69 with a significance of σAME = 6.9, but this is clearly due to a negative CMB fluctuation (ΔTCMB = −60 ± 17 μK). For the largest fitted CMB temperature of ΔTCMB = 603 ± 180 μK in G030.77−00.03, we find an AME amplitude of (194 ± 22) × 1020 cm-2 (8.5σ). Without a CMB component (ΔTCMB = 0), the AME amplitude is (154 ± 20) × 1020 cm-2 (7.6σ). In this case the CMB does not appear to be causing a large bias, although there is a ≈1−2σ bias in a few sources. This justifies our high cut-off threshold of 5σ. We also verify that the general trends presented in our analysis still hold when not taking into account the CMB.
In summary, we are confident in the robustness of our AME detections, particularly those at σAME > 5. We have been conservative with the uncertainties in the photometry, and in most cases our SEDs do not change appreciably when changing the details of the analysis. In fact, we believe that many of the regions with σAME = 2−5 (“semi-significant”) are likely to be “real” detections of AME, which can be seen in many of the subsequent plots to be consistent with the higher-significance AME sources.
5. Statistical study of AME regions
In this section we study statistically a number of the observational-based parameters and correlations in AME and non-AME regions, and try to investigate the nature of the AME sources and the role that the environment plays.
5.1. Nature of the sources
5.1.1. Angular sizes
First, we would like to know whether the sources are extended or compact relative to the analysis resolution of 1°. We have seen already that there is visual evidence that the strongest AME regions appear to be extended. This tendency for AME/spinning dust to originate mostly from the diffuse/extended emission has been seen in several previous studies. The majority of AME sources are diffuse, including the Perseus and ρ Ophiuchi clouds; Tibbs et al. (2010) found that in the Perseus molecular cloud at least 90% of the AME comes from diffuse extended emission. Surveys at higher resolution do not appear to detect strong AME; Scaife et al. (2008) found little or no detectable AME from a sample of relatively compact (≲1′) H ii regions.
To estimate the size of each source, an elliptical Gaussian is fitted to the pixels
within the photometric aperture of radius 1°, taking into account an offset and gradient in the background. We
take the average size, defined as the mean of the major and minor FWHM axes derived from
the Gaussian fit to the Planck 28.4 GHz map, and deconvolve this from
the map resolution, as 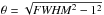 ; these values are listed in Table 3. The uncertainties are estimated from the average
noise level at 28.4 GHz. We repeat the analysis at other frequencies and obtain similar
results, with most sources agreeing in size to within
; these values are listed in Table 3. The uncertainties are estimated from the average
noise level at 28.4 GHz. We repeat the analysis at other frequencies and obtain similar
results, with most sources agreeing in size to within
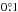 –
–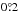 . Derived values greater than
2° are not found to be
very robust, but they nevertheless indicate that the source is very extended.
. Derived values greater than
2° are not found to be
very robust, but they nevertheless indicate that the source is very extended.
Figure 10 shows the distribution of deconvolved
sizes for the entire sample. There is a clear tendency for the AME sources to be more
extended, while non-AME sources tend to be compact, relative to the beam. The AME
sources have a mean size of 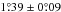 , while the non-AME sources are at
, while the non-AME sources are at
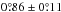 , with many of them essentially
unresolved in maps at 1°
resolution. Semi-significant sources have a mean size of
, with many of them essentially
unresolved in maps at 1°
resolution. Semi-significant sources have a mean size of
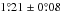 . As mentioned earlier, this is a
trend that is becoming increasingly apparent in studies of AME. It could of course be a
selection effect, since the dust grains around young and therefore compact H ii
regions are known to be different to the dust grains in the ISM environment away from
hot OB stars. For example, the PAH population is depleted in close proximity to hot OB
stars (Boulanger et al. 1988; Povich et al. 2007). This could be important for
understanding the dust grain population and environments responsible for exciting the
grain rotation. Indeed, Planck Collaboration XXI
(2011) found that there was little or no AME associated with the warm neutral
medium (WNM) or WIM phases.
. As mentioned earlier, this is a
trend that is becoming increasingly apparent in studies of AME. It could of course be a
selection effect, since the dust grains around young and therefore compact H ii
regions are known to be different to the dust grains in the ISM environment away from
hot OB stars. For example, the PAH population is depleted in close proximity to hot OB
stars (Boulanger et al. 1988; Povich et al. 2007). This could be important for
understanding the dust grain population and environments responsible for exciting the
grain rotation. Indeed, Planck Collaboration XXI
(2011) found that there was little or no AME associated with the warm neutral
medium (WNM) or WIM phases.
 |
Fig. 10 Histogram of average deconvolved FWHM sizes for AME and non-AME sources, as derived from Gaussian fitting to the Planck 28.4 GHz map at 1° resolution. Sources with FWHM> 2°are plotted as having a FWHM = 2°. The most significant AME sources are shown as the hatched histogram, while the non-significant (non-AME) sources are shown as the grey histogram. The strongest AME sources are, in general, extended, while non-AME sources tend to be relatively compact. |
5.1.2. AME fraction and IRE – H ii or molecular dust clouds?
We would like to establish how much of the total emission, at a given frequency, is due to AME. At frequencies near 30 GHz, the dominant emission will be due to either AME or free-free emission. H ii regions will exhibit strong free-free emission from warm (Te ≈ 104 K) ionized gas, while dust clouds without massive star formation will have little or no associated free-free emission.
To calculate the AME fraction we subtract the non-AME components at 28.4 GHz and
propagate the uncertainties to leave the 28.4 GHz AME residual,
 , and its uncertainty,
, and its uncertainty,
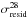 . We then estimate the AME fraction from
the ratio of the AME residual to the total flux density at 28.4 GHz. The histogram of
the 28.4 GHz AME fraction is shown in Fig. 11. As
expected, the AME sources exhibit a much higher fraction of AME at 28.4 GHz; in many, at
least half of the 28.4 GHz flux density could be due to AME.
. We then estimate the AME fraction from
the ratio of the AME residual to the total flux density at 28.4 GHz. The histogram of
the 28.4 GHz AME fraction is shown in Fig. 11. As
expected, the AME sources exhibit a much higher fraction of AME at 28.4 GHz; in many, at
least half of the 28.4 GHz flux density could be due to AME.
 |
Fig. 11 Histogram of the AME fraction, |
The weighted mean AME fractions are 0.50 ± 0.02 (AME) and 0.06 ± 0.02 (non-AME).This can be compared with the study of H ii regions by Todorović et al. (2010), who found an average AME fraction at 30 GHz of 0.41 ± 0.10. Dickinson et al. (2009) found that approximately half the 30 GHz flux density from the H ii region RCW175 was due to AME. The average value in the Galactic plane appears to be lower; Planck Collaboration XXI (2011) found that 0.25 ± 0.05 of the 30 GHz flux density was due to AME within the inner Galactic plane, while Planck Collaboration (in prep.) found a value of 0.42 ± 0.02. Although this is a considerable fraction, it is less than what has been observed in the diffuse Galactic foreground at high latitudes, where the dust-correlated AME is the dominant component and accounts for approximately 75% of the total 30 GHz emission (Davies et al. 2006; Ghosh et al. 2012). On the other hand, other measurements (Dickinson et al. 2007; Scaife et al. 2008) have found much less or no AME as a fraction of the total flux density. Sources with a smaller AME fraction (≲20%) may be prevalent, but are much more difficult to detect since the other non-AME components must be accurately removed first. The weighted average AME fraction for the semi-significant AME sources is 0.25 ± 0.02 in this study.
Most of our sources appear to be associated with H ii regions as well as molecular clouds within giant molecular complexes (GMCs). The fact that most bright FIR sources are coincident with H ii regions is well-known (e.g., Myers et al. 1986); however, a few AME sources in our sample appear to have very little free-free emission, leaving the bulk of 23 GHz emission as AME. These regions tend to be associated with dark nebula (Lynds 1962) with no known H ii regions present. The highest significance examples of these are LDN137/141 (G004.24+18.09), LDN134 (G005.40+36.50), LDN1557 (G180.18+04.30), and LDN1582/1584 (G192.34−11.37). Many of the other AME regions do have strong free-free emission and can be associated with H ii regions. The most notable associations of dark nebulae and H ii regions are given in the Notes in Table 3.
To investigate the nature of the heating of the dust, we estimate the infrared excess, defined by Mezger (1978) as IRE ≡ LFIR/LLyα. The IRE is a measure of the heating of dust associated with H ii regions. If IRE = 1, the FIR luminosity can be explained by stellar Lyα photons, which, after absorption by the gas and degradation to Lyα, are absorbed by dust grains. If IRE > 1, either direct dust absorption of stellar photons or additional stars producing little ionization, or both, are needed (Myers et al. 1986).
As a proxy for LFIR, we estimate the total flux in the FIR by integrating the best-fitting thermal dust model across all frequencies. As a proxy for LLyα, we use the best-fitting free-free model to calculate the 5 GHz flux density. Both these quantities depend on the square of the distance, which cancels out in the IRE. Figure 12 shows these two quantities plotted against each other. There is a wide range of IRE values covering 1 to greater than 100. Sources with IRE > 100 are unlikely to harbour strong H ii regions, and are mostly molecular dust clouds with no high-mass star formation; ρ Ophiuchi lies in this region. AME sources tend to have higher IRE values compared to the rest of the sample with most AME sources at IRE ≳ 4, with a median value of 14.8; most of the non-AME sources are at IRE < 10, with a median value of 2.6. This suggests that AME comes from the molecular cloud dust or PDR, but not from within H ii regions themselves. This fits with the general idea that PAHs are destroyed in H ii gas, and that AME emissivity is lower in the ionized phase of the ISM.
 |
Fig. 12 Integrated FIR flux (proxy for FIR luminosity) plotted against the free-free flux density at 5 GHz (proxy for Lyα luminosity). Symbols are as in Fig. 6. Perseus (P) and ρ Ophiuchi (R) clouds are marked. IRE values of 1, 10, and 100 are shown as straight lines. Most AME sources have IRE > 4. |
5.1.3. Dust properties
Next we look at the basic dust properties from the fitted model of thermal and spinning dust components and IRAS colour ratios. We emphasize that the dust properties are strictly related to the big dust grains and are not thought to be directly responsible for the AME, which will be from the smallest dust grains and PAHs if due to spinning dust. Furthermore, for some sources it is possible that the FIR dust emission is not spatially coincident with the AME. Nevertheless, we expect that the global dust properties will be indicative of the environment close to where the AME is originating.
Figure 13 shows the dust temperature (Td) against the fitted thermal dust emissivity index (βd). The dust temperatures are as expected for evolved diffuse H ii regions and molecular clouds, in the range ≈15−30 K, with a weighted mean of 18.5 K. This is slightly cooler than the average expected for typical H ii regions, and is close to the average value found in the diffuse ISM (Planck Collaboration XI 2014). This is probably due to the fact that we are measuring the average temperature over a relatively large area, and are therefore sensitive to the diffuse dust in the large-scale environment, as opposed to the dust in the direct vicinity of hot stars. The dust emissivity index is also in the expected range (for a single component fit) of βd = 1.4−2.4, with a weighted mean of 1.76. This is similar to the value of 1.78 found in nearby molecular clouds in Planck Collaboration XXV (2011). We note that more recent studies have found a flattening of the thermal dust emissivity index at frequencies around 100 GHz to values in the range 1.5−1.7 (Planck Collaboration, in prep.). This may make a small difference to the overall fits presented here, but will have a very small or negligible impact on the AME flux density at frequencies of 20−60 GHz.
 |
Fig. 13 Big grain dust temperature (Td) vs. thermal dust emissivity index (βd). The symbols are as in Fig. 6. Perseus (P) and ρ Ophiuchi (R) clouds are marked. There is no strong trend with βd, while the most significant AME regions (filled black circles) tend to be associated with colder dust. |
Figure 13 shows two trends. First, the most significant AME sources tend to be associated with cooler dust temperatures. Most of the AME sources are in the range 14 ≤ Td ≤ 20 K, with a weighted mean of 16.6 K, compared to 22.0 K for the non-AME regions. This is in line with the results of Planck Collaboration XXI (2011), in which it was found that the AME sources are dominated by emission from the molecular phase and that hotter dust has little or no AME. However, it is the opposite of what is found at smaller angular scales in the Perseus molecular cloud (Tibbs et al. 2011), where the AME-dominated regions are slightly warmer on average, (20.2 ± 0.5) K, than the non-AME regions (17.7 ± 0.7) K. The Perseus AME clouds are within the range of temperatures for AME sources in our sample. Second, there is a trend of the AME amplitude with increasing dust temperature, which is related to the interstellar radiation field (ISRF) G0. This will be discussed in Sect. 5.4.
In terms of the dust emissivity index, there is no strong correlation, except that the
AME regions tend to have a higher value of βd that the non-AME regions; AME
regions have 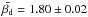 , while the non-AME regions have
, while the non-AME regions have
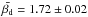 . The non-AME regions are dominated by
bright H ii regions, and the emissivity index range is similar to those found
by Dupac et al. (2003) for clouds with relatively
cool temperature (T =
11−20 K). For the ionized gas associated with pure H ii
regions, there should be less AME (Planck Collaboration
XXI 2011).
. The non-AME regions are dominated by
bright H ii regions, and the emissivity index range is similar to those found
by Dupac et al. (2003) for clouds with relatively
cool temperature (T =
11−20 K). For the ionized gas associated with pure H ii
regions, there should be less AME (Planck Collaboration
XXI 2011).
If AME were due to PAHs and small grains, we would naively expect a tighter correlation of AME with the emission from the shorter wavelengths of IRAS; the 12 μm and 25 μm bands trace smaller dust grains; however, H ii regions are known to be depleted of PAHs and the smallest grains, as traced by their 12 μm / 25 μm ratios (Boulanger et al. 1988; Chan & Fich 1995; Povich et al. 2007). Given that spinning dust requires small dust grains, one might expect a separation of AME and non-AME regions via their IRAS ratios.
Previous studies have found that there is an apparent sequence in the IRAS colours given by the 12 μm/25 μm and 60 μm/100 μm ratios. This has been seen in H ii regions, ISM clouds (Chan & Fich 1995; Boulanger et al. 1988), and external galaxies (Helou 1986), where large 60 μm/100 μm ratio means smaller 12 μm/25 μm value and vice versa, i.e., an anti-correlation. The explanation is closely connected to the ISRF and the exciting star(s), since hotter grains have higher 60 μm/100 μm ratios, while close to the star the smallest grains (and PAHs) are destroyed, leading to smaller 12 μm/25 μm ratios. We see the same trend in our sample as a whole, as shown in Fig. 14. This is expected, since a large fraction of our sample contains a component from H ii regions.
 |
Fig. 14 Colour−colour plot of IRAS 60 μm/100 μm vs. IRAS 12 μm/25 μm. Symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are marked. |
It can also be seen that the AME sources generally have a higher 12 μm/25 μm ratio (≈0.6−1.0) than the rest of the sample (≈0.2−0.6). We interpret this as confirmation of the spinning dust model, where the very smallest grains (and PAHs) must be responsible for the bulk of the AME at frequencies ≳20 GHz. At this resolution, we cannot rule out ionic/stellar contamination of the 12 μm IRAS band, although the stellar contribution is expected to be minor. Previous studies (Sellgren et al. 1985; Boulanger & Perault 1988) have shown that in bright nebulae, the bulk of the 12 μm emission comes from the PAH bands at 7.7, 8.8, and 11.3 μm; however, inspection of the sources with the highest 12 μm/25 μm ratios (>0.8) reveals that these are not the brightest free-free emitters of our sample but are in fact some of the most AME-dominated sources. These therefore do not appear to be dominated by ionized gas from H ii regions, which suggests that ionic/stellar contamination is not a prominent effect here. One exception to this is the source G239.40−04.70, which contains the luminous supergiant V∗ VY Canis Majoris, explaining the a 12 μm/25 μm ratio of 1.62; this source should be excluded from any mid-infrared analysis (see Sect. 5.2).
5.1.4. The interstellar radiation field: G0
An important parameter in studies of ISM clouds is the relative strength of the ISRF, G013. This parameter is important for spinning dust, since the ISRF plays a key role in rotationally exciting small grains, charging PAHs, and in the destruction of the smallest grains. While we assume the same form for the shape of the ISRF spectrum here, it should be noted that the intensity and hardness of the ISRF are important.
An estimate of G0 can be obtained from the equilibrium dust temperature of the big grains (TBG) compared to the average value of 17.5 K, i.e., G0 = (TBG/ 17.5 K)(4 + βd). We used the fitted dust temperature from our SEDs as a proxy for the big grain temperature, i.e., TBG ≈ Td. We kept the dust emissivity index constant at βd = 2 to protect against mixing of multiple dust components with a range of dust temperatures that could flatten the index. This allows an estimate of the average G0 for each source (Table 3). As with other FIR properties, we note that in some regions these properties may not be related to the exact environment where the AME is arising.
Figure 15 shows the AME fraction at 28.4 GHz,
defined as the AME residual flux density (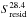 ) divided by the total flux density at
28.4 GHz, against the estimate of G0. The most striking feature is that
sources with low G0 are those with the highest AME
fractions; the majority of strong AME regions are at G0< 4,
while non-AME regions are almost always at G0> 1. There is a general trend of
decreasing AME fraction with G0. When including semi-significant
AME sources, there is also a definite trend of decreasing AME fraction with increasing
G0. The best-fitting power law has a
slope of γ = −0.59 ±
0.11; however, taking only the strongest AME sources yields a slope
of γ = −0.11 ±
0.04. This suggests that there is a much flatter slope for AME strong
sources, and that the AME sources are different in nature to the rest of the sources in
the sample.
) divided by the total flux density at
28.4 GHz, against the estimate of G0. The most striking feature is that
sources with low G0 are those with the highest AME
fractions; the majority of strong AME regions are at G0< 4,
while non-AME regions are almost always at G0> 1. There is a general trend of
decreasing AME fraction with G0. When including semi-significant
AME sources, there is also a definite trend of decreasing AME fraction with increasing
G0. The best-fitting power law has a
slope of γ = −0.59 ±
0.11; however, taking only the strongest AME sources yields a slope
of γ = −0.11 ±
0.04. This suggests that there is a much flatter slope for AME strong
sources, and that the AME sources are different in nature to the rest of the sources in
the sample.
We caution that this trend could be entirely due to selection effects, because AME is more difficult to detect when there is strong free-free emission. Also, the thermal dust could be coming from a different region of space compared to the AME, and thus the relation between G0 and AME might be entirely coincidental. Despite that, the effective free-free EM from our photometry and G0 are positively correlated as one would expect. The role of the ISRF will be discussed further in Sect. 5.4.
 |
Fig. 15 AME fraction at 28.4 GHz as a function of estimated G0. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The best-fitting power laws to the AME regions (solid line) and semi-significant AME regions (dashed line) are overplotted. |
5.1.5. Peak frequency of spinning dust
As discussed in Sect. 3.5, as well as fitting for a spinning dust amplitude, we also fit for a possible shift in the spinning dust peak frequency. This allows us to determine the peak frequency νsp for each SED, which is listed in Table 3 for sources with σAME > 2. Visual inspection of the SEDs indicates that allowing this freedom provides a better fit to the data, where a few sources are clearly not peaking at the starting value of the fitted curve, at 28.1 GHz.
Figure 16 shows the histogram of spinning dust
peak frequencies. The AME sources peak in the range 20−35 GHz, with a weighted mean of 27.9 GHz.
Although the formal uncertainties do not suggest that these are highly statistically
significant, it is clear that the data sometimes prefer spinning dust that is at a
different frequency from the starting value 28.1 GHz. Examples of small shifts can be
seen by careful examination of the SEDs in Fig. 8.
A particularly clear example, previously commented on by Planck Collaboration XX (2011), is G160.60−12.05 (the California nebula/NGC 1499).
The SED is plotted in Fig. 17. The spinning dust
detection is at a level of σAME = 5.1, and the SED shows a peak
at a higher frequency compared to the rest of the sample. The best-fitting peak
frequency is νsp
= (50 ± 17) GHz. Notice that the reduced value is
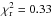 , and thus the significance is likely
underestimated. As discussed earlier, COSMOSOMAS data at 12−18 GHz are not included here because the
filtering required causes problems at frequencies above 100 GHz, resulting in negative
flux densities. This is due to a lack of dust emission in the centre of the nebula where
most of the free-free emission comes from, and nearby dust emission appearing near a
negative lobe caused by the COSMOSOMAS harmonic filtering; however, the shape of the
spectrum at 12−18 GHz is
consistent with a free-free spectrum (Planck
Collaboration XX 2011).
, and thus the significance is likely
underestimated. As discussed earlier, COSMOSOMAS data at 12−18 GHz are not included here because the
filtering required causes problems at frequencies above 100 GHz, resulting in negative
flux densities. This is due to a lack of dust emission in the centre of the nebula where
most of the free-free emission comes from, and nearby dust emission appearing near a
negative lobe caused by the COSMOSOMAS harmonic filtering; however, the shape of the
spectrum at 12−18 GHz is
consistent with a free-free spectrum (Planck
Collaboration XX 2011).
The reality of this shift to higher frequency, and its possible explanation, are not clear and require a more detailed study. Despite that, the conditions in this diffuse H ii region may well be conducive to the production of higher frequency emission. The ISRF comes mostly from the ionizing star ξ Per, where the density is ≈1 cm-3, and goes up to 50 cm-3 on the brightest filaments in the PDR (Boulanger et al. 1988), where the AME may be originating. Similarly, there is a range of temperatures, covering 20−50 K. Our fitted parameters of Td = (21.7 ± 1.6) K, G0 = 3.7 ± 1.7 are an average of these, and may well not be appropriate for conditions in the AME-emitting region, especially as much of the cooler dust emitting at ≈1000 GHz is coming from an adjacent dust cloud. Higher resolution observations of this cloud are needed to investigate this further.
 |
Fig. 16 Histogram of spinning dust peak frequencies, νsp. The unfilled histogram is for both AME and semi-significant AME regions, while the hatched region is for the AME sources only. The best-fitting Gaussians for these two histograms are overplotted. The source at νsp = 50 GHz is G160.60−12.05 (California nebula). |
 |
Fig. 17 SED for G160.60−12.05 (California nebula). The curves and symbols are as in Fig. 8. AME is detected at a level of σAME = 5.0, and the best-fitting spinning dust peak is shifted to νsp = (50 ± 17) GHz. |
Spearman rank correlation coefficients between the AME amplitude (Asp) and IR/submillimetre flux densities.
5.2. Dust correlations
There should be a very strong correlation between the AME and the thermal dust emission, since the AME is thought to be due to spinning dust grains. Figure 18 shows the correlation of the AME amplitude (Asp) with the flux density at 100 μm, 60 μm, and 12 μm from the aperture photometry. A strong correlation is seen between the AME and IR/submillimetre brightness for the AME bright regions (black filled circles). The tight correlation also holds for the semi-significant AME regions (grey filled circles), while non-AME regions (unfilled circles) are weaker and more scattered, partly due to the intrinsic noise.
 |
Fig. 18 Top row: AME amplitude (Asp) as a function of the 100 μm (left), 60 μm (middle), and 12 μm (right) flux density. Bottom row: same as top row, except that the FIR flux densities have been divided by G0. Symbols are as in Fig. 6. The best-fitting slope fitted to the significant AME regions only is plotted. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. There is a strong correlation between the AME intensity and infrared tracers of dust, with an improved correlation after dividing by G0. At 12 μm the fit is made excluding the outlier source G239.40−4.70 (marked). |
To quantify the strength of the correlations, we compute the Spearman rank correlation coefficient (in log space), rs, for the significant AME regions, which are listed in Table 2. This quantity, unlike the Pearson correlation coefficient, does not rely on a linear dependence between two variables (we obtained similar results using either statistic). Average uncertainties on rs are calculated using 1000 Monte Carlo simulations based on their formal uncertainties. There is a relatively strong correlation for sources with significant AME (rs ≈ 0.8), although non-AME sources are not less correlated. For the AME-bright regions, there is no strong preference for them to correlate better with any particular FIR band.
If the AME is due to the smallest dust grains emitting electric dipole radiation, the best correlation should be with the shorter IRAS wavelengths at λ< 60 μm. This has been observed in previous studies at higher angular resolution (e.g., Casassus et al. 2006; Ysard et al. 2010). We do not find such a clear trend, with the worst correlation occurring for the IRAS 12 μm band. Figure 18 shows the correlation of the AME amplitude against the 12 μm flux density. There is a reasonably strong correlation but there is also considerable scatter.
It has been discussed in several works (e.g., Ali-Haïmoud et al. 2009; Ysard et al. 2010) that spinning dust emissivity (per column density) at frequencies 10−30 GHz is not particularly sensitive to the ISRF intensity, G0. On the other hand, the thermal dust emission is strongly dependent on G0, since it is the UV radiation that governs the dust grain temperature. The nanoscale dust particles (PAHs and VSGs) are proportional to G0 (Sellgren et al. 1985) when G0 ≲ 10. Previous studies (e.g., Ysard et al. 2010; Vidal et al. 2011) have found that a better correlation can be obtained with the infrared by dividing far-infrared flux density by G0.
The Spearman rank correlation coefficients for all infrared bands divided by G0 are given in Table 2 in parentheses. In general, we do not see a significant increase in the correlation after dividing by G0. There is a general increase within the sample as a whole (rs ≈ 0.9), but no improvement for the AME sample.
We suspect that some of the correlation scatter with the IRAS bands, particularly at 12 μm and 25 μm, is due to contamination from stellar emission or from fine-structure lines. Shipman & Carey (1996) predicted that for bright H ii regions, line contamination could account for most of the flux densities at 12 μm and might even affect the longer IRAS wavelengths. Sellgren et al. (1985) found that the 12 μm band flux densities in bright reflection nebulae could be explained by approximately equal amounts of continuum and line emission from PAHs. Infrared spectra of the Omega nebula (M17) showed that PAHs dominate the mid-infrared in the neutral PDR beyond the ionized gas of H ii regions (Povich et al. 2007). Also, for many regions in our sample, we are looking at a complex integration of environments including molecular clouds, CNM, and WIM. On the other hand, spinning dust predictions are local (i.e., for a particular environment).
List of 98 candidate AME regions. Names are given by the central Galactic coordinates.
Evidence of a particular example of contamination can be seen in Fig. 18, where there is a source (G239.40−04.70) that has a much higher 12 μm flux density than the rest of the sample. This is due to one of the most luminous supergiants known, V∗ VY Canis Majoris (CMa), which has a 12 μm flux density of 10 000 Jy (Helou & Walker 1988) and accounts for the bulk of the flux density in this band. We therefore omit this source for the correlation values (Table 2) and power-law fits (Fig. 18) at 12 μm and 25 μm. Although this is an extreme object, this clear case of contamination does question the robustness of the IRAS 12 μm flux density, and partly the 25 μm band, for low latitude sight-lines.
We also investigated the ratio of 8 μm / 24 μm using the Spitzer data. This ratio is diagnostic of the PAH fraction compared to that of the small grains. Only 24 sources had coverage and of these only three are AME regions. This makes it difficult to distinguish any trends between AME or non-AME regions. We find no distinction in the 8 μm / 24 μm ratio for AME vs. non-AME regions; however, we note that ρ Ophiuchi has one of the highest ratios, 1.09 ± 0.15, compared to the sample weighted average of 0.28 ± 0.01. One particular outlier is G023.47+08.19, which has a much higher ratio of 10.6 ± 1.5 due to the source being very faint in the Spitzer maps.
5.3. AME emissivity
Next, we would like to compare the AME amplitude to values in the literature. A common way of normalizing the emissivity is to take the ratio of AME flux density to 100 μm (3000 GHz) flux density. Since the far-infrared emission is optically thin for a given dust temperature and composition, this will be proportional to the column density of dust along the line of sight. If AME is due to spinning dust emission, we would therefore expect a strong correlation with the 100 μm brightness (Fig. 18).
We begin by choosing the 28.4 GHz AME flux density, defined as the residual at 28.4 GHz
after subtracting the non-AME components for each source. This allows a comparison with
previous works, where frequencies near 30
GHz have been used extensively. Note that using the 28.4 GHz AME residual
is almost identical to using the AME amplitude (Asp) directly from the fit, since they
are highly correlated. Figure 19 shows the ratio of
28.4 GHz residual flux density to the 100
μm (3000 GHz) flux density as a function of the AME
significance, σAME. The ratio
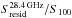 for the AME regions has a large range of
values covering the range (1−15) ×
10-4, with a weighted average of (2.5 ± 0.2) × 10-4. This is
higher than in the H ii regions of Todorović
et al. (2010), but less than the average from high latitude AME (Davies et al. 2006), as shown in Fig. 19. It can be seen that the weighted average is actually
lower than many of the AME regions, due to a few sources having a relatively small
uncertainty and lower emissivity values of (1–2) ×
10-4, including ρ Ophiuchi (G353.05+16.90) at (1.5 ± 0.2) × 104. The unweighted
average is (5.8 ± 0.7) ×
10-4, which is consistent with the 6.2 × 10-4 value of Davies et al. (2006) for the diffuse high latitude AME.
for the AME regions has a large range of
values covering the range (1−15) ×
10-4, with a weighted average of (2.5 ± 0.2) × 10-4. This is
higher than in the H ii regions of Todorović
et al. (2010), but less than the average from high latitude AME (Davies et al. 2006), as shown in Fig. 19. It can be seen that the weighted average is actually
lower than many of the AME regions, due to a few sources having a relatively small
uncertainty and lower emissivity values of (1–2) ×
10-4, including ρ Ophiuchi (G353.05+16.90) at (1.5 ± 0.2) × 104. The unweighted
average is (5.8 ± 0.7) ×
10-4, which is consistent with the 6.2 × 10-4 value of Davies et al. (2006) for the diffuse high latitude AME.
 |
Fig. 19 Ratio of 28.4 GHz residual to the 100 μm flux density as a function of the AME significance. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The weighted and unweighted average ratios for the significant AME regions are shown as the solid horizontal lines. The average ratio from Todorović et al. (2010, dashed line) and Davies et al. (2006, dot-dashed line) are also shown. |
The best-fitting power law to the S100 vs. AME amplitude (Asp) yields a power-law index of + 0.67 ± 0.03 for AME regions, suggesting that there is not a simple, one-to-one ratio between the AME brightness and 100 μm brightness. This is not surprising, given that different dust temperatures will affect a given frequency, particularly near the peak of the thermal dust spectrum where it is very sensitive on the dust temperature (Tibbs et al. 2012b). Instead, as suggested by Finkbeiner (2004), the thermal dust optical depth is expected to be a better diagnostic of the AME emissivity, since it is proportional to the column density of dust via τν = NHκν μmH, where NH is the column density, κ is the dust mass absorption coefficient, μ is the mean molecular weight, and mH is the mass of hydrogen (Boulanger et al. 1996; Martin et al. 2012). The fit against the dust optical depth at a wavelength of 250 μm (τ250), which is proportional to NH, yields a slope much closer to unity (+ 1.03 ± 0.03). This suggests that the AME is emitting at approximately the same level per unit column density in all the bright AME regions chosen in our sample. Planck Collaboration XXI (2011) also found that AME emits at the same level per NH throughout the Galactic plane. We therefore define our default AME emissivity as the AME amplitude divided by the thermal dust optical depth, Asp/τ250. In this case, the units are formally 1020 cm-2, but we note that the interpretation of this value depends on the spinning dust model that is fitted. The actual dust column density calculated from the optical depth depends on the range of dust temperatures along the line-of-sight (Ysard et al. 2012), as well as details of the dust grains including the dust opacity (which in turn depends on many factors such as dust composition).
Figure 20 plots the AME emissivity Asp/τ250 against the significance, σAME. There is considerable scatter in the emissivity, some of which is due to the intrinsic uncertainty in the measurement; however, for AME sources there is more variation than can be accounted for by the uncertainty alone. This will be investigated via correlations with other parameters. Remarkably, unlike the equivalent plot for the 100 μm-based emissivity, there is no clear trend with AME significance. This is an important result. It shows that AME emissivities based on 100 μm data are likely to be biased due to the effect of varying dust temperature. This plot also suggests that AME is emitting at approximately the same level per unit dust column density, not only for the strong AME sources, but for most of the sources within our sample. However, we caution that the uncertainties are large and including an AME component will inevitably result in a positive bias. Furthermore, some sources have a possible contribution from UCH ii regions as well (Table 3). The weighted average emissivity for significant AME sources is (1.36 ± 0.05) × 104, while the non-AME sources are at (2.0 ± 0.5) × 104.
 |
Fig. 20 Ratio of AME amplitude (Asp) to dust optical depth (τ250), as a function of the AME significance σAME. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The horizontal lines represent averages: weighted average of significant AME regions (solid line), unweighted average of significant AME regions (dashed line) and weighted average of non-significant AME regions (dotted line). |
It is worth noting that for the AME regions the weighted average is smaller than the unweighted average of (4.3 ± 0.6) × 104, due to four high significance sources that appear to have a lower emissivity (Asp/τ250< 104) than the rest of the sample. These are G005.40+36.50, G023.47+08.19, G133.27+09.05 and G219.18−08.93. All are associated with dark nebulae (see Table 3 and Sect. 6.2). These sources are high latitude sources with very weak free-free emission and a low intensity radiation field (G0 = 0.3−0.6), leading to cold big grain dust temperatures (Td = 14−16 K).
We have investigated the correlation of AME emissivity with a wide range of parameters and properties in this study. In general, we find little or no correlation with most parameters. Previous works (Lagache 2003; Vidal et al. 2011) found evidence of an anti-correlation of the AME emissivity with the column density. The interpretation is that this is what would be expected with AME arising from small spinning dust grains; as the density (nH) increases, dust grain growth becomes more efficient and thus the small grain population decreases. Figure 21 shows the AME emissivity against the optical depth, τ250. For the significant AME regions, we also find a similar trend. The anti-correlation (rs = −0.72 ± 0.07) has a best-fitting power-law slope of γ = −0.67 ± 0.04, similar to the −0.54 ± 0.10 value found by Vidal et al. (2011).
The effect we see is somewhat surprising given the difficulty of estimating density in the potential complex mix of environments in a 1° beam, especially at low latitudes where there may be multiple objects along the line-of-sight. Nevertheless, this is one of the few observational trends associated with AME that has come to light in several independent studies. It is consistent with small grains as AME carriers, because they are expected to be depleted in denser environments by coagulation onto larger grains.
 |
Fig. 21 Ratio of AME amplitude (Asp) to dust optical depth (τ250), as a function of τ250. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The solid line shows the best-fitting power law for the significant AME regions. |
5.4. The role of the ISRF
The ISRF plays an important role in the ISM. It is a major source of local heating, with UV photons being absorbed by dust grains and re-radiated in the IR. It also has important effects on the composition of the ISM, since it can charge PAHs and also destroy PAHs and VSGs when the intensity is high enough. For spinning dust, the population of PAHs and VSGs is fundamental in determining the AME, and the formation of ions (e.g., C+, H+) can be important for rotationally exciting small dust grains. The ISRF also plays a role in rotationally exciting small dust particles through the absorption of infrared photons; these particles can be dominant in some environments (e.g., when G0 = 1 and nH< 10 cm-3).
In the recent studies by Tibbs et al. (2011,
2012a), the AME brightness was found to
correlate with G0 more than any other parameter,
including the PAH fraction. Figure 22 shows the AME
emissivity as a function of G0 for our sample. We also find that the
AME emissivity is related to G0. For the AME regions there is a
positive correlation (rs = 0.63 ± 0.07) with a fitted
power-law index γ = + 0.74 ±
0.10. We verified that the correlation is due primarily to variations
in Td, and not βd, by setting
βd to the fitted values. We found a
similar positive trend but with larger scatter (rs = 0.49 ± 0.12 and γ = + 1.32 ± 0.10).
Surprisingly, for semi-significant regions (grey filled circles), the same trend is also
visible, but with a flatter slope of γ = + 0.70 ± 0.04, and the non-AME sources are also
correlated. This may suggest that there is AME in many of our sources or that there is a
systematic effect that is driving this result. As before, we only consider the AME sources
with σAME >
5 and 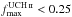 to be reliable. Given the larger scatter,
at this point we can only say that there is a positive correlation with a slope
γ ≈ + 1; we
will adopt this value in Sect. 5.5.
to be reliable. Given the larger scatter,
at this point we can only say that there is a positive correlation with a slope
γ ≈ + 1; we
will adopt this value in Sect. 5.5.
We may not be seeing AME at high G0 (and high Td) because the PAHs/VSGs require radiation to spin, but too much UV destroys them, as happens inside very bright H ii regions (with higher EM, Td and G0). The grains need to be shielded, hence to be close to the PDR of the H ii regions (which is the coldest part of an H ii region). It could also be a selection effect due to brighter free-free emission associated with high values of G0 that would make AME more difficult to detect.
 |
Fig. 22 AME emissivity as a function of G0. The symbols are as in Fig. 6. The straight lines are the best-fitting power laws to the AME (solid line) and including semi-significant AME (dashed line) regions. |
In some environments (e.g., low density), it is expected that as the ISRF increases (up to a certain point), the smaller grains will receive more rotational excitation, resulting in a spinning dust spectrum shifting to higher frequencies (e.g., Ysard et al. 2011). Figure 23 plots the spinning dust peak frequency against G0. Although not strong, there is tentative evidence for a correlation between the two quantities (rs = 0.41 ± 0.15). The majority of the high signal-to-noise ratio detections are clustered near the centre of this plot (νsp = 25–30 GHz and G0 = 1–3), making a slope difficult to constrain; a weighted fit is flat within the uncertainties (dashed line). However, if we make an unweighted fit to the AME sources, assigning median errors for G0 and νsp, we find a positive slope of + 0.18 ± 0.02. Omitting the California nebula, which is driving this fit, gives a slope of + 0.05 ± 0.02. The precise value of the AME emissivity does depend on the assumptions on βd that affect the estimation of G0; however, in this case, using the fitted values for βd actually results in a tighter positive correlation, with rs = 0.65 ± 0.15 and γ = + 0.08 ± 0.02 (omitting the California nebula).
 |
Fig. 23 Spinning dust peak frequency as a function of G0. The symbols are as in Fig. 6. The solid line is the best-fitting power law for the AME regions with all data points equally weighted. The dashed line is the weighted fit to the AME regions, while the dot-dashed line is the weighted fit to AME and semi-significant AME regions. |
As discussed in the next section, the increase of AME emissivity and peak frequency with the increase of G0 is compatible with model predictions. For 0.1 ≲ G0 ≲ 10, gas-grain interactions dominate the process for rotational excitation over photon emission. This might explain why we see a decrease of the AME intensity when Td increases. Alternatively, there could be an observational bias related to the fact that cooler regions, with a weaker radiation field due to less massive stars, will typically have less free-free emission. Thus we may be selecting cool regions preferentially; indeed sources with larger values of Td appear to have larger uncertainties in the AME amplitude. A complete flux-density-limited sample would be required to investigate this possibility. Nevertheless, this result agrees with previous studies that found AME arising preferentially from denser and colder molecular/atomic gas rather than from the ionized gas phase (Planck Collaboration XX 2011; Planck Collaboration XXI 2011).
5.5. Spinning dust modelling
We investigate here whether the behaviour of the AME presently observed can be explained
by spinning dust emission, i.e., rotational emission of PAHs. We focus on the relationship
between the AME and the intensity of the radiation field G0. The present
results indicate a trend between the AME emissivity at 28.4 GHz (noted j28) and
G0 (Fig. 22), where  , with j0 ≃ 3 ×
10-24 MJy sr-1 cm2 per H atom. This trend is found for the significant AME
regions.
, with j0 ≃ 3 ×
10-24 MJy sr-1 cm2 per H atom. This trend is found for the significant AME
regions.
Models show that the spinning dust emissivity increases with G0 and nH, the gas density (Ali-Haïmoud et al. 2009; Ysard & Verstraete 2010; Hoang et al. 2011). In general, the spinning dust emissivity and therefore j28 are functions of nH and G0. In the CNM, excitation of spinning dust by photons and collisions have similar rates. For the present sample, we expect both processes to contribute to the spinning dust emissivity. To model the spinning dust emission in our sample, we describe the emission region in the following way. Observations suggest that PAHs are depleted in the ionized gas (e.g., Salgado et al. 2012; Dobler et al. 2009) and in the case of H ii regions, PAHs are observed to be located in a dense, neutral shell surrounding the ionized gas. We assume that this shell dominates the thermal dust emission and is therefore heated by a mean radiation field of intensity G0. We note that the dust optical depth τ250 does not show any trend with G0 (r = −0.01 ± 0.13), suggesting that the column density of dust is rather constant, probably corresponding to the shell material directly heated by the star. The AME thus comes from a shell around the H ii region with density nH and radiation field G0. From the observed trend of j28 with G0, and assuming that the AME is due to spinning dust, models can constrain the gas density nH.
Using the SPDUST code (Silsbee et al. 2011) and the gas ion scheme of Ysard et al. (2011), we ran model grids for the spinning dust emissivity in the 28.4 GHz LFI band with the following hypotheses. We assume the PAH properties to be the same for all values of G0 and nH, namely that they enclose 65 ppm of carbon and have a log-normal size distribution with centroid 0.6 nm and width 0.4 nm. In addition, we assume the gas temperature to be constant for all nH and G0, namely Tgas = 60 K14. In Fig. 24, we show the relationship between G0 and nH that results from the j28–G0 trend. We see that nH increases with G0, suggesting that density plays an important role in the AME pumping. As expected, higher AME emissivities require higher densities. This trend possibly reflects the presence of more massive stars in denser clouds. The emissivity rises with nH but levels off for nH> 103 cm-3 (see Fig. 8 of Ysard et al. 2011) due to recombination of H+ and C+ ions. When j0 = 6 × 10-24 MJy sr-1 cm2 per H atom, the model emissivity cannot match the observed level even for very high density (nH = 106 cm-3); this is why the dashed curve is interrupted in Fig. 24.
 |
Fig. 24 Density estimates (solid black line) from spinning dust models that follow the observed trend between the AME emissivity j28 and G0. We also show the influence of AME emissivities half (j0 = 1.5 × 10-24 MJy sr-1 cm2 per H atom; triple-dot-dashed line) and twice as large (j0 = 6 × 10-24 MJy sr-1 cm2 per H atom; dashed line). |
We emphasize that this nH–G0 trend is qualitative, because of several important uncertainties. First, while estimating G0 from the emergent dust SED, we may be biased towards low values because of the contribution of large column densities of cold dust. Also, we assume a constant PAH abundance, whereas it is known that PAHs are depleted in dense gas (Arab et al. 2012; Compiègne et al. 2008). This analysis is thus preliminary, and microwave data at higher angular resolution, as well as radiative transfer modelling of such regions, are required to further our understanding of the AME and its possible use in characterizing the physical conditions in the emitting region.
6. Discussion and conclusions
6.1. Detection of AME
In this paper we have increased the number of known candidate AME targets by a factor of several. We have also presented evidence for AME being exhibited in a much larger number of Galactic clouds, albeit at a lower significance. The spectral coverage of radio, submillimetre, and far-infrared data have allowed us to estimate the SED to high precision to determine the continuum components that are contributing at each frequency. These sources are a mix of H ii regions, molecular clouds, and dark clouds, often in cloud complexes. The SEDs can be fitted by a combination of synchrotron (in a few cases), optically thin free-free emission, CMB, thermal dust, and spinning dust.
Of the 98 regions, 42 are highly significant (>5σ) in terms of AME amplitude. Of these 42 sources, 15 contain candidate UCH ii regions (based on IRAS colour ratios) that could be contributing a portion (>25%) of the excess emission and are dropped from the significant AME list. This leaves 27 regions that appear to emit AME. Among the clearest AME detections are the well-known ρ Ophiuchi and Perseus molecular clouds. A further 27 sources are AME significant at the level of 2−5σ. Only 29 of the sample are non-significant (<2σ) although the sample is far from complete.
The AME detections are shown to be robust. In general, we have been conservative in the assignment of uncertainties. The average reduced χ2 value of 0.59 indicates that we may be over-estimating our uncertainties by about 30%; however, given the complexity of assigning flux densities to diffuse emission in the presence of complex and bright backgrounds, we choose to be conservative in this low resolution analysis. We consider the effect of fitting for a CMB component and its relation to a possible flattening of the thermal dust index at frequencies <300 GHz. Although there is some evidence for this effect, it is shown not to be a major effect on the AME properties. The excess emission is readily fitted by spinning dust models that peak at frequencies around 25−30 GHz and have column densities of about 1021 cm-2, reasonable for diffuse ISM clouds. We have not attempted to fit for other components, such as magneto-dipole radiation (Draine & Lazarian 1999; Draine & Hensley 2012, 2013), which could also account for the excess emission.
A number of the sources in the sample have been discussed in the literature. Génova-Santos et al. (2011) used WMAP data to study the reflection nebula associated with the Pleiades (G166.44−24.08) and found (2.15 ± 0.12) Jy at 22.8 GHz in a 1° radius aperture. Of this, the bulk was found to be from AME. In our analysis, we find a similar total flux density of (1.89 ± 0.13) Jy at 22.8 GHz, but the AME level is much lower at (0.83 ± 0.19) Jy. The results are different mostly due to the different level of free-free emission assigned to the cloud due to the large background at low frequencies. Although it does not enter our significant AME list, with σAME = 4.3, this region is likely to be emitting appreciable amounts of AME at frequencies ≈20−40 GHz.
The source G201.62+01.63 was first claimed to emit AME by Finkbeiner et al. (2002), but was later shown by Dickinson et al. (2006) to be consistent with free-free emission on angular scales of 6′ with an upper limit of 24% AME at 31 GHz. More recently, Rubiño-Martín et al. (2012a) detected AME at the 2.8σ level. In the present analysis, this source is highly significant at σAME = 7.4. The analysis of Dickinson et al. (2006) was of the bright, more compact (6′) source in the centre of the nebula, which contains approximately half of the flux density of the more extended region covering 30′. It is possible that most of the AME is originating within this extended region that the 1° analysis is more sensitive to. G204.70−11.80 is associated with LDN1622 and LDN1621, which are both known to be dominated by dust-correlated emission at 31 GHz (Casassus et al. 2006; Dickinson et al. 2010).
6.2. Nature of the sources in our sample
Given the low angular resolution (1°) of the present analysis, it is somewhat difficult to disentangle the various sources and environments for the majority of the AME regions, since in many cases there are multiple sources within the beam. Furthermore, the sample is not complete and there likely remains selection effects and biases. However, in some cases the nature of the source is clear. For example, some of the non-AME regions are clearly dominated by bright H ii regions, such as G209.01−19.38 (M42) and G267.95−1.06 (RCW38).
Of the AME regions, many have a contribution of free-free emission associated with H ii regions. However, a small fraction of these do not have a bright associated H ii region, and a large fraction of the 20−60 GHz flux density is due to AME. These sight-lines do contain known dark nebula and may be responsible for the AME. The best examples of these are G004.24+18.09 (LDN137/141), G005.40+36.50 (LDN134), G023.47+08.19 (LDN462), G133.27+09.05 (LDN1358/1355/1357), G142.35+01.35 (DNe TGU H942), G180.18+04.30 (LDN1557), G192.34−11.37 (LDN1582/1584), G219.18−08.93 (DNe H1544/1546), and G231.83−02.00 (DNe TGU H1593). These sources are dominated by AME at 23 GHz, but the AME emissivity (per unit dust column density) is typically lower than the average for the sample.
The AME regions are, in general, spatially extended even at an angular resolution of 1°, while non-AME regions tend to be relatively compact. This is a trend that is becoming increasingly familiar; AME sources are typically diffuse (e.g., Davies et al. 2006; Casassus et al. 2006, 2008; Dickinson et al. 2010; Planck Collaboration XX 2011; Planck Collaboration XXI 2011), while compact objects show little evidence for AME (e.g., Scaife et al. 2009), or a much smaller fraction of the total flux density (e.g., Dickinson et al. 2007; Tibbs et al. 2010).
A tight correlation is observed between the AME amplitude and dust continuum tracers in the submillimetre (353 GHz) and far-infrared (12, 25, 60, 100 μm). In agreement with other studies, dividing the infrared fluxes by the intensity of the interstellar radiation field G0 improves the correlation. We find that the majority of the AME regions have a high ratio of S12/S25 = 0.06−1.0, compared to the typical range 0.2−0.6. From inspection of these regions, they do not appear to contain a strong ionized component, and therefore probably do not have strong ionic/stellar contamination of the 12 μm band. Instead, we believe that this is indicative of PAHs as the carriers of spinning dust emission. Comparison with Spitzer data is inconclusive because of the limited coverage of the data.
We find that the AME sources favour slightly cooler regions with Td = 14−20 K and a dust emissivity index of βd ≈ + 1.8, while the non-AME sources appear to be warmer (Td = 20−27 K) and prefer a slightly flatter emissivity index βd ≈ + 1.7. This is consistent with the picture that AME is arising primarily from the colder neutral ISM phases, rather than the warmer ionized gas associated with bona fide H ii regions. In H ii regions the PAH population is expected to be depleted, thus reducing the primary carriers of spinning dust emission. The lack of AME associated with the WNM/WIM phase is in agreement with the findings of Planck Collaboration XXI (2011). The ISRF intensity, parameterized by G0, appears to play an important role for AME. We find that most AME sources prefer lower levels of the ISRF in the range 0.3 ≲ G0 ≲ 3, while non-AME regions are generally higher (G0 ≈ 1−10).
For the AME emissivity relative to 100 μm, we find that the levels are similar to those found in the diffuse ISM at high Galactic latitudes, as well as from previous studies of H ii regions, with typical values of a few 10-4. A more robust emissivity is found by forming the ratio between the AME flux density and the thermal dust optical depth τ250, due to its non-dependancy on dust temperature. Remarkably, we find that most of the sources in our sample (AME and non-AME regions) have a similar AME emissivity relative to τ250, although there is a large scatter at all significance levels. This suggests that AME may be inherent to most of the sources in our sample, but for some sources the AME is more difficult to detect, such as when there is a dominant free-free component.
We investigated the AME emissivity with various observational/physical parameters from our sample. In general, we do not find strong trends. We believe this is partly due to the aforementioned complexity and mix of environments and sources within each region, in addition to the relatively small sample size; however, a few weak trends are observed.
In agreement with previous studies (Lagache 2003; Vidal et al. 2011), we find that the AME emissivity decreases with the column density, as traced by the thermal dust optical depth. This might be explained by dust coagulation in denser regions, reducing the population of smallest grains and therefore reducing the number of spinning dust carriers.
We observe a correlation of G0 with the AME emissivity. A weak correlation of G0 with the peak frequency of the spinning dust frequency is also observed. Both these trends may be understood in terms of radiative and collisional excitation of the rotation of small grains; however, we caution that there may also be an observational bias, due to the fact that an increasing G0 generally means an increasing free-free component that makes it more difficult to detect AME. On the other hand, spinning dust modelling of the AME emissivity assuming a fixed small grain abundance suggests that the density increases with G0, a trend expected in massive star forming regions.
Finally, we note that the sources within our sample cover a wide range of distances (from a few kpc to 15 kpc); however, the majority of the significant AME regions (that do not have a potential UCH ii component) tend to be located several degrees away from the Galactic plane, resulting in them being relatively nearby (d< 1 kpc). The semi-significant AME candidates in our sample cover a wide range of Galactocentric distances, showing that AME is not just a local phenomenon, as was previously shown by Planck Collaboration XXI (2011).
6.3. Final remarks
To make further progress in this field it is now vital that we complement these studies in two ways. First, more accurately calibrated data at frequencies not covered in this analysis will help determine more precisely each of the emission components. In particular, more data at frequencies 5−20 GHz (e.g., the 5 GHz C-Band All-Sky Survey, C-BASS; King et al. 2010, or the multi-frequency 11–19 GHz Q-U-I JOint TEnerife CMB experiment, QUIJOTE; Rubiño-Martín et al. 2012b) would improve the constraints on free-free emission, which is a large fraction of the 20−60 GHz brightness in many of the sources under study. Also, the inclusion of the Planck 100 and 217 GHz channels will dramatically improve the constraints where we see evidence of flattening of the low frequency tail of thermal dust, as well as a (minor) contribution from CMB fluctuations on scales of 1°. Second and perhaps more importantly, higher resolution (few arcmin and better) data are required to study different environments in more detail. As discussed earlier, we typically see a mix of environments and multiple sources when working at an angular resolution of 1°. The relationships between the gas and dust can then be inferred and the contribution of AME from different sources can be assessed by comparison with high resolution radio and infrared data. Furthermore, on scales ≪1° the CMB becomes negligible and background emission can, at least in some areas of the sky, be less problematic. High resolution follow-up observations of the AME candidates, such as with AMI (Zwart et al. 2008) at a frequency of 15 GHz, will determine whether the AME is in fact due to diffuse dust and whether UCH ii regions are a major component. With more accurate SEDs and spatial information, we will be able to better constrain important quantities such as the intensity of the radiation field and the abundance of small grains. The polarization properties of AME are also of great importance in identifying the emission mechanisms responsible, such as magneto-dipole radiation (Draine & Hensley 2013). Any significant level of polarized emission, in the frequency range ≈30−300 GHz, will likely be a major foreground for future sensitive CMB B-mode experiments (Rubiño-Martín et al. 2012a; Armitage-Caplan et al. 2012).
National Center for Supercomputing Applications (NCSA), located at the University of Illinois at Urbana-Champaign; http://www.ncsa.illinois.edu
Available from the Bonn Survey Sampler webpage http://www.mpifr-bonn.mpg.de/survey.html
Here we use the approximation given by Draine (2011), which is accurate to better than 1% even up to frequencies of 100 GHz and higher.
The CORNISH 5 GHz source catalogue (Purcell et al. 2013) covering l = 10°–65° has recently been published and provides useful additional information. The two significant AME sources that are covered by CORNISH (G017.00+00.85 and G062.98+00.05) do not contain any bright (>1 Jy) sources at 5 GHz.
Maps downloaded from the SkyView: http://skyview.gsfc.nasa.gov
G0 is a common scaling used for measuring the ISRF, and is integrated between 5 and 13.6 eV (Mathis et al. 1983). A standard value of G0 = 1 is representative of the diffuse ISM (away from hot stars), and corresponds to 1.2 × 10-3 erg s-1 cm-2.
From CLOUDY simulations (as described in Ysard & Verstraete 2010) we find Tgas to be between 50 and 70 K along the nH–G0 trend of Fig. 24.
Acknowledgments
We thank the anonymous referee for providing useful comments. We thank Justin Jonas for providing the 2326 MHz HartRAO map. We acknowledge the use of the MPIfR Survey Sampler website at http://www.mpifr-bonn.mpg.de/survey.html and the Legacy Archive for Microwave Background Data Analysis (LAMBDA); support for LAMBDA is provided by the NASA Office of Space Science. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research also makes use of the SIMBAD database, operated at the CDS, Strasbourg, France. We acknowledge the use of NASA’s SkyView facility (http://skyview.gsfc.nasa.gov) located at NASA Goddard Space Flight Center. C.D. acknowledges an STFC Advanced Fellowship, an EU Marie-Curie IRG grant under the FP7, and an ERC Starting Grant (No. 307209). The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php?project=planck&page=Planck_Collaboration
References
- Acker, A., Marcout, J., Ochsenbein, F., et al. 1992, The Strasbourg-ESO Catalogue of Galactic Planetary Nebulae. Parts I, II (European Southern Observatory) [Google Scholar]
- Ali-Haïmoud, Y., Hirata, C. M., & Dickinson, C. 2009, MNRAS, 395, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armitage-Caplan, C., Dunkley, J., Eriksen, H. K., & Dickinson, C. 2012, MNRAS, 424, 1914 [NASA ADS] [CrossRef] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, Explanatory supplement, 1 [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bersanelli, M., Bensadoun, M., de Amici, G., et al. 1994, ApJ, 424, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulanger, F., & Pérault, M. 1988, ApJ, 330, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Beichman, C., Désert, F. X., et al. 1988, ApJ, 332, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Bourke, T. L., Hyland, A. R., & Robinson, G. 2005, ApJ, 625, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Cabrera, G. F., Förster, F., et al. 2006, ApJ, 639, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Dickinson, C., Cleary, K., et al. 2008, MNRAS, 391, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Castellanos, P., Casassus, S., Dickinson, C., et al. 2011, MNRAS, 411, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, G., & Fich, M. 1995, AJ, 109, 2611 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Abergel, A., Verstraete, L., & Habart, E. 2008, A&A, 491, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J., Broderick, J. J., & Seielstad, G. A. 1991, AJ, 102, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Griffith, M. R., & Wright, A. E. 1993, AJ, 106, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Broderick, J. J., Seielstad, G. A., Douglas, K., & Gregory, P. C. 1994, AJ, 107, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Dickinson, C., Banday, A. J., et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira-Costa, A., Tegmark, M., Davies, R. D., et al. 2004, ApJ, 606, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C. 2013, Adv. Astron., id. 162478 [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Dickinson, C., Casassus, S., Pineda, J. L., et al. 2006, ApJ, 643, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., Bronfman, L., et al. 2007, MNRAS, 379, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., Allison, J. R., et al. 2009, ApJ, 690, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Casassus, S., Davies, R. D., et al. 2010, MNRAS, 407, 2223 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Peel, M., & Vidal, M. 2011, MNRAS, 418, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008, ApJ, 680, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Draine, B., & Finkbeiner, D. P. 2009, ApJ, 699, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: University Press) [Google Scholar]
- Draine, B. T., & Hensley, B. 2012, ApJ, 757, 103 [CrossRef] [Google Scholar]
- Draine, B. T., & Hensley, B. 2013, ApJ, 765, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1999, ApJ, 512, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Schlegel, D. J., Frank, C., & Heiles, C. 2002, ApJ, 566, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Gallegos, J. E., Macías-Pérez, J. F., Gutiérrez, C. M., et al. 2001, MNRAS, 327, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Génova-Santos, R., Rebolo, R., Rubiño-Martín, J. A., López-Caraballo, C. H., & Hildebrandt, S. R. 2011, ApJ, 743, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, T., Banday, A. J., Jaffe, T., et al. 2012, MNRAS, 422, 3617 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Bennett, C. L., Hill, R. S., et al. 2009, ApJS, 180, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2009, Bulletin of the Astronomical Society of India, 37, 45 [Google Scholar]
- Haslam, C., Stoffel, H., Salter, C. J., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G. 1986, ApJ, 311, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., & Walker, D. W. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, 7, 1 [NASA ADS] [Google Scholar]
- Hoang, T., Draine, B. T., & Lazarian, A. 2010, ApJ, 715, 1462 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Lazarian, A., & Draine, B. T. 2011, ApJ, 741, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Jonas, J. L., Baart, E. E., & Nicolson, G. D. 1998, MNRAS, 297, 977 [NASA ADS] [CrossRef] [Google Scholar]
- King, O. G., Copley, C., Davies, R., et al. 2010, in Proc. SPIE, 7741, 1I [Google Scholar]
- Kogut, A., Banday, A. J., Bennett, C. L., et al. 1996, ApJ, 464, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, S. 2002, in Hot Star Workshop III: The Earliest Phases of Massive Star Birth, ed. P. Crowther, ASP Conf. Ser., 267, 81 [Google Scholar]
- Kurtz, S. 2005, in Massive Star Birth: A Crossroads of Astrophysics, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 111 [Google Scholar]
- Kurtz, S., Churchwell, E., & Wood, D. O. S. 1994, ApJS, 91, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G. 2003, A&A, 405, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitch, E. M., Readhead, A. C. S., Pearson, T. J., & Myers, S. T. 1997, ApJ, 486, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Lynds, B. T. 1962, ApJS, 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Macellari, N., Pierpaoli, E., Dickinson, C., & Vaillancourt, J. E. 2011, MNRAS, 418, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Markwardt, C. B. 2009, in ASP Conf. Ser. 411, eds. D. A. Bohlender, D. Durand, & P. Dowler, 251 [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mezger, P. O. 1978, A&A, 70, 565 [NASA ADS] [Google Scholar]
- Miville-Deschênes, M., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M., Ysard, N., Lavabre, A., et al. 2008, A&A, 490, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J., Helou, G., Condon, J. J., et al. 2010a, ApJ, 709, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, T., Sadler, E. M., Ekers, R. D., et al. 2010b, MNRAS, 402, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Dame, T. M., Thaddeus, P., et al. 1986, ApJ, 301, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Paradis, D., Bernard, J.-P., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Dobashi, K., Shimoikura, T., et al. 2012a, A&A, 543, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Paladini, R., Noriega-Crespo, A., et al. 2012b, A&A, 537, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauliny-Toth, I. K., & Shakeshaft, J. R. 1962, MNRAS, 124, 61 [NASA ADS] [Google Scholar]
- Peel, M. W., Dickinson, C., Davies, R. D., et al. 2012, MNRAS, 424, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Perrott, Y. C., Scaife, A. M. M., Hurley-Walker, N., & Grainge, K. J. B. 2013, Adv. Astron. [Google Scholar]
- Planck Collaboration I. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2011, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2011, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2011, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2011, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2011, A&A, 536, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2011, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2011, A&A, 536, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2011, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2011, A&A, 536, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVII. 2011, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2011, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2011, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2011, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2011, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2011, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XII. 2013, A&A, 557, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, submitted [arXiv:1303.5062] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, submitted [arXiv:1312.1300] [Google Scholar]
- Planck Collaboration XII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321580 [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321553 [Google Scholar]
- Planck HFI Core Team. 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team. 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Povich, M. S., Stone, J. M., Churchwell, E., et al. 2007, ApJ, 660, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. R., Hoare, M. G., Cotton, W. D., et al. 2013, ApJS, 205, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ramesh, B., & Sridharan, T. K. 1997, MNRAS, 284, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS] [Google Scholar]
- Reich, P., Testori, J. C., & Reich, W. 2001, A&A, 376, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reich, W. 1982, A&AS, 48, 219 [NASA ADS] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubiño-Martín, J. A., López-Caraballo, C. H., Génova-Santos, R., & Rebolo, R. 2012a, Adv. Astron., 2012, id. 351836 [Google Scholar]
- Rubiño-Martín, J. A., Rebolo, R., Aguiar, M., et al. 2012b, in Proc. SPIE, 8444, 2Y [Google Scholar]
- Salgado, F., Berné, O., Adams, J. D., et al. 2012, ApJ, 749, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Scaife, A., Green, D. A., Battye, R. A., et al. 2007, MNRAS, 377, L69 [NASA ADS] [Google Scholar]
- Scaife, A. M. M., Hurley-Walker, N., Davies, M. L., et al. 2008, MNRAS, 385, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Scaife, A. M. M., Hurley-Walker, N., Green, D. A., et al. 2009, MNRAS, 400, 1394 [NASA ADS] [CrossRef] [Google Scholar]
- Scaife, A. M. M., Green, D. A., Pooley, G. G., et al. 2010a, MNRAS, 403, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Scaife, A. M. M., Nikolic, B., Green, D. A., et al. 2010b, MNRAS, 406, L45 [NASA ADS] [Google Scholar]
- Sellgren, K., Allamandola, L. J., Bregman, J. D., Werner, M. W., & Wooden, D. H. 1985, ApJ, 299, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Shipman, R. F., & Carey, S. J. 1996, ApJ, 469, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Silsbee, K., Ali-Haïmoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tibbs, C. T., Watson, R. A., Dickinson, C., et al. 2010, MNRAS, 402, 1969 [NASA ADS] [CrossRef] [Google Scholar]
- Tibbs, C. T., Flagey, N., Paladini, R., et al. 2011, MNRAS, 418, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Tibbs, C. T., Paladini, R., Compiègne, M., et al. 2012a, ApJ, 754, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Tibbs, C. T., Paladini, R., & Dickinson, C. 2012b, Adv. Astron., id. 124931 [Google Scholar]
- Todorović, M., Davies, R. D., Dickinson, C., et al. 2010, MNRAS, 406, 1629 [NASA ADS] [Google Scholar]
- Vidal, M., Casassus, S., Dickinson, C., et al. 2011, MNRAS, 414, 2424 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, R. A., Rebolo, R., Rubiño-Martín, J. A., et al. 2005, ApJ, 624, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Webster, A. S. 1974, MNRAS, 166, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989a, ApJ, 340, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989b, ApJS, 69, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., & Verstraete, L. 2010, A&A, 509, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Miville-Deschênes, M. A., & Verstraete, L. 2010, A&A, 509, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Juvela, M., & Verstraete, L. 2011, A&A, 535, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Juvela, M., Demyk, K., et al. 2012, A&A, 542, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwart, J. T. L., Barker, R. W., Biddulph, P., et al. 2008 (AMI Consortium), MNRAS, 391, 1545 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Sources of the datasets used in this paper, as well as centre frequencies, angular resolutions, and references.
Spearman rank correlation coefficients between the AME amplitude (Asp) and IR/submillimetre flux densities.
List of 98 candidate AME regions. Names are given by the central Galactic coordinates.
All Figures
 |
Fig. 1 Map of residuals at 28.4 GHz after subtracting off synchrotron, free-free, thermal dust, and CMB components (see text), in mK (R-J) units. A 5°-smoothed version of the map is subtracted to remove extended diffuse emission to more easily identify bright, relatively compact sources. This map is shown in the Mollweide projection, with l = 0° in the centre and increasing to the left. |
| In the text | |
 |
Fig. 2 CMB-subtracted Planck 28.4 GHz map covering the entire Galactic
plane and latitudes | b
| < 30°. The colour scale has a logarithmic stretch. Regions
with the most significant AME are highlighted as thick squares while the rest of the
sample are shown as circles. Regions with significant excess emission but with a
potential UCH ii contribution ( |
| In the text | |
 |
Fig. 3 Example SEDs (see text for description of individual SEDs) of sources with little or no AME (see Fig. 8 for SEDs with significant AME). Data points are shown as circles with errors and are colour-coded for radio data (cyan), WMAP (red), Planck (blue), and DIRBE/ IRAS (black). The best-fitting model of free-free (dotted line), synchrotron (long-dashed line), thermal dust (short-dashed line), CMB (triple-dot-dashed line), and spinning dust (dot-dashed line) are shown. Data included in the fit are shown as filled circles, while the other data are unfilled. The residual spectrum, after subtraction of free-free, synchrotron, CMB and thermal dust components, is shown as an insert. |
| In the text | |
 |
Fig. 4 Histogram of the AME significance values, σAME, for
the sample of 98 sources. The 5σ limit is shown as a dashed line. Sources
that are significant and have a maximum contribution from UCH ii regions
( |
| In the text | |
 |
Fig. 5 Colour−colour plot of IRAS PSC sources (grey plus symbols) that lie within the apertures of all 98 sources in our sample. UCH ii candidates (solid black squares) tend to have ratios log 10(S60/S12) ≥ 1.30 and log 10(S25/S12) ≥ 0.57, corresponding to the top-right hand corner of this plot (marked with a dashed line). |
| In the text | |
 |
Fig. 6 Estimated maximum contribution from UCH ii regions plotted against
28.4 GHz AME residual flux density. The most significant AME sources
(σAME >
5 and |
| In the text | |
 |
Fig. 7 Maps of example sources with significant (σAME > 5) excess emission. Each row is a gnomic map in Galactic coordinates, 5° on a side, and centred on each source, labelled in the 0.408 GHz map. The maps from left to right are 0.408, 1.42, 22.7, 28.4, 44.1, and 143 GHz. The WMAP/Planck maps have been CMB-subtracted. The colour-scale is linear, and ranges from the minimum to maximum value within each map. The aperture is shown as a solid line; the background annulus as dashed lines. The strong AME at frequencies around 30 GHz is evident. |
| In the text | |
 |
Fig. 8 SEDs for the sources with very significant AME and
|
| In the text | |
 |
Fig. 9 Correlation plot between the AME amplitude, Asp, and the fitted CMB fluctuation temperature. Symbols are as in Fig. 6. For most sources, the fitted CMB temperatures are within the expected range shown as dashed lines (| ΔTCMB | < 150 μK) and are not strongly correlated with the AME flux density. However, for some sources, there is a strong positive correlation with CMB temperatures that are higher than expected, but associated with larger uncertainties. |
| In the text | |
 |
Fig. 10 Histogram of average deconvolved FWHM sizes for AME and non-AME sources, as derived from Gaussian fitting to the Planck 28.4 GHz map at 1° resolution. Sources with FWHM> 2°are plotted as having a FWHM = 2°. The most significant AME sources are shown as the hatched histogram, while the non-significant (non-AME) sources are shown as the grey histogram. The strongest AME sources are, in general, extended, while non-AME sources tend to be relatively compact. |
| In the text | |
 |
Fig. 11 Histogram of the AME fraction, |
| In the text | |
 |
Fig. 12 Integrated FIR flux (proxy for FIR luminosity) plotted against the free-free flux density at 5 GHz (proxy for Lyα luminosity). Symbols are as in Fig. 6. Perseus (P) and ρ Ophiuchi (R) clouds are marked. IRE values of 1, 10, and 100 are shown as straight lines. Most AME sources have IRE > 4. |
| In the text | |
 |
Fig. 13 Big grain dust temperature (Td) vs. thermal dust emissivity index (βd). The symbols are as in Fig. 6. Perseus (P) and ρ Ophiuchi (R) clouds are marked. There is no strong trend with βd, while the most significant AME regions (filled black circles) tend to be associated with colder dust. |
| In the text | |
 |
Fig. 14 Colour−colour plot of IRAS 60 μm/100 μm vs. IRAS 12 μm/25 μm. Symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are marked. |
| In the text | |
 |
Fig. 15 AME fraction at 28.4 GHz as a function of estimated G0. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The best-fitting power laws to the AME regions (solid line) and semi-significant AME regions (dashed line) are overplotted. |
| In the text | |
 |
Fig. 16 Histogram of spinning dust peak frequencies, νsp. The unfilled histogram is for both AME and semi-significant AME regions, while the hatched region is for the AME sources only. The best-fitting Gaussians for these two histograms are overplotted. The source at νsp = 50 GHz is G160.60−12.05 (California nebula). |
| In the text | |
 |
Fig. 17 SED for G160.60−12.05 (California nebula). The curves and symbols are as in Fig. 8. AME is detected at a level of σAME = 5.0, and the best-fitting spinning dust peak is shifted to νsp = (50 ± 17) GHz. |
| In the text | |
 |
Fig. 18 Top row: AME amplitude (Asp) as a function of the 100 μm (left), 60 μm (middle), and 12 μm (right) flux density. Bottom row: same as top row, except that the FIR flux densities have been divided by G0. Symbols are as in Fig. 6. The best-fitting slope fitted to the significant AME regions only is plotted. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. There is a strong correlation between the AME intensity and infrared tracers of dust, with an improved correlation after dividing by G0. At 12 μm the fit is made excluding the outlier source G239.40−4.70 (marked). |
| In the text | |
 |
Fig. 19 Ratio of 28.4 GHz residual to the 100 μm flux density as a function of the AME significance. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The weighted and unweighted average ratios for the significant AME regions are shown as the solid horizontal lines. The average ratio from Todorović et al. (2010, dashed line) and Davies et al. (2006, dot-dashed line) are also shown. |
| In the text | |
 |
Fig. 20 Ratio of AME amplitude (Asp) to dust optical depth (τ250), as a function of the AME significance σAME. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The horizontal lines represent averages: weighted average of significant AME regions (solid line), unweighted average of significant AME regions (dashed line) and weighted average of non-significant AME regions (dotted line). |
| In the text | |
 |
Fig. 21 Ratio of AME amplitude (Asp) to dust optical depth (τ250), as a function of τ250. The symbols are as in Fig. 6. The Perseus (P) and ρ Ophiuchi (R) clouds are indicated. The solid line shows the best-fitting power law for the significant AME regions. |
| In the text | |
 |
Fig. 22 AME emissivity as a function of G0. The symbols are as in Fig. 6. The straight lines are the best-fitting power laws to the AME (solid line) and including semi-significant AME (dashed line) regions. |
| In the text | |
 |
Fig. 23 Spinning dust peak frequency as a function of G0. The symbols are as in Fig. 6. The solid line is the best-fitting power law for the AME regions with all data points equally weighted. The dashed line is the weighted fit to the AME regions, while the dot-dashed line is the weighted fit to AME and semi-significant AME regions. |
| In the text | |
 |
Fig. 24 Density estimates (solid black line) from spinning dust models that follow the observed trend between the AME emissivity j28 and G0. We also show the influence of AME emissivities half (j0 = 1.5 × 10-24 MJy sr-1 cm2 per H atom; triple-dot-dashed line) and twice as large (j0 = 6 × 10-24 MJy sr-1 cm2 per H atom; dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.