| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322069 | |
| Published online | 11 April 2014 | |
High-resolution ammonia mapping of the very young protostellar core Chamaeleon-MMS1⋆,⋆⋆
1 Department of Physics, PO Box 64, 00014 University of Helsinki, Finland
e-mail: miikka.vaisala@helsinki.fi
2 Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
3 Aalto University, Department of Information and Computer Science, PO Box 15400, 00076 Aalto, Finland
4 Australia Telescope National Facility, CSIRO, PO Box 76, NSW 1710 Epping, Australia
5 Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
6 Dublin Institute for Advanced Studies (DIAS), 31 Fitzwilliam Place, 2 Dublin, Ireland
Received: 12 June 2013
Accepted: 19 February 2014
Aims. The aim of this study is to investigate the structure and kinematics of the nearby candidate first hydrostatic core Cha-MMS1.
Methods. Cha-MMS1 was mapped in the NH3(1,1) line and the 1.2 cm continuum using the Australia Telescope Compact Array (ATCA). The angular resolution of the ATCA observations is 7″ (~1000 AU), and the velocity resolution is 50 m s-1. The core was also mapped with the 64 m Parkes Telescope in the NH3(1,1) and (2,2) lines. Observations from Herschel Space Observatory and Spitzer Space Telescope were used to help interpretation. The ammonia spectra were analysed using Gaussian fits to the hyperfine structure. A two-layer model was applied in the central parts of the core where the ATCA spectra show signs of self-absorption.
Results. A compact high column density core with a steep velocity gradient (~20 km s-1 pc-1) is detected in ammonia. We derive a high gas density (~106 cm-3) in this region, and a fractional ammonia abundance compatible with determinations towards other dense cores (~10-8). This suggests that the age of the high density core is comparable to the freeze-out timescale of ammonia in these conditions, on the order of 104 years. The direction of the velocity gradient agrees with previous single-dish observations, and the overall velocity distribution can be interpreted as rotation. The rotation axis goes through the position of a compact far-infrared source detected by Spitzer and Herschel. The specific angular momentum of the core, ~10-3km s-1 pc, is typical for protostellar envelopes. A string of 1.2 cm continuum sources is tentatively detected near the rotation axis. The ammonia spectra suggest the presence of warm embedded gas in its vicinity. An hourglass-shaped structure is seen in ammonia at the cloud’s average LSR velocity, also aligned with the rotation axis. Although this structure resembles a pair of outflow lobes the ammonia spectra show no indications of shocked gas.
Conclusions. The observed ammonia structure mainly delineates the inner envelope around the central source. The velocity gradient is likely to originate in the angular momentum of the contracting core, although influence of the outflow from the neighbouring young star IRS4 is possibly visible on one side of the core. The tentative continuum detection and the indications of a warm background component near the rotation axis suggest that the core contains a deeply embedded outflow which may have been missed in previous single-dish CO surveys owing to beam dilution.
Key words: stars: formation / stars: protostars / ISM: individual objects: Cha-MMS1 / ISM: jets and outflows / radio continuum: ISM / radio lines: ISM
Based on observations obtained with the 64 m Parkes radio telescope and the Australia Telescope Compact Array (ATCA). The Parkes radio telescope and ATCA are part of the Australia Telescope National Facility, which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO.
Reduced data used in this paper, Parkes, ATCA (FITS cubes), and Herschel (FITS) data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A99
© ESO, 2014
1. Introduction
The characteristics of a stellar system in formation are determined by the mass and angular momentum distributions of the place of its origin, a collapsing dense molecular cloud core. According to the current view the early phases of the low-mass protostellar collapse can be roughly divided into two stages. The collapse leads initially to the formation of the so-called first hydrostatic core (FHSC, Larson 1969) that, depending on the core rotation, can resemble a disk-like structure. Soon thereafter (within a few thousand years) the dissociation of molecular hydrogen allows the core material to collapse further into the system equator forming a protostar and an accretion disk around it (e.g., Machida et al. 2008a). The system loses mass and angular momentum through outflows, which can be driven by collimated jets or magnetocentrifugally accelerated disk winds (e.g., Pudritz et al. 2007).
The situation can be complicated if the magnetic field and the rotation axis are misaligned, or if the core collapses under an external influence. In view of the fact that most stars form in clusters with various disturbing elements, it is evident that real situations are not simple, and both theoretical modelling and high-resolution observational studies in different environments are needed.
In this paper, we concentrate on gas kinematics in the nearby dense core Cha-MMS1, as probed by ammonia observations with the Australia Telescope Compact Array (ATCA). The core was discovered in the λ = 1.3 mm survey by Reipurth et al. (1996). It is associated with the reflection nebula Cederblad 110 and a small cluster of young stellar objects (YSOs) located in the centre of the Chamaeleon I (Cha I) cloud complex (e.g., Prusti et al. 1991; Persi et al. 2001). The distance to Cha I is ~160 pc (Whittet et al. 1997). Amongst star-forming cores Cha-MMS1 is an interesting specimen in two respects. Firstly, owing to the Spitzer detection at 24 and 70 μm and the lack of high-velocity line emission, the source has been suggested to represent a FHSC (Belloche et al. 2006, 2011; Cordiner et al. 2012; Tsitali et al. 2013). Secondly, the core is obviously hit by a molecular outflow from the neighbouring Class I protostar Ced110 IRS4 (Hiramatsu et al. 2007; Ladd et al. 2011), making it therefore a potential example of externally triggered collapse.
The main motivation of the present study is to use the gas motions to study the evolutionary stage of the core, and to examine the role of the suggested external momentum input. It turns out that the high spectral resolution combined with a reasonably good spatial resolution provided by ATCA reveal a peculiar rotating structure, probably resulting from spin-up during the core contraction, but which has a slight indication of external influence on one side of the core. We also find indirect evidence for an embedded outflow.
In Sect. 2 of this paper, we describe the observing methods and the data reduction, and in Sect. 3, we present the results of the observations. In Sect. 4, we discuss the core kinematics in the light of previous observations and the predictions of recent MHD models for a collapsing rotating core. Finally, in Sect. 5, we present our conclusions.
2. Observations and data reduction
2.1. Parkes mapping
The dense clump around the millimetre source Cha-MMS1 was mapped in the (J,K) = (1,1) and (2,2) inversion lines of NH3 at λ = 1.3 cm using the Parkes 64-m telescope in January 1991. The half-power beam width (HPBW) of the telescope is 80′′ at the wavelength used. The single channel maser receiver was connected to a 1024 channel digital autocorrelator which was split into two bands 512 channels each to record the (1, 1) and (2, 2) spectra simultaneously. The width of each spectral band was 5 MHz, and the velocity resolution was 0.12 km s-1. The observations were done in the position switching mode. The mapped area is about 5′ × 5′. The (0, 0) position was IRAS 11054-7706 C (Cohen & Schwartz 1987) (RA 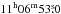 , Dec − 77°22′47″ (J2000)), later identified as Ced 110 IRS4 (Prusti et al. 1991), and the map was extended towards southwest where strong ammonia emission was found. The spacing between map positions was generally 1′, but a spacing of 30″ was used in the vicinity of the ammonia maximum. At the time of the observations the millimetre source was not yet discovered. The calibration was checked by observing standard extragalactic sources at different elevations, and by comparing the ammonia line intensities towards some strong galactic sources also visible from the Effelsberg 100 m telescope in Germany, taking the different beam sizes into account.
, Dec − 77°22′47″ (J2000)), later identified as Ced 110 IRS4 (Prusti et al. 1991), and the map was extended towards southwest where strong ammonia emission was found. The spacing between map positions was generally 1′, but a spacing of 30″ was used in the vicinity of the ammonia maximum. At the time of the observations the millimetre source was not yet discovered. The calibration was checked by observing standard extragalactic sources at different elevations, and by comparing the ammonia line intensities towards some strong galactic sources also visible from the Effelsberg 100 m telescope in Germany, taking the different beam sizes into account.
The two brightest positions in both (1,1) and (2,2) lie at the offsets (+ 10″, − 14″) and (+ 10″, + 16″) from Cha-MMS1a (Reipurth et al. 1996) the coordinates of which are RA 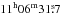 , Dec. − 77°23′32″ (J2000). The (1,1) spectrum towards (+ 10″, − 14″) is shown in Fig. 1, together with the ATCA spectrum convolved to the same angular resolution. These spectra are presented in the intensity unit Jy beam-1. The position (+ 10″, − 14″) is in fact the same as shown in Fig. 6 of Tennekes et al. (2006) from a different observing run1. Analysis of the Parkes data is presented in Sect. 3.1.
, Dec. − 77°23′32″ (J2000). The (1,1) spectrum towards (+ 10″, − 14″) is shown in Fig. 1, together with the ATCA spectrum convolved to the same angular resolution. These spectra are presented in the intensity unit Jy beam-1. The position (+ 10″, − 14″) is in fact the same as shown in Fig. 6 of Tennekes et al. (2006) from a different observing run1. Analysis of the Parkes data is presented in Sect. 3.1.
 |
Fig. 1 NH3(1,1) inversion line spectrum towards the ammonia maximum as observed with the Parkes 64 m telescope (upper spectrum), at the offset (+ 10″, − 14″) from Cha-MMS1a (Reipurth et al. 1996). The corresponding ATCA spectrum “smoothed” to an 80″ resolution is shown at the bottom. The latter is produced by applying a Gaussian taper to the visibility data. |
2.2. ATCA mapping
Observational parameters of the ATCA mapping.
Cha-MMS1 was observed with the ATCA, located near Narrabri, New South Wales, Australia. The observations were made using a single pointing. The image covers a region of about 2′ in diameter around the phase centre at 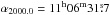 , δ2000.0 = −77°23′42″, which lies 10″ south of the 1.3-mm dust continuum maximum Cha-MMS1a (Reipurth et al. 1996). The observations were made in two 12 h runs on 2003 Sep. 6 and 30, using the array configurations EW367B and EW352. The shortest baselines of these configurations are about 46 and 31 m, respectively. The longest baselines for both configurations are about 4400 m.
, δ2000.0 = −77°23′42″, which lies 10″ south of the 1.3-mm dust continuum maximum Cha-MMS1a (Reipurth et al. 1996). The observations were made in two 12 h runs on 2003 Sep. 6 and 30, using the array configurations EW367B and EW352. The shortest baselines of these configurations are about 46 and 31 m, respectively. The longest baselines for both configurations are about 4400 m.
The phase and bandpass calibration sources were selected from the ATCA Calibrator Source Catalogue (Reynolds et al. 1997). The phase-reference calibrator was quasar PKS 1057–797, and this source was used also for the reference pointing measurement in the beginning of every fourth phase calibrator−target source cycle. The duration of the cycle was 3 + 15 min. The bandpass calibrators were PKS 1921–293 and PKS 1253–055. The planets Jupiter and Mars were observed to provide flux standards. The absolute calibration was done using the predicted visibility functions provided by the Miriad reduction package (Sault et al. 1995).
The correlator was set up to record the NH3(1,1) inversion line and the 1.3 cm continuum. The NH3(1, 1) line has 18 hyperfine components concentrated on 5 groups, the so-called main group and four satellites. The rest frequency of the line centre is about 23 694.5 MHz, and the separation between the outermost satellites is 3.3 MHz. The correlator set-up gave 1) a 4 MHz frequency band with 1024 channels (for lines); and 2) a 112 MHz band divided into 14 channels of 8 MHz (for continuum). The spectral resolution of the narrow band corresponds to 50 m s-1. Both bands were centred at 23 692.5 MHz. The Doppler correction was done off-line in the course of data reduction. The 1.3 cm receivers have orthogonal linearly polarised feeds. The correlator yielded two polarisation products in the narrow band, and all four in the wide band. The observational parameters are summarised in Table 1.
 |
Fig. 2 Integrated intensity map of the NH3(1,1) satellites towards Cha-MMS1 observed with ATCA. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. The synthesised beam is indicated in the top right corner. |
The weather was good on Sep. 6, but at best moderate during the second session on Sep. 30. The theoretical visibility noise in the continuum had an rms of ~0.03 − 0.04 Jy on Sep. 6. On Sep. 30 the rms noise was ~0.07 Jy in the beginning but rose above 0.1 Jy after 6 h of measurements because of high humidity. Only the first half of the second run was used.
The data were calibrated, inverted and cleaned using Miriad. The inversion of the wideband visibility data was performed using all the channel information (i.e., multi-frequency synthesis). The flux densities of the detectected sources were derived from naturally weighted images corrected for the primary beam responses. The noise level at the centre of the image, and the size of the synthesised beam are given in Table 1.
The ATCA spectrum towards (10″, − 14″) smoothed to the angular resolution of Parkes, 80″, is shown in Fig. 1 (lower curve). The smoothed image cube has been produced by weighting (“tapering”) the visibility data by a Gaussian in the inversion. The ATCA data observations miss a substantial part of the flux owing to the lack of baselines shorter than 30 m. Comparing the NH3(1,1) satellites in the Parkes and smoothed ATCA spectra shows that the missing flux is about 50%.
The integrated NH3(1,1) satellite intensity map of Cha-MMS1 observed with with ATCA is shown in Fig. 2. The main group has been excluded here because of its large optical thickness. The analysis of the ATCA wide-band images is described in Sect. 3.2, and the spectra are analysed in Sect. 3.3.
2.3. Herschel data
 |
Fig. 3 Left: intensity of thermal dust emission (MJy sr-1) at the wavelength λ = 250μm in a region of 5′ × 5′ region around Cha-MMS1. The map is centred at the Spitzer 24 μm peak indicated with a red triangle. The red circle in the top right corner corresponds to the average Herschel beamsize (FWHM, 18″) at 250 μm. The small white ellipse shows the synthesised ATCA beam (~7″). Middle: dust temperature, Tdust (K), in the same region. The red circle in the top right corner represents the resolution of the calculated Tdust and H2 column density maps (40″). Right: H2 column density, N(H2) (1022 cm-2) derived from the 250 μm optical thickness, τ250 μm. The dust temperature and column density maps are derived by fitting a modified blackbody function to the Herschel intensity maps at 500, 350, 250, and 160 μm assuming an emissivity index of β = 2.0 (see text). The locations of three prominent young stellar objects (YSOs), Ced110 IRS2 (right), IRS4 (middle), and IRS6 (left), are indicated with asterisks. The plus sign indicates the location of the millimetre source Cha-MMS1a (Reipurth et al. 1996). The white contour shows the integrated intensity level 5 K km s-1 of the NH3(1,1) satellites as observed with ATCA. The yellow contours in the right panel shows the integrated intensity ( |
We used far-infrared (far-IR) and submm maps from the Herschel satellite to inspect the overall distribution of gas and dust in the vicinity of Cha-MMS1. The Herschel maps used in this study were extracted from the extensive mapping of the Chamaeleon I (Cha I) cloud with the Spectral and Photometric Imaging Receiver (SPIRE) and Photodetector Array Camera and Spectrometer (PACS) instruments, as part of the Herschel Gould Belt Survey2 (André et al. 2010; Winston et al. 2012). An overview of the Herschel Space Observatory is given in Pilbratt et al. (2010).The SPIRE and PACS instruments are described in Griffin et al. (2010) and Poglitsch et al. (2010), respectively.
The pipeline-reduced data of Cha I are publicly available at the Herschel Science Archive3. The wavelengths covered in the SPIRE+PACS parallel mode survey are 500, 350, and 250 μm (SPIRE), and 160 and 70 μm (PACS). The full width at half maxium (FWHM) values of the Gaussians fitted to the beam profiles are, in order of decreasing wavelength, 37″, 25″, 18″, 12″ × 16″, and 6″ × 12″, the PACS beams being clearly elongated in observations carried out in the parallel mode. We did not apply any zero-point corrections to the pipeline-reduced maps.
In order to derive the distributions of the dust temperature, Tdust, and the optical thickness„ τλ, of the dust emission, the maps at 500, 350, 250, and 160 μm were convolved with Gaussians to a common resolution of 40″ (FWHM), and the intensity distributions were fitted pixel by pixel with a modified blackbody function, Iν ≈ Bν(Tdust)τν ∝ Bν(Tdust) νβ, where Bν(T) is the Planck function, and τν is the optical thickness of the emitting source at the frequency ν. The modified blackbody function characterises optically thin (τν ≪ 1) thermal dust emission at far-IR and submm wavelengths. We fixed the emissivity/opacity exponent to β = 2.0. The observationally derived values of β are typically close to 2.0 (e.g., Schnee et al. 2010; Juvela et al. 2011), although higher values have been reported for cold regions (e.g. Planck Collaboration 2011b). An average value of ~1.8 was found in a recent study of the Taurus-Auriga molecular cloud, but with significant anticorrelation between dust temperature and the spectral index (Planck Collaboration 2011a).
The pipeline-calibrated in-beam flux densities were colour corrected to monochromatic flux densities at the standard wavelengths in the course of Tdust fitting using the adopted shape of the source spectrum (a modified blackbody spectrum with β = 2.0) and the spectral response functions of SPIRE and PACS photometers for an extended source4. In addition, the SPIRE pipeline flux densities were converted from point source calibration to extended source calibration before the temperature fitting and colour correction.
The errors of Tdust and τ250 μm caused by photometric noise were estimated by a Monte Carlo method using the 1σ error maps provided for the three SPIRE bands and a 7% uncertainty of the absolute calibration for all four bands according to the information given in SPIRE and PACS manuals (SPIRE Observers’ Manual, Version 2.4; PACS Observer’s Manual, Version 2.4). Different realisations of the Tdust and τ250 μm maps were calculated by combining the four intensity maps with the corresponding error maps, assuming that the error in each pixel is normally distributed. The errors in each pixel were obtained from the standard deviation of one thousand realisations. The relative errors of Tdust obtained this way are typically 2−3%, and the errors for τ250 μm are around 10%.
The 250 μm optical thickness map, calculated from τ250 μm = I250 μm/B250 μm(Tdust), is proportional to the molecular hydrogen column density, N(H2). The column density can be obtained from 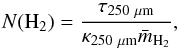 (1)where κ is the dust “opacity”, or absorption cross-section per unit mass of gas, and
(1)where κ is the dust “opacity”, or absorption cross-section per unit mass of gas, and 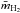 (=2.8 amu) is the average particle mass per H2molecule (assuming 10% He and negligible amout of metals). For the dust opacity at 250 μm we adopt
(=2.8 amu) is the average particle mass per H2molecule (assuming 10% He and negligible amout of metals). For the dust opacity at 250 μm we adopt 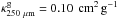 (Hildebrand 1983).
(Hildebrand 1983).
The column density map in a 5′ × 5′ region around Cha-MMS1 is shown in the rightmost panel of Fig. 3. The other panels of Fig. 3 show the 250 μm intensity map (I250 μm, left) and the Tdust map (middle). The YSOs Ced 110 IRS6 (Class I), IRS4 (Class I), and IRS2 (Class III) are surrounded by warm dust and they are visible as local maxima on the Tdust map. The cavity on the western side of IRS2 is partly visible on the Tdust map (see Fig. 4 of Bally et al. (2006)). Cha-MMS1 is situated in a cold region south of IRS2. IRS4 has been found to produce an outflow which probably collides into the Cha-MMS1 core (Hiramatsu et al. 2007; Ladd et al. 2011).
To estimate the effect of the uncertainty related to the adopted emissivity index, β, we repeated the analysis described above using fixed emissivity indices of β = 1.8 and β = 2.2. Lowering β leads to higher dust colour temperatures, and lower optical thicknesses τ250 μm. The effect of increasing β is the opposite. The maximum H2 column density is found slightly southeast of Cha-MMS1a at the offset (+4″, −8″), and the colour temperature minimum lies further southeast at the offset (+23″, −50″). The range of Tdust and N(H2) values at these two positions for β = 1.8 − 2.2 are listed in Table 2.
Tdust and N(H2) values at the temperature minimum and the column density maximum using the emissivity index β = 2.0, and the range β = 1.8−2.2.
The uncertainties owing to photometric noise are about 3% and 10% for Tdust and N(H2), respectively. The change of β by 0.2 has an effect which corresponds to about two times the photometric noise. The line-of-sight inhomogeneities, especially in dense clouds cause further uncertainties as discussed in e.g. Nielbock et al. (2012), Ysard et al. (2012), and Suutarinen et al. (2013).
3. Results
3.1. Parkes results
The NH3(1,1) spectrum observed with Parkes towards the offset (10″, − 14″) from Cha-MMS1a is shown in Fig. 1, and the integrated NH3(1,1) intensity map of the core is shown in Fig. 3, superimposed on the total H2 column density map as derived from thermal dust emission (Sect. 2.3).
The general concept of deriving gas parameters from the hyperfine spectra is presented by Ho et al. (1979). The spectroscopic properties of ammonia can be found, e.g., in the papers of Kukolich (1967), Poynter & Kakar (1975) and in the review by Ho & Townes (1983). The standard method of deriving ammonia column densities from the NH3 inversion lines is described in, e.g., Ungerechts et al. (1986, their Appendix). We have used the CURVEFIT function of IDL (Interactive Data Language5) to fit 18 Gaussians to the hyperfine components of the NH3(1,1) inversion line. The parameters of this fit are the excitation temperature Tex, total optical thickness τtot(1,1) (the sum of the peak optical thicknesses of the 18 components), line-of-sight velocity VLSR and linewidth ΔV. As typical for cold cores, the (2,2) hyperfine satellite groups are very weak also in Cha-MMS1, and the optical thickness of this line cannot be estimated. The (2,2) column density is derived assuming the main group is optically thin and that Tex(2,2) = Tex(1,1).
A hyperfine component fit to the spectrum shown in Fig. 1 gives the following parameters: TMB,peak = 1.9 ± 0.2 K (the main-beam brightness temperature assuming the efficiency ηMB = 0.7), VLSR = 4.42 ± 0.02 km s-1, ΔV = 0.48 ± 0.03 km s-1 (FWHM), τtot = 8.8 ± 1.1. The standard method of deriving the kinetic temperature from the (1,1) to (2,2) comparison gives Tkin = 11.1 ± 1.2 K. Assuming (somewhat unrealistically) uniform beam filling we obtain an excitation temperature of Tex(1,1) = 4.8 ± 0.2 K, and a column density of N(pNH3) = 2.7 ± 0.4 × 1014 cm-2 for para-NH3. In cold clouds N(pNH3) ≈ N(NH3(1,1)) as other metastable para states, (2,2), (4,4), etc. are scarcely populated. The obtained column density represents the average para-NH3 column density within the 80″ Parkes beam. The corresponding H2 column density at (10″, − 14″), as derived from the Herschel observations and smoothed to the same angular resolution, is N(H2) = 3.3 × 1022 cm-2. The implied fractional para-ammonia abundance is X(pNH3) ~ 1 × 10-8.
3.2. ATCA wide-band images
The 112 MHz band covers the sky frequencies of the NH3(1,1) and (2,2) lines. The (1,1) hyperfine groups are split between the two central channels (7 and 8), centred at 23 688.5 and 23 692.5 MHz, and one of the other channels (centred at 23 720.5 MHz) can have contribution from the (2,2) line with the rest frequency 23 722.6 MHz. Three separate images have been formed from the wide-band visibility data using a) the two channels with (1,1) lines; b) the channel with the (2, 2); and c) the remaining 11 line-free channels. The first two (a and b) are shown as pixel images in Fig. 4, and the continuum map (c) is superposed as contours on these.
 |
Fig. 4 ATCA wide-band images. Top: the pixel image shows the intensity distribution of the two central channels covering the NH3(1,1) line. Bottom: the pixel image of the channel containing the (2,2) line. The contour map superimposed on both images represents the true 1.3 cm continuum emission, i.e. wide-band channels without ammonia line contamination. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. |
The intensity in the two central channels is clearly higher than in other channels, and the distribution is similar to that of the integrated satellite intensity shown in Fig. 2. This indicates that emission in channels 7 and 8 comes primarily from the NH3(1,1) line. The channel with the (2,2) line shows faint compact features located in the region with strong (1,1) emission. The distribution is different from that of the pure continuum shown as contours. Also the channel covering the (2,2) line frequency is likely to be dominated by ammonia.
Three emission peaks at a level of 1 mJy beam-1 (corresponding to about 5 K km s-1) can be identified on the (2,2) map. The offsets of the (2,2) peaks with respect to the Cha-MMS1a position, and estimates of the kinetic temperature, Tkin, in these locations are presented in Table 3. Two of the (2,2) peaks (a and c in the Table) coincide with the (1,1) peaks in the bright ridge, while the third peak (b) lies about 10″ east of the line connecting the (1,1) peaks. Position (a) is the brightest in both (1,1) and (2,2) emission, and its coordinates are RA 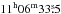 , Dec − 77°23′33″ (J2000). This position lies 4″ west of the Herschel peak given in Table 1 of Winston et al. (2012), and 2″ north of the Spitzer 24 μm maximum.
, Dec − 77°23′33″ (J2000). This position lies 4″ west of the Herschel peak given in Table 1 of Winston et al. (2012), and 2″ north of the Spitzer 24 μm maximum.
Integrated intensities of the NH3(2,2) lines and (1,1) satellites and kinetic temperatures derived from these towards three (2,2) peaks.
The temperature estimates have been derived from the (1,1) and (2,2) intensities following the method first presented by Ho et al. (1979) assuming local thermodynamic equilibrium (LTE) and optically thin emission. The relation derived by Walmsley & Ungerechts (1983) and Danby et al. (1988) have been used to convert the rotational temperature, T12, to the kinetic temperature, Tkin.
From the (1,1) linewidths one can obtain the following upper limits for the kinetic temperatures at the positions listed in Table 3, a: 33 K (Δυ = 0.30 km s-1), b: 23 K (Δυ = 0.25 km s-1), and c: 20 K (Δυ = 0.23 km s-1). These results are consistent with the estimates from the integrated (1,1) and (2,2) intensities suggesting that the maxima of the (2,2) map pin-point warm spots in the core.
The pure continuum map shows a string of weak sources near the ammonia maximum. The intensities of the four peaks near the map centre are only 3−4 times the rms noise in the region, i.e. in the range 0.26 − 0.33 mJy beam-1. The tentative detection remains therefore to be confirmed, or disproved, by a deeper integration. Lehtinen et al. (2003) derived a 3σ upper limit of 0.1 mJy/4″ beam for the intensity of Cha-MMS1 at 3.5 cm. The confirmation of the 1.3 cm maximum intensity quoted above would mean a spectral index of α> 1.2 which would be consistent with optically thick free-free emission.
3.3. ATCA spectral line image
The ATCA narrow-band visibility data from both observing runs were combined and inverted into an xyv-image cube. The original spectral visibility data contain 1024 channels. After dropping 82 channels at both ends of the bandpass the final image cube has 860 velocity (frequency) channels 0.05 km s-1 (3.9 kHz) in width. The frequency range covers all the five hyperfine groups of the (J,K) = (1,1) inversion line. Two NH3(1,1) spectra extracted from the ATCA image cube are shown in Fig. 5. The spectra are Hanning smoothed averages over 3″ × 3″ regions around the indicated positions. The selected positions are (0″,0″) (Cha-MMS1a) and (7″, − 4″) (a local maximum in the 24 μm Spitzer map).
 |
Fig. 5 ATCA NH3(1,1) spectra towards the offsets (0″,0″) and (+ 7″, − 4″) from Cha-MMS1a. The latter position coincides with a Spitzer 24 μm emission peak. The top panels show a Gaussian fit to the four satellite groups of the hyperfine structure (green curve). The column density spectra of ammonia in the rotational level (1,1) derived from these fits are shown on the right of the satellite spectra. The panels in the middle row show two-component fits to the full hyperfine structure including the main group (black curve). In the bottom panels, the modelled emission profiles from the two layers (component 1: red, component 2: blue) are shown separately. The foreground component 2 has a lower excitation temperature than component 1, and causes absorption features. The corresponding NH3(1,1) column density spectra of components 1 (red) and 2 (blue) are shown on the right. The dashed curve shows the combined NH3(1,1) column density spectrum of layers 1 and 2. |
In the optically thin case the integrated intensity of the main group in the centre of the spectrum (including the transitions 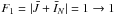 , F1 = 2 → 2, where
, F1 = 2 → 2, where 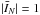 is the nuclear spin of the N nucleus) is equal to the total integrated intensity of the four satellites (from left to right: F1 = 1 → 0, F1 = 1 → 2, F1 = 2 → 1, F1 = 0 → 1). The groups are further split owing to magnetic interactions.
is the nuclear spin of the N nucleus) is equal to the total integrated intensity of the four satellites (from left to right: F1 = 1 → 0, F1 = 1 → 2, F1 = 2 → 1, F1 = 0 → 1). The groups are further split owing to magnetic interactions.
Near the NH3(1,1) maximum the main hyperfine group is sometimes weaker than any of the four satellites. This indicates self-absorption. On the outskirts of the map the spectra look optically thin, the main group being the strongest. The (1,1) satellites are less affected by large column densities than the main group because the total optical thickness of each satellite is about one quarter of that of the main group. In the optically thick limit the five groups have equal intensities.
We have tested three methods of modelling the (1,1) hyperfine structure. The method selected depends on the ratio of the integrated main group intensity to the integrated intensity of the satellites. We denote this ratio by M/S.
-
A)
In the first method, Gaussian fits to all the 18 hyperfinecomponents were made in regions where the optical thicknessdoes not appear to be very large. The method was applied in thepositions whereM / S ≥ 1 / 2. This requirement is fulfilled at the core edges.
-
B)
In the regions where M / S < 1 / 2, we have made Gaussian fits only to the ten hyperfine components of the four satellite groups. For these values of M/S, the optical thickness of the main group is large, and satellite line structure is better reproduced using this model than using method A.
-
C)
In the third method, the spectra with M / S < 1 / 4 (suggesting self-absorption) have been fitted with a function describing emission from two contacting plane-parallel homogeneous layers at different excitation temperatures, Tex,fg and Tex,bg. Here we indicate quantities pertinent to the component in the foreground with “fg”, and those related to the background with “bg”. The two-layer method is discussed in Anderson et al. (1997). Assuming that LTE holds in both layers, and that the radiation impinging on the background layer is the cosmic microwave background (CMB), the brightness temperature spectrum can be written as
![\begin{eqnarray} \begin{array}{lcl} T_{\rm B}(\upsilon) &=& T_{11} \, [F(T_{\rm ex,bg})-F(T_{\rm CMB})] (1-e^{-\tau_{\rm bg}(\upsilon)})e^{-\tau_{\rm fg}(\upsilon)} \\ & &+ T_{11} \, [F(T_{\rm ex,fg})-F(T_{\rm CMB})] (1-e^{-\tau_{\rm fg}(\upsilon)}) , \end{array} \end{eqnarray}](/articles/aa/full_html/2014/04/aa22069-13/aa22069-13-eq158.png) (2)where T11 ≡
hν11/k,
ν11 is the line frequency,
h and
k are
the Planck and Boltzmann constants, TCMB is the cosmic background
temperature, and the function F(T) is defined by
(2)where T11 ≡
hν11/k,
ν11 is the line frequency,
h and
k are
the Planck and Boltzmann constants, TCMB is the cosmic background
temperature, and the function F(T) is defined by 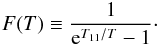 When the background component has a higher
excitation temperature than the foreground component, i.e., when Tex,bg>Tex,fg
the spectra show absorption dips.
When the background component has a higher
excitation temperature than the foreground component, i.e., when Tex,bg>Tex,fg
the spectra show absorption dips.
NH3(1,1) line parameters towards Cha-MMS1a, (0″,0″), the Spitzer 24 μm peak, (7″, − 4″), using the methods A, B, and C explained in the text.
The region where the two-layer fit gives reasonable values, i.e., where the four fit parameters (Tex, τtot, υLSR, and Δυ) are physically meaningful (positive) for both layers, is marked in Fig. 6. The region concentrates around a NW-SE axis going through the Spitzer 24 μm peak and millimetre peak Cha-MMS1a. As discussed in Sect. 3.3.1 this axis can be identified as the rotation axis of the dense nucleus of the core. The absorption occurs at velocities between 4.3 and 4.5 km s-1, around the systemic velocity of the cloud. Strong absorption is not seen on the northeastern nor the southwestern side of the axis because there the inner parts are either blue- or redshifted with respect to the absorbing envelope (see Sect. 3.3.1).
The ammonia spectrum towards the position of the Spitzer 24 μm emission maximum, (7″, −4″), shown in Fig. 5 (right panel) has one of the deepest main group absorption features in the whole map. The two-layer fit (see Table 4) suggests that the underlying component has a clearly higher Tex than the foreground component. Probably also the kinetic temperature of component 1 is elevated with respect to average value of the core, Tkin ~ 11 K, derived from Parkes data (Sect. 3.1), because for thermal emission lines Tex ≤ Tkin. It is evident from Fig. 5 (top panel) that the total column density from the fit to the satellites (method B, with Tex ~ 6.9 K) is substantially higher than that resulting from the two-layer fit. On the other hand, towards the position Cha-MMS1a, (0″,0″), lying somewhat off from the brightest emission, the satellite fit corresponds closely to background component of the two-layer fit, and the total column densities from methods B and C are similar. The average excitation temperatures of the background and foreground components are ⟨ Tex,bg ⟩ = 10.5 K and ⟨ Tex,fg ⟩ = 4.5 K, respectively. The positions where the Tex,bg> 11 K (the average gas kinetic temperature) are marked in Fig. 6 with blue plus signs.
 |
Fig. 6 Top: the region where the two-layer fit (method C) is applicable is shown with white diamonds on the integrated brightness temperature map of the NH3(1,1) satellites. Blue plus signs indicate positions where Tex,bg> 11 K, i.e., where the excitation temperature of the background component exceeds the average kinetic temperature of the core. Bottom: comparison between the NH3(1,1) column densities derived by fits to the hyperfine satellites only (method B, x-axis) and two-layer fits (method C, y-axis). The average uncertainties of the points are indicated in the top left corner. The red line represents the one-to-one correlation. |
A comparison between the NH3(1,1) column densities derived by two-layer fits (method C), and fits to the hyperfine satellites only (method B) is shown in the right panel of Fig. 6. One can see that the two column densities agree reasonably well up to N(1,1) ~ 1015 cm-2, but towards the highest column densities discrepancies occur. Similar effects are seen in comparisons between methods A and B and between methods A and C. Method A tends to overestimate the optical thickness of the line (and the column density) in the region where the main component shows self-absorption. On the other hand, the results from method C (altogether eight parameters for the two components) are uncertain when the radial velocities of the background and foreground components are nearly the same because both components have narrow linewidths. The average uncertainty of the two-layer fits is larger than for the satellite fits (see Fig. 6). Owing to the mentioned uncertainties, we have used a combination of methods A and B, that is, satellite fits in the central region and fits to all the 18 hyperfine components in the outer parts, in the derivation of the NH3(1,1) column density map. This map is shown in Fig. 7. The column density map resulting from a combination of models A, B, and C (the satellite fit replaced by the two-layer fit in the region where the fit parameters are positive) is similar to that shown in Fig. 7, except for a larger number of “bad” pixels deviating from the overall pattern. A comparison between the NH3(1,1) column density map and the 870 μm dust emission map is shown in Fig. 8. The dust continuum map was observed by Belloche et al. (2011) with the LABOCA bolometer array on APEX. In this figure, the ammonia map is smoothed to the angular resolution of the LABOCA map, 21″.
 |
Fig. 7 Column density of NH3 in the rotational level (J,K) = (1,1) in Cha-MMS1. The contour values are 10, 15, and 20 × 1014 cm-2. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. |
The bright integral-shaped ridge (PA 175°) visible in the integrated intensity map (Fig. 2) does not stand out in the column density map. The highest column densities are found on the NE side of the Spitzer 24 μm peak, and in a wiggled, filamentary structure in the southern part of the core. The offsets of the two most prominent maxima from Cha-MMS1a are (+9″,0″) and (+29″, −27″). The column densities of NH3(1,1) at these positions are (2.8 ± 0.5) × 1015 cm-2 and (2.3 ± 0.5) × 1015 cm-2, respectively. Judging from comparison with the Herschel and LABOCA maps (Figs. 3 and 8), the southern ammonia maximum is not associated with an H2 column density maximum, and it may therefore indicate a local enhancement in the ammonia abundance.
 |
Fig. 8 Column density map of the NH3(1,1) smoothed to an angular resolution of 21″ (contours) overlaid on the 870 μm map obtained with LABOCA (Belloche et al. 2011; Tsitali et al. 2013). The contour levels are 5, 7.5, and 10 × 1014 cm-2. The plus sign indicates the 1.2-mm dust emission peak Cha-MMS1a and the triangle shows the location of the Spitzer 24 μm source. |
Because high resolution (2,2) spectra are not available, we have not been able to derive properly the rotational temperature and the total ammonia column density in each position. At low temperatures the (1,1) column density is roughly equal to that of para-NH3. In Sect. 3.4, we use the para-NH3 abundance derived in Sect. 3.1 to make a rough estimate of the mass and other physical parameters of the ammonia core.
3.3.1. Velocity distribution
The NH3(1,1) column density spectra derived in the previous Section were used to study the velocity structure of the core. Velocity channel maps formed from the column density cube are shown in Fig. 9 as contours superposed on the Spitzer 24 μm dust emission map. Each channel covers an interval of 0.1 km s-1 (two correlator channels). The centre velocities range from 3.9 to 5.0 km s-1. Channel maps calculated directly from the spectral cube using the most blueshifted (leftmost) hyperfine group (F1 = 1 → 0, with two close-lying components F = 3 / 2 → 1 / 2 and F = 1 / 2 → 1 / 2) show the same structure but with a higher noise level.
The core has a velocity gradient with the υLSR increasing from the NE to SW. Around the systemic velocity of the cloud, at 4.4 and 4.5 km s-1 one can see a linear structure with a position angle of 130°. The velocity gradient is thus almost planar near the NW-SE axis defined by this structure, and the axis can be identified as the rotation axis of the inner core. Gas components with velocities below 4.5 km s-1 (i.e., blueshifted gas) can be found on the northeastern side of the axis, while the southwestern side has larger velocities (redshifted gas). The most blueshifted gas can be found on the NE side of the ammonia column density maximum and the 24 μm peak. The most redshifted gas lies some 25″ south of the Spitzer position.
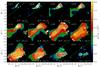 |
Fig. 9 Velocity channel maps of the NH3(1,1) column density in the Cha-MMS1 core. The column densities are shown using a logarithmic colour scale. The LSR velocity in km s-1 of the velocity channel is indicated in the bottom of each panel, and the mass in M⊙ in this channel is indicated in the top left corner. The green line indicates the axis of rotation determined from the velocity distribution. The positions of Cha-MMS1a and the Spitzer 24 μm peak are marked with a plus sign and a triangle, respectively. |
The velocity gradient in the core is also illustrated in Fig. 10 which shows the radial velocity distribution as a pixel image, and position velocity diagrams along two perpendicular axes, one along the suggested rotation axis (PA 130°) and another in the direction of the steepest velocity gradient (PA 40°). The average velocity gradient along the second axis, estimated from the velocities at the ends of the axis, is about 20 km s-1 pc-1 (see Fig. 10c). The two axes intersect at the Spitzer 24 μm peak.
The distribution of the NH3(1,1) linewidths resulting from Gaussian fits to the hyperfine structure is shown in Fig. 11. One can see that the lines are mostly quite narrow, between 0.2 and 0.3 km s-1, but there is a slight increase in the linewidths (ΔV> 0.3km s-1) near the Spitzer 24 μm source.
3.4. Physical parameters of the core
The column density of ammonia in the (1,1) rotational level derived in Sect. 3.3 have been used to estimate the mass and dynamical parameters of the core. In the conversion from N(NH3(1,1)) to N(H2) needed for the mass, we have approximated the para-NH3 column density by the (1,1) column density, and assumed a fractional para-ammonia abundance of X(pNH3) = 1.0 × 10-8 derived from comparison between the Parkes and Herschel data (see Sect. 3.1).
The results of the calculations are presented in Table 5. The parameters given in this Table refer to the region above the column density threshold N(1,1) > 5 × 1014 cm-2. The mass of this structure is ~2 M⊙. This mass is slightly larger than the virial mass implied by the condition Egrav + 2 Ekin = 0, where Egrav is the gravitational potential energy and Ekin is the kinetic energy including the contributions of the thermal and turbulent motions and the core rotation. The specific angular momentum of the core, j = ℒ /M, given in the Table is calculated with respect to axis indicated in Figs. 9 and 10 (PA 130°). The obtained ratio of the rotational and gravitational energies, βrot ~ 0.07, is close to the high end of the range of values determined previously by Goodman et al. (1993), Barranco & Goodman (1998), and Caselli et al. (2002) through single-dish observations. The specific angular momentum is similar to that in the inner part of L1544 as derived from interferometric NH2D data by Crapsi et al. (2007), and an order of magnitude lower than j derived from NH3 in the same target. According to results of previous interferometric surveys the value we obtain in Cha-MMS1, j ~ 10-3 km s-1 pc, is typical for protostellar envelopes and lies clearly below the specific angular momenta derived for prestellar cores (Ohashi 1999; Crapsi et al. 2007). On the other hand, both β and j are higher by about a factor of two than the median values for cores formed in the simulation of Dib et al. (2010) of magnetised, self-gravitating molecular clouds with decaying turbulence. According to the results of Dib et al. (2010) angular momenta derived observationally from projected velocity maps overestimate the true values by a factor of ~10 because of the omission of fluctuations in the 3D velocity field.
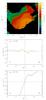 |
Fig. 10 Distribution of the NH3(1,1) line velocities derived from Gaussian fits to the hyperfine structure. Top: the radial velocity map. The VLSR values can be read from the contours and the colour bar on the right. The locations of the Spitzer 24 μm source and the submm source Cha-MMS1a are shown with a triangle and a plus sign, respectively. Middle: velocity profile along the NW-SE oriented axis drawn in yellow on the map, Bottom: velocity profile along the NE-SW oriented axis indicated with green. Also the error bars result from Gaussian fits to the (1,1) hyperfine structure. |
 |
Fig. 11 Map of the NH3(1,1) linewidths derived from Gaussian fits to the hyperfine structure. |
Dynamical parameters of the core derived from the ammonia spectra (see text).
3.5. Spectral energy distribution and evolutionary stage of Cha-MMS1
To characterise the emission arising from Cha-MMS1, we constructed its spectral energy distribution (SED) by combining the Herschel and Spitzer data. The Herschel data were first convolved to the resolution of the SPIRE/500 μm band (37″ or 0.027 pc at the source distance). The PACS and SPIRE flux densities at 160, 250, 350, and 500 μm were then determined in an aperture with a radius of 25″. The corresponding values are 7.7 ± 0.9, 11.6 ± 0.8, 8.7 ± 0.81, and 4.7 ± 0.6 Jy, respectively. The median intensities in an annulus surrounding the aperture up to the radius 50″ was used in the background subtraction. The Spitzer/MIPS 24 and 70 μm flux densities, 3.0 ± 0.4 and 349 ± 44 mJy, were adopted from Tsitali et al. (2013). The Herschel flux densities are smaller than those listed for Cha-MMS1 in Winston et al. (2012), probably because we have used a smaller aperture (the apertures are not given in the paper of Winston et al. 2012).
The SED of Cha-MMS1 was analysed by fitting model SEDs to the observed flux densities from a large pre-computed grid of YSO models (Robitaille et al. 2006, 2007)6. The grid consists of 20 000 two-dimensional YSO radiation transfer models covering a wide range of stellar masses (0.1−50 M⊙) and evolutionary stages. Each model outputs SEDs at 10 different viewing angles (inclinations) ranging from edge-on (90°) to pole-on (0°, resulting in a total of 200 000 SEDs. The model fitter requires a distance range within which to fit the observed data. We assumed that the source distance is in the range 135−165 pc (Whittet et al. 1997). The other assumption we made was that the foreground interstellar extinction is no more than AV = 20. In Fig. 12 we show the SED for Cha-MMS1 along with the best-fitting model and the subsequent nine best-fit models (shown as grey lines).
The models could not fit the 70 μm data point well. We note that inclusion of the 70 μm data point icreases significantly (by a factor of ~9) the 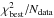 value (Ndata is the number of data points) with respect to the calculation where the 70 μm flux is not used in the fit. Moreover, the models predict slightly higher 160 μm flux densities than the observed value. The resulting model parameters are given in Table 6. In addition to the best-fit model, we show the range of possible parameter values that can be derived from the subsequent nine best models.
value (Ndata is the number of data points) with respect to the calculation where the 70 μm flux is not used in the fit. Moreover, the models predict slightly higher 160 μm flux densities than the observed value. The resulting model parameters are given in Table 6. In addition to the best-fit model, we show the range of possible parameter values that can be derived from the subsequent nine best models.
The best-fit model stellar mass and total luminosity are found to be M⋆ ~ 0.12 M⊙ and Ltot ~ 0.6 L⊙. We note that the latter includes contributions from the central star and accretion, assuming that all the accretion energy is radiated away. Moreover, it is corrected for foreground extinction and does not depend on the viewing angle. The envelope mass, Menv ~ 0.9 M⊙, determined from the long wavelength emission, is about half of the value 2.2 M⊙ derived from NH3, which is a reasonable agreement given the assumptions used in the analysis [e.g., X(NH3)].
Robitaille et al. (2006) defined different stages of evolution based on the value of the stellar mass, M⋆, and the envelope accretion rate, Ṁenv. For Cha-MMS1, we derive the Ṁenv/M⋆ ratio ~4 × 10-4 yr-1 which in this classification scheme suggests that it represents a deeply embedded Stage 0 source (Ṁenv/M⋆ ≫ 10-6 yr-1) seen nearly edge-on (the inclination angle is ~70°). This early evolutionary stage is also characterised by an envelope whose mass is Menv ≫ M⋆ and Mdisk. The derived luminosity, 0.6 L⊙, is higher than the value expected for a candidate FHSC (<0.1 L⊙; e.g., Enoch et al. 2010; Pineda et al. 2011; Chen et al. 2012).
Our results suggest that if the central source is a true protostar, it represents a Class 0 object, an accreting second hydrostatic core at a very early stage of evolution. It should be noted, that the models of Robitaille et al. (2006) only cover YSOs with central temperatures above 2000 K. The model fails to fit the 70 μ flux density which has been found to correlate closely with the internal luminosity of the protostar (Dunham et al. 2008). Based on the correlation found by Dunham et al. (2008) and on the predictions of Commerçon et al. (2012) for the FHSC flux densities at 24 and 70 μm, Tsitali et al. (2013) concluded that the central source of Cha-MMS1 has a very low luminosity, ~0.1 L⊙, and it is likely to be a FHSC. On the other hand, the models of Commerçon et al. (2012) suggest that it is very difficult to distinguish between embedded Class 0 protostars and FHSCs based solely on SED information.
 |
Fig. 12 Spectral energy distribution for Cha-MMS1. The observed flux density values are shown as filled circles. The error bars are smaller than the data points in the figure. Ten best model fits are shown: the solid black line shows the best-fitting model, and the grey lines illustrate the subsequent nine best-fit models. The dashed line shows the SED of the stellar photosphere corresponding to the central source in the best-fitting model (in the absence of circumstellar material). |
Results of SED modelling.
4. Discussion
4.1. The high column density ammonia core
One important conclusion from this work is that with ATCA, we detect a compact high column density structure in the NH3(1,1) line which is “invisible” at single dish (Parkes) resolution. The average para-ammonia column density which we derive (~1 × 1015 cm-2) is likely an underestimate due to high optical depth in the satellite transitions. Such high column densities of ammonia in cold cores are very rare and, actually, we are not aware of any comparable examples. For example, towards L1544, Crapsi et al. (2007) found a total (ortho + para) NH3 column density of 7 × 1014 cm-2 using the VLA. This value is derived assuming thermal relative populations of the ortho and para states, impying that the para-ammonia column density in L1544 is ~1 × 1014 cm-2. This is an order of magnitude less than our value in Cha-MMS1.
One can check this by comparing the 870 μm map of Cha-MMS1 from Belloche et al. (2011) (see also Tsitali et al. 2013) made with the LABOCA receiver on the APEX telescope (HPBW 21″) with our NH3 column density map. This is shown in Fig. 8 where we have smoothed the NH3 to the dust continuum resolution. One sees that the dust continuum and the ammonia column trace somewhat different regions and in fact the ammonia peak is 25″ to the south of the 870 μm peak. This may partly reflect the ATCA missing flux problem discussed in Sect. 2.2. However, it might also indicate a gradient in the ammonia abundance. We have attempted to estimate the ammonia abundance in this area assuming a dust temperature of 12.5 K and a dust opacity of 0.0083 cm2g-1 at λ = 870 μm (which is consistent with the cross-section at λ = 250 μm assumed in Sect. 2.3). We derive a mean H2 column density over the ammonia source of 7.6 × 1022 cm-2 and a mean total ammonia abundance [NH3]/[H2] = 3 × 10-8 (assuming ortho/para ~1). The dust continuum angular resolution does not suffice to make a reliable estimate of the abundance gradient but a difference of a factor 2 from north to south seems plausible. Clearly, higher angular resolution observations of this region in a variety of molecular species and in particular 15NH3 are needed to clarify this situation.
The mean NH3 abundance is quite compatible with past ammonia abundance determinations in cores (e.g., Harju et al. 1993; Dunham et al. 2011) but applies to a region considerably denser than in most previous work (106 cm-3, see Table 5). The timescale for freeze-out of gas phase ammonia on dust grain surfaces at this density is on the order of 104 years suggesting that the age of the high-density ammonia core cannot be much greater than this. In general, the ammonia abundance reflects the molecular nitrogen abundance and ammonia correlates well with N2H+. This suggests that ALMA observations of N2H+ would be a fruitful way of studying the kinematics of the core surrounding Cha-MMS1.
4.2. Core kinematics
The kinematics of the molecular cloud in the neighbourhood of Cha-MMS1 are complex as one realises studying the N2H+(1−0) map of Ladd et al. (2011) which covers an area of roughly 200″ in diameter with an angular resolution of 36″. Our results can also be compared with the data of Tsitali et al. (2013) who present in several tracers the results of cuts parallel and perpendicular to the filamentary structure seen in the APEX LABOCA map (see Tsitali et al. 2013, Fig. 1a). Our ATCA ammonia map covers a more limited region with a higher angular resolution than in the above mentioned studies (see Table 1) and traces the kinematics of high density [n(H2) = 106 cm-3] material. A general aim of such observations is to compare the kinematics of the high density core nucleus with that of the surrounding lower density material. One can expect to find evidence for outflows or accretion associated with embedded protostars as well as for rotation. In the latter case, a naive expectation is that due to angular momentum conservation, the rotation axis is the same for high and low density gas but that angular velocity increases rapidly on small size scales.
We first note that the direction of the velocity gradient found by us is quite different from that found by Tsitali et al. perpendicular to the “filamentary structure” seen in the LABOCA map. The reason for that may lie in the positioning of the cuts, angular resolution, and the molecular probes used by Tsitali et al. Our radial velocities increase from the northeast to the south in the same way as in the single-dish N2H+ map of Ladd et al., but the gradient is steeper in the present NH3 map. This suggests differential rotation with the angular velocity increasing towards the rotation axis. The axis of rotation has a position angle of 130°, and is roughly delineated in the velocity channel centred at 4.5 km s-1 in Fig. 9. The steepness of the velocity gradient corroborates the notion that the ammonia emission traces the central parts of the core.
The bright N-S oriented ridge seen in the integrated intensity map shares the overall velocity gradient of the central region. The largest diameter of the ridge is about 5000 AU, and its symmetry axis is tilted with respect to the overall rotation axis by 45°. This configuration resembles very much the structure observed around the YSO Barnard 1c (Matthews et al. 2006, see their Fig. 8). Unlike Cha-MMS1, Barnard 1c reached an advanced stage with well-developed molecular outflow. The column density map (Fig. 7) shows that the largest ammonia column densities are found in two separate regions, near the northern and southern ends of the ridge. The two most prominent column density maxima lie in the vicinity of the rotation axis, some 30″ (~5000 AU) apart. The northern ammonia maximum lies close to the far-IR peak determining the location of the H2 column density maximum. As discussed above, the southern ammonia maximum is likely to trace a local enhancement in the fractional ammonia abundance.
Both Hiramatsu et al. (2007) and Ladd et al. (2011) suggest that outflow from the neighbouring Class I protostar IRS4, lying about 80″ (~13 000 AU, 0.06 pc) NE from our map centre, is interacting with the Cha-MMS1 core. According to both studies the momentum of the IRS4 outflow is large enough to affect the core dynamics. On the other hand, Ladd et al. (2011) find that the outflow might be deflected from the Cha-MMS1 core, and they suggest that the outflow is not colliding with the core directly but delivers “a glancing blow”.
While it is possible that the outflow from IRS4 has influenced the velocity structure in the northeastern side of the core, and may have contributed to the core collapse through compression it is less likely that the overall velocity gradient could have been directly caused by external momentum input. An outflow cannot easily exert torque on a gaseous body; more likely it will plough its way through the cloud (see Ladd et al. 2011, Sect. 4.2.1). It is therefore difficult to explain the redshifted gas in the southern part by the outflow from IRS4. The most believable explanation for the large velocity gradient is therefore spin-up resulting from (partial) conservation of the angular momentum during the core collapse. Another possibility however is that infall onto the Cha-MMS1 Spitzer source is responsible for the high velocity gradient close to the protostar. Tobin et al. (2012), in their study of Class 0 protostellar envelopes, point out that the kinematic signatures of infall and rotation are similar and hence difficult to distinguish. Therefore, it is certainly possible that the real situation is a combination of the two.
Are there any signs of a molecular outflow along the rotational axis of the core as in the case of Barnard 1c? An elongated, hourglass-shaped structure in the likeness of some previously observed outflow lobes is seen in the channel maps, albeit in a very narrow LSR velocity range of 4.4−4.5 km s-1 (see Fig. 9). The structure is aligned with the approximately northwest-southeast oriented rotation axis (PA 130°) and seems to protrude from the densest part of the core on its southeastern side. A symmetric, elongated ammonia structure and the absence of high-velocity wings could possibly be explained by a dense outflow or by compressed ouflow cavity walls seen nearly side on.
Ammonia has been previously observed to probe cavity walls around evolved molecular outflows (Anglada et al. 1995; Beltrán et al. 2008), and to take part in collimated high-velocity outflows (Bachiller et al. 1993; Tafalla & Bachiller 1995; Curiel et al. 1996). In the latter case, the gas properties (line shapes, kinetic temperatures, enhanced ammonia abundances) show clear evidence for shocks. In the present ammonia data no sign of shocked gas is, however, seen. The ammonia linewidths (see Fig. 11) are below 0.3 km s-1 in the southeastern part of the putative NW-SE “outflow”, but increase to slightly above 0.3 km s-1 in a conical region in the northwest. The analysis of the NH3 profiles suggests the presence of a warm gas component in the neighbourhood of the Spitzer 24 μm source and the rotation axis: a two-layer model with a cool foreground component, and an underlying dense or/and warm component is applicable to this elongated region. The distribution of this component overlaps largely with the region showing 1.2 cm continuum emission, and wide-band NH3(2,2) emission. This coincidence suggests that the present ammonia map partly probes gas heated by an outflow embedded in Cha-MMS1.
Another intriguing structure reminiscent of an outflow is seen in the wide-band (1,1) map (Fig. 4): three maxima, the brightest one associated with the NH3 column density maximum near the far-IR peak, and two others on its southern side. These features lie along the bright ridge seen in the integrated line emission map (PA 175°). The two subsidiary peaks have slightly arc-like shapes suggesting shock compression. Also in these positions ammonia lines are narrow (0.2 − 0.3km s-1), and no trace of pedestals or wings can be seen in the (1,1) high-resolution spectra. The wiggling secondary maximum in the (1, 1) column density map mentioned above is associated with the southernmost wide-band (1,1) peak.
The spectra shown in Fig. 5 as well as other spectra in the vicinity of the Spitzer 24 μm source show no clear evidence for accretion. In fact absorption in this region is blue-shifted with respect to the embedded warmer gas. We note here however that it is also possible that this “self absorption” occurs in the foreground more extended component which is mainly responsible for the lower optical depth emission seen with single dish telescopes.
4.3. On the nature of Cha-MMS1
The SED described in Sect. 3.5 suggests that, if Cha-MMS1 has entered into a protostellar stage, it is still a Class 0-type object. Class 0 protostars are known to drive outflows (e.g. Arce & Sargent 2006), and in such of an object a strongly collimated high-velocity jet can act as the driving force behind the slower velocity molecular outflow. (e.g., Arce et al. 2007). In Cha-MMS1, emission at visual and IR wavelengths from a possible high-velocity jet could be totally obscured by the dense core. The presence of a jet is suggested by the tentative detection of radio continuum emission (Sect. 3.2), which traces free-free emission from shock-ionised gas. The bending of this feature towards north does not agree with the linearity of the NW-SE oriented ammonia structure. On the other hand, three of the continuum peaks lie close to the axis defined by the wide band (1,1) maxima (Fig. 4). The total 1.3 cm flux density of the continuum feature seen in Fig. 4 is 0.8 ± 0.4 mJy. Assuming a spectral index of α = 1.2 (see Sect. 3.2), and using the relationship between the outflow momentum rate and the 6 cm radio continuum luminosity derived by Anglada et al. (1998) we obtain an upper limit for the momentum rate of Ṗ = 5 × 10-6M⊙ yr-1 km s-1. Using the stellar age ~3 × 104 yr derived from the SED modelling (Sect. 3.5), and adopting a velocity of 30 km s-1 for the putative molecular outflow, the mass of the outflow becomes 0.005 M⊙. In the situation where the described outflow is seen side-on, only a fraction of it is seen within a telescope beam, and we estimate that the integrated intensity of the CO(J = 3 − 2) line as observed with a 10-m telescope (like ASTE) would be ∫TMBdυ ~ 0.5 K km s-1, and might remain undetected taking into account blending with the quiescent gas and the outflow from IRS4 (see Fig. 7 of Hiramatsu et al. 2007). On the other hand, in the case of a small inclination angle the same outflow should produce a signal detectable with single-dish telescopes.
Two principal mechanisms have been proposed to drive protostellar jets. Both are based on the magnetocentrifugal mechanism (Blandford & Payne 1982; Shu et al. 1994) but related to different driving sources of the outflow. Firstly, the magnetocentrifugal mechanism can be operational through an accretion disk alone (e.g., Blandford & Payne 1982; Pudritz et al. 2007), assuming that the magnetic field of the disk is twisted enough to form a sufficiently open poloidal field geometry, through which excess matter and angular momentum can escape the system (the disk-wind model). Secondly, the magnetocentrifugal mechanism can also be active in a system consisting of an accretion disk and a protostar (Shu et al. 1994). The rotational interaction between the magnetic fields of a disk and a young star creates open field lines near the equator of the system, where matter is blown out as bipolar jets (the X-wind model). These mechanisms might be relevant in an early stage already. Several numerical MHD models (Tomisaka 1998, 2000, 2002; Banerjee & Pudritz 2006; Machida et al. 2008a) have also shown that a FHSC can produce low-velocity outflows. In these simulations, FHSC outflows have wide opening angles and extend to a distance of a few times the width of the outflow. However, according to the recent model calculations of Price et al. (2012), low-mass FHSCs can generate well-collimated, slow (~2 − 7km s-1) outflows, expanding to several thousand AU.
The projected total length of the hypothetical NW-SE outflow is (based on the structure in Fig. 8) approximately 9000 AU. Adopting the range of the characteristic outflow speeds from Price et al. (2012), this length corresponds to ages between 3000 and 11 000 yr. These times are slightly longer than the expected lifetimes of FHSCs (Commerçon et al. 2012), but comparable to the dynamical time-scale of the outflow associated with the candidate FHSC Per-Bolo 58 (υ = 2.4km s-1, τd = 16 000 yr; Dunham et al. 2011).
There are a number of molecular outflows observed from very young objects. Some of them are suspected to be still at the first core stage and some are likely to be more advanced very low luminosity objects (VeLLOs; see Dunham et al. 2008). Examples of this are L673-7 (Dunham et al. 2010), Per-Bolo 58 (Enoch et al. 2010; Dunham et al. 2011), L1448 IRS 2E (Chen et al. 2010); L1451 (Pineda et al. 2011), CB 17 MMS (Chen et al. 2012), and L1521F-IRS (Takahashi et al. 2013). In general, the resolution and the noise level in the observations towards FHSC candidates are not good enough to exclude a low-luminosity protostar. L1521F-IRS deserves a particular mention as Takahashi et al. (2013) state that they can see two distinct velocity components in their observations: one corresponding to wide slow outflow and more highly collimated fast outflow. They suspect that the slow component originates from the FHSC stage.
The theoretical and observational studies described above show that outflows are characteristic of very young protostars. Several features of Cha-MMS1: a rotating core with an embedded 24 μm continuum source, the tentative detection of radio continuum, the hourglass-shaped ammonia distribution at the nominal velocity of the cloud, suggest the presence of a young molecular outflow. However, in contrast to the VeLLO and candidate FHSC outflows mentioned above, no CO outflow originating in Cha-MMS1 has been detected. If such an outflow exists, the high-velocity wings may still be confined in the very inner regions of the core, and can have escaped the previous single-dish surveys. To confirm or disprove this possibility more detailed and sensitive observations than available so far are needed. High-resolution submm/far-IR continuum observations could be used to study the shape of the compact far-IR source, which may be associated with the FHSC or a protostellar disk. Also, line observations in high-density tracer molecules could help us to understand the velocity structure of the core in more detail. Finally, deep radio continuum observations can confirm the presence of free-free emission from ionised jets.
The rotational speed (Ω ~ 6.5 × 10-13 s-1) and the ratio of rotational and gravitational energies (~7%) derived for the core are large, and rotation is probably influencing strongly the star formation process in Cha-MMS1. Furthermore, the region has been reported to be significantly magnetised, with the large-scale magnetic field oriented roughly in the same way as the rotation axis inferred from the present ammonia data (Whittet et al. 1994; Haikala et al. 2005, their Fig. 8). The combination of fast rotation and magnetic fields should have resulted in the formation of a disk-like first core, probably generating outflows through toroidal magnetic pressure (Tomisaka 1998; Machida et al. 2004; Banerjee & Pudritz 2006).
According to MHD models, the circumstellar disk formed from the first core should be small compared with that in an unmagnetised core because of the removal of the angular momentum by magnetic braking. Nevertheless, a high rotation speed can have led to the fragmentation of the disk and the formation of a protobinary or a multiple object, at a phase (density) determined by the ratio of the rotational and magnetic energies (Machida et al. 2008b; Machida & Matsumoto 2011; Joos et al. 2013). The ammonia data show indications of outflows along two axes with the position angles 130° and 175° (see Sect. 4.2). Jet precession or a double jet associated with a binary would possibly explain these features.
5. Conclusions
We have mapped the Cha-MMS1 core in the NH3(1,1) line and in the 1.2 cm continuum using the Australia Telescope Compact Array at spatial resolution of about 1000 AU. The observations reveal a high-column density ammonia core with a steep (20 km s-1 pc-1) velocity gradient. The gradient can be interpreted as rotation around a NW-SE oriented axis which passes through the position of a Spitzer 24 μm point source. The ammonia spectra are self-absorbed near the rotation axis. A two-layer model used to fit the absorption suggests that the underlying component has an elevated temperature near the Spitzer source. A string of weak 1.2 cm continuum sources are tentatively detected in this region.
It seems natural to explain the presence of warm gas close to the rotation axis in terms heating by an embedded outflow. However, no evidence for high-velocity gas or shocks are found in the spectral lines observed towards this core, so the question about the evolutionary stage of the central source remains open. An analysis of the SED using the models of Robitaille et al. (2006) suggests that if the central source is a YSO it belongs to the Class 0. On the other hand, as pointed out by Tsitali et al. (2013), the 70 μm flux density of the central source implies a very low luminosity which would be consistent with an FHSC, but clearly too low for a true protostar.
Observations at a high spatial resolution of ~100 AU (≤1″) will probably clarify this issue. Besides a search for a compact outflow in CO, probing the distribution and kinematics of dense gas in the neighourhood of the Spitzer source would be useful. The observed ammonia lines have very large optical thicknesses, and it is likely that the fractional abundances of both NH3 and N2H+ are high in the centre of the core. These molecules, and their 15N substituted variants look therefore suitable for probing the interior parts of the core.
See the SPIRE and PACS Observer’s Manuals (Versions 2.4) at http://herschel.esac.esa.int, “Herschel Documentation”.
Distributed by Exelis Visual Information Solutions, Inc. (http://www.exelisvis.com)
The online SED-fitting tool is available at http://caravan.astro.wisc.edu/protostars/
Acknowledgments
We wish to thank the ATCA staff for their help during our observations, and the anonymous referee for very helpful comments. Financial support from the Academy of Finland projects 132291, 141017, and 218159, from the research programme “Active Suns” at the University of Helsinki, and from Jenny and Antti Wihuri Foundation and Finnish Cultural Foundation grants are acknowledged. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) with Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada);NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) with UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM(France); MPIA (Germany); INAFIFSI/ OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). This research has made use of NASA’s Astrophysics Data System.
References
- Anderson, I. M., Harju, J., & Haikala, L. K. 1997, A&A, 326, 366 [NASA ADS] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada, G., Estalella, R., Mauersberger, R., et al. 1995, ApJ, 443, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada, G., Villuendas, E., Estalella, R., et al. 1998, AJ, 116, 2953 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., & Sargent, A. I. 2006, ApJ, 646, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., Shepherd, D., Gueth, F., et al. 2007, in Protostars and Planets V (Tucson: University of Arizona press), 245 [Google Scholar]
- Bachiller, R., Martin-Pintado, J., & Fuente, A. 1993, ApJ, 417, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Walawender, J., Luhman, K. L., & Fazio, G. 2006, AJ, 132, 1923 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Barranco, J. A., & Goodman, A. A. 1998, ApJ, 504, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Parise, B., van der Tak, F. F. S., et al. 2006, A&A, 454, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Wiseman, J., Ho, P. T. P., et al. 2008, A&A, 485, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Arce, H. G., Zhang, Q., et al. 2010, ApJ, 715, 1344 [Google Scholar]
- Chen, X., Arce, H. G., Dunham, M. M., et al. 2012, ApJ, 751, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., & Schwartz, R. D. 1987, ApJ, 316, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Launhardt, R., Dullemond, C., & Henning, T. 2012, A&A, 545, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordiner, M. A., Charnley, S. B., Wirström, E. S., & Smith, R. G. 2012, ApJ, 744, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curiel, S., Rodriguez, L. F., Gomez, J. F., et al. 1996, ApJ, 456, 677 [Google Scholar]
- Danby, G., Flower, D. R., Valiron, P., Schilke, P., & Walmsley, C. M. 1988, MNRAS, 235, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Hennebelle, P., Pineda, J. E., et al. 2010, ApJ, 723, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. K., Rosolowsky, E., Evans, II, N. J., Cyganowski, C., & Urquhart, J. S. 2011, ApJ, 741, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, II, N. J., et al. 2008, ApJS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Evans, N. J., Bourke, T. L., et al. 2010, ApJ, 721, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Chen, X., Arce, H. G., et al. 2011, ApJ, 742, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Lee, J.-E., Harvey, P., Dunham, M. M., & Schnee, S. 2010, ApJ, 722, L33 [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Haikala, L. K., Harju, J., Mattila, K., & Toriseva, M. 2005, A&A, 431, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harju, J., Walmsley, C. M., & Wouterloot, J. G. A. 1993, A&AS, 98, 51 [NASA ADS] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hiramatsu, M., Hayakawa, T., Tatematsu, K., et al. 2007, ApJ, 664, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., Barrett, A. H., Myers, P. C., et al. 1979, ApJ, 234, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Joos, M., Hennebelle, P., Ciardi, A., & Fromang, S. 2013, A&A, 554, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pelkonen, V.-M., et al. 2011, A&A, 527, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kukolich, S. G. 1967, Phys. Rev., 156, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ladd, E. F., Wong, T., Bourke, T. L., & Thompson, K. L. 2011, ApJ, 743, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lehtinen, K., Harju, J., Kontinen, S., & Higdon, J. L. 2003, A&A, 401, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Machida, M. N., & Matsumoto, T. 2011, MNRAS, 413, 2767 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Tomisaka, K., & Matsumoto, T. 2004, MNRAS, 348, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Machida, M. N., Inutsuka, S.-i., & Matsumoto, T. 2008a, ApJ, 676, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Tomisaka, K., Matsumoto, T., & Inutsuka, S.-I. 2008b, ApJ, 677, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. C., Hogerheijde, M. R., Jørgensen, J. K., & Bergin, E. A. 2006, ApJ, 652, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, N. 1999, in Star Formation 1999, ed. T. Nakamoto, 129 [Google Scholar]
- Persi, P., Marenzi, A. R., Gómez, M., & Olofsson, G. 2001, A&A, 376, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Arce, H. G., Schnee, S., et al. 2011, ApJ, 743, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poynter, R. L., & Kakar, R. K. 1975, ApJS, 29, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Tricco, T. S., & Bate, M. R. 2012, MNRAS, 423, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Prusti, T., Clark, F. O., Whittet, D. C. B., Laureijs, R. J., & Zhang, C. Y. 1991, MNRAS, 251, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, in Protostars and Planets V (Tucson: University of Arizona Press), 277 [Google Scholar]
- Reipurth, B., Nyman, L.-Å., & Chini, R. 1996, A&A, 314, 258 [NASA ADS] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schnee, S., Enoch, M., Noriega-Crespo, A., et al. 2010, ApJ, 708, 127 [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Suutarinen, A., Haikala, L. K., Harju, J., et al. 2013, A&A, 555, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., & Bachiller, R. 1995, ApJ, 443, L37 [Google Scholar]
- Takahashi, S., Ohashi, N., & Bourke, T. L. 2013, ApJ, 774, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Tennekes, P. P., Harju, J., Juvela, M., & Tóth, L. V. 2006, A&A, 456, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobin, J. J., Hartmann, L., Bergin, E., et al. 2012, ApJ, 748, 16 [Google Scholar]
- Tomisaka, K. 1998, ApJ, 502, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 2000, ApJ, 528, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 2002, ApJ, 575, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Tsitali, A. E., Belloche, A., Commerçon, B., & Menten, K. M. 2013, A&A, 557, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ungerechts, H., Winnewisser, G., & Walmsley, C. M. 1986, A&A, 157, 207 [NASA ADS] [Google Scholar]
- Walmsley, C. M., & Ungerechts, H. 1983, A&A, 122, 164 [NASA ADS] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Carkner, A. L., et al. 1994, MNRAS, 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS] [Google Scholar]
- Winston, E., Cox, N. L. J., Prusti, T., et al. 2012, A&A, 545, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Juvela, M., Demyk, K., et al. 2012, A&A, 542, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Tdust and N(H2) values at the temperature minimum and the column density maximum using the emissivity index β = 2.0, and the range β = 1.8−2.2.
Integrated intensities of the NH3(2,2) lines and (1,1) satellites and kinetic temperatures derived from these towards three (2,2) peaks.
NH3(1,1) line parameters towards Cha-MMS1a, (0″,0″), the Spitzer 24 μm peak, (7″, − 4″), using the methods A, B, and C explained in the text.
All Figures
 |
Fig. 1 NH3(1,1) inversion line spectrum towards the ammonia maximum as observed with the Parkes 64 m telescope (upper spectrum), at the offset (+ 10″, − 14″) from Cha-MMS1a (Reipurth et al. 1996). The corresponding ATCA spectrum “smoothed” to an 80″ resolution is shown at the bottom. The latter is produced by applying a Gaussian taper to the visibility data. |
| In the text | |
 |
Fig. 2 Integrated intensity map of the NH3(1,1) satellites towards Cha-MMS1 observed with ATCA. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. The synthesised beam is indicated in the top right corner. |
| In the text | |
 |
Fig. 3 Left: intensity of thermal dust emission (MJy sr-1) at the wavelength λ = 250μm in a region of 5′ × 5′ region around Cha-MMS1. The map is centred at the Spitzer 24 μm peak indicated with a red triangle. The red circle in the top right corner corresponds to the average Herschel beamsize (FWHM, 18″) at 250 μm. The small white ellipse shows the synthesised ATCA beam (~7″). Middle: dust temperature, Tdust (K), in the same region. The red circle in the top right corner represents the resolution of the calculated Tdust and H2 column density maps (40″). Right: H2 column density, N(H2) (1022 cm-2) derived from the 250 μm optical thickness, τ250 μm. The dust temperature and column density maps are derived by fitting a modified blackbody function to the Herschel intensity maps at 500, 350, 250, and 160 μm assuming an emissivity index of β = 2.0 (see text). The locations of three prominent young stellar objects (YSOs), Ced110 IRS2 (right), IRS4 (middle), and IRS6 (left), are indicated with asterisks. The plus sign indicates the location of the millimetre source Cha-MMS1a (Reipurth et al. 1996). The white contour shows the integrated intensity level 5 K km s-1 of the NH3(1,1) satellites as observed with ATCA. The yellow contours in the right panel shows the integrated intensity ( |
| In the text | |
 |
Fig. 4 ATCA wide-band images. Top: the pixel image shows the intensity distribution of the two central channels covering the NH3(1,1) line. Bottom: the pixel image of the channel containing the (2,2) line. The contour map superimposed on both images represents the true 1.3 cm continuum emission, i.e. wide-band channels without ammonia line contamination. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. |
| In the text | |
 |
Fig. 5 ATCA NH3(1,1) spectra towards the offsets (0″,0″) and (+ 7″, − 4″) from Cha-MMS1a. The latter position coincides with a Spitzer 24 μm emission peak. The top panels show a Gaussian fit to the four satellite groups of the hyperfine structure (green curve). The column density spectra of ammonia in the rotational level (1,1) derived from these fits are shown on the right of the satellite spectra. The panels in the middle row show two-component fits to the full hyperfine structure including the main group (black curve). In the bottom panels, the modelled emission profiles from the two layers (component 1: red, component 2: blue) are shown separately. The foreground component 2 has a lower excitation temperature than component 1, and causes absorption features. The corresponding NH3(1,1) column density spectra of components 1 (red) and 2 (blue) are shown on the right. The dashed curve shows the combined NH3(1,1) column density spectrum of layers 1 and 2. |
| In the text | |
 |
Fig. 6 Top: the region where the two-layer fit (method C) is applicable is shown with white diamonds on the integrated brightness temperature map of the NH3(1,1) satellites. Blue plus signs indicate positions where Tex,bg> 11 K, i.e., where the excitation temperature of the background component exceeds the average kinetic temperature of the core. Bottom: comparison between the NH3(1,1) column densities derived by fits to the hyperfine satellites only (method B, x-axis) and two-layer fits (method C, y-axis). The average uncertainties of the points are indicated in the top left corner. The red line represents the one-to-one correlation. |
| In the text | |
 |
Fig. 7 Column density of NH3 in the rotational level (J,K) = (1,1) in Cha-MMS1. The contour values are 10, 15, and 20 × 1014 cm-2. The positions of Cha-MMS1a and the Spitzer 24 μm maximum are marked with a plus sign and a triangle, respectively. |
| In the text | |
 |
Fig. 8 Column density map of the NH3(1,1) smoothed to an angular resolution of 21″ (contours) overlaid on the 870 μm map obtained with LABOCA (Belloche et al. 2011; Tsitali et al. 2013). The contour levels are 5, 7.5, and 10 × 1014 cm-2. The plus sign indicates the 1.2-mm dust emission peak Cha-MMS1a and the triangle shows the location of the Spitzer 24 μm source. |
| In the text | |
 |
Fig. 9 Velocity channel maps of the NH3(1,1) column density in the Cha-MMS1 core. The column densities are shown using a logarithmic colour scale. The LSR velocity in km s-1 of the velocity channel is indicated in the bottom of each panel, and the mass in M⊙ in this channel is indicated in the top left corner. The green line indicates the axis of rotation determined from the velocity distribution. The positions of Cha-MMS1a and the Spitzer 24 μm peak are marked with a plus sign and a triangle, respectively. |
| In the text | |
 |
Fig. 10 Distribution of the NH3(1,1) line velocities derived from Gaussian fits to the hyperfine structure. Top: the radial velocity map. The VLSR values can be read from the contours and the colour bar on the right. The locations of the Spitzer 24 μm source and the submm source Cha-MMS1a are shown with a triangle and a plus sign, respectively. Middle: velocity profile along the NW-SE oriented axis drawn in yellow on the map, Bottom: velocity profile along the NE-SW oriented axis indicated with green. Also the error bars result from Gaussian fits to the (1,1) hyperfine structure. |
| In the text | |
 |
Fig. 11 Map of the NH3(1,1) linewidths derived from Gaussian fits to the hyperfine structure. |
| In the text | |
 |
Fig. 12 Spectral energy distribution for Cha-MMS1. The observed flux density values are shown as filled circles. The error bars are smaller than the data points in the figure. Ten best model fits are shown: the solid black line shows the best-fitting model, and the grey lines illustrate the subsequent nine best-fit models. The dashed line shows the SED of the stellar photosphere corresponding to the central source in the best-fitting model (in the absence of circumstellar material). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.