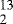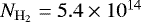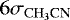| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201935318 | |
| Published online | 23 August 2019 | |
Fragmentation, rotation, and outflows in the high-mass star-forming region IRAS 23033+5951
A case study of the IRAM NOEMA large program CORE★,★★
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: bosco@mpia.de
2
Institute of Astronomy and Astrophysics, University of Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
3
Leiden Observatory, Leiden University,
2300
RA Leiden,
The Netherlands
4
IRAM, 300 rue de la Piscine, Domaine Universitaire,
38406
Saint Martin d’Hères,
France
5
National Astronomical Observatory of China,
Datun Road 20,
Chaoyang,
Beijing, PR China
6
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1,
85748
Garching, Germany
7
Department of Chemistry, Ludwig Maximilian University,
Butenandtstr. 5-13,
81377
Munich,
Germany
8
UK Astronomy Technology Centre, Royal Observatory Edinburgh,
Blackford Hill,
Edinbugh
EH9 3HJ,
UK
9
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
10
Centre for Astrophysics and Planetary Science, University of Kent,
Canterbury,
CT2 7NH,
UK
11
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze,
Italy
12
School of Physics and Astronomy, The University of Leeds,
Woodhouse Lane,
Leeds
LS2 9JT,
UK
13
INAF – Osservatorio Astronomico di Cagliari,
Via della Scienza 5,
09047
Selargius (CA), Italy
14
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Strasse 77,
50937
Köln,
Germany
15
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México,
PO Box 3-72,
58090
Morelia,
Michoacán,
México
16
McMaster University,
1280 MAIN ST W,
L8S 4M1
Hamilton,
ON,
Canada
17
Astrophysics Research Institute, Liverpool John Moores University,
146 Brownlow Hill,
Liverpool
L3 5RF,
UK
Received:
19
February
2019
Accepted:
8
July
2019
Context. The formation process of high-mass stars (>8 M⊙) is poorly constrained, particularly the effects of clump fragmentation creating multiple systems and the mechanism of mass accretion onto the cores.
Aims. We study the fragmentation of dense gas clumps, and trace the circumstellar rotation and outflows by analyzing observations of the high-mass (~500 M⊙) star-forming region IRAS 23033+5951.
Methods. Using the Northern Extended Millimeter Array (NOEMA) in three configurations and the IRAM 30 m single-dish telescope at 220 GHz, we probe the gas and dust emission at an angular resolution of ~0.45′′, corresponding to 1900 au.
Results. In the millimeter (mm) continuum emission, we identify a protostellar cluster with at least four mm-sources, where three of them show a significantly higher peak intensity well above a signal-to-noise ratio of 100. Hierarchical fragmentation from large to small spatial scales is discussed. Two fragments are embedded in rotating structures and drive molecular outflows, traced by 13CO (2–1) emission. The velocity profiles across two of the cores are similar to Keplerian but are missing the highest-velocity components close to the center of rotation, which is a common phenomena from observations like these, and other rotation scenarios are not excluded entirely. Position–velocity diagrams suggest protostellar masses of ~6 and 19 M⊙. Rotational temperatures from fitting CH3CN (12K− 11K) spectra are used for estimating the gas temperature and thereby also the disk stability against gravitational fragmentation, utilizing Toomre’s Q parameter. Assuming that the candidate disk is in Keplerian rotation about the central stellar object and considering different disk inclination angles, we identify only one candidate disk as being unstable against gravitational instability caused by axisymmetric perturbations.
Conclusions. The dominant sources cover different evolutionary stages within the same maternal gas clump. The appearance of rotation and outflows of the cores are similar to those found in low-mass star-forming regions.
Key words: ISM: individual objects: IRAS 23033+5951 / ISM: kinematics and dynamics / ISM: jets and outflows / circumstellar matter / stars: formation / stars: massive
The reduced datacubes and maps are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/629/A10 or alternatively at http://www.mpia.de/core.
Based on observations carried out with the IRAM NOrthern Extended Millimeter Array (NOEMA). IRAM is supported by INSU/ CNRS (France), MPG (Germany), and IGN (Spain).
© F. Bosco et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
High-mass stars with masses exceeding 8 M⊙ contribute asignificant fraction of luminosity of star clusters and galaxies and thus shape their visual appearance (e.g., Motte et al. 2017). They also play a key role in the internal dynamics of stellar clusters, as they affect the motion of lower-mass stars by tidal interactions, which presumably leads to the removal of low-mass stars from the cluster centers, the so-called effect of mass segregation. Still, the formation process of these objects is poorly constrained by observations, which is due to the fact that high-mass stars typically form in a clustered mode and high-mass star-forming regions are on average located at large distances, on the order of a few kiloparsecs, limiting the linear spatial resolution (Zinnecker & Yorke 2007; Beuther et al. 2007; Tan et al. 2014). Also, high-mass stars are rare, have short formation timescales, and reach the main sequence while still deeply embedded in their parental molecular clump.
In the past, different models assuming high-mass star formation (HMSF) to be a consequence of a spherical collapse of a molecular gas clump (e.g., Kahn 1974; Wolfire & Cassinelli 1987) suggested a halting of the mass accretion due to high stellar radiation pressure once the mass of the high-mass protostellar object (HMPO) exceeds 40 M⊙. However, there is consensus in the ongoing discussion that the mass accretion onto the core is not halted immediately by the outward-acting stellar radiation pressure. Instead, HMPOs continue the mass accretion via circumstellar disks and the radiation can escape via outflow cavities (e.g., Yorke & Sonnhalter 2002; Arce et al. 2007; Vaidya et al. 2009; Krumholz et al. 2009; Kuiper et al. 2010, 2011, 2015, 2016; Kuiper & Hosokawa 2018; Klassen et al. 2016). Beltrán & de Wit (2016) summarize the observational properties of accretion disks in HMSF which are embedded in flattened rotating structures (103–104 au) and thereby circumvent the radiation pressure problem for ongoing mass accretion. This suggests that the formation scenario of high-mass objects is analogous to a scaled-up version of the low-mass star-forming process, that is, nonspherical mass accretion via circumstellar disks (e.g., Johnston et al. 2013, 2015; Cesaroni et al. 2014, 2017). Such an accretion scenario is presumably traced by an ordered molecular outflow, which is launched from the disk surface (e.g., Arce et al. 2007), as long as the accretion disk is stable. However, there is evidence from simulations (e.g., Peters et al. 2010a,b; Klassen et al. 2016; Rosen et al. 2016; Harries et al. 2017; Meyer et al. 2017, 2018) that the rotating structures around high-mass stars are unstable against self-gravity and tend to form spiral arms, which at sufficient local density will fragment to form companion objects (cf. the observations by Ilee et al. 2018). Recent work additionally suggests that also episodic accretion events in non-isotropic regions may explain the growth of HMPOs to masses exceeding the assumed mass limit of 40 M⊙ (e.g., Caratti o Garatti et al. 2017; Hunter et al. 2017; Motte et al. 2017). Such episodic accretion events in turn may on the one hand be explained by the accretion of disk fragments, as shown for example by Kratter & Matzner (2006) or Meyer et al. (2017). On the other hand, they may also be introduced by infall events of larger-scale gas streams (e.g., Gómez & Vázquez-Semadeni 2014; Vázquez-Semadeni et al. 2019). For example, Peretto et al. (2013) observed that HMSF regions tend to reside at the hubs of larger-scale (~ 1– 100 pc) filaments, along which material flows into the proto-cluster – predominantly onto the heaviest cores, which accrete the material competitively (see e.g., Tan et al. 2014; André et al. 2014; Motte et al. 2017, for reviews).
The Northern Extended Millimeter Array (NOEMA) large program CORE (Beuther et al. 2018) addresses open questions on fragmentation and disk formation during HMSF by investigating a sample of 20 high-mass star-forming regions at high spatial resolution in the cold dust and gas emission. The survey focuses on the early protostellar phase which is accompanied by molecular outflows and accretion disks within the dense cores of the parental clump. The sample sources were selected to have luminosities exceeding 104 L⊙ and are located within a maximum distance of 6 kpc, enabling a linear spatial resolution ≤ 3000 au for an angular resolution ≲0.5′′. As a pilot study, Beuther et al. (2012, 2013) investigated the HMSF regions NGC 7538 IRS1 and NGC 7538S. The overview paper (Beuther et al. 2018) presents the source sample, the spectral setup, and the goal of the survey, as well as the full continuum data from which they derive the fragmentation statistics in the 1.37 mm dust continuum emission. Mottram et al. (in prep.) investigate the connection of cores to the extended environments in the form of gas inflows by merging the interferometric with single-dish data from the IRAM 30 m telescope for W3IRS4. Furthermore, Ahmadi et al. (2018) provide a detailed description of the variety of molecular transitions covered with the survey setup, using the example of the chemically rich HMSF region W3(H2O), primarily focusing on the disk properties. Gieser et al. (in prep.) investigate the physical structure and chemical composition in the young, early hot core region AFGL2591 by combining IRAM 30 m and NOEMA data with a 1D physical–chemical model.
In this paper, we report the investigation of the high-mass star-forming region IRAS 23033+5951, also listed as G110.0931-00.0641 in the RMS survey catalog (Lumsden et al. 2013). This target is associated with the Cepheus Far molecular cloud complex (Harju et al. 1993). Lumsden et al. (2013) derived a kinematic distance of 4.3 kpc from the source velocity of − 53.1 km s−1 and a bolometric luminosity of Lbol = 1.7 × 104 L⊙. We note that we discard the older distance estimate of 3.5 kpc by Harju et al. (1993) which was assumed in previous publications on this region, since this estimate is based only on the association to the Cepheus Far group located at the less precise distance estimate of 3.5 kpc.
Maud et al. (2015) estimated the clump mass to be ~700 M⊙ based on SCUBA 850 μm data (Di Francesco et al. 2008) and BOLOCAM data (Ginsburg et al. 2013), whereas Beuther et al. (2018) derived a clump mass of ~500 M⊙ from the same SCUBA data. The differences are due to different assumptions on the gas temperature and opacity values. The region is associated with spatially distinct water and methanol masers (Beuther et al. 2002a; Schnee & Carpenter 2009), and with molecular gas emission (e.g., Wouterloot & Walmsley 1986). In particular, Beuther et al. (2002b) report the detection of a molecular outflow in CO emission.
Reid & Matthews (2008) present interferometric observations obtained from the Berkeley-Illinois-Maryland Association (BIMA) array at 3 mm wavelength and angular resolution of ≤5.5′′, revealing the fragmentation of the source into two millimeter (mm) clumps, denoted as MMS1 and MMS2. This fragmentation is also seen in SCUBA 850 μm data (Di Francesco et al. 2008). Schnee & Carpenter (2009) reveal further fragmentation of MMS1 into two major mm sources which we refer to as MMS1a in the north, coincident with a Midcourse Space Experiment (MSX) infrared point source (Reid & Matthews 2008), and MMS1b in the south (cf. Fig. 1). Emission in the centimeter (cm) regime was detected only towards a small region in MMS1 (Sridharan et al. 2002; Rodríguez et al. 2012), coincident with MMS1a, where Rodríguez et al. (2012) report the fragmentation of the 3.6 cm source into three regions, labeled VLA1–3. These latter authors discuss this finding as either condensations of an ionized jet or ultra-compact (UC) H II regions from different ionization sources. Both possibilities indicate the presence of at least one evolved HMPO. However, the conversion of their flux densities yields 8 GHz luminosities on the order of ≲1.1 × 1012 W Hz−1 and a comparison of these values to other cm sources from Fig. 6 of Hoare & Franco (2007) shows that these values are an order of magnitude too low to stem from an UCH II region. These findings therefore suggest that the cm emission traces a high-mass YSO wind or jet. Rodríguez et al. (2012) analyze the positions and velocities of water maser emission towards MMS1b and infer disk rotation. Modeling the data with an inclined disk model, they obtain a radius of 0.03′′ (135 au) and a position angle of 65° ± 1°. The best-fit disk is inclined by 83° ± 1° towards the line of sight and orbits about a central body with a mass of 19 M⊙. Schnee & Carpenter (2009) associate the methanol maser emission at 95 GHz with the emission peak in MMS2.
This paper is organized as follows. We report on the observations and the data reduction in Sect. 2. The observational results from the continuum and spectral line emission are presented in Sect. 3. In Sect. 3.6, we estimate protostellar masses from the disk kinematics and perform extensive tests in Appendix A. We discuss our observational results in the context of clump fragmentation, outflows, and disk stability in Sect. 4 and draw our conclusions in Sect. 5. We provide a summary sketch of our interpretation of the data in the concluding section.
 |
Fig. 1 Continuum emission towards IRAS 23033+5951 at 1.37 mm, with a phase center at RA 23h 05m 25. s00 and Dec +60° 08′ 15.′′49 (J2000.0). The black contours indicate the 5, 10, 15, 20σ levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The corresponding negative values are absent in the presented region. The white + and labels mark the mm sources identified by CLUMPFIND. The green, red, and blue symbols are cm point sources, H2 O masers (both Rodríguez et al. 2012), and methanol masers (Rodríguez-Garza et al. 2017), respectively. The shaded ellipse in the bottom left shows the synthesized beam of 0.45′′ × 0.37′′ (PA 47°). The small panels zoom in on the elongation of the core MMS1a (b,c), MMS1a (d), MMS1b (e), MMS1c (f) and MMS2a (g). |
2 Observations and data reduction
2.1 NOEMA
We observed the high-mass star-forming region IRAS 23033+5951 during five epochs between June 2014 and March 2016 using NOEMA at Plateau de Bure (France) in the A, B, and D array-configurations, with a phase center at RA 23h 05m 25. s00 and Dec +60° 08′ 15.′′49 (J2000.0). These observations are part of the NOEMA large program CORE (Beuther et al. 2018). The projected baselines range from 20 m up to 750 m and an example uv-coverage is presented in the survey overview (Beuther et al. 2018). The receivers were tuned to the 1.3 mm (220 GHz) band. The key molecular transition lines in this spectral window are summarized in Table 1. The spectral resolution of the broadband correlation units is 1.95 MHz or 2.7 km s−1 at 1.37 mm and we have eight narrow band units achieving 0.312 MHz or 0.42 km s−1 for a subset of the transitions. The complete set of spectral lines covered with this setup is described in detail in Ahmadi et al. (2018) and Mottram et al. (in prep.). The NOEMA observations were carried out in track-sharing mode with IRAS 23151+5912 and the calibration sources listed in Table 2.
2.2 IRAM 30 m telescope
Furthermore, IRAS 23033+5951 was observed with the IRAM 30 m telescope at Pico Veleta (Spain) in March 2016 in on-the-fly mode. Merging these single-dish data with the interferometric visibilities yields coverage of the uv -plane in the inner15 m. This is necessary to recover the extended emission which is filtered out by the interferometric observations. The single-dish data by themselves have an angular and spectral resolution of ~ 11′′ and 0.195 MHz or 0.27 km s−1 at 1.37 mm. In this work,only the 13CO (2–1) data were used for the combination. The process of merging the interferometric with the single-dish data is described in detail in Mottram et al. (in prep.).
2.3 Datareduction
The data were calibrated using the GILDAS/CLIC1 software. The respective sources for the calibration process are listed in Table 2. The imaging and deconvolution processes were conducted using GILDAS/MAPPING. The continuum data were imaged with uniform weighting to obtain a high spatial resolution, where the low number of channels containing spectral line emission were excluded by hand. We applied self-calibration on the continuum data using CASA (version 4.7.2, McMullin et al. 2007) to reduce the rms noise from 0.46 to 0.28 mJy beam−1 (cf. Beuther et al. 2018). For the spectral line cubes, we subtracted the continuum emission from the high-resolution narrow band data in the uv -domain and resampled to a spectral resolution of 0.5 km s−1. The resulting tables were imaged applying uniform weighting (robust weighting parameter of 0.1), and CLEANed with the HOGBOM algorithm. With this procedure, we achieved an angular resolution of 0.45′′ × 0.37′′ (position angle, PA 47°) for the continuum image and 0.43′′ × 0.35′′ (PA 61°) for the spectral line cubes. The continuum image has an rms noise of 0.28 mJy beam−1 and the corresponding values for the spectral line cubes are estimated from line-free channels and listed in Table 1. The merged data cube for 13CO (2–1) has an angular resolution of 0.8′′ × 0.67′′ (PA 52°) and a rms noise of 2.15 mJy beam−1.
Molecular line transitions analyzed in this paper.
Calibration sources for the interferometer data.
3 Observational results
3.1 Continuum emission at 1.37 mm
The continuum emission at 1.37 mm towards IRAS 23033+5951 presented in Fig. 1 shows three strong mm cores surrounded by a group of smaller structures. Following the approach conducted for the whole CORE sample in Beuther et al. (2018), we analyze this using the CLUMPFIND algorithm (Williams et al. 1994), with a detection threshold of 10σ = 2.8 mJy beam−1, as applied in Beuther et al. (2018). This algorithm is capable of disentangling substructures within the given threshold contour. The positions of all sources, as identified by CLUMPFIND, are summarized in Table 3 along with their inferred masses and column densities (see Sect. 3.2).
This analysis reveals the fragmentation of the mm sources from Reid & Matthews (2008): MMS1 hosts two of the major cores, denoted in the following as MMS1a in the north and MMS1b in the south, and one smaller condensation above the 10σ detection threshold, denoted as MMS1c. The two major cores are coincident with the northern two sources detected at 3 mm by Schnee & Carpenter (2009). The southern clump MMS2 shows one major core, MMS2a, being coincident with the third source at 3 mm by Schnee & Carpenter (2009). There are groups of 5σ detections towards the east and towards the north and east from MMS1a (panels a and b) and to the west of MMS2a (panel g). Furthermore, the core MMS1a shows some elongation towards the north (panel c). We discuss evidence of further fragmentation along with the insets of Fig. 1 in Sect. 4.1.
Position, mass, and column density estimates for the mm sources.
3.2 Core mass and column density estimates
The dust continuum flux density Sν of a core is proportional to the core mass M (Hildebrand 1983) via the following expression:
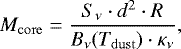 (1)
(1)
with the distance d towards the source, the gas-to-dust mass ratio R, the Planck function Bν as a function of the dust temperature Tdust, and the dust opacity κν. We integrate the flux density within the 5σ contours and compute core masses using the distance estimate of 4.3 kpc from the RMS survey (Lumsden et al. 2013). We note that we (consistent with Beuther et al. 2018) increase the canonical value of 100 for the gas-to-dust mass ratio to 150 to account for the contribution of elements heavier than H (Draine 2011, Table 23.1), which is furthermore reasonable since IRAS 23033+5951 resides at a galactocentric radius of ≳ 10 kpc where higher gas-to-dust mass ratios are expected (Giannetti et al. 2017). We assume the dust opacity to be κ1.37 mm = 0.9 cm2 g−1, which is in agreement with the estimate of Ossenkopf & Henning (1994) for dust grains with thin ice mantles for gas densities of 106 cm−3 of κ1.3 mm = 0.899 cm2 g−1. Beuther et al. (2018) estimated the clump-averaged gas temperature from H2CO spectral line fits and found Tgas = 55 K. Assuming that the dust is thermally coupled to the gas, that is Tdust ≈ Tgas, we use this temperature to estimate core masses and derive additional estimates for the two cores MMS1a and b from the respective core-averaged CH3CN rotational temperatures of Trot ≈ 70 and 100 K; see Sect. 3.5. The core mass estimates are presented in Table 3, along with the beam averaged H2 column densities, which we calculated from the peak intensity Ipeak using the following equation (Schuller et al. 2009):
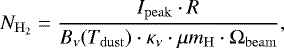 (2)
(2)
where μmH is the product of the mean molecular weight, assumed to be 2.8 (see appendix of Kauffmann et al. 2008), and the mass of atomic hydrogen mH, and Ωbeam is the beam solid angle. We furthermore compute H2 column density maps, presented in Fig. 8, using the map of mm continuum intensity Iν (Fig. 1) and the maps of rotational temperature Trot (Fig. 8, Sect. 3.5). All over the regions, where CH3CN emission is available for tracing gas (and dust) temperatures, the H2 column density values are above 1023 cm−2.
We notethat the inferred mass and column density estimates are only lower limits due to the flux filtering effect of interferometric observations. Beuther et al. (2018) estimate the percentage of missing flux to be 65% for this source and find the absolute flux scale over the entire survey to be correct within 20%; see their Table 3 and Sect. 4. Furthermore, the estimates are based on the assumption of optically thin continuum emission at 1.37 mm, which was confirmed by comparing brightness temperatures (~ 2 K) to rotational temperatures from fitting CH3CN spectra in Sect. 3.5 (see Fig. 8) and the gas temperature of Tgas = 22 K, obtained by Maud et al. (2015) from the analysis of C18O emission. In addition to this, we assume that there is no contribution from free–free emission, which may not necessarily be the case towards MMS1a with cm emission (see Sect. 4.3).
3.3 Spectral line emission: spectra and moment maps
The spectra of the three dominant cores MMS1a,b and 2a in Fig. 2 were averaged over the central 0.5′′ of each core to estimate the respective chemical composition. The parameters in Table 1 are given only for the transitions, which were analyzed in the context of kinematics, and were extracted from the CDMS2 (Müller et al. 2001, 2005; Endres et al. 2016) and LAMDA3 (Schöier et al. 2005) databases. The spectrum of MMS2a only shows spectral lines from comparably simple molecules like 13CO, H2CO, and CH3OH, all having upper energy levels ≲70 K. Compared to the emission from the other two cores, MMS2a emits only weakly <0.03 Jy beam−1. In contrast to this, the northern cores show a variety of species with stronger emission (≲ 0.1 Jy beam−1). Besides the C-bearing species from above, we also detect N-bearing species such as DCN, HC3N, HNCO, and CH3CN, and S-bearing species as SO and OCS towards these cores.
For the analysis of the spatial distribution, we present integrated line intensity maps (zeroth order moment) only for the transitions 13CO (2–1), CH3OH (4+2,2,0–3+1,2,0), DCN (30,0–20,0), H2CO (32,2–22,1) and (30,3–20,2), and SO (56 – 45) in Fig. 3, which all have a high S/N and trace different density regimes; cf. Table 1. Other transitions are not shown, as they do not provide further spatial information. The distribution of CH3CN is implicitly shown in Fig. 4, where the emission from all transitions is stacked and blanked below the 6σ level. As expected, we detect those transitions with a lower critical density in the regions far away from the main dense cores, as well as towards the dense cores where we also detect those transitions with higher critical densities. DCN follows the elongation of MMS1a to the north (panel c in Fig. 1). In the transitions 13CO (2–1), SO (56 –45), and H2CO (30,3–20,2) we identify an elongated structure through MMS1b at a position angle ϕ ≈315° from the north–south axis, marked by the dashed line in Fig. 3. We discuss this structure in the context of molecular outflows in Sect. 3.4.
We probe the kinematics of the clump MMS1 using maps of the intensity-weighted peak velocities (first-order moment), with closer zooms in Fig. 4. Towards MMS1b, we identify a velocity gradient in SO (56 –45), H2CO (30,3–20,2), and CH3OH (4+2,2,0–3+1,2,0) from northeast to southwest (ϕgrad ≈ 130°), from red- to blueshifted emission of ~ 5 km s−1 over an angular distance of ~ 2′′, corresponding to 8600 au. While CH3CN (123 –113) remains inconclusive, a similar gradient is seen in the combined map of the CH3CN (12K–11K) transitions (cf. Fig. 8). The gradient is oriented roughly perpendicular to the elongated structure, seen in the 13CO, H2CO and SO transitions mentioned above. Towards the northern core MMS1a, we identify a velocity gradient in east–west orientation for SO and CH3CN with ϕgrad ≈ 270°. In contrast to this, the remaining maps for the CH3OH, H2CO and DCN transitions do not show specific gradients.
In the right panel of Fig. 4, we present the spectral line width (second order moment). For CH3OH (4+2,2,0–3+1,2,0) and H2CO (30,3–20,2), these maps show larger line widths of 5–7 km s−1 towards the center of the cores, which indicates that the cores are fed by streams of gas and dust material or that YSOs in the cores launch outflows. In the SO (56 – 45) map, we additionally detect larger line widths ≳ 10 km s−1 along the elongated structure, where several velocity components from Fig. 5 are overlapping.
Towards the third core, MMS2a, we only report the detection of 13CO, H2CO and CH3OH transitions, as in the core-averaged spectra, at a similar systemic velocity. Due to the overall low S/N, we do not work on the kinematics of this core.
 |
Fig. 2 Spectra towards the three major cores from the broadband correlator unit data obtained from averaging the central 0.5′′ around the continuum emission peak. The spectral resolution in these bands is ~ 2.7 km s−1 or ~ 1.95 MHz. The molecule labels are given for the chemically rich core MMS1b. We note that the flux scale is smaller for MMS2a. Lines labeled with numbers are: (1) and (3) unidentified, (2) 33SO, (4) SO2, (5) 34SO2, (6) and (9) HNCO, (7) H |
3.4 Molecular outflows
Beuther et al. (2002b) report a large-scale outflow structure. They observed the emission of CO (2–1) towards IRAS 23033+5951 with the IRAM 30 m telescope, with an angular resolution of 11′′, corresponding to ~47 300 au. Their data show redshifted emission towards the southeast and blueshifted emission centered around the northern part of the clump with some tailing emission towards the northwest. We use 13CO (2–1) and SO (65–54) emission to identify and distinguish molecular outflows based on their collimation degree and to relate the outflows to the mm sources.
In Fig. 5, we present channel maps of the two transitions 13CO (2–1) and SO (56–45), tracing low-density gas. Furthermore, we make use of our merged data cube from NOEMA interferometric and the 30 m single-dish telescope data. We integrate the blue and redshifted line wings from − 70 to − 60 km s−1 and from − 46 to − 36 km s−1, respectively, i.e., over a range of Δv = 10 km s−1 each starting 7 km s−1 from the vLSR, and plot them over the continuum intensity, yielding Fig. 6. These velocity intervals contain the respective intervals for the blue and red outflow lobes from Beuther et al. (2002b).
In the channel maps in Fig. 5 we identify in several channels an elongated structure which is connected to MMS1b in both species. This structure is highlighted by blue and red arrows for blue and redshifted emission, respectively, and is elongated in the northwest to southeast direction (ϕout ≈ 315°, starting at the blueshifted side). The detection of blue- and redshifted velocity components on both sides of the core suggests that we see an outflow almost perpendicular to the line of sight (Cabrit & Bertout 1986; Cabrit et al. 1988). In contrast to this, the northern core MMS1a is not connected to components with velocities higher than ± 1 km s−1 from the vLSR. However, the analysis of the merged data set presented in Fig. 6 suggests the possibility that the blueshifted emission to the north belongs to a blue outflow lobe launched from MMS1a, where the respective red lobe matches the leftover red emission to the south. This candidate outflow appears to be considerably less collimated than the one launched from MMS1b and is seen under a projected position angle of ϕout ≈ 350°. This disentanglement is further discussed with the overall gas kinematics in Sect. 4.2.
The overall structure is in good agreement with the extended H2 emission found by Navarete et al. (2015; Fig. A130), observing the source with an H2 narrow band filter (λ = 2.122 μm, Δλ = 0.032 μm). In addition to the northwest to southeast elongation seen in 13CO emission, they detect additional emission towards the east of MMS1, but there is no information on whether this represents another outflow launched from this clump.
 |
Fig. 3 Spectral line emission from selected molecular species towards IRAS 23033+5951. For the integrated intensity (zeroth order moment) maps, the intensity was integrated over the ± 10 km s−1 around the vLSR = −53.1 km s−1 and above the 5σ threshold of each respective molecule. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The dashed ellipses in the lower left corner of each panel show the respective synthesized beam ≈ 0.43′′ × 0.35′′ (PA 61°). The dashed lines indicate an elongated structure through MMS1b. |
 |
Fig. 4 Spectral line emission towards IRAS 23033+5951. For the first (intensity-weighted peak velocity, left panels) and second-order moment maps (line width, right panels), the flux was integrated over the velocity range vLSR ± 10 km s−1, with vLSR = −53.1 km s−1, considering emission above the 5 σ threshold of each respective molecule. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The dashed ellipses in the lower left corner of each panel show the respective synthesized beam ≈ 0.43′′ × 0.35′′ (PA 61°). |
 |
Fig. 5 Channel maps of 13CO (2–1, top panels) and SO (56–45, bottom panels) emission in the interferometric data. The black contours are the 5, 10, and 15σ levels for the respective molecule, and the blue dotted contours are the corresponding negative values. The black + signs mark the position of the mm emission peaks of MMS1a and b. The blue and red arrows guide the eye to the direction of the respective Doppler-shifted emission. The shaded ellipse in the lower left corners indicate the synthesized beam of 0.44′′ × 0.36′′ (PA 61°) for both data cubes. |
3.5 Spectral line emission: derivation of gas properties and kinematics
The methyl cyanide CH3CN (12K–11K) transition set is a well-known tracer for the rotational temperature (Green 1986; Zhang et al. 1998; Araya et al. 2005). This quantity is a good approximation of the temperature of the surrounding gas and dust if the medium is in local thermodynamic equilibrium (LTE) and if CH3CN is coupled to the ambient medium. This is presumably the case for densities above the critical density ncrit ~ 4 × 106 cm−3 (Loren & Mundy 1984). We use the equivalent core radii from Beuther et al. (2018) to transfer the column densities from Table 3 into volume densities and obtain values ~ 5.0 × 107cm−3, well above the critical value, which confirms that the medium is in LTE.
We use XCLASS (eXtended CASA Line Analysis Software Suite, Möller et al. 2017) for fitting the CH3CN spectra. This package solves the radiative transfer equations for a medium in LTE, using the VAMDC4 and CDMS5 databases (Müller et al. 2001, 2005; Endres et al. 2016). From the XCLASS package, we use the XCLASSMAPFIT function, which fits the spectra from a data cube pixel-by-pixel, yielding best-fit parameter maps for rotational temperature, column density, peak velocity, and velocity dispersion.
Since significant emission, >6σ, is detected only towards small regions around the continuum emission peaks of the two major cores MMS1a and b, we consider only a 2.2′′ × 2.2′′ area around each core and extract the corresponding regions from the CH3CN (12K–11K, K = 0–6) data cube. Tests revealed that good fitting is achieved by a sequence of 300 iterations of the genetic algorithm and another 50 iterations of the Levenberg-Marquardt algorithm (see Möller et al. 2017, for descriptions). We note that the map fits include also the isotopologs of methyl cyanide and that we furthermore assume that the beam filling factor is 1 or, equivalently that the source size is much larger than the beam.
An example spectrum from the MMS1b continuum emission peak is presented in Fig. 7 along with the corresponding best fit. This fit shows slight systematic deviations from the data as it underestimates the peaks of the emission lines. A possible explanation for this are the “shoulder” features towards lower frequencies, indicating a second velocity component of the gas. However, not all spectra can be properly fitted with two distinct velocity components and we thus decided to adopt a single-component fit to obtain self-consistent parameter maps. An improvement was achieved only in a region of 5 × 5 pixels around the continuum emission peak, corresponding to about one synthesized beam. In this region the χ2 was reduced by ≤30%.
We present the resulting maps of the rotational temperature Trot in Fig. 8. The respective results for the relative velocity and line width are shown in the CH3CN panels in both Figs. 4 and 8. The general temperature structure towards both cores shows values as low as ~70 and ~ 100 K in the center, for MMS1a and b, respectively, and higher temperatures towards the edges up to ~ 300 K. Such strong deviations towards larger radii from the emission peak however are probably due to the lower S/N where the emission is just above the 6σ detection threshold. This makes it more difficult for the fitting procedure to solve the parameter ambiguity, for instance between gas column density and temperature, and the procedure may tend towards the limits of the parameter range, 600 K in this case. As deviations from the general trend, we identify no temperature increase towards the south and west of MMS1a and only a slight increase towards the east. Towards MMS1b the temperature estimates decrease from the central values down to ~ 40 K, towards the east, and to ~ 70 K, to the south-west. The analysis of the central 7 × 7 pixels of the cores yields temperatures of 70 ± 20 and 100 ± 40 K for MMS1a and b, respectively. We note that, although CH3CN may not be optically thin and therefore may trace slightly different layers of the region than the dust continuum emission, at the given high densities (~5.0 × 107cm−3) gas and dust should be closely coupled. Therefore, in the following we assume coupling of dust and gas and hence the same temperaturefor both.
 |
Fig. 6 Multiple outflow structures towards IRAS 23033+5951 as traced by 13CO (2–1)emission in the merged data cube. The gray-scale in the background shows the continuum intensity from Fig. 1. The blue and red contours present the integrated line wing emission from 13CO for the intervals of − 70 to − 60 km s−1 and − 46 to − 36 km s−1 (vLSR = −53.1 km s−1), respectively, starting at 55% and increasing in steps of 10% of the peak intensities Ipeak,blue = 0.78 Jy beam−1 km s−1 and Ipeak,red = 0.25 Jy beam−1 km s−1. The green contours show the continuum emission at 3.6 cm, reported by Beuther et al. (2002a), starting at 4 σ and increasing in steps of σ = 41.5 μJy beam−1 with an angular resolution of 1.04′′ × 0.62′′, and the yellow diamonds towards MMS1a mark the positions of the 3.6 cm emission peaks (Rodríguez et al. 2012) with an angular resolution of 0.31′′ × 0.25′′. The blue and red arrows are drawn by eye to guide the reader to the outflow lobes from MMS1a and b. The solid lines across the cores are drawn perpendicular and indicate the corresponding inferred disk major axes. The shaded ellipse in the lower left corner indicates the synthesized beam of 0.8′′ × 0.67′′ (PA 52°) of the merged 13CO (2–1) data. |
 |
Fig. 7 Spectrum of the CH3CN (12K – 11K,
K = 0– 6) transitions towards the continuum emission peak in MMS1b. The red curve indicates the best fit as obtained from the XCLASS procedures, with Trot = 85 K and |
 |
Fig. 8 Results of the radiative transfer modeling with XCLASS of the CH3CN (12K – 11K, K = 0– 6) data. The maps cover 2.2′′ × 2.2′′ extracted around the two major cores MMS1a and b, where pixels with flux below
|
 |
Fig. 9 Position–velocity diagrams for the H2CO (30,3 –20,2) transition towards the two major cores MMS1a and b from the NOEMA data, with a synthesized beam of ≈ 0.43′′ × 0.35′′ (PA 61°). The cut directions are shown in Fig. 8. The bottom right PV diagram is from a cut through MMS1b, perpendicular to the left cut and along the inferred outflow axis (see Sect. 3.4). The white contour shows the 4σ detection threshold. The black vertical and horizontal bars indicate the position of the continuum emission peak and the systemic velocity, respectively. Their lengths correspond to 1′′ ≈ 4300 au and 14 km s−1. The black dots indicate the detection with the most extreme velocity at each position. The black solid curves indicate the Keplerian velocities, corresponding to the mass estimates in Table 4. The black crosses in the lower right corners indicate the resolution elements along both axes. |
3.6 Position–velocity diagrams: protostellar mass estimates
We analyze the velocity structure by means of position–velocity (PV) diagrams (see Fig. 9) along the gradients in Fig. 4, where the PV cuts follow the arrows in the kinematics overview in Fig. 8. Before deriving protostellar mass estimates, we need to characterize the velocity profiles in the corresponding PV diagrams since the kinematic mass estimates presented below are based on the assumption that the material is in disk-like Keplerian rotation around the central young stellar object (YSO).
3.6.1 Characterization of velocity profiles
In Fig. 9, we plot PV diagrams of H2CO (30,3–20,2), which is a good tracer of the outer (rotating) structure. We note that we postpone the analysis of more typical high-density gas tracers such as CH3CN to the appendix (Appendix A.3.1) due to their comparably weak emission towards IRAS 23033+5951. Furthermore, the strong low-K emission lines of this molecule are blended, leaving only the weaker high-K lines for the analysis. Due to the lack of an unambiguous velocity gradient towards MMS1a, we present in Fig. 9 two PV diagrams for this core,with ϕ = 240° (counting from north to east, solid black line in Fig. 8) and ϕ =290° (dashed black line), where the second is motivated by the 13CO and CH3CN velocity gradient and the first is roughly perpendicular to the outflow axis and to the elongation of the cm emission.
We compare the PV diagrams in Fig. 9 to the results from Ohashi et al. (1997). In their Fig. 11, these latter authors show PV diagrams for rigid body rotation with and without infalling material and also the signature of Keplerian rotation without infall. In the infall-only scenario, the diagram is expected to be symmetric about both axes, which is only roughly the case in the 240° plot of MMS1a. However, the emission in the lower left and upper right quadrants dominate their counterparts, which is an indicator of rotation about the central YSO and also apparent in the other plots. At this point, we note that we cannot distinguish clearly between rigid body rotation with infall and Keplerian rotation, where both scenarios are expected to show emission almost only in two of the four quadrants. This is because of the spread of intensity due to the finite beam size – we find the highest velocities distributed over ~ 0.5′′ along the positional axis, which is roughly the beam size – which indicates that emission is spread into the other quadrants and that the underlying profile is thereby obscured.
The black curves in the plots indicate Keplerian rotation for a given protostellar mass (see Sect. 3.6.2 for details). The respective intensity distribution in the three plots is in qualitative agreement with a Keplerian rotation profile, but we do not detect emission at the highest expected velocities in the very center at the given sensitivities. This lack of the most extreme velocities may occur due to the limited sensitivity and spatial (and spectral) resolution – as Krumholz et al. (2007) showed with synthetic observations – or due to optical depth effects, either in the continuum or the lines, close to the central position such that emission from the central region is hidden. The effect of the limited spatial resolution was mentioned above and suggests that we may detect the highest velocities from the center but spread over the size of the synthesized beam. For both sources, we find the structure to follow the Keplerian velocity profile up to a radius of ~ 1′′ (4300 au). A comparison to other rotating disks and toroids around high-mass stars (Beltrán & de Wit 2016, Table 2) shows that this is a typical scale for objects of similar mass.
3.6.2 Kinematic mass estimates
Now assuming the scenario of Keplerian disk-like rotation around a central YSO, the mass of the latter is traced by the velocity distribution of the material, since the highest velocity at a given radial distance r to the center of mass is limited by the Kepler orbital velocity vKepler(r):
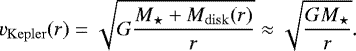 (3)
(3)
In this equation, G is the gravitational constant, M⋆ is the mass of the central object(s), and Mdisk(r) is the mass of the disk, enclosed inside the radius r. At this point, we assume that the gravitational potential is dominated by the central YSO and hence we neglect the disk-mass term in Eq. (3), where we conduct an a posteriori check on this assumption in the last paragraph of this subsection.
Seifried et al. (2016) presented a method for estimating the highest velocity at a given radial distance from the central object by evaluating PV diagrams. In Sect. 4.2 of this latter paper, the authors propose to start at the most extreme velocities for each position and iterate over the velocity channels until the first position–velocity pixel above a certain threshold is found. They find this method to be the most robust among those they tested on synthetic PV data where the true YSO mass was known.
We apply this method to the PV diagrams in Fig. 9 to estimate the highest velocity as a function of the radial distance to the central YSO (black diamonds) and to finally fit the result with a function of Keplerian tangential velocity, according to Eq. (3). For the fitting procedure, we use the PYTHON package ASTROPY.MODELING6 (Astropy Collaboration 2013). We add the parameters v0 ≈ vLSR and r0 to the model function to account for deviations in the local standard of rest (LSR) and for the resolution-limited position of the central object. A detailed description of the fit procedure is presented in Appendix A along with a variety of tests of this method to explore the effects of various parameters of the imaging process, such as the weighting parameter. The code is made available online7.
The curves in the PV diagrams of the H2CO (30,3–20,2) transition were obtained from this method choosing a detection threshold of 4σ. The best-fit parameters of the modeling procedure are listed in Table 4. The velocity and position offsets do not differ significantly from the literature value of vLSR = −53.1 km s−1 and the mm emission peak, varying only by fractions of a pixel size.
Mass estimates obtained from this method are uncertain (see Appendix A). An obvious source of uncertainty is the yet unconstrained disk inclination i, as we obtain only a fraction of the protostellar mass Mfit = M⋆ ⋅ sin2i (cf. e.g., Fig. 7 in Jankovic et al. 2019, for PV diagrams for three different inclinations). In fact, a comparison between the 240° panel of MMS1a with the panels for inclinations of i = 30° in Figs. 6 and 7 of Jankovic et al. (2019) suggests that we detect rotation under significant inclination towards this core, since we do not detect an emission gap around the vLSR between blue- and redshifted emission, which is expected for edge-on disk inclinations (cf. their Figs. 6 and 7). Deducing the presence of spiral arms from the substructure of emission in the diagram however, seems to be unreasonable due to the limited spatial resolution. This makes our mass estimate a lower limit with respect to inclination. A less accessible source of uncertainty however is the effect of the size of the synthesized beam or of line broadening, as mentioned above. These spread the emission in the spatial and velocity direction, respectively, thereby populating more extreme pixels in the PV diagrams, where the larger spread clearly provides larger mass estimates (cf. Fig. A.3). However, we refrain from characterizing this effect as we would need a deconvolution of the image prior to selecting the PV pixels from the data cube, and postpone a more extensive study of the uncertainties to a following paper by Ahmadi et al. (in prep.).
To improve the robustness of our estimate, we also include the transitions CH3CN (123 –113) and CH3OH (4+2,2,0–3+1,2,0) and compute the average mass from all estimates for a given core; see bottom rows in Table 4, where we weight with the respective model error. These provide significantly lower mass estimates than the H2CO-only estimates, because most of the molecules do not show such extended emission as H2CO and the overall S/N is lower, especially towards the more extreme velocities. For the core MMS1a, we included both PV cut angles in the averaging process and find that the ϕ = 290° estimate from H2CO of 6.3 ± 0.8M⊙ is in better agreement with the average estimate of 5.8 ± 0.3M⊙, in contrast to the ϕ = 240° estimate of 8.6 ± 0.6M⊙. Both estimates for the core MMS1b are in agreement with the 19 M⊙ YSO mass estimate, which Rodríguez et al. (2012) obtained from modeling H2 O maser emission.
We conduct an a posteriori check on the assumption from above that the contribution of the disk mass to the gravitational potential is negligible compared to the YSO mass M⋆. Therefore, we assume a typical gas density structure and  , neglecting the envelope contribution to the core mass. We assess a lower limit for the radius rdom out to which the rotating structure should be dominated by the central YSO, that is, M⋆ ≤ Mdisk(rdom). We use the core masses from Table 3 and the core radii of 5081 and 3915 au for MMS1a and b, respectively (Beuther et al. 2018, Table 5). If we now compare this to our YSO mass estimates from Table 4, we get an a posteriori confirmation and obtain that in MMS1b, the gravitational potential in the core should be completely dominated by the YSO, whereas in the case of MMS1a this is only true out to half the core radius, ~2000 au. However, this is only a lower limit as the MMS1a kinematic mass estimate should only be treated as a lower limit and thereby we argue that the disk mass should indeed be negligible in the analysis of these two cores. Still, we have to note that also the core masses are only lower limits due to the flux filtering effect.
, neglecting the envelope contribution to the core mass. We assess a lower limit for the radius rdom out to which the rotating structure should be dominated by the central YSO, that is, M⋆ ≤ Mdisk(rdom). We use the core masses from Table 3 and the core radii of 5081 and 3915 au for MMS1a and b, respectively (Beuther et al. 2018, Table 5). If we now compare this to our YSO mass estimates from Table 4, we get an a posteriori confirmation and obtain that in MMS1b, the gravitational potential in the core should be completely dominated by the YSO, whereas in the case of MMS1a this is only true out to half the core radius, ~2000 au. However, this is only a lower limit as the MMS1a kinematic mass estimate should only be treated as a lower limit and thereby we argue that the disk mass should indeed be negligible in the analysis of these two cores. Still, we have to note that also the core masses are only lower limits due to the flux filtering effect.
Best-fit parameters from the H2CO (30,3 –20,2) PV diagram evaluation.
3.6.3 Accelerating or decelerating material
We investigate the H2CO (30,3–20,2) emission forsignatures of in- or outflowing material. Therefore we create a PV diagram (see bottom right panel in Fig. 9) for this transition along the presumable MMS1b outflow axis (ϕ = 220°), obtained from the analysis in Sect. 3.4. We identify a signature in the lower-right quadrant of the corresponding PV diagramwith more blueshifted velocities towards larger radii to the northwest. This indicates that gas is either accelerating outwards or decelerating inwards, relative to the central velocity. Thus, this PV diagram suggests that the elongated structure represents either a feeding flow onto the core or a molecular outflow (see Sect 4.2 for further discussion).
4 Analysis and discussion
4.1 Hierarchical fragmentation
From the continuum emission at 1.37 mm in Fig. 1, we infer the fragmentation of IRAS 23033+5951, where the angular resolution of0.45′′ × 0.37′′ corresponds to a spatial resolution element of ~1900 au, at a distance of 4.3 kpc. In Sect. 3.1, we report that the mm source MMS1 (detected at an angular resolution of ~ 5′′, Reid & Matthews 2008), fragments into at least two cores. The three major cores, MMS1a, MMS1b, and MMS2a, are coincident with the 3 mm detections by Schnee & Carpenter (2009), but the lower-intensity structures, such as MMS1c, appear only in the high-angular-resolution, sensitive interferometric data presented in this work. We obtain a hierarchy of three levels of fragmentation in the HMSFR IRAS 23033+5951:
- 1.
Large-scale clumps with connected 1.37 mm continuum emission above the 5 σ detection limit: within the map of continuum emission, we have the two mm emission clumps MMS1 and MMS2, separated from each other by a projected distance of more than 20 000 au ≈ 0.1 pc.
- 2.
Separated cores within the major clumps: as identified by the CLUMPFIND algorithm, we find the MMS1 clump to be composed of at least two cores. The projected separations of the emission peaks are on the order 5000–9000 au.
- 3.
Indications towards further fragmentation: as mentioned above, we find indications of further clump fragments, that is, 5σ detections separated from the major cores by ~0.5−1.0″, corresponding to 2000–4000 au; see panels (b) and (g) in Fig. 1. However, with the given data there is no clear evidence for protostellar cores within these groups of weak sources.
4.1.1 Comparison to Jeans fragmentation
We derive the Jeans fragmentation length λJ and mass MJ using the mean density estimate for IRAS 23033+5951 from Beuther et al. (2002c) of 3.6 × 105 cm−3. We compute λJ and MJ for three dust temperature regimes, namely for cold dust with Tdust = 22 K (Maud et al. 2015), for the 55 K estimate from Beuther et al. (2018), and for the hot core dust temperatures Tdust ≈ 100 K, from Sect. 3.5. We note that the above dust temperatures are inferred from gas temperatures under the assumption that gas and dust are well coupled (i.e., Tdust ≈ Tgas), which is reasonable at the given high densities. We obtain 6000 au and 0.32 M⊙, 9500 au and 1.27 M⊙, and 12 500 au and 3.1 M⊙ for the three temperature regimes, respectively. The mass estimates of the three major cores (see Table 3) are significantly larger than the corresponding Jeans masses of the hot core temperature regime while the faint core MMS1c roughly has the Jeans mass for the intermediate temperature regime. This core is relatively close to MMS1b, at a projected distance of ~ 5200 au, and the projected distance between MMS1a and b of 9000 au is also smaller than expected from the Jeans analysis. However, we must note that the mass estimates from above entail large uncertainties due to the various underlying assumptions. A more extensive study of the fragmentation of a larger number of clumps is presented in Beuther et al. (2018).
4.1.2 Preferred axis of structure and fragmentation
Interestingly, the structure of IRAS 23033+5951 appears to be elongated along an axis from the north-northeast to the south-southwest. All three major structures lie on this axis and the minor cores are located not further away than 2′′. We seek larger-scale patterns and compare this to far-infrared (FIR) data from the Hi-GAL survey (Molinari et al. 2010); see Fig. 10 for the 160 μm emission. Inthese data, we find another source, IRAS 23031+5948, to be located along this axis, at about 3′ (corresponding to ~4 pc) to the south-southwest, with some intermediate emission forming a “bridge” between the two IRAS sources. In the IRAM 30 m single-dish observations, covering a field of view of 1.5′ × 1.5′, we find that the 13CO and C18O emission extends from the central clump towards the south-southwest, confirming a molecular connection to the other source.
Reid & Matthews (2008) analyze PV data along this axis, across IRAS 23033+5951, and report on a velocity gradient of ~ 4 km s−1 over ~ 40′′, seen in H13CO+ interferometric data. They interpret this as a large-scale rotation of a flattened structure with a major axis of about 0.5 pc. In the context of the larger-scale FIR emission, this may now also be interpreted as some kind of molecular accretion flow along a filamentary structure onto the major cores. A large-scale structure with a comparable velocity gradient towards G35.20-0.74N has been suggested to resemble either a flattened rotating object or a filamentary structure, where Sánchez-Monge et al. (2014) find the latter hypothesis to be the more plausible explanation for the regular fragmentation pattern. Another similar example of such a molecular flow onto high-mass protostellar cores on slightly smaller scales is presented by Mottram et al. (in prep.), reporting the flow of material along a molecular stream across several cores onto the most luminous core in W3 IRS4. Other examples of similar accretion flows are reported by, for example, Fernández-López et al. (2014), Peretto et al. (2014), and Tackenberg et al. (2014), or more recently by Lu et al. (2018), Veena et al. (2018), and Yuan et al. (2018).
However, further observational data covering the large-scale environment of IRAS 23033+5951 at a decent velocity resolution ≲ 1 km s−1 are required to analyze the gas kinematics and to finally address the question, whether or not this indeed indicates a larger-scale filamentary flow or a fragmentation scheme which is inherited from the larger scales.
 |
Fig. 10 Herschel/PACS observations at 160 μm towards IRAS 23033+5951 and IRAS 23031+5948, from the Hi-GAL survey (Molinari et al. 2010). |
4.2 Kinematics of the molecular gas
The mm source MMS1 shows a complex kinematic structure which is likely dominated by the two cores MMS1a and b at the scale of the angular resolution of the presented data (~ 0.45′′, corresponding to 1900 au).
4.2.1 Disentanglement of molecular outflows and characterization of velocity gradients
To disentangle the complex kinematic structure of this region, we consider the velocity gradients from Sect. 3.3, the PV diagrams from Fig. 9, and the molecular outflow structure from Sect. 3.4 along with the continuum emission at 3.6 cm (Beuther et al. 2002a; Rodríguez et al. 2012) and the maser analysis by Rodríguez et al. (2012) for the following cores.
The core MMS2a
Molecular outflows are often found as symmetric structures centered around their launching core. The emission of the outflow-tracing species 13CO and SO however does not reveal any outflow structure towards the position of the core MMS2. Therefore, we have no evidence that MMS2a has already launched a molecular outflow. Interesting is, however, the detection of Class I methanol masers at 44 GHz (70 – 61, Rodríguez-Garza et al. 2017) and 95 GHz (80–71, Schnee & Carpenter 2009), exclusively towards the west and north-east of MMS2a but not towards MMS1 (cf. Fig. 1). These Class I masers indicate the presence of shocked gas (e.g., Leurini et al. 2016), an implication that is difficult to address for MMS2a with our data. Furthermore, the emission of the dense-gas tracers is too weak towards this core to infer any velocity gradient in the dense gas. In the following, we therefore focus on the northern two cores MMS1a and b, both hosting outflow-driving protostellar candidates.
The core MMS1b
The characterization of the core MMS1b is the least ambiguous one, since we have identified a well-defined outflow axis at a projected position angle ϕout ≈ 315°. The interpretation as a molecular outflow is consistent with 13CO and SO channel maps and the outwards-accelerating structure, which we found in the corresponding panel of the H2CO PV diagrams along the outflow axis. Furthermore, we see a strong velocity gradient of ~ 5 km s−1 over ~ 2′′ across this core (black arrow in Fig. 8), which is oriented perpendicular to the presumed outflow axis at ϕgrad ≈ 230°. Rodríguez et al. (2012) analyzed the H2O maser group M1 in terms of disk rotation. The best-fit disk model has a radius of 0.03′′, corresponding to 135 au, and a position angle of 65° ± 1° which is in agreement with the inferred velocity gradient in the outer rotating structure. We note that the position of this maser group (Rodríguez et al. 2012) deviates slightly from the MMS1b mm emission peak. However, this deviation of only half the beam width is below the resolution of our data.
The collected information suggests an outflow axis roughly perpendicular to the rotating structure in the core with Δϕ = 70°–85°. Since outflows are launched from circumstellar disks (e.g., Kölligan & Kuiper 2018), these findings consistently suggest the presence of a disk-outflow system in MMS1b.
However, it is not clear yet to what extent the velocity gradient stems from a circumstellar disk in Keplerian rotation and/or from the rotation of the protostellar envelope. To address this question, we can use the emission of dense gas tracing molecules like CH3OH and CH3CN. In the zoomed-in velocity maps in Fig. 4, we see the gradient for CH3CN, with ϕgrad ≈ 225° (cf. Fig. 8), whereas the lower-density gas tracing molecules differ in the position angle. This indicates that the signal from these latter molecules has some contributionfrom envelope material either flowing inward to be accreted onto the core or flowing outward to be removed from the core in form of a molecular outflow.
The core MMS1a
In contrast to MMS1b, we do not clearly identify an elongated but narrow molecular emission structure towards the core MMS1a in the integrated intensity maps in Fig. 3 or in the channel maps in Fig. 5. If we assume that the blue- and redshifted emission, which does not appear to belong to the collimated outflow from MMS1b, stems from an outflow from MMS1a, then we can reconstruct the outflow axis in Fig. 6. As these two lobes cover large areas, we state the position angle as ϕout ≈ 350° with large uncertainties of ~ ±30°. A comparison of these two lobes in Fig. 6 to the large-scale outflow lobes from Fig. 1 in Beuther et al. (2002b) suggests that MMS1a and MMS1b together form the large-scale outflow structure seen in their data with lower spatial resolution. In this picture, MMS1a launches a large-scale and less collimated outflow, in contrast to the scenario in which MMS1b launches a collimated outflow. However, the jet-scenario for the cm emission does not support this outflow axis, as the VLA1–VLA3 axis is tilted by 70–80° with respectto it (see Fig. 8). This latter finding is in better agreement with cm emission stemming from an ionized disk-like structure, but this is discussed further in Sect. 4.3.
4.2.2 Stability of Keplerian disks
Simulations of the formation of high-mass stars suggest that these objects accrete mass via massive disks, which tend to form spiral arms and fragment under self-gravity (e.g., Meyer et al. 2017, 2018). In this section, we now analyze the rotating structures in the dominant cores in terms of fragmentation by the gravitational collapse due to possible instabilities against axisymmetric perturbations. Implicitly, we assume that the rotating structures are disks in equilibrium and in Keplerian rotation, which is a reasonable assumption from the results in Sect. 3.6. For this analysis, we make use of the stability criterion for a self-gravitating disk, derived by Toomre (1964):
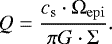 (4)
(4)
In this equation, cs is the local speed of sound, Ωepi is the epicyclic frequency, G is the gravitational constant and Σ is the disk surface density. Toomre (1964) found that rotating disks are unstable against axisymmetric perturbations for Q ≲ Qcrit = 1. We note that the exact critical value is under current debate, as for example Binney & Tremaine (2008) report critical values up to Qcrit ~ 2, when applying different assumptions on the disk temperature and density profiles. In contrast to this, the studies by for example Behrendt et al. (2015) showed that the critical value drops below 0.7 for sech2 density profiles of the disk in z direction. Takahashi et al. (2016) revised the general picture towards spiral arm formation in protoplanetary disks for Q ≲ 1, where these spiral arms fragment only if the arm-internal Q drops below 0.6; see their Fig. 1. This value has been confirmed by the simulations of Klassen et al. (2016) and Meyer et al. (2018), who found that only regions with Q < 0.6 indeed startfragmentation. With the discussion above in mind, we conduct the following Toomre Q stability analysis with Qcrit = 1 and a stable (unstable) regime for a larger (smaller) values of Q, where the unstable regime indicates potential spiral arm formation, eventually leading to fragmentation, if the local Q drops below 0.6.
We calculate maps of the Q parameter for the inner 2.2′′ × 2.2′′ around the peaks of mm continuum emission for the two major cores MMS1a and b. Again, we exclude MMS2a from the analysis due to the absence of CH3CN emission, resulting in insufficient information on the gas excitation temperature towards this core. We compute maps for each of the three variables, using the following equations:
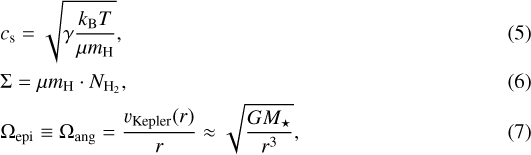
with the adiabatic coefficient γ ≈ 7∕5 for primarily diatomic gas, Boltzmann’s constant kB, the dust temperature T, the mean molecular mass μmH, the molecular hydrogen column density 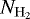 , the Keplerian angular velocity Ωang, and the Kepler orbital velocity vKepler(r) from above. For the map of the speed of sound, we again use the temperature maps in Fig. 8 which we assume to be equal to the dust temperature, as discussed above. We obtain the surface density Σ by multiplying the H2 column density map in Fig. 8 with the mean molecular weight μmH, where we again emphasize that we computed the H2 column density under the assumption of thermal coupling between the CH3CN line emitting gas and the dust. The epicyclic frequency is identically equal to the angular velocity Ωang, in the case of Keplerian rotation (Pringle & King 2007), where this is computed from the mass estimates in Table 4 and a map of the orbital distance to the central HMPO. We note that the epicyclic frequency is treated as a lower limit, since the kinematic mass estimates are lower limits, as mentioned above, and that the surface density is treated as lower limits due to flux filtering effects. Further considerations on the computation of the individual parameters are presented in Appendix B.
, the Keplerian angular velocity Ωang, and the Kepler orbital velocity vKepler(r) from above. For the map of the speed of sound, we again use the temperature maps in Fig. 8 which we assume to be equal to the dust temperature, as discussed above. We obtain the surface density Σ by multiplying the H2 column density map in Fig. 8 with the mean molecular weight μmH, where we again emphasize that we computed the H2 column density under the assumption of thermal coupling between the CH3CN line emitting gas and the dust. The epicyclic frequency is identically equal to the angular velocity Ωang, in the case of Keplerian rotation (Pringle & King 2007), where this is computed from the mass estimates in Table 4 and a map of the orbital distance to the central HMPO. We note that the epicyclic frequency is treated as a lower limit, since the kinematic mass estimates are lower limits, as mentioned above, and that the surface density is treated as lower limits due to flux filtering effects. Further considerations on the computation of the individual parameters are presented in Appendix B.
In the next step, we plug all three maps into Eq. (4) and estimate a pixel-by-pixel map of Toomre’s Q parameter for the two main mm sources, as presented in Fig. 11 for the three disk inclination angles i = 10°, 45° and 80°. In the resulting Toomre Q parameter maps (Fig. 11), the stable regions are colored blue, the critical values are shown in yellow, and the unstable regions are shown in red. We note that the presented values are physically relevant only inside the dashed ellipses indicating the projected extent of the disk, as traced by rotation (cf. Fig. 9).
Considering the almost face-on disk scenario (i = 10°, top panels in Fig. 11), the two cores already differ significantly. For the southern core MMS1b, the Q values drop into the critical regime only in the outer parts of the candidate disk, see the solid and dashed ellipses indicating assumed disk radii of 2150 and 4300 au, respectively. In contrast to this, the candidate disk around MMS1a shows Q values in the yellowish critical regime of ~1, especially the one towards the southwest, thereby indicating the potential for spiral arm formation.
Towards intermediate disk inclinations i ~ 45°, the Q values tend to decrease globally, as the deprojection of the orbital distance and the HMPO mass cause the epicyclic frequency Ωepi to decrease towards larger orbital distances and especially faster along the disk minor axis due to the deprojection of r (see mid panels in Fig. 11). In these maps, we identify the MMS1a disk to be essentially in a critical to unstable condition in the inner parts, and also for MMS1b we identify parts of the inner disk region to be partially in the critical regime. However, the Q parameters tend to increase again towards higher disk inclinations, i ~ 80°, as the deprojection of the column density reduces the disk surface density significantly, yielding higher values for Q. The maps are comparable to the low-i maps as the region inside the inner ellipses only shows values in the critical to stable regime for MMS1b, and for MMS1a we find a similar structure as for i ~ 10°. However, due to the deprojection, most parts of both images are now located at radial distances beyond 4000 au, making it unlikely that they are still part of a disk-like structure. We furthermore note that the outflow and the disk models for MMS1b of Rodríguez et al. (2012) suggest the corresponding candidate disk to be highly inclined with i ≳ 80° and therefore make it likely that the candidate disk in this core is stable against such a fragmentation at the spatial resolution of our observations. Still, we note that the presented Toomre analysis is highly uncertain, especially towards nearly edge-on (i > 80°) disk scenarios due to the deprojection terms (see Eq. (B.3)).
In summary, we find that only the rotating structure in MMS1a may be unstable to axisymmetric perturbations eventually forming spiral-arm features and fragmenting due to local gravitational collapse under the assumptions that (1) it is a disk in equilibrium and in ordered, Keplerian-like rotation and (2) that the CH3CN line-emitting gas is well thermally coupled to the dust and can therefore accurately trace the dust temperature. However, though we identify potentially unstable regions, we do not find evidence for actually ongoing disk fragmentation in our data.
4.3 Origin of the cm emission
Beuther et al. (2002a) and Rodríguez et al. (2012) reported emission at 3.6 cm towards MMS1a, with an angular resolution of 1.04′′ × 0.62′′ and 0.31′′ × 0.25′′, respectively. This radio emission structure is elongated in the east–west direction with a position angle of ϕcm ≈ 285° and Rodríguez et al. (2012) found it to be fragmented into three sources VLA1–3. The intermediate source, VLA2, is coincident with the emission peak of MMS1a and Obonyo et al. (2019) found that the spectral index of αCQ = 0.33 ± 0.14 of this source closely matches the thermal emission, where these latter authors derive the index by comparison of C- (6 cm) and Q-band (7 mm) flux. The other two cm sources VLA1 and 3, however, have slightly negative spectral indices of αCQ = −0.11 ± 0.07 and − 0.14 ± 1.49 (Obonyo et al. 2019). The uncertainties are sufficiently high as to prevent us from solving the ambiguity of whether these two sources trace an ionized jet (as suggested by Rodríguez et al. 2012) or rather an ionized disk wind (as suggested by the conversion of their flux densities to 8 GHz luminosities on the order of ≲ 1.1 × 1012W Hz−1 and a comparison of these values to other cm sources from Fig. 6 of Hoare & Franco 2007). We note that these 8 GHz luminosities of VLA1 are two orders of magnitude lower than typical UCH II regions and thus make this option unlikely; nonetheless, they indicate the presence of at least one high-mass YSO.
We furthermore note that the 3.6 cm emission is not well aligned with the still uncertain outflow axis of MMS1a but is well aligned with the velocity gradient seen in CH3CN (see Fig. 8). This suggests that either both trace circumstellar rotation with the cm emission originating from the disk surface, or both follow an acceleration, where the cm emission originates from a jet and the CH3CN gas is tracing potentially entrained gas (as also found by Leurini et al. 2011; Busquet et al. 2014; Palau et al. 2017). This scenario indicates that MMS1a may be launching two outflows, one seen in 13CO and the other one traced by the cm emission, where this latter one is also capable of explaining the additional H2 emission to the east, observed by Navarete et al. (2015). Even though the latter scenario appears to be the more likely one, we do not find clear evidence for excluding one of the two scenarios.
 |
Fig. 11 Maps of Toomre’s Q parameter towards MMS1a and b. The color scale indicates the value of Toomre’sQ parameter, where blue is Toomre-stable, yellow is critical, and red regions are gravitationally unstable against axisymmetric perturbations, where the level of Qcrit = 1 is indicated by the red dashed contours. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The solid and dashed gray ellipses show the deprojected radii of the disks with diameter 4300 and 8600 au, respectively. The black diamonds in the MMS1a panels mark the positions of the emission peaks at 3.6 cm (Rodríguez et al. 2012). Top panels: Q parameter maps of the two cores for the rotating disk structures seen almost face-on (i = 10°). Motivated by the disk inclination estimate of iMMS1b ~ 80° (Rodríguez et al. 2012), we also present maps for such disk inclinations (bottom panels) and intermediate values (i = 45°, middle panels). For the deprojection process, the angles of the disk major axes of ϕmaj,MMS1a ≈ 240° and ϕmaj,MMS1b ≈ 230° (relative to the north–south axis, see text) were used. The shaded ellipse in the lower right corner indicates the synthesized beam of the CH3CN data of 0.42′′ × 0.35′′ (PA 61°). |
 |
Fig. 12 Summary of the structure of IRAS 23033+5951. The fragmentation into four cores in two groups is depicted by the black spheres. Circumstellar rotation is indicated by arrows and the inferred outflow lobes are indicated by blue and red cones. The masses of the cores MMS1a–c and 2a are 23.5, 10.0, 1.2, and 11.4 M⊙. The three high-mass cores show evidence to be in more and more evolved stages, going from south to north. |
4.4 Evolutionary stages
Throughout the previous analysis, we found evidence for differences in the evolutionary stages of the three dominant cores. The chemical composition indicates an early, rather cool evolutionary stage of MMS2a, as we do not detect transition lines with upper state energies larger than 70 K. Along with missing signatures of outflowing material (cf. Sect. 4.2.1 and the summary Fig. 12), this suggests that MMS2a is still in a deeply embedded and cooler stage than the other two sources and is presumably in the earliest evolutionary stage of the three major cores.
In contrast to this, we detect CH3CN transitions towards MMS1b with upper-state energy levels ≳ 100 K. This core shows a richer chemical composition with N- and S-bearing molecules and a probable disk-outflow system, where the outflow is collimated, suggesting a stable circumstellar disk or rotating structure. Rodríguez et al. (2012) traced this disk structure at the scales <200 au with H2O (22 GHz) maser emission.
The third core, MMS1a, again differs significantly from the other two as there is cm emission and no maser emission. Even though we cannot clearly distinguish whether the cm emission stems from a jet or disk winds, this detection suggests that the YSO within this core is in a later evolutionary stage than those in the other two cores. The detection of CH3CN is weaker in this source than towards MMS1b presumably due to radiation destroying the more complex molecules, but may also be explained by an overall lower core temperature.
The above-mentioned sequence is reminiscent of the situation in the star-forming clump NGC 7538S (Feng et al. 2016), one of the pathfinder sources for the CORE program. NGC 7538S was also resolved into three cores along one main direction with an apparent evolutionary age gradient.
Finally, we discuss the cores in IRAS 23033+5951 in the context of the evolution of outflow structure. In their Fig. 4, Beuther & Shepherd (2005) suggested that the appearance of outflows evolves along with the following two observables of the HMPO, the evolution of the surrounding H II region, and the spectral type of the HMPO, where less compact H II regions and earlier spectral types tend to have less collimated outflow cavities. This evolution, that is the outflow broadening with time, is confirmed by simulations (e.g., Peters et al. 2011; Vaidya et al. 2011; Kuiper et al. 2015, 2016; Kuiper & Hosokawa 2018; Kölligan & Kuiper 2018) showing that strong ionizing stellar flux makes it less likely to build up a stable disk and thereby a stable magnetic field which is crucial to the launching process of a jet. The low collimation of the molecular outflow may also be due to unresolved binaries or multiple-star systems in which the massive bodies disturb the outflow-launching region with the same result (Peters et al. 2014). These authors furthermore find that the collimated outflows from a group of YSOs, which share similar outflow axes due to the conservation of angular momentum from earlier phases, eventually add up to form what is observed as a poorly collimated outflow. Thereby, the finding of this outflow structure may point towards the presence of multiple YSOs in a given core. In Sect. 4.2.1, we assign two outflows, one to each of the mm sources MMS1a and b. We discussed above that MMS1a with the less collimated large-scale outflow and with cm emission is likely in a more evolved stage than the YSO(s) within MMS1b. This is consistent with the outflow evolution with time or evolutionary stage as suggested by Beuther & Shepherd (2005).
5 Conclusion
We studied the high-mass star-forming region IRAS 23033+5951, addressing open questions to the formation of high-mass stars. As part of the CORE survey, the region was observed with NOEMA in the A, B, and D configurations with short spacings from the IRAM 30 m single-dish telescope, in the 220 GHz or 1.37 mm spectral window.
The dust continuum emission was used for estimating core masses and H2 column densities, and the molecular gas emission for analyzing the kinematic components of the cloud. For instance, the 13CO (2–1) transition was used for investigating the outflow structure and the H2CO (30,3–20,2) transition was used for studying rotating structures. The masses of embedded protostars were investigated by analyzing PV diagrams across these rotating objects. For the two most massive cores, we carried out radiative transfer modeling of a methyl cyanide (12K–11K) cube with XCLASS and the resulting maps of rotational temperature were used for the calculation of pixel-by-pixel Toomre Q parameter maps.
The 1.37 mm dust continuum observations reveal hierarchical fragmentation of the parental cloud into a group of at least four mm sources, where the inferred structure is summarized in Fig. 12 along with rotation and outflow features of particular cores. The source MMS1c is of low mass (1.2M⊙) and is an order of magnitude less dense than the other cores (3.2 × 1023 cm−2). The other three pre- or protostellar cores have H2 column densities from 1.62 to 4.28× 1024 cm−2 and dominate the mm emission. They indicate three different evolutionary stages within one maternal gas clump:
-
Towards the southern core MMS2a (M = 11.4M⊙), we detect only emission of spectral lines excited at low temperatures (<70 K). We identify no significant rotation of the core and no connection to a molecular outflow. This suggests that the core is in the earliest evolutionary stage of the three most massive cores.
-
Compared to this, MMS1b (M = 10.0M⊙) is warmer, as spectral lines are detected with upper energy levels ≳ 100 K, and is chemically rich, as N- and S-bearing species are also detected. The molecular emission indicates core rotation and the PV diagram shows a Keplerian-like rotation profile tracing a candidate disk, which is essentially Toomre-stable against gravitational fragmentation at the spatial scales traced by our observations. Furthermore, this object drives a rather collimated outflow, seen in 13CO and SO.
-
The analysis of the presumably most evolved core, MMS1a (M = 23.5M⊙), suggests that the central object(s) is (are) driving an outflow with a wide opening angle, indicating the presence of one or more HMPOs. Associated with this core, the cm emission likely indicates nonthermal emission in the close vicinity of the HMPO(s). The candidate disk indicates Toomre-instability in the inner 2000 au.
The spatial resolution of the presented observations, ~ 0.45′′ ≈ 1900 au, cannot reveal fragmentation at smaller scales relevant for the analysis of the typically high multiplicity of high-mass stars. The results of this work support a scenario where high-mass stars form by similar processes to their low-mass counterparts, only scaled up, where the mass accretion onto the protostars continues via disk-like rotating structures and the outflows decollimate with protostellar evolution.
Acknowledgements
We thank the referee for the suggestions, which significantly clarified the analysis and structure of the paper. F.B., H.B., A.A. and J.C.M. acknowledge support from the European Research Council under the Horizon 2020 Framework Program via the ERC Consolidator Grant CSF-648505. Furthermore, the team thanks IRAM and its staff for conducting the large program CORE. R.K. acknowledges financial support via the Emmy Noether Research Group on Accretion Flows and Feedback in Realistic Models of Massive Star Formation funded by the German Research Foundation (DFG) under grant no. KU 2849/3-1 and KU2849/3-2. D.S. acknowledges support by the Deutsche Forschungsgemeinschaft through SPP 1833: “Building a Habitable Earth” (SE 1962/6-1). A.S.M. is partially supported by the German Research Foundation (DFG) through grant SFB956 (subproject A6). A.P. acknowledges financial support from UNAM-PAPIIT IN113119 grant, México.
Appendix A Position–velocity diagram fits
A.1 Estimating extreme velocities
The Keplerian velocity profile is described by Eq. (3) and is an upper limit to the line-of-sight velocity at a given radial distance from the center of rotation, the supposed protostellar object. Seifried et al. (2016) present an approach using this relation for an estimate of the protostellar mass. They compare different methods for estimating the maximum velocity at a given distance to the protostellar object from PV diagrams and find that the most robust one is the following (see their Sect. 4.2):
- 1.
estimate the noise level σ;
- 2.
estimatethe two (opposing) quadrants with the strongest emission;
- 3.
iterate over positions:
- (a)
begin with the channel of highest (lowest) velocity while being in the quadrant of positions with higher (lower) velocities than the vLSR;
- (b)
iterate towards lower (higher) velocity channels until the first pixel with flux above a chosen threshold, for example 4 σ, is found;
- (c)
add the PV coordinates of this pixel to a list (for later analysis).
- (a)
A.2 Fitting a Keplerian velocity profile
We follow this method and collect a set of radial positions and corresponding maximum velocities, which we pass to a PYTHON least-squares optimization function. To account for the uncertainties in the core position and the systemic velocity vLSR, we expand Eq. (3) by the positional shift r0 and the velocity shift v0 = vLSR. Furthermore, we introduce a sign-function to account for the opposite velocity difference from the vLSR of the blue- and redshifted emission on the respective sides of the emission peak, and a “±” representing the sign change due to the respective positive or negative velocity offset at the starting position. Thus, we yield the following expression:
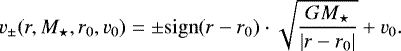 (A.1)
(A.1)
We use the PYTHON package ASTROPY.MODELING8 (Astropy Collaboration 2013) and create a custom model for v(r, M⋆, r0, v0) from Eq. (A.1). This model is fitted to the PV data via Levenberg-Marquardt least-squares fitting, within the PYTHON package KEPLERFIT9. We collect the best-fit parameters, the respective standard deviations, and the integrated χ2 as a measure of the residuals.
A.3 Analysis of uncertainties
The outcome of this fitting procedure depends strongly on the input parameters. Therefore, we tested how the detection threshold, the different chemical species, the size of a flagged central region, and the imaging of the data themselves affect the fit estimates.
A.3.1 Effect of detection threshold and chemical species
The estimate of the extreme velocities is dependent on the detection threshold. Therefore, if we choose a lower detection threshold (e.g., 3σ) the algorithm estimates higher relative velocity offsets and the derived YSO mass is expected to be higher. In contrast to this, the absolute velocity offset vLSR is supposed to be the same, since the relative velocity offsets should increase symmetrically. We see this effect in the parameters in Fig. A.1, where the mass estimates for the 4 σ detection threshold are smaller or similar to the corresponding 3 σ estimates. The absolute velocity offsets agree well in general, but for MMS1a we see a Δv ~ 0.8 km s−1 in the H2CO transition. This difference may be due to the strong asymmetry between blue- and redshifted emission for MMS1a.
 |
Fig. A.1 Best-fit estimates of kinematic mass (top) and systemic velocity (bottom) for thresholds of 3 and 4 σ for the YSO mass and velocity (vLSR), respectively.The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
Different molecular transition lines usually trace different regimes of density and temperature; see for instance Table 1. Therefore, we compare the fit of the H2CO (30,3–20,2) low-temperature gas-tracing line to the CH3CN (123 –113) high-temperature gas-tracing line. We expect that the H2CO is detected towards larger distances from the YSO, whereas the CH3CN line should trace the closer rotational structure. We see this detection constraint in the results, where CH3CN gives mass estimates a factor of ~ 2 lower than the corresponding H2CO fit. This is expected to be due to the overall lower S/N in the CH3 CN data.
A.3.2 Effect of flagging the innermost data points
The PV diagrams in Fig. 9 do not show the highest velocities close to the center of rotation which are expected from the assumption of Keplerian rotation. This may be due to filtering effects during the observation (Krumholz et al. 2007). A second explanation for this nondetection may be the suppression of the highest velocity due to a presence of an unresolved binary or multiple YSO system (Peters et al. 2014) or due to higher optical thickness in line or continuum emission towards the central region. Therefore, we test how flagging these innermost data points affects the outcome of the fit, applying a detection threshold of 4 σ.
Parameters for synthesized beam and rms noise of the images from different weighting schemes and the merged data set.
While this yields a significant decrease in the fit residual (bottom panel in Fig. A.2), thereis a trend of the mass estimate for both cores, as we obtain a higher mass estimate (≳ 20%). The velocity offset differs only on the order of 0.4 km s−1 and the position offset r0 varies well below the resolution limit ~1900 au. Therefore, we suggest to flag the innermost data points in the case of a constant extreme velocity in the center, while keeping in mind that the mass estimate from the nonflagged fit yields a lower limit.
A.3.3 Effect of the merging and imaging process
The H2CO (30,3–20,2) is also covered in the IRAM 30 m single-dish data. Therefore, we are able to test how merging the data (in different weighting schemes) affects the outcome of the fit. In general, more natural weighting schemes result in larger beam sizes, which smooths outthe resulting image, and in a higher S/N. On the other hand, the more extended and lower-density structures are represented by the shorter baselines which are better represented in the more natural weighting scheme. We compare the results from three weighting schemes: natural and robust with the two weight thresholds of 1 and 0.1 (corresponding to uniform weighting) for both the interferometric-only data set and the merged data set. The size of the synthesized beams and the rms noise are given in Table A.1 for all of these images.
The results of this comparison are presented in Fig. A.3. We see the expected trend from the variation of the weighting schemes, where the flux filtering effect and the lower S/N should be the main reasons for the lower mass estimates towards the more robust weighting schemes. In the fits to the merged data sets, we usually do not identify the highest velocities close to the candidate YSO, since the flux is smoothed over the positions. This results in lower mass estimates when comparing the merged to the interferometric-only data. In contrast to this, the deviations of the position and velocity offsets are weak and show no trend. Both stay well below or close to the resolution limits of 1900 au and 0.5 km s−1. In the plot of the residuals however, we see a clear trend towards lower χ2 values for the more robust weighting schemes, which is due to the detection of the higher velocities towards the center, whereas for the naturally weighted images this nondetection yields a significant deviation between data and fit, close to r0.
 |
Fig. A.2 Best-fit results for the tests of flagging the inner region around the YSO. The routine was applied to the PV diagrams from the H2CO (30,3 –20,2) image. The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
We suggest that a robust weighting scheme should be preferred to a natural one, since the Keplerian velocity distribution is only seen in the (dense-material tracing) robust weighting schemes. This yields a lower limit which we find to be a factor of 3 ± 1.5 below the corresponding larger estimates from the other weighting schemes.
 |
Fig. A.3 Best-fit results for PV diagrams from different weighting schemes. The results are presented for three weighting parameters of the merged data set and for the interferometric data. Within both series, the weighting schemes are natural, robust with a weight threshold of 1 and robust with a weight threshold of 0.1 (uniform); see Table A.1. The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
A.4 Dependency on disk inclination
From the velocity field in the candidate disks, only the radial component is traced in red- and blueshifted fractions of the emission lines. Therefore, the inclination acts as a limit to the mass estimate described above. In this section we derive the dependence of this estimate on the disk inclination i relative to the line of sight. For consistency, we stick to the definition from Sect. 4.2.2 and define the inclination of the disk to be 0° if the disk is seen face-on. In this case, the radial component vrad of the velocity field decreases to almost zero, since the Keplerian velocity component acts only in the plane of rotation:
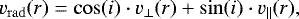 (A.2)
(A.2)
where the component v∥ = vKepler is the Keplerian velocity component in the disk plane and where the perpendicular component assumed to be negligible (v⊥ ≈ 0). Thus, we indeed measure Mfit = M ⋅ sin2i with that method:
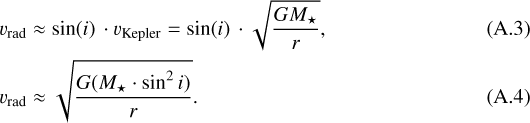
We note that this mass scaling factor should not make a significant difference for the estimate of protostellar mass for MMS1b, since the high disk inclination causes only a factor of sin 2(80°) ≈ 0.97. For the northern source MMS1a however, the mass may be underestimated by a factor of 1∕ sin2(45°) = 2 or even more.
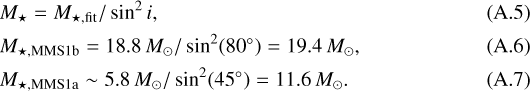
We summarize that this method yields only a lower limit to the YSO mass for cases in which the disk inclination is not known.
Appendix B Toomre Q maps
In this section, we describe in detail how we compute the parameter maps for the Toomre Q analysis taking into account the a priori unknown disk inclination.
The computation of disk surface density Σ and epicyclic frequency Ωepi maps is less straight-forward than for the map for the speed of sound, as both quantities are affected by the yet poorly constrained disk inclination i, where we define i to have value 0° for disks seen face-on and 90° for disks seen edge-on. The mass estimate to be plugged into Eq. (7) relates to the inclination i as M⋆ = Mfit∕sin2i. On the other hand, the projected orbital distance  to the YSOat the mm emission peak in the image can be computed from the distances Δx and Δy in pixel coordinates which are converted into a projected physical distance by the pixel size and the source distance of 4300 pc. We use a disk model as sketched in Fig. B.1, where the position angle ϕ0 of the disk major axis is given with respect to the north–south axis (y-axis) and counterclockwise. We compute the deprojected orbital distance by scaling up the distance in the direction perpendicular to the disk major axis,
to the YSOat the mm emission peak in the image can be computed from the distances Δx and Δy in pixel coordinates which are converted into a projected physical distance by the pixel size and the source distance of 4300 pc. We use a disk model as sketched in Fig. B.1, where the position angle ϕ0 of the disk major axis is given with respect to the north–south axis (y-axis) and counterclockwise. We compute the deprojected orbital distance by scaling up the distance in the direction perpendicular to the disk major axis, 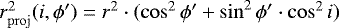 , where ϕ′ is the position angle in the rotated system, with
, where ϕ′ is the position angle in the rotated system, with 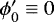 . This expression yields r = rproj for i = 0° and diverges for i ~ 90° towards directions perpendicular to the disk major axis, that is, towards ϕ′ ~ 90°.
. This expression yields r = rproj for i = 0° and diverges for i ~ 90° towards directions perpendicular to the disk major axis, that is, towards ϕ′ ~ 90°.
 |
Fig. B.1 Sketch of the inclined disk ellipse model for the initialization of the map of the deprojected radius, which was used to obtain a map of the epicyclic frequency Ωepi. |
The computation of a map for the disk column density is uncertain as we cannot distinguish the contributions from the protostellar envelope or the disk material to the observed column density Σobs. At this point we assume that the largest fraction originates from the rotating disk material. However, we note that this remains a source of large uncertainty in our disk stability analysis, as the Q parameter increases with smaller disk column density, where this would result from removing the protostellar envelope contribution. We also note that the column density traces the disk column density best in a face-on disk scenario. We address this deprojection by applying the low-order approximation Σdisk ≈ cos i ⋅ Σobs, which was found to be a fair approximation for disks with typical density vertical and horizontal density structures (Kee et al. 2018). For large disk inclinations however, the columns trace a range of disk radii simultaneously and therefore only allow for rough estimates of the local disk column density, presumably rendering the analysis impossible for disks seen under an inclination i > 80°.
Summarizing the above considerations regarding the effect of the inclination i, we obtain the following relation:
![\begin{align*} Q_{\mathrm{obs}} &= \frac{c_{\mathrm{s}} \cdot \Omega_{\mathrm{epi,obs}}(i, \phi')}{\pi G \cdot \Sigma_{\mathrm{obs}}(i)} \\[1pt] &= \frac{c_{\mathrm{s}} \cdot \Omega_{\mathrm{epi}}}{\pi G \cdot \Sigma} \cdot \frac{\sin i \cdot \left( \cos^2 \phi' + \sin^2 \phi' \cos^2 i \right)^{-3/4}}{\cos^{-1} i} \\[1pt] &= Q_{\mathrm{real}} \cdot \frac{\sin i \cdot \cos i}{\left( \cos^2 \phi' + \sin^2 \phi' \cos^2 i \right)^{3/4}}.\end{align*}](/articles/aa/full_html/2019/09/aa35318-19/aa35318-19-eq15.png)
References
- Ahmadi, A., Beuther, H., Mottram, J. C., et al. 2018, A&A, 618, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 27 [Google Scholar]
- Araya, E., Hofner, P., Kurtz, S., Bronfman, L., & DeDeo, S. 2005, ApJS, 157, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., Shepherd, D., Gueth, F., et al. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 245 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Behrendt, M., Burkert, A., & Schartmann, M. 2015, MNRAS, 448, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., & de Wit, W. J. 2016, A&ARv, 24, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Shepherd, D. 2005, Astrophys. Space Sci. Lib., 324, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Walsh, A., Schilke, P., et al. 2002a, A&A, 390, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002b, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002c, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 165 [Google Scholar]
- Beuther, H., Linz, H., & Henning, T. 2012, A&A, 543, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Linz, H., & Henning, T. 2013, A&A, 558, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Mottram, J. C., Ahmadi, A., et al. 2018, A&A, 617, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton: Princeton University Press) [Google Scholar]
- Busquet, G., Lefloch, B., Benedettini, M., et al. 2014, A&A, 561, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrit, S., & Bertout, C. 1986, ApJ, 307, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., Goldsmith, P. F., & Snell, R. L. 1988, ApJ, 334, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Caratti o Garatti, A., Stecklum, B., Garcia Lopez, R., et al. 2017, Nat. Phys., 13, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Galli, D., Neri, R., & Walmsley, C. M. 2014, A&A, 566, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R., Sánchez-Monge, Á., Beltrán, M. T., et al. 2017, A&A, 602, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Francesco, J., Johnstone, D., Kirk, H., MacKenzie, T., & Ledwosinska, E. 2008, ApJS, 175, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, S., Beuther, H., Semenov, D., et al. 2016, A&A, 593, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernández-López, M., Arce, H. G., Looney, L., et al. 2014, ApJ, 790, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Giannetti, A., Leurini, S., König, C., et al. 2017, A&A, 606, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Glenn, J., Rosolowsky, E., et al. 2013, ApJS, 208, 14 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gómez, G. C., & Vázquez-Semadeni, E. 2014, ApJ, 791, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S. 1986, ApJ, 309, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Harju, J., Walmsley, C. M., & Wouterloot, J. G. A. 1993, A&AS, 98, 51 [NASA ADS] [Google Scholar]
- Harries, T. J., Douglas, T. A., & Ali, A. 2017, MNRAS, 471, 4111 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hoare, M. G., & Franco, J. 2007, Astrophys. Space Sci. Proc., 1, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Brogan, C. L., MacLeod, G., et al. 2017, ApJ, 837, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Ilee, J. D., Cyganowski, C. J., Brogan, C. L., et al. 2018, ApJ, 869, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Jankovic, M. R., Haworth, T. J., Ilee, J. D., et al. 2019, MNRAS, 482, 4673 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. G., Shepherd, D. S., Robitaille, T. P., & Wood, K. 2013, A&A, 551, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, K. G., Robitaille, T. P., Beuther, H., et al. 2015, ApJ, 813, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Kahn, F. D. 1974, A&A, 37, 149 [NASA ADS] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kee, N. D., Owocki, S., & Kuiper, R. 2018, MNRAS, 479, 4633 [NASA ADS] [CrossRef] [Google Scholar]
- Klassen, M., Pudritz, R. E., Kuiper, R., Peters, T., & Banerjee, R. 2016, ApJ, 823, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kölligan, A., & Kuiper, R. 2018, A&A, 620, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K. M., & Matzner, C. D. 2006, MNRAS, 373, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2007, ApJ, 665, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuiper, R., & Hosokawa, T. 2018, A&A, 616, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2010, ApJ, 722, 1556 [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2011, ApJ, 732, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Yorke, H. W., & Turner, N. J. 2015, ApJ, 800, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Turner, N. J., & Yorke, H. W. 2016, ApJ, 832, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Leurini, S., Codella, C., Zapata, L., et al. 2011, A&A, 530, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Menten, K. M., & Walmsley, C. M. 2016, A&A, 592, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loren, R. B., & Mundy, L. G. 1984, ApJ, 286, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, X., Zhang, Q., Liu, H. B., et al. 2018, ApJ, 855, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Hoare, M. G., Urquhart, J. S., et al. 2013, ApJS, 208, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Maud, L. T., Lumsden, S. L., Moore, T. J. T., et al. 2015, MNRAS, 452, 637 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
- Meyer, D. M. A., Vorobyov, E. I., Kuiper, R., & Kley, W. 2017, MNRAS, 464, L90 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M.-A., Kuiper, R., Kley, W., Johnston, K. G., & Vorobyov, E. 2018, MNRAS, 473, 3615 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Möller, T., Endres, C., & Schilke, P. 2017, A&A, 598, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Louvet, F., & Nguyen Lu’O’Ng, Q. 2017, in Formation, Evolution, and Survival of Massive Star Clusters, eds. C. Charbonnel & A. Nota, IAU Symp., 316, 9 [NASA ADS] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Navarete, F., Damineli, A., Barbosa, C. L., & Blum, R. D. 2015, MNRAS, 450, 4364 [NASA ADS] [CrossRef] [Google Scholar]
- Obonyo, W. O., Lumsden, S. L., Hoare, M. G., et al. 2019, MNRAS, 486, 3664 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, N., Hayashi, M., Ho, P. T. P., & Momose, M. 1997, ApJ, 475, 211 [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palau, A., Walsh, C., Sánchez-Monge, Á., et al. 2017, MNRAS, 467, 2723 [NASA ADS] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Fuller, G. A., André, P., et al. 2014, A&A, 561, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., et al. 2010a, ApJ, 711, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Klessen, R. S., Mac Low, M.-M., & Banerjee, R. 2010b, ApJ, 725, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., & Mac Low, M.-M. 2011, ApJ, 729, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Klaassen, P. D., Mac Low, M.-M., et al. 2014, ApJ, 788, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & King, A. 2007, Astrophysical Flows (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Reid, M. A., & Matthews, B. C. 2008, ApJ, 675, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, T., Trinidad, M. A., & Migenes, V. 2012, ApJ, 755, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Garza, C. B., Kurtz, S. E., Gómez-Ruiz, A. I., et al. 2017, ApJS, 233, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, A. L., Krumholz, M. R., McKee, C. F., & Klein, R. I. 2016, MNRAS, 463, 2553 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Monge, Á., Beltrán, M. T., Cesaroni, R., et al. 2014, A&A, 569, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnee, S., & Carpenter, J. M. 2009, ApJ, 698, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., Sánchez-Monge, Á., Walch, S., & Banerjee, R. 2016, MNRAS, 459, 1892 [Google Scholar]
- Shirley, Y. L. 2015, PASP, 127, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Schilke, P., Menten, K. M., & Wyrowski, F. 2002, ApJ, 566, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Tackenberg, J., Beuther, H., Henning, T., et al. 2014, A&A, 565, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, S. Z., Tsukamoto, Y., & Inutsuka, S. 2016, MNRAS, 458, 3597 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 149 [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Vaidya, B., Fendt, C., & Beuther, H. 2009, ApJ, 702, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Vaidya, B., Fendt, C., Beuther, H., & Porth, O. 2011, ApJ, 742, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Veena, V. S., Vig, S., Mookerjea, B., et al. 2018, ApJ, 852, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Palau, A., Ballesteros-Paredes, J., Gómez, G. C., & Zamora-Avilés, M. 2019, MNRAS, submitted [arXiv:1903.11247] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., & Cassinelli, J. P. 1987, ApJ, 319, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Wouterloot, J. G. A., & Walmsley, C. M. 1986, A&A, 168, 237 [NASA ADS] [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, J., Li, J.-Z., Wu, Y., et al. 2018, ApJ, 852, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Ho, P. T. P., & Ohashi, N. 1998, ApJ, 494, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
Grenoble Image and Line Data Analysis Software, www.iram.fr/IRAMFR/GILDAS/
Cologne Database for Molecular Spectroscopy, www.cdms.de
Leiden Atomic and Molecular Database, www.strw.leidenuniv.nl/~moldata
VAMDC consortium, http://www.vamdc.org
Cologne Database for Molecular Spectroscopy, www.cdms.de
PYTHON package ASTROPY.MODELING, http://docs.astropy.org/en/stable/modeling/
KEPLERFIT, https://github.com/felixbosco/KeplerFit
PYTHON package ASTROPY.MODELING, http://docs.astropy.org/en/stable/modeling/
KEPLERFIT, https://github.com/felixbosco/KeplerFit
All Tables
Parameters for synthesized beam and rms noise of the images from different weighting schemes and the merged data set.
All Figures
 |
Fig. 1 Continuum emission towards IRAS 23033+5951 at 1.37 mm, with a phase center at RA 23h 05m 25. s00 and Dec +60° 08′ 15.′′49 (J2000.0). The black contours indicate the 5, 10, 15, 20σ levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The corresponding negative values are absent in the presented region. The white + and labels mark the mm sources identified by CLUMPFIND. The green, red, and blue symbols are cm point sources, H2 O masers (both Rodríguez et al. 2012), and methanol masers (Rodríguez-Garza et al. 2017), respectively. The shaded ellipse in the bottom left shows the synthesized beam of 0.45′′ × 0.37′′ (PA 47°). The small panels zoom in on the elongation of the core MMS1a (b,c), MMS1a (d), MMS1b (e), MMS1c (f) and MMS2a (g). |
| In the text | |
 |
Fig. 2 Spectra towards the three major cores from the broadband correlator unit data obtained from averaging the central 0.5′′ around the continuum emission peak. The spectral resolution in these bands is ~ 2.7 km s−1 or ~ 1.95 MHz. The molecule labels are given for the chemically rich core MMS1b. We note that the flux scale is smaller for MMS2a. Lines labeled with numbers are: (1) and (3) unidentified, (2) 33SO, (4) SO2, (5) 34SO2, (6) and (9) HNCO, (7) H |
| In the text | |
 |
Fig. 3 Spectral line emission from selected molecular species towards IRAS 23033+5951. For the integrated intensity (zeroth order moment) maps, the intensity was integrated over the ± 10 km s−1 around the vLSR = −53.1 km s−1 and above the 5σ threshold of each respective molecule. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The dashed ellipses in the lower left corner of each panel show the respective synthesized beam ≈ 0.43′′ × 0.35′′ (PA 61°). The dashed lines indicate an elongated structure through MMS1b. |
| In the text | |
 |
Fig. 4 Spectral line emission towards IRAS 23033+5951. For the first (intensity-weighted peak velocity, left panels) and second-order moment maps (line width, right panels), the flux was integrated over the velocity range vLSR ± 10 km s−1, with vLSR = −53.1 km s−1, considering emission above the 5 σ threshold of each respective molecule. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The dashed ellipses in the lower left corner of each panel show the respective synthesized beam ≈ 0.43′′ × 0.35′′ (PA 61°). |
| In the text | |
 |
Fig. 5 Channel maps of 13CO (2–1, top panels) and SO (56–45, bottom panels) emission in the interferometric data. The black contours are the 5, 10, and 15σ levels for the respective molecule, and the blue dotted contours are the corresponding negative values. The black + signs mark the position of the mm emission peaks of MMS1a and b. The blue and red arrows guide the eye to the direction of the respective Doppler-shifted emission. The shaded ellipse in the lower left corners indicate the synthesized beam of 0.44′′ × 0.36′′ (PA 61°) for both data cubes. |
| In the text | |
 |
Fig. 6 Multiple outflow structures towards IRAS 23033+5951 as traced by 13CO (2–1)emission in the merged data cube. The gray-scale in the background shows the continuum intensity from Fig. 1. The blue and red contours present the integrated line wing emission from 13CO for the intervals of − 70 to − 60 km s−1 and − 46 to − 36 km s−1 (vLSR = −53.1 km s−1), respectively, starting at 55% and increasing in steps of 10% of the peak intensities Ipeak,blue = 0.78 Jy beam−1 km s−1 and Ipeak,red = 0.25 Jy beam−1 km s−1. The green contours show the continuum emission at 3.6 cm, reported by Beuther et al. (2002a), starting at 4 σ and increasing in steps of σ = 41.5 μJy beam−1 with an angular resolution of 1.04′′ × 0.62′′, and the yellow diamonds towards MMS1a mark the positions of the 3.6 cm emission peaks (Rodríguez et al. 2012) with an angular resolution of 0.31′′ × 0.25′′. The blue and red arrows are drawn by eye to guide the reader to the outflow lobes from MMS1a and b. The solid lines across the cores are drawn perpendicular and indicate the corresponding inferred disk major axes. The shaded ellipse in the lower left corner indicates the synthesized beam of 0.8′′ × 0.67′′ (PA 52°) of the merged 13CO (2–1) data. |
| In the text | |
 |
Fig. 7 Spectrum of the CH3CN (12K – 11K,
K = 0– 6) transitions towards the continuum emission peak in MMS1b. The red curve indicates the best fit as obtained from the XCLASS procedures, with Trot = 85 K and |
| In the text | |
 |
Fig. 8 Results of the radiative transfer modeling with XCLASS of the CH3CN (12K – 11K, K = 0– 6) data. The maps cover 2.2′′ × 2.2′′ extracted around the two major cores MMS1a and b, where pixels with flux below
|
| In the text | |
 |
Fig. 9 Position–velocity diagrams for the H2CO (30,3 –20,2) transition towards the two major cores MMS1a and b from the NOEMA data, with a synthesized beam of ≈ 0.43′′ × 0.35′′ (PA 61°). The cut directions are shown in Fig. 8. The bottom right PV diagram is from a cut through MMS1b, perpendicular to the left cut and along the inferred outflow axis (see Sect. 3.4). The white contour shows the 4σ detection threshold. The black vertical and horizontal bars indicate the position of the continuum emission peak and the systemic velocity, respectively. Their lengths correspond to 1′′ ≈ 4300 au and 14 km s−1. The black dots indicate the detection with the most extreme velocity at each position. The black solid curves indicate the Keplerian velocities, corresponding to the mass estimates in Table 4. The black crosses in the lower right corners indicate the resolution elements along both axes. |
| In the text | |
 |
Fig. 10 Herschel/PACS observations at 160 μm towards IRAS 23033+5951 and IRAS 23031+5948, from the Hi-GAL survey (Molinari et al. 2010). |
| In the text | |
 |
Fig. 11 Maps of Toomre’s Q parameter towards MMS1a and b. The color scale indicates the value of Toomre’sQ parameter, where blue is Toomre-stable, yellow is critical, and red regions are gravitationally unstable against axisymmetric perturbations, where the level of Qcrit = 1 is indicated by the red dashed contours. The black contours indicate the 5, 10, 15, 20σ continuum emission levels and increase further in steps of 20σ, where σ = 0.28 mJy beam−1. The solid and dashed gray ellipses show the deprojected radii of the disks with diameter 4300 and 8600 au, respectively. The black diamonds in the MMS1a panels mark the positions of the emission peaks at 3.6 cm (Rodríguez et al. 2012). Top panels: Q parameter maps of the two cores for the rotating disk structures seen almost face-on (i = 10°). Motivated by the disk inclination estimate of iMMS1b ~ 80° (Rodríguez et al. 2012), we also present maps for such disk inclinations (bottom panels) and intermediate values (i = 45°, middle panels). For the deprojection process, the angles of the disk major axes of ϕmaj,MMS1a ≈ 240° and ϕmaj,MMS1b ≈ 230° (relative to the north–south axis, see text) were used. The shaded ellipse in the lower right corner indicates the synthesized beam of the CH3CN data of 0.42′′ × 0.35′′ (PA 61°). |
| In the text | |
 |
Fig. 12 Summary of the structure of IRAS 23033+5951. The fragmentation into four cores in two groups is depicted by the black spheres. Circumstellar rotation is indicated by arrows and the inferred outflow lobes are indicated by blue and red cones. The masses of the cores MMS1a–c and 2a are 23.5, 10.0, 1.2, and 11.4 M⊙. The three high-mass cores show evidence to be in more and more evolved stages, going from south to north. |
| In the text | |
 |
Fig. A.1 Best-fit estimates of kinematic mass (top) and systemic velocity (bottom) for thresholds of 3 and 4 σ for the YSO mass and velocity (vLSR), respectively.The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
| In the text | |
 |
Fig. A.2 Best-fit results for the tests of flagging the inner region around the YSO. The routine was applied to the PV diagrams from the H2CO (30,3 –20,2) image. The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
| In the text | |
 |
Fig. A.3 Best-fit results for PV diagrams from different weighting schemes. The results are presented for three weighting parameters of the merged data set and for the interferometric data. Within both series, the weighting schemes are natural, robust with a weight threshold of 1 and robust with a weight threshold of 0.1 (uniform); see Table A.1. The error bars are the standard deviations from the least-squares fits. The horizontal line in the velocity plot is the systemic velocity of the source IRAS 23033+5951. |
| In the text | |
 |
Fig. B.1 Sketch of the inclined disk ellipse model for the initialization of the map of the deprojected radius, which was used to obtain a map of the epicyclic frequency Ωepi. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.