| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321058 | |
| Published online | 13 March 2013 | |
Radio to gamma-ray variability study of blazar S5 0716+714
1 Max-Planck-Institut für Radioastronomie (MPIfR), Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: brani@mpifr-bonn.mpg.de
2 Astrophysical Institute, Department of Physics and Astronomy, Ohio University Athens, OH 45701, USA
3 Centre for Space Research, North-West University, Potchefstroom Campus, 2531 Potchefstroom, South Africa
4 Université Bordeaux 1, CNRS/IN2p3, Centre d’Études Nucléaires de Bordeaux-Gradignan, 33175 Gradignan, France
5 Astronomy Department, University of Michigan, Ann Arbor, MI 48109-1042, USA
6 Istituto Nazionale di Fisica Nucleare, Sezione di Padova, 35131 Padova, Italy
7 Dipartimento di Fisica e Astronomia, Università di Padova, 35131 Padova, Italy
8 Dept. of Astronomy and Astrophysics, Penn State University, University Park, PA 16802, USA
9 Department of Physical Sciences, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, 739-8526 Hiroshima, Japan
10 FÖMI Satellite Geodetic Observatory, PO Box 585, 1592 Budapest, Hungary
11 Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences, 1121 Budapest, Hungary
12 Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, 263 129 Nainital, India
13 Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA
14 Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, 739-8526 Hiroshima, Japan
15 IRAM, 300 rue de la piscine, 38406 Saint-Martin d’Hères, France
16 Aalto University Metsähovi Radio Observatory, Kylmälä, Finland
17 Xinjiang Astronomical Observatory, Chinese Academy of Sciences, 150 Science 1-Street, 830011 Urumqi, PR China
18 Cahill Center for Astronomy and Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA
19 Instituto de Radioastronomía Milimétrica (IRAM), Avenida Divina Pastora 7, Local 20, 18012 Granada, Spain
20 CAB, INTA-CSIC, Ctra. de Torrejón a Ajalvir, km 4, 28850, Torrejón de Ardoz, Madrid, Spain
21 Purdue University, Department of Physics, 525 Northwestern Ave, West Lafayette, IN 47907, USA
22 Department of Astronomy, Kyoto University, Kitashirakawa-Oiwake-cho, Sakyo-ku, 606-8502 Kyoto, Japan
23 Astro Space Center of Lebedev Physical Institute, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received: 8 January 2013
Accepted: 29 January 2013
We present the results of a series of radio, optical, X-ray, and γ-ray observations of the BL Lac object S50716+714 carried out between April 2007 and January 2011. The multifrequency observations were obtained using several ground- and space-based facilities. The intense optical monitoring of the source reveals faster repetitive variations superimposed on a long-term variability trend on a time scale of ~350 days. Episodes of fast variability recur on time scales of ~60−70 days. The intense and simultaneous activity at optical and γ-ray frequencies favors the synchrotron self-Compton mechanism for the production of the high-energy emission. Two major low-peaking radio flares were observed during this high optical/γ-ray activity period. The radio flares are characterized by a rising and a decaying stage and agrees with the formation of a shock and its evolution. We found that the evolution of the radio flares requires a geometrical variation in addition to intrinsic variations of the source. Different estimates yield robust and self-consistent lower limits of δ ≥ 20 and equipartition magnetic field Beq ≥ 0.36 G. Causality arguments constrain the size of emission region θ ≤ 0.004 mas. We found a significant correlation between flux variations at radio frequencies with those at optical and γ-rays. Theoptical/GeV flux variations lead the radio variability by ~65 days. The longer time delays between low-peaking radio outbursts and optical flares imply that optical flares are the precursors of radio ones. An orphan X-ray flare challenges the simple, one-zone emission models, rendering them too simple. Here we also describe the spectral energy distribution modeling of the source from simultaneous data taken through different activity periods.
Key words: galaxies: active / BL Lacertae objects: individual: S5 0716+714 / gamma rays: galaxies / X-rays: galaxies / radio continuum: galaxies
© ESO, 2013
1. Introduction
The BL Lac object S5 0716+714 is among the most extremely variable blazars. The optical continuum of the source is so featureless that it is hard to estimate its redshift. Nilsson et al. (2008) claims a value of z = 0.31 ± 0.08 based on the photometric detection of the host galaxy. Very recently, the detection of intervening Lyα systems in the ultra-violet spectrum of the source has confirmed the earlier estimates with a redshift value 0.2315 < z < 0.3407 (Danforth et al. 2012). This source has been classified as an intermediate-peaked blazar (IBL) by Giommi et al. (1999), as the frequency of the first spectral energy distribution (SED) peak varies between 1014 and 1015 Hz, and thus does not fall into the wavebands specified by the usual definitions of low and high energy peaked blazars (i.e. LBLs and HBLs).
S5 0716+714 is one of the brightest BL Lacs in the optical bands and has an optical intraday variability (IDV) duty cycle of nearly one (Wagner & Witzel 1995). Unsurprisingly, this source has been the subject of several optical monitoring campaigns on intraday (IDV) timescales (e.g. Wagner et al. 1996; Rani et al. 2011; Montagni et al. 2006; Gupta et al. 2009, 2012, and references therein). The source has shown five major optical outbursts separated roughly by ~3.0 ± 0.3 years (Raiteri et al. 2003). High optical polarization of ~20%−29% has also been observed in the source (Takalo et al. 1994; Fan et al. 1997). Gupta et al. (2009) analyzed the excellent intraday optical light curves of the source observed by Montagni et al. (2006) and reports good evidence of nearly periodic oscillations ranging between 25 and 73 min on several different nights. Good evidence of ~15-min periodic oscillations at optical frequencies has been reported by Rani et al. (2010a). A detailed multiband short-term optical flux and color variability study of the source is reported in Rani et al. (2010b). There we found that the optical spectra of the source tend to be bluer with increasing brightness.
There is a series of papers covering flux variability studies (Quirrenbach et al. 1991; Wagner et al. 1996, and references therein) and morphological/kinematic studies at radio frequencies (Witzel et al. 1988; Jorstad et al. 2001; Antonucci et al. 1986; Bach et al. 2005; Rastorgueva et al. 2011, and references therein). Intraday variability at radio wavelengths is likely to be a mixture of intrinsic and extrinsic mechanisms (due to interstellar scintillation). A significant correlation between optical – radio flux variations on day-to-day timescales has been reported by Wagner et al. (1996). The frequency dependence of the variability index at radio bands is not found to be consistent with interstellar scintillation (Fuhrmann et al. 2008), which implies the presence of very small emitting regions within the source. However, the IDV time scale does show evidence of an annual modulation, suggesting that the IDV of S5 0716+714 could be dominated by interstellar scintillation (Liu et al. 2012).
EGRET onboard the Compton Gamma-ray Observatory (CGRO) detected high-energy γ-ray (>100 MeV) emission from S5 0716+714 several times from 1991 to 1996 (Hartman et al. 1999; Lin et al. 1995). Two strong γ-ray flares in September and October 2007 were detected in the source with AGILE (Chen et al. 2008). These authors have also carried out SED modeling of the source with two synchrotron self-Compton (SSC) emitting components, representative of a slowly and a rapidly variable component, respectively. Observations by BeppoSAX (Tagliaferri et al. 2003) and XMM-Newton (Foschini et al. 2006) provide evidence of a concave X-ray spectrum in the 0.1−10 keV band, a signature of the presence of both the steep tail of the synchrotron emission and the flat part of the inverse Compton (IC) spectrum. Recently, the MAGIC collaboration has reported the first detection of VHE γ-rays from the source at the 5.8σ significance level (Anderhub et al. 2009). The discovery of S5 0716+714 as a VHE γ-ray BL Lac object was triggered by its very high optical state, suggesting a possible correlation between VHE γ-ray and the optical emissions. This source is also among the bright blazars in the Fermi/LAT (Large Area Telescope) Bright AGN Sample (LBAS) (Abdo et al. 2010a), whose GeV spectra are governed by a broken power law. The combined GeV−TeV spectrum of the source displays absorption-like features in 10−100 GeV energy range (Senturk et al. 2011).
The broadband flaring behavior of the source is even more complex. A literature study reveals that the broadband flaring activity of the source is not simultaneous at all frequencies (Chen et al. 2008; Villata et al. 2008; Vittorini et al. 2009; Ostorero et al. 2006). Also, it is hard to explain both the slow modes of variability at radio and hard X-ray bands and the rapid variability observed in the optical, soft X-ray, and γ-ray bands using a single-component SSC model (see Villata et al. 2008; Giommi et al. 2008; Chen et al. 2008; Vittorini et al. 2009). The X-ray spectrum of the source contains contributions from both synchrotron and IC emission (Foschini et al. 2006; Ferrero et al. 2006) and the simultaneous optical-GeV variations favor an SSC emission mechanism (Chen et al. 2008; Vittorini et al. 2009).
Despite several efforts to understand the broadband flaring activity of the source, we still do not have clear knowledge of the emission mechanisms responsible for its origin. In particular, the location and the mechanism responsible for the high-energy emission and the relation between the variability at different wavelengths are not yet well understood. Therefore, it is important to investigate whether a correlation exists between optical and radio emissions, which are both ascribed to synchrotron radiation from relativistic electrons in a plasma jet. If the same photons are up-scattered to high energies, simultaneous variability features could be expected at optical – GeV frequencies. But the observed variability often challenges such scenarios. To explore the broadband variability features and to understand the underlying emission mechanism, an investigation of long-term variability over several decades of frequencies is crucial. The aim of the broadband variability study reported in this paper is to provide a general physical scenario which allows us to put each observed variation of the source across several decades of frequencies in a coherent context.
Here, we report on a broadband variability study of the source spanning a time period of April 2007 to January 2011. The multifrequency observations comprise GeV monitoring by Fermi/LAT, X-ray observations by Swift/XRT, as well as optical and radio monitoring by several ground-based telescopes. More explicitly, we investigate the correlation of γ-ray activity with the emission at lower frequencies, focusing on the individual flares observed between August 2008 and January 2011. The evolution of radio (cm and mm) spectra is tested in the context of a standard shock-in-jet model. The broadband SED of the source is investigated using a one-zone synchrotron self-Compton (SSC) model and also with a hybrid SSC plus external radiation Compton model. In short, this study allows us to shed light on the broadband radio-to-γ-ray flux and spectral variability during a flaring activity phase of the source over this period.
This paper is structured as follows. Section 2 provides a brief description of the multifrequency data we employed. In Sect. 3, we report the statistical analysis and its results. Our discussion is given in Sect. 4, and we present our conclusions in Sect. 5.
2. Multifrequency data
From April 2007 to February 2011, S5 0716+714 was observed using both ground- and space-based observing facilities. These multifrequency observations of the source extend over a frequency range between radio and γ-rays including optical and X-rays. In the following subsections, we summarize the observations and data reduction.
 |
Fig. 1 Radio to mm wavelength light curves of S5 0716+714 observed over the past ~3 years. For clarity, the light curves at different frequencies are shown with arbitrary offsets (indicated by a “Frequency + x Jy” label). The major radio flares are labeled as “R0”, “R6” and “R8” (see Fig. 2 for the details of labeling). |
Ground-based radio observatories.
2.1. Radio and mm data
We collected 2.7 to 230 GHz radio wavelength data of the source over a time period of April 2007 to January 2011 (JD′1 = 200 to 1600) using the 9 radio telescopes listed in Table 1. The cm/mm radio light curves of the source were observed as a part of observations within the framework of F-GAMMA program (Fermi-GST related monitoring program of γ-ray blazars, Fuhrmann et al. 2007; Angelakis et al. 2008). The overall frequency range spans from 2.7 GHz to 230 GHz using the Effelsberg 100 m telescope (2.7 to 43 GHz) and the IRAM 30 m Telescope at the Pico Veleta (PV) Observatory (86 to 230 GHz). These flux measurements were performed quasi-simultaneously using the cross-scan method slewing over the source position, in azimuth and elevation direction with adaptive number of sub-scans for reaching the desired sensitivity. Subsequently, atmospheric opacity correction, pointing off-set correction, gain correction and sensitivity correction have been applied to the data.
This source is also a part of an ongoing blazar monitoring program at 15 GHz at the Owens Valley Radio Observatory (OVRO) 40-m radio telescope which provides the radio data sampled at 15 GHz. We have also used the combined data from the University of Michigan Radio Astronomy Observatory (UMRAO; 4.8, 8 and 14.5 GHz, Aller et al. 1985) and the Metsähovi Radio Observatory (MRO; 22 and 37 GHz; Teräsranta et al. 1998, 2004), which provide us with radio light curves at 5, 8, 15 and 37 GHz. Additional flux monitoring at 5, 8, 22 and 43 GHz radio bands is obtained using 32 m telescope at NOTO radio observatory. The Urumqi 25 m radio telescope monitors the source at 5 GHz. The 230 and 345 GHz data are provided by the Submillimeter Array (SMA) Observer Center2 data base (Gurwell et al. 2007), complemented by some measurements from PV and the Plateau de Bure Interferometer (PdBI). The radio light curves of the source are shown in Fig. 1. The mm observations are closely coordinated with the more general flux density monitoring conducted by IRAM, and data from both programs are also included.
 |
Fig. 2 Light curves of 0716+714 from γ-ray to radio wavelengths a) GeV light curve at E > 100 MeV; b) X-ray light curve at 0.3−10 KeV; c) optical V passband light curve and d) 5 to 230 GHz radio light curves. Vertical dotted lines are marked w.r.t. different optical flares labeling the broadband flares as “G” for γ-rays, “X” for X-rays, “O” for optical and “R” for Radio followed by the number close to flare. The yellow area represents the period for which we construct the broadband SEDs of the source (see Sect. 3.5 for details). |
2.2. Optical data
Optical V passband data of the source were obtained from the observations at the 1.5-m Kanata Telescope located on Higashi-Hiroshima Observatory over a time period of February 14, 2009 to June 01, 2010 (JD′ = 877 to 1349). The Triple Range Imager and SPECtrograph (Watanabe et al. 2005) was used for the observations from JD′ = 612 to 1228. Then, the HOWPol (Hiroshima One-shot Wide-field Polarimeter, Kawabata et al. 2008) was used from JD′ 1434 to 2233 with the V-band filter. Exposure times for an image ranged from 10 to 80 s, depending on the magnitude of the object and the condition of sky. The photometry on the CCD images was performed in a standard procedure: after bias subtraction and flat-field division, the magnitudes were calculated using the aperture photometry technique.
Additional optical V-passband data were obtained from the 2.3 m Bok Telescope of Steward Observatory from April 28, 2009 through June 2, 2010 (JD′ = 950−1350). These data are from the public data archive that provides the results of polarization and flux monitoring of bright γ-ray blazars selected from the Fermi/LAT-monitored blazar list3. We have also included optical V passband archival data extracted from the American Association of Variable Star Observers (AAVSO)4 over a period September 2008 to January 2011 (JD′ = 710−1600). The combined optical V passband flux light curve of S5 0716+714 is shown in Fig. 2c.
2.3. X-ray data
The X-ray (0.3−10 keV) data were obtained by Swift/XRT over a time period of September 2008 to January 2011 (JD′ = 710−1600). The Swift/XRT data were processed using the most recent versions of the standard Swift tools: Swift Software version 3.8, FTOOLS version 6.11 and XSPEC version 12.7.0 (see Kalberla et al. 2005, and references therein).
All of the observations were obtained in photon counting (PC) mode. Circular and annular regions are used to describe the source and background areas, respectively, and the radii of both regions depend on the measured count rate using the FTOOLS script xrtgrblc. Spectral fitting was done with an absorbed power-law with NH = 0.31 × 1021 cm-2 set to the Galactic value found by Kalberla et al. (2005). For three of the observations, there were more than 100 counts in the source region, and a chi-squared statistic is used with a minimum bin size of 20 cts/bin. For the bin centered on JD′ = 1214, only 62 counts were found in the source region, and the unbinned data are fitted using C-statistics as described by Cash (1979). One sigma errors in the de-absorbed flux were calculated assuming that they share the same percentage errors as the absorbed flux for the same time and energy range. The X-ray light curve of the source is shown in Fig. 2b.
2.4. γ-ray data
We employ γ-ray (100 MeV−300 GeV) data collected between a time period August 08, 2008 to January 30, 2011 (JD′ = 686–1592) in survey mode by Fermi/LAT. The LAT data are analyzed using the standard ScienceTools (software version v9.23.1) and the instrument response function P7V65. Photons in the Source event class are selected for this analysis. We select γ-rays with zenith angles less than 100 deg to avoid contamination from γ-rays produced by cosmic ray interactions in the upper atmosphere. The diffuse emission from our Galaxy is modeled using a spatial model6 (gal_2yearp7v6_v0.fits) which was derived with Fermi/LAT data taken during the first two years of operation. The extragalactic diffuse and residual instrumental backgrounds are modeled as an isotropic component (isotropic_p7v6source.txt) with both flux and spectral photon index left free in the model fit. The data analysis is done with an unbinned maximum likelihood technique (Mattox et al. 1996) using the publicly available tools7. We analyzed a Region of Interest (RoI) of 10° in radius, centered on the position of the γ-ray source associated with S5 0716+714, using the maximum-likelihood algorithm implemented in gtlike. In the RoI model, we include all the 24 sources within 10° with their model parameters fixed to their 2FGL catalog values, as none of these sources are reported to be variable (see Nolan et al. 2012, for details). The contribution of these 24 sources within the RoI model to the observed variability of the source is negligible as they are very faint compared to S5 0716+714. The LAT instrument-induced variability is tested with bright pulsars and is ~2% and is much smaller than the statistical errors reported for the source (Ackermann et al. 2012).
Source variability is investigated by producing the light curves (E > 100 MeV) by likelihood analysis with time bins of 1-, 7- and 30-day. The bin-to-bin exposure time variation is less than 7%. The light curves are produced by modeling the spectra over each bin by a simple power law which provide a good fit over these small bins of time. Here, we set both the photon index and integral flux as free parameters. We will use the weekly averaged light curves for the multifrequency analysis, as the daily averaged flux points have a low TS (Test Statistics) value (<9). In a similar way, we construct the GeV spectrum of the source over different time periods (see Sect. 3.5 for details). We split the 0.1 to 100 GeV spectra into 5 different energy bins: 0.1−0.3, 0.3−1.0, 1.0−3.0, 3.0−10.0 and 10.0−100.0 GeV. A simple power law with constant photon index Γ (the best fit value obtained for the entire energy range) provides a good estimate of integral flux over each energy bin. The GeV spectrum of the source is investigated over four different time periods, which represent different brightness states of the source and will be used in broadband spectral modeling. The details of the broadband spectral analysis are given in Sect. 3.5.
3. Analysis and results
3.1. Light curve analysis
3.1.1. Radio frequencies
Figure 1 displays the 2.7−230 GHz radio band light curves of the source observed over the past ~3 years. The source exhibits significant variability, being more rapid and pronounced towards higher frequencies over this period with two major outbursts. Towards lower frequencies (<10 GHz) the individual flares appear less pronounced and broaden in time.
To quantify the strength of variability at different radio frequencies, we extract the time scale of variability (tvar) from the observed light curves. We employed the structure function (SF) (Simonetti et al. 1985) analysis method following Rani et al. (2009). The radio SF curves are shown in Fig. 3.
Variability time scales at radio wavelengths.
 |
Fig. 3 Top: structure functions at radio frequencies. The solid curves represent the best fitted power laws. The dotted lines in each plot indicate the timescale of variability (tvar). Bottom: structure functions at optical and γ-ray frequencies. |
 |
Fig. 4 SF vs. frequency at GHz frequencies for a structure function time =100 days. |
At 15 GHz and higher radio frequencies, the SF curve follow a continuous rising trend showing a peak at tvar1, following a plateau and again reaching a maximum at tvar2. However, the SF curve at 10 GHz and lower frequencies do not reveal a sharp break in the slope as the variability features seem to be milled out at these frequencies. We do not consider variability features at time lags longer than half of the length of the observations due to the increasing statistical uncertainty of the SF values in this region. To extract the variability timescales, we fitted a power law (P(f) ~ fβ) to the two rising parts of the SF curves. The variability timescale is given by a break in the slope of the power-law fits. In Fig. 3 (top), the red curves represent the fitted power-law to rising trend of SF curves and the vertical dotted lines stand for tvar1 and tvar2. The best fitted values of the power-law slopes and the estimated timescale of variability are given in Table 2. Thus, the SF curve reveals two different variability time scales, one which reflects the short-term variability (tvar1) while the other one refers to the long-term variability (tvar2).
The SF value is proportional to the square of the amplitude of variability, so to compare the strength of the variability at different frequencies, we produce SF vs. frequency plots at different time lags. In Fig. 4, we show the SF vs. frequency plot at a time lag of 100 days. The source displays more pronounced and faster variability at higher radio frequencies compared to lower ones, peaking at a frequency of 43 GHz, and have similar amplitude at higher frequencies. It seems that the radio variability saturates above this frequency. We notice a similar trend at 50 and 200 day time lags. Thus, for different time lags the variability strength exhibits a similar frequency dependence.
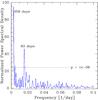 |
Fig. 5 LSP analysis curve showing a peak at a period of 63 and 359 days. |
 |
Fig. 6 Optical V passband light curve of S5 0716+714 with different time binning. The light curve appears as a superposition of fast flares on a modulated base level varying on a (350 ± 9) day timescale. These slower variations can be clearly seen in 75-day binned light curve (error bar represents variations in flux over the binned period). The dashed line represents a spline interpolation through the 75-day binned light curve. Dotted lines are obtained by shifting the spline by ±0.65 mag. |
3.1.2. Optical frequencies
The source exhibits multi-flaring behavior at optical frequencies with each flare roughly separated by 60−70 days (see Fig. 2c). The optical V band SF curve in Fig. 3 (bottom) shows rapid variability with multiple cycles of rises and declines. The first peak in SF curve appears at a timescale tvar ~ 30 days which is followed by a dip at ~60 days. This peak corresponds to the fastest variability timescale. The peaks in the optical SF curve at tvar = 90, 180, 240 and 300 days represent the long-term variability timescales. This indicates a possible superposition of a short 30−40 day time scale variability with the long-term variability trend.
Multiple cycles in the optical SF curve represent the nearly periodic variations at ~60 days timescale. We used the Lomb-Scargle periodogram (LSP) (Lomb 1976; Rani et al. 2009) method to test the presence of this harmonic. The LSP analysis of the whole data set is displayed in Fig. 5. The LSP analysis reveals two significant (>99.9999% confidence level) peaks at 359 and 63 days. The peak at 359 days is close to half of the duration of observations, so it is hard to claim this frequency due to limited number of cycles. The nearly annual periodicity could also be affected by systematic effects due to annual observing cycle. A visual inspection of the light curve indicates a total of 7 rapid flares separated by 60−70 days. Also, the LSP is only sensitive for a dominant white-noise process (PN(f) ∝ f0). It is for this reason that we further inspect the significance of this frequency with the Power Spectral Density (PSD) analysis method (Vaughan 2005) which is a powerful tool to search for periodic signals in time series, including those contaminated by white noise and/or red noise. To achieve a uniform sampling in the optical data, we adopt a time-average binning of 3-day. We found that the significance of the period at ~60 days is only 2σ. We therefore can not claim a significant detection of a quasi-periodic variability feature at this frequency.
We also notice that during the course of our optical monitoring, the peak-to-peak amplitude of the short-term variations remains almost constant, ~1.3 mag. Hence, the variability trend traced by the minima is very similar to that by the maxima of the light curve during the course of ~2 years of our monitoring. The constant variability trend is displayed in Fig. 6. In this figure, the dashed line denotes a spline through the 75-day binned light curve and the dotted lines are obtained by shifting the spline by ± 0.65 mag. So, the observed variations fall within a constant variation area. A constant variability amplitude in magnitudes implies that the flux variation amplitude is proportional to the flux level itself (following m1 − m2 ∝ log 10(f1/f2)). This can be easily interpreted in terms of variations of the Doppler boosting factor, δ = [Γ(1 − β cos θ)] -1 (Raiteri et al. 2003). In such a scenario, the observed flux is relativistically boosted by a factor of δ3 and requires a variation in δ by a factor of ~1.2. Such a change in δ can be due to either a viewing angle (θ) variation or a change of the bulk Lorentz factor (Γ) or may be a combination of both. A change in δ by a factor of 1.2 can be easily interpreted as a few degree variation in θ while it requires a noticeable change of the bulk Lorentz factor. Therefore, it is more likely that the long-term flux base-level modulations are dominated by a geometrical effect than by an energetic one.
Hence, we consider that the optical variability amplitude remains almost constant during our observations. A similar variability trend was also observed in this source by Raiteri et al. (2003). They also noticed a possibility of nearly periodic oscillations at a timescale of 3.0 ± 0.3 years, but due to the limited time coverage this remains uncertain. The optical light curve of the source also displays fast flares with a rising timescales of ~30 day. However, the rising timescale of the radio flares is of the order of 60 days (see Table 5). Thus, the optical variability features are very rapid compared to those at radio wavelengths.
3.1.3. X-ray frequencies
Figure 2b displays the 0.3−10 keV light curve of S5 0716+714. Although the X-ray light curve is not as well sampled as those at other frequencies, the data indicate a flare at keV energies between JD′ = 1122 to 1165. Due to large gap in the data train, it is not possible to locate the exact peak time of this flare. Still, it is interesting to note that this orphan X-ray flare is not simultaneous with any of the GeV flares nor with the optical flares. Its occurrence coincides with the optical – GeV minimum after the major flares at these frequencies (O5/G5, see Fig. 2).
3.1.4. Gamma-ray frequencies
The GeV light curve observed by Fermi/LAT is extracted over the time period of August 2008 to February 2011. Figure 7 shows the weekly and monthly averaged γ-ray light curves integrated over the energy range 100 MeV to 300 GeV. There is a significant enhancement in the weekly averaged γ-ray flux over the time period of JD′ = 900 to 1110, peaking at JD′ ~ 1110, with a peak flux value of (0.57 ± 0.05) × 10-6 ph cm-2 s-1, which is ~6 times brighter than the minimum flux and ~3 times brighter than the average flux value. Later it decays, reaching a minimum at JD′ = 1150, and then it remains in a quiescent state until JD′ = 1200. The quiescent state is followed by another sequence of flares. The source displays similar variability features in the constant uncertainty light curve obtained using the adaptive binning analysis method following Lott et al. (2012). A more detailed discussion of GeV variability is given in Rani et al. (2012).
The source exhibits a marginal spectral softening during the quiescent state in the monthly averaged light curve. The γ-ray photon index (Γ) changes from ~2.08 ± 0.03 (II) to 2.16 ± 0.02 (III), then again to 2.04 ± 0.04 (IV). Different activity states of the source are separated by vertical lines in Fig. 7. We notice no clear spectral variation in the weekly averaged light curve due to large uncertainty and scatter of individual data points.
The SF curve of the source at GeV frequencies is shown in Fig. 3 (bottom). The variability timescales are extracted using the power-law fitting method as described above, which gives a break at ~30 and 180 days. We notice that the variability features at tvar ~ 180 days are also observed at radio and optical frequencies. However, the faster variability (tvar ~ 30 days) observed at optical and γ-ray frequencies does not extend to radio wavelengths. A similar long-term variability timescale at γ-ray, optical and radio frequencies provides a possible hint of a co-spatial origin. In the following sections, we will search for such possible correlations.
 |
Fig. 7 Gamma-ray flux and photon index light curve of S5 0716+714 measured with the Fermi/LAT for a time period between August 04, 2008 to February 07, 2011. The blue symbols show the weekly averaged flux while monthly averaged values are plotted in red. Different activity states of the source are separated by vertical green lines. A marginal softening of spectrum over the quiescent state can be seen here. |
 |
Fig. 8 DCF curves among the different radio frequency light curves. The solid curves represent the best-fit Gaussian function. |
3.2. Correlation analysis
The multifrequency light curves of S5 0716+714 are presented in Fig. 2. The analysis presented in this section is focused on a time period between JD′ = 800 to 1400, which covers the two major radio flares and the respective optical-to–γ-ray flaring activity. The source displayed multiple flares across the whole electromagnetic spectrum over this period, which we label as follows. We mark the vertical dotted lines w.r.t. different optical flares, labeling the broadband flares as “G” for γ-rays, “X” for X-rays, “O” for optical and “R” for radio followed by the number adjacent to them. For example, the optical flares should be read as “O1” to “O9”.
To search for possible time lags and to quantify the correlation among the multifrequency light curves of the source, we computed discrete cross-correlation functions (DCFs) following the method described by (Edelson & Krolik 1988). The details of this method are also discussed by Rani et al. (2009). In the following sections, we will discuss in detail the correlation between the observed light curves.
3.2.1. Radio correlation
At radio wavelengths, the source exhibits significant flux variability, being more rapid and pronounced towards higher frequencies. We label the two major outbursts as “R6” and “R8” (see Fig. 2). Apparently, the mm flares are observed a few days earlier than the cm flares. Our dense frequency coverage facilitates a cross-correlation analysis between the different observing bands. Owing to its better time sampling, we have chosen the 15 GHz light curve as a reference. Figure 8 shows the DCF curves adopting a binning of 10-day.
We used a Gaussian profile fitting technique to estimate the time lag and respective cross-correlation coefficient value for the DCF curves. Around the peak, the DCF curve as a function of time lag t can be reasonably well described by a Gaussian of the form: ![\hbox{${\rm DCF}(t) = a \times ~\exp\left [\frac{-(t-b)^{2}}{2c^{2}}\right]$}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq58.png) , where a is the peak value of the DCF, b is the time lag at which the DCF peaks and c characterizes the width of the Gaussian function. The calculated parameter (a, b and c) values for each frequency are listed in Table 3. The solid curve represents the fitted Gaussian function in Fig. 8.
, where a is the peak value of the DCF, b is the time lag at which the DCF peaks and c characterizes the width of the Gaussian function. The calculated parameter (a, b and c) values for each frequency are listed in Table 3. The solid curve represents the fitted Gaussian function in Fig. 8.
Our analysis confirms the existence of a significant correlation across all observed radio-band light curves till 15 GHz with formal delays listed in Table 3 (parameter b). However, no pronounced delayed flux variations are observed at 10 GHz and lower frequencies. Also, the flux variations at 2.7 GHz seem to be less correlated with those at 15 GHz, which is obvious as the flaring behavior is not clearly visible below 15 GHz.
Correlation analysis results among radio frequencies.
Radio correlation analysis results for individual flares.
The long term radio light curve shows three major radio flares, labeled as R0, R6 and R8 in Fig. 1. In the correlation analysis of the entire light curves, these flares are blended and folded into a single DCF. In order to separate the flares from each other, we performed a correlation analysis over three different time bins which cover the time ranges of the individual radio flares: JD′ = 500 to 750 (R0 flare), JD′ = 1000 to 1210 (R6 flare) and JD′ = 1210 to 1400 (R8 flare). The time lags of these flares relative to the 15 GHz data are estimated as above. However due to sparse data sampling, it was not possible to estimate the time lags for R8 directly using the DCF method. So, for this flare, we first interpolate the data through a spline function and then perform the DCF analysis, except at 23 GHz and 33 GHz (due to long data gaps). The calculated time lags of each flare are given in Table 4.
In Fig. 9, we report the calculated time lags as a function of frequency with 15 GHz as the reference frequency. The estimated time lag using the entire light curves are shown with blue circles. As we see in Fig. 9, the time lag increases with an increase in frequency and seems to follow a power law. Consequently, we fitted a power law, P(f) = Nfα to the time lag vs. frequency curve. The best fitted parameters are N = 1.71 ± 0.43, α = 0.30 ± 0.08. For the individual flares, we find: N = 1.07 ± 0.06, α = 0.32 ± 0.01 for the R0, N = 1.45 ± 0.61, α = 0.32 ± 0.08 for R6, and N = 1.33 ± 0.01, α = 0.29 ± 0.03 for R8. We conclude that a common trend in the time lag (with 15 GHz as the reference frequency) vs. frequency curve is seen for all the three radio flares (R0, R6 and R8) with an average slope of 0.30.
 |
Fig. 9 Time lag vs. frequency, using 15 GHz as the reference frequency. Time lag vs. frequency curves for individual flares are shown with different colors. The solid lines represent the best fitted power law in each case. |
 |
Fig. 10 Modeled radio flare, R6. The blue points are the observed data while the red curve represent the fit. |
We also followed an alternative approach to estimate the time shift of the radio flares at each frequency w.r.t. 15 GHz. The flares at each frequency can be modeled with an exponential rise and decay of the form: ![\begin{eqnarray} f(t)&=&f_0 + f_{\max}~\exp[(t-t_0)/t_{\rm r}], ~~~~{\rm for} ~t<t_0, {\rm and} \\ &=&f_0 + f_{\max}~\exp[-(t-t_0)/t_{\rm d}] ~~~~ {\rm for} ~t>t_0\nonumber \end{eqnarray}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq71.png) (1)where f0 is the background flux level that stays constant over the corresponding interval, fmax is the amplitude of the flare, t0 is the epoch of the peak, and tr and td are the rise and decay time scales, respectively. Since R6 is the most pronounced and best sampled flare, we model this flare in order to cross-check the frequency vs. time lags results obtained by the DCF method. As the flaring behavior is not clearly visible below 15 GHz, so we restrict this analysis to frequencies above 15 GHz. As there is no observation available during the flaring epoch at 23 and 86 GHz, we fix tr and td using the fit parameters from the adjacent frequencies. The best fit of the function f(t) for the R6 flare is shown in Fig. 10 and the parameters are given in Table 5. The estimated time shift around the R6 flare at each frequency w.r.t. 15 GHz are shown in Fig. 9 (red symbols) and the fitted power law parameters are N = 1.17 ± 0.13, α = −0.31 ± 0.03. Thus, this alternative estimate of the power law slope using the model fitting technique confirms the results obtained by the DCF analysis.
(1)where f0 is the background flux level that stays constant over the corresponding interval, fmax is the amplitude of the flare, t0 is the epoch of the peak, and tr and td are the rise and decay time scales, respectively. Since R6 is the most pronounced and best sampled flare, we model this flare in order to cross-check the frequency vs. time lags results obtained by the DCF method. As the flaring behavior is not clearly visible below 15 GHz, so we restrict this analysis to frequencies above 15 GHz. As there is no observation available during the flaring epoch at 23 and 86 GHz, we fix tr and td using the fit parameters from the adjacent frequencies. The best fit of the function f(t) for the R6 flare is shown in Fig. 10 and the parameters are given in Table 5. The estimated time shift around the R6 flare at each frequency w.r.t. 15 GHz are shown in Fig. 9 (red symbols) and the fitted power law parameters are N = 1.17 ± 0.13, α = −0.31 ± 0.03. Thus, this alternative estimate of the power law slope using the model fitting technique confirms the results obtained by the DCF analysis.
Fitted model parameters for R6 flare.
3.2.2. Radio vs. optical correlation
S5 0716+714 exhibits multiple flares at optical frequencies. The flares are roughly separated by 60−70 days. We labeled the different optical flares as O1−O9 as shown in Fig. 2. During this multi-flaring activity period two major flares are observed at radio wavelengths. The radio flare R6 apparently coincides in time with O6 and R8 with O8. To investigate the possible correlation among the flux variations at optical and radio frequencies, we perform a DCF analysis using the 2-year-long simultaneous optical and radio data trains between JD′ = 680 to 1600 (see Fig. 2). Note that the strength of flux variability increases towards higher frequencies, peaking at 43 GHz (see Fig. 3). Therefore, we choose two radio frequencies, 37 GHz and 230 GHz, in order to compare the strength of radio – optical correlation above and below the saturation frequency (43 GHz). The optical vs. radio DCF analysis curves are shown in Fig. 11a. Multiple peaks in the DCF may reflect a QPO behavior at optical frequencies. As the formal errors, we use half of the binning time. We summarize the optical vs. 230 GHz and 37 GHz DCF analysis results in Table 6.
Fitted model parameters for R6 flare.
 |
Fig. 11 a) DCF curve for optical V passband vs. 37 GHz (in blue) and 230 GHz (in red) flux with a bin size of 5-day. b) Radio flux vs. optical V-band flux. c) Time shifted radio flux vs. optical V-band flux. The blue symbols show the time shifted 230 GHz (t-65 days) data while 37 GHz (t-68 days) data are shown in red. |
The maximum correlation of the optical V passband with the 230 GHz light curve occurs at a 65 day time lag. However a second peak with lower peak coefficient also occurs close to zero time lag (see Fig. 11). The analysis shows that the cross-correlation coefficient of the simultaneous radio – optical flare peaks O6-R6 and O8-R8 is lower than the cross-correlation coefficient of the O5-R6 and O7-R8 flare peaks. In both cases the optical flares O5 and O7 are observed ~65 days earlier than the radio flares R6 and R8, respectively. The observed time lag between the optical and radio flares is consistent with the extrapolated frequency dependent time shift (as shown in Fig. 9) to optical wavelengths. In Sect. 4.1, we will discuss this in detail.
In order to quantify the correlation among optical and radio data, we generate flux – flux plots, which are shown in Figs. 11b−c. For the following analysis we used a 1-day binning. Figure 11c shows the time shifted 230 GHz (t-63) and 37 GHz (t-66) flux plotted vs. the optical V-band flux. The time-shifted radio and optical V-band fluxes fall on a straight line, indicating a correlation. A Pearson correlation analysis reveals a significant correlation between the two data trains. We obtain the following values: rP = 0.59 and 99.93% confidence level for 230 GHz (t-65) vs. V-band and rP = 0.43 and 99.3% confidence level for 37 GHz (t-65) vs. V-band, where rP is the linear Pearson correlation coefficient. Thus, we found a significant correlation among the time shifted radio vs. optical V-band flux at a confidence level >99%.
In contrast to this, the radio (with no time shift) vs. optical V-band correlations are found to be not significant. Figure 11c shows 230 GHz and 37 GHz vs. V-band flux-flux plots, and the correlation statistics are: 230 GHz vs. V-band: rP = 0.40, 91% confidence level and 37 GHz vs. V-band: rP = 0.15, 74% confidence level. Thus, the confidence level of the correlations is lower than 95% in these cases. We also check the significance of the correlation statistics with a time shift of ~120 and 180 days and do not find a correlation to have a significance greater than 2σ in any case.
Hence, using DCF and linear Pearson correlation statistics, we have found a significant correlation among the flux variations at optical and radio frequencies with the optical V-band leading the radio fluxes at 230 and 37 GHz by ~63 and ~66 days, respectively. We therefore conclude that flux variations at optical and radio frequencies are correlated such that the optical variability is leading the radio with a time lag of about two months.
 |
Fig. 12 Top: DCF curve of the γ-ray light curve w.r.t. the 230 GHz radio light curve. The solid curve is the best fitted Gaussian function to the 11-day binned DCF curve. Bottom: flux-flux plot of the shifted radio vs. γ-ray data. The blue symbols show the time shifted 230 GHz data while 37 GHz data are shown in red. |
 |
Fig. 13 Top: weekly averaged normalized flux at γ-ray and optical V band frequencies plotted vs. time. The flux variations at these two frequencies seem to have a one-to-one correlation with each other. Bottom left: γ-ray vs. optical flux. Bottom right: the DCF curve of γ-ray vs. optical V passband flux using a bin size of 10-day in each case. A: using the complete data as shown in Fig. 2; B: after removing the data covering the duration of the optical flare O6; C: using the data before flare O6. |
3.2.3. Radio vs. gamma-ray correlation
We apply the DCF analysis method to investigate a possible correlation among flux variations at radio and γ-ray frequencies. In Fig. 12, we report the DCF analysis results of the weekly averaged γ-ray light curve with the 230 GHz radio data with a time bin size of 11 days. As the flux variations at 37 GHz are delayed by ~3 days w.r.t. those at 230 GHz, we only show the DCF analysis curve w.r.t 230 GHz. To estimate the possible peak DCF value and respective time lag, we fit a Gaussian function to the DCF curve with a bin size of 11 days. The best-fit function is shown in Fig. 12 and the fit parameters are a = 0.94 ± 0.30, b = (67 ± 3) days and c = (7 ± 2) days. This indicates a clear correlation between the γ-ray and 230 GHz radio light curves of the source with the GeV flare leading the radio flare by (67 ± 3) days.
Optical vs. γ-ray cross-correlation analysis results.
To check the significance of the γ-ray vs. radio correlation, we produce flux-flux plots of the time shifted radio vs. γ-ray flux. Since the γ-ray flux is weekly averaged, we use a time binning equal to seven-day. The weekly averaged flux-flux plots of the time shifted 230 GHz (t + 67 days) and 37 GHz (t + 70 days) vs. γ-ray are shown in Fig. 12 (bottom) and the correlation statistics are: 230 GHz (t + 67 days) vs. γ-ray: rP = 0.37, 97.7% confidence level and 37 GHz (t + 70 days) vs. γ-ray: rP = 0.33, 97.3% confidence level. Thus, in each case the confidence level of the correlation is higher than 95%. This supports a possible correlation among the flux variations at γ-ray and radio frequencies with γ-rays leading the radio emission by ~67 days. We also note that the time shifts are very similar to the time shifts observed between radio and optical bands (see Sect. 3.2.2). We therefore expect a very short or no time delay between the flux variations at optical and γ-ray frequencies. This will be investigated in the next section.
3.2.4. Optical vs. gamma-ray correlation
Visual inspection of variability curves in Fig. 2 shows an apparent correlation between the various flux density peaks of the GeV light curve and the optical peaks (O1 to O9, except O6). The flaring pattern at γ-rays is similar to the QPO-like behavior observed at optical frequencies. In addition, the long-term variability features are also simultaneous at the two frequencies. To compare the flaring behavior of the source at optical and γ-ray frequencies, we plot the normalized weekly averaged optical and γ-ray light curves on top of each other (see Fig. 13 top). A consistent and simultaneous flaring behavior can be seen between JD′ = 680 to 1200, however the γ-ray variability is less correlated later. In Fig. 13 (middle), we show a flux-flux plot of the weekly averaged γ-ray vs. optical V-band data. A clear correlation among the two can be seen, which is confirmed by a linear correlation analysis, yielding rP = 0.36 and 99.996% confidence level. The correlation is even stronger in part I, for which we find rP = 0.66 and 99.9999% confidence level. Here, we have used the weekly averaged optical flux for the analysis, and the uncertainty represents variation of the flux over this period.
In Fig. 13 (bottom), we show the cross-correlation analysis results of the γ-ray and optical data trains. We consider three different cases to investigate the possible correlation and summarize the results in Table 7. This analysis reveals that the two-year-long GeV and optical data trains are strongly correlated with each other with no time lag longer than one week. It is also important to note that the strength of correlation is higher before the end of the O5/G5 flares than after those flares.
3.2.5. The orphan X-ray flare
In order to investigate the origin of the X-ray flare (JD′ = 1120−1210, Fig. 2), we explore the correlation between X-ray photon index and flux. We do not see any systematic change in the X-ray photon index (ΓX - ray) w.r.t. a change in the flux. The X-ray photon index vs. flux plot over the flaring period between “5−8” (see Fig. 2 for labeling) is shown in Fig. 14 (top) and the estimated correlation coefficient rP is 0.25 with a confidence level of 69%. Thus, as per correlation statistics, the X-ray photon index and flux are not significantly correlated with each other. We also notice that the flaring amplitude is similar at soft and hard X-rays as shown in Fig. 14 (bottom). The percentage fractional variability is 22.5 and 25 in the soft and hard X-ray bands, respectively. The comparable fractional variability implies that the X-ray flare is equally attributed to emission from the soft and the hard X-ray bands.
Although the X-ray light curve of the source is the least sampled one among all the multifrequency light curves, we notice a flare peaking between “5” and “6” [JD′ = 1000 to 1200] (see Fig. 2). However, due to the gap in the observations it is hard to determine the exact peak time of the flare. If we consider that the maximum in the X-ray light curve (say X6) is close to the peak of the flare, then this epoch coincides with a minimum in the optical/GeV flux and it is observed ~50 days after the O5/G5 flares (see Fig. 2).
The DCFs of the X-ray light curve with γ-ray and radio frequency light curves do not follow any particular trend as there are very few observations available in the X-ray band. A formal X-ray vs. optical DCF curve (Fig. 15) shows a peak at a time lag =− (60 ± 3) days and another peak at (15 ± 3) days. The large DCF error bars are due to sparse data sampling of the X-ray light curve. In the former case, a negative time lag means that optical variations lead the X-ray ones, while in the other case the opposite occurs. An overall inspection of the light curves in Fig. 2 reveals that the optical flare (O5) is observed ~55 days earlier than the X-ray flare X6, and O6 appears ~12 days later. This indicates that the X-ray variability is governed by some other effect than the major optical/GeV flares (O5/G5), which appear strongly correlated.
 |
Fig. 14 Top: X-ray photon index vs. flux at 0.3−10 keV. The data points in the box belong to a phase of brightening shown in the bottom figure. The X-ray photon index of the source is almost constant at 2.25 ± 0.25 (shown by a dashed line) over the flaring period. Bottom: soft and hard X-ray light curves of the source over the period of high X-ray activity. The flaring activity is similar in the two X-ray bands. |
 |
Fig. 15 DCF curve of X-ray vs. optical V passband flux using a bin size of 3-day. |
3.3. Radio spectral analysis
In the following sections, we will study the spectral variability of S5 0716+714 during the different flaring episodes with a focus on the good spectral coverage in the radio bands.
3.3.1. Modeling the radio spectra
The multifrequency radio data allow a detailed study of the spectral evolution of the two major radio flares, R6 and R8. We construct quasi-simultaneous radio spectra using 2.7 to 230 GHz data. To perform a spectral analysis of the light curves simultaneous data points are needed. This is achieved by performing a linear interpolation between the flux density values from observations. A time sampling Δt = 5 days is selected for the interpolation. We interpolate the data between the two adjacent observations to predict the flux if the data gap is not longer than 5 days; however for longer gaps we drop such data points. In Fig. 16, we report the spectral evolution of the R6 and R8 radio flares. In this figure, the flux densities are averaged values over the 5-day binning period and the uncertainties in the fluxes represent their variation over this period.
The observed radio spectrum is thought to result from the superposition of emission from the steady state (unperturbed region) and the perturbed (shocked) regions of the jet. We constructed the quiescent spectrum using the lowest flux level during the course of our observations. Emission from a steady jet is better characterized by a relatively flat spectrum, so we choose the steepest one observed on February 17, 2008. The quiescent spectrum is shown in Fig. 16b. The flux densities were fitted by a power law F(ν) = Cq(ν/ GHz)αq with Cq = (0.92 ± 0.02) Jy and αq = −(0.062 ± 0.007).
We fitted the radio spectra using a synchrotron self-absorbed spectrum. A synchrotron self-absorbed (SSA) spectrum can be described as (see Türler et al. 2000; Fromm et al. 2011, for details) : 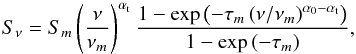 (2)where
(2)where 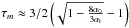 is the optical depth at the turnover frequency, Sm is the turnover flux density, νm is the turnover frequency and αt and α0 are the spectral indices for the optically thick and optically thin parts of the spectrum, respectively (S ~ να).
is the optical depth at the turnover frequency, Sm is the turnover flux density, νm is the turnover frequency and αt and α0 are the spectral indices for the optically thick and optically thin parts of the spectrum, respectively (S ~ να).
Best-fit spectral parameters for the evolution of radio flares using a one-component SSA model.
For the spectral analysis, we first subtract the contribution of the quiescent spectrum from the data and then used Eq. (2) for fitting. The uncertainties of the remaining flaring spectrum are calculated taking into account the errors of the interpolated data points and the uncertainties of the quiescent spectrum. We tried two independent approaches to model the radio spectra: (i) a one-component SSA model; (ii) a two-component SSA model.
One-component SSA model: during the fitting process we allowed all four parameters (Sm, νm, αt, α0) (see Eq. (2)) to vary. In Fig. 16a we show the 230 GHz light curve with labels (“numbers”), marking the time of best spectral coverage, for which spectra can be calculated. A typical spectrum (for time bin “4”) is shown in Fig. 16c. In Table 8 we list the spectral parameters of the one-component SSA fit for all spectral epochs (bin 1 to 18). In a homogeneous emission region, the spectrum is described by characteristic shapes Iν ∝ ν5/2 and Iν ∝ ν− (s − 1)/2 for the optically thick and thin domain (s is the power law index of the relativistic electrons), respectively. Thus, the theoretically expected value of the optically thick spectral index, αt is 2.5. While fitting the spectra with a single-component SSA model, we find that αt varies between 0.32 to 1.56. This deviation of αt from 2.5 indicates that the emission region is not homogeneous, and it may be composed of more than one homogeneous components. We also notice that the radio spectra over the period between the two radio flares R6 and R8 (from bin9 to bin12) can not be described by such a spectral model at all. Apparently, these spectra seem to be composed of two different components, one peaking near 30 GHz (low-frequency component) and the other one at ~100 GHz (high-frequency component). Consequently, we consider a two-component model.
 |
Fig. 16 Evolution of the radio spectra: a) 230 GHz light curve showing different periods over which the spectra are constructed. b) Quiescent radio spectrum; c) results of a single component spectral fitting at time bin “4”, the dotted line corresponds to the quiescent spectrum, the dashed one to the flaring spectrum and the solid line to the total spectrum. d) The same spectrum fitted by a two-component synchrotron self-absorbed model, with the green dashed line showing the individual components and the blue solid line showing a combination of the two. A single component model curve is displayed with a dotted-dashed red curve for comparison. e) and f) The time evolution of Smax vs. νmax for the R6 and R8 radio flares. The spectral evolution extracted using a single-component model is shown by blue symbols and the red symbols denote a two-component model (see text for details). |
Best fitted spectral parameters over the evolution of radio flares using a two component SSA model.
Two-component SSA model: since the flux densities at cm wavelengths are much higher than the extrapolation of the mm-flux with a spectral index αt = 2.5 for the optically thick branch of a homogeneous synchrotron source, we assume that besides the mm-submm emitting component, there is an additional spectral component which is responsible for the cm emission. We therefore fit the radio spectra with a two-component model. This allows us to fix αt, and set it to 2.5 for both of the components. We also fix the peak frequency of the lower frequency component to 20 GHz, as the low-frequency νm varies between 18−25 GHz and the fitting improves only marginally if we allow this parameter to vary. Hence, we study the spectral evolution of the radio spectra by fixing αt(l)8 = αt(h) = 2.5 and νml = 20 GHz. Such a scenario appears reasonable and is motivated by the idea of a synchrotron self-absorbed “Blandford-Königl” jet (Blandford & Königl 1979) and a more variable core or shock component. The fitted spectrum using this restricted two-component model is shown in Fig. 16 (d) and the best fit parameters are given in Table 9. A variable low-frequency component provides a better fit over bin 9−12. Therefore, we consider that both the low- and high- frequency components are varying over the time period between the two flares. The two-component SSA model describes the radio spectra much better than a single-component model. We therefore conclude that the radio spectra are at least composed of two components, one peaking at cm wavelengths and the other at mm-submm wavelengths.
3.3.2. Evolution of radio flares
In the following we adopt a model of spectral evolution as described by Marscher & Gear (1985) which considers the evolution of a traveling shock wave in a steady state jet. The typical evolution of a flare in turnover frequency – turnover flux density (Sm − νm) plane can be obtained by inspecting the R (radius of jet)-dependence of the turnover frequency, νm, and the turnover flux density, Sm (see Fromm et al. 2011, for details). During the first stage, Compton losses are dominant and νm, decreases with increasing radius, R, while Sm, increases. In the second stage, where synchrotron losses are the dominating energy loss mechanism, the turnover frequency continues to decrease while the turnover flux density remains constant. Both the turnover frequency and turnover flux density decrease in the final, adiabatic stage. We studied the evolution of the radio flares using the results obtained from both one- and two-component SSA models and in each case, we obtained similar results. The evolution of the R6 and R8 flares in Sm − νm plane are shown in Figs. 16e−f.
In a standard shock in jet model, 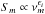 (Fromm et al. 2011; Marscher & Gear 1985) where ϵi depends upon the variation of physical quantities i.e. magnetic field (B), Doppler factor (δ) and energy of relativistic electrons (see Fromm et al. 2011; Marscher & Gear 1985, for details). The estimated ϵi values for both the one- and two-component SSA models are given in Table 10.
(Fromm et al. 2011; Marscher & Gear 1985) where ϵi depends upon the variation of physical quantities i.e. magnetic field (B), Doppler factor (δ) and energy of relativistic electrons (see Fromm et al. 2011; Marscher & Gear 1985, for details). The estimated ϵi values for both the one- and two-component SSA models are given in Table 10.
Marscher & Gear (1985) predicted a value of ϵCompton = −2.5 and Fromm et al. (2011) obtain −1.21, whereas Björnsson & Aslaksen (2000) obtained ϵCompton = −0.43 using a modified expression for the shock width. The estimated ϵCompton value for the R8 flare lies between these values, while for the R6 flare it is too high to be explained by the simple assumptions of a standard shock-in-jet model (see Table 10). For the adiabatic stage Marscher & Gear (1985) derived an exponent ϵadiabatic = 0.69 (assuming s = 3) and Fromm et al. (2011) found ϵadiabatic = 0.77. We obtain ϵadiabatic ~ 2 for the R8 flare and ~10 for the R6 flare which is again too steep. The spectral evolution of the R8 radio flare can be well interpreted in terms of a standard shock-in-jet model based on intrinsic effects. The rapid rise and decay of Sm w.r.t. νm in the case of the R6 (see Fig. 16) flare rule out these simple assumptions of a standard shock-in-jet model considered by Marscher & Gear (1985) with a constant Doppler factor (δ).
We argue that the spectral evolution of the radio flare, R6 (in Sm − νm plane) need to be investigated by considering both the intrinsic variation and the variation in the Doppler factor (δ) of the emitting region. Qian et al. (1996) studied the intrinsic evolution of the superluminal components in 3C 345 with its beaming factor variation being taken into account with a typical variation of the viewing angle by 2−8°. In the study of the spectral evolution of the IR-mm flare in 3C 273, Qian et al. (1999) found that the bulk acceleration of the flaring component improves the fit of the spectral evolution at lower frequencies. Therefore, it is worthwhile to include a variation of δ along the jet axis in our model, which we parametrize as δ ∝ Rb. Such an approach could easily explain the large variation in the observed turnover flux density, while the observed turnover frequency kept a nearly constant value or changed only slightly (Fromm et al. 2011).
We consider the evolution of radio flares in the framework of dependencies of physical parameters a, s and d following Lobanov & Zensus (1999). Here, a, s and d parametrize the variations of δ ∝ Rb, B ∝ R− a and N(γ) ∝ γ− s along jet radius. Since it is evident that ϵ values do not differ much for different choices of a and s (Lobanov & Zensus 1999), we assume for simplicity that s ≈ constant and for two extreme values of a = 1 and 2, we investigate the variations in b. The calculated values of b for different stages of evolution of radio flares are given in Table 10. It is important to note that the Doppler factor varies significantly along jet radius during the evolution of the two radio flares.
Moreover, the turnover frequency between the Compton and synchrotron stages (νr) and the synchrotron and adiabatic stages (νf) in the Sm − νm plane characterize the observed behavior of the radio outbursts (Valtaoja et al. 1992). In a shock induced flare, the shock strength reaches its maximal development at νr and the decay stage starts at νf. In Figs. 16e−f, we display by dashed lines the frequencies νr and νf. The shock reaches its maximal development at 80 GHz for the R6 flare and at 74 GHz for the R8 flare. The observed behavior of the outburst depends on νr. In a shock induced flare, the observed frequency (νobs) is less than νr in the case of low-peaking flares, while νobs > νr for high-peaking flares (Valtaoja et al. 1992). We therefore conclude that both the R6 and R8 radio outbursts are low-peaking radio flares and are in quantitative agreement with the formation of a shock and its evolution.
Different states of spectral evolution and their characteristics.
3.3.3. Synchrotron spectral break
The source was observed at IR frequencies with the Spitzer Space Telescope on December 06, 2007. We obtained the IRAC+MIPS photometric measurements at 5−40 μm from the Spitzer archive9. Since the source has been observed at radio wavelengths over this period, we combine the cm – mm and IR observations to construct a more complete broadband synchrotron spectrum. The combined radio – IR spectrum is shown in Fig. 17. The red curve represents the best fitted synchrotron self-absorbed spectrum with a break at a frequency of νb = (1.3 ± 0.1) × 104 GHz. The best-fit parameters are: Sm = (1.03 ± 0.02) Jy, νm = (45.74 ± 3.12) GHz, αt = (0.33 ± 0.01) and the spectral index of the optically thin part (α0) is − (0.38 ± 0.09) and − (0.66 ± 0.07) above and below the break, respectively. Hence, modeling of the radio – IR spectrum provides strong evidence for a break in the synchrotron spectrum at νb ~ 1.3 × 104 GHz with a spectral break Δα = 0.28 ± 0.1. We can also include the optical V passband flux from the AASVO (see Sect. 2.2) to estimate the spectral break. This leads to a steeper spectral index with α0 = −0.88 ± 0.03 and a break Δα = 0.51 ± 0.09.
The spectral break could be attributed to synchrotron loss of the high energy electrons. It is widely accepted that synchrotron losses result in a steepening of the particle spectrum by one power and a steepening of the emitted synchrotron spectrum by a half-power (Reynolds 2009; Kardashev 1962). Also, synchrotron-loss spectral breaks differing from 0.5 could be produced naturally in an inhomogeneous source (Reynolds 2009). As νb is mainly determined by synchrotron loss, it depends on the magnetic field strength. One can estimate the minimum-energy magnetic field strength using the following relation given by Heavens & Meisenheimer (1987): 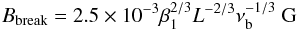 (3)where β1.c is the speed of the upstream gas related to the shock, L is the length of the emission region in kpc (at ν < νb) and νb is the break frequency in GHz. For relativistic shocks β1 is close to 1. We constrain the length of the emission region L using the variability timescales at 230 GHz as this is the closest radio frequency to νb. Using L ≤ 0.04 × 10-3 kpc (see Sect. 3.4.3), we found Bbreak ≥ 0.14 G. The minimum energy condition implies equipartition of energy, which means Bbreak ~ Beq (equipartition magnetic field).
(3)where β1.c is the speed of the upstream gas related to the shock, L is the length of the emission region in kpc (at ν < νb) and νb is the break frequency in GHz. For relativistic shocks β1 is close to 1. We constrain the length of the emission region L using the variability timescales at 230 GHz as this is the closest radio frequency to νb. Using L ≤ 0.04 × 10-3 kpc (see Sect. 3.4.3), we found Bbreak ≥ 0.14 G. The minimum energy condition implies equipartition of energy, which means Bbreak ~ Beq (equipartition magnetic field).
 |
Fig. 17 Radio-IR spectra using Spitzer observations. The red curve is the best fitted synchrotron self-absorbed spectra with a break at (1.3 ± 0.1) × 104 GHz with a spectral break Δα = 0.28 ± 0.1. The green line represents the spectral fitting including optical data point and this leads to spectral break Δα = 0.51 ± 0.09. |
3.4. Brightness temperature, size of emission region and jet Doppler factors
3.4.1. Brightness temperature 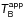
The observed rapid variability implies a very compact emission region and hence a high brightness temperature if the variations are intrinsic to the source. Assuming a spherical brightness distribution for the variable source and that the triggered flux variations propagate isotropically through the source, then the light travel time argument implies a radius d ≤ cΔt for the emission region where Δt is the time interval of expansion. So, the flux variability observed in radio bands allows us to estimate the brightness temperature of the source using the relation (see Ostorero et al. 2006; Fuhrmann et al. 2008, for details). 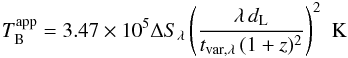 (4)where ΔSλ is the change in flux density (Jy) over time tvar,λ (years), dL is the luminosity distance in Mpc, λ is wavelength in cm and z is the redshift of the source. Here and in the following calculations we will use z = 0.31, which yields a luminosity distance, dL = 1510 Mpc (see Fuhrmann et al. 2008, for details).
(4)where ΔSλ is the change in flux density (Jy) over time tvar,λ (years), dL is the luminosity distance in Mpc, λ is wavelength in cm and z is the redshift of the source. Here and in the following calculations we will use z = 0.31, which yields a luminosity distance, dL = 1510 Mpc (see Fuhrmann et al. 2008, for details).
Two major outbursts (R6 and R8) are observed in the source at 15 GHz and at higher radio frequencies. To calculate the brightness temperature, we have used the rising time of the flares (see Table 5) separately for the two flares at 15, 37, 86 and 230 GHz, as these are the best sampled light curves. The radio flares follow a slow rising and fast decaying trend, so we calculate tvar for both the rising and the decay phases of the flares. The calculated tvar for the two radio flares are listed in Col. 2 of Table 11 and the apparent brightness temperatures (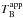 ) are in Col. 3.
) are in Col. 3.
3.4.2. Doppler factor from variability timescales δvar
The calculated 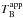 is one to two orders of magnitude higher than the IC-limit
is one to two orders of magnitude higher than the IC-limit 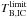 of TB ~ 1012 K (Kellermann & Pauliny-Toth 1969) at all frequencies up to 230 GHz. We notice that
of TB ~ 1012 K (Kellermann & Pauliny-Toth 1969) at all frequencies up to 230 GHz. We notice that 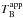 exceeds
exceeds 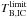 even at short-mm bands. The excessive brightness temperature can be interpreted by relativistic boosting of the radiation, which gives to a lower limit of the Doppler factor of the emitting region
even at short-mm bands. The excessive brightness temperature can be interpreted by relativistic boosting of the radiation, which gives to a lower limit of the Doppler factor of the emitting region ![\begin{equation} \delta_{\rm var} = (1+z)~\left [\frac{T_{\rm B}^{\rm app}}{10^{12}} \right ] ^{\frac{1}{3 + \alpha}}\cdot \end{equation}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq202.png) (5)Here α is the spectral index of the optically thin part of the radio spectrum. We obtained αthin = −0.23 to − 0.91 for the R6 radio flare and αthin = −0.20 to − 0.41 for the R8 flare (see Sect. 4.1 for details). The calculated δvar values are listed in column 4 of Table 11. We obtain δvar ≥ 14 for the two radio flares.
(5)Here α is the spectral index of the optically thin part of the radio spectrum. We obtained αthin = −0.23 to − 0.91 for the R6 radio flare and αthin = −0.20 to − 0.41 for the R8 flare (see Sect. 4.1 for details). The calculated δvar values are listed in column 4 of Table 11. We obtain δvar ≥ 14 for the two radio flares.
Variability brightness temperatures.
In addition, we can also use the intrinsic brightness temperature limit based on the equipartition between particle energy and field energy (Scott & Readhead 1977): TB,eq ~ 5 × 1010 K which is derived on the basis of an argument that this limit better reflects the stationary state of a synchrotron source which for many sources yields TB ≲ 1011 K (e.g., Readhead 1994). In this case, the calculated Doppler factor values using the equipartition limit, ![\hbox{$\delta_{\rm var,eq}=(1+z)\sqrt[3+\alpha]{T_{\rm B}^{\rm app}/5\times10^{10}}$}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq212.png) , become higher by a factor of 4.47 i.e. δvar,eq = 4.47 × δvar.
, become higher by a factor of 4.47 i.e. δvar,eq = 4.47 × δvar.
3.4.3. Size of the emission region θ
One can obtain the size of the emission region using the calculated Doppler factors (δ) and variability time scales (tvar): 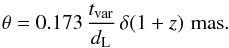 (6)The angular size θ calculated using δvar,IC are listed Col. 5 of Table 11. We obtain that the estimated value of the angular dimension θ lies between 0.004−0.09 mas. Again, θ will be a factor of 4.47 higher if we use δvar,eq. In linear dimensions, the size of the emission region ranges between (0.6−12.1) × 1017 cm.
(6)The angular size θ calculated using δvar,IC are listed Col. 5 of Table 11. We obtain that the estimated value of the angular dimension θ lies between 0.004−0.09 mas. Again, θ will be a factor of 4.47 higher if we use δvar,eq. In linear dimensions, the size of the emission region ranges between (0.6−12.1) × 1017 cm.
3.4.4. Inverse Compton Doppler factor δIC
One can constrain the inverse Compton Doppler factor (δIC) by comparing the expected and observed fluxes at high energies (see Ghisellini et al. 1993, for details). The IC Doppler factor is defined as ![\begin{eqnarray} \delta_{\rm IC}\!=\!\left[f(\alpha)S_{m}(1+z)\right]^{(4-2\alpha)/(10-6\alpha)}\left(\frac{\ln(\nu_{\rm c}/\nu_{m})\nu_{\gamma}^{\alpha}} {S_{\gamma}\theta^{(6-4\alpha)}\nu_{m}^{(5-3\alpha)}}\right)^{1/(10-6\alpha)}.\label{doppler_IC_2} \end{eqnarray}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq220.png) (7)where νc is the synchrotron high frequency cut-off in GHz, Sm the flux density in Jy at the synchrotron turnover frequency νm, SIC the observed γ-ray flux in Jy (assumed to arise from the IC process) at νγ in keV, α is the spectral index of the optically thin part of the spectrum, θν the source’s angular size in mas and f(α) ≃ 0.14 − 0.08α. The apparent variability size is calculated using Eq. (6). For the high energy cut-off we follow Fuhrmann et al. (2008) and use νc ~ 5.5 × 105 GHz.
(7)where νc is the synchrotron high frequency cut-off in GHz, Sm the flux density in Jy at the synchrotron turnover frequency νm, SIC the observed γ-ray flux in Jy (assumed to arise from the IC process) at νγ in keV, α is the spectral index of the optically thin part of the spectrum, θν the source’s angular size in mas and f(α) ≃ 0.14 − 0.08α. The apparent variability size is calculated using Eq. (6). For the high energy cut-off we follow Fuhrmann et al. (2008) and use νc ~ 5.5 × 105 GHz.
For these calculations, we used tvar equals 9 days, which is the fastest variability timescale for the R6 flare at 86 GHz. α is obtained from the SSA modeling (see Sect. 3.3.1) and the estimated values are given in Table 12. δIC is calculated for the same four time bins which we use to model the broadband SEDs of the source (see Sect. 3.5). The estimated values for δIC are given in Table 12. We find that during the four different activity states of the source δIC ≥ 20.
Brightness temperature.
3.4.5. Gamma-ray Doppler factor δγ
It is also possible to obtain a limit on the Doppler factor δ by considering that the high-energy γ-ray photons can collide with the softer radiation to produce e± pairs with the assumption that the bulk of the high-energy emission (γ-rays and X-rays) is produced in the same emission region. The cross-section of this process is maximized at ~σT/5 (see Svensson 1987, for details), where σT is the Thomson scattering cross-section. This leads to a lower limit on δ with the requirement that τγγ(ν) < 1 (Dondi & Ghisellini 1995; Finke et al. 2008): ![\begin{equation} \delta_{\gamma}>\left[\frac{2^{a-1} (1+z)^{2-2a}\sigma_{\rm T} D_{\rm L}^2}{m_{\rm e} c^4 t_{\rm var}} \epsilon f_{\epsilon^{-1}}^{\rm syn} \right]^\frac{1}{6 - 2a} \end{equation}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq260.png) (8)where a is the power law index of the synchrotron spectrum i.e.
(8)where a is the power law index of the synchrotron spectrum i.e. 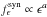 , σT is the scattering Thomson cross-section, me is the electron mass, ϵ1 = E/(mec2) is the dimensionless energy of a γ-ray photon with energy E for which the optical depth of the emitting region τγγ = 1. For the highest energy GeV (207 GeV) photon observed in the source (Rani et al. 2012), we obtain ϵ = 207 GeV/(5.11 × 10-4 GeV) = 4 × 104 and ϵ-1 = 2.4 × 10-6. Using
, σT is the scattering Thomson cross-section, me is the electron mass, ϵ1 = E/(mec2) is the dimensionless energy of a γ-ray photon with energy E for which the optical depth of the emitting region τγγ = 1. For the highest energy GeV (207 GeV) photon observed in the source (Rani et al. 2012), we obtain ϵ = 207 GeV/(5.11 × 10-4 GeV) = 4 × 104 and ϵ-1 = 2.4 × 10-6. Using 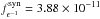 ergs cm-2 s-1, we obtain δγ ≥ 9.1. The detection of the source at above 400 GeV (Anderhub et al. 2009) constrains δγ ≥ 9.8.
ergs cm-2 s-1, we obtain δγ ≥ 9.1. The detection of the source at above 400 GeV (Anderhub et al. 2009) constrains δγ ≥ 9.8.
3.4.6. Magnetic field from synchrotron self-absorption
It is also possible to constrain the magnetic field using the standard synchrotron self-absorption expressions. Following Marscher (1987), an expression for the magnetic field B in a homogeneous synchrotron self-absorbed region is given by: ![\begin{eqnarray} B_{\rm SA}\,[{\rm G}]\,=10^{-5} b(\alpha) \theta^{4}\nu_{m}^{5}S_{m}^{-2}\left(\frac{\delta}{1+z}\right), \label{B} \end{eqnarray}](/articles/aa/full_html/2013/04/aa21058-13/aa21058-13-eq271.png) (9)where b(α) depends on the optically thin spectral index αthin (see Table 1 in Marscher 1987), Sm is the flux density, θ is the source’s angular size at the synchrotron turnover frequency νm and δ is the Doppler factor. The size of the emitting region responsible for the observed variations can be constrained using mm-VLBI measurements of the core region of S5 0716+714 by Bach et al. (2006): θ < 0.04 mas. Using b(α) = 3.13, Sm = 3.89 Jy, νm = 80 GHz, we calculate a lower limit of the magnetic field BSA in the range of (0.0078−0.0198)δ mG. Using δ ≥ 7 at νm ~ 80 GHz (see Table 11), we obtained BSA ≥ 0.05 to 0.14 G. The size of the emission region constrained using the causality arguments, θ ~ 0.0027 mas at νm ~ 80 GHz (see Table 11) gives BSA ≥ 0.03 G. These calculations constrain BSA ≥ 0.03 − 0.14 G
(9)where b(α) depends on the optically thin spectral index αthin (see Table 1 in Marscher 1987), Sm is the flux density, θ is the source’s angular size at the synchrotron turnover frequency νm and δ is the Doppler factor. The size of the emitting region responsible for the observed variations can be constrained using mm-VLBI measurements of the core region of S5 0716+714 by Bach et al. (2006): θ < 0.04 mas. Using b(α) = 3.13, Sm = 3.89 Jy, νm = 80 GHz, we calculate a lower limit of the magnetic field BSA in the range of (0.0078−0.0198)δ mG. Using δ ≥ 7 at νm ~ 80 GHz (see Table 11), we obtained BSA ≥ 0.05 to 0.14 G. The size of the emission region constrained using the causality arguments, θ ~ 0.0027 mas at νm ~ 80 GHz (see Table 11) gives BSA ≥ 0.03 G. These calculations constrain BSA ≥ 0.03 − 0.14 G
3.4.7. Equipartition magnetic field and Doppler factor
The equipartition magnetic field Beq, which minimizes the total energy Etot = (1 + k)Ee + EB (with relativistic particle energy Ee ~ B-1.5 and energy of the magnetic field EB ~ B2), is given by the following expression (e.g. Bach et al. 2005; Fuhrmann et al. 2008): 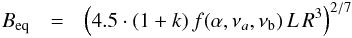 (10)here k is the energy ratio between electrons and heavy particles, L is the synchrotron luminosity of the source given by
(10)here k is the energy ratio between electrons and heavy particles, L is the synchrotron luminosity of the source given by 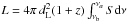 , R is the size of the component in cm, Sm is the synchrotron peak flux in Jy, νm is the synchrotron peak frequency in GHz and f(α,νa,νb) is a tabulated function depending on the upper and lower synchrotron frequency cutoffs νa,νb. Using νa = 107 Hz, νb = 5.5 × 1014 Hz, and f( − 0.5,107,1011) = 1.6 × 107, we obtain
, R is the size of the component in cm, Sm is the synchrotron peak flux in Jy, νm is the synchrotron peak frequency in GHz and f(α,νa,νb) is a tabulated function depending on the upper and lower synchrotron frequency cutoffs νa,νb. Using νa = 107 Hz, νb = 5.5 × 1014 Hz, and f( − 0.5,107,1011) = 1.6 × 107, we obtain 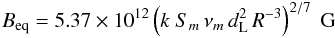 (11)Using Beq ≥ 0.14 (see Sect. 3.3.3), Sm = 3.89 Jy, νm = 80 GHz, R = 2.90 × 1016 − 1.2 × 1018 cm (estimated using tvar = 25 days at νm = 86 GHz), the above expression yields k = 1. A small value of k implies that the jet is mainly composed of electron-positron plasma.
(11)Using Beq ≥ 0.14 (see Sect. 3.3.3), Sm = 3.89 Jy, νm = 80 GHz, R = 2.90 × 1016 − 1.2 × 1018 cm (estimated using tvar = 25 days at νm = 86 GHz), the above expression yields k = 1. A small value of k implies that the jet is mainly composed of electron-positron plasma.
Equations (9) and (11) give different dependencies of the magnetic field on δ, i.e. BSA ~ δ and Beq ~ δ2/7α + 1. This yields 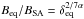 . Adopting the above numbers, we obtain Doppler factors δeq,B in the range of 14−20 (for α = −(0.35 to 0.7)).
. Adopting the above numbers, we obtain Doppler factors δeq,B in the range of 14−20 (for α = −(0.35 to 0.7)).
3.4.8. Comparison of the estimated parameters
The apparent brightness temperature TB obtained from the day-to-day variations exceeds the theoretical limits by several orders of magnitudes. Although TB decreases towards the mm-bands, it is still higher than the IC-limit (1012 K). TB exceeds 1014 K at 15 GHz and 1012 K at 230 GHz. We have obtained lower limits to the Doppler factor of the source using different methods as discussed in the earlier sections. These methods reveal a range of consistent lower limits to the Doppler factor with δvar ≥ 14, δIC ≥ 20, δγ ≥ 10 and δeq,B ≥ 20. Comparing the Doppler factor estimates obtained with different methods seems to suggest that δ ≥ 20. An independent approach to estimate δ is spectral modeling of the broadband SEDs, and this gives δ = 25 (see Sect. 3.5), which is in agreement with the former values. These limits are in good agreement with the estimates based on the recent kinematical VLBI studies of the source (Bach et al. 2006) and the IC Doppler factor limits obtained by Fuhrmann et al. (2008). As δeq,B agrees fairly well with the δ values derived from the other methods, we conclude that the emission region is in a state of equilibrium.
The estimated magnetic field value from the broadband spectral modeling lies between 0.05 and 1 G. A break in the optically thin power-law slope at a wavelength of ~23 μm constrains the equipartition magnetic field to Beq ≥ 0.36 G. We obtained BSA ≥ 0.14 G from the synchrotron self-absorption calculation. The size of the emission region (θ) derived on the basis of causality arguments lies between 0.004−0.091 mas which agrees fairly well with the size of emission region constrained using mm-VLBI measurements (Bach et al. 2006).
Parameters of SSC and EC fits to SED of S5 0716+714.
 |
Fig. 18 Broad band SEDs of S5 0716+714. Each SED is constructed using 10-day averaged multifrequency data. The error bars represent the variation of flux over 10 days in each bin. Pure SSC models are shown as thick dashed curves. For EC fits, the total model SEDs are the thick solid curves; the synchrotron components are dotted, the SSC components are dot-dashed, and the EC components are thin dashed curves. |
3.5. The complete spectral energy distribution
The broadband monitoring of the source over several decades of frequencies allows us to construct multiple quasi-simultaneous SEDs. The SEDs of the source constructed over 4 different periods of time are shown in Fig. 18. These time bins (tbin) reflect different brightness states of the source and each time bin has a width of 10-day. The variation in flux over the bin width is shown as error bars in the SED plots. We construct the broadband SEDs for the following activity periods:
-
Bin110: Radio-mm(steady), optical(high), X-ray(steady),GeV (low).
-
Bin2: Radio-mm(low), optical(flaring), X-ray(low), GeV (flaring).
-
Bin3: Radio-mm(flaring), optical(flaring), X-ray(flaring), GeV (low).
-
Bin4: Radio-mm(steady), optical(low), X-ray(steady), GeV (steady).
The double-humped structures of the broadband SEDs can usually be modeled by both leptonic and hadronic models (e.g. Boettcher et al. 2012). Here we have used a quasi-equilibrium version of a leptonic one-zone jet model as described by Boettcher et al. (2012). In this model, the observed radiation is assumed to be originating from the ultra-relativistic electrons (and positrons) in a spherical emission region of co-moving radius RB propagating with relativistic speed βΓc (Γ is bulk Lorentz factor) along the jet, which is offset by an angle θ w.r.t the line-of-sight. We fix θ to be such that the bulk Lorentz factor, Γ equals the Doppler factor, δ, which, for highly relativistic motion (Γ ≫ 1) implies θ = 1/Γ. The emitting electrons are assumed to be instantaneously accelerated into a power-law distribution of electron energy, Ee = γmec2, of the form Q(γ) = Q0γ− q with q being the injection electron spectral index and γ1 and γ2 are the low- and the high-energy cutoffs.
An equilibrium in the emission region between particle injection, radiative cooling, and escape of particles from the emission region yields a temporary quasi-equilibrium state described by a broken power law. The particle escape is parametrized through an escape timescale parameter η > 1 so that tesc = ηR/c. The balance between the particle escape and radiative cooling will lead to a break in the equilibrium particle distribution at a break Lorentz factor γb, where tesc = tcool(γ). The cooling timescale is calculated
self-consistently taking into account synchrotron, SSC and EC cooling. Depending on whether γb is greater than or less than γ1, the system will be in the slow cooling or fast cooling regime, respectively, leading to different spectral indices of the equilibrium electron distribution Böttcher & Chiang (2002).
In the fitted model the number density of injected particles is normalized to the resulting power in ultra-relativistic electrons propagating along the jet given by, 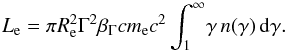 (12)The magnetic field is considered as a free parameter in the emission region. The Poynting flux along jet is
(12)The magnetic field is considered as a free parameter in the emission region. The Poynting flux along jet is 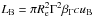 , where uB = B2/(8π) is the magnetic field energy density. The equipartition parameter eB = LB/Le is calculated for each fitted model.
, where uB = B2/(8π) is the magnetic field energy density. The equipartition parameter eB = LB/Le is calculated for each fitted model.
After evaluation of the quasi-equilibrium particle distribution in the emission region, our code calculates the radiative output from the synchrotron, SSC, and EC emissions self-consistently with the radiative cooling rates. The external radiation field, which serves as seed photons for EC scattering, is assumed to be isotropic in the stationary AGN rest frame. Its spectrum can be chosen to be a thermal blackbody with temperature Text and radiation energy density uext, or a line-dominated spectrum (or a combination of the two). The direct emission from this external radiation field is added to the emission from the jet to yield the total modeled SED, which we fit to the observations.
We first tried to fit the SEDs with a pure SSC model, as this has fewer free parameters than the EC version of the model. However, except for the SED of bin 1 (see below), pure SSC models typically fail to reproduce the Fermi/LAT spectra of the SEDs. Also a detailed study of the γ-ray spectrum of the source (Rani et al. 2013), shows a significant correlation between detection of the high energy GeV photons and change in spectral slope below and above the break energy, which suggests that BLR opacity has a significant impact on the observed spectral breaks. Therefore, we included an external radiation component, as outlined above, to produce SSC+EC fits.
The fitted models are shown in Fig. 18 and the best-fit parameters are given in Table 13. The pure SSC model does a moderately good job in describing the SEDs of the low states, although the γ-ray spectra appear systematically too steep. The SED of Bin1 is well fitted with the SSC model, while for the other time bins an EC component is required to fit the GeV spectra. The high-state is very problematic for the SSC model as it would require a much lower magnetic field (far below equipartition) and – in the case of Bin 2 – a very large emission region, in conflict with the often observed intraday optical variability. All the low-state fits are possible with parameters close to equipartition between relativistic electrons and the magnetic field. A model including external Compton generally does a better job in reproducing the entire SEDs (including the γ-ray spectrum), if one uses an external radiation field dominated by Ly-α emission from a putative broad line region (BLR). For S5 0716+714, we found that the radiation field energy density of this external field varies between 10-6 to 10-5 ergs cm-3, which is a factor of ~1000 lower than what we expect for a typical quasar. However, this is a reasonable value for a BL Lac like S5 0716+714 which is known to have a featureless spectrum. Furthermore, this low BLR energy density value naturally explains the origin of γ-ray spectral breaks observed in the source. Moreover, the low BLR energy density is consistent with the non-detection of emission lines. Parameters close to equipartition can be used for all time bins, including the high states.
At first glance the fits look good, but in more detail the fit to the radio data for some bins is relatively poor. In the EC model, the model fits the cm-radio data quite well, but is much below the mm data for Bin3. The model for Bin4 does not fit the radio data at all (see Fig. 18). So, in general the model under-predicts the radio flux at mm and cm bands. This indicates the possibility of a missing spectral component at cm-mm wavelengths. We have seen in Sect. 3.3.1 that a two-component model better describes the radio spectra. Therefore, we conclude that an additional synchrotron component is required to fit the broadband SED at mm to cm wavelengths.
4. Discussion
The densely sampled multifrequency observations of the BL Lac object S5 0716+714 over the past three years allow us to study its broadband flaring behavior and probe into the physical process, location and size of the emission regions. We found a direct connection between GeV and optical flares, and major flares propagate down to radio wavelengths. The radio outbursts seem to be smeared out at 10 GHz and lower frequencies. An orphan X-ray flare lags the major optical-GeV flare (O5-G5) by ~55 days and the X-ray emission is produced by both synchrotron and inverse Compton mechanisms. It seems that the interaction of shocks with the underlying jet structure might be responsible for optical and high energy emission, and opacity plays a key role in the time-delayed emission at radio wavelengths.
4.1. Broadband correlation alignment
Following the broadband cross-correlation analysis (3.2), we plot the estimated time lag as a function of frequency in Fig. 19. Figure 19a shows the plot of the time lag measurements at different frequencies for the R6 flare using 15 GHz as the reference frequency (see Fig. 2). It has become evident in Sect. 3.2.1 that the time lags (w.r.t. 15 GHz) increase with frequency and follow a power-law as a function of frequency with a slope ~0.3. If we extend the fitted power law to optical frequencies, then the R6 flare meets the O5 flare, which is observed ~60 days earlier than the R6 flare. A formal cross-correlation between optical and radio frequency light curves indicates a significant correlation with a delay of ~60 days at radio wavelengths. The dashed line in Fig. 19a connects the simultaneous optical – GeV flares. The optical-GeV correlation shows no time lag among the flares at the two frequencies, i.e. O5 correlates with G5 and O4 with G4; but there is no respective GeV flare for O6. The nearby optical, X-ray and GeV flares are shown with their possible time lags w.r.t. R6. The allowed time range of the peak of the X-ray flare is marked with an arrow. In Fig. 19b, we show a similar plot for the R8 flare. Both of these figures provide a one-to-one connection of the broadband flares based on our analysis.
 |
Fig. 19 a) Time lag measurements vs. frequency using 15 GHz as the reference frequency for the radio flare R6. The best fitted power law at radio and mm frequencies is extended up to the optical wavelengths. The near by optical, X-ray and GeV flares are shown with their possible time lags w.r.t. R6. b) The same for the R8 flare (see Fig. 2 for flare labeling) In both plots, the dashed lines indicate the SSC process with simultaneous optical-γ-ray events. |
4.2. Origin of optical variability
During our observations, the source was highly active at optical frequencies showing multiple flares roughly separated from each other by ~60−70 days, superimposed on a long-term variability trend at a ~350 day timescale. The periodogram analysis reveals two significant peaks at ~63 and 359 day timescales. A more robust analysis using the power spectrum density method implies that the significance of a detection of a quasi-periodic signal at the frequency corresponding to these timescales is only 2σ. Thus, the significance of detection remains marginal. However, it is important to note that periodic variations at a year timescale has also been observed earlier in the source (Raiteri et al. 2003).
During the two years of our observations, we found that the long-term variability amplitude of the source remains almost constant at about 1.3 mag. A constant variability amplitude can be interpreted in terms of variations of the Doppler boosting factor (Raiteri et al. 2003). The change in δ can be due to either a viewing angle (θ) variation or a change of the bulk Lorentz factor (Γ) or maybe a combination of both. We notice that a change in δ by a factor of 1.2 can be easily interpreted as a few degree variation in θ, while it requires a noticeable change of the bulk Lorentz factor. We therefore propose that the geometry significantly affects the long-term flux base-level modulations. Such variations are very likely originating as a relativistic shock traces a spiral path through the jet (Marscher 1996).
4.3. Origin of γ-rays
The source displays substantial activity at γ-rays during the high optical activity period. This is to be expected in leptonic models, as the same electrons radiating the optical synchrotron photons would emit γ-rays through the inverse Compton scattering process. Here, we observe a similar flaring behavior at the two frequencies. We also found that the flux variations at optical and GeV frequencies are significantly correlated with each other (on weekly timescales) and corresponding to each optical flare “O1” to “O9” (except O6) there is a local maximum “G1” to “G9” at GeV frequencies. In addition to that the variability timescales (both short and long) are also comparable for optical and GeV light curves. We note that the ratio between the high and low γ-ray flux levels is about 15, while in the optical band the same ratio is of the order of 3.7. Thus, the γ-ray flux density appears to vary as the square of change in the optical flux density. This reflects a quadratic dependence of the GeV flux variations compared to optical variability. This favors a SSC interpretation. However, we would also like point out that a weak EC contribution is also required in order to model the GeV spectrum of the source.
4.4. Opacity and delay at radio wavelengths
The source reaches a maximum in simultaneous optical – GeV flaring activity at “5” (see Fig. 2, flares: O5-G5). This maximum coincides with the beginning of a major radio outburst “R6” at 230 GHz. The R6 radio flare is observed ~65 days later than the optical flare O5 at 230 GHz. The R6 flare is followed by another radio flare, R8, with a moderate level of flux activity between the two. The two major 230 GHz radio outbursts (R6 and R8) are smoothed and delayed at lower radio frequencies till 15 GHz. The flaring activity seems to be completely washed out at ≤10 GHz. The estimated time lag (using 15 GHz as reference frequency) at each frequency as a function of frequency follows a power law with a slope ~0.3. Delayed emission at lower frequencies is a clear indication of opacity effects due to synchrotron self-absorption (Kudryavtseva et al. 2011).
As per the cross-correlation analysis, the optical – radio variability is found to be significantly correlated, with the flux variations at optical frequencies leading those at radio bands by ~60 days (see Sect. 3.2.2). Most earlier studies on the radio – optical correlation have shown that the radio events lag behind the optical ones by several weeks or months (e.g. Tornikoski et al. 1994; Clements et al. 1995; Villata et al. 2007; Raiteri et al. 2003; Jorstad et al. 2010; Agudo et al. 2011, and references therein). Similar variability timescales (~90 and 180 days) at optical and radio frequencies again hint at a co-spatial origin of variability. It is worth pointing out that the long term variability timescales are common at optical (and also at γ-rays) and radio frequencies. The fast repetitive optical/γ-ray flares are not observed at radio wavelengths. Therefore, it is not unreasonable to suggest that the long term variability features observed at optical/GeV frequencies propagate down to radio frequencies with a time lag of ~60 days. As we notice in Sect. 3.3.1, the two radio outbursts are low-peaking flares. Thus, a 60 day time delay between the optical and radio activity emphasizes the optical flares being the precursor of the radio flares (Valtaoja et al. 1992).
4.5. Origin of the orphan X-ray flare
When the source is flaring at optical – GeV frequencies, it is quiet at X-rays. Although it is hard to locate the exact peak time of the X-ray flare, it is obvious that the maximum of the X-ray flux peaks ~50 days later than the major optical – GeV flares (O5-G5) (see Fig. 2). At this epoch, the source was in a relatively steady state at optical/GeV frequencies while there is another bright optical flare lagging the X-ray maximum by ~10 days. We also notice that the fractional variability of the source is comparable at soft (22.5%) and hard (25%) X-rays. Interestingly, we do not find any significant correlation among the X-ray spectral index and flux. This may be due to the poor data sampling or may be intrinsic to the source. The concave shape of the X-ray spectrum (see Sect. 3.5), suggests that the X-ray emission shows a combination of synchrotron and inverse Compton mechanisms which could prevent the source from exhibiting any steepening or hardening trend during the flare.
A similar orphan X-ray flare was also observed in the blazar 3C 279 by Abdo et al. (2010b) with X-ray flaring activity lagging optical – GeV flares by 60 days. The authors argued that X-ray photons are produced further down to the jet compared to optical – GeV photons. Hayashida et al. (2012) argued in the context of a two component model; the X-ray flare is produced by the low-frequency component which is less variable compared to the high-frequency component. Although we do not completely understand the origin of the orphan X-ray flare in S5 0716+714, it appears possible that the X-ray emission is not co-spatial with the optical/γ-ray emission in this event. We notice some low level flux activity (mini flare, say R7) in between the two major radio flares (“R6” and “R8”, see Fig. 2). While modeling the radio spectra of the source, we also noticed that a two-component model better describes the synchrotron spectra of the source over this period. This indicates that either multiple shocks are hitting the emission region which at first produces the major flare “O5/G5-R6”, then “X6/O6-R7” and later “O7/G7-R8”, or the radiation is contributed by two synchrotron components with the low-frequency component producing the X-ray flare.
5. Conclusions
In this paper we presented the results of the radio to γ-ray monitoring of S5 0716+714 from April 2007 to January 2011. The source was very active at optical and higher frequencies. Two major radio outbursts were observed during this high activity period. From the rapid rise and decay, we derive variability brightness temperatures exceeding the IC limit, which at least for mm flares is a very unique behavior.
A long-term variability trend (~350 days timescale) is visible in the optical light curves which is superimposed with repetitive variations on shorter time scales (~60 day). A comparison of the various flaring episodes of S5 0716+714 strongly indicates a one-to-one correlation between the strength of the γ-ray emission and the strength of the optical emission. A quadratic dependence of the amplitude of the γ-ray variability with respect to that of the optical favors an SSC explanation.
The high-energy (optical – GeV) flares propagate down to radio frequencies with a time delay of ~65 days following a power-law dependence on frequency with a slope ~0.3. This indicates that opacity plays a key role in producing time delays among light curves at optically thin and thick wavelengths. Since the radio outbursts are low-peaking flares, such a long time lag is only possible in the case of optical flares being the precursors of radio ones. The evolution of the radio flares are in agreement with the generalized shock model proposed by Valtaoja et al. (1992). The evolution of the flare in the turnover frequency – turnover flux density (νm − Sm) plane shows a very steep rise and decay over the Compton and adiabatic stages with a slope too high to be expected from intrinsic variations, requiring an additional Doppler factor variation along the jet. For the two flares, we notice that δ changes as R0.7 during the rise and as R2.6 during the decay of R6 flare. The evolution of the R8 flare is governed by δ ∝ R0.4 during the rising phase and δ ∝ R-2.0 during the decay phase of the flare.
An orphan X-ray flare is observed ~50 days after the major optical – GeV flares. The detection of an isolated X-ray flare challenges the simple one-zone emission models, rendering them too simple. The lack of substantial observations over the flaring epoch makes it even more complicated to understand. We found that this flare has equal contributions from both the synchrotron and the high-energy (inverse Compton in a leptonic model interpretation) emission mechanisms.
We model the broadband SEDs of the source using two different versions of leptonic models: a pure SSC and SSC+EC. We found that the low activity states of the source are well described by a pure SSC model while an EC contribution is required to reproduce the SEDs for high states. The SSC+EC model returns magnetic field parameter value closer to equipartition, providing a satisfactory description of the broadband SEDs. We found that satisfactory model fits can be achieved if the external radiation field is dominated by Ly-α emission from the broad-line region. This model nicely describes the broadband SEDs of the source at optical and higher frequencies, but under-predicts the cm−mm spectra at least for few time periods. A separate synchrotron component seems required to fit the cm−mm radio fluxes. This may also provide a hint towards the origin of the orphan X-ray flare.
See http://www.aavso.org/ for more information.
Acknowledgments
The Fermi/LAT Collaboration acknowledges the generous support of a number of agencies and institutes that have supported the Fermi/LAT Collaboration. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. This research is partly based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. This work has made use of observations with the IRAM 30-m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. The observations made use of the Noto telescope operated by INAF − Istituto di Radioastronomia. B.R. gratefully acknowledges the travel support the COSPAR Capacity-Building Workshop fellowship program. I.N. was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. N.M. is funded by an ASI fellowship under contract number I/005/11/0. We also acknowledge the Swift Team and the Swift/XRT monitoring program efforts, as well as analysis supported by NASA Fermi GI grants NNX10AU14G. L.X. is supported by the National Natural Science Foundation of China (No. 11273050). Work at UMRAO has been supported by a series of grants from the NSF and from NASA. Support for operation of the observatory was provided by the University of Michigan. I.A. acknowledges funding by the “Consejería de Economía, Innovación y Ciencia” of the Regional Government of Andalucía through grant P09-FQM-4784, an by the “Ministerio de Economía y Competitividad” of Spain through grant AYA2010-14844. The Metsähovi team acknowledges the support from the Academy of Finland to our observing projects (numbers 212656, 210338, 121148, and others). We thank Ivan Agudo for his contribution at the 30 m telescope and for discussion. We would like to thank Marcello Giroletti, the internal referee from Fermi/LAT team for his useful suggestions and comments. We thank the referee for several helpful suggestions. We would also like to thank Jeff Hodgson for the help in finalizing the text.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 710, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Marscher, A. P., Jorstad, S. G., et al. 2011, ApJ, 735, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, H. D., Aller, M. F., Latimer, G. E., & Hodge, P. E. 1985, ApJS, 59, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Anderhub, H., Antonelli, L. A., Antoranz, P., et al. 2009, ApJ, 704, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Angelakis, E., Fuhrmann, L., Marchili, N., Krichbaum, T. P., & Zensus, J. A. 2008, Mem. Soc. Astron. It., 79, 1042 [NASA ADS] [Google Scholar]
- Antonucci, R. R. J., Hickson, P., Olszewski, E. W., & Miller, J. S. 1986, AJ, 92, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bach, U., Krichbaum, T. P., Ros, E., et al. 2005, A&A, 433, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bach, U., Krichbaum, T. P., Kraus, A., Witzel, A., & Zensus, J. A. 2006, A&A, 452, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Björnsson, C.-I., & Aslaksen, T. 2000, ApJ, 533, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Boettcher, M., Harris, D. E., & Krawczynski, H. 2012, Relativistic Jets from Active Galactic Nuclei [Google Scholar]
- Böttcher, M., & Chiang, J. 2002, ApJ, 581, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, A. W., D’Ammando, F., Villata, M., et al. 2008, A&A, 489, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clements, S. D., Smith, A. G., Aller, H. D., & Aller, M. F. 1995, AJ, 110, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Danforth, C. W., Nalewajko, K., France, K., & Keeney, B. A. 2012, ArXiv e-prints [Google Scholar]
- Dondi, L., & Ghisellini, G. 1995, MNRAS, 273, 583 [NASA ADS] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Cheng, K. S., Zhang, L., & Liu, C. H. 1997, A&A, 327, 947 [NASA ADS] [Google Scholar]
- Ferrero, E., Wagner, S. J., Emmanoulopoulos, D., & Ostorero, L. 2006, A&A, 457, 133 [Google Scholar]
- Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Tagliaferri, G., Pian, E., et al. 2006, A&A, 455, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2011, A&A, 531, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, L., Zensus, J. A., Krichbaum, T. P., Angelakis, E., & Readhead, A. C. S. 2007, in The First GLAST Symposium, eds. S. Ritz, P. Michelson, & C. A. Meegan, AIP Conf. Ser., 921, 249 [Google Scholar]
- Fuhrmann, L., Krichbaum, T. P., Witzel, A., et al. 2008, A&A, 490, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Giommi, P., Massaro, E., Chiappetti, L., et al. 1999, A&A, 351, 59 [NASA ADS] [Google Scholar]
- Giommi, P., Colafrancesco, S., Cutini, S., et al. 2008, A&A, 487, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, A. C., Srivastava, A. K., & Wiita, P. J. 2009, ApJ, 690, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Krichbaum, T. P., Wiita, P. J., et al. 2012, MNRAS, 425, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Gurwell, M. A., Peck, A. B., Hostler, S. R., Darrah, M. R., & Katz, C. A. 2007, in From Z-Machines to ALMA: (Sub)Millimeter Spectroscopy of Galaxies, eds. A. J. Baker, J. Glenn, A. I. Harris, et al., ASP Conf. Ser., 375, 234 [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashida, M., Madejski, G. M., Nalewajko, K., et al. 2012, ApJ, 754, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., & Meisenheimer, K. 1987, MNRAS, 225, 335 [NASA ADS] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJ, 556, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Larionov, V. M., et al. 2010, ApJ, 715, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kardashev, N. S. 1962, Soviet Astron., 6, 317 [Google Scholar]
- Kawabata, K. S., Nagae, O., Chiyonobu, S., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kudryavtseva, N. A., Gabuzda, D. C., Aller, M. F., & Aller, H. D. 2011, MNRAS, 415, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y. C., Bertsch, D. L., Dingus, B. L., et al. 1995, ApJ, 442, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Song, H.-G., Marchili, N., et al. 2012, A&A, 543, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Lott, B., Escande, L., Larsson, S., & Ballet, J. 2012, A&A, 544, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 1987, in Superluminal Radio Sources, eds. J. A. Zensus, & T. J. Pearson, 280 [Google Scholar]
- Marscher, A. P. 1996, in Blazar Continuum Variability, eds. H. R. Miller, J. R. Webb, & J. C. Noble, ASP Conf. Ser., 110, 248 [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Montagni, F., Maselli, A., Massaro, E., et al. 2006, A&A, 451, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, K., Pursimo, T., Sillanpää, A., Takalo, L. O., & Lindfors, E. 2008, A&A, 487, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ostorero, L., Wagner, S. J., Gracia, J., et al. 2006, A&A, 451, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, S. J., Krichbaum, T. P., Zensus, J. A., Steffen, W., & Witzel, A. 1996, A&A, 308, 395 [NASA ADS] [Google Scholar]
- Qian, S., Witzel, A., Krichbaum, T. P., et al. 1999, in BL Lac Phenomenon, eds. L. O. Takalo, & A. Sillanpää, ASP Conf. Ser., 159, 443 [Google Scholar]
- Quirrenbach, A., Witzel, A., Wagner, S., et al. 1991, ApJ, 372, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Tosti, G., et al. 2003, A&A, 402, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Wiita, P. J., & Gupta, A. C. 2009, ApJ, 696, 2170 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., Ganesh, S., & Wiita, P. J. 2010a, ApJ, 719, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, B., Gupta, A. C., Strigachev, A., et al. 2010b, MNRAS, 404, 1992 [NASA ADS] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., Ganesh, S., & Wiita, P. J. 2011, MNRAS, 413, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, B., Krichbaum, T. P., Fuhrmann, L., et al. 2013, ASR, submitted [Google Scholar]
- Rastorgueva, E. A., Wiik, K. J., Bajkova, A. T., et al. 2011, A&A, 529, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Readhead, A. C. S. 1994, ApJ, 426, 51 [Google Scholar]
- Reynolds, S. P. 2009, ApJ, 703, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, M. A., & Readhead, A. C. S. 1977, MNRAS, 180, 539 [NASA ADS] [Google Scholar]
- Senturk, G. D., Errando, M., Boettcher, M., et al. 2011 [arXiv:1111.0378] [Google Scholar]
- Simonetti, J. H., Cordes, J. M., & Heeschen, D. S. 1985, ApJ, 296, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, R. 1987, MNRAS, 227, 403 [NASA ADS] [Google Scholar]
- Tagliaferri, G., Ravasio, M., Ghisellini, G., et al. 2003, A&A, 400, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takalo, L. O., Sillanpaeae, A., & Nilsson, K. 1994, A&AS, 107, 497 [NASA ADS] [Google Scholar]
- Teräsranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teräsranta, H., Achren, J., Hanski, M., et al. 2004, A&A, 427, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tornikoski, M., Valtaoja, E., Teraesranta, H., & Okyudo, M. 1994, A&A, 286, 80 [NASA ADS] [Google Scholar]
- Türler, M., Courvoisier, T. J.-L., & Paltani, S. 2000, A&A, 361, 850 [NASA ADS] [Google Scholar]
- Valtaoja, E., Terasranta, H., Urpo, S., et al. 1992, A&A, 254, 71 [NASA ADS] [Google Scholar]
- Vaughan, S. 2005, A&A, 431, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Aller, M. F., et al. 2007, A&A, 464, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2008, A&A, 481, L79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vittorini, V., Tavani, M., Paggi, A., et al. 2009, ApJ, 706, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., Witzel, A., Heidt, J., et al. 1996, AJ, 111, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, M., Nakaya, H., Yamamuro, T., et al. 2005, PASP, 117, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, A., Schalinski, C. J., Johnston, K. J., et al. 1988, A&A, 206, 245 [NASA ADS] [Google Scholar]
All Tables
Best-fit spectral parameters for the evolution of radio flares using a one-component SSA model.
Best fitted spectral parameters over the evolution of radio flares using a two component SSA model.
All Figures
 |
Fig. 1 Radio to mm wavelength light curves of S5 0716+714 observed over the past ~3 years. For clarity, the light curves at different frequencies are shown with arbitrary offsets (indicated by a “Frequency + x Jy” label). The major radio flares are labeled as “R0”, “R6” and “R8” (see Fig. 2 for the details of labeling). |
| In the text | |
 |
Fig. 2 Light curves of 0716+714 from γ-ray to radio wavelengths a) GeV light curve at E > 100 MeV; b) X-ray light curve at 0.3−10 KeV; c) optical V passband light curve and d) 5 to 230 GHz radio light curves. Vertical dotted lines are marked w.r.t. different optical flares labeling the broadband flares as “G” for γ-rays, “X” for X-rays, “O” for optical and “R” for Radio followed by the number close to flare. The yellow area represents the period for which we construct the broadband SEDs of the source (see Sect. 3.5 for details). |
| In the text | |
 |
Fig. 3 Top: structure functions at radio frequencies. The solid curves represent the best fitted power laws. The dotted lines in each plot indicate the timescale of variability (tvar). Bottom: structure functions at optical and γ-ray frequencies. |
| In the text | |
 |
Fig. 4 SF vs. frequency at GHz frequencies for a structure function time =100 days. |
| In the text | |
 |
Fig. 5 LSP analysis curve showing a peak at a period of 63 and 359 days. |
| In the text | |
 |
Fig. 6 Optical V passband light curve of S5 0716+714 with different time binning. The light curve appears as a superposition of fast flares on a modulated base level varying on a (350 ± 9) day timescale. These slower variations can be clearly seen in 75-day binned light curve (error bar represents variations in flux over the binned period). The dashed line represents a spline interpolation through the 75-day binned light curve. Dotted lines are obtained by shifting the spline by ±0.65 mag. |
| In the text | |
 |
Fig. 7 Gamma-ray flux and photon index light curve of S5 0716+714 measured with the Fermi/LAT for a time period between August 04, 2008 to February 07, 2011. The blue symbols show the weekly averaged flux while monthly averaged values are plotted in red. Different activity states of the source are separated by vertical green lines. A marginal softening of spectrum over the quiescent state can be seen here. |
| In the text | |
 |
Fig. 8 DCF curves among the different radio frequency light curves. The solid curves represent the best-fit Gaussian function. |
| In the text | |
 |
Fig. 9 Time lag vs. frequency, using 15 GHz as the reference frequency. Time lag vs. frequency curves for individual flares are shown with different colors. The solid lines represent the best fitted power law in each case. |
| In the text | |
 |
Fig. 10 Modeled radio flare, R6. The blue points are the observed data while the red curve represent the fit. |
| In the text | |
 |
Fig. 11 a) DCF curve for optical V passband vs. 37 GHz (in blue) and 230 GHz (in red) flux with a bin size of 5-day. b) Radio flux vs. optical V-band flux. c) Time shifted radio flux vs. optical V-band flux. The blue symbols show the time shifted 230 GHz (t-65 days) data while 37 GHz (t-68 days) data are shown in red. |
| In the text | |
 |
Fig. 12 Top: DCF curve of the γ-ray light curve w.r.t. the 230 GHz radio light curve. The solid curve is the best fitted Gaussian function to the 11-day binned DCF curve. Bottom: flux-flux plot of the shifted radio vs. γ-ray data. The blue symbols show the time shifted 230 GHz data while 37 GHz data are shown in red. |
| In the text | |
 |
Fig. 13 Top: weekly averaged normalized flux at γ-ray and optical V band frequencies plotted vs. time. The flux variations at these two frequencies seem to have a one-to-one correlation with each other. Bottom left: γ-ray vs. optical flux. Bottom right: the DCF curve of γ-ray vs. optical V passband flux using a bin size of 10-day in each case. A: using the complete data as shown in Fig. 2; B: after removing the data covering the duration of the optical flare O6; C: using the data before flare O6. |
| In the text | |
 |
Fig. 14 Top: X-ray photon index vs. flux at 0.3−10 keV. The data points in the box belong to a phase of brightening shown in the bottom figure. The X-ray photon index of the source is almost constant at 2.25 ± 0.25 (shown by a dashed line) over the flaring period. Bottom: soft and hard X-ray light curves of the source over the period of high X-ray activity. The flaring activity is similar in the two X-ray bands. |
| In the text | |
 |
Fig. 15 DCF curve of X-ray vs. optical V passband flux using a bin size of 3-day. |
| In the text | |
 |
Fig. 16 Evolution of the radio spectra: a) 230 GHz light curve showing different periods over which the spectra are constructed. b) Quiescent radio spectrum; c) results of a single component spectral fitting at time bin “4”, the dotted line corresponds to the quiescent spectrum, the dashed one to the flaring spectrum and the solid line to the total spectrum. d) The same spectrum fitted by a two-component synchrotron self-absorbed model, with the green dashed line showing the individual components and the blue solid line showing a combination of the two. A single component model curve is displayed with a dotted-dashed red curve for comparison. e) and f) The time evolution of Smax vs. νmax for the R6 and R8 radio flares. The spectral evolution extracted using a single-component model is shown by blue symbols and the red symbols denote a two-component model (see text for details). |
| In the text | |
 |
Fig. 17 Radio-IR spectra using Spitzer observations. The red curve is the best fitted synchrotron self-absorbed spectra with a break at (1.3 ± 0.1) × 104 GHz with a spectral break Δα = 0.28 ± 0.1. The green line represents the spectral fitting including optical data point and this leads to spectral break Δα = 0.51 ± 0.09. |
| In the text | |
 |
Fig. 18 Broad band SEDs of S5 0716+714. Each SED is constructed using 10-day averaged multifrequency data. The error bars represent the variation of flux over 10 days in each bin. Pure SSC models are shown as thick dashed curves. For EC fits, the total model SEDs are the thick solid curves; the synchrotron components are dotted, the SSC components are dot-dashed, and the EC components are thin dashed curves. |
| In the text | |
 |
Fig. 19 a) Time lag measurements vs. frequency using 15 GHz as the reference frequency for the radio flare R6. The best fitted power law at radio and mm frequencies is extended up to the optical wavelengths. The near by optical, X-ray and GeV flares are shown with their possible time lags w.r.t. R6. b) The same for the R8 flare (see Fig. 2 for flare labeling) In both plots, the dashed lines indicate the SSC process with simultaneous optical-γ-ray events. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


