| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 55 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220610 | |
| Published online | 15 April 2013 | |
Improved photometric calibration of the SNLS and the SDSS supernova surveys⋆,⋆⋆
1 LPNHE, CNRS-IN2P3 and Université Paris 6 & 7, 4 place Jussieu, Paris Cedex 05, France
e-mail: betoule@lpnhe.in2p3.fr
2 PCCP, 10 rue Alice Domont et Léonie Duquet, Paris Cedex 13, France
3 Center for Particle Astrophysics, Fermi National Accelerator Laboratory, PO Box 500, Batavia, IL 60510, USA
4 Canada-France-Hawaii Telescope Corp., Kamuela, HI 96743, USA
5 Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
6 Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue Chicago, IL 60637, USA
7 Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street Philadelphia, PA 19104-6396, USA
Received: 22 October 2012
Accepted: 15 December 2012
Context. We present a combined photometric calibration of the Supernova Legacy Survey (SNLS) and the SDSS supernova survey, which results from a joint effort of the SDSS and the SNLS collaborations.
Aims. Our primary motivation is to eventually sharpen cosmological constraints derived from type Ia supernova measurements by improving the accuracy of the photometric calibration. We deliver fluxes calibrated to the HST spectrophotometric star network for large sets of tertiary stars that cover the science fields of both surveys in all photometric bands. We also cross-calibrate directly the two surveys and demonstrate their consistency.
Methods. For each survey the flat-fielding is revised based on the analysis of dithered star observations. The calibration transfer from the HST spectrophotometric standard stars to the multi-epoch tertiary standard star catalogs in the science fields follows three different paths: observations of primary standard stars with the SDSS PT telescope; observations of Landolt secondary standard stars with SNLS MegaCam instrument at CFHT; and direct observation of faint HST standard stars with MegaCam. In addition, the tertiary stars for the two surveys are cross-calibrated using dedicated MegaCam observations of stripe 82. This overlap enables the comparison of these three calibration paths and justifies using their combination to improve the calibration accuracy.
Results. Flat-field corrections have improved the uniformity of each survey as demonstrated by the comparison of photometry in overlapping fields: the rms of the difference between the two surveys is 3 mmag in gri, 4 mmag in z and 8 mmag in u. We also find a remarkable agreement (better than 1%) between the SDSS and the SNLS calibration in griz. The cross-calibration and the introduction of direct calibration observations bring redundancy and strengthen the confidence in the resulting calibration. We conclude that the surveys are calibrated to the HST with a precision of about 0.4% in griz. This precision is comparable to the external uncertainty affecting the color of the HST primary standard stars.
Key words: cosmology: observations / techniques: photometric / methods: observational
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products available at the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
Photometric catalogs for stars in the CFTHLS deep fields and the SDSS stripe 82, and measurements of the MegaPrime transmission curves are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/cgi-bin/qcat?J/A+A/552/A124
© ESO, 2013
1. Introduction
Substantial efforts have been spent in the last few years to improve the accuracy of the calibration of large photometric surveys (e.g. Ivezić et al. 2007; Padmanabhan et al. 2008, for SDSS Regnault et al. 2009, for SNLS Schlafly et al. 2012, for Pan-STARRS), establishing large catalogs of stars with broadband magnitudes known with an accuracy of 1 or 2%. The scientific goals pursued cover a broad domain from stellar physics to cosmology. One of the main drivers for precision photometry is the quest for precise cosmological constraints from the Hubble diagram of type Ia supernovae.
In spite of the vast improvements in photometric calibration over the last decade, calibration uncertainties remain the dominant source of systematic error limiting the precision of cosmological constraints obtained from more than 400 well-measured type-Ia supernova (SN Ia) light curves (see e.g. the discussion of systematics in Conley et al. 2011). As an illustration, the accuracy of the measurement of the dark energy equation of state parameter w provided in Sullivan et al. (2011) is about 8% while it would reach 5.7% with a perfect photometric calibration. The calibration accuracy is likely to remain a serious issue in upcoming surveys expecting an order of magnitude increase in the number of supernovae.
The photometric component of the Supernova Legacy Survey (SNLS) was conducted at the Canada France Hawaii Telescope (CFHT) using the wide field MegaPrime/MegaCam camera. During its five years of survey operations (2003−2008), about 1000 multi-band SN Ia light curves were discovered in the redshift range 0.2 < z < 1, 500 of which were spectroscopically identified. The first three years of the data sample are analyzed and published in Guy et al. (2010), Conley et al. (2011), Sullivan et al. (2011). The Sloan Digital Sky Survey II (SDSS-II) SN Survey was one of the three components of the SDSS-II project. During three three-month seasons of survey operations (Fall 2005−2008), the SDSS SN survey discovered multi-band light curves for 500 spectroscopically confirmed SNe Ia in the redshift range 0.01 < z < 0.45. The processing and analysis of the first year sample are given in Holtzman et al. (2008), Kessler et al. (2009).
This work is part of the SDSS+SNLS joint analysis. It presents the collaborative effort made to improve the accuracy of photometric calibration. Previous calibrations for the two surveys are described in Holtzman et al. (2008) and Regnault et al. (2009, hereafter R09) respectively. This paper supersedes both by providing a common and consistent calibration for the two surveys. We exploit dedicated CFHT observations that complement the usual calibration data. The complementary data consists of direct observations of primary spectrophotometric standard stars and of SDSS science fields.
The advantage of these complementary observations is threefold: 1) they provide a direct cross-calibration of the tertiary standard stars used to calibrate the supernova measurement in both surveys; 2) they enable an accurate consistency check of the photometry between both instruments; and 3) they provide redundant paths, subject to different systematics, to anchor the common cross-calibrated set of tertiary standards on the flux scale defined by the HST white dwarfs (Bohlin et al. 2001). The various calibration paths to the HST system are illustrated in Fig. 1, where the red dashed lines show the paths enabled by the complementary CFHT observations.
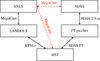 |
Fig. 1 Schematic view of calibration data used in the present work. Each box represents a set of standard stars established in that photometric system. Each arrow shows the available cross-calibration data corresponding to the measurement of flux ratios between the two different sets of standards. The two new sets of SNLS measurements introduced in this paper are indicated with red dashed lines. |
Since the publication of the SNLS calibration in R09, we use additional calibration data including a factor of two more data to map the photometric response and data to calibrate the replacement i band filter that was installed in 2007. In addition, the consistency checks introduced in this work showed subtle problems in the flat-fielding of both surveys that required corrections. As a consequence, this paper also describes a reanalysis of the original calibration data for the two surveys.
The paper is organized as follows. An overview of the subject is given in Sect. 2. The determination of the MegaCam flat-fielding solution, the determination of a consistent set of tertiary standards in the SNLS fields, and the calibration of the SNLS are detailed in Sects. 3–5. Sections 6 and 7 describe a redetermination of the photometric calibration of the SDSS supernova survey. Section 8 describes the analysis of the dedicated cross-calibration data that anchor the two surveys to the same flux scale. We gather all the relevant data to provide a combined calibration solution to both surveys in Sect. 9. Finally, in Sect. 10 we summarize the properties of the calibration products and discuss the consistency of the available calibration data. We conclude by identifying survey and detector design limitations and present perspectives for future improvements.
2. Overview
2.1. Definitions
The purpose of photometric calibration is to relate the instrumental fluxes measured in the image pixels to the physical fluxes of the observed objects. Instrumental magnitudes are defined as mADU = −2.5log 10φADU. The calibration is commonly divided in two steps. The first step consists in the compensation of the variation of the effective instrument throughput (in space and time) to deliver a homogeneous and consistent set of measurements. The second step consists in the delivery of a model relating the homogenized quantities to the physical flux of the astrophysical objects.
The results of these two steps are calibrated broadband magnitudes (m) of objects in a photometric system whose interpretation in terms of physical fluxes is given by 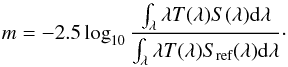 (1)S(λ) is the spectral energy density (SED) of the object above the earth’s atmosphere in units of erg-1 cm-2 Å-1, T(λ) is the overall instrument throughput (including the atmosphere) that defines the natural photometric system, and Sref is a reference flux scale to which the object flux is compared. T(λ) is expressed as the detector response to incident photons and its normalization is irrelevant because it cancels in the ratio. The factor λ is required to convert the SED to a function proportional to the number of photons per unit wavelength.
(1)S(λ) is the spectral energy density (SED) of the object above the earth’s atmosphere in units of erg-1 cm-2 Å-1, T(λ) is the overall instrument throughput (including the atmosphere) that defines the natural photometric system, and Sref is a reference flux scale to which the object flux is compared. T(λ) is expressed as the detector response to incident photons and its normalization is irrelevant because it cancels in the ratio. The factor λ is required to convert the SED to a function proportional to the number of photons per unit wavelength.
In what follows we refer to the AB magnitude system as defined in Fukugita et al. (1996), unless otherwise specified. Accordingly, Sref = Sab where Sab is: 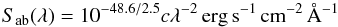 (2)with the wavelength λ expressed in angstrom and c the speed of light expressed in Å s-1.
(2)with the wavelength λ expressed in angstrom and c the speed of light expressed in Å s-1.
The model describing the physical interpretation of the instrumental fluxes has two components. The first is the determination of the effective passband corresponding to the instrument measurements up to a normalization factor. The second is the determination of the flux scale of the homogeneous measurements in each passband. The latter is obtained from a comparison to a flux reference, which we choose to be the HST-CALSPEC stellar library (see the CALSPEC website1 and references therein).
Our primary goal is the calibration of the SNLS and the SDSS supernova surveys. The main output of this work consists of calibrated AB natural magnitudes for large sets of stars selected in the science fields. These stars constitute in-situ photometric references directly usable to calibrate supernova flux measurements. They will be referred to as the tertiary standards, while in the same terminology, the spectrophotometric standards established by the HST constitute the primary standards, and stars used in the calibration transfer from the HST to the science fields are referred to as secondary standards.
We also deliver an estimate of uncertainties related to this calibration that can be propagated to the cosmological result. Accurately measuring the flux ratios between different photometric bands is of paramount importance for cosmological constraints, as this enables the comparison of supernova luminosity at different redshifts. Since cosmological constraints are insensitive to a global calibration offset on the flux scale, we concentrate on the accuracy of the relative calibration between the different photometric bands in the two surveys. We do not include the uncertainty on the global flux scale of the calibration reference (see e.g. Bohlin & Gilliland 2004).
2.2. Description of Instruments and Surveys
The SNLS covers the four low extinction fields of the CFHT Legacy Survey Deep component (hereafter D1 to D4). They were repeatedly imaged in the 4 photometric bands gMrMiMzM every 3–4 nights during dark astronomical time2. Photometry in the uM band is also available for those fields but was not part of the supernova survey. The original iM filter was broken in July 2007 and replaced by a slightly different iM filter in October of the same year. We will refer to the photometric band defined by the replacement filter as i2M. The MegaPrime instrument is mounted on the CFHT prime focus and hosts the MegaCam camera, a mosaic of 36 e2v 2048 × 4612 CCDs, that covers a field of 0.96 × 0.94 deg2 (Boulade et al. 2003). Raw MegaCam images are processed by the Elixir pipeline (Magnier & Cuillandre 2004) that handles bias subtraction, flat-fielding and defringing in iM and zM bands.
The SDSS-II Supernova Survey primary instrument is the SDSS CCD camera (Gunn et al. 1998) mounted on a dedicated 2.5-m telescope (Gunn et al. 2006) at Apache Point Observatory (APO), New Mexico. The focal plane hosts a CCD array organized as six columns of 5 CCDs. Each CCD of the column records images in one of five broad optical bands: ugriz (Fukugita et al. 1996). The camera was used in time-delay-and-integrate (or drift scan) mode, which provides efficient sky coverage. The Supernova Survey scanned at the normal (sidereal) SDSS survey rate, which yielded 55 s integrated exposures in each passband. The survey covers a 300 square-degree region (2.5° wide over 8 h in right ascension) that was repeatedly observed (every fourth day in average) over the course of three three-month seasons. The region is centered on the celestial equator and is referred to as “Stripe 82”.
Many aspects of the analysis are complicated by two instrumental effects: spatial variation of the instrument passband response, and stray light which adversely affects common flat-fielding methods. Below we describe these two issues.
2.2.1. Varying passbands
It was realized in R09 that spatial variations of the passband response resulted in non-negligible color terms between photometric measurements obtained at different positions on the MegaCam focal plane. The size of the color terms between the center and the edge of the focal plane is about 0.02 (depending on the band) for main sequence stars indexed by their g − i color (cf. Sect. 3 and Fig. 3). The major contribution to this variation is related to the manufacturing process of the large MegaCam interference filters (30 × 30 cm2). The variation was found to follow an almost perfect radial pattern, with the filters being redder at the center of the focal plane than at their edge. The typical variation of the filter transmission’s mean wavelength amounts to a few nanometers. Other expected contributors to variations of the effective passband are differences of quantum efficiency between CCDs (they were found small enough to be neglected), and variations in time of the spectral shape of the atmospheric extinction (that average out over multi-epoch measurements and will not be considered).
The measurement of SDSS effective passbands are described in Doi et al. (2010). Small differences (at most 2 nm variations of the effective wavelength against the average transmission for ugri, 4 nm in z band) were found between the individual filters mounted on the different columns of the camera. The SDSS calibration strategy is such that this issue can generally be neglected in the calibration transfer.
Varying passbands bring two complications to the analysis of photometric measurements. First, the flux interpretation of a broadband magnitude (Eq. (1)) depends on the position of the measurement on the focal plane of the instrument. Defining x as the focal plane position and T|x as the passpand response at x, magnitudes in the natural (and position dependent) photometric system are denoted by  S(\lambda) {\rm d}\lambda}{\int_\lambda \lambda \cmag[T](\lambda) S_\ab(\lambda) {\rm d}\lambda}\cdot \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq35.png) (3)Second, the variation of response depends on the object SED and therefore it is not possible to ensure the uniformity of the instrument response for objects with an arbitrary SED. There is thus a degree of freedom in the choice of the spectrum for which the response of the instrument is made uniform (refer to Sect. 3.3 for further discussion).
(3)Second, the variation of response depends on the object SED and therefore it is not possible to ensure the uniformity of the instrument response for objects with an arbitrary SED. There is thus a degree of freedom in the choice of the spectrum for which the response of the instrument is made uniform (refer to Sect. 3.3 for further discussion).
2.2.2. Stray light in the wide field corrector
In addition to the problem of the passbands varying with the position on the focal plane, there are other position dependent optical effects that complicate the determination of the instrument photometric response. Parasitic reflections between filters and optical elements of the wide-field corrector are the most problematic because they cannot be modeled and subtracted easily. These effects produce stray light that pollutes the images obtained by observation of uniform illumination sources such as twilight sky, dome screen, or night sky background. These techniques thus cannot be used directly to produce the instrument flat-fields3.
2.3. Current state of the SNLS and SDSS calibration
2.3.1. Absolute calibration transfer
The original calibration strategies for both the SDSS (Stoughton et al. 2002) and the SNLS (Astier et al. 2006; Regnault et al. 2009) photometric surveys follow roughly the same scheme. As neither survey telescope could directly observe the primary spectrophotometric standard available at that time, they relied on third party observations, to which they anchored via a set of secondary standard stars.
In the SNLS, the secondary standard stars are those established in Landolt (1992). The SDSS secondary star network was built using a dedicated instrument called the photometric telescope (PT) (Tucker et al. 2006). The PT was used to determine a nightly photometric solution and to deliver calibrated secondary standards. These secondary standards are distributed in square patches of 0.36 sq-deg throughout the SDSS survey area. The supernova survey area (Stripe 82) is covered with an average of one PT-calibrated patch every 3 degrees in right ascension.
These two-step calibration strategies have limitations. First, they accumulate the photometric and systematic uncertainties of two measurements. Second, and more importantly, the secondary standard stars provide only broadband photometric references rather than spectrophotometric references. Since the secondary star photometric system is different from that of the science system (i.e, SNe Ia), this difference ultimately limits the precision of the absolute calibration to the accuracy of photometric color transformations between those two systems (i.e. to some kind of interpolation between quantities integrated over different passbands).
The passbands in the Landolt UBVRI system differ from the MegaCam uMgMrMiMzM, and the transmission functions of the Landolt filters actually used are not precisely known. The resulting color transformations are difficult to model and have significant uncertainties, ranging between 0.3 to 2% depending on the band. These uncertainties were the limiting factor in the previous release of the SNLS calibration.
The strategy of the SDSS may appear more favorable as the PT was specifically designed to use a filter set identical to the 2.5 m science telescope. However, the filter sets differ significantly primarily because of the differences in the environment (vacuum vs. air) as explained in Doi et al. (2010). In addition, repeated, in situ measurements enabled Doi et al. (2010) to detect a significant change in the u-band filter response after the 2001 measurement. The PT filter responses, however, were not measured as frequently or as carefully, and we are again forced to rely on empirically determined color transformations to tie the two systems together. The problem with the determination of the color transformations is further complicated by errors in the PT flat-fielding as discussed in Sect. 6.
2.3.2. Survey uniformity
The characterization of the MegaPrime response is based on twilight flat-fields, corrected, at large scale, for the optical effects induced by stray light and plate-scale distortion. This photometric correction is measured on dithered observations of dense stellar fields following the scheme presented in R09. Although this measurement does not depend on assumptions about the telescope optics, we found that it is sensitive to variations in the atmospheric conditions during the dithered observation sequences.
The determination of the instrument response presented in R09 covers the period 2003−2006, and a significant evolution of the response is attributable to changes in the telescope optical setup. An extension of this R09 study is thus required for the analysis of observations after 2006, in particular observations made with the i2M replacement filter. In addition, since the determination of the photometric corrections are affected by random variations in the atmospheric conditions, we expect some improvement from including new independent observations.
SDSS imaging data was obtained using drift scanning: each point on the sky was sampled by each CCD row so that the effective response is averaged over all rows. The flat-field is therefore represented by a 1-dimensional array of values holding the relative average response between pixel columns. Such solutions were determined by different techniques in Ivezić et al. (2007) and Padmanabhan et al. (2008). The first technique relies on a combination of stellar locus analysis and comparison of the Sloan photometry to PT secondary patches. The second technique solves for the flat-field vector by cross-correlating normal observations, scanned in the right ascension direction, with infrequent observations that scanned the sky approximately along declination.
The flat-fielding of the supernova survey currently relies on the PT-based solution, while the cross-scan based solution is applied to the main survey since the eighth data release (DR8). Small but significant discrepancies between the two solutions can be found when comparing the photometry of stars in the Stripe 82 (see Sect. 6).
2.4. Project for this work
In this paper, we review, control and improve the original calibration paths of both surveys, and we provide an important cross-check by directly inter-calibrating the two surveys. We also describe direct observations of suitably faint primary standard stars (now available in the CALSPEC database) with MegaCam on the CFHT, providing an alternative path to anchor the SNLS to the HST scale.
The various calibration paths exploited in this paper are summarized in the schematic view presented in Fig. 1. The two new MegaCam calibration and inter-calibration measurements (shown by red-dashed lines in Fig. 1) provide a redundancy in the calibration of both surveys to the HST standards. The original “Landolt” and “PT” calibration paths involve very large numbers of measurements accumulated over the course of the surveys. These calibrations are essentially free from statistical uncertainty, but, as already discussed, they are limited by the accuracy of color transformations. On the contrary, the direct path provides direct observation of spectrophotometric standards in the MegaCam photometric system and eliminates this dominant systematic for SNLS. The direct path, however, involves a smaller number of observations, potentially affected by systematics related to the difficulty of observing bright stars.
A general agreement between all the available measurements conducted with different instruments and subject to different sources of uncertainty would strongly support the conclusion that systematics are controlled and correctly estimated. In addition, the data gathered for the direct cross-calibration of the SDSS and the SNLS provide high-quality photometry in both systems for a large number of stars. Those measurements sample a wide range of stellar types and a large part of both focal planes. Such data can deliver two important by-products. First, a consistency assessment of the uniformity and quality of the photometry in both surveys. Second, a precise determination of the color transformations between the two systems. The latter can be compared with expectations to provide a sensitive check of the passband transmissions.
This work is presented as follows. A new determination of the MegaCam photometric response extending over the entire survey is described in Sect. 3. It is used to build an average catalog of photometric tertiary standards in Sect. 4. On the SDSS side, the question of the discrepancy between the two available flat-field solutions is investigated in Sect. 6. Identifying evidence of an error in the nominal PT flat-field (Appendix A), we opt for using the cross-scan solution which is independent of the PT. The stripe 82 tertiary catalog is corrected accordingly.
Validation of the uniformity of the resulting tertiary catalogs is given by the analysis of the cross-calibration data (Sect. 8, see in particular Fig. 28 page ). Constraints binding together the flux scales of both tertiary catalogs are also derived in Sect. 8.
Measurements anchoring tertiary catalogs to the HST primary standards are described in Sect. 5.1 for the path using Landolt secondary standards, in Sect. 5.2 for the direct measurements of HST standards with MegaCam, and in Sect. 7 for the path using the SDSS PT secondary patches. The combination of all available data to provide a common and improved calibration of the SDSS and SNLS surveys as well as the full estimate of the associated uncertainties is described in Sect. 9. The reader can skip the details of the analysis and jump directly to Sect. 10 where we discuss the consistency between the different calibration paths (see in particular Fig. 29) and describe the calibration products.
3. MegaCam/MegaPrime instrument model
This section is dedicated to the determination of the two key ingredients characterizing the effective model of MegaPrime measurements: the effective transmission T|x(λ), and the photometric flat-field solution F(x) corresponding to our aperture photometry method. While these two subjects are usually treated separately, they are correlated in MegaPrime due to the continuous variation of the filter transmission with position.
Figure 2 shows an overview of the data samples involved in the determination of the instrument model, and highlights the main steps of the analysis. In Sect. 3.1, we gather independent characterizations of the optical components to build a model of the instrument passband transmissions. The resulting transmission functions T|x(λ) vary continuously with the distance from the focal plane center x (hereafter referred to as the radius). In Sect. 3.2 we use synthetic photometry to compute the small color transformations relating stellar observations obtained at different radii. We compute photometric corrections to the instrument response maps delivered by the usual twilight observations in Sect. 3.3. Those corrections are obtained from dithered observations of dense stellar fields under photometric conditions. We use the color transformations from Sect. 3.2 to make sure that the resulting photometric response maps F(x) make the instrument response constant for an (hypothetical) object whose SED corresponds to the AB spectrum Sab. With this choice of reference SED, the relation between the instrumental and AB magnitudes is a single calibration constant (the AB zero point) that is valid across the entire focal plane. The uncertainties on the results are discussed in Sect. 3.4.
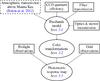 |
Fig. 2 Overview of the MegaPrime photometric response determination. Boxes figure the various data sets involved in the construction of the model (dashed for external data). Ellipses figure the main steps of the analysis. |
A comprehensive model of the MegaCam effective passband transmissions has already been released in R09. The main modification since then is the replacement, in October 2007, of the interference filter defining band iM after its accidental destruction on July 20th 2007. This reanalysis was triggered by this incident and aims mainly at providing calibration data for the slightly different replacement filter (hereafter i2M). We also propagate improvements to other bands, mainly the benefits of an extended data set and better understanding of the instrument model. A summary of main differences is provided at the end of this section.
3.1. Instrument passbands
3.1.1. Passband model
The effective transmission model for photometric band b results from the product of 5 components: ![\begin{equation} \label{eq:11} \cmag[T]^b(\lambda) = T_b^{\rm f}(\lambda, \x) T_{\rm c}(\lambda) R_{\rm m}(\lambda) T_{\rm a}(\lambda) \epsilon_\text{ccd}(\lambda), \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq41.png) (4)where
(4)where 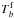 is the position dependent transmission of the interference filter, Tc the transmission of the wide field corrector, Rm the primary mirror reflectivity, Ta the average atmospheric transmission at Mauna Kea (at a typical airmass of 1.25) as measured by the SNFactory (Buton et al. 2012) and ϵccd the measured quantum efficiency (QE) of the MegaCam e2v CCDs. Note that Ta differs quite significantly from the preliminary version used in R09.
is the position dependent transmission of the interference filter, Tc the transmission of the wide field corrector, Rm the primary mirror reflectivity, Ta the average atmospheric transmission at Mauna Kea (at a typical airmass of 1.25) as measured by the SNFactory (Buton et al. 2012) and ϵccd the measured quantum efficiency (QE) of the MegaCam e2v CCDs. Note that Ta differs quite significantly from the preliminary version used in R09.
The measurements of quantum efficiency for individual CCDs display slight variations between chips. They do not introduce noticeable modification of the effective passband transmission in any photometric band except for gM and uM. In these two bands, we measure a maximum shift of mean wavelength between the reddest and the bluest CCD of 1.5 nm and 2.3 nm, respectively. The use of per chip QE curves in place of the average one published in R09 has a negligible impact on the calibration. In addition, they marginally improve the agreement between synthetic and measured color terms between chips, which may indicate uncorrected weaknesses in the individual measurements. Since the per chip QE curves do not improve the calibration, they are not used in this release of the calibration and instead we use the mean QE model4.
3.1.2. Laboratory measurements of filter transmission
The transmissions of our interference filters under normal incidence were measured by their manufacturers at several positions. Measurements for the original filter set, manufactured by SAGEM/REOSC, are published in R09. Measurements are available for each filter at several positions: at the center of the filter, and at 23, 47, 70, 93, 117, 140, 163, 186 and 210 mm away from the center. Transmission curves are linearly interpolated between measurements as a function of radius to provide the continuous model function, 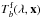 .
.
For the i2M filter, measurements of the transmission provided by the manufacturer, BARR associates, are available at the center of the filter and at 20, 40, 60, 80, 100, 120, 140, 160, 180 mm away from the center. The potential existence of leaks outside the main passband is not excluded by these measurements that cover only the expected wavelength range of the main passband. The 180 mm measurements were repeated for each corner of the filter. The mean wavelength varies along the radius from 761.2 nm on one side of the filter to 764.9 nm close to the center, which makes it more uniform than the original filter. There are indications that the filter transmission function may not follow a radial pattern. Measurements at the 4 corners display small discrepancies, with variations between the two extreme sides of the filter reaching 1.7 nm. However, without complementary measurements at intermediate radii, it was not possible to build an alternative to a radially variable filter model. Deviations from the radial symmetry are barely noticeable in the observational data (cf. Sect. 3.4).
The normal incidence measurements are blue-shifted to account for the average incident angle of the CFHT f/4 beam. As in R09, this shift is done using the approximate relation, 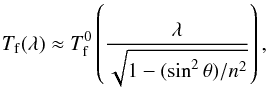 (5)where θ is the incidence angle, and n is an effective index of refraction for the filter.
(5)where θ is the incidence angle, and n is an effective index of refraction for the filter.
The transmission curves of the original filters were measured again at CFHT in 2006 at 5 angles ranging from 0 to 8° at a few locations. This allowed us to check that the above formula applies and to determine the refractive index n for each filter. We then integrated the transmission function over the telescope beam for each location in the focal plane.
As the replacement filter i2M transmission was never measured under non-normal incidence, the exact value of its refractive index n cannot be directly determined. We used the value measured on the original iM filter, n = 1.6. The validity of this choice is indirectly assessed in Sect. 8.3.
Last, the comparison of the manufacturer transmission curves with the 2006 measurement at CFHT for the original filter set is provided in Appendix B. It revealed an important discrepancy (an 8 nm shift of the red cut-off) in iM and rM, while measurements in the other bands were found in nearly perfect agreement. As discussed in Appendix B, we believe that the CFHT measurements provide a better description of the survey filters and we therefore corrected the iM and rM transmission curves accordingly. The validity of this correction could not be directly tested on the whole spatial extension of the filters. An indirect assessment using stellar locus is provided in Sects. 3.4.2 and 8.3.
The resulting transmission curves are given in Tables E.3–E.8 at several radii away from the center. A sufficiently accurate mapping between object coordinates and position on the filter is obtained by considering the filter close to the focal plane and using the focal distance of the instrument, F = 14.89 m.
3.2. Stellar measurements across the focal plane
While slightly variable, the MegaCam natural photometric system remains sufficiently similar between different focal plane positions that precise transformations between stellar measurements can be derived for a large range of the stellar population. Passband transmission models have been used to compute synthetic values of the color transformations between the natural system at a given radius and the uniform system defined as the natural system at the center of the focal plane (denoted x0). The relations take the form ![\begin{equation} \label{eq:4} \umag \approx \cmag - \dk(\x) \left(\umag[c]-c^0(x)\right) \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq59.png) (6)where c|x0 is the color index of the star, c0 is the reference color for the linear transformation, and
(6)where c|x0 is the color index of the star, c0 is the reference color for the linear transformation, and 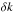 is the color term adjusted to a given stellar population5. The choice of c|x0 is arbitrary, and we choose (g − i)|x0 because it is well measured for most stars and it is a good proxy of the star temperature.
is the color term adjusted to a given stellar population5. The choice of c|x0 is arbitrary, and we choose (g − i)|x0 because it is well measured for most stars and it is a good proxy of the star temperature.
The primary use of these transformations lies in the process of determining the photometric flat-field solution (cf. Sect. 3.3) for MegaCam, using measurements calibrated on Landolt stars. Since this calibration procedure delivers magnitudes in an approximate Vega system, we determine transformations in that system as described in R09, and we make use of the primary spectrophotometric standard BD +17 4708 as a flux scale reference. More specifically, in this system the synthetic magnitudes are defined as  S(\lambda) {\rm d}\lambda}{\int_\lambda \lambda \cmag[T](\lambda) S^V_\text{ref}(\lambda) {\rm d}\lambda}\,,\label{eq:28} \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq64.png) (7)where
(7)where
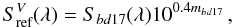 with Sbd17 the SED of the star BD +17 47086 and mbd17 the MegaCam magnitude of this star inferred from Landolt observations (see Sect. 5.1). As those scaling constants (mbd17) are close to the Vega magnitudes of BD +17 4708, this system is by construction an approximate Vega system. To avoid confusion with the AB magnitudes that we use everywhere else in this paper, magnitudes in this system will be, when needed, distinguished as
with Sbd17 the SED of the star BD +17 47086 and mbd17 the MegaCam magnitude of this star inferred from Landolt observations (see Sect. 5.1). As those scaling constants (mbd17) are close to the Vega magnitudes of BD +17 4708, this system is by construction an approximate Vega system. To avoid confusion with the AB magnitudes that we use everywhere else in this paper, magnitudes in this system will be, when needed, distinguished as 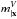 where the V superscript stands for Vega.
where the V superscript stands for Vega.
The relations defined by Eq. (6) were adjusted in a limited color range on synthetic magnitudes computed from the Pickles (1998) and Gunn & Stryker (1983) stellar libraries. As an illustration, the adjustment of synthetic transformations between the center and the edge of the focal plane are shown on Fig. 3. The selected color range corresponds to a region where the linear approximation is sufficiently accurate.
The uncertainty on the slope of the transformation, evaluated from the difference obtained between the two libraries, is smaller than 2 mmag per color unit. The dispersion around the fitted transformation is typically smaller than 3 mmag.
We also evaluated the sensitivity of the fitted transformation to extinction by interstellar dust. Spectra have been reddened according to a Cardelli et al. (1989) law to account for the mean extinction of the stellar population. The extinction vector is nearly co-linear to the stellar locus in the selected color-range. For a value of E(B − V) = 0.4, the modification of the slope is typically negligible in all bands except z, where it reaches 3 mmag per color unit. We conclude that, in fields with relatively low extinction, it is safe to translate measurements of stars lying in the selected color range across the focal plane using the fitted transformation7.
 |
Fig. 3 Synthetic color transformation between the center and the corner of the filters (17 cm from the center) in each band. Dots are synthetic magnitudes computed for stellar spectra from the Gunn & Stryker (1983) spectral library. Linear color transformation (solid line) are adjusted in the range delimited by vertical dashed lines. The color index is a Vega MegaCam color. The red square figures the synthesized transformation of the spectrophotometric standard star BD +17 4708 computed from its STIS spectrum available from the CALSPEC database. |
3.3. Determination of the photometric flat-field
A common way to measure the instrumental response is the observation of the twilight sky, assumed to be a uniform source of light. A first complication preventing the direct use of this technique is the variation of filter passband transmission across the Megacam focal plane. This effect makes the response variation slightly dependent on the SED of the observed objects. Consequently, the strict uniformity of the response can only be ensured for a single class of objects sharing the same SED shape. Our first concern here is that the twilight images are functions of the twilight color which is not a useful reference for stellar photometry.
Putting aside this complication, the twilight images do not deliver satisfying results for the photometric uniformity of point-like objects, and is due to differences in the optical response to isotropic and parallel illuminations (see e.g. Manfroid 1995). In MegaCam, two major contributions are identified (Magnier & Cuillandre 2004): 1) distortions of the plate-scale and 2) parasitic reflections on the various components of the wide field corrector. The combination of both effects leads to differences of around 10% between stellar fluxes measured at the edge or center of flat-fielded images.
It is, however, expected that those purely instrumental effects are smooth and fairly stable in time, so that the determination of the photometric flat-field can take the form of a large-scale stable correction to the twilight flat-field. The twilight flat-field thus corrects for small-scales and time variations of the instrument response, while the response at large scales is to be determined by other means. We will refer to this correction as the photometric flat-field correction in what follows.
Smaller deviations (around 1%) also arise from variations of the point spread function (PSF) across the field that may not be correctly handled by the photometry method. While small, such effects make the flat-field definition ultimately dependent on the photometry method. We choose to measure fluxes in twilight flat-fielded images8, leading to instrumental magnitudes written 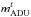 , where the t superscript denotes the use of twilight flat-field. Those magnitudes are related to natural magnitudes by
, where the t superscript denotes the use of twilight flat-field. Those magnitudes are related to natural magnitudes by 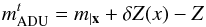 (8)where
(8)where 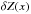 is the photometric flat-field correction, and
is the photometric flat-field correction, and 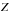 is a per-exposure global calibration offset (the zero point). Due to the variation of passbands the correction depends on the flux reference chosen: roughly speaking, the color of the twilight spectrum relative to the reference spectrum.
is a per-exposure global calibration offset (the zero point). Due to the variation of passbands the correction depends on the flux reference chosen: roughly speaking, the color of the twilight spectrum relative to the reference spectrum.
3.3.1. The “grid” observations
A comprehensive model of this correction could in principle be built from the knowledge of optical distortions, reflections and of the spectral shape of the twilight. The alternative strategy that we follow in this work is to measure 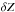 from a set of specifically designed observations (similarly to what was done in R09). To implement this strategy, the CFHT has gathered sequences of 13 dithered observations of a dense stellar field in every passband. Since the beginning of MegaCam observations, 2 stellar fields have been observed in this manner on a yearly basis and also after each major intervention on the telescope optics.
from a set of specifically designed observations (similarly to what was done in R09). To implement this strategy, the CFHT has gathered sequences of 13 dithered observations of a dense stellar field in every passband. Since the beginning of MegaCam observations, 2 stellar fields have been observed in this manner on a yearly basis and also after each major intervention on the telescope optics.
The characteristics of those 2 dense stellar fields are given in Table 1. Some attention has been paid to potential effects related to Galactic dust extinction in these low galactic latitude fields. The analysis of the average color locus of the stellar population showed that the typical value of the dust extinction corresponds to E(B − V) = 0.1 in the summer field (hereafter grid-2), and E(B − V) = 0.4 in the winter field (hereafter grid-1), with noticeable variations.
A summary of those observations, hereafter the “grid” observations, as well as associated telescope events is given in Table A.1. The dithering pattern followed by the observations is described in Table A.2. It consists roughly of 13 exposures spaced by logarithmically increasing step sizes in right-ascension and in declination.
Dense stellar fields observed to model the photometric flat-field correction.
3.3.2. Constraining a model of the instrumental response with grid observations
An appropriate model for the twilight flat-fielded observations (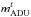 ) is given by Eq. (8). The natural magnitudes m|x of the grid stars are not known and have to be determined from the observations themselves, up to a global offset. Also, due to the variation of the effective passbands, the natural magnitude of a star is not expected to be constant across the focal plane. The only tractable way to obtain a closed system is to rely on approximate color transformation. Unlike what has been done in R09, we do not fit for color transformations and flat-field corrections at the same time. We choose to rely on the linear transformationfrom Sect. 3.2. For stars lying in the validity range of those transformations, Eq. (8) translates to the linear model already described in R09,
) is given by Eq. (8). The natural magnitudes m|x of the grid stars are not known and have to be determined from the observations themselves, up to a global offset. Also, due to the variation of the effective passbands, the natural magnitude of a star is not expected to be constant across the focal plane. The only tractable way to obtain a closed system is to rely on approximate color transformation. Unlike what has been done in R09, we do not fit for color transformations and flat-field corrections at the same time. We choose to rely on the linear transformationfrom Sect. 3.2. For stars lying in the validity range of those transformations, Eq. (8) translates to the linear model already described in R09, ![\begin{equation} \label{eq:30} \madu^t - \dk(\x) \left[\umag[g]-\umag[i] - c^0(\x)\right] = \umag + \dzp(\x) - \zp\,. \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq87.png) (9)Free parameters in this model are the reference instrumental magnitudes of all stars at the center of the focal plane m|x0, the zero points of each exposure in the sequence
(9)Free parameters in this model are the reference instrumental magnitudes of all stars at the center of the focal plane m|x0, the zero points of each exposure in the sequence 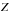 , and the shape of
, and the shape of 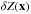 that has to be parameterized. We also need the reference g|x0 − i|x0 colors of the stars. It is however sufficient to have this color determined only approximately, because it appears multiplied by
that has to be parameterized. We also need the reference g|x0 − i|x0 colors of the stars. It is however sufficient to have this color determined only approximately, because it appears multiplied by 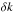 which is typically small (
which is typically small (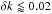 ). The construction of an approximate catalog for the grid-field stars, neglecting in a first pass the impact of filter changes on the flat-fielding, is the subject of Sect. 3.3.3.
). The construction of an approximate catalog for the grid-field stars, neglecting in a first pass the impact of filter changes on the flat-fielding, is the subject of Sect. 3.3.3.
An irrelevant constant can be exchanged between the 3 terms of the right-end side of Eq. (9). We therefore assume 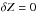 at the center of the focal plane and
at the center of the focal plane and 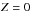 for the first exposure. However, this system remains poorly constrained because of a partial degeneracy between the flat-field correction and the variation of
for the first exposure. However, this system remains poorly constrained because of a partial degeneracy between the flat-field correction and the variation of 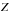 between dithered exposures. The degeneracy issue making the construction of photometric flat-field (or “superflats”) for a CCD camera difficult is investigated in Manfroid (1996). A simple solution is to make the assumption that the whole sequence is photometric, i.e. to assume that
between dithered exposures. The degeneracy issue making the construction of photometric flat-field (or “superflats”) for a CCD camera difficult is investigated in Manfroid (1996). A simple solution is to make the assumption that the whole sequence is photometric, i.e. to assume that 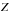 is constant during the sequence. This assumption is hard to satisfy experimentally, even for the clearest nights, mainly because of variations in the PSF between exposures inducing variations in the aperture corrections.
is constant during the sequence. This assumption is hard to satisfy experimentally, even for the clearest nights, mainly because of variations in the PSF between exposures inducing variations in the aperture corrections.
To account for part of the aperture correction variations we used aperture photometry with reasonably large radii scaled with the image quality (IQ). The IQ is computed as the average sigma of a Gaussian fit to stars on each CCD9. We then perform the photometry in apertures of radius 7.5 × IQ.
Second order variations of aperture corrections, as well as variations of the atmospheric extinction between successive exposures are to be expected at some level so that only a part of the zero point variation is corrected. Still, we rely on the assumption of photometricity during the observation sequence to alleviate the degeneracy problem and we expect that the resulting error will average out with several determinations obtained from uncorrelated sequences. This issue is further discussed in Sect. 3.4.
The exact shape of the 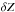 correction is unknown and thus has to be parameterized. The scheme adopted in R09 was to subdivide the focal plane into 1296 cells of 512 × 512 pixels on which
correction is unknown and thus has to be parameterized. The scheme adopted in R09 was to subdivide the focal plane into 1296 cells of 512 × 512 pixels on which 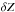 is assumed constant in each cell, leading to a pixelized representation of the correction. Here we build a nearly equivalent model with a smaller number of parameters from the following considerations: 1) optical effects are expected to be a smooth continuous function of the focal plane position; 2) discontinuities between CCDs are introduced by the IQ-scaled aperture photometry method because different aperture radii are used to process different CCDs on the same image; 3) variations of quantum efficiency shape from one chip to another may introduce discontinuities between CCDs if the twilight color is significantly different from that of the standard reference and 4) occasional jumps of the amplifier gains were noted in R09, and have to be accounted for. As a consequence we choose to expand
is assumed constant in each cell, leading to a pixelized representation of the correction. Here we build a nearly equivalent model with a smaller number of parameters from the following considerations: 1) optical effects are expected to be a smooth continuous function of the focal plane position; 2) discontinuities between CCDs are introduced by the IQ-scaled aperture photometry method because different aperture radii are used to process different CCDs on the same image; 3) variations of quantum efficiency shape from one chip to another may introduce discontinuities between CCDs if the twilight color is significantly different from that of the standard reference and 4) occasional jumps of the amplifier gains were noted in R09, and have to be accounted for. As a consequence we choose to expand 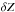 as the sum of a smooth function decomposed on a uniform cubic B-Spline basis plus a discrete step function δG accounting for differences between amplifiers:
as the sum of a smooth function decomposed on a uniform cubic B-Spline basis plus a discrete step function δG accounting for differences between amplifiers: 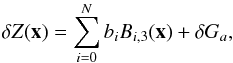 (10)where a indexes the 72 amplifiers. We impose separately δG26 = 0 for the amplifier 26 that lies close to the center of the focal plane and
(10)where a indexes the 72 amplifiers. We impose separately δG26 = 0 for the amplifier 26 that lies close to the center of the focal plane and 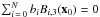 . The choice of N, which sets the number of model parameters, is discussed in Sect. 3.3.4.
. The choice of N, which sets the number of model parameters, is discussed in Sect. 3.3.4.
Measurements are mostly affected by photon noise, which is approximately modeled as a Gaussian process whose variance is given by the flux integrated in the aperture. Only measurements with a signal to noise ratio exceeding 10 are kept and a weighted least-square minimization is used to estimate model parameters. Although the stellar instrumental reference magnitudes contribute a very large number of nuisance parameters, the problem remains tractable if its sparsity is correctly taken into account10.
3.3.3. Construction of grid field catalogs
The transformation of instrumental magnitudes to the reference system requires the approximate knowledge of the star color in the reference system. On a first pass, a calibrated catalog of the grid fields is built from all the gathered observations of those fields. These observations comprise a greater number of epochs than the grid dataset alone as those fields were routinely observed to measure the PSF of the CFHT instrument. The latter set of observations is usually slightly deeper than the nominal grid observations.
The flat-fielding of the observations is made using an approximate version of the flat-field correction 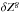 ignoring the effect of varying passbands. The simplified model is
ignoring the effect of varying passbands. The simplified model is 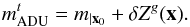 (11)Besides the approximate flat-fielding, the averaging procedure adopted to build grid field catalogs is identical to the one used to establish the tertiary star catalogs, and is extensively described in Sect. 4. Once obtained, the average catalogs are calibrated to the Landolt system using same-night observations of the Landolt secondary patches as described in Sect. 5.1. The catalogs are cleaned a posteriori to keep measurements with error below 5% and with reduced χ2 < 2 (which excludes some variable stars). The color−color diagrams of the resulting catalogs are shown in Fig. 4.
(11)Besides the approximate flat-fielding, the averaging procedure adopted to build grid field catalogs is identical to the one used to establish the tertiary star catalogs, and is extensively described in Sect. 4. Once obtained, the average catalogs are calibrated to the Landolt system using same-night observations of the Landolt secondary patches as described in Sect. 5.1. The catalogs are cleaned a posteriori to keep measurements with error below 5% and with reduced χ2 < 2 (which excludes some variable stars). The color−color diagrams of the resulting catalogs are shown in Fig. 4.
 |
Fig. 4 Stellar population within the two grid fields. The green dashed line is a synthetic stellar locus computed from the Pickles stellar library. Spectra have been reddened to match the average extinction measured in the field. The black arrow shows the corresponding extinction vector. |
Our primary interest lies in the measurement of the gM − iM color of the stars. This measurement is affected by the uncertainty on the gM and iM calibration. From the dispersion between the different calibration epochs, we estimate that the global uncertainty on gM − iM is below 0.008 and 0.004 for the grid-1 and grid-2 catalogs, respectively. Another error is induced by the approximate flat-field applied to the observations and by the difference between the natural color g|x − i|x that we measure and the uniform color g|x0 − i|x0 that we use to index color transformations. For stars in the color range considered the maximum difference between g|x − i|x and g|x0 − i|x0 is expected to be 0.01. Finally, the noise on the gM − iM color is expected to reach at most 0.07 rms for the faintest stars in the sample. As the 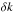 color term between the natural and uniform system is at most 0.027, all error terms have a negligible impact on the translation of star magnitudes to the reference system (at most 2 mmag rms for the noisiest stars). We will hence neglect the errors induced by the color transformation in what follows.
color term between the natural and uniform system is at most 0.027, all error terms have a negligible impact on the translation of star magnitudes to the reference system (at most 2 mmag rms for the noisiest stars). We will hence neglect the errors induced by the color transformation in what follows.
3.3.4. Results
The color transformations determined in Sect. 3.2 are readily applicable to colors calibrated on the Landolt system. Grid measurements are matched to the color catalogs described above, and we use measurements of stars lying in the color range where the linear color transformation 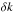 is valid. The model (9) is then fit to the selected data.
is valid. The model (9) is then fit to the selected data.
In all bands, we have computed solutions with increasing resolution of the spline basis. Increasing the resolution above N = 12 × 12 splines for the focal plane does not bring a significant χ2 improvement nor significant changes to the solution. We thus selected this resolution to compute all flat-field corrections. The systematic error on the flat-field induced by the inability of the chosen parameterization to describe the actual shape of the photometric correction is below 0.001 mag.
The main advantage of the parameterization adopted here is to decrease the number of parameters needed to describe the flat-field correction. The typical number of parameters for the selected resolution of the spline basis is Nampli + Nspline = 214, compared to 1295 in the scheme adopted in R09. The statistical uncertainty on the reconstruction of the flat-fielding solution is below 1 mmag, compared to ~4 mmag in the previous R09 scheme.
We checked the sensitivity to outliers using simulations with 2% photometric outliers11 uniformly distributed in the range [ − 2; + 2] mag. The simulation with and without outliers gives the same result, showing the efficiency of the procedure to discard outliers.
As already stated, the model does not include varying photometric conditions during the observation of the grid sequence. Unfortunately, while high quality photometric time has been dedicated to the grid observations, very few sequences were found to exhibit a stable IQ. The flat-field solutions from the grid sequences with the most stable IQ are displayed on Fig. 5.
The error induced by variation of the photometric zero point between exposures is expected to dominate the error on the determination of the flat-field correction. The selection of data to minimize the impact of zero point variations is discussed in the next section.
 |
Fig. 5 Maps of photometric corrections (relative to the twilight flat-field). Each panel displays a low resolution map (36 × 36 super-pixels of 256 × 256 real pixels, i.e. a resolution of about 2′) of the |
Finally, the flat-fielding correction that satisfies Eq. (8) depends on the flux reference of the magnitude system. The corrections derived so far refer to the system defined by Eq. (7). By construction, those corrections make the natural magnitude of BD +17 4708 independent of focal plane position. Corrections needed to ensure the same property in an AB system are readily obtained (up to an irrelevant constant that can be chosen to ensure 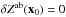 ) as:
) as:  S_\ab(\lambda) {\rm d}\lambda}{\int \lambda \cmag[T](\lambda) S_\text{ref}^V(\lambda) {\rm d}\lambda}\cdot \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq124.png) (12)Once the corrections are obtained, photometrically flat-fielded instrumental magnitudes are given by:
(12)Once the corrections are obtained, photometrically flat-fielded instrumental magnitudes are given by: 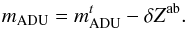 (13)Since the correction is bound to a photometry method (IQ-scaled here) and a photometric system (AB in the rest of this paper), it is generally advisable to keep the image pixels scaled by the twilight flat-field and to apply needed corrections to catalogs.
(13)Since the correction is bound to a photometry method (IQ-scaled here) and a photometric system (AB in the rest of this paper), it is generally advisable to keep the image pixels scaled by the twilight flat-field and to apply needed corrections to catalogs.
3.4. Discussion
We now turn to a discussion of uncertainties associated with our determination of the instrument response. Noise does not constitute a limiting factor in any of the measurements required to build the response model. Instead, the most significant errors are expected to arise from imperfect verification of the assumptions that the model is built on. Explicitly, we have made the following hypotheses:
-
1.
the transmission of the instrument as a function of wavelengthdoes not evolve with time;
-
2.
the transmission of the instrument as a function of wavelength depends solely on the focal plane radius, and this dependency is correctly mapped;
-
3.
the photometric response can be obtained as a stable photometric correction to the twilight flat-fields;
-
4.
the observations of dense stellar fields that constrain the photometric correction are obtained under stable photometric conditions.
In what follows, we quantitatively evaluate the validity of each assumption. We also discuss the resulting errors on the photometric response map.
3.4.1. Filter aging
The transmission model for the original Sagem/REOSC filters was based on early measurements by the manufacturer, prior to delivery in 2002. Later measurements of these filters have been conducted at CFHT in 2006 and display perfect agreement with the manufacturer findings in the uM, gM and zM bands. However, quite significant discrepancies between different measurements of the rM and iM filters were found, and thus a potential aging effect of these filters has been investigated (cf. Sect. 3.1.2).
To investigate this effect, we formed independent catalogs of the D3 field on a yearly basis, and looked for time-dependent color terms between the partial and the reference catalogs. The computed color terms are displayed in Fig. 6. The possible variation in filter response is less than 0.001 per unit of gM − iM color and it can be safely neglected. This test excludes a significant continuous variation of the filters over the course of the survey. In particular, this negligible change in the filters cannot explain the discrepancy between the 2002 and 2006 measurements of the transmission curves; if these measurements corresponded to a real change, we would have seen a color term of about 0.005 mag per unit of g − i. The filter measurements could both be correct, however, if the filter response changed after the first measurements were taken but before the survey began.
We conclude from this study that the passbands did not significantly evolve during the survey and that the 2006 measurements should be representative of the survey filters. This justifies our decision to correct the 2002 measurements so that they now match the 2006 measurements at the few positions where the latter are available (see Appendix B).
We recall, however, that this choice does not make the filter model entirely consistent. As an example, some spatial discrepancies between the predicted and measured color-terms for the rM filter are presented in the next section and are visible in Fig. 7. This discrepancy indicates that the model for this filter is still not fully accurate, which has consequences on the absolute calibration (cf. Sect. 9) and on the response map as discussed below.
 |
Fig. 6 Color terms between tertiary catalogs averaged over different periods. The survey observations in the D3 field have been divided into 5 periods covering about a year. Each data point is the fit of a linear color term between the catalog obtained from a single year and the catalog obtained from the whole survey. The stellar population is indexed by the g − i color. |
3.4.2. Consistency of the model of passband variations
A first argument in favor of the adequacy of our varying passband model is that the introduction of the color term in the model of grid observations given by Eq. (9) indeed improves the fit to the grid data set without the addition of free parameters. To go one step further and be more quantitative, one can leave 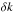 as a free parameter in the adjustment to the grid dataset. This was done in R09 using a coarse parameterization of the
as a free parameter in the adjustment to the grid dataset. This was done in R09 using a coarse parameterization of the 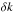 variation in cells of 1536 × 1024 pixels. The
variation in cells of 1536 × 1024 pixels. The 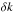 maps have been redetermined independently on all available grid epochs. The measured
maps have been redetermined independently on all available grid epochs. The measured 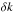 are compared to synthetic ones as a function of distance to the focal plane center in Fig. 7.
are compared to synthetic ones as a function of distance to the focal plane center in Fig. 7.
We have displayed the results from the two grid fields separately on this figure to distinguish potential effects related to reddening by dust. One can note that while the two grid fields suffer different dust extinction, the synthetic color terms, accounting for extinction, are almost indistinguishable. The fitted color terms agree as well, and there is no reason to question the results from the dusty grid-1 field.
The agreement between the model and the observations is generally satisfying. It deteriorates a bit in band rM at large radius, where the synthetic color-term becomes the most dependent on the selected color range. The observations also suggest that the i2M filter may be a bit more variable than measured.
Quantitatively, the standard deviations of the residuals of the measured to the synthetic 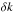 maps are 0.014, 0.004, 0.003, 0.003, 0.004, 0.002 in band uM, gM, rM, iM, i2M and zM respectively. Residuals maps are shown on Fig. 8. The most prominent features are the radial deviations in band rM and i2M already noticed on the radially averaged plot. Otherwise the residuals are consistent with noise in the observations. The boundaries between different chips are also visible in band u and g, which can be explained by slight differences in quantum efficiency curves from one CCD to another12.
maps are 0.014, 0.004, 0.003, 0.003, 0.004, 0.002 in band uM, gM, rM, iM, i2M and zM respectively. Residuals maps are shown on Fig. 8. The most prominent features are the radial deviations in band rM and i2M already noticed on the radially averaged plot. Otherwise the residuals are consistent with noise in the observations. The boundaries between different chips are also visible in band u and g, which can be explained by slight differences in quantum efficiency curves from one CCD to another12.
Although statistically significant, the discrepancy between the calculations and measurements are negligible for our purposes. We stick to the modeled color terms as they provide some consistency with the flux interpretation of the magnitudes, and significantly reduce the noise of flat-field.
One can also note that the examination of the various epochs independently exclude significant evolution of the pattern with time. The test is however insensitive to global variations of the mean passband with time which has been investigated above using tertiary stars.
 |
Fig. 7 Difference between measured and modeled color terms (relating the natural and reference photometric system) as a function of radius. Solid points show the average value of the |
 |
Fig. 8 Maps of residuals between the predicted and measured color term to the reference system. The synthetic color terms are computed on reddened spectra from the Pickles stellar library, to reflect the effect of the extinction measured in field grid-1. The measured |
3.4.3. Stability of the photometric flat-field corrections
Twilight flat-fields are assembled independently for each run of MegaCam (every lunation). In contrast, the photometric correction is determined about twice a year from a set of dedicated observations. We now want to assess the hypothesis that this correction is appropriate to other runs than the one it was derived for.
There are three main issues to consider. First, whether the differential response between point-like and uniform illumination (what is mapped by the photometric correction) is stable. Second, whether the successive twilight flat-fields consistently map the instrument response to uniform illumination. Third, whether the variations of the instrument response occur on time scales smaller than a MegaCam run. Below we qualitatively discuss each of these issues.
Changes in the instrumental setup:
the origin of a difference between instrument responses to point-like and uniform illumination is attributed to three main effects: 1) the spatial variation of the plate-scale; 2) the pollution of twilight images by stray light; and 3) the distortion of the PSF that varies the fraction of flux recovered by the photometry. Each of these effects is related to the optical configuration of the instrument and should be fairly stable.
However, several important adjustments to the telescope setup have been made during the survey, and these may have modified its response. We have investigated the stability of the instrument response using the repeated observations of the SNLS deep fields. The compatibility between the observations conducted at different epochs provide a stringent monitoring of changes in the survey uniformity. The analysis is fully described in Appendix A, and shows that telescope modifications indeed affect the photometry. A single photometric correction is thus not suitable to flat-field the entire survey.
We identified three telescope events with a noticeable impact on the flat-field corrections. The first is the flip of the L3 lens in the image corrector that produced a noticeable improvement of the uniformity of the image quality across the focal plane13. The second is the unfortunate accumulation of metal shavings on the top optical surface below the filter mechanism until its identification and cleaning at the end of the year 2006. The last is the accidental breaking of the iM filter in July 2007. These events define roughly 5 epochs: the beginning of the survey with the original telescope setup, the improved setup, the period of noticeable dust accumulation, the short period between the dust cleaning and the filter breakout, and the end of the survey. The exact dates of the telescope events are given in Table A.1.
Grid observations were accumulated sufficiently often to account for each of these major events. We can determine a photometric correction suitable for each epoch of the survey. However, this scheme can account only for abrupt changes in the telescope setup. The accumulation of metal dust is harder to handle because this effect is likely to change slowly with time but only a single grid observation was taken during this period (shortly before the cleaning when the effect was at its maximum). That being said, we can use the monitoring of the instrument response provided by deep-field observations (see Appendix A) to argue that, once corrected with the available grids, the instrument response appears compatible across all epochs at the 5 mmag level and does not display a significantly stronger dispersion during the period of dust accumulation than during the other periods.
Variations in the twilight flat-field:
aside from the twilight noise, which is negligible at large scales, there is one expected contribution to systematic differences between different runs: the twilight images contain a color-dependent term as noted in Sect. 3.3. If the effective color of the observed twilight varies significantly from one run to another, the photometric correction would have to be modified to compensate the variations induced on the twilight flat-field.
The procedure of taking twilight flats is automated so we expect the average twilight colors to be rather stable. We checked this by studying twilight flat-fields in the time period 04 Sep. 2007 through 05 Sep. 2008 when no intervention on the telescope optics occurred. We computed the ratio of each flat-field image obtained during this time period to the average flat-field image over the period. Defining an effective twilight color as the correlation coefficient between the twilight flat and the 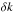 maps, we have measured variations of colors between successive flat-fields with standard deviations of 0.04, 0.15, 0.11, 0.15 and 0.45 in units of the
maps, we have measured variations of colors between successive flat-fields with standard deviations of 0.04, 0.15, 0.11, 0.15 and 0.45 in units of the 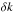 maps for uMgMrMiM and zM bands respectively.
maps for uMgMrMiM and zM bands respectively.
The fraction of those variations unrelated to changes in the twilight color (but simply to actual changes in the instrument response following roughly a similar pattern) is difficult to estimate. Nevertheless, those variations can be used to set an upper bound on the effect: in all cases a variation of the twilight color by the quoted amount contributes a flat-field error that reaches at most 5 mmag. The effect is small and will be smoothed out by averaging different photometric corrections; hence it can be safely neglected.
Variations of the instrument response on short time scale:
last, variations of the amplifier gain arise on time-scales shorter than the run and cannot be properly accounted for by the twilight flat-field. A prominent example of an amplifier gain variation is clearly visible on the 2005-10-09 grid displayed in Fig. 5. One amplifier (the left side) on the last CCD of the second row pops out. This feature is present in all bands for this epoch, but since it is not reproduced on other grid epochs we interpret this effect as a variation of the gain between the acquisition of twilight and the observation of the grid.
Such features normally contribute a small extra noise that averages out on several lunations. However, when an amplifier jump alter a photometric flat-field correction, all the images flat-fielded using this correction are coherently affected. The jumps of the amplifier gains are estimated to be generally small from a preliminary analysis of a monitoring experiment of the MegaCam gains conducted with the SNDICE experiment (Guyonnet et al., in prep.)14. As such deviations are expected to randomly affect different determinations of the photometric correction, a practical way to handle this difficulty is again to rely on the averaging of several determinations.
Compatibility between different epochs:
from all the considerations above we conclude that the assumption of a stable photometric correction is mostly valid, at the 5 mmag level, over large periods during the survey. We adopt the subdivision of the survey in five periods, as defined above, and we attribute a range of validity to photometric corrections determined during a given period that extends over the whole period. Remaining deviations, due either to the instrument response evolving slowly within each period, to variations in the twilight flat-field, or to variations of amplifier gains are difficult to characterize with a high level of confidence. A reliable estimate is provided by the fact that the photometric corrections bring the different survey epochs in agreement at the 5 mmag level. An important point is that the remaining deviations should be smoothed out by averaging the observations over the 5 periods.
3.4.4. Errors in the photometric flat-field correction
The measurement noise contributes about 1 mmag to the flat-field correction uncertainty and is therefore negligible. The main weakness of the grid method is the inability to adjust variations of the photometric response during the ~17 min observation sequences.
The statistical properties of the variations of the overall zero point during short sequences can be obtained from the main survey observation sequences that consist of half-hour long visits split into 5−6 exposures on the same field (with a negligible dithering). The zero point is found to be fairly stable during clear nights with an rms typically smaller than 5 mmag (see Sect. 4.1 for the determination of zero points and Fig. 10 for the distribution of zero points variations). Most of this variation is uncorrelated from one sequence to another. However, a small systematic shift of about + 2 ± 0.5 mmag per hour can be measured.
We used the measured shift and rms as inputs to simulations in order to evaluate the impact of such variations on the determination of the photometric correction. We checked for the influence of a random variation of the photometric zero point with an rms of 5 mmag and a systematic shift of 2 mmag per hour. The systematic shift results in a negligible (below 1 mmag peak-to-peak) gradient on the focal plane. The random photometric zero point produces a more significant error on individual solutions taking the form of large-scale variations with a peak-to-peak amplitude of about 1%. However, this random error is smoothed out as expected when several independent determinations of the photometric correction are averaged together.
Some epochs display stronger (and time correlated) variations of the observing conditions than what is typically observed. We took the conservative approach of discarding observations where conditions were not stable. Epochs were not used to flat-field the survey if the seeing variations were greater than 50% peak to peak, or variations of measured aperture corrections were greater than 1.1% peak to peak. Those epochs are likely to display zero points variations greater than the 5 mmag rms assumed in the simulations. This cut removes 18, 23, 30, 28, 40 and 20% of the available epochs in uM,gM,rM,iM, i2M and zM band, respectively. Valid observations are displayed in bold face in Table A.1. While this choice is somewhat arbitrary, excluding or keeping the observations made under variable conditions has a small impact on the uniformity of the tertiary star catalogs. When included, the catalogs are modified by about 1% peak-to-peak (or 3 mmag rms).
3.4.5. Internal estimate of the flat-field uncertainty
The typical r.m.s scatter of the selected grid solutions across epochs is 6, 6, 7, 7, 2 and 9 mmag in band uM,gM,rM,iM and zM, respectively. The structure of the variation is visible in Fig. 9. In all bands (but i2M that was installed after the cleaning), the accumulation of dust in the optics during the year 2006, visible at the lower right corner of the focal plane, dominates the variation. The pattern of noisy amplifiers also shows up on the variation map. Beyond these recognizable features it is difficult to distinguish between what is attributable to actual modifications of the telescope response, and what should be considered as part of the flat-fielding error.
As discussed above, the most reliable internal estimate of the remaining flat-fielding error is determined by the agreement between different periods of the deep survey. The typical rms σff of the spatial discrepancies between individual exposures are obtained in Appendix A and summarized in Table 2. Assuming that the errors are smoothed out when different photometric corrections covering the 5 periods are averaged, one concludes that a rough estimate of the residual uncertainty on the tertiary star flat-fielding is given by 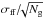 , where Ng is the number of independent determinations of the photometric correction. An independent cross-check of the flat-fielding quality is obtained by comparison with the SDSS in Sect. 8.4; it gives similar numbers.
, where Ng is the number of independent determinations of the photometric correction. An independent cross-check of the flat-fielding quality is obtained by comparison with the SDSS in Sect. 8.4; it gives similar numbers.
Internal consistency of the photometric flat-field.
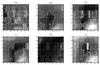 |
Fig. 9 Variation of the photometric flat-field corrections. Each panel displays a low resolution map (36 × 36 super-pixels of 256 × 256 real pixels, i.e. a resolution of about 2′) of the rms between all the determinations of the photometric grid corrections in a given photometric band. CCD boundaries are shown by white dotted lines. Note that all photometric correction maps are normalized to be zero at the center of the focal plane. As a consequence the rms across epochs is null at the center by construction. Noisy amplifiers are easily seen in rM and zM bands. In all bands (but i2M that was not available), the variation of response induced by the 2006 deposit of metal dust is clearly visible at the bottom right of the focal plane. |
3.5. Summary
We have built a model of the effective MegaPrime passband corresponding to the new i2M replacement filters. The iM and rM models have also been significantly revised with respect to the previous R09 release of the SNLS calibration using the more reliable 2006 filter measurement data.
The flat-field processing has been slightly updated with respect to R09. The most significant change is the use of modeled color terms rather than measured color terms to translate measurements when fitting the photometric corrections. This update is not expected to introduce significant changes in natural magnitudes except in rM at the corners of the focal plane, where the effect alters the flat-fielding by 0.5%. We also choose to make the instrument response constant for objects having an AB spectrum rather than for the primary spectrophotometric standard BD +17 4708. This convention makes the derivation of AB magnitudes from instrumental magnitudes more straightforward. Another change is a smooth parameterization of the instrument response which is expected to provide a slight decrease in the flat-fielding noise.
The main benefits for flat-fielding accuracy are related to the extension of the data sample (except for the broken iM filter). Most sources of flat-fielding error are uncorrelated between different epochs, and these errors are thus smoothed out with the addition of new grid observations. To avoid biasing the average we introduced a quality cut to remove epochs strongly affected by varying observation conditions.
An upper bound on the flat-fielding error is provided by the variability of the photometric corrections determined on independent data samples. It is below 1% in all bands. Assuming the error is uncorrelated between epochs, this also sets an upper bound of typically 0.3% rms on the uniformity of the resulting catalogs. We study the consequences of flat-fielding uncertainties on calibration in Sect. 4.3.2.
4. SNLS tertiary star catalogs
4.1. Multi-epoch average photometry of tertiary stars
A large number of exposures have been accumulated on the CFHTLS deep fields. A small dithering is generally applied to the observations for the purpose of filling gaps between CCDs. Its typical amplitude is between 80 and 120 pixels in right ascension and 300 to 360 pixels in declination. This dither is small enough that position dependent changes in filter response can be neglected. We thus assume that a given star is always observed through the same effective filter. This assumption simplifies the construction of a multi-epoch photometric catalog using natural magnitudes for the selected tertiary stars in the deep fields.
We use the stars selected as described in Sect. 11.1 of R09. We first determine aperture flux measurements for all stars in all the survey images, and then apply photometric flat-field corrections (Sect. 3.3) to the individual measurements according to Eq. (13). The survey is split into five periods, corresponding to noticeable changes in the instrument configuration. An independent determination of the photometric correction is applied to each epoch. The exact mapping between measurements and corrections is described in Appendix A and illustrated in Fig. A.2.
The model for the measured flux Ys,t of non-variable stars after flat-fielding is: 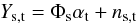 (14)where t indexes the exposure, s indexes the star, Φs = 10− 0.4m|x is the local broadband flux of star s,
(14)where t indexes the exposure, s indexes the star, Φs = 10− 0.4m|x is the local broadband flux of star s, 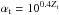 is the photometric zero point of exposure t, and ns,t is the measurement noise. The overall scales of Φs and α are not constrained from the data. Setting the scale of the Φs to correspond to physical flux requires calibration data, and is the subject of Sect. 5. At this stage, we are only interested in delivering an homogeneous set of measurements, and we will fit the model to the data with the constraint ⟨ αt ⟩ = 1. We work in flux space rather than in magnitude space because at low S/N, averaging logarithms causes a bias.
is the photometric zero point of exposure t, and ns,t is the measurement noise. The overall scales of Φs and α are not constrained from the data. Setting the scale of the Φs to correspond to physical flux requires calibration data, and is the subject of Sect. 5. At this stage, we are only interested in delivering an homogeneous set of measurements, and we will fit the model to the data with the constraint ⟨ αt ⟩ = 1. We work in flux space rather than in magnitude space because at low S/N, averaging logarithms causes a bias.
 |
Fig. 10 Top panel: distribution of zero point variations during an observation sequence (typically 6 exposures of 220 s in the same band in a row). Nights displaying a variability larger than 1% are discarded from the averaging. While the plot is cut at 0.025, numerous sequences (about 20%) taken under non-photometric conditions display a much larger variation. The zero point is defined as |
We opt for a two-step, iterative method. We start from a first estimate of 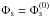 , obtained as the median of instrumental flux over all epochs for each star, and then we iterate the following steps until convergence:
, obtained as the median of instrumental flux over all epochs for each star, and then we iterate the following steps until convergence:
-
1.
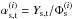 using the current estimate of Φs, and solve for αt in the linear model:
using the current estimate of Φs, and solve for αt in the linear model: 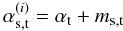 where the measurement noise on
where the measurement noise on 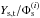 is modeled as an independent random Gaussian variable ms,t centered around 0 with variance
is modeled as an independent random Gaussian variable ms,t centered around 0 with variance 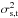 .
. -
2.
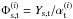 and improve the estimate of Φs as the (non-weighted) mean of
and improve the estimate of Φs as the (non-weighted) mean of 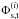 across a subset of photometric exposures.
across a subset of photometric exposures.
In this procedure, ± 4σs,t outliers are flagged and discarded. We model the relative flux uncertainty 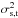 as
as 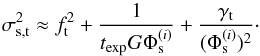 (15)Accurate values of
(15)Accurate values of 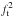 , and to a smaller extent, γt, are difficult to derive from first principles. We thus derived robust estimates of these parameters for each exposure by fitting the rms of
, and to a smaller extent, γt, are difficult to derive from first principles. We thus derived robust estimates of these parameters for each exposure by fitting the rms of 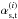 computed in bins of
computed in bins of 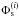 .
.
The major contributor to the γt term, which dominates the measurement error at low fluxes, comes from the Poisson fluctuation of the sky background. Its theoretically expected value is 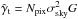 where Npix is the number of pixels in the aperture (≲700),
where Npix is the number of pixels in the aperture (≲700), 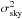 is the variance of the background fluctuation, and G ~ 1.6 e−/ADU is the gain of the readout electronics. This theoretical estimate, however, is typically significantly smaller than the fitted γt value because it does not account for contamination by structured residuals in the background (PSF tails, ghost reflections...), especially in the iM and zM bands where subtraction residuals from fringing can be important.
is the variance of the background fluctuation, and G ~ 1.6 e−/ADU is the gain of the readout electronics. This theoretical estimate, however, is typically significantly smaller than the fitted γt value because it does not account for contamination by structured residuals in the background (PSF tails, ghost reflections...), especially in the iM and zM bands where subtraction residuals from fringing can be important.
The other important contribution to the measurement error is related to the flat-field error, ft. The major components of this term are the error in the flat-field estimate, the variations of amplifier gains, and potential structures in the atmospheric extinction (clouds). Such errors are typically correlated among observations within the same night or the same run. This error term dominates the measurement error at the bright end: the error on individual measurements of star magnitudes asymptotically reaches 1.08ft/αt, which typically amounts to 6 mmag for clear nights.
The large number of epochs over a long time period makes it possible to control systematic errors by applying stringent selection criteria (cuts) on the measurements entering in the averaging process. We applied two cuts based on the relative variations of the zero point: 1) the time stability of the zero point during each observation sequence; and 2) the spatial uniformity of the zero point in each exposure.
The distribution of the standard deviation of αt from its mean value for the night is displayed in Fig. 10. The stability of the zero point is generally better than 1% for photometric sequences, with typical values of 2 − 3 mmag. We discarded observations for nights with a relative variation of αt greater that 1% because they might have been affected by clouds; this requirement removes 15 to 30% of the nights.
We also compute the relative variation of the zero point 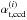 on a per CCD basis, and compute
on a per CCD basis, and compute 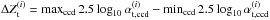 . The distribution of
. The distribution of  is shown in Fig. 11: it is generally below 4%, with a typical value of 2%. This result shows that the various flat-field corrections are in agreement at this level, although there are occasional outliers related to atmospheric conditions or amplifier gain variability. These outliers are identified and discarded by a cut on
is shown in Fig. 11: it is generally below 4%, with a typical value of 2%. This result shows that the various flat-field corrections are in agreement at this level, although there are occasional outliers related to atmospheric conditions or amplifier gain variability. These outliers are identified and discarded by a cut on  . We discuss further the variation of
. We discuss further the variation of 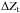 with time in Appendix A.
with time in Appendix A.
 |
Fig. 11 Distribution of the peak-to-peak zero point variation across the focal plane. Exposures displaying a peak-to-peak variation greater than 3% (6% in uM and zM) are discarded from the averaging. Vertical dashed lines show the cuts applied in the averaging process. |
We did not attempt to correct the catalog for selection bias. Biases arise for faint objects due to the higher selection efficiency of positive fluctuations, and for bright objects that saturate some pixels on nights with good seeing, leaving only nights with poor seeing conditions. Completeness of the catalog, defined as the fraction of nights a given star is used, is shown in Fig. 12. Completeness does not reach 100% on average due to the dithering needed to fill gaps between CCDs, contamination of apertures by cosmic rays, and occasional defects in the instrument (part of the CCD mosaic being non operational at a given time). We did not apply cuts to the catalog to discard stars potentially affected by selection bias.
 |
Fig. 12 Measurement completeness in the tertiary star catalogs. Each plot displays the ratio of selected measurements to the number of exposures as a function of the star magnitude in each band. The plateau at ~85% reflects mostly the ratio of the usable area in the focal plane to the total area covered by the catalog. |
4.2. Anchoring to the Landolt system
Nine fields containing a large subset of the Landolt equatorial secondary standards were routinely observed by the CFHT for calibration purposes. Those observations can be used to derive zero points for a large number of nights and tie the tertiary catalogs to the Landolt system.
The basic assumption underlying our strategy is that, besides the most obvious systematic differences between observations (such as airmass differences or systematic differences in the PSF)15, variations of observing conditions are uncorrelated from one night to another, and therefore these variations will average out with many repeated measurement of the flux ratios. We are thus modeling the exposure zero point as: 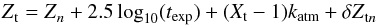 (16)where
(16)where  is the zero point of a given exposure t,
is the zero point of a given exposure t,  is the mean zero point for night n, (Xt − 1)katm is the average extinction at airmass Xt and
is the mean zero point for night n, (Xt − 1)katm is the average extinction at airmass Xt and 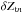 accounts for a variation of the photometric response in exposure t with respect to the average of the night
accounts for a variation of the photometric response in exposure t with respect to the average of the night 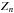 . In the calibration process, we treat this latter term as a noise that is independent for each night, and whose average is zero over many nights. Deviations from this hypothesis, related to systematic differences between calibration and science exposures, are discussed in Sect 4.3.
. In the calibration process, we treat this latter term as a noise that is independent for each night, and whose average is zero over many nights. Deviations from this hypothesis, related to systematic differences between calibration and science exposures, are discussed in Sect 4.3.
Following the scheme described in R09, we assume that the transformation between the Landolt system and the reference MegaCam system follows an approximate piece-wise linear color relation fL: 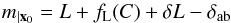 (17)where L is the Landolt magnitude of the star in the closest photometric band, C is the Landolt color index of the star, and δL accounts for small deviations of individual stars with respect to the single parameter relation fL. The calibration offset δab sets the magnitude system to the AB flux scale, and is determined by referring to a primary standard which is the subject of Sect. 5. For now we ignore δab and set the photometric calibration of the tertiary catalogs to a common but arbitrary scale, close to a Vega system.
(17)where L is the Landolt magnitude of the star in the closest photometric band, C is the Landolt color index of the star, and δL accounts for small deviations of individual stars with respect to the single parameter relation fL. The calibration offset δab sets the magnitude system to the AB flux scale, and is determined by referring to a primary standard which is the subject of Sect. 5. For now we ignore δab and set the photometric calibration of the tertiary catalogs to a common but arbitrary scale, close to a Vega system.
The large number of observations allows us to solve simultaneously for the transformation and the exposure zero points. We impose the constraint that δL = 0 on average, and find no significant degeneracy between parameters. The complete model for a photometrically flat-fielded Landolt star measurement is: ![\begin{eqnarray} \label{eq:22} \madu - \dk(x) (\umag[c] - c^0(x)) &=& L + \LtoM(C) + \delta L - \zp_n \nonumber\\ &&\quad - 2.5 \log_{10}(t_\text{exp}) - (X_{\rm t}-1)k_{\rm atm}. \end{eqnarray}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq198.png) (18)The relation fL is parameterized as:
(18)The relation fL is parameterized as:
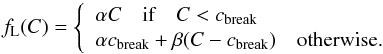 The free parameters include the two slopes for the piece-wise linear color transform (α and β), the airmass correction term katm, the zero point for each night
The free parameters include the two slopes for the piece-wise linear color transform (α and β), the airmass correction term katm, the zero point for each night 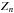 , and the deviation δL for each star. We impose the constraint ⟨ δL ⟩ ≈ 0 by adding a prior term
, and the deviation δL for each star. We impose the constraint ⟨ δL ⟩ ≈ 0 by adding a prior term 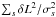 to the χ2 function. We choose σs = 0.01 to match the observed dispersion of the MegaCam to Landolt relation. The adjusted transformations are shown in Fig. 13.
to the χ2 function. We choose σs = 0.01 to match the observed dispersion of the MegaCam to Landolt relation. The adjusted transformations are shown in Fig. 13.
 |
Fig. 13 Color transformation between the Landolt system and the reference MegaCam system. Open black circles show the MegaCam and Landolt measurements of the Landolt secondary standards. The overall scale is set by the magnitudes of the primary spectrophotometric standard star BD +17 4708 (solid red square). Measurements of BD +17 4708 magnitudes in the Landolt system are provided by Landolt & Uomoto (2007). Since BD +17 4708 cannot be directly observed with MegaCam, its MegaCam magnitudes are inferred from the average color transformation (black line) determined from the secondary standard measurements. Potential deviations from this average color transformation are examined in R09 (see Sect. 5.1). Other primary standards from Landolt & Uomoto (2007) are displayed as red crosses; they are not close enough to the bulk of secondary standards to be reliably transformed with the average transformation. Observations of the Landolt standards in i2M were not numerous enough to deliver a robust measurement of the i2|x0 − I transformation (refer to Sect. 5.3 for the i2M calibration). |
Corresponding values for the transform parameters are given in Table 3.
The fit of Landolt observations delivers measurements of zero points 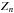 for a significant subset of the nights with observations of the SNLS fields (see Table 4). These zero points can be used to anchor the flux scale of the multi-epoch catalogs of the 4 fields to a common scale (relative to the Landolt system) according to the model given by Eq. (16)16. Non-photometric nights that were discarded in the analysis of the multi-epoch catalog (see Sect. 4.1) were also rejected in this averaging. Since a significant time period can occasionally separate the calibration exposures and the science exposures, this cut does not exclude all calibration observations affected by non-photometric conditions. A more robust assessment of the photometricity is possible when several calibration exposures are available for a single night, as is the case for about a third of the nights. We also discarded nights displaying a zero point that is significantly lower (by more than 0.05 mag) than the average zero point observed in a 10-night rolling average. Finally, we discarded nights displaying 3σ zero point outliers when applying the calibration model from Eq. (16) to calibrate the deep field exposures. Table 4 summarizes the number of photometric nights with concomitant observations of the Landolt and science fields, the observed dispersion between the independent measurements of the catalog scale provided by each night, and the resulting statistical uncertainty. The smaller number of zM nights is partly related to fewer Landolt observations in zM and cuts. Observations in uM were not part of the supernova survey and were not cadenced.
for a significant subset of the nights with observations of the SNLS fields (see Table 4). These zero points can be used to anchor the flux scale of the multi-epoch catalogs of the 4 fields to a common scale (relative to the Landolt system) according to the model given by Eq. (16)16. Non-photometric nights that were discarded in the analysis of the multi-epoch catalog (see Sect. 4.1) were also rejected in this averaging. Since a significant time period can occasionally separate the calibration exposures and the science exposures, this cut does not exclude all calibration observations affected by non-photometric conditions. A more robust assessment of the photometricity is possible when several calibration exposures are available for a single night, as is the case for about a third of the nights. We also discarded nights displaying a zero point that is significantly lower (by more than 0.05 mag) than the average zero point observed in a 10-night rolling average. Finally, we discarded nights displaying 3σ zero point outliers when applying the calibration model from Eq. (16) to calibrate the deep field exposures. Table 4 summarizes the number of photometric nights with concomitant observations of the Landolt and science fields, the observed dispersion between the independent measurements of the catalog scale provided by each night, and the resulting statistical uncertainty. The smaller number of zM nights is partly related to fewer Landolt observations in zM and cuts. Observations in uM were not part of the supernova survey and were not cadenced.
Statistical uncertainty (in magnitudes) on the calibration to the Landolt system.
4.3. Systematic uncertainties in the calibration to the Landolt system
We now turn to a review of potential sources of systematic uncertainty in the calibration path through Landolt observations. Here we only discuss uncertainties that affect the determination of the absolute flux scale of the tertiary catalog. These uncertainties are summarized in Table 5.
4.3.1. Systematic differences in aperture corrections
The first is from potential systematic differences in the photometry of standard and tertiary stars. The brightness of standard stars requires a short integration time (2–3 s) to avoid saturation. During the course of the survey, a small defocus (smearing the PSF core by about 1 pixel) on Landolt fields has also been applied to observe the brightest secondary standards of the Smith et al. (2002) set. It is likely that this defocus introduces systematic differences between the effective PSF of tertiary star observations and primary or secondary standard observations, resulting in slightly different aperture corrections.
To first order, PSF variations are approximately accounted for by the scaling of aperture radius in our photometry method. We statistically investigated deviations to this correction by computing aperture corrections between aperture of radius 7.5 and 20 times the image quality. We found a remaining variation of aperture corrections with image quality, and offsets between Landolt and deep field exposures dependent on the defocusing of Landolt observations.
The change in aperture corrections with image quality is illustrated in Fig. 14. The changes for tertiary standards and Landolt stars are similar, except for the offset related to defocusing. The IQ dependence is approximately linear with a small positive slope in the gM band and a negative slope in the other bands.
 |
Fig. 14 Variation of aperture correction from small to large apertures as a function of the image quality, IQ, defined as sigma of a Gaussian fit to the PSF (in pixels). Apertures are scaled with the IQ: small apertures correspond to a radius of 7.5 × IQ and large apertures to a radius of 20 × IQ. The aperture corrections are computed as φ7.5/φ20 − 1 where φ7.5 and φ20 denote instrumental fluxes in the small and large aperture, respectively. Data points correspond to the median of aperture corrections in bins of IQ over all the exposures in the survey. Results for short (and slightly out-of-focus) exposures on Landolt fields (black circles) and long exposures on deep fields (black squares) are displayed separately. |
The observation strategy of the Landolt fields slightly evolved over the course of the survey. Calibration stars were originally exposed for 3 s with the telescope in focus. The exposure time was reduced to 2 s in February 2005 and the telescope focus was offset by 0.5 mm with respect to the nominal focus to avoid saturation of the brightest stars. The amount of defocus was later reduced to 0.3 mm in August 2007. We therefore have three distinct time periods corresponding to different observational setups. We computed the average aperture correction offset between Landolt and deep field observations in bins corresponding to each time period. The measured offsets, shown in Fig. 15, were applied to the calibrated magnitudes to correct for the systematic differences on aperture corrections in the determination of the zero points.
A reliable estimate of the error on this correction is difficult to obtain. The correction is based on the assumption that the total flux loss is indeed proportional to the aperture correction, or in other words, that the fraction of flux captured in the larger aperture is stable. Whether this assumption is verified or not is a tricky question. A model independent hint on the accuracy of this correction is indicated by the agreement between the three time periods once the correction is applied, and by the residual dispersion of the calibration as a function of seeing difference. The different periods are statistically compatible. To be conservative, we took the difference between the two periods with the greater statistical accuracy (2003−2005 and 2005−2007) as a reasonable upper bound on the systematic related to aperture correction.
4.3.2. Flat-field error
The first effect of the flat-field error is to degrade the uniformity of the tertiary catalogs as discussed in Sect. 4.1 and in Appendix A. It can also result in an error on the average calibration because secondary standards are observed preferentially at the center of the focal plane. The Landolt calibration is made with sufficient statistics to provide a strict limit on this effect. The dispersion of the calibration residuals as a function of the flat-field solution applied is shown in Fig. 16. Each point on the plot corresponds to a mostly independent realization of the SNLS calibration, as it involves disjoint data samples for both the determination of the flat-field and the zero points. The measured dispersion is between 1 and 3 mmag in all bands. This dispersion is dominated by the statistical uncertainty on each point, and can be used to set an upper bound on the contribution from the flat-field error. Since the flat-field error is likely to be uncorrelated between different observations of the grid fields (cf. Sect. 3.4), we divided the measured dispersion by the square-root of the number of grid observations to estimate the flat-field error in Table 5.
Uncertainty budget in the cross-calibration between SNLS and the HST via the observation of Landolt secondary standards.
 |
Fig. 15 Average aperture correction (between 7.5 and 20 IQ radius) is shown for the 3 periods corresponding to different observational setups. Landolt stars (short exposures, slightly out of focus) are shown in black circles, and deel fields (long exposures) are shown in black squares. The statistical uncertainties on the averages are negligible. |
 |
Fig. 16 Catalog zero point as a function of the grid solution. The error bars reflect the statistical uncertainty on the mean estimated from the dispersion of measurements in the period. |
4.3.3. Shutter precision
The precision of the MegaPrime shutter could bias the photometric ratio between short and long exposures. The uncertainty on the exposure time was estimated in R09 to be less than 3 ms. For photometric standards exposed for 2 s, this uncertainty affects the flux by at most 0.15%.
4.3.4. Residual background contamination
The sky background subtraction is a difficult problem for aperture photometry. Our background estimate is based on the distribution of image pixels in tiles of 256 × 256 pixels after application of a mask discarding objects up to a given contamination level. The final estimate is a smooth interpolated version of the resulting low-resolution background map. Higher frequency structure remains in the background subtracted maps, in particular, the PSF tails from bright objects. Since R09 showed significant hints for background residuals in the aperture photometry of tertiary stars, we investigated the origin of this bias.
The basic idea is the following: structure in the background is expected at scales smaller than 256 pixels. Important contributors to such structure are PSF tails from bright objects and residuals from fringe subtraction in the i and z bands. These structures remain in the background subtracted images and contaminate aperture photometry. This is an intrinsic limitation of the aperture photometry method which assumes isolated objects on a background with noise expected to be zero on average, an hypothesis not verified in practice.
PSF tails are particularly annoying in our case as they make the average level of aperture contamination dependent on the star location. For our tertiary stars, which are selected to be fairly isolated objects, one expects the average contamination of apertures to be lower than for randomly distributed objects. Therefore, our hypothesis to explain the bias spotted in R09 is that the background subtraction algorithm is ill-suited to the specific locations of our tertiary stars (typically an overestimate as they are isolated).
We seek a quantitative estimate of this effect. Let us denote b(x) the residual background level at a given position x in the image after background subtraction, and C(x) the flux carried to this position by the PSF tails of neighboring objects. According to the discussion above, b and C are related. This relation is rather complex as the specifics of the background subtraction algorithm comes into play to suppress the large scales of the structure. In addition, the value of C is difficult to obtain because it requires knowledge of the PSF far out in the tails. Estimating the effect from first principles is thus not feasible.
We can characterize the residual background statistically by measuring an empirical relation between b and a quantity crudely related to C. We define a contamination index 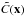 as:
as: 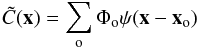 (19)where ψ is an approximation of the PSF normalized to 1, o runs across objects detected in the image and Φo is the flux of object o. The actual value of
(19)where ψ is an approximation of the PSF normalized to 1, o runs across objects detected in the image and Φo is the flux of object o. The actual value of 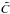 does not have a clear physical interpretation because it depends on the number of objects included in the sum and on the approximation used to describe the PSF. We can expect, however, that positions corresponding to larger
does not have a clear physical interpretation because it depends on the number of objects included in the sum and on the approximation used to describe the PSF. We can expect, however, that positions corresponding to larger 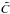 correspond to positions with greater residuals.
correspond to positions with greater residuals.
To determine the empirical relation between b and 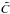 , we sampled the deep field images in the survey at uniformly spaced positions. For each position x we compute two quantities. First we estimate b(x) from the average residual sky level (after background subtraction) in a 32 × 32 pixel aperture centered at this position. Second, the contamination index
, we sampled the deep field images in the survey at uniformly spaced positions. For each position x we compute two quantities. First we estimate b(x) from the average residual sky level (after background subtraction) in a 32 × 32 pixel aperture centered at this position. Second, the contamination index 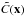 is computed under the assumption that the PSF follows a Moffat function (Moffat 1969) with parameters adjusted on the images. The top panel of Fig. 17 shows clear evidence for the dependence between the residual background level and the isolation of the location.
is computed under the assumption that the PSF follows a Moffat function (Moffat 1969) with parameters adjusted on the images. The top panel of Fig. 17 shows clear evidence for the dependence between the residual background level and the isolation of the location.
The average contamination in tertiary standard measurements is obtained as follows: we first compute the contamination index (Eq. (19)) for the positions of our tertiary standards, excluding the contribution of the tertiary star itself. We then convert each contamination index into a residual background level according to the relation shown in Fig. 17, and compute the average over all tertiary star positions. The distribution of the contamination index of tertiary stars is shown on the bottom panel of Fig. 17. As expected, the tertiary standards are well isolated objects with other image objects adding less than a fraction of an ADU per pixel. We found an average of 0.06, 0, − 0.26 and 0.01 ADU/pixel, respectively, in the gMrMiM and zM bands.
Those contamination numbers are in perfect agreement with the estimate of background residuals obtained in R09 Sect. 4.2 by studying aperture corrections as a function of flux. We thus conclude that the proposed mechanism explains the observed background subtraction bias. To account for the resulting bias on aperture magnitudes, we subtracted the average contamination level to the aperture flux measurements. Note that this is only an average correction, accounting for the overall bias introduced by background residuals. Contamination of apertures by background structure still contributes noise on individual aperture measurements. The distribution of this noise has a positive skewness (whose significance depends on the magnitude range considered) and some caution should be exercised when using the aperture catalog for calibration.
 |
Fig. 17 Background residuals as a function of the contamination index. The contamination index at a given location for a given aperture is defined as the flux in the aperture expected from objects detected in the field, assuming they have a Moffat PSF profile (see Eq. (19)). The top figure displays the average background level (in ADU per pixel) in random apertures as a function of this contamination index. We concentrate on random positions with low contamination index (apertures expected to be mostly empty), sampling the background level far from detected objects. The shape of the curves reflect the remaining structure in the background due to PSF tails. The bottom plot displays the distribution of the contamination indexes at the position of tertiary stars (excluding the contribution from the tertiary star itself). Horizontal lines in the top plot display the average value of the curve weighted for tertiaries, i.e. the expected per-pixel background offset for tertiaries. |
To illustrate the amplitude of the remaining effect, we give a comparison of catalog magnitudes with PSF photometry. The PSF photometry software independently adjusts and subtracts a background offset for each measurement, and is thus insensitive to residual background fluctuations. A known chromatic effect (see Guy et al. 2010), attributed to wavelength-dependent changes in the PSF that were neglected in the PSF photometry method17, has to be accounted for before performing the comparison. The dispersion of the difference between aperture and PSF photometry of the tertiary stars as a function of the star color are displayed in Fig. 18. The chromatic difference is easily seen in the gM band. Smaller but significant trends are also visible in the rM and iM bands.
After removing the chromatic trend and correcting the aperture magnitudes for the average background contamination computed above, the PSF and aperture magnitudes agree as a function of the star magnitude. As illustrated in Fig. 19, there is excellent agreement in the magnitude range 16–21 for the gM and rM bands, indicating that the average aperture contamination is mostly removed. The range of agreement appears a bit smaller in the iM and zM bands: 16–19.5. To obtain the most precise calibration, we suggest using stars only in the above confidence ranges.
Applying the same analysis to the Landolt measurements, we found that the residual background level in short time exposures is consistently positive and varies around a mean value of 0.1 ADU/pixels. This is attributed to a small biasing of our background estimator, which is based on a combination of the mean and the median of pixel values. It delivers biased estimates on the asymmetric distribution of background pixels in short exposures. The impact of such a bias on the determination of zero points is smaller than 1 mmag and is included in the systematic error budget.
 |
Fig. 18 Difference between PSF and aperture photometry for tertiary stars as a function of star color. The black line displays a linear fit of the chromatic trend observed. |
 |
Fig. 19 Difference between PSF and aperture photometry for tertiary stars as a function of star magnitudes (with the chromatic trend from Fig. 18 and the average background contamination of apertures subtracted). Black circles display the average of data points in bins of magnitudes. Averages are computed with a clipping at 2.5σ as used in the calibration of SNLS supernovae light-curves (Guy et al. 2010). |
 |
Fig. 20 Top: color−color diagram of the 4 SNLS tertiary star catalogs. Bottom: residuals to a linear fit of the average stellar locus in the range 0.2 < g − i < 1.2. The residuals for the 4 deep fields are displayed separately (D1: red crosses, D2: green squares, D3: black circles, D4: blue asterisks). |
4.3.5. Survey uniformity
The uniformity of the photometry between the 4 SN fields relies on the uniformity of the photometry of Landolt equatorial standards. The dispersion of zero points between individual Landolt fields has been estimated in R09 to be 0.002 in gri and 0.004 in z. As the true error is likely to have some spatial correlation, we use these numbers as estimates of the systematic uncertainty induced by non uniformity in the secondary network. Note that this error potentially affects the average calibration as the photometric standard observations are calibrated against a subset of the secondary standards.
The uniformity is confirmed by the generally good agreement of stellar locus between fields as displayed in Fig. 20. The dispersion of the stellar locus is compatible with the statistical uncertainty on the zero point in each field.
5. MegaCam absolute calibration measurements
The straightforward way to set the physical flux scale of the star catalog is to equate synthetic magnitudes of spectrophotometric standard stars with their corresponding magnitudes in the system defined by the catalog. Unfortunately, no such standards are currently present in the SNLS fields, although several pure hydrogen white-dwarves have been identified (Limboz et al. 2008; Lidman et al. 2013) that might serve this purpose in the future. For now, our absolute flux calibration relies on external observations of spectrophotometric standard stars.
Measurements from the Hubble Space Telescope imaging spectrograph (STIS) provide the best available set of spectrophotometric standard stars in the visible part of the spectrum. The calibrated spectra of HST fundamental standards are part of the CALSPEC database. Most of these stars are too bright for MegaCam to routinely and reliably observe. Therefore, until now, observations of the Landolt equatorial secondary standards (Landolt 1992) have been the preferred method to set the SNLS field absolute calibration, with anchoring to the HST flux scale indirectly provided by Landolt & Uomoto (2007) observations of HST standards in the Landolt system.
However, recent work (Bohlin & Cohen 2008) has extended the CALSPEC database to include redder and fainter standards. Direct MegaCam observation of these new standards opens an alternate calibration path for the SNLS fields.
We start this section by deriving AB offsets for the tertiary catalogs from the Landolt calibration observations. We then explore the possibility of direct calibration through observations of three solar analogs. Cross-calibration with the SDSS, presented in Sect. 8, offers yet a third calibration alternative. We devote Sect. 9 to the comparison of these various options.
5.1. Absolute calibration through Landolt observations
5.1.1. Transformation of Landolt standard measurements
We have used MegaCam observations of Landolt secondary standards to adjust the color relation shown in Eq. (17). This relation can be used to transform Landolt system measurements of stars (particularly measurements of standard stars) to the tertiary standard-defined SNLS system. Calibration constraints can be obtained by applying this relation to a spectrophotometric standard whose expected MegaCam AB magnitude ![\hbox{$\umag[\tilde m]$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq303.png) can be synthesized from the calibrated CALSPEC spectrum. This gives:
can be synthesized from the calibrated CALSPEC spectrum. This gives: ![\begin{equation} \label{eq:landaboffset} \delta_\ab = L + \LtoM(C) + \delta L - \umag[\tilde m] . \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq304.png) (20)Any of the Landolt & Uomoto (2007) Primary Spectrophotometric Standard Stars (hereafter PSSS) can be used to set the unknown calibration coefficient δab, provided the corresponding δL are known. The red crosses on Fig. 13 show primary standards from the CALSPEC database with accurate Landolt system magnitudes.
(20)Any of the Landolt & Uomoto (2007) Primary Spectrophotometric Standard Stars (hereafter PSSS) can be used to set the unknown calibration coefficient δab, provided the corresponding δL are known. The red crosses on Fig. 13 show primary standards from the CALSPEC database with accurate Landolt system magnitudes.
The average color transformation fL is adjusted so that ⟨ δL ⟩ = 0 on average for Landolt secondary stars. As shown in Fig. 13, the only spectrophotometric standard with Landolt magnitudes sufficiently close in color to the average of Landolt secondary standards (so that the corresponding δL is expected to be small) is BD +17 4708. R09 has done a careful estimate of the BD +17 4708 δL values, reproduced here in Table 3. We use these values to compute estimates of the calibration offsets according to Eq. (20). These calibration offsets are given in Table 6.
5.1.2. Uncertainties on the MegaCam magnitudes of BD + 17 4708
The dominant contribution to the systematic error budget is the uncertainty on δL, the term quantifying a star’s departure from the average transformation between the Landolt system and the MegaCam system. Intrinsic dispersion around the average transformation is expected due to variations in the SED of individual stars. Without any further assumptions, the dispersion of Landolt secondary standards around the average color transformation gives an estimate of the related uncertainty. Dispersion ranges from 13 mmag rms in band gM to 20 mmag in band zM.
As already stated, a more precise determination of δL, i.e. of the exact position of BD +17 4708 with respect to the bulk of the Landolt secondaries in the Fig. 13 Color−color diagram, was attempted in R09. This work used synthetic photometry on stellar libraries to model the small deviations induced by specific properties of BD +17 4708 (extinction, metallicity, log g, binarity) with respect to the mean properties of the Landolt standards, leading theoretically to a precise determination of δL and hence, to accurate magnitudes for the standards in the MegaCam system. Unfortunately a few contributions, like the effect of a faint companion to BD +17 4708, were difficult to estimate accurately and quite large uncertainties remain on the BD +17 4708 MegaCam magnitudes, especially in zM. The R09 δL values are given in the last column of Table 3; R09 uncertainty estimates on δL are shown in the “Landolt to Megacam transformation” row of Table 5.
Determination of the calibration offsets for the SNLS catalogs.
In band uM the value of δL has very large uncertainty, large enough that its determination was not even attempted by R09. Consequently, we quote the dispersion of the secondary standards around the color transformation as the uncertainty on the MegaCam magnitude of BD +17 470818. It amounts to 0.02 mag in uM.
The Landolt measurements of BD +17 4708 magnitudes are also affected by a small statistical uncertainty (about 0.002) that we include in the systematic error budget. The uncertainties affecting the Landolt observations calibration method (including relevant uncertainties discussed in Sect. 4.3) are summarized in Table 5.
5.2. Direct calibration to the HST
5.2.1. Observations of 3 solar analogs
The addition of fainter standards to the CALSPEC database raises the prospect of a more straightforward calibration method. We investigated the possibility of using direct observations of the faintest PSSS to set the photometric calibration of the SNLS. Three stars, SNAP-2, P177D and P330E, lie close enough to the D3 field to be easily observed together in a single short observing block with a potentially small airmass lever arm.
Observations were conducted at CFHT in June 2011 in short sequences, with exposures of standard stars bracketing a single exposure on D3. To avoid saturation and to study the behavior of aperture corrections on out-of-focus exposures, two exposures (one in focus, one out-of-focus) were taken of the brighter stars P177D and P330E. Exposures on SNAP-2 begin and close the sequence, enabling the monitoring of atmospheric extinction stability. Standard fields are exposed for 3 s; D3 fields are exposed for 120 s.
Images were processed by the standard Elixir pipeline and aperture photometry was performed in several predefined radii. Images were flat-fielded using the appropriate grid solution. Standard stars were observed on CCD #22. D3 flux measurements are matched with the tertiary star catalog and used to determined a zero point for the sequence. The zero point is then used to calibrate the standard star measurements, correcting for the effect of different airmasses. This allows us to determine the offset between the Landolt based calibration and an AB system by: ![\begin{equation} \label{eq:32} \delta_\ab = -2.5\logdec(\madu[\phi]/t_\text{exp}) + \zp + k_\text{atm} (X_{\rm D} - X_{\rm S}) - \cmaga \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq341.png) (21)where φADU/texp is the instrumental aperture flux corrected for PSF variations between the current exposure and the deep field exposure on which the sequence zero point
(21)where φADU/texp is the instrumental aperture flux corrected for PSF variations between the current exposure and the deep field exposure on which the sequence zero point 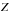 has been determined, XD and XS are the respective airmasses of the deep field and the standard star, katm is the average linear correction for atmospheric extinction and
has been determined, XD and XS are the respective airmasses of the deep field and the standard star, katm is the average linear correction for atmospheric extinction and 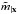 is the natural AB magnitude of the standard star at the observed position synthesized from its CALSPEC spectrum. Again, we use the notation
is the natural AB magnitude of the standard star at the observed position synthesized from its CALSPEC spectrum. Again, we use the notation 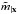 in place of m|x to distinguish synthetic from measured magnitudes.
in place of m|x to distinguish synthetic from measured magnitudes.
5.2.2. Error model
We build an error model for these measurements by considering the following sources of uncertainty: the photon noise of the standard star measurements, the flat-field noise, the tertiary measurement noise, the time variation of the zero point during the sequence and the uncertainty on the airmass correction. We are only interested in uncertainties affecting the flux measurements, for now. Any error on the calibration offset related to uncertainties affecting the synthetic magnitude 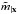 , such as uncertainties on passbands and error on the reference spectra, will be discussed later (in Sect. 9) and are not considered in what follows.
, such as uncertainties on passbands and error on the reference spectra, will be discussed later (in Sect. 9) and are not considered in what follows.
The photon noise can be readily determined from the sky level and the magnitude of the star. The typical contribution of background residuals to aperture contamination has been measured on the numerous observations of the Landolt fields. We use the measurements from the D3 exposure to estimate the size of the flat-field noise for the sequence. We adjust the error model (15) to the dispersion of measurements with respect to the magnitude of the corresponding tertiary catalog star. Typically, the corresponding flat-fielding error term (f) is found to be smaller than 0.4%.
The 72 tertiary stars on CCD # 22 allow a zero point determination with typical statistical uncertainties of 2 mmag in bands gMrMiM, and 5 mmag in bands zM and uM. This error affects all measurements of the sequence in the same way but is expected to be uncorrelated from one night to another.
The photometric ratio between the two SNAP-2 exposures bracketing each sequence was used to estimate gray atmospheric extinction variation for the corresponding set of observations. The extra noise contribution of this component is found to be smaller than 2 mmag.
Due to external constraints in the observing schedule, the deep field observation airmasses tend to be higher, on average, than the primary standard observation airmasses. This is unfortunate as it makes the final measurement sensitive to the variations of the atmospheric extinction around its average value katm (cf. Table 3).
Computations of the night-to-night dispersion of the SNLS zero point were used to estimate the typical variation of extinction around its average value. Magnitude variations were found to be 0.028, 0.009, 0.01, 0.01, 0.015 in ugriz bands, respectively. These estimates do incorporate contributions unrelated to atmospheric extinction such as instrumental effects, variation of the PSF uncorrected by the IQ scaling rule, and noise from the zero point determination itself. Therefore, effective variation of atmospheric extinction on clear nights may actually be somewhat smaller. On the other hand, these numbers are in good agreement with similar SNFactory measurements (Buton et al. 2012), except for zM where our estimate is significantly larger than the SNFactory estimate (about 0.3%), and uM where they found a variability closer to 4%. We used the largest numbers in each band as a conservative estimate of the uncertainty on the airmass correction term.
5.2.3. Systematic errors on the solar analog measurements
The solar analog-based measurement of the SNLS tertiary catalog AB offsets is also affected by systematic differences in the PSF between short and long exposures, uncertainty on short exposure durations, residual contamination of apertures, and, as the observations are coupled only with the SNLS deep field D3, non-uniformity in the survey.
We carefully monitored the variation of aperture corrections between exposures by computing aperture photometry in a large panel of radii. We choose to use 16-pixel radius aperture measurements to limit the background noise contribution to individual measurements. We also measure the median photometric ratio between these apertures and a 43-pixel radius aperture, which is assumed to capture a stable fraction of the total flux. All measurements were corrected by this measured photometric ratio. The statistical uncertainty on this aperture correction for individual exposures is typically smaller than 1 mmag and is included as extra noise.
The important matter is how well the 43-pixel aperture is representative of the total flux. A hint is given by the variation of the photometric ratio between the first and last exposures of the sequence. Figure 21 displays this photometric ratio for the 43-pixel aperture as a function of the difference in image quality between the two exposures. While the seeing can vary a lot, the photometric ratio is typically stable, with a rms of 2.3 mmag. This sets an upper bound on the combined contribution of the atmospheric extinction variation, shutter noise and variation of the flux loss outside the 43-pixel aperture. We conservatively use this number as a (pessimistic) estimate of the systematic flux difference between photometry on short and long exposures.
 |
Fig. 21 Stability of the flux measurements during the calibration sequences in gMrMiM bands. The difference of instrumental magnitudes in an aperture of 43 pixels between the first and the last exposure of the sequence is displayed as a function of the seeing evolution between the exposures. |
The background residual is measured for each exposure on a per CCD basis and all measurements are corrected for it. The extra noise introduced by the contamination of individual apertures is included in the measurement covariance matrices.
The uniformity of the survey has been discussed in Sect. 4.3.5. We use the statistical uncertainty on the average zero points of the individual SNLS D3 field, as given in Table 4, as an estimate of the departure of this field from the average survey system.
Finally, as for the previous calibration method, the shutter precision potentially biases the flux estimate of the short standard exposures. However, no field has been exposed less than 3 s, decreasing the impact of this systematic to less than 1 mmag.
5.2.4. Calibration offsets from the solar analogs.
Our error estimates were used to build a covariance matrix R of measurement errors accounting for correlation between the different error sources. The final AB offset measurement is obtained as the least-square average of the individual measurements 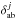 :
:
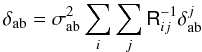 where
where 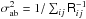 is the variance of the final estimate.
is the variance of the final estimate.
The results are summarized in Table 6. The offset can be compared to the offset inferred from Landolt observations of BD +17 4708. The results are further discussed in Sect. 9 where they are compared and combined with the other calibration measurements.
5.3. Intercalibration of iM and i2M catalogs
The number of epochs with coincident observations of Landolt and SNLS fields in band i2M is small. Consequently, no accurate calibration of the i2M band measurements can be obtained in this manner. On the other hand, no direct measurements of the HST standards were obtained before the breaking of the iM filter. Even so, a relatively precise cross-calibration of the iM and i2M catalogs is possible due to the similarity of the two filters.
We measured the average transformation between i|x0 and i2|x0 for stars in the color range 0 < g|x0 − i|x0 < 1 encompassing the BD +17 4708 color (g − i = 0.34). The measured color term between the two bands is i2|x0 − i|x0 = 0.025( ± 0.001) × (g|x0 − i|x0). The dispersion around this linear transformation is measured to be 4 mmag for stars brighter than iM < 18. This is comparable to the expected measurement error of 3.5 mmag, dominated by the flat-field induced error. Therefore, intrinsic dispersion is expected to be no larger than 2 mmag. Applying this transformation to BD+17 allows us to infer the i2M magnitude of the primary standard from its gM and iM magnitudes with a precision better than 2 mmag, thus anchoring together the catalog flux scales in the i2M and iM bands.
6. SDSS tertiary star catalog
The SDSS follows a calibration scheme similar to what was presented for the SNLS. To calibrate individual supernova measurements, a high-accuracy photometric catalog of non-variable stars was generated from a coaddition of repeated observations of stripe 82. The construction of this catalog is described in Ivezić et al. (2007). For brevity, this star catalog will be referred to as the “coadd” catalog.
A comparison of MegaCam Stripe 82 observations (described in Sect. 8) and the coadd catalog revealed evidence for a percent-level residual non-uniformity in the final flat-fielding solution of the coadd catalog. While the effect on individual SN photometry is negligible and the errors tend to average out when cosmological parameters are determined, the non-uniformity triggered investigations of the origin of the flat-fielding error and its possible impact on calibration. We start this section by summarizing the key steps of the construction of the coadd catalog and then describe a revision of the coadd flat-fielding.
6.1. Construction of the SDSS coadd catalog
The coadd catalog was obtained by averaging SDSS measurements of 58 photometric runs from Stripe 82 delivering on average 10 measurements per star. Quality cuts based on the repeatability of the measurements were applied to discard variable stars. The version used in the SN processing consists of 681 301 stars.
The flat-fielding of the SDSS camera is simplified by the drift scanning technique used to obtain imaging data. In drift scanning, each point on the sky is sampled by each CCD row; therefore, the effective response is averaged over all rows. However, row averaging does not eliminate spatial and temporal variations of the atmospheric transparency. Long term drift is controlled by anchoring the catalog photometry to the PT secondary patches placed throughout the SDSS survey area. Stripe 82 has an unusually high density of these secondary patches: on average, one every 4 degrees in RA but they are not uniformly spaced and there is a gap of 29 degrees between RA = 60 and RA = 89.
Averaging over photometric runs improves measurement noise and several sources of systematics, most notably variations in atmospheric transparency. However, declination pointings remain similar from run to run, such that Stripe 82 stars are only observed in a narrow range of pixel columns. Therefore, cross-scan variations (including flat-fielding errors and passband differences) are not smoothed out by run averaging.
The original technique for flat-fielding the images based on sky levels proved to be problematic for reasons similar to those preventing the direct use of twilights in MegaCam. A new procedure that determined flat-field vectors for the SDSS camera based on the Ivezić et al. (2004) stellar locus was then implemented19. This technique stems from the observation that most of the stellar population lines up in a narrow locus in the 4D ugriz color-space. The stellar colors are projected onto 4 color−color diagrams where the bulk of the stellar population is tightly clustered around a line in color−color space. The requirement that the stellar locus be independent of the position on the focal plane can be used to determine differences in flat-fields between the bands.
To apply the stellar locus technique to the Stripe 82 observations, average principal colors have been computed in bins of 0.01 degrees in declination, over a region spanning Galactic coordinates. It is assumed that all bins probe mostly the same population of stars, thanks to the narrow range of declination of stripe 82, so that differences in principal color are not induced by changes in the stellar population. The flat-field differences were adjusted to ensure constant principal colors across declination bins.
The technique only determines the difference in flat field between different filter bands. To determine the overall “gray” scale as a function of declination, Ivezić et al. (2007) relied on the calibration provided by the PT. The 2.5 m photometry in band gri is compared to the PT photometry of secondary stars, and the average difference is used as the reference flat-field vector for r-band. In this procedure, any error in the PT flat-fielding is transferred to the 2.5 meter telescope as an error common to all the passbands.
One last correction was applied to improve the uniformity of the catalog by taking into account the differences in the filter passbands for the different camera columns. In the published version20, all stellar measurements were transformed to the system defined by the official SDSS transmission curves21. The present work is based on an earlier (unpublished) version of the catalog that was used by (Holtzman et al. 2008) to calibrate the photometry of the supernova light curves. In this earlier version, no color transformation is attempted and all magnitudes are delivered in the natural system.
The coadd catalog photometric scale is anchored to the PT secondary patches by the SDSS pipeline. The PT photometry, in turn, is tied to the USNO star network Smith et al. (2002). The calibration of the secondary patches is based on the PT observations of 3 HST CALSPEC standards (Holtzman et al. 2008) so we do not rely on the calibration of the USNO star network. We do rely on its uniformity and suitability to provide an accurate measurement of atmospheric extinction. Observations are transformed from the PT natural system to the 2.5 m natural system using canonical color transformations. Standard star observations have been conducted with the target object roughly at the center of the camera image, whereas the color transformations have been derived from measurements over the entire image. In this observational setup, non-uniformity in the PT photometry may result in some calibration bias. In addition, the color transformations were determined quite early in the survey and were not monitored closely.
As variations of the PT response as large as 2% were found (cf. Appendix C), the following sections describe our determination of a flat-fielding correction to the coadd catalog which removes most of the sensitivity to PT photometry. In Sect. 7, we will use this uniform catalog to determine corrections to the PT flat-field, update the PT to 2.5 m transformation equation and revise the AB offsets for the corrected catalog from PT observations of HST photometric standards.
6.2. Corrected SDSS flat-field
A separate effort (Padmanabhan et al. 2008) sought to enforce the uniformity of the SDSS survey with naturally overlapping fields and special crossing scans that observed the sky in directions that were approximately perpendicular to the SDSS Stripes. The observation of stars in different camera columns allowed a recalibration of the SDSS that did not rely directly on the PT flat-fielding. In addition, it calibrated each filter separately and did not rely on the stellar locus or other assumptions about the objects being observed. This technique was used for the SDSS Data Release 822. This catalog will be referred to as DR8 and was retrieved from the SDSS database using the query given in appendix D.
The DR8 catalog is based on a single observation of each star. Consequently it is statistically less precise than the coadd catalog. In addition, typical SDSS observations take place at low airmass making it difficult to determine the atmospheric extinction from the SDSS 2.5 m data alone, requiring some additional assumptions. In contrast, the PT routinely measures standard stars at both low and high airmass and measures atmospheric extinction with much better accuracy.
Since we know that the PT flat-field has significant errors we want to use the DR8 data to correct the coadd catalog as a function of declination. We correct the coadd catalog, rather than using DR8 directly, because the multiple star observations incorporated into the coadd catalog greatly decrease the photometric errors and make it possible to eliminate various types of outliers. In the following, we will refer to the resulting catalog as the “corrected” catalog. Corresponding magnitudes will be denoted with a c subscript.
6.2.1. Matching the coadd and DR8 catalogs
We analyzed the differences between the two catalogs. The results of the analysis are restricted to the resulting catalog of matched stars. The matching criteria were:
-
The separation of two objects in the coadd and DR8 catalogs is lessthan 1′′.
-
There is no other object in the coadd catalog that is within 3.6′′ in both right ascension and declination.
-
The object in the coadd catalog is not within 3.6′′ in both right ascension and declination of any other object in the DR8 catalog.
A star must have 4 or more observations in the g, r, and i bands to be included in the catalog. In the following analysis, the measured u and z magnitudes are used only if there are 4 or more observations. We have also chosen to require 14.0 < r < 20.4.
6.2.2. Right ascension trend
Figure 22 shows the difference in the two catalogs as a function of right ascension. The data show a clear trend that is approximately linear in right ascension (α). We fit the data for each filter to the form 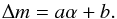 (22)The results of the fits for each filter are shown in Table 7.
(22)The results of the fits for each filter are shown in Table 7.
 |
Fig. 22 The difference in magnitude (coadd−DR8) for the 5 SDSS filters is shown as a function of right ascension. |
Given the significant trend in the difference, the question arises as to which catalog is more nearly correct. The SDSS DR8 procedure (Padmanabhan et al. 2008) assumes the extinction to be of the form 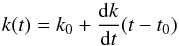 (23)where k0 and dk/dt are constants, t is the time of observation and t0 a reference time (in this case 0700UT). The assumed mean values and dispersion of dk/dt are taken from Padmanabhan et al. (2008), converted into mmag/deg and shown in the “DR8” column of Table 7 assuming an airmass of 1.2, a typical airmass for a Stripe 82 run. The slope of the difference between the coadd and DR8 are similar to the values assumed by DR8, but not identical.
(23)where k0 and dk/dt are constants, t is the time of observation and t0 a reference time (in this case 0700UT). The assumed mean values and dispersion of dk/dt are taken from Padmanabhan et al. (2008), converted into mmag/deg and shown in the “DR8” column of Table 7 assuming an airmass of 1.2, a typical airmass for a Stripe 82 run. The slope of the difference between the coadd and DR8 are similar to the values assumed by DR8, but not identical.
 |
Fig. 23 Difference between the coadd catalog and DR8 as a function of declination. The symbols represent the binned data and the lines are a cubic spline function fit to the data with 71 control points. |
The mtPipe calibration (Tucker et al. 2006) used for SDSS data production does not include any time-dependent terms although occasionally different photometric solutions were used for different time intervals during the night. The PT calibration is imprinted on the SDSS 2.5 m data through the secondary patches. Thus, we would expect a time variation-induced calibration error in the SDSS catalog data with the effect being proportional, on average, to the difference in time between the 2.5 m observations and the PT observations. A typical scan of Stripe 82 starts in the early evening at approximately −60° and ends in the early morning at +60°, resulting in a tight correlation between RA and the time of night. In contrast, the 178 Stripe 82 secondary PT patches used to calibrate the coadd catalog were taken throughout the night at more-or-less random times.
Trend line fits in RA.
Given the number of patches and their distribution in time of observation, it seems likely that the secondary patches should provide a good average over observing conditions throughout the night. Seasonal variations could produce a bias in calibration as a function of right ascension since higher right-ascension patches tend to be observed later in the season, but any variation that is slower than a night should be removed by the nightly calibration. We therefore assume that the PT patches have no bias as a function of right ascension.
In the processing of the 2.5 m data a single zeropoint is computed for each CCD so changes in atmospheric extinction could result in a bias in calibration as a function of right ascension. On the other hand, a typical photometric run in the stripe 82 catalog is often much shorter than the maximum of 8 h: the average run length is 3 h. Thus the effect of any change in atmospheric extinction should be substantially reduced for the shorter run. Regardless of what we might expect from the SDSS photometric processing, we can examine the agreement between the coadd catalog and the PT patches, which weassume to be unbiased with respect to right ascension. For each PT patch we determine the average difference between coadd and PT observations of the same stars. We then fit a line to the data as a function of RA. The results are shown in Table 7. The individual PT patches show considerably more scatter than would be expected from the statistical errors; presumably this is due to small time variations in atmospheric extinction (which was assumed to be constant over the course of the night). We characterize the distributions by fitting straight lines whose slopes are reported in the last column of Table 7. The quoted uncertainties are computed from the scatter of the data, not the statistical errors on the individual points. Also given in Table 7 are the slopes expected if the DR8 trend were correct. The fitted slopes are consistent with zero and, for all bands except u, are significantly different from the slopes suggested by the DR8 catalog. We conclude that this comparison disfavors the trends of the DR8 catalog and we remove the slopes reported in Table 7 from the DR8 data, bringing it into agreement with the coadd.
There are remaining trends in the data that are not well fit by the straight-line approximation.The origin of these variations is likely to be fluctuations inatmospheric transparency which affect the DR8 single epoch photometry more than the coadd catalog. However, we are primarily interested in the flat-fielding as a function of declination, and the major effect of remaining trends on the flat-fielding is a slight increase of the dispersion.
 |
Fig. 24 SDSS 2.5 m to PT measured color transformations. The individual stellar measurements are averaged in color bins of 0.05 width for clarity. The error bars display the 1σ uncertainty on the average estimated from the dispersion of individual measurements. The straight black line is the linear fit to the data. |
6.2.3. Flat-field correction
Figure 23 shows the comparison between the DR8 catalog and the coadd as a function of declination after the linear trend in RA has been removed from DR8. The data are binned into 226 declination ranges (each bin is approximately 0.01° wide). The catalog differences display similar patterns from band to band (particularly in r, i, and z), reinforcing the notion that the PT flat-field is a significant source of error in the coadd catalog. However, the bands also exhibit significant trends and the pattern of residuals does not show the exact 0.6 degree periodicity that would be expected if a gray scale error in the PT were the only effect.
The solid lines on Fig. 23 are cubic B-spline curves, each of which has 71 control points determined by a fit to the binned data. The decision to use 71 control points was somewhat arbitrary but puts the angular resolution at about 0.03. The analysis of the PT flat field leads us to expect a sharp discontinuity where the secondary patches abut one another. This would argue for a large number of control points in order to adjust those expected discontinuities. However, it was suspected that the binning of data to produce the coadd originally may have introduced some numerical noise, so the number of control points was chosen to be smaller than the number of data bins in order to produce some smoothing effect. The χ2 of the fit decreases slowly as the number of bins is increased and doesn’t seem to offer any useful clues as to an appropriate cutoff.
We correct the coadd catalog by subtracting the fitted smooth correction. Because we redetermine a (small) absolute calibration offset for the corrected catalog (described in the next section), we do not require the average correction to be zero. The residual difference between the DR8 and the corrected coadd catalogs shows a rapid 2 mmag rms fluctuation on small angular scales but is constant over larger scales. An assessment of the flat-fielding quality of the corrected catalog is given by the comparison with MegaCam measurements in Sect. 8.4. In particular, Fig. 28 suggests that the flat-fielding is now correct at the 0.5% level in griz.
7. SDSS PT calibration measurements
We now turn to the determination of AB offsets for the corrected coadd catalog using SDSS PT observations of HST standards. The non-uniformity of the PT response has a potential impact on this calibration transfer and must be corrected for. The basic idea is to use the uniformity of the corrected coadd catalog to improve the flat-field of the PT, redetermine the color relation between the corrected coadd catalog and the corrected PT photometry, and use those corrected relations to transform PT observations of the primary standards to the 2.5 m photometric system.
7.1. Correction of PT measurements
The calibration of the 2.5 m telescope native system to the absolute (AB) system relies on repeated SDSS PT observations of the HST CALSPEC23 standard stars (Bohlin & Cohen 2008). The PT measurements are calibrated against the set of USNO standard stars and transformed to the SDSS 2.5 m natural system using fixed color transformations. The PT calibration is robustly transferred to the 2.5 m telescope through the PT secondary patches.
With the discovery of photometric errors in the PT, it becomes important to redetermine (or check) the transformation equations between the two systems. We did so by looking for corrections to the already transformed magnitudes taking the form: 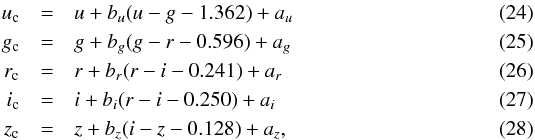 Here we denote the magnitude coming from the corrected coadd catalog with the subscript mc, to avoid confusion with the PT measurements transformed to the ugriz using the nominal color transformations.
Here we denote the magnitude coming from the corrected coadd catalog with the subscript mc, to avoid confusion with the PT measurements transformed to the ugriz using the nominal color transformations.
As we are fitting for corrections, we would recover b = a = 0 in all filters if the nominal transformation described the data perfectly. In order to compute these transformations the PT observations of secondary stars are matched with the corrected catalog of 2.5 m observations with the following criteria:
-
Match within 0.001 degrees.
-
Matches must be unique.
Since we know that the PT is subject to flat-fielding errors we want to allow for the possibility that a varies with position on the focal plane. The color term b, however, is likely to be nearly constant. So, we fit our data to Eqs. (24)–(28) in two steps. First, we determine the color term using the central portion of the PT CCD and the following criteria:
-
Valid PT magnitude and SDSS magnitudes for color.
-
At least 4 observations in the corrected catalog.
-
2.5 m r-band magnitude in the range 14.0 < r < 19.0.
-
The star must be in the center of the PT focal plane (400 < x < 1448 and 400 < y < 1448), where x and y are the pixel coordinates of the 2048 × 2048 pixel CCD.
-
Color in the range given by Table 8.
The fit is iterated and any magnitude that deviates by more than 5σ is dropped from the fit. The data are shown in Fig. 24 and the results of the fits are given in Table 9. In general, the color terms and offsets between the two systems are quite small. While some of the b terms are statistically significant their magnitudes are small.
Color range used to compute the color transformations.
PT color transforms.
PT measurements of HST standard star magnitudes.
PT focal plane offsets.
Next, we determine a position dependent a term by fitting the data in bins of a uniformly spaced 7 × 7 grid across the CCD focal plane. Although the b terms are not significant, the data is corrected for color prior to determining position dependent a terms. The resulting pattern of a terms is shown in Fig. 25. The main feature is a ~4% gradient between the 2 opposite corner of the CCD and has a similar shape in all the bands.
 |
Fig. 25 PT flat-field corrections. |
7.2. Absolute calibration
We can now use the PT measurements to update the SDSS supernova survey calibration. The original HST standard star PT measurements are displayed in Table 10. They are reported, as usual, in the 2.5 m photometric system by the application of the nominal (uncorrected) color transformations. Table 12 lists the same PT measurements in the corrected catalog system, obtained by applying Eqs. (24)−(28) to the original (Table 10) magnitudes.As described earlier in the text, these corrections are PT focal plane position-dependent, and compensate for the non-uniformity of the PT response.AB offsets calculated from the corrected HST standard measurements are given in Table 11.
HST spectra and SDSS filter responses (Doi et al. 2010) are used to compute expected magnitudes for the HST standard stars via the synthetic magnitude formula given in Eq. (1). Results of this calculation are given in Table 13. As the CALSPEC version somewhat affects the resulting magnitudes, Table 13 also notes the specific files used. Given in Table 14, the differences between the synthetic and the measured magnitudes are the AB offsets of the SDSS photometric system. The standard calibration uses the solar analogs because their colors are well within the range of validity of the PT→SDSS system color transformation. The dispersion in the results of the 3 solar analogs gives an estimate of the error in the AB offset – about 0.002 to 0.003 magnitudes – although this does not include any systematic effects that might result in common errors to the solar analogs. We also show BD +17 4708, which serves as the primary reference for the SDSS photometryas well as for several other experiments. The difference between BD +17 4708 and the solar analogs is another indication of AB offset errors. The WD result is also shown. However, WD colors are far beyond the region of validity for the color transformation thus their computed AB offsets should not be regarded as reliable.
7.3. Discussion
Besides the hints given by the variation of the calibration as a function of the selected standard, we can try to review and quantify the sources of uncertainty affecting the calibration of the corrected catalog. As for the SNLS, our concern here are the uncertainties affecting the measured magnitudes of the HST standards. The discussion of the spectra uncertainties is common to both surveys and delayed to Sect. 9.
7.3.1. Survey uniformity
The PT calibration can be affected by a spatial non-uniformity in the USNO star network. In particular, non-uniformity in the network could result in a systematic difference between the calibration of the solar analog measurements (α ≈ 15 h) and the calibration of the secondary patches (20 h < α < 4 h). The question is thus how much error there might be in transferring the calibration 12 h ahead (or behind) in RA. Possible non-uniformities are not directly discussed in the literature but the USNO network is expected to be especially robust because of nearly continuous measurements of the primary standards over a two year period of observation. From the uncertainties quoted in Smith et al. (2002) for the primary standard star measurements in the global fit, we estimate that the relative uncertainty in uniformity is less than 1.5 mmag in u band and 1 mmag in the other bands.
The PT observation program was designed so that the USNO standard stars were observed at the center of the focal plane. In contrast to the measurements of the HST standards, the non-uniformity of the response thus has no impact on the PT calibration to the USNO standard star network.
7.3.2. Color transformation
The color transformation from the PT to the 2.5 m system introduces some uncertainty on the precision to which the 2.5 m magnitudes of the standard stars are known. Two effects must be considered: the fact that individual stars do not fall exactly on the average color transformation, and the fact that in the SDSS camera each CCD has its own filter.
We found the intrinsic dispersion around the average transformation by looking at the dispersion of magnitudes synthesized in both systems from a stellar spectral atlas (Gunn-Stryker-Bruzal). We use this dispersion to estimate how much spectral variations of the HST standards might vary from the average stellar population which determines the color transformations. This dispersion is probably an overestimate because we ignore the effects of noise in the spectral atlas. In addition, the spectral diversity is likely over represented by the spectral atlas.
Standard star magnitudes in the SDSS system after all corrections.
Synthetic magnitudes of HST standard stars.
An alternative estimate of the magnitude of this error can be obtained from the variation of the AB-offset with the spectral type and color of the standard considered (available from Table 14). We obtain similar numbers, except for u band where the variation is inflated by the fact that the blue WDs clearly lie outside the validity range of the linear color transformation, and g band where the dispersion in the atlas seems artificially high. However, we do not attempt to correct the dispersion measured from the atlas and accept this dispersion as a conservative error estimate. This error dominates the uncertainty budget for the PT-based calibration as shown in Table 16. This is similar to the situation in SNLS, where the transformation of the BD +17 4708 Landolt magnitudes dominates the uncertainty on the Landolt-based calibration.
The color transformation is adjusted using data covering the entire width of the SDSS camera. As a consequence it translates PT measurements to the “average” SDSS photometric system. Our corrected tertiary catalog stems from a version of the coadd catalog with star magnitudes reported in the native SDSS photometric system. The flat-fielding correction applied to match the DR8 photometry does not use any color-dependent term, and leaves magnitudes in the natural system. This calibration procedure should adjust the zeropoint of each camera column so that a star of average color (as is nearly the case for solar analogs) will have the same magnitude in each camera column in the native system24.
The filters have been measured independently. Table 15 shows the synthetic magnitudes for the 6 camera columns for one of the HST white dwarfs and one of the solar analogs. The differences in magnitudes are small (1%) but not completely negligible. The variation of the AB magnitude of the solar analog around its nominal value illustrates the variation of the calibration offset effectively applicable to individual columns. Neglecting the filter changes adds a calibration noise (centered on zero) of 6, 4, 1, 0.2 and 0.6 mmag rms in ugri and z bands, perfectly negligible for SN measurements.
As far as we are only interested in accurate calibration on average (which is the case for SN-Ia science), the global AB offsets are adequate, and we do not account for any related effect in our systematic budget. When considering only a subset of the camera columns however, some attention should be paid to the change of photometric system, and calibration offsets for individual columns may have to be determined from Table 15.
8. SDSS/SNLS direct cross-calibration
8.1. Cross-calibration dataset
In theory, several overlapping areas between the CFHTLS and the SDSS (in particular the CFHTLS deep fields D2 and D3) could be used to tighten both surveys’ photometric calibration. However, the utility of existing published data sets is limited by two factors: the precision of the SDSS zero point determination for single epoch photometry and the difficult-to-evaluate precision of the inter-calibration between the D2-D3 DR8 and the Stripe 82 observations. In this work we rely instead on a specially designed observation program of Stripe 82 with MegaCam.
The original program, called MAPC (for MegaCam absolute calibration program), imaged the CFHTLS deep fields D1 and D4 and 2 fields in Stripe 82 (hereafter SDSS36 and SDSS326) in short “observing blocks”. Each observing block (OB) was observed in about half an hour in two bands. Since switching filters with MegaCam takes about 2 min, all the OB targets were first observed in one band, then another filter was selected to re-observe all the targets. To enable the monitoring of extinction stability, each observing block begins and ends with an exposure of the same field. Observations extended from December 2006 to February 2008. The cross-calibration data set was complemented by an early-2011 program of joint observations of D1 and SDSS36 alone (hereafter OB_D1_ext) with a reduced scope.
AB offsets for SDSS.
Synthetic and natural SDSS magnitudes of HST standard stars by camera column.
Systematic uncertainty budget for SDSS.
In the original program, 5 successive exposures of Stripe 82 were taken with a coarse dithering applied. This allowed us to map a slightly larger field (− 0.8° to 0.8° in declination, covering two thirds of the width of Stripe 82) while providing a cross check of the MegaCam flat-fielding. The position offsets applied to each exposure are given in Table 19 and roughly correspond to half of the focal plane size. Short exposures on standard fields were also included in the original program to provide an alternative determination of the MegaCam absolute calibration, but this method proved more sensitive to observation systematics than the one presented in Sect. 5.2. Both of these complications were dropped from the complementary program to shorten the observing block as much as possible. The definition and specifics of observing blocks for the two programs can be found in Table 18.
From this data sample we derive Stripe 82 star catalogs in MegaCam natural magnitudes, calibrated on the SNLS deep fields that can be readily compared to the SDSS catalog.
8.2. Calibrated MegaCam measurements of the Stripe 82 fields
Images from the cross-calibration data are processed using the standard SNLS photometric pipeline. Each resulting catalog is then matched (regarding astrometry) to the tertiary star catalog of the corresponding field, namely the SNLS tertiary star catalog described in Sect. 4 for SNLS deep fields and the corrected coadd SDSS catalog described in Sect. 6 for Stripe 82 fields. A matching radius of 1 arcsec was used and a few other selection criteria were applied to the SDSS corrected catalog:
-
The number of z band observations of the star must be greater than 4.
-
The rms of the gri band star measurements must be less than 30 mmag.
From studying MegaCam photometric flat-field corrections, we know that the accuracy of single epoch flat-fields are limited by errors that are expected to average out in the construction of the deep field tertiary star catalogs. A simple way to propagate this improvement to single epoch photometry is to align the photometry of deep field exposures on the corresponding tertiary star catalog. For each observing group we compute a rough flattening correction to the photometry by computing a zero point deviation per chip in addition to the global zero point. The following model is adjusted to the deep field observations available in the observing group.
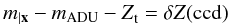 where m|x designates the magnitude reported in the tertiary catalogs, mADU the flat-fielded instrumental magnitudes and
where m|x designates the magnitude reported in the tertiary catalogs, mADU the flat-fielded instrumental magnitudes and 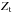 has been adjusted for each exposure in a first pass neglecting the
has been adjusted for each exposure in a first pass neglecting the 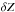 term. The fit is done in flux and measurements are weighted according to the error model introduced in Sect. 4.1. The
term. The fit is done in flux and measurements are weighted according to the error model introduced in Sect. 4.1. The 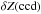 corrections are then applied to all images of the observing group.
corrections are then applied to all images of the observing group.
The procedure described in Sect. 4.1 is applied to build averaged MegaCam catalogs of the 2 Southern Stripe fields. Separate catalogs are built for different pointings. The catalogs are then calibrated according to the zero points computed on deep field exposures. The uncertainty on the catalog zero point is estimated as the night-to-night dispersion of the fit residuals, divided by the square root of the number of nights.
Direct comparison with the SDSS is enabled by the transformation of the measurements to the SNLS uniform photometric system. This is done using the transformation derived in Sect. 3.2 for stars lying in the valid color range of the transformation.
This procedure results in two sets of roughly 2000 and 6000 stars with natural SDSS magnitudes (denoted m2.5) and uniform SNLS magnitude (denoted m|x0). Depending on the pointing and photometric band between 2 and 9 nights are averaged (see Table 18). For such short observing blocks, the rms of the nightly zero points is typically below 5 mmag.
Field definition in the MAPC program.
8.3. Passband consistency
The first outputs obtained from the comparison of SNLS and SDSS measurements of the Stripe 82 stars are precise color transformations between the two systems. We determined linear color-transformations between SDSS and SNLS measurements for stars in the color range 0.5 < g − i < 1.5 according to the model: 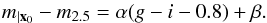 (29)Measurements are weighted according to the errors reported in both catalogs added in quadrature. To account for residual variation in the catalog zero point, independent β are determined for each MegaCam pointing. The transformations are illustrated in Fig. 26 and the measured slopes are given in Table 20. We emphasize that these equations describe transformations of the reference MegaCam system (filters at the center of the focal plane) to the SDSS system. The reference MegaCam system is not equivalent to and should not be confused with the average natural MegaCam system.
(29)Measurements are weighted according to the errors reported in both catalogs added in quadrature. To account for residual variation in the catalog zero point, independent β are determined for each MegaCam pointing. The transformations are illustrated in Fig. 26 and the measured slopes are given in Table 20. We emphasize that these equations describe transformations of the reference MegaCam system (filters at the center of the focal plane) to the SDSS system. The reference MegaCam system is not equivalent to and should not be confused with the average natural MegaCam system.
 |
Fig. 26 Linear color transformations between the SDSS and SNLS uniform magnitude system. The black lines represent the best linear fit of the data, whereas the red lines are based on synthetic magnitudes of the Gunn-Stryker-Bruzal stellar library and the SNLS and SDSS transmission models described in Sect. 2.2.1. |
These transformations can be compared to synthetic photometry-based predictions as a relative assessment of the accuracy of both instruments’ effective passbands. We synthesized stellar magnitudes for the 2 photometric systems from 2 stellar libraries, and determined a linear relationship for the resulting color−color plots. The slopes are given in Table 20 and over-plotted in red on Fig. 26. They are to be compared with the fitted slope in black. We report the statistical uncertainty on the slope determined on the Gunn-Stryker-Bruzal library, and the difference of slope obtained with respect to the Pickles library as an estimate of the systematic uncertainty on this quantity.
The discrepancy between the expected and measured slopes can be used to estimate the uncertainty on the passband knowledge. We provide in Table 20 the wavelength shift to be applied to the SNLS passbands to explain the whole effect. As can be seen the agreement is good in all bands, except in rM and i2M where a 3σ shift is detected. Note that the uM measurement does not provide useful constraints on the filter model.
Observing group description in the MAPC program and its extension.
The dithering pattern in MAPC.
The effective SDSS passbands actually vary slightly from one chip to another. In order to investigate whether passband differences may account for some of the observed discrepancies, we subdivided the sample into declination slices roughly corresponding to the 4 SDSS camera columns covered by our measurements. We compare these results to slopes determined separately for the camera columns using the independent passband determinations from Doi et al. (2010) in Fig. 27. There may be some correlation between the small observed and predicted slope variations from one camera column to another, but the flat-fielding uncertainty and other systematics make this comparison problematic. This is especially the case in uM, where both the predicted and measured color terms are affected by large uncertainties, making the comparison inconclusive. However, the measurements consistently disagree with the models in rM and i2M bands, indicating that SDSS camera column transmission variations cannot explain the discrepancies noticed in Table 20. It is more likely that these discrepancies originate from real deficiencies in the MegaPrime passband models. We further discuss passband uncertainties and their impact on the calibration in Sect. 9.
 |
Fig. 27 Comparison between synthetic and measured stellar locus slopes in the SNLS-SDSS color diagram for the 4 SDSS camcols covered in the observation program. |
8.4. Uniformity of the photometry
As they are subject to different systematics, a thorough assessment of the photometry uniformity can be delivered by the comparison of the two measurement sets. Due to the drift-scanning of the SDSS observations, the uniformity of the SDSS photometry is expected to be excellent at small scales in right ascension. In contrast, no specific direction is expected to be preferred in MegaCam observations.
Transformation equation between SNLS and SDSS systems.
This study led to the discovery of the flat-field problem in the PT and triggered the recalibration of the SDSS coadd catalog. The photometry residuals (after correction of the Stripe 82 catalog) are shown as a function of right ascension, declination and MegaCam radius in Fig. 28. Errors in SDSS flat-fielding would be expected to be most prominently seen when plotted versus declination while SNLS flat-fielding errors could appear in any of the plots. The radial plots correspond to an approximate MegaCam symmetry and exhibit some residual structure in r and z bands. The rms of residuals in bins of right ascension are 4, 1, 2, 3, 2 and 3 mmag in uMgMrMiMi2M and zM. Those numbers agree with the expected large-scale flat-fielding accuracy of the SNLS tertiary catalogs.
 |
Fig. 28 Relative uniformity of SNLS and SDSS photometry. |
8.5. Average offsets
We can now tie the SNLS and SDSS calibrations together. Ultimately, the quantity of interest is the flux interpretation of a calibrated measurement. As filters themselves have uncertainties, the error on this quantity depends on the SED of the object itself (to first order in its color). We discuss this question in the next section. We display in Table 21 the offset between the two surveys for a star of color g − i = 0.8 (defined as the β term in Eq. (29)).
The offset is computed separately on each field. The statistical uncertainty is estimated from the night-to-night dispersion of measurements divided by the square root of the number of observation nights. We then combine the two numbers and use the difference between the two fields as an estimate of the uncertainty on the mean related to the residual non-uniformity of the surveys.
9. Combined calibration
The calibration products for both surveys consist of:
-
measured natural magnitudes for a set of tertiary standards m3, in an arbitrary magnitude system;
-
magnitudes of primary spectrophotometric standards ms in the same magnitude system, affected by some measurement and systematic errors ns.
The primary spectrophotometric standards are to be used to set the actual flux scale (equivalently determining a magnitude offset to the AB system δab) of the first by equating the measured magnitude of the standard ms, with its expected magnitude 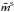 synthesized from the spectrophotometric reference measurement:
synthesized from the spectrophotometric reference measurement: 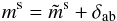 (30)with:
(30)with:
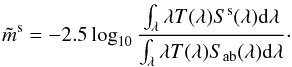 The result is affected by uncertainties on the effective instrument passbands T and on the SED Ss of the reference, as well as the error on the measured magnitude ns.
The result is affected by uncertainties on the effective instrument passbands T and on the SED Ss of the reference, as well as the error on the measured magnitude ns.
In our case we have at our disposal:
-
59 direct measurements of 3 solar-analogs (P330E, P177D andSNAP2) performed with MegaCam and calibrated to the SNLSsystem (see Sect. 5.2).
-
Landolt & Uomoto (2007) measurements of the star BD +17 4708, color transformed to the SNLS system in 5 bands (see Sect. 5.1).
-
PT measurements of 4 photometric standards (BD +17 4708, P330E, P177D, P041C) color-transformed to the 2.5 m system in the 5 photometric bands (see Sect. 7). We do not use the PT observations of bluer standards as they are outside the valid range of the PT→SDSS system color transformation.
In addition, the cross-calibration data described in Sect. 8 yields 6 constraints on the relation between the two surveys’ tertiary catalog flux scales, and a straightforward constraint on the iM and i2M magnitudes is given by the comparison of tertiary star magnitudes in these two bands (see Sect. 5.3). Altogether, we have a total of 91 measurements (or pseudo-measurements) and associated uncertainty estimates with which to constrain the AB offsets of the tertiary catalogs in the 11 photometric bands considered.
Our purpose here is to optimally combine the entire set of calibration data, to check its consistency, and to derive a reliable estimate of the uncertainty on the resulting calibration. As we want to combine several standard stars measured in different photometric systems related by linear transformations, we start by discussing and parametrizing the uncertainty on the instrument passbands and primary standard SEDs.
9.1. Uncertainties on passbands
The uncertainty on the effective instrument passband comes from various sources and may take some arbitrarily complex form. For instance, the portion of passband uncertainty from optical elements whose transmissions can be measured should approximately reduce to the uncertainty of the wavelength calibration of the monochromator (i.e. a global wavelength shift). On the other hand, the portion of passband uncertainty due to other elements, like the CCD QE, can be harder to characterize. The determination of the average atmospheric transmission is also affected by uncertainties, which primarily impact the u band calibration. In what follows, we assume that we can parametrize the error affecting the effective passband defining the photometric band b by a shift in the passband’s mean wavelength ![\hbox{$\wshift[b]$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq491.png) . In other words, when performing first order computations in the next section, we will assume that passband uncertainties result from a global shift of the filter. We now attempt to derive an estimate of the amplitude of the uncertainty on the mean wavelength
. In other words, when performing first order computations in the next section, we will assume that passband uncertainties result from a global shift of the filter. We now attempt to derive an estimate of the amplitude of the uncertainty on the mean wavelength 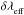 .
.
9.1.1. SDSS passbands
Measurement errors on the SDSS passbands are not completely characterized by Doi et al. (2010), but we will estimate the uncertainty from data in that paper. The accuracy of the monochromator calibration is given as ±3 Å, which we assume is a constant error for all wavelengths in a given filter band. The ability to reproduce an independent quantum efficiency measurement (Fig. 2 in Doi et al. 2010) suggests that the amplitude error is less than 2%. Assuming a ± 2% error that is linear in wavelength across the band, we calculate an error in the mean filter wavelength that is 0.3% of the filter bandwidth. Using 1500 Å for the filter width and combining that uncertainty with the monochromator uncertainty, results in a 6 Å uncertainty in mean filter response. The 1500 Å width is slightly too large for g, r, and i bands and a factor of 3 too large for u and z. However, we don’t decrease the error estimate for these bands because there are probably other (unquantified) uncertainties for these bands (e.g. the difficulty of determining the UV transmission and the red cutoff in z).
9.1.2. SNLS passbands
The lack of monitoring for the MegaCam passbands proved to be a weak point in the SNLS survey. It was only recently realized that two of the interference filters may have undergone significant alteration in their early days.
The REOSC filters were measured twice (in 2002 and 2006) and both measurements appear to be in rough agreement in all bands but iM and rM. Two arguments support the hypothesis that the 2006 measurements yield a better representation of the survey passbands: first, the stability of the color locus of tertiary stars during the 5 years of the survey, presented in Sect. 3.4.1, excludes the hypothesis of a slow aging of the filters between 2003 and 2008. Second, recent lab measurements of pieces of the broken iM filter were found to be in agreement with the 2006 measurement while incompatible with the 2002 ones. Because the 2006 measurements only cover the outer edge of the filters (12−15 cm away from the center), it was not possible to use them directly. Instead, we opt for applying a correction to the 2002 iM and rM measurements (see Appendix B). The unaltered 2002 measurements are used as-is for the uM, gM, and zM filters. We now try to quantify the size of the uncertainty on the mean passbands resulting from these choices.
The mean wavelength shift between the 2002 and 2006 measurements provides an estimate of the error at a specific position (about 15 cm away from the center). The measured differences amount to 5, 3, − 37, − 31 and 6 Å in uM, gM, rM, iM and zM bands respectively. The spatial consistency of the filter model is then ensured by the agreement of modeled and measured color terms between different positions (as illustrated on Fig. 7). A noticeable exception is the rM filter for which the measured and modeled color terms start to disagree at radii greater than 10 cm. Without proper measurements of the rM filter at radius smaller than 10 cm, it is thus not possible to trust the corrected filter model more than the uncorrected model. Therefore, we assign an uncertainty of 37 Å to the rM filter passband. The situation appears a bit better for the iM filter, since the accuracy of the 2006 measurement has been checked (cf. Appendix B), and the agreement between predicted and measured color-terms is quite good. Nevertheless, it seems premature to assign an uncertainty smaller than 31 Å to the iM passband without better understanding the source of the filter change. For the uM, gM, and zM filters, we also use the quoted differences between the two available measurements, namely 5, 3 and 6 Å, as an estimate of the measurement uncertainty.
The i2M BARR filter was never completely measured. In particular its effective refraction index is unknown and assumed to be similar to that of the iM filter. We base our estimate of the i2M passband uncertainty on the stellar locus in the plane i2M − i vs. g − i which has been well-constrained by observations of Stripe 82 stars and synthetic photometry predictions (see Sect. 8.3). The comparison between synthetic predictions and measurements suggests an i2M shift of − 30 Å (Table 20).
The uncertainty on the average atmospheric extinction curve is estimated in Buton et al. (2012) to be smaller than 0.02 mag/airmass. This has a negligible impact on the definition of any of the passbands. A noteworthy exception is the zM filter, which covers a region of strong H2O absorption (8916−9929 Å). Errors in the modeling of the average extinction could cause the mean wavelength of the effective filter to shift by a few angstroms. However, the error is unlikely to exceed the uncertainty quoted for this filter. Given their high throughput and the smoothness of their transmission, we do not expect significant contributions to a wavelength shift from any of the instrument elements besides the interference filters.
9.2. SED of the primary standard stars
Five spectrophotometric standard stars from the CALSPEC database are being considered in our final calibration data: the F sub-dwarf BD +17 4708 and the 4 G-type stars P041C, P177D, P330E and SNAP2. All these stars have STIS spectra calibrated by the model spectra of the white dwarfs G191B2B, GD153, and GD71. Any error in the spectral modeling of those three fundamental standard stars would equally affect our 5 standard stars.
The calibration reference is affected by both the white dwarf atmosphere model error and uncertainties in the determination of the primary standard surface gravity and effective temperature from observations of their Balmer line profiles. Following R09, we base our estimate on considerations from Bohlin & Hartig (2002) and adopt a 0.5% slope uncertainty (1σ) over the range 3000 Å−10 000 Å. Relative to g band25, the resulting (correlated) uncertainties are 0.7, 1.1, 2.2 and 3.2 mmag in u, r, i and z bands respectively.
In addition, some measurement error is expected to affect the individual measurements. Similarly to what was done in R09, our estimate of the covariance of broadband magnitudes synthesized from STIS spectra is based on the repeatability of the monitoring spectra of AGK +81 266. The individually measured spectra were integrated in the MegaCam and SDSS passbands and an empirical covariance matrix of the measurements was built. We found a repeatability of 5, 4, 5, 6 and 11 mmag in broadband magnitudes ugriz for both instruments, with significant correlation between neighboring bands, and (as expected) nearly perfect correlation between overlapping bands. The full covariance matrix is delivered in Table E.10. Some of the standard spectra were established with several independent measurements. When determining the expected broadband noise of the star measurement the covariance matrix is divided by the number of observations.
9.3. Mixing calibration data
For each available measurement (or pseudo-measurement in the case of a color-transformed magnitude) of a photometric standard s in a photometric band b, denoted 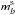 , the corresponding expected standard AB magnitude
, the corresponding expected standard AB magnitude 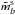 can be calculated from its CALSPEC spectrum. The model for the calibration data is:
can be calculated from its CALSPEC spectrum. The model for the calibration data is: 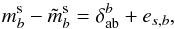 (31)where e is the error term affecting the estimate of
(31)where e is the error term affecting the estimate of 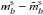 . It is further decomposed as:
. It is further decomposed as: ![\begin{equation} e_{s,b} = n_{s,b} + c_{s,b} + \frac {\partial \tilde m^{\rm s}_b}{\partial \weff[b]} \wshift[b]\,, \label{eq:35} \end{equation}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq514.png) (32)where ns,b is the measurement error affecting
(32)where ns,b is the measurement error affecting 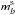 (including systematic uncertainties on the measurement), cs,b is the uncertainty affecting the broadband CALSPEC magnitudes, and
(including systematic uncertainties on the measurement), cs,b is the uncertainty affecting the broadband CALSPEC magnitudes, and ![\hbox{$\frac {\partial \tilde m^{\rm s}_b}{\partial \weff[b]} \wshift[b]$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq517.png) describe the first order impact of the filter uncertainty on
describe the first order impact of the filter uncertainty on 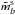 .
.
The cross-calibration data (between SNLS and SDSS as well as between bands iM and i2M) adds further constraints. These take the generic form of approximate linear relations between very similar filters, applicable on average to the tertiary stars: 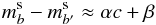 (33)with some uncertainty on α and β26. As before, we translate these color relations into cross-calibration constraints by assuming that those relations also apply to a spectrophotometric standard lying in the color range of the transformation. The extra error coming from the dispersion around the color transformation has to be estimated from stellar libraries. We thus add to our model the following terms:
(33)with some uncertainty on α and β26. As before, we translate these color relations into cross-calibration constraints by assuming that those relations also apply to a spectrophotometric standard lying in the color range of the transformation. The extra error coming from the dispersion around the color transformation has to be estimated from stellar libraries. We thus add to our model the following terms: 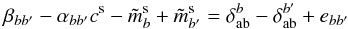 (34)where (b,b′) ranges over { (uM,u), (gM,g), (rM,r), (iM,i), (i2M,i), (zM,z), (i2M,iM) }. Again the error term is compound:
(34)where (b,b′) ranges over { (uM,u), (gM,g), (rM,r), (iM,i), (i2M,i), (zM,z), (i2M,iM) }. Again the error term is compound: ![\begin{eqnarray*} e_{bb'} = c_{s,b} - c_{s,b'} + \frac {\partial m^{\rm s}_b}{\partial \weff[b]} \wshift[b] - \frac {\partial m^{\rm s}_{b'}}{\partial \weff[b']} \wshift[b'] + e_\alpha c + e_\beta + d, \end{eqnarray*}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq528.png) where d is an uncertainty term accounting for the dispersion of stars around the color relation. We obtain the expected rms of the d term by measuring the dispersion around the average transformation of magnitudes synthesized from a stellar spectrum library. We find 48, 6, 2, 4, 3 and 2 mmag of dispersion around the relations between the SNLS and corresponding SDSS band for uM,gM,rM,iM,i2M,zM respectively.
where d is an uncertainty term accounting for the dispersion of stars around the color relation. We obtain the expected rms of the d term by measuring the dispersion around the average transformation of magnitudes synthesized from a stellar spectrum library. We find 48, 6, 2, 4, 3 and 2 mmag of dispersion around the relations between the SNLS and corresponding SDSS band for uM,gM,rM,iM,i2M,zM respectively.
To ease the handling of correlated uncertainties between all the measurements, we can gather the 91 calibration measurements into a single vector y and write the linear model for the calibration data in matrix form: 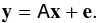 (35)We want to solve for the vector of calibration offsets
(35)We want to solve for the vector of calibration offsets 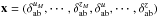 . The Jacobian matrix A relates each measurement to the corresponding offset (or a difference between two offsets in the case of cross-calibration constraints), and e is the vector of error terms.
. The Jacobian matrix A relates each measurement to the corresponding offset (or a difference between two offsets in the case of cross-calibration constraints), and e is the vector of error terms.
9.4. Covariance matrix of calibration data
Most of the measurement systematic uncertainties coherently affect different measurements (even across different bands). Neglecting the correlations would significantly underestimate the true error. We thus formed the full covariance matrix R = cov(e) of the calibration measurements accounting for all the error terms in the model above.
We already described the computation of the covariance of broadband CALSPEC magnitudes in Sect. 9.2. The computation of the resulting contribution to R accounts for the STIS measurement error and the uncertainty on white dwarf primary calibration differently. The STIS measurement errors are assumed to be uncorrelated from one star to another and divided by the number of observations for each star. The calibration error is assumed to be a systematic error that produces the same error for all the measurements of all the stars.
The error affecting the determination of the filter effective wavelength is assumed unrelated from one filter to another. Its contribution RF to R is obtained as:
where H is the matrix holding the terms ![\hbox{$\frac {\partial m^{\rm s}_b}{\partial \weff[b]}$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq540.png) corresponding to each measurement.
corresponding to each measurement.
Due to the large number of systematic uncertainties to be accounted for, the construction of the covariance matrix of the measurement error terms is less straightforward. In brief, we have assumed that all statistical uncertainties arising from measurement noise (photon noise or flat-field noise) are uncorrelated from one measurement to another, whereas part of the systematic uncertainties affect measurements coherently and are therefore taken to be fully correlated. Full details of the assumptions made in the covariance matrix computation are given in Appendix E.4.
9.5. Least-square estimate of the calibration
Correlation matrix of the final calibration.
We derived the combined estimate of the calibration offsets through weighted least-square minimization. The resulting offsets are given in Table 23, along with the diagonal component of their covariance matrix. The corresponding correlation matrix is given in Table 22. The offsets are applied to the catalog of tertiary standard stars to provide our best estimate of their AB magnitudes.
The global χ2 of the fit is 79.8 for 80 degrees of freedom. Note that we are mainly manipulating actual systematic uncertainties rather than Gaussian-distributed random variables. A better assessment of the agreement between the different sets of primary standard measurements is provided by Fig. 29. We defer the discussion of these results to the next section of the paper.
10. Results
10.1. Calibration products
We deliver natural broadband AB magnitudes for a large set of selected stars (the tertiary standards) in the SNLS and SDSS science fields. These tertiary standards will be used to calibrate the science images of the surveys and may be useful for other, similar purposes.
The calibration of the catalogs to the AB system results from the combination of all the calibration data gathered in this work. The details of the combination are described in Sect. 9. Briefly, we combined calibration constraints coming from observations of 5 different spectrophotometric standard stars from the CALSPEC database. Those observations were conducted following 3 mostly independent paths presented in Sect. 2.4 and described respectively in Sects. 5.1, 5.2 and 7. In addition, the SNLS and SDSS tertiary catalogs are tied together by a cross-calibration measurement described in Sect. 8.
We emphasize that the magnitudes are delivered in the natural photometric systems of the corresponding instrument, as defined in Sect. 2.2.1. As a consequence, their correct interpretation is given by Eq. (3) using the effective filters corresponding to the average position of the star observation in the field of view. We deliver a model of MegaCam passbands along with this paper and refer the reader to the work from Doi et al. (2010) for the SDSS effective passbands.
Another consequence of the variation of the natural photometric system with the position in the field of view is that, for calibration purposes, the reference catalogs are best matched with exposures sharing a compatible pointing (same pointing for MegaCam or same declination for SDSS). In other cases, small color terms accounting for the slight differences in the effective filters may have to be considered to obtain accurate zero points.
One may also note that the catalogs have been established using IQ-scaled aperture photometry in the case of SNLS and the usual PSF photometry algorithm in the case of SDSS. While the result does not depend on the photometry method to first order, small spatial or chromatic effects may need to be accounted for when comparing to measurements obtained using different photometry methods (see e.g. Sect. 4.3.3).
SDSS and SNLS combined AB offsets.
 |
Fig. 29 Agreement between complementary determinations of the SNLS AB offsets. SNLS BD+17 and SNLS SA lines refer to the SNLS calibration on Landolt standards and direct solar analog measurements respectively (cf. Sect. 4). The SDSS SA and SDSS BD+17 lines refer to the calibration obtained by translating the PT measurements of the solar analogs and BD +17 4708 respectively, to the SNLS system via the relations obtained in Sect. 8. The data points correspond to the calibration offset relative to the combined calibration including all the measurements and are not independent. The shaded region illustrates the uncertainty on the combined calibration. |
For most comparison purposes, it is also convenient to report MegaCam measurements in a single photometric system, close to the natural system. In this paper, we follow the convention adopted in R09 and define the MegaCam uniform magnitudes as the natural magnitudes that would have been observed for objects at the center of the focal plane27. We have derived color transformations between the natural and uniform system (see Sect. 3.2) and include in the catalog MegaCam uniform magnitudes for all stars that can be accurately transformed.
Finally, we determine measured color terms between the uniform MegaCam photometric system and the average SDSS system in Sect. 8.3. These facilitate comparison of other data specifically obtained in these photometric systems.
Catalogs can be found in Tables E.1 and E.228. AB offsets given in Table 23 are already applied to the released catalogs. The covariance matrix associated with this calibration is given in Tables 23 and 22. Finally the Megacam effective transmission models to be used in Eq. (2) are given in Tables E.3−E.829. What follows is a general discussion of these results.
10.2. Agreement between the available calibration paths
A key feature of this work is the redundancy between several calibration paths established independently and subject to different systematics. An illustration of the agreement between the different paths is provided by Fig. 29.
The agreement between the SNLS and SDSS calibration appears better than one percent in the gri and z bands. There is an apparent offset of about 4% in u which is still compatible with the low precision of the cross-calibration data in this band. Internally, there is a small tension between the Landolt and solar analog calibrations of the SNLS in iM/i2M and rM (~1.9 and 1.3%). To a lesser extent, a similar trend is visible in the SDSS which suggests that at least a part of the tension may be explained by an actual calibration difference between the BD +17 4708 and the solar analog CALSPEC reference spectra.
Overall, we reckon that the whole data sample is compatible with the modeled uncertainties. Consequently we opted for combining the whole data sample to set the flux scale of the tertiary catalogs and we believe that the uncertainties resulting from the combination are reliable.
10.3. Uncertainties on the combined calibration
A few points pertaining to the calibration uncertainties ought to be discussed.
First, one can observe from the correlation matrix in Table 22 that the cross-calibration data brings significant correlations in the calibration of all the SNLS and the SDSS overlapping bands but u and g, where the accuracy of the cross-calibration is limited by the less-similar filters and the higher dispersion of the stellar population about the color-tranformations. Consequently, flux measurements in the two surveys can now be compared with low cross-calibration uncertainty.
It is also interesting to compare the relative importance of the various contributions to the global calibration uncertainty. The last row of Table 23 shows that the uncertainty on the primary standard spectra amounts for about half the uncertainty (in variance) for the redder bands (riz). The imperfect knowledge of filters impacts mostly the u and uM band calibration due to the large variation of the standard star spectra in this wavelength region and the rM band due to the larger uncertainty remaining on the transmission of this filter.
Evidence for potential evolution of the rM and iM filters has been found and the resulting uncertainty on the filter passbands is discussed in Sect. 9.1. We emphasize that the impact of filter passband uncertainty depends on the color of the object whose flux is being determined. Specifically, this error cancels for objects whose spectrum is close to the spectrum of our standard stars (main sequence stars of color g − i ~ 0.55). This is why the poor knowledge of MegaCam iM and rM passbands only minimally affects AB calibration accuracy: the primary standards we observe have SEDs close to the AB spectrum in those bands (stars with g − i ~ 0.55 have r − i ~ 0.1). This is not the case for type Ia supernovae; therefore, the impact of filter passband uncertainty on their flux measurements is bound to be much larger.
10.4. Comparison with SNLS3
For the four photometric bands already calibrated in R09, we compared uniformity and absolute calibrations between the new and prior tertiary catalogs. A sign mistake affecting the R09 catalog was discovered in this comparison. It contributes to a slight deterioration of the catalog uniformity and shifts the average flux scale of the catalog by 8, 5, 6, 3 mmag on average for band gM,rM,iM and zM respectively. Once the error sign is corrected, the remaining offsets are given in Table 24. The comparison of calibrated magnitude differences as a function of the distance to the center of the focal plane is given in Fig. 30.
Calibration offset between R09 and the present release of the SNLS calibration.
 |
Fig. 30 Difference between SNLS-calibrated tertiary star magnitudes and previous R09 release as a function of the distance to the focal plane center. The 4 deep fields are compared separately (D1: red plus, D2: green squares, D3: black circles, D4: blue crosses.) |
10.5. Comparison with the previous calibration of the SDSS SN survey
Following the discovery of a non-uniformity in the SDSS PT flat-field, this work introduces two changes to the SDSS tertiary catalogs. The first is a correction of the tertiary catalog flat-fielding based on the Data Release 8 SDSS catalog (Padmanabhan et al. 2008) flat-fielding solution. The second is the new determination of the corresponding AB offsets. The previous calibration of the SDSS SN survey was based on the uncorrected version of the coadd catalog scaled to the AB system by the application of AB offsets from Holtzman et al. (2008, Table 1). As supernovae are uniformly distributed in declination, the calibration offset to be expected from this release is readily given by the weighted average of magnitude differences between the two calibrated catalogs. This offset is given in Table 25.
Calibration offsets between first and third year release of the SDSS-II SN survey.
The difference in the average photometry is fairly small compared to the size of the PT flat-field correction. This is a fortunate consequence of the fact that the effect is close to symmetric with respect to the center of the PT focal plane, where standard stars were observed. The row labeled rms in Table 25 gives an estimate of the gain in photometric precision that is to be expected from the improved flat-fielding.
10.6. Comparison with other work
While we have achieved excellent agreement with the SNLS and SDSS supernova surveys we did not attempt to compare our photometry with any other survey. The SDSS SN photometry has been compared with CSP (Mosher et al. 2012), where good agreement was found. The Pan-STARRS survey (Hodapp et al. 2004) has recently reported a small discrepancy with the SDSS stellar photometry (Tonry et al. 2012), but larger than might be expected on the basis of this work. Their analysis used the publicly available SDSS catalogs which lack the corrections applied in this paper and they did not use the filter transmission measurements of Doi, et al. However, the discrepancy in photometry might very well persist even with our revised catalog.
11. Conclusion
We have delivered updates to the tertiary standard star catalogs that define the photometric calibration of the SNLS and the SDSS supernovae surveys. The catalogs provide standard star calibrated AB magnitudes, in the natural photometric system of both instruments. The products are fully described in Sect. 10.1.
The flux calibration is based on the observation of 5 different HST primary spectrophotometric standard stars from the CALSPEC database. In addition, the SNLS and SDSS tertiary standard stars are now tied together by specifically designed cross-calibration observations. Three independent routes, each subject to different observational systematics, were used to transfer the HST primary standard star calibration to the tertiary standard stars. Good agreement was found between these 3 routes, which were then combined to provide the final products. In particular, the offsets derived in Sect. 9 from simultaneously fitting all available information have been applied to the delivered catalogs. These offsets have been determined with CALSPEC version 3 spectra, and may be updated as new CALSPEC versions are released. See Appendix E for more details.
With respect to previous releases, the photometric calibration evolved by less than 1% in all photometric bands but u. Major improvements arise from better flat-fielding processes (that also improve the uniformity of the resulting catalogs), and the introduction of more data to constrain the calibration transfer.
The calibration transfer from HST standard stars to stars in supernovae fields is thought to be accurate to about 3 mmag in the riz photometric bands. This is comparable, or better than the error related to the calibration uncertainty of the primary standard stars themselves. The error in band g is about 4 mmag and remains dominated by the error in the calibration transfer. The uncertainty on the u band calibration amounts to about 1% in the SDSS and 2% in the SNLS, dominated by the uncertainty on the instrument effective passbands.
The photometric calibration was complicated by the need to overcome several instrumental effects as well as weaknesses ininstrument or survey designs. The most important complications are summarized here:
-
Uniform illumination of wide-field instruments is not enough toachieve accurate flat-fielding; internal reflections in the opticalpath must be accounted for. At least two elements, CCDs andfilters, are reflective enough to feed significant amounts of lightback into the wide-field corrector optics. Reflected by convexlens surfaces, this light causes ghosting as well as diffuse andstructured contamination in the flat-fields. For this reason,photometric uniformity of both the SDSS and SNLS instrumentsultimately relies on the analysis of dithered stellar observations.The variation of atmospheric conditions during the observationsequences ultimately limits the flat-field solution accuracy.
-
Similarly, small-angle scattering of light caused by dust or defects in the optics can affect the photometry of point sources while leaving the flat-field twilight images unchanged. A remarkable illustration of such a phenomenon occurred during the SNLS survey: the progressive deposit of metal dust from the filter jukebox on one corner of the top corrector lens caused a local 6% deterioration of the effective throughput of the photometry, and was only detected and measured through dithered stellar observations. Such effects can also be detected by monitoring apparent star brightness in often-visited fields.
-
For SNLS, spatial variations of the instrument effective passbands had to be accounted for in order to accurately conduct the calibration transfer and deliver relevant flat-fielding solutions. An extensive survey of the filters’ transmission would make the calibration more accurate.
-
The characterization of the SNLS photometric system would have been simplified by the implementation of a well-planned filter passband monitoring program. Nonetheless, no significant chromatic differences have been observed in repeat stellar photometry over the course of the survey, providing direct evidence of the photometric system’s long-term stability.
-
Slight readout electronics instabilities cause percent-level noise in the MegaCam flat-fielding. For the SNLS, this effect is mitigated by repeated measurements over the long duration of the survey; for shorter surveys, this effect would have been difficult to overcome. Reproducible illumination provided by artificial light sources might provide more reliable monitoring of the instrument throughput.
-
The SDSS calibration relied on a separate telescope (the PT), but neither the flat-field nor the filter throughput waswell-characterized enough for the precision photometry goals of this paper. Instead we had to rely on empirical color-transformations and correct the flat-field from external data.
Most of these effects were overcome by introducing redundancy in the measurements, or by the analysis of specifically designed additional observations. While such strategies allowed us to reach an accuracy of 0.3%, it would be prohibitively time-consuming to reduce this accuracy further. Future photometric surveys such as SkyMapper (Keller et al. 2007), DES (Bernstein et al. 2012) and LSST (LSST Science Collaborations et al. 2009) might take advantage of current developments regarding instrumental calibration with artificial calibration sources. Information provided by the SNDICE illumination prototype (Barrelet & Juramy 2008), Guyonnet et al. (in prep.) installed at the CFHT has already proved immensely valuable in understanding MegaPrime instrumental effects such as flat-field pollution with ghosts and readout electronics gain variations. Ongoing analysis of SNDICE data may also give us a final understanding of the MegaCam filter passbands. A comparable device (Stubbs et al. 2010) has aided in the calibration of the Pan-STARRS instrument; the Dark Energy Survey is taking a similar approach with DECal (Rheault et al. 2012).
Another effect that must be accounted for when computing the photometric response from images of uniform illumination is the distortion of the plate-scale (see Fig. 4 in R09). This distortion can be easily computed from the astrometry. Other effects can also arise from the variation of the PSF across the focal plane. When not properly accounted for by the photometry method, the effective fraction of the flux captured by the photometry can vary. This makes the effective throughput spatially variable in a way that depends on the photometry method.
The version used in this paper can be found at ftp://ftp.stsci.edu/cdbs/currenT_calspec/bd_17d4708_stisnic_003.ascii
The parameters of the linear color transformation and their dependence on the focal plane position are available in electronic form at http://supernovae.in2p3.fr/snls_sdss/
We use the sparse Cholesky factorization routine from the CHOLMOD library (Chen et al. 2008) to solve for the normal equation.
Although measurements of individual chips quantum efficiency are available, they are known to be affected by problems such as ice condensation in the cryostat. Using them in the model does not improve the agreement with measurements and occasionally deteriorates it. As a consequence, we stick to the average QE model.
To be discussed in Sect. 4.3.
Anchoring to the Landolt system also enables the use of spectrophotometric standards measured in the Landolt system to set the absolute scale of the catalogs (see Sect. 5.1).
This is handled in SNLS by interpreting the PSF magnitudes in a modified photometric system (see Guy et al. 2010, for further discussion).
See http://www.sdss.org/dr7/algorithms/flatfield.html for a detailed description of the DR7 flat-fielding.
Available from http://www.sdss.org/dr5/instruments/imager/index.html#filters
A complete interpretation of these relations is not trivial as it requires some spectral model of the stellar population composing the tertiary standard stars. The estimation of resulting uncertainties would be somewhat complex. We prefer to rely on a star with available and reliable spectrophotometry and model how it deviates from the average stellar population.
Full catalogs can be retrieved from the CDS or the dedicated webpage http://supernovae.in2p3.fr/snls_sdss/
Acknowledgments
The authors heartily acknowledge the fruitful collaboration of the Canada France Hawaii telescope team, in gathering part of the data required for the present effort. We warmly thank the SNDICE collaboration for their help in the measurement of the SNLS passbands as well as for enlightening discussions on instrumental effects. We thank C. Buton and the SNF Collaboration for providing us early versions of their atmospheric transmission curve prior to publication. We are grateful to D. Tucker for giving us details about the SDSS calibration. This work was supported in part by the US Department of Energy under contract number DE-AC0276SF00515. Part of the data reduction was carried out at the Centre de Calcul de l’IN2P3 (CCIN2P3, Lyon, France).
References
- Abell, P. A., Allison, & J. 2009, LSST Science Collaborations [arXiv:0912.0201] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrelet, E., & Juramy, C. 2008, Nucl. Instruments Meth. Phys. Res. A, 585, 93 [Google Scholar]
- Bernstein, J. P., Kessler, R., Kuhlmann, S., et al. 2012, ApJ, 753, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Cohen, M. 2008, AJ, 136, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 127, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Hartig, G. 2002, HRC and WFC Flat Fields: Dispersors, Anomalies, and Photometric Stability, Tech. rep., ACS [Google Scholar]
- Bohlin, R. C., Dickinson, M. E., & Calzetti, D. 2001, AJ, 122, 2118 [NASA ADS] [CrossRef] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 72 [Google Scholar]
- Buton, C., Copin, Y., Aldering, G., et al. 2013, A&A, 549, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Davis, T. A., Hager, W. W., & Rajamanickam, S. 2008, ACM Trans. Math. Softw., 35, 22:1 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Stryker, L. L. 1983, ApJS, 52, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodapp, K. W., Kaiser, N., Aussel, H., et al. 2004, Astron. Nachr., 325, 636 [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Z., Lupton, R. H., Schlegel, D., et al. 2004, Astron. Nachr., 325, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Smith, J. A., Miknaitis, G., et al. 2007, AJ, 134, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJSS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U., & Uomoto, A. K. 2007, AJ, 133, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Lidman, C., Ruhlmann-Kleider, V., Sullivan, M., et al. 2013, PASA, 30, e001 [NASA ADS] [CrossRef] [Google Scholar]
- Limboz, F., Karataş, Y., Kilic, M., Benoist, C., & Aliş, S. 2008, MNRAS, 383, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Manfroid, J. 1995, A&AS, 113, 587 [NASA ADS] [Google Scholar]
- Manfroid, J. 1996, A&AS, 118, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Mosher, J., Sako, M., Corlies, L., et al. 2012, AJ, 144, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, N., Schlegel, D. J., Finkbeiner, D. P., et al. 2008, ApJ, 674, 1217 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rheault, J.-P., DePoy, D. L., Marshall, J. L., et al. 2012, in Am. Astron. Soc. Meet. Abstracts, 219, #248.02 [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., Juric, M., et al. 2012, ApJ, 756, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Stubbs, C. W., Doherty, P., Cramer, C., et al. 2010, ApJS, 191, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, D. L., Kent, S., Richmond, M. W., et al. 2006, Astron. Nachr., 327, 821 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Monitoring of the MegaCam flat-field variability from deep fields
Variations of the instrumental response are determined by the time distribution of thephotometric coefficient  (where t indexes the exposures, and ccd indexes the 36 MegaCam chips. We recall that
(where t indexes the exposures, and ccd indexes the 36 MegaCam chips. We recall that 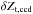 is computed for each deep field by building an average photometric catalog of non-variable stars as described in Sect. 4. We then compute for each available exposure a zero point relative to the average catalog. Once the exposure t is scaled by this zero point, we recompute a zero point offset for each CCD (
is computed for each deep field by building an average photometric catalog of non-variable stars as described in Sect. 4. We then compute for each available exposure a zero point relative to the average catalog. Once the exposure t is scaled by this zero point, we recompute a zero point offset for each CCD (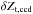 ) relative to the average catalog. Non-zero offsets indicate that the throughput of the instrument has varied non uniformly. This can be due either to clouds or to a variation of the instrument response that is not corrected by the twilight flat-fielding.
) relative to the average catalog. Non-zero offsets indicate that the throughput of the instrument has varied non uniformly. This can be due either to clouds or to a variation of the instrument response that is not corrected by the twilight flat-fielding.
Grid observations and associated telescope events.
Dithering pattern of the grid exposures.
For each exposure t we compute the rms of 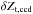 of the 36 CCDs. The statistical uncertainty on the determination of
of the 36 CCDs. The statistical uncertainty on the determination of 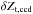 is typically 2 mmag, so that sets the minimum expected value. The rms values observed throughout the survey are displayed in Fig. A.1. The measured rms is typically about 5 mmag. The observed excess relative to the minimum value of 2 mmag is to be expected for at least 3 reasons: 1) structured variations of the atmospheric transparency, such as clouds, affect the observations, 2) the gains of some CCDs amplifiers vary on time scales shorter than a single run, and therefore can’t be calibrated by a single twilight flat-field, and 3) telescope modifications can have an impact on the photometric response, while leaving the twilight observations virtually unchanged. The effects of 1) and 3) can be observed directly in Fig. A.1, while 2) is a noise that contributes to a global increase of the measured rms.
is typically 2 mmag, so that sets the minimum expected value. The rms values observed throughout the survey are displayed in Fig. A.1. The measured rms is typically about 5 mmag. The observed excess relative to the minimum value of 2 mmag is to be expected for at least 3 reasons: 1) structured variations of the atmospheric transparency, such as clouds, affect the observations, 2) the gains of some CCDs amplifiers vary on time scales shorter than a single run, and therefore can’t be calibrated by a single twilight flat-field, and 3) telescope modifications can have an impact on the photometric response, while leaving the twilight observations virtually unchanged. The effects of 1) and 3) can be observed directly in Fig. A.1, while 2) is a noise that contributes to a global increase of the measured rms.
Clouds are occasionally responsible for a large increase in the measured rms. These non-photometric conditions are easily detected and excluded from the averaging of the tertiary catalogs. Exposures detected as non photometric are displayed as black dots on Fig. A.1.
 |
Fig. A.1 Standard deviation of the relative CCD zero points for each exposure in the survey. Black dots denote exposures that were excluded from the average because of cuts on the stability of the observing conditions or on the uniformity of the effective instrument response. Exposures are ordered by increasing observation date. The vertical gray dotted lines indicate the separation between different MegaCam runs (roughly one run per lunation). The twilight flat-field is common to all observations in a run. The vertical red lines indicate significant changes to the telescope. The letters refer to the events described in Table A.1. In this figure, the same photometric flat-field correction, determined from observations on 2005-10-09 (black vertical line), is applied to all the observations. |
We have displayed telescope modifications that had a noticeable impact on the uniformity of the photometry as red vertical lines. The beginning of the survey was marked by continuous adjustment of the optical setup. We retained only the main modification (that had the greatest impact on the image quality): the flip of the third lens in the wide field corrector. It is denoted as event A on the graph. The rms of exposures obtained prior to this event can be seen to be higher. The second and most significant phenomenon was the accumulation of metal dust on a corner of the wide field corrector optics. Its effect was the scattering at small angles of a growing part of the light, decreasing progressively the flux fraction contained in the core of the PSF (and hence the throughput of the photometry), while leaving the twilight images essentially unchanged. The effect is clearly visible in Fig. A.1 as a progressive increase of the rms during the year 2006. Its detection and cleaning occurred at the end of 2006 and is denoted as event C. The beginning of the accumulation is harder to determine. We approximately determined that the effect becomes sufficiently important at the middle of 2006 (event B). The last events are the destruction (D) and replacement (E) of the iM filter in 2007. Exposures in gM and rM were apparently also affected by the same event (D), but we do not understand why they changed.
The events are summarized in Table A.1. They define 5 periods for which independent photometric corrections can be determined. The application of our set of photometric corrections to the survey flat-fielding is illustrated in Fig. A.2. This figure is similar to Fig. A.1, but made after the application of photometric corrections. After correction, the measurements are consistent within an error σff, which is estimated as the average rms of 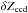 . Values of σff were given in Table 2 in the main text.
. Values of σff were given in Table 2 in the main text.
 |
Fig. A.2 Same as Fig. A.1, but different photometric flat-field corrections were used for the different periods of the survey. The vertical black lines indicate the date of grid observations used to compute the photometric corrections. The changes of data point color indicate the different flat-field corrections applied. These corrections were used to produce the multi-epoch tertiary catalogs described in Sect. 4. |
Appendix B: MegaCam filters measurements
 |
Fig. B.1 Comparison of available measurements of the REOSC filter transmission curves at a distance of 15cm from the center. |
The transmission curves of the original Sagem/REOSC MegaCam filters were measured twice: the first time by the manufacturer before their installation in MegaCam in 2002, and the second time in 2006 by the CFHT operational team. The 2006 measurements are available only at positions close to the border of the filter due to limitations in the bench clearance, and their spectral resolution is coarser. Comparison between the two measurements at 15 cm from the center (after convolution of the REOSC measurements to match resolutions) is given in Fig. B.1. The position of the rM and iM filter cut-offs can be seen to be shifted ~8 nm redder in the 2006 measurements. The origin of these discrepancies and the reason why only two filters are affected are unclear.
A confirmation of the 2006 measurements was recently given by the measurement of the transmission of one of the broken pieces of the iM filter. The measurement was conducted on the calibration bench of the SNDICE illumination device (Barrelet & Juramy 2008), and display a perfect agreement with the 2006 transmission curves 12 cm away from the center (the appropriate curve for the broken piece).
The possibility of a continuous (slow) aging of the filters is excluded by the examination of color-terms between the beginning and the end of the survey (cf. Sect. 3.4.1). It is thus likely that the 2006 measurements are the most representative of the state of MegaCam filters during the survey. The lack for measurements at the center of the filters in the 2006 data requires additional data or assumptions. We opt for correcting the iM and rM REOSC measurements to make them match the 2006 transmission curves. The application of a linear stretch in wavelength of the form:
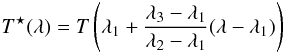 was found to reconcile both measurement sets. We used (λ1,λ2,λ3) = (5300 Å, 6837 Å, 6891 Å) for rM and (6600 Å, 8464 Å, 8539 Å) for iM. The resulting transmission model at 15 cm is shown as a dashed black line in Fig. B.1; similar agreement is obtained with the 12 cm data.
was found to reconcile both measurement sets. We used (λ1,λ2,λ3) = (5300 Å, 6837 Å, 6891 Å) for rM and (6600 Å, 8464 Å, 8539 Å) for iM. The resulting transmission model at 15 cm is shown as a dashed black line in Fig. B.1; similar agreement is obtained with the 12 cm data.
Appendix C: SDSS Photometric Telescope (PT) flat-field
There are some overlapping secondary patches in stripe 82 that can be used to check for deviations from a uniform response of the PT. This section provides an analysis of that data.
The data sample consists of the 13 secondary patches listed in Table C.1. The fields labeled A, B, C, and D are the standard locations in declination for secondary patches in stripe 82. The field of view is 40 arcmin (2/3 degree), so there is no overlap between the A, B, C, and D secondary patches. The fields labeled E, F, and G are special patches that were placed approximately half-way in declination between the standard locations, providing a 50% overlap with the standard patches. The camera pointings are all in the same relative orientation with East-West being in the CCD column direction.
The analysis involved matching stars in the overlapping pointings and computing the difference in magnitude. The data come from the SDSS data processing (mtPipe) (Tucker et al. 2006). The differences in magnitude measure the difference in response of the focal plane between a given column and another one that is displaced by 1/2 the size of the CCD. If the response is uniform all the differences would be zero. It is convenient to measure the distance along the focal plane in terms of degrees of declination. We determine this distance as the declination of a matched star minus the reported declination of the telescope pointing. The matching star is nominally at a declination lower by 20 arcmin.
The results are summarized in Table C.2. The table gives the total number of comparison stars that were found and a fit to the equation 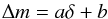 (C.1)where Δm is the magnitude difference, δ is the position on the focal plane in units of degrees of declination, and a and b are fit parameters. A χ2 is given for each fit. The fit is made to 6 binned data points so there are 4 degrees of freedom for each fit, except for the combined fit to g, r, and i (last line in Table C.2). This fit is performed on 18 binned data points from g, r, and i so there are 16 degrees of freedom for that fit. The chi-squared’s are generally good although they could probably be improved by the addition of a quadratic term. However, it was felt that a quadratic term was unnecessary and possibly sensitive to unknown systematic errors. Every filter shows a consistent trend of positive residuals and a negative slope with declination. However, the fits are quite precise and there are statistically significant differences between the filters.
(C.1)where Δm is the magnitude difference, δ is the position on the focal plane in units of degrees of declination, and a and b are fit parameters. A χ2 is given for each fit. The fit is made to 6 binned data points so there are 4 degrees of freedom for each fit, except for the combined fit to g, r, and i (last line in Table C.2). This fit is performed on 18 binned data points from g, r, and i so there are 16 degrees of freedom for that fit. The chi-squared’s are generally good although they could probably be improved by the addition of a quadratic term. However, it was felt that a quadratic term was unnecessary and possibly sensitive to unknown systematic errors. Every filter shows a consistent trend of positive residuals and a negative slope with declination. However, the fits are quite precise and there are statistically significant differences between the filters.
The PT data with secondary patch overlaps in SDSS stripe 82.
The results of PT fits.
The results above only give the difference in response between the two halves of the PT. Determining the actual response requires additional data or assumptions. There seem to be two obvious models that could explain some features of the data:
-
The CCD readout uses different amplifiers for the two halves ofthe chip we are considering. It is possible that the gain differencebetween the two amplifiers has not been properly calibrated.Such a mis-calibration could occur, for example, if the light levelsin the flat-field exposures resulted in a non-linear amplifierresponse that was different for the two amplifiers while normalexposure levels remained in the linear regime. This scenariocould explain the offset between the two halves of the CCD butdoesn’t seem very plausible and would not explain the observedslopes.
-
The illumination of the flat-field exposures may be non-uniform. This would lead to an error in the calibration of the CCD response. The non-uniformity is most likely to be a slowly varying function of position.
In any case the data are not compatible with a uniform photometric response in the PT flat-fielded exposures. The PT flat-field error has two consequences. First it is transferred to the 2.5 m as a flat-fielding error. It should imprint a periodic pattern 0.6 degrees wide in declination on the photometry. Second, as primary standard stars are observed preferentially at the center of the focal plane, it can bias the calibration relative to the tertiary stars that are observed throughout the focal plane. It is thus necessary to provide a correction of the 2.5 m flat-field independent of the PT and to characterize the PT flat-field error to derive accurate calibration from its measurement.
Appendix D: DR8 catalog retrieval
The Stripe 82 DR8 catalog has been retrieved from the DR8 database using the following query: select psfmag_u, psfmag_g, psfmag_r, psfmag_i, psfmag_z, ra, dec, run, camcol, psfmagerr_u, psfmagerr_g, psfmagerr_r, psfmagerr_i, psfmagerr_z into mydb.MyTable from phototag where dec between − 1.3 and 1.3 and ((ra between 300 and 360) or (ra between 0 and 60)) and type = 6 and mode = 1 and psfmag r < 22.5.
Appendix E: SNLS and SDSS calibration products
Our main delivery are catalogs of natural magnitudes for a large set of tertiary standard stars calibrated to the AB flux scale. We also provide the material required for the interpretation of those magnitudes in term of physical fluxes (instrument transmission functions) as well as the material required to update the AB calibration as new CALSPEC spectra for our primary standards are released.
All the material described below is available from the SNLS and SDSS joint calibration webpage: http://supernovae.in2p3.fr/snls_sdss/
Appendix E.1: Tertiary stars catalogs
We provide catalogs of natural AB magnitudes in each of the MegaCam filters for selected tertiary standard stars in the four CFHTLS deep fields in the natural MegaCam photometric system. This system is described in Sect. 3.1 and the corresponding transmission curves are given below (Sect. E.2). Note that the transmission depends on the location on the focal plane. A subsample of the D1 catalog is given in Table E.2.
Similarly, we deliver natural SDSS AB magnitudes for selected tertiaries in the Stripe 82. The magnitudes are given for the average filter response as given by Doi et al. (2010), i.e., they should not be adjusted for the small differences in the filter responses of the different CCD columns. An excerpt from the catalog is given in Table E.1.
In both cases the released magnitudes are already placed on the AB system by the addition of the zero points given in Table 14. Full catalogs in electronic format can be retrieved from the CDS or from the SNLS and SDSS joint calibration webpage.
Appendix E.2: MegaCam transmission functions
Low resolution version of the Megacam effective transmission curves are tabulated in Tables E.3−E.8. Higher resolution versions are available on the joint calibration webpage.
As described in Sect. 3.1, the transmission functions depends on the location in the MegaCam focal plane. Assuming that the transmission vary continuously with the radius from the focal plane center provides an effective description. We deliver tabulated measurements at regularly spaced radii. Those measurements can be linearly interpolated to other positions.
Appendix E.3: HST standard measured magnitudes
The tertiary catalogs define a magnitude system. This system has been anchored to the AB flux scale according to a calibration reference. We choose to use, as our reference, 5 stars from the HST CALSPEC database for which direct or indirect magnitudes in the system defined by the tertiary catalogs were available. Therefore, our calibration reference is the current release (stinic_003) of the CALSPEC spectra for those 5 stars.
The natural magnitudes of the measured HST standards are given in Table E.9. Those measurements can be used to update the AB calibration of the catalogs, given revised synthetic magnitudes for these stars. Measurements in Table E.9 are delivered in the same photometric system than the published tertiary standards catalog, i.e. with the AB offsets derived in this work (Table 23) already applied. Therefore, any offset computed, according to Eq. (31), from the difference between a measurement given in Table E.9 and the synthetic AB magnitude for the corresponding star readily applies to the published catalog.
When computing synthetic AB magnitudes for a star in the MegaCam focal plane, the peculiar position of the star in the focal plane must be taken into account. Also, we describe in Sect. E.4 the constitution of the covariance matrix for measurements in Table E.9. This matrix can be used to combine all measurements similarly to what has been done in Sect. 9.
Appendix E.4: Covariance matrices
The assumptions made to build the covariance matrix of systematic measurement errors in the calibration data follows.
In SNLS, we assume that the shutter bias affects identically all measurements of flux ratios between short and long exposures. The error resulting from aperture corrections is assumed to affect coherently the measurements of the solar analogs in a given band, and without correlation from one band to another. We account for the aperture correction residuals in the Landolt-based BD +17 4708 measurements independently as the observation strategy was different and the derivations of the corrections were independent. The survey non-uniformity affects coherently the measurement of solar analogs that are related to the survey through the SNLS D3 field. The Landolt non-uniformity is included to account for a potential departure of the BD +17 4708 measurements from the average Landolt system. The errors on the color transformation of BD +17 4708 are assumed to be independent from one band to another. This may not be fully justified, but this error matters only in band z and potential correlations with other bands are negligible.
In SDSS, the statistical uncertainty on the color transformation between the PT and 2.5 m system affects coherently all the measurements in a given band. Star-to-star dispersion around the color transformation is assumed independent from one star to another. The non uniformity of the Smith catalog coherently affects the measurement of solar analogs as they lie at approximately the same hour angle.
The resulting covariance matrix of measurements in Table E.9 (including measurement noise and systematics) is available from the SNLS/SDSS calibration webpage.
As described in Sect. 9, when combining the available measurements to provide the final calibration, we account for other contributions to the covariance of the AB offsets: the HST-STIS spectrum measurement error, the STIS calibration error, and the uncertainty on instrument filters. A corresponding covariance matrix for each of these contributions is also available from the SNLS/SDSS calibration webpage.
The estimation of the STIS measurement error is discussed in Sect. 9.2. The corresponding covariance matrix for a single epoch STIS measurement is displayed in Table E.10.
Catalog of natural AB SDSS magnitudes for selected tertiary standards in the Stripe 82.
Catalog of natural AB MegaCam magnitudes for selected tertiary standards in the D1 field.
uM transmission curve at an airmass of 1.25.
gM transmission curve at an airmass of 1.25.
rM transmission curve at an airmass of 1.25.
iM transmission curve at an airmass of 1.25.
i2M transmission curve at an airmass of 1.25.
zM transmission curve at an airmass of 1.25.
Measured magnitudes for CALSPEC standards.
Covariance matrix of synthetic STIS magnitudes.
All Tables
Statistical uncertainty (in magnitudes) on the calibration to the Landolt system.
Uncertainty budget in the cross-calibration between SNLS and the HST via the observation of Landolt secondary standards.
Calibration offsets between first and third year release of the SDSS-II SN survey.
Catalog of natural AB SDSS magnitudes for selected tertiary standards in the Stripe 82.
Catalog of natural AB MegaCam magnitudes for selected tertiary standards in the D1 field.
All Figures
 |
Fig. 1 Schematic view of calibration data used in the present work. Each box represents a set of standard stars established in that photometric system. Each arrow shows the available cross-calibration data corresponding to the measurement of flux ratios between the two different sets of standards. The two new sets of SNLS measurements introduced in this paper are indicated with red dashed lines. |
| In the text | |
 |
Fig. 2 Overview of the MegaPrime photometric response determination. Boxes figure the various data sets involved in the construction of the model (dashed for external data). Ellipses figure the main steps of the analysis. |
| In the text | |
 |
Fig. 3 Synthetic color transformation between the center and the corner of the filters (17 cm from the center) in each band. Dots are synthetic magnitudes computed for stellar spectra from the Gunn & Stryker (1983) spectral library. Linear color transformation (solid line) are adjusted in the range delimited by vertical dashed lines. The color index is a Vega MegaCam color. The red square figures the synthesized transformation of the spectrophotometric standard star BD +17 4708 computed from its STIS spectrum available from the CALSPEC database. |
| In the text | |
 |
Fig. 4 Stellar population within the two grid fields. The green dashed line is a synthetic stellar locus computed from the Pickles stellar library. Spectra have been reddened to match the average extinction measured in the field. The black arrow shows the corresponding extinction vector. |
| In the text | |
 |
Fig. 5 Maps of photometric corrections (relative to the twilight flat-field). Each panel displays a low resolution map (36 × 36 super-pixels of 256 × 256 real pixels, i.e. a resolution of about 2′) of the |
| In the text | |
 |
Fig. 6 Color terms between tertiary catalogs averaged over different periods. The survey observations in the D3 field have been divided into 5 periods covering about a year. Each data point is the fit of a linear color term between the catalog obtained from a single year and the catalog obtained from the whole survey. The stellar population is indexed by the g − i color. |
| In the text | |
 |
Fig. 7 Difference between measured and modeled color terms (relating the natural and reference photometric system) as a function of radius. Solid points show the average value of the |
| In the text | |
 |
Fig. 8 Maps of residuals between the predicted and measured color term to the reference system. The synthetic color terms are computed on reddened spectra from the Pickles stellar library, to reflect the effect of the extinction measured in field grid-1. The measured |
| In the text | |
 |
Fig. 9 Variation of the photometric flat-field corrections. Each panel displays a low resolution map (36 × 36 super-pixels of 256 × 256 real pixels, i.e. a resolution of about 2′) of the rms between all the determinations of the photometric grid corrections in a given photometric band. CCD boundaries are shown by white dotted lines. Note that all photometric correction maps are normalized to be zero at the center of the focal plane. As a consequence the rms across epochs is null at the center by construction. Noisy amplifiers are easily seen in rM and zM bands. In all bands (but i2M that was not available), the variation of response induced by the 2006 deposit of metal dust is clearly visible at the bottom right of the focal plane. |
| In the text | |
 |
Fig. 10 Top panel: distribution of zero point variations during an observation sequence (typically 6 exposures of 220 s in the same band in a row). Nights displaying a variability larger than 1% are discarded from the averaging. While the plot is cut at 0.025, numerous sequences (about 20%) taken under non-photometric conditions display a much larger variation. The zero point is defined as |
| In the text | |
 |
Fig. 11 Distribution of the peak-to-peak zero point variation across the focal plane. Exposures displaying a peak-to-peak variation greater than 3% (6% in uM and zM) are discarded from the averaging. Vertical dashed lines show the cuts applied in the averaging process. |
| In the text | |
 |
Fig. 12 Measurement completeness in the tertiary star catalogs. Each plot displays the ratio of selected measurements to the number of exposures as a function of the star magnitude in each band. The plateau at ~85% reflects mostly the ratio of the usable area in the focal plane to the total area covered by the catalog. |
| In the text | |
 |
Fig. 13 Color transformation between the Landolt system and the reference MegaCam system. Open black circles show the MegaCam and Landolt measurements of the Landolt secondary standards. The overall scale is set by the magnitudes of the primary spectrophotometric standard star BD +17 4708 (solid red square). Measurements of BD +17 4708 magnitudes in the Landolt system are provided by Landolt & Uomoto (2007). Since BD +17 4708 cannot be directly observed with MegaCam, its MegaCam magnitudes are inferred from the average color transformation (black line) determined from the secondary standard measurements. Potential deviations from this average color transformation are examined in R09 (see Sect. 5.1). Other primary standards from Landolt & Uomoto (2007) are displayed as red crosses; they are not close enough to the bulk of secondary standards to be reliably transformed with the average transformation. Observations of the Landolt standards in i2M were not numerous enough to deliver a robust measurement of the i2|x0 − I transformation (refer to Sect. 5.3 for the i2M calibration). |
| In the text | |
 |
Fig. 14 Variation of aperture correction from small to large apertures as a function of the image quality, IQ, defined as sigma of a Gaussian fit to the PSF (in pixels). Apertures are scaled with the IQ: small apertures correspond to a radius of 7.5 × IQ and large apertures to a radius of 20 × IQ. The aperture corrections are computed as φ7.5/φ20 − 1 where φ7.5 and φ20 denote instrumental fluxes in the small and large aperture, respectively. Data points correspond to the median of aperture corrections in bins of IQ over all the exposures in the survey. Results for short (and slightly out-of-focus) exposures on Landolt fields (black circles) and long exposures on deep fields (black squares) are displayed separately. |
| In the text | |
 |
Fig. 15 Average aperture correction (between 7.5 and 20 IQ radius) is shown for the 3 periods corresponding to different observational setups. Landolt stars (short exposures, slightly out of focus) are shown in black circles, and deel fields (long exposures) are shown in black squares. The statistical uncertainties on the averages are negligible. |
| In the text | |
 |
Fig. 16 Catalog zero point as a function of the grid solution. The error bars reflect the statistical uncertainty on the mean estimated from the dispersion of measurements in the period. |
| In the text | |
 |
Fig. 17 Background residuals as a function of the contamination index. The contamination index at a given location for a given aperture is defined as the flux in the aperture expected from objects detected in the field, assuming they have a Moffat PSF profile (see Eq. (19)). The top figure displays the average background level (in ADU per pixel) in random apertures as a function of this contamination index. We concentrate on random positions with low contamination index (apertures expected to be mostly empty), sampling the background level far from detected objects. The shape of the curves reflect the remaining structure in the background due to PSF tails. The bottom plot displays the distribution of the contamination indexes at the position of tertiary stars (excluding the contribution from the tertiary star itself). Horizontal lines in the top plot display the average value of the curve weighted for tertiaries, i.e. the expected per-pixel background offset for tertiaries. |
| In the text | |
 |
Fig. 18 Difference between PSF and aperture photometry for tertiary stars as a function of star color. The black line displays a linear fit of the chromatic trend observed. |
| In the text | |
 |
Fig. 19 Difference between PSF and aperture photometry for tertiary stars as a function of star magnitudes (with the chromatic trend from Fig. 18 and the average background contamination of apertures subtracted). Black circles display the average of data points in bins of magnitudes. Averages are computed with a clipping at 2.5σ as used in the calibration of SNLS supernovae light-curves (Guy et al. 2010). |
| In the text | |
 |
Fig. 20 Top: color−color diagram of the 4 SNLS tertiary star catalogs. Bottom: residuals to a linear fit of the average stellar locus in the range 0.2 < g − i < 1.2. The residuals for the 4 deep fields are displayed separately (D1: red crosses, D2: green squares, D3: black circles, D4: blue asterisks). |
| In the text | |
 |
Fig. 21 Stability of the flux measurements during the calibration sequences in gMrMiM bands. The difference of instrumental magnitudes in an aperture of 43 pixels between the first and the last exposure of the sequence is displayed as a function of the seeing evolution between the exposures. |
| In the text | |
 |
Fig. 22 The difference in magnitude (coadd−DR8) for the 5 SDSS filters is shown as a function of right ascension. |
| In the text | |
 |
Fig. 23 Difference between the coadd catalog and DR8 as a function of declination. The symbols represent the binned data and the lines are a cubic spline function fit to the data with 71 control points. |
| In the text | |
 |
Fig. 24 SDSS 2.5 m to PT measured color transformations. The individual stellar measurements are averaged in color bins of 0.05 width for clarity. The error bars display the 1σ uncertainty on the average estimated from the dispersion of individual measurements. The straight black line is the linear fit to the data. |
| In the text | |
 |
Fig. 25 PT flat-field corrections. |
| In the text | |
 |
Fig. 26 Linear color transformations between the SDSS and SNLS uniform magnitude system. The black lines represent the best linear fit of the data, whereas the red lines are based on synthetic magnitudes of the Gunn-Stryker-Bruzal stellar library and the SNLS and SDSS transmission models described in Sect. 2.2.1. |
| In the text | |
 |
Fig. 27 Comparison between synthetic and measured stellar locus slopes in the SNLS-SDSS color diagram for the 4 SDSS camcols covered in the observation program. |
| In the text | |
 |
Fig. 28 Relative uniformity of SNLS and SDSS photometry. |
| In the text | |
 |
Fig. 29 Agreement between complementary determinations of the SNLS AB offsets. SNLS BD+17 and SNLS SA lines refer to the SNLS calibration on Landolt standards and direct solar analog measurements respectively (cf. Sect. 4). The SDSS SA and SDSS BD+17 lines refer to the calibration obtained by translating the PT measurements of the solar analogs and BD +17 4708 respectively, to the SNLS system via the relations obtained in Sect. 8. The data points correspond to the calibration offset relative to the combined calibration including all the measurements and are not independent. The shaded region illustrates the uncertainty on the combined calibration. |
| In the text | |
 |
Fig. 30 Difference between SNLS-calibrated tertiary star magnitudes and previous R09 release as a function of the distance to the focal plane center. The 4 deep fields are compared separately (D1: red plus, D2: green squares, D3: black circles, D4: blue crosses.) |
| In the text | |
 |
Fig. A.1 Standard deviation of the relative CCD zero points for each exposure in the survey. Black dots denote exposures that were excluded from the average because of cuts on the stability of the observing conditions or on the uniformity of the effective instrument response. Exposures are ordered by increasing observation date. The vertical gray dotted lines indicate the separation between different MegaCam runs (roughly one run per lunation). The twilight flat-field is common to all observations in a run. The vertical red lines indicate significant changes to the telescope. The letters refer to the events described in Table A.1. In this figure, the same photometric flat-field correction, determined from observations on 2005-10-09 (black vertical line), is applied to all the observations. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but different photometric flat-field corrections were used for the different periods of the survey. The vertical black lines indicate the date of grid observations used to compute the photometric corrections. The changes of data point color indicate the different flat-field corrections applied. These corrections were used to produce the multi-epoch tertiary catalogs described in Sect. 4. |
| In the text | |
 |
Fig. B.1 Comparison of available measurements of the REOSC filter transmission curves at a distance of 15cm from the center. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



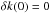
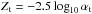
![\hbox{$\umag[c^0]\approx 0$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq1232.png)
![\hbox{$IQ= \sqrt[4]{\det \langle M \rangle }$}](/articles/aa/full_html/2013/04/aa20610-12/aa20610-12-eq1233.png)