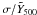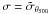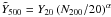EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 536 (December 2011) A&A, 536 (2011) A12 Full HTML
Planck early results
Free Access
Issue
A&A
Volume 536, December 2011
Planck early results
Article Number A12
Number of page(s) 10
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201116489
Published online 01 December 2011

© ESO, 2011

1. Introduction

Galaxy cluster properties follow simple scaling laws (see e.g. Rosati et al. 2002; Voit 2005, for recent reviews). This attests to a remarkable consistency in the cluster population and motivates the use of clusters as cosmological probes. These scaling laws also provide important clues to cluster formation, and relations involving optical properties, in particular, help uncover the processes driving galaxy evolution.

The Sunyaev-Zeldovich (SZ) effect (Sunyaev & Zeldovich 1972; Birkinshaw 1999) opens a fresh perspective on cluster scaling laws, and the advent of large-area SZ surveys furnishes us with a powerful new tool (Carlstrom et al. 2002). Proportional

to ICM mass and temperature, the thermal SZ effect probes the gas in a manner complementary to X-ray measurements, giving a more direct view of the gas mass and energy content. Ground-based instruments, such as the Atacama Cosmology Telescope (ACT, Swetz et al. 2008), the South Pole Telescope (SPT, Carlstrom et al. 2011) and APEX-SZ (Dobbs et al. 2006), are harvesting a substantial crop of scientific results and producing, for the first time, SZ-selected catalogues and using them to constrain cosmological parameters (Staniszewski et al. 2009; Marriage et al. 2011; Sehgal et al. 2011; Vanderlinde et al. 2010; Hand et al. 2011; Williamson et al. 2011).

The Planck1 consortium has published its first scientific results (Planck Collaboration 2011a) and released the Planck Early Release Compact Source Catalogue (ERCSC) (Planck Collaboration 2011c), which includes the Planck early SZ (ESZ) all-sky cluster list (Planck Collaboration 2011d). Planck (Tauber et al. 2010; Planck Collaboration 2011a) is the third generation space mission to measure the anisotropy of the cosmic microwave background (CMB). It observes the sky in nine frequency bands covering 30–857 GHz with high sensitivity and angular resolution from 31′–5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1K. Polarization is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration 2011b). Two Data Processing Centres (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for galactic and extragalactic astrophysics, as well as cosmology. Early astrophysics results are given in Planck Collaboration (2011d)-Planck Collaboration (2011u).

Planck early results on clusters of galaxies are presented in this paper and in (Planck Collaboration 2011d–g). In the present work, we use Planck SZ measurements at the locations of MaxBCG clusters (Koester et al. 2007a) to extract the SZ signal-richness scaling relation. There are several optical cluster catalogs (Wen et al. 2009; Hao et al. 2010; Szabo et al. 2011) available from the Sloan Digital Sky Survey (York et al. 2000, SDSS). For this initial study, we chose the MaxBCG catalogue for its large sample size, wide mass range and well-characterized selection function, and because its properties have been extensively studied. In particular, we benefit from weak-lensing mass measurements and mass-richness relations (Johnston et al. 2007; Mandelbaum et al. 2008a; Sheldon et al. 2009; Rozo et al. 2009). A combined SZ-optical study over such a large catalogue is unprecedented and Planck is a unique SZ instrument for this task, as its all-sky coverage encompasses the complete SDSS area and the full MaxBCG cluster sample.

Our analysis methodology follows that of the accompanying paper on the SZ properties of X-ray selected clusters (Planck Collaboration 2011f). Although the individual SZ measurements in both cases generally have low signal-to-noise, we extract the statistical properties of the ICM – mean relations and their dispersion – by averaging over the large sample. The approach enables us to study the properties of a much larger and representative sample of clusters than otherwise possible.

The SZ-richness relation adds a new entry to the complement of cluster scaling laws and additional constraints on cluster and galaxy evolution models. With a mass-richness relation, we can also derive the SZ signal-mass relation. This is a central element in predictions for the diffuse SZ power spectrum and SZ cluster counts. Poor knowledge of the relation represents an important source of modeling uncertainty. Low mass systems, for example, contribute a large fraction of the SZ power, but we know very little about their SZ signal.

We organise the paper as follows: the next section presents the data used, both the Planck maps and the MaxBCG catalogue and pertinent characteristics. Section 3 details our SZ measurements based on a multi-frequency matched filter, and outlines some of the systematic checks. In Sect. 4 we present our basic results and in Sect. 5 compare them to model expectations. Section 6 concludes.

1.1. Conventions and notation

In the following, we adopt a flat fiducial cosmology with ΩM = 0.3 with the remainder of the critical density made up by a cosmological constant. We express the Hubble parameter at redshift z as with h = 0.7. Cluster radii are expressed in terms of RΔ, the radius inside of which the mean mass overdensity equals Δ × ρc(z), where ρc(z) = 3H2(z) / 8πG is the critical density at redshift z. Similarly, we quote masses as 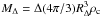MΔ=Δ(4π/3)RΔ3ρc\hbox{$M_\Delta=\Delta (4\pi/3)R^3_\Delta\rho_{\rm c}$}. We note that, in contrast, optical cluster studies, and in particular the MaxBCG group, frequently employ radii and masses scaled to the mean matter density, rather than the critical density. For example, it is standard practice to refer to quantities measured within R200b, where the overdensity of 200 is defined with respect to the background density (this corresponds to R60 at z = 0 and R155 at z = 1). For richness we will use the MaxBCG N200, defined as the number of red galaxies with L > 0.4 L ∗  within R200b. Richness N200 is the only quantity in this work defined relative to the mean background density.

We characterize the SZ signal with the Compton-y parameter integrated over a sphere of radius R500 and expressed in arcmin2: 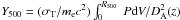Y500=(σT/mec2)∫0R500PdV/DA2(z)\hbox{$Y_{500}= (\sigma_{\rm T}/m_{\rm e} c^2)\int_0^{R_{500}}\; P {\rm d}V/\Dang^2(z)$}, where DA denotes angular distance, σT is the Thomson cross-section, c the speed of light, me the electron rest mass and P = nekT is the pressure, defined as the product of the electron number density and temperature, k being the Boltzmann constant. The use of this spherical, rather than cylindrical, quantity is possible because we adopt a template SZ profile when using the matched filter (discussed below). We bring our measurements to z = 0 and a fiducial angular distance assuming self-similar scaling in redshift. To this end, we introduce the intrinsic cluster quantity (an “absolute SZ signal strength”) 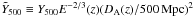˜Y500≡Y500E−2/3(z)(DA(z)/500 Mpc)2\hbox{$\Yscaled\equiv Y_{500} E^{-2/3}(z)(\Dang(z)/500\, {\rm Mpc})^2$}, also expressed in arcmin2.

2. Data sets

We base our study on Planck SZ measurements at the positions of clusters in the published MaxBCG cluster catalogue.

2.1. The MaxBCG optical cluster catalogue

The MaxBCG catalogue (Koester et al. 2007b,a) is derived from Data Release 5 (DR5) of the Sloan Digital Sky Survey (York et al. 2000), covering an area of 7500  deg2 in the Northern hemisphere. Galaxy cluster candidates were extracted by color, magnitude and a spatial filter centered on galaxies identified as the brightest cluster galaxy (BCG). The catalogue provides position, redshift, richness and total luminosity for each candidate. In the following we will only use the richness N200, defined as the number of red-sequence galaxies with L > 0.4   L ∗  and within a projected radius at which the cluster interior mean density equals 200 times the mean background density at the redshift of the cluster (see Koester et al. 2007a, for details and the remark in Sect. 1.1). The catalogue consists of 13823 galaxy clusters over the redshift range 0.1 < z < 0.3, with 90% purity and 85% completeness for 10 < N200 < 190 as determined from simulations.

A valuable characteristic for our study is the wide mass range spanned by the catalogue. Another is the fact that numerous authors have studied the catalogue, providing extensive information on its properties. In particular, Sheldon et al. (2009) and Mandelbaum et al. (2008a) have published mass estimates from weak gravitational lensing analyses, which Johnston et al. (2007) and Rozo et al. (2009) use to construct mass-richness (M500 − N200) relations. We apply this relation, as outlined below, to adapt our SZ filter measurements for each individual cluster according to its given richness, N200, as well as in our model predictions.

In their discussion, Rozo et al. (2009) identify the differences between the Sheldon et al. (2009) and Mandelbaum et al. (2008a) mass estimates and the impact on the deduced mass-richness relation. They trace the systematically higher mass estimates of Mandelbaum et al. (2008a) to these authors’ more detailed treatment of photometric redshift uncertainties (Mandelbaum et al. 2008b). Moreover, they note that Johnston et al. (2007), when employing the Sheldon et al. (2009) measurements, used an extended MaxBCG catalogue that includes objects with N200 < 10, where the catalogue is known to be incomplete. These two effects lead Rozo et al. (2009) to propose a flatter mass-richness relation with higher normalisation than the original Johnston et al. (2007) result. In the following, we perform our analysis with both relations; specifically, using the fit in Table 10 for the M500 − N200 relation of Johnston et al. (2007), and Eqs. (4), (A.20) and (A.21) of Rozo et al. (2009).

2.2. Planck data

We use the six HFI channel temperature maps (prior to CMB removal) provided by the DPC and whose characteristics are given in Planck HFI Core Team (2011b). These maps correspond to the observations of intensity in the first ten months of survey by Planck, still allowing complete sky coverage. Hence, they give us access to the entire SDSS survey area and complete MaxBCG catalogue. After masking bad pixels and contaminated regions (e.g., areas where an individual frequency map has a point source at  > 10σ), we have Planck observations for 13104 of the 13823 clusters in the MaxBCG catalogue.

3. SZ measurements

We extract the SZ signal at the position of each MaxBCG cluster by applying a multi-frequency matched filter (Herranz et al. 2002; Melin et al. 2006) to the six Planck temperature maps. The technique maximises the signal-to-noise of objects having the known frequency dependence of the thermal SZ effect and the expected angular profile. The filter returns the amplitude of the template, which we then convert into integrated SZ signal, Y500, within R500. It also returns an estimate of the local noise through the filter, σθ500, due to instrumental noise and astrophysical emissions. The same procedure is used in Planck Collaboration (2011f). We refer the reader to Melin et al. (2006, 2011) for details.

3.1. SZ model template

For the filter’s spatial template we adopt the empirical universal pressure profile of Arnaud et al. (2010), deduced from X-ray studies of the REXCESS cluster sample (Böhringer et al. 2007): 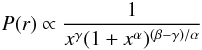P(r)∝1xγ(1+xα)(β−γ)/α\begin{equation} P(r) \propto \frac{1}{x^\gamma (1+x^\alpha)^{(\beta-\gamma)/\alpha}} \end{equation}(1)where the physical radius r is scaled to x = r / rs, with rs = R500 / c500. For the standard self-similar case (ST case in Appendix B of Arnaud et al. 2010), c500 = 1.156 and the exponents are α = 1.0620, β = 5.4807, γ = 0.3292. The normalisation is arbitrary for purposes of the matched filter. The SZ signal being proportional to the gas pressure, we find the filter template by integrating along the line-of-sight and expressing the result in terms of projected angles: x = θ / θs. We truncate the filter at 5θ500, containing more than 95% of the signal for the model.

3.2. Application of the filter

We apply the matched filter to each cluster in the MaxBCG catalogue, using the mass-richness relation, M500 − N200, to define R500 and set the angular scale θ500 = R500 / DA(z). The filter effectively samples the cluster SZ signal along a cone out to a transverse angular radius of 5θ500, and returns the normalisation for the template. We apply a geometric factor based on the template SZ profile to convert the deduced total SZ signal along the cone to an equivalent Y500 value, the SZ signal integrated within a sphere of physical radius R500. To account for the redshift range of the catalogue, we scale these measurements according to self-similar expectations to redshift z = 0 and a fiducial angular distance of 500 Mpc: 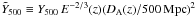˜Y500≡Y500 E−2/3(z)(DA(z)/500 Mpc)2\hbox{$\Yscaled\equiv Y_{500}\,E^{-2/3}(z)(\Dang(z)/500\,{\rm Mpc})^2$}. We accordingly adapt the estimated filter noise σθ500 to uncertainty 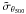˜σθ500\hbox{$\sigscaled$} on these scaled SZ signal measurements. The results of this procedure when using the Johnston et al. (2007) mass-richness relation are shown in Fig. 1.

3.3. Systematic effects

As in the other four Planck SZ papers (Planck Collaboration 2011d–g), we have carried out various tests to ensure the robustness of the Planck SZ measurements. They included investigation of the cluster size-flux degeneracy, evaluation of the impact of the assumed pressure profile used for the Planck cluster detection, of beam-shape effects, color corrections, potential contamination by point sources, as well as an overall error budget estimation. We refer the reader to Sect. 6 of Planck Collaboration (2011d) for an extensive description of this common analysis.

To complete this investigation in the present work, we repeated our entire analysis, changing both the instrument beams and adopted SZ profiles. In the former instance, we varied the beams at all frequencies together to the extremes of their associated uncertainties as specified by the DPC (Planck HFI Core Team 2011b). All beams were increased or all decreased in lock-step to maximize any effect. To investigate the profile, we re-extracted the SZ signal using a non-standard SZ signal-mass scaling, and separately for cool-core and morphologically disturbed SZ profiles (based on the work of Arnaud et al. 2010). In all cases, the impact on the measurements was of order a few percent and thus negligibly impacts our conclusions.

thumbnail Fig.1

Individual scaled SZ signal measurements, ˜Y500\hbox{$\Yscaled$}, for the MaxBCG catalogue as a function of richness N200. We do not plot individual error bars to avoid saturating the figure. The error bar drawn in the upper left represents the median uncertainty over the entire population; in general, the uncertainty increases towards low richness. The SZ signal measurements are expressed as the Compton y parameter integrated over a sphere out to R500, scaled in redshift according to the self-similar model and placed at a fiducial angular distance of 500 Mpc. Each point represents the result of the matched filter applied to an individual cluster in the catalogue. Upward pointing arrows indicate values beyond the plotted range. The radius R500, and hence the filter size, is set from the mass of each cluster determined via the weak-lensing calibrated M500 − N200 relation given by Johnston et al. (2007). The results are nearly the same for the relation given by Rozo et al. (2009).

thumbnail Fig.2

Scaled SZ signal measurements, ˜Y500\hbox{$\Yscaled$}, binned by richness, N200. The left-hand panel presents the results for the Johnston et al. (2007)M500 − N200 relation, the right-hand panel for the Rozo et al. (2009) relation. In each case, the red diamonds show the bin-average, redshift-scaled ˜Y500\hbox{$\Yscaled$} calculated as the weighted mean of all individual measurements (e.g., Fig. 1) in the bin, where the weights are taken from the estimated filter noise. The thick error bars show the corresponding uncertainty on the bin-average SZ signal, while the lighter error bars indicate the uncertainty found by bootstrap analysis; they are larger due to the presence of intrinsic scatter within the bins, most notable at high richness (see Fig. 4). The blue points represent the model prediction for each bin found by averaging, with the same weights as the data, the SZ signal expected from the Y500 − M500 (Arnaud et al. 2010, STD case) and corresponding M500 − N200 relations. The Planck measurements are little affected by choice of mass-richness relation, while the model points move significantly upward with the Rozo et al. (2009) mass calibration. Dashed lines in both panels show the best fit power-law to the Planck individual cluster data points (i.e., prior to binning, as shown in Fig. 1); the parameters for these fits are given in Table 2.

thumbnail Fig.3

Null test performed by randomising the angular positions of the clusters. The red diamonds show the bin-average, redshift-scaled measurements, ˜Y500\hbox{$\Yscaled$}, as reported in the left-hand side of Fig. 2 with their corresponding measurement and bootstrap uncertainties; blue stars are the same model points. The green triangles present the bin-averages for the randomised catalogue with uncertainties given only by the SZ measurement errors. Results for the randomised catalogue are consistent with zero within their uncertainties. By comparison, the values for the real catalogue represent highly significant detections of the SZ signal in all richness bins. Left-hand panel: results over the full richness range. Right-hand panel: zoom into the region indicated by the dotted lines in the left-hand panel to highlight the low-richness end.

4. Results

Our basic measurements are the set of individual scaled SZ signal values 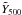˜Y500\hbox{$\Yscaled$} for each MaxBCG cluster, given as a function of richness N200 in Fig. 1 for the Johnston et al. (2007) mass calibration. At high richness we can detect by eye a slight upturn of the points. Except for the most massive objects, however, the signal-to-noise of the individual measurements is small, in most cases well below unity. This is as expected given the masses of the clusters and the Planck noise levels.

To extract the signal, we bin these 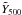˜Y500\hbox{$\Yscaled$} values by richness and calculate the bin averages as the noise-weighted mean of all individual i = 1,..,Nb measurements falling within the bin: 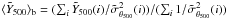⟨˜Y500⟩b=(∑i˜Y500(i)/σθ5002˜(i))/(∑i1/σθ5002˜(i))\hbox{$\langle \Yscaled\rangle_{\rm b} = (\sum_i \Yscaled(i)/\sigscaled^2(i))/(\sum_i 1/\sigscaled^2(i))$}. We plot the result as the red diamonds in Fig. 2. The bold error bars represent only the statistical uncertainty associated with the SZ signal measurements: 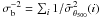σb-2=∑i1/σθ5002˜(i)\hbox{$\sigma^{-2}_{\rm b} = \sum_i 1/\sigscaled^2(i)$} (in some cases the error bars are hidden by the size of the data point in the figure). The left-hand panel of the figure shows results using the Johnston et al. (2007) mass calibration, while the right-hand side gives results for the Rozo et al. (2009) mass calibration. The individual SZ signal measurements are not sensitive to this choice: the different calibrations do modify the adopted filter size, but the impact on the measured signal is small.

We quantify the significance of the SZ detection using a null test: we perform an identical analysis on the MaxBCG catalogue after first randomising the cluster angular positions within the SDSS DR5 footprint. In this analysis we are therefore attempting to measure SZ signal with the same set of filters, but now positioned randomly within the SDSS survey. The result is shown in Fig. 3 by the green triangles, to be compared to the actual MaxBCG measurement given by the red diamonds. The left-hand panel presents the null test over the full richness range, while the right-hand panel affords an expanded view of the low mass end. The analysis on the randomised catalog remains consistent with zero (no detection) to within the SZ measurement uncertainty over the entire richness range. The actual measurements of the MaxBCG clusters, on the other hand, deviate by many σ from zero. We reject the null hypothesis in all bins at high significance.

Figure 4 summarises our analysis of the uncertainty and intrinsic scatter as a function of richness. In the left panel we show the uncertainty on the mean signal 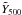˜Y500\hbox{$\Yscaled$} in each bin, expressed as a fraction of 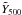˜Y500\hbox{$\Yscaled$}. The red solid red line traces the uncertainty on the mean signal due to just the measurement error, i.e., the noise level in the filter. The blue dashed line gives the uncertainty on the mean assuming that the measurements within a bin are Gaussian distributed about the mean with variance equal to the empirical in-bin variance. We show the relative uncertainty calculated from a bootstrap analysis of the entire catalogue as the dot-dashed, green curve. We perform our full analysis on 10000 bootstrap realisations from the actual catalogue and use the distribution of the resulting bin averages to find the relative uncertainty. The difference between the bootstrap and measurement uncertainties (red line) towards higher richness represents a detection of intrinsic scatter in those bins. At N200 < 30, this difference is small and any intrinsic scatter is difficult to distinguish from the measurement errors.

Table 1

Scaled Planck SZ signal measurements 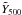˜Y500\hbox{$\Yscaled$} binned by N200 for the Rozo et al. (2009) mass-richness relation.

thumbnail Fig.4

Dispersion analysis. Left-hand panel: relative uncertainty on the mean versus richness. The relative uncertainty is expressed as a fraction of the bin-average redshift-scaled SZ signal: σ/˜Y500\hbox{$\sigma/\Yscaled$}. The lower red curve corresponds to pure measurement uncertainties from the matched filter noise estimations; they are the solid error bars of Fig. 2. The upper blue curve traces the uncertainty on the mean assuming the points within a richness bin are normally distributed according to the observed in-bin dispersion. Bootstrap uncertainties are given as the middle green line, found as the dispersion in the mean ˜Y500\hbox{$\Yscaled$} in each bin calculated over 10000 bootstrap realisations of the entire MaxBCG catalogue. The numbers given in the legend indicate the number of objects in each richness bin. Right-hand panel: fractional intrinsic scatter as a function of richness. The blue dot-dashed line (connecting the blue triangles) shows the raw dispersion in each richness bin, while the green dash-three-dotted line (connecting the green crosses) gives the calculated statistical dispersion from the measurement error on the scaled SZ signal ˜Y500\hbox{$\Yscaled$}. The red dashed line with error bars is our estimation of the intrinsic scatter as a function of richness. For this calculation we have eliminated outliers in each bin at  > 5σ, with σ=˜σθ500\hbox{$\sigma = \sigscaled$} for each cluster. We only calculate the intrinsic scatter at N200 > 30, because at lower richness it becomes difficult to separate the intrinsic dispersion from the scatter due to pure measurement error.

In the right-hand panel of Fig. 4 we show our estimate of the intrinsic scatter in the scaling relation as a function of richness for N200 > 30. This is expressed as a fraction of the mean, 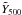˜Y500\hbox{$\Yscaled$}. The dot-dashed, blue line traces the empirical, or raw, dispersion around the average signal of each bin. The three-dot-dashed, green line gives the dispersion corresponding to pure SZ measurement noise. To find the intrinsic scatter, we use the estimator: Σb2=1Nb−1∑i=1Nb(˜Y500(i)−[˜Y500]arith)2−1Nb∑i=1Nbσθ5002˜(i)\begin{equation} \Sigma^2_{\rm b} = \frac{1}{N_{\rm b}-1}\sum_{i=1}^{N_{\rm b}}\left(\Yscaled(i)-[\Yscaled]_{\rm arith}\right)^2 - \frac{1}{N_{\rm b}}\sum_{i=1}^{N_{\rm b}}\sigscaled^2(i) \end{equation}(2)where [˜Y500]arith\hbox{$[\Yscaled]_{\rm arith}$} is the straight arithmetic mean in the bin. 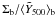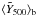In the figure we plot Σb/⟨˜Y500⟩b\hbox{$\Sigma_{\rm b}/\langle \Yscaled \rangle_{\rm b}$}, with ⟨˜Y500⟩b\hbox{$\langle\Yscaled\rangle_{\rm b}$} being the weighted mean, as above. For this calculation we clip all outliers at  > 5σ, where σ is the individual cluster SZ signal error. The final result, especially at low richness, depends on the chosen clipping threshold. The scatter is not Gaussian, as the large fractional intrinsic scatter at low richness suggests. Below N200 ≈ 30, it becomes difficult to draw clear conclusions concerning the scatter, as can be appreciated by the fact that the bootstrap and pure SZ measurement uncertainties begin to overlap in the left-hand panel. For this reason, we only calculate the intrinsic scatter for the five highest richness bins in the right-hand panel.

In conclusion, we detect a signal down to the lowest mass systems in the MaxBCG catalog with high statistical significance. This is the central result of our study. According to the mass calibration from Johnston et al. (2007), we observe the SZ signal in objects of mass as low as M500 = (4 − 5) × 1013 M⊙.

5. Discussion

Figure 2 summarises the central results of our study. There are two notable aspects: firstly, we detect the SZ signal at high significance over the entire mass range; moreover, simple power laws adequately represent the observed scaling relations. Secondly, we see a discrepancy in the 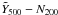˜Y500−N200\hbox{$\Yscaled-N_{200}$} relation relative to expectations based on X-ray models and either the Johnston et al. (2007) or Rozo et al. (2009) mass calibrations.

Fitting a power law of the form 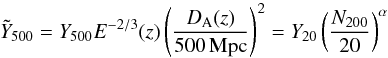˜Y500=Y500E−2/3(z)(DA(z)500 Mpc)2=Y20(N20020)α\begin{equation} \label{eq:YNrelation} \Yscaled = Y_{500}E^{-2/3}(z)\left(\frac{\Dang(z)}{500\,{\rm Mpc}}\right)^2= \YN\left(\frac{N_{200}}{20}\right)^{\aN} \end{equation}(3)directly to the individual scaled measurements (e.g., Fig. 1), we obtain the results summarised in Table 2. The Rozo et al. (2009) mass calibration assigns a larger mass to the clusters, increasing the filter scale and augmenting the measured SZ signal, which we see as the slightly higher normalisation. These fits are plotted as the dashed lines in Fig. 2. The power laws satisfactorily represent the bin-average trends. The reduced χ2 = 1.16 (13104-2 degrees-of-freedom) in both cases is poor; this reflects the presence of the intrinsic scatter, also evident by the larger uncertainties on the fit from the bootstrap analysis.

Table 2

The SZ signal-richness relation fit to a power law of the form ˜Y500=Y20N200(/20)α\hbox{$\Yscaled=\YN\left(N_{200}/20 \right)^\aN$} (see Eq. (3)) for the two mass-richness relations.

The blue stars in Fig. 2 represent the predictions of a model based on the Y500 − M500 relation from Arnaud et al. (2010) and the Johnston et al. (2007) (left) or Rozo et al. (2009) (right) M500 − N200 mean scaling relation. It assumes a self-similar Y500 − M500 scaling relation (STD case) calibrated on X-ray observations of the REXCESS cluster sample (Böhringer et al. 2007). This calibration is also consistent with WMAP observations (Melin et al. 2011) and with the Planck analysis (Planck Collaboration 2011f,g). In each bin we average the model predictions in the same way as the Planck observations: we find the model bin-average redshift-scaled SZ signal as the inverse-error-weighted (pure SZ measurement error) average, assigning each cluster in the bin the same error as the actual observation of that object. Note that in the observation plane (˜Y500,N200)\hbox{$(\Yscaled, N_{200})$}, the model (blue) points change with the mass calibration much more than the measurements.

We see a clear discrepancy between the model and the Planck SZ measurements for both mass calibrations. In the case of the Johnston et al. (2007) mass calibration, the discrepancy manifests as a shift in normalisation that we can characterise by a 25% mass shift at given SZ signal: M −  → 0.75M; the slope of the observed relation remains consistent with the self-similar prediction. The Rozo et al. (2009) mass calibration, on the other hand, flattens the mass-richness relation and predicts a shallower power law, as well as a higher normalisation; at N200 = 50 there is a factor of 2 between the predicted and observed amplitudes.

We now discuss some possible explanations for this discrepancy. Weak lensing mass estimates are difficult, and as we have seen there is an important difference in the two mass calibrations. Rozo et al. (2009), building on earlier work by Mandelbaum et al. (2008b), discuss some of the issues when measuring the weak-lensing signal for the MaxBCG catalogue. However, it seems unlikely that the weak-lensing mass calibration would be in error to the extent needed to explain the discrepancy seen in Fig. 2. The discrepancy is in fact larger for the Rozo et al. (2009) result, which should be the more robust mass calibration.

Our model predictions use a series of non-linear, mean relations between observables which in reality have scatter that may also be non-Gaussian. The largest scatter is expected to be in the mass-richness relation. If the scatter is large enough, it could bias the predictions. We have investigated the effect of a 45% log-normal scatter in mass at fixed richness (e.g., Rozo et al. 2009) and of a Poissonian distribution in richness at fixed mass. These are realistic expectations for the degree of scatter in the relations. The effect on the predicted, binned SZ signal is at most 20%, not enough to explain the factor of two discrepancy we see.

Contamination of the MaxBCG catalogue with a fraction, f, of objects that do not contribute an SZ signal (e.g., projection effects in the optical) would bias the measured signal low by about 1 − f. The level of contamination needed to explain the magnitude of the discrepancy with the Rozo et al. (2009) calibration (f ≈ 0.5) seems unlikely. The catalogue is estimated, instead, to be close to 90% pure for N200 > 10. Moreover, contamination would also lower the weak-lensing mass calibration by about 1 − f, at given N200. Since the predicted SZ signal scales as M5 / 3, the model SZ signal would drop by an even larger amount than the observed signal.

thumbnail Fig.5

The ˜Y500−N200\hbox{$\Yscaled-N_{200}$} relation for the MCXC X-ray subsample. Thick lines give the statistical errors, while the thin bars are the bootstrap uncertainties. We find that the MCXC X-ray subsample matches the model predictions much better than the full sample, which maintains a clear offset relative to the model, as seen in in Fig. 2.

To investigate this discrepancy further we analyse, in the same manner, a subsample of the MaxBCG clusters with X-ray data from the MCXC catalogue (Piffaretti et al. 2011). This represents an X-ray detected subsample of the MaxBCG. The results are given in Fig. 5 for the Rozo et al. (2009) mass calibration and with our usual notation. We see that this X-ray subsample, of 189 clusters, matches the model predictions much better. This argues that, at least for this subsample, the weak-lensing mass calibration is not significantly biased. The result also indicates the presence of a range of ICM properties at fixed richness. This is consistent with the study by Rozo et al. (2009), obtained by adapting the approach of Rykoff et al. (2008b), who find a large scatter in X-ray luminosity at fixed N200.

Splitting the catalogue according to the luminosity of the BCG lends support to the presence of populations with different ICM properties. In each bin, we divide the catalogue into a BCG-dominated sample, where the fraction of the cluster luminosity contributed by the BCG is larger than the average for that bin, and its complement sample. The BCG-dominated sample has a notably higher normalisation, closer to the predicted relation, than the complement sample.

We also compare our results to the X-ray results from Rykoff et al. (2008a) who stacked ROSAT photons around MaxBCG clusters according to richness. As with our SZ observations, their individual X-ray fluxes had low signal-to-noise, but they extracted mean luminosities from each image stack (Rykoff et al. 2008b). They report luminosities, L200, over the 0.1 − 2.4 keV band and within R200 for each N200 richness bin. Their analysis revealed a discrepancy between the observed mean luminosities and the X-ray model predictions, using the Johnston et al. (2007) mass calibration.

To compare we re-binned into the same richness bins as Rykoff et al. (2008b), calculating the new, bin-average, redshift-scaled ˜Y500\hbox{$\Yscaled$}. We also convert their luminosities to L500 using the X-ray profile adopted in Arnaud et al. (2010); the conversion factor is 0.91. In addition, we apply the self-similar redshift luminosity scaling of E − 7 / 3(z = 0.25) to bring the Rykoff et al. (2008a) measurements to equivalent z = 0 values from the values at their median redshift, z = 0.25. The resulting points are shown in Fig. 6.

The model line in the figure is calculated from the z = 0, X-ray luminosities using the X-ray based scaling laws in Arnaud et al. (2010). In this plane the model matches the observations well, demonstrating consistency between the SZ and X-ray observations. Remarkably, the ICM quantities remain in agreement with the model despite the individual discrepancies (SZ and X-ray luminosity) with richness.

The intrinsic scatter in the scaling relation, given in Fig. 4, starts at about 60% and rises to over 100% at N200 ≈ 30. This was calculated by clipping all outliers at  > 5σ; the result depends on the choice of clipping threshold, indicative of a non-Gaussian distribution. This dispersion should be compared to the estimated log-normal scatter in the mass-richness relation of 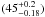(45-0.18+0.2)\hbox{$(45_{-0.18}^{+0.2})$}% found by Rozo et al. (2009). Assuming that the dispersion in the SZ signal-mass relation is much smaller, we would expect a dispersion of order 75%, not far from what we find and within the uncertainties. Such large fractional dispersion implies a non-Gaussian distribution skewed toward high SZ signal values, particularly at low richness.

6. Conclusions

We have measured with high significance the mean SZ signal for MaxBCG clusters binned by richness, even the poorest systems. The observed SZ signal-richness relation, based on 13104 of the MaxBCG clusters observed by Planck, is well represented by a power law. This adds another scaling relation to the list of such relations known to exist among cluster properties and that present important constraints on cluster and galaxy evolution models.

The observed relation has a significantly lower amplitude than predicted by X-ray models coupled with the mass-richness relation from weak-lensing observations. The origin of this discrepancy remains unclear. Bias in the weak-lensing mass measurements and/or a high contamination of the catalogue are potential explanations; another would be a bias in hydrostatic X-ray masses relative to weak-lensing based masses (Borgani et al. 2004; Piffaretti & Valdarnini 2008), although the required level of bias would be much larger than expected from simulations. In general, we would expect a wide range of ICM properties at fixed richness (e.g., for example by Rykoff et al. 2008a; Rozo et al. 2009) of which only the more X-ray luminous objects are readily found in X-ray samples used to establish the X-ray model. This is consistent with the better agreement of the model with a subsample of the MaxBCG catalogue with X-ray observations. Remarkably, the relation between mean SZ signal and mean X-ray luminosity for the entire catalogue does conform to model predictions despite discrepant SZ signal-richness and X-ray luminosity-richness relations; properties of the gas halo appear more stably related than either to richness.

We find large intrinsic scatter in the SZ signal-richness relation, although consistent with the major contribution arising from scatter in the mass-richness relation. The uncertainties, however, are important. Such large scatter implies a non-Gaussian distribution of SZ signal at given richness, skewed towards higher signal strengths. This is consistent with the idea of a wide range of ICM properties at fixed richness, with X-ray detected objects preferentially at the high SZ signal end.

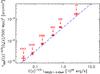thumbnail Fig.6

Comparison of our bin-average redshift-scaled SZ signal measurements with the mean X-ray luminosities found by Rykoff et al. (2008a). For this comparison, we re-bin into the same bins as Rykoff et al. (2008a) and plot the results as the red diamonds with error bars. The X-ray luminosities are brought to equivalent z = 0 values using the self-similar scaling of E − 7 / 3(z = 0.25) applied at the quoted z = 0.25 median redshift. The dashed blue line shows the predictions of the X-ray model. Our notation for the error bars follows previous figures. The numbers in the figure indicate the number of clusters in each bin.

The 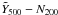˜Y500−N200\hbox{$\Yscaled-N_{200}$} relation, and by consequence the 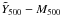˜Y500−M500\hbox{$\Yscaled-M_{500}$} relation, is an important part of our understanding of the cluster population and a key element in its use as a cosmological probe. Predictions of both the number counts of SZ-detected clusters and the diffuse SZ power spectrum depend sensitively on the 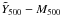˜Y500−M500\hbox{$\Yscaled-M_{500}$} relation. The amplitude of the SZ power spectrum varies as the square of the normalisation, while the counts depend on it exponentially. In both instances, this relation represents a significant theoretical uncertainty plaguing models.

Our study of the SZ signal-richness relation is a step towards reducing this uncertainty, and it presents a new cluster scaling relation as a useful constraint for theories of cluster and galaxy evolution. Concerning the latter, we find no obvious sign of an abrupt change in the ICM properties of optically selected clusters over a wide range of richness, hence mass, as might be expected from strong feedback models. Future research with Planck will extend this work to other catalogues and a greater redshift range.

1

Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.

Acknowledgments

The authors from the consortia funded principally by CNES, CNRS, ASI, NASA, and Danish Natural Research Council acknowledge the use of the pipeline running infrastructures Magique3 at Institut d’Astrophysique de Paris (France), CPAC at Cambridge (UK), and USPDC at IPAC (USA). We acknowledge the use of the HEALPix package (Górski et al. 2005). A description of the Planck Collaboration and a list of its members, indicating which technical or scientific activities they have been involved in, can be found at http://www.rssd.esa.int/Planck.

References

  1. Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Birkinshaw, M. 1999, Phys. Rep., 310, 97 [NASA ADS] [CrossRef] [Google Scholar]
  4. Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Borgani, S., Murante, G., Springel, V., et al. 2004, MNRAS, 348, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  6. Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
  7. Carlstrom, J. E., Holder, G. P., & Reese, E. D. 2002, ARA&A, 40, 643 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dobbs, M., Halverson, N. W., Ade, P. A. R., et al. 2006, New A Rev., 50, 960 [Google Scholar]
  9. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hand, N., Appel, J. W., Battaglia, N., et al. 2011, 2011, ApJ, 736, 39 [NASA ADS] [CrossRef] [Google Scholar]
  11. Hao, J., McKay, T. A., Koester, B. P., et al. 2010, ApJS, 191, 254 [NASA ADS] [CrossRef] [Google Scholar]
  12. Herranz, D., Sanz, J. L., Hobson, M. P., et al. 2002, MNRAS, 336, 1057 [NASA ADS] [CrossRef] [Google Scholar]
  13. Johnston, D. E., Sheldon, E. S., Tasitsiomi, A., et al. 2007 [arXiv:0709.1159] [Google Scholar]
  14. Koester, B. P., McKay, T. A., Annis, J., et al. 2007a, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
  15. Koester, B. P., McKay, T. A., Annis, J., et al. 2007b, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Mandelbaum, R., Seljak, U., & Hirata, C. M. 2008a, J. Cosmology Astropart. Phys., 8, 6 [Google Scholar]
  19. Mandelbaum, R., Seljak, U., Hirata, C. M., et al. 2008b, MNRAS, 386, 781 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
  21. Marriage, T. A., Acquaviva, V., Ade, P. A. R., et al. 2011, ApJ, 737, 61 [NASA ADS] [CrossRef] [Google Scholar]
  22. Melin, J., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Melin, J., Bartlett, J. G., Delabrouille, J., et al. 2011, A&A, 525, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Planck Collaboration 2011b, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Planck Collaboration 2011c, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Planck Collaboration 2011d, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Planck Collaboration 2011e, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Planck Collaboration 2011f, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Planck Collaboration 2011g, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Planck Collaboration 2011h, A&A, 536, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Planck Collaboration 2011i, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Planck Collaboration 2011j, A&A, 536, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Planck Collaboration 2011k, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Planck Collaboration 2011l, A&A, 536, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Planck Collaboration 2011m, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Planck Collaboration 2011n, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Planck Collaboration 2011o, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Planck Collaboration 2011p, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Planck Collaboration 2011q, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Planck Collaboration 2011r, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Planck Collaboration 2011s, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Planck Collaboration 2011t, A&A, 536, A24 [Google Scholar]
  47. Planck Collaboration 2011u, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Planck Collaboration 2011v, The Explanatory Supplement to the Planck Early Release Compact Source Catalogue (ESA) [Google Scholar]
  49. Planck Collaboration 2011w, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Planck HFI Core Team 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Planck HFI Core Team 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Rozo, E., Rykoff, E. S., Evrard, A., et al. 2009, ApJ, 699, 768 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rykoff, E. S., Evrard, A. E., McKay, T. A., et al. 2008a, MNRAS, 387, L28 [NASA ADS] [Google Scholar]
  56. Rykoff, E. S., McKay, T. A., Becker, M. R., et al. 2008b, ApJ, 675, 1106 [NASA ADS] [CrossRef] [Google Scholar]
  57. Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sheldon, E. S., Johnston, D. E., Scranton, R., et al. 2009, ApJ, 703, 2217 [NASA ADS] [CrossRef] [Google Scholar]
  59. Staniszewski, Z., Ade, P. A. R., Aird, K. A., et al. 2009, ApJ, 701, 32 [CrossRef] [Google Scholar]
  60. Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments on Astrophys. Space Phys., 4, 173 [Google Scholar]
  61. Swetz, D. S., Ade, P. A. R., Allen, C., et al. 2008, in Presented at the SPIE Conf. Ser., 7020 [Google Scholar]
  62. Szabo, T., Pierpaoli, E., Dong, F., Pipino, A., & Gunn, J. E. 2011, ApJ, 736, 21 [NASA ADS] [CrossRef] [Google Scholar]
  63. Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Vanderlinde, K., Crawford, T. M., de Haan, T., et al. 2010, ApJ, 722, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  65. Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
  66. Wen, Z. L., Han, J. L., & Liu, F. S. 2009, ApJS, 183, 197 [NASA ADS] [CrossRef] [Google Scholar]
  67. Williamson, R., Benson, B. A., High, F. W., et al. 2011, ApJ, 738, 139 [NASA ADS] [CrossRef] [Google Scholar]
  68. York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
  69. Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Scaled Planck SZ signal measurements 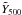˜Y500\hbox{$\Yscaled$} binned by N200 for the Rozo et al. (2009) mass-richness relation.

In the text
Table 2

The SZ signal-richness relation fit to a power law of the form ˜Y500=Y20N200(/20)α\hbox{$\Yscaled=\YN\left(N_{200}/20 \right)^\aN$} (see Eq. (3)) for the two mass-richness relations.

In the text

All Figures

thumbnail Fig.1

Individual scaled SZ signal measurements, ˜Y500\hbox{$\Yscaled$}, for the MaxBCG catalogue as a function of richness N200. We do not plot individual error bars to avoid saturating the figure. The error bar drawn in the upper left represents the median uncertainty over the entire population; in general, the uncertainty increases towards low richness. The SZ signal measurements are expressed as the Compton y parameter integrated over a sphere out to R500, scaled in redshift according to the self-similar model and placed at a fiducial angular distance of 500 Mpc. Each point represents the result of the matched filter applied to an individual cluster in the catalogue. Upward pointing arrows indicate values beyond the plotted range. The radius R500, and hence the filter size, is set from the mass of each cluster determined via the weak-lensing calibrated M500 − N200 relation given by Johnston et al. (2007). The results are nearly the same for the relation given by Rozo et al. (2009).
In the text
thumbnail Fig.2

Scaled SZ signal measurements, ˜Y500\hbox{$\Yscaled$}, binned by richness, N200. The left-hand panel presents the results for the Johnston et al. (2007)M500 − N200 relation, the right-hand panel for the Rozo et al. (2009) relation. In each case, the red diamonds show the bin-average, redshift-scaled ˜Y500\hbox{$\Yscaled$} calculated as the weighted mean of all individual measurements (e.g., Fig. 1) in the bin, where the weights are taken from the estimated filter noise. The thick error bars show the corresponding uncertainty on the bin-average SZ signal, while the lighter error bars indicate the uncertainty found by bootstrap analysis; they are larger due to the presence of intrinsic scatter within the bins, most notable at high richness (see Fig. 4). The blue points represent the model prediction for each bin found by averaging, with the same weights as the data, the SZ signal expected from the Y500 − M500 (Arnaud et al. 2010, STD case) and corresponding M500 − N200 relations. The Planck measurements are little affected by choice of mass-richness relation, while the model points move significantly upward with the Rozo et al. (2009) mass calibration. Dashed lines in both panels show the best fit power-law to the Planck individual cluster data points (i.e., prior to binning, as shown in Fig. 1); the parameters for these fits are given in Table 2.
In the text
thumbnail Fig.3

Null test performed by randomising the angular positions of the clusters. The red diamonds show the bin-average, redshift-scaled measurements, ˜Y500\hbox{$\Yscaled$}, as reported in the left-hand side of Fig. 2 with their corresponding measurement and bootstrap uncertainties; blue stars are the same model points. The green triangles present the bin-averages for the randomised catalogue with uncertainties given only by the SZ measurement errors. Results for the randomised catalogue are consistent with zero within their uncertainties. By comparison, the values for the real catalogue represent highly significant detections of the SZ signal in all richness bins. Left-hand panel: results over the full richness range. Right-hand panel: zoom into the region indicated by the dotted lines in the left-hand panel to highlight the low-richness end.
In the text
thumbnail Fig.4

Dispersion analysis. Left-hand panel: relative uncertainty on the mean versus richness. The relative uncertainty is expressed as a fraction of the bin-average redshift-scaled SZ signal: σ/˜Y500\hbox{$\sigma/\Yscaled$}. The lower red curve corresponds to pure measurement uncertainties from the matched filter noise estimations; they are the solid error bars of Fig. 2. The upper blue curve traces the uncertainty on the mean assuming the points within a richness bin are normally distributed according to the observed in-bin dispersion. Bootstrap uncertainties are given as the middle green line, found as the dispersion in the mean ˜Y500\hbox{$\Yscaled$} in each bin calculated over 10000 bootstrap realisations of the entire MaxBCG catalogue. The numbers given in the legend indicate the number of objects in each richness bin. Right-hand panel: fractional intrinsic scatter as a function of richness. The blue dot-dashed line (connecting the blue triangles) shows the raw dispersion in each richness bin, while the green dash-three-dotted line (connecting the green crosses) gives the calculated statistical dispersion from the measurement error on the scaled SZ signal ˜Y500\hbox{$\Yscaled$}. The red dashed line with error bars is our estimation of the intrinsic scatter as a function of richness. For this calculation we have eliminated outliers in each bin at  > 5σ, with σ=˜σθ500\hbox{$\sigma = \sigscaled$} for each cluster. We only calculate the intrinsic scatter at N200 > 30, because at lower richness it becomes difficult to separate the intrinsic dispersion from the scatter due to pure measurement error.
In the text
thumbnail Fig.5

The ˜Y500−N200\hbox{$\Yscaled-N_{200}$} relation for the MCXC X-ray subsample. Thick lines give the statistical errors, while the thin bars are the bootstrap uncertainties. We find that the MCXC X-ray subsample matches the model predictions much better than the full sample, which maintains a clear offset relative to the model, as seen in in Fig. 2.
In the text
thumbnail Fig.6

Comparison of our bin-average redshift-scaled SZ signal measurements with the mean X-ray luminosities found by Rykoff et al. (2008a). For this comparison, we re-bin into the same bins as Rykoff et al. (2008a) and plot the results as the red diamonds with error bars. The X-ray luminosities are brought to equivalent z = 0 values using the self-similar scaling of E − 7 / 3(z = 0.25) applied at the quoted z = 0.25 median redshift. The dashed blue line shows the predictions of the X-ray model. Our notation for the error bars follows previous figures. The numbers in the figure indicate the number of clusters in each bin.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.