| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014120 | |
| Published online | 03 March 2011 | |
Abell 611
II. X-ray and strong lensing analyses
1 Dipartimento di AstronomiaUniversità
di Bologna, via Ranzani
1, 40127 Bologna, Italy
e-mail: annamaria.donnarumm2@unibo.it
2 INAF - Osservatorio Astronomico di
Bologna, via Ranzani 1, 40127
Bologna,
Italy
3 INFN, Sezione di Bologna, viale Berti
Pichat 6/2, 40127
Bologna,
Italy
4 Institut d'Astrophysique de Paris, CNRS UMR 7095, 98bis Bd Arago, 75014 Paris, France
5 UPMC Université Paris 06, UMR 7095, 75014 Paris, France
6 Dipartimento di Fisica, Università La
Sapienza, Piazzale
A.Moro
00185
Roma,
Italy
7 INAF - Osservatorio Astronomico di
Roma, via Frascati 33, 00044 Monte Porzio Catone, Roma, Italy
8 INAF - Osservatorio Astronomico di
Napoli, via Moiariello 16, 80131
Napoli,
Italy
9 INAF - Osservatorio Astronomico di
Padova, vicolo dell’Osservatorio 5, 35122
Padova,
Italy
10 Key Lab for Astrophysics, Shanghai
Normal University, 100 Guilin Road,
200234
Shanghai, PR
China
11 Department of Physics, Institute
for Computational Cosmology, Durham University, South Road, Durham
DH1 3LE,
UK
Received: 22 January 2010
Accepted: 17 October 2010
We present the results of our analyses of the X-ray emission and of the strong lensing systems in the galaxy cluster Abell 611 [z = 0.288]. This cluster is an optimal candidate for a comparison of the mass reconstructions obtained through X-ray and lensing techniques, because of its very relaxed dynamical appearance and its exceptional strong lensing system. We infer the X-ray mass estimate deriving the density and temperature profile of the intra-cluster medium within the radius r ≃ 700 kpc through a non-parametric approach, taking advantage of the high spatial resolution of a Chandra observation. Assuming that the cluster is in hydrostatic equilibrium and adopting a matter density profile, we can recover the total mass distribution of Abell 611 via the X-ray data. Moreover, we derive the total projected mass in the central regions of Abell 611 performing a parametric analysis of its strong lensing features through the publicly available analysis software Lenstool. As a final step we compare the results obtained with both methods. We derive a good agreement between the X-ray and strong lensing total mass estimates in the central regions where the strong lensing constraints are present (i.e. within the radius r ≃ 100 kpc), while a marginal disagreement is found between the two mass estimates when extrapolating the strong lensing results in the outer spatial range. We suggest that in this case the X-ray/strong lensing mass disagreement can be explained by an incorrect estimate of the relative contributions of the baryonic component and of the dark matter, caused by the intrinsic degeneracy between the different mass components in the strong lensing analysis. We discuss the effect of some possible systematic errors that influence both mass estimates. We find a slight dependence of the measurements of the X-ray temperatures (and therefore of the X-ray total masses) on the background adopted in the spectral analysis, with total deviations on the value of M200 of the order of the 1σ statistical error. The strong lensing mass results are instead sensitive to the parameterisation of the galactic halo mass in the central regions, in particular to the modelling of the brightest cluster galaxy (BCG) baryonic component, which induces a significant scatter in the strong lensing mass results.
Key words: gravitational lensing: strong / X-ray: galaxies: clusters / galaxies: clusters: general / galaxies: clusters: individual Abell 611
© ESO, 2011
1. Introduction
Testing the accuracy of the several approaches used to estimate the mass of galaxy clusters is necessary to assess the reliability of methods involving clusters as cosmological probes. For example, the comparison of the cluster baryon fractions fb to the cosmic baryon fraction can provide a direct constraint on the mean mass density of the Universe, ΩM (Ettori et al. 2009; Allen et al. 2008; Ettori et al. 2003), while the evolution of the cluster mass function can tightly constrain ΩΛ and the dark energy equation-of-state parameter w (Vikhlinin et al. 2009).
 |
Fig. 1 (Left panel) F606W ACS/HST image of the cluster Abell 611 (see Table 3 for the observation summary). The X-ray isophotes derived from the Chandra image (shown in the middle panel) are overlaid in white. The green cross indicates the X-ray centroid. (Middle panel) The Chandra X-ray image of Abell 611 in the energy range [0.25–7.0] keV. The image was smoothed with a 3 pixel FWHM Gaussian filter, and is not exposure-corrected. The contours derived from the HST image (shown in the left panel) are overlaid in white to facilitate the comparison between the images. Here again the green cross marks the X-ray centroid. (Right panel) Pseudo-colour composite image of Abell 611, obtained combining r and g-SLOAN images, taken with the Large Binocular Camera mounted at LBT. The three panels are WCS-aligned; the size of the field of view is ≃ [1.6 × 1.8] arcmin. |
Cluster mass profiles can be probed through several independent techniques, relying on different physical mechanisms and requiring different assumptions. The comparison of results obtained with different methods and the (dis)agreement between them provide a useful check, and can give additional insights on the inner structure of clusters. For example, cluster masses can be estimated through the projected phase-space distribution and velocity dispersion of cluster galaxies (Biviano & Poggianti 2009; Diaferio et al. 2005); the dynamical studies, however, are affected by the strong degeneracy between the mass density profile and the velocity dispersion anisotropy profile, and thus require strong assumptions on the form of the velocity dispersion tensor.
Measurements of the Sunyaev-Zel’dovich effect (hereafter SZE; Sunyaev & Zel’dovich 1972) towards galaxy clusters yield a direct measurement of the pressure distribution of the cluster gas: the total gravitational mass can thus be determined combining this information with the intra-cluster medium (hereafter ICM) temperature, estimated for example through the X-ray spectral analysis (Grego et al. 2001). Because it is independent of the cluster redshift, the SZE can be an extremely powerful tool to investigate the mass of high-redshift clusters (Hincks et al. 2009), but accurate measurements of the SZE are still a challenge because of intrinsic limitations and systematic biases (faint signal extending over a large angular size and subject to several sources of contamination).
So far, the analysis of the cluster X-ray emission and of the gravitational lensing effect are among the most promising techniques to estimate galaxy cluster masses.
The X-ray mass estimate is less biased compared with lensing-derived masses by projection effects, because the X-ray emission is traced by the square of the gas density (Gavazzi 2005; Wu 2000). However, X-ray measurements of cluster masses imply the assumption of hydrostatic equilibrium of the ICM with the dark matter potential and of spherical symmetry of the cluster mass distribution. Hence the total mass profile can be inferred from the radial profiles of gas temperature and density.
On the other hand, the gravitational lensing effect allows for the determination of the projected surface mass density of the lens, regardless of its dynamical state or the nature of the intervening matter. This effect is determined by all massive structures along the line of sight, so lensing mass measurements are subject to foreground and background contaminations. Moreover, the lensing effect is sensitive to features of the mass distribution such as its ellipticity and asymmetry and to the presence of substructures (Meneghetti et al. 2007a).
The combination of X-ray and lensing results could verify and strengthen the findings on the cluster physics and masses (see for example Allen 1998; Ettori & Lombardi 2003; Bradač et al. 2008); but so far several works in literature claimed a significant disagreement between strong lensing and X-ray mass estimates, (Wu & Fang 1996; Smail et al. 1997; Ota et al. 2004; Voigt & Fabian 2006; Gitti et al. 2007; Halkola et al. 2008) which would prevent any joint analysis. Many convincing explanations, even if not conclusive, have been suggested.
It is therefore clear that a comparison between independent mass estimates for galaxy clusters can provide a vital check of the assumptions adopted in the cluster analysis, and will possibly give us additional insights into the underlying physics of these objects. In particular, the comparison between lensing and X-ray mass in galaxy clusters is also directly related to the cosmological parameters, since their ratio depends on the cosmic density parameter, ΩM, and the cosmological constant, ΩΛ, for their different dependence on the angular diameter distances, which are smaller in an ΩΛ dominated universe, as pointed out by Wu (2000).
Targets for a comparative analysis should be relaxed, unperturbed objects to avoid biases deriving from the incorrect assumption of hydrostatic equilibrium (X-ray analysis) or from the contamination of secondary mass clumps or unresolved substructures (lensing analysis).
An ideal candidate for this kind of analysis is Abell 611. It is a rich, cool-core cluster at z = 0.288 (Struble & Rood 1999); its X-ray emission peak is well centred on the Brightest Cluster Galaxy (hereafter BCG; see left and central panels of Fig. 1), and the X-ray isophotes appear quite regular, with a low degree of ellipticity. These characteristics are generally considered good indicators of a relaxed dynamical state. Relaxed objects are quite rare at this redshift, so a detailed study of the properties of Abell 611 is even more appealing.
In this work we will focus on the comparison between the X-ray and strong lensing mass estimates. A weak lensing analysis of large field of view data, obtained with the Large Binocular Camera (LBC) mounted at the Large Binocular Telescope (LBT), is presented in Romano et al. (2010) (hereafter Paper I). Here we present new X-ray and strong lensing mass estimates, based on a non-parametric reconstruction of gas density and temperature profiles obtained through the analysis of a Chandra observation, and on a strong lensing reconstruction respectively, which was performed with the Lenstool analysis software (Kneib et al. 1996; Jullo et al. 2007).
This paper is organised as follows. In Sect. 2 we will introduce our X-ray analysis, focusing on the data reduction and on the method applied to recover the total and gas mass profiles, and discuss some possible systematic errors associated with the X-ray analysis. The strong lensing analysis is presented in Sect. 3, where we will briefly discuss our main findings. We will compare the X-ray and strong lensing results in Sect. 4: a comparison with previous analyses can be found in Sect. 5. Finally, we will summarise our results and draw our conclusions in Sect. 6. Throughout this work we will assume a flat ΛCDM cosmology: the matter density parameter will have the value Ωm = 0.3, the cosmological constant density parameter ΩΛ = 0.7, and the Hubble constant will be H0 = 70 km s-1 Mpc-1. At the cluster redshift and for the assumed cosmological parameters, 1 arcsec is equivalent to 4.329 kpc. Unless otherwise stated, all uncertainties are referred to a 68% confidence level.
2. X-ray analysis
2.1. X-ray data reduction
The X-ray analysis of Abell 611 returns several indicators of a relaxed dynamical state, such as the absence of substructures in the X-ray emission (which appears isotropic over elliptical isophotes), a well-defined cool-core, and a smooth surface brightness profile. The X-ray emission is centred on the BCG: the distance between the X-ray centroid and the BCG centre is ≃ 1 arcsec (the uncertainty on this measure is comparable to the smoothing scale applied to the X-ray image to determine the centroid, i.e. 3 pixels ≃ 1.5 arcsec). Moreover, Abell 611 appears to be a radio-quiet cluster, because the Giant Metrewave Radio Telescope (GMRT) Radio Halo Survey (Venturi et al. 2007, 2008,see Sect. 5) failed to detect any extended radio emission associated with this cluster. Since giant radio halos are the most relevant examples of non-thermal activity in galaxy clusters (Brunetti et al. 2009), the absence of a radio halo supports the hypothesis of thermal pressure support, connected to the hydrostatic equilibrium assumption required in the X-ray analysis.
Observation summary of the Chandra exposure used for the X-ray analysis.
This cluster can therefore be considered an ideal candidate to highlight any issue with the current analysis techniques: it fullfills the assumptions of thermal pressure support and of spherical symmetry, so it is unlikely that potential biases in the results are related to the limiting assumptions underlying the X-ray analysis. We performed our X-ray analysis on the only Chandra data set available, retrieved from the public archive (see Table 1 for observation log). We reduced the data using the CIAO data analysis package – version 4.0 – and the calibration database CALDB 3.5.01. We will summarise here briefly the reduction procedure.
The Chandra observation was tele-metered in very faint mode and was performed through both back-illuminated (BI) and front-illuminated (FI) chips. The cluster centre was imaged in the S3 BI chip. The level-1 event files were reprocessed to apply the appropriate gain maps and calibration products and to reduce the ACIS quiescent background2. We used the acis_process_events tool to check for cosmic-ray background events and to correct for eventual spatial gain variations caused by charge transfer inefficiency to re-compute the event grades. We applied the standard event selection, including only the events flagged with grades 0,2,3,4, and filtered for the Good Time Intervals associated with the observation. The bright point sources were masked out, and a geometrical correction for the masked areas was applied; the point sources were identified using the script vtpdetect, and the result was then checked through visual inspection.
A careful screening of the background light curve is necessary for a correct background subtraction (Markevitch et al. 2003), to discard contaminating flare events, which could have a non-negligible influence on the inferred cluster spectral properties. We extracted the background light curve, applying a time binning of about 1 ks, in the energy range [2.5–7] keV, which is the most effective band to individuate common flares for S3 chip. We applied the script lc_clean to include only the time periods within a factor 1.2 of the mean quiescent rate. We compared the S3 background light curve with the light curve extracted in the S1 chip using the energy range [2.5–6] keV, to check for faint, long flares, which were not identified. The S3 background light curve was examined using the ChIPS facilities to identify and exclude further flaring events. The net exposure time after the light curve screening is about 31 ks (see Table 1).
 |
Fig. 2 (Top left panel) Deprojected gas density profile. The red circles indicate the values determined by the normalisation of the thermal spectra, while diamonds represent the values obtained combining both spectral and surface brightness measurements: the dashed line shows the best-fit profile. (Bottom left panel) ICM temperature profile. The figure shows the projected temperature values, directly inferred from the spectral analysis (red filled circles) and the deprojected values, which were rebinned to the same binning of the spectral profile (diamonds). The dashed line shows the deprojected best-fit profile. (Right panel) The projected (black empty diamonds) and deprojected (red filled circles) metallicity profile for Abell 611 inferred from the X-ray analysis. The dotted line represents the mean metallicity value Z = (0.45 ± 0.1) Z⊙, as determined through the fit of the spectrum extracted in the area with radius R = 2.9 arcmin, i.e. the cluster area covered by our spectral analysis. The grey region indicates the 1σ confidence level. |
2.2. X-ray analysis
In order to derive a reliable cluster mass estimate through the X-ray analysis, a primary issue is to avoid any bias in the temperature estimate, because cluster masses derived by assuming hydrostatic equilibrium are dependent on the temperature profile, as demonstrated by Rasia et al. (2006). For this purpose, a correct background modelling is crucial. The X-ray background is often estimated through the blank-sky background data sets provided by the ACIS calibration team. The blank-sky observations are reduced similarly to the source data sets to be compatible with the cluster event files; the former are then re-normalised by comparing the blank-sky count rate in a given energy range (generally kT > 8.0 keV, since in this band the Chandra effective area is negligible) with the local background count rate. One of the advantages of this modus operandi is that the derived ARF and RESPONSE matrices will be consistent both for the source and the background spectrum. However, the background in the X-ray soft band can vary both in time and in space, so it is important to verify whether the background derived by the blank-sky datasets is consistent with the “real” one.
For this purpose, we extracted a spectrum from the Chandra observation in a region where the cluster emission is negligible: we compared the former to a spectrum derived in the same region of the blank-field data set. We tried to fit the residuals in the [0.4–3] keV band with a MEKAL model, without an absorption component and broadening the normalisation fitting range to negative values. This comparison shows some differences between the two spectra. For this reason, we decided to proceed in the spectral fitting utilising both a local background estimate and a blank-sky estimate. The effect of the background choice in the mass estimate results will be discussed in Sect. 2.5.
2.3. Spectral fitting
The spectra were extracted on concentric annuli centred on the X-ray surface brightness centroid, each one containing at least 2500 net source counts, to infer an estimate of the ICM metallicity. We selected six annuli with adequate S/N ratio, up to Rspec = 2.9 arcmin. We used the CIAO specextract tool to extract the source and background spectra and to construct ancillary-response and response matrices. The spectra were fitted in the 0.6–7.0 keV range except for the last two annuli, in which, due to the higher background level, we restricted the analysis to the range 0.6–5.0 keV. We performed the spectral analysis using the XSPEC software package (Arnaud 1996). We adopted an optically-thin plasma emission model (the mekal model; Mewe et al. 1985; Kaastra & Mewe 1993) with an absorption component (the Tübingen-Boulder model tbabs; Wilms et al. 2000).
We fixed the Galactic absorption to the value inferred from radio HI maps in Dickey & Lockman (1990), i.e. 4.99 × 1020 cm-2. The free parameters in the spectral fitting model are the temperature, the metallicity and the normalisation of the thermal spectrum.
The metal abundance profile presents a central peak with a quite scattered trend (see the right panel of Fig. 2). The metallicity profile is not directly involved in the X-ray mass reconstruction: but we still verified whether a bias in its measurement can influence the derived mass estimate. The results of this check will be presented in Sect. 2.5.
2.4. X-ray mass profile
The gas temperature and density profiles are recovered without any parameterisation of the ICM properties, but relying on the assumptions of spherical symmetry and hydrostatic equilibrium and on the choice of a model for the total mass.
The method that was applied is briefly resumed in the following; the reader can refer to Ettori et al. (2002); Morandi et al. (2007); Morandi & Ettori (2007) for full details.
 |
Fig. 3 (Left panel) Mass profiles for Abell 611 as determined through the X-ray analysis. The black solid line and the red dashed line indicate the total mass and the gas mass profile, respectively. (Right panel) Confidence levels determined through the X-ray analysis for the NFW profile parameters rs and c200. The red circle indicates the best-fit values, while the contours represent the 1σ,2σ, and 3σ confidence levels. |
Best-fit values for the total mass parameters obtained through the X-ray analysis.
In this section, the subscript “ring” will indicate a projected quantity measured in concentric rings (equivalently, spectral bins), whereas the subscript “shell” will point to a deprojected quantity measured in volume shells. The projected gas temperature Tring, metal abundance Zring and the normalisation Kring of the model for each annulus are derived through the spectral analysis. In particular, the normalisation of the thermal spectrum provides an estimate for the emission integral 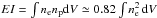 .
.
To deproject the former quantities, we need to derive the intersection of each volume shell with the spectral annuli, which can be calculated through an upper triangular matrix 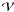 , whose last pivot represents the outermost annulus if we assume spherical symmetry (Kriss et al. 1983; Buote 2000).
, whose last pivot represents the outermost annulus if we assume spherical symmetry (Kriss et al. 1983; Buote 2000).
To calculate the deprojected density profile, we combined the spectral information and the cluster X-ray surface brightness (SB) profile, composed by 15 bins with 1000 counts each. The SB provides an estimate of the volume-counts emissivity 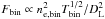 , where DL is the luminosity distance of the cluster. By comparing this observed profile with the values predicted by a thermal plasma model, with temperature and metallicity equal to the measured spectral quantities and taking into account the absorption effect, we can solve for the electron density and obtain a gas density profile better resolved than a “spectral-only” one (see the top panel of Fig. 2).
, where DL is the luminosity distance of the cluster. By comparing this observed profile with the values predicted by a thermal plasma model, with temperature and metallicity equal to the measured spectral quantities and taking into account the absorption effect, we can solve for the electron density and obtain a gas density profile better resolved than a “spectral-only” one (see the top panel of Fig. 2).
The total gravitating mass was then constrained as follows: the observed deprojected temperature profile in volume shells Tshell was obtained through 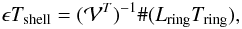 (1)where
(1)where 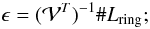 (2)here the symbol # indicates a matrix product,
(2)here the symbol # indicates a matrix product, 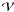 is the volume matrix and Lring is the cluster luminosity measured in concentric rings. We compare it to the predicted temperature profile Tmodel, obtained by inverting the equation of hydrostatic equilibrium between the dark matter and the intracluster plasma, i.e.:
is the volume matrix and Lring is the cluster luminosity measured in concentric rings. We compare it to the predicted temperature profile Tmodel, obtained by inverting the equation of hydrostatic equilibrium between the dark matter and the intracluster plasma, i.e.: 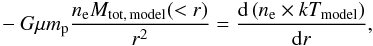 (3)where ne is the deprojected electron density. Our best-fit mass model was determined by comparing the observed temperature profile T obs with the predicted profile T model, which depends on the mass model parameters: accordingly we minimised the quantity:
(3)where ne is the deprojected electron density. Our best-fit mass model was determined by comparing the observed temperature profile T obs with the predicted profile T model, which depends on the mass model parameters: accordingly we minimised the quantity: 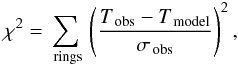 (4)where the Tmodel profile was rebinned to match the observed temperature profile. In the bottom panel of Fig. 2 we show the projected temperature profile as determined through the spectral analysis, the deprojected best-fit profile and the deprojected profile, rebinned to the spectral intervals.
(4)where the Tmodel profile was rebinned to match the observed temperature profile. In the bottom panel of Fig. 2 we show the projected temperature profile as determined through the spectral analysis, the deprojected best-fit profile and the deprojected profile, rebinned to the spectral intervals.
We assumed the NFW profile as the total mass functional; this profile can be expressed as: 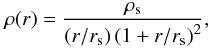 (5)where ρs is the characteristic density and rs is the scale radius. We will describe the NFW profile through the scale radius and the concentration parameter c200; the former can be defined as
(5)where ρs is the characteristic density and rs is the scale radius. We will describe the NFW profile through the scale radius and the concentration parameter c200; the former can be defined as 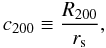 (6)where R200 is the radius within which the mean matter density of the halo is 200 times the critical density of the Universe. Assuming a mass model, the best-fitting values of its parameters are determined by minimising the quantity defined in Eq. (4). The NFW profile parameters were optimised in the ranges
(6)where R200 is the radius within which the mean matter density of the halo is 200 times the critical density of the Universe. Assuming a mass model, the best-fitting values of its parameters are determined by minimising the quantity defined in Eq. (4). The NFW profile parameters were optimised in the ranges 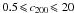 and
and 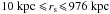 , where the scale radius upper limit is the outer radius of the surface brightness profile. The gas and total mass profiles are shown in Fig. 3; the inferred mass model parameters are listed in Table 2. The confidence levels for the NFW parameters are shown in the right panel of Fig. 3.
, where the scale radius upper limit is the outer radius of the surface brightness profile. The gas and total mass profiles are shown in Fig. 3; the inferred mass model parameters are listed in Table 2. The confidence levels for the NFW parameters are shown in the right panel of Fig. 3.
2.5. Systematic effects in the X-ray mass profile
In this section we will briefly assess if our X-ray mass estimate of Abell 611 can be affected by some analysis choices.
The choice of the X-ray background estimate, as discussed in Sect. 2.2, could have a non-negligible impact on the derived temperature profile, and consequently on the total mass measurement. Moreover, we verified whether considering the ICM metallicity as a free parameter in the spectral analysis can impact the X-ray mass estimate of Abell 611, since (as shown in Fig. 2) its inferred metallicity profile is quite irregular. We thus re-ran the spectral analysis by fixing the metallicity Z to the typical value of 0.3 Z⊙ (see e.g. Balestra et al. 2007); we then derived a new X-ray mass estimate adopting the spectral profiles obtained under the assumption of a constant metallicity.
Therefore we derived the mass of Abell 611 through the X-ray analysis:
- 1.
by estimating the X-ray background through the spectra extracted from the blank-sky dataset (opportunely reprocessed and re-normalised to be consistent with the source observations) in the same image regions used for the source spectra (case 1);
- 2.
by estimating the X-ray background from peripheral regions of the S3 chip in the source dataset (case 2);
- 3.
as in the previous case, but by fixing the metallicity Z to the value 0.3 Z⊙ (case 3).
The results obtained in the first two cases mutually agree within the 1σ range, even if the temperature profile derived in the latter case is systematically higher (see Fig. 4). Moreover, the best-fit parameters obtained in the third case (i.e. fixing the metallicity to 0.3 Z⊙: see case 3 in Table 2) agree with the values obtained by including the metallicity as a free parameter in the fitting: the choice of estimating or fixing the metallicity in the spectral analysis has a negligible impact on the derived cluster mass.
 |
Fig. 4 Comparison between the temperature profile determined by estimating the X-ray background through the blank-sky dataset (red dashed line) or using a local background component (black solid line). |
3. Strong lensing analysis
3.1. Imaging data
Our strong lensing analysis of Abell 611 benefits from the high-resolution imaging data obtained with the Hubble Space Telescope (HST), which allowed an unambiguous identification of several lensed systems. Abell 611 was observed with the Advanced Camera for Surveys (ACS) mounted on HST. We retrieved the ACS association data of Abell 611 from the Multimission Archive at STScI (MAST)3; the details of the HST observation of Abell 611 are summarised in Table 3.
Observation summary of the ACS/HST image used for the strong lensing analysis.
Best-fit parameters obtained by modelling the galaxy luminosity with the Sérsic profile (Sersic 1968).
The HST archival data for Abell 611 are already processed following the ACS pipeline and combined using the multidrizzle software (Koekemoer et al. 2002), with a final pixel scale of 0.05 arcsec; consequently no additional basic data reduction is necessary. But we used the softwares SExtractor (Bertin & Arnouts 1996), Scamp (Bertin 2006) and Swarp4 (Bertin et al. 2002), developed at the TERAPIX data reduction centre to derive the object catalogue for the Abell 611 HST imaging data, re-compute an astrometric solution and finally resample the image to derive a more accurate astrometric matching and to equalise the background level. The WCS coordinates reported in the present work are given with regard to the HST data and refer to the astrometric solution that we re-derived. Abell 611 was also observed during the Science Demonstration Time for the Blue Channel of the Large Binocular Camera (LBC), mounted at the Large Binocular Telescope (LBT) (located at the Mt. Graham International Observatory, Arizona), in good seeing conditions (FWHM of the seeing disc ~ 0.6 arcsec). The observations were made with the g-SLOAN and r filters; the total exposure times of the two coadded images are 3.6 ks and 0.9 ks, respectively. The LBT data were reduced according to the data reduction pipeline developed at the INAF/OAR centre5; the astrometric solution was derived with the ASTROMC software (Radovich et al. 2008). The final plate scale of the LBC images is 0.225 arcsec/pixel. Further details on the LBC/LBT data and on their reduction can be found in Paper I and in Giallongo et al. (2008); a comparison with the weak lensing mass estimate obtained in Paper I is presented in Sect. 5. The pseudo-colour image of Abell 611, obtained by combining the two LBT observations, is shown in Fig. 1. We relied on the g-SLOAN and r LBT observations both to verify whether the candidate conjugated images have similar colours, as it should be because of the intrinsic surface brightness conservation in gravitational lensing, and to select the cluster galaxies, in order to account for their mass in the lens modelling (see Sect. 3.5).
 |
Fig. 5 Overview of the strong lensing system of Abell 611. The knots that we used as constraints are marked as red crosses on the F606W ACS/HST image; enlarged images are shown in Fig. A.1. The magenta crosses indicate the perturber galaxies that were optimised singularly (see Case 6 in Table 5). The blue crosses correspond to a likely lensed system, identified by R09, which is not yet confirmed spectroscopically. We discuss our selection of the input images and its effect on the results in Sect. 3.2 and Sect. 3.7. The coordinates of all the systems are listed in Table A.1. The size of the field of view is ≃ 50 × 42.5 arcsec; the image was smoothed with a 2 pixel FWHM Gaussian filter (1 pixel = 0.05 arcsec). |
3.2. Strong lensing system
Abell 611 exhibits an outstanding strong lensing system. The most evident lensed feature is the giant tangential arc located at about 15.5 arcsec from the BCG centre (see Fig. 5). The curvature of the arc significantly changes in the proximity of some cluster galaxies, which locally perturb the critical lines and possibly the magnification and the multiplicity of the lensed images (Keeton 2003; Amara et al. 2006; Meneghetti et al. 2007b; Peirani et al. 2008; Puchwein & Hilbert 2009).
Richard et al. (2010) (hereafter R09) obtained the optical spectra of three surface brightness spots along the tangential arc, deriving a redshift estimate of z = 0.908 ± 0.005 for all of them. The arc appears to be formed by three merging images (A.1, A.2 and A.3 in Fig. 5), as in a typical cusp configuration.
Another confirmed lensed system is a fold system (hereafter called system B). Richard et al. (2010) reported the spectroscopic redshifts obtained for images B.2 and B.3 in Fig. 5, confirming that both of them are lensed images of a source at redshift z = 2.06 ± 0.02. The images labelled B.1 and B.4/B.5 can be safely considered as their counter-images. More specifically, the image B.5 appears to be an additional image produced by the position of the source B, lying totally or partially inside the caustic of the nearby galaxy (galaxy n.1 in Table 4). The g-r colours of all images of system B are similar (see Fig. 1).
A third lensed system was serendipitously identified by R09. They were able to derive the redshift zC.1 = 2.59 ± 0.01. of image C.1 (see Fig. 5) thanks to its strong Lyman-alpha emission. The image C.2 (see Fig. 5) was considered by R09 to be the counter-image of C.1. We agree with their identification and included both images as constraints.
Finally, the images labelled D.1 to D.4 in Fig. 5 were identified by R09 and by Newman et al. (2009) (hereafter N09; see Sect. 5 for more details about their recent study of Abell 611) as a lensed system, from the similarity of the morphologies of images D.1 and D.2. However, this system is not yet confirmed spectroscopically, so we decided not to include it in the strong lensing analysis, but we verified if and how the best-fitting results would be modified by considering it as an additional constraint (see Sect. 3.7).
3.3. Strong lensing modelling
We performed a parametric reconstruction of the mass distribution of Abell 611 with the Lenstool analysis software6 (Kneib et al. 1996; Jullo et al. 2007).
Our lens model consists of the superposition of a smooth cluster-scale potential and of galaxy-scale halos, associated with early-type cluster galaxies. The details of the cluster scale halo modelling will be discussed in Sect. 3.4, whereas we will discuss the galaxy-scale component in Sect. 3.5; finally the BCG modelling will be discussed separately in Sect. 3.6.
We constrained the lens model for Abell 611 by identifying in each image system, consisting of the multiple images of the same source, some elliptical regions or knots, which are likely to be multiple images of the same source area. The knots were identified through visual inspection of the ACS/HST observation by selecting the local peaks in the surface brightness, which are detectable in the strong lensing images of Abell 611. The surface brightness spots were then grouped into sets of conjugated knots by evaluating characteristics such as their relative positions with respect to the location of the critical lines and their brightness ratios.
We assumed an astrometric positional error of σpos = 0.2 arcsec. The adopted error affects the χ2 estimator computed in the source plane by Lenstool: 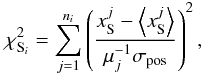 (7)where
(7)where 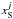 is the position of the source corresponding to the observed image j,
is the position of the source corresponding to the observed image j, 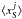 the barycenter of the ni source positions (corresponding to the ni conjugated images or knots of the image system i), and μj the magnification for the lensed image j; the final χ2 is then obtained by combining the individual
the barycenter of the ni source positions (corresponding to the ni conjugated images or knots of the image system i), and μj the magnification for the lensed image j; the final χ2 is then obtained by combining the individual 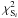 computed for each image system.
computed for each image system.
Between the several optimisation methods available in Lenstool we adopted the Bayesian optimisation method, with a convergence speed parameter equal to 0.4; this method, although slower than the other optimisation options, is less sensitive to local minima in the parameter space.
3.4. Cluster-scale component
We modelled the cluster scale component assuming an elliptical NFW profile as mass functional. The initial values for the centre, ellipticity e and position angle θ of the cluster halo were inferred from the BCG luminosity profile. The centre was allowed to vary ± 5 arsec, while the ellipticity and the position angle were optimised in the ranges 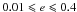 and
and 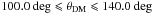 , respectively. The optimisation range of the cluster position angle is asymmetric in order to take into account the orientation of the X-ray isophotes. The optimisation ranges for the NFW profile parameters were c200 ∈ [0.5 − 14.0] and rs ∈ [50.0 − 800.0] kpc.
, respectively. The optimisation range of the cluster position angle is asymmetric in order to take into account the orientation of the X-ray isophotes. The optimisation ranges for the NFW profile parameters were c200 ∈ [0.5 − 14.0] and rs ∈ [50.0 − 800.0] kpc.
3.5. Galaxy-scale components
3.5.1. Selection of cluster galaxies
Several authors demonstrated that the inclusion of galaxy-scale halos in the lens modelling (in particular the galaxies whose projected position is within the region probed by strong lensing) is necessary to account for their effect on the lensing cross section and on the appearance of the lensed images that fall close to the perturbers (Natarajan et al. 2007; Amara et al. 2006; Meneghetti et al. 2003; Keeton 2003; Bradač et al. 2002). Although gravitational lensing is sensitive to all massive structures distributed along the line of sight, the main galactic mass budget is constituted of the massive early-type cluster galaxies; we will thus consider only this galactic population in our lens modelling.
The cluster members were selected through the characteristic cluster red-sequence, which allows us to identify the red early-type galaxies (Bell et al. 2004) and which is clearly detected in the colour-magnitude diagram (see Fig. 6). We will assume in the modelling that all the red-sequence galaxies belong to the cluster, and thus lie at its same redshift. The diagram was derived by extracting the object catalogues from the two LBT observations, using the SExtractor software in single and dual-image mode.
Even if the total exposure time of the red image is 0.9 ks, which is one fourth of the g-Sloan observation exposure time, the former filter allows an easier deblending of the redder cluster galaxies from the bluer lensed features. For this reason we used the r filter image for the detection of the sources in the dual-image mode. Moreover, even if the higher spatial resolution of ACS data would guarantee a more accurate deblending of contiguous sources, we decided to use the LBC data, which cover a wider area, to derive the cluster galaxy catalogue.
Only galaxies located within 100 arcsec ( ≃ 433 kpc) from the BCG centre and whose magnitude mR is lower than 23 were included in the lens modelling; a total of 97 galaxies were selected adopting these criteria. We added to the catalogue the galaxy located between system B.2 and B.3 in Fig. 5 that could affect the lensed images due to its position. The colour–magnitude diagram, the cluster red-sequence and the galaxies included in the lens modelling are shown in Fig. 6.
 |
Fig. 6 Colour–magnitude diagram of Abell 611. The black lines define the cluster red-sequence, while the blue filled squares indicate the red sequence galaxies lying within 100 arcsec from the BCG centre, which were included in the lens modelling. The black circle indicates the galaxy located between the lensed images B.1 and C.1 (see Fig. 5), which was included in the lens modelling for its position; the magnitude estimate derived for this galaxy from the LBT data is contaminated by the flux contribution of the nearby lensed feature (see text for details). |
3.5.2. Estimate of cluster galaxy parameters
We used the two-dimensional fitting algorithm GALFIT7 (Peng et al. 2002) to model and subtract the BCG as well as seven galaxies located within ≃ 17 arcsec from the BCG centre and with magnitude in the ACS F606W filter lower than 22 for a better identification of the multiple lensed images and to extract the BCG surface brightness profile. All galaxies were fitted simultaneously; the lensed features and the point-like sources were masked out. We modelled the galaxy light profile adopting both a Sérsic and a de Vaucouleurs profile. The Sérsic profile (Sersic 1968) has the functional form ![\begin{equation} \Sigma(r)=\Sigma_{\rm e} \exp{\left[-\kappa \left(\left({\frac{r}{r_{\rm e}}}\right)^{1/n} - 1\right)\right]}, \label{eq:sersic} \end{equation}](/articles/aa/full_html/2011/04/aa14120-10/aa14120-10-eq168.png) (8)where Σe is the pixel surface brightness at the effective radius re, the latter defined as the radius that encloses half of the total flux, and n is the Sérsic index. The de Vaucouleurs profile (de Vaucouleurs 1948) has the same analytical form as the Sérsic profile, but the index has the fixed value of 4.
(8)where Σe is the pixel surface brightness at the effective radius re, the latter defined as the radius that encloses half of the total flux, and n is the Sérsic index. The de Vaucouleurs profile (de Vaucouleurs 1948) has the same analytical form as the Sérsic profile, but the index has the fixed value of 4.
The galaxy models were convolved with the HST PSF image created using the TinyTim software 8 (Krist 1993). The reduced χ2 of the best-fitting models obtained adopting either the Sérsic or the de Vaucouleurs profile are similar, 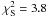 and
and 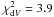 , respectively. However, the galaxy-subtracted image derived fitting the galaxy light profile with a de Vaucouleurs model shows larger residuals in the central area for some of the fitted galaxies, in particular for the galaxy labelled 1 in Table 4. For this reason we chose a Sérsic profile to model and subtract from the HST image the galaxies located within ≃ 17 arcsec from the BCG centre. The best-fitting parameters for the galaxy profiles are listed in Table 4; the corresponding galaxies are indicated in Fig. 5 with the same numbering sequence as in Table 4. Snapshots of the galaxy-subtracted HST image are shown in Fig. A.1.
, respectively. However, the galaxy-subtracted image derived fitting the galaxy light profile with a de Vaucouleurs model shows larger residuals in the central area for some of the fitted galaxies, in particular for the galaxy labelled 1 in Table 4. For this reason we chose a Sérsic profile to model and subtract from the HST image the galaxies located within ≃ 17 arcsec from the BCG centre. The best-fitting parameters for the galaxy profiles are listed in Table 4; the corresponding galaxies are indicated in Fig. 5 with the same numbering sequence as in Table 4. Snapshots of the galaxy-subtracted HST image are shown in Fig. A.1.
3.5.3. Mass profiles of cluster galaxies
In order to reduce the number of parameters to an adequate number we need to relate the total mass of cluster galaxies to an observable quantity; we will thus assume a scaling relation that links the mass of a galaxy to its luminosity. We will also assume that the morphological parameters of the underlying galaxy halo match the values inferred from the galaxy luminosity; this is a reasonable assumption because of the tight correlation between light and mass profile in early-type galaxies (see e.g. Gavazzi et al. 2007; Koopmans et al. 2006). For this reason, the galaxy centroid, ellipticity and position angle were fixed to the values obtained from the analysis performed with SExtractor of the r filter LBC images. However, the parameters derived from the LBC data for some of the galaxies close to the lensed images or to the BCG appear to be incorrect, because of an inefficient de-blending for the lower spatial resolution of LBC images. In these cases we adopted the parameters (namely centroid coordinates, position angle, major/minor axis length and magnitude) estimated through SExtractor from the HST F606W image.
We parameterised the mass of cluster galaxies with the dual pseudo isothermal elliptical mass distribution (hereafter dPIE, Kassiola & Kovner 1993; Kneib et al. 1996), following Jullo et al. (2007); Brainerd et al. (1996) and several other authors. The dPIE profile is given by 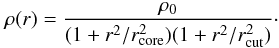 (9)The dPIE cut radius can be roughly considered as the half mass radius9. The two-dimensional surface mass density distribution is obtained by integrating Eq. (9) (see also Limousin et al. 2005):
(9)The dPIE cut radius can be roughly considered as the half mass radius9. The two-dimensional surface mass density distribution is obtained by integrating Eq. (9) (see also Limousin et al. 2005): 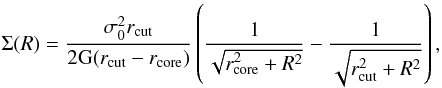 (10)where σ0 is a characteristic central velocity dispersion, which cannot be simply related to the measured velocity dispersion (Elíasdóttir et al. 2007).
(10)where σ0 is a characteristic central velocity dispersion, which cannot be simply related to the measured velocity dispersion (Elíasdóttir et al. 2007).
The free parameters in the dPIE model are thus the core radius rcore, the truncation radius rcut, and the characteristic velocity dispersion σ0. For elliptical galaxies, the Faber-Jackson relation (hereafter FJ, Faber & Jackson 1976) predicts that the central velocity dispersion σ0 is proportional to the galaxy luminosity L following the scaling relation  (11)where L ⋆ is a given arbitrary galaxy luminosity and
(11)where L ⋆ is a given arbitrary galaxy luminosity and 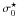 is its corresponding dPIE velocity dispersion; our reference magnitude is
is its corresponding dPIE velocity dispersion; our reference magnitude is 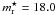 . We will assume the following scaling relations for the characteristic radii of the dPIE profile:
. We will assume the following scaling relations for the characteristic radii of the dPIE profile: 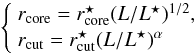 (12)here again
(12)here again 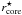 and
and 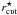 are the dPIE scale parameters for a L ⋆ galaxy. The exponent of the scaling relation for rcut determines how the mass scales with respect to the light distribution. If α = 0.5 the mass-to-light ratio (ML) of the galaxy is constant and independent of its luminosity, as usually assumed in strong and weak lensing analyses (Richard et al. 2007; Hoekstra et al. 2004). Assuming α = 0.8 one obtains that the mass-to-light ratio scales with luminosity according to ML ∝ L0.3 (Halkola et al. 2006; Natarajan & Kneib 1997). In this paper we will assume α = 0.5, but in Sect. 3.7 we will compare the results obtained under this assumption with those obtained by assuming α = 0.8. We did not test alternative scaling relations for the cluster galaxy core radius, since we did not identify any reliable constraint on the galaxy inner mass distribution.
are the dPIE scale parameters for a L ⋆ galaxy. The exponent of the scaling relation for rcut determines how the mass scales with respect to the light distribution. If α = 0.5 the mass-to-light ratio (ML) of the galaxy is constant and independent of its luminosity, as usually assumed in strong and weak lensing analyses (Richard et al. 2007; Hoekstra et al. 2004). Assuming α = 0.8 one obtains that the mass-to-light ratio scales with luminosity according to ML ∝ L0.3 (Halkola et al. 2006; Natarajan & Kneib 1997). In this paper we will assume α = 0.5, but in Sect. 3.7 we will compare the results obtained under this assumption with those obtained by assuming α = 0.8. We did not test alternative scaling relations for the cluster galaxy core radius, since we did not identify any reliable constraint on the galaxy inner mass distribution.
The galaxy parameters optimised in the lens modelling are the central velocity dispersion and the truncation radius, whereas the other dPIE parameters (ellipticity, position and orientation of the halo) were tied to the values inferred from the analysis of the galaxy light profile.
The normalisation for the core radius scaling was set to 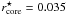 arcsec ≃ 0.15 kpc, while for the velocity dispersion normalisation
arcsec ≃ 0.15 kpc, while for the velocity dispersion normalisation 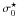 we adopted the uniform prior [120.0–200.0] km s-1. Following the relation between luminosity and velocity dispersion found by Bernardi et al. (2003), our reference magnitude corresponds to a velocity dispersion ≃ 170 km s-1 for an early-type galaxy. The prior
we adopted the uniform prior [120.0–200.0] km s-1. Following the relation between luminosity and velocity dispersion found by Bernardi et al. (2003), our reference magnitude corresponds to a velocity dispersion ≃ 170 km s-1 for an early-type galaxy. The prior ![\hbox{$\sigma_0^\star\in [120.0{-}200.0]$}](/articles/aa/full_html/2011/04/aa14120-10/aa14120-10-eq193.png) km s-1 adopts a conservative upper limit; the lower limit was decreased to 120.0 km s-1 to take into account the recent findings of Natarajan et al. (2009) about the difference in the dPIE velocity dispersion between cluster galaxies in the core or in the outer regions.
km s-1 adopts a conservative upper limit; the lower limit was decreased to 120.0 km s-1 to take into account the recent findings of Natarajan et al. (2009) about the difference in the dPIE velocity dispersion between cluster galaxies in the core or in the outer regions.
The truncation radius normalisation determines the steepness of the galaxy mass profile. A common and reasonable approach is to fix it to a likely value (see R09 and Limousin et al. 2009), since usually the strong lensing system does not provide enough constraints on the mass distribution of the small scale perturbers. However, the mass distribution of early-type galaxies in high-density environment is likely to be truncated compared to field galaxies with an equivalent luminosity (Halkola et al. 2007; Limousin et al. 2007; Natarajan et al. 2002). For this reason, the truncation of cluster galaxy halos could be different from one case to another.
Thanks to the peculiar lensing system of Abell 611, an estimate of the truncation radius normalisation will be derived in one dedicated tests (see Sect. 3.7). The perturbing galaxy labelled 1 in Fig. 5 was optimised singularly, since the strong constraints on its Einstein radius provided by the conjugate systems B.4/B.5 enable a reliable estimate of its mass distribution. Because however neither R09 or Newman et al. (2009) unlinked this galaxy from the cluster member catalogue, we ran a test to verify if and how this single perturber can affect the global test results.
3.6. Modelling of the BCG
The BCG itself was included in the lens modelling as a dPIE halo. However, although the BCG was parameterised with the same mass functional as the cluster members, its mass model refers only to its baryonic content, while for cluster galaxies what is actually modelled is the total mass. As pointed out in the work of Miralda-Escude (1995) (see also Limousin et al. 2008; Dubinski 1998; Mellier et al. 1993), the dark matter halo of the BCG is indistinguishable from the cluster halo in the lens modelling.
For this reason a direct comparison of the measured central velocity dispersion of the BCG to the fitted σ0,dPIE would lead to incorrect conclusions: the former is determined by the combined contribution of the dark and baryonic matter, while the latter is a fitting parameter referred to as a “stellar-only” BCG component.
The dPIE mass parameters – characteristic central velocity dispersion σ0,dPIE and truncation radius rcut – were optimised for the BCG in the ranges [100.0–350.0] km s-1 and [8.0–31.0] arcsec ( ≃ [34.6–134.2] kpc), respectively: these ranges take into account the results obtained through a strong lensing analysis by R09 and by N09, to allow a comparison with their results (see Sect. 5).
The degeneracy between the central baryonic mass budget and the dark matter content with regard to the strong lensing results is currently well established. It is still to be discussed whether the choice of the BCG mass profile can impact the derived cluster mass parameters. To assess this point, we ran a dedicated test adopting the Sérsic profile to parametrise the BCG mass. The Sérsic mass profile has the same functional form as Eq. (8), but the parameter Σe refers to the mass density at the effective radius re.
For the modelling of the BCG we adopted the morphological parameters derived from the two-dimensional fitting of the BCG luminosity profile obtained with Galfit, listed in Table 4. We optimised the Sérsic index within ± 10% of the best-fitting value, to take into account the measurement errors. After some preliminary tests, we chose as lower limit to the Σe optimisation range the value of 2 × 108 M⊙ kpc-2 to derive a total mass for the BCG similar to the mass derived when modelling the BCG as a dPIE profile, for a safer comparison between the results obtained in both cases (see the total projected mass maps and the surface mass density profiles shown in Fig. 7).
 |
Fig. 7 (Top Panels) Comparison between the projected mass maps obtained when modelling the BCG with a dPIE profile (left panel, case 1 in Table 5) or with a Sérsic profile (right panel, case 7 in Table 5). See Table 5 and the text for further details. (Bottom Panels) Comparison between the surface mass density profiles for the BCG halo (left panel) and the NFW cluster scale halo (right panel) derived when modelling the BCG with a dPIE profile (red solid line, case 1) or with a Sérsic profile (green dashed line, case 7). |
3.7. Strong lensing results
We present in this section the results of the parametric analysis of the strong lensing system in Abell 611. In order to assess the effect of the galaxy parameterisation on the best-fitting results for the cluster-scale halo we performed several tests, changing the manner of including the cluster galaxies.
Median values for the total mass parameters, obtained with the strong lensing analysis.
 |
Fig. 8 Scatter plots for the NFW parameters rs and c200 obtained for some representative cases. The numbering of the cases corresponds to the numbering in Table 5. The red point distribution marks the 3σ confidence level for the two parameters. The green stars indicate the best-fit values; the error-bars refer to the 1σ statistical uncertainty. We used the same knot systems as inputs and the same priors on the cluster halo mass distribution in all the six cases; the only differences were the modelling and the parameterisation of the cluster galaxies and of the BCG. The probability distribution in case 4 appears squeezed because it crushed on the lower limit for the BCG characteristic central velocity dispersion. The lens model results for the cases shown here are listed in Table 5. |
We list below the characteristics of the lens modelling for the cases presented in Table 5.
-
Case 1: both the reference truncation radius and the reference central velocity dispersion for the cluster–galaxy scaling relation were optimised in the ranges [4–12] arcsec and [120.0–200.0] km s-1, respectively. In this case, and when not otherwise stated, the mass parameters of galaxy n. 1 in Fig. 5 were individually optimised (the optimization ranges were rcut ∈ [0.5–8.0] arcsec and σ0 ∈ [90.0–190.0] km s-1) and the exponent α in Eq. (12) was set equal to 0.5.
-
Case 2: the reference central velocity dispersion was optimised, whereas the reference truncation radius was fixed to the value of
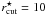 arcsec. The exponent α in
Eq. (12) was assumed to be equal
to 0.8 (therefore the Mass to Light ratio ML is ∝ 0.3).
arcsec. The exponent α in
Eq. (12) was assumed to be equal
to 0.8 (therefore the Mass to Light ratio ML is ∝ 0.3). -
Case 3: as in case 2, but we assumed that α = 0.5 (therefore ML is constant and independent of the galaxy luminosity).
-
Case 4: a constant ML scaling relation was assumed for all cluster galaxies. This is the only case in which the galaxy n. 1 in Fig. 5 was not individually optimised.
-
Case 5: we adopted the same lens model as in case 3, but we included as constraint the candidate lens system individuated by R09 and by N09, labelled D in Fig. 5 and in Table A.1 in the Appendix.
-
Case 6: a constant ML scaling relation was adopted for all the cluster galaxies, with the exception of those that can be tested through the strong lensing analysis, for their direct effect on some lensed images (galaxies 1 to 6 in Fig. 5), which were individually optimised.
-
Case 7: the same lens model as in case 1 was assumed, but the BCG was modelled with an elliptical Sérsic profile.
The results of the strong lensing analysis of Abell 611 for the aforementioned cases are listed in Table 5. The critical and the caustic lines and the images predicted in all tested cases are shown in the Fig. B.1 in the Appendix. Evidently depending on the different lens modelling the results on the cluster total mass can change by up to 15%, so the parameterisation of the perturber galaxies and of the BCG has a non-negligible impact on the strong lensing results; the degeneracy between cluster and galaxy mass parameters is shown in Fig. 8. In particular, a strong degeneracy is found between the fiducial BCG central velocity dispersion and the cluster concentration/total mass (see the top panels in Fig. 9).
It is remarkable that the resulting NFW cluster parameters depend not only on the BCG baryonic mass, but also on the BCG mass profile. In case 1 and in case 7 we show the results obtained by modelling the BCG with a dPIE or with a Sérsic profile, respectively; the corresponding projected mass maps and surface mass density profiles are shown in Fig. 7. The BCG mass derived in both cases is similar, but the inferred cluster parameters are significantly different. In particular, the cluster total mass is larger and the NFW concentration parameter lower when modelling the BCG with a Sérsic profile. This result can be explained by considering that, in this case, the surface mass density of the best-fitting Sérsic profile in the BCG central region is larger compared with the best-fitting dPIE profile (see the bottom left panel in Fig. 7). The inferred concentration for the cluster scale halo in the latter case will thus be higher because of the degeneracy between the cluster halo and the BCG mass with respect to the lens total mass, which is the quantity constrained by the gravitational lensing.
However, the estimates of the total mass in the central regions (where the strong lensing constraints are found) derived in the different cases mutually agree, (see the discussion in Sect. 4); the modelling of the galactic component appears to have a negligible impact on the total mass results in the central region. Conversely, the differences among several of the test cases arise when the cluster mass is extrapolated outside the region that is accessible through the strong lensing analysis.
This is another evidence that the modelling of the BCG stellar mass can directly affect the cluster total mass results: in order to obtain reliable mass estimates through a parametric strong lensing analysis, it is crucial to break the degeneracy between the different lens components.
 |
Fig. 9 Scatter plots of cluster-halo parameters (c200 and Mtot) versus parameters of the modelling of either the BCG or the perturber galaxy n.1 (hereafter P1, see text for details). Here we show the posterior probability distributions obtained in a representative case (case 1 in Table 5). The plotted parameters are: 1. the NFW concentration parameter c200 versus the BCG fiducial central velocity dispersion σ0,BCG (top left panel); 2. the cluster halo mass Mtot versus σ0,BCGtop right panel); 3. the NFW concentration parameter c200 versus the fiducial central velocity dispersion σ0,P1 of the galaxy P1 (bottom left panel); 4. the cluster halo mass Mtot versus σ0,P1 (bottom right panel). The contours show the 68%, 95% and 99% confidence levels. The colour code refers to the value of the χ2 estimator. |
Despite the difference in the best-fitting results, all models return probability regions in the parameter space that are marginally consistent with each other. As previously found for the X-ray analysis, the strong lensing results appears relatively stable against possible systematic errors, which in this case are mainly constituted by modelling uncertainties.
As stated before, the perturber galaxy n.1 (see Fig. 5) was individually optimised in all the tests that we ran, except in case 4, due to the tight constraint on its mass distribution provided by the conjugated images B.4 and B.5. We found a mild degeneracy between the mass of this galaxy, the mass of the stellar content of the BCG, and the concentration of the NFW halo, as expected given the proximity of this perturber to the BCG (see the bottom panels in Fig. 9).
 |
Fig. 10 Median values of the dPIE truncation radius rcut vs. the characteristic dPIE central velocity dispersion σ0 for the galaxies that perturb the strong lensing system of Abell 611. The red triangles show the results obtained linking the galaxy parameters to the same scaling relation in the lens modelling (Case 4 in Table 5), while the blue stars represent the results obtained optimising the galaxies individually (Case 6 in Table 5). The grey dashed lines show the iso-density contours. The error bars indicate the 1σ uncertainty, while the cyan boxes indicate the 3σ confidence region for the results which refer to Case 4. |
Moreover, in case 6 we optimised singularly the galaxies whose mass distribution can be constrained through the strong lensing effect alone. As it is evident from Fig. 10, optimising in wide ranges the dPIE parameters for these perturber galaxies returns, as expected, large uncertainties in the mass parameters. However, for some perturbers the parameters inferred through an individual optimisation appear to be incongruous with those predicted assuming the parameter scaling derived from the Faber-Jackson relation. It is reasonable to question whether neglecting the scatter associated to the galaxy parameter scaling relations in the strong lensing analysis could bias the inferred results.
It seems likely that in most cases this bias, if any, can be safely negligible, as it is obvious by comparing case 1 to case 6. Nonetheless, in the presence of galaxies that strongly affect the strong lensing features, the biasing effect on the final results could be more significant (again, this is the case of the perturber galaxy labelled n.1 in this work, as can be seen by comparing case 1 to case 4).
Regarding the strong lensing systems, all our models predict that the tangential arc (system A) originates by the large deformation of a single source located on a “naked cusp”, i.e. a tangential caustic extending outside the radial caustic (Kormann et al. 1994; Bartelmann & Loeb 1998; Rusin & Ma 2001). Naked cusps are a quite rare caustic configuration which mainly occurrs in highly elliptical lens systems whose surface density is only moderately above the critical surface density required for the production of multiple images (“marginal lenses”, Blandford & Kochanek 1987; Bartelmann 2000), with a few naked cusps detected so far (Lewis et al. 2002; Oguri et al. 2008). Sources placed within the exposed tangential caustic form only three magnified images on the same side of the lens: this explains why the tangential arc in Abell 611 has no counter-image.
The position and the shape of the observed images are well reproduced by all our models, as is obvious from the low scatter both in the image and in the source plane resulting from the best-fit models: all tests returned low values of the reduced χ2 (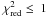 ) and of the image plane root-mean-square (rmsi ≤ 0.5 arcsec) (see also the fitting results for a representative case – Case 1 – listed in Table 6).
) and of the image plane root-mean-square (rmsi ≤ 0.5 arcsec) (see also the fitting results for a representative case – Case 1 – listed in Table 6).
Fitting results of the source-plane optimisation.
In particular, the lens models of cases 4 and 7 (see Table 5) predict a central image for the system B in a position almost coincident with a radial-oriented feature lying close to the centre of the BCG (see Fig. 11 and the predicted central image in Fig. B.1; this central image was also indentified and interpreted by N09). However, since the detection of this feature is not certain, we did not include it as an additional constraint.
 |
Fig. 11 ACS/HST snapshot of a radial-oriented feature, likely a central counter-image corresponding to System B; the BCG is visible [subtracted] in the left [right] panel. |
Regarding the third system C, our identification of the positive parity counter-image, which follows R09, appears reliable owing to the very low scatter resulting for this system. Our models predict three additional counter-images: two of them should be located close to the BCG and to the galaxy n.1, and are predicted to be demagnified with respect to the identified image, so they are likely not detectable. A negative parity counter-image is predicted at about 2–3 arcsec (depending on the different lens models) above the observed one. In that area there are no evident counter-images, but a faint one, identified with SExtractor (S/N ≃ 3.9), whose position could be marginally compatible with the location of the predicted image. The flux ratio derived when modelling the BCG as a dPIE halo does not match the observed one well, while the images predicted when modelling the BCG with a Sérsic profile follow the observed flux ratio more closely (see Fig. 12), because of the difference in the inferred mass for the galactic perturbers. This evidence would seem to favour the modelling of the BCG with a Sérsic profile over the dPIE profile: but we aim to highlight that other explanations could be possible to the observed mismatch in the flux ratios for the images of the third system. For example, the effect of unresolved substructures along the line of sight would cause the dimming of the negative-parity image in cusp systems (Keeton 2003) (see also Oguri et al. 2008). Another explanation could be the misidentification of the counter-image C.2, which would cause its predicted magnification to be incorrect.
The candidate system D looks plausible considering the low scatter in the observed and predicted positions. The redshift estimates of the four knot systems are marginally consistent. However, the results of the cluster mass parameters are not significantly changed by including this system.
4. Comparison between X-ray and strong lensing results
We will compare here the results obtained with the strong lensing and the X-ray analyses for the galaxy cluster Abell 611. The left panel in Fig. 13 shows the probability distributions of the NFW profile parameters obtained with both analyses, while the right panel compares the corresponding projected mass profiles. For the strong lensing analysis we show the 3σ region, marginalised over the other fit parameters, derived in case 1 and in case 7 of Table 5. The best-fit values for the NFW profile parameters and for the corresponding mass are listed in Table 7.
 |
Fig. 12 Comparison between the ACS/HST F606W observation (left panel), smoothed with a 3 FWHM pixel Gaussian filter for a better visualisation of the faint lensed image C.1 (marked with a white circle), and the reconstructed image systems predicted from the lens models in case 1 ((middle panel): in this case the BCG was modelled as a dPIE potential) and case 7 ((right panel): the BCG was parametrised with a Sérsic profile – see Table 5). The white circles in the middle and right panels mark the centre of the predicted counter-images. The black circle in the left panel indicates a candidate counter-image of C.1, indentified with SExtractor. The three images are WCS-aligned; the flux scale of the second and the third panel is the same. |
To unfold this issue, higher resolution observations of the Sunyaev-Zel’dovich effect measurements towards this cluster would play a crucial role, because they would allow us with the X-ray data to estimate the projected axis ratio along the line of sight. Obviously the best-fit values for the scale radius and the concentration parameter derived with the X-ray and the strong lensing analyses are consistent within a 2 − σ range; however, the results derived from the strong lensing analysis in case 7 better agree with the X-ray estimates. In particular, the strong lensing mass estimates for Abell 611 are lower than the mass derived through our X-ray analysis which is lower by up to a factor of two.
Comparison of the mass results obtained with the X-ray and the strong lensing analyses.
This result is somehow surprising, since so far the discrepancies found between strong lensing and X-ray mass estimates have the opposite trend, with the smaller X-ray masses (see e.g. Richard et al. 2009; Peng et al. 2009; Gitti et al. 2007; Medezinski et al. 2007). However, the mass estimates for Abell 611 derived in three representative cases agree very well in the region where the strong lensing constraints are found (approximately R ≤ 100 kpc), as is obvious from the right panel of Fig. 13. On the other hand, the strong lensing mass is smaller than the X-ray one when extrapolating the mass profile in the cluster peripheral regions.
This result confirms that strong lensing provides a robust estimate of the total mass of the cluster (DM plus baryonic component) in the central region; it moreover suggests that the disagreement between the X-ray and the strong lensing masses can be related to the incorrect estimate of the total baryonic mass budget (for example, the reader can compare the results obtained in case 4 and in case 1 in Table 5) or of its radial profile, because the resulting cluster mass distribution will be incorrectly steepened (with a higher concentration parameter and a smaller scale radius) to account for the missing baryonic mass component.
 |
Fig. 13 (Left panel) Comparison of the NFW parameter probability distribution obtained with our X-ray and strong lensing analyses. The X-ray and the strong lensing contours show the 3-σ confidence level (the strong lensing results were marginalised over the other fit parameters). The X-ray contours were obtained deriving the X-ray background from the blank-sky data-set, while the strong lensing result refers to case 1 and to case 7 in Table 5. For an easier comparison we overplotted some previous recent results. We show in the plot the results obtained through a strong lensing analysis by Richard et al. (2010) (label SL-R09), through a weak and a strong lensing analysis by Newman et al. (2009) (labels WL-N09 and SL-N09, respectively) and in Paper I through a weak lensing analysis (label WL-Ro09; the results shown here were obtained by adopting a spherical NFW profile; the shear catalogue in this case was derived through the shapelet decomposition technique). The bars show the 1-σ errors. (Top right panel) Projected 2D mass profiles obtained with the X-ray (red solid line) and with the strong lensing analyses when modelling the BCG as a dPIE (green dashed line) or a Sérsic halo (blue dashed line). The vertical lines mark the spatial range of the strong lensing (black dotted line) and X-ray (red solid line) constraints. The X-ray (strong lensing) profile was derived by measuring the enclosed mass in cylinders centred on the X-ray emission centroid [BCG]. The distance between the X-ray centroid and the BCG centre is ≃ 1 ± 1.5 arcsec. The mass map derived from the strong lensing analysis was extrapolated up to a radius of 200 arcsec from the mass measurements obtained in the central regions. The statistical errors on the strong lensing profiles were determined computing the standard deviation from 300 mass map realizations. As a comparison, we report the estimates of the projected total mass within 250 kpc obtained by Richard et al. (2010) through a strong lensing analysis (label SL-R09, marked with a filled black circle) and through an X-ray analysis by Sanderson et al. (2009a) (label X-ray-S09, marked with a filled orange square). (Bottom right panel) Ratios between the X-ray and the strong lensing projected mass estimates; the strong lensing estimates were obtained by modelling the BCG through a dPIE (red solid line) or a Sérsic (blue dotted line) profile. |
While this possible source of systematic errors in the strong lensing mass estimate was already observed in other studies, the dependence of the derived cluster total mass on the assumed BCG mass profile is a new evidence in the strong lensing analysis of real galaxy clusters, which was already observed through the analysis of simulated galaxy clusters by Meneghetti et al. (2010). A similar but less significant effect is related to the scaling of the ML relation, which is assumed to derive the cluster galaxy masses, as is evident by comparing case 2 and case 3 in Table 5.
Another explanation of the X-ray/strong lensing mass mismatch for Abell 611 could be an oblate-like cluster geometry: as demonstrated in Gavazzi (2005) (see also Morandi et al. 2011, 2010; Corless et al. 2009; Meneghetti et al. 2010), the orientation of the halo along the plane of the sky would cause the lensing mass to under-estimate the true one. On the contrary, the X-ray derived masses are the most stable against possible projection effects because of the cluster asphericity (see again Gavazzi 2005).
5. Comparison with previous studies
A combined analysis of X-ray data and of Sunyaev-Zel’dovich effect measurements was performed by De Filippis et al. (2005) to recover the three-dimensional potential distribution for a sample of 25 massive clusters. They estimated that the elongation of Abell 611 along the line of sight is elos ≃ 1.05 ± 0.37, while its maximum axial ratio is ≃ 1.19 ± 0.27, so neither an oblate nor a prolate orientation of Abell 611 can be excluded.
Morandi et al. (2007) and Morandi & Ettori (2007) analysed Chandra X-ray data for a sample of 24 X-ray luminous clusters to derive the scaling relations between their X-ray properties and the Sunyaev-Zel’dovich effect measurements (in Morandi et al. 2007) and the profiles and the scaling properties of their gas entropy (in Morandi & Ettori 2007). They analysed the same Chandra observation of Abell 611 as we (see Table 1 for more details on the Chandra dataset) by adopting a technique similar to the method followed here. Their estimate of the total mass of Abell 611 is M500 = (5.18 ± 2.15) × 1014 M⊙ at the radius R500 = (1.1 ± 0.2) Mpc which agrees very well with our X-ray result of M500 = (6.77 ± 0.84) × 1014 M⊙ at the radius R500 = (1.2 ± 0.1) Mpc.
A very recent re-analysis of the Chandra data for Abell 611 is presented in Sanderson et al. (2009a) (see also Sanderson & Ponman 2010; Sanderson et al. 2009b). The mass estimate for Abell 611 at R500 = (1.3 ± 0.1) Mpc derived in their work is M500 = (9.23 ± 2.8) × 1014 M⊙, which again agrees well with our results.
An analysis of the weak gravitational lensing effect induced by this cluster was performed by Dahle (2006) through observations in the I and V bands obtained with the University of Hawaii Telescope and the Nordic Optical Telescope. Assuming an NFW profile to model the radial density distribution and a concentration parameter as predicted by Bullock et al. (2001), they obtained a mass value of M180 = (5.21 ± 3.47) × 1014 M⊙ within R180. The same data were reanalysed by Pedersen & Dahle (2007), who derived an estimate of M500 = (3.83 ± 2.89) × 1014 M⊙.
A very recent study of the weak lensing effect in Abell 611 is presented in Paper I. This work takes advantage of the imaging data obtained through the Large Binocular Camera (LBC) mounted at the Large Binocular Telescope (LBT), which were presented in Sect. 3. Their weak lensing analysis benefits by the wide field of view of the LBC ( ≃ 23 arcmin × 25 arcmin) and two different methods of extracting the shear signal, the well known KSB approach (Kaiser et al. 1995) and the shapelet decomposition technique, proposed more recently by Refregier (2003); Refregier & Bacon (2003) and Massey & Refregier (2005). Their model-indepent estimates of the total projected mass within a radius of ≃ 1.5 Mpc are Mprojec, WL, 1 = (7.7 ± 3.3) × 1014 M⊙ and Mprojec, WL, 2 = (8.4 ± 3.8) × 1014 M⊙ when adopting the KSB or the shapelet method, respectively. These results agree very well with our X-ray mass estimate, i.e. Mprojec, X - ray = [9.8 ± 1.4] × 1014 M⊙ at the radius R ≃ 1.5 Mpc, while our strong lensing mass estimate is lower (see the discussion in the previous section and the right panel of Fig. 13).
They also derived a model-dependent estimate by assuming that the total mass profile of the cluster can be parameterised through the NFW profile. The best-fitting results were a total cluster mass of ![\hbox{$ M_{200} = 5.6^{+4.7}_{-2.7} [5.9^{+2.2}_{-1.7}] \times 10^{14}\ M_{\odot}$}](/articles/aa/full_html/2011/04/aa14120-10/aa14120-10-eq362.png) , at the radius
, at the radius ![\hbox{$ R_{200} = 1.54^{+0.34}_{-0.31} \ [1.57^{+0.18}_{-0.17}]$}](/articles/aa/full_html/2011/04/aa14120-10/aa14120-10-eq363.png) Mpc, and a concentration parameter of
Mpc, and a concentration parameter of ![\hbox{$c_{200} = 3.13^{+4.67}_{-1.74} [2.95^{+1.80}_{-1.05}]$}](/articles/aa/full_html/2011/04/aa14120-10/aa14120-10-eq364.png) when adopting the KSB (Shapelets) approach.
when adopting the KSB (Shapelets) approach.
For an easier comparison, the best-fitting values of the cluster-scale NFW profile derived in the former case are overplotted in Fig. 13. These results seems to agree better with our X-ray mass results as regards the strong lensing estimates.
Recently, Richard et al. (2010) (R09) published the results of a strong lensing analysis performed on a subsample of 10 massive clusters extracted from the Local Cluster Substructure Survey (LoCuSS), which included Abell 611.
Another study dedicated to the analysis of the matter distribution in Abell 611 was recently performed by Newman et al. (2009) (N09). They reconstructed the cluster mass distribution by combining weak and strong lensing analyses and dynamical data, taking advantage of Subaru, HST, and Keck data, respectively. The strong lensing parametric analyses of both R09 and N09 were performed with the software Lenstool. We overplotted their results for an NFW profile fit in Fig. 13.
Richard et al. (2010) considered as constraints to the lens optimisation both the confirmed (labelled A, B, and C in our notation) and the candidate (labelled D) systems (as in the case 5 in Table 5), but including only one set of conjugated knots for the tangential arc (system A in our notation). Their results are consistent with our strong lensing findings, which are obtained modelling the BCG as a dPIE halo within the 3σ confidence range, while a larger mismatch is found with our X-ray results and with the strong lensing results in case 7. The discussion in Sect. 4 could likely also be applied to a comparison between the strong lensing results of R09 and the X-ray and weak lensing mass estimates of Abell 611.
Regarding the results obtained by N09 through the fit of a NFW profile to the strong lensing data, their best-fitting values show an even higher discrepancy with our mass results: for example, they derive a concentration parameter significantly higher than the concentration derived from both our X-ray and our strong lensing analyses. An extensive comparison of our results with the findings of R09 and N09 is beyond the aims of this comparative section. One of the differences in the strong lensing modelling that could have an impact on the final results is the number of adopted constraints, because N09 included only the brightest knots of the systems A, B, and D in their strong lensing analysis. It could be that using as input all or most of the constraints that can be derived from the morphology of the lensed images in Abell 611 could decrease the discrepancy between their results and ours. Indeed, it is apparent that their results follow the degeneracies expected in the strong lensing parameter estimates between the cluster halo parameters and the central stellar component, which can be reduced by forcing the best-fitting lens model to reproduce realistic reconstructions of the observed lensed images. Moreover, it is interesting that the SL best-fit parameters reported in N09 agree better with the results we obtained by linking all the perturber cluster galaxies to the same relation (case 4 in Table 5). This evidence reinforces our conclusions about the significant impact that the modelling of the galactic component can have in the strong lensing analysis of Abell 611, and it could suggest that adopting the same scaling relation for the cluster galaxies in this case could be inadequate.
The weak lensing results of N09, instead, agree within the 3σ errors with both our strong lensing and X-ray mass estimates.
6. Conclusions and discussion
We presented new mass estimates for the relaxed cluster Abell 611, derived through the analysis of the cluster X-ray emission and of its exceptional strong lensing system. We performed a non-parametric reconstruction of the gas density and temperature profile through the only Chandra observation available to date. The cluster total mass was then estimated adopting the NFW profile as mass functional, under the assumptions of spherical symmetry and of hydrostatic equilibrium.
Our X-ray estimates of the cluster total mass are M200 = 9.32 ± 1.39 × 1014 M⊙ and M200 = 11.11 ± 2.06 × 1014 M⊙ when deriving the X-ray background through the blank-field observations or through the source dataset, respectively, thus demonstrating the effect of the X-ray background treatment on the cluster mass estimate. The inclusion of the metallicity as free parameter in the spectral fitting was found to have a negligible impact on the cluster mass results.
We reconstructed the projected mass distribution in the central region of Abell 611 through a parametric analysis of its remarkable strong lensing system, using the publicly available software Lenstool. We used as constraints to the lens optimisation a detailed system of conjugated lensed images, indentifying 14 sets of knots in three different lensed systems. We adopted an elliptical NFW profile to parametrise the smooth cluster halo; moreover we added the small-scale perturbers constituted by the cluster galaxies by adopting a scaling relation that links their total mass to their luminosity. We ran several tests to verify if and how the strong lensing cluster mass estimate is dependent on the modelling of the galactic component, in particular on the distribution of the BCG baryonic mass component.
We found that the extrapolated strong lensing mass for Abell 611 is
-
moderately sensitive to the mass modelling of the galaxy-scaleperturbers that determine the peculiar characteristics of thestrong lensing system in Abell 611; indeed, weobtained that the different cluster galaxy parametrisations caninduce a scatter of up to 10% on the total mass estimate (when extrapolating the SL mass up to R200) with respect to the mean value (comparing Cases 1 to 6 in Table 5);
-
more significantly affected by the inferred BCG baryonic mass budget (because of the degeneracy between the cluster halo mass and the BCG baryonic mass) and by the assumed mass profile for the BCG baryonic halo. The deviation of the extrapolated total mass with respect to the mean value can be as high as 40% when adopting different mass profiles for the BCG stellar mass distribution (comparing cases 1 to 7 in Table 5).
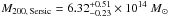 , when assuming the Sérsic profile as the BCG mass functional. The baryonic BCG mass inferred in both cases is similar, and both estimates are dependent on the optimisation limits imposed to the BCG mass parameters.
, when assuming the Sérsic profile as the BCG mass functional. The baryonic BCG mass inferred in both cases is similar, and both estimates are dependent on the optimisation limits imposed to the BCG mass parameters.
Our X-ray and strong lensing mass estimates agree well in the central regions, where the total projected mass can actually be constrained through the strong lensing analysis, while we find a significant difference between the X-ray mass and the extrapolated SL mass in the cluster outer region. This result suggests that the observed mismatch between the X-ray and the strong lensing mass could be caused by the incorrect estimate of the BCG stellar mass content or of the total mass of cluster galaxies in the central regions, because gravitational lensing alone cannot separate the mass of the different lens components.
However, even with these caveats in the interpretation of the results, the X-ray and strong lensing mass estimates for Abell 611 in the most opportune cases are consistent within the 3σ error range. These findings support the hypothesis that taking into account the possible sources of errors and deepening our knowledge of the current limitations of the X-ray and strong lensing analyses, both techniques return robust results. Their reliability can be increased even more by extending the detailed analysis of possible systematic biases affecting the mass estimates to other appropriate objects, i.e. massive, relaxed galaxy clusters like Abell 611.
See the CIAO analysis guides for the data reduction: cxc.harvard.edu/ciao/guides/.
For a complete discussion on this topic, see cxc.harvard.edu/cal/Acis/Cal_prods/vfbkgrnd/index.html.
The software SExtractor, Scamp and Swarp can be found at the url: astromatic.iap.fr/software/sextractor, astromatic.iap.fr/software/scamp and astromatic.iap.fr/software/swarp, respectively.
The Lenstool software package is available at www.oamp.fr/cosmology/lenstool.
The GALFIT software is publicly available at the url users.obs.carnegiescience.edu/peng/work/galfit/galfit.html.
The TinyTim software is available at the url www.stsci.edu/software/tinytim/tinytim.html.
The cut radius corresponds to the 3-D half mass radius for a null core radius (Elíasdóttir et al. 2007).
Acknowledgments
These results are based on observations made with the NASA/ESA Hubble Space telescope, with the Chandra X-ray Observatory and with the Large Binocular Telescope. We thank the anonymous referee for carefully reading the article, and for useful comments and suggestions that improved the presentation of our results. We thank Jean Paul Kneib and the Lenstool developers for making their lensing software public. A.D. acknowledges the support of European Association for Research in Astronomy (MEST-CT-2004-504604 Marie Curie – EARA EST fellowship). A.D., S.E. and M.M. acknowledge the financial contribution from contracts ASI-INAF I/023/05/0, I/088/06/0 and I/016/07/0. L.F. and M.R. acknowledge the support of the European Commission Programme 6-th framework, Marie Curie Training and Research Network “DUEL”, contract number MRTN-CT-2006-036133. LF is partly supported by the Chinese National Science Foundation Nos. 10878003 & 10778725, 973 Program No. 2007CB 815402, Shanghai Science Foundations and Leading Academic Discipline Project of Shanghai Normal University (DZL805).
References
- Allen, S. W. 1998, MNRAS, 296, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Amara, A., Metcalf, R. B., Cox, T. J., & Ostriker, J. P. 2006, MNRAS, 367, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M. 2000, A&A, 357, 51 [NASA ADS] [Google Scholar]
- Bartelmann, M., & Loeb, A. 1998, ApJ, 503, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Sheth, R. K., Annis, J., et al. 2003, AJ, 125, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, ed. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, ed. D. A. Bohlender, D. Durand, & T. H. Handley, ASP Conf. Ser., 281, 228 [Google Scholar]
- Biviano, A., & Poggianti, B. M. 2009, A&A, 501, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Kochanek, C. S. 1987, ApJ, 321, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Schneider, P., Steinmetz, M., et al. 2002, A&A, 388, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradač, M., Schrabback, T., Erben, T., et al. 2008, ApJ, 681, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Buote, D. A. 2000, ApJ, 539, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., King, L. J., & Clowe, D. 2009, MNRAS, 393, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Dahle, H. 2006, ApJ, 653, 954 [NASA ADS] [CrossRef] [Google Scholar]
- De Filippis, E., Sereno, M., Bautz, M. W., & Longo, G. 2005, ApJ, 625, 108 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Ann. d’Astrophys., 11, 247 [Google Scholar]
- Diaferio, A., Geller, M. J., & Rines, K. J. 2005, ApJ, 628, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dubinski, J. 1998, ApJ, 502, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007 [arXiv:0710.5636] [Google Scholar]
- Ettori, S., & Lombardi, M. 2003, A&A, 398, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., De Grandi, S., & Molendi, S. 2002, A&A, 391, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Tozzi, P., & Rosati, P. 2003, A&A, 398, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R. 2005, A&A, 443, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Ragazzoni, R., Grazian, A., et al. 2008, A&A, 482, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Piffaretti, R., & Schindler, S. 2007, A&A, 472, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grego, L., Carlstrom, J. E., Reese, E. D., et al. 2001, ApJ, 552, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Seitz, S., & Pannella, M. 2006, MNRAS, 372, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Seitz, S., & Pannella, M. 2007, ApJ, 656, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Hildebrandt, H., Schrabback, T., et al. 2008, A&A, 481, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hincks, A. D., Acquaviva, V., Ade, P., et al. 2010, ApJS, 191, 423 [Google Scholar]
- Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kaastra, J. S., & Mewe, R. 1993, A&AS, 97, 443 [NASA ADS] [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2003, ApJ, 584, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Fruchter, A. S., Hook, R. N., & Hack, W. 2002, in The 2002 HST Calibration Workshop: Hubble after the Installation of the ACS and the NICMOS Cooling System, ed. S. Arribas, A. Koekemoer, & B. Whitmore, 337 [Google Scholar]
- Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
- Kriss, G. A., Cioffi, D. F., & Canizares, C. R. 1983, ApJ, 272, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 536 [Google Scholar]
- Lewis, G. F., Carilli, C., Papadopoulos, P., & Ivison, R. J. 2002, MNRAS, 330, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Kneib, J.-P., & Natarajan, P. 2005, MNRAS, 356, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Kneib, J. P., Bardeau, S., et al. 2007, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Richard, J., Kneib, J., et al. 2008, A&A, 489, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Jullo, E., Richard, J., et al. 2010, A&A, 524, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markevitch, M., Bautz, M. W., Biller, B., et al. 2003, ApJ, 583, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., & Refregier, A. 2005, MNRAS, 363, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Medezinski, E., Broadhurst, T., Umetsu, K., et al. 2007, ApJ, 663, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Mellier, Y., Fort, B., & Kneib, J. 1993, ApJ, 407, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bartelmann, M., & Moscardini, L. 2003, MNRAS, 346, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Argazzi, R., Pace, F., et al. 2007a, A&A, 461, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Bartelmann, M., Jenkins, A., & Frenk, C. 2007b, MNRAS, 381, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [Google Scholar]
- Miralda-Escude, J. 1995, ApJ, 438, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., & Ettori, S. 2007, MNRAS, 380, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Ettori, S., & Moscardini, L. 2007, MNRAS, 379, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Pedersen, K., & Limousin, M. 2010, ApJ, 713, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Pedersen, K., & Limousin, M. 2011, ApJ, 729, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., & Kneib, J.-P. 1997, MNRAS, 287, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J.-P., & Smail, I. 2002, ApJ, 580, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., De Lucia, G., & Springel, V. 2007, MNRAS, 376, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J., Smail, I., et al. 2009, ApJ, 693, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2009, ApJ, 706, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Ofek, E. O., Inada, N., et al. 2008, ApJ, 676, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, N., Pointecouteau, E., Hattori, M., & Mitsuda, K. 2004, ApJ, 601, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Pedersen, K., & Dahle, H. 2007, ApJ, 667, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Peirani, S., Alard, C., Pichon, C., Gavazzi, R., & Aubert, D. 2008, MNRAS, 390, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, E., Andersson, K., Bautz, M. W., & Garmire, G. P. 2009, ApJ, 701, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., & Hilbert, S. 2009, MNRAS, 398, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Radovich, M., Puddu, E., Romano, A., Grado, A., & Getman, F. 2008, A&A, 487, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasia, E., Ettori, S., Moscardini, L., et al. 2006, MNRAS, 369, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Refregier, A. 2003, MNRAS, 338, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Refregier, A., & Bacon, D. 2003, MNRAS, 338, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Kneib, J., Jullo, E., et al. 2007, ApJ, 662, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Kneib, J., Limousin, M., Edge, A., & Jullo, E. 2009, MNRAS, L365 [Google Scholar]
- Richard, J., Smith, G. P., Kneib, J., et al. 2010, MNRAS, 404, 325 [NASA ADS] [Google Scholar]
- Romano, A., Fu, L., Giordano, F., et al. 2010, A&A, 514, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rusin, D., & Ma, C.-P. 2001, ApJ, 549, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, A. J. R., & Ponman, T. J. 2010, MNRAS, 402, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, A. J. R., Edge, A. C., & Smith, G. P. 2009a, MNRAS, 398, 1698 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, A. J. R., O’Sullivan, E., & Ponman, T. J. 2009b, MNRAS, 395, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes (Sersic, J. L.) [Google Scholar]
- Smail, I., Ellis, R. S., Dressler, A., et al. 1997, ApJ, 479, 70 [Google Scholar]
- Struble, M. F., & Rood, H. J. 1999, ApJS, 125, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Voigt, L. M., & Fabian, A. C. 2006, MNRAS, 368, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-P. 2000, MNRAS, 316, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-P., & Fang, L.-Z. 1996, ApJ, 467, L45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Multiple-image systems
We list in this Appendix the coordinates of the input multiple image systems that we used to constrain the lens model for Abell 611. The position of the knots for the image systems corresponding to source A and B are shown in Fig. A.1.
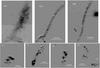 |
Fig. A.1 Details of the images used as constraints for the lens optimisation corresponding to the sources A and B (see Table A.1). The first three panels on the left show the location of the knots selected along the tangential arc, while the last four panels on the right show the conjugate knots identified in the quintuplet system. All panels were selected in the galaxy-subtracted image, obtained through the two-dimensional fitting algorithm GALFIT (Peng et al. 2002). The images were smoothed with a 2 pixel FWHM Gaussian filter for a better visualisation. |
Coordinates of the multiple images used as constraints in the lens model optimisation.
Appendix B: Comparison between predicted image configurations
In this Appendix we compare the observed strong lensing system of Abell 611 to the lensed images predicted by our best-fit models. The top left panel shows the ACS/HST image of Abell 611 (filter F606W), in which the galaxies were subtracted through the software Galfit. The last seven panels show the images predicted by our best-fitting lens models, corresponding to the cases listed in Table 5.
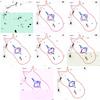 |
Fig. B.1 Comparison between the images predicted by our best-fit models and the observed lensed features. (Top left panel) Galaxy-subtracted ACS/HST image of Abell 611. The identified (A,B,C) and candidate (D) lensed systems are marked in green, magenta, cyan, and red. (Top middle, top right, middle and bottom panels) The predicted critical (caustic) lines are overlaid in red (blue) on the images predicted by the best-fit models listed in Table 5. They refer to a source plane at redshift zA = 0.908. The predicted sources are drawn in the last seven panels with the same colour as the corresponding image system in the top left panel. The conjugated knots used as constraints are shown in Fig. 5, whereas their coordinates are listed in Table A.1. The field dimensions of the panels are ≃ [35.2 × 35.1] arcsec; all fields are WCS-aligned. The flux scale is the same in the last seven panels. |
All Tables
Best-fit values for the total mass parameters obtained through the X-ray analysis.
Best-fit parameters obtained by modelling the galaxy luminosity with the Sérsic profile (Sersic 1968).
Median values for the total mass parameters, obtained with the strong lensing analysis.
Comparison of the mass results obtained with the X-ray and the strong lensing analyses.
Coordinates of the multiple images used as constraints in the lens model optimisation.
All Figures
 |
Fig. 1 (Left panel) F606W ACS/HST image of the cluster Abell 611 (see Table 3 for the observation summary). The X-ray isophotes derived from the Chandra image (shown in the middle panel) are overlaid in white. The green cross indicates the X-ray centroid. (Middle panel) The Chandra X-ray image of Abell 611 in the energy range [0.25–7.0] keV. The image was smoothed with a 3 pixel FWHM Gaussian filter, and is not exposure-corrected. The contours derived from the HST image (shown in the left panel) are overlaid in white to facilitate the comparison between the images. Here again the green cross marks the X-ray centroid. (Right panel) Pseudo-colour composite image of Abell 611, obtained combining r and g-SLOAN images, taken with the Large Binocular Camera mounted at LBT. The three panels are WCS-aligned; the size of the field of view is ≃ [1.6 × 1.8] arcmin. |
| In the text | |
 |
Fig. 2 (Top left panel) Deprojected gas density profile. The red circles indicate the values determined by the normalisation of the thermal spectra, while diamonds represent the values obtained combining both spectral and surface brightness measurements: the dashed line shows the best-fit profile. (Bottom left panel) ICM temperature profile. The figure shows the projected temperature values, directly inferred from the spectral analysis (red filled circles) and the deprojected values, which were rebinned to the same binning of the spectral profile (diamonds). The dashed line shows the deprojected best-fit profile. (Right panel) The projected (black empty diamonds) and deprojected (red filled circles) metallicity profile for Abell 611 inferred from the X-ray analysis. The dotted line represents the mean metallicity value Z = (0.45 ± 0.1) Z⊙, as determined through the fit of the spectrum extracted in the area with radius R = 2.9 arcmin, i.e. the cluster area covered by our spectral analysis. The grey region indicates the 1σ confidence level. |
| In the text | |
 |
Fig. 3 (Left panel) Mass profiles for Abell 611 as determined through the X-ray analysis. The black solid line and the red dashed line indicate the total mass and the gas mass profile, respectively. (Right panel) Confidence levels determined through the X-ray analysis for the NFW profile parameters rs and c200. The red circle indicates the best-fit values, while the contours represent the 1σ,2σ, and 3σ confidence levels. |
| In the text | |
 |
Fig. 4 Comparison between the temperature profile determined by estimating the X-ray background through the blank-sky dataset (red dashed line) or using a local background component (black solid line). |
| In the text | |
 |
Fig. 5 Overview of the strong lensing system of Abell 611. The knots that we used as constraints are marked as red crosses on the F606W ACS/HST image; enlarged images are shown in Fig. A.1. The magenta crosses indicate the perturber galaxies that were optimised singularly (see Case 6 in Table 5). The blue crosses correspond to a likely lensed system, identified by R09, which is not yet confirmed spectroscopically. We discuss our selection of the input images and its effect on the results in Sect. 3.2 and Sect. 3.7. The coordinates of all the systems are listed in Table A.1. The size of the field of view is ≃ 50 × 42.5 arcsec; the image was smoothed with a 2 pixel FWHM Gaussian filter (1 pixel = 0.05 arcsec). |
| In the text | |
 |
Fig. 6 Colour–magnitude diagram of Abell 611. The black lines define the cluster red-sequence, while the blue filled squares indicate the red sequence galaxies lying within 100 arcsec from the BCG centre, which were included in the lens modelling. The black circle indicates the galaxy located between the lensed images B.1 and C.1 (see Fig. 5), which was included in the lens modelling for its position; the magnitude estimate derived for this galaxy from the LBT data is contaminated by the flux contribution of the nearby lensed feature (see text for details). |
| In the text | |
 |
Fig. 7 (Top Panels) Comparison between the projected mass maps obtained when modelling the BCG with a dPIE profile (left panel, case 1 in Table 5) or with a Sérsic profile (right panel, case 7 in Table 5). See Table 5 and the text for further details. (Bottom Panels) Comparison between the surface mass density profiles for the BCG halo (left panel) and the NFW cluster scale halo (right panel) derived when modelling the BCG with a dPIE profile (red solid line, case 1) or with a Sérsic profile (green dashed line, case 7). |
| In the text | |
 |
Fig. 8 Scatter plots for the NFW parameters rs and c200 obtained for some representative cases. The numbering of the cases corresponds to the numbering in Table 5. The red point distribution marks the 3σ confidence level for the two parameters. The green stars indicate the best-fit values; the error-bars refer to the 1σ statistical uncertainty. We used the same knot systems as inputs and the same priors on the cluster halo mass distribution in all the six cases; the only differences were the modelling and the parameterisation of the cluster galaxies and of the BCG. The probability distribution in case 4 appears squeezed because it crushed on the lower limit for the BCG characteristic central velocity dispersion. The lens model results for the cases shown here are listed in Table 5. |
| In the text | |
 |
Fig. 9 Scatter plots of cluster-halo parameters (c200 and Mtot) versus parameters of the modelling of either the BCG or the perturber galaxy n.1 (hereafter P1, see text for details). Here we show the posterior probability distributions obtained in a representative case (case 1 in Table 5). The plotted parameters are: 1. the NFW concentration parameter c200 versus the BCG fiducial central velocity dispersion σ0,BCG (top left panel); 2. the cluster halo mass Mtot versus σ0,BCGtop right panel); 3. the NFW concentration parameter c200 versus the fiducial central velocity dispersion σ0,P1 of the galaxy P1 (bottom left panel); 4. the cluster halo mass Mtot versus σ0,P1 (bottom right panel). The contours show the 68%, 95% and 99% confidence levels. The colour code refers to the value of the χ2 estimator. |
| In the text | |
 |
Fig. 10 Median values of the dPIE truncation radius rcut vs. the characteristic dPIE central velocity dispersion σ0 for the galaxies that perturb the strong lensing system of Abell 611. The red triangles show the results obtained linking the galaxy parameters to the same scaling relation in the lens modelling (Case 4 in Table 5), while the blue stars represent the results obtained optimising the galaxies individually (Case 6 in Table 5). The grey dashed lines show the iso-density contours. The error bars indicate the 1σ uncertainty, while the cyan boxes indicate the 3σ confidence region for the results which refer to Case 4. |
| In the text | |
 |
Fig. 11 ACS/HST snapshot of a radial-oriented feature, likely a central counter-image corresponding to System B; the BCG is visible [subtracted] in the left [right] panel. |
| In the text | |
 |
Fig. 12 Comparison between the ACS/HST F606W observation (left panel), smoothed with a 3 FWHM pixel Gaussian filter for a better visualisation of the faint lensed image C.1 (marked with a white circle), and the reconstructed image systems predicted from the lens models in case 1 ((middle panel): in this case the BCG was modelled as a dPIE potential) and case 7 ((right panel): the BCG was parametrised with a Sérsic profile – see Table 5). The white circles in the middle and right panels mark the centre of the predicted counter-images. The black circle in the left panel indicates a candidate counter-image of C.1, indentified with SExtractor. The three images are WCS-aligned; the flux scale of the second and the third panel is the same. |
| In the text | |
 |
Fig. 13 (Left panel) Comparison of the NFW parameter probability distribution obtained with our X-ray and strong lensing analyses. The X-ray and the strong lensing contours show the 3-σ confidence level (the strong lensing results were marginalised over the other fit parameters). The X-ray contours were obtained deriving the X-ray background from the blank-sky data-set, while the strong lensing result refers to case 1 and to case 7 in Table 5. For an easier comparison we overplotted some previous recent results. We show in the plot the results obtained through a strong lensing analysis by Richard et al. (2010) (label SL-R09), through a weak and a strong lensing analysis by Newman et al. (2009) (labels WL-N09 and SL-N09, respectively) and in Paper I through a weak lensing analysis (label WL-Ro09; the results shown here were obtained by adopting a spherical NFW profile; the shear catalogue in this case was derived through the shapelet decomposition technique). The bars show the 1-σ errors. (Top right panel) Projected 2D mass profiles obtained with the X-ray (red solid line) and with the strong lensing analyses when modelling the BCG as a dPIE (green dashed line) or a Sérsic halo (blue dashed line). The vertical lines mark the spatial range of the strong lensing (black dotted line) and X-ray (red solid line) constraints. The X-ray (strong lensing) profile was derived by measuring the enclosed mass in cylinders centred on the X-ray emission centroid [BCG]. The distance between the X-ray centroid and the BCG centre is ≃ 1 ± 1.5 arcsec. The mass map derived from the strong lensing analysis was extrapolated up to a radius of 200 arcsec from the mass measurements obtained in the central regions. The statistical errors on the strong lensing profiles were determined computing the standard deviation from 300 mass map realizations. As a comparison, we report the estimates of the projected total mass within 250 kpc obtained by Richard et al. (2010) through a strong lensing analysis (label SL-R09, marked with a filled black circle) and through an X-ray analysis by Sanderson et al. (2009a) (label X-ray-S09, marked with a filled orange square). (Bottom right panel) Ratios between the X-ray and the strong lensing projected mass estimates; the strong lensing estimates were obtained by modelling the BCG through a dPIE (red solid line) or a Sérsic (blue dotted line) profile. |
| In the text | |
 |
Fig. A.1 Details of the images used as constraints for the lens optimisation corresponding to the sources A and B (see Table A.1). The first three panels on the left show the location of the knots selected along the tangential arc, while the last four panels on the right show the conjugate knots identified in the quintuplet system. All panels were selected in the galaxy-subtracted image, obtained through the two-dimensional fitting algorithm GALFIT (Peng et al. 2002). The images were smoothed with a 2 pixel FWHM Gaussian filter for a better visualisation. |
| In the text | |
 |
Fig. B.1 Comparison between the images predicted by our best-fit models and the observed lensed features. (Top left panel) Galaxy-subtracted ACS/HST image of Abell 611. The identified (A,B,C) and candidate (D) lensed systems are marked in green, magenta, cyan, and red. (Top middle, top right, middle and bottom panels) The predicted critical (caustic) lines are overlaid in red (blue) on the images predicted by the best-fit models listed in Table 5. They refer to a source plane at redshift zA = 0.908. The predicted sources are drawn in the last seven panels with the same colour as the corresponding image system in the top left panel. The conjugated knots used as constraints are shown in Fig. 5, whereas their coordinates are listed in Table A.1. The field dimensions of the panels are ≃ [35.2 × 35.1] arcsec; all fields are WCS-aligned. The flux scale is the same in the last seven panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


