| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | A289 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202553923 | |
| Published online | 16 July 2025 | |
Gaps in stellar streams as a result of globular cluster flybys
The case of Palomar 5
1
LIRA, Observatoire de Paris, Université PSL, Sorbonne Université, Université Paris Cité, CY Cergy Paris Université, CNRS,
92190
Meudon,
France
2
Department of Physics, University of Rome “La Sapienza”,
Piazzale Aldo Moro 5,
00185
Rome,
Italy
3
Institute for Complex Systems CNR,
Piazzale Aldo Moro 2,
00185
Rome,
Italy
4
Dipartimento di Fisica e Astronomia. “Galileo Gallilei” Università di Padova,
Vicolo dell’Osservatorio 3
Padova
35122,
Italy
5
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg,
UMR 7550,
67000
Strasbourg,
France
6
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
7
UNIDIA, Observatoire de Paris, Université PSL, CNRS,
92190
Meudon,
France
8
DTIS, ONERA, Université Paris Saclay,
91123
Palaiseau,
France
9
LUX, CNRS UMR 8252, Observatoire de Paris, PSL,
61 Avenue de l’Observatoire,
75014
Paris,
France
10
Department of Physics and Astronomy, University of Exeter,
Stocker Rd,
Exeter
EX4 4QL,
UK
★ Corresponding author: salvatore.ferrone@obspm.fr
Received:
27
January
2025
Accepted:
26
May
2025
Context. Thin stellar streams, such as those resulting from the tidal disruption of globular clusters, have long been known and used as probes of the gravitational potential of our Galaxy, both its visible and dark contents. The literature commonly interprets the presence of underdensity regions, or gaps, along these streams as being due to the close passage of dark matter subhalos.
Aims. In this work, we investigate the perturbations induced on streams by the passage of dense stellar systems, such as globular clusters themselves, to test the possibility that they may cause the formation of gaps as well. In particular, we focus on the study of the stream generated by a cluster with characteristics (mass, size, and orbit) similar to those of Palomar 5, a well-known globular cluster in the Galactic halo that has particularly long tidal tails.
Methods. For this purpose, we used a particle-test code to simulate the formation and evolution of the stream when subjected to the Galaxy’s gravitational field plus its whole system of globular clusters.
Results. Our study shows that such a stream can be strongly perturbed by the close passage of other clusters, in particular NGC 2808, NGC 7078, and NGC 104, and that these perturbations induce the formation of gaps in the tails.
Conclusions. The results of this work show that globular clusters can induce gaps in cold streams–just as it has been demonstrated in the literature for that other baryonic components, such as giant molecular clouds and the Galactic bar. Therefore, a future work that attempts to infer the dark matter subhalo distribution from stellar stream gaps must include the contributions from globular clusters.
Key words: globular clusters: general / Galaxy: kinematics and dynamics / globular clusters: individual: Palomar 5
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Stellar streams are several-kiloparsecs-long structures formed by the tidal disruption of globular clusters or dwarf galaxies orbiting a host galaxy. These tidal forces arise due to differential gravitational pulls across extended objects, causing stars farther from the galactic center to lag behind, while those closer to the center speed up. This stretching creates two tidal tails that trace the cluster’s orbit unless in the closest vicinity to the object (Montuori et al. 2007).
Numerical predictions of this phenomenon have existed since the 1970s (see, e.g., Keenan & Innanen 1975). These predictions occurred well before the first detections of Galactic globular cluster tidal tails (Grillmair et al. 1995). Interestingly, Grillmair et al. (1995)’s detections were made nearly contemporaneously with the discovery of the Sagittarius stellar stream by Ibata et al. (1994), which is the closest example of a stream emerging from a dwarf satellite currently interacting with the Milky Way.
Subsequent studies1 extended Grillmair’s findings to other globular cluster streams but were often limited to the detections of stars still close to the cluster tidal radius, until the discovery made by Odenkirchen et al. (2001, 2002, 2003) of long and thin tails outside the Palomar 5 globular cluster. With a mass of 1.34 ± 0.24 × 104 M⊙ (Baumgardt et al. 2019), Palomar 5 is one of the least massive globular clusters in the Galaxy. Odenkirchen et al. (2003) showed that its tails contain more mass than the cluster. The works of Grillmair & Dionatos (2006a) and Kuzma et al. (2015) showed that the tails have an extent of more than 20° degrees in the sky. The discovery of its prominent tails stimulated a vigorous and successful search in the following years. New streams were discovered, mostly taking advantage of Sloan Digital Sky Survey data, but Pan-STARRS and ATLAS were also used (Grillmair & Dionatos 2006b; Belokurov et al. 2006; Grillmair 2009; Bonaca et al. 2012; Grillmair et al. 2013; Grillmair 2014; Grillmair et al. 2015; Bernard et al. 2014, 2016; Grillmair 2017; Koposov et al. 2014).
Bonaca & Price-Whelan (2025) provides a review of stellar stream astronomy, which has entered a new era since the publication of the data from the Gaia astrometric mission (Gaia Collaboration 2016). Gaia’s characterization of billions of stars in the Milky Way enables the search for these structures by coupling photometry, astrometry, and spectroscopy for the brightest stars. The possibility given by Gaia to track stars with coherent movements over the entirety of the sky has led to the discovery of dozens of new streams. In addition, Malhan & Ibata (2018) developed the streamfinder algorithm and applied it across a series of works (Malhan et al. 2018; Ibata et al. 2018, 2019) to discover a multitude of streams.
The possibility of combining Gaia data with spectroscopic surveys has extended the study of stellar streams beyond the quantification of their orbital properties to a full chemical characterization (Li et al. 2019; Ji et al. 2020; Li et al. 2021, 2022; Usman et al. 2024). Currently, about a hundred stellar streams are known in our Galaxy. Mateu (2023) compiled their tracks on the sky into a catalog. Interestingly, only about 20 streams are associated with known Galactic globular clusters.
One of the interests in studying stellar streams is that they can constrain the gravitational field of their host galaxies, particularly the Milky Way. Compared to the measurement of the HI rotation curve, stellar streams offer the opportunity to investigate the potential of the host galaxy over a wide range of distances, reaching the outermost regions of the halo. For example, Varghese et al. (2011) demonstrated how stellar streams can be used to infer the mass and scale parameters of dark matter halos, utilizing various amounts of observational data, ranging from basic right ascension and declination to full six-dimensional phase space information. Bonaca & Hogg (2018) reviewed this concept from an information-theoretic point of view, identifying which orbits and configurations of stellar streams yield the most information about the Galactic potential. However, using single streams to constrain the potential led to ambiguous and non-converging results. For example, Law & Majewski (2010) made use of the Sagittarius stream to infer that the dark matter halo of our Galaxy has a triaxial shape (see also Helmi 2004; Johnston et al. 2005; Law et al. 2005), but Bovy et al. (2016) concluded that the dark matter halo of our Galaxy is nearly spherical at the distances of the Palomar 5 and GD-1 streams. The two contrasting results could indicate that the halo is triaxial at one distance but spherical at another, highlighting the need for streams at different distances to map the halo shape. Recently, Ibata et al. (2024) constructed a Milky Way model by applying a Markov chain Monte-Carlo (MCMC) fitting procedure. This method identified the set of potential parameters in an axisymmetric model of the Milky Way that best reproduces all observed stellar streams.
Beyond the global visible and dark mass distribution streams, streams can also be used to infer the granularity of the dark matter, that is, the mass and density of the subhalos populating our Galaxy. According to simulations by Springel et al. (2008), the Λ cold dark matter (ΛCDM) model predicts that galaxies grow hierarchically, with dark matter clumps forming at a wide range of masses and sizes. These clumps, or subhalos, are predicted to follow a mass distribution with a power-law slope slightly shallower than −2.0. Vegetti et al. (2012) detected the smallest observed dark matter halo through gravitational lensing in an Einstein ring with a mass of 108 solar masses. However, some models predict that dark matter clumps could exist down to at least the mass of Earth-like planets (see Green et al. 2005, and discussion in Amorisco (2021)).
Ibata et al. (2002) first suggested that dark matter subhalos could influence stellar streams by diffusing their orbital elements. Later, Carlberg (2012) expanded this idea, proposing that subhalos could create gaps in stellar streams during flyby encounters, where a subhalo approaches closely enough to a segment of a stream and significantly changes the orbits of the closest stars. Carlberg & Grillmair (2013) applied this idea and looked for the presence of gaps in the well-known Palomar 5 and GD-1 streams, concluding that the density variations found in their streams were consistent with expectations from ΛCDM models. Bonaca et al. (2019) provided further observational evidence for this idea, identifying a gap and a spur in the GD-1 stream that they could not explain by known objects, such as globular clusters, and which they suggested was due to the close passage of a dark matter subhalo. Interestingly enough, as stated in Bonaca et al. (2019), the recovered properties of this subhalo (mass and size) were denser than those with the ΛCDM masssize relationship presented in Moliné et al. (2017). The works mentioned are only a few examples of the extensive literature that has explored the impact of dark matter subhalos in simulated streams (Helmi & Koppelman 2016; Hermans et al. 2021; Banik et al. 2021; Hilmi et al. 2024; Nibauer et al. 2025) or searched for their traces in observed streams (Thomas et al. 2016; Erkal et al. 2017; Bonaca et al. 2020b,a).
In contrast, a limited number of works have explored whether other structures, such as those from baryonic matter, can cause variations in the density of streams and gaps that can be confused with those produced by dark matter subhalos. Among these works, it is worth mentioning the results of Pearson et al. (2017), which suggest that the presence of the bar at the center of the Galaxy can perturb the characteristics of a stream, such as Palomar 5, and generate gaps along its tail. That the Galactic bar could have an influence on stream morphology was also discussed by Hattori et al. (2016) and Price-Whelan et al. (2016), in the case of the Ophiuchus stream (Bernard et al. 2014). Besides the Galactic bar, giant molecular clouds can also produce gaps in stellar streams, as shown by Amorisco et al. (2016). All of these works thus indicate that baryonic structures can play an important role in tail morphology. In this context, an extensive numerical study specifically focused on modeling the tails of Palomar 5 under the influence of the Galactic bar, spiral arms, giant molecular clouds, and globular clusters, has been realized by Banik & Bovy (2019), who concluded that both the influence of the bar and that of the giant molecular clouds can leave imprints on Palomar 5 tidal tails similar to those left by dark matter subhalos. In contrast, they found the effect of globular clusters to be negligible.
Few studies have specifically investigated the effect of globular clusters on stellar streams. Erkal et al. (2017) concluded that globular clusters could not be responsible for the observed density variations in the tails of Palomar 5. Their analysis focused on the characteristics of the observed gaps and involved constraining progenitor properties using reconstructive modeling. By trial and error, they identified a specific configuration of masses, sizes, impact parameters, times of impact, and relative velocities for two perturbers that successfully reproduced the observed density distribution. However, as we do in this work, their method does not perform full forward modeling of the entire globular cluster system on Palomar 5’s stream. While they suggest that the impact rate of globular clusters is likely less significant – given their lower abundance compared to the expected dark matter subhalos population – they do not explore this aspect in detail. However, they state that it is an avenue for future investigation.
More recently, Doke & Hattori (2022) have examined the possibility that gaps in the GD-1 stellar stream could be due to the close passage of globular clusters, concluding that this scenario is improbable. These first works suggest that the impact of globular clusters on stellar streams is negligible. This result does not necessarily need to be the general case, especially for streams of clusters such as Palomar 5, which live in the inner 20 kpc of the Galaxy, where many other globular clusters also orbit. For example, Khoperskov et al. (2018), Mastrobuono-Battisti et al. (2019), and Ishchenko et al. (2023b) showed that globular clusters can even collide with other clusters, which implies that cluster stream collisions should happen much more frequently since streams are far more extended than clusters.
In this study, we aim to fill this gap in the literature on numerically modeling cluster-stream interactions. We seek to quantify the impact of passing globular clusters in the vicinity of streams to understand whether these systems can also be effective and how frequently they alter the distribution of stars in the tails, producing underdense regions or gaps. To this end, in the following pages, we present the results of simulations of the streams of Palomar 5 subject to the gravitational interaction with the set of 165 Galactic globular clusters for which positions and velocities are known to date and for which orbits can therefore be reconstructed (Baumgardt & Vasiliev 2021). We chose to simulate streams formed from a cluster with the current characteristics of Palomar 5 because it is a halo cluster with extended tails, and because it is a cluster for which the effect of baryonic structures on its stream has already been studied. As we show, and in tension with previous claims, the close passage of other clusters with such a stream is not rare. Indeed, in the 50 simulations we ran, we found the formation of numerous gaps, averaging 1.5 gaps per simulation, generated by 18 different clusters across the entire system of Galactic globular clusters.
2 Methods
The most accurate model of the Palomar 5 stream would involve full modeling of the internal dynamics of the cluster, which would mean computing N-body interactions with a 𝒪 (N2) computation time, stellar evolution, supernovae, an initial mass distribution, treatment of binary star systems, etc. (for such an example, see Gieles et al. 2021; Wang et al. 2016). Instead, we opt for solving the restricted-three-body problem, also known as the particle-test method, as we did for Ferrone et al. (2023), which we describe here for completeness. As demonstrated by Mastrobuono-Battisti et al. (2012), although the restricted threebody problem neglects the internal evolution of the cluster, it still reproduces very similar stream properties since the model captures key extracluster physics, such as disk shocking and epicyclic stripping.
Below, we first present the approach used to include the Galactic globular cluster system in our modeling (Sect. 2.1), highlighting the similarities and differences with respect to what we did in Ferrone et al. (2023); we then summarize the method used to model the mass loss from the cluster (Sect. 2.2) and finally discuss the quality of the numerical integration (Sect. 2.3).
2.1 Numerical methodology
We begin by extracting positions in the sky, proper motions, line-of-sight velocities, and distances, as well as masses and half-mass radii, of 165 globular clusters from the Galactic globular cluster catalog by Baumgardt & Vasiliev (2021)2. We then convert the initial conditions from sky coordinates into a Galactocentric reference frame, by adopting a velocity for the local standard of rest of vLSR = 240 km s−1 and a peculiar velocity of the Sun equal to (U⊙, V⊙, W⊙) = (11.1, 12.24, 7.25) km s−1, as reported by Schönrich (2012). We set the Sun’s position to (x⊙, y⊙, z⊙) = (−8.34, 0, 0.027) kpc. We took the vertical position above the disk from Chen et al. (2001) and the distance of the Sun to the Galactic center from Reid et al. (2014). These transformations were performed using astropy (Astropy Collaboration 2013).
For the Galactic potential, we employed the second model from Pouliasis et al. (2017), a superposition of a thin disk, thick disk, and dark matter halo, with masses and scale lengths provided in Table 1 of Ferrone et al. (2023). This model is timeindependent throughout our simulations. This model satisfies a series of observational constraints such as local solar, stellar density, the Galactic rotation curve, similarly to other Galactic models such as MWpotential2014 from Bovy (2015) and McMillian2017 from McMillan (2017). However, we use only one Galactic potential to balance data volume and computation time, which should suffice. Vasiliev & Baumgardt (2021) found that only a few outer globular clusters are strongly affected by different potential models. Generally, kinematic uncertainties are the dominant factor in differences between orbital solutions per cluster. Similarly, Grondin et al. (2024) generated a globular cluster mass-loss catalog using seven different potential models and found that their debris distributions were rather modelindependent, similar to those of Ferrone et al. (2023). While the clusters’ exact positions in time may depend on the model, we assert that interaction rates and stream formation are largely independent of the choice of the Galactic potential model.
Lastly, we select an integration time of 5 Gyr as a compromise between maximizing interaction statistics and modeling the Galaxy as a time-independent, constant mass distribution. Ishchenko et al. (2023a) analyzed the orbits of the Galactic cluster population using the same initial conditions as in this work within five live Milky Way-like potentials from IllustrisTNG (Pillepich et al. 2018). They found that in all sampled potentials, orbital changes remain minimal over 5 Gyr, becoming significant only at earlier look-back times when the host galaxy had significantly less mass or was undergoing a merger event.
2.1.1 Full simulations
There is a primary methodological departure from Ferrone et al. (2023). In that work, globular clusters evolved under the gravitational effect of the Galaxy alone. In contrast, now we also consider the effect of all other Galactic globular clusters by taking into account the direct N-body interactions between them. First, all clusters are represented by Plummer spheres, each with its own mass and half-mass radius as reported in the Baumgardt catalog (Baumgardt & Vasiliev 2021). For the remainder of this paper, the full simulations consider the gravitational forces from the globular cluster interactions.
For these simulations, we proceeded in two steps:
First, starting from the Galactocentric positions and velocities of all 165 Galactic globular clusters, we integrate their orbits back in time for 5 Gyr under the influence of the Galaxy itself and their mutual influence. In the back-ward integration, the system of equations of motion for the globular clusters is thus:
![\[\frame{\overset{}{\mathop r} _i} = - \nabla \frame{\text{\Phi }} + \mathop \sum \limits_\frame{j \ne i}^\frame{\frame{N_\frame{GC}}} \frac{\frame{G\frame{m_j}}}{\frame{\frame{\frame{\left(\nolbrace \frame{\frame{\frame{\left|\nolbrace \frame{\frame{r_j} - \frame{r_i}} \norbrace\right|}^2} + b_j^2} \norbrace\right)}^\frame{3/2}}}}\left(\nolbrace \frame{\frame{r_j} - \frame{r_i}} \norbrace\right),\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq1.png) (1)
where r indicates the Galactocentric position vector, the index i indicates the globular cluster of interest; the index j indicates the other globular clusters that are summed over. NGC is the total number of globular clusters, which in this study is 165, mj is the mass of the j-th cluster in the sample, bj is its Plummer scale radius, and r j is its Galactocentric position. Φ represents the same Galactic smooth potential that we discussed previously (Pouliasis et al. 2017, Model II, in the present case). Note that the masses and sizes of the globular clusters are kept constant in these simulations and are not allowed to vary with time, which means that we do not consider their internal evolution. In Sect. 4, we discuss the implications of the modeling limitations.
(1)
where r indicates the Galactocentric position vector, the index i indicates the globular cluster of interest; the index j indicates the other globular clusters that are summed over. NGC is the total number of globular clusters, which in this study is 165, mj is the mass of the j-th cluster in the sample, bj is its Plummer scale radius, and r j is its Galactocentric position. Φ represents the same Galactic smooth potential that we discussed previously (Pouliasis et al. 2017, Model II, in the present case). Note that the masses and sizes of the globular clusters are kept constant in these simulations and are not allowed to vary with time, which means that we do not consider their internal evolution. In Sect. 4, we discuss the implications of the modeling limitations.Once we found the positions and velocities of the entire globular cluster, we sampled Palomar 5 with 100 000 particles from a Plummer distribution, taking the mass and halfmass radius from the Baumgardt catalog: 1.3 × 104 M⊙ and 27.6 pc. We then integrated the evolution of these particles forward in time to the present day, taking into account that each particle feels the gravitational potential of the Galaxy, its host cluster, and that of all the other clusters in the Galaxy. Note that we do not account for self-gravity among particles. The particles experience the gravitational field yet do not contribute to it, a common assumption in galactic dynamics, as the mass of an individual star is negligible compared to the mass of the larger dynamical system. The equation of motion of a generic particle among the 100 000 that populate Palomar 5 is thus:
![\[\frame{\overset{}{\mathop r} _p} = - \nabla \frame{\text{\Phi }} + \mathop \sum \limits_j^\frame{\frame{N_\frame{GC}}} \frac{\frame{G\frame{m_j}}}{\frame{\frame{\frame{\left(\nolbrace \frame{\frame{\frame{\left|\nolbrace \frame{\frame{r_j}(t) - \frame{r_p}} \norbrace\right|}^2} + b_j^2} \norbrace\right)}^\frame{3/2}}}}\left(\nolbrace \frame{\frame{r_j}(t) - \frame{r_p}} \norbrace\right),\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq2.png) (2)
(2)
where the index p represents one of the 100 000 particles of interest, rp being its position, and j indexes over the globular clusters as in Eq. (1). We note that in Eq. (2), the positions of the globular clusters are time-dependent since they are being loaded during this step and not computed, unlike Eq. (1).
The procedure described so far has been repeated 50 times, generating a new set of initial conditions each time, given the uncertainties on proper motions, line-of-sight velocities, distances to the Sun, and masses of all clusters, as reported in the Baumgardt catalog. We handle these uncertainties through a Monte-Carlo approach by sampling them with a Gaussian distribution and considering the covariance term between the proper motions. We use the most probable values for the initial conditions in the first simulation. We sample the uncertainties for all globular clusters. Additionally, for each resampling of Palomar 5’s mass, we also resample the distribution of the 100 000 star particles.
During the integration, we save intermediate snapshots to facilitate the analysis of stellar streams and the effects of cluster impacts. Specifically, for each realization of the Palomar 5 stream, we saved 5000 in snapshots, equivalent to a temporal resolution of 1 million years. We provide the parameters that specify our data volume in Table 1. Using single precision floating point numbers, the size of our simulations is approximately:
![\[\frame{N_p} \times \frame{N_\frame{\frame{\text{ts}}}} \times \frame{N_\frame{\frame{\text{phase~}}}} \times \frame{N_\frame{\frame{\text{sampling~}}}} \times 4~\frame{\text{bytes}}~ \approx 600\,\frame{\text{Gb}}.\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq3.png) (3)
(3)
Parameters determining the data volume.
2.1.2 Reference simulations
To quantify the impact of globular cluster passages on the density of the Palomar 5 stream, we performed a second set of simulations, which we refer to as the reference simulations in this paper. These reference simulations use the same 50 sets of initial conditions as the full simulations, the same Galactic potential, but exclude mutual interactions between globular clusters. The approach adopted for this second set of simulations is thus equivalent to that adopted already in Ferrone et al. (2023). In Eq. (1), only the gradient of the Galactic potential is considered. In Eq. (2), of the second term on the right side of the equation, only the influence of Palomar 5’s Plummer sphere on Palomar 5’s particles is considered. In other words, the sum iterates over only one globular cluster, the host. We omit all interactions with the other clusters.
2.2 Mass loss
Each of the 100 000 particles that initially populate the cluster undergoes experiences the forces from Pal 5 and the Galactic potential. The mass and radius of Pal 5 are held constant over time. At each time step, a certain number of particles will therefore acquire sufficient energy to no longer be gravitationally bound to the cluster itself and thus go on to populate the streams, whose mass and spatial extent grow over time. It is important to note that in the approach used:
The masses and sizes of the clusters (and therefore the parameters of the Plummer potentials) do not change over time, which is an oversimplification, because in a self-consistent approach, these parameters would vary.
We use the same initial conditions for Pal 5 progenitor as it has today, and this is also a simplification, since Pal 5 – 5 Gyr years ago – must have contained at least part of the mass estimated today in its tails3.
The assumption in point 2 is a direct consequence of the approach described in point 1. Starting from a cluster with a mass and size similar to the current ones can lead to streams with lower velocity dispersions than those we would obtain if we had used a self-consistent approach. In a future article, we will report on the study of gap survival times depending on the masses and sizes of progenitor clusters (Ferrone et al, in prep.). We note, however, that simplifications of this kind are not uncommon in literature. Pearson et al. (2017) discussed the formation of gaps in the Pal 5 tails and assumed a time-independent mass of 50 000 M⊙ for Pal 5, over the last 4 Gyr; Erkal et al. (2017) adopted a N-body approach to simulate Pal 5 stream, but used Pal 5 current conditions as their progenitor’s initial conditions; Banik & Bovy (2019) simulated the Pal 5 stream as emerging from a stellar system with a velocity dispersion of 0.5 km/s (similar to that of particles escaping from our cluster, as we have verified).
The characteristics of the streams modeled in this paper may be considered more representative of those of clusters that are now completely dispersed, i.e., it is conceivable that completely dispersed globular clusters that left behind a population of ‘orphan’ streams passed through characteristics similar to those of Pal 5 today (small masses and extended radii). In this sense, the initial conditions chosen (in terms of internal parameters) may be more representative of those of streams for which the progenitor is now dissolved (see, for example, the population of streams without progenitors described by Ibata et al. 2024) than those currently typical of Galactic globular clusters than those currently typical of Galactic globular clusters4.
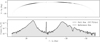 |
Fig. 1 Simulated Palomar 5 stream created by modeling the host cluster as a Plummer sphere disrupting within an axis-symmetric Galactic potential plus the gravitational effect of 164 other Galactic globular clusters. The top panel shows the distribution of star particles that escaped the cluster due to tidal forces. The bottom panel shows the 1D density profile marginalized over longitude. The gray fill shows a reference simulation that uses the same conditions to produce the stream but does not include the other globular clusters. The large central peak in density is composed of particles still bound to Palomar 5. ℓ0, b0 are located Palomar 5’s cluster’s center of mass. Two large gaps are present due to the passage of two globular clusters. Np indicates the number of particles in a bin, while N is the total number of particles, which is 100 000. |
2.3 Numerical stability
We used a leapfrog integrator because of its ability to preserve phase-space volume and conserve the Hamiltonian with each integration step. For instance, this method is preferable to a Runge-Kutta scheme, which can introduce non-physical and significant numerical errors in systems that require long-term stability and energy conservation. One drawback of the leapfrog integrator is that it requires a uniform time step throughout the entire computation, resulting in unnecessary computations for a particle after it has escaped from the host cluster. However, energy conservation and phase-space volume preservation are paramount when modeling stellar streams. The time step was therefore set to be small enough to conserve energy for the most interior particles within the cluster – ensuring that a higher mass loss did not arise from numerical error. We found that a time-step of 10 000 years was adequate to maintain energy conservation, with a median variation of ![\[\frame{10^\frame{ - 12}}\frac{\frame{\frame{\text{\Delta }}E}}{\frame{\frame{E_0}}}\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq4.png) , where E0 is a particle’s initial energy, and ΔE is the difference between its final and initial energy.
, where E0 is a particle’s initial energy, and ΔE is the difference between its final and initial energy.
We also checked the reverse integrability of the globular cluster system for the reference simulations. By reverse integrability, we mean the integrator’s capability to track the cluster backward in time and then re-integrate it forward along the same trajectory. Integrating point masses in a static axis-symmetric potential conserves Lz and E, which create regular periodic and non-chaotic orbits. Therefore, any drift would arise from purely numerical error. We selected a timestamp for which the drift in the final position after forward integration, compared to the initial position from the backward integration, was consistently at least two orders of magnitude smaller than the Plummer scale radius used for Palomar 5. This high precision ensures that no fictitious numerical forces influence the system, preventing any artificial mass loss or retention of star particles.
3 Results
3.1 Overview
The presence of the other globular clusters affects the properties of the Palomar 5 stream. Fig. 1 presents an obvious example of this effect, which we selected for its prominent gaps. Two of these gaps are visible in Galactic coordinates and become even more apparent when marginalizing over latitude to reconstruct the 1D density profile of the stream as a function of longitude.
Regarding the shape of the density distribution, the central peak corresponds to the still-intact globular cluster whose stars have not yet escaped. The stream’s density peaks are of the same order as the cluster itself, which is inconsistent with reality; the cluster’s peak density should be higher than that of the stream. Of course, this discrepancy is a result of our modeling choices. Since we use the present-day mass and radius for Palomar 5 for the whole simulation duration, the system is less dense than it should have been. In turn, our simulations have a strong initial mass loss, which adds to the amplitudes of the profile density peaks of Fig. 1. This inaccuracy is acceptable for the scope of this work. First, Palomar 5’s tails indeed have more mass than the cluster itself. Ibata et al. (2017) reports that there could be three times as much mass in Palomar 5’s tails as the cluster itself. Secondly, the exact form of the density distribution is less important than having a population of particles present that can probe a cluster flyby event.
To compare the reference and full simulations more quantitatively, we work in the tail coordinate system, in which the stream’s central axis aligns with the cluster’s orbit. We based this coordinate system on the work of Dehnen et al. (2004) and present it in Fig. A.1. Briefly, in this system, the xtail coordinate represents the position of a particle along the orbit relative to the globular cluster. Positive values of xtail are ahead of the cluster, while negative xtail is behind the cluster. The ytail coordinate measures the particle’s distance within the orbital plane, where positive values indicate that the particle is farther from the Galactic center and negative values indicate that it is closer. Fig. 2 shows a comparison between one of the 50 realizations of the Palomar 5 stream, taking into account the gravitational interactions with all other globular clusters in the Galaxy (top panel) and omitting them (bottom panel). This comparison clearly shows the presence of two wide (∼100 pc and ∼1 kpc) gaps in the leading tail and of a more subtle underdensity at xtail ∼ 5 kpc (we refer the reader to Appendix A for a detailed description of the underdensities and gaps detection method).
To determine which globular clusters were responsible for creating these gaps and when close passages occurred, we estimated the gravitational acceleration along the orbit of Palomar 5. We represented it in the (t, τ) space. t is the simulation time, and τ indicates how long it will take for Palomar 5 to reach a given point in its orbit or how long ago it passed. The use of τ is advantageous because the growth of the stream is approximately linear in τ.
On the other hand, streams in physical space are modulated by their orbital eccentricity with periodic expansion and contraction depending on the orbital phase (see the top panel of Fig. 5. Sanders et al. 2016, for an example). Adopting this time-space and reporting the gravitational acceleration along the Palomar 5 orbit in this space, identifying the globular clusters that produced the perturbation and the time at which it occurred becomes straightforward. We refer the reader to Appendix B for a detailed description of the procedure. In this way, we can identify that the clusters responsible for creating gaps in the simulation of the Palomar 5 stream, as reported in Fig. 2, are NGC 2808, NGC 7078, and NGC 104. Their close passages occurred 200 Myr, − 1.9, and − 2.1 Gyr ago, respectively.
To further investigate whether the three clusters above are responsible for producing the gaps observed in this simulation, we conducted additional experiments by including only the perturbation of each cluster at a time, while neglecting the gravitational perturbations of all the other clusters in the Galaxy.
To verify that the three suspected clusters are responsible for producing the gaps, we conducted experiments by including one perturbed at a time and excluding all others. We present these results in the middle panels of Fig. 2 and clearly show that NGC 2808, NGC 7078, and NGC 104 are the clusters responsible for creating the underdense regions observed in the leading tails of Palomar 5. It is worth noting that the times at which the passages of these clusters occurred, according to our analysis, are in agreement with the observed width of the corresponding gaps: the encounter with NGC 2808 being very recent (only 200 Myr ago), its induced gap is still very thin, because it takes time for a perturbation to grow into an extended gap, as it is the case for those induced by the passages of NGC 7078 and NGC 104, which occurred in earlier times. It is also interesting to emphasize that gaps as thin as those generated by the passage of NGC 2808, 200 Myr ago, can be detected by working in the tail coordinate system and by making a comparative analysis (full versus reference simulations): they are so thin that they cannot be directly identified in Galactic coordinates (see Fig. 1). The analysis presented in Fig. 2 has been repeated for the whole set of simulations, and online appendix reports all of them for completeness. For all the streams, morphologically speaking, the only changes appear to be the existence of gaps or their absence. We do not observe a thickening of the streams due to an increased velocity dispersion.
From this analysis, we can derive a statistical view of (1) the number of gaps generated on the Palomar 5 stream by the system of Galactic globular clusters, (2) the clusters that generated these gaps, and the time history of these perturbations. From this, we can then quantify (3) the properties of the perturbers (their masses, sizes, and orbital parameters) as well as (4) the impact geometry of the encounters, which allows us to understand which encounters are more favorable for generating gaps in the Palomar 5 stream. In the following, we will present the results of this analysis, addressing points (1) and (2).
3.2 The history and statistics of gap creations in the Palomar 5 stream
By applying the methodology described above to the whole set of simulations, we can reconstruct the history of close passages of Galactic globular clusters to Palomar 5’s stream in the last 5 Gyr, which – we remind the reader – is the time interval investigated in our simulations. Fig. 3 and Table 2 present results of this analysis. NGC 2808 impacted Palomar 5’s stream about 200 Myr ago in 44 out of 50 simulations, creating a small gap at a similar position to the one reported in Fig. 2 in each case. Since this interaction occurred less than one orbital period ago, despite the uncertainties, the orbital solutions remain similar and thus produce consistent results across all simulations. However, as we continue to turn back time further, the uncertainties in the initial conditions allow the various orbital solutions to diverge from one another. Thus, in one configuration, a cluster can impact the stream at a given time, and yet at the same moment, in a different set of initial conditions, it could be on the other side of the Galaxy. We will discuss the necessary conditions for creating a gap in Appendix D.
In total, we report the finding of 73 gaps across our 50 simulations, which averages to 1.5 gaps per simulation. Eighteen different perturbers provoke the gaps. Table 3 presents the distribution of the number of gaps appearing per simulation.
If we consider NGC 2808 an outlier and exclude it from the experiment, we observe an average of 0.6 gaps per simulation.
We need a more sophisticated statistic to compare our results to other simulations, so we turn to the gap creation rate developed by Carlberg (2012). The gap creation rate is the number of gaps that appear per unit time and is normalized by the stream’s length. For our simulations, this rate is given by:
![\[\frame{\mathcal{R}_\frame{\frame{\text{Pal}}\,\frame{\text{5}}}} = \frac{1}{T}\frame{\smallint ^}_0^T\frame{l^\frame{ - 1}}(t)\underset{i}{\mathop \frame{\frame{\sum ^}}} \delta \left(\nolbrace \frame{t - \frame{t_i}} \norbrace\right)\frame{\text{d}}t,\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq5.png) (4)
where T is the total integration time, l(t) is the length of the stream, and ∑i δ(t − ti) sums over the gap occurrences, with i indexing over the number of gaps in a given simulation. Here, δ represents the Dirac delta function. This expression can be simplified to:
(4)
where T is the total integration time, l(t) is the length of the stream, and ∑i δ(t − ti) sums over the gap occurrences, with i indexing over the number of gaps in a given simulation. Here, δ represents the Dirac delta function. This expression can be simplified to:
![\[\frame{\mathcal{R}_\frame{\frame{\text{Pal}}\,5}} = \frac{1}{T}\underset{i}{\mathop \frame{\frame{\sum ^}}} \frac{1}{\frame{l\left(\nolbrace \frame{\frame{t_i}} \norbrace\right)}}.\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq6.png) (5)
(5)
This computation allowed us to analyze the distribution of gap creation rates across all simulations. Notice that since the gap creation rate adds in parallel, naturally, gaps that occur at earlier times when the stream was shorter are weighted higher than those that occur when the stream is longer. Fig. 4 presents these results which are is roughly consistent with a simple estimate of the average gap creation rate: with 73 gaps over 5 Gyr of integration time for a stream about 20 kpc in length, the naive estimate is approximately 0.015 km s−1 kpc−2 (which is roughly equivalent to 0.015 Gyr−1kpc−1). This naive estimate is about double the weighted mean gap creation rate of 0.009 km s−1 kpc−2 and is higher because it does not account for the growth of the stream over time, unlike Eq. (4).
Lastly, we note that of the 73 observed gaps, only eight are in the trailing tail, and the rest are in the leading tail, which is a surprising result. A priori, since the star particles escape at similar rates from the L1 and L2 Lagrange points, each tail is of similar length and density. The main difference between the two tails is that the leading tail is closer to the Galactic center than the trailing tail by about 400 pc. Since the lengths are equal, and the offset between the tails is slight compared to the Galactocentric distance of about 10 kpc, we expected the gaps in each tail to be more or less the same. We can compute the probability of observing the unequal occurrences through the binomial distribution. First, since the 44 gaps linked to NGC 2808 are the result of the same flyby, they are not independent events. We remove them from this consideration, which leaves 21 gaps in the leading tail and 8 in the trailing. The probability of observing up to 8 successes in 29 trials, given a 50% chance of success, is 1.2% – unlikely, but possible. Additionally, other perturbers impact at consistent times, which may violate the assumption of independent events, as seen with NGC 2808.
 |
Fig. 2 Density maps of Palomar 5’s stream in the tail coordinate system, where x′is the integrated arc length along the cluster’s orbit and y′ is the distance within the orbital plane. The color scale represents normalized particle counts (total: 100 000). The top panel shows the full simulation with three gaps on the stream’s right-hand side. The next three panels depict simulations with identical initial conditions but exclude the gravitational influence of all clusters except those forming a given gap. The Reference simulation omits the influence from other globular clusters. The bottom panel compares Palomar 5’s observed stream length to the Reference simulation, using the same Monte-Carlo realization as Fig. 1 and Sampling 009 (as seen in the online appendix). |
 |
Fig. 3 Simulation time when the impacts occurred for all gap-causing flybys summed over all 50 simulations. Each perturbing cluster is labeled and color-consistent. We report the time axis in simulation units, with 1 s kpc km −1 corresponding to roughly 1 Gyr. We note that the plot breaks the y-axis to accommodate the large number of encounters from NGC 2808 without overshadowing the other interactions. |
Number of gaps created by each perturber across all 50 simulations.
Occurrence of gaps in Palomar 5 streams, in our simulations.
 |
Fig. 4 Distribution of the number of gaps normalized over the total integration time and unit stream length as described by Eq. (4) for the whole set of 50 full simulations. |
3.3 Impact geometry and parameters of the perturbers
With the perturbers identified, we perform statistical analysis to understand the conditions necessary for a globular cluster to induce a gap in the Palomar 5 stream. We turn to impact theory, which in its simplest form is presented in works such as Binney & Tremaine (2008). Consider two particles: one stationary and the other moving past it. The impact parameter is the distance between the two particles at the point of their closest approach. The impulse approximation is employed, which assumes that the velocity of the perturber remains unchanged during the interaction. This assumption simplifies the computation.
To understand how the impacted particle is perturbed, one needs to compute its change in momentum, which is determined by integrating the force acting on the particle throughout the interaction. A useful approximation for this change in momentum, per unit mass, is the force at the closest approach multiplied by an estimate of the interaction time:
![\[\frame{\text{\Delta }}p \approx ~\frame{\text{Force}}~ \times \frame{\text{~interaction~time}}~ = \frac{\frame{GM}}{\frame{\frame{b^2}}} \times 2\frac{b}{\frame{\delta v}} = 2\frac{\frame{GM}}{\frame{b\delta v}},\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq7.png) (6)
where M is the mass of the perturber, b is the impact parameter, δυ is the relative velocity of the perturber with respect to the particle, and G is the gravitational constant.
(6)
where M is the mass of the perturber, b is the impact parameter, δυ is the relative velocity of the perturber with respect to the particle, and G is the gravitational constant.
This equation asserts that a more massive perturber, passing closer to the particle and moving more slowly, will have a greater impact. It is important to note that the momentum change is inversely proportional to the velocity of the perturber. Note that this contrasts with the intuition from elastic collisions, such as those between billiard balls, where higher velocities result in greater impacts.
Erkal & Belokurov (2015) extended this impact theory from one point mass impacting another to studying how an extended body impacts a stream by quantifying the change in momentum of a given particle as a function of its distance from the point of greatest impact along the stream. Erkal & Belokurov (2015) models their perturber as a Plummer sphere, like in our simulations. Since a stream is not a point but has length and an orientation in space, one needs to consider the parallel and perpendicular components of the velocity to describe the impact fully. Consequently, five parameters determine the change in velocity of a given stream particle: M, rp, b, W∥, and W⊥, which are the mass of the perturber, size of the perturber, impact parameter, parallel and perpendicular components of the relative velocity. As detailed in Appendix C, we calculated these parameters for all our full simulations by selecting – for each of them – the strongest five flybys of a perturber with the Palomar 5 stream. Thus, we compute 250 impacts and flag those that give way to gaps.
Visual inspection of the five key impact parameters (M, rp, b, W∥, and W⊥) did not reveal a clear distinction between flybys that create gaps and those that do not. Therefore, we only present the quantities from Eq. (6) in Fig. 5. Note that this figure displays the total relative velocity rather than separating the parallel and perpendicular components, as no specific trends were observed when plotting the two velocity components separately. We also excluded the characteristic cluster radius, which showed little correlation with the results, likely due to the narrow range of globular cluster radii (see Fig. 7). This factor might be more significant for dark matter subhalos, where size variation is greater.
While Fig. 5 demonstrates that mass, relative velocity, or impact parameter alone cannot predict gap formation, one interesting result emerges: impact parameters greater than 300 pc do not create gaps. The stream widths are roughly 200 pc, as seen in the online appendix. This finding is even more evident when examining the b-M plane. A series of perturbers at roughly ∼ 8 × 105 M⊙ highlights NGC 2808’s flybys, where all encounters with impact parameters under 200 pc result in gaps, while those beyond this distance do not. In other words, even the most massive globular clusters with masses greater than about 106 M⊙ cannot cause gaps if their impact parameters are greater than roughly 300 pc. Interestingly, even fast encounters (δυ > 300 km/s) can produce gaps for impact parameter values below this threshold. Perhaps this is not surprising, since the range of possible relative velocities is much less than that of mass and impact parameters, which vary by two and three orders of magnitude, respectively. In contrast, the relative velocities only vary by about a factor of three.
Once all the key impact parameters are estimated, we can use Eq. (6) and calculate Δp, the change in momentum (per unit mass) imparted by a cluster flyby on Palomar 5 stream. Fig. 6 shows the distribution of imparted change in momentum for all impacts that produce a gap compared to those that do not. On average, encounters that lead to gap creation impart a change in momentum on stream particles, which is a factor of 10 higher than encounters that do not form gaps (but with some overlap in the low-velocity tail). Interestingly, changes in momentum, which lead to gap creations, extend over a large range in velocities. There is a factor of about 100 between the smallest and largest changes with NGC 2808 (orange color in the histogram) imparting changes in the velocity of stream particles, which redistribute over the whole range of Δp.
In addition to characterizing the parameters governing cluster encounters with the stream, since we know which clusters have produced gaps on the tail of Palomar 5, we can also verify their orbital and structural properties. Fig. 7 shows just this, where we first show the clusters’ mass and size (i.e., half-mass radius) that cause gaps on the tails of Palomar 5, dividing them from those that do not. As can be seen, no cluster with mass below 105 M⊙ causes gaps on the Palomar 5 stream, and all perturbers, except FSR 1758, have a half-mass radius below 10 pc. Even more interesting is their distribution in the E-Lz plane, which shows that the clusters that cause gaps are on both direct and retrograde orbits (negative and positive values of Lz). However, all of the perturbers exist in an energy interval between −2 and −1 × 105 km2s−2, which is because only clusters within Palomar 5’s orbital space can interact with the stream: clusters with higher orbital energies tend to have larger apocenters than that of Palomar 5 and thus spend most of their time away from Palomar 5’s orbital volume.
Finally, it is worth noting the location of impacts with the stream, specifically whether they occur when Palomar 5 is near its pericenter. Fig. 7’s bottom panel shows that encounters can occur at all orbital phases of Palomar 5, when it is close to the pericenter, but also very far away from it, at the outskirts of its orbital space. However, when taken all together, the location of gap-creating impacts shows a strong negative correlation with the Galactocentric radius r, with the number N of encounters favorable to gap formation going as N = − 2.5r + 50 (with a Pearson coefficient of − 0.86). While there are more clusters near the Galactic center, clusters naturally spend more time near their apocenters, and the lower relative velocities in these regions should favor gap creation. However, this result suggests that the cluster Galactic number density outweighs these factors when determining the number of gaps. The results are for Palomar 5 only, and a future study would need to investigate streams along various orbits before generalizing this conclusion.
3.4 Comparison to observations
We briefly compare our simulated gaps to the literature on Palomar 5. In the bottom panel of Fig. 2, we compare the tracks of Palomar 5 that were compiled in galstreams by Mateu (2023). The mid-point positions of the streams do not have the same Galactocentric positions as Palomar 5 from Baumgardt’s catalog, and this difference creates an offset when projected into tail coordinates. Moreover, since we sample the distances to Palomar 5, the Galactocentric position within the Baumgardt catalog varies. To combat this, we position the mid-point of the Galstream tracks at the cluster’s center of mass, allowing us to compare the length of the observed tracks to our simulated streams. We use the three tracks Pal5-PW19, Pal5-S20, and Pal5-I21 from Price-Whelan et al. (2019), Sollima (2020), and Ibata et al. (2021), respectively. For each track, we found the distance from the cluster in both directions, counting the number of gaps within this range, and we present this in Fig. 8. In the maximum limit, many gaps could appear at a rate of about one per realization. However, only a few gaps occur at the shortest reported stream length. We note that the gap generated by the recent perturbation induced on the stream by the passage of NGC 2808 (whose occurrence is very likely according to our models) sits in a portion of the simulated tail which is at the edge of the observed one (see bottom panel in Fig. 2). This element and the fact that this gap is skinny, because it is very recent, probably make its detection difficult.
We observe no gaps within 3 kpc of the cluster in our simulation. There may be a few reasons for the absence of gaps in the portion of the tails closer to the cluster center. First, as Sanders et al. (2016) demonstrated, the dispersion of action-frequencies in the stream plays a role. For instance, the frequency corresponding to the azimuthal action, Jϕ, is ![\[~\frame{\dot \theta _\phi } = - \frac{\frame{\partial \mathcal{H}}}{\frame{\partial \frame{J_\phi }}}\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq8.png) and where θϕ is the angle describing the position of the particle phase space between momentum (pϕ) and position (ϕ) axes – where ϕ is the azimuthal angle between the x-y axes in physical space. Stream regions with well-separated frequencies are more susceptible to gap formation, while those with a wide frequency range (near the cluster) tend to erase the history of impacts. Thus, for a gap to form, the imparted change in frequency must exceed the range of frequencies in the impacted region. Therefore, the strong flybys close to the cluster were inconsequential for gap formation.
and where θϕ is the angle describing the position of the particle phase space between momentum (pϕ) and position (ϕ) axes – where ϕ is the azimuthal angle between the x-y axes in physical space. Stream regions with well-separated frequencies are more susceptible to gap formation, while those with a wide frequency range (near the cluster) tend to erase the history of impacts. Thus, for a gap to form, the imparted change in frequency must exceed the range of frequencies in the impacted region. Therefore, the strong flybys close to the cluster were inconsequential for gap formation.
Another possible explanation is the different thicknesses of the simulated tails at different distances from the cluster’s center. At distances less than 3 kpc from Palomar 5, the tails are skinny, with a typical thickness of less than 100 pc. To cause gaps in these regions, the clusters would have to pass close to the stream, with impact parameters similar to the thickness itself. We note that the thinness of the tails at these distances is probably a direct consequence of the initial parameters we chose for the simulation. For Palomar 5, 5 Gyr years ago, we assumed the same internal parameters (mass and size) as the cluster today. With such parameters, after 5 Gyr of evolution, our system has lost most of its mass, and therefore, the part of the tails closest to the cluster itself, whose density depends mainly on the most recent mass loss (see, for example, Fig. A.3 in Mastrobuono-Battisti et al. 2012), is necessarily very thin because the simulated cluster has essentially no more mass to lose. This last point also has a consequence in the gap creation rate, which we derived at the end of Sect. 3.3: with only 70% of the tail (∼14 kpc over 20 kpc, excluding the innermost ± 3 kpc from the cluster center) suitable for forming gaps, the gap creation rates are about 50% higher than those estimated in the previous section, where values have been derived taking into account the full tail extent. This gap creation rate would still not be high enough to reproduce the number of gaps in Palomar 5’s tails, as reported by Carlberg et al. (2012). Their study suggested the presence of five gaps with a 99% detection confidence, leading to a gap creation rate of 0.17 Gyr−1 kpc−1. If correct, this rate would be too high to be explained by Galactic globular clusters only.
An additional explanation for the absence of gaps in the inner regions of a stream is given in Appendix D. Briefly, the eccentricity of an orbit induces tidal shocking at the pericenter passages that cause episodes of increased mass loss where the escaped stars leave with a higher mean velocity and greater velocity dispersion. In essence, streams from progenitors on eccentric orbits are made of two components: a continuous flow of stars plus many packets of stars that burst out from pericenter passages. The gap impact occurs at a single position, creating a gap in each subpopulation. However, the gaps have different drift rates across the groups, and they eventually go out of phase, erasing the impact’s signature. The packets of stars disperse with time. However, bursts contribute to more escaped stars as the simulation evolves than the continuous outflow. As a result, at late stages of the simulation, the region nearest to the globular cluster is made of distinct yet overlapping populations. After an impact in this location, the impact site between the groups quickly goes out of phase.
 |
Fig. 5 Distribution and relationship between the impact variables from Eq. (6) for all close flybys considered. The colors indicate the encounters that cause gaps and are the same as Fig. 3, with white edges for visibility and binned in red for the histograms. The black histogram shows the close encounters that did not lead to gaps. Indeed, no obvious trend has emerged that delimits these planes into gap-producing or non-gap-producing ones. |
 |
Fig. 6 Distribution of imparted change in momentum (per unit mass) from a cluster flyby given by Eq. (6). The data set includes the top 5 strongest flybys from each simulation. Those that cause gaps are colored, stacked, and overlaid atop those that do not – this is the gray distribution. We note the meaning of the colors is the same as in Fig. 3. |
4 Discussion
The simulations presented in this paper suggest that, in the last 5 Gyr of evolution, Palomar 5’s stream could have experienced multiple close encounters with other Galactic globular clusters, some of which can create gaps – even a few kiloparsecs wide – in its tails. Currently, the literature debates whether or not a gap exists in the observed portion of Palomar 5 tails. Ibata et al. (2016) found no statistically significant gap in Palomar 5 tails, while Erkal et al. (2017), analyzing the same dataset as Ibata et al. (2016), suggested the presence of a few dips and gaps in the tails, at angular distances between 2° and 9° from the cluster center (see also Bonaca et al. 2020b). While our simulations produced 73 gaps across 50 realizations, only about 22 are beyond the current length of the observed portion of the stream, which means, on average, we obtain at least one gap from a globular cluster within the past 5 Gyr. However, we did not attempt to create mock observations or simulate a full detection process accounting for the challenges of disentangling field stars from stream stars. While such an analysis would be valuable, it is beyond the scope of this study.
Our simulations produce a stream for Palomar 5 that is longer than the currently observed extent. In simulations, stream detections are straightforward because we can use reference runs to clearly separate stream particles from the field and compare against a known “true” structure. In contrast, observational data are inherently more challenging due to magnitude limits, contamination from field stars, and the lack of a ground truth for comparison.
The factors mentioned above could lead one to conclude that the number of gaps identified in this study could represent an upper limit. However, this conclusion is incomplete. Globular clusters lose mass and evaporate over time, leading to an incomplete catalog of perturbers. Moreover, the present-day masses used in our simulations are likely lower than the historical masses of these clusters. For example, Pearson et al. (2024) conducted a study simulating the dissolution of a realistic globular cluster population to identify how many stellar streams we should expect in the Milky Way and used a mock catalog of globular clusters with masses above 104 M⊙ totaling about 10 000 clusters. Their setup implies that more perturbers could have been present in the past, potentially increasing the frequency and number of gaps in Palomar 5’s stream.
We note that our results seem to be in tension with the conclusions of Banik & Bovy (2019), who presented a numerical study of Palomar 5 tails, orbiting a Milky Way-like potential, where both dark matter subhalos and baryonic sub-structures (Galactic bar, spiral arms, giant molecular clouds, globular clusters) were taken into account to quantify the importance of these latter in density variations in Pal5 streams. While their methods are extremely similar to ours, their analysis diverges significantly. Specifically, Banik & Bovy (2019) focused on examining power spectra, analyzing variations in the one-dimensional stream density in stellar counts along the length of the stream. Upon comparison with our simulations, we observe that the power spectra from our full simulations that include globular clusters and the reference simulations that do not significantly differ. We suggest that this may be due to the signal from only one or two gaps caused by globular clusters not being sufficient to produce notable differences in the overall power spectrum. Additionally, Banik & Bovy (2019) may not have inspected the profiles for individual gaps, which may be why they did not report them. Further investigations would be needed to confirm this interpretation and thoroughly assess the impact of globular clusters on stream density profiles.
Erkal et al. (2017) also present a study about the impact of globular clusters in producing gaps on the Pal 5 stream. In section 6.3 of their article, Erkal et al. (2017) discuss the fact that globular clusters with masses greater than 106 M⊙ are rare in the Galaxy, especially at distances compatible with the orbit of Pal 5, while – based on previous works – they estimate that subhalos of dark matter of similar mass are at least three times greater in number. This difference leads them to conclude that the gaps they report in the Pal 5 streams are more likely to be induced by dark matter subhalos than by globular clusters.
However, as we show in this paper, even clusters with masses below 106 M⊙ can produce gaps. The clusters perturbing the Pal 5 stream are clusters with masses up to 10 times lower than those considered by Erkal et al. (2017). It is thus possible that Erkal et al. (2017) have underestimated the impact of globular clusters’ close passages on a stream such as Pal 5. It is more difficult, however, to make a comparative analysis between the role of clusters and subhalos at equal stellar mass. Being less dense than globular clusters, subhalos should produce less intense perturbations on streams (for fixed impact parameters and relative velocities). We can derive from Sanders et al. (2016)’s third figure that a more concentrated system delivers a higher velocity kick but over a shorter distance, while a more spread out system will affect more stars yet perturb them less. A systematic comparative analysis to quantify the role of clusters and subhalos in producing gaps and perturbations in stellar streams still needs to be done.
The impact of globular clusters’ close interactions with stellar streams has also been the object of another recent paper by Doke & Hattori (2022), who concluded that the chance for GD-1 gaps, which have been reported in several works (see, for example, Bonaca et al. 2019; de Boer et al. 2018, 2020) to be produced by globular clusters is very low. This result is not necessarily in contradiction with ours since GD-1 has a pericenter which is almost twice that of Palomar 5 (see, for example Malhan & Ibata 2019). As discussed in Sect. 3.3, the number, N, of close encounters that lead to gap creation is anti-correlated with the distance r to the Galactic center. If we naively use the same radial dependence of gaps from Palomar 5 for GD-1 by swapping a pericenter from 6 kpc to 16 kpc, we would reduce the number of gap-favorable impacts by more than a factor of 2. Moreover, we note that Doke & Hattori (2022) pre-selects the globular clusters that could have experienced a close encounter with the GD-1 stream by selecting only clusters that pass at a distance of less than 0.5 kpc from the stream, having a relative velocity smaller than 300 km/s. As shown in our Fig. 5, bottom-left panel, in the case of Palomar 5, this choice would lead to excluding most of the encounters favorable to gap creation, which turn out to have relative velocities above 300 km/s, reducing the total to just 19 gaps. It would be interesting to repeat a similar study as the one made by Doke & Hattori (2022) for GD-1, imposing no selection on possible candidate clusters.
As already suggested in previous works which have studied the impact of baryonic structures on Palomar 5 tails (Pearson et al. 2017; Banik & Bovy 2019), this cluster may lie in a region of the phase-space which is not favorable to distinguish gaps created by dark matter subhalos from gaps created by baryonic structures, such as the Galactic bar and giant molecular clouds. Our study shows that close encounters with globular clusters constitute a further element that confuses a simple interpretation of the observed Palomar 5 stream gaps (if any). Other clusters and streams in the orbital energy range of Palomar 5 may suffer from the same difficulty. Going to lower orbital energies worsens the situation because the effect of the Galactic bar, giant molecular clouds, and interactions with globular clusters becomes even more efficient. In the innermost regions of the Galaxy, where the density of dark matter subhalos is maximal, globular cluster streams are intrinsically more difficult to find, in addition to the fact that the dynamical times in these regions become so small that the stars lost from globular clusters do not redistribute themselves for the most part into thin structures (see Ferrone et al. 2023). It is thus probably only at larger distances from the Galactic center than those spanned by Palomar 5’s orbit that the impact of dark matter subhalos may become dominant, but one should bear in mind that at these distances, the number density of subhalos also decreases. In the future, it will be interesting to apply the type of study conducted here to the whole set of streams to quantify the regime in which they are favorable to the creation of gaps from baryonic structures.
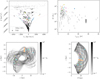 |
Fig. 7 Top left: energy-angular momentum space of the globular clusters in the simulations, with 50 × 165 data points representing all sampled initial conditions. Clusters impacting Palomar 5 are shown with colored markers, large for the samplings that induce a gap and small for those that do not. The small gray dots represent the non-gap-causing clusters. The 50 white dots indicate Palomar 5’s sampled initial conditions for the current day position. The light-pink dashed curve shows the circular velocity curve. Top right: mass-size plane of the globular clusters in the simulations, with uncertainties on the masses indicated as vertical lines. We remind the reader that the globular cluster catalog currently does not provide uncertainties for the characteristic radii of clusters. Bottom left: Palomar 5’s orbit in the Galactocentric xy plane. The gray scale represents all 50 stacked orbits, with 𝒫 indicating the probability of Palomar 5’s position, normalized to 𝒫max = 1. The colored markers indicate the position of the perturber when it impacted the stream and not its present-day position. Bottom right: same as the bottom left but in the meridional plane. In all panels, the colors of the markers and histogram bars correspond to specific perturbers as specified in Fig. 3. |
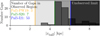 |
Fig. 8 Distribution of gaps as a function of absolute distance from the center of mass of Palomar 5’s globular cluster. We count the number of gaps within the observable range on an individual track basis, with track lengths determined by the minimum and maximum x′-coordinates from the bottom panel of Fig. 2. The ranges for Price-Whelan et al. (2019), Sollima (2020), and Ibata et al. (2021) are shown for their respective dimensions, and the number of gaps within these ranges is indicated in the figure. Vertical bars mark the x′ > 0 limit of the stream – we only show the right-hand side instead of both for clarity, as most gaps are located on the right-hand side of the stream in any case. |
5 Conclusions
Our study demonstrates that globular cluster flybys can produce density gaps in the stellar streams of Palomar 5. The occurrence and characteristics of these gaps depend on the stream’s dynamical and structural properties, the perturber’s mass, and the impact parameter. While our simulations predict the formation of gaps in Palomar 5’s tails, the predicted gaps do not align with the regions of the stream currently observed. Several factors contribute to the absence of simulated gaps in the observed portions of Palomar 5’s tails, including the stream’s varying thickness, the dispersion of action frequencies near the cluster, and the initial conditions adopted in our simulations.
The broader implications of our findings indicate that globular cluster interactions add a layer of complexity to interpreting stellar stream substructures, complicating efforts to distinguish between baryonic and dark matter-induced gaps. While Palomar 5’s phase-space region may not be ideal for isolating the impact of dark matter subhalos, extending this analysis to other streams, particularly those at larger Galactocentric distances, could provide clearer insights.
Future work should involve a systematic comparison of gap creation rates across various Galactic potentials and extend the scope to a wider range of streams and globular clusters. Such a work could disentangle regimes where baryonic and dark matter-induced substructures can dominate gap creation, shedding light on the elusive influence of dark matter subhalos on stellar streams. Additionally, we can continue to add realistic physics to the Galactic environment, such as the merger of the Sagittarius dwarf galaxy, the passages of the Large and Small Magellanic clouds, as well as a time-evolving globular cluster population that compensates for the clusters’ mass loss, evaporation, and similarly add members from the current incomplete census.
Data availability
The code used to produce the data in these simulations is available at github.com/salvatore-ferrone/tstrippy. Examples of the installation and use of the code are provided at tstrippy.readthedocs.io. The gallery of gaps, i.e., our online appendix of the figures of all 50 simulations in which the gaps were identified, is available on Zenodo at https://doi.org/10.5281/zenodo.15528089
Acknowledgements
This work has made use of the computational resources available at the Paris Observatory, as well as those obtained through the DARI grant A1020410154 (PI: P. Di Matteo) and of the Astropy, Numpy, and Matplotlib libraries (Astropy Collaboration 2013, 2018; Harris et al. 2020; Hunter 2007). S.F., P.D.M., and M.M. thank the École Doctorale 127 for its financial support. M.M. thanks the CNR STM program, thanks to which the collaboration on this research topic began.
Appendix A Gap detection
For each of the 50 simulations, we compare the final snapshots between the reference and full simulations using the tail coordinate system, as shown in Fig. A.1. We only saved the reference simulations at the final time stamps, thus from Eq. 3 where Nts=1, leading to a data volume of about one hundred measly megabytes. We inspected these differences by generating 2D density maps of the streams. Additionally, we marginalized over the y′-coordinate to produce 1D density profiles along the x′-axis. We show these comparisons in the results section (see Fig. A.2).
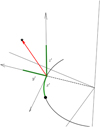 |
Fig. A.1 Demonstration of the transformation from Galactocentric coordinates to tail coordinates. The black dot represents the globular cluster, while the thick black line shows a segment of its orbit. The star symbol indicates a star particle. The red vector points from the nearest point on the cluster’s orbit to the star particle. The Galactocentric position vector is the y′-axis. The local orbital plane, the cross-product between the orbit’s local position and velocity vector, defines the z′-axis. We project the red vector on each of these axes. We measure the x’ coordinate as the path length along the orbit from the cluster to the nearest point. Positive x′, y′, z′ indicate that a star is ahead of the cluster, farther from the Galactic center, and above the orbital plane, respectively. |
To construct the 1D density profiles, we binned the data using the ![\[\sqrt N \]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq9.png) rule, where N is the number of data points (Np = 105). After binning the 1D profiles, we apply a median boxcar smoothing technique. At each bin, we select a number of adjacent data points from both sides, place them in a list, and replace the central value of the bin with the median. We use 10 adjacent points per side, corresponding to a smoothing length of approximately 1 kpc. This procedure reduces high-frequency noise and smooths the profiles. For instance, notice the absence of a high mass peak indicating the center of mass in the bottom panel of Fig. A.2.
rule, where N is the number of data points (Np = 105). After binning the 1D profiles, we apply a median boxcar smoothing technique. At each bin, we select a number of adjacent data points from both sides, place them in a list, and replace the central value of the bin with the median. We use 10 adjacent points per side, corresponding to a smoothing length of approximately 1 kpc. This procedure reduces high-frequency noise and smooths the profiles. For instance, notice the absence of a high mass peak indicating the center of mass in the bottom panel of Fig. A.2.
With the smoothed 1D density profiles in hand, we search regions where the full simulations are significantly underdense compared to reference simulations, surpassing stochastic fluctuations. We first impose a signal-to-noise ratio threshold, 𝒮𝒩ℛ. The signal is the log of the counts per bin from the reference 1D density profile; we propagate errors assuming a Poisson distribution. We then compute a threshold for the number of counts in the reference simulation, Nv, using the transcendental equation:
![\[\mathcal{S}\mathcal{N}\mathcal{R} = \ln (10)\frame{\log _\frame{10}}\left(\nolbrace \frame{\frame{N_v}} \norbrace\right)\sqrt \frame{\frame{N_v}} .\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq10.png) (A.1)
(A.1)
By setting 𝒮𝒩ℛ = 5, we solve for N using scipy.optimize.fsolve, finding that N must be greater than 7. After discarding insignificant bins (i.e., those with counts below the threshold), we computed the log ratio of the counts between the reference and full simulations:
![\[\frame{\mathcal{R}_i} = \frame{\log _\frame{10}}\left(\nolbrace \frame{\frac{\frame{\frame{N_\frame{f,i}}}}{\frame{\frame{N_\frame{v,i}}}}} \norbrace\right),\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq11.png) (A.2)
(A.2)
where ℛi is the log ratio, Nf,i are the counts from the full simulation, and Nυ,i are the counts from the reference simulation for each bin i. We then analyze the i distribution. If the differences between the density profiles are primarily due to stochastic processes of similar magnitude, this distribution should resemble a Gaussian, as expected from the central limit theorem. Thus, we flag all regions where the density is underdense by more than two standard deviations, which should highlight regions whose underdensity is unlikely to be the result of the sum of stochastic processes but rather the passage of another globular cluster.
However, this method has its limitations, especially when detecting smaller gaps. As outlined by Erkal & Belokurov (2015), since gap growth is a dispersion phenomenon, a small gap is not indicative of a weak impact but a recent one. Additionally, since our streams have finite width, some gaps are oblique with respect to the stream axis. In such cases, marginalizing over y′ erases the gap’s signal, making it impossible to detect in a 1D profile. This limitation is particularly evident in gaps caused by NGC 2808, as discussed in the results. Therefore, this quantitative analysis serves as an aid to visual inspection rather than a complete substitute for it. This method helps with significant, subtle gaps that the eye does not notice in the 2D maps. The online appendix presents these profiles.
Appendix B Perturber identification
We aim to identify the origin of the gaps observed at the end of the simulation. To this end, we examine the evolution of stream density over time. Instead of using the x’-coordinate, we introduce τ, which represents time rather than distance. Specifically, τ indicates how long a cluster will take to reach a given point in its orbit or how long ago it passed. This choice of coordinates is advantageous because the growth of the stream is approximately linear in τ. In contrast, in physical space, streams on eccentric orbits expand and contract depending on the orbital phase.
Sanders et al. (2016) extended the analysis of Erkal & Belokurov (2015), demonstrating that action-angle variables provide a useful coordinate system for analyzing stream evolution, as actions are conserved quantities and their associated angles grow linearly over time. Although we became aware of this work only after completing our analysis, we note that τ is a suitable approximation and behaves similarly to the angle variable corresponding to the azimuthal action: τ ≈ θϕ,i − θϕ,GC.
The core of our analysis is presented in Fig. B.1. The bottom panel shows the evolution of the stream density over time. To avoid extremely low-density regions at the stream’s edges, we applied the same density threshold as from Eq. A.1 to focus on the more significant areas of the stream. Next, we modeled Palomar 5’s orbit as a proxy for its stream and sampled points along the orbit to measure the gravitational force exerted by other globular clusters. The top panel of Fig. B.1 shows how the total gravitational acceleration on Palomar 5’s stream evolves over its length throughout the simulation.
 |
Fig. A.2 Comparison between the density maps and profiles of the full and reference simulations is presented. The blue vertical bars highlight the locations where the full simulation is less dense than the reference simulation by 2-σ. We do not consider bins below the noise threshold when measuring the differences between the two 1D profiles. We smoothed the 1D profiles with a median box-car filter. |
We then used scipy’s ndimage (Virtanen et al. 2020) package to identify the top five local maxima in the data space of gravitational acceleration g as a function of time t and the stream coordinate τ. First, we smooth the data space by taking a 5-point moving average kernel. Secondly, we use a maximum filter to locate coordinates in the (t, τ) data plane that are local maxima to at least 10 adjacent data points. We order these locations and save the top five strongest interactions. Then, we iterated over the contributions of individual globular clusters to determine which cluster contributed the most to each peak in g. We label each significant peak with the corresponding globular cluster.
Afterward, we cross-referenced these peaks with the locations of the gaps identified by studying the density maps and profiles from Fig. A.2. The impact leaves a low-density wake in the (t, τ) plane for large gaps resulting from strong interactions. the bottom panel of Fig. B.1 shows the wakes corresponding to the impacts of NGC 104 and NGC 7808.
Fig. B.1 contains some interesting information. Notice the periodic ribbons of force in the (t, τ) plane. The ribbons are due to pericenter passages where Palomar 5 is getting closer to the center of mass of the globular cluster system. Additionally, for the impacts of NGC 104 and NGC 7078, wakes can be observed in the density map. Another important aspect is that the strongest peak in gravitational force does not necessarily create a gap.
Notice how NGC 5272, which was labeled with 0 to indicate that it has the greatest local maxima, does not have a gap. The reason for this is manifold. For instance, the force needs to be modulated with time since the change in momentum is the determining factor and not the peak magnitude of the force. Additionally, there is an offset of about 200 pc between the stream and the orbit, as seen when viewing the stream in tail coordinates, so peaks upon the orbit are good proxies for the stream but are not definitive. We found that the top five greatest impacts accounted for all gaps, except for Sampling 014 as shown in Fig. 3 of our extended list of figures, whose gap from NGC 6584 corresponded to the 7th peak.
We compile the results of this analysis into a table. Each row of the table corresponds to a gap; its corresponding suspects are the columns. The culprit is labeled as TRUE. For a handful of simulations, to double-check that we make the correct verdict, we recompute the simulations, yet individually adding one globular cluster at a time. As a result, we can confirm that singular gaps arise from the suspected clusters. Fig. 2 shows one such example.
Appendix C Reconstruction of the impact geometry
As discussed in Sect 3.3, five parameters determine the change in velocity of a given stream particle: M, rp, b, W∥, and W⊥. In the following, we describe how we estimated these parameters during impacts in our simulations. To achieve this, we identify the impact of the most significant clusters, as determined in the previous analysis in Sect. B. Then, we refine these estimates to pinpoint the exact location of the impact along the stream and the precise moment it occurred. To do so, we fit a third-order parametric polynomial to the stream using the saved snapshots from our simulations:
![\[s(\tau ) = \{ \begin{array}{{c}} \frame{x(\tau ) = \frame{a_0} + \frame{a_1}\tau + \frame{a_2}\frame{\tau ^2} + \frame{a_3}\frame{\tau ^3}} \hfill \\ \frame{y(\tau ) = \frame{b_0} + \frame{b_1}\tau + \frame{b_2}\frame{\tau ^2} + \frame{b_3}\frame{\tau ^3}} \hfill \\ \frame{z(\tau ) = \frame{c_0} + \frame{c_1}\tau + \frame{c_2}\frame{\tau ^2} + \frame{c_3}\frame{\tau ^3},} \hfill \\ \end{array} \]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq12.png) (C.1)
(C.1)
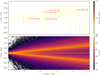 |
Fig. B.1 Demonstration of how we determined which globular clusters were responsible for the gaps. The y-axis is τ, a coordinate in units of time that indicates how far ahead or behind it is from a globular cluster. The x-axis is the simulation time, t, where 0 s km kpc−1 indicates the present time. The bottom plot showcases the evolution of the stream density over simulation time. We used the density to determine a suitable stream length. Subsequently, we used this length to extract a piece of Palomar 5’s orbit. This orbital segment approximates the stream. Then, we compute the gravitational force from all other stream stand-in clusters, shown in the top plot. The gravitational force is measured in acceleration and is given in integration units: km2 kpc−1 s−2. Moments of high acceleration indicate the passage of another cluster. The red circles indicate the top 5 strongest passages, as well as the names of the clusters. The example shown in this plot is the same simulation as Fig. 1. |
where x, y, and z represent the parametric line describing the stream in Galactocentric coordinates, τ is the stream coordinate in time as described in the Appendix B, and is used as the independent variable to parameterize the position along the stream. The coefficients ai, bi, and ci are the polynomial coefficients. We found that a second-order polynomial was insufficient to capture the curvature along the full length of the stream, with divergence at the ends of the tails. A third-order polynomial was sufficient and desirable, as the lowest order adequately captures the stream’s path over the entire length under consideration.
In this analysis, we only consider one side of the stream. For instance, if the impact candidate was in the leading tail, only the star particles with τ > 0 are used to constrain the stream track. The polynomial coefficients were determined through a minimization method using the Nelder-Mead algorithm from scipy’s optimization package.
Since we saved the simulation snapshots at a temporal resolution of 1 Myr – rather than at the integration time-step, which would have generated excessive data, we must interpolate between snapshots to more precisely estimate the impact geometry. We fit the stream’s shape with a parametric third-order polynomial at the five time steps surrounding the approximate impact time. This time is a period of 5 Myr, sufficiently covering the interaction time. The interaction time can be estimated as ![\[t \approx \frac{\frame{100\,\frame{\text{pc}}}}{\frame{300\,\frac{\frame{\frame{\text{km}}}}{\frame{\text{s}}}}} \approx 0.3\,\frame{\text{Myr}}\frame{\text{.}}\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq13.png) .
.
Then, we used a cubic spline interpolation for the coefficients describing the stream’s shape, which allows us to describe each polynomial coefficient as a function of time. Consequently, we can parameterize the stream as a function of both simulation time and position along the stream:
![\[s(t,\tau ) = \{ \begin{array}{{c}} \frame{x(t,\tau ) = \frame{a_0}(t) + \frame{a_1}(t)\tau + \frame{a_2}(t)\frame{\tau ^2} + \frame{a_3}(t)\frame{\tau ^3}} \hfill \\ \frame{y(t,\tau ) = \frame{b_0}(t) + \frame{b_1}(t)\tau + \frame{b_2}(t)\frame{\tau ^2} + \frame{b_3}(t)\frame{\tau ^3}} \hfill \\ \frame{z(t,\tau ) = \frame{c_0}(t) + \frame{c_1}(t)\tau + \frame{c_2}(t)\frame{\tau ^2} + \frame{c_3}(t)\frame{\tau ^3}.} \hfill \\ \end{array} \]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq14.png) (C.2)
(C.2)
The values of the coefficients as a function of time are obtained through linear interpolation, ensuring that the coefficients at the snapshot times match the values constrained by the simulation data.
Next, we fit the trajectory of the perturber with a secondorder polynomial. With equations for both the stream and the perturber as functions of time, we identify the time and location of impact by minimizing a cost function, defined as the distance between the stream and the perturber:
![\[b(t,\tau ) = \|s(t,\tau ) - p(t)\|,\]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq15.png) (C.3)
where s(t, τ) is the Galactocentric position of a point on the stream, p(t) is the position of the perturber, and b is the distance between the two. The minimum value of b, denoted as min(b), represents the impact parameter. We performed the minimization using scipy’s optimization package with the L-BFGS-B method, which allowed us to place bounds on t and τ, ensuring no extrapolation occurs (Davidon 1991).
(C.3)
where s(t, τ) is the Galactocentric position of a point on the stream, p(t) is the position of the perturber, and b is the distance between the two. The minimum value of b, denoted as min(b), represents the impact parameter. We performed the minimization using scipy’s optimization package with the L-BFGS-B method, which allowed us to place bounds on t and τ, ensuring no extrapolation occurs (Davidon 1991).
Once this minimization is done, determining the relative velocity becomes straightforward. Since the minimization provides the impact parameter, time of impact, and the corresponding value of τ, we can compute the derivatives of the parametric equations at tmin and τmin. The parallel and perpendicular components of the perturber’s velocity relative to the stream are given by:
![\[\begin{array}{{c}} \frame{\delta v = \frame{\upsilon _p} - \frame{\upsilon _s},} \hfill \\ \frame{\frame{w_\|} = (\delta \upsilon ) \cdot \frame{\frame{\hat \upsilon }_s},} \hfill \\ \frame{\frame{w_ \bot } = \sqrt \frame{\frame{\text{\Delta }}\frame{\upsilon ^2} - w_\|^2,} } \hfill \\ \end{array} \]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq16.png) (C.4)
where υp and υs are the velocities of the perturber and the stream, respectively. We compute the strongest five flybys for each of the 50 simulations. Thus, we created a sample of 250 impacts and flagged those that give rise to gaps. We refer the reader to Sect. 3.3 for the presentation and discussion of the results.
(C.4)
where υp and υs are the velocities of the perturber and the stream, respectively. We compute the strongest five flybys for each of the 50 simulations. Thus, we created a sample of 250 impacts and flagged those that give rise to gaps. We refer the reader to Sect. 3.3 for the presentation and discussion of the results.
Appendix D Survival of gaps in streams emerging from more massive globular clusters
In Section 2.2, we emphasized that the conditions chosen to simulate the formation and evolution of streams around Pal 5 are probably unrealistic. By choosing, as we did, the same values for the mass and size of the cluster 5 billion years ago as the cluster has today, we did not take into account the loss of mass and internal evolution of the cluster over time. In particular, the velocity dispersion of the stars in a cluster and the velocity dispersion of the stars leaving the cluster and entering the stream depend on the cluster’s mass. It is therefore legitimate to ask whether, using a progenitor with a different mass and/or size, the gaps survive and whether, in particular, gaps formed several billion years ago can still be visible today.
 |
Fig. D.1 We dissect the one-dimensional density of the stream from the bottom panel of Fig. D.2. We divide the stars into two categories: the multiple groups that are shocked out at different pericenter passages, or those that leak out of the cluster continuously. The bottom panel shows the leaked population in blue, and each group that was shocked out at each pericenter passage is color-coded by the escape time. The sum of the leaked and shocked outflow gives the total profile density, which is shown in black. The top four panels display the first shocked groups from different pericenter passages, shown individually. Each group shows the gap resulting from the impact of NGC 7078 ∼2.5 Gyr ago, yet they are progressively offset as explained in the text. |
While we anticipate that a specific study on this aspect is in preparation (Ferrone et al., in prep), we would like to preview a few results here, particularly regarding the gap decoherence phenomenon presented in Fig. D.1. First, Fig. D.2 shows two streams with the same orbital parameters that were impacted by NGC 7078. The top panel shows a stream originating from a host mass of ∼10, 000 M⊙, while in the second panel we increased the mass to ∼ 40, 000 M⊙. For simplicity, both clusters have the same half-mass radius of 27 pc. The encounter occurred about two and a half billion years ago with NGC 7078, which has a mass of 5.16 × 105 M⊙. The gap persists for the lighter host, yet is barely visible in the case of the more massive host.
 |
Fig. D.2 Both simulations use identical orbital conditions for the globular clusters, with a half-mass radius of 27 pc. In the lower panel, Pal 5’s mass is increased relative to the upper one. Although both streams are perturbed by NGC 7078 approximately 2.5 Gyr ago, the resulting gap is attenuated in the more massive model. |
Fig. D.1 dissects the more massive stream of Fig. D.2 and explains why the gap does not persist. The bottom panel shows the total density distribution, decomposed into two profiles: stars that are either leaked or shocked out of the cluster. By shocked, we mean stars that are lost during pericenter passages. Tidal forces generally scale with r−3, and thus significantly intensify during pericenter passages (see Fig. 3 of Dehnen et al. (2004) for an illustration of the magnitude of tidal forces along an orbit). A consequence of these passages is that many more stars escape, fleeing with higher mean velocity and velocity dispersion–this can be visualized in the “Christmas tree” illustration in Fig. A.3 of Mastrobuono-Battisti et al. (2012). We consider the continuous outflow of stars between pericenter passages to be leaked stars. We identify pericenter passages by computing each local minimum of the cluster’s Galactocentric 3D radius using scipy.signal.find_peaks. The duration of each shock is given by ![\[\frame{t_\frame{\frame{\text{shock~}}}} = 2\sqrt \frame{r/\left|\nolbrace \frame{\nabla \frame{\text{\Phi }}} \norbrace\right|} \]](/articles/aa/full_html/2025/07/aa53923-25/aa53923-25-eq17.png) , where r is the Galactocentric radius and |∇Φ| is the magnitude of the acceleration from the Galactic potential. Stars within this time range around a given pericenter passage are all given the same color and shown as individual groups in the first through fourth panels of Fig. D.1.
, where r is the Galactocentric radius and |∇Φ| is the magnitude of the acceleration from the Galactic potential. Stars within this time range around a given pericenter passage are all given the same color and shown as individual groups in the first through fourth panels of Fig. D.1.
References
- Amorisco, N. C. 2021, arXiv e-prints [arXiv:2111.01148] [Google Scholar]
- Amorisco, N. C., Gómez, F. A., Vegetti, S., & White, S. D. M. 2016, MNRAS, 463, L17 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banik, N., & Bovy, J. 2019, MNRAS, 484, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Banik, N., Bovy, J., Bertone, G., Erkal, D., & de Boer, T. J. L. 2021, J. Cosmology Astropart. Phys., 2021, 043 [Google Scholar]
- Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2019, MNRAS, 482, 5138 [Google Scholar]
- Baumgardt, H., Sollima, A., & Hilker, M. 2020, PASA, 37, e046 [Google Scholar]
- Belokurov, V., Evans, N. W., Irwin, M. J., Hewett, P. C., & Wilkinson, M. I. 2006, ApJ, 637, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Schlafly, E. F., et al. 2014, MNRAS, 443, L84 [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Schlafly, E. F., et al. 2016, MNRAS, 463, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Bonaca, A., & Hogg, D. W. 2018, ApJ, 867, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Geha, M., & Kallivayalil, N. 2012, ApJ, 760, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Hogg, D. W., Price-Whelan, A. M., & Conroy, C. 2019, ApJ, 880, 38 [Google Scholar]
- Bonaca, A., Conroy, C., Hogg, D. W., et al. 2020a, ApJ, 892, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Pearson, S., Price-Whelan, A. M., et al. 2020b, ApJ, 889, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., & Price-Whelan, A. M. 2025, New A Rev., 100, 101713 [Google Scholar]
- Bovy, J. 2014, ApJ, 795, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Bahmanyar, A., Fritz, T. K., & Kallivayalil, N. 2016, ApJ, 833, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G. 2012, ApJ, 748, 20 [Google Scholar]
- Carlberg, R. G., & Grillmair, C. J. 2013, ApJ, 768, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Grillmair, C. J., & Hetherington, N. 2012, ApJ, 760, 75 [Google Scholar]
- Chen, B., Stoughton, C., Smith, J. A., et al. 2001, ApJ, 553, 184 [Google Scholar]
- Davidon, W. C. 1991, SIAM J. Optimiz., 1, 1 [Google Scholar]
- de Boer, T. J. L., Belokurov, V., Koposov, S. E., et al. 2018, MNRAS, 477, 1893 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T., Gieles, M., & Erkal, D. 2020, AAS Meeting Abs., 235, 336.07 [Google Scholar]
- Dehnen, W., Odenkirchen, M., Grebel, E. K., & Rix, H.-W. 2004, AJ, 127, 2753 [NASA ADS] [CrossRef] [Google Scholar]
- Doke, Y., & Hattori, K. 2022, ApJ, 941, 129 [Google Scholar]
- Erkal, D., & Belokurov, V. 2015, MNRAS, 450, 1136 [Google Scholar]
- Erkal, D., Koposov, S. E., & Belokurov, V. 2017, MNRAS, 470, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrone, S., Di Matteo, P., Mastrobuono-Battisti, A., et al. 2023, A&A, 673, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieles, M., Erkal, D., Antonini, F., Balbinot, E., & Peñarrubia, J. 2021, Nat. Astron., 5, 957 [Google Scholar]
- Green, A. M., Hofmann, S., & Schwarz, D. J. 2005, J. Cosmology Astropart. Phys., 2005, 003 [Google Scholar]
- Grillmair, C. J. 2009, ApJ, 693, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J. 2014, ApJ, 790, L10 [Google Scholar]
- Grillmair, C. J. 2017, ApJ, 847, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006a, ApJ, 641, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006b, ApJ, 643, L17 [Google Scholar]
- Grillmair, C. J., Freeman, K. C., Irwin, M., & Quinn, P. J. 1995, AJ, 109, 2553 [Google Scholar]
- Grillmair, C. J., Cutri, R., Masci, F. J., et al. 2013, ApJ, 769, L23 [Google Scholar]
- Grillmair, C. J., Hetherington, L., Carlberg, R. G., & Willman, B. 2015, ApJ, 812, L26 [Google Scholar]
- Grondin, S. M., Webb, J. J., Lane, J. M. M., Speagle, J. S., & Leigh, N. W. C. 2024, MNRAS, 528, 5189 [Google Scholar]
- Hattori, K., Erkal, D., & Sanders, J. L. 2016, MNRAS, 460, 497 [CrossRef] [Google Scholar]
- Helmi, A. 2004, MNRAS, 351, 643 [Google Scholar]
- Helmi, A., & Koppelman, H. H. 2016, ApJ, 828, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Hermans, J., Banik, N., Weniger, C., Bertone, G., & Louppe, G. 2021, MNRAS, 507, 1999 [Google Scholar]
- Hilmi, T., Erkal, D., Koposov, S. E., et al. 2024, arXiv e-prints [arXiv:2404.02953] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
- Ibata, R. A., Lewis, G. F., Irwin, M. J., & Quinn, T. 2002, MNRAS, 332, 915 [Google Scholar]
- Ibata, R. A., Lewis, G. F., & Martin, N. F. 2016, ApJ, 819, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Thomas, G., Martin, N. F., & Chapman, S. 2017, ApJ, 842, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Malhan, K., Martin, N. F., & Starkenburg, E. 2018, ApJ, 865, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Malhan, K., & Martin, N. F. 2019, ApJ, 872, 152 [Google Scholar]
- Ibata, R., Malhan, K., Martin, N., et al. 2021, ApJ, 914, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Malhan, K., Tenachi, W., et al. 2024, ApJ, 967, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ishchenko, M., Sobolenko, M., Berczik, P., et al. 2023a, A&A, 673, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishchenko, M., Sobolenko, M., Berczik, P., et al. 2023b, A&A, 678, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ji, A. P., Li, T. S., Hansen, T. T., et al. 2020, AJ, 160, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Law, D. R., & Majewski, S. R. 2005, ApJ, 619, 800 [Google Scholar]
- Keenan, D. W., & Innanen, K. A. 1975, AJ, 80, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Mastrobuono-Battisti, A., Di Matteo, P., & Haywood, M. 2018, A&A, 620, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koposov, S. E., Irwin, M., Belokurov, V., et al. 2014, MNRAS, 442, L85 [Google Scholar]
- Kuzma, P. B., Da Costa, G. S., Keller, S. C., & Maunder, E. 2015, MNRAS, 446, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., & Majewski, S. R. 2010, ApJ, 718, 1128 [Google Scholar]
- Law, D. R., Johnston, K. V., & Majewski, S. R. 2005, ApJ, 619, 807 [Google Scholar]
- Lee, K. H., Lee, H. M., Fahlman, G. G., & Lee, M. G. 2003, AJ, 126, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, I., & Scholz, R. D. 1997, A&A, 320, 776 [NASA ADS] [Google Scholar]
- Leon, S., Meylan, G., & Combes, F. 2000, A&A, 359, 907 [NASA ADS] [Google Scholar]
- Li, T. S., Koposov, S. E., Zucker, D. B., et al. 2019, MNRAS, 490, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. S., Koposov, S. E., Erkal, D., et al. 2021, ApJ, 911, 149 [CrossRef] [Google Scholar]
- Li, T. S., Ji, A. P., Pace, A. B., et al. 2022, ApJ, 928, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., & Ibata, R. A. 2018, MNRAS, 477, 4063 [Google Scholar]
- Malhan, K., & Ibata, R. A. 2019, MNRAS, 486, 2995 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., Ibata, R. A., & Martin, N. F. 2018, MNRAS, 481, 3442 [Google Scholar]
- Mastrobuono-Battisti, A., Di Matteo, P., Montuori, M., & Haywood, M. 2012, A&A, 546, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastrobuono-Battisti, A., Khoperskov, S., Di Matteo, P., & Haywood, M. 2019, A&A, 622, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateu, C. 2023, MNRAS, 520, 5225 [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Moliné, Á., Sánchez-Conde, M. A., Palomares-Ruiz, S., & Prada, F. 2017, MNRAS, 466, 4974 [Google Scholar]
- Montuori, M., Capuzzo-Dolcetta, R., Di Matteo, P., Lepinette, A., & Miocchi, P. 2007, ApJ, 659, 1212 [Google Scholar]
- Nibauer, J., Bonaca, A., Spergel, D. N., et al. 2025, ApJ, 983, 68 [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., et al. 2002, AAS Meeting Abstracts, 200, 10.01 [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., et al. 2003, AJ, 126, 2385 [Google Scholar]
- Pearson, S., Price-Whelan, A. M., & Johnston, K. V. 2017, Nat. Astron., 1, 633 [Google Scholar]
- Pearson, S., Bonaca, A., Chen, Y., & Gnedin, O. Y. 2024, ApJ, 976, 54 [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Pouliasis, E., Di Matteo, P., & Haywood, M. 2017, A&A, 598, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price-Whelan, A. M., Sesar, B., Johnston, K. V., & Rix, H.-W. 2016, ApJ, 824, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Mateu, C., Iorio, G., et al. 2019, AJ, 158, 223 [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Sanders, J. L., Bovy, J., & Erkal, D. 2016, MNRAS, 457, 3817 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R. 2012, MNRAS, 427, 274 [Google Scholar]
- Siegel, M. H. 2001, AAS Meeting Abstracts, 199, 109.06 [Google Scholar]
- Sollima, A. 2020, MNRAS, 495, 2222 [Google Scholar]
- Sollima, A., Martínez-Delgado, D., Valls-Gabaud, D., & Peñarrubia, J. 2011, ApJ, 726, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Martínez Delgado, D., Muñoz, R. R., et al. 2018, MNRAS, 476, 4814 [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [Google Scholar]
- Testa, V., Zaggia, S. R., Andreon, S., et al. 2000, A&A, 356, 127 [NASA ADS] [Google Scholar]
- Thomas, G. F., Ibata, R., Famaey, B., Martin, N. F., & Lewis, G. F. 2016, MNRAS, 460, 2711 [Google Scholar]
- Usman, S. A., Ji, A. P., Li, T. S., et al. 2024, MNRAS, 529, 2413 [Google Scholar]
- Varghese, A., Ibata, R., & Lewis, G. F. 2011, MNRAS, 417, 198 [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., Lagattuta, D. J., McKean, J. P., et al. 2012, Nature, 481, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wang, L., Spurzem, R., Aarseth, S., et al. 2016, MNRAS, 458, 1450 [Google Scholar]
For more subsequent observation detections of tidal debris, i.e., globular cluster stars beyond the tidal radius see the works of: Lehmann & Scholz (1997); Testa et al. (2000); Leon et al. (2000); Siegel (2001); Lee et al. (2003); Sollima et al. (2011, 2018); Sollima (2020).
The Baumgardt catalog has been assembled across a series of works, see: Baumgardt et al. (2020, 2019); Baumgardt & Hilker (2018). The catalog can be found on the World Wide Web at https://people.smp.uq.edu.au/HolgerBaumgardt/globular/
In this regard, we recall that Bovy (2014) modeled the GD-1 stream as the result of the dissolution of a cluster with a mass of 2 × 104 M⊙, and a tidal radius of 0.07 kpc.
All Tables
All Figures
 |
Fig. 1 Simulated Palomar 5 stream created by modeling the host cluster as a Plummer sphere disrupting within an axis-symmetric Galactic potential plus the gravitational effect of 164 other Galactic globular clusters. The top panel shows the distribution of star particles that escaped the cluster due to tidal forces. The bottom panel shows the 1D density profile marginalized over longitude. The gray fill shows a reference simulation that uses the same conditions to produce the stream but does not include the other globular clusters. The large central peak in density is composed of particles still bound to Palomar 5. ℓ0, b0 are located Palomar 5’s cluster’s center of mass. Two large gaps are present due to the passage of two globular clusters. Np indicates the number of particles in a bin, while N is the total number of particles, which is 100 000. |
| In the text | |
 |
Fig. 2 Density maps of Palomar 5’s stream in the tail coordinate system, where x′is the integrated arc length along the cluster’s orbit and y′ is the distance within the orbital plane. The color scale represents normalized particle counts (total: 100 000). The top panel shows the full simulation with three gaps on the stream’s right-hand side. The next three panels depict simulations with identical initial conditions but exclude the gravitational influence of all clusters except those forming a given gap. The Reference simulation omits the influence from other globular clusters. The bottom panel compares Palomar 5’s observed stream length to the Reference simulation, using the same Monte-Carlo realization as Fig. 1 and Sampling 009 (as seen in the online appendix). |
| In the text | |
 |
Fig. 3 Simulation time when the impacts occurred for all gap-causing flybys summed over all 50 simulations. Each perturbing cluster is labeled and color-consistent. We report the time axis in simulation units, with 1 s kpc km −1 corresponding to roughly 1 Gyr. We note that the plot breaks the y-axis to accommodate the large number of encounters from NGC 2808 without overshadowing the other interactions. |
| In the text | |
 |
Fig. 4 Distribution of the number of gaps normalized over the total integration time and unit stream length as described by Eq. (4) for the whole set of 50 full simulations. |
| In the text | |
 |
Fig. 5 Distribution and relationship between the impact variables from Eq. (6) for all close flybys considered. The colors indicate the encounters that cause gaps and are the same as Fig. 3, with white edges for visibility and binned in red for the histograms. The black histogram shows the close encounters that did not lead to gaps. Indeed, no obvious trend has emerged that delimits these planes into gap-producing or non-gap-producing ones. |
| In the text | |
 |
Fig. 6 Distribution of imparted change in momentum (per unit mass) from a cluster flyby given by Eq. (6). The data set includes the top 5 strongest flybys from each simulation. Those that cause gaps are colored, stacked, and overlaid atop those that do not – this is the gray distribution. We note the meaning of the colors is the same as in Fig. 3. |
| In the text | |
 |
Fig. 7 Top left: energy-angular momentum space of the globular clusters in the simulations, with 50 × 165 data points representing all sampled initial conditions. Clusters impacting Palomar 5 are shown with colored markers, large for the samplings that induce a gap and small for those that do not. The small gray dots represent the non-gap-causing clusters. The 50 white dots indicate Palomar 5’s sampled initial conditions for the current day position. The light-pink dashed curve shows the circular velocity curve. Top right: mass-size plane of the globular clusters in the simulations, with uncertainties on the masses indicated as vertical lines. We remind the reader that the globular cluster catalog currently does not provide uncertainties for the characteristic radii of clusters. Bottom left: Palomar 5’s orbit in the Galactocentric xy plane. The gray scale represents all 50 stacked orbits, with 𝒫 indicating the probability of Palomar 5’s position, normalized to 𝒫max = 1. The colored markers indicate the position of the perturber when it impacted the stream and not its present-day position. Bottom right: same as the bottom left but in the meridional plane. In all panels, the colors of the markers and histogram bars correspond to specific perturbers as specified in Fig. 3. |
| In the text | |
 |
Fig. 8 Distribution of gaps as a function of absolute distance from the center of mass of Palomar 5’s globular cluster. We count the number of gaps within the observable range on an individual track basis, with track lengths determined by the minimum and maximum x′-coordinates from the bottom panel of Fig. 2. The ranges for Price-Whelan et al. (2019), Sollima (2020), and Ibata et al. (2021) are shown for their respective dimensions, and the number of gaps within these ranges is indicated in the figure. Vertical bars mark the x′ > 0 limit of the stream – we only show the right-hand side instead of both for clarity, as most gaps are located on the right-hand side of the stream in any case. |
| In the text | |
 |
Fig. A.1 Demonstration of the transformation from Galactocentric coordinates to tail coordinates. The black dot represents the globular cluster, while the thick black line shows a segment of its orbit. The star symbol indicates a star particle. The red vector points from the nearest point on the cluster’s orbit to the star particle. The Galactocentric position vector is the y′-axis. The local orbital plane, the cross-product between the orbit’s local position and velocity vector, defines the z′-axis. We project the red vector on each of these axes. We measure the x’ coordinate as the path length along the orbit from the cluster to the nearest point. Positive x′, y′, z′ indicate that a star is ahead of the cluster, farther from the Galactic center, and above the orbital plane, respectively. |
| In the text | |
 |
Fig. A.2 Comparison between the density maps and profiles of the full and reference simulations is presented. The blue vertical bars highlight the locations where the full simulation is less dense than the reference simulation by 2-σ. We do not consider bins below the noise threshold when measuring the differences between the two 1D profiles. We smoothed the 1D profiles with a median box-car filter. |
| In the text | |
 |
Fig. B.1 Demonstration of how we determined which globular clusters were responsible for the gaps. The y-axis is τ, a coordinate in units of time that indicates how far ahead or behind it is from a globular cluster. The x-axis is the simulation time, t, where 0 s km kpc−1 indicates the present time. The bottom plot showcases the evolution of the stream density over simulation time. We used the density to determine a suitable stream length. Subsequently, we used this length to extract a piece of Palomar 5’s orbit. This orbital segment approximates the stream. Then, we compute the gravitational force from all other stream stand-in clusters, shown in the top plot. The gravitational force is measured in acceleration and is given in integration units: km2 kpc−1 s−2. Moments of high acceleration indicate the passage of another cluster. The red circles indicate the top 5 strongest passages, as well as the names of the clusters. The example shown in this plot is the same simulation as Fig. 1. |
| In the text | |
 |
Fig. D.1 We dissect the one-dimensional density of the stream from the bottom panel of Fig. D.2. We divide the stars into two categories: the multiple groups that are shocked out at different pericenter passages, or those that leak out of the cluster continuously. The bottom panel shows the leaked population in blue, and each group that was shocked out at each pericenter passage is color-coded by the escape time. The sum of the leaked and shocked outflow gives the total profile density, which is shown in black. The top four panels display the first shocked groups from different pericenter passages, shown individually. Each group shows the gap resulting from the impact of NGC 7078 ∼2.5 Gyr ago, yet they are progressively offset as explained in the text. |
| In the text | |
 |
Fig. D.2 Both simulations use identical orbital conditions for the globular clusters, with a half-mass radius of 27 pc. In the lower panel, Pal 5’s mass is increased relative to the upper one. Although both streams are perturbed by NGC 7078 approximately 2.5 Gyr ago, the resulting gap is attenuated in the more massive model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


