| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A287 | |
| Number of page(s) | 17 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202452349 | |
| Published online | 24 January 2025 | |
Unified multiwavelength data analysis workflow with gammapy
Constraining the broadband emission of the flat-spectrum radio quasar OP 313
1
Instituto de Astrofísica de Canarias (IAC),
C/ Vía Láctea s/n,
38205
La Laguna,
Tenerife,
Spain
2
Universidad de La Laguna (ULL),
Avda. Astrofísico Francisco Sánchez s/n,
38206
La Laguna,
Tenerife,
Spain
3
FSLAC IRL 2009, CNRS/IAC,
La Laguna,
Tenerife,
Spain
4
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris,
91191
Gif-sur-Yvette,
France
5
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
6
Istituto Nazionale di Fisica Nucleare, Sezione di Padova,
35131
Padova,
Italy
7
APC, Université de Paris, CNRS, CEA, Observatoire de Paris,
10 rue Alice Domon et Léonie Duquet,
75013
Paris,
France
8
Max Planck Institute for Physics (MPP),
Boltzmannstr. 8,
85748
Garching/Munich,
Germany
★ Corresponding author; mnievas@iac.es
Received:
23
September
2024
Accepted:
8
December
2024
Context. The flat-spectrum radio quasar (FSRQ) OP 313 entered an enhanced activity phase in November 2023 and has undergone multiple flares since then. This activity has motivated the organization of several large multi-wavelength campaigns, including two deep observations from the hard X-ray telescope NuSTAR. We investigate the broadband emission from OP 313 during these two observations, based on a new unified analysis framework, with data in the optical to γ rays.
Aims. Traditional methods for analyzing blazar emission often rely on proprietary software tailored to specific instruments, making it challenging to integrate and interpret data from multiwavelength campaigns in a comprehensive way. This study demonstrates the feasibility of utilizing gammapy, an open-source Python package, together with common data formats originally developed for γ-ray instrumentation to perform a consistent multi-instrument analysis. This enables a forward-folding approach that fully incorporates source observations, detector responses, and various instrumental and astrophysical backgrounds. This methodology has been applied to an example set of recent data collected from the distant quasar OP 313.
Methods. We present a comprehensive data reconstruction and analysis for instruments including the Liverpool Telescope’s IO:O detector, Swift-UVOT, Swift-XRT, NuSTAR, and Fermi-LAT. The resulting spectral analysis has been validated against the native tools for each instrument. Additionally, we developed a multiwavelength phenomenological model of the source emission, encompassing the optical to γ-ray bands and incorporating absorption components across different energy regimes.
Results. We have introduced and validated a new unified framework for multiwavelength forward-folding data analysis based on gammapy and open data formats, demonstrating its application to spectral data from the quasar OP 313. This approach provides a more statistically correct treatment of the data than fitting a collection of flux points extracted from the different instruments. This study is the first to use a common event data format and analysis tool covering 11 orders of magnitude in energy, from approximately 1 eV to 100 GeV. The high-level event data, instrument response functions, and models are provided in a gammapy-compatible format, ensuring accessibility and reproducibility of scientific results. A brief discussion on the origin of the broadband emission of OP 313 is also included in this work.
Key words: acceleration of particles / astroparticle physics / methods: data analysis / methods: statistical / galaxies: high-redshift / quasars: individual: FSRQ OP 313
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Active galactic nuclei (AGNs), in particular those with large- scale jets of ultra-relativistic particles, are the primary extragalactic sources of γ-ray photons. Their nonthermal emission extends over the entire electromagnetic spectrum, from radio to γ rays; however, the driving physical mechanism that explains the radiation in each band is different. At low energies, from radio to optical (in some cases up to X-rays), the emission is often attributed to synchrotron radiation from relativistic electrons (Konigl 1981). At higher energies, the situation is less clear and diverse mechanisms are assumed to explain the emission, from an inverse Compton of the same electrons with the synchrotron radiation (synchrotron-self-Compton or SSC; see Maraschi et al. 1992) or with external thermal photons from the AGN structure (external Compton or EC; e.g., Dermer & Schlickeiser 1993) to various hadronic processes: protonsynchrotron or proton-proton (see e.g., Aharonian 2002).
Flat-spectrum radio quasars (FSRQs) are a subclass of AGNs characterized by jets closely aligned with the line of sight and strong thermal radiation components from the AGN accretion disk in the optical-UV band. This radiation is partially reprocessed into thermal emission by the dusty torus in the infrared and into Doppler-broadened emission lines in the broad line region (BLR). These thermal radiation fields are significant targets for Compton (up)scattering, making FSRQs often very luminous in the γ-ray band, especially during flares. This process is a major cooling mechanism for the accelerated electrons, as the electrons lose energy by scattering photons to higher energies. The high luminosity and close jet alignment makes FSRQs detectable at greater distances compared to BL Lac objects, which lack strong thermal components.
However, detecting very-high-energy (VHE; E > 100 GeV) γ-ray emission from AGNs (especially for those found at high redshifts) is challenging, due to the attenuation from the extragalactic background light (EBL; e.g., Domínguez et al. 2011; Saldana-Lopez et al. 2021), which absorbs γ rays from distant sources. It comprises an irreducible background that encodes important information about the star formation history in the Universe. The induced absorption produces an energydependent imprint on the blazar spectrum, significantly reducing the observable γ-ray flux in the VHE band. At the same time, it provides an opportunity to constrain the density of the EBL indirectly, provided that we can infer the intrinsic spectrum of the source. For sources at a redshift of ɀ ~ 1 and sub-TeV photons, the most relevant part of the spectrum of the EBL is the so-called cosmic optical background component.
OP 313 is a FSRQ at a redshift of ɀ = 0.997 (Schneider et al. 2010), which has experienced several flaring states over the past 15 years, as evidenced by the continuous monitoring with the Fermi-LAT γ-ray space telescope. In November 2023, OP 313 entered a multi-month high state, with daily energy flux often exceeding F(> 100 MeV) ≳ 10−10 ergcm−2 s−1 in the Fermi light curve repository (Abdollahi et al. 2023), representing the brightest flare for this source since Fermi’s launch in 2008, more than two orders of magnitude above the quiescent state flux. Around February 29, 2024 (MJD60369), the source reached a record high of (2.96 ± 0.57) × 10−9 ergcm−2 s−1. At ɀ = 0.997, this flaring episode makes OP 313 one of the most luminous AGNs ever recorded in γ rays. Follow-up observations with the Large-Sized Telescope prototype (LST-1) Cherenkov telescope began in December 2023 and led to the first detection of this source at VHEs, making OP 313 the most distant AGN ever detected by a Cherenkov telescope (Cortina & CTAO LST Collaboration 2023). Since then, the CTAO LST Collaboration has led a very intense multiwavelength monitoring campaign of the source, which has driven the development of new analysis techniques like the one presented in this work. The detection of such a bright and distant source, coupled with the methodologies described herein, offers a unique opportunity to constrain the dynamic emission of the source and provide a good benchmarking tool to test EBL models using physically motivated intrinsic emission models.
In this work, we aim to validate a new analysis and data management workflow using the OGIP format1 (Corcoran et al. 1995), the Gamma Astro Data Formats (GADF) initiative (Deil et al. 2017; Nigro et al. 2021), and the open-source tool gammapy (Donath et al. 2023). We want to deliver a working prototype data archive for the source, retaining the instrument response metadata for reproducibility in future analyses and the interpretation of these observations. This paper is focused on demonstrating and validating a novel methodology for multiwavelength analysis. For this demonstration, we combined datasets from a small coordinated multiwavelength follow-up campaign on OP 313 developed on March 4, 2024 (MJD60373) and March 15, 2024 (MJD60384), utilizing public data from Swift-UVOT, Swift-XRT, NuSTAR, and Fermi-LAT, and data from Liverpool IO:O in the optical regime. The resulting data products, in standard OGIP/GADF formats compatible with gammapy, are readily available in Zenodo (Nievas Rosillo et al. 2024) and GitHub2. They are described in more detail in Appendix A. We defer the integration of this dataset with a larger campaign, including proprietary VHE γ-ray data from LST-1 and MAGIC, as well as additional optical, infrared, and radio results, for a separate work coordinated by the CTAO LST Collaboration. To keep the main body of the paper as focused as possible, we refer to the data and results from the first observing night on March 4, 2024 (MJD60373). We also comment briefly on the results of the application of the analysis framework to the second night on March 15, 2024 (MJD60384) in Appendix F.
Our proposed method involves a forward modeling approach within a unified framework for all multiwavelength datasets, covering near-infrared (ɀ-band) to high-energy (HE, 100 MeV < E < 100 GeV) γ-rays, spanning nearly 11 orders of magnitude in energy. The mathematical representation of this method is as follows:
![$\eqalign{ & N(E,X) = \sum\limits_{{\rm{sources }}} {\cal R} \left( {E,{E_{{\rm{true }}}},X} \right)*{\cal P}\left( {{E_{{\rm{true }}}},X,{X_{{\rm{true }}}}} \right) \cr & & \,\,\,\,\,\,\,\,\,*\left[ {{\cal E}\left( {{E_{{\rm{true }}}},{X_{{\rm{true }}}}} \right) \times \phi \left( {{E_{{\rm{true }}}}} \right)} \right], \cr} $](/articles/aa/full_html/2025/01/aa52349-24/aa52349-24-eq1.png) (1)
(1)
where the number of expected excess event density N(E, X) (in space and energy) is given as a function of the sum over a number of finite emitters of the differential spectrum ϕ(Etrue) of each source times the exposure ℰ(Etrue, Xtrue) at its location, convoluted with the PSF Ƥ(Etrue, X, Xtrue). It offers information on the actual distribution of the measured counts given a location in the detector and sky, possibly as a function of energy, and a redistribution or migration matrix of ℛ(E, Etrue, X). The latter provides the redistribution between the true energy and the measured energy of the event, as a function of the location in the detector X and the sky Xtrue.
This paper is structured as follows. Section 2 details the motivation for developing a new method for analyzing and archiving high-level data across multiple bands. Section 3 describes the different instruments and procedures used to build the datasets and instrument response functions (IRFs). Section 4 presents the validation of the data formats and analysis methods, along with a phenomenological model of the emission of the source. The discussion of limitations, possible extensions, and prospects for a future work is included in Sect. 5. The main results are summarized in Sect. 6. Wherever applicable, we use a flat ΛCDM cosmology, with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and TCMB,0 = 2.725 K.
2 Motivation
Accurately modeling the spectral energy distribution (SED) of flaring AGNs across multiple wavelengths is a complex task due to the inherent challenges in handling diverse data types and formats. The traditional approach isolates each instrument or energy regime to “reconstruct” (or estimate) flux points and upper limits (ULs), followed by a reinterpretation of the same points using physically motivated models (see e.g., Ahnen et al. 2015; MAGIC Collaboration 2023). However, this method has several limitations.
First, storing flux points in tables or plots often results in significant information loss. This approach typically fails to account for the energy resolution of the instruments if no unfolding (Schmitt 2017) is performed (a process that is inherently ill- posed). Consequently, the flux points may become correlated.
Additionally, errors are commonly treated as Gaussian, which is inappropriate for instruments that operate in low-count regimes where Poisson statistics are more suitable (see e.g., Yamada et al. 2019). Overall, ULs are frequently represented as single values at specific confidence levels, resulting in the loss of information contained in the underlying probability distributions. This practice can lead to biased interpretations, especially when statistical fluctuations, ULs and non-detections are ignored (e.g., Essey & Kusenko 2014).
Moreover, current methods fall short in handling multiplicative models in SED flux points, such as correcting for hydrogen column density (NH) in X-ray data, Galactic extinction in the optical/UV, or EBL absorption in the γ-ray regime. Typically, these corrections are applied to the reconstructed flux points, which can hinder accurate statistical correction for absorption components in the SED, particularly if the correction is applied differently for each dataset (this is sometimes the case for works based on archival data samples, e.g., Nievas Rosillo et al. 2022).
Recent advancements have explored moving away from flux points towards forward-folding techniques, which have demonstrated promising results in characterizing the EBL (Acciari et al. 2019) using VHE data. This forward-folding approach offers a more comprehensive statistical analysis of multiwavelength datasets, addressing many shortcomings of traditional flux-point methods. One key distinction is that flux-point fitting loses access to instrument-specific information (e.g., energy resolution, effective area, instrumental backgrounds, and PSF), while forward-folding incorporates these details as an essential part of the analysis convolving complete emission models with the IRFs to calculate the likelihood. By adopting the forward modeling technique, emission, and absorption models can be seamlessly integrated into the analysis. This enables a better handling of uncertainties in parameters, such as hydrogen column density, and EBL. Despite its advantages, forward-folding presents practical challenges, such as the need to install and configure analysis tools for each instrument and manage the orchestration of communication between them to compute the multi-instrument likelihood.
Our immediate goal is therefore to integrate high-level data from various photon-counting experiments into a unified analysis framework. To facilitate this, we propose using the standardized format for high-level data products, which ensures easier distribution of the data and instrument description, as well as the reproducibility of the results. As an open-source Python package based on the popular libraries numpy (Harris et al. 2020) and astropy (Astropy Collaboration 2013, 2018, 2022, 2024), gammapy (Acero et al. 2024) is particularly well-suited for this task. As the official science tool for the Cherenkov Telescope Array Observatory (CTAO), gammapy is actively developed and compatible with both OGIP (X-ray) and GADF (γ-ray) data formats. This makes it an ideal choice for our analysis, enabling the joint analysis of different types of datasets, whether onedimensional (1D) if only a distribution of counts as a function of energy is stored, or three-dimensional (3D) where data cubes of three dimensions (two spatial coordinates and one energy coordinate) are available. Finally, we show that even in the case of single-channel photometric datasets the proposed format is well suited to describe the data.
Furthermore, gammapy allows for the incorporation of physically motivated models through external emission libraries (including synchrotron, inverse Compton, and absorption components; e.g., EBL absorption) or even extend it with models from the X-ray library sherpa (Freeman et al. 2001; Doe et al. 2007; Burke et al. 2024) to add hydrogen absorption and interstellar extinction. Public radiation processes modeling codes like agnpy (Nigro et al. 2022; Nigro et al. 2023), jetset (Tramacere et al. 2009; Tramacere et al. 2011; Tramacere 2020), and naima (Zabalza 2015) offer a more accurate representation of underlying physical processes compared to traditional functional or empirical models available in standard X-ray analysis packages like xspec (Arnaud 1996) and sherpa. This capability allows for a more accurate and statistically robust comparison of different models.
The proposed workflow can be compared with the MultiMission Maximum Likelihood framework (3ML, Vianello et al. 2015; Burgess et al. 2021), a versatile tool designed to facilitate multiwavelength analysis by integrating various software packages tailored for different types of observational data (see e.g., Albert et al. 2023; Klinger et al. 2024). However, 3ML requires a complex setup involving the installation and configuration of multiple software tools within a common environment to “export” the likelihood functionality for each instrument. This integration involves ensuring seamless communication between tools such as xspec for X-ray data, Fermipy or gammapy for γ-ray analysis, and other domain-specific software for optical photometric data. In contrast, while our method requires the preliminary construction of IRFs, it provides a unified data format and analysis workflow that supports the integration of multiwavelength data without the need for multiple software environments. By design, the proposed methodology simplifies the analysis setup, enhances portability, and improves reproducibility compared to the arguably more cumbersome process required by 3ML.
In the following sections, we detail the components of our methodology and describe the dataset and IRF generation for the case of study of the flaring blazar OP 313. Our proposed framework aims to enhance the accuracy of SED modeling and streamline the analysis process across diverse astrophysical datasets and improve the reproducibility of the results. This work focuses on the technical implementation and presents validation tests in comparison to the standard analysis tools and methods used for each instrument.
3 Dataset construction
3.1 Fermi-LAT data reduction
The Large Area Telescope (LAT, Atwood et al. 2009) onboard the Fermi satellite is a space-based, pair-conversion telescope surveying the sky in the high-energy γ-ray band (≲100 MeV to ≳100 GeV). It covers 20% of the sky instantaneously and surveys the entire sky approximately every ~3 hours, making it an excellent instrument for studying transient phenomena, including AGN flares.
3.1.1 Data reduction
We collected Fermi-LAT Pass 8 SOURCE class events involving energies higher than 100 MeV within a region of interest (ROI) of 15 deg radius around the OP 313 position from October 1, 2023 to April 1, 2024 (183 days). Nightly binned analyses, centered at 00:00 UTC, were performed with the Fermi Science Tools (Fermi Science Support Development Team 2019), using enrico (Sanchez & Deil 2015) as a high-level wrapper to manage the individual jobs. We utilized the latest available version of LAT’s IRFs (P8R3_SOURCE_V3) and applied a conservative zenith cut of 90 deg to avoid Earth’s limb contamination and a DATA_QUAL==1 && LAT_CONFIG==1 filter to ensure that only good quality events were analyzed, following the recommendations in Cicerone3.
The sky model for the analysis was generated using the Fermi-LAT 14-Year Point Source Catalog (4FGL-DR4 Abdollahi et al. 2022; Ballet et al. 2023), incorporating sources within a 20 deg radius around OP 313. Because we only integrate 24 h per analysis, we adopted a simple power-law (PWL) spectral model for OP 313, including the EBL absorption model from Domínguez et al. (2011). Positions and extensions of all sources from the 4FGL-DR4 were kept fixed, leaving only the spectral parameters of OP 313 (normalization and spectral index) and the normalization of the isotropic background component as free parameters. Spectral parameters for weak sources (<10 σ significance) and distant sources (>5 deg) were kept fixed, except for normalizations.
 |
Fig. 1 Long term evolution of the nightly high-energy gamma-ray flux emitted by OP 313. Left: Fermi-LAT light curve (1-day binning) of OP 313 above 100 MeV during the major 2023–2024 flare episode, for integral flux and spectral index. Blue and red bars mark the two nights with NuSTAR observations that are the focus of this study. Right: spectral index as a function of the integral flux for each night over six months of LAT data. The density of points is color-coded, with yellow points showing larger number density of nights and purple-blue tones indicating more isolated bins. |
3.1.2 Long-term analysis of the high-energy flare
In addition to focusing on two specific nights with comprehensive multiwavelength coverage, we examined the broader activity of OP 313 to contextualize its emission during these nights within a longer-term flare that persisted over several months in 2023–2024. Figure 1 shows the evolution of the nightly flux above 100 MeV for OP 313, with 24-hour bins centered at midnight UTC. It also depicts the evolution of the spectral index in the Fermi-LAT energy band and its correlation with the estimated flux, hinting that during high emission states, the spectrum of OP 313 becomes harder, with an index in the LAT band smaller than ~2. Figure 1 shows that the source entered an intermediate γ-ray activity plateau phase following a very strong flare at the end of February.
3.1.3 Dataset and IRFs
For Fermi-LAT, the dataset is managed as a 3D MapDataset in gammapy, which includes spatial (two coordinates) and energy (one coordinate) dimensions. Figure 2 shows 2D and 1D projected representations of the different parts giving shape to the Dataset. From first row (left) to second row (right) the following information is shown:
- (a)
Integral counts map: a 2D representation of the underlying “counts cube” summed over the entire energy range and smoothed with a Gaussian kernel of 0.2 deg to enhance visibility of sources;
- (b)
Initial model map convolved with the IRFs to produce the predicted counts (npred map) and again integrated over the entire energy range just for visualization purposes. The original 3D version of this model is fit to the data (counts cube) by gammapy;
- (c)
Containment radius: 1D representation of the PSF corresponding to 68% and 95% of the events contained as a function of energy, indicating the spatial resolution of the LAT. As opposed to the native analysis, Fermitools, our conversion to gammapy format assumes a non-varying PSF. For the analysis of a bright point-like source in a 20° region, the impact of spatial variations of the PSF of LAT is negligible;
- (d)
Energy dispersion: distribution of reconstructed energies versus true energies, providing information on how accurately the instrument measures the energy of γ-ray events and energy bias (significant at the lowest energies, E ≲ 100 MeV);
- (e)
Exposure map: 2D projection of the exposure (effective area multiplied by livetime) at 30.6 GeV, illustrating the spatial variation in exposure across the FoV;
- (f)
Exposure at the FoV center: 1D projection of the exposure as a function of true energy at the center of the field of view, showing the energy dependence of LAT’s sensitivity.
3.2 NuSTAR data reduction
The Nuclear Spectroscopic Telescope Array (NuSTAR, Harrison et al. 2013) is a focusing high-energy X-ray telescope operating in the 3–79 keV energy range. NuSTAR is a telescope array consisting of two twin modules (NuSTAR A and NuSTAR B), each made of four cadmium-zinc-tellurium detectors.
The standard data products provided to the observer are similar to other X-ray and gamma-ray space telescopes and consist of an event list with the reconstructed position, energy, and time of arrival of arrival of each detected photon.
The typical data reduction procedure used in X-ray astronomy is to define a spatial region for spectral extraction and an OFF region to estimate the spectral background. The data reduction and first stages of the analysis were performed with nustardas v2.1.2. The data were obtained from the quick-look area4 for observation IDs 91002609002 (night of March 4, 2024) and 91002609004 (night of March 15, 2024).
We ran nupipeline to process the data through Stage 1 (data calibration) and Stage 2 (data screening) for each of the nights and each of the telescope modules.
In a second step, we ran nuproducts (Stage 3) over the Level 2 event files to extract the integrated bandpass images (3– 79 keV), the source spectrum and light curves. Each NuSTAR module and sector has slightly different properties, therefore the background extraction regions were optimized for each module in shape and location to maximize background statistics, but keeping it within the limits of the same sector in which the source is located (see Fig. 3). From this point, we focus only on the spectral analysis of the Level 3 data produced by nuproducts, consisting of: (i) PHA files (energy spectra) for the source and background; (ii) ARF file (ancillary response file), which contains the effective area; and (iii) RMF file (response or redistribution matrix file), containing the energy migration matrix, a 2D array that gives the probabilities of assigning the photon to a given PHA channel for each input photon energy.
 |
Fig. 2 Fermi-LAT dataset description for the first selected night. From top left to bottom right: (a) Integral counts map, smoothed with a Gaussian kernel of 0.2°. (b) Initial model map, convolved with the IRFs (npred map). (c) 68% and 95% containment radius as a function of energy. (d) Energy dispersion (reconstructed energy as a function of true energy). (e) Exposure map at 10.6 GeV. (f) Exposure at the FoV center as a function of true energy. |
 |
Fig. 3 NuSTAR A/B counts map for the first observation night, together with the signal extraction region (blue dashed circle) and background extraction region (orange dashed box minus the signal extraction circle). |
3.2.1 Background model
Two analyses of the spectral data were considered, each with different background assumptions. The first analysis uses the ON-OFF method with W-statistics (W-statistics, wstat5, or Poisson data with a Poisson background). In this approach, the background is estimated measuring the number of events in the OFF region (see Fig. 3), assuming that it is the same as in the source region once correcting for the region size differences. This method is straightforward but cannot account for any spatial variation of the background (e.g., instrumental lines). In addition, it is statistically limited, as the W-statistic estimator can produce inaccurate results in low-count regimes, particularly if the background reaches zero counts in a given energy bin. To mitigate these issues, we re-binned the data into coarser energy bins (by a factor of 32) to increase the statistics per bin.
The second approach involves using a background model for NuSTAR data. We employed the cosmic X-ray background (CXB) simulation tool nuskybgd (Wik et al. 2014) to estimate the background (using C-statistics, cstat, or Poisson data with a background model). Compared to a directly measured background via the OFF background method, the predicted background from nuskybgd effectively addresses issues related to very low statistics at high energies. At the cost of the complexity added by nuskybgd, this approach retains the spectral resolution better, while fully utilizing the energy range of NuSTAR and accounts for the spatial variation of instrumental background. A detailed comparison of the impact of the choice of the background method is presented in Appendix D.
 |
Fig. 4 gammapy dataset representation of NuSTAR A for night 1 is shown here. NuSTAR B for this observation and NuSTAR A/B for night 2 are similar. From top-left to bottom-right: (a) estimated distribution of background events from the OFF rectangular region of Fig. 3 and the ON event distribution from the signal extraction region. (b) Estimated distribution of background events from nuskybgd. ON event distribution identical to the previous case. (c) NuSTAR A exposure (effective area × livetime) as a function of true energy. (d) NuSTAR A energy dispersion matrix. |
3.2.2 Dataset and IRFs
An overall view of the datasets for the NuSTAR A module on the first of the two available nights, with both the Poisson measured background (gammapy’s SpectrumDatasetOnOff object) and the one with nuskybgd background model (gammapy’s SpectrumDataset object), is shown in Fig. 4.
3.3 Swift-XRT data reduction
The X-Ray Telescope (XRT, Burrows et al. 2004) onboard the Swift satellite is an X-ray CCD imaging spectrometer designed to measure the position, spectrum, and brightness of astronomical objects in the range of 0.2, to 10, keV, with a dynamic range spanning more than seven orders of magnitude in flux. XRT has an effective area of approximately 135 cm2 at 1.5 keV and a detection sensitivity of 2 × 10−14 erg cm−2 s−1 in 10 ks of observing time.
The FoV is 23.6 × 23.6 arcmin, with an angular resolution of 18 arcsec (half-energy width; HEW). XRT operates in two readout modes: windowed timing (WT) and photon counting (PC). The WT mode bins 10 rows into a single row, focusing on the central 200 columns to improve time resolution to 1.7 ms (ideal for bright sources). The PC mode retains full imaging and spectroscopic capabilities but with a slower time resolution of 2.5 s, and is limited by pileup effects at high count rates (≳0.6 c/s, Vaughan et al. 2006). OP 313 is a relatively weak X-ray source with a modest count rate of ≲0.2 c/s, well within the capabilities of XRT in PC mode; therefore, this work focuses exclusively on this mode.
3.3.1 Data reduction
Swift-XRT data for OP 313 were downloaded from the UK Swift Science Data Centre6. Of all available data from the telescope, this work focuses on data collected during the nights of March 4th, 2024 and March 15th, 2024, with Swift observation IDs 00036384074 (2.96 ks) and 00089816002 (3.16 ks), respectively. We used Heasoft 6.32.1 and xrtdas v3.7.0 for data reduction. Spectra were extracted using xrtproducts for a fixed source extraction region of 40” radius, and a surrounding annular region of 80” and 300” radii for the background (see Fig. 5). This process results in two separate PHA files, along with the corresponding ARF. The RMF file was downloaded from HEASARC’s calibration database (CALDB).
 |
Fig. 5 Swift-XRT dataset representation after energy bin grouping to avoid background spectra dominated by zeros. (a) Swift-XRT image of OP 313. Blue circle and orange annulus show the signal and background extraction regions, respectively. (b) Distribution of events for both regions as a function of energy, corrected for the different region sizes. (c) Swift-XRT exposure (effective area × livetime) as a function of true energy. (d) Swift-XRT energy dispersion matrix (also known as redistribution matrix or migration matrix). |
3.3.2 Dataset and IRFs
The source and background PHA files, together with the RMF and ARF, were used to generate gammapy’s SpectrumDatasetOnOff objects, represented in Fig. 5. Following the discussion for NuSTAR on background statistics, we re-binned the spectral data into coarser energy bins with 30 channels each, to avoid zero counts in the background bins and therefore preserving the accuracy of the W-statistics assumption.
3.4 Swift-UVOT data reduction
The Ultraviolet/Optical Telescope (UVOT, Roming et al. 2005) onboard the Swift satellite is a diffraction-limited 30 cm modified Ritchey–Chrétien telescope with a limiting magnitude of 22.3 in 1 ks exposures. The UVOT detector, identical to XMM- Newton’s microchannel-plate intensified CCD, operates in photon counting mode over the range of 170 to 650 nm with 7 filters (V, B, U in the visible band; UVW1, UVM2, and UVW2 in the UV band; and a white or full-passband filter).
3.4.1 Data reduction
Data reduction for Swift-UVOT is performed using HEASoft v6.32.1. After downloading the target images from HEASARC’s repository, source extraction regions were defined as circular apertures. We used an exceptionally large radius of 25″ as one Swift gyroscope gradually degraded since July 2023 until failing in March 2024, increasing the likelihood of star tracker “loss of lock” after long slews (Cenko 2024a,b). The effect was particularly strong in the second night. The source regions are initially centered on the nominal position of OP 313 and finetuned based on centroid calculations. A background extraction region is then defined as an annulus with an inner radius of 40″ and an outer radius of 100″, centered on the source region. An example of the source and background regions, overlaid on top of the cutout of the Swift-UVOT images for different filters, is shown in Fig. 6. OP 313 is a distant, strongly Doppler-boosted source that appears point-like in most energy bands, including optical and UV. Consequently, UVOT data are analyzed using the same strategy used for XRT and NuSTAR. The result is the production of PHA source and background files (containing the integrated number of counts) for each filter. UVOT Response files (RSP) are downloaded directly from CALDB.
 |
Fig. 6 Swift-UVOT dataset representation. First row: Swift-UVOT images in two of the photometric filters available for the first selected night, indicated by dashed blue circles (signal) and orange annuli (background), respectively. Second row: effective collection area for each of the available Swift-UVOT filters. |
3.4.2 Dataset and IRFs
In imaging mode (i.e., without using the grisms) and for pointlike sources, we treat UVOT as a single-channel detector with a response determined by the selected photometric filter. The RSP files provide effective area information for each filter (see Fig. 6, second row). A dummy redistribution matrix is generated on the fly to match gammapy’s expected format definition. These redistribution matrices consist of a row of constant values, indicating that all photon energies contribute to the single-channel detector.
3.5 Liverpool-IO:O Data reduction
The Liverpool Telescope (LT, Steele et al. 2004), located on the Canary island of La Palma, is a fully robotic 2-meter telescope operated by Liverpool John Moores University. Its robotic capabilities allow for seamless transitions between different observing programs and instruments, which is crucial for time-sensitive observations of transient phenomena such as γ- ray bursts and supernovae. The Infrared-Optical:Optical camera (IO:O, see Barnsley et al. 2016) camera on the LT is equipped with a charge-coupled device (CCD) and a range of photometric filters. This camera includes a complete Sloan filter set: u, 𝑔, i, r, ɀ, making it a valuable lower-energy complement to the Swift-UVOT.
We developed a custom data analysis pipeline using the photutils (Bradley et al. 2022) Python package to process LT IO:O calibrated images through differential aperture photometry. This pipeline reduces each image into a SpectrumDatasetOnOff compatible format in gammapy, calculating signal and background counts in ON and OFF regions, respectively. The exposure or instrument response is estimated with the same images, using a differential photometry technique consisting on measuring the flux of several calibration stars in the FoV and comparing it to their known flux densities in reference catalogs.
3.5.1 Calibration stars
For each image, the pipeline utilizes the WCS information in the FITS header to identify potential calibration stars. These stars are matched with a clean star sample from the SDSS-DR18 catalog (Almeida et al. 2023), downloaded using astroquery (Ginsburg et al. 2019) with a custom SQL query to select all bright stars (mu,𝑔,r,i,ɀ < 21) in the FoV of the LT images; the exceptions include: those with non-clean flags, stars close to the edges of the SDSS images, stars affected by cosmic rays, blended stars with non-robust photometry, and those with large PSF magnitude errors or saturated pixels. An additional query to the Pan-STARRS PS1 catalog (Chambers et al. 2016; Flewelling et al. 2020) is performed to remove variable stars, as this catalog provides a measurement of the star magnitude dispersion (in bands 𝑔, r, i, and ɀ) for different observations of the same field. For each of the surviving stars (nine for our images), we assemble an astropy Table object containing the coordinates, magnitudes in the five selected bands and errors in the magnitudes. The magnitudes reported in the SDSS-DR18 are in the AB system, therefore conversion to flux densities, Fν, is given by:
![${m_{{\rm{AB}}}} = - 2.5{\log _{10}}\left[ {{{{F_v}} \over {{\rm{erg}}{\rm{c}}{{\rm{m}}^{ - 2}}{{\rm{s}}^{ - 1}}{\rm{H}}{{\rm{z}}^{ - 1}}}}} \right] - 48.60.$](/articles/aa/full_html/2025/01/aa52349-24/aa52349-24-eq2.png) (2)
(2)
3.5.2 Exposure estimation
The expected number of excess counts Nsrc,tot for an ON/OFF dataset in a given energy window can be expressed, following Eq. (1), in terms of the exposure ℰ(Etrue) and the differential spectrum ф(Etrue) as:
![${N_{{\rm{src,tot }}}} = \int_E {\cal R} \left( {E,{E_{{\rm{true }}}}} \right)*\left[ {{\cal E}\left( {{E_{{\rm{true }}}}} \right) \times \phi \left( {{E_{{\rm{true }}}}} \right)} \right]d{E_{{\rm{true }}}}.$](/articles/aa/full_html/2025/01/aa52349-24/aa52349-24-eq3.png) (3)
(3)
For optical ground-based instruments, characterizing ℰ(Etrue) is complex due to the need to account for both optical elements and atmospheric effects, the latter particularly hard to assess and only accounted for as an energy-averaged scaling factor of the exposure which is derived directly from star photometry. We approximate the energy-dependence of the exposure (effective area multiplied by livetime, as per gammapy definition) by the detector throughput curves provided in Barnsley et al. (2016), consisting of the product of filter transmission times cryostat transmission times CCD quantum efficiency (see Fig. 7). This approximation assumes that the photometric band is narrow enough for the source spectrum to be approximated by the photon density Fν/νc, where νc is the effective frequency of the photometric band and Fν is the flux density. Rewriting Eq. (3) in terms of wavelength, we get:
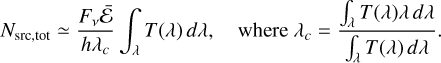 (4)
(4)
For each image, multiple stars are used to combine exposure estimates into a single value using a weighted average. The weights are the inverse of the estimated exposure variance. The final error on the exposure is obtained by adding the statistical uncertainty from the weighted average in quadrature to the standard deviation of all measurements:
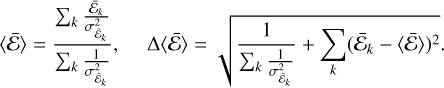 (5)
(5)
The exposure is then defined as 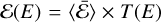 , where T(E) is interpolated from the known detector throughput dependency on wavelength, T(λ).
, where T(E) is interpolated from the known detector throughput dependency on wavelength, T(λ).
 |
Fig. 7 Liverpool IO:O dataset representation. Top row: LT IO:O images in two of the photometric filters available for the first selected night, with the signal and background extraction regions represented by blue and orange dashed circles and annuli, respectively. Bottom row: throughput for each of the available LT IO:O bands (transmission of the filter multiplied by the cryostat window transmission, CW, and the quantum efficiency of the CCD, QE) as dashed curves, and for CW and CW×QE alone. For completeness, the reconstructed effective area for each calibration star and each filter are shown as solid colored curves. |
3.5.3 Dataset and IRFs
For the LT IO:O observations of OP 313, we constructed SpectrumDatasetOnOff-style datasets, integrating photons over a region in the sky where the source is located for each filter (see Fig. 7). This approach resulted in 1D datasets for each image, losing spatial information. The exposure is estimated using the method described earlier, with the RMF generated following the same process as in UVOT, consisting of a row of constant values due to the single-channel nature of each image.
In contrast to space-borne photon-counting instruments, the flux calibration relies on differential photometry using calibration stars within the FoV. Variations in star spectra introduce systematic uncertainties in the effective areas. In a classical analysis method, based on flux point generation, these systematics are commonly added in quadrature to the statistical uncertainty.
In the forward-folding approach described here, an alternative method is utilized to include normalization models for each dataset or each filter (e.g., using a PiecewiseNormSpectralModel with normalization factors defined at filter-center energies). Gaussian priors are applied to account for the measured systematic uncertainties, with the widths of the Gaussian priors set to the standard deviation of the relative errors in the exposure with respect to the calculated mean. These relative errors range from less than 0.1 mag for the ɀ- and i-bands to more than 0.3 mag for the u-band, where fewer reference stars are detectable. A more detailed discussion on the practical differences between the two methods and the effect of adding the systematic in quadrature to the statistical uncertainty is provided in Appendix E.
 |
Fig. 8 Temporal coverage of the first observation night. |
4 Results
4.1 Summary of observational data and analysis
We present the results from the broadband emission analysis of OP 313, spanning from optical to high-energy γ rays. The instruments used, listed in decreasing order of energy coverage, are: Fermi-LAT, NuSTAR, Swift-XRT, Swift-UVOT, and the LT with the IO:O camera. Our analysis aims to interpret the data in a multiwavelength context and evaluate the capabilities of our new multi-instrument data management workflow. Before testing broadband modeling of the joint dataset, we carried out a technical validation of the analysis of data for each instrument separately, comparing in each case the spectral reconstruction of gammapy against that of the analysis tools native to each instrument. The details of this validation can be found in Appendix C. This section is divided into three parts:
Phenomenological broadband emission model: we define the model for the broadband emission of OP 313, which also serves as a benchmark for the analyses;
Comparison of fitting approaches: we compare the results obtained from the canonical flux point fitting method with those from the forward-folding approach;
Physical interpretation of the emission: we discuss the physical implications of the emission model and its consistency with the observed data.
4.2 Broadband emission modeling
4.2.1 Emission components
To model the broadband emission from OP 313, we employed a phenomenological approach using two power-laws with exponential cut-offs with a fixed index of α = 1:
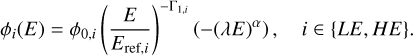 (6)
(6)
In this model, фLE(E) represents the synchrotron emission (low energy component), and фHE(E) represents the inverse Compton emission (high energy component) in a simplified leptonic scenario. The λ parameter refers to the inverse cut-off energy.
4.2.2 Absorption components
Absorption models were applied as follows:
ISM extinction: relevant for optical and especially UV energies. Given OP 313’s Galactic latitude of +83.34° and a color excess of EB−V ≈ 0.0125 (Schlegel et al. 1998), interstellar medium (ISM) extinction is minimal below 10 eV. At ~5 eV (UVOT’s UVM2 filter), the transparency is approximately 90% (Cardelli et al. 1989);
Hydrogen I absorption: relevant for X-ray energies below ~1 keV. Parameterized using the neutral hydrogen (HI) column density Wilms et al. (2000), which is 1.25 × 1020 cm−2 for OP 313 (HI4PI Collaboration 2016);
EBL absorption: significant at energies above ~10 GeV. We use the model from Saldana-Lopez et al. (2021), which can be regarded as an update over Domínguez et al. (2011).
4.3 Forward folding fitting method
We employed two distinct fitting methodologies to analyze the data from the participating instruments:
Flux-point fitting: This traditional method fits the model to observed flux points derived from analyzing each instrument’s data separately. Although it simplifies the fitting and can be computationally faster, it is observed to be more sensitive to the choice of initial parameters. Additionally, this approach may introduce errors due to differences in flux estimation and instrument calibration methodologies. It also overlooks upper limits and correlations between flux points;
Forward-folding technique: This method fits the model directly to the counts or event data from the instruments, convolving with the IRFs in each iteration. It allows for the background components and full instrumental effects to be incorporated.
Figure 9 illustrates the best-fit models and their confidence bands for both fitting methods, while Fig. 10 shows the correlations between the model parameters estimated from the covariance matrix for each fit. Both methods yield consistent results with well behaved residuals across the electromagnetic spectrum, confirming that the phenomenological model effectively captures the emission from OP 313 from optical to the γ-ray band. However, the forward folding technique shows better exploitation of the data, as it is able to use data beyond the last significant bins in both NuSTAR and Fermi-LAT.
Other notable differences between the two methods include the treatment of instrumental effects and background components, more accurate in the forward folding case as the method directly incorporates energy redistribution and provides a more uniform representation of the emission in the observed counts space. In the NuSTAR case, bins for which the effective area of the instrument is approximately zero can still provide useful constraints to the instrumental background model. As opposed to directly fitting instrumental background components during the forward folding, the classical method inadequately performs a fit to ‘flux points’ implying that the background is either fixed or subtracted. A similar problem occurs with Fermi-LAT skymodel, consisting on the sum of diffuse components (isotropic component, galactic diffuse emission) and a number of pointlike source lying close to OP 313. In the classical method, the contributions of such components are “frozen,” as opposed to fitted in the forward folding. Finally, the proposed workflow reduces systematic uncertainties associated with the conversion of counts to fluxes in the optical band as information coming from different filters is indirectly accounted for in the counts-flux conversion, likely improving the accuracy of the fit.
 |
Fig. 9 Joint multi-instrument forward-folding fit and joint fit using fluxpoints employing a phenomenological model with two distinct emission components and three absorption components. Top panel: individual datasets fitted with simple models (power-laws, log-parabolas, powerlaws with exponential cutoffs) and corresponding reconstructed flux points, and joint fits (flux points, forward folding). Middle panel: residuals, calculated as the ratio of reconstructed differential spectrum to model prediction for the flux points fit (residual PF, open markers), and as the significance or ratio of the difference between the excess counts and model predicted counts to the square root of the model predictions for each bin in the forward folding case (Residuals FF, small filled circles). For clarity, and due to the large amount of energy bins in the X-ray datasets, only one every five bins is shown for NuSTAR and one every three bins is shown for XRT. Bottom panel: multiplicative absorption components. |
4.4 Physical interpretation of the broadband emission
The continuous spectral connection from X-rays to γ-rays observed in Fig. 9 suggests a coherent emission scenario likely originating from a single emission zone. This points to a single inverse Compton process to explain both the X-ray and γ-ray emissions.
The data also favors an external inverse Compton model for OP 313 due to the large ratio of peak energy fluxes in the high energy component of the SED to that of the low-energy component (Compton dominance). In a synchrotron-self-Compton scenario, achieving such a high Compton dominance would require overly low magnetic fields, unrealistically high Doppler factors, and/or electron densities. In contrast, the external Compton scenario can naturally result in large values for that ratio as electrons scatter the highly dense photon field from external components such as the accretion disk, the dusty torus or the broad line region of the AGN.
To further identify the specific external radiation field responsible for the Compton upscattering, additional data in the VHE regime would be necessary. Observations with instruments such as LST-1 or MAGIC could provide this information. This aspect is beyond the scope of this work, and will be explored in a forthcoming publication including VHE observations from these two instruments.
 |
Fig. 10 Corner plot showing the error ellipses calculated with a bootstrap method for the best-fit (free) parameters of the flux-point based fit and the full forward-folding joint fit. The model used for the LE is highly degenerate because of the limited amount of available data to constrain that component. |
5 Discussion
In the preceding sections, we describe the process of evaluating a flexible data format designed to streamline both archival and analysis processes. This format, based on OGIP and the GADF initiative, integrates direct observations (e.g., event counts, spectra and the energy distributions of counts, or spatially-resolved data cubes) with IRFs from a diverse range of instruments, from space-borne γ-ray observatories like Fermi-LAT to groundbased optical telescopes such as the LT.
5.1 Flexibility and modeling capabilities
This method excels at providing flexibility for data modeling. We tested a phenomenological model with two simple power-laws with exponential cutoffs as emission components, aimed at representing synchrotron and inverse Compton emissions from a relativistic particle population in a jet. This model was complemented with fixed absorption components (extinction, neutral hydrogen, and EBL) and various background sources (diffuse radiation fields, additional sources in Fermi-LAT, and instrumental backgrounds in NuSTAR). Despite leaving many of these additional components free (normalizations of the spectral components of bright Fermi-LAT sources, Fermi-LAT isotropic and galactic diffuse components, and instrumental backgrounds in NuSTAR-A and NuSTAR-B), the minimization converged within a reasonable computing time using the proposed forward folding technique, offering advantages over traditional methods that rely on reconstructed flux points.
The approach proposed here for multiwavelength fitting is particularly beneficial for the X-ray data analysis part in this broadband context. Classical tools, such as xspec, are unfortunately often misused in the γ-ray community to produce flux points that are later fitted in the multiwavelength context (e.g., Nigro et al. 2022; Alfaro et al. 2022), despite not being technically designed for that purpose. In the case of NuSTAR, this is especially relevant since its instrumental background model is a complex sum of multiple components, making it almost impossible to extract for the source of interest flux points using xspec, as it would require us to remove the contribution to the total flux from each of the other components. The proposed flexible framework, based on gammapy, removes the need for multiwavelength flux points. It can potentially enable a 3D analysis of XRT and NuSTAR data. The latter could be particularly advantageous for extended sources, or for a point source on top of an extended source (e.g., a halo), especially for instruments with limited angular resolution like NuSTAR. Therefore, the method tested in this work presents natural extensions and improvements.
5.2 Main challenges and practical limits
The increased flexibility and accuracy naturally comes with tradeoffs. The method involves a more complex workflow and a larger parameter space. It also requires a more detailed modeling of observational data to incorporate all effects (astrophysical and instrumental backgrounds) and has to fold spectral models with various IRFs in each iteration to predict “observables” (counts, spectra, or data cubes) that are fit to the data. This complexity results in a higher computation time and practical limits for the method’s application are yet to be fully assessed.
For Fermi-LAT, our analysis assumes that the PSF depends only on energy and that it is constant within the FoV. This is a potential limitation with respect to its native analysis pipeline, Fermitools. Fortunately, for bright point-like sources like OP 313, where the contribution of other sources in the FoV is almost negligible, this effect should be small. Being gammapy an active developed tool, this drawback may be addressed in the future.
As photon-counting devices, Swift-XRT and Swift-UVOT are subject to the effects of pile-up and coincidence loss, which happen when the photon flux is large enough that two or more photons have a significant probability of being detected at the same position within a single CCD readout frame. In such cases, the detector registers the multiple events as a single event, with the recorded energy being the sum of the overlapping photons. This phenomenon skews the observed energy distribution and modifies the statistical properties of the data, deviating from pure Poissonian behavior and affecting the accuracy of count rate uncertainties.
The treatment of these effects varies per instrument. For UVOT, a correction for coincidence loss is implemented in uvotsource, effective as long as the field is not crowded and the source remains point-like (Breeveld et al. 2010). In the case of XRT, pile-up is less common in windowed timing (WT) mode unless the source is very bright, which requires specialized treatment when it does occur (Mineo et al. 2006). In photon counting (PC) mode (Vaughan et al. 2006), a common approach to mitigate pile-up involves defining an annular extraction region to mask the brightest central pixels and estimate the source counts from the wings of the PSF. As in UVOT, this approach is feasible only for isolated, point-like sources with minimal background contamination. More complex scenarios, such as extended sources or crowded fields, would likely require a more sophisticated spatial and spectral modeling of the emission and pile-up effects, well beyond the scope of this work.
5.3 Considerations for optical instruments
In the optical band, we tested a simplified IRF implementation tailored for relatively broad “filter” photometry. This approach represents a significant improvement over classical methods, which often just multiply the measured flux densities obtained through differential photometry techniques by an effective frequency of the band calculated under some assumption (typically flat photon spectrum or flat energy spectrum), ignoring the actual spectrum of the source. For steep spectra such as that of OP 313 in the UV band, the real photon distribution is typically skewed, shifting the effective frequency of the band.
The approximate IRFs we introduced in this work omit critical factors such as how atmospheric extinction, mirror reflectivity, aging of mirror coatings, and CCD defects modify the effective band profile. Including these elements in the IRFs (while technically challenging) would improve the accuracy of the spectral reconstruction. We did not explore a spectral data analysis in the optical band due to the additional complexities involved, such as calibrating both wavelengths and fluxes, which could compromise the Poisson statistics of the observed data.
6 Conclusions
The results presented in Sect. 4 demonstrate the effectiveness of the forward-folding technique for astrophysical data analysis in the context of complex multiwavelength studies involving several instruments. This method not only shows that it is possible to organize, store, and analyze data from different instruments together in a consistent manner, but it also offers practical advantages over the classical flux-point fitting technique in terms of robustness. Furthermore, it allows for a more accurate statistical comparison of different modeling hypotheses, thereby simplifying the interpretation of the physical processes at play for a source such as the FSRQ OP 313.
The resulting multi-instrument datasets and analysis code are stored in a format that is convenient for distribution and archiving. This format not only facilitates the reproduction of the results obtained in this specific study, but also supports further research on OP 313 with public datasets, as well as serve to make future validation tests for gammapy. Future works could involve a detailed modeling of the spectral energy distribution using physical models via codes such as jetset (Tramacere et al. 2009; Tramacere et al. 2011), agnpy (Nigro et al. 2022), Bjet_MCMC (Hervet et al. 2024; Hervet 2024), or SOPRANO (Gasparyan et al. 2022, 2023) or by exploring nested sampling methods (Buchner 2021).
This study provides a largely static view of OP 313 for two specific nights. Including variability studies and time-evolving models that account for particle injection and cooling will enhance our understanding of the emission of the source, in particular, and blazars in general. In this regard, the proposed simplified handling of instrument datasets will ensure greater consistency and reduce errors, compared to classical methods that use data in disparate formats. Hopefully this approach can provide one of the first comprehensive multiwavelength blazar datasets built over standardized data formats and open-source analysis tools.
Acknowledgements
We acknowledge the Fermi-LAT, NuSTAR, Swift-XRT, and Swift-UVOT teams for providing open-access data and analysis tools, as well as their support during this target-of-opportunity observation campaign. We also thank the Liverpool Telescope team for their prompt response and access to their robotic observations through reactive time. We are also grateful to the gammapy team for their extremely versatile and open-source analysis pipeline, which played a fundamental role in this multi-instrument, multiwavelength project. M.N.R. acknowledges support from the Agencia Estatal de Investigación del Ministerio de Ciencia, Innovación y Universidades (MCIU/AEI) under grant PARTICIPACIÓN DEL IAC EN EL EXPERIMENTO AMS and the European Regional Development Fund (ERDF) with reference PID2022- 137810NB-C22/DIO 10.13039/501100011033. J.O.S. and D.M. acknowledge financial support from the projetct ref. AST22_00001_9 with founding from the European Union – NextGenerationEU, the Ministerio de Ciencia, Innovación y Universidades, Plan de Recuperación, Transformación y Resiliencia, the Consejería de Universidad, Investigación e Innovación from the Junta de Andalucía and the Consejo Superior de Investigaciones Científicas. J.O.S. also acknowledges financial support through the Severo Ochoa grant CEX2021-001131-S funded by MCIN/AEI/ 10.13039/501100011033 and through grants PID2019- 107847RB-C44 and PID2022-139117NB-C44 and founding from INFN Cap. U.1.01.01.01.009. F.A. acknowledge support from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158) and support by CNES, focused on methodology for X-ray analysis.
Appendix A Software description and data repository
This work is based on the open-source analysis tool gammapy and open data formats initiatives (GADF, OGIP). Only two new code implementations were required to conduct the analysis as presented in this manuscript. The first is a reader for standard OGIP files generated by HEASARC’s native tools like uvot2pha, xrtproducts, and nuproducts. This reader was originally developed by Giunti & Terrier (2022) for XMM, and it was extended to also support NuSTAR, Swift-XRT, and Swift- UVOT. The second implementation is a set of PYTHON classes that perform an optical point-like photometric reduction of Liverpool Telescope IO:O data, producing OGIP-compliant files from optical images using a set of reference stars with known photometry from Sloan’s SDSS DR18 and PanSTARR’s PS1 catalogs.
Additionally, we provide Jupyter notebooks (Perez & Granger 2007; Ragan-Kelley et al. 2014) to illustrate the details of the construction of the gammapy-compliant datasets, as well as the analysis of each individual dataset and the joint analysis of the broadband datasets. These codes, along with the resulting gammapy-compliant data files, are available in a GitHub repository (Nievas 2024) for easy access and reproducible results. The structure of this repository is as follows:
Notebooks/DatasetGenerator
Notebooks/DatasetAnalysis
Helpers
Models
Figures
Within the Notebooks/DatasetGenerator/ directory (with one subdirectory for each night of observations), we stored notebooks (one per instrument) that compile all the steps to generate the gammapy-compliant 1D and 3D binned datasets, as described in Sect. 3. Similarly, Notebooks/DatasetAnalysis/ contains notebooks with the analysis of the datasets from individual instruments and the joint analysis of the multiwavelength (MWL) datasets. The Helpers/ directory contains functions for generating gammapy native multiplicative models for dust extinction, neutral hydrogen, and EBL absorption. It also includes classes for fetching photometry data from the PS1 and SDSS DR18 catalogs, as well as various file handling and plotting functions used across the analysis notebooks. The Models/ directory contains the tabular absorption models for EBL (Domínguez et al. 2011; Saldana-Lopez et al. 2021), the neutral hydrogen absorption exported from xspec’s TBabs model (Wilms et al. 2000; NASA 2024), and the dust extinction extracted from xspec’s redden (Cardelli et al. 1989; NASA 2024). Finally, the Figures/ directory (one subdirectory per observing night) contains plots and figures presented in this work.
Appendix B Reproducibility and analysis tools
To ensure reproducibility of the multiwavelength analysis presented in this work, detailed information is provided on the software tools (including versions), calibration files, and observation IDs used for each instrument. The data were processed using publicly available software and calibrated with the most up-to- date instrument response files. The following tables summarize the relevant details for each instrument.
Details for Fermi-LAT data analysis.
Details for NuSTAR data analysis.
Details for Swift-XRT data analysis.
B.1 Fermi-LAT
Fermi-LAT data were analyzed using the Fermitools package version 2.2.0, using the latest available diffuse models for PASS8 and the most recent 4FGL-DR4 catalog release at the time. The analysis settings are shown in Table B.1.
B.2 NuSTAR
NuSTAR observations were analyzed using the nustardas package version 2.1.2, as part of the HEASoft 6.31.1 software suite. The instrumental background modeling was performed with nuskybgd. The observation IDs and analysis details are listed in Table B.2
B.3 Swift-XRT
The X-ray Telescope (XRT) data were analyzed using the tools provided in the HEASoft package, version 6.32.1. Specific details on the software versions, observations, and response files are reported in Table B.3.
B.4 Swift-UVOT
The UVOT data were processed using the UVOT software suite within HEASoft 6.32.1, and the final data products were extracted using uvot2pha, which internally uses uvotproduct and uvotsource. Specific details are summarized in Table B.4.
Details for Swift-UVOT data analysis.
B.5 Liverpool IO:O
The Liverpool IO:O was provided in already reduced format by Liverpool’s automatic reduction, and the final photometric analysis was performed with a custom-made code, provided in the Notebooks folder of the GitHub repository, which is based on common python packages like astropy or photutils, and public catalogs from Sloan and Pan-STARRS
Details for Liverpool IO:O data analysis.
Appendix C Dataset analysis validation
This appendix shows the comparison between the analyses conducted using native tools specific to each instrument (i.e., xspec for NuSTAR and XRT, Fermitools/enrico for Fermi- LAT) and those performed on the OGIP- and GADF-compliant datasets using gammapy. This comparison is needed for validating the consistency and reliability of the gammapy-based analysis, and will turn crucial to later extend the full statistical forward folding technique across different wavelength regimes.
For high-energy instruments like Fermi-LAT, NuSTAR, and Swift-XRT, we directly compared in Fig. C.1 the best-fit spectral energy distribution confidence bands and corresponding flux points. To keep the comparison straightforward and the parameter space limited to just two variables, we used a simple power-law in each band, with either EBL absorption in γ rays or neutral hydrogen absorption in X-rays. Even though Fermi-LAT γ-ray data hints significant curvature in that band, using a simple model is enough to test the validity of the method, and only a power-law with exponential cut-off was used in Fig. 9 for the broadband analysis.
The results shown in figures C.1a, C.1b and C.1c indicate that the best-fit model and contours obtained with gammapy are indistinguishable from those obtained with the native tools, demonstrating the potential of gammapy as a multiwavelength data analysis framework.
In addition, we show in Fig. C.1b the spectral reconstruction with both the instrumental background and the Poisson background estimate, matching well below ∼30 keV. We note however that xspec has two severe limitations. The first is linked to the definition of a the power-law, whose pivot energy in xspec is fixed to 1 keV and cannot be changed. To avoid impacting the results with a reference energy that is outside the energy range of NuSTAR, we redefined the power-law so that the normalization is done with respect to the the integral flux in the 3–70 keV band, instead of at a specific energy. The second limitation is that xspec is not designed to produce flux points as we noted in Sect. 5.1, and only in simple cases with few spectral components (NuSTAR and Swift-XRT when doing an OFF background analysis with Poisson background statistics) it was feasible to estimate some sort of flux points for different energy bins. For more sophisticated cases, such as NuSTAR with the complex instrumental background model produced by nuskybgd, the flux points estimated with xspec do not correspond to the source component but to the total sky model, including the systematic background. Removing the additional background components (which are not fixed) is not straightforward; therefore, in Fig. C.1b, we only report the SED confidence band from xspec without the flux points. We also checked the parameter error contours in the amplitude versus the spectral index parameter space in Fig. C.2, noting a very good agreement for the three instruments.
Finally, to validate the analysis on single-channel datasets, we estimated the all-channel best-fit spectral model for both Swift-UVOT and Liverpool IO:O, together with reconstructed flux points for each filter individually. The latter are compared to the flux derived from the native analysis, namely, the output of uvotsource for Swift-UVOT, and the differential photometry fluxes reconstructed with our photutils-based pipeline for Liverpool IO:O. The resulting SEDs are shown in figures C.3a and C.3b respectively. To reduce the effect introduced by the ambiguity in the selection of the reference energy of the band (estimated differently for gammapy and the native analyses), figures C.4a and C.4b compare the ratio of each flux point over the best model prediction at the reference energy of the flux point.
Appendix D Background estimation for NuSTAR
Two different methods for estimating the background in 1D datasets were explored for NuSTAR observations. The first method is the general Poisson or OFF background estimate. This method makes minimal assumptions about the structure of the background spectra, primarily that the background spectrum is identical in the OFF region as in the ON region. While this approach offers significant flexibility, it has the downside that Poisson fluctuations can dominate the often weak emission from the source, particularly at higher energies. Moreover, the assumption of Poisson statistics requires all background spectral bins to have non-zero counts to ensure a correctly defined likelihood function. This can pose a problem for photon-counting instruments like NuSTAR, especially when integrating over short exposure times. To mitigate issues arising from zero-count bins, it often becomes necessary to group the data into coarser energy bins, which can compromise spectral resolution.
The second method involves modeling the background, a technique extensively used in the analysis of data from instruments like Fermi-LAT, where detailed background models such as diffuse galactic emission maps and isotropic emission spectra have been developed. In this work, we employ a similar approach for NuSTAR by using instrumental background spectral models generated by the nuskybgd tool. This method provides an alternative to the Poisson background estimate by incorporating a more structured model of the instrumental background into the analysis.
Comparison of parameter values for the best-fits of the native tools (fermitools+minuit/migrad for Fermi-LAT data, xspec’s Levenberg- Marquardt algorithm for NuSTAR and Swift-XRT) with the same results obtained with gammapy with the default minuit/migrad as minimizer and algorithm. For simplicity, a classical power-law with absorption with amplitude defined as the photon density at a reference energy was used for Fermi-LAT and Swift-XRT (including also EBL absorption for Fermi-LAT following in this case Domínguez et al. (2011) as it is included in the Fermitools, and neutral hydrogen for Swift-XRT as implemented in xspec’s TBabs code). For NuSTAR, a power-law with integral as amplitude parameter was utilised as xspec does not allow us to change the default reference energy, which is fixed at 1 keV and therefore out of the energy range of the instrument. Switching to migrad inxspec showed a completely negligible impact on the estimated minima.
 |
Fig. C.1 Best-fit power-law models (with EBL absorption in Fermi-LAT and neutral hydrogen absorption for NuSTAR and Swift-XRT) fitted to each dataset with native tools (xspec or Fermitools depending on the case) and gammapy. For reference, the spectral reconstruction with the OFF Background estimate in NuSTAR (second panel) is shown in blue for reference. Upper limits are calculated at a 95% confidence level from the cstat/wstat likelihood profiles. |
 |
Fig. C.2 Parameter error ellipses on the amplitude (integral flux for NuSTAR) and spectral index for the power-law fit to the Fermi-LAT, NuSTAR A+B and Swift-XRT datasets. Contours in black correspond to gammapy, while the native tool contours are shown in red. For NuSTAR, the contours obtained with the Poisson or OFF background estimate are shown in blue for reference. |
A direct comparison between the reconstructed spectra of the FSRQ OP 313 obtained using the two methods is shown in Fig. C.1, with the OFF background estimation results depicted in blue and the model background prediction results in black. Additionally, Fig. C.2 presents the best-fit parameter error ellipses for both methods. The comparison reveals that at lower energies, where photon statistics are robust, the results from both methods are fully compatible. However, discrepancies begin to emerge at energies above 30 keV. Notably, in the 60–70 keV range, the OFF background estimate only provides an upper limit (with less than a 2 σ excess), while the model background based analysis continues to reconstruct a flux point with a significance exceeding 2 σ.
These findings suggest that while both methods are viable, the choice of background estimation method can significantly impact the results at higher energies, particularly when the source signal is weak compared to the background. The model background method, with its more sophisticated modeling of the instrumental and astrophysical background, may offer advantages in these regimes, potentially yielding more accurate spectral reconstructions where the OFF background method falls short.
 |
Fig. C.3 Best-fit spectra (log-parabola with dust extinction) and flux points reconstructed using gammapy – based on counts and IRFs – and with native tools using flux densities multiplied by the effective filter frequency center. Flux points in gammapy are evaluated over the geometrical center of the bin (black filled circles) and at the effective mean energy of the band with open diamond symbols (under the assumption of a flat source photon spectrum, to be roughly comparable to the classical method). LT datasets from the same filter were stacked together using gammapy’s stack_reduce method, that co-adds the counts, background and exposures for datasets with compatible energy axes. For the native analysis, weighted averages are shown instead as red boxes. Dashed gray error bars depict the total error once incorporating systematic uncertainties. |
 |
Fig. C.4 Comparison of reconstructed ‘relative’ flux values using native photometry tools (reconstructed flux densities multiplied by the filter’s effective frequency) and those obtained with gammapy (using counts and instrument response functions). All ‘relative’ fluxes are shown as a ratio to the best-fit gammapy model of the joint datasets, evaluated at the corresponding point energy. |
Appendix E Systematic Uncertainties in Liverpool Telescope Data
In the classical analysis, systematic uncertainties related to errors in the zero-point estimation (star-to-star variations) are typically propagated in quadrature to the final error estimate of the source flux. While this method is model-independent, it does not take full advantage of the detailed broadband spectrum of the source, which becomes more apparent as additional data across different energy bands are incorporated.
In this work, we explore an alternative approach using the PiecewiseNormSpectralModel in gammapy. This model adds an energy-dependent multiplicative component to our source’s spectral model, allowing the normalization parameters at each fixed energy node to be free. To avoid creating a highly degenerate model by leaving these parameters completely unconstrained, we impose Gaussian priors on each normalization factor. These priors are centered at 1, with widths corresponding to the systematic uncertainties arising from star-to-star variations in the calculated exposure.
When this component together with the source spectrum is fitted to the data, it causes a deformation of the assumed spectrum (e.g., a log-parabola), enabling the model to better align with the actual measurements (excess counts) by subtly adjusting the shape of the spectrum (see Fig. C.3, light gray curve and black diamond markers). By removing this component, we can recover the underlying estimate of the true spectrum (dark gray), free from the influence of systematic errors. For clarity, in this figure we stacked together observations using the same filter, which in gammapy it is technically implemented in the stack_reduce method by co-adding the counts, background, and exposures for datasets with compatible axes. The equivalent stacking is achieved for the native (classical) analysis by performing a weighted average of the flux points, where the weights are set to the inverse of the square of the statistical uncertainties of the points.
Appendix F Second night analysis (MJD60384)
The body of this manuscript primarily discusses the methodology used to create gammapy-compatible datasets, with data from the first night of NuSTAR observations (March 4th, 2024, MJD 60373) presented as an example of the reconstruction achievable using our analysis framework. In this appendix we briefly report the results of applying the same analysis to the second night of NuSTAR observations (March 15th, 2024, MJD 60384). The corresponding temporal coverage is still consistent across all instruments, as seen in Fig. F.1.
To keep this section short and focused on the final results, we focus on the two main figures from Sect. 4.4. The first figure is the best-fit models, shown in Fig. F.2, using the same sum of two power-laws with exponential cut-offs as in Fig. 9. We note that Swift-UVOT has a single observation with filter UM2, but more importantly, as discussed in Sect. 3.4, Swift was affected by a noticeable degradation in the pointing accuracy caused by noise in one gyroscope (Cenko 2024a,b). This is in fact hinted in our Swift-XRT data, whose integrated PC-mode image shows a larger PSF than usual, and it is readily visible in UVOT, where OP 313 images are elongated and distorted, requiring an abnormally large source integration region of 25” radius to fully contain the signal. The standard 5” radius yields an underestimation of the source flux by a factor ∼2.
The corresponding corner plot, representing the error ellipses for each pair of free model parameters for the source emission component, is displayed in Fig. F.3. Compared to Fig. 10, we observe a similar degree of degeneracy between the parameters for the low-energy (LE) component. Moreover, despite our efforts to enlarge the source extraction region in both Swift-XRT and Swift-UVOT to accommodate their poorer PSF, a notable discrepancy persists between Swift-XRT and the spectral reconstruction from NuSTAR and Fermi-LAT. This inconsistency leads to less stable fitting process and different best-fit solutions for the low-energy component between the flux point fitting analysis and the forward folding technique.
It is worth noting that both the significant model degeneracies and fit convergence issues are common challenges faced when working with large and diverse datasets. However, these issues could potentially be mitigated by adopting a modern, fully Bayesian nested sampling inference engine such as UltraNest (Buchner 2021), which efficiently explores the entire prior parameter space to build robust posterior probability distributions for model parameters, even if the distribution is multimodal. With the full dataset exported into a standard framework and the construction of a full forward folding likelihood, we are already halfway to exploring this approach.
 |
Fig. F.1 Temporal coverage of the second observation night. |
 |
Fig. F.2 Joint multi-instrument forward-folding fit and joint fit using flux-points from the night of March 15, 2024 (MJD60384) with the similar structure as in Fig. 9. Note that Swift data were affected by a severe “loss of lock” problem that night. |
 |
Fig. F.3 Corner plot showing the error ellipses calculated with a bootstrap method for the best-fit (free) parameters of the flux-point based fit and the full forward-folding joint fit. The model used for the LE is highly degenerate because of the limited amount of available data to constrain that component. |
References
- Abdollahi, S., Acero, F., Baldini, L., et al. 2022, ApJS, 260, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Abdollahi, S., Ajello, M., Baldini, L., et al. 2023, ApJS, 265, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Ansoldi, S., Antonelli, L. A., et al. 2019, MNRAS, 486, 4233 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Bernete, J., Biederbeck, N., et al. 2024, https://doi.org/10.5281/zenodo.10726484 [Google Scholar]
- Aharonian, F. A. 2002, MNRAS 332, 215 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2015, ApJ, 815, L23 [Google Scholar]
- Albert, A., Alfaro, R., Alvarez, C., et al. 2023, ApJ, 942, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Alfaro, R., Alvarez, C., Arteaga-Velázquez, J. C., et al. 2022, ApJ, 934, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Almeida, A., Anderson, S. F., Argudo-Fernández, M., et al. 2023, ApJS, 267, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Society of the Pacific Conference Series, 101, Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, 17 [NASA ADS] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2024, https://doi.org/10.5281/zenodo.13860849 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Ballet, J., Bruel, P., Burnett, T. H., Lott, B., & The Fermi-LAT collaboration. 2023, arXiv e-prints [arXiv:2307.12546] [Google Scholar]
- Barnsley, R. M., Jermak, H. E., Steele, I. A., et al. 2016, J. Astron. Telesc. Instrum. Syst., 2, 015002 [Google Scholar]
- Bradley, L., Sipo? cz, B., Robitaille, T., et al. 2022, https://doi.org/10.5281/zenodo.6825092 [Google Scholar]
- Breeveld, A. A., Curran, P. A., Hoversten, E. A., et al. 2010, MNRAS, 406, 1687 [NASA ADS] [Google Scholar]
- Buchner, J. 2021, J. Open Source Softw. 6, 3001 [CrossRef] [Google Scholar]
- Burgess, J. M., Fleischhack, H., Vianello, G., et al. 2021, https://doi.org/10.5281/zenodo.5646954 [Google Scholar]
- Burke, D., Laurino, O., wmclaugh, et al. 2024, https://doi.org/10.5281/zenodo.13909532 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2004, SPIE Conf. Ser., 5165, 201 [NASA ADS] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ 345, 245 [Google Scholar]
- Cenko, B. 2024a, GRB Coordinates Network 35953, 1 [NASA ADS] [Google Scholar]
- Cenko, B. 2024b, GRB Coordinates Network 36033, 1 [NASA ADS] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, arXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Corcoran, M. F., Angelini, L., George, I., et al. 1995, in Astronomical Society of the Pacific Conference Series, 77, Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, 219 [NASA ADS] [Google Scholar]
- Cortina, J., & CTAO LST Collaboration 2023, ATel, 16381, 1 [NASA ADS] [Google Scholar]
- Deil, C., Boisson, C., Kosack, K., et al. 2017, in American Institute of Physics Conference Series, 1792, 6th International Symposium on High Energy Gamma-Ray Astronomy (AIP), 070006 [NASA ADS] [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ 416, 458 [Google Scholar]
- Doe, S., Nguyen, D., Stawarz, C., et al. 2007, in Astronomical Society of the Pacific Conference Series, 376, Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, 543 [NASA ADS] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [Google Scholar]
- Donath, A., Terrier, R., Remy, Q., et al. 2023, A&A, 678, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Essey, W., & Kusenko, A. 2014, Astropart. Phys. 57, 30 [CrossRef] [Google Scholar]
- Fermi Science Support Development Team 2019, Fermitools: Fermi Science Tools, Astrophysics Source Code Library [record ascl:1905.011] [Google Scholar]
- Flewelling, H. A., Magnier, E. A., Chambers, K. C., et al. 2020, ApJS, 251, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, P., Doe, S., & Siemiginowska, A. 2001, SPIE Conf. Ser. 4477, 76 [NASA ADS] [Google Scholar]
- Gasparyan, S., Bégué, D., & Sahakyan, N. 2022, MNRAS 509, 2102 [Google Scholar]
- Gasparyan, S., Bégué, D., & Sahakyan, N. 2023, in The Sixteenth Marcel Grossmann Meeting. On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, eds. R. Ruffino. & G. Vereshchagin, 429 [Google Scholar]
- Ginsburg, A., Sipo? cz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Giunti, L., & Terrier, R. 2022, https://github.com/registerrier/gammapy-ogip-spectra [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- Hervet, O. 2024, https://doi.org/10.5281/zenodo.13129296 [Google Scholar]
- Hervet, O., Johnson, C. A., & Youngquist, A. 2024, ApJ 962, 140 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klinger, M., Taylor, A. M., Parsotan, T., et al. 2024, MNRAS, 529, L47 [Google Scholar]
- Konigl, A. 1981, ApJ 243, 700 [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2023, A&A, 670, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ 397, L5 [CrossRef] [Google Scholar]
- Mineo, T., Romano, P., Mangano, V., et al. 2006, Nuovo Cimento B Ser., 121, 1521 [Google Scholar]
- NASA 2024, https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/ [Google Scholar]
- Nievas, M. 2024, https://github.com/mireianievas/gammapy_mwl_workflow [Google Scholar]
- Nievas Rosillo, M., Domínguez, A., Chiaro, G., et al. 2022, MNRAS, 512, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Nievas Rosillo, M., Acero, F., Otero Santos, J., et al. 2024, https://doi.org/10.5281/zenodo.14033304 [Google Scholar]
- Nigro, C., Hassan, T., & Olivera-Nieto, L. 2021, Universe 7, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Nigro, C., Sitarek, J., Gliwny, P., et al. 2022, A&A, 660, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nigro, C., Sitarek, J., Gliwny, P., et al. 2023, https://doi.org/10.5281/zenodo.7633553 [Google Scholar]
- Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng. 9, 21 [Google Scholar]
- Ragan-Kelley, M., Perez, F., Granger, B., et al. 2014, in AGU Fall Meeting Abstracts, 2014, H44D–07 [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
- Saldana-Lopez, A., Domínguez, A., Pérez-González, P. G., et al. 2021, MNRAS, 507, 5144 [CrossRef] [Google Scholar]
- Sanchez, D., & Deil, C. 2015, Enrico: Python package to simplify Fermi-LAT analysis, Astrophysics Source Code Library [record ascl:1501.008] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ 500, 525 [Google Scholar]
- Schmitt, S. 2017, in European Physical Journal Web of Conferences, 137, 11008 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [Google Scholar]
- Steele, I. A., Smith, R. J., Rees, P. C., et al. 2004, SPIE Conf. Ser., 5489, 679 [Google Scholar]
- Tramacere, A. 2020, JetSeT: Numerical modeling and SED fitting tool for relativistic jets, Astrophysics Source Code Library [record ascl:2009.001] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, E., & Taylor, A. M. 2011, ApJ 739, 66 [Google Scholar]
- Vaughan, S., Goad, M. R., Beardmore, A. P., et al. 2006, ApJ, 638, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Vianello, G., Lauer, R. J., Younk, P., et al. 2015, arXiv e-prints [arXiv:1507.08343] [Google Scholar]
- Wik, D. R., Hornstrup, A., Molendi, S., et al. 2014, ApJ, 792, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ 542, 914 [Google Scholar]
- Yamada, S., Axelsson, M., Ishisaki, Y., et al. 2019, PASJ, 71, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V. 2015, in 34th International Cosmic Ray Conference (ICRC2015), 922 [Google Scholar]
Note that in xspec, no name distinctions are made between cstat and wstat, see https://heasarc.gsfc.nasa.gov/docs/xanadu/xspec/manual/XSappendixStatistics.html
All Tables
Comparison of parameter values for the best-fits of the native tools (fermitools+minuit/migrad for Fermi-LAT data, xspec’s Levenberg- Marquardt algorithm for NuSTAR and Swift-XRT) with the same results obtained with gammapy with the default minuit/migrad as minimizer and algorithm. For simplicity, a classical power-law with absorption with amplitude defined as the photon density at a reference energy was used for Fermi-LAT and Swift-XRT (including also EBL absorption for Fermi-LAT following in this case Domínguez et al. (2011) as it is included in the Fermitools, and neutral hydrogen for Swift-XRT as implemented in xspec’s TBabs code). For NuSTAR, a power-law with integral as amplitude parameter was utilised as xspec does not allow us to change the default reference energy, which is fixed at 1 keV and therefore out of the energy range of the instrument. Switching to migrad inxspec showed a completely negligible impact on the estimated minima.
All Figures
 |
Fig. 1 Long term evolution of the nightly high-energy gamma-ray flux emitted by OP 313. Left: Fermi-LAT light curve (1-day binning) of OP 313 above 100 MeV during the major 2023–2024 flare episode, for integral flux and spectral index. Blue and red bars mark the two nights with NuSTAR observations that are the focus of this study. Right: spectral index as a function of the integral flux for each night over six months of LAT data. The density of points is color-coded, with yellow points showing larger number density of nights and purple-blue tones indicating more isolated bins. |
| In the text | |
 |
Fig. 2 Fermi-LAT dataset description for the first selected night. From top left to bottom right: (a) Integral counts map, smoothed with a Gaussian kernel of 0.2°. (b) Initial model map, convolved with the IRFs (npred map). (c) 68% and 95% containment radius as a function of energy. (d) Energy dispersion (reconstructed energy as a function of true energy). (e) Exposure map at 10.6 GeV. (f) Exposure at the FoV center as a function of true energy. |
| In the text | |
 |
Fig. 3 NuSTAR A/B counts map for the first observation night, together with the signal extraction region (blue dashed circle) and background extraction region (orange dashed box minus the signal extraction circle). |
| In the text | |
 |
Fig. 4 gammapy dataset representation of NuSTAR A for night 1 is shown here. NuSTAR B for this observation and NuSTAR A/B for night 2 are similar. From top-left to bottom-right: (a) estimated distribution of background events from the OFF rectangular region of Fig. 3 and the ON event distribution from the signal extraction region. (b) Estimated distribution of background events from nuskybgd. ON event distribution identical to the previous case. (c) NuSTAR A exposure (effective area × livetime) as a function of true energy. (d) NuSTAR A energy dispersion matrix. |
| In the text | |
 |
Fig. 5 Swift-XRT dataset representation after energy bin grouping to avoid background spectra dominated by zeros. (a) Swift-XRT image of OP 313. Blue circle and orange annulus show the signal and background extraction regions, respectively. (b) Distribution of events for both regions as a function of energy, corrected for the different region sizes. (c) Swift-XRT exposure (effective area × livetime) as a function of true energy. (d) Swift-XRT energy dispersion matrix (also known as redistribution matrix or migration matrix). |
| In the text | |
 |
Fig. 6 Swift-UVOT dataset representation. First row: Swift-UVOT images in two of the photometric filters available for the first selected night, indicated by dashed blue circles (signal) and orange annuli (background), respectively. Second row: effective collection area for each of the available Swift-UVOT filters. |
| In the text | |
 |
Fig. 7 Liverpool IO:O dataset representation. Top row: LT IO:O images in two of the photometric filters available for the first selected night, with the signal and background extraction regions represented by blue and orange dashed circles and annuli, respectively. Bottom row: throughput for each of the available LT IO:O bands (transmission of the filter multiplied by the cryostat window transmission, CW, and the quantum efficiency of the CCD, QE) as dashed curves, and for CW and CW×QE alone. For completeness, the reconstructed effective area for each calibration star and each filter are shown as solid colored curves. |
| In the text | |
 |
Fig. 8 Temporal coverage of the first observation night. |
| In the text | |
 |
Fig. 9 Joint multi-instrument forward-folding fit and joint fit using fluxpoints employing a phenomenological model with two distinct emission components and three absorption components. Top panel: individual datasets fitted with simple models (power-laws, log-parabolas, powerlaws with exponential cutoffs) and corresponding reconstructed flux points, and joint fits (flux points, forward folding). Middle panel: residuals, calculated as the ratio of reconstructed differential spectrum to model prediction for the flux points fit (residual PF, open markers), and as the significance or ratio of the difference between the excess counts and model predicted counts to the square root of the model predictions for each bin in the forward folding case (Residuals FF, small filled circles). For clarity, and due to the large amount of energy bins in the X-ray datasets, only one every five bins is shown for NuSTAR and one every three bins is shown for XRT. Bottom panel: multiplicative absorption components. |
| In the text | |
 |
Fig. 10 Corner plot showing the error ellipses calculated with a bootstrap method for the best-fit (free) parameters of the flux-point based fit and the full forward-folding joint fit. The model used for the LE is highly degenerate because of the limited amount of available data to constrain that component. |
| In the text | |
 |
Fig. C.1 Best-fit power-law models (with EBL absorption in Fermi-LAT and neutral hydrogen absorption for NuSTAR and Swift-XRT) fitted to each dataset with native tools (xspec or Fermitools depending on the case) and gammapy. For reference, the spectral reconstruction with the OFF Background estimate in NuSTAR (second panel) is shown in blue for reference. Upper limits are calculated at a 95% confidence level from the cstat/wstat likelihood profiles. |
| In the text | |
 |
Fig. C.2 Parameter error ellipses on the amplitude (integral flux for NuSTAR) and spectral index for the power-law fit to the Fermi-LAT, NuSTAR A+B and Swift-XRT datasets. Contours in black correspond to gammapy, while the native tool contours are shown in red. For NuSTAR, the contours obtained with the Poisson or OFF background estimate are shown in blue for reference. |
| In the text | |
 |
Fig. C.3 Best-fit spectra (log-parabola with dust extinction) and flux points reconstructed using gammapy – based on counts and IRFs – and with native tools using flux densities multiplied by the effective filter frequency center. Flux points in gammapy are evaluated over the geometrical center of the bin (black filled circles) and at the effective mean energy of the band with open diamond symbols (under the assumption of a flat source photon spectrum, to be roughly comparable to the classical method). LT datasets from the same filter were stacked together using gammapy’s stack_reduce method, that co-adds the counts, background and exposures for datasets with compatible energy axes. For the native analysis, weighted averages are shown instead as red boxes. Dashed gray error bars depict the total error once incorporating systematic uncertainties. |
| In the text | |
 |
Fig. C.4 Comparison of reconstructed ‘relative’ flux values using native photometry tools (reconstructed flux densities multiplied by the filter’s effective frequency) and those obtained with gammapy (using counts and instrument response functions). All ‘relative’ fluxes are shown as a ratio to the best-fit gammapy model of the joint datasets, evaluated at the corresponding point energy. |
| In the text | |
 |
Fig. F.1 Temporal coverage of the second observation night. |
| In the text | |
 |
Fig. F.2 Joint multi-instrument forward-folding fit and joint fit using flux-points from the night of March 15, 2024 (MJD60384) with the similar structure as in Fig. 9. Note that Swift data were affected by a severe “loss of lock” problem that night. |
| In the text | |
 |
Fig. F.3 Corner plot showing the error ellipses calculated with a bootstrap method for the best-fit (free) parameters of the flux-point based fit and the full forward-folding joint fit. The model used for the LE is highly degenerate because of the limited amount of available data to constrain that component. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


