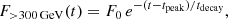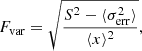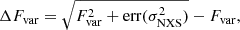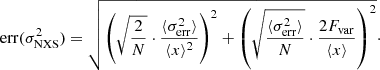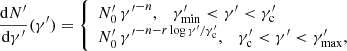| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347845 | |
| Published online | 09 February 2024 | |
Multi-year characterisation of the broad-band emission from the intermittent extreme BL Lac 1ES 2344+514
1
Japanese MAGIC Group: Institute for Cosmic Ray Research (ICRR), The University of Tokyo, Kashiwa, 277-8582 Chiba, Japan
2
Instituto de Astrofísica de Canarias and Dpto. de Astrofísica, Universidad de La Laguna, 38200 La Laguna, Tenerife, Spain
3
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
4
National Institute for Astrophysics (INAF), 00136 Rome, Italy
5
Università di Udine and INFN Trieste, 33100 Udine, Italy
6
Max-Planck-Institut für Physik, 80805 München, Germany
7
Università di Padova and INFN, 35131 Padova, Italy
8
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology (BIST), 08193 Bellaterra, Barcelona, Spain
9
Technische Universität Dortmund, 44221 Dortmund, Germany
10
Croatian MAGIC Group: University of Zagreb, Faculty of Electrical Engineering and Computing (FER), 10000 Zagreb, Croatia
11
IPARCOS Institute and EMFTEL Department, Universidad Complutense de Madrid, 28040 Madrid, Spain
12
Centro Brasileiro de Pesquisas Físicas (CBPF), 22290-180 URCA, Rio de Janeiro, RJ, Brazil
13
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, 28040 Madrid, Spain
14
ETH Zürich, 8093 Zürich, Switzerland
15
Departament de Física, and CERES-IEEC, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
16
Università di Pisa and INFN Pisa, 56126 Pisa, Italy
17
Universitat de Barcelona, ICCUB, IEEC-UB, 08028 Barcelona, Spain
18
Department for Physics and Technology, University of Bergen, Bergen, Norway
19
INFN MAGIC Group: INFN Sezione di Catania and Dipartimento di Fisica e Astronomia, University of Catania, 95123 Catania, Italy
20
INFN MAGIC Group: INFN Sezione di Torino and Università degli Studi di Torino, 10125 Torino, Italy
21
INFN MAGIC Group: INFN Sezione di Bari and Dipartimento Interateneo di Fisica dell’Università e del Politecnico di Bari, 70125 Bari, Italy
22
Croatian MAGIC Group: University of Rijeka, Faculty of Physics, 51000 Rijeka, Croatia
23
University of Geneva, Chemin d’Ecogia 16, 1290 Versoix, Switzerland
24
Japanese MAGIC Group: Physics Program, Graduate School of Advanced Science and Engineering, Hiroshima University, 739-8526 Hiroshima, Japan
25
Armenian MAGIC Group: ICRANet-Armenia, 0019 Yerevan, Armenia
26
University of Lodz, Faculty of Physics and Applied Informatics, Department of Astrophysics, 90-236 Lodz, Poland
27
Croatian MAGIC Group: Josip Juraj Strossmayer University of Osijek, Department of Physics, 31000 Osijek, Croatia
28
Universität Würzburg, 97074 Würzburg, Germany
29
Finnish MAGIC Group: Finnish Centre for Astronomy with ESO, University of Turku, 20014 Turku, Finland
30
Japanese MAGIC Group: Department of Physics, Tokai University, Hiratsuka, 259-1292 Kanagawa, Japan
31
Università di Siena and INFN Pisa, 53100 Siena, Italy
32
Saha Institute of Nuclear Physics, A CI of Homi Bhabha National Institute, Kolkata, 700064 West Bengal, India
33
Inst. for Nucl. Research and Nucl. Energy, Bulgarian Academy of Sciences, 1784 Sofia, Bulgaria
34
Japanese MAGIC Group: Department of Physics, Yamagata University, Yamagata 990-8560, Japan
35
Finnish MAGIC Group: Space Physics and Astronomy Research Unit, University of Oulu, 90014 Oulu, Finland
36
Japanese MAGIC Group: Chiba University, ICEHAP, 263-8522 Chiba, Japan
37
Japanese MAGIC Group: Institute for Space-Earth Environmental Research and Kobayashi-Maskawa Institute for the Origin of Particles and the Universe, Nagoya University, 464-6801 Nagoya, Japan
38
Japanese MAGIC Group: Department of Physics, Kyoto University, 606-8502 Kyoto, Japan
39
INFN MAGIC Group: INFN Sezione di Perugia, 06123 Perugia, Italy
40
INFN MAGIC Group: INFN Roma Tor Vergata, 00133 Roma, Italy
41
Japanese MAGIC Group: Department of Physics, Konan University, Kobe, Hyogo 658-8501, Japan
42
International Center for Relativistic Astrophysics (ICRA), Rome, Italy
43
Institute for Astro- and Particle Physics, University of Innsbruck, 6020 Innsbruck, Austria
44
Port d’Informació Científica (PIC), 08193 Bellaterra, Barcelona, Spain
45
Institute for Astro- and Particle Physics, University of Innsbruck, 6020 Innsbruck, Austria
46
Department of Physics, University of Oslo, Oslo, Norway
47
Dipartimento di Fisica, Università di Trieste, 34127 Trieste, Italy
48
Max-Planck-Institut für Physik, 80805 München, Germany
49
INAF Padova, Padova, Italy
50
Japanese MAGIC Group: Institute for Cosmic Ray Research (ICRR), The University of Tokyo, Kashiwa, 277-8582 Chiba, Japan
51
Space Science Data Center (SSDC) – ASI, Via del Politecnico, s.n.c., 00133 Roma, Italy
52
INAF – Osservatorio Astronomico di Roma, Via di Frascati 33, 00040 Monteporzio, Italy
53
Italian Space Agency, ASI, Via del Politecnico snc, 00133 Roma, Italy
54
School of Astrophysics, Presidency University, 86/1 College Street, Kolkata 700073, India
55
INAF-Osservatorio Astrofisico di Torino, 10025 Pino Torinese, TO, Italy
56
Institute of Astronomy and National Astronomical Observatory, Bulgarian Academy of Sciences, Sofia, Bulgaria
57
Department of Physics and Astronomy, Faculty of Natural Sciences, University of Shumen, 115, Universitetska Str., 9712 Shumen, Bulgaria
58
Astronomical Observatory, Volgina 7, 11060 Belgrade, Serbia
59
Saint Petersburg State University, 7/9 Universitetskaya nab., St. Petersburg 199034, Russia
60
Pulkovo Observatory, St.-Petersburg 196140, Russia
61
Special Astrophysical Observatory, Russian Academy of Sciences, 369167 Nizhnii Arkhyz, Russia
62
Graduate Institute of Astronomy, National Central University, 300 Zhongda Road, Zhongli 32001, Taiwan
63
Institute for Astrophysical Research, Boston University, 725 Commonwealth Ave, Boston, MA 02215, USA
64
Astronomical Institute of St. Petersburg State University, 28 Universitetskij Pr., 198504 St. Petersburg, Russia
65
EPT Observatories, Tijarafe, 38780 La Palma, Spain
66
INAF, TNG Fundaci ón Galileo Galilei, 38712 La Palma, Spain
67
Abastumani Observatory, Mt. Kanobili, 0301 Abastumani, Georgia
68
Zentrum für Astronomie der Universitüt Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
69
Engelhardt Astronomical Observatory, Kazan Federal University, Tatarstan, Russia
70
School of Cosmic Physics, Dublin Institute For Advanced Studies, Dublin, Ireland
71
Section of Astrophysics, Astronomy and Mechanics, Department of Physics, National and Kapodistrian University of Athens, 15784 Zografos, Athens, Greece
72
Finnish Centre for Astronomy with ESO (FINCA), University of Turku, 20014 Turku, Finland
73
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
74
Owens Valley Radio Observatory, California Institute of Technology, Pasadena, CA 91125, USA
75
Institute of Astrophysics, Foundation for Research and Technology-Hellas, 71110 Heraklion, Greece
76
Department of Physics, Univ. of Crete, 70013 Heraklion, Greece
77
Department of Astronomy, University of California, Berkeley, CA 94720-3411, USA
78
INAF – Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italy
79
Faculty of Physics and Astronomy, Astronomical Institute (AIRUB), Ruhr University Bochum, 44780 Bochum, Germany
Received:
31
August
2023
Accepted:
28
September
2023
Aims. The BL Lac 1ES 2344+514 is known for temporary extreme properties characterised by a shift of the synchrotron spectral energy distribution (SED) peak energy νsynch, p above 1 keV. While those extreme states have only been observed during high flux levels thus far, additional multi-year observing campaigns are required to achieve a coherent picture. Here, we report the longest investigation of the source from radio to very high energy (VHE) performed so far, focussing on a systematic characterisation of the intermittent extreme states.
Methods. We organised a monitoring campaign covering a 3-year period from 2019 to 2021. More than ten instruments participated in the observations in order to cover the emission from radio to VHE. In particular, sensitive X-ray measurements by XMM-Newton, NuSTAR, and AstroSat took place simultaneously with multi-hour MAGIC observations, providing an unprecedented constraint of the two SED components for this blazar.
Results. While our results confirm that 1ES 2344+514 typically exhibits νsynch, p > 1 keV during elevated flux periods, we also find periods where the extreme state coincides with low flux activity. A strong spectral variability thus happens in the quiescent state, and is likely caused by an increase in the electron acceleration efficiency without a change in the electron injection luminosity. On the other hand, we also report a strong X-ray flare (among the brightest for 1ES 2344+514) without a significant shift of νsynch, p. During this particular flare, the X-ray spectrum is among the softest of the campaign. It unveils complexity in the spectral evolution, where the common harder-when-brighter trend observed in BL Lacs is violated. By combining Swift-XRT and Swift-UVOT measurements during a low and hard X-ray state, we find an excess of the UV flux with respect to an extrapolation of the X-ray spectrum to lower energies. This UV excess implies that at least two regions significantly contribute to the infrared/optical/ultraviolet/X-ray emission. Using the simultaneous MAGIC, XMM-Newton, NuSTAR, and AstroSat observations, we argue that a region possibly associated with the 10 GHz radio core may explain such an excess. Finally, we investigate a VHE flare, showing an absence of simultaneous variability in the 0.3−2 keV band. Using time-dependent leptonic modelling, we show that this behaviour, in contradiction to single-zone scenarios, can instead be explained by a two-component model.
Key words: radiation mechanisms: non-thermal / galaxies: active / BL Lacertae objects: individual: 1ES 2344+514
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
The source 1ES 2344+514 (RA = 23h47′04.837″, Dec = +51°42′17.878″, J2000; Gaia Collaboration 2020) is a nearby BL Lacertae (BL Lac) object located at a redshift of z = 0.044 (Perlman et al. 1996). It is a member of the blazar category – an active galactic nucleus (AGN) whose relativistic plasma jet is aligned with the observer’s line of sight (Romero et al. 2017). As is typically observed in blazars, the spectral energy distribution (SED) displays two broad emission components. The low-energy component ranges from radio to X-rays, and the high-energy component is located in the gamma-ray band. The low-energy component peaks above 1015 Hz, implying that it belongs to the subcategory of high-frequency BL Lac (HBL) objects (Padovani & Giommi 1995). The source 1ES 2344+514 is one of the first extragalactic objects detected at very high energy (VHE; E > 100 GeV). The first VHE detection was achieved by the Whipple 10 m telescope during a bright flare in 1996 with a peak flux of ∼60% of the Crab Nebula flux above 350 GeV (Catanese et al. 1998). Allen et al. (2017) reported an average flux above 350 GeV of ∼4% of the Crab Nebula between 2008 and 2015 in the absence of any flaring activity. In what follows, we consider such a flux level as representative of the quiescent VHE activity of 1ES 2344+514. We note however that the VHE flux can vary within a factor ∼2 down to daily timescales (Albert et al. 2007; Allen et al. 2017; Acciari et al. 2011). Regarding the X-ray band, the 2−10 keV flux lies around 10−11 erg cm−2 s−1 in quiescent states (Acciari et al. 2011; Aleksić et al. 2013).
Giommi et al. (2000) reported strong spectral variability of the X-ray spectrum on a timescale of 5 ks during a flaring state: the peak energy of the low-energy SED component shifted by a factor of more than 30, and reached energies above 10 keV. Blazars with a low-energy component peaking above 1 keV are dubbed as extreme high-frequency BL Lacs (EHBLs; Costamante et al. 2001; Biteau et al. 2020). Recently, MAGIC Collaboration (2020a) published a multi-wavelength study of 1ES 2344+514 in a flaring period that happened in 2016. The source again temporarily behaved as an EHBL. The broad-band SED could be well modelled both with leptonic and hadronic scenarios. In leptonic models, the low-energy SED component originates from electron-synchrotron radiation, while the high-energy component is attributed to electron inverse-Compton (IC) scattering off the synchrotron photons. This model is commonly dubbed as the synchrotron self-Compton (SSC) model (see, e.g. Maraschi et al. 1992). In the hadronic model, the low-energy component still originates from electron-synchrotron radiation, but the high-energy component is ascribed to proton-synchrotron radiation (see, e.g. Mücke & Protheroe 2001; Cerruti et al. 2015). During the quiescent activity, the peak energy of 1ES 2344+514 was estimated to be around 0.1 keV (Aleksić et al. 2013; Nilsson et al. 2018; Ajello et al. 2020). This blazar is thus characterised by an EHBL behaviour occurring on a temporary basis, which seems to happen mostly during high emission states.
As highlighted by Biteau et al. (2020), the EHBL population is not homogeneous. While some of the members are EHBL-like only temporarily (e.g. 1ES 2344+514), other EHBLs display extreme properties on a constant basis (e.g. 1ES 1426+428). In addition to that, several EHBLs are not only extreme in the synchrotron domain but also in the VHE band with a high-energy SED component peaking above 1 TeV (e.g. 1ES 0229+200). Those sources are commonly called extreme-TeV EHBLs and are particularly challenging for standard blazar acceleration and emission models (Kaufmann et al. 2011). In general, EHBLs represent the most energetic class of blazars and their study is particularly relevant in the context of particle acceleration mechanisms in AGN jets.
The intermittent EHBL nature of 1ES 2344+514 is still poorly characterised owing to the low amount of multi-year broad-band campaigns performed so far. This prevents a detailed understanding of the physical origin of these extreme states and how exactly the EHBL state correlates with the flux activity. This work presents the longest multi-year study from radio to VHE of 1ES 2344+514 performed so far. A dense multi-wavelength campaign was organised between 2019 and 2021 by involving more than ten different instruments. We emphasise that most of the observing campaign was organised through an unbiased monitoring of the source, without triggering observations on particular flaring events, in order to get a systematic investigation of the spectral evolution. A detailed characterisation of the X-ray emission was obtained using XMM-Newton, Nuclear Spectroscopic Telescope Array (NuSTAR), and AstroSat deep exposures. The latter observations are accompanied by multi-hour MAGIC exposures with the aim to acquire a precise determination of the two SED components. Furthermore, thanks to a dense monitoring from the Neil Gehrels Swift Observatory (Swift) and MAGIC telescopes, we carry out a systematic investigation of the intermittent EHBL state in the synchrotron and VHE gamma-ray regimes. This paper also discusses an intriguing flare that was detected in 2019, during which the emission characteristics suggest at least two separate emitting components contributing to the SED from infrared (IR) to X-rays. Finally, the results are interpreted within theoretical leptonic models, which are able to successfully describe the SEDs.
The paper is structured in the following way. Section 2 describes the observations and data reduction, Sect. 3 discusses the multi-wavelength variability and the observed correlation trends over the campaign, and Sect. 4 presents the spectral analysis in the X-ray and VHE bands. The theoretical modelling of the deep exposures with simultaneous MAGIC, NuSTAR, XMM-Newton, and AstroSat data is shown in Sect. 5, a general discussion of the different results is presented in Sect. 6, and the conclusions are drawn in Sect. 7.
2. Dataset and analysis
2.1. MAGIC
The VHE observations were performed by the Florian Goebel Major Atmospheric Gamma Imaging Cherenkov telescopes (MAGIC) array, which consists of two 17 m diameter imaging atmospheric Cherenkov telescopes located at an altitude of 2231 m above the sea level, on the Canary Island of La Palma at the Roque de los Muchachos Observatory. The integral sensitivity of MAGIC for point-source observations above 220 GeV is (0.66 ± 0.03)% of the Crab Nebula flux1 in 50 h (Aleksić et al. 2016).
The MAGIC observations of 1ES 2344+514 covered a ∼2.5 yr period from August 2019 until December 2021. After data-quality selection, a total of about 32 h of effective observation time was collected in 25 nights. The source was observed with zenith angles ranging from 20° to 62°. We use the standard analysis tools from the MAGIC Analysis and Reconstruction Software (MARS; Zanin et al. 2013; Aleksić et al. 2016) to process the data. A fraction of the observations are affected by the presence of the Moon, which leads to an increased night-sky background light contamination (Ahnen et al. 2017). In order to take into account these varying observational conditions, the data are first split into several subsets according to the level of moonlight contamination. Then, the analysis is carried out by adopting Monte Carlo simulations tuned to match the corresponding conditions of the different data subsets (Ahnen et al. 2017).
The MAGIC fluxes are computed above 300 GeV in daily and yearly binning. They are plotted in Fig. 1. The typical exposure of a single MAGIC observation lies between 0.5 h and 2 h. However, two nights have a significantly larger exposure of ∼5 h, July 23, 2020 (MJD 59053) and August 6, 2021 (MJD 59432). In the following, they are referred to as “deep exposure 1” and “deep exposure 2”. They are marked in Fig. 1 with orange and brown dashed vertical lines, respectively. Those deep exposures took place simultaneously with sensitive X-ray observations by XMM-Newton, NuSTAR, and AstroSat with the aim of obtaining precise simultaneous measurements of the low- and high-energy SED components of 1ES 2344+514. Table 1 lists the corresponding exact observing times of MAGIC as well as of the accompanying X-ray instruments. Regarding deep exposure 1, the MAGIC detection is significant and about 5.6σ (the measured flux is about 4% of the Crab Nebula). As for the deep exposure 2 epoch, the flux is lower (2% of the Crab Nebula above 300 GeV), leading to a detection significance of only 2σ. No significant intranight VHE variability is detected in the MAGIC data on these two dates. The corresponding fluxes and spectra are thus averaged over their respective observation time. In this work, all MAGIC spectra and best-fit parameters are computed using a forward-folding method to take into account the finite energy resolution of the instrument (Zanin et al. 2013).
 |
Fig. 1. Multi-wavelength light curves between December 23, 2018 (MJD 58475) and January 21, 2022 (MJD 59600). The vertical dashed blue line highlights the date of the VHE flare detected by MAGIC in August 2019. The orange and maroon dashed vertical lines highlight the dates of the deep exposure 1 (July 23, 2020 – MJD 59053) and deep exposure 2 (August 6, 2021 – MJD 59432) epochs that contain simultaneous long observations from MAGIC, XMM-Newton, NuSTAR, and AstroSat. The top panel shows the MAGIC fluxes above 300 GeV in daily (black markers) and yearly binning (pink markers). The horizontal dashed-grey line represents 4% of the Crab Nebula flux above 300 GeV. The second panel from the top reports the Fermi-LAT fluxes in the 0.3−300 GeV band in monthly binning. An upper limit at 95% confidence level is quoted for time bins with TS < 5. The maroon markers are fluxes in 2-day binning around the VHE flare. In the third panel from the top, the Swift-XRT fluxes are shown in the 0.3−2 keV (light-green markers) and 2−10 keV (dark-green markers) bands. The NuSTAR (cyan), XMM-Newton (pink), and AstroSat-SXT2022). The grey bands correspond to the three (light red) fluxes are shown in the 3−79 keV, 2−10 keV, and 0.7−7 keV bands, respectively. The fourth panel from the top displays the UV fluxes from the Swift-UVOT instrument in the UVW1, UVM2, and UVW2 filters. The fifth panel from the top reports the fluxes in the R band from GASP-WEBT, KAIT, and Tuorla. Finally, the bottom panel shows the OVRO fluxes measured at 15 GHz. |
Summary of the observing times of the VHE and X-ray instruments during the two long exposures in July 2020 and August 2021.
2.2. Fermi-LAT
The Large Area Telescope (LAT) instrument is a pair-conversion telescope onboard the Fermi satellite (Atwood et al. 2009; Ackermann et al. 2012). Fermi-LAT surveys the gamma-ray sky in the 20 MeV to E > 300 GeV energy range with an all-sky coverage on a ∼3 h timescale. The analysis for this work is performed using an unbinned-likelihood approach with tools from the FERMITOOLS software2 v2.0.8isert. We adopt the instrument response function P8R3_SOURCE_V2 and the diffuse background models3 gll_iem_v07 and iso_P8R3_SOURCE_V3_v1.
We select Source class events between 0.3 GeV and 300 GeV in a circular region of interest (ROI) with a radius of 15° around 1ES 2344+514. The events with a zenith angle > 90° are discarded to limit the contribution from gamma rays grazing Earth’s limb. To model the field sources, we consider all sources from the fourth Fermi-LAT source catalogue Data Release 2 (4FGL-DR2; Abdollahi et al. 2020; Ballet et al. 2020) that are located within the ROI plus an annulus of 5°. A simple power-law function is used to model 1ES 2344+514. In order to build light curves, the source model is fitted to the data by setting the normalisation and the spectral index of all the sources within 7° from the target as free parameters. Above 7° all parameters are fixed to the 4FGL-DR2 values. The normalisations of the background components are left as free parameters. When the fit does not converge, the model parameters are fixed to the 4FGL-DR2 values for sources detected with a test statistic (TS; Mattox et al. 1996) below 4. If after that the fit still does not converge, we gradually increase the TS threshold below which the model parameters are fixed, until a convergence is achieved. Additionally, the power-law index of 1ES 2344+514 is fixed to the 4FGL-DR2 value if the source is detected with TS < 15. Finally, for each time bin resulting in TS < 5, a flux upper limit at 95% confidence level is quoted in the light curve.
The light curve is computed in monthly time bins, which is the exposure time needed by Fermi-LAT to detect 1ES 2344+514 during quiescent emission states (F0.3 − 300 GeV ≈ 0.5 × 10−8 cm−2 s−1). The light curve is computed in 2-day bins close to a VHE flare detected in August 2019 (see Sect. 3).
2.3. Swift-XRT
To accompany the MAGIC monitoring, we organised many simultaneous X-ray observations by the Swift X-ray Telescope (XRT; Burrows et al. 2005). The Swift-XRT observations were performed in the Windowed Timing (WT) and Photon Counting (PC) readout modes depending on the source flux. The data are processed using the XRTDAS software package (v.3.7.0) developed by the ASI Space Science Data Center4 (SSDC), released by the NASA High Energy Astrophysics Archive Research Center (HEASARC) in the HEASoft package (v.6.30.1). The calibration files from Swift-XRT CALDB (version 20210915) are used within the xrtpipeline to calibrate and clean the events.
The X-ray spectrum from each observation is extracted from the calibrated and cleaned event file. For both WT and PC modes data, the events for the spectral analysis is selected within a circle of 20 pixel (∼47″) radius. The background is extracted from a nearby circular region with the same radius. The ancillary response files are generated with the xrtmkarf task applying corrections for point spread function (PSF) losses and CCD defects using the cumulative exposure map.
The 0.3−10 keV source spectra are binned using the grppha task to ensure a minimum of 20 counts per bin, and then modelled in XSPEC using power-law and log-parabola models (with a pivot energy fixed at 1 keV). Additionally, and for each X-ray analysis presented in this work, a photoelectric absorption component is included considering a column density fixed to NH = 1.41 × 1021 cm−2 (HI4PI Collaboration 2016). In the vast majority of the observations, the statistical preference for a log-parabola model is not significant. We compute fluxes in the energy bands 0.3−2 keV and 2−10 keV.
2.4. XMM-Newton EPIC
We organised two X-ray observations of 1ES 2344+514 from XMM-Newton (Jansen et al. 2001) during the MAGIC multi-hour observations on July 23, 2020 (deep exposure 1) and August 6, 2021 (deep exposure 2). Table 1 summarises the exact observing windows as well as the duration. All three EPIC cameras (pn, MOS1, and MOS2) were operated in Large Window mode. The data are reduced using the XMM-Newton Science Analysis System (SAS v20.0.0) following standard procedures. Time intervals with strong background flaring are filtered out following standard procedures using the high-energy light curves with cuts of 0.4 and 0.35 counts s−1 for the pn and MOS, respectively. The total good exposure times after the filtering are 18.9, 26.7, and 26.7 ks in 2020 and 19.4, 27.4, and 27.3 ks in 2021 for the pn, MOS1, and MOS2, respectively. Source and background spectra are extracted from circular regions of radius 34″ for all three detectors. All spectra are binned to contain at least 20 counts per bin and not to oversample the intrinsic energy resolution by more than a factor of three. The empirical correction of the EPIC effective area based on simultaneous NuSTAR observations is applied by setting applyabsfluxcorr = yes in the arfgen task5. The spectra are finally modelled with a log-parabola function in the 0.4−10 keV range using XSPEC (with a pivot energy fixed at 1 keV).
2.5. NuSTAR
NuSTAR (Harrison et al. 2013) observed 1ES 2344+514 in the 3−79 keV band during the MAGIC long exposure on July 23, 2020 (deep exposure 1) with its two coaligned X-ray telescopes and corresponding focal planes, focal plane module A (FPMA) and B (FPMB). The total observing time is 21 ks (see Table 1). The Level-1 data products are processed with the NuSTAR Data Analysis Software (nustardas, v1.9.7) within the HEAsoft software. Cleaned event files (Level-2 data products) are produced and calibrated using standard filtering criteria with the nupipeline software module, and the OPTIMIZED parameter for the exclusion of the South Atlantic Anomaly (SAA) passages. We use the calibration files available in the NuSTAR CALDB version 20220510.
Spectra of the source are extracted for the whole observation from the cleaned event files using a circle of 26 pixel (∼60″) radius, while the background is extracted from a nearby circular region of 26 pixel radius on the same chip of the source. The choice of the extraction region size optimises the signal-to-noise ratio, but alternative choices do not affect the results. The ancillary response files are generated with the numkarf task, applying corrections for the PSF losses, exposure maps, and vignetting. The spectra are rebinned with a minimum of 20 counts per energy bin to allow for χ2 spectrum fitting.
2.6. AstroSat
Between August 5, 2021 and August 7, 2021, we obtained a deep exposure from the Soft X-ray Telescope (SXT), which is an X-ray imaging instrument onboard the AstroSat satellite (Singh et al. 2016, 2017). The observation encompasses the one from MAGIC and XMM-Newton during the deep exposure 2 epoch.
Level-1 data are stored, in FITS format, in the AstroSat data archive6. The Level-2 data are generated from the Level-1 data by running the sxtpipeline tool provided by the SXT data-analysis package (AS1SXTLevel2-1.4b). After merging the cleaned event files of individual orbits together by sxtpyjuliamerger we use the xselect tool of HEASoft to extract the images, light curves and spectra from the merged clean event files in the range 0.7−7 keV. We select the source region as a circle of radius 12′ centred at the point source. As background we use the file SkyBkg_comb_EL3p5_Cl_Rd16p0_v01.pha provided by SXT POC team. The fluxes (in the 0.7−7 keV band) and spectral parameters were computed using XSPEC using a log-parabola model. Table 1 summarises the exact observing window and exposure of AstroSat-SXT.
2.7. Swift-UVOT
We obtained ultraviolet (UV) data coverage with the Swift UV/Optical Telescope (UVOT; Roming et al. 2005) observations between January 2019 and December 2021 performed in the W1, M2, and W2 filters. Over this time range, a total of 67 observations of 1ES 2344+514 are selected after quality checks. We perform photometry over the total exposures of each observation in the sample extracted from the official archive, applying the same apertures for source counts (the standard with 5″ radius) and background (mostly three or four circles of ∼16″ radii off the source) estimation. The photometry is obtained executing the task within the official software included in the HEAsoft 6.23 package, from HEASARC, and then applying the official calibrations (Breeveld et al. 2011) included in the more recent CALDB release (20201026). The fluxes are dereddened considering a mean interstellar extinction curve taken from Fitzpatrick (1999) and a Galactic E(B − V) value of 0.1805 mag (Schlegel et al. 1998; Schlafly & Finkbeiner 2011).
2.8. XMM-Newton OM
In addition to the X-ray observations from the three XMM-Newton EPIC cameras, we process the data collected simultaneously by the Optical Monitor (OM) in the B, U, W1, M2, and W2 filters. The data reduction is performed using the SAS task omichain. The transformation from count rate to flux is achieved by using the conversion factors given in the SAS watchout dedicated page7. Magnitudes are finally corrected for Galactic extinction using an E(B − V) value of 0.1805 mag (Schlafly & Finkbeiner 2011).
2.9. Optical
At optical wavelengths, we profited from R-band observations carried out by the Tuorla blazar monitoring programme8 between January 3, 2019 (MJD 58486) and November 30, 2021 (MJD 59458). The data were acquired by the Kungliga Vetenskapsakademien (KVA; 35 cm primary mirror diameter) telescope and Joan Oró Telescope (TJO; 80 cm primary mirror diameter). The KVA is located on the island of La Palma, in Spain, at the Roque de los Muchachos Observatory, while the TJO telescope is placed at the Montsec Astronomical Observatory, also in Spain. Data reduction is performed following the differential photometry method described by Nilsson et al. (2018) with an aperture radius of 7.5″. The contributions of the host galaxy and nearby companions are subtracted from the observed fluxes, and we apply a correction for the Galactic extinction.
Additional R-band observations were performed by the Whole Earth Blazar Telescope9 (WEBT; e.g. Villata et al. 2007; Raiteri et al. 2017) consortium. The observations were made within the GLAST-AGILE Support Program (GASP; e.g. Villata et al. 2009), which provides mainly optical, but also radio and near-IR support to blazar observations by gamma-ray satellites. Optical data for this paper are taken at the Abastumani, Athens, Crimean10, Haleakala, Lulin, McDonald, Perkins, Rozhen, Skinakas, St. Petersburg, Teide, Tijarafe, and Vidojevica Observatories. The R-band flux densities of the source are corrected for a quantity accounting for the contribution by the host galaxy and nearby companions, the Galactic extinction, and intercalibration among the different datasets. For the latter, we use the data by the Tuorla blazar monitoring programme as a reference.
Finally, we also make use of R-band observations from the 0.76 m Katzman Automatic Imaging Telescope (KAIT; Filippenko et al. 2001) at Lick Observatory on Mt. Hamilton, CA, USA. The data are first reduced adopting the custom pipeline presented by Ganeshalingam et al. (2010). Then, the photometry is carried out using a 9-pixel aperture (corresponding to 7.2″). Several nearby stars are chosen from the Pan-STARRS111 catalogue for calibration, and their magnitudes are transformed into the Landolt (1983, 1990) system using the empirical prescription presented by Tonry et al. (2012), Eq. (6). Data from KAIT are corrected for Galactic extinction, and the contribution of the host galaxy (plus nearby companions) is subtracted with the procedure described above.
2.10. OVRO
The radio observations were performed by the Owens Valley Radio Observatory (OVRO) 40 m telescope within the blazar monitoring programme (Richards et al. 2011). OVRO employs an off-axis dual-beam optics and a cryogenic pseudo-correlation receiver with a 15 GHz centre frequency and 3 GHz bandwidth. The calibration is done using a temperature-stable diode noise source in order to remove receiver gain drifts. Finally, the flux-density scale is derived from observations of 3C 286 assuming a value of 3.44 Jy at 15.0 GHz from Baars et al. (1977). The flux-density scale has a systematic uncertainty of ∼5%, which is not included in the error bars of data points shown later. More details about the OVRO data reduction and calibration are provided by Richards et al. (2011).
3. Multi-wavelength light curves
In Fig. 1 the multi-wavelength light curves between December 23, 2018 (MJD 58475) and January 21, 2022 (MJD 59600) are displayed from radio to VHE. In the top panel, the MAGIC fluxes above 300 GeV are plotted with daily binning (dark markers) and yearly binning (pink markers). The horizontal grey dashed line depicts 4% of the Crab Nebula flux, which is a good approximation of the quiescent state of 1ES 2344+514 at VHE. It corresponds to the average flux level reported by Allen et al. (2017) between 2008 and 2015 when no VHE flaring activity was detected. A VHE flare is observed in August 2019 and is highlighted with a vertical blue dashed line. This flare is studied in greater detail in Sects. 3.1 and 6.3. During the rest of the campaign, no strong flare is detected at VHE. The 2020 average flux above 300 GeV is (3.5 ± 0.4)% of the Crab Nebula, in agreement with the quiescent state. For 2021, the average flux drops to (1.9 ± 0.6)% of that of the Crab Nebula and is one of the lowest states measured for 1ES 2344+514.
In the second panel from the top, the Fermi-LAT fluxes in the 0.3−300 GeV band are shown with monthly binning in dark-yellow markers. Throughout the campaign the monthly fluxes fluctuate around the quiescent state of the source. The comparison of the 2019–2021 emission with the long-term behaviour can be seen in Fig. A.1, which presents a Fermi-LAT light curve starting from 2008. Close to the VHE flare in August 2019, the monthly emission shows little variability. However, a 2-days binned light curve simultaneous with the flare (maroon markers in Fig. 1) indicates a clear flux increase on shorter timescale (see also Sect. 3.1).
In the X-ray, the Swift-XRT fluxes in the 0.3−2 keV and 2−10 keV bands are binned observation-wise (with a typical exposure time around 1−2 ks) and show variability on a daily timescale. The 2−10 keV flux varies around 1 × 10−11 − 2 × 10−11 erg cm−2 s−1, which is the typical dynamical range for 1ES 2344+514 in quiescent activity (Acciari et al. 2011; Aleksić et al. 2013). Nonetheless, a bright flare in the 0.3−2 keV band is visible on October 5, 2019 (MJD 58761), while the 2−10 keV flux remains at the quiescent state. This particular night appears as an outlier with respect to the other nights and is discussed in more detail in Sect. 4.1.
The two long X-ray exposures accompanying the multi-hour MAGIC observations are highlighted in Fig. 1 with vertical orange and maroon dashed lines. The first one, labelled as deep exposure 1 (on July 23, 2020), includes simultaneous XMM-Newton and NuSTAR pointings, and the second one, labelled as deep exposure 2 (on August 6, 2021) comprises simultaneous XMM-Newton and AstroSat pointings (see Table 1). The XMM-Newton and NuSTAR fluxes are plotted in pink and cyan colours, respectively. During these two epochs the VHE flux source is low: about 4% of the Crab Nebula for the deep exposure 1 epoch and about 2% of the Crab Nebula regarding deep exposure 2.
The organisation of multiband long exposures represents the only possibility to search for flux variations down to sub-hour scales, being the timescale over which blazars are known to vary. Such investigations are also essential to provide constraints on the source dimension based on causality arguments. Our data reveal no strong variability at VHE nor in the X-ray during both deep exposure 1 and deep exposure 2 epochs. The MAGIC fluxes are fully consistent with a constant behaviour, while the X-ray emission (in XMM-Newton, NuSTAR, or AstroSat data) varies at the level of 10% only. Nonetheless, we exploit these observations to achieve a precise spectral characterisation of the low activity of the source, which is studied in detail in Sects. 4.1 and 5.
In the UV, optical, and radio wavebands, no apparent flaring episode is noted throughout the multi-wavelength campaign. As discussed and quantified in Sect. 3.2, those energy regions of the spectrum show a smaller variability strength compared to the X-ray and VHE bands.
Eventually, we search for correlated variability between the different bands between 2019 and 2021. Marginal hints of correlation are found between the VHE and X-ray, and the results are shown in Sect. 3.3. No significant correlation is found between the other bands over the multi-wavelength campaign presented in this work. In Sect. 3.4 we search for correlation between the Fermi-LAT and OVRO fluxes using ∼13 yr of data, revealing a marginal hint.
3.1. Zoom on the August 2019 flare
Figure 2 is a zoom around the VHE flare detected with MAGIC in 2019. The top panel displays the MAGIC fluxes. The highest flux is measured on August 6, 2019 (MJD 58701), and is about 20% of the Crab Nebula above 300 GeV. This is ≳5 times larger than the quiescent state of 1ES 2344+514 at VHE (Allen et al. 2017). The subsequent daily measurements show a continuous flux dimming, which is inconsistent with a constant-flux hypothesis at the level of 3σ. We estimate the decay timescale, tdecay, by fitting an exponential function (see e.g. Abdo et al. 2010):
 |
Fig. 2. Multi-wavelength light curves around the VHE flare detected by MAGIC in August 2019. The top panel shows the MAGIC fluxes above 300 GeV in daily binning. The dashed curve is a fit of an exponential function using Eq. (1) in order to estimate the variability timescale (see text for more details). The horizontal dashed-grey line represents 4% of the Crab Nebula flux above 300 GeV. The second panel from the top displays the Fermi-LAT fluxes in the 0.3−300 GeV band in monthly binning (dark-yellow markers) and 2-day binning (maroon markers). In case the source is detected with TS < 5, an upper limit at 95% confidence level is quoted. In the third panel from the top are the Swift-XRT fluxes in the 0.3−2 keV (light-green markers) and 2−10 keV (dark-green markers) bands. The fourth panel from the top displays the UV fluxes from the Swift-UVOT instrument in the UVW1, UVM2, and UVW2 filters. Finally, the bottom panel shows the R-band fluxes from GASP-WEBT and Tuorla. |
where tpeak is the time of the maximum flux that we fix to the centre of the first MAGIC observation. Based on Eq. (1), we find tdecay = 1.7 ± 0.5 day. The result of the fit is shown as a black dotted line in the MAGIC panel of Fig. 2.
The Fermi-LAT fluxes in brown markers are binned in 2 days and also show a hint of a roughly daily timescale flare simultaneous with the VHE. The estimated flux for the time bin centred on August 6, 2019 (the first MAGIC observation) is the highest and about 5 times the monthly average (dark-yellow markers). The hint of the flare is strengthened by the fact that on the date of the highest Fermi-LAT flux, the source is significantly detected with TS ≈ 45 (∼7σ) over a only 2-days integration time. We also find TS < 18 for the other 2-days bins around the VHE flare. In fact, a significant Fermi-LAT detection (i.e. TS ≈ 25) of 1ES 2344+514 requires an integration time on roughly weekly timescale for its quiescent 0.3−300 GeV flux of ∼0.5 × 10−8 cm−2 s−1.
In the X-ray, the flux evolution is statistically consistent with a constant hypothesis within 2σ both in the 0.3−2 keV and 2−10 keV bands. A hint of flux decay is nevertheless apparent in the 2−10 keV regime. Regarding the optical and UV, here also the flux is consistent with a constant evolution. As argued later in Sects. 3.3 and 6.3, this broad-band behaviour is difficult to reconcile with a single one-zone leptonic model and requires an additional emission component developing in the jet. A time-dependent modelling of the three consecutive days is performed in Sect. 6.3.
3.2. Variability
The variability of the source throughout the spectrum is characterised using the fractional variability Fvar (Vaughan et al. 2003) in different wavebands. The fractional variability is essentially the normalised variance of the flux after subtracting statistical fluctuations. It is defined as:
where S is the standard deviation of the flux for N measurements, ⟨x⟩ is the average flux and 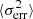 is the corresponding mean square error. Following the prescription of Poutanen et al. (2008), the uncertainty in Fvar is estimated as:
is the corresponding mean square error. Following the prescription of Poutanen et al. (2008), the uncertainty in Fvar is estimated as:
where,
The results are shown in Fig. 3. We consider the full light curves displayed in Fig. 1, meaning using all data between December 23, 2018 (MJD 58475) and January 21, 2022 (MJD 59600).
 |
Fig. 3. Fractional variability as a function of energy for the multi-wavelength light curves in Fig. 1. |
We note that Fvar shows a roughly monotonic increase from the radio to the X-ray (corresponding to the low-energy SED component of 1ES 2344+514) as well as from the MeV to TeV energies (corresponding to the high-energy SED component). The highest variability is found in the MAGIC fluxes. Such a two-peak structure of Fvar(E) is typical in HBLs (see e.g. Aleksić et al. 2015) and the locations of the two local maxima match roughly the peak frequency of the two SED components, located in the X-ray (probed by Swift-XRT) and VHE bands (probed by MAGIC), respectively. This behaviour of Fvar(E) is attributed to the fact that towards higher energies in the respective SED components, the flux is radiated by particles with increasing energy (for instance, the characteristic synchrotron frequency is ν ∝ B′γ′2, where B′ and γ′ are the magnetic field and electron Lorentz factor, respectively). More energetic particles suffer from stronger and faster cooling (from synchrotron and IC emission), hence leading to higher variability with increasing photon energy.
3.3. VHE versus X-ray correlation
We characterise the VHE versus X-ray correlation over the full campaign using the MAGIC and Swift-XRT observations. We correlate the MAGIC flux above 300 GeV with the Swift-XRT flux estimated in the 0.3−2 keV and 2−10 keV bands. In order to remove biases due to nonsimultaneity, only pairs of measurements that took place within 4 h are taken into account. Such a time window falls well below the minimum variability timescale measured in the VHE and X-ray regimes along the campaign. The results are shown in Fig. 4. The blue data points highlight the measurements during the August 2019 flare, and the arrows show the corresponding direction of time. In order to quantify the correlation, we use the Pearson’s coefficient as well as the discrete correlation function (DCF; Edelson & Krolik 1988). The resulting values for each energy combination are listed in Table 2.
 |
Fig. 4. VHE flux versus X-ray flux over the multi-wavelength campaign using MAGIC and Swift-XRT data. Fluxes are nightly binned. Only pairs of measurements within 4 h are considered. The blue measurements correspond to the flaring state in August 2019 and the arrows show the direction of time. The Pearson coefficients and DCF computed over the full data sample are shown in Table 2. |
The results do not reveal any significant VHE versus X-ray correlation. In the case of > 300 GeV versus 0.3−2 keV, the Pearson’s coefficient is only  with a low significance of 0.9σ. Regarding > 300 GeV versus 2−10 keV, the Pearson’s coefficient and the significance are slightly higher (
with a low significance of 0.9σ. Regarding > 300 GeV versus 2−10 keV, the Pearson’s coefficient and the significance are slightly higher (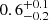 , 2.7σ), although the trend remains marginal. Along most of the campaign, the source is in a low state and the dynamic range of flux values is relatively small. This may be a main reason explaining the low level of correlation.
, 2.7σ), although the trend remains marginal. Along most of the campaign, the source is in a low state and the dynamic range of flux values is relatively small. This may be a main reason explaining the low level of correlation.
The three consecutive measurements during the flare, highlighted with blue markers, shows an interesting correlated behaviour. Between the first and the third day of the flare, the VHE flux decayed by a factor of ∼3.5. From, Fig. 4, a hint of a simultaneous decay is also noticeable in the 2−10 keV band. On the other hand, in the 0.3−2 keV band the flux shows a roughly constant behaviour without any indication of a decay. Such different trends between two very nearby energy regions (0.3−2 keV and 2−10 keV) are difficult to reconcile with a single-zone model. In fact, it suggests that the VHE flare coincides with a region dominating the X-ray emission only at ≳2 keV, while the ≲2 keV flux originates from a different emitting region possibly unrelated to the flare. In Sect. 6.3, we successfully interpret the flare using a two-component leptonic model in a time-dependent approach.
3.4. Radio versus MeV–GeV gamma-ray correlation
For several blazars, studies have unveiled a positive correlation between the flux in the MeV–GeV and radio bands (see, e.g. Marscher et al. 2008; Pushkarev et al. 2010; Fuhrmann et al. 2014). The correlation typically occurs with a delay where the radio band lags behind the MeV–GeV with a time lag ranging from a few tens to a few hundreds of days (Max-Moerbeck et al. 2014a). We search for such correlation pattern in 1ES 2344+514 by taking advantage of the simultaneous long-term OVRO and Fermi-LAT monitoring (∼13 yr). The long-term light curves of OVRO and Fermi-LAT are shown in Fig. A.1. The Fermi-LAT fluxes are computed with monthly binning, in the same fashion as in Fig. 1. We correlate the two bands and search for a time lag using the DCF (Edelson & Krolik 1988). Regarding the Fermi-LAT fluxes, only bins with a detection significance above 2σ (i.e. TS > 4) are considered. The results are shown in Fig. 5 in red markers. The DCF is evaluated in time-lag bins of 30 days, being the smallest bin size of the two light curves. The highest DCF value (∼0.43) is found at a lag of 90 days. A positive lag means that the radio is delayed behind the MeV–GeV band.
 |
Fig. 5. DCF between OVRO and Fermi-LAT versus the time lag. Positive lags mean that the OVRO fluxes lag behind the Fermi-LAT ones. The horizontal dashed lines represent the 2σ (light blue), 3σ (dark blue) and 4σ (magenta) confidence bands using Monte-Carlo simulations (see text). |
We evaluate the significance of the DCF using dedicated Monte-Carlo simulations. First, the slope of the power spectral density (PSD; see, e.g. Max-Moerbeck et al. 2014b) of the two light curves is estimated. For this we adopted the same approach as the one described by MAGIC Collaboration (2021). We obtain a PSD power-law index of βLAT = −0.9 for the Fermi-LAT data, and βOVRO = −2.1. Those values match the one generally found in BL Lac type objects (Max-Moerbeck et al. 2014a). Using these PSD shapes, 105 realistic and uncorrelated light curves are simulated with the same temporal sampling and binning as the data. From this set of simulations, the distribution of the DCF is extracted in each lag bin to derive 2σ, 3σ, and 4σ confidence bands. They are plotted in cyan, blue, and magenta dashed lines, respectively. We note that the light curves are simulated using the Timmer & Koenig (1995) method, which is valid only for Gaussian-distributed fluxes. This assumption is valid for the OVRO data. For the Fermi-LAT light curve, the fluxes are not exactly Gaussian-distributed. Because of that, we also simulated the light curves using the prescription of Emmanoulopoulos et al. (2013), which preserves any underlying flux distribution. However, the results do not show a significant difference. In conclusion, our simulations indicate that the correlation is at the level of 3σ.
In order to estimate the time-lag uncertainty, we follow the common method of Peterson et al. (1998, 2004). We generate 2000 pairs of light curves in both energy bands using flux randomisation and random subset selection. For each of these light-curve pairs, the DCF is computed and the centroid of the lags above 80% of the maximum DCF value is calculated. The centroid is computed within a range of 320 days around the peak seen at τlag ≈ 90 days in Fig. 5. Finally, the 1σ confidence band for the lag is estimated from the 68% containment of the centroid distribution. Using this method, we obtain a 1σ confidence band of τlag ∈ [30, 106] days.
4. Spectral evolution and study of the intermittent EHBL behaviour
4.1. X-ray spectral evolution
1ES 2344+514 is known for its intermittent EHBL behaviour in the synchrotron domain, with a synchrotron peak frequency shifting above 1 keV (i.e. ≳2.4 × 1017 Hz) temporarily. The shift seems to occur primarily during flaring episodes, as observed in 1996 by Giommi et al. (2000) and more recently in 2016 by MAGIC Collaboration (2020a). This behaviour follows the common harder-when-brighter trend observed in other BL Lac type objects (Krawczynski et al. 2004; Acciari et al. 2021; MAGIC Collaboration 2021). With the Swift-XRT observations gathered during the multi-wavelength campaign presented in this work we study the X-ray spectral variability over a ∼3 yr time frame and characterise in deeper detail the occurrence of intermittent EHBL states.
In Fig. 6 we show the Swift-XRT power-law index ΓXRT versus the 0.3−2 keV and 2−10 keV fluxes over the entire campaign. ΓXRT is obtained by fitting the power-law model dN/dE ∝ E−ΓXRT over the 0.3−10 keV range. We note that 68 out of 72 Swift-XRT fits have a χ2 yielding a p-value below 2σ, indicating that a simple power-law model provides a satisfactory description of the spectrum in the vast majority of cases. Only two observations reveal a preference for a log-parabolic model at a significance above 3σ. For the 0.3−2 keV band, the spectral hardness does not show any hint of correlation with the flux. On the other hand, in the 2−10 keV band evidence of a harder-when-brighter trend is found. The Pearson’s correlation coefficient is −0.5 ± 0.1 with a significance of 4.6σ. The three days during the 2019 flare at VHE are highlighted in blue, and show a softening of the emission throughout the flux-decaying phase. The fact that the harder-when-brighter trend is mostly visible when looking at the 2−10 keV band may be due to a larger variability in the latter band compared to the 0.3−2 keV band. For completeness, we list in Appendix B the spectral results of each Swift-XRT observation both using a power-law and a log-parabola model.
 |
Fig. 6. X-ray power-law index versus flux over the multi-wavelength campaign using Swift-XRT data. Fluxes are nightly binned. The blue measurements correspond to the flaring state in August 2019 and the arrows show the direction of time. The green and violet markers correspond to the “soft flare” (October 5, 2019) and “hard low state” (September 20, 2020) periods. |
A significant fraction of the measurements have ΓXRT < 2, suggesting a synchrotron peak frequency located above or around 1 keV, in agreement with an EHBL behaviour. The hint of anticorrelation in the right panel of Fig. 6 suggests that an increased 2−10 keV flux generally correlates with an EHBL state. Nevertheless, throughout the campaign several outliers exist pointing towards a more complex phenomenology. In Fig. 6, we highlight two emblematic outliers. The first one is a soft X-ray flare that occurred on October 5, 2019 (MJD 58761) and it is plotted with a magenta diamond marker. The second one is a hard low state on September 20, 2020 (MJD 59112), plotted with a green square marker.
The soft X-ray flare is identified by a 0.3−2 keV flux of ∼3.5 × 10−11 erg cm−2 s−1, which is by far the highest flux measured in this band over the campaign. Also, the 2−10 keV state is among the highest measured. On the other hand, it shows one of the softest states during the campaign and ΓXRT ≈ 2.17, implying a synchrotron peak below 1 keV despite the high state. The measurement clearly stands out from the rest of the points in Fig. 6. It is worth mentioning that on that day, a simultaneous MAGIC measurement yields a flux above 300 GeV around 8% of the Crab Nebula, which is twice the nonflaring state of 1ES 2344+514 (Allen et al. 2017). The analysis of Fermi-LAT data averaged over one day centred around October 5, 2019 yields a ∼4.3σ detection and a flux in the 0.3−300 GeV band of (5.2 ± 2.9)×10−8 cm−2 s−1. This is about 5 times the monthly average around that date, although the relatively large uncertainty prevents us from firmly claiming the presence of an MeV–GeV flare. In any case, such a flare would not be surprising since in leptonic models the electrons emitting in the 0.3−2 keV band are also responsible for the MeV–GeV flux (Tavecchio et al. 1998).
Regarding the hard low state day, both the 0.3−2 keV and 2−10 keV fluxes are relatively low, around 10−11 erg cm−2 s−1. On the other hand, it shows one of the hardest spectra with ΓXRT ≈ 1.8. The source is thus in an EHBL state despite the low activity. In fact, the X-ray spectrum exhibited a similar hardness as during the VHE flare. A VHE measurement performed a few hours after Swift reveals a low flux of 4% of the Crab Nebula. The X-ray spectral evolution during those two peculiar epochs goes against the typical harder-when-brighter relation. An EHBL state in 1ES 2344+514 thus occurs independently from the flux activity. We note that a comparable hard low state is visible in Fig. 7 at ΓXRT ≈ 1.75 with a 0.3−2.0 keV flux of ∼10−11 erg cm−2 s−1. The later measurement, which has one of the lowest 0.3−2 keV fluxes, indicates that an EHBL state in low activity is a feature that repeats over time. No simultaneous MAGIC data are available.
 |
Fig. 7. Optical/UV and X-ray emission during specific states. The violet markers depict the Swift spectrum during a soft flare on October 5, 2019, during which the power-law index is above 2, indicating a synchrotron peak energy below 1 keV. The green markers display the Swift spectrum during a low but hard state on September 20, 2020. During the latter day, the source is in an EHBL state despite the particularly low flux. An extrapolation of the X-ray best-fit power-law model to lower energy (shown with a green dashed line) suggests a UV excess and possibly indicates a second component contributing to the synchrotron SED. The orange and maroon markers correspond to the deep exposure 1 and deep exposure 2 SEDs. The blue markers represent the Swift spectrum during the VHE flare on August 6, 2019. Grey points are archival measurements from the SSDC database for comparison purposes. The black dotted line is the host-galaxy template, also taken from the SWIRE database. |
In Fig. 7, the Swift-XRT SEDs for those two selected outliers are plotted, together with the Swift-UVOT measurements to obtain a comprehensive view of the synchrotron component. The flare state on August 6, 2019 is also plotted with blue markers. Fig. 7 emphasises a strong X-ray spectral variability, inconsistent with the harder-when-brighter evolution (as already mentioned).
4.1.1. Evidence of a UV excess
Another interesting result from Fig. 7 stems from an apparent mismatch between the X-ray and UV fluxes during the hard low state (green markers). In other words, the extrapolation to lower energies of the Swift-XRT spectrum falls significantly below the Swift-UVOT data points (by a factor ∼2.5). In Fig. 7, a green dashed line shows the extrapolation to lower energies of the best-fit power-law model. The corresponding X-ray power-law index is significantly below 2 (ΓXRT = 1.82 ± 0.05), while the energy flux around the low-energy Swift-XRT points is at the level or even below the Swift-UVOT measurements. In addition to that, the fluxes in the three Swift-UVOT filters point towards a relatively hard spectrum in the UV, further confirming the mismatch between the Swift-XRT and Swift-UVOT data. Using a two-point photon index formula, 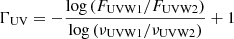 (see e.g. Foschini et al. 2015), we estimate the spectral index in the UV to be ΓUV = 1.7 ± 0.4 (we neglect in this computation the host-galaxy contribution). For the other days shown in Fig. 7, the evidence for an excess is less apparent. The combination of a hard and particularly low X-ray state on September 20, 2020 renders its detection easier. The other hard low state visible in Fig. 7 mentioned in the previous section, which is characterised by ΓXRT ≈ 1.75 and a 0.3−2.0 keV flux of ∼10−11 erg cm−2 s−1, displays the same mismatch between the UV data and the Swift-XRT spectrum.
(see e.g. Foschini et al. 2015), we estimate the spectral index in the UV to be ΓUV = 1.7 ± 0.4 (we neglect in this computation the host-galaxy contribution). For the other days shown in Fig. 7, the evidence for an excess is less apparent. The combination of a hard and particularly low X-ray state on September 20, 2020 renders its detection easier. The other hard low state visible in Fig. 7 mentioned in the previous section, which is characterised by ΓXRT ≈ 1.75 and a 0.3−2.0 keV flux of ∼10−11 erg cm−2 s−1, displays the same mismatch between the UV data and the Swift-XRT spectrum.
The contribution from the host galaxy plotted as a black dotted line in Fig. 7 is negligible in the UV band (≲10%; Raiteri et al. 2014), in particular for the UVOT W2 filter, and cannot explain the UV excess. We consider here a host template of a 13 Gyr old elliptical galaxy taken from the SWIRE12 library Polletta et al. (2007). Using different elliptical templates, such as the one from Kinney et al. (1996), indicates a similar host contribution in the UV band, and thus leads to the same conclusions. Overall, such a spectral feature indicates two different electron populations contributing to the UV and X-ray emission of 1ES 2344+514 (see Sects. 5 and 6).
4.1.2. XMM-Newton, NuSTAR, and AstroSat deep exposures
This section presents the spectral results of the long X-ray exposures that took place simultaneously with multi-hour MAGIC observations, deep exposure 1 and deep exposure 2. The first one took place on July 23, 2020 and includes X-ray data from XMM-Newton and NuSTAR. The second exposure includes XMM-Newton and AstroSat-SXT X-ray data and happened on August 6, 2021. Table 1 summarises the exposures for each instrument. The combination of XMM-Newton, NuSTAR, and AstroSat provides an unprecedented characterisation of the synchrotron emission around the SED peak frequency for 1ES 2344+514.
The spectra are fitted with a fixed Galactic column density of hydrogen (NH = 1.41 × 1021 cm−2) using a power-law and a log-parabola model: dN/dE ∝ (E/E0)−Γ and dN/dE ∝ (E/E0)−α − β log E/E0, with E0 = 1 keV as the pivot energy. For all instruments, we average the spectrum over the entire exposure time given the low flux variability and the absence of significant intraday spectral variability. The XMM-Newton spectral parameters are derived by simultaneously fitting the EPIC PN, MOS1, and MOS2 data. Regarding the deep exposure 1 epoch, the parameters are obtained from XMM-Newton-only data as well as the combined XMM-Newton+NuSTAR spectra given that the two instruments complement each other in energy. In all cases and for both nights, from the XMM-Newton fits the power-law model is significantly rejected (> 5σ), implying the detection of a curvature in the 0.3−10 keV range. In what follows, we thus only consider and discuss the log-parabola model.
The results of the fits are listed in Table 3. The last column is the extracted synchrotron peak frequency, νsynch, p, that is obtained in XSPEC using the eplogpar model (which is essentially the same function as the log parabola defined earlier, but refactored such that νsynch, p becomes an explicit parameter of the model). Deep exposure 1, where the 2−10 keV flux is slightly higher, shows a harder α with respect to the deep exposure 2 epoch (α = 1.94 ± 0.01 versus α = 2.07 ± 0.01 from the XMM-Newton data). In addition, the curvature β is significantly more pronounced during deep exposure 2. Such harder-when-brighter evolution is confirmed by the evolution of νsynch, p. The fits yield a small, but significant shift of νsynch, p between the two epochs. We find νsynch, p = 1.32 ± 0.04 keV for deep exposure 1 while during deep exposure 2 XMM-Newton and AstroSat consistently unveil a lower value: νsynch, p = 0.82 ± 0.03 keV for XMM-Newton and νsynch, p = 0.97 ± 0.12 keV using AstroSat. It is worth noting that despite the low activity νsynch, p is larger than 1 keV for deep exposure 1, thus within the EHBL family according to the definition of Costamante et al. (2001). In conclusion, similarly to what is discussed in the previous section, 1ES 2344+514 can show EHBL behaviour also in low states. In Fig. 7 we show the XMM-Newon and NuSTAR SEDs. For XMM-Newton only the data from EPIC-pn camera are used to build the SED for simplicity and also given the larger number of counts compared to the ones in the MOS1 and MOS2 cameras. The UV data at ν > 1015 Hz (obtained from the XMM-Newton OM instrument) receive negligible contribution from the host galaxy (Raiteri et al. 2014).
X-ray spectral parameters from XMM-Newton, NuSTAR, and AstroSat-SXT observations using a log-parabola model during the deep exposures with MAGIC.
Regarding deep exposure 1 the difference in the parameters between the XMM-Newton-only and XMM-Newton/NuSTAR-combined fits is not significant. This indicates a smooth connection between the soft X-ray band (up to ∼10 keV) covered by XMM-Newton and the hard X-ray band covered by NuSTAR (≳10 keV). We also stress that the cross-calibration factors (derived from the fits in Xspec) between XMM-Newton and NuSTAR are all below 15%, thus within the systematics of the scientific instrumentation onboard these two spacecrafts (Madsen et al. 2017). For the deep exposure 2 epoch, the AstroSat-SXT spectral parameters (derived in the 0.7−7 keV range) are consistent with the ones obtained in the 0.4−10 keV band by XMM-Newton.
4.2. VHE spectral evolution
The MAGIC observations are used to probe the spectral variability in the VHE band. Unfortunately, given the low flux, the VHE spectral slope cannot be resolved with high resolution on a single snapshot for most of the MAGIC observing nights. A meaningful VHE spectral study on a daily timescale over the full campaign is thus not possible (unlike in the X-ray with Swift-XRT, XMM-Newton, NuSTAR, and AstroSat). Thus, we limit the VHE spectral study to a few specific epochs of interest: the VHE flaring period, the soft X-ray flare, and the deep exposures nights simultaneous with XMM-Newton, NuSTAR, and AstroSat. We also compute a VHE spectrum using a MAGIC observation close to the hard low state in the X-ray discussed earlier. The corresponding MAGIC observation is not strictly simultaneous with the Swift-XRT one, but took place roughly 14 h after. All spectra are fitted between 100 GeV and 2 TeV with a simple power-law spectrum, dN/dE = f0(E/E0)−ΓVHE, with E0 = 500 GeV the normalisation energy. This simple function provides a satisfactory description of the data, and the preference for a log-parabola model (one additional degree of freedom) is always below 3σ. All parameters are computed after correcting the spectra for extragalactic background light (EBL) absorption using the template EBL model from Domínguez et al. (2011).
Table 4 lists the resulting best-fit parameters. Evidence of daily timescale spectral variability is measured between the first and the second days of the flare. On August 6, 2019, the brightest day of the flare, the spectrum is hard with ΓVHE = 1.9 ± 0.2. On the night after, August 7, 2019, the spectrum steepens to ΓVHE = 2.5 ± 0.2 together with the flux. This harder-when-brighter trend closely follows what is also measured in the X-ray (see blue points in Fig. 6 and Sect. 4.1). During the flaring event in 2016 discussed by MAGIC Collaboration (2020a), the power-law index is around 2.0−2.1 (depending on the exact day), being consistent with what we report here for the peak activity of the August 2019 flare. Regarding the soft X-ray flare night, the spectrum is similarly hard (ΓVHE = 1.8 ± 0.3), although the VHE flux is close to the quiescent state (8% of the Crab Nebula). Regarding the night close to the hard low state in the X-ray band, the uncertainty of the slope (ΓVHE = 2.1 ± 0.5) does not allow us to make any strong claim about the VHE spectral shape.
MAGIC spectral parameters for epochs of interest obtained from a power-law fit (dN/dE = f0(E/E0)−ΓVHE) between 100 GeV and 2 TeV.
During the deep exposure nights (together with XMM-Newton, NuSTAR, and AstroSat), ΓVHE is around 2.4−2.5 and remains consistent within statistical uncertainties. Differently from the X-ray (see previous section), no VHE spectral variability is measured during those nights, which may also be due to the limited sensitivity of MAGIC compared to XMM-Newton, NuSTAR, and AstroSat.
In Table 4 we also show the power-law index derived for the entire 2020 year, during which we do not find any significant flare. The best-fit index is ΓVHE = 2.4 ± 0.1, similar to the deep exposure nights as well as to the days following the peak VHE activity on August 6, 2019. Within (statistical and systematic) uncertainties, such an average slope is consistent with previous measurements during quiescent states (Albert et al. 2007; Aleksić et al. 2013; Allen et al. 2017). During 2021, the total detection significance is only ∼2σ, preventing a precise determination of the average spectral hardness. The corresponding best-fit index is ΓVHE = 2.3 ± 0.4, consistent with the 2020 average.
Overall, the MAGIC observations unveil VHE spectral variability, although moderate. Except during the August 2019 VHE flare and soft X-ray flare in October 2019, the measured power law is typically around ΓVHE ≈ 2.4 − 2.5 (consistent with published work during quiescent states). In Appendix C, we overlaid the best-fit MAGIC power-law models in order to better appreciate the spectral variability.
5. Multi-wavelength characterisation of the quiescent activity and its broad-band modelling
Figure 8 shows the broad-band SEDs during the deep exposure 1 and deep exposure 2 epochs. The corresponding VHE emission is at the level of ∼4% and ∼2% of the Crab Nebula above 300 GeV, respectively (see Table 4). The 2−10 keV fluxes are close to 10−11 erg cm−2 s−1 (see Table 3). As highlighted in the Sect. 1, such flux levels correspond to the quiescent activity of the source. The MAGIC spectra are corrected for the EBL absorption effects. In view of the low detection significance by MAGIC for deep exposure 2, the corresponding VHE SED contains only one point with a ∼2σ signal. We thus complement the VHE spectrum with a butterfly envelope indicating the 1σ statistical uncertainty on the spectral shape derived from the power-law fit. In the radio, we use the closest OVRO measurements, which took place ≲1 day away from the one of MAGIC but can be assumed as simultaneous given the low variability at such energies (see Sect. 3.2). For the UV data, we consider the fluxes from the XMM-Newton OM instrument that were obtained simultaneously with the X-ray measurements. Regarding Fermi-LAT, the SEDs are averaged over 1 month around the deep exposure 1 observation and over 2 months around deep exposure 2. Such integration times are needed to achieve a significant detection (TS > 25). The grey data points are the archival measurements retrieved from the SSDC. A comparison with the archival data reveals that the source is probed in one of its lowest VHE gamma-ray states measured so far. For deep exposure 2, the X-ray flux is also among the lowest.
 |
Fig. 8. Broad-band SEDs during the simultaneous MAGIC, XMM-Newton, NuSTAR, and AstroSat observations. The panel on the left shows the SED from the deep exposure 1 epoch (July 23, 2020) while the panel on the right is during the deep exposure 2 epoch (August 6, 2021). The results of the 2-component SSC modelling is also shown: the dashed dark-blue line is the emission from the core region, while the violet dash-dotted line is the emission from the variable region (see text for more details). The sum of the two components is plotted in a continuous light-blue line. The parameter values of the model are listed in Table 5. The large bump in the optical domain (black dashed curve) is the emission from the host galaxy modelled with the template from the SWIRE database (Polletta et al. 2007). As in Fig. 7, grey points are archival measurements from the SSDC database. |
The extensive multi-wavelength coverage allows us to model the emission assuming a leptonic scenario (Maraschi et al. 1992; Tavecchio et al. 1998; Krawczynski et al. 2004) in order to constrain the physical properties of the quiescent state of 1ES 2344+514. The leptonic scenario considered here involves synchrotron radiation by a population of relativistic electrons as well as IC scattering off the synchrotron photons (the so-called SSC model). The particle interaction processes are computed using routines from the JetSeT software (Massaro et al. 2006; Tramacere et al. 2009, 2011; Tramacere 2020).
In light of the results presented in Sect. 4.1, which provides strong evidence that two separate particle populations contribute to the synchrotron emission, we consider a two-component model. The two components consist of two spherical regions homogeneously filled with electrons that are spatially separated and, thus, not interacting with each other. Further, we assume that each component is embedded in a homogeneous magnetic field. One region, dubbed as “variable”, dominates the emission from optical to VHE. The second region, that we call “core”, dominates mostly in the radio but brings a quite relevant contribution to the IR/optical/UV spectrum such that it is responsible for the UV excess reported in Sect. 4.1. For simplicity, we assume that the two components are streaming down the jet with the same speed, and both having a Doppler factor of δ = 10. This value is in reasonable agreement with those derived by Hovatta et al. (2009) and Lister et al. (2021) with Very Long Baseline Interferometry (VLBI) observations, from the variability brightness temperature in the radio (Liodakis et al. 2018a), as well as those obtained from SED modelling of BL Lac type objects (Tavecchio et al. 2010).
The electron distribution in the variable component is modelled as a broken power-law distribution,
where 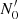 is a normalisation constant. The corresponding electron energy density is given by
is a normalisation constant. The corresponding electron energy density is given by 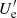 (in [erg cm−3]). Also,
(in [erg cm−3]). Also, 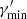 ,
, 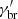 , and
, and 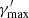 are defined as the minimum, break, and maximum Lorentz factor, respectively. We stress that a simple power-law model, which has one degree of freedom less, provides a significantly worse description of the X-ray spectrum. Hence, such a simple function is not a solution here and a model including a break (or any kind of steepening) is required to describe the X-ray emission. The size of the variable component is set to R′ = 2 × 1016 cm. It is in agreement with the constraint from causality arguments, R′≲δ ⋅ c ⋅ tvar, obs (Tavecchio et al. 1998), where tvar, obs is the observed variability timescale, being tvar, obs ∼ 1 day in the X-ray and VHE (see Sect. 3). As described in the previous paragraph, δ is fixed to 10.
are defined as the minimum, break, and maximum Lorentz factor, respectively. We stress that a simple power-law model, which has one degree of freedom less, provides a significantly worse description of the X-ray spectrum. Hence, such a simple function is not a solution here and a model including a break (or any kind of steepening) is required to describe the X-ray emission. The size of the variable component is set to R′ = 2 × 1016 cm. It is in agreement with the constraint from causality arguments, R′≲δ ⋅ c ⋅ tvar, obs (Tavecchio et al. 1998), where tvar, obs is the observed variability timescale, being tvar, obs ∼ 1 day in the X-ray and VHE (see Sect. 3). As described in the previous paragraph, δ is fixed to 10.
Regarding the core component, the electron distribution is modelled with a simple power-law function, 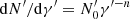 with
with 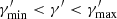 , since the sparsity of the data between the radio and optical/UV does not allow us to constrain functions with a higher degree of complexity. To limit the degrees of freedom, we set
, since the sparsity of the data between the radio and optical/UV does not allow us to constrain functions with a higher degree of complexity. To limit the degrees of freedom, we set 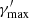 to the value at which the synchrotron cooling break occurs. For this, we equate the synchrotron cooling time to the advection time (or effective escape time) of the electrons given by
to the value at which the synchrotron cooling break occurs. For this, we equate the synchrotron cooling time to the advection time (or effective escape time) of the electrons given by 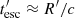 (Inoue & Takahara 1996).
(Inoue & Takahara 1996).
The core component from our model is considered as the radio core of 1ES 2344+514 unveiled by VLBI data. Hence, the radius is fixed to R′ = 1017 cm, similar to the size of the radio core at 15.4 GHz. Based on VLBI data, Aleksić et al. (2013) reported a size for the 15.4 GHz core of 0.07 ± 0.04 mas, equivalent to ∼2 × 1017 cm at the distance of 1ES 2344+514. As an additional constraint, we require the core component to be at equipartition – the electron energy density is equal to that of the magnetic field, 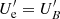 . Between the two epochs modelled here, the physical parameters of the core component are identical given the low flux variability observed in the radio (see Sect. 3.2).
. Between the two epochs modelled here, the physical parameters of the core component are identical given the low flux variability observed in the radio (see Sect. 3.2).
The resulting models are shown in Fig. 8: the dark-blue dashed line is the emission from the core, the violet dash-dotted line is the emission from the variable region, and the light-blue solid line is the sum of both components. The dark dotted line, around ∼1014 − 1015 Hz, is the contribution from the host galaxy estimated with an elliptical galaxy template borrowed from SWIRE database and scaled to the redshift of 1ES 2344+514. The values of the model parameters derived for both days and both emitting components are listed in Table 5. The model is able to describe the data from radio to VHE satisfactorily. The core component only dominates in the radio, and is clearly negligible in the gamma rays with respect to the variable region.
Parameters of the two-components SSC models obtained for the MAGIC, XMM-Newton, NuSTAR, and AstroSat simultaneous observing nights.
By construction and as mentioned previously, the parameters of the core component are assumed to be the same between the two days. This assumption seems to be reasonable as it provides an appropriate prediction of the radio flux (at 15 GHz as measured by OVRO). Regarding the variable region, the most significant differences in the parameters between the deep exposure 1 and deep exposure 2 models are related to the electron population. More specifically, the high-energy slope of the electron distribution (given by n2) is softer during deep exposure 2. Additionally, 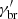 is slightly lower on the latter day: this is consistent with the harder-when-brighter trend reported in Sect. 4.1.2.
is slightly lower on the latter day: this is consistent with the harder-when-brighter trend reported in Sect. 4.1.2.
The break in the electron distribution in the variable region for the deep exposure 1 SED is n2 − n1 = 1.06 and occurs at 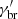 = 4.9 × 105. Homogeneous models (as the one considered here) predict an electron cooling break due to synchrotron radiation of n2 − n1 = 1, similar to the value obtained here. Furthermore, assuming an electron advection time of
= 4.9 × 105. Homogeneous models (as the one considered here) predict an electron cooling break due to synchrotron radiation of n2 − n1 = 1, similar to the value obtained here. Furthermore, assuming an electron advection time of 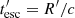 (see, e.g. Inoue & Takahara 1996), the theoretical break location falls within ∼25% from the value of our model. We stress that the location and the strength of the break are derived directly from X-ray data and not fixed a priori based on physical assumptions. The break observed during the deep exposure 1 epoch may thus be associated with synchrotron cooling. For deep exposure 2, although
(see, e.g. Inoue & Takahara 1996), the theoretical break location falls within ∼25% from the value of our model. We stress that the location and the strength of the break are derived directly from X-ray data and not fixed a priori based on physical assumptions. The break observed during the deep exposure 1 epoch may thus be associated with synchrotron cooling. For deep exposure 2, although 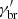 agrees well with synchrotron cooling (within ∼25%), its strength is greater (n2 − n1 ≈ 1.8) than theoretically expected if caused solely by synchrotron radiation. Either additional effects related to the source geometry (for instance, inhomogeneities in the emitting region; see Reynolds 2009) are taking place, or the break may also be intrinsic to the underlying acceleration process.
agrees well with synchrotron cooling (within ∼25%), its strength is greater (n2 − n1 ≈ 1.8) than theoretically expected if caused solely by synchrotron radiation. Either additional effects related to the source geometry (for instance, inhomogeneities in the emitting region; see Reynolds 2009) are taking place, or the break may also be intrinsic to the underlying acceleration process.
The extrapolation to lower energies of the X-ray emission from the variable region falls below the UV data points, leading to a similar UV excess reported in Sect. 4.1. In our model, the UV excess is due to a significant contribution by the core region to the UV flux. The additional core component contributes to the total UV flux at the level of 45% for both epochs.
As an alternative to the broken power-law function to model the electron distribution, we test a log-parabolic model with a low-energy power-law branch (LPPL; Massaro et al. 2006):
where r quantifies the curvature, and 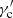 is the energy above which the curvature occurs in the distribution. The motivation for testing this alternative function is twofold. First, several works showed that a log-parabola distribution may naturally arise in case of stochastic acceleration in magnetic turbulence or any acceleration process in which the acceleration probability is energy dependent (Kardashev 1962; Massaro et al. 2004a, 2006; Tramacere et al. 2009). The power-law branch in the low-energy part of the distribution may originate from first-order Fermi acceleration (diffusive shock acceleration). The LPPL function is thus physically motivated by simultaneous Fermi first-order and second-order (i.e. stochastic) acceleration processes. Second, as shown in Sect. 4.1.2, the sensitive X-ray observations clearly indicate a curved spectrum in agreement with a log-parabola shape.
is the energy above which the curvature occurs in the distribution. The motivation for testing this alternative function is twofold. First, several works showed that a log-parabola distribution may naturally arise in case of stochastic acceleration in magnetic turbulence or any acceleration process in which the acceleration probability is energy dependent (Kardashev 1962; Massaro et al. 2004a, 2006; Tramacere et al. 2009). The power-law branch in the low-energy part of the distribution may originate from first-order Fermi acceleration (diffusive shock acceleration). The LPPL function is thus physically motivated by simultaneous Fermi first-order and second-order (i.e. stochastic) acceleration processes. Second, as shown in Sect. 4.1.2, the sensitive X-ray observations clearly indicate a curved spectrum in agreement with a log-parabola shape.
In order to model the SEDs with Eq. (6), the slope of the low-energy power-law branch (n) is fixed to n1, being the index of the low-energy part of the broken power-law model used previously (see Table 5). Further, 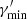 and
and 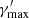 are fixed to the same values as in Table 5. The fitting routines of JetSeT are eventually used to find the best-fit parameters for the electron distribution.
are fixed to the same values as in Table 5. The fitting routines of JetSeT are eventually used to find the best-fit parameters for the electron distribution.
Both SEDs are well described with the LPPL function as a model for the electron distribution. The data do not allow us to find a significant preference between the broken power-law and LPPL models. For deep exposure 1, we find r = 1.00 and 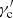 = 2.86 × 105. Regarding deep exposure 2, we obtain r = 2.17 and
= 2.86 × 105. Regarding deep exposure 2, we obtain r = 2.17 and 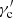 = 2.50 × 105. We summarised in Appendix D the resulting values for all the modelling parameters. From these results, two interesting aspects deserve to be stressed. First, one finds that r ≈ 4β, where β is the curvature of the log-parabola fit to the XMM-Newton and NuSTAR spectra (see Table 3). This relationship is in good agreement with the expected relationship between the synchrotron spectrum curvature and the electron distribution curvature parameter if one assumes the δ-approximation for the computation of the synchrotron flux (see, e.g. Massaro et al. 2004b). Second, the curvature r is anticorrelated with the location of the synchrotron peak energy: r is twice as high on deep exposure 2 with respect to deep exposure 1, while the synchrotron peak energy is lower (νsynch, p = 0.8 keV versus νsynch, p = 1.3 keV; see Table 3). This anticorrelation trend is consistent with a regime in which stochastic acceleration is the dominant factor responsible for the flux and spectral variability Tramacere et al. (2011).
= 2.50 × 105. We summarised in Appendix D the resulting values for all the modelling parameters. From these results, two interesting aspects deserve to be stressed. First, one finds that r ≈ 4β, where β is the curvature of the log-parabola fit to the XMM-Newton and NuSTAR spectra (see Table 3). This relationship is in good agreement with the expected relationship between the synchrotron spectrum curvature and the electron distribution curvature parameter if one assumes the δ-approximation for the computation of the synchrotron flux (see, e.g. Massaro et al. 2004b). Second, the curvature r is anticorrelated with the location of the synchrotron peak energy: r is twice as high on deep exposure 2 with respect to deep exposure 1, while the synchrotron peak energy is lower (νsynch, p = 0.8 keV versus νsynch, p = 1.3 keV; see Table 3). This anticorrelation trend is consistent with a regime in which stochastic acceleration is the dominant factor responsible for the flux and spectral variability Tramacere et al. (2011).
6. Discussions
6.1. Intermittent EHBL behaviour
One of the primary goals of our study is a systematic characterisation of the X-ray and VHE spectral evolution over a multi-year period to better assess the origin of the intermittent EHBL characteristics. Previous works showed that drastic spectral changes implying an EHBL nature can correlate with outburst phases, although the picture remains elusive given that these studies were performed over short time ranges (unlike the one presented here) and also mostly focussed on flaring states (e.g. Giommi et al. 2000; MAGIC Collaboration 2020a).
Using almost three years of Swift-XRT data, our results indeed confirm a general harder-when-brighter evolution in the X-ray with an EHBL behaviour in the synchrotron domain more likely to occur in higher emission states. The anticorrelation between the power-law index ΓXRT and the 2−10 keV flux is significant at the level of 4.6σ (see Sect. 4.1). Above a 2−10 keV flux of ∼1.7 × 10−11 erg cm−2 s−1, all spectra display ΓXRT < 2, that is, a synchrotron peak energy ≥1 keV and thus 1ES 2344+514 is behaving as an EHBL. During the deep exposure 1 and deep exposure 2 epochs, the synchrotron peak frequency is precisely determined thanks to XMM-Newton, NuSTAR, and AstroSat data. A small but significant shift of the peak frequency is indeed visible between these epochs and correlates positively with the flux. In conclusion, this means that flux enhancements are likely accompanied by an injection of freshly accelerated electrons in the radiation zone or due to some reacceleration process (see, for instance, Zech & Lemoine 2021).
Nonetheless, the unbiased data sample from Swift-XRT unveils several outliers to this trend, calling for more complexity. First, one of the softest X-ray spectra from this campaign (on October 5, 2019) actually coincides with the highest 0.3−2 keV flux (by far) and also close to the highest 2−10 keV flux. This outburst has to be caused by an underlying mechanism that differs from the one driving the general harder-when-brighter trend visible throughout the campaign. It must be a process that remains achromatic or only slightly chromatic, like a change in the electron density or in the Doppler factor δ. Another interesting outlier is September 20, 2020, where despite the low X-ray flux the Swift-XRT index is ΓXRT ≈ 1.8, implying a synchrotron peak energy significantly above 1 keV. Figure 7 shows a comparison of the corresponding X-ray SED (green markers) with the deep exposures by XMM-Newton and NuSTAR during other low-activity epochs, which are significantly softer. It is interesting to see in Fig. 7 evidence of an anticorrelation between the soft X-ray (∼1017 Hz) and the hard X-ray points (∼1018 Hz) when comparing the green (September 20, 2020) and maroon (deep exposure 2 – August 6, 2021) SEDs. This implies relatively strong changes in the acceleration or cooling efficiency of the electrons without a significant change in the flux level.
An increase in the acceleration efficiency without a significant change in the electrons injection luminosity in the emitting region could qualitatively explain this behaviour. In such a case, the whole electron distribution would shift to higher energies, thus amplifying the flux at higher energies and decreasing the one at lower energies. Another possibility could be a variation of the magnetic field, while keeping the acceleration efficiency constant: assuming a system close to equilibrium in which synchrotron radiation and adiabatic expansion are the dominant cooling processes, a decrease in B′ over time would shift the cooling break in the electron distribution to higher energy, hence leading to an anticorrelation between the rising and falling edges of the synchrotron bump. MAGIC Collaboration (2021) put forward such a scenario to explain a 3σ anticorrelation in Mrk 421 between the UV and X-ray emission (which correspond to the rising and falling edge of the synchrotron SED component).
We note that intermittent shifts of the synchrotron peak above 1 keV in low activity is particularly rare, and to our knowledge it was only found in Mrk 501 so far (Ahnen et al. 2018). In conclusion, our results consolidate the hypothesis that being an EHBL is a temporary feature instead of an intrinsic characteristic (at least for a subset of EHBLs).
As for the spectral evolution at VHE, the MAGIC data do not allow us to perform a systematic spectral study on a daily timescale. The lower-than-usual VHE state throughout most the campaign, below 4% Crab Nebula, prevents sufficient photon statistics to build daily SEDs with meaningful constraints on the spectral slope for the majority of the days. It is not possible to firmly identify if shifts of the gamma-ray component to higher energies systematically coincide (or not) with the one observed in the synchrotron part. At least, during the VHE flare in August 2019, the MAGIC spectrum could be determined and the power-law slope shows an indication of harder-when-brighter, as observed simultaneously in the X-ray. The hardest spectrum is Γ = 1.9 ± 0.2, thus still in agreement with a gamma-ray peak below 1 TeV. Overall, we do not find indication that the source behaved as an extreme-TeV EHBL despite significant shift of the synchrotron SED component above 1 keV. From this point of view, 1ES 2344+514 differs from 1ES 0229+200 or 1ES 1426+426, which have similar synchrotron peak frequencies but a gamma-ray component peaking above 1 TeV (Foffano et al. 2019; Biteau et al. 2020).
6.2. Origin of the UV excess and modelling of the quiescent state
In this work, we report strong evidence of (at least) two emitting components contributing to the synchrotron flux from the IR to the X-ray. It is suggested from the detection of a UV excess during a hard low state in the X-ray on September 20, 2020: the UV flux as measured by Swift-UVOT lies significantly above the extrapolation to lower energies of the Swift-XRT spectrum. The SED modelling of the two long exposures with sensitive X-ray data from XMM-Newton and NuSTAR (July 23, 2020 and August 6, 2021) also indicates the presence of such an excess, as discussed earlier. The excess is especially apparent on September 20, 2020 with respect to the other days, which is likely due to the combination of a low, but hard X-ray spectrum on this particular date.
A discontinuity in the low-energy SED component was previously noted in the low-frequency peak BL Lac (LBL) object AO 0235+16 (Raiteri et al. 2006). The UV-to-X-ray spectrum of AO 0235+16 may be reconciled by introducing a thermal component. The latter hypothesis is, however, highly improbable for 1ES 2344+514 (see below). Regarding HBLs and EHBLs, some evidence was found in 1ES 0229+200, RGB 0710+591 (Costamante et al. 2018), and Mrk 501 (MAGIC Collaboration 2020b) based on SED modelling. Nevertheless, the UV/X-ray mismatch shown here for 1ES 2344+514 is quite pronounced and evident: the energy flux around the low-energy end of the hard Swift-XRT spectrum on September 20, 2020 is equal to or even below the one in the Swift-UVOT filters, which was not the case in the studies mentioned before.
The host galaxy is unlikely to be the origin of the UV excess given that in the UV the contribution is negligible (in particular in the UVM2 and UVW2 filters). As also discussed by Costamante et al. (2018), an unaccounted UV thermal component from the host (e.g. because of a burst of massive star formation following a recent merger) is very unlikely since this emission would need to be more than an order of magnitude larger than the template used in this work to model the thermal emission from a giant elliptical galaxy. Instead, a more natural solution is that this excess originates from a second population of nonthermal electrons. Such a second population might be less energetic than the one emitting the X-ray/gamma-ray flux and located in larger regions, possibly in downstream parts of the jet.
To investigate the latter scenario, we use the two MAGIC observations simultaneous with NuSTAR, XMM-Newton, and AstroSat (July 23, 2020 and August 6, 2021), which provide the most detailed broad-band view of the quiescent activity of this source (see Sect. 5). We find that a two-component scenario like the one mentioned above is able to well describe the SEDs. In our model, the IR/optical to VHE flux is dominated by a relatively compact region (dubbed as variable) filled with highly energetic electrons (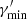 = 2 × 103 and
= 2 × 103 and 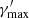 = 8 × 106). The second component (dubbed as core) is then introduced to explain the UV excess. The corresponding electron population is less energetic than in the variable region (
= 8 × 106). The second component (dubbed as core) is then introduced to explain the UV excess. The corresponding electron population is less energetic than in the variable region (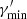 = 10 and
= 10 and 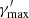 = 9 × 104). Its synchrotron SED peaks in the UV band, while in the gamma-ray band it is subdominant by more than an order of magnitude with respect to the variable region.
= 9 × 104). Its synchrotron SED peaks in the UV band, while in the gamma-ray band it is subdominant by more than an order of magnitude with respect to the variable region.
Further, our modelling supports the idea that this second component responsible for the UV excess can be attributed to the 10 GHz radio core. As seen in Fig. 8, it well explains the flux measured by OVRO at 15 GHz, and the region radius (∼10−1 pc) is in agreement with VLBI observations at similar frequencies. We also note that a break happens in the model below ∼1011 Hz (see Fig. 8), which is due to synchrotron self-absorption (Konigl 1981). Based on the parameters of the core component, we find that the self-absorption optical depth τν becomes ∼1 at a frequency of about 5 GHz. Since the surface of unity optical depth is a defining property of a radio core (Blandford & Königl 1979), this further suggests that the UV excess comes from the radio core at a frequency close to 10 GHz.
Lindfors et al. (2016) presented a study of the optical (R-band) and radio (15 GHz data from OVRO) emission from a sample of VHE-emitting BL Lac type objects. By exploiting the variability patterns, Lindfors et al. (2016) extracted information about the different regions contributing to the jet emission. In 1ES 2344+514, it was concluded that at least 25% of the optical flux is radiated in the same region as the one responsible for the 15 GHz emission. The model we present in Sect. 5 is in good agreement with this conclusion as it predicts that ∼40% of the total (host-galaxy subtracted) R-band flux comes from the region describing the radio data.
In Sect. 3.4, we report a 3σ positive correlation between OVRO and Fermi-LAT. A 2σ indication was reported by Liodakis et al. (2018b), also using OVRO and Fermi-LAT, but over a ∼9 yr period. In this work, using a more extensive set over ∼13 yr, the significance is marginally higher. The highest correlation occurs at a time lag of ∼90 days (meaning the radio lags behind the gamma rays), but the uncertainty is large and the lag is not precisely constrained. Future long-term monitoring is needed to confirm the existence of a correlation and to obtain a better constraint on the time lag that is needed to narrow down the underling physical process. A positive correlation with the radio lagging behind the gamma rays is relatively common in BL Lacs (Max-Moerbeck et al. 2014a). One plausible explanation is the evolution of the electron population, which first emits the gamma-ray flux and then cools down to lower energies to radiate radio photons. The cooling time thus drives the radio/gamma-ray lag, which can reach monthly timescales (see, e.g. Hovatta et al. 2015). In an alternative scenario, the lag is explained by an evolution of the optical transparency throughout the jet. The gamma-ray emitting zone starts opaque at radio frequencies (because of synchrotron self-absorption), and due to (for example) adiabatic expansion (for detailed modelling, see Tramacere et al. 2022), gradually becomes transparent to the radio. In the framework of our modelling for the low state presented above, the former scenario is favoured. The high 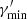 in the variable region (∼103) implies that the emission in the 15 GHz band is essentially negligible compared to the core region and, thus, the radio opacity does not play a role.
in the variable region (∼103) implies that the emission in the 15 GHz band is essentially negligible compared to the core region and, thus, the radio opacity does not play a role.
6.3. Time-dependent modelling of the 2019 flaring activity
The VHE flare that occurred in August 2019 reveals complex emission patterns, as discussed in Sect. 3.3. The VHE flux shows a hint of correlated variability with the 2−10 keV flux, but not with the 0.3−2 keV emission, which is stable throughout the flare despite a decay of the VHE flux by a factor of ∼3.5 (see Fig. 4). The VHE flare appears orphan when one considers only the 0.3−2 keV energies. In the other bands, no outburst is measured in the UV, optical, and radio. However, the Fermi-LAT measurements unveil an approximately daily timescale flare in the 0.3−300 GeV band coinciding with the VHE. Below, we argue that such multi-wavelength variability features are at odds with a one-zone SSC scenario, and two emitting components (at least) must be invoked to describe the multi-wavelength behaviour in a leptonic approach.
First, the absence of significant variability in the 0.3−2 keV regime naturally points towards a corresponding emitting region different than the one responsible for the gamma-ray flare. The indication of variability in the 2−10 keV band (by a factor ∼2) may be reconciled by considering that the flaring region remains subdominant in the soft X-ray (0.3−2 keV), but brings a sizable contribution to the 2−10 keV flux. In principle, changes affecting only the highest energy part of the electron distribution could induce a variability of the synchrotron flux in the 2−10 keV band but not in the 0.3−2 keV band. However, this scenario would have issues for explaining a Fermi-LAT flare (that we report here) given that the electrons radiating MeV–GeV photons (via IC scattering) emit synchrotron photons at much lower energies than ∼1 keV. Katarzyński et al. (2005) investigated the VHE versus X-ray correlation behaviour in (TeV-emitting) BL Lac type objects using a one-zone SSC model. By evolving different physical parameters driving the flux variability, the authors came to the conclusion that the VHE/X-ray correlation is mostly linear or quadratic. Although the exact correlated behaviour is parameter-dependent and sensitive to the precise energy ranges under consideration, any correlation above a quadratic relationship, as we clearly see here between the > 300 GeV and 0.3−2 keV emission, demands either an unphysical scenario or a strong fine-tuning of the parameters. Finally, the evidence of a Fermi-LAT flare but not in the UV/optical also points towards (at least) two emitting regions since those SED regions are expected to originate from the same electron population within typical one-zone SSC models applied to TeV BL Lacs (Tavecchio et al. 1998). In summary, within a leptonic scenario, it is highly improbable that the SED from optical/UV to > 1 TeV is dominated by a single component during the flare.
Following the above arguments, we attempt to describe the flare using a time-dependent leptonic model involving several emitting components. We carry out the modelling over the three-days time span during which we gathered simultaneous MAGIC and Swift data (August 6–8, 2019 – MJD 58701, MJD 58702, and MJD 58703). We consider a “quiescent” component describing the emission state before the flare state and a “flaring” component responsible for the gamma-ray flare. The quiescent component is assumed to be in a steady state, while the flaring component is evolving with time. The JetSeT modelling code is used to evolve the electron distribution in time. In our scenario, the two components are not cospatial, and thus not interacting with each other.
In order to limit the degrees of freedom in the model, the radius R′ and the Doppler factor δ of the quiescent component are fixed to the values adopted in Sect. 5 (i.e. R′ = 2 × 1016 cm and δ = 10). As for the electron distribution, a simple power-law model (without break) is used, 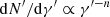 with
with 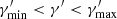 . No XMM-Newton or NuSTAR data are available over this time period to precisely constrain the SED below and above the synchrotron peak, which would be needed to constrain a possible break in dN′/dγ′. The total electron energy density is given as
. No XMM-Newton or NuSTAR data are available over this time period to precisely constrain the SED below and above the synchrotron peak, which would be needed to constrain a possible break in dN′/dγ′. The total electron energy density is given as 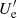 .
.
In the flaring component a power-law distribution of electrons is instantaneously injected at t0 = MJD 58701 with a slope of 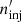 and with Lorentz factors between
and with Lorentz factors between 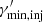 and
and 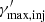 . The initial energy density is
. The initial energy density is 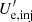 . The electrons subsequently cool, leading to the decay of the flux as observed in the data. We take into account synchrotron, IC, and adiabatic cooling mechanisms. Following Tramacere et al. (2022), the adiabatic expansion of the flaring component occurs at a constant velocity
. The electrons subsequently cool, leading to the decay of the flux as observed in the data. We take into account synchrotron, IC, and adiabatic cooling mechanisms. Following Tramacere et al. (2022), the adiabatic expansion of the flaring component occurs at a constant velocity 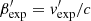 such that the adiabatic cooling timescale becomes
such that the adiabatic cooling timescale becomes 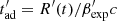 . We define
. We define 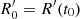 as the initial radius of the flaring component. Owing to energy conservation (Begelman et al. 1984), the magnetic field depends on R′(t) as
as the initial radius of the flaring component. Owing to energy conservation (Begelman et al. 1984), the magnetic field depends on R′(t) as 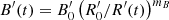 , where
, where 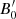 is the initial magnetic field strength. We fix here mB = 1, implying a fully toroidal configuration of the magnetic field (Begelman et al. 1984). This assumption is in agreement with the results of Tramacere et al. (2022), who performed a long-term time-dependent modelling of TeV HBL objects. We assume a value of δ = 20 for the Doppler factor, twice the one of the quiescent component but still within the standard range of values found in modelling TeV BL Lac objects (Tavecchio et al. 2010).
is the initial magnetic field strength. We fix here mB = 1, implying a fully toroidal configuration of the magnetic field (Begelman et al. 1984). This assumption is in agreement with the results of Tramacere et al. (2022), who performed a long-term time-dependent modelling of TeV HBL objects. We assume a value of δ = 20 for the Doppler factor, twice the one of the quiescent component but still within the standard range of values found in modelling TeV BL Lac objects (Tavecchio et al. 2010).
The adopted parameter values for the quiescent and flaring components are listed in Tables 6 and 7. The resulting model is plotted in Fig. 9. The emission from the flaring component is plotted in a dashed line for each day. The emission from the quiescent component is shown with a grey dotted-dash line. Finally, the contribution from the core region introduced in Sect. 5 is also added, using the same parameters as the one obtained in Sect. 5, Table 5. The sum of all components is given with continuous solid lines. We plot with different colours the daily simultaneous SEDs. Regarding Fermi-LAT, the SEDs are averaged over two days for August 6, and August 7, 2019. For August 8, 2019, a two-week integration period is adopted given the absence of significant signal over several days around that day.
 |
Fig. 9. Leptonic modelling of the August 2019 flare. The dash-dotted grey line is the emission from the quiescent component adopting the parameters listed in Table 6. The long dash line is the emission from the flaring component, using the parameters listed in Table 7. While the quiescent component is assumed to be constant over time, the flaring component evolves with time (see text for more details). The short dash blue line depicts the emission from the core component using the same parameters as the one obtained in Sect. 5, Table 5. The dotted black line is the host-galaxy contribution, using a template from the SWIRE database (Polletta et al. 2007). The solid lines are the sum of all components. Each day is plotted with a different colour, while the data from the respective instruments are displayed with distinct markers according to the legend. |
Model parameters of the quiescent component for the modelling of the August 2019 flare.
Model parameters of the flaring component for the modelling of the August 2019 flare.
In general, a relatively good description of the data is achieved from X-ray to TeV. All data points lie within ≲2σ from the modelling curves. The UV data (from Swift-UVOT) is explained by the emission from the core and quiescent component, in analogy to the modelling performed in Sect. 5.
Given the multi-wavelength coverage and temporal sampling, it is challenging to obtain a precise constraint on the adiabatic expansion velocity  . Nonetheless, it is interesting to remark that the adopted value,
. Nonetheless, it is interesting to remark that the adopted value, 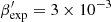 , is within the 1σ uncertainty band obtained by Tramacere et al. (2022), who modelled long-term light curves of the HBL Mrk 421 using a time-dependent SSC scenario. In our model, values significantly larger,
, is within the 1σ uncertainty band obtained by Tramacere et al. (2022), who modelled long-term light curves of the HBL Mrk 421 using a time-dependent SSC scenario. In our model, values significantly larger, 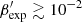 , are excluded as this leads to a decay of the overall IC flux that would be faster than the observed daily timescale variability. The adiabatic expansion gives rise to a drop of the IC flux that is particularly pronounced owing to a combination of the increasing electron volume and reduction of the target photon density.
, are excluded as this leads to a decay of the overall IC flux that would be faster than the observed daily timescale variability. The adiabatic expansion gives rise to a drop of the IC flux that is particularly pronounced owing to a combination of the increasing electron volume and reduction of the target photon density.
The flaring component is significantly Compton dominated. Relative to the quiescent zone, it remains subdominant in the X-ray up to ∼10 keV but it dominates in the gamma-ray regime, particularly during the first two days (August 6, and August 7, 2019). The corresponding Compton dominance, defined as AC = LIC, peak/Lsynch, peak, where LIC, peak is the luminosity at the IC peak and Lsynch, peak is the one at the synchrotron peak, is around AC ≈ 4 − 5 throughout the three days modelled here. Such a high AC is achieved by invoking an emitting region that is more compact and with a higher electron energy density than the quiescent zone. The strong Compton dominance leads to an important impact of the IC cooling effects (taken into account in our model), which is even the dominant timescale for electrons with Lorentz factors γ′≈105 − 106. Regarding the quiescent component, we have AC ≈ 0.5, typical of BL Lacs type objects in nonflaring states (Finke 2013).
The injected electron distribution in the flaring component is softer (ninj = 2.65) with respect to the one in the quiescent zone (n = 2.38). ninj is somewhat constrained by the Fermi-LAT observations since a harder injected spectrum (for instance, with ninj < 2.5) would start to underpredict the Fermi-LAT measurements. Those derived indices are somewhat larger than the canonical index of ∼2.23 expected in shock acceleration (Kirk et al. 2000). On the other hand, in the case of oblique shocks (as in a recollimation scenario, for instance), the index of the particle distribution may well be larger, > 2.5 (see Baring et al. 2016, and references therein). Interestingly, Zech & Lemoine (2021) showed that oblique shocks are able to reproduce the SED of EHBLs. Electron acceleration may also be caused in magnetic reconnection events (Sironi & Spitkovsky 2014), although the relatively low magnetisation of the flaring component in the model (B′≈10−2 G) tends to disfavour such an acceleration process.
7. Concluding remarks
This paper presents an extensive multi-wavelength characterisation of 1ES 2344+514 over a 3 yr period from radio to VHE. The source is known for its strong spectral variability in the X-ray band and shows intermittent EHBL characteristics. While being among the first extragalactic sources detected at VHE, and also among the closest BL Lac objects, the published multi-wavelength campaigns only focus either on flaring states or on small timescales (of a few months). We have organised a VHE monitoring by MAGIC, accompanied especially by simultaneous Swift, XMM-Newton, NuSTAR, and AstroSat observations, in order to obtain a systematic and detailed broad-band characterisation of the intermittent EHBL properties. The gathered observations also allowed to study with unprecedented accuracy the low-emission state.
Our results confirm the previously harder-when-brighter trend in the X-ray band, with a higher probability to find the source in an EHBL state during enhanced flux periods. Nonetheless, several nights also exhibit EHBL-like characteristics during low activity epochs, indicating strong shift of the synchrotron component independently from the source activity. These results likely imply significant changes of the electron acceleration efficiency, orphan from a significant change in the electron injection luminosity. We also observed an X-ray flaring event (one of the brightest for 1ES 2344+514) which is not characterised by an EHBL-like state, in clear contradiction with the harder-when-brighter trend. In turn, several flaring mechanisms must coexist, some being chromatic, others being achromatic.
During a hard but low X-ray emission state, we find that the UV flux is above the extrapolation to lower energies of the Swift-XRT data. This UV excess cannot be caused by a thermal component and must be of nonthermal origin. Likely, two separate electron populations (at least) significantly contribute to the synchrotron SED. Using a two-component leptonic model applied to the broad-band SEDs with simultaneous MAGIC, XMM-Newton, NuSTAR, and AstroSat observations, we propose that this UV excess could originate from the ∼10 GHz radio core.
We do not find significant (> 5σ) VHE versus X-ray correlation along the campaign. During a bright VHE flare in August 2019, the > 300 GeV flux shows a hint of correlation with the 2−10 keV band, while nothing is apparent in the 0.3−2 keV range. In fact, the 0.3−2 keV flux is constant despite a decay of the VHE flux by more than a factor 3. We argue that this behaviour is not in agreement with a single-zone leptonic scenario. Instead, using a time-dependent modelling approach, we investigate an alternative multi-zone model in which the flare is caused by a very compact emitting region that remains subdominant in the X-ray (in particular below ∼2 keV) but dominates the VHE emission. This scenario is in agreement with the flare properties, although it requires a flaring region heavily out of equipartition between the electron and magnetic energy densities.
For a given energy threshold, the Crab Nebula flux is defined as the integral flux of the Crab Nebula spectrum above the threshold energy. Throughout this work, we consider the Crab Nebula spectrum from Aleksić et al. (2016).
Acknowledgments
A. Arbet Engels: project leadership, paper drafting and editing, coordination of multi-wavelength observations and analysis, MAGIC and Fermi-LAT data analysis, variability analysis, theoretical modelling and interpretation; R. Chatterjee: AstroSat data analysis; F. D’Ammando: XMM-Newton and NuSTAR data analysis, paper drafting and editing; S. Das: AstroSat data analysis; D. Dorner: organisation of multi-wavelength observations; A. V. Filippenko: KAIT data analysis, paper editing; S. Fukami: paper editing, theoretical modelling and interpretation; T. Hovatta: OVRO data analysis; S. Kiehlmann: OVRO data analysis; C. Leto: Swift-UVOT data analysis; P. Majumdar: organisation of multi-wavelength observations; M. Manganaro: organisation of multi-wavelength observations; H. A. Mondal: paper drafting and editing, MAGIC and AstroSat data analysis, variability analysis; M. Perri: Swift-XRT data analysis; C. M. Raiteri: WEBT campaign management and data analysis, paper editing; A. C. S. Readhead: OVRO data analysis; F. Verrecchia: Swift-UVOT data analysis; M. Villata: WEBT campaign management and data analysis; W. Zheng: KAIT data acquisition and analysis. The rest of the authors have contributed in one or several of the following ways: design, construction, maintenance, and operation of the instrument(s); preparation and/or evaluation of the observation proposals; data acquisition, processing, calibration and/or reduction; production of analysis tools and/or related Monte Carlo simulations; discussion and approval of the contents of the draft. We would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF, MPG and HGF; the Italian INFN and INAF; the Swiss National Fund SNF; the grants PID2019-104114RB-C31, PID2019-104114RB-C32, PID2019-104114RB-C33, PID2019-105510GB-C31, PID2019-107847RB-C41, PID2019-107847RB-C42, PID2019-107847RB-C44, PID2019-107988GB-C22 funded by the Spanish MCIN/AEI/10.13039/501100011033; the Indian Department of Atomic Energy; the Japanese ICRR, the University of Tokyo, JSPS, and MEXT; the Bulgarian Ministry of Education and Science, National RI Roadmap Project DO1-400/18.12.2020 and the Academy of Finland grant #320045 are gratefully acknowledged. This work has also been supported by Centros de Excelencia “Severo Ochoa” y Unidades “María de Maeztu” programme of the Spanish MCIN/AEI/10.13039/501100011033 (SEV-2016-0588, CEX2019-000920-S, CEX2019-000918-M, CEX2021-001131-S, MDM-2015-0509-18-2) and by the CERCA institution of the Generalitat de Catalunya; by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project uniri-prirod-18-48; by the Deutsche Forschungsgemeinschaft (SFB1491 and SFB876); the Polish Ministry Of Education and Science grant #2021/WK/08; and by the Brazilian MCTIC, CNPq and FAPERJ. A.A.E. and D.P. acknowledge support from the Deutsche Forschungs gemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311 This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by the National Aeronautics and Space Administration (NASA). We thank the NuSTAR Operations, Software, and Calibration teams for support with the execution and analysis of these observations. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC; Italy) and the California Institute of Technology (USA). This research has also made use of the XRT Data Analysis Software (XRTDAS) developed under the responsibility of the ASI Science Data Center (ASDC), Italy. This work has used data from the Indian Space Science Data Centre (ISSDC) under the AstroSat mission of the Indian Space Research Organisation (ISRO). We acknowledge the POC teams of the SXT and LAXPC instruments for archiving data and providing the necessary software tools. S.D. and R.C. thank ISRO for support under the AstroSat archival data utilization programme, and IUCAA for their hospitality and usage of their facilities during their stay at different times as part of the university associateship programme. The Abastumani team acknowledges financial support by the Shota Rustaveli NSF of Georgia under contract FR-19-6174. The R-band photometric data from the University of Athens Observatory (UOAO) were obtained after utilising the robotic and remotely controlled instruments at the facilities (Gazeas 2016). The research at Boston University was supported in part by NASA Fermi GI grant 80NSSC22K1571 and US National Science Foundation (NSF) grant AST-2108622. This study was based (in part) on observations conducted using the 1.8 m Perkins Telescope Observatory (PTO) in Arizona (USA), which is owned and operated by Boston University. This research was partially supported by the Bulgarian National Science Fund of the Ministry of Education and Science under grants KP-06-H38/4 (2019), KP-06-KITAJ/2 (2020) and KP-06-H68/4 (2022). The Skinakas Observatory is a collaborative project of the University of Crete, the Foundation for Research and Technology – Hellas, and the Max-Planck-Institut für Extraterrestrische Physik. G.D., O.V., M.D.J., and M.S. acknowledge support by the Astronomical station Vidojevica, funding from the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (contract #451-03-47/2023-01/200002), by the EC through project BELISSIMA (call FP7-REGPOT-2010-5, #256772), the observing and financial grant support from the Institute of Astronomy and Rozhen NAO BAS through the bilateral SANU-BAN joint research project Gaia astrometry and fast variable astronomical objects, and support by the SANU project F-187. This paper used observations made with the IAC-80 telescope operated on the island of Tenerife by the Instituto de Astrofísica de Canarias in the Spanish Observatorio del Teide and also observations made with the LCOGT 0.4 m telescope network, one of whose nodes is located in the Spanish Observatorio del Teide. This research has made use of data from the OVRO 40 m monitoring programme (Richards et al. 2011), supported by private funding from the California Institute of Technology and the Max Planck Institute for Radio Astronomy, and by NASA grants NNX08AW31G, NNX11A043G, and NNX14AQ89G and NSF grants AST-0808050 and AST-1109911. S.K. acknowledges support from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme under grant agreement #771282. KAIT and its ongoing operation were made possible by donations from Sun Microsystems, Inc., the Hewlett-Packard Company, AutoScope Corporation, the Lick Observatory, the US NSF, the University of California, the Sylvia & Jim Katzman Foundation, and the TABASGO Foundation. Research at Lick Observatory is partially supported by a generous gift from Google. A.V.F.’s group at U.C. Berkeley is grateful for financial assistance from the Christopher R. Redlich Fund, Alan Eustace (W.Z. is a Eustace Specialist in Astronomy), and many other donors.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 738, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Ansoldi, S., Antonelli, L. A., et al. 2021, MNRAS, 504, 1427 [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017, Astropart. Phys., 94, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2018, A&A, 620, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ajello, M., Angioni, R., Axelsson, M., et al. 2020, ApJ, 892, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 662, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2013, A&A, 556, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015, A&A, 576, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [Google Scholar]
- Allen, C., Archambault, S., Archer, A., et al. 2017, MNRAS, 471, 2117 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Ballet, J., Burnett, T. H., Digel, S. W., & Lott, B. 2020, arXiv e-prints [arXiv:2005.11208] [Google Scholar]
- Baring, M. G., Böttcher, M., & Summerlin, E. J. 2016, MNRAS, 464, 4875 [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [Google Scholar]
- Biteau, J., Prandini, E., Costamante, L., et al. 2020, Nat. Astron., 4, 124 [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in Gamma Ray Bursts 2010, eds. J. E. McEnery, J. L. Racusin, & N. Gehrels, AIP Conf. Ser., 1358, 373 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [Google Scholar]
- Catanese, M., Akerlof, C. W., Badran, H. M., et al. 1998, ApJ, 501, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Cerruti, M., Zech, A., Boisson, C., & Inoue, S. 2015, MNRAS, 448, 910 [Google Scholar]
- Costamante, L., Ghisellini, G., Giommi, P., et al. 2001, A&A, 371, 512 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costamante, L., Bonnoli, G., Tavecchio, F., et al. 2018, MNRAS, 477, 4257 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [Google Scholar]
- Emmanoulopoulos, D., McHardy, I. M., & Papadakis, I. E. 2013, MNRAS, 433, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Li, W. D., Treffers, R. R., & Modjaz, M. 2001, in IAU Colloq. 183: Small Telescope Astronomy on Global Scales, eds. B. Paczynski, W. P. Chen, & C. Lemme, ASP Conf. Ser., 246, 121 [NASA ADS] [Google Scholar]
- Finke, J. D. 2013, ApJ, 763, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Foffano, L., Prandini, E., Franceschini, A., & Paiano, S. 2019, MNRAS, 486, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Berton, M., Caccianiga, A., et al. 2015, A&A, 575, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, L., Larsson, S., Chiang, J., et al. 2014, MNRAS, 441, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
- Ganeshalingam, M., Li, W., Filippenko, A. V., et al. 2010, ApJS, 190, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Gazeas, K. 2016, Rev. Mex. Astron. Astrofis. Conf. Ser., 48, 22 [NASA ADS] [Google Scholar]
- Giommi, P., Padovani, P., & Perlman, E. 2000, MNRAS, 317, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Petropoulou, M., Richards, J. L., et al. 2015, MNRAS, 448, 3121 [Google Scholar]
- Inoue, S., & Takahara, F. 1996, ApJ, 463, 555 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kardashev, N. S. 1962, Soviet Astron., 6, 317 [NASA ADS] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufmann, S., Wagner, S. J., Tibolla, O., & Hauser, M. 2011, A&A, 534, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ, 542, 235 [Google Scholar]
- Konigl, A. 1981, ApJ, 243, 700 [Google Scholar]
- Krawczynski, H., Hughes, S. B., Horan, D., et al. 2004, ApJ, 601, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1983, AJ, 88, 439 [Google Scholar]
- Landolt, A. U. 1990, PASP, 102, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Lindfors, E. J., Hovatta, T., Nilsson, K., et al. 2016, A&A, 593, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liodakis, I., Hovatta, T., Huppenkothen, D., et al. 2018a, ApJ, 866, 137 [Google Scholar]
- Liodakis, I., Romani, R. W., Filippenko, A. V., et al. 2018b, MNRAS, 480, 5517 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Homan, D. C., Kellermann, K. I., et al. 2021, ApJ, 923, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Beardmore, A. P., Forster, K., et al. 2017, AJ, 153, 2 [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2020a, MNRAS, 496, 3912 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2020b, A&A, 637, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2021, A&A, 655, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., Nesci, R., & Verrecchia, F. 2004a, A&A, 422, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004b, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [Google Scholar]
- Max-Moerbeck, W., Hovatta, T., Richards, J. L., et al. 2014a, MNRAS, 445, 428 [Google Scholar]
- Max-Moerbeck, W., Richards, J. L., Hovatta, T., et al. 2014b, MNRAS, 445, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., & Protheroe, R. J. 2001, Astropart. Phys., 15, 121 [Google Scholar]
- Nilsson, K., Lindfors, E., Takalo, L. O., et al. 2018, A&A, 620, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, P., & Giommi, P. 1995, ApJ, 444, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Stocke, J. T., Schachter, J. F., et al. 1996, ApJS, 104, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical Recipes in C++: The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Pushkarev, A. B., Kovalev, Y. Y., & Lister, M. L. 2010, ApJ, 722, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Kadler, M., et al. 2006, A&A, 452, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Carnerero, M. I., et al. 2014, MNRAS, 442, 629 [Google Scholar]
- Raiteri, C. M., Villata, M., Acosta-Pulido, J. A., et al. 2017, Nature, 552, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P. 2009, ApJ, 703, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [Google Scholar]
- Romero, G. E., Boettcher, M., Markoff, S., & Tavecchio, F. 2017, Space Sci. Rev., 207, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Singh, K. P., Stewart, G. C., Chandra, S., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, T. Takahashi, & M. Bautz, SPIE Conf. Ser., 9905, 99051E [Google Scholar]
- Singh, K. P., Stewart, G. C., Westergaard, N. J., et al. 2017, JApA, 38, 29 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [Google Scholar]
- Tavecchio, F., Ghisellini, G., Ghirlanda, G., Foschini, L., & Maraschi, L. 2010, MNRAS, 401, 1570 [Google Scholar]
- Timmer, J., & Koenig, M. 1995, A&A, 300, 707 [NASA ADS] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [Google Scholar]
- Tramacere, A. 2020, Astrophysics Source Code Library [record ascl:2009.001] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, E., & Taylor, A. M. 2011, ApJ, 739, 66 [Google Scholar]
- Tramacere, A., Sliusar, V., Walter, R., Jurysek, J., & Balbo, M. 2022, A&A, 658, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Villata, M., Raiteri, C. M., Aller, M. F., et al. 2007, A&A, 464, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Gurwell, M. A., et al. 2009, A&A, 504, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanin, R., Carmona, E., Sitarek, J., et al. 2013, Proceedings of the 33rd International Cosmic Ray Conference (ICRC2013), Rio de Janeiro, Brazil, July 2–9, 0773 [Google Scholar]
- Zech, A., & Lemoine, M. 2021, A&A, 654, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Fermi-LAT and OVRO long-term light curves
This section presents the long-term light curves from Fermi-LAT (0.3–300 GeV) and OVRO (15 GHz) between 2008 and the end of 2021. The Fermi-LAT fluxes are computed with a monthly binning. An upper limit at 95% confidence level is quoted in case the TS is below 5 (see Sect. 2). The light curves are shown in Fig. A.1. The grey vertical band highlights the period of time corresponding to the 2019–2021 multi-wavelength campaign, which is the focus of this work. Based on these light curves, the correlation between the gamma-ray and radio emission is investigated, and the results are displayed in Sect. 3.4.
 |
Fig. A.1. Long-term Fermi-LAT (0.3–300 GeV) and OVRO (15 GHz) light curves, from 2008 until the end of 2021. The Fermi-LAT fluxes are monthly binned. See Sect. 2 and Sect. 3 for more details about the analysis. |
Appendix B: Swift-XRT spectral fit parameters
This section presents the spectral parameters of all the Swift-XRT observations performed throughout the campaign, using power-law and log-parabola models. The models assume a photoelectric absorption by a fixed column density of NH = 1.41 × 1021 cm−2 (HI4PI Collaboration 2016). The results are listed in Table B.1.
Swift-XRT analysis results.
Appendix C: MAGIC spectra for epochs of interest
In this section, we show plots of the MAGIC best-fit spectra during the epochs of interest discussed in Sec. 4.2. As described Sec. 4.2, the data is fitted with a power-law model between 100 GeV and 2 TeV. The best fit parameters can be found in Table 4. We plot the spectra obtained during the VHE flare period in August 2019, during the soft X-ray flare & hard low X-ray state as well as during the deep exposures (on July 23, 2020 and August 6, 2021). They are shown in Fig. C.1, C.2 and C.3, respectively. For comparison purposes, we also show the average spectra from 2020 and 2021. For each fit the butterfly represents the 1-σ uncertainty band.
 |
Fig. C.1. Best-fit power-law models from MAGIC observations during the VHE flare period of August 2019. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
 |
Fig. C.2. Best-fit power-law models from MAGIC observations during the soft X-ray flare and the hard low X-ray state. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
 |
Fig. C.3. Best-fit power-law models from MAGIC observations during deep exposure 1 and deep exposure 2. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
Appendix D: Modelling of the quiescent activity using a LPPL function for the electron distribution
We also modelled the MAGIC, XMM-Newton, NuSTAR, and AstroSat simultaneous nights using a LPPL function (instead of a broken power-law function) to describe the electron distribution within the variable region. The LPPL function, originally introduced by Massaro et al. (2006), is defined in Eq. 6. The resulting parameter values are listed in Table D.1. We refer the reader to Sect. 5 for a detailed description of the respective parameters (as well as the procedure to constrain them).
Parameters of the two-components SSC models obtained for the MAGIC, XMM-Newton, NuSTAR, and AstroSat simultaneous observing nights using a LPPL function for the electron distribution in the variable region.
All Tables
Summary of the observing times of the VHE and X-ray instruments during the two long exposures in July 2020 and August 2021.
X-ray spectral parameters from XMM-Newton, NuSTAR, and AstroSat-SXT observations using a log-parabola model during the deep exposures with MAGIC.
MAGIC spectral parameters for epochs of interest obtained from a power-law fit (dN/dE = f0(E/E0)−ΓVHE) between 100 GeV and 2 TeV.
Parameters of the two-components SSC models obtained for the MAGIC, XMM-Newton, NuSTAR, and AstroSat simultaneous observing nights.
Model parameters of the quiescent component for the modelling of the August 2019 flare.
Model parameters of the flaring component for the modelling of the August 2019 flare.
Parameters of the two-components SSC models obtained for the MAGIC, XMM-Newton, NuSTAR, and AstroSat simultaneous observing nights using a LPPL function for the electron distribution in the variable region.
All Figures
 |
Fig. 1. Multi-wavelength light curves between December 23, 2018 (MJD 58475) and January 21, 2022 (MJD 59600). The vertical dashed blue line highlights the date of the VHE flare detected by MAGIC in August 2019. The orange and maroon dashed vertical lines highlight the dates of the deep exposure 1 (July 23, 2020 – MJD 59053) and deep exposure 2 (August 6, 2021 – MJD 59432) epochs that contain simultaneous long observations from MAGIC, XMM-Newton, NuSTAR, and AstroSat. The top panel shows the MAGIC fluxes above 300 GeV in daily (black markers) and yearly binning (pink markers). The horizontal dashed-grey line represents 4% of the Crab Nebula flux above 300 GeV. The second panel from the top reports the Fermi-LAT fluxes in the 0.3−300 GeV band in monthly binning. An upper limit at 95% confidence level is quoted for time bins with TS < 5. The maroon markers are fluxes in 2-day binning around the VHE flare. In the third panel from the top, the Swift-XRT fluxes are shown in the 0.3−2 keV (light-green markers) and 2−10 keV (dark-green markers) bands. The NuSTAR (cyan), XMM-Newton (pink), and AstroSat-SXT2022). The grey bands correspond to the three (light red) fluxes are shown in the 3−79 keV, 2−10 keV, and 0.7−7 keV bands, respectively. The fourth panel from the top displays the UV fluxes from the Swift-UVOT instrument in the UVW1, UVM2, and UVW2 filters. The fifth panel from the top reports the fluxes in the R band from GASP-WEBT, KAIT, and Tuorla. Finally, the bottom panel shows the OVRO fluxes measured at 15 GHz. |
| In the text | |
 |
Fig. 2. Multi-wavelength light curves around the VHE flare detected by MAGIC in August 2019. The top panel shows the MAGIC fluxes above 300 GeV in daily binning. The dashed curve is a fit of an exponential function using Eq. (1) in order to estimate the variability timescale (see text for more details). The horizontal dashed-grey line represents 4% of the Crab Nebula flux above 300 GeV. The second panel from the top displays the Fermi-LAT fluxes in the 0.3−300 GeV band in monthly binning (dark-yellow markers) and 2-day binning (maroon markers). In case the source is detected with TS < 5, an upper limit at 95% confidence level is quoted. In the third panel from the top are the Swift-XRT fluxes in the 0.3−2 keV (light-green markers) and 2−10 keV (dark-green markers) bands. The fourth panel from the top displays the UV fluxes from the Swift-UVOT instrument in the UVW1, UVM2, and UVW2 filters. Finally, the bottom panel shows the R-band fluxes from GASP-WEBT and Tuorla. |
| In the text | |
 |
Fig. 3. Fractional variability as a function of energy for the multi-wavelength light curves in Fig. 1. |
| In the text | |
 |
Fig. 4. VHE flux versus X-ray flux over the multi-wavelength campaign using MAGIC and Swift-XRT data. Fluxes are nightly binned. Only pairs of measurements within 4 h are considered. The blue measurements correspond to the flaring state in August 2019 and the arrows show the direction of time. The Pearson coefficients and DCF computed over the full data sample are shown in Table 2. |
| In the text | |
 |
Fig. 5. DCF between OVRO and Fermi-LAT versus the time lag. Positive lags mean that the OVRO fluxes lag behind the Fermi-LAT ones. The horizontal dashed lines represent the 2σ (light blue), 3σ (dark blue) and 4σ (magenta) confidence bands using Monte-Carlo simulations (see text). |
| In the text | |
 |
Fig. 6. X-ray power-law index versus flux over the multi-wavelength campaign using Swift-XRT data. Fluxes are nightly binned. The blue measurements correspond to the flaring state in August 2019 and the arrows show the direction of time. The green and violet markers correspond to the “soft flare” (October 5, 2019) and “hard low state” (September 20, 2020) periods. |
| In the text | |
 |
Fig. 7. Optical/UV and X-ray emission during specific states. The violet markers depict the Swift spectrum during a soft flare on October 5, 2019, during which the power-law index is above 2, indicating a synchrotron peak energy below 1 keV. The green markers display the Swift spectrum during a low but hard state on September 20, 2020. During the latter day, the source is in an EHBL state despite the particularly low flux. An extrapolation of the X-ray best-fit power-law model to lower energy (shown with a green dashed line) suggests a UV excess and possibly indicates a second component contributing to the synchrotron SED. The orange and maroon markers correspond to the deep exposure 1 and deep exposure 2 SEDs. The blue markers represent the Swift spectrum during the VHE flare on August 6, 2019. Grey points are archival measurements from the SSDC database for comparison purposes. The black dotted line is the host-galaxy template, also taken from the SWIRE database. |
| In the text | |
 |
Fig. 8. Broad-band SEDs during the simultaneous MAGIC, XMM-Newton, NuSTAR, and AstroSat observations. The panel on the left shows the SED from the deep exposure 1 epoch (July 23, 2020) while the panel on the right is during the deep exposure 2 epoch (August 6, 2021). The results of the 2-component SSC modelling is also shown: the dashed dark-blue line is the emission from the core region, while the violet dash-dotted line is the emission from the variable region (see text for more details). The sum of the two components is plotted in a continuous light-blue line. The parameter values of the model are listed in Table 5. The large bump in the optical domain (black dashed curve) is the emission from the host galaxy modelled with the template from the SWIRE database (Polletta et al. 2007). As in Fig. 7, grey points are archival measurements from the SSDC database. |
| In the text | |
 |
Fig. 9. Leptonic modelling of the August 2019 flare. The dash-dotted grey line is the emission from the quiescent component adopting the parameters listed in Table 6. The long dash line is the emission from the flaring component, using the parameters listed in Table 7. While the quiescent component is assumed to be constant over time, the flaring component evolves with time (see text for more details). The short dash blue line depicts the emission from the core component using the same parameters as the one obtained in Sect. 5, Table 5. The dotted black line is the host-galaxy contribution, using a template from the SWIRE database (Polletta et al. 2007). The solid lines are the sum of all components. Each day is plotted with a different colour, while the data from the respective instruments are displayed with distinct markers according to the legend. |
| In the text | |
 |
Fig. A.1. Long-term Fermi-LAT (0.3–300 GeV) and OVRO (15 GHz) light curves, from 2008 until the end of 2021. The Fermi-LAT fluxes are monthly binned. See Sect. 2 and Sect. 3 for more details about the analysis. |
| In the text | |
 |
Fig. C.1. Best-fit power-law models from MAGIC observations during the VHE flare period of August 2019. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
| In the text | |
 |
Fig. C.2. Best-fit power-law models from MAGIC observations during the soft X-ray flare and the hard low X-ray state. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
| In the text | |
 |
Fig. C.3. Best-fit power-law models from MAGIC observations during deep exposure 1 and deep exposure 2. For comparison purposes, the average spectra of 2020 and 2021 are also shown. More details on the analysis can be found in Sect. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.