| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347988 | |
| Published online | 11 April 2024 | |
First characterization of the emission behavior of Mrk 421 from radio to very high-energy gamma rays with simultaneous X-ray polarization measurements⋆
1
Japanese MAGIC Group: Institute for Cosmic Ray Research (ICRR), The University of Tokyo, Kashiwa, 277-8582 Chiba, Japan
2
ETH Zürich, 8093 Zürich, Switzerland
3
Instituto de Astrofísica de Canarias and Dpto. de Astrofísica, Universidad de La Laguna, 38200 La Laguna, Tenerife, Spain
4
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
5
National Institute for Astrophysics (INAF), 00136 Rome, Italy
6
Università di Udine and INFN Trieste, 33100 Udine, Italy
7
Max-Planck-Institut für Physik, 85748 Garching, Germany
8
Università di Padova and INFN, 35131 Padova, Italy
9
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology (BIST), 08193 Bellaterra (Barcelona), Spain
10
Croatian MAGIC Group: University of Zagreb, Faculty of Electrical Engineering and Computing (FER), 10000 Zagreb, Croatia
11
IPARCOS Institute and EMFTEL Department, Universidad Complutense de Madrid, 28040 Madrid, Spain
12
Centro Brasileiro de Pesquisas Físicas (CBPF), 22290-180 URCA Rio de Janeiro (RJ), Brazil
13
University of Lodz, Faculty of Physics and Applied Informatics, Department of Astrophysics, 90-236 Lodz, Poland
14
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, 28040 Madrid, Spain
15
Departament de Física, and CERES-IEEC, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
16
Università di Pisa and INFN Pisa, 56126 Pisa, Italy
17
Universitat de Barcelona, ICCUB, IEEC-UB, 08028 Barcelona, Spain
18
Department for Physics and Technology, University of Bergen, Norway
19
INFN MAGIC Group: INFN Sezione di Torino and Università degli Studi di Torino, 10125 Torino, Italy
20
INFN MAGIC Group: INFN Sezione di Catania and Dipartimento di Fisica e Astronomia, University of Catania, 95123 Catania, Italy
21
INFN MAGIC Group: INFN Sezione di Bari and Dipartimento Interateneo di Fisica dell’Università e del Politecnico di Bari, 70125 Bari, Italy
22
Croatian MAGIC Group: University of Rijeka, Faculty of Physics, 51000 Rijeka, Croatia
23
Technische Universität Dortmund, 44221 Dortmund, Germany
24
University of Geneva, Chemin d’Ecogia 16, 1290 Versoix, Switzerland
25
Japanese MAGIC Group: Physics Program, Graduate School of Advanced Science and Engineering, Hiroshima University, 739-8526 Hiroshima, Japan
26
Deutsches Elektronen-Synchrotron (DESY), 15738 Zeuthen, Germany
27
Armenian MAGIC Group: ICRANet-Armenia, 0019 Yerevan, Armenia
28
Croatian MAGIC Group: University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture (FESB), 21000 Split, Croatia
29
Universität Würzburg, 97074 Würzburg, Germany
30
Croatian MAGIC Group: Josip Juraj Strossmayer University of Osijek, Department of Physics, 31000 Osijek, Croatia
31
Finnish MAGIC Group: Finnish Centre for Astronomy with ESO, University of Turku, 20014 Turku, Finland
32
Japanese MAGIC Group: Department of Physics, Tokai University, Hiratsuka, 259-1292 Kanagawa, Japan
33
Università di Siena and INFN Pisa, 53100 Siena, Italy
34
Saha Institute of Nuclear Physics, A CI of Homi Bhabha National Institute, Kolkata, 700064 West Bengal, India
35
Inst. for Nucl. Research and Nucl. Energy, Bulgarian Academy of Sciences, 1784 Sofia, Bulgaria
36
Japanese MAGIC Group: Department of Physics, Yamagata University, Yamagata 990-8560, Japan
37
Finnish MAGIC Group: Space Physics and Astronomy Research Unit, University of Oulu, 90014 Oulu, Finland
38
Japanese MAGIC Group: Chiba University, ICEHAP, 263-8522 Chiba, Japan
39
Japanese MAGIC Group: Institute for Space-Earth Environmental Research and Kobayashi-Maskawa Institute for the Origin of Particles and the Universe, Nagoya University, 464-6801 Nagoya, Japan
40
Japanese MAGIC Group: Department of Physics, Kyoto University, 606-8502 Kyoto, Japan
41
INFN MAGIC Group: INFN Sezione di Perugia, 06123 Perugia, Italy
42
INFN MAGIC Group: INFN Roma Tor Vergata, 00133 Roma, Italy
43
Japanese MAGIC Group: Department of Physics, Konan University, Kobe, Hyogo 658-8501, Japan
44
Also at International Center for Relativistic Astrophysics (ICRA), Rome, Italy
45
Now at Institute for Astro- and Particle Physics, University of Innsbruck, 6020 Innsbruck, Austria
46
Also at Port d’Informació Científica (PIC), 08193 Bellaterra, (Barcelona), Spain
47
Also at Institute for Astro- and Particle Physics, University of Innsbruck, 6020 Innsbruck, Austria
48
Also at Department of Physics, University of Oslo, Norway
49
Also at Dipartimento di Fisica, Università di Trieste, 34127 Trieste, Italy
50
Max-Planck-Institut für Physik, 85748 Garching, Germany
51
Also at INAF, 35122 Padova, Italy
52
Japanese MAGIC Group: Institute for Cosmic Ray Research (ICRR), The University of Tokyo, Kashiwa, 277-8582 Chiba, Japan
53
INAF Istituto di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
54
Finnish Centre for Astronomy with ESO, 20014 University of Turku, Finland
55
Institute for Astrophysical Research, Boston University, 725 Commonwealth Avenue, Boston, MA 02215, USA
56
ASI – Agenzia Spaziale Italiana, Via del Politecnico snc, 00133 Roma, Italy
57
INAF Istituto di Astrofisica e Planetologia Spaziali, Via del Fosso del Cavaliere 100, 00133 Roma, Italy
58
Dipartimento di Fisica, Università degli Studi di Roma “La Sapienza”, Piazzale Aldo Moro 5, 00185 Roma, Italy
59
Dipartimento di Fisica, Università degli Studi di Roma “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Roma, Italy
60
Space Science Data Center, Agenzia Spaziale Italiana, Via del Politecnico snc, 00133 Roma, Italy
61
INAF Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone (RM), Italy
62
Quasar Science Resource S.L. for the European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
63
Foundation for Research and Technology – IESL Hellas, Greece
64
Institute of Astrophysics, Voutes, 7110 Heraklion, Greece
65
Department of Physics, University of Crete, 70013 Heraklion, Greece
66
Institute of Astrophysics, Foundation for Research and Technology-Hellas, 71110 Heraklion, Greece
67
Owens Valley Radio Observatory, California Institute of Technology, MC 249-17, Pasadena, CA 91125, USA
68
Department of Physics, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
69
Department of Physics, Graduate School of Advanced Science and Engineering, Hiroshima University Kagamiyama, 1-3-1 Higashi-Hiroshima, Hiroshima 739-8526, Japan
70
Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan
71
Core Research for Energetic Universe (Core-U), Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan
72
Planetary Exploration Research Center, Chiba Institute of Technology, 2-17-1 Tsudanuma, Narashino, Chiba 275-0016, Japan
73
Institut de Radioastronomie Millimétrique, Avenida Divina Pastora, 7, Local 20, 18012 Granada, Spain
74
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
75
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
76
Aalto University Department of Electronics and Nanoengineering, PO Box 15500 00076 Aalto, Finland
77
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
78
NASA Marshall Space Flight Center, Huntsville, AL 35812, USA
79
Also affiliated at Physik Department, Technische Universität München, James-Franck-Str. 1, 85748 Garching, Germany
Received:
15
September
2023
Accepted:
16
December
2023
Aims. We have performed the first broadband study of Mrk 421 from radio to TeV gamma rays with simultaneous measurements of the X-ray polarization from IXPE.
Methods. The data were collected as part of an extensive multiwavelength campaign carried out between May and June 2022 using MAGIC, Fermi-LAT, NuSTAR, XMM-Newton, Swift, and several optical and radio telescopes to complement IXPE data.
Results. During the IXPE exposures, the measured 0.2–1 TeV flux was close to the quiescent state and ranged from 25% to 50% of the Crab Nebula without intra-night variability. Throughout the campaign, the very high-energy (VHE) and X-ray emission are positively correlated at a 4σ significance level. The IXPE measurements reveal an X-ray polarization degree that is a factor of 2–5 higher than in the optical/radio bands; that implies an energy-stratified jet in which the VHE photons are emitted co-spatially with the X-rays, in the vicinity of a shock front. The June 2022 observations exhibit a rotation of the X-ray polarization angle. Despite no simultaneous VHE coverage being available during a large fraction of the swing, the Swift-XRT monitoring reveals an X-ray flux increase with a clear spectral hardening. This suggests that flares in high synchrotron peaked blazars can be accompanied by a polarization angle rotation, as observed in some flat spectrum radio quasars. Finally, during the polarization angle rotation, NuSTAR data reveal two contiguous spectral hysteresis loops in opposite directions (clockwise and counterclockwise), implying important changes in the particle acceleration efficiency on approximately hour timescales.
Key words: radiation mechanisms: non-thermal / galaxies: active / BL Lacertae objects: individual: mrk421 / gamma rays: general / X-rays: galaxies
All data shown in Figs. 1, 2, 5, 7, and 8 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A127
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
Blazars are a class of jetted active galactic nuclei (AGNs) where the relativistic plasma jet is oriented at a small angle to the line of sight from Earth. They emit across the full electromagnetic spectrum, from the radio to very high-energy (VHE) gamma rays (E > 100 GeV). Blazars with no or very faint emission lines in the optical band are referred to as BL Lac-type objects (Urry & Padovani 1995).
The spectral energy distribution (SED) of BL Lac-type objects is dominated by the nonthermal radiation emission from the jet. The SED shows two large components, one peaking from the radio to X-rays and a second component located in the gamma rays. It is widely accepted, based on spectral and polarization characteristics, that the first component originates from synchrotron radiation produced by relativistic electrons and/or positrons in the magnetic field within the jet. The exact origin of the second component is difficult to determine and still under debate. A possible scenario is electron inverse Compton (IC) scattering on synchrotron photons making up the first component, the synchrotron self-Compton (SSC) model (Maraschi et al. 1992; Madejski et al. 1999). In some cases, an additional target photon field for IC scattering is introduced to properly describe the SED of BL Lacs (e.g., Madejski et al. 1999; Böttcher et al. 2013). Scenarios involving hadronic particles also provide possible explanations for the gamma-ray emission (Mannheim 1993; Cerruti et al. 2015). A common approach for classifying BL Lac-type objects is by the peak frequency of their synchrotron component (Urry & Padovani 1995; Padovani et al. 2017). Following the nomenclature of Abdo et al. (2010a), blazars showing a synchrotron peak frequency νs < 1014 Hz are labeled low synchrotron peaked blazars (LSPs). Intermediate synchrotron peaked blazars (ISPs) show peak frequencies of 1014 Hz < νs < 1015 Hz. Blazars with νs > 1015 Hz are defined as high synchrotron peaked (HSPs).
Markarian 421 (Mrk 421; RA = 11h4′27.31″, Dec = 38°12′31.8″, J2000, z = 0.031) is an archetypal HSP and among the closest and most extensively studied extragalactic sources in the VHE sky (e.g., Horan et al. 2009; Baloković et al. 2016; Acciari et al. 2021). Nevertheless, the exact processes for the acceleration of high-energy particles and the resulting emission mechanisms in Mrk 421, and blazars generally, remain unclear. One promising approach for testing acceleration and emission scenarios in HSPs is to measure the linear polarization throughout the spectrum (Marscher & Gear 1985; Zhang & Böttcher 2013; Tavecchio 2021). Polarization measurements also provide important clues about the magnetic field ordering.
Prior blazar polarization measurements fell short of HSP synchrotron peak frequencies, extending only up to optical
frequencies. Optical polarization measurements are thus not sufficient to probe the most energetic electrons freshly accelerated inside the jet. Since December 9, 2021, the Imaging X-ray Polarimetry Explorer (IXPE) has been in orbit (Weisskopf 2022) and is able to perform measurements of the linear polarization of blazars between 2 and 8 keV. The first detection of X-ray polarization from the blazar Markarian 501 (Mrk 501) by IXPE was reported in Liodakis et al. (2022). A high degree of linear polarization, at the level of 10%, was detected without significant polarization variability. The X-ray polarization was in fact found to be significantly higher than in the optical and radio bands. These properties suggest a shock acceleration model with an energy-stratified electron population. IXPE observed Mrk 421 in May and June 2022. Part of the results were published in Di Gesu et al. (2022) and Di Gesu (2023). Similarly to Mrk 501, a high degree of linear polarization was detected in the X-ray compared to the optical and radio.
Since 2009, the blazar Mrk 421 has been the focus of a multiyear program consisting of dedicated half-year observations with a number of instruments covering the broadband emission from the radio to VHE gamma rays. The first publication of this extensive observation program was Abdo et al. (2011). Triggered by the planned observations of Mrk 421 by IXPE, the multi-instrument observations related to the extensive campaign on Mrk 421 were intensified during (as well as before and after) the times when IXPE observed Mrk 421. This intensified monitoring was particularly important for the Florian Goebel Major Atmospheric Gamma Imaging Cherenkov (MAGIC). In this work we present the first observations of a blazar in VHE gamma rays accompanied by simultaneous X-ray polarization measurements. We have coordinated observations from a great number of instruments, complementing the IXPE and VHE measurements with detailed coverage in X-rays by the Neil Gehrels Swift Observatory (Swift), the X-ray Multi-Mirror Mission (XMM-Newton), and the Nuclear Spectroscopic Telescope Array (NuSTAR). High-energy gamma-ray observations are provided by the Large Area Telescope (LAT) on board the Fermi Gamma-ray Space Telescope (Fermi-LAT).
This paper is structured as follows: in Sect. 2 we describe the observations and data analysis conducted with the different instruments. In Sect. 3 we provide a detailed characterization of the multiwavelength (MWL) emission during the IXPE observations, focusing on the spectral evolution, polarization features, and intra-night variability. In Sect. 4 we investigate the MWL behavior and correlations across the full campaign, spanning from May to June 2022. Finally, in Sect. 5 we summarize and discuss the experimental findings of this study.
2. Observations and data processing
2.1. MAGIC
The MAGIC telescopes consist of two 17-meter imaging atmospheric Cherenkov telescopes, MAGIC I and MAGIC II, located at the Observatorio del Roque de los Muchachos (ORM; 28.762°N 17.890°W, 2200 m above sea level) on the Canary Island of La Palma. Stereoscopic observations have been performed since 2009, enabling the detection of gamma rays with energies from about 30 GeV up to ≳100 TeV (Aleksić et al. 2016; MAGIC Collaboration 2020).
During the full time period covered by this work, we observed Mrk 421 for 20.2 h in total. The analysis is performed using the MAGIC Analysis and Reconstruction Software (MARS; Zanin et al. 2013; Aleksić et al. 2016), in the zenith angle range between 5° and 62°. After applying quality cuts to remove data taken at too high of a zenith angle and during adverse weather conditions, 17.3 h of data remained. The data were taken under low moonlight conditions, thus limiting contamination from night sky background light (Ahnen et al. 2017b). Thanks to the brightness and proximity of Mrk 421, two separate light curves can be obtained in the VHE regime covering an energy range from 0.2–1 TeV and above 1 TeV. The former light curve only contains data taken with a zenith angle of up to 50° due to the increasing energy threshold at larger zeniths (Aleksić et al. 2016), while the latter includes the entire zenith range.
The spectral analysis of the MAGIC data was performed by fitting the data with a log-parabolic model defined as follows:
The normalization constant is given by f0, α is the photon index at a normalization energy E0, and β is the curvature parameter. For the normalization energy, E0, a fixed value of 300 GeV was chosen. Flux points were obtained by performing the Tikhonov unfolding procedure as described in Albert et al. (2007). All obtained parameters and flux points were corrected for the extragalactic background light absorption following the model of Domínguez et al. (2011).
2.2. Fermi-LAT
The LAT instrument is a pair-conversion telescope on board the Fermi satellite (Atwood et al. 2009; Ackermann et al. 2012) surveying the gamma-ray sky in the 20 MeV to > 300 GeV energy range. For this work, we performed an unbinned-likelihood analysis using tools from the FERMITOOLS software1 v2.0.8. We used the instrument response function P8R3_SOURCE_V2 and the diffuse background models2 gll_iem_v07 and iso_P8R3_SOURCE_V3_v1.
We selected Source class events between 0.3 GeV and 300 GeV in a circular region of interest (ROI) with a radius of 20° around Mrk 421. The events with a zenith angle > 90° were discarded to limit the contribution from limb gamma rays. To build the source model, we included all sources from the fourth Fermi-LAT source catalog Data Release 2 (4FGL-DR2; Abdollahi et al. 2020; Ballet et al. 2020) that are found within the ROI plus an annulus of 5°. Mrk 421 was modeled with a simple power-law function. In order to build light curves, the source model was fitted to the data by letting free to vary the normalization and the spectral parameters of all sources within 7° of the target. Above 7°, all spectral parameters were fixed to the 4FGL-DR2 values. The normalizations of the diffuse background components were left as free parameters. When the fit did not converge, the model parameters were fixed to the 4FGL-DR2 values for sources detected with a test statistic (TS; Mattox et al. 1996) below 4. If after that the fit still did not converge, we gradually increased the TS threshold below which the model parameters are fixed, until convergence is achieved.
We produced a light curve in the 0.3–300 GeV3 band using 3-day time bins. In all time bins, the source is detected with TS > 25 (i.e., > 5σ). Finally, we computed a SED around each IXPE observation by averaging the data over 7 days. This time bin choice is a good compromise solution, given the flux variability observed in the light curves, and the limited sensitivity of LAT to measure gamma-ray spectra over short time intervals.
2.3. NuSTAR
This work comprises two multi-hour exposures from the Nuclear Spectroscopic Telescope Array (NuSTAR; Harrison et al. 2013), which consists of two co-aligned X-ray telescopes focusing on two independent focal plane modules, FPMA and FPMB. The instrument provides unprecedented sensitivity in the 3–79 keV band. The observations took place June 4-5, 2022 (MJD 59734 to MJD 59735) and June 7–8, 2022 (MJD 59737 to MJD 59738; observation ID 60702061002 and 60702061004, respectively), with a total exposure time of 21 ksec and 23 ksec, respectively. The raw data were processed using the NuSTAR Data Analysis Software (NuSTARDAS) package v.2.1.1 and CALDB version 20220912. The events were screened in the nupipeline process with the flags tentacle=yes and saamode=optimized in order to remove any potential background increase caused by the South Atlantic Anomaly passages. The source counts were obtained from a circular region centered around Mrk 421 with a radius of ≈140″. The background events were extracted from a source-free nearby circular region having the same radius. The spectra were then grouped with the grppha task to obtain at least 20 counts in each energy bin.
For both exposures, the source spectra dominate over the background up to roughly ≈30 keV. Hence, in this work we decided to quote fluxes only up to 30 keV, and in two separate energy bands: 3–7 keV and 7–30 keV. The best-fit spectral parameters averaged over the respective observations were obtained in the full NuSTAR bandpass, 3–79 keV. We fitted the spectra using XSPEC (Arnaud 1996) assuming a log-parabolic function with a normalization energy fixed to 1 keV. A simple power-law model provides a significantly worse description of the spectra (at a level > 5σ based on the χ2) and a curvature is detected during both observations. Here, and for the rest of the X-ray analysis performed in this work, a photoelectric absorption component was added to the model assuming an equivalent hydrogen column density fixed to NH = 1.34 × 1020 cm−2 (HI4PI Collaboration 2016). The fluxes and spectral parameters were computed by fitting simultaneously FPMA and FPMB. The cross-calibration factor between the two focal plane modules is for all bins within 0.95 and 1.05, thus well inside the expected systematics (Madsen et al. 2015).
2.4. Swift-XRT
We organized several X-ray pointings from the Swift X-ray Telescope (XRT; Burrows et al. 2005). A special effort was put to schedule the observations simultaneously to the MAGIC exposures. The Swift-XRT observations were performed in both Windowed Timing (WT) and Photon Counting (PC) readout modes. We processed the data using the XRTDAS software package (v.3.7.0) developed by the ASI Space Science Data Center4 (SSDC), released by the NASA High Energy Astrophysics Archive Research Center (HEASARC) in the HEASoft package (v.6.30.1). In order to calibrate and clean the events, data were reprocessed with the xrtpipeline script and using calibration files from Swift-XRT CALDB (version 20210915) within the xrtpipeline.
For each observation, the X-ray spectrum was extracted from the calibrated and cleaned event file. In both WT and PC modes, the events were selected within a circle of 20-pixel (∼47 arcsec) radius. The background was then extracted from a nearby, source-free, circular region with a 40-pixel radius. The ancillary response files (ARF) were generated with the xrtmkarf task applying corrections for point spread function losses and charge coupled device (CCD) defects using the cumulative exposure map.
The 0.3 − 10 keV source spectra were binned using the grppha task by requiring at least 20 counts per energy bin. We then used XSPEC using both a power-law and log-parabola models (with a pivot energy fixed at 1 keV). In the vast majority of the observations, the statistical preference for a log-parabola model is significant (> 5σ). The fluxes were extracted in the 0.3–2 keV, and 2–10 keV energy bands.
2.5. XMM-Newton
The XMM-Newton observatory carries on board several co-aligned X-ray instruments: the European Photon Imaging Camera (EPIC) and two reflection grating spectrometers (RGS1 and RGS2; Jansen et al. 2001). The EPIC cameras consist of two metal oxide semiconductors (EPIC-MOS1 and MOS2; Turner et al. 2001) and one pn junction (EPIC-pn, Strüder et al. 2001) CCD arrays operating in the 0.2–10 keV energy band. All XMM-Newton observations presented in this paper were taken with the EPIC camera under TIMING mode with the THICK filter. Data are available in the EPIC-pn and EPIC-MOS2 cameras. Observing times per observation range between ∼17 ksec and ∼47 ksec. Our sample was analyzed using the XMM-Newton standard Science Analysis System (SAS; v20.0.0; Gabriel et al. 2004) and most updated calibration files. Event lists were produced for the two EPIC cameras following the standard SAS reduction procedure. Periods of high-background activity were removed following the standard method (Lumb et al. 2002).
The source and background regions for the EPIC-pn and EPIC-MOS2 cameras were extracted following the same method as described in de la Calle Pérez et al. (2021). We extracted spectra in the full energy range (0.2–10 keV) with an energy resolution of 5 eV. The spectra were re-binned to avoid over sampling the intrinsic energy resolution of the EPIC cameras by a factor larger than 3, while making sure that each spectral channel contains at least 25 background-subtracted counts. Spectral fits were performed with the XSPEC package (Arnaud 1996) in the energy range 0.6–10 keV (a minimum fit energy of ≈0.6 keV is recommended by the official SAS documentation5 for TIMING mode observations to avoid low energy noise distorting the spectra). For every observation, we performed spectral fits and derived spectral parameters from the combined EPIC instruments available (i.e., EPIC-pn and EPIC-MOS2). All spectra were fitted using a log-parabola model (with a pivot energy set at 1 keV).
The most updated comparison of X-ray satellite observations shows that EPIC-pn data slightly differ from the NuSTAR and Swift data both in flux and slope (Madsen et al. 2017). The EPIC-pn fluxes are significantly lower than the NuSTAR fluxes, typically by the order of 20%. Although, based on the analysis performed so far, it is not possible to elucidate which instrument recovers the correct X-ray fluxes, the XMM-Newton Science Operation Center has proposed a correction to the XMM-Newton EPIC data that can be applied for observations performed simultaneously with NuSTAR. This correction has been applied to all the EPIC data that has simultaneous data with NuSTAR. The correction was applied in the ARF generation and can be done using the standard SAS task arfgen including the parameter applyabsfluxcorr=yes.6
2.6. IXPE
The IXPE telescope (Weisskopf 2022) is the first instrument capable of resolving the X-ray polarization degree and angle in blazars. Here, we exploited the first three IXPE observations of Mrk 421, which took place in the first half of 2022 and were accompanied by the simultaneous MAGIC monitoring. The first observation spanned from May 4, 2022 10:00 UTC (MJD 59703) until May 6, 2022 11:10 UTC (MJD 59705), for a total exposure of 97 ksec. The two additional observations took place in June 2022: from June 4, 2022 10:56 UTC until June 6, 2022 11:08 UTC (MJD 59734 to MJD 59736; 96 ksec exposure time), and from June 7, 2022 08:49 UTC until June 9, 2022 09:51 UTC (MJD 59737 to MJD 59739; 86 ksec exposure time). All results shown in this paper were taken from Di Gesu et al. (2022, May observation) and Di Gesu (2023, June observations). We refer the reader to these two works for details about the analysis procedure.
During the first IXPE observation, in May 2022, no variability of the polarization degree and angle is measured (Di Gesu et al. 2022), and the values averaged over the full exposure are considered. Regarding the two observations in June 2022, the polarization angle exhibits a large rotation (Di Gesu 2023) at a speed of 80 ± 9°/day (June 4–6, 2022; MJD 59734 to MJD 59736) and 91 ± 8°/day (June 7–9, 2022; MJD 59737 to MJD 59739). The rotation is evident when considering the data binned in 3 h intervals. Based on simulations, Di Gesu (2023) estimated that the probability of detecting these rotations due to random walks is about 2%, and thus, it is highly unlikely to have occurred by chance. As described in Di Gesu (2023), the polarization degree remains consistent with a constant behavior hypothesis.
2.7. Swift-UVOT
We obtained a coverage in the UV band from the Swift UV/Optical Telescope (UVOT; Roming et al. 2005). We considered observations between April 26, 2022 (MJD 59695) and June 27, 2022 (MJD 59757) with the W1, M2 and W2 filters. We selected a sample of 43 observations of Mrk 421 from the official data archive, by applying standard quality checks to all observations in the chosen time interval, excluding those with unstable attitude or affected by contamination from a nearby star light (51 UMa). For each observation, we performed photometry over the total exposures in each filter. The same apertures for source counts (the standard with 5 arcsec radius) and background estimation (mostly three-four circles of ∼16 arcsec radii off the source) were applied to all. We used the official software included in the HEASoft 6.23 package, from HEASARC, to perform the photometry extraction and then applied the official calibrations (Breeveld et al. 2011) included in the recent CALDB release (20201026). Finally, we de-reddened source fluxes according to a mean interstellar extinction curve (Fitzpatrick 1999) and the mean Galactic E(B − V) value of 0.0123 mag (Schlegel et al. 1998; Schlafly & Finkbeiner 2011).
2.8. Optical observations
In the optical, we exploited R-band photometric and polarimetric observations from the RoboPol (Skinakas Observatory, Greece; King et al. 2014; Ramaprakash et al. 2019), Nordic Optical Telescope (NOT; ORM, Spain), and KANATA (Higashi-Hiroshima observatory, Japan) telescopes. We also made use of H-band (infrared; IR) data from the Perkins telescope (Perkins Telescope Observatory, Flagstaff, AZ). All these data were published in Di Gesu et al. (2022) and Di Gesu (2023), where more details on the analysis procedures can be found. Additional polarimetric and photometric observations of the source in the Johnson Cousins R band were performed at Sierra Nevada Observatory, Granada, Spain, with a four-unit polarized filter-wheel mounted at the 0.9 m telescope (here after dubbed T90). Unpolarized standard stars were also observed to compute the instrumental polarization that was subtracted from the actual data. Standard pre-reduction and analysis steps were performed.
All the polarization and photometric data were corrected for the contribution of the host galaxy using the host fluxes reported in Nilsson et al. (2007). The intrinsic polarization degree was obtained using the following formula: Pdeg, intr = Pdeg, obs ⋅ I/(I − Ihost), where Pdeg, obs the observed polarization degree, I the observed flux and Ihost the host flux. Finally, the flux densities were also corrected for a galactic extinction of 0.033 mag according to the NASA/IPAC Extragalactic Database (NED).7
2.9. Radio observations
We collected data in the microwave band at 3.5 mm (86.24 GHz) and 1.3 mm (230 GHz) wavelengths with the 30 m telescope of the Institut de Radioastronomie Millimetrique (IRAM) that is located at the Pico Veleta Observatory (Sierra Nevada, Granada, Spain). The observations were performed within the Polarimetric Monitoring of AGN at Millimeter Wavelengths (POLAMI) program8 (Agudo et al. 2018a,b). The four Stokes parameters (I, Q, U, and V) were recorded simultaneously using the XPOL procedure (Thum et al. 2008). The data reduction and calibration was achieved following the POLAMI procedure described in Agudo et al. (2018a).
Additional radio observations were performed by the Metsähovi telescope. A detailed description of the data reduction and analysis can be found in Teraesranta et al. (1998). In short, observations at 37 GHz are conducted using the 13.7 m Metsähovi telescope. Under optimal conditions the detection limit of the telescope at 37 GHz is approximately 0.2 Jy. For the flux density, DR 21 is used as the primary calibrator, and NGC 7027, 3C 274, and 3C 84 are used as secondary calibrators. The flux density errors include the uncertainty in the absolute flux calibration as well as the root mean square of the measurement. We considered as detections only the observations with a signal-to-noise ratio greater than four.
Finally, we collected millimeter radio polarimetric measurements at 1.3 mm (approximately 230 GHz) with the Submillimeter Array (SMA; Ho et al. 2004). The observations were conducted within the SMA Monitoring of AGNs with POLarization (SMAPOL) program in full polarization mode using SMA polarimeter (Marrone & Rao 2008) and SWARM correlator (Primiani et al. 2016). The polarized intensity, position angle, and polarization percentage were derived from the Stokes I, Q, and U visibilities and calibrated with the MIR software package9 using MWC 349 A, Callisto (total flux calibrators), and 3C 286 (polarized calibrator).
3. Characterization of the VHE to radio behavior during IXPE observations
Figure 1 shows the MWL light curves from MJD 59695 (April 26, 2022) to MJD 59760 (June 30, 2022), which encompasses all IXPE observing periods. In the top row, the VHE energy bands (0.2–1 TeV and > 1 TeV) are shown. As previously mentioned, data observed at a zenith above 50° were excluded from the 0.2–1 TeV energy band, while for the > 1 TeV fluxes no cut on the zenith distance was applied. The cut on the zenith distance is necessary because the energy threshold increases to above 0.2 TeV for zenith angles greater than 50°, and hence we would introduce artificial downward fluctuations in the reported fluxes (e.g., by producing a light curve above 0.2 TeV when using data with an energy threshold well above this energy). In any case, this selection cut only removed a small fraction of the data from the 0.2–1 TeV light curve (it affects only three nights, removing a total of ≈2 h), and no intra-night variability was found in any of the two bands. Thus, the slightly different underlying data selection does not affect in any significant manner the hardness ratio. Measurements from Fermi-LAT in the 0.3–300 GeV band are portrayed in the second panel from the top. The Fermi-LAT fluxes are computed in 3-day bins, providing a good trade-off between flux uncertainty and temporal resolution. In X-rays, third panel, a dense temporal coverage is given by Swift-XRT in two energy bands (0.3–2 keV and 2–10 keV). On selected days during the IXPE observations, additional data by NuSTAR and XMM-Newton are available. We quantified the corresponding spectral evolution using the hardness ratio in X-rays, defined as the ratio of the 2 − 10 keV flux to the 0.3 − 2 keV flux, in the fourth panel. Additionally, the hardness ratio of the VHE data (defined as the ratio of the > 1 TeV flux to the 0.2 − 1 TeV flux) is shown. UV observations from Swift-UVOT in the W1, M2 and W2 filters are shown in the fifth panel from the top. We complement the MWL light curves with further data in the optical/IR and radio, which are plotted in the sixth and seventh panel, respectively. The last two panels at the bottom of Fig. 1 display the evolution of the polarization degree and polarization angle in the radio, optical, IR and X-ray.
 |
Fig. 1. MWL light curve for Mrk 421 covering the whole campaign from MJD 59695 (April 26, 2022) to MJD 59757 (June 27, 2022). The gray bands correspond to the three IXPE observations. Top to bottom: MAGIC fluxes in daily bins for two energy bands (note the two different y-axes); Fermi-LAT fluxes in 3 day bins; X-ray fluxes in daily bins including Swift-XRT, NuSTAR and IXPE; hardness ratio between the high- and low-energy fluxes of Swift-XRT and between the two VHE bands of MAGIC (note the two different y-axes); optical R-band data from NOT, RoboPol KANATA; IR H-band data from Perkins; radio data from IRAM and polarization degree and polarization angle observations in the optical to radio from NOT, RoboPol, KANATA, Perkins, IRAM, SMA and in X-rays from IXPE. |
3.1. IXPE observation in May 2022
The first observation of Mrk 421 by IXPE occurred between May 4 and May 6, 2022 (MJD 59703.42–MJD 59705.47) and is shown as the first gray band in Fig. 1. Here and in the following, this epoch will be referred to as IXPE 1.
The MAGIC telescopes achieved a continuous daily coverage over the entire IXPE exposure. In both VHE energy bands, the flux exhibits a constant behavior throughout the specified time period, showing a flux slightly below 10% of the emission of the Crab Nebula10 in the range above 1 TeV, and around 25% for the 0.2–1 TeV range. We do not find significant flux or spectral variability on daily and sub-daily timescales. A simultaneous X-ray characterization is obtained thanks to Swift-XRT as well as a long exposure from XMM-Newton on MJD 59704 (May 5, 2022). The flux in both energy bands of the Swift-XRT instrument exhibits moderate daily variability. In the 0.3–2 keV band, a flux increase at the level of 20% is observed, while it is 40% in the 2–10 keV band. The hardness ratio rises from 0.23 ± 0.01 up to almost 0.35 ± 0.01, indicating a harder-when-brighter trend in agreement with previous observations of Mrk 421 (see for instance Aleksić et al. 2015a; Acciari et al. 2021; MAGIC Collaboration 2021). Regarding the multi-hour XMM-Newton pointing, the average 2–10 keV flux (pink marker in Fig. 1) is consistent with Swift-XRT results. During the observation, little variability is observed. A 500 s binned XMM-Newton light curve is shown in Fig. A.1. The concurrent optical/IR (R band and H band) and radio flux data in Fig. 1 around IXPE 1 show small variability although the limited temporal coverage prevents a detailed variability characterization.
The degree of polarization from radio to optical shows slightly fluctuating values around 3%. The results of the IXPE observation (taken from Di Gesu et al. 2022) show a much higher constant degree of polarization of 15 ± 2 % in the X-ray band. The polarization angle determined by IXPE is 215 ± 4° (or 35 ± 4°, if one considers the 180° ambiguity in polarization angle measurements) and is in agreement with the angles measured in radio to optical, which range from around 200° up to 230° and also remains constant throughout the observation period.
3.2. IXPE observation in June 2022
The second and third IXPE observations of Mrk 421 were performed between June 4 and 6, 2022 (MJD 59734.46–MJD 59736.46) and between June 7 and 9, 2022 (MJD 59737.36–MJD 59739.41). In the following, these two observing epochs are dubbed IXPE 2 and IXPE 3, respectively. They are highlighted with vertical gray bands in Fig. 1.
MAGIC could only observe during the first day of the IXPE 2 period as well as two days before, for a total of 3.3 h of observation. Over the course of three days, the flux in the 0.2–1 TeV band is close to ≈50% of the Crab Nebula and ≈20% above 1 TeV, indicating about twice as much flux as during IXPE 1.
In X-rays, a significantly higher activity is also observed throughout the entire IXPE 2 and IXPE 3 windows with respect to IXPE 1, and the source exhibits clear spectral and flux variability. Between the IXPE 2 epoch and the start of the IXPE 3 epoch, the 2–10 keV flux shows a steady increase by a factor of ≈2.6, together with a clear hardening of the emission that is highlighted by the hardness ratio evolution (a more detailed spectral analysis is presented in Sect. 3.3). The peak activity in the 2–10 keV band is about five times the average flux level observed during IXPE 1. Although this flux state is still below previous X-ray outbursts of Mrk 421 (see for instance the March 2010 flare reported in Aleksić et al. 2015b), this activity is among the highest states recorded during 2022. The flux then decreases during the last Swift-XRT observation simultaneous to IXPE 3. The XMM-Newton analysis confirms the higher X-ray activity compared to IXPE 1. The observation took place at the beginning of the IXPE 2 epoch, slightly before the clear flux increase witnessed by Swift-XRT. In addition to Swift-XRT and XMM-Newton, a precise hard X-ray characterization was obtained thanks to two multi-hour NuSTAR exposures during both IXPE 2 and IXPE 3. In the third panel from the top of Fig. 1, we show the NuSTAR fluxes in the 3–7 keV and 7–30 keV bands using 1 h time bins. For IXPE 2, the NuSTAR observation was simultaneous to MAGIC. The corresponding intra-night VHE versus X-ray correlation is investigated in Sect. 3.5. During both NuSTAR pointings, a moderate flux change is observed on hour timescales (at the level of 30%). Nonetheless, a detailed study unveils spectral hysteresis patterns. This analysis is presented in Sect. 3.6.
Regarding the MeV-GeV band, the Fermi-LAT analysis shows a similar flux state as during IXPE 1, and is close to the average activity for Mrk 421 (Abdo et al. 2011). For the UV, optical, IR, and radio emission, the emission does not reveal significant evolution with respect to IXPE 1 either.
The bottom panels of Fig. 1 show the evolution of the polarization degree and angle in the X-ray 2–8 keV band (pink markers; the data are taken from Di Gesu 2023). During IXPE 2 and IXPE 3, the averaged degree is 10 ± 1%. While the polarization degree is consistent with a constant behavior (see also Sect. 3.6), the polarization angle exhibits an evident rotation, which seems continuous between the two IXPE 2 and IXPE 3 epochs. During IXPE 2, the angle rotates at an average angular velocity of 80 ± 9°/day amounting to a total rotation of 120°. The rotation continued at a compatible rate of 91 ± 8°/day during IXPE 3, for a total rotation of 140°. The significant X-ray flux increase and spectral hardening measured by Swift-XRT is thus accompanied by a rotation of the polarization angle. In Sect. 3.6, we investigate the short timescale spectral variability in the hard X-rays during the polarization angle rotation using simultaneous NuSTAR data.
It is interesting to note that at lower frequencies, in the radio, IR and optical bands, neither the flux nor polarization properties show any prominent variability. The polarization degree in the optical and IR fluctuates around 5% while the radio polarization is slightly lower, around 2% both for the 86 GHz and 230 GHz bands.
3.3. Spectral evolution throughout the IXPE observing epochs
Figure 2 presents the simultaneous broadband SEDs during each of the IXPE periods from the IR up to VHE gamma rays. In comparison, the average state of Mrk 421 taken from Abdo et al. (2011) is plotted in light gray. Since the VHE flux level reported in Abdo et al. (2011) is close to the average state found by Whipple over a time span of 14 years (45% of the Crab Nebula flux, Acciari et al. 2014), we considered the broadband SED of Abdo et al. (2011) as an average activity state and used it as a reference for comparison. MAGIC VHE flux points from IXPE 1 were obtained by averaging all data within the corresponding IXPE exposures since we find no significant spectral no flux variability. Regarding IXPE 2, a single MAGIC observation is available and it took place at the beginning of the IXPE window, while IXPE 3 is lacking VHE coverage (see Fig. 1 and previous section). The Fermi-LAT SEDs were averaged over 7 days, centered around the IXPE windows. In X-rays, for IXPE 1, we show the Swift-XRT SED on MJD 59704.02 (May 5, 2022), which is close to the center of the IXPE window and simultaneous to the XMM-Newton observation. Regarding IXPE 2 and IXPE 3, we plot for each epoch the Swift-XRT SEDs that were first recorded within the IXPE windows. These SEDs are also accompanied by simultaneous XMM-Newton (for IXPE 2 only) and NuSTAR data (for both IXPE 2 and IXPE 3). We add Swift-XRT SEDs corresponding to the last pointing before the end of the IXPE windows in order to illustrate the daily timescale variability along the IXPE exposure. For the optical and IR data, we used measurements that are the closest in time to each of the X-ray observations.
 |
Fig. 2. Broadband SED around the three IXPE observations. Data from MAGIC were corrected for the extragalactic background light absorption using the model outlined in Domínguez et al. (2011). In plain colored markers, the Swift-XRT data correspond to the pointing that happened first within the IXPE windows. The Swift-XRT data in diamond markers with a face color in white are from the subsequent observation. For comparison, the SED of an average emission state of Mrk 421 from Abdo et al. (2011) is shown in light gray. |
Compared to the average state of Abdo et al. (2011), the IXPE 1 epoch (blue markers) displays a VHE and X-ray emission that is significantly lower. The X-ray SED is also softer, indicating a shift of the synchrotron peak toward lower frequencies. Based on a log-parabola fit in the SED space (νFν ∝ 10−b(log(ν/νp))2), we derived a peak frequency located at νp = (2.00 ± 0.07)×1016 Hz, while the state from Abdo et al. (2011) suggests νp ≈ 1017 Hz. Throughout the IXPE 2 and IXPE 3, Fig. 2 highlights clearly the spectral changes occurring during the polarization angle swing reported by IXPE. At the beginning of IXPE 2 (plain violet color markers), the emission is roughly comparable to the typical state at all frequencies. Compared to IXPE 1, the synchrotron peak frequency increases marginally to νp = (2.27 ± 0.09)×1016 Hz. The emission increases significantly during the subsequent X-ray SED, which shows a flux well above the typical state as well as an harder emission. The maximum observed brightness is reached at the start of IXPE 3 (green markers), which coincides with the second NuSTAR observation and shows an enhanced emission state throughout the full synchrotron peak accompanied by a significant shift of the synchrotron peak toward a higher frequency (νp = (7.6 ± 1.3)×1016 Hz). A decrease is then observed the following day (shown with a white marker).
Owing to the dependence of the peak frequencies on the adopted fitting function, we also determined the synchrotron peak frequency following the phenomenological description of Ghisellini et al. (2017). We obtained values of νp higher by a factor of 2–3 compared to the log-parabola fit. Since the peak is not well covered for IXPE 1 and IXPE 2, and rather flat for IXPE 3, these model-dependent differences are expected. The clear trend of a synchrotron peak shifting toward higher values for IXPE 3 is still present.
The obtained spectral parameters in X-rays and VHE gamma rays are listed in Table 1. As for Fig. 2, the MAGIC spectral fits are performed after averaging all nights within the IXPE windows. For all IXPE epochs, the MAGIC data show a preference for a log-parabola model (see Eq. (1)) over a simple power-law function. The preference is above 3σ for IXPE 1 and at the level of 2σ for IXPE 2. We do not observe significant variability of the curvature parameter β, which stays consistent with β = 0.50. Thus, throughout this work, the MAGIC spectra simultaneous to the IXPE observations were fitted using a log-parabola model using a fixed curvature β = 0.50. This choice removes any correlation between α and β (see Eq. (1)), providing a better assessment of the hardness evolution during the different epochs. The normalization energy was fixed to 300 GeV. The resulting best fit spectral indices of MAGIC are shown in the first primary row of Table 1.
Spectral parameters from the VHE and X-ray observations around the three IXPE observing epochs.
The Swift-XRT spectra show a significant preference for a log-parabola model over a power law. As in the MAGIC spectral study, the data were fitted using a log-parabola with fixed curvature in order to obtain a better characterization of the hardness evolution throughout the IXPE epochs. We used here β = 0.29, which is the average curvature over the campaign. The second primary row of Table 1 presents the best fit parameters for each exposure simultaneous to IXPE (the pivot energy of the log-parabola model is 1 keV).
Regarding XMM-Newton and NuSTAR, the spectral parameters are derived in the 0.6–10 keV and 3–79 keV bands, respectively. Similarly to the fits for MAGIC and Swift-XRT, we fixed the curvature in the log-parabola model to β = 0.2 for XMM-Newton and to β = 0.45 for NuSTAR. For both instruments, the pivot energy was set to 1 keV.
Overall, the spectral evolution is consistent with the typical harder-when-brighter trend found frequently in Mrk 421 (Acciari et al. 2021; MAGIC Collaboration 2021). At VHE, α during IXPE 2 is smaller compared to IXPE 1 (α = −2.30 ± 0.08 versus α = −2.64 ± 0.06 for IXPE 1), while the emitted flux doubled. A similar behavior is found in X-rays with Swift-XRT, XMM-Newton and NuSTAR data and confirmed by the visual trend in Fig. 2. The spectral hardening is particularly evident between IXPE 2 and IXPE 3 when the X-ray polarization angle rotates. Both in Swift-XRT and NuSTAR the spectral parameter α hardens by ≈0.3 − 0.4 (see Table 1).
Most of the spectral variability in X-rays occurs on an approximately daily timescale. The shorter timescales variability can be probed thanks to the multi-hour exposures from XMM-Newton and NuSTAR. Figures A.1 and A.2 show the 0.3–2 keV the 2–10 keV fluxes (binned in 500 s) as well as the hardness ratio obtained during the observations of XMM-Newton. The ratios do not reveal any prominent spectral evolution over approximately hour timescales for either day. The NuSTAR analysis, however, reveals a moderate spectral change on approximately hour timescales, although spectral hysteresis behavior is apparent. A more detailed analysis is presented in Sect. 3.6.
3.4. Broadband evolution of the polarization degree between the IXPE epochs
Figure 3 summarizes the polarization degree as a function of the frequency for all IXPE observing epochs. The bottom panel shows the ratio to the X-ray polarization degree. For the optical and IR, we performed a weighted average of the measurements within the IXPE observing windows. In the radio, we considered all measurements within the IXPE windows as well as those that took place less than half a day before the start or after the end of the IXPE observing times (i.e., all radio observations within MJD 59702.96 to MJD 59706.04, MJD 59733.99 to MJD 59736.94 and MJD 59736.90 to MJD 59739.88; May 3–7, 2022, June 3–6, 2022, and June 6–9, 2022). This more relaxed simultaneity criteria allows one to include radio measurements for IXPE 2 and IXPE 3 epochs, which do not contain strictly simultaneous radio polarimetry coverage. We note that the variability of the radio polarization throughout this campaign is anyhow low and happens on timescales longer than 1 day. Figure 3 highlights the energy dependence of the polarization degree, with an evident increase in the X-ray band, as already reported by Di Gesu et al. (2022) and Liodakis et al. (2022), both in Mrk 421 and Mrk 501.
 |
Fig. 3. Frequency dependency of the polarization degree. Top: MWL polarization degree as a function of frequency during all three IXPE epochs. Bottom: ratio of the frequency-dependent polarization degree to the corresponding X-ray polarization degree. |
All epochs share the common characteristics of a significantly higher polarization in X-rays compared to lower frequencies. This highlights the value of combining X-ray, optical and radio polarization data. We do not find any significant correlation of the polarization degree with the flux or spectral hardness in the individual energy bands. On the other hand, the ratio between the optical and IR polarization degree and the one in the X-ray band is significantly lower during IXPE 1 than during IXPE 2 and IXPE 3 (bottom panel of Fig. 3).
It is interesting to compare the broadband behavior of the polarization degree with the one of the fractional variability (Fvar; Vaughan et al. 2003). We computed Fvar using all observations inside the IXPE windows, using the prescription of Poutanen et al. (2008) to estimate the corresponding uncertainties. The results are presented in Fig. 4. As for Fig. 3, we considered in the radio a slightly relaxed simultaneity criteria and also included measurements that took place less than half a day before the start or after the end of the IXPE observing times to compute Fvar. The Fvar in the radio can only be computed with data from IRAM in the 86.24 GHz band since it is the only one that has more than one measurement (that is the minimum requirement for a computation of Fvar). In X-rays, we used Swift-XRT fluxes binned observation-wise in the 0.3–2 keV and 2–10 keV ranges. We complemented them with those from the XMM-Newton (0.3–2 keV and 2–10 keV) and NuSTAR (3–7 keV and 7–30 keV) long exposures. In these two cases, the results are plotted in gray markers to differentiate between them. Indeed, neither of the two instruments have simultaneous data for all IXPE epochs (unlike Swift-XRT), and given the generally stronger variability at those energies, this different temporal coverage biases the results and explains the discrepancy relative to the Swift-XRT Fvar.
 |
Fig. 4. Fractional variability (Fvar) as a function of the frequency during the IXPE epochs. Fvar is computed using all data from Fig. 1 that are within the IXPE time windows. In the radio, we consider slightly relaxed simultaneity criteria and also include measurements that took place less than half a day before the start or after the end of the IXPE observing times (see the main text for more details). Radio, optical, IR, and Swift data are daily binned. We include the Fvar from the NuSTAR and XMM-Newton multi-hour exposures using ≈30 min binning. These measurements are plotted in the gray since the two instruments did not gather data for all IXPE epochs, which biases the comparison with other wavebands. |
Similarly to the polarization degree, Fvar shows a significant increase in X-rays, while the optical and radio band are compatible within 1σ. This trend, previously reported in Mrk 421 and other HSPs (Aleksić et al. 2015a; Patel et al. 2018), potentially suggests an underlying physical origin common to the one explaining the broadband behavior of the polarization degree. A discussion on this aspect is given in Sect. 5.
3.5. Intra-night MAGIC and NuSTAR light curves during IXPE 2
During the night of June 5-6, 2022 (MJD 59734 to MJD 59735), MAGIC observations took place strictly simultaneously with NuSTAR. The light curves obtained are shown in Fig. 5. The data were divided into bins of around 30 min. Due to the otherwise limited exposure time by NuSTAR, the first bin was extended to ≈40 min. The upper panel shows the MAGIC fluxes, with an energy threshold of 400 GeV. This minimum energy is slightly higher than in Fig. 1 since some of the time bins contain observations taken under a zenith distance of up to 60°, which increases the energy threshold of the MAGIC stereo system. The NuSTAR fluxes were extracted in the 3–7 keV and 7–30 keV bands.
 |
Fig. 5. MAGIC and NuSTAR intra-night light curve between June 4, 2022 (MJD 59734) and June 5, 2022 (MJD 59735), corresponding to the IXPE 2 epoch. Upper panel: Light curve above 400 GeV obtained with MAGIC. A constant model fit is showed in dashed gray with the corresponding reduced χ2. Lower panel: Light curves for the 3–7 keV and the 7–30 keV band taken by NuSTAR, and constant fits for both. Fluxes from both instruments are computed in ≈30 min time bins, except for the first bin that is ≈40 min long due to a limited exposure of NuSTAR around at the start of the MAGIC observation. |
No significant intra-night variability can be claimed for the MAGIC observations. On the other hand, NuSTAR detects significant variability in both energy bands. By fitting the data with a constant model, the hypothesis of a non-variable emission is rejected at a significance above 5σ for the 3–7 keV band and above 3σ for the 7–30 keV band.
The flux measured by MAGIC is plotted against the flux of both NuSTAR energy bands in Fig. 6. The correlation coefficient between each pair of energy bands is given by the Pearson’s r coefficient. For the correlation between the 3–7 keV and > 400 GeV flux a coefficient of r = 0.74, and between 7–30 keV and > 400 GeV of r = 0.66 is found. Both cases suggest a light positive correlation. In order to evaluate the significance of the correlation, we used Monte Carlo simulated light curves. Each simulated flux point was produced by assuming a Gaussian distribution by taking the flux values of the actual data as a mean of the distribution and the uncertainty on the flux as the corresponding standard deviation. New light curves were then drawn and additionally the temporal information was shuffled in order to obtain pairs of “realistic” uncorrelated light curves. We simulated 106 pairs of light curves and derived p-values of the correlation coefficient r of the data based on the distribution of the r coefficients given by the simulations. We find a p-value of 0.068 (equivalent to ≈1.8σ) between the 3–7 keV and > 400 GeV bands and a p-value of 0.102 (equivalent to ≈1.6σ) for 7–30 keV and > 400 GeV. Due to the relatively large statistical uncertainties in the VHE light curve, no significant correlation can be claimed and only an indication of correlation at best can be proposed.
 |
Fig. 6. MAGIC flux versus NuSTAR flux and quantification of the correlation during the IXPE 2 epoch. The MAGIC flux is computed above 400 GeV while the X-ray flux is evaluated in two different energy bands: 3–7 keV for the left panel and 7–30 keV for the right panel. In each panel, the obtained Pearson’s r coefficient is indicated. We specify below the p-value that describes the probability of obtaining the observed r coefficient for two uncorrelated light curves. This p-value was estimated based on Monte Carlo toy simulations (see the main text for more details). |
In Sect. 4 we extend the search for correlation over longer timescale by including data from the entire MWL campaign between April 2022 and June 2022.
3.6. Evidence of X-ray spectral hysteresis simultaneous to a polarization angle swing during IXPE 2 and IXPE 3
Using the multi-hour exposure of NuSTAR, we investigate in detail the X-ray spectral evolution during the period where a polarization angle swing is detected by IXPE in the X-rays (see Sect. 3.2 and Fig. 1). Figure 7 is a zoomed-in view of around the polarization angle swing, showing the NuSTAR measurements together with the polarization degree and angle in the radio, optical and IR. For IXPE, the polarization degree and angle were binned in ∼3 h.
 |
Fig. 7. Zoomed-in view of the NuSTAR light curves in the 3–7 keV and 7–30 keV bands during the IXPE 2 and IXPE 3 epochs. The top panel report the fluxes in 1 h bins. The second panel from the top is the α index evolution derived from fits of the NuSTAR spectra. The last two panels show the simultaneous polarization degree and polarization angle in the X-ray band (IXPE), optical and radio bands. |
The top panel shows the NuSTAR fluxes in the 3–7 keV and 7–30 keV bands, in 1 h time bins. Small variability is noted during the observation from June 5 to 6, 2022 (MJD 59734 to MJD 59735, simultaneous to IXPE 2), but more structured variability patterns can be seen during the observation simultaneous to IXPE 3, between June 8 and 9, 2022 (MJD 59737 to MJD 59738). In particular, the light curve displays two “humps” caused by two consecutive flux rise and decay phases, which thus reveal variability on ∼1 h timescale.
The NuSTAR spectra were fitted in the 3–30 keV band adopting a log-parabola model (pivot energy fixed at 1 keV). By fitting the spectra with a 1 h temporal binning, we find that the curvature parameter β shows little variability throughout the observations. The derived β values range from 0.27 to 0.57, but for each time bin they are within less than ≈2σ from the weighted average over the two observations, which yields βavg = 0.45. Consequently, we performed a second series of fits with a 1 h binning after fixing β = 0.45 to remove any correlation between α and β in order to obtain a more straightforward assessment of the spectral hardness evolution. We stress that fixing β = 0.45 does not significantly degrades the fit statistics (the beta-free spectral model is preferred at a significance below 2.5σ in each of the bins). The resulting index α as a function of time in 1 h bins is plotted in the second panel from the top in Fig. 7.
For the observation simultaneous to the IXPE 2 period (around MJD 59735 – June 5, 2022), we do not find strong spectral change. The index α varies by at most 5% around a value of ≈ − 2.35, during a quasi-monotonic flux decay of ≈30%. We do not detect any significant correlation between α and flux, nor any spectral hysteresis pattern.
Regarding the NuSTAR observations taken at the same time as the IXPE 3 period, a similar spectral variability amplitude is observed, although hysteresis patterns can be seen when α is reported as a function of the flux. Figure 8 shows the value of α versus the 3–7 keV and 7–30 keV fluxes in 1 h bins during IXPE 3. The gray arrows indicate the direction of time. During the first part of the observation, the data points (both in the 3–7 keV and 7–30 keV bands) display a spectral hysteresis in a clockwise direction (i.e., decay phase has softer spectrum than in the rising phase). On the other hand, the second part of the observations exhibits a spectral hysteresis in counterclockwise direction (i.e., decay phase has a harder spectrum than in the rising phase). Spectral hysteresis, in both the clockwise and counterclockwise direction, has been previously detected in Mrk 421 (Brinkmann et al. 2003; Ravasio et al. 2004). Nonetheless, it is the first time that two continuous clockwise and counterclockwise rotations are detected over an hour timescale. A more detailed discussion of these results is given in Sect. 5.
 |
Fig. 8. Log-parabola photon index, α, versus 3–7 keV and 7–30 keV flux as measured by NuSTAR during the third IXPE observation (IXPE 3 period). The data are 1 h binned and α is obtained by fitting a log-parabola function that has a fixed curvature parameter β = 0.45. The gray arrows show the direction of time, and the blue and red arrows in the middle of the panels depict the clockwise and counterclockwise directions observed in the data, respectively. |
As unveiled by the bottom panels of Fig. 7, no significant variability is observed in the polarization degree simultaneous to the NuSTAR hysteresis patterns. Based on a constant fit, the data are consistent with a stable X-ray polarization hypothesis within 3σ (both for IXPE 2 and IXPE 3 periods). Regarding the X-ray polarization angle, the large angular swing mentioned before happens at a constant speed of ∼80°/day despite the NuSTAR flux and variability patterns discussed above.
4. MWL evolution and correlation throughout the observing campaign
As commonly seen in HSPs such as Mrk 421, the flux (Fig. 1) displays the strongest variability in the X-ray and VHE regimes. A noticeable feature in the MAGIC light curves is an enhanced VHE state period between MJD 59719 (May 20, 2022) and MJD 59723 (May 24, 2022). A peak flux of ∼1.4 C.U. is measured on MJD 59722 (May 23, 2022) in both the 0.2–1 TeV and > 1 TeV bands (equivalent to ≈3 times the typical state). A simultaneous significant flux increase is noted in X-rays, as revealed by the Swift-XRT light curves (third panel from the top). This high state also coincides with a hardening of both the VHE and X-ray spectrum, as illustrated by the hardness ratio plotted in the fourth panel from the top. This behavior, already seen within the IXPE observing epochs in the earlier section, is consistent with the harder-when-brighter trend previously detected in Mrk 421 (Aleksić et al. 2015a; Acciari et al. 2021; MAGIC Collaboration 2021). At lower energies, no simultaneous outburst is detected in the UV and optical (seventh and eighth panel from the top). On the other hand, it is interesting to remark that a RoboPol measurement (R-band) simultaneous to the peak activity at VHE on MJD 59722 (May 23, 2022) shows a rotation of the polarization angle by about 60° compared to an observation conducted a few days earlier (∼MJD 59718 – May 19, 2022). Such a swing of the polarization angle of comparable amplitude and on similar timescales (i.e., an approximately daily timescale) was reported by Marscher & Jorstad (2021) in 2017, also for Mrk 421. The sparse sampling of the RoboPol light curve prevents, however, a strong claim on the association of the optical polarization angle rotation with the VHE and X-ray flare. Besides the enhanced state around MJD 59722 (May 23, 2022), the emission in the X-ray and VHE bands along the campaigns remains comparable to the quiescent activity. In fact, during previous outbursts, the VHE and X-ray fluxes were more than an order of magnitude higher than the average value from the campaign discussed in this work (Acciari et al. 2020; Abeysekara et al. 2020).
In the 0.3–300 GeV band, the Fermi-LAT light curve exhibits a flux variability by a factor of ∼3 around an average state of ∼8 × 10−8 cm−2 s−1, which is close to the typical flux level for Mrk 421 (Aleksić et al. 2015a). As for the spectral evolution, no significant variability of the Fermi-LAT power-law index is detected.
In the UV band, despite moderate variability, the Swift-UVOT fluxes display an interesting quasi-monotonic increase starting from MJD ∼59710 (May 11, 2022) to MJD ∼59760 (June 30, 2022). The highest UV state is registered on MJD 59753 (June 23, 2022), and slightly more than twice the minimum state is measured on MJD 59717 (May 18, 2022). The R-band measurements show a similar increasing trend over this period. Over the same period, the X-ray band shows an opposite evolution with an overall decay of the 0.3–2 keV and 2–10 keV fluxes. This behavior is accompanied by a simultaneous drop of the X-ray hardness ratio (see the fourth panel from the top in Fig. 1). Such a behavior points toward an anticorrelation between the X-ray and UV bands, possibly caused by a shift of the entire synchrotron component to lower frequencies. The quantification of the anticorrelation significance is performed in Sect. 4.2.
4.1. VHE–X-ray correlation over the entire campaign
In Sect. 3.5 we reported an indication of positive correlation between the MAGIC and NuSTAR fluxes during the IXPE 2 observations. The low significance (estimated around 2σ between the 3–7 keV and > 400 GeV bands) is partly due to the relatively large uncertainties on the VHE gamma-ray fluxes measured in these short timescales. In this section, we extend the VHE versus X-ray correlation study over the entire campaign by making use of the MAGIC and Swift-XRT measurements. We correlated the daily binned MAGIC fluxes (in the 0.2–1 TeV and > 1 TeV bands) with the Swift-XRT fluxes binned observation-wise (0.3–2 keV and 2–10 keV bands), and computed the discrete correlation coefficient (DCF; Edelson & Krolik 1988) in a series of 2-day binned time lags. The significance of the DCF was estimated based on Monte Carlo simulations. The simulations were performed in a similar fashioned to what is described in MAGIC Collaboration (2021). We summarize below the procedure.
The significance bands were obtained by first simulating a large number (104) of uncorrelated light curves for each of the energy bands considered. The light curves were simulated using the prescription from Emmanoulopoulos et al. (2013) in order to preserve the probability distribution function of the observed fluxes. Furthermore, the simulated light curves were produced by assuming a power spectral density (PSD) function that follows a power-law model. The slopes of the PSD models in X-rays were taken directly from MAGIC Collaboration (2021) and are −1.45 for the 0.3–2 keV band and −1.3 for the 2–10 keV band. These slopes (derived with Swift-XRT data in 2016-2017 that cover a longer time span than the one considered in this work) were found to be in agreement with the 2022 observations and thus represent a good proxy to estimate the significance. Regarding the simulations of VHE light curves, it was not possible to directly extract the PSD slope in a reliable manner using the MAGIC data of this work due to the relatively sparse sampling. We therefore adopted the PSD slope of −1.3 that was reported by (Aleksić et al. 2015a) using Whipple observations during a campaign organized in 2009. The fake light curves were generated with a temporal resolution matching the typical exposure time of the observations, and the same temporal sampling as the data was then applied to the simulations. Finally, we computed the DCF as a function of time lag for all pairs of simulated light curves. The 2σ, 3σ, and 4σ confidence bands were derived from the distribution of the simulated DCF values in each time-lag bin.
Figures 9 and 10 show the DCF obtained from MAGIC 0.2–1 TeV versus Swift-XRT 2–10 keV and MAGIC > 1 TeV versus Swift-XRT 2–10 keV, respectively. The dashed lines depict the 2σ (light blue), 3σ (dark blue), 4σ (magenta) confidence bands. A positive correlation can be seen at zero time lag with a significance of 4σ, further strengthening the reported in Sect. 3.5. As for the correlation of the MAGIC fluxes with the 0.3–2 keV band, the significance is somewhat lower, around 3σ. The results are shown in Figs. B.1 and B.2. This suggests that the 2–10 keV flux is more closely related to the VHE flux compared to the 0.3–2 keV band during this period of time.
 |
Fig. 9. DCF computed for the MAGIC 0.2 − 1 TeV and Swift-XRT 2–10 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue, and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
 |
Fig. 10. DCF computed for the MAGIC > 1 TeV and Swift-XRT 2–10 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue, and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
4.2. Investigation of the UV and optical versus X-ray anticorrelation
Figure 1 suggests an anticorrelation between the UV and X-ray fluxes between MJD 59710 (May 11, 2022) and MJD 59760 (June 30, 2022). We quantify this trend by computing the DCF between the Swift-XRT data (using both the 0.3–2 keV and 2–10 keV fluxes) and the Swift-UVOT W1 measurements. For simplicity, only the data in the Swift-UVOT W1 band were considered for this correlation study. In fact, the fluxes in the M2 and W2 Swift-UVOT filters give very similar results, which is expected given their proximity in frequency with W1. The resulting plots are shown in Figs. C.1 and C.2 for the 0.3–2 keV and 2–10 keV bands, respectively. The significance bands were obtained with the exact same method described in the previous section. The PSD slopes were taken from MAGIC Collaboration (2021): −1.45 for Swift-UVOT W1 and Swift-XRT 0.3–2 keV and −1.3 for Swift-XRT 2–10 keV. We find that the significance of the anticorrelation observed in the data is at the level of 2 − 3σ, and can only be considered marginal evidence. The significance is marginally higher in the Swift-UVOT W1 versus Swift-XRT 2–10 keV case than in the Swift-UVOT W1 versus Swift-XRT 0.3–2 keV case. The peak at a positive time lag of ∼16 days in both figures, can be considered an artifact resulting from the sampling and short overall time period.
We repeated the above exercise after including Swift data from the entire MWL campaign (i.e., from MJD 59695 to MJD 59760; April 26, 2022, to June 30, 2022). The results – shown in Figs. C.3 and C.4 – reveal a decrease in the significance below 2σ. The marginal evidence of anticorrelation is thus only observed over a 1.5-month period between MJD ∼59710 (May 1, 2022) and MJD ∼59760 (June 30, 2022).
This is the third time that an indication of anticorrelation between UV and X-ray fluxes is reported in Mrk 421. The first two hints were observed during MWL campaigns organized during 2009 (Aleksić et al. 2015a) and 2017 (MAGIC Collaboration 2021), and were also happening over an approximately monthly timescale. These repeating trends point toward some physical connection between the UV and X-ray emitting regions, which is particularly relevant in the context of the recent IXPE results that suggest energy-stratified emitting regions.
The anticorrelation is not significantly detected during the first part of the 2022 campaign, which might be explained by a low variability. Alternatively, the physical mechanism responsible for the anticorrelation may only take place temporarily. MAGIC Collaboration (2021) investigated the anticorrelation between X-ray and UV as well as X-ray and optical over several months. They also found that such a trend became significant on ∼monthly timescales, possibly indicating that it is not a permanent feature of Mrk 421.
4.3. Optical polarization evolution throughout the entire campaign
The R-band flux, which is close to the UV in frequency, also displays an increase throughout the campaign, in particular during the second part (between MJD 59710 and MJD 59760; May 11, 2022, to June 30, 2022), corroborating the anticorrelation hinted at by the Swift-UVW1 measurements. The R-band data are unfortunately too sparse to properly quantify the trend in that waveband. The rise in the optical flux seems to be accompanied by an increase in the polarization degree. In Fig. 11, we present the correlation between the polarization degree and flux using strictly simultaneous R-band measurements. We considered all data from RoboPol, NOT and T90 along the campaign. The KANATA measurements were discarded because of their very large flux uncertainties, in comparison to the measurements from the other instruments. We stress that the data mostly cover the MJD 59710 to MJD 59760 period (i.e., during the UV and X-ray anticorrelation hint period; May 11, 2022, to June 30, 2022), except for a single NOT measurement that took place before (on MJD 59703 – May 4, 2022). We find a positive correlation with a Pearson’s r of r = 0.8 ± 0.1. Using the same method as in Sect. 3.5, we estimated an associated p-value of pvalue = 1 × 10−5, corresponding to a correlation significance of ≈4σ. By fitting a linear function (see the dotted black line), the slope of the correlation is a = 0.51 ± 0.09. The same results are derived if one considers data between MJD 59710 to MJD 59760 (i.e., after removing the NOT measurement on MJD 59703).
 |
Fig. 11. Correlation between the polarization degree and flux in the R band over the entire campaign. The dotted black line is a linear fit, yielding a best-fit slope of a = 0.52 ± 0.09. The Pearson’s r of the correlation is r = 0.8 ± 0.1. The associated p-value is pvalue = 1 × 10−5. |
Overall, the combination of the UV versus X-ray anticorrelation on approximately monthly timescales and the rise in the R-band polarization degree observed over similar timescales potentially implies a general change in the physical properties of the source. The interpretation of this observation is given in Sect. 5.
5. Discussion and summary
This work reports on an extensive MWL observation campaign of Mrk 421 organized in 2022 from the radio to VHE gamma rays, including, for the first time, a simultaneous characterization of the X-ray polarization behavior. The VHE observations were carried out using the MAGIC telescopes and are accompanied by observations from Fermi-LAT, NuSTAR, XMM-Newton, and Swift as well as multiple instruments covering the optical to radio bands.
The daily coverage from MAGIC during the first IXPE observation in May 2022 (IXPE 1) reveals a low emission state at VHEs (≈25% of the Crab Nebula in the 0.2–1 TeV band) without any significant variability on either day or hour timescales. Moderate daily variability is noted in the X-ray band, which reveals an emission state lower than the average activity of Mrk 421 (Abdo et al. 2011). The optical, UV and MeV-GeV fluxes remain close to the typical activity. As for the broadband polarization characteristics, the polarization degree is significantly stronger in X-rays than at lower frequencies. This illustrates the importance of combining X-ray, optical and radio polarization data. As discussed in Di Gesu et al. (2022) and Liodakis et al. (2022), these results are in line with an energy-stratified jet, where the most energetic particles (emitting X-ray photons) are located in smaller regions that possess a more ordered magnetic field, close to the acceleration site. The energy dependence and the slow variability of the polarization degree strongly point toward a shock acceleration scenario. Electrons subsequently cool and diffuse in larger regions, where the field is more turbulent, and continue to emit from optical to radio frequencies. During IXPE 1, there is no significant variation in the polarization angle (Di Gesu et al. 2022) at any energy. In particular, the X-ray polarization angle is compatible with that measured in the optical and radio.
The IXPE 2 and 3 epochs (June 2022) are also characterized by a constant X-ray polarization degree that is significantly higher compared to lower frequencies. Such a general broadband feature of the polarization degree shares some similarities with the variability strength (quantified with the fractional variability, Fvar), which also shows an increase with energy. The Fvar during the IXPE exposures is indeed significantly higher in the X-ray band compared to the optical and radio data. This behavior may partially be caused by an X-ray emission dominated by (a single or a few) compact regions whose temporary appearance within the jet drives the observed variability, while emission at lower frequencies receives simultaneous contributions from several broader regions that decrease the overall variability. Such a scenario corroborates the energy stratification of the jet implied by the energy dependence of the polarization strength.
While the IXPE 2 and 3 epochs are consistent with a constant polarization degree, the polarization angle exhibits an evident rotation in X-rays during these two IXPE exposures. The rotation proceeds at a constant angular velocity (see also Di Gesu 2023) between the two epochs, and hence is highly suggestive of a single rotation event observed during the two consecutive IXPE 2 and 3 exposures. The optical and radio observations do not show a simultaneous angle rotation.
We managed to characterize the VHE state only at the very beginning of the polarization angle rotation. During that time period, we find that the VHE emission state is higher (and the spectrum is harder) than during IXPE 1, albeit comparable to the average for the source (≈50% of the Crab Nebula in the 0.2–1 TeV band; Abdo et al. 2011). Starting from the second half of the IXPE 2 epoch and during IXPE 3, the activity in X-rays increases and hardens significantly, simultaneously with the angle rotation. The emission reaches a maximum well above the Mrk 421 quiescent state. The VHE gamma rays usually show a strong correlation with X-rays, especially during X-ray flaring activities, as observed during IXPE 3 (see, e.g., Acciari et al. 2020), but the lack of simultaneous observations with MAGIC prevents us from evaluating this characteristic during this specific flaring activity in June 2022.
Previous campaigns on LSP and ISP objects have shown that rotations of the polarization angle in the optical can be associated with flares (Ahnen et al. 2017a; MAGIC Collaboration 2018; Abdo et al. 2010b; Gupta et al. 2019; Chandra et al. 2015; Marscher et al. 2008). In LSPs and ISPs, the synchrotron peak is located around the optical band, while in HSPs (as Mrk 421) it is located in the X-ray regime. One would thus naively expect that X-ray flares in HSPs can similarly be associated with X-ray polarization angle swings. Even if the enhanced X-ray state during IXPE 2 and 3 remains below that of previous notable outbursts of Mrk 421 (see for instance the March 2010 flare reported in Aleksić et al. 2015b), the evident X-ray flux rise and hardening, temporally coincident with a polarization angle swing, may share a common physical origin with the angular swings observed in lower synchrotron peaked blazars.
The absence of a simultaneous polarization angle swing in the optical, IR and radio may be explained by the following scenario: the smaller region radiating the X-ray photons (where the B field is more ordered) is streaming down the jet following helical field lines, leading to an apparent rotation of the polarization angle (Di Gesu 2023), while at lower frequencies, the emitting regions are larger and do not closely follow a helical path, unlike the X-ray region.
The movement of a compact region through a helical path inside the jet induces changes in the Doppler factor, which then lead to significant observed flux variability. We thus investigated whether such a scenario, proposed to explain the angle rotation, is (roughly) consistent with the observed variability amplitude in the X-rays (that is, the energy range with the best temporal coverage during the rotation). The viewing angle, ψ, of a region streaming down a helical path is given by (see, e.g., Larionov et al. 2013)
where θ is the jet axis angle to the line of sight, ζ the pitch angle of the helical field, and ϕ the phase of the spiral rotation. If the region moves at a Lorentz factor of Γb, the associated Doppler factor is δ = [Γb(1−β cos ψ]−1. In the observer’s frame, the intrinsic flux, Fintr, transforms as (Rybicki & Lightman 1979)
where p is the photon index, which we found to be around −2.4 in the 3–7 keV band of NuSTAR during the rotation. According to Di Gesu (2023), the rotation rate can be reproduced if the emitting feature travels with a velocity component parallel to the jet axis of 0.9975c and a transverse component of 0.05c. Based on this estimation, the corresponding pitch angle of the helical field is ≈2.9°. Assuming a typical Lorentz factor of Γb = 20, the expected flux variability amplitude solely introduced by an evolution of the Doppler factor due to the movement on a helical path is plotted in the top panel of Fig. 12. The variability is plotted as a function of the phase of the rotation. The curves are plotted for a set of θ ranging from 0° to 3°, which is typical for blazars. The variability amplitude, being a few orders of magnitude higher for θ = 3°, is strongly dependent on the jet viewing axis. The horizontal dotted blue line displays the observed flux amplitude in the 3–7 keV band, which can be explained by the change in Doppler factor if θ ≈ 0.5°. The low apparent speed of radio knots in Mrk 421 suggests that very long baseline radio observations mostly probe the sheath of the jet instead of the central part (i.e., the spine; see, e.g., Ghisellini et al. 2005; Weaver et al. 2022). We note, however, that Weaver et al. (2022) estimated θ ∼ 1°, which is relatively consistent with Fig. 12. One concludes that, assuming relatively standard parameters, the observed flux changes are not in contradiction with the variability caused by the evolution of the Doppler factor (as the zone travels on helical field lines). It is important to note that the flux variability is also likely affected by acceleration and cooling processes, as suggested by the spectral changes observed on approximately day to hour timescales in the NuSTAR data during IXPE 2 and 3. Hence, the MWL data tell us that the changes in the δ cannot be the only reason for the observed flux variability.
 |
Fig. 12. Relativistic beaming effects due to the travel along a helical path within the jet. Top panel: Flux variability amplitude caused by the evolution of the Doppler factor, δ, when an emitting zone is traveling downstream along a helical path. The variability amplitude is plotted as a function of the phase of the spiral rotation. The horizontal dotted blue line gives the observed variability amplitude in the 3–7 keV band. Bottom panel: Corresponding Doppler factor, δ, as a function of the spiral rotation phase. The curves are produced for different jet axis angles (θ) relative to the line of sight. The zone is assumed to move with a Lorentz factor Γb = 20 in a helical field with a pitch angle of 2.9° (see the main text for more details). |
The observations by NuSTAR simultaneous to the polarization angle swing during IXPE 3 reveal two contiguous spectral hysteresis loops in opposite directions over a single exposure (see Fig. 8). The first loop, in a clockwise direction, is likely the signature of synchrotron cooling causing a delay of the low-energy X-ray photons with respect to the high-energy ones (soft lag). The subsequent counterclockwise loop indicates a delay of the high-energy X-ray photons compared to the low-energy ones (hard lag), suggesting a system observed at energies for which the acceleration timescale is comparable to the cooling timescale, 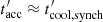 (Kirk et al. 1998).
(Kirk et al. 1998).
Within a framework of shock acceleration, as suggested by the multiband polarization properties, the acceleration timescale in the co-moving frame (primed quantities) of an electron with Lorentz factor γ can be approximated as follows (Drury 1983; Blandford & Eichler 1987; Kusunose et al. 2000):
where 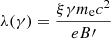 is the mean free path of electrons, parameterized as a fraction, ξ, of the Larmor radius. The parameter ξ, sometimes dubbed the gyro-factor, is related to the efficiency in the acceleration of the high-energy particle population and is always ≥1. In the so-called Bohm limit, the acceleration is the most efficient because it occurs over a mean free path similar to the Larmor radius, and ξ = 1. Within this framework, the acceleration efficiency is proportional to ξ−1, and ξ > 1 indicates an acceleration efficiency lower than that in the Bohm limit. B′ is the magnetic field inside the emitting region and us the speed of the shock, which we assume to be relativistic, us ∼ c. The synchrotron cooling time is given by
is the mean free path of electrons, parameterized as a fraction, ξ, of the Larmor radius. The parameter ξ, sometimes dubbed the gyro-factor, is related to the efficiency in the acceleration of the high-energy particle population and is always ≥1. In the so-called Bohm limit, the acceleration is the most efficient because it occurs over a mean free path similar to the Larmor radius, and ξ = 1. Within this framework, the acceleration efficiency is proportional to ξ−1, and ξ > 1 indicates an acceleration efficiency lower than that in the Bohm limit. B′ is the magnetic field inside the emitting region and us the speed of the shock, which we assume to be relativistic, us ∼ c. The synchrotron cooling time is given by
where σT is the Thomson cross section and 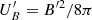 the magnetic field energy density. By expressing the timescales in terms of the observed photon energy, and considering that electrons emit most of their synchrotron photons at an observed frequency of
the magnetic field energy density. By expressing the timescales in terms of the observed photon energy, and considering that electrons emit most of their synchrotron photons at an observed frequency of 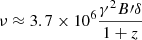 , where δ is the Doppler factor of the emitting region, one finds that the ratio tacc/tcool, synch is in fact independent of B′ (Zhang et al. 2002):
, where δ is the Doppler factor of the emitting region, one finds that the ratio tacc/tcool, synch is in fact independent of B′ (Zhang et al. 2002):
where E is the photon energy in keV units. The counterclockwise loop observed by NuSTAR implies tacc/tcool, synch ≈ 1 at E ≈ 10 keV, which is the characteristic energy probed by NuSTAR. Assuming a typical δ = 30 for Mrk 421, one thus derives ξ ≈ 8 × 104 for the second part of the NuSTAR observation during the IXPE 3 epoch.
On the other hand, the first part of the NuSTAR observation in the IXPE 3 epoch, where a clockwise loop is observed, suggests a regime in which tacc/tcool, synch ≪ 1 since synchrotron cooling is likely the driver of soft lags. The acceleration must take place in a significantly more effective manner. During this part of the observation, ξ must therefore be at least an order of magnitude smaller, ξ ≲ 8 × 103. While the range of values we derive for ξ stays within the estimates of Baring et al. (2017), where it is discussed in a broader theoretical context, the consecutive clockwise and counterclockwise loops during IXPE 3 imply an increase in the gyro-factor, ξ, of at least one order of magnitude over approximately hour timescales.
The above calculations and estimations of ξ do not consider IC cooling. We verified that such a simplification does not significantly affect our results. Using a SSC model (Maraschi et al. 1992; Madejski et al. 1999) that we constrained using the X-ray and VHE spectra during the IXPE epochs, we estimate that the IC cooling timescale is longer than the synchrotron cooling timescale, as one would in any case expect from the lower luminosity of the IC bump in comparison to that of the synchrotron bump. Our model in fact shows a synchrotron cooling timescale that is about twice shorter than the IC cooling. Hence, the synchrotron cooling is sufficient to estimate the dynamics of the electrons, and Eq. (6) remains a valid approximation for estimating ξ. A detailed description of the model and the computation is given in Appendix D.
The modeling performed in Appendix D constrains the magnetic field to be B′∼0.04 G in the X-ray and VHE emitting region with a blob radius of R′≈2 × 1016 cm. These values imply a synchrotron cooling time (Eq. (5)) longer than the light-crossing time ( ) for electrons emitting up to ≈10 keV, which is well within the NuSTAR bandwidth. The modeling parameters are thus clearly in agreement with a NuSTAR variability regulated by cooling (and/or acceleration) mechanisms, instead of the light-crossing time effects, in line with what is suggested by the observed hysteresis loops. If the light travel time is significantly longer than the cooling and/or acceleration timescale, the variability will be dominated via the former.
) for electrons emitting up to ≈10 keV, which is well within the NuSTAR bandwidth. The modeling parameters are thus clearly in agreement with a NuSTAR variability regulated by cooling (and/or acceleration) mechanisms, instead of the light-crossing time effects, in line with what is suggested by the observed hysteresis loops. If the light travel time is significantly longer than the cooling and/or acceleration timescale, the variability will be dominated via the former.
As a final consideration, we combined Eq. (5) with the characteristic synchrotron frequency (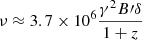 ) to derive the expected cooling timescale in the observer’s frame (Zhang et al. 2002):
) to derive the expected cooling timescale in the observer’s frame (Zhang et al. 2002):
The parameters from the modeling in Appendix D give  h and
h and  h, which is again consistent with the flux doubling and/or halving timescale derived by the NuSTAR data.
h, which is again consistent with the flux doubling and/or halving timescale derived by the NuSTAR data.
Within the IXPE observing windows, there is an indication of stronger optical and IR polarization for IXPE 2 and IXPE 3 compared to IXPE 1. IXPE 2 and 3 also exhibit a ratio between the optical, IR and X-ray polarization degree that is significantly higher. In the configuration of an energy-stratified jet, this possibly indicates that the optical emission originates from regions that are closer to the shock, where the magnetic field is more ordered (i.e., closer to the X-ray emitting region), while for IXPE 1 the optical flux is emitted farther downstream in the jet.
By exploiting data from the entire MWL campaign, we find a positive correlation at the level of 4σ between X-rays and VHE gamma rays without any time delay between the MAGIC energy bands and the 2–10 keV band of Swift-XRT. The correlation is at the level of 3σ with the 0.3–2 keV band. The positive correlation without a time lag supports leptonic scenarios in which the same electron population produces the X-ray and VHE emission, via the SSC process. Positive correlations at zero time lags were also reported in several previous studies (MAGIC Collaboration 2021; Arbet-Engels et al. 2021; Acciari et al. 2021; Aleksić et al. 2015a). Such a positive correlation suggests that VHE gamma rays are also emitted close to the shock front (co-spatially to the X-rays). The higher significance obtained when using the X-ray 2–10 keV band instead of the 0.3–2 keV band suggests that the VHE emission has a tighter relation with the X-ray fluxes above a few keVs rather than below that. Looking at Fig. 2, this implies that the falling edge of the high-energy SED component is mostly dominated by electrons that emit synchrotron photons well above νp, which is in agreement with the expectation of leptonic scenarios (Tavecchio et al. 1998).
At lower energies, we find marginal evidence of an anticorrelation between the X-ray and UV fluxes from May 2022 to June 2022. In this time span, while the X-ray emission shows a long-term flux decay and spectral softening, the UV emission is rising with a quasi-monotonic trend. We find that the marginal evidence of correlation happens at a zero time lag, without any indication of a delay. Although the significance is estimated to be ∼2.5σ using Monte Carlo simulations, this suggestion is interesting in the context of previous results as well as the newly available X-ray polarization measurements. First, we stress that this is the third time that an indication of X-ray versus UV anticorrelation is reported for Mrk 421 (Aleksić et al. 2015a; MAGIC Collaboration 2021), and each previous indication shows a similar anticorrelation trend over approximately monthly timescales. Secondly, the direct implication of an anticorrelation is a physical connection between the X-ray, UV and optical emitting regions. While the IXPE results strongly suggest that those regions are not co-spatial, the anticorrelation further supports a scenario in which particles are first accelerated close to a shock front and then advect (and cool) toward a broader region in the jet and dominate the observed UV and optical emission.
A possible scenario explaining the anticorrelation is a long-term evolution of the acceleration efficiency while the electron injection luminosity stays roughly constant. In this configuration, a decrease in the acceleration efficiency would increase the relative proportion of lower-energy electrons and shift the synchrotron SED toward lower frequencies (as suggested by the data), while keeping the amplitude of the SED peak at a roughly similar level. This scenario is thus expected to generate an increase in the UV and optical flux (rising edge of the synchrotron component) and a decrease in the X-ray flux (falling edge of the synchrotron component).
Angelakis et al. (2016) find an indication of anticorrelation between the optical polarization degree and the synchrotron peak frequencies, νp, for a sample of BL Lac objects. This behavior was qualitatively explained by the fact that, in the case of BL Lac objects with lower νp (such as LSPs), the synchrotron peak is close to the optical band, which is emitted by freshly accelerated electrons near the shock. For HSPs, the optical range is farther from νp and thus comprises emission radiated by electrons that had time to advect away. It is downstream from the shock, where the level of magnetic field disorder increases, thus reducing the observed optical polarization degree. In the case where the anticorrelation between the UV and X-rays described above is caused by a shift in νp toward lower frequencies, one would thus expect a simultaneous rise in the optical polarization degree over time, with a value approaching 1 in the X-rays. Consistently, the period during which we report an indication of anticorrelation is accompanied by an increase in the optical polarization degree (see Sect. 4.3). The higher optical polarization degree would also explain the relatively high ratio between the optical/IR and X-ray polarization degree throughout the IXPE 2 and IXPE 3 epochs (which are within the time range where a hint of UV versus X-ray anticorrelation is reported).
Alternatively, the rise in the optical polarization degree during the UV versus X-ray anticorrelation time range may be caused by a progressive increase in the relative dominance of a few emitting zones radiating the optical and UV flux. Indeed, in the case where the optical flux receives contributions from many regions with different magnetic field configurations, the polarization degree would decrease.
The threshold energy of 0.3 GeV was preferred over the usual 0.1 GeV in order to exploit the improved angular resolution of Fermi-LAT at higher energies. A higher energy threshold also reduces background contamination, which leads to an overall improvement of the signal-to-noise ratio for hard sources such as Mrk 421 (photon index > −2).
The flux of the Crab Nebula used in this work is taken from Aleksić et al. (2016).
Acknowledgments
The MAGIC Collaboration would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF, MPG and HGF; the Italian INFN and INAF; the Swiss National Fund SNF; the grants PID2019-104114RB-C31, PID2019-104114RB-C32, PID2019-104114RB-C33, PID2019-105510GB-C31, PID2019-107847RB-C41, PID2019-107847RB-C42, PID2019-107847RB-C44, PID2019-107988GB-C22 funded by the Spanish MCIN/AEI/10.13039/501100011033; the Indian Department of Atomic Energy; the Japanese ICRR, the University of Tokyo, JSPS, and MEXT; the Bulgarian Ministry of Education and Science, National RI Roadmap Project DO1-400/18.12.2020 and the Academy of Finland grant nr. 320045 is gratefully acknowledged. This work was also been supported by Centros de Excelencia “Severo Ochoa” y Unidades “María de Maeztu” program of the Spanish MCIN/AEI/ 10.13039/501100011033 (SEV-2016-0588, CEX2019-000920-S, CEX2019-000918-M, CEX2021-001131-S, MDM-2015-0509-18-2) and by the CERCA institution of the Generalitat de Catalunya; by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project uniri-prirod-18-48; by the Deutsche Forschungsgemeinschaft (SFB1491 and SFB876); the Polish Ministry of Education and Science grant No. 2021/WK/08; and by the Brazilian MCTIC, CNPq and FAPERJ. A.A.E. and D.P. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) under Germany’s Excellence Strategy EXC-2094–390783311. The Imaging X-ray Polarimetry Explorer (IXPE) is a joint US and Italian mission. The US contribution is supported by the National Aeronautics and Space Administration (NASA) and led and managed by its Marshall Space Flight Center (MSFC), with industry partner Ball Aerospace (contract NNM15AA18C). The Italian contribution is supported by the Italian Space Agency (Agenzia Spaziale Italiana, ASI) through contract ASI-OHBI-2017-12-I.0, agreements ASI-INAF-2017-12-H0 and ASI-INFN-2017.13-H0, and its Space Science Data Center (SSDC), and by the Istituto Nazionale di Astrofisica (INAF) and the Istituto Nazionale di Fisica Nucleare (INFN) in Italy. This research used data products provided by the IXPE Team (MSFC, SSDC, INAF, and INFN) and distributed with additional software tools by the High-Energy Astrophysics Science Archive Research Center (HEASARC), at NASA Goddard Space Flight Center (GSFC). The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This work performed in part under DOE Contract DE-AC02-76SF00515. The IAA-CSIC group acknowledges financial support from the Spanish “Ministerio de Ciencia e Innovación” (MCIN/AEI/ 10.13039/501100011033) through the Center of Excellence Severo Ochoa award for the Instituto de Astrofísica de Andalucía-CSIC (CEX2021-001131-S), and through grants PID2019-107847RB-C44 and PID2022-139117NB-C44. The POLAMI observations were carried out at the IRAM 30 m Telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). Some of the data are based on observations collected at the Observatorio de Sierra Nevada, owned and operated by the Instituto de Astrofísica de Andalucía (IAA-CSIC). Further data are based on observations collected at the Centro Astronómico Hispano en Andalucía (CAHA), operated jointly by Junta de Andalucía and Consejo Superior de Investigaciones Científicas (IAA-CSIC). Some of the data reported here are based on observations made with the Nordic Optical Telescope, owned in collaboration with the University of Turku and Aarhus University, and operated jointly by Aarhus University, the University of Turku, and the University of Oslo, representing Denmark, Finland, and Norway, the University of Iceland and Stockholm University at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. E. L. was supported by Academy of Finland projects 317636 and 320045. The data presented here were obtained (in part) with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOT. We acknowledge funding to support our NOT observations from the Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Finland (Academy of Finland grant nr 306531). We are grateful to Vittorio Braga, Matteo Monelli, and Manuel Sänchez Benavente for performing the observations at the Nordic Optical Telescope. The research at Boston University was supported in part by National Science Foundation grant AST-2108622, NASA Fermi Guest Investigator grants 80NSSC21K1917 and 80NSSC22K1571, and NASA Swift Guest Investigator grant 80NSSC22K0537. This research was conducted in part using the Mimir instrument, jointly developed at Boston University and Lowell Observatory and supported by NASA, NSF, and the W.M. Keck Foundation. We thank D. Clemens for guidance in the analysis of the Mimir data. This research has made use of data from the RoboPUol program, a collaboration between Caltech, the University of Crete, IA-FORTH, IUCAA, the MPIfR, and the Nicolaus Copernicus University, which was conducted at Skinakas Observatory in Crete, Greece. D.B., S.K., R.S., N.M., acknowledge support from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program under grant agreement No. 771282. C.C. acknowledges support from the European Research Council (ERC) under the HORIZON ERC Grants 2021 program under grant agreement No. 101040021. This study used observations conducted with the 1.8 m Perkins Telescope (PTO) in Arizona (USA), which is owned and operated by Boston University. This work was supported by NSF grant AST-2109127. We acknowledge the use of public data from the Swift data archive. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. This publication makes use of data obtained at Metsähovi Radio Observatory, operated by Aalto University in Finland. The Submillimetre Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. Mauna Kea, the location of the SMA, is a culturally important site for the indigenous Hawaiian people; we are privileged to study the cosmos from its summit. This work was supported by JST, the establishment of university fellowships toward the creation of science and technology innovation, Grant Number JPMJFS2129. This work was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP21H01137. This work was also partially supported by the Optical and Near-Infrared Astronomy Inter-University Cooperation Program from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. We are grateful to the observation and operating members of the Kanata Telescope. S.K. acknowledges support from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program under grant agreement No. 771282.
References
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Nature, 463, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, 131 [Google Scholar]
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
- Abeysekara, A. U., Benbow, W., Bird, R., et al. 2020, ApJ, 890, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Arlen, T., Aune, T., et al. 2014, Astropart. Phys., 54, 1 [Google Scholar]
- Acciari, V. A., Ansoldi, S., Antonelli, L. A., et al. 2020, ApJS, 248, 29 [Google Scholar]
- Acciari, V. A., Ansoldi, S., Antonelli, L. A., et al. 2021, MNRAS, 504, 1427 [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [Google Scholar]
- Agudo, I., Thum, C., Molina, S. N., et al. 2018a, MNRAS, 474, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Thum, C., Ramakrishnan, V., et al. 2018b, MNRAS, 473, 1850 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017a, A&A, 603, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017b, Astropart. Phys., 94, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, Nucl. Instrum. Methods Phys. Res. A, 583, 494 [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015a, A&A, 576, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015b, A&A, 578, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [Google Scholar]
- Angelakis, E., Hovatta, T., Blinov, D., et al. 2016, MNRAS, 463, 3365 [NASA ADS] [CrossRef] [Google Scholar]
- Arbet-Engels, A., Baack, D., Balbo, M., et al. 2021, A&A, 647, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Ballet, J., Burnett, T. H., Digel, S. W., & Lott, B. 2020, arXiv e-prints [arXiv:2005.11208] [Google Scholar]
- Baloković, M., Paneque, D., Madejski, G., et al. 2016, ApJ, 819, 156 [Google Scholar]
- Baring, M. G., Böttcher, M., & Summerlin, E. J. 2017, MNRAS, 464, 4875 [CrossRef] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Böttcher, M., Reimer, A., Sweeney, K., & Prakash, A. 2013, ApJ, 768, 54 [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, Am. Inst. Phys. Conf. Ser., 1358, 373 [NASA ADS] [Google Scholar]
- Brinkmann, W., Papadakis, I. E., den Herder, J. W. A., & Haberl, F. 2003, A&A, 402, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [Google Scholar]
- Cerruti, M., Zech, A., Boisson, C., & Inoue, S. 2015, MNRAS, 448, 910 [Google Scholar]
- Chandra, S., Zhang, H., Kushwaha, P., et al. 2015, ApJ, 809, 130 [CrossRef] [Google Scholar]
- de la Calle Pérez, I., Álvarez Crespo, N., Racero, E., & Rouco, A. 2021, A&A, 655, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Gesu, L., Donnarumma, I., Tavecchio, F., et al. 2022, ApJ, 938, L7 [CrossRef] [Google Scholar]
- Di Gesu, L., Marshall, H. L., Ehlert, S. R., et al. 2023, Nat. Astron., 7, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [Google Scholar]
- Emmanoulopoulos, D., McHardy, I. M., & Papadakis, I. E. 2013, MNRAS, 433, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, ASP Conf. Ser., 314, 759 [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Righi, C., Costamante, L., & Tavecchio, F. 2017, MNRAS, 469, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Gaur, H., Wiita, P. J., et al. 2019, AJ, 157, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., Moran, J. M., & Lo, K. Y. 2004, ApJ, 616, L1 [Google Scholar]
- Horan, D., Acciari, V. A., Bradbury, S. M., et al. 2009, ApJ, 695, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, O. G., Blinov, D., Ramaprakash, A. N., et al. 2014, MNRAS, 442, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452 [NASA ADS] [Google Scholar]
- Kirk, J. G., Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ, 542, 235 [Google Scholar]
- Kusunose, M., Takahara, F., & Li, H. 2000, ApJ, 536, 299 [Google Scholar]
- Larionov, V. M., Jorstad, S. G., Marscher, A. P., et al. 2013, ApJ, 768, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Liodakis, I., Marscher, A. P., Agudo, I., et al. 2022, Nature, 611, 677 [CrossRef] [Google Scholar]
- Lumb, D. H., Warwick, R. S., Page, M., & De Luca, A. 2002, A&A, 389, 93 [CrossRef] [EDP Sciences] [Google Scholar]
- Madejski, G. M., Sikora, M., Jaffe, T., et al. 1999, ApJ, 521, 145 [CrossRef] [Google Scholar]
- Madsen, K. K., Harrison, F. A., Markwardt, C. B., et al. 2015, ApJS, 220, 8 [Google Scholar]
- Madsen, K. K., Beardmore, A. P., Forster, K., et al. 2017, AJ, 153, 2 [Google Scholar]
- MAGIC Collaboration (Ahnen, M. L., et al.) 2018, A&A, 619, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2020, A&A, 635, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2021, A&A, 655, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannheim, K. 1993, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [CrossRef] [Google Scholar]
- Marrone, D. P., & Rao, R. 2008, Proc. SPIE, 7020, 70202B [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [Google Scholar]
- Marscher, A. P., & Jorstad, S. G. 2021, Galaxies, 9, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [Google Scholar]
- Nilsson, K., Pasanen, M., Takalo, L. O., et al. 2007, A&A, 475, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&A Rev., 25, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, S. R., Shukla, A., Chitnis, V. R., et al. 2018, A&A, 611, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [Google Scholar]
- Primiani, R. A., Young, K. H., Young, A., et al. 2016, J. Astron. Instrum., 5, 1641006a [NASA ADS] [CrossRef] [Google Scholar]
- Ramaprakash, A. N., Rajarshi, C. V., Das, H. K., et al. 2019, MNRAS, 485, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Ravasio, M., Tagliaferri, G., Ghisellini, G., & Tavecchio, F. 2004, A&A, 424, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
- Tavecchio, F. 2021, Galaxies, 9, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [Google Scholar]
- Teraesranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thum, C., Wiesemeyer, H., Paubert, G., Navarro, S., & Morris, D. 2008, PASP, 120, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Weaver, Z. R., Jorstad, S. G., Marscher, A. P., et al. 2022, ApJS, 260, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. 2022, AAS/High Energy Astrophysics Division, 54, 301.01 [NASA ADS] [Google Scholar]
- Zanin, R., Carmona, E., Sitarek, J., et al. 2013, Int. Cosmic Ray Conf., 33, 2937 [NASA ADS] [Google Scholar]
- Zhang, H., & Böttcher, M. 2013, ApJ, 774, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H., Treves, A., Celotti, A., et al. 2002, ApJ, 572, 762 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: XMM-Newton fine-binned light curves
In this section, we present the fine-binned light curves from both of the XMM-Newton exposures analyzed in this work. The fluxes were computed using the EPIC-MOS2 camera (which has the largest exposure time among the operating instruments on board XMM-Newton) in the 0.3-2 keV and 2-10 keV bands using a temporal binning of 500 s. The SAS task epiclccorr was used to produce background-subtracted source count rates corrected for the inefficiencies of the instrument (vignetting, chip gaps, point spread functions, etc.) and time corrections (dead time, GTIs...). The count rates were then converted to energy fluxes (i.e., in erg/cm2/s units) assuming the best-fit log parabola model over the entire exposure. The light curve for the IXPE 1 and the IXPE 2 epochs are shown in Fig. A.1 and Fig. A.2, respectively. The bottom panel present the ratio between the 2-10 keV and the 0.3-2 keV fluxes.
 |
Fig. A.1. XMM-Newton light curve from the EPIC-MOS2 camera in the 0.3-2 keV and 2-10 keV bands during the IXPE 1 epoch. The lower panel is the ratio between the 2-10 keV and 0.3-2 keV fluxes. |
 |
Fig. A.2. XMM-Newton light curve from the EPIC-MOS2 camera in the 0.3-2 keV and 2-10 keV bands during the IXPE 2 epoch. The lower panel is the ratio between the 2-10 keV and 0.3-2 keV fluxes. |
Appendix B: VHE versus 0.2-3 keV DCF analysis
This section presents the results of the DCF analysis between the VHE fluxes and the 0.3-2 keV band from Swift-XRT. Figures B.1 and B.2 show the DCF when the VHE flux is computed in the 0.2-1 TeV and > 1 TeV ranges, respectively. The dashed lines are the confidence bands based on Monte Carlo simulations (see Sect. 4 for more details).
 |
Fig. B.1. DCF computed for the MAGIC 0.2 − 1 TeV and Swift-XRT 0.3-2 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
 |
Fig. B.2. DCF computed for the MAGIC > 1 TeV and Swift-XRT 0.3-2 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
Appendix C: UV versus X-ray correlation
This section presents the results of the DCF analysis between the X-ray and the UV fluxes in the Swift-UVOT W1 filter. Figures C.1 and C.2 show the DCF when the X-ray flux is computed in the 0.3-2 keV and 2-10 keV ranges, respectively, using data between MJD 59710 and MJD 59740 (i.e., corresponding to the second part of the MWL campaign presented in this work; May 11, 2022, to June 10, 2022). The dashed lines are the confidence bands based on Monte Carlo simulations (see Sect. 4 for more details about the procedure). In Fig. C.3 and Fig. C.4, we display the results after repeating the exercise when data from the entire MWL campaign were included (i.e., from MJD 59695 to MJD 59740; April 26, 2022, to June 10, 2022).
 |
Fig. C.1. DCF computed for the Swift-UVOT W1 and Swift-XRT 0.3-2 keV light curves over the second part of the MWL campaign, between MJD 59710 (May 11, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
 |
Fig. C.2. DCF computed for the Swift-UVOT W1 and Swift-XRT 2-10 keV light curves over the second part of the MWL campaign, between MJD 59710 (May 11, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
 |
Fig. C.3. DCF computed for the Swift-UVOT W1 and Swift-XRT 0.3-2 keV light curves over the full MWL campaign, between MJD 59695 (April 26, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
 |
Fig. C.4. DCF computed for the Swift-UVOT W1 and Swift-XRT 2-10 keV light curves over the full campaign, between MJD 59695 (April 26, 2022) to MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
Appendix D: Modeling of the X-ray and VHE spectra during the IXPE epochs
In Sect. 5 we present calculations of the ratio between the cooling and acceleration timescales of X-ray-emitting electrons during the hysteresis loops that we detect in the NuSTAR data during IXPE 3. The ratio between the two timescales is then used to estimate the gyro-factorξ. For simplification, only synchrotron cooling is considered, and IC cooling is neglected. In this section, we address the validity of this assumption.
Following the notation of Tavecchio et al. (1998), the IC cooling timescale is estimated as
where  is the available target photon density for IC process (below the Klein-Nishina limit; see Eq. 20 in Tavecchio et al. 1998) within the emitting zone. The estimation of
is the available target photon density for IC process (below the Klein-Nishina limit; see Eq. 20 in Tavecchio et al. 1998) within the emitting zone. The estimation of 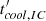 requires the knowledge of
requires the knowledge of 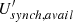 , which we extracted with a simple modeling of the SED by considering a one-zone SSC model (Maraschi et al. 1992; Madejski et al. 1999). For this exercise, we aim at describing the X-ray and VHE spectra only for the following reasons. First, a description of the radio-to-VHE data would require a more complex modeling that takes into account the energy stratification of the jet implied by the broadband polarization data. This effort lies beyond the scope of this work. Secondly, describing the X-ray and VHE spectra in a one-zone SSC approach is motivated by the tight X-ray versus VHE correlation at zero time lag. Since only IXPE 1 and IXPE 2 have simultaneous X-ray and VHE data we are forced to focus on those two epochs to constrain physical parameters of the source during IXPE 3, where the hysteresis loops actually happened. This represents a caveat for the following analysis since the source parameters may have evolved between the different epochs.
, which we extracted with a simple modeling of the SED by considering a one-zone SSC model (Maraschi et al. 1992; Madejski et al. 1999). For this exercise, we aim at describing the X-ray and VHE spectra only for the following reasons. First, a description of the radio-to-VHE data would require a more complex modeling that takes into account the energy stratification of the jet implied by the broadband polarization data. This effort lies beyond the scope of this work. Secondly, describing the X-ray and VHE spectra in a one-zone SSC approach is motivated by the tight X-ray versus VHE correlation at zero time lag. Since only IXPE 1 and IXPE 2 have simultaneous X-ray and VHE data we are forced to focus on those two epochs to constrain physical parameters of the source during IXPE 3, where the hysteresis loops actually happened. This represents a caveat for the following analysis since the source parameters may have evolved between the different epochs.
We first fixed the radius of the emitting region to R′ = 2 × 1016 cm. This was derived from the constraints using causality arguments, R′≲δ ⋅ c ⋅ tvar, obs (Tavecchio et al. 1998), where tvar, obs is the observed variability timescale and δ the Doppler factor, which we fixed to 30 (a typical value adopted for Mrk 421 in previous modeling; see, e.g. Tavecchio et al. 1998; Baloković et al. 2016; MAGIC Collaboration 2021). Here, we set tvar, obs = 7 hr, which is the halving and/or doubling time that we measured in the NuSTAR band. We modeled the electron distribution with a broken power law,
where 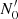 is a normalization constant.
is a normalization constant. 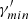 ,
, 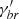 , and
, and 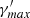 are defined as the minimum, break, and maximum Lorentz factor, respectively. Differently from n2, n1 cannot be constrained by the X-ray and VHE data, so we fix n1 = 2.0, close to the predictions of shock acceleration (Kirk et al. 2000). The overall electron energy density is given by
are defined as the minimum, break, and maximum Lorentz factor, respectively. Differently from n2, n1 cannot be constrained by the X-ray and VHE data, so we fix n1 = 2.0, close to the predictions of shock acceleration (Kirk et al. 2000). The overall electron energy density is given by 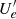 . The resulting models are shown in Fig. D.1, and exhibit a reasonable description of the X-ray and VHE data. We list in Table D.1 and Table D.2 the obtained parameters. The optical/UV and MeV-GeV data are purposely under-predicted. In fact, the energy stratification of jet suggested by the polarization data strongly implies that optical, UV and MeV-GeV fluxes receive a significant contribution from broader and separate regions than the X-ray and VHE one. Hence, our one-zone modeling does not intend to describe the entire SED.
. The resulting models are shown in Fig. D.1, and exhibit a reasonable description of the X-ray and VHE data. We list in Table D.1 and Table D.2 the obtained parameters. The optical/UV and MeV-GeV data are purposely under-predicted. In fact, the energy stratification of jet suggested by the polarization data strongly implies that optical, UV and MeV-GeV fluxes receive a significant contribution from broader and separate regions than the X-ray and VHE one. Hence, our one-zone modeling does not intend to describe the entire SED.
 |
Fig. D.1. Results of a one-zone SSC model applied to the IXPE 1 (top panel) and IXPE 2 (bottom panel) epochs in order to constrain the physical parameters of the X-ray and VHE emitting region. The data are plotted with cyan markers, and the model is shown as a solid blue line. The obtained modeling parameters are listed in Tables D.1 and D.2. The reader is referred to Appendix D for more details on the model. |
Model parameters of the one-zone SSC model applied to the IXPE 1 epoch.
Model parameters of the one-zone SSC model applied to the IXPE 2 epoch.
The modeling yields 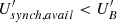 in both epochs. From Eq. D.1 and Eq. 5, one thus concludes that IC cooling timescale is longer than the synchrotron cooling timescale. Only considering synchrotron cooling is thus a reasonable simplification to assess the cooling dynamics of the electrons during the hysteresis loops that we report and discuss in Sects. 3.6 and 5.
in both epochs. From Eq. D.1 and Eq. 5, one thus concludes that IC cooling timescale is longer than the synchrotron cooling timescale. Only considering synchrotron cooling is thus a reasonable simplification to assess the cooling dynamics of the electrons during the hysteresis loops that we report and discuss in Sects. 3.6 and 5.
All Tables
Spectral parameters from the VHE and X-ray observations around the three IXPE observing epochs.
All Figures
 |
Fig. 1. MWL light curve for Mrk 421 covering the whole campaign from MJD 59695 (April 26, 2022) to MJD 59757 (June 27, 2022). The gray bands correspond to the three IXPE observations. Top to bottom: MAGIC fluxes in daily bins for two energy bands (note the two different y-axes); Fermi-LAT fluxes in 3 day bins; X-ray fluxes in daily bins including Swift-XRT, NuSTAR and IXPE; hardness ratio between the high- and low-energy fluxes of Swift-XRT and between the two VHE bands of MAGIC (note the two different y-axes); optical R-band data from NOT, RoboPol KANATA; IR H-band data from Perkins; radio data from IRAM and polarization degree and polarization angle observations in the optical to radio from NOT, RoboPol, KANATA, Perkins, IRAM, SMA and in X-rays from IXPE. |
| In the text | |
 |
Fig. 2. Broadband SED around the three IXPE observations. Data from MAGIC were corrected for the extragalactic background light absorption using the model outlined in Domínguez et al. (2011). In plain colored markers, the Swift-XRT data correspond to the pointing that happened first within the IXPE windows. The Swift-XRT data in diamond markers with a face color in white are from the subsequent observation. For comparison, the SED of an average emission state of Mrk 421 from Abdo et al. (2011) is shown in light gray. |
| In the text | |
 |
Fig. 3. Frequency dependency of the polarization degree. Top: MWL polarization degree as a function of frequency during all three IXPE epochs. Bottom: ratio of the frequency-dependent polarization degree to the corresponding X-ray polarization degree. |
| In the text | |
 |
Fig. 4. Fractional variability (Fvar) as a function of the frequency during the IXPE epochs. Fvar is computed using all data from Fig. 1 that are within the IXPE time windows. In the radio, we consider slightly relaxed simultaneity criteria and also include measurements that took place less than half a day before the start or after the end of the IXPE observing times (see the main text for more details). Radio, optical, IR, and Swift data are daily binned. We include the Fvar from the NuSTAR and XMM-Newton multi-hour exposures using ≈30 min binning. These measurements are plotted in the gray since the two instruments did not gather data for all IXPE epochs, which biases the comparison with other wavebands. |
| In the text | |
 |
Fig. 5. MAGIC and NuSTAR intra-night light curve between June 4, 2022 (MJD 59734) and June 5, 2022 (MJD 59735), corresponding to the IXPE 2 epoch. Upper panel: Light curve above 400 GeV obtained with MAGIC. A constant model fit is showed in dashed gray with the corresponding reduced χ2. Lower panel: Light curves for the 3–7 keV and the 7–30 keV band taken by NuSTAR, and constant fits for both. Fluxes from both instruments are computed in ≈30 min time bins, except for the first bin that is ≈40 min long due to a limited exposure of NuSTAR around at the start of the MAGIC observation. |
| In the text | |
 |
Fig. 6. MAGIC flux versus NuSTAR flux and quantification of the correlation during the IXPE 2 epoch. The MAGIC flux is computed above 400 GeV while the X-ray flux is evaluated in two different energy bands: 3–7 keV for the left panel and 7–30 keV for the right panel. In each panel, the obtained Pearson’s r coefficient is indicated. We specify below the p-value that describes the probability of obtaining the observed r coefficient for two uncorrelated light curves. This p-value was estimated based on Monte Carlo toy simulations (see the main text for more details). |
| In the text | |
 |
Fig. 7. Zoomed-in view of the NuSTAR light curves in the 3–7 keV and 7–30 keV bands during the IXPE 2 and IXPE 3 epochs. The top panel report the fluxes in 1 h bins. The second panel from the top is the α index evolution derived from fits of the NuSTAR spectra. The last two panels show the simultaneous polarization degree and polarization angle in the X-ray band (IXPE), optical and radio bands. |
| In the text | |
 |
Fig. 8. Log-parabola photon index, α, versus 3–7 keV and 7–30 keV flux as measured by NuSTAR during the third IXPE observation (IXPE 3 period). The data are 1 h binned and α is obtained by fitting a log-parabola function that has a fixed curvature parameter β = 0.45. The gray arrows show the direction of time, and the blue and red arrows in the middle of the panels depict the clockwise and counterclockwise directions observed in the data, respectively. |
| In the text | |
 |
Fig. 9. DCF computed for the MAGIC 0.2 − 1 TeV and Swift-XRT 2–10 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue, and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. 10. DCF computed for the MAGIC > 1 TeV and Swift-XRT 2–10 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue, and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. 11. Correlation between the polarization degree and flux in the R band over the entire campaign. The dotted black line is a linear fit, yielding a best-fit slope of a = 0.52 ± 0.09. The Pearson’s r of the correlation is r = 0.8 ± 0.1. The associated p-value is pvalue = 1 × 10−5. |
| In the text | |
 |
Fig. 12. Relativistic beaming effects due to the travel along a helical path within the jet. Top panel: Flux variability amplitude caused by the evolution of the Doppler factor, δ, when an emitting zone is traveling downstream along a helical path. The variability amplitude is plotted as a function of the phase of the spiral rotation. The horizontal dotted blue line gives the observed variability amplitude in the 3–7 keV band. Bottom panel: Corresponding Doppler factor, δ, as a function of the spiral rotation phase. The curves are produced for different jet axis angles (θ) relative to the line of sight. The zone is assumed to move with a Lorentz factor Γb = 20 in a helical field with a pitch angle of 2.9° (see the main text for more details). |
| In the text | |
 |
Fig. A.1. XMM-Newton light curve from the EPIC-MOS2 camera in the 0.3-2 keV and 2-10 keV bands during the IXPE 1 epoch. The lower panel is the ratio between the 2-10 keV and 0.3-2 keV fluxes. |
| In the text | |
 |
Fig. A.2. XMM-Newton light curve from the EPIC-MOS2 camera in the 0.3-2 keV and 2-10 keV bands during the IXPE 2 epoch. The lower panel is the ratio between the 2-10 keV and 0.3-2 keV fluxes. |
| In the text | |
 |
Fig. B.1. DCF computed for the MAGIC 0.2 − 1 TeV and Swift-XRT 0.3-2 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. B.2. DCF computed for the MAGIC > 1 TeV and Swift-XRT 0.3-2 keV light curves between MJD 59700 (May 1, 2022) and MJD 59740 (June 10, 2022) with a time binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue, dark blue and pink dashed lines show the 2σ, 3σ and 4σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. C.1. DCF computed for the Swift-UVOT W1 and Swift-XRT 0.3-2 keV light curves over the second part of the MWL campaign, between MJD 59710 (May 11, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. C.2. DCF computed for the Swift-UVOT W1 and Swift-XRT 2-10 keV light curves over the second part of the MWL campaign, between MJD 59710 (May 11, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. C.3. DCF computed for the Swift-UVOT W1 and Swift-XRT 0.3-2 keV light curves over the full MWL campaign, between MJD 59695 (April 26, 2022) and MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. C.4. DCF computed for the Swift-UVOT W1 and Swift-XRT 2-10 keV light curves over the full campaign, between MJD 59695 (April 26, 2022) to MJD 59760 (June 30, 2022), with a time-lag binning of 2 days. The red points are the obtained DCF values and their uncertainties. The light blue and dark blue dashed lines show the 2σ and 3σ significance bands, respectively (see the main text for more details). |
| In the text | |
 |
Fig. D.1. Results of a one-zone SSC model applied to the IXPE 1 (top panel) and IXPE 2 (bottom panel) epochs in order to constrain the physical parameters of the X-ray and VHE emitting region. The data are plotted with cyan markers, and the model is shown as a solid blue line. The obtained modeling parameters are listed in Tables D.1 and D.2. The reader is referred to Appendix D for more details on the model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



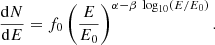
![$$ \begin{aligned} \psi = \arccos { \left[ \cos {\theta } \cos {\zeta } +\sin {\theta } \sin {\zeta } \cos {\phi } \right] } ,\end{aligned} $$](/articles/aa/full_html/2024/04/aa47988-23/aa47988-23-eq17.gif)