EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A334 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A334
Number of page(s) 18
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202451395
Published online 21 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Abundance gradients along the Galactic disk can provide a fundamental constraint for studies of the formation and chemical evolution of the Galaxy. Different stellar and nebular Galactic tracers that correspond to different epochs in the evolution of our Galaxy have been used to probe radial abundance gradients. These are open clusters (OCs, e.g. Randich et al. 2003, 2022; Magrini et al. 2010; Yong et al. 2012), HII regions (e.g. Balser et al. 2011; Esteban et al. 2017; Méndez-Delgado et al. 2022), young massive O and B stars (e.g. Daflon & Cunha 2004; Bragança et al. 2019), classical Cepheids (CCs, e.g. Lemasle et al. 2007, 2008; Luck & Lambert 2011; Genovali et al. 2015; Kovtyukh et al. 2022), planetary nebulae (PNe, e.g. Maciel et al. 2003; Henry et al. 2010; Stanghellini & Haywood 2010, 2018), as well as field stars with precise stellar ages (e.g. Anders et al. 2017; Santos-Peral et al. 2021).

The plethora of information from all these tracers has been carefully interpreted by means of models, allowing us to understand fundamental properties for the Milky Way (MW) disk formation. These include: the inside-out mechanism (e.g. Matteucci & Francois 1989; Chiappini et al. 2001; Schönrich & McMillan 2017), variable star formation efficiency (SFE) that is higher in the inner regions than in the outer ones (e.g. Colavitti et al. 2009; Grisoni et al. 2018; Palla et al. 2020b), and radial gas flows (e.g. Portinari & Chiosi 2000; Spitoni & Matteucci 2011; Bilitewski & Schönrich 2012; Cavichia et al. 2014). Moreover, studies on tracers of the ‘old’ stellar gradients have given important information on the impact of the process of stellar radial migration (e.g. Minchev et al. 2018; Willett et al. 2023).

On the other side, the analysis of spectroscopic data from ground based surveys, such as APOGEE (e.g. Hayden et al. 2015; Queiroz et al. 2020), Gaia-ESO (GES, e.g. Recio-Blanco et al. 2014; Kordopatis et al. 2015; Rojas-Arriagada et al. 2016), and GALAH (Buder et al. 2019, 2021), the accurate asteroseismic stellar ages (e.g. Pinsonneault et al. 2014, 2018; Miglio et al. 2021) and the kinematics and dynamical properties provided by the Gaia mission (Gaia Collaboration 2016, 2018, 2021, 2023b) have pointed towards the existence of two sequences of stars in the [α/Fe]1 versus [Fe/H] abundance pattern in the MW disk: the so-called high-α and low-α sequences.

To explain the wealth of these data, Palla et al. (2020b); Palla et al. (2022, see also Spitoni et al. 2019, 2021) suggested the that presence of this feature (also known as α-bimodality) may be connected to to a delayed (≳3 Gyr) accretion of gas. The latter forges the low-α sequence of stars, while high-α stars are formed promptly in a gas infall episode occurring in the first phases of Galactic formation. This scenario is confirmed by several models and simulations of the evolution of galactic disks (e.g. Noguchi 2018; Grand et al. 2018; Mackereth et al. 2018; Buck 2020), which suggested that the bimodality may be strictly connected to a delayed accretion of gas of a primordial and/or metal-poor chemical composition.

To reproduce the chemical abundances from Gaia DR3 Radial Velocity Spectrometer (RVS) spectra in the solar vicinity (Gaia Collaboration 2023a; Recio-Blanco et al. 2023) and, in particular, a population of massive stars with evidences of a recent chemical impoverishment, Spitoni et al. (2023) recently suggested a novel scenario of chemical evolution. In it the low- α population of stars is generated by two distinct gas accretion episodes, with the latter infall happening at very recent times (<3 Gyr of age). This scenario is constrained by the star formation histories for disk stars inferred from Gaia DR1 and DR2 color-magnitude diagrams (CMDs, Bernard 2017; Ruiz-Lara et al. 2020), which show evidence for short episodes of enhanced star formation (hereafter, SF) in recent times. In this model, the enhanced SF is triggered by the gas infall, which in turn causes the visible chemical impoverishment in the young stellar population as observed by Gaia RVS.

In the light of these recent development for the MW disk formation and evolution, we exploited the OCs from the last data release of the Gaia-ESO survey (Randich et al. 2022) to investigate the late evolution of radial chemical gradients in the Galaxy. In fact, OCs are considered excellent tracers of the chemical properties of the disk stellar populations of our Galaxy, including the spatial distribution of elemental abundances, especially when observed with high-resolution spectroscopy (Spina et al. 2022). In this regard, the Gaia-ESO survey (Gilmore et al. 2012, 2022; Randich et al. 2013, 2022) is the only survey performed on a 8 m-class telescope, which put a specific focus on the population of Galactic OCs. Gaia-ESO targeted OCs over a wide range of ages, distances, masses, and metallicities, observing large unbiased samples of cluster candidates, with a well-defined selection function (Bragaglia et al. 2022; Randich et al. 2022).

From this sample, Magrini et al. (2023) selected 62 OCs, with extended radial (up to R>15 kpc) and age (up to 7 Gyr) ranges, analysing the shape of radial gradients in chemical elements spanning different nucleosynthetic origin (from oxygen to europium) and their time evolution. They found that the gradients of most of chemical elements, including the metal- licity [Fe/H], can be better approximated with a two-slope shape that is steeper in the inner regions and rather flat in the outer ones. Shallower gradient slopes in outer regions were also observed in other studies using different tracers (OCs, e.g. Carbajo-Hijarrubia et al. 2024; CCs, e.g. da Silva et al. 2023), suggesting a flat SFE law for large Galactocentric distances at variance with previously theorised (e.g. Grisoni et al. 2018; Palla et al. 2020b). In addition, Magrini et al. (2023) found that the youngest clusters in the sample (age 1 Gyr) have lower metallic- ity than their older counterpart, even though the effect could be mitigated by avoid considering stars with low surface gravity.

In this work, we compare the above-mentioned data sample with detailed chemical evolution models, which also account for the effect of stellar radial migration. We started from well- tested models under the revised two-infall scenario (Palla et al. 2020b; da Silva et al. 2023), which successfully reproduce data from high-resolution surveys in different Galactocentric regions (see also Spitoni et al. 2021) and were already adopted in the context of radial abundance gradients (Palla et al. 2020b; da Silva et al. 2023). To better investigate the observed behaviour in Gaia-ESO OCs, we then extended the comparison to the newly proposed scenario of the three-infall model (Spitoni et al. 2023), expanding this framework for the first time to the whole MW disk and discussing its feasibility in the context of the adopted dataset.

The paper is organised as follows. In Section 2 we describe the Gaia-ESO OC sample and the additional dataset adopted in this work. In Section 3, we present the model framework used, that is, from the model scenarios to the nucleosynthesis and radial migration prescriptions. In Section 4, we present the comparison between the different model predictions and the observations, also discussing the implications of the obtained results. Finally, in Section 5, we draw some conclusions.

2 Observational data

2.1 Gaia-ESO open clusters

Gaia-ESO is a large public spectroscopic survey that observed the major components of our Galaxy with VLT/FLAMES from 2011–2018 (see Randich et al. 2022; Gilmore et al. 2022, for a full description of the survey). The final release DR5.1 is public and available at the ESO website from June 2023. Gaia-ESO made use of FLAMES with both the high-resolution spectrograph UVES (operating at a resolving power of R=47 000) and the medium-resolution spectrograph GIRAFFE (R∼20 000). It observed open star clusters for about 30% of its 340 nights. The observed clusters cover a wide range in age, distance, mass and metallicity (see Randich et al. 2022), with an unbiased selection of cluster candidates. Each cluster was observed with both UVES and GIRAFFE. In particular, UVES spectra cover a wide spectral range from 480.0 to 680.0 nm (U580) or from 420.0 to 620.0 nm (U520). The large spectral interval, combined with the high signal-to-noise ratios (S/N) and with the high-resolution, have enabled an unprecedented characterisation of a large sample of open clusters, observed and analysed in a homogeneous way (Bragaglia et al. 2022; Hourihane et al. 2023). For the about 80 observed clusters, it was possible to obtain precise stellar parameters and abundances of more than 30 different ions, including those of elements belonging to all the main nucleosynthesis channels, from the lightest ones, such as Li to the heaviest one, such as Eu. The detailed chemistry of the open cluster sample in Gaia-ESO, combined with uniform ages and precise distances from Gaia (e.g. Cantat-Gaudin et al. 2020), has been applied, for instance, to calibrated age-sensitive abundance ratios, known as so-called chemical clocks (Casali et al. 2019, 2020b; Viscasillas Vázquez et al. 2022). The goal has been to investigate the nucleosynthesis of neutron-capture elements (Magrini et al. 2018, 2022; Van der Swaelmen et al. 2023; Molero et al. 2023), to study the evolution of Li abundance (Randich et al. 2020; Romano et al. 2021; Magrini et al. 2021b,a), and to study the shape and the evolution of the radial abundance gradients (Jacobson et al. 2016; Overbeek et al. 2017; Magrini et al. 2017; Spina et al. 2017, 2022; Magrini et al. 2023; da Silva et al. 2023).

In the present work, we make us of the sample of open clusters used in Magrini et al. (2023, hereafter Ma23), where the abundances for 25 chemical elements were provided for the 62 Gaia-ESO OCs older than 100 Myr. The adopted cluster ages are the same as in Viscasillas Vázquez et al. (2022) and are derived from the homogeneous analysis of Gaia photometric and astrometric data by Cantat-Gaudin et al. (2020) by means of an artificial neural network trained on a set of objects with well-determined parameters in the literature. Here, we consider the guiding radius (Rguide) as tracer of the OCs Galactocentic distance. These are computed according to the process defined by Halle et al. (2015, 2018), namely, as the average between the minimum and maximum radius of the orbits. For the latter, we calculate them by using the GALPY code with the axisymmetric potential MWPOTENTIAL2014 (Bovy 2015). For further information on the sample cluster parameters, as well as their distribution in different quantities, we refer to Viscasillas Vázquez et al. (2022). For each cluster, the membership analysis was done using both radial velocities from Gaia-ESO and proper motions and parallaxes from Gaia EDR3 (Gaia Collaboration 2021), as described in Magrini et al. (2021b), Viscasillas Vázquez et al. (2022), and Jackson et al. (2022).

2.2 A restricted sample to avoid observational biases

From a purely observational point of view, the cluster sample in Ma23 showed an unexpected behaviour regarding the evolution with time of the metallicity gradient: the youngest clusters (age < 1 Gyr) in the inner disk have lower metallicity than their older counterparts and they outline a flatter gradient below that of the older population

To distinguish the real evolution of the gradient from possible spectral analysis effects, Ma23 restricted the sample of member stars per cluster. In fact, an investigation of the internal abundances of each cluster showed that there are trends of [Fe/H] versus stellar parameters; in particular, gravity and microturbulence. These trends are not specific to Gaia-ESO but are present in all the considered spectroscopic surveys (see Fig. 10 and Appendix in Ma23). This might be due to two effects: 1) the former is related to problems in modelling the atmospheres of giant stars, which affect the spectral analysis of low-gravity giant stars, as already noted in Casali et al. (2020a) and Spina et al. (2022), and the latter to the effects of magnetic activity in young massive giant stars. Hence, the spectral analysis of giants (log g < 2.5) likely underestimates their [Fe/H] of about 0.1–0.2 dex due to the combination of these effects.

Therefore, in a conservative approach, in order to preserve the actual mean abundance of clusters, we consider a restricted sample of member stars, where only stars with log g > 2.5 and ξ < 1.8 km–1 are taken into account to compute the mean cluster abundances. The average abundances used in the present work, restricted in stellar parameters, are reported in Table C.1. In this table, we also report the different cluster parameters (i.e. age, distances, orbital parameters), which are the same as the ones introduced in Section 2.1 for the original Gaia-ESO OC sample.

2.3 Additional data sets

2.3.1 Gaia-ESO field stars

We selected a sample of about 3800 field stars in Gaia-ESO DR5.1 following the criteria of Viscasillas Vázquez et al. (2022), which we refer to for a complete description. Here we present the basic steps of our selection and the computation of their ages. Our set of field stars is composed by both field stars (GES_FLD keywords GES_MW for general MW fields, GES_MW_BL for fields in the direction of the Galactic bulge, GES_K2 for stars observed in Kepler2 (K2) fields, GES_CR for stars observed in CoRoT fields) and non members of the 62 open clusters considered in this work (age > 100 Myr). We applied some further quality selections: S/N > 20; eTeff < 150 K, elog 𝑔 < 0.25, e[Fe/H] < 0.20, and eξ < 0.20 km s–1. We also applied a further cut in abundance errors, considering only those values that have an eA(El) < 0.1.

The selection function adopted in the Gaia-ESO survey for UVES observations (see Stonkute˙ et al. 2016) favours the main sequence turn-off (MSTO), which makes up the majority of the sample. By construction, the sample of field stars has a limited extent in Galactocentric distances and it is therefore used in our analysis for comparison with the model in the [X/Fe] vs. [Fe/H] plane.

2.3.2 Classical Cepheids in da Silva et al. (2023)

Recently, da Silva et al. (2023, hereafter DS23) provided the largest (1118 spectra, 356 objects) and most homogeneous spectroscopic sample for Galactic CCs with measured metallicity from optical high-resolution, high-S/N spectra. The sample is distributed across the four Galactic quadrants and it ranges from the inner (R ∼ 5 kpc) to the outer (R ∼ 25 kpc) disk. For the distances, measurements were based either on trigonometric parallaxes from Gaia DR3 or on near-infrared period-luminosity relations (Ripepi et al. 2022). Due to the steadily variation in target’s physical properties due to their natural radial oscillations, special care was dedicated to the estimate of the different atmospheric parameters (Teff, log 𝑔, ξ), which were verified using different approaches and/or diagnostics (see also da Silva et al. 2022). In this work, we have taken advantage of the CC sample from DS23 to have an additional observational probe for present-day metallicity gradients, in addition to the young OCs from Ma23.

3 Chemical evolution of the Milky Way disk

In this section, we present the main assumptions and features of the multi-zone chemical evolution models adopted in this work. In particular, in Section 3.1, we provide the details of the revised two-infall model proposed by Palla et al. (2020b) (see also DS23). In Section 3.2, we describe the details of the three- infall framework from Spitoni et al. (2023), which we expand upon throughout this work.

For both of the chemical evolution models listed above, the basic equations that describe the chemical evolution of a given element i are: 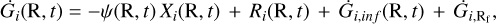G˙i(R,t)=−ψ(R,t)Xi(R,t)+Ri(R,t)+G˙i,inf(R,t)+G˙i,Rf,${\dot G_i}({\rm{R}},t) = - \psi ({\rm{R}},t){X_i}({\rm{R}},t) + {R_i}({\rm{R}},t) + {\dot G_{i,inf}}({\rm{R}},t) + {\dot G_{i,{{\rm{R}}_{\rm{f}}}}},$(1)

where Gi(R, t) = Xi(R, t) G(R, t) is the fraction of the gas mass in the form of an element i and G(R, t) is the fractional gas mass; Xi(R, t) represents the abundance fraction in mass of a given element i, with the summation over all elements in the gas mixture being equal to unity.

The first term on the right-hand side of Eq. (1) corresponds to the rate at which an element i is removed from the ISM due to star formation. The star formation rate (hereafter, SFR) is parametrised according to the Schmidt-Kennicutt law (Kennicutt 1998): 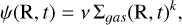ψ(R,t)=vΣgas(R,t)k,$\psi ({\rm{R}},t) = v{\Sigma _{gas}}{({\rm{R}},t)^k},$(2)

where Σ𝑔as is the surface gas density, k = 1.5 is the law index and ν is the star formation efficiency (SFE). Furthermore, Ri(R, t) (see Palla et al. 2020a for the complete expression) takes into account the nucleosynthesis from low-intermediate mass stars (LIMS, m < 8M⊙), core collapse (CC) SNe (Type II and Ib/c, m > 8 M⊙) and Type Ia SNe. For the latter, we assume the singledegenerate scenario and in particular the delay-time-distribution (DTD) by Matteucci & Recchi (2001). This choice can be considered a good compromise to describe the delayed pollution from the entire Type Ia SN population as it enables us to obtain abundance patterns that are similar to those obtained with other DTDs (see Palla 2021 for details). The Ri(R, t) output is also weighted by the initial mass function (IMF). Here, we adopt the IMF by Kroupa et al. (1993), which is preferred to reproduce the characteristics of the MW disk (Romano et al. 2005).

The last term of Eq. (1) refers to radial inflows of gas, which here are implemented following Portinari & Chiosi (2000, see also Palla et al. 2020b for a detailed description of the implementation). In our models, we used a constant speed pattern, namely, with vflow = 1 km s–1 across all radii, as suggested by Palla et al. (2020b). Low speeds (i.e. small radial inflow motion) have also been suggested by previous chemical evolution studies (e.g. Bilitewski & Schönrich 2012; Mott et al. 2013; Vincenzo & Kobayashi 2020) as well as by observations of external galaxies (e.g. Wong et al. 2004; Di Teodoro & Peek 2021).

In general, we have ignored the effect of Galactic winds on chemical evolution of the MW disk. In fact, by studying the Galactic fountains originated by the explosions of Type II SNe in OB associations, Melioli et al. (2008, 2009) and Spitoni et al. (2009) found that metals fall back to approximately the same Galactocentric region from where they were ejected. Moreover, Spitoni et al. (2009) computed the typical timescale of the fallback of this material, finding a value of 0.1 Gyr. These results were also later supported by cosmological simulation of galactic discs of virial mass >1011 M⊙, namely, encompassing the MW, which showed that the majority of the mass ejected by the disc is reaccreted on short timescales and close to the ejection location (e.g. Hopkins et al. 2023 and references therein). Therefore, galactic winds are likely to produce a negligible effect on the global chemical evolution of the Galaxy.

Table 1

Summary of the main parameters of the two-infall model (2INF) adopted in this study.

3.1 Two-infall model

In the two-infall model formalism, the model assumes two consecutive gas accretion episodes feeding the MW disk, forming the so-called high-α and low-α sequences observed in the Galactic disk. Therefore, the third term on the right-hand side of Eq. (1) can be expressed in this way: 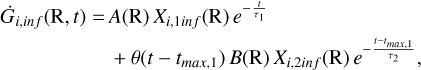G˙i,inf(R,t)=A(R)Xi,1inf(R)e−tτ1+θ(t−tmax,1)B(R)Xi,2inf(R)e−t−tmax,1τ2,$\matrix{ {{{\dot G}_{i,inf}}({\rm{R}},t) = } \hfill & {A({\rm{R}}){X_{i,1inf}}({\rm{R}}){e^{ - {t \over {{\tau _1}}}}}} \hfill \cr {} \hfill & { + \theta \left( {t - {t_{max,1}}} \right)B({\rm{R}}){X_{i,2inf}}({\rm{R}}){e^{ - {{t - {t_{{\rm{max}},1}}} \over {{\tau _2}}}}},} \hfill \cr } $(3)

where Gi,inf (R, t) is the infalling material in the form of element i and Xi,Jinf is the abundance of the same element for the J-th infall. Then, τ1 and τ2 are the timescales of the two infall episodes, while tmax,1 indicates the time of maximum infall, which is also the delay between the first and the second infall episodes. θ is the Heavyside step function, while A(R) and B(R) coefficients are set to reproduce the present-day total surface mass density of the high-α and low-α disks at different Galac- tocentric radii. These latter are assumed to have exponential profiles, in this way: 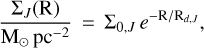ΣJ(R)M⊙pc−2=Σ0,Je−R/Rd,J,${{{\Sigma _J}({\rm{R}})} \over {{{\rm{M}}_ \odot }{\rm{p}}{{\rm{c}}^{ - 2}}}} = {\Sigma _{0,J}}{e^{ - {\rm{R}}/{{\rm{R}}_{d,J}}}},$(4)

where the disk scale length Rd,J is 3.5 kpc for the low-α disk (J = 2) and 2.3 kpc for the high-α one (J = 1, see Palla et al. 2020b and references therein). The quantities Σ0,J are tuned to reproduce the total surface mass density in the solar neighbourhood as provided by McKee et al. (2015) of 47.1 ± 3.4 M⊙ pc–2.

In this work, we take advantage of the model prescriptions adopted in Palla et al. (2020b) and later revised in DS23. The model is thus a revised version of the two-infall paradigm (see also Spitoni et al. 2019) in which two consecutive gas accretion episodes are separated by a delay of tmax,1 = 3.25 Gyr. The fairly large delay relative to the ’classical’ two-infall paradigm (of 1 Gyr, see Chiappini et al. 1997; Romano et al. 2010) allows us to reproduce [α/Fe] vs. [Fe/H] abundance diagrams (e.g. Palla et al. 2020b; Spitoni et al. 2021) throughout the MW disk, as well as the stellar ages trends (e.g. Spitoni et al. 2019; Nissen et al. 2020) in the solar vicinity.

Going into more detail, in the first infall (forging the high-α sequence) the timescale of gas accretion is fixed at τ1 =1 Gyr at all radii, with also a fixed SFE of ν = 2 Gyr–1. For the second gas-infall episode (forming the low-α sequence), the timescale for gas accretion τ2 increases linearly with radius according to the inside-out scenario (following Romano et al. 2000; Chiappini et al. 2001 law). In order to reproduce the slope observed in radial abundance gradients of CCs in DS23, as well as the gradients in other physical quantities such as SFR and gas density (e.g. Stahler & Palla 2005; Nakanishi & Sofue 2003, 2006), the SFE of the second infall episode is variable depending on the galac- tocentric radius, with values between ν = 5 Gyr–1 (at R= 4 kpc) and ν = 0.4 Gyr–1 (from R> 12 kpc). In addition, inward radial gas flows with a constant velocity of vflow = 1 km s–1 are also needed to reproduce the gradients, as discussed above. A summary of all the main parameters adopted in this work for the two-infall model are listed in Table 1.

3.2 Three-infall model

In their recent work, Spitoni et al. (2023, hereafter Sp23) proposed a new chemical evolution framework for the Galactic disk components, constrained by the star formation histories inferred from CMD analyses in Gaia DR1 and DR2 (Bernard 2017; Ruiz-Lara et al. 2020). These works revealed enhanced SF activity within the last 2–3 Gyr. This is mimicked in the chemical evolution model by including a recent (age < 3 Gyr) gas infall episode, which triggers this enhanced SF at late times. In this way, Sp23 were also able to reproduce the new abundance ratios provided by the General Stellar Parametriser-spectroscopy module for Gaia DR3 (Gaia Collaboration 2023a; Recio-Blanco et al. 2023). These results show a chemical impoverishment in the young population of stars in the solar neighbourhood. In this work, we extend the approach presented in Sp23 to the whole MW disk, in order to investigate abundance gradients.

In this model, the functional form of the gas infall rate is: 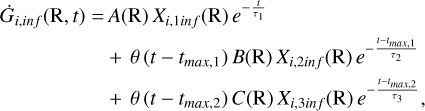G˙i,inf(R,t)=A(R)Xi,1inf(R)e−tτ1+θ(t−tmax,1))B(R)Xi,2inf(R)e−t−tmax,1τ2+θ(t−tmax,2)C(R)Xi,3inf(R)e−t−tmax,2τ3,$\matrix{ {{{\dot G}_{i,inf}}({\rm{R}},t) = } \hfill & {A({\rm{R}}){X_{i,1inf}}({\rm{R}}){e^{ - {t \over {{\tau _1}}}}}} \hfill \cr {} \hfill & { + \theta \left( {t - {t_{max,1)}}} \right)B({\rm{R}}){X_{i,2inf}}({\rm{R}}){e^{ - {{t - {t_{max,1}}} \over {{\tau _2}}}}}} \hfill \cr {} \hfill & { + \theta \left( {t - {t_{max,2}}} \right)C({\rm{R}}){X_{i,3inf}}({\rm{R}}){e^{ - {{t - {t_{max,2}}} \over {{\tau _3}}}}},} \hfill \cr } $(5)

where τ3 is the timescales of the third gas accretion episode, tmax,2 is the Galactic time associated to the start of the third infall, and C(R) is the coefficient to reproduce the present-day total surface density of the third accretion episode Σ3. Here, the sum between the latter and the total surface density of the second infall (Σ2) is equal to the density profile as described in Section 3.1 for the low-α disk in the two-infall model. All the other variables are as in Eq. (3). In fact, the new model uses the framework presented in Section 3.1, but split the low-α sequence into two distinct gas accretion episodes in order to mimic the recent enhanced SF activity. Therefore, we leave all the parameters adopted for the first two infall episodes unchanged, such as the infall timescales and the SFEs at different Galactocentric radii, as well as the IMF (from Kroupa et al. 1993).

For what concern the third additional gas accretion, instead, we set its starting time at tmax,2 = 11 Gyr (as in Sp23) for all the Galactocentric radii. For the other parameters, namely, the SFE, ν3, the timescale of infall, τ3, and the total surface mass density accreted by the third gas infall, we test different parametrisations, which are listed in Table 2:

  1. First, we adopted a setup that is very similar to the one proposed by Sp23 (3INF-1), shown in Table 2 (upper row). Here, the parameters of the third infall, i.e. tmax,2, τ3, Σ2/Σ3 are the same of the latter paper. Concerning the SFE ν3, rather than fixing the value adopted in Sp23, we fixed the proportion between the SFE in the second and third infall episode to be similar to the one used in that paper;

  2. To test further the viability of the three-infall scenario in the context of radial gradients, we allow the third infall parameters relative to the values adopted in the model 3INF- 1 to vary. While leaving constant the starting time of the third infall (to be consistent with SF peaks as shown e.g. by Ruiz-Lara et al. 2020), we acted on all the other physical parameters, namely, the infall timescale, τ3, the SFE, ν3, and for the ratio between the baryonic mass accreted by the second and third infall Σ2/Σ3. The parameter for this setup (3INF-2) are shown in Table 2 (bottom row).

Table 2

Third infall parameters adopted in the models in this paper.

3.3 Nucleosynthesis prescriptions

The nucleosynthesis prescriptions and the implementation of the stellar yields are fundamental ingredients for chemical evolution models. LIMS, massive stars, and Type Ia SNe play a fundamental role in shaping the [X/Fe] versus [Fe/H] abundance patterns as well as radial abundance gradients of the elements of the periodic table.

In this work, we mainly adopt the prescriptions listed below:

However, underlying uncertainties in stellar evolution and nucleosynthesis theory may limit our chances of getting a firm grasp on the evolutionary scenario for the Galaxy. For this reason, we also test other stellar yields for massive stars and Type Ia SNe. In particular, we ran additional models taking advantage of the stellar yields from Kobayashi et al. (2006, 2011) for massive stars. Concerning Type Ia SNe, instead, we also adopted either yields from Leung & Nomoto (2018, benchmark model), or Leung & Nomoto (2020, bubble detonation pattern model). These represent some of the most recent Type Ia SN models for different progenitor classes, namely, near-Chandrasekhar mass white dwarfs (near-MCh, Leung & Nomoto 2018) and subChandrasekhar mass white dwarfs (sub-MCh, Leung & Nomoto 2020, see Kobayashi et al. 2020; Palla 2021 for more details).

3.4 Accounting for migration and observational uncertainties

The overall picture of the MW shows also evident signatures of stellar migration, both on theoretical and observational scales (e.g. Schönrich & Binney 2009; Minchev et al. 2011, 2018; Kordopatis et al. 2015), even when specifically focusing on OCs (e.g. Anders et al. 2017; Spina et al. 2021; Myers et al. 2022). Therefore, we included stellar radial migration prescriptions from the literature to account for this phenomenon in the models. In particular, we implemented migration in the chemical evolution model by adopting the approach already tested in Palla et al. (2022) for MW disk stars. It is worth noting that OCs are more massive than single stars; therefore, the effect of the interactions with perturbing structures should be (in principle) less pronounced than for field stars (e.g. Zhang et al. 2021; Ma23), especially for young-intermediate ages (see Viscasillas Vázquez et al. 2023). However, a model for radial migration valid for field stars is appropriate within our work. It gives at least a robust upper limit on the effect of radial migration on OCs, which is a necessary mechanism to properly explain their radii, abundances, and age trends in the Galactic disk.

In the following, we provide some details on the implementation, which is extensively described in Frankel et al. (2018). Here, migration is seen as a result of a diffusion process, which is the effect of repeated and transient torques on stars by features such as spiral arms or a bar and it is treated in a parametrical way. Following Sanders & Binney (2015) and adapting their parameterization to a Galactocentric radius coordinate, the probability for a star to currently be located at a Galactocentric radius Rf, given that it was born at a radius, R0 , and at a certain age can be written as: 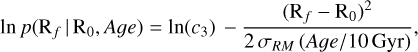lnp(Rf∣R0,Age)=ln(c3)−(Rf−R0)22σRM(Age/10 Gyr),$\ln p\left( {{{\rm{R}}_f}\mid {{\rm{R}}_0},Age} \right) = \ln \left( {{c_3}} \right) - {{{{\left( {{{\rm{R}}_f} - {{\rm{R}}_0}} \right)}^2}} \over {2{\sigma _{RM}}(Age/10\,{\rm{Gyr}})}},$(6)

where σRM is the radial migration strength and c3 a normalization constant ensuring that stars do not migrate to negative radii. For σRM, we adopted a value of 3, as found by Frankel et al. (2020) as a result of their Bayesian fitting procedure of APOGEE red clump stars in the low-α disk. The value above mentioned refers to the churning3 strength, as we already account for blurring effect by considering OCs guiding radius (Rguide) rather than their present-day Galactocentric radius RGC.

It is worth noting that the migration framework adopted is in 1D, i.e. it is not considering azimuthal variations in migration strength. In this way, it can be fully integrated within the chemical evolution models described previously in this Section. The 1D assumption is robust, as various works showed rather small azimuthal abundance variations in galaxies ISM (e.g. Kreckel et al. 2019). Another possible limitation of the adopted migration model is the assumption of no radial or temporal dependence on the migration strength. However, including these dependencies means adding further and uncertain assumptions on the inventory of speeds and strengths of spiral and bar patterns during Galactic evolution (see Frankel et al. 2018). In any case, the calibration of the model parameters on a sample of low-α disc stars extending up to radii ≃15 kpc (Frankel et al. 2020) allows for a radial and temporally averaged estimate of migration in a radial range that comprises all the OCs described in Section 2, except one (Br29).

We also accounted for the effect of observational uncertainties on the chemical abundances of the predicted stellar populations in our model. In particular, we added at each Galactic time, t, a random error to the abundances of the stars formed at t (see also Spitoni et al. 2019; Palla et al. 2022). In this way, we have for each chemical element a ‘new abundance’, defined as: [X/H]new (t)=[X/H](t)+N([X/H],σ[X/H]),${[{\rm{X}}/{\rm{H}}]_{new{\rm{}}}}(t) = [{\rm{X}}/{\rm{H}}](t) + {\cal N}\left( {[{\rm{X}}/{\rm{H}}],{\sigma _{[{\rm{X}}/{\rm{H}}]}}} \right),$(7)

where N is a random function with normal distribution. To make a fair comparison with the Ma23 data set adopted in this study, we set the standard deviation σ[X/H] to correspond to the average spread observed within the OCs in the age intervals of interest, namely, 0.1 < Age/Gyr< 1, 1 < Age/Gyr< 3, 3 < Age/Gyr< 7.

thumbnail Fig. 1

Time evolution of the radial [Fe/H] gradient as predicted by the two-infall model. Filled circles with errorbars are the OC sample by Magrini et al. (2023), which are divided in three age bins: young (Age < 1 Gyr, blue points), intermediate (1 < Age/Gyr < 3, green points), and old (Age > 3 Gyr, red points). Solid lines are the results for the [Fe/H] gradient, as predicted by the two-infall model at 0.5 Gyr (blue lines), 2 Gyr (green lines), and 5 Gyr (red lines). In this plot, and in the following Figures, we use the guiding radius of the orbit, computed as the average between the Apogalacticon and Perigalacticon radii (see Section 2.1), as an indication of the location of each cluster in the disk.

4 Results

In this section, we show the results of the comparison between the models presented in Section 3 and the Ma23 OC sample. In particular, in Section 4.1, we look at the prediction of the two-infall model. In Secton 4.2, we instead show the gradients obtained by means of the three-infall scenario in the light of the data at disposal, discussing such a scenario in Section 4.3.

4.1 Comparing observed gradients with the standard two-infall scenario

In Fig. 1, we show the time evolution of the [Fe/H] as predicted by the two-infall model and compared to the OC data presented in Ma23. From this sample, we removed the Blanco 1 cluster due to its extremely high internal spread observed in metallicity (σ > 0.5 dex), which may hide problems in terms of the abundance derivations for their members. Coming back to Fig. 1, we see that the model captures the general trend of the data: the gradient slope clearly decreases going towards larger radii, in agreement with the trend shown by OCs. This result confirms the conclusion reported in DS23 of a flattening of the gradient at R ≳ 12 kpc, which requires a flat behavior of the SFE at large Galactocentric radii.

However, if we focus on different age bins, we note that OCs with Age < 1 Gyr (blue points) are clearly below the prediction from the model. Moreover, we note that the metallicity of these OCs is lower than that of older clusters, namely, the ones with 1 < Age/Gyr < 3 (green points). Therefore, such a decrease in metallicity with decreasing age cannot be reproduced by genuine chemical evolution model predictions in a scenario of continuous SF, as that of the two-infall model in the age ranges investigated in this study: subsequent stellar generations are progressively enriching the ISM in metals, as demonstrated by the model lines in Fig. 1.

For this reason, we tried to investigate whether the inclusion of effect of stellar migration and abundance uncertainties/spread within OCs (see Section 3.4 for details) may reconcile predictions and observations. The results are shown in Fig. 2. Here, the density plots represent the probability of finding a star with an abundance [X/H] at a Galactocentric radius R in a certain age bin, namely, Age > 3 Gyr (left panel) 1 < Age/Gyr < 3 (central panel), and Age < 1 Gyr (right panel), according to the predictions by the two-infall model. In order to highlight the spread caused by the inclusion of the different effects, the density plot in Fig. 2 (as well as subsequent figures) is represented in log scale. By looking at the left and central panels of the figure, we can see that the model predictions generally capture the observed slope and spread within Ma23 OC sample well, with just the exception of few objects with 10 ≲ R/kpc ≲ 12 in the intermediate-age bin. On the other hand, the right panel clearly shows that young clusters are clearly overestimated by model predictions at different radii. This is also demonstrated by the plotted solid and dashed contour lines, showing the limits in which are contained the 68 and 95% of the predicted stars, respectively. Almost all the observed clusters are, in fact, outside the 2σ of the distribution.

However, as noted by Ma23, abundances in stars with lower surface gravity log g and higher mictroturbolence parameter ξ are susceptible to artifacts in stellar spectral analysis (see Section 2.2). In turn, this may affect the reliability of the obtained OC abundances especially for young clusters, which are more prone to contain such stars. Therefore, we decide to remove stars with log g < 2.5 and ξ > 1.8 km s-1, as suggested by Ma23, to minimise the possible bias introduced in stellar abundance determination within clusters. Despite such a choice costs a not negligible number of OCs for the data-model comparison, this is the only way we can assure robust estimations for different chemical abundances.

In Fig. 3, we show the comparison between the models already shown in Fig. 2 and the Ma23 OC sample with imposed cuts on individual stellar parameters (hereafter, restricted sample). As mentioned above, the old and intermediate age bins are barely affected by the cut in stellar parameters and therefore the data-model comparison the left and central panel is very similar to what already shown in Fig. 2. For the right panel, we see instead that the restricted sample shows in general larger metal- licities than those observed in the full OC sample. Nonetheless, the observed [Fe/H] are still clearly overestimated by the prediction of two-infall model, with most of the clusters still outside the 2σ of the predicted distribution.

This is also highlighted in Table 3, where we show intercepts and slopes of gradient linear fits for the full and restricted OC samples and the two-infall model predictions in different age bins. The fits were obtained in the radial range below R < 12 kpc: this choice was made to avoid the influence of the gradient flattening at large radii, which is found to start around this Galactocentric distance (see, e.g. Carraro et al. 2007; Magrini et al. 2017; Donor et al. 2020; DS23). For the young age bin, the restricted sample shows a significant increase in the fit intercept relative to the full sample, but still this is around 0.2 dex lower than what predicted by the two-infall model. Therefore, even by considering stellar migration and abundance uncertainties effects, these are not sufficient to explain the low [Fe/H] imprinted in the data sample.

We also checked whether uncertainties on cluster ages can be a source of bias for such a result. We considered either the cases of (i) ‘internal’ uncertainties for the age derivation method adopted in this work and (ii) adoption of different isochrones grids and/or different photometric datasets to derive ages. For (i), we performed 1000 Monte Carlo resamplings of the age of the clusters according to their uncertainties. We consider an age uncertainty of log(Age) = 0.2 dex, as found in Cantat-Gaudin et al. (2020) for clusters older than log(Age/yr) > 8.5 in their validation sample4. Even by randomly perturbing the cluster ages according to the uncertainties, we still find a decrease >0.15 dex (precisely, from 0.70 to 0.52 dex) between the intercepts in the intermediate and young age bins relative to the ones shown in Table 3 for the restricted sample. For (ii), instead, we refer to Jeffries et al. (2023), who compared different sets of age determinations for OCs in Gaia-ESO, including a large fraction of the OCs used in this work. We find that the difference between the mean literature ages (from Jeffries et al. 2023) and the ages adopted in this work is always lower than the uncertainty of log(Age) = 0.2 dex adopted for our resampling test: therefore, the distribution of gradient in different age bins will remain similar even when changing the ingredients in the age derivation.

To further inspect the low [Fe/H] abundances by OCs at young ages, we also considered the metallicities derived for the CC sample in DS23 (see Section 2). It is worth noting that the latter sample provided homogeneous derivation of Fe abundances relative to the OC sample adopted here, preventing any additional observational bias. Both the datasets are shown in Fig. 4, together with the prediction for the young age bin by the two-infall model. We note that here (and in the following figures), we have avoided showing the contours of the predicted stellar distribution to avoid overcrowding the plots. Despite the much larger abundance spread observed in DS23 sample, the figure shows that the bulk of Cepheids observed in DS23 up to a radius about ∼10 kpc are also underabundant relative to the model predictions. For larger radii instead, the very large spread in [Fe/H] and the relevant abundance uncertainties for distant Cepheids (we do not show them here for sake of readability, but they arrive up to 0.25 dex) do not allow us to draw strong conclusions, despite the hint of a flattening of the radial metallicity gradient at large Galactocentric distances remains (see DS23 and references therein). In any case, the superposition between the two datasets, which we recall have been obtained using different gradient tracers, strengthen the findings described in this section.

As described in Section 3.3, we also ran additional simulations using different yields for massive stars and Type Ia SNe. In this way, we were able to test the dependence of the observed present-day gradient overestimation on nucleosynthetic calculations.

The results for these runs are shown in Appendix A. They highlight that the theoretical predictions with different stellar yields are very similar, with an overestimation of the present-day gradient in the two-infall model and a similar evolution of the predicted gradient through cosmic time. This denotes that the conclusions of the evolutionary scenarios on the [Fe/H] gradient are marginally affected by the nucleosynthesis prescriptions. Therefore, in the rest of paper, we proceed by using the sets of yields adopted throughout this section.

thumbnail Fig. 2

Time evolution of the radial [Fe/H] gradient as predicted by the two-infall model at Age > 3 Gyr (left panel), 1 < Age/Gyr < 3 (central panel), and Age < 1 Gyr (right panel) for the two-infall model, including stellar migration and abundance uncertainties (see Sect. 3.4). Density plots show the normalised density (in log scale) of stars as predicted by the model in given Galactocentric bin of 0.2 kpc width. White contour lines show the limits within are contained the 68% (solid) and the 95% (dashed) of the predicted stellar distribution in a given radial bin. Solid lines show the results for the [Fe/H] gradient as predicted by the genuine chemical tracks, i.e. the ones shown in Fig. 1, at Ages=0.5 Gyr (cyan line), 2 Gyr (green line) and 5 Gyr (magenta line). Data are the same as in Fig. 1
thumbnail Fig. 3

Same as Fig. 2, but with data restricted to OCs members with log g >2.5 and ξ < 1.8 km s–1 (restricted sample).
Table 3

Comparison between OC sample by Magrini et al. (2023) and two-infall model [Fe/H] gradients at different ages.

thumbnail Fig. 4

Same as Fig. 3, but showing only the results for the young age bin (<1 Gyr), with the addition of Classical Cepheids data sample from da Silva et al. (2023) (pink filled circles).

4.2 Late-time metal dilution: Three-infall model

To explain the unexpected decrease in the [Fe/H] gradient at late times, we explore the scenario proposed by Sp23 for the solar vicinity, where a late-time burst of SF (suggested by Gaia CMD analysis, e.g. Ruiz-Lara et al. 2020) is fueled by gas accretion; this, in turn, causes a metal dilution in the ISM gas. In particular, we have extended such a scenario to the whole disk than the solar neighbourhood.

We started by adopting a setup for the third gas accretion very similar to the one by Spitoni et al. (2023), which is shown in Table 2 (upper row). Here, the parameters of the third infall are the same of the latter paper; the only exception is SFE, ν3, for which we fixed the proportion between the SFE in the second and third infall episode to be similar to the one used in Spitoni et al. (2023). In this way, we were able to preserve the gradient slope observed in the data at different ages, namely: if we apply a flat SFE with radius for the third infall, this will significantly decrease the gradient slope, which is not really seen in the observations (see Table 3). Finally, at variance with Sp23, we adopted a primordial chemical composition for the third gas infall. However, we also perform an additional run with an infall enrichment as in Sp23 (1/5 enriched with an abundance pattern as the one predicted for the high-α phase at [Fe/H]= –0.75 dex), finding negligible differences.

In Fig. 5, we show the predicted evolution of the [Fe/H] gradient by the three-infall model with parameters as for the 3INF-1 setup. The results are shown for the last 3 Gyr, namely, the ages at which this late gas accretion episode is actually acting and changing the gradient evolution. Fig. 5 shows that the effect of metal dilution by the gas accretion is too strong. In particular, the upper panel highlights that we miss to reproduce the metalrich stars in the intermediate-age bin. This is due to the very strong gas dilution happening 2.7 Gyr ago, which leads the bulk of stellar production at subsolar metallicity, even at small Galac- tocentric radii. Rather, this is not seen in OC observations which, despite of the spread seen at individual radial distances, only marginally cover the region where the model would expect to find most of the data.

This is also reflected by looking at Fig. 6, where we show the Age-[Fe/H] relation as predicted by the model 3INF-1 in different radial bins, namely, the inner (R < 7 kpc, left panel), solar (7 < R/kpc < 9, central panel), and outer (R > 9 kpc, right panel). Even accounting for migration and abundance uncertainties effects (see density bins in the figure), the prominent metal dilution prevents a good agreement with the data. This is especially evident at small Galactocentric radii (left panel), where the model fails to reproduce the age-metallicity trend within the last 3 Gyr. The situation is less dramatic at larger radii, where a large fraction of the OCs falls within the range of values allowed by the predictions. However, in the central and right panels, we also observe that the genuine chemical evolution predictions by the model at 8 and 10 kpc (solid lines in the central and left panels, respectively), slightly underestimate the metal content observed in young clusters. The slight underestimation of the present-day gradient by the model 3INF-1 can be observed in Fig. 5 (lower panel).

To test further the viability of the three-infall scenario in the context of radial gradients, we allowed the third infall parameters relative to the values proposed in Sp23 to vary. While leaving the starting time of the third infall constant (to be consistent with the SF peaks, as shown by e.g. Ruiz-Lara et al. 2020) we acted on all the other physical parameters, namely, the infall timescale, τ3, the SFE ν3 and for the ratio between the baryonic mass accreted by the second and third infall Σ2/Σ3, as already shown in Table 2 (bottom row).

In addition, we allowed for a mild chemical enrichment for the infalling gas during the third gas accretion, with half of the gas enriched at a level of [Fe/H]=–0.75 dex, with an abundance pattern that is the same as the one predicted for the high-α phase at that metallicity. This assumption is justified in the light of two possible invoked physical mechanisms behind the observed recent peak in SF (e.g. Isern 2019; Mor et al. 2019; Ruiz-Lara et al. 2020). On one hand, it is suggested a tight connection between the SF peak and the last pericentric passage of Sagittarius dSph (Ruiz-Lara et al. 2020; Roca-Fàbrega et al. 2021). In particular, the gas retained by Sagittarius after its first encounter with the Galaxy may have been definitely stripped in its second pericentric passage, contributing to the gas accretion together with steady cooling flow of gas from the hot corona. On the other hand, Nepal et al. (2024) proposed that the peak in MW disk SF was triggered by intense MW bar activity, which was shown to trigger enhanced SF in galaxies both from a theoretical (e.g. Baba & Kawata 2020) and observational (with integral field spectroscopy on local galaxies, e.g. Lin et al. 2020) points of view. Without discriminating between the two scenarios, it is therefore likely that a mild chemical enrichment have to be present in this late stage of Galactic evolution.

In Fig. 7, we show the predicted evolution of the [Fe/H] gradient by the three-infall model with parameters as for the 3INF-2 setup. In the upper panel, based the metallicity gradients in the 1–3 Gyr age bin, we note that the dilution effect is milder relative to what seen in Fig. 5. This is highlighted by the green solid and dashed lines, showing that the chemical evolution track before and almost 1 Gyr after the onset of the third infall, which have a metallicity difference of around 0.2 dex. The smaller dilution allows us to capture the trend and spread observed in OCs in this age range: here, the location of data points broadly correspond to the regions with a higher predicted probability density of stars; this is at variance with what is seen in Fig. 5. The good agreement between OC data and the 3INF-2 model is also seen in Fig. 7 (lower panel), with all the OCs in the youngest age bin falling within the range of values allowed by the model.

As done for model 3INF-1, we also compare the observed age-metallicity relations at different radii with the prediction of the model 3INF-2. These are shown in Fig. 8. As already noted in Fig. 7, here the dilution by the third gas accretion episode is much less prominent relative to the one seen in Fig. 6 for the model 3INF-1. This difference can be explained by the larger infall timescale for model 3INF-2: here, the slower gas accumulation allows dying stars to progressively pollute with metals the ISM, leaving a more prolonged but less marked decrease in metallicty. This behaviour better reproduces the observed age-metallicity trends, as no sharp dilution effects are seen in our restricted sample. Moreover, the slightly larger SFE ν3 in model 3INF-2 allows for a better agreement between the chemical evolution tracks at different radii (solid and dashed lines in Fig. 8) and the metal content in young clusters, which is instead underestimated by model 3INF-1.

To probe the three-infall scenario even further, we also looked at other chemical elements than Fe. However, in doing this we are more prone to the intrinsic uncertainties in models related to stellar nucleosynthesis, which are less significant when probing the Fe gradient (see Appendix A). To limit this problem as much as possible, we set our focus on two α-elements whose [α/Fe] versus [Fe/H] abundance patterns are generally well reproduced throughout the whole MW metallicity range with the main sets of yield adopted in this work (see Section 3.3); namely: O and Si (see Prantzos et al. 2018; Romano et al. 2019). Other α-elements, such as Mg, are severely underestimated when adopting massive stars Limongi & Chieffi (2018) prescriptions (Prantzos et al. 2018; Palla et al. 2022), while most of Fe-peak elements also suffer of the additional uncertainty on the progenitor nature of Type Ia SNe, which severely alters the abundance trends (Kobayashi et al. 2020; Palla 2021).

In Fig. 9, we show the evolution of [O/H] (upper panels) and [Si/H] (lower panels) as predicted by the model 3INF-2, compared with our restricted sample. The figure highlights a global agreement between the model scenario and the data. [Si/H] gradient resembles the trends already described in this section for Fe, sharing similar gradients slopes with the [Fe/H] gradient in different age ranges. This reflects in a rather flat [Si/Fe] gradient throghout the last Gyr of galactic evolution. On the other hand, the predicted and observed [O/H] gradient is much shallower, resulting in a positive [O/Fe] gradient. For the O gradient, we also note that in the 1–3 Gyr age bin (Fig. 9 upper left panel) all OC abundances lay in the upper end of the range of values allowed by the model, not showing any sign of particular spread as opposed to Fe and Si. However, it is worth noting that for O in general we have to rely on a much lower number of abundance data, which limit us in understanding the real motivation of this discrepancy. Nonetheless, the [O/H] gradient in the youngest age bin (Fig. 9 upper right panel) is reproduced by the model predictions. This is well in agreement with our proposed scenario.

In Fig. 10, we also report the evolution of the OCs and the three-infall scenario in the [X/Fe] vs. [Fe/H] diagram in different radial regions at different ages. In particular, we show the results for Si, as we can rely on a much larger sampling of OCs, for a more thorough comparison relative to O. In Fig. 10 (upper panels) we show the comparison for ages larger than 3 Gyr, namely, before the onset of the third infall. Here, the model predictions including the effects of migration and abundance uncertainties are shown in each radial region with colored areas. Moreover, to guide the eye, the genuine chemical tracks at 6, 8, 10 kpc (in the left, central, and right panels, respectively) are highlighted in color between 3 and 7 Gyr (i.e. the age range considered in these panels). Also, the tracks for 4 and 12 kpc in the age range considered are shown in the left and right panels. Despite of the small data sampling in this age range, we can say that data are well within the predicted [Si/Fe] versus [Fe/H] ranges considering migration and abundance uncertainties effects. In Fig. 10 (lower panel), we show instead the predictions for ages below 3 Gyr, which are the ones affected by late gas accretion. As for the upper panel, we highlight the parts of the tracks with ages <3 Gyr in color. Also in this case, the agreement between predictions and observations is remarkable, with all the clusters falling within the range of values allowed by model predictions.

thumbnail Fig. 5

Time evolution of the radial [Fe/H] gradients at 1 < Age/Gyr < 3 (upper panel) and Age < 1 Gyr (lower panel) for the model 3INF-1, including stellar migration and average OC spread (see Sect. 3.4). Lines show the results for the [Fe/H] gradient as predicted by the model at Ages=0.5 Gyr (cyan line), 1.8 Gyr (green dashed line), and 2.8 Gyr (green solid line). Data are the same as in Fig. 3.
thumbnail Fig. 6

Age-[Fe/H] relation for the model 3INF-1 in different radial ranges, i.e. R < 7 kpc (left panel), 7 < R/kpc < 9 (central panel), and R > 9 kpc (right panel), including stellar migration and OC spread (see Sact. 3.4). The density plot show the normalised density of stars (in log scale) as predicted by the model in a given age bin of 0.25 Gyr width. Lines are genuine chemical tracks at 6, 8, and 10 kpc (solid) and 4 and 12 kpc (dashed). Filled circles represent the restricted sample within OCs in Magrini et al. (2023).
thumbnail Fig. 7

Same as Fig. 5, but for the model 3INF-2.
thumbnail Fig. 8

Same as Fig. 6, but for the model 3INF-2.
thumbnail Fig. 9

Radial and [O/H] (upper panels) and [Si/H] (lower panels) gradients at 1 < Age/Gyr < 3 (left panels) and Age < 1 Gyr (right panels) for the model 3INF-2, including stellar migration and average OC spread (see Section 3.4). Lines show the results for the [Fe/H] gradient as predicted by the model at Ages=0.5 Gyr (cyan lines), 1.8 Gyr (green dashed lines), and 2.8 Gyr (green solid lines). Filled circles represent the restricted sample within OCs in Magrini et al. (2023).
thumbnail Fig. 10

[Si/Fe] versus [Fe/H] evolution for the model 3INF-2 in different radial ranges, namely: R < 7 kpc (left panels), 7 < R/kpc < 9 (central panels), and R > 9 kpc (right panels). The upper panels show results for ages> 3 Gyr, while the lower panels for ages< 3 Gyr. The shaded cyan, light green, and magenta areas are the model prediction in a certain radial range taking into account the effect of stellar migration and OC spread (see Section 3.4). The solid lines represent genuine chemical evolution tracks at 6, 8, and 10 kpc and are colored in the age range considered in the respective panel. Colored dashed lines are the same as colored solid lines but for the radii of 4 kpc (left panels) and 12 kpc (right panel). Colored filled circles represent the restricted sample within OCs in Magrini et al. (2023). Grey points are selected field stars from the Gaia-ESO survey.

4.3 Discussion

Throughout this work we investigated the behaviour in radial abundance gradients, as traced by Ma23 Gaia-ESO OCs, which show a decrease in their metal content towards the youngest population. Within the framework of our models of chemical evolution, that also include the effects of stellar radial migration (following Frankel et al. 2018, 2020), we observe that the observed metal impoverishment of young OCs is expected to mainly be caused by a chemical dilution from a recent gas infall episode, which, in turn, is triggering a late enhanced SF activity. These results confirm the conclusion reported in Sp23, where a very late (≲3 Gyr of age) gas accretion episode was assumed to explain the abundance ratios in the solar neighbourhood observed in Gaia DR3 RVS spectra – and extend it to a much broader range of Galactocentric radii.

However, our preferred scenario generally requires a milder metal dilution than in Sp23 in this late gas infall phase. In particular, our best scenario results to be more similar to the ‘weak dilution’ scenario detailed in Sp23, with smaller contribution of the late infall to the total mass budget and larger SFE relative to their best model. The difference in the results can be explained by the different data set adopted in this work to calibrate our best model. In fact, in Sp23 the model was tuned to reproduce the abundances from young massive stars from Gaia RVS spectra (Gaia Collaboration 2023a; Recio-Blanco et al. 2023) and crossmatched targets in APOGEE DR17 (Abdurro’uf et al. 2022, see their Fig. 14). Ma23 showed that such a class of objects may suffer of biases in the determination of stellar abundances, with an evident decrease in their metallic content. This, in turn, critically influence our view on [X/Fe] vs. [Fe/H] diagrams and abundance gradients. This is also shown in this work, where we see how massive giants with low log g can influence our view on the gradients of young stellar populations (see Section 4.1). As shown in Magrini et al. (2023), this problem concerns spectral analysis in general and is present in various surveys (e.g. APOGEE, GALAH) regardless of the analysis method and spectral range. An effort is needed to improve the model atmospheres of low gravity giant stars, and to include the effect of the magnetic field to advance the analysis of these stars. Spectral analyses of these stars will have even more implications in the future because in the ELT era the brightest giant stars will give us detailed information about chemical abundances in distant galaxies (Roederer et al. 2024).

In the current situation, the choice of imposing motivated cuts in the stellar parameters of OC members allows us to be confident of being less prone to abundance systematics. Moreover, we compared the results of our model with all the different diagnostics available, namely, the abundance gradients in different chemical abundances as well as age-metallicity relations and [X/Fe] versus [Fe/H] abundance patterns in different Galacto- centric regions. All of them have demonstrated a good agreement between the data and models. We also verify that the proposed scenario agrees with the observed values at solar radius and gradients of different physical quantities, such as SFR and gas surface densities (see Appendix B). In this way, we ensure that our proposed scenario of chemical evolution is robust in the context of the MW disk formation.

Nonetheless, the search for unbiased samples with abundances from high-resolution spectroscopy comes at expenses of the sample size. In fact, our results are still limited by the moderate sample size of OCs within our restricted sample (≃50). More data are certainly needed to better probe the three-infall scenario of chemical evolution, imposing more stringent limits, along with a possible revision of the physical parameter values adopted in this work. In particular, further sampling in age and in Galactocentric radii will be fundamental to pursue this goal. As for example, it is worth noting that for moderate to young ages we clearly lack of data at R ≳ 12 kpc. This crucially limits our ability to draw firm conclusions on the evolution of Galactic outer regions, whose evolutionary trends are only suggested following a framework similar to that found for the innermost disk. However, reliable tracers of gradient evolution as OCs are clearly missing from the outer galaxy (see e.g. Cantat-Gaudin et al. 2020) The CCs have started to be observed with high statistical significance also in the outermost regions of the Galaxy (e.g. da Silva et al. 2023; Trentin et al. 2024), but these objects only inform us on the present-day situation. Therefore, accurate abundances and ages of the stellar populations of the outermost Galaxy are needed, and planned (e.g. 4MOST, de Jong et al. 2012; WEAVE, Jin et al. 2024; PLATO, Rauer et al. 2022) and proposed (e.g. WST, Mainieri et al. 2024) facilities will undoubtedly help us in this search.

5 Summary and conclusions

In this paper, we study the evolution of radial abundance gradients in the Milky Way (MW) by taking advantage of the sample of open clusters (OCs) from the last data release of the Gaia- ESO survey (Randich et al. 2022; Magrini et al. 2023). In fact, OCs are among the best tracers of the shape and time evolution of the radial metallicity gradient due to their ages and distances, which can be properly measured by isochrone fitting of the complete sequence, as well as to high-resolution spectroscopic observations that provide precise abundances. Gaia-ESO dedicated about 30% of its observing time to provide the largest sample of precise and homogeneous stellar parameters and abundances of member stars in Galactic OCs.

From a theoretical perspective, we started from the well- tested, revised two-infall model of chemical evolution (e.g. Palla et al. 2020b, see also Spitoni et al. 2019), which successfully reproduces data from high-resolution surveys, such as APOGEE (Ahumada et al. 2020). We extended the comparison to the newly proposed scenario of the three-infall model (Spitoni et al. 2023), proposed in the light of constraints given by Gaia star formation history (e.g. Ruiz-Lara et al. 2020) and abundance ratios (Gaia Collaboration 2023a). For all the probed scenarios, our models take into account the effects of stellar radial migration by including well tested prescriptions from the literature (Frankel et al. 2018, 2020), allowing us to directly see its impact on the late evolution of radial abundance gradients.

Our main considerations and conclusions are thus summarised as follows:

  1. Conservatively, we excluded stars whose spectral analyses may generate a metallicity bias. This choice reduces the trends between stellar parameters and metallicity within the same cluster. This solution does not solve the problem of analysing massive and/or low-gravity giants; however, it allows us to circumvent this issue until progress is made on atmosphere models for these stars and including magnetic activity.

  2. Despite restricting the OC sample to stars which should not hide biases in spectroscopic analysis, we still find a metallic- ity decrease between intermediate age (1–3 Gyr) and young (<1 Gyr) OCs. We show that the radial metallicity gradient as traced by young OCs is overestimated by the predictions of the two-infall scenario, even when accounting for the effect of stellar migration in the model. We also checked whether the adoption of different nucleosynthetic yields for massive stars and Type Ia SNe (i.e. the main contributors to Fe enrichment) may affect this result. We find negligible differences between the different runs, confirming our conclusion.

  3. To explain the observed low metallic content in young clusters, we propose that a late gas accretion episode that triggered a metal dilution would have taken place. This is in agreement with the proposed scenario of the three-infall model by Spitoni et al. (2023) for the solar vicinity. This explains the recent star formation history and abundance ratios as derived by Gaia satellite, as a consequence of recent gas infall episode triggering enhanced SF at recent ages. It is worth noting that in this work, for the first time, we have extended the three-infall scenario to the whole MW disk.

  4. At variance with the best model presented in Spitoni et al. (2023), we invoked a milder metal dilution for this late gas infall episode. In particular, our best scenario requires smaller contribution of the late infall to the mass budget forging the low-α disk (factor ∼1.5–4 lower), while larger infall timescale (τ3 ≃ 1 Gyr instead of τ3 ≃ 0.1 Gyr) and star formation efficiency (ν3 ≃ (2/3)ν2 instead of ν3 ≃ (1/2)ν2). The difference in these results can be explained by the different data sample adopted in this work. In fact, our models are thought to reproduce a sample of OCs cleaned of stars subject to biases in chemical abundance determination (Magrini et al. 2023; see also point 1 of this section), whose class is instead considered in Spitoni et al. (2023, see Gaia Collaboration 2023a; Recio-Blanco et al. 2023).

Further data are definitely needed to probe the new three-infall scenario of chemical evolution on the whole MW disk, imposing more stringent limits, along with a possible revision of the physical parameter values that have been adopted in this work. However, the constraints coming from high-resolution, unbiased chemical abundances, precise ages, and star formation histories from multiple tracers (e.g. Isern 2019; Mor et al. 2019; Ruiz-Lara et al. 2020) allow us to consider the proposed model as a robust and viable scenario for MW disk formation.

Data availability

Full Table C.1 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/A334

Acknowledgements

The authors thank the referee for the careful reading of the manuscript and the useful comments improving the paper content. M.P. acknowledges financial support from the project “LEGO – Reconstructing the building blocks of the Galaxy by chemical tagging” granted by the Italian MUR through contract PRIN2022LLP8TK_001. L.M., E.S., M.F., and S.R. thank INAF for the support (Large Grant EPOCH) and M.P., L.M., and C.V.V. for the MiniGrant Checs. L.M., M.F., and S.R. acknowledge financial support under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2.2.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenera- tionEU– Project ‘Cosmic POT’ Grant Assignment Decree No. 2022X4TM3H by the Italian Ministry of Ministry of University and Research (MUR). MM thanks the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 279384907 – SFB 1245, the State of Hessen within the Research Cluster ELEMENTS (Project ID 500/10.006) for financial support. This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’ s Excellence Strategy - EXC-2094 – 390783311. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programmes 188.B- 3002, 193.B-0936, and 197.B-1074. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the Gaia-ESO Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council. This work makes use of results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia.

Appendix A Probing present-day gradient overestimations with different yield sets

As mentioned in Sections 3.3 and 4.1, we perform additional model runs testing different massive stars and Type Ia SN yields than the reference ones used in this paper (Limongi & Chieffi 2018 and Iwamoto et al. 1999, respectively).

In the following figures, we show the results of this experiment, by reporting the gradient evolution (top panels) and the gradient in the young age bin considering the effects of stellar migration and abundance uncertainties in the model (bottom panels) In particular, Fig. A.1 shows the predicted radial [Fe/H] gradient obtained by adopting the massive star yields from Kobayashi et al. (2006) instead of those from Limongi & Chieffi (2018). In Fig. A.2, we instead report on the predicted radial [Fe/H] gradient obtained by adopting the Type Ia SN yields from an equal mixture of Leung & Nomoto (2018) (near-MCh progenitors) and Leung & Nomoto (2020) (sub-MCh progenitors) instead of those Iwamoto et al. (1999). Regarding the latter Figure, it is worth mentioning that no significant changes are obtained by employing different mixtures in Type Ia yields.

thumbnail Fig. A.1

Predicted radial [Fe/H] gradient from the model 2INF using Kobayashi et al. (2006) instead of Limongi & Chieffi (2018) yields for massive stars. Top panel: same as Fig. 1, but showing the data for the restricted OC sample. Bottom panel: same of Fig. 3, but showing only the results for the young age bin (< 1 Gyr).
thumbnail Fig. A.2

Predicted radial [Fe/H] gradient from the model 2INF using Leung & Nomoto (2018, 2020) instead of Iwamoto et al. (1999) yields for Type Ia SNe. Top panel: same as Fig. 1, but showing the data for the restricted OC sample. Bottom panel: same of Fig. 3, but showing only the results for the young age bin (< 1 Gyr).

Appendix B Gradients in physical quantities from the three-infall model

As mentioned in Section 4.3, we checked whether our three- infall scenario reproduces the constraints in other gradients than those in chemical abundances, i.e. the present-day gradients in the physical quantities.

Results of the comparison between our best model 3INF-2 and literature constraints are shown in Fig. B.1 and B.2. In Fig. B.1, we show the prediction of the model for the SFR surface density. In the left panel, we show the time evolution of this quantity at different radii, with the present-day SFR observed in the solar vicinity (see Prantzos et al. 2018) shown as reference. In the right panel, we show instead the comparison between the predicted present-day gradient and measurements from the literature (Rana 1991; Stahler & Palla 2005; Green 2014). In Fig. B.2, we display the same scheme as Fig. B.1, but for the gas surface density, where the reference value for the solar vicinity and the observed gradients are taken from Dame (1993); Nakanishi & Sofue (2003, 2006). For a detailed discussion on the adopted data sets, we refer to Palla et al. (2020b).

thumbnail Fig. B.1

Left panel: SFR surface density time evolution at 4, 8, 12, and 16 kpc (left). The present-day observed value for the solar vicinity is taken from Prantzos et al. (2018). Right panel: present-day radial SFR surface density gradient. Data are from Rana (1991) (black points with errorbar), Stahler & Palla (2005) (black squares with errorbar), Green (2014) (black crosses).
thumbnail Fig. B.2

Left panel: gas surface density time evolution at 4, 8, 12, and 16 kpc. The present-day observed value for the solar vicinity is taken from Dame (1993); Nakanishi & Sofue (2003, 2006). Right panel: present-day radial gas surface density gradient. The dashed curve is the average between the Dame (1993) and Nakanishi & Sofue (2003, 2006) data sets. The grey shaded region represents the typical uncertainty at each radius (see Palla et al. 2020b for more details).

Appendix C Restricted OC sample

As described in Section 2.2, to avoid observational biases in the computation of the mean abundance of OCs, we build a restricted sample of member stars, where only stars with log g > 2.5 and ξ < 1.8 km-1 are considered to compute the mean cluster abundances. In Table C.1, we provide the average abundances obtained with this membership selection, as well as all the obtained cluster parameters (see also Viscasillas Vázquez et al. 2022).

Table C.1

Excerpt from the list mean cluster abundances and cluster parameters from our adopted restricted sample (see 2.2).

References

  1. Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [CrossRef] [Google Scholar]
  2. Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
  3. Anders, F., Chiappini, C., Minchev, I., et al. 2017, A&A, 600, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Baba, J., & Kawata, D. 2020, MNRAS, 492, 4500 [NASA ADS] [CrossRef] [Google Scholar]
  5. Balser, D. S., Rood, R. T., Bania, T. M., & Anderson, L. D. 2011, ApJ, 738, 27 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bernard, E. J. 2017, in SF2A-2017: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, P. Di Matteo, F. Herpin, E. Lagadec, A. Lançon, Z. Meliani, & F. Royer, Di [Google Scholar]
  7. Bilitewski, T., & Schönrich, R. 2012, MNRAS, 426, 2266 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bragaglia, A., Alfaro, E. J., Flaccomio, E., et al. 2022, A&A, 659, A200 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bragança, G. A., Daflon, S., Lanz, T., et al. 2019, A&A, 625, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Buck, T. 2020, MNRAS, 491, 5435 [NASA ADS] [CrossRef] [Google Scholar]
  12. Buder, S., Lind, K., Ness, M. K., et al. 2019, A&A, 624, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cantat-Gaudin, T., Anders, F., Castro-Ginard, A., et al. 2020, A&A, 640, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Carbajo-Hijarrubia, J., Casamiquela, L., Carrera, R., et al. 2024, A&A, 687, A239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Carraro, G., Geisler, D., Villanova, S., Frinchaboy, P. M., & Majewski, S. R. 2007, A&A, 476, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Casali, G., Magrini, L., Tognelli, E., et al. 2019, A&A, 629, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Casali, G., Magrini, L., Frasca, A., et al. 2020a, A&A, 643, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Casali, G., Spina, L., Magrini, L., et al. 2020b, A&A, 639, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Cavichia, O., Mollá, M., Costa, R. D. D., & Maciel, W. J. 2014, MNRAS, 437, 3688 [NASA ADS] [CrossRef] [Google Scholar]
  21. Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [Google Scholar]
  22. Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  23. Colavitti, E., Cescutti, G., Matteucci, F., & Murante, G. 2009, A&A, 496, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. da Silva, R., Crestani, J., Bono, G., et al. 2022, A&A, 661, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. da Silva, R., D’Orazi, V., Palla, M., et al. 2023, A&A, 678, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dame, T. M. 1993, AIP Conf. Ser., 278, 267 [Google Scholar]
  28. de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, SPIE Conf. Ser., 8446, 84460T [Google Scholar]
  29. Di Teodoro, E. M., & Peek, J. E. G. 2021, ApJ, 923, 220 [NASA ADS] [CrossRef] [Google Scholar]
  30. Donor, J., Frinchaboy, P. M., Cunha, K., et al. 2020, AJ, 159, 199 [NASA ADS] [CrossRef] [Google Scholar]
  31. Esteban, C., Fang, X., García-Rojas, J., & Toribio San Cipriano, L. 2017, MNRAS, 471, 987 [NASA ADS] [CrossRef] [Google Scholar]
  32. Frankel, N., Rix, H.-W., Ting, Y.-S., Ness, M., & Hogg, D. W. 2018, ApJ, 865, 96 [NASA ADS] [CrossRef] [Google Scholar]
  33. Frankel, N., Sanders, J., Ting, Y.-S., & Rix, H.-W. 2020, ApJ, 896, 15 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gaia Collaboration (Recio-Blanco, A., et al.) 2023a, A&A, 674, A38 [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A&A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
  41. Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Grand, R. J. J., Bustamante, S., Gómez, F. A., et al. 2018, MNRAS, 474, 3629 [NASA ADS] [CrossRef] [Google Scholar]
  43. Green, D. A. 2014, IAU Symp., 296, 188 [NASA ADS] [Google Scholar]
  44. Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
  45. Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2015, A&A, 578, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2018, A&A, 616, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [Google Scholar]
  48. Henry, R. B. C., Kwitter, K. B., Jaskot, A. E., et al. 2010, ApJ, 724, 748 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hopkins, P. F., Gurvich, A. B., Shen, X., et al. 2023, MNRAS, 525, 2241 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hourihane, A., François, P., Worley, C. C., et al. 2023, A&A, 676, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Isern, J. 2019, ApJ, 878, L11 [NASA ADS] [CrossRef] [Google Scholar]
  52. Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
  53. Jackson, R. J., Jeffries, R. D., Wright, N. J., et al. 2022, MNRAS, 509, 1664 [Google Scholar]
  54. Jacobson, H. R., Friel, E. D., Jílková, L., et al. 2016, A&A, 591, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Jeffries, R. D., Jackson, R. J., Wright, N. J., et al. 2023, MNRAS, 523, 802 [NASA ADS] [CrossRef] [Google Scholar]
  56. Jin, S., Trager, S. C., Dalton, G. B., et al. 2024, MNRAS, 530, 2688 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kennicutt, Robert C., J. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [Google Scholar]
  60. Kobayashi, C., Leung, S.-C., & Nomoto, K. 2020, ApJ, 895, 138 [CrossRef] [Google Scholar]
  61. Kordopatis, G., Binney, J., Gilmore, G., et al. 2015, MNRAS, 447, 3526 [Google Scholar]
  62. Kovtyukh, V., Lemasle, B., Bono, G., et al. 2022, MNRAS, 510, 1894 [Google Scholar]
  63. Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
  64. Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
  65. Lemasle, B., François, P., Bono, G., et al. 2007, A&A, 467, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Lemasle, B., François, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Leung, S.-C., & Nomoto, K. 2018, ApJ, 861, 143 [Google Scholar]
  68. Leung, S.-C., & Nomoto, K. 2020, ApJ, 888, 80 [Google Scholar]
  69. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lin, L., Li, C., Du, C., et al. 2020, MNRAS, 499, 1406 [NASA ADS] [CrossRef] [Google Scholar]
  71. Luck, R. E., & Lambert, D. L. 2011, AJ, 142, 136 [Google Scholar]
  72. Maciel, W. J., Costa, R. D. D., & Uchida, M. M. M. 2003, A&A, 397, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Mackereth, J. T., Crain, R. A., Schiavon, R. P., et al. 2018, MNRAS, 477, 5072 [NASA ADS] [CrossRef] [Google Scholar]
  74. Magrini, L., Randich, S., Zoccali, M., et al. 2010, A&A, 523, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A&A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Magrini, L., Spina, L., Randich, S., et al. 2018, A&A, 617, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Magrini, L., Smiljanic, R., Franciosini, E., et al. 2021a, A&A, 655, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Magrini, L., Vescovi, D., Casali, G., et al. 2021b, A&A, 646, L2 [EDP Sciences] [Google Scholar]
  79. Magrini, L., Vázquez, C. V., Casali, G., et al. 2022, Universe, 8, 64 [NASA ADS] [CrossRef] [Google Scholar]
  80. Magrini, L., Viscasillas Vázquez, C., Spina, L., et al. 2023, A&A, 669, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Mainieri, V., Anderson, R. I., Brinchmann, J., et al. 2024, arXiv e-prints [arXiv:2403.05398] [Google Scholar]
  82. Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
  83. Matteucci, F., & Recchi, S. 2001, ApJ, 558, 351 [NASA ADS] [CrossRef] [Google Scholar]
  84. McKee, C. F., Parravano, A., & Hollenbach, D. J. 2015, ApJ, 814, 13 [Google Scholar]
  85. Melioli, C., Brighenti, F., D’Ercole, A., & de Gouveia Dal Pino, E. M. 2008, MNRAS, 388, 573 [Google Scholar]
  86. Melioli, C., Brighenti, F., D’Ercole, A., & de Gouveia Dal Pino, E. M. 2009, MNRAS, 399, 1089 [Google Scholar]
  87. Méndez-Delgado, J. E., Amayo, A., Arellano-Córdova, K. Z., et al. 2022, MNRAS, 510, 4436 [CrossRef] [Google Scholar]
  88. Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Minchev, I., Anders, F., Recio-Blanco, A., et al. 2018, MNRAS, 481, 1645 [NASA ADS] [CrossRef] [Google Scholar]
  91. Molero, M., Magrini, L., Matteucci, F., et al. 2023, MNRAS, 523, 2974 [NASA ADS] [CrossRef] [Google Scholar]
  92. Mor, R., Robin, A. C., Figueras, F., Roca-Fàbrega, S., & Luri, X. 2019, A&A, 624, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Mott, A., Spitoni, E., & Matteucci, F. 2013, MNRAS, 435, 2918 [Google Scholar]
  94. Myers, N., Donor, J., Spoo, T., et al. 2022, AJ, 164, 85 [NASA ADS] [CrossRef] [Google Scholar]
  95. Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [Google Scholar]
  96. Nakanishi, H., & Sofue, Y. 2006, PASJ, 58, 847 [NASA ADS] [Google Scholar]
  97. Nepal, S., Chiappini, C., Guiglion, G., et al. 2024, A&A, 681, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Nissen, P. E., Christensen-Dalsgaard, J., Mosumgaard, J. R., et al. 2020, A&A, 640, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Noguchi, M. 2018, Nature, 559, 585 [Google Scholar]
  100. Overbeek, J. C., Friel, E. D., Donati, P., et al. 2017, A&A, 598, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Palla, M. 2021, MNRAS, 503, 3216 [Google Scholar]
  102. Palla, M., Matteucci, F., Calura, F., & Longo, F. 2020a, ApJ, 889, 4 [NASA ADS] [CrossRef] [Google Scholar]
  103. Palla, M., Matteucci, F., Spitoni, E., Vincenzo, F., & Grisoni, V. 2020b, MNRAS, 498, 1710 [Google Scholar]
  104. Palla, M., Santos-Peral, P., Recio-Blanco, A., & Matteucci, F. 2022, A&A, 663, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, 19 [Google Scholar]
  106. Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., et al. 2018, ApJS, 239, 32 [Google Scholar]
  107. Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
  108. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
  109. Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2020, A&A, 638, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Rana, N. C. 1991, ARA&A, 29, 129 [Google Scholar]
  111. Randich, S., Sestito, P., & Pallavicini, R. 2003, A&A, 399, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
  113. Randich, S., Pasquini, L., Franciosini, E., et al. 2020, A&A, 640, L1 [EDP Sciences] [Google Scholar]
  114. Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Rauer, H., Aerts, C., Deleuil, M., et al. 2022, Euro. Planet. Sci. Cong., EPSC2022, 453 [Google Scholar]
  116. Recio-Blanco, A., de Laverny, P., Kordopatis, G., et al. 2014, A&A, 567, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Ripepi, V., Chemin, L., Molinaro, R., et al. 2022, MNRAS, 512, 563 [NASA ADS] [CrossRef] [Google Scholar]
  119. Roca-Fàbrega, S., Llorente de Andrés, F., Chavero, C., Cifuentes, C., & de la Reza, R. 2021, A&A, 656, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Roederer, I. U., Alvarado-Gómez, J. D., Allende Prieto, C., et al. 2024, Exp. Astron., 57, 17 [NASA ADS] [CrossRef] [Google Scholar]
  121. Rojas-Arriagada, A., Recio-Blanco, A., de Laverny, P., et al. 2016, A&A, 586, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  122. Romano, D., Matteucci, F., Salucci, P., & Chiappini, C. 2000, ApJ, 539, 235 [CrossRef] [Google Scholar]
  123. Romano, D., Chiappini, C., Matteucci, F., & Tosi, M. 2005, A&A, 430, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Romano, D., Matteucci, F., Zhang, Z.-Y., Ivison, R. J., & Ventura, P. 2019, MNRAS, 490, 2838 [NASA ADS] [CrossRef] [Google Scholar]
  126. Romano, D., Magrini, L., Randich, S., et al. 2021, A&A, 653, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Ruiz-Lara, T., Gallart, C., Bernard, E. J., & Cassisi, S. 2020, Nat. Astron., 4, 965 [NASA ADS] [CrossRef] [Google Scholar]
  128. Sanders, J. L., & Binney, J. 2015, MNRAS, 449, 3479 [NASA ADS] [CrossRef] [Google Scholar]
  129. Santos-Peral, P., Recio-Blanco, A., Kordopatis, G., Fernández-Alvar, E., & de Laverny, P. 2021, A&A, 653, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Schönrich, R., & Binney, J. 2009, MNRAS, 399, 1145 [Google Scholar]
  131. Schönrich, R., & McMillan, P. J. 2017, MNRAS, 467, 1154 [NASA ADS] [Google Scholar]
  132. Spina, L., Randich, S., Magrini, L., et al. 2017, A&A, 601, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Spina, L., Ting, Y. S., De Silva, G. M., et al. 2021, MNRAS, 503, 3279 [CrossRef] [Google Scholar]
  134. Spina, L., Magrini, L., & Cunha, K. 2022, Universe, 8, 87 [NASA ADS] [CrossRef] [Google Scholar]
  135. Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Spitoni, E., Matteucci, F., Recchi, S., Cescutti, G., & Pipino, A. 2009, A&A, 504, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
  139. Spitoni, E., Recio-Blanco, A., de Laverny, P., et al. 2023, A&A, 670, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Stahler, S. W., & Palla, F. 2005, The Formation of Stars (Hoboken: Wiley-VCH) [Google Scholar]
  141. Stanghellini, L., & Haywood, M. 2010, ApJ, 714, 1096 [NASA ADS] [CrossRef] [Google Scholar]
  142. Stanghellini, L., & Haywood, M. 2018, ApJ, 862, 45 [Google Scholar]
  143. Stonkute, E., Koposov, S. E., Howes, L. M., et al. 2016, MNRAS, 460, 1131 [CrossRef] [Google Scholar]
  144. Trentin, E., Catanzaro, G., Ripepi, V., et al. 2024, A&A, 690, A246 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  145. Van der Swaelmen, M., Viscasillas Vázquez, C., Cescutti, G., et al. 2023, A&A, 670, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  146. Ventura, P., Di Criscienzo, M., Carini, R., & D’Antona, F. 2013, MNRAS, 431, 3642 [Google Scholar]
  147. Ventura, P., Karakas, A., Dell’Agli, F., García-Hernández, D. A., & Guzman-Ramirez, L. 2018, MNRAS, 475, 2282 [NASA ADS] [Google Scholar]
  148. Ventura, P., Dell’Agli, F., Lugaro, M., et al. 2020, A&A, 641, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Vincenzo, F., & Kobayashi, C. 2020, MNRAS, 496, 80 [NASA ADS] [CrossRef] [Google Scholar]
  150. Viscasillas Vázquez, C., Magrini, L., Casali, G., et al. 2022, A&A, 660, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Viscasillas Vázquez, C., Magrini, L., Spina, L., et al. 2023, A&A, 679, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  152. Willett, E., Miglio, A., Mackereth, J. T., et al. 2023, MNRAS, 526, 2141 [NASA ADS] [CrossRef] [Google Scholar]
  153. Wong, T., Blitz, L., & Bosma, A. 2004, ApJ, 605, 183 [NASA ADS] [CrossRef] [Google Scholar]
  154. Yong, D., Carney, B. W., & Friel, E. D. 2012, AJ, 144, 95 [Google Scholar]
  155. Zhang, M., Xiang, M., Zhang, H.-W., et al. 2021, ApJ, 922, 145 [NASA ADS] [CrossRef] [Google Scholar]
1

[X/Y] = log(X/Y) - log(X⊙ /Y⊙), where X, Y are the abundances of the object studied and X⊙, Y⊙ are solar abundances.

2

In Limongi & Chieffi (2018), different yield grids considering different stellar rotation velocities vrot were built.

3

For churning (also known as cold torquing), we mean the change in orbit angular momentum that change orbit’s radius. For blurring, we intend the increase the radial oscillation amplitudes around the guiding radius of the orbit.

4

Cantat-Gaudin et al. (2020) actually found an uncertainty range between 0.1 and 0.2 dex in log(Age), but we leave 0.2 dex also to account for the age precision in the adopted training set, i.e. of log(Age) = 0.1 dex.

All Tables

Table 1

Summary of the main parameters of the two-infall model (2INF) adopted in this study.

In the text
Table 2

Third infall parameters adopted in the models in this paper.

In the text
Table 3

Comparison between OC sample by Magrini et al. (2023) and two-infall model [Fe/H] gradients at different ages.

In the text
Table C.1

Excerpt from the list mean cluster abundances and cluster parameters from our adopted restricted sample (see 2.2).

In the text

All Figures

thumbnail Fig. 1

Time evolution of the radial [Fe/H] gradient as predicted by the two-infall model. Filled circles with errorbars are the OC sample by Magrini et al. (2023), which are divided in three age bins: young (Age < 1 Gyr, blue points), intermediate (1 < Age/Gyr < 3, green points), and old (Age > 3 Gyr, red points). Solid lines are the results for the [Fe/H] gradient, as predicted by the two-infall model at 0.5 Gyr (blue lines), 2 Gyr (green lines), and 5 Gyr (red lines). In this plot, and in the following Figures, we use the guiding radius of the orbit, computed as the average between the Apogalacticon and Perigalacticon radii (see Section 2.1), as an indication of the location of each cluster in the disk.
In the text
thumbnail Fig. 2

Time evolution of the radial [Fe/H] gradient as predicted by the two-infall model at Age > 3 Gyr (left panel), 1 < Age/Gyr < 3 (central panel), and Age < 1 Gyr (right panel) for the two-infall model, including stellar migration and abundance uncertainties (see Sect. 3.4). Density plots show the normalised density (in log scale) of stars as predicted by the model in given Galactocentric bin of 0.2 kpc width. White contour lines show the limits within are contained the 68% (solid) and the 95% (dashed) of the predicted stellar distribution in a given radial bin. Solid lines show the results for the [Fe/H] gradient as predicted by the genuine chemical tracks, i.e. the ones shown in Fig. 1, at Ages=0.5 Gyr (cyan line), 2 Gyr (green line) and 5 Gyr (magenta line). Data are the same as in Fig. 1
In the text
thumbnail Fig. 3

Same as Fig. 2, but with data restricted to OCs members with log g >2.5 and ξ < 1.8 km s–1 (restricted sample).
In the text
thumbnail Fig. 4

Same as Fig. 3, but showing only the results for the young age bin (<1 Gyr), with the addition of Classical Cepheids data sample from da Silva et al. (2023) (pink filled circles).
In the text
thumbnail Fig. 5

Time evolution of the radial [Fe/H] gradients at 1 < Age/Gyr < 3 (upper panel) and Age < 1 Gyr (lower panel) for the model 3INF-1, including stellar migration and average OC spread (see Sect. 3.4). Lines show the results for the [Fe/H] gradient as predicted by the model at Ages=0.5 Gyr (cyan line), 1.8 Gyr (green dashed line), and 2.8 Gyr (green solid line). Data are the same as in Fig. 3.
In the text
thumbnail Fig. 6

Age-[Fe/H] relation for the model 3INF-1 in different radial ranges, i.e. R < 7 kpc (left panel), 7 < R/kpc < 9 (central panel), and R > 9 kpc (right panel), including stellar migration and OC spread (see Sact. 3.4). The density plot show the normalised density of stars (in log scale) as predicted by the model in a given age bin of 0.25 Gyr width. Lines are genuine chemical tracks at 6, 8, and 10 kpc (solid) and 4 and 12 kpc (dashed). Filled circles represent the restricted sample within OCs in Magrini et al. (2023).
In the text
thumbnail Fig. 7

Same as Fig. 5, but for the model 3INF-2.
In the text
thumbnail Fig. 8

Same as Fig. 6, but for the model 3INF-2.
In the text
thumbnail Fig. 9

Radial and [O/H] (upper panels) and [Si/H] (lower panels) gradients at 1 < Age/Gyr < 3 (left panels) and Age < 1 Gyr (right panels) for the model 3INF-2, including stellar migration and average OC spread (see Section 3.4). Lines show the results for the [Fe/H] gradient as predicted by the model at Ages=0.5 Gyr (cyan lines), 1.8 Gyr (green dashed lines), and 2.8 Gyr (green solid lines). Filled circles represent the restricted sample within OCs in Magrini et al. (2023).
In the text
thumbnail Fig. 10

[Si/Fe] versus [Fe/H] evolution for the model 3INF-2 in different radial ranges, namely: R < 7 kpc (left panels), 7 < R/kpc < 9 (central panels), and R > 9 kpc (right panels). The upper panels show results for ages> 3 Gyr, while the lower panels for ages< 3 Gyr. The shaded cyan, light green, and magenta areas are the model prediction in a certain radial range taking into account the effect of stellar migration and OC spread (see Section 3.4). The solid lines represent genuine chemical evolution tracks at 6, 8, and 10 kpc and are colored in the age range considered in the respective panel. Colored dashed lines are the same as colored solid lines but for the radii of 4 kpc (left panels) and 12 kpc (right panel). Colored filled circles represent the restricted sample within OCs in Magrini et al. (2023). Grey points are selected field stars from the Gaia-ESO survey.
In the text
thumbnail Fig. A.1

Predicted radial [Fe/H] gradient from the model 2INF using Kobayashi et al. (2006) instead of Limongi & Chieffi (2018) yields for massive stars. Top panel: same as Fig. 1, but showing the data for the restricted OC sample. Bottom panel: same of Fig. 3, but showing only the results for the young age bin (< 1 Gyr).
In the text
thumbnail Fig. A.2

Predicted radial [Fe/H] gradient from the model 2INF using Leung & Nomoto (2018, 2020) instead of Iwamoto et al. (1999) yields for Type Ia SNe. Top panel: same as Fig. 1, but showing the data for the restricted OC sample. Bottom panel: same of Fig. 3, but showing only the results for the young age bin (< 1 Gyr).
In the text
thumbnail Fig. B.1

Left panel: SFR surface density time evolution at 4, 8, 12, and 16 kpc (left). The present-day observed value for the solar vicinity is taken from Prantzos et al. (2018). Right panel: present-day radial SFR surface density gradient. Data are from Rana (1991) (black points with errorbar), Stahler & Palla (2005) (black squares with errorbar), Green (2014) (black crosses).
In the text
thumbnail Fig. B.2

Left panel: gas surface density time evolution at 4, 8, 12, and 16 kpc. The present-day observed value for the solar vicinity is taken from Dame (1993); Nakanishi & Sofue (2003, 2006). Right panel: present-day radial gas surface density gradient. The dashed curve is the average between the Dame (1993) and Nakanishi & Sofue (2003, 2006) data sets. The grey shaded region represents the typical uncertainty at each radius (see Palla et al. 2020b for more details).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.