| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348886 | |
| Published online | 08 July 2024 | |
The phase curve of the ultra-hot Jupiter WASP-167b as seen by TESS
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, HUN-REN, MTA Centre of Excellence,
Konkoly-Thege Miklós út 15–17.,
1121,
Hungary
e-mail: kalman.szilard@csfk.org
2
HUN-REN-ELTE Exoplanet Research Group,
Szombathely,
Szent Imre h. u. 112.,
9700,
Hungary
3
ELTE Eötvös Loránd University, Doctoral School of Physics,
Budapest,
Pázmány Péter sétány 1/A,
1117,
Hungary
4
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory,
Szombathely,
Szent Imre h. u. 112.,
9700,
Hungary
5
MTA-ELTE Lendület “Momentum” Milky Way Research Group,
Szombathely,
Szent Imre h. u. 112.,
9700,
Hungary
6
Deutsches Zentrum für Luft- und Raumfahrt, Institute of Planetary Research,
Rutherfordstrasse 2,
12489
Berlin,
Germany
7
HUN-REN-SZTE Stellar Astrophysics Research Group,
6500
Baja,
Szegedi út, Kt. 766,
Hungary
8
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
9
University of Szeged, Doctoral School of Physics,
Dóm tér 9,
6720
Szeged,
Hungary
10
Baja Astronomical Observatory of University of Szeged,
6500
Baja,
Szegedi út, Kt. 766,
Hungary
Received:
8
December
2023
Accepted:
30
March
2024
Context. Ultra-hot Jupiters (UHJs) orbiting pulsating A/F stars represent an important subset of the exoplanetary demographic. They are excellent candidates for the study of exoplanetary atmospheres, and are astrophysical laboratories for the investigation of planet-to- star interactions.
Aims. We analysed the TESS light curve of the WASP-167 system, consisting of an F1V star and a substellar companion on a ~2.02 day orbit.
Methods. We modelled the combination of the ellipsoidal variability and the Doppler beaming to measure the mass of WASP-167b, and the reflection effect to obtain constraints on the geometric albedo, while placing a special emphasis on noise separation. We implemented a basic model to determine the dayside (TDay), nightside (TNight), and intrinsic (TInternal) temperatures of WASP-167b, and put a constraint on its Bond albedo.
Results. We confirm the transit parameters of the planet seen in the literature. We find that a resonant ~2P−1 stellar signal (which may originate from planet-to-star interactions) interferes with the phase curve analysis. After careful and thought-out treatment of this signal, we find Mp = 0.34 ± 0.22 MJ. We measure a dayside temperature of 2790 ± 100 K, classifying WASP-167b as an UHJ. We find a 2σ upper limit of 0.51 on its Bond albedo, and determine the geometric albedo at 0.34 ± 0.11 (1σ uncertainty).
Conclusions. With an occultation depth of 106.8 ± 27.3 ppm in the TESS passband, the UHJ WASP-167b is an excellent target for atmospheric studies, especially those at thermal wavelength ranges, where the stellar pulsations are expected to be less influential.
Key words: techniques: photometric / planets and satellites: atmospheres / planets and satellites: detection / planets and satellites: general / planets and satellites: individual: WASP-167b
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Close-in, substellar mass companions orbiting pulsating host stars of A/F spectral types, such as WASP-33b (Christian et al. 2006; Collier Cameron et al. 2010; Herrero et al. 2011), HAT-P-2b (Bakos et al. 2007; de Wit et al. 2017), HD 31221b (Kálmán et al. 2023a), HAT-P-57 (Hartman et al. 2015), and KOI-976 (Ahlers et al. 2019), represent a small fraction of the entire exoplanet population (see e.g. Hey et al. 2021). On the one hand, these systems are analogous to those binary stars where the pulsation of one of the stars is influenced by the tidal forces of its companion, such as V453 Cyg (Southworth et al. 2020) or RS Cha (Steindl et al. 2021). Planet-to-star interactions of this kind have been observed in several of these systems, including HAT-P-2 (de Wit et al. 2017), WASP-33 (Kálmán et al. 2022), and HD 31221 (Kálmán et al. 2023a). Recently, Bryan et al. (2024) explored the potential of these resonances in revealing the evolution of exoplanets, primarily the highly eccentric HAT-P-2b. The emerging class of interacting pulsators and their planetary companions is expected to yield new opportunities in stellar characterisation as well (Bryan et al. 2024). On the other hand, due to the strong irradiation, these systems are prime candidates for atmospheric studies via phase curve analyses. The ultra-hot Jupiter (UHJ) WASP-33b, being the epitome of these systems, is the subject of many such studies, including analyses based on the occultation detections (e.g. Smith et al. 2011; Deming et al. 2012; von Essen et al. 2015; Haynes et al. 2015) and the full phase curve (e.g. Zhang et al. 2018). Both of these require careful treatment of the stellar pulsations, which is enabled by the continuous photometry done by space-borne observatories such as Kepler (Borucki et al. 2010) or Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015), as seen in von Essen et al. (2020). Steindl et al. (2021) explored the known δ Scuti population in the Kepler field and found no UHJ companions of these stars. This suggests that these objects are rare and all-sky surveys, such as TESS or PLAnetary Transits and Oscillations of stars (PLATO; Rauer et al. 2014) might provide a more in-depth insight into these objects.
The host stars in question typically present δ Scuti, γ Doradus, or hybrid δ Scuti–γ Doradus pulsations. These objects often rotate rapidly (Ahlers et al. 2022), leading to spin-orbit misalignment detectable by Doppler tomography, a technique also pioneered on the WASP-33 system (Collier Cameron et al. 2010; Johnson et al. 2015). A continuous monitoring of the stellar obliquity λ also allows the detection of nodal precession (e.g. Johnson et al. 2015; Szabó et al. 2020; Stephan et al. 2022; Watanabe et al. 2022).
In the WASP-167 system (also known as KELT-13, TOI-748, TIC 104024556, Gaia DR3 6154982877300947840) Temple et al. (2017) discovered a hot Jupiter with an orbital period of 2.0219596 ± 0.0000006 days and a radius of 1.58 ± 0.05 RJ. The mass measurement of WASP-167b through radial velocities (RVs) was inconclusive as the star is both line-poor and broad-lined, owing to its spectral type (Teff = 6900 ± 150 K) and rapid rotation (v sin i⋆ = 52 ± 8 km s−1; Temple et al. 2017). Based on Doppler tomography, Temple et al. (2017) established that WASP-167b/KELT-13b has a misaligned retrograde orbit, determined by the spin-orbit angle λ = −165 ± 5°. The line-profile tomography also led the authors to conclude that the host star presents pulsations of either δ Scuti or γ Doradus type, which presents further difficulties in the mass measurements to the ones discussed above (see e.g. Lehmann et al. 2015).
We present an analysis of WASP-167b based solely on its TESS light curve (LC). This paper is structured as follows. In Sect. 2, we describe the LC pre-processing and fitting. In Sect. 3, we present the best-fit parameters, describing both the out-of-transit variations and the transits, and we give constraints on the mass of WASP-167b. We also explore how the pulsations of the host affect the determination of these parameters. In Sect. 4, we characterise the pulsations of the host star, discuss the possibilities of planet-to-star interactions and the possible effects of the pulsations on the precision and accuracy of the retrieved parameters, and estimate the dayside and nightside temperatures of WASP-167b. We provide a summary and draw our conclusions in Sect. 5.
2 Methods
2.1 Light curve preparation
We downloaded the short-cadence simple aperture photometry (SAP) light curves obtained in Sectors 10, 37, and 64 by TESS using the lightkurve software (Lightkurve Collaboration 2018), utilising the astroquery and astropy packages (Ginsburg et al. 2019; Astropy Collaboration 2022). We removed all data points with a non-zero quality flag, and corrected for the third light contamination via the CRWDSAP keyword. The obtained light curves are shown in Fig. 1. We then proceeded to mask apparent anomalies and remove a linear trend from the data of all three sectors. We also corrected for the jitter in the pointing of the telescope. This was done by subtracting the best-fit linear model of the centroid position of the point spread function (PSF) of WASP-167 in terms of row and column pixels.
After the initial preparatory steps, we examined the Fourier spectra of the light curves using Period04 (Lenz & Breger 2005). We identified a critical frequency (~0.98 d−1, see Sect. 4 for details) that is close to being in resonance with the second orbital harmonic of WASP-167b. To explore the effect of the stellar pulsations on the stability of the phase curve parameters, we prepared 17 different light curves, 16 of which were pre-whitened by the 16 highest-amplitude sinusoidal signals from the LCs of the three sectors and the original one (i.e. without whitening). To do this, we first masked the transits. We then computed the Fourier spectrum of the LCs. Breger et al. (1993) suggest that in order to consider a peak in the power spectrum significant, a S /N ≥ 4 is required. Relying on this criterion is a common practice in the analysis of pulsating stars (e.g. Derekas et al. 2009, 2017; Aerts et al. 2018; Bowman et al. 2020; Samadi-Ghadim et al. 2024; Sowicka et al. 2023). We identified 16 peaks with S/N ≥ 4 using Period04, separately for all three sectors. The whitened light curves are then given as
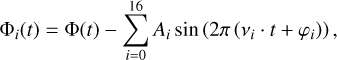 (1)
(1)
where Φ(t) is the original detrended SAP light curve, and Ai, vi, and φi are the amplitudes, frequencies, and phases of the individual Fourier terms, and their values are taken from the Fourier analysis. The pre-whitening process was done for each sector individually. The light curve corresponding to Φ16 is shown in Fig. 1, and it contains 32 transits and 32 full occultations as we fitted the data from the three sectors jointly. We note that the sole purpose of this initial Fourier analysis is to enable a consistent phase curve modelling. The Fourier spectrum after the subtraction of the first 16 highest-amplitude sinusoidal curves is shown in Fig. 2. For the more in-depth discussion of the astrophysical aspect of the pulsations (Sect. 4), we need a stable LC model that can take advantage of a dataset that does not need masked transits.
2.2 Analysis of the light curves
We made use of the Transit and Light Curve Modeller (TLCM; Csizmadia 2020) to model the light variations induced by the presence of WASP-167b. TLCM uses a model similar to that proposed by Mandel & Agol (2002) to describe the transits. It is characterised by the relative planetary radius (Rp/R⋆); the impact parameter, which is related to the orbital inclination via b = a/R⋆ cos ip (ip being the orbital inclination of the planet relative to the line of sight); the time of mid-transit (tC); and the scaled semi-major axis (a/R⋆). The stellar parameters listed in Table 1 were taken into account via the isochrones of Hurley et al. (2000). We calculated the theoretical values for the u1 and u2 quadratic limb-darkening coefficients in the TESS passband with PyLDTK (Parviainen & Aigrain 2015), which uses the PHOENIX library of stellar atmospheres (Husser et al. 2013). The stellar parameters used in these calculations were adopted from Temple et al. (2017) and are listed in Table 1. We implemented a reparametrisation of the quadratic limb-darkening law (based on principal component analysis) by fitting the two coefficients A and B, defined as
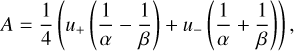 (2)
(2)
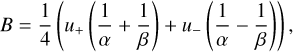 (3)
(3)
where 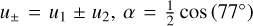 , and
, and 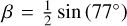 . We note that TLCM uses this definition of limb darkening coefficients in its latest version. We also applied Gaussian priors on A and B, around their theoretical values, in the form of 𝒩(0.91,0.10) and 𝒩(1.40,0.10).
. We note that TLCM uses this definition of limb darkening coefficients in its latest version. We also applied Gaussian priors on A and B, around their theoretical values, in the form of 𝒩(0.91,0.10) and 𝒩(1.40,0.10).
We modelled the out-of-transit variations including the Doppler beaming, the ellipsoidal variability (Zucker et al. 2007; Faigler & Mazeh 2011, and references therein), and the reflection effect, as described in Csizmadia (2020) and Csizmadia et al. (2023b). Both the Doppler beaming and the ellipsoidal variations can be used to estimate the mass of WASP-167b: the former is characterised by the (photometric) RV semi-amplitude Kphot, while the latter introduces the ellipsoidal mass ratio, qell, as a fitting parameter. The contribution of these two effects to the photometric baseline variations depend on the stellar parameters and are taken into account according to the description in Csizmadia (2020). The reflection of the stellar light from the planetary atmosphere was taken into account via a Lambertian phase function:
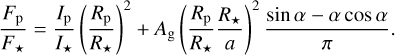 (4)
(4)
Here Ip/I★ is the surface brightness ratio of the planet and the star, Ag is the geometric albedo, and Fp and F★ are respectively the planetary and stellar fluxes. The phase angle α is related to the true anomaly υ by
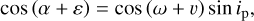 (5)
(5)
where ω is the argument of periastron and ε is the offset of the brightest point on the planetary surface from the substel-lar point. We assumed that WASP-167b has a circular orbit, as expected for a hot Jupiter. An additional free parameter was the orbital period P. Furthermore, we applied the so-called height correction, denoted by the fitting parameter h (see Eq. (47) in Csizmadia 2020). This parameter describes an offset in flux that is designed to perform renormalisation in a similar way to third light contamination.
 |
Fig. 1 TESS simple aperture photometry light curve of WASP-167 (top row, grey dots) from Sectors 10 (left), 37 (middle), and 64 (right). The masked, detrended, and centroid-corrected LC is shown in black. The pulsation model, constructed from the 16 highest amplitude sinusoidal curves, is shown in the second row as a solid magenta line. The blue dots in the third row represent the LC when these 16 highest amplitude pulsations have been removed, while the best-fit combination of time-correlated noise and phase curve models are shown in red. The residuals, along with their root mean square error (RMSE) are shown in the bottom row. |
Stellar parameters of WASP-167, adopted from Temple et al. (2017).
 |
Fig. 2 Fourier spectrum after subtracting the 16 highest-amplitude sinusoidal curves for Sectors 10 (left), 37 (middle), and 64 (left). The solid red line corresponds to the noise level as estimated by Period04. The window function is shown in the top right corner of each panel. |
2.3 Time-correlated noise
In their systematic phase curve study of the TESS data, Wong et al. (2020) excluded WASP-167 specifically due to the stellar variability, which introduces difficulties to the analysis of both the transits and the out-of-transit variations. One possible way to account for this was presented in the case of WASP-33 by von Essen et al. (2020), where the δ Scuti-type and γ Doradus-type stellar oscillations had been removed from the light curve as simple sinusoidal signals, computed via a periodogram. TLCM incorporates the wavelet-based routines of Carter & Winn (2009) to account for time-correlated noise (Csizmadia 2020; Csizmadia et al. 2023b). By treating the residual stellar oscillations and the remaining systematic effects (Fig. 1) in this way, we were able to improve the precision and accuracy of the fitted parameters, as was demonstrated in Csizmadia et al. (2023b), Kálmán et al. (2023b) and Bókon et al. (2023). Stellar pulsations in the case of WASP-33 were also accounted for successfully via this noise filtering approach in Kálmán et al. (2022). These routines introduce two additional parameters to describe the noise: σr and σw for the red and white components, respectively.
We used these wavelets to account for any systematic effects and residual stellar pulsations for the 16 pre-whitened light curves and the original one. In every case, we ran the MCMC analysis for a maximum number of 100,000 steps, with 10 chains (also known as walkers) and a thinning factor of 10.
3 Results
3.1 Influence of the stellar pulsations on the out-of-transit variability
In order to explore the effect that the stellar pulsation has on the precision and accuracy of the out-of-transit variations, we show the behaviour of Ag, Ip/I★, ε, the occultation depth, Kphot, and qell as a function of the number of sinusoidal curves removed as described in Eq. (1). As a check for consistency, we also show the estimated Rp/R★ in every case. The parameters are shown in Fig. 3. The occultation depth can be calculated as follows. First, we divide the best-fit model (including the transits, occultations, and the out-of-transit variations) by the sum of Eq. (4), the ellipsoidal distortion, and the Doppler boosting. The median flux level during the (total) occultation can then be compared to the median of the flat baseline that is out-of-transit and out-of-occultation. The uncertainty of the occultation depth can be estimated as the standard deviation divided by the square root of the number of LC points during the occultation and the standard deviation divided by the square root of the number of points out-of-transit and out-of-occultation, added in quadrature.
In TLCM, the Doppler beaming and ellipsoidal variations are fitted simultaneously to constrain each other (Csizmadia 2020). As discussed in Sect. 2.1, one component of the stellar variability is close to the second orbital harmonic of WASP-167b, the same time-dependence as the ellipsoidal effect. The wavelet-based noise filtering of Carter & Winn (2009), as implemented in TLCM (Csizmadia 2020; Csizmadia et al. 2023b), force the LC into the most likely shape. Given the additional signal around the 2/P frequency region, this component of the stellar variability can yield an inaccurate mass for WASP-167b (either underestimated or overestimated). Theoretically, it would be possible to rely on the Doppler boosting alone for the mass estimation (Mazeh et al. 2012). However, as Csizmadia (2020) pointed out, that effect is often degenerate with the model for the light reflected from the planetary atmosphere. Although Csizmadia (2020) suggests using radial velocity data to break this degeneracy between the out-of-transit parameters, the available measurements from Temple et al. (2017) imply that for this system, the mass of the companion cannot be determined with adequate precision from the present data. The two parameters representing these two effects (beaming and ellipsoidal variations), Kphot and qell, do not change significantly after subtracting the sinusoidal curve corresponding to the frequency near 2/P (Fig. 4, Table A.1); however, they are consistent with each other when modelling Φ2(t) − Φ16(t).
When we model Φ2(t), the offset between the brightest point on the stellar surface and the substellar point (ε) is <−90º (i.e. on the nightside of the planet), assuming tidal locking. This case also corresponds to the shallowest occultation (Fig. 3, Table A.1). This value of ε is non-physical. All of the best-fit parameters are consistent with each other when extracted from Φ3(t)−Φ16(t) (Figs. 4 and 3). The marginal detection of an eastward offset1 between the brightest point on the planetary surface and the substellar point observed in Φ15(t) and Φ16(t) are within 1.8σ of the respective values from Φ3(t) and within 2σ of 0º.
To decide which set of parameters to accept, we calculated the Bayesian information criterion (BIC) for all 17 light curve solutions (Table A.1). When calculating the BIC values, we used the best-fit model without the correlated noise identified via the wavelets in comparison to Φ0(t)−Φ16(t). The total number of parameters was therefore 13 + 3i, where i is the number of sinusoidal curves subtracted, which are described by three independent parameters: their frequency, amplitude, and phase (without σw and σr). The BIC analysis suggests that the Φ16(t) light curve produces the optimal set of parameters, and we therefore adopted this one. We note that Rp/R★ does not change significantly across the 17 tested cases. This is expected since the transits have higher S/N than the out-of-transit variability, and the transit depths can therefore be estimated with higher precision and accuracy in comparison to other parameters (Csizmadia et al. 2023b). We further emphasise that the uncertainties of the analysed parameters are also consistent with each other (Table A.1).
The uniform priors (also known as searchboxes) used in the analysis for each individual parameter were the same throughout the analysis of the 17 light curves. These are shown in Table 2. The combination of the best-fit model for the planetary transits, occultations, out-of-transit variability and the red noise (for Φ16(t)) is plotted in Fig. 1.
 |
Fig. 3 Best-fit Ag, Ip/I★, ε, occultation depth, and Rp/R★ as a function of the number of sinusoidal curves subtracted from the light curve. The dashed lines correspond to the 1σ uncertainty of the parameters obtained from the Φ16(t) LC. |
 |
Fig. 4 Best-fit Kphot and qell as a function of the number of sinusoidal curves subtracted from the light curve. There is a change in the scale of the y-axis after the subtraction of one sinusoidal curve (i.e. before and after the break). The dashed lines correspond to the uncertainty of the parameters obtained from the Φ16(t) LC. |
Fitted and derived parameters from the Φ16(t) light curve.
3.2 System parameters
We applied the same uniform priors for the free parameters (Table 2) on all 17 light curves, with the exception of the two limb darkening coefficients, where the same Gaussian priors were used. The best-fitting light curve model, obtained from Φ16(t), is shown in Fig. 5 and the corresponding parameters are shown in Table 2. The basic transit parameters, including a/R★, Rp/R★, and b, agree within 1σ with the respective values presented in the discovery paper of Temple et al. (2017) after converting those values to the formalism used in our analysis. A slight discrepancy (≲ 1.7σ) can be observed in the measurements of ip, which may be attributed to the differ-ent treatment of limb darkening. The results of Temple et al. (2017) are based on the four-parameter law (Claret 2000, 2004) with theoretical coefficients, the applicability of which is dis-putable for moderately fast rotating, pulsating stars, such as WASP-167. It is also possible that the transit chord is mov-ing due to nodal precession, as in the case of WASP-33b (e.g. Johnson et al. 2015; Stephan et al. 2022), KELT-9b (Stephan et al. 2022), or Kepler-13Ab (e.g. Szabó et al. 2014, 2020; Herman et al. 2018). The planetary radius of 1.621 ± 0.059 RJ is also in good agreement with the size reported in Temple et al. (2017). We also present a slight improvement in the precision of these parameters from the TESS data alone.
The well-known degeneracies between the scaled semi-major axis, the relative planetary radius and the impact parameter are observable in Fig. C.1. These can be quantified via the correlation coefficients from the posteriors: r = −0.49 (between a/R★ and Rp/R★), −0.95 (between a/R★ and b), and 0.51 (between Rp/R★ and b). The reparametrisation of the quadratic limb-darkening coefficients, expressed in Eqs. (2) and (3) yield no significant degeneracies between these and the transit parameters discussed above.
Temple et al. (2017) provide an upper limit of 8 MJ on the mass of WASP-167 by analysing the radial velocity curve. Our adopted set of solutions suggest that the mass is considerably lower at 0.37 ± 0.28 MJ or 0.34 ± 0.22 MJ, as obtained by mod-elling the Doppler beaming effect and the ellipsoidal variability, respectively, placing the planet in the mass regime of Saturn. We note however that due to the stellar signal near the second orbital harmonic (Fig. 6), these masses, obtained from the marginal detection of the two effects, should not be taken at face value. Furthermore, the correlation between the posteriors (Fig. C.1) of Kphot and qell (r = 0.83) also implies that caution must be taken when considering the mass of this object. The true mass of WASP-167b may be estimated by modelling these two effects from infrared light curve observations, where the stellar activity is known to be less significant.
The observed occultation depth of 106.8 ± 27.3 ppm is well below the upper limit of 1100 ppm in z′ band, as obtained from TRAPPIST observations (Temple et al. 2017) (see Ricker et al. 2015, for comparison of the passbands). Incidentally, this result also emphasises the necessity of space-based observations in the study of exoplanets. This occultation depth is detected with p = 1.12 × 10−6, based on the two-sample t-test in which the out-of-transit and out-of-occultation flat baseline is compared to the signal level during the occultation. We also measure a slight eastward offset in the brightest point of the planetary sur-face at 17.7° ± 11.2°, a value that is similar to that observed by von Essen et al. (2020) for WASP-33b. The posteriors of the parameters describing the observed light variation of WASP-167b are not correlated with each other, or the mass measuring parameters (Fig. C.1).
The wavelet-based noise fitting in TLCM is constrained by pre-scribing that the standard deviation of the residuals (of the LC and red noise models) must be equal to the average photomet-ric uncertainty (Csizmadia et al. 2023b). This implies that the efficiency of the noise treatment is dependent on, among other things, the brightness of the star (in this case, V = 10.52 mag). Accordingly, some autocorrelated effects may be present in the residuals, as seen in Fig. 5. To rule out the possibility that the residuals seen in Fig. 5 are caused by an overestimation of the ellipsoidal variability (and consequently, the mass of WASP-167b), we ran another test with the beaming and ellipsoidal effects turned off (i.e. a mass-less case) on the Φ16 LC. The resultant parameters are also shown in Table 2. All of the best-fit parameters are in excellent agreement with the case when we also modelled the two mass-related effects. We measure an increase in Ip/I★, which is a consequence of the lack of a (near) constant signal that would have been the sum of the beaming and ellipsoidal effects. The surface brightness ratio is therefore enlarged (yet still consistent with the uncertainty range from the original analysis) to account for the underlying occultation depth (which is observed to be 108.8 ± 27.3 ppm). The resultant (zero mass) LC model is shown in Fig. B.1. The same auto-correlated effects are present in the residuals of this modelling as in the case of Fig. 5, implying that the mass of WASP-167b is not overestimated in the original calculations. Consequently, we adopt the more thorough massive case for the rest of the analysis.
As an additional check for consistency, we also modelled the light curves from Sectors 10, 37, and 64 separately, for all 17 stages of pre-whitening. We fitted the same parameters over the same intervals as in the global analysis (Table 2). The resultant parameters (Table B.1) are shown in Figs. B.2 and B.3. None of the parameters extracted in this way differ by more than 3σ from the adopted values. The mass-related parameters (Fig. B.2) from Sector 10 are always consistent with a zero-mass object. The effect of the critical frequency F2 is, however, present in the Kphot and qell values from Sectors 37 and 64. As in the case of the global analysis, the relevant values from Φ2 to Φ16 are also consistent with zero in all three sectors. Certain ɛ values are non-physical (B.3), yielding negative occultation depths (as in the case of Φ15 and Φ16 from Sector 37). They are, however, consistent with 0 within the estimated uncertainty range (Table B.1), implying that the out-of-transit variability cannot be distinguished from the time-correlated noise in these cases. The pre-whitening process is not perfectly efficient at the removal of all quasi-periodic noise features (Fig. 1). Consequently, its residuals (third row of Fig. 1) show variability on timescales comparable to the orbital period, but much shorter than the duration of the light curve of the three combined sectors. As a result, in our global fit, these quasi-periodic events get averaged out, yielding parameters that are fundamentally more precise and accurate. This phenomenon can also be observed in the case of WASP-33b, where Lehmann et al. (2015) used a large number of radial velocity observations to deal with the effects of stellar pulsations (in contrast with Kovács et al. 2013, who only had access to 12 data points in total). We note that because of the deep transits (yielding high S/N for the transit depth), the Rp /R★ are always consistent with each other within 1σ. We also note that in general, Sector 10 yields the highest uncertainties for any given parameter, corresponding to the highest RMSE seen in the data from these three sectors (Fig. 1).
We further note that the height correction parameter h is not degenerated with any other fitting parameter (Fig. C.1). This implies that its use is effective in treating any possible light contamination that is not corrected for via the CROWDSAP keyword during the photometry.
 |
Fig. 5 Full phase curve model of WASP-167b (solid red line). The top panel shows the Φ16(t) light curve with the fitted red noise subtracted via the wavelet-based filtering algorithm. The occultation is clearly visible in the zoomed-in middle panel, with the reflection effect, ellipsoidal variability, and Doppler beaming separated (magenta, blue, and orange lines, respectively). The residuals are shown in the bottom panel. The white circles and the respective error bars represent bins of 500 data points each. The less opaque red lines corresponding to 1000 model LCs were randomly selected from the uncertainty ranges of each of the parameters. |
 |
Fig. 6 Fourier spectrum of the residuals of the LC model of WASP-167 from Sectors 10, 37, and 64 (left, middle, and right panel). The plots in the insets show the spectral windows. The dashed red line marks the second orbital harmonic of WASP-167b, demonstrating the critical frequency that influences primarily the mass measurements of the planet. The noise level, as calculated by Period04, is shown as a solid red line. |
4 Discussion
4.1 Stellar signal
The analysis of the stellar pulsations generally requires uninterrupted light curves. To this end, we subtracted the phase curve model (including the transits, occultations, and out-oftransit effects) obtained by the analysis of Φ16(t) from Φ0(t). We then proceeded with calculating the Fourier spectrum of these residuals using Period04, separately for the LCs of the three sectors. These spectra are shown in Fig. 6. The frequencies, amplitudes, and phases, which are the result of the Fourier analysis, are presented in Table 3 for peaks with S /N ≳ 4. In all three sectors, we extracted data from 22 peaks with the highest amplitudes. While a detailed analysis of the stellar signal is beyond the scope of this paper, several observations can be made from the Fourier spectra. First, there are no significant peaks in the data beyond ~3.5 d−1. Second, there is a peak in the Fourier spectra (F2 from Table 3) that almost exactly coincides with the second orbital harmonic of WASP-167b in all three sectors (Fig. 6). In comparison to the best-fit orbital frequency ( forb = (0.49547000 ± 1.3 ⋅ 10−7) d−1), we find that F2 can be expressed as 1.996, 1.958, and 1.996 times forb in the three Sectors 10, 37, and 64, respectively. A similar commensurability was noted by von Essen et al. (2014) and later confirmed by Kálmán et al. (2022) in the case of the WASP-33 system. Finally, the frequencies and amplitudes of the spectral peaks vary considerably from sector to sector, with the exception of F2, known as the critical frequency. Given the incompatible nature of the Fourier spectra in the three sectors, searching for a phase shift in the individual sinusoidal curves (e.g. von Essen et al. 2014) is not feasible.
We find that 2forb matches F2 within ≈3σ (in Sectors 10 and 64) and within 15σ (in Sector 37) when using the formal uncertainties of the pulsational frequencies, calculated via Period04. These calculations are based on the idealistic case where the pulsations can be expressed as simple sinusoidal signals with constant phases, amplitudes, and frequencies. As we demonstrate in this paper, this is not the case for WASP-167 and, as a consequence, these uncertainties may be considerably underestimated. We constructed a simple test to investigate the possibility that the critical frequency only appears close to 2 forb without underlying tidal interactions. To that end, similarly to von Essen et al. (2014) and Kálmán et al. (2023a), we constructed 105 synthetic frequency spectra, each consisting of 22 frequencies (corresponding to the number of peaks identified and presented in Table 3), drawn from a uniform distribution between 0 d-1 and 3.5 d−1. We then proceeded to match these to 2forb to within 3 ⋅0.0015 d−1, or roughly the average uncertainty in the frequencie from Table 3, thus providing a conservative estimate for the synthetic F2. We found that commensurability defined in this way only arises in 5.6% of the cases. This statistic further serves as evidence for tidal interactions between WASP-167b and its host.
The frequency range in which the stellar activity presents itself means that the observing windows might not be sufficient for a detailed characterisation of its nature. If it originates from pulsations, as stated in Temple et al. (2017), then WASP-167b is a γ Doradus pulsator. Instability for this type of stellar pulsation may be expected on the timescales available through the TESS photometry (e.g. Bravo et al. 2014; Kurtz et al. 2015). Although they are generally not expected for Teff ≈ 7000 K, stellar spots can also produce variability compatible with our observations (Fig. 6), and they might offer a better explanation for the apparent changes in the frequencies and amplitudes that are seen in the Fourier decomposition. It is also possible that the star presents both γ Dor type pulsations and spots. Future studies focusing on the Zeeman effect (Babcock 1947), or more precise photometric observations with longer baselines (e.g. with PLATO; Rauer et al. 2014) may help us to understand the origins of the stellar variability of WASP-167. We note, however, that the accurate interpretation of the stellar signal depends strongly on the phase curve model of the planet (Fig. 5), as the latter is also comprised of sinusoidal terms with comparable amplitudes to the ones from stellar oscillational frequencies (Table 3).
The peak in the Fourier spectra near the second orbital harmonic (Fig. 6) is likely composed of both stellar variability (regardless of its nature) and the ellipsoidal effect. As discussed in Sect. 3.2, this implies that the mass measurements of WASP-167b might be inaccurate. This issue might be solved by obtaining more higher-quality radial velocity data than that presented in Temple et al. (2017), as in the case of WASP-33 (Lehmann et al. 2015). It is also possible that, as stated in Sect. 3.2, IR observations, for example performed by Ariel (Tinetti et al. 2021), may be able to provide more reliable mass constraints since the pulsational amplitudes are known to be lower at higher wavelengths (e.g. Derekas et al. 2009).
We also see that the F2 frequency is present in the Fourier spectra from all three sectors (Fig. 6) with similar amplitudes. This suggests that WASP-167b is influencing the activity of its host. To examine the intra-sector stability, we used a time-frequency method known as the discrete wavelet transform (Foster 1996) after filling in the data downlink gaps (seen in Fig. 1) with zeros. The wavelet maps of Fig. 7 show the 0.25–2 day−1 frequency regime (thus incorporating F2). There is clear amplitude modulation around F2, with a period of ~4 days, or ~2P. A similar behaviour has also been observed in the case of WASP-33b and its host star Kálmán et al. (2022). This timescale is well above the estimated orbital period ≤1.81 d−1, suggesting that the origin of this particular signal is not related to stellar rotation. We also observe that in the ≤0.8 d−1 frequency regime there are considerable amplitude and phase curve modulations both intra-sector, and from sector to sector. However, the long-term effects, such as detector systematics, would also be observable in this range, and they cannot be distinguished from the stellar activity via the light curves used in this analysis. A deeper exploration of the stellar signal would need to carefully remove all of the known instrumental effects from the light curves; however, such a study is beyond the scope of this paper. Instrumental noise sources could therefore be a possible explanation for the inter-sector variability in the Fourier spectrum (Fig. 6 and Table 3). Another possibility might be the instability of the pulsational or spot patterns of the star, at least on the timescales at which the three observed sectors sample the LC.
Frequencies, amplitudes, phases, and the respective S/N values extracted from the Fourier transform.
 |
Fig. 7 Wavelet maps of the stellar activity from Sectors 10 (left), 37 (middle), and 64 (right). |
4.2 Dayside, nightside, and intrinsic temperature of WASP-167b
In the phase curve parametrisation of Eq. (4), the second term, characterised by the geometric albedo, is made up of light that is reflected from the planetary atmosphere (determined by the Bond albedo, AB) and light that is emitted from the dayside. To constrain the dayside and nightside temperatures, we used the toy model presented in Csizmadia et al. (2023a) and used in Kálmán et al. (2024) for the energy budget of WASP-167b to distinguish between the two phenomena. In a thermodynamical equilibrium we can state that the incoming and outgoing luminosities are related to each other by
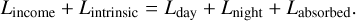 (6)
(6)
In this formulation, Lintrinsic is the result of the intrinsic planetary heat. The incident luminosity is related to the bolometric stellar luminosity via
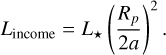 (7)
(7)
By definition, the reflected light from the planetary surface can be characterised as
 (8)
(8)
Assuming blackbody radiation for the dayside and nightside hemispheres of the planet, we obtain
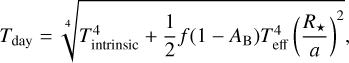 (9)
(9)
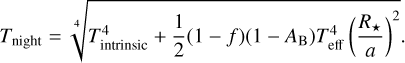 (10)
(10)
Here Tintrinsic, Tday, and Tnight are the internal, dayside, and nightside temperature of WASP-167b, respectively. The heat redistribution efficiency, ƒ, determines the amount of incident stellar luminosity that passes through to the nightside of the planet.
The amplitude of the phase curve in Eq. (4) is the combination of emitted and reflected light. By neglecting the marginal eastward offset, the theoretical geometric albedo can be characterised as
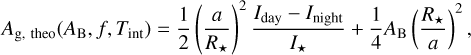 (11)
(11)
where Iday are the passband-specific luminosities of a unit-sized surface area. The surface brightness (Ip/I★) ratio of Eq. (4), taken from Φ16 (t) (Table 2), can be matched to Inight/I★.
There are therefore two observable quantities and three parameters (AB, ƒ, and Tintrinsic) that need to be determined from them. Thus, no unique solution can be found for these via observations in a single passband. We therefore carried out a Monte Carlo integration by generating a sample of 2 × 106 independent random values for AB, ƒ, and Tintrinsic, within intervals of [0, 1], [0.5, 1], and [0 K, 5000 K], respectively, with a uniform distribution. The uncertainties of Teff and a/R★ (Tables 1 and 2) were taken into account via an additional 2 ⋅ 106 independent random values, with Gaussian distributions (with means and standard deviations taken from Tables 1 and 2). We then proceeded by matching Ag,theo and Inight /I★ to the 2σ uncertainty ranges for Ag and Ip/I★ from Table 2.
The resultant distributions of the Bond albedo, intrinsic temperature, and the heat redistribution efficiency are shown in Fig. 8. From these distributions we can draw the following conclusions. WASP-167b/KELT- 13b has a moderately low Bond albedo, with AB < 0.51 at the 2σ level. This is generally in line with what is expected from a hot Jupiter based on empirical studies (e.g. Rowe et al. 2008; Knutson et al. 2009; Cowan & Agol 2011; Deming & Knutson 2020; Singh et al. 2024; Kálmán et al. 2024) and theoretical predictions (e.g. Sudarsky et al. 2000). We also place a lower limit on the heat redistribution efficiency of ƒ > 0.74 (at 2σ), implying that the atmosphere of the planet is structured in a way that it retains the majority of the incident (and absorbed) stellar flux on the dayside, similarly to WASP-18 Ab (Nymeyer et al. 2011). We find that the intrinsic temperature of WASP-167b is ≤2340 K, with 1470 ± 640 K representing the median and standard deviation of the distribution shown in Fig. 8. Combining these facts with the 5.6 L⊙ stellar luminosity (in the TESS passband) implies that the dayside temperature of the planet (Fig. 9) is 2790 ± 100 K, in turn implying that WASP-167b is an ultra-hot Jupiter. We also placed an upper limit on the nightside temperature (Fig. 9) of 2360 K, with the uncertainty range estimated as 1780 ± 380 K. Given that our Ip/I★ estimates are consistent with 0 in the majority of the cases (Fig. 3), it is safe to assume that all of the atmospheric parameters provided here can be regarded as upper limits. We note that AB, ƒ, and Tintrinsic are heavily degenerate, which is the consequence of analysing data in a single passband. Similarly to the nature of the stellar signal, future observations (e.g. with PLATO or Ariel) will have the possibility of a more in-depth exploration of the atmospheric temperature regimes of this planet.
We emphasise that all of the solutions represented in Fig. 8 satisfy the requirements for Ag and Ip/I★ equally well, and that no solutions were found beyond the limits for AB and ƒ presented above. The 2σ uncertainty range stems from taking the 2σ uncertainties for Ag and Ip/I★.
To put our results into context, we adopted the dayside, nightside, and equilibrium temperatures, defined as 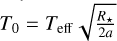 , of several well-studied exoplanets from Bell et al. (2021). We compare the derived Tday and Tnight to these values in Figs. 10 and 11. From these temperatures we can conclude that our results are clear outliers from the planet population. Slight discrepancies might occur due to differences in the surface gravity on the planets or deviations from blackbody radiation. The latter effect could be enhanced, as Bell et al. (2021) present results from infrared phase curves, whereas this study is based on data from the optical range. We also note that the data adopted from Bell et al. (2021) is not compiled in a homogeneous way and, as was presented in Kálmán et al. (2023b), untreated time-correlated noise can induce biases in the modelling parameters. This would imply that such a direct comparison between different studies is not ideal. A further possibility for the observed deviation of our results from the overall population would be that we overestimate Tday and Tnight, by overestimating Tintrinsic, which is related to Ip/I★. The posterior distribution (Fig. C.1) suggest that Ip/I★ is compatible with 0 and, by using the median of this distribution in our analysis, we might overestimate the amount of light emitted by the planet. A deeper exploration of the population statistics is beyond the scope of this paper.
, of several well-studied exoplanets from Bell et al. (2021). We compare the derived Tday and Tnight to these values in Figs. 10 and 11. From these temperatures we can conclude that our results are clear outliers from the planet population. Slight discrepancies might occur due to differences in the surface gravity on the planets or deviations from blackbody radiation. The latter effect could be enhanced, as Bell et al. (2021) present results from infrared phase curves, whereas this study is based on data from the optical range. We also note that the data adopted from Bell et al. (2021) is not compiled in a homogeneous way and, as was presented in Kálmán et al. (2023b), untreated time-correlated noise can induce biases in the modelling parameters. This would imply that such a direct comparison between different studies is not ideal. A further possibility for the observed deviation of our results from the overall population would be that we overestimate Tday and Tnight, by overestimating Tintrinsic, which is related to Ip/I★. The posterior distribution (Fig. C.1) suggest that Ip/I★ is compatible with 0 and, by using the median of this distribution in our analysis, we might overestimate the amount of light emitted by the planet. A deeper exploration of the population statistics is beyond the scope of this paper.
Although the Tintrinsic of WASP-167b is poorly constrained, we explore the possible sources for the intrinsic heat. We list several possibilities in Csizmadia et al. (2023a) and Kálmán et al. (2024); however, at the 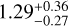 Gyr age of the system (Temple et al. 2017), with a planet on a circular orbit with a λ = −167 ± 5° stellar obliquity, we assume that it originates from the so-called obliquity tides. Levrard et al. (2007) and Millholland (2019) expressed the thermal contribution of this heating process as
Gyr age of the system (Temple et al. 2017), with a planet on a circular orbit with a λ = −167 ± 5° stellar obliquity, we assume that it originates from the so-called obliquity tides. Levrard et al. (2007) and Millholland (2019) expressed the thermal contribution of this heating process as
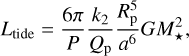 (12)
(12)
where k2 and Qp are the Love number and tidal dissipation factor of the planet. The Love number can be measured by accounting for the slight changes in the shape of the transit (e.g. Hellard et al. 2019, 2020; Barros et al. 2022a, b) or, for eccentric orbits, via the modelling of the apsidal motion (Csizmadia et al. 2019). A direct k2 measurement for WASP-167b is beyond the scope of this paper, and we therefore adopt k2 = 0.61 from Csizmadia et al. (2019), a value which is also in line with k2 measurements of Jupiter (e.g. Durante et al. 2020). We find that the ~10−4 L⊙ intrinsic luminosity of the planet yields Qp = (7.2 ± 1.3) × 105, which is in line with Csizmadia et al. (2023a) and the direct measurements for the giant planets of the Solar System (Goldreich & Soter 1966).
 |
Fig. 8 Distribution of the Bond albedo, the heat redistribution parameter, and the intrinsic temperature. Their combination reproduces the observed phase curve of WASP-167b. |
 |
Fig. 9 Distribution of the dayside and nightside temperatures that reproduce the observed phase curve of WASP-167b. |
 |
Fig. 10 Dayside temperature as a function of the equilibrium temperature from Bell et al. (2021) (black dots and error bars). Our result for WASP-167 is shown in red. |
 |
Fig. 11 Nightside temperature as a function of the equilibrium temperature from Bell et al. (2021) (black dots and error bars). Our result for WASP-167 is shown in red. |
5 Summary and conclusions
We presented the phase curve study of the WASP-167/KELT-13 system, discovered by Temple et al. (2017), based on its TESS photometry from Sectors 10, 37, and 64. We confirm that the system hosts a hot Jupiter on a ~2.022-day orbit, and with a radius ~1.6 RJ (Table 2). We also present refined transit parameters. Previous attempts at constraining its mass from radial velocity data were unsuccessful due to the moderately rapid rotation (52 ± 8 km s−1), spectral type, and activity of the host star. We found a peak in the Fourier spectrum of WASP-167 that is in near-resonance with the second orbital harmonic ~0.989 d−1 (Fig. 6) of its companion, the same time dependence as the ellipsoidal variability caused by WASP-167b.
To analyse how the stellar pulsations affect the precision and accuracy of the transit parameters, we prepared 17 LCs, with an increasing number of sinusoidal components subtracted from them, according to Eq. (1). The parameters of these harmonics were obtained via the Fourier transform using Period04. The sets of examined out-of-transit parameters are shown in Figs. 4 and 3. Using the Bayesian information criterion, we find that subtracting 16 sinusoidal curves yields the optimal solution. This is coincidentally the total number of harmonics that can be determined from the Fourier transform, with the commonly used S/N ≥ 4 criterion. This process of whitening the data yields self-consistent results, with the caveat that we may be overcom-pensating for the ellipsoidal variability. Thus, the obtained mass of WASP-167b at 0.34 ± 0.22 MJ may be considerably underestimated. We also raise the possibility that the critical frequency influencing the mass estimates of WASP-167b may arise from planet-to-star interactions. If the stellar signal originates from pulsations, then the WASP-167 system shows similarities with HAT-P-2 (de Wit et al. 2017), or WASP-33 (Kálmán et al. 2022) and HD 31221b (Kálmán et al. 2023a), depending on whether its orbit has a small (but non-zero) eccentricity or not. On the other hand, if the variability of WASP-167 originates from spots, then it is similar to AU Mic (Szabó et al. 2021) in this regard.
We also present the occultation of WASP-167b (Fig. 5), and its dependence on the stellar pulsations (Fig. 3) via modelling the phase curve of the planet. The resultant occultation depth of 106.8 ± 27.3 ppm and the corresponding dayside temperature of 2790 ± 100 K is well below the limits provided by Temple et al. (2017) from ground-based data. It also raises the possibility that WASP-167b is an ultra-hot Jupiter, similar to WASP-33 (Smith et al. 2011). We measure a geometric albedo of 0.34 ± 0.11 and an eastward offset of the brightest point on the planetary surface of 17.2° ± 11.2°, similarly to WASP-33 in the same passband (von Essen et al. 2020). Furthermore, we obtain (2σ) upper limits on the nightside and intrinsic temperature (2360 K and 2340 K, respectively) and the Bond albedo (0.51), and discuss the possible combinations of Bond albedos and heat redistribution efficiencies (Fig. 8) that can reproduce the observed phase curve (Fig. 5).
Acknowledgements
This work was supported by the PRODEX Experiment Agreement No. 4000137122 between the ELTE Eötvös Loránd University and the European Space Agency (ESA-D/SCI-LE-2021-0025). Support of the KKP-137523 'SeismoLab' Élvonal grant as well as the grant K-138962 of the Hungarian Research, Development and Innovation Office (NKFIH) are acknowledged. This project has been supported by the LP2021-9 Lendiilet grant of the Hungarian Academy of Sciences. Project no. C1746651 has been implemented with the support provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, financed under the NVKDP-2021 funding scheme. This project has received funding from the HUN-REN Hungarian Research Network under grant number KMP-2023/79. Supported by the DKOP-23 Doctoral Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund.
Appendix A Influence of the stellar pulsations on the out-of-transit parameters
Behaviour of the monitored out-of-transit parameters and Rp /RS with respect to the number of subsequent sinusoidal curves (with decreasing amplitudes) used in the whitening process.
In order to test how the stellar pulsations affect the precision and accuracy of out-of-transit parameters, we prepared 17 LCs according to Eq. (1). The monitored parameters include the amplitude of the Doppler beaming (Kphot), the ellipsoidal mass ratio (qell), the geometric albedo (Ag), the surface brightness ratio (Ip/I★), the offset between the brightest point on the dayside hemisphere and the substellar point (ɛ), and the occultation depth. The behaviour of the relative planetary radius is also observed for consistency, and are listed in Table A.1. In order to distinguish between the 17 sets of solutions, we utilised the Bayesian information criterion (BIC), defined as
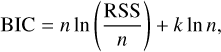 (A.1)
(A.1)
where n is the number of LC points and k is number of parameters (13 plus three times the number of sinusiodial curves subtracted). We establish that the LC solutions computed from Φ16(t) have the lowest BIC value, and accept this set of parameters.
Appendix B Consistency check
We performed a check for consistency for the phase curve analysis by excluding the Doppler beaming and the ellipsoidal variability from the modelling. The resultant LC model is shown in Fig. B.1.
We then performed a second consistency check, where we modelled the data from the three sectors independently from each other, from 00 to 016. We monitored the behaviour of the same parameters as in Figs. 4 and 3.
 |
Fig. B.2 Behaviour of the best-fit Kphot and qell parameters with respect to the pre-whitening. The dark blue dots with error bars and the red dashed lines are the same as in Fig. 4. The respective parameters from Sector 10, 37, and 64 are shown in grey, light blue, and pink, respectively. The pink points and error bars are also slightly offset on the x-axis for better visibility. |
 |
Fig. B.3 Behaviour of the best-fit Ag, Ip/I★, occultation depth and Rp/R★ parameters with respect to the pre-whitening. The dark blue dots with error bars and the red dashed lines are the same as in Fig. 3. The respective parameters from Sector 10, 37, and 64 are shown in grey, light blue, and pink, respectively. The pink points and error bars are also slightly offset on the x-axis for better visibility. |
System parameters from Sectors 10, 37, and 64.
Appendix C Posterior distribution
The posterior distribution from the Markov chain Monte Carlo light curve sampling, prepared via the routines of Foreman-Mackey et al. (2017), are shown in Fig. C.1.
 |
Fig. C.1 Corner plot showing the posterior distribution from the Φ16 light curve modelling. |
References
- Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [Google Scholar]
- Ahlers, J. P., Barnes, J. W., & Myers, S. A. 2019, AJ, 158, 88 [CrossRef] [Google Scholar]
- Ahlers, J. P., Fromont, E. F., Kopparappu, R., Cauley, P. W., & Haqq-Misra, J. 2022, ApJ, 928, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Babcock, H. W. 1947, ApJ, 105, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Kovács, G., Torres, G., et al. 2007, ApJ, 670, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022a, A&A, 657, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022b, A&A, 658, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, T. J., Dang, L., Cowan, N. B., et al. 2021, MNRAS, 504, 3316 [NASA ADS] [CrossRef] [Google Scholar]
- Bókon, A., Kálmán, S., Bíró, I. B., & Szabó, M. G. 2023, A&A, 674, A186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Bowman, D. M., Burssens, S., Simón-Díaz, S., et al. 2020, A&A, 640, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bravo, J. P., Roque, S., Estrela, R., Leão, I. C., & De Medeiros, J. R. 2014, A&A, 568, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Bryan, J., de Wit, J., Sun, M., de Beurs, Z. L., & Townsend, R. H. D. 2024, arXiv e-prints, [arXiv:2403.08014] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [Google Scholar]
- Christian, D. J., Pollacco, D. L., Skillen, I., et al. 2006, MNRAS, 372, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [Google Scholar]
- Csizmadia, S. 2020, MNRAS, 496, 4442 [Google Scholar]
- Csizmadia, S., Hellard, H., & Smith, A. M. S. 2019, A&A, 623, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csizmadia, S., Smith, A. M. S., Cabrera, J., et al. 2023a, A&A, submitted [Google Scholar]
- Csizmadia, S., Smith, A. M. S., Kálmán, S., et al. 2023b, A&A, 675, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., & Knutson, H. A. 2020, Nat. Astron., 4, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Fraine, J. D., Sada, P. V., et al. 2012, ApJ, 754, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Derekas, A., Kiss, L. L., Bedding, T. R., et al. 2009, MNRAS, 394, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Derekas, A., Plachy, E., Molnár, L., et al. 2017, MNRAS, 464, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, J., Lewis, N. K., Knutson, H. A., et al. 2017, ApJ, 836, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Durante, D., Parisi, M., Serra, D., et al. 2020, Geophys. Res. Lett., 47, e86572 [NASA ADS] [CrossRef] [Google Scholar]
- Faigler, S., & Mazeh, T. 2011, MNRAS, 415, 3921 [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
- Foster, G. 1996, AJ, 112, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Ginsburg, A., Sipocz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Buchhave, L. A., et al. 2015, AJ, 150, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, K., Mandell, A. M., Madhusudhan, N., Deming, D., & Knutson, H. 2015, ApJ, 806, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hellard, H., Csizmadia, S., Padovan, S., et al. 2019, ApJ, 878, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Hellard, H., Csizmadia, S., Padovan, S., Sohl, F., & Rauer, H. 2020, ApJ, 889, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Herman, M. K., de Mooij, E. J. W., Huang, C. X., & Jayawardhana, R. 2018, AJ, 155, 13 [Google Scholar]
- Herrero, E., Morales, J. C., Ribas, I., & Naves, R. 2011, A&A, 526, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hey, D. R., Montet, B. T., Pope, B. J. S., Murphy, S. J., & Bedding, T. R. 2021, AJ, 162, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, M. C., Cochran, W. D., Collier Cameron, A., & Bayliss, D. 2015, ApJ, 810, L23 [Google Scholar]
- Kálmán, S., Bókon, A., Derekas, A., et al. 2022, A&A, 660, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kálmán, S., Derekas, A., Csizmadia, S., et al. 2023a, A&A, 673, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kálmán, S., Szabó, G. M., & Csizmadia, S. 2023b, A&A, 675, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kálmán, S., Csizmadia, S., Derekas, A., et al. 2024, AJ, submitted [Google Scholar]
- Knutson, H. A., Charbonneau, D., Cowan, N. B., et al. 2009, ApJ, 703, 769 [CrossRef] [Google Scholar]
- Kovács, G., Kovács, T., Hartman, J. D., et al. 2013, A&A, 553, A44 [Google Scholar]
- Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., & Bowman, D. M. 2015, MNRAS, 450, 3015 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, H., Guenther, E., Sebastian, D., et al. 2015, A&A, 578, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [Google Scholar]
- Levrard, B., Correia, A. C. M., Chabrier, G., et al. 2007, A&A, 462, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- Mazeh, T., Nachmani, G., Sokol, G., Faigler, S., & Zucker, S. 2012, A&A, 541, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millholland, S. 2019, ApJ, 886, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Nymeyer, S., Harrington, J., Hardy, R. A., et al. 2011, ApJ, 742, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rowe, J. F., Matthews, J. M., Seager, S., et al. 2008, ApJ, 689, 1345 [Google Scholar]
- Samadi-Ghadim, A., Lampens, P., & Gizon, L. 2022, A&A, 667, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, V., Scandariato, G., Smith, A. M. S., et al. 2024, A&A, 683, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, A. M. S., Anderson, D. R., Skillen, I., Collier Cameron, A., & Smalley, B. 2011, MNRAS, 416, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
- Sowicka, P., Handler, G., Jones, D., et al. 2023, ApJS, 269, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Steindl, T., Zwintz, K., & Bowman, D. M. 2021, A&A, 645, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephan, A. P., Wang, J., Cauley, P. W., et al. 2022, ApJ, 931, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Sudarsky, D., Burrows, A., & Pinto, P. 2000, ApJ, 538, 885 [Google Scholar]
- Szabó, G. M., Simon, A., & Kiss, L. L. 2014, MNRAS, 437, 1045 [CrossRef] [Google Scholar]
- Szabó, G. M., Pribulla, T., Pál, A., et al. 2020, MNRAS, 492, L17 [CrossRef] [Google Scholar]
- Szabó, G. M., Gandolfi, D., Brandeker, A., et al. 2021, A&A, 654, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Temple, L. Y., Hellier, C., Albrow, M. D., et al. 2017, MNRAS, 471, 2743 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Eccleston, P., Haswell, C., et al. 2021, arXiv e-prints, [arXiv:2104.04824] [Google Scholar]
- von Essen, C., Czesla, S., Wolter, U., et al. 2014, A&A, 561, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Mallonn, M., Albrecht, S., et al. 2015, A&A, 584, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Mallonn, M., Borre, C. C., et al. 2020, A&A, 639, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, N., Narita, N., Palle, E., et al. 2022, MNRAS, 512, 4404 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Shporer, A., Daylan, T., et al. 2020, AJ, 160, 155 [Google Scholar]
- Zhang, M., Knutson, H. A., Kataria, T., et al. 2018, AJ, 155, 83 [Google Scholar]
- Zucker, S., Mazeh, T., & Alexander, T. 2007, ApJ, 670, 1326 [NASA ADS] [CrossRef] [Google Scholar]
According to Csizmadia et al. (2023b), positive ε values correspond to eastward shift, while negative values imply a westward shift, under the assumption that the planet has a prograde rotation.
All Tables
Frequencies, amplitudes, phases, and the respective S/N values extracted from the Fourier transform.
Behaviour of the monitored out-of-transit parameters and Rp /RS with respect to the number of subsequent sinusoidal curves (with decreasing amplitudes) used in the whitening process.
All Figures
 |
Fig. 1 TESS simple aperture photometry light curve of WASP-167 (top row, grey dots) from Sectors 10 (left), 37 (middle), and 64 (right). The masked, detrended, and centroid-corrected LC is shown in black. The pulsation model, constructed from the 16 highest amplitude sinusoidal curves, is shown in the second row as a solid magenta line. The blue dots in the third row represent the LC when these 16 highest amplitude pulsations have been removed, while the best-fit combination of time-correlated noise and phase curve models are shown in red. The residuals, along with their root mean square error (RMSE) are shown in the bottom row. |
| In the text | |
 |
Fig. 2 Fourier spectrum after subtracting the 16 highest-amplitude sinusoidal curves for Sectors 10 (left), 37 (middle), and 64 (left). The solid red line corresponds to the noise level as estimated by Period04. The window function is shown in the top right corner of each panel. |
| In the text | |
 |
Fig. 3 Best-fit Ag, Ip/I★, ε, occultation depth, and Rp/R★ as a function of the number of sinusoidal curves subtracted from the light curve. The dashed lines correspond to the 1σ uncertainty of the parameters obtained from the Φ16(t) LC. |
| In the text | |
 |
Fig. 4 Best-fit Kphot and qell as a function of the number of sinusoidal curves subtracted from the light curve. There is a change in the scale of the y-axis after the subtraction of one sinusoidal curve (i.e. before and after the break). The dashed lines correspond to the uncertainty of the parameters obtained from the Φ16(t) LC. |
| In the text | |
 |
Fig. 5 Full phase curve model of WASP-167b (solid red line). The top panel shows the Φ16(t) light curve with the fitted red noise subtracted via the wavelet-based filtering algorithm. The occultation is clearly visible in the zoomed-in middle panel, with the reflection effect, ellipsoidal variability, and Doppler beaming separated (magenta, blue, and orange lines, respectively). The residuals are shown in the bottom panel. The white circles and the respective error bars represent bins of 500 data points each. The less opaque red lines corresponding to 1000 model LCs were randomly selected from the uncertainty ranges of each of the parameters. |
| In the text | |
 |
Fig. 6 Fourier spectrum of the residuals of the LC model of WASP-167 from Sectors 10, 37, and 64 (left, middle, and right panel). The plots in the insets show the spectral windows. The dashed red line marks the second orbital harmonic of WASP-167b, demonstrating the critical frequency that influences primarily the mass measurements of the planet. The noise level, as calculated by Period04, is shown as a solid red line. |
| In the text | |
 |
Fig. 7 Wavelet maps of the stellar activity from Sectors 10 (left), 37 (middle), and 64 (right). |
| In the text | |
 |
Fig. 8 Distribution of the Bond albedo, the heat redistribution parameter, and the intrinsic temperature. Their combination reproduces the observed phase curve of WASP-167b. |
| In the text | |
 |
Fig. 9 Distribution of the dayside and nightside temperatures that reproduce the observed phase curve of WASP-167b. |
| In the text | |
 |
Fig. 10 Dayside temperature as a function of the equilibrium temperature from Bell et al. (2021) (black dots and error bars). Our result for WASP-167 is shown in red. |
| In the text | |
 |
Fig. 11 Nightside temperature as a function of the equilibrium temperature from Bell et al. (2021) (black dots and error bars). Our result for WASP-167 is shown in red. |
| In the text | |
 |
Fig. B.1 Same as Fig. 5, but with 0 mass assumed for WASP-167b. |
| In the text | |
 |
Fig. B.2 Behaviour of the best-fit Kphot and qell parameters with respect to the pre-whitening. The dark blue dots with error bars and the red dashed lines are the same as in Fig. 4. The respective parameters from Sector 10, 37, and 64 are shown in grey, light blue, and pink, respectively. The pink points and error bars are also slightly offset on the x-axis for better visibility. |
| In the text | |
 |
Fig. B.3 Behaviour of the best-fit Ag, Ip/I★, occultation depth and Rp/R★ parameters with respect to the pre-whitening. The dark blue dots with error bars and the red dashed lines are the same as in Fig. 3. The respective parameters from Sector 10, 37, and 64 are shown in grey, light blue, and pink, respectively. The pink points and error bars are also slightly offset on the x-axis for better visibility. |
| In the text | |
 |
Fig. C.1 Corner plot showing the posterior distribution from the Φ16 light curve modelling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


