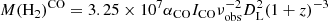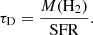| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A288 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348623 | |
| Published online | 22 July 2024 | |
Dark progenitors and massive descendants: A first ALMA perspective of radio-selected near-IR-dark galaxies in the COSMOS field
1
University of Bologna, Department of Physics and Astronomy (DIFA), Via Gobetti 93/2, 40129 Bologna, Italy
e-mail: fabrizio.gentile3@unibo.it
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Gobetti 93/3, 40129 Bologna, Italy
3
CEA, IRFU, DAp, AIM, Université Paris-Saclay, Université Paris Cité, Sorbonne Paris Cité, CNRS, 91191 Gif-sur-Yvette, France
4
SISSA, Via Bonomea 265, 34136 Trieste, Italy
5
IFPU – Institute for fundamental physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
6
INFN-Sezione di Trieste, Via Valerio 2, 34127 Trieste, Italy
7
INAF/IRA, Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
8
INAF, Istituto di Radioastronomia – Italian ARC, Via Piero Gobetti 101, 40129 Bologna, Italy
9
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
10
Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France
11
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20121, Milano, Italy & Via Bianchi 46, 23807 Merate, Italy
12
Caltech/IPAC, MS314-6, 1200 E. California Blvd, Pasadena, CA 91125, USA
13
Inter-University Institute for Data Intensive Astronomy, Department of Astronomy, University of Cape Town, 7701 Rondebosch, Cape Town, South Africa
14
Inter-University Institute for Data Intensive Astronomy, Department of Physics and Astronomy, University of the Western Cape, 7535 Bellville, Cape Town, South Africa
15
Department of Physics, University of Zagreb, Bijenicka cesta 32, 10002 Zagreb, Croatia
Received:
15
November
2023
Accepted:
10
May
2024
We present the first spectroscopic ALMA follow-up for a pilot sample of nine radio-selected near-IR-dark galaxies in the COSMOS field. These sources were initially selected as radio-detected sources (S3 GHz > 12.65 μJy) without an optical or near-IR (NIR) counterpart in the COSMOS2015 catalog (Ks ≳ 24.7 mag), and just three of them were subsequently detected in the deeper COSMOS2020. Several studies highlighted that this selection could provide a population of highly dust-obscured, massive, and star-bursting galaxies. With these new ALMA observations, we assess the spectroscopic redshifts of this pilot sample of sources and improve the quality of the physical properties estimated through SED-fitting. Moreover, we measure the quantity of molecular gas inside these galaxies and forecast their potential evolutionary path, finding that the radio-selected NIR-dark galaxies might likely represent a population of high-z progenitors of the massive and passive galaxies that were discovered at z ∼ 3. Finally, we present some initial constraints on the kinematics of the interstellar medium within the analyzed galaxies, reporting a high fraction (∼55%) of double-peaked lines that can be interpreted as the signature of a rotating structure in our targets or as the presence of major mergers in our sample. The results we present here show the scientific potential of (sub)mm observations for this elusive population of galaxies and highlight the potential contribution of these sources to the evolution of the massive and passive galaxies at high z.
Key words: galaxies: evolution / galaxies: high-redshift / galaxies: ISM / galaxies: starburst / infrared: galaxies / submillimeter: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
One of the largest puzzles of modern astronomy is the recent discovery of a significant population of massive (M⋆ ∼ 1011 M⊙) and passive (sSFR < 10−11 yr−1) galaxies that were in place at z ∼ 3 (see some examples in Straatman et al. 2014; Schreiber et al. 2018; Valentino et al. 2020b).
This discovery challenges our galaxy evolution models for two main reasons. On the one hand, these galaxies assembled most of their stellar mass at z > 3, in a period of the cosmic time at which, according to studies based at optical and NIR wavelengths (see Madau & Dickinson 2014 and references therein), the cosmic star formation rate density (SFRD; i.e., the average amount of stellar mass created in the Universe per each year and each comoving Mpc3) was lower by at least one order of magnitude than at the so-called cosmic noon (z ∼ 3). On the other hand, at higher redshifts, we would expect to detect a significant population of massive and star-forming galaxies on the way to quench their star formation (the progenitors of these massive and passive galaxies; see, e.g., Valentino et al. 2020b). However, the galaxies selected at these redshifts in the optical and NIR regimes (mostly Lyman-break galaxies; LBGs; see Giavalisco 2002 and references therein) show a population of galaxies whose stellar masses and star formation rates are too low for them to be progenitors of these sources. In addition, the number density of LBGs at z > 3 is generally found to be lower by one or two orders of magnitude than that of massive and passive galaxies at z = 3 (e.g., Stark et al. 2009; Toft et al. 2014; Valentino et al. 2020b).
Before invoking a dramatic change in our galaxy evolution models, we must exclude any bias in our samples of high-z galaxies. A possible issue might, for instance, reside in the wavelength in which these sources are selected. In the past decades, several studies (e.g., Smail et al. 1999, 2002; Frayer et al. 2004; Simpson et al. 2014; Franco et al. 2018; Wang et al. 2019; Gruppioni et al. 2020; Smail et al. 2021; Talia et al. 2021; Manning et al. 2022; Enia et al. 2022; Behiri et al. 2023) unveiled a significant population of dark galaxies that were constantly missed by optical or NIR surveys. These are the so-called dusty star-forming galaxies (DSFGs; see, e.g., the review by Casey et al. 2014). These sources are characterized by significant amounts of dust in their interior, which causes them to be extremely faint (or even undetected) at short wavelengths.
Several studies selecting these sources at longer wavelengths (i.e., where the effect of dust is negligible, or where we can take advantage of its bright thermal emission, mainly in the FIR and (sub)mm) have assessed how they could represent a population of massive and star-forming galaxies whose estimated number densities are comparable with those reported for massive and passive galaxies at z ∼ 3 (e.g., Toft et al. 2014; Valentino et al. 2020b; Talia et al. 2021; Behiri et al. 2023). Moreover, the inclusion of these sources in the cosmic census of high-z galaxies could be significant enough to change the behavior of the cosmic SFRD at z > 3 (see, e.g., Rowan-Robinson et al. 2016; Gruppioni et al. 2020; Talia et al. 2021; Behiri et al. 2023; Traina et al. 2024).
The main drawback of these studies when performed at FIR and sub(mm) wavelengths is the size of the analyzed samples. When previous-generation instruments such as the Submillimetre Common-User Bolometer Array (SCUBA) on the James Clerk Maxwell Telescope (e.g., Smail et al. 1997; Hughes et al. 1998; Dunlop et al. 2004), the Photodetecting Array Camera and Spectrometer, or the Spectral and Photometric Imaging Receiver (PACS and SPIRE) cameras on the Herschel Space Observatory (e.g., Gruppioni et al. 2013; Burgarella et al. 2013) were employed, the low sensitivity of these instruments biased these samples toward the most extreme objects. In addition, their coarse resolution made it difficult to associate the correct multiwavelength counterpart to the FIR emission without a high-resolution follow-up (see, e.g., Simpson et al. 2015, 2020; Stach et al. 2019; Dudzevičiūtė et al. 2021).
All these issues might in principle be solved through using current state-of-the-art facilities that observe at these wavelengths, such as the Atacama Large (sub)Millimeter Array (ALMA) or the Northern Extended Millimeter Array (NOEMA), which have a higher sensitivity and a better spatial resolution. These instruments are not designed to perform wide blind surveys, however: their small field of view means that the observation of statistically significant volumes of the Universe is very time-consuming (see some noteworthy examples in Dunlop et al. 2017; Franco et al. 2018; Casey et al. 2021).
A possible solution to all these problems could reside in a radio selection. Because radio photons can be generated by free-free emission in HII regions and synchrotron emission from relativistic electrons accelerated in supernovae remnants, they represent a tracer of star formation that is not biased by dust (see, e.g., Kennicutt & Evans 2012 and references therein). As shown for the first time by Chapman et al. (2001), the selection of faint radio sources without an optical or NIR counterpart can provide a sample of likely DSFGs (Chapman et al. 2002, 2004), but the selection can take advantage of the large FOVs and optimal spatial resolution of modern radio interferometers. Moreover, the high sensitivity reached by deep radio surveys can unveil samples of galaxies with less extreme properties than what is commonly obtained through FIR or (sub)mm selections (see, e.g., Chapman et al. 2002, 2004; Talia et al. 2021; Behiri et al. 2023; Gentile et al. 2024).
The drawback of this radio selection is the possible contribution by AGN, however, because nuclear activity can also produce radio emission. This issue can be partly solved with a multiwavelength approach by focusing on extragalactic fields in which a broad photometric coverage is available, which enables a search for the characteristic signatures of AGN at frequencies other than radio (see, e.g., the discussions in Enia et al. 2022 and Gentile et al. 2024; see also the review by Hickox & Alexander 2018 and references therein).
By focusing on deep radio surveys and requiring no counterparts in deeper NIR surveys (as was initially employed by Chapman et al. 2001; see, e.g., Talia et al. 2021, Enia et al. 2022, Behiri et al. 2023, van der Vlugt et al. 2023, and Gentile et al. 2024), we can collect so-called radio-selected NIR-dark galaxies1 (RS NIR-dark galaxies hereafter). The first studies analyzing these sources (Talia et al. 2021; Enia et al. 2022; Behiri et al. 2023; Gentile et al. 2024) reported a series of interesting results that we list below.
-
The RS NIR-dark galaxies represent a population of highly dust-obscured (Av ∼ 4 mag), massive (M⋆ ∼ 1011 M⊙), and star-forming (SFR ∼ 500 M⊙ yr−1) galaxies. The bulk of the population is located at z ∼ 3, and there is a significant tail of high-z sources at z > 4.5.
-
When compared with other galaxies in the same redshift ranges, the RS NIR-dark galaxies always lie above the main sequence of star-forming galaxies, and nearly half of them lie in the starburst regime.
-
Their number density at z > 3.5 (not corrected for incompleteness or for the expected duty cycle) is higher than n = (3.3 ± 0.9)×10−6 Mpc−3. This differs moderately with what was reported by Straatman et al. (2014), Schreiber et al. (2018), and Valentino et al. (2020b) for the massive and passive galaxies at z ∼ 3.
-
Their contribution to the cosmic SFRD at z > 4.5 could be as high as 20–40% of the contribution that is obtained when only optically or NIR-selected galaxies are considered.
When these results increase the scientific potential of the RS NIR-dark galaxies, they cause new questions. First, all these results are based on photometric redshifts and spectral energy distribution (SED) fitting. Because the photometry of these sources is mostly constrained by upper limits in the optical and NIR regimes, a spectroscopic confirmation of the redshift is necessary to decrease the degeneracies affecting the physical properties estimated through this procedure. Second, if the number density of the RS NIR-dark galaxies is compatible with the passive galaxies at z ∼ 3, we need to constrain their evolutionary path to establish the possible relation between the progenitors and the descendants. Finally, we must explain their location in the SFR-stellar mass plane and unveil the physical processes taking place in their ISM that cause the intense star formation.
Clearly, most of these questions cannot be addressed by relying on existing photometry alone that was analyzed in previous studies of these sources: we need to collect more data. Given the elusive nature of the RS NIR-dark galaxies, our choice is limited to the new facilities observing at longer wavelengths: ALMA, NOEMA, and the James Webb Space Telescope (JWST). As noted by several previous studies, (sub)mm observations can be highly useful in assessing the true nature of dark galaxies selected at other wavelengths, allowing us to constrain their dust and gas content (e.g., Chapman et al. 2001, 2002, 2004) and to prove their obscured star formation (e.g., Wang et al. 2019).
This paper is focused on the first ALMA follow-up of a pilot sample of nine RS NIR-dark galaxies selected in the COSMOS field by Talia et al. (2021) that was analyzed by Behiri et al. (2023) and Gentile et al. (2024). The first results involving an accepted NOEMA follow-up and the first JWST data obtained through the COSMOS-Web survey (Casey et al. 2023) will be described in following papers (Gentile et al., in prep.).
This study is structured as follows. In Sect. 2, we introduce our targets, the ancillary photometry available for them, and the new ALMA observations. In Sect. 3, we describe the analysis of the ALMA cubes, the identification of any bright emission line in our targets, and our modeling of the spectroscopic redshifts. Moreover, we present some initial insights into the ISM kinematics and derive the physical properties of our pilot sample of galaxies through SED fitting. Then, in Sect. 4, we discuss our results, estimate the gas mass in our sources, and forecast a possible evolutionary path for them. Finally, we draw our conclusions in Sect. 5. Throughout this paper, we assume a Chabrier (2003) initial mass function (IMF) and a flat ΛCDM cosmology with [Ωm, ΩΛ, h]=[0.3, 0.7, 0.7].
2. Data
2.1. ALMA observations and data reduction
The main focus of this study is on the observations carried out by ALMA during its cycle 8 as a part of the observing program 2021.1.01467.S (PI: M. Talia). The required observations consisted of a spectroscopic follow-up at millimeter wavelengths for a pilot sample of nine RS NIR-dark galaxies (Table 1). These sources were initially selected in the COSMOS field by Talia et al. (2021) among those located in the high-z tail of the redshift distribution (photo-z > 4.5), with the best-sampled SEDs (i.e., with at least one significant detection at S/N > 3 at FIR or (sub)mm wavelengths), and with a reliable SED fitting. Following the selection by Talia et al. (2021), these objects were part of a sample of 476 galaxies that were robustly detected (S3 GHz > 12.65 μJy; S/N > 5.5) in the catalog of the VLA-COSMOS 3GHz Large Project (Smolčić et al. 2017) and lacked an optical and NIR counterpart in the COSMOS2015 catalog (Laigle et al. 2016), that is, the most recent NIR-selected catalog of the COSMOS field at the time of that study. As highlighted by Gentile et al. (2024), the public release of the deeper COSMOS2020 catalog (∼1 mag deeper in the Ks band and with the detection operated in a more complete detection image; see Weaver et al. 2022) allowed us to associate an optical or NIR counterpart with ∼150 sources analyzed in Talia et al. (2021). The targets with a counterpart in the COSMOS2020 catalog are highlighted with an appropriate flag in Table 12.
Main observational properties of the nine targets.
The main scientific goal of the observing program was to assess the spectroscopic redshifts of the nine targets. Therefore, we requested a spectral setup covering the whole band 3 of ALMA (i.e., all the frequencies between ∼84 and ∼115 GHz). This setup, analogous to the setups employed in similar studies in the current literature (see, e.g., Walter et al. 2016; Jin et al. 2019, 2022; Cox et al. 2023), ensures that at least one line of the CO and [CI] transitions should be detected for almost all the redshifts in the range 0 < z < 8. Moreover, this spectral scan provides the possible detection of two lines for most of the redshifts higher than 3, allowing an unambiguous determination of the spec-z (see Fig. 1). To cover the whole band 3 with ALMA, five settings were required. By estimating the integrated fluxes of the expected CO and [CI] lines observable in our setup, we requested a sensitivity of 0.32 mJy beam−1 per stacked channel for a total of 27h of ALMA observing time. The observations were performed in service mode between March and September 2022, when the interferometer was in its C–4/C–3 configurations (i.e., with baselines between 15 and 500/784 m, an expected beam size of 1.4″/0.92″, and a maximum recoverable scale of 16.2″/11.2″). The calibration was performed by the Alma Regional Center through the ALMA standard pipeline. After the calibrated measurement sets were obtained, we merged the multiple observations through the Common Astronomy Software Applications package (CASA v6.1; CASA Team et al. 2022). Finally, to achieve the sensitivity originally requested in the proposal, we resampled the native spectral resolution to obtain ∼0.02 GHz channels (∼50 km s−1 at the reference frequency of 100 GHz). After a first cleaning (performed with the task TCLEAN and employing natural weighting to maximize the sensitivity; see Högbom 1974), we verified that the median rms across the stacked channels was 0.2 mJy beam−1 (i.e., slightly better than requested in the original proposal), increasing toward higher frequencies due to the decreasing transmissivity of the ALMA band 3 up to 0.4 mJy beam−1. The various settings have some overlap in frequency, and therefore, these (overlapping) ranges have a better rms. The beam shape is quite uniform across the channels: it can be modeled as an ellipse with a half-power beam width equal to 1.45″ × 1.31″ position angle of ∼ − 70°.
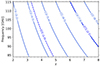 |
Fig. 1. Spectral setup adopted for the ALMA observations. This configuration allowed us to observe at least one line of the CO and [CI] transition for all the redshifts below 8. For most of the redshifts higher than 3, two lines are detectable at the observed frequencies. |
2.2. Ancillary data
The nine galaxies we analyze are located in the Cosmic Evolution Survey field (COSMOS; one of the most famous extragalactic fields in modern astronomy that was observed by most of the main telescopes in the past decades: see, e.g., Scoville et al. 2007; Koekemoer et al. 2007; Laigle et al. 2016; Civano et al. 2016; Weaver et al. 2022; Euclid Collaboration 2022; Casey et al. 2023). They are therefore almost completely covered in multiple wavelengths from radio to X-rays. Most of the photometry for these sources is described in Gentile et al. (2024) and is briefly summarized here. The fluxes in the optical-to-MIR regime were extracted from the scientific maps employed by Weaver et al. (2022) to build the COSMOS2020 catalog. These maps were produced by the Hyper Supreme-Cam (HSC), VISTA InfraRed CAMera (VIRCAM), and Infrared Array Camera (IRAC) instruments mounted on the Subaru, VISTA, and Spitzer telescopes. Gentile et al. (2024) analyzed these maps through the pipeline called photometry extractor for blended objects (PHOEBO). This pipeline implements a modified version of the algorithm introduced by Labbé et al. (2006) that has been employed in several studies (see, e.g., Endsley et al. 2021; Whitler et al. 2023), but it was optimized for the deblending of RS NIR-dark galaxies. It mainly relies on a double prior from the radio and NIR maps, employing a PSF-matching between the high- (radio and NIR) and low-resolution maps (mainly those produced by IRAC) to deblend the different sources and extract forced photometry. Further details of the algorithm and its validation are presented in Gentile et al. (2024), and the algorithm is freely available in a GitHub repository3. Additional photometry at longer wavelengths was retrieved through cross-matching with preexisting catalogs. The photometry at FIR wavelengths was obtained from the SuperDeblended catalog (v20201010; Jin et al. 2018), containing deblended photometry from MIPS/Spitzer, PACS and SPIRE/Herschel, and the SCUBA-2/JCMT instruments and telescopes. The fluxes at (sub)mm wavelengths were retrieved through cross-matching with the catalog from the Automated Mining of the ALMA Archive in the COSMOS Field (A3COSMOS) survey (v.20200310; Liu et al. 2019). Finally, radio fluxes at 1.28, 1.4, and 3 GHz were obtained from the catalogs of the COSMOS-VLA large program (Schinnerer et al. 2010; Smolčić et al. 2017) and of the MIGHTEE Early Science Data Release (Jarvis et al. 2016; Heywood et al. 2022). A shallow X-ray coverage is also available for the COSMOS field in the public catalogs by Elvis et al. (2009) and Civano et al. (2016). This latter information was employed in Gentile et al. (2024) to ensure that none of the sources analyzed in this work hosts a powerful and unobscured AGN (Lx > 1042 erg s−1).
3. Analysis of the datacubes
3.1. Continuum images
The first analysis performed on the calibrated MSs consisted of the production of a continuum image (see Fig. 2), which is useful to study the properties of dust in our targets. This procedure was performed through the CASA task tclean in multifrequency synthesis (mfs) mode after masking any bright line that could contaminate the continuum emission. To maximize the sensitivity of the cleaned image, we employed a natural weighting throughout this procedure. To estimate the continuum fluxes, we performed aperture photometry with CARTA (Comrie et al. 2021), for which we employed an aperture corresponding to the 2σ contour of the continuum image. We verified that this estimate is compatible within the estimated uncertainties with the flux estimated through a 2D profile-fitting performed with the CASA task IMFIT. The results of this procedure are reported in Table 2. We obtained that six out of nine targets are robustly detected (S/N > 3) in the continuum images.
 |
Fig. 2. Continuum maps of the nine targets. The black contours are in steps of 2σ starting from 3σ. All the images have a 7.5″ side, while the synthetized beam is reported in the lower left corner of each image. |
Continuum fluxes for the RS NIR-dark galaxies analysed in this study.
3.2. Line identification and reliability
The emission lines inside our datacubes were unveiled through a line-finding algorithm analogous to the algorithms employed in several previous studies (e.g., Daddi et al. 2015; Walter et al. 2016; Coogan et al. 2018; Puglisi et al. 2019; Jin et al. 2019, 2022). We summarize it below.
-
We obtained a continuum-subtracted MS for each source through the CASA task UVCONTSUB. We modeled the continuum as a first-grade polynomial whose slope was fit in the whole frequency range covered by our observations after any bright line was massked that could contaminate the continuum estimation.
-
We computed the zeroth moment of the continuum-subtracted MS through the CASA task IMMOMENTS to unveil the spatial region of the datacube with a significant line emission. In all targets we analyzed, the zeroth moment significantly overlaps with the radio emission at 3 GHz, as visible in the maps by Smolčić et al. (2017). This result ensures that the millimeter emission can be safely associated with our targets.
-
We performed the imaging of the continuum-subtracted visibilities through the CASA task TCLEAN. We employed a natural weighting to maximize the sensitivity of the cleaned images.
-
We convolved the cleaned datacube with a series of boxcar kernels with variable widths between one and 13 channels (i.e., between 60 and 780 km s−1 at a representative frequency of 100 GHz).
-
For each convolved datacube, we produced an S/N cube by dividing each channel by the relative rms. This quantity was computed through a sigma clipping performed on the inner region of the primary beam to avoid possible biases due to significant emission and higher noise far from the phase center.
-
Finally, we extracted an S/N spectrum for each convolved datacube through the Python library INTERFEROPY (Boogaard et al. 2021). We employed as extracting region the 2σ contour of the zeroth-moment map obtained in step 2.
This procedure resulted in a list of possible lines, with the related S/N and full width at zero intensity (FWZI)4. However, given the nature of the noise in interferometric data, it is generally needed to establish the reliability of each line R = 1 − p (where p is the probability of a spurious detection). Since several methods exist to compute this quantity for interferometric data, we followed two complementary approaches. Firstly, following Jin et al. (2019), we computed the spurious probability of each line as
where R0 is the reliability expected in the Gaussian case (which therefore approaches unity toward higher S/N), and NEff is the number of effective searches. Through an extensive series of simulations, Jin et al. (2019) estimated that this quantity can be approximated through the relation
where Ntotal, ch is the total number of channels inside the datacube, Nline, ch is the number of channels in which the line is detected, and 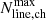 and
and 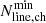 are the minimum and maximum width of the boxcar kernels employed during the line search (see point 4), respectively. While this approach is based on simulations and does not depend on the properties of the actual cube, it relies on the hypothesis that the noise at the phase center of our observations is approximately Gaussian (a reasonable assumption given the almost complete uv coverage generally produced by ALMA). We also computed the reliability of each line following Walter et al. (2016), through the FINDCLUMPS algorithm as implemented in the Python library INTERFEROPY. This method estimates the reliability as
are the minimum and maximum width of the boxcar kernels employed during the line search (see point 4), respectively. While this approach is based on simulations and does not depend on the properties of the actual cube, it relies on the hypothesis that the noise at the phase center of our observations is approximately Gaussian (a reasonable assumption given the almost complete uv coverage generally produced by ALMA). We also computed the reliability of each line following Walter et al. (2016), through the FINDCLUMPS algorithm as implemented in the Python library INTERFEROPY. This method estimates the reliability as
where NP and NN are the number of positive and negative peaks in the whole datacube in a given S/N bin, respectively. This approach does not rely on any assumption about the nature of the noise in our datacubes, but it could be biased by the small statistics that affects the number of pixels in our observations.
Both the procedures described here allowed us to identify at least one bright (S/N > 6) line (see Table 3) in all targets. The S/N of all the detected lines is high, and we were therefore able to estimate a spurious probability lower than 10−6 for all of them, following Jin et al. (2019). Similarly, because their S/N is higher than every negative peak in the analyzed datacubes, we can estimate for all of them a 100% reliability following Walter et al. (2016). By producing the zeroth moment of each (continuum-subtracted) line through the CASA task IMMOMENTS, we obtained the maps reported in the insets in Fig. 3. Moreover, by performing aperture photometry with CARTA on the 2σ contour of these maps, we measured the integrated line fluxes reported in Table 4.
 |
Fig. 3. Spectrum of the various lines identified through the procedure discussed in Sects. 3.2 and 3.3 in our targets. To increase the visibility of the lines, we resampled the original spectral resolution employed in the study up to ∼180 km s−1. For each line, we report in the upper right corner the ID of the galaxy and our modeling as CO or [CI] transitions. The insets show the moment zero of each line (7.5″ side) centered on the radio position measured from the 3 GHz maps, with the contours in steps of 2σ starting from 3σ. In each line, we also report in red the Gaussian modeling with one or two components as described in Sect. 3.4. In the lines modeled with a double Gaussian, we also show the two subcomponents with a dashed orange line. |
 |
Fig. 3. continued. |
Integrated fluxes of the lines detected in our sources.
3.3. Redshift estimation
After the different lines in our datacubes were detected, we estimated the spectroscopic redshift of our sources following Jin et al. (2019). To do this, we considered the line with the highest S/N in each cube (i.e., the line with the highest reliability) and modeled it as each of the CO transitions that should be visible in the redshift range 0 < z < 8 (see Fig. 1). For all redshifts higher than 3, for most of which a second line is expected, we searched for a detection at the expected frequency in the line list produced in Sect. 3.2. Through the S/N of each detection, we computed the reliability of the tentative second lines through Eq. (1). It is crucial to underline that for the second line, the number of effective searches (NEff) was much lower than those employed in Sect. 3.2. In this case, we did not perform an active search of the line throughout the whole spectrum, but we only analyzed the frequencies allowed by the first line. Therefore, the NEff just corresponds to the number of possible CO transitions with which we can model the first line. For each redshift, we finally estimated a joint spurious probability given by the product between the spurious probability of the first and second line. The redshift with the highest reliability was assumed to be the spectroscopic redshift of our sources.
This approach was sufficient for all the galaxies in which two lines were robustly detected. However, for four of our targets, no second line is detected at a sufficiently high S/N in the spectra we analyzed. For these galaxies, we assessed the redshift based on additional information from the photometry. After the continuum datapoint at 3 mm (Table 2) was added to the photometry presented in Sect. 2.2 (or an upper limit for the galaxies that were undetected in the continuum images), we performed an SED fitting through the code CIGALE (Boquien et al. 2019; see more details of the employed models in Sect. 3.5) by fixing the redshift to all the spec-z allowed by the single line identified in the spectrum. Hence, we assumed the redshift with the best agreement between the modeled SED and the photometry as the final value for the spec-z (i.e., the redshift with the lowest χ2). Remarkably, for one of the remaining galaxies (RSN-182), the redshifts estimated through this procedure fall in a small frequency range at z ∼ 4.7 where a single line (CO(5–4)) is expected. Similarly, three targets (RSN-41, RSN-247, and RSN-456) have a redshift lower than 3, where according to our spectral setup no second line is expected to be observed. We also report a tentative second line in RSN-361 at ν = 88.13 GHz. Even though this detection falls exactly where the [CI](1–0) line would be expected for a galaxy at z = 4.585, the low S/N ∼ 3.5 and the spatial offset with the robustly detected line at ν = 103.19 GHz make the line identification unsure. Finally, we underline that the continuum image (see Fig. 2) shows a quite irregular morphology for this source, suggesting the a possible major merger (which might explain the spatial offset of the tentative [CI](1–0) line). It is important to note that these redshifts based on a single detected line are clearly more uncertain than those relying on a double detection. We cannot exclude that a fainter line (e.g., a [CI](1–0)) would be observed in our frequency range with deeper observations. For instance, given the redshift estimated through CO(4–3) and CO(5–4) in RSN-298, we would expect a [CI](1–0) line at ν = 95.57 GHz in that source, even though nothing is detected at that frequency at S/N higher than 1σ. For the other galaxies where a single line is detected, however, these solutions would be disfavored by the photometry.
3.4. Initial insights into the ISM kinematics
As shown in Table 3, most of our targets have quite broad lines (FWHMs of several hundreds of km/s). This result is familiar for high-z DSFGs and ULIRGs in general (see, e.g., Jin et al. 2019, 2022; Cox et al. 2023), and it is generally explained through an ISM that is much more turbulent than what is commonly observed in local galaxies. In this study, however, we perform a more detailed analysis of some targets because the FWHM of the lines is much larger than the spectral resolution requested in our observation. This property allowed us to infer some initial insights into the ISM kinematics inside our galaxies. As shown in Fig. 3, most of the lines observed in our targets have a peculiar morphology that suggests the possible presence of two peaks in the observed line spectrum. This result could be explained by a kinematically decoupled component such as in a disk or in the later stage of a merger. To decide in a statistically motivated way whether our lines should be modeled with a single or double component, we performed a test hypothesis. In our case, the null hypothesis consisted of modeling the line with a single Gaussian, while the alternative hypothesis consisted of a modeling with two Gaussians. We employed two nested models (with four and seven free parameters because we allowed a residual continuum component), and performed a partial F-test (e.g., Bevington & Robinson 2003) employing a threshold of 0.05 for the level of significance to reject the null hypothesis. Considering only the highest S/N line in each spectrum, we obtained that a double component is statistically significant for five out of nine targets (∼55%). For most galaxies in which two lines are detected (with the notable exception of RSN-84), the lower S/N of the second line prevented us from concluding that the additional component is statistically required for a correct modeling. For all the lines for which the double model is statistically motivated, we report the best-fitting parameters in Table 5. A comparison of the fraction of double-peaked lines with other similar studies in the current literature presenting spectroscopic follow-up of SMGs at (sub)mm wavelengths shows that our percentage is higher than the ∼30% reported by Bothwell et al. (2013) (detecting CO emission in a large sample of 32 SMGs in the redshift range 1.2 < z < 4.1) and Aravena et al. (2016) (observing 17 lensed DSFGs at 2.5 < z < 5.7). and the ∼40% of double-peaked profiled reported by Birkin et al. (2021) (studying 61 ALMA-detected SMGs). Unfortunately, the limited size of our sample prevents us from unambiguously establishing whether this difference is due to the different selections or a consequence of the different S/N achieved by the different observations. The two components with different velocities in our galaxies can be explained with a rotating structure or as the signature of the late stage of a major merger. These hypotheses are also strengthened by the first moments of the CO and [CI] lines within three of our targets (those with the highest S/N in the CO-lines, RSN-84, RSN-121, and RSN-235. In RSN-84, the same structure is visible in the CO(4–3) and [CI](1–0) lines; see Fig. 4). Unfortunately, the spatial resolution of our observations is not sufficient to distinguish between the two possible models (i.e., a disk or a merger). Similarly, the coarse spatial and spectral resolution prevents us from performing a proper modeling of the possible disk (see, e.g., Di Teodoro & Fraternali 2015; Roman-Oliveira et al. 2023). Constraining the deprojected velocity of the gas and its velocity dispersion would allow us to determine whether the structure is stable. This result would be of crucial importance to constrain some of the evolutionary models of massive galaxies (see Sect. 4.4).
 |
Fig. 4. Moment-one maps (2.5″ × 2.5″) of the lines detected in three of the targets. According to our modeling, the maps show clear evidence of a rotating structure or a late stage of a merger. |
3.5. SED fitting
After we assessed the spectroscopic redshift of our sources, we estimated their physical properties through an SED fitting with the code CIGALE (Boquien et al. 2019). To account for all the processes taking place inside our targets, we employed several libraries, following the same strategy as employed in Gentile et al. (2024). First, we included the stellar emission through the stellar population libraries by Bruzual & Charlot (2003), combined through an exponentially declining star formation history with random bursts of star formation. The stellar attenuation was modeled following Charlot & Fall (2000), and the dust thermal emission was included in the templates through the Draine et al. (2014) models. Finally, radio emission was treated as described in Boquien et al. (2019). We also explored the possible presence of AGN within our sources by adding a dusty torus component as modeled by Fritz et al. (2006). For all the models, we employed the parameters used by Donevski et al. (2020) in the analysis of their sample of DSFGs with CIGALE. The results of the SED fitting and all the physical properties estimated with CIGALE are summarized in Fig. 5 and in Table 6. Through the SED fitting, we estimated the stellar mass (M⋆), the infrared luminosity (LIR), and the dust attenuation (Av). Because the photometric coverage in the FIR-to-radio regime for our targets is significantly better than in the optical and NIR ones, we estimated the SFR from the LIR through the relation by Kennicutt & Evans (2012), rescaled to a Chabrier (2003) IMF. A last interesting parameter estimated through SED fitting is the AGN fraction (fAGN), defined as the ratio of the luminosity of the host galaxy to that of the AGN in the wavelength range [5, 40] μm. Interestingly, CIGALE reports a fAGN = 0 for all our targets, and we can therefore safely conclude that the photometry of our galaxies is correctly reproduced without a dusty torus component. Another indication for the lack of a strong AGN contribution in our sample comes from the estimation of the qTIR from the infrared luminosity (computed through the SED fitting) and the radio flux (see, e.g., Helou et al. 1985) The latter was converted into a 1.4 GHz radio luminosity through the spectroscopic redshift and the radio slope measured through the radio fluxes at 3 GHz and 1.4 or 1.28 GHz. For the galaxies without a second radio detection (RSN-41, RSN-235, and RSN-298), we assumed the median slope computed for the rest of the sample. We obtain that all the qTIR are in the range [2.45,2.55], which agrees well with what is commonly measured for star-forming galaxies (e.g., Yun et al. 2001).
 |
Fig. 5. Best-fitting SEDs of our targets as computed by CIGALE (Boquien et al. 2019). The different emissions in the galaxies are color-coded. Attenuated stellar emission is reported as an orange line. The dust emission is reported in red, and the radio emission is reported in purple. Finally, the solid black line shows the best-fitting SED. |
Physical properties for our sources derived through SED fitting.
4. Results and discussion
4.1. Analysis of the spec-z
As visible in Table 3, the nine galaxies analyzed in this paper have a spec-z between 2.8 and 4.7, with a median value of ∼3.52. By comparing these values with the photometric redshifts estimated following Gentile et al. (2024) (when the continuum point at 3 mm obtained in Sect. 3.1 is added), we note that the agreement is quite good (see Fig. 6). More quantitatively, we can measure the accuracy of our photo-z as
 |
Fig. 6. Comparison of the photometric redshift following Gentile et al. (2024) and the spectroscopic redshifts measured in this study. The one-to-one relation is reported as the dotted black line, and the shaded gray area shows the galaxies with |Δz|/(1 + z) < 0.15. The galaxies with a spec-z obtained from the modeling of two lines are highlighted with an additional box. |
when considering all the spec-z assessed in Sect. 3.3. This result validates the procedure followed in Gentile et al. (2024) for estimating the photometric redshift of the RS NIR-dark galaxies, and it is quite encouraging for future follow-ups for the high-z candidates reported in that study. Finally, we underline that because for three of our galaxies with at least one line, we have a counterpart in the COSMOS2020 catalog (see Table 1), we can retrieve three photo-z from that catalog (z = 3.6 ± 0.3, z = 2.8 ± 0.3, and 4.6 ± 0.3 for RSN-84, RSN-247, and RSN-361, respectively). These quantities were computed by Weaver et al. (2022) with the two SED-fitting codes EAZY (Brammer et al. 2008) and LEPHARE (Arnouts et al. 1999; Ilbert et al. 2006) on the optical and NIR bands included in the COSMOS2020 catalog and on the first two channels of IRAC, and they agree perfectly with the spectroscopic redshift estimated through (sub)mm spectroscopy (see Table 3). A last interesting comparison can be performed with the photometric redshifts computed by Talia et al. (2021) that were employed to select the targets for these ALMA observations. Unfortunately, most of the sources are located at a lower redshift than expected from that study (see Table 3). This difference can be explained by the several improvements in the photometry extraction and in the photo-z estimation employed in Gentile et al. (2024) with respect to Talia et al. (2021). We expect that most of the differences arise because of the new deblending procedure based on the PHOEBO algorithm (allowing us to better extract the photometry from low-resolution maps; e.g., the four IRAC channels), the deeper IRAC images employed in Gentile et al. (2024), and the more stringent upper limits employed in the photometric bands without detections. A full comparison of the two procedures can be found in Gentile et al. (2024). We expect this difference in the photo-z computed by Gentile et al. (2024) and Talia et al. (2021) to produce different constraints on the contribution of the RS NIR-dark galaxies to the cosmic SFRD (especially at z > 4.5, where most of the targets were located according to the previous photo-z). This point will be addressed in detail through the analysis of the full sample of RS NIR-dark galaxies in COSMOS in a forthcoming paper (Gentile et al., in prep.)
4.2. Analysis of the physical properties
The results obtained through SED fitting in Sect. 3.5 allow us to confirm one of the main results established in Gentile et al. (2024). In that study, we assessed that the RS NIR-dark galaxy selection produces a sample of star-bursting DSFGs. However, since this result was based on an SED fitting in which the redshift was a free parameter, the quantities estimated through this procedure were affected by significant uncertainties due to the several degeneracies between the shape of the SED and the redshift. By assuming the spec-z measured through our ALMA observations, we can decrease the uncertainty on these quantities. First of all, the median properties estimated with the improved SED fitting are broadly compatible with those estimated by Gentile et al. (2024) for the whole sample (see also the results discussed in Talia et al. 2021 and Behiri et al. 2023 regarding a smaller subset of the same sample). We underline, however, that since the galaxies in the proposal were selected from those with at least one secure detection in the FIR or (sub)mm regimes, we do not expect the median properties of our sample to be necessarily similar to those of the whole sample of RS NIR-dark sources. A second interesting comparison of this study and that by Gentile et al. (2024) resides in the comparison of the SFR and stellar mass computed through the new SED fitting and the main sequence of the star-forming galaxies. As shown in Fig. 7, most of the targets are still located above the main sequence by Schreiber et al. (2015), close to the star-bursting regime (i.e., galaxies with an SFR at least three times higher than what is expected from a main-sequence source with the same mass and in the same redshift bin). We underline, however, that the location on the main sequence strongly relies on the estimated stellar mass, which is quite uncertain for our targets because the rest-frame optical continuum is highly obscured by the dust. Nevertheless, the employment of the CIGALE code, relying on the energy balance principle between dust absorption and emission, allowed us to obtain some indirect constraint on the dust extinction from the infrared and radio coverage. More stringent constraints on the stellar mass will be provided for most of the galaxies in the whole sample of RS NIR-dark galaxies in COSMOS by the deep NIR imaging provided by JWST as part of the COSMOS-Web survey (Casey et al. 2023, Gentile et al., in prep.). Figure 7 also reports for comparison the location of other populations of dark DSFGs in the stellar mass versus SFR plane: the H-dropouts by Wang et al. (2019) and the NIRfaint SMGs by Smail et al. (2021). While the overlap between our RS NIR-dark galaxies and the H-dropouts has already been studied in Gentile et al. (2024), the availability of the new (sub)mm data allowed us to study more quantitatively how many of our sources would be selected with the criteria employed by Smail et al. (2021). We recall that these sources are part of a sample of 707 SMGs collected in the Ultra Deep Survey by reimaging a sample of galaxies initially detected in the 850 μm maps produced with the SCUBA2 camera (Geach et al. 2017) with ALMA (in band 7, i.e., at a representative frequency of 870 μm; Stach et al. 2019). The sample studied by Smail et al. (2021) contains all5 the sources with Ks > 25.3 mag (at 5σ). Since the Ks limiting magnitudes in the UDS and in COSMOS are similar, we studied the overlap between the two populations by comparing the (sub)mm flux at 850 μm. For our sources, only RSN-84 has an ALMA flux at the same frequency (see Table 2). Three of the other galaxies have analogous fluxes from the deblending of the SCUBA2 maps (Jin et al. 2018), while the others have only upper limits (S/N < 3σ, since the uncertainties in the SuperDeblended catalog also account for the deblending procedure). For these sources, we employed the best-fitting fluxes at 850 μm computed with CIGALE. On the other hand, the sources in Smail et al. (2021) were initially selected for having an S/N > 4σ (equivalent to S850 μm ≥ 3.8 mJy) in the original SCUBA2 maps. However, the higher resolution achieved by ALMA in the Stach et al. (2019) follow-up allowed the discovery of multiple fainter sources that contribute to the original sources detected by SCUBA2 up to S850 μm > 1 mJy and with a median value of 3.8 ± 0.3 mJy. Therefore, even though four out of nine sources in our sample would not have been selected by the original SCUBA2 survey because they are too faint for the limited sensitivity of that instrument (see Table 2), all of them would have been detected by the deeper ALMA follow-up.
 |
Fig. 7. Comparison of the physical properties estimated through CIGALE and the main sequence of star-forming galaxies by Schreiber et al. (2015) (solid gray line; the shaded area is its 1σ = 0.3 dex its scatter). The targets are reported as colored stars, with the same color-code as employed in Fig. 6. The dotted gray line reports our threshold for identifying the star-bursting galaxies (i.e., those whose SFR is higher than three times that expected from a main-sequence galaxy). For reference, we also report the location of the RS NIR-dark galaxies around z ∼ 3.5 studied in Gentile et al. (2024), the NIR-faint SMGs by Smail et al. (2021), and the H-dropout galaxies by Wang et al. (2019). |
4.3. Gas mass and depletion time
Several studies highlighted that the [CI](1–0) and the CO(1–0) lines can be employed as good tracers of the molecular gas inside galaxies (e.g., Papadopoulos et al. 2004; Valentino et al. 2020a; Gururajan et al. 2023). For four galaxies in our sample (see Table 3), we observed the [CI](1–0) line and directly estimated the molecular gas mass in our objects by employing the relation by Papadopoulos et al. (2004),
where DL is the luminosity distance of our target expressed in Mpc, ICO is the integrated line flux, and A10 = 0.793 × 10−7 s−1 is the Einstein coefficient. Q10 and X10 are the [CI] excitation factor and the [CI]/H2 abundance ratio, respectively. For these quantities, we employed literature standard values of XCI = 3 × 10−5 and Q10 = 0.6 (Papadopoulos et al. 2004; Bothwell et al. 2017). Through Eq. (5), we estimated the gas masses for RSN-84, RSN-121, RSN-235, and RSN-361 reported in Table 6. For all the other targets in which we did not detect the [CI](1–0) line, we derived the gas mass from the CO(1–0) line through the relation
(see, e.g., Bolatto et al. 2013 and references therein). It is well known that the value of αCO is highly uncertain and strongly depends on the specific property of each galaxy. We chose a literature value of 0.8 M⊙ [K km s−1 pc−2]−1, which is usually employed for star-bursting galaxies (see, e.g., Bolatto et al. 2013; Gururajan et al. 2023). In order to use Eq. (6), we rescaled the measured fluxes of our CO lines to the CO(1–0) transition by assuming a CO spectral line energy distribution (SLED). Several studies highlighted that the CO-SLED of galaxies is strongly affected by AGN (see, e.g., Vallini et al. 2019) and evolves with redshift (e.g., Boogaard et al. 2020). Since the previous test performed on our targets by Talia et al. (2021) and Gentile et al. (2024) (together with the null AGN fraction obtained through SED fitting with CIGALE; Sect. 3.5) excluded strong nuclear activity, we chose the CO-SLED obtained by Bothwell et al. (2013) for a sample of DSFGs in the redshift range 1.2 − 4.1 (i.e., compatible with the spec-z of our targets). We employed R31 = 2.3 ± 0.3, R41 = 3.0 ± 0.4, and R51 = 3.8 ± 0.7, where Rn1 is the ratio of the integrated line flux in the nth CO transition and the CO(1–0). The gas mass obtained through these relations is reported in Table 6. For the galaxies with both a CO and a [CI] line, we report both estimates of the gas mass. However, since the values estimated from the [CI](1–0) line rely on fewer assumptions than those based on the CO lines (i.e., they do not relie on the assumed CO-SLED, but still depend on the conversion factor between the [CI](1–0), as uncertain as the αCO value), we employed these gas masses in the following analyses. The information about the gas content of our galaxies can be combined with the SFR estimated in Sect. 3.5 and is reported in Table 6 to assess the depletion time of our galaxies. This quantity is defined as the amount of time in which each object would transform its whole gas mass into stars assuming a constant SFR,
For our galaxies, we obtained the depletion times reported in the last column of Table 6. The values for the galaxies in our sample range from 80 to 300 Myr. These quantities can be compared with other populations of galaxies in the current literature, as shown in Fig. 8. The depletion time of our targets can be compared with that expected from main-sequence galaxies. Saintonge et al. (2013) reported a τD that evolved with redshift as τD = 1.5(1 + z)α, with several collaborations finding different values for the exponent, spanning from α = −1.0 (Davé et al. 2012) to α = −1.5 (Magnelli et al. 2013). Our targets have a shorter depletion time than main-sequence galaxies. This result represents a further confirmation (independent of the more uncertain stellar mass) of the star-bursting nature of our sources. Similarly, we can compare the gas mass and the SFR of our RS NIR-dark galaxies with several SMGs in the current literature (those analyzed by Walter et al. 2011, Bothwell et al. 2017, and Cañameras et al. 2018). For all these sources, we retrieved the infrared luminosity and the [CI](1-0) line fluxes from the study by Valentino et al. (2020a). Following the relations by Kennicutt & Evans (2012) and Papadopoulos et al. (2004), we estimated the SFR and gas mass in a consistent way with those derived from our targets. We obtain that our RS NIR-dark galaxies are more gas rich on average than the SMGs analyzed in those studies in the low-SFR tail of their distribution and therefore have a longer depletion time.
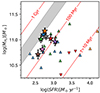 |
Fig. 8. Depletion time and star formation rate for our targets. The RS NIR-dark galaxies are reported as colored stars, following the same color-code as in Fig. 6. The colored triangles are other populations of SMGs, namely those collected by Bothwell et al. (2017), Cañameras et al. (2018), and Walter et al. (2011), reported in blue, orange, and green, respectively. We also report some confirmed QSOs from the same studies as reversed red triangles. The shaded gray area reports the depletion time expected from main-sequence galaxies at z ∼ 3.5 following the relation τD = 1.5(1 + z)α found by Saintonge et al. (2013), with α spanning from −1.0 (Davé et al. 2012) to −1.5 (Magnelli et al. 2013), rescaled to a Chabrier (2003) IMF. |
4.4. Possible evolutionary path
The gas mass and depletion times estimated in Sect. 4.3 allow us to forecast a possible evolutionary path for our sources. We employed the same simplistic model as was used to define the depletion time: We assumed that the SFR remains constant inside our sources until all the gas mass is converted into stars. Clearly, this model does not account for any quenching mechanism (e.g., due to possible AGN feedback; see, e.g., Fabian 2012) or gas accretion from the intergalactic medium (e.g., Sancisi et al. 2008). With this model, we assumed that our galaxies evolve from an initial state characterized by z0 = zspec and M⋆, 0 = M⋆ to a final state with zf = zspec − Δz and M⋆, f = M⋆ + MH2, where Δz is the difference in redshift elapsed during the depletion time. The results of this simplistic model applied to our targets are shown in Fig. 9, where we consider all the uncertainties on the involved quantities through a Monte Carlo integration. We compared the final stage of our galaxies with the redshift and stellar mass of the massive and passive galaxies discovered by Schreiber et al. (2018) at z ∼ 3. We note a significant overlap between the two populations. This result, combined with the number densities estimated by Talia et al. (2021), Behiri et al. (2023), and Gentile et al. (2024), suggest that the RS NIR-dark galaxies could represent a significant fraction of the progenitors of the massive and passive galaxies at z ∼ 3. In the broader context of galaxy evolution studies, this result confirms the idea that the dust-obscured galaxies play a significant role in the evolution of the most massive galaxies in the Universe (see, e.g., Casey et al. 2014; Toft et al. 2014; Valentino et al. 2020b). In addition, the components with different velocities detected in our targets in Sect. 3.4 could support two possible evolutionary scenarios for our galaxies. On the one hand, they could be the signature of a significant fraction of major mergers within our sample. This result would confirm the so-called merger-driven scenario for the formation of massive galaxies, where these objects are formed through a series of major mergers (see, e.g., Hopkins et al. 2008b,a). On the other hand, the double component in our galaxies could be due to the presence of a rotating disk. In this case, this result would support the so-called in situ scenario, where the build-up of massive galaxies occurs via the rapid compaction of a gaseous outer disk triggering a huge burst of star formation, and via the subsequent stellar and AGN feedback processes quenching it within a relatively short timescale (< 1 Gyr; see e.g Lapi et al. 2014, Pantoni et al. 2019). The possibility of shedding new light on these alternative scenarios increases the scientific interest in the RS NIR-dark galaxies and the need for high-resolution follow-up for these sources.
 |
Fig. 9. Possible evolutionary paths of our targets, assuming a simple evolutionary model with a constant star formation and a final stage in which all the molecular gas has been transformed into stars. The uncertainties are considered through a Monte Carlo integration. The color map is the same as employed for Fig. 6, For reference, the shaded red stars report the stellar mass and the redshifts for the massive and passive galaxies at z ∼ 3 discovered by Schreiber et al. (2018). |
5. Summary
We presented the first spectroscopic follow-up at millimeter wavelengths for a pilot sample of nine RS NIR-dark galaxies in the COSMOS field. These sources were initially selected by Talia et al. (2021) as radio-detected sources at 3 GHz without an optical or NIR counterpart in the COSMOS2015 catalog, even though three of them (see Table 1) were subsequently detected in the deeper COSMOS2020. Through a new series of ALMA observations, we identified at least one bright emission line in all the targets and two lines in five out of nine objects. From the analysis of the new ALMA data, we obtained the results we list below.
-
Modeling the detected lines as CO and [CI] transitions, we estimated a spectroscopic redshift for all the galaxies in our sample. These values agree well with those estimated through SED fitting in Gentile et al. (2024).
-
The new availability of a spectroscopic redshift allowed us to decrease the degeneracies in the SED-fitting procedure. This improved SED fitting confirmed one of the main results forthe RS NIR-dark galaxies: They represent a population of highly obscured (Av ∼ 4), massive (M⋆ ∼ 1011 M⊙), and star-forming (SFR ∼ 500 M⊙ yr−1) galaxies.
-
The same improved SED fitting, together with preexisting data, allowed us to estimate the flux of our sources at 870 μm. This value is analogous to that reported by Smail et al. (2021) for their sample of NIR-faint SMGs, suggesting that our radio selection is able to provide a similar population of DSFGs as those obtained from (sub)mm selections. A similar conclusion was reached by observing the overlap between the physical properties (stellar mass and SFR) computed through SED fitting for the two samples.
-
The good spectral resolution of the new ALMA observations allowed us to assess a high fraction (∼55%) of double-peaked profiles in the lines detected in our targets. We explained this result with the possible presence of a rotating structure within our galaxies or with major mergers in our sample. High-resolution follow-up with ALMA or JWST are needed to distinguish between these two possibilities.
-
Based on the CO and [CI] lines detected in our targets, we estimated the gas mass and the depletion time of our galaxies. These results allowed us to forecast a possible evolutionary path for our objects. This strongly suggests that the RS NIR-dark galaxies might represent a significant fraction of the progenitors of the massive and passive galaxies at z ∼ 3 and that they are excellent probes for testing galaxy evolution models.
Since these sources were detected in the COSMOS2020 catalog, they are not part of the sample analyzed in Gentile et al. (2024). For these sources, we performed the same analysis (photometry extraction and SED-fitting) as described in that study.
The FWZI is an immediate product of the procedure employed to identify the lines in the extracted spectra since it corresponds to the binning maximizing the S/N of the line. However, in Table 3, we report the more common full width at half maximum (FWHM) obtained through the Gaussian modeling described in Sect. 3.4.
The original sample of NIR-faint sources by Smail et al. (2021) would contain another 50 sources that are not included in that study because the photometry at optical and NIR frequencies is contaminated. We assumed that the 30 galaxies analyzed by Smail et al. (2021) are representative of the full sample.
Acknowledgments
We thank the anonymous referee for their comments that improved the initial version of this paper. F.G. thanks Gayathri Gururajan for the insightful conversations about the gas tracers, Anton Koekemoer and Ian Smail for the careful reading of the manuscript and for the useful comments, and Roberto Decarli for the precious feedback on an early version of this paper. F.G., M.T., A.L., M.M. and A.C. acknowledge the support from grant PRIN MIUR 2017-20173ML3WW_001. ‘Opening the ALMA window on the cosmic evolution of gas, stars, and supermassive black holes’. I.D. acknowledges support from INAF Minigrant “Harnessing the power of VLBA towards a census of AGN and star formation at high redshift”. M.V. acknowledges financial support from the Inter-University Institute for Data Intensive Astronomy (IDIA), a partnership of the University of Cape Town, the University of Pretoria and the University of the Western Cape, and from the South African Department of Science and Innovation’s National Research Foundation under the ISARP RADIOSKY2020 and RADIOMAP Joint Research Schemes (DSI-NRF Grant Numbers 113121 and 150551) and the SRUG HIPPO Projects (DSI-NRF Grant Numbers 121291 and SRUG22031677). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2021.1.01467.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Aravena, M., Spilker, J. S., Bethermin, M., et al. 2016, MNRAS, 457, 4406 [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [Google Scholar]
- Behiri, M., Talia, M., Cimatti, A., et al. 2023, ApJ, 957, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data Reduction and Error Analysis for the Physical Sciences, 3rd edn. (New York, NY: McGraw-Hill) [Google Scholar]
- Birkin, J. E., Weiss, A., Wardlow, J. L., et al. 2021, MNRAS, 501, 3926 [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Boogaard, L., Meyer, R. A., & Novak, M. 2021, Astrophysics Source Code Library [record ascl:2112.005] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Bothwell, M. S., Aguirre, J. E., Aravena, M., et al. 2017, MNRAS, 466, 2825 [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [Google Scholar]
- CASA Team (Bean, B., et al.) 2022, PASP, 134, 114501 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
- Casey, C. M., Zavala, J. A., Manning, S. M., et al. 2021, ApJ, 923, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Kartaltepe, J. S., Drakos, N. E., et al. 2023, ApJ, 954, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chapman, S. C., Richards, E. A., Lewis, G. F., Wilson, G., & Barger, A. J. 2001, ApJ, 548, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Lewis, G. F., Scott, D., Borys, C., & Richards, E. 2002, ApJ, 570, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Smail, I., Blain, A. W., & Ivison, R. J. 2004, ApJ, 614, 671 [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [Google Scholar]
- Comrie, A., Wang, K.-S., Hsu, S.-C., et al. 2021, Astrophysics Source Code Library [record ascl:2103.031] [Google Scholar]
- Coogan, R. T., Daddi, E., Sargent, M. T., et al. 2018, MNRAS, 479, 703 [NASA ADS] [Google Scholar]
- Cox, P., Neri, R., Berta, S., et al. 2023, A&A, 678, A26 [Google Scholar]
- Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davé, R., Finlator, K., & Oppenheimer, B. D. 2012, MNRAS, 421, 98 [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [Google Scholar]
- Donevski, D., Lapi, A., Małek, K., et al. 2020, A&A, 644, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2021, MNRAS, 500, 942 [Google Scholar]
- Dunlop, J. S., McLure, R. J., Yamada, T., et al. 2004, MNRAS, 350, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [Google Scholar]
- Euclid Collaboration (Moneti, A., et al.) 2022, A&A, 658, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [Google Scholar]
- Endsley, R., Stark, D. P., Charlot, S., et al. 2021, MNRAS, 502, 6044 [NASA ADS] [CrossRef] [Google Scholar]
- Enia, A., Talia, M., Pozzi, F., et al. 2022, ApJ, 927, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frayer, D. T., Reddy, N. A., Armus, L., et al. 2004, AJ, 127, 728 [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Geach, J. E., Dunlop, J. S., Halpern, M., et al. 2017, MNRAS, 465, 1789 [Google Scholar]
- Gentile, F., Talia, M., Behiri, M., et al. 2024, ApJ, 962, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M. 2002, ARA&A, 40, 579 [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS, 432, 23 [Google Scholar]
- Gruppioni, C., Béthermin, M., Loiacono, F., et al. 2020, A&A, 643, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gururajan, G., B’ethermin, M., Sulzenauer, N., et al. 2023, A&A, 676, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Heywood, I., Jarvis, M. J., Hale, C. L., et al. 2022, MNRAS, 509, 2150 [Google Scholar]
- Hickox, R. C., & Alexander, D. M. 2018, ARA&A, 56, 625 [Google Scholar]
- Högbom, J. A. 1974, A&AS, 15, 417 [Google Scholar]
- Hopkins, P. F., Cox, T. J., Kereš, D., & Hernquist, L. 2008a, ApJS, 175, 390 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008b, ApJS, 175, 356 [Google Scholar]
- Hughes, D. H., Serjeant, S., Dunlop, J., et al. 1998, Nature, 394, 241 [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M., Taylor, R., Agudo, I., et al. 2016, MeerKAT Science: On the Pathway to the SKA, 6 [Google Scholar]
- Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
- Jin, S., Daddi, E., Magdis, G. E., et al. 2019, ApJ, 887, 144 [Google Scholar]
- Jin, S., Daddi, E., Magdis, G. E., et al. 2022, A&A, 665, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [Google Scholar]
- Labbé, I., Bouwens, R., Illingworth, G. D., & Franx, M. 2006, ApJ, 649, L67 [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Lapi, A., Raimundo, S., Aversa, R., et al. 2014, ApJ, 782, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Lang, P., Magnelli, B., et al. 2019, ApJS, 244, 40 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Magnelli, B., Popesso, P., Berta, S., et al. 2013, A&A, 553, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manning, S. M., Casey, C. M., Zavala, J. A., et al. 2022, ApJ, 925, 23 [CrossRef] [Google Scholar]
- Pantoni, L., Lapi, A., Massardi, M., Goswami, S., & Danese, L. 2019, ApJ, 880, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W. F., & Viti, S. 2004, MNRAS, 351, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Puglisi, A., Daddi, E., Liu, D., et al. 2019, ApJ, 877, L23 [Google Scholar]
- Roman-Oliveira, F., Fraternali, F., & Rizzo, F. 2023, MNRAS, 521, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Oliver, S., Wang, L., et al. 2016, MNRAS, 461, 1100 [Google Scholar]
- Saintonge, A., Lutz, D., Genzel, R., et al. 2013, ApJ, 778, 2 [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Glazebrook, K., Nanayakkara, T., et al. 2018, A&A, 618, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [Google Scholar]
- Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015, ApJ, 799, 81 [CrossRef] [Google Scholar]
- Simpson, J. M., Smail, I., Dudzevičiūtė, U., et al. 2020, MNRAS, 495, 3409 [Google Scholar]
- Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Ivison, R. J., Kneib, J. P., et al. 1999, MNRAS, 308, 1061 [Google Scholar]
- Smail, I., Owen, F. N., Morrison, G. E., et al. 2002, ApJ, 581, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Dudzevičiūtė, U., Stach, S. M., et al. 2021, MNRAS, 502, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017, A&A, 602, A1 [Google Scholar]
- Stach, S. M., Dudzevičiūtė, U., Smail, I., et al. 2019, MNRAS, 487, 4648 [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Straatman, C. M. S., Labbé, I., Spitler, L. R., et al. 2014, ApJ, 783, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Talia, M., Cimatti, A., Giulietti, M., et al. 2021, ApJ, 909, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [Google Scholar]
- Traina, A., Gruppioni, C., Delvecchio, I., et al. 2024, A&A, 681, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020a, ApJ, 890, 24 [Google Scholar]
- Valentino, F., Tanaka, M., Davidzon, I., et al. 2020b, ApJ, 889, 93 [Google Scholar]
- Vallini, L., Tielens, A. G. G. M., Pallottini, A., et al. 2019, MNRAS, 490, 4502 [CrossRef] [Google Scholar]
- van der Vlugt, D., Hodge, J. A., Jin, S., et al. 2023, ApJ, 951, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Weiß, A., Downes, D., Decarli, R., & Henkel, C. 2011, ApJ, 730, 18 [Google Scholar]
- Walter, F., Decarli, R., Aravena, M., et al. 2016, ApJ, 833, 67 [Google Scholar]
- Wang, T., Schreiber, C., Elbaz, D., et al. 2019, Nature, 572, 211 [Google Scholar]
- Weaver, J. R., Kauffmann, O. B., Ilbert, O., et al. 2022, ApJS, 258, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Whitler, L., Stark, D. P., Endsley, R., et al. 2023, MNRAS, 519, 5859 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1. Full ALMA spectra for the nine targets. For each source, we highlight the detected lines, and we report our modeling as CO/[CI] transitions for each of them. |
 |
Fig. A.1. (Continue) |
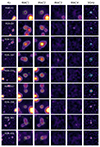 |
Fig. A.2. Cutouts (10” × 10”) in the main NIR-to-MIR bands for the nine targets. We report the 3 and 5 σ contours. Moreover, for each galaxy, we overplot in green the 3 and 5 σ contours of the brightest line on the IRAC ch1 and ch2 images. Similarly, the same contours of the continuum emission are overplotted in cyan on the 3 GHz images. |
All Tables
All Figures
 |
Fig. 1. Spectral setup adopted for the ALMA observations. This configuration allowed us to observe at least one line of the CO and [CI] transition for all the redshifts below 8. For most of the redshifts higher than 3, two lines are detectable at the observed frequencies. |
| In the text | |
 |
Fig. 2. Continuum maps of the nine targets. The black contours are in steps of 2σ starting from 3σ. All the images have a 7.5″ side, while the synthetized beam is reported in the lower left corner of each image. |
| In the text | |
 |
Fig. 3. Spectrum of the various lines identified through the procedure discussed in Sects. 3.2 and 3.3 in our targets. To increase the visibility of the lines, we resampled the original spectral resolution employed in the study up to ∼180 km s−1. For each line, we report in the upper right corner the ID of the galaxy and our modeling as CO or [CI] transitions. The insets show the moment zero of each line (7.5″ side) centered on the radio position measured from the 3 GHz maps, with the contours in steps of 2σ starting from 3σ. In each line, we also report in red the Gaussian modeling with one or two components as described in Sect. 3.4. In the lines modeled with a double Gaussian, we also show the two subcomponents with a dashed orange line. |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. Moment-one maps (2.5″ × 2.5″) of the lines detected in three of the targets. According to our modeling, the maps show clear evidence of a rotating structure or a late stage of a merger. |
| In the text | |
 |
Fig. 5. Best-fitting SEDs of our targets as computed by CIGALE (Boquien et al. 2019). The different emissions in the galaxies are color-coded. Attenuated stellar emission is reported as an orange line. The dust emission is reported in red, and the radio emission is reported in purple. Finally, the solid black line shows the best-fitting SED. |
| In the text | |
 |
Fig. 6. Comparison of the photometric redshift following Gentile et al. (2024) and the spectroscopic redshifts measured in this study. The one-to-one relation is reported as the dotted black line, and the shaded gray area shows the galaxies with |Δz|/(1 + z) < 0.15. The galaxies with a spec-z obtained from the modeling of two lines are highlighted with an additional box. |
| In the text | |
 |
Fig. 7. Comparison of the physical properties estimated through CIGALE and the main sequence of star-forming galaxies by Schreiber et al. (2015) (solid gray line; the shaded area is its 1σ = 0.3 dex its scatter). The targets are reported as colored stars, with the same color-code as employed in Fig. 6. The dotted gray line reports our threshold for identifying the star-bursting galaxies (i.e., those whose SFR is higher than three times that expected from a main-sequence galaxy). For reference, we also report the location of the RS NIR-dark galaxies around z ∼ 3.5 studied in Gentile et al. (2024), the NIR-faint SMGs by Smail et al. (2021), and the H-dropout galaxies by Wang et al. (2019). |
| In the text | |
 |
Fig. 8. Depletion time and star formation rate for our targets. The RS NIR-dark galaxies are reported as colored stars, following the same color-code as in Fig. 6. The colored triangles are other populations of SMGs, namely those collected by Bothwell et al. (2017), Cañameras et al. (2018), and Walter et al. (2011), reported in blue, orange, and green, respectively. We also report some confirmed QSOs from the same studies as reversed red triangles. The shaded gray area reports the depletion time expected from main-sequence galaxies at z ∼ 3.5 following the relation τD = 1.5(1 + z)α found by Saintonge et al. (2013), with α spanning from −1.0 (Davé et al. 2012) to −1.5 (Magnelli et al. 2013), rescaled to a Chabrier (2003) IMF. |
| In the text | |
 |
Fig. 9. Possible evolutionary paths of our targets, assuming a simple evolutionary model with a constant star formation and a final stage in which all the molecular gas has been transformed into stars. The uncertainties are considered through a Monte Carlo integration. The color map is the same as employed for Fig. 6, For reference, the shaded red stars report the stellar mass and the redshifts for the massive and passive galaxies at z ∼ 3 discovered by Schreiber et al. (2018). |
| In the text | |
 |
Fig. A.1. Full ALMA spectra for the nine targets. For each source, we highlight the detected lines, and we report our modeling as CO/[CI] transitions for each of them. |
| In the text | |
 |
Fig. A.1. (Continue) |
| In the text | |
 |
Fig. A.2. Cutouts (10” × 10”) in the main NIR-to-MIR bands for the nine targets. We report the 3 and 5 σ contours. Moreover, for each galaxy, we overplot in green the 3 and 5 σ contours of the brightest line on the IRAC ch1 and ch2 images. Similarly, the same contours of the continuum emission are overplotted in cyan on the 3 GHz images. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



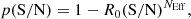
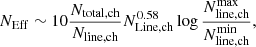
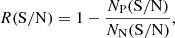
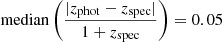
![$$ \begin{aligned} M(\mathrm{H}_2)^{[\mathrm{CI}]}=1375.8\times 10^{-12}\frac{D_{\rm L}^2 I_{[\mathrm{CI}](1-0)}}{(1+z)A_{10}Q_{10}X_{\mathrm{CI}}}[M_\odot ], \end{aligned} $$](/articles/aa/full_html/2024/07/aa48623-23/aa48623-23-eq10.gif)