| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348128 | |
| Published online | 17 May 2024 | |
The cold interstellar medium of a normal sub-L⋆ galaxy at the end of reionization
1
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
2
Cosmic Dawn Center (DAWN), Copenhagen N, Denmark
e-mail: francesco.valentino@eso.org
3
Department of Astronomy, The University of Texas at Austin, Austin, TX, USA
4
Niels Bohr Institute, University of Copenhagen, Jagtvej 128, 2200 Copenhagen N, Denmark
5
Institute of Astronomy, Graduate School of Science, The University of Tokyo, 2-21-1, Osawa, Mitaka, Tokyo, 181-0015, Japan
6
Research Center for Early Universe, Graduate School of Science, The University of Tokyo, 7-3-1, Hongo, Bunkyo-ku, Tokyo, 113-0033, Japan
7
Steward Observatory, University of Arizona, 933 N. Cherry Ave., Tucson, AZ, 85721, USA
8
Kapteyn Astronomical Institute, University of Groningen, 9700 AV Groningen, The Netherlands
9
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Campus San Joaquín, Av. Vicuña Mackenna 4860, Macul Santiago, 7820436, Chile
10
Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica de Chile, Campus San Joaquín, Av. Vicuña Mackenna 4860, Macul Santiago, 7820436, Chile
11
Millennium Institute of Astrophysics, Nuncio Monseñor Sótero Sanz 100, Of 104, Providencia, Santiago, Chile
12
Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO, 80301, USA
13
Dipartimento di Fisica, Sapienza, Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
14
INFN, Sezione di Roma I, Piazzale Aldo Moro 2, 00185 Roma, Italy
15
INAF/Osservatorio Astronomico di Roma, Via di Frascati 33, 00078 Monte Porzio Catone, Italy
16
Departamento de Física Teórica y del Cosmos, Campus de Fuentenueva, Edificio Mecenas, Universidad de Granada, 18071 Granada, Spain
17
Instituto Carlos I de Física Teórica y Computacional, Facultad de Ciencias, 18071 Granada, Spain
18
DTU-Space, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
19
Department of Astronomy, University of Geneva, Chemin Pegasi 51, 1290 Versoix, Switzerland
20
Purple Mountain Observatory and Key Laboratory for Radio Astronomy, Chinese Academy of Sciences, Nanjing, PR China
21
School of Astronomy and Space Science, University of Science and Technology of China, Hefei, PR China
22
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD, 21218, USA
23
Institute for Cosmic Ray Research, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba, 277-8582, Japan
24
Kavli IPMU (WPI), The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba, 277-8583, Japan
25
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo, 181-8588, Japan
26
Department of Physics & Astronomy, Johns Hopkins University, 3400 North Charles Street, Baltimore, MD, 21218, USA
27
Max-Planck-Institut für Extraterrestrische Physik (MPE), Giessenbachstraße 1, 85748 Garching, Germany
28
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia
29
International Centre for Radio Astronomy Research (ICRAR), University of Western Australia, Crawley, WA, 6009, Australia
30
Institute for Advanced Research, Nagoya University, Furocho, Chikusa, Nagoya, 464-8602, Japan
31
Department of Physics, Graduate School of Science, Nagoya University, Furocho, Chikusa, Nagoya, 464-8602, Japan
32
Cahill Center for Astronomy and Astrophysics, California Institute of Technology, MS 249-17, Pasadena, CA, 91125, USA
33
Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), No. 1, Sec. 4, Roosevelt Rd., Taipei, 10617, Taiwan
Received:
2
October
2023
Accepted:
19
February
2024
We present the results of a ∼60-h multiband observational campaign with the Atacama Large Millimeter Array targeting a spectroscopically confirmed and lensed sub-L⋆ galaxy at z = 6.07, first identified during the ALMA Lensing Cluster Survey (ALCS). We sampled the dust continuum emission from rest frame 90–370 μm at six different frequencies and set constraining upper limits on the molecular gas line emission and content by targeting the CO (7 − 6) and [C I](3P2−3P1) transitions in two lensed images with μ ≳ 20. Complementing these submillimeter observations with deep optical and near-IR photometry and spectroscopy with JWST, we find this galaxy to form stars at a rate of SFR ∼ 7 M⊙ yr−1, ∼50 − 70% of which is obscured by dust. This is consistent with what one would predict for a M⋆ ∼ 7.5 × 108 M⊙ object by extrapolating the relation between the fraction of the obscured star formation rate and stellar mass at z < 2.5 and with observations of IR-detected objects at 5 < z < 7. The light-weighted dust temperature of Tdust ∼ 50 K is similar to that of more massive galaxies at similar redshifts, although with large uncertainties and with possible negative gradients. We measure a dust mass of Mdust ∼ 1.5 × 106 M⊙ and, by combining [C I], [C II], and a dynamical estimate, a gas mass of Mgas ∼ 2 × 109 M⊙. Their ratio (δDGR) is in good agreement with predictions from models and empirical relations in the literature. The dust-to-stellar mass fraction of fdust ∼ 0.002 and the young stellar age (100 − 200 Myr) are consistent with efficient dust production via supernovae, as predicted by existing models and simulations of dust evolution. Also, the expected number density of galaxies with Mdust ∼ 106 M⊙ at z = 6 from a subset of these models is in agreement with the observational estimate that we set from the parent ALCS survey. The combination of gravitational lensing and deep multiwavelength observations allowed us to probe luminosity and mass regimes up to two orders of magnitude lower than what has been explored so far for field galaxies at similar redshifts. Our results serve as a benchmark for future observational endeavors of the high-redshift and faint sub-L⋆ galaxy population that might have driven the reionization of the Universe.
Key words: gravitational lensing: strong / galaxies: evolution / galaxies: formation / galaxies: high-redshift / galaxies: ISM / galaxies: star formation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Over the past few years, the number of galaxies confirmed at redshift z > 6 and deeper into the reionization epoch has soared. Interferometric (sub)millimeter observations and ground-based and, more recently, space-based optical and near-IR spectroscopy have been instrumental in allowing us to start exploring the physics regulating the growth of the first galaxies. Truly multiwavelength studies proved to be necessary to observe and connect all components in galaxies and provide a complete view of these systems. However, for reasons of opportunity and observing time cost, priority has been given to the brightest and rarest targets that could maximize the detection rates – but in doing so we have been missing more numerous, typical galaxy populations at z > 6.
In light of the possible preponderant role played by average, rather than exceptional, galaxy populations in the reionization of the Universe (Robertson 2022), there has been a renewed focus on spectroscopic studies of faint sources around or below the knee of the luminosity function (L⋆) and on the main sequence of star formation (Daddi et al. 2007) at these redshifts, particularly after the launch of the James Webb Space Telescope (JWST). Moreover, observational campaigns of faint objects are even more affordable when the Universe comes to our aid with the gravitational lensing effect. This phenomenon provides a unique window onto the formation of faint galaxies on small scales, which would otherwise be impossible to probe without the presence of massive objects along the line of sight.
Here we attempt to push the existing boundaries for deep multiwavelength extragalactic studies at high redshifts by leveraging state-of-the-art instruments and the lensing effect. Our primary objective is to start exploring a new portion of the cold gas and dust parameter space at intrinsic low stellar masses, star formation rates (SFRs), and metallicities. These regimes are critical to understanding the first phases of galaxy formation. The availability of cold gas reservoirs and the impact of intense, hard radiation feedback from young stars with low metallicities ultimately regulate the growth of the numerous population of low-mass galaxies and their ability to reionize the Universe. Furthermore, these processes are intricately linked to the rate at which metals and dust accumulate, and the relationship between these two components in the earliest phases of galaxy assembly remains itself a debated topic (see, e.g., Péroux & Howk 2020; Popping et al. 2023; Heintz et al. 2023a; Konstantopoulou et al. 2024; Schneider & Maiolino 2023). Fortunately, both dust and metals can now be traced in early galaxies. Thanks to JWST, we can directly measure the metallicity of large samples of very distant sources (e.g., Curti et al. 2024). In contrast, over the past few years, observations with the Atacama Large Millimeter Array (ALMA) have revealed the existence of dust-rich, and in some cases seemingly over-abundant, galaxies within a few hundred million years of the Big Bang (see Witstok et al. 2023 for a recent compilation). This has sparked discussions on the creation and maintenance of dust grains in early galaxies. The short timescales involved seem to preclude a dominant role for asymptotic giant branch (AGB) stars, leaving supernovae (SNe) and grain growth in the interstellar medium (ISM) as the most viable alternatives for dust production, contending against destruction via reverse shocks (Gall et al. 2011; Popping et al. 2017; Schneider & Maiolino 2023). Different flavors of these mechanisms have been incorporated into models and simulations, yet the ever increasing body of observations persistently challenges their predictions.
In this work we delve into these subjects, concentrating our investigation on a faint sub-L⋆ galaxy at z = 6.072, positioned in projection behind the cluster RXJ0600–2007 (Fujimoto et al. 2021; Laporte et al. 2021, F21 and L21 hereafter; Sun et al. 2022). An extensive observational campaign to characterize the full spectrum of this source commenced soon after its discovery (Fujimoto et al. 2024) and is still ongoing. Here we present the initial findings from a series of programs conducted with ALMA. With the latter we accumulated approximately ∼60 h of observations, which were complemented by Hubble Space Telescope (HST) and JWST imaging as well as integral field near-IR spectroscopy from JWST. Armed with this rich dataset, we also aim to provide a reference for further studies involving larger samples of similar galaxies whose spectroscopic confirmation is now within reach (e.g., Khullar et al. 2021; Glazer et al. 2023; Fudamoto et al. 2024).
Details on the data reduction and analysis are presented in Sects. 2 and 3. In Sect. 4 we report on the obscured SFR, its fraction of the total value, the dust mass and temperature (Mdust and Tdust), the cold gas mass and properties as traced by dust, neutral and ionized atomic carbon (C I and C II), carbon monoxide (CO), dynamics, and direct estimates of dust-to-stellar and dust-to-gas ratios (δDGR), and we put them in the context of the literature values for brighter UV galaxies and models at similar redshifts. Our conclusions are presented in Sect. 5. The reader can find detailed descriptions of the whole dataset (Fujimoto et al. 2024) and a focused analysis of the JWST photometry (Giménez-Arteaga et al. 2024) in companion papers. The study of the properties of the photon-dominated regions traced by multiple far-IR (FIR) lines is left to a dedicated work (Lee et al., in prep.).
Throughout this work we make use of the AB system to report magnitudes. Unless otherwise specified, we adopt a Chabrier (2003) initial mass function (IMF) and a Λ cold dark matter cosmology with Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
2. Data
2.1. The target
The target presented in this study was discovered serendipitously during the mapping of dust emission at λobs = 1.1 mm within and around 33 clusters from legacy surveys using HST and the Spitzer Space Telescope – the ALMA Lensing Cluster Survey (ALCS; Kohno et al. 2023; Fujimoto et al. 2021, 2023; Kokorev et al. 2022). Five lensed images of this galaxy are now securely spectroscopically confirmed. In particular, a highly magnified arc composed of two images of a peripheral region of the source (dubbed “z6.1-6.2”; magnification factor μ ∼ 100) crosses a caustic line and stands out as one of the brightest observed [C II]158 μm emitters at z > 6 (F21). The emission of a second lensed image (“z6.3”), approximately 15″ distant from the arc, is also strongly boosted (μ ∼ 20) and offers an excellent view of global properties of this galaxy. This has already allowed for investigations of resolved properties in the UV wavelength regime down to < 300 pc with HST observations. Its total intrinsic absolute UV rest-frame magnitude is ∼3× fainter than the knee of the luminosity function of Lyman break galaxies at z = 6 (F21).
2.2. ALMA multiwavelength observations
The goal of our ALMA campaign is to characterize the properties of the cold ISM in this sub-L⋆ galaxy as completely as possible. We thus followed up its lensed images in Bands 3, 5, 6, 7, and 81, targeting known FIR and submillimeter lines and their underlying dust continuum emission. A summary of observations, their integration time, observed and rest-frame frequency and wavelengths, depths, and beam sizes is provided in Table 1. The ALMA data were consistently reduced and calibrated using the Common Astronomy Software Applications (CASA) package version 6.2.1.7 (McMullin et al. 2007) with the standard pipeline script. TCLEAN was used to produce the continuum maps averaging all channels in the spectral windows not dominated by bright lines (whose expected position is accurately known from the robust redshift estimate). The TCLEAN routines were executed down to the 2σ level. We chose a pixel scale approximately ten times smaller than the beam size and adopted a common spectral channel bin of 40 km s−1. The final natural-weighted map has synthesized beams and continuum sensitivities listed in Table 1. More details about the individual ALMA programs and the data reduction can be found in Fujimoto et al. (2024).
Summary of the ALMA observations presented here.
2.3. Ancillary datasets
RXJ0600–2007 (z = 0.43) has been observed as part of the Reionization Lensing Cluster Survey (RELICS; Coe et al. 2019) and the Massive Cluster Survey (MACS; Ebeling et al. 2001). It thus benefits from ample UV to near-IR photometric coverage with the HST and Spitzer. A homogeneous data reduction of all programs targeting this cluster and a consistent re-extraction of the photometry is presented in Kokorev et al. (2022) as part of the Complete Hubble Archive for Galaxy Evolution (CHArGE) initiative. It has been recently complemented by JWST observations with the Near-Infrared Camera (NIRCam; Rieke et al. 2005) and Spectrograph (NIRSpec; Jakobsen et al. 2022) integral field unit (#GO 1567, PI: S. Fujimoto). The imaging was taken with the F115W, F150W, F277W, F356W, and F444W filters. The data reduction is performed following the same steps described in Valentino et al. (2023). NIRCam images of the arc and the z6.3 images at 4.5 μm are shown in Fig. 1. The integral field spectroscopy came at high spectral resolution with the G395H/F290LP combination (R ∼ 2700, λobs ∼ 2.9 − 5.1 μm), thus covering the redshifted optical rest-frame emission of lines from the ionized gas (notably including Hα, Hβ, [O III]λλ4959, 5007, [N II]λλ6549, 6584, [S II]λλ6716, 6731, the auroral line [O III]λ4364, and many others). For further details about the JWST and HST imaging and spectroscopy, we refer the reader to the companion papers (Giménez-Arteaga et al. 2024; Fujimoto et al. 2024).
 |
Fig. 1. ALMA continuum bands of the arc (top rows, 7.5″ side) and the z6.3 image (bottom rows, 5″ side). The rest-frame wavelength of each map is labeled. The ALMA images are color-scaled within ±5 times the rms per pixel in each band. Solid (positive) and dashed (negative) blue contours are at ±3, 5, 7, and 9σ. The solid red line and shaded area indicate the aperture adopted to extract the photometry. The beam size is shown in the bottom-right corner of each cutout. The bottom-right panel of each series shows the JWST/NIRCam image at 4.5 μm. In the latter, the point spread function has a full width at half maximum of |
3. Analysis
3.1. Dust continuum photometric extraction
We extracted the photometry within elliptical apertures in the continuum emission ALMA maps. We ran the pythonic version of SOURCE EXTRACTOR (Bertin & Arnouts 1996), SEP (v1.2.1, Barbary 2016), to detect the centroid, orientation, and ellipticity of the apertures in each band independently. We measured total flux densities within adaptively scaled (Kron 1980) apertures (FLUX_AUTO in SOURCE EXTRACTOR’s nomenclature). To ensure that we measured flux densities across wavelengths within consistent portions of each lensed image, in every band we fixed our fiducial aperture to that retrieved for Band 7 in the 122 μm rest frame, where the S/N of the detection is high (10 and 14 for z6.3 and the arc, respectively). We show the extent of such an aperture in every map in Fig. 1. The resulting dust continuum emission flux densities for z6.3 and the arc are reported in Table 2, together with available upper limits on Herschel photometry (de-blended and extracted as described in Sun et al. 2022). The uncertainties are computed from the rms per beam in each continuum image scaled by the number of independent beams within the aperture (e.g., Béthermin et al. 2020).
ALMA continuum photometry and Band 3 line measurements.
When observing in Bands 6, 7, and 8, we separately pointed each lensed image. Given the larger field of view in Bands 3 and 5, the pointing was centered between z6.3 and the arc. In this case, the lensed images are well within the inner portions of the primary beam. Therefore, a correction for the primary beam was not needed. In the case of Band 6, we obtained observations in two configurations (C2 and C5), which allows us to test for possible flux lost on the full arc scale (the maximum recoverable scale for Band 6 in C5 is of ∼3″). Independent measurements of the continuum emission in the two configurations are consistent (Table 2). We thus combined these datasets with CASA for our final measurements, improving the signal-to-noise of the detection.
Choosing Bands 5 or 6, where the detections are also robust, as references to determine the aperture instead of Band 7 does not appreciably impact the measurements. Also, we excluded possible strong biases due to widely different spatial distribution of the dust emission across bands by measuring total flux densities independently at each frequency, obtaining consistent results.
Finally, we counterchecked our aperture photometry against modeling of the emission with the task IMFIT in CASA and single Gaussians profiles. The results are overall in good agreement with those from aperture photometry especially when detections are robust (Table 2). Low signal-to-noise estimates and upper limits are also consistent (e.g., Band 8). We note that the assumption of a single, smooth profile captures reasonably well the global light emission from each lensed image, but clumping on smaller scales is likely present. This is evident from the optical rest-frame emission captured by JWST (Fig. 1) and, to a lesser extent, by the highest resolution ALMA map in Band 6. Also, the assumption of a Gaussian light distribution is arguably not apt for the highly stretched arc, where two distinct peaks have been identified in the [C II] maps at low spatial resolution (F21). Yet, the total flux densities are consistent with those from aperture photometry, which are robust against clumping and spatial inhomogeneities. This suggests that the spatial variations are not fully captured by ALMA at the current spatial resolution and depths in most bands, but this does not affect our conclusions.
3.2. Spectral extraction
We extracted the spectra of the lensed images over the same apertures used to measure the continuum emission in order to derive consistent ratios. Here we focus particularly on Band 3 observations targeting the [C I](3P2−3P1) (νrest = 809.34 GHz) and CO (7 − 6) (νrest = 806.65 GHz) lines, proxies of the molecular gas of the galaxy, and we defer detailed analyses of photon-dominated regions to future work (Lee et al., in prep.). We show the extracted Band 3 spectra around the expected location of the [C I] and CO line emission in Fig. 2. We do not detect any line emissions. We thus set upper limits on the fluxes integrated on the [C II] line width from low spatial resolution measurements (Δv = FWHM = 180 km s−1, F21). Based on spectra binned at dv = 40 km s−1, we obtain 3σ upper limits on the line fluxes as 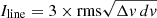 , where rms is the aperture noise per channel in the spectral window where the lines fall. We applied a mild clipping at 3σ to remove outliers, which resulted in a 6% lower rms. The limits on line fluxes and luminosities are reported in Table 2. We note that the upper limits on z6.3 and the arc differ because of the areas that we considered to estimate the rms.
, where rms is the aperture noise per channel in the spectral window where the lines fall. We applied a mild clipping at 3σ to remove outliers, which resulted in a 6% lower rms. The limits on line fluxes and luminosities are reported in Table 2. We note that the upper limits on z6.3 and the arc differ because of the areas that we considered to estimate the rms.
 |
Fig. 2. Observed Band 3 spectra of the arc (top) and the z6.3 image (bottom). The expected positions of the [C I](3P2−3P1) and CO (7 − 6) lines are marked. |
3.3. Long-wavelength spectral energy distribution modeling
We modeled the ALMA and Herschel photometry using the Bayesian code MERCURIUS (Witstok et al. 2022, 2023). We assumed optically thin dust emission and initially left the dust temperature (Tdust) and emissivity slope (β) free to vary. For consistency with the literature compilation presented in Witstok et al. (2023), a primary reference later in this work, we adopted their same priors. For the dust temperature, we used the default gamma distribution with shape parameter a = 1.5 and shifted it to start at the temperature of the cosmic microwave background (CMB, TCMB); for β, we imposed a Gaussian prior centered at 1.8 and with a standard deviation of 0.25. These priors reflect the belief that Tdust is less likely to be extremely high and the known distribution of β across redshifts (Witstok et al. 2022, 2023). The effect of the CMB is taken into account in the modeling (da Cunha et al. 2013). We adopt the built-in dust emissivity coefficient κ = κ0(ν/ν0)β with κ0 = 8.94 cm2 g−1 at ν0 = 1900 GHz (∼158 μm, Hirashita et al. 2014), consistent with the choice in several recent works (Schouws et al. 2022; Witstok et al. 2022, 2023; Valentino et al. 2022). The choice of different emissivity coefficients has an obvious systematic impact on the final fit estimates with differences amounting up to an order of magnitude. The best-fit models for z6.3 and the arc are shown in Fig. 3 and the parameters are reported in Table 3. We also attempted alternative models at fixed β = 1.5, 2 – typical choices when fewer data points are available – and implementing a self-consistent calculation of the wavelength λ0 at which the dust emission becomes optically thin (i.e., optical depth τ = 1), given the knowledge of the intrinsic source size from high-spatial resolution measurements (effective radius 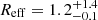 kpc measured in the source plane after de-lensing, F21). The results are overall consistent with the free parameter fit. On the one hand, the absence of strong observational constraints at short wavelengths does not allow for a robust determination of Tdust, as expected. On the other hand, the multiple ALMA detections in the Rayleigh-Jeans tail of the dust emission better constrain Mdust. The range spanned by the best-fit solutions, also subject to the choice of the priors, reflects the systematic uncertainties hindering the modeling of the long-wavelength spectral energy distributions (SEDs) – here and in the rest of the literature. For completeness and transparency, we report on a different selection of priors and treatment of the optical depth in Appendix A.
kpc measured in the source plane after de-lensing, F21). The results are overall consistent with the free parameter fit. On the one hand, the absence of strong observational constraints at short wavelengths does not allow for a robust determination of Tdust, as expected. On the other hand, the multiple ALMA detections in the Rayleigh-Jeans tail of the dust emission better constrain Mdust. The range spanned by the best-fit solutions, also subject to the choice of the priors, reflects the systematic uncertainties hindering the modeling of the long-wavelength spectral energy distributions (SEDs) – here and in the rest of the literature. For completeness and transparency, we report on a different selection of priors and treatment of the optical depth in Appendix A.
 |
Fig. 3. FIR SED modeling for z6.3 (left) and z6.1–6.2 (arc, right). Black circles and arrows indicate detections and 3σ upper limits on the observed photometry. The dashed line and shaded areas mark the best-fit model with MERCURIUS under the assumption of an optically thin emission. |
Physical properties.
We estimate Tdust ∼ 37 and ∼50 K for the arc and z6.3, respectively. Both are consistent with typical Tdust values at z ∼ 6 for more massive UV-, optical-, and IR-selected sources (Witstok et al. 2023). We note that, in principle, gradients in Tdust or dust composition (thus, β) could be present (Akins et al. 2022) and potentially detectable, given the lensing configuration. As described in F21, the arc strongly magnifies (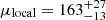 ) a peripheral region of the source plane and it can be used to gauge possible gradients within the galaxy. On the contrary, z6.3 is the brightest lensed image that captures the global properties of the intrinsic source. Marginally higher Tdust are indeed preferred for z6.3, suggesting the presence of a negative dust temperature gradient. However, in practice the resolution and S/N of the integrated detections in crucial ALMA bands at the shortest and longest wavelengths do not allow for a full-fledged resolved analysis at this stage and current speculations on the presence of gradient will have to be tested against new observations. For reference, in the rest of this work we make use of the best-fit parameters with free β under the optically thin assumption and we focus on the global properties of the galaxy from the z6.3 image. For completeness, the measurements for the arc are shown in figures and reported in tables.
) a peripheral region of the source plane and it can be used to gauge possible gradients within the galaxy. On the contrary, z6.3 is the brightest lensed image that captures the global properties of the intrinsic source. Marginally higher Tdust are indeed preferred for z6.3, suggesting the presence of a negative dust temperature gradient. However, in practice the resolution and S/N of the integrated detections in crucial ALMA bands at the shortest and longest wavelengths do not allow for a full-fledged resolved analysis at this stage and current speculations on the presence of gradient will have to be tested against new observations. For reference, in the rest of this work we make use of the best-fit parameters with free β under the optically thin assumption and we focus on the global properties of the galaxy from the z6.3 image. For completeness, the measurements for the arc are shown in figures and reported in tables.
3.4. Modeling of optical and near-IR observations
We modeled the JWST photometry as described in detail in the companion paper by Giménez-Arteaga et al. (2024) and previous works (Giménez-Arteaga et al. 2023). Briefly, we first point-spread-function-matched the observations to the lowest available resolution in NIRCam F444W (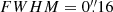 ) and then we modeled the emission with BAGPIPES (Carnall et al. 2018). Since we cannot consistently resolve the molecular gas and dust emission within the galaxy with ALMA (especially that at the longest wavelengths to determine Mdust), we made use of the SED modeling of the integrated fluxes. However, we encourage the reader interested in the details of a pixel-by-pixel analysis of z6.3 to consult the dedicated companion paper.
) and then we modeled the emission with BAGPIPES (Carnall et al. 2018). Since we cannot consistently resolve the molecular gas and dust emission within the galaxy with ALMA (especially that at the longest wavelengths to determine Mdust), we made use of the SED modeling of the integrated fluxes. However, we encourage the reader interested in the details of a pixel-by-pixel analysis of z6.3 to consult the dedicated companion paper.
We adopted Bruzual & Charlot (2003) single stellar population models2, a grid of CLOUDY (Ferland et al. 2017) emission line grids extended to higher ionization parameters (up to log(U)= − 1), and a Calzetti et al. (2000) attenuation curve. We imposed uniform priors on the attenuation (AV = 0 − 3), metallicity (Z = 0 − Z⊙), formed stellar mass (M = 105 − 1011 M⊙). We finally adopted the stellar mass estimate obtained with a double power-law star formation history (SFH) that is a robust choice against the “outshining” effect of young stellar populations (Sect. 4.2). The M⋆ estimate is consistent with those from other parameterizations of the SFHs on resolved scales, while that of SFR is notoriously dependent on the shape of the formation history and the time window to average for the calculation. We thus refrained from using the SFR from optical/near-IR SED modeling in this work.
Finally, we derived the gas-phase metallicity and unobscured SFR on global scales by integrating the measurements of the ionized line emissions in the NIRSpec spectrum (Fujimoto et al. 2024) and the stellar continuum in the far-UV (FUV) range of the z6.3 image. The former, expressed as the oxygen gas-phase abundance [12+log(O/H)], was derived via the “direct method” based on the electron temperature Te and the detection of the [O III]λ4364 auroral line. The global resulting metallicity is 12 + log(O/H) = 8.11 ± 0.20 (Z ∼ 0.25 Z⊙ for a solar abundance of 12 + log(O/H) = 8.69; Asplund et al. 2009). In Sect. 4.3, we return to a discussion of the SFR from the Hα Balmer line, sensitive to the formation of stars on timescales of ≲10 Myr.
4. A view of the cold gas and dust properties of a sub-L⋆ galaxy at z = 6
4.1. Gas and dust emission tracers
We show ALMA-derived observables (or closely related quantities) in context of what is available in the literature in Fig. 4. The data compilation is briefly described in Appendix B. In the space of observables, the upper limits on CO (7 − 6) and [C I](3P2−3P1) are consistent with the loci of L′/LIR ratios (and their scatter) of variously selected IR-emitting galaxies spread across the last 13 Gyr of cosmic time. This is true also for the ![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i} ]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq26.gif) /Mdust ratio, both tracers of the cold gas mass in galaxies. The combination of lensing and deep observations allows for the exploration of LIR and line ratios typical of local IR-detected objects – but at the end of reionization. This is a jump of ∼2 orders of magnitude in intrinsic LIR at z ∼ 6. The exact location of the intrinsic values in Fig. 4 is of course dependent on the lensing models and it is affected by their uncertainties (Table 3), but these are confidently smaller than the jump in LIR. The ratios of line and continuum emissions are also affected by uncertainties on differential lensing, but this effect seems limited especially for z6.3 (Fujimoto et al. 2024), our anchor to derive the global properties of this galaxy.
/Mdust ratio, both tracers of the cold gas mass in galaxies. The combination of lensing and deep observations allows for the exploration of LIR and line ratios typical of local IR-detected objects – but at the end of reionization. This is a jump of ∼2 orders of magnitude in intrinsic LIR at z ∼ 6. The exact location of the intrinsic values in Fig. 4 is of course dependent on the lensing models and it is affected by their uncertainties (Table 3), but these are confidently smaller than the jump in LIR. The ratios of line and continuum emissions are also affected by uncertainties on differential lensing, but this effect seems limited especially for z6.3 (Fujimoto et al. 2024), our anchor to derive the global properties of this galaxy.
 |
Fig. 4. Observed L′/LIR for CO (7 − 6) (top), [C I](3P2−3P1) (center), and |
The ratios shown in Fig. 4 start telling us the story of our target. In broad terms, CO (7 − 6) traces the dense and warm star-forming molecular gas and linearly correlates with LIR, a classical tracer of the obscured SFR. The [C I](3P2−3P1) luminosity correlates with the total molecular gas content (Yang et al. 2017; Valentino et al. 2020b), despite its exact calibration being sensitive to (here unknown) excitation corrections (Dunne et al. 2022). The ![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq32.gif) /LIR ratio is thus a proxy for the depletion timescale in the galaxy (τdepl = Mgas/SFR). Since the dust mass is also a tracer of the cold gas mass in galaxies (Magdis et al. 2012), the
/LIR ratio is thus a proxy for the depletion timescale in the galaxy (τdepl = Mgas/SFR). Since the dust mass is also a tracer of the cold gas mass in galaxies (Magdis et al. 2012), the ![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq33.gif) /Mdust ratio can serve as a proxy of the (inverse of the) dust-to-gas ratio (δDGR). Figure 4 thus suggests that the z = 6 sub-L⋆ galaxy is generally consistent with the observed or extrapolated properties and trends of IR-detected galaxies in terms of depletion timescales and dust-to-gas ratios as a function of the obscured SFR.
/Mdust ratio can serve as a proxy of the (inverse of the) dust-to-gas ratio (δDGR). Figure 4 thus suggests that the z = 6 sub-L⋆ galaxy is generally consistent with the observed or extrapolated properties and trends of IR-detected galaxies in terms of depletion timescales and dust-to-gas ratios as a function of the obscured SFR.
4.2. Gas and dust masses
We computed the total gas mass of our galaxy by leveraging the measurements available for z6.3. We converted the [C I](3P2−3P1) upper limit to Mgas as (Papadopoulos & Greve 2004)
where DL is the luminosity distance in Mpc, Q21 is the excitation factor, Sν Δv the upper limit on the velocity-integrated line flux, A21 = 2.68 × 10−7 s−1 the Einstein coefficient, and X[CI] the neutral atomic carbon abundance. The excitation correction is a major factor of uncertainty and it is unknown for this object. In order to obtain an upper limit on Mgas, we considered Q21 = [0.05 − 0.4], the range expected for Tdust ∼ 50 K (Papadopoulos et al. 2022). Similarly, we do not know the abundance X[CI]. We thus adopted the value for lower redshift main-sequence objects with solar-like metallicity (∼1.5 × 10−5, Valentino et al. 2018, similar to the average obtained by Dunne et al. 2022 for their literature sample) and assumed that it scales linearly with metallicity to our ∼25% Z⊙ estimate from NIRSpec (Glover & Clark 2016; Heintz & Watson 2020). For reference, the metallicity scaling in Heintz & Watson (2020) has an intrinsic scatter of ∼0.2 dex. With these variety of assumptions, the upper limit on ![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq35.gif) is converted into μMgas < (0.1 − 1.0)×1010 M⊙.
is converted into μMgas < (0.1 − 1.0)×1010 M⊙.
We calculated an alternative estimate of the gas mass from the [C II] emission. This bright line is well detected in our source (F21, Lee et al., in prep.), so the uncertainty must be due to the calibration itself. By assuming the conversion factor in Zanella et al. (2018), we find μMgas([CII])=30 × LCII = (6.9 ± 0.6)×1010 M⊙ (F21). More recently, lower conversion factors for specific galaxy populations have also been suggested (α[CII] ≲ 10 M⊙/L⊙
Rizzo et al. 2021; Sommovigo et al. 2021). Heintz et al. (2021) proposed a metallicity-dependent calibration to the neutral atomic gas mass M(HI) based on a sample of local dwarf galaxies and distant gamma-ray bursts with [C II] in absorption in the rest-frame UV. By applying this conversion, we obtain ![$ \mu M_{\mathrm{HI}} (\mathrm{[CII]}) = 2.2^{+1.5}_{-0.9}\times10^{11}\,M_{\odot} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq36.gif) , where the uncertainties include those on the metallicity and the calibration.
, where the uncertainties include those on the metallicity and the calibration.
The gas dynamics derived in F21 offer an upper limit on Mgas independent of the assumptions on these calibrations. The subtraction of the intrinsic M⋆ from the dynamical mass estimate Mdyn = (3 ± 1)×109 M⊙ leaves (2 ± 1)×109 M⊙ for all the remaining components. Neglecting dark matter and dust as major contributors to the total mass of the central disk, this value can be ascribed to cold gas. The upper limits from [C I](3P2−3P1) are consistent with the dynamical estimate (Mgas([CI])< (0.6 − 4.8) × 108 M⊙) and so is Mgas([CII])=(3 ± 1) × 109 M⊙ following Zanella et al. (2018) (F21). The metallicity-dependent calibration from Heintz et al. (2021) exceeds the current limit set by dynamical arguments (![$ M_{\mathrm{HI}}(\mathrm{[CII]}) = 1.0^{+0.7}_{-0.4}\times10^{10}\,M_{\odot} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq37.gif) ). However, it is useful to remind that the distribution and extension of [C II] H I, and H2 gas might differ. An extended H I disk might not be accounted for by the dynamical modeling as traced by the [C II] emission. Also, the calibration of H I([C II]) partially relies on absorption measurements in gamma ray bursts. These measurements are sensitive to the integrated column density and might be representative of the dense central cores of galaxies. These factors should be borne in mind when comparing these calibrations (see Heintz et al. 2023b for a discussion in the case of a similar low-metallicity galaxy at high redshift).
). However, it is useful to remind that the distribution and extension of [C II] H I, and H2 gas might differ. An extended H I disk might not be accounted for by the dynamical modeling as traced by the [C II] emission. Also, the calibration of H I([C II]) partially relies on absorption measurements in gamma ray bursts. These measurements are sensitive to the integrated column density and might be representative of the dense central cores of galaxies. These factors should be borne in mind when comparing these calibrations (see Heintz et al. 2023b for a discussion in the case of a similar low-metallicity galaxy at high redshift).
Figure 5 shows the global dust-to-gas mass ratio, δDGR, as a function of metallicity based on the Mgas estimates described above. The upper limits on Mgas([CI]) (under two sets of excitation conditions) reflect the location of z6.3 in the ![$ L_{\mathrm{IR}}{-}L^{\prime}_{{[\mathrm{C}\,\textsc{I}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq38.gif) /Mdust ratio shown in Fig. 4. For the fiducial galaxy-integrated metallicity 12 + log(O/H)=(8.11 ± 0.20) measured via the direct method, the δDGR is generally consistent with models and empirical relations in the literature (Rémy-Ruyer et al. 2014; De Vis et al. 2019; Magdis et al. 2012; Vijayan et al. 2019; Mauerhofer & Dayal 2023; Popping et al. 2017, 2023; Popping & Péroux 2022 furthermore, the results from De Vis et al. 2019 are consistent with the predictions from Li et al. 2019). We note that no strong evolution in the δGDR–metallicity relation is seen as a function of redshift and estimates from distant absorption systems are in agreement with local measurements (Péroux & Howk 2020; Popping & Péroux 2022; Heintz et al. 2023a). Reversing the argument, δDGR ∼ 0.001 (∼10× lower than typical values of massive dusty star-forming galaxies, Magdis et al. 2012) is consistent with the detection of [C II] and upper limits on [C I](3P2−3P1), under the assumptions on the calibrations mentioned above.
/Mdust ratio shown in Fig. 4. For the fiducial galaxy-integrated metallicity 12 + log(O/H)=(8.11 ± 0.20) measured via the direct method, the δDGR is generally consistent with models and empirical relations in the literature (Rémy-Ruyer et al. 2014; De Vis et al. 2019; Magdis et al. 2012; Vijayan et al. 2019; Mauerhofer & Dayal 2023; Popping et al. 2017, 2023; Popping & Péroux 2022 furthermore, the results from De Vis et al. 2019 are consistent with the predictions from Li et al. 2019). We note that no strong evolution in the δGDR–metallicity relation is seen as a function of redshift and estimates from distant absorption systems are in agreement with local measurements (Péroux & Howk 2020; Popping & Péroux 2022; Heintz et al. 2023a). Reversing the argument, δDGR ∼ 0.001 (∼10× lower than typical values of massive dusty star-forming galaxies, Magdis et al. 2012) is consistent with the detection of [C II] and upper limits on [C I](3P2−3P1), under the assumptions on the calibrations mentioned above.
 |
Fig. 5. Dust-to-gas mass ratio as a function of metallicity. Purple triangles indicate the 3σ lower limits from [C I](3P2−3P1) under high- and low-excitation conditions. The gold and blue stars indicate Mgas from [C II] using the conversions in Zanella et al. (2018) and Heintz et al. (2021), respectively. The red star shows the maximum amount of gas allowed by [C II] dynamics (F21). The points are slightly offset along the X axis for clarity. The uncertainty on the metallicity is represented by the horizontal red bar. The blue lines mark the (extrapolated) relations from Magdis et al. (2012), Rémy-Ruyer et al. (2014), De Vis et al. (2019), Popping & Péroux (2022), and Popping et al. (2023), and the models from Mauerhofer & Dayal (2023), Popping et al. (2017), Li et al. (2019), and Vijayan et al. (2019). |
However, we note that the uncertainties on the measurements, the intrinsic scatter of the relations involved in Fig. 5, and the fact that we are reporting measurements for a single object certainly do not allow us to exclude any models or trends. Also, given the original blind detection in [C II] and dust, we might be selecting an intrinsically dust-rich object – yet, consistent with the scaling relations shown so far. In addition, as for every global measure in this and common in the literature, we are averaging measurements on large spatial regions. The derived quantities are thus luminosity-weighted and this might introduce biases (an “outshining” effect, Sawicki & Yee 1998; Papovich et al. 2001; Giménez-Arteaga et al. 2023). In this case, the most metal-poor and least dust-obscured regions dominate the emission of the [O III] auroral line used to estimate the metallicity. These might not be the same regions emitting in the FIR. There are indeed hints of different FIR and optical emission distributions when we compare the highest ALMA resolution maps and those from JWST (Fig. 1) and across the JWST photometry itself (Giménez-Arteaga et al. 2024). The geometric distributions of gas (H2, H I, and H II) and dust and their spatial overlap (or lack-of) are factors in the calculation of δDGR. However, we are not in the position to fully explore the presence of gradients in the ALMA maps, given their resolution. Future work on higher spatial resolution data will trace the dust distribution within the galaxy and allow for the quantification of the “outshining” effect at long wavelengths.
4.3. Dust-obscured SFR
The SED modeling described in Sect. 3.3 returns LIR, a direct tracer of the dust-obscured SFR(IR). The latter is computed as log(SFR(IR)/M⊙ yr−1)=log(LIR/erg s−1)−43.41 (Murphy et al. 2011; Kennicutt & Evans 2012). We did not apply any further correction to homogenize the Kroupa (2001) and Chabrier (2003) IMFs, given their similarity. The significant uncertainties on Tdust propagate on LIR and on SFR(IR) (Table 3). Given the well-established linear correlation between LIR and 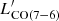 (Greve et al. 2014; Liu et al. 2015; Lu et al. 2017; Kamenetzky et al. 2016), we derived an alternative constraint on SFR(IR) from the upper limit on CO (7 − 6) (Fig. 4). For this calculation, we adopted the parameterization:
(Greve et al. 2014; Liu et al. 2015; Lu et al. 2017; Kamenetzky et al. 2016), we derived an alternative constraint on SFR(IR) from the upper limit on CO (7 − 6) (Fig. 4). For this calculation, we adopted the parameterization:
with an intrinsic scatter of 0.16 dex (Valentino et al. 2020a). The 3σ upper limit on μSFR(IR, CO(7–6)) < 53 M⊙ yr−1 is ∼3× more stringent than the loosely constrained central value from the SED modeling for z6.3 (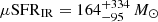 yr−1), but consistent with it. The higher upper limit derived for the arc, which is a direct consequence of the larger projected area for the flux integration (Sect. 3.2), is also consistent with the estimate from the FIR photometry. We note that the lower estimates of LIR and SFR(IR) derived by rescaling Band 6 observations in F21, L21, and Sun et al. (2022) are in full agreement with those in Table 3 – unsurprisingly, at least for the arc image whose best-fit Tdust ∼ 37 K and β ∼ 1.6 are similar to the shape assumed in these works.
yr−1), but consistent with it. The higher upper limit derived for the arc, which is a direct consequence of the larger projected area for the flux integration (Sect. 3.2), is also consistent with the estimate from the FIR photometry. We note that the lower estimates of LIR and SFR(IR) derived by rescaling Band 6 observations in F21, L21, and Sun et al. (2022) are in full agreement with those in Table 3 – unsurprisingly, at least for the arc image whose best-fit Tdust ∼ 37 K and β ∼ 1.6 are similar to the shape assumed in these works.
4.4. Unobscured and total SFR
We computed the unobscured SFR from the FUV stellar continuum of z6.3 captured by JWST. We estimated the 1500 Å rest-frame emission by convolving our blueshifted best-fit modeling of NIRCam imaging with the GALEX FUV filter and converting it into 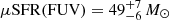 yr−1 as log(SFR(FUV)/M⊙ yr−1)=log(LFUV/erg s−1)−43.35 (Murphy et al. 2011). We obtain a similar
yr−1 as log(SFR(FUV)/M⊙ yr−1)=log(LFUV/erg s−1)−43.35 (Murphy et al. 2011). We obtain a similar 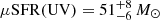 yr−1 from the total UV luminosity (LUV = 1.5νLν with ν = ν(λrest = 2800 Å)) following Bell et al. (2005). We note that no dust correction was applied to these estimates. We further computed a total SFR estimate (i.e., corrected for the dust attenuation) of
yr−1 from the total UV luminosity (LUV = 1.5νLν with ν = ν(λrest = 2800 Å)) following Bell et al. (2005). We note that no dust correction was applied to these estimates. We further computed a total SFR estimate (i.e., corrected for the dust attenuation) of 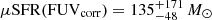 yr−1 from FUV luminosities following Hao et al. (2011), in which the correction to SFR(FUV)obs is less than that applied in Murphy et al. (2011). This value is in close agreement with
yr−1 from FUV luminosities following Hao et al. (2011), in which the correction to SFR(FUV)obs is less than that applied in Murphy et al. (2011). This value is in close agreement with 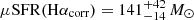 yr−1 using the same set of calibrations (log(SFR(Hα)/M⊙ yr−1)=log(L(Hα)/erg s−1)−41.27 (Murphy et al. 2011), but including a 2.5× correction for the Z ∼ 25% Z⊙ metallicity measured for z6.3 (Fujimoto et al. 2024). In fact, these calibrations are valid under the assumptions of a constant SFH over 100 Myr timescales and solar metallicity. On the one hand, a correction for the metallicity will decrease the Hα-based SFR by ∼0.3 − 0.4 dex (a factor of ∼2 − 2.5) because of higher production efficiency of ionizing photons by lower-metallicity, massive, and binary stellar systems (the exact conversion depends on the assumed models, e.g., Kennicutt & Evans 2012; Theios et al. 2019; Shapley et al. 2023). The metallicity effect only mildly affects the FUV output (Kennicutt & Evans 2012). The IR emission should follow that in the FUV, but the dust opacity decreases at low metallicity, reducing the IR emission at fixed SFR. The total SFR(Hαcorr) value is broadly consistent with the sum of the IR and (uncorrected) FUV-based SFR estimate (Table 2). These total values are in slight excess, but consistent with that in F21. This also confirms that this galaxy is consistent with the locus of the main-sequence in the M⋆–SFR plane at z ∼ 6, as argued in F21.
yr−1 using the same set of calibrations (log(SFR(Hα)/M⊙ yr−1)=log(L(Hα)/erg s−1)−41.27 (Murphy et al. 2011), but including a 2.5× correction for the Z ∼ 25% Z⊙ metallicity measured for z6.3 (Fujimoto et al. 2024). In fact, these calibrations are valid under the assumptions of a constant SFH over 100 Myr timescales and solar metallicity. On the one hand, a correction for the metallicity will decrease the Hα-based SFR by ∼0.3 − 0.4 dex (a factor of ∼2 − 2.5) because of higher production efficiency of ionizing photons by lower-metallicity, massive, and binary stellar systems (the exact conversion depends on the assumed models, e.g., Kennicutt & Evans 2012; Theios et al. 2019; Shapley et al. 2023). The metallicity effect only mildly affects the FUV output (Kennicutt & Evans 2012). The IR emission should follow that in the FUV, but the dust opacity decreases at low metallicity, reducing the IR emission at fixed SFR. The total SFR(Hαcorr) value is broadly consistent with the sum of the IR and (uncorrected) FUV-based SFR estimate (Table 2). These total values are in slight excess, but consistent with that in F21. This also confirms that this galaxy is consistent with the locus of the main-sequence in the M⋆–SFR plane at z ∼ 6, as argued in F21.
4.5. Fraction of obscured SFR
Combining these estimates, we derive the obscured SFR fraction for z6.3 of 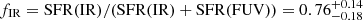 . Based on the upper limit on LIR(CO (7 − 6)), this fraction decreases to fIR < 0.52. These values are in agreement with the individual IR-detections for z ∼ 7 UV-selected sources in Algera et al. (2023) at M⋆ ≳ 109 M⊙ (see also Inami et al. 2022; Mitsuhashi et al. 2023a). Our more constraining upper limit on LIR(CO (7 − 6)) better agrees with their fIR from stacking of the whole sample at similar M⋆, including non-IR detections. Similar values are reported also for more massive galaxies on the main-sequence at z ∼ 5 (Fudamoto et al. 2020; Mitsuhashi et al. 2023b) and are in overall agreement with the fIR estimates for mass-complete samples at z < 2.5 (Whitaker et al. 2017). This is also consistent with the absence of strong Lyα emission from the lensed images (rest-frame equivalent width (Lyα) ≲4 Å for both z6.3 and the arc at 3σ, F21). Nonetheless, as mentioned above, it is useful to remember that our target was serendipitously discovered as a strong [C II] and dust continuum emitter in the first place and not preselected based on its UV emission or some rest-frame UV or optical line emission (which might miss dusty objects) as for the samples in Algera et al. (2023) and Fudamoto et al. (2020). Therefore, it does not suffer from the same selection biases of these literature works and might be a suitable representative of the more dust-rich population of sub-L⋆ galaxies at these redshifts.
. Based on the upper limit on LIR(CO (7 − 6)), this fraction decreases to fIR < 0.52. These values are in agreement with the individual IR-detections for z ∼ 7 UV-selected sources in Algera et al. (2023) at M⋆ ≳ 109 M⊙ (see also Inami et al. 2022; Mitsuhashi et al. 2023a). Our more constraining upper limit on LIR(CO (7 − 6)) better agrees with their fIR from stacking of the whole sample at similar M⋆, including non-IR detections. Similar values are reported also for more massive galaxies on the main-sequence at z ∼ 5 (Fudamoto et al. 2020; Mitsuhashi et al. 2023b) and are in overall agreement with the fIR estimates for mass-complete samples at z < 2.5 (Whitaker et al. 2017). This is also consistent with the absence of strong Lyα emission from the lensed images (rest-frame equivalent width (Lyα) ≲4 Å for both z6.3 and the arc at 3σ, F21). Nonetheless, as mentioned above, it is useful to remember that our target was serendipitously discovered as a strong [C II] and dust continuum emitter in the first place and not preselected based on its UV emission or some rest-frame UV or optical line emission (which might miss dusty objects) as for the samples in Algera et al. (2023) and Fudamoto et al. (2020). Therefore, it does not suffer from the same selection biases of these literature works and might be a suitable representative of the more dust-rich population of sub-L⋆ galaxies at these redshifts.
4.6. Dust production
The direct dust detection with ALMA and the fraction of obscured star formation point at efficient dust formation in this sub-L⋆ galaxy at z = 6. The fdust = Mdust/M⋆ fraction can offer an indication of the necessary dust yields. Considering the young average age of the galaxy (100 − 200 Myr, Giménez-Arteaga et al. 2024), the dust production via SNe is a more plausible channel than via longer-timescale AGB stars. Following the recipe for a Chabrier (2003) IMF presented in Michałowski (2015), the galaxy-integrated 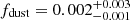 from z6.3 is converted into a yield of
from z6.3 is converted into a yield of 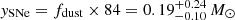 . This yield is in agreement with that reported in L21 (
. This yield is in agreement with that reported in L21 (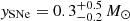 ). The magnified Mdust and M⋆ are consistent with observed values in the local Universe and with the locus of efficient SNe dust production computed by Di Cesare et al. (2023) and Witstok et al. (2023) under similar assumptions as those adopted here.
). The magnified Mdust and M⋆ are consistent with observed values in the local Universe and with the locus of efficient SNe dust production computed by Di Cesare et al. (2023) and Witstok et al. (2023) under similar assumptions as those adopted here.
In Fig. 6, we draw a comparison with more complex dust formation models and observations of objects at z = 5 − 7 available in the literature (Di Cesare et al. 2023, and references therein), complemented with a few more recent works. We corrected the stellar mass estimates of the observations and models derived under the assumption of a Salpeter (1955) IMF to the prescriptions in Chabrier (2003) or Kroupa (2001), which are similar. We did not attempt to correct Mdust for the different IMFs (e.g., influencing the rate of SNe) in the models, given the complex relations among parameters. The choice of different IMFs, along with SFHs, stellar population synthesis models, and several other assumptions in the SED modeling, does remain a major source of systematic uncertainties that inflates the scatter of the distribution in Fig. 6. We highlight the reanalysis of high-redshift sources in Witstok et al. (2022, 2023) as we used a consistent approach, code, and priors to model the FIR emission, and thus a direct comparison can be drawn in terms of Mdust. Both the global and localized measurements in the periphery of the galaxy from the z6.3 and arc images, respectively, are broadly consistent with the existing models and can be explained by SNe without invoking the contribution of AGB or efficient grain growth. Nevertheless, a contribution from growth in the ISM to the dust mass budget is not excluded if we reasonably consider destruction processes such as SN shocks, astration, or ejection (see Fig. 9 in Di Cesare et al. 2023 for a depiction of the dust mass budget for combination of processes at work at high redshift).
 |
Fig. 6. Dust mass as a function of stellar mass at 5 < z < 7. The red stars indicate the arc and z6.3 images of our galaxy, as labeled. Red arrows show the direction of the correction for the lensing magnification. The open blue symbols mark observed galaxies from the works in the legend. The empirical estimates are from Graziani et al. (2020), Pozzi et al. (2021), Sommovigo et al. (2021, 2022), and Witstok et al. (2022, 2023); the models are from Popping et al. (2017), Imara et al. (2018), Vijayan et al. (2019), Triani et al. (2020), Di Cesare et al. (2023), Mushtaq et al. (2023), Dayal et al. (2022), and Mauerhofer & Dayal (2023). Arrows indicate upper limits. Blue lines show the predictions for the models listed in the legend. |
Finally, we cannot avoid noting that we are at a stage where systematic errors totally dominate the uncertainties on Mdust and M⋆ from observations. Even with a common set of observations, the derived physical quantities may vary by up to 1 dex. This currently hinders a critical test of theoretical models and simulations – the latter predicting M⋆/Mdust ratios that vary by up to one order of magnitude at M⋆ ≲ 109 M⊙.
4.7. The cosmological context
Given the promising increase in new ALMA detections of intrinsically low-mass and faint UV galaxies at z ∼ 6 (Glazer et al. 2023; Fudamoto et al. 2024), we attempted to place our results in a broader cosmological framework. F21 and Fujimoto et al. (2023) already discussed how our target compares with brighter IR emitters in context of 1.1 mm number counts and the derived LIR luminosity function. Here we took advantage of the better constraints on Mdust enabled by the multiple ALMA detections in the Rayleigh-Jeans tail of the SED. Figure 7 shows the constraint on the dust mass function at 6 ≲ z ≲ 7.5 that we derived from our measurement at intrinsic low masses (i.e., after applying the magnification correction to z6.3). The number statistics are identical to those in Fujimoto et al. (2023) to facilitate the comparison, where the volume has been corrected for the lensing effect and the Poissonian error bars are computed following Gehrels (1986). For reference, we show the results for the serendipitous detections in the REBELS survey at z ∼ 7 (Fudamoto et al. 2021; Bouwens et al. 2022), where we considered the published estimates of Mdust, comoving volume, and correction for clustering. We opted to show this as a lower limit, considering the uncertainties on its derivation (Algera et al. 2023 for a comparison among different estimates on the SFR density from a similar set of observations from REBELS). Still following Sect. 6.1 in Fujimoto et al. (2023), we added constraints from sources in cosmological fields and with the Rayleigh-Jeans tail of the SED sampled by two or more bands. These include a source at z = 7.13 (Watson et al. 2015; we adopt Mdust from Bakx et al. 2021 and increased it by ∼40% to account for the extended emission as in Akins et al. 2022) and a dust-enshrouded quasar at z = 7.19 (Fujimoto et al. 2022). Finally, we show the dust mass functions from a handful of theoretical models (Popping et al. 2017; Vijayan et al. 2019; Di Cesare et al. 2023; DELPHI, Dayal et al. 2022; Mauerhofer & Dayal 2023). For thoroughness, within the supplementary material, we present an alternative perspective of this figure through cumulative number counts3.
 |
Fig. 7. Dust mass function. The blue lines show the predictions of the models at z = 6, as labeled (Popping et al. 2017; Vijayan et al. 2019; Di Cesare et al. 2023; DELPHI, Dayal et al. 2022; Mauerhofer & Dayal 2023). For reference, the dashed gray line marks the dust mass function from the fiducial model in Popping et al. (2017) at z = 0. The filled red star and open circles indicate the observational constraints based on our target and other surveys at high redshifts, as labeled (Watson et al. 2015; Bakx et al. 2021; Akins et al. 2022; Fudamoto et al. 2021; Fujimoto et al. 2022; ϕ values estimated in Fujimoto et al. 2023). |
Considering all the caveats and uncertainties discussed throughout this work and the low number statistics (dominant over the exact choice of the log-bin size in the case of single sources), we find that the models shown in Fig. 7 are in the right ballpark of the constraints set by our blind survey at z = 6 and targeted surveys at slightly higher redshifts. A significant drop of the number density of low-Mdust galaxy is expected beyond the peak of the cosmic SFR density. For reference, in Fig. 7 we show the evolution of the dust mass function from z = 0 to 6 (∼12.5 Gyr) predicted by the fiducial model by Popping et al. (2017), able to broadly reproduce the observational estimates at z = 0 up to Mdust ∼ 108.3 M⊙ (e.g., Vlahakis et al. 2005; Dunne et al. 2011; Clemens et al. 2013; Pozzi et al. 2020). A decrease by a factor of ∼10 in the number density of Mdust ∼ 106 M⊙ galaxies is expected, consistent with the predictions from alternative models and with our fiducial estimate at face value. Our constraint, being formally consistent with scattered observational estimates at z = 0 (Fig. 7 in Popping et al. 2017; Pozzi et al. 2021), is currently not sufficient to pinpoint any redshift evolution (or shape of the mass function). However, it is a first step in the right direction: forthcoming blind surveys and detailed multiband follow-up to determine Mdust will populate Fig. 7 and inform us on the global dust formation in a cosmological context.
5. Conclusions
We have presented a detailed physical characterization of the global properties of a sub-L⋆ lensed galaxy at z = 6 with particular emphasis on the cold dust and gas components. Dust and gas were traced in a 60-hour ALMA campaign that covered the emission from ∼90 to ∼370 μm rest-frame wavelengths and several gas-tracing emission lines. Based on these and ample ancillary data, including JWST imaging and integral field spectroscopy:
-
We derive a total SFR (unobscured from FUV and Hα lines, obscured from the FIR SED modeling and with an upper limit on CO (7 − 6)) of μSFR ∼ 140 M⊙ yr−1 (lensing-corrected to ∼7 M⊙ yr−1). Coupled with an updated estimate of μM⋆ ∼ 1.5 × 1010 M⊙ (M⋆ ∼ 7.5 × 108 M⊙ de-lensed), this source falls on the locus of main-sequence galaxies, while being intrinsically ∼3 times fainter than the knee of the luminosity function at z = 6.
-
We detect the rest-frame FIR continuum emission at six different wavelengths with ALMA, robustly confirming the presence of dust and obscured star formation at low stellar masses and metallicities (Z ∼ 25% Z⊙ from JWST/NIRSpec).
-
We estimate dust temperatures in the range Tdust ∼ 37 − 50 K, the lower end being observed in a highly magnified peripheral region of the galaxy. This might suggest the presence of a negative Tdust gradient, but the resolution, S/N, and lack of detections close to the peak of the dust emission currently hamper our ability to constrain Tdust and its possible spatial variations.
-
We constrain the amount of obscured star formation to fIR ≲ 50 − 70%, which is consistent with trends at lower redshifts and a handful of detections and stacking at 5 < z < 7. The main uncertainties in this calculation are on Tdust and, by extension, on the SFR(IR).
-
We estimate a dust mass of μMdust ∼ 0.3 × 108M⊙ (Mdust ∼ 1.5 × 106 M⊙ de-lensed) and a dust-to-stellar mass fraction of fdust ∼ 0.002. This amount of dust is consistent with a rapid production from SNe without invoking AGB stars, which are unlikely to contribute due to the young age of the galaxy. Our measurements are broadly consistent with the wide range of predictions from more complex models of dust evolution.
-
We estimate a total gas mass, or upper limits, based on [C I](3P2−3P1), [C II], and dynamical modeling. The dynamical modeling sets an intrinsic maximum amount of Mgas ∼ 2 × 109 M⊙, consistent with the upper limit on [C I](3P2−3P1) and some of the calibrations of the [C II]–Mgas relation. This implies a dust-to-gas mass ratio, δDGR, on the order of ∼10−3, in good agreement with models and empirical Z − δDGR relations in the literature.
-
Armed with an estimate of Mdust more robust and lower than typical values in the literature at these redshifts, we placed a constraint on the dust mass function at the low-Mdust end. Encouragingly, we find the predictions of a few recent dust formation models to be in the ballpark of our observational constraint despite all the caveats and uncertainties.
This is an example of how the synergy among cutting-edge instruments collecting deep observations across the electromagnetic spectrum opens a window onto the physics of numerous low-luminosity, low-mass, low-SFR, and low-metallicity galaxies at reionization. Future works in preparation and planned targeted observations (e.g., a ALMA high-frequency follow-up to pin down Tdust or at higher angular resolutions) will allow us to explore the cold gas and dust properties on sub-galactic scales. Larger samples will eventually be assembled and will be the key to constraining correlations and models, including the global production of dust in a cosmological framework, a task currently impossible given their scatter and the low number of galaxies with data of the necessary quality and coverage.
As detailed in Giménez-Arteaga et al. (2024), a Kroupa (2001) IMF was used to model the JWST/NIRCam photometry. The stellar mass estimates are similar to those derived using a Chabrier (2003) prescription.
Available on Zenodo: https://doi.org/10.5281/zenodo.10703293
Acknowledgments
We thank the referee for their insightful comments that improved this article. We are grateful to Aswin Vijayan, Pratika Dayal, and Valentin Mauerhofer for sharing their models and predictions. F.V. warmly thanks Joris Witstok for help and support in using the fitting code MERCURIUS; Kasper Heintz, Gergö Popping, and the rest of the GESO team at the European Southern Observatory for useful discussions while preparing this manuscript. The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant No. 140. S.F. acknowledges the support from NASA through the NASA Hubble Fellowship grant HST-HF2-51505.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. F.E.B. acknowledges support from ANID Millennium Science Initiative Program – ICN12_009, CATA-BASAL – FB210003, and FONDECYT Regular – 1200495 (FEB); D.E. acknowledges support from a Beatriz Galindo senior fellowship (BG20/00224) from the Spanish Ministry of Science and Innovation, projects PID2020-114414GB-100 and PID2020-113689GB-I00 financed by MCIN/AEI/10.13039/501100011033, project P20-00334 financed by the Junta de Andalucía, and project A-FQM-510-UGR20 of the FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades. G.E.M. acknowledges the Villum Fonden research grants 13160 and 37440. This paper makes use of the following ALMA data: ADS/JAO.ALMA# 2021.0.00055.S, 2021.0.00181.S, 2021.0.00247.S, and 2022.0.00195.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The research is also based in part on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program #1567.
References
- Akins, H. B., Fujimoto, S., Finlator, K., et al. 2022, ApJ, 934, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Algera, H. S. B., Inami, H., Oesch, P. A., et al. 2023, MNRAS, 518, 6142 [Google Scholar]
- Andreani, P., Retana-Montenegro, E., Zhang, Z.-Y., et al. 2018, A&A, 615, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Sommovigo, L., Carniani, S., et al. 2021, MNRAS, 508, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Barbary, K. 2016, J. Open Source Softw., 1, 58 [Google Scholar]
- Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [Google Scholar]
- Berta, S., Lutz, D., Genzel, R., Förster-Schreiber, N. M., & Tacconi, L. J. 2016, A&A, 587, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [Google Scholar]
- Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Smit, R., Schouws, S., et al. 2022, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., & Davé, R. 2018, MNRAS, 480, 4379 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Clemens, M. S., Negrello, M., De Zotti, G., et al. 2013, MNRAS, 433, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Salmon, B., Bradač, M., et al. 2019, ApJ, 884, 85 [Google Scholar]
- Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A&A, 634, L14 [EDP Sciences] [Google Scholar]
- Curti, M., Maiolino, R., Curtis-Lake, E., et al. 2024, A&A, 684, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Decarli, R., Pensabene, A., Venemans, B., et al. 2022, A&A, 662, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
- Dunne, L., Gomez, H. L., da Cunha, E., et al. 2011, MNRAS, 417, 1510 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Maddox, S. J., Papadopoulos, P. P., Ivison, R. J., & Gomez, H. L. 2022, MNRAS, 517, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020, A&A, 643, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Schouws, S., et al. 2021, Nature, 597, 489 [CrossRef] [Google Scholar]
- Fudamoto, Y., Inoue, A. K., Coe, D., et al. 2024, ApJ, 961, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Oguri, M., Brammer, G., et al. 2021, ApJ, 911, 99 [Google Scholar]
- Fujimoto, S., Brammer, G. B., Watson, D., et al. 2022, Nature, 604, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Kohno, K., Ouchi, M., et al. 2023, ApJS, submitted [arXiv:2303.01658] [Google Scholar]
- Fujimoto, S., Ouchi, M., Kohno, K., et al. 2024, arXiv e-prints [arXiv:2402.18543] [Google Scholar]
- Gall, C., Hjorth, J., & Andersen, A. C. 2011, A&A Rev., 19, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [Google Scholar]
- Giménez-Arteaga, C., Oesch, P. A., Brammer, G. B., et al. 2023, ApJ, 948, 126 [CrossRef] [Google Scholar]
- Giménez-Arteaga, C., Fujimoto, S., Valentino, F., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202349135 [Google Scholar]
- Glazer, K., Bradac, M., Sanders, R. L., et al. 2023, MNRAS, submitted [arXiv:2309.11548] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2016, MNRAS, 456, 3596 [Google Scholar]
- Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Gururajan, G., Béthermin, M., Theulé, P., et al. 2022, A&A, 663, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gururajan, G., Bethermin, M., Sulzenauer, N., et al. 2023, A&A, 676, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hagimoto, M., Bakx, T. J. L. C., Serjeant, S., et al. 2023, MNRAS, 521, 5508 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [Google Scholar]
- Harrington, K. C., Weiss, A., Yun, M. S., et al. 2021, ApJ, 908, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, K. E., & Watson, D. 2020, ApJ, 889, L7 [Google Scholar]
- Heintz, K. E., Watson, D., Oesch, P. A., Narayanan, D., & Madden, S. C. 2021, ApJ, 922, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, K. E., De Cia, A., Thöne, C. C., et al. 2023a, A&A, 679, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heintz, K. E., Giménez-Arteaga, C., Fujimoto, S., et al. 2023b, ApJ, 944, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., Ferrara, A., Dayal, P., & Ouchi, M. 2014, MNRAS, 443, 1704 [NASA ADS] [CrossRef] [Google Scholar]
- Imara, N., Loeb, A., Johnson, B. D., Conroy, C., & Behroozi, P. 2018, ApJ, 854, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Inami, H., Algera, H. S. B., Schouws, S., et al. 2022, MNRAS, 515, 3126 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Montillaud, J., Ysard, N., & Lunttila, T. 2013, A&A, 556, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamenetzky, J., Rangwala, N., Glenn, J., Maloney, P. R., & Conley, A. 2016, ApJ, 829, 93 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Khullar, G., Gozman, K., Lin, J. J., et al. 2021, ApJ, 906, 107 [CrossRef] [Google Scholar]
- Kohno, K., Fujimoto, S., Tsujita, A., et al. 2023, arXiv e-prints [arXiv:2305.15126] [Google Scholar]
- Kokorev, V., Brammer, G., Fujimoto, S., et al. 2022, ApJS, 263, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Konstantopoulou, C., De Cia, A., Ledoux, C., et al. 2024, A&A, 681, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, N., Zitrin, A., Ellis, R. S., et al. 2021, MNRAS, 505, 4838 [Google Scholar]
- Lei, H., Valentino, F., Magdis, G. E., et al. 2023, A&A, 673, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Q., Narayanan, D., & Davé, R. 2019, MNRAS, 490, 1425 [CrossRef] [Google Scholar]
- Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Daddi, E., Schinnerer, E., et al. 2021, ApJ, 909, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, N., Zhao, Y., Díaz-Santos, T., et al. 2017, ApJS, 230, 1 [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Mauerhofer, V., & Dayal, P. 2023, MNRAS, 526, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Michałowski, M. J. 2015, A&A, 577, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitsuhashi, I., Harikane, Y., Bauer, F. E., et al. 2023a, ApJ, submitted [arXiv:2311.16857] [Google Scholar]
- Mitsuhashi, I., Tadaki, K.-i., Ikeda, R., et al. 2023b, A&A, submitted [arXiv:2311.17671] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [Google Scholar]
- Mushtaq, M., Ceverino, D., Klessen, R. S., Reissl, S., & Puttasiddappa, P. H. 2023, MNRAS, 525, 4976 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Cañameras, R., Kneissl, R., et al. 2019, A&A, 624, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadopoulos, P. P., & Greve, T. R. 2004, ApJ, 615, L29 [Google Scholar]
- Papadopoulos, P., Dunne, L., & Maddox, S. 2022, MNRAS, 510, 725 [Google Scholar]
- Papovich, C., Dickinson, M., & Ferguson, H. C. 2001, ApJ, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., & Howk, J. C. 2020, ARA&A, 58, 363 [CrossRef] [Google Scholar]
- Popping, G., & Péroux, C. 2022, MNRAS, 513, 1531 [CrossRef] [Google Scholar]
- Popping, G., Somerville, R. S., & Galametz, M. 2017, MNRAS, 471, 3152 [NASA ADS] [CrossRef] [Google Scholar]
- Popping, G., Shivaei, I., Sanders, R. L., et al. 2023, A&A, 670, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzi, F., Calura, F., Zamorani, G., et al. 2020, MNRAS, 491, 5073 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzi, F., Calura, F., Fudamoto, Y., et al. 2021, A&A, 653, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
- Riechers, D. A., Hodge, J. A., Pavesi, R., et al. 2020, ApJ, 895, 81 [Google Scholar]
- Rieke, M. J., Kelly, D., & Horner, S. 2005, in Cryogenic Optical Systems and Instruments XI, eds. J. B. Heaney, & L. G. Burriesci, SPIE Conf. Ser., 5904, 1 [NASA ADS] [Google Scholar]
- Rizzo, F., Vegetti, S., Fraternali, F., Stacey, H. R., & Powell, D. 2021, MNRAS, 507, 3952 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E. 2022, ARA&A, 60, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, M. J. F., van der Werf, P. P., Aalto, S., et al. 2015, ApJ, 801, 72 [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sawicki, M., & Yee, H. K. C. 1998, AJ, 115, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., & Maiolino, R. 2023, A&ARv, 32, 2 [Google Scholar]
- Schouws, S., Stefanon, M., Bouwens, R., et al. 2022, ApJ, 928, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Sanders, R. L., Reddy, N. A., Topping, M. W., & Brammer, G. B. 2023, ApJ, 954, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Carniani, S., et al. 2021, MNRAS, 503, 4878 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]
- Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [Google Scholar]
- Sun, F., Egami, E., Fujimoto, S., et al. 2022, ApJ, 932, 77 [CrossRef] [Google Scholar]
- Theios, R. L., Steidel, C. C., Strom, A. L., et al. 2019, ApJ, 871, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Triani, D. P., Sinha, M., Croton, D. J., Pacifici, C., & Dwek, E. 2020, MNRAS, 493, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2018, ApJ, 869, 27 [Google Scholar]
- Valentino, F., Daddi, E., Puglisi, A., et al. 2020a, A&A, 641, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2020b, ApJ, 890, 24 [Google Scholar]
- Valentino, F., Brammer, G., Fujimoto, S., et al. 2022, ApJ, 929, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Valentino, F., Brammer, G., Gould, K. M. L., et al. 2023, ApJ, 947, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahakis, C., Dunne, L., & Eales, S. 2005, MNRAS, 364, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Weiß, A., Downes, D., Decarli, R., & Henkel, C. 2011, ApJ, 730, 18 [Google Scholar]
- Watson, D., Christensen, L., Knudsen, K. K., et al. 2015, Nature, 519, 327 [Google Scholar]
- Whitaker, K. E., Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Witstok, J., Smit, R., Maiolino, R., et al. 2022, MNRAS, 515, 1751 [Google Scholar]
- Witstok, J., Jones, G. C., Maiolino, R., Smit, R., & Schneider, R. 2023, MNRAS, 523, 3119 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanella, A., Daddi, E., Magdis, G., et al. 2018, MNRAS, 481, 1976 [Google Scholar]
Appendix A: Tests on the photometric extraction and SED modeling
In Figure A.1, we show the results of the best-fit elliptical Gaussian modeling with CASA/IMFIT (Section 3.1). For detections of both the arc and the z6.3 image, the total flux density from this modeling is consistent with that from aperture photometry (Figure A.2). This suggests that the clumping evident in Bands observed at higher resolution (Band 6 at 158 μm and shorter rest-frame wavelengths mapped by JWST) does not introduce major bias in our global estimates. Also, the detection at 370 μm rest frame is less significant than in every other band except at 88 μm. The elongated western tail in the arc image is consistent with noise.
 |
Fig. A.1. Dust continuum maps, best-fit Gaussian modeling, and residuals for the lensed z6.1-6.2 (arc, top rows) and z6.3 (bottom rows) images. The side of each cutout is 10". The rest-frame wavelengths of each map are labeled. Blue contours are at 2, 3, 5, and 10σ (rms). The images are color-scaled within ±5 times the rms per pixel in each band. The beam is shown in the bottom-right corner of the cutouts of the residuals. |
Furthermore, we tested variations on modeling of the FIR/millimeter SEDs with an alternative choice for the prior on β (flat within [1, 5]) and adopting the self-consistent treatment to estimate the wavelength at which the optical depth reaches unity (λ0(τ = 1), Witstok et al. 2023). We applied this treatment to z6.3 after de-lensing and adopting the intrinsic effective radius in the source plane (Section 3.3). This approach confirms that, on average, the optical thin assumption holds for our target and that the ensuing best-fit parameters are consistent with those listed in Table 3 for a fixed sets of priors. Concerning the choice of the priors on the dust emissivity slope, β, the best-fit estimates (i.e., the median of the posterior distribution) determined using a uniform distribution are 15% higher and 20% lower for z6.3 and the arc, respectively, than using the physically informed Gaussian distribution. The error bars (i.e., the 16 − 84% inter-percentile range) also generally increase and the final estimates are overall consistent with the values presented in Table 3. The uncertainties connected with the exact choice on the priors (or fixed values) are known (Juvela et al. 2013; Bakx et al. 2021; Algera et al. 2023) and add up to the error budget and systematics when comparing different works in the literature. All corner plots for the SED models discussed in this work are available online4.
 |
Fig. A.2. Photometric extractions. Filled circles indicate the ratio between the observed photometry extracted in Kron apertures and that from modeling with CASA/IMFIT. Large arrows show the 2σ upper limits on aperture photometry. Small gray arrows are 3σ upper limits on Herschel/SPIRE from Sun et al. (2022). For reference, we show both the measured Band 6 flux densities in configuration C2 and the combined C2+C5 (offset to improve the readability). Left: Arc (z6.1-6.2). Center: z6.3. Right: Aperture photometry of both lensed images. The flux densities are normalized to that in Band 7 (122 μm rest frame) for clarity and to avoid introducing the uncertainties on the magnification factor. The measurements in Band 6 (158 μm rest frame) from Fujimoto et al. (2021) are shown as orange squares. |
Appendix B: Literature sample
In Figure 4, we show the measurements for our z=6 sub-L⋆ galaxy in comparison with literature samples with available CO (7 − 6), [C I](3P2 − 3P1) luminosities, and reliable dust continuum detections to derive LIR and Mdust. LIR refers to the total IR luminosity integrated between 8 and 1000 μm. Estimates of FIR luminosities integrated over narrower ranges (e.g., 40-122 μm) have been corrected to total with an average correction factor of ∼1.3. We note that similar corrections might apply depending on the exact models used in the FIR SED modeling (e.g., a modified black body predicts lower LIR luminosities than physically motivated Draine & Li (2007) models, Berta et al. 2016; Valentino et al. 2018). Corrections for lensing were generally not applied. The samples include those already described in Valentino et al. 2020a, expanded to more recent results: local galaxies from the Herschel-FTS archive (Liu et al. 2015, 2021) and the HerCULES (Rosenberg et al. 2015) survey; main-sequence galaxies at z ∼ 1.5 (Valentino et al. 2020b, 2020a); blindly detected sources from ASPECS (Boogaard et al. 2020); variously selected submillimeter and IR-bright galaxies at z = 2 − 6, including quasars (Walter et al. 2011; Strandet et al. 2017; Cañameras et al. 2018; Nesvadba et al. 2019; Yang et al. 2017; Andreani et al. 2018; Cortzen et al. 2020; Riechers et al. 2020; Harrington et al. 2021; Gururajan et al. 2022; Decarli et al. 2022; Lei et al. 2023; Gururajan et al. 2023; Hagimoto et al. 2023).
All Tables
All Figures
 |
Fig. 1. ALMA continuum bands of the arc (top rows, 7.5″ side) and the z6.3 image (bottom rows, 5″ side). The rest-frame wavelength of each map is labeled. The ALMA images are color-scaled within ±5 times the rms per pixel in each band. Solid (positive) and dashed (negative) blue contours are at ±3, 5, 7, and 9σ. The solid red line and shaded area indicate the aperture adopted to extract the photometry. The beam size is shown in the bottom-right corner of each cutout. The bottom-right panel of each series shows the JWST/NIRCam image at 4.5 μm. In the latter, the point spread function has a full width at half maximum of |
| In the text | |
 |
Fig. 2. Observed Band 3 spectra of the arc (top) and the z6.3 image (bottom). The expected positions of the [C I](3P2−3P1) and CO (7 − 6) lines are marked. |
| In the text | |
 |
Fig. 3. FIR SED modeling for z6.3 (left) and z6.1–6.2 (arc, right). Black circles and arrows indicate detections and 3σ upper limits on the observed photometry. The dashed line and shaded areas mark the best-fit model with MERCURIUS under the assumption of an optically thin emission. |
| In the text | |
 |
Fig. 4. Observed L′/LIR for CO (7 − 6) (top), [C I](3P2−3P1) (center), and |
| In the text | |
 |
Fig. 5. Dust-to-gas mass ratio as a function of metallicity. Purple triangles indicate the 3σ lower limits from [C I](3P2−3P1) under high- and low-excitation conditions. The gold and blue stars indicate Mgas from [C II] using the conversions in Zanella et al. (2018) and Heintz et al. (2021), respectively. The red star shows the maximum amount of gas allowed by [C II] dynamics (F21). The points are slightly offset along the X axis for clarity. The uncertainty on the metallicity is represented by the horizontal red bar. The blue lines mark the (extrapolated) relations from Magdis et al. (2012), Rémy-Ruyer et al. (2014), De Vis et al. (2019), Popping & Péroux (2022), and Popping et al. (2023), and the models from Mauerhofer & Dayal (2023), Popping et al. (2017), Li et al. (2019), and Vijayan et al. (2019). |
| In the text | |
 |
Fig. 6. Dust mass as a function of stellar mass at 5 < z < 7. The red stars indicate the arc and z6.3 images of our galaxy, as labeled. Red arrows show the direction of the correction for the lensing magnification. The open blue symbols mark observed galaxies from the works in the legend. The empirical estimates are from Graziani et al. (2020), Pozzi et al. (2021), Sommovigo et al. (2021, 2022), and Witstok et al. (2022, 2023); the models are from Popping et al. (2017), Imara et al. (2018), Vijayan et al. (2019), Triani et al. (2020), Di Cesare et al. (2023), Mushtaq et al. (2023), Dayal et al. (2022), and Mauerhofer & Dayal (2023). Arrows indicate upper limits. Blue lines show the predictions for the models listed in the legend. |
| In the text | |
 |
Fig. 7. Dust mass function. The blue lines show the predictions of the models at z = 6, as labeled (Popping et al. 2017; Vijayan et al. 2019; Di Cesare et al. 2023; DELPHI, Dayal et al. 2022; Mauerhofer & Dayal 2023). For reference, the dashed gray line marks the dust mass function from the fiducial model in Popping et al. (2017) at z = 0. The filled red star and open circles indicate the observational constraints based on our target and other surveys at high redshifts, as labeled (Watson et al. 2015; Bakx et al. 2021; Akins et al. 2022; Fudamoto et al. 2021; Fujimoto et al. 2022; ϕ values estimated in Fujimoto et al. 2023). |
| In the text | |
 |
Fig. A.1. Dust continuum maps, best-fit Gaussian modeling, and residuals for the lensed z6.1-6.2 (arc, top rows) and z6.3 (bottom rows) images. The side of each cutout is 10". The rest-frame wavelengths of each map are labeled. Blue contours are at 2, 3, 5, and 10σ (rms). The images are color-scaled within ±5 times the rms per pixel in each band. The beam is shown in the bottom-right corner of the cutouts of the residuals. |
| In the text | |
 |
Fig. A.2. Photometric extractions. Filled circles indicate the ratio between the observed photometry extracted in Kron apertures and that from modeling with CASA/IMFIT. Large arrows show the 2σ upper limits on aperture photometry. Small gray arrows are 3σ upper limits on Herschel/SPIRE from Sun et al. (2022). For reference, we show both the measured Band 6 flux densities in configuration C2 and the combined C2+C5 (offset to improve the readability). Left: Arc (z6.1-6.2). Center: z6.3. Right: Aperture photometry of both lensed images. The flux densities are normalized to that in Band 7 (122 μm rest frame) for clarity and to avoid introducing the uncertainties on the magnification factor. The measurements in Band 6 (158 μm rest frame) from Fujimoto et al. (2021) are shown as orange squares. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq27.gif)
![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq29.gif)
![$ L^{\prime}_{{[\mathrm{C}\,\textsc{i}]}^3P_2{-} ^3P_1} $](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq30.gif)
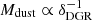
![$$ \begin{aligned} M_{\rm gas}(\mathrm{[CI]}) = 1375.8 \times 10^{-12} \, \frac{D_{\rm L}^2 \, Q_{21}\,S_{\rm \nu }\,\Delta v}{(1+z)\,A_{21} X_{\rm [CI]}} ,\end{aligned} $$](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq34.gif)
![$$ \begin{aligned} \mathrm{log}(L\prime _{\rm CO(7{-}6)} / [\mathrm{K\,km^{-1}\,s^{-1}\,pc^2}])&= (0.94 \pm 0.01) \times \mathrm{log}(L_{\rm IR} / L_\odot ) \nonumber \\ \quad&+ (-2.34\pm 0.09) \end{aligned} $$](/articles/aa/full_html/2024/05/aa48128-23/aa48128-23-eq40.gif)