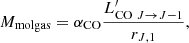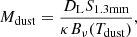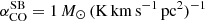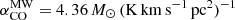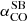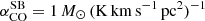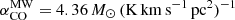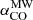Unveiling dust, molecular gas, and high star-formation efficiency in extremely UV bright star-forming galaxies at z ∼ 2.1–3.6

M. Dessauges-Zavadsky; R. Marques-Chaves; D. Schaerer; M.-Y. Xiao; L. Colina; J. Alvarez-Marquez; I. Pérez-Fournon

doi:10.1051/0004-6361/202451832

Home

All issues

Volume 693 (January 2025)

A&A, 693 (2025) A17

Full HTML

Open Access

Issue		A&A Volume 693, January 2025


Article Number		A17
Number of page(s)		21
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/202451832
Published online		23 December 2024

A&A, 693, A17 (2025)

Unveiling dust, molecular gas, and high star-formation efficiency in extremely UV bright star-forming galaxies at z ∼ 2.1–3.6

M. Dessauges-Zavadsky¹^⋆, R. Marques-Chaves¹, D. Schaerer¹^,2, M.-Y. Xiao¹, L. Colina³, J. Alvarez-Marquez³ and I. Pérez-Fournon⁴^,5

¹ Département d’Astronomie, Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
² CNRS, IRAP, 14 Avenue E. Belin, 31400 Toulouse, France
³ Centro de Astrobiología (CAB), CSIC-INTA, Ctra. de Ajalvir km 4, Torrejón de Ardoz, 28850 Madrid, Spain
⁴ Instituto de Astrofísica de Canarias, C/Vía Láctea, s/n, 38205 San Cristóbal de La Laguna, Tenerife, Spain
⁵ Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain

^⋆ Corresponding author; miroslava.dessauges@unige.ch

Received: 7 August 2024
Accepted: 21 October 2024

Abstract

We analysed the Atacama Large Millimetre/submillimetre Array (ALMA) far-infrared (FIR), 1.3 mm, dust continuum and CO emission of 12 starburst galaxies at z ∼ 2.1 − 3.6 selected for their extreme brightness in the rest-frame UV, with absolute magnitudes of −23.4 to −24.7. We also analysed their Very Large Telescope (VLT) High Acuity Wide field K-band Imager (HAWK-I) H- and K_s-band images. The targeted galaxies are characterised by negligible dust attenuations with blue UV spectral slopes (−2.62 to −1.84), very young stellar populations of ∼10 Myr, and powerful starbursts with a high mean specific star-formation rate of 112 Gyr⁻¹, placing them ∼1.5 dex above the main sequence at similar redshifts and stellar masses (M_stars ∼ (1.5 − 4.6)×10⁹ M_⊙). The FIR dust continuum emission revealed in nine galaxies gives IR luminosities of (5.9 − 28.3)×10¹¹ L_⊙, with six galaxies remaining dominated by unobscured UV star-formation rates, and high dust masses barely produced by supernovae within the 10 Myr timescale. The CO emission detected in eight galaxies leads to molecular gas masses higher than stellar masses, with the mean molecular gas mass fraction as high as 82%. The corresponding star-formation efficiencies reach ≳40%, with amazingly short molecular gas depletion timescales between less than 13 Myr and 71 Myr. These unique properties never reported in previously studied galaxies highlight that these galaxies are likely caught at the very beginning of their stellar mass build-up and undergo a very efficient and fast conversion of gas into stars that can only result from the gas collapse within a very short free-fall time. We find that the feedback-free starburst model seems to be able to explain the formation of these galaxies. To reconcile the co-spatial FIR dust emission with the UV-bright unattenuated emission, we speculate about the presence of radiation-driven outflows that can temporarily remove dust at the location of the starburst and expel it at large distances in line with the measured high FIR effective radii (1.7 kpc to 5 kpc) in comparison to the very compact stellar radii of a few hundred parsecs.

Key words: dust / extinction / ISM: molecules / galaxies: high-redshift / galaxies: starburst / galaxies: star formation

© The Authors 2024

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The census of star-forming galaxies at high redshifts (z > 2) has been ongoing for decades, and different observational techniques have been developed to identify galaxies either as Lyman break galaxies (LBGs) or Lyman-α emitters (LAEs). Large volumes of space have been probed to investigate their space density as a function of their ultraviolet luminosity through luminosity functions (e.g. Reddy & Steidel 2009; Sobral et al. 2018a). The bright end of the luminosity function (LF) of the UV and Lyα emission corresponds to massive star formation and high production of ionising photons. However, the identification of the most UV- or Lyα-luminous star-forming galaxies remains challenging for three possible reasons: vigorous episodes of star formation are simply rare phenomena; galaxies with high star-formation rates (SFRs) consume their gas quickly, implying short timescales for their UV- or Lyα-luminous phases; or galaxies at the bright end of the LF produce significant quantities of dust during their intense star formation so that these most vigorous and intrinsically luminous star-forming galaxies quickly have their emission at UV wavelengths heavily obscured by dust (e.g. Casey et al. 2014).

Probing the bright end of UV and Lyα LFs thus requires wide-area surveys. Several dedicated surveys at z ∼ 2 − 3 covering a few square degrees (1 − 4 deg²) have searched for extremely UV-luminous galaxies but failed to discover galaxies more luminous than two times the typical luminosity (L^⋆) of UV and Lyα of LBGs and LAEs, which corresponds to the unobscured absolute magnitude 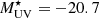$M_{UV}^{⋆} = - 20.7$ $M^{\star}_{\mathrm{UV}} = -20.7$ and $log (L_{Ly α}^{⋆} / erg s^{- 1}) = 42.8$ $\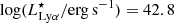log(L^{\star}_{\mathrm{Ly\alpha}}/\rm erg\,s^{-1}) = 42.8$ , respectively (e.g. Ouchi et al. 2008; Zheng et al. 2016; Sobral et al. 2018b). The Baryon Oscillation Spectroscopic Survey Emission-Line Lens Survey for the GALaxy-Lyα EmitteR sYstems (BELLS GALLERY; Shu et al. 2016) led to the discovery of five LAEs at 2 < z < 3 with intrinsic M_UV above 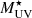$M_{UV}^{⋆}$ $M^{\star}_{\mathrm{UV}}$ , with two of them being brighter than M_UV < −23 and having 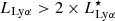$L_{Ly α} > 2 \times L_{Ly α}^{⋆}$ $L_{\mathrm{Ly\alpha}} > 2\times L^{\star}_{\mathrm{Ly\alpha}}$ , and this was without the need to invoke an active galactic nucleus (AGN) component (Marques-Chaves et al. 2017, 2020a). Additionally, five strongly lensed UV-luminous non-active LBGs with −23.5 < M_UV < −21.1 were also reported in the literature but with, on average, strongly suppressed Lyα lines, higher metallicities, stronger interstellar medium (ISM) absorption lines, and redder slopes, suggesting higher dust attenuation than the extremely UV-bright LAEs (Pettini et al. 2000; Quider et al. 2009, 2010; Dessauges-Zavadsky et al. 2010, 2011; Patrício et al. 2016; Marques-Chaves et al. 2018).

Remarkably, UV-luminous galaxies above 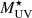$M_{UV}^{⋆}$ $M^{\star}_{\mathrm{UV}}$ are also detected at z > 6 (Sobral et al. 2015; Matsuoka et al. 2018; Hashimoto et al. 2019; Endsley et al. 2021; Bouwens et al. 2022a), and recent works now include the highest redshift sources known at the epoch of reionisation (EoR) discovered with the James Webb Space Telescope (JWST), leading to important and unexpected implications (e.g. Bouwens et al. 2023; Atek et al. 2023; Bunker et al. 2023; Casey et al. 2023; Castellano et al. 2024; Carniani et al. 2024). The volume density inferred for these UV-luminous sources with M_UV reaching −22.5 is much higher by factors of ∼10 − 100 than that predicted by models (e.g. Mason et al. 2018), implying steeper UV LFs than predicted such that the bright end of the LFs does not significantly evolve between 8 < z < 16 (e.g. Naidu et al. 2022; Finkelstein et al. 2024; Chemerynska et al. 2024). The excess of these UV-bright sources at the EoR, which still needs to be confirmed with spectroscopic redshift assessments, currently puts strain on the standard ΛCDM cosmology unless new concepts in our understanding of star-formation processes and baryon physics are invoked (Boylan-Kolchin 2023). Different scenarios have thus been proposed to explain the extremely UV-luminous and massive galaxies detected at the EoR and their excess, including a feedback-free starburst yielding a very high star-formation efficiency, namely a very efficient conversion of accreted gas into stars within a very short free-fall timescale (Dekel et al. 2023; Li et al. 2024); a temporary removal of dust as a consequence of radiation-driven outflows that yields very low dust attenuation and makes the galaxies appear brighter (Ferrara et al. 2023; Ziparo et al. 2023; Ferrara 2024); a top-heavy IMF boosting the UV radiation and the luminosity to mass ratio (e.g. Bekki & Tsujimoto 2023; Trinca et al. 2024); and a stochastic variability of the SFR (e.g. Mirocha & Furlanetto 2023; Gelli et al. 2024). Which of these scenarios holds now needs to be determined. Finally, although AGN contamination could possibly also explain the excess of these UV-bright sources at the EoR, this scenario was discarded by Finkelstein & Bagley (2022) and only the exceptionally UV-luminous galaxy GN-z11 at z = 10.6 potentially hosts an AGN (Maiolino et al. 2024).

The recent search for extremely UV-luminous galaxies with M_UV < −23 undertaken at z ≳ 2 within the ∼ 9000 deg²-wide extended Baryon Oscillation Spectroscopic Survey (eBOSS; Abolfathi et al. 2018) of the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2011) delivered about 70 galaxies at the very bright end of the UV LF, and they are among the most UV-bright galaxies known at cosmic noon (Marques-Chaves et al., in prep.). The first detailed studies of 13 of these galaxies are presented in Marques-Chaves et al. (2020b), Álvarez-Márquez et al. (2021), Marques-Chaves et al. (2021), Marques-Chaves et al. (2022), and Upadhyaya et al. (2024). We selected 12 of the most UV-luminous galaxies with M_UV ranging from −23.4 to −24.5 at z = 2.08 − 3.61, accessible for observations with ALMA. They are characterised by unattenuated starlight with steep UV spectral slopes ranging from −2.62 to −1.84 and are dominated by young stellar populations with average ages of ∼10 Myr, as testified by their rest-frame UV spectra revealing pure stellar features. Powered by powerful starbursts with very high specific SFRs (∼ 100 Gyr⁻¹), the corresponding stellar masses are in the range of (1.47 − 4.59)×10⁹ M_⊙, and they have sub-solar metallicities. Evidence of outflows, and even inflows, is found for some of these galaxies, as well as signatures of very massive stars (VMSs) with masses of 100 M_⊙ − 400 M_⊙. Two galaxies are identified as very strong Lyman continuum (LyC) leakers. Considering these physical properties altogether, the galaxies are interpreted as being in an intense starburst phase with the bulk of their stellar mass being formed in a few million years.

Globally, most of the physical properties of these galaxies resemble the recently discovered galaxies at the EoR. Therefore, the scenarios proposed to explain the UV brightness and excess of galaxies out at z > 8 could also explain the tremendous UV luminosities of these vigorous starburst galaxies at cosmic noon. The ALMA observations we acquired in the far-infrared (FIR) dust continuum at 1.3 mm (band 6) and in the CO(3–2) or CO(4–3) line emission (band 3) are key to inferring their dust and cold molecular gas masses – two physical parameters that are essential to fully probe the star-formation process ongoing in the galaxies and bring answers to the questions as to how much dust was produced within the ∼10 Myr burst timescale, where dust is located so that it is reconciled with the steep UV spectral slopes, how much obscured star formation contributes to the whole SFR budget in these highly star-forming galaxies, how much molecular gas mass is available to feed their star formation, what are the subsequent molecular gas mass depletion timescale and star-formation efficiency, with the latter expected to be higher with respect to that of nearby galaxies given the high stellar mass build-up achieved within 10 Myr only. Efficiencies higher than 20% are indeed advocated by different studies to explain diverse observational findings at very high redshifts (e.g. Xiao et al. 2024; de Graaff et al. 2024; Weibel et al. 2024) and make them compatible with simulations (e.g. Kannan et al. 2023; Boylan-Kolchin 2023). These answers are helpful to determine whether the molecular gas mass reservoir is consumed rapidly so that galaxies quench by starvation or, on the contrary, the molecular gas mass reservoir is massive enough to produce high amounts of dust so that galaxies turn into luminous dusty star-forming galaxies.

In Sect. 2 we describe the selection and the physical properties of the 12 UV-bright star-forming galaxies at z = 2.08 − 3.61 studied in this work. In Sect. 3 we present their ALMA and Very Large Telescope (VLT) HAWK-I observations and the corresponding data reduction and imaging. We then analyse the CO line, the FIR dust continuum, and the rest-frame UV or optical emission, and we measure CO luminosities, molecular gas masses, IR luminosities, dust masses, and FIR dust continuum as well as the rest-frame UV/optical sizes. Section 4 discusses the derived measurements in the general context of main sequence (MS) star-forming galaxies and starburst galaxies at similar and higher redshifts. We focus on the dust-obscured star formation in Sect. 4.1, the molecular gas mass content and depletion timescale in Sect. 4.2, the star-formation efficiency in Sect. 4.3, the dust mass content in Sect. 4.4, the FIR dust continuum and rest-frame UV/optical sizes in Sect. 4.5, and the rest-frame UV/optical morphology and spatial offsets in Sect. 4.6. In Sect. 5 we try to obtain a complete understanding of these extremely UV-luminous galaxies, considering all of their physical properties. Finally, in Sect. 6 we summarize our results.

Throughout the paper, we assume the ΛCDM cosmology with Ω_m = 0.3, Ω_Λ = 0.7, and H₀ = 70 km s⁻¹ Mpc⁻¹. We adopt the Chabrier (2003) initial mass function (IMF).

2. Target sample and their properties

This work presents ALMA and VLT HAWK-I observations of 12 extremely UV-bright star-forming galaxies at z = 2.08 − 3.61. These sources are part of a large sample of about 70 UV-luminous galaxies (Marques-Chaves et al. in prep.) selected from the ∼ 9000 deg²-wide eBOSS/SDSS survey (Abolfathi et al. 2018) to have high UV absolute magnitudes and narrow Lyα emission profiles in their BOSS spectra (covering the spectral range λ ≃ 3600 − 10 000 Å with a resolving power R ≃ 2000). The targets studied here were selected for ALMA and HAWK-I observations with declinations ≤30° and other properties that are representative of the parent sample. They show extremely bright M_UV ranging from −23.4 to −24.6, Lyα luminosities of log(L_Lyα/erg s⁻¹) = 42.9 − 44.1, and Lyα rest-frame equivalent widths of EWL_Lyα = 12 − 55 Å. The rest-frame UV and optical properties of a fraction (7/12) of these targets were analysed in detail in previous works through deep spectroscopy with the 10.4 m Gran Telescopio Canarias (Marques-Chaves et al. 2020b, 2021, 2022, 2024; Álvarez-Márquez et al. 2021; Upadhyaya et al. 2024), and for the remaining targets through shallow SDSS spectroscopy. We measured steep UV spectral slopes (β_UV) from −2.62 to −1.84, suggesting residual/low dust attenuations E(B − V)≤0.1 when assuming the Calzetti et al. (2000) extinction law with an intrinsic β₀ = −2.44.

In the references listed above it is also shown that the rest-frame UV spectra of the galaxies studied here reveal pure stellar features, such as wind lines and photospheric absorption, known to be produced only by the atmospheres of the most massive stars; as such, they are characterised by very young stellar populations with an average age of ∼10 Myr for the whole sample (but some galaxies are even younger and some slightly older). They have metallicities in the range of 12 + log(O/H) = 8.13 − 8.49, with a mean of 8.36, that is, Z/Z_⊙ ≃ 0.5. Using their UV luminosities (L_UV), we measured high unobscured star-formation rates SFR_UV = 104 − 415 M_⊙ yr⁻¹ by applying the specific L_UV–SFR_UV conversion factor κ_UV = 1.3 × 10⁻⁸ M_⊙ yr⁻¹/(erg s⁻¹ Hz⁻¹), derived using the Binary Population and Spectral Synthesis (BPASS) binary models (Eldridge et al. 2017; Stanway & Eldridge 2018; Byrne et al. 2022), and assuming a continuous star formation over 10 Myr, a metallicity of 0.5 Z_⊙, and the Chabrier (2003) IMF. However, one needs to keep in mind that κ_UV is strongly dependent on the burst age for 10 Myr and below, such that SFR_UV gets more than twice higher for a two times shorter continuous star formation, as explained in Marques-Chaves et al. (2024). The stellar masses of the young stellar population were then derived following M_stars = SFR_UV × 10 Myr, where SFR_UV were corrected for the dust attenuation using the observed β_UV; we obtained M_stars = (1.47 − 4.59)×10⁹ M_⊙. Analysing the spectral energy distributions (SEDs) of the galaxies, Marques-Chaves et al. (2020b, 2021, 2022) find that the SEDs are dominated by a young and intense burst of star formation, and could only infer loose upper limits on the mass of the old stellar population 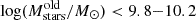$log (M_{stars}^{old} / M_{⊙}) < 9.8 - 10.2$ $\log (M_{\mathrm{stars}}^{\mathrm{old}}/M_{\odot}) < 9.8{-}10.2$ (3σ). The new Hubble Space Telescope (HST) photometry recently acquired for J1316+2614 provides a more stringent upper limit on 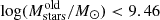$log (M_{stars}^{old} / M_{⊙}) < 9.46$ $\log (M_{\mathrm{stars}}^{\mathrm{old}}/M_{\odot}) < 9.46$ (3σ), yielding a fraction of the starburst mass to the total (young+old) stellar mass > 62% (see Fig. 9 Marques-Chaves et al. 2024). The absence of relevant old stellar population in these galaxies is interpreted as indicating that the galaxies are in an intense starburst phase with the bulk of their stellar mass being formed in a few million years. Table 1 summarizes all the rest-frame UV physical properties derived for our galaxies.

Table 1.

Rest-frame UV properties of the galaxy sample.

The galaxies studied here also appear as very strong producers of ionising radiation given their extreme M_UV, and two are confirmed to be strong LyC leakers (Marques-Chaves et al. 2021, 2022), with J1316+2614 at z = 3.6122 reaching a LyC escape fraction as high as f_esc(LyC)≃90%. Moreover, they have complex gas kinematics, showing signatures of outflows from the weak ISM absorption lines having blueshifted centroids with respect to the systemic redshift (Álvarez-Márquez et al. 2021; Marques-Chaves et al. 2021), and even signatures of inflow for J1316+2614 from the blue-dominated Lyα emission with respect to the systemic redshift (Marques-Chaves et al. 2022).

3. Observations and data analysis

3.1. ALMA data reduction and imaging

The 12 targets are part of two ALMA observing programmes. The first programme 2018.1.00932.S (PI: R. Marques-Chaves) includes J0146–0220, J0850+1549, J1220+0842, and J1157+0113, and was observed in Cycle 6 in bands 3 and 6 in the configurations C43-4 and C43-3, respectively, with short on-source integration times per target between 5 and 35 minutes. The second programme 2021.1.01438.S (PI: R. Marques-Chaves) includes J1322+0423, J1415+2036, J1249+1550, J0006+2452, J1220–0051, J0950+0523, J0121+0025, and J1316+2614, and was observed in Cylcle 8 also in bands 3 and 6 in the configurations C43-5 and C43-1 (C43-2 for J0950+0523), respectively, with on-source integration times of about 40 minutes per target. The band 3 observations were tuned to the CO(3–2) emission line, except for the 2 highest redshift targets at z > 3, J1316+2614 and J0121+0025, that were tuned to the CO(4–3) emission line. The band 6 observations were aimed for the 240 GHz (1.3 mm) FIR dust continuum solely and therefore were not tuned to a specific frequency. The spectral resolution was set to 31.25 MHz (i.e. ∼ 45 km s⁻¹) for both band 3 and 6 observations.

The ALMA data were calibrated with the standard observatory pipeline, and imaged using the Common Astronomy Software Application (CASA, version 6.2.1.7; McMullin et al. 2007). We imaged the band 6 calibrated visibilities of continuum over the four spectral windows with the multi-frequency synthesis, applying a pixel size of 0.1″ (for the 2018.1.00932.S targets) or 0.15″ (for the 2021.1.01438.S targets), and the natural weighting. The clean was repeated down to the threshold of 4× the RMS noise level of the dirty images using the tclean routine in CASA. We then applied the primary beam correction on the cleaned continuum emission maps. The corresponding FIR continuum maps are shown in Figs. 1, A.1, and A.2 (left panels).

Fig. 1.

Images showing the FIR dust continuum emission, the H- or K_s-band continuum emission, the CO(3–2) or CO(4–3) emission, and the related spectra (if CO is detected) of our 12 extreme starburst galaxies ordered by increasing redshift from top to bottom. Left panels: 23″ × 23″ ALMA band 6 1.3 mm (240 GHz) FIR dust continuum images of our targeted galaxies. Contour levels start at ±4σ and are in steps of 1σ up to 10σ and in larger steps above. The respective synthesised beam size and orientation are indicated by the red filled ellipse in the bottom-left corner. The cross in each panel corresponds to the coordinates of the HAWK-I continuum emission peak (except for J0850+1549 and J0121+0025 for which we consider, respectively, the CFHT MegaCam and Subaru continuum emission peak) and is ±3″ in size. Middle-left panels: 10″ × 10″ VLT HAWK-I seeing-limited H-band or AO K_s-band images of our starburst galaxies in greyscale with the ALMA band 6 FIR dust continuum contours overlaid in red. For J0850+1549 and J0121+0025, we show, respectively, the CFHT MegaCam and Subaru seeing-limited R-band images. Contour levels start at ±4σ and are in steps of 2σ, except for J0146–0220, J1249+1550, and J0850+1549 where contour levels are the same as in the left panels. The PSF is shown by the black filled circle in bottom-left corner, and the ALMA synthesised beam by the red filled ellipse in the bottom-right corner. The cross is the same as in the left panels. Middle-right panels: 10″ × 10″ ALMA CO(3–2) or CO(4–3) velocity-integrated intensity moment-0 maps of our galaxies. The maps were integrated over the cyan-shaded spectral channels shown in the right panels. Contour levels start at ±4σ and are in steps of 1σ. The respective synthesised beam size and orientation are indicated by the red filled ellipse in the bottom-right corner. The cross is the same as in the other panels. Right panels: ALMA CO(3–2) or CO(4–3) emission line spectra of our galaxies, plotted when detected, in steps of ∼ 45 km s⁻¹ and with the zero velocity centred on the redshifts derived from optical nebular emission lines (Table 1). The cyan-shaded regions correspond to the velocity channels optimising the CO detections, as described in Sect. 3.1. The dashed orange lines correspond to the RMS noise level of spectra. The solid red lines are the multi-component Gaussian best-fits to the observed CO line profiles. The vertical bars mark the positions of the fitted Gaussian components. The rest of the figure is available in Appendix A.

For the CO(3–2) and CO(4–3) emission imaging we used the pixel size of 0.1″ (for the 2018.1.00932.S targets) or 0.05″ (for the 2021.1.01438.S targets). The Briggs weighting with the robust factor of 1.0 was applied for the few galaxies with a high S/N CO detection, otherwise we applied the natural weighting. Similarly to the continuum maps, we cleaned all channels with the tclean routine down to the threshold of 4× the RMS noise level of the dirty cubes, and a primary beam correction was applied. Finally, we also imaged the band 3 calibrated visibilities of continuum over the four spectral windows, excluding channels contaminated by the CO emission. No band 3 (100 GHz) continuum was detected in any target. The resulting band 3 (CO emission) and band 6 (continuum emission) synthesised beam sizes and RMS noise levels for the 12 targets are listed in Tables 2 and 3, respectively.

Table 2.

CO emission line observations (ALMA band 3).

The CO moment-0 maps, that is, the velocity-integrated CO line intensity maps, were obtained by averaging the cleaned cube over the spectral channels where the CO emission is detected, using the immoments routine in CASA. We adopted the optimum channel range as the one that is maximising the S/N of the 1D spectrum of the CO emission line by iteratively testing different channel ranges (following the method of, e.g. Daddi et al. 2015; Zanella et al. 2018). For each channel range tested, the CO emission was extracted within a custom (polygonal) aperture including all the flux above the RMS noise level and typically bigger than the synthesised beam size. No band 3 continuum was subtracted beforehand, since undetected. The corresponding CO moment-0 maps and the CO line spectra are shown in Figs. 1, A.1, and A.2 (middle-right and right panels).

3.2. From the CO emission line to molecular gas masses

The CO emission is successfully detected close to the phase centre and at the expected frequency for eight targets. J0146–0220, J1249+1550, J0006+2452, J1220–0051, J0950+0523, and J1157+0113 show robust CO detections above 5σ, while J1415+2036 and J0121+0025 show patchy CO emission peaks at 4 − 5σ significance level spread over < 3″ (i.e. < 25 kpc) around the phase centre (Figs. 1, A.1, and A.2, middle-right panels). Four of the robust CO detections in J0006+2452, J1220–0051, J0950+0523, and J1157+0113 are spatially resolved, while J0146–0220 and J1249+1550 are unresolved/marginally resolved with their CO emission being comparable to the ALMA synthesised beam size. All the CO line profiles are complex, most are characterised by double-peaks and J1157+0113 even shows a triple-peak (Figs. 1, A.1, and A.2, right panels). They are difficult to interpret (between rotation/mergers) with the current data which do not allow us to perform a detailed kinematic analysis via velocity (moment-1) and dispersion (moment-2) maps given that all our galaxies are not sufficiently resolved.

We measured the CO velocity-integrated intensities (I_CO) from the CO moment-0 maps integrating all the signal located around the phase centre, above the surrounding RMS noise level. No aperture correction was needed as the customised apertures used were all bigger than the synthesised beam. The derived I_CO agree very well with those determined from the Gaussian fitting of the CO line profiles. To fit the complex CO line profiles, we performed multi-component Gaussian fitting using the nonlinear χ² minimisation and the Levenberg-Marquardt algorithm. Errors on the values of CO redshifts (z_CO), full-width half maximum (FWHM_CO), and I_CO were estimated using the Monte Carlo approach by perturbing the observed spectrum with 1000 random realisations. For the CO non-detections, upper limits on I_CO were derived from the 4σ RMS noise level of moment-0 maps integrated over ∼ 350 km s⁻¹, the typical FWHM measured for the detected CO emission lines of our targets. We then used Eq. (3) from Solomon et al. (1997) to derive the CO luminosities (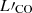 $L'_{CO}$ $L\prime_{\mathrm{CO}}$ ) from the respective I_CO. The resulting measurements can be found in Table 2.

The molecular gas mass (M_molgas) is then expressed as

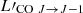$\begin{matrix} M_{molgas} = α_{CO} \frac{L_{CO J \to J - 1}^{'}}{r_{J, 1}}, \end{matrix}$ $\begin{aligned} M_{\rm molgas} = \alpha _{\rm CO} \frac{L^{\prime }_{\mathrm{CO}~J\rightarrow J-1}}{r_{J,1}}, \end{aligned}$ (1)

where $L'_{CO J \to J - 1}$ $L\prime_{\mathrm{CO}~J\rightarrow J-1}$ in K km s⁻¹ is the luminosity of a given CO transition, r_J, 1 is the CO luminosity correction for this transition to the fundamental CO(1–0) transition, and α_CO in M_⊙ (K km s⁻¹ pc²)⁻¹ is the conversion factor between the CO(1–0) luminosity and the H₂ gas mass.

To convert the CO(3–2) and CO(4–3) luminosities to the fundamental CO(1–0) luminosity, which ultimately gives the total H₂ molecular gas mass, we applied the CO luminosity correction factors r_3, 1 = 0.77 ± 0.14 and r_4, 1 = 0.61 ± 0.13, respectively, derived by Boogaard et al. (2020) from the stacking of CO-flux-limited star-forming galaxies at z ∼ 2.5 from the ALMA SPECtroscopic Survey (ASPECS). Overall, the adopted CO excitation (i.e. CO spectral line energy distribution) is comparable to the one of a lensed star-forming galaxy at z ∼ 3.6 with a similar IR luminosity to our targets (Dessauges-Zavadsky et al. 2017) and z ∼ 2.5 starburst galaxies (Xiao et al. 2022). 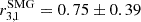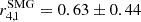It is also comparable to the recently derived CO excitation of IR-luminous sub-mm galaxies (SMGs) at z = 2 − 5 ( $r_{3, 1}^{SMG} = 0.75 \pm 0.39$ $r_{3,1}^{\mathrm{SMG}} = 0.75\pm 0.39$ and $r_{4, 1}^{SMG} = 0.63 \pm 0.44$ $r_{4,1}^{\mathrm{SMG}} = 0.63\pm 0.44$ ; Frias Castillo et al. 2023), in contrast with the initially higher CO excitation derived for SMGs at z = 1 − 4 (Bothwell et al. 2013).

As for the CO-to-H₂ conversion factor, hereafter we favour the value derived for nearby starburst galaxies, 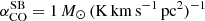$α_{CO}^{SB} = 1 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}} = 1\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ , given the starburst nature of our targets (Sect. 2). The corresponding M_molgas measurements are summarised in Table 4. In Sects. 4.2 and 4.3 we discuss the impact of α_CO values between 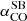$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ and the Milky Way value 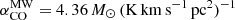$α_{CO}^{MW} = 4.36 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}} = 4.36\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ (including the factor of 1.36 to account for heavy elements, primarily Helium; Bolatto et al. 2013).

3.3. From the FIR dust continuum to IR luminosities and dust masses

The 1.3 mm (240 GHz) band 6 FIR dust continuum emission is robustly detected at the phase centre for nine targets: J0146–0220, J1249+1550, J0006+2452, J0850+1549, J1220–0051, J0950+0523, J1157+0113, J0121+0025, and J1316+2614 (Figs. 1, A.1, and A.2, left panels). All the continuum detections are spatially resolved, except in J0146–0220 whose continuum emission is comparable to the ALMA synthesised beam size.

We measured the FIR fluxes (S_1.3mm) from the 1.3 mm (240 GHz) continuum emission maps using customised apertures big enough to include for each emission all the signal located around the phase centre, above the surrounding RMS noise level (no aperture correction was needed as the apertures used were all bigger than the synthesised beam). The derived S_1.3mm agree very well with those determined from the fitting of the continuum emission in the uv plane by adopting the Fourier transform of the elliptical Gaussian 2D model. The fits were done using the UV_FIT routine from the GILDAS software package (Guilloteau & Lucas 2000), leaving the centre coordinates, flux, FWHM_major, FWHM_minor, and position angle of the Gaussian 2D model as free parameters. The fit in the uv plane did not converge for one target J1157+0113, certainly because of the complex shape of its emission in the continuum map that could not be approximated by the elliptical Gaussian 2D model. For the continuum non-detections, we considered 4σ upper limits estimated from the RMS noise level of the continuum dirty images. The resulting S_1.3mm measurements are listed in Table 3.

Table 3.

Far-infrared dust continuum observations (ALMA band 6) and rest-frame UV/optical ground-based observations.

We used the results of the uv fits to derive the deconvolved FIR dust continuum sizes of the spatially resolved targets (except for J1157+0113). We computed the effective radius (R_eff, FIR), defined as the radius enclosing half of the total emission, following 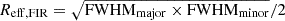$R_{eff, FIR} = \sqrt{{FWHM}_{major} \times {FWHM}_{minor}} / 2$ $R_{\mathrm{eff,FIR}} = \sqrt{\mathrm{FWHM_{major} \times FWHM_{minor}}}/2$ , where the square root of the product of the deconvolved full-width half maximum along the major and minor axes of the Gaussian 2D most precise fits of the FIR continuum emission corresponds to the circularised FWHM radius. The resulting R_eff, FIR are listed in Table 3.

Since our galaxies have a low dust attenuation E(B − V)≤0.1 (Sect. 2), we assumed that the emission models for these galaxies should be optically thin. Therefore, to determine the IR luminosity (L_IR) we scaled the optically thin modified black-body (MBB) function (Casey 2012) to the measured 1.3 mm (240 GHz) continuum flux of each target, and integrated over the wavelength range between 8 μm and 1000 μm. We derived the dust mass (M_dust) from S_1.3mm in Jy by following Casey (2012)

$\begin{matrix} M_{dust} = \frac{D_{L} S_{1.3 mm}}{κ B_{ν} (T_{dust})}, \end{matrix}$ $\begin{aligned} M_{\rm dust} = \frac{D_{\rm L} S_{\rm 1.3mm}}{\kappa B_{\nu }(T_{\rm dust})}, \end{aligned}$ (2)

where D_L in m is the luminosity distance, and B_ν(T_dust) in Jy sr⁻¹ is the Planck function at the dust temperature (T_dust) and the observer-frame frequency (ν = 240 GHz). We assumed T_dust = 40 K for the dust associated with the starburst regions of our targets at z ∼ 2.1 − 3.6 (e.g. Schreiber et al. 2018; Sommovigo et al. 2022; Viero et al. 2022; Witstok et al. 2023). For the dust mass absorption coefficient 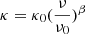$κ = κ_{0} {(\frac{ν}{ν_{0}})}^{β}$ $\kappa = \kappa_0 (\frac{\nu}{\nu_0})^{\beta}$ , where β is the dust emissivity index and κ₀ the dust opacity at ν₀ (λ₀), we assumed β = 1.4, κ₀ = 40 cm² g⁻¹, and λ₀ = 100 μm (Bianchi & Schneider 2007). We then derived the uncertainties on L_IR and M_dust as the median absolute deviations (mad) obtained when averaging over T_dust = 30 K, 35 K, 40 K, and 45 K and seven different κ models of dust composition listed in Ginolfi et al. (2019, Table 2), each of them providing a combination of parameters β, κ₀, and λ₀ selected from the literature (Weingartner & Draine 2001; Bertoldi et al. 2003; Robson et al. 2004; Beelen et al. 2006; Bianchi & Schneider 2007; Galliano et al. 2011; Jones et al. 2017). The resulting uncertainties are big but allow us to place our L_IR and M_dust estimates on the conservative side given the poorly constrained FIR SED with one single band continuum measurement. They are also big enough to encompass the ≳5 − 10% correction factor potentially needed to derive the intrinsic dust emission detected against the cosmic microwave background at the redshift of our galaxies (which we have not applied) computed by da Cunha et al. (2013). In Table 3 we summarize the derived L_IR, and M_dust can be found in Table 4.

Table 4.

Dust and molecular gas properties of the galaxy sample.

3.4. VLT HAWK-I data reduction and analysis

The near-IR imaging was obtained in H- and K_s-bands for 10 targets with HAWK-I on the VLT UT4. These observations were conducted between March 2023 and February 2024 in service mode as part of the programme 111.251K.001 (PI: R. Marques-Chaves). The H-band observations were taken under very good seeing conditions of 0.4″ − 0.6″ (FWHM). The K_s-band observations were obtained with the GRound layer Adaptive optics system Assisted by Lasers (GRAAL), enhancing the final image quality down to 0.3″ − 0.4″ (FWHM). For each target, the total on-source exposure times were 560 seconds and 1350 seconds in the H- and K_s-bands, respectively. Data were reduced using the standard ESO pipeline version 2.4.12¹ and were flux calibrated against 2MASS stars in the field. The astrometry was calibrated using the GAIA DR3 catalogue (Gaia Collaboration 2023) yielding an RMS precision of 0.10″ − 0.13″, which is roughly similar to the HAWK-I native pixel-scale (0.107″ per pixel).

Given the very good HAWK-I image quality, we investigated the morphology and sizes of the galaxies². We used GALFIT (Peng et al. 2002) to fit the light distribution of each galaxy with the 2D Gaussian function convolved to the instrumental point spread function (PSF) that was measured from bright stars in the HAWK-I field-of-view. The fitting process was performed on 10″ × 10″ background-subtracted cutouts centred on each target, shown in Figs. 1, A.1, and A.2 (middle-left panels). Overall, a single 2D Gaussian profile fitted well the observed light profiles for most of our galaxies, except for J0146–0220 and J0006+2452 that required an additional component. We find that eight galaxies are resolved in the HAWK-I images, for which we derived the rest-frame UV or optical effective radius (R_{eff, UV/opt}) measurements. The two remaining galaxies, J0950+0523 and J1316+2614, are unresolved with effective radii as small as R_eff, UV < 0.55 kpc for J1316+2614. J0146–0220 and J0006+2452 show a bright and unresolved component beside the extended and resolved component.

For the two targets with no HAWK-I observations, J0850+1549 and J0121+0025, we used, respectively, the public CFHT MegaCam and Subaru seeing-limited R-band images to infer their sizes, following the same methodology as described for HAWK-I images. The rest-frame UV or optical effective radii of our 12 UV-bright galaxies are summarised in Table 3.

4. Results

4.1. Dust-obscured star formation

As summarised in Sect. 2, our galaxies are intense starburst galaxies with very high unobscured star-formation rates for their M_stars and redshifts, ranging between SFR_UV = 104 M_⊙ yr⁻¹ and 415 M_⊙ yr⁻¹ (uncorrected for dust attenuation; Table 1). The measured L_IR (Table 3), moreover, show that most of these UV-bright galaxies reside in the regime of luminous IR galaxies (LIRGs; 10¹¹ < L_IR/L_⊙ < 10¹²) and 3 galaxies reside at the faint end of ultra-luminous IR galaxies (ULIRGs; 10¹² < L_IR/L_⊙ < 10¹³). They provide a measure of the obscured star-formation rates, defined as SFR_IR = L_IR/10¹⁰, following the calibration of Kennicutt (1998) for the Chabrier (2003) IMF. They reach SFR_IR = 59 M_⊙ yr⁻¹ to 238 M_⊙ yr⁻¹, with three upper limits below 57 M_⊙ yr⁻¹ (Table 4). The resulting total SFR (SFR_UV+IR = SFR_UV + SFR_IR) place our galaxies well above the MS of star-forming galaxies at similar z ∼ 2.5 and with similar stellar masses, with very high MS offsets of Δ_MS = SFR_UV+IR/⟨SFR_MS⟩ ∼ 30 (e.g. Speagle et al. 2014; Leslie et al. 2020). Obviously, the offsets could be lower in presence of old, yet currently poorly evidenced, stellar populations (Sect. 2).

In Fig. 2 we show the comparison of the unobscured SFR_UV and obscured SFR_IR of our galaxies. The bulk of these extreme starbursts are dominated by the unobscured SFR_UV and have obscured fractions of star formation (f_obscured = SFR_IR/SFR_UV+IR) ranging between ≲14% and 42%. Only three galaxies, J0006+2452, J0950+0523, and J1157+0113, have f_obscured moderately above 50%, with at most 57%. Based on different galaxy samples and exploring the possible effects of the assumed FIR SED template in the determination of SFR_IR values, Whitekar et al. (2017) showed that f_obscured is highly mass dependent but redshift independent for galaxies at 0 < z < 2.5. Half of our extreme starburst galaxies follows their f_obscured–M_stars relation, while the other half of galaxies with f_obscured < 25% is located a factor of two below the empirical relation. The latter galaxies have among the lowest f_obscured measurements known at their M_stars, and this even in comparison to stacks of UV-selected galaxies at z ∼ 5 (Fudamoto et al. 2020b) and z ∼ 7 (Algera et al. 2023). The deviation from the mean f_obscured–M_stars relation would be all the more significant if the stellar masses of our galaxies are underestimated (see Sect. 2). Among these low f_obscured galaxies, we find the two strong LyC leaking galaxies, J0121+0025 and J1316+2614, at z > 3 (Marques-Chaves et al. 2021, 2022), both with FIR dust continuum detections.

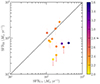Fig. 2.

Comparison of the unobscured SFR_UV (uncorrected for dust attenuation) and obscured SFR_IR of our galaxies, colour-coded by redshift. The majority of our galaxies is dominated by the unobscured SFR_UV, such that the corresponding obscured fractions of star formation range between f_obscured < 14% and 42%, and is above 50% for three galaxies only. The dashed line traces the one-to-one relationship.

In Fig. 3 we show the IR excess (IRX = L_IR/L_UV) as a function of the UV spectral slope of our galaxies. This is another empirical relation commonly studied for star-forming galaxies used to evaluate their dust attenuation, which does not evidence significant redshift evolution at least for galaxies at z ≲ 4 (e.g. Meurer et al. 1999; Whitekar et al. 2014; Bouwens et al. 2016; Fudamoto et al. 2017; Álvarez-Márquez et al. 2016, 2019). In comparison to the existing galaxy samples around the cosmic noon era, our galaxies are characterised by very blue β_UV < −1.8 and low IRX < + 0.5 because of their particularly high L_UV dominating over the LIRG/ULIRG regime. These two characteristics are more typical of very high redshift UV-selected galaxies at z ∼ 4.5 − 7.7 (e.g. Fudamoto et al. 2020b; Inami et al. 2022; Bowler et al. 2024); in particular, mean β_UV between −2.2 and −2.6 were derived from about a thousand of 5 < z < 13 galaxies (Roberts-Borsani et al. 2024; Heintz et al. 2024). As a result, similarly to the z ∼ 4.5 − 7.7 galaxies, most of our galaxies deviate from the canonical IRX–β_UV relation derived by Meurer et al. (1999) for nearby starburst galaxies with an intrinsic UV continuum slope β₀ = −2.23 (solid line in Fig. 3). Reddy et al. (2018) computed IRX–β_UV relations assuming a constant star formation with an age of 100 Myr and including nebular continuum emission for a low stellar metallicity of Z = 0.14 Z_⊙, assumed to better characterise high redshift galaxies expected to have different physical conditions from nearby starburst galaxies with younger stellar populations and lower metallicities, yielding bluer β₀ = −2.62 relative to the canonical relation of Meurer et al. (1999). The resulting IRX–β_UV predictions with β₀ = −2.62 were found to agree with stacks of UV-selected galaxies at z > 4.5 (e.g. Fudamoto et al. 2020b). In Fig. 3 we show the corresponding IRX–β_UV predictions obtained for the Small Magellanic Cloud (SMC; Gordon et al. 2003) extinction curve (dashed line) and the Calzetti et al. (2000) attenuation curve (dotted line). For three of our galaxies we observe a good match with the SMC and β₀ = −2.62 prediction, although the Meurer et al. (1999) IRX–β_UV relation remains consistent within the measurement uncertainties. Six galaxies are clearly offset to bluer β_UV values, and are most precisely reproduced by the Calzetti et al. (2000) and β₀ = −2.62 prediction.

Fig. 3.

Infrared excess as a function of the UV spectral slope of our galaxies, colour-coded by redshift. Our galaxies are all characterised by very blue β_UV < −1.8 and low IRX < + 0.5. Most of them deviate from the canonical IRX–β_UV relation (solid line; Meurer et al. 1999), and are better reproduced with the bluer intrinsic UV continuum slope β₀ = −2.62 as computed by Reddy et al. (2018) for the SMC (dashed line) and Calzetti et al. (2000) (dotted line) extinction curves.

Another well-studied empirical relation that links dust attenuation and stellar masses of galaxies is the IRX–M_stars relation, which is expected because M_stars is the outcome of past star-formation activity responsible for producing dust in supernovae (SNe) and pulsating moderate-mass asymptotic giant branch (AGB) stars, and is also suggested by simulations (Graziani et al. 2020). Different parametrisations are reported for samples of MS galaxies at z ∼ 1.5 − 4, showing, on average, that MS galaxies follow a relatively tight and shallow IRX–M_stars correlation with small variations from one sample to another (e.g. Heinis et al. 2014; Bouwens et al. 2016; Álvarez-Márquez et al. 2016; Koprowski et al. 2018), with the exception of the study of Fudamoto et al. (2020a) where they report a significantly steeper IRX–M_stars relation for their sample of z = 2.5 − 4.0 MS galaxies. Starburst galaxies at similar redshifts are found above the IRX–M_stars relation of MS galaxies with ∼ + 0.5 dex higher IRX values, indicating that starbursts are more dust extinct at a fixed M_stars (Fudamoto et al. 2020a). Our extreme starburst galaxies are among the few galaxies known with individual IRX measurements at stellar masses as low as log(M_stars/M_⊙) = 9.17 − 9.66. Half of them follows more or less the shallow IRX–M_stars parametrisation, and the other half lies in between, that is, above the steep Fudamoto et al. (2020a) parametrisation and below the shallow parametrisation, and even below the parametrisation from Heinis et al. (2014) specifically derived from stacks of high L_UV MS galaxies (log L_UV/L_⊙ = 10.64 − 10.94, which, nevertheless, are lower than the UV luminosities of our galaxies). Consequently, the currently still debated IRX–M_stars relation of MS galaxies, particularly for low stellar masses (M_stars/M_⊙ < 10¹⁰), makes it difficult to bring definitive conclusions on the dust attenuation of our extreme starburst galaxies with respect to MS galaxies with similar M_stars. Globally, our galaxies populate the IRX and M_stars parameter space encompassed by the relations extrapolated from individual measurements and stacks of different samples of more massive MS galaxies at comparable redshifts. Nevertheless, they seem to agree particularly well with the new IRX–M_stars parametrisation recently derived by Bowler et al. (2024) for the very high redshift galaxies (z ∼ 4.5 − 7.7).

4.2. Molecular gas mass content and depletion timescale

The measurements (and upper limits) of the molecular gas masses of our galaxies, derived from the CO(3–2) or CO(4–3) luminosities, range between M_molgas < 0.63 × 10¹⁰ M_⊙ and 3.67 × 10¹⁰ M_⊙ when derived with 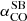$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ (Table 4). As shown in Fig. 4, whatever α_CO, our extreme starburst galaxies have significantly higher SFR_UV+IR than MS galaxies at comparable M_molgas, or, inversely, have significantly lower M_molgas than MS galaxies at comparable SFR_UV+IR (if these latter exist). This is in line with the integrated Kennicutt-Schmidt (KS) star-formation law and its M_molgas–SFR parametrisations determined by Sargent et al. (2014) for MS galaxies (solid line in Fig. 4 derived from nearby and cosmic noon galaxies) and starburst galaxies (dashed line in Fig. 4 derived from nearby and z < 0.1 ULIRGs), as also reported by Daddi et al. (2010) and Genzel et al. (2010). Our galaxies actually represent the first sample of high redshift galaxies that shows an offset from MS galaxies high enough, when assuming 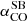$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ , to lie on the starburst M_molgas–SFR relation offset by more than 1 dex from the MS relation. Both the sample of massive starburst galaxies at z ∼ 1.6 studied by Silverman et al. (2015, 2018) and SMGs at z ∼ 1 − 5 (e.g. Bothwell et al. 2013; Calistro Rivera et al. 2018; Liu et al. 2019; Frias Castillo et al. 2023) do not reach the starburst star-formation regime even with 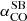$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ . On the other hand, our galaxies still satisfy the empirical relation defined between L_IR and 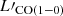$L'_{CO (1 - 0)}$ $L\prime_{\mathrm{CO(1-0)}}$ established for diverse galaxy types from nearby galaxies (disks, dwarfs, starbursts) to ULIRGs, MS galaxies, SMGs, and quasars at z ∼ 0 − 5 (e.g. Carilli & Walter 2013; Dessauges-Zavadsky et al. 2015). This means that, for their IR luminosities, our starburst galaxies have the expected CO luminosities. They thus end up in the extreme starbursting regime mostly because of their very high unobscured SFR_UV (see also Sect. 4.1).

Fig. 4.

Molecular gas mass as a function of the total (unobscured plus obscured) star-formation rate of our galaxies, colour-coded by redshift. The filled circles correspond to M_molgas determined with $α_{CO}^{SB} = 1 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}} = 1\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ , and the dotted red segments show the range of possible M_molgas with higher CO-to-H₂ conversion factors up to $α_{CO}^{MW} = 4.36 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}} = 4.36\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ . Whatever α_CO, our extreme starburst galaxies have significantly higher SFR_UV+IR than MS galaxies at comparable M_molgas (see the solid line as derived by Sargent et al. 2014). For $α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ our galaxies are the first galaxies known at high redshift to reach the starburst M_molgas–SFR relation (dashed line) offset by > 1 dex from the MS relation, according to the parametrisation of Sargent et al. (2014) based on nearby and z < 0.1 ULIRGs.

The high SFR_UV+IR of our galaxies yield very short molecular gas depletion timescales (t_depl = M_molgas/SFR_UV+IR) with a mean of 49 Myr ± 12 Myr for 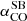$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ (Table 4). As shown in the left panel of Fig. 5, these t_depl are significantly shorter by more than one order of magnitude than those measured in MS galaxies at any redshift (e.g. Béthermin et al. 2015; Liu et al. 2019; Tacconi et al. 2020; Dessauges-Zavadsky et al. 2020). They are also shorter than those reported for the massive starburst galaxies at z ∼ 1.6 with their mean t_depl ∼ 60 Myr (Silverman et al. 2015, 2018) and for the SMGs with their mean t_depl ∼ 200 Myr (e.g. Bothwell et al. 2013; Calistro Rivera et al. 2018; Frias Castillo et al. 2023), considering the same 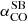$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ . The upper limit on t_depl derived for J1316+2614, our highest redshift galaxy, even suggests that all its molecular gas mass (M_molgas < 6.3 × 10⁹ M_⊙) is depleted in < 13 Myr! This remains true despite the uncertain L_IR measurements (Sect. 3.3) affecting SFR_UV+IR: if SFR_UV+IR are underestimated the t_depl values would be even shorter, and if, on the other hand, SFR_UV+IR are overestimated they would need to be overestimated by a factor of more than 10 to bring our galaxies to the t_depl values of MS galaxies at similar redshifts, which is implausible as SFR_UV+IR are dominated by SFR_UV and not by the uncertain SFR_IR. Consequently, our extreme starburst galaxies are really vigorously consuming their molecular gas mass reservoir and are rapidly building up their stellar mass.

Fig. 5.

Molecular gas depletion timescale (left) and molecular gas mass fraction (right) as a function of the redshift of our galaxies shown by the red filled circles. Similarly to Fig. 4, the dotted red segments represent the range of possible t_depl and f_molgas measurements of our galaxies as derived with CO-to-H₂ conversion factors sampling values from $α_{CO}^{SB} = 1 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}} = 1\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ to $α_{CO}^{MW} = 4.36 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}} = 4.36\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ . The t_tepl and f_molgas means, errors on the means, and standard deviations obtained for the CO-detected MS galaxies from the compilation of Dessauges-Zavadsky et al. (2020) are shown by the black/grey crosses in five redshift bins 0 < z < 0.1, 0.1 < z < 1, 1 < z < 1.5, 1.5 < z < 2.5, and 2.5 < z < 3.7. The light-grey shaded area corresponds to t_tepl and f_molgas derived by Béthermin et al. (2015) from the FIR SED stacks of MS galaxies. For all MS galaxy measurements compiled here, the same $α_{CO}^{MW}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}}$ conversion factor is assumed. Our extreme starburst galaxies have significantly shorter t_depl than those measured in MS galaxies at any redshift (left). This indicates that they are vigorously consuming their molecular gas mass reservoir to build up their stellar mass. On the other hand, they have very high f_molgas (right), in excess with respect to MS galaxies at similar redshifts, showing that their mass remains dominated by the molecular gas mass over the stellar mass.

In the right panel of Fig. 5 we show the molecular gas mass fractions (f_molgas = M_molgas/(M_molgas + M_stars)) of our galaxies as a function of redshift that we compare to MS galaxies. We observe that our galaxies have very high f_molgas with a mean of 82%±10% for 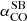$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ (Table 4). This reveals that their baryonic mass is dominated by the cold molecular gas mass over the stellar mass, with the mean molecular gas mass to stellar mass ratio (μ_molgas = M_molgas/M_stars) of 6 ± 3, and this despite the observed very rapid molecular gas consumption timescales (Fig. 5, left panel). This suggests that our extreme starburst galaxies are caught at the very beginning of their stellar mass build-up, or that cosmic gas inflows are actively feeding these galaxies. The measured f_molgas of our galaxies are in significant excess with respect to those of MS galaxies at similar redshifts, and still higher than those of MS galaxies with similar M_stars (and z) despite the existing steep f_molgas–M_stars anticorrelation (e.g. Béthermin et al. 2015; Liu et al. 2019; Tacconi et al. 2020; Dessauges-Zavadsky et al. 2020). The stellar masses of our galaxies would need to be underestimated by, on average, a factor of ∼3 − 4 to reach the upper end of the f_molgas distribution of MS galaxies at z ∼ 2.5. The same is true for them to reach the mean f_molgas ∼ 50% of the massive starburst galaxies at z ∼ 1.6 of Silverman et al. (2015, 2018) and even more to reach the mean f_molgas ∼ 40% of SMGs (e.g. Bothwell et al. 2013; Calistro Rivera et al. 2018; Frias Castillo et al. 2023), considering the same α_CO.

4.3. Star-formation efficiency

Our extreme starburst galaxies are dominated by very young stellar populations of ∼10 Myr, with the bulk of their stellar mass being assembled within this short timescale given the absence of relevant old stellar populations, as described in Sect. 2. Upadhyaya et al. (2024), moreover, showed that their rest-frame UV spectra resemble those of nearby young star clusters (R136–Crowther et al. 2016 and SB179 Senchyna et al. 2017) and the Sunburst star cluster at z ≃ 2.4 (Meštrić et al. 2023). As a result, in contrast to most of the galaxies at cosmic noon whose stellar populations are a mixed bag of young and old populations dominated by old populations, our galaxies represent rare objects whose stellar populations are dominated by young populations representing > 30% to 62% of the total stellar mass of our galaxies (Marques-Chaves et al. 2020b, 2021, 2022, 2024).

We can thus measure the star-formation efficiency (ϵ_SF) of our galaxies, defined as the fraction of molecular gas mass converted into the recently formed stellar mass, namely here over the past ∼10 Myr, following 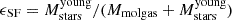$ϵ_{SF} = M_{stars}^{young} / (M_{molgas} + M_{stars}^{young})$ $\epsilon_{\mathrm{SF}} = M_{\mathrm{stars}}^{\mathrm{young}}/(M_{\mathrm{molgas}}+M_{\mathrm{stars}}^{\mathrm{young}})$ (Evans et al. 2009; Dessauges-Zavadsky et al. 2019, 2023). We find ϵ_SF ranging from 8% to 37% (Table 4), with a mean of 18%±9% for 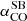$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ . J1249+1550 has the highest measured ϵ_SF approaching 40%, together with J1316+2614 with its lower limit ϵ_SF > 40%. They both are associated with very short molecular gas depletion timescales of 36 Myr and < 13 Myr, respectively, among the shorter in our galaxy sample (Table 4). One needs to keep in mind that the derived ϵ_SF likely are lower limits, as we do not know whether all the measured M_molgas is associated with the star formation taking place in the compact starburst UV-bright component of our galaxies revealed by the HST and HAWK-I rest-frame UV/optical images (see Sect. 4.6).

The derived ϵ_SF of our extreme starburst galaxies are higher in comparison to those of a few percent only (≲5%) measured in nearby galaxies (e.g. Schruba et al. 2019; Utomo et al. 2018; Kim et al. 2023). On the other hand, they agree with the ϵ_SF values of ∼30% inferred for two strongly lensed MS galaxies at z ≃ 1 from the analysis of giant molecular clouds and their association with star-forming regions (Dessauges-Zavadsky et al. 2019, 2023). These enhanced ϵ_SF are comparable to those proposed in ultra-massive (M_stars > 10¹¹ M_⊙) optically dark and quenched galaxies recently discovered at z ∼ 5 − 6 (Xiao et al. 2024; de Graaff et al. 2024), whose existence can be explained by invoking very high star-formation efficiencies (≳20% to 100%). Similarly, Weibel et al. (2024) suggested that an increasing ϵ_SF with redshift, reaching values of ϵ_SF ∼ 30% at z ∼ 7 − 8, is required to explain the high-mass end of the stellar mass functions at z ≥ 4 − 9 as determined with JWST observations. On the simulation side, MillenniumTNG simulations also find that ϵ_SF of about 10%−30% are necessary in the early Universe to solve the observed excess of luminous/massive galaxies at z ≳ 8 discovered with JWST (Kannan et al. 2023). Values of ϵ_SF ≥ 57% are even invoked by Boylan-Kolchin (2023) to reconcile the standard ΛCDM cosmological model with the observed excess.

4.4. Dust mass content

The detected dust continuum emission in the Rayleigh-Jeans tail of the FIR SED (λ_rest > 230 μm) was used to estimate the dust mass content of our galaxies, as described in Sect. 3.3. However, the derived M_dust ranging from < 1.1 × 10⁷ M_⊙ to 1.1 × 10⁸ M_⊙ (Table 4) have to be considered with some caution given their large uncertainties coming from the poorly constrained FIR SED with one single band continuum measurement and the large number of free parameters entering in the dust composition models. The corresponding dust-to-gas mass ratios (δ_DGR = M_dust/M_molgas) are spread out between log(δ_DGR) < − 2.9 and −2.1 for 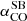$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ . This spread is comparable to the dispersion of δ_DGR measurements reported in the literature at a given metallicity and the various extrapolated δ_DGR–metallicity relations that diverge even more at 12+log(O/H) < 8 (e.g. Magdis et al. 2012; Rémy-Ruyer et al. 2014; De Vis et al. 2019; Popping et al. 2023; Valentino et al. 2024). The observed δ_DGR–metallicity correlation is also found in semi-analytic models of galaxy formation that include the tracking of dust formation and destruction over cosmic time (e.g. Popping et al. 2017). Globally, the inferred δ_DGR of our galaxies lower than 10⁻² (the typical δ_DGR value measured around solar metallicity) favour sub-solar metallicities in agreement with the metallicity measurements of our galaxies (12+log(O/H) = 8.13 − 8.49; Sect. 2).

In Fig. 6 we compare the dust masses of our extreme starburst galaxies to different empirical M_dust–M_stars relations presented in Kokorev et al. (2021, their Fig. 12) for MS galaxies at similar redshifts but extrapolated from more massive galaxies (log(M_stars/M_⊙) > 10). Our galaxies agree with the M_dust–M_stars relation derived by Magnelli et al. (2020) as shown by the solid black line, but are well below the relations of Liu et al. (2019) and Kokorev et al. (2021) shown by the dotted and dashed black lines, respectively, which predict much higher M_dust for the low-M_stars MS galaxies at z ∼ 2.5. The M_dust estimates of our extreme starburst galaxies in fact resemble those of z ∼ 4 − 7 galaxies with comparable stellar masses (Pozzi et al. 2021; Sommovigo et al. 2022; Witstok et al. 2023; Valentino et al. 2024).

Fig. 6.

Dust mass as a function of the stellar mass of our extreme starburst galaxies, colour-coded by redshift. Our galaxies agree with the M_dust–M_stars relation derived by Magnelli et al. (2020) as shown by the solid black line, but are well below the relations of Liu et al. (2019) and Kokorev et al. (2021) shown by the dotted and dashed black lines, respectively. The grey shaded zone defines the SN dust production as predicted by Gall & Hjorth (2019), which is barely sufficient to reproduce M_dust of most of our galaxies. The thick dashed-dotted green line defines the start of the AGB star contribution to the dust production (Witstok et al. 2023).

The efficiency of dust production of our galaxies can be assessed by comparing their M_dust and M_stars with dust production models. In Fig. 6 the grey shaded zone defines the SN dust production as predicted by the model of Gall & Hjorth (2019), which assumes that the dust is produced during a star-formation episode lasting over Δt with a mean SFR and with SNe (or their massive star progenitors³) producing a fraction η of solar masses of dust, with the rate of SNe being proportional to SFR with the proportionality factor γ; such that the produced dust mass can be expressed as M_dust = γηSFRΔt. Gall & Hjorth (2019) computed the dust productivity μ_dust = γη and derived μ_dust = 0.004 ± 0.002 for the Chabrier (2003) IMF. The product SFRΔt gives the stellar mass assembled during the star-formation episode, which for our galaxies is computed over a burst age of ∼ 10 Myr as described in Sect. 2. The SN dust production can hence be expressed as M_dust = (0.004 ± 0.002)M_stars. This simple model indicates that SNe (or massive stars) alone barely produce enough dust (without considering dust destruction) during the short burst timescale of our extreme starburst galaxies (see the grey shaded zone in Fig. 6) to enable to reproduce their dust masses. For four galaxies, despite their big and conservative M_dust uncertainties (Sect. 3.3), their M_dust measurements even clearly step outside the predicted SN dust production, unless a top-heavy IMF is invoked, or the (young) stellar masses of these galaxies are underestimated by a factor of up to ∼4. On longer timescales, but relatively rapidly (for Δt ≳ 40 Myr), AGB stars start to contribute to the dust production in addition to SNe (Schneider & Maiolino 2024, their Fig. 1), as delimited by the thick dash-dotted green line in Fig. 6 derived by Witstok et al. (2023, following the simulations of Di Cesare et al. 2023). With respect to other dust formation models, only those by Imara et al. (2018) and Vijayan et al. (2019) predict the formation of enough dust to reproduce M_dust of all the low-M_stars galaxies in our sample; models of Popping et al. (2017) at z ∼ 2 − 3 globally follow the same trend as the SN dust production of Gall & Hjorth (2019).

4.5. FIR dust continuum and rest-frame UV/optical sizes

The FIR dust continuum sizes were measured in the uv plane for seven galaxies of our sample using the ALMA 1.3 mm band 6 observations (Sect. 3.3). They range between R_eff, FIR = 1.7 kpc and 5.0 kpc (Table 3), and are shown as a function of L_IR in Fig. 7. The dependence of the FIR dust sizes of high redshift galaxies (1 < z < 6) on L_IR is still debated between, on one hand, the positive correlation (plotted as the dark-grey shaded area) reported by Fujimoto et al. (2017, based on a thousand of ALMA archival galaxies) that is in line with the stellar rest-frame UV size–luminosity correlation for star-forming galaxies (e.g. Shibuya et al. 2015), and, on the other hand, the anti-correlation (light-grey shaded area) proposed by Jin et al. (2022, based on a much smaller compilation of massive dusty galaxies, but with a better dynamical range towards lower L_IR, from Valentino et al. 2020, Franco et al. 2020, and Gómez-Guijarro et al. 2022). In both studies, the big R_eff, FIR 1 σ scatter (∼ 0.3 − 0.5 dex) at a given L_IR weakens the significance of the respective correlations. We observe that R_eff, FIR of our galaxies, on average, better agree with the relation of Jin et al. (2022).

Fig. 7.

Far-infrared dust continuum effective radius as a function of the IR luminosity of our galaxies, colour-coded by redshift. Our extreme starburst galaxies agree better with the R_eff, FIR–L_IR anti-correlation (light-grey shaded area) found by Jin et al. (2022) than with the R_eff, FIR–L_IR correlation (dark-grey shaded area) of Fujimoto et al. (2017).

A dependence of R_eff, FIR on stellar mass was also reported for massive galaxies at 1.5 < z < 4.5 by Gómez-Guijarro et al. (2022) as shown in Fig. 8 by the solid and dashed black lines at z < 2.5 and z > 2.5, respectively. Its slope is comparable to the slope of the stellar rest-frame UV effective radius versus M_stars relation derived for late-type galaxies (LTG) at similar redshifts z ∼ 2.5 (blue shaded area) but its normalisation is much lower by a factor of ∼3 − 4 (van der Wel et al. 2014). Fujimoto et al. (2017) also found that the FIR dust continuum sizes of high redshift galaxies are more compact than those at UV/optical wavelengths, albeit with a less different normalisation factor. Our galaxies have much higher R_eff, FIR (filled circles) with respect to the Gómez-Guijarro et al. (2022) relations, and in fact very much agree with the stellar rest-frame UV sizes of LTG at z ∼ 2.5. TNG50 simulations from Popping et al. (2022) predict FIR dust continuum (850 μm rest-frame) sizes as a function of the stellar mass of MS galaxies from z = 1 to z = 5, which at z ∼ 2 − 3 approximately match R_eff, FIR of our galaxies, but clearly overpredict the R_eff, FIR–M_stars relations proposed by Gómez-Guijarro et al. (2022).

Fig. 8.

Far-infrared dust continuum effective radius (filled circles) and rest-frame UV/optical effective radius (filled stars) as a function of the stellar mass of our galaxies, colour-coded by redshift. All our galaxies have systematically higher R_eff, FIR than R_{eff, UV/opt}. As a result, R_eff, FIR of our galaxies strongly deviate from the R_eff, FIR–M_stars relations of Gómez-Guijarro et al. (2022) at z < 2.5 and z > 2.5, shown by the solid and dashed black lines, respectively, as they are more extended. On the other hand, their R_{eff, UV/opt} agree with the R_eff, UV–M_stars relation (blue shaded area) derived for LTG at z ∼ 2.5 by van der Wel et al. (2014). The green shaded area corresponds to the R_eff, UV–M_stars relation of z ∼ 2.5 early-type galaxies (ETG; van der Wel et al. 2014).

In Fig. 8 we furthermore compare R_eff, FIR (filled circles) with the rest-frame UV or optical effective radii (filled stars) derived from our HAWK-I seeing-limited H-band or AO K_s-band observations⁴, respectively (Sect. 3.4 and Table 3). We observe that half of our galaxies have R_{eff, UV/opt} in agreement with those of LTG at z ∼ 2.5 (van der Wel et al. 2014), and the other half is considerably more compact. However, globally, all our extremely UV-luminous galaxies have R_eff, FIR systematically higher than their R_{eff, UV/opt}. As a result, the mean R_{eff, UV/opt}/R_eff, FIR = 0.43 ± 0.17 ratio of our galaxies contrasts with what is reported in the literature for galaxies at comparable redshifts 1 < z < 4, R_eff, HST/R_eff, ALMA ∼ 1.6 and ∼2.4 for, respectively, ALMA archival galaxies from Fujimoto et al. (2017) and massive galaxies from Franco et al. (2020). Our galaxies actually share one additional physical property in common with very high redshift UV-selected galaxies at 4.5 < z < 6, because these latter are also characterised by relatively extended FIR dust continuum sizes with respect to the compact UV sizes (≲1.5 kpc) with R_eff, HST/R_eff, ALMA = 0.39 ± 0.15 as recently measured by Pozzi et al. (2024, see also Mitsuhashi et al. 2024).

4.6. Rest-frame UV/optical morphology and spatial offsets

As shown in the middle-left panels of Figs. 1, A.1, and A.2, most of our extremely UV-luminous galaxies are characterised by a simple ‘roundish’ rest-frame UV or optical morphology with one main bright component with R_{eff, UV/opt} ranging from 0.79 kpc to 2.01 kpc (Table 3). Two galaxies, J0950+0523 and J1316+2614, are particularly compact with R_eff, opt < 0.74 kpc and < 0.55 kpc, respectively, unresolved in the HAWK-I AO K_s-band images. Only two galaxies, J0146–0220 and J0006+2452, show more complex rest-frame optical morphologies with one main bright and compact component with R_eff, opt < 0.8 kpc (unresolved in HAWK-I AO K_s-band observations), centred on the phase centre, and a more diffuse component extended over > 2 kpc in radius and offset in one direction with respect to the main component. A second tiny component seems also to be present on top of the diffuse component in J0146–0220. The detected rest-optical diffuse emission can be interpreted as a possible signature of either a diffuse underlying old stellar population or diffuse outflowing gas as the HAWK-I K_s-band emission can instead trace the nebular Hα emission at the redshift of these two galaxies.

The recently acquired HST images of J1415+2036, J0850+1549, and J1316+2614 confirm that the rest-frame UV morphology of our extreme starburst galaxies is a mixed bag between one single component for J1316+2614 (Marques-Chaves et al. 2024) and multi-components with J1415+2036 and J0850+1549 showing, respectively, two and three very compact components (Marques-Chaves et al. in prep.) that are blended in ground-based observations (Figs. 1 and A.1, middle-left panels). The HST images also reveal that the extreme L_UV we measure mostly comes from a very compact component, which is barely resolved even at the HST resolution. The galaxy J1316+2614 appears as the most extreme case in our sample, because it is composed of one single very compact HST component with an effective radius as small as 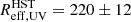$R_{eff, UV}^{HST} = 220 \pm 12$ $R_{\mathrm{eff,UV}}^{\mathrm{HST}} = 220\pm 12$ pc, co-spatial with the extended FIR dust continuum emission, and without any sign of underlying HST diffuse emission (Marques-Chaves et al. 2024).

In both J0146–0220 and J0006+2452 galaxies, the FIR dust continuum emission is co-spatial with the CO emission, but is offset from the main rest-optical component, whereas it aligns with the extended diffuse rest-optical emission. The offsets between the main rest-optical component and the FIR emission are 0.66″ and 0.59″, that is, about 5.5 kpc and 4.9 kpc, in J0146–0220 and J0006+2452, respectively. The possible origin of this offset is discussed in Sect. 5. J1249+1550 and J0850+1549 also seem to have their FIR emission slightly offset by ≲0.25 − 0.3″ from the bright rest-optical and rest-UV emission, respectively, but these offsets remain within the synthesised beam and PSF uncertainties and need to be confirmed. Thus, for seven out of nine galaxies one can assume that the UV/optical bright component is co-spatial with the more extended FIR emission and the CO emission (when detected) as shown in the middle-left and middle-right panels of Figs. 1, A.1, and A.2.

J1415+2036 and J0121+0025 show patchy CO emission peaks at 4 − 5σ significance level spread within < 3″ (i.e. < 25 kpc) around the phase centre (Figs. 1 and A.2, middle-right panels). Their integrated CO line detections nevertheless seem relatively robust, especially for J1415+2036, as shown by their respective CO line spectra plotted in the right panels of Figs. 1 and A.2. However, how this patchy CO emission with its relatively big spatial extent relates to the rest-frame UV/optical emission remains unclear, especially in J0121+0025 where the escaping LyC radiation (Marques-Chaves et al. 2021) needs to be reconciled with the presence of cold molecular gas. The other leaker, J1316+2614 (Marques-Chaves et al. 2022), is undetected in the CO emission with a stringent upper limit on its very depleted M_molgas < 6.3 × 10⁹ M_⊙ (Fig. 4).

5. Discussion

The studied sample consists of the 12 most UV-bright galaxies known at z ≃ 2.1 − 3.6 with M_UV = −23.40 to −24.65 (Sect. 2 and Table 1), surpassing by 2 − 3 magnitudes the recently detected JWST UV-luminous galaxies at 7 < z < 16 brighter than 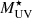$M_{UV}^{⋆}$ $M^{\star}_{\mathrm{UV}}$ (e.g. Bouwens et al. 2023; Atek et al. 2023; Bunker et al. 2023; Casey et al. 2023; Castellano et al. 2024; Carniani et al. 2024). They also outshine by far the brightest stellar clusters known in the Sunburst (M_UV ∼ −19) at z ≃ 2.4 and Sunrise (M_UV ∼ −18) at z ≃ 6 galaxies (Vanzella et al. 2022, 2023). They are dominated by very young stellar populations of ∼10 Myr (as assessed from the rest-frame UV spectroscopy) and are powerful starbursts with a mean specific SFR (sSFR = SFR/M_stars) of 112 Gyr⁻¹ (± 45 Gyr⁻¹), placing them ∼1.5 dex above the MS for their redshifts and stellar masses (M_stars ∼ (1.47 − 4.59)×10⁹ M_⊙). They show unattenuated starlight with blue UV spectral slopes between β_UV = −2.62 and −1.84, similar to those observed in several UV-bright galaxies at z > 7 (Roberts-Borsani et al. 2024; Heintz et al. 2024). They present complex gas kinematics showing signatures of outflows and inflows. Furthermore, they are not only very efficient at producing ionising radiation given their luminous M_UV, but some of them leak high amounts of LyC photons (Marques-Chaves et al. 2021), including the record-holder J1316+2614 at z = 3.6122 with a LyC escape fraction of f_esc(LyC) ≃ 90% (Marques-Chaves et al. 2022). In summary, our galaxies possibly experience very early stages of vigorous starbursts with a fast mode of stellar mass build-up, likely resembling the major bursts of star formation taking place in the UV-luminous galaxies recently discovered with JWST at the EoR.

The ALMA observations, analysed in this paper, furthermore reveal the relatively bright FIR dust continuum emission for nine of our galaxies, placing these extremely UV-luminous galaxies in the LIRG regime, and even the ULIRG regime for three galaxies, with L_IR = (5.9 − 28.3)×10¹¹ L_⊙ (Table 3). All galaxies in the LIRG regime remain nevertheless dominated by the unobscured SFR_UV, and half of them even have f_obscured < 25%, much lower than UV-selected galaxies at z ∼ 4.5 − 7.7 (Sect. 4.1). The resulting IRX ratios together with the blue β_UV best match the IRX–β_UV relations determined for young stellar populations (Fig. 3), in line with their very young ages of ∼10 Myr derived from rest-frame UV spectra.

Large amounts of CO molecular gas in eight of our galaxies are also shown by ALMA observations, with much higher (up to an order of magnitude) molecular gas masses than their stellar masses, yielding very high f_molgas between 63% and 92% (Table 4 and Sect. 4.2). In what follows we refer to the M_molgas measurements derived using the CO-to-H₂ conversion factor 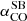$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ , but our conclusions do not change when considering the ∼4 times higher 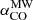$α_{CO}^{MW}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}}$ instead. ϵ_SF reliably estimated for our galaxies thanks to their dominant very young (∼10 Myr) stellar populations, show that very efficient star formation is taking place in our galaxies with ϵ_SF values reaching up to ∼40% (Sect. 4.3). Those are likely even higher if only part of the detected M_molgas is associated with the star formation ongoing in the compact UV-bright component of our galaxies. This can, in particular, be the case for galaxies showing spatial offsets between the main UV-bright component and CO emission, currently evidenced in J1415+2036 and J0121+0025 (Sect. 4.6). The high ϵ_SF are a unique physical property characterising our galaxies together with their amazingly short t_depl between 36 Myr and 71 Myr (Table 4 and Sect. 4.2), which highlight a very efficient and fast conversion of gas into stars that can only result from the gas collapse within a very short free-fall time.

In their model, Dekel et al. (2023) suggest the formation of feedback-free starbursts (FFB) through the collapse of gas clouds within very short free-fall times, approaching the monolithic collapse model, in high density (> 10³ cm⁻³ and > 2 × 10³ M_⊙ pc⁻¹) and low metallicity (Z ≤ 0.2 Z_⊙) environments. This makes star formation very efficient, because the cloud collapse occurs before the onset of stellar winds and SNe feedback, allowing the formation of massive galaxies within a few million years; and this also makes galaxies appear blue with none to little dust attenuation. A significant fraction of gas mass (∼80%) is predicted to be in massive gas clouds shielded against feedback and which can hence participate in the FFB star formation. More specifically, Li et al. (2024) showed that globally the star-formation history (SFH) in an FFB galaxy occurs in several generations separated by about 10 Myr, which consist of a peak of nearly simultaneous FFB starbursts lasting for about 2 − 5 Myr and ending in low amounts of gas left over, followed by a period of gas accumulation until the onset of the following generation of bursts. The dispersion of the f_molgas and ϵ_SF measurements could be linked to the different SFH evolutionary stages of our galaxies following this model.

The stellar mass surface densities of our galaxies, defined as ΣM_stars = M_stars/(2πR_eff²), range between ΣM_stars = 80 M_⊙ pc⁻¹ and 1170 M_⊙ pc⁻² when measured with the ground-based rest-frame UV/optical effective radii listed in Table 3. However, as discussed in Sect. 4.6, the extreme L_UV of our galaxies emerge from a compact component which is unresolved in the HAWK-I images (even with AO; R_eff, opt < 0.8 kpc) and is barely resolved in the recently acquired HST images with 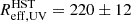$R_{eff, UV}^{HST} = 220 \pm 12$ $R_{\mathrm{eff,UV}}^{\mathrm{HST}} = 220\pm 12$ pc measured in J1316+2614 (Marques-Chaves et al. 2024). The derived M_stars also come from these compact UV-bright components (see Sect. 2), and represent > 30% to > 62% of the total stellar mass of our galaxies (Marques-Chaves et al. 2020b, 2021, 2022, 2024). As a result, the starbursting UV-bright components⁵, for an average 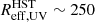$R_{eff, UV}^{HST} \sim 250$ $R_{\mathrm{eff,UV}}^{\mathrm{HST}} \sim 250$ pc, have very high ΣM_stars ∼ (0.37−1.2) × 10⁴ M_⊙ pc⁻²⁶ well in line with the surface density threshold required for an FFB to occur⁷ (Dekel et al. 2023). Most of the physical properties of our extremely UV-bright galaxies at z ∼ 2.5 actually seem to be naturally explained in the context of the FFB model, and this despite their Z ∼ 0.5 Z_⊙ metallicities (Upadhyaya et al. 2024) while the FFB model was so far validated at Z ≤ 0.2 Z_⊙. However, the measured metallicities should reflect the chemical enrichment of the starbursts over the past ∼10 Myr, potentially differing from the gas metallicity in the pre-FFB phase.

What furthermore needs to be understood is the relatively bright FIR dust continuum emission detected in nine of our galaxies (Sect. 4.4), and which we find co-spatial with the main rest-frame UV/optical component in seven galaxies (Sect. 4.6) in contrast with their very blue (β_UV < −1.84) unattenuated starlight. A possible simple explanation could be geometrical, such that the UV-bright emission is located in front of the dust layer, hence appearing unaffected by dust obscuration. However, this specific geometrical alignment appears surprisingly too common given its high occurrence for seven out of nine galaxies.

Another interpretation could follow the Ferrara et al. (2023) model (see also Ziparo et al. 2023; Ferrara 2024) which suggests a temporary removal of dust (and gas) cleared by radiation-driven outflows that develop when galaxy luminosities become super-Eddington, making galaxies appear UV brighter and bluer with very low dust attenuation (A_V ≲ 0.02), and having an impact on the occurrence of huge LyC leakage. All our galaxies (see Table 1) can potentially develop such radiation-driven outflows given their sSFR well above the super-Eddington sSFR > 25 Gyr⁻¹ threshold⁸ computed by Ferrara (2024), in contrast to MS galaxies that reach this super-Eddington limit only at very high redshifts of z > 7 (Faisst et al. 2016; Bouwens et al. 2022b; Bradley et al. 2023; Stefanon et al. 2022, 2023).

Evidence of outflowing gas was reported in two of our galaxies so far, J1220+0842 (Álvarez-Márquez et al. 2021) and J0121+0025 (Marques-Chaves et al. 2021), from ISM absorption lines showing blueshifted centroids with respect to the systemic redshift by −400 km s⁻¹ and −450 km s⁻¹, respectively, in line with their Lyα profiles. The Lyα profiles of two other galaxies, J1249+1550 and J0850+1549, also support outflows. And, evidence of dust being possibly blown away in our galaxies is maybe best highlighted in J0146–0220 and J0006+2452, where the FIR emission is spatially offset from the main compact rest-optical component along with the diffuse rest-optical emission (Sect. 4.6). For the seven other galaxies with co-spatial FIR dust continuum emission, we can speculate that the dust is expelled out spherically creating a ‘hole’ in the FIR emission at the location of the UV-bright component and with a size of at least the UV-bright component’s radius (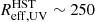 $R_{eff, UV}^{HST} \sim 250$ $R_{\mathrm{eff,UV}}^{\mathrm{HST}} \sim 250$ pc; see above), currently unresolved at the angular resolution of our ALMA observations. The recent discovery of the Lyα hole in J1316+2614 at the location of the stellar UV emission while the Lyα emission extends out to ∼6 kpc (Marques-Chaves et al. 2024) provides support to a comparable FIR dust emission hole, because dust should follow the same distribution as the Lyα emission that is tracing neutral gas. Moreover, the particularly big R_eff, FIR > 1.7 kpc (higher than R_{eff, UV/opt}) of the FIR dust emission of our galaxies (Table 3) are also in line with dust being pushed beyond the radius of ∼2 − 3 kpc at which it becomes optically thin (as predicted by Ferrara 2024). Same is likely true for the gas that is also expected to be removed by outflows, and the CO emission is indeed found co-spatial with the FIR dust emission (Figs. 1, A.1, and A.2). Nevertheless, we do not observe any evidence of outflowing molecular gas in any of the currently available CO line profiles (no broad CO line component is detected; see Figs. 1, A.1, and A.2, right panels).

Menon et al. (2024) also demonstrated in their radiation hydrodynamical numerical simulations that localised starbursts can evacuate (local) surrounding dust/gas through radiation-driven outflows in very high stellar/gas surface density conditions (Σ > 10³ M_⊙ pc²) in line with the ΣM_stars measured for our starbursting UV-bright components (see above). Their results are slightly different from the Ferrara et al. (2023) model which invokes a global galaxy-scale radiation-driven outflow, whereas their simulations suggest a picture where ‘localised’ outflows (at tens of parsecs scale) enable the UV-emitting stellar populations to be visible, while other regions can still be obscured, resulting in co-spatial UV/FIR emission when viewed with large apertures.

The origin of the dust detected in our galaxies remains to be explained. Dust could be produced by SNe at the end of the FFB phase, or have an independent origin before the onset of the FFB. As discussed in Sect. 4.4, the inferred dust masses (Table 4) – however relatively uncertain since derived from single band continuum measurements at 1.3 mm – can barely be produced by SNe (or massive stars) during the ∼10 Myr starburst phase (Gall & Hjorth 2019) for most of our galaxies and are clearly in excess in four galaxies, at least with the standard Chabrier (2003) IMF. This suggests that some dust was probably already produced prior to the burst of star formation by an older stellar population (from AGB stars and previous SNe). However, the evidence of an old stellar population currently remains elusive. So far, the SED analysis supports the absence of significant old stellar populations in these galaxies (Marques-Chaves et al. 2020b, 2021, 2022, 2024), and the nature of the underlying diffuse rest-frame optical emission detected with HAWK-I in at least two galaxies, J0146–0220 and J0006+2452, still needs to be understood (Sect. 4.6).

Other dust production mechanisms can be invoked, such as the rapid grain growth in the galaxy ISM (Graziani et al. 2020; Dayal et al. 2022; Schneider & Maiolino 2024) that would bypass the need of an old stellar population. Moreover, recently Higgins et al. (2023) reported that VMSs with masses of some 200 M_⊙ can eject 100 times more heavy elements in their winds than 50 M_⊙ stars and hence possibly produce more dust. Evidence of VMSs in some of our extreme starburst galaxies is obtained from the detection of intense and broad He IIλ1640 emission lines, with equivalent widths of EW₀ = 3 − 5 Å (Upadhyaya et al. 2024; Marques-Chaves et al. 2020b, 2021, 2022), that is, much stronger than that typically found in normal star-forming galaxies (EW₀ ≃ 1 Å; Shapley et al. 2003). Such high EW₀ are difficult to explain by standard stellar models with an IMF upper mass cut-off M_upp = 100 M_⊙, but are reproduced well by evolutionary models and atmospheres of VMSs with masses from 100 M_⊙ to 400 M_⊙ (Martins & Palacios 2022). If such populations including VMSs can produce sufficient amounts of dust as those observed in our galaxies remains to be worked out.

Marques-Chaves et al. (2020b) speculated on the fate of these extreme starburst galaxies and proposed two scenarios. Either these are the progenitors of compact present-day ellipticals (the so-called red nuggets; e.g. Dekel & Burkert 2014) in case the star formation quenches right after the starburst phase, or these are ultra-/hyper-luminous dusty star-forming galaxies (DSFGs; Santini et al. 2010) caught in their very early evolutionary stage (∼10 Myr), before their dust-poor extremely UV-luminous phase gets obscured by dust, in case the intense SFR activity lasts over a few hundreds of million years if located in gas-rich environments. The t_depl measurements derived in this work now provide a constraint on the gas consumption timescales of our galaxies. They highlight that most of our galaxies have enough gas to sustain the SFR over a few dozens of million years, that is, a factor of around three to seven longer than the current ∼10 Myr age of the burst. As a result, over these timescales they will more than triple their M_stars, and produce large amounts of dust by more than tripling their M_dust just from the SN dust production (reaching M_dust/M_⊙ ≳ 10⁸ − 10⁹ according to Gall & Hjorth 2019). They could hence turn into FIR-bright DSFGs, heavily obscured in the UV. On the other hand, galaxies with t_depl comparable to the burst age (∼10 Myr), and especially J1316+2614 with t_depl < 13 Myr, are expected to quench rapidly by starvation even before reaching the SMG phase, likely representing the very initial phases in the evolution of massive quiescent galaxies.

6. Summary and conclusions

In this study, we performed an analysis of the ALMA FIR 1.3 mm (240 GHz) dust continuum and the CO(3–2) or CO(4–3) emission of 12 starburst galaxies at z = 2.08 − 3.61 selected for their extreme brightness in the rest-frame UV with absolute magnitudes M_UV = −23.4 to −24.7. We also analysed the HAWK-I seeing-limited H-band and AO K_s-band images acquired for ten targets. The rest-frame UV and optical properties of seven of these targets have already been analysed in detail in previous works (Marques-Chaves et al. 2020b, 2021, 2022, 2024; Álvarez-Márquez et al. 2021; Upadhyaya et al. 2024). All the galaxies are characterised by steep UV spectral slopes β_UV = −2.62 to −1.84 and dominated by very young stellar populations of ∼10 Myr, indicating that the bulk of their stellar mass M_stars = (1.47 − 4.59)×10⁹ M_⊙ was formed in an intense starburst phase over ∼10 Myr given the absence of relevant old stellar populations. They have sub-solar metallicities ranging between 12 + log(O/H) = 8.13 and 8.49. Signatures of very massive stars with masses from 100 M_⊙ to 400 M_⊙ are revealed in their rest-frame UV spectra (Upadhyaya et al. 2024) from the strong and broad He IIλ1640 emission line (e.g. Crowther et al. 2016; Martins et al. 2023; Schaerer et al. 2024), suggesting an IMF with possibly a higher upper mass cut-off and likely also boosting their L_UV (Schaerer et al. 2024). Several targets in our sample present complex gas kinematics showing evidence of outflows and even inflows for one galaxy (J1316+2614). They are all strong producers of ionising radiation given their very luminous M_UV, and two of them are identified as strong LyC leakers (J0121+0025 and J1316+2614). Placed at the EoR, these galaxies alone would be able to ionise their environment.

Detected in nine galaxies, the ALMA FIR dust continuum emission provides constraints on their IR luminosities, obscured SFR_IR, and dust masses, and the CO emission detected in eight galaxies provides constraints on their molecular gas masses:

With L_IR = (5.9 − 28.3)×10¹¹ L_⊙ our galaxies populate the LIRG regime, and even the ULIRG regime for three galaxies. All the LIRG-type galaxies remain dominated by the unobscured SFR_UV. For half of the galaxies, the obscured fractions of star formation are less than 25%, placing them a factor of two below the empirical f_obscured–M_stars relation of Whitekar et al. (2017), that is, even below the UV-selected galaxies at z ∼ 4.5 − 7.7 (Fudamoto et al. 2020b; Algera et al. 2023).
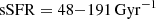The resulting total SFR_UV+IR bring these UV-bright galaxies considerably above (a factor of ∼30) the main sequence of star-forming galaxies for similar redshifts and stellar masses (e.g. Speagle et al. 2014), confirming they are powerful starbursts with specific SFRs as high as $sSFR = 48 - 191 {Gyr}^{- 1}$ $\rm sSFR = 48{-}191\,Gyr^{-1}$ .
The blue UV spectral slopes and luminous L_UV, implying IRX < + 0.5, shift our extreme starburst galaxies away from the canonical IRX–β_UV relation of Meurer et al. (1999) to relations expected for younger and lower metallicity stellar populations (Reddy et al. 2018), in agreement with their ∼10 Myr ages derived from rest-frame UV spectroscopy and sub-solar metallicities. Our galaxies are among the few with individual IRX measurements at their low stellar masses. They populate the IRX–M_stars parameter space between the relations found for main sequence galaxies at z ∼ 1.5 − 4 when extrapolated to lower M_stars (e.g. Bouwens et al. 2016; Fudamoto et al. 2020a) and agree best with the relation derived for very high redshift UV-selected galaxies at z ∼ 4.5 − 7.7 (Bowler et al. 2024), but they definitely disagree with starburst galaxies at comparable redshifts that have a much higher IRX at fixed M_stars (Fudamoto et al. 2020a).
The high dust masses M_dust = (2.3 − 11.1)×10⁷ M_⊙ of our galaxies (to be confirmed with a better FIR SED sampling) support an efficient dust production given their ∼10 Myr ages. Indeed, SNe alone barely produce such dust amounts during this short timescale (Gall & Hjorth 2019) and even fail for four galaxies unless a top-heavy IMF is invoked. Other dust production mechanisms can be invoked, for instance the rapid grain growth in the ISM, VMSs, or AGB stars in the presence of an old stellar population that remains elusive (Schneider & Maiolino 2024; Higgins et al. 2023).
The dust-to-gas mass ratios of our UV-bright galaxies range between < 10^−2.9 and 10^−2.1 (for 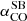$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ ) and are consistent with different δ_DGR–12 + log(O/H) relations when extrapolated to their sub-solar metallicities (e.g. Popping et al. 2023).
Our extreme starburst galaxies are offset from the integrated KS M_molgas–SFR_UV+IR relation of main sequence galaxies and match the starburst regime as defined by Sargent et al. (2014). Their high SFR_UV+IR with respect to their M_molgas give unprecedentedly short molecular gas depletion timescales between t_depl < 13 Myr and 71 Myr (for 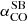$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ ). On the other hand, their baryonic masses remain dominated by the cold molecular gas over stars, which results in very high molecular gas mass fractions between f_molgas < 60% and 92% (for 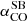$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ ), in significant excess with respect to those of main sequence galaxies (e.g. Tacconi et al. 2020). This suggests that these extreme starburst galaxies are caught at the very beginning of their intense starburst phase while vigorously consuming their still high molecular gas mass reservoir to build up their stellar mass.
Dominated by very young stellar populations of ∼10 Myr, we obtained direct star-formation efficiency measurements of our galaxies ranging from ϵ_SF = 8% to > 40% (for 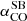$α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ ); these are much higher than ϵ_SF < 5% measured in nearby galaxies (e.g. Kim et al. 2023). The derived ϵ_SF should even be considered as lower limits given that only a percentage of the detected CO gas may be involved in the ongoing star formation. These high ϵ_SF, together with very short t_depl, highlight the amazingly efficient and fast conversion of gas into stars of these UV-bright galaxies.
The FIR dust continuum effective radii of our galaxies range between R_eff, FIR = 1.7 kpc and 5 kpc, and are bigger than their R_{eff, UV/opt}. The corresponding mean R_{eff, UV/opt}/R_eff, FIR = 0.43 ± 0.17 is in contrast to what is typically observed for galaxies at comparable redshifts (Fujimoto et al. 2017) but in agreement with the size properties of very high redshift UV-selected galaxies at 4.5 < z < 6 (Mitsuhashi et al. 2024; Pozzi et al. 2024).
Our extremely UV-luminous galaxies are mostly characterised by a simple rest-frame UV/optical morphology, as assessed from HAWK-I observations, composed of one main bright component with R_{eff, UV/opt} < 0.55 kpc to 2.01 kpc. Only two galaxies, J0146–0220 and J0006+2452, have more complex rest-frame optical morphologies with one main bright compact component (R_eff, opt < 0.8 kpc) and a diffuse component extended over R_eff, opt > 2 kpc that is offset in one direction with respect to the main component. A second tiny component is also present in J0146–0220. The diffuse emission could either trace an underlying old stellar population or outflowing gas as the HAWK-I K_s-band is contaminated by the nebular Hα emission at the redshift of these two galaxies. HST images acquired for three of our galaxies confirmed the multi-component morphology (blended in the ground-based images) for two other galaxies, J1415+2036 and J0850+1549, whereas J1316+2614 remains composed of one single extremely UV-bright and compact component. All of these components are barely resolved even at the HST resolution ( 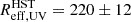$R_{eff, UV}^{HST} = 220 \pm 12$ $R_{\mathrm{eff,UV}}^{\mathrm{HST}} = 220\pm 12$ pc for J1316+2614; Marques-Chaves et al. 2024).
For seven galaxies, the main rest-UV/optical bright component is co-spatial with the more extended FIR dust continuum emission and the CO emission (when detected). This is quite surprising given their very blue unattenuated starlight. Only two galaxies, J0146–0220 and J0006+2452, have their FIR and CO emissions offset from the main rest-optical component but aligned with the extended diffuse rest-optical emission.

The extremely UV-luminous galaxies studied in this paper are recognised as being among the brightest UV galaxies known with M_UV = −23.4 to −24.6 and among the most powerful starbursts, harbouring very young stellar populations of about 10 Myr. Their high star-formation efficiencies and very short molecular gas depletion timescales, together with their still very high molecular gas masses dominating over their stellar masses, strongly suggest that these galaxies are caught at the very beginning of their stellar mass build-up in an incredibly intense, rapid, and efficient gas-to-stars conversion phase. We find that the feedback-free starburst model of Dekel et al. (2023) seems to be able to explain the unique physical properties of our galaxies through the collapse of gas clouds within very short free-fall times before the onset of stellar winds and SN feedback. However, in addition to this, our galaxies are characterised by a relatively bright FIR dust continuum emission that is found to be co-spatial with the main rest-UV/optical bright component in seven out of nine galaxies. This is in strong contrast with their blue unattenuated starlight, as one would rather expect the galaxy to be dust obscured. To reconcile these physical properties, the Ferrara et al. (2023) model of dust removal by radiation-driven outflows taking place above the super-Eddington threshold at the location of the starburst appears to be a viable option and would also explain the big FIR effective radii of our galaxies in comparison to their stellar effective radii (see also Menon et al. 2024). Finally, the measured dust masses seem to require dust production mechanisms that are more rapid and efficient than SNe given the short 10 Myr timescale available for their formation.

While these extremely UV-luminous starburst galaxies are rare at z = 2.1 − 3.6, with only about 70 of them found in the ∼ 9000 deg²-wide eBOSS survey, corresponding to a number density of 10⁻⁹ Mpc⁻³ (Marques-Chaves et al., in prep.), intrinsically they are certainly not so rare. The detection of some of them at z > 6 (e.g. Sobral et al. 2015; Matsuoka et al. 2018; Hashimoto et al. 2019) and, more recently, their unexpected overabundance discovered at 7 < z < 16 with JWST, implying steeper UV luminosity functions than predicted (e.g. Bouwens et al. 2023; Atek et al. 2023; Bunker et al. 2023; Casey et al. 2023; Castellano et al. 2024; Carniani et al. 2024), show that galaxies towards the EoR are more often experiencing such UV-luminous and still unobscured phases, with high sSFRs. As discussed in Sect. 1, different scenarios were invoked to explain the UV-luminous starburst galaxies at the EoR and their number excess. Among these scenarios are the very efficient star formation following the Dekel et al. (2023) model and the Ferrara et al. (2023, see also Ziparo et al. 2023, Ferrara 2024) model of temporary dust removal as a consequence of radiation-driven outflows, for which the molecular gas and FIR dust continuum analysis of our galaxies provides some support. Alternatively, a modified IMF (towards a top-heavy one) boosting the UV radiation and the luminosity-to-mass ratio of galaxies was also proposed (e.g. Bekki & Tsujimoto 2023; Trinca et al. 2024) as well as a stochastic variability of the SFR (e.g. Mirocha & Furlanetto 2023; Gelli et al. 2024). Currently, we have no evidence supporting a modified IMF except possibly an IMF with a higher upper mass cut-off given that our galaxies host VMSs (Upadhyaya et al. 2024) that can also lead to high UV luminosity increases (Schaerer et al. 2024).

In summary, these galaxies show several similarities with the galaxies recently unveiled at the EoR with JWST. They hence possibly represent a sample of lower redshift ‘analogues’ that benefit from the advantage of a rich dataset and data to come that will be difficult to acquire for galaxies at z > 7. Our UV-bright galaxies at cosmic noon thus are ideal laboratories to test different scenarios proposed to explain what triggers the extreme UV luminosities and starbursts of galaxies and their number excess at the EoR.

¹

https://www.eso.org/sci/software/pipelines/hawki/hawki-pipe-recipes.html

²

However, one needs to keep in mind that the HAWK-I images at the redshift of our galaxies are likely dominated by the strong rest-frame optical lines, [O III]+Hβ or Hα.

³

The model of Gall & Hjorth (2019) does not specify how exactly the dust is produced in SNe or in massive stars prior the SN explosion.

⁴

For J0850+1549 and J0121+0025 we used the CFHT MegaCam and Subaru seeing-limited R-band observations, respectively.

⁵

The corresponding SFR_UV surface densities of the UV-bright components are also huge with ΣSFR_UV ∼ (0.27−1.1) × 10³ M_⊙ yr⁻¹ kpc⁻². Only a few massive stellar clusters at sub-10 pc scales, hosted in the Sunburst and Sunrise high redshift galaxies, have such extreme ΣSFR_UV (Vanzella et al. 2022, 2023; Messa et al. 2024).

⁶

Such high ΣM_stars were only reported for very few star-forming galaxies with similar M_stars and redshifts, and are more common for more massive compact star-forming galaxies (Barro et al. 2017), as well as for young star-forming clumps at 1 < z < 3 yet typically having two orders of magnitude lower stellar masses (e.g. Claeyssens et al. 2023; Messa et al. 2024).

⁷

For one of our galaxies, J1220+0842, Marques-Chaves et al. (2020b) could even measure its density from the [O II] λ3729/λ3726 and C III] λ1906/λ1908 line ratios that is > 10³ cm⁻³, namely in agreement with the FFB density threshold.

⁸

The super-Eddington limit from Ferrara (2024) was reassessed by Li et al. (2024), who found that super-Eddington ejections potentially take place at z > 16 only.

Acknowledgments

This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00932.S and 2021.1.01438.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This paper is also based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 111.251K.001.

References

Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
Algera, H. S. B., Inami, H., Oesch, P. A., et al. 2023, MNRAS, 518, 6142 [Google Scholar]
Álvarez-Márquez, J., Burgarella, D., Heinis, S., et al. 2016, A&A, 587, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Álvarez-Márquez, J., Burgarella, D., Buat, V., Ilbert, O., & Pérez-González, P. G. 2019, A&A, 630, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Álvarez-Márquez, J., Marques-Chaves, R., Colina, L., & Pérez-Fournon, I. 2021, A&A, 647, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Atek, H., Shuntov, M., Furtak, L., et al. 2023, MNRAS, 519, 1201 [Google Scholar]
Barro, G., Faber, M., Koo, D. C., et al. 2017, ApJ, 840, 47 [CrossRef] [Google Scholar]
Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef] [Google Scholar]
Bekki, K., & Tsujimoto, T. 2023, MNRAS, 526, L26 [NASA ADS] [CrossRef] [Google Scholar]
Bertoldi, F., Carilli, C. L., Cox, P., et al. 2003, A&A, 406, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [Google Scholar]
Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]
Bouwens, R. J., Illingworth, G. D., van Dokkum, P. G., et al. 2022a, ApJ, 927, 81 [NASA ADS] [CrossRef] [Google Scholar]
Bouwens, R. J., Smit, R., Schouws, S., et al. 2022b, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]
Bouwens, R. J., Stefanon, M., Brammer, G., et al. 2023, MNRAS, 523, 1009 [NASA ADS] [CrossRef] [Google Scholar]
Bowler, R. A. A., Inami, H., Sommovigo, L., et al. 2024, MNRAS, 527, 5808 [Google Scholar]
Boylan-Kolchin, M. 2023, Nat. Astron., 7, 731 [NASA ADS] [CrossRef] [Google Scholar]
Bradley, L. D., Coe, D., Brammer, G., et al. 2023, ApJ, 955, 13 [CrossRef] [Google Scholar]
Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Byrne, C. M., Stanway, E. R., Eldridge, J. J., McSwiney, L., & Townsend, O. T. 2022, MNRAS, 512, 5329 [NASA ADS] [CrossRef] [Google Scholar]
Calistro Rivera, G., Hodge, J. A., Smail, I., et al. 2018, ApJ, 863, 56 [Google Scholar]
Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
Carniani, S., Hainline, K., D’Eugenio, F., et al. 2024, Nature, 633, 318 [CrossRef] [Google Scholar]
Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]
Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
Casey, C. M., Kartaltepe, J. S., Drakos, N. E., et al. 2023, ApJ, 954, 31 [NASA ADS] [CrossRef] [Google Scholar]
Castellano, M., Napolitano, L., Fontana, A., et al. 2024, ApJ, 972, 143 [Google Scholar]
Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
Chemerynska, I., Atek, H., Furtak, L. J., et al. 2024, MNRAS, 531, 2615 [NASA ADS] [CrossRef] [Google Scholar]
Claeyssens, A., Adamo, A., Richard, J., Mahler, G., Messa, M., & Dessauges-Zavadsky, M. 2023, MNRAS, 520, 2180 [NASA ADS] [CrossRef] [Google Scholar]
Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [Google Scholar]
da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]
de Graaff, A., Setton, D. J., Brammer, G., et al. 2024, arXiv e-prints [arXiv:2404.05683] [Google Scholar]
Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [Google Scholar]
Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Liet, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
Dessauges-Zavadsky, M., D’Odorico, S., Schaerer, D., et al. 2010, A&A, 510, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dessauges-Zavadsky, M., Christensen, L., D’Odorico, S., Schaerer, D., & Richard, J. 2011, A&A, 533, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dessauges-Zavadsky, M., Zamojski, M., Schaerer, D., et al. 2015, A&A, 577, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dessauges-Zavadsky, M., Zamojski, M., Rujopakarn, W., et al. 2017, A&A, 605, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dessauges-Zavadsky, M., Richard, J., Combes, F., et al. 2019, Nat. Astron., 3, 1115 [NASA ADS] [CrossRef] [Google Scholar]
Dessauges-Zavadsky, M., Ginolfi, M., Pozzi, F., et al. 2020, A&A, 643, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dessauges-Zavadsky, M., Richard, J., Combes, F., et al. 2023, MNRAS, 519, 6222 [NASA ADS] [CrossRef] [Google Scholar]
De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]
Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, 58 [NASA ADS] [CrossRef] [Google Scholar]
Endsley, R., Stark, D. P., Chevallard, J., & Charlot, S. 2021, MNRAS, 500, 5229 [Google Scholar]
Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [Google Scholar]
Faisst, A. L., Capak, P., Hsieh, B. C., et al. 2016, ApJ, 821, 122 [Google Scholar]
Ferrara, A. 2024, A&A, 684, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ferrara, A., Pallottini, A., & Dayal, P. 2023, MNRAS, 522, 3986 [NASA ADS] [CrossRef] [Google Scholar]
Finkelstein, S. L., & Bagley, M. B. 2022, ApJ, 938, 25 [NASA ADS] [CrossRef] [Google Scholar]
Finkelstein, S. L., Leung, G. C. K., Bagley, M. B., et al. 2024, ApJL, 969, L2 [NASA ADS] [CrossRef] [Google Scholar]
Franco, M., Elbaz, D., Zhou, L., et al. 2020, A&A, 643, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Frias Castillo, M., Hodge, J., Rybak, M., et al. 2023, ApJ, 945, 128 [NASA ADS] [CrossRef] [Google Scholar]
Fudamoto, Y., Oesch, P. A., Schinnerer, E., et al. 2017, MNRAS, 472, 483 [Google Scholar]
Fudamoto, Y., Oesch, P. A., Magnelli, B., et al. 2020a, MNRAS, 491, 4724 [Google Scholar]
Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020b, A&A, 643, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [Google Scholar]
Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gall, C., & Hjorth, J. 2019, ApJ, 868, 62 [Google Scholar]
Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gelli, V., Mason, C., & Hayward, C. C. 2024, arXiv e-prints [arXiv:2405.13108] [Google Scholar]
Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
Ginolfi, M., Schneider, R., Valiante, R., et al. 2019, MNRAS, 483, 1256 [NASA ADS] [CrossRef] [Google Scholar]
Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022, A&A, 659, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]
Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
Guilloteau, S., & Lucas, R. 2000, ASP Conf. Ser., 217, 299 [Google Scholar]
Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019, PASJ, 71, 71 [Google Scholar]
Heinis, S., Buat, V., Béthermin, M., et al. 2014, MNRAS, 437, 1268 [Google Scholar]
Heintz, K. E., Brammer, G. B., Watson, D., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202450243 [Google Scholar]
Higgins, E. R., Vink, J. S., Hirschi, R., Laird, A. M., & Sabhahit, G. N. 2023, MNRAS, 526, 534 [NASA ADS] [CrossRef] [Google Scholar]
Imara, N., Loeb, A., Johnson, B. D., Conroy, C., & Behroozi, P. 2018, ApJ, 854, 36 [NASA ADS] [CrossRef] [Google Scholar]
Inami, H., Algera, H. S. B., Schouws, S., et al. 2022, MNRAS, 515, 3126 [NASA ADS] [CrossRef] [Google Scholar]
Jin, S., Daddi, E., Magdis, G. E., et al. 2022, A&A, 665, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kannan, R., Springel, V., Hernquist, L., et al. 2023, MNRAS, 524, 2594 [CrossRef] [Google Scholar]
Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
Kim, J., Chevance, M., Kruijssen, J. M. D., et al. 2023, ApJ, 944, L20 [NASA ADS] [CrossRef] [Google Scholar]
Kokorev, V. I., Magdis, G. E., Davidzon, I., et al. 2021, ApJ, 921, 40 [NASA ADS] [CrossRef] [Google Scholar]
Koprowski, M. P., Coppin, K. E. K., Geach, J. E., et al. 2018, MNRAS, 479, 4355 [NASA ADS] [CrossRef] [Google Scholar]
Leslie, S. K., Schinnerer, E., Liu, D., et al. 2020, ApJ, 899, 58 [Google Scholar]
Li, Z., Dekel, A., Sarkar, K. C., et al. 2024, A&A, 690, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Liu, D., Schinnerer, E., Groves, B., et al. 2019, ApJ, 887, 235 [Google Scholar]
Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
Magnelli, B., Boogaard, L., Decarli, R., et al. 2020, ApJ, 892, 66 [NASA ADS] [CrossRef] [Google Scholar]
Maiolino, R., Scholtz, J., Witstok, J., et al. 2024, Nature, 627, 59 [NASA ADS] [CrossRef] [Google Scholar]
Marques-Chaves, R., Pérez-Fournon, I., Shu, Y., et al. 2017, ApJ, 834, L18 [NASA ADS] [CrossRef] [Google Scholar]
Marques-Chaves, R., Pérez-Fournon, I., Gavazzi, R., et al. 2018, ApJ, 854, 151 [Google Scholar]
Marques-Chaves, R., Pérez-Fournon, I., Shu, Y., et al. 2020a, MNRAS, 492, 1257 [Google Scholar]
Marques-Chaves, R., Álvarez-Márquez, J., Colina, L., et al. 2020b, MNRAS, 499, L105 [Google Scholar]
Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2021, MNRAS, 507, 524 [NASA ADS] [CrossRef] [Google Scholar]
Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2022, MNRAS, 517, 2972 [CrossRef] [Google Scholar]
Marques-Chaves, R., Schaerer, D., Vanzella, E., et al. 2024, A&A, 691, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Martins, F., & Palacios, A. 2022, A&A, 659, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Martins, F., Schaerer, D., Marques-Chaves, R., & Upadhyaya, A. 2023, A&A, 678, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mason, C. A., Treu, T., Dijkstra, M., et al. 2018, ApJ, 856, 2 [Google Scholar]
Matsuoka, Y., Onoue, M., Kashikawa, N., et al. 2018, PASJ, 70, S35 [Google Scholar]
McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
Menon, S. H., Burkhart, B., Somerville, R. S., Thompson, T. A., & Sternberg, A. 2024, arXiv e-prints [arXiv:2408.14591] [Google Scholar]
Messa, M., Dessauges-Zavadsky, M., Adamo, A., Richard, J., & Claeyssens, A. 2024, MNRAS, 529, 2162 [CrossRef] [Google Scholar]
Meštrić, U., Vanzella, E., Upadhyaya, A., et al. 2023, A&A, 673, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]
Mirocha, J., & Furlanetto, S. R. 2023, MNRAS, 519, 843 [Google Scholar]
Mitsuhashi, I., Tadaki, K.-I., Ikeda, R., et al. 2024, A&A, 690, A197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Naidu, R. P., Oesch, P. A., van Dokkum, P., et al. 2022, ApJ, 940, L14 [NASA ADS] [CrossRef] [Google Scholar]
Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [Google Scholar]
Patrício, V., Richard, J., Verhamme, A., et al. 2016, MNRAS, 456, 4191 [Google Scholar]
Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
Pettini, M., Steidel, C. C., Adelberger, K. L., Dickinson, M., & Giavalisco, M. 2000, ApJ, 528, 96 [Google Scholar]
Popping, G., Somerville, R. S., & Galametz, M. 2017, MNRAS, 471, 3152 [NASA ADS] [CrossRef] [Google Scholar]
Popping, G., Pillepich, A., Calistro Rivera, G., et al. 2022, MNRAS, 510, 3321 [CrossRef] [Google Scholar]
Popping, G., Shivaei, I., Sanders, R. L., et al. 2023, A&A, 670, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pozzi, F., Calura, F., Fudamoto, Y., et al. 2021, A&A, 653, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pozzi, F., Calura, F., D’Amato, Q., et al. 2024, A&A, 686, A187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Quider, A. M., Pettini, M., Shapley, A. E., & Steidel, C. C. 2009, MNRAS, 398, 1263 [Google Scholar]
Quider, A. M., Shapley, A. E., Pettini, M., Steidel, C. C., & Stark, D. P. 2010, MNRAS, 402, 1467 [Google Scholar]
Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [Google Scholar]
Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]
Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
Roberts-Borsani, G., Treu, T., Shapley, A., et al. 2024, arXiv e-prints [arXiv:2403.07103] [Google Scholar]
Robson, I., Priddey, R. S., Isaak, K. G., & McMahon, R. G. 2004, MNRAS, 351, L29 [NASA ADS] [CrossRef] [Google Scholar]
Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
Schaerer, D., Guibert, J., Marques-Chaves, R., & Martins, F. 2024, A&A, submitted [arXiv:2407.12122] [Google Scholar]
Schneider, R., & Maiolino, R. 2024, A&ARv, 32, 2 [NASA ADS] [CrossRef] [Google Scholar]
Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schruba, A., Kruijssen, J. M. D., & Leroy, A. K. 2019, ApJ, 883, 2 [NASA ADS] [CrossRef] [Google Scholar]
Senchyna, P., Stark, D. P., Vidal-García, A., et al. 2017, MNRAS, 472, 2608 [NASA ADS] [CrossRef] [Google Scholar]
Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [Google Scholar]
Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]
Shu, Y., Bolton, A. S., Kochaneket, C. S., et al. 2016, ApJ, 824, 86 [NASA ADS] [CrossRef] [Google Scholar]
Silverman, J. D., Daddi, E., Rodighiero, G., et al. 2015, ApJ, 812, L23 [NASA ADS] [CrossRef] [Google Scholar]
Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]
Sobral, D., Matthee, J., Darvish, B., et al. 2015, ApJ, 808, 139 [Google Scholar]
Sobral, D., Santos, S., Matthee, J., et al. 2018a, MNRAS, 476, 4725 [Google Scholar]
Sobral, D., Matthee, J., Darvish, B., et al. 2018b, MNRAS, 477, 2817 [Google Scholar]
Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]
Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 479, 75 [NASA ADS] [CrossRef] [Google Scholar]
Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2022, ApJ, 927, 48 [CrossRef] [Google Scholar]
Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2023, ApJ, 943, 81 [NASA ADS] [CrossRef] [Google Scholar]
Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
Trinca, A., Schneider, R., Valiante, R., et al. 2024, MNRAS, 529, 3563 [NASA ADS] [CrossRef] [Google Scholar]
Upadhyaya, A., Marques-Chaves, R., Schaerer, D., et al. 2024, A&A, 686, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Utomo, D., Sun, J., Leroy, A. K., et al. 2018, ApJ, 861, L18 [NASA ADS] [CrossRef] [Google Scholar]
Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]
Valentino, F., Fujimoto, S., Giménez-Arteaga, C., et al. 2024, A&A, 685, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]
Vanzella, E., Castellano, M., Bergamini, P., et al. 2022, A&A, 659, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vanzella, E., Claeyssens, A., Welch, B., et al. 2023, ApJ, 945, 53 [NASA ADS] [CrossRef] [Google Scholar]
Viero, M. P., Sun, G., Chung, D. T., Moncelsi, L., & Condon, S. S. 2022, MNRAS, 516, L30 [NASA ADS] [CrossRef] [Google Scholar]
Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [NASA ADS] [CrossRef] [Google Scholar]
Weibel, A., Oesch, P. A., Barrufet, L., et al. 2024, MNRAS, 533, 1808 [NASA ADS] [CrossRef] [Google Scholar]
Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
Whitekar, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
Whitekar, K. E., Alexandra Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]
Witstok, J., Jones, G. C., Maiolino, R., Smit, R., & Schneider, R. 2023, MNRAS, 523, 3119 [NASA ADS] [CrossRef] [Google Scholar]
Xiao, M.-Y., Wang, T., Elbaz, D., et al. 2022, A&A, 664, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Xiao, M. Y., Oesch, P., Elbaz, D., et al. 2024, arXiv e-prints [arXiv:2309.02492] [Google Scholar]
Zanella, A., Daddi, E., Magdis, G., et al. 2018, MNRAS, 481, 1976 [Google Scholar]
Zheng, Z.-Y., Malhotra, S., Rhoads, J. E., et al. 2016, ApJS, 226, 23 [Google Scholar]
Ziparo, F., Ferrara, A., Sommovigo, L., & Kohandel, M. 2023, MNRAS, 520, 2445 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Figure 1 continued

Fig. A.1.

See Fig. 1 for the description of panels.

Fig. A.2.

See Fig. 1 for the description of panels.

All Tables

Table 1.

Rest-frame UV properties of the galaxy sample.

In the text

Table 2.

CO emission line observations (ALMA band 3).

In the text

Table 3.

Far-infrared dust continuum observations (ALMA band 6) and rest-frame UV/optical ground-based observations.

In the text

Table 4.

Dust and molecular gas properties of the galaxy sample.

In the text

All Figures

Fig. 1.

Images showing the FIR dust continuum emission, the H- or K_s-band continuum emission, the CO(3–2) or CO(4–3) emission, and the related spectra (if CO is detected) of our 12 extreme starburst galaxies ordered by increasing redshift from top to bottom. Left panels: 23″ × 23″ ALMA band 6 1.3 mm (240 GHz) FIR dust continuum images of our targeted galaxies. Contour levels start at ±4σ and are in steps of 1σ up to 10σ and in larger steps above. The respective synthesised beam size and orientation are indicated by the red filled ellipse in the bottom-left corner. The cross in each panel corresponds to the coordinates of the HAWK-I continuum emission peak (except for J0850+1549 and J0121+0025 for which we consider, respectively, the CFHT MegaCam and Subaru continuum emission peak) and is ±3″ in size. Middle-left panels: 10″ × 10″ VLT HAWK-I seeing-limited H-band or AO K_s-band images of our starburst galaxies in greyscale with the ALMA band 6 FIR dust continuum contours overlaid in red. For J0850+1549 and J0121+0025, we show, respectively, the CFHT MegaCam and Subaru seeing-limited R-band images. Contour levels start at ±4σ and are in steps of 2σ, except for J0146–0220, J1249+1550, and J0850+1549 where contour levels are the same as in the left panels. The PSF is shown by the black filled circle in bottom-left corner, and the ALMA synthesised beam by the red filled ellipse in the bottom-right corner. The cross is the same as in the left panels. Middle-right panels: 10″ × 10″ ALMA CO(3–2) or CO(4–3) velocity-integrated intensity moment-0 maps of our galaxies. The maps were integrated over the cyan-shaded spectral channels shown in the right panels. Contour levels start at ±4σ and are in steps of 1σ. The respective synthesised beam size and orientation are indicated by the red filled ellipse in the bottom-right corner. The cross is the same as in the other panels. Right panels: ALMA CO(3–2) or CO(4–3) emission line spectra of our galaxies, plotted when detected, in steps of ∼ 45 km s⁻¹ and with the zero velocity centred on the redshifts derived from optical nebular emission lines (Table 1). The cyan-shaded regions correspond to the velocity channels optimising the CO detections, as described in Sect. 3.1. The dashed orange lines correspond to the RMS noise level of spectra. The solid red lines are the multi-component Gaussian best-fits to the observed CO line profiles. The vertical bars mark the positions of the fitted Gaussian components. The rest of the figure is available in Appendix A.

In the text

Fig. 2.

Comparison of the unobscured SFR_UV (uncorrected for dust attenuation) and obscured SFR_IR of our galaxies, colour-coded by redshift. The majority of our galaxies is dominated by the unobscured SFR_UV, such that the corresponding obscured fractions of star formation range between f_obscured < 14% and 42%, and is above 50% for three galaxies only. The dashed line traces the one-to-one relationship.

In the text

Fig. 3.

Infrared excess as a function of the UV spectral slope of our galaxies, colour-coded by redshift. Our galaxies are all characterised by very blue β_UV < −1.8 and low IRX < + 0.5. Most of them deviate from the canonical IRX–β_UV relation (solid line; Meurer et al. 1999), and are better reproduced with the bluer intrinsic UV continuum slope β₀ = −2.62 as computed by Reddy et al. (2018) for the SMC (dashed line) and Calzetti et al. (2000) (dotted line) extinction curves.

In the text

Fig. 4.

Molecular gas mass as a function of the total (unobscured plus obscured) star-formation rate of our galaxies, colour-coded by redshift. The filled circles correspond to M_molgas determined with $α_{CO}^{SB} = 1 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}} = 1\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ , and the dotted red segments show the range of possible M_molgas with higher CO-to-H₂ conversion factors up to $α_{CO}^{MW} = 4.36 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}} = 4.36\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ . Whatever α_CO, our extreme starburst galaxies have significantly higher SFR_UV+IR than MS galaxies at comparable M_molgas (see the solid line as derived by Sargent et al. 2014). For $α_{CO}^{SB}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}}$ our galaxies are the first galaxies known at high redshift to reach the starburst M_molgas–SFR relation (dashed line) offset by > 1 dex from the MS relation, according to the parametrisation of Sargent et al. (2014) based on nearby and z < 0.1 ULIRGs.

In the text

Fig. 5.

Molecular gas depletion timescale (left) and molecular gas mass fraction (right) as a function of the redshift of our galaxies shown by the red filled circles. Similarly to Fig. 4, the dotted red segments represent the range of possible t_depl and f_molgas measurements of our galaxies as derived with CO-to-H₂ conversion factors sampling values from $α_{CO}^{SB} = 1 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{SB}} = 1\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ to $α_{CO}^{MW} = 4.36 M_{⊙} {(K km s^{- 1} {pc}^{2})}^{- 1}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}} = 4.36\,M_{\odot}\,\rm (K\,km\,s^{-1}\,pc^2)^{-1}$ . The t_tepl and f_molgas means, errors on the means, and standard deviations obtained for the CO-detected MS galaxies from the compilation of Dessauges-Zavadsky et al. (2020) are shown by the black/grey crosses in five redshift bins 0 < z < 0.1, 0.1 < z < 1, 1 < z < 1.5, 1.5 < z < 2.5, and 2.5 < z < 3.7. The light-grey shaded area corresponds to t_tepl and f_molgas derived by Béthermin et al. (2015) from the FIR SED stacks of MS galaxies. For all MS galaxy measurements compiled here, the same $α_{CO}^{MW}$ $\alpha_{\mathrm{CO}}^{\mathrm{MW}}$ conversion factor is assumed. Our extreme starburst galaxies have significantly shorter t_depl than those measured in MS galaxies at any redshift (left). This indicates that they are vigorously consuming their molecular gas mass reservoir to build up their stellar mass. On the other hand, they have very high f_molgas (right), in excess with respect to MS galaxies at similar redshifts, showing that their mass remains dominated by the molecular gas mass over the stellar mass.

In the text

Fig. 6.

Dust mass as a function of the stellar mass of our extreme starburst galaxies, colour-coded by redshift. Our galaxies agree with the M_dust–M_stars relation derived by Magnelli et al. (2020) as shown by the solid black line, but are well below the relations of Liu et al. (2019) and Kokorev et al. (2021) shown by the dotted and dashed black lines, respectively. The grey shaded zone defines the SN dust production as predicted by Gall & Hjorth (2019), which is barely sufficient to reproduce M_dust of most of our galaxies. The thick dashed-dotted green line defines the start of the AGB star contribution to the dust production (Witstok et al. 2023).

In the text

	Fig. 7. Far-infrared dust continuum effective radius as a function of the IR luminosity of our galaxies, colour-coded by redshift. Our extreme starburst galaxies agree better with the R_eff, FIR–L_IR anti-correlation (light-grey shaded area) found by Jin et al. (2022) than with the R_eff, FIR–L_IR correlation (dark-grey shaded area) of Fujimoto et al. (2017).
In the text

Fig. 8.

Far-infrared dust continuum effective radius (filled circles) and rest-frame UV/optical effective radius (filled stars) as a function of the stellar mass of our galaxies, colour-coded by redshift. All our galaxies have systematically higher R_eff, FIR than R_{eff, UV/opt}. As a result, R_eff, FIR of our galaxies strongly deviate from the R_eff, FIR–M_stars relations of Gómez-Guijarro et al. (2022) at z < 2.5 and z > 2.5, shown by the solid and dashed black lines, respectively, as they are more extended. On the other hand, their R_{eff, UV/opt} agree with the R_eff, UV–M_stars relation (blue shaded area) derived for LTG at z ∼ 2.5 by van der Wel et al. (2014). The green shaded area corresponds to the R_eff, UV–M_stars relation of z ∼ 2.5 early-type galaxies (ETG; van der Wel et al. 2014).

In the text

	Fig. A.1. See Fig. 1 for the description of panels.
In the text

	Fig. A.2. See Fig. 1 for the description of panels.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]

[2] Algera, H. S. B., Inami, H., Oesch, P. A., et al. 2023, MNRAS, 518, 6142 [Google Scholar]

[3] Álvarez-Márquez, J., Burgarella, D., Heinis, S., et al. 2016, A&A, 587, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[4] Álvarez-Márquez, J., Burgarella, D., Buat, V., Ilbert, O., & Pérez-González, P. G. 2019, A&A, 630, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[5] Álvarez-Márquez, J., Marques-Chaves, R., Colina, L., & Pérez-Fournon, I. 2021, A&A, 647, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[6] Atek, H., Shuntov, M., Furtak, L., et al. 2023, MNRAS, 519, 1201 [Google Scholar]

[7] Barro, G., Faber, M., Koo, D. C., et al. 2017, ApJ, 840, 47 [CrossRef] [Google Scholar]

[8] Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef] [Google Scholar]

[9] Bekki, K., & Tsujimoto, T. 2023, MNRAS, 526, L26 [NASA ADS] [CrossRef] [Google Scholar]

[10] Bertoldi, F., Carilli, C. L., Cox, P., et al. 2003, A&A, 406, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[11] Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [Google Scholar]

[12] Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]

[13] Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]

[14] Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]

[15] Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]

[16] Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]

[17] Bouwens, R. J., Illingworth, G. D., van Dokkum, P. G., et al. 2022a, ApJ, 927, 81 [NASA ADS] [CrossRef] [Google Scholar]

[18] Bouwens, R. J., Smit, R., Schouws, S., et al. 2022b, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]

[19] Bouwens, R. J., Stefanon, M., Brammer, G., et al. 2023, MNRAS, 523, 1009 [NASA ADS] [CrossRef] [Google Scholar]

[20] Bowler, R. A. A., Inami, H., Sommovigo, L., et al. 2024, MNRAS, 527, 5808 [Google Scholar]

[21] Boylan-Kolchin, M. 2023, Nat. Astron., 7, 731 [NASA ADS] [CrossRef] [Google Scholar]

[22] Bradley, L. D., Coe, D., Brammer, G., et al. 2023, ApJ, 955, 13 [CrossRef] [Google Scholar]

[23] Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[24] Byrne, C. M., Stanway, E. R., Eldridge, J. J., McSwiney, L., & Townsend, O. T. 2022, MNRAS, 512, 5329 [NASA ADS] [CrossRef] [Google Scholar]

[25] Calistro Rivera, G., Hodge, J. A., Smail, I., et al. 2018, ApJ, 863, 56 [Google Scholar]

[26] Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]

[27] Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]

[28] Carniani, S., Hainline, K., D’Eugenio, F., et al. 2024, Nature, 633, 318 [CrossRef] [Google Scholar]

[29] Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]

[30] Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]

[31] Casey, C. M., Kartaltepe, J. S., Drakos, N. E., et al. 2023, ApJ, 954, 31 [NASA ADS] [CrossRef] [Google Scholar]

[32] Castellano, M., Napolitano, L., Fontana, A., et al. 2024, ApJ, 972, 143 [Google Scholar]

[33] Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]

[34] Chemerynska, I., Atek, H., Furtak, L. J., et al. 2024, MNRAS, 531, 2615 [NASA ADS] [CrossRef] [Google Scholar]

[35] Claeyssens, A., Adamo, A., Richard, J., Mahler, G., Messa, M., & Dessauges-Zavadsky, M. 2023, MNRAS, 520, 2180 [NASA ADS] [CrossRef] [Google Scholar]

[36] Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [Google Scholar]

[37] da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]

[38] Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]

[39] Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[40] Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]

[41] de Graaff, A., Setton, D. J., Brammer, G., et al. 2024, arXiv e-prints [arXiv:2404.05683] [Google Scholar]

[42] Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [Google Scholar]

[43] Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Liet, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]

[44] Dessauges-Zavadsky, M., D’Odorico, S., Schaerer, D., et al. 2010, A&A, 510, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Dessauges-Zavadsky, M., Christensen, L., D’Odorico, S., Schaerer, D., & Richard, J. 2011, A&A, 533, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[46] Dessauges-Zavadsky, M., Zamojski, M., Schaerer, D., et al. 2015, A&A, 577, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[47] Dessauges-Zavadsky, M., Zamojski, M., Rujopakarn, W., et al. 2017, A&A, 605, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[48] Dessauges-Zavadsky, M., Richard, J., Combes, F., et al. 2019, Nat. Astron., 3, 1115 [NASA ADS] [CrossRef] [Google Scholar]

[49] Dessauges-Zavadsky, M., Ginolfi, M., Pozzi, F., et al. 2020, A&A, 643, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[50] Dessauges-Zavadsky, M., Richard, J., Combes, F., et al. 2023, MNRAS, 519, 6222 [NASA ADS] [CrossRef] [Google Scholar]

[51] De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[52] Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]

[53] Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]

[54] Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, 58 [NASA ADS] [CrossRef] [Google Scholar]

[55] Endsley, R., Stark, D. P., Chevallard, J., & Charlot, S. 2021, MNRAS, 500, 5229 [Google Scholar]

[56] Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [Google Scholar]

[57] Faisst, A. L., Capak, P., Hsieh, B. C., et al. 2016, ApJ, 821, 122 [Google Scholar]

[58] Ferrara, A. 2024, A&A, 684, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[59] Ferrara, A., Pallottini, A., & Dayal, P. 2023, MNRAS, 522, 3986 [NASA ADS] [CrossRef] [Google Scholar]

[60] Finkelstein, S. L., & Bagley, M. B. 2022, ApJ, 938, 25 [NASA ADS] [CrossRef] [Google Scholar]

[61] Finkelstein, S. L., Leung, G. C. K., Bagley, M. B., et al. 2024, ApJL, 969, L2 [NASA ADS] [CrossRef] [Google Scholar]

[62] Franco, M., Elbaz, D., Zhou, L., et al. 2020, A&A, 643, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[63] Frias Castillo, M., Hodge, J., Rybak, M., et al. 2023, ApJ, 945, 128 [NASA ADS] [CrossRef] [Google Scholar]

[64] Fudamoto, Y., Oesch, P. A., Schinnerer, E., et al. 2017, MNRAS, 472, 483 [Google Scholar]

[65] Fudamoto, Y., Oesch, P. A., Magnelli, B., et al. 2020a, MNRAS, 491, 4724 [Google Scholar]

[66] Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020b, A&A, 643, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[67] Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [Google Scholar]

[68] Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[69] Gall, C., & Hjorth, J. 2019, ApJ, 868, 62 [Google Scholar]

[70] Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[71] Gelli, V., Mason, C., & Hayward, C. C. 2024, arXiv e-prints [arXiv:2405.13108] [Google Scholar]

[72] Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]

[73] Ginolfi, M., Schneider, R., Valiante, R., et al. 2019, MNRAS, 483, 1256 [NASA ADS] [CrossRef] [Google Scholar]

[74] Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022, A&A, 659, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[75] Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]

[76] Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]

[77] Guilloteau, S., & Lucas, R. 2000, ASP Conf. Ser., 217, 299 [Google Scholar]

[78] Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019, PASJ, 71, 71 [Google Scholar]

[79] Heinis, S., Buat, V., Béthermin, M., et al. 2014, MNRAS, 437, 1268 [Google Scholar]

[80] Heintz, K. E., Brammer, G. B., Watson, D., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202450243 [Google Scholar]

[81] Higgins, E. R., Vink, J. S., Hirschi, R., Laird, A. M., & Sabhahit, G. N. 2023, MNRAS, 526, 534 [NASA ADS] [CrossRef] [Google Scholar]

[82] Imara, N., Loeb, A., Johnson, B. D., Conroy, C., & Behroozi, P. 2018, ApJ, 854, 36 [NASA ADS] [CrossRef] [Google Scholar]

[83] Inami, H., Algera, H. S. B., Schouws, S., et al. 2022, MNRAS, 515, 3126 [NASA ADS] [CrossRef] [Google Scholar]

[84] Jin, S., Daddi, E., Magdis, G. E., et al. 2022, A&A, 665, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[85] Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[86] Kannan, R., Springel, V., Hernquist, L., et al. 2023, MNRAS, 524, 2594 [CrossRef] [Google Scholar]

[87] Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]

[88] Kim, J., Chevance, M., Kruijssen, J. M. D., et al. 2023, ApJ, 944, L20 [NASA ADS] [CrossRef] [Google Scholar]

[89] Kokorev, V. I., Magdis, G. E., Davidzon, I., et al. 2021, ApJ, 921, 40 [NASA ADS] [CrossRef] [Google Scholar]

[90] Koprowski, M. P., Coppin, K. E. K., Geach, J. E., et al. 2018, MNRAS, 479, 4355 [NASA ADS] [CrossRef] [Google Scholar]

[91] Leslie, S. K., Schinnerer, E., Liu, D., et al. 2020, ApJ, 899, 58 [Google Scholar]

[92] Li, Z., Dekel, A., Sarkar, K. C., et al. 2024, A&A, 690, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[93] Liu, D., Schinnerer, E., Groves, B., et al. 2019, ApJ, 887, 235 [Google Scholar]

[94] Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]

[95] Magnelli, B., Boogaard, L., Decarli, R., et al. 2020, ApJ, 892, 66 [NASA ADS] [CrossRef] [Google Scholar]

[96] Maiolino, R., Scholtz, J., Witstok, J., et al. 2024, Nature, 627, 59 [NASA ADS] [CrossRef] [Google Scholar]

[97] Marques-Chaves, R., Pérez-Fournon, I., Shu, Y., et al. 2017, ApJ, 834, L18 [NASA ADS] [CrossRef] [Google Scholar]

[98] Marques-Chaves, R., Pérez-Fournon, I., Gavazzi, R., et al. 2018, ApJ, 854, 151 [Google Scholar]

[99] Marques-Chaves, R., Pérez-Fournon, I., Shu, Y., et al. 2020a, MNRAS, 492, 1257 [Google Scholar]

[100] Marques-Chaves, R., Álvarez-Márquez, J., Colina, L., et al. 2020b, MNRAS, 499, L105 [Google Scholar]

[101] Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2021, MNRAS, 507, 524 [NASA ADS] [CrossRef] [Google Scholar]

[102] Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2022, MNRAS, 517, 2972 [CrossRef] [Google Scholar]

[103] Marques-Chaves, R., Schaerer, D., Vanzella, E., et al. 2024, A&A, 691, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[104] Martins, F., & Palacios, A. 2022, A&A, 659, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[105] Martins, F., Schaerer, D., Marques-Chaves, R., & Upadhyaya, A. 2023, A&A, 678, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[106] Mason, C. A., Treu, T., Dijkstra, M., et al. 2018, ApJ, 856, 2 [Google Scholar]

[107] Matsuoka, Y., Onoue, M., Kashikawa, N., et al. 2018, PASJ, 70, S35 [Google Scholar]

[108] McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]

[109] Menon, S. H., Burkhart, B., Somerville, R. S., Thompson, T. A., & Sternberg, A. 2024, arXiv e-prints [arXiv:2408.14591] [Google Scholar]

[110] Messa, M., Dessauges-Zavadsky, M., Adamo, A., Richard, J., & Claeyssens, A. 2024, MNRAS, 529, 2162 [CrossRef] [Google Scholar]

[111] Meštrić, U., Vanzella, E., Upadhyaya, A., et al. 2023, A&A, 673, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[112] Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]

[113] Mirocha, J., & Furlanetto, S. R. 2023, MNRAS, 519, 843 [Google Scholar]

[114] Mitsuhashi, I., Tadaki, K.-I., Ikeda, R., et al. 2024, A&A, 690, A197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[115] Naidu, R. P., Oesch, P. A., van Dokkum, P., et al. 2022, ApJ, 940, L14 [NASA ADS] [CrossRef] [Google Scholar]

[116] Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [Google Scholar]

[117] Patrício, V., Richard, J., Verhamme, A., et al. 2016, MNRAS, 456, 4191 [Google Scholar]

[118] Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]

[119] Pettini, M., Steidel, C. C., Adelberger, K. L., Dickinson, M., & Giavalisco, M. 2000, ApJ, 528, 96 [Google Scholar]

[120] Popping, G., Somerville, R. S., & Galametz, M. 2017, MNRAS, 471, 3152 [NASA ADS] [CrossRef] [Google Scholar]

[121] Popping, G., Pillepich, A., Calistro Rivera, G., et al. 2022, MNRAS, 510, 3321 [CrossRef] [Google Scholar]

[122] Popping, G., Shivaei, I., Sanders, R. L., et al. 2023, A&A, 670, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[123] Pozzi, F., Calura, F., Fudamoto, Y., et al. 2021, A&A, 653, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[124] Pozzi, F., Calura, F., D’Amato, Q., et al. 2024, A&A, 686, A187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[125] Quider, A. M., Pettini, M., Shapley, A. E., & Steidel, C. C. 2009, MNRAS, 398, 1263 [Google Scholar]

[126] Quider, A. M., Shapley, A. E., Pettini, M., Steidel, C. C., & Stark, D. P. 2010, MNRAS, 402, 1467 [Google Scholar]

[127] Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [Google Scholar]

[128] Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]

[129] Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]

[130] Roberts-Borsani, G., Treu, T., Shapley, A., et al. 2024, arXiv e-prints [arXiv:2403.07103] [Google Scholar]

[131] Robson, I., Priddey, R. S., Isaak, K. G., & McMahon, R. G. 2004, MNRAS, 351, L29 [NASA ADS] [CrossRef] [Google Scholar]

[132] Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[133] Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]

[134] Schaerer, D., Guibert, J., Marques-Chaves, R., & Martins, F. 2024, A&A, submitted [arXiv:2407.12122] [Google Scholar]

[135] Schneider, R., & Maiolino, R. 2024, A&ARv, 32, 2 [NASA ADS] [CrossRef] [Google Scholar]

[136] Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[137] Schruba, A., Kruijssen, J. M. D., & Leroy, A. K. 2019, ApJ, 883, 2 [NASA ADS] [CrossRef] [Google Scholar]

[138] Senchyna, P., Stark, D. P., Vidal-García, A., et al. 2017, MNRAS, 472, 2608 [NASA ADS] [CrossRef] [Google Scholar]

[139] Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [Google Scholar]

[140] Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]

[141] Shu, Y., Bolton, A. S., Kochaneket, C. S., et al. 2016, ApJ, 824, 86 [NASA ADS] [CrossRef] [Google Scholar]

[142] Silverman, J. D., Daddi, E., Rodighiero, G., et al. 2015, ApJ, 812, L23 [NASA ADS] [CrossRef] [Google Scholar]

[143] Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]

[144] Sobral, D., Matthee, J., Darvish, B., et al. 2015, ApJ, 808, 139 [Google Scholar]

[145] Sobral, D., Santos, S., Matthee, J., et al. 2018a, MNRAS, 476, 4725 [Google Scholar]

[146] Sobral, D., Matthee, J., Darvish, B., et al. 2018b, MNRAS, 477, 2817 [Google Scholar]

[147] Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]

[148] Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]

[149] Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]

[150] Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 479, 75 [NASA ADS] [CrossRef] [Google Scholar]

[151] Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2022, ApJ, 927, 48 [CrossRef] [Google Scholar]

[152] Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2023, ApJ, 943, 81 [NASA ADS] [CrossRef] [Google Scholar]

[153] Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]

[154] Trinca, A., Schneider, R., Valiante, R., et al. 2024, MNRAS, 529, 3563 [NASA ADS] [CrossRef] [Google Scholar]

[155] Upadhyaya, A., Marques-Chaves, R., Schaerer, D., et al. 2024, A&A, 686, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[156] Utomo, D., Sun, J., Leroy, A. K., et al. 2018, ApJ, 861, L18 [NASA ADS] [CrossRef] [Google Scholar]

[157] Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]

[158] Valentino, F., Fujimoto, S., Giménez-Arteaga, C., et al. 2024, A&A, 685, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[159] van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]

[160] Vanzella, E., Castellano, M., Bergamini, P., et al. 2022, A&A, 659, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[161] Vanzella, E., Claeyssens, A., Welch, B., et al. 2023, ApJ, 945, 53 [NASA ADS] [CrossRef] [Google Scholar]

[162] Viero, M. P., Sun, G., Chung, D. T., Moncelsi, L., & Condon, S. S. 2022, MNRAS, 516, L30 [NASA ADS] [CrossRef] [Google Scholar]

[163] Vijayan, A. P., Clay, S. J., Thomas, P. A., et al. 2019, MNRAS, 489, 4072 [NASA ADS] [CrossRef] [Google Scholar]

[164] Weibel, A., Oesch, P. A., Barrufet, L., et al. 2024, MNRAS, 533, 1808 [NASA ADS] [CrossRef] [Google Scholar]

[165] Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]

[166] Whitekar, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]

[167] Whitekar, K. E., Alexandra Pope, A., Cybulski, R., et al. 2017, ApJ, 850, 208 [NASA ADS] [CrossRef] [Google Scholar]

[168] Witstok, J., Jones, G. C., Maiolino, R., Smit, R., & Schneider, R. 2023, MNRAS, 523, 3119 [NASA ADS] [CrossRef] [Google Scholar]

[169] Xiao, M.-Y., Wang, T., Elbaz, D., et al. 2022, A&A, 664, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[170] Xiao, M. Y., Oesch, P., Elbaz, D., et al. 2024, arXiv e-prints [arXiv:2309.02492] [Google Scholar]

[171] Zanella, A., Daddi, E., Magdis, G., et al. 2018, MNRAS, 481, 1976 [Google Scholar]

[172] Zheng, Z.-Y., Malhotra, S., Rhoads, J. E., et al. 2016, ApJS, 226, 23 [Google Scholar]

[173] Ziparo, F., Ferrara, A., Sommovigo, L., & Kohandel, M. 2023, MNRAS, 520, 2445 [NASA ADS] [CrossRef] [Google Scholar]